thesis frame

• The OB1 AXS Custom
• The OB1 À La Carte

The OB1 Frameset

• Free Fit Consult
• Find Your Frame Size
• Unboxing & Setup Guides
• What They're Saying
• Warranty & Returns

While our original spec results in our idea of the perfect bike, we can’t wait to see what yours looks like.  Whether you’re looking to run vintage XTR with bar end shifters for touring, you’re a Campy person, or you want to migrate parts over from a past bike, our frameset lets you build your unique version of the OB1. 

Frameset includes:

• Frame and fork (including bolts and spare frame hardware)
• Spare derailleur hanger (we'd hate to leave you hanging)

Compatible with mechanical 1x, electronic 1x and 2x drivetrains only. Not compatible with mechanical front derailleurs

Want help building your perfect bike? Schedule a consult with one of our resident bike nerds to discuss your fit and chat about your build.

Overview                    Specs                    Geometry                    FAQ

With nimble yet stable endurance geometry, the OB1 is truly a do it all machine.

Chase down roadies, explore some new singletrack, or load up for a long adventure. Join the N=1 revolution.

Current lead time:  Frames ship in 2-4 weeks depending on size and color.  Frame modules require full assembly. We strongly suggest using a professional mechanic to build your bike to ensure you get a safe and reliable machine.

Why you'll love the OB1

• Endurance road geometry for all day comfort and balanced handling.
• Dropper post  compatible 27.2mm seat tube.
• Clearance for high volume tires  up to 650B x 47mm and 700C x 40mm for exceptional traction and a smooth ride.

Click on the name of each component to learn more about why we chose it.  Every detail is chosen for the optimal balance of performance, durability, and serviceability.

To learn more about our approach, check out how we built a high-end carbon dream bike .

• Spirited yet stable endurance road geometry
• Clearance for 650B x 47mm or 700C x 40mm
• Mounting points for (5)  cages , fenders, a bento, and more
• Up to 46T or 50/34T chainrings
• Round 27.2 seat tube with traditional seat post clamp
• Construction: Reinforced Toray 800/700
• 1145g +/-5% (medium black w/o hardware)

WHY WE CHOSE IT

• Accommodations for fenders, headlight, and cages
• Clearance for 650B x 47mm and 700C x 40mm tires
• Steersafe-reinforced carbon steerer
• 12x100mm thru-axle dropouts
• Reinforced Toray 800/700 carbon construction
• 445g fork | 45g SteerSafe

• Hollow bolt-on
• 6mm hex head
• Strong and durable 7075 alloy
• Just ~80g per set
• Integrated look
• Traditional clamping interface for even distribution of forces
• Stainless steel cartridge bearings
• Sealed upper cap
• Split crown race
• Upper: 41.8x30.5x8 | 45°x45°
• Lower: 51.9x40x8 | 45°x45°
• Rigid for use with long-cage derailleurs
• Axle threads directly into the hanger
• Extra included just in case
• 2 bottle mounts in the front triangle
• 1 bottle mount below the downtube
• 1 bento mount on the top tube
• 2 bottle mounts on the fork blades
• Front and rear fender mounts (seat stay bridge included)
• Wide central clamping area on handlebar

Have a question? Check out our FAQ or reach out to us directly at [email protected] to talk to a real human. We're always happy to talk bikes.  

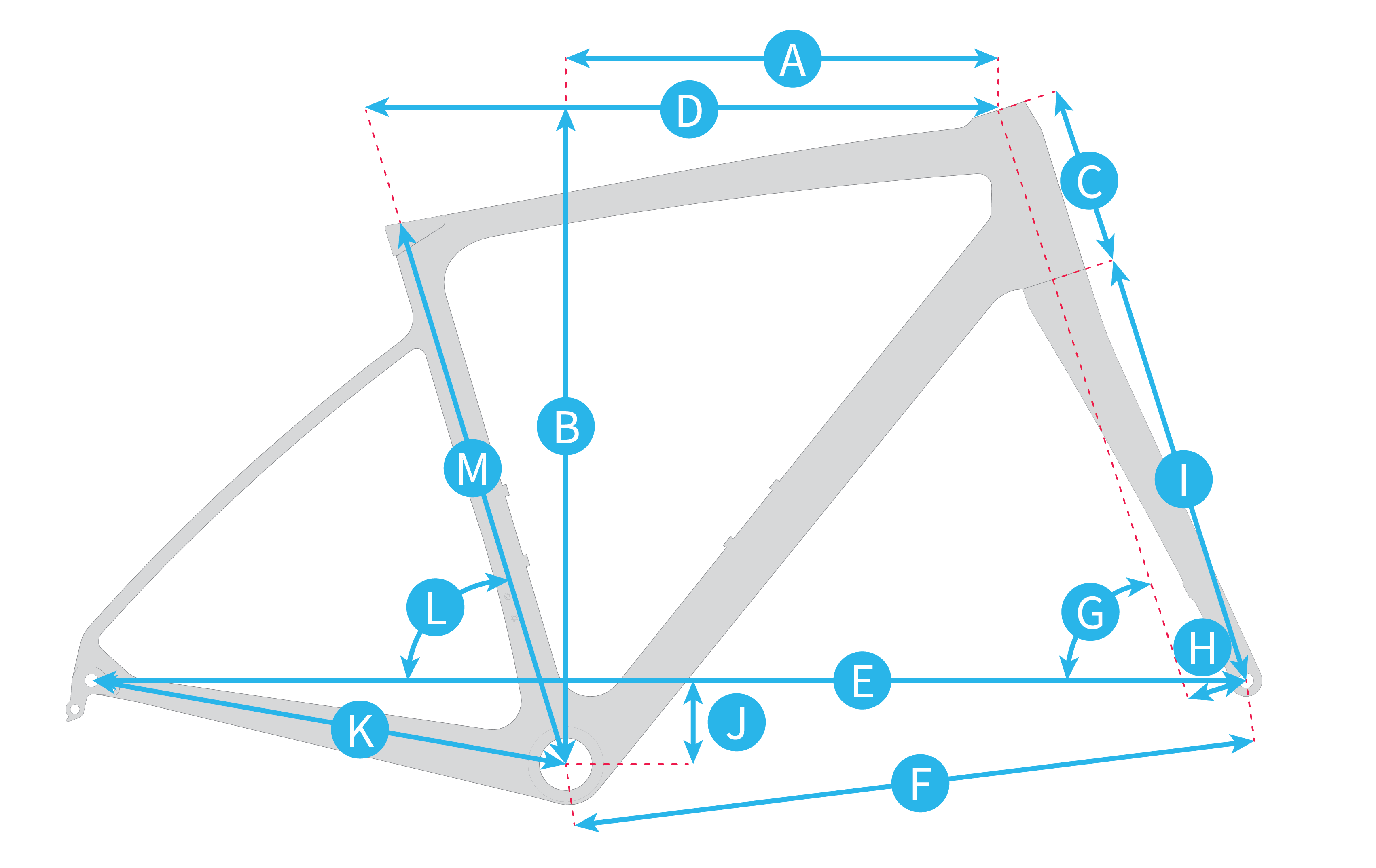
All figures in millimeters unless otherwise indicated.

What they're saying about the OB1

"I've been playing bikes for over twenty years now. This bike inspires a mix of speed, fun and confidence I've never felt before. I had high expectations for this bike, and I’m happy to say it has blown me away." - Rachel C.

“I've been loving my OB1. It's opened up a whole other world of riding for me with many new places to explore. Every time I'm on a new trail, I'm blown away by the beauty of the new places I'm discovering, excited to go out and try a route I've never done before and very thankful I have the OB1 to take me to all these places I previously couldn't go to before.” - Andy W.

Join our newsletter

"Exceeds all expectations. The bike is basically perfect. Smashed a bunch of PRs. This thing is a thoroughbread."

- Joshua S.  

Purdue Online Writing Lab Purdue OWL® College of Liberal Arts

Tips and Examples for Writing Thesis Statements

Welcome to the Purdue OWL

This page is brought to you by the OWL at Purdue University. When printing this page, you must include the entire legal notice.

Copyright ©1995-2018 by The Writing Lab & The OWL at Purdue and Purdue University. All rights reserved. This material may not be published, reproduced, broadcast, rewritten, or redistributed without permission. Use of this site constitutes acceptance of our terms and conditions of fair use.

This resource provides tips for creating a thesis statement and examples of different types of thesis statements.

Tips for Writing Your Thesis Statement

1. Determine what kind of paper you are writing:

• An analytical paper breaks down an issue or an idea into its component parts, evaluates the issue or idea, and presents this breakdown and evaluation to the audience.
• An expository (explanatory) paper explains something to the audience.
• An argumentative paper makes a claim about a topic and justifies this claim with specific evidence. The claim could be an opinion, a policy proposal, an evaluation, a cause-and-effect statement, or an interpretation. The goal of the argumentative paper is to convince the audience that the claim is true based on the evidence provided.

If you are writing a text that does not fall under these three categories (e.g., a narrative), a thesis statement somewhere in the first paragraph could still be helpful to your reader.

2. Your thesis statement should be specific—it should cover only what you will discuss in your paper and should be supported with specific evidence.

3. The thesis statement usually appears at the end of the first paragraph of a paper.

4. Your topic may change as you write, so you may need to revise your thesis statement to reflect exactly what you have discussed in the paper.

Thesis Statement Examples

Example of an analytical thesis statement:

The paper that follows should:

• Explain the analysis of the college admission process
• Explain the challenge facing admissions counselors

Example of an expository (explanatory) thesis statement:

• Explain how students spend their time studying, attending class, and socializing with peers

Example of an argumentative thesis statement:

• Present an argument and give evidence to support the claim that students should pursue community projects before entering college

10.5 Writing Process: Creating a Position Argument

Learning outcomes.

By the end of this section, you will be able to:

• Demonstrate brainstorming processes and tools as means to discover topics, ideas, positions, and details.
• Apply recursive strategies for organizing drafting, collaborating, peer reviewing, revising, rewriting, and editing.
• Compose a position argument that integrates the writer’s ideas with those from appropriate sources.
• Give and act on productive feedback to works in progress.
• Apply or challenge common conventions of language or grammar in composing and revising.

Now is the time to try your hand at writing a position argument. Your instructor may provide some possible topics or a singular topic. If your instructor allows you to choose your own topic, consider a general subject you feel strongly about and whether you can provide enough support to develop that subject into an essay. For instance, suppose you think about a general subject such as “adulting.” In looking back at what you have learned while becoming an adult, you think of what you wish you had known during your early teenage years. These thoughts might lead you to brainstorm about details of the effects of money in your life or your friends’ lives. In reviewing your brainstorming, you might zero in on one topic you feel strongly about and think it provides enough depth to develop into a position argument. Suppose your brainstorming leads you to think about negative financial concerns you or some of your friends have encountered. Thinking about what could have helped address those concerns, you decide that a mandated high school course in financial literacy would have been useful. This idea might lead you to formulate your working thesis statement —first draft of your thesis statement—like this: To help students learn how to make sensible financial decisions, a mandatory class in financial literacy should be offered in high schools throughout the country.

Once you decide on a topic and begin moving through the writing process, you may need to fine-tune or even change the topic and rework your initial idea. This fine-tuning may come as you brainstorm, later when you begin drafting, or after you have completed a draft and submitted it to your peers for constructive criticism. These possibilities occur because the writing process is recursive —that is, it moves back and forth almost simultaneously and maybe even haphazardly at times, from planning to revising to editing to drafting, back to planning, and so on.

Summary of Assignment

Write a position argument on a controversial issue that you choose or that your instructor assigns to you. If you are free to choose your own topic, consider one of the following:

• The legal system would be strengthened if ______________________.
• The growing use of technology in college classrooms is weakening _____________.
• For safety reasons, public signage should be _________________.
• For entrance into college, standardized testing _________________________.
• In relation to the cost of living, the current minimum wage _______________________.
• During a pandemic, America __________________________.
• As a requirement to graduate, college students __________________________.
• To guarantee truthfulness of their content, social media platforms have the right to _________________.
• To ensure inclusive and diverse representation of people of all races, learning via virtual classrooms _________________.
• Segments of American cultures have differing rules of acceptable grammar, so in a college classroom ___________________.

In addition, if you have the opportunity to choose your own topic and wish to search further, take the lead from trailblazer Charles Blow and look to media for newsworthy “trends.” Find a controversial issue that affects you or people you know, and take a position on it. As you craft your argument, identify a position opposing yours, and then refute it with reasoning and evidence. Be sure to gather information on the issue so that you can support your position sensibly with well-developed ideas and evidence.

Another Lens. To gain a different perspective on your issue, consider again the people affected by it. Your position probably affects different people in different ways. For example, if you are writing that the minimum wage should be raised, then you might easily view the issue through the lens of minimum-wage workers, especially those who struggle to make ends meet. However, if you look at the issue through the lens of those who employ minimum-wage workers, your viewpoint might change. Depending on your topic and thesis, you may need to use print or online sources to gain insight into different perspectives.

For additional information about minimum-wage workers, you could consult

• printed material available in your college library;
• databases in your college library; and
• pros and cons of raising the minimum wage;
• what happens after the minimum wage is raised;
• how to live on a minimum-wage salary;
• how a raise in minimum wage is funded; and
• minimum wage in various U.S. states.

To gain more insight about your topic, adopt a stance that opposes your original position and brainstorm ideas from that viewpoint. Begin by gathering evidence that would help you refute your previous stance and appeal to your audience.

Quick Launch: Working Thesis Frames and Organization of Ideas

After you have decided on your topic, the next step is to arrive at your working thesis. You probably have a good idea of the direction your working thesis will take. That is, you know where you stand on the issue or problem, but you are not quite sure of how to word your stance to share it with readers. At this point, then, use brainstorming to think critically about your position and to discover the best way to phrase your statement.

For example, after reading an article discussing different state-funded community college programs, one student thought that a similar program was needed in Alabama, her state. However, she was not sure how the program worked. To begin, she composed and answered “ reporters’ questions ” such as these:

• What does a state-funded community college program do? pays for part or all of the tuition of a two-year college student
• Who qualifies for the program? high school graduates and GED holders
• Who benefits from this? students needing financial assistance, employers, and Alabama residents
• Why is this needed? some can’t afford to go to college; tuition goes up every year; colleges would be more diverse if everyone who wanted to go could afford to go
• Where would the program be available? at all public community colleges
• When could someone apply for the program? any time
• How can the state fund this ? use lottery income, like other states

The student then reviewed her responses, altered her original idea to include funding through a lottery, and composed this working thesis:

student sample text To provide equal educational opportunities for all residents, the state of Alabama should create a lottery to completely fund tuition at community colleges. end student sample text

Remember that a strong thesis for a position should

• state your stance on a debatable issue;
• reflect your purpose of persuasion; and
• be based on your opinion or observation.

When you first consider your topic for an argumentative work, think about the reasoning for your position and the evidence you will need—that is, think about the “because” part of your argument. For instance, if you want to argue that your college should provide free Wi-Fi for every student, extend your stance to include “because” and then develop your reasoning and evidence. In that case, your argument might read like this: Ervin Community College should provide free Wi-Fi for all students because students may not have Internet access at home.

Note that the “because” part of your argument may come at the beginning or the end and may be implied in your wording.

As you develop your thesis, you may need help funneling all of your ideas. Return to the possibilities you have in mind, and select the ideas that you think are strongest, that recur most often, or that you have the most to say about. Then use those ideas to fill in one of the following sentence frames to develop your working thesis. Feel free to alter the frame as necessary to fit your position. While there is no limit to the frames that are possible, these may help get you started.

________________ is caused/is not caused by ________________, and _____________ should be done.

Example: A declining enrollment rate in college is caused by high tuition rates, and an immediate freeze on the cost of tuition should be applied.

______________ should/should not be allowed (to) ________________ for a number of reasons.

Example: People who do not wear masks during a pandemic should not be allowed to enter public buildings for a number of reasons.

Because (of) ________________, ___________________ will happen/continue to happen.

Example: Because of a lack of emphasis on STEAM (Science, Technology, Engineering, the Arts, and Mathematics) education in public schools, America will continue to lag behind many other countries.

_____________ is similar to/nothing like ________________ because ______________.

Example: College classes are nothing like high school classes because in college, more responsibility is on the student, the classes are less frequent but more intense, and the work outside class takes more time to complete.

______________ can be/cannot be thought of as __________________ because ______________.

Example: The Black Lives Matter movement can be thought of as an extension of the Civil Rights movement from the 1950s and 1960s because it shares the same mission of fighting racism and ending violence against Black people.

Next, consider the details you will need to support your thesis. The Aristotelian argument structure, named for the Greek philosopher Aristotle , is one that may help you frame the draft of your position argument. For this method, use something like the following chart. In Writing Process: Creating a Position Argument, you will find a similar organizer that you can copy and use for your assignment.

Drafting: Rhetorical Appeals and Types of Supporting Evidence

To persuade your audience to support your position or argument, consider various rhetorical appeals— ethos, logos, pathos, and kairos—and the types of evidence to support your sound reasoning. See Reasoning Strategies: Improving Critical Thinking for more information on reasoning strategies and types of evidence.

Rhetorical Appeals

To establish your credibility, to show readers you are trustworthy, to win over their hearts, and to set your issue in an appropriate time frame to influence readers, consider how you present and discuss your evidence throughout the paper.

• Appeal to ethos . To establish credibility in her paper arguing for expanded mental health services, a student writer used these reliable sources: a student survey on mental health issues, data from the International Association of Counseling Services (a professional organization), and information from an interview with a campus mental health counselor.
• Appeal to logos . To support her sound reasoning, the student writer approached the issue rationally, using data and credible evidence to explain the current situation and its effects.
• Appeal to pathos . To show compassion and arouse audience empathy, the student writer shared the experience of a student on her campus who struggled with anxiety and depression.
• Appeal to kairos . To appeal to kairos, the student emphasized the immediate need for these services, as more students are now aware of their particular mental health issues and trying to deal with them.

The way in which you present and discuss your evidence will reflect the appeals you use. Consider using sentence frames to reflect specific appeals. Remember, too, that sentence frames can be composed in countless ways. Here are a few frames to get you thinking critically about how to phrase your ideas while considering different types of appeals.

Appeal to ethos: According to __________________, an expert in ______________, __________________ should/should not happen because ________________________.

Appeal to ethos: Although ___________________is not an ideal situation for _________________, it does have its benefits.

Appeal to logos: If ____________________ is/is not done, then understandably, _________________ will happen.

Appeal to logos: This information suggests that ____________________ needs to be investigated further because ____________________________.

Appeal to pathos: The story of _____________________ is uplifting/heartbreaking/hopeful/tragic and illustrates the need for ____________________.

Appeal to pathos: ___________________ is/are suffering from ________________, and that is something no one wants.

Appeal to kairos: _________________ must be addressed now because ________________ .

Appeal to kairos: These are times when ______________ ; therefore, _____________ is appropriate/necessary.

Types of Supporting Evidence

Depending on the point you are making to support your position or argument, certain types of evidence may be more effective than others. Also, your instructor may require you to include a certain type of evidence. Choose the evidence that will be most effective to support the reasoning behind each point you make to support your thesis statement. Common types of evidence are these:

Renada G., a junior at Powell College South, worked as a waitress for 15 hours a week during her first three semesters of college. But in her sophomore year, when her parents were laid off during the pandemic, Renada had to increase her hours to 35 per week and sell her car to stay in school. Her grades started slipping, and she began experiencing symptoms of depression and anxiety. When she called the campus health center to make an appointment for counseling, Renada was told she would have to wait two weeks before she could be seen.

Here is part of how Lyndon B. Johnson defined the Great Society: “But most of all, the Great Society is not a safe harbor, a resting place, a final objective, a finished work. It is a challenge constantly renewed, beckoning us toward a destiny where the meaning of our lives matches the marvelous products of our labor.”

Bowen Lake is nestled in verdant foothills, lush with tall grasses speckled with wildflowers. Around the lake, the sweet scent of the purple and yellow flowers fills the air, and the fragrance of the hearty pines sweeps down the hillsides in a westerly breeze. Wood frogs’ and crickets’ songs suddenly stop, as the blowing of moose calling their calves echoes across the lake’s soundless surface. Or this was the scene before the deadly destruction of fires caused by climate change.

When elaborating on America’s beauty being in danger, Johnson says, “The water we drink, the food we eat, the very air that we breathe, are threatened with pollution. Our parks are overcrowded, our seashores overburdened. Green fields and dense forests are disappearing.”

Speaking about President Lyndon B. Johnson and the Vietnam War, noted historian and Johnson biographer Doris Kearns Goodwin said, “It seemed the hole in his heart from the loss of work was too big to fill.”

Charles Blow has worked at the Shreveport Times , The Detroit News , National Geographic , and The New York Times .

When interviewed by George Rorick and asked about the identities of his readers, Charles Blow said that readers’ emails do not elaborate on descriptions of who the people are. However, “the kinds of comments that they offer are very much on the thesis of the essay.”

In his speech, Lyndon B. Johnson says, “The Great Society is a place where every child can find knowledge to enrich his mind and to enlarge his talents.”

To support the need for change in classrooms, Johnson uses these statistics: “Each year more than 100,000 high school graduates, with proved ability, do not enter college because they cannot afford it. And if we cannot educate today’s youth, what will we do in 1970 when elementary school enrollment will be five million greater than 1960?”

• Visuals : graphs, photographs, charts, or maps used in addition to written or spoken information.

Brainstorm for Supporting Points

Use one or more brainstorming techniques, such as a web diagram as shown in Figure 10.8 or the details generated from “because” statements, to develop ideas or particular points in support of your thesis. Your goal is to get as many ideas as possible. At this time, do not be concerned about how ideas flow, whether you will ultimately use an idea (you want more ideas than will end up in your finished paper), spelling, or punctuation.

When you have finished, look over your brainstorming. Then circle three to five points to incorporate into your draft. Also, plan to answer “ reporters’ questions ” to provide readers with any needed background information. For example, the student writing about the need for more mental health counselors on her campus created and answered these questions:

What is needed? More mental health counseling is needed for Powell College South.

Who would benefit from this? The students and faculty would benefit.

• Why is this needed? The college does not have enough counselors to meet all students’ needs.
• Where are more counselors needed? More counselors are needed at the south campus.
• When are the counselors needed? Counselors need to be hired now and be available both day and night to accommodate students’ schedules.
• How can the college afford this ? Instead of hiring daycare workers, the college could use students and faculty from the Early Childhood Education program to run the program and use the extra money to pay the counselors.

Using Logic

In a position argument, the appropriate use of logic is especially important for readers to trust what you write. It is also important to look for logic in material you read and possibly cite in your paper so that you can determine whether writers’ claims are reasonable. Two main categories of logical thought are inductive reasoning and deductive reasoning .

• Inductive reasoning moves from specific to broad ideas. You begin by collecting details, observations, incidents, or facts; examining them; and drawing a conclusion from them. Suppose, for example, you are writing about attendance in college classes. For three weeks, you note the attendance numbers in all your Monday, Wednesday, and Friday classes (specific details), and you note that attendance is lower on Friday than on the other days (a specific detail). From these observations, you determine that many students prefer not to attend classes on Fridays (your conclusion).
• Deductive reasoning moves from general to specific ideas. You begin with a hypothesis or premise , a general concept, and then examine possibilities that would lead to a specific and logical conclusion. For instance, suppose you think that opportunities for foreign students at your college are inadequate (general concept). You examine the specific parts of that concept (e.g., whether your college provides multicultural clubs, help with language skills, or work-study opportunities) and determine that those opportunities are not available. You then determine that opportunities for foreign students are lacking at your college.

Logical Fallacies and Propaganda

Fallacies are mistakes in logic. Readers and writers should be aware of these when they creep into writing, indicating that the points the writers make may not be valid. Two common fallacies are hasty generalizations and circular arguments. See Glance at Genre: Rhetorical Strategies for more on logical fallacies.

• A hasty generalization is a conclusion based on either inadequate or biased evidence. Consider this statement: “Two students in Math 103 were nervous before their recent test; therefore, all students in that class must have text anxiety.” This is a hasty generalization because the second part of the statement (the generalization about all students in the class) is inadequate to support what the writer noted about only two students.
• A circular argument is one that merely restates what has already been said. Consider this statement: “ The Hate U Give is a well-written book because Angie Thomas, its author, is a good novelist.” The statement that Thomas is a good novelist does not explain why her book is well written.

In addition to checking work for fallacies, consider propaganda , information worded so that it endorses a particular viewpoint, often of a political nature. Two common types of propaganda are bandwagon and fear .

• In getting on the bandwagon , the writer encourages readers to conform to a popular trend and endorse an opinion, a movement, or a person because everyone else is doing so. Consider this statement: “Everyone is behind the idea that 7 a.m. classes are too early and should be changed to at least 8 a.m. Shouldn’t you endorse this sensible idea, too?”
• In using fear, the writer presents a dire situation, usually followed by what could be done to prevent it. Consider this statement: “Our country is at a turning point. Enemies threaten us with their power, and our democracy is at risk of being crushed. The government needs a change, and Paul Windhaus is just the man to see we get that change.” This quotation appeals to fear about the future of the country and implies that electing a certain individual will solve the predicted problems.

Organize the Paper

To begin, write your thesis at the top of a blank page. Then select points from your brainstorming and reporters’ questions to organize and develop support for your thesis. Keep in mind that you can revise your thesis whenever needed.

To begin organizing her paper on increased mental health services on her college campus, the student wrote this thesis at the top of a page:

student sample text Because mental health is a major concern at Powell College South, students could benefit from expanding the services offered . end student sample text

Next she decided the sequence in which to present the points. In a position or an argument essay, she could choose one of two methods: thesis-first organization or delayed-thesis organization.

Thesis-First Organization

Leading with a thesis tells readers from the beginning where you stand on the issue. In this organization, the thesis occupies both the first and last position in the essay, making it easy for readers to remember.

Introduce the issue and assert your thesis. Make sure the issue has at least two debatable sides. Your thesis establishes the position from which you will argue. Writers often state their thesis as the last sentence in the first paragraph, as the student writer has done:

student sample text The problem of mental health has become front-page news in the last two months. Hill’s Herald , Powell College South’s newspaper, reported 14 separate incidents of students who sought counseling but could not get appointments with college staff. Since mental health problems are widespread among the student population, the college should hire more health care workers to address this problem. end student sample text

Summarize the counterclaims . Before elaborating on your claims, explain the opposition’s claims. Including this information at the beginning gives your argument something to focus on—and refute—throughout the paper. If you ignore counterclaims, your argument may appear incomplete, and readers may think you have not researched your topic sufficiently. When addressing a counterclaim, state it clearly, show empathy for those who have that view, and then immediately refute it with support developed through reasoning and evidence. Squeezing the counterclaims between the thesis and the evidence reserves the strongest places—the opening and closing—for your position.

student sample text Counterclaim 1 : Powell College South already employs two counselors, and that number is sufficient to meet the needs of the student population. end student sample text

student sample text Counterclaim 2 : Students at Powell College South live in a metropolitan area large enough to handle their mental health needs. end student sample text

Refute the counterclaims. Look for weak spots in the opposition’s argument, and point them out. Use your opponent’s language to show you have read closely but still find problems with the claim. This is the way the writer refuted the first counterclaim:

student sample text While Powell College South does employ two counselors, those counselors are overworked and often have no time slots available for students who wish to make appointments. end student sample text

State and explain your points, and then support them with evidence. Present your points clearly and precisely, using Reasoning Strategies: Improving Critical Thinking to explain and cite your evidence. The writer plans to use a problem-solution reasoning strategy to elaborate on these three points using these pieces of evidence:

student sample text Point 1: Wait times are too long. end student sample text

student sample text Kay Payne, one of the campus counselors, states that the wait time for an appointment with her is approximately 10 days. end student sample text

student sample text Point 2: Mental health issues are widespread within the student community. end student sample text

student sample text In a recent on-campus student survey, 75 percent of 250 students say they have had some kind of mental health issues at some point in their life. end student sample text

student sample text Point 3: The staff-to-student ratio is too high. end student sample text

student sample text The International Accreditation of Counseling Services states that the recommended ratio is one full-time equivalent staff member for every 1,000 to 1,500 students. end student sample text

Restate your position as a conclusion. Near the end of your paper, synthesize your accumulated evidence into a broad general position, and restate your thesis in slightly different language.

student sample text The number of students who need mental health counseling is alarming. The recent news articles that attest to their not being able to schedule appointments add to the alarm. While Powell College South offers some mental health counseling, the current number of counselors and others who provide health care is insufficient to handle the well-being of all its students. Action must be taken to address this problem. end student sample text

Delayed-Thesis Organization

In this organizational pattern, introduce the issue and discuss the arguments for and against it, but wait to take a side until late in the essay. By delaying the stance, you show readers you are weighing the evidence, and you arouse their curiosity about your position. Near the end of the paper, you explain that after carefully considering both pros and cons, you have arrived at the most reasonable position.

Introduce the issue. Here, the writer begins with action that sets the scene of the problem.

student sample text Tapping her foot nervously, Serena looked at her watch again. She had been waiting three hours to see a mental health counselor at Powell College South, and she did not think she could wait much longer. She had to get to work. end student sample text

Summarize the claims for one position. Before stating which side you support, explain how the opposition views the issue. This body paragraph presents evidence about the topic of more counselors:

student sample text Powell College South has two mental health counselors on staff. If the college hires more counselors, more office space will have to be created. Currently Pennington Hall could accommodate those counselors. Additional counselors would allow more students to receive counseling. end student sample text

Refute the claims you just stated. Still not stating your position, point out the other side of the issue.

student sample text While office space is available in Pennington Hall, that location is far from ideal. It is in a wooded area of campus, six blocks from the nearest dorm. Students who would go there might be afraid to walk through the woods or might be afraid to walk that distance. The location might deter them from making appointments. end student sample text

Now give the best reasoning and evidence to support your position. Because this is a delayed-thesis organization, readers are still unsure of your stance. This section should be the longest and most carefully documented part of the paper. After summarizing and refuting claims, the writer then elaborates on these three points using problem-solution reasoning supported by this evidence as discussed in Reasoning Strategies: Improving Critical Thinking, implying her position before moving to the conclusion, where she states her thesis.

student sample text The International Association of Counseling Services states that one full-time equivalent staff member for every 1,000 to 1,500 students is the recommended ratio. end student sample text

State your thesis in your conclusion. Your rhetorical strategy is this: after giving each side a fair hearing, you have arrived at the most reasonable conclusion.

student sample text According to the American Psychological Association, more than 40 percent of all college students suffer from some form of anxiety. Powell College South students are no different from college students elsewhere: they deserve to have adequate mental health counseling. end student sample text

Drafting begins when you organize your evidence or research notes and then put them into some kind of written form. As you write, focus on building body paragraphs through the techniques presented in Reasoning Strategies: Improving Critical Thinking that show you how to support your position and then add evidence. Using a variety of evidence types builds credibility with readers. Remember that the recursiveness of the writing process allows you to move from composing to gathering evidence and back to brainstorming ideas or to organizing your draft at any time. Move around the writing process as needed.

Keep in mind that a first draft is just a beginning—you will revise it into a better work in later drafts. Your first draft is sometimes called a discovery draft because you are discovering how to shape your paper: which ideas to include and how to support those ideas. These suggestions and graphic organizer may be helpful for your first draft:

• Write your thesis at the top of the paper.
• Compose your body paragraphs: those that support your argument through reasoning strategies and those that address counterclaims.
• Leave your introduction, conclusion, and title for later drafts.

Use a graphic organizer like Table 10.1 to focus points, reasoning, and evidence for body paragraphs. You are free to reword your thesis, reasoning, counterclaim(s), refutation of counterclaim(s), concrete evidence, and explanation/elaboration/clarification at any time. You are also free to adjust the order in which you present your reasoning, counterclaim(s), and refuting of counterclaim(s).

Develop a Writing Project through Multiple Drafts

Your first draft is a kind of experiment in which you are concerned with ideas and with getting the direction and concept of the paper clear. Do not think that your first draft must be perfect; remind yourself that you are just honing your work. In most serious writing, every phase of the process can be considered recursive, helping you shape the best paper possible.

Peer Review: Critical Thinking and Counterclaims

After you have completed the first draft, begin peer review. Peer reviewers can use these sentence starters when thinking critically about overall strengths and developmental needs.

• One point about your position that I think is strong is ______ because ________.
• One point about your position that I think needs more development is _____ because _______.
• One area that I find confusing is _____________; I was confused about _______.
• One major point that I think needs more explanation or detail is _______.
• In my opinion, the purpose of your paper is to persuade readers _______.
• In my opinion, the audience for your paper is _______.
• One area of supporting evidence that I think could use more development is _______.
• One counterclaim you include is ________________.
• Your development of the counterclaim is __________________ because ________________.

Refuting Counterclaims

Peer reviewers are especially helpful with position and argument writing when it comes to refuting counterclaims. Have your peer reviewer read your paper again and look for supporting points and ideas to argue against , trying to break down your argument. Then ask your reviewer to discuss the counterclaims and corresponding points or ideas in your paper. This review will give you the opportunity to think critically about ways to refute the counterclaims your peer reviewer suggests.

As preparation for peer review, match each of the following arguments with their counterarguments.

Revising: Reviewing a Draft and Responding to Counterclaims

Revising means reseeing, rereading, and rethinking your thoughts on paper until they fully match your intention. Mentally, it is conceptual work focused on units of meaning larger than the sentence. Physically, it is cutting, pasting, deleting, and rewriting until the ideas are satisfying. Be ready to spend a great deal of time revising your drafts, adding new information and incorporating sources smoothly into your prose.

The Revising Process

To begin revising, return to the basic questions of topic ( What am I writing about? ), purpose ( Why am I writing about this topic? ), audience ( For whom am I writing? ), and culture ( What is the background of the people for whom I am writing? ).

• What is the general scope of my topic? __________________________________
• What is my thesis? __________________________________________________
• Does my thesis focus on my topic? ______________________________________
• Does my thesis clearly state my position? ______________________
• What do I hope to accomplish in writing about this topic? ____________________
• Do all parts of the paper advance this purpose? ____________________________
• Does my paper focus on my argument or position? _________________________
• What does my audience know about this subject? _______________________
• What does my audience need to know to understand the point of my paper? _______________________________________________________________

What questions or objections do I anticipate from my audience? ___________

________________________________________________________________

• What is the culture of the people for whom I am writing? Do all readers share the same culture? ________________________________________________________

How do my beliefs, values, and customs differ from those of my audience?

____________________________________________________________________

• How do the cultures of the authors of sources I cite differ from my culture or the culture(s) of my audience? ______________________________________________

Because of the recursivity of the writing process, returning to these questions will help you fine-tune the language and structure of your writing and target the support you develop for your audience.

Responding to Counterclaims

The more complex the issue, the more opposing sides it may have. For example, a writer whose position is that Powell College South Campus should offer daycare to its students with children might find opposition for different reasons. Someone may oppose the idea out of concern for cost; someone else may support the idea if the daycare is run on a volunteer basis; someone else may support the idea if the services are offered off campus.

As you revise, continue studying your peer reviewer’s comments about counterclaims. If you agree with any counterclaim, then say so in the paragraph in which you address counterclaims. This agreement will further establish your credibility by showing your fairness and concern for the issue. Look over your paper and peer review comments, and then consider these questions:

• In what ways do you address realistic counterclaims? What other counterclaims should you address? Should you add to or replace current counterclaims?
• In what ways do you successfully refute counterclaims? What other refutations might you include?
• Are there any counterclaims with which you agree? If so, how do you concede to them in your paper? In what ways does your discussion show fairness?

After completing your peer review and personal assessment, make necessary revisions based on these notes. See Annotated Student Sample an example of a student’s argumentative research essay. Note how the student

• presents the argument;
• supports the viewpoint with reasoning and evidence;
• includes support in the form of facts, opinions, paraphrases, and summaries;
• provides citations (correctly formatted) about material from other sources in the paper;
• uses ethos, pathos, and logos throughout the paper; and
• addresses counterclaims (dissenting opinions).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/writing-guide/pages/1-unit-introduction

• Authors: Michelle Bachelor Robinson, Maria Jerskey, featuring Toby Fulwiler
• Publisher/website: OpenStax
• Book title: Writing Guide with Handbook
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/writing-guide/pages/1-unit-introduction
• Section URL: https://openstax.org/books/writing-guide/pages/10-5-writing-process-creating-a-position-argument

© Dec 19, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• College University and Postgraduate
• Academic Degrees
• Doctoral Studies
• Theses and Dissertations

How to Write a Thesis Statement

Last Updated: February 27, 2024 Fact Checked

This article was reviewed by Gerald Posner . Gerald Posner is an Author & Journalist based in Miami, Florida. With over 35 years of experience, he specializes in investigative journalism, nonfiction books, and editorials. He holds a law degree from UC College of the Law, San Francisco, and a BA in Political Science from the University of California-Berkeley. He’s the author of thirteen books, including several New York Times bestsellers, the winner of the Florida Book Award for General Nonfiction, and has been a finalist for the Pulitzer Prize in History. He was also shortlisted for the Best Business Book of 2020 by the Society for Advancing Business Editing and Writing. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 3,198,656 times.

Whether you’re writing a short essay or a doctoral dissertation, your thesis statement can be one of the trickiest sentences to formulate. Fortunately, there are some basic rules you can follow to ensure your thesis statement is effective and interesting, including that it must be a debatable analytical point, not a general truism.

Crafting Great Thesis Statements

• Thesis: "Computers allow fourth graders an early advantage in technological and scientific education."
• ' Thesis: "The river comes to symbolize both division and progress, as it separates our characters and country while still providing the best chance for Huck and Jim to get to know one another."
• Thesis: "Through careful sociological study, we've found that people naturally assume that "morally righteous" people look down on them as "inferior," causing anger and conflict where there generally is none."

• Ex. "This dynamic between different generations sparks much of the play’s tension, as age becomes a motive for the violence and unrest that rocks King Lear."
• Ex. "The explosion of 1800s philosophies like Positivism, Marxism, and Darwinism undermined and refuted Christianity to instead focus on the real, tangible world."
• Ex. "Without the steady hand and specific decisions of Barack Obama, America would never have recovered from the hole it entered in the early 2000s."

• "While both sides fought the Civil War over the issue of slavery, the North fought for moral reasons while the South fought to preserve its own institutions."
• "The primary problem of the American steel industry is the lack of funds to renovate outdated plants and equipment."
• "Hemingway's stories helped create a new prose style by employing extensive dialogue, shorter sentences, and strong Anglo-Saxon words."

• "After the third and fourth time you see him beat himself, one finally realizes that Huck Finn is literature's first full-blown sadomasochist."
• "The advent of internet technology has rendered copyright laws irrelevant -- everyone can and should get writing, movies, art, and music for free."
• "Though they have served admirably for the past two centuries, recent research shows that America needs to ditch the two-party system, and quickly."

• "By owning up to the impossible contradictions, embracing them and questioning them, Blake forges his own faith, and is stronger for it. Ultimately, the only way for his poems to have faith is to temporarily lose it."
• "According to its well-documented beliefs and philosophies, an existential society with no notion of either past or future cannot help but become stagnant."
• "By reading “Ode to a Nightingale” through a modern deconstructionist lens, we can see how Keats viewed poetry as shifting and subjective, not some rigid form."
• "The wrong people won the American Revolution." While striking and unique, who is "right" and who is "wrong" is exceptionally hard to prove, and very subjective.
• "The theory of genetic inheritance is the binding theory of every human interaction." Too complicated and overzealous. The scope of "every human interaction" is just too big
• "Paul Harding's novel Tinkers is ultimately a cry for help from a clearly depressed author." Unless you interviewed Harding extensively, or had a lot of real-life sources, you have no way of proving what is fact and what is fiction."

Getting it Right

• is an assertion, not a fact or observation. Facts are used within the paper to support your thesis.
• takes a stand, meaning it announces your position towards a particular topic.
• is the main idea and explains what you intend to discuss.
• answers a specific question and explains how you plan to support your argument.
• is debatable. Someone should be able to argue an alternate position, or conversely, support your claims.

• "Because of William the Conqueror's campaign into England, that nation developed the strength and culture it would need to eventually build the British Empire."
• "Hemingway significantly changed literature by normalizing simplistic writing and frank tone."

Finding the Perfect Thesis

• A clear topic or subject matter
• A brief summary of what you will say
• [Something] [does something] because [reason(s)].
• Because [reason(s)], [something] [does something].
• Although [opposing evidence], [reasons] show [Something] [does something].
• The last example includes a counter-argument, which complicates the thesis but strengthens the argument. In fact, you should always be aware of all counter-arguments against your thesis. Doing so will refine your thesis, and also force you to consider arguments you have to refute in your paper.

• There are two schools of thought on thesis timing. Some people say you should not write the paper without a thesis in mind and written down, even if you have to alter it slightly by the end. The other school of thought says that you probably won't know where you're going until you get there, so don't write the thesis until you know what it should be. Do whatever seems best to you.

• Never frame your thesis as a question . The job of a thesis is to answer a question, not ask one.
• A thesis is not a list. If you're trying to answer a specific question, too many variables will send your paper off-focus. Keep it concise and brief.
• Never mention a new topic that you do not intend to discuss in the paper.
• Do not write in the first person. Using sentences such as, "I will show...," is generally frowned upon by scholars.
• Do not be combative. The point of your paper is to convince someone of your position, not turn them off, and the best way to achieve that is to make them want to listen to you. Express an open-minded tone, finding common ground between different views.

Sample Thesis and List of Things to Include

Community Q&A

• Think of your thesis as a case a lawyer has to defend. A thesis statement should explain to your readers the case you wish to make and how you will accomplish that. You can also think of your thesis as a contract. Introducing new ideas the reader is not prepared for may be alienating. Thanks Helpful 1 Not Helpful 0
• An effective thesis statement controls the entire argument. It determines what you cannot say. If a paragraph does not support your thesis, either omit it or change your thesis. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ https://wts.indiana.edu/writing-guides/how-to-write-a-thesis-statement.html
• ↑ https://owl.purdue.edu/owl/general_writing/the_writing_process/thesis_statement_tips.html
• ↑ https://writingcenter.unc.edu/tips-and-tools/thesis-statements/
• ↑ http://www.writing.utoronto.ca/advice/planning-and-organizing/thesis-statements
• ↑ https://writingcenter.uagc.edu/writing-a-thesis

About This Article

To write an effective thesis statement, choose a statement that answers a general question about your topic. Check that your thesis is arguable, not factual, and make sure you can back it up your with evidence. For example, your thesis statement could be something like "Computers allow fourth graders an early advantage in technological and scientific education." To learn about writing thesis statements for different types of essays or how to incorporate them into your essay, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Alysia Van Gelder

Oct 26, 2017

Did this article help you?

Aug 12, 2016

Aug 14, 2019

Sophie Parks

May 5, 2016

Anna Fryman

Mar 28, 2021

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

• Privacy Policy

Buy Me a Coffee

Home » Thesis – Structure, Example and Writing Guide

Thesis – Structure, Example and Writing Guide

Table of contents.

Definition:

Thesis is a scholarly document that presents a student’s original research and findings on a particular topic or question. It is usually written as a requirement for a graduate degree program and is intended to demonstrate the student’s mastery of the subject matter and their ability to conduct independent research.

History of Thesis

The concept of a thesis can be traced back to ancient Greece, where it was used as a way for students to demonstrate their knowledge of a particular subject. However, the modern form of the thesis as a scholarly document used to earn a degree is a relatively recent development.

The origin of the modern thesis can be traced back to medieval universities in Europe. During this time, students were required to present a “disputation” in which they would defend a particular thesis in front of their peers and faculty members. These disputations served as a way to demonstrate the student’s mastery of the subject matter and were often the final requirement for earning a degree.

In the 17th century, the concept of the thesis was formalized further with the creation of the modern research university. Students were now required to complete a research project and present their findings in a written document, which would serve as the basis for their degree.

The modern thesis as we know it today has evolved over time, with different disciplines and institutions adopting their own standards and formats. However, the basic elements of a thesis – original research, a clear research question, a thorough review of the literature, and a well-argued conclusion – remain the same.

Structure of Thesis

The structure of a thesis may vary slightly depending on the specific requirements of the institution, department, or field of study, but generally, it follows a specific format.

Here’s a breakdown of the structure of a thesis:

This is the first page of the thesis that includes the title of the thesis, the name of the author, the name of the institution, the department, the date, and any other relevant information required by the institution.

This is a brief summary of the thesis that provides an overview of the research question, methodology, findings, and conclusions.

This page provides a list of all the chapters and sections in the thesis and their page numbers.

Introduction

This chapter provides an overview of the research question, the context of the research, and the purpose of the study. The introduction should also outline the methodology and the scope of the research.

Literature Review

This chapter provides a critical analysis of the relevant literature on the research topic. It should demonstrate the gap in the existing knowledge and justify the need for the research.

Methodology

This chapter provides a detailed description of the research methods used to gather and analyze data. It should explain the research design, the sampling method, data collection techniques, and data analysis procedures.

This chapter presents the findings of the research. It should include tables, graphs, and charts to illustrate the results.

This chapter interprets the results and relates them to the research question. It should explain the significance of the findings and their implications for the research topic.

This chapter summarizes the key findings and the main conclusions of the research. It should also provide recommendations for future research.

This section provides a list of all the sources cited in the thesis. The citation style may vary depending on the requirements of the institution or the field of study.

This section includes any additional material that supports the research, such as raw data, survey questionnaires, or other relevant documents.

How to write Thesis

Here are some steps to help you write a thesis:

• Choose a Topic: The first step in writing a thesis is to choose a topic that interests you and is relevant to your field of study. You should also consider the scope of the topic and the availability of resources for research.
• Develop a Research Question: Once you have chosen a topic, you need to develop a research question that you will answer in your thesis. The research question should be specific, clear, and feasible.
• Conduct a Literature Review: Before you start your research, you need to conduct a literature review to identify the existing knowledge and gaps in the field. This will help you refine your research question and develop a research methodology.
• Develop a Research Methodology: Once you have refined your research question, you need to develop a research methodology that includes the research design, data collection methods, and data analysis procedures.
• Collect and Analyze Data: After developing your research methodology, you need to collect and analyze data. This may involve conducting surveys, interviews, experiments, or analyzing existing data.
• Write the Thesis: Once you have analyzed the data, you need to write the thesis. The thesis should follow a specific structure that includes an introduction, literature review, methodology, results, discussion, conclusion, and references.
• Edit and Proofread: After completing the thesis, you need to edit and proofread it carefully. You should also have someone else review it to ensure that it is clear, concise, and free of errors.
• Submit the Thesis: Finally, you need to submit the thesis to your academic advisor or committee for review and evaluation.

Example of Thesis

Example of Thesis template for Students:

Title of Thesis

Table of Contents:

Chapter 1: Introduction

Chapter 2: Literature Review

Chapter 3: Research Methodology

Chapter 4: Results

Chapter 5: Discussion

Chapter 6: Conclusion

References:

Appendices:

Note: That’s just a basic template, but it should give you an idea of the structure and content that a typical thesis might include. Be sure to consult with your department or supervisor for any specific formatting requirements they may have. Good luck with your thesis!

Application of Thesis

Thesis is an important academic document that serves several purposes. Here are some of the applications of thesis:

• Academic Requirement: A thesis is a requirement for many academic programs, especially at the graduate level. It is an essential component of the evaluation process and demonstrates the student’s ability to conduct original research and contribute to the knowledge in their field.
• Career Advancement: A thesis can also help in career advancement. Employers often value candidates who have completed a thesis as it demonstrates their research skills, critical thinking abilities, and their dedication to their field of study.
• Publication : A thesis can serve as a basis for future publications in academic journals, books, or conference proceedings. It provides the researcher with an opportunity to present their research to a wider audience and contribute to the body of knowledge in their field.
• Personal Development: Writing a thesis is a challenging task that requires time, dedication, and perseverance. It provides the student with an opportunity to develop critical thinking, research, and writing skills that are essential for their personal and professional development.
• Impact on Society: The findings of a thesis can have an impact on society by addressing important issues, providing insights into complex problems, and contributing to the development of policies and practices.

Purpose of Thesis

The purpose of a thesis is to present original research findings in a clear and organized manner. It is a formal document that demonstrates a student’s ability to conduct independent research and contribute to the knowledge in their field of study. The primary purposes of a thesis are:

• To Contribute to Knowledge: The main purpose of a thesis is to contribute to the knowledge in a particular field of study. By conducting original research and presenting their findings, the student adds new insights and perspectives to the existing body of knowledge.
• To Demonstrate Research Skills: A thesis is an opportunity for the student to demonstrate their research skills. This includes the ability to formulate a research question, design a research methodology, collect and analyze data, and draw conclusions based on their findings.
• To Develop Critical Thinking: Writing a thesis requires critical thinking and analysis. The student must evaluate existing literature and identify gaps in the field, as well as develop and defend their own ideas.
• To Provide Evidence of Competence : A thesis provides evidence of the student’s competence in their field of study. It demonstrates their ability to apply theoretical concepts to real-world problems, and their ability to communicate their ideas effectively.
• To Facilitate Career Advancement : Completing a thesis can help the student advance their career by demonstrating their research skills and dedication to their field of study. It can also provide a basis for future publications, presentations, or research projects.

When to Write Thesis

The timing for writing a thesis depends on the specific requirements of the academic program or institution. In most cases, the opportunity to write a thesis is typically offered at the graduate level, but there may be exceptions.

Generally, students should plan to write their thesis during the final year of their graduate program. This allows sufficient time for conducting research, analyzing data, and writing the thesis. It is important to start planning the thesis early and to identify a research topic and research advisor as soon as possible.

In some cases, students may be able to write a thesis as part of an undergraduate program or as an independent research project outside of an academic program. In such cases, it is important to consult with faculty advisors or mentors to ensure that the research is appropriately designed and executed.

It is important to note that the process of writing a thesis can be time-consuming and requires a significant amount of effort and dedication. It is important to plan accordingly and to allocate sufficient time for conducting research, analyzing data, and writing the thesis.

Characteristics of Thesis

The characteristics of a thesis vary depending on the specific academic program or institution. However, some general characteristics of a thesis include:

• Originality : A thesis should present original research findings or insights. It should demonstrate the student’s ability to conduct independent research and contribute to the knowledge in their field of study.
• Clarity : A thesis should be clear and concise. It should present the research question, methodology, findings, and conclusions in a logical and organized manner. It should also be well-written, with proper grammar, spelling, and punctuation.
• Research-Based: A thesis should be based on rigorous research, which involves collecting and analyzing data from various sources. The research should be well-designed, with appropriate research methods and techniques.
• Evidence-Based : A thesis should be based on evidence, which means that all claims made in the thesis should be supported by data or literature. The evidence should be properly cited using appropriate citation styles.
• Critical Thinking: A thesis should demonstrate the student’s ability to critically analyze and evaluate information. It should present the student’s own ideas and arguments, and engage with existing literature in the field.
• Academic Style : A thesis should adhere to the conventions of academic writing. It should be well-structured, with clear headings and subheadings, and should use appropriate academic language.

Advantages of Thesis

There are several advantages to writing a thesis, including:

• Development of Research Skills: Writing a thesis requires extensive research and analytical skills. It helps to develop the student’s research skills, including the ability to formulate research questions, design and execute research methodologies, collect and analyze data, and draw conclusions based on their findings.
• Contribution to Knowledge: Writing a thesis provides an opportunity for the student to contribute to the knowledge in their field of study. By conducting original research, they can add new insights and perspectives to the existing body of knowledge.
• Preparation for Future Research: Completing a thesis prepares the student for future research projects. It provides them with the necessary skills to design and execute research methodologies, analyze data, and draw conclusions based on their findings.
• Career Advancement: Writing a thesis can help to advance the student’s career. It demonstrates their research skills and dedication to their field of study, and provides a basis for future publications, presentations, or research projects.
• Personal Growth: Completing a thesis can be a challenging and rewarding experience. It requires dedication, hard work, and perseverance. It can help the student to develop self-confidence, independence, and a sense of accomplishment.

Limitations of Thesis

There are also some limitations to writing a thesis, including:

• Time and Resources: Writing a thesis requires a significant amount of time and resources. It can be a time-consuming and expensive process, as it may involve conducting original research, analyzing data, and producing a lengthy document.
• Narrow Focus: A thesis is typically focused on a specific research question or topic, which may limit the student’s exposure to other areas within their field of study.
• Limited Audience: A thesis is usually only read by a small number of people, such as the student’s thesis advisor and committee members. This limits the potential impact of the research findings.
• Lack of Real-World Application : Some thesis topics may be highly theoretical or academic in nature, which may limit their practical application in the real world.
• Pressure and Stress : Writing a thesis can be a stressful and pressure-filled experience, as it may involve meeting strict deadlines, conducting original research, and producing a high-quality document.
• Potential for Isolation: Writing a thesis can be a solitary experience, as the student may spend a significant amount of time working independently on their research and writing.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Conceptual and Theoretical Frameworks for Thesis Studies: What you must know

A theoretical framework is a conceptual model that provides a systematic and structured way of thinking about a research problem or question. It helps to identify key variables and the relationships between them and to guide the selection and interpretation of data. Theoretical frameworks draw on existing theories and research and can be used to develop new hypotheses or test existing ones. They provide a foundation for research design, data collection, and analysis and can help to ensure that research is relevant, rigorous, and coherent. Theoretical frameworks are common in many disciplines, including social sciences, natural sciences, and humanities, and are essential for building knowledge and advancing understanding in a field.

This article explains the importance of frameworks in a thesis study and the differences between conceptual frameworks and theoretical frameworks. It provides guidelines on how to write a thesis framework, definitions of variable types, and examples of framework types.

What is a research framework and why do I need one?

When planning your thesis study, you need to justify your research and explain its design to your readers. This is called the research framework.

When planning your thesis study, you need to justify your research and explain its design to your readers. This is called the research framework. Think of it as the foundation of a building. A good building needs a strong foundation. Similarly, your research needs to be supported by reviewing and explaining the existing knowledge in the field, describing how your research study will fit within or contribute to the existing literature (e.g., it could challenge or test an existing theory or address a knowledge gap), and informing the reader how your study design aligns with your thesis question or hypothesis.

Important components of the framework are a literature review of recent studies associated with your thesis topic as well as theories/models used in your field of research. The literature review acts as a filtering tool to select appropriate thesis questions and guide data collection, analysis, and interpretation of your findings. Think broadly! Apart from reviewing relevant published papers in your field of research, also explore theories that you have come across in your undergraduate courses, other published thesis studies, encyclopedias, and handbooks.

There are two types of research frameworks: theoretical and conceptual .

What is a conceptual framework?

A conceptual framework is a written or visual representation that explains the study variables and their relationships with each other. The starting point is a literature review of existing studies and theories about your topic.

Steps to develop a conceptual framework

• Clarify your study topic by identifying and defining key concepts in your thesis problem statement and thesis question. Essentially, your thesis should address a knowledge gap.
• Perform a literature review to provide a background to interpret and explain the study findings. Also, draw on empirical knowledge that you have gained from personal experience.
• Identify crucial variables from the literature review and your empirical knowledge, classify them as dependent or independent variables, and define them.
• Brainstorm all the possible factors that could affect each dependent variable.
• Propose relationships among the variables and determine any associations that exist between all variables.
• Use a flowchart or tree diagram to present your conceptual framework.

Types of variables

When developing a conceptual framework, you will need to identify the following:

• Independent variables
• Dependent variables
• Moderating variables
• Mediating variables
• Control variables

First, identify the independent (cause) and dependent (effect) variables in your study. Then, identify variables that influence this relationship, such as moderating variables, mediating variables, and control variables. A moderating variable changes the relationship between independent and dependent variables when its value increases or decreases. A mediating variable links independent and dependent variables to better explain the relationship between them. A control variable could potentially impact the cause-and-effect relationship but is kept constant throughout the study so that its effects on the findings/outcomes can be ruled out.

Example of a conceptual framework

You want to investigate the hours spent exercising (cause) on childhood obesity (effect).

Now, you need to consider moderating variables that affect the cause-and-effect relationship. In our example, the amount of junk food eaten would affect the level of obesity.

Next, you need to consider mediating variables. In our example, the maximum heart rate during exercise would affect the child’s weight.

Finally, you need to consider control variables. In this example, because we do not want to investigate the role of age in obesity, we can use this as a control variable. Thus, the study subjects would be children of a specific age (e.g., aged 6–10 years).

What is a theoretical framework?

A theoretical framework provides a general framework for data analysis. It defines the concepts used and explains existing theories and models in your field of research.

A theoretical framework provides a general framework for data analysis. It defines the concepts used and explains existing theories and models in your field of research. It also explains any assumptions that were used to inform your approach and your choice of specific rationales. Theoretical frameworks are often used in the fields of social sciences.

Purpose of a theoretical framework

• Test and challenge existing theories
• Establish orderly connections between observations and facts
• Predict and control situations
• Develop hypotheses

Steps to develop a theoretical framework

• Identify and define key concepts in your thesis problem statement and thesis question.
• Explain and evaluate existing theories by writing a literature review that describes the concepts, models, and theories that support your study.
• Choose the theory that best explains the relationships between the key variables in your study.
• Explain how your research study fills a knowledge gap or fits into existing studies (e.g., testing if an established theory applies to your thesis context).
• Discuss the relevance of any theoretical assumptions and limitations.

A thesis topic can be approached from a variety of angles, depending on the theories used.

• In psychology, a behavioral approach would use different methods and assumptions compared with a cognitive approach when treating anxiety.
• In literature, a book could be analyzed using different literary theories, such as Marxism or poststructuralism.

Structuring a theoretical framework

The structure of a theoretical framework is fluid, and there are no specific rules that need to be followed, as long as it is clearly and logically presented.

The theoretical framework is a natural extension of your literature review. The literature review should identify gaps in the field of your research, and reviewing existing theories will help to determine how these can be addressed. The structure of a theoretical framework is fluid, and there are no specific rules that need to be followed, as long as it is clearly and logically presented. The theoretical framework is sometimes integrated into the literature review chapter of a thesis, but it can also be included as a separate chapter, depending on the complexity of the theories.

Example of a theoretical framework

The sales staff at Company X are unmotivated and struggling to meet their monthly targets. Some members of the management team believe that this could be achieved by implementing a comprehensive product-training program, but others believe that introducing a sales commission structure will help.

Company X is not achieving their monthly sales targets

To increase monthly sales.

Research question:

How can Company X motivate their sales team to achieve its monthly sales targets?

Sub-questions:

• Why do the sales staff feel unmotivated?
• What is the relationship between motivation and monetary rewards?
• Do the sales staff feel that they have sufficient product knowledge?

Theoretical framework:

A literature search will need to be performed to understand the background of the many different theories of motivation in psychology. For example, Maslow’s Hierarchy of Needs (basic human needs—physiological, safety, love/belonging, esteem, and self-actualization—have to be fulfilled before one can live up to their true potential), Vroom’s Theory of Expectancy (people decide upon their actions based on the outcomes they expect), and Locke’s Goal-Setting Theory (goals are a key driver of one’s behavior). These theories would need to be investigated to determine which would be the best approach to increase the motivation of the sales staff in Company X so that the monthly sales targets are met.

A robust conceptual or theoretical framework is crucial when writing a thesis/dissertation. It defines your research gap, identifies your approach, and guides the interpretation of your results.

A thesis is the most important document you will write during your academic studies. For professional thesis editing and thesis proofreading services, check out Enago's Thesis Editing service s for more information.

Editor’s pick

Get free updates.

Subscribe to our newsletter for regular insights from the research and publishing industry!

What type of framework is used in the Humanities and Social Sciences (HSS) domain? +

Theoretical frameworks are typically used in the HSS domain, while conceptual frameworks are used in the Sciences domain.

What is the difference between mediating versus moderating variables? +

The difference between mediators and moderators can be confusing. A moderating variable is unaffected by the independent variable and can increase or decrease the strength of the relationship between the independent and dependent variables. A mediating variable is affected by the independent variable and can explain the relationship between the independent and dependent variables. T he statistical correlation between the independent and dependent variables is higher when the mediating variable is excluded.

What software should I use to present my conceptual framework? +

The software program Creately provides some useful templates that can help you get started. Other recommended programs are SmartDraw , Inkscape , and diagrams.net .

thesis frame

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Thesis frame

Thesis Statement Practice | Sentence Frames to Track Character Development

Counterclaim and thesis sentence frame anchor chart glue in

Thesis Statement Practice: Sentence Frames to Analyze Craft, or Literary Devices

Rhetorical Analysis Thesis Frame Statements | AP Lang

Thesis Frames : Easy to Follow Guides

Thesis Statement Practice: Sentence Frames Trace the Shifting Meaning of a Motif

Frankenstein Argument Essay | Scaffold | Thesis & Topic Sentence Frames

To Kill a Mockingbird Essay - Thesis & Topic Sentence Frames

• Google Docs™

Opinion Writing Sentence Frames Paragraph Templates & Posters

How to Write Thesis Statements - Common Core Aligned

Argumentative - Research Report - 5 Paragraph Frames - Essay Organizer

Writing the Synthesis Essay for AP Lang: Sentence Frames

Thesis Statement Worksheets Digital Bundle: Topic Sentences Practice

Pastel Rainbow Number Posters With Ten Frames 1 - 30

Botanical (Eucalyptus) Number Posters with Ten Frames 1-30

Character Analysis Essay Lesson Plan + Sentence Frames

Blue Rainbow Number Posters with Ten Frames 1-30

Summarizing Conflict | Summary Statement Sentence Frames | Embedded Vocabulary

Orange Creamsicle Number Posters with Ten Frames 1-30

Argumentative Essay Frame Version 1

Argumentative Essay Frame Version 2

Sweet Treats Decor Numbers and Tens Frames Posters

Ten Frame Number Posters Outdoor Adventure Camping Theme

Addition to 10 using Ten Frames

• Google Slides™
• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

• All Courses
• Louisiana ELA Guidebooks
• Frequently Asked Questions
• Book Resources
• Resource Library
• Get Involved
• 10th Anniversary

Customizable Templates Overview

Watch an overview of the new customizable templates, which can easily be customized to fit your content and set your students up for success.

Speech Thesis Statement

In the realm of effective communication, crafting a well-structured and compelling speech thesis statement is paramount. A speech thesis serves as the bedrock upon which impactful oratory is built, encapsulating the core message, purpose, and direction of the discourse. This exploration delves into diverse speech thesis statement examples, offering insights into the art of formulating them. Moreover, it provides valuable tips to guide you in crafting speeches that resonate powerfully with your audience and leave a lasting impact.

What is a Speech Thesis Statement? – Definition

A speech thesis statement is a succinct and focused declaration that encapsulates the central argument, purpose, or message of a speech. It outlines the primary idea the speaker intends to convey to the audience, serving as a guide for the content and structure of the speech.

What is an Example of Speech Thesis Statement?

“In this speech, I will argue that implementing stricter gun control measures is essential for reducing gun-related violence and ensuring public safety. By examining statistical data, addressing common misconceptions, and advocating for comprehensive background checks, we can take meaningful steps toward a safer society.”

In this example, the speech’s main argument, key points (statistics, misconceptions, background checks), and the intended impact (safer society) are all succinctly conveyed in the thesis statement.

100 Speech Thesis Statement Examples

• “Today, I will convince you that renewable energy sources are the key to a sustainable and cleaner future.”
• “In this speech, I will explore the importance of mental health awareness and advocate for breaking the stigma surrounding it.”
• “My aim is to persuade you that adopting a plant-based diet contributes not only to personal health but also to environmental preservation.”
• “In this speech, I will discuss the benefits of exercise on cognitive function and share practical tips for integrating physical activity into our daily routines.”
• “Today, I’ll argue that access to quality education is a fundamental right for all, and I’ll present strategies to bridge the educational gap.”
• “My speech centers around the significance of arts education in fostering creativity, critical thinking, and overall cognitive development in students.”
• “Through this speech, I’ll shed light on the impact of plastic pollution on marine ecosystems and inspire actionable steps toward plastic reduction.”
• “My aim is to persuade you that stricter regulations on social media platforms are imperative to combat misinformation and protect user privacy.”
• “Today, I’ll discuss the importance of empathy in building strong interpersonal relationships and provide techniques to cultivate empathy in daily interactions.”
• “In this speech, I’ll present the case for implementing universal healthcare, emphasizing its benefits for both individual health and societal well-being.”
• “My speech highlights the urgency of addressing climate change and calls for international collaboration in reducing carbon emissions.”
• “I will argue that the arts play a crucial role in fostering cultural understanding, breaking down stereotypes, and promoting global harmony.”
• “Through this speech, I’ll advocate for the preservation of endangered species and offer strategies to contribute to wildlife conservation efforts.”
• “Today, I’ll discuss the power of effective time management in enhancing productivity and share practical techniques to prioritize tasks.”
• “My aim is to convince you that raising the minimum wage is vital to reducing income inequality and improving the overall quality of life.”
• “In this speech, I’ll explore the societal implications of automation and artificial intelligence and propose strategies for a smooth transition into the future.”
• “Through this speech, I’ll emphasize the significance of volunteering in community development and suggest ways to get involved in meaningful initiatives.”
• “I will argue that stricter regulations on fast food advertising are necessary to address the growing obesity epidemic among children and adolescents.”
• “Today, I’ll discuss the importance of financial literacy in personal empowerment and provide practical advice for making informed financial decisions.”
• “My speech focuses on the value of cultural diversity in enriching society, fostering understanding, and promoting a more inclusive world.”
• “In this speech, I’ll present the case for investing in renewable energy technologies to mitigate the adverse effects of climate change on future generations.”
• “I will argue that embracing failure as a stepping stone to success is crucial for personal growth and achieving one’s fullest potential.”
• “Through this speech, I’ll examine the impact of social media on mental health and offer strategies to maintain a healthy online presence.”
• “Today, I’ll emphasize the importance of effective communication skills in professional success and share tips for honing these skills.”
• “My aim is to persuade you that stricter gun control measures are essential to reduce gun-related violence and ensure public safety.”
• “In this speech, I’ll discuss the significance of cultural preservation and the role of heritage sites in maintaining the identity and history of communities.”
• “I will argue that promoting diversity and inclusion in the workplace leads to enhanced creativity, collaboration, and overall organizational success.”
• “Through this speech, I’ll explore the impact of social media on political engagement and discuss ways to critically evaluate online information sources.”
• “Today, I’ll present the case for investing in public transportation infrastructure to alleviate traffic congestion, reduce pollution, and enhance urban mobility.”
• “My aim is to persuade you that implementing mindfulness practices in schools can improve students’ focus, emotional well-being, and overall academic performance.”
• “In this speech, I’ll discuss the importance of supporting local businesses for economic growth, community vibrancy, and sustainable development.”
• “I will argue that fostering emotional intelligence in children equips them with crucial skills for interpersonal relationships, empathy, and conflict resolution.”
• “Through this speech, I’ll emphasize the need for comprehensive sex education that addresses consent, healthy relationships, and informed decision-making.”
• “Today, I’ll explore the benefits of embracing a minimalist lifestyle for mental clarity, reduced stress, and a more mindful and sustainable way of living.”
• “My aim is to persuade you that sustainable farming practices are essential for preserving ecosystems, ensuring food security, and mitigating climate change.”
• “In this speech, I’ll discuss the importance of civic engagement in democracy and provide strategies for individuals to get involved in their communities.”
• “I will argue that investing in early childhood education not only benefits individual children but also contributes to a stronger and more prosperous society.”
• “Through this speech, I’ll examine the impact of social media on body image dissatisfaction and offer strategies to promote body positivity and self-acceptance.”
• “Today, I’ll present the case for stricter regulations on e-cigarette marketing and sales to curb youth vaping and protect public health.”
• “My aim is to persuade you that exploring nature and spending time outdoors is essential for mental and physical well-being in our technology-driven world.”
• “In this speech, I’ll discuss the implications of automation on employment and suggest strategies for reskilling and preparing for the future of work.”
• “I will argue that embracing failure as a valuable learning experience fosters resilience, innovation, and personal growth, leading to ultimate success.”
• “Through this speech, I’ll emphasize the significance of media literacy in discerning credible information from fake news and ensuring informed decision-making.”
• “Today, I’ll explore the benefits of implementing universal healthcare, focusing on improved access to medical services and enhanced public health outcomes.”
• “My aim is to persuade you that embracing sustainable travel practices can minimize the environmental impact of tourism and promote cultural exchange.”
• “In this speech, I’ll present the case for criminal justice reform, highlighting the importance of alternatives to incarceration for nonviolent offenders.”
• “I will argue that instilling a growth mindset in students enhances their motivation, learning abilities, and willingness to face challenges.”
• “Through this speech, I’ll discuss the implications of artificial intelligence on the job market and propose strategies for adapting to automation-driven changes.”
• “Today, I’ll emphasize the importance of digital privacy awareness and provide practical tips to safeguard personal information online.”
• “My aim is to persuade you that investing in renewable energy sources is crucial not only for environmental sustainability but also for economic growth.”
• “In this speech, I’ll discuss the significance of cultural preservation and the role of heritage sites in maintaining a sense of identity and history.”
• “I will argue that promoting diversity and inclusion in the workplace leads to improved creativity, collaboration, and overall organizational performance.”
• “Through this speech, I’ll explore the impact of social media on political engagement and offer strategies to critically assess online information.”
• “Today, I’ll present the case for investing in public transportation to alleviate traffic congestion, reduce emissions, and enhance urban mobility.”
• “My aim is to persuade you that implementing mindfulness practices in schools can enhance students’ focus, emotional well-being, and academic achievement.”
• “In this speech, I’ll discuss the importance of supporting local businesses for economic growth, community vitality, and sustainable development.”
• “I will argue that fostering emotional intelligence in children equips them with essential skills for healthy relationships, empathy, and conflict resolution.”
• “Through this speech, I’ll emphasize the need for comprehensive sex education that includes consent, healthy relationships, and informed decision-making.”
• “My aim is to persuade you that sustainable farming practices are vital for preserving ecosystems, ensuring food security, and combating climate change.”
• “In this speech, I’ll discuss the importance of civic engagement in democracy and provide strategies for individuals to actively participate in their communities.”
• “I will argue that investing in early childhood education benefits not only individual children but also contributes to a stronger and more prosperous society.”
• “Through this speech, I’ll examine the impact of social media on body image dissatisfaction and suggest strategies to promote body positivity and self-acceptance.”
• “Today, I’ll present the case for stricter regulations on e-cigarette marketing and sales to combat youth vaping and protect public health.”
• “My aim is to persuade you that connecting with nature and spending time outdoors is essential for mental and physical well-being in our technology-driven world.”
• “In this speech, I’ll discuss the implications of automation on employment and suggest strategies for reskilling and adapting to the changing job landscape.”
• “I will argue that embracing failure as a valuable learning experience fosters resilience, innovation, and personal growth, ultimately leading to success.”
• “Through this speech, I’ll emphasize the significance of media literacy in discerning credible information from fake news and making informed decisions.”
• “Today, I’ll explore the benefits of implementing universal healthcare, focusing on improved access to medical services and better public health outcomes.”
• “My aim is to persuade you that adopting sustainable travel practices can minimize the environmental impact of tourism and promote cultural exchange.”
• “I will argue that instilling a growth mindset in students enhances their motivation, learning abilities, and readiness to tackle challenges.”
• “Through this speech, I’ll discuss the implications of artificial intelligence on the job market and propose strategies for adapting to the changing landscape.”
• “Today, I’ll emphasize the importance of digital privacy awareness and provide practical tips to safeguard personal information in the online world.”
• “My aim is to persuade you that investing in renewable energy sources is essential for both environmental sustainability and economic growth.”
• “In this speech, I’ll discuss the transformative power of art therapy in promoting mental well-being and share real-life success stories.”
• “I will argue that promoting gender equality not only empowers women but also contributes to economic growth and social progress.”
• “Through this speech, I’ll explore the impact of technology on interpersonal relationships and offer strategies to maintain meaningful connections.”
• “Today, I’ll present the case for sustainable fashion choices, emphasizing their positive effects on the environment and ethical manufacturing practices.”
• “My aim is to persuade you that investing in early childhood education is an investment in the future, leading to a more educated and equitable society.”
• “In this speech, I’ll discuss the significance of community service in building strong communities and share personal stories of volunteering experiences.”
• “I will argue that fostering emotional intelligence in children lays the foundation for a harmonious and empathetic society.”
• “Through this speech, I’ll emphasize the importance of teaching critical thinking skills in education and how they empower individuals to navigate a complex world.”
• “Today, I’ll explore the benefits of embracing a growth mindset in personal and professional development, leading to continuous learning and improvement.”
• “My aim is to persuade you that conscious consumerism can drive positive change in industries by supporting ethical practices and environmentally friendly products.”
• “In this speech, I’ll present the case for renewable energy as a solution to energy security, reduced carbon emissions, and a cleaner environment.”
• “I will argue that investing in mental health support systems is essential for the well-being of individuals and society as a whole.”
• “Through this speech, I’ll discuss the role of music therapy in enhancing mental health and promoting emotional expression and healing.”
• “Today, I’ll emphasize the importance of embracing cultural diversity to foster global understanding, harmony, and peaceful coexistence.”
• “My aim is to persuade you that incorporating mindfulness practices into daily routines can lead to reduced stress and increased overall well-being.”
• “In this speech, I’ll discuss the implications of genetic engineering and gene editing technologies on ethical considerations and future generations.”
• “I will argue that investing in renewable energy infrastructure not only mitigates climate change but also generates job opportunities and economic growth.”
• “Through this speech, I’ll explore the impact of social media on political polarization and offer strategies for promoting constructive online discourse.”
• “Today, I’ll present the case for embracing experiential learning in education, focusing on hands-on experiences that enhance comprehension and retention.”
• “My aim is to persuade you that practicing gratitude can lead to improved mental health, increased happiness, and a more positive outlook on life.”
• “In this speech, I’ll discuss the importance of teaching financial literacy in schools to equip students with essential money management skills.”
• “I will argue that promoting sustainable agriculture practices is essential to ensure food security, protect ecosystems, and combat climate change.”
• “Through this speech, I’ll emphasize the need for greater awareness of mental health issues in society and the importance of reducing stigma.”
• “Today, I’ll explore the benefits of incorporating arts and creativity into STEM education to foster innovation, critical thinking, and problem-solving.”
• “My aim is to persuade you that practicing mindfulness and meditation can lead to improved focus, reduced anxiety, and enhanced overall well-being.”

Speech Thesis Statement for Introduction

Introductions set the tone for impactful speeches. These thesis statements encapsulate the essence of opening remarks, laying the foundation for engaging discourse.

• “Welcome to an exploration of the power of storytelling and its ability to bridge cultures and foster understanding across diverse backgrounds.”
• “In this introductory speech, we delve into the realm of artificial intelligence, examining its potential to reshape industries and redefine human capabilities.”
• “Join us as we navigate the fascinating world of space exploration and the role of technological advancements in uncovering the mysteries of the universe.”
• “Through this speech, we embark on a journey through history, highlighting pivotal moments that have shaped civilizations and continue to inspire change.”
• “Today, we embark on a discussion about the significance of empathy in our interactions, exploring how it can enrich our connections and drive positive change.”
• “In this opening address, we dive into the realm of sustainable living, exploring practical steps to reduce our environmental footprint and promote eco-consciousness.”
• “Join us as we explore the evolution of communication, from ancient symbols to modern technology, and its impact on how we connect and convey ideas.”
• “Welcome to an exploration of the intricate relationship between art and emotion, uncovering how artistic expression transcends language barriers and unites humanity.”
• “In this opening statement, we examine the changing landscape of work and career, discussing strategies to navigate career transitions and embrace lifelong learning.”
• “Today, we delve into the concept of resilience and its role in facing adversity, offering insights into how resilience can empower us to overcome challenges.”

Speech Thesis Statement for Graduation

Graduation speeches mark significant milestones. These thesis statements encapsulate the achievements, aspirations, and challenges faced by graduates as they move forward.

• “As we stand on the threshold of a new chapter, let’s reflect on our journey, celebrate our achievements, and embrace the uncertainties that lie ahead.”
• “In this graduation address, we celebrate not only our academic accomplishments but also the personal growth, resilience, and friendships that have enriched our years here.”
• “As we step into the world beyond academia, let’s remember that learning is a lifelong journey, and the skills we’ve honed will propel us toward success.”
• “Today, we bid farewell to the familiar and embrace the unknown, armed with the knowledge that every challenge we face is an opportunity for growth.”
• “In this commencement speech, we acknowledge the collective accomplishments of our class and embrace the responsibility to contribute positively to the world.”
• “As we graduate, let’s carry with us the values instilled by our education, applying them not only in our careers but also in shaping a more just and compassionate society.”
• “Join me in celebrating the diversity of talents and perspectives that define our graduating class, and let’s channel our unique strengths to make a meaningful impact.”
• “Today, we honor the culmination of our academic pursuits and embrace the journey of continuous learning that will shape our personal and professional paths.”
• “In this graduation address, we acknowledge the support of our families, educators, and peers, recognizing that our successes are a testament to shared effort.”
• “As we don our caps and gowns, let’s remember that our education equips us not only with knowledge but also with the power to effect positive change in the world.”

Speech Thesis Statement For Acceptance

Acceptance speeches express gratitude and acknowledge achievements. These thesis statements capture the essence of acknowledgment, appreciation, and commitment.

• “I am humbled and honored by this recognition, and I pledge to use this platform to amplify the voices of the marginalized and work toward equity.”
• “As I accept this award, I express my gratitude to those who believed in my potential, and I commit to using my skills to contribute meaningfully to our community.”
• “Receiving this honor is a testament to the collaborative efforts that make achievements possible. I am dedicated to sharing this success with those who supported me.”
• “Accepting this award, I am reminded of the responsibility that accompanies it. I vow to continue striving for excellence and inspiring those around me.”
• “As I receive this recognition, I extend my deepest appreciation to my mentors, colleagues, and family, and I promise to pay it forward by mentoring the next generation.”
• “Accepting this accolade, I recognize that success is a team effort. I commit to fostering a culture of collaboration and innovation in all my endeavors.”
• “Receiving this honor, I am reminded of the privilege I have to effect change. I dedicate myself to leveraging this platform for the betterment of society.”
• “Accepting this award, I am grateful for the opportunities that have shaped my journey. I am committed to using my influence to uplift others and drive positive change.”
• “As I stand here, I am deeply moved by this recognition. I pledge to use this honor as a catalyst for making a meaningful impact on the lives of those I encounter.”
• “Accepting this distinction, I embrace the responsibility it brings. I promise to uphold the values that guided me to this moment and channel my efforts toward progress.”

Speech Thesis Statement in Extemporaneous

Extemporaneous speeches require quick thinking and concise communication. These thesis statements capture the essence of on-the-spot analysis and delivery.

• “On the topic of technological disruption, we explore its effects on job markets, emphasizing the importance of upskilling for the workforce’s evolving demands.”
• “In this impromptu speech, we dissect the complexities of global climate agreements, assessing their impact on environmental sustainability and international cooperation.”
• “Addressing the issue of cyberbullying, we examine its psychological consequences, potential legal remedies, and strategies to create safer online spaces.”
• “Discussing the merits of universal basic income, we weigh its potential to alleviate poverty, stimulate economic growth, and reshape the social safety net.”
• “As we delve into the debate on genetically modified organisms, we consider the benefits of increased crop yields, while also evaluating environmental and health concerns.”
• “On the topic of urbanization, we analyze its benefits in fostering economic growth and cultural exchange, while addressing challenges of infrastructure and inequality.”
• “Delving into the controversy surrounding artificial intelligence, we explore its transformative potential in various sectors, touching on ethical considerations and fears of job displacement.”
• “In this impromptu speech, we examine the impact of social media on political discourse, highlighting the role of echo chambers and the need for critical thinking.”
• “Addressing the issue of mental health stigma, we discuss the societal barriers that prevent seeking help, while advocating for open conversations and destigmatization.”
• “Discussing the concept of ethical consumerism, we weigh the impact of consumer choices on industries, environment, and labor rights, emphasizing the power of informed purchasing.”

Speech Thesis Statement in Argumentative Essay

Argumentative speeches present clear stances on contentious topics. These thesis statements assert positions while indicating the direction of the ensuing debate.

• “In this argumentative speech, we assert that mandatory voting fosters civic participation and strengthens democracy by ensuring diverse voices are heard.”
• “Advocating for stricter gun control, we contend that regulations on firearm access are vital for public safety, reducing gun violence, and preventing tragedies.”
• “Arguing for the benefits of school uniforms, we posit that uniforms promote a focused learning environment, reduce socioeconomic disparities, and enhance school spirit.”
• “In this persuasive speech, we assert that capital punishment should be abolished due to its potential for wrongful executions, lack of deterrence, and ethical concerns.”
• “Taking a stand against standardized testing, we argue that these assessments stifle creativity, promote rote learning, and fail to measure true intellectual potential.”
• “Defending the benefits of renewable energy, we assert that transitioning to sustainable sources will mitigate climate change, create jobs, and reduce dependence on fossil fuels.”
• “Addressing the merits of open borders, we contend that welcoming immigrants bolsters cultural diversity, contributes to economic growth, and upholds humanitarian values.”
• “In this persuasive speech, we argue against the use of animal testing, asserting that modern alternatives exist to ensure scientific progress without unnecessary suffering.”
• “Advocating for comprehensive sex education, we assert that teaching about contraception, consent, and healthy relationships equips students to make informed choices.”
• “Arguing for universal healthcare, we posit that accessible medical services are a basic human right, contributing to improved public health, reduced disparities, and economic stability.”

These examples offer a range of thesis statements for various types of speeches, catering to different contexts and styles of presentation. Tailor them to fit your specific needs and adjust the content as necessary to create impactful speeches.

Is There a Thesis Statement in a Speech?

Yes, a thesis statement is an essential component of a speech. Just like in written essays, a thesis statement in a speech serves as the central point or main idea that the speaker wants to convey to the audience. It provides focus, direction, and a preview of the content that will follow in the speech. A well-crafted thesis statement helps the audience understand the purpose of the speech and what they can expect to learn or gain from listening.

What is the Thesis Structure of a Speech?

The structure of a thesis statement in a speech is similar to that of a thesis statement in an essay, but it’s adapted for the spoken format. A speech thesis generally consists of:

• Topic: Clearly state the topic or subject of your speech. This provides the context for your thesis and gives the audience an idea of the subject matter.
• Main Idea or Argument: Present the main point you want to make or the central argument you’ll be discussing in your speech. This should be a concise and focused statement that encapsulates the essence of your message.
• Supporting Points: Optionally, you can include a brief overview of the main supporting points or arguments that you’ll elaborate on in the body of your speech. This gives the audience an outline of what to expect.

How Do You Write a Speech Thesis Statement? – Step by Step Guide

• Choose Your Topic: Select a topic that is relevant to your audience and aligns with the purpose of your speech.
• Identify Your Main Message: Determine the central message or argument you want to convey. What is the key takeaway you want your audience to remember?
• Craft a Concise Statement: Write a clear and concise sentence that captures the essence of your main message. Make sure it’s specific and avoids vague language.
• Consider Your Audience: Tailor your thesis statement to your audience’s level of understanding and interests. Use language that resonates with them.
• Review and Refine: Read your thesis statement aloud to ensure it sounds natural and engaging. Refine it as needed to make it compelling.

Tips for Writing a Speech Thesis Statement

• Be Specific: A strong thesis statement is specific and focused. Avoid vague or general statements.
• Avoid Jargon: Use language that your audience can easily understand, avoiding complex jargon or technical terms unless you explain them.
• One Main Idea: Stick to one main idea or argument. Multiple ideas can confuse your audience.
• Preview Supporting Points: If applicable, briefly preview the main supporting points you’ll cover in your speech.
• Reflect the Purpose: Your thesis should reflect the purpose of your speech—whether it’s to inform, persuade, entertain, or inspire.
• Keep It Concise: A thesis statement is not a paragraph. Keep it to a single sentence that encapsulates your message.
• Practice Pronunciation: If your thesis statement includes challenging words or terms, practice pronouncing them clearly.
• Test for Clarity: Ask someone to listen to your thesis statement and summarize what they understood from it. This can help you gauge its clarity.
• Revise as Necessary: Don’t be afraid to revise your thesis statement as you refine your speech. It’s important that it accurately represents your content.
• Capture Interest: Craft your thesis statement in a way that captures the audience’s interest and curiosity, encouraging them to listen attentively.

Remember, the thesis statement sets the tone for your entire speech. It should be well-crafted, engaging, and reflective of the main message you want to communicate to your audience.

Speech Thesis Statement Generator

Text prompt

• Instructive
• Professional

Create a Speech Thesis Statement on the importance of voting

Write a Speech Thesis Statement for a talk on renewable energy benefits

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Dissertation

How to Write a Thesis or Dissertation Conclusion

Published on September 6, 2022 by Tegan George and Shona McCombes. Revised on November 20, 2023.

The conclusion is the very last part of your thesis or dissertation . It should be concise and engaging, leaving your reader with a clear understanding of your main findings, as well as the answer to your research question .

In it, you should:

• Clearly state the answer to your main research question
• Summarize and reflect on your research process
• Make recommendations for future work on your thesis or dissertation topic
• Show what new knowledge you have contributed to your field
• Wrap up your thesis or dissertation

Instantly correct all language mistakes in your text

Upload your document to correct all your mistakes in minutes

Table of contents

Discussion vs. conclusion, how long should your conclusion be, step 1: answer your research question, step 2: summarize and reflect on your research, step 3: make future recommendations, step 4: emphasize your contributions to your field, step 5: wrap up your thesis or dissertation, full conclusion example, conclusion checklist, other interesting articles, frequently asked questions about conclusion sections.

While your conclusion contains similar elements to your discussion section , they are not the same thing.

Your conclusion should be shorter and more general than your discussion. Instead of repeating literature from your literature review , discussing specific research results , or interpreting your data in detail, concentrate on making broad statements that sum up the most important insights of your research.

As a rule of thumb, your conclusion should not introduce new data, interpretations, or arguments.

Prevent plagiarism. Run a free check.

Depending on whether you are writing a thesis or dissertation, your length will vary. Generally, a conclusion should make up around 5–7% of your overall word count.

An empirical scientific study will often have a short conclusion, concisely stating the main findings and recommendations for future research. A humanities dissertation topic or systematic review , on the other hand, might require more space to conclude its analysis, tying all the previous sections together in an overall argument.

Your conclusion should begin with the main question that your thesis or dissertation aimed to address. This is your final chance to show that you’ve done what you set out to do, so make sure to formulate a clear, concise answer.

• Don’t repeat a list of all the results that you already discussed
• Do synthesize them into a final takeaway that the reader will remember.

An empirical thesis or dissertation conclusion may begin like this:

A case study –based thesis or dissertation conclusion may begin like this:

In the second example, the research aim is not directly restated, but rather added implicitly to the statement. To avoid repeating yourself, it is helpful to reformulate your aims and questions into an overall statement of what you did and how you did it.

Your conclusion is an opportunity to remind your reader why you took the approach you did, what you expected to find, and how well the results matched your expectations.

To avoid repetition , consider writing more reflectively here, rather than just writing a summary of each preceding section. Consider mentioning the effectiveness of your methodology , or perhaps any new questions or unexpected insights that arose in the process.

You can also mention any limitations of your research, but only if you haven’t already included these in the discussion. Don’t dwell on them at length, though—focus on the positives of your work.

• While x limits the generalizability of the results, this approach provides new insight into y .
• This research clearly illustrates x , but it also raises the question of y .

The only proofreading tool specialized in correcting academic writing - try for free!

The academic proofreading tool has been trained on 1000s of academic texts and by native English editors. Making it the most accurate and reliable proofreading tool for students.

Try for free

You may already have made a few recommendations for future research in your discussion section, but the conclusion is a good place to elaborate and look ahead, considering the implications of your findings in both theoretical and practical terms.

• Based on these conclusions, practitioners should consider …
• To better understand the implications of these results, future studies could address …
• Further research is needed to determine the causes of/effects of/relationship between …

When making recommendations for further research, be sure not to undermine your own work. Relatedly, while future studies might confirm, build on, or enrich your conclusions, they shouldn’t be required for your argument to feel complete. Your work should stand alone on its own merits.

Just as you should avoid too much self-criticism, you should also avoid exaggerating the applicability of your research. If you’re making recommendations for policy, business, or other practical implementations, it’s generally best to frame them as “shoulds” rather than “musts.” All in all, the purpose of academic research is to inform, explain, and explore—not to demand.

Make sure your reader is left with a strong impression of what your research has contributed to the state of your field.

Some strategies to achieve this include:

• Returning to your problem statement to explain how your research helps solve the problem
• Referring back to the literature review and showing how you have addressed a gap in knowledge
• Discussing how your findings confirm or challenge an existing theory or assumption

Again, avoid simply repeating what you’ve already covered in the discussion in your conclusion. Instead, pick out the most important points and sum them up succinctly, situating your project in a broader context.

The end is near! Once you’ve finished writing your conclusion, it’s time to wrap up your thesis or dissertation with a few final steps:

• It’s a good idea to write your abstract next, while the research is still fresh in your mind.
• Next, make sure your reference list is complete and correctly formatted. To speed up the process, you can use our free APA citation generator .
• Once you’ve added any appendices , you can create a table of contents and title page .
• Finally, read through the whole document again to make sure your thesis is clearly written and free from language errors. You can proofread it yourself , ask a friend, or consider Scribbr’s proofreading and editing service .

Here is an example of how you can write your conclusion section. Notice how it includes everything mentioned above:

V. Conclusion

The current research aimed to identify acoustic speech characteristics which mark the beginning of an exacerbation in COPD patients.

The central questions for this research were as follows: 1. Which acoustic measures extracted from read speech differ between COPD speakers in stable condition and healthy speakers? 2. In what ways does the speech of COPD patients during an exacerbation differ from speech of COPD patients during stable periods?

All recordings were aligned using a script. Subsequently, they were manually annotated to indicate respiratory actions such as inhaling and exhaling. The recordings of 9 stable COPD patients reading aloud were then compared with the recordings of 5 healthy control subjects reading aloud. The results showed a significant effect of condition on the number of in- and exhalations per syllable, the number of non-linguistic in- and exhalations per syllable, and the ratio of voiced and silence intervals. The number of in- and exhalations per syllable and the number of non-linguistic in- and exhalations per syllable were higher for COPD patients than for healthy controls, which confirmed both hypotheses.

However, the higher ratio of voiced and silence intervals for COPD patients compared to healthy controls was not in line with the hypotheses. This unpredicted result might have been caused by the different reading materials or recording procedures for both groups, or by a difference in reading skills. Moreover, there was a trend regarding the effect of condition on the number of syllables per breath group. The number of syllables per breath group was higher for healthy controls than for COPD patients, which was in line with the hypothesis. There was no effect of condition on pitch, intensity, center of gravity, pitch variability, speaking rate, or articulation rate.

This research has shown that the speech of COPD patients in exacerbation differs from the speech of COPD patients in stable condition. This might have potential for the detection of exacerbations. However, sustained vowels rarely occur in spontaneous speech. Therefore, the last two outcome measures might have greater potential for the detection of beginning exacerbations, but further research on the different outcome measures and their potential for the detection of exacerbations is needed due to the limitations of the current study.

Checklist: Conclusion

I have clearly and concisely answered the main research question .

I have summarized my overall argument or key takeaways.

I have mentioned any important limitations of the research.

I have given relevant recommendations .

I have clearly explained what my research has contributed to my field.

I have  not introduced any new data or arguments.

You've written a great conclusion! Use the other checklists to further improve your dissertation.

If you want to know more about AI for academic writing, AI tools, or research bias, make sure to check out some of our other articles with explanations and examples or go directly to our tools!

Research bias

• Survivorship bias
• Self-serving bias
• Availability heuristic
• Halo effect
• Hindsight bias
• Deep learning
• Generative AI
• Machine learning
• Reinforcement learning
• Supervised vs. unsupervised learning

 (AI) Tools

• Grammar Checker
• Paraphrasing Tool
• Text Summarizer
• AI Detector
• Plagiarism Checker
• Citation Generator

In a thesis or dissertation, the discussion is an in-depth exploration of the results, going into detail about the meaning of your findings and citing relevant sources to put them in context.

The conclusion is more shorter and more general: it concisely answers your main research question and makes recommendations based on your overall findings.

While it may be tempting to present new arguments or evidence in your thesis or disseration conclusion , especially if you have a particularly striking argument you’d like to finish your analysis with, you shouldn’t. Theses and dissertations follow a more formal structure than this.

All your findings and arguments should be presented in the body of the text (more specifically in the discussion section and results section .) The conclusion is meant to summarize and reflect on the evidence and arguments you have already presented, not introduce new ones.

For a stronger dissertation conclusion , avoid including:

• Important evidence or analysis that wasn’t mentioned in the discussion section and results section
• Generic concluding phrases (e.g. “In conclusion …”)
• Weak statements that undermine your argument (e.g., “There are good points on both sides of this issue.”)

Your conclusion should leave the reader with a strong, decisive impression of your work.

The conclusion of your thesis or dissertation shouldn’t take up more than 5–7% of your overall word count.

The conclusion of your thesis or dissertation should include the following:

• A restatement of your research question
• A summary of your key arguments and/or results
• A short discussion of the implications of your research

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

George, T. & McCombes, S. (2023, November 20). How to Write a Thesis or Dissertation Conclusion. Scribbr. Retrieved April 2, 2024, from https://www.scribbr.com/dissertation/write-conclusion/

Is this article helpful?

Tegan George

Other students also liked, how to write a discussion section | tips & examples, how to write an abstract | steps & examples, how to write a thesis or dissertation introduction, unlimited academic ai-proofreading.

✔ Document error-free in 5minutes ✔ Unlimited document corrections ✔ Specialized in correcting academic texts