math problem solving what is

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• How to Use Math Journals in Class
• The Frayer Model for Math
• Algorithms in Mathematics and Beyond
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Critical Thinking Definition, Skills, and Examples
• Graphic Organizers in Math
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• Christmas Word Problem Worksheets
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests
• 7 Steps to Math Success

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

The home of mathematics education in New Zealand.

• Forgot password ?
• Teaching material
• Problem solving activities
• Problem Solving Information
• What is Problem Solving?

What is problem solving?

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

On this page we discuss "What is problem polving?" under three headings: introduction, four stages of problem solving, and the scientific approach.

Introduction

Naturally enough, problem solving is about solving problems. And we’ll restrict ourselves to thinking about mathematical problems here even though problem solving in school has a wider goal. When you think about it, the whole aim of education is to equip students to solve problems. 

But problem solving also contributes to mathematics itself. Mathematics consists of skills and processes. The skills are things that we are all familiar with. These include the basic arithmetical processes and the algorithms that go with them. They include algebra in all its levels as well as sophisticated areas such as the calculus. This is the side of the subject that is largely represented in the Strands of Number and Algebra, Geometry and Measurement and Statistics.

On the other hand, the processes of mathematics are the ways of using the skills creatively in new situations. Mathematical processes include problem solving, logic and reasoning, and communicating ideas. These are the parts of mathematics that enable us to use the skills in a wide variety of situations.

It is worth starting by distinguishing between the three words "method", "answer" and "solution". By "method" we mean the means used to get an answer. This will generally involve one or more Problem Solving Strategies . On the other hand, we use "answer" to mean a number, quantity or some other entity that the problem is asking for. Finally, a "solution" is the whole process of solving a problem, including the method of obtaining an answer and the answer itself.

method + answer = solution

But how do we do Problem Solving? There are four basic steps. Pólya enunciated these in 1945 but all of them were known and used well before then. Pólya’s four stages of problem solving are listed below.

Four stages of problem solving                             

1. Understand and explore the problem  2. Find a strategy  3. Use the strategy to solve the problem  4. Look back and reflect on the solution.

Although we have listed the four stages in order, for difficult problems it may not be possible to simply move through them consecutively to produce an answer. It is frequently the case that students move backwards and forwards between and across the steps.

You can't solve a problem unless you can first understand it. This requires not only knowing what you have to find but also the key pieces of information that need to be put together to obtain the answer.

Students will often not be able to absorb all the important information of a problem in one go. It will almost always be necessary to read a problem several times, both at the start and while working on it. With younger students it is worth repeating the problem and then asking them to put the question in their own words. Older students might use a highlighter to mark the important parts of the problem.

Finding a strategy tends to suggest that it is a simple matter to think of an appropriate strategy. However, for many problems students may find it necessary to play around with the information before they are able to think of a strategy that might produce a solution. This exploratory phase will also help them to understand the problem better and may make them aware of some piece of information that they had neglected after the first reading.

Having explored the problem and decided on a strategy, the third step, solve the problem , can be attempted. Hopefully now the problem will be solved and an answer obtained. During this phase it is important for the students to keep a track of what they are doing. This is useful to show others what they have done and it is also helpful in finding errors should the right answer not be found.

At this point many students, especially mathematically able ones, will stop. But it is worth getting them into the habit of looking back over what they have done. There are several good reasons for this. First of all it is good practice for them to check their working and make sure that they have not made any errors. Second, it is vital to make sure that the answer they obtained is in fact the answer to the problem. Third, in looking back and thinking a little more about the problem, students are often able to see another way of solving the problem. This new solution may be a nicer solution than the original and may give more insight into what is really going on. Finally, students may be able to generalise or extend the problem.

Generalising a problem means creating a problem that has the original problem as a special case. So a problem about three pigs may be changed into one which has any number of pigs.

In Problem 4 of What is a Problem? , there is a problem on towers. The last part of that problem asks how many towers can be built for any particular height. The answer to this problem will contain the answer to the previous three questions. There we were asked for the number of towers of height one, two and three. If we have some sort of formula, or expression, for any height, then we can substitute into that formula to get the answer for height three, for instance. So the "any" height formula is a generalisation of the height three case. It contains the height three case as a special example.

Extending a problem is a related idea. Here though, we are looking at a new problem that is somehow related to the first one. For instance, a problem that involves addition might be looked at to see if it makes any sense with multiplication. A rather nice problem is to take any whole number and divide it by two if it’s even and multiply it by three and add one if it’s odd. Keep repeating this manipulation. Is the answer you get eventually 1? We’ll do an example. Let’s start with 34. Then we get

34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1

We certainly got to 1 then. Now it turns out that no one in the world knows if you will always get to 1 this way, no matter where you start. That’s something for you to worry about. But where does the extension come in? Well we can extend this problem, by just changing the 3 to 5. So this time instead of dividing by 2 if the number is even and multiplying it by three and adding one if it’s odd, try dividing by 2 if the number is even and multiplying it by 5 and adding one if it’s odd. This new problem doesn’t contain the first one as a special case, so it’s not a generalisation. It is an extension though – it’s a problem that is closely related to the original. 

It is by this method of generalisation and extension that mathematics makes great strides forward. Up until Pythagoras’ time, many right-angled triangles were known. For instance, it was known that a triangle with sides 3, 4 and 5 was a right-angled triangle. Similarly people knew that triangles with sides 5, 12 and 13, and 7, 24 and 25 were right angled. Pythagoras’ generalisation was to show that EVERY triangle with sides a, b, c was a right-angled triangle if and only if a 2 + b 2 = c 2 .

This brings us to an aspect of problem solving that we haven’t mentioned so far. That is justification (or proof). Your students may often be able to guess what the answer to a problem is but their solution is not complete until they can justify their answer.

Now in some problems it is hard to find a justification. Indeed you may believe that it is not something that any of the class can do. So you may be happy that the students can find an answer. However, bear in mind that this justification is what sets mathematics apart from every other discipline. Consequently the justification step is an important one that shouldn’t be missed too often.

Scientific approach                                   

Another way of looking at the Problem Solving process is what might be called the scientific approach. We show this in the diagram below.

Here the problem is given and initially the idea is to experiment with it or explore it in order to get some feeling as to how to proceed. After a while it is hoped that the solver is able to make a conjecture or guess what the answer might be. If the conjecture is true it might be possible to prove or justify it. In that case the looking back process sets in and an effort is made to generalise or extend the problem. In this case you have essentially chosen a new problem and so the whole process starts over again.

Sometimes, however, the conjecture is wrong and so a counter-example is found. This is an example that contradicts the conjecture. In that case another conjecture is sought and you have to look for a proof or another counterexample.

Some problems are too hard so it is necessary to give up. Now you may give up so that you can take a rest, in which case it is a ‘for now’ giving up. Actually this is a good problem solving strategy. Often when you give up for a while your subconscious takes over and comes up with a good idea that you can follow. On the other hand, some problems are so hard that you eventually have to give up ‘for ever’. There have been many difficult problems throughout history that mathematicians have had to give up on.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

Powerful online learning at your pace

What IS Problem-Solving?

Ask teachers about problem-solving strategies, and you’re opening a can of worms! Opinions about the “best” way to teach problem-solving are all over the board. And teachers will usually argue for their process quite passionately.

When I first started teaching math over 25 years ago, it was very common to teach “keywords” to help students determine the operation to use when solving a word problem. For example, if you see the word “total” in the problem, you always add. Rather than help students become better problem solvers, the use of keywords actually resulted in students who don’t even feel the need to read and understand the problem–just look for the keywords, pick out the numbers, and do the operation indicated by the keyword.

This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.

Another common strategy for teaching problem-solving is the use of acrostics that students can easily remember to perform the “steps” in problem-solving. CUBES is an example. Just as with keywords, however, students often follow the steps with little understanding. As an example, a common step is to underline or highlight the question. But if you ask students why they are underlining or highlighting the question, they often can’t tell you. The question is , in fact, super important, but they’ve not been told why. They’ve been told to underline the question, so they do.

The problem with both keywords and the rote-step strategies is that both methods try to turn something that is inherently messy into an algorithm! It’s way past time that we leave both methods behind.

First, we need to broaden the definition of problem-solving. Somewhere along the line, problem-solving became synonymous with “word problems.” In reality, it’s so much more. Every one of us solves dozens or hundreds of problems every single day, and most of us haven’t solved a word problem in years. Problem-solving is often described as  figuring out what to do when you don’t  know what to do.  My power went out unexpectedly this morning, and I have work to do. That’s a problem that I had to solve. I had to think about what the problem was, what my options were, and formulate a plan to solve the problem. No keywords. No acrostics. I’m using my phone as a hotspot and hoping my laptop battery doesn’t run out. Problem solved. For now.

If you want to get back to what problem-solving really is, you should consult the work of George Polya. His book, How to Solve It , which was first published in 1945, outlined four principles for problem-solving. The four principles are: understand the problem, devise a plan, carry out the plan, and look back. This document from UC Berkeley’s Mathematics department is a great 4-page overview of Polya’s process. You can probably see that the keyword and rote-steps strategies were likely based on Polya’s method, but it really got out of hand. We need to help students think , not just follow steps.

I created both primary and intermediate posters based on Polya’s principles. Grab your copies for free here !

I would LOVE to hear your comments about problem-solving!

Similar Posts

First, I have a quiz for you. If you speak and write Hindi, you can skip this quiz. For the rest of you, look at the symbols below. Can you…

Building a Wacky Hundred Chart!

What could be better than getting kids up and moving during the school day? How about helping them develop number sense as they build a wacky hundred chart? This post…

An Interview with Sherry Parrish, author of Number Talks

In 2014, I had the pleasure of hearing Sherry Parrish and Ann Dominick speak at the NCTM Annual Meeting in New Orleans. My campus had been using Number Talks in…

Telling Time to the Hour and Half Hour

The math standards are carefully aligned to gradually develop concepts over a period of time. A great example is telling time. In First Grade, students are required to tell time…

Practicing +10 and -10

Ever wonder why we practice the patterns of +1/-1 and +10/-10 using a hundred chart? Well, we’re adding and subtracting tens and ones, so it actually supports place value understanding….

Place Value, CRA Style

What is CRA you ask? It stands for concrete, representational, and abstract, and it’s a research-based instructional sequence that results in a deeper understanding of mathematics concepts. Concrete learning is…

Do you tutor teachers?

I do professional development for district and schools, and I have online courses.

You make a great point when you mentioned that teaching students to look for “keywords” is not teaching students to become better problem solvers. I was once guilty of using the CUBES strategy, but have since learned to provide students with opportunity to grapple with solving a problem and not providing them with specified steps to follow.

I think we’ve ALL been there! We learn and we do better. 🙂

Love this article and believe that we can do so much better as math teachers than just teaching key words! Do you have an editable version of this document? We are wanting to use something similar for our school, but would like to tweak it just a bit. Thank you!

I’m sorry, but because of the clip art and fonts I use, I am not able to provide an editable version.

Hi Donna! I am working on my dissertation that focuses on problem-solving. May I use your intermediate poster as a figure, giving credit to you in my citation with your permission, for my section on Polya’s Traditional Problem-Solving Steps? You laid out the process so succinctly with examples that my research could greatly benefit from this image. Thank you in advance!

Absolutely! Good luck with your dissertation!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2008 Revised 2011

What Is Problem Solving?

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created: May 19, 2022

Last updated: January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

Math for Kids

Guess and Check

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

After-School Math Program

• Boost Math Skills After School!
• Join our Math Program, Ideal for Students in Grades 1-8!

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!

Related posts

April 18, 2022

Learn How to Teach Multiplication to Children in a Few Simple Steps

The task of teaching multiplication to children often falls on adults. Following their understanding and appreciation of addition and subtraction, children must also demonstrate proficiency in multiplication. Kids understand multiplication when you explain it to them simply, even if it seems complicated at first. 6 Creative Steps for Teaching Kids Multiplication Different approaches provide various […]

May 6, 2022

How to Use a Protractor?

By the 4th grade, kids begin learning types of angles. They advance to measuring angles with the help of tools like a protractor. But for many children, a protractor is a confusing semicircle with dashes and numbers, so they need detailed guidelines to learn how to use a protractor to measure and draw angles. Teachers […]

February 16, 2022

How to Teach Subtraction to Little Kids: Four Proven Methods

Most adults can subtract numbers in seconds, even though it’s more complicated than addition. Sometimes, you can instantly solve 10 – 9 or 14 – 6 because you have learned subtraction facts by heart in school. Meanwhile, little kids do their best to grasp the basics. How do you teach kids to calculate two-digit numbers […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

March 12, 2024

The Simplest Math Problem Could Be Unsolvable

The Collatz conjecture has plagued mathematicians for decades—so much so that professors warn their students away from it

By Manon Bischoff

Mathematicians have been hoping for a flash of insight to solve the Collatz conjecture.

James Brey/Getty Images

At first glance, the problem seems ridiculously simple. And yet experts have been searching for a solution in vain for decades. According to mathematician Jeffrey Lagarias, number theorist Shizuo Kakutani told him that during the cold war, “for about a month everybody at Yale [University] worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.”

The Collatz conjecture—the vexing puzzle Kakutani described—is one of those supposedly simple problems that people tend to get lost in. For this reason, experienced professors often warn their ambitious students not to get bogged down in it and lose sight of their actual research.

The conjecture itself can be formulated so simply that even primary school students understand it. Take a natural number. If it is odd, multiply it by 3 and add 1; if it is even, divide it by 2. Proceed in the same way with the result x : if x is odd, you calculate 3 x + 1; otherwise calculate x / 2. Repeat these instructions as many times as possible, and, according to the conjecture, you will always end up with the number 1.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example: If you start with 5, you have to calculate 5 x 3 + 1, which results in 16. Because 16 is an even number, you have to halve it, which gives you 8. Then 8 / 2 = 4, which, when divided by 2, is 2—and 2 / 2 = 1. The process of iterative calculation brings you to the end after five steps.

Of course, you can also continue calculating with 1, which gives you 4, then 2 and then 1 again. The calculation rule leads you into an inescapable loop. Therefore 1 is seen as the end point of the procedure.

Following iterative calculations, you can begin with any of the numbers above and will ultimately reach 1.

Credit: Keenan Pepper/Public domain via Wikimedia Commons

It’s really fun to go through the iterative calculation rule for different numbers and look at the resulting sequences. If you start with 6: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1. Or 42: 42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, you always seem to end up with 1. There are some numbers, such as 27, where it takes quite a long time (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...), but so far the result has always been 1. (Admittedly, you have to be patient with the starting number 27, which requires 111 steps.)

But strangely there is still no mathematical proof that the Collatz conjecture is true. And that absence has mystified mathematicians for years.

The origin of the Collatz conjecture is uncertain, which is why this hypothesis is known by many different names. Experts speak of the Syracuse problem, the Ulam problem, the 3 n + 1 conjecture, the Hasse algorithm or the Kakutani problem.

German mathematician Lothar Collatz became interested in iterative functions during his mathematics studies and investigated them. In the early 1930s he also published specialist articles on the subject , but the explicit calculation rule for the problem named after him was not among them. In the 1950s and 1960s the Collatz conjecture finally gained notoriety when mathematicians Helmut Hasse and Shizuo Kakutani, among others, disseminated it to various universities, including Syracuse University.

Like a siren song, this seemingly simple conjecture captivated the experts. For decades they have been looking for proof that after repeating the Collatz procedure a finite number of times, you end up with 1. The reason for this persistence is not just the simplicity of the problem: the Collatz conjecture is related to other important questions in mathematics. For example, such iterative functions appear in dynamic systems, such as models that describe the orbits of planets. The conjecture is also related to the Riemann conjecture, one of the oldest problems in number theory.

Empirical Evidence for the Collatz Conjecture

In 2019 and 2020 researchers checked all numbers below 2 68 , or about 3 x 10 20 numbers in the sequence, in a collaborative computer science project . All numbers in that set fulfill the Collatz conjecture as initial values. But that doesn’t mean that there isn’t an outlier somewhere. There could be a starting value that, after repeated Collatz procedures, yields ever larger values that eventually rise to infinity. This scenario seems unlikely, however, if the problem is examined statistically.

An odd number n is increased to 3 n + 1 after the first step of the iteration, but the result is inevitably even and is therefore halved in the following step. In half of all cases, the halving produces an odd number, which must therefore be increased to 3 n + 1 again, whereupon an even result is obtained again. If the result of the second step is even again, however, you have to divide the new number by 2 twice in every fourth case. In every eighth case, you must divide it by 2 three times, and so on.

In order to evaluate the long-term behavior of this sequence of numbers , Lagarias calculated the geometric mean from these considerations in 1985 and obtained the following result: ( 3 / 2 ) 1/2 x ( 3 ⁄ 4 ) 1/4 x ( 3 ⁄ 8 ) 1/8 · ... = 3 ⁄ 4 . This shows that the sequence elements shrink by an average factor of 3 ⁄ 4 at each step of the iterative calculation rule. It is therefore extremely unlikely that there is a starting value that grows to infinity as a result of the procedure.

There could be a starting value, however, that ends in a loop that is not 4 → 2 → 1. That loop could include significantly more numbers, such that 1 would never be reached.

Such “nontrivial” loops can be found, for example, if you also allow negative integers for the Collatz conjecture: in this case, the iterative calculation rule can end not only at –2 → –1 → –2 → ... but also at –5 → –14 → –7 → –20 → –10 → –5 → ... or –17 → –50 → ... → –17 →.... If we restrict ourselves to natural numbers, no nontrivial loops are known to date—which does not mean that they do not exist. Experts have now been able to show that such a loop in the Collatz problem, however, would have to consist of at least 186 billion numbers .

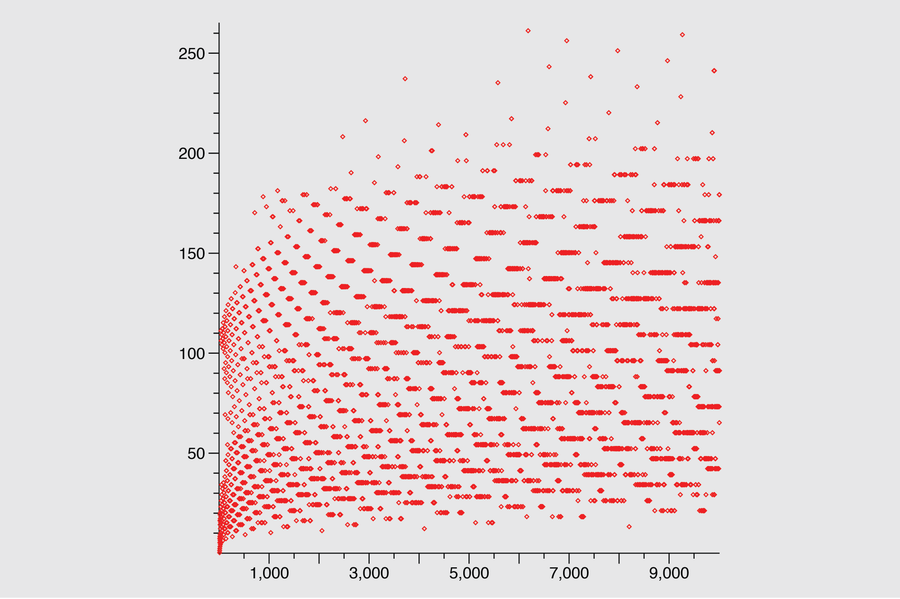
The length of the Collatz sequences for all numbers from 1 to 9,999 varies greatly.

Credit: Cirne/Public domain via Wikimedia Commons

Even if that sounds unlikely, it doesn’t have to be. In mathematics there are many examples where certain laws only break down after many iterations are considered. For instance,the prime number theorem overestimates the number of primes for only about 10 316 numbers. After that point, the prime number set underestimates the actual number of primes.

Something similar could occur with the Collatz conjecture: perhaps there is a huge number hidden deep in the number line that breaks the pattern observed so far.

A Proof for Almost All Numbers

Mathematicians have been searching for a conclusive proof for decades. The greatest progress was made in 2019 by Fields Medalist Terence Tao of the University of California, Los Angeles, when he proved that almost all starting values of natural numbers eventually end up at a value close to 1.

“Almost all” has a precise mathematical meaning: if you randomly select a natural number as a starting value, it has a 100 percent probability of ending up at 1. ( A zero-probability event, however, is not necessarily an impossible one .) That’s “about as close as one can get to the Collatz conjecture without actually solving it,” Tao said in a talk he gave in 2020 . Unfortunately, Tao’s method cannot generalize to all figures because it is based on statistical considerations.

All other approaches have led to a dead end as well. Perhaps that means the Collatz conjecture is wrong. “Maybe we should be spending more energy looking for counterexamples than we’re currently spending,” said mathematician Alex Kontorovich of Rutgers University in a video on the Veritasium YouTube channel .

Perhaps the Collatz conjecture will be determined true or false in the coming years. But there is another possibility: perhaps it truly is a problem that cannot be proven with available mathematical tools. In fact, in 1987 the late mathematician John Horton Conway investigated a generalization of the Collatz conjecture and found that iterative functions have properties that are unprovable. Perhaps this also applies to the Collatz conjecture. As simple as it may seem, it could be doomed to remain unsolved forever.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

Jump to navigation

Usable Math: Math Learning through Problem Solving and Design

Usable Math is a free and accessible online interactive math problem solving platform for elementary school-age children and their teachers, tutors, caregivers, and families. It is being developed by a team of UMass Amherst researchers led by Sharon Edwards in the College of Education. Our workshop will highlight the site's design and functions, including:

• 17 problem solving modules featuring essential math concepts taught in elementary schools.
• Use of virtual coaches to support students' math thinking and learning.
• Motivation strategies to engage and sustain student learning.
• Storytelling modules connecting math with science, history and English/language arts.
• Students writing their own math problems and solving strategies
• GenAI-enhancements for teachers.
• Sharon A. Edwards, Clinical Faculty
•  Robert W. Maloy, Senior Lecturer
•  Sai Gattupalli, Doctoral Candidate
• Aubrey Coyne, Undergraduate Project Assistant

Department of Physics

• Find us on Facebook
• Subscribe to us on YouTube
• Connect with us on LinkedIn
• Make a Gift

Can you solve NASA's Pi Day 2024 challenge?

Hungry for Pi? Check out NASA's Pi Day challenge and put your wits to the test solving problems just like NASA scientists and engineers.

Happy Pi Day 2024!

Have you ever wondered what it would be like to solve problems for NASA to help with the exploration of other planets in the solar system ? 

In celebration of Pi Day 2024 , you can do just that and take the annual NASA Pi Day Challenge . This is a fun way to put on your scientist and engineer thinking cap and try your best at a series of questions all surrounding the mathematical constant, pi. 

Related: What is the smallest known planet?

What is pi? If you recall from mathematics class back in grade school, it's approximately 3.14159 and can be used to figure out the circumference of a circle of the volume of a square. 

While there are many uses for it in different STEM jobs and fields, it's also very important for engineers and scientists at NASA to help study not just our planet but others across the solar system and even other galaxies .

This challenge is a tradition that has been on-going for the last decade put on by NASA's Jet Propulsion Laboratory's Education Office and features numerous math problems you have to solve using pi. 

Some of the questions you can answer this year pertain to missions including the Deep Space Optical Communications technology on NASA's Psyche spacecraft , the Double Asteroid Redirection Test (DART) spacecraft, Earth-orbiting satellites, rovers on the Moon, and even the Hubble Space Telescope and James Webb Space Telescope .

—  As scientists find real exoplanets, sci-fi writers change their vision of alien worlds

 — 10 surprising facts about pi

— Pi Day turns 35: The circle of mathematics needs more diversity, advocates say

So, let's get solving! You can find each of the problems with an accompanying worksheet you can do all your work online and the answers will be posted by NASA so you can check your work! 

There are nearly four dozen different questions you can figure out, so try a few or do them all to "cook up" a unique way to get space-y and celebrate Pi Day 2024! 

Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: [email protected].

Get the Space.com Newsletter

Breaking space news, the latest updates on rocket launches, skywatching events and more!

Meredith is a regional Murrow award-winning Certified Broadcast Meteorologist and science/space correspondent. She most recently was a Freelance Meteorologist for NY 1 in New York City & the 19 First Alert Weather Team in Cleveland. A self-described "Rocket Girl," Meredith's personal and professional work has drawn recognition over the last decade, including the inaugural Valparaiso University Alumni Association First Decade Achievement Award, two special reports in News 12's Climate Special "Saving Our Shores" that won a Regional Edward R. Murrow Award, multiple Fair Media Council Folio & Press Club of Long Island awards for meteorology & reporting, and a Long Island Business News & NYC TV Week "40 Under 40" Award.

Scientists may have just caught 7 exotic 'ghost particles' as they pierced through Earth

What is the smallest known planet?

India's Chandrayaan-3 lunar lander barely kicked up any moon dust. Here's why that matters

Most Popular

By Meredith Garofalo March 16, 2024

By Elizabeth Howell March 16, 2024

By Keith Cooper March 15, 2024

By Elizabeth Howell March 15, 2024

By Mike Wall March 15, 2024

By Tereza Pultarova March 15, 2024

By Robert Lea March 15, 2024

By Jeff Spry March 15, 2024

By Daisy Dobrijevic March 15, 2024

• 2 The James Webb Space Telescope is digging deep into the mysteries of gas planets
• 3 Sony FE 16-35mm f/2.8 GM II vs Canon RF 15-35mm f/2.8 L IS USM
• 4 Sleeping subduction zone could awaken and form a new 'Ring of Fire' that swallows the Atlantic Ocean
• 5 Lego Creator 3-in-1 Space Astronaut review

Equation Solver

Enter the Equation you want to solve into the editor.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

Algebra AI: Solve Math Problem 4+

Homework helper with ai tutor, picking machine, designed for iphone.

• Offers In-App Purchases

iPhone Screenshots

Description.

Unlock the power of learning with Algebra AI, the ultimate math solving companion designed for students from middle school through university. Whether you're tackling algebra, calculus, or any math problem in between, Algebra AI is here to guide you through with precise, step-by-step solutions. Powered by advanced AI technology, this app transforms the way you learn and approach math problems. ____________ WHY ALGEBRA AI? INSTANT PROBLEM SOLVING: Simply scan your math homework, and receive accurate, step-by-step solutions within seconds. Our AI-powered solver deciphers handwritten and printed problems alike, making your study sessions more efficient and productive. COMPREHENSIVE MATH SUPPORT: Algebra AI covers a wide range of mathematical domains, from basic algebra to complex calculus, ensuring no problem is too big or too small for the app to handle. LEARN AT YOUR PACE: With detailed explanations for each step, you can grasp the underlying concepts at your own pace. This personalized learning approach helps reinforce your understanding and boosts your confidence in math. INTERACTIVE LEARNING EXPERIENCE: Engage with interactive problems and get instant feedback to improve your problem-solving skills. Algebra AI is not just a solver; it's a tool that teaches you how to tackle math problems on your own. 24/7 HOMEWORK HELPER: Algebra AI is your round-the-clock study companion. Whether you're burning the midnight oil or squeezing in a study session between classes, the app is always ready to assist you. ____________ DISCOVER THE FEATURES YOU NEED: AI-POWERED SOLUTIONS: Get fast and reliable answers to all your math questions. Our AI algorithm is constantly learning and improving to provide you with the best possible solutions. WIDE RANGE OF MATH TOPICS: From geometry to trigonometry, Algebra AI has got you covered. The app supports multiple math subjects, catering to a diverse student base. HANDWRITING RECOGNITION: Our sophisticated handwriting recognition technology ensures that you can get solutions to handwritten problems just as easily as printed ones. STEP-BY-STEP EXPLANATIONS: Understand the 'how' and 'why' behind each solution. Algebra AI breaks down complex problems into manageable steps, making it easier for you to learn and apply the concepts. USER-FRIENDLY INTERFACE: With a clean, intuitive design, navigating through the app is a breeze. Find solutions, learn new concepts, and track your progress with just a few taps. ____________ Transform your math learning experience with Algebra AI, the smart, efficient, and interactive way to solve math problems and master concepts. Download now and start conquering your math challenges today! Privacy Policy: https://www.kovalee.app/privacy-policy Terms of use: https://www.apple.com/legal/internet-services/itunes/dev/stdeula/

Version 1.1.0

Bug fixes and performance improvements

App Privacy

The developer, Picking Machine , indicated that the app’s privacy practices may include handling of data as described below. For more information, see the developer’s privacy policy .

Data Used to Track You

The following data may be used to track you across apps and websites owned by other companies:

Data Not Linked to You

The following data may be collected but it is not linked to your identity:

• Identifiers
• Diagnostics

Privacy practices may vary based on, for example, the features you use or your age. Learn More

Information

• Unlimited school problems R99.99
• App Support
• Privacy Policy

More By This Developer

Habyy: Daily Habit Tracker

WINGMAN: Rizz GPT Dating AI

Football Coach: Elite Workout

Basketball Coach: Pro Workout

You Might Also Like

AI Math Helper: Scan & Solve

Solver: AI Math Scan & Solve

Pi - Math AI Solver

Sailor Compass

10 Helpful Worksheet Ideas for Primary School Math Lessons

M athematics is a fundamental subject that shapes the way children think and analyze the world. At the primary school level, laying a strong foundation is crucial. While hands-on activities, digital tools, and interactive discussions play significant roles in learning, worksheets remain an essential tool for reinforcing concepts, practicing skills, and assessing understanding. Here’s a look at some helpful worksheets for primary school math lessons.

Comparison Chart Worksheets

Comparison charts provide a visual means for primary school students to grasp relationships between numbers or concepts. They are easy to make at www.storyboardthat.com/create/comparison-chart-template , and here is how they can be used:

• Quantity Comparison: Charts might display two sets, like apples vs. bananas, prompting students to determine which set is larger.
• Attribute Comparison: These compare attributes, such as different shapes detailing their number of sides and characteristics.
• Number Line Comparisons: These help students understand number magnitude by placing numbers on a line to visualize their relative sizes.
• Venn Diagrams: Introduced in later primary grades, these diagrams help students compare and contrast two sets of items or concepts.
• Weather Charts: By comparing weather on different days, students can learn about temperature fluctuations and patterns.

Number Recognition and Counting Worksheets

For young learners, recognizing numbers and counting is the first step into the world of mathematics. Worksheets can offer:

• Number Tracing: Allows students to familiarize themselves with how each number is formed.
• Count and Circle: Images are presented, and students have to count and circle the correct number.
• Missing Numbers: Sequences with missing numbers that students must fill in to practice counting forward and backward.

Basic Arithmetic Worksheets

Once students are familiar with numbers, they can start simple arithmetic. 

• Addition and Subtraction within 10 or 20: Using visual aids like number lines, counters, or pictures can be beneficial.
• Word Problems: Simple real-life scenarios can help students relate math to their daily lives.
• Skip Counting: Worksheets focused on counting by 2s, 5s, or 10s.

Geometry and Shape Worksheets

Geometry offers a wonderful opportunity to relate math to the tangible world.

• Shape Identification: Recognizing and naming basic shapes such as squares, circles, triangles, etc.
• Comparing Shapes: Worksheets that help students identify differences and similarities between shapes.
• Pattern Recognition: Repeating shapes in patterns and asking students to determine the next shape in the sequence.

Measurement Worksheets

Measurement is another area where real-life application and math converge.

• Length and Height: Comparing two or more objects and determining which is longer or shorter.
• Weight: Lighter vs. heavier worksheets using balancing scales as visuals.
• Time: Reading clocks, days of the week, and understanding the calendar.

Data Handling Worksheets

Even at a primary level, students can start to understand basic data representation.

• Tally Marks: Using tally marks to represent data and counting them.
• Simple Bar Graphs: Interpreting and drawing bar graphs based on given data.
• Pictographs: Using pictures to represent data, which can be both fun and informative.

Place Value Worksheets

Understanding the value of each digit in a number is fundamental in primary math.

• Identifying Place Values: Recognizing units, tens, hundreds, etc., in a given number.
• Expanding Numbers: Breaking down numbers into their place value components, such as understanding 243 as 200 + 40 + 3.
• Comparing Numbers: Using greater than, less than, or equal to symbols to compare two numbers based on their place values.

Fraction Worksheets

Simple fraction concepts can be introduced at the primary level.

• Identifying Fractions: Recognizing half, quarter, third, etc., of shapes or sets.
• Comparing Fractions: Using visual aids like pie charts or shaded drawings to compare fractions.
• Simple Fraction Addition: Adding fractions with the same denominator using visual aids.

Money and Real-Life Application Worksheets

Understanding money is both practical and a great way to apply arithmetic.

• Identifying Coins and Notes: Recognizing different denominations.
• Simple Transactions: Calculating change, adding up costs, or determining if there’s enough money to buy certain items.
• Word Problems with Money: Real-life scenarios involving buying, selling, and saving.

Logic and Problem-Solving Worksheets

Even young students can hone their problem-solving skills with appropriate challenges.

• Sequences and Patterns: Predicting the next item in a sequence or recognizing a pattern.
• Logical Reasoning: Simple puzzles or riddles that require students to think critically.
• Story Problems: Reading a short story and solving a math-related problem based on the context.

Worksheets allow students to practice at their own pace, offer teachers a tool for assessment, and provide parents with a glimpse into their child’s learning progression. While digital tools and interactive activities are gaining prominence in education, the significance of worksheets remains undiminished. They are versatile and accessible and, when designed creatively, can make math engaging and fun for young learners.

The post 10 Helpful Worksheet Ideas for Primary School Math Lessons appeared first on Mom and More .

Help | Advanced Search

Mathematics > General Mathematics

Title: series for even powers of pi by generalization euler's method for solving the basel problem.

Abstract: The purpose of this paper is to present series expansions for even powers of the number $\pi$. This is accomplished by generalizing Euler's method for solving the Basel Problem, which was published in 1735. We employ elementary symmetric polynomials, transform them into nested sums, and thereby derive nice series formulas for even powers of the number $\pi$ such as \[ \frac{\pi^2}{3!}= \sum_{\ell_1=1}^\infty\frac{1}{\ell_1^2} \;;\quad\quad \frac{\pi^4}{5!} = \sum_{\ell_2=2}^\infty \sum_{\ell_1=1}^{\ell_2-1} \frac{1}{\ell_1^2\cdot\ell_2^2} \;;\quad\quad \frac{\pi^6}{7!}= \sum_{\ell_3=3}^\infty \sum_{\ell_2=2}^{\ell_3-1} \sum_{\ell_1=1}^{\ell_2-1}\frac{1}{\ell_1^2\cdot\ell_2^2\cdot\ell_3^2} \;;\quad\cdots \] Many of these formulas do not seem to be widely known. -- In dieser Abhandlung stellen wir ein Verfahren vor, das die Berechnung von Reihen für geradzahlige Potenzen von $\pi$ ermöglicht. Die Grundidee ist eine Verallgemeinerung des Verfahrens von Euler, mit dem er 1735 das Basler Problem löste. Wir stellen elementar-symmetrische Polynome durch mehrfach verschachtelte Summen dar und leiten davon Reihen für geradzahlige Potenzen der Kreiszahl $\pi$ ab. Die meisten der angegebenen Reihen scheinen nicht so bekannt zu sein.

Submission history

Access paper:.

• Download PDF
• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .