homework 2 powers of monomials and geometric applications

Have an account?

Unit 6 Homework 2: Powers of Monomials

9th - 12th grade, mathematics.

10 questions

Introducing new   Paper mode

No student devices needed.   Know more

Simplify the following monomial:    ( x 4 ) 2 \left(x^4\right)^2 ( x 4 ) 2    

  x 2 x^2 x 2    

  x 6 x^6 x 6    

  x 8 x^8 x 8    

  ( m 2 n 7 ) 3 \left(m^2n^7\right)^3 ( m 2 n 7 ) 3    Simplify the following monomial:

  m 6 n 21 m^6n^{21} m 6 n 2 1    

  m 21 n 6 m^{21}n^6 m 2 1 n 6    

  m − 1 n 4 m^{-1}n^4 m − 1 n 4    

Simplify the following monomial:    ( 2 w 3 ) 6 \left(2w^3\right)^6 ( 2 w 3 ) 6    

  64 w 18 64w^{18} 6 4 w 1 8    

  12 w 9 12w^9 1 2 w 9    

  6 w 6 6w^6 6 w 6    

  ( − 4 x 2 ) 2 \left(-4x^2\right)^2 ( − 4 x 2 ) 2    Simplify the following monomial:

  16 x 4 16x^4 1 6 x 4    

  − 8 x 2 -8x^2 − 8 x 2    

  − 4 x 4 -4x^4 − 4 x 4    

Simplify the following monomial:    ( − 5 y 3 ) 3 \left(-5y^3\right)^3 ( − 5 y 3 ) 3    

  − 125 y 9 -125y^9 − 1 2 5 y 9    

  − 15 y 3 -15y^3 − 1 5 y 3    

  − 5 y 6 -5y^6 − 5 y 6    

 Simplify the following monomial:     ( 1 2 x 4 ) 7 \left(\frac{1}{2}x^4\right)^7 ( 2 1 ​ x 4 ) 7    

  1 128 x 28 \frac{1}{128}x^{28} 1 2 8 1 ​ x 2 8    

  2 x 7 2x^7 2 x 7    

  1 14 x 28 \frac{1}{14}x^{28} 1 4 1 ​ x 2 8    

Simplify the following monomial:    1 2 ( 4 k 5 ) 2 \frac{1}{2}\left(4k^5\right)^2 2 1 ​ ( 4 k 5 ) 2    

  8 k 10 8k^{10} 8 k 1 0    

  16 k 10 16k^{10} 1 6 k 1 0    

  8 k 5 8k^5 8 k 5    

  ( m 5 n 3 ) 7 × m 2 n \left(m^5n^3\right)^7\times m^2n ( m 5 n 3 ) 7 × m 2 n    Simplify the following monomial:

  m 37 n 22 m^{37}n^{22} m 3 7 n 2 2    

  m 70 n 21 m^{70}n^{21} m 7 0 n 2 1    

  m 35 n 23 m^{35}n23 m 3 5 n 2 3    

  ( 2 x 3 y 2 z 2 ) 3 ( x 2 z ) 4 \left(2x^3y^2z^2\right)^3\left(x^2z\right)^4 ( 2 x 3 y 2 z 2 ) 3 ( x 2 z ) 4    Simplify the following monomial:

  8 x 17 y 6 z 10 8x^{17}y^6z^{10} 8 x 1 7 y 6 z 1 0    

  8 x 15 z 10 8x^{15}z^{10} 8 x 1 5 z 1 0    

  8 x 17 z 10 8x^{17}z^{10} 8 x 1 7 z 1 0    

  ( − 4 m n ) 3 × ( − 2 m 2 ) 3 \left(-4mn\right)^3\times\left(-2m^2\right)^3 ( − 4 m n ) 3 × ( − 2 m 2 ) 3    Simplify the following monomial:

  512 m 9 n 3 512m^9n^3 5 1 2 m 9 n 3    

  − 512 m 9 n 3 -512m^9n^3 − 5 1 2 m 9 n 3    

  − 72 m 9 n 3 -72m^9n^3 − 7 2 m 9 n 3    

Explore all questions with a free account

Continue with email

Continue with phone

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2.4: Powers of Monomials and Binomials

• Last updated
• Save as PDF
• Page ID 130850

Learning Objectives

By the end of this section, you will be able to: 

• Expand a positive integer power of monomial and binomial expressions
• Identify coefficients of terms of a positive integer powers of a binomial expression

Be Prepared

Before we get started, take this readiness quiz.

1. Expand \((2x-3)^2 \).

2. Simplify \((3\cdot 5\).

3. Evaluate \((5x^3\) at \(x=2\).

Powers of Monomials

Now let’s look at an exponential expression that contains a power raised to a power. Let's see if we can discover a general property.

Notice the 6 is the product of the exponents, 2 and 3. We see that \((x^2)^3\) is \(x^{2\cdot 3}\) or \(x^6\). We can also see that

In this example we multiplied the exponents.

We can check various examples to see that this leads us to the Power Property for Positive Integer Exponents.

Power Property for Integer Exponents

If \(a\) is a real number and \(m\) and \(n\) are positive integers, then

\[(a^m)^n=a^{mn}. \nonumber \]

To raise a power to a power, multiply the exponents.

Example \(\PageIndex{1}\)

Simplify each expression:

a. \((y^5)^9\)

b. \((4^{4})^7\)

c. \((y^3)^6(y^5)^4\)

Try It \(\PageIndex{2}\)

a. \((b^7)^5\)

b. \((5^4)^{3}\)

c. \((a^4)^5(a^7)^4\)

a. \(b^{35}\)

b. \(5^{12}\)

c. \(a^{48}\)

Try It \(\PageIndex{3}\)

a. \((z^6)^9\)

b. \((3^{7})^7\)

c. \((q^4)^5(q^3)^3\)

a. \(z^{54}\)

b. \(3^{49}\)

c. \(q^{29}\)

We will now look at an expression containing a product that is raised to a power. Can we find this pattern?

Notice that each factor was raised to the power and \((2x)^3\) is \(2^3x^3\).

The exponent applies to each of the factors! We can say that the exponent distributes over multiplication. If we were to check various examples with exponents we would find the same pattern emerges. This leads to the Product to a Power Property for Postive Integer Exponents.

Product to a Power Property for Integer Exponents

If \(a\) and \(b\) are real numbers and \(m\) is a positive integer, then

\[(ab)^m=a^mb^m \nonumber. \]

To raise a product to a power, raise each factor to that power.

Example \(\PageIndex{4}\)

a. \((−3mn)^3\)

b. \((6k^3)^{2}\)

c. \((5x^{3})^2\)

Try It \(\PageIndex{5}\)

a. \((2wx)^5\)

b. \((2b^3)^{4}\)

c. \((8a^{4})^2\)

a. \(32w^5x^5\)

b. \(16b^{12}\)

c. \(64a^8\)

Try It \(\PageIndex{6}\)

a. \((−3y)^3\)

b. \((−4x^4)^{2}\)

c. \((2c^{4})^3\)

a. \(−27y^3\)

b. \(16x^8\)

c. \(8c^{12}\)

• The Binomial Theorem

In this section we consider powers of binomial expressions like

$$(x+y)^5, (x+3)^4, \text{ or }(2x-3)^{10}.\nonumber$$

These are polynomials with degree equal to the exponent.

Let's consider

$$(x+y)^3=(x+y)(x+y)(x+y).\nonumber$$

To distribute, we take one term from each factor and multiply.  We repeat for all possible choices then add the results.

$$(x+y)^3=(x+y)(x+y)(x+y)=xxx+xxy+xyx+yxx+xyy+yxy+yyx+yyy=x^3+3x^2y+3xy^2+y^3.\nonumber$$

If we consider the coefficient of the \(x^2y\) term, we see it is the number of ways we can choose two \(x\)'s and one \(y\).  Similarly, for the other coefficients.

It turns out these are well known numbers and we have

The Binomial Theorem \(\PageIndex{7}\)

 \[(x+y)^n=a_0x^n+a_1x^{n-1}y+\cdots+a_{n-1}xy^{n-1}+a_ny^n,\nonumber\]

where the coefficients come from the \(n\)th row (counting from \(0\) of the Pascal's triangle):

See  Pascal's triangle - Wikipedia   -- The first paragraph.  The image above is from the same.

To get from one row to the next you add the two numbers above (or 1 in the case of the first and last number).  For example on the 4th row (counting from zero), above the 4 are 3 and 1, above the 6 is 3 and 3, and the ends have only 1 above.

For example,

\[\begin{align*}(x+2)^4&=x^4+4x^3\cdot 2+6x^2\cdot 2^2+4 x \cdot 2^3+2^4\\ &=x^4+8x^3+24 x^2+32 x+16.\end{align*}\]

Note that the numbers in Pascal's triangle are called binomial coefficients.  The details are beyond the scope of the book but more information and many applications can be found in the Wikipedia article on the topic.

Example \(\PageIndex{8}\)

Find the coefficient of \(x^3\) in the expression \((2x-3)^6\).

Note that the exponent on \(x\) is 3.  We find the 4th number in the 7th line of Pascal's triangle (this is because with Pascal's triangle the counting starts at 0).  Thus, we see it is 20.

So the relevant term is \(20 (2x)^3(-3)^3\) (noting that the exponents add to \(6\)).  Therefore, the coefficient of \(x^3\) is 

\[20\cdot 2^3\cdot(-3)^3=-4320.\nonumber\]

Try It \(\PageIndex{9}\)

Find the coefficient of

a. \(x^4\) in \((2-x)^7\)

b. \(xy^2\) in \((x-3y)^3\)

c. \(x^4y^3\) in \((2y-x^2)^5\)

Writing Exercises \(\PageIndex{10}\)

• Explain by writing out the full meaning why \((2^3)^4\).
• Why is \((2^3)^4=(2^4)^3\)?
• Verify the expansion of \((x+1)^4\) by evaluating at \(x=1\).

Exit Problem

• Simplify \((3x^4)^3\) and check by evaluating this expression and your simplification at \(x=2\).
• What is the coefficient of \(x^5y^2\) in \(2x-y)^7\)

Key Concepts

• Power of a monomial
• Power of a binomial
• Pascal's triangle

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Powers Of Monomials And Geometric Applications

Powers Of Monomials And Geometric Applications - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Power of monomials homework practice answers, Exponent rules review work, Power of monomials homework practice answers, Power of monomials homework practice answers, Middle school, Power of monomials homework practice answers, Study guide and intervention workbook, Polynomial functions.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Power Of Monomials Homework Practice Answers

2. exponent rules review worksheet, 3. power of monomials homework practice answers, 4. power of monomials homework practice answers, 5. middle school, 6. power of monomials homework practice answers, 7. study guide and intervention workbook, 8. polynomial functions -.

RWM102: Algebra

Unit 7: operations with monomials.

As we have seen, algebra involves the use of variables to represent unknown quantities in equations. Here we will begin the study of expressions that primarily consist of variables.

The rules that govern operations with these expressions arise from the properties of operations with numbers, such as the distributive property and the order of operations. In this unit we focus on monomials, which are expressions that contain only one term. We will learn how to multiply, divide, and apply rules of exponents to monomials.

Completing this unit should take you approximately 3 hours.

Upon successful completion of this unit, you will be able to:

• apply the rules of exponents to simplify algebraic exponential expressions; and
• multiply, divide, and simplify the powers of monomials.

7.1: Algebraic Exponential Expressions

The first mathematical functions we will explore are the exponential functions of monomials.

Read this article through the section on the product of powers property. This page reviews writing and solving exponential expressions. Pay attention to how we multiply monomials with exponents, the products of powers property, and example 2.

After you read, complete questions 2, 3, 6, 7, 8, 25, 26, 27 and 28 in the practice set and check your answers.

7.2: Manipulating Exponents

In this section, we will look at important rules for manipulating exponents.

Read this article, which shows the rules for multiplying exponents, taking the power of an exponent, and taking the exponent of a product. It may help to write a list of these properties to keep track of them. Watch the video to see a few examples.

After you read, complete questions 2, 3, 6, 7, 14, 15, 25, 26, 33, and 34 in the practice set and check your answers.

7.3: Quotient of Exponents and Power of a Quotient

The next important operation is the quotient of exponents, which is what we use when dividing monomials with exponents.

Read this article and pay attention to the quotient of powers property and the power of a quotient property in examples 1 and 2.

After you read, complete questions 1, 2, 5, 6, 12, and 13 in the practice set and check your answers.

7.4: Negative Exponents

In this section, we learn how to use negative exponents and how to translate between negative exponents and fractions.

Watch these videos, which walk you through the logic of why negative exponents can be written as fractions.

After you watch, complete this assessment and check your answers.

7.5: Multiplying Monomials

Now that you are comfortable with the rules of exponents, you are ready to apply them to functions of monomials. In this section, we will discuss multiplying monomials.

Read the section on multiplying monomials and the solution for example 6.26.

After you read, complete example 6.27 and check your answer.

7.6: Dividing Monomials

The last function we must apply to monomials is division.

This article gives an excellent review of the properties of monomials and exponents, as well as how to divide monomials. Review the summary of exponent properties, which goes over everything we discussed in this unit. After you read, complete examples 6.72 through 6.75 and check your work.

Powers of monomials

Here we explain how to find the power of a monomial. Also, you will see several examples of powers of monomials and exercises with solutions to practice.

Table of Contents

How to calculate the power of a monomial

To calculate the power of a monomial, raise each element of the monomial to the exponent of the power. That is, the power of a monomial consists of raising the coefficient and the variable of the monomial to the exponent of the power.

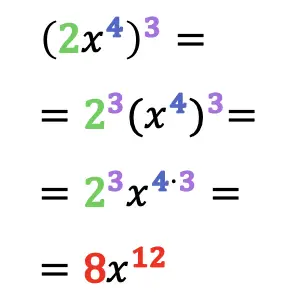
Remember from the properties of powers that when we raise a term that is already raised, the two exponents multiply each other. That is why in the powers of monomials the exponent of each variable (letter) is always multiplied by the exponent that indicates the power.

Note that the result of the power of a monomial depends on the sign of the monomial:

• The power of a positive monomial always results in another positive monomial, regardless of the parity of the exponent:
• A negative monomial raised to an even power equals to a positive monomial:
• A negative monomial raised to an odd power is always equal to another negative monomial:

Examples of powers of monomials

So that you can fully understand how to compute the power of a monomial, below we leave you with several examples of this type of operation with monomials:

Practice problems on powers of monomials

Below you have several practice problems on finding powers of monomials to understand better how to do this operation.

Calculate the following powers of monomials

Solve the following powers of monomials

Simplify the following powers of fractions with monomials as much as possible:

See: how to divide monomials

To simplify the rational expressions we have to apply the following property of powers:

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Copyright © 1999-2020 themathlab.com

Powers of Monomials - Process & Examples - Expii

Powers of monomials - process & examples, explanations (3), raise normal terms, multiply exponents.

When working with complicated monomials (expressions that with a bunch of variables and numbers multiplied together, with no addition or subtraction), you might see something like this:

This monomial has an exponent . This means you need to take the power of the whole monomial, internal exponents and all. This is called powers of monomials. The simplest way to do this is to:

• Raise each term in the monomial to the power.

Let's try out the rules on the expression above.

When a term doesn't have a visible exponent , what can we say that term's power is?

Related Lessons

Example walk through.

Taking a monomial to a power is not so different from taking a constant to a power. Start with a few warm up questions:

24= (x2)4= (2x)4= (2x2)4=

Now, take a look at this one: (2x3y2)4=

This expression looks more complicated than the warm up questions, but it is still manageable. Disregard the power outside of the parenthesis for a moment and treat each base as its own little unit: in this case, we have 2, x3 and y2.

Then, take a look at the power outside of the parenthesis and distribute it to each unit we just identified. This simple breakdown will allow you to solve the powers of monomials!

Image source: by Caroline Kulczycky

Now, try a problem to test your understanding.

(3x2y5z)3 Evaluate.

(Video) Powers of Monomials

by TeacherTube Math

This video by TeacherTube Math covers powers of monomials.

We can evaluate terms with exponents that are then raised to another power . Raise each piece of the term (coefficients and each individual variable) by that power. If the variable has an exponent, then you multiply the power of the expression by the power of the exponent . This is called the power of monomials.

Let's see this in action with an example. The first she looks at is: (x2)3 Here, we have a variable squared being raised to the third power. We simplify an exponent raised to a power by multiplying the powers . (x2)3=x2⋅3=x6

The next example is: (2x4)6 We have a coefficient, 2, and a variable raised to the fourth power. We simplify by raising each of these to the sixth power.

(2x4)6=26×x46=64×x4⋅6=64x24

The third example is: (3p2r3t)3 This example has multiple variables. We raise each of these to the third power. (3p2r3t)3=33×p23×r33×t3=27×p2⋅3×r3⋅3×t3=27p6r9t3

Test Yourself: (3x3y4)2

• Get started
• Pre-Algebra

A quicker path to better grades

We have gathered all your curriculum-based courses, assignments, hints, tests, and solutions in one easy-to-use place

• Integrated I
• Integrated II
• Integrated III

Can't find your textbook?

More math. less studying.

A personal private tutor for each student. Free from preassure and study anxiety.

Powers of Monomials

Abilities covered in this lesson, lesson settings, catch-up and review.

Here are a few recommended readings before getting started with this lesson.

• Degree of a Monomial

Finish Your Homework Before Playing!

Kriz wants to play some video games with their little cousin. However, Kriz's cousin has not finished his homework yet.

Kriz does not want to spill out the answer right away. They want to help their cousin understand math! Kriz's cousin only knows how to use multiplication tables.

Power of a Power Property

A power with a non-zero base a and an integer exponent m that is raised to another integer exponent n can be written as a power with base a and exponent m* n.

(a^m)^n = a^(m* n)

Power of a Product Property

A power with an integer exponent m whose base is the product of two non-zero factors a and b can be written as the product of two powers with bases a and b and the same exponent m.

(ab)^m = a^m b^m

Bonus for Same Color

While waiting for their cousin to finish his homework,Kriz plays a single-player game video game.

This game might look familiar! Kriz is particularly good at this video game, so they decide to try a new challenge level. In this level, Kriz's score is represented by a monomial. x^2y^3 Each time Kriz completes a line of the same color , their score is raised by a power.

Use the Power of a Product Property and the Power of a Power Property .

(a * b)^m=a^m* b^m

(a^m)^n=a^(m* n)

Zero Exponent Property

Any non-zero real number raised to the power of 0 is equal to 1.

Negative Exponent Property

If a is a non-zero real number and n is a positive integer , then a raised to the power of - n is equal to 1 over a raised to the power of n.

a^(- n)=1/a^n

Watch the Boosters!

Use the Product of Powers Property and the Zero Exponent Property . Remember, any number or expression multiplied by 1 is equal to itself.

a^m*a^n=a^(m+n)

a+(- b)=a-b

Subtract term

The Cousins Play the Hardest Level

Kriz's cousin has finally finished his homework, so they can play a cooperative game together.

Use the Quotient of Powers Property and the Negative Exponent Property to reach the final answer.

a^m/a^n= a^(m-n)

a^(- m)=1/a^m

Solving the Problem With a Table

Kriz's cousin needs to finish his homework. He is down to the last multiplication problem.

Note that both 16 and 9 are perfect squares. This can be shown in the multiplication table.

Rewrite 16 as 4^2

Rewrite 9 as 3^2

a^m* b^m=(a * b)^m

Finally, the answer can be given using only information from the multiplication table.

Recommended exercises

Snapsolve any problem by taking a picture. Try it in the Numerade app?

How Do You Take the Power of a Monomial?

Taking a monomial to a power isn't so hard, especially if you watch this tutorial about the power of a monomial rule!

• power of a monomial
• raising a power
• parentheses
• power of a power
• multiply exponents

Background Tutorials

Introduction to algebraic expressions.

What is a Variable?

You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!

Rules of Exponents

What's the Power of a Power Rule?

Sometimes you'll see a number with an exponent raised to another exponent, and the first time you see it, you probably think it's a typo! But it's not a typo, it's a real thing, and there's a really nice trick for making it simpler that you'll see in the video.

What's a Monomial?

If you learn about algebra, then you'll see monomials everywhere! Watch this tutorial and learn what makes a monomial, and what does not.

Further Exploration

How Do You Solve a Word Problem by Taking a Monomial to a Power?

This tutorial shows you how to find the volume of a cube box. The fun part? The measurement of each side is a monomial! Watch this tutorial to see how to cube a monomial.

How Do You Take a Monomial to a Power?

Got a monomial raised to a power? Want to simplify it? You could use the power of a product rule. You may also need the power of a power rule too. In this tutorial, you'll see how to simplify a monomial raise to a power.

• Terms of Use

6.5 Divide Monomials

Learning objectives.

By the end of this section, you will be able to:

• Simplify expressions using the Quotient Property for Exponents
• Simplify expressions with zero exponents
• Simplify expressions using the quotient to a Power Property
• Simplify expressions by applying several properties
• Divide monomials

Be Prepared 6.9

Before you get started, take this readiness quiz.

Simplify: 8 24 . 8 24 . If you missed this problem, review Example 1.65 .

Be Prepared 6.10

Simplify: ( 2 m 3 ) 5 . ( 2 m 3 ) 5 . If you missed this problem, review Example 6.23 .

Be Prepared 6.11

Simplify: 12 x 12 y . 12 x 12 y . If you missed this problem, review Example 1.67 .

Simplify Expressions Using the Quotient Property for Exponents

Earlier in this chapter, we developed the properties of exponents for multiplication. We summarize these properties below.

Summary of Exponent Properties for Multiplication

If a and b a and b are real numbers, and m and n m and n are whole numbers, then

Now we will look at the exponent properties for division. A quick memory refresher may help before we get started. You have learned to simplify fractions by dividing out common factors from the numerator and denominator using the Equivalent Fractions Property. This property will also help you work with algebraic fractions—which are also quotients.

Equivalent Fractions Property

If a , b , and c a , b , and c are whole numbers where b ≠ 0 , c ≠ 0 b ≠ 0 , c ≠ 0 ,

As before, we’ll try to discover a property by looking at some examples.

Notice, in each case the bases were the same and we subtracted exponents.

When the larger exponent was in the numerator, we were left with factors in the numerator.

When the larger exponent was in the denominator, we were left with factors in the denominator—notice the numerator of 1.

This leads to the Quotient Property for Exponents .

Quotient Property for Exponents

If a a is a real number, a ≠ 0 a ≠ 0 , and m and n m and n are whole numbers, then

A couple of examples with numbers may help to verify this property.

Example 6.59

Simplify: ⓐ x 9 x 7 x 9 x 7 ⓑ 3 10 3 2 . 3 10 3 2 .

To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.

Try It 6.117

Simplify: ⓐ x 15 x 10 x 15 x 10 ⓑ 6 14 6 5 . 6 14 6 5 .

Try It 6.118

Simplify: ⓐ y 43 y 37 y 43 y 37 ⓑ 10 15 10 7 . 10 15 10 7 .

Example 6.60

Simplify: ⓐ b 8 b 12 b 8 b 12 ⓑ 7 3 7 5 . 7 3 7 5 .

Try It 6.119

Simplify: ⓐ x 18 x 22 x 18 x 22 ⓑ 12 15 12 30 . 12 15 12 30 .

Try It 6.120

Simplify: ⓐ m 7 m 15 m 7 m 15 ⓑ 9 8 9 19 . 9 8 9 19 .

Notice the difference in the two previous examples:

• If we start with more factors in the numerator, we will end up with factors in the numerator.
• If we start with more factors in the denominator, we will end up with factors in the denominator.

The first step in simplifying an expression using the Quotient Property for Exponents is to determine whether the exponent is larger in the numerator or the denominator.

Example 6.61

Simplify: ⓐ a 5 a 9 a 5 a 9 ⓑ x 11 x 7 . x 11 x 7 .

Try It 6.121

Simplify: ⓐ b 19 b 11 b 19 b 11 ⓑ z 5 z 11 . z 5 z 11 .

Try It 6.122

Simplify: ⓐ p 9 p 17 p 9 p 17 ⓑ w 13 w 9 . w 13 w 9 .

Simplify Expressions with an Exponent of Zero

A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like a m a m a m a m . From your earlier work with fractions, you know that:

In words, a number divided by itself is 1. So, x x = 1 x x = 1 , for any x ( x ≠ 0 ) x ( x ≠ 0 ) , since any number divided by itself is 1.

The Quotient Property for Exponents shows us how to simplify a m a n a m a n when m > n m > n and when n < m n < m by subtracting exponents. What if m = n m = n ?

Consider 8 8 8 8 , which we know is 1.

Now we will simplify a m a m a m a m in two ways to lead us to the definition of the zero exponent. In general, for a ≠ 0 a ≠ 0 :

We see a m a m a m a m simplifies to a 0 a 0 and to 1. So a 0 = 1 a 0 = 1 .

Zero Exponent

If a a is a non-zero number, then a 0 = 1 a 0 = 1 .

Any nonzero number raised to the zero power is 1.

In this text, we assume any variable that we raise to the zero power is not zero.

Example 6.62

Simplify: ⓐ 9 0 9 0 ⓑ n 0 . n 0 .

The definition says any non-zero number raised to the zero power is 1.

Try It 6.123

Simplify: ⓐ 15 0 15 0 ⓑ m 0 . m 0 .

Try It 6.124

Simplify: ⓐ k 0 k 0 ⓑ 29 0 . 29 0 .

Now that we have defined the zero exponent, we can expand all the Properties of Exponents to include whole number exponents.

What about raising an expression to the zero power? Let’s look at ( 2 x ) 0 ( 2 x ) 0 . We can use the product to a power rule to rewrite this expression.

This tells us that any nonzero expression raised to the zero power is one.

Example 6.63

Simplify: ⓐ ( 5 b ) 0 ( 5 b ) 0 ⓑ ( −4 a 2 b ) 0 . ( −4 a 2 b ) 0 .

Try It 6.125

Simplify: ⓐ ( 11 z ) 0 ( 11 z ) 0 ⓑ ( −11 p q 3 ) 0 . ( −11 p q 3 ) 0 .

Try It 6.126

Simplify: ⓐ ( −6 d ) 0 ( −6 d ) 0 ⓑ ( −8 m 2 n 3 ) 0 . ( −8 m 2 n 3 ) 0 .

Simplify Expressions Using the Quotient to a Power Property

Now we will look at an example that will lead us to the Quotient to a Power Property.

Notice that the exponent applies to both the numerator and the denominator.

This leads to the Quotient to a Power Property for Exponents .

Quotient to a Power Property for Exponents

If a a and b b are real numbers, b ≠ 0 b ≠ 0 , and m m is a counting number, then

To raise a fraction to a power, raise the numerator and denominator to that power.

An example with numbers may help you understand this property:

Example 6.64

Simplify: ⓐ ( 3 7 ) 2 ( 3 7 ) 2 ⓑ ( b 3 ) 4 ( b 3 ) 4 ⓒ ( k j ) 3 . ( k j ) 3 .

Try It 6.127

Simplify: ⓐ ( 5 8 ) 2 ( 5 8 ) 2 ⓑ ( p 10 ) 4 ( p 10 ) 4 ⓒ ( m n ) 7 . ( m n ) 7 .

Try It 6.128

Simplify: ⓐ ( 1 3 ) 3 ( 1 3 ) 3 ⓑ ( −2 q ) 3 ( −2 q ) 3 ⓒ ( w x ) 4 . ( w x ) 4 .

Simplify Expressions by Applying Several Properties

We’ll now summarize all the properties of exponents so they are all together to refer to as we simplify expressions using several properties. Notice that they are now defined for whole number exponents.

Summary of Exponent Properties

Example 6.65.

Simplify: ( y 4 ) 2 y 6 . ( y 4 ) 2 y 6 .

Try It 6.129

Simplify: ( m 5 ) 4 m 7 . ( m 5 ) 4 m 7 .

Try It 6.130

Simplify: ( k 2 ) 6 k 7 . ( k 2 ) 6 k 7 .

Example 6.66

Simplify: b 12 ( b 2 ) 6 . b 12 ( b 2 ) 6 .

Try It 6.131

Simplify: n 12 ( n 3 ) 4 . n 12 ( n 3 ) 4 .

Try It 6.132

Simplify: x 15 ( x 3 ) 5 . x 15 ( x 3 ) 5 .

Example 6.67

Simplify: ( y 9 y 4 ) 2 . ( y 9 y 4 ) 2 .

Try It 6.133

Simplify: ( r 5 r 3 ) 4 . ( r 5 r 3 ) 4 .

Try It 6.134

Simplify: ( v 6 v 4 ) 3 . ( v 6 v 4 ) 3 .

Example 6.68

Simplify: ( j 2 k 3 ) 4 . ( j 2 k 3 ) 4 .

Here we cannot simplify inside the parentheses first, since the bases are not the same.

Try It 6.135

Simplify: ( a 3 b 2 ) 4 . ( a 3 b 2 ) 4 .

Try It 6.136

Simplify: ( q 7 r 5 ) 3 . ( q 7 r 5 ) 3 .

Example 6.69

Simplify: ( 2 m 2 5 n ) 4 . ( 2 m 2 5 n ) 4 .

Try It 6.137

Simplify: ( 7 x 3 9 y ) 2 . ( 7 x 3 9 y ) 2 .

Try It 6.138

Simplify: ( 3 x 4 7 y ) 2 . ( 3 x 4 7 y ) 2 .

Example 6.70

Simplify: ( x 3 ) 4 ( x 2 ) 5 ( x 6 ) 5 . ( x 3 ) 4 ( x 2 ) 5 ( x 6 ) 5 .

Try It 6.139

Simplify: ( a 2 ) 3 ( a 2 ) 4 ( a 4 ) 5 . ( a 2 ) 3 ( a 2 ) 4 ( a 4 ) 5 .

Try It 6.140

Simplify: ( p 3 ) 4 ( p 5 ) 3 ( p 7 ) 6 . ( p 3 ) 4 ( p 5 ) 3 ( p 7 ) 6 .

Example 6.71

Simplify: ( 10 p 3 ) 2 ( 5 p ) 3 ( 2 p 5 ) 4 . ( 10 p 3 ) 2 ( 5 p ) 3 ( 2 p 5 ) 4 .

Try It 6.141

Simplify: ( 3 r 3 ) 2 ( r 3 ) 7 ( r 3 ) 3 . ( 3 r 3 ) 2 ( r 3 ) 7 ( r 3 ) 3 .

Try It 6.142

Simplify: ( 2 x 4 ) 5 ( 4 x 3 ) 2 ( x 3 ) 5 . ( 2 x 4 ) 5 ( 4 x 3 ) 2 ( x 3 ) 5 .

Divide Monomials

You have now been introduced to all the properties of exponents and used them to simplify expressions. Next, you’ll see how to use these properties to divide monomials. Later, you’ll use them to divide polynomials.

Example 6.72

Find the quotient: 56 x 7 ÷ 8 x 3 . 56 x 7 ÷ 8 x 3 .

Try It 6.143

Find the quotient: 42 y 9 ÷ 6 y 3 . 42 y 9 ÷ 6 y 3 .

Try It 6.144

Find the quotient: 48 z 8 ÷ 8 z 2 . 48 z 8 ÷ 8 z 2 .

Example 6.73

Find the quotient: 45 a 2 b 3 −5 a b 5 . 45 a 2 b 3 −5 a b 5 .

Try It 6.145

Find the quotient: −72 a 7 b 3 8 a 12 b 4 . −72 a 7 b 3 8 a 12 b 4 .

Try It 6.146

Find the quotient: −63 c 8 d 3 7 c 12 d 2 . −63 c 8 d 3 7 c 12 d 2 .

Example 6.74

Find the quotient: 24 a 5 b 3 48 a b 4 . 24 a 5 b 3 48 a b 4 .

Try It 6.147

Find the quotient: 16 a 7 b 6 24 a b 8 . 16 a 7 b 6 24 a b 8 .

Try It 6.148

Find the quotient: 27 p 4 q 7 −45 p 12 q . 27 p 4 q 7 −45 p 12 q .

Once you become familiar with the process and have practiced it step by step several times, you may be able to simplify a fraction in one step.

Example 6.75

Find the quotient: 14 x 7 y 12 21 x 11 y 6 . 14 x 7 y 12 21 x 11 y 6 .

Be very careful to simplify 14 21 14 21 by dividing out a common factor, and to simplify the variables by subtracting their exponents.

Try It 6.149

Find the quotient: 28 x 5 y 14 49 x 9 y 12 . 28 x 5 y 14 49 x 9 y 12 .

Try It 6.150

Find the quotient: 30 m 5 n 11 48 m 10 n 14 . 30 m 5 n 11 48 m 10 n 14 .

In all examples so far, there was no work to do in the numerator or denominator before simplifying the fraction. In the next example, we’ll first find the product of two monomials in the numerator before we simplify the fraction. This follows the order of operations. Remember, a fraction bar is a grouping symbol.

Example 6.76

Find the quotient: ( 6 x 2 y 3 ) ( 5 x 3 y 2 ) ( 3 x 4 y 5 ) . ( 6 x 2 y 3 ) ( 5 x 3 y 2 ) ( 3 x 4 y 5 ) .

Try It 6.151

Find the quotient: ( 6 a 4 b 5 ) ( 4 a 2 b 5 ) 12 a 5 b 8 . ( 6 a 4 b 5 ) ( 4 a 2 b 5 ) 12 a 5 b 8 .

Try It 6.152

Find the quotient: ( −12 x 6 y 9 ) ( −4 x 5 y 8 ) −12 x 10 y 12 . ( −12 x 6 y 9 ) ( −4 x 5 y 8 ) −12 x 10 y 12 .

Access these online resources for additional instruction and practice with dividing monomials:

• Rational Expressions
• Dividing Monomials
• Dividing Monomials 2

Section 6.5 Exercises

Practice makes perfect.

In the following exercises, simplify.

ⓐ x 18 x 3 x 18 x 3 ⓑ 5 12 5 3 5 12 5 3

ⓐ y 20 y 10 y 20 y 10 ⓑ 7 16 7 2 7 16 7 2

ⓐ p 21 p 7 p 21 p 7 ⓑ 4 16 4 4 4 16 4 4

ⓐ u 24 u 3 u 24 u 3 ⓑ 9 15 9 5 9 15 9 5

ⓐ q 18 q 36 q 18 q 36 ⓑ 10 2 10 3 10 2 10 3

ⓐ t 10 t 40 t 10 t 40 ⓑ 8 3 8 5 8 3 8 5

ⓐ b b 9 b b 9 ⓑ 4 4 6 4 4 6

ⓐ x x 7 x x 7 ⓑ 10 10 3 10 10 3

Simplify Expressions with Zero Exponents

ⓐ 20 0 20 0 ⓑ b 0 b 0

ⓐ 13 0 13 0 ⓑ k 0 k 0

ⓐ − 27 0 − 27 0 ⓑ − ( 27 0 ) − ( 27 0 )

ⓐ − 15 0 − 15 0 ⓑ − ( 15 0 ) − ( 15 0 )

ⓐ ( 25 x ) 0 ( 25 x ) 0 ⓑ 25 x 0 25 x 0

ⓐ ( 6 y ) 0 ( 6 y ) 0 ⓑ 6 y 0 6 y 0

ⓐ ( 12 x ) 0 ( 12 x ) 0 ⓑ ( −56 p 4 q 3 ) 0 ( −56 p 4 q 3 ) 0

ⓐ 7 y 0 7 y 0 ( 17 y ) 0 ( 17 y ) 0 ⓑ ( −93 c 7 d 15 ) 0 ( −93 c 7 d 15 ) 0

ⓐ 12 n 0 − 18 m 0 12 n 0 − 18 m 0 ⓑ ( 12 n ) 0 − ( 18 m ) 0 ( 12 n ) 0 − ( 18 m ) 0

ⓐ 15 r 0 − 22 s 0 15 r 0 − 22 s 0 ⓑ ( 15 r ) 0 − ( 22 s ) 0 ( 15 r ) 0 − ( 22 s ) 0

ⓐ ( 3 4 ) 3 ( 3 4 ) 3 ⓑ ( p 2 ) 5 ( p 2 ) 5 ⓒ ( x y ) 6 ( x y ) 6

ⓐ ( 2 5 ) 2 ( 2 5 ) 2 ⓑ ( x 3 ) 4 ( x 3 ) 4 ⓒ ( a b ) 5 ( a b ) 5

ⓐ ( a 3 b ) 4 ( a 3 b ) 4 ⓑ ( 5 4 m ) 2 ( 5 4 m ) 2

ⓐ ( x 2 y ) 3 ( x 2 y ) 3 ⓑ ( 10 3 q ) 4 ( 10 3 q ) 4

( a 2 ) 3 a 4 ( a 2 ) 3 a 4

( p 3 ) 4 p 5 ( p 3 ) 4 p 5

( y 3 ) 4 y 10 ( y 3 ) 4 y 10

( x 4 ) 5 x 15 ( x 4 ) 5 x 15

u 6 ( u 3 ) 2 u 6 ( u 3 ) 2

v 20 ( v 4 ) 5 v 20 ( v 4 ) 5

m 12 ( m 8 ) 3 m 12 ( m 8 ) 3

n 8 ( n 6 ) 4 n 8 ( n 6 ) 4

( p 9 p 3 ) 5 ( p 9 p 3 ) 5

( q 8 q 2 ) 3 ( q 8 q 2 ) 3

( r 2 r 6 ) 3 ( r 2 r 6 ) 3

( m 4 m 7 ) 4 ( m 4 m 7 ) 4

( p r 11 ) 2 ( p r 11 ) 2

( a b 6 ) 3 ( a b 6 ) 3

( w 5 x 3 ) 8 ( w 5 x 3 ) 8

( y 4 z 10 ) 5 ( y 4 z 10 ) 5

( 2 j 3 3 k ) 4 ( 2 j 3 3 k ) 4

( 3 m 5 5 n ) 3 ( 3 m 5 5 n ) 3

( 3 c 2 4 d 6 ) 3 ( 3 c 2 4 d 6 ) 3

( 5 u 7 2 v 3 ) 4 ( 5 u 7 2 v 3 ) 4

( k 2 k 8 k 3 ) 2 ( k 2 k 8 k 3 ) 2

( j 2 j 5 j 4 ) 3 ( j 2 j 5 j 4 ) 3

( t 2 ) 5 ( t 4 ) 2 ( t 3 ) 7 ( t 2 ) 5 ( t 4 ) 2 ( t 3 ) 7

( q 3 ) 6 ( q 2 ) 3 ( q 4 ) 8 ( q 3 ) 6 ( q 2 ) 3 ( q 4 ) 8

( −2 p 2 ) 4 ( 3 p 4 ) 2 ( −6 p 3 ) 2 ( −2 p 2 ) 4 ( 3 p 4 ) 2 ( −6 p 3 ) 2

( −2 k 3 ) 2 ( 6 k 2 ) 4 ( 9 k 4 ) 2 ( −2 k 3 ) 2 ( 6 k 2 ) 4 ( 9 k 4 ) 2

( −4 m 3 ) 2 ( 5 m 4 ) 3 ( −10 m 6 ) 3 ( −4 m 3 ) 2 ( 5 m 4 ) 3 ( −10 m 6 ) 3

( −10 n 2 ) 3 ( 4 n 5 ) 2 ( 2 n 8 ) 2 ( −10 n 2 ) 3 ( 4 n 5 ) 2 ( 2 n 8 ) 2

In the following exercises, divide the monomials.

56 b 8 ÷ 7 b 2 56 b 8 ÷ 7 b 2

63 v 10 ÷ 9 v 2 63 v 10 ÷ 9 v 2

−88 y 15 ÷ 8 y 3 −88 y 15 ÷ 8 y 3

−72 u 12 ÷ 1 2 u 4 −72 u 12 ÷ 1 2 u 4

45 a 6 b 8 −15 a 10 b 2 45 a 6 b 8 −15 a 10 b 2

54 x 9 y 3 −18 x 6 y 15 54 x 9 y 3 −18 x 6 y 15

15 r 4 s 9 18 r 9 s 2 15 r 4 s 9 18 r 9 s 2

20 m 8 n 4 30 m 5 n 9 20 m 8 n 4 30 m 5 n 9

18 a 4 b 8 −27 a 9 b 5 18 a 4 b 8 −27 a 9 b 5

45 x 5 y 9 −60 x 8 y 6 45 x 5 y 9 −60 x 8 y 6

64 q 11 r 9 s 3 48 q 6 r 8 s 5 64 q 11 r 9 s 3 48 q 6 r 8 s 5

65 a 10 b 8 c 5 42 a 7 b 6 c 8 65 a 10 b 8 c 5 42 a 7 b 6 c 8

( 10 m 5 n 4 ) ( 5 m 3 n 6 ) 25 m 7 n 5 ( 10 m 5 n 4 ) ( 5 m 3 n 6 ) 25 m 7 n 5

( −18 p 4 q 7 ) ( −6 p 3 q 8 ) −36 p 12 q 10 ( −18 p 4 q 7 ) ( −6 p 3 q 8 ) −36 p 12 q 10

( 6 a 4 b 3 ) ( 4 a b 5 ) ( 12 a 2 b ) ( a 3 b ) ( 6 a 4 b 3 ) ( 4 a b 5 ) ( 12 a 2 b ) ( a 3 b )

( 4 u 2 v 5 ) ( 15 u 3 v ) ( 12 u 3 v ) ( u 4 v ) ( 4 u 2 v 5 ) ( 15 u 3 v ) ( 12 u 3 v ) ( u 4 v )

Mixed Practice

ⓐ 24 a 5 + 2 a 5 24 a 5 + 2 a 5 ⓑ 24 a 5 − 2 a 5 24 a 5 − 2 a 5 ⓒ 24 a 5 · 2 a 5 24 a 5 · 2 a 5 ⓓ 24 a 5 ÷ 2 a 5 24 a 5 ÷ 2 a 5

ⓐ 15 n 10 + 3 n 10 15 n 10 + 3 n 10 ⓑ 15 n 10 − 3 n 10 15 n 10 − 3 n 10 ⓒ 15 n 10 · 3 n 10 15 n 10 · 3 n 10 ⓓ 15 n 10 ÷ 3 n 10 15 n 10 ÷ 3 n 10

ⓐ p 4 · p 6 p 4 · p 6 ⓑ ( p 4 ) 6 ( p 4 ) 6

ⓐ q 5 · q 3 q 5 · q 3 ⓑ ( q 5 ) 3 ( q 5 ) 3

ⓐ y 3 y y 3 y ⓑ y y 3 y y 3

ⓐ z 6 z 5 z 6 z 5 ⓑ z 5 z 6 z 5 z 6

( 8 x 5 ) ( 9 x ) ÷ 6 x 3 ( 8 x 5 ) ( 9 x ) ÷ 6 x 3

( 4 y ) ( 12 y 7 ) ÷ 8 y 2 ( 4 y ) ( 12 y 7 ) ÷ 8 y 2

27 a 7 3 a 3 + 54 a 9 9 a 5 27 a 7 3 a 3 + 54 a 9 9 a 5

32 c 11 4 c 5 + 42 c 9 6 c 3 32 c 11 4 c 5 + 42 c 9 6 c 3

32 y 5 8 y 2 − 60 y 10 5 y 7 32 y 5 8 y 2 − 60 y 10 5 y 7

48 x 6 6 x 4 − 35 x 9 7 x 7 48 x 6 6 x 4 − 35 x 9 7 x 7

63 r 6 s 3 9 r 4 s 2 − 72 r 2 s 2 6 s 63 r 6 s 3 9 r 4 s 2 − 72 r 2 s 2 6 s

56 y 4 z 5 7 y 3 z 3 − 45 y 2 z 2 5 y 56 y 4 z 5 7 y 3 z 3 − 45 y 2 z 2 5 y

Everyday Math

Memory One megabyte is approximately 10 6 10 6 bytes. One gigabyte is approximately 10 9 10 9 bytes. How many megabytes are in one gigabyte?

Memory One gigabyte is approximately 10 9 10 9 bytes. One terabyte is approximately 10 12 10 12 bytes. How many gigabytes are in one terabyte?

Writing Exercises

Jennifer thinks the quotient a 24 a 6 a 24 a 6 simplifies to a 4 a 4 . What is wrong with her reasoning?

Maurice simplifies the quotient d 7 d d 7 d by writing d 7 d = 7 d 7 d = 7 . What is wrong with his reasoning?

When Drake simplified − 3 0 − 3 0 and ( −3 ) 0 ( −3 ) 0 he got the same answer. Explain how using the Order of Operations correctly gives different answers.

Robert thinks x 0 x 0 simplifies to 0. What would you say to convince Robert he is wrong?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra-2e/pages/6-5-divide-monomials

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.