null hypothesis large sample

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base
Null and Alternative Hypotheses | Definitions & Examples

Null & Alternative Hypotheses | Definitions, Templates & Examples

Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

Null hypothesis ( H 0 ): There’s no effect in the population .
Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:

The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

Academic style
Vague sentences
Style consistency

See an example

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

They’re both answers to the research question.
They both make claims about the population.
They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

General template sentences

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
Alternative hypothesis ( H a ): Independent variable affects dependent variable.

Test-specific template sentences

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved April 16, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/

Is this article helpful?

Shaun Turney

Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

10.2: Understanding Null Hypothesis Testing

Last updated
Save as PDF
Page ID 20196

Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton

Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton
Kwantlen Polytechnic U., Washington State U., & Texas A&M U.—Texarkana
Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive summary data (e.g., means, correlation coefficients) for those variables. These descriptive data for the sample are called statistics . In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing (often called null hypothesis significance testing or NHST) is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-zero”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the probability of the sample result or a more extreme result if the null hypothesis were true (Lakens, 2017). [1] This probability is called the p value . A low p value means that the sample or more extreme result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample or more extreme result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value criterion be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result at least as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [2] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.

You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

Role of Sample Size and Relationship Strength

Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table $\PageIndex{1}$ shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2.

Although Table $\PageIndex{1}$ provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table $\PageIndex{1}$ illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [3] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

Lakens, D. (2017, December 25). About p -values: Understanding common misconceptions. [Blog post] Retrieved from https://correlaid.org/en/blog/understand-p-values/ ↵
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13.1 Understanding Null Hypothesis Testing

Learning objectives.

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994). Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

Role of Sample Size and Relationship Strength

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant

Although Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007). The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.

Practice: Use Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” to decide whether each of the following results is statistically significant.

The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003.

Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science , 16 , 259–263.

Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Biochem Med (Zagreb)
v.31(1); 2021 Feb 15

Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies

Ceyhan ceran serdar.

1 Medical Biology and Genetics, Faculty of Medicine, Ankara Medipol University, Ankara, Turkey

Murat Cihan

2 Ordu University Training and Research Hospital, Ordu, Turkey

Doğan Yücel

3 Department of Medical Biochemistry, Lokman Hekim University School of Medicine, Ankara, Turkey

Muhittin A Serdar

4 Department of Medical Biochemistry, Acibadem Mehmet Ali Aydinlar University, Istanbul, Turkey

Calculating the sample size in scientific studies is one of the critical issues as regards the scientific contribution of the study. The sample size critically affects the hypothesis and the study design, and there is no straightforward way of calculating the effective sample size for reaching an accurate conclusion. Use of a statistically incorrect sample size may lead to inadequate results in both clinical and laboratory studies as well as resulting in time loss, cost, and ethical problems. This review holds two main aims. The first aim is to explain the importance of sample size and its relationship to effect size (ES) and statistical significance. The second aim is to assist researchers planning to perform sample size estimations by suggesting and elucidating available alternative software, guidelines and references that will serve different scientific purposes.

Introduction

Statistical analysis is a crucial part of a research. A scientific study must include statistical tools in the study, beginning from the planning stage. Developed in the last 20-30 years, information technology, along with evidence-based medicine, increased the spread and applicability of statistical science. Although scientists have understood the importance of statistical analysis for researchers, a significant number of researchers admit that they lack adequate knowledge about statistical concepts and principles ( 1 ). In a study by West and Ficalora, more than two-thirds of the clinicians emphasized that “the level of biostatistics education that is provided to the medical students is not sufficient” ( 2 ). As a result, it was suggested that statistical concepts were either poorly understood or not understood at all ( 3 , 4 ). Additionally, intentionally or not, researchers tend to draw conclusions that cannot be supported by the actual study data, often due to the misuse of statistics tools ( 5 ). As a result, a large number of statistical errors occur affecting the research results.

Although there are a variety of potential statistical errors that might occur in any kind of scientific research, it has been observed that the sources of error have changed due to the use of dedicated software that facilitates statistics in recent years. A summary of main statistical errors frequently encountered in scientific studies is provided below ( 6 - 13 ):

Flawed and inadequate hypothesis;
Improper study design;
Lack of adequate control condition/group;
Spectrum bias;
Overstatement of the analysis results;
Spurious correlations;
Inadequate sample size;
Circular analysis (creating bias by selecting the properties of the data retrospectively);
Utilization of inappropriate statistical studies and fallacious bending of the analyses;
p-hacking ( i.e. addition of new covariates post hoc to make P values significant);
Excessive interpretation of limited or insignificant results (subjectivism);
Confusion (intentionally or not) of correlations, relationships, and causations;
Faulty multiple regression models;
Confusion between P value and clinical significance; and
Inappropriate presentation of the results and effects (erroneous tables, graphics, and figures).

Relationship among sample size, power, P value and effect size

In this review, we will concentrate on the problems associated with the relationships among sample size, power, P value, and effect size (ES). Practical suggestions will be provided whenever possible. In order to understand and interpret the sample size, power analysis, effect size, and P value, it is necessary to know how the hypothesis of the study was formed. It is best to evaluate a study for Type I and Type II errors ( Figure 1 ) through consideration of the study results in the context of its hypotheses ( 14 - 16 ).

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f1.jpg

Illustration of Type I and Type II errors.

A statistical hypothesis is the researcher’s best guess as to what the result of the experiment will show. It states, in a testable form the proposition the researcher plans to examine in a sample to be able to find out if the proposition is correct in the relevant population. There are two commonly used types of hypotheses in statistics. These are the null hypothesis (H0) and the alternative (H1) hypothesis. Essentially, the H1 is the researcher’s prediction of what will be the situation of the experimental group after the experimental treatment is applied. The H0 expresses the notion that there will be no effect from the experimental treatment.

Prior to the study, in addition to stating the hypothesis, the researcher must also select the alpha (α) level at which the hypothesis will be declared “supported”. The α represents how much risk the researcher is willing to take that the study will conclude H1 is correct when (in the full population) it is not correct (and thus, the null hypothesis is really true). In other words, alpha represents the probability of rejecting H0 when it actually is true. (Thus, the researcher has made an error by reporting that the experimental treatment makes a difference, when in fact, in the full population, that treatment has no effect.)

The most common α level chosen is 0.05, meaning the researcher is willing to take a 5% chance that a result supporting the hypothesis will be untrue in the full population. However, other alpha levels may also be appropriate in some circumstances. For pilot studies, α is often set at 0.10 or 0.20. In studies where it is especially important to avoid concluding a treatment is effective when it actually is not, the alpha may be set at a much lower value; it might be set at 0.001 or even lower. Drug studies are examples for studies that often set the alpha at 0.001 or lower because the consequences of releasing an ineffective drug can be extremely dangerous for patients.

Another probability value is called “the P value”. The P value is simply the obtained statistical probability of incorrectly accepting the alternate hypothesis. The P value is compared to the alpha value to determine if the result is “statistically significant”, meaning that with high probability the result found in the sample will also be true in the full population. If the P value is at or lower than alpha, H1 is accepted. If it is higher than alpha, the H1 is rejected and H0 is accepted instead.

There are actually two types of errors: the error of accepting H1 when it is not true in the population; this is called a Type I error; and is a false positive. The alpha defines the probability of a Type I error. Type I errors can happen for many reasons, from poor sampling that results in an experimental sample quite different from the population, to other mistakes occurring in the design stage or implementation of the research procedures. It is also possible to make an erroneous decision in the opposite direction; by incorrectly rejecting H1 and thus wrongly accepting H0. This is called a Type II error (or a false negative). The β defines the probability of a Type II error. The most common reason for this type of error is small sample size, especially when combined with moderately low or low effect sizes. Both small sample sizes and low effect sizes reduce the power in the study.

Power, which is the probability of rejecting a false null hypothesis, is calculated as 1-β (also expressed as “1 - Type II error probability”). For a Type II error of 0.15, the power is 0.85. Since reduction in the probability of committing a Type II error increases the risk of committing a Type I error (and vice versa ), a delicate balance should be established between the minimum allowed levels for Type I and Type II errors. The ideal power of a study is considered to be 0.8 (which can also be specified as 80%) ( 17 ). Sufficient sample size should be maintained to obtain a Type I error as low as 0.05 or 0.01 and a power as high as 0.8 or 0.9.

However, when power value falls below < 0.8, one cannot immediately conclude that the study is totally worthless. In parallel with this, the concept of “cost-effective sample size” has gained importance in recent years ( 18 ).

Additionally, the traditionally chosen alpha and beta error limits are generally arbitrary and are being used as a convention rather than being based on any scientific validity. Another key issue for a study is the determination, presentation and discussion of the effect size of the study, as will be discussed below in detail.

Although increasing the sample size is suggested to decrease the Type II errors, it will increase the cost of the project and delay the completion of the research activities in a foreseen period of time. In addition, it should not be forgotten that redundant samples may cause ethical problems ( 19 , 20 ).

Therefore, determination of the effective sample size is crucial to enable an efficient study with high significance, increasing the impact of the outcome. Unfortunately, information regarding sample size calculations are not often provided by clinical investigators in most diagnostic studies ( 21 , 22 ).

Calculation of the sample size

Different methods can be utilized before the onset of the study to calculate the most suitable sample size for the specific research. In addition to manual calculation, various nomograms or software can be used. The Figure 2 illustrates one of the most commonly used nomograms for sample size estimation using effect size and power ( 23 ).

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f2.jpg

Nomogram for sample size and power, for comparing two groups of equal size. Gaussian distributions assumed. Standardized difference (effect size) and aimed power values are initially selected on the nomogram. The line connecting these values cross the significance level region of the nomogram. The intercept at the appropriate significance value presents the required sample size for the study. In the above example, for effect size = 1, power = 0.8 and alpha value = 0.05, the sample size is found to be 30. (Adapted from reference 16 ).

Although manual calculation is preferred by the experts of the subject, it is a bit complicated and difficult for the researchers that are not statistics experts. In addition, considering the variety of the research types and characteristics, it should be noted that a great number of calculations will be required with too many variables ( Table 1 ) ( 16 , 24 - 30 ).

In recent years, numerous software and websites have been developed which can successfully calculate sample size in various study types. Some of the important software and websites are listed in Table 2 and are evaluated based both on the remarks stated in the literature and on our own experience, with respect to the content, ease of use, and cost ( 31 , 32 ). G-Power, R, and Piface stand out among the listed software in terms of being free-to use. G-Power is a free-to use tool that be used to calculate statistical power for many different t-tests, F-tests, χ 2 tests, z-tests and some exact tests. R is an open source programming language which can be tailored to meet individual statistical needs, by adding specific program modules called packages onto a specific base program. Piface is a java application specifically designed for sample size estimation and post-hoc power analysis. The most professional software is PASS (Power Analysis and Sample Size). With PASS, it is possible to analyse sample size and power for approximately 200 different study types. In addition, many websites provide substantial aid in calculating power and sample size, basing their methodology on scientific literature.

The sample size or the power of the study is directly related to the ES of the study. What is this important ES? The ES provides important information on how well the independent variable or variables predict the dependent variable. Low ES means that, independent variables don’t predict well because they are only slightly related to the dependent variable. Strong ES means that, independent variables are very good predictors of the dependent variable. Thus, ES is clinically important for evaluating how efficiently the clinicians can predict outcomes from the independent variables.

The scale of the ES values for different types of statistical tests conducted in different study types are presented in Table 3 .

In order to evaluate the effect of the study and indicate its clinical significance, it is very important to evaluate the effect size along with statistical significance. P value is important in the statistical evaluation of the research. While it provides information on presence/absence of an effect, it will not account for the size of the effect. For comprehensive presentation and interpretation of the studies, both effect size and statistical significance (P value) should be provided and considered.

It would be much easier to understand ES through an example. For example, assume that independent sample t-test is used to compare total cholesterol levels for two groups having normal distribution. Where X, SD and N stands for mean, standard deviation and sample size, respectively. Cohen’s d ES can be calculated as follows:

Mean (X), mmol/L Standard deviation (SD) Sample size (N)

Group 1 6.5 0.5 30

Group 2 5.2 0.8 30

Cohen d ES results represents: 0.8 large, 0.5 medium, 0.2 small effects). The result of 1.94 indicates a very large effect. Means of the two groups are remarkably different.

In the example above, the means of the two groups are largely different in a statistically significant manner. Yet, clinical importance of the effect (whether this effect is important for the patient, clinical condition, therapy type, outcome, etc .) needs to be specifically evaluated by the experts of the topic.

Power, alpha values, sample size, and ES are closely related with each other. Let us try to explain this relationship through different situations that we created using G-Power ( 33 , 34 ).

The Figure 3 shows the change of sample size depending on the ES changes (0.2, 1 and 2.5, respectively) provided that the power remains constant at 0.8. Arguably, case 3 is particularly common in pre-clinical studies, cell culture, and animal studies (usually 5-10 samples in animal studies or 3-12 samples in cell culture studies), while case 2 is more common in clinical studies. In clinical, epidemiological or meta-analysis studies, where the sample size is very large; case 1, which emphasizes the importance of smaller effects, is more commonly observed ( 33 ).

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f3.jpg

Relationship between effect size and sample size. P – power. ES - effect size. SS - sample size. The required sample size increases as the effect size decreases. In all cases, P value is set to 0.8. The sample sizes (SS) when ES is 0.2, 1, or 2.5; are 788, 34 and 8, respectively. The graphs at the bottom represent the influence of change in the sample size on the power.

In Figure 4 , case 4 exemplifies the change in power and ES values when the sample size is kept constant ( i.e. as low as 8). As can be seen here, in studies with low ES, working with few samples will mean waste of time, redundant processing, or unnecessary use of laboratory animals.

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f4.jpg

Relationship between effect size and power. Two different cases are schematized where the sample size is kept constant either at 8 or at 30. When the sample size is kept constant, the power of the study decreases as the effect size decreases. When the effect size is 2.5, even 8 samples are sufficient to obtain power = ~0.8. When the effect size is 1, increasing sample size from 8 to 30 significantly increases the power of the study. Yet, even 30 samples are not sufficient to reach a significant power value if effect size is as low as 0.2.

Likewise, case 5 exemplifies the situation where the sample size is kept constant at 30. In this case, it is important to note that when ES is 1, the power of the study will be around 0.8. Some statisticians arbitrarily regard 30 as a critical sample size. However, case 5 clearly demonstrates that it is essential not to underestimate the importance of ES, while deciding on the sample size.

Especially in recent years, where clinical significance or effectiveness of the results has outstripped the statistical significance; understanding the effect size and power has gained tremendous importance ( 35 – 38 ).

Preliminary information about the hypothesis is eminently important to calculate the sample size at intended power. Usually, this is accomplished by determining the effect size from the results of a previous study or a preliminary study. There are software available which can calculate sample size using the effect size

We now want to focus on sample size and power analysis in some of the most common research areas.

Determination of sample size in pre-clinical studies

Animal studies are the most critical studies in terms of sample size. Especially due to ethical concerns, it is vital to keep the sample size at the lowest sufficient level. It should be noted that, animal studies are radically different from human studies because many animal studies use inbred animals having extremely similar genetic background. Thus, far fewer animals are needed in the research because genetic differences that could affect the study results are kept to a minimum ( 39 , 40 ).

Consequently, alternative sample size estimation methodologies were suggested for each study type ( 41 - 44 ). If the effect size is to be determined using the results from previous or preliminary studies, sample size estimation may be performed using G-Power. In addition, Table 4 may also be used for easy estimation of the sample size ( 40 ).

In addition to sample size estimations that may be computed according to Table 4 , formulas stated in Table 1 and the websites mentioned in Table 2 may also be utilized to estimate sample size in animal studies. Relying on previous studies pose certain limitations since it may not always be possible to acquire reliable “pooled standard deviation” and “group mean” values.

Arifin et al. proposed simpler formulas ( Table 5 ) to calculate sample size in animal studies ( 45 ). In group comparison studies, it is possible to calculate the sample size as follows: N = (DF/k)+1 (Eq. 4).

Based on acceptable range of the degrees of freedom (DF), the DF in formulas are replaced with the minimum ( 10 ) and maximum ( 20 ). For example, in an experimental animal study where the use of 3 investigational drugs are tested minimum number of animals that will be required: N = (10/3)+1 = 4.3; rounded up to 5 animals / group, total sample size = 5 x 3 = 15 animals. Maximum number of animals that will be required: N = (20/3)+1 = 7.7; rounded down to 7 animals / group, total sample size = 7 x 3 = 21 animals.

In conclusion, for the recommended study, 5 to 7 animals per group will be required. In other words, a total of 15 to 21 animals will be required to keep the DF within the range of 10 to 20.

In a compilation where Ricci et al. reviewed 15 studies involving animal models, it was noted that the sample size used was 10 in average (between 6 and 18), however, no formal power analysis was reported by any of the groups. It was striking that, all studies included in the review have used parametric analysis without prior normality testing ( i.e. Shapiro-Wilk) to justify their statistical methodology ( 46 ).

It is noteworthy that, unnecessary animal use could be prevented by keeping the power at 0.8 and selecting one-tailed analysis over two-tailed analysis with an accepted 5% risk of making type I error as performed in some pharmacological studies, reducing the number of required animals by 14% ( 47 ).

Neumann et al. proposed a group-sequential design to minimize animal use without a decrease in statistical power. In this strategy, researchers started the experiments with only 30% of the animals that were initially planned to be included in the study. After an interim analysis of the results obtained with 30% of the animals, if sufficient power is not reached, another 30% is included in the study. If results from this initial 60% of the animals provide sufficient statistical power, then the rest of the animals are excused from the study. If not, the remaining animals are also included in the study. This approach was reported to save 20% of the animals in average, without leading to a decrease in statistical power ( 48 ).

Alternative sample size estimation strategies are implemented for animal testing in different countries. As an example, a local authority in southwestern Germany recommended that, in the absence of a formal sample size estimation, less than 7 animals per experimental group should be included in pilot studies and the total number of experimental animals should not exceed 100 ( 48 ).

On the other hand, it should be noted that, for a sample size of 8 to 10 animals per group, statistical significance will not be accomplished unless a large or very large ES (> 2) is expected ( 45 , 46 ). This problem remains as an important limitation for animal studies. Software like G-Power can be used for sample size estimation. In this case, results obtained from a previous or a preliminary study will be required to be used in the calculations. However, even when a previous study is available in literature, using its data for a sample size estimation will still pose an uncertainty risk unless a clearly detailed study design and data is provided in the publication. Although researchers suggested that reliability analyses could be performed by methods such as Markov Chain Monte Carlo, further research is needed in this regard ( 49 ).

The output of the joint workshop held by The National Institutes of Health (NIH), Nature Publishing Group and Science; “Principles and Guidelines for Reporting Preclinical Research” that was published in 2014, has since been acknowledged by many organizations and journals. This guide has shed significant light on studies using biological materials, involving animal studies, and handling image-based data ( 50 ).

Another important point regarding animal studies is the use of technical repetition (pseudo replication) instead of biological repetition. Technical repetition is a specific type of repetition where the same sample is measured multiple times, aiming to probe the noise associated with the measurement method or the device. Here, no matter how many times the same sample is measured, the actual sample size will remain the same. Let us assume a research group is investigating the effect of a therapeutic drug on blood glucose level. If the researchers measure the blood glucose level of 3 mice receiving the actual treatment and 3 mice receiving placebo, this would be a biological repetition. On the other hand, if the blood glucose level of a single mouse receiving the actual treatment and the blood glucose level of a single mouse receiving placebo are each measured 3 times, this would be technical repetition. Both designs will provide 6 data points to calculate P value, yet the P value obtained from the second design would be meaningless since each treatment group will only have one member ( Figure 5 ). Multiple measurements on single mice are pseudo replication; therefore do not contribute to N. No matter how ingenious, no statistical analysis method can fix incorrectly selected replicates at the post-experimental stage; replicate types should be selected accurately at the design stage. This problem is a critical limitation, especially in pre-clinical studies that conduct cell culture experiments. It is very important for critical assessment and evaluation of the published research results ( 51 ). This issue is mostly underestimated, concealed or ignored. It is striking that in some publications, the actual sample size is found to be as low as one. Experiments comparing drug treatments in a patient-derived stem cell line are specific examples for this situation. Although there may be many technical replications for such experiments and the experiment can be repeated several times, the original patient is a single biological entity. Similarly, when six metatarsals are harvested from the front paws of a single mouse and cultured as six individual cultures, another pseudo replication is practiced where the sample size is actually 1, instead of 6 ( 52 ). Lazic et al . suggested that almost half of the studies (46%) had mistaken pseudo replication (technical repeat) for genuine replication, while 32% did not provide sufficient information to enable evaluation of appropriateness of the sample size ( 53 , 54 ).

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f5.jpg

Technical vs biological repeat.

In studies providing qualitative data (such as electrophoresis, histology, chromatography, electron microscopy), the number of replications (“number of repeats” or “sample size”) should explicitly be stated.

Especially in pre-clinical studies, standard error of the mean (SEM) is frequently used instead of SD in some situations and by certain journals. The SEM is calculated by dividing the SD by the square root of the sample size (N). The SEM will indicate how variable the mean will be if the whole study is repeated many times. Whereas the SD is a measure of how scattered the scores within a set of data are. Since SD is usually higher than SEM, researchers tend to use SEM. While SEM is not a distribution criterion; there is a relation between SEM and 95% confidence interval (CI). For example, when N = 3, 95% CI is almost equal to mean ± 4 SEM, but when N ≥ 10; 95% CI equals to mean ± 2 SEM. Standard deviation and 95% CI can be used to report the statistical analysis results such as variation and precision on the same plot to demonstrate the differences between test groups ( 52 , 55 ).

Given the attrition and unexpected death risk of the laboratory animals during the study, the researchers are generally recommended to increase the sample size by 10% ( 56 ).

Sample size calculation for some genetic studies

Sample size is important for genetic studies as well. In genetic studies, calculation of allele frequencies, calculation of homozygous and heterozygous frequencies based on Hardy-Weinberg principle, natural selection, mutation, genetic drift, association, linkage, segregation, haplotype analysis are carried out by means of probability and statistical models ( 57 - 62 ). While G-Power is useful for basic statistics, substantial amount of analyses can be conducted using genetic power calculator ( http://zzz.bwh.harvard.edu/gpc/ ) ( 61 , 62 ). This calculator, which provides automated power analysis for variance components (VC) quantitative trait locus (QTL) linkage and association tests in sibships, and other common tests, is significantly effective especially for genetics studies analysing complex diseases.

Case-control association studies for single nucleotide polymorphisms (SNPs) may be facilitated using OSSE web site ( http://osse.bii.a-star.edu.sg/ ). As an example, let us assume the minor allele frequencies of an SNP in cases and controls are approximately 15% and 7% respectively. To have a power of 0.8 with 0.05 significance, the study is required to include 239 samples both for cases and controls, adding up to 578 samples in total ( Figure 6 ).

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f6.jpg

Interface of Online Sample Size Estimator (OSSE) Tool. (Available at: http://osse.bii.a-star.edu.sg/ ).

Hong and Park have proposed tables and graphics in their article for facilitating sample size estimation ( 57 ). With the assumption of 5% disease prevalence, 5% minor allele frequency and complete linkage disequilibrium (D’ = 1), the sample size in a case-control study with a single SNP marker, 1:1 case-to-control ratio, 0.8 statistical power, and 5% type I error rate can be calculated according to the genetic models of inheritance (allelic, additive, dominant, recessive, and co-dominant models) and the odd ratios of heterozygotes/rare homozygotes ( Table 6 ). As demonstrated by Hong and Park among all other types of inheritance, dominant inheritance requires the lowest sample size to achieve 0.8 statistical power. Whereas, testing a single SNP in a recessive inheritance model requires a very large sample size even with a high homozygote ratio, that is practically challenging with a limited budget ( 57 ). The Table 6 illustrates the difficulty in detecting a disease allele following a recessive mode of inheritance with moderate sample size.

Sample size and power analyses in clinical studies

In clinical research, sample size is calculated in line with the hypothesis and study design. The cross-over study design and parallel study design apply different approaches for sample size estimation. Unlike pre-clinical studies, a significant number of clinical journals necessitate sample size estimation for clinical studies.

The basic rules for sample size estimation in clinical trials are as follows ( 63 , 64 ):

Error level (alpha): It is generally set as < 0.05. The sample size should be increased to compensate for the decrease in the effect size.
Power must be > 0.8: The sample size should be increased to increase the power of the study. The higher the power, the lower the risk of missing an actual effect.

An external file that holds a picture, illustration, etc.
Object name is bm-31-1-010502-f7.jpg

The relationship among clinical significance, statistical significance, power and effect size. In the example above, in order to provide a clinically significant effect, a treatment is required to trigger at least 0.5 mmol/L decreases in cholesterol levels. Four different scenarios are given for a candidate treatment, each having different mean total cholesterol change and 95% confidence interval. ES - effect size. N – number of participant. Adapted from reference 65 .

Similarity and equivalence: The sample size required demonstrating similarity and equivalence is very low.

Sample size estimation can be performed manually using the formulas in Table 1 as well as software and websites in Table 2 (especially by G-Power). However, all of these calculations require preliminary results or previous study outputs regarding the hypothesis of interest. Sample size estimations are difficult in complex or mixed study designs. In addition: a) unplanned interim analysis, b) planned interim analysis and

adjustments for common variables may be required for sample size estimation.

In addition, post-hoc power analysis (possible with G-Power, PASS) following the study significantly facilitates the evaluation of the results in clinical studies.

A number of high-quality journals emphasize that the statistical significance is not sufficient on its own. In fact, they would require evaluation of the results in terms of effect size and clinical effect as well as statistical significance.

In order to fully comprehend the effect size, it would be useful to know the study design in detail and evaluate the effect size with respect to the type of the statistical tests conducted as provided in Table 3 .

Hence, the sample size is one of the critical steps in planning clinical trials, and any negligence or shortcomings in its estimate may lead to rejection of an effective drug, process, or marker. Since statistical concepts have crucial roles in calculating the sample size, sufficient statistical expertise is of paramount importance for these vital studies.

Sample size, effect size and power calculation in laboratory studies

In clinical laboratories, software such as G-Power, Medcalc, Minitab, and Stata can be used for group comparisons (such as t-tests, Mann Whitney U, Wilcoxon, ANOVA, Friedman, Chi-square, etc. ), correlation analyses (Pearson, Spearman, etc .) and regression analyses.

Effect size that can be calculated according to the methods mentioned in Table 3 is important in clinical laboratories as well. However, there are additional important criteria that must be considered while investigating differences or relationships. Especially the guidelines (such as CLSI, RiliBÄK, CLIA, ISO documents) that were established according to many years of experience, and results obtained from biological variation studies provide us with essential information and critical values primarily on effect size and sometimes on sample size.

Furthermore, in addition to the statistical significance (P value interpretation), different evaluation criteria are also important for the assessment of the effect size. These include precision, accuracy, coefficient of variation (CV), standard deviation, total allowable error, bias, biological variation, and standard deviation index, etc . as recommended and elaborated by various guidelines and reference literature ( 66 - 70 ).

In this section, we will assess sample size, effect size, and power for some analysis types used in clinical laboratories.

Sample size in method and device comparisons

Sample size is a critical determinant for Linear, Passing Bablok, and Deming regression studies that are predominantly being used in method comparison studies. Sample size estimations for the Passing-Bablok and Deming method comparison studies are exemplified in Table 7 and Table 8 respectively. As seen in these tables, sample size estimations are based on slope, analytical precision (% CV), and range ratio (c) value ( 66 , 67 ). These tables might seem quite complicated for some researchers that are not familiar with statistics. Therefore, in order to further simplify sample size estimation; reference documents and guidelines have been prepared and published. As stated in CLSI EP09-A3 guideline, the general recommendation for the minimum sample size for validation studies to be conducted by the manufacturer is 100; while the minimum sample size for user-conducted verification is 40 ( 68 ). In addition, these documents clearly explain the requirements that should be considered while collecting the samples for method/device comparison studies. For instance, samples should be homogeneously dispersed covering the whole detection range. Hence, it should be kept in mind that randomly selected 40-100 sample will not be sufficient for impeccable method comparison ( 68 ).

Additionally, comparison studies might be carried out in clinical laboratories for other purposes; such as inter-device, where usage of relatively few samples is suggested to be sufficient. For method comparison studies to be conducted using patient samples; sample size estimation, and power analysis methodologies, in addition to the required number of replicates are defined in CLSI document EP31-A-IR. The critical point here is to know the values of constant difference, within-run standard deviation, and total sample standard deviation ( 69 ). While studies that compare devices having high analytical performance would suffice lower sample size; studies comparing devices with lower analytical performance would require higher sample size.

Lu et al. used maximum allowed differences for calculating sample sizes that would be required in Bland Altman comparison studies. This type of sample size estimation, which is critically important in laboratory medicine, can easily be performed using Medcalc software ( 70 ).

Sample size in lot to lot variation studies

It is acknowledged that lot-to-lot variation may influence the test results. In line with this, method comparison is also recommended to monitor the performance of the kit in use, between lot changes. To aid in the sample size estimation of these studies; CLSI has prepared the EP26-A guideline “User evaluation of between-reagent lot variation; approved guideline”, which provides a methodology like EP31-A-IR ( 71 , 72 ).

The Table 9 presents sample size and power values of a lot-to-lot variation study comparing glucose measurements at 3 different concentrations. In this example, if the difference in the glucose values measured by different lots is > 0.2 mmol/L, > 0.58 mmol/L and > 1.16 mmol/L at analyte concentrations of 2.77 mmol/L, 8.32 mmol/L and 16.65 mmol/L respectively, lots would be confirmed to be different. In a scenario where one sample is used for each concentration; if the lot-to-lot variation results obtained from each of the three different concentrations are lower than the rejection limits (meaning that the precision values for the tested lots are within the acceptance limits), then the lot variation is accepted to lie within the acceptance range. While the example for glucose measurements presented in the guideline suggests that “1 sample” would be sufficient at each analyte concentration, it should be noted that sample size might vary according to the number to devices to be tested, analytical performance results of the devices ( i.e. precision), total allowable error, etc. For different analytes and scenarios ( i.e. for occasions where one sample/concentration is not sufficient), researchers need to refer CLSI EP26-A ( 71 ).

Some researchers find CLSI EP26-A and CLSI EP31 rather complicated for estimating the sample size in lot-to-lot variation and method comparison studies (which are similar to a certain extent). They instead prefer to use the sample size (number of replicates) suggested by Mayo Laboratories. Mayo Laboratories decided that lot-to-lot variation studies may be conducted using 20 human samples where the data are analysed by Passing-Bablok regression and accepted according to the following criteria: a) slope of the regression line will lie between 0.9 and 1.1; b) R2 coefficient of determination will be > 0.95; c) the Y-intercept of the regression line will be < 50% of the lowest reportable concentration, d) difference of the means between reagent lots will be < 10% ( 73 ).

Sample size in verification studies

Acceptance limits should be defined before the verification and validation studies. These could be determined according to clinical cut-off values, biological variation, CLIA criteria, RiliBÄK criteria, criteria defined by the manufacturer, or state of the art criteria. In verification studies, the “sample size” and the “minimum proportion of the observed samples required to lie within the CI limits” are proportional. For instance, for a 50-sample study, 90% of the samples are required to lie within the CI limits for approval of the verification; while for a 200-sample study, 93% is required ( Table 10 ). In an example study whose total allowable error (TAE) is specified as 15%; 50 samples were measured. Results of the 46 samples (92% of all samples) lied within the TAE limit of 15%. Since the proportion of the samples having results within the 15% TAE limit (92% of the samples) exceeds the minimum proportion required to lie within the TAE limits (90% of the samples), the method is verified ( 74 ).

Especially in recent years, researchers tend to use CLSI EP15-A3 or alternative strategies relying on EP15-A3, for verification analyses. While the alternative strategies diverge from each other in many ways, most of them necessitate a sample size of at least 20 ( 75 - 78 ). Yet, for bias studies, especially for the ones involving External Quality Control materials, even lower sample sizes ( i.e. 10) may be observed ( 79 ). Verification still remains to be one of the critical problems for clinical laboratories. It is not possible to find a single criteria and a single verification method that fits all test methods ( i.e. immunological, chemical, chromatographical, etc. ).

While sample size for qualitative laboratory tests may vary according to the reference literature and the experimental context, CLSI EP12 recommends at least 50 positive and 50 negative samples, where 20% of the samples from each group are required to fall within cut-off value +/- 20% ( 80 , 81 ). According to the clinical microbiology validation/verification guideline Cumitech 31A, the minimum number of the samples in positive and negative groups is 100/each group for validation studies, and 10/each group for verification studies ( 82 ).

Sample size in diagnostic and prognostic studies

ROC analysis is the most important statistical analysis in diagnostic and prognostic studies. Although sample size estimation for ROC analyses might be slightly complicated; Medcalc, PASS, and Stata may be used to facilitate the estimation process. Before the actual size estimations, it is a prerequisite for the researcher to calculate potential area under the curve (AUC) using data from previous or preliminary studies. In addition, size estimation may also be calculated manually according to Table 1 , or using sensitivity (or TPF) and 1-specificity (FPF) values according to Table 11 which is adapted from CLSI EP24-A2 ( 83 , 84 ).

As is known, X-axis of the ROC curve is FPF, and Y-axis is TPF. While TPF represents sensitivity, FPF represents 1-specificity. Utilizing Table 11 , for a 0.85 sensitivity, 0.90 specificity and a maximum allowable error of 5% (L = 0.05), 196 positive and 139 negative samples are required. For the scenarios not included in this table, reader should refer to the formulas given under “diagnostic prognostic studies” subsection of Table 1 .

Standards for reporting of diagnostic accuracy studies (STARD) checklist may be followed for diagnostic studies. It is a powerful checklist whose application is explained in detail by Cohen et al. and Flaubaut et al. ( 85 , 86 ). This document suggests that, readers demand to understand the anticipated precision and power of the study and whether authors were successful in recruiting the sufficient number of participants; therefore it is critical for the authors to explain the intended sample size of their study and how it was determined. For this reason, in diagnostic and prognostic studies, sample size and power should clearly be stated.

As can be seen here, the critical parameters for sample size estimation are AUC, specificity and sensitivity, and their 95% CI values. The table 12 demonstrates the relationship of sample size with sensitivity, specificity, negative predictive value (NPV) and positive predictive value (PPV); the lower the sample size, the higher is the 95% CI values, leading to increase in type II errors ( 87 ). As can be seen here, confidence interval is narrowed as the sample size increases, leading to a decrease in type II errors.

Like all sample size calculations, preliminary information is required for sample size estimations in diagnostic and prognostic studies. Yet, variation occurs among sample size estimates that are calculated according to different reference literature or guidelines. This variation is especially prominent depending on the specific requirements of different countries and local authorities.

While sample size calculations for ROC analyses may easily be performed via Medcalc, the method explained by Hanley et al. and Delong et al. may be utilized to calculate sample size in studies comparing different ROC curves ( 88 , 89 ).

Sample size for reference interval determination

Both IFCC working groups and the CLSI guideline C28-A3c offer suggestions regarding sample size estimations in reference interval studies ( 90 - 93 ). These references mainly suggest at least 120 samples should be included for each study sub-group ( i.e., age-group, gender, race, etc. ). In addition, the guideline also states that, at least 20 samples should be studied for verification of the determined reference intervals.

Since extremes of the observed values may under/over-represent the actual percentile values of a population in nonparametric studies, care should be taken not to rely solely on the extreme values while determining the nonparametric 95% reference interval. Reed et al. suggested a minimum sample size of 120 to be used for 90% CI, 146 for 95% CI, and 210 for 99% CI (93). Linnet proposed that up to 700 samples should be obtained for results having highly skewed distributions ( 94 ). The IFCC Committee on Reference Intervals and Decision Limits working group recommends a minimum of 120 reference subjects for nonparametric methods, to obtain results within 90% CI limits ( 90 ).

Due to the inconvenience of the direct method, in addition to the challenges encountered using paediatric and geriatric samples as well as the samples obtained from complex biological fluids ( i.e. cerebrospinal fluid); indirect sample size estimations using patient results has gained significant importance in recent years. Hoffmann method, Bhattacharya method or their modified versions may be used for indirect determination of the reference intervals ( 95 - 101 ). While a specific sample size is not established, sample size between 1000 and 10.000 is recommended for each sub-group. For samples that cannot be easily acquired ( i.e. paediatric and geriatric samples, and complex biological fluids), sample sizes as low as 400 may be used for each sub-group ( 92 , 100 ).

Sample size in survey studies

The formulations given on Table 1 and the websites mentioned on Table 2 will be particularly useful for sample size estimations in survey studies which are dependent primarily on the population size ( 101 ).

Three critical aspects should be determined for sample size determination in survey studies:

Population size
Confidence Interval (CI) of 95% means that, when the study is repeated, with 95% probability, the same results will be obtained. Depending on the hypothesis and the study aim, confidence interval may lie between 90% and 99%. Confidence interval below 90% is not recommended.

For a given CI, sample size and ME is inversely proportional; sample size should be increased in order to obtain a narrower ME. On the contrary, for a fixed ME, CI and sample size is directly proportional; in order to obtain a higher CI, the sample size should be increased. In addition, sample size is directly proportional to the population size; higher sample size should be used for a larger population. A variation in ME causes a more drastic change in sample size than a variation in CI. As exemplified in Table 13 , for a population of 10,000 people, a survey with a 95% CI and 5% ME would require at least 370 samples. When CI is changed from 95% to 90% or 99%, the sample size which was 370 initially would change into 264 or 623 respectively. Whereas, when ME is changed from 5% to 10% or 1%; the sample size which was initially 370 would change into 96 or 4900 respectively. For other ME and CI levels, the researcher should refer to the equations and software provided on Table 1 and Table 2 .

The situation is slightly different for the survey studies to be conducted for problem detection. It would be most appropriate to perform a preliminary survey with a small sample size, followed by a power analysis, and completion of the study using the appropriate number of samples estimated based on the power analysis. While 30 is suggested as a minimum sample size for the preliminary studies, the optimal sample size can be determined using the formula suggested in Table 14 which is based on the prevalence value ( 103 ). It is unlikely to reach a sufficient power for revealing of uncommon problems (prevalence 0.02) at small sample sizes. As can be seen on the table, in the case of 0.02 prevalence, a sample size of 30 would yield a power of 0.45. In contrast, frequent problems ( i.e. prevalence 0.30) were discovered with higher power (0.83) even when the sample size was as low as 5. For situations where power and prevalence are known, effective sample size can easily be estimated using the formula in Table 1 .

Does big sample size always increase the impact of a study?

While larger sample size may provide researchers with great opportunities, it may create problems in interpretation of statistical significance and clinical impact. Especially in studies with big sample sizes, it is critically important for the researchers not to rely only on the magnitude of the regression (or correlation) coefficient, and the P value. The study results should be evaluated together with the effect size, study efficiencies ( i.e. basic research, clinical laboratory, and clinical studies) and confidence interval levels. Monte Carlo simulations could be utilized for statistical evaluations of the big data results ( 18 , 104 ).

As a result, sample size estimation is a critical step for scientific studies and may show significant differences according to research types. It is important that sample size estimation is planned ahead of the study, and may be performed through various routes:

If a similar previous study is available, or preliminary results of the current study are present, their results may be used for sample size estimations via the websites and software mentioned in Table 1 and Table 2 . Some of these software may also be used to calculate effect size and power.
If the magnitude of the measurand variation that is required for a substantial clinical effect is available ( i.e. significant change is 0.51 mmol/L for cholesterol, 26.5 mmol/L for creatinine, etc. ), it may be used for sample size estimation ( Figure 7 ). Presence of Total Allowable Error, constant and critical differences, biological variations, reference change value (RCV), etc. will further aid in sample size estimation process. Free software (especially G-Power) and web sites presented on Table 2 will facilitate calculations.
If effect size can be calculated by a preliminary study, sample size estimations may be performed using the effect size ( via G-Power, Table 4 , etc. )
In the absence of a previous study, if a preliminary study cannot be performed, an effect size may be initially estimated and be used for sample size estimations
If none of the above is available or possible, relevant literature may be used for sample size estimation.
For clinical laboratories, especially CLSI documents and guidelines may prove useful for sample size estimation ( Table 9,11 9,11 ).

Sample size estimations may be rather complex, requiring advanced knowledge and experience. In order to properly appreciate the concept and perform precise size estimation, one should comprehend properties of different study techniques and relevant statistics to certain extend. To assist researchers in different fields, we aimed to compile useful guidelines, references and practical software for calculating sample size and effect size in various study types. Sample size estimation and the relationship between P value and effect size are key points for comprehension and evaluation of biological studies. Evaluation of statistical significance together with the effect size is critical for both basic science, and clinical and laboratory studies. Therefore, effect size and confidence intervals should definitely be provided and its impact on the laboratory/clinical results should be discussed thoroughly.

Potential conflict of interest

None declared.

5: Hypothesis Testing, Part 1

Identify and write null and alternative hypotheses
Describe randomization procedures
Determine p-values using randomization methods in StatKey and Minitab
Interpret p-values
Make conclusions on the basis of a p-value

In Lesson 4 we used data from samples to construct confidence intervals for population parameters. When constructing confidence intervals the population parameters were unknown and we were estimating them. In this lesson we will continue to study statistical inference, but here we will be focusing on testing specific hypotheses. Now, we have a hypothesized population parameter to test. This changes how we construct our sampling distribution. Instead of having a distribution centered on the observed sample statistic, we will construct a distribution centered on the hypothesized population parameter.

This lesson corresponds to Sections 4.1, 4.2, and 4.3 in the Lock 5 textbook.

Hypothesis tests use data from a sample to make an inference about the value of a population parameter. In this lesson we will be conducting hypothesis tests with the following parameters:

We can also conduct hypothesis tests with paired means. If data are paired, and the response variable is quantitative, then the outcome of interest is the mean difference. In a population this is $\mu_d$ and in a sample $\overline x_d$. We would first compute the differences for each case, then treat those differences as if they are the variable of interest and conduct a single sample mean test.

5.1 - Introduction to Hypothesis Testing

Previously we used confidence intervals to estimate unknown population parameters. We compared confidence intervals to specified parameter values and when the specific value was contained in the interval, we concluded that there was not sufficient evidence of a difference between the population parameter and the specified value. In other words, any values within the confidence intervals were reasonable estimates of the population parameter and any values outside of the confidence intervals were not reasonable estimates. Here, we are going to look at a more formal method for testing whether a given value is a reasonable value of a population parameter. To do this we need to have a hypothesized value of the population parameter.

In this lesson we will compare data from a sample to a hypothesized parameter. In each case, we will compute the probability that a population with the specified parameter would produce a sample statistic as extreme or more extreme to the one we observed in our sample. This probability is known as the p-value and it is used to evaluate statistical significance.

A test is considered to be statistically significant when the p-value is less than or equal to the level of significance, also known as the alpha ($\alpha$) level. For this class, unless otherwise specified, $\alpha=0.05$; this is the most frequently used alpha level in many fields.

Sample statistics vary from the population parameter randomly. When results are statistically significant, we are concluding that the difference observed between our sample statistic and the hypothesized parameter is unlikely due to random sampling variation.

5.2 - Writing Hypotheses

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis ($H_0$) and an alternative hypothesis ($H_a$).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

At this point we can write hypotheses for a single mean ($\mu$), paired means($\mu_d$), a single proportion ($p$), the difference between two independent means ($\mu_1-\mu_2$), the difference between two proportions ($p_1-p_2$), a simple linear regression slope ($\beta$), and a correlation ($\rho$).
The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., $\mu_0$ and $p_0$). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., $p$ and $\mu$). The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

5.2.1 - Examples

Example: rent.

Research question : Is the average monthly rent of a one-bedroom apartment in State College, Pennsylvania less than \$900?

In this question we are comparing the mean of all State College one-bedroom apartments (i.e. $\mu$) to the value of \$900. This is a single sample mean test. We want to know if the population mean is less than \$900, so this is a left-tailed test. Our hypotheses are:

$H_0:\mu=\$900$
$H_a: \mu < \$900$

Example: IQ Scores

Research question : Is the average IQ score of all World Campus STAT 200 students higher than the national average of 100?

In this question we are comparing the mean of all World Campus STAT 200 students (i.e. $\mu$) to the given value of 100. This is a single sample mean test. We want to know if the population mean is greater than 100, so this is a right-tailed test. Our hypotheses are:

$H_0:\mu = 100$
$H_a: \mu > 100$

Example: Weight Loss

Research question: Do participants lose weight following a weight-loss intervention?

Data were collected from one group of participants before and after a weight-loss intervention. Data were paired by participant. Assuming that $x_1$ is an individual's weight before the intervention and $x_2$ is their weight at the end of the study, if they lost weight then $x_1-x_2$ would be a positive number (i.e., greater than 0). Thus, this is a right-tailed test. Because we are testing their mean difference, the parameter that we should write in our hypotheses is $\mu_d$ where $\mu_d$ is the mean weight change (before-after) in the population.

Our hypotheses are:

$H_0: \mu_d=0$
$H_a:\mu_d > 0 $

Example: Gender of College of Science Students

Research question : Is the percent of students enrolled in Penn State's College of Science who identify as women different from 50%?

In this question we are comparing the proportion of all Penn State College of Science students (i.e. $p$) to the given value of 0.5. This is a single sample proportion test. We want to know if the population proportion is different from 0.5, so this is a two-tailed test. Our hypotheses are:

$H_0:p=0.5$
$H_a: p ≠ 0.5$

Example: Dog Ownership

Research question : Do the majority of all World Campus STAT 200 students own a dog?

If the majority of all students own a dog, then more than 50% own a dog. In this question we are comparing the population proportion for all World Campus STAT 200 students (i.e. $p$) to the value of 0.5. This is a single sampling proportion test. We want to know if the proportion is greater than 0.5, so this is a right-tailed test. Our hypotheses are:

$H_a: p > 0.5$

Example: Weights of Boys and Girls

Research question : In preschool, are the weights of boys and girls different?

We are comparing the weights of two independent groups: boys and girls. Weight is a quantitative variable so the parameter we are testing is $\mu$. Our research question does not hypothesize which group has the larger weight, so this is a two-tailed test. Our hypotheses are:

$H_0: \mu_b = \mu_g$
$H_a: \mu_b \ne \mu_g$

Note: This is equivalent to $H_0: \mu_b - \mu_g = 0$ and $H_a: \mu_b - \mu_g \ne 0$.

Example: Smoking by Gender

Research question : Is the proportion of men who smoke cigarettes different from the proportion of women who smoke cigarettes in the United States?

In this question we are comparing two independent groups: men and women. The response variable, smoking, is categorical therefore we are comparing proportions. Our research question does not suggest which group smokes more, so we have a two-tailed test. Our hypotheses are:

$H_0: p_1=p_2$
$H_a: p_1 \ne p_2$

Note: This is equivalent to $H_0: p_1 - p_2 =0$ and $H_a: p_1 - p_2 \ne 0$

Example: Predicting SAT-Math using IQ

Research question : Can IQ scores be used to predict SAT-Math scores in the population of all American high school seniors?

SAT-Math and IQ scores are both quantitative variables. Our research question is about prediction, so we are going to use simple linear regression. The parameter we are testing is $\beta$. Our research question does not state whether we expect the slope to be positive or negative, therefore this is a two-tailed test. Our hypotheses are:

$H_0: \beta = 0$
$H_a: \beta \ne 0$

Example: Relation Between Height and Weight

Research question : Is there a positive relationship between height and weight in the population of all American adults age 25 and older?

The relationship between two quantitative variables is measured using correlation (Pearson's r). The parameter we are testing is $\rho$. A positive relationship would be indicated by a positive correlation coefficient, therefore this is a right-tailed test. Our hypotheses are:

$H_0: \rho = 0$

$H_a: \rho > 0$

5.3 - Randomization Procedures

Like bootstrapping procedures, randomization procedures use resampling techniques to construct a sampling distribution that can be used to make inferences about the population. What makes a randomization distribution different is that it is constructed given that the null hypothesis is true. The randomization distribution will be centered on the value in the null hypothesis.

StatKey can be used to construct a randomization distribution for a single mean, single proportion, difference in means, difference in proportions, the slope of a simple linear regression model, or a correlation (Pearson's r ). Minitab can conduct a randomization test for a single mean, single proportion, or difference in means.

The video below walks through an example of using StatKey to construct a randomization distribution. It also looks ahead to the next section and uses that randomization distribution to determine the p-value.

These are the steps that we will be using to conduct hypothesis tests this semester:

Determine what type of test you need to conduct and write the hypotheses.
Construct a randomization distribution under the assumption that the null hypothesis is true.
Use the randomization distribution to find the p-value.
Decide if you should reject or fail to reject the null hypothesis.
State a real-world conclusion in relation to the original research question.

Here, you learned how to complete Step 2. On the next page you will learn how to use this randomization distribution to complete Steps 3 through 5.

5.3.1 - StatKey Randomization Methods (Optional)

The following information goes beyond what you are expected to know for this course. Here, details about all of the randomization procedure options available in StatKey are covered. In STAT 200 you will always be using the default randomization methods. The information here is optional and is meant to provide extra details to individuals who are interested in learning more, beyond what is required of most introductory statistics courses.

Randomization Test for One Mean

In StatKey there is only one method for conducting a randomization test for one mean. The sample is shifted so that the sample mean equals the hypothesized population mean (i.e., the value in the null hypothesis). Samples of the same size as the original sample are drawn with replacement from the shifted distribution and the mean of each randomization sample is recorded on the randomization distribution dotplot.

Randomization Test for One Proportion

In StatKey there is only one method for conducting a randomization test for one proportion. Samples of the same size as the original sample are drawn from a theoretical distribution with a proportion equal to the hypothesized population proportion (i.e., the value in the null hypothesis).The sample proportion in each randomization sample is recorded on the randomization distribution dotplot.

Randomization Test for a Difference in Means

StatKey offers three randomization methods when comparing the means of two independent groups: reallocate groups, shift groups, and combine groups. In this course we will always be using the default method of reallocating groups. For larger sample sizes results will be relatively consistent across the three methods. In practice, the method that is most appropriate may depend on the design of the research study. For example, the reallocation method may be preferred in studies where participants were randomly assigned to different conditions.

Reallocate Groups This is the default method in StatKey. In this course, this is always the method that will be used. Using the reallocate method, all cases in the samples are combined and then randomly assigned to the two groups with the same sample sizes as the original samples. This is done without replacement. The mean of each reallocated sample is recorded. The difference between those reallocated sample's means is recorded on the randomization distribution dotplot.
Shift Groups The two groups are shifted until their observed sample means are equal. This is similar to the method used for one sample mean. After the groups are shifted, cases are randomly selected from the first group, with replacement, until a randomization sample of the same size as the first group's original sample is obtained. This procedure is followed for the second group as well. The difference between the mean of the first group and the mean of the second group is recorded on the randomization distribution plot.
Combine Groups All cases in the samples are combined and then randomly selected with replacement. Again, the sample sizes for each group will be equal to each group's original sample size. The difference between this combine groups method and the default reallocate groups method is that this method resamples with replacement so an original case can appear more than once in a group, in both groups, or not at all.

Randomization Test for a Difference in Proportions

StatKey offers two randomization methods when comparing the proportions of two independent groups: reallocation and resampling. In this course we will be using the default reallocation method.

Reallocation This procedure is the same as the reallocate groups procedure for two group means. All cases are combined and then randomly assigned to between the two groups with the same sample sizes as the original samples. This is done without replacement so the total number of successes between the two groups will always be equal to the total number of successes between the two groups.
Resampling The two groups are combined and the overall observed proportion is computed. Samples of the same size as the original samples are drawn from a theoretical distribution with a proportion equal to the overall observed proportion. The differences between the sample proportions in the two randomization samples are recorded on the randomization distribution dotplot.

Randomization Test for a Slope, Correlation

The randomization methods used for testing the slope and correlation are the same as both procedures involve two quantitative variables. In each case, the pairs of x and y variables are separated and randomly assigned to new pairs. The slope or correlation between those new pairs is computed and recorded on the randomization distribution plot. Like the other reallocation methods, this is done without replacement so each case's x value and y value are only selected once.

Online discussion including textbook author Robin Lock https://groups.google.com/forum/#!topic/lock5stat/AG45cIcy018
Lock Morgan, K., Lock, R. H., Frazer Lock, P., Lock, E. F., Lock, D. F. (2014). StatKey: Online tools for bootstrap intervals and randomization tests. Paper presented at the International Conference on Teaching Statistics (ICOTS9). Flagstaff, AZ. https://iase-web.org/icots/9/proceedings/pdfs/ICOTS9_9B2_LOCKMORGAN.pdf

5.4 - p-values

We can use a randomization distribution to determine how likely our sample statistic is given that the null hypothesis is true. This probability is known as the p-value . The p-value is the proportion of samples on the randomization distribution that are more extreme than our observed sample in the direction of the alternative hypothesis. The p-value is compared to the alpha level (typically 0.05).

Making a Decision

If $p > \alpha$ then we "fail to reject the null hypothesis" and conclude that there is not enough evidence of a difference in the population. This does not mean that the null hypothesis is true, it only means that we do not have sufficient evidence to say that it is likely false. These results are not statistically significant.

If $p \leq \alpha$ then we "reject the null hypothesis" and conclude that there is a difference in the population. These results are statistically significant.

5.5 - Randomization Test Examples in StatKey

The following pages contain examples of conducting randomization tests using StatKey .

5.5.1 - Single Proportion Example: PA Residency

This example uses data collected from World Campus STAT 200 students at the beginning of the Fall 2016 semester. You can download this Minitab file here: fall2016stdata.mpx

Research question : Are less than half of all World Campus STAT 200 students Pennsylvania residents?

This research question is asking if there is evidence that the population proportion is less than 0.50 which can be translated to the following hypotheses:

$H_0: p=0.50$

$H_a: p \lt 0.50$

Step 1 : We are comparing the proportion in one group to 0.50. This is a one sample proportion test.

Step 2 : We used StatKey to construct a randomization distribution.

Step 3 : $p<0.001$

Step 4 : $p \leq 0.05$, reject the null hypothesis

Step 5 : There is evidence that the proportion of all World Campus STAT 200 students who are Pennsylvania residents is less than 0.50.

5.5.2 - Paired Means Example: Age

Research question: On average, are husbands older than their wives?

Step 1: The data are paired by couple. This is a paired means test.

$H_0: \mu_d=0$

$H_a: \mu_d > 0$

Step 2: We constructed a randomization distribution in StatKey using the built in dataset.

Step 3: $p < 0.001$

Step 4: Reject the null hypothesis

Step 5: There is evidence that in the population, on average, husbands are older than their wives.

5.5.3 - Difference in Means Example: Exercise by Biological Sex

Do males and females differ in terms of how many hours per week they exercise? This example uses a dataset that is built in to StatKey .

Step 1 : Hours exercised per week is a quantitative variable and we are comparing two independent groups. We should conduct a hypothesis test for the differences in means.

$H_0: \mu_m = \mu_f$

$H_a: \mu_m \ne \mu_f$

Step 2 : We constructed the randomization distribution given that there is not a difference between the means of males and females.

Step 3 : $p = 0.114+0.114=0.228$

Step 4 : $p>0.05$, we should fail to reject the null hypothesis

Step 5 : There is not enough evidence that the mean number of hours per week exercised by males and females is different in the population. Our results are not statistically significant.

5.5.4 - Correlation Example: Quiz & Exam Scores

Using the sample data in:

We want to know if there is evidence of a positive relationship between quiz scores and final exam scores in the population of all World Campus STAT 200 students. If there is a positive relationship, then the population correlation would be greater than zero. This can be translated to the following hypotheses:

Step 1 : We are examining the relationship between two quantitative variables. We should compute and test Pearson's r which is a correlation coefficient.

Step 2 : We constructed a randomization distribution given that the correlation in the population is 0.

Step 3 : $p<0.001$

Step 4 : $p\leq 0.05$, we should reject the null hypothesis

Step 5 : There is evidence of a positive relationship between quiz scores and final exam scores in the population of all World Campus STAT 200 students.

5.6 - Lesson 5 Summary

Identify and write null and alternative hypotheses.
Describe randomization procedures.
Determine p-values using randomization methods in StatKey and Minitab.
Interpret p-values.
Make conclusions on the basis of a p-value.

Let's review the randomization test procedures that you learned in this lesson:

Determine what type of test you need to conduct and write the hypotheses
Construct a randomization distribution under the assumption that the null hypothesis is true
Use the randomization distribution to find the p-value
Decide if you should reject or fail to reject the null hypothesis (see below)
State a real-world conclusion in relation to the original research question

If $p>\alpha$ then we fail to reject the null hypothesis and there is not enough evidence to support the alternative hypothesis. These results are said to be not statistically significant. If $p \le \alpha$ then we reject the null hypothesis and conclude that there is enough evidence to support the alternative hypothesis. These results are statistically significant. Unless otherwise stated, $\alpha$ of 0.05 should be used.

We will be using these same hypothesis testing steps in all of the remaining lessons.

Statistics Made Easy

The Large Sample Condition: Definition & Example

In statistics, we’re often interested in using samples to draw inferences about populations through hypothesis tests or confidence intervals .

Most of the formulas that we use in hypothesis tests and confidence intervals make the assumption that a given sample roughly follows a normal distribution .

However, in order to safely make this assumption we need to make sure our sample size is large enough. Specifically, we need to make sure that the Large Sample Condition is met.

The Large Sample Condition: The sample size is at least 30.

Note: In some textbooks, a “large enough” sample size is defined as at least 40 but the number 30 is more commonly used.

When this condition is met, it can be assumed that the sampling distribution of the sample mean is approximately normal. This assumption allows us to use samples to draw inferences about the populations from which they came from.

The reason why the number 30 is used is based upon the Central Limit Theorem. You can read more about that in this blog post .

Example: Verifying the Large Sample Condition

Suppose a certain machine creates crackers. The distribution of the weight of these cookies is skewed to the right with a mean of 10 ounces and a standard deviation of 2 ounces. If we take a simple random sample of 100 cookies produced by this machine, what is the probability that the mean weight of the cookies in this sample is less than 9.8 ounces?

In order to answer this question, we can use the Normal CDF Calculator , but we first need to verify that the sample size is large enough in order to assume that the distribution of the sampling mean is normal.

In this example, our sample size is n = 100 , which is much larger than 30. Despite the fact that the true distribution of the weight of the cookies is skewed to the right, since our sample size is “large enough” we can assume that the distribution of the sampling mean is normal. Thus, we would be safe to use the Normal CDF Calculator to solve this problem.

Modifications to the Large Sample Condition

Often a sample size is considered “large enough” if it’s greater than or equal to 30, but this number can vary a bit based on the underlying shape of the population distribution.

In particular:

If the population distribution is symmetric, sometimes a sample size as small as 15 is sufficient.
If the population distribution is skewed, generally a sample size of at least 30 is needed.
If the population distribution is extremely skewed, then a sample size of 40 or higher may be necessary.

Depending on the shape of the population distribution, you may require more or less than a sample size of 30 in order for the Central Limit Theorem to apply.

Additional Resources

Introduction to the Central Limit Theorem Introduction to Sampling Distributions

Published by Zach

Learning Objectives

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

The Misunderstood p Value

Null Hypothesis. Image description available.

Role of Sample Size and Relationship Strength

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [3] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

Image Description

“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]

“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]

Media Attributions

Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
Lakens, D. (2017, December 25). About p -values: Understanding common misconceptions. [Blog post] Retrieved from https://correlaid.org/en/blog/understand-p-values/ ↵
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Descriptive data that involves measuring one or more variables in a sample and computing descriptive summary data (e.g., means, correlation coefficients) for those variables.

Corresponding values in the population.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error (often symbolized H0 and read as “H-zero”).

An alternative to the null hypothesis (often symbolized as H1), this hypothesis proposes that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

A decision made by researchers using null hypothesis testing which occurs when the sample relationship would be extremely unlikely.

A decision made by researchers in null hypothesis testing which occurs when the sample relationship would not be extremely unlikely.

The probability of obtaining the sample result or a more extreme result if the null hypothesis were true.

The criterion that shows how low a p-value should be before the sample result is considered unlikely enough to reject the null hypothesis (Usually set to .05).

An effect that is unlikely due to random chance and therefore likely represents a real effect in the population.

Refers to the importance or usefulness of the result in some real-world context.

Research Methods in Psychology Copyright © 2019 by Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

13.1 Understanding Null Hypothesis Testing

Learning objectives.

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

“Null Hypothesis” retrieved from http://imgs.xkcd.com/comics/null_hypothesis.png (CC-BY-NC 2.5)

Role of Sample Size and Relationship Strength

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

“Conditional Risk” retrieved from http://imgs.xkcd.com/comics/conditional_risk.png (CC-BY-NC 2.5)

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Share This Book

Increase Font Size

Null Hypothesis Examples

ThoughtCo / Hilary Allison

Scientific Method
Chemical Laws
Periodic Table
Projects & Experiments
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

The null hypothesis —which assumes that there is no meaningful relationship between two variables—may be the most valuable hypothesis for the scientific method because it is the easiest to test using a statistical analysis. This means you can support your hypothesis with a high level of confidence. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating the dependent variable or due to chance.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable) and the independent variable . You do not need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect that there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses, the null hypothesis is written as H 0 (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95 percent or 99 percent is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

What Is a Hypothesis? (Science)
What 'Fail to Reject' Means in a Hypothesis Test
What Are the Elements of a Good Hypothesis?
Scientific Method Vocabulary Terms
Null Hypothesis Definition and Examples
Definition of a Hypothesis
Six Steps of the Scientific Method
Hypothesis Test for the Difference of Two Population Proportions
Understanding Simple vs Controlled Experiments
What Is the Difference Between Alpha and P-Values?
Null Hypothesis and Alternative Hypothesis
What Are Examples of a Hypothesis?
What It Means When a Variable Is Spurious
Hypothesis Test Example
How to Conduct a Hypothesis Test
What Is a P-Value?

Power and Sample Size Determination

1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11

Issues in Estimating Sample Size for Hypothesis Testing

Ensuring that a test has high power.

All Modules

In the module on hypothesis testing for means and proportions, we introduced techniques for means, proportions, differences in means, and differences in proportions. While each test involved details that were specific to the outcome of interest (e.g., continuous or dichotomous) and to the number of comparison groups (one, two, more than two), there were common elements to each test. For example, in each test of hypothesis, there are two errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. In the first step of any test of hypothesis, we select a level of significance, α , and α = P(Type I error) = P(Reject H 0 | H 0 is true). Because we purposely select a small value for α , we control the probability of committing a Type I error. The second type of error is called a Type II error and it is defined as the probability we do not reject H 0 when it is false. The probability of a Type II error is denoted β , and β =P(Type II error) = P(Do not Reject H 0 | H 0 is false). In hypothesis testing, we usually focus on power, which is defined as the probability that we reject H 0 when it is false, i.e., power = 1- β = P(Reject H 0 | H 0 is false). Power is the probability that a test correctly rejects a false null hypothesis. A good test is one with low probability of committing a Type I error (i.e., small α ) and high power (i.e., small β, high power).

Here we present formulas to determine the sample size required to ensure that a test has high power. The sample size computations depend on the level of significance, aα, the desired power of the test (equivalent to 1-β), the variability of the outcome, and the effect size. The effect size is the difference in the parameter of interest that represents a clinically meaningful difference. Similar to the margin of error in confidence interval applications, the effect size is determined based on clinical or practical criteria and not statistical criteria.

The concept of statistical power can be difficult to grasp. Before presenting the formulas to determine the sample sizes required to ensure high power in a test, we will first discuss power from a conceptual point of view.

Suppose we want to test the following hypotheses at aα=0.05: H 0 : μ = 90 versus H 1 : μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the alternative hypothesis or not. This is done by computing a test statistic and comparing the test statistic to an appropriate critical value. If the null hypothesis is true (μ=90), then we are likely to select a sample whose mean is close in value to 90. However, it is also possible to select a sample whose mean is much larger or much smaller than 90. Recall from the Central Limit Theorem (see page 11 in the module on Probability ), that for large n (here n=100 is sufficiently large), the distribution of the sample means is approximately normal with a mean of

If the null hypothesis is true, it is possible to observe any sample mean shown in the figure below; all are possible under H 0 : μ = 90.

Normal distribution of X when the mean of X is 90. A bell-shaped curve with a value of X-90 at the center.

Rejection Region for Test H 0 : μ = 90 versus H 1 : μ ≠ 90 at α =0.05

Standard normal distribution showing a mean of 90. The rejection areas are in the two tails at the extremes above and below the mean. If the alpha level is 0.05, then each tail accounts for an arean of 0.025.

The areas in the two tails of the curve represent the probability of a Type I Error, α= 0.05. This concept was discussed in the module on Hypothesis Testing .

Now, suppose that the alternative hypothesis, H 1 , is true (i.e., μ ≠ 90) and that the true mean is actually 94. The figure below shows the distributions of the sample mean under the null and alternative hypotheses.The values of the sample mean are shown along the horizontal axis.

Two overlapping normal distributions, one depicting the null hypothesis with a mean of 90 and the other showing the alternative hypothesis with a mean of 94. A more complete explanation of the figure is provided in the text below the figure.

If the true mean is 94, then the alternative hypothesis is true. In our test, we selected α = 0.05 and reject H 0 if the observed sample mean exceeds 93.92 (focusing on the upper tail of the rejection region for now). The critical value (93.92) is indicated by the vertical line. The probability of a Type II error is denoted β, and β = P(Do not Reject H 0 | H 0 is false), i.e., the probability of not rejecting the null hypothesis if the null hypothesis were true. β is shown in the figure above as the area under the rightmost curve (H 1 ) to the left of the vertical line (where we do not reject H 0 ). Power is defined as 1- β = P(Reject H 0 | H 0 is false) and is shown in the figure as the area under the rightmost curve (H 1 ) to the right of the vertical line (where we reject H 0 ).

Note that β and power are related to α, the variability of the outcome and the effect size. From the figure above we can see what happens to β and power if we increase α. Suppose, for example, we increase α to α=0.10.The upper critical value would be 92.56 instead of 93.92. The vertical line would shift to the left, increasing α, decreasing β and increasing power. While a better test is one with higher power, it is not advisable to increase α as a means to increase power. Nonetheless, there is a direct relationship between α and power (as α increases, so does power).

β and power are also related to the variability of the outcome and to the effect size. The effect size is the difference in the parameter of interest (e.g., μ) that represents a clinically meaningful difference. The figure above graphically displays α, β, and power when the difference in the mean under the null as compared to the alternative hypothesis is 4 units (i.e., 90 versus 94). The figure below shows the same components for the situation where the mean under the alternative hypothesis is 98.

Overlapping bell-shaped distributions - one with a mean of 90 and the other with a mean of 98

Notice that there is much higher power when there is a larger difference between the mean under H 0 as compared to H 1 (i.e., 90 versus 98). A statistical test is much more likely to reject the null hypothesis in favor of the alternative if the true mean is 98 than if the true mean is 94. Notice also in this case that there is little overlap in the distributions under the null and alternative hypotheses. If a sample mean of 97 or higher is observed it is very unlikely that it came from a distribution whose mean is 90. In the previous figure for H 0 : μ = 90 and H 1 : μ = 94, if we observed a sample mean of 93, for example, it would not be as clear as to whether it came from a distribution whose mean is 90 or one whose mean is 94.

In designing studies most people consider power of 80% or 90% (just as we generally use 95% as the confidence level for confidence interval estimates). The inputs for the sample size formulas include the desired power, the level of significance and the effect size. The effect size is selected to represent a clinically meaningful or practically important difference in the parameter of interest, as we will illustrate.

The formulas we present below produce the minimum sample size to ensure that the test of hypothesis will have a specified probability of rejecting the null hypothesis when it is false (i.e., a specified power). In planning studies, investigators again must account for attrition or loss to follow-up. The formulas shown below produce the number of participants needed with complete data, and we will illustrate how attrition is addressed in planning studies.

return to top | previous page | next page

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.2: Large Sample Tests for a Population Mean

Last updated
Save as PDF
Page ID 520

Learning Objectives

To learn how to apply the five-step test procedure for a test of hypotheses concerning a population mean when the sample size is large.
To learn how to interpret the result of a test of hypotheses in the context of the original narrated situation.

In this section we describe and demonstrate the procedure for conducting a test of hypotheses about the mean of a population in the case that the sample size $n$ is at least $30$. The Central Limit Theorem states that $\overline{X}$ is approximately normally distributed, and has mean $\mu _{\overline{X}}=\mu$ and standard deviation $\sigma _{\overline{X}}=\sigma /\sqrt{n}$, where $\mu$ and $\sigma$ are the mean and the standard deviation of the population. This implies that the statistic

\[\frac{\bar{x}-\mu }{\sigma /\sqrt{n}} \nonumber \]

has the standard normal distribution, which means that probabilities related to it are given in Figure 7.1.5 and the last line in Figure 7.1.6.

If we know $\sigma$ then the statistic in the display is our test statistic. If, as is typically the case, we do not know $\sigma$, then we replace it by the sample standard deviation $s$. Since the sample is large the resulting test statistic still has a distribution that is approximately standard normal.

Standardized Test Statistics for Large Sample Hypothesis Tests Concerning a Single Population Mean

If $\sigma$ is known: $Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}$
If $\sigma$ is unknown: $Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}$

The test statistic has the standard normal distribution.

The distribution of the standardized test statistic and the corresponding rejection region for each form of the alternative hypothesis (left-tailed, right-tailed, or two-tailed), is shown in Figure $\PageIndex{1}$.

Distribution of the Standardized Test Statistic and the Rejection Region

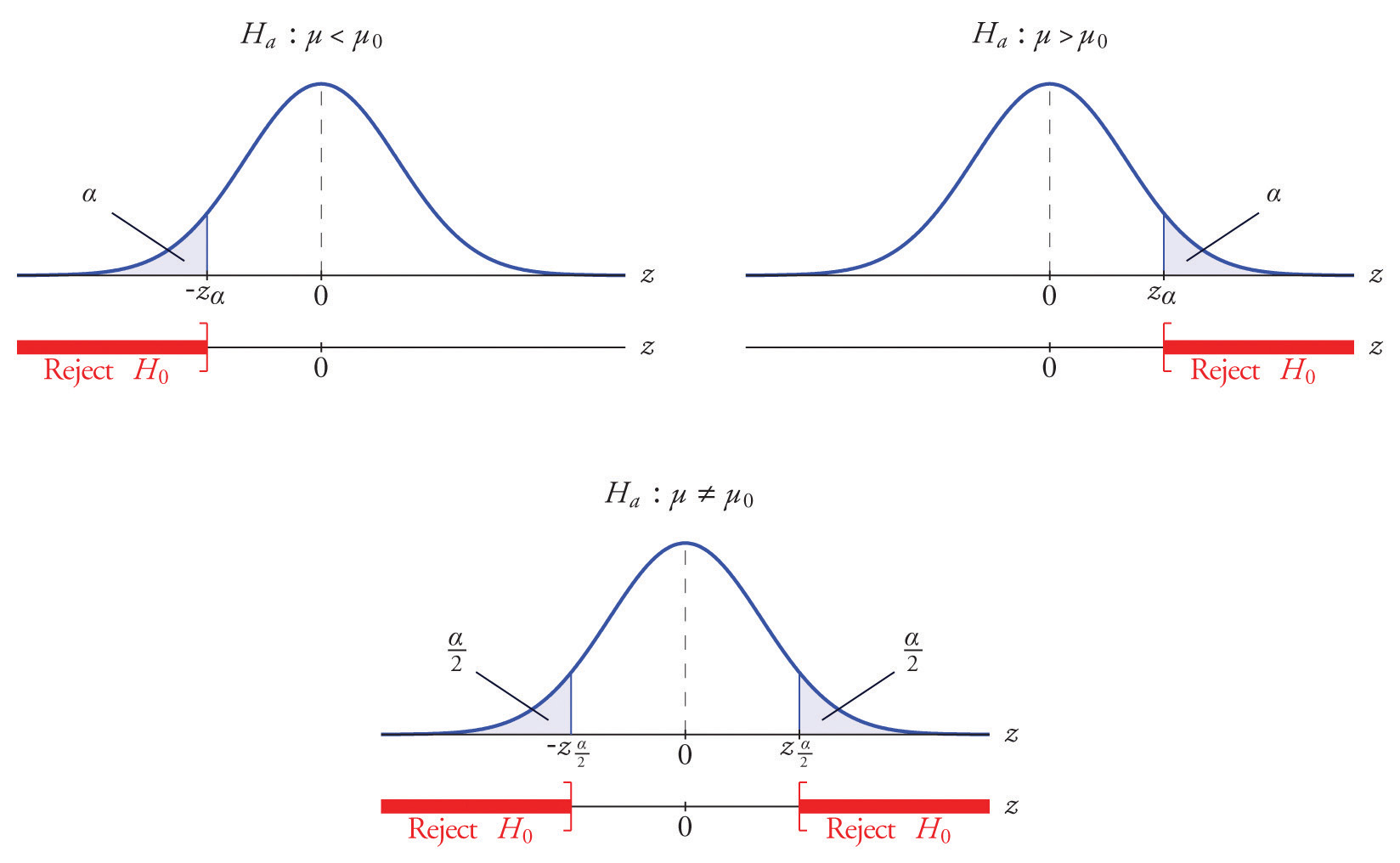
Example $\PageIndex{1}$

It is hoped that a newly developed pain reliever will more quickly produce perceptible reduction in pain to patients after minor surgeries than a standard pain reliever. The standard pain reliever is known to bring relief in an average of $3.5$ minutes with standard deviation $2.1$ minutes. To test whether the new pain reliever works more quickly than the standard one, $50$ patients with minor surgeries were given the new pain reliever and their times to relief were recorded. The experiment yielded sample mean $\bar{x}=3.1$ minutes and sample standard deviation $s=1.5$ minutes. Is there sufficient evidence in the sample to indicate, at the $5\%$ level of significance, that the newly developed pain reliever does deliver perceptible relief more quickly?

We perform the test of hypotheses using the five-step procedure given at the end of Section 8.1.

Step 1 . The natural assumption is that the new drug is no better than the old one, but must be proved to be better. Thus if $\mu$ denotes the average time until all patients who are given the new drug experience pain relief, the hypothesis test is \[H_0: \mu =3.5\\ \text{vs}\\ H_a:\mu <3.5\; @\; \alpha =0.05 \nonumber \]
Step 2 . The sample is large, but the population standard deviation is unknown (the $2.1$ minutes pertains to the old drug, not the new one). Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the standard normal distribution.
Step 3 . Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{3.1-3.5}{1.5/\sqrt{50}}=-1.886 \nonumber \]
Step 4 . Since the symbol in $H_a$ is “$<$” this is a left-tailed test, so there is a single critical value, $-z_\alpha =-z_{0.005}$, which from the last line in Figure 7.1.6 we read off as $-1.645$. The rejection region is $(-\infty ,-1.645]$.
Step 5 . As shown in Figure $\PageIndex{2}$ the test statistic falls in the rejection region. The decision is to reject $H_0$. In the context of the problem our conclusion is:

The data provide sufficient evidence, at the $5\%$ level of significance, to conclude that the average time until patients experience perceptible relief from pain using the new pain reliever is smaller than the average time for the standard pain reliever.

Example $\PageIndex{2}$

A cosmetics company fills its best-selling $8$ ounce jars of facial cream by an automatic dispensing machine. The machine is set to dispense a mean of $8.1$ ounces per jar. Uncontrollable factors in the process can shift the mean away from $8.1$ and cause either underfill or overfill, both of which are undesirable. In such a case the dispensing machine is stopped and recalibrated. Regardless of the mean amount dispensed, the standard deviation of the amount dispensed always has value $0.22$ ounce. A quality control engineer routinely selects $30$ jars from the assembly line to check the amounts filled. On one occasion, the sample mean is $\bar{x}=8.2$ ounces and the sample standard deviation is $s=0.25$ ounce. Determine if there is sufficient evidence in the sample to indicate, at the $1\%$ level of significance, that the machine should be recalibrated.

Step 1 . The natural assumption is that the machine is working properly. Thus if $\mu$ denotes the mean amount of facial cream being dispensed, the hypothesis test is \[H_0: \mu =8.1\\ \text{vs}\\ H_a:\mu \neq 8.1\; @\; \alpha =0.01 \nonumber \]
Step 2 . The sample is large and the population standard deviation is known. Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}} \nonumber \] and has the standard normal distribution.
Step 3 . Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}=\frac{8.2-8.1}{0.22/\sqrt{30}}=2.490 \nonumber \]
Step 4 . Since the symbol in $H_a$ is “$\neq$” this is a two-tailed test, so there are two critical values, $\pm z_{\alpha /2}=\pm z_{0.005}$, which from the last line in Figure 7.1.6 "Critical Values of " we read off as $\pm 2.576$. The rejection region is $(-\infty ,-2.576]\cup [2.576,\infty )$.
Step 5 . As shown in Figure $\PageIndex{3}$ the test statistic does not fall in the rejection region. The decision is not to reject $H_0$. In the context of the problem our conclusion is:

The data do not provide sufficient evidence, at the $1\%$ level of significance, to conclude that the average amount of product dispensed is different from $8.1$ ounce. We conclude that the machine does not need to be recalibrated.

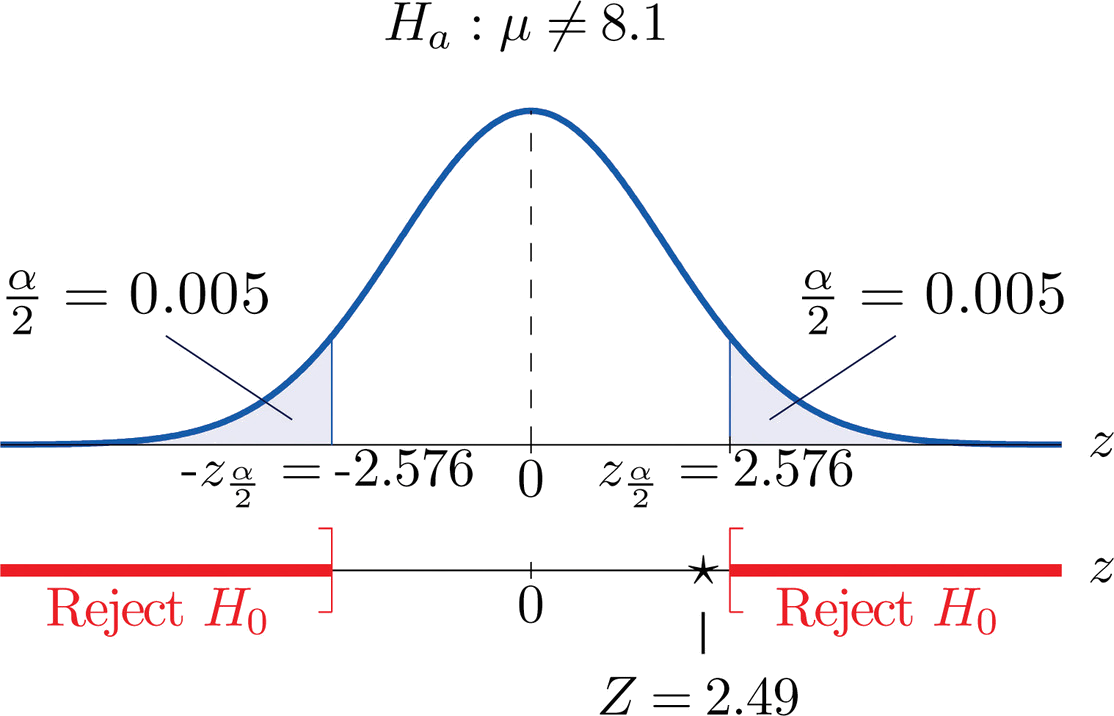
Key Takeaway

There are two formulas for the test statistic in testing hypotheses about a population mean with large samples. Both test statistics follow the standard normal distribution.
The population standard deviation is used if it is known, otherwise the sample standard deviation is used.
The same five-step procedure is used with either test statistic.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 13: Inferential Statistics

Understanding Null Hypothesis Testing

Learning Objectives

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Long Descriptions

Media Attributions

Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Values in a population that correspond to variables measured in a study.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.

The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.

When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.

The probability that, if the null hypothesis were true, the result found in the sample would occur.

How low the p value must be before the sample result is considered unlikely in null hypothesis testing.

When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.6: Hypothesis Test of a Single Population Mean with Examples

Last updated
Save as PDF
Page ID 130297

Steps for performing Hypothesis Test of a Single Population Mean

Step 1: State your hypotheses about the population mean. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure

Find or identify the sample size, n, the sample mean, $\bar{x}$ and the sample standard deviation, s .

The sampling distribution for the one-mean test statistic is, approximately, T- distribution if the following conditions are met

Sample is random with independent observations .
Sample is large. The population must be Normal or the sample size must be at least 30.

Step 3: Perform the procedure based on the assumption that $H_{0}$ is true

Find the Estimated Standard Error: $SE=\frac{s}{\sqrt{n}}$.
Compute the observed value of the test statistic: $T_{obs}=\frac{\bar{x}-\mu_{0}}{SE}$.
Check the type of the test (right-, left-, or two-tailed)
Find the p-value in order to measure your level of surprise.

Step 4: Make a decision about $H_{0}$ and $H_{a}$

Do you reject or not reject your null hypothesis?

Step 5: Make a conclusion

What does this mean in the context of the data?

The following examples illustrate a left-, right-, and two-tailed test.

Example $\pageindex{1}$.

$H_{0}: \mu = 5, H_{a}: \mu < 5$

Test of a single population mean. $H_{a}$ tells you the test is left-tailed. The picture of the $p$-value is as follows:

$Normal distribution curve of a single population mean with a value of 5 on the x-axis and the p-value points to the area on the left tail of the curve.$

Exercise $\PageIndex{1}$

$H_{0}: \mu = 10, H_{a}: \mu < 10$

Assume the $p$-value is 0.0935. What type of test is this? Draw the picture of the $p$-value.

left-tailed test

$alt$

Example $\PageIndex{2}$

$H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2$

This is a test of a single population proportion. $H_{a}$ tells you the test is right-tailed . The picture of the p -value is as follows:

$Normal distribution curve of a single population proportion with the value of 0.2 on the x-axis. The p-value points to the area on the right tail of the curve.$

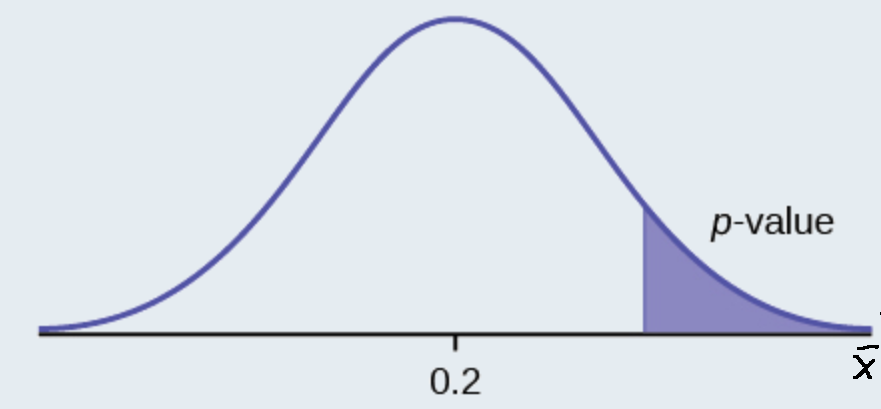
Exercise $\PageIndex{2}$

$H_{0}: \mu \leq 1, H_{a}: \mu > 1$

Assume the $p$-value is 0.1243. What type of test is this? Draw the picture of the $p$-value.

right-tailed test

$alt$

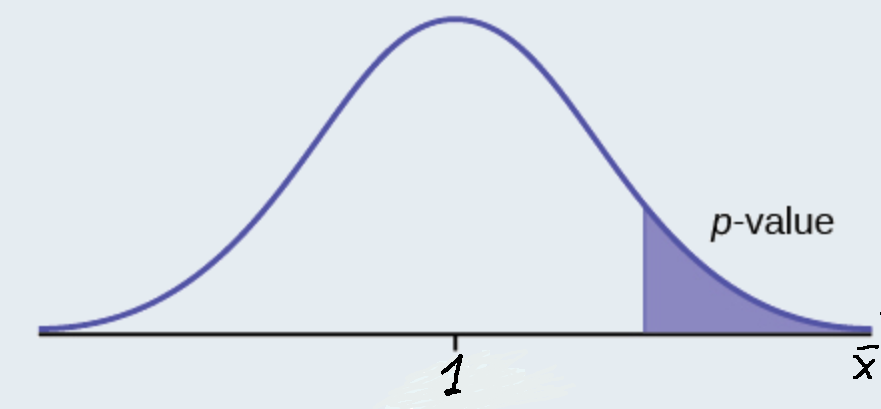
Example $\PageIndex{3}$

$H_{0}: \mu = 50, H_{a}: \mu \neq 50$

This is a test of a single population mean. $H_{a}$ tells you the test is two-tailed . The picture of the $p$-value is as follows.

$Normal distribution curve of a single population mean with a value of 50 on the x-axis. The p-value formulas, 1/2(p-value), for a two-tailed test is shown for the areas on the left and right tails of the curve.$

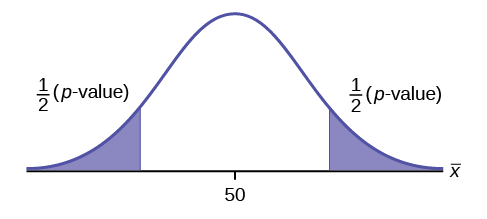
Exercise $\PageIndex{3}$

$H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5$

Assume the p -value is 0.2564. What type of test is this? Draw the picture of the $p$-value.

two-tailed test

$alt$

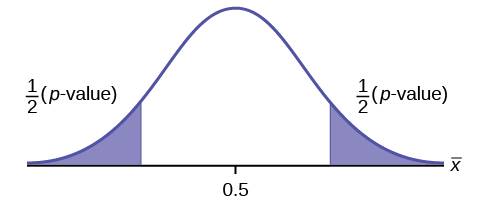
Full Hypothesis Test Examples

Example $\pageindex{4}$.

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that $\alpha = 0.05$. This is a test of a single population mean .

$H_{0}: \mu = 65 H_{a}: \mu > 65$

Since the instructor thinks the average score is higher, use a "$>$". The "$>$" means the test is right-tailed.

Determine the distribution needed:

Random variable: $\bar{X} =$ average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given $n = 10$ sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's $t$.

Use $t_{df}$. Therefore, the distribution for the test is $t_{9}$ where $n = 10$ and $df = 10 - 1 = 9$.

The sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Calculate the $p$-value using the Student's $t$-distribution:

\[t_{obs} = \dfrac{\bar{x}-\mu_{\bar{x}}}{\left(\dfrac{s}{\sqrt{n}}\right)}=\dfrac{67-65}{\left(\dfrac{3.1972}{\sqrt{10}}\right)}\]

Use the T-table or Excel's t_dist() function to find p-value:

$p\text{-value} = P(\bar{x} > 67) =P(T >1.9782 )= 1-0.9604=0.0396$

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

$Normal distribution curve of average scores on the first statistic tests with 65 and 67 values on the x-axis. A vertical upward line extends from 67 to the curve. The p-value points to the area to the right of 67.$

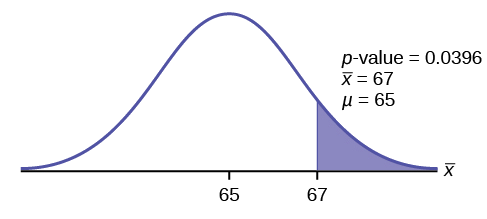
Compare $\alpha$ and the $p-\text{value}$:

Since $α = 0.05$ and $p\text{-value} = 0.0396$. $\alpha > p\text{-value}$.

Make a decision: Since $\alpha > p\text{-value}$, reject $H_{0}$.

This means you reject $\mu = 65$. In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The $p\text{-value}$ can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for $\mu_{0}$, the name of the list where you put the data, and 1 for Freq: . Arrow down to $\mu$: and arrow over to $> \mu_{0}$. Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the $p\text{-value}$ (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. $\mu > 65$ is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with $t = 1.9781$ (test statistic) and $p = 0.0396$ ($p\text{-value}$). Make sure when you use Draw that no other equations are highlighted in $Y =$ and the plots are turned off.

Exercise $\PageIndex{4}$

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

$H_{0}: \mu = 5$
$H_{a}: \mu < 5$
$p = 0.0082$

Because $p < \alpha$, we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example $\PageIndex{5}$

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

$H_{0}: \mu \leq 1$
$H_{a}: \mu > 1$
Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
Do the calculations : $p\text{-value} ( = 0.036)$

4. State the Conclusions : Since the $p\text{-value} (= 0.036)$ is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

The hypothesis test itself has an established process. This can be summarized as follows:

Determine $H_{0}$ and $H_{a}$. Remember, they are contradictory.
Determine the random variable.
Determine the distribution for the test.
Draw a graph, calculate the test statistic, and use the test statistic to calculate the $p\text{-value}$. (A t -score is an example of test statistics.)
Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use $\alpha$ and not $\beta$. $\beta$ is needed to help determine the sample size of the data that is used in calculating the $p\text{-value}$. Remember that the quantity $1 – \beta$ is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
Data from Growing by Degrees by Allen and Seaman.
Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
“Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

COMMENTS

Null & Alternative Hypotheses
The null and alternative hypotheses offer competing answers to your research question. When the research question asks "Does the independent variable affect the dependent variable?": The null hypothesis ( H0) answers "No, there's no effect in the population.". The alternative hypothesis ( Ha) answers "Yes, there is an effect in the ...
Null Hypothesis: Definition, Rejecting & Examples
When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A.. Null Hypothesis H 0: No effect exists in the population.; Alternative Hypothesis H A: The effect exists in the population.; In every study or experiment, researchers assess an effect or relationship.
How to Write a Null Hypothesis (5 Examples)
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
9.1: Null and Alternative Hypotheses
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with $H_{0}$.The null is not rejected unless the hypothesis test shows otherwise.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
25.3
As is always the case, we need to start by finding a threshold value $c$, such that if the sample mean is larger than $c$, we'll reject the null hypothesis: That is, in order for our hypothesis test to be conducted at the $\alpha=0.05$ level, the following statement must hold (using our typical $Z$ transformation):
8.5: Large Sample Tests for a Population Proportion
where p p denotes the proportion of all adults who prefer the company's beverage over that of its competitor's beverage. Step 2. The test statistic (Equation 8.5.1 8.5.1) is. Z = p^ −p0 p0q0 n− −−−√ Z = p ^ − p 0 p 0 q 0 n. and has the standard normal distribution. Step 3. The value of the test statistic is.
4.4: Hypothesis Testing
The right tail describes the probability of observing such a large sample mean if the null hypothesis is true. The shaded tail in Figure 4.15 represents the chance of observing such a large mean, conditional on the null hypothesis being true. That is, the shaded tail represents the p-value. We shade all means larger than our sample mean, \(\bar ...
10.2: Understanding Null Hypothesis Testing
The Logic of Null Hypothesis Testing. Null hypothesis testing (often called null hypothesis significance testing or NHST) is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H0 and read as "H-zero").
13.1 Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
Sample size, power and effect size revisited: simplified and practical
The sample size critically affects the hypothesis and the study design, and there is no straightforward way of calculating the effective sample size for reaching an accurate conclusion. Use of a statistically incorrect sample size may lead to inadequate results in both clinical and laboratory studies as well as resulting in time loss, cost, and ...
Large sample proportion hypothesis testing
Video transcript. We want to test the hypothesis that more than 30% of U.S. households have internet access with a significance level of 5%. We collect a sample of 150 households, and find that 57 have access. So to do our hypothesis test, let's just establish our null hypothesis and our alternative hypothesis.
5: Hypothesis Testing, Part 1
The sample is shifted so that the sample mean equals the hypothesized population mean (i.e., the value in the null hypothesis). Samples of the same size as the original sample are drawn with replacement from the shifted distribution and the mean of each randomization sample is recorded on the randomization distribution dotplot.
The Large Sample Condition: Definition & Example
The Large Sample Condition: Definition & Example. In statistics, we're often interested in using samples to draw inferences about populations through hypothesis tests or confidence intervals. Most of the formulas that we use in hypothesis tests and confidence intervals make the assumption that a given sample roughly follows a normal distribution.
Understanding Null Hypothesis Testing
The Logic of Null Hypothesis Testing. Null hypothesis testing (often called null hypothesis significance testing or NHST) is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H0 and read as "H-zero").
13.1 Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that ...
Examples of the Null Hypothesis
The null hypothesis—which assumes that there is no meaningful relationship between two variables—may be the most valuable hypothesis for the scientific method because it is the easiest to test using a statistical analysis. This means you can support your hypothesis with a high level of confidence. Testing the null hypothesis can tell you whether your results are due to the effect of ...
Are large data sets inappropriate for hypothesis testing?
$\begingroup$ If a large sample makes you think hypothesis testing was the wrong tool, then hypothesis testing wasn't actually answering the right question at smaller samples either -- that it was wrong just became more obvious at large sample sizes, but the same considerations are relevant. If a significant result at a very small effect size makes you say "well, that's not what I wanted, I ...
Issues in Estimating Sample Size for Hypothesis Testing
Suppose we want to test the following hypotheses at aα=0.05: H 0: μ = 90 versus H 1: μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the ...
8.2: Large Sample Tests for a Population Mean
The sample is large and the population standard deviation is known. Thus the test statistic is. Z = x¯ −μ0 σ/ n−−√ Z = x ¯ − μ 0 σ / n. and has the standard normal distribution. Step 3. Inserting the data into the formula for the test statistic gives. Z = x¯ −μ0 σ/ n−−√ = 8.2 − 8.1 0.22/ 30−−√ = 2.490 Z = x ...
Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
8.6: Hypothesis Test of a Single Population Mean with Examples
Steps for performing Hypothesis Test of a Single Population Mean. Step 1: State your hypotheses about the population mean. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure. Find or identify the sample size, n, the sample mean, ˉx. x ¯.
Z Test: Uses, Formula & Examples
Related posts: Null Hypothesis: Definition, Rejecting & Examples and Understanding Significance Levels. Two-Sample Z Test Hypotheses. Null hypothesis (H 0): Two population means are equal (µ 1 = µ 2).; Alternative hypothesis (H A): Two population means are not equal (µ 1 ≠ µ 2).; Again, when the p-value is less than or equal to your significance level, reject the null hypothesis.
How to Find P Value from a Test Statistic
A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis, so you reject it. A large p-value (> 0.05) indicates weak evidence against the null hypothesis, so you fail to reject it. P-values very close to the cutoff (0.05) are considered to be marginal (could go either way).

Have a language expert improve your writing

Null & Alternative Hypotheses | Definitions, Templates & Examples

Table of contents

Receive feedback on language, structure, and formatting

Examples of null hypotheses

Examples of alternative hypotheses

Here's why students love Scribbr's proofreading services

General template sentences

Test-specific template sentences

Cite this Scribbr article

Is this article helpful?

Shaun Turney

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

10.2: Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

13.1 Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Key Takeaways

Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies

Murat Cihan

Doğan Yücel

Muhittin A Serdar

Introduction

Relationship among sample size, power, P value and effect size

Calculation of the sample size

Mean (X), mmol/L Standard deviation (SD) Sample size (N)

Determination of sample size in pre-clinical studies

Sample size calculation for some genetic studies

Sample size and power analyses in clinical studies

Sample size, effect size and power calculation in laboratory studies

Sample size in method and device comparisons

Sample size in lot to lot variation studies

Sample size in verification studies

Sample size in diagnostic and prognostic studies

Sample size for reference interval determination

Sample size in survey studies

Does big sample size always increase the impact of a study?

5: Hypothesis Testing, Part 1

5.1 - Introduction to Hypothesis Testing

5.2 - Writing Hypotheses

5.2.1 - Examples

Example: IQ Scores

Example: Weight Loss

Example: Gender of College of Science Students

Example: Dog Ownership

Example: Weights of Boys and Girls

Example: Smoking by Gender

Example: Predicting SAT-Math using IQ

Example: Relation Between Height and Weight

5.3 - Randomization Procedures

5.3.1 - StatKey Randomization Methods (Optional)

5.4 - p-values

Making a Decision

5.5 - Randomization Test Examples in StatKey

5.5.1 - Single Proportion Example: PA Residency

5.5.2 - Paired Means Example: Age

5.5.3 - Difference in Means Example: Exercise by Biological Sex

5.5.4 - Correlation Example: Quiz & Exam Scores

5.6 - Lesson 5 Summary

The Large Sample Condition: Definition & Example

Example: Verifying the Large Sample Condition

Modifications to the Large Sample Condition

Additional Resources

Published by Zach

Learning Objectives

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

The Misunderstood p Value