manifold hypothesis paper

Testing the manifold hypothesis

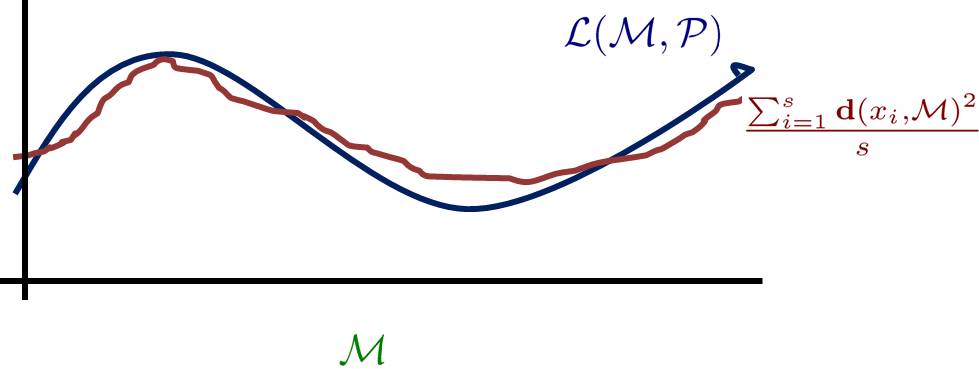
The hypothesis that high dimensional data tend to lie in the vicinity of a low dimensional manifold is the basis of manifold learning. The goal of this paper is to develop an algorithm (with accompanying complexity guarantees) for testing the existence of a manifold that fits a probability distribution supported in a separable Hilbert space, only using i.i.d samples from that distribution. More precisely, our setting is the following. Suppose that data are drawn independently at random from a probability distribution 𝒫 𝒫 \mathcal{P} supported on the unit ball of a separable Hilbert space ℋ ℋ \mathcal{H} . Let 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) be the set of submanifolds of the unit ball of ℋ ℋ \mathcal{H} whose volume is at most V 𝑉 V and reach (which is the supremum of all r 𝑟 r such that any point at a distance less than r 𝑟 r has a unique nearest point on the manifold) is at least τ 𝜏 \tau . Let ℒ ​ ( ℳ , 𝒫 ) ℒ ℳ 𝒫 \mathcal{L}(\mathcal{M},\mathcal{P}) denote mean-squared distance of a random point from the probability distribution 𝒫 𝒫 \mathcal{P} to ℳ ℳ \mathcal{M} . We obtain an algorithm that tests the manifold hypothesis in the following sense.

The algorithm takes i.i.d random samples from 𝒫 𝒫 \mathcal{P} as input, and determines which of the following two is true (at least one must be):

There exists ℳ ∈ 𝒢 ​ ( d , C ​ V , τ C ) ℳ 𝒢 𝑑 𝐶 𝑉 𝜏 𝐶 \mathcal{M}\in\mathcal{G}(d,CV,\frac{\tau}{C}) such that ℒ ​ ( ℳ , 𝒫 ) ≤ C ​ ϵ . ℒ ℳ 𝒫 𝐶 italic-ϵ \mathcal{L}(\mathcal{M},\mathcal{P})\leq C{\epsilon}.

There exists no ℳ ∈ 𝒢 ​ ( d , V / C , C ​ τ ) ℳ 𝒢 𝑑 𝑉 𝐶 𝐶 𝜏 \mathcal{M}\in\mathcal{G}(d,V/C,C\tau) such that ℒ ​ ( ℳ , 𝒫 ) ≤ ϵ C . ℒ ℳ 𝒫 italic-ϵ 𝐶 \mathcal{L}(\mathcal{M},\mathcal{P})\leq\frac{{\epsilon}}{C}.

The answer is correct with probability at least 1 − δ 1 𝛿 1-\delta .

1. Introduction

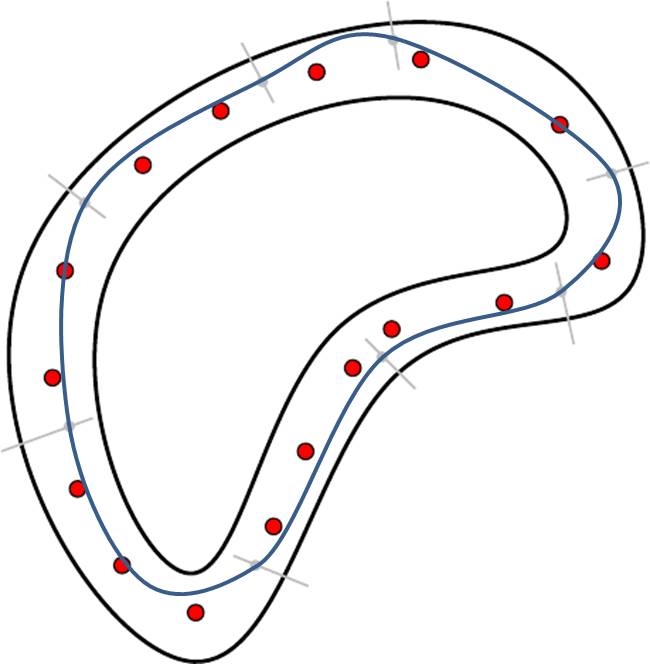
We are increasingly confronted with very high dimensional data from speech, images, and genomes and other sources. A collection of methodologies for analyzing high dimensional data based on the hypothesis that data tend to lie near a low dimensional manifold is now called "Manifold Learning". (see Figure  1 ) We refer to the underlying hypothesis as the "manifold hypothesis." Manifold Learning has been an area of intense activity over the past two decades. We refer the interested reader to a limited set of papers associated with this field; see [ 1 , 4 , 5 , 6 , 9 , 14 , 16 , 17 , 26 , 27 , 28 , 30 , 32 , 34 , 38 ] and the references therein.

The goal of this paper is to develop an algorithm that tests the manifold hypothesis.

Examples of low-dimensional manifolds embedded in high-dimensional spaces include: image vectors representing 3D objects under different illumination conditions, and camera views and phonemes in speech signals. The low-dimensional structure typically arises due to constraints arising from physical laws. A recent empirical study  [ 4 ] of a large number of 3 × \times 3 images represented as points in ℝ 9 superscript ℝ 9 \mathbb{R}^{9} revealed that they approximately lie on a two-dimensional manifold knows as the Klein bottle.

One of the characteristics of high-dimensional data of the type mentioned earlier is that the number of dimensions is comparable, or larger than, the number of samples. This has the consequence that the sample complexity of function approximation can grow exponentially. On the positive side, the data exhibits the phenomenon of “concentration of measure”  [ 8 , 18 ] and asymptotic analysis of statistical techniques is possible. Standard dimensional reduction techniques such as Principal Component Analysis and Factor Analysis, work well when the data lies near a linear subspace of high-dimensional space. They do not work well when the data lies near a nonlinear manifold embedded in the high-dimensional space.

Recently, there has been considerable interest in fitting low-dimensional nonlinear manifolds from sampled data points in high-dimensional spaces. These problems have been viewed as optimization problems generalizing the projection theorem in Hilbert Space. One line of research starts with principal curves/surfaces  [ 14 ] and topology preserving networks  [ 21 ] . The main ideas is that information about the global structure of a manifold can be obtained by analyzing the “interactions” between overlapping local linear structures. The so-called Local Linear Embedding method (local PCA) constructs a local geometric structure that is invariant to translation and rotation in the neighborhood of each data point  [ 29 ] .

In another line of investigation  [ 35 ] , pairwise geodesic distances of data points with respect to the underlying manifold are estimated and multi-dimensional scaling is used to project the data points on a low-dimensional space which best preserves the estimated geodesics. The tangent space in the neighborhood of a data point can be used to represent the local geometry and then these local tangent spaces can be aligned to construct the global coordinate system of the nonlinear manifold  [ 39 ] .

In order to state the problem more precisely, we need to describe the class of manifolds within which we will search for the existence of a manifold which satisfies the manifold hypothesis.

Let ℳ ℳ {\mathcal{M}} be a submanifold of ℋ ℋ \mathcal{H} . The reach τ > 0 𝜏 0 \tau>0 of ℳ ℳ {\mathcal{M}} is the largest number such that for any 0 < r < τ 0 𝑟 𝜏 0<r<\tau , any point at a distance r 𝑟 r of ℳ ℳ {\mathcal{M}} has a unique nearest point on ℳ ℳ {\mathcal{M}} .

Let 𝒢 e = 𝒢 e ​ ( d , V , τ ) subscript 𝒢 𝑒 subscript 𝒢 𝑒 𝑑 𝑉 𝜏 {\mathcal{G}}_{e}={\mathcal{G}}_{e}(d,V,\tau) be the family of d 𝑑 d -dimensional 𝒞 2 − limit-from superscript 𝒞 2 \mathcal{C}^{2}- submanifolds of the unit ball in ℋ ℋ \mathcal{H} with volume ≤ V absent 𝑉 \leq V and reach ≥ τ absent 𝜏 \geq\tau .

Let 𝒫 𝒫 \mathcal{P} be an unknown probability distribution supported in the unit ball of a separable (possibly infinite-dimensional) Hilbert space and let ( x 1 , x 2 , … ) subscript 𝑥 1 subscript 𝑥 2 … (x_{1},x_{2},\ldots) be i.i.d random samples sampled from 𝒫 𝒫 \mathcal{P} .

The test for the Manifold Hypothesis answers the following affirmatively: Given error ε 𝜀 \varepsilon , dimension d 𝑑 d , volume V 𝑉 V , reach τ 𝜏 \tau and confidence 1 − δ 1 𝛿 1-\delta , is there an algorithm that takes a number of samples depending on these parameters and with probability 1 − δ 1 𝛿 1-\delta distinguishes between the following two cases (as least one must hold): (a) Whether there is a

(b) Whether there is no manifold

Here d ​ ( M , x ) 𝑑 𝑀 𝑥 d(M,x) is the distance from a random point x 𝑥 x to the manifold ℳ ℳ {\mathcal{M}} , C 𝐶 C is a constant depending only on d 𝑑 d .

The basic statistical question is:

What is the number of samples needed for testing the hypothesis that data lie near a low-dimensional manifold?

The desired result is that the sample complexity of the task depends only on the “intrinsic” dimension, volume and reach, but not the “ambient” dimension.

We approach this by considering the Empirical Risk Minimization problem.

and define the Empirical Loss

We need to determine how large s 𝑠 s needs to be so that

The answer to this question is given by Theorem 1 in the paper.

The proof of the theorem proceeds by approximating manifolds using point clouds and then using uniform bounds for k − limit-from 𝑘 k- means (Lemma  11 of the paper).

The uniform bounds for k − limit-from 𝑘 k- means are proven by getting an upper bound on the Fat Shattering Dimension of a certain function class and then using an integral related to Dudley’s entropy integral. The bound on the Fat Shattering Dimension is obtained using a random projection and the Sauer-Shelah Lemma. The use of random projections in this context appears in Chapter 4, [ 20 ] and [ 25 ] , however due to the absence of chaining, the bounds derived there are weaker.

The Algorithmic question can be stated as follows:

where C 𝐶 C is some constant depending only on d. (b) Whether there is no manifold ℳ ∈ 𝒢 e = 𝒢 e ​ ( d , V / C , C ​ τ ) ℳ subscript 𝒢 𝑒 subscript 𝒢 𝑒 𝑑 𝑉 𝐶 𝐶 𝜏 {\mathcal{M}}\in{\mathcal{G}}_{e}={\mathcal{G}}_{e}(d,V/C,C\tau) such that

where C 𝐶 C is some constant depending only on d.

The key step to solving this problem is to translate the question of optimizing the squared-loss over a family of manifolds to that of optimizing over sections of a disc bundle. The former involves an optimization over a non-parameterized infinite dimensional space, while the latter involves an optimization over a parameterized (albeit infinite dimensional) set.

We introduce the notion of a cylinder packet in order to define a disc bundle. A cylinder packet is a finite collection of cylinders satisfying certain alignment constraints. An ideal cylinder packet corresponding to a d − limit-from 𝑑 d- manifold ℳ ℳ \mathcal{M} of reach τ 𝜏 \tau (see Definition  1 ) in ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} is obtained by taking a net (see Definition  5 ) of the manifold and for every point p 𝑝 p in the net, throwing in a cylinder centered at p 𝑝 p isometric to 2 ​ τ ¯ ​ ( B d × B n − d ) 2 ¯ 𝜏 subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 2\bar{\tau}(B_{d}\times B_{n-d}) whose d − limit-from 𝑑 d- dimensional central cross-section is tangent to ℳ ℳ \mathcal{M} . Here τ ¯ = c ​ τ ¯ 𝜏 𝑐 𝜏 \bar{\tau}=c\tau for some appropriate constant c 𝑐 c depending only on d 𝑑 d , B d subscript 𝐵 𝑑 B_{d} and B n − d subscript 𝐵 𝑛 𝑑 B_{n-d} are d − limit-from 𝑑 d- dimensional and ( n − d ) − limit-from 𝑛 𝑑 (n-d)- dimensional balls respectively.

For every cylinder cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} in the packet, we define a function f i subscript 𝑓 𝑖 f_{i} that is the squared distance to the d − limit-from 𝑑 d- dimensional central cross section of cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} . These functions are put together using a partition of unity defined on ∪ i cyl i subscript 𝑖 subscript cyl 𝑖 \cup_{i}{\texttt{cyl}}_{i} . The resulting function f 𝑓 f is an “approximate-squared-distance-function" (see Definition  14 ). The base manifold is the set of points x 𝑥 x at which the gradient ∇ f ∇ 𝑓 \nabla f is orthogonal to every eigenvector corresponding to values in [ c , C ] 𝑐 𝐶 [c,C] of the Hessian Hess ​ f ​ ( x ) Hess 𝑓 𝑥 \,\texttt{Hess}\,f(x) . Here c 𝑐 c and C 𝐶 C are constants depending only on the dimension d 𝑑 d of the manifold. The fiber of the disc bundle at a point x 𝑥 x on the base manifold is defined to be the ( n − d ) − limit-from 𝑛 𝑑 (n-d)- dimensional Euclidean ball centered at x 𝑥 x contained in the span of the aforementioned eigenvectors of the Hessian. The base manifold and its fibers together define the disc bundle.

The optimization over sections of the disc bundle proceeds as follows. We fix a cylinder cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} of the cylinder packet. We optimize the squared loss over local sections corresponding to jets whose C 2 − limit-from superscript 𝐶 2 C^{2}- norm is bounded above by c 1 τ ¯ subscript 𝑐 1 ¯ 𝜏 \frac{c_{1}}{\bar{\tau}} , where c 1 subscript 𝑐 1 c_{1} is a controlled constant. The corresponding graphs are each contained inside cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} . The optimization over local sections is performed by minimizing squared loss over a space of C 2 − limit-from superscript 𝐶 2 C^{2}- jets (see Definition  20 ) constrained by inequalities developed in [ 13 ] . The resulting local sections corresponding to various i 𝑖 i are then patched together using the disc bundle and a partition of unity supported on the base manifold. The last step is performed implicitly, since we do not actually need to produce a manifold, but only need to certify the existence or non-existence a manifold possessing certain properties. The results of this paper together with those of [ 13 ] lead to an algorithm fitting a manifold to the data as well; the main additional is to construct local sections from jets, rather than settling for the existence of good local sections as we do here.

Such optimizations are performed over a large ensemble of cylinder packets. Indeed the the size of this ensemble is the chief contribution in the complexity bound.

1.1. Definitions

Definition 1 (reach) ..

Let ℳ ℳ \mathcal{M} be a subset of ℋ ℋ \mathcal{H} . The reach of ℳ ℳ \mathcal{M} is the largest number τ 𝜏 \tau to have the property that any point at a distance r < τ 𝑟 𝜏 r<\tau from ℳ ℳ \mathcal{M} has a unique nearest point in ℳ ℳ \mathcal{M} .

Definition 2 (Tangent Space) .

Let ℋ ℋ \mathcal{H} be a separable Hilbert space. For a closed A ⊆ ℋ 𝐴 ℋ A\subseteq\mathcal{H} , and a ∈ A 𝑎 𝐴 a\in A , let the “tangent space" T ​ a ​ n 0 ​ ( a , A ) 𝑇 𝑎 superscript 𝑛 0 𝑎 𝐴 Tan^{0}(a,A) denote the set of all vectors v 𝑣 v such that for all ϵ > 0 italic-ϵ 0 {\epsilon}>0 , there exists b ∈ A 𝑏 𝐴 b\in A such that 0 < | a − b | < ϵ 0 𝑎 𝑏 italic-ϵ 0<|a-b|<{\epsilon} and | v / | v | − b − a | b − a | | < ϵ 𝑣 𝑣 𝑏 𝑎 𝑏 𝑎 italic-ϵ \big{|}v/{|v|}-\frac{b-a}{|b-a|}\big{|}<{\epsilon} . For a set X ⊆ ℋ 𝑋 ℋ X\subseteq\mathcal{H} and a point a ∈ ℋ 𝑎 ℋ a\in\mathcal{H} let 𝐝 ​ ( a , X ) 𝐝 𝑎 𝑋 \mathbf{d}(a,X) denote the Euclidean distance of the nearest point in X 𝑋 X to a 𝑎 a . Let T ​ a ​ n ​ ( a , A ) 𝑇 𝑎 𝑛 𝑎 𝐴 Tan(a,A) denote the set of all x 𝑥 x such that x − a ∈ T ​ a ​ n 0 ​ ( a , A ) 𝑥 𝑎 𝑇 𝑎 superscript 𝑛 0 𝑎 𝐴 x-a\in Tan^{0}(a,A) .

The following result of Federer (Theorem 4.18, [ 11 ] ), gives an alternate characterization of the reach.

Proposition 1 .

Let A 𝐴 A be a closed subset of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} . Then,

Definition 3 ( C r − limit-from superscript 𝐶 𝑟 C^{r}- submanifold) .

We obtain an algorithm that tests the manifold hypothesis in the following sense.

The number of data points required is of the order of

and the number of arithmetic operations is

The number of calls made to ℬ ℬ \mathcal{B} is O ​ ( n 2 ) 𝑂 superscript 𝑛 2 O(n^{2}) .

1.2. A note on controlled constants

2. sample complexity of manifold fitting.

In this section, we show that if instead of estimating a least-square optimal manifold using the probability measure, we randomly sample sufficiently many points and then find the least square fit manifold to this data, we obtain an almost optimal manifold.

Definition 4 (Sample Complexity) .

We state below, a sample complexity bound when mean-squared error is minimized over 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) .

Theorem 1 .

For r > 0 𝑟 0 r>0 , let

Suppose s ≥ s 𝒢 ​ ( ϵ , δ ) 𝑠 subscript 𝑠 𝒢 italic-ϵ 𝛿 s\geq s_{\mathcal{G}}({\epsilon},{\mathbf{\delta}}) and x = { x 1 , … , x s } 𝑥 subscript 𝑥 1 … subscript 𝑥 𝑠 x=\{x_{1},\dots,x_{s}\} be a set of i.i.d points from 𝒫 𝒫 \mathcal{P} and 𝒫 X subscript 𝒫 𝑋 \mathcal{P}_{X} is the uniform probability measure over X 𝑋 X . Let ℳ e ​ r ​ m subscript ℳ 𝑒 𝑟 𝑚 \mathcal{M}_{erm} denote a manifold in 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) that approximately minimizes the quantity

Let ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) . For x ∈ ℳ 𝑥 ℳ x\in\mathcal{M} denote the orthogonal projection from ℋ ℋ \mathcal{H} to the affine subspace T ​ a ​ n ​ ( x , ℳ ) 𝑇 𝑎 𝑛 𝑥 ℳ Tan(x,\mathcal{M}) by Π x subscript Π 𝑥 \Pi_{x} . We will need the following claim to prove Theorem  1 .

Suppose that ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) . Let

3. Proof of Claim  1

3.1. constants:, 3.2. d − limit-from 𝐷 d- planes:.

One checks easily that ( D ​ P ​ L , d ​ i ​ s ​ t ) 𝐷 𝑃 𝐿 𝑑 𝑖 𝑠 𝑡 (DPL,dist) is a metric space. We write Π ⟂ superscript Π perpendicular-to \Pi^{\perp} to denote the orthocomplement of Π Π \Pi in ℋ ℋ \mathcal{H} .

3.3. Patches:

Suppose B Π ​ ( 0 , r ) subscript 𝐵 Π 0 𝑟 B_{\Pi}(0,r) is the ball of radius r 𝑟 r about the origin in a D − limit-from 𝐷 D- plane Π Π \Pi , and suppose

a patch of radius r 𝑟 r over Π Π \Pi centered at 0 0 . We define

is a linear map, and for linear maps A : Π → Π ⟂ : 𝐴 → Π superscript Π perpendicular-to A:\Pi\rightarrow\Pi^{\perp} , we define ‖ A ‖ norm 𝐴 \|A\| as

subscript Γ 0 𝑧 ℋ \Gamma=\Gamma_{0}+z\subset\mathcal{H} a patch of radius r 𝑟 r over Π Π \Pi , centered at z 𝑧 z . If Γ 0 subscript Γ 0 \Gamma_{0} is tangent to Π Π \Pi at its center 0 0 , then we say that Γ Γ \Gamma is tangent to Π Π \Pi at its center z 𝑧 z .

The following is an easy consequence of the implicit function theorem in fixed dimension ( D 𝐷 D or 2 ​ D 2 𝐷 2D ).

Let Γ 1 subscript Γ 1 \Gamma_{1} be a patch of radius r 1 subscript 𝑟 1 r_{1} over Π 1 subscript Π 1 \Pi_{1} centered at z 1 subscript 𝑧 1 z_{1} and tangent to Π 1 subscript Π 1 \Pi_{1} at z 1 subscript 𝑧 1 z_{1} . Let z 2 subscript 𝑧 2 z_{2} belong to Γ 1 subscript Γ 1 \Gamma_{1} and suppose ‖ z 2 − z 1 ‖ < c 0 ​ r 1 . norm subscript 𝑧 2 subscript 𝑧 1 subscript 𝑐 0 subscript 𝑟 1 \|z_{2}-z_{1}\|<c_{0}r_{1}. Assume

Let Π 2 ∈ D ​ P ​ L subscript Π 2 𝐷 𝑃 𝐿 \Pi_{2}\in DPL with d ​ i ​ s ​ t ​ ( Π 2 , Π 1 ) < c 0 . 𝑑 𝑖 𝑠 𝑡 subscript Π 2 subscript Π 1 subscript 𝑐 0 dist(\Pi_{2},\Pi_{1})<c_{0}. Then there exists a patch Γ 2 subscript Γ 2 \Gamma_{2} of radius c 1 ​ r 1 subscript 𝑐 1 subscript 𝑟 1 c_{1}r_{1} over Π 2 subscript Π 2 \Pi_{2} centered at z 2 subscript 𝑧 2 z_{2} with

Here c 0 subscript 𝑐 0 c_{0} and c 1 subscript 𝑐 1 c_{1} are small constants depending only on D 𝐷 D , and by rescaling, we may assume without loss of generality that r 1 = 1 subscript 𝑟 1 1 r_{1}=1 when we prove Lemma  2 .

The meaning of Lemma  2 is that if Γ Γ \Gamma is the graph of a map

3.4. Imbedded manifolds:

Let ℳ ⊂ ℋ ℳ ℋ \mathcal{M}\subset\mathcal{H} be a "compact imbedded D − limit-from 𝐷 D- manifold" (for short, just a "manifold") if the following hold:

ℳ ℳ \mathcal{M} is compact.

There exists an r 1 > r 2 > 0 subscript 𝑟 1 subscript 𝑟 2 0 r_{1}>r_{2}>0 such that for every z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} , there exists T z ​ ℳ ∈ D ​ P ​ L subscript 𝑇 𝑧 ℳ 𝐷 𝑃 𝐿 T_{z}\mathcal{M}\in DPL such that ℳ ∩ B ℋ ​ ( z , r 2 ) = Γ ∩ B ℋ ​ ( z , r 2 ) ℳ subscript 𝐵 ℋ 𝑧 subscript 𝑟 2 Γ subscript 𝐵 ℋ 𝑧 subscript 𝑟 2 \mathcal{M}\cap B_{\mathcal{H}}(z,r_{2})=\Gamma\cap B_{\mathcal{H}}(z,r_{2}) for some patch Γ Γ \Gamma over T z ​ ( ℳ ) subscript 𝑇 𝑧 ℳ T_{z}(\mathcal{M}) of radius r 1 subscript 𝑟 1 r_{1} , centered at z 𝑧 z and tangent to T z ​ ( ℳ ) subscript 𝑇 𝑧 ℳ T_{z}(\mathcal{M}) at z 𝑧 z . We call T z ​ ( ℳ ) subscript 𝑇 𝑧 ℳ T_{z}(\mathcal{M}) the tangent space to ℳ ℳ \mathcal{M} at z 𝑧 z .

3.5. Growing a Patch

Lemma 3 ("growing patch") ..

ℳ \Gamma\subset\Gamma^{+}\subset\mathcal{M}.

Corollary 4 .

Let ℳ ℳ \mathcal{M} be a manifold with infinitesimal reach ≥ 1 absent 1 \geq 1 and suppose 0 ∈ ℳ 0 ℳ 0\in\mathcal{M} . Then there exists a patch Γ Γ \Gamma of radius c ^ ^ 𝑐 \hat{c} over T 0 ​ ℳ subscript 𝑇 0 ℳ T_{0}\mathcal{M} such that Γ ⊂ ℳ Γ ℳ \Gamma\subset\mathcal{M} .

Lemma  3 implies Corollary  4 . Indeed, we can start with a tiny patch Γ Γ \Gamma (centered at 0 0 ) over T 0 ​ ℳ subscript 𝑇 0 ℳ T_{0}\mathcal{M} , with Γ ⊂ ℳ Γ ℳ \Gamma\subset\mathcal{M} . Such Γ Γ \Gamma exists because ℳ ℳ \mathcal{M} is a manifold. By repeatedly applying the Lemma, we can repeatedly increase the radius of our patch by a fixed amount c ​ r 2 𝑐 subscript 𝑟 2 cr_{2} ; we can continue doing so until we arrive at a patch of radius ≥ c ^ absent ^ 𝑐 \geq\hat{c} .

Proof of Lemma  3 .

Without loss of generality, we can take ℋ = ℝ D ⊕ ℋ ′ ℋ direct-sum superscript ℝ 𝐷 superscript ℋ ′ \mathcal{H}=\mathbb{R}^{D}\oplus\mathcal{H}^{\prime} for a Hilbert space ℋ ′ superscript ℋ ′ \mathcal{H}^{\prime} ; and we may assume that

Our patch Γ Γ \Gamma is then a graph

with Ψ ​ ( 0 ) = 0 , Ψ 0 0 \Psi(0)=0, ∇ Ψ ​ ( 0 ) = 0 , ∇ Ψ 0 0 \nabla\Psi(0)=0, and

\Psi^{+} is simply the union of the graphs of

Also, for each y ∈ B ℝ D ​ ( 0 , r ) 𝑦 subscript 𝐵 superscript ℝ 𝐷 0 𝑟 y\in B_{\mathbb{R}^{D}}(0,r) , the point ( y , Ψ ​ ( y ) ) 𝑦 Ψ 𝑦 (y,\Psi(y)) belongs to

𝑟 superscript 𝑐 ′′′ subscript 𝑟 2 r+c^{\prime\prime\prime}r_{2} over T 0 ​ ℳ subscript 𝑇 0 ℳ T_{0}\mathcal{M} centered at 0 0 . That proves the lemma. ∎

3.6. Global Reach

For a real number τ > 0 𝜏 0 \tau>0 , A manifold ℳ ℳ \mathcal{M} has reach ≥ τ absent 𝜏 \geq\tau if and only if every x ∈ ℋ 𝑥 ℋ x\in\mathcal{H} such that 𝐝 ​ ( x , ℳ ) < τ 𝐝 𝑥 ℳ 𝜏 \mathbf{d}(x,\mathcal{M})<\tau has a unique closest point of ℳ ℳ \mathcal{M} . By Federer’s characterization of the reach in Proposition  1 , if the reach is greater than one, the infinitesimal reach is greater than 1 1 1 as well.

Let ℳ ℳ \mathcal{M} be a manifold of reach ≥ 1 absent 1 \geq 1 , with 0 ∈ ℳ 0 ℳ 0\in\mathcal{M} . Then, there exists a patch Γ Γ \Gamma of radius c ^ ^ 𝑐 \hat{c} over T 0 ​ ℳ subscript 𝑇 0 ℳ T_{0}\mathcal{M} centered at 0 0 , such that

There is a patch Γ Γ \Gamma of radius c ^ ^ 𝑐 \hat{c} over T 0 ​ ℳ subscript 𝑇 0 ℳ T_{0}\mathcal{M} centered at 0 0 such that

(See Lemma  3 .) For any x ∈ Γ ∩ B ℋ ​ ( 0 , c ♯ ) 𝑥 Γ subscript 𝐵 ℋ 0 superscript 𝑐 ♯ x\in\Gamma\cap B_{\mathcal{H}}(0,c^{\sharp}) , there exists a tiny ball B x subscript 𝐵 𝑥 B_{x} (in ℋ ℋ \mathcal{H} ) centered at x 𝑥 x such that Γ ∩ B x = ℳ ∩ B x Γ subscript 𝐵 𝑥 ℳ subscript 𝐵 𝑥 \Gamma\cap B_{x}=\mathcal{M}\cap B_{x} ; that’s because ℳ ℳ \mathcal{M} is a manifold.

It follows that the distance from

is strictly positive.

Suppose Γ n ​ o subscript Γ 𝑛 𝑜 \Gamma_{no} intersects B H ​ ( 0 , c ♯ 100 ) subscript 𝐵 𝐻 0 superscript 𝑐 ♯ 100 B_{H}(0,\frac{c^{\sharp}}{100}) ; say y n ​ o ∈ B ℋ ​ ( 0 , c ♯ 100 ) ∩ Γ n ​ o subscript 𝑦 𝑛 𝑜 subscript 𝐵 ℋ 0 superscript 𝑐 ♯ 100 subscript Γ 𝑛 𝑜 y_{no}\in B_{\mathcal{H}}(0,\frac{c^{\sharp}}{100})\cap\Gamma_{no} . Also, 0 ∈ B ℋ ​ ( 0 , c ♯ 100 ) ∩ Γ y ​ e ​ s . 0 subscript 𝐵 ℋ 0 superscript 𝑐 ♯ 100 subscript Γ 𝑦 𝑒 𝑠 0\in B_{\mathcal{H}}(0,\frac{c^{\sharp}}{100})\cap\Gamma_{yes}.

The continuous function B ℋ ​ ( 0 , c ♯ 100 ) ∋ y ↦ 𝐝 ​ ( y , Γ n ​ o ) − 𝐝 ​ ( y , Γ y ​ e ​ s ) contains subscript 𝐵 ℋ 0 superscript 𝑐 ♯ 100 𝑦 maps-to 𝐝 𝑦 subscript Γ 𝑛 𝑜 𝐝 𝑦 subscript Γ 𝑦 𝑒 𝑠 B_{\mathcal{H}}(0,\frac{c^{\sharp}}{100})\ni y\mapsto\mathbf{d}(y,\Gamma_{no})-\mathbf{d}(y,\Gamma_{yes}) is positive at y = 0 𝑦 0 y=0 and negative at y = y n ​ o 𝑦 subscript 𝑦 𝑛 𝑜 y=y_{no} . Hence at some point,

It follows that y H ​ a ​ m subscript 𝑦 𝐻 𝑎 𝑚 y_{Ham} has two distinct closest points in ℳ ℳ \mathcal{M} and yet

since 0 ∈ ℳ 0 ℳ 0\in\mathcal{M} and y H ​ a ​ m ∈ B ℋ ​ ( 0 , c ♯ 100 ) . subscript 𝑦 𝐻 𝑎 𝑚 subscript 𝐵 ℋ 0 superscript 𝑐 ♯ 100 y_{Ham}\in B_{\mathcal{H}}(0,\frac{c^{\sharp}}{100}). That contradicts our assumption that ℳ ℳ \mathcal{M} has reach ≥ 1 absent 1 \geq 1 . Hence our assumption that Γ n ​ o subscript Γ 𝑛 𝑜 \Gamma_{no} intersects B ℋ ​ ( 0 , c ♯ 100 ) subscript 𝐵 ℋ 0 superscript 𝑐 ♯ 100 B_{\mathcal{H}}(0,\frac{c^{\sharp}}{100}) must be false. Therefore, by definition of Γ n ​ o subscript Γ 𝑛 𝑜 \Gamma_{no} we have

it follows that

proving the lemma. ∎

This completes the proof of Claim  1 .

4. A bound on the size of an ϵ − limit-from italic-ϵ {\epsilon}- net

Definition 5 ..

Let ( X , 𝐝 ) 𝑋 𝐝 (X,\mathbf{d}) be a metric space, and r > 0 𝑟 0 r>0 . We say that Y 𝑌 Y is an r − limit-from 𝑟 r- net of X 𝑋 X if Y ⊆ X 𝑌 𝑋 Y\subseteq X and for every x ∈ X 𝑥 𝑋 x\in X , there is a point y ∈ Y 𝑦 𝑌 y\in Y such that 𝐝 ​ ( x , y ) < r 𝐝 𝑥 𝑦 𝑟 \mathbf{d}(x,y)<r .

Corollary 6 .

be given by

Let ℳ ∈ 𝒢 ℳ 𝒢 \mathcal{M}\in\mathcal{G} , and ℳ ℳ \mathcal{M} be equipped with the metric 𝐝 ℋ subscript 𝐝 ℋ \mathbf{d}_{\mathcal{H}} of the ℋ ℋ \mathcal{H} . Then, for any r > 0 𝑟 0 r>0 , there is an τ ​ r − limit-from 𝜏 𝑟 \sqrt{\tau r}- net of ℳ ℳ \mathcal{M} consisting of no more than U 𝒢 ​ ( 1 / r ) subscript 𝑈 𝒢 1 𝑟 U_{\mathcal{G}}(1/r) points.

𝑘 1 y_{k+1} be an arbitrary member of this set. Else declare the construction of Y 𝑌 Y to be complete.

By Claim  1 for each y ∈ Y 𝑦 𝑌 y\in Y , there are controlled constants 0 < c < 1 / 2 0 𝑐 1 2 0<c<1/2 and 0 < c ′ 0 superscript 𝑐 ′ 0<c^{\prime} such that for any r ∈ ( 0 , τ ] 𝑟 0 𝜏 r\in(0,\tau] , the volume of ℳ ∩ B ℋ ​ ( y , c ​ r ) ℳ subscript 𝐵 ℋ 𝑦 𝑐 𝑟 \mathcal{M}\cap B_{\mathcal{H}}(y,cr) is greater than c ′ ​ r d superscript 𝑐 ′ superscript 𝑟 𝑑 c^{\prime}r^{d} .

Since the volume of

is less or equal to V 𝑉 V the cardinality of Y 𝑌 Y is less or equal to V c ′ ​ r d 𝑉 superscript 𝑐 ′ superscript 𝑟 𝑑 \frac{V}{c^{\prime}r^{d}} for all r ∈ ( 0 , τ ] . 𝑟 0 𝜏 r\in(0,\tau]. The corollary follows. ∎

4.1. Fitting k 𝑘 k affine subspaces of dimension d 𝑑 d

A natural generalization of k-means was proposed in [ 3 ] wherein one fits k 𝑘 k d − limit-from 𝑑 d- dimensional planes to data in a manner that minimizes the average squared distance of a data point to the nearest d − limit-from 𝑑 d- dimensional plane. For more recent results on this kind of model, with the average p t ​ h superscript 𝑝 𝑡 ℎ p^{th} powers rather than squares, see [ 19 ] . We can view k − limit-from 𝑘 k- means as a 0 − limit-from 0 0- dimensional special case of k − limit-from 𝑘 k- planes.

In this section, we derive an upper bound for the generalization error of fitting k − limit-from 𝑘 k- planes. Unlike the earlier bounds for fitting manifolds, the bounds here are linear in the dimension d 𝑑 d rather than exponential in it. The dependence on k 𝑘 k is linear up to logarithmic factors, as before. In the section, we assume for notation convenience that the dimension m 𝑚 m of the Hilbert space is finite, though the results can be proved for any separable Hilbert space.

We wish to obtain a probabilistic upper bound on

where { x i } 1 s superscript subscript subscript 𝑥 𝑖 1 𝑠 \{x_{i}\}_{1}^{s} is the train set and 𝔼 𝒫 ​ F ​ ( x ) subscript 𝔼 𝒫 𝐹 𝑥 \mathbb{E}_{\mathcal{P}}F(x) is the expected value of F 𝐹 F with respect to 𝒫 𝒫 \mathcal{P} . Due to issues of measurability, ( 2 ) need not be random variable for arbitrary ℱ ℱ \mathcal{F} . However, in our situation, this is the case because ℱ ℱ \mathcal{F} is a family of bounded piecewise quadratic functions, smoothly parameterized by ℋ b × k superscript subscript ℋ 𝑏 absent 𝑘 \mathcal{H}_{b}^{\times k} , which has a countable dense subset, for example, the subset of elements specified using rational data. We obtain a bound that is independent of m 𝑚 m , the ambient dimension.

Theorem 7 .

where A i subscript 𝐴 𝑖 A_{i} is defined by the condition that for any vector z 𝑧 z , ( z − ( A i ​ z ) ) † superscript 𝑧 subscript 𝐴 𝑖 𝑧 † \left(z-(A_{i}z)\right)^{{\dagger}} and A i ​ z subscript 𝐴 𝑖 𝑧 A_{i}z are the components of z 𝑧 z parallel and perpendicular to H i subscript 𝐻 𝑖 H_{i} , and c i subscript 𝑐 𝑖 c_{i} is the point on H i subscript 𝐻 𝑖 H_{i} that is the nearest to the origin (it could have been any point on H i subscript 𝐻 𝑖 H_{i} ). Thus

Now, define vector valued maps Φ Φ \Phi and Ψ Ψ \Psi whose respective domains are the space of d 𝑑 d dimensional affine subspaces and ℋ ℋ \mathcal{H} respectively.

where A i † ​ A i superscript subscript 𝐴 𝑖 † subscript 𝐴 𝑖 A_{i}^{{\dagger}}A_{i} and x ​ x † 𝑥 superscript 𝑥 † xx^{{\dagger}} are interpreted as rows of m 2 superscript 𝑚 2 m^{2} real entries.

is equal to

We see that since ‖ x ‖ ≤ 1 norm 𝑥 1 \|x\|\leq 1 , ‖ Ψ ​ ( x ) ‖ ≤ 1 norm Ψ 𝑥 1 \|\Psi(x)\|\leq 1 . The Frobenius norm ‖ A i † ​ A i ‖ 2 superscript norm superscript subscript 𝐴 𝑖 † subscript 𝐴 𝑖 2 \|A_{i}^{{\dagger}}A_{i}\|^{2} is equal to T ​ r ​ ( A i ​ A i † ​ A i ​ A i † ) , 𝑇 𝑟 subscript 𝐴 𝑖 superscript subscript 𝐴 𝑖 † subscript 𝐴 𝑖 superscript subscript 𝐴 𝑖 † Tr(A_{i}A_{i}^{{\dagger}}A_{i}A_{i}^{{\dagger}}), which is the rank of A i subscript 𝐴 𝑖 A_{i} since A i subscript 𝐴 𝑖 A_{i} is a projection. Therefore,

Uniform bounds for classes of functions of the form min i ⁡ Φ ​ ( H i ) ⋅ Ψ ​ ( x ) ⋅ subscript 𝑖 Φ subscript 𝐻 𝑖 Ψ 𝑥 \min_{i}\Phi(H_{i})\cdot\Psi(x) follow from Lemma  11 . We infer from Lemma  11 that if

𝑑 5 italic-ϵ 1 𝛿 \mathbb{P}\left[\sup\limits_{F\in\mathcal{F}_{k,d}}\Bigg{|}\frac{\sum_{i=1}^{s}F(x_{i})}{s}-\mathbb{E}_{\mathcal{P}}F(x)\Bigg{|}<\sqrt{3(d+5)}{\epsilon}\right]>1-{\mathbf{\delta}}. The last statement can be rephrased as follows. If

5. Tools from empirical processes

In order to prove a uniform bound of the form

it suffices to bound a measure of the complexity of ℱ ℱ \mathcal{F} known as the Fat-Shattering dimension of the function class ℱ ℱ \mathcal{F} . The metric entropy (defined below) of ℱ ℱ \mathcal{F} can be bounded using the Fat-Shattering dimension, leading to a uniform bound of the form of ( 3 ).

Definition 6 (metric entropy) .

Given a metric space ( Y , ρ ) 𝑌 𝜌 (Y,\rho) , we call Z ⊆ Y 𝑍 𝑌 Z\subseteq Y an η − limit-from 𝜂 \eta- net of Y 𝑌 Y if for every y ∈ Y 𝑦 𝑌 y\in Y , there is a z ∈ Z 𝑧 𝑍 z\in Z such that ρ ​ ( y , z ) < η . 𝜌 𝑦 𝑧 𝜂 \rho(y,z)<\eta. Given a measure 𝒫 𝒫 \mathcal{P} supported on a metric space X 𝑋 X , and ℱ ℱ \mathcal{F} a class of functions from X 𝑋 X to ℝ ℝ \mathbb{R} . Let N ​ ( η , ℱ , ℒ 2 ​ ( 𝒫 ) ) 𝑁 𝜂 ℱ subscript ℒ 2 𝒫 N(\eta,\mathcal{F},\mathcal{L}_{2}(\mathcal{P})) denote the minimum number of elements that an η − limit-from 𝜂 \eta- net of ℱ ℱ \mathcal{F} could have, with respect to the metric imposed by the Hilbert space ℒ 2 ​ ( 𝒫 ) subscript ℒ 2 𝒫 \mathcal{L}_{2}(\mathcal{P}) , wherein the distance between f 1 : X → ℝ : subscript 𝑓 1 → 𝑋 ℝ f_{1}:X\rightarrow\mathbb{R} and f 2 : X → ℝ : subscript 𝑓 2 → 𝑋 ℝ f_{2}:X\rightarrow\mathbb{R} is

We call ln ⁡ N ​ ( η , ℱ , ℒ 2 ​ ( 𝒫 ) ) 𝑁 𝜂 ℱ subscript ℒ 2 𝒫 \ln N(\eta,\mathcal{F},\mathcal{L}_{2}(\mathcal{P})) the metric entropy of ℱ ℱ \mathcal{F} at scale η 𝜂 \eta with respect to ℒ 2 ​ ( 𝒫 ) subscript ℒ 2 𝒫 \mathcal{L}_{2}(\mathcal{P}) .

Definition 7 (Fat-shattering dimension) .

We will also need to use the notion of VC dimension, and some of its properties. These appear below.

Definition 8 .

The following result concerning the VC dimension of halfspaces is well known (Corollary 13.1, [ 7 ] ).

Theorem 8 .

𝑔 1 VC_{\Lambda}=g+1 .

We state the Sauer-Shelah Lemma below.

Lemma 9 (Theorem 13.2, [ 7 ] ) .

For V ​ C Λ > 2 𝑉 subscript 𝐶 Λ 2 VC_{\Lambda}>2 , ∑ i = 0 V ​ C Λ ( k i ) ≤ k V ​ C Λ superscript subscript 𝑖 0 𝑉 subscript 𝐶 Λ binomial 𝑘 𝑖 superscript 𝑘 𝑉 subscript 𝐶 Λ \sum_{i=0}^{VC_{\Lambda}}{k\choose i}\leq k^{VC_{\Lambda}} .

The lemma below follows from existing results from the theory of Empirical Processes in a straightforward manner, but does not seem to have appeared in print before. We have provided a proof in the appendix.

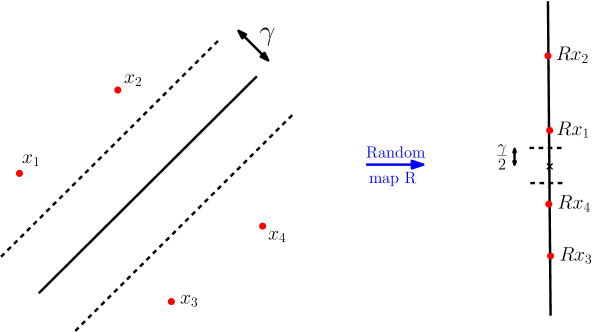
A key component in the proof of the uniform bound in Theorem  1 is an upper bound on the fat-shattering dimension of functions given by the maximum of a set of minima of collections of linear functions on a ball in ℋ ℋ \mathcal{H} . We will use the Johnson-Lindenstrauss Lemma [ 15 ] in its proof.

Let J 𝐽 J be a finite dimensional vectorspace of dimension greater or equal to g 𝑔 g . In what follows, by "uniformly random g − limit-from 𝑔 g- dimensional subspace in J 𝐽 J ," we mean a random variable taking taking values in the set of g − limit-from 𝑔 g- dimensional subspaces of J 𝐽 J , possessing the following property. Its distribution is invariant under the action of the orthogonal group acting on J 𝐽 J .

• 𝑘 ℓ 𝐶 𝑘 ℓ superscript 𝛾 2 superscript 2 𝐶 𝑘 ℓ superscript 𝛾 2 \mathrm{fat}_{\gamma}(\mathcal{F}_{k,\ell})\leq\frac{Ck\ell}{\gamma^{2}}\log^{2}\frac{Ck\ell}{\gamma^{2}}.
• 𝑘 ℓ subscript 𝔼 subscript 𝜇 𝑠 𝑓 subscript 𝑥 𝑖 subscript 𝔼 𝜇 𝑓 italic-ϵ 1 𝛿 \mathbb{P}\left[\sup_{f\in\mathcal{F}_{k,\ell}}\big{|}\mathbb{E}_{\mu_{s}}f(x_{i})-\mathbb{E}_{\mu}f\big{|}\geq{\epsilon}\right]\leq 1-{\mathbf{\delta}}.

𝑠 𝑘 ℓ g:=C_{1}\left({\gamma}^{-2}\log(s+k\ell)\right) for a sufficiently large universal constant C 1 subscript 𝐶 1 C_{1} . Consider a particular 𝒜 ∈ X 𝒜 𝑋 {\mathcal{A}}\in X and f ​ ( x ) := max j ⁡ min i ⁡ v i ​ j ⋅ x assign 𝑓 𝑥 subscript 𝑗 subscript 𝑖 ⋅ subscript 𝑣 𝑖 𝑗 𝑥 f(x):=\max_{j}\min_{i}v_{ij}\cdot x that satisfies ( 7 ) and ( 8 ).

Let R 𝑅 R be an orthogonal projection onto a uniformly random g − limit-from 𝑔 g- dimensional subspace of s ​ p ​ a ​ n ​ ( X ∪ V ) 𝑠 𝑝 𝑎 𝑛 𝑋 𝑉 span(X\cup V) ; we denote the family of all such linear maps ℜ \Re . Let R ​ X 𝑅 𝑋 RX denote the set { R ​ x 1 , … , R ​ x s } 𝑅 subscript 𝑥 1 … 𝑅 subscript 𝑥 𝑠 \{Rx_{1},\dots,Rx_{s}\} and likewise, R ​ V 𝑅 𝑉 RV denote the set { R ​ v 11 , … , R ​ v k ​ l } 𝑅 subscript 𝑣 11 … 𝑅 subscript 𝑣 𝑘 𝑙 \{Rv_{11},\dots,Rv_{kl}\} . Since all vectors in X ∪ V 𝑋 𝑉 X\cup V belong to the unit ball B ℋ subscript 𝐵 ℋ B_{\mathcal{H}} , by the Johnson-Lindenstrauss Lemma, with probability greater than 1 / 2 1 2 {1/2} , the inner product of every pair of vectors in R ​ X ∪ R ​ V 𝑅 𝑋 𝑅 𝑉 RX\cup RV multiplied by m g 𝑚 𝑔 \frac{m}{g} is within γ 𝛾 \gamma of the inner product of the corresponding vectors in X ∪ V 𝑋 𝑉 X\cup V .

Therefore, we have the following.

Observation 1 .

With probability at least 1 2 1 2 \frac{1}{2} the following statements are true.

Let R ∈ ℜ 𝑅 R\in\Re be a projection onto a uniformly random g − limit-from 𝑔 g- dimensional subspace in s ​ p ​ a ​ n ​ ( X ∪ V ) 𝑠 𝑝 𝑎 𝑛 𝑋 𝑉 span(X\cup V) . Let J := span ​ ( R ​ X ) assign 𝐽 span 𝑅 𝑋 J:=\mathrm{span}(RX) and let t J : J → ℝ : superscript 𝑡 𝐽 → 𝐽 ℝ t^{J}:J\rightarrow\mathbb{R} be the function given by

𝑔 2 𝑘 ℓ s^{O((g+2)k\ell)} .

Proof of Claim  2 .

𝑔 2 𝑘 ℓ s^{(g+2)k\ell} .

𝑠 𝑘 ℓ C_{1}\left({\gamma}^{-2}\log(s+k\ell)\right) for g 𝑔 g , we see that

implying that

Therefore by Lemma  10 , if

Let t = ln ⁡ ( k ​ ℓ γ ) 𝑡 𝑘 ℓ 𝛾 t=\ln\left(\frac{\sqrt{k\ell}}{\gamma}\right) . Then the integral in ( 13 ) equals

U:\mathbb{R}^{+}\rightarrow\mathbb{Z}^{+} be a real-valued function. Let 𝒢 ~ ~ 𝒢 \mathcal{\tilde{G}} be any family of subsets of the unit ball B ℋ subscript 𝐵 ℋ B_{\mathcal{H}} in a Hilbert space ℋ ℋ \mathcal{H} such that for all r > 0 𝑟 0 r>0 every element ℳ ∈ 𝒢 ~ ℳ ~ 𝒢 \mathcal{M}\in\mathcal{\tilde{G}} can be covered using U ​ ( 1 r ) 𝑈 1 𝑟 U(\frac{1}{r}) open Euclidean balls.

A priori, it is unclear if

is a random variable, since the supremum of a set of random variables is not always a random variable (although if the set is countable this is true). Let 𝐝 𝚑𝚊𝚞𝚜 subscript 𝐝 𝚑𝚊𝚞𝚜 \mathbf{d}_{\mathtt{haus}} represent Hausdorff distance. For each n ≥ 1 𝑛 1 n\geq 1 , 𝒢 ~ n subscript ~ 𝒢 𝑛 \mathcal{\tilde{G}}_{n} be a countable set of finite subsets of ℋ ℋ \mathcal{H} , such that for each ℳ ∈ 𝒢 ~ ℳ ~ 𝒢 \mathcal{M}\in\mathcal{\tilde{G}} , there exists ℳ ′ ∈ 𝒢 ~ n superscript ℳ ′ subscript ~ 𝒢 𝑛 \mathcal{M}^{\prime}\in\mathcal{\tilde{G}}_{n} such that 𝐝 𝚑𝚊𝚞𝚜 ​ ( ℳ , ℳ ′ ) ≤ 1 / n , subscript 𝐝 𝚑𝚊𝚞𝚜 ℳ superscript ℳ ′ 1 𝑛 \mathbf{d}_{\mathtt{haus}}(\mathcal{M},\mathcal{M}^{\prime})\leq 1/n, and for each ℳ ′ ∈ 𝒢 ~ n superscript ℳ ′ subscript ~ 𝒢 𝑛 \mathcal{M}^{\prime}\in\mathcal{\tilde{G}}_{n} , there is an ℳ ′′ ∈ 𝒢 ~ superscript ℳ ′′ ~ 𝒢 \mathcal{M}^{\prime\prime}\in\mathcal{\tilde{G}} such that 𝐝 𝚑𝚊𝚞𝚜 ​ ( ℳ ′′ , ℳ ′ ) ≤ 1 / n subscript 𝐝 𝚑𝚊𝚞𝚜 superscript ℳ ′′ superscript ℳ ′ 1 𝑛 \mathbf{d}_{\mathtt{haus}}(\mathcal{M}^{\prime\prime},\mathcal{M}^{\prime})\leq 1/n . For each n 𝑛 n , such a 𝒢 ~ n subscript ~ 𝒢 𝑛 \mathcal{\tilde{G}}_{n} exists because ℋ ℋ \mathcal{H} is separable. Now ( 14 ) is equal to

and for each n 𝑛 n , the supremum in the limits is over a countable set; thus, for a fixed n 𝑛 n , the quantity in the limits is a random variable. Since the pointwise limit of a sequence of measurable functions (random variables) is a measurable function (random variable), this proves that

is a random variable.

U_{\mathcal{G}}:\mathbb{R}^{+}\rightarrow\mathbb{R}^{+} be a function taking values in the positive reals. Suppose every ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) can be covered by the union of some U 𝒢 ​ ( 1 r ) subscript 𝑈 𝒢 1 𝑟 U_{\mathcal{G}}(\frac{1}{r}) open Euclidean balls of radius r ​ τ 16 𝑟 𝜏 16 \frac{\sqrt{r\tau}}{16} , for every r > 0 𝑟 0 r>0 . If

Given a collection 𝐜 := { c 1 , … , c k } assign 𝐜 subscript 𝑐 1 … subscript 𝑐 𝑘 \mathbf{c}:=\{c_{1},\dots,c_{k}\} of points in ℋ ℋ \mathcal{H} , let

Let ℱ k subscript ℱ 𝑘 \mathcal{F}_{k} denote the set of all such functions for

B ℋ subscript 𝐵 ℋ B_{\mathcal{H}} being the unit ball in the Hilbert space.

Consider ℳ ∈ 𝒢 := 𝒢 ​ ( d , V , τ ) ℳ 𝒢 assign 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}:=\mathcal{G}(d,V,\tau) . Let 𝐜 ​ ( ℳ , ϵ ) = { c ^ 1 , … , c ^ k ^ } 𝐜 ℳ italic-ϵ subscript ^ 𝑐 1 … subscript ^ 𝑐 ^ 𝑘 \mathbf{c}(\mathcal{M},{\epsilon})=\{\hat{c}_{1},\dots,\hat{c}_{\hat{k}}\} be a set of k ^ := U 𝒢 ​ ( 1 / ϵ ) assign ^ 𝑘 subscript 𝑈 𝒢 1 italic-ϵ \hat{k}:=U_{\mathcal{G}}(1/{\epsilon}) points in ℳ ℳ \mathcal{M} , such that ℳ ℳ \mathcal{M} is contained in the union of Euclidean balls of radius τ ​ ϵ / 16 𝜏 italic-ϵ 16 \sqrt{\tau{\epsilon}}/16 centered at these points. Suppose x ∈ B ℋ 𝑥 subscript 𝐵 ℋ x\in B_{\mathcal{H}} . Since c ​ ( ℳ , ϵ ) ⊆ ℳ 𝑐 ℳ italic-ϵ ℳ c(\mathcal{M},{\epsilon})\subseteq\mathcal{M} , we have 𝐝 ​ ( x , ℳ ) ≤ 𝐝 ​ ( x , c ​ ( ℳ , ϵ ) ) 𝐝 𝑥 ℳ 𝐝 𝑥 𝑐 ℳ italic-ϵ \mathbf{d}(x,\mathcal{M})\leq\mathbf{d}(x,c(\mathcal{M},{\epsilon})) . To obtain a bound in the reverse direction, let y ∈ ℳ 𝑦 ℳ y\in\mathcal{M} be a point such that | x − y | = 𝐝 ​ ( x , ℳ ) 𝑥 𝑦 𝐝 𝑥 ℳ |x-y|=\mathbf{d}(x,\mathcal{M}) , and let z ∈ 𝐜 ​ ( ℳ , ϵ ) 𝑧 𝐜 ℳ italic-ϵ z\in\mathbf{c}(\mathcal{M},{\epsilon}) be a point such that | y − z | < τ ​ ϵ / 16 𝑦 𝑧 𝜏 italic-ϵ 16 |y-z|<\sqrt{\tau{\epsilon}}/16 . Let z ′ superscript 𝑧 ′ z^{\prime} be the point on T ​ a ​ n ​ ( y , ℳ ) 𝑇 𝑎 𝑛 𝑦 ℳ Tan(y,\mathcal{M}) that is closest to z 𝑧 z . By the reach condition, and Proposition  1 ,

Since τ < 1 𝜏 1 \tau<1 , this shows that

Inequality ( 15 ) reduces the problem of deriving uniform bounds over a space of manifolds to a problem of deriving uniform bounds for k − limit-from 𝑘 k- means. (For the best previously known bound for k − limit-from 𝑘 k- means, see [ 23 ] .)

map a point x ∈ ℋ 𝑥 ℋ x\in\mathcal{H} to one in ℋ ⊕ ℝ direct-sum ℋ ℝ \mathcal{H}\oplus\mathbb{R} , which we equip with the natural Hilbert space structure. For each i 𝑖 i , let

The factor of 2 − 1 / 2 superscript 2 1 2 2^{-1/2} (which could have been replaced by a slightly larger constant) is present because we want c ~ i subscript ~ 𝑐 𝑖 {\tilde{c}}_{i} to belong to to the unit ball. Then,

Let ℱ Φ subscript ℱ Φ \mathcal{F}_{\Phi} be the set of functions of the form 4 ​ min i = 1 k ⁡ Φ ​ ( x ) ⋅ c ~ i ⋅ 4 superscript subscript 𝑖 1 𝑘 Φ 𝑥 subscript ~ 𝑐 𝑖 4\min_{i=1}^{k}\Phi(x)\cdot{\tilde{c}}_{i} where c ~ i subscript ~ 𝑐 𝑖 {\tilde{c}}_{i} is given by ( 16 ) and

Proof of Theorem  1 .

This follows immediately from Corollary  6 and Lemma  12 . ∎

6. Dimension reduction

Suppose that X = { x 1 , … , x s } 𝑋 subscript 𝑥 1 … subscript 𝑥 𝑠 X=\{x_{1},\dots,x_{s}\} is a set of i.i.d random points drawn from 𝒫 𝒫 \mathcal{P} , a probability measure supported in the unit ball B ℋ subscript 𝐵 ℋ B_{\mathcal{H}} of a separable Hilbert space ℋ ℋ \mathcal{H} . Let ℳ e ​ r ​ m ​ ( X ) subscript ℳ 𝑒 𝑟 𝑚 𝑋 \mathcal{M}_{erm}(X) denote a manifold in 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) that (approximately) minimizes

Suppose ϵ < c ​ τ italic-ϵ 𝑐 𝜏 {\epsilon}<c\tau . Let W 𝑊 W denote an arbitrary 2 ​ s 𝒢 ​ ( ϵ , δ ) 2 subscript 𝑠 𝒢 italic-ϵ 𝛿 2s_{\mathcal{G}}({\epsilon},{\mathbf{\delta}}) dimensional linear subspace of ℋ ℋ \mathcal{H} containing X 𝑋 X . Then

Let ℳ 2 ∈ 𝒢 := 𝒢 ​ ( d , V , τ ) subscript ℳ 2 𝒢 assign 𝒢 𝑑 𝑉 𝜏 \mathcal{M}_{2}\in\mathcal{G}:=\mathcal{G}(d,V,\tau) achieve

Let N ϵ subscript 𝑁 italic-ϵ N_{\epsilon} denote a set of no more than s G ​ ( ϵ , δ ) subscript 𝑠 𝐺 italic-ϵ 𝛿 s_{G}({\epsilon},{\mathbf{\delta}}) points contained in ℳ 2 subscript ℳ 2 \mathcal{M}_{2} that is an ϵ − limit-from italic-ϵ {\epsilon}- net of ℳ 2 subscript ℳ 2 \mathcal{M}_{2} . Thus for every x ∈ ℳ 2 𝑥 subscript ℳ 2 x\in\mathcal{M}_{2} , there is y ∈ N ϵ 𝑦 subscript 𝑁 italic-ϵ y\in N_{\epsilon} such that | x − y | < ϵ 𝑥 𝑦 italic-ϵ |x-y|<{\epsilon} . Let O 𝑂 O denote a unitary transformation from ℋ ℋ \mathcal{H} to ℋ ℋ \mathcal{H} that fixes each point in X 𝑋 X and maps every point in N ϵ subscript 𝑁 italic-ϵ N_{\epsilon} to some point in W 𝑊 W . Let Π W subscript Π 𝑊 \Pi_{W} denote the map from ℋ ℋ \mathcal{H} to W 𝑊 W that maps x 𝑥 x to the point in W 𝑊 W nearest to x 𝑥 x . Let ℳ 3 := O ​ ℳ 2 . assign subscript ℳ 3 𝑂 subscript ℳ 2 \mathcal{M}_{3}:=O\mathcal{M}_{2}. Since O 𝑂 O is an isometry that fixes X 𝑋 X ,

Since 𝒫 X subscript 𝒫 𝑋 \mathcal{P}_{X} is supported in the unit ball and the Hausdorff distance between Π W ​ ℳ 3 subscript Π 𝑊 subscript ℳ 3 \Pi_{W}\mathcal{M}_{3} and ℳ 3 subscript ℳ 3 \mathcal{M}_{3} is at most ϵ italic-ϵ {\epsilon} ,

By Lemma  14 , we see that Π W ​ ℳ 3 subscript Π 𝑊 subscript ℳ 3 \Pi_{W}\mathcal{M}_{3} belongs to 𝒢 ​ ( d , V , τ ​ ( 1 − c ) ) 𝒢 𝑑 𝑉 𝜏 1 𝑐 \mathcal{G}(d,V,\tau(1-c)) , thus proving the lemma. ∎

By Lemma  13 , it suffices to find a manifold 𝒢 ​ ( d , V , τ ) ∋ M ~ e ​ r ​ m ​ ( X ) ⊆ V contains 𝒢 𝑑 𝑉 𝜏 subscript ~ 𝑀 𝑒 𝑟 𝑚 𝑋 𝑉 \mathcal{G}(d,V,\tau)\ni\tilde{M}_{erm}(X)\subseteq V such that

Let ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) , and let Π Π \Pi be a map that projects ℋ ℋ \mathcal{H} orthogonally onto a subspace containing the linear span of a c ​ ϵ ​ τ − limit-from 𝑐 italic-ϵ 𝜏 {c{\epsilon}}\tau- net S ¯ ¯ 𝑆 \bar{S} of ℳ ℳ \mathcal{M} . Then, the image of ℳ ℳ \mathcal{M} , is a d − limit-from 𝑑 d- dimensional submanifold of ℋ ℋ \mathcal{H} and

The volume of Π ​ ( ℳ ) Π ℳ \Pi(\mathcal{M}) is no more than the volume of ℳ ℳ \mathcal{M} because Π Π \Pi is a contraction. Since ℳ ℳ \mathcal{M} is contained in the unit ball, Π ​ ( ℳ ) Π ℳ \Pi(\mathcal{M}) is contained in the unit ball.

First suppose that | x − y | < ϵ ​ τ 𝑥 𝑦 italic-ϵ 𝜏 |{x}-y|<\sqrt{{\epsilon}}\tau . Choose x ~ ∈ S ¯ ~ 𝑥 ¯ 𝑆 \tilde{x}\in\bar{S} that satisfies

𝑥 𝑦 𝑥 italic-ϵ 𝜏 𝑦 𝑥 z:=x+\frac{(y-x)\sqrt{{\epsilon}}\tau}{|y-x|} . By linearity and Proposition  1 ,

Therefore, there is a point y ^ ∈ T ​ a ​ n ​ ( x , ℳ ) ^ 𝑦 𝑇 𝑎 𝑛 𝑥 ℳ \hat{y}\in Tan(x,\mathcal{M}) such that

By Claim  1 , there is a point y ¯ ∈ ℳ ¯ 𝑦 ℳ \bar{y}\in\mathcal{M} such that

Let y ~ ∈ S ¯ ~ 𝑦 ¯ 𝑆 \tilde{y}\in\bar{S} satisfy

Consequently,

We now have

Since x ~ ~ 𝑥 \tilde{x} and y ~ ~ 𝑦 \tilde{y} belong to the range of Π Π \Pi , it follows from ( 24 ) and ( 27 ) that

𝑥 ~ 𝑥 𝑦 ~ 𝑦 2 𝑐 italic-ϵ 𝜏 |x-\tilde{x}|+|y-\tilde{y}|<2c{\epsilon}\tau . Then,

and the claim follows since x ~ ~ 𝑥 \tilde{x} and y ~ ~ 𝑦 \tilde{y} belong to the range of Π Π \Pi . ∎

By Claim  3 , we see that

the lemma follows. ∎

7. Overview of the algorithm

Given a set X := { x 1 , … , x s } assign 𝑋 subscript 𝑥 1 … subscript 𝑥 𝑠 X:=\{x_{1},\dots,x_{s}\} of points in ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} , we give an overview of the algorithm that finds a nearly optimal interpolating manifold.

Definition 9 .

Let ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) be called an ϵ − limit-from italic-ϵ {\epsilon}- optimal interpolant if

where C 𝐶 C is some constant depending only on d 𝑑 d .

With probability greater than 1 − δ 1 𝛿 1-{\mathbf{\delta}} , ℳ ℳ \mathcal{M} is an ϵ − limit-from italic-ϵ {\epsilon}- optimal interpolant and

As a consequence of ( 33 ) and the lower bounds on the reaches of ℳ ℳ \mathcal{M} and ℳ ′ superscript ℳ ′ \mathcal{M}^{\prime} , it follows (as has been shown in Lemma  17 ) that ℳ ℳ \mathcal{M} must be the graph of a section of D ′ superscript 𝐷 ′ D^{\prime} . In other words ℳ ℳ \mathcal{M} intersects each fiber of D ′ superscript 𝐷 ′ D^{\prime} in a unique point. We use convex optimization to find good local sections, and patch them up to find a good global section. Thus, our algorithm involves two main phases:

Construct a set 𝒟 ¯ norm superscript ¯ 𝒟 norm \mathcal{\bar{D}}^{\texttt{norm}} of disc bundles over manifolds in 𝒢 ​ ( d , C ​ V , τ / C ) 𝒢 𝑑 𝐶 𝑉 𝜏 𝐶 \mathcal{G}(d,CV,\tau/C) is rich enough that every ϵ − limit-from italic-ϵ {\epsilon}- optimal interpolant is a section of some member of 𝒟 ¯ norm superscript ¯ 𝒟 norm \mathcal{\bar{D}}^{\texttt{norm}} .

Given D norm ∈ 𝒟 ¯ norm superscript 𝐷 norm superscript ¯ 𝒟 norm D^{\texttt{norm}}\in\mathcal{\bar{D}}^{\texttt{norm}} , use convex optimization to find a minimal ϵ ^ ^ italic-ϵ \hat{{\epsilon}} such that D norm superscript 𝐷 norm D^{\texttt{norm}} has a section (i. e. a small transverse perturbation of the base manifold of D norm superscript 𝐷 norm D^{{\texttt{norm}}} ) which is a ϵ ^ − limit-from ^ italic-ϵ \hat{{\epsilon}}- optimal interpolant. This is achieved by finding the right manifold in the vicinity of the base manifold of D norm superscript 𝐷 norm D^{\texttt{norm}} by finding good local sections (using results from [ 12 , 13 ] ) and then patching these up using a gentle partition of unity supported on the base manifold of D norm . superscript 𝐷 norm D^{\texttt{norm}}.

8. Disc Bundles

The following definition specifies the kind of bundles we will be interested in. The constants have been named so as to be consistent with their appearance in ( 102 ) and Observation  4 . Recall the parameter r 𝑟 r from Definition  3 .

Definition 10 .

Definition 11 ..

D norm superscript 𝐷 norm D^{\texttt{norm}} is a disc bundle over the manifold ℳ ∈ 𝒢 ​ ( d , τ ^ , V ^ ) ℳ 𝒢 𝑑 ^ 𝜏 ^ 𝑉 \mathcal{M}\in\mathcal{G}(d,\hat{\tau},\hat{V}) .

• subscript 𝑧 0 ℳ direct-sum 0 superscript ℝ 𝑛 𝑑 Nor_{z_{0},\mathcal{M}}=\{0\}\oplus\mathbb{R}^{n-d} . Then, D norm ∩ B ​ ( z 0 , c ¯ 11 ​ τ ^ ) superscript 𝐷 norm 𝐵 subscript 𝑧 0 subscript ¯ 𝑐 11 ^ 𝜏 D^{\texttt{norm}}\cap B(z_{0},\overline{c}_{11}\hat{\tau}) is a bundle over a graph { ( z , Ψ ​ ( z ) ) } z ∈ Ω z 0 subscript 𝑧 Ψ 𝑧 𝑧 subscript Ω subscript 𝑧 0 \{(z,\Psi(z))\}_{z\in\Omega_{z_{0}}} where the domain Ω z 0 subscript Ω subscript 𝑧 0 \Omega_{z_{0}} is an open subset of T ​ a ​ n ​ ( z 0 , ℳ ) 𝑇 𝑎 𝑛 subscript 𝑧 0 ℳ Tan(z_{0},\mathcal{M}) .

𝑥 Ψ 𝑥 𝑣 (x,\Psi(x))+v with x ∈ B d ​ ( z 0 , c ¯ 10 ​ τ ^ ) , v ∈ Π ( x , Ψ ​ ( x ) ) ​ B n − d ​ ( x , c ¯ 10 ​ τ ^ 2 ) . formulae-sequence 𝑥 subscript 𝐵 𝑑 subscript 𝑧 0 subscript ¯ 𝑐 10 ^ 𝜏 𝑣 subscript Π 𝑥 Ψ 𝑥 subscript 𝐵 𝑛 𝑑 𝑥 subscript ¯ 𝑐 10 ^ 𝜏 2 x\in B_{d}(z_{0},\overline{c}_{10}\hat{\tau}),v\in\Pi_{(x,\Psi(x))}B_{n-d}(x,\frac{\overline{c}_{10}\hat{\tau}}{2}). Moreover, x 𝑥 x and v 𝑣 v here are 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smooth functions of z ∈ B n ​ ( x , c ¯ 11 ​ τ ^ ) 𝑧 subscript 𝐵 𝑛 𝑥 subscript ¯ 𝑐 11 ^ 𝜏 z\in B_{n}(x,\overline{c}_{11}\hat{\tau}) , with derivatives up to order k − 2 𝑘 2 {k-2} bounded by C 𝐶 C in absolute value.

Let x ∈ B d ​ ( z 0 , c ¯ 10 ​ τ ^ ) 𝑥 subscript 𝐵 𝑑 subscript 𝑧 0 subscript ¯ 𝑐 10 ^ 𝜏 x\in B_{d}(z_{0},\overline{c}_{10}\hat{\tau}) , and let v ∈ Π ( x , Ψ ​ ( x ) ) ​ ℝ n . 𝑣 subscript Π 𝑥 Ψ 𝑥 superscript ℝ 𝑛 v\in\Pi_{(x,\Psi(x))}\mathbb{R}^{n}. Then, we can express v 𝑣 v in the form

where v # ∈ { 0 } ⊕ ℝ n − d superscript 𝑣 # direct-sum 0 superscript ℝ 𝑛 𝑑 v^{\#}\in\{0\}\oplus\mathbb{R}^{n-d} and | v # | ≤ 2 ​ | v | superscript 𝑣 # 2 𝑣 |v^{\#}|\leq 2|v| .

Definition 12 .

For any D norm → ℳ base ∈ 𝒟 ¯ ​ ( d , τ ^ , V ^ ) → superscript 𝐷 norm subscript ℳ base ¯ 𝒟 𝑑 ^ 𝜏 ^ 𝑉 D^{\texttt{norm}}\rightarrow\mathcal{M}_{\texttt{base}}\in\mathcal{\bar{D}}(d,\hat{\tau},\hat{V}) , and α ∈ ( 0 , 1 ) , 𝛼 0 1 \alpha\in(0,1), let α ​ 𝒟 ¯ ​ ( d , τ ^ , V ^ ) 𝛼 ¯ 𝒟 𝑑 ^ 𝜏 ^ 𝑉 \alpha\mathcal{\bar{D}}(d,\hat{\tau},\hat{V}) denote a bundle over ℳ base subscript ℳ base \mathcal{M}_{\texttt{base}} , whose every fiber is a scaling by α 𝛼 \alpha of the corresponding fiber of D norm superscript 𝐷 norm D^{\texttt{norm}} .

9. A key lemma

Given a function with prescribed smoothness, the following key lemma allows us to construct a bundle satisfying certain conditions, as well as assert that the base manifold has controlled reach. We decompose ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} as ℝ d ⊕ ℝ n − d direct-sum superscript ℝ 𝑑 superscript ℝ 𝑛 𝑑 \mathbb{R}^{d}\oplus\mathbb{R}^{n-d} . When we write ( x , y ) ∈ ℝ n 𝑥 𝑦 superscript ℝ 𝑛 (x,y)\in\mathbb{R}^{n} , we mean x ∈ ℝ d 𝑥 superscript ℝ 𝑑 x\in\mathbb{R}^{d} and y ∈ ℝ n − d 𝑦 superscript ℝ 𝑛 𝑑 y\in\mathbb{R}^{n-d} .

Let the following conditions hold.

Suppose F : B n ​ ( 0 , 1 ) → ℝ : 𝐹 → subscript 𝐵 𝑛 0 1 ℝ F:B_{n}(0,1)\rightarrow\mathbb{R} is 𝒞 k − limit-from superscript 𝒞 𝑘 \mathcal{C}^{k}- smooth.

for ( x , y ) ∈ B n ​ ( 0 , 1 ) 𝑥 𝑦 subscript 𝐵 𝑛 0 1 (x,y)\in B_{n}(0,1) and | α | ≤ k 𝛼 𝑘 |\alpha|\leq k .

For x ∈ ℝ d 𝑥 superscript ℝ 𝑑 x\in\mathbb{R}^{d} and y ∈ ℝ n − d 𝑦 superscript ℝ 𝑛 𝑑 y\in\mathbb{R}^{n-d} and ( x , y ) ∈ B n ​ ( 0 , 1 ) 𝑥 𝑦 subscript 𝐵 𝑛 0 1 (x,y)\in B_{n}(0,1) , suppose also that

• subscript 𝐶 0 subscript 𝑐 1 subscript 𝐶 1 𝑘 𝑛 C_{0},c_{1},C_{1},k,n .

𝛼 subscript Π ℎ 𝑖 𝑧 𝐶 |\partial^{\alpha}\Pi_{hi}(z)|\leq C for z ∈ B n ​ ( 0 , c 2 ) , | α | ≤ k − 2 . formulae-sequence 𝑧 subscript 𝐵 𝑛 0 subscript 𝑐 2 𝛼 𝑘 2 z\in B_{n}(0,c_{2}),|\alpha|\leq{k-2}. Thus, N ​ ( z ) 𝑁 𝑧 \mathit{N}(z) depends 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smoothly on z 𝑧 z .

There is a 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smooth map

with the following properties

on B d ​ ( 0 , c 4 ) , subscript 𝐵 𝑑 0 subscript 𝑐 4 B_{d}(0,c_{4}), for 1 ≤ | α | ≤ k − 2 1 𝛼 𝑘 2 1\leq|\alpha|\leq{k-2} . Then, the set of all z = ( x , y ) ∈ B d ​ ( 0 , c 4 ) × B n − d ​ ( 0 , c 3 ) , 𝑧 𝑥 𝑦 subscript 𝐵 𝑑 0 subscript 𝑐 4 subscript 𝐵 𝑛 𝑑 0 subscript 𝑐 3 z=(x,y)\in B_{d}(0,c_{4})\times B_{n-d}(0,c_{3}), such that

is a 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smooth graph.

𝑥 Ψ 𝑥 𝑣 z=(x,\Psi(x))+v , with x ∈ B d ​ ( 0 , c 5 ) , v ∈ N ​ ( x , Ψ ​ ( x ) ) ∩ B n ​ ( 0 , c 6 ) formulae-sequence 𝑥 subscript 𝐵 𝑑 0 subscript 𝑐 5 𝑣 𝑁 𝑥 Ψ 𝑥 subscript 𝐵 𝑛 0 subscript 𝑐 6 x\in B_{d}(0,c_{5}),v\in\mathit{N}(x,\Psi(x))\cap B_{n}(0,c_{6}) . Define

𝑥 Ψ 𝑥 𝑣 z=(x,\Psi(x))+v . Then, Φ d subscript Φ 𝑑 \Phi_{d} and Φ n − d subscript Φ 𝑛 𝑑 \Phi_{n-d} are 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- functions of z 𝑧 z and their derivatives of order up to k − 2 𝑘 2 {k-2} are at most C 𝐶 C in absolute value.

We first study the gradient and Hessian of F 𝐹 F . Taking ( x , y ) = ( 0 , 0 ) 𝑥 𝑦 0 0 (x,y)=(0,0) in ( 36 ), we see that

A standard lemma in analysis asserts that non-negative F 𝐹 F satisfying ( 35 ) must also satisfy

𝐹 superscript 𝜌 2 F+\rho^{2} , we find that

superscript 𝑥 2 superscript 𝑦 2 1 2 superscript 𝜌 2 3 (|x|^{2}+|y|^{2})^{\frac{1}{2}}\leq\rho^{\frac{2}{3}} , for z = ( z 1 , … , z n ) = ( x , y ) , 𝑧 subscript 𝑧 1 … subscript 𝑧 𝑛 𝑥 𝑦 z=(z_{1},\dots,z_{n})=(x,y), estimates ( 35 ) and ( 41 ) and Taylor’s theorem yield

Hence, ( 36 ) implies that

𝑖 𝑗 2 𝐹 0 \left(\partial_{ij}^{2}F(0)\right) satisfies

That is, the matrices

are positive definite, real and symmetric. If ( A i ​ j ) subscript 𝐴 𝑖 𝑗 \left(A_{ij}\right) is positive definite, real and symmetric, then

for i ≠ j 𝑖 𝑗 i\neq j , since the two–by–two submatrix

must also be positive definite and thus has a positive determinant. It follows from ( 47 ) that

if i ≤ d 𝑖 𝑑 i\leq d , and

for any j 𝑗 j . Therefore, if i ≤ d 𝑖 𝑑 i\leq d and j > d 𝑗 𝑑 j>d , then

𝑑 1 𝑗 𝑛 d+1\leq j\leq n . Without loss of generality, we can rotate the last n − d 𝑛 𝑑 n-d coordinate axes in ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} , so that the matrix

is diagonal, say,

For an n × n 𝑛 𝑛 n\times n matrix A = ( a i ​ j ) 𝐴 subscript 𝑎 𝑖 𝑗 A=(a_{ij}) , let

Then ( 47 ) and ( 48 ) show that

𝑑 1 … 𝑛 j=d+1,\dots,n. We can pick controlled constants so that ( 53 ), ( 54 ) and ( 35 ), ( 37 ) imply the following.

Notation 1 .

For λ j subscript 𝜆 𝑗 \lambda_{j} satisfying ( 54 ), let c # superscript 𝑐 # c^{\#} be a sufficiently small controlled constant. Let Ω Ω \Omega be the set of all real symmetric n × n 𝑛 𝑛 n\times n matrices A 𝐴 A such that

Definition 13 .

If A ∈ Ω 𝐴 Ω A\in\Omega , let Π h ​ i ​ ( A ) : ℝ n → ℝ n : subscript Π ℎ 𝑖 𝐴 → superscript ℝ 𝑛 superscript ℝ 𝑛 \Pi_{hi}(A):\mathbb{R}^{n}\rightarrow\mathbb{R}^{n} be the orthogonal projection from ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} to the span of the eigenspaces of A 𝐴 A that correspond to eigenvalues in [ c ¯ 2 , C ¯ 3 ] , subscript ¯ 𝑐 2 subscript ¯ 𝐶 3 [\overline{c}_{2},\overline{C}_{3}], and let Π l ​ o : ℝ n → ℝ n : subscript Π 𝑙 𝑜 → superscript ℝ 𝑛 superscript ℝ 𝑛 \Pi_{lo}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n} be the orthogonal projection from ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} onto the span of the eigenspaces of A 𝐴 A that correspond to eigenvalues in [ − c ¯ 1 , c ¯ 1 ] . subscript ¯ 𝑐 1 subscript ¯ 𝑐 1 [-\overline{c}_{1},\overline{c}_{1}].

Then, A ↦ Π h ​ i ​ ( A ) maps-to 𝐴 subscript Π ℎ 𝑖 𝐴 A\mapsto\Pi_{hi}(A) and A ↦ Π l ​ o ​ ( A ) maps-to 𝐴 subscript Π 𝑙 𝑜 𝐴 A\mapsto\Pi_{lo}(A) are smooth maps from the compact set Ω Ω \Omega into the space of all real symmetric n × n 𝑛 𝑛 n\times n matrices. For a matrix A 𝐴 A , let | A | 𝐴 |A| denote its spectral norm, i. e.

Then, in particular,

for A ∈ Ω , | α | ≤ k . formulae-sequence 𝐴 Ω 𝛼 𝑘 A\in\Omega,|\alpha|\leq k. Let

for z < c ¯ 4 𝑧 subscript ¯ 𝑐 4 z<\overline{c}_{4} , which make sense, thanks to the comment following ( 59 ). Also, we define projections Π d : ℝ n → ℝ n : subscript Π 𝑑 → superscript ℝ 𝑛 superscript ℝ 𝑛 \Pi_{d}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n} and Π n − d : ℝ n → ℝ n : subscript Π 𝑛 𝑑 → superscript ℝ 𝑛 superscript ℝ 𝑛 \Pi_{n-d}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n} by setting

From ( 53 ) 53 (\ref{eq:ch8}) and ( 60 ) 60 (\ref{eq:ch12}) we see that

Also, ( 35 ) and ( 61 ) together give

for | z | < c ¯ 4 , | α | ≤ k − 2 formulae-sequence 𝑧 subscript ¯ 𝑐 4 𝛼 𝑘 2 |z|<\overline{c}_{4},|\alpha|\leq{k-2} . From ( 66 ), ( 67 ) and ( 37 ), we have

2 𝐹 𝑧 \partial^{2}F(z) with ( n − d ) 𝑛 𝑑 (n-d) highest eigenvalues; this holds for | z | < c ¯ 4 𝑧 subscript ¯ 𝑐 4 |z|<\overline{c}_{4} . Now set

for | z | < c ¯ 4 𝑧 subscript ¯ 𝑐 4 |z|<\overline{c}_{4} . Thus

𝑑 1 … 𝑛 𝑧 subscript ¯ 𝑐 4 i=d+1,\dots,n,|z|<\overline{c}_{4} . Here, [ Π h ​ i ​ ( z ) ] i ​ j subscript delimited-[] subscript Π ℎ 𝑖 𝑧 𝑖 𝑗 [\Pi_{hi}(z)]_{ij} is the i ​ j 𝑖 𝑗 ij entry of the matrix Π h ​ i ​ ( z ) subscript Π ℎ 𝑖 𝑧 \Pi_{hi}(z) . From ( 67 ) and ( 35 ) we see that

for | z | < c ¯ 4 , | α | ≤ k − 2 formulae-sequence 𝑧 subscript ¯ 𝑐 4 𝛼 𝑘 2 |z|<\overline{c}_{4},|\alpha|\leq{k-2} . Also, since Π n − d subscript Π 𝑛 𝑑 \Pi_{n-d} and Π h ​ i ​ ( z ) subscript Π ℎ 𝑖 𝑧 \Pi_{hi}(z) are orthogonal projections from ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} to subspaces of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} , ( 42 ) and ( 69 ) yield

From ( 71 ), we have

for z = 0 𝑧 0 z=0 . Also, from ( 66 ) and ( 53 ), we see that

𝑑 1 … 𝑛 z=0,i=d+1,\dots,n,j=d+1,\dots,n;

𝑑 1 … 𝑛 \ell=d+1,\dots,n .

In view of the above remarks, ( 74 ) shows that

with the following properties:

on B d ​ ( 0 , c ¯ 6 ) , subscript 𝐵 𝑑 0 subscript ¯ 𝑐 6 B_{d}(0,\overline{c}_{6}), for | α | ≤ k − 2 𝛼 𝑘 2 |\alpha|\leq{k-2} .

Let z = ( x , y ) ∈ B d ​ ( 0 , c ¯ 6 ) × B n − d ​ ( 0 , c ¯ 5 ) . 𝑧 𝑥 𝑦 subscript 𝐵 𝑑 0 subscript ¯ 𝑐 6 subscript 𝐵 𝑛 𝑑 0 subscript ¯ 𝑐 5 z=(x,y)\in B_{d}(0,\overline{c}_{6})\times B_{n-d}(0,\overline{c}_{5}). Then

𝐹 𝑧 0 \Pi_{hi}(z)\partial F(z)=0 . Consequently, after replacing c ¯ 5 subscript ¯ 𝑐 5 \overline{c}_{5} and c ¯ 6 subscript ¯ 𝑐 6 \overline{c}_{6} in ( 76 ), ( 77 ), ( 78 ), ( 79 ) by smaller controlled constants c ¯ 9 < c ¯ 8 < 1 2 ​ c ¯ 7 subscript ¯ 𝑐 9 subscript ¯ 𝑐 8 1 2 subscript ¯ 𝑐 7 \overline{c}_{9}<\overline{c}_{8}<\frac{1}{2}\overline{c}_{7} , we obtain the following results:

is a 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smooth map;

on B d ​ ( 0 , c ¯ 9 ) subscript 𝐵 𝑑 0 subscript ¯ 𝑐 9 B_{d}(0,\overline{c}_{9}) for | α | ≤ k − 2 𝛼 𝑘 2 |\alpha|\leq k-2 ;

𝑑 1 … subscript 𝑣 𝑛 direct-sum 0 superscript ℝ 𝑛 𝑑 v=(0,\dots,0,v_{d+1},\dots,v_{n})\in\{0\}\oplus\mathbb{R}^{n-d} , we define

From ( 67 ) and ( 77 ), we have

𝑑 1 … 𝑛 i=d+1,\dots,n, ( 84 ) gives

𝑑 1 𝑥 … subscript Ψ 𝑛 𝑥 superscript ℝ 𝑛 𝑑 \Psi(x)=(\Psi_{d+1}(x),\dots,\Psi_{n}(x))\in\mathbb{R}^{n-d}. We study the first partials of E i ​ ( x , v ) subscript 𝐸 𝑖 𝑥 𝑣 E_{i}(x,v) at ( x , v ) = ( 0 , 0 ) . 𝑥 𝑣 0 0 (x,v)=(0,0). From ( 86 ), we find that

for i ∈ { 1 , … , d } 𝑖 1 … 𝑑 i\in\{1,\dots,d\} and j ∈ { 1 , … , n } 𝑗 1 … 𝑛 j\in\{1,\dots,n\} . Therefore, another application of ( 86 ) yields

𝑑 1 … 𝑛 i\in[d],j\in\{d+1,\dots,n\} and ( x , v ) = ( 0 , 0 ) 𝑥 𝑣 0 0 (x,v)=(0,0) . Similarly, from ( 89 ) we obtain

𝑑 1 … 𝑛 j=d+1,\dots,n . Therefore, from ( 87 ), we have

𝑑 1 … subscript 𝑣 𝑛 𝐸 𝑥 𝑣 (x_{1},\dots,x_{d},v_{d+1},\dots,v_{n})\mapsto E(x,v) at the origin is given by

where I d subscript 𝐼 𝑑 I_{d} and I n − d subscript 𝐼 𝑛 𝑑 I_{n-d} denote (respectively) the d × d 𝑑 𝑑 d\times d and ( n − d ) × ( n − d ) 𝑛 𝑑 𝑛 𝑑 (n-d)\times(n-d) identity matrices, O ​ ( ρ 1 / 3 ) 𝑂 superscript 𝜌 1 3 O(\rho^{1/3}) denotes a matrix whose entries have absolute values at most C ​ ρ 1 / 3 𝐶 superscript 𝜌 1 3 C\rho^{1/3} ; and O ​ ( 1 ) 𝑂 1 O(1) denotes a matrix whose entries have absolute values at most C 𝐶 C . A matrix of the form ( 96 ) is invertible, and its inverse matrix has norm at most C 𝐶 C . (Here, we use ( 37 ).) Note also that that | E ​ ( 0 , 0 ) | = | ( 0 , Ψ ​ ( 0 ) ) | ≤ C ​ ρ . 𝐸 0 0 0 Ψ 0 𝐶 𝜌 |E(0,0)|=|(0,\Psi(0))|\leq C\rho. Consequently, the inverse function theorem (see Section 3 of [ 24 ] ) and ( 85 ) imply the following.

There exist controlled constants c ¯ 10 subscript ¯ 𝑐 10 \overline{c}_{10} and c ¯ 11 subscript ¯ 𝑐 11 \overline{c}_{11} with the following properties:

is well-defined.

Moreover, we may pick c ¯ 10 subscript ¯ 𝑐 10 \overline{c}_{10} in ( 97 ) small enough that the following holds.

Observation 2 .

Observation 3 ..

~ 𝑥 Ψ ~ 𝑥 ~ 𝑣 (x,\Psi(x))+v=(\tilde{x},\Psi(\tilde{x}))+\tilde{v} , then x = x ~ 𝑥 ~ 𝑥 x=\tilde{x} and v = v ~ 𝑣 ~ 𝑣 v=\tilde{v} .

Observation 4 .

𝑥 Ψ 𝑥 𝑣 (x,\Psi(x))+v with x ∈ B d ​ ( 0 , c ¯ 10 ) , v ∈ Π h ​ i ​ ( x , Ψ ​ ( x ) ) ​ ℝ n ∩ B n − d ​ ( 0 , c ¯ 10 2 ) . formulae-sequence 𝑥 subscript 𝐵 𝑑 0 subscript ¯ 𝑐 10 𝑣 subscript Π ℎ 𝑖 𝑥 Ψ 𝑥 superscript ℝ 𝑛 subscript 𝐵 𝑛 𝑑 0 subscript ¯ 𝑐 10 2 x\in B_{d}(0,\overline{c}_{10}),v\in\Pi_{hi}(x,\Psi(x))\mathbb{R}^{n}\cap B_{n-d}(0,\frac{\overline{c}_{10}}{2}). Moreover, x 𝑥 x and v 𝑣 v here are 𝒞 k − 2 − limit-from superscript 𝒞 𝑘 2 \mathcal{C}^{{k-2}}- smooth functions of z ∈ B n ​ ( 0 , c ¯ 11 ) 𝑧 subscript 𝐵 𝑛 0 subscript ¯ 𝑐 11 z\in B_{n}(0,\overline{c}_{11}) , with derivatives up to order k − 2 𝑘 2 {k-2} bounded by C 𝐶 C in absolute value.

10. Constructing a disc bundle possessing the desired characteristics

10.1. approximate squared distance functions.

Suppose that ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) is a submanifold of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} . Let

For τ ~ > 0 , ~ 𝜏 0 \tilde{\tau}>0, let

Let d ~ ~ 𝑑 \tilde{d} be a suitable large constant depending only on d 𝑑 d , and which is a monotonically increasing function of d 𝑑 d . Let

We use a basis for ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} that is such that ℝ d ¯ superscript ℝ ¯ 𝑑 \mathbb{R}^{\bar{d}} is the span of the first d ¯ ¯ 𝑑 \bar{d} basis vectors, and ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} is the span of the first d 𝑑 d basis vectors. We denote by Π d ¯ subscript Π ¯ 𝑑 \Pi_{\bar{d}} , the corresponding projection of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} onto ℝ d ¯ superscript ℝ ¯ 𝑑 \mathbb{R}^{\bar{d}} .

Definition 14 .

Let a ​ s ​ d ​ f ℳ τ ¯ 𝑎 𝑠 𝑑 superscript subscript 𝑓 ℳ ¯ 𝜏 {asdf}_{\mathcal{M}}^{\bar{\tau}} denote the set of all functions F ¯ : ℳ τ ¯ → ℝ : ¯ 𝐹 → subscript ℳ ¯ 𝜏 ℝ \bar{F}:\mathcal{M}_{\bar{\tau}}\rightarrow\mathbb{R} such that the following is true. For every z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} , there exists an isometry Θ z subscript Θ 𝑧 \Theta_{z} of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} that fixes the origin, and maps ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} to a subspace parallel to the tangent plane at z 𝑧 z such that F ^ z : B n ​ ( 0 , 1 ) → ℝ : subscript ^ 𝐹 𝑧 → subscript 𝐵 𝑛 0 1 ℝ \hat{F}_{z}:B_{n}(0,1)\rightarrow\mathbb{R} given by

satisfies the following.

𝑟 2 r+2 , r 𝑟 r being the number in Definition  3 .

There is a function F z : ℝ d ¯ → ℝ : subscript 𝐹 𝑧 → superscript ℝ ¯ 𝑑 ℝ F_{z}:\mathbb{R}^{\bar{d}}\rightarrow\mathbb{R} such that for any w ∈ B n ​ ( 0 , 1 ) 𝑤 subscript 𝐵 𝑛 0 1 w\in B_{n}(0,1) ,

where ℝ d ⊆ ℝ d ¯ ⊆ ℝ n superscript ℝ 𝑑 superscript ℝ ¯ 𝑑 superscript ℝ 𝑛 \mathbb{R}^{d}\subseteq\mathbb{R}^{\bar{d}}\subseteq\mathbb{R}^{n} .

where Π h ​ i subscript Π ℎ 𝑖 \Pi_{hi} is as in Lemma  15 applied to the function F ^ z subscript ^ 𝐹 𝑧 \hat{F}_{z} .

Let F ¯ ¯ 𝐹 \bar{F} be in a ​ s ​ d ​ f ℳ τ ¯ 𝑎 𝑠 𝑑 superscript subscript 𝑓 ℳ ¯ 𝜏 {asdf}_{\mathcal{M}}^{\bar{\tau}} and let Γ z subscript Γ 𝑧 \Gamma_{z} and Θ z subscript Θ 𝑧 \Theta_{z} be as in Definition  14 .

The graph Γ z subscript Γ 𝑧 \Gamma_{z} is contained in ℝ d ¯ superscript ℝ ¯ 𝑑 \mathbb{R}^{\bar{d}} .

Let c 4 subscript 𝑐 4 c_{4} and c 5 subscript 𝑐 5 c_{5} be the constants appearing in ( 38 ) in Lemma  15 , once we fix C 0 subscript 𝐶 0 C_{0} in ( 35 ) to be 10 10 10 , and the constants c 1 subscript 𝑐 1 c_{1} and C 1 subscript 𝐶 1 C_{1} ( 36 ) to 1 / 10 1 10 1/10 and 10 10 10 respectively. The "putative" submanifold

has a reach greater than c ​ τ 𝑐 𝜏 c\tau , where c 𝑐 c is a controlled constant depending only on d 𝑑 d .

Here Π h ​ i ​ ( z ) subscript Π ℎ 𝑖 𝑧 \Pi_{hi}(z) is the orthogonal projection onto the eigenspace corresponding to eigenvalues in the interval [ c ¯ 2 , C ¯ 2 ] subscript ¯ 𝑐 2 subscript ¯ 𝐶 2 [\overline{c}_{2},\overline{C}_{2}] that is specified in Definition  13 .

subscript ^ 𝐹 𝑧 𝑤 \partial\hat{F}_{z}(w) . Therefore

We proceed to the second part of the Lemma. We choose c ¯ 12 subscript ¯ 𝑐 12 \overline{c}_{12} to be a small enough monotonically decreasing function of d ¯ ¯ 𝑑 \bar{d} (by ( 104 ) and the assumed monotonicity of d ~ ~ 𝑑 \tilde{d} , c ¯ 12 subscript ¯ 𝑐 12 \overline{c}_{12} is consequently a monotonically decreasing function of d 𝑑 d ) such that for every point z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} , F z subscript 𝐹 𝑧 F_{z} given by ( 106 ) satisfies the hypotheses of Lemma  15 with ρ < c ~ ​ τ ¯ C 2 𝜌 ~ 𝑐 ¯ 𝜏 superscript 𝐶 2 \rho<\frac{\tilde{c}{\bar{\tau}}}{C^{2}} where C 𝐶 C is the constant in Equation  39 and where c ~ ~ 𝑐 \tilde{c} is a sufficiently small controlled constant. Suppose that there is a point z ^ ^ 𝑧 \hat{z} in ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} such that 𝐝 ​ ( z ^ , ℳ ) 𝐝 ^ 𝑧 ℳ \mathbf{d}(\hat{z},\mathcal{M}) is greater than m ​ i ​ n ​ ( c 4 , c 5 ) ​ τ ¯ 2 𝑚 𝑖 𝑛 subscript 𝑐 4 subscript 𝑐 5 ¯ 𝜏 2 \frac{min(c_{4},c_{5})\bar{\tau}}{2} , where c 4 subscript 𝑐 4 c_{4} and c 5 subscript 𝑐 5 c_{5} are the constants in ( 38 ). Let z 𝑧 z be the unique point on ℳ ℳ \mathcal{M} nearest to z ^ ^ 𝑧 \hat{z} . We apply Lemma  15 to F z subscript 𝐹 𝑧 F_{z} . By Equation  39 in Lemma  15 , there is a point z ~ ∈ ℳ p ​ u ​ t ~ 𝑧 subscript ℳ 𝑝 𝑢 𝑡 \tilde{z}\in\mathcal{M}_{put} such that

The constant c l ​ e ​ m subscript 𝑐 𝑙 𝑒 𝑚 c_{lem} is controlled by c ~ ~ 𝑐 \tilde{c} and can be made as small as needed provided it is ultimately controlled by d 𝑑 d alone. We have an upper bound of C 𝐶 C on the first-order derivatives of Ψ Ψ \Psi in Equation  39 , which is a function whose graph corresponds via Θ z subscript Θ 𝑧 \Theta_{z} to ℳ ℳ \mathcal{M} in a τ ¯ 2 − limit-from ¯ 𝜏 2 {\frac{\bar{\tau}}{2}}- neighborhood of z 𝑧 z . Any unit vector v ∈ T ​ a ​ n 0 ​ ( z ) 𝑣 𝑇 𝑎 superscript 𝑛 0 𝑧 v\in Tan^{0}(z) , is nearly orthogonal to z ~ − z ^ ~ 𝑧 ^ 𝑧 \tilde{z}-\hat{z} in that

Ψ |\partial\Psi| from Equation  39 .

This shows that for every z ^ ∈ ℳ p ​ u ​ t ^ 𝑧 subscript ℳ 𝑝 𝑢 𝑡 \hat{z}\in\mathcal{M}_{put} its distance to ℳ ℳ \mathcal{M} satisfies

Recall that

Therefore, for every point z ^ ^ 𝑧 \hat{z} in ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} , there is a point z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} such that

We have now shown that ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} lies not only in ℳ min ⁡ ( c 4 , c 5 ) ​ τ ¯ subscript ℳ subscript 𝑐 4 subscript 𝑐 5 ¯ 𝜏 \mathcal{M}_{{\min(c_{4},c_{5})\bar{\tau}}} but also in ℳ min ⁡ ( c 4 , c 5 ) ​ τ ¯ 2 subscript ℳ subscript 𝑐 4 subscript 𝑐 5 ¯ 𝜏 2 \mathcal{M}_{\frac{\min(c_{4},c_{5})\bar{\tau}}{2}} . This fact, in conjunction with ( 39 ) and Proposition  1 implies that ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} is a manifold with reach greater than c ​ τ 𝑐 𝜏 c\tau .

be the bundle over ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} wherein the fiber at a point z ^ ∈ ℳ p ​ u ​ t ^ 𝑧 subscript ℳ 𝑝 𝑢 𝑡 \hat{z}\in\mathcal{M}_{put} , consists of all points z 𝑧 z such that

| z ^ − z | ≤ c ¯ 12 ​ τ ^ 𝑧 𝑧 subscript ¯ 𝑐 12 𝜏 |\hat{z}-z|\leq\overline{c}_{12}\tau , and

z − w 𝑧 𝑤 z-w lies in the span of the top n − d 𝑛 𝑑 n-d eigenvectors of the Hessian of F ¯ ¯ 𝐹 \bar{F} evaluated at z ^ ^ 𝑧 \hat{z} .

Observation 5 .

11. constructing cylinder packets.

We wish to construct a family of functions ¯ ​ ℱ ¯ absent ℱ \bar{}\mathcal{F} defined on open subsets of B n ​ ( 0 , 1 ) subscript 𝐵 𝑛 0 1 B_{n}(0,1) such that for every ℳ ∈ 𝒢 ​ ( d , V , τ ) ℳ 𝒢 𝑑 𝑉 𝜏 \mathcal{M}\in\mathcal{G}(d,V,\tau) such that ℳ ⊆ B n ​ ( 0 , 1 ) ℳ subscript 𝐵 𝑛 0 1 \mathcal{M}\subseteq B_{n}(0,1) , there is some F ^ ∈ ¯ ​ ℱ ^ 𝐹 ¯ absent ℱ \hat{F}\in\bar{}\mathcal{F} such that the domain of F ^ ^ 𝐹 \hat{F} contains ℳ τ ¯ subscript ℳ ¯ 𝜏 \mathcal{M}_{\bar{\tau}} and the restriction of F ^ ^ 𝐹 \hat{F} to ℳ τ ¯ subscript ℳ ¯ 𝜏 \mathcal{M}_{\bar{\tau}} is contained in a ​ s ​ d ​ f ℳ τ ¯ 𝑎 𝑠 𝑑 superscript subscript 𝑓 ℳ ¯ 𝜏 {asdf}_{\mathcal{M}}^{\bar{\tau}} .

Let ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} and ℝ n − d superscript ℝ 𝑛 𝑑 \mathbb{R}^{n-d} respectively denote the spans of the first d 𝑑 d vectors and the last n − d 𝑛 𝑑 n-d vectors of the canonical basis of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} . Let B d subscript 𝐵 𝑑 B_{d} and B n − d subscript 𝐵 𝑛 𝑑 B_{n-d} respectively denote the unit Euclidean balls in ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} and ℝ n − d superscript ℝ 𝑛 𝑑 \mathbb{R}^{n-d} . Let Π d subscript Π 𝑑 \Pi_{d} be the map given by the orthogonal projection from ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} onto ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} . Let cyl := τ ¯ ​ ( B d × B n − d ) assign cyl ¯ 𝜏 subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 {\texttt{cyl}}:={\bar{\tau}}(B_{d}\times B_{n-d}) , and cyl 2 = 2 ​ τ ¯ ​ ( B d × B n − d ) superscript cyl 2 2 ¯ 𝜏 subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 {\texttt{cyl}}^{{2}}={2\bar{\tau}}(B_{d}\times B_{n-d}) . Suppose that for any x ∈ 2 ​ τ ¯ ​ B d 𝑥 2 ¯ 𝜏 subscript 𝐵 𝑑 x\in 2{\bar{\tau}}B_{d} and y ∈ 2 ​ τ ¯ ​ B n − d 𝑦 2 ¯ 𝜏 subscript 𝐵 𝑛 𝑑 y\in 2{\bar{\tau}}B_{n-d} , ϕ cyl 2 : ℝ d ⊕ ℝ n − d → ℝ : subscript italic-ϕ superscript cyl 2 → direct-sum superscript ℝ 𝑑 superscript ℝ 𝑛 𝑑 ℝ \phi_{{\texttt{cyl}}^{2}}:\mathbb{R}^{d}\oplus\mathbb{R}^{n-d}\rightarrow\mathbb{R} is given by

and for any z ∉ cyl 2 𝑧 superscript cyl 2 z\not\in{{\texttt{cyl}}^{2}} ,

Suppose for each i ∈ [ N ¯ ] := { 1 , … , N ¯ } 𝑖 delimited-[] ¯ 𝑁 assign 1 … ¯ 𝑁 i\in[\bar{N}]:=\{1,\dots,\bar{N}\} , x i ∈ B n ​ ( 0 , 1 ) subscript 𝑥 𝑖 subscript 𝐵 𝑛 0 1 x_{i}\in B_{n}(0,1) and o i subscript 𝑜 𝑖 o_{i} is a proper rigid body motion, i. e. the composition of a proper rotation and translation of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} and that o i ​ ( 0 ) = x i subscript 𝑜 𝑖 0 subscript 𝑥 𝑖 o_{i}(0)=x_{i} .

For each i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] , let cyl i := o i ​ ( cyl ) , assign subscript cyl 𝑖 subscript 𝑜 𝑖 cyl {\texttt{cyl}}_{i}:=o_{i}({\texttt{cyl}}), and cyl i 2 := o i ​ ( cyl 2 ) . assign subscript superscript cyl 2 𝑖 subscript 𝑜 𝑖 superscript cyl 2 {\texttt{cyl}}^{2}_{i}:=o_{i}({\texttt{cyl}}^{2}). Note that x i subscript 𝑥 𝑖 x_{i} is the center of cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} .

We say that a set of cylinders C p := { cyl 1 2 , … , cyl N ¯ 2 } assign subscript 𝐶 𝑝 superscript subscript cyl 1 2 … superscript subscript cyl ¯ 𝑁 2 C_{p}:=\{{\texttt{cyl}}_{1}^{2},\dots,{\texttt{cyl}}_{\bar{N}}^{2}\} (where each cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} is isometric to cyl 2 superscript cyl 2 {\texttt{cyl}}^{2} ) is a cylinder packet if the following conditions hold true for each i 𝑖 i .

Let S i := { cyl i 1 2 , … , cyl i | S i | 2 } assign subscript 𝑆 𝑖 superscript subscript cyl subscript 𝑖 1 2 … superscript subscript cyl subscript 𝑖 subscript 𝑆 𝑖 2 S_{i}:=\{{\texttt{cyl}}_{i_{1}}^{2},\dots,{\texttt{cyl}}_{i_{|S_{i}|}}^{2}\} be the set of cylinders that intersect cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} . Translate the origin to the center of cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} (i. e.  x i subscript 𝑥 𝑖 x_{i} ) and perform a proper Euclidean transformation that puts the d − limit-from 𝑑 d- dimensional central cross-section of cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} in ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} .

For each j ∈ [ | S i | ] 𝑗 delimited-[] subscript 𝑆 𝑖 j\in[|S_{i}|] , T ​ r i j ​ U i j ​ cyl i j 2 𝑇 subscript 𝑟 subscript 𝑖 𝑗 subscript 𝑈 subscript 𝑖 𝑗 subscript superscript cyl 2 subscript 𝑖 𝑗 Tr_{i_{j}}U_{i_{j}}{\texttt{cyl}}^{2}_{i_{j}} is a translation of cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} by a vector contained in ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} .

| ( I ​ d − U i j ) ​ v | < c 12 ​ τ ¯ ​ | v − x i j | 𝐼 𝑑 subscript 𝑈 subscript 𝑖 𝑗 𝑣 subscript 𝑐 12 ¯ 𝜏 𝑣 subscript 𝑥 subscript 𝑖 𝑗 \big{|}\left(Id-U_{i_{j}}\right)v\big{|}<c_{12}{\bar{\tau}}|v-x_{i_{j}}| , for each j 𝑗 j in { 1 , … , | S j | } 1 … subscript 𝑆 𝑗 \{1,\dots,|S_{j}|\}

| T ​ r i j ​ ( 0 ) | < C ​ τ ¯ 2 τ 𝑇 subscript 𝑟 subscript 𝑖 𝑗 0 𝐶 superscript ¯ 𝜏 2 𝜏 |Tr_{i_{j}}(0)|<C\frac{{\bar{\tau}}^{2}}{\tau} for each j 𝑗 j in { 1 , … , | S j | } 1 … subscript 𝑆 𝑗 \{1,\dots,|S_{j}|\} .

⋃ j ( T ​ r i j ​ U i j ​ cyl j ) ⊇ B d ​ ( 0 , 3 ​ τ ¯ ) subscript 𝐵 𝑑 0 3 ¯ 𝜏 subscript 𝑗 𝑇 subscript 𝑟 subscript 𝑖 𝑗 subscript 𝑈 subscript 𝑖 𝑗 subscript cyl 𝑗 \bigcup_{j}(Tr_{i_{j}}U_{i_{j}}{\texttt{cyl}}_{j})\supseteq B_{d}(0,3\bar{\tau}) .

We call { o 1 , … , o N ¯ } subscript 𝑜 1 … subscript 𝑜 ¯ 𝑁 \{o_{1},\dots,o_{\bar{N}}\} a packet if { o 1 ​ ( cyl ) , … , o N ​ ( cyl ) } subscript 𝑜 1 cyl … subscript 𝑜 𝑁 cyl \{o_{1}({\texttt{cyl}}),\dots,o_{N}({\texttt{cyl}})\} is a cylinder packet.

12. Constructing an exhaustive family of disc bundles

We now show how to construct a set D ¯ ¯ 𝐷 \bar{D} of disc bundles rich enough that any manifold ℳ ∈ 𝒢 ​ ( d , τ , V ) ℳ 𝒢 𝑑 𝜏 𝑉 \mathcal{M}\in\mathcal{G}(d,\tau,V) corresponds to a section of at least one disc bundle in D ¯ ¯ 𝐷 \bar{D} . The constituent disc bundles in D ¯ ¯ 𝐷 \bar{D} will be obtained from cylinder packets.

to be a bump function that has the following properties for any fixed k 𝑘 k for a controlled constant C 𝐶 C .

For all α 𝛼 \alpha such that 0 < | α | ≤ k 0 𝛼 𝑘 0<|\alpha|\leq k , for all x ∈ { 0 } ∪ { x | | x | ≥ 1 } 𝑥 0 conditional-set 𝑥 𝑥 1 x\in\{0\}\cup\{x|\,|x|\geq 1\}

and for all x ∈ { x | | x | ≥ 1 } 𝑥 conditional-set 𝑥 𝑥 1 x\in\{x|\,|x|\geq 1\}

for all x , 𝑥 x,

and for | x | < 1 4 𝑥 1 4 |x|<\frac{1}{4} ,

Definition 15 .

Given a Packet o ¯ := { o 1 , … , o N ¯ } assign ¯ 𝑜 subscript 𝑜 1 … subscript 𝑜 ¯ 𝑁 \bar{o}:=\{o_{1},\dots,o_{\bar{N}}\} , define F o ¯ : ⋃ i cyl i → ℝ : superscript 𝐹 ¯ 𝑜 → subscript 𝑖 subscript cyl 𝑖 ℝ F^{\bar{o}}:\bigcup_{i}{\texttt{cyl}}_{i}\rightarrow\mathbb{R} by

Definition 16 .

Let A 1 subscript 𝐴 1 A_{1} and A 2 subscript 𝐴 2 A_{2} be two d − limit-from 𝑑 d- dimensional affine subspaces of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} for some n ≥ 1 𝑛 1 n\geq 1 , that respectively contain points x 1 subscript 𝑥 1 x_{1} and x 2 subscript 𝑥 2 x_{2} . We define ∢ ​ ( A 1 , A 2 ) ∢ subscript 𝐴 1 subscript 𝐴 2 \sphericalangle(A_{1},A_{2}) , the "angle between A 1 subscript 𝐴 1 A_{1} and A 2 subscript 𝐴 2 A_{2} ", by

Let ℳ ℳ \mathcal{M} belong to 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) . Let Y := { y 1 , … , y N ¯ } assign 𝑌 subscript 𝑦 1 … subscript 𝑦 ¯ 𝑁 Y:=\{y_{1},\dots,y_{\bar{N}}\} be a maximal subset of ℳ ℳ \mathcal{M} with the property that no two distinct points are at a distance of less than τ ¯ 2 ¯ 𝜏 2 \frac{\bar{\tau}}{2} from each other. We construct an ideal cylinder packet { cyl 1 2 , … , cyl N ¯ 2 } superscript subscript cyl 1 2 … superscript subscript cyl ¯ 𝑁 2 \{{\texttt{cyl}}_{1}^{2},\dots,{\texttt{cyl}}_{\bar{N}}^{2}\} by fixing the center of cyl i 2 superscript subscript cyl 𝑖 2 {\texttt{cyl}}_{i}^{2} to be y i subscript 𝑦 𝑖 y_{i} , and fixing their orientations by the condition that for each cylinder cyl i 2 subscript superscript cyl 2 𝑖 {\texttt{cyl}}^{2}_{i} , the d − limit-from 𝑑 d- dimensional central cross-section is a tangent disc to the manifold at y i subscript 𝑦 𝑖 y_{i} . Given an ideal cylinder packet, an admissible cylinder packet corresponding to ℳ ℳ \mathcal{M} is obtained by perturbing the the center of each cylinder by less than c 12 ​ τ ¯ subscript 𝑐 12 ¯ 𝜏 c_{12}{\bar{\tau}} and applying arbitrary unitary transformations to these cylinders whose difference with the identity has a norm less than C ​ τ ¯ 2 τ . 𝐶 superscript ¯ 𝜏 2 𝜏 C\frac{{\bar{\tau}}^{2}}{\tau}.

Let ℳ ℳ \mathcal{M} belong to 𝒢 ​ ( d , V , τ ) 𝒢 𝑑 𝑉 𝜏 \mathcal{G}(d,V,\tau) and let { cyl 1 , … , cyl N ¯ } subscript cyl 1 … subscript cyl ¯ 𝑁 \{{\texttt{cyl}}_{1},\dots,{\texttt{cyl}}_{\bar{N}}\} be an admissible packet corresponding to ℳ ℳ \mathcal{M} .

Recall that a ​ s ​ d ​ f ℳ τ ¯ 𝑎 𝑠 𝑑 superscript subscript 𝑓 ℳ ¯ 𝜏 {asdf}_{\mathcal{M}}^{\bar{\tau}} denotes the set of all F ¯ : ℳ τ ¯ → ℝ : ¯ 𝐹 → subscript ℳ ¯ 𝜏 ℝ \bar{F}:\mathcal{M}_{\bar{\tau}}\rightarrow\mathbb{R} (where τ ¯ = c ¯ 12 ​ τ ¯ 𝜏 subscript ¯ 𝑐 12 𝜏 \bar{\tau}=\overline{c}_{12}\tau and ℳ τ ¯ subscript ℳ ¯ 𝜏 \mathcal{M}_{\bar{\tau}} is a τ ¯ − limit-from ¯ 𝜏 \bar{\tau}- neighborhood of ℳ ℳ \mathcal{M} ) for which the following is true:

For every z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} , there exists an isometry Θ Θ \Theta of ℋ ℋ \mathcal{H} that fixes the origin, and maps ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} to a subspace parallel to the tangent plane at z 𝑧 z satisfying the conditions below. Let F ^ z : B n ​ ( 0 , 1 ) → ℝ : subscript ^ 𝐹 𝑧 → subscript 𝐵 𝑛 0 1 ℝ \hat{F}_{z}:B_{n}(0,1)\rightarrow\mathbb{R} be given by

Then, F ^ z subscript ^ 𝐹 𝑧 \hat{F}_{z}

𝑟 2 k=r+2 .

For any w ∈ B n 𝑤 subscript 𝐵 𝑛 w\in B_{n} ,

where ℝ n ⊇ ℝ d ¯ ⊇ ℝ d superset-of-or-equals superscript ℝ 𝑛 superscript ℝ ¯ 𝑑 superset-of-or-equals superscript ℝ 𝑑 \mathbb{R}^{n}\supseteq\mathbb{R}^{\bar{d}}\supseteq\mathbb{R}^{d} , and Π d ¯ subscript Π ¯ 𝑑 \Pi_{\bar{d}} is the projection of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} onto ℝ d ¯ superscript ℝ ¯ 𝑑 \mathbb{R}^{\bar{d}} .

For any fixed z ∈ ℳ 𝑧 ℳ z\in\mathcal{M} , it suffices to check that there exists a proper isometry Θ Θ \Theta of ℋ ℋ \mathcal{H} such that :

The hypotheses of Lemma  15 are satisfied by

We begin by checking the condition (A). It is clear that F ^ z o ¯ : B n ​ ( 0 , 1 ) → ℝ : superscript subscript ^ 𝐹 𝑧 ¯ 𝑜 → subscript 𝐵 𝑛 0 1 ℝ \hat{F}_{z}^{\bar{o}}:B_{n}(0,1)\rightarrow\mathbb{R} is 𝒞 k − limit-from superscript 𝒞 𝑘 \mathcal{C}^{k}- smooth.

Thus, to check condition (A), it suffices to establish the following claim.

There is a constant C 0 subscript 𝐶 0 C_{0} depending only on d 𝑑 d and k 𝑘 k such that

• 𝑥 𝑦 superscript subscript ^ 𝐹 𝑧 ¯ 𝑜 𝑥 𝑦 subscript 𝐶 0 \partial^{\alpha}_{x,y}\hat{F}_{z}^{\bar{o}}(x,y)\leq C_{0} for ( x , y ) ∈ B n ​ ( 0 , 1 ) 𝑥 𝑦 subscript 𝐵 𝑛 0 1 (x,y)\in B_{n}(0,1) and 1 ≤ | α | ≤ k 1 𝛼 𝑘 1\leq|\alpha|\leq k .

For ( x , y ) ∈ B n ​ ( 0 , 1 ) 𝑥 𝑦 subscript 𝐵 𝑛 0 1 (x,y)\in B_{n}(0,1) ,

• subscript 𝐶 0 subscript 𝑐 1 subscript 𝐶 1 𝑘 𝑑 C_{0},c_{1},C_{1},k,{d} .

That the first part of the claim, i. e. ( C4.1 ) is true follows from the chain rule and the definition of F ^ z o ¯ ​ ( x , y ) superscript subscript ^ 𝐹 𝑧 ¯ 𝑜 𝑥 𝑦 \hat{F}_{z}^{\bar{o}}(x,y) after rescaling by τ ¯ ¯ 𝜏 \bar{\tau} . We proceed to show ( C4.2 ). For any i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] and any vector v 𝑣 v in ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} , For ρ 𝜌 \rho taken to be the value from Lemma  15 , we see that for a sufficiently small value of c ¯ 12 = τ ¯ τ subscript ¯ 𝑐 12 ¯ 𝜏 𝜏 \overline{c}_{12}=\frac{\bar{\tau}}{\tau} (controlled by d 𝑑 d alone), and a sufficiently small controlled constant as the value of c 12 subscript 𝑐 12 c_{12} , ( 116 ) and ( 117 ) follow because ℳ ℳ \mathcal{M} is a manifold of reach greater or equal to τ 𝜏 \tau , and consequently Proposition  1 holds true.

The inequalities ( 116 ), ( 117 ) and ( 118 ) imply ( C4.2 ), completing the proof of the claim. ∎

Definition 17 .

Let ¯ ​ ℱ ¯ absent ℱ \bar{}\mathcal{F} be set of all functions F o ¯ superscript 𝐹 ¯ 𝑜 F^{\bar{o}} obtained as { cyl i 2 } i ∈ [ N ¯ ] subscript subscript superscript cyl 2 𝑖 𝑖 delimited-[] ¯ 𝑁 \{{\texttt{cyl}}^{2}_{i}\}_{i\in[\bar{N}]} ranges over all cylinder packets centered on points of a lattice whose spacing is a controlled constant multiplied by τ 𝜏 \tau and the orientations are chosen arbitrarily from a net of the Grassmannian manifold G ​ r d n 𝐺 superscript subscript 𝑟 𝑑 𝑛 Gr_{d}^{n} (with the usual Riemannian metric) of scale that is a sufficiently small controlled constant.

By Lemma  17 ¯ ​ ℱ ¯ absent ℱ \bar{}\mathcal{F} has the following property:

Corollary 18 .

For every ℳ ∈ 𝒢 ℳ 𝒢 \mathcal{M}\in\mathcal{G} that is a 𝒞 r − limit-from superscript 𝒞 𝑟 \mathcal{C}^{r}- submanifold, there is some F ^ ∈ ¯ ​ ℱ ^ 𝐹 ¯ absent ℱ \hat{F}\in\bar{}\mathcal{F} that is an approximate-squared-distance-function for ℳ ℳ \mathcal{M} , i. e. the restriction of F ^ ^ 𝐹 \hat{F} to ℳ τ ¯ subscript ℳ ¯ 𝜏 \mathcal{M}_{\bar{\tau}} is contained in a ​ s ​ d ​ f ℳ τ ¯ 𝑎 𝑠 𝑑 superscript subscript 𝑓 ℳ ¯ 𝜏 {asdf}_{\mathcal{M}}^{\bar{\tau}} .

13. Finding good local sections

Definition 18 ..

is an ϵ − limit-from italic-ϵ {\epsilon}- optimal interpolant if the 𝒞 r − limit-from superscript 𝒞 𝑟 \mathcal{C}^{r}- norm of f 𝑓 f (see Definition  20 )) satisfies

where c 𝑐 c and C > 1 𝐶 1 C>1 are some constants depending only on d 𝑑 d .

13.1. Basic convex sets

We will denote the codimension n − d 𝑛 𝑑 n-d by n ¯ ¯ 𝑛 \bar{n} . It will be convenient to introduce the following notation. For some i ∈ ℕ 𝑖 ℕ i\in\mathbb{N} , an " i − limit-from 𝑖 i- Whitney field" is a family P → = { P x } x ∈ E → 𝑃 subscript superscript 𝑃 𝑥 𝑥 𝐸 \vec{P}=\{P^{x}\}_{x\in E} of i 𝑖 i dimensional vectors of real-valued polynomials P x subscript 𝑃 𝑥 P_{x} indexed by the points x 𝑥 x in a finite set E ⊆ ℝ d 𝐸 superscript ℝ 𝑑 E\subseteq\mathbb{R}^{d} . We say that P → = ( P x ) x ∈ E → 𝑃 subscript subscript 𝑃 𝑥 𝑥 𝐸 \vec{P}=(P_{x})_{x\in E} is a Whitney field "on E 𝐸 E ", and we write Wh r n ¯ ​ ( E ) subscript superscript Wh ¯ 𝑛 𝑟 𝐸 \texttt{Wh}^{\bar{n}}_{r}(E) for the vector space of all n ¯ − limit-from ¯ 𝑛 \bar{n}- Whitney fields on E 𝐸 E of degree at most r 𝑟 r .

Definition 19 .

Let 𝒞 r ​ ( ℝ d ) superscript 𝒞 𝑟 superscript ℝ 𝑑 \mathcal{C}^{r}(\mathbb{R}^{d}) denote the space of all real functions on ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} that are r − limit-from 𝑟 r- times continuously differentiable and

For a closed subset U ∈ ℝ d 𝑈 superscript ℝ 𝑑 U\in\mathbb{R}^{d} such that U 𝑈 U is the closure of its interior U o superscript 𝑈 𝑜 U^{o} , we define the 𝒞 r − limit-from superscript 𝒞 𝑟 \mathcal{C}^{r}- norm of a function f : U → ℝ : 𝑓 → 𝑈 ℝ f:U\rightarrow\mathbb{R} by

When U 𝑈 U is clear from context, we will abbreviate ‖ f ‖ 𝒞 r ​ ( U ) subscript norm 𝑓 superscript 𝒞 𝑟 𝑈 \|f\|_{\mathcal{C}^{r}(U)} to ‖ f ‖ 𝒞 r subscript norm 𝑓 superscript 𝒞 𝑟 \|f\|_{\mathcal{C}^{r}} .

Definition 20 .

We define 𝒞 r ​ ( B d , B n ¯ ) superscript 𝒞 𝑟 subscript 𝐵 𝑑 subscript 𝐵 ¯ 𝑛 \mathcal{C}^{r}(B_{d},B_{\bar{n}}) to consist of all f : B d → B n ¯ : 𝑓 → subscript 𝐵 𝑑 subscript 𝐵 ¯ 𝑛 f:B_{d}\rightarrow B_{\bar{n}} such that f ​ ( x ) = ( f 1 ​ ( x ) , … , f n ¯ ​ ( x ) ) 𝑓 𝑥 superscript 𝑓 1 𝑥 … superscript 𝑓 ¯ 𝑛 𝑥 f(x)=(f^{1}(x),\dots,f^{\bar{n}}(x)) and for each i ∈ n ¯ 𝑖 ¯ 𝑛 i\in\bar{n} , f i : B d → ℝ : subscript 𝑓 𝑖 → subscript 𝐵 𝑑 ℝ f_{i}:B_{d}\rightarrow\mathbb{R} belongs to 𝒞 r ​ ( B d ) superscript 𝒞 𝑟 subscript 𝐵 𝑑 \mathcal{C}^{r}(B_{d}) . We define the 𝒞 r − limit-from superscript 𝒞 𝑟 \mathcal{C}^{r}- norm of f ​ ( x ) := ( f 1 ​ ( x ) , … , f n ¯ ​ ( x ) ) assign 𝑓 𝑥 superscript 𝑓 1 𝑥 … superscript 𝑓 ¯ 𝑛 𝑥 f(x):=(f^{1}(x),\dots,f^{\bar{n}}(x)) by

Suppose F ∈ 𝒞 r ​ ( B d ) 𝐹 superscript 𝒞 𝑟 subscript 𝐵 𝑑 F\in\mathcal{C}^{r}(B_{d}) , and x ∈ B d 𝑥 subscript 𝐵 𝑑 x\in B_{d} , we denote by J x ​ ( F ) subscript 𝐽 𝑥 𝐹 J_{x}(F) the polynomial that is the r t ​ h superscript 𝑟 𝑡 ℎ r^{th} order Taylor approximation to F 𝐹 F at x 𝑥 x , and call it the “jet of F 𝐹 F at x 𝑥 x ".

𝑥 P_{x}=P^{+}_{x} . We define a C r − limit-from superscript 𝐶 𝑟 C^{r}- norm on n ¯ − limit-from ¯ 𝑛 \bar{n}- Whitney fields as follows. If P → ∈ Wh r n ¯ ​ ( E ) → 𝑃 subscript superscript Wh ¯ 𝑛 𝑟 𝐸 \vec{P}\in\texttt{Wh}^{\bar{n}}_{r}(E) , we define

where the infimum is taken over all F ∈ 𝒞 r ​ ( B d , B n ¯ ) 𝐹 superscript 𝒞 𝑟 subscript 𝐵 𝑑 subscript 𝐵 ¯ 𝑛 F\in\mathcal{C}^{r}(B_{d},B_{\bar{n}}) such that F 𝐹 F agrees with P → → 𝑃 \vec{P} .

We are interested in the set of all f ∈ 𝒞 r ​ ( B d , B n ¯ ) 𝑓 superscript 𝒞 𝑟 subscript 𝐵 𝑑 subscript 𝐵 ¯ 𝑛 f\in\mathcal{C}^{r}(B_{d},B_{\bar{n}}) such that ‖ f ‖ 𝒞 r ​ ( B d , B n ¯ ) ≤ 1 subscript norm 𝑓 superscript 𝒞 𝑟 subscript 𝐵 𝑑 subscript 𝐵 ¯ 𝑛 1 \|f\|_{\mathcal{C}^{r}(B_{d},B_{\bar{n}})}\leq 1 . By results of Fefferman (see page 19, [ 13 ] ) we have the following.

Theorem 19 .

E^{+} and a convex set K 𝐾 K having the following properties.

Here K 𝐾 K is the intersection of m ¯ ≤ exp ⁡ ( C / ϵ ) ​ | E | ¯ 𝑚 𝐶 italic-ϵ 𝐸 \bar{m}\leq\exp(C/{\epsilon})|E| sets { x | ( α i ​ ( x ) ) 2 ≤ β i } conditional-set 𝑥 superscript subscript 𝛼 𝑖 𝑥 2 subscript 𝛽 𝑖 \{x|(\alpha_{i}(x))^{2}\leq\beta_{i}\} , where α i ​ ( x ) subscript 𝛼 𝑖 𝑥 \alpha_{i}(x) is a real valued linear function such that α ​ ( 0 ) = 0 𝛼 0 0 \alpha(0)=0 and β i > 0 subscript 𝛽 𝑖 0 \beta_{i}>0 . Thus

𝐾 \vec{P}^{+}\in K , that agrees with P → → 𝑃 \vec{P} on E 𝐸 E .

1 italic-ϵ \|\vec{P}\|_{\mathcal{C}^{r}(E)}\leq 1+{\epsilon}.

For our purposes, it would suffice to set the above ϵ italic-ϵ {\epsilon} to any controlled constant. To be specific, we set ϵ italic-ϵ {\epsilon} to 2 2 2 . By Theorem 1 of [ 12 ] we know the following.

Theorem 20 .

There exists a linear map T 𝑇 T from 𝒞 r ​ ( E ) superscript 𝒞 𝑟 𝐸 \mathcal{C}^{r}(E) to 𝒞 r ​ ( ℝ d ) superscript 𝒞 𝑟 superscript ℝ 𝑑 \mathcal{C}^{r}(\mathbb{R}^{d}) and a controlled constant C 𝐶 C such that T ​ f | E = f evaluated-at 𝑇 𝑓 𝐸 𝑓 {T}f\big{|}_{E}=f and ‖ T ​ f ‖ 𝒞 r ​ ( ℝ d ) ≤ C ​ ‖ f ‖ 𝒞 r ​ ( E ) subscript norm 𝑇 𝑓 superscript 𝒞 𝑟 superscript ℝ 𝑑 𝐶 subscript norm 𝑓 superscript 𝒞 𝑟 𝐸 \|{T}f\|_{\mathcal{C}^{r}(\mathbb{R}^{d})}\leq C\|f\|_{\mathcal{C}^{r}(E)} .

Definition 21 .

x_{i}\in\texttt{Wh}_{r}^{1}(E^{+}) ) such that for each i ∈ [ m ¯ ] 𝑖 delimited-[] ¯ 𝑚 i\in[\bar{m}]

\texttt{Wh}_{r}^{\bar{n}}(E^{+}) via the natural isomorphism. Then, from Theorem   19 and Theorem  20 we obtain the following.

Corollary 21 .

There is a controlled constant C 𝐶 C depending on r 𝑟 r and d 𝑑 d such that

¯ 𝐾 \vec{P}^{+}\in\bar{K} , that agrees with P → → 𝑃 \vec{P} on E 𝐸 E .

¯ 𝐾 \vec{P}^{+}\in\bar{K} that agrees with P → → 𝑃 \vec{P} on E 𝐸 E , then ‖ P → ‖ 𝒞 r ​ ( E , ℝ n ¯ ) ≤ C . subscript norm → 𝑃 superscript 𝒞 𝑟 𝐸 superscript ℝ ¯ 𝑛 𝐶 \|\vec{P}\|_{\mathcal{C}^{r}(E,\mathbb{R}^{\bar{n}})}\leq C.

13.2. Preprocessing

Let ϵ ¯ > 0 ¯ italic-ϵ 0 \bar{{\epsilon}}>0 be an error parameter.

Notation 2 .

For n ∈ ℕ 𝑛 ℕ n\in\mathbb{N} , we denote the set { 1 , … , n } 1 … 𝑛 \{1,\dots,n\} by [ n ] delimited-[] 𝑛 [n] . Let { x 1 , … , x N } ⊆ ℝ d subscript 𝑥 1 … subscript 𝑥 𝑁 superscript ℝ 𝑑 \{x_{1},\dots,x_{N}\}\subseteq\mathbb{R}^{d} .

Let S 1 := { 1 } assign subscript 𝑆 1 1 S_{1}:=\{1\} and p ​ ( 1 ) := 1 assign 𝑝 1 1 p(1):=1 . For any i > 1 𝑖 1 i>1 ,

if { j : j ∈ S i − 1 ​ and ​ | x j − x i | < ϵ ¯ } ≠ ∅ conditional-set 𝑗 𝑗 subscript 𝑆 𝑖 1 and subscript 𝑥 𝑗 subscript 𝑥 𝑖 ¯ italic-ϵ \{j:j\in S_{i-1}\,\text{and}\,|x_{j}-x_{i}|<\bar{{\epsilon}}\}\neq\emptyset , set p ​ ( i ) 𝑝 𝑖 p(i) to be an arbitrary element of { j : j ∈ S i − 1 ​ and ​ | x j − x i | < ϵ ¯ } conditional-set 𝑗 𝑗 subscript 𝑆 𝑖 1 and subscript 𝑥 𝑗 subscript 𝑥 𝑖 ¯ italic-ϵ \{j:j\in S_{i-1}\,\text{and}\,|x_{j}-x_{i}|<\bar{{\epsilon}}\} , and set S i := S i − 1 assign subscript 𝑆 𝑖 subscript 𝑆 𝑖 1 S_{i}:=S_{i-1} ,

and otherwise set p ​ ( i ) := i assign 𝑝 𝑖 𝑖 p(i):=i and set S i := S i − 1 ∪ { i } assign subscript 𝑆 𝑖 subscript 𝑆 𝑖 1 𝑖 S_{i}:=S_{i-1}\cup\{i\} .

Finally, set S := S N assign 𝑆 subscript 𝑆 𝑁 S:=S_{N} , N ^ = | S | ^ 𝑁 𝑆 \hat{N}=|S| and for each i 𝑖 i , let

For i ∈ S 𝑖 𝑆 i\in S , let μ i := N − 1 ​ | h ​ ( i ) | assign subscript 𝜇 𝑖 superscript 𝑁 1 ℎ 𝑖 \mu_{i}:=N^{-1}\big{|}h(i)\big{|} , and let

It is clear from the construction that for each i ∈ [ N ] 𝑖 delimited-[] 𝑁 i\in[N] , | x p ​ ( i ) − x i | ≤ ϵ ¯ subscript 𝑥 𝑝 𝑖 subscript 𝑥 𝑖 ¯ italic-ϵ |x_{p(i)}-x_{i}|\leq\bar{{\epsilon}} . The construction of S 𝑆 S ensures that the distance between any two points in S 𝑆 S is at least ϵ ¯ ¯ italic-ϵ \bar{{\epsilon}} . The motivation for sketching the data in this manner was that now, the extension problem involving E = { x i | i ∈ S } 𝐸 conditional-set subscript 𝑥 𝑖 𝑖 𝑆 E=\{x_{i}|i\in S\} that we will have to deal with will be better conditioned in a sense explained in the following subsection.

13.3. Convex program

Let the indices in [ N ] delimited-[] 𝑁 [N] be permuted so that S = [ N ^ ] 𝑆 delimited-[] ^ 𝑁 S=[\hat{N}] . For any f 𝑓 f such that ‖ f ‖ 𝒞 2 ≤ C − 1 ​ c subscript norm 𝑓 superscript 𝒞 2 superscript 𝐶 1 𝑐 \|f\|_{\mathcal{C}^{2}}\leq C^{-1}c , and | x − y | < ϵ ¯ 𝑥 𝑦 ¯ italic-ϵ |x-y|<\bar{{\epsilon}} , we have | f ​ ( x ) − f ​ ( y ) | < ϵ ¯ 𝑓 𝑥 𝑓 𝑦 ¯ italic-ϵ |f(x)-f(y)|<\bar{{\epsilon}} , (and so the grouping and averaging described in the previous section do not affect the quality of our solution), therefore we see that in order to find a ϵ ¯ − limit-from ¯ italic-ϵ \bar{{\epsilon}}- optimal interpolant, it suffices to minimize the objective function

\vec{P}\in\bar{K}\subseteq\texttt{Wh}_{r}^{\bar{n}}(E^{+}) , to within an additive error of ϵ ¯ ¯ italic-ϵ \bar{{\epsilon}} , and to find the corresponding point in K ¯ ¯ 𝐾 \bar{K} . We note that ζ 𝜁 \zeta is a convex function over K ¯ ¯ 𝐾 \bar{K} .

\vec{P}\in\texttt{Wh}_{r}^{1}(E^{+}) has the property that for each x ∈ E 𝑥 𝐸 x\in E , every coefficient of P x subscript 𝑃 𝑥 P_{x} is bounded above by c ′ ​ ϵ ¯ 2 superscript 𝑐 ′ superscript ¯ italic-ϵ 2 c^{\prime}\bar{{\epsilon}}^{2} . Then, if c ′ superscript 𝑐 ′ c^{\prime} is less than some controlled constant depending on d 𝑑 d ,

By the properties of θ 𝜃 \theta listed above, we see that f 𝑓 f agrees with P → → 𝑃 \vec{P} and that ‖ f ‖ 𝒞 2 ​ ( ℝ d ) ≤ 1 subscript norm 𝑓 superscript 𝒞 2 superscript ℝ 𝑑 1 \|f\|_{\mathcal{C}^{2}(\mathbb{R}^{d})}\leq 1 if c ′ superscript 𝑐 ′ c^{\prime} is bounded above by a sufficiently small controlled constant. ∎

Let z o ​ p ​ t ∈ K ¯ subscript 𝑧 𝑜 𝑝 𝑡 ¯ 𝐾 z_{opt}\in\bar{K} be any point such that

Observation 6 .

By Lemma  22 we see that the set K 𝐾 K contains a Euclidean ball of radius c ′ ​ ϵ ¯ 2 superscript 𝑐 ′ superscript ¯ italic-ϵ 2 c^{\prime}\bar{{\epsilon}}^{2} centered at the origin, where c ′ superscript 𝑐 ′ c^{\prime} is a controlled constant depending on d 𝑑 d .

E^{+} are bounded by C 𝐶 C , every point in K ¯ ¯ 𝐾 \bar{K} is at a Euclidean distance of at most C ​ N ^ 𝐶 ^ 𝑁 C\hat{N} from the origin. We can bound N ^ ^ 𝑁 \hat{N} from above as follows:

Thanks to Observation  6 and facts from Computer Science, we will see in a few paragraphs that the relevant optimization problems are tractable.

13.4. Complexity

Since we have an explicit description of K ¯ ¯ 𝐾 \bar{K} as in intersection of cylinders, we can construct a “separation oracle", which, when fed with z 𝑧 z , does the following.

If z ∈ K ¯ 𝑧 ¯ 𝐾 z\in\bar{K} then the separation oracle outputs “Yes."

ℝ a:\texttt{Wh}_{r}^{\bar{n}}(E^{+})\rightarrow\mathbb{R} such that a ​ ( z ) < 0 𝑎 𝑧 0 a(z)<0 and ∀ z ′ ∈ K ¯ for-all superscript 𝑧 ′ ¯ 𝐾 \forall z^{\prime}\in\bar{K} a ​ ( z ′ ) > 0 𝑎 superscript 𝑧 ′ 0 a(z^{\prime})>0 .

x_{j}\in\texttt{Wh}_{r}^{1}(E^{+}) .

If, for each i ∈ [ m ¯ ] 𝑖 delimited-[] ¯ 𝑚 i\in[\bar{m}] ,

holds, then declare that x ∈ K ¯ 𝑥 ¯ 𝐾 x\in\bar{K} .

Else, let there be some i 0 ∈ [ m ¯ ] subscript 𝑖 0 delimited-[] ¯ 𝑚 i_{0}\in[\bar{m}] such that

Output the following separating half-space :

The complexity A 0 subscript 𝐴 0 A_{0} of answering the above query is the complexity of evaluating α i ​ ( x j ) subscript 𝛼 𝑖 subscript 𝑥 𝑗 \alpha_{i}(x_{j}) for each i ∈ [ m ¯ ] 𝑖 delimited-[] ¯ 𝑚 i\in[\bar{m}] and each j ∈ [ n ¯ ] 𝑗 delimited-[] ¯ 𝑛 j\in[\bar{n}] . Thus

For some a ∈ K ¯ 𝑎 ¯ 𝐾 a\in\bar{K} ,

1 ¯ italic-ϵ L\leq C(1+|\log(\bar{{\epsilon}})|) .

By Observation  6 , we see that the diameter of K ¯ ¯ 𝐾 \bar{K} is at most C ​ ϵ ¯ − d 𝐶 superscript ¯ italic-ϵ 𝑑 C\bar{{\epsilon}}^{-d} and K ¯ ¯ 𝐾 \bar{K} contains a ball B L subscript 𝐵 𝐿 B_{L} of radius 2 − L superscript 2 𝐿 2^{-L} . Let the convex hull of B L subscript 𝐵 𝐿 B_{L} and the point z o ​ p ​ t subscript 𝑧 𝑜 𝑝 𝑡 z_{opt} be K h subscript 𝐾 ℎ K_{h} . Then,

\vec{P}\in\texttt{Wh}_{r}^{\bar{n}}(E^{+}) at which

ℝ f:\texttt{Wh}_{r}^{\bar{n}}(E^{+})\rightarrow\mathbb{R} given by

where | ⋅ | |\cdot| denotes the Euclidean norm. We see that the magnitude of the gradient of ζ 𝜁 \zeta is bounded above by C ​ N ^ 𝐶 ^ 𝑁 C\hat{N} at z o ​ p ​ t subscript 𝑧 𝑜 𝑝 𝑡 z_{opt} , and the Hessian of ζ 𝜁 \zeta is bounded above by the Identity. Therefore,

We note that

where the right hand side denotes the intersection of K h subscript 𝐾 ℎ K_{h} with a Euclidean ball of radius ϵ ¯ 2 ​ C ​ N ^ ¯ italic-ϵ 2 𝐶 ^ 𝑁 \frac{\bar{{\epsilon}}}{2C\hat{N}} and center z o ​ p ​ t subscript 𝑧 𝑜 𝑝 𝑡 z_{opt} . By the definition of K h subscript 𝐾 ℎ K_{h} , K h ∩ B ​ ( z o ​ p ​ t , ϵ ¯ 2 ​ C ​ N ^ ) subscript 𝐾 ℎ 𝐵 subscript 𝑧 𝑜 𝑝 𝑡 ¯ italic-ϵ 2 𝐶 ^ 𝑁 K_{h}\cap B\left(z_{opt},\frac{\bar{{\epsilon}}}{2C\hat{N}}\right) contains a ball of radius 2 − 2 ​ L superscript 2 2 𝐿 2^{-2L} . This proves the claim. ∎

Given a separation oracle for K ¯ ∈ ℝ n ¯ ​ ( dim ( K ) ) ¯ 𝐾 superscript ℝ ¯ 𝑛 dimension 𝐾 \bar{K}\in\mathbb{R}^{\bar{n}(\dim(K))} and the guarantee that for some a ∈ K ¯ 𝑎 ¯ 𝐾 a\in\bar{K} ,

¯ italic-ϵ 𝜁 subscript 𝑧 𝑜 𝑝 𝑡 {\epsilon}>\bar{{\epsilon}}+\zeta(z_{opt}) , Vaidya’s algorithm (see [ 36 ] ) finds a point in K ¯ ∩ { z | ζ ​ ( z ) < ϵ } ¯ 𝐾 conditional-set 𝑧 𝜁 𝑧 italic-ϵ \bar{K}\cap\{z|\zeta(z)<{\epsilon}\} using

arithmetic steps, where L ′ ≤ C ( L + | log ( ϵ ¯ ) ) | ) L^{\prime}\leq C(L+|\log(\bar{{\epsilon}}))|) . Here A 0 subscript 𝐴 0 A_{0} is the number of arithmetic operations required to answer a query to the separation oracle.

Let ϵ v ​ a subscript italic-ϵ 𝑣 𝑎 {\epsilon}_{va} denote the smallest real number such that

For any ϵ > ϵ v ​ a italic-ϵ subscript italic-ϵ 𝑣 𝑎 {\epsilon}>{\epsilon}_{va} , Vaidya’s algorithm finds a point in K ¯ ∩ { z | ζ ​ ( z ) < ϵ } ¯ 𝐾 conditional-set 𝑧 𝜁 𝑧 italic-ϵ \bar{K}\cap\{z|\zeta(z)<{\epsilon}\} using

arithmetic steps, where L ′ ≤ C ( 1 + | log ( ϵ ¯ ) ) | ) L^{\prime}\leq C(1+|\log(\bar{{\epsilon}}))|) .

𝐿 ¯ italic-ϵ C(L+|\ln\bar{{\epsilon}}|) calls to Vaidya’s algorithm.

14. Patching local sections together

For any i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] , recall the cylinders cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} and Euclidean motions o i subscript 𝑜 𝑖 o_{i} from Section  11 .

Let base ​ ( cyl i ) := o i ​ ( cyl ∩ ℝ d ) assign base subscript cyl 𝑖 subscript 𝑜 𝑖 cyl superscript ℝ 𝑑 \texttt{base}({\texttt{cyl}}_{i}):=o_{i}({\texttt{cyl}}\cap\mathbb{R}^{d}) and stalk ​ ( cyl i ) := o i ​ ( cyl ∩ ℝ n − d ) assign stalk subscript cyl 𝑖 subscript 𝑜 𝑖 cyl superscript ℝ 𝑛 𝑑 \texttt{stalk}({\texttt{cyl}}_{i}):=o_{i}({\texttt{cyl}}\cap\mathbb{R}^{n-d}) . Let f ˇ i : B d → B n − d : subscript ˇ 𝑓 𝑖 → subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 \check{f}_{i}:B_{d}\rightarrow B_{n-d} be an arbitrary C 2 superscript 𝐶 2 C^{2} function such that

Let f i : base ​ ( cyl ) → stalk ​ ( cyl ) : subscript 𝑓 𝑖 → base cyl stalk cyl f_{i}:\texttt{base}({\texttt{cyl}})\rightarrow\texttt{stalk}({\texttt{cyl}}) be given by

Now, fix an i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] . Without loss of generality, we will drop the subscript i 𝑖 i (having fixed this i 𝑖 i ), and assume that o i := i ​ d assign subscript 𝑜 𝑖 𝑖 𝑑 o_{i}:=id , by changing the frame of reference using a proper rigid body motion. Recall that F ^ o ¯ superscript ^ 𝐹 ¯ 𝑜 \hat{F}^{\bar{o}} was defined by ( 115 ), i. e.

(now 0 0 and o i = i ​ d subscript 𝑜 𝑖 𝑖 𝑑 o_{i}=id play the role that z 𝑧 z and Θ Θ \Theta played in ( 115 )). Let N ​ ( z ) 𝑁 𝑧 \mathit{N}(z) be the linear subspace spanned by the top n − d 𝑛 𝑑 n-d eigenvectors of the Hessian of F ^ o ¯ superscript ^ 𝐹 ¯ 𝑜 \hat{F}^{\bar{o}} at a variable point z 𝑧 z . Let the intersection of

be locally expressed as the graph of a function g i subscript 𝑔 𝑖 g_{i} , where

For this fixed i 𝑖 i , we drop the subscript and let g : B d ​ ( 0 , 1 ) → ℝ n − d : 𝑔 → subscript 𝐵 𝑑 0 1 superscript ℝ 𝑛 𝑑 g:B_{d}(0,1)\rightarrow\mathbb{R}^{n-d} be given by

As in ( 10.1 ), we see that

lies in ℝ d ¯ , superscript ℝ ¯ 𝑑 \mathbb{R}^{\bar{d}}, and the manifold ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} obtained by patching up all such manifolds for i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] is, as a consequence of Proposition  1 and Lemma  15 a submanifold, whose reach is at least c ​ τ 𝑐 𝜏 c\tau . Let

be the bundle over ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} defined by ( 111 ).

Let s i subscript 𝑠 𝑖 s_{i} be the local section of D ¯ norm := D ¯ F o ¯ norm assign superscript ¯ 𝐷 norm subscript superscript ¯ 𝐷 norm superscript 𝐹 ¯ 𝑜 \bar{D}^{\texttt{norm}}:=\bar{D}^{\texttt{norm}}_{{F^{\bar{o}}}} defined by

where U := U i ⊆ ℳ p ​ u ​ t assign 𝑈 subscript 𝑈 𝑖 subscript ℳ 𝑝 𝑢 𝑡 U:=U_{i}\subseteq\mathcal{M}_{put} is an open set fixed by ( 129 ). The choice of τ ¯ τ ¯ 𝜏 𝜏 \frac{\bar{\tau}}{\tau} in ( 125 ) is small enough to ensure that there is a unique open set U 𝑈 U and a unique s i subscript 𝑠 𝑖 s_{i} such that ( 129 ) holds (by Observations 2 , 3 and 4 ). We define U j subscript 𝑈 𝑗 U_{j} for any j ∈ [ N ¯ ] 𝑗 delimited-[] ¯ 𝑁 j\in[\bar{N}] analogously. Next, we construct a partition of unity on ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} . For each j ∈ [ N ¯ ] 𝑗 delimited-[] ¯ 𝑁 j\in[\bar{N}] , let θ ~ j : ℳ p ​ u ​ t → [ 0 , 1 ] : subscript ~ 𝜃 𝑗 → subscript ℳ 𝑝 𝑢 𝑡 0 1 \tilde{\theta}_{j}:\mathcal{M}_{put}\rightarrow[0,1] be an element of a partition of unity defined as follows. For x ∈ cyl j 𝑥 subscript cyl 𝑗 x\in{\texttt{cyl}}_{j} ,

where θ 𝜃 \theta is defined by ( 112 ). Let

We use the local sections { s j | j ∈ [ N ¯ ] } conditional-set subscript 𝑠 𝑗 𝑗 delimited-[] ¯ 𝑁 \{s_{j}|j\in[\bar{N}]\} , defined separately for each j 𝑗 j by ( 129 ) and the partition of unity { θ i } i ∈ N ¯ subscript subscript 𝜃 𝑖 𝑖 ¯ 𝑁 \{\theta_{i}\}_{i\in\bar{N}} , to obtain a global section s 𝑠 s of D o ¯ norm subscript superscript 𝐷 norm ¯ 𝑜 D^{\texttt{norm}}_{\bar{o}} defined as follows for x ∈ U i 𝑥 subscript 𝑈 𝑖 x\in U_{i} .

We also define f : V i → B n − d : 𝑓 → subscript 𝑉 𝑖 subscript 𝐵 𝑛 𝑑 f:V_{i}\rightarrow B_{n-d} by

The above equation fixes an open set V i subscript 𝑉 𝑖 V_{i} in ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} . The graph of s 𝑠 s , i. e.

is the output manifold. We see that ( 133 ) defines a manifold ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} , by checking this locally. We will obtain a lower bound on the reach of ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} in Section  15 .

15. The reach of the output manifold

Recall that F ^ o ¯ superscript ^ 𝐹 ¯ 𝑜 \hat{F}^{\bar{o}} was defined by ( 115 ), i. e.

(now 0 0 and o i = i ​ d subscript 𝑜 𝑖 𝑖 𝑑 o_{i}=id play the role that z 𝑧 z and Θ Θ \Theta played in ( 115 )). We place ourselves in the context of Observation  4 . By construction, F o ¯ : B n → ℝ : superscript 𝐹 ¯ 𝑜 → subscript 𝐵 𝑛 ℝ {F}^{\bar{o}}:B_{n}\rightarrow\mathbb{R} satisfies the conditions of Lemma  15 , therefore there exists a map

satisfying the following condition.

Also, x 𝑥 x and v 𝑣 v are C r − limit-from superscript 𝐶 𝑟 C^{r}- smooth functions of z ∈ B n ​ ( 0 , c ¯ 11 ) 𝑧 subscript 𝐵 𝑛 0 subscript ¯ 𝑐 11 z\in B_{n}(0,\bar{c}_{11}) . with derivatives of order up to r 𝑟 r bounded above by C 𝐶 C . Let

𝑥 𝑔 𝑥 x+g(x) is the disc

By Lemma  23 below, we can ensure, by setting c ¯ 12 ≤ c ¯ subscript ¯ 𝑐 12 ¯ 𝑐 \overline{c}_{12}\leq\bar{c} for a sufficiently small controlled constant c ¯ ¯ 𝑐 \bar{c} , that the derivatives of Φ − i ​ d Φ 𝑖 𝑑 \Phi-id of order less or equal to r = k − 2 𝑟 𝑘 2 r=k-2 are bounded above by a prescribed controlled constant c 𝑐 c .

For any controlled constant c 𝑐 c , there is a controlled constant c ¯ ¯ 𝑐 \bar{c} such that if c ¯ 12 ≤ c ¯ subscript ¯ 𝑐 12 ¯ 𝑐 \overline{c}_{12}\leq\bar{c} , then for each i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] , and each | α | ≤ 2 𝛼 2 |\alpha|\leq 2 the functions Φ Φ \Phi and g 𝑔 g , respectively defined in ( 134 ) and ( 128 ) satisfy

Proof of Lemma  23 .

We would like to apply Lemma  15 here, but its conclusion would not directly help us, since it would give a bound of the form

where C 𝐶 C is some controlled constant. To remedy this, we are going to use a simple scaling argument. We first provide an outline of the argument. We change scale by "zooming out", then apply Lemma  15 , and thus obtain a bound of the the desired form

We replace each cylinder cyl j = o j ​ ( cyl ) subscript cyl 𝑗 subscript 𝑜 𝑗 cyl {\texttt{cyl}}_{j}=o_{j}({\texttt{cyl}}) by cyl ˇ j := o j ​ ( τ ¯ ​ ( B d × ( C ˇ ​ B n − d ) ) ) assign subscript ˇ cyl 𝑗 subscript 𝑜 𝑗 ¯ 𝜏 subscript 𝐵 𝑑 ˇ 𝐶 subscript 𝐵 𝑛 𝑑 \check{{\texttt{cyl}}}_{j}:=o_{j}(\bar{\tau}(B_{d}\times(\check{C}B_{n-d}))) . Since the guarantees provided by Lemma  15 have an unspecified dependence on d ¯ ¯ 𝑑 \bar{d} (which appears in ( 114 )), we require an upper bound on the "effective dimension" that depends only on d 𝑑 d and is independent of C ˇ ˇ 𝐶 \check{C} . If we were only to "zoom out", this unspecified dependence on d ¯ ¯ 𝑑 \bar{d} renders the bound useless. To mitigate this, we need to modify the cylinders that are far away from the point of interest. More precisely, we consider a point x ∈ c ​ y ​ l ˇ i 𝑥 subscript ˇ 𝑐 𝑦 𝑙 𝑖 x\in\check{cyl}_{i} and replace each cyl j subscript cyl 𝑗 {\texttt{cyl}}_{j} that does not contribute to Φ ​ ( x ) Φ 𝑥 \Phi(x) by cyl ˇ j subscript ˇ cyl 𝑗 \check{{\texttt{cyl}}}_{j} , a suitable translation of

This ensures that the dimension of

is bounded above by a controlled constant depending only on d 𝑑 d . We then apply Lemma  15 to the function F ˇ o ˇ ​ ( w ) superscript ˇ 𝐹 ˇ 𝑜 𝑤 \check{F}^{\check{o}}(w) defined in ( 138 ). This concludes the outline; we now proceed with the details. Recall that we have fixed our attention to c ​ y ​ l ˇ i subscript ˇ 𝑐 𝑦 𝑙 𝑖 \check{cyl}_{i} . Let

where C ˇ ˇ 𝐶 \check{C} is an appropriate (large) controlled constant, whose value will be specified later.

Given a Packet o ¯ := { o 1 , … , o N ¯ } assign ¯ 𝑜 subscript 𝑜 1 … subscript 𝑜 ¯ 𝑁 \bar{o}:=\{o_{1},\dots,o_{\bar{N}}\} , define a collection of cylinders

in the following manner. Let

𝑥 𝑣 x+v . For any j ∈ T ˇ ∖ S ˇ 𝑗 ˇ 𝑇 ˇ 𝑆 j\in\check{T}\setminus\check{S} , let

Next, for any j ∈ T ˇ 𝑗 ˇ 𝑇 j\in\check{T} , let

For each j ∈ T ˇ 𝑗 ˇ 𝑇 j\in\check{T} , let cyl ˇ j := o ˇ j ​ ( cyl ˇ ) . assign subscript ˇ cyl 𝑗 subscript ˇ 𝑜 𝑗 ˇ cyl \check{{\texttt{cyl}}}_{j}:=\check{o}_{j}(\check{{\texttt{cyl}}}). Define F o ˇ : ⋃ j ∈ T ˇ cyl ˇ j → ℝ : superscript 𝐹 ˇ 𝑜 → subscript 𝑗 ˇ 𝑇 subscript ˇ cyl 𝑗 ℝ F^{\check{o}}:\bigcup_{j\in\check{T}}\check{{\texttt{cyl}}}_{j}\rightarrow\mathbb{R} by

Taking c ¯ 12 subscript ¯ 𝑐 12 \overline{c}_{12} to be a sufficiently small controlled constant depending on C ˇ ˇ 𝐶 \check{C} , we see that

restricted to B n subscript 𝐵 𝑛 B_{n} , satisfies the requirements of Lemma  15 . Choosing C ˇ ˇ 𝐶 \check{C} to be sufficiently large, for each | α | ∈ [ 2 , k ] 𝛼 2 𝑘 |\alpha|\in[2,k] , the function Φ Φ \Phi defined in ( 134 ) satisfies

for each | α | ∈ [ 0 , k − 2 ] 𝛼 0 𝑘 2 |\alpha|\in[0,k-2] , the function g 𝑔 g defined in ( 134 ) satisfies

Observe that we can choose j ∈ [ N ¯ ] ∖ [ N ˇ ] 𝑗 delimited-[] ¯ 𝑁 delimited-[] ˇ 𝑁 j\in[\bar{N}]\setminus[\check{N}] such that | o ˇ j ​ ( 0 ) | < 10 ​ τ subscript ˇ 𝑜 𝑗 0 10 𝜏 |\check{o}_{j}(0)|<10\tau , and for this j 𝑗 j , cyl ˇ j ∩ cyl ˇ = ∅ subscript ˇ cyl 𝑗 ˇ cyl \check{{\texttt{cyl}}}_{j}\cap\check{{\texttt{cyl}}}=\emptyset and so

The Lemma follows from Taylor’s Theorem, in conjunction with ( 139 ), ( 140 ) and ( 141 ).

Observation 7 .

By choosing C ˇ ≥ 2 / c ¯ 11 ˇ 𝐶 2 subscript ¯ 𝑐 11 \check{C}\geq 2/\overline{c}_{11} we find that the domains of both Φ Φ \Phi and Φ − 1 superscript Φ 1 \Phi^{-1} may be extended to contain the cylinder ( 3 2 ) ​ B d × B n − d 3 2 subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 \left(\frac{3}{2}\right)B_{d}\times B_{n-d} , while satisfying ( 134 ).

𝛼 superscript Φ 1 𝐼 𝑑 𝑤 𝑐 |\partial^{\alpha}(\Phi^{-1}-Id)(w)|\leq c for | α | ≤ r 𝛼 𝑟 |\alpha|\leq r and w ∈ B d × B n − d 𝑤 subscript 𝐵 𝑑 subscript 𝐵 𝑛 𝑑 w\in B_{d}\times B_{n-d} . For the remainder of this section, we will assume a scale where τ ¯ = 1 ¯ 𝜏 1 \bar{\tau}=1 .

For u ∈ U i 𝑢 subscript 𝑈 𝑖 u\in U_{i} , we have the following equality which we restate from ( 131 ) for convenience.

Let Π p ​ s ​ e ​ u ​ d subscript Π 𝑝 𝑠 𝑒 𝑢 𝑑 \Pi_{pseud} (for "pseudonormal bundle") be the map from a point x 𝑥 x in cyl to the basepoint belonging to ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} of the corresponding fiber. The following relation exists between Π p ​ s ​ e ​ u ​ d subscript Π 𝑝 𝑠 𝑒 𝑢 𝑑 \Pi_{pseud} and Φ Φ \Phi :

We define the C k − 2 superscript 𝐶 𝑘 2 C^{k-2} norm of a local section s j subscript 𝑠 𝑗 s_{j} over U ⊆ U j ∩ U i 𝑈 subscript 𝑈 𝑗 subscript 𝑈 𝑖 U\subseteq U_{j}\cap U_{i} by

Suppose for a specific x 𝑥 x and t 𝑡 t ,

where t 𝑡 t belongs to U j ∩ U i subscript 𝑈 𝑗 subscript 𝑈 𝑖 U_{j}\cap U_{i} . Applying Π p ​ s ​ e ​ u ​ d subscript Π 𝑝 𝑠 𝑒 𝑢 𝑑 \Pi_{pseud} to both sides,

Substituting back, we have

By definition  18 , we have the bound ‖ f j ‖ C k − 2 ​ ( ϕ j − 1 ​ ( U i ∩ U j ) ) ≤ c subscript norm subscript 𝑓 𝑗 superscript 𝐶 𝑘 2 superscript subscript italic-ϕ 𝑗 1 subscript 𝑈 𝑖 subscript 𝑈 𝑗 𝑐 \|f_{j}\|_{C^{k-2}(\phi_{j}^{-1}(U_{i}\cap U_{j}))}\leq c . We have

which gives the bound

Therefore, from ( 142 ),

From the preceding two equations, it follows that

The cutoff functions θ j subscript 𝜃 𝑗 \theta_{j} satisfy

Therefore, by ( 131 ),

which we rewrite as

We will now show that

By ( 132 ) in view of τ ¯ = 1 ¯ 𝜏 1 \bar{\tau}=1 , for u ∈ U i 𝑢 subscript 𝑈 𝑖 u\in U_{i} , there is an x ∈ V i 𝑥 subscript 𝑉 𝑖 x\in V_{i} such that

This gives us

𝛼 Φ 𝐼 𝑑 𝑥 𝑐 |\partial^{\alpha}(\Phi-Id)(x)|\leq c for | α | ≤ r 𝛼 𝑟 |\alpha|\leq r , we see that

By ( 149 ),( 150 ) and ( 148 ), we have ‖ f ∘ ψ ‖ C k − 2 ​ ( U i ) ≤ c . subscript norm 𝑓 𝜓 superscript 𝐶 𝑘 2 subscript 𝑈 𝑖 𝑐 \|f\circ\psi\|_{C^{k-2}(U_{i})}\leq c.

By ( 150 ), we have

16. The mean-squared distance of the output manifold from a random data point

Let ℳ o ​ p ​ t subscript ℳ 𝑜 𝑝 𝑡 \mathcal{M}_{opt} be an approximately optimal manifold in that

Suppose that o ¯ ¯ 𝑜 \bar{o} is the packet from the previous section and that the corresponding function F o ¯ superscript 𝐹 ¯ 𝑜 F^{\bar{o}} belongs to a ​ s ​ d ​ f ​ ( ℳ o ​ p ​ t ) 𝑎 𝑠 𝑑 𝑓 subscript ℳ 𝑜 𝑝 𝑡 {asdf}(\mathcal{M}_{opt}) . We need to show that the ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} constructed using o ¯ ¯ 𝑜 \bar{o} serves the purpose it was designed for; namely that the following Lemma holds.

Let us examine the manifold ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} . Recall that ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} was constructed from a collection of local sections { s i } i ∈ N ¯ subscript subscript 𝑠 𝑖 𝑖 ¯ 𝑁 \{s_{i}\}_{i\in\bar{N}} , one for each i 𝑖 i such that o i ∈ o ¯ subscript 𝑜 𝑖 ¯ 𝑜 o_{i}\in\bar{o} . These local sections were obtained from functions f i : base ​ ( cyl i ) → stalk ​ ( cyl i ) : subscript 𝑓 𝑖 → base subscript cyl 𝑖 stalk subscript cyl 𝑖 f_{i}:\texttt{base}({\texttt{cyl}}_{i})\rightarrow\texttt{stalk}({\texttt{cyl}}_{i}) . The s i subscript 𝑠 𝑖 s_{i} were patched together using a partition of unity supported on ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} .

Let 𝒫 i ​ n subscript 𝒫 𝑖 𝑛 \mathcal{P}_{in} be the measure obtained by restricting 𝒫 𝒫 \mathcal{P} to ∪ i ∈ [ N ¯ ] cyl i subscript 𝑖 delimited-[] ¯ 𝑁 subscript cyl 𝑖 \cup_{i\in[\bar{N}]}{\texttt{cyl}}_{i} . Let 𝒫 o ​ u ​ t subscript 𝒫 𝑜 𝑢 𝑡 \mathcal{P}_{out} be the measure obtained by restricting 𝒫 𝒫 \mathcal{P} to ( ∪ i ∈ [ N ¯ ] cyl i ) c superscript subscript 𝑖 delimited-[] ¯ 𝑁 subscript cyl 𝑖 𝑐 \left(\cup_{i\in[\bar{N}]}{\texttt{cyl}}_{i}\right)^{c} . Thus,

For any ℳ ∈ 𝒢 ℳ 𝒢 \mathcal{M}\in\mathcal{G} ,

We will separately analyze the two terms on the right when ℳ ℳ \mathcal{M} is ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} . We begin with 𝔼 𝒫 o ​ u ​ t ​ 𝐝 ​ ( x , ℳ f ​ i ​ n ) 2 subscript 𝔼 subscript 𝒫 𝑜 𝑢 𝑡 𝐝 superscript 𝑥 subscript ℳ 𝑓 𝑖 𝑛 2 \mathbb{E}_{\mathcal{P}_{out}}\mathbf{d}(x,\mathcal{M}_{fin})^{2} . We make two observations:

By ( 125 ), the function f ˇ i subscript ˇ 𝑓 𝑖 \check{f}_{i} , satisfies

By Lemma  23 , the fibers of the disc bundle D norm superscript 𝐷 norm D^{{\texttt{norm}}} over ℳ p ​ u ​ t ∩ cyl i subscript ℳ 𝑝 𝑢 𝑡 subscript cyl 𝑖 \mathcal{M}_{put}\cap{\texttt{cyl}}_{i} are nearly orthogonal to base ​ ( cyl i ) base subscript cyl 𝑖 \texttt{base}({\texttt{cyl}}_{i}) .

Therefore, no point outside the union of the cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} is at a distance less than τ ¯ ​ ( 1 − 2 ​ τ ¯ τ ) ¯ 𝜏 1 2 ¯ 𝜏 𝜏 \bar{\tau}(1-\frac{2\bar{\tau}}{\tau}) to ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} .

Since F o ¯ superscript 𝐹 ¯ 𝑜 F^{\bar{o}} belongs to a ​ s ​ d ​ f ​ ( ℳ o ​ p ​ t ) 𝑎 𝑠 𝑑 𝑓 subscript ℳ 𝑜 𝑝 𝑡 {asdf}(\mathcal{M}_{opt}) , we see that no point outside the union of the cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} is at a distance less than τ ¯ ​ ( 1 − C ​ c 12 ) ¯ 𝜏 1 𝐶 subscript 𝑐 12 \bar{\tau}(1-Cc_{12}) to ℳ o ​ p ​ t subscript ℳ 𝑜 𝑝 𝑡 \mathcal{M}_{opt} . Here C 𝐶 C is a controlled constant.

For any given controlled constant c 𝑐 c , by choosing c ¯ 11 subscript ¯ 𝑐 11 \bar{c}_{11} (i. e.  τ ¯ τ ¯ 𝜏 𝜏 \frac{\bar{\tau}}{\tau} ) and c 12 subscript 𝑐 12 c_{12} appropriately, we can arrange for

Consider terms involving 𝒫 i ​ n subscript 𝒫 𝑖 𝑛 \mathcal{P}_{in} now. We assume without loss of generality that 𝒫 𝒫 \mathcal{P} possesses a density, since we can always find an arbitrarily small perturbation of 𝒫 𝒫 \mathcal{P} (in the ℓ 2 − limit-from superscript ℓ 2 \ell^{2}- Wasserstein metric) that is supported in a ball and also possesses a density. Let

be the projection which maps a point in ∪ i ∈ N ¯ cyl i subscript 𝑖 ¯ 𝑁 subscript cyl 𝑖 \cup_{i\in\bar{N}}{\texttt{cyl}}_{i} to the unique nearest point on ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} . Let μ p ​ u ​ t subscript 𝜇 𝑝 𝑢 𝑡 \mu_{put} denote the d − limit-from 𝑑 d- dimensional volume measure on ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} .

Let { 𝒫 i ​ n z } z ∈ ℳ p ​ u ​ t subscript superscript subscript 𝒫 𝑖 𝑛 𝑧 𝑧 subscript ℳ 𝑝 𝑢 𝑡 \{\mathcal{P}_{in}^{z}\}_{z\in\mathcal{M}_{put}} denote the natural measure induced on the fiber of the normal disc bundle of radius 2 ​ τ ¯ 2 ¯ 𝜏 2\bar{\tau} over z 𝑧 z .

Using the partition of unity { θ j } j ∈ [ N ¯ ] subscript subscript 𝜃 𝑗 𝑗 delimited-[] ¯ 𝑁 \{\theta_{j}\}_{j\in[\bar{N}]} supported in ℳ p ​ u ​ t subscript ℳ 𝑝 𝑢 𝑡 \mathcal{M}_{put} , we split the right hand side of ( 154 ).

For x ∈ cyl i 𝑥 subscript cyl 𝑖 x\in{\texttt{cyl}}_{i} , let ℕ x subscript ℕ 𝑥 \mathbb{N}_{x} denote the unique fiber of D norm superscript 𝐷 norm D^{\texttt{norm}} that x 𝑥 x belongs to. Observe that ℳ f ​ i ​ n ∩ ℕ x subscript ℳ 𝑓 𝑖 𝑛 subscript ℕ 𝑥 \mathcal{M}_{fin}\cap\mathbb{N}_{x} consists of a single point. Define 𝐝 ~ ​ ( x , ℳ f ​ i ​ n ) ~ 𝐝 𝑥 subscript ℳ 𝑓 𝑖 𝑛 \tilde{\mathbf{d}}(x,\mathcal{M}_{fin}) to be the distance of x 𝑥 x to this point, i. e.

We proceed to examine the right hand side in ( 155 ).

For each i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] , let ℳ f ​ i ​ n i subscript superscript ℳ 𝑖 𝑓 𝑖 𝑛 \mathcal{M}^{i}_{fin} denote manifold with boundary corresponding to the graph of f i subscript 𝑓 𝑖 f_{i} , i. e. let

Since the quadratic function is convex, the average squared "distance" (where "distance" refers to 𝐝 ~ ~ 𝐝 \tilde{\mathbf{d}} ) to ℳ f ​ i ​ n subscript ℳ 𝑓 𝑖 𝑛 \mathcal{M}_{fin} is less or equal to the average of the squared "distances" to the local sections in the following sense.

Next, we will look at the summands of the right hand side. Lemma  23 tells us that ℕ x subscript ℕ 𝑥 \mathbb{N}_{x} is almost orthogonal to o i ​ ( ℝ d ) subscript 𝑜 𝑖 superscript ℝ 𝑑 o_{i}(\mathbb{R}^{d}) . By Lemma  23 , and the fact that each f i subscript 𝑓 𝑖 f_{i} satisfies ( 151 ), we see that

We now fix i ∈ [ N ¯ ] 𝑖 delimited-[] ¯ 𝑁 i\in[\bar{N}] . Let 𝒫 i superscript 𝒫 𝑖 \mathcal{P}^{i} be the measure which is obtained, by the translation via o i − 1 superscript subscript 𝑜 𝑖 1 o_{i}^{-1} of the restriction of 𝒫 𝒫 \mathcal{P} to cyl i subscript cyl 𝑖 {\texttt{cyl}}_{i} . In particular, 𝒫 i superscript 𝒫 𝑖 \mathcal{P}^{i} is supported on cyl .

Let μ b ​ a ​ s ​ e i subscript superscript 𝜇 𝑖 𝑏 𝑎 𝑠 𝑒 \mu^{i}_{base} be the push-forward of 𝒫 i superscript 𝒫 𝑖 \mathcal{P}^{i} onto base ​ ( cyl ) base cyl \texttt{base}({\texttt{cyl}}) under Π d subscript Π 𝑑 \Pi_{d} . For any x ∈ cyl i 𝑥 subscript cyl 𝑖 x\in{\texttt{cyl}}_{i} , let v ​ ( x ) ∈ ℳ f ​ i ​ n i 𝑣 𝑥 subscript superscript ℳ 𝑖 𝑓 𝑖 𝑛 v(x)\in\mathcal{M}^{i}_{fin} be the unique point such that x − v ​ ( x ) 𝑥 𝑣 𝑥 x-v(x) lies in o i ​ ( ℝ n − d ) subscript 𝑜 𝑖 superscript ℝ 𝑛 𝑑 o_{i}(\mathbb{R}^{n-d}) . In particular,

By Lemma  23 , we see that

Recall that ℳ f ​ i ​ n i subscript superscript ℳ 𝑖 𝑓 𝑖 𝑛 \mathcal{M}^{i}_{fin} is the graph of a function f i : base ​ ( cyl ) → stalk ​ ( cyl ) : subscript 𝑓 𝑖 → base cyl stalk cyl f_{i}:\texttt{base}({\texttt{cyl}})\rightarrow\texttt{stalk}({\texttt{cyl}}) . In Section  13 , we have shown how to construct f i subscript 𝑓 𝑖 f_{i} so that it satisfies ( 125 ) and ( 158 ), where ϵ ^ = c ​ ϵ N ¯ ^ italic-ϵ 𝑐 italic-ϵ ¯ 𝑁 \hat{{\epsilon}}=\frac{c{\epsilon}}{\bar{N}} , for some sufficiently small controlled constant c 𝑐 c .

Let f i o ​ p ​ t : base ​ ( cyl ) → stalk ​ ( cyl ) : superscript subscript 𝑓 𝑖 𝑜 𝑝 𝑡 → base cyl stalk cyl f_{i}^{opt}:\texttt{base}({\texttt{cyl}})\rightarrow\texttt{stalk}({\texttt{cyl}}) denote the function (which exists because of the bound on the reach of ℳ o ​ p ​ t subscript ℳ 𝑜 𝑝 𝑡 \mathcal{M}_{opt} ) with the property that

By ( 158 ), we see that

Lemma  23 and the fact that each f i subscript 𝑓 𝑖 f_{i} satisfies ( 151 ), and ( 158 ) show that

The proof follows from ( 152 ), ( 153 ) and ( 160 ). ∎

17. Number of arithmetic operations

After the dimension reduction of Section  6 , the ambient dimension is reduced to

The number of times that local sections are computed is bounded above by the product of the maximum number of cylinders in a cylinder packet, (i. e.  N ¯ ¯ 𝑁 \bar{N} , which is less or equal to C ​ V τ d 𝐶 𝑉 superscript 𝜏 𝑑 \frac{CV}{\tau^{d}} ) and the total number of cylinder packets contained inside B n ∩ ( c 12 ​ τ ) − 1 ​ ℤ n . subscript 𝐵 𝑛 superscript subscript 𝑐 12 𝜏 1 subscript ℤ 𝑛 B_{n}\cap(c_{12}\tau)^{-1}\mathbb{Z}_{n}. The latter number is bounded above by ( c 12 ​ τ ) − n ​ N ¯ superscript subscript 𝑐 12 𝜏 𝑛 ¯ 𝑁 (c_{12}\tau)^{-n\bar{N}} . Each optimization for computing a local section requires only a polynomial number of computations as discussed in Subsection  13.4 . Therefore, the total number of arithmetic operations required is bounded above by

18. Conclusion

We developed an algorithm for testing if data drawn from a distribution supported in a separable Hilbert space has an expected squared distance of O ​ ( ϵ ) 𝑂 italic-ϵ O({\epsilon}) to a submanifold (of the unit ball) of dimension d 𝑑 d , volume at most V 𝑉 V and reach at least τ 𝜏 \tau . The number of data points required is of the order of

and the number of arithmetic operations and calls to the black-box that evaluates inner products in the ambient Hilbert space is

19. Acknowledgements

We are grateful to Alexander Rakhlin and Ambuj Tiwari for valuable feedback and for directing us to material related to Dudley’s entropy integral. We thank Stephen Boyd, Thomas Duchamp, Sanjeev Kulkarni, Marina Miela, Thomas Richardson, Werner Stuetzle and Martin Wainwright for valuable discussions.

• [1] Belkin, M., and Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15 , 6 (2003), 1373–1396.
• [2] Bousquet, O., Boucheron, S., and Lugosi, G. Introduction to statistical learning theory. In Advanced Lectures on Machine Learning (2003), pp. 169–207.
• [3] Bradley, P., and Mangasarian, O. L. k-plane clustering. Journal of Global Optimization 16 (2000), 23–32.
• [4] Carlsson, G. Topology and data. Bulletin of the American Mathematical Society 46 (January 2009), 255–308.
• [5] Christopher R. Genovese, Marco Perone-Pacifico, I. V., and Wasserman, L. Manifold estimation and singular deconvolution under hausdorff loss. Annals of Statistics 40 , 2 (2012).
• [6] Dasgupta, S., and Freund, Y. Random projection trees and low dimensional manifolds. In Proceedings of the 40th annual ACM symposium on Theory of computing (2008), STOC ’08, pp. 537–546.
• [7] Devroye, L., Györfi, L., and Lugosi, G. A probabilistic theory of pattern recognition . Springer, 1996.
• [8] Donoho, D. L. Aide-memoire. high-dimensional data analysis: The curses and blessings of dimensionality, 2000.
• [9] Donoho, D. L., and Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proceedings of the National Academy of Sciences 100 , 10 (May 2003), 5591–5596.
• [10] Dudley, R. M. Uniform central limit theorems , vol. 63 of Cambridge Studies in Advanced Mathematics . Cambridge University Press, Cambridge, 1999.
• [11] Federer, H. Curvature measures. Transactions of the American Mathematical Society 93 (1959).
• [12] Fefferman, C. Interpolation and extrapolation of smooth functions by linear operators. Rev. Mat. Iberoamericana 21 , 1 (2005), 313–348.
• [13] Fefferman, C. The c m superscript 𝑐 𝑚 c^{m} norm of a function with prescribed jets ii. Rev. Mat. Iberoamericana 25 , 1 (2009), 275–421.
• [14] Hastie, T. J., and Stuetzle, W. Principal curves. Journal of the American Statistical Association 84 (1989), 502–516.
• [15] Johnson, W., and Lindenstrauss, J. Extensions of lipschitz mappings into a hilbert space. Contemporary Mathematics 26 (1984), 419–441.
• [16] Kambhatla, A., and Leen, T. K. Fast non-linear dimension reduction. In In IEEE International Conference on Neural Networks (1993), IEEE, pp. 1213–1218.
• [17] Kégl, B., Krzyzak, A., Linder, T., and Zeger, K. Learning and design of principal curves. IEEE Transactions on Pattern Analysis and Machine Intelligence 22 (2000), 281–297.
• [18] Ledoux, M. The Concentration of Measure Phenomenon , vol. 87. Math. Surveys and Monographs, AMS, 2001.
• [19] Lerman, G., and Zhang, T. Probabilistic recovery of multiple subspaces in point clouds by geometric ℓ p subscript ℓ 𝑝 \ell_{p} minimization. Annals of Statistics 39 , 5 (2011), 2686–2715.
• [20] Ma, Y., and Fu, Y.
• [21] Martinetz, T., and Schulten, K. Topology representing networks. Neural Netw. 7 , 3 (Mar. 1994), 507–522.
• [22] Massart, P. Some applications of concentration inequalities to statistics. Annales de la facult des sciences de Toulouse 9 , 2 (2000), 245–303.
• [23] Maurer, A., and Pontil, M. K -dimensional coding schemes in hilbert spaces. IEEE Transactions on Information Theory 56 , 11 (2010), 5839–5846.
• [24] Narasimhan, R. Lectures on Topics in Analysis . Tata Institute of Fundamental Research, Bombay, 1965.
• [25] Narayanan, H., and Mitter, S. On the sample complexity of testing the manifold hypothesis. In NIPS (2010).
• [26] Narayanan, H., and Niyogi, P. On the sample complexity of learning smooth cuts on a manifold. In Proc. of the 22nd Annual Conference on Learning Theory (COLT) (June 2009).
• [27] Niyogi, P., Smale, S., and Weinberger, S. Finding the homology of submanifolds with high confidence from random samples. Discrete & Computational Geometry 39 , 1-3 (2008), 419–441.
• [28] Perrault-Joncas, D., and Meila, M. Metric learning and manifolds: Preserving the intrinsic geometry. submitted .
• [29] Polito, M., and Perona, P. Grouping and dimensionality reduction by locally linear embedding. In Advances in Neural Information Processing Systems 14 (2001), MIT Press, pp. 1255–1262.
• [30] Roweis, S. T., and Saul, L. K. Nonlinear dimensionality reduction by locally linear embedding. Science 290 (2000), 2323–2326.
• [31] Rudelson, M., and Vershynin, R. Combinatorics of random processes and sections of convex bodies. Annals of Mathematics 164 (2006), 603–648.
• [32] Smola, A. J., and Williamson, R. C. Regularized principal manifolds. In In Computational Learning Theory: 4th European Conference (2001), Springer, pp. 214–229.
• [33] Sridharan, K., and Srebro, N. Note on refined dudley integral covering number bound.
• [34] Tenenbaum, J. B., Silva, V., and Langford, J. C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 290 , 5500 (2000), 2319–2323.
• [35] Tenenbaum, J. B., Silva, V. d., and Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. 2319–2323.
• [36] Vaidya, P. M. A new algorithm for minimizing convex functions over convex sets. Mathematical Programming 73 , 3 (1996), 291–341.
• [37] Vapnik, V. Estimation of Dependences Based on Empirical Data: Springer Series in Statistics (Springer Series in Statistics) . Springer-Verlag New York, Inc., Secaucus, NJ, USA, 1982.
• [38] Weinberger, K. Q., and Saul, L. K. Unsupervised learning of image manifolds by semidefinite programming. Int. J. Comput. Vision 70 , 1 (2006), 77–90.
• [39] Zhang, Z., and Zha, H. Principal manifolds and nonlinear dimension reduction via local tangent space alignment. SIAM Journal of Scientific Computing 26 (2002), 313–338.

Appendix A Proof of Lemma  10

Definition 22 (rademacher complexity) ..

Given a class ℱ ℱ \mathcal{F} of functions f : X → ℝ : 𝑓 → 𝑋 ℝ f:X\rightarrow\mathbb{R} a measure μ 𝜇 \mu supported on X 𝑋 X , and a natural number n ∈ ℕ 𝑛 ℕ n\in\mathbb{N} , and an n − limit-from 𝑛 n- tuple of points ( x 1 , … ​ x n ) subscript 𝑥 1 … subscript 𝑥 𝑛 (x_{1},\dots x_{n}) , where each x i ∈ X subscript 𝑥 𝑖 𝑋 x_{i}\in X we define the empirical Rademacher complexity R n ​ ( ℱ , x ) subscript 𝑅 𝑛 ℱ 𝑥 R_{n}(\mathcal{F},x) as follows. Let σ = ( σ 1 , … , σ n ) 𝜎 subscript 𝜎 1 … subscript 𝜎 𝑛 \sigma=(\sigma_{1},\dots,\sigma_{n}) be a vector of n 𝑛 n independent Rademacher (i. e. unbiased { − 1 , 1 } − limit-from 1 1 \{-1,1\}- valued) random variables. Then,

We will use Rademacher complexities to bound the sample complexity from above. We know (see Theorem 3.2 3.2 3.2 , [ 2 ] ) that for all δ > 0 𝛿 0 {\mathbf{\delta}}>0 ,

Using a “chaining argument" the following Claim is proved below.

When ϵ italic-ϵ {\epsilon} is taken to equal 0 0 , the above is known as Dudley’s entropy integral [ 10 ] .

A result of Rudelson and Vershynin (Theorem 6.1, page 35 [ 31 ] ) tells us that the integral in ( 162 ) can be bounded from above using an integral involving the square root of the fat-shattering dimension (or in their terminology, combinatorial dimension.) The precise relation that they prove is

for universal constants c 𝑐 c and C 𝐶 C .

From Equations ( 161 ), ( 162 ) and ( 163 ), we see that if

Appendix B Proof of Claim  6

We begin by stating the finite class lemma of Massart ( [ 22 ] , Lemma 5.2).

where f ^ 0 = 0 subscript ^ 𝑓 0 0 \hat{f}_{0}=0 . Now, choose N 𝑁 N such that e ​ p ​ s 2 ≤ M ​ 2 − N < ϵ 𝑒 𝑝 𝑠 2 𝑀 superscript 2 𝑁 italic-ϵ \frac{eps}{2}\leq M2^{-N}<{\epsilon} ,

We use Cauchy-Schwartz on the first term to give

We use Massart’s Lemma to bound the second term,

Now, from equations ( 168 ), ( 170 ) and ( 175 ),

• Help & FAQ

Testing the manifold hypothesis

• Mathematics

Research output : Contribution to journal › Article › peer-review

The hypothesis that high dimensional data tend to lie in the vicinity of a low dimensional manifold is the basis of manifold learning. The goal of this paper is to develop an algorithm (with accompanying complexity guarantees) for testing the existence of a manifold that fits a probability distribution supported in a separable Hilbert space, only using i.i.d. samples from that distribution. More precisely, our setting is the following. Suppose that data are drawn independently at random from a probability distribution P supported on the unit ball of a separable Hilbert space H. Let G(d.V.T)be the set of submanifolds of the unit ball of H whose volume is at most Vand reach (which is the supremum of all rsuch that any point at a distance less than rhas a unique nearest point on the manifold) is at least T. Let L(M.P) denote the mean-squared distance of a random point from the probability distribution Pto M. We obtain an algorithm that tests the manifold hypothesis in the following sense. The algorithm takes i.i.d. random samples from Pas input and determines which of the following two is true (at least one must be): There exists M ∈ G(d,CV,T/C) such that L(M,P)≤C∈ There exists no M ∈ G(d,V/C,CT) such that L(M,P) ≤ ∈/C The answer is correct with probability at least 1-δ.

All Science Journal Classification (ASJC) codes

• General Mathematics
• Applied Mathematics

Access to Document

• 10.1090/jams/852

Other files and links

• Link to publication in Scopus
• Link to the citations in Scopus

Fingerprint

• Probability distributions Engineering & Materials Science 100%
• Hilbert spaces Engineering & Materials Science 93%
• Testing Mathematics 74%
• Probability Distribution Mathematics 65%
• Separable Hilbert Space Mathematics 58%
• Unit ball Mathematics 49%
• High-dimensional Data Mathematics 30%
• Supremum Mathematics 26%

T1 - Testing the manifold hypothesis

AU - Fefferman, Charles

AU - Mitter, Sanjoy

AU - Narayanan, Hariharan

N1 - Publisher Copyright: © 2016 American Mathmatical Society.

PY - 2016/10

Y1 - 2016/10

N2 - The hypothesis that high dimensional data tend to lie in the vicinity of a low dimensional manifold is the basis of manifold learning. The goal of this paper is to develop an algorithm (with accompanying complexity guarantees) for testing the existence of a manifold that fits a probability distribution supported in a separable Hilbert space, only using i.i.d. samples from that distribution. More precisely, our setting is the following. Suppose that data are drawn independently at random from a probability distribution P supported on the unit ball of a separable Hilbert space H. Let G(d.V.T)be the set of submanifolds of the unit ball of H whose volume is at most Vand reach (which is the supremum of all rsuch that any point at a distance less than rhas a unique nearest point on the manifold) is at least T. Let L(M.P) denote the mean-squared distance of a random point from the probability distribution Pto M. We obtain an algorithm that tests the manifold hypothesis in the following sense. The algorithm takes i.i.d. random samples from Pas input and determines which of the following two is true (at least one must be): There exists M ∈ G(d,CV,T/C) such that L(M,P)≤C∈ There exists no M ∈ G(d,V/C,CT) such that L(M,P) ≤ ∈/C The answer is correct with probability at least 1-δ.

AB - The hypothesis that high dimensional data tend to lie in the vicinity of a low dimensional manifold is the basis of manifold learning. The goal of this paper is to develop an algorithm (with accompanying complexity guarantees) for testing the existence of a manifold that fits a probability distribution supported in a separable Hilbert space, only using i.i.d. samples from that distribution. More precisely, our setting is the following. Suppose that data are drawn independently at random from a probability distribution P supported on the unit ball of a separable Hilbert space H. Let G(d.V.T)be the set of submanifolds of the unit ball of H whose volume is at most Vand reach (which is the supremum of all rsuch that any point at a distance less than rhas a unique nearest point on the manifold) is at least T. Let L(M.P) denote the mean-squared distance of a random point from the probability distribution Pto M. We obtain an algorithm that tests the manifold hypothesis in the following sense. The algorithm takes i.i.d. random samples from Pas input and determines which of the following two is true (at least one must be): There exists M ∈ G(d,CV,T/C) such that L(M,P)≤C∈ There exists no M ∈ G(d,V/C,CT) such that L(M,P) ≤ ∈/C The answer is correct with probability at least 1-δ.

UR - http://www.scopus.com/inward/record.url?scp=84979774604&partnerID=8YFLogxK

UR - http://www.scopus.com/inward/citedby.url?scp=84979774604&partnerID=8YFLogxK

U2 - 10.1090/jams/852

DO - 10.1090/jams/852

M3 - Article

AN - SCOPUS:84979774604

SN - 0894-0347

JO - Journal of the American Mathematical Society

JF - Journal of the American Mathematical Society

Manifold Hypothesis

What is the Manifold Hypothesis?

The Manifold Hypothesis states that real-world high-dimensional data lie on low-dimensional manifolds embedded within the high-dimensional space.

This hypothesis is better explained in examples, however.

Let's tackle the "embedded manifold" bit first, before we get to how it applies to machine learning and data.

A manifold is really just a technical term that is used to classify spaces of arbitrary dimension. For every whole number there exists a flat space called Euclidean space that has characteristics very similar to the cartesian plane. For example the Pythagorean theorem holds and thus the shortest distance between points is a straight line (in contrast, this is not true on a circle or sphere).  The dimension of a Euclidean space is essentially the number of (independent) degrees of freedom - basically, the number of (orthogonal) directions one can "move" inside the space).  A line has one such dimension, an infinite plane has 2, and an  infinite volume has 3, and so n.  A manifold is essentially a generalization of Euclidean space such that locally (small areas) are approximately the same as Euclidean space but the entire space fails to be have the same properties of Euclidean space when observed in its entirety.  This theoretical framework always mathematicians and other quantitively motivated scientists to describe spaces, like spheres, tori (donut-shaped spaces) and mobius bands, in a precise way and even allows a whole plethora of mathematical machinery, including calculus, to be used in a meaningful way.  The upshot is that now the classes of spaces upon which calculus now makes sense is expanded to include spaces that may be curved in arbitrary ways, or even have holes like the torus. 

So now we take this idea, and apply it to high-dimensional data.   Imagine we are interested in classify all (black and white) mages with mxn pixels.  Each pixel has a numerical value, and each can vary depending on what the image is, which could correspond to anything from an award wining photo to meaningless noise.  The point is that we have mxn degrees of freedom so we can treat an image of mxn pixels as being a single point in living in a space (manifold)  of dimension N = mn ,  Now, imagine the set of all mxn imagines that are photos of Einstein.  Clearly we now have some restriction on the choice of values for the pixels if we want the images to be photos of Einstein rather than something else.  Obviously random choices will not generate such images.  Therefore, we expect there to be less freedom of choice and hence:

The manifold hypothesis states that that this subset should actually live in an (ambient) space of lower dimension, in fact a dimension much, much smaller than  N . 

Why This Hypothesis is Important in Artificial Intelligence? 

The Manifold Hypothesis explains ( heuristically ) why machine learning techniques are able to find useful features and produce accurate predictions from datasets that have a potentially large number of dimensions ( variables).    The fact that the actual data set of interest actually lives on in a space of low dimension, means that a given machine learning model only needs to learn to focus on a few key features of the dataset to make decisions.  However these key features may turn out to be complicated functions of the original variables.  Many of the algorithms behind machine learning techniques focus on ways to determine these (embedding) functions.

MIT has an excellent paper  on testing the hypothesis. We also recommend checking out  Colah’s blog .

The world's most comprehensive data science & artificial intelligence glossary

Please sign up or login with your details

Generation Overview

AI Generator calls

AI Video Generator calls

AI Chat messages

Genius Mode messages

Genius Mode images

AD-free experience

Private images

• Includes 500 AI Image generations, 1750 AI Chat Messages, 30 AI Video generations, 60 Genius Mode Messages and 60 Genius Mode Images per month. If you go over any of these limits, you will be charged an extra $5 for that group.
• For example: if you go over 500 AI images, but stay within the limits for AI Chat and Genius Mode, you'll be charged $5 per additional 500 AI Image generations.
• Includes 100 AI Image generations and 300 AI Chat Messages. If you go over any of these limits, you will have to pay as you go.
• For example: if you go over 100 AI images, but stay within the limits for AI Chat, you'll have to reload on credits to generate more images. Choose from $5 - $1000. You'll only pay for what you use.

Out of credits

Refill your membership to continue using DeepAI

Share your generations with friends

Subscribe to the PwC Newsletter

Join the community, edit social preview.

Add a new code entry for this paper

Remove a code repository from this paper, mark the official implementation from paper authors, add a new evaluation result row.

• ADVERSARIAL PURIFICATION
• ADVERSARIAL ROBUSTNESS
• VARIATIONAL INFERENCE

Remove a task

Add a method, remove a method.

• VARIATIONAL INFERENCE -

Edit Datasets

Adversarial purification with the manifold hypothesis.

26 Oct 2022  ·  Zhaoyuan Yang , Zhiwei Xu , Jing Zhang , Richard Hartley , Peter Tu · Edit social preview

In this work, we formulate a novel framework for adversarial robustness using the manifold hypothesis. This framework provides sufficient conditions for defending against adversarial examples. We develop an adversarial purification method with this framework. Our method combines manifold learning with variational inference to provide adversarial robustness without the need for expensive adversarial training. Experimentally, our approach can provide adversarial robustness even if attackers are aware of the existence of the defense. In addition, our method can also serve as a test-time defense mechanism for variational autoencoders.

Code Edit Add Remove Mark official

Tasks edit add remove, datasets edit.

Results from the Paper Edit

Methods edit add remove.

Failures Forecast on Overhead Lines from Wind Loads in the Krasnodar Krai of Russia

• Conference paper
• First Online: 10 February 2024
• Cite this conference paper

• Oleg Loktionov   ORCID: orcid.org/0000-0002-4669-8729 12 &
• Olga Kondrateva   ORCID: orcid.org/0000-0002-5462-3612 12  

Part of the book series: Lecture Notes in Networks and Systems ((LNNS,volume 733))

Included in the following conference series:

• International Scientific Conference Fundamental and Applied Scientific Research in the Development of Agriculture in the Far East

151 Accesses

The need to consider the climatic loads is directly related to the maintenance and development of the power industry infrastructure and ensuring energy security, and the vulnerability of the electric grid complex to climate manifestations is due to a significant amount of infrastructure affected by meteorological factors. The aim of the study is to forecasting the number of accidents on the overhead lines of PJSC “Rosseti Kuban” in Krasnodar Krai for various wind speeds for the period up to 2030. It was carried out a detailed analysis of the technological failures causes on overhead lines in the selected area and was estimated the distribution of accidents associated with wind exposure for various voltage classes.It was determined the number of phenomena with a maximum wind speed averaged over a 10-min time interval by classes corresponding to the Beaufort scale and were formed forecast estimates until 2030. A mathematical model has been developed for estimating the uptime probability of overhead lines depending on the exposure level of wind speed based on the lognormal distribution function, which is used to determine the forecast values of the number of accidents. The obtained results can be used to form recommendations for the implementation of organizational and technical measures to prevention and increase the stability of the electric grid complex. The developed methodological approach is significant, both for individual regions of Russia and for all electric grid companies, for the introduction of critical infrastructure facilities into climate adaptation plans.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Wind regime change over the russian territory and the accident rate of overhead power lines, failure probability estimation of overhead transmission lines considering the spatial and temporal variation in severe weather.

Impact of Wind Power Integration on the Moroccan Electrical Grid Reliability

Brockway AM, Wang L, Dunn LN, Callaway D, Jones A (2022) Climate-aware decision-making: lessons for electric grid infrastructure planning and operations. Environ Res Lett 17(7):073002

Article   Google Scholar  

Gerlak AK, Weston J, McMahan B, Murray RL, Mills-Novoa M (2018) Climate risk management and the electricity sector. Clim Risk Manag 19:12–22

McMahan B, Gerlak AK (2020) Climate risk assessment and cascading impacts: risks and opportunities for an electrical utility in the U.S. Southwest. Clim Risk Manage 29:100240

Google Scholar  

Rezaei SN, Chouinard L, Langlois S, Legeron F (2016) Analysis of the effect of climate change on the reliability of overhead transmission lines. Sustain Cities Soc 27:137–144

Loktionov OA, Kondrateva OE, Fedotova EV (2022) Analysis of prerequisites for changing wind load standards for electric grid facilities. In: Paper presented at the 4th international youth conference on radio electronics, electrical and power engineering

Yang SC, Liu TJ, Hong HP (2019) Reliability of tower and tower-line systems under spatiotemporally varying wind or earthquake loads. Am Soc Civil Eng 143:1–13

Scherb A, Garre L, Straub D (2019) Evaluating component importance and reliability of power transmission networks subject to windstorms: methodology and application to the Nordic grid. Reliab Eng Syst Saf 119:1–11

Li Z, Jiangjun R, Zhiye D, Daochun H, Yongqing D (2022) Transmission line tower failure warning based on FBG strain monitoring and prediction model. Electr Power Syst Res 214:1–8

Kubelwa YD, Swanson AG, Papailiou KO, Dorrell DG (2022) On the Euler-Lagrange formalism to compute power line bundle conductors subject to aeolian vibrations. Mech Syst Signal Process 163:108099

Klimenko VV, Kondratyeva OE, Tereshin AG et al (2021) Wind regime change over the Russian territory and the accident rate of overhead power lines. Dokl Phys 66(3):80–87

Loktionov OA, Kondrateva OE, Fedotova EV et al (2020) Analysis of dangerous wind loads influence on 110–220 kV power grid reliability in Yamalo-Nenets Autonomous district of Russian Federation. In: Paper presented at the 2nd international youth conference on radio electronics, electrical and power engineering

Kondrateva O, Myanikova E, Loktionov O (2021) Analysis of the climatic factors influence on the overhead transmission lines reliability. Environ Clim Technol 24(3):201–214

Khasanov SR, Gracheva EI, Toshkhodzhaeva MI, Dadabaev ST, Mirkhalikova DS (2020) Reliability modeling of high-voltage power lines in a sharply continental climate. In: E3S web of conferences: 2020 high speed turbomachines and electrical drives conference, p 01051

Xiaoxun Z, Zixu X, Yu W et al (2023) Research on wind speed behavior prediction method based on multi-feature and multi-scale integrated learning. Energy 263:125593

Fu X, Li H-N, Li G et al (2021) Failure analysis of a transmission line considering the joint probability distribution of wind speed and rain intensity. Eng Struct 233:1–13

Lee S, Ham Y (2021) Probabilistic framework for assessing the vulnerability of power distribution infrastructures under extreme wind conditions. Sustain Cities Soc 65:1–11

Rocchetta R, Zio E, Patelli E (2018) A power-flow emulator approach for resilience assessment of repairable power grids subject to weather-induced failures and data deficiency. Appl Energy 210:339–350

Costa IC, Venturini LF, Da Rosa MA (2019) Wind speed severity scale model applied to overhead line reliability simulation. Electr Power Syst Res 171:240–250

Hasse L (2015) Basic atmospheric structure and concepts | Beaufort wind scale. In: Encyclopedia of atmospheric sciences, 2nd edn. Academic Press

World Meteorological Organization (2017) WMO guidelines on the calculation of climate normal. WMO-No. 1203, Geneva

Download references

Acknowledgements

This work was supported by the Russian Science Foundation (project No. 22-79-00042).

Author information

Authors and affiliations.

National Research University “Moscow Power Engineering Institute”, 14, Krasnokazaramennaya Street, Moscow, 111250, Russia

Oleg Loktionov & Olga Kondrateva

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Oleg Loktionov .

Editor information

Editors and affiliations.

University of Chinese Academy of Sciences, Beijing, China

Khasanov Sayidjakhon Zokirjon ugli

Far Eastern State Agrarian University, Blagoveshchensk, Russia

Aleksei Muratov

ITMO University, St. Petersburg, Russia

Svetlana Ignateva

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Loktionov, O., Kondrateva, O. (2024). Failures Forecast on Overhead Lines from Wind Loads in the Krasnodar Krai of Russia. In: Zokirjon ugli, K.S., Muratov, A., Ignateva, S. (eds) Fundamental and Applied Scientific Research in the Development of Agriculture in the Far East (AFE-2022). AFE 2023. Lecture Notes in Networks and Systems, vol 733. Springer, Cham. https://doi.org/10.1007/978-3-031-37978-9_45

Download citation

DOI : https://doi.org/10.1007/978-3-031-37978-9_45

Published : 10 February 2024

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-37977-2

Online ISBN : 978-3-031-37978-9

eBook Packages : Intelligent Technologies and Robotics Intelligent Technologies and Robotics (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research