problem solving strategy act it out

Problem Solving Strategies

The following are some examples of problem solving strategies.

Explore it//Act it/Try it (EAT) method (Basic)

Explore it//Act it/Try it (EAT) method (Intermediate )

Explore it//Act it/Try it (EAT) method (Advanced)

Finding a Pattern (Basic)

Finding a Pattern (Intermediate)

Finding a Pattern (Advanced)

Explore It/Act It/Try It (EAT) Method (Basic)

In this lesson, we will look at some basic examples of the Explore it//Act it/Try it (EAT) method of problem solving strategy.

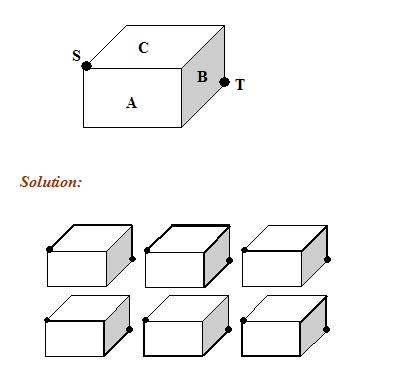
A plumber has to connect a pipe from a storage tank at the corner, S , of the roof to a tap at the diagonally opposite corner, T , in the figure below. Find the number of paths for the pipe if the pipe can only run along the edges of walls A , B , or roof C .

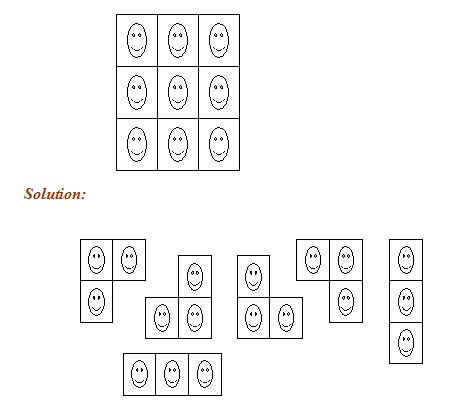
Three stamps are to be torn from a sheet of nine stamps as shown below. The three stamps must be intact so that each stamp is joined to another stamp along at least one edge. Find the possible patterns for these three stamps.

Rachel has to spend exactly $100 on the following gifts. What are the combinations of gifts that she can buy?

B, E, F or B, D

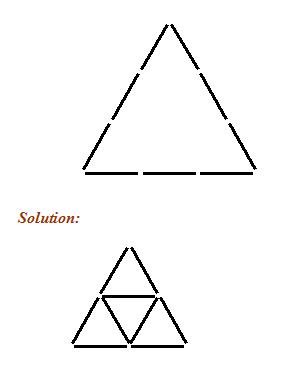
The figure below shows 9 matchsticks arranged as an equilateral triangle. Rearrange exactly 5 of the matchsticks to form 5 equilateral triangles, without leaving any stray matchsticks.

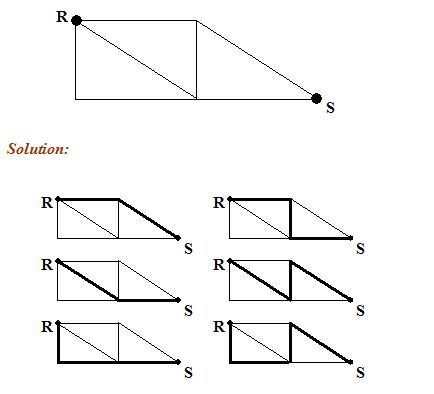
The figure below shows the roads linking cities R and S . What are the different routes to travel from R to S ?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Book a Demo

Struggling to overcome challenges in your life? We all face problems, big and small, on a regular basis.

So how do you tackle them effectively? What are some key problem-solving strategies and skills that can guide you?

Effective problem-solving requires breaking issues down logically, generating solutions creatively, weighing choices critically, and adapting plans flexibly based on outcomes. Useful strategies range from leveraging past solutions that have worked to visualizing problems through diagrams. Core skills include analytical abilities, innovative thinking, and collaboration.

Want to improve your problem-solving skills? Keep reading to find out 17 effective problem-solving strategies, key skills, common obstacles to watch for, and tips on improving your overall problem-solving skills.

Key Takeaways:

• Effective problem-solving requires breaking down issues logically, generating multiple solutions creatively, weighing choices critically, and adapting plans based on outcomes.
• Useful problem-solving strategies range from leveraging past solutions to brainstorming with groups to visualizing problems through diagrams and models.
• Core skills include analytical abilities, innovative thinking, decision-making, and team collaboration to solve problems.
• Common obstacles include fear of failure, information gaps, fixed mindsets, confirmation bias, and groupthink.
• Boosting problem-solving skills involves learning from experts, actively practicing, soliciting feedback, and analyzing others’ success.
• Onethread’s project management capabilities align with effective problem-solving tenets – facilitating structured solutions, tracking progress, and capturing lessons learned.

What Is Problem-Solving?

Problem-solving is the process of understanding an issue, situation, or challenge that needs to be addressed and then systematically working through possible solutions to arrive at the best outcome.

It involves critical thinking, analysis, logic, creativity, research, planning, reflection, and patience in order to overcome obstacles and find effective answers to complex questions or problems.

The ultimate goal is to implement the chosen solution successfully.

What Are Problem-Solving Strategies?

Problem-solving strategies are like frameworks or methodologies that help us solve tricky puzzles or problems we face in the workplace, at home, or with friends.

Imagine you have a big jigsaw puzzle. One strategy might be to start with the corner pieces. Another could be looking for pieces with the same colors. 

Just like in puzzles, in real life, we use different plans or steps to find solutions to problems. These strategies help us think clearly, make good choices, and find the best answers without getting too stressed or giving up.

Why Is It Important To Know Different Problem-Solving Strategies?

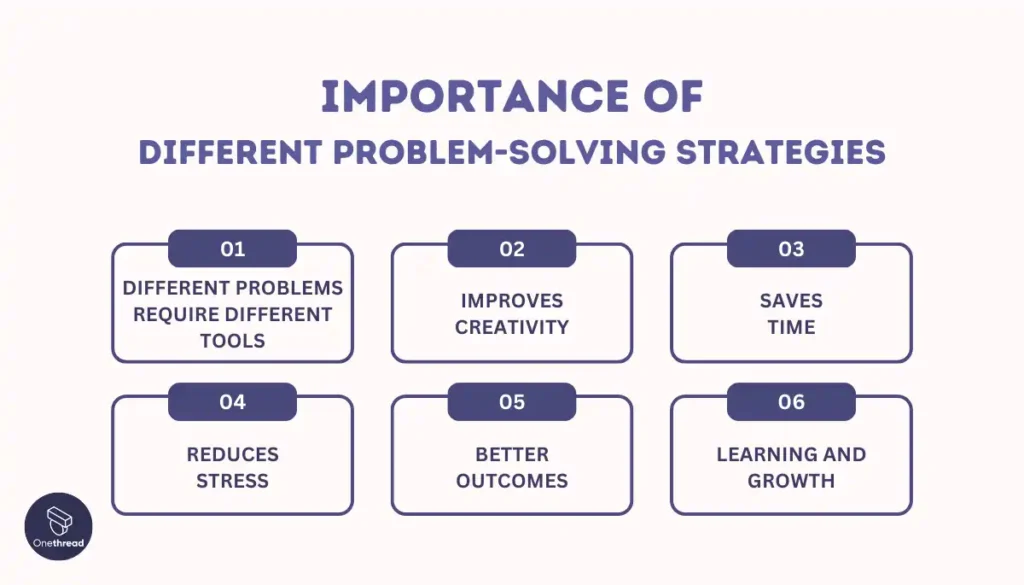
Knowing different problem-solving strategies is important because different types of problems often require different approaches to solve them effectively. Having a variety of strategies to choose from allows you to select the best method for the specific problem you are trying to solve.

This improves your ability to analyze issues thoroughly, develop solutions creatively, and tackle problems from multiple angles. Knowing multiple strategies also aids in overcoming roadblocks if your initial approach is not working.

Here are some reasons why you need to know different problem-solving strategies:

• Different Problems Require Different Tools: Just like you can’t use a hammer to fix everything, some problems need specific strategies to solve them.
• Improves Creativity: Knowing various strategies helps you think outside the box and come up with creative solutions.
• Saves Time: With the right strategy, you can solve problems faster instead of trying things that don’t work.
• Reduces Stress: When you know how to tackle a problem, it feels less scary and you feel more confident.
• Better Outcomes: Using the right strategy can lead to better solutions, making things work out better in the end.
• Learning and Growth: Each time you solve a problem, you learn something new, which makes you smarter and better at solving future problems.

Knowing different ways to solve problems helps you tackle anything that comes your way, making life a bit easier and more fun!

17 Effective Problem-Solving Strategies

Effective problem-solving strategies include breaking the problem into smaller parts, brainstorming multiple solutions, evaluating the pros and cons of each, and choosing the most viable option. 

Critical thinking and creativity are essential in developing innovative solutions. Collaboration with others can also provide diverse perspectives and ideas. 

By applying these strategies, you can tackle complex issues more effectively.

Now, consider a challenge you’re dealing with. Which strategy could help you find a solution? Here we will discuss key problem strategies in detail.

1. Use a Past Solution That Worked

This strategy involves looking back at previous similar problems you have faced and the solutions that were effective in solving them.

It is useful when you are facing a problem that is very similar to something you have already solved. The main benefit is that you don’t have to come up with a brand new solution – you already know the method that worked before will likely work again.

However, the limitation is that the current problem may have some unique aspects or differences that mean your old solution is not fully applicable.

The ideal process is to thoroughly analyze the new challenge, identify the key similarities and differences versus the past case, adapt the old solution as needed to align with the current context, and then pilot it carefully before full implementation.

An example is using the same negotiation tactics from purchasing your previous home when putting in an offer on a new house. Key terms would be adjusted but overall it can save significant time versus developing a brand new strategy.

2. Brainstorm Solutions

This involves gathering a group of people together to generate as many potential solutions to a problem as possible.

It is effective when you need creative ideas to solve a complex or challenging issue. By getting input from multiple people with diverse perspectives, you increase the likelihood of finding an innovative solution.

The main limitation is that brainstorming sessions can sometimes turn into unproductive gripe sessions or discussions rather than focusing on productive ideation —so they need to be properly facilitated.

The key to an effective brainstorming session is setting some basic ground rules upfront and having an experienced facilitator guide the discussion. Rules often include encouraging wild ideas, avoiding criticism of ideas during the ideation phase, and building on others’ ideas.

For instance, a struggling startup might hold a session where ideas for turnaround plans are generated and then formalized with financials and metrics.

3. Work Backward from the Solution

This technique involves envisioning that the problem has already been solved and then working step-by-step backward toward the current state.

This strategy is particularly helpful for long-term, multi-step problems. By starting from the imagined solution and identifying all the steps required to reach it, you can systematically determine the actions needed. It lets you tackle a big hairy problem through smaller, reversible steps.

A limitation is that this approach may not be possible if you cannot accurately envision the solution state to start with.

The approach helps drive logical systematic thinking for complex problem-solving, but should still be combined with creative brainstorming of alternative scenarios and solutions.

An example is planning for an event – you would imagine the successful event occurring, then determine the tasks needed the week before, two weeks before, etc. all the way back to the present.

4. Use the Kipling Method

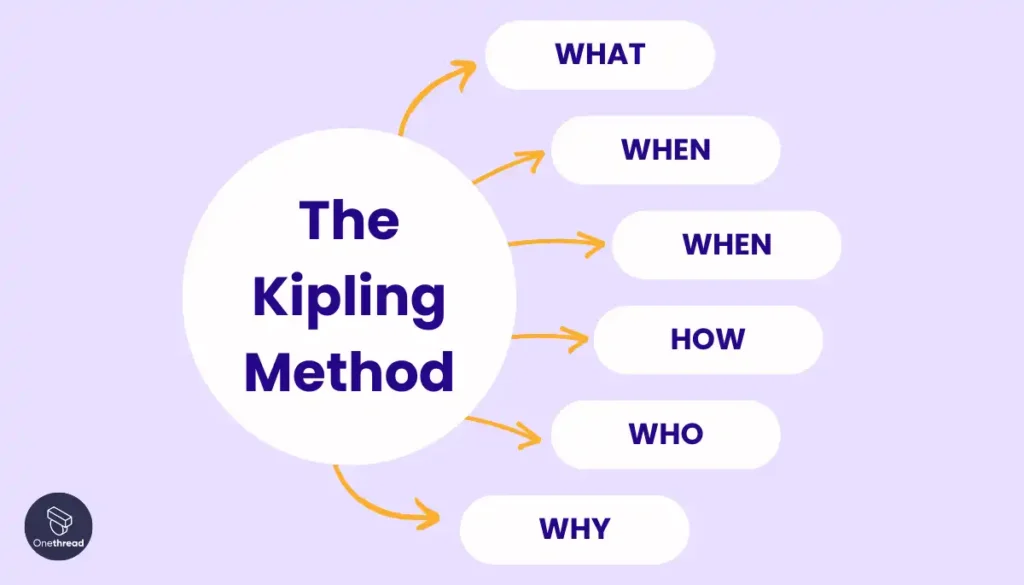
This method, named after author Rudyard Kipling, provides a framework for thoroughly analyzing a problem before jumping into solutions.

It consists of answering six fundamental questions: What, Where, When, How, Who, and Why about the challenge. Clearly defining these core elements of the problem sets the stage for generating targeted solutions.

The Kipling method enables a deep understanding of problem parameters and root causes before solution identification. By jumping to brainstorm solutions too early, critical information can be missed or the problem is loosely defined, reducing solution quality.

Answering the six fundamental questions illuminates all angles of the issue. This takes time but pays dividends in generating optimal solutions later tuned precisely to the true underlying problem.

The limitation is that meticulously working through numerous questions before addressing solutions can slow progress.

The best approach blends structured problem decomposition techniques like the Kipling method with spurring innovative solution ideation from a diverse team. 

An example is using this technique after a technical process failure – the team would systematically detail What failed, Where/When did it fail, How it failed (sequence of events), Who was involved, and Why it likely failed before exploring preventative solutions.

5. Try Different Solutions Until One Works (Trial and Error)

This technique involves attempting various potential solutions sequentially until finding one that successfully solves the problem.

Trial and error works best when facing a concrete, bounded challenge with clear solution criteria and a small number of discrete options to try. By methodically testing solutions, you can determine the faulty component.

A limitation is that it can be time-intensive if the working solution set is large.

The key is limiting the variable set first. For technical problems, this boundary is inherent and each element can be iteratively tested. But for business issues, artificial constraints may be required – setting decision rules upfront to reduce options before testing.

Furthermore, hypothesis-driven experimentation is far superior to blind trial and error – have logic for why Option A may outperform Option B.

Examples include fixing printer jams by testing different paper tray and cable configurations or resolving website errors by tweaking CSS/HTML line-by-line until the code functions properly.

6. Use Proven Formulas or Frameworks (Heuristics)

Heuristics refers to applying existing problem-solving formulas or frameworks rather than addressing issues completely from scratch.

This allows leveraging established best practices rather than reinventing the wheel each time.

It is effective when facing recurrent, common challenges where proven structured approaches exist.

However, heuristics may force-fit solutions to non-standard problems.

For example, a cost-benefit analysis can be used instead of custom weighting schemes to analyze potential process improvements.

Onethread allows teams to define, save, and replicate configurable project templates so proven workflows can be reliably applied across problems with some consistency rather than fully custom one-off approaches each time.

Try One thread

Experience One thread full potential, with all its features unlocked. Sign up now to start your 14-day free trial!

7. Trust Your Instincts (Insight Problem-Solving)

Insight is a problem-solving technique that involves waiting patiently for an unexpected “aha moment” when the solution pops into your mind.

It works well for personal challenges that require intuitive realizations over calculated logic. The unconscious mind makes connections leading to flashes of insight when relaxing or doing mundane tasks unrelated to the actual problem.

Benefits include out-of-the-box creative solutions. However, the limitations are that insights can’t be forced and may never come at all if too complex. Critical analysis is still required after initial insights.

A real-life example would be a writer struggling with how to end a novel. Despite extensive brainstorming, they feel stuck. Eventually while gardening one day, a perfect unexpected plot twist sparks an ideal conclusion. However, once written they still carefully review if the ending flows logically from the rest of the story.

8. Reverse Engineer the Problem

This approach involves deconstructing a problem in reverse sequential order from the current undesirable outcome back to the initial root causes.

By mapping the chain of events backward, you can identify the origin of where things went wrong and establish the critical junctures for solving it moving ahead. Reverse engineering provides diagnostic clarity on multi-step problems.

However, the limitation is that it focuses heavily on autopsying the past versus innovating improved future solutions.

An example is tracing back from a server outage, through the cascade of infrastructure failures that led to it finally terminating at the initial script error that triggered the crisis. This root cause would then inform the preventative measure.

9. Break Down Obstacles Between Current and Goal State (Means-End Analysis)

This technique defines the current problem state and the desired end goal state, then systematically identifies obstacles in the way of getting from one to the other.

By mapping the barriers or gaps, you can then develop solutions to address each one. This methodically connects the problem to solutions.

A limitation is that some obstacles may be unknown upfront and only emerge later.

For example, you can list down all the steps required for a new product launch – current state through production, marketing, sales, distribution, etc. to full launch (goal state) – to highlight where resource constraints or other blocks exist so they can be addressed.

Onethread allows dividing big-picture projects into discrete, manageable phases, milestones, and tasks to simplify execution just as problems can be decomposed into more achievable components. Features like dependency mapping further reinforce interconnections.

Using Onethread’s issues and subtasks feature, messy problems can be decomposed into manageable chunks.

10. Ask “Why” Five Times to Identify the Root Cause (The 5 Whys)

This technique involves asking “Why did this problem occur?” and then responding with an answer that is again met with asking “Why?” This process repeats five times until the root cause is revealed.

Continually asking why digs deeper from surface symptoms to underlying systemic issues.

It is effective for getting to the source of problems originating from human error or process breakdowns.

However, some complex issues may have multiple tangled root causes not solvable through this approach alone.

An example is a retail store experiencing a sudden decline in customers. Successively asking why five times may trace an initial drop to parking challenges, stemming from a city construction project – the true starting point to address.

11. Evaluate Strengths, Weaknesses, Opportunities, and Threats (SWOT Analysis)

This involves analyzing a problem or proposed solution by categorizing internal and external factors into a 2×2 matrix: Strengths, Weaknesses as the internal rows; Opportunities and Threats as the external columns.

Systematically identifying these elements provides balanced insight to evaluate options and risks. It is impactful when evaluating alternative solutions or developing strategy amid complexity or uncertainty.

The key benefit of SWOT analysis is enabling multi-dimensional thinking when rationally evaluating options. Rather than getting anchored on just the upsides or the existing way of operating, it urges a systematic assessment through four different lenses:

• Internal Strengths: Our core competencies/advantages able to deliver success
• Internal Weaknesses: Gaps/vulnerabilities we need to manage
• External Opportunities: Ways we can differentiate/drive additional value
• External Threats: Risks we must navigate or mitigate

Multiperspective analysis provides the needed holistic view of the balanced risk vs. reward equation for strategic decision making amid uncertainty.

However, SWOT can feel restrictive if not tailored and evolved for different issue types.

Teams should view SWOT analysis as a starting point, augmenting it further for distinct scenarios.

An example is performing a SWOT analysis on whether a small business should expand into a new market – evaluating internal capabilities to execute vs. risks in the external competitive and demand environment to inform the growth decision with eyes wide open.

12. Compare Current vs Expected Performance (Gap Analysis)

This technique involves comparing the current state of performance, output, or results to the desired or expected levels to highlight shortfalls.

By quantifying the gaps, you can identify problem areas and prioritize address solutions.

Gap analysis is based on the simple principle – “you can’t improve what you don’t measure.” It enables facts-driven problem diagnosis by highlighting delta to goals, not just vague dissatisfaction that something seems wrong. And measurement immediately suggests improvement opportunities – address the biggest gaps first.

This data orientation also supports ROI analysis on fixing issues – the return from closing larger gaps outweighs narrowly targeting smaller performance deficiencies.

However, the approach is only effective if robust standards and metrics exist as the benchmark to evaluate against. Organizations should invest upfront in establishing performance frameworks.

Furthermore, while numbers are invaluable, the human context behind problems should not be ignored – quantitative versus qualitative gap assessment is optimally blended.

For example, if usage declines are noted during software gap analysis, this could be used as a signal to improve user experience through design.

13. Observe Processes from the Frontline (Gemba Walk)

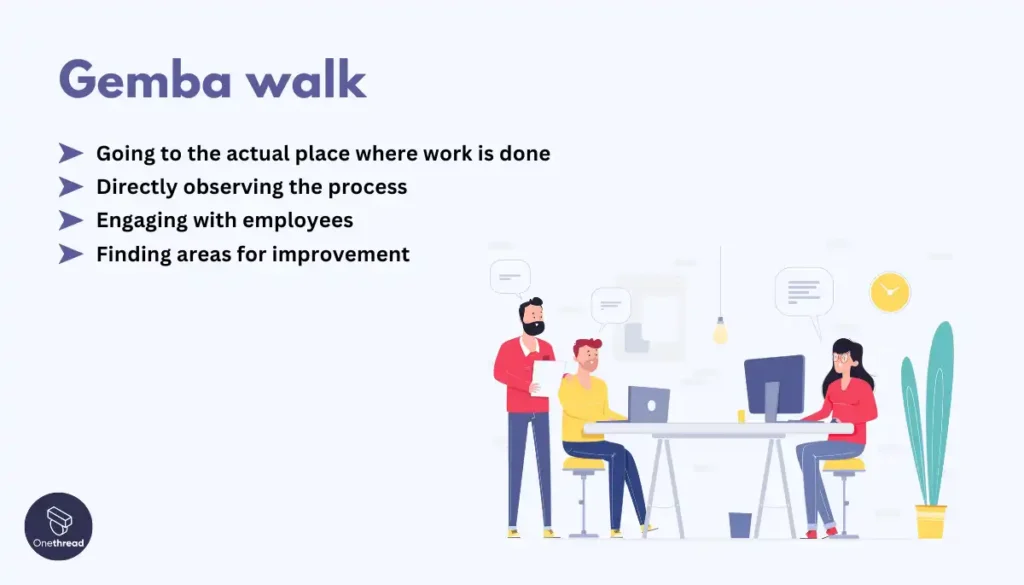
A Gemba walk involves going to the actual place where work is done, directly observing the process, engaging with employees, and finding areas for improvement.

By experiencing firsthand rather than solely reviewing abstract reports, practical problems and ideas emerge.

The limitation is Gemba walks provide anecdotes not statistically significant data. It complements but does not replace comprehensive performance measurement.

An example is a factory manager inspecting the production line to spot jam areas based on direct reality rather than relying on throughput dashboards alone back in her office. Frontline insights prove invaluable.

14. Analyze Competitive Forces (Porter’s Five Forces)

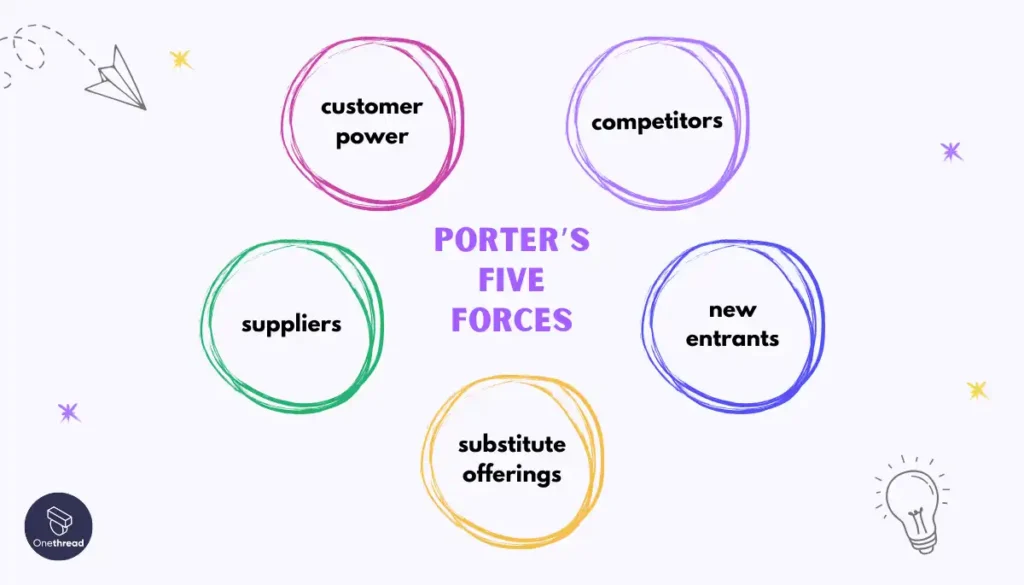
This involves assessing the marketplace around a problem or business situation via five key factors: competitors, new entrants, substitute offerings, suppliers, and customer power.

Evaluating these forces illuminates risks and opportunities for strategy development and issue resolution. It is effective for understanding dynamic external threats and opportunities when operating in a contested space.

However, over-indexing on only external factors can overlook the internal capabilities needed to execute solutions.

A startup CEO, for example, may analyze market entry barriers, whitespace opportunities, and disruption risks across these five forces to shape new product rollout strategies and marketing approaches.

15. Think from Different Perspectives (Six Thinking Hats)

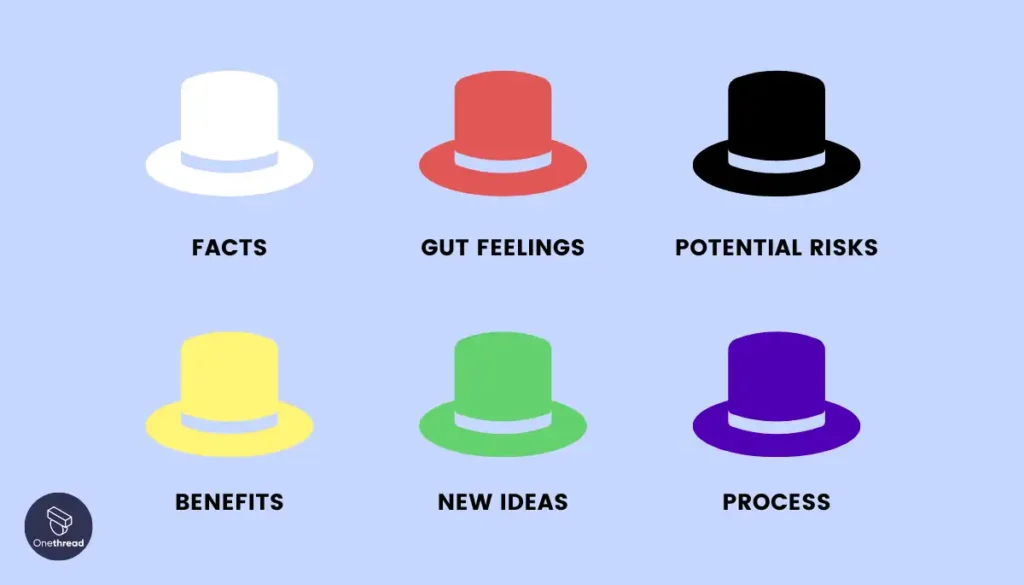
The Six Thinking Hats is a technique developed by Edward de Bono that encourages people to think about a problem from six different perspectives, each represented by a colored “thinking hat.”

The key benefit of this strategy is that it pushes team members to move outside their usual thinking style and consider new angles. This brings more diverse ideas and solutions to the table.

It works best for complex problems that require innovative solutions and when a team is stuck in an unproductive debate. The structured framework keeps the conversation flowing in a positive direction.

Limitations are that it requires training on the method itself and may feel unnatural at first. Team dynamics can also influence success – some members may dominate certain “hats” while others remain quiet.

A real-life example is a software company debating whether to build a new feature. The white hat focuses on facts, red on gut feelings, black on potential risks, yellow on benefits, green on new ideas, and blue on process. This exposes more balanced perspectives before deciding.

Onethread centralizes diverse stakeholder communication onto one platform, ensuring all voices are incorporated when evaluating project tradeoffs, just as problem-solving should consider multifaceted solutions.

16. Visualize the Problem (Draw it Out)

Drawing out a problem involves creating visual representations like diagrams, flowcharts, and maps to work through challenging issues.

This strategy is helpful when dealing with complex situations with lots of interconnected components. The visuals simplify the complexity so you can thoroughly understand the problem and all its nuances.

Key benefits are that it allows more stakeholders to get on the same page regarding root causes and it sparks new creative solutions as connections are made visually.

However, simple problems with few variables don’t require extensive diagrams. Additionally, some challenges are so multidimensional that fully capturing every aspect is difficult.

A real-life example would be mapping out all the possible causes leading to decreased client satisfaction at a law firm. An intricate fishbone diagram with branches for issues like service delivery, technology, facilities, culture, and vendor partnerships allows the team to trace problems back to their origins and brainstorm targeted fixes.

17. Follow a Step-by-Step Procedure (Algorithms)

An algorithm is a predefined step-by-step process that is guaranteed to produce the correct solution if implemented properly.

Using algorithms is effective when facing problems that have clear, binary right and wrong answers. Algorithms work for mathematical calculations, computer code, manufacturing assembly lines, and scientific experiments.

Key benefits are consistency, accuracy, and efficiency. However, they require extensive upfront development and only apply to scenarios with strict parameters. Additionally, human error can lead to mistakes.

For example, crew members of fast food chains like McDonald’s follow specific algorithms for food prep – from grill times to ingredient amounts in sandwiches, to order fulfillment procedures. This ensures uniform quality and service across all locations. However, if a step is missed, errors occur.

The Problem-Solving Process

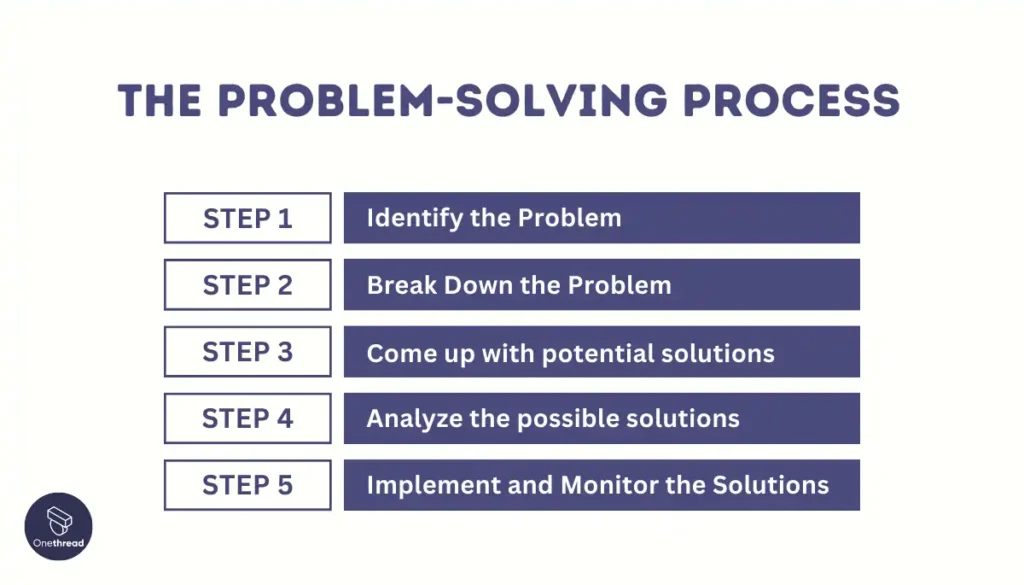
The problem-solving process typically includes defining the issue, analyzing details, creating solutions, weighing choices, acting, and reviewing results.

In the above, we have discussed several problem-solving strategies. For every problem-solving strategy, you have to follow these processes. Here’s a detailed step-by-step process of effective problem-solving:

Step 1: Identify the Problem

The problem-solving process starts with identifying the problem. This step involves understanding the issue’s nature, its scope, and its impact. Once the problem is clearly defined, it sets the foundation for finding effective solutions.

Identifying the problem is crucial. It means figuring out exactly what needs fixing. This involves looking at the situation closely, understanding what’s wrong, and knowing how it affects things. It’s about asking the right questions to get a clear picture of the issue. 

This step is important because it guides the rest of the problem-solving process. Without a clear understanding of the problem, finding a solution is much harder. It’s like diagnosing an illness before treating it. Once the problem is identified accurately, you can move on to exploring possible solutions and deciding on the best course of action.

Step 2: Break Down the Problem

Breaking down the problem is a key step in the problem-solving process. It involves dividing the main issue into smaller, more manageable parts. This makes it easier to understand and tackle each component one by one.

After identifying the problem, the next step is to break it down. This means splitting the big issue into smaller pieces. It’s like solving a puzzle by handling one piece at a time. 

By doing this, you can focus on each part without feeling overwhelmed. It also helps in identifying the root causes of the problem. Breaking down the problem allows for a clearer analysis and makes finding solutions more straightforward. 

Each smaller problem can be addressed individually, leading to an effective resolution of the overall issue. This approach not only simplifies complex problems but also aids in developing a systematic plan to solve them.

Step 3: Come up with potential solutions

Coming up with potential solutions is the third step in the problem-solving process. It involves brainstorming various options to address the problem, considering creativity and feasibility to find the best approach.

After breaking down the problem, it’s time to think of ways to solve it. This stage is about brainstorming different solutions. You look at the smaller issues you’ve identified and start thinking of ways to fix them. This is where creativity comes in. 

You want to come up with as many ideas as possible, no matter how out-of-the-box they seem. It’s important to consider all options and evaluate their pros and cons. This process allows you to gather a range of possible solutions. 

Later, you can narrow these down to the most practical and effective ones. This step is crucial because it sets the stage for deciding on the best solution to implement. It’s about being open-minded and innovative to tackle the problem effectively.

Step 4: Analyze the possible solutions

Analyzing the possible solutions is the fourth step in the problem-solving process. It involves evaluating each proposed solution’s advantages and disadvantages to determine the most effective and feasible option.

After coming up with potential solutions, the next step is to analyze them. This means looking closely at each idea to see how well it solves the problem. You weigh the pros and cons of every solution.

Consider factors like cost, time, resources, and potential outcomes. This analysis helps in understanding the implications of each option. It’s about being critical and objective, ensuring that the chosen solution is not only effective but also practical.

This step is vital because it guides you towards making an informed decision. It involves comparing the solutions against each other and selecting the one that best addresses the problem.

By thoroughly analyzing the options, you can move forward with confidence, knowing you’ve chosen the best path to solve the issue.

Step 5: Implement and Monitor the Solutions

Implementing and monitoring the solutions is the final step in the problem-solving process. It involves putting the chosen solution into action and observing its effectiveness, making adjustments as necessary.

Once you’ve selected the best solution, it’s time to put it into practice. This step is about action. You implement the chosen solution and then keep an eye on how it works. Monitoring is crucial because it tells you if the solution is solving the problem as expected. 

If things don’t go as planned, you may need to make some changes. This could mean tweaking the current solution or trying a different one. The goal is to ensure the problem is fully resolved. 

This step is critical because it involves real-world application. It’s not just about planning; it’s about doing and adjusting based on results. By effectively implementing and monitoring the solutions, you can achieve the desired outcome and solve the problem successfully.

Why This Process is Important

Following a defined process to solve problems is important because it provides a systematic, structured approach instead of a haphazard one. Having clear steps guides logical thinking, analysis, and decision-making to increase effectiveness. Key reasons it helps are:

• Clear Direction: This process gives you a clear path to follow, which can make solving problems less overwhelming.
• Better Solutions: Thoughtful analysis of root causes, iterative testing of solutions, and learning orientation lead to addressing the heart of issues rather than just symptoms.
• Saves Time and Energy: Instead of guessing or trying random things, this process helps you find a solution more efficiently.
• Improves Skills: The more you use this process, the better you get at solving problems. It’s like practicing a sport. The more you practice, the better you play.
• Maximizes collaboration: Involving various stakeholders in the process enables broader inputs. Their communication and coordination are streamlined through organized brainstorming and evaluation.
• Provides consistency: Standard methodology across problems enables building institutional problem-solving capabilities over time. Patterns emerge on effective techniques to apply to different situations.

The problem-solving process is a powerful tool that can help us tackle any challenge we face. By following these steps, we can find solutions that work and learn important skills along the way.

Key Skills for Efficient Problem Solving

Efficient problem-solving requires breaking down issues logically, evaluating options, and implementing practical solutions.

Key skills include critical thinking to understand root causes, creativity to brainstorm innovative ideas, communication abilities to collaborate with others, and decision-making to select the best way forward. Staying adaptable, reflecting on outcomes, and applying lessons learned are also essential.

With practice, these capacities will lead to increased personal and team effectiveness in systematically addressing any problem.

 Let’s explore the powers you need to become a problem-solving hero!

Critical Thinking and Analytical Skills

Critical thinking and analytical skills are vital for efficient problem-solving as they enable individuals to objectively evaluate information, identify key issues, and generate effective solutions. 

These skills facilitate a deeper understanding of problems, leading to logical, well-reasoned decisions. By systematically breaking down complex issues and considering various perspectives, individuals can develop more innovative and practical solutions, enhancing their problem-solving effectiveness.

Communication Skills

Effective communication skills are essential for efficient problem-solving as they facilitate clear sharing of information, ensuring all team members understand the problem and proposed solutions. 

These skills enable individuals to articulate issues, listen actively, and collaborate effectively, fostering a productive environment where diverse ideas can be exchanged and refined. By enhancing mutual understanding, communication skills contribute significantly to identifying and implementing the most viable solutions.

Decision-Making

Strong decision-making skills are crucial for efficient problem-solving, as they enable individuals to choose the best course of action from multiple alternatives. 

These skills involve evaluating the potential outcomes of different solutions, considering the risks and benefits, and making informed choices. Effective decision-making leads to the implementation of solutions that are likely to resolve problems effectively, ensuring resources are used efficiently and goals are achieved.

Planning and Prioritization

Planning and prioritization are key for efficient problem-solving, ensuring resources are allocated effectively to address the most critical issues first. This approach helps in organizing tasks according to their urgency and impact, streamlining efforts towards achieving the desired outcome efficiently.

Emotional Intelligence

Emotional intelligence enhances problem-solving by allowing individuals to manage emotions, understand others, and navigate social complexities. It fosters a positive, collaborative environment, essential for generating creative solutions and making informed, empathetic decisions.

Leadership skills drive efficient problem-solving by inspiring and guiding teams toward common goals. Effective leaders motivate their teams, foster innovation, and navigate challenges, ensuring collective efforts are focused and productive in addressing problems.

Time Management

Time management is crucial in problem-solving, enabling individuals to allocate appropriate time to each task. By efficiently managing time, one can ensure that critical problems are addressed promptly without neglecting other responsibilities.

Data Analysis

Data analysis skills are essential for problem-solving, as they enable individuals to sift through data, identify trends, and extract actionable insights. This analytical approach supports evidence-based decision-making, leading to more accurate and effective solutions.

Research Skills

Research skills are vital for efficient problem-solving, allowing individuals to gather relevant information, explore various solutions, and understand the problem’s context. This thorough exploration aids in developing well-informed, innovative solutions.

Becoming a great problem solver takes practice, but with these skills, you’re on your way to becoming a problem-solving hero. 

How to Improve Your Problem-Solving Skills?

Improving your problem-solving skills can make you a master at overcoming challenges. Learn from experts, practice regularly, welcome feedback, try new methods, experiment, and study others’ success to become better.

Learning from Experts

Improving problem-solving skills by learning from experts involves seeking mentorship, attending workshops, and studying case studies. Experts provide insights and techniques that refine your approach, enhancing your ability to tackle complex problems effectively.

To enhance your problem-solving skills, learning from experts can be incredibly beneficial. Engaging with mentors, participating in specialized workshops, and analyzing case studies from seasoned professionals can offer valuable perspectives and strategies. 

Experts share their experiences, mistakes, and successes, providing practical knowledge that can be applied to your own problem-solving process. This exposure not only broadens your understanding but also introduces you to diverse methods and approaches, enabling you to tackle challenges more efficiently and creatively.

Improving problem-solving skills through practice involves tackling a variety of challenges regularly. This hands-on approach helps in refining techniques and strategies, making you more adept at identifying and solving problems efficiently.

One of the most effective ways to enhance your problem-solving skills is through consistent practice. By engaging with different types of problems on a regular basis, you develop a deeper understanding of various strategies and how they can be applied. 

This hands-on experience allows you to experiment with different approaches, learn from mistakes, and build confidence in your ability to tackle challenges.

Regular practice not only sharpens your analytical and critical thinking skills but also encourages adaptability and innovation, key components of effective problem-solving.

Openness to Feedback

Being open to feedback is like unlocking a secret level in a game. It helps you boost your problem-solving skills. Improving problem-solving skills through openness to feedback involves actively seeking and constructively responding to critiques. 

This receptivity enables you to refine your strategies and approaches based on insights from others, leading to more effective solutions. 

Learning New Approaches and Methodologies

Learning new approaches and methodologies is like adding new tools to your toolbox. It makes you a smarter problem-solver. Enhancing problem-solving skills by learning new approaches and methodologies involves staying updated with the latest trends and techniques in your field. 

This continuous learning expands your toolkit, enabling innovative solutions and a fresh perspective on challenges.

Experimentation

Experimentation is like being a scientist of your own problems. It’s a powerful way to improve your problem-solving skills. Boosting problem-solving skills through experimentation means trying out different solutions to see what works best. This trial-and-error approach fosters creativity and can lead to unique solutions that wouldn’t have been considered otherwise.

Analyzing Competitors’ Success

Analyzing competitors’ success is like being a detective. It’s a smart way to boost your problem-solving skills. Improving problem-solving skills by analyzing competitors’ success involves studying their strategies and outcomes. Understanding what worked for them can provide valuable insights and inspire effective solutions for your own challenges. 

Challenges in Problem-Solving

Facing obstacles when solving problems is common. Recognizing these barriers, like fear of failure or lack of information, helps us find ways around them for better solutions.

Fear of Failure

Fear of failure is like a big, scary monster that stops us from solving problems. It’s a challenge many face. Because being afraid of making mistakes can make us too scared to try new solutions. 

How can we overcome this? First, understand that it’s okay to fail. Failure is not the opposite of success; it’s part of learning. Every time we fail, we discover one more way not to solve a problem, getting us closer to the right solution. Treat each attempt like an experiment. It’s not about failing; it’s about testing and learning.

Lack of Information

Lack of information is like trying to solve a puzzle with missing pieces. It’s a big challenge in problem-solving. Because without all the necessary details, finding a solution is much harder. 

How can we fix this? Start by gathering as much information as you can. Ask questions, do research, or talk to experts. Think of yourself as a detective looking for clues. The more information you collect, the clearer the picture becomes. Then, use what you’ve learned to think of solutions. 

Fixed Mindset

A fixed mindset is like being stuck in quicksand; it makes solving problems harder. It means thinking you can’t improve or learn new ways to solve issues. 

How can we change this? First, believe that you can grow and learn from challenges. Think of your brain as a muscle that gets stronger every time you use it. When you face a problem, instead of saying “I can’t do this,” try thinking, “I can’t do this yet.” Look for lessons in every challenge and celebrate small wins. 

Everyone starts somewhere, and mistakes are just steps on the path to getting better. By shifting to a growth mindset, you’ll see problems as opportunities to grow. Keep trying, keep learning, and your problem-solving skills will soar!

Jumping to Conclusions

Jumping to conclusions is like trying to finish a race before it starts. It’s a challenge in problem-solving. That means making a decision too quickly without looking at all the facts. 

How can we avoid this? First, take a deep breath and slow down. Think about the problem like a puzzle. You need to see all the pieces before you know where they go. Ask questions, gather information, and consider different possibilities. Don’t choose the first solution that comes to mind. Instead, compare a few options. 

Feeling Overwhelmed

Feeling overwhelmed is like being buried under a mountain of puzzles. It’s a big challenge in problem-solving. When we’re overwhelmed, everything seems too hard to handle. 

How can we deal with this? Start by taking a step back. Breathe deeply and focus on one thing at a time. Break the big problem into smaller pieces, like sorting puzzle pieces by color. Tackle each small piece one by one. It’s also okay to ask for help. Sometimes, talking to someone else can give you a new perspective. 

Confirmation Bias

Confirmation bias is like wearing glasses that only let you see what you want to see. It’s a challenge in problem-solving. Because it makes us focus only on information that agrees with what we already believe, ignoring anything that doesn’t. 

How can we overcome this? First, be aware that you might be doing it. It’s like checking if your glasses are on right. Then, purposely look for information that challenges your views. It’s like trying on a different pair of glasses to see a new perspective. Ask questions and listen to answers, even if they don’t fit what you thought before.

Groupthink is like everyone in a group deciding to wear the same outfit without asking why. It’s a challenge in problem-solving. It means making decisions just because everyone else agrees, without really thinking it through. 

How can we avoid this? First, encourage everyone in the group to share their ideas, even if they’re different. It’s like inviting everyone to show their unique style of clothes. 

Listen to all opinions and discuss them. It’s okay to disagree; it helps us think of better solutions. Also, sometimes, ask someone outside the group for their thoughts. They might see something everyone in the group missed.

Overcoming obstacles in problem-solving requires patience, openness, and a willingness to learn from mistakes. By recognizing these barriers, we can develop strategies to navigate around them, leading to more effective and creative solutions.

What are the most common problem-solving techniques?

The most common techniques include brainstorming, the 5 Whys, mind mapping, SWOT analysis, and using algorithms or heuristics. Each approach has its strengths, suitable for different types of problems.

What’s the best problem-solving strategy for every situation?

There’s no one-size-fits-all strategy. The best approach depends on the problem’s complexity, available resources, and time constraints. Combining multiple techniques often yields the best results.

How can I improve my problem-solving skills?

Improve your problem-solving skills by practicing regularly, learning from experts, staying open to feedback, and continuously updating your knowledge on new approaches and methodologies.

Are there any tools or resources to help with problem-solving?

Yes, tools like mind mapping software, online courses on critical thinking, and books on problem-solving techniques can be very helpful. Joining forums or groups focused on problem-solving can also provide support and insights.

What are some common mistakes people make when solving problems?

Common mistakes include jumping to conclusions without fully understanding the problem, ignoring valuable feedback, sticking to familiar solutions without considering alternatives, and not breaking down complex problems into manageable parts.

Final Words

Mastering problem-solving strategies equips us with the tools to tackle challenges across all areas of life. By understanding and applying these techniques, embracing a growth mindset, and learning from both successes and obstacles, we can transform problems into opportunities for growth. Continuously improving these skills ensures we’re prepared to face and solve future challenges more effectively.

Let's Get Started with Onethread

Onethread empowers you to plan, organise, and track projects with ease, ensuring you meet deadlines, allocate resources efficiently, and keep progress transparent.

By subscribing you agree to our  Privacy Policy .

Giving modern marketing teams superpowers with short links that stand out.

• Live Product Demo

© Copyright 2023 Onethread, Inc

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Overview of the Problem-Solving Mental Process

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Rachel Goldman, PhD FTOS, is a licensed psychologist, clinical assistant professor, speaker, wellness expert specializing in eating behaviors, stress management, and health behavior change.

• Identify the Problem
• Define the Problem
• Form a Strategy
• Organize Information
• Allocate Resources
• Monitor Progress
• Evaluate the Results

Frequently Asked Questions

Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue.

The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything they can about the issue and then using factual knowledge to come up with a solution. In other instances, creativity and insight are the best options.

It is not necessary to follow problem-solving steps sequentially, It is common to skip steps or even go back through steps multiple times until the desired solution is reached.

In order to correctly solve a problem, it is often important to follow a series of steps. Researchers sometimes refer to this as the problem-solving cycle. While this cycle is portrayed sequentially, people rarely follow a rigid series of steps to find a solution.

The following steps include developing strategies and organizing knowledge.

1. Identifying the Problem

While it may seem like an obvious step, identifying the problem is not always as simple as it sounds. In some cases, people might mistakenly identify the wrong source of a problem, which will make attempts to solve it inefficient or even useless.

Some strategies that you might use to figure out the source of a problem include :

• Asking questions about the problem
• Breaking the problem down into smaller pieces
• Looking at the problem from different perspectives
• Conducting research to figure out what relationships exist between different variables

2. Defining the Problem

After the problem has been identified, it is important to fully define the problem so that it can be solved. You can define a problem by operationally defining each aspect of the problem and setting goals for what aspects of the problem you will address

At this point, you should focus on figuring out which aspects of the problems are facts and which are opinions. State the problem clearly and identify the scope of the solution.

3. Forming a Strategy

After the problem has been identified, it is time to start brainstorming potential solutions. This step usually involves generating as many ideas as possible without judging their quality. Once several possibilities have been generated, they can be evaluated and narrowed down.

The next step is to develop a strategy to solve the problem. The approach used will vary depending upon the situation and the individual's unique preferences. Common problem-solving strategies include heuristics and algorithms.

• Heuristics are mental shortcuts that are often based on solutions that have worked in the past. They can work well if the problem is similar to something you have encountered before and are often the best choice if you need a fast solution.
• Algorithms are step-by-step strategies that are guaranteed to produce a correct result. While this approach is great for accuracy, it can also consume time and resources.

Heuristics are often best used when time is of the essence, while algorithms are a better choice when a decision needs to be as accurate as possible.

4. Organizing Information

Before coming up with a solution, you need to first organize the available information. What do you know about the problem? What do you not know? The more information that is available the better prepared you will be to come up with an accurate solution.

When approaching a problem, it is important to make sure that you have all the data you need. Making a decision without adequate information can lead to biased or inaccurate results.

5. Allocating Resources

Of course, we don't always have unlimited money, time, and other resources to solve a problem. Before you begin to solve a problem, you need to determine how high priority it is.

If it is an important problem, it is probably worth allocating more resources to solving it. If, however, it is a fairly unimportant problem, then you do not want to spend too much of your available resources on coming up with a solution.

At this stage, it is important to consider all of the factors that might affect the problem at hand. This includes looking at the available resources, deadlines that need to be met, and any possible risks involved in each solution. After careful evaluation, a decision can be made about which solution to pursue.

6. Monitoring Progress

After selecting a problem-solving strategy, it is time to put the plan into action and see if it works. This step might involve trying out different solutions to see which one is the most effective.

It is also important to monitor the situation after implementing a solution to ensure that the problem has been solved and that no new problems have arisen as a result of the proposed solution.

Effective problem-solvers tend to monitor their progress as they work towards a solution. If they are not making good progress toward reaching their goal, they will reevaluate their approach or look for new strategies .

7. Evaluating the Results

After a solution has been reached, it is important to evaluate the results to determine if it is the best possible solution to the problem. This evaluation might be immediate, such as checking the results of a math problem to ensure the answer is correct, or it can be delayed, such as evaluating the success of a therapy program after several months of treatment.

Once a problem has been solved, it is important to take some time to reflect on the process that was used and evaluate the results. This will help you to improve your problem-solving skills and become more efficient at solving future problems.

A Word From Verywell​

It is important to remember that there are many different problem-solving processes with different steps, and this is just one example. Problem-solving in real-world situations requires a great deal of resourcefulness, flexibility, resilience, and continuous interaction with the environment.

Get Advice From The Verywell Mind Podcast

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares how you can stop dwelling in a negative mindset.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

You can become a better problem solving by:

• Practicing brainstorming and coming up with multiple potential solutions to problems
• Being open-minded and considering all possible options before making a decision
• Breaking down problems into smaller, more manageable pieces
• Asking for help when needed
• Researching different problem-solving techniques and trying out new ones
• Learning from mistakes and using them as opportunities to grow

It's important to communicate openly and honestly with your partner about what's going on. Try to see things from their perspective as well as your own. Work together to find a resolution that works for both of you. Be willing to compromise and accept that there may not be a perfect solution.

Take breaks if things are getting too heated, and come back to the problem when you feel calm and collected. Don't try to fix every problem on your own—consider asking a therapist or counselor for help and insight.

If you've tried everything and there doesn't seem to be a way to fix the problem, you may have to learn to accept it. This can be difficult, but try to focus on the positive aspects of your life and remember that every situation is temporary. Don't dwell on what's going wrong—instead, think about what's going right. Find support by talking to friends or family. Seek professional help if you're having trouble coping.

Davidson JE, Sternberg RJ, editors.  The Psychology of Problem Solving .  Cambridge University Press; 2003. doi:10.1017/CBO9780511615771

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. Published 2018 Jun 26. doi:10.3389/fnhum.2018.00261

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

My Learning Springboard

School Planning | Academic Tutoring | Test Preparation

A Multidisciplinary Educational Consulting Firm

More results...

Problem-Solving Strategies

January 26, 2021 Brad Hoffman Leave a Comment

Certainly, many students find that it is possible to solve a given word problem with minimal consideration of how to approach it. People have varying degrees of “math sense.” Some find most math problems mysterious. Some, however, can very easily see what to do to find solutions; it almost seems obvious to them. But even for students with strong “math sense,” there come those situations when they don’t intuitively know what to do. For all learners, the recognition of specific problem-solving strategies to solve math problems is useful. Thinking about our own thinking (aka metacognition) is important in developing flexibility so that we can see more than one way to solve a particular problem. Math journaling supports this thinking and development.

Below you will find a list of some very useful problem-solving strategies . One thing that is particularly beneficial about this set of strategies is that they are, in fact, universal. In other words, they will work regardless of the math program a student might be using. Whether it’s Singapore Math or Everyday Math or something else entirely , these problem-solving strategies can provide a clear path toward solutions. Interestingly, they can even extend to problem-solving outside the area of math! Becoming familiar with them and comfortable using them can be a big help to students as they wend their way through problems, be they less or more complex.

10 Problem-Solving Strategies

• Make a model/Act out
• Draw a diagram or picture
• Look for a pattern
• Make an organized list
• Make a table
• Guess & Check
• Make it simpler
• Work backwards
• Use logical reasoning

Here are some examples of problems and how to use these strategies.

“How many complete turns does the hour hand on a clock make in one day?”

From the list of problem-solving strategies above, “make a model or act it out” is an excellent choice for this problem. A student could use a model or a real analog clock and turn the hands and count. Distinguishing between the minute and the hour hand and recognizing that the clock only shows 12 of the 24 hours in a day lets the student see that the hour hand makes two complete turns. A physical clock that a student can actually turn provides an important concrete experience that may prove helpful for finding the solution.

“Using each of the digits 0, 1, 2, 3, 4 only once, make a two-digit number times a three-digit number multiplication problem with the greatest product.”

Students can “ draw a diagram or picture” of an “empty” multiplication problem with a box for each digit. Consider which two digits give the largest product and put them in the highest place value spots. Then, if it’s not immediately evident to the student, use one of the other problem-solving strategies — “ guess and check” — to place the remaining digits in the remaining spots. Check by multiplying the results to identify which is actually the largest (e.g. Is it 430 x 21 or 320 x 41?)

“How many even numbers are there between 201 and 351?”

In this instance, “ look for a pattern” would be especially helpful from the list of problem-solving strategies. Either write all numbers from 201 through 351 and notice the pattern that there are 5 in every set of 10 numbers (e.g. 201-210), and then count how many sets of 10 numbers there are and multiply that by 5, or simply write one set of 10 numbers and identify the 5 in 10 pattern without writing out all of them. Either way is valid.

“You have two noses and three hats. How many different nose-hat disguises can you wear?”

For this problem, “ make an organized list ” from the problem-solving strategies listed above works well. The list will start with Hat A and match with each nose (2), then Hat B with each nose (2), then Hat C with each nose (2). This gives a total of 6 disguises.

“How many numbers between 10 and 30 give a remainder of 2 when divided by 3?” You could “ make a table” to find the solution.

As the Table continues, a pattern becomes evident (“ look for a pattern ” — overlapping strategy!) in which every third number gives a remainder of 2. Count them for a solution.

“If 25 Glinks equal a Glonk, and 15 Glonks equal a Glooie, how many Glinks equal 2 Glooies?”

Please, “ make it simpler”! That strategy is an especially good choice from the list of problem solving-strategies. Let’s look at a simpler, but similar, problem. It’s simpler because the numbers are smaller, and you could even draw a picture to prove it’s correct.

If 3 Glinks equal a Glonk. And 2 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 3×2, which equals 6.

So, if 6 Glinks equal a Glooie, then how many Glinks equal 2 Glooies? Multiply 6×2, which equals 12. So, 12 Glinks equal 2 Glooies.

Now with the larger numbers:

If 25 Glinks equal a Glonk. And 15 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 15×25, which equals 750. So, 750 Glinks equal a Glooie.

Then, how many Glinks equal 2 Glooies? Multiply 750×2, which equals 1500. So, there are 1500 Glinks in 2 Glooies.

It’s the same process, with bigger numbers! Much simpler!

“If I add 10 to my age and double it, I am 90. How old am I?”

From the list of problem-solving strategies, this problem begs for the student to “ work backwards”. Simply un-double the 90 and subtract ten. 90 divided by 2 = 45 and 45-10=35. Voilà! The answer is 35 years old! Then reverse again to confirm that the answer is correct.

“Arrange these digits and symbols to make a true number sentence (equation.) 3,1,4,9,+,/,= (Note: the forward slash  [/] signifies “divided by”.)

“ Use logical reasoning ” to realize that any order is possible, but a larger number needs to be divided by a smaller number with no remainder (9/3=3) Then 3+1=4, so the sentence 9/3+1=4 is the solution.

For the problems that seem absolutely impossible to solve, your best option is to “ brainstorm” , and that’s on the above list of problem-solving strategies! Try various ideas; work with a partner; explore to see what might work; try everything you can think of! It’s amazing how good ideas will sometimes just pop into one’s head!

As a student works with these problem-solving strategies, it becomes clear that they often overlap (as in the “ draw a picture” / “guess and check” example above, problem #2). Or a student becomes especially attached to a few particular strategies that often work well. Some problems seem to be especially suitable for a particular strategy, while others can be approached from several directions. Having the flexibility to move from one strategy to another helps avoid the serious “I’m STUCK!” situation. Also, using more than one strategy on the same problem allows students to check solutions more efficiently before moving on. Again, however, THINKING about how we are THINKING is very beneficial in developing skills in this area. We call this metacognition .

Solving word problems can be fun, like being a detective who has unusual insight. There are solutions! Enjoy finding them! And make effective use of problem-solving strategies!

By Jean Snyder and Brad Hoffman , Elementary Math Specialists

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Notify me of follow-up comments by email.

Notify me of new posts by email.

Company Overview

School Planning

Private Tutoring

Test Preparation

Math Interventions

• Introduction
• Subitizing Interventions
• Counting Interventions: Whole Numbers Less Than 30
• Counting Interventions: Whole Numbers Greater Than 30 (Place Value)
• Counting Interventions: Fractions
• Counting Interventions: Decimals
• Composing and Decomposing Numbers Interventions
• Rounding Interventions
• Number Sense Lesson Plans
• Addition and Subtraction Facts
• Multiplication and Division Facts
• Computational Fluency Lesson Plans
• Understanding the Problem Interventions
• Planning and Executing a Solution Interventions

Planning & Executing

Response to error: planning & executing, feedback during the lesson, strategies to try after the lesson.

• Monitoring Progress & Reflecting on a Solution Interventions
• Problem-Solving Process Interventions
• Problem-Solving Lesson Plans
• Identifying Essential Variables Interventions
• Direct Models Interventions
• Counting On/Back Interventions
• Deriving Interventions
• Interpreting the Results Interventions
• Mathematical Modeling Lesson Plans
• Math Rules and Concepts Interventions
• Math Rules and Concepts Lesson Plans

The second step to solving a problem is planning and executing a strategy. In this step, the student must predict the outcome, choose a familiar approach, and implement that approach systematically to solve the problem. This page includes intervention strategies that you can use to support your students in this area. As you read, consider which of these interventions best aligns with your student's strengths and needs in the whole-learner domains.

Explicit Instruction

If you are intervening to support your students' ability to plan and execute a problem, you should start by explicitly teaching the skill. This sounds like:

• Explain the Skill/Concept.  Define planning and executing, and explain the activity. ( "Once we understand what the problem is asking, we need to plan and execute a strategy for solving it. Planning means choosing the best strategy to solve the problem  and try ing that strategy out." "Today, we'll be practicing planning and executing strategies to solve problems."  )
• Model Skill with Examples.  Think aloud about planning and executing a strategy.  ( "Since I know the problem — The boy had one apple. The girl had two apples. How many did they have together? — is asking me to figure out how many they have if you join the boy's apples and the girl's apples, I think I can plan to solve this strategy by drawing it. First, I'll draw one apple. Then, I'll draw two more. Now, I can solve it: One, Two, Three apples all together! )
• Model Skill with Non-Examples.  Think aloud about executing a strategy without planning it appropriately. ( "What if I just decided to solve the problem without planning my strategy out? I know! I can write an equation. Hmmm... I'll write 3-1 =? Hmm... This strategy doesn't match my story because I don't really know how to write equations yet. This is not the best strategy for me to use. By planning and thinking about what strategy I'll use , I can make sure that I'm choosing a strategy that I understand, and one that will help me solve the problem." )
• Practice the Skill.  Engage in one or more of the activities below to practice the skill with your student, providing feedback as necessary. ( "Now you try. I'm going to give you a problem ..." )

Activity A: Teach Story Problem Schematics

If a student understands what the problem is asking, but is having difficulty figuring out how to plan to solve it, you can teach him to diagram the information in the story by creating a schematic. This hand-drawn graphic organizer can help him clarify how quantities in the story are related to one another .

There are many different types of word problems, and each one has a different logic. Forbinger and Fuchs (2014) illustrate how most  addition, subtraction, multiplication, and division story problem types can be modeled in terms of part/whole relationships  here .  

Teach Story Problem Schematics in Action

In the video below, Emily Art explicitly models how to use a graphic organizer to organize known and unknown information in a story problem. She does this to introduce the skill to an intervention student. 

As you watch, consider: Why might modeling the information in this way support understanding of the problem?

If your student knows the steps in the problem-solving process but is still having difficulty solving a new problem, you may need to intervene to support his understanding of the range of approaches one might take to solve a problem. When a student encounters a new story type, he may understand the problem but not yet know an appropriate strategy for solving it. A strong problem-solver will begin to model what he does know in an attempt to solve the problem, whereas a weak problem-solver might just give up. You can support a struggling problem-solver's ability to plan and execute a problem by teaching him a series of reliable strategies to choose from when approaching a new problem type (Burns, 2007).

Such strategies might include:

• Look for a pattern : See if you can figure out if there is a logical connection between the numbers in the problem
• Make an organized list: Write down the information that you know in the problem, which will help you identify what is yet unknown
• Act it out: Represent the problem through motions or actions
• Draw a picture: Represent the problem through a visual
• Use objects: Use cubes to represent the numbers in the problem
• Guess and check: Try a number, and then put it back into the problem to check your answer
• Work backward: Start at the end of the problem, and work your way back to the beginning
• Write an equation: See if you can take the numbers from the problem and turn them into an equation
• Solve a simpler (or similar) problem: See if you can use more basic numbers (such as rounding to the nearest ten) to solve the problem
• Make a model: Represent the problem by constructing a model

Each of these strategies should be explicitly taught in isolation   and practiced with the student. After each strategy is mastered, it should be posted somewhere for easy reference. Click here for a document that defines and gives examples of attack strategies.

Explicitly Teach a Range of Problem Attack Strategies in Action  Introduce one problem-solving strategy at a time, from most to least concrete. After introducing a new strategy, have the student read the problem, and choose between the attack strategies she knows to identify one that would work best to solve the problem. The following strategy refers to the problem below. There were some birds on the telephone wire; 3 flew away, and now there are 9 on the wire and 3 on the tree. How many birds were on the wire before any flew away? Teacher: Now you know three attack strategies: Act It Out, Use Objects, and Draw a Picture. Read the problem. Then, we'll consider the best attack strategy for planning and executing this problem. Student reads problem.  Teacher: What strategy, out of the ones we've learned (teacher points to Act It Out, Use Objects, and Draw a Picture), would work best here?

Student: I think Draw a Picture because I can see the story in my head, and I think it will help me figure out how many birds were on the wire before. 

Activity C: Make a Prediction Another strategy to use if your student is struggling to understand the story and choose an attack strategy is called Make a Prediction. In this strategy, the student predicts whether the answer is going to be bigger or smaller than one of the numbers in the story and tries to explain why. This type of prediction helps ensure that he has a clear understanding of the action in the story and of the ways that the quantities are related to one another or changing in the story .

Make a Prediction in Action (Model)

In this video, Emily Art explicitly models how to make a prediction to check her understanding of a story. As you watch, consider: How does this intervention help a student plan the best strategy to use to solve a problem?

In this video, the student practices making a prediction so that he can plan the best way to solve the problem. As you watch, consider: What prompts does Emily use to help the student use text evidence to check his prediction?

Think about the following scenario, which takes place after a teacher has explicitly taught a student strategies for planning and executing a problem. This example refers to the following problem.

There were some birds on the telephone wire, 3 flew away, now there are 9 on the wire and 3 on the tree. How many birds were on the wire before any flew away?      Teacher: "How might you solve this problem?"      Student: " I don't know what to do. I give up." 

In such a case, what might you do? 

When you are planning your lessons, you should anticipate that your student will make errors throughout. Here are a series of prompts that you can use to respond to errors. Keep in mind that all students are different, and that students might respond better to some types of feedback than to others.

If your student struggles to meet your objective, there are various techniques that you might try in order to adjust the activity so as best to meet your student's needs. 

• << Previous: Understanding the Problem Interventions
• Next: Monitoring Progress & Reflecting on a Solution Interventions >>
• Last Updated: Feb 14, 2024 6:46 PM
• URL: https://relay.libguides.com/math-interventions

The home of mathematics education in New Zealand.

• Forgot password ?
• Teaching material
• Problem solving activities
• Problem Solving Information
• Problem Solving Strategies

Problem solving strategies

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

What are problem solving strategies?

Strategies are things that Pólya would have us choose in his second stage of problem solving and use in his third stage ( What is Problem Solving? ). In actual fact he called them heuristics . They are a collection of general approaches that might work for a number of problems. 

There are a number of common strategies that students of primary age can use to help them solve problems. We discuss below several that will be of value for problems on this website and in books on problem solving. 

Common Problem Solving Strategies

• Guess (includes guess and check, guess and improve)
• Act It Out (act it out and use equipment)
• Draw (this includes drawing pictures and diagrams)
• Make a List (includes making a table)
• Think (includes using skills you know already)

We have provided a copymaster for these strategies so that you can make posters and display them in your classroom. It consists of a page per strategy with space provided to insert the name of any problem that you come across that uses that particular strategy (Act it out, Draw, Guess, Make a List). This kind of poster provides good revision for students. 

An in-depth look at strategies                 

We now look at each of the following strategies and discuss them in some depth. You will see that each strategy we have in our list includes two or more subcategories.

• Guess and check is one of the simplest strategies. Anyone can guess an answer. If they can also check that the guess fits the conditions of the problem, then they have mastered guess and check. This is a strategy that would certainly work on the Farmyard problem described below but it could take a lot of time and a lot of computation. Because it is so simple, you may have difficulty weaning some students away from guess and check. As problems get more difficult, other strategies become more important and more effective. However, sometimes when students are completely stuck, guessing and checking will provide a useful way to start to explore a problem. Hopefully that exploration will lead to a more efficient strategy and then to a solution.
• Guess and improve is slightly more sophisticated than guess and check. The idea is that you use your first incorrect guess to make an improved next guess. You can see it in action in the Farmyard problem. In relatively straightforward problems like that, it is often fairly easy to see how to improve the last guess. In some problems though, where there are more variables, it may not be clear at first which way to change the guessing.  
• Young students especially, enjoy using Act it Out . Students themselves take the role of things in the problem. In the Farmyard problem, the students might take the role of the animals though it is unlikely that you would have 87 students in your class! But if there are not enough students you might be able to include a teddy or two. This is an effective strategy for demonstration purposes in front of the whole class. On the other hand, it can also be cumbersome when used by groups, especially if a largish number of students is involved.  Sometimes the students acting out the problem may get less out of the exercise than the students watching. This is because the participants are so engrossed in the mechanics of what they are doing that they don’t see the underlying mathematics. 
• Use Equipment is a strategy related to Act it Out. Generally speaking, any object that can be used in some way to represent the situation the students are trying to solve, is equipment. One of the difficulties with using equipment is keeping track of the solution. The students need to be encouraged to keep track of their working as they manipulate the equipment. Some students need to be encouraged and helped to use equipment. Many students seem to prefer to draw. This may be because it gives them a better representation of the problem in hand. Since there are problems where using equipment is a better strategy than drawing, you should encourage students' use of equipment by modelling its use yourself from time to time.  
• It is fairly clear that a picture has to be used in the strategy Draw a Picture . But the picture need not be too elaborate. It should only contain enough detail to help solve the problem. Hence a rough circle with two marks is quite sufficient for chickens and a blob plus four marks will do a pig. All students should be encouraged to use this strategy at some point because it helps them ‘see’ the problem and it can develop into quite a sophisticated strategy later.
• It’s hard to know where Drawing a Picture ends and Drawing a Diagram begins. You might think of a diagram as anything that you can draw which isn’t a picture. But where do you draw the line between a picture and a diagram? As you can see with the chickens and pigs, discussed above, regular picture drawing develops into drawing a diagram. Venn diagrams and tree diagrams are particular types of diagrams that we use so often they have been given names in their own right.  
• There are a number of ways of using Make a Table . These range from tables of numbers to help solve problems like the Farmyard, to the sort of tables with ticks and crosses that are often used in logic problems. Tables can also be an efficient way of finding number patterns.
• When an Organised List is being used, it should be arranged in such a way that there is some natural order implicit in its construction. For example, shopping lists are generally not organised. They usually grow haphazardly as you think of each item. A little thought might make them organised. Putting all the meat together, all the vegetables together, and all the drinks together, could do this for you. Even more organisation could be forced by putting all the meat items in alphabetical order, and so on. Someone we know lists the items on her list in the order that they appear on her route through the supermarket.  
• Being systematic may mean making a table or an organised list but it can also mean keeping your working in some order so that it is easy to follow when you have to go back over it. It means that you should work logically as you go along and make sure you don’t miss any steps in an argument. And it also means following an idea for a while to see where it leads, rather than jumping about all over the place chasing lots of possible ideas.
• It is very important to keep track of your work. We have seen several groups of students acting out a problem and having trouble at the end simply because they had not kept track of what they were doing. So keeping track is particularly important with Act it Out and Using Equipment. But it is important in many other situations too. Students have to know where they have been and where they are going or they will get hopelessly muddled. This begins to be more significant as the problems get more difficult and involve more and more steps.
• In many ways looking for patterns is what mathematics is all about. We want to know how things are connected and how things work and this is made easier if we can find patterns. Patterns make things easier because they tell us how a group of objects acts in the same way. Once we see a pattern we have much more control over what we are doing.
• Using symmetry helps us to reduce the difficulty level of a problem. Playing Noughts and crosses, for instance, you will have realised that there are three and not nine ways to put the first symbol down. This immediately reduces the number of possibilities for the game and makes it easier to analyse. This sort of argument comes up all the time and should be grabbed with glee when you see it.
• Finally working backwards is a standard strategy that only seems to have restricted use. However, it’s a powerful tool when it can be used. In the kind of problems we will be using in this web-site, it will be most often of value when we are looking at games. It frequently turns out to be worth looking at what happens at the end of a game and then work backward to the beginning, in order to see what moves are best.
• Then we come to use known skills .  This isn't usually listed in most lists of problem solving strategies but as we have gone through the problems in this web site, we have found it to be quite common.  The trick here is to see which skills that you know can be applied to the problem in hand. One example of this type is Fertiliser (Measurement, level 4).  In this problem, the problem solver has to know the formula for the area of a rectangle to be able to use the data of the problem.  This strategy is related to the first step of problem solving when the problem solver thinks 'have I seen a problem like this before?'  Being able to relate a word problem to some previously acquired skill is not easy but it is extremely important.

Uses of strategies                                           

Different strategies have different uses. We’ll illustrate this by means of a problem.

The Farmyard Problem : In the farmyard there are some pigs and some chickens. In fact there are 87 animals and 266 legs. How many pigs are there in the farmyard?

Some strategies help you to understand a problem. Let’s kick off with one of those. Guess and check . Let’s guess that there are 80 pigs. If there are they will account for 320 legs. Clearly we’ve over-guessed the number of pigs. So maybe there are only 60 pigs. Now 60 pigs would have 240 legs. That would leave us with 16 legs to be found from the chickens. It takes 8 chickens to produce 16 legs. But 60 pigs plus 8 chickens is only 68 animals so we have landed nearly 20 animals short.

Obviously we haven’t solved the problem yet but we have now come to grips with some of the important aspects of the problem. We know that there are 87 animals and so the number of pigs plus the number of chickens must add up to 87. We also know that we have to use the fact that pigs have four legs and chickens two, and that there have to be 266 legs altogether.

Some strategies are methods of solution in themselves. For instance, take Guess and improve . Supposed we guessed 60 pigs for a total of 240 legs. Now 60 pigs imply 27 chickens, and that gives another 54 legs. Altogether then we’d have 294 legs at this point.

Unfortunately we know that there are only 266 legs. So we’ve guessed too high. As pigs have more legs than hens, we need to reduce the guess of 60 pigs. How about reducing the number of pigs to 50? That means 37 chickens and so 200 + 74 = 274 legs.

We’re still too high. Now 40 pigs and 47 hens gives 160 + 94 = 254 legs. We’ve now got too few legs so we need to guess more pigs.

You should be able to see now how to oscillate backwards and forwards until you hit on the right number of pigs. So guess and improve is a method of solution that you can use on a number of problems.

Some strategies can give you an idea of how you might tackle a problem. Making a table illustrates this point. We’ll put a few values in and see what happens.

From the table we can see that every time we change the number of pigs by one, we change the number of legs by two. This means that in our last guess in the table, we are five pigs away from the right answer. Then there have to be 46 pigs.

Some strategies help us to see general patterns so that we can make conjectures. Some strategies help us to see how to justify conjectures. And some strategies do other jobs. We’ll develop these ideas on the uses of strategies as this web-site grows.

What strategies can be used at what levels?

In the work we have done over the last few years, it seems that students are able to tackle and use more strategies as they continue with problem solving. They are also able to use them to a deeper level. We have observed the following strategies being used in the stated Levels.

Levels 1 and 2

• Draw a picture
• Use equipment
• Guess and check

Levels 3 and 4

• Draw a diagram
• Guess and improve
• Make a table
• Make an organised list

It is important to say here that the research has not been exhaustive. Possibly younger students can effectively use other strategies. However, we feel confident that most students at a given Curriculum Level can use the strategies listed at that Level above. As problem solving becomes more common in primary schools, we would expect some of the more difficult strategies to come into use at lower Levels.

Strategies can develop in at least two ways. First students' ability to use strategies develops with experience and practice. We mentioned that above. Second, strategies themselves can become more abstract and complex. It’s this development that we want to discuss here with a few examples.

Not all students may follow this development precisely. Some students may skip various stages. Further, when a completely novel problem presents itself, students may revert to an earlier stage of a strategy during the solution of the problem.

Draw: Earlier on we talked about drawing a picture and drawing a diagram. Students often start out by giving a very precise representation of the problem in hand. As they see that it is not necessary to add all the detail or colour, their pictures become more symbolic and only the essential features are retained. Hence we get a blob for a pig’s body and four short lines for its legs. Then students seem to realise that relationships between objects can be demonstrated by line drawings. The objects may be reduced to dots or letters. More precise diagrams may be required in geometrical problems but diagrams are useful in a great many problems with no geometrical content.

The simple "draw a picture" eventually develops into a wide variety of drawings that enable students, and adults, to solve a vast array of problems.

Guess: Moving from guess and check to guess and improve, is an obvious development of a simple strategy. Guess and check may work well in some problems but guess and improve is a simple development of guess and check.

But guess and check can develop into a sophisticated procedure that 5-year-old students couldn’t begin to recognise. At a higher level, but still in the primary school, students are able to guess patterns from data they have been given or they produce themselves. If they are to be sure that their guess is correct, then they have to justify the pattern in some way. This is just another way of checking.

All research mathematicians use guess and check. Their guesses are called "conjectures". Their checks are "proofs". A checked guess becomes a "theorem". Problem solving is very close to mathematical research. The way that research mathematicians work is precisely the Pólya four stage method ( What is Problem Solving? ). The only difference between problem solving and research is that in school, someone (the teacher) knows the solution to the problem. In research no one knows the solution, so checking solutions becomes more important.

So you see that a very simple strategy like guess and check can develop to a very deep level.

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

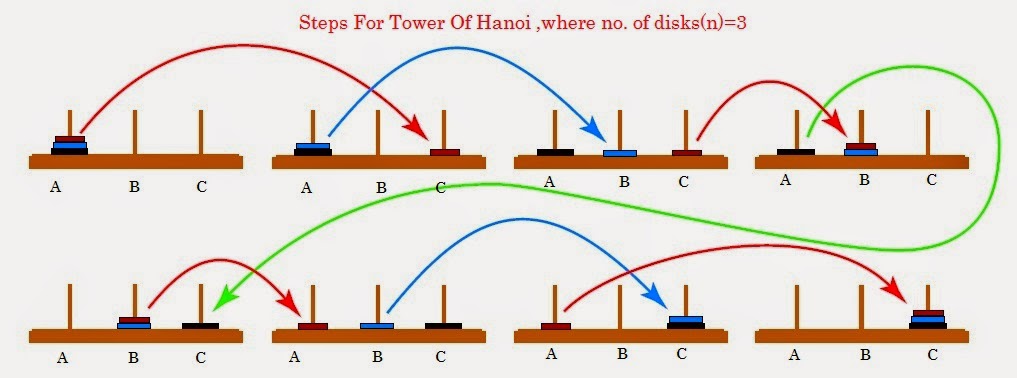
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size