random assignment and sampling

Random Assignment in Psychology: Definition & Examples

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

In psychology, random assignment refers to the practice of allocating participants to different experimental groups in a study in a completely unbiased way, ensuring each participant has an equal chance of being assigned to any group.

In experimental research, random assignment, or random placement, organizes participants from your sample into different groups using randomization. 

Random assignment uses chance procedures to ensure that each participant has an equal opportunity of being assigned to either a control or experimental group.

The control group does not receive the treatment in question, whereas the experimental group does receive the treatment.

When using random assignment, neither the researcher nor the participant can choose the group to which the participant is assigned. This ensures that any differences between and within the groups are not systematic at the onset of the study. 

In a study to test the success of a weight-loss program, investigators randomly assigned a pool of participants to one of two groups.

Group A participants participated in the weight-loss program for 10 weeks and took a class where they learned about the benefits of healthy eating and exercise.

Group B participants read a 200-page book that explains the benefits of weight loss. The investigator randomly assigned participants to one of the two groups.

The researchers found that those who participated in the program and took the class were more likely to lose weight than those in the other group that received only the book.

Importance 

Random assignment ensures that each group in the experiment is identical before applying the independent variable.

In experiments , researchers will manipulate an independent variable to assess its effect on a dependent variable, while controlling for other variables. Random assignment increases the likelihood that the treatment groups are the same at the onset of a study.

Thus, any changes that result from the independent variable can be assumed to be a result of the treatment of interest. This is particularly important for eliminating sources of bias and strengthening the internal validity of an experiment.

Random assignment is the best method for inferring a causal relationship between a treatment and an outcome.

Random Selection vs. Random Assignment 

Random selection (also called probability sampling or random sampling) is a way of randomly selecting members of a population to be included in your study.

On the other hand, random assignment is a way of sorting the sample participants into control and treatment groups. 

Random selection ensures that everyone in the population has an equal chance of being selected for the study. Once the pool of participants has been chosen, experimenters use random assignment to assign participants into groups. 

Random assignment is only used in between-subjects experimental designs, while random selection can be used in a variety of study designs.

Random Assignment vs Random Sampling

Random sampling refers to selecting participants from a population so that each individual has an equal chance of being chosen. This method enhances the representativeness of the sample.

Random assignment, on the other hand, is used in experimental designs once participants are selected. It involves allocating these participants to different experimental groups or conditions randomly.

This helps ensure that any differences in results across groups are due to manipulating the independent variable, not preexisting differences among participants.

When to Use Random Assignment

Random assignment is used in experiments with a between-groups or independent measures design.

In these research designs, researchers will manipulate an independent variable to assess its effect on a dependent variable, while controlling for other variables.

There is usually a control group and one or more experimental groups. Random assignment helps ensure that the groups are comparable at the onset of the study.

How to Use Random Assignment

There are a variety of ways to assign participants into study groups randomly. Here are a handful of popular methods: 

• Random Number Generator : Give each member of the sample a unique number; use a computer program to randomly generate a number from the list for each group.
• Lottery : Give each member of the sample a unique number. Place all numbers in a hat or bucket and draw numbers at random for each group.
• Flipping a Coin : Flip a coin for each participant to decide if they will be in the control group or experimental group (this method can only be used when you have just two groups) 
• Roll a Die : For each number on the list, roll a dice to decide which of the groups they will be in. For example, assume that rolling 1, 2, or 3 places them in a control group and rolling 3, 4, 5 lands them in an experimental group.

When is Random Assignment not used?

• When it is not ethically permissible: Randomization is only ethical if the researcher has no evidence that one treatment is superior to the other or that one treatment might have harmful side effects. 
• When answering non-causal questions : If the researcher is just interested in predicting the probability of an event, the causal relationship between the variables is not important and observational designs would be more suitable than random assignment. 
• When studying the effect of variables that cannot be manipulated: Some risk factors cannot be manipulated and so it would not make any sense to study them in a randomized trial. For example, we cannot randomly assign participants into categories based on age, gender, or genetic factors.

Drawbacks of Random Assignment

While randomization assures an unbiased assignment of participants to groups, it does not guarantee the equality of these groups. There could still be extraneous variables that differ between groups or group differences that arise from chance. Additionally, there is still an element of luck with random assignments.

Thus, researchers can not produce perfectly equal groups for each specific study. Differences between the treatment group and control group might still exist, and the results of a randomized trial may sometimes be wrong, but this is absolutely okay.

Scientific evidence is a long and continuous process, and the groups will tend to be equal in the long run when data is aggregated in a meta-analysis.

Additionally, external validity (i.e., the extent to which the researcher can use the results of the study to generalize to the larger population) is compromised with random assignment.

Random assignment is challenging to implement outside of controlled laboratory conditions and might not represent what would happen in the real world at the population level. 

Random assignment can also be more costly than simple observational studies, where an investigator is just observing events without intervening with the population.

Randomization also can be time-consuming and challenging, especially when participants refuse to receive the assigned treatment or do not adhere to recommendations. 

What is the difference between random sampling and random assignment?

Random sampling refers to randomly selecting a sample of participants from a population. Random assignment refers to randomly assigning participants to treatment groups from the selected sample.

Does random assignment increase internal validity?

Yes, random assignment ensures that there are no systematic differences between the participants in each group, enhancing the study’s internal validity .

Does random assignment reduce sampling error?

Yes, with random assignment, participants have an equal chance of being assigned to either a control group or an experimental group, resulting in a sample that is, in theory, representative of the population.

Random assignment does not completely eliminate sampling error because a sample only approximates the population from which it is drawn. However, random sampling is a way to minimize sampling errors. 

When is random assignment not possible?

Random assignment is not possible when the experimenters cannot control the treatment or independent variable.

For example, if you want to compare how men and women perform on a test, you cannot randomly assign subjects to these groups.

Participants are not randomly assigned to different groups in this study, but instead assigned based on their characteristics.

Does random assignment eliminate confounding variables?

Yes, random assignment eliminates the influence of any confounding variables on the treatment because it distributes them at random among the study groups. Randomization invalidates any relationship between a confounding variable and the treatment.

Why is random assignment of participants to treatment conditions in an experiment used?

Random assignment is used to ensure that all groups are comparable at the start of a study. This allows researchers to conclude that the outcomes of the study can be attributed to the intervention at hand and to rule out alternative explanations for study results.

Further Reading

• Bogomolnaia, A., & Moulin, H. (2001). A new solution to the random assignment problem .  Journal of Economic theory ,  100 (2), 295-328.
• Krause, M. S., & Howard, K. I. (2003). What random assignment does and does not do .  Journal of Clinical Psychology ,  59 (7), 751-766.

Related Articles

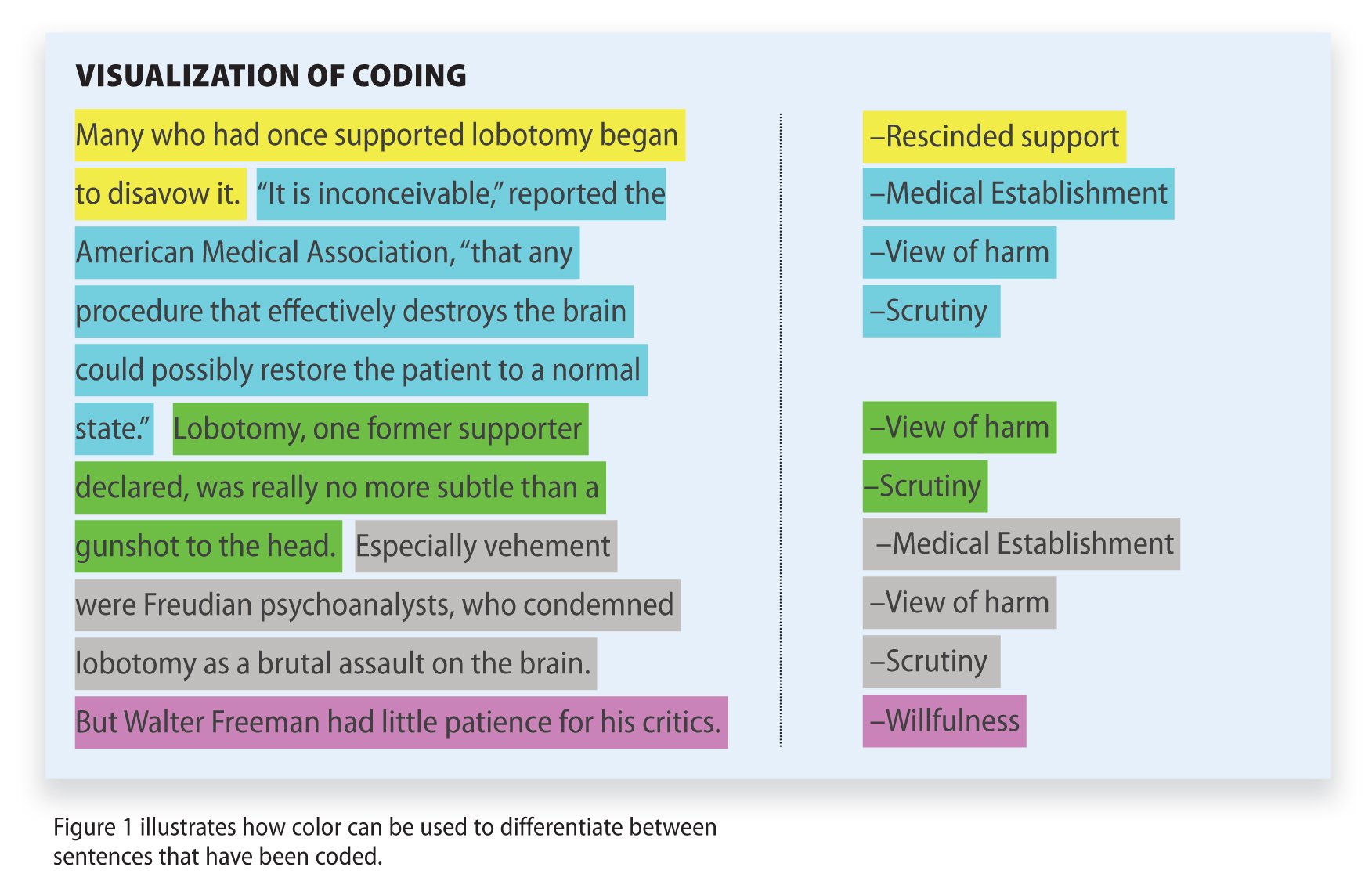
Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 6.

• Introduction to experiment design
• Matched pairs experiment design
• The language of experiments
• Principles of experiment design
• Experiment designs

Random sampling vs. random assignment (scope of inference)

• (Choice A)   Just the residents involved in Hilary's study. A Just the residents involved in Hilary's study.
• (Choice B)   All residents in Hilary's town. B All residents in Hilary's town.
• (Choice C)   All residents in Hilary's country. C All residents in Hilary's country.
• (Choice A)   Yes A Yes
• (Choice B)   No B No
• (Choice A)   Just the residents in Hilary's study. A Just the residents in Hilary's study.

Want to join the conversation?

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

The Definition of Random Assignment According to Psychology

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Emily is a board-certified science editor who has worked with top digital publishing brands like Voices for Biodiversity, Study.com, GoodTherapy, Vox, and Verywell.

Materio / Getty Images

Random assignment refers to the use of chance procedures in psychology experiments to ensure that each participant has the same opportunity to be assigned to any given group in a study to eliminate any potential bias in the experiment at the outset. Participants are randomly assigned to different groups, such as the treatment group versus the control group. In clinical research, randomized clinical trials are known as the gold standard for meaningful results.

Simple random assignment techniques might involve tactics such as flipping a coin, drawing names out of a hat, rolling dice, or assigning random numbers to a list of participants. It is important to note that random assignment differs from random selection .

While random selection refers to how participants are randomly chosen from a target population as representatives of that population, random assignment refers to how those chosen participants are then assigned to experimental groups.

Random Assignment In Research

To determine if changes in one variable will cause changes in another variable, psychologists must perform an experiment. Random assignment is a critical part of the experimental design that helps ensure the reliability of the study outcomes.

Researchers often begin by forming a testable hypothesis predicting that one variable of interest will have some predictable impact on another variable.

The variable that the experimenters will manipulate in the experiment is known as the independent variable , while the variable that they will then measure for different outcomes is known as the dependent variable. While there are different ways to look at relationships between variables, an experiment is the best way to get a clear idea if there is a cause-and-effect relationship between two or more variables.

Once researchers have formulated a hypothesis, conducted background research, and chosen an experimental design, it is time to find participants for their experiment. How exactly do researchers decide who will be part of an experiment? As mentioned previously, this is often accomplished through something known as random selection.

Random Selection

In order to generalize the results of an experiment to a larger group, it is important to choose a sample that is representative of the qualities found in that population. For example, if the total population is 60% female and 40% male, then the sample should reflect those same percentages.

Choosing a representative sample is often accomplished by randomly picking people from the population to be participants in a study. Random selection means that everyone in the group stands an equal chance of being chosen to minimize any bias. Once a pool of participants has been selected, it is time to assign them to groups.

By randomly assigning the participants into groups, the experimenters can be fairly sure that each group will have the same characteristics before the independent variable is applied.

Participants might be randomly assigned to the control group , which does not receive the treatment in question. The control group may receive a placebo or receive the standard treatment. Participants may also be randomly assigned to the experimental group , which receives the treatment of interest. In larger studies, there can be multiple treatment groups for comparison.

There are simple methods of random assignment, like rolling the die. However, there are more complex techniques that involve random number generators to remove any human error.

There can also be random assignment to groups with pre-established rules or parameters. For example, if you want to have an equal number of men and women in each of your study groups, you might separate your sample into two groups (by sex) before randomly assigning each of those groups into the treatment group and control group.

Random assignment is essential because it increases the likelihood that the groups are the same at the outset. With all characteristics being equal between groups, other than the application of the independent variable, any differences found between group outcomes can be more confidently attributed to the effect of the intervention.

Example of Random Assignment

Imagine that a researcher is interested in learning whether or not drinking caffeinated beverages prior to an exam will improve test performance. After randomly selecting a pool of participants, each person is randomly assigned to either the control group or the experimental group.

The participants in the control group consume a placebo drink prior to the exam that does not contain any caffeine. Those in the experimental group, on the other hand, consume a caffeinated beverage before taking the test.

Participants in both groups then take the test, and the researcher compares the results to determine if the caffeinated beverage had any impact on test performance.

A Word From Verywell

Random assignment plays an important role in the psychology research process. Not only does this process help eliminate possible sources of bias, but it also makes it easier to generalize the results of a tested sample of participants to a larger population.

Random assignment helps ensure that members of each group in the experiment are the same, which means that the groups are also likely more representative of what is present in the larger population of interest. Through the use of this technique, psychology researchers are able to study complex phenomena and contribute to our understanding of the human mind and behavior.

Lin Y, Zhu M, Su Z. The pursuit of balance: An overview of covariate-adaptive randomization techniques in clinical trials . Contemp Clin Trials. 2015;45(Pt A):21-25. doi:10.1016/j.cct.2015.07.011

Sullivan L. Random assignment versus random selection . In: The SAGE Glossary of the Social and Behavioral Sciences. SAGE Publications, Inc.; 2009. doi:10.4135/9781412972024.n2108

Alferes VR. Methods of Randomization in Experimental Design . SAGE Publications, Inc.; 2012. doi:10.4135/9781452270012

Nestor PG, Schutt RK. Research Methods in Psychology: Investigating Human Behavior. (2nd Ed.). SAGE Publications, Inc.; 2015.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Statistics Made Easy

Random Selection vs. Random Assignment

Random selection and random assignment  are two techniques in statistics that are commonly used, but are commonly confused.

Random selection  refers to the process of randomly selecting individuals from a population to be involved in a study.

Random assignment  refers to the process of randomly  assigning  the individuals in a study to either a treatment group or a control group.

You can think of random selection as the process you use to “get” the individuals in a study and you can think of random assignment as what you “do” with those individuals once they’re selected to be part of the study.

The Importance of Random Selection and Random Assignment

When a study uses  random selection , it selects individuals from a population using some random process. For example, if some population has 1,000 individuals then we might use a computer to randomly select 100 of those individuals from a database. This means that each individual is equally likely to be selected to be part of the study, which increases the chances that we will obtain a representative sample – a sample that has similar characteristics to the overall population.

By using a representative sample in our study, we’re able to generalize the findings of our study to the population. In statistical terms, this is referred to as having  external validity – it’s valid to externalize our findings to the overall population.

When a study uses  random assignment , it randomly assigns individuals to either a treatment group or a control group. For example, if we have 100 individuals in a study then we might use a random number generator to randomly assign 50 individuals to a control group and 50 individuals to a treatment group.

By using random assignment, we increase the chances that the two groups will have roughly similar characteristics, which means that any difference we observe between the two groups can be attributed to the treatment. This means the study has  internal validity  – it’s valid to attribute any differences between the groups to the treatment itself as opposed to differences between the individuals in the groups.

Examples of Random Selection and Random Assignment

It’s possible for a study to use both random selection and random assignment, or just one of these techniques, or neither technique. A strong study is one that uses both techniques.

The following examples show how a study could use both, one, or neither of these techniques, along with the effects of doing so.

Example 1: Using both Random Selection and Random Assignment

Study:  Researchers want to know whether a new diet leads to more weight loss than a standard diet in a certain community of 10,000 people. They recruit 100 individuals to be in the study by using a computer to randomly select 100 names from a database. Once they have the 100 individuals, they once again use a computer to randomly assign 50 of the individuals to a control group (e.g. stick with their standard diet) and 50 individuals to a treatment group (e.g. follow the new diet). They record the total weight loss of each individual after one month.

Results:  The researchers used random selection to obtain their sample and random assignment when putting individuals in either a treatment or control group. By doing so, they’re able to generalize the findings from the study to the overall population  and  they’re able to attribute any differences in average weight loss between the two groups to the new diet.

Example 2: Using only Random Selection

Study:  Researchers want to know whether a new diet leads to more weight loss than a standard diet in a certain community of 10,000 people. They recruit 100 individuals to be in the study by using a computer to randomly select 100 names from a database. However, they decide to assign individuals to groups based solely on gender. Females are assigned to the control group and males are assigned to the treatment group. They record the total weight loss of each individual after one month.

Results:  The researchers used random selection to obtain their sample, but they did not use random assignment when putting individuals in either a treatment or control group. Instead, they used a specific factor – gender – to decide which group to assign individuals to. By doing this, they’re able to generalize the findings from the study to the overall population but they are  not  able to attribute any differences in average weight loss between the two groups to the new diet. The internal validity of the study has been compromised because the difference in weight loss could actually just be due to gender, rather than the new diet.

Example 3: Using only Random Assignment

Study:  Researchers want to know whether a new diet leads to more weight loss than a standard diet in a certain community of 10,000 people. They recruit 100 males athletes to be in the study. Then, they use a computer program to randomly assign 50 of the male athletes to a control group and 50 to the treatment group. They record the total weight loss of each individual after one month.

Results:  The researchers did not use random selection to obtain their sample since they specifically chose 100 male athletes. Because of this, their sample is not representative of the overall population so their external validity is compromised – they will not be able to generalize the findings from the study to the overall population. However, they did use random assignment, which means they can attribute any difference in weight loss to the new diet.

Example 4: Using Neither Technique

Study:  Researchers want to know whether a new diet leads to more weight loss than a standard diet in a certain community of 10,000 people. They recruit 50 males athletes and 50 female athletes to be in the study. Then, they assign all of the female athletes to the control group and all of the male athletes to the treatment group. They record the total weight loss of each individual after one month.

Results:  The researchers did not use random selection to obtain their sample since they specifically chose 100 athletes. Because of this, their sample is not representative of the overall population so their external validity is compromised – they will not be able to generalize the findings from the study to the overall population. Also, they split individuals into groups based on gender rather than using random assignment, which means their internal validity is also compromised – differences in weight loss might be due to gender rather than the diet.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• J Athl Train
• v.43(2); Mar-Apr 2008

Issues in Outcomes Research: An Overview of Randomization Techniques for Clinical Trials

Minsoo kang.

1 Middle Tennessee State University, Murfreesboro, TN

Brian G Ragan

2 University of Northern Iowa, Cedar Falls, IA

Jae-Hyeon Park

3 Korea National Sport University, Seoul, Korea

To review and describe randomization techniques used in clinical trials, including simple, block, stratified, and covariate adaptive techniques.

Background:

Clinical trials are required to establish treatment efficacy of many athletic training procedures. In the past, we have relied on evidence of questionable scientific merit to aid the determination of treatment choices. Interest in evidence-based practice is growing rapidly within the athletic training profession, placing greater emphasis on the importance of well-conducted clinical trials. One critical component of clinical trials that strengthens results is random assignment of participants to control and treatment groups. Although randomization appears to be a simple concept, issues of balancing sample sizes and controlling the influence of covariates a priori are important. Various techniques have been developed to account for these issues, including block, stratified randomization, and covariate adaptive techniques.

Advantages:

Athletic training researchers and scholarly clinicians can use the information presented in this article to better conduct and interpret the results of clinical trials. Implementing these techniques will increase the power and validity of findings of athletic medicine clinical trials, which will ultimately improve the quality of care provided.

Outcomes research is critical in the evidence-based health care environment because it addresses scientific questions concerning the efficacy of treatments. Clinical trials are considered the “gold standard” for outcomes in biomedical research. In athletic training, calls for more evidence-based medical research, specifically clinical trials, have been issued. 1 , 2

The strength of clinical trials is their superior ability to measure change over time from a treatment. Treatment differences identified from cross-sectional observational designs rather than experimental clinical trials have methodologic weaknesses, including confounding, cohort effects, and selection bias. 3 For example, using a nonrandomized trial to examine the effectiveness of prophylactic knee bracing to prevent medial collateral ligament injuries may suffer from confounders and jeopardize the results. One possible confounder is a history of knee injuries. Participants with a history of knee injuries may be more likely to wear braces than those with no such history. Participants with a history of injury are more likely to suffer additional knee injuries, unbalancing the groups and influencing the results of the study.

The primary goal of comparative clinical trials is to provide comparisons of treatments with maximum precision and validity. 4 One critical component of clinical trials is random assignment of participants into groups. Randomizing participants helps remove the effect of extraneous variables (eg, age, injury history) and minimizes bias associated with treatment assignment. Randomization is considered by most researchers to be the optimal approach for participant assignment in clinical trials because it strengthens the results and data interpretation. 4 – , 9

One potential problem with small clinical trials (n < 100) 7 is that conventional simple randomization methods, such as flipping a coin, may result in imbalanced sample size and baseline characteristics (ie, covariates) among treatment and control groups. 9 , 10 This imbalance of baseline characteristics can influence the comparison between treatment and control groups and introduce potential confounding factors. Many procedures have been proposed for random group assignment of participants in clinical trials. 11 Simple, block, stratified, and covariate adaptive randomizations are some examples. Each technique has advantages and disadvantages, which must be carefully considered before a method is selected. Our purpose is to introduce the concept and significance of randomization and to review several conventional and relatively new randomization techniques to aid in the design and implementation of valid clinical trials.

What Is Randomization?

Randomization is the process of assigning participants to treatment and control groups, assuming that each participant has an equal chance of being assigned to any group. 12 Randomization has evolved into a fundamental aspect of scientific research methodology. Demands have increased for more randomized clinical trials in many areas of biomedical research, such as athletic training. 2 , 13 In fact, in the last 2 decades, internationally recognized major medical journals, such as the Journal of the American Medical Association and the BMJ , have been increasingly interested in publishing studies reporting results from randomized controlled trials. 5

Since Fisher 14 first introduced the idea of randomization in a 1926 agricultural study, the academic community has deemed randomization an essential tool for unbiased comparisons of treatment groups. Five years after Fisher's introductory paper, the first randomized clinical trial involving tuberculosis was conducted. 15 A total of 24 participants were paired (ie, 12 comparable pairs), and by a flip of a coin, each participant within the pair was assigned to either the control or treatment group. By employing randomization, researchers offer each participant an equal chance of being assigned to groups, which makes the groups comparable on the dependent variable by eliminating potential bias. Indeed, randomization of treatments in clinical trials is the only means of avoiding systematic characteristic bias of participants assigned to different treatments. Although randomization may be accomplished with a simple coin toss, more appropriate and better methods are often needed, especially in small clinical trials. These other methods will be discussed in this review.

Why Randomize?

Researchers demand randomization for several reasons. First, participants in various groups should not differ in any systematic way. In a clinical trial, if treatment groups are systematically different, trial results will be biased. Suppose that participants are assigned to control and treatment groups in a study examining the efficacy of a walking intervention. If a greater proportion of older adults is assigned to the treatment group, then the outcome of the walking intervention may be influenced by this imbalance. The effects of the treatment would be indistinguishable from the influence of the imbalance of covariates, thereby requiring the researcher to control for the covariates in the analysis to obtain an unbiased result. 16

Second, proper randomization ensures no a priori knowledge of group assignment (ie, allocation concealment). That is, researchers, participants, and others should not know to which group the participant will be assigned. Knowledge of group assignment creates a layer of potential selection bias that may taint the data. Schulz and Grimes 17 stated that trials with inadequate or unclear randomization tended to overestimate treatment effects up to 40% compared with those that used proper randomization. The outcome of the trial can be negatively influenced by this inadequate randomization.

Statistical techniques such as analysis of covariance (ANCOVA), multivariate ANCOVA, or both, are often used to adjust for covariate imbalance in the analysis stage of the clinical trial. However, the interpretation of this postadjustment approach is often difficult because imbalance of covariates frequently leads to unanticipated interaction effects, such as unequal slopes among subgroups of covariates. 18 , 19 One of the critical assumptions in ANCOVA is that the slopes of regression lines are the same for each group of covariates (ie, homogeneity of regression slopes). The adjustment needed for each covariate group may vary, which is problematic because ANCOVA uses the average slope across the groups to adjust the outcome variable. Thus, the ideal way of balancing covariates among groups is to apply sound randomization in the design stage of a clinical trial (before the adjustment procedure) instead of after data collection. In such instances, random assignment is necessary and guarantees validity for statistical tests of significance that are used to compare treatments.

How To Randomize?

Many procedures have been proposed for the random assignment of participants to treatment groups in clinical trials. In this article, common randomization techniques, including simple randomization, block randomization, stratified randomization, and covariate adaptive randomization, are reviewed. Each method is described along with its advantages and disadvantages. It is very important to select a method that will produce interpretable, valid results for your study.

Simple Randomization

Randomization based on a single sequence of random assignments is known as simple randomization. 10 This technique maintains complete randomness of the assignment of a person to a particular group. The most common and basic method of simple randomization is flipping a coin. For example, with 2 treatment groups (control versus treatment), the side of the coin (ie, heads  =  control, tails  =  treatment) determines the assignment of each participant. Other methods include using a shuffled deck of cards (eg, even  =  control, odd  =  treatment) or throwing a die (eg, below and equal to 3  =  control, over 3  =  treatment). A random number table found in a statistics book or computer-generated random numbers can also be used for simple randomization of participants.

This randomization approach is simple and easy to implement in a clinical trial. In large trials (n > 200), simple randomization can be trusted to generate similar numbers of participants among groups. However, randomization results could be problematic in relatively small sample size clinical trials (n < 100), resulting in an unequal number of participants among groups. For example, using a coin toss with a small sample size (n  =  10) may result in an imbalance such that 7 participants are assigned to the control group and 3 to the treatment group ( Figure 1 ).

Block Randomization

The block randomization method is designed to randomize participants into groups that result in equal sample sizes. This method is used to ensure a balance in sample size across groups over time. Blocks are small and balanced with predetermined group assignments, which keeps the numbers of participants in each group similar at all times. According to Altman and Bland, 10 the block size is determined by the researcher and should be a multiple of the number of groups (ie, with 2 treatment groups, block size of either 4 or 6). Blocks are best used in smaller increments as researchers can more easily control balance. 7 After block size has been determined, all possible balanced combinations of assignment within the block (ie, equal number for all groups within the block) must be calculated. Blocks are then randomly chosen to determine the participants' assignment into the groups.

For a clinical trial with control and treatment groups involving 40 participants, a randomized block procedure would be as follows: (1) a block size of 4 is chosen, (2) possible balanced combinations with 2 C (control) and 2 T (treatment) subjects are calculated as 6 (TTCC, TCTC, TCCT, CTTC, CTCT, CCTT), and (3) blocks are randomly chosen to determine the assignment of all 40 participants (eg, one random sequence would be [TTCC / TCCT / CTTC / CTTC / TCCT / CCTT / TTCC / TCTC / CTCT / TCTC]). This procedure results in 20 participants in both the control and treatment groups ( Figure 2 ).

Although balance in sample size may be achieved with this method, groups may be generated that are rarely comparable in terms of certain covariates. 6 For example, one group may have more participants with secondary diseases (eg, diabetes, multiple sclerosis, cancer) that could confound the data and may negatively influence the results of the clinical trial. Pocock and Simon 11 stressed the importance of controlling for these covariates because of serious consequences to the interpretation of the results. Such an imbalance could introduce bias in the statistical analysis and reduce the power of the study. 4 , 6 , 8 Hence, sample size and covariates must be balanced in small clinical trials.

Stratified Randomization

The stratified randomization method addresses the need to control and balance the influence of covariates. This method can be used to achieve balance among groups in terms of participants' baseline characteristics (covariates). Specific covariates must be identified by the researcher who understands the potential influence each covariate has on the dependent variable. Stratified randomization is achieved by generating a separate block for each combination of covariates, and participants are assigned to the appropriate block of covariates. After all participants have been identified and assigned into blocks, simple randomization occurs within each block to assign participants to one of the groups.

The stratified randomization method controls for the possible influence of covariates that would jeopardize the conclusions of the clinical trial. For example, a clinical trial of different rehabilitation techniques after a surgical procedure will have a number of covariates. It is well known that the age of the patient affects the rate of healing. Thus, age could be a confounding variable and influence the outcome of the clinical trial. Stratified randomization can balance the control and treatment groups for age or other identified covariates.

For example, with 2 groups involving 40 participants, the stratified randomization method might be used to control the covariates of sex (2 levels: male, female) and body mass index (3 levels: underweight, normal, overweight) between study arms. With these 2 covariates, possible block combinations total 6 (eg, male, underweight). A simple randomization procedure, such as flipping a coin, is used to assign the participants within each block to one of the treatment groups ( Figure 3 ).

Although stratified randomization is a relatively simple and useful technique, especially for smaller clinical trials, it becomes complicated to implement if many covariates must be controlled. 20 For example, too many block combinations may lead to imbalances in overall treatment allocations because a large number of blocks can generate small participant numbers within the block. Therneau 21 purported that a balance in covariates begins to fail when the number of blocks approaches half the sample size. If another 4-level covariate was added to the example, the number of block combinations would increase from 6 to 24 (2 × 3 × 4), for an average of fewer than 2 (40 / 24  =  1.7) participants per block, reducing the usefulness of the procedure to balance the covariates and jeopardizing the validity of the clinical trial. In small studies, it may not be feasible to stratify more than 1 or 2 covariates because the number of blocks can quickly approach the number of participants. 10

Stratified randomization has another limitation: it works only when all participants have been identified before group assignment. This method is rarely applicable, however, because clinical trial participants are often enrolled one at a time on a continuous basis. When baseline characteristics of all participants are not available before assignment, using stratified randomization is difficult. 7

Covariate Adaptive Randomization

Covariate adaptive randomization has been recommended by many researchers as a valid alternative randomization method for clinical trials. 9 , 22 In covariate adaptive randomization, a new participant is sequentially assigned to a particular treatment group by taking into account the specific covariates and previous assignments of participants. 9 , 12 , 18 , 23 , 24 Covariate adaptive randomization uses the method of minimization by assessing the imbalance of sample size among several covariates. This covariate adaptive approach was first described by Taves. 23

The Taves covariate adaptive randomization method allows for the examination of previous participant group assignments to make a case-by-case decision on group assignment for each individual who enrolls in the study. Consider again the example of 2 groups involving 40 participants, with sex (2 levels: male, female) and body mass index (3 levels: underweight, normal, overweight) as covariates. Assume the first 9 participants have already been randomly assigned to groups by flipping a coin. The 9 participants' group assignments are broken down by covariate level in Figure 4 . Now the 10th participant, who is male and underweight, needs to be assigned to a group (ie, control versus treatment). Based on the characteristics of the 10th participant, the Taves method adds marginal totals of the corresponding covariate categories for each group and compares the totals. The participant is assigned to the group with the lower covariate total to minimize imbalance. In this example, the appropriate categories are male and underweight, which results in the total of 3 (2 for male category + 1 for underweight category) for the control group and a total of 5 (3 for male category + 2 for underweight category) for the treatment group. Because the sum of marginal totals is lower for the control group (3 < 5), the 10th participant is assigned to the control group ( Figure 5 ).

The Pocock and Simon method 11 of covariate adaptive randomization is similar to the method Taves 23 described. The difference in this approach is the temporary assignment of participants to both groups. This method uses the absolute difference between groups to determine group assignment. To minimize imbalance, the participant is assigned to the group determined by the lowest sum of the absolute differences among the covariates between the groups. For example, using the previous situation in assigning the 10th participant to a group, the Pocock and Simon method would (1) assign the 10th participant temporarily to the control group, resulting in marginal totals of 3 for male category and 2 for underweight category; (2) calculate the absolute difference between control and treatment group (males: 3 control – 3 treatment  =  0; underweight: 2 control – 2 treatment  =  0) and sum (0 + 0  =  0); (3) temporarily assign the 10th participant to the treatment group, resulting in marginal totals of 4 for male category and 3 for underweight category; (4) calculate the absolute difference between control and treatment group (males: 2 control – 4 treatment  =  2; underweight: 1 control – 3 treatment  =  2) and sum (2 + 2  =  4); and (5) assign the 10th participant to the control group because of the lowest sum of absolute differences (0 < 4).

Pocock and Simon 11 also suggested using a variance approach. Instead of calculating absolute difference among groups, this approach calculates the variance among treatment groups. Although the variance method performs similarly to the absolute difference method, both approaches suffer from the limitation of handling only categorical covariates. 25

Frane 18 introduced a covariate adaptive randomization for both continuous and categorical types. Frane used P values to identify imbalance among treatment groups: a smaller P value represents more imbalance among treatment groups.

The Frane method for assigning participants to either the control or treatment group would include (1) temporarily assigning the participant to both the control and treatment groups; (2) calculating P values for each of the covariates using a t test and analysis of variance (ANOVA) for continuous variables and goodness-of-fit χ 2 test for categorical variables; (3) determining the minimum P value for each control or treatment group, which indicates more imbalance among treatment groups; and (4) assigning the participant to the group with the larger minimum P value (ie, try to avoid more imbalance in groups).

Going back to the previous example of assigning the 10th participant (male and underweight) to a group, the Frane method would result in the assignment to the control group. The steps used to make this decision were calculating P values for each of the covariates using the χ 2 goodness-of-fit test represented in the Table . The t tests and ANOVAs were not used because the covariates in this example were categorical. Based on the Table , the lowest minimum P values were 1.0 for the control group and 0.317 for the treatment group. The 10th participant was assigned to the control group because of the higher minimum P value, which indicates better balance in the control group (1.0 > 0.317).

Probabilities From χ 2 Goodness-of-Fit Tests for the Example Shown in Figure 5 (Frane 18 Method)

Covariate adaptive randomization produces less imbalance than other conventional randomization methods and can be used successfully to balance important covariates among control and treatment groups. 6 Although the balance of covariates among groups using the stratified randomization method begins to fail when the number of blocks approaches half the sample size, covariate adaptive randomization can better handle the problem of increasing numbers of covariates (ie, increased block combinations). 9

One concern of these covariate adaptive randomization methods is that treatment assignments sometimes become highly predictable. Investigators using covariate adaptive randomization sometimes come to believe that group assignment for the next participant can be readily predicted, going against the basic concept of randomization. 12 , 26 , 27 This predictability stems from the ongoing assignment of participants to groups wherein the current allocation of participants may suggest future participant group assignment. In their review, Scott et al 9 argued that this predictability is also true of other methods, including stratified randomization, and it should not be overly penalized. Zielhuis et al 28 and Frane 18 suggested a practical approach to prevent predictability: a small number of participants should be randomly assigned into the groups before the covariate adaptive randomization technique being applied.

The complicated computation process of covariate adaptive randomization increases the administrative burden, thereby limiting its use in practice. A user-friendly computer program for covariate adaptive randomization is available (free of charge) upon request from the authors (M.K., B.G.R., or J.H.P.). 29

Conclusions

Our purpose was to introduce randomization, including its concept and significance, and to review several randomization techniques to guide athletic training researchers and practitioners to better design their randomized clinical trials. Many factors can affect the results of clinical research, but randomization is considered the gold standard in most clinical trials. It eliminates selection bias, ensures balance of sample size and baseline characteristics, and is an important step in guaranteeing the validity of statistical tests of significance used to compare treatment groups.

Before choosing a randomization method, several factors need to be considered, including the size of the clinical trial; the need for balance in sample size, covariates, or both; and participant enrollment. 16 Figure 6 depicts a flowchart designed to help select an appropriate randomization technique. For example, a power analysis for a clinical trial of different rehabilitation techniques after a surgical procedure indicated a sample size of 80. A well-known covariate for this study is age, which must be balanced among groups. Because of the nature of the study with postsurgical patients, participant recruitment and enrollment will be continuous. Using the flowchart, the appropriate randomization technique is covariate adaptive randomization technique.

Simple randomization works well for a large trial (eg, n > 200) but not for a small trial (n < 100). 7 To achieve balance in sample size, block randomization is desirable. To achieve balance in baseline characteristics, stratified randomization is widely used. Covariate adaptive randomization, however, can achieve better balance than other randomization methods and can be successfully used for clinical trials in an effective manner.

Acknowledgments

This study was partially supported by a Faculty Grant (FRCAC) from the College of Graduate Studies, at Middle Tennessee State University, Murfreesboro, TN.

Minsoo Kang, PhD; Brian G. Ragan, PhD, ATC; and Jae-Hyeon Park, PhD, contributed to conception and design; acquisition and analysis and interpretation of the data; and drafting, critical revision, and final approval of the article.

Chapter 6: Experimental Research

6.2 experimental design, learning objectives.

• Explain the difference between between-subjects and within-subjects experiments, list some of the pros and cons of each approach, and decide which approach to use to answer a particular research question.
• Define random assignment, distinguish it from random sampling, explain its purpose in experimental research, and use some simple strategies to implement it.
• Define what a control condition is, explain its purpose in research on treatment effectiveness, and describe some alternative types of control conditions.
• Define several types of carryover effect, give examples of each, and explain how counterbalancing helps to deal with them.

In this section, we look at some different ways to design an experiment. The primary distinction we will make is between approaches in which each participant experiences one level of the independent variable and approaches in which each participant experiences all levels of the independent variable. The former are called between-subjects experiments and the latter are called within-subjects experiments.

Between-Subjects Experiments

In a between-subjects experiment , each participant is tested in only one condition. For example, a researcher with a sample of 100 college students might assign half of them to write about a traumatic event and the other half write about a neutral event. Or a researcher with a sample of 60 people with severe agoraphobia (fear of open spaces) might assign 20 of them to receive each of three different treatments for that disorder. It is essential in a between-subjects experiment that the researcher assign participants to conditions so that the different groups are, on average, highly similar to each other. Those in a trauma condition and a neutral condition, for example, should include a similar proportion of men and women, and they should have similar average intelligence quotients (IQs), similar average levels of motivation, similar average numbers of health problems, and so on. This is a matter of controlling these extraneous participant variables across conditions so that they do not become confounding variables.

Random Assignment

The primary way that researchers accomplish this kind of control of extraneous variables across conditions is called random assignment , which means using a random process to decide which participants are tested in which conditions. Do not confuse random assignment with random sampling. Random sampling is a method for selecting a sample from a population, and it is rarely used in psychological research. Random assignment is a method for assigning participants in a sample to the different conditions, and it is an important element of all experimental research in psychology and other fields too.

In its strictest sense, random assignment should meet two criteria. One is that each participant has an equal chance of being assigned to each condition (e.g., a 50% chance of being assigned to each of two conditions). The second is that each participant is assigned to a condition independently of other participants. Thus one way to assign participants to two conditions would be to flip a coin for each one. If the coin lands heads, the participant is assigned to Condition A, and if it lands tails, the participant is assigned to Condition B. For three conditions, one could use a computer to generate a random integer from 1 to 3 for each participant. If the integer is 1, the participant is assigned to Condition A; if it is 2, the participant is assigned to Condition B; and if it is 3, the participant is assigned to Condition C. In practice, a full sequence of conditions—one for each participant expected to be in the experiment—is usually created ahead of time, and each new participant is assigned to the next condition in the sequence as he or she is tested. When the procedure is computerized, the computer program often handles the random assignment.

One problem with coin flipping and other strict procedures for random assignment is that they are likely to result in unequal sample sizes in the different conditions. Unequal sample sizes are generally not a serious problem, and you should never throw away data you have already collected to achieve equal sample sizes. However, for a fixed number of participants, it is statistically most efficient to divide them into equal-sized groups. It is standard practice, therefore, to use a kind of modified random assignment that keeps the number of participants in each group as similar as possible. One approach is block randomization . In block randomization, all the conditions occur once in the sequence before any of them is repeated. Then they all occur again before any of them is repeated again. Within each of these “blocks,” the conditions occur in a random order. Again, the sequence of conditions is usually generated before any participants are tested, and each new participant is assigned to the next condition in the sequence. Table 6.2 “Block Randomization Sequence for Assigning Nine Participants to Three Conditions” shows such a sequence for assigning nine participants to three conditions. The Research Randomizer website ( http://www.randomizer.org ) will generate block randomization sequences for any number of participants and conditions. Again, when the procedure is computerized, the computer program often handles the block randomization.

Table 6.2 Block Randomization Sequence for Assigning Nine Participants to Three Conditions

Random assignment is not guaranteed to control all extraneous variables across conditions. It is always possible that just by chance, the participants in one condition might turn out to be substantially older, less tired, more motivated, or less depressed on average than the participants in another condition. However, there are some reasons that this is not a major concern. One is that random assignment works better than one might expect, especially for large samples. Another is that the inferential statistics that researchers use to decide whether a difference between groups reflects a difference in the population takes the “fallibility” of random assignment into account. Yet another reason is that even if random assignment does result in a confounding variable and therefore produces misleading results, this is likely to be detected when the experiment is replicated. The upshot is that random assignment to conditions—although not infallible in terms of controlling extraneous variables—is always considered a strength of a research design.

Treatment and Control Conditions

Between-subjects experiments are often used to determine whether a treatment works. In psychological research, a treatment is any intervention meant to change people’s behavior for the better. This includes psychotherapies and medical treatments for psychological disorders but also interventions designed to improve learning, promote conservation, reduce prejudice, and so on. To determine whether a treatment works, participants are randomly assigned to either a treatment condition , in which they receive the treatment, or a control condition , in which they do not receive the treatment. If participants in the treatment condition end up better off than participants in the control condition—for example, they are less depressed, learn faster, conserve more, express less prejudice—then the researcher can conclude that the treatment works. In research on the effectiveness of psychotherapies and medical treatments, this type of experiment is often called a randomized clinical trial .

There are different types of control conditions. In a no-treatment control condition , participants receive no treatment whatsoever. One problem with this approach, however, is the existence of placebo effects. A placebo is a simulated treatment that lacks any active ingredient or element that should make it effective, and a placebo effect is a positive effect of such a treatment. Many folk remedies that seem to work—such as eating chicken soup for a cold or placing soap under the bedsheets to stop nighttime leg cramps—are probably nothing more than placebos. Although placebo effects are not well understood, they are probably driven primarily by people’s expectations that they will improve. Having the expectation to improve can result in reduced stress, anxiety, and depression, which can alter perceptions and even improve immune system functioning (Price, Finniss, & Benedetti, 2008).

Placebo effects are interesting in their own right (see Note 6.28 “The Powerful Placebo” ), but they also pose a serious problem for researchers who want to determine whether a treatment works. Figure 6.2 “Hypothetical Results From a Study Including Treatment, No-Treatment, and Placebo Conditions” shows some hypothetical results in which participants in a treatment condition improved more on average than participants in a no-treatment control condition. If these conditions (the two leftmost bars in Figure 6.2 “Hypothetical Results From a Study Including Treatment, No-Treatment, and Placebo Conditions” ) were the only conditions in this experiment, however, one could not conclude that the treatment worked. It could be instead that participants in the treatment group improved more because they expected to improve, while those in the no-treatment control condition did not.

Figure 6.2 Hypothetical Results From a Study Including Treatment, No-Treatment, and Placebo Conditions

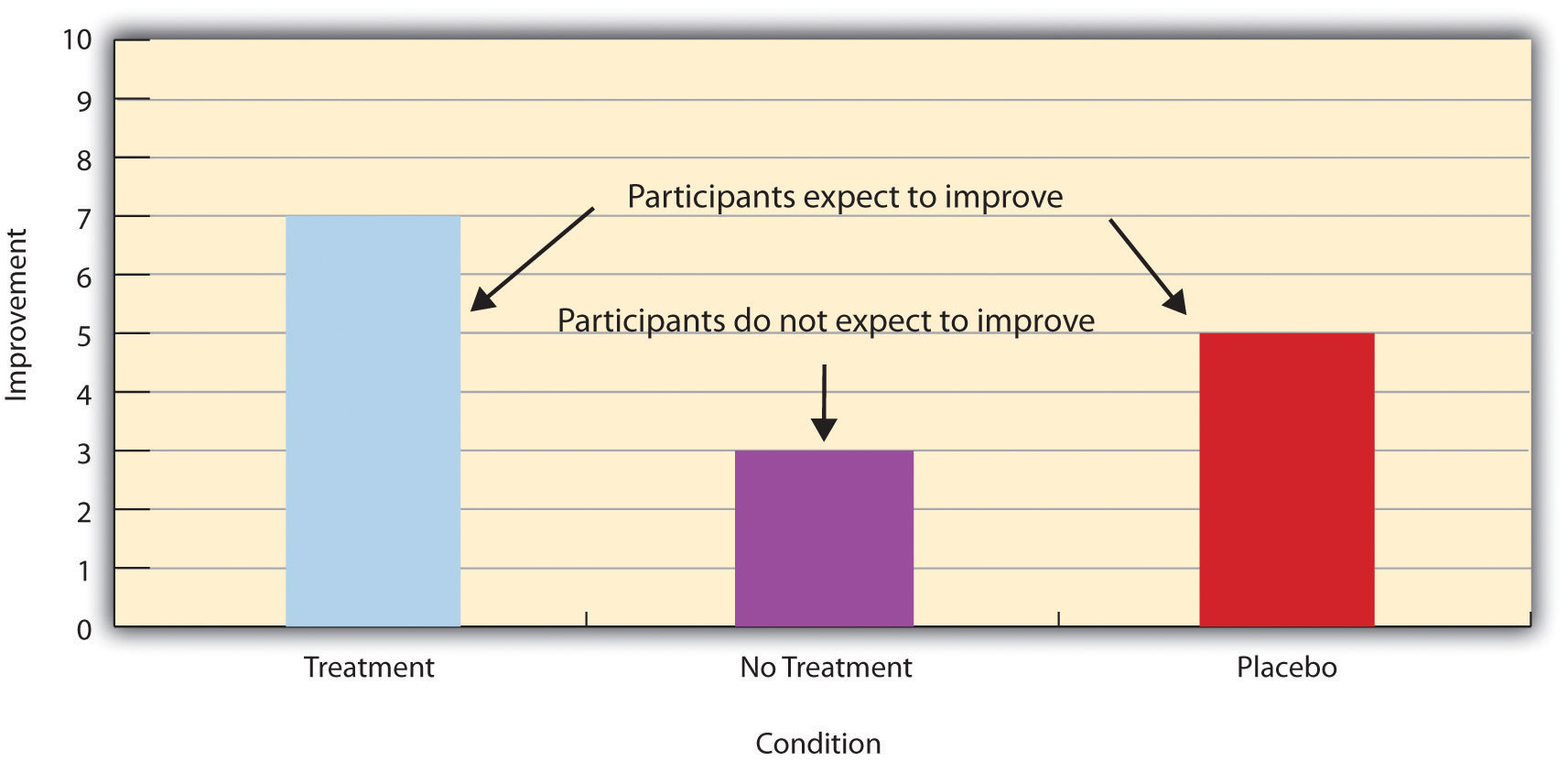
Fortunately, there are several solutions to this problem. One is to include a placebo control condition , in which participants receive a placebo that looks much like the treatment but lacks the active ingredient or element thought to be responsible for the treatment’s effectiveness. When participants in a treatment condition take a pill, for example, then those in a placebo control condition would take an identical-looking pill that lacks the active ingredient in the treatment (a “sugar pill”). In research on psychotherapy effectiveness, the placebo might involve going to a psychotherapist and talking in an unstructured way about one’s problems. The idea is that if participants in both the treatment and the placebo control groups expect to improve, then any improvement in the treatment group over and above that in the placebo control group must have been caused by the treatment and not by participants’ expectations. This is what is shown by a comparison of the two outer bars in Figure 6.2 “Hypothetical Results From a Study Including Treatment, No-Treatment, and Placebo Conditions” .

Of course, the principle of informed consent requires that participants be told that they will be assigned to either a treatment or a placebo control condition—even though they cannot be told which until the experiment ends. In many cases the participants who had been in the control condition are then offered an opportunity to have the real treatment. An alternative approach is to use a waitlist control condition , in which participants are told that they will receive the treatment but must wait until the participants in the treatment condition have already received it. This allows researchers to compare participants who have received the treatment with participants who are not currently receiving it but who still expect to improve (eventually). A final solution to the problem of placebo effects is to leave out the control condition completely and compare any new treatment with the best available alternative treatment. For example, a new treatment for simple phobia could be compared with standard exposure therapy. Because participants in both conditions receive a treatment, their expectations about improvement should be similar. This approach also makes sense because once there is an effective treatment, the interesting question about a new treatment is not simply “Does it work?” but “Does it work better than what is already available?”

The Powerful Placebo

Many people are not surprised that placebos can have a positive effect on disorders that seem fundamentally psychological, including depression, anxiety, and insomnia. However, placebos can also have a positive effect on disorders that most people think of as fundamentally physiological. These include asthma, ulcers, and warts (Shapiro & Shapiro, 1999). There is even evidence that placebo surgery—also called “sham surgery”—can be as effective as actual surgery.

Medical researcher J. Bruce Moseley and his colleagues conducted a study on the effectiveness of two arthroscopic surgery procedures for osteoarthritis of the knee (Moseley et al., 2002). The control participants in this study were prepped for surgery, received a tranquilizer, and even received three small incisions in their knees. But they did not receive the actual arthroscopic surgical procedure. The surprising result was that all participants improved in terms of both knee pain and function, and the sham surgery group improved just as much as the treatment groups. According to the researchers, “This study provides strong evidence that arthroscopic lavage with or without débridement [the surgical procedures used] is not better than and appears to be equivalent to a placebo procedure in improving knee pain and self-reported function” (p. 85).

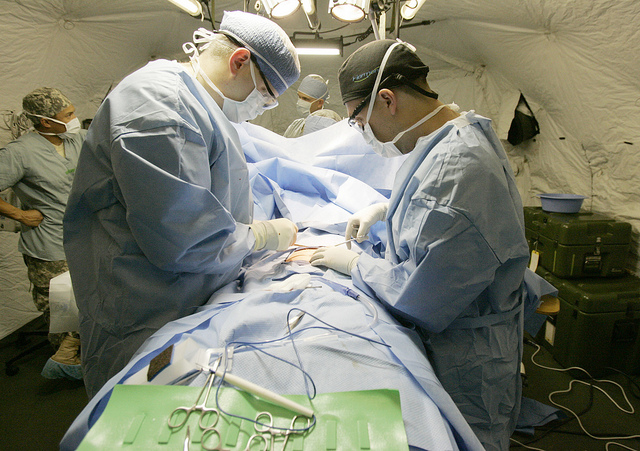
Research has shown that patients with osteoarthritis of the knee who receive a “sham surgery” experience reductions in pain and improvement in knee function similar to those of patients who receive a real surgery.

Army Medicine – Surgery – CC BY 2.0.

Within-Subjects Experiments

In a within-subjects experiment , each participant is tested under all conditions. Consider an experiment on the effect of a defendant’s physical attractiveness on judgments of his guilt. Again, in a between-subjects experiment, one group of participants would be shown an attractive defendant and asked to judge his guilt, and another group of participants would be shown an unattractive defendant and asked to judge his guilt. In a within-subjects experiment, however, the same group of participants would judge the guilt of both an attractive and an unattractive defendant.

The primary advantage of this approach is that it provides maximum control of extraneous participant variables. Participants in all conditions have the same mean IQ, same socioeconomic status, same number of siblings, and so on—because they are the very same people. Within-subjects experiments also make it possible to use statistical procedures that remove the effect of these extraneous participant variables on the dependent variable and therefore make the data less “noisy” and the effect of the independent variable easier to detect. We will look more closely at this idea later in the book.

Carryover Effects and Counterbalancing

The primary disadvantage of within-subjects designs is that they can result in carryover effects. A carryover effect is an effect of being tested in one condition on participants’ behavior in later conditions. One type of carryover effect is a practice effect , where participants perform a task better in later conditions because they have had a chance to practice it. Another type is a fatigue effect , where participants perform a task worse in later conditions because they become tired or bored. Being tested in one condition can also change how participants perceive stimuli or interpret their task in later conditions. This is called a context effect . For example, an average-looking defendant might be judged more harshly when participants have just judged an attractive defendant than when they have just judged an unattractive defendant. Within-subjects experiments also make it easier for participants to guess the hypothesis. For example, a participant who is asked to judge the guilt of an attractive defendant and then is asked to judge the guilt of an unattractive defendant is likely to guess that the hypothesis is that defendant attractiveness affects judgments of guilt. This could lead the participant to judge the unattractive defendant more harshly because he thinks this is what he is expected to do. Or it could make participants judge the two defendants similarly in an effort to be “fair.”

Carryover effects can be interesting in their own right. (Does the attractiveness of one person depend on the attractiveness of other people that we have seen recently?) But when they are not the focus of the research, carryover effects can be problematic. Imagine, for example, that participants judge the guilt of an attractive defendant and then judge the guilt of an unattractive defendant. If they judge the unattractive defendant more harshly, this might be because of his unattractiveness. But it could be instead that they judge him more harshly because they are becoming bored or tired. In other words, the order of the conditions is a confounding variable. The attractive condition is always the first condition and the unattractive condition the second. Thus any difference between the conditions in terms of the dependent variable could be caused by the order of the conditions and not the independent variable itself.

There is a solution to the problem of order effects, however, that can be used in many situations. It is counterbalancing , which means testing different participants in different orders. For example, some participants would be tested in the attractive defendant condition followed by the unattractive defendant condition, and others would be tested in the unattractive condition followed by the attractive condition. With three conditions, there would be six different orders (ABC, ACB, BAC, BCA, CAB, and CBA), so some participants would be tested in each of the six orders. With counterbalancing, participants are assigned to orders randomly, using the techniques we have already discussed. Thus random assignment plays an important role in within-subjects designs just as in between-subjects designs. Here, instead of randomly assigning to conditions, they are randomly assigned to different orders of conditions. In fact, it can safely be said that if a study does not involve random assignment in one form or another, it is not an experiment.

There are two ways to think about what counterbalancing accomplishes. One is that it controls the order of conditions so that it is no longer a confounding variable. Instead of the attractive condition always being first and the unattractive condition always being second, the attractive condition comes first for some participants and second for others. Likewise, the unattractive condition comes first for some participants and second for others. Thus any overall difference in the dependent variable between the two conditions cannot have been caused by the order of conditions. A second way to think about what counterbalancing accomplishes is that if there are carryover effects, it makes it possible to detect them. One can analyze the data separately for each order to see whether it had an effect.

When 9 Is “Larger” Than 221

Researcher Michael Birnbaum has argued that the lack of context provided by between-subjects designs is often a bigger problem than the context effects created by within-subjects designs. To demonstrate this, he asked one group of participants to rate how large the number 9 was on a 1-to-10 rating scale and another group to rate how large the number 221 was on the same 1-to-10 rating scale (Birnbaum, 1999). Participants in this between-subjects design gave the number 9 a mean rating of 5.13 and the number 221 a mean rating of 3.10. In other words, they rated 9 as larger than 221! According to Birnbaum, this is because participants spontaneously compared 9 with other one-digit numbers (in which case it is relatively large) and compared 221 with other three-digit numbers (in which case it is relatively small).

Simultaneous Within-Subjects Designs

So far, we have discussed an approach to within-subjects designs in which participants are tested in one condition at a time. There is another approach, however, that is often used when participants make multiple responses in each condition. Imagine, for example, that participants judge the guilt of 10 attractive defendants and 10 unattractive defendants. Instead of having people make judgments about all 10 defendants of one type followed by all 10 defendants of the other type, the researcher could present all 20 defendants in a sequence that mixed the two types. The researcher could then compute each participant’s mean rating for each type of defendant. Or imagine an experiment designed to see whether people with social anxiety disorder remember negative adjectives (e.g., “stupid,” “incompetent”) better than positive ones (e.g., “happy,” “productive”). The researcher could have participants study a single list that includes both kinds of words and then have them try to recall as many words as possible. The researcher could then count the number of each type of word that was recalled. There are many ways to determine the order in which the stimuli are presented, but one common way is to generate a different random order for each participant.

Between-Subjects or Within-Subjects?

Almost every experiment can be conducted using either a between-subjects design or a within-subjects design. This means that researchers must choose between the two approaches based on their relative merits for the particular situation.

Between-subjects experiments have the advantage of being conceptually simpler and requiring less testing time per participant. They also avoid carryover effects without the need for counterbalancing. Within-subjects experiments have the advantage of controlling extraneous participant variables, which generally reduces noise in the data and makes it easier to detect a relationship between the independent and dependent variables.

A good rule of thumb, then, is that if it is possible to conduct a within-subjects experiment (with proper counterbalancing) in the time that is available per participant—and you have no serious concerns about carryover effects—this is probably the best option. If a within-subjects design would be difficult or impossible to carry out, then you should consider a between-subjects design instead. For example, if you were testing participants in a doctor’s waiting room or shoppers in line at a grocery store, you might not have enough time to test each participant in all conditions and therefore would opt for a between-subjects design. Or imagine you were trying to reduce people’s level of prejudice by having them interact with someone of another race. A within-subjects design with counterbalancing would require testing some participants in the treatment condition first and then in a control condition. But if the treatment works and reduces people’s level of prejudice, then they would no longer be suitable for testing in the control condition. This is true for many designs that involve a treatment meant to produce long-term change in participants’ behavior (e.g., studies testing the effectiveness of psychotherapy). Clearly, a between-subjects design would be necessary here.

Remember also that using one type of design does not preclude using the other type in a different study. There is no reason that a researcher could not use both a between-subjects design and a within-subjects design to answer the same research question. In fact, professional researchers often do exactly this.

Key Takeaways

• Experiments can be conducted using either between-subjects or within-subjects designs. Deciding which to use in a particular situation requires careful consideration of the pros and cons of each approach.
• Random assignment to conditions in between-subjects experiments or to orders of conditions in within-subjects experiments is a fundamental element of experimental research. Its purpose is to control extraneous variables so that they do not become confounding variables.
• Experimental research on the effectiveness of a treatment requires both a treatment condition and a control condition, which can be a no-treatment control condition, a placebo control condition, or a waitlist control condition. Experimental treatments can also be compared with the best available alternative.

Discussion: For each of the following topics, list the pros and cons of a between-subjects and within-subjects design and decide which would be better.

• You want to test the relative effectiveness of two training programs for running a marathon.
• Using photographs of people as stimuli, you want to see if smiling people are perceived as more intelligent than people who are not smiling.
• In a field experiment, you want to see if the way a panhandler is dressed (neatly vs. sloppily) affects whether or not passersby give him any money.
• You want to see if concrete nouns (e.g., dog ) are recalled better than abstract nouns (e.g., truth ).
• Discussion: Imagine that an experiment shows that participants who receive psychodynamic therapy for a dog phobia improve more than participants in a no-treatment control group. Explain a fundamental problem with this research design and at least two ways that it might be corrected.

Birnbaum, M. H. (1999). How to show that 9 > 221: Collect judgments in a between-subjects design. Psychological Methods, 4 , 243–249.

Moseley, J. B., O’Malley, K., Petersen, N. J., Menke, T. J., Brody, B. A., Kuykendall, D. H., … Wray, N. P. (2002). A controlled trial of arthroscopic surgery for osteoarthritis of the knee. The New England Journal of Medicine, 347 , 81–88.

Price, D. D., Finniss, D. G., & Benedetti, F. (2008). A comprehensive review of the placebo effect: Recent advances and current thought. Annual Review of Psychology, 59 , 565–590.

Shapiro, A. K., & Shapiro, E. (1999). The powerful placebo: From ancient priest to modern physician . Baltimore, MD: Johns Hopkins University Press.

• Research Methods in Psychology. Provided by : University of Minnesota Libraries Publishing. Located at : http://open.lib.umn.edu/psychologyresearchmethods . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

Privacy Policy

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

34.4 - creating random assignments.

We now turn our focus from randomly sampling a subset of observations from a data set to that of generating a random assignment of treatments to experimental units in a randomized, controlled experiment. The good news is that the techniques used to sample without replacement can easily be extended to generate such random assignment plans.

It's probably a good time to remind you of the existence of the PLAN procedure. As I mentioned earlier, due to time constraints of the course and the complexity of the PLAN procedure, we will not use it to accomplish any of our random assignments. You should be aware, however, of its existence should you want to explore it on your own in the future.

Example 34.15 Section  

Suppose we are interested in conducting an experiment so that we can compare the effects of two drugs (A and B) and one placebo on headache pain. We have 30 subjects enrolled in our study but need to determine a plan for randomly assigning 10 of the subjects to treatment A, 10 of the subjects to treatment B, and 10 of the subjects to the placebo. The following program does just that for us. That is, it creates a random assignment for 30 subjects in a completely randomized design with one factor having 3 levels:

Okay, let's first launch and run    the SAS program, so you can review the resulting output to convince yourself that the code did indeed generate the desired treatment plan. You should see that 10 of the subjects were randomly assigned to treatment A, 10 to treatment B, and 10 to the placebo.

Now, let's walk ourselves through the program to make sure we understand how it works. The first DATA step merely uses a simple DO loop to create a temporary data set called exper1 that contains one observation for each of the experimental units (in our case, the experimental units are subjects). The only variable in the data set, unit , contains an arbitrary label 1, 2, ..., 30 assigned to each of the experimental units.

The remainder of the code generates a random assignment. To do so, the code from Example 34.5 is simply extended. That is:

• The second DATA step uses the ranuni function to generate a uniform random number between 0 and 1 for each observation in the exper1 data set. The result is stored in a temporary data set called random1 .
• The random1 data set is sorted in order of the random number.
• The third DATA step uses an IF-THEN-ELSE construct to assign the first ten units in sorted order to Group 1, the second ten to Group 2, and the last ten to Group 3.
• A FORMAT is defined to label the groups meaningfully.
• The final randomization list is printed.

Example 34.16 Section  

To create a random assignment for a completely randomized design with two factors , you can just modify the IF statement in the previous example. The following program generates a random assignment of treatments to 30 subjects, in which Factor A has 2 levels and Factor B has 3 levels (and hence 6 treatments). The code is similar to the code from the previous example except the IF statement now divides the 30 subjects into 6 treatment groups and (arbitrarily) assigns the levels of factors A and B to the groups:

First, my apologies for the formatting that makes the IF-THEN-ELSE statement a little difficult to read. I needed to format it as such so that I could easily capture the image of the program for you.

Again, it's probably best if you first launch and run    the SAS program, so you can review the resulting output to convince yourself that the code did indeed generate the desired treatment plan. You should see that five of the subjects were randomly assigned to the A=1, B=1 group, five to the A=1, B=2 group, five to the A=1, B=3 group, and so on.

Then, if you compare the code to the code from the previous example, the only substantial difference you should see is the difference between the two IF statements. As previously mentioned, the IF statement here divides the 30 subjects into 6 treatment groups and (arbitrarily) assigns the levels of factors A and B to the groups:

Example 34.17 Section  

Thus far, our random assignments have not involved dealing with a blocking factor. As you know, it is natural in some experiments to block some of the experimental units together in an attempt to reduce unnecessary variability in your measurements that might otherwise prevent you from making good treatment comparisons. Suppose, for example, that your workload would prevent you from making more than nine experimental measurements in a day. Then, it would be a good idea then to treat the day as a blocking factor. The following program creates a random assignment for 27 subjects in a randomized block design with one factor having three levels.

Again, my apologies about the formatting that makes the program a little more difficult than usual to read. I needed to format it as such so that I could easily capture the image of the program for you.

It's probably going to be best if you first launch and run    the SAS program, so you can first review the contents of the initial exper2 data set:

EXPER2: Definition of Experimental Units

and then the resulting output that contains the desired treatment plan... first in block-treatment order:

Random Assignments for RBD: Sorted in BLOCK-TRT order

and then in block-unit order:

Random Assignments for RBD: Sorted in BLOCK-UNIT order

As you can see, the exper2 data set is created to contain one observation for each of the experimental units (27 subjects here). The variable unit contains an arbitrary label (1, 2, ..., 30) assigned to each of the experimental units. The variable block , which identifies the block number (1, 2, and 3), divides the experimental units into three equal-sized blocks of nine.

Now, to create the random assignment:

• We use the ranuni function to generate a uniform random number between 0 and 1 for each observation.
• Then, within each block, we sort the data in order of the random number.
• Then, we create a counter variable to count the number of observations within each block: for the first observation within each block ("if first.block "), we set the counter ( k ) to 0; otherwise, we increase the counter by 1 for each observation within the block. (For this to work, we must retain k from iteration to iteration).
• Using an IF-THEN-ELSE construct, within each block , assign the first three units in sorted order ( k =0,1,2) to group 1, the second three ( k =3,4,5) to group 2, and the last three ( k =6,7,8) to group 3.

Depending on how the experiment will be conducted, you can print the random assignment in different orders:

• First, the randomization is printed in order of treatment within each block. This will accommodate experiments for which it is natural to perform the treatments in groups on the randomized experimental units.
• Then, the randomization is printed in order of units within the block. This will accommodate experiments for which it is natural to perform the treatments in random order on consecutive experimental units.

The Plagiarism Checker Online For Your Academic Work

Start Plagiarism Check

Editing & Proofreading for Your Research Paper

Get it proofread now

Online Printing & Binding with Free Express Delivery

Configure binding now

• Academic essay overview
• The writing process
• Structuring academic essays
• Types of academic essays
• Academic writing overview
• Sentence structure
• Academic writing process
• Improving your academic writing
• Titles and headings
• APA style overview
• APA citation & referencing
• APA structure & sections
• Citation & referencing
• Structure and sections
• APA examples overview
• Commonly used citations
• Other examples
• British English vs. American English
• Chicago style overview
• Chicago citation & referencing
• Chicago structure & sections
• Chicago style examples
• Citing sources overview
• Citation format
• Citation examples
• College essay overview
• Application
• How to write a college essay
• Types of college essays
• Commonly confused words
• Definitions
• Dissertation overview
• Dissertation structure & sections
• Dissertation writing process
• Graduate school overview
• Application & admission
• Study abroad
• Master degree
• Harvard referencing overview
• Language rules overview
• Grammatical rules & structures
• Parts of speech
• Punctuation
• Methodology overview
• Analyzing data
• Experiments
• Observations
• Inductive vs. Deductive
• Qualitative vs. Quantitative
• Types of validity
• Types of reliability
• Sampling methods
• Theories & Concepts
• Types of research studies
• Types of variables
• MLA style overview
• MLA examples
• MLA citation & referencing
• MLA structure & sections
• Plagiarism overview
• Plagiarism checker
• Types of plagiarism
• Printing production overview
• Research bias overview
• Types of research bias
• Example sections
• Types of research papers
• Research process overview
• Problem statement
• Research proposal
• Research topic
• Statistics overview
• Levels of measurment
• Frequency distribution
• Measures of central tendency
• Measures of variability
• Hypothesis testing
• Parameters & test statistics
• Types of distributions
• Correlation
• Effect size
• Hypothesis testing assumptions
• Types of ANOVAs
• Types of chi-square
• Statistical data
• Statistical models
• Spelling mistakes
• Tips overview
• Academic writing tips
• Dissertation tips
• Sources tips
• Working with sources overview
• Evaluating sources
• Finding sources
• Including sources
• Types of sources

Your Step to Success

Plagiarism Check within 10min

Printing & Binding with 3D Live Preview

Random Assignment – A Simple Introduction with Examples

How do you like this article cancel reply.

Save my name, email, and website in this browser for the next time I comment.

Completing a research or thesis paper is more work than most students imagine. For instance, you must conduct experiments before coming up with conclusions. Random assignment, a key methodology in academic research, ensures every participant has an equal chance of being placed in any group within an experiment. In experimental studies, the random assignment of participants is a vital element, which this article will discuss.

Inhaltsverzeichnis

• 1 Random Assignment – In a Nutshell
• 2 Definition: Random assignment
• 3 Importance of random assignment
• 4 Random assignment vs. random sampling
• 5 How to use random assignment
• 6 When random assignment is not used

Random Assignment – In a Nutshell

• Random assignment is where you randomly place research participants into specific groups.
• This method eliminates bias in the results by ensuring that all participants have an equal chance of getting into either group.
• Random assignment is usually used in independent measures or between-group experiment designs.

Definition: Random assignment

Pearson Correlation is a descriptive statistical procedure that describes the measure of linear dependence between two variables. It entails a sample, control group , experimental design , and randomized design. In this statistical procedure, random assignment is used. Random assignment is the random placement of participants into different groups in experimental research.

Importance of random assignment

Random assessment is essential for strengthening the internal validity of experimental research. Internal validity helps make a casual relationship’s conclusions reliable and trustworthy.

In experimental research, researchers isolate independent variables and manipulate them as they assess the impact while managing other variables. To achieve this, an independent variable for diverse member groups is vital. This experimental design is called an independent or between-group design.

Example: Different levels of independent variables

• In a medical study, you can research the impact of nutrient supplements on the immune (nutrient supplements = independent variable, immune = dependent variable)

Three independent participant levels are applicable here:

• Control group (given 0 dosages of iron supplements)
• The experimental group (low dosage)
• The second experimental group (high dosage)

This assignment technique in experiments ensures no bias in the treatment sets at the beginning of the trials. Therefore, if you do not use this technique, you won’t be able to exclude any alternate clarifications for your findings.

In the research experiment above, you can recruit participants randomly by handing out flyers at public spaces like gyms, cafés, and community centers. Then:

• Place the group from cafés in the control group
• Community center group in the low prescription trial group
• Gym group in the high-prescription group

Even with random participant assignment, other extraneous variables may still create bias in experiment results. However, these variations are usually low, hence should not hinder your research. Therefore, using random placement in experiments is highly necessary, especially where it is ethically required or makes sense for your research subject.

Random assignment vs. random sampling

Simple random sampling is a method of choosing the participants for a study. On the other hand, the random assignment involves sorting the participants selected through random sampling. Another difference between random sampling and random assignment is that the former is used in several types of studies, while the latter is only applied in between-subject experimental designs.

Your study researches the impact of technology on productivity in a specific company.

In such a case, you have contact with the entire staff. So, you can assign each employee a quantity and apply a random number generator to pick a specific sample.

For instance, from 500 employees, you can pick 200. So, the full sample is 200.

Random sampling enhances external validity, as it guarantees that the study sample is unbiased, and that an entire population is represented. This way, you can conclude that the results of your studies can be accredited to the autonomous variable.

After determining the full sample, you can break it down into two groups using random assignment. In this case, the groups are:

• The control group (does get access to technology)
• The experimental group (gets access to technology)

Using random assignment assures you that any differences in the productivity results for each group are not biased and will help the company make a decision.

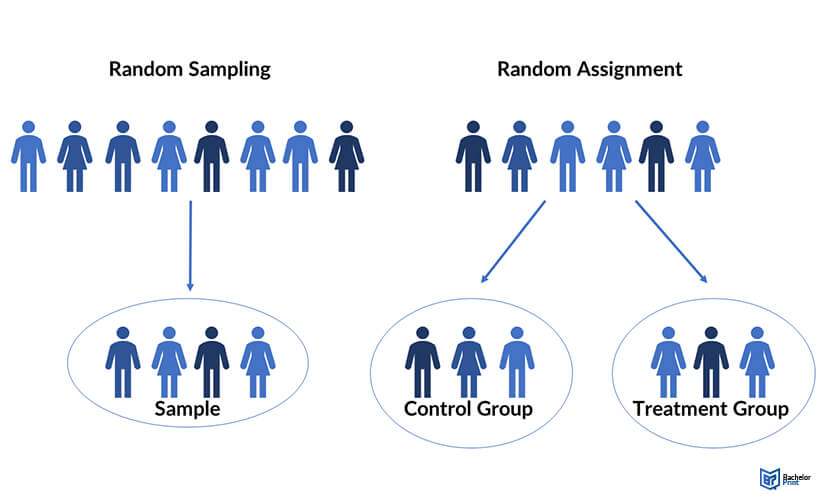
How to use random assignment

Firstly, give each participant a unique number as an identifier. Then, use a specific tool to simplify assigning the participants to the sample groups. Some tools you can use are:

Random member assignment is a prevailing technique for placing participants in specific groups because each person has a fair opportunity of being put in either group.

Random assignment in block experimental designs

In complex experimental designs , you must group your participants into blocks before using the random assignment technique.

You can create participant blocks depending on demographic variables, working hours, or scores. However, the blocks imply that you will require a bigger sample to attain high statistical power.

After grouping the participants in blocks, you can use random assignments inside each block to allocate the members to a specific treatment condition. Doing this will help you examine if quality impacts the result of the treatment.

Depending on their unique characteristics, you can also use blocking in experimental matched designs before matching the participants in each block. Then, you can randomly allot each partaker to one of the treatments in the research and examine the results.

When random assignment is not used

As powerful a tool as it is, random assignment does not apply in all situations. Like the following:

Comparing different groups

When the purpose of your study is to assess the differences between the participants, random member assignment may not work.

If you want to compare teens and the elderly with and without specific health conditions, you must ensure that the participants have specific characteristics. Therefore, you cannot pick them randomly.

In such a study, the medical condition (quality of interest) is the independent variable, and the participants are grouped based on their ages (different levels). Also, all partakers are tried similarly to ensure they have the medical condition, and their outcomes are tested per group level.

No ethical justifiability

Another situation where you cannot use random assignment is if it is ethically not permitted.

If your study involves unhealthy or dangerous behaviors or subjects, such as drug use. Instead of assigning random partakers to sets, you can conduct quasi-experimental research.

When using a quasi-experimental design , you examine the conclusions of pre-existing groups you have no control over, such as existing drug users. While you cannot randomly assign them to groups, you can use variables like their age, years of drug use, or socioeconomic status to group the participants.

What is the definition of random assignment?

It is an experimental research technique that involves randomly placing participants from your samples into different groups. It ensures that every sample member has the same opportunity of being in whichever group (control or experimental group).

When is random assignment applicable?

You can use this placement technique in experiments featuring an independent measures design. It helps ensure that all your sample groups are comparable.

What is the importance of random assignment?

It can help you enhance your study’s validity . This technique also helps ensure that every sample has an equal opportunity of being assigned to a control or trial group.

When should you NOT use random assignment

You should not use this technique if your study focuses on group comparisons or if it is not legally ethical.

We use cookies on our website. Some of them are essential, while others help us to improve this website and your experience.

• External Media

Individual Privacy Preferences

Cookie Details Privacy Policy Imprint

Here you will find an overview of all cookies used. You can give your consent to whole categories or display further information and select certain cookies.

Accept all Save

Essential cookies enable basic functions and are necessary for the proper function of the website.

Show Cookie Information Hide Cookie Information

Statistics cookies collect information anonymously. This information helps us to understand how our visitors use our website.

Content from video platforms and social media platforms is blocked by default. If External Media cookies are accepted, access to those contents no longer requires manual consent.

Privacy Policy Imprint

4 Types of Random Sampling Techniques Explained

“Why should I care about random sampling?”

Here’s why: If you’re a data scientist and want to develop models, you need data. And if you need data, someone needs to collect that data. And if someone is collecting data, they need to make sure that it isn’t biased or it will be extremely costly in the long run.

Therefore, if you want to collect unbiased data, then you need to know about random sampling.

4 Types of Random Sampling Techniques

• Simple random sampling.
• Stratified random sampling.
• Cluster random sampling.
• Systematic random sampling.

More From Terence Shin 10 Advanced SQL Concepts You Should Know for Data Science Interviews

What Is Random Sampling?

Random sampling simply describes a state wherein every element in a population has an equal chance of being chosen for the sample.  Sounds simple, right? Well, it’s a lot easier said than done because you must consider a lot of logistics in order to minimize bias. These  four types of random sampling techniques will allow you to do just that.

1. Simple Random Sampling

Simple random sampling requires the use of randomly generated numbers to choose a sample. More specifically, it initially requires a sampling frame, which is a list or database of all members of a population. You can then randomly generate a number for each element, using Excel for example, and take the first n number of samples that you require.

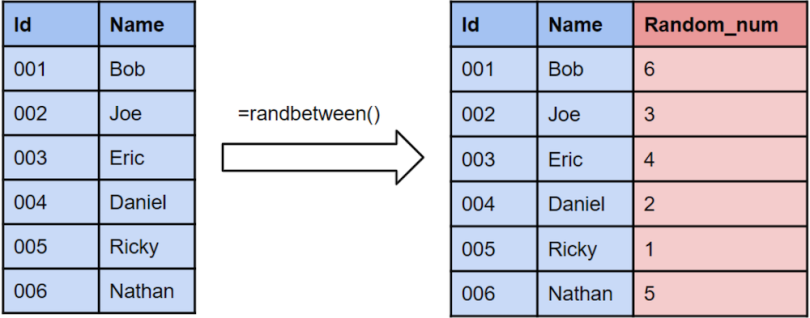
To give an example, imagine the table on the right was your sampling frame. Using software like Excel, you can then generate random numbers for each element in the sampling frame. If you need a sample size of three, then you would take the samples with the random numbers from one to three.

2. Stratified Random Sampling

Stratified random sampling involves dividing a population into groups with similar attributes and randomly sampling each group.

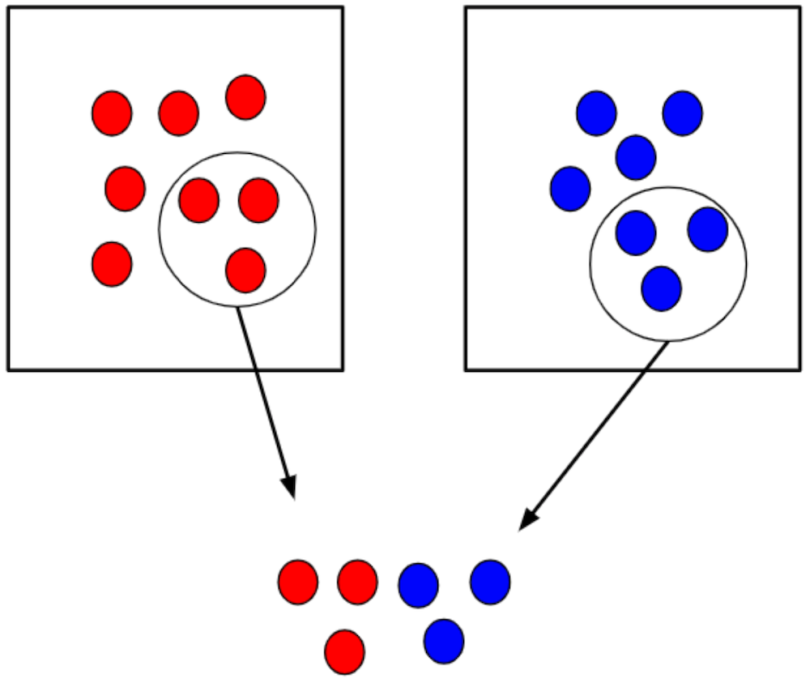
This method ensures that different segments in a population are equally represented. To give an example, imagine a survey is conducted at a school to determine overall satisfaction. Here, stratified random sampling can equally represent the opinions of students in each department.

3. Cluster Random Sampling

Cluster sampling starts by dividing a population into groups or clusters. What makes this different from stratified sampling is that each cluster must be representative of the larger population. Then, you randomly select entire clusters to sample.

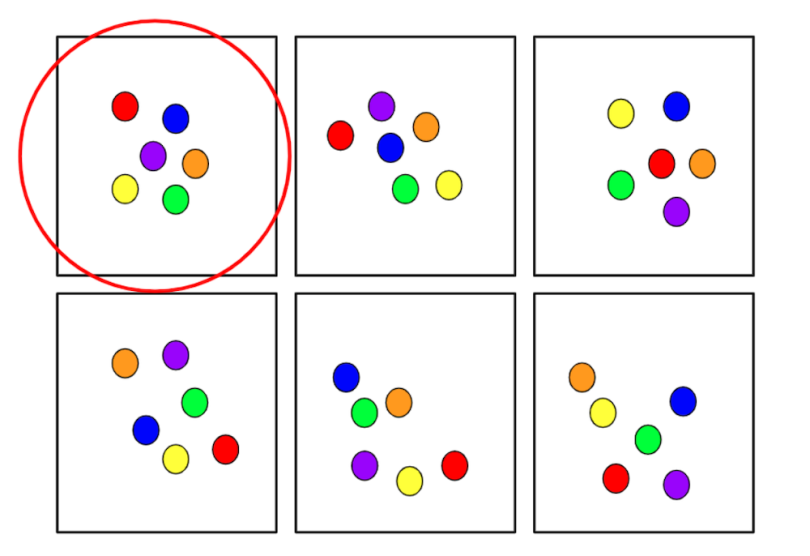
For example, if a school had five different eighth grade classes, cluster random sampling means any one class would serve as a sample.

4. Systematic Random Sampling

Systematic random sampling is a common technique in which you sample every k th element. For example, if you were conducting surveys at a mall, you might survey every 100th person that walks in.

If you have a sampling frame, then you would divide the size of the frame, N , by the desired sample size, n , to get the index number, k . You would then choose every k th element in the frame to create your sample.

Using the same charts from the first example, if we wanted a sample size of two this time, then we would take every third row in the sampling frame.

More in Data Science How to Create a Search Engine With Python and Laravel

Random Sampling Explained

You should now have an understanding of what random sampling is and several common techniques for conducting it. Mastering this concept is extremely important to minimize bias and create better models.

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

We're sorry, but some features of Research Randomizer require JavaScript. If you cannot enable JavaScript, we suggest you use an alternative random number generator such as the one available at Random.org .

RESEARCH RANDOMIZER

Random sampling and random assignment made easy.

Research Randomizer is a free resource for researchers and students in need of a quick way to generate random numbers or assign participants to experimental conditions. This site can be used for a variety of purposes, including psychology experiments, medical trials, and survey research.

GENERATE NUMBERS

In some cases, you may wish to generate more than one set of numbers at a time (e.g., when randomly assigning people to experimental conditions in a "blocked" research design). If you wish to generate multiple sets of random numbers, simply enter the number of sets you want, and Research Randomizer will display all sets in the results.

Specify how many numbers you want Research Randomizer to generate in each set. For example, a request for 5 numbers might yield the following set of random numbers: 2, 17, 23, 42, 50.

Specify the lowest and highest value of the numbers you want to generate. For example, a range of 1 up to 50 would only generate random numbers between 1 and 50 (e.g., 2, 17, 23, 42, 50). Enter the lowest number you want in the "From" field and the highest number you want in the "To" field.

Selecting "Yes" means that any particular number will appear only once in a given set (e.g., 2, 17, 23, 42, 50). Selecting "No" means that numbers may repeat within a given set (e.g., 2, 17, 17, 42, 50). Please note: Numbers will remain unique only within a single set, not across multiple sets. If you request multiple sets, any particular number in Set 1 may still show up again in Set 2.

Sorting your numbers can be helpful if you are performing random sampling, but it is not desirable if you are performing random assignment. To learn more about the difference between random sampling and random assignment, please see the Research Randomizer Quick Tutorial.

Place Markers let you know where in the sequence a particular random number falls (by marking it with a small number immediately to the left). Examples: With Place Markers Off, your results will look something like this: Set #1: 2, 17, 23, 42, 50 Set #2: 5, 3, 42, 18, 20 This is the default layout Research Randomizer uses. With Place Markers Within, your results will look something like this: Set #1: p1=2, p2=17, p3=23, p4=42, p5=50 Set #2: p1=5, p2=3, p3=42, p4=18, p5=20 This layout allows you to know instantly that the number 23 is the third number in Set #1, whereas the number 18 is the fourth number in Set #2. Notice that with this option, the Place Markers begin again at p1 in each set. With Place Markers Across, your results will look something like this: Set #1: p1=2, p2=17, p3=23, p4=42, p5=50 Set #2: p6=5, p7=3, p8=42, p9=18, p10=20 This layout allows you to know that 23 is the third number in the sequence, and 18 is the ninth number over both sets. As discussed in the Quick Tutorial, this option is especially helpful for doing random assignment by blocks.

Please note: By using this service, you agree to abide by the SPN User Policy and to hold Research Randomizer and its staff harmless in the event that you experience a problem with the program or its results. Although every effort has been made to develop a useful means of generating random numbers, Research Randomizer and its staff do not guarantee the quality or randomness of numbers generated. Any use to which these numbers are put remains the sole responsibility of the user who generated them.

Note: By using Research Randomizer, you agree to its Terms of Service .