assignment fill in the blank exercise 9.02

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

Completing the square.

• Worked example: Completing the square (intro)
• Completing the square (intro)
• Worked example: Rewriting expressions by completing the square
• Worked example: Rewriting & solving equations by completing the square
• Completing the square (intermediate)

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.2: Exercise

• Last updated
• Save as PDF
• Page ID 105827

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

PART 1: DIFFUSION & OSMOSIS

Diffusion is the movement of molecules from an area in which they are high in concentration to an area in which they are low in concentration. Molecules move down a concentration gradient until they are equally distributed, or equilibrium is reached (Fig. 1). At equilibrium, there is no concentration gradient. Molecules still move once equilibrium is reached, but there is no net movement in any one direction.

Osmosis is a specific type of diffusion : the diffusion of water molecules across a semipermeable membrane. Like other molecules, water molecules diffuse down a concentration gradient, from an area of higher free water concentration to an area of lower free water concentration. This means that water will move across a semipermeable membrane, like the cell membrane, in the direction of the higher solute concentration. (In solution, high solute concentration = low free water concentration; conversely, low solute concentration = high free water concentration.) You will observe this concept in Part 2: Osmosis & Tonicity .

In living organisms, most substances are transported as solutes , dissolved in water, a solvent . For example, if we dissolve salt (\(\ce{NaCl}\)) in a beaker of water, salt (\(\ce{NaCl}\)) is the solute and water is the solvent. Examples of solutes in the human body include glucose, small proteins, and electrolytes like calcium and sodium ions. Waste products, such as \(\ce{CO2}\) and urea are also transported as solutes. Solutes are carried by body fluids, such as blood plasma, and pass into and out of cells through passive and active transport . In either case, the cell membrane will either inhibit or facilitate the process of diffusion: some molecules can easily diffuse across a plasma membrane and some cannot. For example, small, nonpolar molecules (such as \(\ce{CO2}\) and \(\ce{O2}\)) can cross a membrane by simple diffusion. Large molecules or polar molecules, however, cannot easily diffuse across a membrane. Cells must have specialized membrane-bound proteins that function to transport such substances across the membrane.

In Part 1: Diffusion & Osmosis , you will learn about diffusion and osmosis using dialysis membrane, a selectively permeable sheet of cellulose that permits the passage of water and small solutes, but does not allow larger molecules to diffuse across. This is because the membrane has microscopic pores that only allow small molecules through; anything larger than the size of the pores is prevented from crossing. Some of the solutes in this experiment, sucrose (\(\ce{C12H22O11}\)) and starch (\(\ce{(C6H10O5})n}\) are too large to pass through the pores of the dialysis tubing, but the solvent molecules (\(\ce{H2O}\)) and glucose (\(\ce{C12H22O11}\)), are small enough to pass easily.

Exercise 1: Molecular Weight and Diffusion Rate

Molecular weight is an indication of the mass and size of a molecule. The purpose of this experiment is to determine the relationship between molecular weight and the rate of diffusion through a semisolid gel. You will investigate two dyes, methylene blue and potassium permanganate.

Employing Steps in the Scientific Method:

• Record the Question that is being investigated in this experiment. ________________________________________________________________
• Record a Hypothesis for the question stated above. ________________________________________________________________
• Predict the results of the experiment based on your hypothesis (if/then). ________________________________________________________________
• Perform the experiment below and collect your data.
• Petri dish of agar semi-solid gel (Mueller Hinton agar plates, 150 x 15 mm) - make sure the agar has been allowed to come to room temperature
• Methylene blue solution (0.2% in 25% EtOH)
• Potassium permanganate solution (0.1% KMnO4)
• Small straws
• Small plastic metric ruler

1. Obtain a petri dish of agar

2. Take the plastic straw and gently stick it down into one side of the agar. Lift up the straw, withdrawing a small plug of agar. Repeat on the other side of the dish.

3. Using a 1mL transfer pipet, place a single drop of each dye into the appropriate agar well. (Fig. 2).

4. After 20 minutes, place a small, clear metric ruler underneath the Petri dish to measure the distance (diameter) that the dye has moved. Enter the data in Table 1.

5. Repeat step 4 at 40, 60, and 80 minutes.

• What is the relationship between molecular weight and the rate of diffusion? Explain. ________________________________________________________________
• Go back and look at your initial hypothesis. Does your data support this hypothesis? Explain. _______________________________________________________________

Extension Activity: (Optional)

The results of this experiment can be presented graphically. The presentation of your data in a graph will assist you in interpreting your results. Based on your results, you can complete the final step of scientific investigation, in which you must be able to propose a logical argument that either allows you to support or reject your initial hypothesis.

• Graph your results using the data from Table 1.
• What is the dependent variable? Which axis is used to graph this data? ______________________________________________________________________
• What is your independent variable? Which axis is used to graph this data? ______________________________________________________________________

Exercise 2: Diffusion Across a Membrane

• Dialysis tubing
• Plastic clips or string
• 5 x 400 mL beakers (or plastic cups)
• Electronic balance
• Weigh boats
• 15% Sucrose solution (MW sucrose = 342 g/mol)
• 30% Sucrose solution (MW sucrose = 342 g/mol)
• 30% Glucose solution (MW glucose = 180 g/mol)
• Graduated cylinders (10 mL and 100 mL)
• Wax pencil or sharpie
• 15% starch solution (MW = variable)
• Iodine solution (MW = 166 g/mol)
• Benedict’s reagent
• Hot plate or heat block
• Cut 5 pieces of dialysis membrane approximately 10 cm long. Soak the pieces in tap water until they are soft and pliable (3-5 minutes). *This step may be done for you; check with your instructor.
• Obtain 5 beakers (plastic cups) and label them #1 - 5. Fill each beaker with 150 mL of a solution as follows:
• Beaker #1 – H2O
• Beaker #2 – H2O
• Beaker #3 – H2O
• Beaker #4 – 30% sucrose solution
• Beaker #5 - H2O and 1mL Iodine solution
• Set beakers aside.
• Remove one piece of dialysis membrane from the soaking water and open it, forming a tube. Close one end of the tube with a plastic clip, a piece of string, or simply tie it with a knot (Fig. 3)

• Fill the bag with 10 mL of H2O. Remove excess air, and close the other end of the bag with a plastic clip, a piece of string, or tie with a knot. Set aside on a paper towel.
• Repeat steps 4 and 5 for the 4 remaining dialysis tubes, filling them with 10 mL of a solution as follows:

• Bag #2 – 15% sucrose

• Bag #3 – 30% sucrose

• Bag #4 – H2O

• Bag #5 - 5 mL 30% glucose solution and 5 mL 15% starch solution

• Rinse off the outside of the bags with water and carefully blot dry.
• Weigh bags #1 - 4 to the nearest 0.5g. Record the weights in Table 1 below, in the column labeled “0 min.”
• Place each bag in the corresponding beaker (Bag #1 in Beaker #1, etc.). Make sure each bag is fully submerged in the solution.
• Set a timer for 5 minutes.
• At the end of 5 minutes, remove bags 1 - 4 from their beakers, blot excess fluid, and record the mass (in grams) in Table 1.
• Return the bags to the appropriate beaker, and wait another 5 minutes.
• Repeat steps 11 - 13 every 5 minutes and record the weights in Table 1.
• Calculate the total weight change (weight change = final weight – initial weight) for each bag. Record the values in Table 2. Calculate the rate (g/min) of osmosis for each bag by dividing the weight change by the time change. Since all 4 bags were recorded for a total of 20 minutes, the time change for all 4 bags is 20 minutes. Record the rate of osmosis for all 4 bags in Table 2.
• Make observations about bag #5 and beaker #5 in Table 3.
• Remove several mL of liquid from bag #5 and beaker #5 and add each to separate test tubes.
• Add several drops of Benedict's solution to each of the two test tubes and heat to 100 degrees Celsius in a boiling water bath or heat block for 2 - 5 minutes. Record the test results in Table 3.
• Did the weight of each bag (#1 - #4) change significantly over 20 minutes? Explain.
• In which bag(s) was there a net movement of water?
• Explain what is meant by “net movement”.
• Which carbohydrate molecules (glucose, sucrose, starch) were not able to move across the membrane? Explain.
• In terms of solvent (water) concentration, water moved from the area of _______________ concentration to the area of __________________ concentration across a selectively permeable membrane, which is defined as ________________________.
• What can you conclude about the movement of Iodine, glucose, and starch across the dialysis membrane based on your results in Table 3? Support your answers for each with the observation from bag #5 and beaker #5.
• We used the dialysis tubing to simulate a cell membrane. How is the dialysis tubing functionally the same as a cell membrane?
• We used the dialysis tubing to simulate a cell membrane. How is the dialysis tubing functionally different from a cell membrane?
• Prepare a line graph using the data from Table 2.

PART 2: OSMOSIS & TONICITY

Tonicity is the relative concentration of solute (particles), and therefore also a solvent (water), outside the cell compared with inside the cell.

• An isotonic solution has the same concentration of solute (and therefore of free water) as the cell. When cells are placed in an isotonic solution, there is no net movement of water.

• A hypertonic solution has a higher solute (therefore, lower free water) concentration than the cell. When cells are placed in a hypertonic solution, water moves out of the cell into the lower free water solution.

• A hypotonic solution has a lower solute (therefore, higher free water) concentration than the cell. When cells are placed in a hypotonic solution, water moves into the cell from the higher free water solution.

IMPORTANT NOTE: Notice that all of the above definitions have ‘solution’ as the noun. Sometimes the noun will refer to the cell instead of the solution. For example, a hypotonic cell will experience a net movement of water out of the cell. What this means is that if the ‘solution’ is hypotonic, the cell is hypertonic and vice versa.

Exercise 1: Observing Osmosis in Potato Strips

• Wax pencil or Sharpie
• Metric ruler
• 10% NaCl solution
• 0.9% NaCl solution
• Forceps and scalpel
• Obtain a potato and use a cork borer to prepare 3 cylinders of potato. Push the borer through the length of the potato. When the borer is filled, use the flat end of a wooden skewer to gently push out the potato cylinder into the petri dish. Use the scalpel to cut each potato cylinder into a length of 5 cm.
• With a wax pencil or Sharpie, label 3 test tubes (#1, #2, #3).
• Using the metric ruler, mark each tube at the 10 cm mark level from the bottom of the tube.
• Tube #1 - distilled water
• Tube #2 - 10% sodium chloride (NaCl)
• Tube #3 - 0.9% NaCl
• Place one potato cylinder into each test tube and allow them to soak for about 15 minutes in the solutions.
• You can now move on to Exercises 2 and 3 while your potatoes soak.
• After the elapsed time, observe each strip for limpness (water loss, flaccid) or stiffness (water gain,turgor).
• Which tube contained the limp (flaccid) potato strip? Explain.
• Which tube contained the stiff (turgid) potato strip? Explain.
• Which solution is isotonic to the inside of the potato cell?
• What happened to the potato strip in the isotonic solution?

Osmoregulation in Living Cells

Some organisms, known as osmoregulators , have special adaptations to keep tight control over their internal osmotic conditions while still others, known as osmoconformers , are able to live in a variety of osmotic conditions. Most living cells, however, are often at the mercy of their surrounding osmotic environment. Many freshwater plants live in an isotonic or hypotonic environment, so they have no adaptations to protect them from a hypertonic environment. Likewise, mammalian red blood cells live in the isotonic plasma inside your circulatory system so they have no protection from either a hypertonic nor a hypotonic environment.

A plant cell is surrounded by a rigid cell wall, so when the cell is placed in a hypotonic environment, the net flow of water is from the surrounding medium into the cell, and it simply expands to the cell wall and becomes turgid. When the same plant cell is placed in a hypertonic environment, water leaves the central vacuole and the cytoplasm shrinks. This causes the cell membrane to pull away from the cell wall. In this situation, the plant cell will undergo plasmolysis and die. Animal cells have no cell wall so when they are in a hypotonic environment they will expand and fill with water until they burst in a condition known as lysis. Figures 4 and 5 demonstrate these conditions.

Exercise 2: Observing Osmosis in Elodea Cells

• Blank slides and coverslips
• 10% salt solution
• Elodea leaf
• Place a drop of water onto a clean microscope slide.
• Using the forceps, gently tear off a small leaf from the Elodea plant.
• Prepare a wet mount by placing the Elodea leaf into the drop of water on your slide.
• Place a coverslip onto the slide.
• Use the scanning (4x) objective to bring the Elodea cells into focus. You may not be able to observe individual cells at this power.
• Switch to the low power (10x) objective. The Elodea cell walls should be visible. They will look like dark green grid lines. Use the fine focus adjustment to focus the specimen.
• Once you think you have located an Elodea cell, switch to the high power (40x) objective and refocus using the fine focus adjustment.
• Next, add several drops of 10% salt (NaCl) solution to the edge of the coverslip to allow the salt to diffuse under the coverslip. Observe what happens to the cells (this may require you to search around along the edges of the leaf). Look for cells that have been visibly altered.
• Record your observations in the following table. The cells in distilled water should look similar to the figure below.

• Which solution is hypertonic to an Elodea cell? Use your observations to support your answer.
• Would you expect pond water to be isotonic, hypotonic, or hypertonic to Elodea cells? Explain your answer.
• Explain what happens to a plant cell that undergoes plasmolysis.

Exercise 3: Observing Osmosis in Red Blood Cells (Erythrocytes)

• Sheep red blood cells
• Obtain 3 test tubes and label them (#1, #2, #3) with a wax pencil or Sharpie.
• Tube #1 - Distilled water
• Tube #2 - 10% NaCl
• Using a new transfer pipette, add 2 drops of sheep blood to each tube and swirl gently to mix the contents.
• Hold each test tube up to a sheet of paper with printed text. Attempt to read the print through each tube and record your results in the following table.
• Label 3 microscope slides (#1, #2, #3) with a wax pencil or Sharpie.
• Prepare wet mounts of each tube by placing a drop of the solution in each tube (#1 - 3) on the appropriate microscope slide (#1 -3). Add a coverslip to each slide.
• View slide #1 through the microscope using the scanning (4x) objective first. Focus the image using the coarse adjustment. Then view the blood cells under low power and then high power. Only use the fine focus adjustment to focus the specimen.
• Observe slide #2 and slide #3 in the same manner.
• Record the appearance of the red blood cells in each solution in the following table.
• Which solution allowed you to read print through the solution? Explain.
• Which solution is hypertonic to the RBCs? Use your observations to support your answer.
• Which solution is hypotonic to the RBCs? Use your observations to support your answer.
• Which solution is isotonic to the RBCs? Use your observations to support your answer.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.2: Exercises

• Last updated
• Save as PDF
• Page ID 40907

• Allen B. Downey
• Olin College via Green Tea Press

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

There are solutions to these exercises in the next section. You should at least attempt each one before you read the solutions.

Exercise \(\PageIndex{1}\)

Write a program that reads words.txt and prints only the words with more than 20 characters (not counting whitespace).

Exercise \(\PageIndex{2}\)

In 1939 Ernest Vincent Wright published a 50,000 word novel called Gadsby that does not contain the letter “e”. Since “e” is the most common letter in English, that’s not easy to do.

In fact, it is difficult to construct a solitary thought without using that most common symbol. It is slow going at first, but with caution and hours of training you can gradually gain facility.

All right, I’ll stop now.

Write a function called has_no_e that returns True if the given word doesn’t have the letter “e” in it.

Write a program that reads words.txt and prints only the words that have no “e”. Compute the percentage of words in the list that have no “e”.

Exercise \(\PageIndex{3}\)

Write a function named avoids that takes a word and a string of forbidden letters, and that returns True if the word doesn’t use any of the forbidden letters.

Write a program that prompts the user to enter a string of forbidden letters and then prints the number of words that don’t contain any of them. Can you find a combination of 5 forbidden letters that excludes the smallest number of words?

Exercise \(\PageIndex{4}\)

Write a function named uses_only that takes a word and a string of letters, and that returns True if the word contains only letters in the list. Can you make a sentence using only the letters acefhlo ? Other than “Hoe alfalfa”?

Exercise \(\PageIndex{5}\)

Write a function named uses_all that takes a word and a string of required letters, and that returns True if the word uses all the required letters at least once. How many words are there that use all the vowels aeiou ? How about aeiouy ?

Exercise \(\PageIndex{6}\)

Write a function called is_abecedarian that returns True if the letters in a word appear in alphabetical order (double letters are ok). How many abecedarian words are there?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.2E: Hyperbolas (Exercises)

• Last updated
• Save as PDF
• Page ID 22299

• David Lippman & Melonie Rasmussen
• The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

section 9.2 exercises

Section 9.2 Exercises

In problems 1–4, match each graph to equations A–D.

A. \(\dfrac{x^2}{4} - \dfrac{y^2}{9} = 1\)

B. \(\dfrac{x^2}{9} - \dfrac{y^2}{4} = 1\)

C. \(y^2 - \dfrac{x^2}{9} = 1\)

D. \(\dfrac{y^2}{9} - x^2 = 1\)

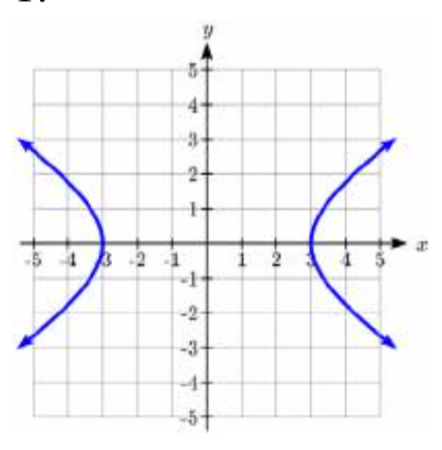
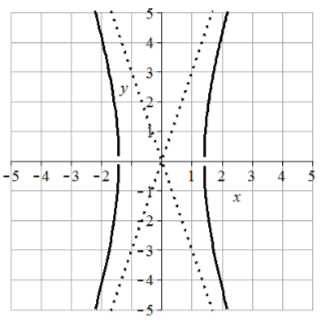
In problems 5–14, find the vertices, length of the transverse axis, and equations of the asymptotes. Sketch the graph. Check using a graphing utility.

5. \(\dfrac{x^2}{4} - \dfrac{y^2}{25} = 1\)

6. \(\dfrac{y^2}{16} - \dfrac{x^2}{9} = 1\)

7. \(y^2 - \dfrac{x^2}{4} = 1\)

8. \(x^2 - \dfrac{y^2}{25} = 1\)

9. \(x^2 - 9y^2 = 9\)

10. \(y^2 - 4x^2 = 4\)

11. \(9y^2 - 16x^2 = 144\)

12. \(16x^2 - 25y^2 = 400\)

13. \(9x^2 - y^2 = 18\)

14. \(4y^2 - x^2 = 12\)

In problems 15–16, write an equation for the graph.

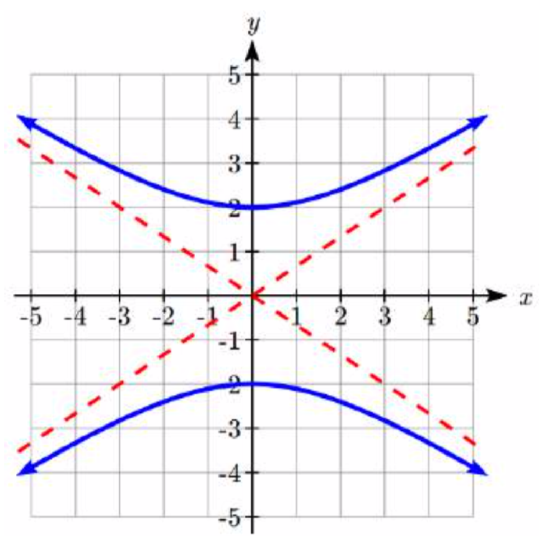
In problems 17–22, find the standard form of the equation for a hyperbola satisfying the given conditions.

17. Vertices at (0, 4) and (0, -4); asymptote \(y = \dfrac{1}{2}x\)

18. Vertices at (-6, 0) and (6, 0); asymptote \(y = 3x\)

19. Vertices at (-3, 0) and (3, 0); passes through (5, 8)

20. Vertices at (0, 4) and (0, -4); passes through (6, 5)

21. Asymptote \(y = x\); passes through (5, 3)

22. Asymptote \(y = x\); passes through (12, 13)

In problems 23–30, match each graph to equations A–H.

A. \(\dfrac{\left( x - 1 \right)^2}{9} - \dfrac{\left( y - 2 \right)^2}{4} = 1\)

B. \(\dfrac{\left( x + 1 \right)^2}{9} - \dfrac{\left( y + 2 \right)^2}{4} = 1\)

C. \(\dfrac{\left( x + 1 \right)^2}{9} - \dfrac{\left( y + 2 \right)^2}{16} = 1\)

D. \(\dfrac{\left( x - 1 \right)^2}{9} - \dfrac{\left( y - 2 \right)^2}{16} = 1\)

E. \(\dfrac{\left( y - 2 \right)^2}{4} - \dfrac{\left( x - 1 \right)^2}{9} = 1\)

F. \(\dfrac{\left( y + 2 \right)^2}{4} - \dfrac{\left( x + 1 \right)^2}{9} = 1\)

G. \(\dfrac{\left( y + 2 \right)^2}{4} - \dfrac{\left( x + 1 \right)^2}{16} = 1\)

H. \(\dfrac{\left( y - 2 \right)^2}{4} - \dfrac{\left( x - 1 \right)^2}{16} = 1\)

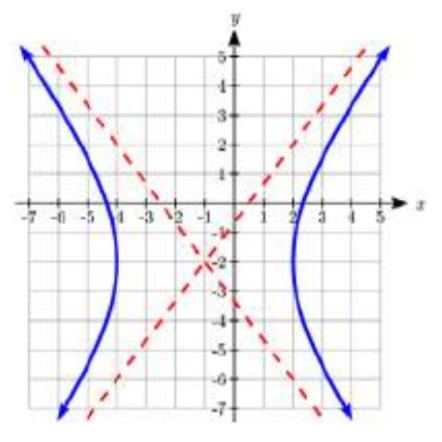
31. \(\dfrac{\left( x - 1 \right)^2}{25} - \dfrac{\left( y + 2 \right)^2}{4} = 1\)

32. \(\dfrac{\left( y - 3 \right)^2}{16} - \dfrac{\left( x + 5 \right)^2}{36} = 1\)

33. \(\dfrac{\left( y - 1 \right)^2}{9} - \left( x + 2 \right)^2 = 1\)

34. \(\dfrac{\left( x - 1 \right)^2}{25} - \left( y - 6 \right)^2 = 1\)

35. \(4x^2 - 8x - y^2 = 12\)

36. \(4y^2 + 16y - 9x^2 = 20\)

37. \(4y^2 - 16y - x^2 - 2x = 1\)

38. \(4x^2 - 16x - y^2 + 6y = 29\)

39. \(9x^2 + 36x - 4y^2 + 8y = 4\)

40. \(9y^2 + 36y - 16x^2 - 96x = - 36\)

In problems 41–42, write an equation for the graph.

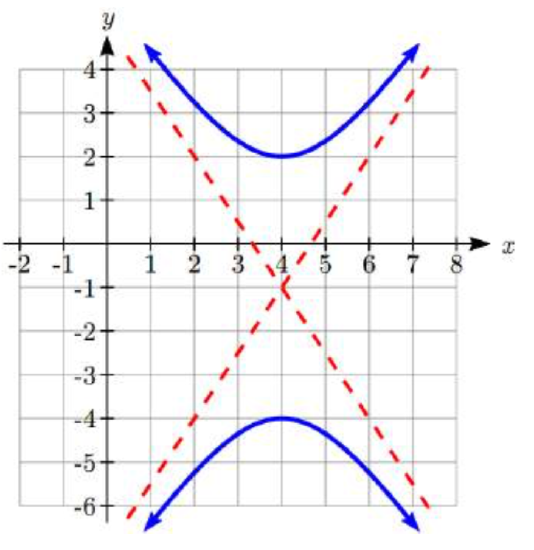
In problems 43–44, find the standard form of the equation for a hyperbola satisfying the given conditions.

43. Vertices (-1,-2) and (-1,6); asymptote \(y - 2 = 2\left( {x + 1} \right)\)

44. Vertices (-3,-3) and (5,-3); asymptote \(\;y + 3 = \dfrac{1}{2}\left( {x - 1} \right)\)

In problems 45–48, find the center, vertices, length of the transverse axis, and equations of the asymptotes. Sketch the graph. Check using a graphing utility.

45. \(y = \pm 4\sqrt {9x^2 - 1} \)

46. \(y = \pm \dfrac{1}{4}\sqrt {9x^2 + 1} \)

47. \(y = 1 \pm \dfrac{1}{2}\sqrt {9x^2 + 18x + 10} \)

48. \( = - 1 \pm 2\sqrt {9x^2 - 18x + 8} \)

In problems 49–54, find the foci.

49. \(\dfrac{y^2}{6} - \dfrac{x^2}{19} = 1\)

50. \(x^2 - \dfrac{y^2}{35} = 1\)

51. \(\dfrac{\left( x - 1 \right)^2}{15} - \left( y - 6 \right)^2 = 1\)

52. \(\dfrac{\left( y - 3 \right)^2}{47} - \dfrac{\left( x + 5 \right)^2}{2} = 1\)

53. \(y = 1 \pm \dfrac{4}{3}\sqrt {x^2 + 8x + 25} \)

54. \(y = - 3 \pm \dfrac{12}{5}\sqrt {x^2 - 4x - 21} \)

In problems 55–66, find the standard form of the equation for a hyperbola satisfying the given conditions.

55. Foci (5, 0) and (-5, 0), vertices (4, 0) and (4, 0)

56. Foci (0, 26) and (0, -26), vertices (0, 10) and (0, -10)

57. Focus (0, 13), vertex (0, 12), center (0, 0)

58. Focus (15, 0), vertex (12, 0), center (0, 0)

59. Focus (17, 0) and (-17, 0), asymptotes \(y = \dfrac{8}{15}x\) and \(y = - \dfrac{8}{15}x\)

60. Focus (0, 25) and (0, 25), asymptotes \(y = \dfrac{24}{7}x\) and \(y = - \dfrac{24}{7}x\)

61. Focus (10, 0) and (-10, 0), transverse axis length 16

62. Focus (0, 34) and (0, -34), transverse axis length 32

63. Foci (1, 7) and (1, -3), vertices (1, 6) and (1,-2)

64. Foci (4, -2) and (-6, -2), vertices (2, -2) and (-4, -2)

65. Focus (12, 3), vertex (4, 3), center (-1, 3)

66. Focus (-3, 15), vertex (-3, 13), center (-3, -2)

67. LORAN Stations A and B are 100 kilometers apart and send a simultaneous radio signal to a ship. The signal from A arrives 0.0002 seconds before the signal from B. If the signal travels 300,000 kilometers per second, find an equation of the hyperbola on which the ship is positioned if the foci are located at A and B.

68. Thunder and Lightning Anita and Samir are standing 3050 feet apart when they see a bolt of light strike the ground. Anita hears the thunder 0.5 seconds before Samir does. Sound travels at 1100 feet per second. Find an equation of the hyperbola on which the lighting strike is positioned if Anita and Samir are located at the foci.

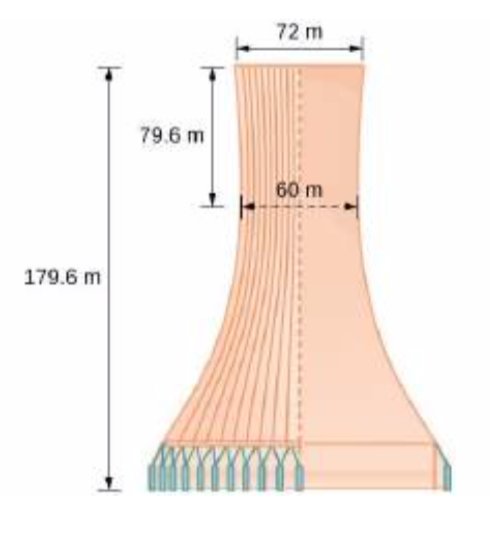
69. Cooling Tower The cooling tower for a power plant has sides in the shape of a hyperbola. The tower stands 179.6 meters tall. The diameter at the top is 72 meters. At their closest, the sides of the tower are 60 meters apart. Find an equation that models the sides of the cooling tower.

70. Calibration A seismologist positions two recording devices 340 feet apart at points A and B. To check the calibration, an explosive is detonated between the devices 90 feet from point A. The time the explosions register on the devices is noted and the difference calculated. A second explosion will be detonated east of point A. How far east should the second explosion be positioned so that the measured time difference is the same as for the first explosion?

71. Target Practice A gun at point A and a target at point B are 200 feet apart. A person at point C hears the gun fire and hit the target at exactly the same time. Find an equation of the hyperbola on which the person is standing if the foci are located at A and B. A fired bullet has a velocity of 2000 feet per second. The speed of sound is 1100 feet per second.

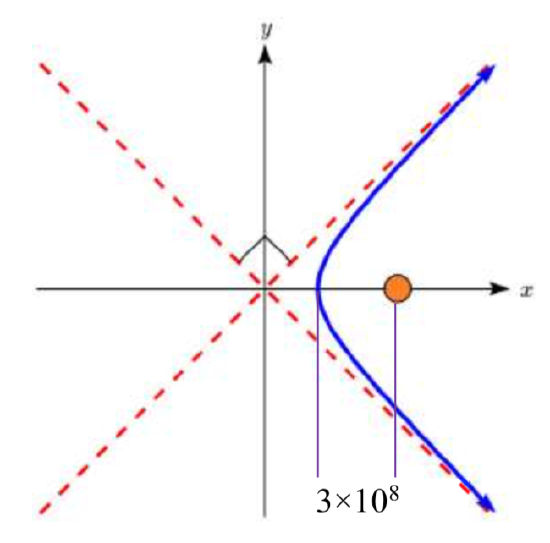
72. Comet Trajectories A comet passes through the solar system following a hyperbolic trajectory with the sun as a focus. The closest it gets to the sun is 3×108 miles. The figure shows the trajectory of the comet, whose path of entry is at a right angle to its path of departure. Find an equation for the comet’s trajectory. Round to two decimal places

73. The conjugate of the hyperbola \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = - 1\). Show that \(5y^2 - x^2 + 25 = 0\) is the conjugate of \(x^2 - 5y^2 + 25 = 0\).

74. The eccentricity \(e\) of a hyperbola is the ratio \(\dfrac{c}{a}\), where \(c\) is the distance of a focus from the center and \(a\) is the distance of a vertex from the center. Find the eccentricity of \(\dfrac{x^2}{9} - \dfrac{y^2}{16} = 1\).

75. An equilateral hyperbola is one for which a = b. Find the eccentricity of an equilateral hyperbola.

76. The latus rectum of a hyperbola is a line segment with endpoints on the hyperbola that passes through a focus and is perpendicular to the transverse axis. Show that \(\dfrac{2b^2}{a}\)is the length of the latus rectum of \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\).

77. Confocal hyperbolas have the same foci. Show that, for \(0 < k < 6\), all hyperbolas of the form \(\dfrac{x^2}{k} - \dfrac{y^2}{6 - k} = 1\) are confocal.

5. Vertices \((\pm 2, 0)\), transverse length = 4, asymptotes \(y = \pm 5/2x\),

7. Vertices \((0, \pm 1)\), transverse length = 2, asymptotes \(y = \pm 1/2x\),

9. Vertices \((\pm 3,0)\) transverse length = 6, asymptotes \(y =\pm 1/3x\),

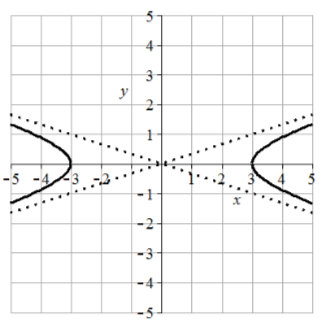
11. Vertices \((0, \pm 4)\), transverse length = 8, asymptotes \(y = \pm 4/3x\)

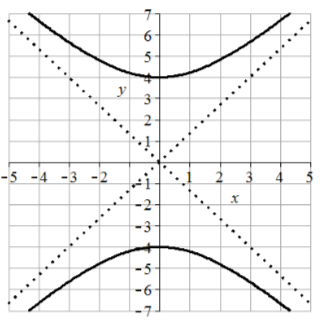
13. Vertices \((\pm \sqrt{2}, 0)\), transverse length = \(2\sqrt{2}\), asymptotes \(y = \pm 3x\),

15. \(\dfrac{y^2}{4} - \dfrac{x^2}{9} = 1\)

17. \(\dfrac{y^2}{16} - \dfrac{x^2}{64} = 1\)

19. \(\dfrac{y^2}{9} - \dfrac{x^2}{36} = 1\)

21. \(\dfrac{y^2}{16} - \dfrac{x^2}{16} = 1\)

31. Center (1, -2), vertices (6, -2) and (-4, -2), transverse length = 10, asymptotes \(y = \pm 2/5(x - 1) - 2\)

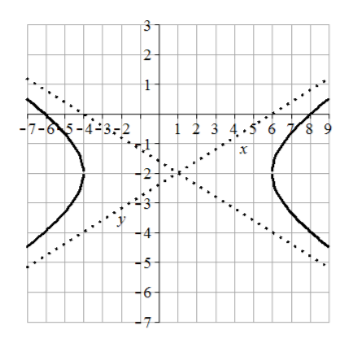
33. Center (-2, 1), vertices (-2, 4) and (-2, -2), transverse length = 6, asymptotes \(y = \pm 3(x + 2) + 1\)

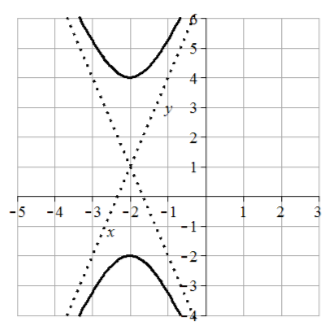
35. Center (1, 0), vertices (3, 0) and (-1, 0), transverse length = 4, asymptotes \(y =\pm 2(x-1)\)

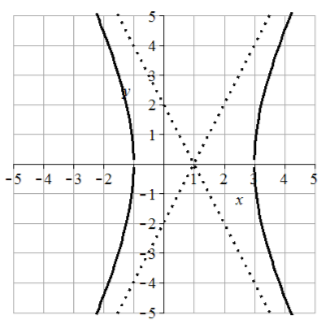
37. Center (-1, 2), vertices (-1, 4) and (-1, 0), transverse length = 4, asymptotes \(y = \pm 1/2(x + 1) + 2\)

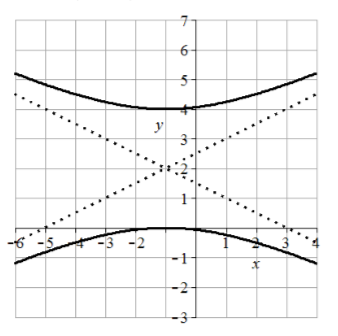
39. Center (-2, 1), vertices (0, 1) and (-4, 1), transverse length = 4, asymptotes \(y = \pm 3/2(x + 2) + 1\)

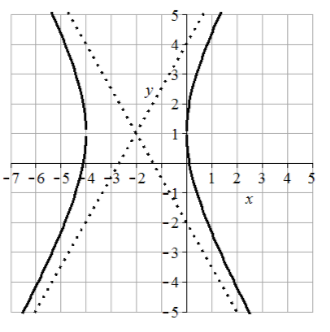
41. \(\dfrac{(y + 1)^2}{9} - \dfrac{(x - 4)^2}{4} = 1\)

43. \(\dfrac{(y - 2)^2}{16} - \dfrac{(x + 1)^2}{4} = 1\)

45. Center (0,0), vertices \((\pm 1/3,0)\), transverse length = 2/3, asymptotes \(y = \pm 12 x\)

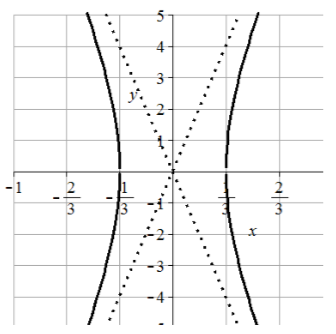
46. Center (-1, 1), vertices (-1, 3/2) and (-1, 1/2), transverse length = 1, asymptotes \(y = \pm 3/2 (x + 1) + 1\)

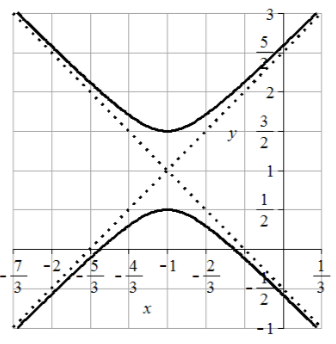
49. Foci \((0, \pm 5)\)

51. Foci (5, 6) and (-3, 6)

53. Foci (-4, 6) and (-4, -4)

55. \(\dfrac{x^2}{16} - \dfrac{y^2}{9} = 1\)

57. \(\dfrac{y^2}{144} - \dfrac{x^2}{25} = 1\)

59. \(\dfrac{x^2}{225} - \dfrac{y^2}{64} = 1\)

61. \(\dfrac{x^2}{64} - \dfrac{y^2}{36} = 1\)

63. \(\dfrac{(y - 2)^2}{16} - \dfrac{(x - 1)^2}{9} = 1\)

65. \(\dfrac{(x + 1)^2}{25} - \dfrac{(y - 3)^2}{144} = 1\)

67. \(\dfrac{x^2}{900} - \dfrac{y^2}{1600} = 1\)

69. \(\dfrac{x^2}{900} - \dfrac{y^2}{14400.3636} = 1\)

71. \(\dfrac{x^2}{3025} - \dfrac{y^2}{6975} = 1\)

73. \(5y^2 - x^2 + 25 = 0\) can be put in the form \(\dfrac{y^2}{5} - \dfrac{x^2}{25} = -1\). \(x^2 - 5y^2 + 25 = 0\) can be put in the form \(\dfrac{y^2}{5} - \dfrac{x^2}{25} = 1\) showing they are conjugate.

75. \(\sqrt{2}\)

77. No matter the value of \(k\), the foci are at \((\pm \sqrt{6}, 0)\)