problem solving maps math

Problem Solving Maps International Summit

Listen to 39 different presentations done by teachers using the Problem Solving Maps approach to teach mathematics

Free for teachers, parents, and educational consultants!

What is the problem solving maps method.

Problem Solving Maps (PSM) are graphical representations of critical thinking processes needed to solve math problems successfully. The maps are 1) Example-Conclusion Map, 2) the Multi-Rule Map and 3) the Math-Breaker Map.  The purpose of these maps is twofold: 1) to provide support in learning a specific topic and 2) to map out problem-solving strategies that are generic enough to be used on a large variety of math content.

• Instructors, tutors or parents can use PSM to teach a large variety of topics
• PSM do not take a long time to learn
• Students learn thinking and problems solving skills that are transferable from one math topic to the next
• PSM are very effective to diagnose where students are having trouble
• With PSM, students can have better notes to study
• With PSM, student can improve self confidence and performance

Listen to 39 presentations of teachers using Problem Solving Maps

  Extending and Completing a Pattern by Elisa T. Maramag

Visualizing, Representing, And Converting Liter And Milliliter From Larger To Smaller Unit And Vice-Versa by Jhoanna Marie T. Teru

Ordering Numbers with the Multi-Rule Map by Jamaica F. Lacson

Square Of A Binomial by Jean Aiko C. Domingo

Finding The Surface Area Of A Cylinder  by Darwin B. Lico, PhD Order Of Operations PEMDAS Rule Using The Multi Rule Map  by Myrna B. Mallanao Teaching Mathematics Using PSM Approach: Finding The Area Of A Composite Figure  by   Mary Jean A. Nalunat   The Effectivity Of Problem Solving Maps To Improve Academic Performance Of Grade 6 Learners In Mathematics  by   Rowena R. Yumul

Product Of Cube Of Binomial Multiplication Of Integers (Using Example Conclusion Map) by Arjon Paul D. Dela Paz Multiplication Of Integers (Using Example Conclusion Map) by Jonah M. Asuncion   Factoring Perfect Square Trinomials Teaching Complementary And Supplementary Angles Using The 3 Problem Solving Maps (PSM) by Novy H. Facun Teaching Complementary and Supplementary Angles Using the 3 Problem Solving Maps (PSM) by  Katherine A. Matarlo   Solving Problems Involving Sides And Angles Of A Polygon by Reina Ross Yumul Solomo   Measures Of Variability Of Ungroup Data by Fatima L. Tambago   Teaching Laws Of Exponents Using Example Conclusion Map by Anna Lisa T. Dela Rosa   Improving Mathematics Aptitude Of Grade 7 Students Of Sauyo High School Through Problem-Solving Maps by Grace D. Gutano

Solving Systems Of Linear Equations By Elimination Method Using Problem Solving Maps by Evelyn C. Torrefranca Fundamental Counting Principle by Aimee Rose A. Galicia Integrating Problem Solving Maps In A Video Lesson On Grade 8 Mathematics, Triangle Congruence Postulates by Joshua P. Salazar Proving The Congruence Of Triangles Using SAS Postulate by Mary Ann L. Abundo Proving Triangle Congruence Using Multi Rule Maps by Aileen D. Canonicato

Angle Of Elevation And Angle Of Depression by Lahlyn G. Unica Problem Solving Maps (PSM) A Problem Solving Strategy To Lessen The Mathematics Anxiety Level Of Grade 9 Students by John Richard L. Quiambao Transforming Standard Form Of Quadratic Function Into Vertex Form by Charnel D. Santos Enhancing Student's Performance In Variation With The Use Of Problem Solving Maps (PSM) On Selected Grade 9 Students by Elmer L. Cinco PSM Completing The Square by Sherrelle Francisco Mendoza Maxie And Minnie Application Of Maximum And Minimum Of Quadratic Functions by Sheryl F. Dullano Solving Problems Involving Trigonometric Ratios Using MRM And MBM by Queenie Pearl E. Domasig Law Of Sines by Ken-Ken A. Bormate Addition And Subtraction Of Radicals by Jonofre M. Borja

Synthetic Division by Karen T. Basada Math Breaker As A Tool In Solving Problems Involving Permutations by Randy Dela Vega Utilizing Math-Breaker Maps To Improve Performance In Mathematics And Self-Efficacy Of Students In Online Distance Learning by Joshua P. Salazar Investigating The Use Of Example-Conclusion Maps For Mathematics Enhancement Program by Benigno F. Baluyut The Use Of Math - Breaker Maps In Improving The Performance Of Grade 10 Mathematics Learners In Solving Problems Involving Probability by Zenaida W. Halili Geometric Mean by Charisma T. Banag Solving Problems Involving Probability Of Union Of Two Events And Joint Events by Jona M. Zapata Circle Theorems (Angles In A Circle) by Rhon C. Suliva

  Rational Inequalities by Rachelle Anne Marie S. Adriano

Praises for Problem Solving Maps

 "We are glad that we turned to the Problem Solving Maps (PSM) system as one of one of our strategies to improve students' quantitative thinking skills in the Philippines.  We have been able to positively impact thousands of students in our schools." 

Dr. Jeni Corpuz Superintendent, Department of Education - Philippines

 "I attribute much of the success of my Math students to the use of the Problem Solving Maps (PSM). This mathematical tool helped my students understand different concepts in Math, which are crucial to their success not only in school but in preparation for the Math portion of the ACT and SAT Tests as well". 

Felesia M. Harrel Johnson Founder, College Bound Academic Center - USA

 "We have observed that with Problem Solving Maps (PSM) students get a deeper and quicker understanding of math concepts for topics that are usually challenging.  PSM methods are without a doubt a cutting edge process to teach quantitative and logical reasoning skills." 

Maciej Winiarek Critical Thinking Specialist - Poland

 "The Problem Solving Maps are helping our students make concrete their thinking about abstract concepts. This process also allows teachers to clearly see where students are struggling so they can address these concerns easily and directly."

Vikki Wandmacher Principal, White Pine Middle School - USA

 "The [PSM] math tools enable us to organize our thought by a pattern. Learning a thinking pattern makes life much easier, not only in studying math but also in various aspects of everyday life." 

Motoi Tobita, Ph.D., Master Lead Facilitator, TOCFE - Japan

 "With the Problem Solving Map (PSM) system, it is very easy to find out the gaps students have in their knowledge.  I am glad I learned PSM so I can help my students being successful." 

Karyna Lopez Award Winning Math Teacher-Mexico

How the summit works

Fill out the registration form, you will be added automatically to the summit site and receive a welcome email, follow the email instructions to set your password, you will have access to the presentations, leave a comment for your fellow teachers who made the effort to create their presentations, you will have access to watch the presentations at any time, macatangay, ma. rossell b. macatangay.

Review of PSM

I would like to commend the preparation of different insightful presentation that will definitely be a big help to teachers. Congratulations!

Onuorich De Lara

Congratulations to all the presenters, I learned a lot from the presentation. Here I realized how lucky are the pupils if all the teachers learned this PSM.

Niña Resan Niña Resan

I would like to congratulate all the presenters for a job well done! Watching all the presentations made me want to use PSM in my lessons for better understanding of my students. Thank you for this free summit. Iearned a lot ?

Rosette S. Dela Cruz

Watching all the presentations inspired and motivates me to use PSM in my classes. After watching, the presentation, it made me realize that it is doable for me.

Congratulations to all. The first summit show how teachers apply the PSM in different lessons in Math. To make math enjoyable and easy to understand. (Sobrang gagaling nyo pong lahat ma'am and sir)

Ludivina A. Porcare

PSM review.

Congratulations to all presenters. The strategies presented will surely be a big help to teachers in teaching the subject. Kudos to all presenter and organizer of this summit.

Rate this course

Choose your rating

Sign up for our newsletter!

Want to stay up-to-date on industry trends?

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

"Improving Students' Problem Solving Skills in Mathematics using PROBLEM SOLVING MAPS in Grade 4 pupils of Plaridel Elementary School"

Problem Solving Skills is one of the most important factors for students to solve problems in Mathematics and think critically. The skills that we need in order to be able to think critically are varied and include observation, reflection, evaluation, inference, explanation, problem solving and decision making. This Action Research describes the implementation of PROBLEM SOLVING MAPS to enhance students thinking skills of Grade 4 Pupils in Plaridel Elementary School. The Classroom Action Research was conducted last quarter of the grading period. As the result of application using Problem Solving Map, it is found out that 39 out of 44 pupils or 88.64% of the pupils have showed improvement in Problem Solving Skills and only 5 pupils or 11.36% of the pupils needs more appropriate practice and remediation program. Several factors may be contributed to Problem Solving Skills difficulties. One factor is that most pupils are struggling in basic mathematical operations and reluctant to solve mathematics problems. It is for this reason that the researcher conducted an action research to find some teaching strategies that will improve the problem solving skills of Grade 4 pupils of PlaridelElementary School using PROBLEM SOLVING MAPS. Introduction:

Related Papers

IOSR Journals publish within 3 days

Critical thinking is one of the important indicators for students to be competing in the world of work and personal life, students must have the ability to solve problems and must be able to think critically. One effort to improve critical thinking skills, especially in math lessons is to implement problem-solving learning. This article describes the implementation of problem-solving learning in improving students' critical thinking skills of grade VIII SMP Negeri 5 Bulukumba obtained through classroom action research that is conducted for 2 cycles with the result that with the application of learning problem solving can improve the ability of critical thinking as seen from the indicators the success of 35 people or 87.5% of students have completed learning mathematics and as many as 5 people or 12.5% of students have not finished learning math. In addition, the activity of students in the learning process also achieved the success indicator that overall there is 70.5% in the first cycle increased to 88.5% in cycle II and the implementation of learning (the ability of teachers in managing class and student activities) increased in the same category the good category.

Rahmah Johar

This study investigated pre-service teachers’ perception of the effectiveness of teachers’ effort on developing democratic classroom in video excerpts. Pre-service teachers watched video excerpts of teacher efforts on developing democratic classroom. There are 30 participants in the second year of the teacher education program in Aceh, Indonesia, provided data for the study. They enrolled in a Teaching and Learning Mathematics Strategy II for primary school. They fill observation form. The data indicated that many pre-service teachers struggled to identify evidence of democratic classroom. According to the evidence proposed, it was most likely that the pre-service teachers considered democratic means teacher should listen to their students. Most of the pre-service teachers also thought that rule and its penalty should be proposed by teacher. However, as they observed more videos, they became more aware of democratic classroom, thus they can provide more evidence and more ideas about how to improve a better democratic environment in classroom.

International Symposium on Mathematics Teaching Published Proceedings

Megan Burton

This study examines the evaluation of student thinking by teacher candidates when they are observing and when they are engaged in the practice of teaching during a mediated field experience. Teacher candidates co-led elementary science, technology, engineering, and mathematics summer experiences for three weeks. Data from three teacher candidates in one classroom of eighteen children ages seven to eight were examined. Teacher candidates observed students when peers were teaching and also examined work and took anecdotal notes during their own teaching experiences. These data were analyzed using Interpretative Phenomenological Analysis. Findings provide insight into teacher candidates’ perceptions of elementary students’ mathematical thinking when in various field experience roles. This insight can help teacher educators plan experiences that deepen teacher candidate understandings of student thinking.

PROJECT-BASED EDUCATION AND OTHER ACTIVATING STRATEGIES IN SCIENCE EDUCATION XVI

Martin Rusek

This contribution aims at the actual meaning of results gained from student testing via problem tasks. According to Koreneková (2018), positive responses do not necessarily mean that students managed to solve the problem tasks and reached the expected outcomes defined in the national curriculum. Concurrent think-aloud method was used to identify strategies students (N = 16) used to solve problem tasks. The results were worse than in the pilot testing of the same tasks. Many false-positive results were identified which puts the original test results into question.

Proceedings of the Seventh Conference on Research in Mathematics Education in Ireland (MEI 7)

Aisling Twohill

It is with great pleasure that we present the following proceedings from the Seventh Conference on Research in Mathematics Education in Ireland (MEI 7), which took place in Dublin City University in October, 2019. Our conference theme Mathematical Literacy, throughout and beyond education aims to foreground learners’ engagement with mathematics at all stages of the education system, and their development of mathematical proficiency within and beyond formal classroom settings. Mathematical literacy encompasses a learner’s proficiency to engage fluently with mathematical concepts, and to apply mathematical thinking in non-routine and novel situations. Mathematically literate children and adults recognise the mathematics in a situation, and understand how to mathematise a scenario in order to problem solve. Equally, mathematical literacy includes the capacity to interpret and analyse scenarios presented through mathematics. Mathematically literate individuals are thus less vulnerable to being convinced by inaccurate interpretations of data and mathematics. A key aspect of mathematical literacy is fluency in expressing one’s mathematical thinking in a clear and convincing manner. The notion of what it means to be mathematically literate is to a large extent dependent on the context in which mathematics is used. Some consider performance in examinations to be a determinant of the level of mathematical literacy. However, successfully completing daily activities and routines such as travelling and cooking all rely on fundamental mathematical literacy, for example, knowledge of distance, time, weight and temperature. For educators, mathematical literacy encompasses far more than an ability to do mathematics oneself, but also to be able to ascertain where the learner is at in their mathematical understanding and to scaffold and extend that learning. The education system in Ireland plays a key role in developing the mathematical literacy of all learners, to support full engagement with 21st century society. Central to such active citizenship is the propensity to apply mathematical concepts beyond the walls of the various classrooms where mathematics is taught; at primary, secondary and third levels. In these proceedings of MEI 7, we present papers that reflect a broad variety of mathematical research that is taking place in Ireland and further afield. Collectively, the authors seek to solidify and progress the research field of mathematics education, throughout and beyond Ireland.

September 2018

JEGYS Journal

The purpose of this analytical review was to investigate the uses of the TASC model to teach gifted students and develop their creativity. The researcher decided to select studies of the TASC model, which were not used by Maker, Alhusaini, Zimmerman, Pease, Schiever, and Whitford (2014) in the Saudi project. The studies included 30 out of 367 studies that were chosen for the Saudi project. Out of the 30 studies, the researcher selected 15, which he identified as school-based projects in which the TASC model was specifically used or described in teaching. The researcher also added six books that were written by Belle Wallace and colleagues. All of the reviewed publications suggested that the TASC model has been an effective, useful, and practical method with all students from different grade levels and of different abilities (especially with those who were gifted), as well as in all different content areas, to teach students and develop their creativity. The researcher identified limitations across the reviewed studies and publications, such as omissions of data collection procedures, data analysis processes, and lack of information about the participants as well as the interventions. Also, most of the studies provided qualitative results with no further discussion or explanation. More high quality research is needed to improve the scholarly conversation around this model.

Journal of Indian Education

seema shukla ojha

History is a written record of human experiences across time and space. The learners of history need to relate various kind of available sources to understand historical events and concepts. It is however observed that the classroom teaching in history is blended with a collection of facts, rote memorisation leading to boredom, leaving very little space for critical thinking among students. It is pertinent for teachers to evolve effective ways of learning history to generate and retain interest in the subject. How we can make the teaching-learning of history effective in schools, is a question frequently asked in different forums. This paper is the outcome of an educational intervention, with an objective to explore the effectiveness of integrating student-centred measures in a social science classroom at the elementary stage as a medium to enhance critical thinking skills and student engagement.

Mohammed Al-Amri , Abdullah Ambusaidi

The idea of integrated curricula is one of the ideas which have been suggested for developing curricula and improving teaching methods and techniques, especially the ones associated with young children. The integration between science and art has a long history since both subjects are highly interrelated to each other. Science benefits from art in many ways such as explaining scientific phenomena, drawing and building sciences' models, whereas art benefits from science by using scientific phenomena as a source for developing: (1) drawing and painting and (2) children's imagination. The aim of the current study is to investigate the impact of using the integration approach between science and art to develop science process skills among 5th grade female students. The sample consisted of 58 female students which were divided into two groups; the experimental group (N=29) which was taught the science content by the integration approach and the control group (N=29) which was taug...

Muhammad Yaumi

This study was designed to promote teachers’ understanding of the learner-centered approach through training the multiple intelligences-based instructions, improve teachers’ performance in designing learner-oriented instruction, and improve teachers’ performance in implementing instruction. This study used proactive action research involving 126 teachers (informants) as trainees and instructional design members, came from 10 elementary Madrasah in Indonesia, 36 of them were mentored, and 192 students participated in a focus group discussion. There were 10 principals and two supervisors to be research collaborators. Teachers’ understanding and performance improvement through training multiple intelligence-based instructions, designing student-centered approach, and mentoring the implementation of student-centered learning indicated significant contribution. The teachers’ understanding of multiple intelligence-based instruction was the majority in the good category. The activity of designing the student-centered approach gave a good contribution to the capability of designing every single one of the multiple intelligences-based strategies. The mentoring system improved teachers’ performance greater than those of training and instructional design. Implementation of training, instructional design, and the mentoring system implies improving learning processes and outcomes. Strengthening the recruitment system of teachers and performance improvement, capacity building of educators to design models, approaches, strategies, methods, and learning activities, as well as establishing togetherness on all lines; government, principals, supervisors, community, and teachers as the primary element.

Dawood Al-abri

RELATED PAPERS

Mustafa SOZBILIR

Asmuni Asmuni , Asmuni Asmuni

International Group for the Psychology of M athematics …

Ann Gervasoni

MARILYN CASTRO

PATT36, Research and Practice in Technology Education: Perspectives on Human Capacity and Development

Belinda von Mengersen

Fariza Khalid

Laurie D Edwards

Marjannah Mangotara

Kaca Cihakova

TEACHERS AND TEACHING …

Claudia Melear

University of St. Lasalle

Melalyn Parales

Julan Daguil

Proceedings of the 29th Conference of the …

FERNANDO HITT

International Group for the Psychology of M …

Núria Planas

Juliet Ampoful

Rashida Kapadia

Jerry Becker

Asmuni Asmuni

Monte Claro Elementary

Pedagogical Research

Ifigenia Iliopoulou

diani nurhajati

Dharel Acut

Kafoussi, S

Journal of Analysis and Computation (JAC)

Rajadurai Rajkumar

Isabel Vale

Roman Dorczak

Ali Delice , Eyup Sevimli

Ana Campina

Isabel Cabrita

International Group for the Psychology of …

International Group for the …

Libreriauniversitaria.it Edizioni

Florian Meyer

Maryna Rafalska

Jovanni De Guia

Jovan De Guia

Edlight Mutungwe

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Mathematics Assessment Project

Professional development modules, 3: problem solving lessons.

JavaScript and Flash Player are needed to access the video and software - but you can download the print materials from here.

Print materials:

Do i stand back and watch, or intervene and tell them what to do.

The Formative Assessment Lessons are of two types; those that focus on the development of conceptual understanding and those that focus on problem solving. Concept Development lessons are intended to assess and develop students’ understanding of fundamental concepts through activities that engage them in classifying and defining, representing concepts in multiple ways, testing and challenging common misconceptions and exploring structure. Problem Solving FALs are intended to assess and develop students’ capacity to select and deploy their mathematical knowledge in non-routine contexts and typically involve students in comparing and critiquing alternative approaches to solving a problem.

In this PD module, we focus on Problem Solving lessons. In most Mathematics classrooms, students are provided with structured tasks and are told precisely which techniques to use: students learn by following instructions. Even tasks described as ‘problem solving’ often amount to mathematical exercises rephrased in ‘plain English’, with a well-defined ‘correct’ solution method. Problems and situations that arise in the world , however, are rarely exercises in the use of a particular skill or concept. Such problems require students to make simplifications, model situations, choose appropriate knowledge and processes from their ‘toolkit’, and test whether their solution is ‘good enough’ for the purpose in hand. If students are to learn to use their skills autonomously in their future lives, they will need opportunities to work on less structured problems in their classrooms.

About the MAP PD Modules

These modules have been developed by the Shell Center team at the Center for Research in Mathematics Education , University of Nottingham. They draw on successful materials developed by the team for Bowland Maths and Improving Learning in Mathematics .

Getting started

Download the print materials (links on the left) and read the main Module Guide .

Use the tabs at the top of the screen to browse the video which accompanies this module.

© 2012 The University of Nottingham. Distributed under the Creative Commons Attribution Noncommercial Share-Alike license .

Includes material adapted from Bowland Maths ( www.bowlandmaths.org.uk ) © 2008-2010 Bowland Charitable Trust.

Mathematics Problem Solving

Mathematics has a language of its own based on the number system, but it is also based on students begin able to see patterns in number, and in data, and then solve problems that are based in real life contexts. The research in this section is anchored by the research by a middle school teacher (and Christa McAuliff scholar) who systematically used Thinking Maps with her underachieving students. In addition, Kathy Ernst, a national leader in mathematics instruction describes in detail and shows how she uses Thinking Maps to coach and mentor math teachers. We strongly suggest you look into her book co-written with Sarah Ryan: Success from the Start: Your First Years Teaching Elementary Mathematics” published by the National Council of Teachers of Mathematics.

Click on the PDF icon to download

Student Successes With Thinking Maps® David Hyerle and Larry Alper coeditors Corwin Press, Second Edition, January 2011, Thousand Oaks, California

Chapter 8: Meeting the Challenge of High Stakes Testing in Middle School Mathematics Janie B. MacIntyre, M.Ed.

Thinking Maps allow you to see where you have made your mistake, and how to show your math in words that make sense’ - Student

The statistics indicate considerable growth in mathematical achievement, so how and why does applying thinking maps in math instruction improve math ability as measured on these tests?

Key sections from the chapter The Challenge of High Stakes Testing in Middle School Mathematics with excerpts above include:

Facing Myself and My Students

Beyond Intuition

Results: Gains in Developmental Growth

Thinking Maps: A Bridge to Success

Beyond Test Scores

Janie B. MacIntyre, M.Ed. is a middle school teacher, researcher, and educational consultant who was named as a USA Today Teacher Team member and a Christa McAuliffe Scholar.

An Evaluation of Students’ Perception of Thinking Maps® in the Middle School Mathematics Classroom By Heather A. Mors, Kennesaw State University, Atlanta, United States. 2015

The findings of this research indicate that students are using Thinking Maps® for knowledge acquisition, namely in the form of note taking.  In addition, Thinking Maps® provide a bridge between prior knowledge and targeted knowledge by breaking problems down into parts that the students can understand.  Finally, students report that Thinking Maps® helped them answer complex math problems by breaking the problems into smaller parts and showing the steps to solve problems. The findings of this research should be used to guide teacher practices.  Regardless of their feelings, most of the students perceived the benefits of using Thinking Maps®.  Students recognized that Thinking Maps® helped them solve math problems, break problems down and make problems easier to understand.  The data from the survey is consistent with the interview data with 54.4% of students agreeing or strongly agreeing that Thinking Maps® is beneficial for solving math problems and 64.9% of the students agreeing or strongly agreeing that Thinking Maps® are beneficial for answering critical thinking questions.  Additionally, students were very interested in the electronic platform of Thinking Maps that allows the students to focus less on the map construction. 

The Relationship Between Thinking Maps® and Florida Comprehensive Assesment Test® Reading and Mathematics Scores in Two Urban Middle Schools By Ana Delgado Diaz, University of Central Florida, Orlando, United States. 2010

Statistical analysis did not result in significant differences in the use of Thinking Maps® as measured by FCAT but there were percentage differences that may indicate educational significance for Hispanic, economically disadvantaged and English language learners in FCAT Reading and for white, black and students with disabilities in FCAT Mathematics. Results of this study should not discourage the implementation of Thinking Maps® instruction as visual tools for learning. FCAT may not be an appropriate instrument to measure if an instructional visual tool such as Thinking Maps® makes a difference in student achievement. A better measurement tool would be for teachers to develop rubrics that can be used to assess student generated Thinking Maps® or use rubrics provided in the Thinking Maps ®: A Language for Learning (Hyerle & Yeager, 2007) training manual. 

Chapter 17 : Mentoring Mathematics Teaching and Learning Kathy Ernst, M.S.

“So many people have come into my classroom with vague advice and comments that have just made things worse. This is the first time anyone’s given me concrete suggestions about what I can do. This has been really helpful—thank you.” Teacher (after Kathy and colleague used the Flow and Multi-Flow Maps in post-conference supervision conversation)

Key sections from the chapter Mentoring Mathematics Teaching and Learning with excerpts above include:

Tools For Focused Observation and Reflection

Tools For Explicit Coaching In Model Lessons

Part 1: Lesson Planning/Orientation

Part 2: Lesson Observation

Part 3 Reflective Conversation

Imagining the Possibilities

Kathy Ernst, M.S. has spent 30 years teaching children and teachers in elementary and middle schools and has served on the faculty of the Leadership in Mathematics Education Program at Bank Street College of Education. She has facilitated the implementation of standards-based mathematics curricula in schools, working with teachers to support children’s construction of mathematical ideas.

2004 Final Report Thinking Maps North Carolina School Study By Nancy Cook Smith, Ph.D., North Carolina, United States, 2005

This study compares the gains in standardized test scores made by North Carolina schools that adopted Thinking Maps after 1997 and before 2002 and those gains made by comparable schools that did not adopt the intervention. North Carolina state assessment data from 1997 to 2002 were evaluated to ascertain the percentage of students at four performance levels for each school. Schools that adopted Thinking Maps showed statistically significant gains in students in the proficient performance level and parallel significant drops in the percent of students performing at the lowest performance level. The two groups of schools were comparable in geographic location and percent of students at the lowest socio-economic level (eligible for free or reduced lunch).

Thinking About Learning By Jacqueline Grennon Brooks, Hofstra University, New York, United States.

It is widely recog- nized that what students learn in school is rarely generalized into applications, theories and principles subject to further investigation. Therefore, deep understanding is often absent and, with it, a basis for reasoning and explanation (Schoenfeld, 1988). In order to further educational practice targeted at promoting pattern recognition and also generate a research approach that studies learners’ pattern recognition and conceptual change, the Thinking Maps® language (Hyerle, 1996) is a useful tool.

Professional books for additional research and documentation on Thinking Schools, Visual Tools and Thinking Maps®

Pathways to Thinking Schools

Visual Tools for Transforming Information into Knowledge

Student Successes with Thinking Maps®

Developing Connective Leadership

Growing Thinking Students in Thinking Schools

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

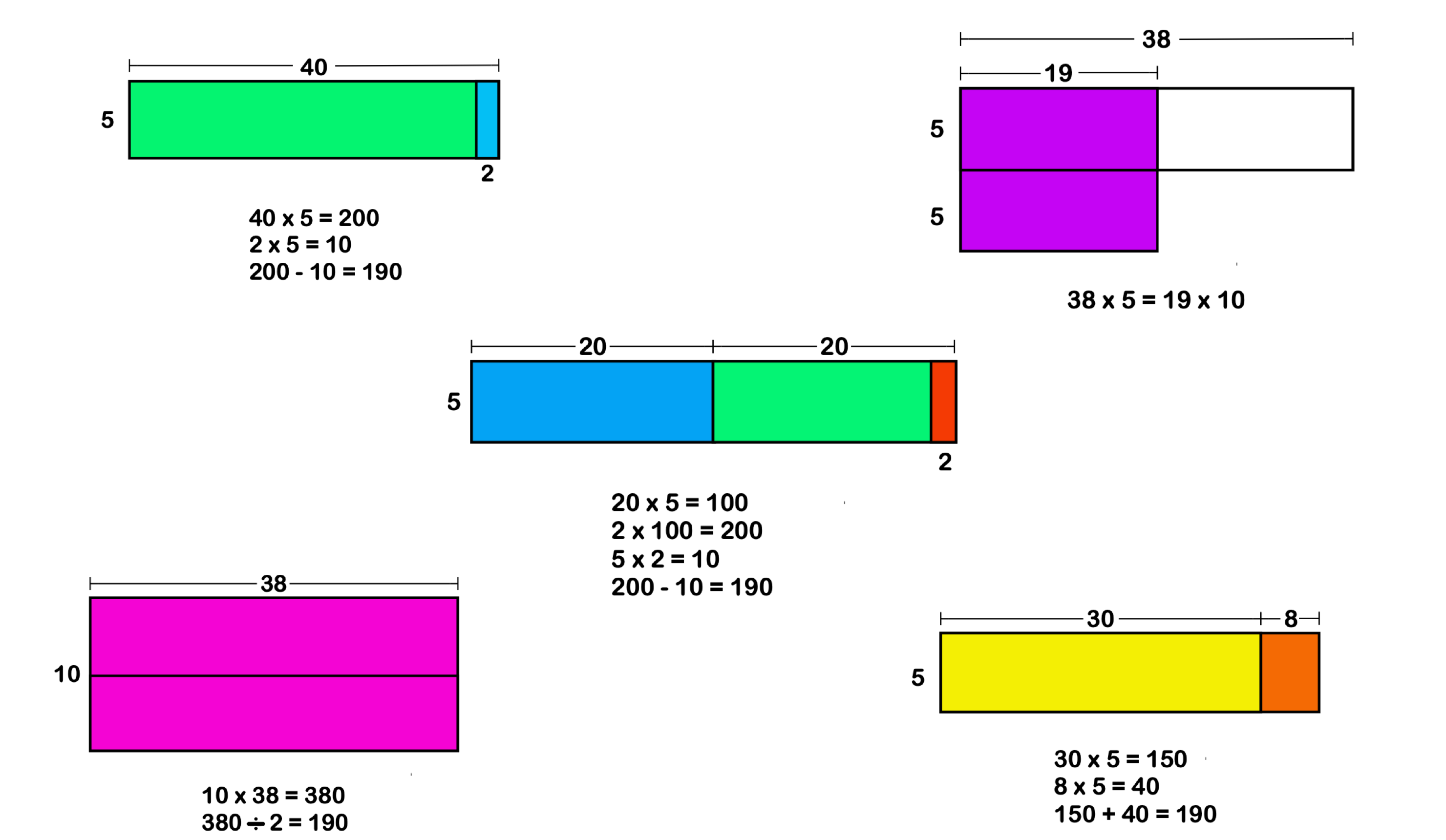
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

The Algebra Problem: How Middle School Math Became a National Flashpoint

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Sign up for The Morning newsletter from the New York Times

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system.

Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly 4 in 5 poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class.

San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’ administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12% of Black and Latino eighth graders do, compared with roughly 24% of white pupils, a federal report found.

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research. A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Massachusetts, the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80% from 60%. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100%, yes,” he added. “That was not something that I could live with.”

c.2024 The New York Times Company

Recommended Stories

Nba playoffs: luka dončić, mavericks power past anthony edwards to take a 3-0 lead over timberwolves.

The Mavericks are now just one win away from their first NBA Finals trip since 2011.

'Today I was carded — I'm 49': This anti-aging eye cream helps users turn back the clock, and it's down to $20

Loved by over 14,000 reviewers, the formula targets dark circles, puffiness and wrinkles.

Trump tried to woo Libertarian voters and got booed. Here's what happened.

“If we unite, we will be unstoppable," Trump pitched to the crowd of third-party voters.

Kyle Larson's Indy-Charlotte double in jeopardy because of rain-delayed Indianapolis 500

Larson said during a rain delay that racing in the Indy 500 was the "priority."

Women in AI: Miriam Vogel stresses the need for responsible AI

To give AI-focused women academics and others their well-deserved — and overdue — time in the spotlight, TechCrunch has been publishing a series of interviews focused on remarkable women who’ve contributed to the AI revolution. Miriam Vogel is the CEO of EqualAI, a nonprofit created to reduce unconscious bias in AI and promote responsible AI governance. As a board member at the Responsible AI Institute and senior advisor to the Center for Democracy and Technology, Vogel's advised White House leadership on initiatives ranging from women, economic, regulatory and food safety policy to matters of criminal justice.

Will Biden be on the Ohio ballot in November? Why the state's Republican governor says they're 'running out of time' to make sure he is.

After missing their deadline, Ohio politicians are discussing ways to certify Biden as the 2024 Democratic nominee for president in their state.

This bestselling hair-strengthening oil has 63,500+ fans: 'Fuller than it has been in years'

It includes rosemary and mint, which users say not only bolsters strands, but leaves them soft and shiny.

'Ended up returning my Skims': This tummy-taming bodysuit is down to $17 for Memorial Day weekend

'Not only does it snatch your waist, but it's not uncomfortable either!' says one fan.

Voters historically have short memories about the economy. Inflation might be different.

The Biden campaign is hoping voters' minds aren't fully set as it wrestles with a polling deficit and dismal economic ratings. But inflation could test those hopes.

Memorial Day steal: Shoppers in their 50s and 60s gush about this top-selling SPF moisturizer, and it’s down to $15

When the sun's out, this is the cream that over 63,000 rave reviewers reach for.

Families of Uvalde shooting victims sue Activision and Meta

The families of victims of the shooting at Robb Elementary School in Uvalde, Texas are suing Activision and Meta, as well as gun manufacturer Daniel Defense. The families bringing the lawsuits are represented by attorney Josh Koskoff, who previously won a settlement from Remington for the families of Sandy Hook shooting victims. The suit against the technology companies claims, "Over the last 15 years, two of America’s largest technology companies ... have collaborated with the firearms industry in a scheme that makes the Joe Camel campaign look laughably harmless, even quaint."

Junkyard Gem: 1999 Mitsubishi Galant GTZ

A 1999 Mitsubishi Galant GTZ-V6 sedan found in a North Carolina junkyard.

These slimming Levi's jeans are up to 60% off for Memorial Day weekend — some styles start at just $22

Let us be your jean genie — grab this top-quality denim before these deals go poof.

'Fitted in the right spots': This 'wonderfully flattering' T-shirt is down to just $17

More than 27,000 five-star shoppers say this is the summer staple you need in multiple colors.

Angel Reese thanks Alyssa Thomas for flagrant foul: 'I got back up and I kept going and kept pushing'

Angel Reese said she wanted to get "knocked down" at the next level, and she got her wish.

Y Combinator’s Garry Tan supports some AI regulation but warns against AI monopolies

Garry Tan, president and CEO of Y Combinator, told a crowd at The Economic Club of Washington, D.C. this week that “regulation is likely necessary” for artificial intelligence. Tan spoke with Teresa Carlson, a General Catalyst board member as part of a one-on-one interview where he discussed everything from how to get into Y Combinator to AI, noting that there is “no better time to be working in technology than right now.” Tan said he was “overall supportive” of the National Institute of Standards and Technology (NIST) attempt to construct an GenAI risk mitigation framework, and said that “large parts of the EO by the Biden Administration are probably on the right track.”

'Makes my skin feel young': Shoppers in their 60s and 70s say their secret to looking younger is this $9 collagen cream

4,900+ shoppers swear by this age-defying, wallet-friendly formula.

Memorial Day sales 2024: We found the best deals at Amazon, Walmart, Target and more

The holiday weekend runs May 24-27, but you can already save big on your favorite brands.

The Fed's favored inflation gauge highlights shortened trading week: What to know this week

The Fed's preferred inflation gauge will test a stock market near record highs in a holiday-shortened trading week.

How Americans view the economy depends on whether they rent or own

How’s the economy doing? Your answer may depend on whether you own your home.

Game Central

Similar problems from web search.

• Trending Blogs
• Geeksforgeeks NEWS
• Geeksforgeeks Blogs
• Tips & Tricks
• Website & Apps
• ChatGPT Blogs
• ChatGPT News
• ChatGPT Tutorial
• How to use Chat-GPT to solve Coding Problems?
• 10 Best ChatGPT Prompts to Solve Complex Math Problems
• How to Use ChatGPT Prompts for Effective Study Sessions
• NCERT Solutions for Class 12 Maths -Chapter Wise with PDF
• Google Code to Learn Contest 2021 - For Class 05-12 Students!
• RD Sharma Class 8 Solutions for Maths: Chapter Wise PDF
• NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry
• NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
• How to Add a Google Form to Google Classroom
• NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
• Java Program to Find the Perimeter of a Circle
• How to prove that the area of a circle is pi r squared?
• NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles
• What are Mathematical Puzzles and How to solve them?
• Tricks To Solve Age-Based Problems
• Descartes' Circle Theorem with implementation
• How to prepare for Infosys - The Complete guide
• How to Draw a Circle of Given Radius R in MATLAB?
• Top Maths Apps for College Students in 2024

How to Solve Maths Problems with Google Circle for Students

Math can be a challenging subject for many students. Between understanding word problems and applying the right formulas, getting stuck is a common experience. Google has introduced a powerful tool called Google Circle, designed to help students solve math problems with confidence.

Read In Short: What Google Circle is and how it can help students solve math problems. How to use Google Circle to break down and solve different types of math problems. Additional tips and tricks to maximize your learning experience with Google Circle

What is Google Circle?

Google Circle is a feature within the Google Search app for Android devices . It allows you to solve math problems directly from your phone or tablet. Instead of simply providing answers, Google Circle focuses on math problem-solving by offering step-by-step guidance. This makes it a valuable tool for understanding the concepts behind the calculations, not just getting the final answer.

How Does Google Circle Work

Using Google Circle is incredibly simple. Here’s how it goes:

Step 1: Open the Google Search app on your Android device.

Step 2: find the math problem you’re working on., step 3: circle the specific problem you want help with using your finger., step 4: google circle will recognize it and use its artificial intelligence to analyze it., how to enable circle to search, step 1: open settings on your phone, step 2: scroll down and select display, step 3: scroll down and select navigation bar, step 4: select the toggle and turn on circle to search, which devices are getting the circle to search update.

Below is the list of android which is getting Google Circle App

• Samsung Galaxy S24, S24 Plus, and S24 Ultra
• Samsung Galaxy S23, S23 Plus, and S23 Ultra
• Samsung Galaxy S23 FE
• Samsung Galaxy Z Fold 5
• Samsung Galaxy Z Flip 5
• Samsung Galaxy Tab S9, S9 Plus, and S9 Ultra
• Google Pixel 8 and Pixel 8 Pro
• Google Pixel 7 and Pixel 7 Pro
• Google Pixel 6 and Pixel 6 Pro
• Google Pixel 7a
• Google Pixel 6a
• Google Pixel Fold
• Google Pixel Tablet

What Types of Math Problems Can Google Circle Solve?

Currently, Google Circle is particularly helpful with math word problems. These can be some of the trickiest problems to tackle, as they require translating real-world situations into mathematical terms.

Google Circle excels at helping students understand the key information in a word problem, identify the relevant mathematical concepts, and apply the appropriate formulas to reach the solution.

Here are some specific areas where Google Circle can be helpful:

• Algebra: Solve for variables, manipulate equations, and understand linear relationships.
• Geometry: Calculate areas, and volumes, and understand geometric shapes and their properties.
• Statistics: Analyze data sets, calculate measures of central tendency, and interpret graphs.

How to Solve Math Probelm Using Google Search

Step 1: activate circle to search.

On your Android smartphone or tablet, activate the Circle to Search feature.

Step 2: Circle the Problem

Find the math problem you’re stuck on and circle it on your screen. This prompts the feature to focus on that particular problem.

Step 3: Get Step-by-Step Instructions

The feature breaks down the problem and provides step-by-step instructions to solve it

Google Circle Vs Photomath Vs Socratic by Google

Tips for getting the most out of google circle.

• Practice makes perfect: Don’t just rely on Google Circle for the answer. Use it as a guide to understand the steps and then try solving similar problems on your own. This will solidify your learning and build your confidence.
• Focus on understanding, not just answers: While getting the right answer is important, the true power of Google Circle lies in its explanations. Pay attention to why each step is taken and how the concepts are applied.
• Don’t be afraid to experiment: Google Circle can handle various math problems. Try circling different parts of a word problem to see how it breaks down the information and guides you toward the solution.
• Take notes: As Google Circle explains the steps, jot down important points or formulas for future reference. This will create a personal study guide tailored to your learning needs.
• Combine it with other resources: Google Circle is a powerful tool, but it shouldn’t be your only resource. Use it alongside your textbook, class notes, or online tutorials for a well-rounded understanding.

Google Circle is a new tool designed to help students to become independent math problem solvers. By using its step-by-step guidance and clear explanations, you can transform your approach to math, gaining a deeper understanding of concepts and building the confidence to tackle even the most challenging problems. So, next time you’re stuck on a math question, don’t hesitate to circle it with Google Circle and watch your problem-solving skills soar!

Google Circle for Students – FAQs

Is google circle available on iphones.

Unfortunately, as of now, Google Circle is only available on Android devices within the Google Search app. However, there might be plans for future expansion to other platforms.

Is Google Circle safe to use?

Google Circle is a feature within the official Google Search app, making it a safe and reliable tool. However, it’s always a good practice to be mindful of the information you share online and only use it for educational purposes.

What if Google Circle can’t solve my math problem?

While Google Circle is constantly learning and expanding its capabilities, it might encounter problems it can’t handle yet. In such cases, don’t hesitate to consult your teacher, a tutor, or online resources for alternative solutions.

Will Google Circle do my math homework for me?

Google Circle is not a magic shortcut. It’s designed to be a learning tool. While it can guide you through the problem-solving process, it’s still important for you to understand the steps and concepts involved.

Please Login to comment...

Similar reads.

• School Learning News
• Latest News
• School Learning
• Websites & Apps

Improve your Coding Skills with Practice

What kind of Experience do you want to share?