probability class 12 case study questions 2023

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 12 Maths Chapter 13 Probability

• Last modified on: 1 year ago
• Reading Time: 6 Minutes

[PDF] Download Case Study Questions for Class 12 Maths Chapter 13 Probability

Here we are providing case study questions for class 12 maths. In this article, we are sharing Class 12 Maths Chapter 13 Probability case study questions. All case study questions of class 12 maths are solved so that students can check their solutions after attempting questions.

Case Study Questions for Class 12 Maths

Case study questions are a type of question that is commonly used in academic and professional settings to evaluate a person’s ability to analyze, interpret, and solve problems based on a given scenario or case study.

Typically, a case study question presents a real-world situation or problem that requires the individual to apply their knowledge and skills to identify the issues, consider various solutions, and recommend a course of action.

Case study questions are designed to test critical thinking skills, problem-solving abilities, and the capacity to work through complex and ambiguous situations.

Preparing for case study questions involves developing a deep understanding of the subject matter, being able to analyze and synthesize information quickly, and being able to communicate ideas clearly and effectively.

Importance of Solving Case Study Questions for Class 12 Maths

Solving case study questions for Class 12 Maths is extremely important as it provides students with an opportunity to apply the mathematical concepts they have learned to real-world scenarios. These questions present a situation or problem that requires students to use their problem-solving skills and critical thinking abilities to arrive at a solution.

The importance of solving case study questions for Class 12 Maths can be summarized as follows:

• Enhances problem-solving skills: Case study questions challenge students to think beyond textbook examples and apply their knowledge to real-world situations. This enhances their problem-solving skills and helps them develop a deeper understanding of the mathematical concepts.
• Improves critical thinking abilities: Case study questions require students to analyze and evaluate information, and draw conclusions based on their understanding of the situation. This helps them develop their critical thinking abilities, which are essential for success in many areas of life.
• Helps in retaining concepts: Solving case study questions helps students retain the concepts they have learned for a longer period of time. This is because they are more likely to remember the concepts when they have applied them to a real-world situation.
• Better preparation for exams: Many competitive exams, including the Class 12 Maths board exam, contain case study questions. Solving these questions helps students become familiar with the format of the questions and the skills required to solve them, which can improve their performance in exams.

In conclusion, solving case study questions for Class 12 Maths is important as it helps students develop problem-solving and critical thinking skills, retain concepts better, and prepare for exams.

Related Posts

Category lists (all posts).

All categories of this website are listed below with number of posts in each category for better navigation. Visitors can click on a particular category to see all posts related to that category.

• Full Form (1)
• Biography of Scientists (1)
• Assertion Reason Questions in Biology (37)
• Case Study Questions for Class 12 Biology (14)
• DPP Biology for NEET (12)
• Blog Posts (35)
• Career Guidance (1)
• Assertion Reason Questions for Class 10 Maths (14)
• Case Study Questions for Class 10 Maths (15)
• Extra Questions for Class 10 Maths (12)
• Maths Formulas for Class 10 (1)
• MCQ Questions for Class 10 Maths (15)
• NCERT Solutions for Class 10 Maths (4)
• Quick Revision Notes for Class 10 Maths (14)
• Assertion Reason Questions for Class 10 Science (16)
• Case Study Questions for Class 10 Science (14)
• Evergreen Science Book Solutions for Class 10 (17)
• Extra Questions for Class 10 Science (23)
• HOTS for Class 10 Science (17)
• Important Questions for Class 10 Science (10)
• Lakhmir Singh Class 10 Biology Solutions (4)
• Lakhmir Singh Class 10 Chemistry Solutions (5)
• Lakhmir Singh Class 10 Physics Solutions (5)
• MCQ Questions for Class 10 Science (20)
• NCERT Exemplar Solutions for Class 10 Science (16)
• NCERT Solutions for Class 10 Science (15)
• Quick Revision Notes for Class 10 Science (4)
• Study Notes for Class 10 Science (17)
• Assertion Reason Questions for Class 10 Social Science (14)
• Case Study Questions for Class 10 Social Science (24)
• MCQ Questions for Class 10 Social Science (3)
• Topicwise Notes for Class 10 Social Science (4)
• CBSE CLASS 11 (1)
• Assertion Reason Questions for Class 11 Chemistry (14)
• Case Study Questions for Class 11 Chemistry (11)
• Free Assignments for Class 11 Chemistry (1)
• MCQ Questions for Class 11 Chemistry (8)
• Very Short Answer Questions for Class 11 Chemistry (7)
• Assertion Reason Questions for Class 11 Entrepreneurship (8)
• Important Questions for CBSE Class 11 Entrepreneurship (1)
• Assertion Reason Questions for Class 11 Geography (24)
• Case Study Questions for Class 11 Geography (24)
• Assertion Reason Questions for Class 11 History (12)
• Case Study Questions for Class 11 History (12)
• Assertion and Reason Questions for Class 11 Maths (16)
• Case Study Questions for Class 11 Maths (16)
• Formulas for Class 11 Maths (6)
• MCQ Questions for Class 11 Maths (17)
• NCERT Solutions for Class 11 Maths (8)
• Case Study Questions for Class 11 Physical Education (11)
• Assertion Reason Questions for Class 11 Physics (15)
• Case Study Questions for Class 11 Physics (12)
• Class 11 Physics Study Notes (5)
• Concept Based Notes for Class 11 Physics (2)
• Conceptual Questions for Class 11 Physics (10)
• Derivations for Class 11 Physics (3)
• Extra Questions for Class 11 Physics (13)
• MCQ Questions for Class 11 Physics (16)
• NCERT Solutions for Class 11 Physics (16)
• Numerical Problems for Class 11 Physics (4)
• Physics Formulas for Class 11 (7)
• Revision Notes for Class 11 Physics (11)
• Very Short Answer Questions for Class 11 Physics (11)
• Assertion Reason Questions for Class 11 Political Science (20)
• Case Study Questions for Class 11 Political Science (20)
• CBSE CLASS 12 (8)
• Extra Questions for Class 12 Biology (14)
• MCQ Questions for Class 12 Biology (13)
• Case Studies for CBSE Class 12 Business Studies (13)
• MCQ Questions for Class 12 Business Studies (1)
• Revision Notes for Class 12 Business Studies (10)
• Assertion Reason Questions for Class 12 Chemistry (15)
• Case Study Based Questions for Class 12 Chemistry (14)
• Extra Questions for Class 12 Chemistry (5)
• Important Questions for Class 12 Chemistry (15)
• MCQ Questions for Class 12 Chemistry (8)
• NCERT Solutions for Class 12 Chemistry (16)
• Revision Notes for Class 12 Chemistry (7)
• Assertion Reason Questions for Class 12 Economics (9)
• Case Study Questions for Class 12 Economics (9)
• MCQ Questions for Class 12 Economics (1)
• MCQ Questions for Class 12 English (2)
• Assertion Reason Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Geography (18)
• Assertion Reason Questions for Class 12 History (8)
• Case Study Questions for Class 12 History (13)
• Assertion Reason Questions for Class 12 Informatics Practices (13)
• Case Study Questions for Class 12 Informatics Practices (11)
• MCQ Questions for Class 12 Informatics Practices (5)
• Assertion and Reason Questions for Class 12 Maths (14)
• Case Study Questions for Class 12 Maths (13)
• Maths Formulas for Class 12 (5)
• MCQ Questions for Class 12 Maths (14)
• Problems Based on Class 12 Maths (1)
• RD Sharma Solutions for Class 12 Maths (1)
• Assertion Reason Questions for Class 12 Physical Education (11)
• Case Study Questions for Class 12 Physical Education (11)
• MCQ Questions for Class 12 Physical Education (10)
• Assertion Reason Questions for Class 12 Physics (16)
• Case Study Based Questions for Class 12 Physics (14)
• Class 12 Physics Conceptual Questions (16)
• Class 12 Physics Discussion Questions (1)
• Class 12 Physics Latest Updates (2)
• Derivations for Class 12 Physics (8)
• Extra Questions for Class 12 Physics (4)
• Important Questions for Class 12 Physics (8)
• MCQ Questions for Class 12 Physics (14)
• NCERT Solutions for Class 12 Physics (18)
• Numerical Problems Based on Class 12 Physics (16)
• Physics Class 12 Viva Questions (1)
• Revision Notes for Class 12 Physics (7)
• Assertion Reason Questions for Class 12 Political Science (16)
• Case Study Questions for Class 12 Political Science (16)
• Notes for Class 12 Political Science (1)
• Assertion Reason Questions for Class 6 Maths (13)
• Case Study Questions for Class 6 Maths (13)
• Extra Questions for Class 6 Maths (1)
• Worksheets for Class 6 Maths (1)
• Assertion Reason Questions for Class 6 Science (16)
• Case Study Questions for Class 6 Science (16)
• Extra Questions for Class 6 Science (1)
• MCQ Questions for Class 6 Science (9)
• Assertion Reason Questions for Class 6 Social Science (1)
• Case Study Questions for Class 6 Social Science (26)
• NCERT Exemplar for Class 7 Maths (13)
• NCERT Exemplar for Class 7 Science (19)
• NCERT Exemplar Solutions for Class 7 Maths (12)
• NCERT Exemplar Solutions for Class 7 Science (18)
• NCERT Notes for Class 7 Science (18)
• Assertion Reason Questions for Class 7 Maths (14)
• Case Study Questions for Class 7 Maths (14)
• Extra Questions for Class 7 Maths (5)
• Assertion Reason Questions for Class 7 Science (18)
• Case Study Questions for Class 7 Science (17)
• Extra Questions for Class 7 Science (19)
• Assertion Reason Questions for Class 7 Social Science (1)
• Case Study Questions for Class 7 Social Science (30)
• Assertion Reason Questions for Class 8 Maths (7)
• Case Study Questions for Class 8 Maths (17)
• Extra Questions for Class 8 Maths (1)
• MCQ Questions for Class 8 Maths (6)
• Assertion Reason Questions for Class 8 Science (16)
• Case Study Questions for Class 8 Science (11)
• Extra Questions for Class 8 Science (2)
• MCQ Questions for Class 8 Science (4)
• Numerical Problems for Class 8 Science (1)
• Revision Notes for Class 8 Science (11)
• Assertion Reason Questions for Class 8 Social Science (27)
• Case Study Questions for Class 8 Social Science (23)
• CBSE Class 9 English Beehive Notes and Summary (2)
• Assertion Reason Questions for Class 9 Maths (14)
• Case Study Questions for Class 9 Maths (14)
• MCQ Questions for Class 9 Maths (11)
• NCERT Notes for Class 9 Maths (6)
• NCERT Solutions for Class 9 Maths (12)
• Revision Notes for Class 9 Maths (3)
• Study Notes for Class 9 Maths (10)
• Assertion Reason Questions for Class 9 Science (16)
• Case Study Questions for Class 9 Science (15)
• Evergreen Science Book Solutions for Class 9 (15)
• Extra Questions for Class 9 Science (22)
• MCQ Questions for Class 9 Science (11)
• NCERT Solutions for Class 9 Science (15)
• Revision Notes for Class 9 Science (1)
• Study Notes for Class 9 Science (15)
• Topic wise MCQ Questions for Class 9 Science (2)
• Topicwise Questions and Answers for Class 9 Science (15)
• Assertion Reason Questions for Class 9 Social Science (15)
• Case Study Questions for Class 9 Social Science (19)
• CHEMISTRY (8)
• Chemistry Articles (2)
• Daily Practice Problems (DPP) (3)
• Books for CBSE Class 9 (1)
• Books for ICSE Class 10 (3)
• Editable Study Materials (8)
• Exam Special for CBSE Class 10 (3)
• H. C. Verma (Concepts of Physics) (13)
• Study Materials for ICSE Class 10 Biology (14)
• Extra Questions for ICSE Class 10 Chemistry (1)
• Study Materials for ICSE Class 10 Chemistry (5)
• Study Materials for ICSE Class 10 Maths (16)
• Important Questions for ICSE Class 10 Physics (13)
• MCQ Questions for ICSE Class 10 Physics (4)
• Study Materials for ICSE Class 10 Physics (8)
• Study Materials for ICSE Class 9 Maths (7)
• Study Materials for ICSE Class 9 Physics (10)
• Topicwise Problems for IIT Foundation Mathematics (4)
• Challenging Physics Problems for JEE Advanced (2)
• Topicwise Problems for JEE Physics (1)
• DPP for JEE Main (1)
• Integer Type Questions for JEE Main (1)
• Integer Type Questions for JEE Chemistry (6)
• Chapterwise Questions for JEE Main Physics (1)
• Integer Type Questions for JEE Main Physics (8)
• Physics Revision Notes for JEE Main (4)
• JEE Mock Test Physics (1)
• JEE Study Material (1)
• JEE/NEET Physics (6)
• CBSE Syllabus (1)
• Maths Articles (2)
• NCERT Books for Class 12 Physics (1)
• NEET Chemistry (13)
• Important Questions for NEET Physics (17)
• Topicwise DPP for NEET Physics (5)
• Topicwise MCQs for NEET Physics (32)
• NTSE MAT Questions (1)
• Physics (1)
• Alternating Current (1)
• Electrostatics (6)
• Fluid Mechanics (2)
• PowerPoint Presentations (13)
• Previous Years Question Paper (3)
• Products for CBSE Class 10 (15)
• Products for CBSE Class 11 (10)
• Products for CBSE Class 12 (6)
• Products for CBSE Class 6 (2)
• Products for CBSE Class 7 (5)
• Products for CBSE Class 8 (1)
• Products for CBSE Class 9 (3)
• Products for Commerce (3)
• Products for Foundation Courses (2)
• Products for JEE Main & Advanced (10)
• Products for NEET (6)
• Products for ICSE Class 6 (1)
• Electrostatic Potential and Capacitance (1)
• Topic Wise Study Notes (Physics) (2)
• Topicwise MCQs for Physics (2)
• Uncategorized (138)

Test series for students preparing for Engineering & Medical Entrance Exams are available. We also provide test series for School Level Exams. Tests for students studying in CBSE, ICSE or any state board are available here. Just click on the link and start test.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Privacy Policy
• Terms and Conditions

• Web Stories

Friday, February 4, 2022

Case study questions class 12 maths chapter 13 probability cbse board term 2.

0 comments:

Post a comment.

Please do not enter any spam link in the comment box.

Warning: Do Not Copy!

• Blog Archives

• Best Books for IIT JEE
• Best Colleges Of India
• class 10 Case Study Based questions
• Class 10 Maths MCQ
• Class 11 Maths Case Study Questions
• Class 11 Maths MCQ
• Class 12 Math Case Study questions
• Class 12 Maths MCQ
• JEE MAIN MCQ
• Maths Strategy JEE
• News for Students

Blog Archive

• ►  April (3)
• ►  March (2)
• Case Study Questions Class 12 MATHS Chapter 13 Pro...
• ►  January (5)
• ►  December (9)
• ►  November (5)
• ►  October (6)
• ►  September (5)
• ►  April (4)
• ►  March (3)
• ►  October (2)
• ►  September (7)
• ►  August (2)
• ►  July (4)

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

Case Based Questions (MCQ)

• Miscellaneous
• Probability Distribution
• Bernoulli Trial

Question 1 - Case Based Questions (MCQ) - Chapter 13 Class 12 Probability

Last updated at April 16, 2024 by Teachoo

A coach is training 3 players. He observes that the player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots.

From this situation answer the following:.

Let the target is hit by A, B and C. Then, the probability that A, B and, C all will hit, is

(a) 4/5 , (b) 3/5 , (c) 2/5 .

Referring to (i), what is the probability that B, C will hit and A will lose?

(a) 1/10 , (b) 3/10 , (c) 7/10 .

With reference to the events mentioned in (i), what is the probability that ‘any two of A, B and C will hit?

(a) 1/30 , (b) 11/30 , (c) 17/30 .

What is the probability that ‘none of them will hit the target’?

(b) 1/60 , (c) 1/15 .

What is the probability that at least one of A, B or C will hit the target?

(a) 59/60 , (b) 2/5 , (c) 3/5 .

Question A coach is training 3 players. He observes that the player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots. From this situation answer the following:P(A) = Probability of A hitting the target = 𝟒/𝟓 P(B) = Probability of B hitting the target = 𝟑/𝟒 P(C) = Probability of C hitting the target = 𝟐/𝟑 Question 1 Let the target is hit by A, B and C. Then, the probability that A, B and, C all will hit, is (a) 4/5 (b) 3/5 (c) 2/5 (d) 1/5P(all hit) = Probability A will hit × Probability B will hit × Probability C will hit = 4/5 × 3/4 × 2/3 = 𝟐/𝟓 So, the correct answer is (c) Question 2 Referring to (i), what is the probability that B, C will hit and A will lose? (a) 1/10 (b) 3/10 (c) 7/10 (d) 4/10P(B and C will hit and A will lose) = Probability A will not hit × Probability B will hit × Probability C will hit = (𝟏−𝟒/𝟓)"×" 𝟑/𝟒 × 𝟐/𝟑 = 1/5 × 3/4 × 2/3 = 𝟏/𝟏𝟎 So, the correct answer is (a) Question 3 With reference to the events mentioned in (i), what is the probability that ‘any two of A, B and C will hit? (a) 1/30 (b) 11/30 (c) 17/30 (d) 13/30 P(any two will hit) = P(A will not hit) × P(B will hit) × P(C will hit) + P(A will hit) × P(B will not hit) × P(C will hit) + P(A will hit) × P(B will hit) × P(C will not hit) = (1−4/5)"×" 3/4 × 2/3 + 4/5 "×" (1−3/4)× 2/3 +4/5 "×" 3/4 × (1−2/3) = 1/5 "×" 3/4 × 2/3 + 4/5 "×" 1/4 × 2/3 +4/5 "×" 3/4 × 1/3 = 1/10+2/15+1/5 = 𝟏𝟑/𝟑𝟎 So, the correct answer is (d) Question 4 What is the probability that ‘none of them will hit the target’? (a) 1/30 (b) 1/60 (c) 1/15 (d) 2/15P(none will hit) = Probability A will not hit × Probability B will not hit × Probability C will not hit = (𝟏−𝟒/𝟓) × (𝟏−𝟑/𝟒)×(𝟏−𝟐/𝟑) = 1/5×1/4×1/3 = 𝟏/𝟔𝟎 So, the correct answer is (b) Question 5 What is the probability that at least one of A, B or C will hit the target? (a) 59/60 (b) 2/5 (c) 3/5 (d) 1/60P( at least one will hit) = P(exactly one will hit) + P(exactly two will hit) + P(all will hit) P(exactly one will hit) P(exactly one will hit) = P(A will hit)×P(B will not hit) × P(C will not hit) + P (A will not hit) × P (B will hit) × P (C will not hit) + P (A will not hit)× P (B will not hit) × P (C will hit) = 4/5×(1−3/4)×(1−2/3) +(1−4/5)×3/4×(1−2/3) +(1−4/5)×(1−3/4)×2/3= 4/5 "×" 1/4 × 1/3 + 1/5 "×" 3/4× 1/3 +1/5 "×" 1/4 × 2/3 = 1/15+1/20+1/30 = 𝟗/𝟔𝟎P(exactly two will hit) This is calculated in Question 3 P(exactly two will hit) = 𝟏𝟑/𝟑𝟎 P(all will hit) This is calculated in Question 1 P(all will hit) = 𝟐/𝟓Now, P(at least one will hit) = P(exactly one will hit) + P(exactly two will hit) + P(all will hit) = 9/60+13/30+2/5 = 𝟓𝟗/𝟔𝟎 So, the correct answer is (a)

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

• Online Class
• Ask Doubt on Whatsapp
• Search Doubtnut

CASE STUDY/PASSAGE BASED QUESTIONS from MTG GUIDE PROBABILITY for Class 12

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

All Exercises from MTG GUIDE Class 12 MATHS PROBABILITY

• CASE STUDY/PASSAGE BASED QUESTIONS

• Neet Online Test Pack

12th Standard stateboard question papers & Study material

தமிழ் subjects.

கணினி பயன்பாடுகள்

கணினி அறிவியல்

வணிகக் கணிதம் மற்றும் புள்ளியியல்.

கணினி தொழில்நுட்பம்

கணக்குப்பதிவியல்

English Subjects

Computer Science

Business Maths and Statistics

Accountancy

Computer Applications

Computer Technology

11th Standard stateboard question papers & Study material

9th Standard stateboard question papers & Study material

Social Science

சமூக அறிவியல்

6th standard stateboard question papers & study material.

10th Standard stateboard question papers & Study material

7th Standard stateboard question papers & Study material

8th Standard stateboard question papers & Study material

கணிதம் - old

12th Standard CBSE Subject Question Paper & Study Material

Introductory Micro and Macroeconomics

Business Studies

Indian Society

Physical Education

Bio Technology

Engineering Graphics

Entrepreneurship

Hindi Elective

Home Science

Legal Studies

Political Science

11th Standard CBSE Subject Question Paper & Study Material

Mathematics

Enterprenership

Applied Mathematics

10th standard cbse subject question paper & study material.

9th Standard CBSE Subject Question Paper & Study Material

8th Standard CBSE Subject Question Paper & Study Material

7th Standard CBSE Subject Question Paper & Study Material

6th Standard CBSE Subject Question Paper & Study Material

School Exams

Tamil Nadu State Board Exams

Scholarship Exams

Study Materials , News and Scholarships

Stateboard Tamil Nadu

Free Online Tests

Educational News

Scholarships

Entrance Exams India

Video Materials

12th Standard CBSE

Class 12th Maths - Probability Case Study Questions and Answers 2022 - 2023

Class 12th Maths - Probability Case Study Questions and Answers 2022 - 2023 Study Materials Sep-08 , 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12 Maths Subject - Probability, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

A PHP Error was encountered

Severity: Warning

Message: in_array() expects parameter 2 to be array, null given

Filename: material/details.php

Line Number: 1436

Message: Use of undefined constant EXAM - assumed 'EXAM' (this will throw an Error in a future version of PHP)

Line Number: 1438

QB365 - Question Bank Software

Probability case study questions with answer key.

Final Semester - June 2015

(ii) P (B I C) =

(iii) P (A ⋂ B I C) =

(iv) P (A I C) =

(v) P (A ∪ B I C) =

(ii) What is the probability that the first ball is yellow and the second ball is red?

(iii) What is the probability that both the balls are red?

(iv) What is the probability that the first ball is green and the second ball is not yellow?

(v) What is the probability that both the balls are not blue?

(ii) P (A  \(\cup\)  B) =

(iii) P (B  |  A) =

(iv) P (A  |  B) =

(v) P ( not A and not B ) =

(ii) When the doctor arrives late, what is the probability that he comes by cab?

(iii) When the doctor arrives late, what is the probability that he comes by bike?

(iv) When the doctor arrives late, what is the probability that he comes by other means of transport?

(v) What is the probability that the doctor is late by any means?

(ii) What is the probability that the average study time of students is not more than 1 hour?

(iii) What is the probability that the average study time of students is at least 3 hours?

(iv) What is the probability that the average study time of students is exactly 2 hours?

(v) What is the probability that the average study time of students is at least 1 hour?

(ii) Probability that puzzle is solved by Ravi but not by Priya, is

(iii) Find the probability that puzzle is solved.

(iv) Probability that exactly one of them solved the puzzle, is

(v) Probability that none of them solved the puzzle, is

(ii) The probability of drawing two diamonds, given that a card of heart is missing, is

(iii) Let A be the event of drawing two diamonds from remaining 51 cards and E 1 , E 2 , E 3 and E 4 be the events that lost card is of diamond, club, spade and heart respectively, then the approximate value of  \(\sum_{i=1}^{4} P\left(A \mid E_{i}\right) \text { is }\)

(iv) All of a sudden, missing card is found and, then two cards are drawn simultaneously without replacement. Probability that both drawn cards are king is

(v) If two cards are drawn from a well shuffled pack of 52 cards, one by one with replacement, then probability of getting not a king in 1 st and 2 nd draw is

(ii) The probability that it does not rain on chosen day is

(iii) The probability that the weatherman predicts correctly is

(iv) The probability that it will rain on the chosen day, if weatherman predict rain for that day, is

(v) The probability that it will not rain on the chosen day, if weatherman predict rain for that day, is

(ii) Probability that all children are boys, if two elder children are boys, is

(iii) Find the probability that two middle children are boys, if it is given that eldest child is a girl.

(iv) Find the probability that all children are boys, if it is given that at most one of the children is a girl.

(v) Find the probability that all children are boys, if it is given that at least three of the children are boys.

(ii) Teacher ask Mivaan, what is the probability that both tickets drawn by Aadya shows odd number?

(iii) Teacher ask Deepak, what is the probability that tickets drawn by Mivaan, shows a multiple of 4 on one ticket and a multiple 5 on other ticket?

(iv) Teacher ask Archit, what is the probability that tickets are drawn by Deepak, shows a prime number on one ticket and a multiple of 4 on other ticket?

(v) Teacher ask Aadya, what is the probability that tickets drawn by Vrinda, shows an even number on first ticket and an odd' number on second ticket?

(ii) If the wife is watching television, the probability that husband is also watching television, is

(iii) The probability that both husband and wife are watching television during prime time, is

(iv) The probability that the wife is watching television during prime time, is

(v) If the wife is watching television, then the probability that husband is not watching television, is

(ii) The probability that India losing the third match, if India has already loose the first two matches is

(iii) The probability th-.at India losing the first two matches is

(iv) The probability that India winning the first three matches is

(v) The probability that India winning exactly one of the first three matches is

(ii) The value of ab + bc + ac - 2abc is

(iii) The value of abc is

(iv) The value of ab + bc + dc is

(v) The value of a + b + c is

(ii) Probability that defective bolt drawn is manufactured by machine B, is

(iii) Probability that defective bolt drawn is manufactured by machine C, is

(iv) Probability that defective bolt is not manufactured by machine B, is

(v) Probability that defective bolt is not manufactured by machine C, is

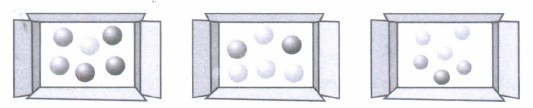
(ii) Probability of occurrence of event E, given that the balls drawn are from box II, is

(iii) Probability of occurrence of event E, given that balls drawn are from box III, is

(iv) The value of  \(\sum_{i=1}^{3} P\left(E \mid E_{i}\right)\)  is equal to

(v) The probability that the balls drawn are from box II, given that event E has already occurred, is

(ii) The probability that none of them is selected, is

(iii) The probability that only one of them is selected, is

(iv) The probability that atleast one of them is selected, is

(v) Suppose Nisha is selected by the manager and told her about two posts I and II for which selection is independent. If the probability of selection for post I is  \(\frac{1}{6}\) and for post II is \(\frac{1}{5}\)  then the probability that Nisha is selected for at least one post, is

(ii) The probability that X = 4 equals

(iii) The probability that X ≥ 2 equals

(iv) The value of P(X ≥ 6) is

(v) The probability that X > 3 equals

(ii) The probability that the selected student has failed in Mathematics, if it is known that he has failed in Economics, is

(iii) The probability that the selected student has passed in at least one of the two subjects, is

(iv) The probability that the selected student has failed in at least one of the two subjects, is

(v) The probability that the selected student has passed in Mathematics, if it is known that he has failed in Economics, is

(ii) Find the probability that mother is at right end, given that son and daughter are together.

(iii) Find the probability that father and mother are in the middle, given that son is at right end.

(iv) Find the probability that father and son are standing together, given that mother and daughter are standing together.

(v) Find the probability that father and mother are on either of the ends, given that son is at second position from the right end.

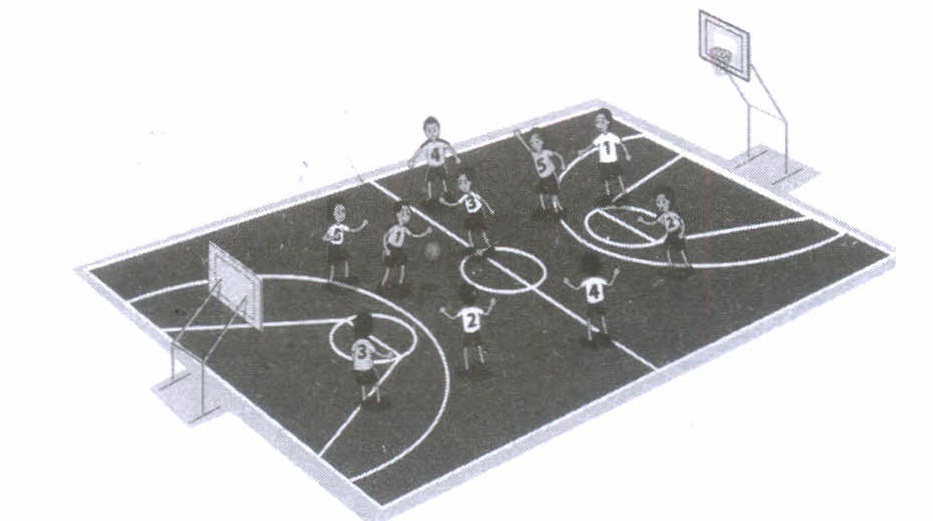
(ii) P(T 2 drawing a match against T 1 ) is equal to

(iii) P(X > Y) is equal to

(iv) P(X = Y) is equal to

(v) P(X + Y = 8) is equal to

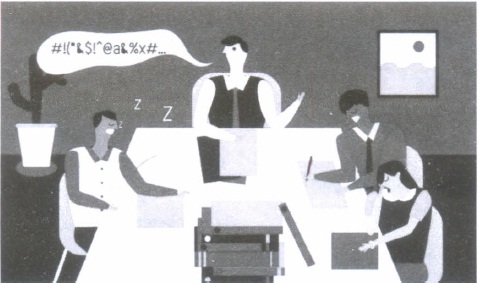
(ii) The probability that Sonia processed the form and committed an error is

(iii) The total probability of committing an error in processing the form is

(iv) The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms: If the form selected at random has an error, the probability that the form is NOT processed by Vinay is

(v) Let A be the event of committing an error in processing the form and let E 1 , E 2 and E 3 be the events that Vinay, Sonia and Iqbal processed the form. The value of  \(\sum_{i=1}^{3} P\left(E_{i} \mid A\right) \text { is }\)

*****************************************

• Previous Class 12th Maths - Three Dimensional Geometry Case Study Questions and Answers 2...
• Next Class 12th Maths - Linear Case Study Questions and Answers 2022 - 2023

Reviews & Comments about Class 12th Maths - Probability Case Study Questions and Answers 2022 - 2023

Write your Comment

12th Standard CBSE Maths Videos

CBSE 12th Maths Sample Model Question Paper with Answer Key 2023

12th Standard CBSE Maths Usefull Links

• 10th Standard

Other 12th Standard CBSE Subjects

Other 12th Standard CBSE Maths Study material

Class 12th maths - three dimensional geometry ... click to view, class 12th maths - linear case study questions and answers 2022 - 2023 click to view, class 12th maths - probability case study questions and answers 2022 - 2023 click to view, class 12th maths - vector algebra case study questions and answers 2022 - 2023 click to view, class 12th maths - differential equations case ... click to view, class 12th maths - application of integrals ... click to view, class 12th maths - application of derivatives ... click to view, class 12th maths - continuity and differentiability ... click to view, class 12th maths - determinants case study questions and answers 2022 - 2023 click to view, class 12th maths - matrices case study questions and answers 2022 - 2023 click to view, class 12th maths - relations and functions ... click to view, test click to view, 12th standard cbse mathematics public model question paper iv 2019 - 2020 click to view, 12th standard cbse mathematics public model question paper iii 2019 - 2020 click to view, 12th standard cbse mathematics public model question paper ii 2019 - 2020 click to view, register & get the solution for class 12th maths - probability case study questions and answers 2022 - 2023.

• Bihar Board

RBSE Result 2024

Srm university.

• Goa Board Result 2024
• Maharashtra HSC Result
• Maharashtra SSC Result
• RBSE 10th Result 2024
• RBSE 12th Result 2024
• CBSE Board Result 2024
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 12

CBSE Class 12 Maths Exam 2024 Important Case Study Based Questions

Case study questions for class 12 maths: check here the important case study based questions of section e in the cbse class 12 maths exam 2024 for last minute preparation..

CBSE Class 12 Maths Exam 2024 Important Questions: The Central Board of Secondary Education is the largest and one of the most famed school boards in India, and lakhs of students are currently enrolled in it. The CBSE conducts the Class 12 board exams annually. The next paper is arguably the most important for science and commerce stream students: Maths on 9 March. Maths is essential for non-medical science and commerce aspirants and is also required in subjects like physics, statistics and accounts. CBSE Class 12 Maths requires extensive practice, especially important topics like Calculus and Algebra. There will be five sections in the 2024 CBSE Class 12 Maths exam, and the last section E will comprise two case study-based questions of 4 marks. These questions are quite important from the exam point of view, and you can check and practice the solved versions here.

CBSE Class 12   Maths   Unit Wise Marks Distribution 2024

CBSE Maths Previous Year Question Paper Class 12

CBSE Class 12 Maths Case Study Questions 2023

Q uestion 1:  Ramesh is   elder brother of Suresh. Ramesh wants to help his younger brother Suresh to solve the following problems of integrals. Write the suitable substitution by which Ramesh can help him.

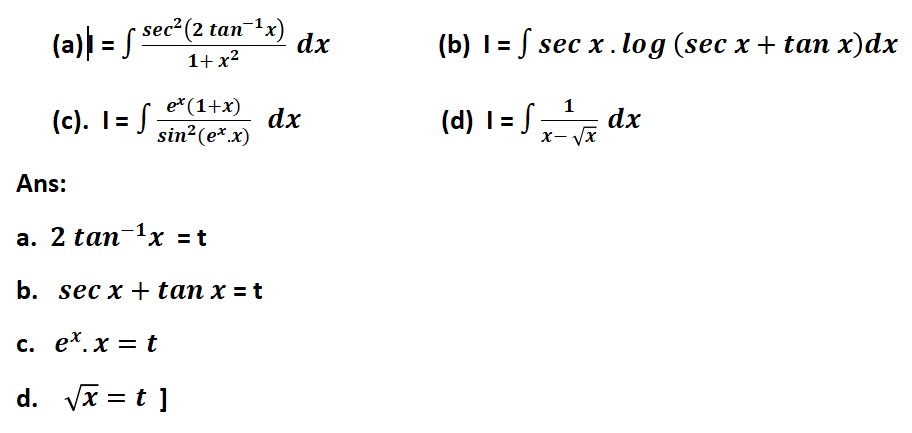
Question 2: Mr Shashi, who is an architect, designs a building for a small company. The design of window on the ground floor is proposed to be different than other floors. The window   is in the shape of a rectangle which is surmounted by a semi-circular opening. This window is having a perimeter of 10 m as shown below :

Based on the above information answer the following :

(i) If 2x and 2y represents the length and breadth of the rectangular portion of the windows, then the relation between the variables is:      

(ii) The combined area (A) of the rectangular region and semi-circular region of the window expressed as a function of x is:

(iii) The maximum value of area A, of the whole window is

The owner of this small company is interested in maximizing the area of the whole window so that maximum light input is possible.

For this to happen, the length of rectangular portion of the window should be

(i) 4y = 10 - (2 + π)x

(ii) A = 10x - (2 + 12π)x 2

(iii) 50/4 + π

20/4 + π  

Question 3:  Read the following and answer the questions given below 

The front gate of a building is in the shape of a trapezium as shown below. Its three sides other than base are of 10 m each. The height of the gate is h meter. On the basis of below figure, answer the following questions:

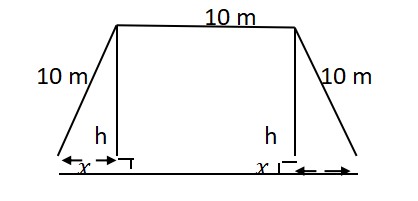
(i)  Write the Area (A) of the gate in terms of   .

(ii) Write the value of  when Area (A)  is maximum.

(iii) Write the value of h when Area (A) is maximum .

      Write the Maximum value of Area (A) .

(i) (10 + x)√100 - x 2

(iii) 5√3m OR 75√3/m.m2

Question 4 : Read the following and answer the questions given below 

Given three identical boxes 1 st,  2 nd  and 3 rd  each containing two coins. In 1 st  box both coins are gold coins, in 2 nd  box both are silver coins and in 3 rd  box there is one gold and one silver coin. A person chooses a box at random and takes out a coin.

On the basis of above information, answer the following questions:    

(i)   What is the probability of choosing 1 st  box  ?

(ii)  What is the probability of getting gold coin from 3 rd  box ?

(iii)  What is the total probability of drawing gold coin ?

       If drawn coin is of gold the probability that other coin in the box is also of gold?

(iii) 1/2  Or  2/3            

Question 5:  Read the following and answer the questions given below

Sand is pouring from a pipe at the rate of 12 cm 3 / second the falling sand forms a cone on the ground in such a way that the height of the cone is always 1/6 th of the radius of the base. Based on above information answer the following:

(i)  Write the expression for volume in terms of height only.

(ii)   What is the rate of Change of height, when height is 4 cm?

i)  12πh 3

(ii) 1/48 cm/s

Question 6: There are two antiaircraft guns, named as A and B. The probabilities that the shell fired from them hits an airplane are 0.3 and 0.2 respectively. Both of them fired one shell at an airplane at the same time.

(i) What is the probability that the shell fired from exactly one of them hit the plane?

(ii) If it is known that the shell fired from exactly one of them hit the plane, then what is the probability that it was fired from B?

• CBSE Class 12 Maths Deleted Syllabus 2023-24
• NCERT Solutions 12th Maths PDF

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• JAC 9th, 11th रिजल्ट 2024
• JAC 9th रिजल्ट 2024
• JAC Result 2024
• jac.jharkhand.gov.in 11th Result 2024
• JAC 11वीं रिजल्ट 2024 रोल नंबर
• GBSHSE SSC Result 2024
• SSC Result 2024 Goa
• CDS 2 Notification 2024
• results.gbshsegoa.net Result 2024
• CBSE 10th Result 2024
• CBSE Class 12 QnA

Latest Education News

UP Board Class 11 Syllabus 2024-25 OUT: Download Syllabus PDF for All Subject

JEE Advanced Complete Syllabus 2024 Released! Find Detailed Syllabus Chapter, Topics-wise & Download PDF

UPSC NDA Application Form 2024: यूपीएससी एमडीए परीक्षा के लिए रजिस्ट्रेशन शुरू, upsc.gov.in करें Apply

Vikram University Result 2024 Out: विक्रम यूनिवर्सिटी रिजल्ट vikramuniv.ac.in पर जारी, ये रहा Direct Link

Vikram University Result 2024 OUT at vikramuniv.ac.in: Direct Link to Download UG and PG Marksheet

[डायरेक्ट लिंक] jac.jharkhand.gov.in 9th, 11th Result 2024: झारखंड बोर्ड 9वीं और 11वीं का रिजल्ट jacresults.com पर घोषित, यहां Roll Number से तुुरंत करें चेक

भारत के 10 सबसे अधिक लोकसभा सीटों वाले राज्यों की सूची, पढ़ें

भारत में पंचवर्षीय योजनाओं की सूची, यहां पढ़ें

[LIVE] RBSE 10th, 12th Result 2024: बड़ी खबर! राजस्थान बोर्ड 10वीं, 12वीं रिजल्ट rajeduboard.rajasthan.gov.in पर जल्द, ये रहा Direct Link

Jharkhand Board 9th, 11th Result 2024 LIVE: जारी हुए झारखण्ड बोर्ड 9वीं, 11वीं रिजल्ट ऑनलाइन लिंक jac.jharkhand.gov.in, रोल नंबर, रोल कोड से मार्क शीट डाउनलोड करें

[रिजल्ट लिंक] JAC 9th Result 2024 OUT: कोडरमा जिला रहा अव्वल, jac.jharkhand.gov.in पर इस Link से तुरंत डाउनलोड करें अपनी Marksheet

CUET UG Exam Analysis 2024, May 17: Check Detailed Paper Review, Difficulty Level, and Good Attempts

JAC 11वीं रिजल्ट 2024 रोल नंबर: ऑफिसियल वेबसाइट jac.jharkhand.gov.in पर फटाफट देखें झारखण्ड बोर्ड 11वीं आर्ट्स, साइंस और कॉमर्स का रिजल्ट

Upcoming Government Jobs 2024 LIVE: Employment News May (11-17) 2024, Notifications, Admit Card, Exam Date, Result and much more

[लिंक एक्टिव] JAC 9th, 11th Result 2024 OUT: झारखंड बोर्ड के नतीजे 9वीं और 11वीं बोर्ड परीक्षा के नतीजे jacresults.com पर जारी

CHSE Odisha 12th Result 2024 Expected Soon, Check Latest Updates Here

[रिजल्ट लिंक] JAC Result 2024 LIVE: Jharkhand Board 9th and 11th Results Declared on jacresults.com, Check Marks Online by Roll Number, Roll Code

CUET UG Answer Key May 17, 2024: Download Set Wise Answer Sheet PDF

CMAT Exam Analysis 2024, Shift 1, 2: Check Paper Review, Difficulty Level, Questions Asked

UPSC EPFO Personal Assistant Syllabus 2024: PDF Download For Important Topics, Check Exam Pattern

Talk to our experts

1800-120-456-456

• Important Questions for CBSE Class 12 Maths Chapter 13 - Probability 2024-25

CBSE Class 12 Maths Chapter-13 Important Questions - Free PDF Download

Free PDF download of Important Questions for CBSE Class 12 Maths Chapter 13 - Probability prepared by expert Maths teachers from latest edition of CBSE(NCERT) books . Register online for Maths tuition on Vedantu.com to score more marks in CBSE board examination .

Download CBSE Class 12 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 12 Maths Important Questions for other chapters:

Related Chapters

Study Important Questions for Class 12 Mathematics Chapter 13 – Probability

Very Short Answer Question (1 Mark)

1. Find $P\left( {A}/{B}\; \right)$ if $P\left( A \right)=0.4$, $P\left( B \right)=0.8$ and $P\left( {B}/{A}\; \right)=0.6$.

Ans: It is given that,

$P\left( A \right)=0.4$

$P\left( B \right)=0.8$

$P\left( {B}/{A}\; \right)=0.6$

It is known that,

$P\left( {B}/{A}\; \right)=\frac{P\left( A\cap B \right)}{P\left( A \right)}$

$\Rightarrow P\left( A\cap B \right)=0.4\times 0.6=0.24$

$P\left( {A}/{B}\; \right)=\frac{P\left( A\cap B \right)}{P\left( B \right)}$

$\Rightarrow P\left( {A}/{B}\; \right)=\frac{0.24}{0.8}=0.3$

Therefore, $P\left( {A}/{B}\; \right)=0.3$

2. Find $P\left( A\cap B \right)$ if $A$ and $B$ are two events such that $P\left( A \right)=0.5$, $P\left( B \right)=0.6$ and $P\left( A\cup B \right)=0.8$.

$P\left( A \right)=0.5$

$P\left( B \right)=0.6$

$P\left( A\cup B \right)=0.8$

$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ 

$\Rightarrow 0.8=0.5+0.6-P\left( A\cap B \right)$

$\Rightarrow P\left( A\cap B \right)=1.1-0.8=0.3$

Therefore, $P\left( A\cap B \right)=0.3$

3. A soldier fires three bullets at the enemy. The probability that the enemy will be killed by one bullet is $0.7$. What is the probability that the enemy is still alive?

Probability that the enemy will be killed by one bullet is $0.7$

Probability that the enemy will be alive after one bullet is fired $=1-0.7=0.3$

Probability that the enemy is still alive after three bullets is fired$=0.3\times 0.3\times 0.3=0.027$ 

Therefore, the probability that the enemy is still alive is $0.027$.

4. What is the probability that a leap year has $53$ Sundays?

Ans: It is known that a leap year has $366$ days.

It means that there are $52$ weeks and $2$ extra days.

The $52$ weeks have $52$ Sundays.

The possibilities for two extra days are  $\left\{ Monday,Tuesday \right\}$, $\left\{ Tuesday,Wednesday \right\}$, $\left\{ Wednesday,Thursday \right\}$, $\left\{ Thursday,Friday \right\}$, $\left\{ Friday,Saturday \right\}$, $\left\{ Saturday,Sunday \right\}$and $\left\{ Saturday,Sunday \right\}$

The possibility of having Sunday in the other days is $\left\{ Saturday,Sunday \right\}$ and$\left\{ Saturday,Sunday \right\}$

The number of favourable outcomes will be $2$ 

Total number of outcomes is $7$ 

Probability of an event $A$: $P\left( A \right)=\frac{Favourable\text{ }Outcomes}{\text{Total }Outcomes}$ 

$\Rightarrow P\left( A \right)=\frac{2}{7}$ 

Probability that a leap year has $53$ Sundays is $\frac{2}{7}$ .

5. $20$ cards are numbered $1$ to $20$. One card is drawn at random. What is the probability that the number on the card will be a multiple of $4$?

Sample space, $S=1,2,3,.........,20$ 

Total number of outcomes in the sample space, $n\left( S \right)=20$

Let $A$ be the event of getting multiple of $4$,$A=4,8,12,16,20$ 

Total number of favourable outcomes, $n\left( A \right)=5$

Probability of an event $A$: $P\left( A \right)=\frac{n\left( A \right)}{n\left( S \right)}$ 

$\Rightarrow P\left( A \right)=\frac{5}{20}=0.25$ 

The probability that the number on the card will be a multiple of $4$is $0.25$.

6. Three coins are tossed once. Find the probability of getting at least one head.

Ans: Sample space, $S=\left\{ HHH,HHT,HTH,THH,HTT,THT,TTH,TTT \right\}$ 

Total number of outcomes in the sample space, $n\left( S \right)=8$

Let $A$ be the event of getting at least one head,$A=\left\{ HHH,HHT,HTH,THH,HTT,THT,TTH \right\}$ 

Total number of favourable outcomes, $n\left( A \right)=7$

$\Rightarrow P\left( A \right)=\frac{7}{8}$ 

Therefore, the probability of getting at least one head is $\frac{7}{8}$.

7. The probability that a student is not a swimmer is $\frac{1}{5}$. Find the probability that out of $5$ students, $4$ are swimmers.

The probability that a student is not a swimmer $=\frac{1}{5}$

The probability that a student is a swimmer $=1-\frac{1}{5}=\frac{4}{5}$

Probability that out of $5$ students, $4$ are swimmers:

From Binomial distribution:$P\left( X=x \right)={}^{n}{{C}_{x}}{{p}^{x}}{{q}^{n-x}}$ 

Here, $x=4$, $n=5$, $p=\frac{4}{5}$ and $q=\frac{1}{5}$ 

$\Rightarrow P\left( X=4 \right)={}^{5}{{C}_{4}}{{\left( \frac{4}{5} \right)}^{4}}{{\left( \frac{1}{5} \right)}^{5-4}}$ 

$\Rightarrow P\left( X=4 \right)=\frac{5!}{4!\left( 5-4 \right)!}{{\left( \frac{4}{5} \right)}^{4}}{{\left( \frac{1}{5} \right)}^{1}}$

$\Rightarrow P\left( X=4 \right)=5{{\left( \frac{4}{5} \right)}^{4}}\left( \frac{1}{5} \right)$

$\Rightarrow P\left( X=4 \right)={{\left( \frac{4}{5} \right)}^{4}}$

The probability that out of $5$ students, $4$ are swimmers is ${{\left( \frac{4}{5} \right)}^{4}}$.

8. Find $P\left( {A}/{B}\; \right)$ if $P\left( B \right)=0.5$ and $P\left( A\cap B \right)=0.32$.

$P\left( B \right)=0.5$

$P\left( A\cap B \right)=0.32$

$\Rightarrow P\left( {A}/{B}\; \right)=\frac{P\left( A\cap B \right)}{P\left( B \right)}$

$\Rightarrow P\left( {A}/{B}\; \right)=\frac{0.32}{0.50}=\frac{16}{25}$

Therefore, $P\left( {A}/{B}\; \right)=\frac{16}{25}$

9. A random variable $X$ has the following probability distribution.

Find the value of $k$.

Ans: It is known that the sum of all the probabilities of a random variable is equal to $1$ i.e. $\sum{P\left( X \right)=1}$.

$\Rightarrow \frac{1}{15}\times 0+k\times 1+\frac{15k-2}{15}\times 2+k\times 3+\frac{15k-1}{15}\times 4+\frac{1}{15}\times 5=1$ 

$\Rightarrow 9k-\frac{3}{15}=1$

$\Rightarrow 4k=1+\frac{1}{15}$

$\Rightarrow 4k=\frac{16}{15}$

$\Rightarrow k=\frac{4}{15}$

10. A random variable $X$ taking values $0$, $1$, $2$ has the following probability distribution for some number $k$.

P(X)=\begin{cases}k &if & X = 0\\2k &if & X = 1,find &k.\\3k &if & X = 2\end{cases}

Ans: It is known that the sum of probabilities of a random variable is equal to $1$.

$\Rightarrow k+2k+3k=1$ 

$\Rightarrow 6k=1$ 

$\Rightarrow k=\frac{1}{6}$ 

Therefore, the value of $k$ is $\frac{1}{6}$.

Long Answer Questions (4 Marks)

11. A problem in Mathematics is given to three students whose chance of solving it are $\frac{1}{2}$, $\frac{1}{3}$ and $\frac{1}{4}$. What is the probability that the problem is solved?

Ans: Let $A,B,C$ be the events of solving the problem.

$\bar{A},\bar{B},\bar{C}$ be the event  of not solving the problem.

It is known that, $\bar{A},\bar{B},\bar{C}$ are independent events.

From the given data,

$P\left( A \right)=\frac{1}{2}\Rightarrow P\left( {\bar{A}} \right)=\frac{1}{2}$ 

$P\left( B \right)=\frac{1}{3}\Rightarrow P\left( {\bar{B}} \right)=\frac{2}{3}$

\[P\left( C \right)=\frac{1}{4}\Rightarrow P\left( {\bar{C}} \right)=\frac{3}{4}\]

$P\left( None\text{ }solving\text{ }the\text{ }problem \right)=P(\bar{A}\text{ }and\text{ }\bar{B}\text{ }and\text{ }\bar{C})$

$\Rightarrow P(None\text{ }solving\text{ }the\text{ }problem)=P(\bar{A}\cap \bar{B}\cap \bar{C})$ 

$\Rightarrow P(None\text{ }solving\text{ }the\text{ }problem)=P(\bar{A})P(\bar{B})P(\bar{C})$

$\Rightarrow P(None\text{ }solving\text{ }the\text{ }problem)=\frac{1}{2}\times \frac{2}{3}\times \frac{3}{4}=\frac{1}{4}$

$P(The\text{ problem will b}e\text{ solved})=1-P(None\text{ }solving\text{ }the\text{ }problem)$ 

$P(The\text{ problem will b}e\text{ solved})=1-\frac{1}{4}=\frac{3}{4}$

Therefore, the probability that the problem is solved is $\frac{3}{4}$.

12. A die is rolled. If the outcome is an even number, what is the probability that it is a prime?

Ans: Sample space when a die is rolled, $S=\left\{ 1,2,3,4,5,6 \right\}$ 

Let $A$ be the event of getting an even number.

Let $B$ be the event of getting a prime number.

$A=\left\{ 1,3,5 \right\}$ $B=\left\{ 2,3,5 \right\}$ $A\cap B=\left\{ 3,5 \right\}$ 

Conditional probability, $P\left( {B}/{A}\; \right)=\frac{P\left( A\cap B \right)}{P\left( A \right)}$ 

$\Rightarrow P\left( {B}/{A}\; \right)=\frac{\frac{2}{6}}{\frac{3}{6}}=\frac{2}{3}$

Therefore, when a die is rolled if the outcome is an even number the probability that it is prime is $\frac{2}{3}$.

13. If $A$ and $B$ are two events such that $P\left( A \right)=\frac{1}{4}$, $P\left( B \right)=\frac{1}{2}$ and $P\left( A\cap B \right)=\frac{1}{8}$. Find $P$(not $A$ and not $B$).

Ans: Given,

$P\left( A \right)=\frac{1}{4}$

$P\left( B \right)=\frac{1}{2}$

$P\left( A\cap B \right)=\frac{1}{8}$

\[P\left( not~A~\And \text{ n}ot~\text{B} \right)=P\left( A'\cap B' \right)\] 

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=P\left( A\cup B \right)'\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=1-P\left( A\cup B \right)\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=1-\left[ P\left( A \right)+P\left( B \right)-P\left( A\cap B \right) \right]\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=1-\left[ \frac{1}{4}+\frac{1}{2}-\frac{1}{8} \right]\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=1-\left[ \frac{2}{8}+\frac{4}{8}-\frac{1}{8} \right]\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=1-\frac{5}{8}\]

\[\Rightarrow P\left( not~A~\And \text{ n}ot~\text{B} \right)=\frac{3}{8}\]

Therefore, \[P\left( not~A~\And \text{ n}ot~\text{B} \right)=\frac{3}{8}\]

14. In a class of $25$ students with roll numbers $1$ to $25$, a student is picked up at random to answer a question. Find the probability that the roll number of the selected student is either a multiple of $5$ or of $7$.

Ans: Sample space, $S=\left\{ 1,2,3,4,........25 \right\}$

Total number of outcomes in the sample space, $n\left( S \right)=25$

Let $A$ be the event that the roll number of selected student is either a multiple of $5$ or of $7$,$A=\left\{ 5,7,10,14,15,20,21,25 \right\}$ 

Total number of favourable outcomes, $n\left( A \right)=8$

$\Rightarrow P\left( A \right)=\frac{8}{25}$ 

Therefore, the probability that the roll number of the selected student is either a multiple of $5$ or of $7$is $\frac{8}{25}$.

15. A can hit a target $4$ times in $5$ shots $B$ three times in $4$ shots and $C$ twice in $3$ shots. They fire a volley. What is the probability that at least two shots hit.

Ans: Fire a volley means that $A$, $B$ and $C$ all try to hit the target simultaneously.

At least two shots hit the target:

$A$ and $B$ hit and $C$ fails to hit.

$A$ and $C$ hit and $B$ fails to hit.

$B$ and $C$ hit and $A$ fails to hit.

$A$, $B$ ,$C$ all three hit the target.

The chance of hitting by $A,P\left( A \right)=\frac{4}{5}$ and of not hitting by $A,P\left( A' \right)=1-\frac{4}{5}=\frac{1}{5}$

The chance of hitting by $B,P\left( B \right)=\frac{3}{4}$ and of not hitting by $B,P\left( B' \right)=1-\frac{3}{4}=\frac{1}{4}$

The chance of hitting by $C,P\left( C \right)=\frac{2}{3}$ and of not hitting by $C,P\left( C' \right)=1-\frac{2}{3}=\frac{1}{3}$

Probability of $\left( I \right)$ is $P\left( ABC' \right)=\frac{4}{5}\times \frac{3}{4}\times \frac{1}{3}=\frac{1}{5}$ 

Probability of $\left( II \right)$ is $P\left( ACB' \right)=\frac{4}{5}\times \frac{2}{3}\times \frac{1}{4}=\frac{2}{15}$ 

Probability of $\left( III \right)$ is $P\left( BC'A \right)=\frac{3}{4}\times \frac{2}{3}\times \frac{1}{5}=\frac{1}{10}$

Probability of $\left( IV \right)$ is $P\left( ABC \right)=\frac{4}{5}\times \frac{3}{4}\times \frac{2}{3}=\frac{2}{5}$

$Total\text{ }probability=\frac{1}{5}+\frac{2}{15}+\frac{1}{10}+\frac{2}{5}$  

$Total\text{ }probability=\frac{6}{30}+\frac{4}{30}+\frac{3}{30}+\frac{12}{30}$

$Total\text{ }probability=\frac{25}{30}=\frac{5}{6}$

Therefore, the probability that at least two shots hit the target is $\frac{5}{6}$.

16. Two dice are thrown once. Find the probability of getting an even number on the first die or a total of $8$ .

Ans: Sample space, $S=\left\{ 1,2,3,4,........36 \right\}$

Total number of outcomes in the sample space, $n\left( S \right)=36$

Let $A$ be the event of getting even number on the first die$A=\left\{ \left( 2,1 \right),\left( 2,2 \right),...,\left( 2,6 \right),\left( 4,1 \right),\left( 4,2 \right),...,\left( 4,6 \right),\left( 6,1 \right),\left( 6,2 \right),...,\left( 6,6 \right) \right\}$ 

Total number of favourable outcomes, $n\left( A \right)=18$

Let $B$ be the event of getting a total of $8$, $B=\left\{ \left( 2,6 \right),\left( 3,5 \right),\left( 4,4 \right),\left( 5,3 \right),\left( 6,2 \right) \right\}$ 

Total number of favourable outcomes, $n\left( B \right)=5$

Let $A\cap B$ be the event of getting an even number on first die and a total of $8$,$A\cap B=\left\{ \left( 2,6 \right),\left( 4,4 \right),\left( 6,2 \right) \right\}$ 

Total number of favourable outcomes, $n\left( A\cap B \right)=3$

Probability of an event $A$: $P\left( A \right)=\frac{n\left( A \right)}{n\left( S \right)}=\frac{18}{36}$ 

Probability of an event $B$: $P\left( A \right)=\frac{n\left( B \right)}{n\left( S \right)}=\frac{5}{36}$ 

Probability of an event $A\cap B$: $P\left( A\cap B \right)=\frac{n\left( A\cap B \right)}{n\left( S \right)}=\frac{3}{36}$ 

$P\left( A\cup B \right)=\frac{18}{36}+\frac{5}{36}-\frac{3}{36}$

$P\left( A\cup B \right)=\frac{20}{36}=\frac{5}{9}$

Therefore, the probability of getting an even number on the first die or a total of $8$ is $\frac{5}{9}$.

17. $A$ and $B$ throw a die alternatively till one of them throws a $'6'$ and wins the game. Find their respective probabilities of winning, if $A$ starts the game.

Ans: Let $S$ be the success of getting $6$ and $F$ be the failure of not getting $6$.

$\Rightarrow P\left( S \right)=p=\frac{1}{6}$ 

$\Rightarrow P\left( F \right)=q=\frac{5}{6}$

\[P\left( A\text{ }wins\text{ }in\text{ }first\text{ }throw \right)=P\left( S \right)=p\] 

\[P\left( A\text{ }wins\text{ }in\text{ third }throw \right)=P\left( FFS \right)=qqp\]

\[P\left( A\text{ }wins\text{ }in\text{ fifth }throw \right)=P\left( FFFFS \right)=qqqqp\]

\[P\left( A\text{ }wins \right)=p+qqp+qqqqp+......\]

\[\Rightarrow P\left( A\text{ }wins \right)=p\left( 1+{{q}^{2}}+{{q}^{4}}+...... \right)\]

\[\Rightarrow P\left( A\text{ }wins \right)=\frac{p}{1-{{q}^{2}}}\]

\[\Rightarrow P\left( A\text{ }wins \right)=\frac{\frac{1}{6}}{1-\frac{25}{36}}=\frac{36}{6\times 11}=\frac{6}{11}\] 

\[P\left( \text{B }wins \right)=1-P\left( \text{A }wins \right)\]

\[P\left( \text{B }wins \right)=1-\frac{6}{11}=\frac{5}{11}\]

Therefore, \[P\left( \text{A }wins \right)=\frac{6}{11}\]and \[P\left( \text{B }wins \right)=\frac{5}{11}\].

18. If $A$and $B$ are events such that $P\left( A \right)=\frac{1}{2}$ , $P\left( A\bigcup B \right)=\frac{3}{5}$ and $P\left( B \right)=p$ find p if events are

a. mutually exclusive

Ans: It is given that, 

$P\left( A \right)=\frac{1}{2}$

 $P\left( B \right)=p$ 

$P\left( A\cup B \right)=\frac{3}{5}$

It is known that, if two events $A$ and $B$ are mutually exclusive then$P\left( A\cap B \right)=0$.

$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$

$\Rightarrow \frac{3}{5}=\frac{1}{2}+p-0$

$\Rightarrow p=\frac{3}{5}-\frac{1}{2}$

$\Rightarrow p=\frac{1}{10}$

Therefore, the value of $p$ is $\frac{1}{10}$.

b. independent

 $P\left( A \right)=\frac{1}{2}$

 $P\left( B \right)=p$

 $P\left( A\cup B \right)=\frac{3}{5}$

We know that if two events $A$ and $B$ are independent then $P\left( A\cap B \right)=P\left( A \right)P\left( B \right)$

$\Rightarrow \frac{3}{5}=\frac{1}{2}+p-\frac{p}{2}$ $\left[ P\left( A \right)P\left( B \right)=\frac{p}{2} \right]$

$\Rightarrow \frac{p}{2}=\frac{3}{5}-\frac{1}{2}$

$\Rightarrow p=\frac{2}{10}=\frac{1}{5}$

Therefore, the value of $p$ is $\frac{1}{5}$.

19. A man takes a step forward with probability $0.4$ and backward with probability $0.6$ . Find the probability that at the end of eleven steps he is one step away from the starting point.

Ans: Let, a step forward be the success $S$ and a step backward be the failure $F$ .

$\Rightarrow P\left( S \right)=p=0.4$ 

$\Rightarrow P\left( F \right)=q=0.6$

In eleven steps he will be one step away from the starting point if the number of successes and failures differ by $1$.

Therefore there are two chances i.e,

Number of successes$=6$ 

Number of failures$=5$ OR

Number of successes$=5$ 

Number of failures$=6$

Required probability$={}^{11}{{C}_{6}}{{p}^{6}}{{q}^{5}}+{}^{11}{{C}_{5}}{{p}^{5}}{{q}^{6}}$ 

$\Rightarrow \frac{11!}{6!5!}{{\left( 0.4 \right)}^{6}}{{\left( 0.6 \right)}^{5}}+\frac{11!}{6!5!}{{\left( 0.4 \right)}^{5}}{{\left( 0.6 \right)}^{6}}$

$\Rightarrow \frac{11!}{6!5!}{{\left( 0.4 \right)}^{5}}{{\left( 0.6 \right)}^{5}}\left[ 0.4+0.5 \right]$

$\Rightarrow \frac{11\times 10\times 9\times 8\times 7}{5\times 4\times 3\times 2\times 1}{{\left( 0.4 \right)}^{5}}{{\left( 0.6 \right)}^{5}}\left( 1 \right)=0.3678$

20. Two cards are drawn from a pack of well shuffled $52$ cards one by one with replacement. Getting an ace or a spade is considered a success. Find the probability distribution for the number of successes.

Ans: Let $A$ be the event of a number of aces and spades.

$\Rightarrow n(A)=16$ 

Number of outcomes in sample space,$n(S)=52$ 

Probability of picking an Ace or a spade, $P(A)=\frac{4}{13}$ 

Probability of not picking an Ace or a spade, $P(A')=1-\frac{4}{13}=\frac{9}{13}$ 

Let $X$ be the event of number of aces or spades

When $X=0$ 

$P\left( X=0 \right)=P(A')\times P(A')$ 

$\Rightarrow P\left( X=0 \right)=\frac{9}{13}\times \frac{9}{13}=\frac{81}{169}$

When $X=1$ 

$P\left( X=1 \right)=P(A)\times P(A')$ 

$\Rightarrow P\left( X=1 \right)=\frac{4}{13}\times \frac{9}{13}=\frac{36}{169}$

When $X=2$ 

$P\left( X=2 \right)=P(A)\times P(A)$ 

$\Rightarrow P\left( X=0 \right)=\frac{4}{13}\times \frac{4}{13}=\frac{16}{169}$

Therefore, the probability distribution for the number of successes is:

21. In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/losses.

Ans: The following cases will be obtained from the given scenario:

Man gets $6$in the first throw

Man doesn’t get $6$ in the first throw, gets $6$ in the second throw

Man doesn’t get $6$ in the first and second throws, gets $6$ in the third throw

Man doesn’t get $6$ in the first, second and third throws

Case I: Man gets $6$in the first throw

Probability of getting $6$$=\frac{1}{6}$ 

Amount won$=1$ 

Case II: Man doesn’t get $6$ in the first throw, gets $6$ in the second throw

Probability of getting $6$$=\frac{5}{6}\times \frac{1}{6}=\frac{5}{36}$ 

Amount won$=-1+1=0$ 

Case III: Man doesn’t get $6$ in the first and second throws, gets $6$ in the third throw

Probability of getting $6$$=\frac{5}{6}\times \frac{5}{6}\times \frac{1}{6}=\frac{25}{216}$ 

Amount won$=-1-1+1=-1$ 

Case IV: Man doesn’t get $6$ in the first, second and third throws

Probability of getting $6$$=\frac{5}{6}\times \frac{5}{6}\times \frac{5}{6}=\frac{125}{216}$ 

Amount won$=-1-1-1=-3$ 

\[Expected\text{ }value=Amount\text{ }won\text{ }\times \text{ }Probability\text{ }for\text{ }all\text{ }four\text{ }throws\] 

\[Expected\text{ }value=\left( 1\times \frac{1}{6} \right)+\left( 0\times \frac{5}{36} \right)+\left( -1\times \frac{25}{216} \right)+\left( -3\times \frac{125}{216} \right)\]

\[Expected\text{ }value=\frac{1}{6}+0-\frac{25}{216}-\frac{125}{216}\]

\[Expected\text{ }value=\frac{36-25-125}{216}\]

\[Expected\text{ }value=\frac{36-400}{216}\]

\[Expected\text{ }value=\frac{-364}{216}=\frac{-91}{54}\]

Therefore, the expected value of the amount he wins or loses is $\frac{-91}{54}$.

22. Suppose that $10\%$ of men and $5\%$ women have grey hair. A grey haired person is selected at random. What is the probability that the selected person is male assuming that there are $60\%$ males and $40\%$  females?

Ans: Let $A$ be the event that the person selected has grey hair

Let ${{E}_{1}}$ be the event that the person selected is male

Let ${{E}_{2}}$ be the event that the person selected is female

$\Rightarrow P\left( {{E}_{1}} \right)=\frac{60}{100}=\frac{3}{5}$ 

$\Rightarrow P\left( {{E}_{2}} \right)=\frac{40}{100}=\frac{2}{5}$

Probability that the selected is male with grey hair:$P\left( {A}/{{{E}_{1}}}\; \right)=\frac{10}{100}=\frac{1}{10}$ 

Probability that the selected is male with grey hair:$P\left( {A}/{{{E}_{2}}}\; \right)=\frac{5}{100}=\frac{1}{20}$ 

From Bayes theorem:\[P\left( {{{E}_{1}}}/{A}\; \right)=\frac{P({{E}_{1}})P\left( {A}/{{{E}_{1}}}\; \right)}{P({{E}_{1}})P\left( {A}/{{{E}_{1}}}\; \right)+P({{E}_{2}})P\left( {A}/{{{E}_{2}}}\; \right)}\] 

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{3}{5}\times \frac{1}{10}}{\frac{3}{5}\times \frac{1}{10}+\frac{2}{5}\times \frac{1}{20}}\] 

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{3}{3+1}=\frac{3}{4}\]

Therefore, the probability that the selected person is male is $\frac{3}{4}$.

23. A card from a pack of $52$ cards are lost. From the remaining cards of the pack, two cards are drawn. What is the probability that they both are diamonds?

Ans: Let ${{E}_{1}}$ be the event that the lost cad is diamond

In a pack of $52$ there are $13$ diamonds$\Rightarrow P({{E}_{1}})=\frac{13}{52}=\frac{1}{4}$ 

Let ${{E}_{2}}$ be the event that the lost cad is not a diamond

$\Rightarrow P({{E}_{2}})=1-P({{E}_{1}})=1-\frac{1}{4}=\frac{3}{4}$ 

Let $A$ be the event that the two cards drawn are both diamonds

Number of ways of drawing 2 diamond cards

\[\Rightarrow P\left( {A}/{{{E}_{1}}}\; \right)=\frac{Number\text{ }of\text{ }ways\text{ }of\text{ }drawing\text{ }2\text{ }diamond\text{ }cards}{Total\text{ }Number\text{ }of\text{ }ways\text{ }of\text{ }drawing\text{ }2\text{ }cards}\]

$\Rightarrow P\left( {A}/{{{E}_{1}}}\; \right)=\frac{{}^{12}{{C}_{2}}}{{}^{51}{{C}_{2}}}=\frac{66}{1275}$ 

$\Rightarrow P\left( {A}/{{{E}_{2}}}\; \right)=\frac{{}^{13}{{C}_{2}}}{{}^{51}{{C}_{2}}}=\frac{78}{1275}$

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{66}{1275}\times \frac{1}{4}}{\frac{66}{1275}\times \frac{1}{4}+\frac{78}{1275}\times \frac{3}{4}}=\frac{66}{66+224}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{66}{1275}\times \frac{1}{4}}{\frac{66}{1275}\times \frac{1}{4}+\frac{78}{1275}\times \frac{3}{4}}=\frac{66}{66+234}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{66}{300}=\frac{11}{50}\]

Therefore, the probability that they both are diamonds is $\frac{11}{50}$.

24. Ten eggs are drawn successively with replacement from a lot containing $10\%$  defective eggs. Find the probability that there is at least one defective egg.

Probability of defective eggs$=10%$ 

$\Rightarrow p=\frac{10}{100}=\frac{1}{10}$ 

Probability of good eggs$=q$ 

$\Rightarrow q=1-\frac{1}{10}=\frac{9}{10}$ 

Probability that at least one egg is defective out of $=p(1)+p(2)+p(3)+.......$ 

$\Rightarrow \left[ p(0)+p(1)+p(2)+.....+p(10) \right]-p(0)$

$\Rightarrow 1-p(0)=1-{{\left( \frac{9}{10} \right)}^{10}}$ 

Therefore, the probability that there is at least one defective egg is $1-{{\left( \frac{9}{10} \right)}^{10}}$.

25. Find the variance of the number obtained on a throw of an unbiased die.

Ans: Let the number obtained on an unbiased die is $X$.

The probability of getting each number is equal in an unbiased die. Here, it is $\frac{1}{6}$

Probability distribution in an unbiased die:

Mean Expectation value is $E(X)=\sum\limits_{i=1}^{n}{{{x}_{i}}{{p}_{i}}}$ 

$\Rightarrow E(X)=1\times \frac{1}{6}+2\times \frac{1}{6}+3\times \frac{1}{6}+4\times \frac{1}{6}+5\times \frac{1}{6}+6\times \frac{1}{6}$

$\Rightarrow E(X)=\frac{21}{6}$

Variance: $Var(X)=E\left( {{X}^{2}} \right)-{{\left[ E\left( X \right) \right]}^{2}}$ 

$E({{X}^{2}})=\sum\limits_{i=1}^{n}{{{x}_{i}}^{2}{{p}_{i}}}$

$\Rightarrow E({{X}^{2}})={{1}^{2}}\times \frac{1}{6}+{{2}^{2}}\times \frac{1}{6}+{{3}^{2}}\times \frac{1}{6}+{{4}^{2}}\times \frac{1}{6}+{{5}^{2}}\times \frac{1}{6}+{{6}^{2}}\times \frac{1}{6}$

$\Rightarrow E({{X}^{2}})=\frac{1+4+9+16+25+36}{6}$

\[\Rightarrow E({{X}^{2}})=\frac{91}{6}\]

$Var(X)=E\left( {{X}^{2}} \right)-{{\left[ E\left( X \right) \right]}^{2}}$

$\Rightarrow Var(X)=\frac{91}{6}-{{\left[ \frac{21}{6} \right]}^{2}}$

$\Rightarrow Var(X)=\frac{91}{6}-\frac{441}{36}$

$\Rightarrow Var(X)=\frac{546-441}{36}=\frac{105}{36}$

$\Rightarrow Var(X)=\frac{35}{12}$

Therefore, the variance of the number obtained on a throw of an unbiased die is $\frac{35}{12}$.

Long Answer Questions (6 Marks)

26. In a hurdle race, a player has to cross $8$ hurdles. The probability that he will clear a hurdle is $\frac{4}{5}$, what is the probability that he will knock down in fewer than $2$  hurdles?

Ans: Let $X$ be the event of a number of hurdles that the player knocks down.

From Binomial distribution,

$P\left( X=x \right)={}^{n}{{C}_{x}}{{q}^{n-x}}{{p}^{x}}$ 

It is given that,

Number of hurdles, $n=8$ 

Probability that he will clear the hurdle, $q=\frac{4}{5}$ 

Probability that he will not clear the hurdle, $p=1-\frac{4}{5}=\frac{1}{5}$

$P\left( X=x \right)={}^{8}{{C}_{x}}{{\left( \frac{4}{5} \right)}^{8-x}}{{\left( \frac{1}{5} \right)}^{x}}$

Probability that he will knock down fewer than $2$ hurdles:

$\Pr obability=P\left( Knock\text{ }0\text{ }hurdles \right)+P\left( Knock\text{ 1 }hurdles \right)$ 

$\Rightarrow \Pr obability=P\left( X=0 \right)+P\left( X=1 \right)$

$\Rightarrow \Pr obability={}^{8}{{C}_{0}}{{\left( \frac{4}{5} \right)}^{8-0}}{{\left( \frac{1}{5} \right)}^{0}}+{}^{8}{{C}_{1}}{{\left( \frac{4}{5} \right)}^{8-1}}{{\left( \frac{1}{5} \right)}^{1}}$

$\Rightarrow \Pr obability=1\times {{\left( \frac{4}{5} \right)}^{8}}\times 1+8\times {{\left( \frac{4}{5} \right)}^{7}}\times \left( \frac{1}{5} \right)$

$\Rightarrow \Pr obability={{\left( \frac{4}{5} \right)}^{7}}\left[ \left( \frac{4}{5} \right)+8\times \left( \frac{1}{5} \right) \right]$

$\Rightarrow \Pr obability={{\left( \frac{4}{5} \right)}^{7}}\left[ \frac{12}{5} \right]$

Therefore, the probability that he will knock down in fewer than $2$  hurdles is $\frac{12}{5}{{\left( \frac{4}{5} \right)}^{7}}$.

27. Bag $A$ contains $4$ red, $3$ white and $2$ black balls. Bag $B$ contains $3$ red, $2$ white and $3$ black balls. One ball is transferred from bag $A$ to bag $B$  and then a ball is drawn from bag $B$. The ball so drawn is found to be red. Find the probability that the transferred ball is black.

Ans: Consider the following notations:

${{A}_{1}}$ : One red ball is transferred from bag $A$ to bag $B$ 

${{A}_{2}}$ : One white ball is transferred from bag $A$ to bag $B$

${{A}_{3}}$ : One black ball is transferred from bag $A$ to bag $B$

$E$ : Drawing a red ball from bag $B$

\[P\left( {{A}_{1}} \right)=\frac{Number\text{ }of\text{ }red\text{ }balls\text{ }in\text{ }bag\text{ }A}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ }A}\] 

\[\Rightarrow P\left( {{A}_{1}} \right)=\frac{4}{4+3+2}=\frac{4}{9}\]

\[P\left( {{A}_{2}} \right)=\frac{Number\text{ }of\text{ white }balls\text{ }in\text{ }bag\text{ A}}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ }A}\] 

\[\Rightarrow P\left( {{A}_{2}} \right)=\frac{3}{4+3+2}=\frac{3}{9}\]

\[P\left( {{A}_{3}} \right)=\frac{Number\text{ }of\text{ black }balls\text{ }in\text{ }bag\text{ A}}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ }A}\] 

\[\Rightarrow P\left( {{A}_{3}} \right)=\frac{3}{4+3+2}=\frac{2}{9}\]

If event ${{A}_{1}}$ occurs, number of red balls in bag $B$ $=(3+1)=4$ 

Total number of balls in bag $B=(3+2+3)+1=9$

$P\left( {E}/{{{A}_{1}}}\; \right)=\frac{Number\text{ }of\text{ red }balls\text{ }in\text{ }bag\text{ B}}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ B}}$ 

$\Rightarrow P\left( {E}/{{{A}_{1}}}\; \right)=\frac{4}{9}$

If event ${{A}_{2}}$ occurs, number of red balls in bag $B$ $=3$ 

$P\left( {E}/{{{A}_{2}}}\; \right)=\frac{Number\text{ }of\text{ black }balls\text{ }in\text{ }bag\text{ B}}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ B}}$ 

$\Rightarrow P\left( {E}/{{{A}_{2}}}\; \right)=\frac{3}{9}$

If event ${{A}_{3}}$ occurs, number of red balls in bag $B$ $=3$ 

$P\left( {E}/{{{A}_{3}}}\; \right)=\frac{Number\text{ }of\text{ black }balls\text{ }in\text{ }bag\text{ B}}{Total\text{ }number\text{ }of\text{ }balls\text{ }in\text{ }bag\text{ B}}$ 

$\Rightarrow P\left( {E}/{{{A}_{3}}}\; \right)=\frac{3}{9}$

From Bayes theorem: \[P\left( {{{A}_{3}}}/{E}\; \right)=\frac{P({{A}_{3}})P\left( {E}/{{{A}_{3}}}\; \right)}{P({{A}_{1}})P\left( {E}/{{{A}_{1}}}\; \right)+P({{A}_{2}})P\left( {E}/{{{A}_{2}}}\; \right)+P({{A}_{3}})P\left( {E}/{{{A}_{3}}}\; \right)}\] 

\[\Rightarrow P\left( {{{A}_{3}}}/{E}\; \right)=\frac{\frac{2}{9}\times \frac{3}{9}}{\frac{4}{9}\times \frac{4}{9}+\frac{3}{9}\times \frac{3}{9}+\frac{2}{9}\times \frac{3}{9}}\]

\[\Rightarrow P\left( {{{A}_{3}}}/{E}\; \right)=\frac{6}{16+9+6}=\frac{6}{31}\]

28. If a fair coin is tossed $10$ times, find the probability of getting.

a. exactly six heads, 

Ans: Let $X$ be the number of heads obtained.

Number of tosses, $n=10$ 

Probability of head, $p=\frac{1}{2}$ 

Probability of no getting head,$q=1-p=\frac{1}{2}$ 

From binomial distribution: $P\left( X=x \right)={}^{n}{{C}_{x}}{{q}^{n-x}}{{p}^{x}}$ 

Here, $x=6$ 

\[\Rightarrow P\left( X=6 \right)={}^{10}{{C}_{6}}{{\left( \frac{1}{2} \right)}^{10-6}}{{\left( \frac{1}{2} \right)}^{6}}\] 

$\Rightarrow P\left( X=6 \right)=\frac{10!}{\left( 10-6 \right)!6!}{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P\left( X=6 \right)=\frac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P\left( X=6 \right)=\frac{105}{512}$

b. at least six heads,

Ans: At least six heads means that$\Rightarrow P(x\ge 6)$ 

$P(x\ge 6)=P(x=6)+P(x=7)+P(x=8)+P(x=9)+P(x=10)$ 

$\Rightarrow P(x\ge 6)={}^{10}{{C}_{6}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{7}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{8}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{9}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{10}}{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\ge 6)=\left[ {}^{10}{{C}_{6}}+{}^{10}{{C}_{7}}+{}^{10}{{C}_{8}}+{}^{10}{{C}_{9}}+{}^{10}{{C}_{10}} \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\ge 6)=\left[ \frac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}+\frac{10\times 9\times 8}{3\times 2\times 1}+\frac{10\times 9}{2\times 1}+10+1 \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\ge 6)=\left[ 210+120+45+10+1 \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\ge 6)=\frac{193}{512}$

c. at most six heads.

Ans: At most six heads means that$\Rightarrow P(x\le 6)$ 

$P(x\le 6)=P(x=6)+P(x=5)+P(x=4)+P(x=3)+P(x=2)+P(x=1)+P(x=0)$

$P(x\le 6)={}^{10}{{C}_{6}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{5}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{4}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{3}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{2}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{1}}{{\left( \frac{1}{2} \right)}^{10}}+{}^{10}{{C}_{0}}{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\le 6)=\left[ {}^{10}{{C}_{6}}+{}^{10}{{C}_{5}}+{}^{10}{{C}_{4}}+{}^{10}{{C}_{3}}+{}^{10}{{C}_{2}}+{}^{10}{{C}_{1}}+{}^{10}{{C}_{0}} \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\le 6)=\left[ \frac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}+\frac{10\times 9\times 8\times 7\times 6}{5\times 4\times 3\times 2\times 1}+\frac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}+\frac{10\times 9\times 8}{3\times 2\times 1}+\frac{10\times 9}{2\times 1}+10+1 \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\le 6)=\left[ 210+252+210+120+45+10+1 \right]{{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\le 6)=\left( 848 \right){{\left( \frac{1}{2} \right)}^{10}}$

$\Rightarrow P(x\le 6)=\frac{53}{64}$

29. A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter by other means of transport are respectively $\frac{3}{13}$, $\frac{1}{5}$, $\frac{1}{10}$ and $\frac{2}{5}$. The probabilities that he will be late are $\frac{1}{4}$, $\frac{1}{3}$and $\frac{1}{12}$ if he comes by train, bus and scooter respectively but if comes by other means of transport, then he will not be late. When he arrives, he is late. What is the probability that he comes by train?

 $E$ : Event that the doctor visits the patient late

${{T}_{1}}$ : Event that the doctor comes by train, $\Rightarrow P\left( {{T}_{1}} \right)=\frac{3}{10}$

${{T}_{2}}$ : Event that the doctor comes by bus, $\Rightarrow P\left( {{T}_{2}} \right)=\frac{1}{5}$

${{T}_{3}}$ : Event that the doctor comes by scooter, $\Rightarrow P\left( {{T}_{3}} \right)=\frac{1}{10}$

${{T}_{4}}$ : Event that the doctor comes by other means of transport, $\Rightarrow P\left( {{T}_{4}} \right)=\frac{2}{5}$

Probability that the doctor arriving late comes by train, $P\left( {E}/{{{T}_{1}}}\; \right)=\frac{1}{4}$ 

Probability that the doctor arriving late comes by bus, $P\left( {E}/{{{T}_{2}}}\; \right)=\frac{1}{3}$ 

Probability that the doctor arriving late comes by scooter, $P\left( {E}/{{{T}_{3}}}\; \right)=\frac{1}{12}$ 

Probability that the doctor arriving late comes by other transport, $P\left( {E}/{{{T}_{4}}}\; \right)=0$ 

From Baye’s theorem: \[P\left( {{{T}_{1}}}/{E}\; \right)=\frac{P({{T}_{1}})P\left( {E}/{{{T}_{1}}}\; \right)}{P({{T}_{1}})P\left( {E}/{{{T}_{1}}}\; \right)+P({{T}_{2}})P\left( {E}/{{{T}_{2}}}\; \right)+P({{T}_{3}})P\left( {E}/{{{T}_{3}}}\; \right)+P({{T}_{4}})P\left( {E}/{{{T}_{4}}}\; \right)}\]

\[\Rightarrow P\left( {{{T}_{1}}}/{E}\; \right)=\frac{\frac{3}{10}\times \frac{1}{4}}{\frac{3}{10}\times \frac{1}{4}+\frac{1}{5}\times \frac{1}{3}+\frac{1}{10}\times \frac{1}{12}+\frac{2}{5}\times 0}\]

\[\Rightarrow P\left( {{{T}_{1}}}/{E}\; \right)=\frac{\frac{3}{40}}{\frac{3}{40}+\frac{1}{15}+\frac{1}{120}+0}\]

\[\Rightarrow P\left( {{{T}_{1}}}/{E}\; \right)=\frac{\frac{3}{40}}{\frac{18}{120}}=\frac{1}{2}\]

Therefore, the probability that the doctor arrives late by train is $\frac{1}{2}$. 

30. A man is known to speak the truth $3$ out of $4$ times. He throws a die and reports that it is six. Find the probability that it is actually a six.

Ans: Let $A$ be the event that the number on die is $6$.

Probability that the man speaks truth, $P(T)=\frac{3}{4}$ 

Probability that the man lies, $P(F)=1-\frac{3}{4}=\frac{1}{4}$ 

Probability of getting $6,P\left( {A}/{T}\; \right)=\frac{1}{6}$ 

Probability of not getting $6,P\left( {A}/{F}\; \right)=1-\frac{1}{6}=\frac{5}{6}$ 

From Bayes theorem: \[P\left( {T}/{A}\; \right)=\frac{P(T)P\left( {A}/{T}\; \right)}{P(T)P\left( {A}/{T}\; \right)+P(F)P\left( {A}/{F}\; \right)}\]

\[\Rightarrow P\left( {T}/{A}\; \right)=\frac{\frac{3}{4}\times \frac{1}{6}}{\frac{3}{4}\times \frac{1}{6}+\frac{1}{4}\times \frac{5}{6}}\]

\[\Rightarrow P\left( {T}/{A}\; \right)=\frac{3}{3+5}=\frac{3}{8}\]

Therefore, Probability that its actually $6$ is $\frac{3}{8}$.

31. An insurance company insured $2000$ scooter drivers, $4000$ car drivers and $6000$ truck drivers. The probability of an accidents are $0.01$, $0.03$and$0.15$respectively if one of the insured persons meets with an accident. What is the probability that he is a scooter driver?

$E$ : The event when the driver drives scooter 

$F$ :  The event when the driver drives car

$G$ : The event when the driver drives truck

$K$ : The event that the driver meets accident

From the given data:

$P\left( E \right)=\frac{2000}{12000}$

$P\left( F \right)=\frac{4000}{12000}$

$P\left( G \right)=\frac{6000}{12000}$

$P\left( K\left| E \right. \right)=\frac{1}{100}$ $\left( K\left| E \right. \right)$: The driver meets accident provided he drives scooter

$P\left( K\left| F \right. \right)=\frac{3}{100}$ $\left( K\left| F \right. \right)$: The driver meets accident provided he drives car

$P\left( K\left| G \right. \right)=\frac{15}{100}$ $\left( K\left| G \right. \right)$: The driver meets accident provided he drives truck

From Bayes theorem:

$P\left( E\left| K \right. \right)=\frac{P\left( E \right)P\left( K\left| E \right. \right)}{P\left( E \right)P\left( K\left| E \right. \right)+P\left( F \right)P\left( K\left| F \right. \right)+P\left( G \right)P\left( K\left| G \right. \right)}$

\[\Rightarrow P\left( E\left| K \right. \right)=\frac{\frac{1}{6}\times \frac{1}{100}}{\frac{1}{6}\times \frac{1}{100}+\frac{1}{3}\times \frac{3}{100}+\frac{1}{2}\times \frac{15}{100}}\]

\[\Rightarrow P\left( E\left| K \right. \right)=\frac{\frac{1}{6}}{\frac{1}{6}+1+\frac{15}{2}}\]

\[\Rightarrow P\left( E\left| K \right. \right)=\frac{1}{52}\]

Therefore, the probability that the accidental person is a scooter driver is $\frac{1}{52}$.

32. Two cards from a pack of $52$ cards are lost. One card is drawn from the remaining cards. If a drawn card is a heart, find the probability that the lost cards were both hearts.

Ans: Consider the following events:

${{E}_{1}}$ be the event both lost cards are hearts.

${{E}_{2}}$ be the event both lost cards are non hearts.

${{E}_{3}}$ be the event one lost card is non heart and one is heart.

$A$ be the event of picking a heart from remaining  $50$ cards.

$P\left( {{E}_{1}} \right)=\frac{{}^{13}{{C}_{2}}}{{}^{52}{{C}_{2}}}=\frac{13\times 12}{52\times 51}$ 

$\Rightarrow P\left( {{E}_{1}} \right)=\frac{1}{17}$

$P\left( \frac{A}{{{E}_{1}}} \right)=\frac{11}{50}$ 

$P\left( {{E}_{2}} \right)=\frac{{}^{39}{{C}_{2}}}{{}^{52}{{C}_{2}}}=\frac{39\times 38}{52\times 51}$ 

$\Rightarrow P\left( {{E}_{2}} \right)=\frac{19}{34}$

\[P\left( \frac{A}{{{E}_{2}}} \right)=\frac{13}{50}\] 

$P\left( {{E}_{3}} \right)=\frac{(One~~heart)~and\left( One~~non~heart \right)}{{}^{52}{{C}_{2}}}$

$P\left( {{E}_{3}} \right)=\frac{13\times 39}{{}^{52}{{C}_{2}}}=\frac{13\times 39\times 2}{52\times 51}$ 

$\Rightarrow P\left( {{E}_{3}} \right)=\frac{39}{102}$

$P\left( \frac{A}{{{E}_{3}}} \right)=\frac{12}{50}$ 

From Baye’s theorem:\[P\left( {{{E}_{1}}}/{A}\; \right)=\frac{P({{E}_{1}})P\left( {A}/{{{E}_{1}}}\; \right)}{P({{E}_{1}})P\left( {A}/{{{E}_{1}}}\; \right)+P({{E}_{2}})P\left( {A}/{{{E}_{2}}}\; \right)+P({{E}_{3}})P\left( {A}/{{{E}_{3}}}\; \right)}\] 

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{1}{17}\times \frac{11}{50}}{\frac{1}{17}\times \frac{11}{50}+\frac{19}{34}\times \frac{13}{50}+\frac{39}{102}\times \frac{12}{50}}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{11}{11+\frac{247}{2}+78}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{22}{22+247+156}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{22}{425}\]

Therefore, the probability that the lost cards were both hearts is $\frac{22}{425}$.

33. A box $X$ contains $2$ white and $3$ red balls and a bag $Y$ contains $4$ white and $5$ red balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn from bag $Y$.

Ans: Let the event of selecting a red ball be $R$.

Let the event of selecting the bag $X$ be $X$.

Let the event of selecting the bag $Y$ be $Y$.

Bag $X$ has $2$ white and $3$ red balls.

Bag $Y$ has $4$ white and $5$ red balls.

$\Rightarrow P\left( X \right)=P\left( Y \right)=\frac{1}{2}$ 

$P\left( {R}/{X}\; \right)=\frac{3}{5}$ 

$P\left( {R}/{Y}\; \right)=\frac{5}{9}$

From Bayes theorem: \[P\left( {Y}/{R}\; \right)=\frac{P(Y)P\left( {R}/{Y}\; \right)}{P(X)P\left( {R}/{X}\; \right)+P(Y)P\left( {R}/{Y}\; \right)}\]

\[\Rightarrow P\left( {Y}/{R}\; \right)=\frac{\frac{5}{9}\times \frac{1}{2}}{\frac{3}{5}\times \frac{1}{2}+\frac{5}{9}\times \frac{1}{2}}\]

\[\Rightarrow P\left( {Y}/{R}\; \right)=\frac{25}{27+25}=\frac{25}{52}\]

Therefore, the probability that the ball is red and drawn from bag $Y$is$\frac{25}{52}$.

34. In answering a question on a multiple choice, a student either knows the answer or guesses. Let $\frac{3}{4}$ be the probability that he knows the answer and $\frac{1}{4}$ be the probability that he guesses. Assuming that a student who guesses at the answer will be incorrect with probability $\frac{1}{4}$. What is the probability that the student knows the answer, given that he answered correctly?

Ans: Let ${{E}_{1}}$ and ${{E}_{2}}$ be the respective events in which the student knows the answer and guesses the answer.

Let $A$ be the event that the answer is correct.

$P\left( {{E}_{1}} \right)=\frac{3}{4}$ 

$P\left( {{E}_{2}} \right)=\frac{1}{4}$

The probability that the student answered correctly by knowing the answer is $1$.

$\Rightarrow P\left( {A}/{{{E}_{1}}}\; \right)=1$  

The probability that the student answered correctly by guessing the answer is $\frac{1}{4}$

$\Rightarrow P\left( {A}/{{{E}_{2}}}\; \right)=\frac{1}{4}$  

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{3}{4}\times 1}{\frac{3}{4}\times 1+\frac{1}{4}\times \frac{1}{4}}=\frac{\frac{3}{4}}{\frac{3}{4}+\frac{1}{16}}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{\frac{3}{4}}{\frac{13}{16}}\]

\[\Rightarrow P\left( {{{E}_{1}}}/{A}\; \right)=\frac{12}{13}\]

Therefore, the probability that the student answers correctly by knowing the answer is $\frac{12}{13}$.

35. Suppose a girl throws a die. If she gets $5$ or $6$She tosses a coin three times and notes the number of heads. If she gets $1$, $2$, $3$ or $4$ She tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head. What is the probability that she throws $1$, $2$, $3$ or $4$ with the die?

$E$ : The event when $5\text{ or 6}$ come

$F$ :  The event when $\text{1,2,3 or 4}$ come

$K$ : The event that the coin shows exactly one head

$P\left( E \right)=\frac{2}{6}$

$P\left( F \right)=\frac{4}{6}$

$P\left( K\left| E \right. \right)=\frac{3}{8}$ $\left( K\left| E \right. \right)$: The event that the coin shows exactly one head provided $5\text{ or 6}$come

$P\left( K\left| F \right. \right)=\frac{1}{2}$ $\left( K\left| F \right. \right)$: The event that the single throw of coin shows exactly one head provided $\text{1,2,3 or 4}$come

From Bayes theorem 

$P\left( F\left| K \right. \right)=\frac{P\left( F \right)P\left( K\left| F \right. \right)}{P\left( E \right)P\left( K\left| E \right. \right)+P\left( F \right)P\left( K\left| F \right. \right)}$

\[\Rightarrow P\left( F\left| K \right. \right)=\frac{\frac{4}{6}\times \frac{1}{2}}{\frac{2}{6}\times \frac{3}{8}+\frac{4}{6}\times \frac{1}{2}}\]

\[\Rightarrow P\left( F\left| K \right. \right)=\frac{2}{\frac{3}{4}+2}=\frac{8}{11}\]

Therefore, the probability that the item is produced from the second group is $\frac{8}{11}$.

36. In a bolt factory machines $A$, $B$ and $C$ manufacture $60%$, $30%$ and $10%$ of the total bolts respectively, $2%$, $5%$ and $10%$ of the bolts produced by them respectively are defective. A bolt is picked up at random from the product and is found to be defective. What is the probability that it has been manufactured by machine $A$?

In a bolt factory machines $A$, $B$ and $C$ manufacture $60%$, $30%$ and $10%$ of the total bolts.

Let total bolts be $x$.

Number of bolts in Machine $A=x\times \frac{60}{100}=0.6x$ 

Number of bolts in Machine $B=x\times \frac{30}{100}=0.3x$ 

Number of bolts in Machine $C=x\times \frac{10}{100}=0.1x$ 

Probability of picking a bolt from $A$, $P\left( A \right)=\frac{0.6x}{0.6x+0.3x+0.1x}=0.6x$ 

Probability of picking a bolt from $B$, $P\left( B \right)=\frac{0.3x}{0.6x+0.3x+0.1x}=0.3x$ 

Probability of picking a bolt from $C$, $P\left( C \right)=\frac{0.1x}{0.6x+0.3x+0.1x}=0.1x$ 

Let $D$ be the event of a bolt picked up at random from the product and is found to be defective.

$P\left( {D}/{A}\; \right)=\frac{2}{100}=0.02$ 

$P\left( {D}/{B}\; \right)=\frac{5}{100}=0.05$

\[P\left( {D}/{C}\; \right)=\frac{10}{100}=0.1\]

From Baye’s theorem:\[P\left( {A}/{D}\; \right)=\frac{P(A)P\left( {D}/{A}\; \right)}{P(A)P\left( {D}/{A}\; \right)+P(B)P\left( {D}/{B}\; \right)+P(C)P\left( {D}/{C}\; \right)}\]

\[\Rightarrow P\left( {A}/{D}\; \right)=\frac{0.6\times 0.02}{0.6\times 0.02+0.3\times 0.05+0.1\times 0.1}\]

\[\Rightarrow P\left( {A}/{D}\; \right)=\frac{12}{12+15+10}\]

\[\Rightarrow P\left( {A}/{D}\; \right)=\frac{12}{37}\]

Therefore, probability of a bolt picked up at random from the product and is found to be defective and is from machine $A$is $\frac{12}{37}$.

37. Two urns $A$ and $B$ contain $6$ black and $4$ white, $4$ black and $6$ white balls respectively. Two balls are drawn from one of the urns. If both the balls drawn are white, find the probability that the balls are drawn from urn $B$.

Ans: Let $E$be the event of drawing two white balls.

Urn $A$contains $6$ black and $4$ white balls.

Urn $B$contains $4$ black and $6$ white balls.

Probability of choosing Urn $A$or Urn $B$ is $P(A)=P(B)=\frac{1}{2}$

Probability of choosing two white balls from \[A=P\left( {E}/{A}\; \right)\] 

\[\Rightarrow P\left( {E}/{A}\; \right)=\frac{{}^{4}{{C}_{2}}}{{}^{10}{{C}_{2}}}=\frac{6}{45}\]

Probability of choosing two white balls from \[B=P\left( {E}/{B}\; \right)\] 

\[\Rightarrow P\left( {E}/{B}\; \right)=\frac{{}^{6}{{C}_{2}}}{{}^{10}{{C}_{2}}}=\frac{15}{45}\]

From Bayes theorem:\[P\left( {B}/{E}\; \right)=\frac{P(B)P\left( {E}/{B}\; \right)}{P(A)P\left( {E}/{A}\; \right)+P(B)P\left( {E}/{B}\; \right)}\]

\[\Rightarrow P\left( {B}/{E}\; \right)=\frac{\frac{1}{2}\times \frac{15}{45}}{\frac{1}{2}\times \frac{6}{45}+\frac{1}{2}\times \frac{15}{45}}=\frac{15}{6+15}\]

\[\Rightarrow P\left( {B}/{E}\; \right)=\frac{15}{21}=\frac{5}{7}\]

Therefore, the probability that the balls are drawn from urn $B$ is $\frac{5}{7}$.

38. Two cards are drawn from a well shuffled pack of $52$ cards. Find the mean and variance for the number of face cards obtained.

Ans: Let $X$ be the event of the number of face cards. 

When two cards are picked with replacement there are chances of getting either \[0,1or\text{ 2}\]face cards.

Number of face cards in a deck$=12$ 

Number of events in sample space, $n\left( S \right)=52$

$P\left( N \right)$ be the probability of not picking face card , $P\left( N \right)=\frac{40}{52}$

$P\left( F \right)$ be the probability of picking a face card , $P\left( F \right)=\frac{12}{52}$

For $X=0$: 

Probability, $P\left\{ NN \right\}=\frac{40}{52}\times \frac{40}{52}$

$\Rightarrow P\left\{ NN \right\}=\frac{40}{52}\times \frac{40}{52}=\frac{100}{169}$

For $X=1$:  

Probability, \[P\left( NF\text{ or }FN \right)=P(N)P(F)+P(F)P(N)\] 

\[\Rightarrow P\left( NF\text{ or }FN \right)=2\times \frac{40}{52}\times \frac{12}{52}=\frac{60}{169}\]

For $X=2$: 

Probability, \[P\left( FF \right)=\frac{12}{52}\times \frac{12}{52}\] 

\[\Rightarrow P\left( FF \right)=\frac{9}{169}\]

Probability distribution:

Mean Expectation value is $\mu =E(X)=\sum\limits_{i=1}^{n}{{{x}_{i}}{{p}_{i}}}$ 

$\Rightarrow \mu =0\times \frac{100}{169}+1\times \frac{60}{169}+2\times \frac{9}{169}$

$\Rightarrow \mu =0+\frac{100}{169}+\frac{60}{169}+\frac{18}{169}$

$\Rightarrow \mu =\frac{78}{169}=\frac{6}{13}$

Therefore, the mean number of heads is $\frac{6}{13}$.

$\Rightarrow E({{X}^{2}})={{0}^{2}}\times \frac{100}{169}+{{1}^{2}}\times \frac{60}{169}+{{2}^{2}}\times \frac{9}{169}$

$\Rightarrow E({{X}^{2}})=\frac{0+60+36}{169}$

\[\Rightarrow E({{X}^{2}})=\frac{96}{169}\]

$\Rightarrow Var(X)=\frac{96}{169}-{{\left[ \frac{6}{13} \right]}^{2}}$

$\Rightarrow Var(X)=\frac{96-36}{169}$

$\Rightarrow Var(X)=\frac{60}{169}$

Therefore, the variance of the number of heads is $\frac{60}{169}$.

39. Write the probability distribution for the number of heads obtained when three coins are tossed together. Also, find the mean and variance of the number of heads.

Ans: Let $X$ be the event of the number of heads.

When three coins are tossed simultaneously there are chances of getting either \[0,1,2~or\text{ 3}\]heads.

Sample space, $S=\left\{ TTT,HTT,THT,TTH,HHT,HTH,THH,HHH \right\}$ 

Number of events in sample space, $n\left( S \right)=8$ 

For $X=0$: Possible outcome$\left\{ TTT \right\}$ 

Number of possible outcomes$=1$ 

Probability, \[P\left( X \right)=\frac{1}{8}\] 

For $X=1$: Possible outcome$\left\{ HTT,THT,TTH \right\}$ 

Number of possible outcomes$=3$ 

Probability, \[P\left( X \right)=\frac{3}{8}\] 

For $X=2$: Possible outcome$\left\{ HHT,HTH,THH \right\}$ 

For $X=3$: Possible outcome$\left\{ HHH \right\}$ 

$\Rightarrow \mu =0\times \frac{1}{8}+1\times \frac{3}{8}+2\times \frac{3}{8}+3\times \frac{1}{8}$

$\Rightarrow \mu =0+\frac{3}{8}+\frac{6}{8}+\frac{3}{8}$

$\Rightarrow \mu =\frac{12}{8}=\frac{3}{2}$

Therefore, the mean number of heads is $\frac{3}{2}$.

$\Rightarrow E({{X}^{2}})={{0}^{2}}\times \frac{1}{8}+{{1}^{2}}\times \frac{3}{8}+{{2}^{2}}\times \frac{3}{8}+{{3}^{2}}\times \frac{1}{8}$

$\Rightarrow E({{X}^{2}})=\frac{0+3+12+9}{8}$

\[\Rightarrow E({{X}^{2}})=\frac{24}{8}=3\]

$\Rightarrow Var(X)=3-{{\left[ \frac{3}{2} \right]}^{2}}$

$\Rightarrow Var(X)=\frac{12-9}{4}$

$\Rightarrow Var(X)=\frac{3}{4}$

Therefore, the variance of the number of heads is $\frac{3}{4}$.

40. Two groups are competing for the position on the Board of Directors of a corporation. The probabilities that the first and the second groups will win are $0.6$ and $0.4$ respectively. Further, if the first group wins, the probability of introducing a new product is $0.7$ and the corresponding probability is $0.3$ if the second group wins. Find the probability that the new product introduced was by the second group.

$E$ : The event when the first group wins

$F$ :  The event when the second group wins

$K$ : The event that the new item is produced

$P\left( E \right)=0.6$

$P\left( F \right)=0.4$

$P\left( K\left| E \right. \right)=0.7$ $\left( K\left| E \right. \right)$: The event that the item is introduced by first group 

$P\left( K\left| F \right. \right)=0.3$ $\left( K\left| F \right. \right)$: The event that item is introduced by second group

\[\Rightarrow P\left( F\left| K \right. \right)=\frac{0.4\times 0.3}{0.6\times 0.7+0.4\times 0.3}\]

\[\Rightarrow P\left( F\left| K \right. \right)=\frac{12}{42+12}\]

\[\Rightarrow P\left( F\left| K \right. \right)=\frac{12}{54}=\frac{2}{9}\]

Thus, the probability that the item is produced from the second group is $\frac{2}{9}$.

Important Related Links for CBSE Class 12 Maths 

CBSE Class 12 Maths Important Questions

Cbse study materials.

• Math Article

Probability For Class 12

Probability for class 12 notes.

Probability For Class 12 covers topics like conditional probability, multiplication rule, random variables, Bayes theorem, etc. Probability is defined as the extent to which an event is likely to occur . It is measured as the number of favourable events to occur from the total number of events. It is to be noted that the probability of an event is always 0 ≤ P e  ≤ 1.

For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But if we toss two coins in the air, there could be three possibilities of events to occur, such as both the coins show heads or both show tails or one shows heads and one tail, i.e.(H, H), (H, T),(T, T).

Probability Class 12 Concepts

• Introduction

Conditional Probability

• Multiplication Theorem on Probability

Independent Events

• Bayes’ Theorem

Random Variables and its Probability Distributions

Bernoulli trials and binomial distribution, probability formula.

The probability formula is defined as the likelihood of an event to happen. It is equal to the ratio of the number of favourable results and the total number of outcomes. The formula for the probability of an event to occur is given by;

Conditional Probability is the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome. It simply depends on any event in the past which has already taken place.

If E and F are two events with the same sample space of a random experiment, then the conditional probability of the event E gives that F has occurred, i.e. P(E|F) is,

P(E|F) = P(E ∩ F)/P(F), provided P(F) ≠ 0

Properties of Conditional Probability

Let E and F be events of a sample space S of an experiment, then;

Property 1: P(S|F) = P(F|F) = 1

Property 2 : If A and B are two events in a sample space S and F is an event of S, such that P(F)≠0, then;

P((A ∪ B)|F) = P(A|F) + P(B|F) – P((A ∩ B)|F)

Property 3:  P(E′|F) = 1 − P(E|F)

Multiplication Rule

Let E and F be two events associated with a sample space S. Clearly, the set E ∩ F denotes the event that both E and F have occurred. In other words, E ∩ F denotes the simultaneous occurrence of the events E and F. The event E ∩ F is also written as EF. According to this rule, if E and F are the events in a sample space, then;

P(E ∩ F) = P(E) P(F|E) = P(F) P(E|F)

where P(E) ≠ 0 and P(F) ≠ 0

Two experiments are said to be independent if for every pair of events E and F, where E is associated with the first experiment and F with the second experiment, the probability of the simultaneous occurrence of the events E and F when the two experiments are performed is the product of P(E) and P(F) calculated separately on the basis of two experiments, i.e.,

P (E ∩ F) = P (E).P(F)

Baye’s Theorem

A set of events E 1 , E 2 , …, E n is said to represent a partition of the sample space S if 

(a) E i ∩ E j = φ, i ≠ j, i, j = 1, 2, 3, …, n

(b) E 1 ∪ Ε 2 ∪ … ∪ E n = S and 

(c) P(E i )> 0 for all i = 1, 2, …, n. 

In other words, the events E 1 , E 2 , …, E n represent a partition of the sample space S if they are pairwise disjoint, exhaustive and have nonzero probabilities and A be any event with nonzero probability, then:

\(\begin{array}{l}P(E_{i}|A)=\frac{P(E_{i})P(A|E_{i})}{\sum_{j=1}^{n}P(E_{j})P(A|E_{j})}\end{array} \)

Theorem of total probability 

Let {E 1 , E 2 , …, E n ) be a partition of a sample space and suppose that each of E 1 , E 2 , …, E n has a nonzero probability. Let A be an event associated with S, then

 P(A) = P(E 1 ) P (A|E 1 ) + P (E 2 ) P (A|E 2 ) + … + P (E n ) P(A|E n )

A random variable is a real-valued function whose domain is the sample space of a random experiment.

The probability distribution of a random variable X is the system of numbers:

X: x 1   x 2   … x n

P(X): p 1   p 2   … p n

where p i  > 0,

\(\begin{array}{l}\sum_{i=1}^{n}p_i=1;\ i=1,2,3,…,n\end{array} \)

The real numbers x 1 , x 2 , …, x n are the possible values of the random variable X and p i (i = 1, 2, …, n) is the probability of the random variable X taking the value xi i.e., P(X = x i ) = p i

The mean of a random variable X is also called the expectation of X, denoted by E(X). Thus, 

\(\begin{array}{l}E(X)=\mu=\sum_{i=1}^{n}x_ip_i=x_1p_1+x_2p_2+x_3p_3+…+x_np_n\end{array} \)

Thus, we can write the mean, variance and standard deviation of a random variable X as:

Trials of a random experiment are called Bernoulli trials if they satisfy the following conditions: 

(i) There should be a finite number of trials. 

(ii) The trials should be independent. 

(iii) Each trial has exactly two outcomes: success or failure. 

(iv) The probability of success remains the same in each trial.

The probability distribution of number of successes in an experiment consisting of n Bernoulli trials may be obtained by the binomial expansion of (q + p) n . Hence, we can write this distribution of the number of successes X as:

This probability distribution is known as the binomial distribution with parameters n and p.

From this, the probability of success can be calculated as:

P (X = x) = P(x) =  n C x  q n-x  p x  , x = 0, 1, …, n

n = Total number of trials

p = probability of success q = 1 – p

Probability Solved Examples

Question: If P (A) = 0.8, P (B) = 0.5 and P (B|A) = 0.4, find: (i) P (A ∩ B)

(ii) P (A|B)

(iii) P (A ∪ B)

Solution: Given, P (A) = 0.8, P (B) = 0.5 and P (B|A) = 0.4

(i) We have to find P (A ∩ B)

As we know, by conditional probability,

P(B|A) = P (A ∩ B)/P(A)

P (A ∩ B) = P(B|A).P(A) = 0.4 x 0.8 = 0.32

(ii) We have to find P (A|B)

P(A|B) = P (A ∩ B)/P(B)

P(A|B) = 0.32/0.5 = 0.64

(iii) We have to find P (A ∪ B)

P (A ∪ B) = P(A) + P(B) – P (A ∩ B)

= 0.8 + 0.5 – 0.32

Question 2: If a fair coin is tossed 10 times, find the probability of exactly seven tails.

Given that a fair coin is tossed 10 times.

The repeated tosses of a coin are Bernoulli trials.

Let X be the number of heads in an experiment of 10 trials. 

Here, X has the binomial distribution with n = 10 and p = 1 2

We know that,

x = 7, n = 10, p = ½, q = 1 – (½) = (½)

P(X = 7) =  10 C 7  (1/2) 10-7  (½) 7

=  10 C 3  (½) 10

Therefore, the probability of getting exactly seven tails is 15/128.

Practice Problems

• It is known that 10% of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective?
• Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
• A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
• A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam
• 1. Mathematics
• 3. Chemistry

CBSE Case Study Class 12

While preparing for the board exams, students are being judged on different levels of skills, such as writing, reading, etc. CBSE Case Study Class 12 questions are one of them that helps in assessing critical thinking.

The Central Board of Secondary Education will be asking the case study questions in the Class 12 board examination. Therefore, here on this page, we have provided the CBSE Case Study Class 12 for Maths, Physics, Chemistry, Biology and other subjects. Our subject matter experts have prepared Case Study questions so that Apart from the basic standard questions, students can have a variety of problems to solve. 

Just like MCQs, and other written types questions CBSE Case Study Class 12 questions will impact the overall performance of a student. Therefore for the convenience of the students we have provided the download links here, so that they can easily access the Class 12 Case Study.

Download Subject Wise CBSE Case Study Class 12 Question and Answers PDF 

There are three different streams in class 12th: Science, Arts & Commerce. And all these streams have a variety of subjects therefore, here our subject experts have crafted the Subject Wise Case Study For Class 12. Download Subject Wise CBSE Case Study Class 12 Question and Answers PDF from the below given links.

CBSE Case Study Questions Class 12 for Maths

To learn how to answer CBSE Case Study Class 12 maths questions, it would be a good choice to refer to the separate set of questions in PDF. CBSE Case Study Questions for Class 12 Maths can be quite useful and helpful in understanding how the board will prepare the case based questions for maths. 

The Maths Case studies are distributed into different chapters as per the prescribed syllabus of maths. Each and every chapter contains several number of case studies problems which enable the learners to gain in-depth knowledge in the subject.

The maths case study questions of class 12 are usually based on the formula. If any student wants to get a good score in maths case studies then they have to be well versed with a set of formulas as per the chapters and topics. Case Study Class 12 Maths can be downloaded here on this website for free of cost.

Case Study Questions Class 12 Chapter 1 Relations And Functions

Case Study Questions Class 12 Chapter  3 Matrices

Case Study Questions Class 12 Chapter  4 Determinants

Case Study Questions Class 12 Chapter  5 Continuity And Differentiability

Case Study Questions Class 12 Chapter  6 Application Of Derivatives

Case Study Questions Class 12 Chapter  8 Application Of Integrals

Case Study Questions Class 12 Chapter  9 Differential Equations

Case Study Questions Class 12 Chapter  10 Vector Algebra

Case Study Questions Class 12 Chapter  11 Three Dimensional Geometry

Case Study Questions Class 12 Chapter  12 Linear Programming

Case Study Questions Class 12 Chapter  13 Probability

CBSE Case Study Questions Class 12 for Physics

CBSE Class 12 Physics Case Study for different chapters can be interesting to solve. Class 12th physics case studies generally contain descriptive paragraphs and 4 to 5 different questions are given based on the paragraph. Students are required to read the paragraph thoroughly and understand them as well as observe the given data and information to answer the Class 12 Case Study Questions for Physics. 

In order to solve those questions students are required to have a better understanding of the basic level of physics concepts too, so make sure to use Class 12 Revision Notes of Physics. 

Case Study Questions Class 12 Chapter 1 Electric Charges and Fields

Case Study Questions Class 12 Chapter 2 Electrostatic Potential And Capacitance

Case Study Questions Class 12 Chapter 3 Current Electricity

Case Study Questions Class 12 Chapter 4 Moving Charges And Magnetism

Case Study Questions Class 12 Chapter 5 Magnetism And Matter

Case Study Questions Class 12 Chapter 6 Electromagnetic Induction

Case Study Questions Class 12 Chapter 7 Alternating Current

Case Study Questions Class 12 Chapter 8 Electromagnetic Waves

Case Study Questions Class 12 Chapter 9 Ray Optics & Optical Instruments

Case Study Questions Class 12 Chapter 10 Wave Optics

Case Study Questions Class 12 Chapter 11 Dual Nature Radiation & Matter

Case Study Questions Class 12 Chapter 12 Atoms

Case Study Questions Class 12 Chapter 13 Nuclei

Case Study Questions Class 12 Chapter 14 Semiconductor Electronics - Materials, Devices & Simple Circuits

CBSE Case Study Questions Class 12 for Chemistry

Students opted for Science stream will have to study CBSE Case Study Class 12 Chemistry. The given PDF of CBSE Class 12 Case Study Questions for Chemistry will enable the students to practice tons of questions on a regular basis. It will help them to revise the chemistry questions and its syllabus frequently. The Case study questions allow students to think more creative and find the answers in the quickest way possible. Links to download the PDF file of Class 12 Chemistry Case Study are given here.

Case Study Questions Class 12 Chapter 1 The Solid State

Case Study Questions Class 12 Chapter  2 Solutions

Case Study Questions Class 12 Chapter  3 Electrochemistry

Case Study Questions Class 12 Chapter  4 Chemical Kinetics

Case Study Questions Class 12 Chapter  5 Surface Chemistry  

Case Study Questions Class 12 Chapter  7 The p-Block Elements

Case Study Questions Class 12 Chapter  8 The d- and f-Block Elements

Case Study Questions Class 12 Chapter  9 Coordination Compounds

Case Study Questions Class 12 Chapter  10 Haloalkanes And Haloarenes

Case Study Questions Class 12 Chapter 11 Alcohols, Phenols And Ethers

Case Study Questions Class 12 Chapter  12 Aldehydes. Ketones & Carboxylic Acids

Case Study Questions Class 12 Chapter  13 Amines

Case Study Questions Class 12 Chapter 14 Biomolecules

CBSE Case Study Questions Class 12 for Biology

There are lots of chapters in class 12 Biology from which Class 12 Case Study Questions can be framed. Going through such types of questions help the students to assess their understanding level in the topics discussed in NCERT Class 12 Biology Books. By practicing the Class 12 Case Study Questions for Biology students will be very confident to ace the board exam. Also the Biology case study will be very useful for the NEET exam preparation.

Doing a regular practice of Class 12 Biology Case Study questions is a great way to score higher marks in the board exams as it will help students to develop a grip on the concepts. 

Case Study Questions Class 12 Chapter 2 Sexual Reproduction in Flowering Plants

Case Study Questions Class 12 Chapter 3 Human Reproduction

Case Study Questions Class 12 Chapter 4 Reproductive Health

Case Study Questions Class 12 Chapter 5 Principles of Inheritance & Variation

Case Study Questions Class 12 Chapter 6 Molecular Basic of Inheritance

Case Study Questions Class 12 Chapter 8 Human Health And Diseases

Case Study Questions Class 12 Chapter 10 Microbes in Human Welfare

Case Study Questions Class 12 Chapter 11 Biotechnology - Principles & Processes

Case Study Questions Class 12 Chapter 12 Biotechnology And Its Applications

Case Study Questions Class 12 Chapter 13 Organisms And Populations

Case Study Questions Class 12 Chapter 15 Biodiversity And Conversation

Case study types of questions are generally descriptive that helps to gather more information easily so, it is kinda easy to answer. However, our subject matter experts have given the solutions of all the CBSE Case Study Class 12 Biology questions.

Passage Based Class 12 Case Study Questions in PDF

CBSE Class 12 Case studies are known as Passage Based Questions. These types of problems usually contain a short/long paragraph with 4 to 5 questions. 

Students can easily solve Passage Based Class 12 Case Study Questions by reading those passages. By reading the passage students will get the exact idea of what should be the answers. Because the passage already contains some vital information or data. However a better understanding of the basic concepts that can be learned from the NCERT Class 12 Textbooks will aid in solving the Case based questions or passage based questions.

How to Download CBSE Case Study of Class 12?

Follow the below given simple steps to know how to download CBSE Case Study of Class 12:-

• Open Selfstudys website in your browser
• Go to the navigation menu that look like this
• Now, click on CBSE and then Case Study respectively
• A new page will open, where you have to click on “Class 12”
• Now, you are ready to select the subject for which you want to download the case study questions.

How to Solve Case Study Based Questions of Class 12?

There are very simple methods that a student should keep in mind while solving CBSE Case Study Class 12 for any subject:

• Read each line of paragraph carefully and pay attention to the given data/numbers. Often questions are framed according to the highlighted data of the passage.
• Since case study questions are often framed in Multiple choice questions, students should have the knowledge of elimination methods in MCQs.
• Having a good understanding of the topics that are discussed in CBSE Class 12 Books are ideal to Solve Case Study Based Questions of Class 12.

Features Of Class 12 Case Study Questions And Answers PDF

The three most noticeable features of Class 12 Case Study Questions And Answers Pdf are -

• It Is Free To Use:  Keeping in mind the need of students and to help them in doing Self Study, our team has made all the PDF of CBSE Case Study Class 12 free of cost.
• Answers Are Given:  Not only the PDFs are free provided but answers are given for all the questions of CBSE Case Study Class 12. 
• PDF Can Be Downloaded Or Viewed Online:  Many students don’t like to download the PDFs on their device due to the shortage of storage. Therefore, CBSE Class 12 Case Study questions are made available here in online format, so that students can view them online. However, through the Selfstudys app, a learner can download the PDFs too.

Benefits of Using CBSE Class 12 Case Study Questions and Answers

The CBSE Class 12 Case Study Questions and Answers can help a student in several ways:

• In Exam Preparation:  Those who go through the CBSE Case Study Class 12 will find support during the exam preparation as case based questions are also asked in the CBSE Class 12 Board examination. 
• Help in brushing up the previous learnings:  No matter how brilliant you are, you have to revise the studied topics time and again to keep them refreshed. And in this task, the CBSE Class 12 Case Study Questions and Answers can help a lot.
• To develop the critical thinking:  Able to analyse information and make an objective judgement is a skill that is known as critical thinking. A student of class 12 can use CBSE Case Study Class 12 with answers to develop critical thinking so that they can make better decisions in their life and in the board examination.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.