define hypothesis in math term

A statement that could be true, which might then be tested.

Example: Sam has a hypothesis that "large dogs are better at catching tennis balls than small dogs". We can test that hypothesis by having hundreds of different sized dogs try to catch tennis balls.

Sometimes the hypothesis won't be tested, it is simply a good explanation (which could be wrong). Conjecture is a better word for this.

Example: you notice the temperature drops just as the sun rises. Your hypothesis is that the sun warms the air high above you, which rises up and then cooler air comes from the sides.

Note: when someone says "I have a theory" they should say "I have a hypothesis", because in mathematics a theory is actually well proven.

Mathematicians
Math Lessons
Square Roots
Math Calculators
Hypothesis | Definition & Meaning

JUMP TO TOPIC

Explanation of Hypothesis

Contradiction, simple hypothesis, complex hypothesis, null hypothesis, alternative hypothesis, empirical hypothesis, statistical hypothesis, special example of hypothesis, solution part (a), solution part (b), hypothesis|definition & meaning.

A hypothesis is a claim or statement that makes sense in the context of some information or data at hand but hasn’t been established as true or false through experimentation or proof.

In mathematics, any statement or equation that describes some relationship between certain variables can be termed as hypothesis if it is consistent with some initial supporting data or information, however, its yet to be proven true or false by some definite and trustworthy experiment or mathematical law.

Following example illustrates one such hypothesis to shed some light on this very fundamental concept which is often used in different areas of mathematics.

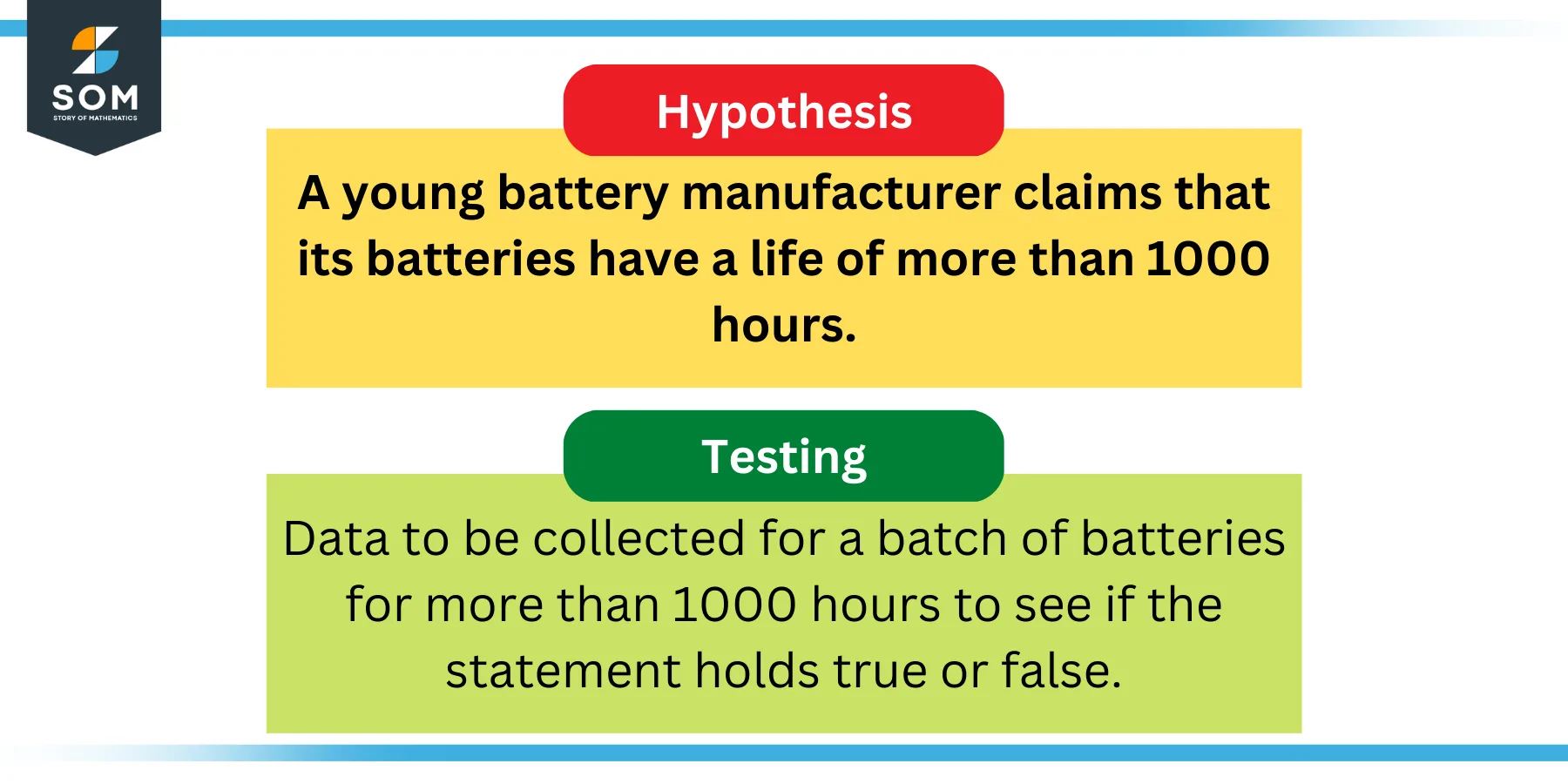
Figure 1: Example of Hypothesis

Here we have considered an example of a young startup company that manufactures state of the art batteries. The hypothesis or the claim of the company is that their batteries have a mean life of more than 1000 hours. Now its very easy to understand that they can prove their claim on some testing experiment in their lab.

However, the statement can only be proven if and only if at least one batch of their production batteries have actually been deployed in the real world for more than 1000 hours . After 1000 hours, data needs to be collected and it needs to be seen what is the probability of this statement being true .

The following paragraphs further explain this concept.

As explained with the help of an example earlier, a hypothesis in mathematics is an untested claim that is backed up by all the known data or some other discoveries or some weak experiments.

In any mathematical discovery, we first start by assuming something or some relationship . This supposed statement is called a supposition. A supposition, however, becomes a hypothesis when it is supported by all available data and a large number of contradictory findings.

The hypothesis is an important part of the scientific method that is widely known today for making new discoveries. The field of mathematics inherited this process. Following figure shows this cycle as a graphic:

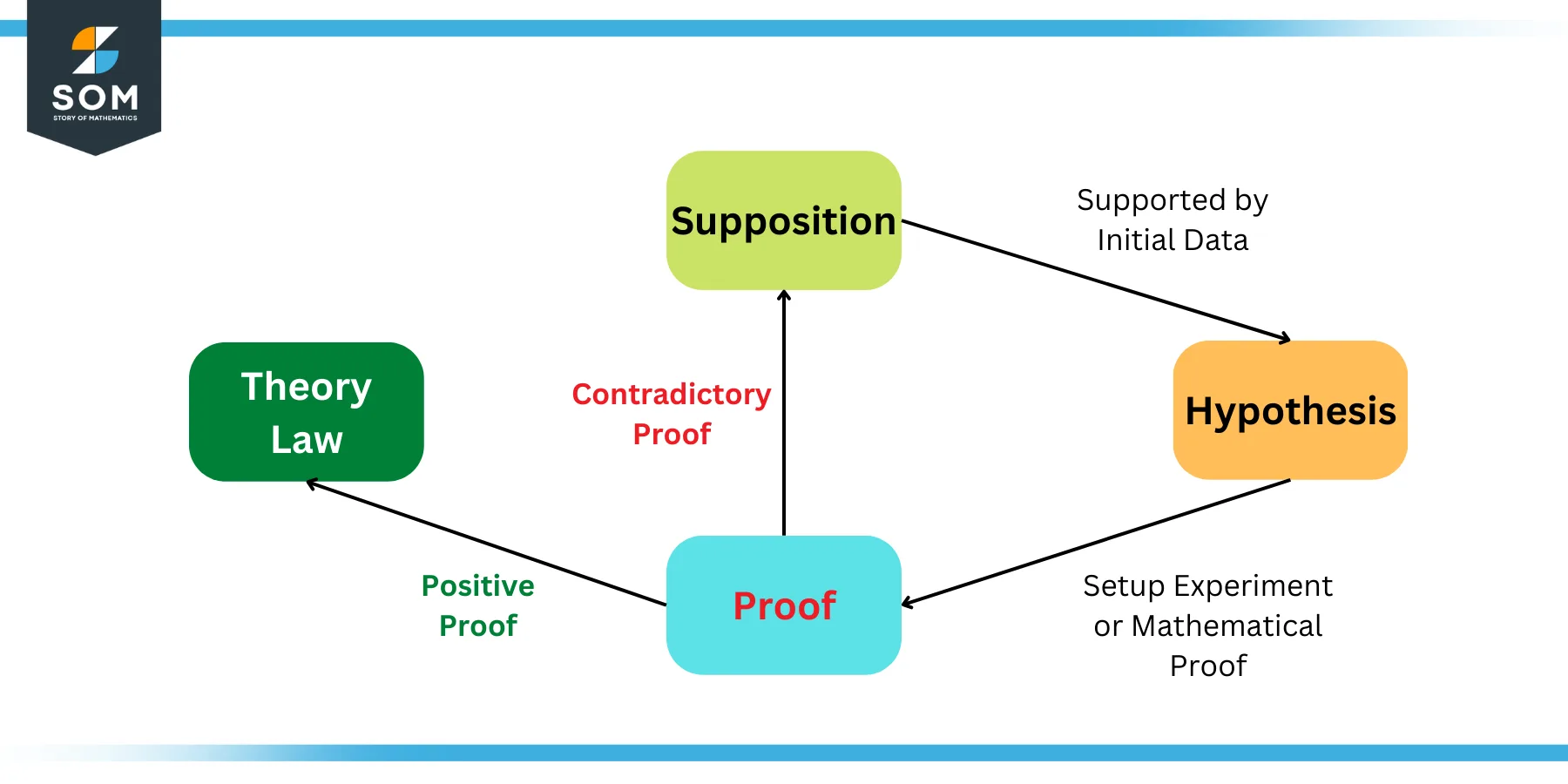
Figure 2: Role of Hypothesis in the Scientific Method

The above figure shows a simplified version of the scientific method. It shows that whenever a supposition is supported by some data, its termed as hypothesis. Once a hypothesis is proven by some well known and widely acceptable experiment or proof, its becomes a law. If the hypothesis is rejected by some contradictory results then the supposition is changed and the cycle continues.

Lets try to understand the scientific method and the hypothesis concept with the help of an example. Lets say that a teacher wanted to analyze the relationship between the students performance in a certain subject, lets call it A, based on whether or not they studied a minor course, lets call it B.

Now the teacher puts forth a supposition that the students taking the course B prior to course A must perform better in the latter due to the obvious linkages in the key concepts. Due to this linkage, this supposition can be termed as a hypothesis.

However to test the hypothesis, the teacher has to collect data from all of his/her students such that he/she knows which students have taken course B and which ones haven’t. Then at the end of the semester, the performance of the students must be measured and compared with their course B enrollments.

If the students that took course B prior to course A perform better, then the hypothesis concludes successful . Otherwise, the supposition may need revision.

The following figure explains this problem graphically.

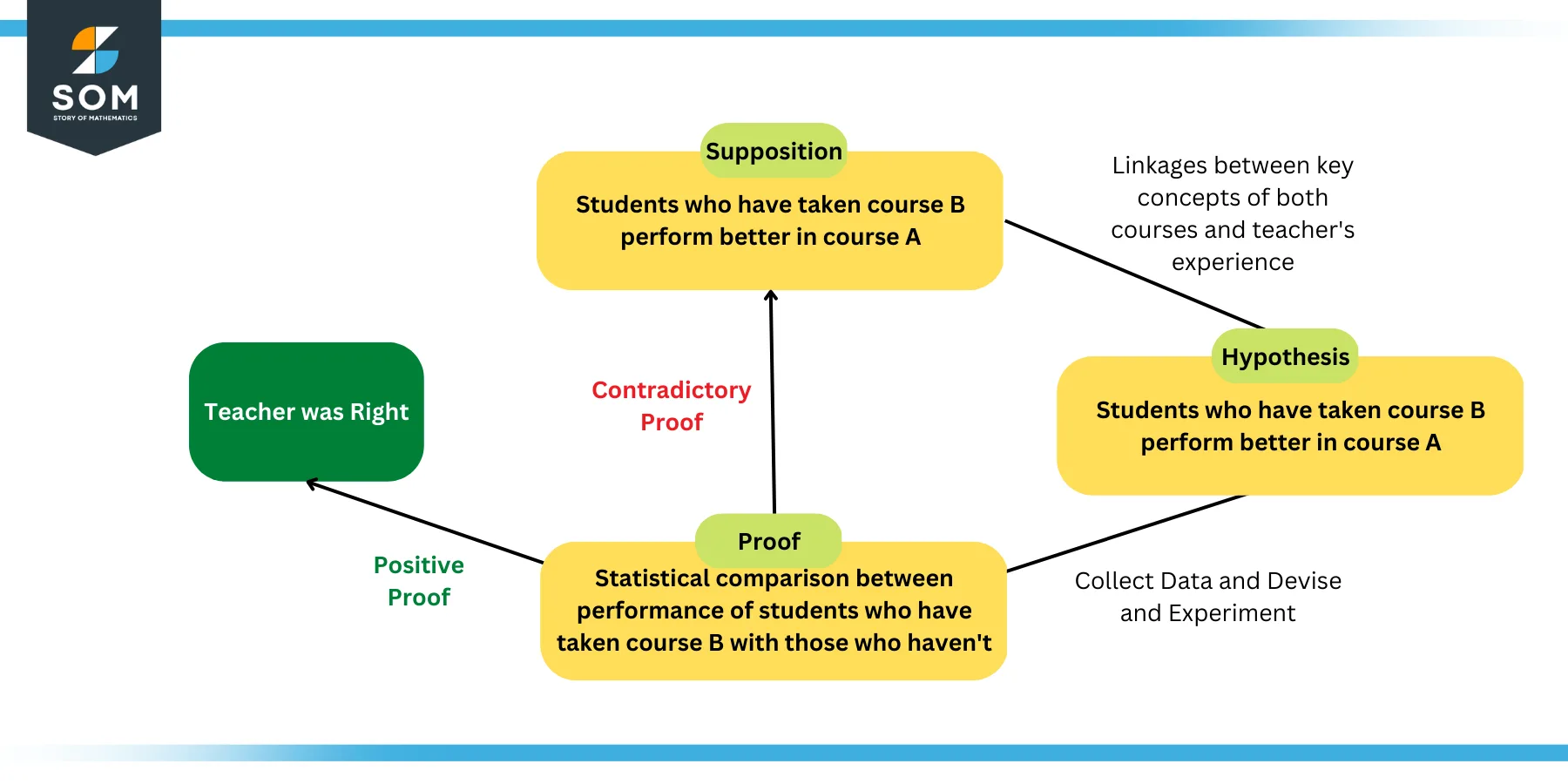
Figure 3: Teacher and Course Example of Hypothesis

Important Terms Related to Hypothesis

To further elaborate the concept of hypothesis, we first need to understand a few key terms that are widely used in this area such as conjecture, contradiction and some special types of hypothesis (simple, complex, null, alternative, empirical, statistical). These terms are briefly explained below:

A conjecture is a term used to describe a mathematical assertion that has notbeenproved. While testing may occasionally turn up millions of examples in favour of a conjecture, most experts in the area will typically only accept a proof . In mathematics, this term is synonymous to the term hypothesis.

In mathematics, a contradiction occurs if the results of an experiment or proof are against some hypothesis. In other words, a contradiction discredits a hypothesis.

A simple hypothesis is such a type of hypothesis that claims there is a correlation between two variables. The first is known as a dependent variable while the second is known as an independent variable.

A complex hypothesis is such a type of hypothesis that claims there is a correlation between more than two variables. Both the dependent and independent variables in this hypothesis may be more than one in numbers.

A null hypothesis, usually denoted by H0, is such a type of hypothesis that claims there is no statistical relationship and significance between two sets of observed data and measured occurrences for each set of defined, single observable variables. In short the variables are independent.

An alternative hypothesis, usually denoted by H1 or Ha, is such a type of hypothesis where the variables may be statistically influenced by some unknown factors or variables. In short the variables are dependent on some unknown phenomena .

An Empirical hypothesis is such a type of hypothesis that is built on top of some empirical data or experiment or formulation.

A statistical hypothesis is such a type of hypothesis that is built on top of some statistical data or experiment or formulation. It may be logical or illogical in nature.

According to the Riemann hypothesis, only negative even integers and complex numbers with real part 1/2 have zeros in the Riemann zeta function . It is regarded by many as the most significant open issue in pure mathematics.

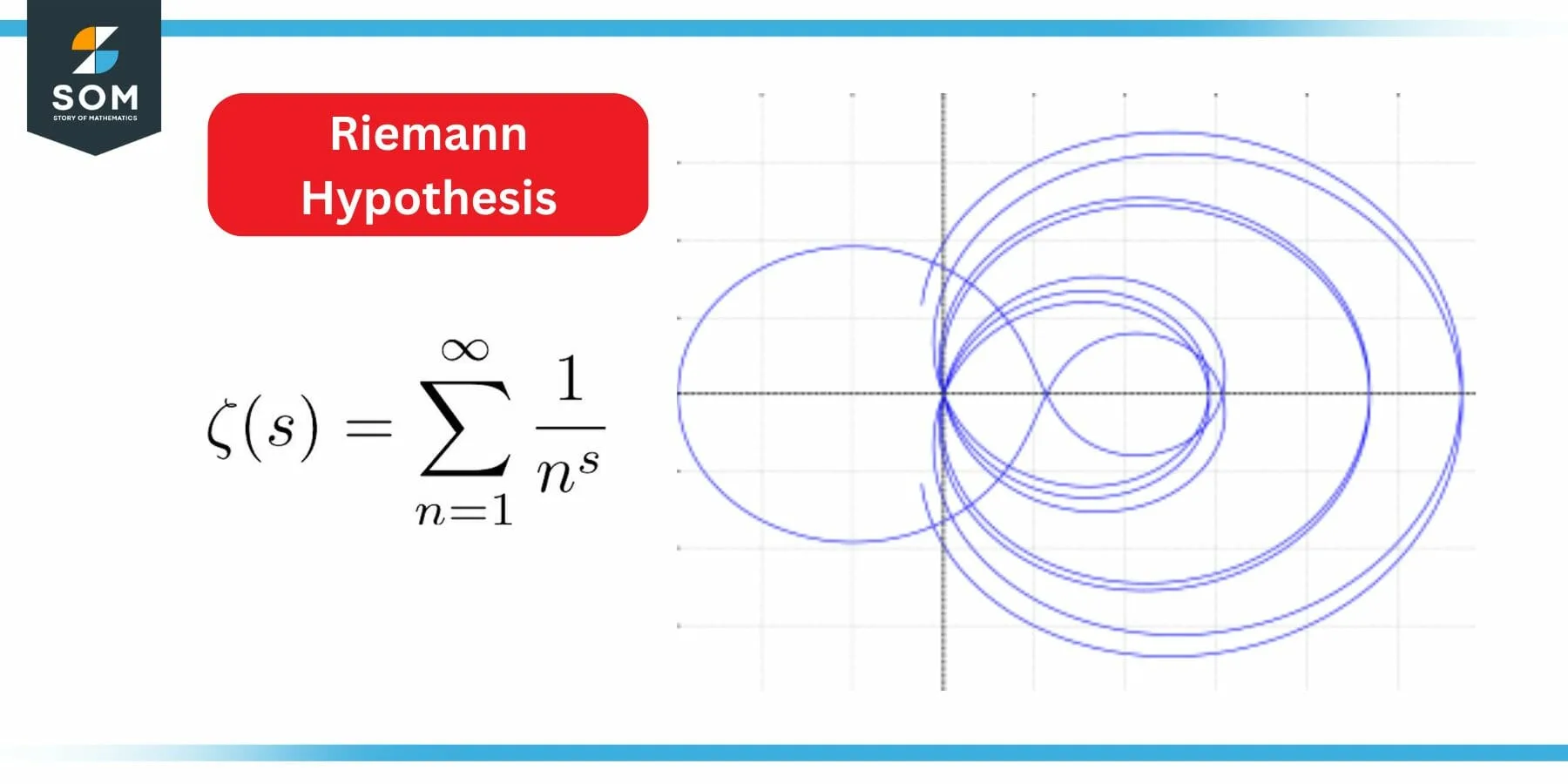
Figure 4: Riemann Hypothesis

The Riemann hypothesis is the most well-known mathematical conjecture, and it has been the subject of innumerable proof efforts.

Numerical Examples

Identify the conclusions and hypothesis in the following given statements. Also state if the conclusion supports the hypothesis or not.

Part (a): If 30x = 30, then x = 1

Part (b): if 10x + 2 = 50, then x = 24

Hypothesis: 30x = 30

Conclusion: x = 10

Supports Hypothesis: Yes

Hypothesis: 10x + 2 = 50

Conclusion: x = 24

All images/mathematical drawings were created with GeoGebra.

Hour Hand Definition < Glossary Index > Identity Definition

Professor: Erika L.C. King Email: [email protected] Office: Lansing 304 Phone: (315)781-3355

The majority of statements in mathematics can be written in the form: "If A, then B." For example: "If a function is differentiable, then it is continuous". In this example, the "A" part is "a function is differentiable" and the "B" part is "a function is continuous." The "A" part of the statement is called the "hypothesis", and the "B" part of the statement is called the "conclusion". Thus the hypothesis is what we must assume in order to be positive that the conclusion will hold.

Whenever you are asked to state a theorem, be sure to include the hypothesis. In order to know when you may apply the theorem, you need to know what constraints you have. So in the example above, if we know that a function is differentiable, we may assume that it is continuous. However, if we do not know that a function is differentiable, continuity may not hold. Some theorems have MANY hypotheses, some of which are written in sentences before the ultimate "if, then" statement. For example, there might be a sentence that says: "Assume n is even." which is then followed by an if,then statement. Include all hypotheses and assumptions when asked to state theorems and definitions!

Still have questions? Please ask!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics > unit 10.

Idea behind hypothesis testing

Examples of null and alternative hypotheses

Writing null and alternative hypotheses
P-values and significance tests
Comparing P-values to different significance levels
Estimating a P-value from a simulation
Estimating P-values from simulations
Using P-values to make conclusions

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Forgot password? New user? Sign up

Existing user? Log in

Hypothesis Testing

Already have an account? Log in here.

A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.

The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the $p$-value to the level of significance (a chosen target). If the $p$-value is less than or equal to the level of significance, then the null hypothesis is rejected.

When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.

Definitions and Methodology

Hypothesis test and confidence intervals.

In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.

The null hypothesis $($denoted $H_0)$ is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis $($denoted $H_1).$ Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted $\alpha$, which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted $\beta$, which is also its probability of occurrence. Also, $\alpha$ is known as the significance level , and $1-\beta$ is known as the power of the test. $H_0$ $\textbf{is true}$$\hspace{15mm}$ $H_0$ $\textbf{is false}$ $\textbf{Reject}$ $H_0$$\hspace{10mm}$ Type I error Correct Decision $\textbf{Reject}$ $H_1$ Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The $p$-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.

Methodologies: Given an estimator $\hat \theta$ of a population statistic $\theta$, following a probability distribution $P(T)$, computed from a sample $\mathcal{S},$ and given a significance level $\alpha$ and test statistic $t^*,$ define $H_0$ and $H_1;$ compute the test statistic $t^*.$ $p$-value Approach (most prevalent): Find the $p$-value using $t^*$ (right-tailed). If the $p$-value is at most $\alpha,$ reject $H_0$. Otherwise, reject $H_1$. Critical Value Approach: Find the critical value solving the equation $P(T\geq t_\alpha)=\alpha$ (right-tailed). If $t^*>t_\alpha$, reject $H_0$. Otherwise, reject $H_1$. Note: Failing to reject $H_0$ only means inability to accept $H_1$, and it does not mean to accept $H_0$.

Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the $p$-value approach with significance level $\alpha=0.05:$ Define $H_0$: $\mu=200$. Define $H_1$: $\mu>200$. Since our values are normally distributed, the test statistic is $z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09$. Using a standard normal distribution, we find that our $p$-value is approximately $0.001$. Since the $p$-value is at most $\alpha=0.05,$ we reject $H_0$. Therefore, we can conclude that the test shows sufficient evidence to support the claim that $\mu$ is larger than $200$ mg/dL.

If the sample size was smaller, the normal and $t$-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.

Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the $p$-value approach with significance level $\alpha=0.05$ and the $t$-distribution with 24 degrees of freedom: Define $H_0$: $\mu=200$. Define $H_1$: $\mu\neq 200$. Using the $t$-distribution, the test statistic is $t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54$. Using a $t$-distribution with 24 degrees of freedom, we find that our $p$-value is approximately $2(0.068)=0.136$. We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the $p$-value is larger than $\alpha=0.05,$ we fail to reject $H_0$. Therefore, the test does not show sufficient evidence to support the claim that $\mu$ is not equal to $200$ mg/dL.

The complement of the rejection on a two-tailed hypothesis test (with significance level $\alpha$) for a population parameter $\theta$ is equivalent to finding a confidence interval $($with confidence level $1-\alpha)$ for the population parameter $\theta$. If the assumption on the parameter $\theta$ falls inside the confidence interval, then the test has failed to reject the null hypothesis $($with $p$-value greater than $\alpha).$ Otherwise, if $\theta$ does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate $($with $p$-value at most $\alpha).$

Statistics (Estimation)
Normal Distribution
Correlation
Confidence Intervals

Problem Loading...

Note Loading...

Set Loading...

Definition Of Hypothesis

Hypothesis is the part of a conditional statement just after the word if.

Examples of Hypothesis

In the conditional, "If all fours sides of a quadrilateral measure the same, then the quadrilateral is a square" the hypothesis is "all fours sides of a quadrilateral measure the same".

Video Examples: Hypothesis

Solved Example on Hypothesis

Ques: in the example above, is the hypothesis "all fours sides of a quadrilateral measure the same" always, never, or sometimes true.

A. always B. never C. sometimes Correct Answer: C

Step 1: The hypothesis is sometimes true. Because, its true only for a square and a rhombus, not for the other quadrilaterals rectangle, parallelogram, or trapezoid.

Related Worksheet

Identifying-and-Describing-Right-Triangles-Gr-4
Points,-Lines,-Line-Segments,-Rays-and-Angles-Gr-4
Two-dimensional-Geometric-Figures-Gr-4
Interpreting-Multiplication-as-Scaling-or-Resizing-Gr-5
Parallel-Lines-and-Transversals-Gr-8

HighSchool Math

MathDictionary
PhysicsDictionary
ChemistryDictionary
BiologyDictionary
MathArticles
HealthInformation

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as $H_{0}$. Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as $H_{1}$ or $H_{a}$. For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, $\alpha$ or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$. $\overline{x}$ is the sample mean, $\mu$ is the population mean, $\sigma$ is the population standard deviation and n is the size of the sample.
t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$. s is the sample standard deviation.
$\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}$. $O_{i}$ is the observed value and $E_{i}$ is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

One sample: z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.
Two samples: z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

One sample: t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$.
Two samples: t = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

$H_{0}$: The population parameter is ≤ some value

$H_{1}$: The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

$H_{0}$: The population parameter is ≥ some value

$H_{1}$: The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

$H_{0}$: the population parameter = some value

$H_{1}$: the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
Step 2: Set up the alternative hypothesis.
Step 3: Choose the correct significance level, $\alpha$, and find the critical value.
Step 4: Calculate the correct test statistic (z, t or $\chi$) and p-value.
Step 5: Compare the test statistic with the critical value or compare the p-value with $\alpha$ to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as $H_{0}$: $\mu$ = 100.

Step 2: The alternative hypothesis is given by $H_{1}$: $\mu$ > 100.

Step 3: As this is a one-tailed test, $\alpha$ = 100% - 95% = 5%. This can be used to determine the critical value.

1 - $\alpha$ = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.

$\mu$ = 100, $\overline{x}$ = 112.5, n = 30, $\sigma$ = 15

z = $\frac{112.5-100}{\frac{15}{\sqrt{30}}}$ = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Probability and Statistics
Data Handling

Important Notes on Hypothesis Testing

Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
It involves the setting up of a null hypothesis and an alternate hypothesis.
There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ > 90 $\overline{x}$ = 110, $\mu$ = 90, n = 5, s = 18. $\alpha$ = 0.05 Using the t-distribution table, the critical value is 2.132 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. $H_{0}$: $\mu$ = 80, $H_{1}$: $\mu$ ≠ 80 $\overline{x}$ = 88, $\mu$ = 80, n = 36, $\sigma$ = 10. $\alpha$ = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ z = $\frac{88-80}{\frac{10}{\sqrt{36}}}$ = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ < 90 $\overline{x}$ = 110, $\mu$ = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = $\frac{82-90}{\frac{18}{\sqrt{6}}}$ t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ and for two samples is z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide $\alpha$ by 2. This is done as there are two rejection regions in the curve.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

9.1: Introduction to Hypothesis Testing

Last updated
Save as PDF
Page ID 10211

Kyle Siegrist
University of Alabama in Huntsville via Random Services

Basic Theory

Preliminaries.

As usual, our starting point is a random experiment with an underlying sample space and a probability measure $\P$. In the basic statistical model, we have an observable random variable $\bs{X}$ taking values in a set $S$. In general, $\bs{X}$ can have quite a complicated structure. For example, if the experiment is to sample $n$ objects from a population and record various measurements of interest, then \[ \bs{X} = (X_1, X_2, \ldots, X_n) \] where $X_i$ is the vector of measurements for the $i$th object. The most important special case occurs when $(X_1, X_2, \ldots, X_n)$ are independent and identically distributed. In this case, we have a random sample of size $n$ from the common distribution.

The purpose of this section is to define and discuss the basic concepts of statistical hypothesis testing . Collectively, these concepts are sometimes referred to as the Neyman-Pearson framework, in honor of Jerzy Neyman and Egon Pearson, who first formalized them.

A statistical hypothesis is a statement about the distribution of $\bs{X}$. Equivalently, a statistical hypothesis specifies a set of possible distributions of $\bs{X}$: the set of distributions for which the statement is true. A hypothesis that specifies a single distribution for $\bs{X}$ is called simple ; a hypothesis that specifies more than one distribution for $\bs{X}$ is called composite .

In hypothesis testing , the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis . The null hypothesis is usually denoted $H_0$ while the alternative hypothesis is usually denoted $H_1$.

An hypothesis test is a statistical decision ; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value $\bs{x}$ of the data vector $\bs{X}$. Thus, we will find an appropriate subset $R$ of the sample space $S$ and reject $H_0$ if and only if $\bs{x} \in R$. The set $R$ is known as the rejection region or the critical region . Note the asymmetry between the null and alternative hypotheses. This asymmetry is due to the fact that we assume the null hypothesis, in a sense, and then see if there is sufficient evidence in $\bs{x}$ to overturn this assumption in favor of the alternative.

An hypothesis test is a statistical analogy to proof by contradiction, in a sense. Suppose for a moment that $H_1$ is a statement in a mathematical theory and that $H_0$ is its negation. One way that we can prove $H_1$ is to assume $H_0$ and work our way logically to a contradiction. In an hypothesis test, we don't prove anything of course, but there are similarities. We assume $H_0$ and then see if the data $\bs{x}$ are sufficiently at odds with that assumption that we feel justified in rejecting $H_0$ in favor of $H_1$.

Often, the critical region is defined in terms of a statistic $w(\bs{X})$, known as a test statistic , where $w$ is a function from $S$ into another set $T$. We find an appropriate rejection region $R_T \subseteq T$ and reject $H_0$ when the observed value $w(\bs{x}) \in R_T$. Thus, the rejection region in $S$ is then $R = w^{-1}(R_T) = \left\{\bs{x} \in S: w(\bs{x}) \in R_T\right\}$. As usual, the use of a statistic often allows significant data reduction when the dimension of the test statistic is much smaller than the dimension of the data vector.

The ultimate decision may be correct or may be in error. There are two types of errors, depending on which of the hypotheses is actually true.

Types of errors:

A type 1 error is rejecting the null hypothesis $H_0$ when $H_0$ is true.
A type 2 error is failing to reject the null hypothesis $H_0$ when the alternative hypothesis $H_1$ is true.

Similarly, there are two ways to make a correct decision: we could reject $H_0$ when $H_1$ is true or we could fail to reject $H_0$ when $H_0$ is true. The possibilities are summarized in the following table:

Of course, when we observe $\bs{X} = \bs{x}$ and make our decision, either we will have made the correct decision or we will have committed an error, and usually we will never know which of these events has occurred. Prior to gathering the data, however, we can consider the probabilities of the various errors.

If $H_0$ is true (that is, the distribution of $\bs{X}$ is specified by $H_0$), then $\P(\bs{X} \in R)$ is the probability of a type 1 error for this distribution. If $H_0$ is composite, then $H_0$ specifies a variety of different distributions for $\bs{X}$ and thus there is a set of type 1 error probabilities.

The maximum probability of a type 1 error, over the set of distributions specified by $ H_0 $, is the significance level of the test or the size of the critical region.

The significance level is often denoted by $\alpha$. Usually, the rejection region is constructed so that the significance level is a prescribed, small value (typically 0.1, 0.05, 0.01).

If $H_1$ is true (that is, the distribution of $\bs{X}$ is specified by $H_1$), then $\P(\bs{X} \notin R)$ is the probability of a type 2 error for this distribution. Again, if $H_1$ is composite then $H_1$ specifies a variety of different distributions for $\bs{X}$, and thus there will be a set of type 2 error probabilities. Generally, there is a tradeoff between the type 1 and type 2 error probabilities. If we reduce the probability of a type 1 error, by making the rejection region $R$ smaller, we necessarily increase the probability of a type 2 error because the complementary region $S \setminus R$ is larger.

The extreme cases can give us some insight. First consider the decision rule in which we never reject $H_0$, regardless of the evidence $\bs{x}$. This corresponds to the rejection region $R = \emptyset$. A type 1 error is impossible, so the significance level is 0. On the other hand, the probability of a type 2 error is 1 for any distribution defined by $H_1$. At the other extreme, consider the decision rule in which we always rejects $H_0$ regardless of the evidence $\bs{x}$. This corresponds to the rejection region $R = S$. A type 2 error is impossible, but now the probability of a type 1 error is 1 for any distribution defined by $H_0$. In between these two worthless tests are meaningful tests that take the evidence $\bs{x}$ into account.

If $H_1$ is true, so that the distribution of $\bs{X}$ is specified by $H_1$, then $\P(\bs{X} \in R)$, the probability of rejecting $H_0$ is the power of the test for that distribution.

Thus the power of the test for a distribution specified by $ H_1 $ is the probability of making the correct decision.

Suppose that we have two tests, corresponding to rejection regions $R_1$ and $R_2$, respectively, each having significance level $\alpha$. The test with region $R_1$ is uniformly more powerful than the test with region $R_2$ if \[ \P(\bs{X} \in R_1) \ge \P(\bs{X} \in R_2) \text{ for every distribution of } \bs{X} \text{ specified by } H_1 \]

Naturally, in this case, we would prefer the first test. Often, however, two tests will not be uniformly ordered; one test will be more powerful for some distributions specified by $H_1$ while the other test will be more powerful for other distributions specified by $H_1$.

If a test has significance level $\alpha$ and is uniformly more powerful than any other test with significance level $\alpha$, then the test is said to be a uniformly most powerful test at level $\alpha$.

Clearly a uniformly most powerful test is the best we can do.

$P$-value

In most cases, we have a general procedure that allows us to construct a test (that is, a rejection region $R_\alpha$) for any given significance level $\alpha \in (0, 1)$. Typically, $R_\alpha$ decreases (in the subset sense) as $\alpha$ decreases.

The $P$-value of the observed value $\bs{x}$ of $\bs{X}$, denoted $P(\bs{x})$, is defined to be the smallest $\alpha$ for which $\bs{x} \in R_\alpha$; that is, the smallest significance level for which $H_0$ is rejected, given $\bs{X} = \bs{x}$.

Knowing $P(\bs{x})$ allows us to test $H_0$ at any significance level for the given data $\bs{x}$: If $P(\bs{x}) \le \alpha$ then we would reject $H_0$ at significance level $\alpha$; if $P(\bs{x}) \gt \alpha$ then we fail to reject $H_0$ at significance level $\alpha$. Note that $P(\bs{X})$ is a statistic . Informally, $P(\bs{x})$ can often be thought of as the probability of an outcome as or more extreme than the observed value $\bs{x}$, where extreme is interpreted relative to the null hypothesis $H_0$.

Analogy with Justice Systems

There is a helpful analogy between statistical hypothesis testing and the criminal justice system in the US and various other countries. Consider a person charged with a crime. The presumed null hypothesis is that the person is innocent of the crime; the conjectured alternative hypothesis is that the person is guilty of the crime. The test of the hypotheses is a trial with evidence presented by both sides playing the role of the data. After considering the evidence, the jury delivers the decision as either not guilty or guilty . Note that innocent is not a possible verdict of the jury, because it is not the point of the trial to prove the person innocent. Rather, the point of the trial is to see whether there is sufficient evidence to overturn the null hypothesis that the person is innocent in favor of the alternative hypothesis of that the person is guilty. A type 1 error is convicting a person who is innocent; a type 2 error is acquitting a person who is guilty. Generally, a type 1 error is considered the more serious of the two possible errors, so in an attempt to hold the chance of a type 1 error to a very low level, the standard for conviction in serious criminal cases is beyond a reasonable doubt .

Tests of an Unknown Parameter

Hypothesis testing is a very general concept, but an important special class occurs when the distribution of the data variable $\bs{X}$ depends on a parameter $\theta$ taking values in a parameter space $\Theta$. The parameter may be vector-valued, so that $\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_n)$ and $\Theta \subseteq \R^k$ for some $k \in \N_+$. The hypotheses generally take the form \[ H_0: \theta \in \Theta_0 \text{ versus } H_1: \theta \notin \Theta_0 \] where $\Theta_0$ is a prescribed subset of the parameter space $\Theta$. In this setting, the probabilities of making an error or a correct decision depend on the true value of $\theta$. If $R$ is the rejection region, then the power function $ Q $ is given by \[ Q(\theta) = \P_\theta(\bs{X} \in R), \quad \theta \in \Theta \] The power function gives a lot of information about the test.

The power function satisfies the following properties:

$Q(\theta)$ is the probability of a type 1 error when $\theta \in \Theta_0$.
$\max\left\{Q(\theta): \theta \in \Theta_0\right\}$ is the significance level of the test.
$1 - Q(\theta)$ is the probability of a type 2 error when $\theta \notin \Theta_0$.
$Q(\theta)$ is the power of the test when $\theta \notin \Theta_0$.

If we have two tests, we can compare them by means of their power functions.

Suppose that we have two tests, corresponding to rejection regions $R_1$ and $R_2$, respectively, each having significance level $\alpha$. The test with rejection region $R_1$ is uniformly more powerful than the test with rejection region $R_2$ if $ Q_1(\theta) \ge Q_2(\theta)$ for all $ \theta \notin \Theta_0 $.

Most hypothesis tests of an unknown real parameter $\theta$ fall into three special cases:

Suppose that $ \theta $ is a real parameter and $ \theta_0 \in \Theta $ a specified value. The tests below are respectively the two-sided test , the left-tailed test , and the right-tailed test .

$H_0: \theta = \theta_0$ versus $H_1: \theta \ne \theta_0$
$H_0: \theta \ge \theta_0$ versus $H_1: \theta \lt \theta_0$
$H_0: \theta \le \theta_0$ versus $H_1: \theta \gt \theta_0$

Thus the tests are named after the conjectured alternative. Of course, there may be other unknown parameters besides $\theta$ (known as nuisance parameters ).

Equivalence Between Hypothesis Test and Confidence Sets

There is an equivalence between hypothesis tests and confidence sets for a parameter $\theta$.

Suppose that $C(\bs{x})$ is a $1 - \alpha$ level confidence set for $\theta$. The following test has significance level $\alpha$ for the hypothesis $ H_0: \theta = \theta_0 $ versus $ H_1: \theta \ne \theta_0 $: Reject $H_0$ if and only if $\theta_0 \notin C(\bs{x})$

By definition, $\P[\theta \in C(\bs{X})] = 1 - \alpha$. Hence if $H_0$ is true so that $\theta = \theta_0$, then the probability of a type 1 error is $P[\theta \notin C(\bs{X})] = \alpha$.

Equivalently, we fail to reject $H_0$ at significance level $\alpha$ if and only if $\theta_0$ is in the corresponding $1 - \alpha$ level confidence set. In particular, this equivalence applies to interval estimates of a real parameter $\theta$ and the common tests for $\theta$ given above .

In each case below, the confidence interval has confidence level $1 - \alpha$ and the test has significance level $\alpha$.

Suppose that $\left[L(\bs{X}, U(\bs{X})\right]$ is a two-sided confidence interval for $\theta$. Reject $H_0: \theta = \theta_0$ versus $H_1: \theta \ne \theta_0$ if and only if $\theta_0 \lt L(\bs{X})$ or $\theta_0 \gt U(\bs{X})$.
Suppose that $L(\bs{X})$ is a confidence lower bound for $\theta$. Reject $H_0: \theta \le \theta_0$ versus $H_1: \theta \gt \theta_0$ if and only if $\theta_0 \lt L(\bs{X})$.
Suppose that $U(\bs{X})$ is a confidence upper bound for $\theta$. Reject $H_0: \theta \ge \theta_0$ versus $H_1: \theta \lt \theta_0$ if and only if $\theta_0 \gt U(\bs{X})$.

Pivot Variables and Test Statistics

Recall that confidence sets of an unknown parameter $\theta$ are often constructed through a pivot variable , that is, a random variable $W(\bs{X}, \theta)$ that depends on the data vector $\bs{X}$ and the parameter $\theta$, but whose distribution does not depend on $\theta$ and is known. In this case, a natural test statistic for the basic tests given above is $W(\bs{X}, \theta_0)$.

What Is a Hypothesis? (Science)

If...,Then...

Angela Lumsden/Getty Images

Scientific Method
Chemical Laws
Periodic Table
Projects & Experiments
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

A hypothesis (plural hypotheses) is a proposed explanation for an observation. The definition depends on the subject.

In science, a hypothesis is part of the scientific method. It is a prediction or explanation that is tested by an experiment. Observations and experiments may disprove a scientific hypothesis, but can never entirely prove one.

In the study of logic, a hypothesis is an if-then proposition, typically written in the form, "If X , then Y ."

In common usage, a hypothesis is simply a proposed explanation or prediction, which may or may not be tested.

Writing a Hypothesis

Most scientific hypotheses are proposed in the if-then format because it's easy to design an experiment to see whether or not a cause and effect relationship exists between the independent variable and the dependent variable . The hypothesis is written as a prediction of the outcome of the experiment.

Null Hypothesis and Alternative Hypothesis

Statistically, it's easier to show there is no relationship between two variables than to support their connection. So, scientists often propose the null hypothesis . The null hypothesis assumes changing the independent variable will have no effect on the dependent variable.

In contrast, the alternative hypothesis suggests changing the independent variable will have an effect on the dependent variable. Designing an experiment to test this hypothesis can be trickier because there are many ways to state an alternative hypothesis.

For example, consider a possible relationship between getting a good night's sleep and getting good grades. The null hypothesis might be stated: "The number of hours of sleep students get is unrelated to their grades" or "There is no correlation between hours of sleep and grades."

An experiment to test this hypothesis might involve collecting data, recording average hours of sleep for each student and grades. If a student who gets eight hours of sleep generally does better than students who get four hours of sleep or 10 hours of sleep, the hypothesis might be rejected.

But the alternative hypothesis is harder to propose and test. The most general statement would be: "The amount of sleep students get affects their grades." The hypothesis might also be stated as "If you get more sleep, your grades will improve" or "Students who get nine hours of sleep have better grades than those who get more or less sleep."

In an experiment, you can collect the same data, but the statistical analysis is less likely to give you a high confidence limit.

Usually, a scientist starts out with the null hypothesis. From there, it may be possible to propose and test an alternative hypothesis, to narrow down the relationship between the variables.

Example of a Hypothesis

Examples of a hypothesis include:

If you drop a rock and a feather, (then) they will fall at the same rate.
Plants need sunlight in order to live. (if sunlight, then life)
Eating sugar gives you energy. (if sugar, then energy)
White, Jay D. Research in Public Administration . Conn., 1998.
Schick, Theodore, and Lewis Vaughn. How to Think about Weird Things: Critical Thinking for a New Age . McGraw-Hill Higher Education, 2002.
Null Hypothesis Definition and Examples
Definition of a Hypothesis
What Are the Elements of a Good Hypothesis?
Six Steps of the Scientific Method
Independent Variable Definition and Examples
What Are Examples of a Hypothesis?
Understanding Simple vs Controlled Experiments
Scientific Method Flow Chart
Scientific Method Vocabulary Terms
What Is a Testable Hypothesis?
Null Hypothesis Examples
What 'Fail to Reject' Means in a Hypothesis Test
How To Design a Science Fair Experiment
What Is an Experiment? Definition and Design
Hypothesis Test for the Difference of Two Population Proportions

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Indian J Crit Care Med
v.23(Suppl 3); 2019 Sep

An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors

Priya ranganathan.

1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India

2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India

The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.

How to cite this article

Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230–S231.

Two papers quoted in this issue of the Indian Journal of Critical Care Medicine report. The results of studies aim to prove that a new intervention is better than (superior to) an existing treatment. In the ABLE study, the investigators wanted to show that transfusion of fresh red blood cells would be superior to standard-issue red cells in reducing 90-day mortality in ICU patients. 1 The PROPPR study was designed to prove that transfusion of a lower ratio of plasma and platelets to red cells would be superior to a higher ratio in decreasing 24-hour and 30-day mortality in critically ill patients. 2 These studies are known as superiority studies (as opposed to noninferiority or equivalence studies which will be discussed in a subsequent article).

SAMPLE VERSUS POPULATION

A sample represents a group of participants selected from the entire population. Since studies cannot be carried out on entire populations, researchers choose samples, which are representative of the population. This is similar to walking into a grocery store and examining a few grains of rice or wheat before purchasing an entire bag; we assume that the few grains that we select (the sample) are representative of the entire sack of grains (the population).

The results of the study are then extrapolated to generate inferences about the population. We do this using a process known as hypothesis testing. This means that the results of the study may not always be identical to the results we would expect to find in the population; i.e., there is the possibility that the study results may be erroneous.

HYPOTHESIS TESTING

A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the “alternate” hypothesis, and the opposite is called the “null” hypothesis; every study has a null hypothesis and an alternate hypothesis. For superiority studies, the alternate hypothesis states that one treatment (usually the new or experimental treatment) is superior to the other; the null hypothesis states that there is no difference between the treatments (the treatments are equal). For example, in the ABLE study, we start by stating the null hypothesis—there is no difference in mortality between groups receiving fresh RBCs and standard-issue RBCs. We then state the alternate hypothesis—There is a difference between groups receiving fresh RBCs and standard-issue RBCs. It is important to note that we have stated that the groups are different, without specifying which group will be better than the other. This is known as a two-tailed hypothesis and it allows us to test for superiority on either side (using a two-sided test). This is because, when we start a study, we are not 100% certain that the new treatment can only be better than the standard treatment—it could be worse, and if it is so, the study should pick it up as well. One tailed hypothesis and one-sided statistical testing is done for non-inferiority studies, which will be discussed in a subsequent paper in this series.

STATISTICAL ERRORS

There are two possibilities to consider when interpreting the results of a superiority study. The first possibility is that there is truly no difference between the treatments but the study finds that they are different. This is called a Type-1 error or false-positive error or alpha error. This means falsely rejecting the null hypothesis.

The second possibility is that there is a difference between the treatments and the study does not pick up this difference. This is called a Type 2 error or false-negative error or beta error. This means falsely accepting the null hypothesis.

The power of the study is the ability to detect a difference between groups and is the converse of the beta error; i.e., power = 1-beta error. Alpha and beta errors are finalized when the protocol is written and form the basis for sample size calculation for the study. In an ideal world, we would not like any error in the results of our study; however, we would need to do the study in the entire population (infinite sample size) to be able to get a 0% alpha and beta error. These two errors enable us to do studies with realistic sample sizes, with the compromise that there is a small possibility that the results may not always reflect the truth. The basis for this will be discussed in a subsequent paper in this series dealing with sample size calculation.

Conventionally, type 1 or alpha error is set at 5%. This means, that at the end of the study, if there is a difference between groups, we want to be 95% certain that this is a true difference and allow only a 5% probability that this difference has occurred by chance (false positive). Type 2 or beta error is usually set between 10% and 20%; therefore, the power of the study is 90% or 80%. This means that if there is a difference between groups, we want to be 80% (or 90%) certain that the study will detect that difference. For example, in the ABLE study, sample size was calculated with a type 1 error of 5% (two-sided) and power of 90% (type 2 error of 10%) (1).

Table 1 gives a summary of the two types of statistical errors with an example

Statistical errors

In the next article in this series, we will look at the meaning and interpretation of ‘ p ’ value and confidence intervals for hypothesis testing.

Source of support: Nil

Conflict of interest: None

Hypothesis Testing

Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.

2. Identify a test statistic that can be used to assess the truth of the null hypothesis .

Explore with Wolfram|Alpha

More things to try:

hypothesis testing mean
1->2, 2->3, 3->1, 3->4, 4->1
complexity class BPP

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Hypothesis Testing." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/HypothesisTesting.html

Subject classifications

Maths Notes Class 12
NCERT Solutions Class 12
RD Sharma Solutions Class 12
Maths Formulas Class 12
Maths Previous Year Paper Class 12
Class 12 Syllabus
Class 12 Revision Notes
Physics Notes Class 12
Chemistry Notes Class 12
Biology Notes Class 12
Domain and Range of Trigonometric Functions
Exponential Graph
Line Integral
Determinant of 2x2 Matrix
Integral of Cos x
Algebra of Matrices
Random Sampling Method
Derivative of Sin 2x
Integration
Derivative of Sec Square x
Derivative Rules
Derivative of Sec x
Systematic Random Sampling
Derivative of Tan Inverse x
Derivative of Arctan
Zero Vector
Triple Integrals
Local Maxima and Minima in Calculus

Hypothesis is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables. Hypothesis is also called Theory, Thesis, Guess, Assumption, or Suggestion. Hypothesis creates a structure that guides the search for knowledge.

In this article, we will learn what is hypothesis, its characteristics, types, and examples. We will also learn how hypothesis helps in scientific research.

What is Hypothesis?

A hypothesis is a suggested idea or plan that has little proof, meant to lead to more study. It’s mainly a smart guess or suggested answer to a problem that can be checked through study and trial. In science work, we make guesses called hypotheses to try and figure out what will happen in tests or watching. These are not sure things but rather ideas that can be proved or disproved based on real-life proofs. A good theory is clear and can be tested and found wrong if the proof doesn’t support it.

Hypothesis Meaning

A hypothesis is a proposed statement that is testable and is given for something that happens or observed.

It is made using what we already know and have seen, and it’s the basis for scientific research.
A clear guess tells us what we think will happen in an experiment or study.
It’s a testable clue that can be proven true or wrong with real-life facts and checking it out carefully.
It usually looks like a “if-then” rule, showing the expected cause and effect relationship between what’s being studied.

Characteristics of Hypothesis

Here are some key characteristics of a hypothesis:

Testable: An idea (hypothesis) should be made so it can be tested and proven true through doing experiments or watching. It should show a clear connection between things.
Specific: It needs to be easy and on target, talking about a certain part or connection between things in a study.
Falsifiable: A good guess should be able to show it’s wrong. This means there must be a chance for proof or seeing something that goes against the guess.
Logical and Rational: It should be based on things we know now or have seen, giving a reasonable reason that fits with what we already know.
Predictive: A guess often tells what to expect from an experiment or observation. It gives a guide for what someone might see if the guess is right.
Concise: It should be short and clear, showing the suggested link or explanation simply without extra confusion.
Grounded in Research: A guess is usually made from before studies, ideas or watching things. It comes from a deep understanding of what is already known in that area.
Flexible: A guess helps in the research but it needs to change or fix when new information comes up.
Relevant: It should be related to the question or problem being studied, helping to direct what the research is about.
Empirical: Hypotheses come from observations and can be tested using methods based on real-world experiences.

Sources of Hypothesis

Hypotheses can come from different places based on what you’re studying and the kind of research. Here are some common sources from which hypotheses may originate:

Existing Theories: Often, guesses come from well-known science ideas. These ideas may show connections between things or occurrences that scientists can look into more.
Observation and Experience: Watching something happen or having personal experiences can lead to guesses. We notice odd things or repeat events in everyday life and experiments. This can make us think of guesses called hypotheses.
Previous Research: Using old studies or discoveries can help come up with new ideas. Scientists might try to expand or question current findings, making guesses that further study old results.
Literature Review: Looking at books and research in a subject can help make guesses. Noticing missing parts or mismatches in previous studies might make researchers think up guesses to deal with these spots.
Problem Statement or Research Question: Often, ideas come from questions or problems in the study. Making clear what needs to be looked into can help create ideas that tackle certain parts of the issue.
Analogies or Comparisons: Making comparisons between similar things or finding connections from related areas can lead to theories. Understanding from other fields could create new guesses in a different situation.
Hunches and Speculation: Sometimes, scientists might get a gut feeling or make guesses that help create ideas to test. Though these may not have proof at first, they can be a beginning for looking deeper.
Technology and Innovations: New technology or tools might make guesses by letting us look at things that were hard to study before.
Personal Interest and Curiosity: People’s curiosity and personal interests in a topic can help create guesses. Scientists could make guesses based on their own likes or love for a subject.

Types of Hypothesis

Here are some common types of hypotheses:

Simple Hypothesis

Complex hypothesis, directional hypothesis.

Non-directional Hypothesis

Null Hypothesis (H0)

Alternative hypothesis (h1 or ha), statistical hypothesis, research hypothesis, associative hypothesis, causal hypothesis.

Simple Hypothesis guesses a connection between two things. It says that there is a connection or difference between variables, but it doesn’t tell us which way the relationship goes.

Complex Hypothesis tells us what will happen when more than two things are connected. It looks at how different things interact and may be linked together.

Directional Hypothesis says how one thing is related to another. For example, it guesses that one thing will help or hurt another thing.

Non-Directional Hypothesis

Non-Directional Hypothesis are the one that don’t say how the relationship between things will be. They just say that there is a connection, without telling which way it goes.

Null hypothesis is a statement that says there’s no connection or difference between different things. It implies that any seen impacts are because of luck or random changes in the information.

Alternative Hypothesis is different from the null hypothesis and shows that there’s a big connection or gap between variables. Scientists want to say no to the null hypothesis and choose the alternative one.

Statistical Hypotheis are used in math testing and include making ideas about what groups or bits of them look like. You aim to get information or test certain things using these top-level, common words only.

Research Hypothesis comes from the research question and tells what link is expected between things or factors. It leads the study and chooses where to look more closely.

Associative Hypotheis guesses that there is a link or connection between things without really saying it caused them. It means that when one thing changes, it is connected to another thing changing.

Causal Hypothesis are different from other ideas because they say that one thing causes another. This means there’s a cause and effect relationship between variables involved in the situation. They say that when one thing changes, it directly makes another thing change.

Hypothesis Examples

Following are the examples of hypotheses based on their types:

Simple Hypothesis Example

Studying more can help you do better on tests.
Getting more sun makes people have higher amounts of vitamin D.

Complex Hypothesis Example

How rich you are, how easy it is to get education and healthcare greatly affects the number of years people live.
A new medicine’s success relies on the amount used, how old a person is who takes it and their genes.

Directional Hypothesis Example

Drinking more sweet drinks is linked to a higher body weight score.
Too much stress makes people less productive at work.

Non-directional Hypothesis Example

Drinking caffeine can affect how well you sleep.
People often like different kinds of music based on their gender.
The average test scores of Group A and Group B are not much different.
There is no connection between using a certain fertilizer and how much it helps crops grow.

Alternative Hypothesis (Ha)

Patients on Diet A have much different cholesterol levels than those following Diet B.
Exposure to a certain type of light can change how plants grow compared to normal sunlight.
The average smarts score of kids in a certain school area is 100.
The usual time it takes to finish a job using Method A is the same as with Method B.
Having more kids go to early learning classes helps them do better in school when they get older.
Using specific ways of talking affects how much customers get involved in marketing activities.
Regular exercise helps to lower the chances of heart disease.
Going to school more can help people make more money.
Playing violent video games makes teens more likely to act aggressively.
Less clean air directly impacts breathing health in city populations.

Functions of Hypothesis

Hypotheses have many important jobs in the process of scientific research. Here are the key functions of hypotheses:

Guiding Research: Hypotheses give a clear and exact way for research. They act like guides, showing the predicted connections or results that scientists want to study.
Formulating Research Questions: Research questions often create guesses. They assist in changing big questions into particular, checkable things. They guide what the study should be focused on.
Setting Clear Objectives: Hypotheses set the goals of a study by saying what connections between variables should be found. They set the targets that scientists try to reach with their studies.
Testing Predictions: Theories guess what will happen in experiments or observations. By doing tests in a planned way, scientists can check if what they see matches the guesses made by their ideas.
Providing Structure: Theories give structure to the study process by arranging thoughts and ideas. They aid scientists in thinking about connections between things and plan experiments to match.
Focusing Investigations: Hypotheses help scientists focus on certain parts of their study question by clearly saying what they expect links or results to be. This focus makes the study work better.
Facilitating Communication: Theories help scientists talk to each other effectively. Clearly made guesses help scientists to tell others what they plan, how they will do it and the results expected. This explains things well with colleagues in a wide range of audiences.
Generating Testable Statements: A good guess can be checked, which means it can be looked at carefully or tested by doing experiments. This feature makes sure that guesses add to the real information used in science knowledge.
Promoting Objectivity: Guesses give a clear reason for study that helps guide the process while reducing personal bias. They motivate scientists to use facts and data as proofs or disprovals for their proposed answers.
Driving Scientific Progress: Making, trying out and adjusting ideas is a cycle. Even if a guess is proven right or wrong, the information learned helps to grow knowledge in one specific area.

How Hypothesis help in Scientific Research?

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

Initiating Investigations: Hypotheses are the beginning of science research. They come from watching, knowing what’s already known or asking questions. This makes scientists make certain explanations that need to be checked with tests.
Formulating Research Questions: Ideas usually come from bigger questions in study. They help scientists make these questions more exact and testable, guiding the study’s main point.
Setting Clear Objectives: Hypotheses set the goals of a study by stating what we think will happen between different things. They set the goals that scientists want to reach by doing their studies.
Designing Experiments and Studies: Assumptions help plan experiments and watchful studies. They assist scientists in knowing what factors to measure, the techniques they will use and gather data for a proposed reason.
Testing Predictions: Ideas guess what will happen in experiments or observations. By checking these guesses carefully, scientists can see if the seen results match up with what was predicted in each hypothesis.
Analysis and Interpretation of Data: Hypotheses give us a way to study and make sense of information. Researchers look at what they found and see if it matches the guesses made in their theories. They decide if the proof backs up or disagrees with these suggested reasons why things are happening as expected.
Encouraging Objectivity: Hypotheses help make things fair by making sure scientists use facts and information to either agree or disagree with their suggested reasons. They lessen personal preferences by needing proof from experience.
Iterative Process: People either agree or disagree with guesses, but they still help the ongoing process of science. Findings from testing ideas make us ask new questions, improve those ideas and do more tests. It keeps going on in the work of science to keep learning things.

People Also View:

Mathematics Maths Formulas Branches of Mathematics

Summary – Hypothesis

A hypothesis is a testable statement serving as an initial explanation for phenomena, based on observations, theories, or existing knowledge. It acts as a guiding light for scientific research, proposing potential relationships between variables that can be empirically tested through experiments and observations. The hypothesis must be specific, testable, falsifiable, and grounded in prior research or observation, laying out a predictive, if-then scenario that details a cause-and-effect relationship. It originates from various sources including existing theories, observations, previous research, and even personal curiosity, leading to different types, such as simple, complex, directional, non-directional, null, and alternative hypotheses, each serving distinct roles in research methodology. The hypothesis not only guides the research process by shaping objectives and designing experiments but also facilitates objective analysis and interpretation of data, ultimately driving scientific progress through a cycle of testing, validation, and refinement.

FAQs on Hypothesis

What is a hypothesis.

A guess is a possible explanation or forecast that can be checked by doing research and experiments.

What are Components of a Hypothesis?

The components of a Hypothesis are Independent Variable, Dependent Variable, Relationship between Variables, Directionality etc.

What makes a Good Hypothesis?

Testability, Falsifiability, Clarity and Precision, Relevance are some parameters that makes a Good Hypothesis

Can a Hypothesis be Proven True?

You cannot prove conclusively that most hypotheses are true because it’s generally impossible to examine all possible cases for exceptions that would disprove them.

How are Hypotheses Tested?

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data

Can Hypotheses change during Research?

Yes, you can change or improve your ideas based on new information discovered during the research process.

What is the Role of a Hypothesis in Scientific Research?

Hypotheses are used to support scientific research and bring about advancements in knowledge.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Math Definitions - Letter H

1» Half
1» Handspan
1» Hect-
1» Hectare (ha)
1» Heft
1» Height
1» Hemisphere
1» Hendecagon
1» Hepta-
1» Heptagon
1» Hexa-
1» Hexadecimal
1» Hexagon
1» Hexahedron
1» Highest Common Factor
1» Hindu-Arabic Number System
1» Histogram
1» Horizontal
1» Horizontal Run
1» Hour
1» Hour Hand
1» Hundredth
1» Hyperbola
1» Hypotenuse
1» Hypothesis

Definition of Hypothesis

A hypothesis is a statement that might be true, but which needs to be tested.

For example, Al forwards the hypothesis that "pink snails move more slowly than brown snails."

Al will be able to test his hypothesis by calculating the speed of hundreds of pink and brown snails, and then analysing the data he has collected to decide which colour of snail is the fastest.

Sometimes scientists will forward hypotheses that cannot be tested, but which seem to be a good explanation of something. It is worth noting that such hypotheses may be wrong. For example, an archaeologist might put forward the hypothesis that an ancient people believed that a certain rock painting was endowed with magical powers. Without a time machine, this hypothesis cannot be tested, but it could be a plausible explanation for the size and position of the rock painting.

Description

The aim of this dictionary is to provide definitions to common mathematical terms. Students learn a new math skill every week at school, sometimes just before they start a new skill, if they want to look at what a specific term means, this is where this dictionary will become handy and a go-to guide for a student.

Year 1 to Year 12 students

Learning Objectives

Learn common math terms starting with letter H

Author: Subject Coach Added on: 6th Feb 2018

You must be logged in as Student to ask a Question.

None just yet!

THANK YOU FOR STOPPING BY!

Worksheets, Videos, Tests, Pretests
Science Projects
Maths Projects
Activity Ideas

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.1: Statements and Conditional Statements

Last updated
Save as PDF
Page ID 7034

Ted Sundstrom
Grand Valley State University via ScholarWorks @Grand Valley State University

Much of our work in mathematics deals with statements. In mathematics, a statement is a declarative sentence that is either true or false but not both. A statement is sometimes called a proposition . The key is that there must be no ambiguity. To be a statement, a sentence must be true or false, and it cannot be both. So a sentence such as "The sky is beautiful" is not a statement since whether the sentence is true or not is a matter of opinion. A question such as "Is it raining?" is not a statement because it is a question and is not declaring or asserting that something is true.

Some sentences that are mathematical in nature often are not statements because we may not know precisely what a variable represents. For example, the equation 2$x$+5 = 10 is not a statement since we do not know what $x$ represents. If we substitute a specific value for $x$ (such as $x$ = 3), then the resulting equation, 2$\cdot$3 +5 = 10 is a statement (which is a false statement). Following are some more examples:

There exists a real number $x$ such that 2$x$+5 = 10. This is a statement because either such a real number exists or such a real number does not exist. In this case, this is a true statement since such a real number does exist, namely $x$ = 2.5.
For each real number $x$, $2x +5 = 2 \left( x + \dfrac{5}{2}\right)$. This is a statement since either the sentence $2x +5 = 2 \left( x + \dfrac{5}{2}\right)$ is true when any real number is substituted for $x$ (in which case, the statement is true) or there is at least one real number that can be substituted for $x$ and produce a false statement (in which case, the statement is false). In this case, the given statement is true.
Solve the equation $x^2 - 7x +10 =0$. This is not a statement since it is a directive. It does not assert that something is true.
$(a+b)^2 = a^2+b^2$ is not a statement since it is not known what $a$ and $b$ represent. However, the sentence, “There exist real numbers $a$ and $b$ such that $(a+b)^2 = a^2+b^2$" is a statement. In fact, this is a true statement since there are such integers. For example, if $a=1$ and $b=0$, then $(a+b)^2 = a^2+b^2$.
Compare the statement in the previous item to the statement, “For all real numbers $a$ and $b$, $(a+b)^2 = a^2+b^2$." This is a false statement since there are values for $a$ and $b$ for which $(a+b)^2 \ne a^2+b^2$. For example, if $a=2$ and $b=3$, then $(a+b)^2 = 5^2 = 25$ and $a^2 + b^2 = 2^2 +3^2 = 13$.

Progress Check 1.1: Statements

Which of the following sentences are statements? Do not worry about determining whether a statement is true or false; just determine whether each sentence is a statement or not.

2$\cdot$7 + 8 = 22.
$(x-1) = \sqrt(x + 11)$.
$2x + 5y = 7$.
There are integers $x$ and $y$ such that $2x + 5y = 7$.
There are integers $x$ and $y$ such that $23x + 27y = 52$.
Given a line $L$ and a point $P$ not on that line, there is a unique line through $P$ that does not intersect $L$.
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$.
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$ for all real numbers $a$ and $b$.
The derivative of $f(x) = \sin x$ is $f' (x) = \cos x$.
Does the equation $3x^2 - 5x - 7 = 0$ have two real number solutions?
If $ABC$ is a right triangle with right angle at vertex $B$, and if $D$ is the midpoint of the hypotenuse, then the line segment connecting vertex $B$ to $D$ is half the length of the hypotenuse.
There do not exist three integers $x$, $y$, and $z$ such that $x^3 + y^2 = z^3$.

Add texts here. Do not delete this text first.

How Do We Decide If a Statement Is True or False?

In mathematics, we often establish that a statement is true by writing a mathematical proof. To establish that a statement is false, we often find a so-called counterexample. (These ideas will be explored later in this chapter.) So mathematicians must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text.

For now, we want to focus on what happens before we start a proof. One thing that mathematicians often do is to make a conjecture beforehand as to whether the statement is true or false. This is often done through exploration. The role of exploration in mathematics is often difficult because the goal is not to find a specific answer but simply to investigate. Following are some techniques of exploration that might be helpful.

Techniques of Exploration

Guesswork and conjectures . Formulate and write down questions and conjectures. When we make a guess in mathematics, we usually call it a conjecture.

For example, if someone makes the conjecture that $\sin(2x) = 2 \sin(x)$, for all real numbers $x$, we can test this conjecture by substituting specific values for $x$. One way to do this is to choose values of $x$ for which $\sin(x)$is known. Using $x = \frac{\pi}{4}$, we see that

$\sin(2(\frac{\pi}{4})) = \sin(\frac{\pi}{2}) = 1,$ and

$2\sin(\frac{\pi}{4}) = 2(\frac{\sqrt2}{2}) = \sqrt2$.

Since $1 \ne \sqrt2$, these calculations show that this conjecture is false. However, if we do not find a counterexample for a conjecture, we usually cannot claim the conjecture is true. The best we can say is that our examples indicate the conjecture is true. As an example, consider the conjecture that

If $x$ and $y$ are odd integers, then $x + y$ is an even integer.

We can do lots of calculation, such as $3 + 7 = 10$ and $5 + 11 = 16$, and find that every time we add two odd integers, the sum is an even integer. However, it is not possible to test every pair of odd integers, and so we can only say that the conjecture appears to be true. (We will prove that this statement is true in the next section.)

Use of prior knowledge. This also is very important. We cannot start from square one every time we explore a statement. We must make use of our acquired mathematical knowledge. For the conjecture that $\sin (2x) = 2 \sin(x)$, for all real numbers $x$, we might recall that there are trigonometric identities called “double angle identities.” We may even remember the correct identity for $\sin (2x)$, but if we do not, we can always look it up. We should recall (or find) that for all real numbers $x$, \[\sin(2x) = 2 \sin(x)\cos(x).\]
We could use this identity to argue that the conjecture “for all real numbers $x$, $\sin (2x) = 2 \sin(x)$” is false, but if we do, it is still a good idea to give a specific counterexample as we did before.
Cooperation and brainstorming . Working together is often more fruitful than working alone. When we work with someone else, we can compare notes and articulate our ideas. Thinking out loud is often a useful brainstorming method that helps generate new ideas.

Progress Check 1.2: Explorations

Use the techniques of exploration to investigate each of the following statements. Can you make a conjecture as to whether the statement is true or false? Can you determine whether it is true or false?

$(a + b)^2 = a^2 + b^2$, for all real numbers a and b.
There are integers $x$ and $y$ such that $2x + 5y = 41$.
If $x$ is an even integer, then $x^2$ is an even integer.
If $x$ and $y$ are odd integers, then $x \cdot y$ is an odd integer.

Conditional Statements

One of the most frequently used types of statements in mathematics is the so-called conditional statement. Given statements $P$ and $Q$, a statement of the form “If $P$ then $Q$” is called a conditional statement . It seems reasonable that the truth value (true or false) of the conditional statement “If $P$ then $Q$” depends on the truth values of $P$ and $Q$. The statement “If $P$ then $Q$” means that $Q$ must be true whenever $P$ is true. The statement $P$ is called the hypothesis of the conditional statement, and the statement $Q$ is called the conclusion of the conditional statement. Since conditional statements are probably the most important type of statement in mathematics, we give a more formal definition.

A conditional statement is a statement that can be written in the form “If $P$ then $Q$,” where $P$ and $Q$ are sentences. For this conditional statement, $P$ is called the hypothesis and $Q$ is called the conclusion .

Intuitively, “If $P$ then $Q$” means that $Q$ must be true whenever $P$ is true. Because conditional statements are used so often, a symbolic shorthand notation is used to represent the conditional statement “If $P$ then $Q$.” We will use the notation $P \to Q$ to represent “If $P$ then $Q$.” When $P$ and $Q$ are statements, it seems reasonable that the truth value (true or false) of the conditional statement $P \to Q$ depends on the truth values of $P$ and $Q$. There are four cases to consider:

$P$ is true and $Q$ is true.
$P$ is false and $Q$ is true.
$P$ is true and $Q$ is false.
$P$ is false and $Q$ is false.

The conditional statement $P \to Q$ means that $Q$ is true whenever $P$ is true. It says nothing about the truth value of $Q$ when $P$ is false. Using this as a guide, we define the conditional statement $P \to Q$ to be false only when $P$ is true and $Q$ is false, that is, only when the hypothesis is true and the conclusion is false. In all other cases, $P \to Q$ is true. This is summarized in Table 1.1 , which is called a truth table for the conditional statement $P \to Q$. (In Table 1.1 , T stands for “true” and F stands for “false.”)

Table 1.1: Truth Table for $P \to Q$

The important thing to remember is that the conditional statement $P \to Q$ has its own truth value. It is either true or false (and not both). Its truth value depends on the truth values for $P$ and $Q$, but some find it a bit puzzling that the conditional statement is considered to be true when the hypothesis P is false. We will provide a justification for this through the use of an example.

Example 1.3:

Suppose that I say

“If it is not raining, then Daisy is riding her bike.”

We can represent this conditional statement as $P \to Q$ where $P$ is the statement, “It is not raining” and $Q$ is the statement, “Daisy is riding her bike.”

Although it is not a perfect analogy, think of the statement $P \to Q$ as being false to mean that I lied and think of the statement $P \to Q$ as being true to mean that I did not lie. We will now check the truth value of $P \to Q$ based on the truth values of $P$ and $Q$.

Suppose that both $P$ and $Q$ are true. That is, it is not raining and Daisy is riding her bike. In this case, it seems reasonable to say that I told the truth and that$P \to Q$ is true.
Suppose that $P$ is true and $Q$ is false or that it is not raining and Daisy is not riding her bike. It would appear that by making the statement, “If it is not raining, then Daisy is riding her bike,” that I have not told the truth. So in this case, the statement $P \to Q$ is false.
Now suppose that $P$ is false and $Q$ is true or that it is raining and Daisy is riding her bike. Did I make a false statement by stating that if it is not raining, then Daisy is riding her bike? The key is that I did not make any statement about what would happen if it was raining, and so I did not tell a lie. So we consider the conditional statement, “If it is not raining, then Daisy is riding her bike,” to be true in the case where it is raining and Daisy is riding her bike.
Finally, suppose that both $P$ and $Q$ are false. That is, it is raining and Daisy is not riding her bike. As in the previous situation, since my statement was $P \to Q$, I made no claim about what would happen if it was raining, and so I did not tell a lie. So the statement $P \to Q$ cannot be false in this case and so we consider it to be true.

Progress Check 1.4: xplorations with Conditional Statements

1 . Consider the following sentence:

If $x$ is a positive real number, then $x^2 + 8x$ is a positive real number.

Although the hypothesis and conclusion of this conditional sentence are not statements, the conditional sentence itself can be considered to be a statement as long as we know what possible numbers may be used for the variable $x$. From the context of this sentence, it seems that we can substitute any positive real number for $x$. We can also substitute 0 for $x$ or a negative real number for x provided that we are willing to work with a false hypothesis in the conditional statement. (In Chapter 2 , we will learn how to be more careful and precise with these types of conditional statements.)

(a) Notice that if $x = -3$, then $x^2 + 8x = -15$, which is negative. Does this mean that the given conditional statement is false?

(b) Notice that if $x = 4$, then $x^2 + 8x = 48$, which is positive. Does this mean that the given conditional statement is true?

(c) Do you think this conditional statement is true or false? Record the results for at least five different examples where the hypothesis of this conditional statement is true.

2 . “If $n$ is a positive integer, then $n^2 - n +41$ is a prime number.” (Remember that a prime number is a positive integer greater than 1 whose only positive factors are 1 and itself.) To explore whether or not this statement is true, try using (and recording your results) for $n = 1$, $n = 2$, $n = 3$, $n = 4$, $n = 5$, and $n = 10$. Then record the results for at least four other values of $n$. Does this conditional statement appear to be true?

Further Remarks about Conditional Statements

Suppose that Ed has exactly $52 in his wallet. The following four statements will use the four possible truth combinations for the hypothesis and conclusion of a conditional statement.

If Ed has exactly $52 in his wallet, then he has $20 in his wallet. This is a true statement. Notice that both the hypothesis and the conclusion are true.
If Ed has exactly $52 in his wallet, then he has $100 in his wallet. This statement is false. Notice that the hypothesis is true and the conclusion is false.
If Ed has $100 in his wallet, then he has at least $50 in his wallet. This statement is true regardless of how much money he has in his wallet. In this case, the hypothesis is false and the conclusion is true.

This is admittedly a contrived example but it does illustrate that the conventions for the truth value of a conditional statement make sense. The message is that in order to be complete in mathematics, we need to have conventions about when a conditional statement is true and when it is false.

If $n$ is a positive integer, then $(n^2 - n + 41)$ is a prime number.

Perhaps for all of the values you tried for $n$, $(n^2 - n + 41)$ turned out to be a prime number. However, if we try $n = 41$, we ge $n^2 - n + 41 = 41^2 - 41 + 41$ $n^2 - n + 41 = 41^2$ So in the case where $n = 41$, the hypothesis is true (41 is a positive integer) and the conclusion is false $41^2$ is not prime. Therefore, 41 is a counterexample for this conjecture and the conditional statement “If $n$ is a positive integer, then $(n^2 - n + 41)$ is a prime number” is false. There are other counterexamples (such as $n = 42$, $n = 45$, and $n = 50$), but only one counterexample is needed to prove that the statement is false.

Although one example can be used to prove that a conditional statement is false, in most cases, we cannot use examples to prove that a conditional statement is true. For example, in Progress Check 1.4 , we substituted values for $x$ for the conditional statement “If $x$ is a positive real number, then $x^2 + 8x$ is a positive real number.” For every positive real number used for $x$, we saw that $x^2 + 8x$ was positive. However, this does not prove the conditional statement to be true because it is impossible to substitute every positive real number for $x$. So, although we may believe this statement is true, to be able to conclude it is true, we need to write a mathematical proof. Methods of proof will be discussed in Section 1.2 and Chapter 3 .

Progress Check 1.5: Working with a Conditional Statement

The following statement is a true statement, which is proven in many calculus texts.

If the function $f$ is differentiable at $a$, then the function $f$ is continuous at $a$.

Using only this true statement, is it possible to make a conclusion about the function in each of the following cases?

It is known that the function $f$, where $f(x) = \sin x$, is differentiable at 0.
It is known that the function $f$, where $f(x) = \sqrt[3]x$, is not differentiable at 0.
It is known that the function $f$, where $f(x) = |x|$, is continuous at 0.
It is known that the function $f$, where $f(x) = \dfrac{|x|}{x}$ is not continuous at 0.

Closure Properties of Number Systems

The primary number system used in algebra and calculus is the real number system . We usually use the symbol R to stand for the set of all real numbers. The real numbers consist of the rational numbers and the irrational numbers. The rational numbers are those real numbers that can be written as a quotient of two integers (with a nonzero denominator), and the irrational numbers are those real numbers that cannot be written as a quotient of two integers. That is, a rational number can be written in the form of a fraction, and an irrational number cannot be written in the form of a fraction. Some common irrational numbers are $\sqrt2$, $\pi$ and $e$. We usually use the symbol $\mathbb{Q}$ to represent the set of all rational numbers. (The letter $\mathbb{Q}$ is used because rational numbers are quotients of integers.) There is no standard symbol for the set of all irrational numbers.

Perhaps the most basic number system used in mathematics is the set of natural numbers . The natural numbers consist of the positive whole numbers such as 1, 2, 3, 107, and 203. We will use the symbol $\mathbb{N}$ to stand for the set of natural numbers. Another basic number system that we will be working with is the set of integers . The integers consist of zero, the positive whole numbers, and the negatives of the positive whole numbers. If $n$ is an integer, we can write $n = \dfrac{n}{1}$. So each integer is a rational number and hence also a real number.

We will use the letter $\mathbb{Z}$ to stand for the set of integers. (The letter $\mathbb{Z}$ is from the German word, $Zahlen$, for numbers.) Three of the basic properties of the integers are that the set $\mathbb{Z}$ is closed under addition , the set $\mathbb{Z}$ is closed under multiplication , and the set of integers is closed under subtraction. This means that

If $x$ and $y$ are integers, then $x + y$ is an integer;
If $x$ and $y$ are integers, then $x \cdot y$ is an integer; and
If $x$ and $y$ are integers, then $x - y$ is an integer.

Notice that these so-called closure properties are defined in terms of conditional statements. This means that if we can find one instance where the hypothesis is true and the conclusion is false, then the conditional statement is false.

Example 1.6: Closure

In order for the set of natural numbers to be closed under subtraction, the following conditional statement would have to be true: If $x$ and $y$ are natural numbers, then $x - y$ is a natural number. However, since 5 and 8 are natural numbers, $5 - 8 = -3$, which is not a natural number, this conditional statement is false. Therefore, the set of natural numbers is not closed under subtraction.
We can use the rules for multiplying fractions and the closure rules for the integers to show that the rational numbers are closed under multiplication. If $\dfrac{a}{b}$ and $\dfrac{c}{d}$ are rational numbers (so $a$, $b$, $c$, and $d$ are integers and $b$ and $d$ are not zero), then $\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}.$ Since the integers are closed under multiplication, we know that $ac$ and $bd$ are integers and since $b \ne 0$ and $d \ne 0$, $bd \ne 0$. Hence, $\dfrac{ac}{bd}$ is a rational number and this shows that the rational numbers are closed under multiplication.

Progress Check 1.7: Closure Properties

Answer each of the following questions.

Is the set of rational numbers closed under addition? Explain.
Is the set of integers closed under division? Explain.
Is the set of rational numbers closed under subtraction? Explain.
Which of the following sentences are statements? (a) $3^2 + 4^2 = 5^2.$ (b) $a^2 + b^2 = c^2.$ (c) There exists integers $a$, $b$, and $c$ such that $a^2 + b^2 = c^2.$ (d) If $x^2 = 4$, then $x = 2.$ (e) For each real number $x$, if $x^2 = 4$, then $x = 2.$ (f) For each real number $t$, $\sin^2t + \cos^2t = 1.$ (g) $\sin x < \sin (\frac{\pi}{4}).$ (h) If $n$ is a prime number, then $n^2$ has three positive factors. (i) 1 + $\tan^2 \theta = \text{sec}^2 \theta.$ (j) Every rectangle is a parallelogram. (k) Every even natural number greater than or equal to 4 is the sum of two prime numbers.
Identify the hypothesis and the conclusion for each of the following conditional statements. (a) If $n$ is a prime number, then $n^2$ has three positive factors. (b) If $a$ is an irrational number and $b$ is an irrational number, then $a \cdot b$ is an irrational number. (c) If $p$ is a prime number, then $p = 2$ or $p$ is an odd number. (d) If $p$ is a prime number and $p \ne 2$ or $p$ is an odd number. (e) $p \ne 2$ or $p$ is a even number, then $p$ is not prime.
Determine whether each of the following conditional statements is true or false. (a) If 10 < 7, then 3 = 4. (b) If 7 < 10, then 3 = 4. (c) If 10 < 7, then 3 + 5 = 8. (d) If 7 < 10, then 3 + 5 = 8.
Determine the conditions under which each of the following conditional sentences will be a true statement. (a) If a + 2 = 5, then 8 < 5. (b) If 5 < 8, then a + 2 = 5.
Let $P$ be the statement “Student X passed every assignment in Calculus I,” and let $Q$ be the statement “Student X received a grade of C or better in Calculus I.” (a) What does it mean for $P$ to be true? What does it mean for $Q$ to be true? (b) Suppose that Student X passed every assignment in Calculus I and received a grade of B-, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (c) Suppose that Student X passed every assignment in Calculus I and received a grade of C-, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (d) Now suppose that Student X did not pass two assignments in Calculus I and received a grade of D, and that the instructor made the statement $P \to Q$. Would you say that the instructor lied or told the truth? (e) How are Parts ( 5b ), ( 5c ), and ( 5d ) related to the truth table for $P \to Q$?

Theorem If f is a quadratic function of the form $f(x) = ax^2 + bx + c$ and a < 0, then the function f has a maximum value when $x = \dfrac{-b}{2a}$. Using only this theorem, what can be concluded about the functions given by the following formulas? (a) $g (x) = -8x^2 + 5x - 2$ (b) $h (x) = -\dfrac{1}{3}x^2 + 3x$ (c) $k (x) = 8x^2 - 5x - 7$ (d) $j (x) = -\dfrac{71}{99}x^2 +210$ (e) $f (x) = -4x^2 - 3x + 7$ (f) $F (x) = -x^4 + x^3 + 9$

Theorem If $f$ is a quadratic function of the form $f(x) = ax^2 + bx + c$ and ac < 0, then the function $f$ has two x-intercepts.

Using only this theorem, what can be concluded about the functions given by the following formulas? (a) $g (x) = -8x^2 + 5x - 2$ (b) $h (x) = -\dfrac{1}{3}x^2 + 3x$ (c) $k (x) = 8x^2 - 5x - 7$ (d) $j (x) = -\dfrac{71}{99}x^2 +210$ (e) $f (x) = -4x^2 - 3x + 7$ (f) $F (x) = -x^4 + x^3 + 9$

Theorem A. If $f$ is a cubic function of the form $f (x) = x^3 - x + b$ and b > 1, then the function $f$ has exactly one $x$-intercept. Following is another theorem about $x$-intercepts of functions: Theorem B . If $f$ and $g$ are functions with $g (x) = k \cdot f (x)$, where $k$ is a nonzero real number, then $f$ and $g$ have exactly the same $x$-intercepts.

Using only these two theorems and some simple algebraic manipulations, what can be concluded about the functions given by the following formulas? (a) $f (x) = x^3 -x + 7$ (b) $g (x) = x^3 + x +7$ (c) $h (x) = -x^3 + x - 5$ (d) $k (x) = 2x^3 + 2x + 3$ (e) $r (x) = x^4 - x + 11$ (f) $F (x) = 2x^3 - 2x + 7$

(a) Is the set of natural numbers closed under division? (b) Is the set of rational numbers closed under division? (c) Is the set of nonzero rational numbers closed under division? (d) Is the set of positive rational numbers closed under division? (e) Is the set of positive real numbers closed under subtraction? (f) Is the set of negative rational numbers closed under division? (g) Is the set of negative integers closed under addition? Explorations and Activities
Exploring Propositions . In Progress Check 1.2 , we used exploration to show that certain statements were false and to make conjectures that certain statements were true. We can also use exploration to formulate a conjecture that we believe to be true. For example, if we calculate successive powers of $2, (2^1, 2^2, 2^3, 2^4, 2^5, ...)$ and examine the units digits of these numbers, we could make the following conjectures (among others): $\bullet$ If $n$ is a natural number, then the units digit of $2^n$ must be 2, 4, 6, or 8. $\bullet$ The units digits of the successive powers of 2 repeat according to the pattern “2, 4, 8, 6.” (a) Is it possible to formulate a conjecture about the units digits of successive powers of $4 (4^1, 4^2, 4^3, 4^4, 4^5,...)$? If so, formulate at least one conjecture. (b) Is it possible to formulate a conjecture about the units digit of numbers of the form $7^n - 2^n$, where $n$ is a natural number? If so, formulate a conjecture in the form of a conditional statement in the form “If $n$ is a natural number, then ... .” (c) Let $f (x) = e^(2x)$. Determine the first eight derivatives of this function. What do you observe? Formulate a conjecture that appears to be true. The conjecture should be written as a conditional statement in the form, “If n is a natural number, then ... .”

Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 : p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that, p 0 is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives.

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data.

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Share Share

Register with BYJU'S & Download Free PDFs

$SplashLearn$

Term in Math – Definition, Examples, Practice Problems, FAQs

What is an algebraic expression, what is a term in math, different terms in algebra, solved examples, practice problems, frequently asked questions.

Algebra is the part of mathematics that helps represent problems or situations in the form of mathematical expressions. For example, Tim’s grandma gave him many candy bars. He ate a few and now had 5 left. So, how many candy bars did Tim eat?

Let us pose this question using algebra:

We know how many candy bars are left, so the number 5 would be called the constant. Constants are numbers that have a fixed numerical value. We do not know how many candy bars Tim’s grandma gave him, so we will call it x . The letter x represents the unknown quantity and is known as a variable . When we subtract the number of uneaten candy bars from the number of candy bars Tim’s grandma gave him, we will learn how many he has eaten already.

$Example of variable and constant$

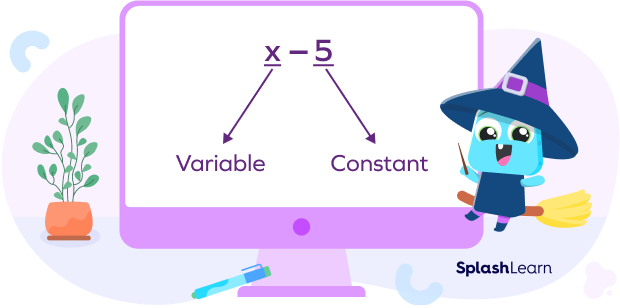
An algebraic expression consists of unknown variables, numbers, and arithmetic operators.

x – 5 is a simple algebraic expression. When we combine constants and variables connected by mathematical operations such as +, -, x, and ÷, we get an algebraic expression .

Let us look at a few more algebraic expressions .

$Example of coefficients$

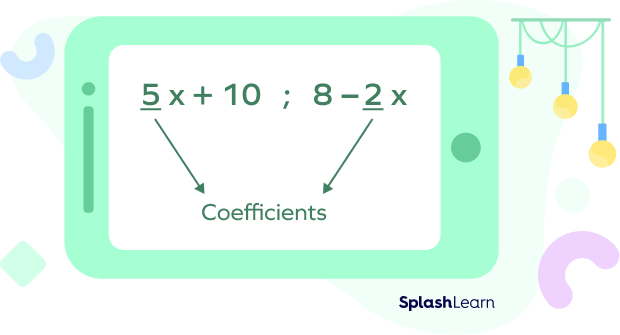
A coefficient is a number multiplied by the variable.The coefficient of 5 x + 10 is 5 and

8 – 2 x is – 2.

In algebra, an algebraic expression is formed by a term or a group of terms together. Term in math is defined as the values on which mathematical operations occur in an algebraic expression. Let’s understand with an example of term.

$Example of terms$

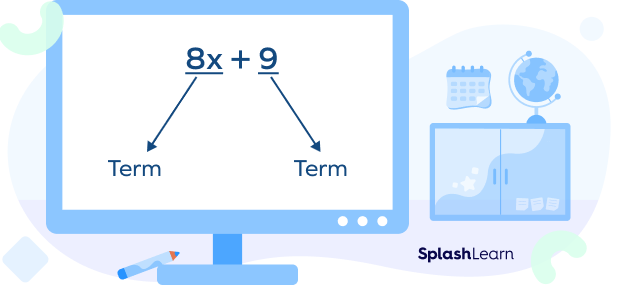
Both 8x and 9 are terms of this algebraic expression.

Related Worksheets

$Determine True or False Worksheet$

What Are the Factors of a Term?

The factors of a term are the numbers or variables that are multiplied to form the term.

For example, the factors of the term 9xy are 9, x, and y.

There are two kinds of terms in algebra: Like Terms and Unlike Terms .

Like Terms: Like terms are terms whose variables and exponent power are the same. They can be simplified by combining them. The operations of addition and subtraction can be performed on them together.

For example, 5x + 8x is an algebraic expression with like terms.

Unlike Terms: Unlike terms are those terms whose variables and their exponents are different from each other. They cannot be simplified by combining them. The operations of addition and subtraction cannot be performed on them together.

For example, 5x + 8y is an algebraic expression with unlike terms.

Let Us Learn about ‘Polynomials’

Polynomial comprises two Greek words: the word “poly” means “many” and “nominal” means “terms”. So, we get the phrase “many terms”. Polynomials are classified into three different types based on the number of terms it consists of.

The three types of polynomials are:

Monomial: It consists of only one term.

Here are a few examples of monomials:

Binomial: It is a polynomial that consists of exactly two terms.

Here are a few examples of binomials:

Trinomial: It is a polynomial that consists of exactly three terms.

Here are a few examples of trinomials:

4x + 27 – 3z
12y -3 + 7z
5z+ 2x + 8y

Example 1: What are the terms, variables, and constants of the algebraic expression:

9x – 7y + 5 ?

In the algebraic expression, 9x – 7y + 5 (Given)

The terms are 9x, -7y and 5

The variables are x and y

Variables are numbers that can take various numerical values.

The constant is the number 5.

Constants are numbers that have a fixed numerical value.

Example 2: What are the factors of the algebraic expression 3abc?

So, the factors of 3abc are 3, a, b, and c.

Example 3: Identify the like and unlike terms:

a) 4p – 7q

b) 12y – 5y

a) 4p – 7q

These are unlike terms. Their variables are different from each other.

b) 12y – 5y These are like terms. Their variables are the same.

Term in Math - Definition With Examples

Attend this quiz & Test your knowledge.

There were x number of sparrows sitting on the branches of a tree. Three flew away. Choose the correct algebraic expression to depict the statements given above.

$Term in Math – Definition, Examples, Practice Problems, FAQs$

What are the terms of the algebraic expression 7x – 9?

What are the factors of the algebraic expression 11yz.

What are the terms in an algebraic expression made up of?

A Term in an algebraic expression can be:

A variable (with or without coefficients )
Both a constant and a variable

The terms add up to form an algebraic expression. So, they are known as the components of the expression.

What are polynomials?

A polynomial comprises two Greek words: “poly” meaning “many” and “nominal” meaning “terms”. So, it makes up the phrase “many terms”.

What are the types of polynomials?

Polynomials are classified into three different types based on the number of terms they consist of. The three types of polynomials are:

Monomial: It consists of only one term. For example, 3a.

Binomial: It is a polynomial that consists of exactly two terms. For example, 3a + 7b Trinomial: It is a polynomial that consists of exactly three terms. For example, 3a + 7b – 5c

Fact Family – Definition Examples, Facts, FAQs, Practice Problems
True – Definition with Examples
Adding Mixed Numbers
Circumference to Diameter: Conversion, Formula, Meaning, Example
Equivalent Fractions – Definition with Examples

$Banner Image$

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

IMAGES

Best Example of How to Write a Hypothesis 2024
Hypothesis
Hypothesis
🏷️ Formulation of hypothesis in research. How to Write a Strong
Hypothesis: Definition, Sources, Uses, Characteristics and Examples
Research Hypothesis: Definition, Types, Examples and Quick Tips

VIDEO

Concept of Hypothesis
What Is A Hypothesis?
Hypothesis Testing
hypothesis Testing
hypothesis testing urdu|directional vs non directional hypothesis|BsN 6th,Post-Rn 2nd|biostatistics|
Stating Hypotheses & Defining Parameters

COMMENTS

Hypothesis Definition (Illustrated Mathematics Dictionary)
Hypothesis. A statement that could be true, which might then be tested. Example: Sam has a hypothesis that "large dogs are better at catching tennis balls than small dogs". We can test that hypothesis by having hundreds of different sized dogs try to catch tennis balls. Sometimes the hypothesis won't be tested, it is simply a good explanation ...
Hypothesis -- from Wolfram MathWorld
A hypothesis is a proposition that is consistent with known data, but has been neither verified nor shown to be false. In statistics, a hypothesis (sometimes called a statistical hypothesis) refers to a statement on which hypothesis testing will be based. Particularly important statistical hypotheses include the null hypothesis and alternative hypothesis. In symbolic logic, a hypothesis is the ...
Hypothesis Definition
Types of Hypothesis. The hypothesis can be broadly classified into different types. They are: Simple Hypothesis. A simple hypothesis is a hypothesis that there exists a relationship between two variables. One is called a dependent variable, and the other is called an independent variable. Complex Hypothesis.
Hypothesis
Definition. A hypothesis is a claim or statement that makes sense in the context of some information or data at hand but hasn't been established as true or false through experimentation or proof. In mathematics, any statement or equation that describes some relationship between certain variables can be termed as hypothesis if it is consistent ...
What is a Hypothesis?
Thus the hypothesis is what we must assume in order to be positive that the conclusion will hold. Whenever you are asked to state a theorem, be sure to include the hypothesis. In order to know when you may apply the theorem, you need to know what constraints you have. So in the example above, if we know that a function is differentiable, we may ...
8.1: The Elements of Hypothesis Testing
Two Types of Errors. The format of the testing procedure in general terms is to take a sample and use the information it contains to come to a decision about the two hypotheses. As stated before our decision will always be either. reject the null hypothesis \ (H_0\) in favor of the alternative \ (H_a\) presented, or.
Examples of null and alternative hypotheses
The null hypothesis is what happens at baseline. It is the uninteresting hypothesis--the boring hypothesis. Usually, it is the hypothesis that assumes no difference. It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove.
9.1: Null and Alternative Hypotheses
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with $H_{0}$.The null is not rejected unless the hypothesis test shows otherwise.
Hypothesis Testing
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators. In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population. The test considers two hypotheses: the ...
Definition and examples of hypothesis
Definition Of Hypothesis. Hypothesis is the part of a conditional statement just after the word if. Examples of Hypothesis. In the conditional, "If all fours sides of a quadrilateral measure the same, then the quadrilateral is a square" the hypothesis is "all fours sides of a quadrilateral measure the same".
Hypothesis Testing
Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant. It involves the setting up of a null hypothesis and an alternate hypothesis. There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
10.2: Null and Alternative Hypotheses
The alternative hypothesis ( Ha H a) is a claim about the population that is contradictory to H0 H 0 and what we conclude when we reject H0 H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample ...
9.1: Introduction to Hypothesis Testing
In hypothesis testing, the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis. The null hypothesis is usually denoted H0 H 0 while the alternative hypothesis is usually denoted H1 H 1. An hypothesis test is a statistical decision; the conclusion will ...
What Is a Hypothesis? The Scientific Method
A hypothesis (plural hypotheses) is a proposed explanation for an observation. The definition depends on the subject. In science, a hypothesis is part of the scientific method. It is a prediction or explanation that is tested by an experiment. Observations and experiments may disprove a scientific hypothesis, but can never entirely prove one.
An Introduction to Statistics: Understanding Hypothesis Testing and
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
Hypothesis Testing -- from Wolfram MathWorld
Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps. 1. Formulate the null hypothesis H_0 (commonly, that the observations are the result of pure chance) and the alternative hypothesis H_a (commonly, that the observations show a real effect combined with a component of chance ...
What is Hypothesis
Alternative Hypothesis is different from the null hypothesis and shows that there's a big connection or gap between variables. Scientists want to say no to the null hypothesis and choose the alternative one. Statistical Hypothesis. Statistical Hypotheis are used in math testing and include making ideas about what groups or bits of them look like.
Hypothesis
Definition of Hypothesis. A hypothesis is a statement that might be true, but which needs to be tested. For example, Al forwards the hypothesis that "pink snails move more slowly than brown snails." Al will be able to test his hypothesis by calculating the speed of hundreds of pink and brown snails, and then analysing the data he has collected ...
hypothesis
Hypothesis. A hypothesis is the 'if' part (antecedent) of a conditional statement.
1.1: Statements and Conditional Statements
Using this as a guide, we define the conditional statement P → Q to be false only when P is true and Q is false, that is, only when the hypothesis is true and the conclusion is false. In all other cases, P → Q is true. This is summarized in Table 1.1, which is called a truth table for the conditional statement P → Q.
What is Hypothesis
Functions of Hypothesis. Following are the functions performed by the hypothesis: Hypothesis helps in making an observation and experiments possible. It becomes the start point for the investigation. Hypothesis helps in verifying the observations. It helps in directing the inquiries in the right direction.
Null Hypothesis
Here, the hypothesis test formulas are given below for reference. The formula for the null hypothesis is: H 0 : p = p 0. The formula for the alternative hypothesis is: H a = p >p 0, < p 0 ≠ p 0. The formula for the test static is: Remember that, p 0 is the null hypothesis and p - hat is the sample proportion.
What is a Term in Math? Definition, Expression, Examples, Facts
In algebra, an algebraic expression is formed by a term or a group of terms together. Term in math is defined as the values on which mathematical operations occur in an algebraic expression. Let's understand with an example of term. Both 8x and 9 are terms of this algebraic expression. View.

Explanation of Hypothesis

Important Terms Related to Hypothesis

Numerical Examples

Hour Hand Definition < Glossary Index > Identity Definition

AP®︎/College Statistics

Examples of null and alternative hypotheses

Want to join the conversation?

Video transcript

Hypothesis Testing

Definitions and Methodology

Definition Of Hypothesis

Examples of Hypothesis

Video Examples: Hypothesis

Solved Example on Hypothesis

Related Worksheet

HighSchool Math

Hypothesis Testing

What is Hypothesis Testing in Statistics?

Hypothesis Testing Definition

Null Hypothesis

Alternative Hypothesis

Hypothesis Testing P Value

Hypothesis Testing Critical region

Hypothesis Testing Formula

Types of Hypothesis Testing

Hypothesis Testing Z Test

Hypothesis Testing t Test

Hypothesis Testing Chi Square

One Tailed Hypothesis Testing

Two Tailed Hypothesis Testing

Hypothesis Testing Steps

Hypothesis Testing Example

Hypothesis Testing and Confidence Intervals

Examples on Hypothesis Testing

FAQs on Hypothesis Testing

What is the z Test in Hypothesis Testing?

What is the t Test in Hypothesis Testing?

What is the formula for z test in Hypothesis Testing?

What is the p Value in Hypothesis Testing?

What is One Tail Hypothesis Testing?

What is the Alpha Level in Two Tail Hypothesis Testing?

9.1: Introduction to Hypothesis Testing

Basic Theory

\(P\)-value

Analogy with Justice Systems

Tests of an Unknown Parameter

Equivalence Between Hypothesis Test and Confidence Sets

Pivot Variables and Test Statistics

What Is a Hypothesis? (Science)

Writing a Hypothesis

Example of a Hypothesis

An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors

How to cite this article

SAMPLE VERSUS POPULATION

HYPOTHESIS TESTING

STATISTICAL ERRORS

Hypothesis Testing

Explore with Wolfram|Alpha

Referenced on Wolfram|Alpha

Subject classifications

What is Hypothesis?

Hypothesis Meaning

Characteristics of Hypothesis

Sources of Hypothesis

Types of Hypothesis

Simple Hypothesis

Null Hypothesis (H0)

Non-Directional Hypothesis

Hypothesis Examples

Simple Hypothesis Example

Complex Hypothesis Example

Directional Hypothesis Example

Non-directional Hypothesis Example

Alternative Hypothesis (Ha)

Functions of Hypothesis

How Hypothesis help in Scientific Research?

People Also View:

Summary – Hypothesis

FAQs on Hypothesis

What are Components of a Hypothesis?