hypothesis testing calculator critical value

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Critical Value Calculator

Use this calculator for critical values to easily convert a significance level to its corresponding Z value, T score, F-score, or Chi-square value. Outputs the critical region as well. The tool supports one-tailed and two-tailed significance tests / probability values.

Related calculators

• Using the critical value calculator
• What is a critical value?
• T critical value calculation
• Z critical value calculation
• F critical value calculation

    Using the critical value calculator

If you want to perform a statistical test of significance (a.k.a. significance test, statistical significance test), determining the value of the test statistic corresponding to the desired significance level is necessary. You need to know the desired error probability ( p-value threshold , common values are 0.05, 0.01, 0.001) corresponding to the significance level of the test. If you know the significance level in percentages, simply subtract it from 100%. For example, 95% significance results in a probability of 100%-95% = 5% = 0.05 .

Then you need to know the shape of the error distribution of the statistic of interest (not to be mistaken with the distribution of the underlying data!) . Our critical value calculator supports statistics which are either:

• Z -distributed (normally distributed, e.g. absolute difference of means)
• T -distributed (Student's T distribution, usually appropriate for small sample sizes, equivalent to the normal for sample sizes over 30)
• X 2 -distributed ( Chi square distribution, often used in goodness-of-fit tests, but also for tests of homogeneity or independence)
• F -distributed (Fisher-Snedecor distribution), usually used in analysis of variance (ANOVA)

Then, for distributions other than the normal one (Z), you need to know the degrees of freedom . For the F statistic there are two separate degrees of freedom - one for the numerator and one for the denominator.

Finally, to determine a critical region, one needs to know whether they are testing a point null versus a composite alternative (on both sides) or a composite null versus (covering one side of the distribution) a composite alternative (covering the other). Basically, it comes down to whether the inference is going to contain claims regarding the direction of the effect or not. Should one want to claim anything about the direction of the effect, the corresponding null hypothesis is direction as well (one-sided hypothesis).

Depending on the type of test - one-tailed or two-tailed, the calculator will output the critical value or values and the corresponding critical region. For one-sided tests it will output both possible regions, whereas for a two-sided test it will output the union of the two critical regions on the opposite sides of the distribution.

    What is a critical value?

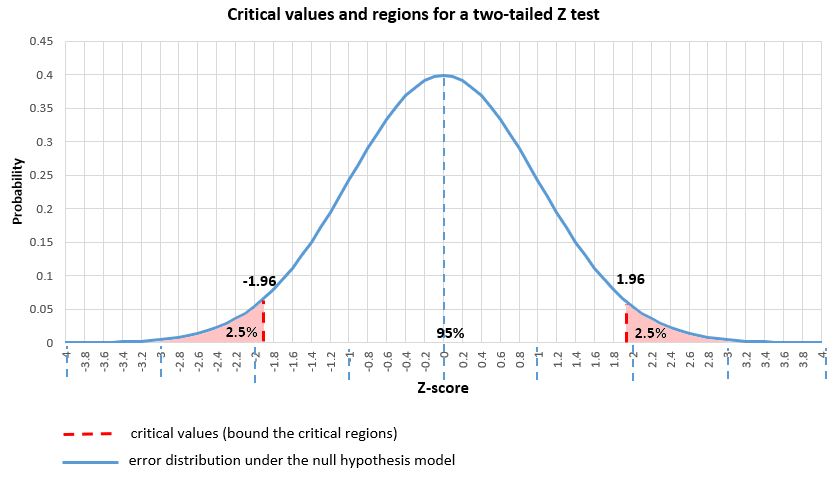
A critical value (or values) is a point on the support of an error distribution which bounds a critical region from above or below. If the statistics falls below or above a critical value (depending on the type of hypothesis, but it has to fall inside the critical region) then a test is declared statistically significant at the corresponding significance level. For example, in a two-tailed Z test with critical values -1.96 and 1.96 (corresponding to 0.05 significance level) the critical regions are from -∞ to -1.96 and from 1.96 to +∞. Therefore, if the statistic falls below -1.96 or above 1.96, the null hypothesis test is statistically significant.

You can think of the critical value as a cutoff point beyond which events are considered rare enough to count as evidence against the specified null hypothesis. It is a value achieved by a distance function with probability equal to or greater than the significance level under the specified null hypothesis. In an error-probabilistic framework, a proper distance function based on a test statistic takes the generic form [1] :

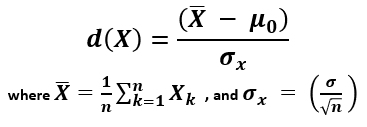
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).

Here is how it looks in practice when the error is normally distributed (Z distribution) with a one-tailed null and alternative hypotheses and a significance level α set to 0.05:

And here is the same significance level when applied to a point null and a two-tailed alternative hypothesis:

The distance function would vary depending on the distribution of the error: Z, T, F, or Chi-square (X 2 ). The calculation of a particular critical value based on a supplied probability and error distribution is simply a matter of calculating the inverse cumulative probability density function (inverse CPDF) of the respective distribution. This can be a difficult task, most notably for the T distribution [2] .

    T critical value calculation

The T-distribution is often preferred in the social sciences, psychiatry, economics, and other sciences where low sample sizes are a common occurrence. Certain clinical studies also fall under this umbrella. This stems from the fact that for sample sizes over 30 it is practically equivalent to the normal distribution which is easier to work with. It was proposed by William Gosset, a.k.a. Student, in 1908 [3] , which is why it is also referred to as "Student's T distribution".

To find the critical t value, one needs to compute the inverse cumulative PDF of the T distribution. To do that, the significance level and the degrees of freedom need to be known. The degrees of freedom represent the number of values in the final calculation of a statistic that are free to vary whilst the statistic remains fixed at a certain value.

It should be noted that there is not, in fact, a single T-distribution, but there are infinitely many T-distributions, each with a different level of degrees of freedom. Below are some key values of the T-distribution with 1 degree of freedom, assuming a one-tailed T test is to be performed. These are often used as critical values to define rejection regions in hypothesis testing.

    Z critical value calculation

The Z-score is a statistic showing how many standard deviations away from the normal, usually the mean, a given observation is. It is often called just a standard score, z-value, normal score, and standardized variable. A Z critical value is just a particular cutoff in the error distribution of a normally-distributed statistic.

Z critical values are computed by using the inverse cumulative probability density function of the standard normal distribution with a mean (μ) of zero and standard deviation (σ) of one. Below are some commonly encountered probability values (significance levels) and their corresponding Z values for the critical region, assuming a one-tailed hypothesis .

The critical region defined by each of these would span from the Z value to plus infinity for the right-tailed case, and from minus infinity to minus the Z critical value in the left-tailed case. Our calculator for critical value will both find the critical z value(s) and output the corresponding critical regions for you.

Chi Square (Χ 2 ) critical value calculation

Chi square distributed errors are commonly encountered in goodness-of-fit tests and homogeneity tests, but also in tests for independence in contingency tables. Since the distribution is based on the squares of scores, it only contains positive values. Calculating the inverse cumulative PDF of the distribution is required in order to convert a desired probability (significance) to a chi square critical value.

Just like the T and F distributions, there is a different chi square distribution corresponding to different degrees of freedom. Hence, to calculate a Χ 2 critical value one needs to supply the degrees of freedom for the statistic of interest.

    F critical value calculation

F distributed errors are commonly encountered in analysis of variance (ANOVA), which is very common in the social sciences. The distribution, also referred to as the Fisher-Snedecor distribution, only contains positive values, similar to the Χ 2 one. Similar to the T distribution, there is no single F-distribution to speak of. A different F distribution is defined for each pair of degrees of freedom - one for the numerator and one for the denominator.

Calculating the inverse cumulative PDF of the F distribution specified by the two degrees of freedom is required in order to convert a desired probability (significance) to a critical value. There is no simple solution to find a critical value of f and while there are tables, using a calculator is the preferred approach nowadays.

    References

1 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

2 Shaw T.W. (2006) – "Sampling Student's T distribution – use of the inverse cumulative distribution function", Journal of Computational Finance 9(4):37-73, DOI:10.21314/JCF.2006.150

3 "Student" [William Sealy Gosset] (1908) - "The probable error of a mean", Biometrika 6(1):1–25. DOI:10.1093/biomet/6.1.1

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Critical Value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/critical-value-calculator.php URL [Accessed Date: 27 Apr, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

• chi-square value

How does t critical value calculator work?

• Enter Significance Level(α) In The Input Box.
• Put the  Degrees Of Freedom In The Input Box.
• Hit The Calculate Button To Find t Critical Value.
• Use The Reset Button To calculate New Values.

How does z critical value calculator work?

• Enter The Significance Level(α) In The Input Box.
• Use The Calculate Button To Get The Z Critical Value.

How does R critical value calculator work?

• Enter Significance Level(α) & Degree of freedom In The Input Boxes.
• Click The Calculate Button.
• Hit The Reset Button To calculate New Values.

How does this calculator work?

• Enter Significance Level(α) & Degree of freedom In Required Input Boxes.
• Press The Reset Button To calculate New Values.

How does F critical value calculator work?

• Enter Significance Level(α)
• Enter Degree of freedom of numerator and denominator in required input boxes.

Give Feedback What do you think of critical value calculator?

Other Calculators

Critical value calculator.

Critical t value calculator enables you to calculate the critical value of z and t at one click. You don’t have to look into hundreds of values in t table or a z table because this z critical value calculator calculates critical values in real time . Keep on reading if you are interested in critical value definition, the difference between t and z critical value, and how to calculate the critical value of t and z without using a critical values calculator.

 Table of Content

What is a critical value, critical value formula, how to find critical values.

• T-Distribution Table

A  critical value is a point on the t-distribution that is compared to the test statistic to determine whether to reject the null hypothesis in hypothesis testing. If the absolute value of the test statistic is greater than the critical value, statistical significance can be declared as well as the null hypothesis can be rejected. Critical value tests can be:

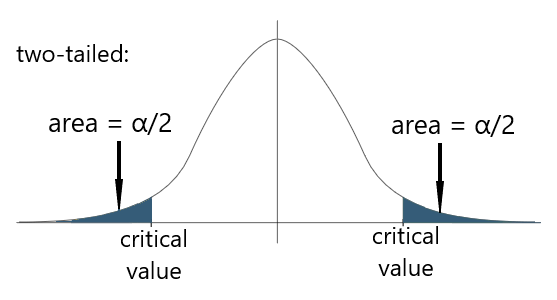
Left-tailed test: Q (α)

Right-tailed test: Q (1 - α)

Two-tailed test: Q (α/2)] ∪ Q (1 - α/2)

What is a t critical value?

T critical value is a point that cuts off the student t distribution . T value is used in a hypothesis test to compare against a calculated t score. The critical value of t helps to decide if a null hypothesis should be supported or rejected.

What is a z critical value?

Z critical value is a point that cuts off an area under the standard normal distribution . The critical value of z can tell what probability any particular variable will have. Z and t critical values are almost identical.

What is f critical value?

F critical value is a value at which the threshold probability α of type-I error (reject a true null hypothesis mistakenly).  The f statistics is the value that follows the f-distribution table.

Here are a few tests that help to calculate the f values.

• Overall significance in regression analysis. k
• Compare two nested regression models. 
• The equality of variances in two normally distributed populations.

All the above tests are right-tailed. F critical value calculator above will help you to calculate the f critical value with a single click.

What is the chi-square value?

In certain hypothesis tests and confidence intervals, chi-square values are thresholds for statistical significance. The Chi-square distribution table is used to evaluate the chi-square critical values. It is rather tough to calculate the critical value by hand, so try a reference table or chi-square critical value calculator above.

The chi-square critical values are always positive and can be used in the following tests.

• Goodness-of-fit tests
• Homogeneity tests
• Tests for independence in contingency tables

Unlike the t & f critical value, Χ 2  (chi-square) critical value needs to supply the degrees of freedom to get the result.

The formula of z and t critical value can be expressed as:

• Q t is the quantile function of t student distribution
• u is the quantile function of the normal distribution
• d refers to the degree of freedom
• α is the significance level

A critical value of t calculator uses all these formulas to produce the exact critical values needed to accept or reject a hypothesis.

Calculating critical value is a tiring task because it involves looking for values into the t-distribution chart. The t-distribution table (student t-test distribution) consists of hundreds of values, so, it is convenient to use t table value calculator above for critical values. However, if you want to find critical values without using t table calculator, follow the examples given below.

How to find t critical value?

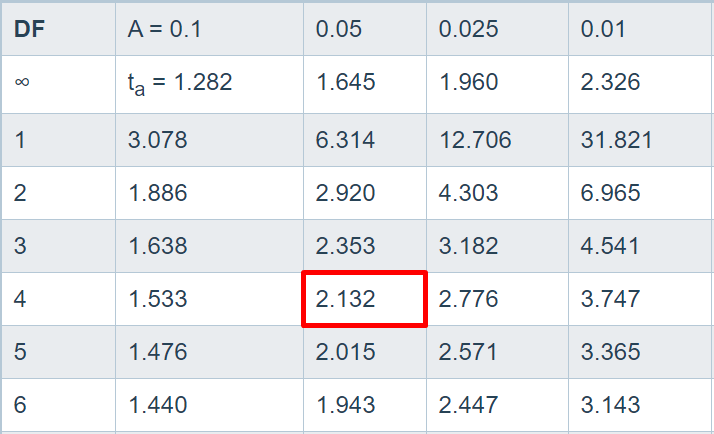
Find the t critical value if the size of the sample is 5 and the significance level is 0.05 .

Subtract 1 from the sample size to get the degree of freedom. Degree of Freedom = N – 1 = 5 – 1 Degree of freedom = 4 α = 0.05

Depending on the test, choose the one-tailed t distribution table or two-tailed t table below.

Look for the degree of freedom in the most left column. Also, look for the significance level α in the top row. Pick the value occurring at the intersection of the mentioned row and column. In this case, the t critical value is 2.132 .

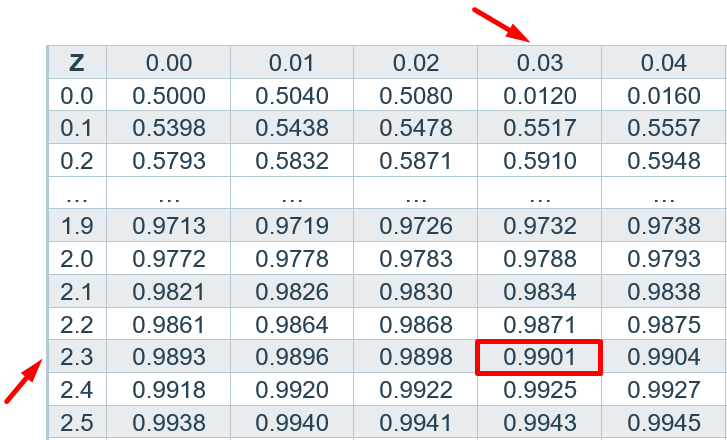
How to find z critical value?

Find the z critical value if the significance level is 0.02 .

Divide the significance level α by 2 α/2 = 0.02/2 α/2 = 0.01

Subtract α/2 from 1. 1 - α/2 = 1 – 0.01 1 - α/2 = 0.99

Search the value 0.99 in the z table given below. Add the values of intersecting row (top) and column (most left) to get the z critical value. 2.3 + 0.03 = 2.33 Z critical value = ±2.33 for the two-tailed test.

T-Distribution Table (One Tail)

The t table for one-tail probability is given below.

T-Distribution Table (Two Tail)

The t table for two-tail probability is given below.

Z table (right-tailed)

The normal distribution table for the right-tailed test is given below.

Z table (left-tailed)

The normal distribution table for the left-tailed test is given below.

• Krista King Math | Online math tutor. 2021. Critical points and the first derivative test — Krista King Math | Online math tutor.
• S.3.1 Hypothesis Testing (Critical Value Approach) | STAT ONLINE. PennState: Statistics Online Courses.
• 7.1.3.1. Critical values and p values. National Institute of Standards and Technology (NIST).

Recent Blogs

F Critical Value: Definition, formula, and Calculations

T Critical Value: Definition, Formula, Interpretation, and Examples

Understanding z-score and z-critical value in statistics: A comprehensive guide

This report is generated by criticalvaluecalculator.com

Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.

Information

• Privacy Policy
• Terms of Services

Critical Value Calculator

To get the result, fill out the calculator form and press the Calculate button.

Table of Content

• 1 What is Critical Value
• 2 Critical Value Formula
• 3 How to calculate critical value? - steps and process
• 4 Common confidence levels and their critical values
• 5 Types of Critical Values
• 6 Critical Value of Z
• 7 Assistance offered by this critical value calculator

What is Critical Value

Any point on a line that divides the graph into two equal parts is considered to have a critical value, to put it simply. Depending on the area in which the value falls, the null hypothesis is either rejected or accepted. One of the two divisions created by the critical value is known as the rejection region. The null hypothesis would not be accepted if the test value were to be found in the rejection region.

Critical Value Formula

The critical value is the point on a test statistic distribution where it is decided whether to reject or not to reject the null hypothesis. The critical value formula depends on the kind of test being run and the level of significance (alpha) picked.

For Example, the critical value formula for a two-tailed z-test with a normal distribution is:

where "alpha" denotes the level of significance and "z" denotes the standard normal distribution (usually 0.05).

The formula for the critical value in a two-tailed t-test is:

where "df" stands for degrees of freedom, "alpha" for level of significance, and "t" stands for the t-distribution.

The formula for a one-tailed test varies depending on which side of the distribution you want to test.

It's crucial to remember that while these formulas provide the critical value for a specific level of significance, the critical value for a specific probability level can also be determined by using the inverse of the cumulative distribution function of the test statistic.

How to Calculate Critical Values: A Step-by-Step Guide

Calculating critical values is an important part of statistical analysis, and understanding the process can help you make better decisions based on data. In this guide, we'll walk you through the steps for calculating critical values.

Step 1: Determine the Type of Hypothesis Test

The first step is to determine whether you are conducting a one-tailed or two-tailed hypothesis test. In a one-tailed test, the null hypothesis is that there is no effect or a specific direction of effect (i.e., "greater than" or "less than"). In a two-tailed test, the null hypothesis is that there is no effect, without specifying the direction of the effect.

Step 2: Choose the Level of Significance

The level of significance, denoted by α (alpha), is the probability of rejecting the null hypothesis when it is true. Common levels of significance are 0.05 (5%) and 0.01 (1%), but the specific value depends on the researcher's preference and the context of the study.

Step 3: Determine the Degrees of Freedom

The degrees of freedom, denoted by df, represent the number of independent pieces of information in the sample that can vary. The formula for degrees of freedom depends on the type of test and the sample size.

For a one-tailed test with a sample size of n, df = n - 1.

For example , if you have a sample size of n = 20, the degrees of freedom for a one-tailed test would be df = 20 - 1 = 19.

For a two-tailed test with a sample size of n, df = n - 2.

For example , if you have a sample size of n = 30, the degrees of freedom for a two-tailed test would be df = 30 - 2 = 28.

Step 4: Look Up the Critical Value

Once you know the type of test, level of significance, and degrees of freedom, you can find the critical value from a statistical table. The critical value is the minimum value of the test statistic that will lead to the rejection of the null hypothesis.

For example , suppose you are conducting a one-tailed test with a level of significance α = 0.05 and degrees of freedom df = 19. From a t-distribution table, the critical value is 1.734.

For a two-tailed test, you need to find the critical value for both tails. The critical values are typically denoted by tα/2 and -tα/2

For example , if α = 0.01 and df = 28, the critical values from a t-distribution table are -2.763 and 2.763, respectively.

Step 5: Calculate the Test Statistic

Calculate the test statistic using the sample data and the null hypothesis. The test statistic is the value used to determine whether to reject or fail to reject the null hypothesis.

For example , suppose you are testing the null hypothesis that the mean weight of a certain population is 50 kg, and your sample mean is 55 kg with a sample standard deviation of 10 kg. The test statistic for a one-tailed test is calculated as:

t = (sample mean - null hypothesis) / (sample standard deviation/sqrt (sample size)) = (55 - 50) / (10 / sqrt(20)) = 3.162

Since the test statistic of 3.162 is greater than the critical value of 1.734, we reject the null hypothesis at the 0.05 level of significance. This means that we have evidence to support the alternative hypothesis that the mean weight of the population is greater than 50 kg.

Common confidence levels and their critical values

In statistical inference, confidence levels are used to quantify the uncertainty associated with estimating a population parameter based on a sample. A confidence level is the probability that a statistical interval, such as a confidence interval, contains the true population parameter. Common confidence levels used in practice include 90%, 95%, and 99%.

The critical values for a given confidence level depend on the distribution of the test statistic and the degrees of freedom. Let's overview some examples of common confidence levels and their corresponding critical values for different distributions.

Normal Distribution

For a normal distribution, the critical values for different confidence levels are given by the z-score. The z-score is the number of standard deviations a value is away from the mean. The critical values for different confidence levels are:

90% confidence level: z = 1.645

95% confidence level: z = 1.96

99% confidence level: z = 2.576

Example : If you want to construct a 95% confidence interval for the population mean based on a sample from a normal distribution, you would use the critical value of z = 1.96

Student's t-Distribution

For small sample sizes or when the population standard deviation is unknown, the t-distribution is used instead of the normal distribution. The critical values for different confidence levels for the t-distribution depend on the degrees of freedom. Some common values are:

90% confidence level: t(df) = 1.645

95% confidence level: t(df) = 1.96

99% confidence level: t(df) = 2.576

Example : If you want to construct a 90% confidence interval for the population mean based on a sample from a t-distribution with 10 degrees of freedom, you would use the critical value of t(10) = 1.645

Chi-Squared Distribution

The chi-squared distribution is used for hypothesis tests and confidence intervals involving the variance of a normally distributed population. The critical values for different confidence levels depend on the degrees of freedom. Some common values are:

90% confidence level: χ²(df) = 14.68

95% confidence level: χ²(df) = 16.92

99% confidence level: χ²(df) = 23.59

Example : If you want to construct a 99% confidence interval for the population variance based on a sample from a normal distribution, you would use the critical value of χ2(n-1) = 23.59, where n is the sample size.

Types of Critical Values

Critical values are specific values that are used to determine whether to reject or fail to reject the null hypothesis. There are different types of critical values used in different statistical tests, and understanding these types can help in making accurate statistical inferences. Below are some types of critical values:

One-tailed critical values

One-tailed critical values are used in hypothesis testing when the alternative hypothesis is directional. To put it another way, the test is made to see if the sample mean differs significantly from the population mean.

Two-tailed critical values

Two-tailed critical values are used in hypothesis testing when the alternative hypothesis is non-directional. Two-tailed critical values are located in the middle of the distribution and correspond to a specified level of significance split between the two tails.

Upper-tailed critical values

Upper-tailed critical values are used in hypothesis testing when the test is designed to determine if the sample mean is significantly greater than the population mean. Upper-tailed critical values are located at the extreme right end of the distribution and correspond to a specified level of significance.

Lower-tailed critical values

Lower-tailed critical values are used in hypothesis testing when the test is designed to determine if the sample mean is significantly less than the population means. A certain level of significance is corresponding to lower-tailed critical values, which are situated at the extreme left end of the distribution.

Critical Value of Z

The critical value of z is a term used in statistics to indicate the value of the standard normal distribution that corresponds to a particular level of significance or alpha (α). The standard normal distribution is a continuous probability distribution that is often used to model random variables that are approximately normal.

As part of a statistical procedure called hypothesis testing, which determines whether there is enough data to support or disprove a null hypothesis, the critical value of z is frequently used. The null hypothesis is a statement that assumes that there is no significant difference between two or more populations or sets of data. For example, suppose you want to perform a two-tailed hypothesis test with a level of significance of 0.05 (i.e., α = 0.05).

The critical value of z at this level of significance is ±1.96. It means that if the test statistic falls outside of the range of -1.96 to 1.96, we can reject the null hypothesis and conclude that there is sufficient evidence to support the alternative hypothesis.

Assistance offered by this critical value calculator

• Calculating critical values for various statistical distributions
• Customizable inputs
• User-friendly interface
• Results in multiple formats

With customizable inputs, users can specify the significance level, degrees of freedom, and other parameters necessary to obtain accurate results. The user-friendly interface of our calculator makes it easy to enter inputs and view results.

Other Calculators

• Standard Deviation Calculator
• Variance Calculator
• Mean Calculator
• Mode Calculator
• Median Calculator
• Arithmetic Mean Calculator
• Harmonic Mean Calculator
• Geometric Mean Calculator
• Mean Absolute Deviation Calculator
• Covariance Calculator
• Correlation Coefficient Calculator
• Sum of Squares Calculator
• Linear Regression Calculator
• Quartile Calculator
• Quadratic Regression
• Five Number Summary Calculator
• Expected Value Calculator
• Chebyshev's Theorem Calculator
• Sample Size Calculator
• Z Score Calculator
• T Test Calculator
• Probability Calculator
• Normal Distribution Calculator
• Confidence Interval Calculator
• Coefficient of Variation Calculator

StatsCalculator.com

T critical value calculator.

• P Value From t Score
• z critical values

Related Tools

• Descriptive Statistics
• Confidence Interval
• Correlation Coefficient
• Outlier Detection
• t-test - 1 Sample
• t-test - 2 Sample

degrees of freedom

For t - Degrees of Freedom is Sample Size - 1

Tool Overview: t Critical Value Calculator

How to find critical values of t.

Planning a statistical experiment and trying to estimate what results you need to accept a hypothesis? In this case, where you need to find the critical values for the t-distribution for a given sample size? You've come to the right place. This critical values calculator is designed to accept your p-value (willingness to accept an incorrect hypothesis) and degrees of freedom. The degrees of freedom for a t-distribution can be derived from the sample size - just subtract one. (degrees of freedom = sample size - 1). You can use this as a critical value calculator with sample size.

Using the critical value calculators

This webpage provides a t critical value calculator with confidence level and sample size (subtract degrees of freedom). Simply enter the requested parameters (alpha level) into the calculator and hit calculate. The critical value represents an associated probability level of the result occurring on the cumulative probability distribution. It generates critical values for both a left tailed test and a two-tailed test (splitting the alpha between the left and right side of the distribution).

How To Conduct Hypothesis Testing

A hypothesis test reduces a statistical question down a single binary proposition. You are using the data points in your sample to assess which of two binary propositions is more likely. The default state is called the null hypothesis - in effect, "nothing to see here", there is no significant difference between your sample data points and sampling distribution for your test. It's just random noise. The other option is refered to the alternative hypothesis - which implies we reject the default state, that the trend in your data is unlikely to be random noise and should be taken seriously. Accepting the alternative hypothesis is dictated by the likelihood that those two samples were drawn from the same population (with the same parameters). We will take a sample, calculate a test statistic and compare it with the expected statistical distribution of that test statistic. When testing the mean of a distribution, you will be comparing the mean value with either the population standard deviation or the sample standard deviation (for large samples).

You're going to hear about another concept here - alpha. You see, we can test our tests - assess the likelhood of the test giving a false positive or a false negative. The alpha value of a given statistical test is the probability of rejecting the null hypothesis when, in fact, the null hypothesis is correct. Eg the probability of a false positive. This alpha is also referred to as the significance level of a test. While there are some common values for alpha (.05, 0.01), I encourage the analyst to carefully think about the cost vs. benefit of running tests at a given level of significance. The real world economics of testing should drive your choice of the correct significance level.

How to calculate critical values

This t score calculator replaces the use of a t distribution table ; it automates the lookup process and can generate a much broader range of values. In the traditional version, you use the t score table and alpha value to find the appropriate critical value for the test. Remember to adjust the alpha value to reflect the nature of the test - one sided or two sided.

critical value calculator with sample size

The degrees of freedom of the t distribution is the sample size - 1. So if you have the sample size, just subtract one and enter that value into the degrees of freedom box.

Other Versions of this T Score Calculator

This version of the t score calculator is used to generate the critical values of t - the cutoff values required to meet specific significance goals for a t test. If you are looking to convert a t statistic into a p value, you will want to use this p value calculator from t . We also have two other calculators you can use to directly compute the t-statistic from sample data: a single sample t test to compare a sample with a hypothesis and a two sample t-test for comparing two samples with each other.

When to Use Standard Normal (Z) vs. Student's T distribution

This t value calculator is good for situations where you're working with small sample sizes. Student's t distribution will converge on the standard normal distribution as the sample size increases. If you are working with a larger sample, you should consider using the version we set up to find critical values of a standard normal . The t distribution is generally perferred for using small samples to analyze the mean of a distribution (eg. use the t value vs. the z score).

About this Website

This t score calculator is part of a larger collection of tools we've assembled as a free replacement to paid statistical packages. The other tools on this site include a descriptive statistics tool , confidence interval generators ( standard normal , proportions ), linear regression tools , and other tools for probability and statistics. Many calculators allow you to save and recycle your data in similar calculations, saving you time and frustration. Bookmark us and come back when you need a good source of free statistics tools. This specific page replaces the need for a critical value calculator with sample size.

Other Tools: P Value From Z Score , P Value From T Score , Z critical value calculator , t critical value calculator

S.3.1 Hypothesis Testing (Critical Value Approach)

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
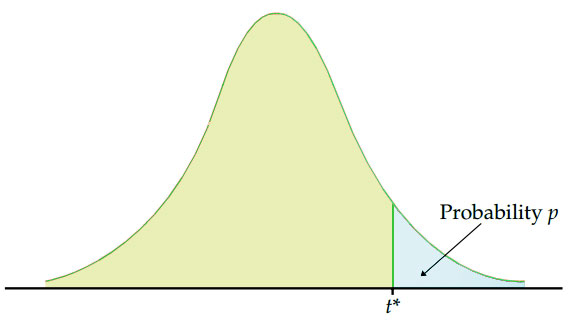
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
• Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

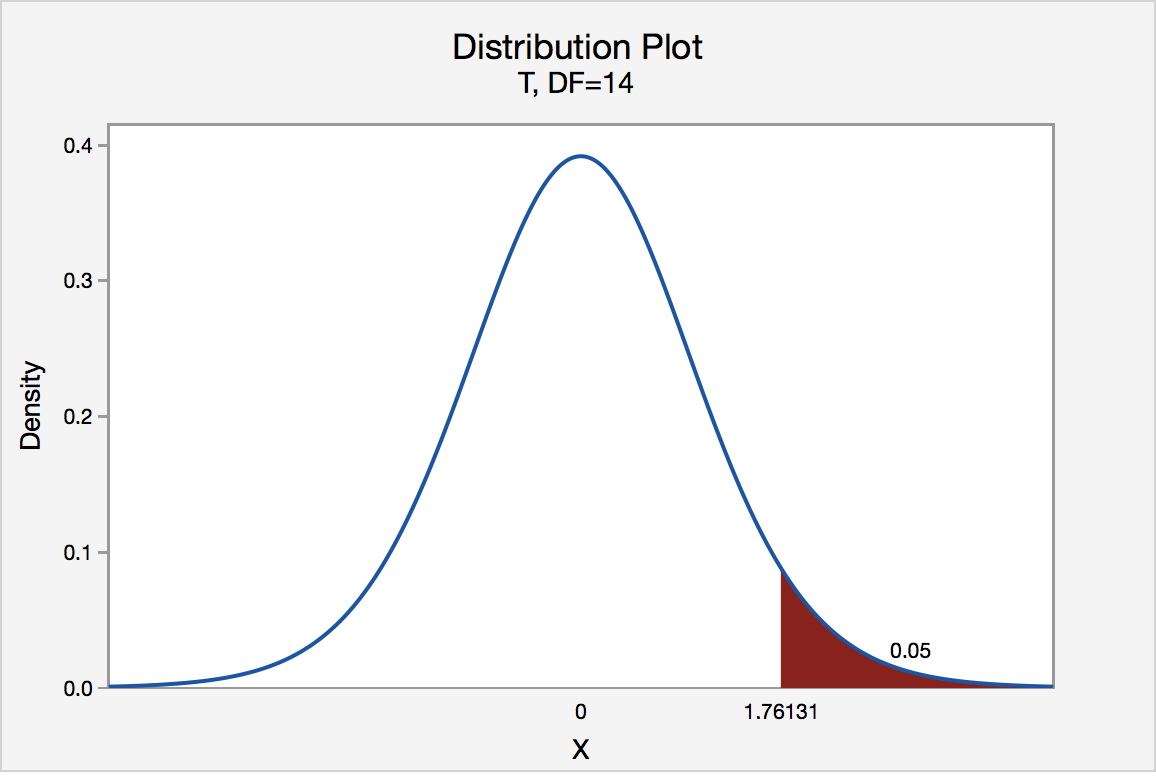
Right-Tailed

The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t \(\alpha\) , n - 1 , such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

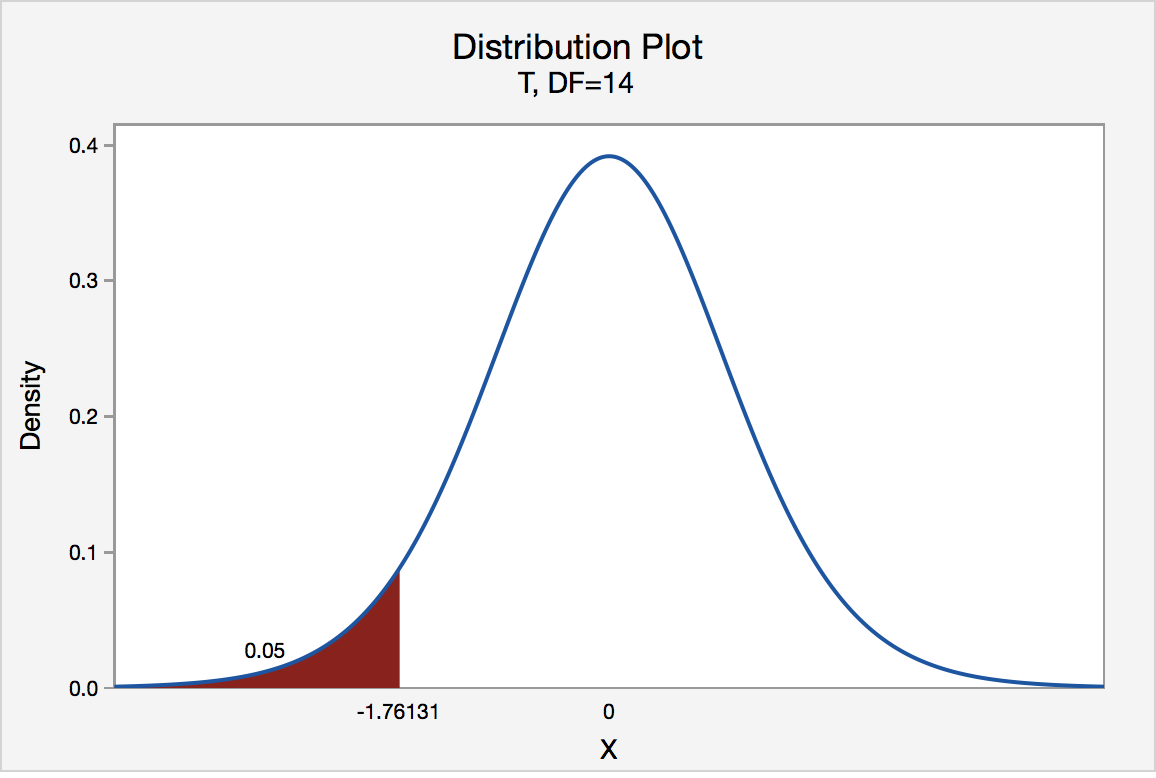
Left-Tailed

The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( \(\alpha\) , n - 1) , such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

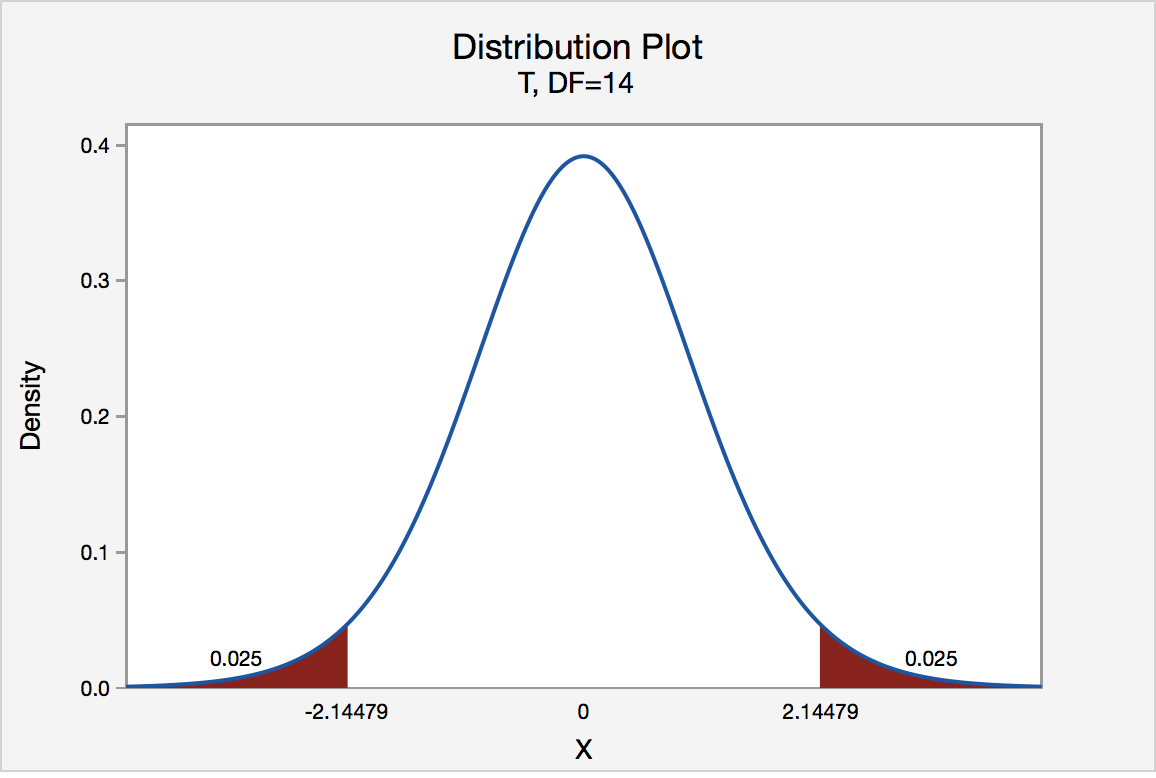
There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( \(\alpha\) / 2, n - 1) and one for the right-tail denoted t ( \(\alpha\) / 2, n - 1) . The value - t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the left of it is \(\alpha\)/2, and the value t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.

How to Calculate Critical Value

Delving into the world of statistics, understanding how to calculate critical value is pivotal for anyone seeking accurate and reliable results in hypothesis testing. In this comprehensive guide, we will unravel the intricacies of critical values, empowering you to make informed decisions based on sound statistical principles.

Unveiling the Mystery: How to Calculate Critical Value

The significance of critical value.

Critical value, a fundamental concept in statistics, dictates the acceptance or rejection of a null hypothesis. It serves as the threshold for statistical significance, guiding researchers and analysts in drawing meaningful conclusions from their data.

Understanding the Formula

To calculate the critical value, one must consider the significance level (alpha) and the degrees of freedom. The formula varies based on the statistical test employed, whether it be a t-test, z-test, or chi-square test. Familiarizing yourself with these formulas is essential for accurate computations.

Step-by-Step Guide

1. identify the statistical test.

Different tests demand different approaches. Determine whether you’re dealing with a t-test, z-test, or another statistical method to choose the correct critical value table.

2. Set the Significance Level

Establish the alpha level, typically denoted as 0.05 or 0.01. This represents the probability of making a Type I error, and adjusting it allows you to control the sensitivity of your test.

3. Find Degrees of Freedom

Degrees of freedom vary based on the nature of your data and the statistical test. Locate the appropriate row and column in the critical value table to pinpoint the critical value.

4. Critical Value Table

Consulting a critical value table specific to your statistical test is crucial. These tables provide precise values corresponding to different alpha levels and degrees of freedom.

Advantages of Mastering Critical Value Calculation

Understanding how to calculate critical value bestows several advantages. It enhances the credibility of your research, ensures accurate hypothesis testing, and enables you to make data-driven decisions with confidence.

Navigating Challenges: Common Pitfalls in Critical Value Calculation

Misinterpretation of alpha.

Failing to grasp the significance of the alpha level can lead to misguided conclusions. A thorough understanding of its role is paramount for precise critical value determination.

Inadequate Knowledge of Degrees of Freedom

Degrees of freedom vary across statistical tests, and miscalculating them can result in erroneous critical values. Take time to familiarize yourself with the specific requirements of your chosen test.

How to Calculate Critical Value: FAQs

Q: Can critical values be negative? Critical values are inherently positive. They represent the thresholds beyond which you reject the null hypothesis, emphasizing the positive nature of these values in hypothesis testing.

Q: How does the critical value relate to p-value? While critical values and p-values are interconnected, they serve distinct roles. Critical values determine the threshold for rejection, whereas p-values indicate the probability of observing results as extreme as the ones obtained.

Q: Is there a universal critical value table? No, critical value tables vary depending on the statistical test and the degrees of freedom. It’s crucial to use a table specific to your chosen method.

Q: Can critical values change based on sample size? Critical values are influenced by the sample size, particularly in t-tests. As sample size increases, critical values tend to approach those of a standard normal distribution.

Q: Are critical values constant across different significance levels? No, critical values change with the chosen significance level. Higher significance levels result in more conservative critical values, influencing the outcome of hypothesis testing.

Q: How frequently should critical values be recalibrated? Critical values should be recalibrated whenever there are changes in the study design, sample size, or chosen significance level. Regular recalibration ensures the accuracy of hypothesis testing.

Navigating the realm of statistics becomes more manageable when armed with the knowledge of how to calculate critical value. This guide has equipped you with a comprehensive understanding of critical values, from their significance to practical applications. Mastering this skill enhances the rigor of your statistical analyses, fostering a data-driven approach to decision-making.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Critical Value Calculator

Step by step calculation, what is the critical value, how to find critical value, left tailed test, right tailed test, z critical value calculator, t critical value calculator, f critical value calculator, chi square critical value calculator, calculators.

• Critical Value

Calculate Critical Z Value

Enter a probability value between zero and one to calculate critical value. Critical values determine what probability a particular variable will have when a sampling distribution is normal or close to normal.

Probability (p): p = 1 - α/2.

Critical Value: Definition and Significance in the Real World

- Guide Authored by Corin B. Arenas , published on October 4, 2019

Ever wondered if election surveys are accurate? How about statistics on housing, health care, and testing scores?  

In this section, we’ll discuss how sample data is tested for accuracy. Read on to learn more about critical value, how it’s used in statistics, and its significance in social science research.

What is a Critical Value?

In testing statistics, a critical value is a factor that determines the margin of error in a distribution graph.

According to Statistics How To , a site headed by math educator Stephanie Glen, if the absolute value of a test statistic is greater than the critical value, then there is statistical significance that rejects an accepted hypothesis.

Critical values divide a distribution graph into sections which indicate ‘rejection regions.’ Basically, if a test value falls within a rejection region, it means an accepted hypothesis (referred to as a null hypothesis) must be rejected. And if the test value falls within the accepted range, the null hypothesis cannot be rejected.

Testing sample data involves validating research and surveys like voting habits, SAT scores, body fat percentage, blood pressure, and all sorts of population data.

Hypothesis Testing and the Distribution Curve

Hypothesis tests check if your data was taken from a sample population that adheres to a hypothesized probability distribution. It is characterized by a null hypothesis and an alternative hypothesis.

In hypothesis testing, a critical value is a point on a distribution graph that is analyzed alongside a test statistic to confirm if a null hypothesis —a commonly accepted fact in a study which researchers aim to disprove—should be rejected.

The value of a null hypothesis implies that no statistical significance exists in a set of given observations. It is assumed to be true unless statistical evidence from an alternative hypothesis invalidates it.  

How does this relate with distribution graphs? A normal distribution curve, which is a bell-shaped curve, is a theoretical representation of how often an experiment will yield a particular result.

Elements of Normal Distribution:

• Has a mean, median, or mode. A mean is the average of numbers in a group, a median is the middle number in a list of numbers, and a mode is a number that appears most often in a set of numbers.
• 50% of the values are less than the mean
• 50% of the values are greater than the mean

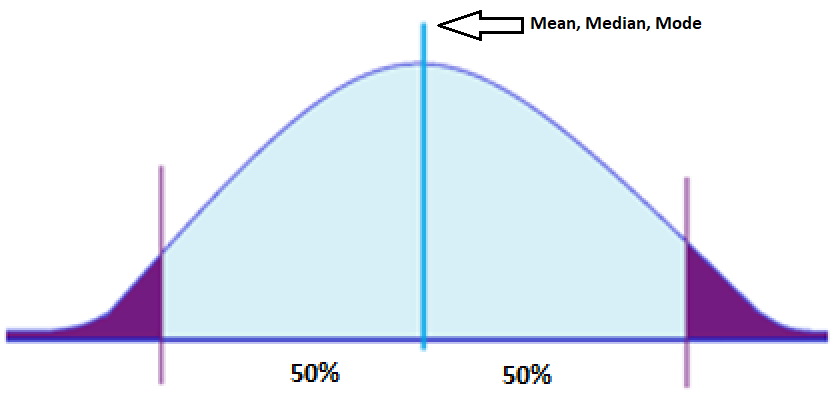
Majority of the data points in normal distribution are relatively similar. A perfectly normal distribution is characterized by its symmetry, meaning half of the data observations fall on either side of the middle of the graph. This implies that they occur within a range of values with fewer outliers on the high and low points of the graph.

Given these implications, critical values do not fall within the range of common data points. Which is why when a test statistic exceeds the critical value, a null hypothesis is forfeited.

Take note: Critical values may look for a two-tailed test or one-tailed test (right-tailed or left-tailed). Depending on the data, statisticians determine which test to perform first.

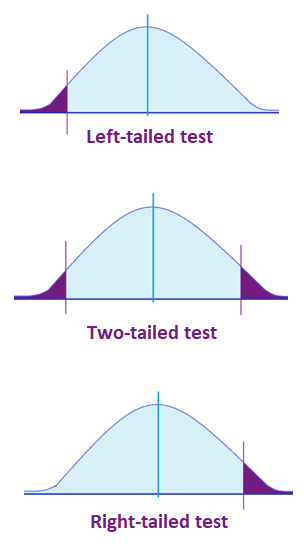
Finding the Critical Value

The standard equation for the probability of a critical value is:

p = 1 – α/2

Where p is the probability and alpha (α) represents the significance or confidence level. This establishes how far off a researcher will draw the line from the null hypothesis.

The alpha functions as the alternative hypothesis. It signifies the probability of rejecting the null hypothesis when it is true. For instance, if a researcher wants to establish a significance level of 0.05, it means there is a 5% chance of finding that a difference exists.

When the sampling distribution of a data set is normal or close to normal, the critical value can be determined as a z score or t score .

Z Score or T Score: Which Should You Use?

Typically, when a sample size is big (more than 40) using z or t statistics is fine. However, while both methods compute similar results, most beginner’s textbooks on statistics use the z score.

When a sample size is small and the standard deviation of a population is unknown, the t score is used. The t score is a probability distribution that allows statisticians to perform analyses on specific data sets using normal distribution. But take note: Small samples from populations that are not approximately normal should not use the t score.

What’s a standard deviation ? This measures how numbers are spread out in a set of values, showing the amount of variation. Low standard deviation means the numbers are close to the mean set, while a high standard deviation signifies numbers are dispersed at a wider range.

Calculating Z Score

The critical value of a z score can be used to determine the margin of error, as shown in the equations below:

• Margin of error = Critical value x Standard deviation of the statistic
• Margin of error = Critical value x Standard error of the statistic

The z score , also known as the standard normal probability score, signifies how many standard deviations a statistical element is from the mean. A z score table is used in hypothesis testing to check proportions and the difference between two means. Z tables indicate what percentage of the statistics is under the curve at any given point.

The basic formula for a z score sample is:

z = (X – μ) / σ

• X is the value of the element
• μ is the population mean
• σ is the standard deviation

Let’s solve an example. For instance, let’s say you have a test score of 85. If the test has a mean (μ) of 45 and a standard deviation (σ) of 23, what’s your z score? X = 85, μ = 45, σ = 23

z = (85 – 45) / 23 = 40 / 23 z = 1.7391

For this example, your score is 1.7391 standard deviations above the mean.

What do the z scores imply?

• If a score is greater than 0, the statistic sample is greater than the mean
• If the score is less than 0, the statistic sample is less than the mean
• If a score is equal to 1, it means the sample is 1 standard deviation greater than the mean, and so on
• If a score is equal to -1, it means the sample is 1 standard deviation less than the mean, and so on

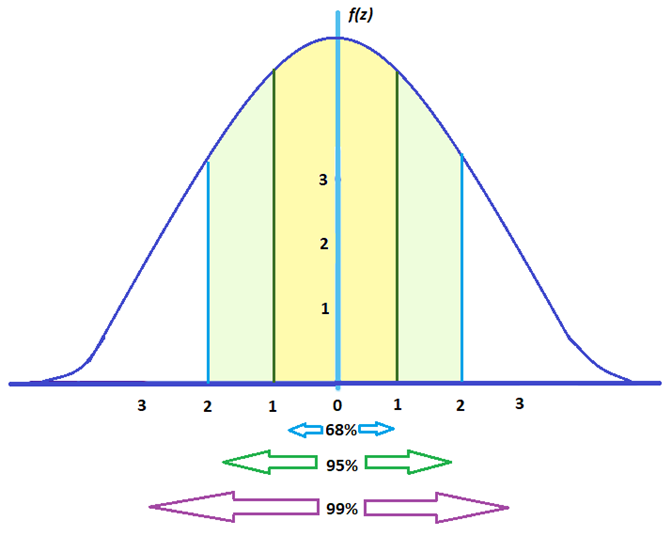
For elements in a large set:

• Around 68% fall between -1 and 1
• Around 95% fall between -2 and 2
• Around 99% fall between -3 and 3

To give you an idea, here’s how spread out statistical elements would look like under a z score graph:

Calculating T Score

On the other hand, here’s the standard formula for the t score:

t = [ x – μ ] / [ s / sqrt( n ) ]

• x is the sample mean
• s is the sample’s standard deviation
• n is the sample size

Then, we account for the degrees of freedom (df) which is the sample size minus 1. df = n – 1

T distribution, also known as the student’s distribution, is associated with a unique cumulative probability. This signifies the chance of finding a sample mean that’s less than or equal to x, based on a random sample size n. Cumulative probability refers to the likelihood that a random variable would fall within a specific range. To express the t statistic with a cumulative probability of 1 – α, statisticians use t α .

Part of finding the t score is locating the degrees of freedom (df) using the t distribution table as a reference. For demonstration purposes, let’s say you have a small sample of 5 and you want to conduct a right-tailed test. Follow the steps below.

5 df, α = 0.05

• Take your sample size and subtract 1. 5 – 1 = 4. df = 4
• For this example, let’s say the alpha level is 5% (0.05).
• Look for the df in the t distribution table along with its corresponding alpha level. You’ll find the critical value where the column and row intersect.

*One-tail t distribution table referenced from How to Statistics. In this example, 5 df, α = 0.05, the critical value is 2.132.

Here’s another example using the t score formula.

A factory produces CFL light bulbs. The owner says that CFL bulbs from their factory lasts for 160 days. Quality specialists randomly chose 20 bulbs for testing, which lasted for an average of 150 days, with a standard deviation of 40 days. If the CFL bulbs really last for 160 days, what is the probability that 20 random CFL bulbs would have an average life that’s less than 150 days?

t = [ 150 – 160 ] / [ 40 / sqrt( 20 ) ] = -10 / [40 / 4.472135] = -10 / 8.94427 t = -1.118034

The degrees of freedom: df = 20 – 1, df = 19

Again, use the variables above to refer to a t distribution table, or use a t score calculator.

For this example, the critical value is 0.1387 . Thus, if the life of a CFL light bulb is 160 days, there is a 13.87% probability that the average CFL bulb for 20 randomly chosen bulbs would be less than or equal to 150 days.

If we were to plot the critical value and shade the rejection region in a graph, it would look like this:

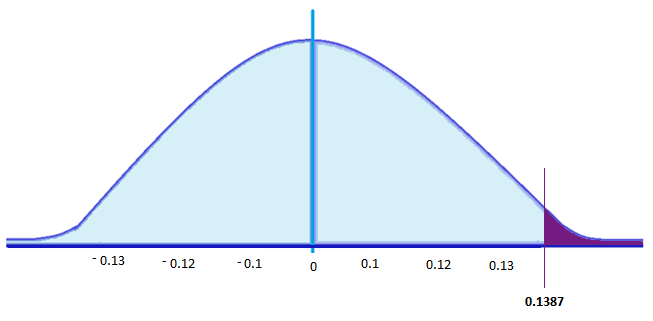
If a test statistic is greater than this critical value, then the null hypothesis, which is ‘CFL light bulbs have a life of 160 days,’ should be rejected. That’s if tests show more than 13.87% of the sample light bulbs (20) have a lifespan of less than or equal 150 days.

Why is Determining Critical Value Important?

Researchers often work with a sample population, which is a small percentage when they gather statistics.

Working with sample populations does not guarantee that it reflects the actual population’s results. To test if the data is representative of the actual population, researchers conduct hypothesis testing which make use of critical values.

What are Real-World Uses for It?

Validating statistical knowledge is important in the study of a wide range of fields. This includes research in social sciences such as economics, psychology, sociology, political science, and anthropology.

For one, it keeps quality management in check. This includes product testing in companies and analyzing test scores in educational institutions.

Moreover, hypothesis testing is crucial for the scientific and medical community because it is imperative for the advancement of theories and ideas.

If you’ve come across research that studies behavior, then the study likely used hypothesis testing and sampling in populations. From the public’s voting behavior, to what type of houses people tend to buy, researchers conduct distribution tests.

Studies such as how male adolescents in certain states are prone to violence, or how children of obese parents are prone to becoming obese, are other examples that use critical values in distribution testing.

In the field of health care, topics like how often diseases like measles, diphtheria, or polio occur in an area is relevant for public safety. Testing would help communities know if there are certain health conditions rising at an alarming rate. This is especially relevant now in the age of anti-vaccine activists .

The Bottom Line

Finding critical values are important for testing statistical data. It’s one of the main factors in hypothesis testing, which can validate or disprove commonly accepted information.

Proper analysis and testing of statistics help guide the public, which corrects misleading or dated information.

Hypothesis testing is useful in a wide range of disciplines, such as medicine, sociology, political science, and quality management in companies.

About the Author

Corin is an ardent researcher and writer of financial topics—studying economic trends, how they affect populations, as well as how to help consumers make wiser financial decisions. Her other feature articles can be read on Inquirer.net and Manileno.com. She holds a Master’s degree in Creative Writing from the University of the Philippines, one of the top academic institutions in the world, and a Bachelor’s in Communication Arts from Miriam College.

How to Excel at Math Cartoon

• Trigonometry
• Percent Off
• Statistical Average
• Standard Deviation
• Correlation
• Probability
• Log/Antilog
• HEX & Binary
• Weight/Mass
• Temperature
• Current Time
• Time Duration
• Balance Equations

Play & Learn

Pin It on Pinterest

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.5: Critical values, p-values, and significance level

• Last updated
• Save as PDF
• Page ID 7117

• Foster et al.
• University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

A low probability value casts doubt on the null hypothesis. How low must the probability value be in order to conclude that the null hypothesis is false? Although there is clearly no right or wrong answer to this question, it is conventional to conclude the null hypothesis is false if the probability value is less than 0.05. More conservative researchers conclude the null hypothesis is false only if the probability value is less than 0.01. When a researcher concludes that the null hypothesis is false, the researcher is said to have rejected the null hypothesis. The probability value below which the null hypothesis is rejected is called the α level or simply \(α\) (“alpha”). It is also called the significance level. If α is not explicitly specified, assume that \(α\) = 0.05.

The significance level is a threshold we set before collecting data in order to determine whether or not we should reject the null hypothesis. We set this value beforehand to avoid biasing ourselves by viewing our results and then determining what criteria we should use. If our data produce values that meet or exceed this threshold, then we have sufficient evidence to reject the null hypothesis; if not, we fail to reject the null (we never “accept” the null).

There are two criteria we use to assess whether our data meet the thresholds established by our chosen significance level, and they both have to do with our discussions of probability and distributions. Recall that probability refers to the likelihood of an event, given some situation or set of conditions. In hypothesis testing, that situation is the assumption that the null hypothesis value is the correct value, or that there is no effect. The value laid out in H0 is our condition under which we interpret our results. To reject this assumption, and thereby reject the null hypothesis, we need results that would be very unlikely if the null was true. Now recall that values of z which fall in the tails of the standard normal distribution represent unlikely values. That is, the proportion of the area under the curve as or more extreme than \(z\) is very small as we get into the tails of the distribution. Our significance level corresponds to the area under the tail that is exactly equal to α: if we use our normal criterion of \(α\) = .05, then 5% of the area under the curve becomes what we call the rejection region (also called the critical region) of the distribution. This is illustrated in Figure \(\PageIndex{1}\).

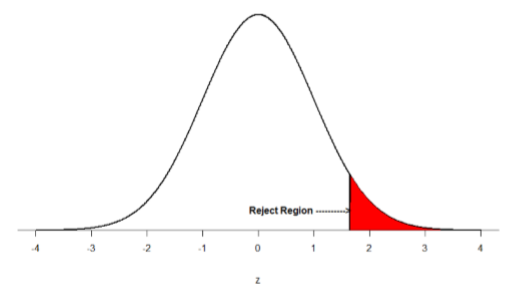
The shaded rejection region takes us 5% of the area under the curve. Any result which falls in that region is sufficient evidence to reject the null hypothesis.

The rejection region is bounded by a specific \(z\)-value, as is any area under the curve. In hypothesis testing, the value corresponding to a specific rejection region is called the critical value, \(z_{crit}\) (“\(z\)-crit”) or \(z*\) (hence the other name “critical region”). Finding the critical value works exactly the same as finding the z-score corresponding to any area under the curve like we did in Unit 1. If we go to the normal table, we will find that the z-score corresponding to 5% of the area under the curve is equal to 1.645 (\(z\) = 1.64 corresponds to 0.0405 and \(z\) = 1.65 corresponds to 0.0495, so .05 is exactly in between them) if we go to the right and -1.645 if we go to the left. The direction must be determined by your alternative hypothesis, and drawing then shading the distribution is helpful for keeping directionality straight.

Suppose, however, that we want to do a non-directional test. We need to put the critical region in both tails, but we don’t want to increase the overall size of the rejection region (for reasons we will see later). To do this, we simply split it in half so that an equal proportion of the area under the curve falls in each tail’s rejection region. For \(α\) = .05, this means 2.5% of the area is in each tail, which, based on the z-table, corresponds to critical values of \(z*\) = ±1.96. This is shown in Figure \(\PageIndex{2}\).

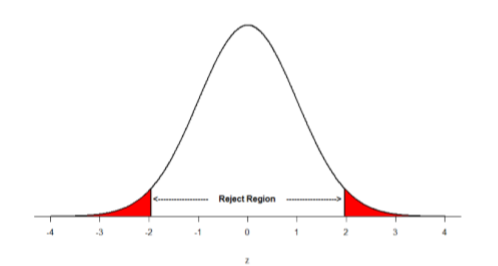
Thus, any \(z\)-score falling outside ±1.96 (greater than 1.96 in absolute value) falls in the rejection region. When we use \(z\)-scores in this way, the obtained value of \(z\) (sometimes called \(z\)-obtained) is something known as a test statistic, which is simply an inferential statistic used to test a null hypothesis. The formula for our \(z\)-statistic has not changed:

\[z=\dfrac{\overline{\mathrm{X}}-\mu}{\bar{\sigma} / \sqrt{\mathrm{n}}} \]

To formally test our hypothesis, we compare our obtained \(z\)-statistic to our critical \(z\)-value. If \(\mathrm{Z}_{\mathrm{obt}}>\mathrm{Z}_{\mathrm{crit}}\), that means it falls in the rejection region (to see why, draw a line for \(z\) = 2.5 on Figure \(\PageIndex{1}\) or Figure \(\PageIndex{2}\)) and so we reject \(H_0\). If \(\mathrm{Z}_{\mathrm{obt}}<\mathrm{Z}_{\mathrm{crit}}\), we fail to reject. Remember that as \(z\) gets larger, the corresponding area under the curve beyond \(z\) gets smaller. Thus, the proportion, or \(p\)-value, will be smaller than the area for \(α\), and if the area is smaller, the probability gets smaller. Specifically, the probability of obtaining that result, or a more extreme result, under the condition that the null hypothesis is true gets smaller.

The \(z\)-statistic is very useful when we are doing our calculations by hand. However, when we use computer software, it will report to us a \(p\)-value, which is simply the proportion of the area under the curve in the tails beyond our obtained \(z\)-statistic. We can directly compare this \(p\)-value to \(α\) to test our null hypothesis: if \(p < α\), we reject \(H_0\), but if \(p > α\), we fail to reject. Note also that the reverse is always true: if we use critical values to test our hypothesis, we will always know if \(p\) is greater than or less than \(α\). If we reject, we know that \(p < α\) because the obtained \(z\)-statistic falls farther out into the tail than the critical \(z\)-value that corresponds to \(α\), so the proportion (\(p\)-value) for that \(z\)-statistic will be smaller. Conversely, if we fail to reject, we know that the proportion will be larger than \(α\) because the \(z\)-statistic will not be as far into the tail. This is illustrated for a one-tailed test in Figure \(\PageIndex{3}\).

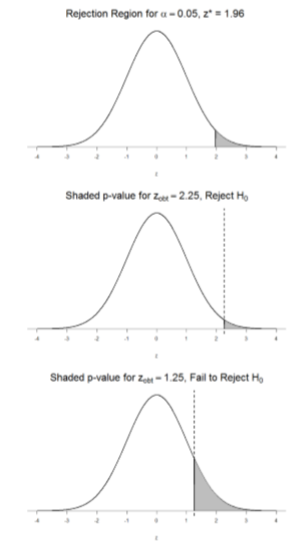
When the null hypothesis is rejected, the effect is said to be statistically significant. For example, in the Physicians Reactions case study, the probability value is 0.0057. Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected. It is very important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what “significant” usually means. When an effect is significant, you can have confidence the effect is not exactly zero. Finding that an effect is significant does not tell you about how large or important the effect is. Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough. Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.

Data Science Society

Data.Platform

Statistical Hypothesis Testing: How to Calculate Critical Values

Testing statistical hypotheses is one of the most important parts of data analysis. It lets the researcher and analyst conclude the whole community from a small sample. In this case, critical values are useful because they help figure out if the results are worthy of attention.

The goal of this article is to define a critical value calculator, talk about why it’s important in statistical hypothesis testing, and show how to use one.

What is statistical hypothesis testing?

Statistical hypothesis testing is a methodical way to draw conclusions about a whole community from a small group of samples. In this step, observed data is compared to an expected or null hypothesis to see if there is a difference that is caused by an effect, chance, or just a human mistake. Hypotheses are put to the test in economics, social studies, and science in order to come to reasonable conclusions.

What are critical values?

In this case, critical values are limits or borders that are used during hypothesis testing to see how important a test statistic is. In hypothesis testing, the critical value is compared to a test statistic that measures the difference between the data that was noticed and the value that was thought to be true. A critical value calculator is used to evaluate if there is sufficient information in the observed results that would make it possible to invalidate the zero hypothesis.

How to calculate critical values

Step 1: identify the test statistic.

Before you can figure out the key values, you need to choose the right test statistic for your hypothesis test. The “test statistic” is a number that shows that the data are different from the “null value.” This is a list of test statistics. Which one to use depends on the data or hypothesis being tested.

Examples of these statistics are the Z-score, T-statistics, F-statistics, and Chi-squared statistics. Here’s a brief overview of when each test statistic is typically used:

Z-score: If you have data that has a normal distribution, you can find out what the group mean and standard deviation are.

T-statistic: The t-statistic is used to test hypotheses when the sample size is small, or the community standard deviation is unknown.

F-statistic: In ANOVA tests, F-statistics are used to find changes between the variances of different groups or treatments.

The chi-squared measure is used for tests that use categorical data, such as the goodness of fit test or the test for independence in a contingency table.

Once you’ve found the best statistic for a hypothesis test, move on to the next step.

Step 2: Determine the degrees of freedom

Degrees of freedom (df) are one of the important things that are used to figure out critical numbers. Freedom of degrees refers to the number of separate factors that are linked to your dataset. The number of degrees of freedom changes based on the test measure that is used.

For example, to find the critical numbers for a T-statistic, one is usually taken away from n to get an idea of the degrees of freedom. An F-statistic in ANOVA, on the other hand, has two sets of degrees of freedom: one for the numerator (which is the difference between groups) and one for the denominator (which is the difference within groups).

Because of this, you need to figure out the right number of degrees of freedom for your analysis and not use the wrong numbers because they lead to wrong results. If you need to find the right degree of freedom values for your test statistic, look at the appropriate statistical tables or sources.

Step 3: One needs to find the critical value in a critical value table

A critical value table is an important part of any hypothesis test. For each degree of freedom and significant level, the table shows the test statistic values that go with them. This critical number sets a limit on how often the null should be rejected.

One example is a two-tailed Z-test with a significance level of 0.05 (alpha = 0.05). If you know the number of degrees of freedom, you can find the critical value that is equal to alpha/2 (0.025) in the

Also, the T-table shows the important number for alpha/2 and your degrees of freedom for the T-distribution with degrees of freedom.

Step 4: Do you believe that the test statistic is bigger than the critical value?

After that, we will compare this test statistic with the critical number we chose from the table. So, you will reject the null hypothesis if your test result is more extreme than what is needed for a significance level (the tail of the distribution above the critical value). This shows that the data that was seen is very different, which means it probably wasn’t just a matter of chance. On the other hand, you can’t reject the null hypothesis if your test statistic doesn’t fall in the rejection area. In this case, the data that was noticed is not enough to show that the value that was hypothesized might be wrong.

In the field of statistical hypothesis testing, researchers and other analysts need to know what key values are and how to find them. So, critical values are a common way to figure out how important the results of tests are. When researchers check to see if the test statistic is greater than or similar to the critical value, they can tell if their data supports the null hypothesis or not.

Always use the right critical value tables, and keep in mind that degrees of freedom are a big part of making sure that statistical analysis is correct and thorough. Using statistical software can also help cut down on mistakes and make the math part of this process easier.

Hypothesis testing is built on important values that help people come to conclusions, make decisions, make progress in science, and learn more. Critical value calculation is a skill that everyone who works with statistics needs to have.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Critical Value Approach in Hypothesis Testing

by Nathan Sebhastian

Posted on Jun 05, 2023

Reading time: 5 minutes

The critical value is the cut-off point to determine whether to accept or reject the null hypothesis for your sample distribution.

The critical value approach provides a standardized method for hypothesis testing, enabling you to make informed decisions based on the evidence obtained from sample data.

After calculating the test statistic using the sample data, you compare it to the critical value(s) corresponding to the chosen significance level ( α ).

The critical value(s) represent the boundary beyond which you reject the null hypothesis. You will have rejection regions and non-rejection region as follows:

Two-sided test

A two-sided hypothesis test has 2 rejection regions, so you need 2 critical values on each side. Because there are 2 rejection regions, you must split the significance level in half.

Each rejection region has a probability of α / 2 , making the total likelihood for both areas equal the significance level.

In this test, the null hypothesis H0 gets rejected when the test statistic is too small or too large.

Left-tailed test

The left-tailed test has 1 rejection region, and the null hypothesis only gets rejected when the test statistic is too small.

Right-tailed test

The right-tailed test is similar to the left-tailed test, only the null hypothesis gets rejected when the test statistic is too large.

Now that you understand the definition of critical values, let’s look at how to use critical values to construct a confidence interval.

Using Critical Values to Construct Confidence Intervals

Confidence Intervals use the same Critical values as the test you’re running.

If you’re running a z-test with a 95% confidence interval, then:

• For a two-sided test, The CVs are -1.96 and 1.96
• For a one-tailed test, the critical value is -1.65 (left) or 1.65 (right)

To calculate the upper and lower bounds of the confidence interval, you need to calculate the sample mean and then add or subtract the margin of error from it.

To get the Margin of Error, multiply the critical value by the standard error:

Let’s see an example. Suppose you are estimating the population mean with a 95% confidence level.

You have a sample mean of 50, a sample size of 100, and a standard deviation of 10. Using a z-table, the critical value for a 95% confidence level is approximately 1.96.

Calculate the standard error:

Determine the margin of error:

Compute the lower bound and upper bound:

The 95% confidence interval is (48.04, 51.96). This means that we are 95% confident that the true population mean falls within this interval.

Finding the Critical Value

The formula to find critical values depends on the specific distribution associated with the hypothesis test or confidence interval you’re using.

Here are the formulas for some commonly used distributions.

Standard Normal Distribution (Z-distribution):

The critical value for a given significance level ( α ) in the standard normal distribution is found using the cumulative distribution function (CDF) or a standard normal table.

z(α) represents the z-score corresponding to the desired significance level α .

Student’s t-Distribution (t-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the t-distribution is found using the inverse cumulative distribution function (CDF) or a t-distribution table.

t(α, df) represents the t-score corresponding to the desired significance level α and degrees of freedom df .

Chi-Square Distribution (χ²-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the chi-square distribution is found using the inverse cumulative distribution function (CDF) or a chi-square distribution table.

where χ²(α, df) represents the chi-square value corresponding to the desired significance level α and degrees of freedom df .

F-Distribution:

The critical value for a given significance level (α), degrees of freedom for the numerator (df₁), and degrees of freedom for the denominator (df₂) in the F-distribution is found using the inverse cumulative distribution function (CDF) or an F-distribution table.

F(α, df₁, df₂) represents the F-value corresponding to the desired significance level α , df₁ , and df₂ .

As you can see, the specific formula to find critical values depends on the distribution and the parameters associated with the problem at hand.

Usually, you don’t calculate the critical values manually as you can use statistical tables or statistical software to determine the critical values.

I will update this tutorial with statistical tables that you can use later.

The critical value is as a threshold where you make a decision based on the observed test statistic and its relation to the significance level.

It provides a predetermined point of reference to objectively evaluate the strength of the evidence against the null hypothesis and guide the acceptance or rejection of the hypothesis.

If the test statistic falls in the critical region (beyond the critical value), it means the observed data provide strong evidence against the null hypothesis.

In this case, you reject the null hypothesis in favor of the alternative hypothesis, indicating that there is sufficient evidence to support the claim or relationship stated in the alternative hypothesis.

On the other hand, if the test statistic falls in the non-critical region (within the critical value), it means the observed data do not provide enough evidence to reject the null hypothesis.

In this case, you fail to reject the null hypothesis, indicating that there is insufficient evidence to support the alternative hypothesis.

Take your skills to the next level ⚡️

I'm sending out an occasional email with the latest tutorials on programming, web development, and statistics. Drop your email in the box below and I'll send new stuff straight into your inbox!

Hello! This website is dedicated to help you learn tech and data science skills with its step-by-step, beginner-friendly tutorials. Learn statistics, JavaScript and other programming languages using clear examples written for people.

Learn more about this website

Connect with me on Twitter

Or LinkedIn

Type the keyword below and hit enter

Click to see all tutorials tagged with:

Critical Value

Critical value is a cut-off value that is used to mark the start of a region where the test statistic, obtained in hypothesis testing, is unlikely to fall in. In hypothesis testing, the critical value is compared with the obtained test statistic to determine whether the null hypothesis has to be rejected or not.

Graphically, the critical value splits the graph into the acceptance region and the rejection region for hypothesis testing. It helps to check the statistical significance of a test statistic. In this article, we will learn more about the critical value, its formula, types, and how to calculate its value.

What is Critical Value?

A critical value can be calculated for different types of hypothesis tests. The critical value of a particular test can be interpreted from the distribution of the test statistic and the significance level. A one-tailed hypothesis test will have one critical value while a two-tailed test will have two critical values.

Critical Value Definition

Critical value can be defined as a value that is compared to a test statistic in hypothesis testing to determine whether the null hypothesis is to be rejected or not. If the value of the test statistic is less extreme than the critical value, then the null hypothesis cannot be rejected. However, if the test statistic is more extreme than the critical value, the null hypothesis is rejected and the alternative hypothesis is accepted. In other words, the critical value divides the distribution graph into the acceptance and the rejection region. If the value of the test statistic falls in the rejection region, then the null hypothesis is rejected otherwise it cannot be rejected.

Critical Value Formula

Depending upon the type of distribution the test statistic belongs to, there are different formulas to compute the critical value. The confidence interval or the significance level can be used to determine a critical value. Given below are the different critical value formulas.

Critical Value Confidence Interval

The critical value for a one-tailed or two-tailed test can be computed using the confidence interval . Suppose a confidence interval of 95% has been specified for conducting a hypothesis test. The critical value can be determined as follows:

• Step 1: Subtract the confidence level from 100%. 100% - 95% = 5%.
• Step 2: Convert this value to decimals to get \(\alpha\). Thus, \(\alpha\) = 5%.
• Step 3: If it is a one-tailed test then the alpha level will be the same value in step 2. However, if it is a two-tailed test, the alpha level will be divided by 2.
• Step 4: Depending on the type of test conducted the critical value can be looked up from the corresponding distribution table using the alpha value.

The process used in step 4 will be elaborated in the upcoming sections.

T Critical Value

A t-test is used when the population standard deviation is not known and the sample size is lesser than 30. A t-test is conducted when the population data follows a Student t distribution . The t critical value can be calculated as follows:

• Determine the alpha level.
• Subtract 1 from the sample size. This gives the degrees of freedom (df).
• If the hypothesis test is one-tailed then use the one-tailed t distribution table. Otherwise, use the two-tailed t distribution table for a two-tailed test.
• Match the corresponding df value (left side) and the alpha value (top row) of the table. Find the intersection of this row and column to give the t critical value.

Test Statistic for one sample t test: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, s is the sample standard deviation and n is the size of the sample.

Test Statistic for two samples t test: \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Decision Criteria:

• Reject the null hypothesis if test statistic > t critical value (right-tailed hypothesis test).
• Reject the null hypothesis if test statistic < t critical value (left-tailed hypothesis test).
• Reject the null hypothesis if the test statistic does not lie in the acceptance region (two-tailed hypothesis test).

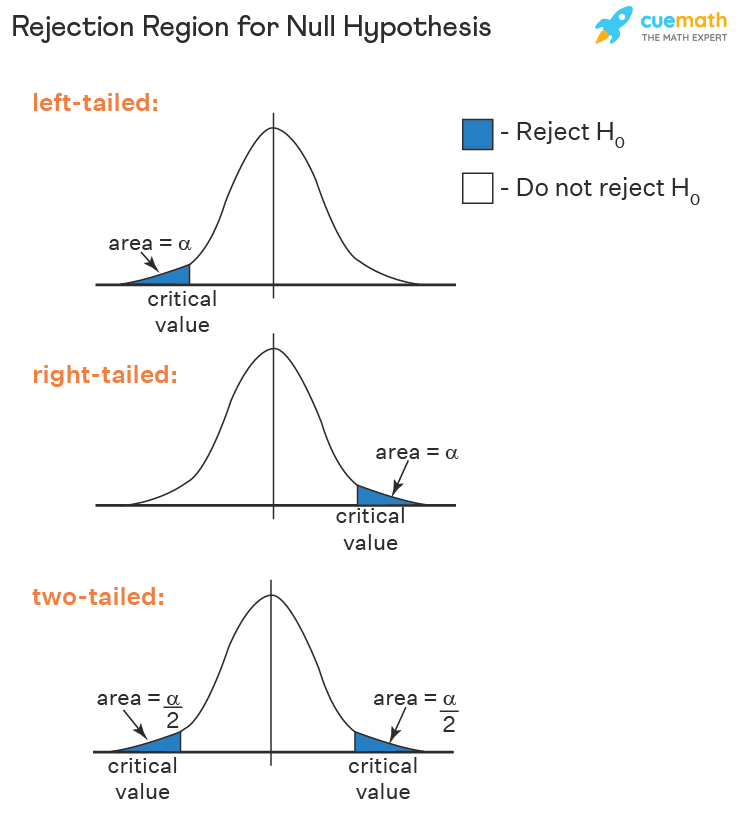
This decision criterion is used for all tests. Only the test statistic and critical value change.

Z Critical Value

A z test is conducted on a normal distribution when the population standard deviation is known and the sample size is greater than or equal to 30. The z critical value can be calculated as follows:

• Find the alpha level.
• Subtract the alpha level from 1 for a two-tailed test. For a one-tailed test subtract the alpha level from 0.5.
• Look up the area from the z distribution table to obtain the z critical value. For a left-tailed test, a negative sign needs to be added to the critical value at the end of the calculation.

Test statistic for one sample z test: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\sigma\) is the population standard deviation.

Test statistic for two samples z test: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

F Critical Value

The F test is largely used to compare the variances of two samples. The test statistic so obtained is also used for regression analysis. The f critical value is given as follows:

• Subtract 1 from the size of the first sample. This gives the first degree of freedom. Say, x
• Similarly, subtract 1 from the second sample size to get the second df. Say, y.
• Using the f distribution table, the intersection of the x column and y row will give the f critical value.

Test Statistic for large samples: f = \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\). \(\sigma_{1}^{2}\) variance of the first sample and \(\sigma_{2}^{2}\) variance of the second sample.

Test Statistic for small samples: f = \(\frac{s_{1}^{2}}{s_{2}^{2}}\). \(s_{1}^{1}\) variance of the first sample and \(s_{2}^{2}\) variance of the second sample.

Chi-Square Critical Value

The chi-square test is used to check if the sample data matches the population data. It can also be used to compare two variables to see if they are related. The chi-square critical value is given as follows:

• Identify the alpha level.
• Subtract 1 from the sample size to determine the degrees of freedom (df).
• Using the chi-square distribution table, the intersection of the row of the df and the column of the alpha value yields the chi-square critical value.

Test statistic for chi-squared test statistic: \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\).

Critical Value Calculation

Suppose a right-tailed z test is being conducted. The critical value needs to be calculated for a 0.0079 alpha level. Then the steps are as follows:

• Subtract the alpha level from 0.5. Thus, 0.5 - 0.0079 = 0.4921
• Using the z distribution table find the area closest to 0.4921. The closest area is 0.4922. As this value is at the intersection of 2.4 and 0.02 thus, the z critical value = 2.42.

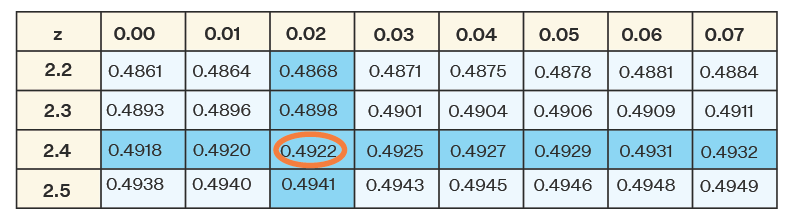
Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Critical Value

• Critical value can be defined as a value that is useful in checking whether the null hypothesis can be rejected or not by comparing it with the test statistic.
• It is the point that divides the distribution graph into the acceptance and the rejection region.
• There are 4 types of critical values - z, f, chi-square, and t.

Examples on Critical Value

Example 1: Find the critical value for a left tailed z test where \(\alpha\) = 0.012.

Solution: First subtract \(\alpha\) from 0.5. Thus, 0.5 - 0.012 = 0.488.

Using the z distribution table, z = 2.26.

However, as this is a left-tailed z test thus, z = -2.26

Answer: Critical value = -2.26

Example 2: Find the critical value for a two-tailed f test conducted on the following samples at a \(\alpha\) = 0.025

Variance = 110, Sample size = 41

Variance = 70, Sample size = 21

Solution: \(n_{1}\) = 41, \(n_{2}\) = 21,

\(n_{1}\) - 1= 40, \(n_{2}\) - 1 = 20,

Sample 1 df = 40, Sample 2 df = 20

Using the F distribution table for \(\alpha\) = 0.025, the value at the intersection of the 40 th column and 20 th row is

F(40, 20) = 2.287

Answer: Critical Value = 2.287

Example 3: Suppose a one-tailed t-test is being conducted on data with a sample size of 8 at \(\alpha\) = 0.05. Then find the critical value.

Solution: n = 8

df = 8 - 1 = 7

Using the one tailed t distribution table t(7, 0.05) = 1.895.

Answer: Crititcal Value = 1.895

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Critical Value

What is the critical value in statistics.

Critical value in statistics is a cut-off value that is compared with a test statistic in hypothesis testing to check whether the null hypothesis should be rejected or not.

What are the Different Types of Critical Value?

There are 4 types of critical values depending upon the type of distributions they are obtained from. These distributions are given as follows:

• Normal distribution (z critical value).
• Student t distribution (t).
• Chi-squared distribution (chi-squared).
• F distribution (f).

What is the Critical Value Formula for an F test?

To find the critical value for an f test the steps are as follows:

• Determine the degrees of freedom for both samples by subtracting 1 from each sample size.
• Find the corresponding value from a one-tailed or two-tailed f distribution at the given alpha level.
• This will give the critical value.

What is the T Critical Value?

The t critical value is obtained when the population follows a t distribution. The steps to find the t critical value are as follows:

• Subtract the sample size number by 1 to get the df.
• Use the t distribution table for the alpha value to get the required critical value.

How to Find the Critical Value Using a Confidence Interval for a Two-Tailed Z Test?

The steps to find the critical value using a confidence interval are as follows:

• Subtract the confident interval from 100% and convert the resultant into a decimal value to get the alpha level.
• Subtract this value from 1.
• Find the z value for the corresponding area using the normal distribution table to get the critical value.

Can a Critical Value be Negative?

If a left-tailed test is being conducted then the critical value will be negative. This is because the critical value will be to the left of the mean thus, making it negative.

How to Reject Null Hypothesis Based on Critical Value?

The rejection criteria for the null hypothesis is given as follows:

• Right-tailed test: Test statistic > critical value.
• Left-tailed test: Test statistic < critical value.
• Two-tailed test: Reject if the test statistic does not lie in the acceptance region.

p-value Calculator

What is p-value, how do i calculate p-value from test statistic, how to interpret p-value, how to use the p-value calculator to find p-value from test statistic, how do i find p-value from z-score, how do i find p-value from t, p-value from chi-square score (χ² score), p-value from f-score.

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

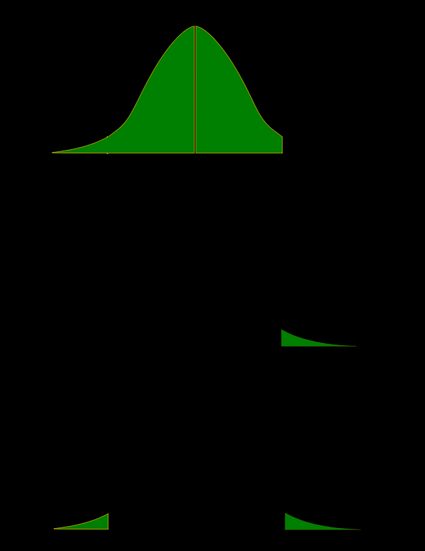
• Non-symmetric case: chi-squared distribution:

In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level .

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

Class width

Implied probability, plastic footprint.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)