measures of center homework

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school statistics

Course: high school statistics   >   unit 1.

• Statistics intro: Mean, median, & mode
• Median in a histogram
• Calculating mean and median from data displays
• Estimating mean and median in data displays

Choosing the "best" measure of center

Part 1: the mean.

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  
• (Choice A)   It represents the "average" score. If each golfer had scored the same, they each would have scored the mean. A It represents the "average" score. If each golfer had scored the same, they each would have scored the mean.
• (Choice B)   It is the middle point in the set of scores. That is, half the team scored higher than the mean, and half the team scored lower than the mean. B It is the middle point in the set of scores. That is, half the team scored higher than the mean, and half the team scored lower than the mean.

Part 2: The median

• (Choice A)   It is the "average" score. That is, if each golfer had scored the same, they each would have scored the median. A It is the "average" score. That is, if each golfer had scored the same, they each would have scored the median.
• (Choice B)   It is the middle point in the set of scores. That is, half the team scored higher than the median, and half the team scored lower than the median. B It is the middle point in the set of scores. That is, half the team scored higher than the median, and half the team scored lower than the median.

Part 3: The "best" measure of center

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Calcworkshop

Measures Of Center 9+ Examples on Mean, Median, Mode

// Last Updated: September 20, 2020 - Watch Video //

Which is better for measuring the center? Mean, median, mode, or standard deviation?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

That’s one of the many questions we’re going to ask in this lesson, as we seek to discover how to measure the center and spread of a distribution.

Now, the mean , sometimes called the arithmetic mean, is the average or the expected value that measures the central value of a data set.

It is found by adding all of the values in the data set and dividing it by the number of values.

While there are several types of means that we will learn about in probability and statistics, the two most important are the population mean and the sample mean.

The sample mean is the average of the values collected, whereas the population mean is the average of all the values in the population.

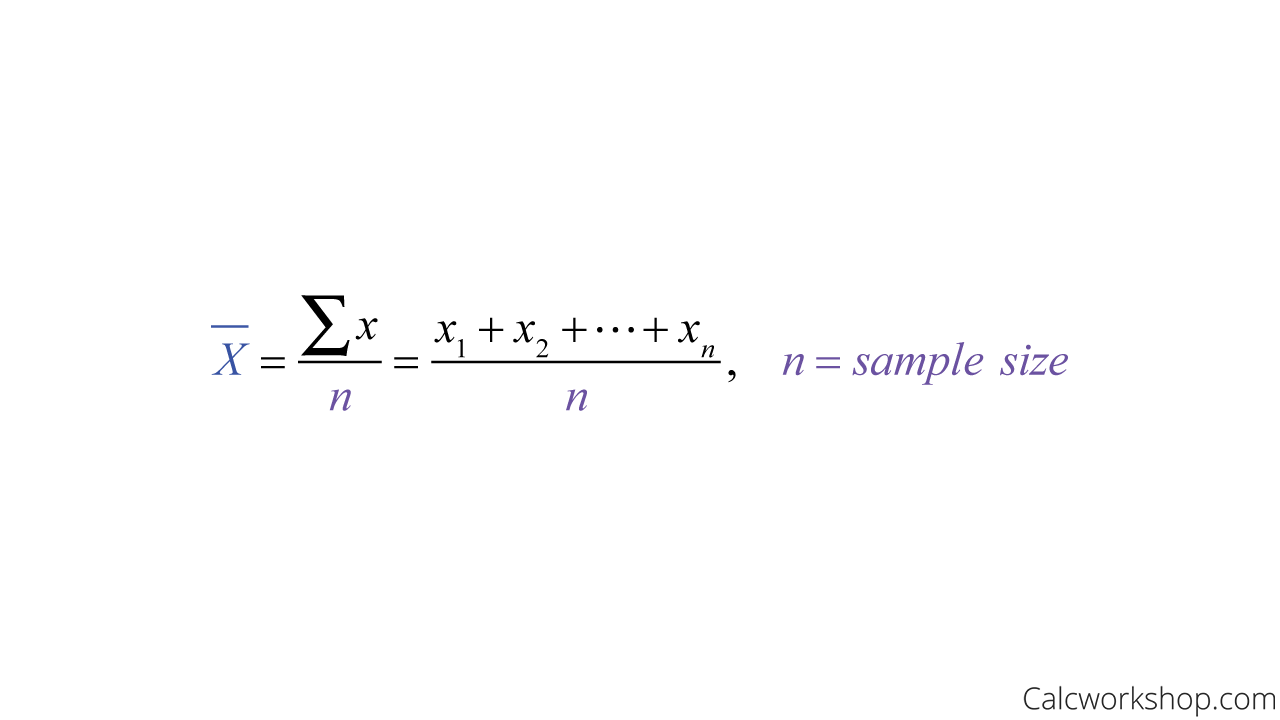
Sample Mean Formula

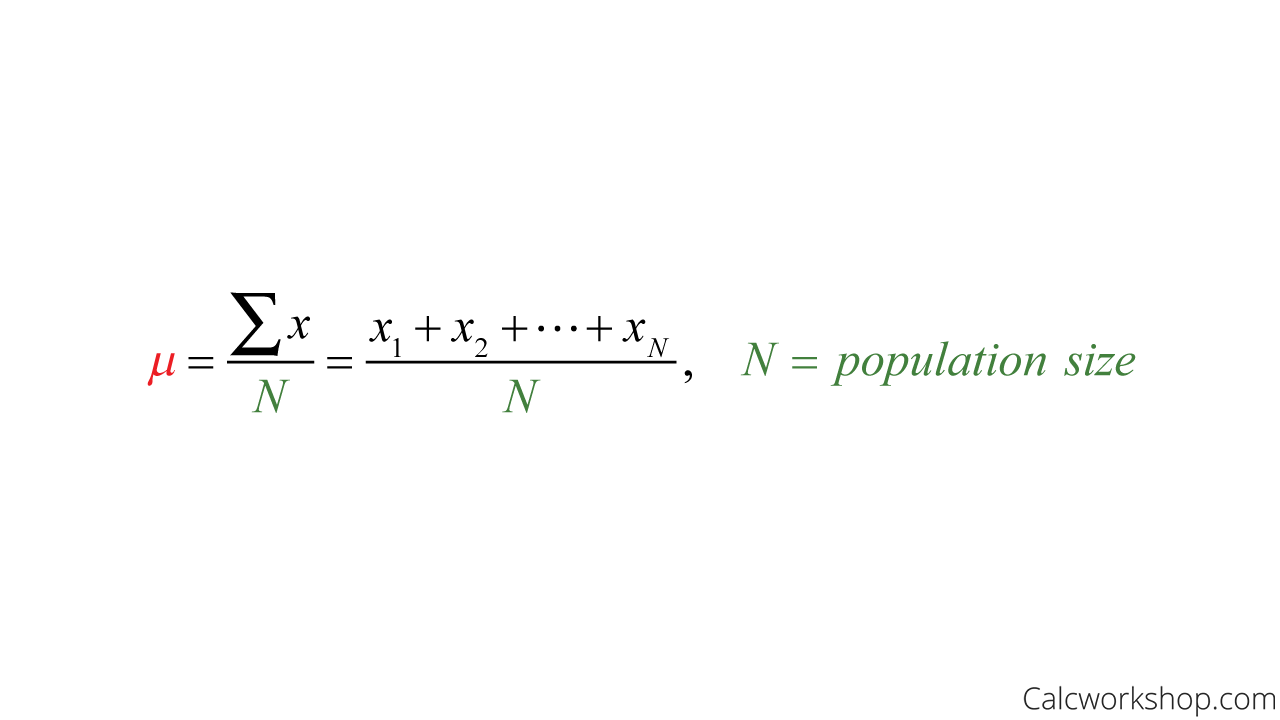
Population Mean Formula

Realistically, the population mean is hard to calculate, so if size of our sample is large enough , the mean becomes a reasonable estimate for the population.

The median is the middle term, or number in a data set ranked in ascending (increasing) order. In other words, it separates the lower half of the data set from the upper half.

What’s important to note is that if the data set has an odd number of values, the median is the middle number. But if the data set has an even number of values, then the median is the average of the two middle terms as Monterey Institute points out, and as the following examples demonstrate.

Median Of Even Set

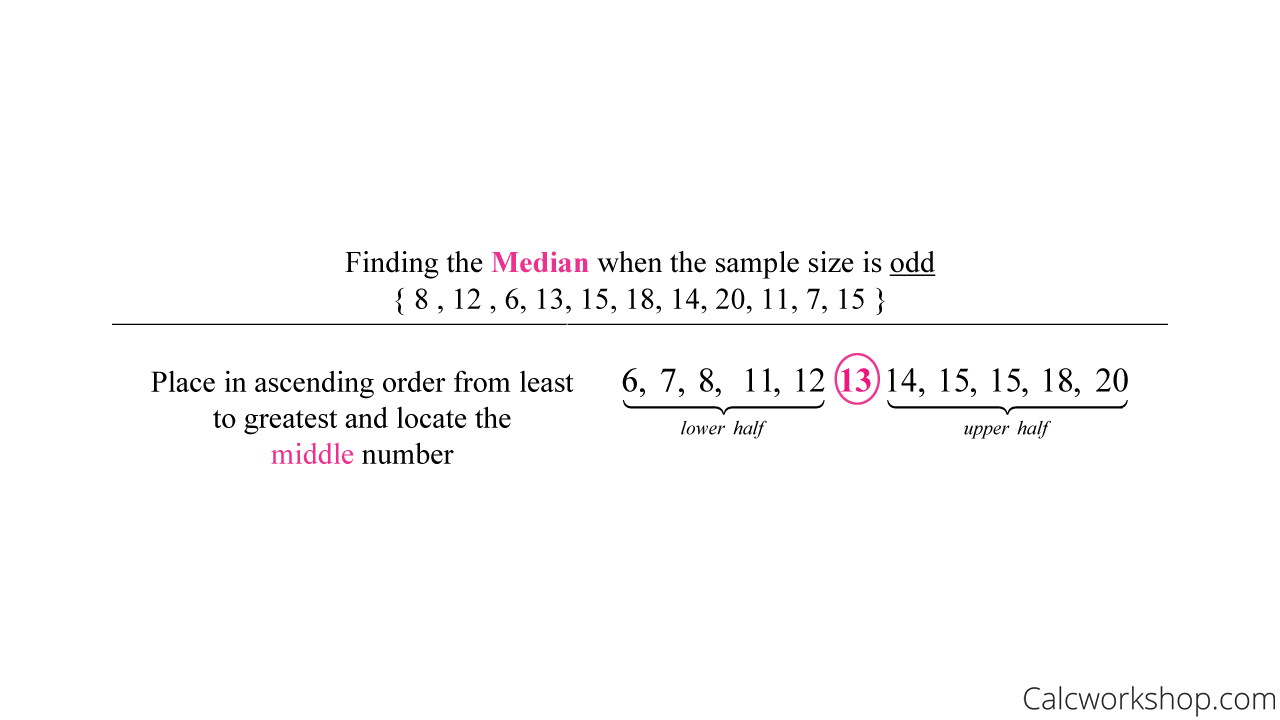
Median Of Odd Numbers

The mode is the value that occurs most frequently in the data set and is considered the most popular number or term. If the data set is unimodal, there will be one mode, but if the data set is bimodal or multimodal, there were will two modes or many modes, respectively.

Unimodal, Bimodal, and Multimodal

Another important value that helps us to understand the center and spread of a distribution is the range. The range is the difference between the maximum value and the minimum value. It’s nothing more than taking the biggest number and then subtracting the smallest number. It gives us a sense of where all the data values exist.

If we have the following data set { 8, 12, 6, 13, 15, 18, 14, 20, 11, 7, 15 }, what do we know?

We know the mode is 15 because it occurs most often, and the range is 14 as it is the value found when we subtract the biggest number, 20, and the smallest number, 6.

Additionally, we can find the Interquartile Range (IQR), which measures the middle 50% of the data and finds the difference between the first and third quartiles. And if you recall, quartiles are the values that divide a dataset into quarters, meaning 25% of the values are below the first quartile, and 75% of the values are below the third quartile, as the example below illustrates.

How To Find IQR

So, the IQR is the difference between the upper quartile (Quartile 3) and the lower quartile (Quartile 1), and by using the example above we find that the interquartile range for this dataset is

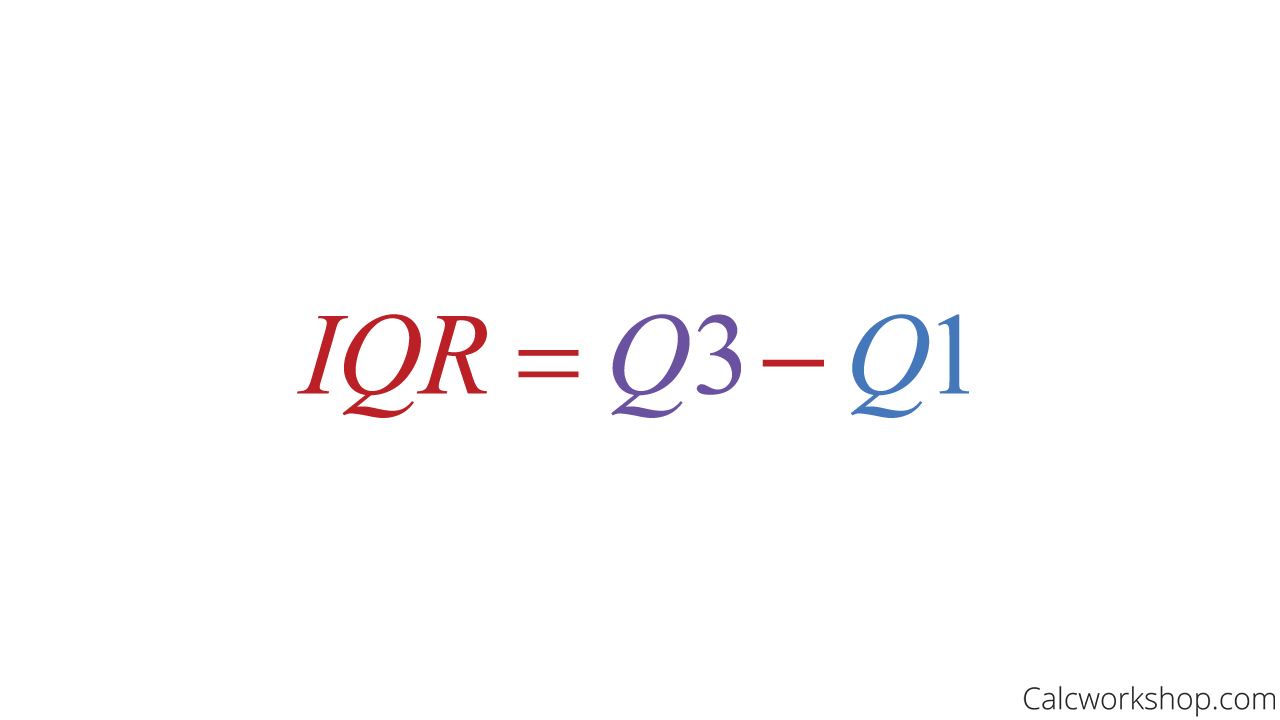
IQR Formula

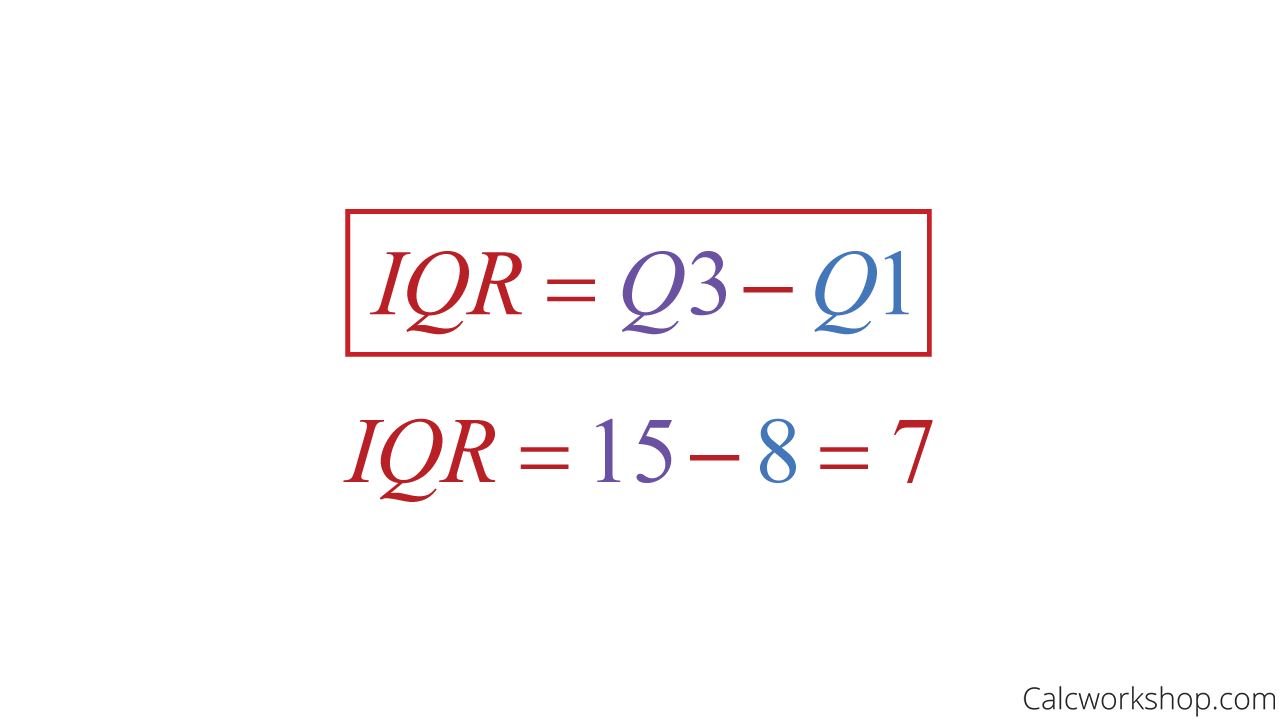
How To Calculate IQR

But did you also know that the IQR is instrumental in identifying outliers?

Outliers are those values that don’t seem to fit the rest of the dataset. To locate outliers, we need to find our “fences,” or those numbers that enclose the data and indicate the acceptable range for our data set. If a number falls outside of the fence, then it is an outlier. We locate our fences by using our upper and lower quartiles and our interquartile range as follows:

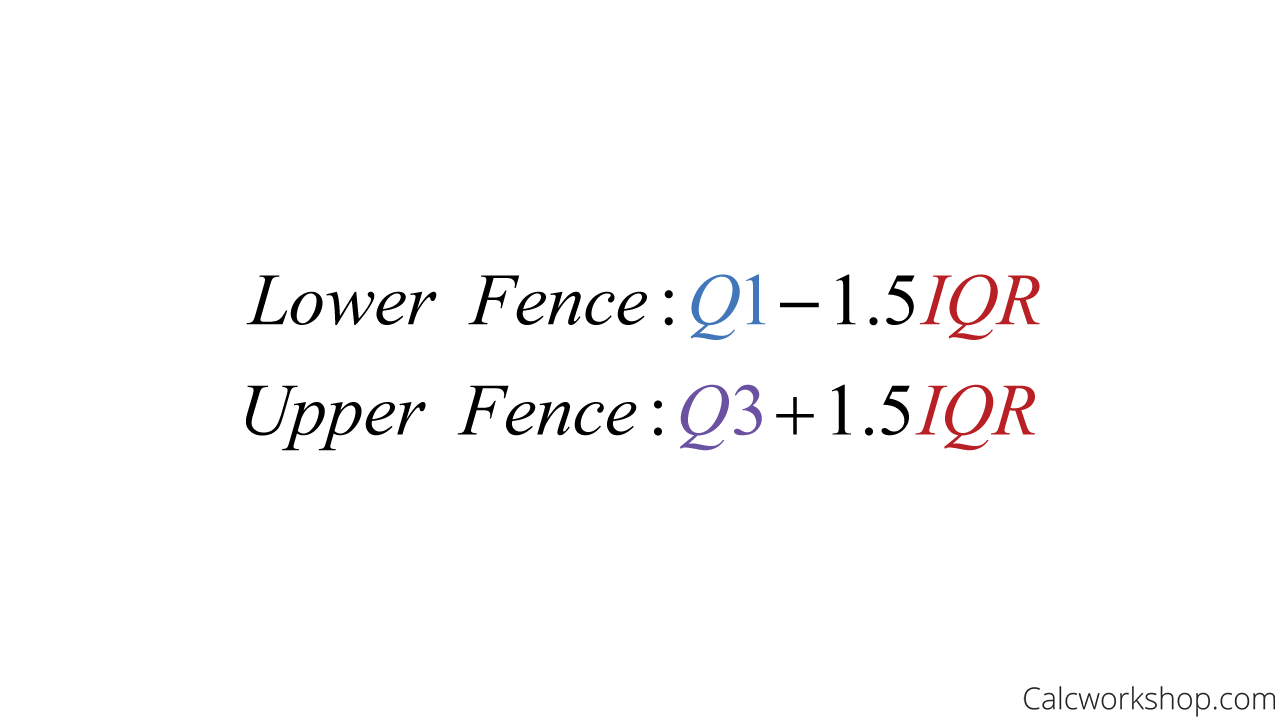
Outlier Formula

So, if we use our previous dataset of { 8, 12, 6, 13, 15, 18, 14, 20, 11, 7, 15 }, where we determined Q1 is 8, Q3 is 15, and the IQR is 7, then our lower and upper fences are:

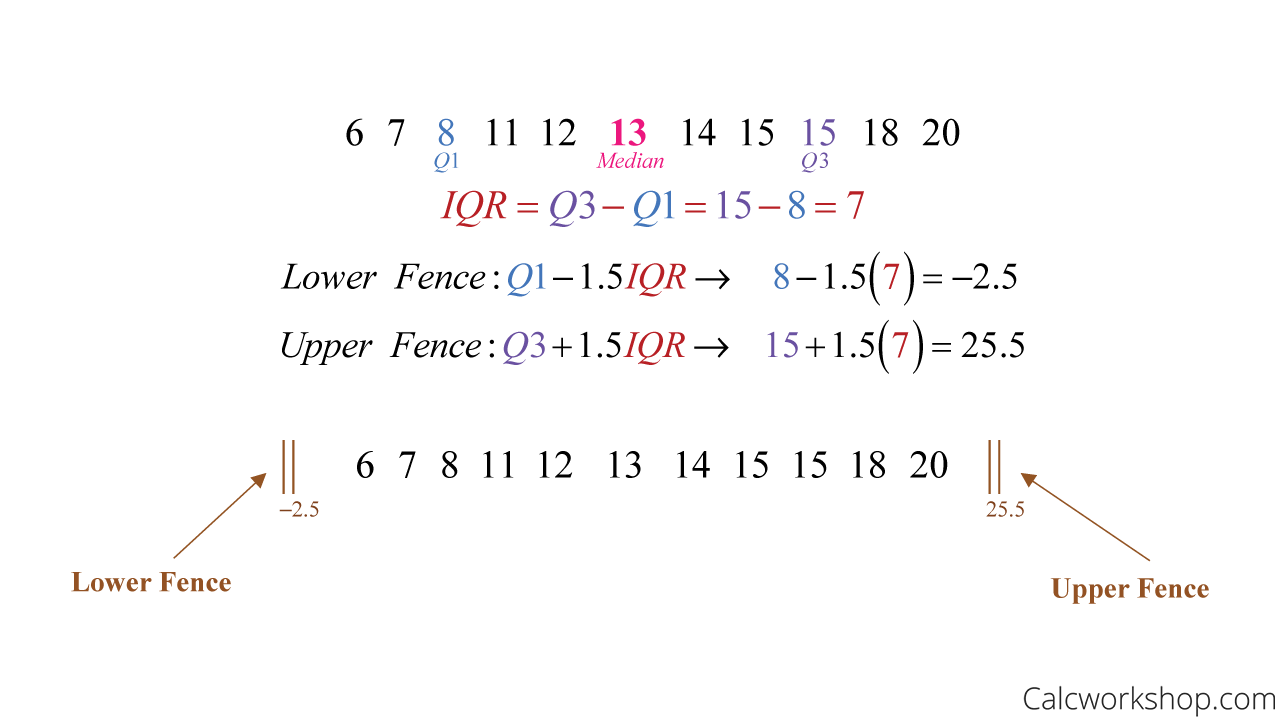
How To Calculate Outliers

As we can see, all of our data set falls within the fences, so we don’t have any outliers!

Measure Of Spread

But we can also describe the distribution in terms of its shape and spread.

The best way to analyze the deviations of each data value in relation to the mean is to find the variance and standard error.

While the quartiles and IQR only use a portion of the dataset, the variance and standard deviation use all the values in the set to measure spread.

So, the variance is a measure of how spread out a data set is.

Standard Deviation

The standard deviation also called the standard error is the square root of the variance and tells us how spread out the data is from the mean.

Meaning, if a dataset has a small standard error, then the data has a narrow spread around the mean and probably fewer extreme values. Conversely, if the standard error is high, the dataset is more spread out and may contain more extreme values.

Worked Example

For example, using our sample data { 8, 12, 6, 13, 15, 18, 14, 20, 11, 7, 15 }, let’s find the mean, variance, and standard error.

Sample Mean, Variance, and Standard Error Calculations

Displaying Quantitative Data

Now it’s time to talk about how best to display the measures of center?

There are five forms for displaying quantitative data:

• Cumulative Frequency Plot
• Box and Whisker Plot

Box And Whisker Plot

The first four we learned in our previous quantitative data video , now it’s time to talk about the Box Plot!

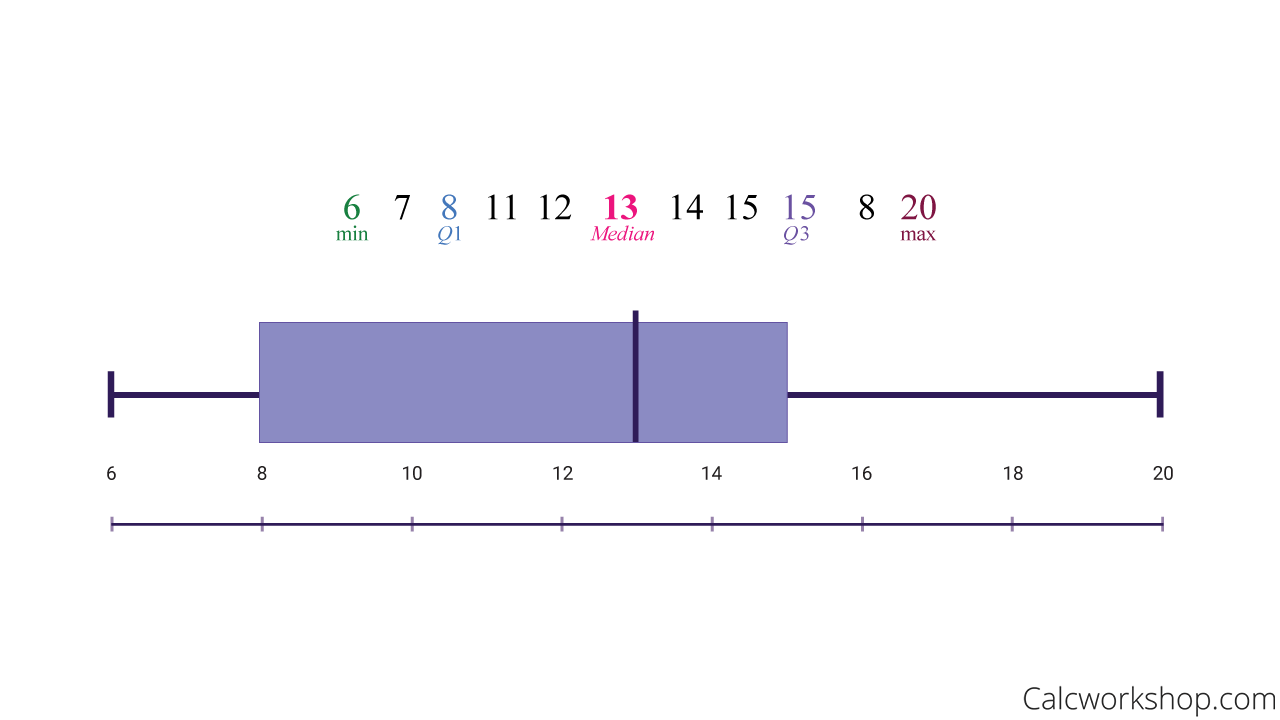
The Box and Whisker Plot also called a box plot, uses the following five-number summary:

The minimum is the smallest number in the dataset, and the maximum is the largest number in the dataset.

We construct a box and whisker plot by first identify our five-number summary. Then we create a box between the first and third quartiles, with the median in the middle. And then, we extend lines from the box to the minimum and maximum values (i.e., the whiskers) to show variability outside the upper and lower quartiles.

In this case, using our current sample data, the box plot is

Additionally, we will also look at how we can describe the distribution using a box plot and how we can modify a box-plot to identify outliers.

And lastly, we will wrap everything up with some words of wisdom on how best to choose the right measure of center and spread for a given distribution and how to draw conclusions based on the center, spread, and shape.

Let’s get to it!

Measures Of Center – Lesson & Examples (Video)

1 hr 10 min

• Introduction to Video: Measuring Center
• 00:00:25 – How do we find the Range, Mean, Median and Mode? with Example 1
• Exclusive Content for Members Only
• 00:09:35 – How do we find the IQR? (Examples #2-3)
• 00:17:23 – How do we use the IQR to determine Outliers? (Example #4)
• 00:26:06 – Creating Box Plots and finding 5-summary statistics (Example #5)
• 00:37:31 – Create a box and whisker plot and identify outliers (Example #6)
• 00:44:31 – Describe the distribution given a box-plot (Example #7)
• 00:48:30 – Finding Variance and Standard Deviation (Example #8)
• 00:59:10 – Find all the measures of center of spread and determine which measures of center should be used for a given distribution (Examples #9-10)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Measures of the Center and Variation of the Data

• Last updated
• Save as PDF
• Page ID 91563

Learning Objectives

• Recognize, describe, and calculate the measures of the center of data.
• Recognize, describe, and calculate the measures of the spread of data.
• Use Chebyshev and Empirical rules to interpret the mean and standard deviation.

Measures of the Center of the Data

The "center" of a data set is also a way of describing the location. The two most widely used measures of the "center" of the data are the mean (average) and the median . To calculate the mean weight of 50 people, add the 50 weights together and divide by 50. To find the median weight of the 50 people, order the data and find the number that splits the data into two equal parts. The median is generally a better measure of the center when there are extreme values or outliers because it is not affected by the precise numerical values of the outliers. The mean is the most common measure of the center. 

The letter used to represent the sample mean is an \(x\) with a bar over it (pronounced “\(x\) bar”): \(\overline{x}\). The Greek letter \(\mu\) (pronounced "mew") represents the population mean . One of the requirements for the sample mean to be a good estimate of the population mean is for the sample taken to be truly random.

The Law of Large Numbers and the Mean

The Law of Large Numbers says that if you take samples of larger and larger sizes from any population, then the mean \(\bar{x}\) of the sample is very likely to get closer and closer to the mean of the population, \(\mu\). This is discussed in more detail later in the text.

When each value in the data set is not unique, the mean can be calculated by multiplying each distinct value by its frequency and then dividing the sum by the total number of data values. To see that both ways of calculating the mean are the same, consider the sample:

1; 1; 1; 2; 2; 3; 4; 4; 4; 4; 4

\[\bar{x} = \dfrac{1+1+1+2+2+3+4+4+4+4+4}{11} = 2.7\]

In the second calculation, the frequencies are 3, 2, 1, and 5.

You can quickly find the location of the median by using the expression

\[\dfrac{n+1}{2}\]

The letter \(n\) is the total number of data values in the sample. If \(n\) is an odd number, the median is the middle value of the ordered data (ordered smallest to largest). If \(n\) is an even number, the median is equal to the average of the two middle values after the data has been ordered. For example, if the total number of data values is 97, then

\[\dfrac{n+1}{2} = \dfrac{97+1}{2} = 49.\]

The median is the 49 th value in the ordered data. If the total number of data values is 100, then

\[\dfrac{n+1}{2} = \dfrac{100+1}{2} = 50.5.\]

The median occurs midway between the 50 th and 51 st values. The location of the median and the value of the median are not the same. The upper case letter \(M\) is often used to represent the median. The next example illustrates the location of the median and the value of the median.

Example \(\PageIndex{1}\)

AIDS data indicating the number of months a patient with AIDS lives after taking a new antibody drug are as follows (smallest to largest):

3; 4; 8; 8; 10; 11; 12; 13; 14; 15; 15; 16; 16; 17; 17; 18; 21; 22; 22; 24; 24; 25; 26; 26; 27; 27; 29; 29; 31; 32; 33; 33; 34; 34; 35; 37; 40; 44; 44; 47

Calculate the mean and the median.

The calculation for the mean is:

\[\bar{x} = \dfrac{[3+4+(8)(2)+10+11+12+13+14+(15)(2)+(16)(2)+...+35+37+40+(44)(2)+47]}{40} = 23.6\]

\[\dfrac{n+1}{2} = \dfrac{40+1}{2} = 20.5\]

Starting at the smallest value, the median is located between the 20 th and 21 st values (the two 24s):

\[M = \dfrac{24+24}{2} = 24\]

Exercise \(\PageIndex{1}\)

The following data show the number of months patients typically wait on a transplant list before getting surgery. The data are ordered from smallest to largest. Calculate the mean and median.

3; 4; 5; 7; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 10; 10; 11; 12; 12; 13; 14; 14; 15; 15; 17; 17; 18; 19; 19; 19; 21; 21; 22; 22; 23; 24; 24; 24; 24

Mean: \(3 + 4 + 5 + 7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 10 + 10 + 10 + 10 + 10 + 11 + 12 + 12 + 13 + 14 + 14 + 15 + 15 + 17 + 17 + 18 + 19 + 19 + 19 + 21 + 21 + 22 + 22 + 23 + 24 + 24 + 24 = 544\)

\[\dfrac{544}{39} = 13.95\]

Median: Starting at the smallest value, the median is the 20 th term, which is 13.

Interactive Exercise \(\PageIndex{1}\)

Another measure of the center is the mode. The mode is the most frequent value. There can be more than one mode in a data set as long as those values have the same frequency and that frequency is the highest. 

Example \(\PageIndex{2}\)

Statistics exam scores for 20 students are as follows:

50; 53; 59; 59; 63; 63; 72; 72; 72; 72; 72; 76; 78; 81; 83; 84; 84; 84; 90; 93

Find the mode.

The most frequent score is 72, which occurs five times. Mode = 72.

Exercise \(\PageIndex{2}\)

The number of books checked out from the library from 25 students are as follows:

0; 0; 0; 1; 2; 3; 3; 4; 4; 5; 5; 7; 7; 7; 7; 8; 8; 8; 9; 10; 10; 11; 11; 12; 12

The most frequent number of books is 7, which occurs four times. Mode = 7.

Interactive Exercise \(\PageIndex{2}\)

It is worth mentioning that the mean and median apply only to quantitative data, whereas the mode can be used with either quantitative or qualitative data. Thus while the mode appears to be the least useful among the three measures of central tendency, it is the only way to assess the center for qualitative data! But when working with quantitative data we still have to choose between the mean and the median. Let’s consider the following example. We have four people Ann, Beth, Connor, and Diana that make the annual salaries $30k, $50k, $50k, $70k respectfully. Their average salary is $50,000 and their median is also $50,000 dollars. Now, let’s say Elon moves in and his salary is $300,000 a year. What effect does this have on the mean and median? The new mean is $100,000 and the new median is still $50,000. Which of the two measures produces a more representative value? In this case, the median is obviously a better choice, for example if Toyota Company was considering building a Lexus or Scion dealership and they were only considering the mean it would appear that an average person in this neighborhood can afford a Lexus when in reality only one person can afford it. So what exactly the difference between the mean and the median? Unlike the mean, the median is not sensitive to the influence of a few extreme observations. Usually, we use the median for house prices and salaries and for everything else we would prefer the mean.

Example \(\PageIndex{3}\)

Suppose that in a small town of 50 people, one person earns $5,000,000 per year and the other 49 each earn $30,000. Which is the better measure of the "center": the mean or the median?

\[\bar{x} = \dfrac{5,000,000+49(30,000)}{50} = 129,400\]

\(M = 30,000\)

(There are 49 people who earn $30,000 and one person who earns $5,000,000.)

The median is a better measure of the "center" than the mean because 49 of the values are 30,000 and one is 5,000,000. The 5,000,000 is an outlier. The 30,000 gives us a better sense of the middle of the data.

Exercise \(\PageIndex{3}\)

In a sample of 60 households, one house is worth $2,500,000 and the rest are worth $280,000. Which is the better measure of the “center”: the mean or the median?

The median is the better measure of the “center” than the mean because 59 of the values are $280,000 and one is $2,500,000. The $2,500,000 is an outlier. The $280,000 gives us a better sense of the middle of the data.

Interactive Exercise \(\PageIndex{3}\)

Measures of variation of the data.

One of the differences between the two data sets that any measure of center doesn't capture is the variety of data within the set. To describe the variation quantitatively, we use measures of variation or measures of spread . Just as there are several different measures of center, there are also several different measures of variation. In this section, we examine two of the most frequently used measures of variation: the range and standard deviation.

Definition: Range

The range of a data set is the difference between the maximum (largest) and minimum (smallest) observations.

Example \(\PageIndex{4}\)

Find the range of the data:

The range of the data is the difference between the largest and the smallest values in the data set: 14−6=8

Interactive Exercise \(\PageIndex{4}\)

Definition: the standard deviation.

The range only measures the total variation and doesn't capture any variation between the minimum and maximum observed values. In contrast to the range, the standard deviation takes into account all the observations. It is the preferred measure of variation when the mean is used as the measure of center. Roughly speaking, the standard deviation measures variation by indicating how far, on average, the observations are from the mean. For a data set with a large amount of variation, the observations will, on average, be far from the mean; so the standard deviation will be large. For a data set with a small amount of variation, the observations will, on average, be close to the mean; so the standard deviation will be small.

Calculating the Standard Deviations

If \(x\) is a number, then the difference "\(x\) – mean" is called its deviation . In a data set, there are as many deviations as there are items in the data set. The deviations are used to calculate the standard deviation. If the numbers belong to a population, in symbols a deviation is \(x - \mu\). For sample data, in symbols a deviation is \(x - \bar{x}\).

The procedure to calculate the standard deviation depends on whether the numbers are the entire population or are data from a sample. The calculations are similar, but not identical. Therefore the symbol used to represent the standard deviation depends on whether it is calculated from a population or a sample. The lower case letter s represents the sample standard deviation and the Greek letter \(\sigma\) (sigma, lower case) represents the population standard deviation. If the sample has the same characteristics as the population, then s should be a good estimate of \(\sigma\).

To calculate the standard deviation, we need to calculate the variance first. The variance is the average of the squares of the deviations (the \(x - \bar{x}\) values for a sample, or the \(x - \mu\) values for a population). The symbol \(\sigma^{2}\) represents the population variance; the population standard deviation \(\sigma\) is the square root of the population variance. The symbol \(s^{2}\) represents the sample variance; the sample standard deviation s is the square root of the sample variance. You can think of the standard deviation as a special average of the deviations.

If the numbers come from a census of the entire population and not a sample, when we calculate the average of the squared deviations to find the variance, we divide by \(N\), the number of items in the population. If the data are from a sample rather than a population, when we calculate the average of the squared deviations, we divide by n – 1 , one less than the number of items in the sample.

Formulas for the Sample Standard Deviation

\[s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}} \label{eq1}\]

\[s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}} \label{eq2}\]

For the sample standard deviation, the denominator is \(n - 1\), that is one less than the sample size.

Formulas for the Population Standard Deviation

\[\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}} \label{eq3} \]

\[\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}} \label{eq4}\]

For the population standard deviation, the denominator is \(N\), the number of items in the population.

In Equations \ref{eq2} and \ref{eq4}, \(f\) represents the frequency with which a value appears. For example, if a value appears once, \(f\) is one. If a value appears three times in the data set or population, \(f\) is three.

Why divide by n-1?

Why divide by (n-1) instead of n? Remember that the main purpose of finding a statistic is to estimate the unknown parameter. If we divide by n instead of (n-1) we will be obtaining a value which is a biased estimator for the population variance. Being biased doesn't necessarily mean bad when we know what the bias is. In this case, \sqrt{\dfrac{\sum(x-\mu)^{2}}{n}} always underestimates the true population variance by the factor of \(\frac{n}{n-1}\). After the correction, we get a desired unbiased estimator for the population variance which we call a sample variance.

Example \(\PageIndex{5}\)

In a fifth grade class, the teacher was interested in the average age and the sample standard deviation of the ages of her students. The following data are the ages for a SAMPLE of n = 20 fifth grade students. The ages are rounded to the nearest half year:

9; 9.5; 9.5; 10; 10; 10; 10; 10.5; 10.5; 10.5; 10.5; 11; 11; 11; 11; 11; 11; 11.5; 11.5; 11.5;

\[\bar{x} = \dfrac{9+9.5(2)+10(4)+10.5(4)+11(6)+11.5(3)}{20} = 10.525 \nonumber\]

The average age is 10.53 years, rounded to two places.

The variance may be calculated by using a table. Then the standard deviation is calculated by taking the square root of the variance. We will explain the parts of the table after calculating s .

The sample variance , \(s^{2}\), is equal to the sum of the last column (9.7375) divided by the total number of data values minus one (20 – 1):

\[s^{2} = \dfrac{9.7375}{20-1} = 0.5125 \nonumber\]

The sample standard deviation s is equal to the square root of the sample variance:

\[s = \sqrt{0.5125} = 0.715891 \nonumber\]

and this is rounded to two decimal places, \(s = 0.72\).

Note that if the 20 students were the entire population then we would use \(\mu\) instead of \(\bar{x}\), \(\sigma^{2}\) instead of \(s^{2}\), and \(\sigma\) instead of \(s\). In such a case, the population variance , \(\sigma^{2}\), is equal to the sum of the last column (9.7375) divided by the total number of data values (20):

\[\sigma^{2} = \dfrac{9.7375}{20} = 0.486875 \nonumber\]

and the population   standard deviation (\sigma\) is equal to the square root of the population variance:

\[\sigma = \sqrt{0.486875} = 0.69776 \nonumber\]

Interactive Exercise \(\PageIndex{5.1}\)

Interactive exercise \(\pageindex{5.2}\).

In practice, USE A CALCULATOR OR COMPUTER SOFTWARE TO CALCULATE THE STANDARD DEVIATION such as this one :

Descriptive Statistics Calculator

Regardless of the tool that you use, you still need to be aware of the context and use the appropriate notation for standard deviation \(\sigma\) or \(s\).

Interactive Exercise \(\PageIndex{5.3}\)

Interpreting the mean and standard deviation together.

The following lists give a few facts that provide a little more insight into what the standard deviation tells us about the distribution of the data.

Chebyshev's Rule

For ANY data set, no matter what the distribution of the data is:

• At least 75% of the data is within two standard deviations of the mean.
• At least 89% of the data is within three standard deviations of the mean.
• At least 95% of the data is within 4.5 standard deviations of the mean.

The Empirical Rule

For data having a distribution that is BELL-SHAPED and SYMMETRIC:

• Approximately 68% of the data is within one standard deviation of the mean.
• Approximately 95% of the data is within two standard deviations of the mean.
• More than 99% of the data is within three standard deviations of the mean.

The empirical rule is also known as the 68-95-99.7 rule. We will learn more about this when studying the "Normal" or "Gaussian" probability distribution in later chapters.

Example \(\PageIndex{6}\)

Suppose \(x\) is from a population with mean 50 and standard deviation 6 with bell-shape distribution.

• About 68% of the x values lie within one standard deviation of the mean. Therefore, about 68% of the x values lie between –1σ = (–1)(6) = –6 and 1σ = (1)(6) = 6 of the mean 50. The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation from the mean 50.
• About 95% of the x values lie within two standard deviations of the mean. Therefore, about 95% of the x values lie between –2σ = (–2)(6) = –12 and 2σ = (2)(6) = 12. The values 50 – 12 = 38 and 50 + 12 = 62 are within two standard deviations from the mean 50.
• About 99.7% of the x values lie within three standard deviations of the mean. Therefore, about 99.7% of the x values lie between –3σ = (–3)(6) = –18 and 3σ = (3)(6) = 18 from the mean 50. The values 50 – 18 = 32 and 50 + 18 = 68 are within three standard deviations of the mean 50.

Exercise \(\PageIndex{6}\)

The population of scores on a college entrance exam have an approximate bell-shape distribution with mean, \(\mu = 52\) points and a standard deviation, \(\sigma = 11\) points.

• About 68% of the \(y\) values lie between what two values? These values are ________________.
• About 95% of the \(y\) values lie between what two values? These values are ________________.
• About 99.7% of the \(y\) values lie between what two values? These values are ________________.

a. About 68% of the values lie between the values 41 and 63.

b. About 95% of the values lie between the values 30 and 74.

c.  About 99.7% of the values lie between the values 19 and 85.

Interactive Exercise \(\PageIndex{6}\)

It is important to note that the Empirical Rule only applies when the shape of the distribution of the data is bell-shaped and symmetric thus allowing us to sketch the following shape of the distribution based only on the two numbers: the mean and the standard deviation:

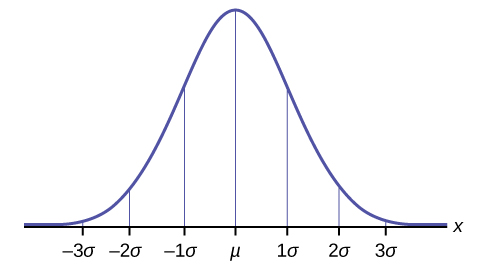
Figure \(\PageIndex{A}\)

Interactive Exercise \(\PageIndex{7}\)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Measures of the Center of the Data

• Last updated
• Save as PDF
• Page ID 10925

The "center" of a data set is also a way of describing location. The two most widely used measures of the "center" of the data are the mean (average) and the median . To calculate the mean weight of 50 people, add the 50 weights together and divide by 50. To find the median weight of the 50 people, order the data and find the number that splits the data into two equal parts. The median is generally a better measure of the center when there are extreme values or outliers because it is not affected by the precise numerical values of the outliers. The mean is the most common measure of the center.

The words “mean” and “average” are often used interchangeably. The substitution of one word for the other is common practice. The technical term is “arithmetic mean” and “average” is technically a center location. However, in practice among non-statisticians, “average" is commonly accepted for “arithmetic mean.”

When each value in the data set is not unique, the mean can be calculated by multiplying each distinct value by its frequency and then dividing the sum by the total number of data values. The letter used to represent the sample mean is an \(x\) with a bar over it (pronounced “\(x\) bar”): \(\overline{x}\).

The Greek letter \(\mu\) (pronounced "mew") represents the population mean . One of the requirements for the sample mean to be a good estimate of the population mean is for the sample taken to be truly random.

To see that both ways of calculating the mean are the same, consider the sample:

1; 1; 1; 2; 2; 3; 4; 4; 4; 4; 4

\[\bar{x} = \dfrac{1+1+1+2+2+3+4+4+4+4+4}{11} = 2.7\]

In the second calculation, the frequencies are 3, 2, 1, and 5.

You can quickly find the location of the median by using the expression

\[\dfrac{n+1}{2}\]

The letter \(n\) is the total number of data values in the sample. If \(n\) is an odd number, the median is the middle value of the ordered data (ordered smallest to largest). If \(n\) is an even number, the median is equal to the two middle values added together and divided by two after the data has been ordered. For example, if the total number of data values is 97, then

\[\dfrac{n+1}{2} = \dfrac{97+1}{2} = 49.\]

The median is the 49 th value in the ordered data. If the total number of data values is 100, then

\[\dfrac{n+1}{2} = \dfrac{100+1}{2} = 50.5.\]

The median occurs midway between the 50 th and 51 st values. The location of the median and the value of the median are not the same. The upper case letter \(M\) is often used to represent the median. The next example illustrates the location of the median and the value of the median.

Example \(\PageIndex{1}\)

AIDS data indicating the number of months a patient with AIDS lives after taking a new antibody drug are as follows (smallest to largest):

3; 4; 8; 8; 10; 11; 12; 13; 14; 15; 15; 16; 16; 17; 17; 18; 21; 22; 22; 24; 24; 25; 26; 26; 27; 27; 29; 29; 31; 32; 33; 33; 34; 34; 35; 37; 40; 44; 44; 47

Calculate the mean and the median.

The calculation for the mean is:

\[\bar{x} = \dfrac{[3+4+(8)(2)+10+11+12+13+14+(15)(2)+(16)(2)+...+35+37+40+(44)(2)+47]}{40} = 23.6\]

\[\dfrac{n+1}{2} = \dfrac{40+1}{2} = 20.5\]

Starting at the smallest value, the median is located between the 20 th and 21 st values (the two 24s):

\[M = \dfrac{24+24}{2} = 24\]

To find the mean and the median, you can use technology to assist you.  Make sure you use the appropriate technology for your class.

Spreadsheets (Microsoft Excel/Google Sheets):

• Enter each datum into its own cell. Usually we use one column for the data.
• To find the mean, in the cell below the data, type: =average(

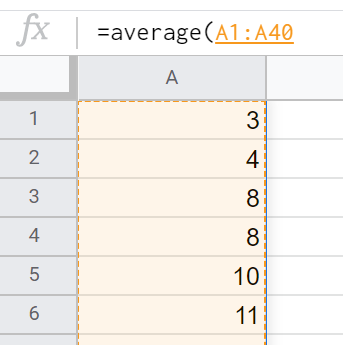
• Hit enter. The spreadsheet should replace your formula with the mean of the data set.
• To find the median, repeat the process, but use the formula: =median(   

TI-83 or TI-84 Graphing Calculator:

• Clear list L1. Pres STAT 4:ClrList. Enter 2nd 1 for list L1. Press ENTER.
• Enter data into the list editor. Press STAT 1:EDIT.
• Put the data values into list L1.
• Press STAT and arrow to CALC. Press 1:1-VarStats. Press 2nd 1 for L1 and then ENTER.
• Press the down and up arrow keys to scroll.

\(\bar{x}\) = 23.6, M = 24

Exercise \(\PageIndex{1}\)

The following data show the number of months patients typically wait on a transplant list before getting surgery. The data are ordered from smallest to largest. Calculate the mean and median.

3; 4; 5; 7; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 10; 10; 11; 12; 12; 13; 14; 14; 15; 15; 17; 17; 18; 19; 19; 19; 21; 21; 22; 22; 23; 24; 24; 24; 24

Mean: \(3 + 4 + 5 + 7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 10 + 10 + 10 + 10 + 10 + 11 + 12 + 12 + 13 + 14 + 14 + 15 + 15 + 17 + 17 + 18 + 19 + 19 + 19 + 21 + 21 + 22 + 22 + 23 + 24 + 24 + 24 = 544\)

\[\dfrac{544}{39} = 13.95\]

Median: Starting at the smallest value, the median is the 20 th term, which is 13.

Example \(\PageIndex{2}\)

Suppose that in a small town of 50 people, one person earns $5,000,000 per year and the other 49 each earn $30,000. Which is the better measure of the "center": the mean or the median?

\[\bar{x} = \dfrac{5,000,000+49(30,000)}{50} = 129,400\]

\(M = 30,000\)

(There are 49 people who earn $30,000 and one person who earns $5,000,000.)

The median is a better measure of the "center" than the mean because 49 of the values are 30,000 and one is 5,000,000. The 5,000,000 is an outlier. The 30,000 gives us a better sense of the middle of the data.

Exercise \(\PageIndex{2}\)

In a sample of 60 households, one house is worth $2,500,000. Half of the rest are worth $280,000, and all the others are worth $315,000. Which is the better measure of the “center”: the mean or the median?

The median is the better measure of the “center” than the mean because 59 of the values are $280,000 and one is $2,500,000. The $2,500,000 is an outlier. Either $280,000 or $315,000 gives us a better sense of the middle of the data.

Another measure of the center is the mode. The mode is the most frequent value. There can be more than one mode in a data set as long as those values have the same frequency and that frequency is the highest. A data set with two modes is called bimodal.

Example \(\PageIndex{3}\)

Statistics exam scores for 20 students are as follows:

50; 53; 59; 59; 63; 63; 72; 72; 72; 72; 72; 76; 78; 81; 83; 84; 84; 84; 90; 93

Find the mode.

The most frequent score is 72, which occurs five times. Mode = 72.

Exercise \(\PageIndex{3}\)

The number of books checked out from the library from 25 students are as follows:

0; 0; 0; 1; 2; 3; 3; 4; 4; 5; 5; 7; 7; 7; 7; 8; 8; 8; 9; 10; 10; 11; 11; 12; 12

The most frequent number of books is 7, which occurs four times. Mode = 7.

Example \(\PageIndex{4}\)

Five real estate exam scores are 430, 430, 480, 480, 495. The data set is bimodal because the scores 430 and 480 each occur twice.

When is the mode the best measure of the "center"? Consider a weight loss program that advertises a mean weight loss of six pounds the first week of the program. The mode might indicate that most people lose two pounds the first week, making the program less appealing.

The mode can be calculated for qualitative data as well as for quantitative data. For example, if the data set is: red, red, red, green, green, yellow, purple, black, blue, the mode is red.

Statistical software will easily calculate the mean, the median, and the mode. Some graphing calculators can also make these calculations. In the real world, people make these calculations using software.

Exercise \(\PageIndex{4}\)

Five credit scores are 680, 680, 700, 720, 720. The data set is bimodal because the scores 680 and 720 each occur twice. Consider the annual earnings of workers at a factory. The mode is $25,000 and occurs 150 times out of 301. The median is $50,000 and the mean is $47,500. What would be the best measure of the “center”?

Because $25,000 occurs nearly half the time, the mode would be the best measure of the center because the median and mean don’t represent what most people make at the factory.

The Law of Large Numbers and the Mean

The Law of Large Numbers says that if you take samples of larger and larger size from any population, then the mean \(\bar{x}\) of the sample is very likely to get closer and closer to \(\mu\). This is discussed in more detail later in the text.

Sampling Distributions and Statistic of a Sampling Distribution

You can think of a sampling distribution as a relative frequency distribution with a great many samples. (See Sampling and Data for a review of relative frequency). Suppose thirty randomly selected students were asked the number of movies they watched the previous week. The results are in the relative frequency table shown below.

If you let the number of samples get very large (say, 300 million or more), the relative frequency table becomes a relative frequency distribution .

A statistic is a number calculated from a sample. Statistic examples include the mean, the median and the mode as well as others. The sample mean \(\bar{x}\) is an example of a statistic which estimates the population mean \(\mu\).

Calculating the Mean of Grouped Frequency Tables

When only grouped data is available, you do not know the individual data values (we only know intervals and interval frequencies); therefore, you cannot compute an exact mean for the data set. What we must do is estimate the actual mean by calculating the mean of a frequency table. A frequency table is a data representation in which grouped data is displayed along with the corresponding frequencies. To calculate the mean from a grouped frequency table we can apply the basic definition of mean:

\[mean = \dfrac{\text{data sum}}{\text{number of data values}}.\]

We simply need to modify the definition to fit within the restrictions of a frequency table.

Since we do not know the individual data values we can instead find the midpoint of each interval. The midpoint is

\[\dfrac{\text{lower boundary+upper boundary}}{2}.\]

We can now modify the mean definition to be

\[\text{Mean of Frequency Table} = \dfrac{\sum{fm}}{\sum{f}}\]

where \(f\) is the frequency of the interval and \(m \) is the midpoint of the interval.

Example \(\PageIndex{5}\)

A frequency table displaying professor Blount’s last statistic test is shown. Find the best estimate of the class mean.

• Find the midpoints for all intervals
• Calculate the sum of the product of each interval frequency and midpoint. \(\sum{fm} 53.25(1) + 59.5(0) + 65.5(4 )+ 71.5(4) + 77.5(2) + 83.5(3) + 89.5(4) + 95.5(1) = 1460.25\)
• \(\mu = \dfrac{\sum{fm}}{\sum{f}} = \dfrac{1460.25}{19} = 76.86\)

Exercise \(\PageIndex{5}\)

Maris conducted a study on the effect that playing video games has on memory recall. As part of her study, she compiled the following data:

What is the best estimate for the mean number of hours spent playing video games?

Find the midpoint of each interval, multiply by the corresponding number of teenagers, add the results and then divide by the total number of teenagers

\[Mean = (1.75)(3) + (5.5)(7) + (9.5)(12) + (13.5)(7) + (17.5)(9) = 409.75\]

• Data from The World Bank, available online at http://www.worldbank.org (accessed April 3, 2013).
• “Demographics: Obesity – adult prevalence rate.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2228&l=en (accessed April 3, 2013).

The mean and the median can be calculated to help you find the "center" of a data set. The mean is the best estimate for the actual data set, but the median is the best measurement when a data set contains several outliers or extreme values. The mode will tell you the most frequently occuring datum (or data) in your data set. The mean, median, and mode are extremely helpful when you need to analyze your data, but if your data set consists of ranges which lack specific values, the mean may seem impossible to calculate. However, the mean can be approximated if you add the lower boundary with the upper boundary and divide by two to find the midpoint of each interval. Multiply each midpoint by the number of values found in the corresponding range. Divide the sum of these values by the total number of data values in the set.

Formula Review

\[\mu = \dfrac{\sum{fm}}{\sum{f}} \]

where \(f\) = interval frequencies and \(m\) = interval midpoints.

Exercise 2.6.6

Find the mean for the following frequency tables.

Exercise 2.6.7

Calculate the mean.

Mean: \(16 + 17 + 19 + 20 + 20 + 21 + 23 + 24 + 25 + 25 + 25 + 26 + 26 + 27 + 27 + 27 + 28 + 29 + 30 + 32 + 33 + 33 + 34 + 35 + 37 + 39 + 40 = 738\);

\(\dfrac{738}{27} = 27.33\)

Exercise 2.6.8

Identify the median.

Exercise 2.6.9

Identify the mode.

The most frequent lengths are 25 and 27, which occur three times. Mode = 25, 27

Use the following information to answer the next three exercises: Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars; nineteen generally sell four cars; twelve generally sell five cars; nine generally sell six cars; eleven generally sell seven cars. Calculate the following:

Exercise 2.6.10

sample mean = \(\bar{x}\) = _______

Exercise 2.6.11

median = _______

Bringing It Together

Exercise 2.6.12

Javier and Ercilia are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information.

• How can you determine which survey was correct ?
• Explain what the difference in the results of the surveys implies about the data.
• If the two histograms depict the distribution of values for each supervisor, which one depicts Ercilia's sample? How do you know?
• If the two box plots depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know? <figure >

Use the following information to answer the next three exercises : We are interested in the number of years students in a particular elementary statistics class have lived in California. The information in the following table is from the entire section.

Exercise 2.6.13

What is the IQR ?

Exercise 2.6.14

What is the mode?

Exercise 2.6.15

Is this a sample or the entire population?

• entire population

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

• International

Trump's hush money trial

University protests

June 24, 2023 - Wagner head says group standing down

By Helen Regan , Andrew Raine , Sophie Tanno, Hafsa Khalil, Tori B. Powell , Adrienne Vogt and Kaanita Iyer , CNN

Moscow mayor says "anti-terrorist measures" are being carried out in the city

From CNN's Mariya Knight

Moscow Mayor Sergei Sobyanin says that "anti-terrorist measures" are being carried out in the city as a result of "incoming information," according to an update on his Telegram group.

The measures include "additional control on the roads" and "limitations on holding public events."

US intel has long assessed the power struggle between Prigozhin and the Russian government

From CNN's Kevin Liptak

US officials determined as early as January that there was an internal power struggle underway between the mercenary Wagner Group and the Russian government, and have been gathering and closely monitoring intelligence on the volatile dynamic ever since.

As Russia’s invasion of Ukraine stalled earlier this year, top American officials said they saw indications of tension between the Kremlin and the Wagner chief Yevgeny Prigozhin. They said they believed those tensions would mount over the coming months.

Officials said their assessments of the situation derived from intelligence, an indication of how seriously the White House and Pentagon took the potential for a power struggle to cause further instability in the ongoing conflict.

In January, a top White House official said Wagner was becoming a “rival power center to the Russian military and other Russian militaries.”

Officials suggested at the time that Prigozhin was working to advance his own interests in Ukraine instead of the broader Russian objectives. 

The Wagner Group, which the West claimed had recruited prison convicts for fighting in Ukraine, was making decisions based on “what they will generate for Prigozhin, in terms of positive publicity,” John Kirby, the National Security Council spokesman, said in January.

Since then, White House and other US national security aides have been highly attuned to what one official said was an “ongoing battle” between Prigozhin and the Russian defense ministry. 

Read more here .

Wagner chief says his fighters are entering Rostov region

From CNN's Mariya Knight

Yevgeny Prigozhin, the chief of the private military group Wagner, said his fighters are entering the Russian Rostov region, which neighbors Ukraine.

“Now we are entering Rostov. The units of the Ministry of Defense, or rather the conscripts, who were thrown to block our road, stepped aside,” Prigozhin said, adding that at the moment his units “have crossed the state border in all places.”

“The border guards came out to meet and hugged our fighters,” he said.

Prigozhin also accused Russian Defense Minister Sergei Shoigu and Chief of the General Staff Valery Gerasimov of “making a decision to destroy the disobedient units (of Wagner PMC) that are ready to protect their Motherland.” 

Prigozhin warned against anyone obstructing him: “We will destroy everything that gets in our way,” he said.

The Wagner chief’s statement comes as Russian state media TASS reported a stepped-up police presence in Rostov late Friday.

CNN cannot independently verify these claims.

"Tumultuous times are coming," adviser to Ukraine’s presidency says in response to Prigozhin news

From CNN's Yulia Kesaieva

Mykhailo Podolyak, an adviser to Ukraine’s presidential administration, reacted on Friday to the frenzy surrounding the Wagner Group leader Yevgeny Prigozhin and his latest claims against Russia's military leadership.

In a tweet posted in English, Podolyak said: "Tumultuous times are coming."

The word  Oprichniki  refers to members of the bodyguard troops established by Ivan the Terrible, which terrorized people who opposed the tsar.

State media: Russia investigating Wagner chief over call for "armed rebellion" and Putin is aware of situation

President Vladimir Putin is aware “of the situation unfolding around Yevgeny Prigozhin,” Russian state media TASS said Friday, referring to the leader of the Wagner Group.

He is also aware that Russia’s Federal Security Service (FSB) initiated a criminal case accusing the mercenary force's chief of calling for "armed rebellion" on Friday, TASS reported.

According to TASS, the National Anti-Terrorism Committee said the allegations spread by Prigozhin “have no basis.”

Kremlin spokesman Dmitry Peskov also said Putin is aware of the situation and "all necessary measures are being taken," according to state media RIA Novosti. 

Some context. Prigozhin on Friday accused Russian military leadership of striking a Wagner military camp and killing a "huge amount" of his mercenary forces. Prigozhin claimed that the Russian Ministry of Defense tricked Wagner and he vowed to "respond to these atrocities." 

Prigozhin and Wagner have played a prominent role in the Ukraine war, and the leader has repeatedly and publicly feuded with Russia's defense heads over what he said was a lack of ammunition, at one point recording a video of him lashing out while standing in front of what he claimed were dead bodies of his fighters.

Wagner chief accuses Russian military leadership of killing "huge amount" of his fighters in strike on camp

From CNN's Lauren Kent and Mariya Knight

The chief of the Wagner private military group, Yevgeny Prigozhin, on Friday accused Russian military leadership of striking a Wagner military camp and killing a "huge amount" of his mercenary forces.

Prigozhin claimed that the Russian Ministry of Defense tricked Wagner and he vowed to "respond to these atrocities." 

"They sneakily deceived us, trying to deprive us of the opportunity to defend our homes and instead hunt down Wagner PMC. We were ready to compromise with the Ministry of Defense to hand over our weapons and find a solution how we will continue to defend our country. But these scumbags did not calm down," Prigozhin said in a voice note posted on Telegram .

"They saw that we weren't broken and they launched strikes on our camps. A huge amount of our fighters were killed, our comrades in arms. We will make a decision about how to respond to these atrocities. The next step is ours," he continued, alleging that "they wiped out dozens."

Russia's Ministry of Defense denied the allegation in a Telegram post Friday, calling the messages and videos spreading on social networks on behalf of Prigozhin about the event "untrue" and "an informational provocation."

Prigozhin claimed that the "evil that is being carried out" by Russia's military leadership "must be stopped" following the alleged attack. "They disregard the lives of soldiers, they have forgotten the word 'justice,'" Prigozhin said in the voice recording. 

"The details started to appear; Minister of Defense arrived to Rostov especially to conduct an operation to destroy Wagner PMC. He used artillerymen and helicopter pilots undercover to destroy us," Prigozhin added. 

Prigozhin vows retaliation : "Many dozens, tens of thousands of lives, of Russian soldiers will be punished," Prigozhin said. "I ask that nobody put up any resistance. Those who show such resistance, we will consider it a threat and destroy them immediately. This includes any roadblocks standing in our way, any aircraft seen over our heads."

He asked people to stay at home and "remain calm, not to be provoked."

In a later Telegram post, Prigozhin said that by criticizing Russian military leadership, he is carrying out a "march of justice" and not a "military coup," alleging that a majority of Russian service members support Wagner.  

"Finally, you will make them supply us with ammunition and make them stop using us as cannon fodder," Prigozhin added.

More background: Earlier on Friday, Prigozhin furthered his ongoing dispute with military leaders in a highly critical video interview where he said Moscow invaded Ukraine under false pretenses devised by the Russian Ministry of Defense, and that Russia is actually losing ground on the battlefield.

And earlier this month, the Wagner boss said he won't sign contracts with Russia’s defense ministry, rejecting an attempt to bring his force in line. His comments came after an announcement by the Russian Ministry of Defense that “volunteer units” and private military groups would be required to sign a contract with the ministry.

Prigozhin and Wagner have played a prominent role in the Ukraine war. In May he said his troops had capture Bakhmut in a costly and largely symbolic gain for Russia.

The Wagner chief has previously  criticized Russia’s traditional military hierarchy , blaming Russian defense chiefs for “tens of thousands” of casualties and stating that divisions could end in a “revolution.”

He also accused Russian military leaders  “sit like fat cats”  in “luxury offices,” while his fighters are “dying,” and later accused the Russian Defense Ministry of trying to  sabotage his troops’ withdrawal from Bakhmut , claiming the ministry laid mines along the exit routes.

CNN's Katharina Krebs, Lindsay Isaac, Uliana Pavlova, Radina Gigova, Josh Pennington contributed reporting to this post.

Please enable JavaScript for a better experience.