problem solving biology example

Browse Course Material

Course info, instructors.

• Prof. Hazel Sive
• Prof. Tyler Jacks
• Dr. Diviya Sinha

Departments

As taught in.

• Biochemistry
• Cell Biology
• Developmental Biology
• Molecular Biology

Learning Resource Types

Introductory biology, problem sets.

In this section, Dr. Diviya Sinha describes how she and the course team create and grade the problem sets for 7.013.

In this course, students are assigned seven long problem sets, roughly one for every two weeks. These problem sets are designed to get students to understand and apply lecture material in order to solve problems. For more discussion about our goals for problem sets, please read Prof. Hazel Sive’s comments on Teaching Students to Solve Problems . This section focuses on how we create the problem sets and their solution keys, and how we grade problem sets.

Developing Problem Set Questions

"I often look at news articles to help me develop the problem set questions."

For each problem set, I think about the key concepts we want to cover and work on developing questions. I often look at news articles to help me develop the problem set questions. For example, we have three lectures on cell biology in 7.013. I came across an article on the MIT homepage titled, “Living cells say: Can you hear me now?” The article discusses how a cell communicates with another neighboring cell. It was written in a very nice way, and the work was done by an MIT professor, so we incorporated it into problem set 4 and problem set 5 . A lot of the problems are similarly grounded in very current research.

Prof. Sive and Prof. Jacks often send me ideas and problems that they would like to include. For example, for the first problem set this semester, Prof. Jacks suggested that we include a question about the DNA that is present in all the cells of just one person: How many trips can you take to the sun with the length of all the DNA present in one person’s body? We incorporated this as a question, and the students really liked it.

I am always in touch with the professors when I’m developing the course materials, and they offer feedback promptly.

Problem Set Solutions

For each problem set, we have an extra staff meeting. When I write problem sets, I eventually become sort of immune to any issues the problem sets might have because I’m so familiar with them. The TAs and I each write out a complete set of answers for all the questions on every problem set. For the most part, the TAs’ answers are the same as mine, but once in a while their solutions have parts that aren’t in my prepared solution key. So, the TAs’ answers can help me understand how I need to improve or add onto each problem set and solution key. I find it very helpful.

Grading responsibilities are split between TAs and undergraduate graders who are undergraduate students who did well in the course in past semesters. If a graduate TA is teaching two recitation sections, the TA might grade the problem sets for one of the recitation sections, and the undergraduate grader might grade the problem sets for the other recitation section. For the next problem set, they switch. This way, the TA gets a picture of how all of the students are doing without having to shoulder all of the grading responsibilities.

This is a big class, and we strive to be consistent when it comes to grading. To promote consistency, the graders, TAs, and I maintain a shared Google document. If a grader or a TA comes across an answer on the problem set that is not part of the solution key and they want to accept it, then they post their comments on the Google document so everyone can see it. If it’s accepted by me or the TA who is in charge of that problem set, then everyone who comes across that same type of answer can accept it.

You are leaving MIT OpenCourseWare

Problem-Solving in Biology Teaching: Students’ Activities and Their Achievement

• Published: 21 July 2023
• Volume 22 , pages 765–785, ( 2024 )

Cite this article

• Nataša Nikolić   ORCID: orcid.org/0000-0001-8460-0430 1 &
• Radovan Antonijević   ORCID: orcid.org/0000-0003-4959-376X 1  

289 Accesses

1 Altmetric

Explore all metrics

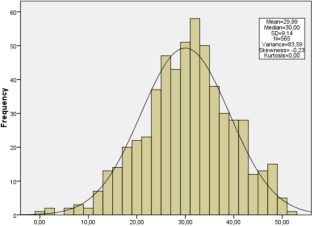
Problem-solving is, by nature, a creative process which, by teaching through the implementation of research and discovery activities, allows students to create their knowledge, revise it and link it to broader systems. The aim of the research was to describe and analyse the process of solving biological problems through activities that are performed during the process of solving them, as well as to study how the implementation of these activities affects the level and quality of student achievement in biology. This study employed a quantitative method research strategy to describe the problem-solving process in biology teaching and determine student achievement. Data collection was by means of survey and testing. A Likert-scale survey and a biology knowledge test were constructed for the purposes of the research. For data analysis, descriptive statistics, factor analysis and the Pearson correlation coefficient were used. The data of eighth-grade students were collected from September 2016 to February 2017, in 72 schools in Serbia (565 students). The factor analysis confirmed that problem-solving activities could be grouped into the following five areas: (1) analysing and planning problem-solving; (2) discovering solution(s) to the problem; (3) problem-solving evaluation activities; (4) additional activities involving the discussion of the problem; (5) the degree of student independence in the process of discovering a solution to a problem. The results show that with the increasing frequency of the realisation of the research problem-solving activities, the achievement of students also increases. With regard to achievement quality, a positive but low correlation was found in all three domains—knowledge acquisition, understanding and application.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Studying the student’s perceptions of engagement and problem-solving skills for academic achievement in chemistry at the higher secondary level

Sankar E. & A. Edward William Benjamin

The Impact of Problem-Based Learning on Students’ Achievement in Mechanical Waves in Secondary Schools

Stella Teddy Kanyesigye, Jean Uwamahoro & Imelda Kemeza

Research mathematicians’ practices in selecting mathematical problems

Morten Misfeldt & Mikkel Willum Johansen

Ali, A. R., Toriman, M. E., & Gasim, M. B. (2014). Academic achievement in biology with suggested solutions in selected secondary schools in Kano State, Nigeria. International Journal of Education and Research, 2 (11), 215–224.

Google Scholar  

Anderson, J. R. (2005). Cognitive Psychology and Its Implications: Sixth Edition . Macmillan.

Aryulina, D., & Riyanto, R. (2016). A problem-based learning model in biology education courses to develop inquiry teaching competency of preservice teachers. Cakrawala Pendidikan, 35 (1), 47–57. https://doi.org/10.21831/cp.v1i1.8364

Article   Google Scholar  

Antonijević, R., & Nikolić, N. (2019). The role of problem-oriented teaching in the process of the development of critical and creative thinking. In V. Orlović Lovren, J. Peeters & N. Matović (Eds.), Quality of education: Global development goals and local strategies (pp. 49–63). Institute for Pedagogy and Andragogy.

Bowden, E. M. (1997). The effect of reportable and unreportable hints on anagram solution and the Aha! experience. Consciousness & Cognition, 6 (4), 545–573. https://doi.org/10.1006/ccog.1997.0325

Article   CAS   Google Scholar  

Bruner, J., Goodnow, J., & Austin, A. (1956). A study of thinking . Wiley.

Cai, J., & Brook, M. (2006). Looking back in problem-solving. Mathematics Teaching, 196 , 42–45.

Chin, C., & Chia, L. G. (2006). Problem-based learning: Using ill-structured problems in biology project work. Science Education, 90 (1), 44–67. https://doi.org/10.1002/sce.20097

Article   ADS   Google Scholar  

Chin, C., & Osborne, J. (2008). Students’ questions: A potential resource for teaching and learning science. Studies in Science Education, 44 (1), 1–39. https://doi.org/10.1080/03057260701828101

Costa, V., & Sarmento, R. P (2019). Confirmatory factor analysis–A case study . Retrieved from https://arxiv.org/ftp/arxiv/papers/1905/1905.05598.pdf

DeVellis, R. F. (1991). Scale development: Theory and applications . Sage Publications Inc.

Dunlap, J. C. (2005). Problem-based learning and self-efficacy: How a capstone course prepares students for a profession. Educational Technology Research and Development, 53 (1), 65–85. https://doi.org/10.1007/BF02504858

Etherington, M. B. (2011). Investigative primary science: A problem-based learning approach. Australian Journal of Teacher Education, 36 (9), 53–74. https://doi.org/10.3316/ielapa.328484780726539

Gagné, E. D., Yekovich, C. W., & Yekovich, F. R. (1993). The cognitive psychology of school learning (2nd ed.). HarperCollins College Publishers.

Gbore, L. O., & Daramola, C. A. (2013). Relative contributions of selected teachers’ variables and students’ attitudes toward academic achievement in biology among senior secondary schools students in Ondo State. Nigeria. Current Issues in Education, 16 (1), 1–11.

Gijbels, D., Dochy, F., Van den Bossche, P., & Segers, M. (2005). Effects of problem-based learning: A meta-analysis from the angle of assessment. Review of Educational Research, 75 (1), 27–61. https://doi.org/10.3102/00346543075001027

Harun, N. G., Yusof, K. H., Jamaludin, M. Z., Helmi, S. A., & Hassan, S. (2012). Motivation in problem-based learning implementation. Procedia-Social and Behavioral Sciences, 56 (2012), 233–242.

Hoskinson, A. M., Caballero, M. D., & Knight, J. K. (2013). How can we improve problem-solving in undergraduate biology? Applying lessons from 30 years of physics education research. CBE Life Sciences Education, 12 (2), 153–161.

Article   PubMed   PubMed Central   Google Scholar  

Hurst, R. W., & Milkent, M. M. (1996). Facilitating successful prediction problem-solving in biology through application of skill theory. Journal of Research in Science Teaching, 33 (5), 541–552.

Jamari, D., Mohamed, H., Abdullah, Z., Mohd Zaid, N., & Aris, B. (2018). Biology problem-solving: The high achiever students. European Proceedings of Social and Behavioural Sciences, 68 , 831–842.

Kapa, E. (2001). A metacognitive support during the process of problem solving in a computerized environment. Educational Studies in Mathematics, 47 (3), 317–336.

Kirui, J. M., & Kaluyu, V. (2018). Influence of selected psychosocial factors on learners’ performance in science subjects: A case of public secondary schools in Moyale Sub-County, Kenya. International Journal of Education and Research, 6 (1), 15–28.

Kolber, B. J. (2011). Extended problem-based learning improves scientific communication in senior biology students. Journal of College Science Teaching, 41 (1), 32–39.

Meiring, S. P. (1980). Problem solving. A basic mathematics goal, parts 1 and 2 . GLC Publishers, Agincourt.

Montague, M. (2005). Math problem solving for upper elementary students with disabilities (p. 8). The Access Center: Improving Outcomes for All Students K.

Nehm, R. H. (2010). Understanding undergraduates’ problem-solving processes. Journal of Microbiology & Biology Education, 11 (2), 119–122. https://doi.org/10.1128/jmbe.v11i2.203

Okoye, N. S., & Okechukwu, R. N. (2006). The effect of concept mapping and problem-solving teaching strategies on achievement in genetics among Nigerian Secondary School Students. African Journal of Educational Studies in Mathematics and Sciences, 4 , 93–98.

Polya, G. (1973). How to solve it: A new aspect of mathematical method  (2nd ed.). Princeton University Press.

Ranjanie, B. (2017). Impact of problem-based learning on teaching biology for higher secondary students. International Journal of Current Research, 9 (12), 62932–62934.

Sabella, M. S., & Redish, E. F. (2007). Knowledge organization and activation in physics problem solving. American Journal of Physics, 75 (11), 1017–1029.

Squires, J. E., Estabrooks, C. A., Newburn-Cook, C. V., & Gierl, M. (2011). Validation of the conceptual research utilization scale: An application of the standards for educational and psychological testing in healthcare. BMC Health Services Research, 11 (1), 1–14.

Stanisavljević, J. D., & Đurić, D. Z. (2012). Efekat primene problemske nastave biologije na trajnost i kvalitet stečenih znanja [The effect of the application of problem-based biology teaching on the durability and quality of acquired knowledge]. Uzdanica, 9 (1), 303–312.

Sungur, S., Tekkaya, C., & Geban, O. (2006). Improving achievement through problem-based learning. Journal of Biological Education, 40 (4), 155–160.

Syafii, W., & Yasin, M. R. (2013). Problem-solving skills and learning achievements through problem-based module in teaching and learning biology in high school. Asian Social Science, 9 (12), 220–228. https://doi.org/10.5539/ass.v9n12p220

Thakur, P., & Dutt, S. (2017). Problem-based learning in biology: Its effect on achievement motivation of students of 9th standard. International Journal of Multidisciplinary Education and Research, 2 (2), 99–104.

Trauth Nare, A., Buck, G., & Beeman-Cadwallader, N. (2016). Promoting student agency in scientific inquiry: A self-study of relational pedagogical practices in science teacher education. In G. Buck & V. Akerson (Eds). Allowing our professional knowledge of pre-service science teacher education to be enhanced by self-study research: Turning a critical eye on our practice (pp. 43–67). Springer.

Woolfolk, A., Hughes, M., and Walkup, V. (2013). Psychology in Education (2nd ed.). Pearson Education.

Xun, G., & Land, S. M. (2004). A conceptual framework for scaffolding III-structured problem-solving processes using question prompts and peer interactions. Educational Technology Research and Development, 52 (2), 5–22. https://doi.org/10.1007/BF02504836

Download references

Author information

Authors and affiliations.

Department of Pedagogy and Andragogy, Faculty of Philosophy, University of Belgrade, Belgrade, Serbia

Nataša Nikolić & Radovan Antonijević

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Nataša Nikolić .

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Nikolić, N., Antonijević, R. Problem-Solving in Biology Teaching: Students’ Activities and Their Achievement. Int J of Sci and Math Educ 22 , 765–785 (2024). https://doi.org/10.1007/s10763-023-10407-5

Download citation

Received : 29 June 2021

Accepted : 07 July 2023

Published : 21 July 2023

Issue Date : April 2024

DOI : https://doi.org/10.1007/s10763-023-10407-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Biology teaching
• Problem-solving
• Problem-solving activities
• Students’ achievement
• Find a journal
• Publish with us
• Track your research

• Publishing Policies
• For Organizers/Editors
• For Authors
• For Peer Reviewers

Biology Problem-Solving: The High Achiever Students

Problem-solving has been acknowledged as one of the compulsory skills needed to face and overcome challenges of the modern world in either learning or everyday life. However, there is limited information regarding the level of problem-solving skills demonstrated by school students in learning biology subject compared to physics and mathematics. This study aims to identify the problem-solving level of 16-year old high achievers in selected boarding school in the Southern and Central Regions of Malaysia. The problem-solving skills of 70 students were measured using a validated open-ended test, UKPM, which consists of general and topic-specific problem-solving questions for biology. These questions focus on the different steps in the problem-solving processes. High achievers from boarding schools were chosen to ensure the homogenous background of the participants. The data were descriptively analysed and the overall score was used to determine the students’ problem-solving level based on the classification in Programme of International Students Assessment (PISA). The result showed that the majority of the participants are low (35%) and intermediate (64%) problem solvers and they showed incompetence in manipulating information and making justifications. They possess high tendency to find the absolute answer, but lack the reflecting ability when answering the test. The criteria and limitations showed that the participants are prone to practise a converged thinking pattern. In this, educators should introduce innovative alternative teaching and learning approach need to enhance the students’ problem-solving skills. Keywords: Problem-solving Skills Problem-solving Processes Biology School

Introduction

Problem-solving (PS) skills refer to a person’s ability to make critical judgment and decision based on the appropriate justification of the problem’s situation and its surrounding ( Kivunja, 2014 ). Solving a problem requires an individual to explore the root cause of a problem and create potential solutions pragmatically by using logic, lateral, and creative thinking ( Ismail & Atan, 2011 ). This approach is parallel with the 21st-century learning that emphasised on the construction of new knowledge, a shift from focusing solely on rote memorisation and classroom knowledge transfer in schools that have become habitual over the years. Problem-solving (PS) PS is not an innate skill ( Bal & Esen, 2016 ) therefore, providing the students with the chance to solve the problem is actually an effective way to develop this skill ( Shute, Ventura, & Ke, 2015 ; Shute & Wang, 2013 ). Learning instruction that emphasises on the understanding of core concept helps in developing students’ PS as this skill is best learnt through the use of domain-specific problem-solving activities that are challenging for students to learn ( Prevost & Lemons, 2016 ). During the process, increasing students’ understanding of the topic will help them to create and relate to the new knowledge. In the aspect of learning and education, the repetition cycle of the PS process through practices will equip them with PS skills that can be applied in different problems regardless of the context, discipline, or situation ( Yang, 2012 ). In this light, PS skills can have long-term benefits and subsequently, help the students to take charge of their profession, personal encounter and everyday hurdles ( Bal & Esen, 2016 ; Syafii & Yasin, 2013 ). Moreover, biologists agreed that students should acquire PS skills in order to learn biology better ( Hoskinson, Caballero, & Knight, 2013 ).

The numerous proposed models on PS stipulate that the basic component of the PS process is to identify problems, to suggest solutions, to apply solutions, and to reflect at the end of the process. One may interpret that the problem-solving process is the sequential steps in a linear process. However, in reality, most individuals demonstrate flexible and inventive approaches based on the different circumstance and they do not adhere to an perpetual linear PS process ( Yu, Fan, & Lin, 2014 ). PS skills are taught through the integration with the teaching of different subjects, fields, domains, or contents, the steps, process, or stages remained unchanged, therefore, understanding the meanings and function of each PS step is crucial for the success of problem-solving. PS step can be used as a guideline on what to observe and measure in evaluating the proficiency of PS. Besides that, teachers will know the types of learning support or scaffolding that have to be given to the students during the teaching and learning process.

PS requires a variety of mental skills, including interpreting information, planning, trying alternative strategies, reflecting and decision-making. However, studies have found that students are not aware of the processes taking place in problem solving ( Yu et al., 2014 ). Early PS studies demonstrated that students have difficulties in PS steps, especially when tackling the orientation stage, which is to identify the problem. In this regard, the first step of PS is vital and students should be taught for a better understanding of this component. Hence, this component should be set as the rubric or benchmark during PS measurement and assessment. Studies done in both general and domain specific PS affirmed that the students’ incapability in solving a problem does not stemmed from their lack of knowledge or skills specific domain, rather, it is due to the failure of properly identifying the source of the problem and its details. This can be seen in PS studies that compared the differences between novice and expert problem solvers where PS performance is highly influenced by individual ability to understand the problem, as well as analysing the potential answer or solution ( Prevost & Lemons, 2016 ). Nevertheless, enhancing students’ PS skills is one of the prior goals of all educational institutions therefore, developing PS skills is necessary in order to improve students’ ability in scientific thinking especially in science subjects, such as biology ( Ulusoy, Turan, Tanriverdi, & Kolayis, 2012 ; Yenice, Ozden, & Evren, 2012 ). In other words, PS skills should be developed early as in the students’ schooling years.

Previous studies have shown that Malaysia students face difficulty in problem-solving ( Abd Razak, Mohd Johar, Andriani, & Yong, 2014 ; Johnny, Abdullah, Abu, Mokhtar, & Atan, 2017 ; Kaus, Phang, Ali, Abu Samah, & Ismail, 2017 ). On the other hand, the term ‘problem-solving’ is commonly synonymous with obvious calculation and this resulted in the lack of study on problem-solving associated with Biology. In this regard, despite the differences in problems’ structure and contents between science subjects, the instructional purpose, which is to elucidate the patterns and processes in the natural world and systems, align comparatively with each other. Research noted that solving biology problem requires the engagement of the same skill practised by physicists and biologists ( Hoskinson et al., 2013 ). Nevertheless, compared to mathematics or physics there is still a prominent gap in the research of PS skills in biology for the past three decades( Kim, Prevost, & Lemons, 2015 ).

Problem Statement

The implementation of PS in pedagogical activities has led to the measurement of PS skills among the students. Studies have shown that there is a significant positive relationship between academic achievement, career success, and certain habits of mind or behaviour with skills competencies ( OECD, 2014 ; Stecher & Hamilton, 2014 ; Wüstenberg, Greiff, & Funke, 2012 ). In this light, it is more challenging to measure the competency level of PS skills compared interpersonal skills, therefore, there are guidelines that can be used in developing the instrument or selecting the rubrics to measure PS skills. On the other hand, these higher-order PS skills are arduous to be measured and the discrepancies on relevant and credible measurement scales are still debatable among the researchers ( McCoy, Braun-Monegan, Bettesworth, & Tindal, 2015 ; Stecher & Hamilton, 2014 ). By observing and measuring these PS processes, this study will obtain valuable information related to the cognitive habit in ones’ mind when solving a task. Observing and measuring these processes during intervention study will provide formative information as well as evidence of the student’s development of PS skills. There is a lack of information about problem-solving skills for biology and how students solve biology problems, among school students is still in its formative stages.

Research Questions

The research questions that lead this study are as follows:

What is the students’ problem-solving competency level for Biology?

How is the students’ performance in non-routine Biology questions in terms of the problem-solving steps in problem-solving process?

Purpose of the Study

For the purposes of this article, domain-specific problem-solving refers to topic Cell Division of secondary school biology syllabus investigate the PS level of the students. Therefore, this study aims to identify the students’ abilities regarding the steps in PS as well as their problem-solving competency level for Biology.

Research Methods

This study was participated by 70 science stream students (39 females and 31 males) who are 16 years old from three high-achieving fully residential schools located in the Central and Southern Regions of Malaysia. The students were chosen to ensure the homogenous background of the participants. Their PS skills for the biology subject were measured using the UKPM, which is a validated open-ended test with 20 topic-specific questions in Section A and 20 general questions in Section B. The topic-specific PS questions are related to cell division, while the general PS questions are related to biology or science as well as questions adapted from the problem-solving domain in Programme for International Student Assessment (PISA). This study referred to the Ge & Land PS Model that comprises four problem-solving steps, which are identifying problems (PS1), giving suggestions and options to solve the problem (PS2), making justification (PS3), and reflecting the action (PS4) ( Bixler, 2007 ). A total of 10 questions were allocated for each PS step and each question focuses on the different steps in the PS process. The maximum score for the UKPM is 120 and the data were analysed descriptively to identify the participants’ performance for each step in the PS process. The assessment rubric was adapted from previous research ( Bixler, 2007 ) while the PS classification of the competency level was done by referring to the OECD or ‘Organisation for Economic Cooperation and Development’ classification that was used in PISA ( OECD, 2014 ). The UKPM was validated prior to the research by experts in the PS domain, as well as against the biology syllabus for the Malaysian secondary school.

Table 2 summarises the participants’ scores. The results show that neither the female nor male participants score excellently in the UKPM test. The mean score for female participants was 42.92, and the difference is not distinct with the male participants with the mean score of 42.42. The overall achievement did not reach 50% of the overall score with only 42.70. The dispersion of the score patterns for all groups is almost similar, with the average of 8. The highest score is 62/120, while the lowest is 26/120. Both extreme scores were obtained by female participants.

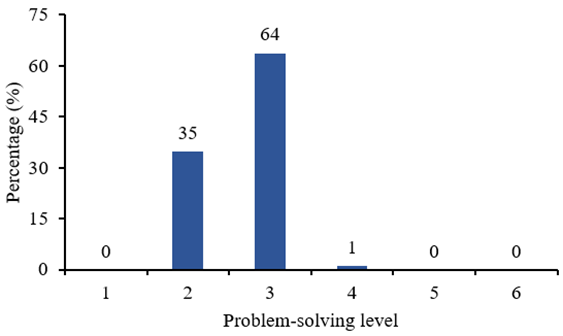
Each individual score was compared and classified according to the six PS competency level as presented by Organisation for Economic Co-operation and Development (2014). Diagram 1 shows the percentage of the number of participants in each competency level; only 1% of the participants could be classified as possessing level 4 competencies. The majority of the participants (64%) could be categorised as level 3 problem solvers, while 35% could be classified as having level 2 competencies.

The level of problem-skill for each gender was compared against and there are only minor differences. Diagram 2 shows that 2% of the female participants possess level 4 competence. Moreover, there is a 4% difference between the number of females (36%) and males (32%) who demonstrated level 2 competence. The same difference was observed in level 3 and there is only a 6% difference between both groups.

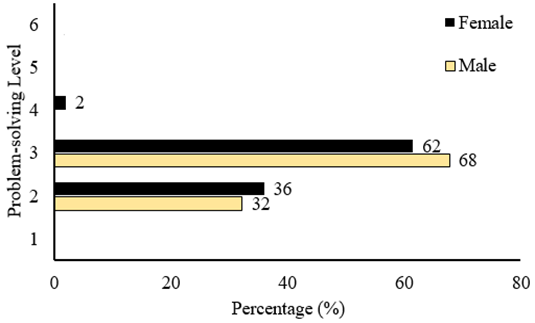
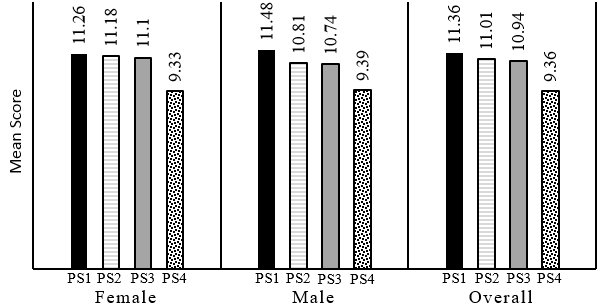
Table 3 describes the score of each PS step in details. Out of the four steps in the PS process, making reflection (PS4) has the lowest mean score of 9.33 ± 3.90 for females and 9.39 ± 3.35 for males. The mean scores show that most participants are capable to obtain at least 10 out of the total 40 marks allocated for PS4 in UKPM. Although the other three steps have higher mean scores, they are still considered to be in the low range as none of the PS steps are able to reach at least 50% of the mean score compared to the allocated marks. The minimum and maximum scores for each PS step are in the lower range as the highest score is 21 (PS4) and the lowest score is 3 (PS2). Diagram 3 summarises the findings related to the PS steps. In this light, there are no major differences in the overall achievement each PS steps between each gender.

The results provide the insights on students’ behaviour when solving problems during the biology subject. The biology subject is different from physics and mathematics; this is because, the calculations only play minimal roles compared to reading and understanding the fact. It was discovered that the participants from both genders have poor knowledge and capabilities in all the PS steps, and consequently, they obtained poor results in the PS domains based on the Programme International Student Assessment (PISA).

It was discovered that the participants did not plan well and did not evaluate the situation in the questions. In one of the PS1 questions, the participants were asked to list all the barriers and factors that they should consider before choosing the most appropriate option and only a small percentage of students managed to list the appropriate answers beyond the question given, while the rest only listed down a few factors that could be found in the question. In another PS1 question, the participants were required to propose an arrangement plan regarding the number of people to be placed in eight rooms. For this question, the participants should consider the criteria given when proposing the arrangement. The researcher expected the participants to perform some calculations, however, the majority of them presented wrong answers even though a draft table was provided to assist them in planning and evaluating the problem by providing specific directions for the key stages. They only provided answers that they are familiar despite the expectation that they would be able to find the solution when they delve deeper into the question. This shows excellent achievement in public school examination will not ensure good competency in non-routine PS as most school examination revolves around routine problem (Abd Razak et al., 2014)

In the meantime, the planning process is seldom practised in answering open-ended problems even though it is commonly used in routine and algorithmic problems. Hence, it should be considered in developing the skills to solve open-ended problems ( Reid & Yang, 2002 ). In this light, most past PS studies only focused on the earlier PS steps, which are identifying the root cause of the problem and planning the solutions and actual success in PS is actually determined based on the capability to determine what is needed to be solved and how to do it effectively ( Ulusoy et al., 2012 ).

Identifying the root cause of the problem and planning the solutions are categorised as knowledge acquisition according to the PS framework in PISA ( OECD, 2014 ) or rule identification and application ( Schweizer, Wüstenberg, & Greiff, 2013 ; Wüstenberg et al., 2012 ). It is assumed that these particular steps are more utilised in higher-order thinking skills (HOTS) compared to the later steps in PS model. Meanwhile, reflections and monitoring require judgement and deep thinking and reflections can be done in most of the PS steps. Due to the huge influence in PS stages, some studies have divided the ‘Identify Problem’ and ‘Solution Planning’ steps into smaller sub-steps (E.g., ‘Gather Info’). Some studies also added other indicators that are relative to these steps (E.g., ‘Avoiding Problem’ and ‘Flexibility’) with a specific checklist of criteria that has to be observed in the study. These additions were based on the researchers’ perspectives and research needs.

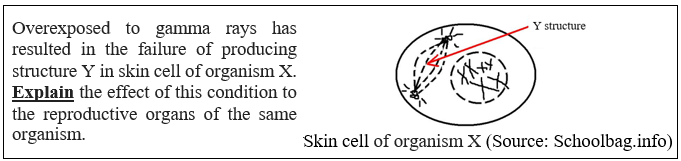
The results revealed that the students are confused and facing difficulties in linking the function of spindle fibre with mitosis or meiosis failure (Figure 4 ). The participants’ lack of understanding of the key concepts has contributed to the poor results for the PS steps. As an example, the question related to the concepts of meiosis and its functions in producing haploid gamete cell which are different in terms of numbers of chromosomes, genetic content due to random desegregation, and crossing over processes. In this light, the students were unable to answer the question even though it is just slightly different from the examination format questions (Figure 5 ). This shows that the students were confused and the students had come out with varied segments of inaccurate response and totally incorrect answers. On the other hand, the success rate was improved when the same question was modified with additional explicit hints or organised to be similar to the pattern of the examination format questions. Without this explicit linkage, the participants had difficulties in linking what they had learnt on the idea of cell division with examination questions. It seems that solving previous exam questions and drill practices are common in a biology lesson so that the students could ace their examination. In this light, despite their impressive results, the students tend to have limitations in terms of their level of thinking skills. These students tend to answer the questions through memorisation, and the drilling practices create a mind model and schema that will be stored in their minds, rather than creating understanding of the principles. In other words, the students memorise the content and they face difficulties when presented with questions in a new context or structure.

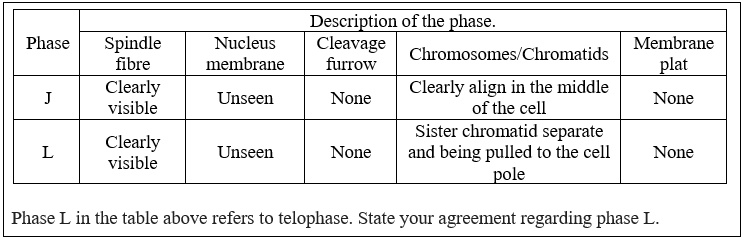
Step four in the PS process is making reflection. In UKPM, questions in PS4 prompt the participants to present their agreement on the topic (Figure 6 ). For example, the students are provided with a formula as a guide for their answers and to answer PS4 questions, students are expected to review and identify the formula and they have to suggest the correct formula when giving their justifications. Unfortunately, there were not many participants who were able to present a sound reflection. Most of them only provide their answers by referring to the given calculation without reflecting and they also provided incorrect answers. As a result, they scored very low for PS4 which affected their overall score. This shows that the learners have low abilities and face difficulties in creating a link between skills and knowledge ( Reid & Yang, 2002 ). Moreover, this study also observed the habit and pattern related to how the participants answer the test. Besides that, at the end of the UKPM test, the researcher had obtained verbal feedbacks from students who seemed to not prefer lengthy questions as they only glanced through the instruction and provide answers without any description, explanation, or justification. It was found that these students are more familiar with routine questions, which only require one right answer and they looked uncomfortable when asked to answer non-routine abstract questions that require giving opinions and justifications and consequently, gave opinions that did not reflect the lesson that they had learnt.

In the meantime, a good problem solver has three characteristics, which are having a good conceptual understanding of the domain involved, including domain-specific skills and being able to adjust wisely to the use of automated skills. This is because PS requires two types of knowledge namely declarative and procedural knowledge that are interdependent during the PS activity ( Yu et al., 2014 ). Expert problem solvers are more mature when performing an integrated mental representation of the problem, as well as demonstrating a better understanding of the core concepts, nature, and form of the problem ( Prevost & Lemons, 2016 ). They need more time to define and understand the issues compared to novice problem solvers who prefer to complete the task impatiently and often ignore the PS steps, including the first and most important step, which is problem identification ( Yu et al., 2014 ). The same pattern could also be observed among primary, secondary, and college students. Novice problem solvers usually seek the solution without the definite understanding of the problem and they lacked the ability to reflect their own performances. They tend to overlook the analysis and reflection process, even though they knew that they were stuck with an inappropriate solution during the process.

The flexible, linear, and sequential PS processes can be practised differently according to the problem solvers’ creativity and needs, as well as the situation. However, the students’ lack of understanding on these PS processes will affect their perceptions on the processes’ progression and nature. Furthermore, research ( Yu et al., 2014 ) reported a similar pattern in the early phase of their study. They found that students lacked the flexibility and creativity as they opted for the linear mode of an incomplete PS process. Therefore, it is important to incorporate effective teaching strategies to enhance the students' understanding on the meaning and function of each PS step, and the students can develop individual skills when solving problems. A good problem solver that practises effective monitoring step would consistently reflect the chosen strategy to ensure that they are on the right track, as well as checking for other solutions. The students should be able to monitor and steer the direction of their own progress, to ask questions among themselves that could help to maximise the effective strategies and to prevent themselves from constantly using the unproductive approach in generating solutions (Jamari, Mohamed, Abdullah, Mohd Zaid, & Aris, 2017b). Choosing an effective strategy without making revisions or having self-correcting mechanisms to monitor the progress of PS is comparable to those who fail to choose good method and strategy right from the start. This issue can contribute to the failure in PS. Therefore, students must be encouraged to make verification by monitoring and reflecting their choice that could increase their HOTS and PS level.

Previous studies suggested that instructional scaffolding is necessary in aiding the students’ problem-solving processes (Jamari, Mohd Zaid, Abdullah, Mohamed, & Aris, 2017a; Kim et al., 2015 ). In this light, it is important to focus on content specific scaffolding, which is also known as conceptual scaffolding in school. This is because mastering the content of the lesson is the ultimate goal of having learning assistance, either with or without instructional materials or the presence of a teacher. Therefore, the teacher is responsible to help students in understanding the function of each step involved in the PS in class regardless of subject or domain ( Yenice et al., 2012 ). The action of mentioning these processes during the teaching and learning process without giving the students with the opportunity to perform activities that require them to think, learn and practise each step will not enhance the students’ PS skills ( Yu et al., 2014 ). The similarities between ill-structured task and common everyday problems make it worthwhile to inculcate and develop the students’ PS skills. PS skills helps to cater the needs of solving multiple tasks in a short term which refers to schooling and learning and at the same time shaping an individual to be a capable problem solver later in life as a long term goal. Since an ill-structured task usually has complex structure and may have numerous potential solutions, this type of task requires more cognitive activity to process all the problems’ information in the attempt to find the best solution.

Promising instructional strategies to enhance HOTS and PS have been widely studied and including the inquiry learning approach and focused on STEM education (Jamari et al., 2017b). However, there are still not much studies being done on these approaches for the Malaysian context although there are plenty of studies done in other countries. Examples of teaching strategies that emphasised on authentic ill-structured problem that can be applied by teachers include case-based learning (CBL) and problem-based learning (PBL). The problem or task does not stem from the textbook, but from the everyday problems which require the application of the similar concepts or principles. CBL and PBL are categorised under inquiry and they are suitable to be used in the environment of science learning due to their potential to attract the interest of students, to spark inquiry, and to encourage them to continue exploring the task ( Herreid, Schiller, & Herreid, 2012 ; Pai et al., 2010 ). Teacher’s face to face or online involvement provides the suitable guidance to help them interpret and accelerate active information transfer processes by providing a learning environment that can develop HOTS and PS skills ( Kivunja, 2014 ; McCoy et al., 2015 ).

Although time is a factor that can affect the development of PS in an individual, it is important to expose the students to PS steps and processes so that they can learn and practise these skills to become a competent citizen. Therefore, teaching approaches and strategies that emphasise on authentic problem and active learning such as Inquiry Learning and STEM (Science, Technology, Engineering and Mathematics) education should be combined with appropriate instructional scaffolding that focuses on the students’ ability to master the lesson, as well as nurturing and developing their PS skills ( Bybee, 2010 ; Moore, Johnson, Peters-Burton, & Guzey, 2016 ; Tseng, Chang, Lai, & Chen, 2013 ). In the meantime, this study has several limitations. One of the limitations is the small number of participants as the study was focused on high achievers. Hence, the sample for this study may not represent the whole population. Nevertheless, the sample provides insights on how high achieving students conduct PS. This information will add to the body of knowledge on problem solving in the context of Malaysian school students. It is assumed that other students are facing the same PS problems as shown by the high achievers, therefore, future research can be implemented on students from different categories and backgrounds. A PS research with more focus on the biology subject can be conducted by replicating this research to other topics in the biology syllabus..

• Abd Razak, N. N. F., Mohd Johar, A., Andriani, D., & Yong, C. Y. (2014). Mathematical Problem Solving Ability Among Form Two Students. Jurnal Pendidikan Matematik, 2(2), 1-13.
• Belgin Bal, İ., & Esen, E. (2016). Problem Solving Skills of Secondary School Students. China-USA Business Review, 15(6). doi:10.17265/1537-1514/2016.06.002
• Bixler, B. A. (2007). The Effects of Scaffolding Students' Problem-Solving Pocess Via Question Prompts on Problem Solving and Intrinsic Motivation In An Online Learning Environment. (Doctor of Philosophy phd thesis), Pennsylvania State University,
• Bybee, R. W. (2010). Advancing STEM Education A 2020 Vision. Technology And Engineering Teacher, 70(1), 30-35.
• Herreid, C. F., Schiller, N. A., & Herreid, K. F. (2012). Science Stories: Using Case Studies to Teach Critical Thinking. VA, USA: National Science Teachers Association.
• Hoskinson, A. M., Caballero, M. D., & Knight, J. K. (2013). How can we improve problem solving in undergraduate biology? Applying lessons from 30 years of physics education research. CBE Life Sci Educ, 12(2), 153-161. doi:10.1187/cbe.12-09-0149
• Ismail, S., & Atan, A. (2011). Aplikasi Pendekatan Penyelesaian Masalah Dalam pengajaran Mata Pelajaran Teknikal dan Vokasional di Fakulti Pendidikan UTM. Journal of Educational Psychology and Counseling, 2, 113-144.
• Jamari, D., Mohamed, H., Abdullah, Z., Mohd Zaid, N., & Aris, B. (2017b). Fostering Higher Order Thinking And Problem Solving Skills Through Social Media. Man In India, 97(12), 1-10.
• Jamari, D., Mohd Zaid, N., Abdullah, Z., Mohamed, H., & Aris, B. (2017a). Instructional Scaffolding To Support Ill-Structured Problem Solving A Review. Sains Humanika, 9(1-4), 33-39.
• Johnny, J., Abdullah, A. H., Abu, M. S., Mokhtar, M., & Atan, N. A. (2017). Difficulties In Reasoning Among High Achievers When Doing Problem Solving In Mathematics. Man In India, 97(12), 61-70.
• Kaus, M. A., Phang, F. A., Ali, M. B., Abu Samah, N., & Ismail, A. K. (2017). Problem Solving And Social Supports: The Roles of Parents. Man In India, 97(12), 279-287.
• Kim, H. S., Prevost, L., & Lemons, P. P. (2015). Students' usability evaluation of a Web-based tutorial program for college biology problem solving. Journal of Computer Assisted Learning, 31(4), 362-377. doi:10.1111/jcal.12102
• Kivunja, C. (2014). Do You Want Your Students to Be Job-Ready with 21st Century Skills? Change Pedagogies: A Pedagogical Paradigm Shift from Vygotskyian Social Constructivism to Critical Thinking, Problem Solving and Siemens’ Digital Connectivism. International Journal of Higher Education, 3(3). doi:10.5430/ijhe.v3n3p81
• McCoy, J. D., Braun-Monegan, J., Bettesworth, L., & Tindal, G. (2015). Do Scaffolded Supports between Aspects of Problem Solving Enhance Assessment Usability? Journal of Education and Practice, 6(36), 175-185.
• Moore, T., Johnson, C. C., Peters-Burton, E. E., & Guzey, S. S. (2016). The need for a STEM road map: A framework for integrated STEM education. In (pp. 33 -12). NY: Routledge Taylor & Francis Froup.
• OECD. (2014). PISA 2012 Results: Creative Problem Solving Students’ skills in tackling real-life problems Volume V. Retrieved from La rue André-Pascal, PARIS
• Pai, A., Benning, T., Woods, N., McGinnis, G., Chu, J., Netherton, J., & Bauerle, C. (2010). The Effectiveness of a Case Study-Based First-Year Biology Class at a Black Women's College. Journal of College Science Teaching, 40(2), 32.
• Prevost, L. B., & Lemons, P. P. (2016). Step by Step: Biology Undergraduates' Problem-Solving Procedures during Multiple-Choice Assessment. CBE Life Sci Educ, 15(4). doi:10.1187/cbe.15-12-0255
• Reid, N., & Yang, M.-J. (2002). Open-ended problem solving in school chemistry: A preliminary investigation. International Journal of Science Education, 24(12), 1313-1332. doi:10.1080/09500690210163189
• Schweizer, F., Wüstenberg, S., & Greiff, S. (2013). Validity of the MicroDYN approach: Complex problem solving predicts school grades beyond working memory capacity. Learning and Individual Differences, 24, 42-52. doi:10.1016/j.lindif.2012.12.011
• Shute, V. J., Ventura, M., & Ke, F. (2015). The power of play: The effects of Portal 2 and Lumosity on cognitive and noncognitive skills. Computers & Education, 80, 58-67. doi:10.1016/j.compedu.2014.08.013
• Shute, V. J., & Wang, L. (2013). Measuring Peoblem Solving Skills In Portal 2. In IADIS International Conference on Cognition and Exploratory Learning in Digital Age (CELDA 2013) (pp. 33-39). Fort Worth, Texas, USA: International Assn for Development of the Information Society (IADIS).
• Stecher, B. M., & Hamilton, L. S. (2014). Measuring Hard-to-Measure Student Competencies A Research and Development Plan (13 978-0-8330-8806-2). Retrieved from Santa Monica, California:
• Syafii, W., & Yasin, R. M. (2013). Problem Solving Skills and Learning Achievements through Problem-Based Module in teaching and learning Biology in High School. Asian Social Science, 9(12). doi:10.5539/ass.v9n12p220
• Tseng, K. H., Chang, C. H., Lai, S. J., & Chen, W. P. (2013). Attitudes towards science, technology, engineering and mathematics (STEM) in a project-based learning (PjBL) environment. International Journal of Technology Design Education, 23, 87-102.
• Ulusoy, Y. O., Turan, H., Tanriverdi, B., & Kolayis, H. (2012). Comparison of Perceived Problem Solving Skills of Trainee Students Graduated from Different. Procedia - Social and Behavioral Sciences, 46, 2099-2103. doi:10.1016/j.sbspro.2012.05.435
• Wüstenberg, S., Greiff, S., & Funke, J. (2012). Complex problem solving — More than reasoning? Intelligence, 40(1), 1-14. doi:10.1016/j.intell.2011.11.003
• Yang, Y. T. C. (2012). Building virtual cities, inspiring intelligent citizens: Digital games for developing students’ problem solving and learning motivation. Computers & Education, 59(2), 365-377. doi:10.1016/j.compedu.2012.01.012
• Yenice, N., Ozden, B., & Evren, B. (2012). Examining of Problem Solving Skills According to Different Variables for Science Teachers Candidates. Procedia - Social and Behavioral Sciences, 46, 3880-3884. doi:10.1016/j.sbspro.2012.06.165
• Yu, K.-C., Fan, S.-C., & Lin, K.-Y. (2014). Enhancing Students’ Problem-Solving Skills through Context-Based Learning. International Journal of Science and Mathematics Education, 13(6), 1377-1401. doi:10.1007/s10763-014-9567-4

Copyright information

About this article

Publication date.

01 May 2018

Article Doi

https://doi.org/10.15405/epsbs.2018.05.68

978-1-80296-039-6

Future Academy

Print ISBN (optional)

Edition number.

1st Edition

Business, innovation, sustainability, environment, green business, environmental issues

Cite this article as:

Jamari, D., Mohamed, H., Abdullah, Z., Zaid, N. M., & Aris, B. (2018). Biology Problem-Solving: The High Achiever Students. In M. Imran Qureshi (Ed.), Technology & Society: A Multidisciplinary Pathway for Sustainable Development, vol 40. European Proceedings of Social and Behavioural Sciences (pp. 831-842). Future Academy. https://doi.org/10.15405/epsbs.2018.05.68

We care about your privacy

We use cookies or similar technologies to access personal data, including page visits and your IP address. We use this information about you, your devices and your online interactions with us to provide, analyse and improve our services. This may include personalising content or advertising for you. You can find out more in our privacy policy and cookie policy and manage the choices available to you at any time by going to ‘Privacy settings’ at the bottom of any page.

Manage My Preferences

You have control over your personal data. For more detailed information about your personal data, please see our Privacy Policy and Cookie Policy .

These cookies are essential in order to enable you to move around the site and use its features, such as accessing secure areas of the site. Without these cookies, services you have asked for cannot be provided.

Third-party advertising and social media cookies are used to (1) deliver advertisements more relevant to you and your interests; (2) limit the number of times you see an advertisement; (3) help measure the effectiveness of the advertising campaign; and (4) understand people’s behavior after they view an advertisement. They remember that you have visited a site and quite often they will be linked to site functionality provided by the other organization. This may impact the content and messages you see on other websites you visit.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• CBE Life Sci Educ
• v.20(1); Spring 2021

The Case for Biocalculus: Improving Student Understanding of the Utility Value of Mathematics to Biology and Affect toward Mathematics

Melissa l. aikens.

† Department of Biological Sciences, University of New Hampshire, Durham, NH 03824

Carrie Diaz Eaton

‡ Digital and Computational Studies Program, Bates College, Lewiston, ME 04240

Hannah Callender Highlander

§ Department of Mathematics, University of Portland, Portland, OR 97203

Associated Data

The next generation of life science professionals will require far more quantitative skills than prior generations. Calculus is important for understanding dynamical systems in biology and, therefore, is often a required course for life science students. However, many life science students do not understand the utility value of mathematics to biology. Therefore, according to expectancy-value theory, life science students may experience lower motivation, which can impact their performance in a calculus course. This study examines how two different biocalculus courses, which integrated calculus and biological concepts and successfully halved the rates of students earning a D, F, or withdrawing (DFW), affected life science students’ utility value, interest, and overall attitudes toward mathematics. Using pre and post surveys, we found that students’ interest in mathematics increased by the end of the semester, and they demonstrated a more sophisticated understanding of how mathematics is used in biology. Students whose attitudes toward mathematics improved primarily attributed these changes to a better understanding of the utility of mathematics to biology, feelings of competence in mathematics, or rapport with the instructor. Thus, communicating the utility value of mathematics to biology through integrated mathematics–biology courses can contribute to improved attitudes toward mathematics that can impact students’ motivation and performance.

INTRODUCTION

Due to an increasing demand for quantitative skills among life scientists, undergraduates in biology today need to demonstrate competency in a variety of quantitative skills ( National Research Council [NRC], 2003 ; Steen, 2005 ; Association of American Medical Colleges–Howard Hughes Medical Institute [AAMC-HHMI], 2009 ; American Association for the Advancement of Science [AAAS], 2011 ). These skills include the ability to create and interpret graphs, the ability to statistically analyze data, and the ability to mathematically model systems ( NRC, 2003 ; AAMC-HHMI, 2009 ; AAAS, 2011 ). Because biological systems are dynamic, calculus plays a key role in the modeling of biological systems. For example, calculus is used in population growth models to account for complex demography ( Ellner and Rees, 2006 ), in Susceptible-Infectious-Removed (SIR) models to understand disease spread (e.g., Buceta and Johnson, 2017 ), and in tumor growth and metastasis models (e.g., Bilous et al. , 2019 ). Therefore, many life science students are required to take a calculus course to satisfy their major or pre-med requirements.

However, life science students are often perceived to be math averse and, therefore, may be less than enthusiastic about taking a calculus course. Although recent work did not demonstrate particularly poor motivational attitudes among life science majors toward the use of mathematics in biology courses, it did reveal a tremendous amount of variation in these attitudes ( Andrews and Aikens, 2018 ). For example, Andrews and Aikens (2018) found that, although the average score for students’ interest in using mathematics to understand biology was 4.5 on a scale from 1 to 7, 1 SD around the mean encompassed values from 2.8 to 6.2. Additionally, one-third of life science students reported high cost (anxiety and effort) of using mathematics in biology courses. Thus, a significant portion of life science students likely enter a calculus course with little interest and some anxiety. Compounding the problem, if calculus courses do not connect the concepts to biological applications, life science students may complete the course without an understanding of why calculus is even required for their major or pre-professional program, making the course feel like a hurdle to overcome rather than a valued learning experience.

Integrated science, technology, engineering, and mathematics (STEM) courses can improve life science students’ affect toward other STEM disciplines. For example, life science students in Introductory Physics for Life Science (IPLS), a course designed to relate principles of physics to biological concepts, reported an increase in their interest in physics at the end of the semester ( Crouch et al. , 2018 ). Students who have taken IPLS report that the biological applications are interesting and relevant to their future careers ( Meredith and Bolker, 2012 ; Crouch et al. , 2018 ). In particular, students report that the physics problems related to biological concepts they have previously encountered in their biology classes are the most interesting, because such problems allow them to see the connections between physics and their biology course work ( Geller et al. , 2018 ). Therefore, one approach to improving life science students’ attitudes toward mathematics, and calculus in particular, is to teach calculus through an integrated biocalculus course in which calculus concepts are applied to biological problems.

Recognizing the value of teaching calculus within a biological context, a number of biocalculus textbooks and courses have been developed (e.g., Adler, 2012 ; Comar, 2013 ; Uhl and Holdener, 2013 ; Bodine et al. , 2014 ; Neuhauser and Roper, 2018 ). However, few studies have examined the extent to which an integrated biocalculus course can improve life science students’ attitudes toward mathematics. In this study, we report on students’ affective outcomes after participating in a biocalculus course designed to intentionally integrate calculus concepts into biological problems. We use expectancy-value theory as a framework for understanding students’ affective experiences, focusing on utility value, as described in the following section.

Theoretical Framework

Expectancy-value theory connects students’ personal values and self-beliefs to their motivation and achievement. Specifically, it posits that students’ expectations of success on a task and their personal values for a task will affect their persistence on a task, particularly challenging tasks, and thus their performance on a task ( Eccles et al. , 1983 ; Wigfield and Eccles, 2000 ). Students who believe that they can successfully complete a task are more likely to persist on a task to completion. However, simply believing a task can be successfully accomplished does not ensure students will persist on a task; they must also find some personal value in that task. Task values include intrinsic value (interest and enjoyment), utility value (usefulness of the task for a future goal), attainment value (importance of doing well on a task for one’s identity), and cost (negative aspects of engaging in a task; Wigfield and Eccles, 2000 ).

Utility value represents students’ perceptions of the importance or usefulness of a task for their future goals ( Eccles et al. , 1983 ). It has been shown to be positively correlated with student performance in a variety of contexts ( Zusho et al. , 2003 ; Cole et al. , 2008 ; Hulleman et al. , 2008 ). Additionally, studies in which students’ utility value is experimentally enhanced through a utility-value intervention have found increases in performance compared with a control group of students ( Hulleman and Harackiewicz, 2009 ; Hulleman et al. , 2010 ). The utility-value intervention also has been shown to narrow achievement gaps between underrepresented and overrepresented groups in science ( Harackiewicz et al. , 2016 ). Therefore, there is strong empirical evidence that students’ perceptions of the usefulness of the material they are learning in their class can play an important role in their course performance.

Experimental research using utility-value interventions has also documented increases in students’ interest in a topic as a result of the intervention (Hulleman and Harackiewicz, 2009; Hulleman et al. , 2010 ). Hidi and Renninger (2006, pp. 113) describe the development of individual interest, an “enduring predisposition to reengage particular content over time,” as resulting from knowledge, positive feelings, and value. Thus, recognizing the value of course material in their lives can contribute to the development of students’ interest in the subject matter ( Hulleman et al. , 2010 ). Interest is an important predictor of academic achievement ( Schiefele et al. , 1992 ) and academic choices, such as courses taken or major ( Harackiewicz et al. , 2002 ). For example, interest in mathematics has been found to predict both grades in mathematics and the number of mathematics courses taken during high school ( Simpkins et al. , 2006 ). It has also been argued that developing students’ interest should be a goal in and of itself, beyond its role in motivation, because interest is fundamental to students’ happiness and well-being ( Harackiewicz and Hulleman, 2010 ).

Redesigning calculus courses to enhance the utility value of mathematics for biological applications may be one way to increase life science students’ interest in mathematics and, ultimately, positively influence their motivation and performance in calculus courses. Cognitive psychologists have demonstrated that students are unable to transfer skills between contexts ( Gick and Holyoak, 1983 ; NRC, 2000 ). Therefore, it is not surprising that when mathematics and biology are not explicitly linked in a curriculum, students have a difficult time envisioning the connection ( Arnett and Van Horn, 2009 ). However, when students’ learning experiences integrate the two disciplines, they are more likely to report that mathematics is important to biology ( Arnett and Van Horn, 2009 ; Thompson et al. , 2010 ). Additionally, placing mathematics in a genuine, real-world context in an interdisciplinary science and mathematics course has led to increases in both students’ perceptions of the importance of mathematics to biology and their enthusiasm for mathematics ( Matthews et al. , 2010 ).

Research Objectives

This study examines changes in students’ utility value, interest, and overall attitudes toward mathematics in two distinct biocalculus courses at two different institutions: the University of Portland (UP) and Unity College (Unity). At UP, the impetus to create a biocalculus course arose out of the observation that biology students were demonstrating generally lower performance in the standard calculus course than their other STEM counterparts and poor quantitative reasoning skills in subsequent courses. Therefore, creating a calculus course that emphasized the relevance of mathematics to biology seemed like a possible avenue to more deeply engage students and improve their performance. Unity designed and implemented a biocalculus course to foster integration between disciplines as part of its larger mission in sustainability science education and transdisciplinary problem solving. The development and structure of both biocalculus courses is described in detail in Diaz Eaton and Highlander (2017) .

In the study by Diaz Eaton and Highlander (2017) , they provided evidence that a carefully designed biocalculus course can improve student performance and retention. Compared with students taking a standard calculus course the same semester, students in the biocalculus course at UP demonstrated higher performance on a common quiz at the end of the semester, despite these students initially having significantly lower performance on a common precalculus quiz at the beginning of the semester. Additionally, rates of students earning a D, F, or withdrawing (DFW rates) were about 50% lower in the redesigned biocalculus courses at both Unity and UP compared with previous years when life science students were in traditional, non-biology calculus courses. In this paper, we build upon those results and show such a course can also improve students’ attitudes toward mathematics by demonstrating the relevance of calculus to biological problems. Specifically, we asked the following questions: 1) To what extent do students’ perceptions of the usefulness of mathematics for their major and their career change after taking a biocalculus course? 2) To what extent does students’ interest in mathematics change after taking a biocalculus course? 3) To what extent do students have more sophisticated views of the utility of mathematics to biology after taking a biocalculus course? 4) What aspects of the biocalculus courses caused students to have generally more positive attitudes about mathematics after taking the course? To answer these questions, we conducted pre and post surveys across multiple sections of the biocalculus classes and analyzed both Likert-type items and open-response items.

Setting and Participants

The study was conducted from 2011 to 2014 in biocalculus courses developed at UP and at Unity. A full description of the courses, the development, and the context can be found in Diaz Eaton and Highlander (2017) . Unity is a small liberal arts college offering only environmental-related majors. At the time the study was conducted, students who took Calculus I typically did so as a major program requirement for earth and environmental science and wildlife biology. Due to the small size of the college, typically one section per semester had been offered. The biocalculus course that was created to fulfill Calculus I requirements has a mixture of lecture, guided-inquiry worksheets, writing, and projects. Modeling ( Diaz Eaton et al. , 2019 ), Excel, metacognition, and communication skills ( Diaz Eaton and Wade, 2014 ) were emphasized, and proofs of major theorems and symbolic calculations “by hand” were de-emphasized.

UP is a small, private Catholic university, with professional schools in business, education, engineering, and nursing and a liberal arts core in the College of Arts and Sciences. Although the UP Biology Department elected in 2010 to remove the calculus requirement for life science majors, many pre-med students were still interested in taking calculus. Therefore, a biocalculus course was created for these students with input from biology faculty. The course included all of the standard Calculus I topics, but with a focus on the applications to modeling biological phenomena, using Fred Adler’s (2012) Modeling the Dynamics of Life: Calculus and Probability for Life Scientists . The course was taught using a more traditional, lecture-based approach, with an emphasis on collaborative problem solving and modeling activities inside and outside class. Students were also required to submit regular journal assignments that asked them to reflect on what they were learning and how, including which concepts they were struggling with and why, and what study methods they were implementing. There were two sections of the course offered each year.

At both institutions, the instructors of the course (C.D.E. and H.C.H.) administered a mathematics attitude survey, modified from Richard Schori’s survey for the Oregon Collaborative for Excellence in the Preparation of Teachers ( Schori, 2015 ). Pre and post surveys were given in class on the first and last days of class to assess any changes in student attitudes toward mathematics. This study was approved by the Institutional Review Board (IRB) at Unity (UCIRB 2012-05) and by the IRB at UP (UPIRB 2011).

Surveys at Unity were collected over four semesters (each semester from Fall 2012 to Spring 2014) and over five different sections of the course (two sections offered in Fall 2012). Surveys at UP were collected over five semesters (each semester from Fall 2011 to Spring 2013 and Spring 2014) and over six different sections of the course (two sections offered in Spring 2014). Only students who completed both the pre and post surveys, whose data were able to be matched between the pre and post surveys, and who were life science majors or pre-med students (four students were not life science majors or pre-med) were included in the analyses. Students were instructed to write individualized codes on each pre and post survey that consisted of a numerical sequence of their birth months, birth dates, and the last two digits of their social security numbers to be used to match the pre and post survey data. Many students at Unity inconsistently reported the coding prompt, making some pre and post data matching impossible. In particular, data from only two students in one Fall 2012 section and one student in another Fall 2012 section could be matched. Because this represented an extremely low response rate for these sections, data from Fall 2012 at Unity were not included in the analyses. The average class size of the biocalculus course at Unity was approximately 14 students, and the average class size of the biocalculus course at UP was approximately 20 students. Response rates, calculated as the number of life science students with pre–post data that could be matched divided by the total number of students in the class section, ranged from 58 to 83% at Unity and 65 to 88% at UP. A total of 32 students from Unity and 87 students from UP are included in the analyses. However, two students were dropped from the quantitative analyses, because they did not report demographic information included as variables in the model-selection process in those analyses. Participant demographics are shown in Table 1 .

Participant demographics by institution ( n = 87 for UP, n = 32 for Unity, total n = 119)

a Gender is missing for one student.

b Final GPA is missing for one student.

Each survey included 25 Likert-type items about students’ mathematics attitudes (five-point scale from “strongly disagree” to “strongly agree”), as well as demographic items (e.g., major, year in school, gender, and self-reported grade point average [GPA]), and short, open-response items (see Supplemental Material for the full pre and post survey). The Likert-type items measuring attitudes were not constructed as scales, which necessitated individual analyses of each item rather than summing or averaging scores across items. For the purposes of this study, we only analyzed a subset of Likert-type, demographic, and open-response items related to our research questions. Among the Likert-type items, we analyzed three items that represented utility value: 1) Mathematics is important for my chosen profession (career utility value 1), 2) The skills I learn in this class will help me in my career after college (career utility value 2), and 3) The skills I learn in this class will help me in other classes for my major (major utility value). We also analyzed one item that represented interest: Mathematics is enjoyable and stimulating to me.

We included the following demographic variables in our analyses: gender (male or female), self-reported GPA at the end of the semester, and year in school (first-year, sophomore, junior, or senior). For GPA, students chose the range in which they believed their GPAs fell: 2.00–2.99, 3.00–3.24, 3.25–3.49, 3.50–3.74, or 3.75–4.00. Thus, GPA is a categorical variable with five levels. Although students reported their GPAs in both the pre and the post survey, many of the students were taking the biocalculus course during their first-year Fall semester. Thus, we chose to use self-reported GPA on the post survey in our analyses because it was not clear to us what a GPA at the beginning of a student’s first semester in college represented.

For the open-response items, we qualitatively analyzed responses to two questions: 1) In your opinion, is the knowledge of mathematics beneficial to biologists? Why or why not? 2) Do you feel that your attitude toward and/or beliefs about mathematics has changed over the course of this semester? Why or why not? If you answered “yes,” what has most influenced any changes in your attitude or beliefs about mathematics? The first question was included on both the pre and post survey, and we used this question to address our third research question related to students’ sophistication in their understanding of the utility value of mathematics for biology. The second question was only on the post survey. We used this question to address our fourth research question, in which we aimed to identify the factors that contributed to a positive change in students’ attitudes.

Data Analysis

Quantitative analysis: likert-type items..

We used ordinal mixed-effects regression models with an adaptive Gauss-Hermite quadrature approximation (10 quadrature points) to determine whether students’ utility value and interest, as measured by the Likert-type items, significantly changed from the beginning to the end of the course. Ordinal regression is more appropriate for Likert-type items than linear regression, because the numbered responses represent ordered categories. Unlike the difference between integers, where the linear distance between 1 and 2 is the same as between 2 and 3, differences between ordered categories may not be equal. In other words, the difference between strongly disagree and disagree may not be the same “distance” as the difference between disagree and neutral ( Theobald et al. , 2019 ). We conducted four separate regressions in which each of the four Likert-type items, representing utility value or interest, served as a dependent variable. Time (categorical variable that is either “pre” or “post”) was included as a predictor variable in all regressions. The time variable is important in repeated-measures mixed-effects models, because it represents differences in scores between the time points (i.e., change in scores). In our model, “pre” was the reference level for the time variable, so the regression output for the time variable indicates the degree to which post scores are different from pre scores. We used model selection to determine whether other predictor variables should be included as fixed effects in each regression. All analyses were conducted in R v. 3.5.0 ( R Core Team, 2018 ) using the ordinal package ( Christensen, 2018 ).

We used mixed-effects models in order to include repeated measures of each student as a random effect. Additionally, we tested whether class section necessitated inclusion as a random effect in each model by calculating the intraclass correlation coefficient (ICC) and by comparing Akaike information criterion values corrected for small sample sizes (AICc) between full and reduced models ( Theobald, 2018 ). ICC is a ratio of between-group variance (i.e., between–class section variance) to total variance, and is calculated for a regression model that includes only the random effect ( Theobald, 2018 ). Small ICC values (<0.05) suggest little variance between groups, and thus a random effect accounting for group variation may not be needed in the model ( Theobald, 2018 ). ICC values for class section in our regression models ranged from 0 to 0.06. For each attitude item, we also compared the AICc value for a full regression model with class section as a random effect to the AICc value for a reduced regression model without class section as a random effect ( Theobald, 2018 ). Lower AICc values indicate a model with better fit, but AICc values within 2 indicate models with similar fit ( Burnham and Anderson, 2002 ). When the difference in AICc values between the full and reduced model was within 2, we kept the simpler model (i.e., the reduced model). For all four of our regressions, the reduced model had a lower AICc value than the full model with class section as a random effect. Moreover, not including class section in the regression models did not change the significance of any predictor variables in our final model. Therefore, although some of the ICC values were slightly above 0.05, we chose to use simpler models in our analyses by not including class section as a random effect.

For each regression model, we also used model selection to determine which predictor variables to include in the model. The full model included categorical main effects, interaction terms, and student as a random effect:

Dependent variable ∼ time (pre or post) + institution (UP or Unity) + gender + final GPA + year in school + time*institution + time*gender + time*final GPA + time*year in school + (1|student)

We compared AICc values among the full model and all possible nested models that included time and student using the dredge function in the package MuMIn ( Bartón, 2018 ). We examined all models with AICc values within 2 of the best models and chose the simplest of these models to run as our final model. In evaluating the significance of the predictor variables in our final models, we adjusted our alpha level using a Bonferroni correction to account for multiple hypothesis tests. Across the four regression models, we conducted hypothesis tests on seven predictor variables, so our alpha was 0.007. Using an alpha of 0.007 as a threshold for significance allows for conservative tests, such that any predictor variable with a p value less than 0.007 is likely not a result of a type I error (false positive).

In ordinal regression, the odds ratio calculated from the regression coefficient represents the odds of increasing from one level of the dependent variable to a higher level of the dependent variable. A major assumption of ordinal regression is that the odds are the same for all levels of the dependent variable. In other words, the odds of moving from the lowest level to a higher level are the same odds as moving from the second-lowest level to a higher level. This is known as the proportional odds assumption. We tested whether our data fit the proportional odds assumption by modeling time and institution as nominal effects, which relaxes the assumption that the odds of each of the variables are the same among all levels ( Christensen, 2018 ). We then used likelihood ratio tests to compare the models including time and institution as nominal effects with our ordinal model in which we assumed proportional odds. For all four models, the likelihood ratio tests indicated the model assuming proportional odds was a better fit, indicating our models met the assumption of proportional odds.

Qualitative Analysis: Open-Response Items.

Responses to the open-response questions were analyzed using deductive and inductive coding. A set of codes were established a priori for whether students thought mathematics was beneficial (three codes: beneficial, not beneficial, not sure) and for whether students’ attitudes changed after taking the biocalculus course (three codes: attitude improved, attitude stayed the same, attitude worsened). However, we used inductive coding, in which we derived codes based on the data in students’ open-response answers ( Saldaña, 2016 ), to code why students reported mathematics was beneficial to biology and why their attitudes changed.

The two questions were analyzed separately, each following the same general procedure for initial coding. First, a subset of 20 responses to the question were coded independently by two researchers (M.L.A. and a biology education graduate student for the first question; M.L.A. and an undergraduate researcher in biology education for the second question). The researchers met and discussed the codes, came to consensus on the codes, and created an initial codebook. The researchers then independently coded another 20 responses to the question and through discussion came to consensus on the codes. They revised the codebook as necessary, either by adding new codes or by revising the definitions, inclusion criteria, or exclusion criteria of the original codes. When codes were added or revised, the researchers reread previously coded responses and recoded as necessary. This iterative cycle of independently coding 20 responses, coming to consensus on codes, revising the codebook, and recoding as necessary was repeated until all responses had been coded.

For the first open-response question asking students whether and how mathematics is beneficial to biologists, we first coded whether students said mathematics was beneficial, mathematics was not beneficial, or they were not sure if mathematics was beneficial. For those students who expressed that mathematics was beneficial, we then coded the explanations they gave for why mathematics was beneficial. We did not code explanations for why mathematics is not beneficial, because only four students, between the pre and post surveys, reported that mathematics was not beneficial, representing a very small sample size on which to base conclusions. We assessed the reliability of our codes by giving 30% of the pre survey and 30% of the post survey responses to H.C.H. to be independently coded. We used Holley and Guilford’s (1964) G index of agreement as a measure of interrater reliability (IRR) due to the high frequencies of some codes and the low frequencies of other codes. When codes demonstrate distributional skew, either because they are used extremely frequently or very rarely, Cohen’s kappa can be quite low even with high interrater agreement ( Xu and Lorber, 2014 ). The G index of agreement is less sensitive to distributional skew in the codes, but still takes into account chance agreement (it assumes an equal probability of choosing a code; Xu and Lorber, 2014 ). All codes had a G greater than 0.80, and only two codes had a G < 0.90. Because we had generated a large number of codes, many of which were found in only a handful of responses, we condensed some of the initial codes into broader categories ( Saldaña, 2016 ). As codes were clustered into categories, all responses within each code were reread to ensure each coded segment reflected the meaning of the broader category. The codebook with the initial codes, categories, and definitions of the codes and categories is included in the Supplemental Material.

For the second open-response question, which asked students if their attitudes had changed and why, we first coded whether students’ attitudes had improved, worsened, or stayed the same. If students’ attitudes stayed the same, we coded whether they had positive or negative mathematics feelings. If students’ attitudes improved or worsened, we coded reasons for these changes. We assessed the reliability of our codes by giving 30% of the student responses (found only on the post survey) to C.D.E. to be independently coded. One code had a G = 0.76, but all other codes had a G > 0.80 (and only one code had a G >0.80 but <0.90). At the end of coding, we had generated 15 codes, only seven of which applied to students whose attitude improved, which is the focus of our study; therefore, we did not condense codes into broader categories. The codebook with the initial codes and definitions of the codes is included in the Supplemental Material.

Model selection resulted in slightly different models for each measure of utility value (Supplemental Table S1), but in no case did utility value significantly change from the beginning to the end of the semester (Supplemental Table S2). Only one of the career utility-value items (Mathematics is important for my chosen profession) demonstrated significant institutional differences, with UP students reporting overall lower scores on this item compared with Unity students; B = −1.69 (±0.56), p = 0.002. Gender was included in the best model explaining major utility value, but it was not significant according to our adjusted alpha value.

In contrast to the results for the utility-value items, students at both Unity and UP reported a significant increase in their interest in mathematics by the end of the semester; B = 1.02 (± 0.29), p = 0.0004 (Supplemental Table S2). The final model for interest included both time and institution as predictors. Overall interest gains were similar between institutions (0.40 at Unity and 0.33 at UP), although Unity had overall lower (though not statistically significant lower) interest scores than UP ( Figure 1 ).

Least-squares means of pre and post scores for the interest survey item: Mathematics is enjoyable and stimulating to me. Error bars represent ± SE.

Qualitative Results: Why Is Mathematics Beneficial to Biology?

In response to the open-ended question asking students whether mathematics is beneficial for biology and why, 94% (111 out of 118 total responses on this question) of students stated that mathematics was beneficial for biology in the pre survey, and 99% (117 out of 118 total responses on this question) of students stated that mathematics was beneficial for biology in the post survey. In the pre survey, 3% of students reported mathematics was not beneficial to biology, and another 3% of students reported they were unsure whether mathematics was beneficial to biology or not. However, only one student (1%) reported mathematics was not beneficial in the post survey.

Students provided a variety of reasons for why mathematics is beneficial to biology that revealed a range of sophistication in understanding the role of mathematics in biology. We describe the seven major categories that emerged from the open-response data: Broad Utility, Biology Utility, Chemistry Utility, Calculations, General Analytical Skills, Science Process Skills, and Specific Applications ( Table 2 ; Figure 2A ). Percentages reported are based on the number of students who reported mathematics was beneficial.

Major categories for students’ responses as to why mathematics is beneficial to biology

(A) Frequency of categories describing why mathematics is beneficial to biology among individuals who reported mathematics to be beneficial to biology ( n = 111 in pre survey; n = 117 in post survey). (B) Frequency of specific science process skill codes (from initial coding) among individuals whose responses to why mathematics is beneficial to biology were categorized under Science Process Skills ( n = 35 in pre survey; n = 56 in post survey). Multiple categories or specific science process skills may have been coded per student, so total percentage sums to greater than 100%.

The Broad Utility and Biology Utility categories represent vague responses for why mathematics is beneficial for biology. Responses in the Broad Utility category did not contain reasons why mathematics was important specifically for understanding biology; rather, students reported that mathematics was broadly important for daily life or for understanding science in general. Overall, these responses indicated that students believed mathematics was important, but they did not demonstrate an explicit connection between mathematics and biology. On the other hand, the Biology Utility category contained student responses in which students stated mathematics was important for broad understanding of biological concepts or processes or for doing biological research but did not clarify in what ways mathematics might be important. Responses did not identify how mathematics may be used in biology, biological concepts or processes for which mathematics may be particularly useful, or any specific practices of biological research that use mathematics, any of which would indicate a deeper understanding of the connection between the disciplines. Overall, the lack of specificity in responses coded as Biology Utility suggests a less sophisticated understanding of the role of mathematics in biology. Together, the Broad Utility and Biology Utility categories encompassed 31% of student responses (16% Broad Utility, 15% Biology Utility) on the pre survey, but only 20% of student responses (11% Broad Utility, 9% Biology Utility) on the post survey ( Figure 2A ).

A small percentage of students (5%) reported on the pre survey that mathematics was useful for understanding chemistry or for specific chemistry applications, such as titrations ( Figure 2A ). Most of these responses reflect students’ perceptions that mathematics is indirectly used in biology through chemistry applications. No students reported mathematics was useful for understanding chemistry on the post survey.

Some students were much more specific in their responses, indicating that mathematics was useful for specific skills used in biology ( Figure 2A ). A small percentage of students indicated that mathematics was important for calculations (pre survey: 8%; post survey: 3%). Many more students indicated that mathematics was useful for more higher-order cognitive skills. Some students responded that mathematics was useful for critical thinking, problem solving, or logical reasoning (pre survey: 7%; post survey 5%). These responses were coded as General Analytical Skills, because they referred to a general set of higher-order cognitive skills identified as important to biology. In contrast, other students reported mathematics was useful for specific skills in reference to conducting biological research, which we have categorized as Science Process Skills. Science Process Skills include collecting data, analyzing data, using or creating models, and making predictions. The number of students reporting a science process skill as a reason why mathematics is beneficial to biology increased from 32% in the pre survey to 48% in the post survey. Among the students who reported a science process skill on the pre survey ( n = 35), 54% reported that mathematics was useful for data analysis in biology research. However, among the students who reported a science process skill in the post survey ( n = 56), almost the same percentages of students reported that mathematics was useful for making predictions (34%), using or creating models (32%), and analyzing data (38%) ( Figure 2B ).

Finally, 15% of students on the pre survey indicated a specific biological example in which mathematics was useful; this increased to 31% of students on the post survey ( Figure 2A ). Most of the examples were related to population growth and dynamics, though drug dosage, game theory, epidemics, and carbon dating were also mentioned by students.

Qualitative Results: Has Your Attitude toward Mathematics Changed? How and Why?

Of the 117 students who wrote responses that could be coded, 47% of students reported that their attitudes toward mathematics improved by the end of the semester, 44% of students reported their attitudes toward mathematics had not changed, and 9% of students reported that their attitudes toward mathematics had worsened. Of the 51 students whose attitudes stayed the same, 31% of students had positive mathematics attitudes, 41% of students had negative mathematics attitudes, and the remaining students did not indicate whether they had positive or negative mathematics attitudes.

Students whose attitudes toward mathematics improved over the semester reported three primary reasons for this change: the relevance and applicability of the material to biology, an ability to comprehend the material, and the professor’s teaching style ( Table 3 and Figure 3 ). Other codes were used only once or twice in student answers and are not discussed here (see Supplemental Material for complete codebook).

Most commonly reported codes reflecting why students’ attitudes toward mathematics improved

Frequency of predominant codes for why students’ attitudes toward mathematics improved among individuals who reported their attitudes improved ( n = 55). Multiple reasons may have been coded per student, so total percentage sums to greater than 100%.

The most common reason reported for a positive change in attitudes was understanding the relevance of mathematics (45% of students whose attitudes improved). Some students emphasized how much they preferred learning about the applications of the calculus concepts rather than simply memorizing mathematical equations. Therefore, explicitly showing students how mathematics could be used within a biological context, that is, demonstrating the utility of mathematics to the field of biology, positively changed how students viewed mathematics.

Another common reason reported for improved attitudes was students’ ability to understand the calculus (35% of students). In some cases, students explicitly mentioned previous struggles with calculus. Students’ responses did not indicate that the restructuring of the calculus course into a biocalculus course was the reason for their ability to understand the material. Rather, it seemed to be related to the instructional style. Regardless, understanding the material appeared to increase students’ perceived competence in their mathematical skills, which promoted a more positive attitude toward mathematics.

Finally, 35% of students whose attitude improved indicated that something about the way the professor taught the course was the underlying reason. This code was found for both instructors in this study, indicating it was not just one particular instructor’s unique teaching methods. Rather, this code included a variety of aspects of an instructor’s teaching style that promoted a positive learning environment. Students mentioned things such as patience, dedication to the students, and the creation of a supportive learning environment as being critical to their improved attitudes. Therefore, student–instructor rapport and classroom climate may be important factors to consider when examining students’ attitudes about a subject.

Life science majors and pre-medical students are often required to take a calculus course, yet many calculus courses do not make explicit, authentic connections between calculus and biology concepts. This can deter students from developing an understanding of the relevance of mathematics to biology and an interest in mathematics, which has been shown to affect student performance. We sought to understand the extent to which two redesigned biocalculus courses for life science students, in which calculus concepts were explicitly rooted in biological problems, would improve students’ utility value and interest in mathematics, and what components of the course were critical for improving overall attitudes toward mathematics. Figure 4 summarizes the relationships we found (solid arrows), as well as relationships we posit based on theory and results from other studies (dashed arrows). Our data suggest that integrating biology and calculus, such that the relevance of calculus to biological contexts is emphasized, can improve students’ understanding of the utility of mathematics for biology, which can promote positive overall attitudes toward mathematics among life science students. Additionally, although we could not test this here, we hypothesize that the observed increase in students’ interest in mathematics was mediated, at least partially, by their more sophisticated understanding of the relevance of mathematics to biology. Our data also demonstrate that students’ perceived competence at mathematics and the rapport they have with the instructor are also important factors that contribute to improved attitudes toward mathematics. Thus, cultivating positive attitudes toward mathematics goes beyond simply demonstrating the relevance of mathematics to biology, but also encompasses instructional techniques and behaviors that cultivate feelings of competence and rapport, such as clarity in explanations, opportunities for students to succeed, enthusiasm for the subject, and approachability.

Factors that contribute to improved affect toward mathematics among life science students in biocalculus courses. Solid arrows represent relationships supported by the results of this study. Dashed arrows represent relationships supported by theory and/or other studies. The arrow from perceived competence to another arrow represents moderation.

Situating Calculus in a Biological Context Improves Students’ Understanding of the Utility of Mathematics to Biology

The biocalculus courses were designed to demonstrate the utility of mathematics to biology through problems that used a biological context. For example, at UP, where most students enrolled in biocalculus were interested in careers in medicine, students developed discrete-time dynamical systems to model the change in chemical concentration within the human lung when an individual breathes in the surrounding air containing a fixed concentration of the chemical. Upon model development, they then used various graphical and analytical tools from calculus to study the resulting equilibrium concentration within the lung. At Unity, where a significant number of students were wildlife biology majors, students worked on deriving a recommendation for a land trust’s lake by using discrete-time models to allow for population growth, stocking, and harvesting. In this project, they were asked to consider additional constraints beyond known biology such as reproductive rate—for example, the target permit numbers for tourism and planning, the amount of investment capital the trust had to invest in stocking, and environmental variability. They then had to write a report of findings to the land trust with a final recommendation.

Because of the applied nature of these courses, we predicted a shift in utility-value scores from the pre survey to the post survey, but these predictions were not borne out by the quantitative data. Examining the pre survey data, we found that students’ utility-value scores were high; approximately 75% of students chose 4 or 5 on a five-point Likert scale for each of the three utility-value items, indicating most students agreed or strongly agreed that mathematics was important for biology before even taking the biocalculus course (Supplemental Figure S1). Therefore, there was little room for improvement in scores on the post survey, and ceiling effects may explain why we did not see a significant increase. Other studies have reported similarly high values for life science students’ perceptions of the importance of mathematics to biology, either before engaging in a quantitative biology curriculum ( Karsai et al. , 2015 ; Hoffman et al. , 2016 ) or in a control group of students who did not engage in a quantitative biology curriculum ( Thompson et al. , 2010 ), suggesting that most life science majors recognize, at least superficially, the importance of mathematics to the biological sciences.

The qualitative data provided deeper insight into students’ utility value of mathematics for biology by asking them how they perceived mathematics to be useful to biology. This question illuminated gaps in students’ understanding of the connection between mathematics and biology that the quantitative data were unable to demonstrate. Notably, on the pre survey, only 45% of students described mathematics as useful for a specific science process skill and/or a specific application in biology, meaning that 55% of students who indicated mathematics was beneficial for biology did not connect mathematics in a meaningful way to the process of biological research or to the understanding of biological phenomena. However, by the end of the course, the percentage of students who cited a science process skill and/or a specific application that requires mathematical knowledge increased to 68%. Together, the quantitative and qualitative data suggest that biology education successfully inculcates in students the idea that mathematics is important for biology, but there is room for improvement in teaching students how mathematics is actually used in biology. Integrated mathematics–biology courses such as biocalculus are one way to effectively fill this knowledge gap in students. These data also point to the limitations of using quantitative measures of utility value and raise the question of the extent to which students need to understand how a task is useful to their future goals for it to meaningfully affect their academic performance and choices.

Among the science process skills, data analysis was most commonly cited in students’ responses in both the pre and post surveys. It is not surprising that many students think of data analysis when they think of mathematics in the biological sciences. Biology labs often incorporate data collection and interpretation into their curricula, and if students have read primary literature for their courses, then they have likely encountered statistics. Additionally, at Unity, most students take statistics before Calculus I. One successful outcome of the biocalculus courses was to broaden students’ perspectives on the way mathematics is used in biology. On the post survey, “using and creating models” and “making predictions” were cited almost as many times as “data analysis” ( Figure 2B ). Because of the courses’ emphasis on mathematical modeling, students gained a greater understanding and appreciation of the role of modeling in the biological sciences, which is a core competency for life science students ( AAAS, 2011 ). Exposing students to a wide array of uses of mathematics within biology can enrich students’ views of how mathematics enhances understanding in the biological sciences.

Understanding of the Utility of Mathematics to Biology and Perceived Competence Promote Positive Attitudes toward Mathematics

It was encouraging that almost half of the students taking the biocalculus courses reported more positive overall attitudes toward mathematics by the end of the semester. Recognizing the relevance and utility of mathematics to biology was one of the main drivers of these improved attitudes ( Figure 3 ). Many students reported that they had developed a better appreciation of or respect for mathematics after seeing how applicable and important it was to biological problems. These results are similar to those found in other integrated STEM courses, such as the IPLS courses ( Meredith and Bolker, 2012 ; Crouch et al. , 2018 ). Although overall attitudes toward mathematics have been found to only weakly correlate to achievement in mathematics ( Ma and Kishor, 1997 ), it seems plausible that improved attitudes may positively affect how students engage with mathematics in their life science courses and careers. As pointed out by Wilkins and Ma (2003, pp. 52) : “A person’s mathematical disposition related to her or his perceptions about and attitude toward mathematics may be as important as content knowledge for making informed decisions in terms of willingness to use this knowledge in everyday life.”

Although some students reported on the open-response question that the application of calculus to biological problems made the mathematics more interesting, we cannot make a causal connection between students’ enhanced views of the utility of mathematics for biology and their increase in interest in mathematics as demonstrated through the quantitative data. However, studies have established that utility-value interventions can result in an increase in interest in the topic ( Hulleman et al. , 2008 , 2010 ; Hulleman and Harackiewicz, 2009). However, this relationship appears to be moderated by students’ perceived competence and whether the utility value is directly communicated or self-generated. When the utility value of a topic to a student’s career is directly communicated, those with lower perceived competence may actually report lower interest in the subject ( Canning and Harackiewicz, 2015 ). In contrast, students with higher perceived competence report greater interest in the task or subject because it reinforces the importance of something at which they are already competent ( Canning and Harackiewicz, 2015 ; Durik et al. , 2015 ). This aligns with Hidi and Renninger’s (2006) concept of interest development, in which positive emotions, such as those generated by feelings of competence, in conjunction with values drive the development of individual interest. Interestingly, in our study, students’ confidence in their ability to understand the calculus concepts and do the problems was an important factor in improving their overall attitudes toward mathematics. Therefore, increasing students’ ability beliefs in mathematics through instruction may be critical for leveraging the utility value communicated through the curriculum of a biocalculus course. Future studies should aim to explore more deeply the relationships among utility value, interest, and perceived competence in integrated STEM courses.

Improving students’ perceptions of the usefulness of mathematics for biology and their interest in using mathematics within a biological context is important for promoting positive student outcomes related to quantitative biology. Many studies have found that students’ utility value or interest in a topic predict, either directly or indirectly, their academic performance ( Durik et al. , 2006 ; Simpkins et al. , 2006 ; Cole et al. 2008 ; Hulleman et al. , 2008 ). Additionally, studies in which interventions have been employed to increase students’ utility value or interest in a topic have led to increases in student performance compared with control groups lacking the intervention (Hulleman and Harackiewicz, 2009; Hulleman et al. , 2010 ; Canning et al. , 2018 ). In this study, we did not collect individual student grades, so we are unable to examine the extent to which changes in interest or students’ understanding of the utility value of mathematics to biology affected student achievement. However, comparing DFW rates in the biocalculus courses at Unity and UP to DFW rates in the standard, non-biology calculus courses that preceded these courses at these institutions demonstrated that DFW rates were halved after implementation of the biocalculus curriculum ( Diaz Eaton and Highlander, 2017 ). Additionally, students in the biocalculus course at UP had significantly higher final common quiz scores than students who were taking the traditional calculus course that same semester ( Diaz Eaton and Highlander, 2017 ). It is important to point out, though, that perceived competence, which is empirically similar to expectancies of success in expectancy-value theory, is also posited to predict performance ( Wigfield and Eccles, 2000 ). Because this was a prevalent code among students whose attitude improved, we cannot discount the idea that changes in students’ perceived competence in the subject matter, rather than utility value or interest, may have factored into the observed changes in DFW rates and quiz scores. Utility value and interest have also been found to predict students’ academic choices, such as course enrollment choices or intentions to remain in a STEM major ( Durik et al. , 2006 ; Simpkins et al. , 2006 ; Canning et al. , 2018 ). Future studies should examine whether changes in students’ interest or understanding of the relationship between mathematics and biology arising from integrated mathematics and biology courses increase their likelihood of taking additional quantitatively focused biology courses.

Instructor–Student Rapport Affects Students’ Attitudes toward the Content

Although not related to the redesign of the calculus courses, the positive influence of the instructor on students’ attitudes toward mathematics must be noted. This result aligns with findings from the social psychology and instructional communication literature on the relationship between instructor behaviors and student affective and cognitive learning outcomes. Students’ affective learning outcomes, or their attitudes toward the instructor and content of the course, have been shown to be affected by instructor immediacy ( Rodriguez et al. , 1996 ; Witt et al. , 2004 ) or behaviors that enhance psychological perceptions of liking and closeness ( Mehrabian, 1971 ). More recently, the importance of instructor–student rapport, or a perception there is a mutual, trusting, prosocial bond between the instructor and student, to learning outcomes has been emphasized ( Frisby and Martin, 2010 ; Frisby and Housley Gaffney, 2015 ). Instructor–student rapport is a perception that results from instructors’ behaviors, such as immediacy, and may therefore serve as a link to explain how instructor behaviors affect student learning outcomes ( Frisby and Martin, 2010 ; Frisby and Housley Gaffney, 2015 ). Responses from our study coded as “Professor” contain descriptions of the professor that correspond to many of the components that have been used to measure instructor–student rapport, such as helpful, enthusiastic, encouraging, and enjoyable ( Wilson et al. , 2010 ). These responses suggest an element of instructor–student rapport was important for improving student attitudes toward the mathematics content. This is an important consideration that should be factored into future studies examining changes in student attitudes of course content.

Limitations and Future Directions

We implemented a pre–post study design that did not have a control group and cannot state with certainty that all changes observed between the pre and post surveys were due to participation in the biocalculus course. In particular, the increase in interest and the change in sophistication of students’ responses about how mathematics is beneficial to biology could be due to general maturation or a shift that would have naturally been seen over this time period regardless of the biocalculus course ( Shadish et al. , 2002 ). Alternatively, we cannot rule out the possibility that the observed changes may have been a result of other experiences the students had over the course of the semester, perhaps in other courses or in a research experience. Additionally, changes in interest may have simply resulted from changes in students’ perceived competence in calculus, rather than from the integrated nature of the course. However, the responses obtained when we queried students directly about the impact of the course on their overall attitudes suggests that at least some change in interest in mathematics is due to the integration of the disciplines. Moreover, many of the responses on the post survey question asking students why mathematics was beneficial for biology referenced specific applications that had been covered in the biocalculus course (e.g., population growth, modeling the concentration of a chemical in a lung over time), suggesting the course content was indeed influencing their views on how mathematics is used in biology. Nevertheless, a control section, in which calculus was taught in a traditional manner to biology students, would have strengthened our conclusions about the effect of integrating mathematics and biology on students’ attitudes toward mathematics.

Additionally, the data collected were from primarily female students in biocalculus courses at two small, predominantly white institutions with two instructors, which limits the generalizability of the data. Importantly, gender and first-generation college status have been found to affect students’ interest in mathematics or their perceptions of the utility of mathematics to their careers ( Gaspard et al. , 2015 ; Andrews and Aikens, 2018 ). We included gender (as a binary variable) in our analyses and did not find it to be a statistically significant predictor of attitudes or of change in attitudes. However, there are two caveats to this finding: 1) model selection results suggested the presence of gender differences in students’ scores for major utility value, but our sample size (overall sample size and sample size of male students) may not have been large enough to detect a statistically significant difference using a Bonferroni-corrected alpha value; and 2) our sample size may not have been large enough to detect an interaction between time and gender, which would indicate changes in attitudes from pre to post differ between the genders. We did not collect demographic data about first/continuing-generation or race/ethnicity from students. Therefore, we recommend that additional studies examine change in affect in a broader diversity of students to more fully understand how attitudes change in different students. Moreover, we recommend examining biocalculus courses at a wide variety of institutions to understand how institutional context may influence changes in affect. For example, class size may affect instructor–student rapport, which may affect the extent to which students’ attitudes change. Studies conducted across diverse contexts with diverse students will ultimately allow for the identification of the critical elements of a biocalculus course necessary to engender positive affect toward mathematics.

Implications for Mathematics and Biology Educators

Understanding biological concepts relies on an understanding of chemistry (e.g., metabolic pathways), physics (e.g., physiological mechanisms), and mathematics (e.g., modeling communities or ecosystems), yet life science students often lack an understanding of how these disciplines are connected to biology and are less enthusiastic about taking these required courses. Our results provide empirical evidence that student attitudes toward mathematics improved after completing a course that highlighted the relevance and applicability of calculus to biology. Creating an integrated mathematics–biology course, such as a biocalculus or biostatistics course, can be one way to achieve this goal. Furthermore, a biocalculus course can contribute to the development of three of the core competencies outlined in Vision and Change ( AAAS, 2011 ) for life science students: the ability to use quantitative reasoning, the ability to use modeling and simulation, and the ability to tap into the interdisciplinary nature of science. Based on reflection as instructors, and to help guide other instructors, we suggest a focus on the following three key items to nurture positive student attitudes toward mathematics: 1) interdisciplinary curricula and conversations, 2) authentic problems for the audience, and 3) intentional metacognition interventions.

Interdisciplinary Curricula and Conversations.

For those interested in how to develop an interdisciplinary biocalculus course, we refer readers to Diaz Eaton and Highlander (2017) . However, we recognize that creating a separate biocalculus course may be beyond the scope of what most departments can do. Therefore, we recommend that both mathematics and biology instructors incorporate examples and problems into their current courses that draw upon the other discipline. Importantly, many curricula have already been developed for that purpose. The QUBES website ( www.qubeshub.org ) has a repository of quantitative biology curricular activities, and CourseSource (coursecourse.org) has quantitative activities listed under some of the learning goals in the Science Process Skills Learning Framework. Duane Nykamp at the University of Minnesota has developed freely available materials, including videos, projects, and in-class worksheets, for a flipped-format biocalculus course ( Nykamp, 2020 ). These materials have been used heavily at UP since Spring 2014. Curricular resources have also been described in a number of papers (e.g., Jungck et al. , 2010 ; Thompson et al. , 2010 ; Schultheis and Kjelvik, 2015 ; Hoffman et al. , 2016 ). However, even though we are mathematical biologists by training, our work in connecting mathematics and biology for students has been deeply enhanced by ongoing interdisciplinary conversations with our biology colleagues and vice versa ( Diaz Eaton et al. , 2019 ). To guide broad collaborative discussions between life scientists and mathematicians, we recommend the special issue “Interdisciplinary Conversations” published in Problems, Resources, and Issues in Undergraduate Mathematics Education ( Ganter et al. 2019a , b ).

Authentic and Relevant Problems.

Critically, when integrating mathematics and biology to enhance life science students’ understanding of the connection between the disciplines, thought must be given to incorporating authentic biological problems. Authentic biological problems do not just use mathematics to solve a problem situated within a biological context, but rather integrate mathematics into a biological problem in a way that allows the student to come to a greater understanding of a biological phenomenon or process ( Watkins et al. , 2012 ). Developing authentic biological problems that integrate mathematics requires expertise from both disciplines and will benefit from time invested in collaborative relationships. To guide the creation and revision of authentic problems, we recommend using the framework presented by Svoboda Gouvea and colleagues (2013) , which can be used to reflect on how the disciplines interact in the problems.

It is also important to consider how to make the problems relevant to the interests of the students. Biology students have diverse interests, ranging from cellular and molecular mechanisms to physiology and medicine to ecology and evolution. Therefore, an understanding of what specific interests the students in a class have can be used to design relevant biocalculus problems. For example, C.D.E. realized that medically oriented time-of-death problems used in the exponential growth and decay section were met with reluctant engagement by her predominantly wildlife biology–focused students. But a colleague in conservation law stopped her in the hallway one day excitedly to tell her about using the same technique and tables to discern the time of death for a deer in a suspected poaching. C.D.E. was able to share this story with the students, relating a newly revised and contextualized problem to concepts learned in other classes and touted by an expert in their desired career, and they anecdotally seemed more interested and engaged (e.g., see Geller et al. , 2018 , which supports this anecdotal evidence). Both H.C.H. and C.D.E. also reflect that conversations with junior and senior biology majors in the class can be similarly helpful in recognizing key linkages between classes and impressing upon younger students the importance of these topics.

Metacognition and Utility-Value Interventions.

Both H.C.H and C.D.E. employed metacognitive interventions at least every other week. For example, H.C.H. regularly shared relevant articles with students and asked them to reflect on the articles in their journals. In one such journal assignment, the prompt was as follows:

Read the article posted on Moodle entitled “The ‘Gift’ of Mathematics in the Era of Biology” and provide a one-paragraph summary of the article. Topics you may want to address include the following:

• What is BIO 2010? What did it urge colleges to do?
• What are some similarities they mention between math and biology?
• What was most surprising in this article?
• Were there parts of the article you didn’t understand or terms you didn’t know? If so, include these in your summary.

C.D.E. presented students with a variety of prompts to encourage reflection. For example, one prompt asked students to read excerpts of news articles and discuss how one excerpt related to the class. Interested readers can find the full set of writing prompts that C.D.E. used on QUBES ( Diaz Eaton, 2020 ).

Utility-value interventions are motivation interventions aimed specifically at boosting students’ utility value. They are relatively easy to implement; students simply write about how what they are learning in class is relevant to their lives (e.g., see Canning and Harackiewicz, 2015 ). Several studies have demonstrated the positive effect of a utility-value intervention on student interest and performance, though these effects appear to primarily occur in students with lower perceived competence (Hulleman and Harackiewicz, 2009; Hulleman et al. , 2010 ). Recent work suggests that the timing of the utility-value intervention is important to consider but that three utility-value interventions over the course of a semester, with written feedback, are ideal, because they allow students multiple opportunities to make connections between the topics and their lives ( Canning et al. , 2018 ).

Our results demonstrate that integrated biocalculus courses can improve life science students’ attitudes toward mathematics by explicitly demonstrating the relevance of mathematics to biological problems. Importantly, by the end of the course, many students had a more sophisticated understanding of how mathematics is used in the biological sciences, and their responses represented a broader perspective on the role mathematics can play in the biological sciences. Therefore, adding a biology-oriented calculus option for life science students can improve students’ understanding of the connection between the disciplines, ultimately improving student motivation for learning and their performance. Recognizing that transforming disciplinary courses into interdisciplinary courses is a significant undertaking, we recommend that instructors of both mathematics and biology courses initiate a dialogue to select and/or design problems that can be included in both types of courses, ensuring they are biologically authentic. Further research on integrated mathematics–biology courses among more diverse student populations and institutions will be invaluable for identifying the instructional and curricular aspects of integrated courses that are critical for improving student motivation and learning. Additionally, documenting longer-term outcomes of integrated mathematics–biology courses, such as how students engage with mathematics in their future courses, will be essential for understanding the extent to which these courses induce long-term change in students’ epistemological beliefs about the role of mathematics in the biological sciences.

Supplementary Material

Acknowledgments.

We thank Richard M. Schori for allowing us to modify and use the attitude survey that he originally developed. We thank Alexis White, Kieu Tran, Kenny Nguyen, and Alexander Kulacki for their assistance with data entry and analysis. We also thank Erin Bodine, Suzanne Lenhart, and Lou Gross and Princeton University Press for the use of the draft versions of their textbook, Lou Gross for feedback on an earlier draft of this paper (which was eventually split into Diaz Eaton and Highlander, 2017 , and this paper), and two anonymous reviewers for their helpful feedback.

• Adler, F. R. (2012). Modeling the dynamics of life: Calculus and probability for life scientists (3rd ed.). Pacific Grove, CA: Brooks Cole. [ Google Scholar ]
• American Association for the Advancement of Science. (2011). Vision and change in undergraduate biology education: A call to action . Washington, DC. [ Google Scholar ]
• Andrews, S. E., Aikens, M. L. (2018). Life science majors’ math-biology task values relate to student characteristics and predict the likelihood of taking quantitative biology courses . Journal of Microbiology & Biology Education , 19 ( 2 ), 1–10. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Arnett, A., Van Horn, D. (2009). Connecting mathematics and science: A learning community that helps math-phobic students . Journal of College Science Teaching , 38 ( 6 ), 30–34. [ Google Scholar ]
• Association of American Medical Colleges–Howard Hughes Medical Institute. (2009). Scientific foundations for future physicians . Washington, DC: Association of American Medical Colleges. [ Google Scholar ]
• Bartoń, K. (2018). MuMIn: Multi-model inference . Retrieved September 6, 2020 from https://CRAN.R-project.org/package=MuMIn
• Bilous, M., Serdjebi, C., Boyer, A., Tomasini, P., Pouypoudat, C., Barbolosi, D., ... & Benzekry, S. (2019). Quantitative mathematical modeling of clinical brain metastasis dynamics in non-small cell lung cancer . Scientific Reports , 9 , 13018. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Bodine, E. N., Lenhart, S., Gross, L. J. (2014). Mathematics for the life sciences . Princeton, NJ: Princeton University Press. [ Google Scholar ]
• Buceta, J., Johnson, K. (2017). Modeling the Ebola zoonotic dynamics: Interplay between enviroclimatic factors and bat ecology . PLoS ONE , 12 ( 6 ), e0179559. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Burnham, K. P., Anderson, D. R. (2002). Model selection and multimodel inference: A practical information-theoretic approach (2nd ed.). New York: Springer. [ Google Scholar ]
• Canning, E. A., Harackiewicz, J. M. (2015). Teach it, don’t preach it: The differential effects of directly-communicated and self-generated utility value information . Motivation Science , 1 ( 1 ), 47–71. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Canning, E. A., Harackiewicz, J. M., Priniski, S. J., Hecht, C. A., Tibbetts, Y., Hyde, J. S. (2018). Improving performance and retention in introductory biology with a utility-value intervention . Journal of Educational Psychology , 110 ( 6 ), 834–849. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Christensen, R. H. B. (2018). Cumulative link models for ordinal regression with the R package ordinal . Retrieved May 24, 2020, from https://cran.r-project.org/web/packages/ordinal/vignettes/clm_article.pdf
• Cole, J. S., Bergin, D. A., Whittaker, T. A. (2008). Predicting student achievement for low stakes tests with effort and task value . Contemporary Educational Psychology , 33 ( 4 ), 609–624. [ Google Scholar ]
• Comar, T. D. (2013). Biocalculus at Benedictine University . In Ledder, G., Carpenter, J. P., Comar, T. D. (Eds.), Undergraduate mathematics for the life sciences: Models, processes, and directions (pp. 17–24). Washington, DC: Mathematical Association of America. [ Google Scholar ]
• Crouch, C. H., Wisittanawat, P., Cai, M., Renninger, K. A. (2018). Life science students’ attitudes, interest, and performance in introductory physics for life science: An exploratory study . Physical Review Physics Education Research , 14 ( 1 ), 10111. [ Google Scholar ]
• Diaz Eaton, C. (2020). Biocalculus writing reflection prompts. Calculus, QUBES Educational Resources . 10.25334/TGCH-TZ24 [ CrossRef ]
• Diaz Eaton, C., Highlander, H. (2017). The case for biocalculus: Design, retention, and student performance . CBE—Life Sciences Education , 16 ( 2 ), ar25. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Diaz Eaton, C., Highlander, H. C., Dahlquist, K. D., Ledder, G., LaMar, M. D., Schugart, R. C. (2019). A “rule-of-five” framework for models and modeling to unify mathematicians and biologists and improve student learning . PRIMUS , 29 ( 8 ), 799–829. [ Google Scholar ]
• Diaz Eaton, C., Wade, S. (2014). Collaborative learning through formative peer review with technology . PRIMUS , 24 ( 6 ), 529–543. [ Google Scholar ]
• Durik, A. M., Shechter, O. G., Noh, M., Rozek, C. S., Harackiewicz, J. M. (2015). What if I can’t? Success expectancies moderate the effects of utility value information on situational interest and performance . Motivation and Emotion , 39 ( 1 ), 104–118. [ Google Scholar ]
• Durik, A. M., Vida, M., Eccles, J. S. (2006). Task values and ability beliefs as predictors of high school literacy choices: A developmental analysis . Journal of Educational Psychology , 98 ( 2 ), 382–393. [ Google Scholar ]
• Eccles, J., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J. L., Midgley, C. (1983). Expectancies, values, and academic behaviors . In Spence, J. T. (Ed.), Achievement and achievement approaches (pp. 74–146). San Francisco, CA: Freeman. [ Google Scholar ]
• Ellner, S. P., Rees, M. (2006). Integral projection models for species with complex demography . American Naturalist , 167 ( 3 ), 410–428. [ PubMed ] [ Google Scholar ]
• Frisby, B. N., Housley Gaffney, A. L. (2015). Understanding the role of instructor rapport in the college classroom . Communication Research Reports , 32 ( 4 ), 340–346. [ Google Scholar ]
• Frisby, B. N., Martin, M. M. (2010). Instructor-student and student-student rapport in the classroom . Communication Education , 59 ( 2 ), 146–164. [ Google Scholar ]
• Ganter, S., Hofrenning, S., Diaz Eaton, C., Piercey, V. (Eds.). (2019a). Interdisciplinary Conversations (Part 1): Models for Interdisciplinary Conversations [Special Issue] . Problems, Resources, and Issues in Undergraduate Mathematics Education , 29 ( 8 ). [ Google Scholar ]
• Ganter, S., Hofrenning, S., Diaz Eaton, C., Piercey, V. (Eds.). (2019b). Special Issue on Interdisciplinary Conversations (Part 2): The Impact of Interdisciplinary Conversations on Courses [Special Issue] . Problems, Resources, and Issues in Undergraduate Mathematics Education , 29 ( 9 ). [ Google Scholar ]
• Gaspard, H., Dicke, A.-L., Flunger, B., Schreier, B., Hafner, I., Trautwein, U., Nagenregast, B. (2015). More value through greater differentiation: Gender differences in value beliefs about math . Journal of Educational Psychology , 107 ( 3 ), 663–677. [ Google Scholar ]
• Geller, B. D., Turpen, C., Crouch, C. H. (2018). Sources of student engagement in Introductory Physics for Life Sciences . Physical Review Physics Education Research , 14 ( 1 ), 010118. [ Google Scholar ]
• Gick, M. L., Holyoak, K. J. (1983). Schema induction and analogical transfer . Cognitive Psychology , 15 , 1–38. [ Google Scholar ]
• Harackiewicz, J. M., Barron, K. E., Tauer, J. M., Elliot, A. J. (2002). Predicting success in college: A longitudinal study of achievement goals and ability measures as predictors of interest and performance from freshman year through graduation . Journal of Educational Psychology , 94 ( 3 ), 562–575. [ Google Scholar ]
• Harackiewicz, J. M., Canning, E. A., Tibbetts, Y., Priniski, S. J., Hyde, J. S. (2016). Closing achievement gaps with a utility-value intervention: Disentangling race and social class . Journal of Personality and Social Psychology , 111 ( 5 ), 745–746. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Harackiewicz, J. M., Hulleman, C. S. (2010). The importance of interest: The role of achievement goals and task values in promoting the development of interest . Social and Personality Psychology Compass , 4 ( 1 ), 42–52. [ Google Scholar ]
• Hidi, S., Renninger, K. A. (2006). The four-phase model of interest development . Educational Psychologist , 41 ( 2 ), 111–127. [ Google Scholar ]
• Hoffman, K., Leupen, S., Dowell, K., Kephart, K., Leips, J. (2016). Development and assessment of modules to integrate quantitative skills in introductory biology courses . CBE—Life Sciences Education , 15 ( 2 ), ar14. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Holley, J. W., Guilford, J. P. (1964). A note on the G index of agreement . Educational and Psychological Measurement , 24 ( 4 ), 749–753. [ Google Scholar ]
• Hulleman, C. S., Durik, A. M., Schweigert, S. A., Harackiewicz, J. M. (2008). Task values, achievement goals, and interest: An integrative analysis . Journal of Educational Psychology , 100 ( 2 ), 398–416. [ Google Scholar ]
• Hulleman, C. S., Godes, O., Hendricks, B. L., Harackiewicz, J. M. (2010). Enhancing interest and performance with a utility value intervention . Journal of Educational Psychology , 102 ( 4 ), 880–895. [ Google Scholar ]
• Hulleman, C. S., Harackiewicz, J. M. (2009). Promoting interest and performance in high school science classes . Science , 326 ( 5958 ), 1410–1412. [ PubMed ] [ Google Scholar ]
• Jungck, J. R., Gaff, H., Weisstein, A. E. (2010). Mathematical manipulative models: In defense of “beanbag biology.” CBE—Life Sciences Education , 9 ( 3 ), 201–211. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Karsai, I., Thompson, K. V., Nelson, K. C. (2015). Modelling and simulation: Helping students acquire this skill using a Stock and Flow approach with MathBench . Letters in Biomathematics , 2 ( 1 ), 1–12. [ Google Scholar ]
• Ma, X., Kishor, N. (1997). Assessing the relationship between attitude toward mathematics and achievement in mathematics: A meta-analysis . Journal for Research in Mathematics Education , 28 ( 1 ), 26–47. [ Google Scholar ]
• Matthews, K. E., Adams, P., Goos, M. (2010). Using the principles of BIO2010 to develop an introductory, interdisciplinary course for biology students . CBE—Life Sciences Education , 9 ( 3 ), 290–297. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Mehrabian, A. (1971). Silent messages . Belmont, CA: Wadsworth. [ Google Scholar ]
• Meredith, D. C., Bolker, J. A. (2012). Rounding off the cow: Challenges and successes in an interdisciplinary physics course for life science students . American Journal of Physics , 80 ( 10 ), 913–922. [ Google Scholar ]
• National Research Council (NRC). (2000). How people learn: Brain, mind, experience and school (expanded ed.). Washington, DC: National Academies Press. [ Google Scholar ]
• NRC. (2003). BIO2010: Transforming undergraduate education for future research biologists . Washington, DC: National Academies Press. [ PubMed ] [ Google Scholar ]
• Neuhauser, C., Roper, M. (2018). Calculus for biology and medicine (4th ed.). Upper Saddle River, NJ: Pearson. [ Google Scholar ]
• Nykamp, D. (2020). Math Insight: Math 1241, Calculus and Dynamical Systems in Biology . Retrieved June 8, 2020, from https://mathinsight.org/thread/math1241
• R Core Team. (2018). R: A language and environment for statistical computing . Vienna, Austria: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org [ Google Scholar ]
• Rodriguez, J. I., Plax, T. G., Kearney, P. (1996). Clarifying the relationship between teacher nonverbal immediacy and student cognitive learning: Affective learning as the central causal mediator . Communication Education , 45 ( 4 ), 293–305. [ Google Scholar ]
• Saldaña, J. (2016). The coding manual for qualitative researchers (3rd ed.). Thousand Oaks, CA: Sage. [ Google Scholar ]
• Schiefele, U., Krapp, A., Winteler, A. (1992). Interest as a predictor of academic achievement: A meta-analysis of research . In Renninger, K. A., Hidi, S., Krapp, A. (Eds.), The role of interest in learning and development (pp. 183–212). Hillsdale, NJ: Erlbaum. [ Google Scholar ]
• Schori, R. (2015). Mathematics Attitude Survey . Retrieved March 25, 2015, from http://people.oregonstate.edu/∼schorir/ocept
• Schultheis, E. H., Kjelvik, M. K. (2015). Data Nuggets: Bringing real data into the classroom to unearth students’ quantitative and inquiry skills . American Biology Teacher , 77 ( 1 ), 19–29. [ Google Scholar ]
• Shadish, W. R., Cook, T. D., Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference . Belmont, CA: Wadsworth Cengage Learning. [ Google Scholar ]
• Simpkins, S. D., Davis-Kean, P. E., Eccles, J. S. (2006). Math and science motivation: A longitudinal examination of the links between choices and beliefs . Developmental Psychology , 42 ( 1 ), 70–83. [ PubMed ] [ Google Scholar ]
• Steen, L. A. (2005). Math & Bio 2010: Linking undergraduate disciplines . Washington, DC: Mathematical Association of America. [ Google Scholar ]
• Svoboda Gouvea, J., Sawtelle, V., Geller, B. D., Turpen, C. (2013). A framework for analyzing interdisciplinary tasks: Implications for student learning and curricular design . CBE—Life Sciences Education , 12 ( 2 ), 187–205. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Theobald, E. (2018). Students are rarely independent: When, why, and how to use random effects in discipline-based education research . CBE—Life Sciences Education , 17 ( 3 ), rm2. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Theobald, E. J., Aikens, M., Eddy, S., Jordt, H. (2019). Beyond linear regression: A reference for analyzing common data types in discipline based education research . Physics Review Physics Education Research , 15 , 020110. [ Google Scholar ]
• Thompson, K. V., Nelson, K. C., Marbach-Ad, G., Keller, M., Fagan, W. F. (2010). Online interactive teaching modules enhance quantitative proficiency of introductory biology students . CBE—Life Sciences Education , 9 ( 3 ), 277–283. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Uhl, J., Holdener, J. (2013). BioCalc at Illinois . In Ledder, G., Carpenter, J. P., Comar, T. D. (Eds.), Undergraduate mathematics for the life sciences: Models, processes, and directions (pp. 5–15). Washington, DC: Mathematical Association of America. [ Google Scholar ]
• Watkins, J., Coffey, J. E., Redish, E. F., Cooke, T. J. (2012). Disciplinary authenticity: Enriching the reforms of introductory physics courses for life-science students . Physical Review Special Topics—Physics Education Research , 8 ( 1 ), 010112. [ Google Scholar ]
• Wigfield, A., Eccles, J. S. (2000). Expectancy–value theory of achievement motivation . Contemporary Educational Psychology , 25 , 68–81. [ PubMed ] [ Google Scholar ]
• Wilkins, J. L., Ma, X. (2003). Modeling change in student attitude toward and beliefs about mathematics . Journal of Educational Research , 97 ( 1 ), 52–63. [ Google Scholar ]
• Wilson, J. H., Ryan, R. G., Pugh, J. L. (2010). Professor-student rapport scale predicts student outcomes . Teaching of Psychology , 37 ( 4 ), 246–251. [ Google Scholar ]
• Witt, P. L., Wheeless, L. R., Allen, M. (2004). A meta-analytical review of the relationship between teacher immediacy and student learning . Communication Monographs , 71 ( 2 ), 184–207. [ Google Scholar ]
• Xu, S., Lorber, M. F. (2014). Interrater agreement statistics with skewed data: Evaluation of alternatives to Cohen’s kappa . Journal of Consulting and Clinical Psychology , 82 ( 6 ), 1219–1227. [ PubMed ] [ Google Scholar ]
• Zusho, A., Pintrich, P. R., Coppola, B. (2003). Skill and will: The role of motivation and cognition in the learning of college chemistry . International Journal of Science Education , 25 ( 9 ), 1081–1094. [ Google Scholar ]

Change Password

Your password must have 8 characters or more and contain 3 of the following:.

• a lower case character, 
• an upper case character, 
• a special character 

Password Changed Successfully

Your password has been changed

• Sign in / Register

Request Username

Can't sign in? Forgot your username?

Enter your email address below and we will send you your username

If the address matches an existing account you will receive an email with instructions to retrieve your username

Successful Problem Solving in Genetics Varies Based on Question Content

• Jennifer S. Avena
• Betsy B. McIntosh
• Oscar N. Whitney
• Ashton Wiens
• Jennifer K. Knight

Department of Molecular, Cellular, and Developmental Biology

School of Education, University of Colorado Boulder, Boulder, CO 80309

Search for more papers by this author

Department of Applied Mathematics, University of Colorado Boulder, Boulder, CO 80309

*Address correspondence to: Jennifer Knight ( E-mail Address: [email protected] ).

Problem solving is a critical skill in many disciplines but is often a challenge for students to learn. To examine the processes both students and experts undertake to solve constructed-response problems in genetics, we collected the written step-by-step procedures individuals used to solve problems in four different content areas. We developed a set of codes to describe each cognitive and metacognitive process and then used these codes to describe more than 1800 student and 149 expert answers. We found that students used some processes differently depending on the content of the question, but reasoning was consistently predictive of successful problem solving across all content areas. We also confirmed previous findings that the metacognitive processes of planning and checking were more common in expert answers than student answers. We provide suggestions for instructors on how to highlight key procedures based on each specific genetics content area that can help students learn the skill of problem solving.

INTRODUCTION

The science skills of designing and interpreting experiments, constructing arguments, and solving complex problems have been repeatedly called out as critical for undergraduate biology students to master ( American Association for the Advancement of Science, 2011 ). Yet each of these skills remains elusive for many students, particularly when the skill requires integrating and evaluating multiple pieces of information ( Novick and Bassok, 2005 ; Bassok and Novick, 2012 ; National Research Council, 2012 ). In this paper, we focus on describing the steps students and experts take while solving genetics problems and determining whether the use of certain processes increases the likelihood of success.

The general process of solving a problem has been described as building a mental model in which prior knowledge can be used to represent ways of thinking through a problem state ( Johnson-Laird, 2010 ). Processes used in problem solving have historically been broken down into two components: those that use domain-general knowledge and those that use domain-specific knowledge. Domain-general knowledge is defined as information that can be used to solve a problem in any field, including such strategies as rereading and identifying what a question is asking ( Alexander and Judy, 1988 ; Prevost and Lemons, 2016 ). Although such steps are important, they are unlikely to be the primary determinants of success when specific content knowledge is required. Domain-specific problem solving, on the other hand, is a theoretical framework that considers one’s discipline-specific knowledge and processes used to solve a problem (e.g., Prevost and Lemons, 2016 ). Domain-specific knowledge includes declarative (knowledge of content), procedural (how to utilize certain strategies), and conditional knowledge (when and why to utilize certain strategies) as they relate to a specific discipline ( Alexander and Judy, 1988 ; Schraw and Dennison, 1994 ; Prevost and Lemons, 2016 ).

Previous studies on problem solving within a discipline have emphasized the importance of domain-specific declarative and conditional knowledge, as students need to understand and be able to apply relevant content knowledge to successfully solve problems ( Alexander et al. , 1989 ; Alexander and Judy, 1988 ; Prevost and Lemons, 2016 ). Our prior work ( Avena and Knight 2019 ) also supported this necessity. After students solved a genetics problem within a content area, they were offered a content hint on a subsequent content-matched question. We found that content hints improved performance overall for students who initially did not understand a concept. In characterizing the students’ responses, we found that the students who benefited from the hint typically used the content language of the hint in their solution. However, we also found that some students who continued to struggle included the content language of the hint but did not use the information in their problem solutions. For example, in solving problems on predicted recombination frequency for linked genes, an incorrect solution might use the correct terms of map units and/or recombination frequency but not actually use map units to solve the problem. Thus, these findings suggest that declarative knowledge is necessary but not sufficient for complex problem solving and also emphasize the importance of procedural knowledge, which includes the “logic” of generating a solution ( Avena and Knight, 2019 ). By definition, procedural knowledge uses both cognitive processes, such as providing reasoning for a claim or executing a task, and metacognitive processes, such as planning how to solve a problem and checking (i.e., evaluating) one’s work (e.g., Kuhn and Udell, 2003 ; Meijer et al. , 2006 ; Tanner, 2012 ). We explore these processes in more detail below.

Cognitive Processing: Reasoning

Generating reasoning requires using one’s knowledge to search for and explain an appropriate set of ideas to support or refute a given model ( Johnson-Laird, 2010 ), so reasoning is likely to be a critical component of solving problems. Toulmin’s original scheme for building a scientific argument ( Toulmin, 1958 ) included generating a claim, identifying supporting evidence, and then using reasoning (warrant) to connect the evidence to the claim. Several studies have demonstrated a positive relationship between general reasoning “ability” ( Lawson, 1978 ), defined as the ability to construct logical links between evidence and conclusions using conceptual principles, and performance ( Cavallo, 1996 ; Cavallo et al. , 2004 ; Johnson and Lawson, 1998 ). As elaborated in more recent literature, there are many specific subcategories of reasoning. Students commonly use memorized patterns or formulas to solve problems: this approach is considered algorithmic and could be used to provide logic for a problem ( Jonsson et al. , 2014 ; Nyachwaya et al. , 2014 ). Such algorithmic reasoning may be used with or without conveying an understanding of how an algorithm is used ( Frey et al. , 2020 ). When an algorithm is not appropriate (or not used) in describing one’s reasoning, but instead the solver provides a generalized explanation of underlying connections, this is sometimes referred to as “explanatory” or “causal” reasoning ( Russ et al. , 2008 ). Distinct from causal reasoning is the domain-specific form of mechanistic reasoning, in which a mechanism of action of a biological principle is elaborated ( Russ et al. , 2008 ; Southard et al. , 2016 ). Another common form of reasoning is quantitative reasoning, which can also be described as statistical or, in other specialized situations, graph-construction reasoning (e.g., Deane et al. , 2016 ; Angra and Gardner, 2018 ). The detailed studies of these specific subcategories of reasoning have usually involved extensive interviews with students and/or very specific guidelines that prompt the use of a particular type of reasoning. Those who have explored students’ unprompted general use of reasoning have found that few students naturally use reasoning to support their ideas ( Zohar and Nemet, 2002 ; James and Willoughby, 2011 ; Schen, 2012 ; Knight et al. , 2015 ; Paine and Knight, 2020 ). However, with explicit training to integrate their knowledge into mental models ( Kuhn and Udell, 2003 ; Osborne, 2010 ) or with repeated cueing from instructors ( Russ et al. , 2008 ; Knight et al. , 2015 ), students can learn to generate more frequent, specific, and robust reasoning.

Metacognitive Processing

Successfully generating possible solutions to problems likely also involves metacognitive thinking . Metacognition is often separated into two components: metacognitive knowledge (knowledge about one’s own understanding and learning) and metacognitive regulation (the ability to change one’s approach to learning; Flavell, 1979 ; Jacobs and Paris, 1987 ; Schraw and Moshman, 1995 ). Metacognitive regulation is usually defined as including such processes as planning, monitoring one’s progress, and evaluating or checking an answer ( Flavell, 1979 ; Jacobs and Paris, 1987 ; Schraw and Moshman, 1995 ; Tanner, 2012 ). Several studies have shown that helping students use metacognitive strategies can benefit learning. For example, encouraging the planning of a possible solution beforehand and checking one’s work afterward helps students generate correct answers during problem solving (e.g., Mevarech and Amrany, 2008 ; McDonnell and Mullally, 2016 ; Stanton et al. , 2015 ). However, especially compared with experts, students rarely use metacognitive processes, despite their value ( Smith and Good, 1984 ; Smith, 1988 ). Experts spend more time orienting, planning, and gathering information before solving a problem than do students, suggesting that experts can link processes that facilitate generating a solution with their underlying content knowledge ( Atman et al. , 2007 ; Peffer and Ramezani, 2019 ). Experts also check their problem-solving steps and solutions before committing to an answer, steps not always seen in student responses ( Smith and Good, 1984 ; Smith, 1988 ). Ultimately, prior work suggests that, even when students understand content and employ appropriate cognitive processes, they may still struggle to solve problems that require reflective and regulative skills.

Theoretical Framework: Approaches to Learning

Developing domain-specific conceptual knowledge requires integrating prior knowledge and new disciplinary knowledge ( Schraw and Dennison, 1994 ). In generating conceptual knowledge, students construct mental models in which they link concepts together to generate a deeper understanding ( Johnson-Laird, 2001 ). These mental constructions involve imagining possible relationships and generating deductions and can be externalized into drawn or written models for communicating ideas ( Chin and Brown, 2000 ; Bennett et al. , 2020 ). Mental models can also trigger students to explain their ideas to themselves (self-explanation), which can also help them solve problems ( Chi et al. , 1989 ).

As our goal is to make visible how students grapple with their knowledge during problem solving, we fit this study into the approaches to learning framework (AtL: Chin and Brown, 2000 ). This framework, derived from detailed interviews of middle-school students solving chemistry problems, defines five elements of how students approach learning and suggests that these components promote deeper learning. Three of these elements are identifiable in the current study: engaging in explanations (employing reasoning through understanding and describing relationships and mechanisms), using generative thinking (application of prior knowledge and analogical transfer), and engaging in metacognitive activity (monitoring progress and modifying approaches). The remaining two elements: question asking (focusing on facts or on understanding) and depth of approaching tasks (taking a deep or a surface approach to learning: Biggs, 1987 ) could not be addressed in our study. However, previous studies showed that students who engage in a deep approach to learning also relate new information to prior knowledge and engage in reasoning (explanations), generate theories for how things work (generative thinking), and reflect on their understanding (metacognitive activity). In contrast, those who engage in surface approaches focus more on memorized, isolated facts than on constructing mental or actual models, demonstrating an absence of the three elements described by this framework. Biggs (1987) also previously provided evidence that intrinsically motivated learners tended to use a deep approach, while those who were extrinsically motivated (e.g., by grades), tended to use a surface approach. Because solving complex problems is, at its core, about how students engage in the learning process, these AtL components helped us frame how students’ learning is revealed by their own descriptions of their thinking processes.

Characterizing Problem-Solving Processes

Thus far, a handful of studies have investigated the processes adult students use in solving biology problems, and how these processes might influence their ability to develop reasonable answers ( Smith and Good, 1984 ; Smith, 1988 ; Nehm, 2010 ; Nehm and Ridgway, 2011 ; Novick and Catley, 2013 ; Prevost and Lemons, 2016 ; Sung et al. , 2020 ). In one study, Prevost and Lemons (2016) collected and analyzed students’ written documentation of their problem-solving procedures when answering multiple-choice questions. Students were taught to document their step-by-step thinking as they answered multiple-choice exam questions that ranged from Bloom’s levels 2 to 4 (understand to analyze; Bloom et al. , 1956 ), describing the steps they took to answer each question. The authors’ qualitative analyses of students’ documented problem solving showed that students frequently used domain-general test-taking skills, such as comparing the language of different multiple-choice distractors. However, students who correctly answered questions tended to use more domain-specific procedures that required knowledge of the discipline, such as analyzing visual representations and making predictions, than unsuccessful students. When students solved problems that required the higher-order cognitive skills of application and analysis, they also used more of these specific procedures than when solving lower-level questions. Another recent study explored how students solved exam questions on the genetic topics of recombination and nondisjunction through in-depth clinical interviews ( Sung et al. , 2020 ). These authors described two approaches that are not conceptual: using algorithms to bypass conceptual thinking and using non–biology specific test-taking strategies (e.g., length of answer, specificity of terminology). They also showed that students sometimes alternate between using an algorithm and a conceptual strategy, defaulting to the algorithm when they do not understand the underlying biological concept.

Research Question 1. How do experts and students differ in their description of problem-solving processes, using a much larger sample size than found in the previous literature (e.g., Chi et al. , 1981 ; Smith and Good, 1984 ; Smith, 1988 ; Atman et al. , 2007 ; Peffer and Ramezani, 2019 ).

Research Question 2. Are certain problem-solving processes more likely to be used in correct than in incorrect student answers?

Research Question 3. Do problem-solving processes differ based on content and are certain combinations of problem-solving processes associated with correct student answers for each content area?

Mixed-Methods Approach

This study used a mixed-methods approach, combining both qualitative and quantitative research methods and analysis to understand a phenomenon more deeply ( Johnson et al. , 2007 ). Our goal was to make student thinking visible by collecting written documentation of student approaches to solving problems (qualitative data), in addition to capturing answer correctness (quantitative data), and integrating these together in our analyses. The student responses serve as a rich and detailed data set that can be interpreted using the qualitative process of assigning themes or codes to student writing ( Hammer and Berland, 2014 ). In a qualitative study, the results of the coding process are unpacked using examples and detailed descriptions to communicate the findings. In this study, we share such qualitative results but also convert the coded results into numerical representations to demonstrate patterns and trends captured in the data. This is particularly useful in a large-scale study, because the output can be analyzed statistically to allow comparisons between categories of student answers and different content areas.

Students in this study were enrolled in an introductory-level undergraduate genetics course for biology majors at the University of Colorado in Spring 2017 ( n = 416). This course is the second in a two-course introductory series, with the first course being Introduction to Cell and Molecular Biology. The students were majority white, 60% female, and 63% were in their first or second year. Ninety percent of the students were majoring in biology or a biology-related field (neuroscience, integrative physiology, biochemistry, biomedical engineering). Of the students enrolled in the course, 295 students consented to be included in the study; some of the student responses have been previously described in the prior study ( Avena and Knight, 2019 ). We recruited experts from the Society for the Advancement of Biology Education Research Listserv by inviting graduate students, postdoctoral fellows, and faculty to complete an anonymous online survey consisting of the same questions that students answered. Of the responses received, we analyzed responses from 52 experts. Due to the anonymous nature of the survey, we did not collect descriptive data about the experts.

Problem Solving

As part of normal course work, students were offered two practice assignments covering four content areas related to each of two course exams (also described in Avena and Knight, 2019 ). Students could answer up to nine questions in blocks of three questions each, in randomized order, for three of the four content areas. Expert participants answered a series of four questions, one in each of the four content areas. All questions were offered online using the survey platform Qualtrics. All participants were asked to document their problem-solving processes as they completed the questions (as in Prevost and Lemons 2016 ), and they were provided with written instructions and an example in the online platform only (see Supplemental Material); no instructions were provided in class, and no explicit discussion of types of problem-solving processes to use were provided in class throughout the semester. Students could receive extra credit up to ∼1% of the course point total, obtaining two-thirds credit for explaining their answer and an additional one-third if they answered correctly. All students who completed the assignment received credit regardless of their consent to participate in the research.

We used questions developed for a prior study ( Avena and Knight, 2019 ) on four challenging genetics topics: calculation of the probability of inheritance across multiple generations (Probability), prediction of the cause of an incorrect chromosome number after meiosis (Nondisjunction), interpretation of a gel and pedigree to determine inheritance patterns (Gel/Pedigree), and prediction of the probability of an offspring’s genotype using linked genes (Recombination; see example in Figure 1 ; all questions presented in Supplemental Material). These content areas have previously been shown to be challenging based on student performance ( Smith et al. , 2008 ; Smith and Knight, 2012 ; Avena and Knight, 2019 ). Each content area contained three isomorphic questions that addressed the same underlying concept, targeted higher-order cognitive processes ( Bloom et al. , 1956 ), and contained the same amount of information with a visual ( Avena and Knight, 2019 ). Each question had a single correct answer and was coded as correct (1) or incorrect (0). For each problem-solving assignment, we randomized 1) the order of the three questions within each content area for each student and 2) the order in which each content area was presented. During each set of three isomorphic questions, while solving one of the isomorphic problems, students also had the option to receive a “content hint,” a single most commonly misunderstood fact for each content area. We do not discuss the effects of the content hints in this paper (instead, see Avena and Knight, 2019 ).

FIGURE 1. Sample problem for students from the Gel/Pedigree content area. Problems in each content area contain a written prompt and an illustrated image, as shown in this example.

Process Coding

Students may engage in processes that they do not document in writing, but we are limited to analyzing only what they do provide in their written step-by-step descriptions. For simplicity, throughout this paper, a “process” is a thought documented by the participant that is coded as a particular process. When we refer to “failure” to use a process, we mean that a participant did not describe this thought process in the answer. Our initial analysis of student processes used a selection of codes from Prevost and Lemons (2016) and Toulmin’s ( 1958 ) original codes of Claim and Reason. We note that all the problems we used can potentially be solved using algorithms, memorized patterns previously discussed and practiced in the class, which may have limited the reasoning students supplied. Because of the complexity of identifying different types of reasoning, we did not further subcategorize the reasoning category in the scheme we present, as this is beyond the scope of this paper. We used an emergent coding process ( Saldana, 2015 ) to identify additional and different processes, including both cognitive and metacognitive actions. Thus, our problem-solving processes (PsP) coding scheme captures the thinking that students document while solving genetics problems (see individual process codes in Table 1 ). We used HyperRESEARCH software (ResearchWare, Inc.) to code each individual’s documented step-by-step processes. A step was typically a sentence and sometimes contained multiple ideas. Each step was given one or more codes, with the exception of reasoning supporting a final conclusion (see Table 2 for examples of coded responses). Each individual process code captures when the student describes that process, regardless of whether the statement is correct or incorrect. Four raters (J.K.K., J.S.A., O.N.W., B.B.M.) coded a total of 24 student answers over three rounds of coding and discussion to reach consensus and identify a final coding scheme. Following agreement on the codes, an additional 12 answers were coded by the four raters to determine interrater agreement. Specifically, in these 12 answers, there were 150 instances in which a code for a step was provided by one or more raters. For each of these 150 instances, we identified the number of raters who agreed. We then calculated a final interrater agreement of 83% by dividing the total number of raters who agreed for all 150 instances (i.e., 524) by the total number of possible raters to agree for four raters in 150 instances (i.e., 600). We excluded answers in which students did not describe their problem-solving steps and those in which students primarily or exclusively used domain-general processes (i.e., individual process codes within the General strategy category in Table 1 ) or made claims without any other supporting codes. The latter two exclusion criteria were used because such responses lacked sufficient description to identify the thought processes. The final data set included a total of 1853 answers from 295 students and 149 answers from 52 experts. We used only correct answers from experts to serve as a comparison to student answers, excluding an additional 29 expert answers that were incorrect.

aExamples of student responses are to a variety of content areas and have been edited for clarity. Each individual process code captures the student’s description, regardless of whether the statement is correct or incorrect.

aThe responses above are all solutions to the question in Figure 1 .

After initial coding and analyses, we identified that student use of drawing was differentially associated with correctness based on content area. Thus, to further characterize drawing use, two raters (J.S.A. and J.K.K.) explored incorrect student answers from Probability and Recombination. One rater examined 33 student answers to identify an initial characterization, and then two raters reviewed a subset of answers to agree upon a final scheme. Each rater then individually categorized a portion of the student answers, and the final interrater agreement on 10 student answers was 90%. Interrater agreement was calculated as described earlier, with each answer serving as one instance, so we divided the total number of raters agreeing for each answer (i.e., 18) by the total possible number of raters agreeing (i.e., 20).

Statistical Analyses

The unit of analysis for all models considered is an individual answer to a problem. We investigate three variations of linear models, specified below. The response variable in all cases is binary (presence/absence of process or correct/incorrect answer). Thus, the models are generalized linear models, and, more specifically, logistic regression models. Because our data contain repeated measures in the form of multiple answers per student, we specifically use generalized linear mixed models (GLMM) to include a random effect on the intercept term in all models, grouped by participant identifier ( Gelman and Hill, 2006 ; Theobald, 2018 ). This component of the model accounts for variability in the baseline outcome between participants. In our case, we can model each student’s baseline probability of answering a problem correctly or each participant’s baseline probability of using a given process (e.g., one student may use Reason more frequently than another student). Accounting for this variation yields better estimates of the fixed effects in the models.

The fitted models give some, but not all, pairwise comparisons among predictor groups. We conducted pairwise post hoc comparisons (e.g., expert vs. correct student, expert vs. incorrect student, correct student vs. incorrect student, or among the four content areas) to draw inferences about the differences among all groups. In particular, we performed Tukey pairwise honestly significant difference (HSD) tests for all pairs of groups, comparing estimated marginal means (estimated using the fitted model) on the logit scale. Using estimated marginal means corrects for unbalanced group sample sizes, and using the Tukey HSD test provides adjusted p values, facilitating comparison to a significance level of α = 0.05.

To ease reproducibility, we use “formula” notation conventionally used in R to specify the models we employ in this paper, which has the following general form: outcome = fixed effect + (1 | group). The random effects component is specified within parentheses, with the random effect on the left of the vertical bar and the grouping variable on the right.

Process present = Expert/Student answer status + (1| ID)

Process present = Content area + (1| ID)

where “Process present” is the response variable as described for model 1; “Content area” is the fixed effect: Factor-level grouping: Probability (1)/Nondisjunction (2)/Gel-Pedigree (3)/Recombination (4); and “(1|ID)” is the random effect as described for model 1.

Student answer correctness = Process 1 + Process 2 + … + Process X + (1| ID)

where “Student answer correctness” is the response variable: incorrect (0)/correct (1); “Process 1 + Process 2 + … + Process X” is the list of process factors entered into the model as the fixed effect: absent (0)/present (1); and “(1|ID)” is the random effect as described for models 1 and 2. We identified which components were associated with correctness by seeing which predictor coefficients remained non-zero in a representative lasso model. We identified a representative model for each content area by first identifying the lasso penalty with the lowest Akaike information criterion (AIC) to reduce variance and then identifying a lasso penalty with a similar AIC that could be used across all content areas. Because a penalty parameter of 25 and the penalty parameter with the lowest AIC for each content area had similar AIC values, we consistently used a penalty parameter of 25. Note that when the penalty parameter is set to zero, the GLMM model is recovered. On the other hand, when the penalty parameter is very large, no predictors are included in the model. Thus, the selected penalty parameter forced many, but not all, coefficients to 0, giving a single representative model for each content area.

All models and tests were performed in R (v. 3.5.1). We used the lme4 package in R ( Bates et al. , 2015 ) for models 1 and 2, and estimation of parameters was performed using residual maximum likelihood. For model 3, we used the glmmLasso package, and the model was fit using the default EM-type estimate. Post hoc pairwise comparisons were performed using the emmeans package.

Human Subjects Approval

Human research was approved by the University of Colorado Institutional Review Board (protocols 16-0511 and 15-0380).

The PsP Coding Scheme Helps Describe Written Cognitive and Metacognitive Processes

We developed a detailed set of codes, which we call the PsP scheme to characterize how individuals describe their solutions to complex genetics problems. Table 1 shows the 18 unique processes along with descriptions and examples for each. With the support of previous literature, we grouped the individual processes into seven strategies, also shown in Table 1 . All strategies characterized in this study were domain specific except the General category, which is domain general. We categorized a set of processes as Orientation based on a previously published taxonomy for think-aloud interviews ( Meijer et al. , 2006 ) and on information management processes from the Metacognitive Awareness Inventory ( Schraw and Dennison, 1994 ). Orienting processes include: Notice (identifying important information in the problem), Recall (activating prior knowledge without applying it), Identify Similarity (among question types), and Identify Concept (the “type” of problem). Orientation processes are relatively surface level, in that information is observed and noted, but not acted on. The Metacognition category includes the three common elements of planning (Plan), monitoring (Assess Difficulty), and evaluating (Check) cited in the metacognitive literature (e.g., Schraw and Moshman, 1995 ; Tanner, 2012 ). The Execution strategy includes actions taken to explicitly solve the problem, including Use Information (apply information related to the problem), Integrate (i.e., linking together two visual representations provided to solve the problem or linking a student’s own drawing to information in the problem), Draw, and Calculate. The Use Information category is distinguished from Recall by a student applying a piece of information (Use Information) rather than just remembering a fact without directly using it in the problem solution (Recall). Students may Recall and then Use Information, just Recall, or just Use Information. If a student used the Integrate process, Use Information was not also coded (i.e., Integrate supersedes Use Information). The Reasoning strategy includes just one general process of Reason, which we define as providing an explanation or rationale for a claim, as previously described in Knight et al. (2013) , Lawson (2010) , and Toulmin (1958) . The Conclusion strategy includes Eliminate and Claim, processes that provide types of responses to address the final answer. The single process within the Error strategy category, Misinterpret, characterizes steps in which students misunderstand the question stem. Finally, the General category includes the codes Clarify, State the Process, and Restate, all of which are generic statements of execution, representing processes that are domain general ( Alexander and Judy, 1988 ; Prevost and Lemons, 2016 ).

To help visualize the series of steps students took and how these steps differed across answers and content areas, we provide detailed examples in Tables 2 and 3 . In Table 2 , we provide three examples of similar-length documented processes to the same Gel/Pedigree problem ( Figure 1 ) from a correct expert, a correct student, and an incorrect student. Note the multiple uses of planning and reasoning in the expert answer, multiple uses of reasoning in the correct student answer, and the absence of both such processes in the incorrect student answer. The reasoning used in each case provides a logical explanation for the claim, which either immediately precedes or follows the reasoning statement. For example, in the second incident of Claim and Reason for Eliot, “because otherwise Zach could not be unaffected” is a logical explanation for the claim “it has to be dominant.” Similarly, for Cassie’s Claim and Reason code, “If both parents are heterozygous for the disease” is a logical explanation for the claim “it is probably inherited in a dominant manner.” Table 3 provides additional examples of correct student answers to the remaining three content areas. Note that for Probability and Recombination questions, the Reason process often explains why a certain genotype or probability is assigned (e.g., “otherwise all or none of the children would have the disease” explains why “Both parents of H and J must be Dd” in Li’s Probability answer) or how a probability is calculated, for example, “using the multiplication rule” (Li’s Probability explanation) or “multiply that by the 100% chance of getting ‘af’ from parent 2” (Preston’s Recombination explanation). In Nondisjunction problems, a student may claim that a nondisjunction occurred in a certain stage of meiosis (the Claim) because it produces certain gamete genotypes consistent with such an error (the Reason), as seen in Gabrielle’s answer.

aResponses edited slightly for clarity. See Table 2 for a correct student documented solution to the Gel/Pedigree problem.

Across All Content Areas, Expert Answers Are More Likely Than Student Answers to Contain Orientation, Metacognition, and Execution Processes

For each category of answers (expert, correct student, and incorrect student), we calculated the overall percent of answers that contained each process and compared these frequencies. Note that, in all cases, frequency represents the presence of a process in an answer, not a count of all uses of that process in an answer. The raw frequency of each process is provided in Table 4 , columns 2–4. To determine statistical significance, we used GLMM to account for individual variability in process use. The predicted likelihood of each process per group and pairwise comparisons between groups from this analysis is provided in Table 4 , columns 5–10. These comparisons show that expert answers were significantly more likely than student answers to contain the processes of Identify concept, Recall, Plan, Check, and Use Information ( Table 4 and Supplemental Table S1). The answers in Table 2 represent some of the typical trends identified for each group. For example, expert Eliot uses both Plan and Check, but these metacognitive processes are not used by either student, Cassie (correct answer) or Ian (incorrect answer).

aPairwise comparison: incorrect students to correct students (i–c), incorrect students to correct experts (i–e), correct students to correct experts (c–e). NA, no comparison made due to predicted probability of 0 in at least one group. *** p < 0.001; ** p < 0.01; * p < 0.05; ns: p > 0.05. See Supplemental Table S1 for standard error of coefficient estimates. Interpretation example: 82.05% and 92.36% of incorrect and correct student answers, respectively, contained Reason. The GLMM, after accounting for individual variability, predicts the probability of an incorrect student using Reason to be 91.80%, while the probability of a correct student using Reason is 96.68%.

Across All Content Areas, Correct Student Answers Are More Likely Than Incorrect Answers to Contain the Processes of Reason and Eliminate

Students most commonly used the processes Use Information, Reason, and Claim, each present in at least 50% of both correct and incorrect student answers ( Table 4 ). The processes Notice, Recall, Calculate, and Clarify were present in 20–50% of both correct and incorrect student answers ( Table 4 ). In comparing correct and incorrect student answers across all content areas, we found that Integrate, Reason, Eliminate, and Clarify were more likely used in correct compared with incorrect answers ( Table 4 ). As illustrated in Table 2 , the problem-solving processes in Cassie’s correct answer include: reasoning for a claim of dominant inheritance and eliminating when ruling out the possibility of an X-linked mode of inheritance. However, in describing the incorrect answer, Ian fails to document use of either of these processes.

Process Use Varies by Question Content

To determine whether student answers contain different processes depending on the content of the problem, we separated answers, regardless of correctness, by content area. We then excluded some processes: we did not analyze the Error and General codes, as well as Claim, which was seen in virtually every answer across content areas. We also excluded the very rarely seen processes of Identify Similarity and Identify Concept, which were present in 5% or fewer of both incorrect and correct student answers. For the remaining 11 processes, we found that each content area elicited different frequencies of use, as shown in Table 5 and Supplemental Table S2. Some processes were nearly absent in a content area: Calculate was rarely seen in answers to Nondisjunction and Gel/Pedigree questions and Eliminate was rarely seen in answers to Probability and Recombination questions. Furthermore, in answering Probability questions, students were more likely to use the processes Plan and Use Information than in any other content area. Recall was most likely in Recombination and least likely in Gel/Pedigree. Examples of student answers showing some of these trends are shown in Table 3 .

aAll student answers (correct and incorrect) are reported. Processes excluded from analyses include Claim, those within the Error and General strategies, processes that were present in 5% or fewer of both incorrect and correct student answers. Pairwise comparisons between: Probability (P), Recombination (R), Nondisjunction (N), and Gel/Pedigree (G). NA: no comparison made due to prevalence of 0% in at least one group. *** p < 0.001; ** p < 0.01; * p < 0.05; ns: p > 0.05. See Supplemental Table S2 for standard errors of coefficient estimates. Interpretation example: In Probability questions, 94.43% of answers contain Reason, while in Nondisjunction, 84.69% of answers contain Reason. Based on GLMM estimates to account for individual variability in process use, a question in the Probability content area had a 97.52% chance of using Reason, and a question in the Nondisjunction content area had an 92.88% chance of using this process.

The Combination of Processes Linked to Correctness Differs by Content Area

Performance varied by content area. Students performed best on Nondisjunction problems (75% correct), followed by Gel/Pedigree (73%), Probability (54%), and then Recombination (45%). Table 6 shows the raw data of process prevalence for correct and incorrect student answers in each of the four content areas. To examine the combination of problem-solving processes associated with correct student answers for each content area, we used a representative GLMM model with a lasso penalty. This type of analysis measures the predictive value of a process on answer correctness, returning a coefficient value. The presence of a factor with a higher positive coefficient increases the probability of answering correctly more than a factor with a lower positive coefficient. With each additional positive factor in the model, the likelihood of answering correctly increases in an additive manner ( Table 7 and Supplemental Table S3). To interpret these values, we show the probability estimates (%) for each process, which represent the probability that an answer will be correct in the presence of one or more processes ( Table 7 ). The strength of association of the process with correctness, measured by positive coefficient size, is listed in descending order. Thus, for each content area, the process with the strongest positive association to a correct answer is listed first. A process with a negative coefficient (a negative association with correctness) is listed last, and models with negative associations are highlighted in gray in Table 7 . An example of how to interpret the GLMM model is as follows. For the content area of Probability, Calculate (strongest association with correctness), Use Information, and Reason (weakest association with correctness) in combination are positively associated with correctness; Draw is the only negative predictor of correctness. For this content area, the intercept indicates a 7.31% likelihood of answering correctly in the absence of any of the processes tested. If an answer contains Calculate only, there is a 40.19% chance the answer will be correct. If an answer contains both Calculate and Use Information, there is a 58.60% chance the answer will be correct, and if the answer contains the three processes of Calculate, Use Information, and Reason combined, there is a 67.56% chance the answer will be correct. If Draw is present in addition to these three processes, the chance the answer will be correct slightly decreases to 66.40%. For Recombination, the processes of Calculate, Recall, Use Information, Reason, and Plan in combination are associated with correctness, and Draw and Assess Difficulty are negatively associated with correctness. For Nondisjunction, the processes of Eliminate, Draw, and Reason in combination are associated with correctness. For Gel/Pedigree, only the process of Reason was associated with correctness. The examples of correct student answers for each content area, as shown in Tables 2 and 3 , were selected to include each of the positively associated processes described.

aAll student answers (correct and incorrect) are reported. Processes excluded from analyses include Claim, those within the Error and General strategies, processes that were present in 5% or fewer of both correct and incorrect student answers.

aBased on a representative GLMM model with a lasso penalty predicting answer correctness with a moderate penalty parameter (lambda = 25). The intercept represents the likelihood of a correct answer in the absence of all processes initially entered into the model: Notice, Plan, Recall, Check, Assess Difficulty, Use Information, Integrate, Draw, Calculate, Reasoning, Eliminate. Shaded rows indicate the inclusion of negative predictors in combination with positive predictors. Probabilities were calculated using the inverse logit of the sum of the combination of log odds coefficient estimates and the intercept from Supplemental Table S3.

To identify why drawing may be detrimental for Probability and Recombination problems, we further characterized how students described their process of Draw in incorrect answers from these two content areas. We identified two categories: Inaccurate drawing and Inappropriate drawing application. Table 8 provides descriptions and student examples for each category. For Probability problems, 49% of the incorrect student answers that used Draw were Inaccurate, as they identified incorrect genotypes or probabilities while drawing a Punnett square. Thirty-one percent of the answers contained Inappropriate drawing applications such as drawing a Punnett square for each generation of a multiple-generation pedigree rather than multiplying probabilities. Five percent of the answers displayed both Inaccurate and Inappropriate drawing ( Figure 2 ). For Recombination, 83% of incorrect student answers using Draw used an Inappropriate drawing application, typically treating linked genes as if they were unlinked by drawing a Punnett square to calculate probability. Ten percent of answers used both Inappropriate and Inaccurate drawing ( Figure 2 ).

FIGURE 2. Drawing is commonly inaccurate or inappropriate in incorrect student answers for Probability and Recombination. Drawing categorization from student answers that used Draw and answered incorrectly for content areas of (A) Probability ( n = 55) and (B) Recombination ( n = 71). Each category is mutually exclusive, so those that have both Inaccurate drawing/Inappropriate drawing are not in the individual use categories. “No drawing error” indicates neither inaccurate nor inappropriate drawings were described. “Cannot determine” indicates not enough information was provided in the students’ written answer to assign a drawing use category.

In this study, we identified and characterized the various processes that a large sample of students and experts used to document their answers to complex genetics problems. Overall, although their frequency of use differed, experts and students used the same set of problem-solving strategies. Experts were more likely to use orienting and metacognitive strategies than students, confirming prior findings on expert–novice differences (e.g., Chi et al. , 1981 ; Smith and Good, 1984 ; Smith, 1988 ; Atman et al. , 2007 ; Smith et al. , 2013 ; McDonnell and Mullally, 2016 ; Peffer and Ramezani, 2019 ). For students, we also identified which strategies were most associated with correct answers. The use of reasoning was consistently associated with correct answers across all content areas combined as well as for each individual content area. Students used other processes more or less frequently depending on the content of the question, and the combination of processes associated with correct answers also varied by content area.

Domain-Specific Problem Solving

We found that most processes students used (i.e., all but those in the General category) were domain specific, relating directly to genetics content. Prevost and Lemons (2016) , who examined students’ process of solving multiple-choice biology problems, found that domain-general processes were more common in answers to lower-order than higher-order questions. They also found that using more domain-specific processes was associated with correctness. In our study, students solved only higher-order problems that asked them to apply or analyze information. Students also had to construct their responses to each problem, rather than selecting from multiple predetermined answer options. These two factors may explain the prevalence of domain-specific processes in the current study, which allowed us to investigate further the types of domain-specific processes that lead to correct answers.

Metacognitive Activity: Orienting and Metacognitive Processes Are Described by Experts but Not Consistently by Students

Our results support several previous findings from the literature comparing the problem-solving tactics of experts and students: experts are more likely to describe orienting and metacognitive problem-solving strategies than students, including planning solutions, checking work, and identifying the concept of the problem.

While some students used planning in their correct answers, experts solving the same problems were more likely to do so. Prior studies of solutions to complex problems in both engineering and science contexts found that experts more often used the orienting/planning behavior of gathering appropriate information compared with novices ( Atman et al. , 2007 ; Peffer and Ramezani, 2019 ). Experts likely have engaged in authentic scientific investigations of their own, and planning is more likely when the problem to be solved is more complex (e.g., Atman et al. , 2007 ), so experts are likely more familiar with and see value in planning ahead before pursuing a certain problem-solving approach.

Experts were much more likely than students to describe their use of checking work, as also shown in previous work ( Smith and Good, 1984 ; Smith, 1988 ; McDonnell and Mullally, 2016 ). McDonnell and Mullally (2016) found greater levels of unprompted checking after students experienced modeling of explicitly checking prompts and were given points for demonstrating checking. These researchers also noted that when students reviewed their work, they usually only checked some problem components, not all. Incomplete checking was associated with incorrect answers, while complete checking was associated with correct answers. In the current study, we did not assess the completeness of checking, and therefore may have missed an opportunity to correlate checking with correctness. However, if most students were generally checking their answers in a superficial way (i.e., only checking one step in the problem-solving process versus checking all steps), this could explain why there were no differences in the presence of checking between incorrect and correct student answers. In contrast to our study, Prevost and Lemons (2016) found checking was the most common domain-specific procedure used by students when answering both lower- and higher-order multiple-choice biology questions. The multiple-choice format may prompt checking, as the answers have already been provided in the scenario. In addition, while that study assessed answers to graded exam questions, we examined answers to extra-credit assignments. Thus, a lack of motivation may have influenced whether the students in the current study reported checking their answers.

Identifying the Concept of a Problem.

Although this strategy was relatively uncommon even among experts, they were more likely than students to describe identifying the concept of a problem in their solutions. This is consistent with previous research showing that nonexperts use superficial features to solve problems ( Chi et al. , 1981 ; Smith and Good, 1984 ; Smith et al. , 2013 ), a tactic also associated with incorrect solutions ( Smith and Good, 1984 ). The process of identifying relevant core concepts in a problem allows experts to identify the appropriate strategies and knowledge needed for any given problem ( Chi et al. , 1981 ). Thus, we suggest that providing students with opportunities to recognize the core concepts of different problems, and thus the similarity of their solutions, could be beneficial for learning successful problem solving.

Engaging in Explanations: Using Reasoning Is Consistently Associated with Correct Answers

Our findings suggest that, although reasoning is frequently used by both correct and incorrect students, it is strongly associated with correct student answers across all content areas. Correct answers were more likely than incorrect answers to use reasoning; furthermore, reasoning was associated with a correct answer for each of the four content areas we explored. This supports previous work showing that reasoning ability in general is associated with overall biology performance ( Cavallo, 1996 ; Johnson and Lawson, 1998 ). Students who use reasoning may be demonstrating their ability to think logically and sequentially connect ideas, essentially building an argument for why their answers make sense. In fact, teaching the skill of argumentation helps students learn to use evidence to provide a reason for a claim, as well as to rebut others’ claims ( Toulmin, 1958 ; Osborne, 2010 ), and can improve their performance on genetics concepts ( Zohar and Nemet, 2002 ). Thus, the genetics students in the current study who were able to explain the rationale behind each of their problem-solving steps are likely to have built a conceptual understanding of the topic that allowed them to construct logical rationales for their answers.

In the future, think-aloud interviews should be used to more closely examine the types of reasoning students use. Students may be more motivated and better able to explain their rationales verbally, or with a combination of drawn and verbal descriptions, than they are inclined to do when typing their answers in a writing-only situation. Interviewers can also ask follow-up questions, confirming student explanations and ideas, something that cannot be obtained from written explanations. In addition, the problems used in this study were near-transfer problems, similar to those that students previously solved during class. Such problems can often be solved using an algorithmic approach, as also recently described by Frey et al. (2020) in chemistry. Future studies could identify whether and when students use more complex approaches such as causal reasoning (providing connections between ideas) or mechanistic reasoning (explaining the biological mechanism as part of making causal connections ( Russ et al. , 2008 ; Southard et al. , 2016 ) in addition to or instead of algorithmic reasoning.

Students Use Different Processes to Answer Questions in Different Content Areas

Overall, students answered 60% of the questions correctly. Some content areas were more challenging than others: Recombination was the most difficult, followed by Probability, then Gel/Pedigree and Nondisjunction (see also Avena and Knight, 2019 ). While our results do not indicate that a certain combination of processes are both necessary and sufficient to solve a problem correctly, they can be useful to instructors wishing to guide students in their strategy use when considering their solutions to certain types of problems. In the following section, we discuss the processes that were specifically associated with correctness in student answers for each content area.

Probability.

Solving a Probability question requires calculation, while many other types of problems do not. To solve the questions in this study, students needed to consider multiple generations from two families to calculate the likelihood of independent events occurring by using the product rule. Smith (1988) found that both successful and unsuccessful students often find this challenging. Our previous work also found that failing to use the product rule, or using it incorrectly, was the second most common error in incorrect student answers ( Avena and Knight, 2019 ). Correctly solving probability problems likely also requires a conceptual understanding of the reasoning behind each calculation (e.g., Deane et al. , 2016 ). This type of reasoning, specific to the mathematical components of a problem, is referred to as statistical reasoning, a suggested competency for biology students ( American Association for the Advancement of Science, 2011 ). The code of Reason includes reasoning about other aspects of the problem (e.g., determining genotypes; see Table 3 ) in addition to reasoning related to calculations. While reasoning was prevalent in both incorrect and correct answers to Probability problems, using reasoning still provided an additional 9% likelihood of answering correctly for students who had also used calculating and applying information in their answers.

Generally, calculation alone was not sufficient to answer a Probability question correctly. When students applied information to solving the specific problem (captured with the Use Information code), such as determining genotypes within the pedigree or assigning a probability, their likelihood of generating a correct answer was 40%. This only increased to 59% if they also used Calculate (see Table 7 ). We previously found that the most common content error in these types of probability problems was mis-assigning a genotype or probability due to incorrectly using information in the pedigree; this error was commonly seen in combination with a product rule error ( Avena and Knight, 2019 ). This correlates with our current findings on the importance of applying procedural knowledge: both Use Information and Calculate, under the AtL element of generating knowledge, contribute to correct problem-solving.

Recombination.

Both the Probability and Recombination questions are fundamentally about calculating probabilities; thus, not surprisingly, Calculate is also associated with correct answers to Recombination questions. Determining map units and determining the frequency of one possible genotype among possible gametes both require calculation. Use of Recall in addition to Calculate increases the likelihood of answering correctly from 18 to 39%. This may be due to the complexity of some of the terms in these problems. As shown previously, incorrect answers to Recombination questions often fail to use map units in their solution ( Avena and Knight, 2019 ). Appropriately using map units thus likely requires remembering that the map unit designation is representative of the probability of recombination and then applying this definition to the problem. When students Used Information, along with Calculate and Recall, their likelihood of answering correctly increased to 63%.

Reasoning and planning also contribute to correct answers in this content area. In their solutions, students needed to consider the genotypes of the offspring and both parents to solve the problem. The multistep nature of the problem may give students the opportunity to plan their possible approaches, either at the very beginning of the problem and/or as they walk through these steps. This was seen in Preston’s solution ( Table 3 ), in which the student sequentially made a short-term plan and then immediately used information in the problem to carry out that plan.

Drawing: A Potentially Misused Strategy in Probability and Recombination Solutions.

Only one process, Drawing, was negatively associated with correct answers in solutions to both Probability and Recombination questions. Drawing is generally considered beneficial in problem solving across disciplines, as it allows students to generate a representation of the problem space and/or of their thinking (e.g., Mason and Singh, 2010 ; Quillin and Thomas, 2015 ; Heideman et al. , 2017 ). However, when students generate inaccurate drawings or use a drawing methodology inappropriately, they are unlikely to reach a correct answer. In a study examining complex meiosis questions, Kindfield (1993) found that students with more incorrect responses provided drawings with features not necessary to solving the problem. In our current study, we found that the helpfulness of a drawing depends on its quality and the appropriateness or context of its use.

When answering Recombination problems, many students described drawing a Punnett square and then calculating the inheritance as if the linked genes were actually genes on separate chromosomes. In doing so, students revealed a misunderstanding of when and why to appropriately use a Punnett square as well as their lack of understanding that the frequency of recombination is connected to the frequency of gametes. Because we have also shown that planning is beneficial in solving Recombination problems, we suggest that instructors emphasize that students first plan to look for certain characteristics in a problem, such as linked versus unlinked genes, to identify how to proceed. For example, noting that genes are linked would suggest not using a Punnett square when solving the problem. Similarly, in Probability questions, students must realize that uncertainty in genotypes over multiple generations of a family can be resolved by multiplying probabilities together rather than by making multiple possible Punnett squares for the outcome of a single individual. These findings connect to the AtL elements of generative thinking and taking a deep approach: drawing can be a generative behavior, but students must also be thinking about the underlying context of the problem rather than a memorized fact.

Nondisjunction.

In Nondisjunction problems, students were asked to predict the cause of an error in chromosome number. Our model for processes associated with correctness in nondisjunction problems ( Table 7 ) suggested that the likelihood of answering correctly in the absence of several processes was 70%. This may explain the higher percent of correct answers in this content area (75%) compared with other content areas. Nonetheless, three processes were shown to help students answer correctly. The process Eliminate, even though used relatively infrequently (10%), provides a benefit. Using elimination when there are a finite number of obvious solutions is a reasonable strategy, and one previously shown to be successful ( Smith and Good, 1984 ). Ideally, this strategy would be coupled with drawing the steps of meiosis and then reasoning about which separation errors could not explain the answer. Drawing was associated with correct answers in this content area, though it was neither required nor sufficient. Instead of drawing, some students may have used a memorized series of steps in their solutions. This is referred to as an “algorithmic” explanation, in which a memorized pattern is used to solve the problem. For example, such a line of explanation may go as follows: “beginning from a diploid cell heterozygous for a certain gene, two of the same alleles being present in one gamete indicates a nondisjunction in meiosis II.” Such algorithms can be applied without a conceptual understanding ( Jonsson et al. , 2014 ; Nyachwaya et al. , 2014 ), and thus students may inaccurately apply them without fully understanding or being able to visualize what is occurring during a nondisjunction event ( Smith and Good, 1984 ; Nyachwaya et al. , 2014 ). Using a drawing may help provide a basis for analytic reasoning, providing logical links between ideas and claims that are thoughtful and deliberate ( Alter et al. , 2007 ). Indeed, in Kindfield’s study ( 1993 ), in which participants (experts and students) were asked to complete complex meiosis questions, they found that those with more accurate models of meiosis used their drawings to assist in their reasoning process. Kindfield (1993) suggested that these drawings allowed for additional working memory space, thus supporting an accurate problem-solving process.

Gel/Pedigree.

Unlike other content areas, the only process associated with correctness in the Gel/Pedigree model was Reasoning, which provided a greater contribution to correct solutions than in any other content area. In these problems, students are asked to find the most likely mode of inheritance given both a pedigree of a family and a DNA gel that shows representations of alleles for each family member. The two visuals, along with the text of the problem, provide students an opportunity to provide logical explanations at many points in the problem. Students use reasoning to support intermediate claims as they think through possible solutions, and again for their final claims, or for why they eliminate an option. Almost half of both correct and incorrect student answers to these questions integrated features from both the gel and pedigree to answer the problem. Even though many correct and incorrect answers integrate, correct answers also reason. We suggest that the presence of two visual aids prompts students to integrate information from both, thus potentially increasing the likelihood of using reasoning.

Limitations

In this study, we captured the problem-solving processes of a large sample of students by asking them to write their step-by-step processes as part of an online assignment. In so doing, we may not have captured the entirety of a student’s thought process. For example, students may have felt time pressure to complete an assignment, may have experienced fatigue after answering multiple questions on the same topic, or simply may not have documented everything they were thinking. Students may also have been less likely to indicate they were engaging in drawing, as they were answering questions using an online text platform; exploring drawing in more detail in the future would require interviews or the collection of drawings as a component of the problem-solving assignment. Additionally, students may not have felt that all the steps they engaged in were worth explaining in words; this may be particularly true for metacognitive processes. Students are not likely accustomed to expressing their metacognitive processes or admitting uncertainty or confusion during assessment situations. However, even given these limitations, we have captured some of the primary components of student thinking during problem solving.

In addition, our expert–student comparison may be biased, as experts had different reasons than students for participating in the study. The experts likely did so because they wanted to be helpful and found it interesting. Students, on the other hand, had very different motivations, such as using the problems for practice in order to perform well on the next exam and/or to get extra credit. Although it is likely not possible to put experts and students in the same affective state while they are solving problems, it is worth realizing that the frequencies of processes they use could reflect their different states while answering the questions.

Finally, the questions in the assignments provided to students were similar to those seen previously during in-class work. The low prevalence of metacognitive processes in their solutions could be due to students’ perception that they have already solved similar questions. This may prevent them from articulating their plans or from checking their work. More complex, far-transfer problems would likely elicit different patterns of processes for successful problem solving.

SUGGESTIONS FOR INSTRUCTION

Calculating: In questions regarding probability, students will need to be familiar with mathematical representations and calculations. Practicing probabilistic thinking is critical.

Drawing: Capturing thought processes with a drawing can help visualize the problem space and can be used to generate supportive reasoning for one’s thinking (e.g., a drawing of the stages of meiosis). However, a cautionary note: drawing can lead to unsuccessful problem solving when used in an inappropriate context, such as a Punnett square when considering linked genes or using multiple Punnett squares when other rules should be used, such as multiplication of probabilities from multiple generations.

Eliminating: In questions with clear alternate final answers, eliminating answers, preferably while explaining one’s reasons, is particularly useful.

Practicing metacognition: Although there were few significant differences in metacognitive processes between correct and incorrect student answers, we still suggest that planning and checking are valuable across content areas, as demonstrated by the more frequent use of these processes by experts.

In summary, we suggest that instructors not only emphasize key pieces of challenging content for each given topic, but also consistently demonstrate possible problem-solving strategies, provide many opportunities for students to practice thinking about how to solve problems, and encourage students to explain to themselves and others why each of their steps makes sense.

ACKNOWLEDGMENTS

This work was supported by the National Science Foundation (DUE 1711348). We are grateful to Paula Lemons, Stephanie Gardner, and Laura Novick for their guidance and suggestions on this project. Special thanks also to the many students and experts who shared their thinking while solving genetics problems.

• American Association for the Advancement of Science . ( 2011 ). Vision and change in undergraduate biology education: A call to action . Washington, DC. Google Scholar
• Bassok, M., & Novick, L. R. ( 2012 ). Problem solving . In Holyoak, K. J.Morrison, R. G. (Eds.), Oxford handbook of thinking and reasoning (pp. 413–432). New York, NY: Oxford University Press. Google Scholar
• Biggs, J. B. ( 1987 ). Student approaches to learning and studying. Research monograph . Hawthorn, Australia: Australian Council for Educational Research. Google Scholar
• Bloom, B. S., Krathwohl, D. R., & Masia, B. B. ( 1956 ). Taxonomy of Educational Objectives: The Classification of Educational Goals . New York, NY: David McKay. Google Scholar
• Gelman, A., & Hill, J. ( 2006 ). Data analysis using regression and multilevel/hierarchical models . Cambridge, England: Cambridge University Press. Google Scholar
• Groll, A. ( 2017 ). glmmLasso: Variable selection for generalized linear mixed models by L1-penalized estimation . R package version , 1 (1), 25. Google Scholar
• Kindfield, A. C. H. ( 1993 ). Biology diagrams: Tools to think with . Journal of the Learning Sciences , 3 (1), 1–36. Google Scholar
• Lemke, J. L. ( 1990 ). Talking science: Language, learning, and values . Norwood, NJ: Ablex Publishing. Retrieved July 30, 2020, from http://eric.ed.gov/?id=ED362379 Google Scholar
• McDonnell, L., & Mullally, M. ( 2016 ). Teaching students how to check their work while solving problems in genetics . Journal of College Science Teaching , 46 (1), 68. Google Scholar
• Novick, L. R., & Bassok, M. ( 2005 ). Problem Solving . In Holyoak, K. J.Morrison, R. G. (Eds.), The Cambridge handbook of thinking and reasoning (pp. 321–349). New York. NY: Cambridge University Press. Google Scholar
• Osborne, J. ( 2010 ). Arguing to learn in science: The role of collaborative, critical discourse . Science , 328 , 463–466. Medline ,  Google Scholar
• Saldana, J. ( 2015 ). The coding manual for qualitative researchers . Los Angeles, CA: Sage. Google Scholar
• Schen, M. ( 2012 , March 25). Assessment of argumentation skills through individual written instruments and lab reports in introductory biology . Paper presented at: Annual Meeting of the National Association for Research in Science Teaching (Indianapolis, IN) . Google Scholar
• Smith, M. K., & Knight, J. K. ( 2012 ). Using the Genetics Concept Assessment to document persistent conceptual difficulties in undergraduate genetics courses . Genetics , 191 , 21–32. Medline ,  Google Scholar
• Smith, M. K., Wood, W. B., & Knight, J. K. ( 2008 ). The Genetics Concept Assessment: A new concept inventory for gauging student understanding of genetics . CBE—Life Sciences Education , 7 (4), 422–430. Link ,  Google Scholar
• Toulmin, S. ( 1958 ). The uses of argument . Cambridge: Cambridge University Press. Google Scholar

Submitted: 21 January 2021 Revised: 16 July 2021 Accepted: 22 July 2021

© 2021 J. S. Avena et al. CBE—Life Sciences Education © 2021 The American Society for Cell Biology. This article is distributed by The American Society for Cell Biology under license from the author(s). It is available to the public under an Attribution–Noncommercial–Share Alike 3.0 Unported Creative Commons License (http://creativecommons.org/licenses/by-nc-sa/3.0).

Biology@Hyndland

Hyndland Science Faculty

National 5 Problem Solving

You can access the National 5 Problem Solving Help Sheet below:

National 5 Problem Solving Help Sheet

You can access the full National 5 Problem Solving Booklet below:

National 5 Problem Solving Booklet Questions

National 5 Problem Solving Booklet Marking Scheme

You can access problem solving questions by category using the links below:

Biological Keys Questions | Biological Keys Marking Scheme

Calculation Questions | Calculations Marking Scheme

Graphs, Charts & Experiments Questions | Graphs, Charts & Experiments Marking Scheme

Ratio Questions | Ratio Marking Scheme

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: The Science of Biology - The Scientific Method

• Last updated
• Save as PDF
• Page ID 12645

Learning Objectives

• Discuss hypotheses and the components of a scientific experiment as part of the scientific method

The Scientific Method

Biologists study the living world by posing questions about it and seeking science -based responses. This approach is common to other sciences as well and is often referred to as the scientific method. The scientific method was used even in ancient times, but it was first documented by England’s Sir Francis Bacon (1561–1626) who set up inductive methods for scientific inquiry. The scientific method can be applied to almost all fields of study as a logical, rational, problem-solving method.

The scientific process typically starts with an observation (often a problem to be solved) that leads to a question. Let’s think about a simple problem that starts with an observation and apply the scientific method to solve the problem. A teenager notices that his friend is really tall and wonders why. So his question might be, “Why is my friend so tall? ”

Proposing a Hypothesis

Recall that a hypothesis is an educated guess that can be tested. Hypotheses often also include an explanation for the educated guess. To solve one problem, several hypotheses may be proposed. For example, the student might believe that his friend is tall because he drinks a lot of milk. So his hypothesis might be “If a person drinks a lot of milk, then they will grow to be very tall because milk is good for your bones.” Generally, hypotheses have the format “If…then…” Keep in mind that there could be other responses to the question; therefore, other hypotheses may be proposed. A second hypothesis might be, “If a person has tall parents, then they will also be tall, because they have the genes to be tall. ”

Once a hypothesis has been selected, the student can make a prediction. A prediction is similar to a hypothesis but it is truly a guess. For instance, they might predict that their friend is tall because he drinks a lot of milk.

Testing a Hypothesis

A valid hypothesis must be testable. It should also be falsifiable, meaning that it can be disproven by experimental results. Importantly, science does not claim to “prove” anything because scientific understandings are always subject to modification with further information. This step—openness to disproving ideas—is what distinguishes sciences from non-sciences. The presence of the supernatural, for instance, is neither testable nor falsifiable. To test a hypothesis, a researcher will conduct one or more experiments designed to eliminate one or more of the hypotheses. Each experiment will have one or more variables and one or more controls. A variable is any part of the experiment that can vary or change during the experiment. The control group contains every feature of the experimental group except it is not given the manipulation that is hypothesized. For example, a control group could be a group of varied teenagers that did not drink milk and they could be compared to the experimental group, a group of varied teenagers that did drink milk. Thus, if the results of the experimental group differ from the control group, the difference must be due to the hypothesized manipulation rather than some outside factor. To test the first hypothesis, the student would find out if drinking milk affects height. If drinking milk has no affect on height, then there must be another reason for the height of the friend. To test the second hypothesis, the student could check whether or not his friend has tall parents. Each hypothesis should be tested by carrying out appropriate experiments. Be aware that rejecting one hypothesis does not determine whether or not the other hypotheses can be accepted. It simply eliminates one hypothesis that is not valid. Using the scientific method, the hypotheses that are inconsistent with experimental data are rejected.

While this “tallness” example is based on observational results, other hypotheses and experiments might have clearer controls. For instance, a student might attend class on Monday and realize she had difficulty concentrating on the lecture. One hypothesis to explain this occurrence might be, “If I eat breakfast before class, then I am better able to pay attention.” The student could then design an experiment with a control to test this hypothesis.

The scientific method may seem too rigid and structured. It is important to keep in mind that although scientists often follow this sequence, there is flexibility. Many times, science does not operate in a linear fashion. Instead, scientists continually draw inferences and make generalizations, finding patterns as their research proceeds. Scientific reasoning is more complex than the scientific method alone suggests.

• In the scientific method, observations lead to questions that require answers.
• In the scientific method, the hypothesis is a testable statement proposed to answer a question.
• In the scientific method, experiments (often with controls and variables) are devised to test hypotheses.
• In the scientific method, analysis of the results of an experiment will lead to the hypothesis being accepted or rejected.
• scientific method : a way of discovering knowledge based on making falsifiable predictions (hypotheses), testing them, and developing theories based on collected data
• hypothesis : an educated guess that usually is found in an “if…then…” format
• control group : a group that contains every feature of the experimental group except it is not given the manipulation that is hypothesized