problem solving with venn diagram

Math teaching support you can trust

resources downloaded

one-on-one tutoring sessions

schools supported

[FREE] Fun Math Games & Activities

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5!

15 Venn Diagram Questions And Practice Problems (Middle & High School): Exam Style Questions Included

Beki christian.

Venn diagram questions involve visual representations of the relationship between two or more different groups of things. Venn diagrams are first covered in elementary school and their complexity and uses progress through middle and high school.

This article will look at the types of Venn diagram questions that might be encountered at middle school and high school, with a focus on exam style example questions and preparing for standardized tests. We will also cover problem-solving questions. Each question is followed by a worked solution.

How to solve Venn diagram questions

Venn diagram questions 6th grade, venn diagram questions 7th grade, venn diagram questions 8th grade, lower ability venn diagram questions, middle ability high school venn diagram questions.

• Looking for more Venn diagram math questions for middle and high school students?

In middle school, sets and set notation are introduced when working with Venn diagrams. A set is a collection of objects. We identify a set using braces. For example, if set A contains the odd numbers between 1 and 10, then we can write this as: 

A = {1, 3, 5, 7, 9}

Venn diagrams sort objects, called elements, into two or more sets.

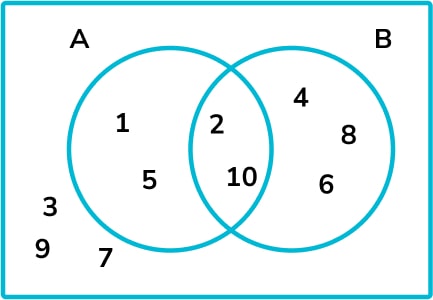
This diagram shows the set of elements 

{1,2,3,4,5,6,7,8,9,10} sorted into the following sets.

Set A= factors of 10 

Set B= even numbers

The numbers in the overlap (intersection) belong to both sets. Those that are not in set A or set B are shown outside of the circles.

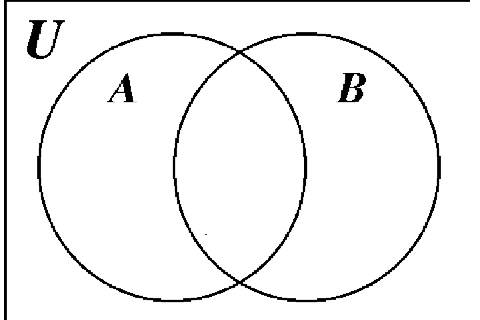
Different sections of a Venn diagram are denoted in different ways.

ξ represents the whole set, called the universal set.

∅ represents the empty set, a set containing no elements.

Venn Diagrams Check for Understanding Quiz

Wondering if your students have fully grasped Venn diagrams? Use this quiz to check their understanding across 10 questions with answers covering all things Venn diagrams!

Let’s check out some other set notation examples!

In middle school and high school, we often use Venn diagrams to establish probabilities.

We do this by reading information from the Venn diagram and applying the following formula.

For Venn diagrams we can say

Middle School Venn diagram questions

In middle school, students learn to use set notation with Venn diagrams and start to find probabilities using Venn diagrams. The questions below are examples of questions that students may encounter in 6th, 7th and 8th grade.

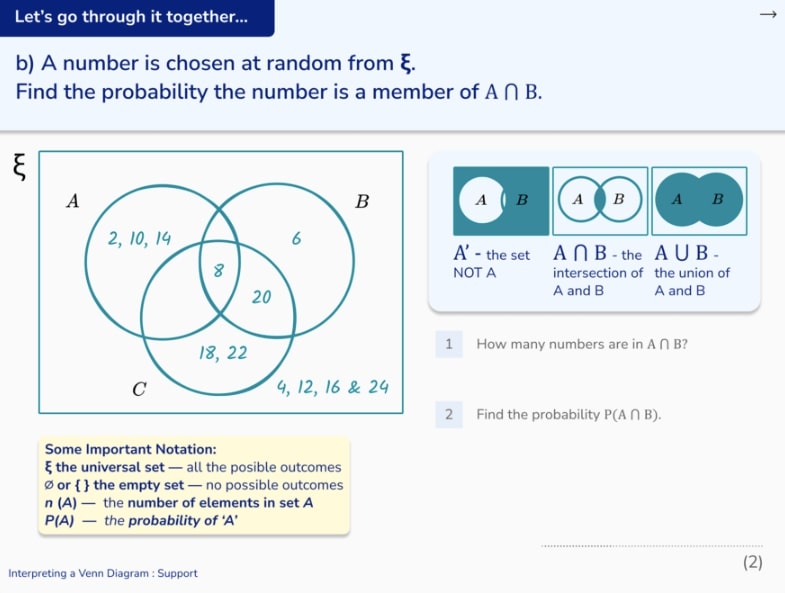
1. This Venn diagram shows information about the number of people who have brown hair and the number of people who wear glasses.

How many people have brown hair and glasses?

The intersection, where the Venn diagrams overlap, is the part of the Venn diagram which represents brown hair AND glasses. There are 4 people in the intersection.

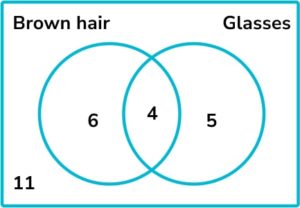
2. Which set of objects is represented by the Venn diagram below?

We can see from the Venn diagram that there are two green triangles, one triangle that is not green, three green shapes that are not triangles and two shapes that are not green or triangles. These shapes belong to set D.

3. Max asks 40 people whether they own a cat or a dog. 17 people own a dog, 14 people own a cat and 7 people own a cat and a dog. Choose the correct representation of this information on a Venn diagram.

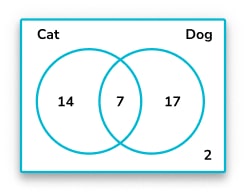
There are 7 people who own a cat and a dog. Therefore, there must be 7 more people who own a cat, to make a total of 14 who own a cat, and 10 more people who own a dog, to make a total of 17 who own a dog.

Once we put this information on the Venn diagram, we can see that there are 7+7+10=24 people who own a cat, a dog or both.

40-24=16 , so there are 16 people who own neither.

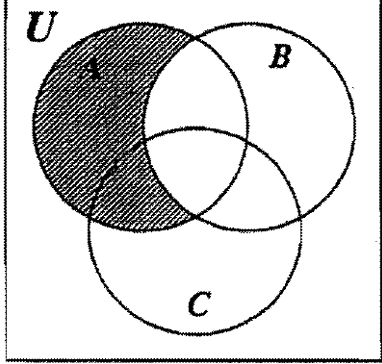
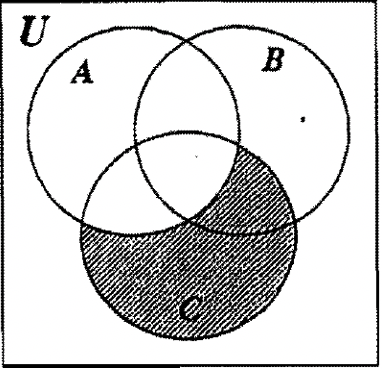
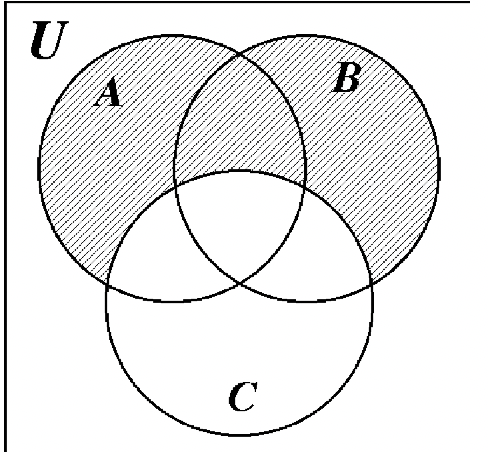
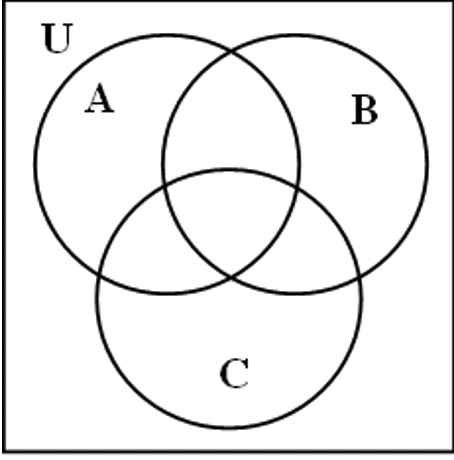
4. The following Venn diagrams each show two sets, set A and set B . On which Venn diagram has A ′ been shaded?

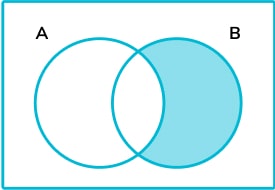
\mathrm{A}^{\prime} means not in \mathrm{A} . This is shown in diagram \mathrm{B.}

5. Place these values onto the following Venn diagram and use your diagram to find the number of elements in the set \text{S} \cup \text{O}.

\xi = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \text{S} = square numbers \text{O} = odd numbers

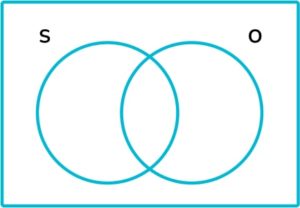
\text{S} \cup \text{O} is the union of \text{S} or \text{O} , so it includes any element in \text{S} , \text{O} or both. The total number of elements in \text{S} , \text{O} or both is 6.

6. The Venn diagram below shows a set of numbers that have been sorted into prime numbers and even numbers.

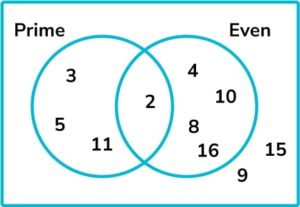
A number is chosen at random. Find the probability that the number is prime and not even.

The section of the Venn diagram representing prime and not even is shown below.

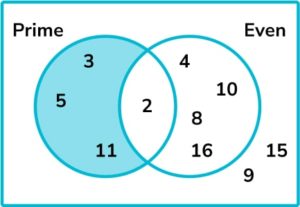
There are 3 numbers in the relevant section out of a possible 10 numbers altogether. The probability, as a fraction, is \frac{3}{10}.

7. Some people visit the theater. The Venn diagram shows the number of people who bought ice cream and drinks in the interval.

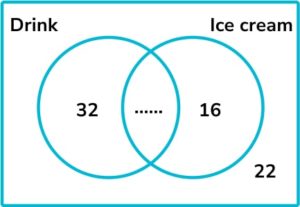
Ice cream is sold for $3 and drinks are sold for $ 2. A total of £262 is spent. How many people bought both a drink and an ice cream?

Money spent on drinks: 32 \times \$2 = \$64

Money spent on ice cream: 16 \times \$3 = \$48

\$64+\$48=\$112 , so the information already on the Venn diagram represents \$112 worth of sales.

\$262-\$112 = \$150 , so another \$150 has been spent.

If someone bought a drink and an ice cream, they would have spent \$2+\$3 = \$5.

\$150 \div \$5=30 , so 30 people bought a drink and an ice cream.

High school Venn diagram questions

In high school, students are expected to be able to take information from word problems and put it onto a Venn diagram involving two or three sets. The use of set notation is extended and the probabilities become more complex.

In advanced math classes, Venn diagrams are used to calculate conditional probability.

8. 50 people are asked whether they have been to France or Spain.

18 people have been to France. 23 people have been to Spain. 6 people have been to both.

By representing this information on a Venn diagram, find the probability that a person chosen at random has not been to Spain or France.

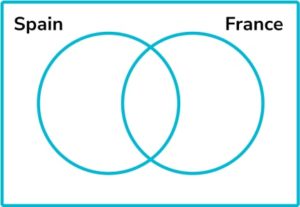
6 people have been to both France and Spain. This means 17 more have been to Spain to make 23  altogether, and 12 more have been to France to make 18 altogether. This makes 35 who have been to France, Spain or both and therefore 15 who have been to neither.

The probability that a person chosen at random has not been to France or Spain is \frac{15}{50}.

9. Some people were asked whether they like running, cycling or swimming. The results are shown in the Venn diagram below.

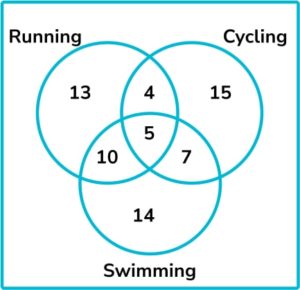
One person is chosen at random. What is the probability that the person likes running and cycling?

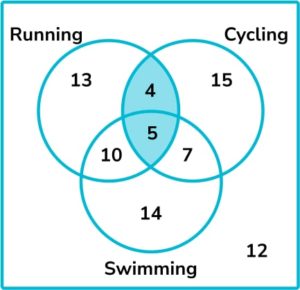
9 people like running and cycling (we include those who also like swimming) out of 80 people altogether. The probability that a person chosen at random likes running and cycling is \frac{9}{80}.

10. ξ = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}

\text{A} = \{ even numbers \}

\text{B} = \{ multiples of 3 \}

By completing the following Venn diagram, find \text{P}(\text{A} \cup \text{B}^{\prime}).

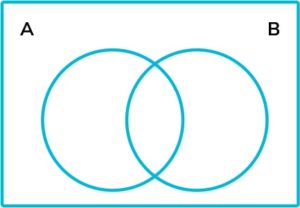
\text{A} \cup \text{B}^{\prime} means \text{A} or not \text{B} . We need to include everything that is in \text{A} or is not in \text{B} . There are 13 elements in \text{A} or not in \text{B} out of a total of 16 elements.

Therefore \text{P}(\text{A} \cup \text{B}^{\prime}) = \frac{13}{16}.

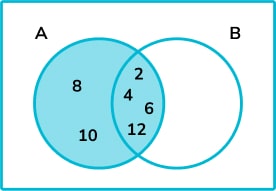
11. ξ = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}

A = \{ multiples of 2 \}

By putting this information onto the following Venn diagram, list all the elements of B.

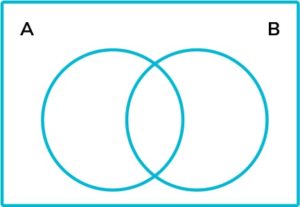
We can start by placing the elements in \text{A} \cap \text{B} , which is the intersection.

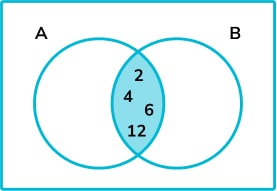
We can then add any other multiples of 2 to set \text{A}.

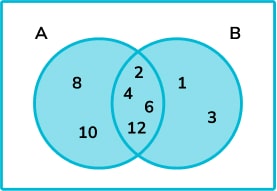
Next, we can add any unused elements from \text{A} \cup \text{B} to \text{B}.

Finally, any other elements can be added to the outside of the Venn diagram.

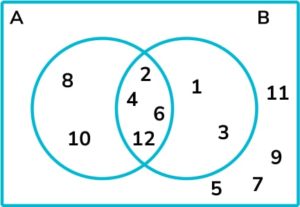
The elements of \text{B} are \{1, 2, 3, 4, 6, 12\}.

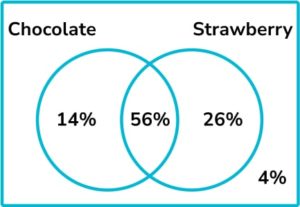
12. Some people were asked whether they like strawberry ice cream or chocolate ice cream. 82% said they like strawberry ice cream and 70% said they like chocolate ice cream. 4% said they like neither.

By putting this information onto a Venn diagram, find the percentage of people who like both strawberry and chocolate ice cream.

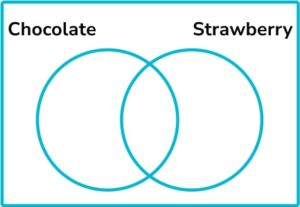
Here, the percentages add up to 156\%. This is 56\% too much. In this total, those who like chocolate and strawberry have been counted twice and so 56\% is equal to the number who like both chocolate and strawberry. We can place 56\% in the intersection, \text{C} \cap \text{S}

We know that the total percentage who like chocolate is 70\%, so 70-56 = 14\%-14\% like just chocolate. Similarly, 82\% like strawberry, so 82-56 = 26\%-26\% like just strawberry.

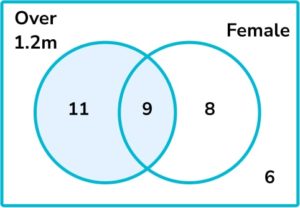
13. The Venn diagram below shows some information about the height and gender of 40 students.

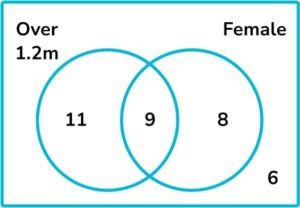
A student is chosen at random. Find the probability that the student is female given that they are over 1.2 m .

We are told the student is over 1.2m. There are 20 students who are over 1.2m and 9 of them are female. Therefore the probability that the student is female given they are over 1.2m is   \frac{9}{20}.

14. The Venn diagram below shows information about the number of students who study history and geography.

H = history

G = geography

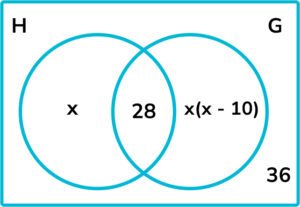
Work out the probability that a student chosen at random studies only history.

We are told that there are 100 students in total. Therefore:

x = 12 or x = -3 (not valid) If x = 12, then the number of students who study only history is 12, and the number who study only geography is 24. The probability that a student chosen at random studies only history is \frac{12}{100}.

15. 50 people were asked whether they like camping, holiday home or hotel holidays.

18\% of people said they like all three. 7 like camping and holiday homes but not hotels. 11 like camping and hotels. \frac{13}{25} like camping.

Of the 27 who like holiday homes, all but 1 like at least one other type of holiday. 7 people do not like any of these types of holiday.

By representing this information on a Venn diagram, find the probability that a person chosen at random likes hotels given that they like holiday homes.

Put this information onto a Venn diagram.

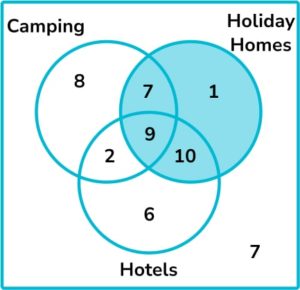
We are told that the person likes holiday homes. There are 27 people who like holiday homes. 19 of these also like hotels. Therefore, the probability that the person likes hotels given that they like holiday homes is \frac{19}{27}.

Looking for more Venn diagram math questions for middle and high school students ?

• Probability questions
• Ratio questions
• Algebra questions
• Trigonometry questions
• Long division questions
• Pythagorean theorem questions

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.

Pythagoras Theorem Questions [FREE]

Downloadable Pythagoras theorem worksheet containing 15 multiple choice questions with a mix of worded problems and deeper problem solving questions.

Includes an answer key and follows variation theory with plenty of opportunities for students to work independently at their own level.

Privacy Overview

Venn Diagram Examples, Problems and Solutions

On this page:

• What is Venn diagram? Definition and meaning.
• Venn diagram formula with an explanation.
• Examples of 2 and 3 sets Venn diagrams: practice problems with solutions, questions, and answers.
• Simple 4 circles Venn diagram with word problems.
• Compare and contrast Venn diagram example.

Let’s define it:

A Venn Diagram is an illustration that shows logical relationships between two or more sets (grouping items). Venn diagram uses circles (both overlapping and nonoverlapping) or other shapes.

Commonly, Venn diagrams show how given items are similar and different.

Despite Venn diagram with 2 or 3 circles are the most common type, there are also many diagrams with a larger number of circles (5,6,7,8,10…). Theoretically, they can have unlimited circles.

Venn Diagram General Formula

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Don’t worry, there is no need to remember this formula, once you grasp the meaning. Let’s see the explanation with an example.

This is a very simple Venn diagram example that shows the relationship between two overlapping sets X, Y.

X – the number of items that belong to set A Y – the number of items that belong to set B Z – the number of items that belong to set A and B both

From the above Venn diagram, it is quite clear that

n(A) = x + z n(B) = y + z n(A ∩ B) = z n(A ∪ B) = x +y+ z.

Now, let’s move forward and think about Venn Diagrams with 3 circles.

Following the same logic, we can write the formula for 3 circles Venn diagram :

n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)

Venn Diagram Examples (Problems with Solutions)

As we already know how the Venn diagram works, we are going to give some practical examples (problems with solutions) from the real life.

2 Circle Venn Diagram Examples (word problems):

Suppose that in a town, 800 people are selected by random types of sampling methods . 280 go to work by car only, 220 go to work by bicycle only and 140 use both ways – sometimes go with a car and sometimes with a bicycle.

Here are some important questions we will find the answers:

• How many people go to work by car only?
• How many people go to work by bicycle only?
• How many people go by neither car nor bicycle?
• How many people use at least one of both transportation types?
• How many people use only one of car or bicycle?

The following Venn diagram represents the data above:

Now, we are going to answer our questions:

• Number of people who go to work by car only = 280
• Number of people who go to work by bicycle only = 220
• Number of people who go by neither car nor bicycle = 160
• Number of people who use at least one of both transportation types = n(only car) + n(only bicycle) + n(both car and bicycle) = 280 + 220 + 140 = 640
• Number of people who use only one of car or bicycle = 280 + 220 = 500

Note: The number of people who go by neither car nor bicycle (160) is illustrated outside of the circles. It is a common practice the number of items that belong to none of the studied sets, to be illustrated outside of the diagram circles.

We will deep further with a more complicated triple Venn diagram example.

3 Circle Venn Diagram Examples:

For the purposes of a marketing research , a survey of 1000 women is conducted in a town. The results show that 52 % liked watching comedies, 45% liked watching fantasy movies and 60% liked watching romantic movies. In addition, 25% liked watching comedy and fantasy both, 28% liked watching romantic and fantasy both and 30% liked watching comedy and romantic movies both. 6% liked watching none of these movie genres.

Here are our questions we should find the answer:

• How many women like watching all the three movie genres?
• Find the number of women who like watching only one of the three genres.
• Find the number of women who like watching at least two of the given genres.

Let’s represent the data above in a more digestible way using the Venn diagram formula elements:

• n(C) = percentage of women who like watching comedy = 52%
• n(F ) = percentage of women who like watching fantasy = 45%
• n(R) = percentage of women who like watching romantic movies= 60%
• n(C∩F) = 25%; n(F∩R) = 28%; n(C∩R) = 30%
• Since 6% like watching none of the given genres so, n (C ∪ F ∪ R) = 94%.

Now, we are going to apply the Venn diagram formula for 3 circles. 

94% = 52% + 45% + 60% – 25% – 28% – 30% + n (C ∩ F ∩ R)

Solving this simple math equation, lead us to:

n (C ∩ F ∩ R)  = 20%

It is a great time to make our Venn diagram related to the above situation (problem):

See, the Venn diagram makes our situation much more clear!

From the Venn diagram example, we can answer our questions with ease.

• The number of women who like watching all the three genres = 20% of 1000 = 200.
• Number of women who like watching only one of the three genres = (17% + 12% + 22%) of 1000 = 510
• The number of women who like watching at least two of the given genres = (number of women who like watching only two of the genres) +(number of women who like watching all the three genres) = (10 + 5 + 8 + 20)% i.e. 43% of 1000 = 430.

As we mentioned above 2 and 3 circle diagrams are much more common for problem-solving in many areas such as business, statistics, data science and etc. However, 4 circle Venn diagram also has its place.

4 Circles Venn Diagram Example:

A set of students were asked to tell which sports they played in school.

The options are: Football, Hockey, Basketball, and Netball.

Here is the list of the results:

The next step is to draw a Venn diagram to show the data sets we have.

It is very clear who plays which sports. As you see the diagram also include the student who does not play any sports (Dorothy) by putting her name outside of the 4 circles.

From the above Venn diagram examples, it is obvious that this graphical tool can help you a lot in representing a variety of data sets. Venn diagram also is among the most popular types of graphs for identifying similarities and differences .

Compare and Contrast Venn Diagram Example:

The following compare and contrast example of Venn diagram compares the features of birds and bats:

Tools for creating Venn diagrams

It is quite easy to create Venn diagrams, especially when you have the right tool. Nowadays, one of the most popular way to create them is with the help of paid or free graphing software tools such as:

You can use Microsoft products such as:

Some free mind mapping tools are also a good solution. Finally, you can simply use a sheet of paper or a whiteboard.

Conclusion:

A Venn diagram is a simple but powerful way to represent the relationships between datasets. It makes understanding math, different types of data analysis , set theory and business information easier and more fun for you.

Besides of using Venn diagram examples for problem-solving and comparing, you can use them to present passion, talent, feelings, funny moments and etc.

Be it data science or real-world situations, Venn diagrams are a great weapon in your hand to deal with almost any kind of information.

If you need more chart examples, our posts fishbone diagram examples and what does scatter plot show might be of help.

About The Author

Silvia Valcheva

Silvia Valcheva is a digital marketer with over a decade of experience creating content for the tech industry. She has a strong passion for writing about emerging software and technologies such as big data, AI (Artificial Intelligence), IoT (Internet of Things), process automation, etc.

Well explained I hope more on this one

WELL STRUCTURED CONTENT AND ENLIGHTNING AS WELL

Leave a Reply Cancel Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed .

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Venn Diagrams: Exercises

Intro Set Not'n Sets Exercises Diag. Exercises

Venn diagram word problems generally give you two or three classifications and a bunch of numbers. You then have to use the given information to populate the diagram and figure out the remaining information. For instance:

Out of forty students, 14 are taking English Composition and 29 are taking Chemistry.

• If five students are in both classes, how many students are in neither class?
• How many are in either class?
• What is the probability that a randomly-chosen student from this group is taking only the Chemistry class?

Content Continues Below

MathHelp.com

There are two classifications in this universe: English students and Chemistry students.

First I'll draw my universe for the forty students, with two overlapping circles labelled with the total in each:

(Well, okay; they're ovals, but they're always called "circles".)

Five students are taking both classes, so I'll put " 5 " in the overlap:

I've now accounted for five of the 14 English students, leaving nine students taking English but not Chemistry, so I'll put " 9 " in the "English only" part of the "English" circle:

I've also accounted for five of the 29 Chemistry students, leaving 24 students taking Chemistry but not English, so I'll put " 24 " in the "Chemistry only" part of the "Chemistry" circle:

This tells me that a total of 9 + 5 + 24 = 38 students are in either English or Chemistry (or both). This gives me the answer to part (b) of this exercise. This also leaves two students unaccounted for, so they must be the ones taking neither class, which is the answer to part (a) of this exercise. I'll put " 2 " inside the box, but outside the two circles:

The last part of this exercise asks me for the probability that a agiven student is taking Chemistry but not English. Out of the forty students, 24 are taking Chemistry but not English, which gives me a probability of:

24/40 = 0.6 = 60%

• Two students are taking neither class.
• There are 38 students in at least one of the classes.
• There is a 60% probability that a randomly-chosen student in this group is taking Chemistry but not English.

Years ago, I discovered that my (now departed) cat had a taste for the adorable little geckoes that lived in the bushes and vines in my yard, back when I lived in Arizona. In one month, suppose he deposited the following on my carpet:

• six gray geckoes,
• twelve geckoes that had dropped their tails in an effort to escape capture, and
• fifteen geckoes that he'd chewed on a little

In addition:

• only one of the geckoes was gray, chewed-on, and tailless;
• two were gray and tailless but not chewed-on;
• two were gray and chewed-on but not tailless.

If there were a total of 24 geckoes left on my carpet that month, and all of the geckoes were at least one of "gray", "tailless", and "chewed-on", how many were tailless and chewed-on, but not gray?

If I work through this step-by-step, using what I've been given, I can figure out what I need in order to answer the question. This is a problem that takes some time and a few steps to solve.

They've given me that each of the geckoes had at least one of the characteristics, so each is a member of at least one of the circles. This means that there will be nothing outside of the circles; the circles will account for everything in this particular universe.

There was one gecko that was gray, tailless, and chewed on, so I'll draw my Venn diagram with three overlapping circles, and I'll put " 1 " in the center overlap:

Two of the geckoes were gray and tailless but not chewed-on, so " 2 " goes in the rest of the overlap between "gray" and "tailless".

Two of them were gray and chewed-on but not tailless, so " 2 " goes in the rest of the overlap between "gray" and "chewed-on".

Since a total of six were gray, and since 2 + 1 + 2 = 5 of these geckoes have already been accounted for, this tells me that there was only one left that was only gray.

This leaves me needing to know how many were tailless and chewed-on but not gray, which is what the problem asks for. But, because I don't know how many were only chewed on or only tailless, I cannot yet figure out the answer value for the remaining overlap section.

I need to work with a value that I don't yet know, so I need a variable. I'll let " x " stand for this unknown number of tailless, chewed-on geckoes.

I do know the total number of chewed geckoes ( 15 ) and the total number of tailless geckoes ( 12 ). After subtracting, this gives me expressions for the remaining portions of the diagram:

only chewed on:

15 − 2 − 1 − x = 12 − x

only tailless:

12 − 2 − 1 − x = 9 − x

There were a total of 24 geckoes for the month, so adding up all the sections of the diagram's circles gives me: (everything from the "gray" circle) plus (the unknown from the remaining overlap) plus (the only-chewed-on) plus (the only-tailless), or:

(1 + 2 + 1 + 2) + ( x )

+ (12 − x ) + (9 − x )

= 27 − x = 24

Solving , I get x = 3 . So:

Three geckoes were tailless and chewed on but not gray.

(No geckoes or cats were injured during the production of the above word problem.)

For more word-problem examples to work on, complete with worked solutions, try this page provided by Joe Kahlig of Texas A&M University. There is also a software package (DOS-based) available through the Math Archives which can give you lots of practice with the set-theory aspect of Venn diagrams. The program is not hard to use, but you should definitely read the instructions before using.

URL: https://www.purplemath.com/modules/venndiag4.htm

Page 1 Page 2 Page 3 Page 4

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Problems Using Venn Diagrams

Venn diagrams are visual tools often used to organize and understand sets and the relationships between them. They're named after John Venn, a British philosopher, and logician who introduced them in the 1880s. Venn diagrams are frequently used in various fields, including mathematics, statistics, logic, computer science, etc. They're handy for solving problems involving sets and subsets, intersections, unions, and complements.

A Step-by-step Guide to Solving Problems Using Venn Diagrams

Here’s a step-by-step guide on how to solve problems using Venn diagrams:

Step 1: Understand the Problem

As with any problem-solving method, the first step is to understand the problem. What sets are involved? How are they related? What are you being asked to find?

Step 2: Draw the Diagram

Draw a rectangle to represent the universal set, which includes all possible elements. Each set within the universal set is represented by a circle. If there are two sets, draw two overlapping circles. If there are three sets, draw three overlapping circles, and so forth. Each section in the overlapping circles represents different intersections of the sets.

Step 3: Label the Diagram

Each circle (set) should be labeled appropriately. If you’re dealing with sets of different types of fruits, for example, one might be labeled “Apples” and another “Oranges”.

Step 4: Fill in the Values

Start filling in the values from the innermost part of the diagram (where all sets overlap) to the outer parts. This helps to avoid double-counting elements that belong to more than one set. Information provided in the problem usually tells you how many elements are in each set or section.

Step 5: Solve the Problem

Now, you can use the diagram to answer the question. This might involve counting the number of elements in a particular set or section of the diagram, or it might involve noticing patterns or relationships between the sets.

Step 6: Check Your Answer

Make sure your answer makes sense in the context of the problem and that you’ve accounted for all elements in the diagram.

by: Effortless Math Team about 10 months ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• How to Solve Negative Exponents and Negative Bases? (+FREE Worksheet!)
• 10 Most Common ACT Math Questions
• TABE Math Practice Test Questions
• Top 10 7th Grade ACT Aspire Math Practice Questions
• How to Use Number Lines to Graph Fractions as Decimals
• A Comprehensive Collection of Free SHSAT Math Practice Tests
• 3rd Grade Georgia Milestones Assessment System Math Practice Test Questions
• Full-Length PSAT 10 Math Practice Test-Answers and Explanations
• The Ultimate PERT Math Course (+FREE Worksheets & Tests)
• How to Graph Inverse Trigonometric Functions?

What people say about "How to Solve Problems Using Venn Diagrams - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos
• Google Play
• Apple Store

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

1.3 Understanding Venn Diagrams

Learning objectives.

After completing this section, you should be able to:

• Utilize a universal set with two sets to interpret a Venn diagram.
• Utilize a universal set with two sets to create a Venn diagram.
• Determine the complement of a set.

Have you ever ordered a new dresser or bookcase that required assembly? When your package arrives you excitedly open it and spread out the pieces. Then you check the assembly guide and verify that you have all the parts required to assemble your new dresser. Now, the work begins. Luckily for you, the assembly guide includes step-by-step instructions with images that show you how to put together your product. If you are really lucky, the manufacturer may even provide a URL or QR code connecting you to an online video that demonstrates the complete assembly process. We can likely all agree that assembly instructions are much easier to follow when they include images or videos, rather than just written directions. The same goes for the relationships between sets.

Interpreting Venn Diagrams

Venn diagrams are the graphical tools or pictures that we use to visualize and understand relationships between sets. Venn diagrams are named after the mathematician John Venn, who first popularized their use in the 1880s. When we use a Venn diagram to visualize the relationships between sets, the entire set of data under consideration is drawn as a rectangle, and subsets of this set are drawn as circles completely contained within the rectangle. The entire set of data under consideration is known as the universal set .

Consider the statement: All trees are plants. This statement expresses the relationship between the set of all plants and the set of all trees. Because every tree is a plant, the set of trees is a subset of the set of plants. To represent this relationship using a Venn diagram, the set of plants will be our universal set and the set of trees will be the subset. Recall that this relationship is expressed symbolically as: Trees ⊂ Plants . Trees ⊂ Plants . To create a Venn diagram, first we draw a rectangle and label the universal set “ U = Plants . U = Plants . ” Then we draw a circle within the universal set and label it with the word “Trees.”

This section will introduce how to interpret and construct Venn diagrams. In future sections, as we expand our knowledge of relationships between sets, we will also develop our knowledge and use of Venn diagrams to explore how multiple sets can be combined to form new sets.

Example 1.18

Interpreting the relationship between sets in a venn diagram.

Write the relationship between the sets in the following Venn diagram, in words and symbolically.

The set of terriers is a subset of the universal set of dogs. In other words, the Venn diagram depicts the relationship that all terriers are dogs. This is expressed symbolically as T ⊂ U . T ⊂ U .

Your Turn 1.18

So far, the only relationship we have been considering between two sets is the subset relationship, but sets can be related in other ways. Lions and tigers are both different types of cats, but no lions are tigers, and no tigers are lions. Because the set of all lions and the set of all tigers do not have any members in common, we call these two sets disjoint sets , or non-overlapping sets.

Two sets A A and B B are disjoint sets if they do not share any elements in common. That is, if a a is a member of set A A , then a a is not a member of set B B . If b b is a member of set B B , then b b is not a member of set A A . To represent the relationship between the set of all cats and the sets of lions and tigers using a Venn diagram, we draw the universal set of cats as a rectangle and then draw a circle for the set of lions and a separate circle for the set of tigers within the rectangle, ensuring that the two circles representing the set of lions and the set of tigers do not touch or overlap in any way.

Example 1.19

Describing the relationship between sets.

Describe the relationship between the sets in the following Venn diagram.

The set of triangles and the set of squares are two disjoint subsets of the universal set of two-dimensional figures. The set of triangles does not share any elements in common with the set of squares. No triangles are squares and no squares are triangles, but both squares and triangles are 2D figures.

Your Turn 1.19

Creating venn diagrams.

The main purpose of a Venn diagram is to help you visualize the relationship between sets. As such, it is necessary to be able to draw Venn diagrams from a written or symbolic description of the relationship between sets.

To create a Venn diagram:

• Draw a rectangle to represent the universal set, and label it U = set name U = set name .
• Draw a circle within the rectangle to represent a subset of the universal set and label it with the set name.

If there are multiple disjoint subsets of the universal set, their separate circles should not touch or overlap.

Example 1.20

Drawing a venn diagram to represent the relationship between two sets.

Draw a Venn diagram to represent the relationship between each of the sets.

• All rectangles are parallelograms.
• All women are people.
• The set of rectangles is a subset of the set of parallelograms. First, draw a rectangle to represent the universal set and label it with U = Parallelograms U = Parallelograms , then draw a circle completely within the rectangle, and label it with the name of the set it represents, R = Rectangles R = Rectangles .

In this example, both letters and names are used to represent the sets involved, but this is not necessary. You may use either letters or names alone, as long as the relationship is clearly depicted in the diagram, as shown below.

• The universal set is the set of people, and the set of all women is a subset of the set of people.

Your Turn 1.20

Example 1.21, drawing a venn diagram to represent the relationship between three sets.

All bicycles and all cars have wheels, but no bicycle is a car. Draw a Venn diagram to represent this relationship.

Step 1: The set of bicycles and the set of cars are both subsets of the set of things with wheels. The universal set is the set of things with wheels, so we first draw a rectangle and label it with U = Things with Wheels U = Things with Wheels .

Step 2: Because the set of bicycles and the set of cars do not share any elements in common, these two sets are disjoint and must be drawn as two circles that do not touch or overlap with the universal set.

Your Turn 1.21

The complement of a set.

Recall that if set A A is a proper subset of set U U , the universal set (written symbolically as A ⊂ U A ⊂ U ), then there is at least one element in set U U that is not in set A A . The set of all the elements in the universal set U U that are not in the subset A A is called the complement of set A A , A ' A ' . In set builder notation this is written symbolically as: A ' = { x ∈ U | x ∉ A } . A ' = { x ∈ U | x ∉ A } . The symbol ∈ ∈ is used to represent the phrase, “is a member of,” and the symbol ∉ ∉ is used to represent the phrase, “is not a member of.” In the Venn diagram below, the complement of set A A is the region that lies outside the circle and inside the rectangle. The universal set U U includes all of the elements in set A A and all of the elements in the complement of set A A , and nothing else.

Consider the set of digit numbers. Let this be our universal set, U = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } . U = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } . Now, let set A A be the subset of U U consisting of all the prime numbers in set U U , A = { 2 , 3 , 5 , 7 } . A = { 2 , 3 , 5 , 7 } . The complement of set A A is A ' = { 0 , 1 , 4 , 6 , 8 , 9 } . A ' = { 0 , 1 , 4 , 6 , 8 , 9 } . The following Venn diagram represents this relationship graphically.

Example 1.22

Finding the complement of a set.

For both of the questions below, A A is a proper subset of U U .

• Given the universal set U = { Billie Eilish, Donald Glover, Bruno Mars, Adele, Ed Sheeran} U = { Billie Eilish, Donald Glover, Bruno Mars, Adele, Ed Sheeran} and set A = { Donald Glover, Bruno Mars, Ed Sheeran} A = { Donald Glover, Bruno Mars, Ed Sheeran} , find A ' . A ' .
• Given the universal set U = { d|d is a dog } U = { d|d is a dog } and B = { b ∈ U|b is a beagle } B = { b ∈ U|b is a beagle } , find B ' . B ' .
• The complement of set A A is the set of all elements in the universal set U U that are not in set A . A . A ' = { Billie Eilish, Adele } A ' = { Billie Eilish, Adele } .
• The complement of set B B is the set of all dogs that are not beagles. All members of set B ′ B ′ are in the universal set because they are dogs, but they are not in set B , B , because they are not beagles. This relationship can be expressed in set build notation as follows: B ′ = { All dogs that are not beagles .} B ′ = { All dogs that are not beagles .} , B ′ = { d ∈ U | d is not a beagle .} B ′ = { d ∈ U | d is not a beagle .} , or B ′ = { d ∈ U | d ∉ B } . B ′ = { d ∈ U | d ∉ B } .

Your Turn 1.22

Check your understanding, section 1.3 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/1-3-understanding-venn-diagrams

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Venn Diagram Examples for Problem Solving

Updated on: 13 September 2022

What is a Venn Diagram?

Venn diagrams define all the possible relationships between collections of sets. The most basic Venn diagrams simply consist of multiple circular boundaries describing the range of sets.

The overlapping areas between the two boundaries describe the elements which are common between the two, while the areas that aren’t overlapping house the elements that are different. Venn diagrams are used often in math that people tend to assume they are used only to solve math problems. But as the 3 circle Venn diagram below shows it can be used to solve many other problems.

Though the above diagram may look complicated, it is actually very easy to understand. Although Venn diagrams can look complex when solving business processes understanding of the meaning of the boundaries and what they stand for can simplify the process to a great extent. Let us have a look at a few examples which demonstrate how Venn diagrams can make problem solving much easier.

Example 1: Company’s Hiring Process

The first Venn diagram example demonstrates a company’s employee shortlisting process. The Human Resources department looks for several factors when short-listing candidates for a position, such as experience, professional skills and leadership competence. Now, all of these qualities are different from each other, and may or may not be present in some candidates. However, the best candidates would be those that would have all of these qualities combined.

The candidate who has all three qualities is the perfect match for your organization. So by using simple Venn Diagrams like the one above, a company can easily demonstrate its hiring processes and make the selection process much easier.

A colorful and precise Venn diagram like the above can be easily created using our Venn diagram software and we have professionally designed Venn diagram templates for you to get started fast too.

Example 2: Investing in a Location

The second Venn diagram example takes things a step further and takes a look at how a company can use a Venn diagram to decide a suitable office location. The decision will be based on economic, social and environmental factors.

In a perfect scenario you’ll find a location that has all the above factors in equal measure. But if you fail to find such a location then you can decide which factor is most important to you. Whatever the priority because you already have listed down the locations making the decision becomes easier.

Example 3: Choosing a Dream Job

The last example will reflect on how one of the life’s most complicated questions can be easily answered using a Venn diagram. Choosing a dream job is something that has stumped most college graduates, but with a single Venn diagram, this thought process can be simplified to a great extent.

First, single out the factors which matter in choosing a dream job, such as things that you love to do, things you’re good at, and finally, earning potential. Though most of us dream of being a celebrity and coming on TV, not everyone is gifted with acting skills, and that career path may not be the most viable. Instead, choosing something that you are good at, that you love to do along with something that has a good earning potential would be the most practical choice.

A job which includes all of these three criteria would, therefore, be the dream job for someone. The three criteria need not necessarily be the same, and can be changed according to the individual’s requirements.

So you see, even the most complicated processes can be simplified by using these simple Venn diagrams.

Join over thousands of organizations that use Creately to brainstorm, plan, analyze, and execute their projects successfully.

More Related Articles

Great article, and all true, but.. I hate venn diagrams! I don’t know why, they’ve just never seemed to work for me. Frustrating!

Hey thanks for writing. It helped me in many ways Thanks again 🙂

Hi Nishadha,

Nice article! I love Venn Diagrams because nothing comes to close to expressing the logical relationships between different sets of elements that well. With Microsoft Word 2003 you can create fantastic looking and colorful Venn Diagrams on the fly, with as many elements and colors as you need.

Hi Worli, Yes, Venn diagrams are a good way to solve problems, it’s a shame that it’s sort of restricted to the mathematics subject. MS Word do provides some nice options to create Venn diagrams, although it’s not the cheapest thing around.

Leave a comment Cancel reply

Please enter an answer in digits: 10 + 7 =

Download our all-new eBook for tips on 50 powerful Business Diagrams for Strategic Planning.

Venn Diagram Word Problems

Related Pages Venn Diagrams Intersection Of Two Sets Intersection Of Three Sets More Lessons On Sets More GCSE/IGCSE Maths Lessons

In these lessons, we will learn how to solve word problems using Venn Diagrams that involve two sets or three sets. Examples and step-by-step solutions are included in the video lessons.

What Are Venn Diagrams?

Venn diagrams are the principal way of showing sets in a diagrammatic form. The method consists primarily of entering the elements of a set into a circle or ovals.

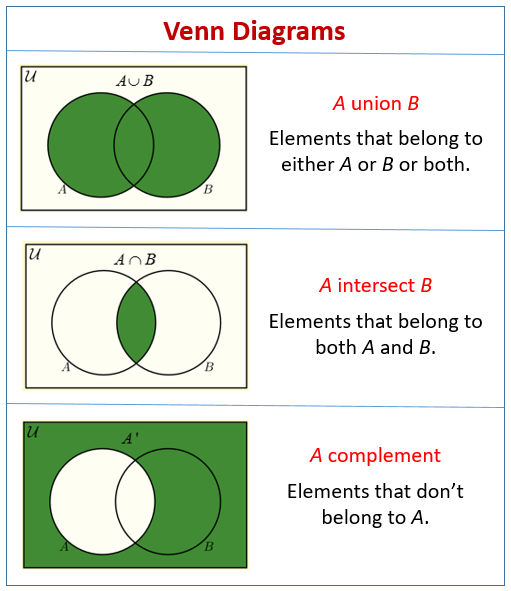
Before we look at word problems, see the following diagrams to recall how to use Venn Diagrams to represent Union, Intersection and Complement.

How To Solve Problems Using Venn Diagrams?

This video solves two problems using Venn Diagrams. One with two sets and one with three sets.

Problem 1: 150 college freshmen were interviewed. 85 were registered for a Math class, 70 were registered for an English class, 50 were registered for both Math and English.

a) How many signed up only for a Math Class? b) How many signed up only for an English Class? c) How many signed up for Math or English? d) How many signed up neither for Math nor English?

Problem 2: 100 students were interviewed. 28 took PE, 31 took BIO, 42 took ENG, 9 took PE and BIO, 10 took PE and ENG, 6 took BIO and ENG, 4 took all three subjects.

a) How many students took none of the three subjects? b) How many students took PE but not BIO or ENG? c) How many students took BIO and PE but not ENG?

How And When To Use Venn Diagrams To Solve Word Problems?

Problem: At a breakfast buffet, 93 people chose coffee and 47 people chose juice. 25 people chose both coffee and juice. If each person chose at least one of these beverages, how many people visited the buffet?

How To Use Venn Diagrams To Help Solve Counting Word Problems?

Problem: In a class of 30 students, 19 are studying French, 12 are studying Spanish and 7 are studying both French and Spanish. How many students are not taking any foreign languages?

Probability, Venn Diagrams And Conditional Probability

This video shows how to construct a simple Venn diagram and then calculate a simple conditional probability.

Problem: In a class, P(male)= 0.3, P(brown hair) = 0.5, P (male and brown hair) = 0.2 Find (i) P(female) (ii) P(male| brown hair) (iii) P(female| not brown hair)

Venn Diagrams With Three Categories

Example: A group of 62 students were surveyed, and it was found that each of the students surveyed liked at least one of the following three fruits: apricots, bananas, and cantaloupes.

34 liked apricots. 30 liked bananas. 33 liked cantaloupes. 11 liked apricots and bananas. 15 liked bananas and cantaloupes. 17 liked apricots and cantaloupes. 19 liked exactly two of the following fruits: apricots, bananas, and cantaloupes.

a. How many students liked apricots, but not bananas or cantaloupes? b. How many students liked cantaloupes, but not bananas or apricots? c. How many students liked all of the following three fruits: apricots, bananas, and cantaloupes? d. How many students liked apricots and cantaloupes, but not bananas?

Venn Diagram Word Problem

Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets.

Problem: 90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers. 5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream. 38 had ice-cream. 8 had a hamburger and ice-cream. How many had nothing? (Errata in video: 90 - (14 + 2 + 3 + 5 + 21 + 7 + 23) = 90 - 75 = 15)

Venn Diagrams With Two Categories

This video introduces 2-circle Venn diagrams, and using subtraction as a counting technique.

How To Use 3-Circle Venn Diagrams As A Counting Technique?

Learn about Venn diagrams with two subsets using regions.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.2: Venn Diagrams

• Last updated
• Save as PDF
• Page ID 82983

• Julie Harland
• MiraCosta College

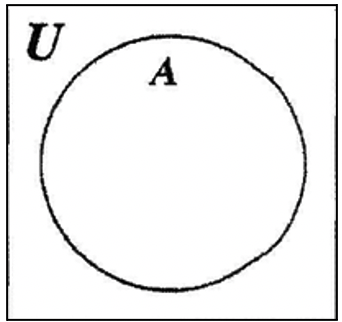
Study the Venn diagrams on this and the following pages. It takes a whole lot of practice to shade or identify regions of Venn diagrams. Be advised that it may be necessary to shade several practice diagrams along the way before you get to the final result.

We shade Venn diagrams to represent sets. We will be doing some very easy, basic Venn diagrams as well as several involved and complicated Venn diagrams.

To find the intersection of two sets, you might try shading one region in a given direction, and another region in a different direction. Then you would look where those shadings overlap. That overlap would be the intersection.

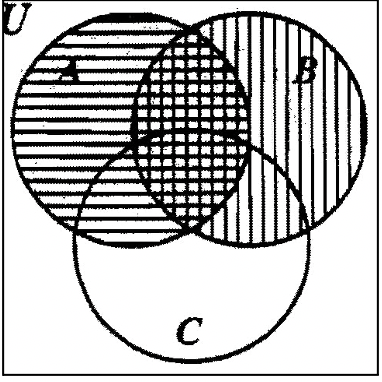
For example, to visualize \(A \cap B\), shade A with horizontal lines and B with vertical lines. Then the overlap is \(A \cap B\). The diagram on the left would be a first step in getting the answer. The shaded part on the diagram to the right shows the final answer.

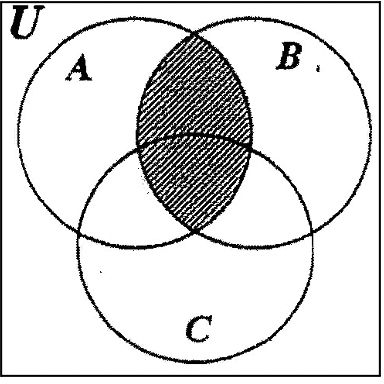
Here are two problems for you to try. Only shade in the final answer for each exercise.

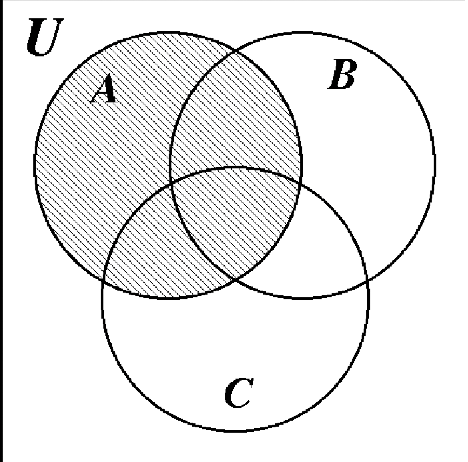
Shade the region that represents \(A \cap C\)

Shade the region that represents \(B \cap C\)

To shade the union of two sets, shade each region completely or shade both regions in the same direction. Thus, to find the union of A and B , shade all of A and all of B .

The final answer is represented by the shaded area in the diagram to the right.

Shade the region that represents \(A \cup C\)

Shade the region that represents \(B \cup C\)

For the complement of a region, shade everything outside the given region. You can think of it as shading everything except that region. On the Venn diagram to the left, the shaded area represents A . On the Venn diagram to the right, the shaded area represents .

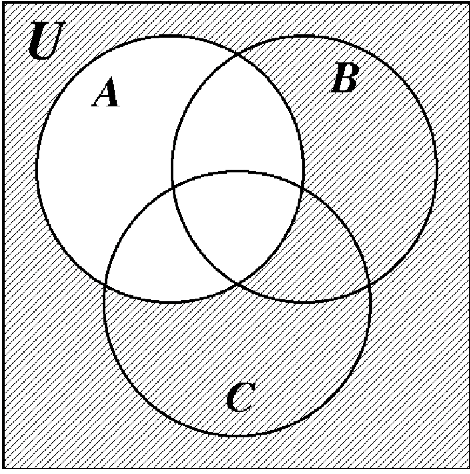
Many people are confused about what part of the Venn diagram represents the universe, U . The universe is the entire Venn diagram, including the sets A , B and C . The three Venn diagrams on the next page illustrate the differences between U , \(U^{c}\) and \((A \cup B \cup C)^{c}\). Carefully note these differences.

Usually, parentheses are necessary to indicate which operation needs to be done first. If there is only union or intersection involved, this isn’t necessary as in ( A \(\cup\) B \(\cup\) C )\(^{c}\) above. Convince yourself that (( A \(\cup\) B ) \(\cup\) C ) = ( A \(\cup\) ( B \(\cup\) C )). Similarly, convince yourself of the analogous fact for intersection by performing the following steps. On the first Venn diagram below, shade A \(\cap\) B with horizontal lines and shade C with vertical lines. Then, the overlap is (( A \(\cap\) B ) \(\cap\) C ). On the second Venn diagram, shade A with lines slanting to the right and B \(\cup\) C with lines slanting to the left. Then the overlap is ( A \(\cap\) ( B \(\cap\) C )). Check to see that the final answer, the overlap in this case, is the same for both. Shade the final answer in the third Venn diagram.

a. ( A \(\cap\) B ) \(\cap\) C

b. ( A \(\cup\) ( B \(\cup\) C ))

c. Shade final answer here.

Now, it's time for you to try a few more diagrams on your own. It may take more than one step to figure out the answer. You might need to do preliminary drawings on scratch paper first. The shadings you show here should be the final answer only, but you should be able to explain and support how you arrived at your answer. Compare your answers with other people in your class and make sure a consensus is reached on the correct answer. Do this for all the Venn diagrams throughout this exercise set. Shade in the region that represents what is written above each of the six Venn diagrams on the following page . Note that in cases involving more than one operation, it is necessary to use parentheses and follow order of operations. Exercises 10 and 11 illustrate why this is necessary.

( C \(\cap\) A )\(^{c}\)

( B \(\cup\) C )\(^{c}\)

( A \(\cap\) B \(\cap\) C )\(^{c}\)

Exercise 10

( A \(\cap\) B ) \(\cap\) C

Exercise 11

( A \(\cap\) ( B \(\cap\) C )

For difference, shade the region coming before the difference sign ( – ) but don’t include or shade any part of the region that follows the difference sign. The Venn on the left represents A–B and the one on the right represents C – A.

Exercise 12

Shade the region that represents A – C

Exercise 13

Shade the region that represents B – C

Study the following Venn diagrams. Make sure you understand how to get the answers.

It's your turn to shade in the region that represents what is written above each diagram.

Exercise 14

( A \(\cap\) C ) – B

Exercise 15

B – ( A \(\cap\) C )

Exercise 16

( A – C ) \(\cup\) ( B – A )

Suppose you wanted to find ((C – A ) \(\cap\) B )\(^{c}\). This would probably take a few steps to get the answer. One approach to finding the correct shading is to notice that the final answer is the complement of ( C – A) \(\cap\) B . That means we would have to first figure out what (C – A) \(\cap\) B looked like. In order to do that, we notice that this is the intersection of two things C – A and B. On the blank Venn diagram to the left below, shade C – A with horizontal lines and B with vertical lines. The overlap would be the intersection. The overlap on your drawing should match the shading shown on the Venn diagram in the middle. Does it? The last step would then be to take the complement of the shading shown on the middle diagram. This is shown on the Venn diagram on the far right. So, it took drawing three Venns to come up with the final answer for this problem. Someone else might be able to do it in fewer steps while someone else might take more steps.

Exercise 17

As mentioned previously, it takes a lot of practice to get good at shading Venn diagrams. It’s even trickier to look at a Venn diagram and describe it, In fact, there is usually more than one way to describe a Venn diagram. For example, the shading for (( C – A ) \(\cap\) B )\(^{c}\) shown on the previous page is the same as it is for (( C \(\cap\) B ) – A )\(^{c}\). What does this mean? We’re so used to only having one correct answer. Well, consider if someone asked you to write an arithmetic problem for which the answer was 2. There would be infinitely many possibilities. For example, 5 - 3 or 1 + 1 or 10/5 would all be acceptable answers. Granted, this kind of question on a test would be harder for a teacher to grade because each student’s response would have to be checked to see if it would work. There isn’t one pat answer. The same goes if a teacher asks you to look at a shading of a Venn diagram and describe it. On the other hand, if a description is given and you are asked to shade the Venn diagram, there is only one correct shading. It is much like being asked to compute an arithmetic problem. The answer to 10 - 8 is 2 and that is the only acceptable answer!

The point of all this is that to master shadings of Venn diagrams and descriptions of Venn diagrams by looking at the shadings takes lots and lots and lots of practice. Give yourself plenty of time to study and work on them and you will accomplish this feat!!!

On the next few pages, you are asked to shade several one, two and three set Venn diagrams. The correct shadings follow. Make sure you try these problems in earnest. Make sure you can explain the steps involved to arrive at the correct shading. After mastering the shadings, see if you can look at a shaded Venn diagram and come up with an accurate description. Again, remember there is more than one way to describe a given Venn diagram.

These Venn diagrams will be helpful when studying for a test. Go back and practice drawing the same Venn diagrams later. Use the answers to see if you can describe them by looking at the picture. Of course, remember that your description might not match exactly since there as more than one way to describe any given Venn diagram. If your description is different, make sure you go through the steps of shading a Venn with your description and see if your shading really matches the Venn diagram you were trying to describe.

Here are a few shaded Venn diagrams. See if you can look at the shadings and come up with a description. I’ve put some possible answers at the bottom of this page.

Here are some possible descriptions for the above Venn diagrams:

Shade the region that represents what is written above each of the one and two set Venn diagrams below. You may need to draw preliminary drawings first for some of them.

Exercise 18

Exercise 19

Exercise 20, exercise 21, exercise 22.

A \(\cap\) B

Exercise 23

A \(\cup\) B

Exercise 24

\(A \cup B^{c}\)

Exercise 25

\((A \cap B)^{c}\)

Exercise 26

\((A \cup B)^{c}\)

Exercise 27

( A \ B ) \(\cup\) ( B \ A )

Exercise 28

\(A^{c} \cup B^{c}\)

Exercise 29

\(A^{c} \cap B^{c}\)

Exercise 30

\((A \cup B)^{c} \cup (A \cap B)\)

Exercise 31

Exercise 32, exercise 33, exercise 34.

( A \(\cap\) B ) – C

Exercise 35

( C \(\cup\) B ) – A

Exercise 36

( A \(\cap\) B ) \(\cup\) C

Exercise 37

( A \(\cup\) B ) \(\cap\) C

Exercise 38

A \(^{c}\) – B

Exercise 39

A \(\cap\) B \(\cap\) C ) – B

Exercise 40

B – ( A \(\cup\) C )

Exercise 41

C – ( A \(\cap\) B )

Exercise 42

( B – A ) \(\cap\) ( B – C )

Exercise 43

( B – A ) \(\cup\) ( B – C )

Exercise 44

( A \(\cup\) B )\(^{c}\)

Exercise 45

A \(^{c}\) \(\cap\) B \(^{c}\)

Exercise 46

A \(^{c}\) – B \(^{c}\)

Exercise 47

( C – B) \(^{c}\)

Exercise 48

( B \(^{c}\) \(\cap\) C ) – A

Exercise 49

( A – ( B \(\cup\) C )) \(\cup\) ( B – ( A \(\cup\) C )) \(\cup\) ( C – ( A \(\cup\) B ))

Exercise 50

( A \(\cap\) C )\(^{c}\)

Exercise 51

(( A \(\cap\) B ) – C ) \(\cap\) ( C – A)

Exercise 52

A \(^{c}\) \(\cup\) C \(^{c}\)

Exercise 53

B \(\cap\) ( C \(\cup\) A \(^{c}\))

Here are the correct shadings to the exercises on the previous pages. After mastering these shadings, reverse the process by looking at the shadings on this page and try to describe them. It takes practice and patience and remember that there may be more than one way to describe some of these. In fact, many times you'll see there is a simpler way to describe them than was on the original exercise!!

In the Material Card section there are blank Venn diagram templates you can use for practice.

Venn Diagram

A Venn diagram is used to visually represent the differences and the similarities between two concepts. Venn diagrams are also called logic or set diagrams and are widely used in set theory, logic, mathematics, businesses, teaching, computer science, and statistics.

Let's learn about Venn diagrams, their definition, symbols, and types with solved examples.

What is a Venn Diagram?

A Venn diagram is a diagram that helps us visualize the logical relationship between sets and their elements and helps us solve examples based on these sets. A Venn diagram typically uses intersecting and non-intersecting circles (although other closed figures like squares may be used) to denote the relationship between sets.

Venn Diagram Example

Let us observe a Venn diagram example. Here is the Venn diagram that shows the correlation between the following set of numbers.

• One set contains even numbers from 1 to 25 and the other set contains the numbers in the 5x table from 1 to 25.
• The intersecting part shows that 10 and 20 are both even numbers and also multiples of 5 between 1 to 25.

Terms Related to Venn Diagram

Let us understand the following terms and concepts related to Venn Diagram, to understand it better.

Universal Set

Whenever we use a set, it is easier to first consider a larger set called a universal set that contains all of the elements in all of the sets that are being considered. Whenever we draw a Venn diagram:

• A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U.
• All the other sets are represented by circles or closed figures within this larger rectangle .
• Every set is the subset of the universal set U.

Consider the above-given image:

• U is the universal set with all the numbers 1-10, enclosed within the rectangle.
• A is the set of even numbers 1-10, which is the subset of the universal set U and it is placed inside the rectangle.
• All the numbers between 1-10, that are not even, will be placed outside the circle and within the rectangle as shown above.

Venn diagrams are used to show subsets. A subset is actually a set that is contained within another set. Let us consider the examples of two sets A and B in the below-given figure. Here, A is a subset of B. Circle A is contained entirely within circle B. Also, all the elements of A are elements of set B.

This relationship is symbolically represented as A ⊆ B. It is read as A is a subset of B or A subset B. Every set is a subset of itself. i.e. A ⊆ A. Here is another example of subsets :

• N = set of natural numbers
• I = set of integers
• Here N ⊂ I, because all-natural numbers are integers .

Venn Diagram Symbols

There are more than 30 Venn diagram symbols. We will learn about the three most commonly used symbols in this section. They are listed below as:

Let us understand the concept and the usage of the three basic Venn diagram symbols using the image given below.

Venn Diagram for Sets Operations

In set theory, we can perform certain operations on given sets. These operations are as follows,

• Union of Set
• Intersection of set
• Complement of set
• Difference of set

Union of Sets Venn Diagram

The union of two sets A and B can be given by: A ∪ B = {x | x ∈ A or x ∈ B}. This operation on the elements of set A and B can be represented using a Venn diagram with two circles. The total region of both the circles combined denotes the union of sets A and B.

Intersection of Set Venn Diagram

The intersection of sets, A and B is given by: A ∩ B = {x : x ∈ A and x ∈ B}. This operation on set A and B can be represented using a Venn diagram with two intersecting circles. The region common to both the circles denotes the intersection of set A and Set B.

Complement of Set Venn Diagram

The complement of any set A can be given as A'. This represents elements that are not present in set A and can be represented using a Venn diagram with a circle. The region covered in the universal set, excluding the region covered by set A, gives the complement of A.

Difference of Set Venn Diagram

The difference of sets can be given as, A - B. It is also referred to as a ‘relative complement’. This operation on sets can be represented using a Venn diagram with two circles. The region covered by set A, excluding the region that is common to set B, gives the difference of sets A and B.

We can observe the above-explained operations on sets using the figures given below,

Venn Diagram for Three Sets

Three sets Venn diagram is made up of three overlapping circles and these three circles show how the elements of the three sets are related. When a Venn diagram is made of three sets, it is also called a 3-circle Venn diagram. In a Venn diagram, when all these three circles overlap, the overlapping parts contain elements that are either common to any two circles or they are common to all the three circles. Let us consider the below given example:

Here are some important observations from the above image:

• Elements in P and Q = elements in P and Q only plus elements in P, Q, and R.
• Elements in Q and R = elements in Q and R only plus elements in P, Q, and R.
• Elements in P and R = elements in P and R only plus elements in P, Q, and R.

How to Draw a Venn Diagram?

Venn diagrams can be drawn with unlimited circles. Since more than three becomes very complicated, we will usually consider only two or three circles in a Venn diagram. Here are the 4 easy steps to draw a Venn diagram:

• Step 1: Categorize all the items into sets.
• Step 2: Draw a rectangle and label it as per the correlation between the sets.
• Step 3: Draw the circles according to the number of categories you have.
• Step 4: Place all the items in the relevant circles.

Example: Let us draw a Venn diagram to show categories of outdoor and indoor for the following pets: Parrots, Hamsters, Cats, Rabbits, Fish, Goats, Tortoises, Horses.

• Step 1: Categorize all the items into sets (Here, its pets): Indoor pets: Cats, Hamsters, and, Parrots. Outdoor pets: Horses, Tortoises, and Goats. Both categories (outdoor and indoor): Rabbits and Fish.
• Step 2: Draw a rectangle and label it as per the correlation between the two sets. Here, let's label the rectangle as Pets.
• Step 3: Draw the circles according to the number of categories you have. There are two categories in the sample question: outdoor pets and indoor pets. So, let us draw two circles and make sure the circles overlap.

• Step 4: Place all the pets in the relevant circles. If there are certain pets that fit both the categories, then place them at the intersection of sets , where the circles overlap. Rabbits and fish can be kept as indoor and outdoor pets, and hence they are placed at the intersection of both circles.

• Step 5: If there is a pet that doesn't fit either the indoor or outdoor sets, then place it within the rectangle but outside the circles.

Venn Diagram Formula

For any two given sets A and B, the Venn diagram formula is used to find one of the following: the number of elements of A, B, A U B, or A ⋂ B when the other 3 are given. The formula says:

n(A U B) = n(A) + n(B) – n (A ⋂ B)

Here, n(A) and n(B) represent the number of elements in A and B respectively. n(A U B) and n(A ⋂ B) represent the number of elements in A U B and A ⋂ B respectively. This formula is further extended to 3 sets as well and it says:

• n (A U B U C) = n(A) + n(B) + n(C) - n(A ⋂ B) - n(B ⋂ C) - n(C ⋂ A) + n(A ⋂ B ⋂ C)

Here is an example of Venn diagram formula.

Example:  In a cricket school, 12 players like bowling, 15 like batting, and 5 like both. Then how many players like either bowling or batting.

Let A and B be the sets of players who like bowling and batting respectively. Then

n(A ⋂ B) = 5

We have to find n(A U B). Using the Venn diagram formula,

n(A U B) = 12 + 15 - 5 = 22.

Applications of Venn Diagram

There are several advantages to using Venn diagrams. Venn diagram is used to illustrate concepts and groups in many fields, including statistics, linguistics, logic, education, computer science, and business.

• We can visually organize information to see the relationship between sets of items, such as commonalities and differences, and to depict the relations for visual communication.
• We can compare two or more subjects and clearly see what they have in common versus what makes them different. This might be done for selecting an important product or service to buy.
• Mathematicians also use Venn diagrams in math to solve complex equations.
• We can use Venn diagrams to compare data sets and to find correlations .
• Venn diagrams can be used to reason through the logic behind statements or equations .

☛ Related Articles:

Check out the following pages related to Venn diagrams:

• Operations on Sets
• Roster Notation
• Set Builder Notation
• Probability

Important Notes on Venn Diagrams:

Here is a list of a few points that should be remembered while studying Venn diagrams:

• Every set is a subset of itself i.e., A ⊆ A.
• A universal set accommodates all the sets under consideration.
• If A ⊆ B and B ⊆ A, then A = B
• The complement of a complement is the given set itself.

Examples of Venn Diagram

Example 1: Let us take an example of a set with various types of fruits, A = {guava, orange, mango, custard apple, papaya, watermelon, cherry}. Represent these subsets using sets notation: a) Fruit with one seed b) Fruit with more than one seed

Solution: Among the various types of fruit, only mango and cherry have one seed.

Answer:    a) Fruit with one seed = {mango, cherry}  b) Fruit with more than one seed = {guava, orange, custard apple, papaya, watermelon}

Note:  If we represent these two sets on a Venn diagram, the intersection portion is empty.

Example 2: Let us take an example of two sets A and B, where A = {3, 7, 9} and B = {4, 8}. These two sets are subsets of the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Find A ∪ B.

Solution: The Venn diagram for the above relations can be drawn as:

Answer:  A ∪ B means, all the elements that belong to either set A or set B or both the sets = {3, 4, 7, 8, 9}

Example 3: Using Venn diagram, find X ∩ Y, given that X = {1, 3, 5}, Y = {2, 4, 6}.

Given: X = {1, 3, 5}, Y = {2, 4, 6}

The Venn diagram for the above example can be given as,

Answer:  From the blue shaded portion of Venn diagram, we observe that, X ∩ Y = ∅ ( null set ).

go to slide go to slide go to slide

Book a Free Trial Class

Venn Diagram Practice Questions

go to slide go to slide

FAQs on Venn Diagrams

What is a venn diagram in math.

In math, a Venn diagram is used to visualize the logical relationship between sets and their elements and helps us solve examples based on these sets.

How do You Read a Venn Diagram?

These are steps to be followed while reading a Venn diagram:

• First, observe all the circles that are present in the entire diagram.
• Every element present in a circle is its own item or data set.
• The intersecting or the overlapping portions of the circles contain the items that are common to the different circles.
• The parts that do not overlap or intersect show the elements that are unique to the different circle.

What is the Importance of Venn Diagram?

Venn diagrams are used in different fields including business, statistics, linguistics, etc. Venn diagrams can be used to visually organize information to see the relationship between sets of items, such as commonalities and differences, and to depict the relations for visual communication.

What is the Middle of a Venn Diagram Called?

When two or more sets intersect, overlap in the middle of a Venn diagram, it is called the intersection of a Venn diagram. This intersection contains all the elements that are common to all the different sets that overlap.

How to Represent a Universal Set Using Venn Diagram?

A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U. All the other sets are represented by circles or closed figures within this larger rectangle that represents the universal set.

What are the Different Types of Venn Diagrams?

The different types of Venn diagrams are:

• Two-set Venn diagram: The simplest of the Venn diagrams, that is made up of two circles or ovals of different sets to show their overlapping properties.
• Three-set Venn diagram: These are also called the three-circle Venn diagram, as they are made using three circles.
• Four-set Venn diagram: These are made out of four overlapping circles or ovals.
• Five-set Venn diagram: These comprise of five circles, ovals, or curves. In order to make a five-set Venn diagram, you can also pair a three-set diagram with repeating curves or circles.

What are the Different Fields of Applications of Venn Diagrams?

There are different cases of applications of Venn diagrams: Set theory, logic, mathematics, businesses, teaching, computer science, and statistics.

Can a Venn Diagram Have 2 Non Intersecting Circles?

Yes, a Venn digram can have two non intersecting circles where there is no data that is common to the categories belonging to both circles.

What is the Formula of Venn Diagram?

The formula that is very helpful to find the unknown information about a Venn diagram is n(A U B) = n(A) + n(B) – n (A ⋂ B), where

• A and B are two sets.
• n(A U B) is the number of elements in A U B.
• n (A ⋂ B) is the number of elements in A ⋂ B.

Can a Venn Diagram Have 3 Circles?

Yes, a Venn diagram can have 3 circles , and it's called a three-set Venn diagram to show the overlapping properties of the three circles.

What is Union in the Venn Diagram?

A union is one of the basic symbols used in the Venn diagram to show the relationship between the sets. A union of two sets C and D can be shown as C ∪ D, and read as C union D. It means, the elements belong to either set C or set D or both the sets.

What is A ∩ B Venn Diagram?

A ∩ B (which means A intersection B) in the Venn diagram represents the portion that is common to both the circles related to A and B.  A ∩ B can be a null set as well and in this case, the two circles will either be non-intersecting or can be represented with intersecting circles having no data in the intersection portion.

Venn Diagram Questions

Venn diagram questions with solutions are given here for students to practice various questions based on Venn diagrams. These questions are beneficial for both school examinations and competitive exams. Practising these questions will develop a skill to solve any problem on Venn diagrams quickly.

Venn diagrams were first introduced by John Venn to represent various propositions in a diagrammatic way. Venn diagrams are used for representing relationships between given sets. For example, natural numbers and whole numbers are subsets of integers represented by the Venn diagram:

Using Venn diagrams, we can easily understand whether given sets are subsets of each other or disjoint sets or have something in common.

• Intersection of Sets
• Union of Sets
• Complement of Set
• Set Operations

Following are some set operations and their meaning useful while solving problems on the Venn diagram:

Some important formulae:

Venn Diagram Questions with Solution

Let us practice some questions based on Venn diagrams.

Question 1: If A and B are two sets such that number of elements in A is 24, number of elements in B is 22 and number of elements in both A and B is 8, find:

(i) n(A ∪ B)

(ii) n(A – B)

(ii) n(B – A)

Given, n(A) = 24, n(B) = 22 and n(A ∩ B) = 8

The Venn diagram for the given information is:

(i) n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 24 + 22 – 8 = 38.

(ii) n(A – B) = n(A) – n(A ∩ B) = 24 – 8 = 16.

(iii) n(B – A) = n(B) – n(A ∩ B) = 22 – 8 = 14.

Question 2: According to the survey made among 200 students, 140 students like cold drinks, 120 students like milkshakes and 80 like both. How many students like atleast one of the drinks?

Number of students like cold drinks = n(A) = 140

Number of students like milkshake = n(B) = 120

Number of students like both = n(A ∩ B) = 80

Number of students like atleast one of the drinks = n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

= 140 + 120 – 80

Question 3: In a group of 500 people, 350 people can speak English, and 400 people can speak Hindi. Find how many people can speak both languages?

Let H be the set of people who can speak Hindi and E be the set of people who can speak English. Then,

n(H ∪ E) = 500

We have to find n(H ∩ E).

Now, n(H ∪ E) = n(H) + n(E) – n(H ∩ E)

⇒ 500 = 400 + 350 – n(H ∩ E)

⇒ n(H ∩ E) = 750 – 500 = 250.

∴ 250 people can speak both languages.

Questions 4: The following Venn diagram shows games played by the number of students in a class:

How many students like only cricket and only football?

As per the given Venn diagram,

Number of students only like cricket = 7

Number of students only like football = 14

∴ Number of students like only cricket and only football = 7 + 14 = 21.

Question 5: In a class of 40 students, 20 have chosen Mathematics, 15 have chosen mathematics but not biology. If every student has chosen either mathematics or biology or both, find the number of students who chose both mathematics and biology and the number of students chose biology but not mathematics.

Let, M ≡ Set of students who chose mathematics

B ≡ Set of students who chose biology

n(M ∪ B) = 40

n(B) = n(M ∪ B) – n(M)

⇒ n(B) = 40 – 20 = 20

n(M – B) = 15

n(M) = n(M – B) + n(M ∩ B)

⇒ 20 = 15 + n(M ∩ B)

⇒ n(M ∩ B) = 20 – 15 = 5

n(B – M) = n(B) – n(M ∩ B)

⇒ n(B – M) = 20 – 5 = 15

Question 6: Represent The following as Venn diagram:

(i) A’ ∩ (B ∪ C)

(ii) A’ ∩ (C – B)

Question 7: In a survey among 140 students, 60 likes to play videogames, 70 likes to play indoor games, 75 likes to play outdoor games, 30 play indoor and outdoor games, 18 like to play video games and outdoor games, 42 play video games and indoor games and 8 likes to play all types of games. Use the Venn diagram to find

(i) students who play only outdoor games

(ii) students who play video games and indoor games, but not outdoor games.

Let V ≡ Play video games

I ≡ Play indoor games

O ≡ Play outdoor games

n(V) = 60, n(I) = 70, n(O) = 75

n(I ∩ O) = 30, n(V ∩ O) = 18, n(V ∩ I) = 42

n(V ∩ I ∩ O) = 8

Hence, by Venn diagram

Number of students only like to play only outdoor games = 35

Number of students like to play video games and indoor games but not outdoor games = 34

Note : Always begin to fill the Venn diagram from the innermost part.

Question 8: Using the Venn diagrams, verify (P ∩ Q) ∪ R = (P ∪ R) ∩ (Q ∪ R).

The shaded portion represents (P ∩ Q) ∪ R in the Venn diagram.

Comparing both the shaded portion in both the Venn diagram, we get (P ∩ Q) ∪ R = (P ∪ R) ∩ (Q ∪ R).

Question 9: Prove using the Venn diagram: (B – A) ∪ (A ∩ B) = B.

From the Venn diagram, it is clear that (B – A) ∪ (A ∩ B) = B

Question 10: In a survey, it is found that 21 people read English newspaper, 26 people read Hindi newspaper, and 29 people read regional language newspaper. If 14 people read both English and Hindi newspapers; 15 people read both Hindi and regional language newspapers; 12 people read both English and regional language newspaper and 8 read all types of newspapers, find:

(i) How many people were surveyed?

(ii) How many people read only regional language newspapers?

Let A ≡ People who read English newspapers.

B ≡ People who read Hindi newspapers.

C ≡ People who read Hindi newspapers.

n(A) = 21, n(B) = 26, n(C) = 29

n(A ∩ B) = 14, n(B ∩ C) = 15, n(A ∩ C) = 12

n(A ∩ B ∩ C) = 8

(i) Number of people surveyed = n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C) = 21 + 26 + 29 – 14 – 15 – 12 + 8 = 43

(ii) By the Venn diagram, number of people who only read regional language newspapers = 10.

Video Lesson on Introduction to Sets

Practice Questions on Venn Diagrams

1. Verify using the Venn diagram:

(i) A – B = A ∩ B C

(ii) (A ∩ B) C = A C ∪ B C

2. For given two sets P and Q, n(P – Q) = 24, n(Q – P) = 19 and n(P ∩ Q) = 11, find:

(iii) n (P ∪ Q)

3. In a group of 65 people, 40 like tea and 10 like both tea and coffee. Find

(i) how many like coffee only and not tea?

(ii) how many like coffee?

4. In a sports tournament, 38 medals were awarded for 500 m sprint, 15 medals were awarded for Javelin throw, and 20 medals were awarded for a long jump. If these medals were awarded to 58 participants and among them only three medals in all three sports, how many received exactly two medals?

Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.