6.4 geometry homework answers

Distances and Circles

Match each equation to its description.

circle centered at \((0,\text-4)\) with a radius of 3

circle centered at \((1,\text-4)\) with a radius of \(\sqrt{3}\)

circle centered at \((1,4)\) with a radius of  \(\sqrt{3}\)

circle centered at \((1,0)\) with a radius of 3

circle centered at \((1,\text-4)\) with a radius of 3

\((x-1)^2+y^2=9\)

\(x^2+(y+4)^2=9\)

\((x-1)^2+(y-4)^2=3\)

\((x-1)^2+(y+4)^2=9\)

\((x-1)^2+(y+4)^2=3\)

For access, consult one of our IM Certified Partners .

Write an equation of a circle that is centered at \((\text-3,2)\) with a radius of 5.

\((x-3)^2+(y+2)^2=5\)

\((x+3)^2+(y-2)^2=5\)

\((x-3)^2+(y+2)^2=25\)

\((x+3)^2+(y-2)^2=25\)

• Plot the circles \(x^2+y^2=4\) and \(x^2+y^2=1\) on the same coordinate plane.
• Find the image of any point on \(x^2+y^2=4\) under the transformation \((x,y) \rightarrow \left(\frac{1}{2}x,\frac{1}{2}y\right)\) .
• What do you notice about \(x^2+y^2=4\) and \(x^2+y^2=1\) ?

\((x,y) \rightarrow (x-3,4-y)\) is an example of a transformation called a glide reflection. Complete the table using the rule.

Does this glide reflection produce a triangle congruent to the original?

The triangle whose vertices are \((1,1), (5,3),\) and \((4,5)\) is transformed by the rule \((x,y) \rightarrow (3x,3y)\) . Is the image similar or congruent to the original figure?

The image is congruent to the original triangle.

The image is similar but not congruent to the original triangle.

The image is neither similar nor congruent to the original triangle.

Match each coordinate rule to a description of its resulting transformation.

\((x,y)\rightarrow(3x,3y)\)

\((x,y)\rightarrow(x-3,y-3)\)

\((x,y)\rightarrow(x+3,y+3)\)

\((x,y)\rightarrow(x-3,y)\)

\((x,y)\rightarrow(x+3,y)\)

\((x,y)\rightarrow(x,y-3)\)

\((x,y)\rightarrow(x,y+3)\)

Translate along the directed line segment from \((0,0)\) to \((\text-3,0)\) .

Translate along the directed line segment from \((0,0)\) to \((0,\text-3)\) .

Translate along the directed line segment from \((0,0)\) to \((3,0)\) .

Translate along the directed line segment from \((0,0)\) to \((0,3)\) .

Translate along the directed line segment from \((0,0)\) to \((3,3)\) .

Translate along the directed line segment from \((0,0)\) to \((\text-3,\text-3)\) .

Dilate using the origin as the center and a scale factor of 3.

A cone-shaped container is oriented with its circular base on the top and its apex at the bottom. It has a radius of 18 inches and a height of 6 inches. The cone starts filling up with water. What fraction of the volume of the cone is filled when the water reaches a height of 2 inches?

\(\frac{1}{729}\)

\(\frac{1}{27}\)

\(\frac19\)

\(\frac13\)

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Big Ideas Math Geometry Answers Chapter 6 Relationships Within Triangles

Need instant homework help for solving all chapter 6 Relationships Within Triangles Questions? Then, don’t worry we have come up with a great study guide and one-stop destination for looking at what you require ie., Big Ideas Math Geometry Answers Chapter 6 Relationships Within Triangles . This BIM Geometry Solution key covered all Chapter 6 Relationships Within Triangles Exercises Questions, Practices, Chapter Review, Chapter Test, Assessments, etc. All you can attain for free of cost and make use of this Ch 6 Relationships Within Triangles Big Ideas Math Geometry Answers for better practice and learning.

Big Ideas Math Book Geometry Answer Key Chapter 6 Relationships Within Triangles

Improve your subject knowledge & clear all your exams with flying colors by taking the help of the BIM Geometry solution key of Ch 6 Relationships Within Triangles . All the questions covered in this study material is very beneficial for students to understand the concept thoroughly. Students who need to learn how to Answer Ch 6 Relationships Within Triangles Questions should definitely go ahead with this page and score maximum marks in the exams. So, here are the links to access Topic-wise Big Ideas Math Geometry Answers Chapter 6 Relationships Within Triangles & ace up your preparation.

• Relationships Within Triangles Maintaining Mathematical Proficiency – Page 299
• Relationships Within Triangles Mathematical Practices – Page 300
• 6.1 Perpendicular And Angle Bisectors – Page 301
• Lesson 6.1 Perpendicular And Angle Bisectors – Page(302-308)
• Exercise 6.1 Perpendicular And Angle Bisectors – Page(306-308)
• 6.2 Bisectors of Triangles – Page 309
• Lesson 6.2 Bisectors of Triangles – Page(310-318)
• Exercise 6.2 Bisectors of Triangles – Page(315-318)
• 6.3 Medians and Altitudes of Triangles – Page 319
• Lesson 6.3 Medians and Altitudes of Triangles – Page(320-326)
• Exercise 6.3 Medians and Altitudes of Triangles – Page(324-326)
• 6.1 and 6.3 Quiz – Page 328
• 6.4 The Triangle Midsegment Theorem – Page 329
• Lesson 6.4 The Triangle Midsegment Theorem – Page (330-334)
• Exercise 6.4 The Triangle Midsegment Theorem – Page(333-334)
• 6.5 Indirect Proof and Inequalities in One Triangle – Page 335
• Lesson 6.5 Indirect Proof and Inequalities in One Triangle – Page(336-342)
• Exercise 6.5 Indirect Proof and Inequalities in One Triangle – Page(340-342)
• 6.6 Inequalities in Two Triangles – Page 343
• Lesson 6.6 Inequalities in Two Triangles – Page(344-348)
• Exercise 6.6 Inequalities in Two Triangles – Page(347-348)
• Relationships Within Triangles Chapter Review – Page(350-352)
• Relationships Within Triangles Chapter Test – Page 353
• Relationships Within Triangles Cumulative Assessment – Page(354-355)

Relationships Within Triangles Maintaining Mathematical Proficiency

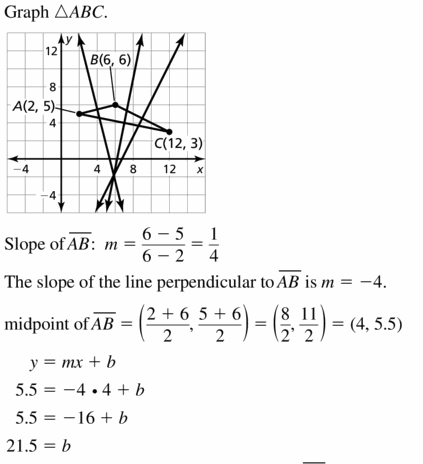
Write an equation of the line passing through point P that is perpendicular to the given line.

Question 1. P(3, 1), y = \(\frac{1}{3}\)x – 5

Answer: y = -3x + 10

Explanation: The slope of the given line is \(\frac { 1 }{ 3 } \). Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line. The slope of the perpendicular line = -3 Substitute the values in y = mx + c 1 = -3(3) + c 1 = -9 + c c = 1 + 9 c = 10 use the slope intercept form of a linear equation again substitute m, c y = -3x + 10

Question 2. P(4, – 3), y = – x – 5

Answer: y = \(\frac { 1 }{ 3 } \)x – \(\frac { 5 }{ 3 } \)

Explanation: The slope of the given line is -3. Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line. The slope of the perpendicular line = \(\frac { 1 }{ 3 } \) Substitute the values in y = mx + c -3 = –\(\frac { 1 }{ 3 } \)(4) + c c = -3 + \(\frac { 4 }{ 3 } \) = \(\frac { -9 + 4 }{ 3 } \) = \(\frac { -5 }{ 3 } \) use the slope intercept form of a linear equation again substitute m, c y = \(\frac { 1 }{ 3 } \)x + \(\frac { -5 }{ 3 } \) y = \(\frac { 1 }{ 3 } \)x – \(\frac { 5 }{ 3 } \)

Question 3. P(- 1, – 2), y = – 4x + 13

Answer: y = \(\frac { 1 }{ 4 } \)x – \(\frac { 7 }{ 4 } \)

Explanation: The slope of the given line is -4. Since the slope of the perpendicular line must be the negative reciprocal of the slope of the given line. The slope of the perpendicular line = \(\frac { 1 }{ 4 } \) Substitute the values in y = mx + c -2 = \(\frac { 1 }{ 4 } \)(-1) + c c = -2 + \(\frac { 1 }{ 4 } \) = \(\frac { -8 + 1 }{ 4 } \) = \(\frac { -7 }{ 4 } \) use the slope intercept form of a linear equation again substitute m, c y = \(\frac { 1 }{ 4 } \)x + \(\frac { -7 }{ 4 } \) y = \(\frac { 1 }{ 4 } \)x – \(\frac { 7 }{ 4 } \)

Write the sentence as an inequality.

Question 4. A number w is at least – 3 and no more than 8.

Answer: -3 ≤ w < 8

Explanation: At least means ≥ and no more than means < w ≥ -3 and w < 8 -3 ≤ w < 8

Question 5. A number m is more than 0 and less than 11.

Answer: 0 < m < 11

Explanation: more than means > and less than means < m > 0 and m < 11 0 < m < 11

Question 6. A number s is less than or equal to 5 or greater than 2.

Answer: 2 < s ≤ 5

Explanation: less than or equal to means ≤ and greater than means > s ≤ 5 or s > 2 2 < s ≤ 5

Question 7. A number d is fewer than 12 or no less than – 7.

Answer: -7 < d < 12

Explanation: fewer than means < no less than means > d < 12 or d > -7 -7 < d < 12

Question 8. ABSTRACT REASONING Is it possible for the solution of a compound inequality to be all real numbers? Explain your reasoning.

Answer: Yes

Relationships Within Triangles Mathematical Practices

Monitoring Progress

Refer to the figures at the top of the page to describe each type of line, ray, or segment in a triangle.

Question 1. perpendicular bisector

Answer: The perpendicular bisector of a side of a triangle is a line perpendicular to the side and passes through its midpoint. Three perpendicular bisectors of sides meet at a point in a triangle.

Question 2. angle bisector

Answer: The angle bisector of an angle in a triangle is a straight line that divides the angle into two congruent angles.

Question 3. median

Answer: It is a line segment from a vertex to the midpoint of the opposite side.

Question 4. altitude

Answer: It is a segment from a vertex of the triangle, perpendicular to the side opposite that vertex of the triangle.

Question 5. midsegment

Answer: It is a segment that connects the mid points of two sides in a triangle.

6.1 Perpendicular and Angle Bisectors

Exploration 1

Points on a Perpendicular Bisector

Work with a partner. Use dynamic geometry software.

a. Draw any segment and label it \(\overline{A B}\). ConStruct the perpendicular bisector of \(\overline{A B}\). Answer:

b. Label a point C that is on the perpendicular bisector of \(\overline{A B}\) but is not on \(\overline{A B}\). Answer:

c. Draw \(\overline{C A}\) and \(\overline{C B}\) and find their lengths. Then move point C to other locations on the perpendicular bisector and note the lengths of \(\overline{C A}\) and \(\overline{C B}\). Answer:

d. Repeat parts (a) – (c) with other segments. Describe any relationships(s) you notice. Answer:

Exploration 2

Points on an Angle Bisector

a. Draw two rays \(\vec{A}\)B and \(\vec{A}\)C to form ∠BAC. Construct the bisector of ∠BAC. Answer:

b. Label a point D on the bisector of ∠BAC. Answer:

c. Construct and find the lengths of the perpendicular segments from D to the sides of ∠BAC. Move point D along the angle bisector and note how the lengths change. Answer:

d. Repeat parts (a)-(c) with other angles. Describe an relationship(s) you notice. USING TOOLS STRATEGICALLY To be proficient in math, you need to visualize the results of varying assumptions, explore consequences, and compare predictions with data. Answer:

Communicate Your Answer

Question 3. What conjectures can you make about a point on the perpendicular bisector of a segment and a point on the bisector of an angle? Answer: It is given a point on the perpendicular bisector of a segment and a point on the bisector of an angle. It is required to give conjectures about a point on the perpendicular bisector of a segment and a point on the bisector of an angle. To do these use the perpendicular bisector and angle bisector theorem.

• By the perpendicular bisector theorem, a perpendicular bisector divides the line into two equal halves and makes a right angle with it. So, it can be said that every point on the perpendicular bisector will be equidistant from both the ends of the line it is bisecting.
• By the angle bisector theorem, a point is equidistant from the sides of the angle if a point is on the bisector of an angle.

Question 4. In Exploration 2. what is the distance from point D to \(\vec{A}\)B when the distance from D to \(\vec{A}\)C is 5 units? Justify your answer. Answer:

Lesson 6.1 Perpendicular and Angle Bisectors

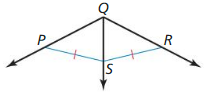
Use the diagram and tile given information to find the indicated measure.

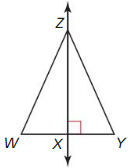
Answer: WZ = 13.75

Explanation: Using the perpendicular bisector theorem YZ = WZ 13.75 = WZ

Answer: YZ = 27

Explanation: Using the perpendicular bisector theorem YZ = WZ n + 17 = 4n – 13 4n – n = 17 + 13 3n = 30 n = 10 YZ = 10 + 17 = 27

Question 3. Find WX when WZ = 20.5. WY = 14.8. and YZ = 20.5.

Answer: WX = 7.4

Explanation: Because WZ = ZY and ZX is the perpendicular bisector of WY by the converse of perpendicular bisector theorem. By the definition of segment sector, WY = 2WX 14.8 = 2WX WX = 7.4

Use the diagram and the given information to find the indicated measure.

Question 4. \(\vec{B}\)D bisects ∠ABC, and DC = 6.9, Find DA.

Answer: DA = 6.9

Explanation: By using the angle bisector theorem DC = DA DA = 6.9

Question 5. \(\vec{B}\)D bisects ∠ABC, AD = 3z + 7, and CD = 2z + 11. Find CD.

Answer: z = 4

Explanation: By using the angle bisector theorem DC = DA 2z + 11 = 3z + 7 3z – 2z = 11 – 7 z = 4

Question 6. Find m∠ABC when AD = 3.2, CD = 3.2, and m∠DBC = 39°.

Answer: m∠DBC = 78°

Explanation: m∠DBC = 39 = m∠DBA m∠ABC = m∠DBC + m∠DBA = 39 + 39 = 78°

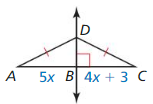
Question 8. Write an equation of the perpendicular bisector of the segment with endpoints (- 1, – 5) and (3, – 1).

Answer: y + 5 = 0

Explanation: Midpoint = (\(\frac { -1 + 3 }{ 2 } \), \(\frac { -5 – 1 }{ 2 } \)) = (\(\frac { 2 }{ 2 } \), \(\frac { -6 }{ 2 } \)) = (1, -3) Slope of the line = \(\frac { -1 + 1 }{ 3 + 5 } \) = 0 Slope of the perpendicular line = 0 Equation of the perpendicular bisector is (y + 5) = 0(x + 1) y + 5 = 0

Exercise 6.1 Perpendicular and Angle Bisectors

Vocabulary and Core Concept Check

Question 2. DIFFERENT WORDS, SAME QUESTION Which is different? Find “both” answers.

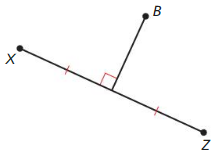
Is point B the same distance from both X and Z?

Answer: Yes.

Is point B equidistant from X and Z?

Is point B collinear with X and Z?

Answer: No.

Is point B on the perpendicular bisector of \(\overline{X Z}\)?

Monitoring Progress and Modeling with Mathematics

In Exercises 3-6, find the indicated measure. Explain your reasoning.

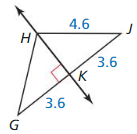
Answer: QR = RS So, QR = 1.3

Answer: UW = 55

Explanation: UV = WU 9x + 1 = 7x + 13 9x – 7x = 13 – 1 2x = 12 x = 6 UW = 7(6) + 13 = 42 + 13 = 55

In Exercises 7-10. tell whether the information in the diagram allows you to conclude that point P lies on the perpendicular bisector of \(\overline{L M}\). Explain your reasoning.

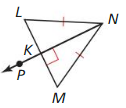
Answer: PN ⊥ LM. So, LN – MN Therefore, point P lies on the LM.

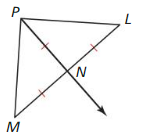
In Exercises 11-14. find the indicated measure. Explain your reasoning.

Answer: PS = RS PS = 12

Answer: FG = 16

Explanation: FG = GH x + 11 = 3x + 1 3x – x = 11 – 1 2x = 10 x = 5 FG = 5 + 11 = 16

In Exercises 15 and 16, tell whether the information in the diagram allows you to conclude that \(\vec{E}\)H bisects ∠FEG. Explain your reasoning.

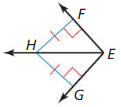
Answer: Yes, because H is equidistant from EF and EG, EH bisects ∠FEG by the Angle Bisector Theorem.

In Exercises 17 and 18, tell whether the information in the diagram allows you to conclude that DB = DC. Explain your reasoning.

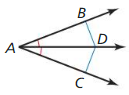
Answer: Yes, because AD is perpendicular to BD and DC. using perpendicular bisector theorem DB = DC.

In Exercises 19-22, write an equation of the perpendicular bisector of the segment with the given endpoints.

Question 20. Q(- 2, 0), R(6, 12)

Answer: An equation of the perpendicular bisector is y = –\(\frac { 3 }{ 7 } \)x + \(\frac { 36 }{ 7 } \)

Explanation: Slope of QR = \(\frac { 12 + 2 }{ 6 – 0 } \) = \(\frac { 7 }{ 3 } \) The slope of the perpendicular line m = –\(\frac { 3 }{ 7 } \) Midpoint of QR = (\(\frac { -2 + 6 }{ 2 } \), \(\frac { 0 + 12 }{ 2 } \) = (-2, 6) y = mx + b 6 = –\(\frac { 3 }{ 7 } \)(-2) + b 6 = \(\frac { 6 }{ 7 } \) + b b = \(\frac { 36 }{ 7 } \) An equation of the perpendicular bisector is y = –\(\frac { 3 }{ 7 } \)x + \(\frac { 36 }{ 7 } \)

Question 22. Y( 10, – 7), Z(- 4, 1)

Answer: An equation of the perpendicular bisector is y = \(\frac { 7 }{ 4 } \)x – \(\frac { 33 }{ 4 } \)

Explanation: Slope of YZ = \(\frac { 1 + 7 }{ -4 – 10 } \) = \(\frac { -4 }{ 7 } \) The slope of the perpendicular line m = \(\frac { 7 }{ 4 } \) Midpoint of YZ = (\(\frac { 10 – 4 }{ 2 } \), \(\frac { -7 + 1 }{ 2 } \)) = (3, -3) y = mx + b -3 = \(\frac { 7 }{ 4 } \)(3) + b b = -3 – \(\frac { 21 }{ 4 } \) = \(\frac { -12 – 21 }{ 4 } \) = \(\frac { -33 }{ 4 } \) An equation of the perpendicular bisector is y = \(\frac { 7 }{ 4 } \)x – \(\frac { 33 }{ 4 } \)

ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in the student’s reasoning.

Answer: CP is not perpendicular to BP. So, x = 5 is wrong.

Answer: PG should be the perpendicular bisector of ∠APB.

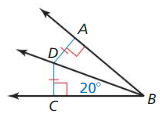
b. How does m∠APB change as the puck gets closer to the goal? Does this change make it easier or more difficult for the goalie to defend the goal? Explain your reasoning. Answer: ∠APB = 2 ∠APG ∠APG = 10° ∠APG = 20°

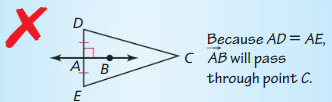
Question 28. WRITING Explain how the Converse of the Perpendicular Bisector Theorem (Theorem 6.2) is related to the construction of a perpendicular bisector.

Answer: The converse of the perpendicular bisector theorem states if a point is equidistant from both the endpoints of the line segments in the same plane, then that point is on the perpendicular bisector of the line segment.

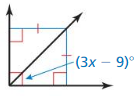
Question 30. REASONING Which point lies on the perpendicular bisector of the segment with endpoints M(7, 5) and m(- 1, 5)? (A) (2, 0) (B) (3, 9) (C) (4, 1) (D) (1, 3)

Answer: (B) (3, 9)

Explanation: The distance from M to (3, 9) is = √(7 – 3)² + (5 – 9)² = √16 + 16 = √32 The distance from m to (3, 9) = √(-1 – 3)² + (5 – 9)² = √16 + 16 = √32

b. Is the museum approximately equidistant from Wilson School and Roosevelt School? Explain your reasoning. Answer: The museum is closer to the Roosevelt school, while for Wilson school it is two blocks north and then two blocks east.

Question 36. THOUGHT PROVOKING The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, is it possible for two lines to be perpendicular but not bisect each other? Explain your reasoning. Answer:

• A line is a great circle that divides the sphere into two equal halves in spherical geometry.
• Any two lines intersecting in two points represent two poles of the spherical lines.
• So, it is not possible for two spherical lines to be perpendicular without bisecting each other.

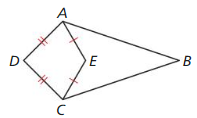
Answer: a. By using the perpendicular bisector theorem \(\overline{X W} \cong \overline{Z W}\) b. By using the perpendicular bisector theorem \(\overline{X V} \cong \overline{Z V}\)

Maintaining Mathematical Proficiency

Classify the triangle by its sides.

Answer: The trinagle is scalene as all the sides have different lengths.

Classify the triangles by its angles.

Answer: The triangle is an obtuse triangle.

6.2 Bisectors of Triangles

Properties of the Perpendicular Bisectors of a Triangle

Work with a partner: Use dynamic geometry software. Draw any ∆ABC. a. Construct the perpendicular bisectors of all three sides of ∆ABC. Then drag the vertices to change ∆ABC. ‘What do you notice about the perpendicular bisectors? Answer:

b. Label a point D at the intersection of the perpendicular bisectors. Answer:

c. Draw the circle with center D through vertex A of ∆ABC. Then drag the vertices to change ∆ABC. What do you notice? Answer:

Properties of the Angle Bisectors of a Triangle

Work with a partner. Use dynamic geometry software. Draw any ∆ABC.

a. Construct the angle bisectors of all three angles of ∆ABC, Then drag the vertices to change ∆ABC. What do you notice about the angle bisectors? Answer:

b. Label a point D at the intersection of the angle bisectors. Answer:

c. Find the distance between D and \(\overline{A B}\). Draw the circle with center D and this distance as a radius. Then drag the vertices to change ∆ABC. What do you notice? LOOKING FOR STRUCTURE To be proficient in math, you need to see complicated things as single objects or as being composed of several objects. Answer:

Question 3. What conjectures can you make about the perpendicular bisectors and the angle bisectors of a triangle? Answer:

Lesson 6.2 Bisectors of Triangles

Find the coordinates of the circumcenter of the triangle with the given vertices.

Question 2. R(- 2, 5), S(- 6, 5), T(- 2, – 1)

Answer: The circumcenter is (4, 7.33)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let R(- 2, 5), S(- 6, 5), T(- 2, – 1) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PR = PS = PT PR² = PS² = PT² PR² = PS² (x + 2)² + (y – 5)² = (x + 6)² + (y – 5)² x² + 4x + 4 + y² – 10x + 25 = x² + 12x + 36 + y² -10y + 25 4x + 4 = 12x + 36 12x – 4x = 36 – 4 8x = 32 x = 4 PS² = PT² (x + 6)² + (y – 5)² = (x + 2)² + (y + 1)² x² + 12x + 36 + y² -10y + 25 = x² + 4x + 4 + y² + 2y + 1 12x – 4x – 10y – 2y + 61 = 5 8x – 12y = -56 8(4) – 12y = -56 32 – 12y = -56 -12y = -56 – 32 -12y = -88 y = 7.33 The circumcenter is (4, 7.33)

Question 3. W(- 1, 4), X(1, 4), Y( 1, – 6)

Answer: The circumcenter is (0.25, -1)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let W(- 1, 4), X(1, 4), Y( 1, – 6) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PW = PX = PY PW² = PY² = PX² PX² = PY² (x – 1)² + (y – 4)² = (x – 1)² + (y + 6)² x² -2x + 1 + y² – 8y + 16 = x² -2x + 1 + y² + 12y + 36 -8y – 12y = 36 – 16 -20y = 20 y = -1 PW² = PX² (x + 1)² + (y – 4)² = (x – 1)² + (y – 4)² x² + 2x + 4 + y² – 8y + 16 = x² – 2x + 1 + y² – 8y + 16 4x = 1 x = 0.25 The circumcenter is (0.25, -1)

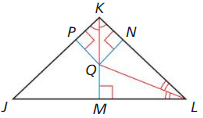
Answer: QP = \(\frac { 23 }{ 2 } \)

Explanation: QM = QN 3x + 8 = 7x + 2 7x – 3x = 8 – 2 4x = 6 x = \(\frac { 3 }{ 2 } \) QP = QN = 7(\(\frac { 3 }{ 2 } \)) + 2 = \(\frac { 23 }{ 2 } \)

Question 5. Draw a sketch to show the location L of the lamppost in Example 4.

Exercise 6.2 Bisectors of Triangles

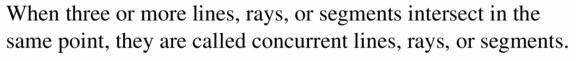
Answer: The third triangle does not belong with the other three. Because the point P in the remaining triangles is the circumcenter. But P is not circumcenter in the third triangle.

In Exercises 3 and 4, the perpendicular bisectors of ∆ABC intersect at point G and are shown in blue. Find the indicated measure.

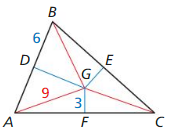
Answer: Because G is the circumcenter of ∆ABC, AG = BG = CG AG = BG = 11 So, AG = 11

In Exercises 5 and 6, the angle bisectors of ∆XYZ intersect at point P and are shown in red. Find the indicated measure.

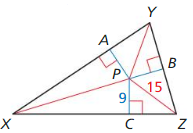
Answer: Because P is the incenter of ∆XYZ, PH = PF = PK Therefore, PK = 15 HP = 15

In Exercises 7-10. find the coordinates of the circumcenter of the triangle with the given vertice

Question 8. D(- 7, – 1), E(- 1, – 1), F(- 7, – 9)

Answer: The circumcenter is (-4, -5)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(- 7, – 1), E(- 1, – 1), F(- 7, – 9) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PD = PE = PF PD² = PE² = PF² PD² = PE² (x + 7)² + (y + 1)² = (x + 1)² + (y + 1)² x² + 14x + 49 + y² + 2y +1 = x² + 2x + 1 + y² + 2y + 1 14x – 2x = 1 – 49 12x = -48 x = -4 PD² = PF² (x + 7)² + (y + 1)² = (x + 7)² + (y + 9)² x² + 14x + 49 + y² + 2y + 1 = x² + 14x + 49 + y² + 18y + 81 18y – 2y = 1 – 81 16y = -80 y = -5 The circumcenter is (-4, -5)

Question 10. L(3, – 6), M(5, – 3) , N (8, – 6)

Answer: The circumcenter is (5.5, -5.5)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let L(3, – 6), M(5, – 3) , N (8, – 6) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PL = PM = PN PL² = PM² = PN² PL² = PN² (x – 3)² + (y + 6)² = (x – 8)² + (y + 6)² x² – 6x + 9 + y² + 12y + 36 = x² -16x + 64 + y² + 12y + 36 -16x + 6x = 9 – 64 -10x = -55 x = 5.5 PL² = PM² (x – 3)² + (y + 6)² = (x – 5)² + (y + 3)² x² – 6x + 9 + y² + 12y + 36 = x² – 10x + 25 + y² + 6y + 9 -6x + 10x + 45 = 6y – 12y + 34 4x = -6y -11 4(5.5) = -6y – 11 22 + 11 = -6y 33 = -6y y = -5.5 The circumcenter is (5.5, -5.5)

In Exercises 11-14, N is the incenter of ∆ABC. Use the given information to find the indicated measure.

Answer: NJ = 9

Explanation: NG = NH = NJ x + 3 = 2x – 3 2x – x = 3 + 3 x = 6 By Incenter theorem, NG = NH = NJ NJ = 6 + 3 = 9

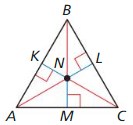
Answer: NS = 4

Explanation: NQ = NR 2x = 3x – 2 3x – 2x = 2 x = 2 NQ = 2 (2) = 4 By Incenter theorem NS = NR = NQ So, NS = 4

Answer: PY = 31

Explanation: PX = PZ 4x + 3 = 6x – 11 6x – 4x = 3 + 11 2x = 14 x = 7 PZ = 6(7) – 11 = 42 – 11 = 31 By the incenter theorem, PX = PZ = PY PY = 31

CONSTRUCTION In Exercises 17-20. draw a triangle of the given type. Find the circumcenter. Then construct the circumscribed circle.

Question 18. obtuse

Question 20. equilateral

CONSTRUCTION In Exercises 21-24, copy the triangle with the given angle measures. Find the incenter. Then construct the inscribed circle.

ERROR ANALYSIS In Exercises 25 and 26. describe and correct the error in identifying equal distances inside the triangle.

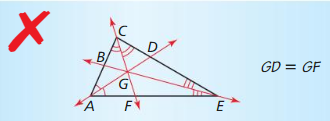
Answer: Because point T is the intersection of the angle bisectors, it is the incenter. But, because TV and TF are not necessarily perpendicular to a side of the trinagle, there is not sufficient evidence to conclude that TV and TZ are congruent. Point T is equidistance from the sides of the triangle.

CRITICAL THINKING In Exercises 29-32, complete the statement with always, sometimes, or never. Explain your reasoning.

Question 30. If the perpendicular bisector of one side of a triangle intersects the opposite vertex. then the triangle is ______________ isosceles.

Answer: If the perpendicular bisector of one side of a triangle intersects the opposite vertex. then the triangle is always isosceles.

Explanation: The Vertex is equidistant to other vertices then.

Question 32. The angle bisectors of a triangle intersect at a point that is ______________ equidistant from the sides of the triangle.

Answer: The angle bisectors of a triangle intersect at a point that is circumcenter equidistant from the sides of the triangle.

CRITICAL THINKING In Exercises 33 and 34, find the coordinates of the circumcenter of the triangle with the given vertices.

Question 34. D(- 9, – 5), E(- 5, – 9), F(- 2, – 2)

Answer: The circumcenter is (4.45, 4.45)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(- 9, – 5), E(- 5, – 9), F(- 2, – 2) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PD = PE = PF PD² = PE² = PF² PD² = PE² (x + 9)² + (y + 5)² = (x + 5)² + (y + 9)² x² + 18x + 81 + y² + 10y + 25 = x² + 10x + 25 + y² + 18y + 81 18x – 10x = 18y – 10y 8x = 8y x = y PE² = PF² (x + 5)² + (y + 9)² = (x + 2)² + (y + 2)² x² + 10x + 25 + y² + 18y + 81 = x² + 4x + 4 + y² + 2y + 4 10x – 4x + 106 = 8 + 2y – 18y 6x + 106 = 8 – 16y 6x + 98 = -16x 22x = -98 x = 4.45 y = 4.45 The circumcenter is (4.45, 4.45)

MATHEMATICAL CONNECTIONS In Exercises 35 and 36. find the a1ue of x that makes N the incenter of the triangle.

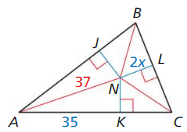
Answer: N the incenter is \(\frac { 12 }{ 2 } \).

Explanation: 25² = 24² + (14x)² 625 = 576 + 196x² 49 = 196x² x = \(\frac { 7 }{ 14 } \) = \(\frac { 1 }{ 2 } \) The value of x will make N the incenter is \(\frac { 12 }{ 2 } \).

Answer: Given ∆ABC, \(\overline{A D}\) bisects∠CAB, \(\overline{B D}\) bisects ∠CBA, \(\overline{D E}\) ⊥ \(\overline{A B}\), \(\overline{D F}\) ⊥ \(\overline{B C}\), and \(\overline{D G}\) ⊥ \(\overline{C A}\) To Prove: The angle bisectors intersect at D, which is equidistant from \(\overline{A B}\), \(\overline{B C}\), and \(\overline{C A}\) It is also given that, AD bisects ∠CAD. So according to the definition of an angle bisector, we can write that∠CAD≅∠BAD. ∠ADP≅∠AFP [Corresponding right angles] And, AP is the common side Thus according to the AAS congruence theorem, we have that, ΔAED≅ΔAGD And, DE≅DG [corresponding parts of congruent triangles] Also, we can write that DE≅DF From the above result, we obtain that the point D is equidistant from the sides AB, BC and CA

Question 40. REASONING Is the incenter of a triangle ever located outside the triangle? Explain your reasoning.

Explanation: Because the incenter is the center of an inscribed circle, it must always be inside the triangle.

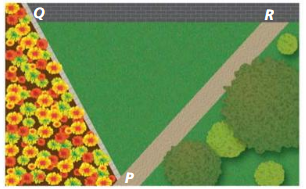
b. Copy the diagram and find the approximate coordinates of the point at which the archaeologists should look for the fire pit.

COMPARING METHODS In Exercises 49 and 50. state whether you would use perpendicular bisectors or angle bisectors. Then solve the problem.

Question 50. On a map of a camp. You need to create a circular walking path that connects the pool at (10, 20), the nature center at (16, 2). and the tennis court at (2, 4). Find the coordinates of the center of the circle and the radius of the circle.

Answer: The center of the circular path is located at (10, 10) and the radius of the circular path is 10 units.

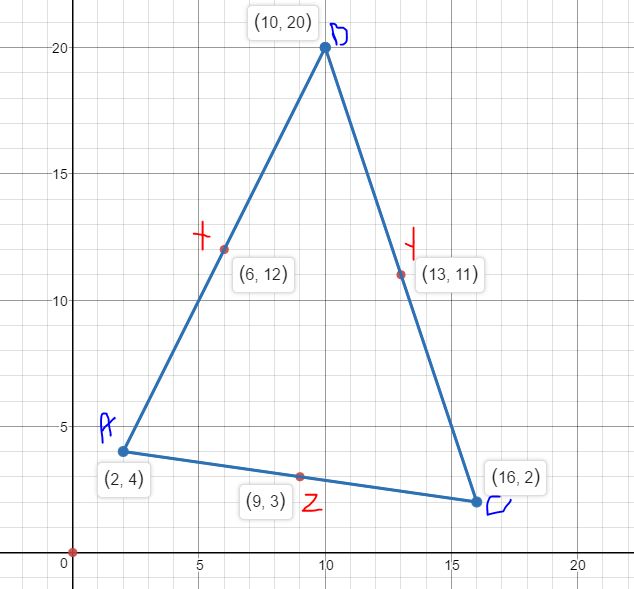
Let the centre of the circle be at O (x, y) Slope of AB = \(\frac { 20 – 4 }{ 10 – 2 } \) = 2 The slope of XO must be \(\frac { -1}{ 2 } \) the negative reciprocal of the slope of AB as the 2 lines are perpendicular Slope of XO = \(\frac { y – 12 }{ x – 6 } \) = \(\frac { -1 }{ 2 } \) y – 12 = -0.5x + 3 0.5x + y = 12 + 3 = 15 x + 2y = 30 The slope of BC = \(\frac { 2 – 20 }{ 16 – 10 } \) = -3 The slope of XO must be \(\frac { 1 }{ 3 } \) = \(\frac { 11 – y }{ 13 – x } \) 33 – 3y = 13 – x x – 3y = -33 + 13 = -20 Subtrcat two equations x + 2y – x + 3y = 30 + 20 y = 10 x – 30 = -20 x = 10 r = √(10 – 2)² + (10 – 4)² r = 10

The endpoints of \(\overline{A B}\) are given. Find the coordinates of the midpoint M. Then find AB. Question 52. A(- 3, 5), B(3, 5)

Answer: AB = 6

Explanation: Midpoint of AB = (\(\frac { -3 + 3 }{ 2 } \), \(\frac { 5 + 5 }{ 2 } \)) = (0, 5) AB = √(3 + 3)² + (5 – 5)² = 6

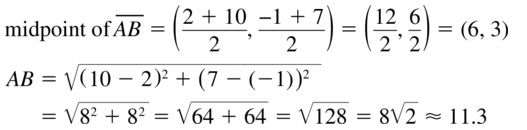
Question 54. A(- 5, 1), B(4, – 5)

Answer: AB = 10.81

Explanation: Midpoint of AB = (\(\frac { -5 + 4 }{ 2 } \), \(\frac { 1 – 5 }{ 2 } \)) = (\(\frac { -1 }{ 2 } \), -2) AB = √(4 + 5)² + (-5 – 1)² = √81 + 36 =  10.81

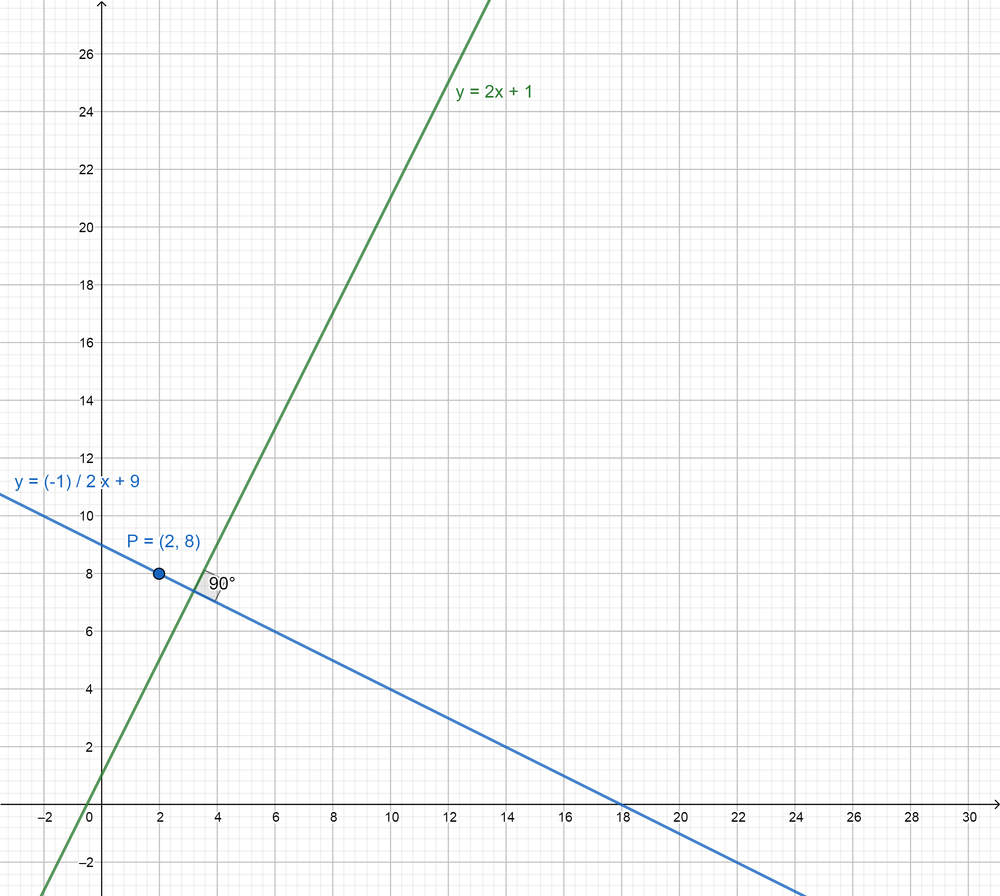
Write an equation of the line passing through point P that is perpendicular to the given line. Graph the equations of the lines to check that they are perpendicular. Question 56. P(2, 8), y = 2x + 1

Answer: y = \(\frac { -1 }{ 2 } \)x + 9

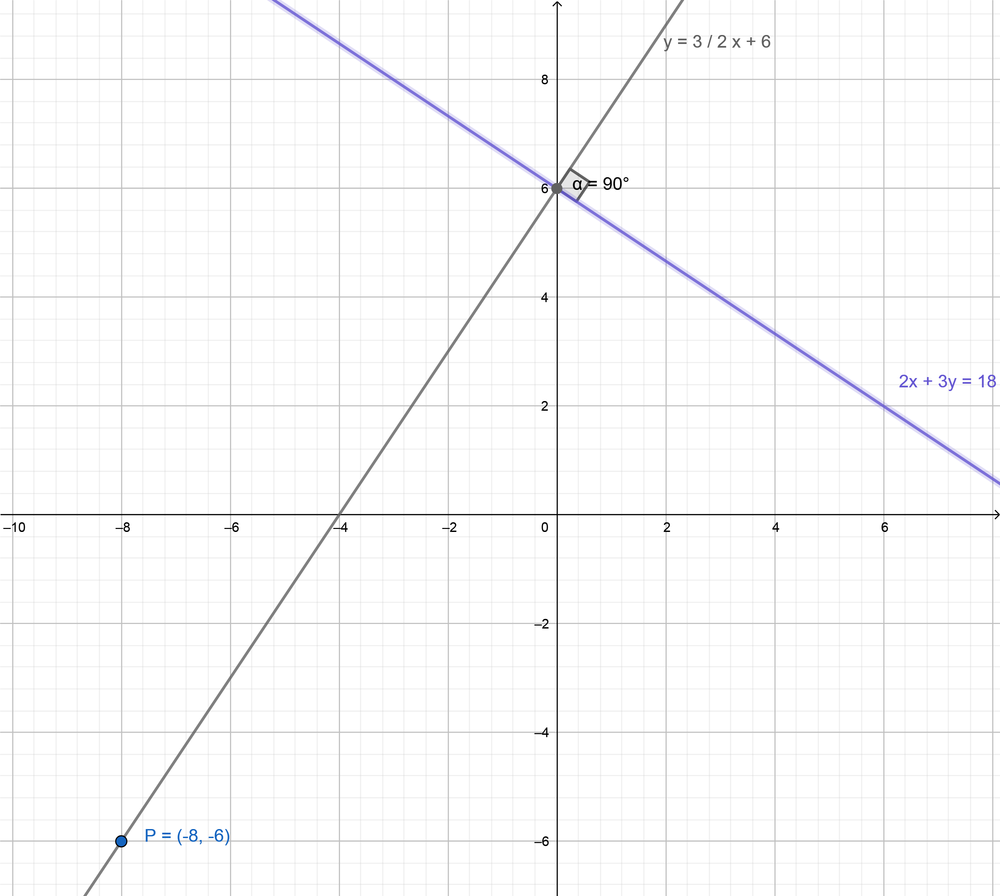
Question 58. P(- 8, – 6), 2x + 3y = 18

Answer: The perpendicular equation is y = \(\frac { 3 }{ 2 } \)x + 6

6.3 Medians and Altitudes of Triangles

Finding Properties of the Medians of a Triangle

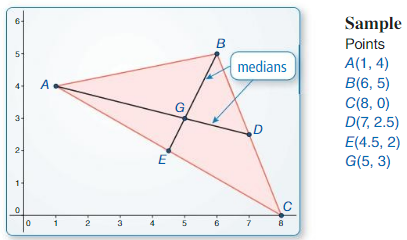
a. Plot the midpoint of \(\overline{B C}\) and label it D, Draw \(\overline{A D}\), which is a median of ABC. Construct the medians to the other two sides of ∆ABC. Answer:

b. What do you notice about the medians? Drag the vertices to change ∆ABC. Use your observations to write a conjecture about the medians of a triangle. Answer:

c. In the figure above, point G divides each median into a shorter segment and a longer segment. Find the ratio of the length of each longer segment to the length of the whole median. Is this ratio always the same? Justify your answer. Answer:

Finding Properties of the Altitudes of a Triangle

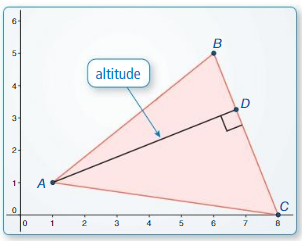
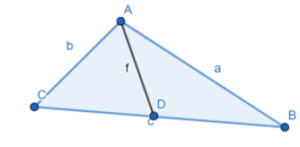
a. Construct the perpendicular segment from vertex A to \(\overline{B C}\). Label the endpoint D. \(\overline{A D}\) is an altitude of ∆ABC. Answer:

b. Construct the altitudes to the other two sides of ∆ABC. What do you notice? Answer:

c. Write a conjecture about the altitudes of a triangle. Test your conjecture by dragging the vertices to change ∆ABC. LOOKING FOR STRUCTURE To be proficient in math, you need to look closely to discern a pattern or structure. Answer:

Lesson 6.3 Medians and Altitudes of Triangles

There are three paths through a triangular park. Each path goes from the midpoint of one edge to the opposite corner. The paths meet at point P.

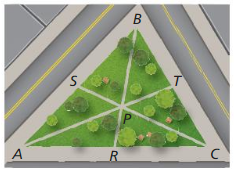
Question 1. Find PS and PC when SC = 2100 feet.

Answer: PS = 700, PC = 2100

Explanation: PC = \(\frac { 2 }{ 3 } \)SC SC = PS + PC SC = PS + \(\frac { 2 }{ 3 } \)SC PS = \(\frac { 1 }{ 3 } \)SC So, PS = \(\frac { 1 }{ 3 } \)(2100) = 700 PC = \(\frac { 2 }{ 3 } \)(2100) = 1400

Question 2. Find TC and BC when BT = 1000 feet.

Answer: BC = 2000 ft, TC = 1000 ft

Explanation: BT = TC So, TC = 1000 ft BC = BT + TC BC = 1000 + 1000 = 2000 ft

Question 3. Find PA and TA when PT = 800 feet.

Answer: PA = 2400 ft, TA = 1600 ft

Explanation: PT = \(\frac { 1 }{ 3 } \)PA PA = 3PT = 3 • 800 = 2400 TA = \(\frac { 2 }{ 3 } \)PA TA = \(\frac { 2 }{ 3 } \)(2400) = 1600

Find the coordinates of the centroid of the triangle with the given vertices.

Question 4. F(2, 5), G(4, 9), H(6, 1)

Answer: The centroid is (4, 5).

Explanation: The centroid of the triangle FGH is O = (\(\frac { 2 + 4 + 6 }{ 3 } \), \(\frac { 5 + 9 + 1 }{ 3 } \)) = (\(\frac { 12 }{ 3 } \), \(\frac { 15 }{ 3 } \)) = (4, 5)

Question 5. X(- 3, 3), Y(1, 5), Z(- 1, – 2)

Answer: The centriod of given triangle is (-1, 2)

Explanation: The centroid of the triangle XYZ is O = (\(\frac { -3 + 1 – 1 }{ 3 } \), \(\frac { 3 + 5 – 2 }{ 3 } \)) = (\(\frac { -3 }{ 3 } \), \(\frac { 6 }{ 3 } \)) = (-1, 2)

Tell whether the orthocenter of the triangle with the given vertices is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.

Question 6. A(0, 3), B(0, – 2), C(6, -3)

Answer: The orthocenter lies outside the triangle.

Explanation: The slope of the line BC = \(\frac { -3 + 2 }{ 6 – 0 } \) = \(\frac { -1 }{ 6 } \) The slope of the perpendicular line = 6 The perpendicular line is (y – 3) = 6(x – 0) y – 3 = 6x y = 6x + 3 The slope of AC = \(\frac { -3 – 3 }{ 6 – 0 } \) = \(\frac { -6 }{ 6 } \) = -1 The slope of the perpendicular line = 1 The equation of perpendicular line (y + 2) = 1(x – 0) y + 2 = x Substitute y = 6x + 3 in above equation 6x + 3 + 2 = x 5x = -5 x = -1 Put x = -1 in y + 2 = x y + 2 = -1 y = -3 The orthocenter is (-1, -3) The orthocenter lies outside the triangle.

Question 7. J(- 3, – 4), K(- 3, 4), L(5, 4)

Answer: The orthocenter lies on the vertex of the triangle.

Explanation: The slope of JL = \(\frac { 4 + 4 }{ 5 + 3 } \) = 2 The slope of perpendicular line is \(\frac { -1 }{ 2 } \) The equation of perpendicular line is (y – 4) = \(\frac { -1 }{ 2 } \)(x + 3) 2y – 8 = -x – 3 x + 2y – 5 = 0 The slope of JK = \(\frac { 4 + 4 }{ -3 + 3 } \) = 0 The slope of the perpendicular line is 0 the equation of perpendicular line is (y – 4) = 0 y = 4 Substitute y = 4 in x + 2y – 5 = 0 x + 2(4) – 5 = 0 x + 3 = 0 x = -3 So, the ortho center is (-3, 4) It lies on the vertex of the triangle.

Question 8. WHAT IF? In Example 4, you want to show that median \(\overline{B D}\) is also an angle bisector. How would your proof be different? Answer: Given ABC is an isosceles triangle and BD is the median. AB = BC AD = CD BD is the common sides ΔABD ≅ ΔBDC ∠ABD = ∠CBD So BD bisects ∠ABC BD is the angle bisector.

Exercise 6.3 Medians and Altitudes of Triangles

Question 2. COMPLETE THE SENTENCE The length of a segment from a vertex to the centroid is ______________ the length of the median from that vertex.

Answer: The length of a segment from a vertex to the centroid is one-third of the length of the median from that vertex.

Monitoring progress and Modeling with Mathematics

In Exercises 3-6, point P is the centroid of ∆LMN. Find PN and QP.

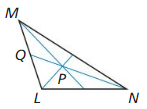
Answer: PN = 14 units, QP = 7 units

Explanation: PN = \(\frac { 2 }{ 3 } \)QN PN = \(\frac { 2 }{ 3 } \)(21) PN = 14 QP = \(\frac { 1 }{ 3 } \)QN = \(\frac { 1 }{ 3 } \)(21) = 7

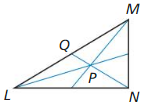
Answer: PN = 28 units, QP = 14 units

Explanation: PN = \(\frac { 2 }{ 3 } \)QN PN = \(\frac { 2 }{ 3 } \)(42) PN = 28 QP = \(\frac { 1 }{ 3 } \)QN = \(\frac { 1 }{ 3 } \)(42) = 14

In Exercises 7-10. point D is the centroid of ∆ ABC. Find CD and CE.

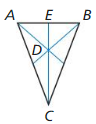
Answer: CD = 22 units, CE = 33 units

Explanation: DE = \(\frac { 1 }{ 3 } \)CE 11 = \(\frac { 1 }{ 3 } \) CE CE = 33 CD = \(\frac { 2 }{ 3 } \) CE CD = \(\frac { 2 }{ 3 } \)(33) CD = 22

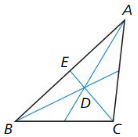
Answer: CE = 45 units, CD = 30

Explanation: DE = \(\frac { 1 }{ 3 } \)CE 15 = \(\frac { 1 }{ 3 } \) CE CE = 45 CD = \(\frac { 2 }{ 3 } \) CE CD = \(\frac { 2 }{ 3 } \)(45) CD = 30

In Exercises 11-14. point G is the centroid of ∆ABC. BG = 6, AF = 12, and AE = 15. Find the length of the segment.

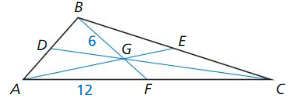
Question 12. \(\overline{B F}\)

Answer: \(\overline{B F}\) = 15

Explanation: All the medians have same length. so, AE = 15 = BF

Question 14. \(\overline{G E}\)

Answer: \(\overline{G E}\) = 5 units

Explanation: AE = AG + GE 15 = 10 + GE GE = 5

In Exercises 15-18. find the coordinates of the centroid of the triangle with the given vertices.

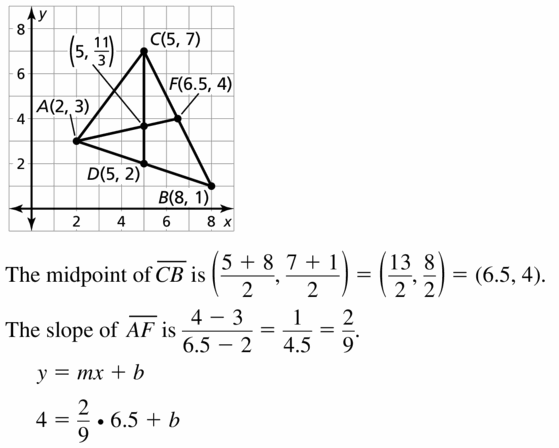
Question 16. F(1, 5), G( – 2, 7), H(- 6, 3)

Answer: The centroid is (\(\frac { -7 }{ 3 } \), 5)

Explanation: The centroid of the trinagle = (\(\frac { 1 – 2 – 6 }{ 3 } \), \(\frac { 5 + 7 + 3 }{ 3 } \)) = (\(\frac { -7 }{ 3 } \), 5)

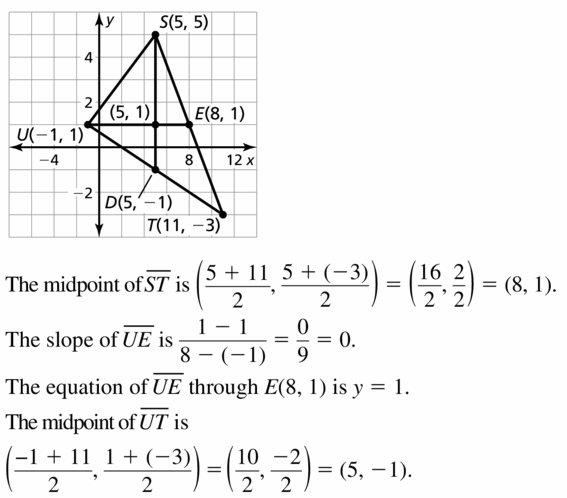
Question 18. X(1, 4), Y(7, 2), Z(2, 3)

Answer: The centroid of the triangle is (\(\frac { 10 }{ 2 } \), 3)

Explanation: The centroid of the trinagle = (\(\frac { 1 + 7 + 2 }{ 3 } \), \(\frac { 4 + 2 + 3 }{ 3 } \)) = (\(\frac { 10 }{ 2 } \), 3)

In Exercises 19-22. tell whether the orthocenter is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.

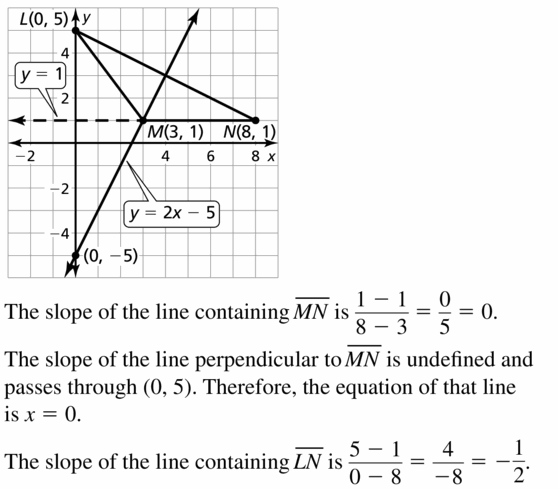
Question 20. X(- 3, 2), Y(5, 2), Z(- 3, 6)

Explanation: The slope of YZ = \(\frac { 6 – 2 }{ -3 – 5 } \) = \(\frac { -1 }{ 2 } \) The slope of the perpendicular line is 2 The equation of perpendicular line is (y – 2) = 2(x + 3) y – 2 = 2x + 6 2x – y + 8 = 0 The slope of XZ = \(\frac { 6 – 2 }{ -3 + 3 } \) = 0 The equation of perpendicular line is (y – 2) = 0 y = 2 Substitute y = 2 in 2x – y + 8 = 0 2x – 2 + 8 = 0 2x + 6 = 0 x = -3 the orthocenter is (-3, 2) The orthocenter lies on the vertex of the triangle.

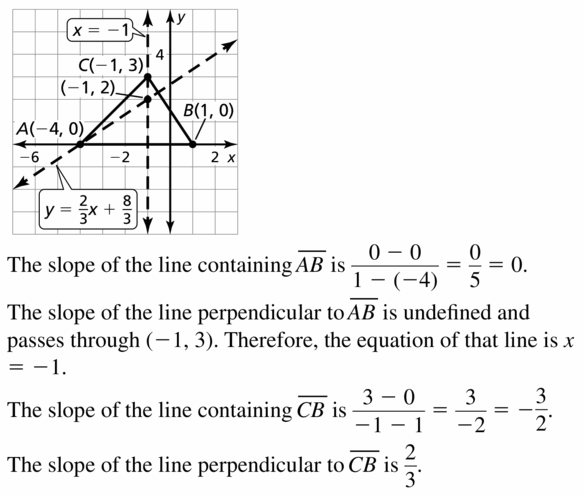
Question 22. T(-2, 1), U( 2, 1), V(0, 4)

Answer: The orthocenter lies inside the triangle ABC.

Explanation: The slope of UV = \(\frac { 4 – 1 }{ 0 – 2 } \) = \(\frac { -3 }{ 2 } \) The slope of the perpendicular line is \(\frac { 2 }{ 3 } \) The equation of the perpendicular line is (y – 1) = \(\frac { 2 }{ 3 } \)(x + 2) 3(y – 1) = 2(x + 2) 3y – 3 = 2x + 2 2x – 3y + 5 = 0 — (i) The slope of TV = \(\frac { 4 – 1 }{ 0 + 2 } \) = \(\frac { 3 }{ 2 } \) The slope of the perpendicular line is \(\frac { -2 }{ 3 } \) The equation of the perpendicular line is (y – 1) = \(\frac { -2 }{ 3 } \)(x – 2) 3(y – 1) = -2(x – 2) 3y – 3 = -2x + 4 2x + 3y – 7 = 0 —(ii) Add two equations 2x – 3y + 5 + 2x + 3y – 7 = 0 4x – 2 = 0 x = 0.5 2x – 1.5 + 5 = 0 x = -1.75 So, the orthocenter is (0, 2.33) The orthocenter lies inside the triangle ABC.

Question 24. obtuse scalene triangle

Question 26. acute isosceles triangle

ERROR ANALYSIS In Exercises 27 and 28, describe and correct the error in finding DE. Point D is the centroid of ∆ABC.

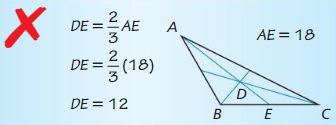
Answer: The length of DE should be 1/3 of length of AE because it is the shorter segment from the centroid DE = \(\frac { 1 }{ 3 } \)AE = \(\frac { 1 }{ 3 } \)(24) = 8 DE = 8

PROOF In Exercises 29 and 30, write a proof of the statement.

Question 30. The altitude from the vertex angle to the base of an isosceles triangle is also a perpendicular bisector. Answer:

CRITICAL THINKING In Exercises 31-36, complete the statement with always, sometimes, or never. Explain your reasoning.

Question 32. The orthocenter is _____________ outside the triangle.

Answer: The orthocenter is always outside the triangle opposite the longest leg, on the same side as the largest angle. The only time all three of these centers fall in the same spot is in the case of an equilateral triangle. In fact, in this case, the incenter falls in the same place as well.

Question 34. An altitude is ______________ the same line segment as an angle bisector.

Answer: An altitude is sometimes the same line segment as an angle bisector.

Question 36. The centroid is ______________ formed by the intersection oÍ the three medians.

Answer: The centroid is a point formed by the intersection oÍ the three medians.

Question 38. WRITING Compare a median. an altitude, and an angle bisector of a triangle.

Answer: Median is a line segment joining a vertex of a triangle with the midoint of the opposite side. Angle bisector is a line segment joining a vertex of a trianglr with the opposite side such that the angle at the vertex split into two equal parts. While altitude is also a line segment joining a vertex of a triangle with opposite side such that the segment is perpendicular to the opposite side. In general, medians, angle bisectors and altitudes drawn from the same vertex of a triangle are different line segments. In an equilateral triagle, altitude, median, and angle bisector drawn from the same vertex overlap. In an isosceles trianglle, the altitude drawn to the base is the median and the angle bisector, the median drawn to the base is the altitude and the angle bisector, the bisector of the angle opposite to the base is the altitude and the median.

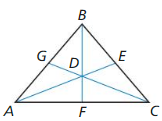
Question 40. ANALYZING RELATIONSHIPS Copy and complete the statement for ∆DEF with centroid K and medians \(\overline{D H}\), \(\overline{E J}\), and \(\overline{F G}\).

a. EJ = ____ KJ

Answer: EJ = 2KJ

b. DK = ____ KH

Answer: DK = 2 KH Since KH is the shorter distance between the two parts of the median, its length is 1/3 of the DH.

c. FG = ___ KF

Answer: FG = \(\frac { 2 }{ 3 } \)KF Since KF is the longest distance between two parts, its length is \(\frac { 2 }{ 3 } \) of FG

d. KG = ___ FG

Answer: KG = 2FG Since KG is the shorter distance between the two parts of the median, its length is 1/3 of the FG.

MATHEMATCAL CONNETIONS In Exercises 41-44, point D is the centroid of ∆ABC. Use the given information to find the value of x.

Question 42. GD = 2x – 8 and GC = 3x + 3

Answer: x = 9

Explanation: GD = \(\frac { 1 }{ 3 } \)GC 2x – 8 = \(\frac { 1 }{ 3 } \)(3x + 3) 2x – 8 = x + 1 x = 9

Question 44. DF = 4x – 1 and BD = 6x + 4

Answer: x = 3

Explanation: BD = 2DF 6x + 4 = 2(4x – 1) 6x + 4 = 8x – 2 2x = 6 x = 3

Question 46. CRITICAL THINKING In what types of triangles can a vertex be one of the points of concurrency of the triangle? Explain your reasoning.

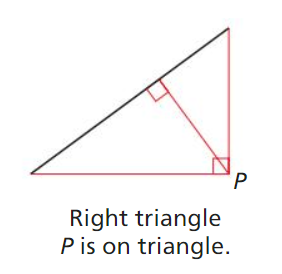
Answer: KM is the median drawn from K to JL.

b. What type of segments is \(\overline{K N}\)? Which point of concurrency lies on \(\overline{K N}\)?

Answer: KN is the altitude drawn from K to JL.

c. Compare the areas of ∆JKM and ∆KLM. Do you think the areas of the triangles formed by the median of any triangle will always compare this way? Explain your reasoning.

Question 50. DRAWING CONCLUSIONS The center of gravity of a triangle, the point where a triangle can balance on the tip of a pencil, is one of the four points of concurrency. Draw and cut out a large scalene triangle on a piece of cardboard. Which of the four points of concurrency is the center of gravity? Explain.

Answer: The median is the balancing line of the triangle The centroid is the point of concurrency of three medians The centroid is the center of gravity of the triangle.

Question 52. THOUGHT PROVOKING Construct an acute scalene triangle. Find the orthocenter, centroid, and circumcenter. What can you conclude about the three points of concurrency?

Answer: The centroid, orthocenter and circumcenter are collinear.

Question 54. PROOF Prove the statements in parts (a)-(c). Given \(\overline{L P}\) and \(\overline{M Q}\) are medians of scalenc ∆LMN. Point R is on \(\vec{L}\)P such that \(\overline{L P} \cong \overline{P R}\). Point S is on \(\vec{M}\)Q such that \(\overline{M Q} \cong \overline{Q S}\). Prove a. \(\overline{N S} \cong \overline{N R}\) b. \(\overline{N S}\) and \(\overline{N R}\) are both parallel to \(\overline{L M}\). c. R, N, and S are collinear. Answer:

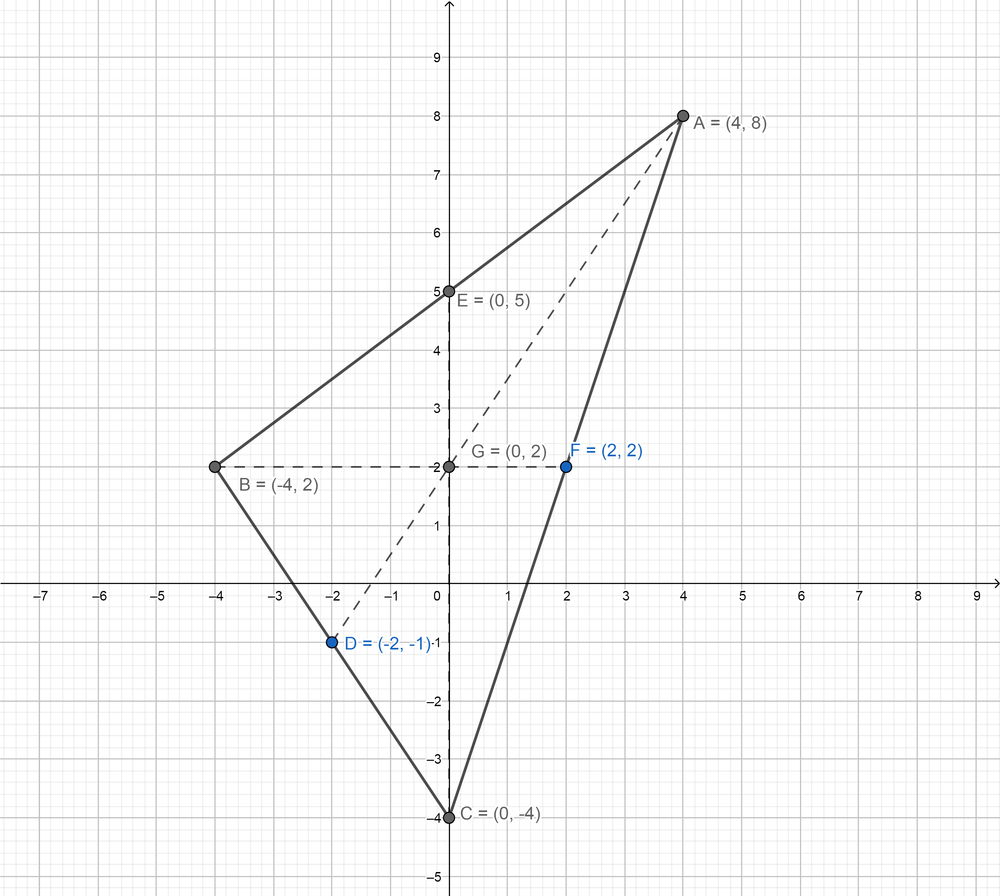
Determine whether \(\overline{A B}\) is parallel to \(\overline{C D}\).

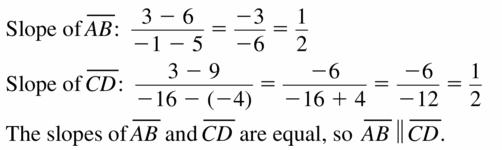
Question 56. A(- 3, 6), B(5, 4), C(- 14, – 10), D(- 2, – 7)

Answer: AB is not parallel to CD.

Explanation: Slope of AB = \(\frac { 4 – 6 }{ 5 + 3 } \) = \(\frac { -1 }{ 4 } \) Slopeof CD = \(\frac { -7 + 10 }{ -2 + 14 } \) = \(\frac { 1 }{ 4 } \) The slopes of AB and CD are not equal. So AB and CD are not parallel.

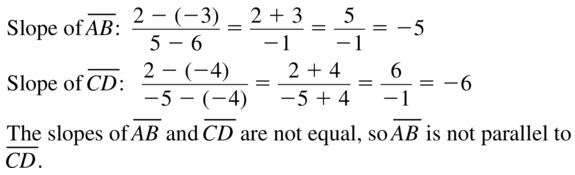
Question 58. A(- 5, 6), B(- 7, 2), C(7, 1), D(4, – 5)

Answer: AB is parallel to CD.

Explanation:, Slope of AB = \(\frac { 2 – 6 }{ -7 + 5 } \) = 2 Slopeof CD = \(\frac { -5 – 1 }{ 4 – 7 } \) = 2 The slopes of AB and CD are equal. So, AB is parallel to CD.

6.1 and 6.3 Quiz

Find the indicated measure. Explain your reasoning.

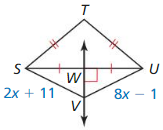
Answer: UV = 15

Explanation: SV = VU 2x + 11 = 8x – 1 8x – 2x = 11 + 1 6x = 12 x = 2 UV = 8(2) – 1 = 15

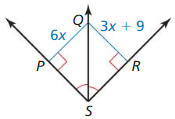
Answer: QP = 18

Explanation: QP = QR 6x = 3x + 9 3x = 9 x = 3 QP = 6(3) = 18

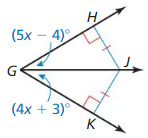
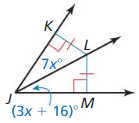
Answer: m∠GJK = 59°

Explanation: 5x – 4 = 4x + 3 x = 7 ∠JGK = 4(7) + 3 = 31 m∠GJK = 180 – (31 + 90) = 180 – 121 = 59

Question 4. A(- 4, 2), B(- 4, – 4), C(0, – 4)

Answer: The circumcenter is (-2, -1)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let A(- 4, 2), B(- 4, – 4), C(0, – 4) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PA = PB = PC PA² = PB² = PC² PA² = PB² (x + 4)² + (y – 2)² = (x + 4)² + (y + 4)² x² + 8x + 16 + y² – 4y + 4 = x² + 8x + 16 + y² + 8y + 16 12y = -12 y = -1 PB² = PC² (x + 4)² + (y + 4)² = (x – 0)² + (y + 4)² x² + 8x + 16 + y² + 8y + 16 = x² + y² + 8y + 16 8x = -16 x = -2 The circumcenter is (-2, -1)

Question 5. D(3, 5), E(7, 9), F(11, 5)

Answer: The circumcenter is (7, 5)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let D(3, 5), E(7, 9), F(11, 5) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PD = PE = PF PD² = PE² = PF² PD² = PE² (x – 3)² + (y – 5)² = (x – 7)² + (y – 9)² x² – 6x + 9 + y² – 10y + 25 = x² – 14x + 49 + y² – 18y + 81 -6x + 14x – 10y + 18y = 130 – 34 8x + 8y = 96 x + y = 12 — (i) PE² = PF² (x – 7)² + (y – 9)² = (x – 11)² + (y – 5)² x² – 14x + 49 + y² – 18y + 81 = x² – 22x + 121 + y² – 10y + 25 -14x + 22x – 18y + 10y = 146 – 130 8x – 8y = 16 x – y = 2 — (ii) Add (i) & (ii) x + y + x – y = 12 + 2 2x = 14 x = 7 Put x = 7 in (i) 7 + y = 12 y = 5 The circumcenter is (7, 5)

The incenter of ∆ABC is point N. Use the given information to find the indicated measure.

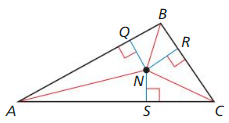
Answer: NS = 11

Explanation: NQ = NR = NS 2x + 1 = 4x – 9 4x – 2x = 10 2x = 10 x = 5 NQ = 10 + 1 = 11 NS = 11

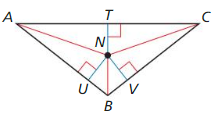
Answer: NT = 15

Explanation: NU = NV = NT -3x + 6 = -5x -3x + 5x = -6 2x = -6 x = -3 NT = -5(-3) = 15

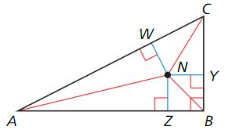
Answer: NW = 26

Explanation: NZ = NY = NW 4x – 10 = 3x – 1 x = 9 NZ = 4(9) – 10 = 36 – 10 = 26 NW = 26

Find the coordinates of the centroid of the triangle wilt the given vertices. Question 9. J(- 1, 2), K(5, 6), L(5, – 2)

Answer: Centroid of the triangle is (3, 2)

Explanation: Centroid of the triangle = (\(\frac { -1 + 5 + 5 }{ 3 } \), \(\frac { 2 + 6 – 2 }{ 3 } \)) = (3, 2)

Question 10. M(- 8, – 6), N(- 4, – 2), P(0, – 4)

Answer: Centroid of the triangle is (-4, -4)

Explanation: Centroid of the triangle = (\(\frac { -8 – 4 + 0 }{ 3 } \), \(\frac { -6 – 2 – 4 }{ 3 } \)) = (-4, -4)

Tell whether the orthocenter is inside, on, or outside the triangle. Then find its coordinates.

Question 11. T(- 2, 5), U(0, 1), V(2, 5)

Answer: The orthocenter lies inside the triangle TUV

Explanation: The slope of TU = \(\frac { 1 – 5 }{ 0 + 2 } \) = -2 The slope of the perpendicular line is \(\frac { 1 }{ 2 } \) The perpendicular line is y – 5 = \(\frac { 1 }{ 2 } \)(x – 2) 2y – 10 = x – 2 x – 2y + 8 = 0 The slope of UV = \(\frac { 5 – 1 }{ 2 – 0 } \) = 2 The slope of the perpendicular line is \(\frac { -1 }{ 2 } \) The perpendicular line is y – 5 = \(\frac { -1 }{ 2 } \)(x + 2) 2y – 10 = -x – 2 x + 2y – 8 = 0 equate both equations x – 2y + 8 = x + 2y – 8 -4y = -16 y = 4 x – 2(4) + 8 = 0 x = 0 So, the orthocenter is (0, 4) The orthocenter lies inside the triangle TUV

Question 12. X(- 1, – 4), Y(7, – 4), Z(7, 4)

Answer: The orthocenter lies on the vertex.

Explanation: The slope of XY = \(\frac { -4 + 4 }{ 7 + 1 } \) = 0 The slope of the perpendicular line is 0 The perpendicular line is y – 4 = 0 y = 4 The slope of XZ =\(\frac { 4 + 4 }{ 7 + 1} \) = 1 The slope of the perpendicular line is -1 The perpendicular line is y + 4 = -1(x – 7) y + 4 = -x + 7 x + y – 3 = 0 x + 4 – 3 = 0 x = -1 So, the orthocenter is (-1, 4) The orthocenter lies on the vertex.

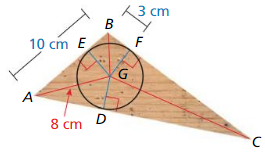
a. Which point of concurrency is the center of the circle? What type of segments are \(\overline{B G}\), \(\overline{C G}\), and \(\overline{A G}\)? Answer:

• The incircle of a triangle touches all sides of the triangle and has the incentre of the triangle as its center. Therefore, it is the largest possible circle that can be fitted inside a triangle.
• So, the wheel is the incircle of the triangle and its center is the incentre of the triangle.
• We know that the point of intersection of the angle bisectors of a triangle is called the incenter of the triangle.
• Since, BG, CG, and AG intersect at the center of the circle which is the incenter of the triangle. So, BG, CG, and AG are the angle bisectors of the triangle ABC.

b. Which theorem can you use to prove that ∆BGF ≅ ∆BGE? Answer: AG, BG, and CG are the angle bisectors of the triangle. As BG is the angle bisector of ∠EBF. ∠FBG = ∠EBG—-(1) ∠GFC = ∠GEA = 90 degrees As ∠GFC forms a linear pair with ∠GFB and ∠GEA forms a linear pair with ∠GEB ∠GFB = 180 – ∠GFC ∠GEB = 180 – ∠GEA ∠GFB = ∠GEB = 90 degrees —-(2) In ΔBGF and ΔBGE ∠GFB ≅ ∠GEB ∠FBG ≅ ∠EBG BG ≅ BG

c. Find the radius of the wheel to the nearest tenth of a centimeter. Justify your answer. Answer: ΔBGF ≅ ΔBGE BF = BE the length of BE is also 3 cm BE + EA = 10 3 + EA = 10 EA = 10 – 3 EA = 7 Apply the Pythagoras theorem in ΔAEG EA² + GE² = AG² 7² + GE² = 8² GE² = 8² – 7² GE² = 64 – 49 GE² = 15 GE = √15 = 3.88 So, the length of GE is 3.88 cm. So, the radius of the wheel to the nearest tenth of cm is 3.9

Question 14. The Deer County Parks Committee plans to build a park at point P, equidistant from the three largest cities labeled X, Y, and Z. The map shown was created b the committee.

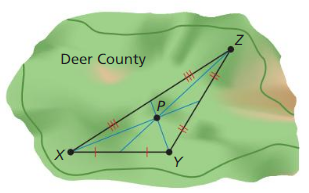
a. Which point of concurrency did the commIttee use as the location of the Park? Answer:

• That committee plans to build a park at point P such that it is at an equal distance from three big cities. We were asked to find which point of concurrency the committee used to locate the park.
• As the three big cities are vertices X, Y, and Z, and point P is equidistant to them, point P must be the point where the perpendicular bisectors of the triangle meet.
• There the committee used the point of concurrency of the perpendicular bisectors.

b. Did the committee use the best point of concurrency for the location of the park? If not, which point would be better to use? Explain. Answer:

• Give is to check whether the committee used the best point of concurrency for the location of the park.
• A point of intersection of perpendicular bisectors is the only point that is at equidistance from all three vertices.
• It is the best point for the location of the park.

6.4 The Triangle Midsegment Theorem

Midsegments of a Triangle

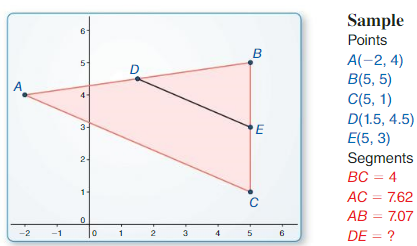
a. Plot midpoint D of \(\overline{A B}\) and midpoint E of \(\overline{B C}\). Draw \(\overline{D E}\), which is a midsegment of ∆ABC. Answer:

b. Compare the slope and length of \(\overline{D E}\) with the slope and length of \(\overline{A C}\). Answer:

c. Write a conjecture about the relationships between the midsegments and sides of a triangle. Test your conjecture by drawing the other midsegments of ∆ABC, dragging vertices to change ∆ABC. and noting whether the relationships hold. Answer:

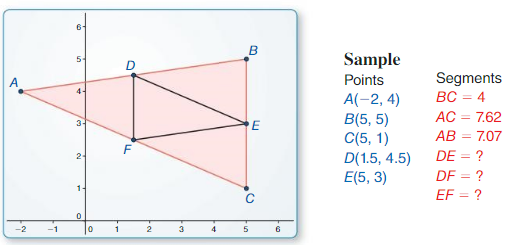
a. Draw all three midsegments of ∆ABC. Answer:

b. Use the drawing to write a Conjecture about the triangle formed by the midsegments of the original triangle. CONSTRUCTING VIABLE ARGUMENTS To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures. Answer:

Question 3. How are the midsegments of a triangle related to the sides of the triangle? Answer:

Question 4. In ∆RST. \(\overline{U V}\) is the rnidsegrnent connecting the midpoints of \(\overline{R S}\) and \(\overline{S T}\). Given UV = 12, find RT. Answer:

Lesson 6.4 The Triangle Midsegment Theorem

Monitoring progress

Use the graph of △ABC.

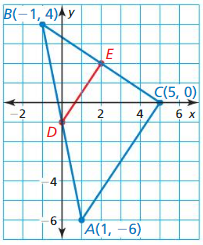
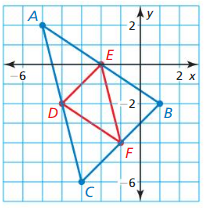
Question 1. In △ABC, show that midsegments \(\overline{D E}\) is parallel to \(\overline{A C}\) and that DE = \(\frac { 1 }{ 2 }\)AC.

Answer: Find the coordinates of D and E by getting the midpoints of AB, BC AB midpoint = D(\(\frac { 1 – 1 }{ 2 } \), \(\frac { 4 – 6 }{ 2 } \)) = D(0, -1) Midpoint of BC = E(\(\frac { 5 – 1 }{ 2 } \), \(\frac { 4 + 0 }{ 2 } \)) = E(2, 2) Slope of AC = \(\frac { 0 + 6 }{ 5 – 1 } \) =\(\frac { 3 }{ 2 } \) Slope of DE = \(\frac { 2 + 1 }{ 2 – 0 } \) = \(\frac { 3 }{ 2 } \) The slopes are same, so the lines are not parallel. DE = √(2 – 0)² + (2 + 1)² = √13 AC = √(5 – 1)² + (0 + 6)² = √16 + 36 = √52 So, DE = \(\frac { 1 }{ 2 }\)AC

Question 2. Find the coordinates of the endpoints of midsegments \(\overline{E F}\), Which opposite \(\overline{A B}\). show that \(\overline{E F}\) is parallel to \(\overline{A B}\) and that EF = \(\frac { 1 }{ 2 }\)AB.

Answer: The coordinates of E = (\(\frac { -1 + 5 }{ 2 } \), \(\frac { 0 + 4 }{ 2 } \)) = (2, 2) The coordinates of F = (\(\frac { 1 + 5 }{ 2 } \), \(\frac { 0 + 6 }{ 2 } \)) = (3, 3) The slope of AB = \(\frac { 4 + 6 }{ -1 – 1 } \) = -5 The slope of EF = \(\frac { 3 – 2 }{ 3 – 2 } \) = 1 The slopes are different. So the lines are not parallel EF = √(3 – 2)² + (3 – 2)² = √2 AB = √(-1 – 1)² + (4 + 6)² = √4 + 100 = √104

Question 3. In Example 2, find the coordinates of F, the midpoint of \(\overline{O C}\). Show that \(\overline{F E}\) || \(\overline{O B}\) and FE = \(\frac { 1 }{ 2 }\)OB.

Answer: The coordinates of F = (\(\frac { 0 + 2p }{ 2 } \), \(\frac { 0 + 0 }{ 2 } \)) = (p, 0) The slope of OB = \(\frac { 2r – 0 }{ 2q – 0 } \) = \(\frac { r }{ q } \) The slope of FE = \(\frac { r – 0 }{ q + p – p }\) = \(\frac { r }{ q }\) The slopes are equal. So, the lines are parallel. FE = √(q + p – p)² + (r – 0)² = √q² + r² OB = √(2q – 0)² + (2r – 0)² = √4q² + 4r²  = 2√q² + r² OB = 2(FE) FE = \(\frac { 1 }{ 2 }\)OB.

Question 4. Copy the diagram in Example 3. Draw and name the third midsegment. Then find the length of \(\overline{V S}\) when the length of the third midsegment is 81 inches.

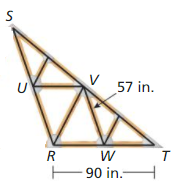
Question 5. In Example 4. if F is the midpoint of \(\overline{C B}\), what do you know about \(\overline{D F}\)?

Answer: DF is parallel to AE.

Question 6. WHAT IF? In Example 5, you jog down Peach Street to Plum Street, over Plum Street to Cherry Street. up Cherry Street to Pear Street. over Pear Street to Peach Street. and then back home up Peach Street. Do you jog more miles in Example 5? Explain.

Answer: The distance you jog = 2.25 + 1.4 + 1.3 + .65 = 5.6

Exercise 6.4 The Triangle Midsegment Theorem

Question 2. COMPLETE THE SENTENCE If \(\overline{D E}\) is the midsegment opposile \(\overline{A C}\) in ∆ABC, then \(\overline{D E}\) || \(\overline{A C}\) and DE = ________ AC by the Triangle Midsegrnent Theorem

Answer: If \(\overline{D E}\) is the midsegment opposile \(\overline{A C}\) in ∆ABC, then \(\overline{D E}\) || \(\overline{A C}\) and DE = \(\frac { 1 }{ 2 } \) AC by the Triangle Midsegrnent Theorem (Theorem 6.8).

In Exercises 3-6, use the graph of ∆ABC with midsegments \(\overline{D E}\), \(\overline{E F}\), and \(\overline{D F}\).

Question 4. Show that \(\overline{D E}\) is parallel to \(\overline{C B}\) and that DE = \(\frac{1}{2}\)CB.

Answer: The slope of DE = \(\frac { 0 + 2 }{ -2 + 4 } \) = 1 The slope of CB = \(\frac { -2 + 6 }{ 1 + 3 } \)  = 1 The slopes are same. So \(\overline{D E}\) is parallel to \(\overline{C B}\) DE = √(-2 + 4)² + (0 + 2)² = √4 + 4 = √8 CB = √(1 + 3)² + (-2 + 6)² = √16 + 16 = √32 So, DE = \(\frac{1}{2}\)CB

Question 6. Show that \(\overline{D F}\) is parallel to \(\overline{A B}\) and that DF = \(\frac{1}{2}\)AB.

Answer: The slope of DF = \(\frac { -4 + 2 }{ -1 + 4 } \) = \(\frac { -2 }{ 3 } \) The slope of AB = \(\frac { -2 – 2 }{ 1 + 5 } \) = \(\frac { -4 }{ 6 } \) = \(\frac { -2 }{ 3 } \) The slopes are equal. So, the lines are parallel. DF = √(-1 + 4)² + (-4 + 2)² = √9 + 4 = √13 AB = √(1 + 5)² + (-2 – 2)² = √36 + 16 = √52 So, DF = \(\frac{1}{2}\)AB.

In Exercises 7-10, \(\overline{D E}\) is a midsegment of ∆ABC Find the value of x.

Answer: x = 10

Explanation: DE = \(\frac { 1 }{ 2 } \)AB 5 = \(\frac { 1 }{ 2 } \)x x = 10

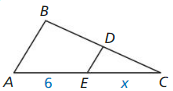
Answer: x = 8

Explanation: BE = EC x = 8

In Exercise 11-16, \(\overline{X J} \cong \overline{J Y}\), \(\overline{Y L} \cong \overline{L Z}\), and \(\overline{X K} \cong \overline{K Z}\). Copy and complete the statement.

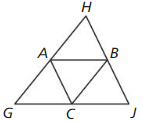
Question 12. \(\overline{X Y}\) || __________

Answer: \(\overline{X Y}\) || KL

Question 14. \(\overline{J L}\) ≅ __________ ≅ __________

Answer: \(\overline{J L}\) ≅ JK ≅ KL

Question 16. \(\overline{J K}\) ≅ __________ ≅ __________

Answer: \(\overline{J K}\) ≅ JL ≅ KL

Question 18. When AC = 3y – 5 and HJ = 4y + 2, what is HB?

Answer: HB = 13

Explanation: AC = 0.5(HJ) 3y – 5 = 0.5(4y + 2) 3y – 5 = 2y + 1 3y – 2y = 1 + 5 y = 6 HB = 0.5(HJ) = 0.5(4(6) + 2) = 0.5(26) = 13

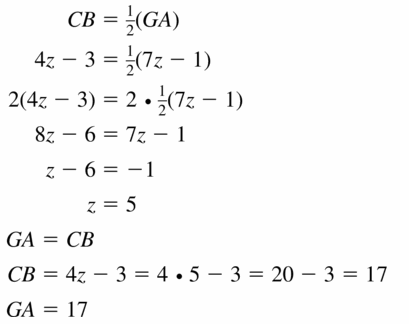
Answer: BC = \(\frac { 1 }{ 2 } \)DE 10 = \(\frac { 12 }{ 2 } \)(5) According to triangle midsegment theorem, AD = DB and AE = EC.

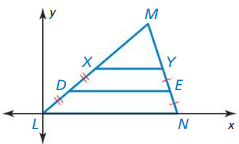
Question 22. PROVING A THEOREM Use the figure from Example 2 to prose the Triangle Midsegment Theorem (Theorem 6.8) for midsegment \(\overline{D F}\), where F is the midpoint of \(\overline{O C}\). Answer:

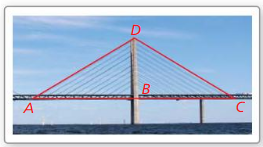
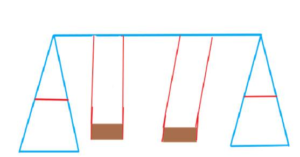
Question 24. THOUGHT PROVOKING Find a real-life object that uses midsegments as part of its structure. Print a photograph of the object and identify the midsegments of one of the triangles in the structure. Answer:

• We have to look for an object which has midsegments in our surroundings. Then identify the midsegment in one of the triangles present in it.
• When we look around, we will see that many structures like swings, rooftops of house, bridges etc, use midsegments in their design.

Answer: Because the yellow triangle vertices are located at the midpoints of the red triangle sides.

Find a counter example to show that the conjecture is false.

Question 28. The difference of two numbers is always less than the greater number.

Answer: When we subtract -3 from 4 i.e 4 -(-3) = 7. The number is greater than the individual integers. So, the subtraction of a negative number from a positive number gives an answer greater than both numbers.

6.5 Indirect Proof and Inequalities in One Triangle

Comparing Angle Measures and Side Lengths

Work with a partner: Use dynamic geometry software. Draw any scalene ∆ABC

b. Order the side lengths. Order the angle measures. What do you observe? Answer:

c. Drug the vertices of ∆ABC to form new triangles. Record the side lengths and angle measures in a table. Write a conjecture about your findings. Answer:

A Relationship of the Side Lengths of a Triangle

a. Find the side lengths of the triangle. Answer:

c. Drag the vertices of ∆ABC to form new triangles and repeat parts (a) and (b). Organize your results in a table. Write a conjecture about your findings. Answer:

Question 3. How are the sides related to the angles of a triangle? How are any two sides of a triangle related to the third side? Answer: The relation between the sides and the angles of the triangle is that in any triangle the largest side and the largest angle of the triangle are always opposite to each other and the shortest side and the shortest angle are always opposite to each other. The relation of the two sides of a triangle to the third side is that the sum of the lengths of any two sides of a triangle is greater than the length of its third side.

Question 4. Is it possible for a triangle to have side lengths of 3, 4, and 10? Explain. Answer: Given side lengths are 3, 4 and 10. 3 + 4 > 10 7 > 10 So, it is not possible to construct a triangle.

Lesson 6.5 Indirect Proof and Inequalities in One Triangle

Question 1. Write in indirect proof that a scalene triangle cannot have two congruent angles. Answer:

• Let us consider the contradiction that a scalene triangle has two congruent angles and no congruent sides. This means that if two angles of a scalene triangle are congruent, then the two sides opposite two these congruent angles also congruent. But this is a contradiction to the above assumption that the triangle has no congruent sides.
• So, we can conclude that a scalene triangle cannot have two congruent angles.

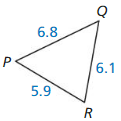
Answer: The sides from the largest to smallest are PQ, QR, PR The angles opposite to sides are ∠R, ∠P, ∠Q The angles from smallest to the largest are ∠Q, ∠P, ∠R

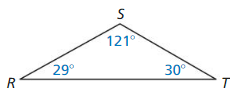
Answer: The angles from shortest to longest are ∠R, ∠T, ∠S

Question 4. A triangle has one side of length 12 inches and another side of length 20 inches. Describe the possible lengths of the third side.

Answer: The length of the third side must be greater than 8 and lesser than 32.

Explanation: Let x represent the length of the third side. Draw diagrams to help visualize the small and large values of x. Then use the Triangle Inequality Theorem to write and solve inequalities. The smallest value of x is x + 12 > 20. So, x > 8 The largest value of x is 12 + 20 > x 32 > x So, 32 > x or 32 < x The length of the third side must be greater than 8 and lesser than 32.

Decide Whether it is possible to construct a triangle with the given side lengths. Explain your reasoning.

Question 5. 4 ft, 9 ft, 10 ft

Answer: It is not possible to construct a triangle.

Explanation: According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. So, 9 + 4 = 13 13 is not greater than 10. So, it is not possible to construct a triangle.

Question 6. 8 ft, 9 ft, 18 ft

Answer: It is possible to construct a triangle.

Explanation: According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. 8 + 9 = 17 > 18 So, it is possible to construct a triangle.

Question 7. 5 cm, 7 cm, 12 cm

Explanation: According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. 7 + 5 = 12 12 is not greater than 12 so, it is not possible to construct a triangle.

Exercise 6.5 Indirect Proof and Inequalities in One Triangle

Question 2. WRITING How can you tell which side of a triangle is the longest Irom the angle measures of the triangle? How can you tell which side is the shortest?

Answer: The angle which is opposite to the longest side is the longest angle.

In Exercises 3-6, write the first step in an indirect proof of the statement.

Question 4. If x and y are odd integers. then xy is odd.

Answer: Assume x = 1, y = 3 xy = 3

Question 6. In ∆JKL, if M is the midpoint of \(\overline{K L}\), then \(\overline{J M}\) is a median.

Answer: Assume temporarily JM is a median.

In Exercises 7 and 8, determine which two statements contradict each other. Explain your reasoning.

Question 8. (A) Both ∠X and ∠Y have measures greater than 20°. (B) Both ∠X and ∠Y have measures less than 30°. (C) m∠X + m∠Y = 62° Answer: B and C. If ∠X and ∠Y are less than 30, then  m∠X + m∠Y is not equal to 62.

In Exercises 9 and 10, use a ruler and protractor to draw the given type of triangle. Mark the largest angle and longest side in red and the smallest angle and shortest side in blue. What do you notice?

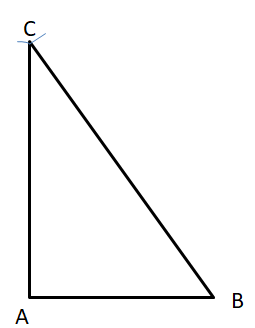
Question 10. right scalene

In Exercises 11 and 12, list the angles of the given triangle from smallest to largest.

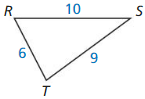
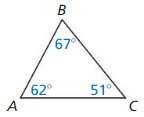
In Exercises 13-16, list the sides of the given triangle from shortest to longest.

In Exercises 17-20, describe the possible lengths of the third side of the triangle given the lengths of the other to sides.

Question 18. 12 feet, 18 feet

Answer: The possible lengths of the third side are greater than 6 and less than 30 ft

Explanation: x + 12 > 18 x > 6 12 + 18 > x 30 > x or x < 30 The possible lengths of the third side are greater than 6 and less than 30 ft

Question 20. 25 meters, 25 meters

Answer: The possible lengths of the third side are greater than 0 and less than 50 m.

Explanation: x + 25 > 25 x > 0 25 + 25 > x 50 > x or x < 50 The possible lengths of the third side are greater than 0 and less than 50 m.

In Exercises 21-23, is it possible to construct a triangle with the given side lengths? If not, explain why not.

Question 22. 3, 6, 9

Explanation: 3 + 6 = 9 → 9 = 9 6 + 9 = 15 → 15 < 9 9 + 3 = 12 → 12 < 9 No, the sum of any two side lengths of a triangle is less than the length of the third side.

Question 24. 35, 120, 125

Answer: 35 + 120 = 155 → 155 < 125 So, No.

Answer: Number 1 is opposite to 90 degrees and 2 is opposite to 60 degrees and the remaining is √3 on the triangle.

Question 28. REASONING Your class has fewer than 30 students. The teacher divides your class into two groups. The first group has 15 students. Use indirect reasoning to show that the second group must have fewer than 15 students.

Answer: The assumption that N2 ≥ 15 is false.

Explanation: The number of students in a class N < 30 The number of students in the first group N1 = 15 The number of students in the second group N2 N = N1 + N2 Assume temporarily that the number of student in the second group has 15 or more students N2 ≥ 15 N1 + N2 ≥ 15 + 15 30 ≥ 30 So, the assumption that N2 ≥ 15 is false.

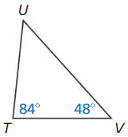
Explanation: ∠R = 180 – (65 + 56) = 180 – 121 = 59, which indicates that ∆RST i isosceles. By the trinagle longer side theorem, ST is 7

Question 32. PROOF Write an indirect proof of the statement “In ∆QRS, if m∠Q + m∠R = 90°, then m∠S = 90°.” Answer:

Question 34. CRITICAL THINKING Is it possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem (Theorem 6. 11)? Explain your reasoning. Answer: Given, Is it possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem? Yes, it is possible to decide if three side lengths form a triangle without checking all three inequalities shown in the Triangle Inequality Theorem. If the sum of the lengths of the two shortest sides is greater than the length of the longest side. then the other two inequalities will also be true.

b. How is your answer to part (a) affected if you know that m∠2 < m∠1 and m∠2 < m∠3? Answer: ∠WXY is smaller than ∠YXZ, ∠YXZ is smaller than ∠WYX, ∠WYX is smaller than ∠XZY and ∠XZY is smaller than ∠XYZ.

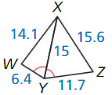
Question 38. MATHEMATICAL CONNECTIONS In ∆DEF, m∠D = (x + 25)°. m∠E = (2x – 4)°, and in m∠F = 63°. List the side lengths and angle measures of the triangle in order from least to greatest.

Answer: sum of angles is 180 degrees x + 25 + 2x – 4 + 63 = 180 3x + 84 = 180 3x = 96 x = 32 m∠D = 32 + 25 = 57 m∠E = 2(32) – 4 = 60 m∠F = 63 The angles from least to greatest are m∠D, m∠E, m∠F and the side lengths are EF, DF, DE.

Question 39. ANALYZING RELATIONSHIPS Another triangle inequality relationship is given by the Exterior Angle Inequality Theorem. It states:

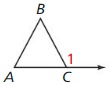
The measures of an exterior angle of a triangle is greater than the measure of either of the nonadjacent interior angles.

MATHEMATICAL CONNECTIONS In Exercises 40 and 41, describe the possible values of x.

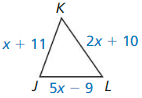
Explanation: JK + JL > KL x + 11 + 5x – 9 > 2x +10 6x + 2 > 2x + 10 4x > 8 x > 2 JK + KL > JL x + 11 + 2x + 10 > 5x – 9 3x + 21 > 5x – 9 30 > 2x 15 > x JL + KL > JK 5x – 9 + 2x + 10 > x + 11 7x + 1 > x + 11 6x > 10 x > \(\frac { 5 }{ 3 } \) The possible values of x are x > \(\frac { 5 }{ 3 } \) and x < 15

Question 44. USING STRUCTURE The length of the base of an isosceles triangle is l. Describe the possible lengths for each leg. Explain our reasoning. Answer: If other lengths are x and x Then, x + x > l 2x > l x > l/2 x + l > x The possible lengths of each leg are l are l/2.

Name the indicated angle between the pair of sides given.

Question 50. \(\overline{A E}\) and \(\overline{B E}\) Answer: The included angle is \(\overline{A E}\) and \(\overline{B E}\) is ∠AEB

Question 52. \(\overline{A D}\) and \(\overline{D C}\) Answer: The included angle is \(\overline{A D}\) and \(\overline{D C}\) is ∠ADC

6.6 Inequalities in Two Triangles

Comparing Measures in Triangles

a. Draw ∆ABC, as shown below. Answer:

b. Draw the circle with center C(3, 3) through the point A(1, 3). Answer:

d. Which two sides of ∆ABC are congruent to two sides of ∆DBC? Justify your answer. Answer:

e. Compare the lengths of \(\overline{A B}\) and \(\overline{D B}\). Then compare the measures of ∠ACB and ∠DCB. Are the results what you expected? Explain. Answer:

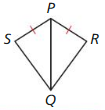
g. Look for a pattern of the measures in our table. Then write a conjecture that summarizes your observations. CONSTRUCTING VIABLE ARGUMENTS To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures. Answer:

Question 3. Explain how you can use the hinge shown at the left to model the concept described in Question 2. Answer:

Lesson 6.6 Inequalities in Two Triangles

Use the diagram

Question 1. If PR = PS and m∠QPR > m∠QPS, which is longer, \(\overline{S Q}\) or \(\overline{R Q}\)?

Answer: Given that, PR = PS and PQ ≅ PQ by the reflexive property of congruence. m∠QPR > m∠QPS. So, two sides of △PSQ are congruent to two sides of △PRQ and included angle in △PRQ is larger. By the hinge theorem RQ > SQ.

Question 2. If PR = PS and RQ < SQ, which is larger, ∠RPQ or ∠SPQ?

Answer: Given that, PR = PS, RQ < SQ PQ ≅ PQ by the reflexive property of congruence theorem. So, two sides of △PSQ are congruent to two sides of △PRQ and third side of △PSQ is longer. By the converse of the hinge theorem, ∠SPQ > ∠RPQ.

Question 3. Write a temporary assumption you can make to prove the Hinge Theorem indirectly. What two cases does that assumption lead to?

Answer: Hinge theorem states that if two sides of the triangle are congruent to two sides of another triangle and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle.

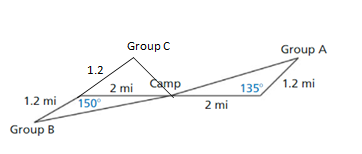
Question 4. WHAT IF? In Example 5, Group C leaves camp and travels 2 miles due north. then turns 40° towards east and travels 1.2 miles. Compare the distances from camp for all three groups.

Exercise 6.6 Inequalities in Two Triangles

Question 2. COMPLETE THE SENTENCE In ∆ABC and ∆DEF, \(\overline{A B} \cong \overline{D E}\), \(\overline{B C} \cong \overline{E F}\). and AC < DF. So m∠_______ > m ∠ _______ by the Converse of the Hinge Theorem

Answer: In ∆ABC and ∆DEF, \(\overline{A B} \cong \overline{D E}\), \(\overline{B C} \cong \overline{E F}\). and AC < DF. So m∠E > m ∠B by the Converse of the Hinge Theorem

In Exercises 3-6, copy and complete the statement with <, >, or = Explain your reasoning.

Answer: m∠1 < m∠2 by the converse of the hinge theorem.

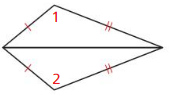
Answer: m∠1 > m∠2 by the converse of the hinge theorem.

In Exercises 7-10. copy and complete the statement with <, >, or =. Explain your reasoning.

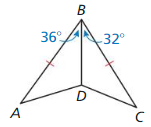
Answer: MN < KL by the converse of the hinge theorem.

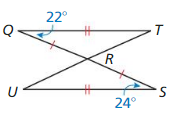
Answer: AC > Dc by the converse of the hinge theorem.

PROOF In Exercises 11 and 12, write a proof.

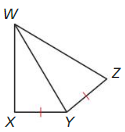
Answer: Given that, AD ≅ BC AC ≅ AC by the reflexive property of congruence theorem DC < AB is given So, m∠BCA > m∠DAC by the hinge theorem.

In Exercises 13 and 14, you and your friend leave on different flights from the same airport. Determine which flight is farther from the airport. Explain your reasoning.

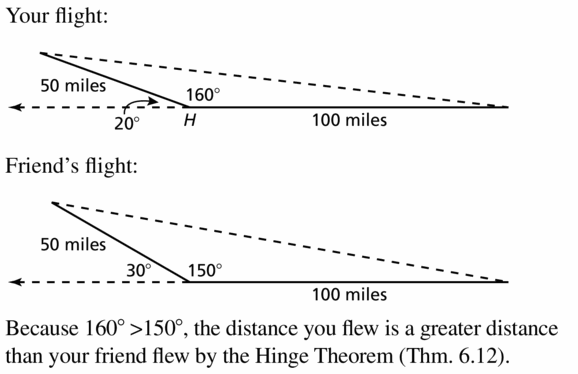
Question 14. Your flight: Flies 21omiles due south, then turns 70° toward west and flies 80 miles. Friend’s flight: Flies 80 miles due north, then turns 50° toward east and flies 210 miles.

Answer: My friend flight is farther from the airport.

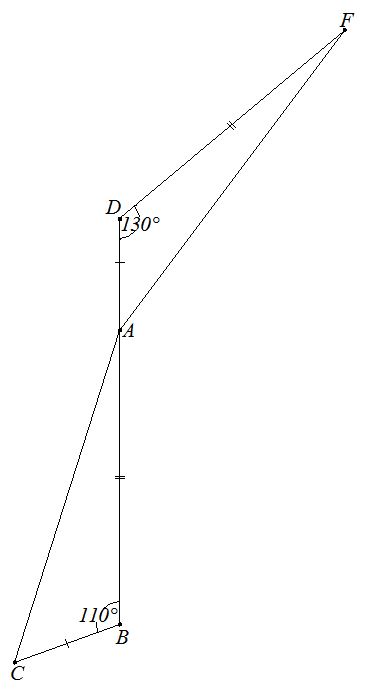
Answer: (D) 35°

Explanation: KL ≅ KJ is given KM ≅ KM by the reflexive property of congruence LM > MJ So, m∠LKM > m∠MKJ 25 > 35

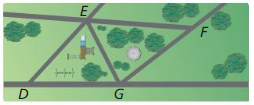
Question 18. ABSTRACT REASONING In ∆EFG, the bisector of ∠F intersects the bisector of ∠G at point H. Explain why \(\overline{F G}\) must be longer than \(\overline{F H}\) or \(\overline{H G}\).

Answer: The sum of interior angles of a triangle is 180 degrees The sum of angles F and G cannot be larger than 180 degrees ∠HFG is half of the measurement of ∠F. ∠HGF is half of the measurement of ∠G. thus, ∠HFG + ∠HGF < 90° ∠FHG = 180° – ∠HGF – ∠HFG > 90°

MATHEMATICAL CONNECTIONS In Exercises 20 and 21, write and solve an inequality for the possible values of x.

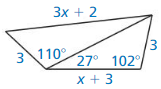
Answer: BC ≅ CD AC ≅ AC by the reflexive property of congruence theorem AB < AD So, m∠ACB < m∠ACD by the converse of the hinge theorem.

Question 24. THOUGHT PROVOKING The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, state an inequality involving the sum of the angles of a triangle. Find a formula for the area of a triangle in spherical geometry.

Maintaining Mathematical proficiency

Find the value of x.

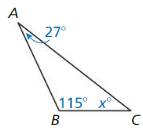
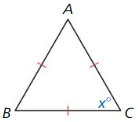
Answer: As two sides are congruent, two angles opposite to the congruent sides are also congruent by the converse of the isosceles trinagle theorem. 36 + x + x = 180 36 + 2x = 180 2x = 144 x = 72

Relationships Within Triangles Chapter Review

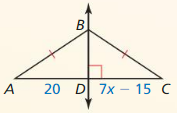
Answer: DC = 20

Explanation: AD = CD 20 = 7x – 15 7x = 35 x = 5 DC = 7(5) – 15 = 20

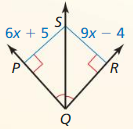
Answer: RS = 23

Explanation: PS = SR 6x + 5 = 9x – 4 9x – 6x = 9 3x = 9 x = 3 RS = 9(3) – 4 = 23

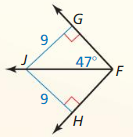
Answer: m∠JFH = 47°

Explanation: m∠JFH = m∠JFG So, m∠JFH = 47°

Question 4. T(- 6, – 5), U(0, – 1), V(0, – 5)

Answer: The circumcenter is (-3, -3)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let T(- 6, – 5), U(0, – 1), V(0, – 5) be the vertices of the given triangle and let P(x,y) be the circumcentre of this triangle. Then PT = PU = PV PT² = PU² = PV² PT² = PU² (x + 6)² + (y + 5)² = (x – 0)² + (y + 1)² x² + 12x + 36 + y² + 10y + 25 = x² + y² + 2y + 1 12x + 8y + 61 = 1 12x + 8y + 60 = 0 3x + 2y + 15 = 0 PU² = PV² (x – 0)² + (y + 1)² = (x – 0)² + (y + 5)² x² + y² + 2y + 1 = x² + y² + 10y + 25 8y + 24 = 0 8y = -24 y = -3 Substitute y = -3 in 3x + 2y + 15 = 0 3x + 2(-3) + 15 = 0 3x – 6 + 15 = 0 3x = -9 x = -3 The circumcenter is (-3, -3)

Question 5. X(- 2, 1), Y(2, – 3), Z(6, – 3)

Answer: The circumcenter is (4, 3)

Explanation: Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let X(- 2, 1), Y(2, – 3), Z(6, – 3) be the vertices of the given triangle and let P(x, y) be the circumcentre of this triangle. Then PX = PY = PZ PX² = PY² = PZ² PX² = PY² (x + 2)² + (y – 1)² = (x – 2)² + (y + 3)² x² + 4x + 4 + y² – 2y + 1 = x² – 4x + 4 + y² + 6y + 9 8x – 8y + 5 = 13 8x – 8y – 8 = 0 x – y = 1 PY² = PZ² (x – 2)² + (y + 3)² = (x – 6)² + (y + 3)² x² – 4x + 4 + y² + 6y + 9 = x² – 12x + 36 + y² + 6y + 9 8x = 32 x = 4 Substitue x = 4 in x – y = 1 4 – y = 1 -y = -3 y = 3 The circumcenter is (4, 3)

Question 6. Point D is the incenter of ∆LMN. Find the value of x.

Answer: x = 13

Question 7. A(- 10, 3), B(- 4, 5), C(- 4, 1)

Answer: The centroid is (-6, 3)

Explanation: The centroid = (\(\frac { -10 – 4 – 4 }{ 3 } \), \(\frac { 3 + 5 + 1 }{ 3 } \)) = (-6, 3)

Question 8. D(2, – 8), E(2, – 2), F(8, – 2)

Answer: The centroid is (4, -4)

Explanation: The centroid = (\(\frac { 2 + 2 + 8 }{ 3 } \), \(\frac { -8 – 2 – 2 }{ 3 } \)) = (4, -4)

Question 9. G(1, 6), H(5, 6), J(3, 1)

Answer: The orthocenter is (3, 5.2) The orthocenter lies inside the triangle.

Explanation: The slope of the line HJ = \(\frac { 1 – 6 }{ 3 – 5} \) = \(\frac { 5 }{ 2 } \) The slope of the perpendicular line = \(\frac { -2 }{ 5 } \) The perpendicular line is (y – 6) = \(\frac { -2 }{ 5 } \)(x – 1) 5(y – 6) = -2(x – 1) 5y – 30 = -2x + 2 2x + 5y – 32 = 0 — (i) The slope of GJ = \(\frac { 1 – 6 }{ 3 – 1 } \) = \(\frac { -5 }{ 2 } \) The slope of the perpendicular line = \(\frac { 2 }{ 5 } \) The equation of perpendicular line (y – 6) = \(\frac { 2 }{ 5 } \)(x – 5) 5(y – 6) = 2(x – 5) 5y – 30 = 2x – 10 2x – 5y + 20 = 0 — (ii) Equate both equations 2x + 5y – 32 = 2x – 5y + 20 10y = 52 y = 5.2 Substitute y = 5.2 in (i) 2x + 5(5.2) – 32 = 0 2x + 26 – 32 = 0 2x = 6 x = 3 The orthocenter is (3, 5.2) The orthocenter lies inside the triangle.

Question 10. K(-8, 5), L(- 6, 3), M(0, 5)

Answer: The othrocenter is (-6, -1) The orthocenter lies outside of the triangle

Explanation: The slope of LM = \(\frac { 5 – 3}{ 0 + 6} \) = \(\frac { 1 }{ 3 } \) The slope of the perpendicular line = -3 The perpendicular line is (y – 5) = -3(x + 8) y – 5 = -3x – 24 3x + y + 19 = 0 —- (ii) The slope of KL = \(\frac { 3 – 5 }{ -6 + 8 } \) = -1 The slope of the perpendicular line = \(\frac { 1 }{ 2 } \) The equation of perpendicular line (y – 5) = \(\frac { 1 }{ 2 } \)(x – 0) 2y – 10 = x —- (ii) Substitute (ii) in (i) 3(2y – 10) + y + 19 = 0 6y – 30 + y + 19 = 0 7y – 11 = 0 y = \(\frac { 11 }{ 7 } \) x = -6 The othrocenter is (-6, -1) The orthocenter lies outside of the triangle

Find the coordinates of the vertices of the midsegment triangle for the triangle with the given vertices.

Question 11. A(- 6, 8), B(- 6, 4), C(0, 4)

Answer: The midsegment of AB = (-6, 6) The midsegment of BC = (-3, 4) The midsegment of AC = (-3, 6)

Explanation: The midsegment of AB = (\(\frac { -6 – 6 }{ 2 } \), \(\frac { 8 + 4 }{ 2 } \)) = (-6, 6) The midsegment of BC = (\(\frac { -6 + 0 }{ 2 } \), \(\frac { 4 + 4 }{ 2 } \)) = (-3, 4) The midsegment of AC = (\(\frac { -6 + 0 }{ 2 } \), \(\frac { 8 + 4 }{ 2 } \)) = (-3, 6)

Question 12. D(- 3, 1), E(3, 5), F(1, – 5)

Answer: The midsegment of DE = (0, 3) The midsegment of EF = (2, 0) The midsegment of DF = (-1, -2)

Explanation: The midsegment of DE = (\(\frac { -3 + 3 }{ 2 } \), \(\frac { 1 + 5 }{ 2 } \)) = (0, 3) The midsegment of EF = (\(\frac { 3 + 1 }{ 2 } \), \(\frac { 5 – 5 }{ 2 } \)) = (2, 0) The midsegment of DF = (\(\frac { -3 + 1 }{ 2 } \), \(\frac { 1 – 5 }{ 2 } \)) = (-1, -2)

Describe the possible lengths of the third side of the triangle given the lengths of the other two sides.

Question 13. 4 inches, 8 inches

Answer: 4 < x < 12

Explanation: 4 + 8 > x 12 > x 4 + x > 8 x > 4 8 + x > 4 x > -4 4 < x < 12

Question 14. 6 meters, 9 meters

Answer: 3 < x < 15

Explanation: 6 + 9 > x 15 > x 6 + x > 9 x > 3 9 + x > 6 x > -3 3 < x < 15

Question 15. 11 feet, 18 feet

Answer: 7 < x < 29

Explanation: 11 + 18 > x 29 > x 11 + x > 18 x > 7 18 + x > 11 x > -7 7 < x < 29

Question 16. Write an indirect proof 0f the statement “In ∆XYZ, if XY = 4 and XZ = 8. then YZ > 4.”

Answer: 4 + 8 > x 12 > x 4 + x > 8 x > 4 8 + x > 4 x > -4 So, 12 > x > 4 Therefore, YZ > 4

Use the diagram.

Question 17. If RQ = RS and m∠QRT > m∠SRT, then how does \(\overline{Q T}\) Compare to \(\overline{S T}\)?

Answer: TQ > ST

Explanation: Given that, RQ = RS and m∠QRT > m∠SRT RT = RT by the reflexive property of congruence theorem TQ > ST by the converse of the hinge theorem.

Question 18. If RQ = RS and QT > ST, then how does ∠QRT compare to ∠SRT?

Answer: Given that, RQ = RS and QT > ST RT = RT by the reflexive property of congruence theorem So, m∠QRT > m∠SRT by the converse of the hinge theorem.

Relationships Within Triangles Chapter Test

In Exercise 1 and 2, \(\overline{M N}\) is a midsegment of ∆JKL. Find the value of x.

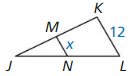
Answer: x = 6

Explanation: KL = 0.5(MN) 12 = 0.5x x = 6

Explanation: JM = ML x = 9

Find the indicated measure. Identify the theorem you use.

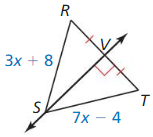
Answer: ST = 17

Explanation: RS = ST by the perpendicular bisector theorem 3x + 8 = 7x – 4 7x – 3x = 12 4x = 12 x = 3 ST = 7(3) – 4 = 21 – 4 = 17

Answer: WY = 32

Explanation: 6x + 2 = 9x – 13 by the angle bisector theorem 3x = 15 x = 5 WY = 6(5) + 2 = 32

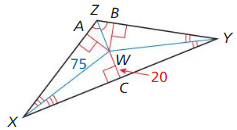
Answer: BW = 20

Explanation: WC = BW = AW by the incenter theorem BW = 20

Copy and complete the statement with <, >, or =.

Question 6. AB _____ CB

Answer: AB > CB

Question 7. m∠1 _____ m∠2

Answer: m∠1 < m∠2 by the converse of the hinge theorem

Question 8. m∠MNP ________ m∠NPM

Answer: m∠MNP < m∠NPM

Question 9. Find the coordinates of the circumcenter, orthocenter, and centroid of the triangle with vertices A(0, – 2), B(4, – 2), and C(0, 6).

Answer: Circumcenter is (1.5, -0.5) orthoceter is (0, -2) centroid is (1.3, 0.7)

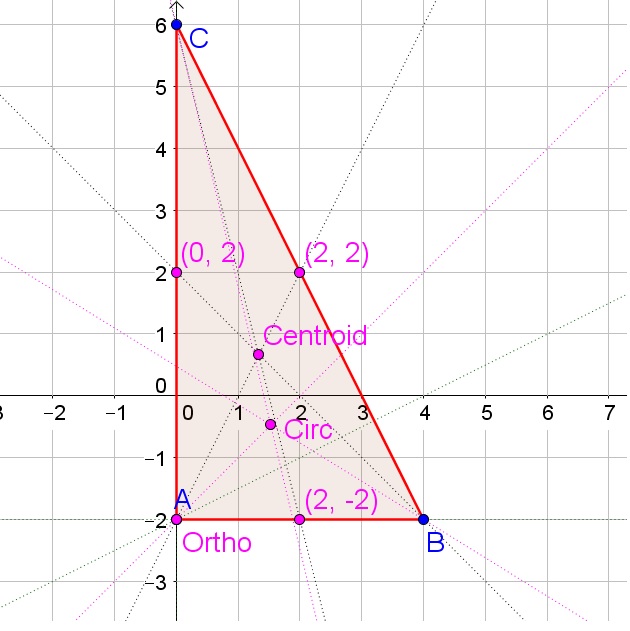
Question 10. Write an indirect proof of the Corollary to the Base Angles Theorem (Corollary 5.2): If ∆PQR is equilateral, then it is equiangular.

Answer: Assume for contradiction that there is an equilateral triangle namely △ABC. So, AB = BC = AC. According to the base angles theorem, if two sides of a triangle are congruent, then the angles opposite them are congruent. Since AB = AC, the base angle theorem tells that m∠B = m∠C Since AB = BC, the base angle theorem tells that m∠A = m∠C By the transitive property of equality m∠A = m∠B = m∠C, which contradicts the assumption that triangle ABC is equiangular. Thus, the corollary is true.

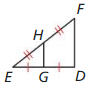
Answer: The area of ∆DEF = A As HG is the midsegment of ∆DEF. Area of ∆GEH = A/2

Question 12. Two hikers start at a visitor center. The first hikes 4 miles hikes due west, then turns 40° toward south and hikes 1.8 miles. The second hikes 4 miles due east, then turns 52° toward north and hikes 1 .8 miles. Which hiker is farther from the visitor center? Explain how you know.

Answer: The second hiker is farther away from the visitor center as all things being equal cos 128 < cos 140 from distance² = 4² + 1.8² — 2 x 4 x 1.8 cos (angle turned)

In Exercises 13-15, use the map.

Question 13. Describe the possible lengths of Pine Avenue.

Answer: The possible lengths of pine avenue are between 2 and 16.

Explanation: 7 + 9 > x 16 > x 7 + x > 9 x > 2 9 + x > 7 x > -2 2 < x < 16 The possible lengths of pine avenue are between 2 and 16.

Question 14. You ride your bike along a trail that represents the shortest distance from the beach to Main Street. You end up exactly halfway between your house and the movie theatre. How long is Pine Avenue? Explain.

Answer: halfway between your house and the movie theatre = 7/2 = 3.5 Pine Avenue is 3.5 mi

Question 15. A market is the same distance from your house, the movie theater, and the beach. Copy the map and locate the market.

Answer: Centroid is the market.

Relationships Within Triangles Cumulative Assessment

Answer: Definition of perpendicular bisector is used to prove the Converse of the Perpendicular Bisector Theorem.

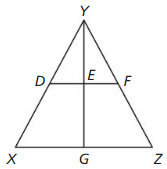
Answer: (B) (3, 5)

Explanation: The coordinates of L(3, 8), M (1, 5), N(5, 2) Centroid = (\(\frac { 3 + 1 + 5 }{ 3 } \), \(\frac { 8 + 5 + 2 }{ 3 } \)) = (3, 5)

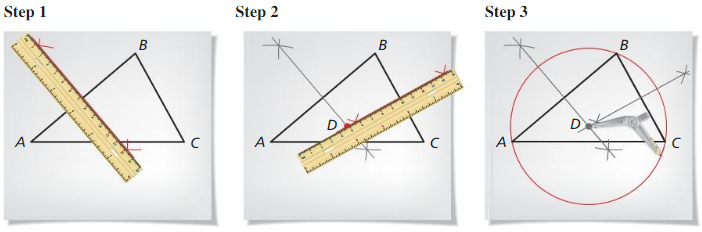
Answer: Draw a perpendicular bisector for AB Draw a perpendicular bisector for BC Extend those bisectors to meet at one point. By taking the point of intersection of perpendicular bisectors as radius, draw a circle that connects three vertices of the triangle.

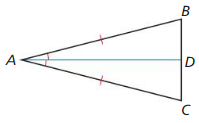
Answer: T(0, 7), U(2, 4), V(-1, 5)

Explanation: The coordinates of Q(-3, 8), R(3, 6), S(1, 2) The midpoint of QR = T = (\(\frac { -3 +3 }{ 2 } \), \(\frac { 8 + 6 }{ 2 } \)) = (0, 7) Midpoint of RS = U = (\(\frac { 3 + 1 }{ 2 } \), \(\frac { 6 + 2 }{ 2 } \)) = (2, 4) Midpoint of SR = V = (\(\frac { 1 – 3 }{ 2 } \), \(\frac { 2 + 8 }{ 2 } \)) = (-1, 5)

b. Show that each midsegment joining the midpoints of two sides is parallel to the third side and is equal to half the length of the third side. Answer: The slope of RS = \(\frac { 2 – 6 }{ 1 – 3 } \) = 2 The slope of TV = \(\frac { 5 – 7 }{ -1 – 0 } \) = 2 As the slopes are same. The lines are parallel. TV = √(-1 – 0)² + (5 – 7)² = √1 + 4 = √5 RS = √(1 – 3)² + (2 – 6)² = √4 + 16 = √20 TV = 0.5(RS)

Question 7. A triangle has vertices X(- 2, 2), Y(1, 4), and Z(2, – 2). Your friend claims that a translation of (x, y) → (x + 2, y – 3) and a translation by a scale factor of 3 will produce a similarity transformation. Do you support our friend’s claim? Explain our reasoning.

Answer: A triangle has vertices X(- 2, 2), Y(1, 4), and Z(2, – 2). The slope of XY m1 = 1-(-2)/4-2 = 3/2 The slope of the side AB, m2 = 3-0/(1-(-1) m2 = 3/2 = 3/2 The slope of the side YZ, m3 = 2-1/(-2-4) = -1/6 The slope of the side BC m4 = 4-3/-5-1 = -1/6 The slope of the side XZ m5 = 4-(-2)/(-2-2) = 4/-4 = -1 The slope of the side AC m6 = 4-0/-5-(-1) = 4/-4 = -1 m1 = m2 m3 = m4 m5 = m6 XY || AB, YZ || BC and XZ || AC Hence ΔABC is a similar transformation of the triangle ΔXYZ.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Homework

• Last updated
• Save as PDF
• Page ID 83000

• Julie Harland
• MiraCosta College

Use the set theory definition of addition or subtraction to add or subtract each of the following. Define appropriate sets and show work. Refer back to pages 2 and 3 for addition and pages 41 and 42 for subtraction if you need help getting started.

Verify each of the following:

State whether each set is closed under addition and/or subtraction of whole numbers. Provide an example if it is closed, or provide a counterexample if it is not closed.

Add the following in the system in which the numbers are given. Show work.

Subtract the following in the system in which the numbers are given. Show work.

For each pair of numbers, add them together. Then subtract the smaller number from the larger number. Show work and check your answer.

\(5432_{\text{six}}\) and \(2453_{\text{six}}\)

\(5T4_{\text{twelve}}\) and \(387_{\text{twelve}}\)

Add 5643 + 7885 using each algorithm from this module. State the method for each.

Subtract 3586 from 8204 each algorithm from this module. State the method for each.

Write the addition table for Base Four.

Someone does the following computation in a certain base, but is making a mistake. What base were they working in and what is the mistake? 132 + 243 = 320. What is the correct answer? Be sure to show work.

Someone used the directed vector to do a subtraction problem. What was the subtraction problem used?

Find the answer to the following subtraction problems by using directed vectors on the number line in conjunction with the missing addend approach. Draw the vectors.

In what number base or bases between 2 and 13 are each of the following calculations valid?