examples of mathematical problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills.  students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• Prodigy Math
• Prodigy English
• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

120 Math Word Problems To Challenge Students Grades 1 to 8

Written by Marcus Guido

Hey teachers! 👋

Use Prodigy to spark a love for math in your students – including when solving word problems!

• Teaching Tools
• Subtraction
• Multiplication
• Mixed operations
• Ordering and number sense
• Comparing and sequencing
• Physical measurement
• Ratios and percentages
• Probability and data relationships

You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.

A jolt of creativity would help. But it doesn’t come.

Whether you’re a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.

This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes.

There are 120 examples in total.

The list of examples is supplemented by tips to create engaging and challenging math word problems.

120 Math word problems, categorized by skill

Addition word problems.

Best for: 1st grade, 2nd grade

1. Adding to 10: Ariel was playing basketball. 1 of her shots went in the hoop. 2 of her shots did not go in the hoop. How many shots were there in total?

2. Adding to 20: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store to get 3 more pieces of gum. How many pieces of gum does Adrianna have now?

3. Adding to 100: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store and got 70 pieces of strawberry gum and 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

4. Adding Slightly over 100: The restaurant has 175 normal chairs and 20 chairs for babies. How many chairs does the restaurant have in total?

5. Adding to 1,000: How many cookies did you sell if you sold 320 chocolate cookies and 270 vanilla cookies?

6. Adding to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In June, the hobby store sold 15,498 more trading cards than normal. In total, how many trading cards did the hobby store sell in June?

7. Adding 3 Numbers: Billy had 2 books at home. He went to the library to take out 2 more books. He then bought 1 book. How many books does Billy have now?

8. Adding 3 Numbers to and over 100: Ashley bought a big bag of candy. The bag had 102 blue candies, 100 red candies and 94 green candies. How many candies were there in total?

Subtraction word problems

Best for: 1st grade, second grade

9. Subtracting to 10: There were 3 pizzas in total at the pizza shop. A customer bought 1 pizza. How many pizzas are left?

10. Subtracting to 20: Your friend said she had 11 stickers. When you helped her clean her desk, she only had a total of 10 stickers. How many stickers are missing?

11. Subtracting to 100: Adrianna has 100 pieces of gum to share with her friends. When she went to the park, she shared 10 pieces of strawberry gum. When she left the park, Adrianna shared another 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

Practice math word problems with Prodigy Math

Join millions of teachers using Prodigy to make learning fun and differentiate instruction as they answer in-game questions, including math word problems from 1st to 8th grade!

12. Subtracting Slightly over 100: Your team scored a total of 123 points. 67 points were scored in the first half. How many were scored in the second half?

13. Subtracting to 1,000: Nathan has a big ant farm. He decided to sell some of his ants. He started with 965 ants. He sold 213. How many ants does he have now?

14. Subtracting to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In July, the hobby store sold a total of 20,777 trading cards. How many more trading cards did the hobby store sell in July compared with a normal month?

15. Subtracting 3 Numbers: Charlene had a pack of 35 pencil crayons. She gave 6 to her friend Theresa. She gave 3 to her friend Mandy. How many pencil crayons does Charlene have left?

16. Subtracting 3 Numbers to and over 100: Ashley bought a big bag of candy to share with her friends. In total, there were 296 candies. She gave 105 candies to Marissa. She also gave 86 candies to Kayla. How many candies were left?

Multiplication word problems

Best for: 2nd grade, 3rd grade

17. Multiplying 1-Digit Integers: Adrianna needs to cut a pan of brownies into pieces. She cuts 6 even columns and 3 even rows into the pan. How many brownies does she have?

18. Multiplying 2-Digit Integers: A movie theatre has 25 rows of seats with 20 seats in each row. How many seats are there in total?

19. Multiplying Integers Ending with 0: A clothing company has 4 different kinds of sweatshirts. Each year, the company makes 60,000 of each kind of sweatshirt. How many sweatshirts does the company make each year?

20. Multiplying 3 Integers: A bricklayer stacks bricks in 2 rows, with 10 bricks in each row. On top of each row, there is a stack of 6 bricks. How many bricks are there in total?

21. Multiplying 4 Integers: Cayley earns $5 an hour by delivering newspapers. She delivers newspapers 3 days each week, for 4 hours at a time. After delivering newspapers for 8 weeks, how much money will Cayley earn?

Division word problems

Best for: 3rd grade, 4th grade, 5th grade

22. Dividing 1-Digit Integers: If you have 4 pieces of candy split evenly into 2 bags, how many pieces of candy are in each bag?

23. Dividing 2-Digit Integers: If you have 80 tickets for the fair and each ride costs 5 tickets, how many rides can you go on?

24. Dividing Numbers Ending with 0: The school has $20,000 to buy new computer equipment. If each piece of equipment costs $50, how many pieces can the school buy in total?

25. Dividing 3 Integers: Melissa buys 2 packs of tennis balls for $12 in total. All together, there are 6 tennis balls. How much does 1 pack of tennis balls cost? How much does 1 tennis ball cost?

26. Interpreting Remainders: An Italian restaurant receives a shipment of 86 veal cutlets. If it takes 3 cutlets to make a dish, how many cutlets will the restaurant have left over after making as many dishes as possible?

Mixed operations word problems

27. Mixing Addition and Subtraction: There are 235 books in a library. On Monday, 123 books are taken out. On Tuesday, 56 books are brought back. How many books are there now?

28. Mixing Multiplication and Division: There is a group of 10 people who are ordering pizza. If each person gets 2 slices and each pizza has 4 slices, how many pizzas should they order?

29. Mixing Multiplication, Addition and Subtraction: Lana has 2 bags with 2 marbles in each bag. Markus has 2 bags with 3 marbles in each bag. How many more marbles does Markus have?

30. Mixing Division, Addition and Subtraction: Lana has 3 bags with the same amount of marbles in them, totaling 12 marbles. Markus has 3 bags with the same amount of marbles in them, totaling 18 marbles. How many more marbles does Markus have in each bag?

Ordering and number sense word problems

31. Counting to Preview Multiplication: There are 2 chalkboards in your classroom. If each chalkboard needs 2 pieces of chalk, how many pieces do you need in total?

32. Counting to Preview Division: There are 3 chalkboards in your classroom. Each chalkboard has 2 pieces of chalk. This means there are 6 pieces of chalk in total. If you take 1 piece of chalk away from each chalkboard, how many will there be in total?

33. Composing Numbers: What number is 6 tens and 10 ones?

34. Guessing Numbers: I have a 7 in the tens place. I have an even number in the ones place. I am lower than 74. What number am I?

35. Finding the Order: In the hockey game, Mitchell scored more points than William but fewer points than Auston. Who scored the most points? Who scored the fewest points?

Fractions word problems

Best for: 3rd grade, 4th grade, 5th grade, 6th grade

36. Finding Fractions of a Group: Julia went to 10 houses on her street for Halloween. 5 of the houses gave her a chocolate bar. What fraction of houses on Julia’s street gave her a chocolate bar?

37. Finding Unit Fractions: Heather is painting a portrait of her best friend, Lisa. To make it easier, she divides the portrait into 6 equal parts. What fraction represents each part of the portrait?

38. Adding Fractions with Like Denominators: Noah walks ⅓ of a kilometre to school each day. He also walks ⅓ of a kilometre to get home after school. How many kilometres does he walk in total?

39. Subtracting Fractions with Like Denominators: Last week, Whitney counted the number of juice boxes she had for school lunches. She had ⅗ of a case. This week, it’s down to ⅕ of a case. How much of the case did Whitney drink?

40. Adding Whole Numbers and Fractions with Like Denominators: At lunchtime, an ice cream parlor served 6 ¼ scoops of chocolate ice cream, 5 ¾ scoops of vanilla and 2 ¾ scoops of strawberry. How many scoops of ice cream did the parlor serve in total?

41. Subtracting Whole Numbers and Fractions with Like Denominators: For a party, Jaime had 5 ⅓ bottles of cola for her friends to drink. She drank ⅓ of a bottle herself. Her friends drank 3 ⅓. How many bottles of cola does Jaime have left?

42. Adding Fractions with Unlike Denominators: Kevin completed ½ of an assignment at school. When he was home that evening, he completed ⅚ of another assignment. How many assignments did Kevin complete?

43. Subtracting Fractions with Unlike Denominators: Packing school lunches for her kids, Patty used ⅞ of a package of ham. She also used ½ of a package of turkey. How much more ham than turkey did Patty use?

44. Multiplying Fractions: During gym class on Wednesday, the students ran for ¼ of a kilometre. On Thursday, they ran ½ as many kilometres as on Wednesday. How many kilometres did the students run on Thursday? Write your answer as a fraction.

45. Dividing Fractions: A clothing manufacturer uses ⅕ of a bottle of colour dye to make one pair of pants. The manufacturer used ⅘ of a bottle yesterday. How many pairs of pants did the manufacturer make?

46. Multiplying Fractions with Whole Numbers: Mark drank ⅚ of a carton of milk this week. Frank drank 7 times more milk than Mark. How many cartons of milk did Frank drink? Write your answer as a fraction, or as a whole or mixed number.

Decimals word problems

Best for: 4th grade, 5th grade

47. Adding Decimals: You have 2.6 grams of yogurt in your bowl and you add another spoonful of 1.3 grams. How much yogurt do you have in total?

48. Subtracting Decimals: Gemma had 25.75 grams of frosting to make a cake. She decided to use only 15.5 grams of the frosting. How much frosting does Gemma have left?

49. Multiplying Decimals with Whole Numbers: Marshall walks a total of 0.9 kilometres to and from school each day. After 4 days, how many kilometres will he have walked?

50. Dividing Decimals by Whole Numbers: To make the Leaning Tower of Pisa from spaghetti, Mrs. Robinson bought 2.5 kilograms of spaghetti. Her students were able to make 10 leaning towers in total. How many kilograms of spaghetti does it take to make 1 leaning tower?

51. Mixing Addition and Subtraction of Decimals: Rocco has 1.5 litres of orange soda and 2.25 litres of grape soda in his fridge. Antonio has 1.15 litres of orange soda and 0.62 litres of grape soda. How much more soda does Rocco have than Angelo?

52. Mixing Multiplication and Division of Decimals: 4 days a week, Laura practices martial arts for 1.5 hours. Considering a week is 7 days, what is her average practice time per day each week?

Comparing and sequencing word problems

Best for: Kindergarten, 1st grade, 2nd grade

53. Comparing 1-Digit Integers: You have 3 apples and your friend has 5 apples. Who has more?

54. Comparing 2-Digit Integers: You have 50 candies and your friend has 75 candies. Who has more?

55. Comparing Different Variables: There are 5 basketballs on the playground. There are 7 footballs on the playground. Are there more basketballs or footballs?

56. Sequencing 1-Digit Integers: Erik has 0 stickers. Every day he gets 1 more sticker. How many days until he gets 3 stickers?

57. Skip-Counting by Odd Numbers: Natalie began at 5. She skip-counted by fives. Could she have said the number 20?

58. Skip-Counting by Even Numbers: Natasha began at 0. She skip-counted by eights. Could she have said the number 36?

59. Sequencing 2-Digit Numbers: Each month, Jeremy adds the same number of cards to his baseball card collection. In January, he had 36. 48 in February. 60 in March. How many baseball cards will Jeremy have in April?

Time word problems

66. Converting Hours into Minutes: Jeremy helped his mom for 1 hour. For how many minutes was he helping her?

69. Adding Time: If you wake up at 7:00 a.m. and it takes you 1 hour and 30 minutes to get ready and walk to school, at what time will you get to school?

70. Subtracting Time: If a train departs at 2:00 p.m. and arrives at 4:00 p.m., how long were passengers on the train for?

71. Finding Start and End Times: Rebecca left her dad’s store to go home at twenty to seven in the evening. Forty minutes later, she was home. What time was it when she arrived home?

Money word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade, 5th grade

60. Adding Money: Thomas and Matthew are saving up money to buy a video game together. Thomas has saved $30. Matthew has saved $35. How much money have they saved up together in total?

61. Subtracting Money: Thomas has $80 saved up. He uses his money to buy a video game. The video game costs $67. How much money does he have left?

62. Multiplying Money: Tim gets $5 for delivering the paper. How much money will he have after delivering the paper 3 times?

63. Dividing Money: Robert spent $184.59 to buy 3 hockey sticks. If each hockey stick was the same price, how much did 1 cost?

64. Adding Money with Decimals: You went to the store and bought gum for $1.25 and a sucker for $0.50. How much was your total?

65. Subtracting Money with Decimals: You went to the store with $5.50. You bought gum for $1.25, a chocolate bar for $1.15 and a sucker for $0.50. How much money do you have left?

67. Applying Proportional Relationships to Money: Jakob wants to invite 20 friends to his birthday, which will cost his parents $250. If he decides to invite 15 friends instead, how much money will it cost his parents? Assume the relationship is directly proportional.

68. Applying Percentages to Money: Retta put $100.00 in a bank account that gains 20% interest annually. How much interest will be accumulated in 1 year? And if she makes no withdrawals, how much money will be in the account after 1 year?

Physical measurement word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade

72. Comparing Measurements: Cassandra’s ruler is 22 centimetres long. April’s ruler is 30 centimetres long. How many centimetres longer is April’s ruler?

73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?

74. Adding Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Micha’s dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?

75. Subtracting Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Micha’s dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?

76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?

77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?

78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?

79. Converting Volume: Shad has a lemonade stand and sold 20 cups of lemonade. Each cup was 500 millilitres. How many litres did Shad sell in total?

80. Converting Length: Stacy and Milda are comparing their heights. Stacy is 1.5 meters tall. Milda is 10 centimetres taller than Stacy. What is Milda’s height in centimetres?

81. Understanding Distance and Direction: A bus leaves the school to take students on a field trip. The bus travels 10 kilometres south, 10 kilometres west, another 5 kilometres south and 15 kilometres north. To return to the school, in which direction does the bus have to travel? How many kilometres must it travel in that direction?

Ratios and percentages word problems

Best for: 4th grade, 5th grade, 6th grade

82. Finding a Missing Number: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?

83. Finding Missing Numbers: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. The difference between the numbers is 12. What are the numbers?

84. Comparing Ratios: The school’s junior band has 10 saxophone players and 20 trumpet players. The school’s senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?

85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?

86. Determining Percent of Change: A decade ago, Oakville’s population was 67,624 people. Now, it is 190% larger. What is Oakville’s current population?

87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?

88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?

Probability and data relationships word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade

89. Understanding the Premise of Probability: John wants to know his class’s favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?

90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?

91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.

92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?

93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Maurita’s 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felice’s 4 tests: 3, 3, 3. If Maurita’s mean for the 4 tests is 1 point higher than Felice’s, what’s the score of Felice’s 4th test?

94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?

95. Writing Equations for Proportional Relationships: Lionel loves soccer, but has trouble motivating himself to practice. So, he incentivizes himself through video games. There is a proportional relationship between the amount of drills Lionel completes, in x , and for how many hours he plays video games, in y . When Lionel completes 10 drills, he plays video games for 30 minutes. Write the equation for the relationship between x and y .

Geometry word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade, 8th grade

96. Introducing Perimeter:  The theatre has 4 chairs in a row. There are 5 rows. Using rows as your unit of measurement, what is the perimeter?

97. Introducing Area: The theatre has 4 chairs in a row. There are 5 rows. How many chairs are there in total?

98. Introducing Volume: Aaron wants to know how much candy his container can hold. The container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. What is the container’s volume?

99. Understanding 2D Shapes: Kevin draws a shape with 4 equal sides. What shape did he draw?

100. Finding the Perimeter of 2D Shapes: Mitchell wrote his homework questions on a piece of square paper. Each side of the paper is 8 centimetres. What is the perimeter?

101. Determining the Area of 2D Shapes: A single trading card is 9 centimetres long by 6 centimetres wide. What is its area?

102. Understanding 3D Shapes: Martha draws a shape that has 6 square faces. What shape did she draw?

103. Determining the Surface Area of 3D Shapes: What is the surface area of a cube that has a width of 2cm, height of 2 cm and length of 2 cm?

104. Determining the Volume of 3D Shapes: Aaron’s candy container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. Bruce’s container is 25 centimetres tall, 9 centimetres long and 9 centimetres wide. Find the volume of each container. Based on volume, whose container can hold more candy?

105. Identifying Right-Angled Triangles: A triangle has the following side lengths: 3 cm, 4 cm and 5 cm. Is this triangle a right-angled triangle?

106. Identifying Equilateral Triangles: A triangle has the following side lengths: 4 cm, 4 cm and 4 cm. What kind of triangle is it?

107. Identifying Isosceles Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 5 cm. What kind of triangle is it?

108. Identifying Scalene Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 6 cm. What kind of triangle is it?

109. Finding the Perimeter of Triangles: Luigi built a tent in the shape of an equilateral triangle. The perimeter is 21 metres. What is the length of each of the tent’s sides?

110. Determining the Area of Triangles: What is the area of a triangle with a base of 2 units and a height of 3 units?

111. Applying Pythagorean Theorem: A right triangle has one non-hypotenuse side length of 3 inches and the hypotenuse measures 5 inches. What is the length of the other non-hypotenuse side?

112. Finding a Circle’s Diameter: Jasmin bought a new round backpack. Its area is 370 square centimetres. What is the round backpack’s diameter?

113. Finding a Circle's Area: Captain America’s circular shield has a diameter of 76.2 centimetres. What is the area of his shield?

114. Finding a Circle’s Radius: Skylar lives on a farm, where his dad keeps a circular corn maze. The corn maze has a diameter of 2 kilometres. What is the maze’s radius?

Variables word problems

Best for: 6th grade, 7th grade, 8th grade

115. Identifying Independent and Dependent Variables: Victoria is baking muffins for her class. The number of muffins she makes is based on how many classmates she has. For this equation, m is the number of muffins and c is the number of classmates. Which variable is independent and which variable is dependent?

116. Writing Variable Expressions for Addition: Last soccer season, Trish scored g goals. Alexa scored 4 more goals than Trish. Write an expression that shows how many goals Alexa scored.

117. Writing Variable Expressions for Subtraction: Elizabeth eats a healthy, balanced breakfast b times a week. Madison sometimes skips breakfast. In total, Madison eats 3 fewer breakfasts a week than Elizabeth. Write an expression that shows how many times a week Madison eats breakfast.

118. Writing Variable Expressions for Multiplication: Last hockey season, Jack scored g goals. Patrik scored twice as many goals than Jack. Write an expression that shows how many goals Patrik scored.

119. Writing Variable Expressions for Division: Amanda has c chocolate bars. She wants to distribute the chocolate bars evenly among 3 friends. Write an expression that shows how many chocolate bars 1 of her friends will receive.

120. Solving Two-Variable Equations: This equation shows how the amount Lucas earns from his after-school job depends on how many hours he works: e = 12h . The variable h represents how many hours he works. The variable e represents how much money he earns. How much money will Lucas earn after working for 6 hours?

How to easily make your own math word problems & word problems worksheets

Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:

• Link to Student Interests:  By framing your word problems with student interests, you’ll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
• Make Questions Topical:  Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
• Include Student Names:  Naming a question’s characters after your students is an easy way make subject matter relatable, helping them work through the problem.
• Be Explicit:  Repeating keywords distills the question, helping students focus on the core problem.
• Test Reading Comprehension:  Flowery word choice and long sentences can hide a question’s key elements. Instead, use concise phrasing and grade-level vocabulary.
• Focus on Similar Interests:  Framing too many questions with related interests -- such as football and basketball -- can alienate or disengage some students.
• Feature Red Herrings:  Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.

A key to differentiated instruction , word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.

Final thoughts about math word problems

You’ll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, they’ll be more relevant to -- and engaging for -- your students.

Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.

The result?

A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Free Mathematics Tutorials, Problems and Worksheets

Thousands of math problems and questions with solutions and detailed explanations are included. Free math tutorials and problems to help you explore and gain deep understanding of math topics such as: Algebra and graphing   ,   Precalculus   ,   Practice tests and worksheets   ,   Calculus   ,   Linear Algebra   ,   Geometry   ,   Trigonometry   ,   Math Videos   ,   Math From Grade 4 to Grade 12   ,   Statistics and Probabilities   ,   Applied Math   ,   Engineering Mathematics   ,   More Math Resources   ,   Math Pages in Different languages and Analyzemath.com in Different Languages

ALGEBRA AND GRAPHING

• Algebra Questions and Problems
• Fractions Questions and Problems with Solutions
• Solving Equation and Inequalities
• Find Domain and Range of Functions
• Complex Numbers
• Step by Step Maths Worksheets Solvers
• Free Graph Paper
• Online Step by Step Algebra Calculators and Solvers

PRECALCULUS

• Graphs of Functions, Equations, and Algebra
• Analytical Tutorials
• Math Problems
• Online Math Calculators and Solvers
• Math Software

PRACTICE TESTS AND WORKSHEETS

• Free Practice for SAT, ACT and Compass Math tests
• Free Practice for quantitative GRE Maths Tests
• Free Math Worksheets to Download
• Differentiation and Derivatives Questions and Problems with Solutions
• Integrals Questions and Problems in Calculus
• Calculus Problem Solving and Applications
• Calculus Tutorials and Problems
• Calculus Questions With Answers
• AP Calculus Questions With Solutions
• Online Step by Step Calculus Calculators and Solvers
• Free Calculus Worksheets to Download

LINEAR ALGEBRA

• Linear Algebra - Questions with Solutions
• Geometry Tutorials and Problems
• Online Geometry Calculators and Solvers
• Online 3D Geometry Calculators and Solvers
• Free Geometry Worksheets to Download

TRIGONOMETRY

• Trigonometry Tutorials and Problems for Self Tests
• Free Trigonometry Questions with Answers
• Free Trigonometry Worksheets to Download
• Online Trigonometry Calculators and Solvers
• Vectors Calculators and Solvers

STATISTICS AND PROBABILITIES

• Elementary Statistics and Probability Tutorials and Problems
• Probabilities
• Statistics Calculators, Solvers and Graphers
• Probability Calculators
• Google Sheets in Math, Statistics and Probabilities

MATH FROM GRADE 4 TO GRADE 12

• Grade 12 Math Problems with Solutions.
• Grade 11 Math Problems with Solutions.
• Grade 10 Math Problems with Solutions.
• Grade 9 Math Problems with Solutions.
• Grade 8 Math Problems with Solutions.
• Grade 7 Math Problems with Solutions.
• Grade 6 Math Problems with Solutions.
• Grade 5 Math Problems with Solutions.
• Grade 4 Math Problems with Solutions.
• High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
• Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
• Primary Math (grades 4 and 5) - Free Questions and Problems With Answers
• Units Conversion and Calculators
• Convert Units of Measurements

APPLIED MATH

• The Applications of Mathematics in Physics and Engineering
• Linear Programming
• Mathematics for Machine Learning
• Mathematical Finance

MORE MATH RESOURCES

• Math Formulas for Mobile Devices
• Engineering Mathematics
• Understanding, Teaching and Learning Mathematics
• HTML5 Applets for iPads
• Math Videos

MATH PAGES IN DIFFERENT LANGUAGES

• Analyzemath.com in Different Languages
• Exercises de Mathematiques Utilisant les Applets
• Mathematics pages in French

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 1: Problem solving with arithmetic

Comparing with multiplication.

• Comparing with multiplication (Opens a modal)
• Comparing with multiplication and addition: giraffe (Opens a modal)
• Comparing with multiplication and addition: money (Opens a modal)
• Comparing with multiplication: magic (Opens a modal)
• Compare with multiplication Get 5 of 7 questions to level up!
• Compare with multiplication word problems Get 3 of 4 questions to level up!

Multiplication, division word problems

• Division word problem: field goals (Opens a modal)
• Multiplication word problem: pizza (Opens a modal)
• Multiplication and division word problems Get 5 of 7 questions to level up!

Multi-step word problems

• No videos or articles available in this lesson
• 2-step estimation word problems Get 3 of 4 questions to level up!
• Represent multi-step word problems using equations Get 3 of 4 questions to level up!
• Multi-step word problems with whole numbers Get 3 of 4 questions to level up!

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• Free Christmas Math Worksheets
• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• How to Use Math Journals in Class
• The Frayer Model for Math
• Algorithms in Mathematics and Beyond
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Critical Thinking Definition, Skills, and Examples
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• Graphic Organizers in Math
• Christmas Word Problem Worksheets
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created: May 19, 2022

Last updated: January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

1:1 Math Lessons

Guess and Check

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

After-School Math Program

• Boost Math Skills After School!
• Join our Math Program, Ideal for Students in Grades 1-8!

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!

Related posts

Best Math Card Games For Kids

In today’s digital age, where screens and devices dominate children’s entertainment and education, it’s essential to find ways to engage young minds in more traditional and interactive ways. Math card games are an excellent avenue to achieve this, offering a blend of entertainment and education to help children develop essential math skills while having a […]

Aug 18, 2023

Everything You Need to Know about Game Based Learning and Its Types

Most times, children do not get enough time to pay attention to teachers as the birds fly past the window. One minute, they are staring at the window. It is a miracle to get children focused on one thing for an extended time, except if it is exciting. As a teacher, you are responsible for […]

May 20, 2022

Safe Learning Environment

The learning environment of students has an immense impact on their learning ability. Whether young or old, you will be affected by how they think if these learners are not in security because psychological influence is there. The following article entails strategies on how to create a safe environment for students in the classroom. What […]

Jun 03, 2022

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Problem Solving, Using and Applying and Functional Mathematics

Problem solving.

The problem-solving process can be described as a journey from meeting a problem for the first time to finding a solution, communicating it and evaluating the route. There are many models of the problem-solving process but they all have a similar structure. One model is given below. Although implying a linear process from comprehension through to evaluation, the model is more of a flow backward and forward, revisiting and revising on the problem-solving journey.

Comprehension

Representation.

• Can they represent the situation mathematically?
• What is it that they are trying to find?
• What do they think the answer might be (conjecturing and hypothesising)?
• What might they need to find out before they can get started?

Planning, analysis and synthesis

Having understood what the problem is about and established what needs finding, this stage is about planning a pathway to the solution. It is within this process that you might encourage pupils to think about whether they have seen something similar before and what strategies they adopted then. This will help them to identify appropriate methods and tools. Particular knowledge and skills gaps that need addressing may become evident at this stage.

Execution and communication

During the execution phase, pupils might identify further related problems they wish to investigate. They will need to consider how they will keep track of what they have done and how they will communicate their findings. This will lead on to interpreting results and drawing conclusions.

Pupils can learn as much from reflecting on and evaluating what they have done as they can from the process of solving the problem itself. During this phase pupils should be expected to reflect on the effectiveness of their approach as well as other people's approaches, justify their conclusions and assess their own learning. Evaluation may also lead to thinking about other questions that could now be investigated.

Using and Applying Mathematics

Aspects of using and applying reflect skills that can be developed through problem solving. For example:

In planning and executing a problem, problem solvers may need to:

• select and use appropriate and efficient techniques and strategies to solve problems
• identify what further information may be required in order to pursue a particular line of enquiry and give reasons for following or rejecting particular approaches
• break down a complex calculation problem into simpler steps before attempting a solution and justify their choice of methods
• make mental estimates of the answers to calculations
• present answers to sensible levels of accuracy; understand how errors are compounded in certain calculations.

During problem solving, solvers need to communicate their mathematics for example by:

• discussing their work and explaining their reasoning using a range of mathematical language and notation
• using a variety of strategies and diagrams for establishing algebraic or graphical representations of a problem and its solution
• moving from one form of representation to another to get different perspectives on the problem
• presenting and interpreting solutions in the context of the original problem
• using notation and symbols correctly and consistently within a given problem
• examining critically, improve, then justifying their choice of mathematical presentation
• presenting a concise, reasoned argument.

Problem solvers need to reason mathematically including through:

• exploring, identifying, and using pattern and symmetry in algebraic contexts, investigating whether a particular case may be generalised further and understanding the importance of a counter-example; identifying exceptional cases
• understanding the difference between a practical demonstration and a proof
• showing step-by-step deduction in solving a problem; deriving proofs using short chains of deductive reasoning
• recognising the significance of stating constraints and assumptions when deducing results
• recognising the limitations of any assumptions that are made and the effect that varying the assumptions may have on the solution to a problem.

Functional Mathematics

Functional maths requires learners to be able to use mathematics in ways that make them effective and involved as citizens, able to operate confidently in life and to work in a wide range of contexts. The key processes of Functional Skills reflect closely the problem solving model but within three phases:

• Making sense of situations and representing them
• Processing and using the mathematics
• Interpreting and communicating the results of the analysis

Mathematical Reasoning & Problem Solving

In this lesson, we’ll discuss mathematical reasoning and methods of problem solving with an eye toward helping your students make the best use of their reasoning skills when it comes to tackling complex problems.

Previously Covered:

• Over the course of the previous lesson, we reviewed some basics about chance and probability, as well as some basics about sampling, surveys, etc. We also covered some ideas about data sets, how they’re represented, and how to interpret the results.

Approaches to Problem Solving

When solving a mathematical problem, it is very common for a student to feel overwhelmed by the information or lack a clear idea about how to get started.

To help the students with their problem-solving “problem,” let’s look at some examples of mathematical problems and some general methods for solving problems:

Identify the following four-digit number when presented with the following information:

• One of the four digits is a 1.
• The digit in the hundreds place is three times the digit in the thousands place.
• The digit in the ones place is four times the digit in the ten’s place.
• The sum of all four digits is 13.
• The digit 2 is in the thousands place.

Help your students identify and prioritize the information presented.

In this particular example, we want to look for concrete information. Clue #1 tells us that one digit is a 1, but we’re not sure of its location, so we see if we can find a clue with more concrete information.

We can see that clue #5 gives us that kind of information and is the only clue that does, so we start from there.

Because this clue tells us that the thousands place digit is 2, we search for clues relevant to this clue. Clue #2 tells us that the digit in the hundreds place is three times that of the thousands place digit, so it is 6.

So now we need to find the tens and ones place digits, and see that clue #3 tells us that the digit in the ones place is four times the digit in the tens place. But we remember that clue #1 tells us that there’s a one somewhere, and since one is not four times any digit, we see that the one must be in the tens place, which leads us to the conclusion that the digit in the ones place is four. So then we conclude that our number is:

If you were following closely, you would notice that clue #4 was never used. It is a nice way to check our answer, since the digits of 2614 do indeed add up to be thirteen, but we did not need this clue to solve the problem.

Recall that the clues’ relevance were identified and prioritized as follows:

• clue #3 and clue #1

By identifying and prioritizing information, we were able to make the information given in the problem seem less overwhelming. We ordered the clues by relevance, with the most relevant clue providing us with a starting point to solve the problem. This method also utilized the more general method of breaking a problem into smaller and simpler parts to make it easier to solve.

Now let’s look at another mathematical problem and another general problem-solving method to help us solve it:

Two trees with heights of 20 m and 30 m respectively have ropes running from the top of each tree to the bottom of the other tree. The trees are 40 meters apart. We’ll assume that the ropes are pulled tight enough that we can ignore any bending or drooping. How high above the ground do the ropes intersect?

Let’s solve this problem by representing it in a visual way , in this case, a diagram:

You can see that we have a much simpler problem on our hands after drawing the diagram. A, B, C, D, E, and F are vertices of the triangles in the diagram. Now also notice that:

b = the base of triangle EFA

h = the height of triangle EFA and the height above the ground at which the ropes intersect

If we had not drawn this diagram, it would have been very hard to solve this problem, since we need the triangles and their properties to solve for h. Also, this diagram allows us to see that triangle BCA is similar to triangle EFC, and triangle DCA is similar to triangle EFA. Solving for h shows that the ropes intersect twelve meters above the ground.

Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods , such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by making it more concrete and approachable.

Let’s try another one.

Given a pickle jar filled with marbles, about how many marbles does the jar contain?

Problems like this one require the student to make and use estimations . In this case, an estimation is all that is required, although, in more complex problems, estimates may help the student arrive at the final answer.

How would a student do this? A good estimation can be found by counting how many marbles are on the base of the jar and multiplying that by the number of marbles that make up the height of the marbles in the jar.

Now to make sure that we understand when and how to use these methods, let’s solve a problem on our own:

How many more faces does a cube have than a square pyramid?

Reveal Answer

The answer is B. To see how many more faces a cube has than a square pyramid, it is best to draw a diagram of a square pyramid and a cube:

From the diagrams above, we can see that the square pyramid has five faces and the cube has six. Therefore, the cube has one more face, so the answer is B.

Before we start having the same problem our model student in the beginning did—that is, being overwhelmed with too much information—let’s have a quick review of all the problem-solving methods we’ve discussed so far:

• Sort and prioritize relevant and irrelevant information.
• Represent a problem in different ways, such as words, symbols, concrete models, and diagrams.
• Generate and use estimations to find solutions to mathematical problems.

Mathematical Mistakes

Along with learning methods and tools for solving mathematical problems, it is important to recognize and avoid ways to make mathematical errors. This section will review some common errors.

Circular Arguments

These involve drawing a conclusion from a premise that is itself dependent on the conclusion. In other words, you are not actually proving anything. Circular reasoning often looks like deductive reasoning, but a quick examination will reveal that it’s far from it. Consider the following argument:

• Premise: Only an untrustworthy man would become an insurance salesman; the fact that insurance salesmen cannot be trusted is proof of this.
• Conclusion: Therefore, insurance salesmen cannot be trusted.

While this may be a simplistic example, you can see that there’s no logical procession in a circular argument.

Assuming the Truth of the Converse

Simply put: The fact that A implies B doesn’t not necessarily mean that B implies A. For example, “All dogs are mammals; therefore, all mammals are dogs.”

Assuming the Truth of the Inverse

Watch out for this one. You cannot automatically assume the inverse of a given statement is true. Consider the following true statement:

If you grew up in Minnesota , you’ve seen snow.

Now, notice that the inverse of this statement is not necessarily true:

If you didn’t grow up in Minnesota , you’ve never seen snow.

Faulty Generalizations

This mistake (also known as inductive fallacy) can take many forms, the most common being assuming a general rule based on a specific instance: (“Bridge is a hard game; therefore, all card games are difficult.”) Be aware of more subtle forms of faulty generalizations.

Faulty Analogies

It’s a mistake to assume that because two things are alike in one respect that they are necessarily alike in other ways too. Consider the faulty analogy below:

People who absolutely have to have a cup of coffee in the morning to get going are as bad as alcoholics who can’t cope without drinking.

False (or tenuous) analogies are often used in persuasive arguments.

Now that we’ve gone over some common mathematical mistakes, let’s look at some correct and effective ways to use mathematical reasoning.

Let’s look at basic logic, its operations, some fundamental laws, and the rules of logic that help us prove statements and deduce the truth. First off, there are two different styles of proofs: direct and indirect .

Whether it’s a direct or indirect proof, the engine that drives the proof is the if-then structure of a logical statement. In formal logic, you’ll see the format using the letters p and q, representing statements, as in:

If p, then q

An arrow is used to indicate that q is derived from p, like this:

This would be the general form of many types of logical statements that would be similar to: “if Joe has 5 cents, then Joe has a nickel or Joe has 5 pennies “. Basically, a proof is a flow of implications starting with the statement p and ending with the statement q. The stepping stones we use to link these statements in a logical proof on the way are called axioms or postulates , which are accepted logical tools.

A direct proof will attempt to lay out the shortest number of steps between p and q.

The goal of an indirect proof is exactly the same—it wants to show that q follows from p; however, it goes about it in a different manner. An indirect proof also goes by the names “proof by contradiction” or reductio ad absurdum . This type of proof assumes that the opposite of what you want to prove is true, and then shows that this is untenable or absurd, so, in fact, your original statement must be true.

Let’s see how this works using the isosceles triangle below. The indirect proof assumption is in bold.

Given: Triangle ABC is isosceles with B marking the vertex

Prove: Angles A and C are congruent.

Now, let’s work through this, matching our statements with our reasons.

• Triangle ABC is isosceles . . . . . . . . . . . . Given
• Angle A is the vertex . . . . . . . . . . . . . . . . Given
• Angles A and C are not congruent . . Indirect proof assumption
• Line AB is equal to line BC . . . . . . . . . . . Legs of an isosceles triangle are congruent
• Angles A and C are congruent . . . . . . . . The angles opposite congruent sides of a triangle are congruent
• Contradiction . . . . . . . . . . . . . . . . . . . . . . Angles can’t be congruent and incongruent
• Angles A and C are indeed congruent . . . The indirect proof assumption (step 3) is wrong
• Therefore, if angles A and C are not incongruent, they are congruent.

“Always, Sometimes, and Never”

Some math problems work on the mechanics that statements are “always”, “sometimes” and “never” true.

Example: x < x 2 for all real numbers x

We may be tempted to say that this statement is “always” true, because by choosing different values of x, like -2 and 3, we see that:

Example: For all primes x ≥ 3, x is odd.

This statement is “always” true. The only prime that is not odd is two. If we had a prime x ≥ 3 that is not odd, it would be divisible by two, which would make x not prime.

• Know and be able to identify common mathematical errors, such as circular arguments, assuming the truth of the converse, assuming the truth of the inverse, making faulty generalizations, and faulty use of analogical reasoning.
• Be familiar with direct proofs and indirect proofs (proof by contradiction).
• Be able to work with problems to identify “always,” “sometimes,” and “never” statements.

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Problem Solving in Mathematics Education

• Open Access
• First Online: 28 June 2016

Cite this chapter

You have full access to this open access chapter

• Peter Liljedahl 6 ,
• Manuel Santos-Trigo 7 ,
• Uldarico Malaspina 8 &
• Regina Bruder 9  

Part of the book series: ICME-13 Topical Surveys ((ICME13TS))

90k Accesses

14 Citations

Problem solving in mathematics education has been a prominent research field that aims at understanding and relating the processes involved in solving problems to students’ development of mathematical knowledge and problem solving competencies. The accumulated knowledge and field developments include conceptual frameworks to characterize learners’ success in problem solving activities, cognitive, metacognitive, social and affective analysis, curriculum proposals, and ways to foster problem solving approaches. In the survey, four interrelated areas are reviewed: (i) the relevance of heuristics in problem solving approaches—why are they important and what research tells us about their use? (ii) the need to characterize and foster creative problem solving approaches—what type of heuristics helps learners think of and practice creative solutions? (iii) the importance for learners to formulate and pursue their own problems; and (iv) the role played by the use of both multiple purpose and ad hoc mathematical action types of technologies in problem solving activities—what ways of reasoning do learners construct when they rely on the use of digital technologies and how technology and technology approaches can be reconciled?

You have full access to this open access chapter,  Download chapter PDF

• Mathematical Problem
• Prospective Teacher
• Creative Process
• Digital Technology
• Mathematical Task

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Mathematical problem solving has long been seen as an important aspect of mathematics, the teaching of mathematics, and the learning of mathematics. It has infused mathematics curricula around the world with calls for the teaching of problem solving as well as the teaching of mathematics through problem solving. And as such, it has been of interest to mathematics education researchers for as long as our field has existed. More relevant, mathematical problem solving has played a part in every ICME conference, from 1969 until the forthcoming meeting in Hamburg, wherein mathematical problem solving will reside most centrally within the work of Topic Study 19: Problem Solving in Mathematics Education. This booklet is being published on the occasion of this Topic Study Group.

To this end, we have assembled four summaries looking at four distinct, yet inter-related, dimensions of mathematical problem solving. The first summary, by Regina Bruder, is a nuanced look at heuristics for problem solving. This notion of heuristics is carried into Peter Liljedahl’s summary, which looks specifically at a progression of heuristics leading towards more and more creative aspects of problem solving. This is followed by Luz Manuel Santos Trigo’s summary introducing us to problem solving in and with digital technologies. The last summary, by Uldarico Malaspina Jurado, documents the rise of problem posing within the field of mathematics education in general and the problem solving literature in particular.

Each of these summaries references in some critical and central fashion the works of George Pólya or Alan Schoenfeld. To the initiated researchers, this is no surprise. The seminal work of these researchers lie at the roots of mathematical problem solving. What is interesting, though, is the diverse ways in which each of the four aforementioned contributions draw on, and position, these works so as to fit into the larger scheme of their respective summaries. This speaks to not only the depth and breadth of these influential works, but also the diversity with which they can be interpreted and utilized in extending our thinking about problem solving.

Taken together, what follows is a topical survey of ideas representing the diversity of views and tensions inherent in a field of research that is both a means to an end and an end onto itself and is unanimously seen as central to the activities of mathematics.

1 Survey on the State-of-the-Art

1.1 role of heuristics for problem solving—regina bruder.

The origin of the word heuristic dates back to the time of Archimedes and is said to have come out of one of the famous stories told about this great mathematician and inventor. The King of Syracuse asked Archimedes to check whether his new wreath was really made of pure gold. Archimedes struggled with this task and it was not until he was at the bathhouse that he came up with the solution. As he entered the tub he noticed that he had displaced a certain amount of water. Brilliant as he was, he transferred this insight to the issue with the wreath and knew he had solved the problem. According to the legend, he jumped out of the tub and ran from the bathhouse naked screaming, “Eureka, eureka!”. Eureka and heuristic have the same root in the ancient Greek language and so it has been claimed that this is how the academic discipline of “heuristics” dealing with effective approaches to problem solving (so-called heurisms) was given its name. Pólya ( 1964 ) describes this discipline as follows:

Heuristics deals with solving tasks. Its specific goals include highlighting in general terms the reasons for selecting those moments in a problem the examination of which could help us find a solution. (p. 5)

This discipline has grown, in part, from examining the approaches to certain problems more in detail and comparing them with each other in order to abstract similarities in approach, or so-called heurisms. Pólya ( 1949 ), but also, inter alia, Engel ( 1998 ), König ( 1984 ) and Sewerin ( 1979 ) have formulated such heurisms for mathematical problem tasks. The problem tasks examined by the authors mentioned are predominantly found in the area of talent programmes, that is, they often go back to mathematics competitions.

In 1983 Zimmermann provided an overview of heuristic approaches and tools in American literature which also offered suggestions for mathematics classes. In the German-speaking countries, an approach has established itself, going back to Sewerin ( 1979 ) and König ( 1984 ), which divides school-relevant heuristic procedures into heuristic tools, strategies and principles, see also Bruder and Collet ( 2011 ).

Below is a review of the conceptual background of heuristics, followed by a description of the effect mechanisms of heurisms in problem-solving processes.

1.1.1 Research Review on the Promotion of Problem Solving

In the 20th century, there has been an advancement of research on mathematical problem solving and findings about possibilities to promote problem solving with varying priorities (c.f. Pehkonen 1991 ). Based on a model by Pólya ( 1949 ), in a first phase of research on problem solving, particularly in the 1960s and the 1970s, a series of studies on problem-solving processes placing emphasis on the importance of heuristic strategies (heurisms) in problem solving has been carried out. It was assumed that teaching and learning heuristic strategies, principles and tools would provide students with an orientation in problem situations and that this could thus improve students’ problem-solving abilities (c.f. for instance, Schoenfeld 1979 ). This approach, mostly researched within the scope of talent programmes for problem solving, was rather successful (c.f. for instance, Sewerin 1979 ). In the 1980s, requests for promotional opportunities in everyday teaching were given more and more consideration: “ problem solving must be the focus of school mathematics in the 1980s ” (NCTM 1980 ). For the teaching and learning of problem solving in regular mathematics classes, the current view according to which cognitive, heuristic aspects were paramount, was expanded by certain student-specific aspects, such as attitudes, emotions and self-regulated behaviour (c.f. Kretschmer 1983 ; Schoenfeld 1985 , 1987 , 1992 ). Kilpatrick ( 1985 ) divided the promotional approaches described in the literature into five methods which can also be combined with each other.

Osmosis : action-oriented and implicit imparting of problem-solving techniques in a beneficial learning environment

Memorisation : formation of special techniques for particular types of problem and of the relevant questioning when problem solving

Imitation : acquisition of problem-solving abilities through imitation of an expert

Cooperation : cooperative learning of problem-solving abilities in small groups

Reflection : problem-solving abilities are acquired in an action-oriented manner and through reflection on approaches to problem solving.

Kilpatrick ( 1985 ) views as success when heuristic approaches are explained to students, clarified by means of examples and trained through the presentation of problems. The need of making students aware of heuristic approaches is by now largely accepted in didactic discussions. Differences in varying approaches to promoting problem-solving abilities rather refer to deciding which problem-solving strategies or heuristics are to imparted to students and in which way, and not whether these should be imparted at all or not.

1.1.2 Heurisms as an Expression of Mental Agility

The activity theory, particularly in its advancement by Lompscher ( 1975 , 1985 ), offers a well-suited and manageable model to describe learning activities and differences between learners with regard to processes and outcomes in problem solving (c.f. Perels et al. 2005 ). Mental activity starts with a goal and the motive of a person to perform such activity. Lompscher divides actual mental activity into content and process. Whilst the content in mathematical problem-solving consists of certain concepts, connections and procedures, the process describes the psychological processes that occur when solving a problem. This course of action is described in Lompscher by various qualities, such as systematic planning, independence, accuracy, activity and agility. Along with differences in motivation and the availability of expertise, it appears that intuitive problem solvers possess a particularly high mental agility, at least with regard to certain contents areas.

According to Lompscher, “flexibility of thought” expresses itself

… by the capacity to change more or less easily from one aspect of viewing to another one or to embed one circumstance or component into different correlations, to understand the relativity of circumstances and statements. It allows to reverse relations, to more or less easily or quickly attune to new conditions of mental activity or to simultaneously mind several objects or aspects of a given activity (Lompscher 1975 , p. 36).

These typical manifestations of mental agility can be focused on in problem solving by mathematical means and can be related to the heurisms known from the analyses of approaches by Pólya et al. (c.f. also Bruder 2000 ):

Reduction : Successful problem solvers will intuitively reduce a problem to its essentials in a sensible manner. To achieve such abstraction, they often use visualisation and structuring aids, such as informative figures, tables, solution graphs or even terms. These heuristic tools are also very well suited to document in retrospect the approach adopted by the intuitive problem solvers in a way that is comprehensible for all.

Reversibility : Successful problem solvers are able to reverse trains of thought or reproduce these in reverse. They will do this in appropriate situations automatically, for instance, when looking for a key they have mislaid. A corresponding general heuristic strategy is working in reverse.

Minding of aspects : Successful problem solvers will mind several aspects of a given problem at the same time or easily recognise any dependence on things and vary them in a targeted manner. Sometimes, this is also a matter of removing barriers in favour of an idea that appears to be sustainable, that is, by simply “hanging on” to a certain train of thought even against resistance. Corresponding heurisms are, for instance, the principle of invariance, the principle of symmetry (Engel 1998 ), the breaking down or complementing of geometric figures to calculate surface areas, or certain terms used in binomial formulas.

Change of aspects : Successful problem solvers will possibly change their assumptions, criteria or aspects minded in order to find a solution. Various aspects of a given problem will be considered intuitively or the problem be viewed from a different perspective, which will prevent “getting stuck” and allow for new insights and approaches. For instance, many elementary geometric propositions can also be proved in an elegant vectorial manner.

Transferring : Successful problem solvers will be able more easily than others to transfer a well-known procedure to another, sometimes even very different context. They recognise more easily the “framework” or pattern of a given task. Here, this is about own constructions of analogies and continual tracing back from the unknown to the known.

Intuitive, that is, untrained good problem solvers, are, however, often unable to access these flexibility qualities consciously. This is why they are also often unable to explain how they actually solved a given problem.

To be able to solve problems successfully, a certain mental agility is thus required. If this is less well pronounced in a certain area, learning how to solve problems means compensating by acquiring heurisms. In this case, insufficient mental agility is partly “offset” through the application of knowledge acquired by means of heurisms. Mathematical problem-solving competences are thus acquired through the promotion of manifestations of mental agility (reduction, reversibility, minding of aspects and change of aspects). This can be achieved by designing sub-actions of problem solving in connection with a (temporarily) conscious application of suitable heurisms. Empirical evidence for the success of the active principle of heurisms has been provided by Collet ( 2009 ).

Against such background, learning how to solve problems can be established as a long-term teaching and learning process which basically encompasses four phases (Bruder and Collet 2011 ):

Intuitive familiarisation with heuristic methods and techniques.

Making aware of special heurisms by means of prominent examples (explicit strategy acquisition).

Short conscious practice phase to use the newly acquired heurisms with differentiated task difficulties.

Expanding the context of the strategies applied.

In the first phase, students are familiarised with heurisms intuitively by means of targeted aid impulses and questions (what helped us solve this problem?) which in the following phase are substantiated on the basis of model tasks, are given names and are thus made aware of their existence. The third phase serves the purpose of a certain familiarisation with the new heurisms and the experience of competence through individualised practising at different requirement levels, including in the form of homework over longer periods. A fourth and delayed fourth phase aims at more flexibility through the transfer to other contents and contexts and the increasingly intuitive use of the newly acquired heurisms, so that students can enrich their own problem-solving models in a gradual manner. The second and third phases build upon each other in close chronological order, whilst the first phase should be used in class at all times.

All heurisms can basically be described in an action-oriented manner by means of asking the right questions. The way of asking questions can thus also establish a certain kind of personal relation. Even if the teacher presents and suggests the line of basic questions with a prototypical wording each time, students should always be given the opportunity to find “their” wording for the respective heurism and take a note of it for themselves. A possible key question for the use of a heuristic tool would be: How to illustrate and structure the problem or how to present it in a different way?

Unfortunately, for many students, applying heuristic approaches to problem solving will not ensue automatically but will require appropriate early and long-term promoting. The results of current studies, where promotion approaches to problem solving are connected with self-regulation and metacognitive aspects, demonstrate certain positive effects of such combination on students. This field of research includes, for instance, studies by Lester et al. ( 1989 ), Verschaffel et al. ( 1999 ), the studies on teaching method IMPROVE by Mevarech and Kramarski ( 1997 , 2003 ) and also the evaluation of a teaching concept on learning how to solve problems by the gradual conscious acquisition of heurisms by Collet and Bruder ( 2008 ).

1.2 Creative Problem Solving—Peter Liljedahl

There is a tension between the aforementioned story of Archimedes and the heuristics presented in the previous section. Archimedes, when submersing himself in the tub and suddenly seeing the solution to his problem, wasn’t relying on osmosis, memorisation, imitation, cooperation, or reflection (Kilpatrick 1985 ). He wasn’t drawing on reduction, reversibility, minding of aspects, change of aspect, or transfer (Bruder 2000 ). Archimedes was stuck and it was only, in fact, through insight and sudden illumination that he managed to solve his problem. In short, Archimedes was faced with a problem that the aforementioned heuristics, and their kind, would not help him to solve.

According to some, such a scenario is the definition of a problem. For example, Resnick and Glaser ( 1976 ) define a problem as being something that you do not have the experience to solve. Mathematicians, in general, agree with this (Liljedahl 2008 ).

Any problem in which you can see how to attack it by deliberate effort, is a routine problem, and cannot be an important discover. You must try and fail by deliberate efforts, and then rely on a sudden inspiration or intuition or if you prefer to call it luck. (Dan Kleitman, participant cited in Liljedahl 2008 , p. 19).

Problems, then, are tasks that cannot be solved by direct effort and will require some creative insight to solve (Liljedahl 2008 ; Mason et al. 1982 ; Pólya 1965 ).

1.2.1 A History of Creativity in Mathematics Education

In 1902, the first half of what eventually came to be a 30 question survey was published in the pages of L’Enseignement Mathématique , the journal of the French Mathematical Society. The authors, Édouard Claparède and Théodore Flournoy, were two Swiss psychologists who were deeply interested in the topics of mathematical discovery, creativity and invention. Their hope was that a widespread appeal to mathematicians at large would incite enough responses for them to begin to formulate some theories about this topic. The first half of the survey centered on the reasons for becoming a mathematician (family history, educational influences, social environment, etc.), attitudes about everyday life, and hobbies. This was eventually followed, in 1904, by the publication of the second half of the survey pertaining, in particular, to mental images during periods of creative work. The responses were sorted according to nationality and published in 1908.

During this same period Henri Poincaré (1854–1912), one of the most noteworthy mathematicians of the time, had already laid much of the groundwork for his own pursuit of this same topic and in 1908 gave a presentation to the French Psychological Society in Paris entitled L’Invention mathématique —often mistranslated to Mathematical Creativity Footnote 1 (c.f. Poincaré 1952 ). At the time of the presentation Poincaré stated that he was aware of Claparède and Flournoy’s work, as well as their results, but expressed that they would only confirm his own findings. Poincaré’s presentation, as well as the essay it spawned, stands to this day as one of the most insightful, and thorough treatments of the topic of mathematical discovery, creativity, and invention.

Just at this time, I left Caen, where I was living, to go on a geological excursion under the auspices of the School of Mines. The incident of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go some place or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuschian functions were identical with those of non-Euclidean geometry. I did not verify the idea; I should not have had the time, as, upon taking my seat in the omnibus, I went on with the conversation already commenced, but I felt a perfect certainty. On my return to Caen, for conscience’ sake, I verified the results at my leisure. (Poincaré 1952 , p. 53)

So powerful was his presentation, and so deep were his insights into his acts of invention and discovery that it could be said that he not so much described the characteristics of mathematical creativity, as defined them. From that point forth mathematical creativity, or even creativity in general, has not been discussed seriously without mention of Poincaré’s name.

Inspired by this presentation, Jacques Hadamard (1865–1963), a contemporary and a friend of Poincaré’s, began his own empirical investigation into this fascinating phenomenon. Hadamard had been critical of Claparède and Flournoy’s work in that they had not adequately treated the topic on two fronts. As exhaustive as the survey appeared to be, Hadamard felt that it failed to ask some key questions—the most important of which was with regard to the reason for failures in the creation of mathematics. This seemingly innocuous oversight, however, led directly to his second and “most important criticism” (Hadamard 1945 ). He felt that only “first-rate men would dare to speak of” (p. 10) such failures. So, inspired by his good friend Poincaré’s treatment of the subject Hadamard retooled the survey and gave it to friends of his for consideration—mathematicians such as Henri Poincaré and Albert Einstein, whose prominence were beyond reproach. Ironically, the new survey did not contain any questions that explicitly dealt with failure. In 1943 Hadamard gave a series of lectures on mathematical invention at the École Libre des Hautes Études in New York City. These talks were subsequently published as The Psychology of Mathematical Invention in the Mathematical Field (Hadameard 1945 ).

Hadamard’s classic work treats the subject of invention at the crossroads of mathematics and psychology. It provides not only an entertaining look at the eccentric nature of mathematicians and their rituals, but also outlines the beliefs of mid twentieth-century mathematicians about the means by which they arrive at new mathematics. It is an extensive exploration and extended argument for the existence of unconscious mental processes. In essence, Hadamard took the ideas that Poincaré had posed and, borrowing a conceptual framework for the characterization of the creative process from the Gestaltists of the time (Wallas 1926 ), turned them into a stage theory. This theory still stands as the most viable and reasonable description of the process of mathematical creativity.

1.2.2 Defining Mathematical Creativity

The phenomena of mathematical creativity, although marked by sudden illumination, actually consist of four separate stages stretched out over time, of which illumination is but one stage. These stages are initiation, incubation, illumination, and verification (Hadamard 1945 ). The first of these stages, the initiation phase, consists of deliberate and conscious work. This would constitute a person’s voluntary, and seemingly fruitless, engagement with a problem and be characterized by an attempt to solve the problem by trolling through a repertoire of past experiences. This is an important part of the inventive process because it creates the tension of unresolved effort that sets up the conditions necessary for the ensuing emotional release at the moment of illumination (Hadamard 1945 ; Poincaré 1952 ).

Following the initiation stage the solver, unable to come up with a solution stops working on the problem at a conscious level and begins to work on it at an unconscious level (Hadamard 1945 ; Poincaré 1952 ). This is referred to as the incubation stage of the inventive process and can last anywhere from several minutes to several years. After the period of incubation a rapid coming to mind of a solution, referred to as illumination , may occur. This is accompanied by a feeling of certainty and positive emotions (Poincaré 1952 ). Although the processes of incubation and illumination are shrouded behind the veil of the unconscious there are a number of things that can be deduced about them. First and foremost is the fact that unconscious work does, indeed, occur. Poincaré ( 1952 ), as well as Hadamard ( 1945 ), use the very real experience of illumination, a phenomenon that cannot be denied, as evidence of unconscious work, the fruits of which appear in the flash of illumination. No other theory seems viable in explaining the sudden appearance of solution during a walk, a shower, a conversation, upon waking, or at the instance of turning the conscious mind back to the problem after a period of rest (Poincaré 1952 ). Also deducible is that unconscious work is inextricably linked to the conscious and intentional effort that precedes it.

There is another remark to be made about the conditions of this unconscious work: it is possible, and of a certainty it is only fruitful, if it is on the one hand preceded and on the other hand followed by a period of conscious work. These sudden inspirations never happen except after some days of voluntary effort which has appeared absolutely fruitless and whence nothing good seems to have come … (Poincaré 1952 , p. 56)

Hence, the fruitless efforts of the initiation phase are only seemingly so. They not only set up the aforementioned tension responsible for the emotional release at the time of illumination, but also create the conditions necessary for the process to enter into the incubation phase.

Illumination is the manifestation of a bridging that occurs between the unconscious mind and the conscious mind (Poincaré 1952 ), a coming to (conscious) mind of an idea or solution. What brings the idea forward to consciousness is unclear, however. There are theories of the aesthetic qualities of the idea, effective surprise/shock of recognition, fluency of processing, or breaking functional fixedness. For reasons of brevity I will only expand on the first of these.

Poincaré proposed that ideas that were stimulated during initiation remained stimulated during incubation. However, freed from the constraints of conscious thought and deliberate calculation, these ideas would begin to come together in rapid and random unions so that “their mutual impacts may produce new combinations” (Poincaré 1952 ). These new combinations, or ideas, would then be evaluated for viability using an aesthetic sieve, which allows through to the conscious mind only the “right combinations” (Poincaré 1952 ). It is important to note, however, that good or aesthetic does not necessarily mean correct. Correctness is evaluated during the verification stage.

The purpose of verification is not only to check for correctness. It is also a method by which the solver re-engages with the problem at the level of details. That is, during the unconscious work the problem is engaged with at the level of ideas and concepts. During verification the solver can examine these ideas in closer details. Poincaré succinctly describes both of these purposes.

As for the calculations, themselves, they must be made in the second period of conscious work, that which follows the inspiration, that in which one verifies the results of this inspiration and deduces their consequences. (Poincaré 1952 , p. 62)

Aside from presenting this aforementioned theory on invention, Hadamard also engaged in a far-reaching discussion on a number of interesting, and sometimes quirky, aspects of invention and discovery that he had culled from the results of his empirical study, as well as from pertinent literature. This discussion was nicely summarized by Newman ( 2000 ) in his commentary on the elusiveness of invention.

The celebrated phrenologist Gall said mathematical ability showed itself in a bump on the head, the location of which he specified. The psychologist Souriau, we are told, maintained that invention occurs by “pure chance”, a valuable theory. It is often suggested that creative ideas are conjured up in “mathematical dreams”, but this attractive hypothesis has not been verified. Hadamard reports that mathematicians were asked whether “noises” or “meteorological circumstances” helped or hindered research [..] Claude Bernard, the great physiologist, said that in order to invent “one must think aside”. Hadamard says this is a profound insight; he also considers whether scientific invention may perhaps be improved by standing or sitting or by taking two baths in a row. Helmholtz and Poincaré worked sitting at a table; Hadamard’s practice is to pace the room (“Legs are the wheels of thought”, said Emile Angier); the chemist J. Teeple was the two-bath man. (p. 2039)

1.2.3 Discourses on Creativity

Creativity is a term that can be used both loosely and precisely. That is, while there exists a common usage of the term there also exists a tradition of academic discourse on the subject. A common usage of creative refers to a process or a person whose products are original, novel, unusual, or even abnormal (Csíkszentmihályi 1996 ). In such a usage, creativity is assessed on the basis of the external and observable products of the process, the process by which the product comes to be, or on the character traits of the person doing the ‘creating’. Each of these usages—product, process, person—is the roots of the discourses (Liljedahl and Allan 2014 ) that I summarize here, the first of which concerns products.

Consider a mother who states that her daughter is creative because she drew an original picture. The basis of such a statement can lie either in the fact that the picture is unlike any the mother has ever seen or unlike any her daughter has ever drawn before. This mother is assessing creativity on the basis of what her daughter has produced. However, the standards that form the basis of her assessment are neither consistent nor stringent. There does not exist a universal agreement as to what she is comparing the picture to (pictures by other children or other pictures by the same child). Likewise, there is no standard by which the actual quality of the picture is measured. The academic discourse that concerns assessment of products, on the other hand, is both consistent and stringent (Csíkszentmihályi 1996 ). This discourse concerns itself more with a fifth, and as yet unmentioned, stage of the creative process; elaboration . Elaboration is where inspiration becomes perspiration (Csíkszentmihályi 1996 ). It is the act of turning a good idea into a finished product, and the finished product is ultimately what determines the creativity of the process that spawned it—that is, it cannot be a creative process if nothing is created. In particular, this discourse demands that the product be assessed against other products within its field, by the members of that field, to determine if it is original AND useful (Csíkszentmihályi 1996 ; Bailin 1994 ). If it is, then the product is deemed to be creative. Note that such a use of assessment of end product pays very little attention to the actual process that brings this product forth.

The second discourse concerns the creative process. The literature pertaining to this can be separated into two categories—a prescriptive discussion of the creativity process and a descriptive discussion of the creativity process. Although both of these discussions have their roots in the four stages that Wallas ( 1926 ) proposed makes up the creative process, they make use of these stages in very different ways. The prescriptive discussion of the creative process is primarily focused on the first of the four stages, initiation , and is best summarized as a cause - and - effect discussion of creativity, where the thinking processes during the initiation stage are the cause and the creative outcome are the effects (Ghiselin 1952 ). Some of the literature claims that the seeds of creativity lie in being able to think about a problem or situation analogically. Other literature claims that utilizing specific thinking tools such as imagination, empathy, and embodiment will lead to creative products. In all of these cases, the underlying theory is that the eventual presentation of a creative idea will be precipitated by the conscious and deliberate efforts during the initiation stage. On the other hand, the literature pertaining to a descriptive discussion of the creative process is inclusive of all four stages (Kneller 1965 ; Koestler 1964 ). For example, Csíkszentmihályi ( 1996 ), in his work on flow attends to each of the stages, with much attention paid to the fluid area between conscious and unconscious work, or initiation and incubation. His claim is that the creative process is intimately connected to the enjoyment that exists during times of sincere and consuming engagement with a situation, the conditions of which he describes in great detail.

The third, and final, discourse on creativity pertains to the person. This discourse is space dominated by two distinct characteristics, habit and genius. Habit has to do with the personal habits as well as the habits of mind of people that have been deemed to be creative. However, creative people are most easily identified through their reputation for genius. Consequently, this discourse is often dominated by the analyses of the habits of geniuses as is seen in the work of Ghiselin ( 1952 ), Koestler ( 1964 ), and Kneller ( 1965 ) who draw on historical personalities such as Albert Einstein, Henri Poincaré, Vincent Van Gogh, D.H. Lawrence, Samuel Taylor Coleridge, Igor Stravinsky, and Wolfgang Amadeus Mozart to name a few. The result of this sort of treatment is that creative acts are viewed as rare mental feats, which are produced by extraordinary individuals who use extraordinary thought processes.

These different discourses on creativity can be summed up in a tension between absolutist and relativist perspectives on creativity (Liljedahl and Sriraman 2006 ). An absolutist perspective assumes that creative processes are the domain of genius and are present only as precursors to the creation of remarkably useful and universally novel products. The relativist perspective, on the other hand, allows for every individual to have moments of creativity that may, or may not, result in the creation of a product that may, or may not, be either useful or novel.

Between the work of a student who tries to solve a problem in geometry or algebra and a work of invention, one can say there is only a difference of degree. (Hadamard 1945 , p. 104).

Regardless of discourse, however, creativity is not “part of the theories of logical forms” (Dewey 1938 ). That is, creativity is not representative of the lock-step logic and deductive reasoning that mathematical problem solving is often presumed to embody (Bibby 2002 ; Burton 1999 ). Couple this with the aforementioned demanding constraints as to what constitutes a problem, where then does that leave problem solving heuristics? More specifically, are there creative problem solving heuristics that will allow us to resolve problems that require illumination to solve? The short answer to this question is yes—there does exist such problem solving heuristics. To understand these, however, we must first understand the routine problem solving heuristics they are built upon. In what follows, I walk through the work of key authors and researchers whose work offers us insights into progressively more creative problem solving heuristics for solving true problems.

1.2.4 Problem Solving by Design

In a general sense, design is defined as the algorithmic and deductive approach to solving a problem (Rusbult 2000 ). This process begins with a clearly defined goal or objective after which there is a great reliance on relevant past experience, referred to as repertoire (Bruner 1964 ; Schön 1987 ), to produce possible options that will lead towards a solution of the problem (Poincaré 1952 ). These options are then examined through a process of conscious evaluations (Dewey 1933 ) to determine their suitability for advancing the problem towards the final goal. In very simple terms, problem solving by design is the process of deducing the solution from that which is already known.

Mayer ( 1982 ), Schoenfeld ( 1982 ), and Silver ( 1982 ) state that prior knowledge is a key element in the problem solving process. Prior knowledge influences the problem solver’s understanding of the problem as well as the choice of strategies that will be called upon in trying to solve the problem. In fact, prior knowledge and prior experiences is all that a solver has to draw on when first attacking a problem. As a result, all problem solving heuristics incorporate this resource of past experiences and prior knowledge into their initial attack on a problem. Some heuristics refine these ideas, and some heuristics extend them (c.f. Kilpatrick 1985 ; Bruder 2000 ). Of the heuristics that refine, none is more influential than the one created by George Pólya (1887–1985).

1.2.5 George Pólya: How to Solve It

In his book How to Solve It (1949) Pólya lays out a problem solving heuristic that relies heavily on a repertoire of past experience. He summarizes the four-step process of his heuristic as follows:

Understanding the Problem

First. You have to understand the problem.

What is the unknown? What are the data? What is the condition?

Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?

Draw a figure. Introduce suitable notation.

Separate the various parts of the condition. Can you write them down?

Devising a Plan

Second. Find the connection between the data and the unknown. You may be obliged to consider auxiliary problems if an immediate connection cannot be found. You should obtain eventually a plan of the solution.

Have you seen it before? Or have you seen the same problem in a slightly different form?

Do you know a related problem? Do you know a theorem that could be useful?

Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.

Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?

Could you restate the problem? Could you restate it still differently? Go back to definitions.

If you cannot solve the proposed problem try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem? Could you solve a part of the problem? Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary? Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or data, or both if necessary, so that the new unknown and the new data are nearer to each other?

Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?

Carrying Out the Plan

Third. Carry out your plan.

Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove that it is correct?

Looking Back

Fourth. Examine the solution obtained.

Can you check the result? Can you check the argument?

Can you derive the solution differently? Can you see it at a glance?

Can you use the result, or the method, for some other problem?

The emphasis on auxiliary problems, related problems, and analogous problems that are, in themselves, also familiar problems is an explicit manifestation of relying on a repertoire of past experience. This use of familiar problems also requires an ability to deduce from these related problems a recognizable and relevant attribute that will transfer to the problem at hand. The mechanism that allows for this transfer of knowledge between analogous problems is known as analogical reasoning (English 1997 , 1998 ; Novick 1988 , 1990 , 1995 ; Novick and Holyoak 1991 ) and has been shown to be an effective, but not always accessible, thinking strategy.

Step four in Pólya’s heuristic, looking back, is also a manifestation of utilizing prior knowledge to solve problems, albeit an implicit one. Looking back makes connections “in memory to previously acquired knowledge [..] and further establishes knowledge in long-term memory that may be elaborated in later problem-solving encounters” (Silver 1982 , p. 20). That is, looking back is a forward-looking investment into future problem solving encounters, it sets up connections that may later be needed.

Pólya’s heuristic is a refinement on the principles of problem solving by design. It not only makes explicit the focus on past experiences and prior knowledge, but also presents these ideas in a very succinct, digestible, and teachable manner. This heuristic has become a popular, if not the most popular, mechanism by which problem solving is taught and learned.

1.2.6 Alan Schoenfeld: Mathematical Problem Solving

The work of Alan Schoenfeld is also a refinement on the principles of problem solving by design. However, unlike Pólya ( 1949 ) who refined these principles at a theoretical level, Schoenfeld has refined them at a practical and empirical level. In addition to studying taught problem solving strategies he has also managed to identify and classify a variety of strategies, mostly ineffectual, that students invoke naturally (Schoenfeld 1985 , 1992 ). In so doing, he has created a better understanding of how students solve problems, as well as a better understanding of how problems should be solved and how problem solving should be taught.

For Schoenfeld, the problem solving process is ultimately a dialogue between the problem solver’s prior knowledge, his attempts, and his thoughts along the way (Schoenfeld 1982 ). As such, the solution path of a problem is an emerging and contextually dependent process. This is a departure from the predefined and contextually independent processes of Pólya’s ( 1949 ) heuristics. This can be seen in Schoenfeld’s ( 1982 ) description of a good problem solver.

To examine what accounts for expertise in problem solving, you would have to give the expert a problem for which he does not have access to a solution schema. His behavior in such circumstances is radically different from what you would see when he works on routine or familiar “non-routine” problems. On the surface his performance is no longer proficient; it may even seem clumsy. Without access to a solution schema, he has no clear indication of how to start. He may not fully understand the problem, and may simply “explore it for a while until he feels comfortable with it. He will probably try to “match” it to familiar problems, in the hope it can be transformed into a (nearly) schema-driven solution. He will bring up a variety of plausible things: related facts, related problems, tentative approaches, etc. All of these will have to be juggled and balanced. He may make an attempt solving it in a particular way, and then back off. He may try two or three things for a couple of minutes and then decide which to pursue. In the midst of pursuing one direction he may go back and say “that’s harder than it should be” and try something else. Or, after the comment, he may continue in the same direction. With luck, after some aborted attempts, he will solve the problem. (p. 32-33)

Aside from demonstrating the emergent nature of the problem solving process, this passage also brings forth two consequences of Schoenfeld’s work. The first of these is the existence of problems for which the solver does not have “access to a solution schema”. Unlike Pólya ( 1949 ), who’s heuristic is a ‘one size fits all (problems)’ heuristic, Schoenfeld acknowledges that problem solving heuristics are, in fact, personal entities that are dependent on the solver’s prior knowledge as well as their understanding of the problem at hand. Hence, the problems that a person can solve through his or her personal heuristic are finite and limited.

The second consequence that emerges from the above passage is that if a person lacks the solution schema to solve a given problem s/he may still solve the problem with the help of luck . This is an acknowledgement, if only indirectly so, of the difference between problem solving in an intentional and mechanical fashion verses problem solving in a more creative fashion, which is neither intentional nor mechanical (Pehkonen 1997 ).

1.2.7 David Perkins: Breakthrough Thinking

As mentioned, many consider a problem that can be solved by intentional and mechanical means to not be worthy of the title ‘problem’. As such, a repertoire of past experiences sufficient for dealing with such a ‘problem’ would disqualify it from the ranks of ‘problems’ and relegate it to that of ‘exercises’. For a problem to be classified as a ‘problem’, then, it must be ‘problematic’. Although such an argument is circular it is also effective in expressing the ontology of mathematical ‘problems’.

Perkins ( 2000 ) also requires problems to be problematic. His book Archimedes’ Bathtub: The Art and Logic of Breakthrough Thinking (2000) deals with situations in which the solver has gotten stuck and no amount of intentional or mechanical adherence to the principles of past experience and prior knowledge is going to get them unstuck. That is, he deals with problems that, by definition, cannot be solved through a process of design [or through the heuristics proposed by Pólya ( 1949 ) and Schoenfeld ( 1985 )]. Instead, the solver must rely on the extra-logical process of what Perkins ( 2000 ) calls breakthrough thinking .

Perkins ( 2000 ) begins by distinguishing between reasonable and unreasonable problems. Although both are solvable, only reasonable problems are solvable through reasoning. Unreasonable problems require a breakthrough in order to solve them. The problem, however, is itself inert. It is neither reasonable nor unreasonable. That quality is brought to the problem by the solver. That is, if a student cannot solve a problem by direct effort then that problem is deemed to be unreasonable for that student. Perkins ( 2000 ) also acknowledges that what is an unreasonable problem for one person is a perfectly reasonable problem for another person; reasonableness is dependent on the person.

This is not to say that, once found, the solution cannot be seen as accessible through reason. During the actual process of solving, however, direct and deductive reasoning does not work. Perkins ( 2000 ) uses several classic examples to demonstrate this, the most famous being the problem of connecting nine dots in a 3 × 3 array with four straight lines without removing pencil from paper, the solution to which is presented in Fig.  1 .

Nine dots—four lines problem and solution

To solve this problem, Perkins ( 2000 ) claims that the solver must recognize that the constraint of staying within the square created by the 3 × 3 array is a self-imposed constraint. He further claims that until this is recognized no amount of reasoning is going to solve the problem. That is, at this point in the problem solving process the problem is unreasonable. However, once this self-imposed constraint is recognized the problem, and the solution, are perfectly reasonable. Thus, the solution of an, initially, unreasonable problem is reasonable.

The problem solving heuristic that Perkins ( 2000 ) has constructed to deal with solvable, but unreasonable, problems revolves around the idea of breakthrough thinking and what he calls breakthrough problems . A breakthrough problem is a solvable problem in which the solver has gotten stuck and will require an AHA! to get unstuck and solve the problem. Perkins ( 2000 ) poses that there are only four types of solvable unreasonable problems, which he has named wilderness of possibilities , the clueless plateau , narrow canyon of exploration , and oasis of false promise . The names for the first three of these types of problems are related to the Klondike gold rush in Alaska, a time and place in which gold was found more by luck than by direct and systematic searching.

The wilderness of possibilities is a term given to a problem that has many tempting directions but few actual solutions. This is akin to a prospector searching for gold in the Klondike. There is a great wilderness in which to search, but very little gold to be found. The clueless plateau is given to problems that present the solver with few, if any, clues as to how to solve it. The narrow canyon of exploration is used to describe a problem that has become constrained in such a way that no solution now exists. The nine-dot problem presented above is such a problem. The imposed constraint that the lines must lie within the square created by the array makes a solution impossible. This is identical to the metaphor of a prospector searching for gold within a canyon where no gold exists. The final type of problem gets its name from the desert. An oasis of false promise is a problem that allows the solver to quickly get a solution that is close to the desired outcome; thereby tempting them to remain fixed on the strategy that they used to get this almost-answer. The problem is, that like the canyon, the solution does not exist at the oasis; the solution strategy that produced an almost-answer is incapable of producing a complete answer. Likewise, a desert oasis is a false promise in that it is only a reprieve from the desolation of the dessert and not a final destination.

Believing that there are only four ways to get stuck, Perkins ( 2000 ) has designed a problem solving heuristic that will “up the chances” of getting unstuck. This heuristic is based on what he refers to as “the logic of lucking out” (p. 44) and is built on the idea of introspection. By first recognizing that they are stuck, and then recognizing that the reason they are stuck can only be attributed to one of four reasons, the solver can access four strategies for getting unstuck, one each for the type of problem they are dealing with. If the reason they are stuck is because they are faced with a wilderness of possibilities they are to begin roaming far, wide, and systematically in the hope of reducing the possible solution space to one that is more manageable. If they find themselves on a clueless plateau they are to begin looking for clues, often in the wording of the problem. When stuck in a narrow canyon of possibilities they need to re-examine the problem and see if they have imposed any constraints. Finally, when in an oasis of false promise they need to re-attack the problem in such a way that they stay away from the oasis.

Of course, there are nuances and details associated with each of these types of problems and the strategies for dealing with them. However, nowhere within these details is there mention of the main difficulty inherent in introspection; that it is much easier for the solver to get stuck than it is for them to recognize that they are stuck. Once recognized, however, the details of Perkins’ ( 2000 ) heuristic offer the solver some ways for recognizing why they are stuck.

1.2.8 John Mason, Leone Burton, and Kaye Stacey: Thinking Mathematically

The work of Mason et al. in their book Thinking Mathematically ( 1982 ) also recognizes the fact that for each individual there exists problems that will not yield to their intentional and mechanical attack. The heuristic that they present for dealing with this has two main processes with a number of smaller phases, rubrics, and states. The main processes are what they refer to as specializing and generalizing. Specializing is the process of getting to know the problem and how it behaves through the examination of special instances of the problem. This process is synonymous with problem solving by design and involves the repeated oscillation between the entry and attack phases of Mason et al. ( 1982 ) heuristic. The entry phase is comprised of ‘getting started’ and ‘getting involved’ with the problem by using what is immediately known about it. Attacking the problem involves conjecturing and testing a number of hypotheses in an attempt to gain greater understanding of the problem and to move towards a solution.

At some point within this process of oscillating between entry and attack the solver will get stuck, which Mason et al. ( 1982 ) refer to as “an honourable and positive state, from which much can be learned” (p. 55). The authors dedicate an entire chapter to this state in which they acknowledge that getting stuck occurs long before an awareness of being stuck develops. They proposes that the first step to dealing with being stuck is the simple act of writing STUCK!

The act of expressing my feelings helps to distance me from my state of being stuck. It frees me from incapacitating emotions and reminds me of actions that I can take. (p. 56)

The next step is to reengage the problem by examining the details of what is known, what is wanted, what can be introduced into the problem, and what has been introduced into the problem (imposed assumptions). This process is engaged in until an AHA!, which advances the problem towards a solution, is encountered. If, at this point, the problem is not completely solved the oscillation is then resumed.

At some point in this process an attack on the problem will yield a solution and generalizing can begin. Generalizing is the process by which the specifics of a solution are examined and questions as to why it worked are investigated. This process is synonymous with the verification and elaboration stages of invention and creativity. Generalization may also include a phase of review that is similar to Pólya’s ( 1949 ) looking back.

1.2.9 Gestalt: The Psychology of Problem Solving

The Gestalt psychology of learning believes that all learning is based on insights (Koestler 1964 ). This psychology emerged as a response to behaviourism, which claimed that all learning was a response to external stimuli. Gestalt psychologists, on the other hand, believed that there was a cognitive process involved in learning as well. With regards to problem solving, the Gestalt school stands firm on the belief that problem solving, like learning, is a product of insight and as such, cannot be taught. In fact, the theory is that not only can problem solving not be taught, but also that attempting to adhere to any sort of heuristic will impede the working out of a correct solution (Krutestkii 1976 ). Thus, there exists no Gestalt problem solving heuristic. Instead, the practice is to focus on the problem and the solution rather than on the process of coming up with a solution. Problems are solved by turning them over and over in the mind until an insight, a viable avenue of attack, presents itself. At the same time, however, there is a great reliance on prior knowledge and past experiences. The Gestalt method of problem solving, then, is at the same time very different and very similar to the process of design.

Gestalt psychology has not fared well during the evolution of cognitive psychology. Although it honours the work of the unconscious mind it does so at the expense of practicality. If learning is, indeed, entirely based on insight then there is little point in continuing to study learning. “When one begins by assuming that the most important cognitive phenomena are inaccessible, there really is not much left to talk about” (Schoenfeld 1985 , p. 273). However, of interest here is the Gestalt psychologists’ claim that focus on problem solving methods creates functional fixedness (Ashcraft 1989 ). Mason et al. ( 1982 ), as well as Perkins ( 2000 ) deal with this in their work on getting unstuck.

1.2.10 Final Comments

Mathematics has often been characterized as the most precise of all sciences. Lost in such a misconception is the fact that mathematics often has its roots in the fires of creativity, being born of the extra-logical processes of illumination and intuition. Problem solving heuristics that are based solely on the processes of logical and deductive reasoning distort the true nature of problem solving. Certainly, there are problems in which logical deductive reasoning is sufficient for finding a solution. But these are not true problems. True problems need the extra-logical processes of creativity, insight, and illumination, in order to produce solutions.

Fortunately, as elusive as such processes are, there does exist problem solving heuristics that incorporate them into their strategies. Heuristics such as those by Perkins ( 2000 ) and Mason et al. ( 1982 ) have found a way of combining the intentional and mechanical processes of problem solving by design with the extra-logical processes of creativity, illumination, and the AHA!. Furthermore, they have managed to do so without having to fully comprehend the inner workings of this mysterious process.

1.3 Digital Technologies and Mathematical Problem Solving—Luz Manuel Santos-Trigo

Mathematical problem solving is a field of research that focuses on analysing the extent to which problem solving activities play a crucial role in learners’ understanding and use of mathematical knowledge. Mathematical problems are central in mathematical practice to develop the discipline and to foster students learning (Pólya 1945 ; Halmos 1994 ). Mason and Johnston-Wilder ( 2006 ) pointed out that “The purpose of a task is to initiate mathematically fruitful activity that leads to a transformation in what learners are sensitized to notice and competent to carry out” (p. 25). Tasks are essential for learners to elicit their ideas and to engage them in mathematical thinking. In a problem solving approach, what matters is the learners’ goals and ways to interact with the tasks. That is, even routine tasks can be a departure point for learners to extend initial conditions and transform them into some challenging activities.

Thus, analysing and characterizing ways in which mathematical problems are formulated (Singer et al. 2015 ) and the process involved in pursuing and solving those problems generate important information to frame and structure learning environments to guide and foster learners’ construction of mathematical concepts and problem solving competences (Santos-Trigo 2014 ). Furthermore, mathematicians or discipline practitioners have often been interested in unveiling and sharing their own experience while developing the discipline. As a results, they have provided valuable information to characterize mathematical practices and their relations to what learning processes of the discipline entails. It is recognized that the work of Pólya ( 1945 ) offered not only bases to launch several research programs in problem solving (Schoenfeld 1992 ; Mason et al. 1982 ); but also it became an essential resource for teachers to orient and structure their mathematical lessons (Krulik and Reys 1980 ).

1.3.1 Research Agenda

A salient feature of a problem solving approach to learn mathematics is that teachers and students develop and apply an enquiry or inquisitive method to delve into mathematical concepts and tasks. How are mathematical problems or concepts formulated? What types of problems are important for teachers/learners to discuss and engage in mathematical reasoning? What mathematical processes and ways of reasoning are involved in understanding mathematical concepts and solving problems? What are the features that distinguish an instructional environment that fosters problem-solving activities? How can learners’ problem solving competencies be assessed? How can learners’ problem solving competencies be characterized and explained? How can learners use digital technologies to understand mathematics and to develop problem-solving competencies? What ways of reasoning do learners construct when they use digital technologies in problem solving approaches? These types of questions have been important in the problem solving research agenda and delving into them has led researchers to generate information and results to support and frame curriculum proposals and learning scenarios. The purpose of this section is to present and discuss important themes that emerged in problem solving approaches that rely on the systematic use of several digital technologies.

In the last 40 years, the accumulated knowledge in the problem solving field has shed lights on both a characterization of what mathematical thinking involves and how learners can construct a robust knowledge in problem solving environments (Schoenfeld 1992 ). In this process, the field has contributed to identify what types of transformations traditional learning scenarios might consider when teachers and students incorporate the use of digital technologies in mathematical classrooms. In this context, it is important to briefly review what main themes and developments the field has addressed and achieved during the last 40 years.

1.3.2 Problem Solving Developments

There are traces of mathematical problems and solutions throughout the history of civilization that explain the humankind interest for identifying and exploring mathematical relations (Kline 1972 ). Pólya ( 1945 ) reflects on his own practice as a mathematician to characterize the process of solving mathematical problems through four main phases: Understanding the problem, devising a plan, carrying out the plan, and looking back. Likewise, Pólya ( 1945 ) presents and discusses the role played by heuristic methods throughout all problem solving phases. Schoenfeld ( 1985 ) presents a problem solving research program based on Pólya’s ( 1945 ) ideas to investigate the extent to which problem solving heuristics help university students to solve mathematical problems and to develop a way of thinking that shows consistently features of mathematical practices. As a result, he explains the learners’ success or failure in problem solving activities can be characterized in terms their mathematical resources and ways to access them, cognitive and metacognitive strategies used to represent and explore mathematical tasks, and systems of beliefs about mathematics and solving problems. In addition, Schoenfeld ( 1992 ) documented that heuristics methods as illustrated in Pólya’s ( 1945 ) book are ample and general and do not include clear information and directions about how learners could assimilate, learn, and use them in their problem solving experiences. He suggested that students need to discuss what it means, for example, to think of and examining special cases (one important heuristic) in finding a closed formula for series or sequences, analysing relationships of roots of polynomials, or focusing on regular polygons or equilateral/right triangles to find general relations about these figures. That is, learners need to work on examples that lead them to recognize that the use of a particular heuristic often involves thinking of different type of cases depending on the domain or content involved. Lester and Kehle ( 2003 ) summarize themes and methodological shifts in problem solving research up to 1995. Themes include what makes a problem difficult for students and what it means to be successful problem solvers; studying and contrasting experts and novices’ problem solving approaches; learners’ metacognitive, beliefs systems and the influence of affective behaviours; and the role of context; and social interactions in problem solving environments. Research methods in problem solving studies have gone from emphasizing quantitative or statistical design to the use of cases studies and ethnographic methods (Krutestkii ( 1976 ). Teaching strategies also evolved from being centred on teachers to the active students’ engagement and collaboration approaches (NCTM 2000 ). Lesh and Zawojewski ( 2007 ) propose to extend problem solving approaches beyond class setting and they introduce the construct “model eliciting activities” to delve into the learners’ ideas and thinking as a way to engage them in the development of problem solving experiences. To this end, learners develop and constantly refine problem-solving competencies as a part of a learning community that promotes and values modelling construction activities. Recently, English and Gainsburg ( 2016 ) have discussed the importance of modeling eliciting activities to prepare and develop students’ problem solving experiences for 21st Century challenges and demands.

Törner et al. ( 2007 ) invited mathematics educators worldwide to elaborate on the influence and developments of problem solving in their countries. Their contributions show a close relationship between countries mathematical education traditions and ways to frame and implement problem solving approaches. In Chinese classrooms, for example, three instructional strategies are used to structure problem solving lessons: one problem multiple solutions , multiple problems one solution , and one problem multiple changes . In the Netherlands, the realistic mathematical approach permeates the students’ development of problem solving competencies; while in France, problem solving activities are structured in terms of two influential frameworks: The theory of didactical situations and anthropological theory of didactics.

In general, problem solving frameworks and instructional approaches came from analysing students’ problem solving experiences that involve or rely mainly on the use of paper and pencil work. Thus, there is a need to re-examined principles and frameworks to explain what learners develop in learning environments that incorporate systematically the coordinated use of digital technologies (Hoyles and Lagrange 2010 ). In this perspective, it becomes important to briefly describe and identify what both multiple purpose and ad hoc technologies can offer to the students in terms of extending learning environments and representing and exploring mathematical tasks. Specifically, a task is used to identify features of mathematical reasoning that emerge through the use digital technologies that include both mathematical action and multiple purpose types of technologies.

1.3.3 Background

Digital technologies are omnipresent and their use permeates and shapes several social and academic events. Mobile devices such as tablets or smart phones are transforming the way people communicate, interact and carry out daily activities. Churchill et al. ( 2016 ) pointed out that mobile technologies provide a set of tools and affordances to structure and support learning environments in which learners continuously interact to construct knowledge and solve problems. The tools include resources or online materials, efficient connectivity to collaborate and discuss problems, ways to represent, explore and store information, and analytical and administration tools to management learning activities. Schmidt and Cohen ( 2013 ) stated that nowadays it is difficult to imagine a life without mobile devices, and communication technologies are playing a crucial role in generating both cultural and technical breakthroughs. In education, the use of mobile artefacts and computers offers learners the possibility of continuing and extending peers and groups’ mathematical discussions beyond formal settings. In this process, learners can also consult online materials and interact with experts, peers or more experienced students while working on mathematical tasks. In addition, dynamic geometry systems (GeoGebra) provide learners a set of affordances to represent and explore dynamically mathematical problems. Leung and Bolite-Frant ( 2015 ) pointed out that tools help activate an interactive environment in which teachers and students’ mathematical experiences get enriched. Thus, the digital age brings new challenges to the mathematics education community related to the changes that technologies produce to curriculum, learning scenarios, and ways to represent, explore mathematical situations. In particular, it is important to characterize the type of reasoning that learners can develop as a result of using digital technologies in their process of learning concepts and solving mathematical problems.

1.3.4 A Focus on Mathematical Tasks

Mathematical tasks are essential elements for engaging learners in mathematical reasoning which involves representing objects, identifying and exploring their properties in order to detect invariants or relationships and ways to support them. Watson and Ohtani ( 2015 ) stated that task design involves discussions about mathematical content and students’ learning (cognitive perspective), about the students’ experiences to understand the nature of mathematical activities; and about the role that tasks played in teaching practices. In this context, tasks are the vehicle to present and discuss theoretical frameworks for supporting the use of digital technology, to analyse the importance of using digital technologies in extending learners’ mathematical discussions beyond formal settings, and to design ways to foster and assess the use of technologies in learners’ problem solving environments. In addition, it is important to discuss contents, concepts, representations and strategies involved in the process of using digital technologies in approaching the tasks. Similarly, it becomes essential to discuss what types of activities students will do to learn and solve the problems in an environment where the use of technologies fosters and values the participation and collaboration of all students. What digital technologies are important to incorporate in problem solving approaches? Dynamic Geometry Systems can be considered as a milestone in the development of digital technologies. Objects or mathematical situations can be represented dynamically through the use of a Dynamic Geometry System and learners or problem solvers can identify and examine mathematical relations that emerge from moving objects within the dynamic model (Moreno-Armella and Santos-Trigo 2016 ).

Leung and Bolite-Frant ( 2015 ) stated that “dynamic geometry software can be used in task design to cover a large epistemic spectrum from drawing precise robust geometrical figures to exploration of new geometric theorems and development of argumentation discourse” (p. 195). As a result, learners not only need to develop skills and strategies to construct dynamic configuration of problems; but also ways of relying on the tool’s affordances (quantifying parameters or objects attributes, generating loci, graphing objects behaviours, using sliders, or dragging particular elements within the configuration) in order to identify and support mathematical relations. What does it mean to represent and explore an object or mathematical situation dynamically?

A simple task that involves a rhombus and its inscribed circle is used to illustrate how a dynamic representation of these objects and embedded elements can lead learners to identify and examine mathematical properties of those objects in the construction of the configuration. To this end, learners are encouraged to pose and pursue questions to explain the behaviours of parameters or attributes of the family of objects that is generated as a result of moving a particular element within the configuration.

1.3.5 A Task: A Dynamic Rhombus

Figure  2 represents a rhombus APDB and its inscribed circle (O is intersection of diagonals AD and BP and the radius of the inscribed circle is the perpendicular segment from any side of the rhombus to point O), vertex P lies on a circle c centred at point A. Circle c is only a heuristic to generate a family of rhombuses. Thus, point P can be moved along circle c to generate a family of rhombuses. Indeed, based on the symmetry of the circle it is sufficient to move P on the semicircle B’CA to draw such a family of rhombuses.

A dynamic construction of a rhombus

1.3.6 Posing Questions

A goal in constructing a dynamic model or configuration of problems is always to identify and explore mathematical properties and relations that might result from moving objects within the model. How do the areas of both the rhombus and the inscribed circle behave when point P is moved along the arc B’CB? At what position of point P does the area of the rhombus or inscribed circle reach the maximum value? The coordinates of points S and Q (Fig.  3 ) are the x -value of point P and as y -value the corresponding area values of rhombus ABDP and the inscribed circle respectively. Figure  2 shows the loci of points S and Q when point P is moved along arc B’CB. Here, finding the locus via the use of GeoGebra is another heuristic to graph the area behaviour without making explicit the algebraic model of the area.

Graphic representation of the area variation of the family of rhombuses and inscribed circles generated when P is moved through arc B’CB

The area graphs provide information to visualize that in that family of generated rhombuses the maximum area value of the inscribed circle and rhombus is reached when the rhombus becomes a square (Fig.  4 ). That is, the controlled movement of particular objects is an important strategy to analyse the area variation of the family of rhombuses and their inscribed circles.

Visualizing the rhombus and the inscribed circle with maximum area

It is important to observe the identification of points P and Q in terms of the position of point P and the corresponding areas and the movement of point P was sufficient to generate both area loci. That is, the graph representation of the areas is achieved without having an explicit algebraic expression of the area variation. Clearly, the graphic representations provide information regarding the increasing or decreasing interval of both areas; it is also important to explore what properties both graphic representations hold. The goal is to argue that the area variation of the rhombus represents an ellipse and the area of the inscribed circle represents a parabola. An initial argument might involve selecting five points on each locus and using the tool to draw the corresponding conic section (Fig.  5 ). In this case, the tool affordances play an important role in generating the graphic representation of the areas’ behaviours and in identifying properties of those representations. In this context, the use of the tool can offer learners the opportunity to problematize (Santos-Trigo 2007 ) a simple mathematical object (rhombus) as a means to search for mathematical relations and ways to support them.

Drawing the conic section that passes through five points

1.3.7 Looking for Different Solutions Methods

Another line of exploration might involve asking for ways to construct a rhombus and its inscribed circle: Suppose that the side of the rhombus and the circle are given, how can you construct the rhombus that has that circle inscribed? Figure  6 shows the given data, segment A 1 B 1 and circle centred at O and radius OD. The initial goal is to draw the circle tangent to the given segment. To this end, segment AB is congruent to segment A 1 B 1 and on this segment a point P is chosen and a perpendicular to segment AB that passes through point P is drawn. Point C is on this perpendicular and the centre of a circle with radius OD and h is the perpendicular to line PC that passes through point C. Angle ACB changes when point P is moved along segment AB and point E and F are the intersection of line h and the circle with centre M the midpoint of AB and radius MA (Fig.  6 ).

Drawing segment AB tangent to the given circle

Figure  7 a shows the right triangle AFB as the base to construct the rhombus and the inscribed circle and Fig.  7 b shows the second solution based on triangle AEB.

a Drawing the rhombus and the inscribed circle. b Drawing the second solution

Another approach might involve drawing the given circle centred at the origin and the segment as EF with point E on the y-axis. Line OC is perpendicular to segment EF and the locus of point C when point E moves along the y-axis intersects the given circle (Fig.  8 a, b). Both figures show two solutions to draw the rhombus that circumscribe the given circle.

a and b Another solution that involves finding a locus of point C

In this example, the GeoGebra affordances not only are important to construct a dynamic model of the task; but also offer learners and opportunity to explore relations that emerge from moving objects within the model. As a result, learners can rely on different concepts and strategies to solve the tasks. The idea in presenting this rhombus task is to illustrate that the use of a Dynamic Geometry System provides affordances for learners to construct dynamic representation of mathematical objects or problems, to move elements within the representation to pose questions or conjectures to explain invariants or patterns among involved parameters; to search for arguments to support emerging conjectures, and to develop a proper language to communicate results.

1.3.8 Looking Back

Conceptual frameworks used to explain learners’ construction of mathematical knowledge need to capture or take into account the different ways of reasoning that students might develop as a result of using a set of tools during the learning experiences. Figure  9 show some digital technologies that learners can use for specific purpose at the different stages of problem solving activities.

The coordinated use of digital tools to engage learners in problem solving experiences

The use of a dynamic system (GeoGebra) provides a set of affordances for learners to conceptualize and represent mathematical objects and tasks dynamically. In this process, affordances such as moving objects orderly (dragging), finding loci of objects, quantifying objects attributes (lengths, areas, angles, etc.), using sliders to vary parameters, and examining family of objects became important to look for invariance or objects relationships. Likewise, analysing the parameters or objects behaviours within the configuration might lead learners to identify properties to support emerging mathematical relations. Thus, with the use of the tool, learners might conceptualize mathematical tasks as an opportunity for them to engage in mathematical activities that include constructing dynamic models of tasks, formulating conjectures, and always looking for different arguments to support them. Similarly, learners can use an online platform to share their ideas, problem solutions or questions in a digital wall and others students can also share ideas or solution methods and engaged in mathematical discussions that extend mathematical classroom activities.

1.4 Problem Posing: An Overview for Further Progress—Uldarico Malaspina Jurado

Problem posing and problem solving are two essential aspects of the mathematical activity; however, researchers in mathematics education have not emphasized their attention on problem posing as much as problem solving. In that sense, due to its importance in the development of mathematical thinking in students since the first grades, we agree with Ellerton’s statement ( 2013 ): “for too long, successful problem solving has been lauded as the goal; the time has come for problem posing to be given a prominent but natural place in mathematics curricula and classrooms” (pp. 100–101); and due to its importance in teacher training, with Abu-Elwan’s statement ( 1999 ):

While teacher educators generally recognize that prospective teachers require guidance in mastering the ability to confront and solve problems, what is often overlooked is the critical fact that, as teachers, they must be able to go beyond the role as problem solvers. That is, in order to promote a classroom situation where creative problem solving is the central focus, the practitioner must become skillful in discovering and correctly posing problems that need solutions. (p. 1)

Scientists like Einstein and Infeld ( 1938 ), recognized not only for their notable contributions in the fields they worked, but also for their reflections on the scientific activity, pointed out the importance of problem posing; thus it is worthwhile to highlight their statement once again:

The formulation of a problem is often more essential than its solution, which may be merely a matter of mathematical or experimental skills. To raise new questions, new possibilities, to regard old questions from a new angle, requires creative imagination and marks real advance in science. (p. 92)

Certainly, it is also relevant to remember mathematician Halmos’s statement ( 1980 ): “I do believe that problems are the heart of mathematics, and I hope that as teachers (…) we will train our students to be better problem posers and problem solvers than we are” (p. 524).

An important number of researchers in mathematics education has focused on the importance of problem posing, and we currently have numerous, very important publications that deal with different aspects of problem posing related to the mathematics education of students in all educational levels and to teacher training.

1.4.1 A Retrospective Look

Kilpatrick ( 1987 ) marked a historical milestone in research related to problem posing and points out that “problem formulating should be viewed not only as a goal of instruction but also as a means of instruction” (Kilpatrick 1987 , p. 123); and he also emphasizes that, as part of students’ education, all of them should be given opportunities to live the experience of discovering and posing their own problems. Drawing attention to the few systematic studies on problem posing performed until then, Kilpatrick contributes defining some aspects that required studying and investigating as steps prior to a theoretical building, though he warns, “attempts to teach problem-formulating skills, of course, need not await a theory” (p. 124).

Kilpatrick refers to the “Source of problems” and points out how virtually all problems students solve have been posed by another person; however, in real life “many problems, if not most, must be created or discovered by the solver, who gives the problem an initial formulation” (p. 124). He also points out that problems are reformulated as they are being solved, and he relates this to investigation, reminding us what Davis ( 1985 ) states that, “what typically happens in a prolonged investigation is that problem formulation and problem solution go hand in hand, each eliciting the other as the investigation progresses” (p. 23). He also relates it to the experiences of software designers, who formulate an appropriate sequence of sub-problems to solve a problem. He poses that a subject to be examined by teachers and researchers “is whether, by drawing students’ attention to the reformulating process and given them practice in it, we can improve their problem solving performance” (p. 130). He also points out that problems may be a mathematical formulation as a result of exploring a situation and, in that sense, “school exercises in constructing mathematical models of a situation presented by the teacher are intended to provide students with experiences in formulating problems.” (p. 131).

Another important section of Kilpatrick’s work ( 1987 ) is Processes of Problem Formulating , in which he considers association, analogy, generalization and contradiction. He believes the use of concept maps to represent concept organization, as cognitive scientists Novak and Gowin suggest, might help to comprehend such concepts, stimulate creative thinking about them, and complement the ideas Brown and Walter ( 1983 ) give for problem posing by association. Further, in the section “Understanding and developing problem formulating abilities”, he poses several questions, which have not been completely answered yet, like “Perhaps the central issue from the point of view of cognitive science is what happens when someone formulates the problem? (…) What is the relation between problem formulating, problem solving and structured knowledge base? How rich a knowledge base is needed for problem formulating? (…) How does experience in problem formulating add to knowledge base? (…) What metacognitive processes are needed for problem formulating?”

It is interesting to realize that some of these questions are among the unanswered questions proposed and analyzed by Cai et al. ( 2015 ) in Chap. 1 of the book Mathematical Problem Posing (Singer et al. 2015 ). It is worth stressing the emphasis on the need to know the cognitive processes in problem posing, an aspect that Kilpatrick had already posed in 1987, as we just saw.

1.4.2 Researches and Didactic Experiences

Currently, there are a great number of publications related to problem posing, many of which are research and didactic experiences that gather the questions posed by Kilpatrick, which we just commented. Others came up naturally as reflections raised in the framework of problem solving, facing the natural requirement of having appropriate problems to use results and suggestions of researches on problem solving, or as a response to a thoughtful attitude not to resign to solving and asking students to solve problems that are always created by others. Why not learn and teach mathematics posing one’s own problems?

1.4.3 New Directions of Research

Singer et al. ( 2013 ) provides a broad view about problem posing that links problem posing experiences to general mathematics education; to the development of abilities, attitudes and creativity; and also to its interrelation with problem solving, and studies on when and how problem-solving sessions should take place. Likewise, it provides information about research done regarding ways to pose new problems and about the need for teachers to develop abilities to handle complex situations in problem posing contexts.

Singer et al. ( 2013 ) identify new directions in problem posing research that go from problem-posing task design to the development of problem-posing frameworks to structure and guide teachers and students’ problem posing experiences. In a chapter of this book, Leikin refers to three different types of problem posing activities, associated with school mathematics research: (a) problem posing through proving; (b) problem posing for investigation; and (c) problem posing through investigation. This classification becomes evident in the problems posed in a course for prospective secondary school mathematics teachers by using a dynamic geometry environment. Prospective teachers posed over 25 new problems, several of which are discussed in the article. The author considers that, by developing this type of problem posing activities, prospective mathematics teachers may pose different problems related to a geometric object, prepare more interesting lessons for their students, and thus gradually develop their mathematical competence and their creativity.

1.4.4 Final Comments

This overview, though incomplete, allows us to see a part of what problem posing experiences involve and the importance of this area in students mathematical learning. An important task is to continue reflecting on the questions posed by Kilpatrick ( 1987 ), as well as on the ones that come up in the different researches aforementioned. To continue progressing in research on problem posing and contribute to a greater consolidation of this research line, it will be really important that all mathematics educators pay more attention to problem posing, seek to integrate approaches and results, and promote joint and interdisciplinary works. As Singer et al. ( 2013 ) say, going back to Kilpatrick’s proposal ( 1987 ),

Problem posing is an old issue. What is new is the awareness that problem posing needs to pervade the education systems around the world, both as a means of instruction (…) and as an object of instruction (…) with important targets in real-life situations. (p. 5)

Although it can be argued that there is a difference between creativity, discovery, and invention (see Liljedahl and Allan 2014 ) for the purposes of this book these will be assumed to be interchangeable.

Abu-Elwan, R. (1999). The development of mathematical problem posing skills for prospective middle school teachers. In A. Rogerson (Ed.), Proceedings of the International Conference on Mathematical Education into the 21st century: Social Challenges, Issues and Approaches , (Vol. 2, pp. 1–8), Cairo, Egypt.

Google Scholar  

Ashcraft, M. (1989). Human memory and cognition . Glenview, Illinois: Scott, Foresman and Company.

Bailin, S. (1994). Achieving extraordinary ends: An essay on creativity . Norwood, NJ: Ablex Publishing Corporation.

Bibby, T. (2002). Creativity and logic in primary-school mathematics: A view from the classroom. For the Learning of Mathematics, 22 (3), 10–13.

Brown, S., & Walter, M. (1983). The art of problem posing . Philadelphia: Franklin Institute Press.

Bruder, R. (2000). Akzentuierte Aufgaben und heuristische Erfahrungen. In W. Herget & L. Flade (Eds.), Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen (pp. 69–78). Berlin: Volk und Wissen.

Bruder, R. (2005). Ein aufgabenbasiertes anwendungsorientiertes Konzept für einen nachhaltigen Mathematikunterricht—am Beispiel des Themas “Mittelwerte”. In G. Kaiser & H. W. Henn (Eds.), Mathematikunterricht im Spannungsfeld von Evolution und Evaluation (pp. 241–250). Hildesheim, Berlin: Franzbecker.

Bruder, R., & Collet, C. (2011). Problemlösen lernen im Mathematikunterricht . Berlin: CornelsenVerlag Scriptor.

Bruner, J. (1964). Bruner on knowing . Cambridge, MA: Harvard University Press.

Burton, L. (1999). Why is intuition so important to mathematicians but missing from mathematics education? For the Learning of Mathematics, 19 (3), 27–32.

Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F.M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp.3–34). Springer.

Churchill, D., Fox, B., & King, M. (2016). Framework for designing mobile learning environments. In D. Churchill, J. Lu, T. K. F. Chiu, & B. Fox (Eds.), Mobile learning design (pp. 20–36)., lecture notes in educational technology NY: Springer.

Chapter   Google Scholar  

Collet, C. (2009). Problemlösekompetenzen in Verbindung mit Selbstregulation fördern. Wirkungsanalysen von Lehrerfortbildungen. In G. Krummheuer, & A. Heinze (Eds.), Empirische Studien zur Didaktik der Mathematik , Band 2, Münster: Waxmann.

Collet, C., & Bruder, R. (2008). Longterm-study of an intervention in the learning of problem-solving in connection with self-regulation. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano, & A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of PME 32 and PME-NA XXX, (Vol. 2, pp. 353–360).

Csíkszentmihályi, M. (1996). Creativity: Flow and the psychology of discovery and invention . New York: Harper Perennial.

Davis, P. J. (1985). What do I know? A study of mathematical self-awareness. College Mathematics Journal, 16 (1), 22–41.

Article   Google Scholar  

Dewey, J. (1933). How we think . Boston, MA: D.C. Heath and Company.

Dewey, J. (1938). Logic: The theory of inquiry . New York, NY: Henry Holt and Company.

Einstein, A., & Infeld, L. (1938). The evolution of physics . New York: Simon and Schuster.

Ellerton, N. (2013). Engaging pre-service middle-school teacher-education students in mathematical problem posing: Development of an active learning framework. Educational Studies in Math, 83 (1), 87–101.

Engel, A. (1998). Problem-solving strategies . New York, Berlin und Heidelberg: Springer.

English, L. (1997). Children’s reasoning processes in classifying and solving comparison word problems. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 191–220). Mahwah, NJ: Lawrence Erlbaum Associates Inc.

English, L. (1998). Reasoning by analogy in solving comparison problems. Mathematical Cognition, 4 (2), 125–146.

English, L. D. & Gainsburg, J. (2016). Problem solving in a 21st- Century mathematics education. In L. D. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (pp. 313–335). NY: Routledge.

Ghiselin, B. (1952). The creative process: Reflections on invention in the arts and sciences . Berkeley, CA: University of California Press.

Hadamard, J. (1945). The psychology of invention in the mathematical field . New York, NY: Dover Publications.

Halmos, P. (1980). The heart of mathematics. American Mathematical Monthly, 87 , 519–524.

Halmos, P. R. (1994). What is teaching? The American Mathematical Monthly, 101 (9), 848–854.

Hoyles, C., & Lagrange, J.-B. (Eds.). (2010). Mathematics education and technology–Rethinking the terrain. The 17th ICMI Study . NY: Springer.

Kilpatrick, J. (1985). A retrospective account of the past 25 years of research on teaching mathematical problem solving. In E. Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 1–15). Hillsdale, New Jersey: Lawrence Erlbaum.

Kilpatrick, J. (1987). Problem formulating: Where do good problem come from? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123–147). Hillsdale, NJ: Erlbaum.

Kline, M. (1972). Mathematical thought from ancient to modern times . NY: Oxford University Press.

Kneller, G. (1965). The art and science of creativity . New York, NY: Holt, Reinhart, and Winstone Inc.

Koestler, A. (1964). The act of creation . New York, NY: The Macmillan Company.

König, H. (1984). Heuristik beim Lösen problemhafter Aufgaben aus dem außerunterrichtlichen Bereich . Technische Hochschule Chemnitz, Sektion Mathematik.

Kretschmer, I. F. (1983). Problemlösendes Denken im Unterricht. Lehrmethoden und Lernerfolge . Dissertation. Frankfurt a. M.: Peter Lang.

Krulik, S. A., & Reys, R. E. (Eds.). (1980). Problem solving in school mathematics. Yearbook of the national council of teachers of mathematics . Reston VA: NCTM.

Krutestkii, V. A. (1976). The psychology of mathematical abilities in school children . University of Chicago Press.

Lesh, R., & Zawojewski, J. S. (2007). Problem solving and modeling. In F. K. Lester, Jr. (Ed.), The second handbook of research on mathematics teaching and learning (pp. 763–804). National Council of Teachers of Mathematics, Charlotte, NC: Information Age Publishing.  

Lester, F., & Kehle, P. E. (2003). From problem solving to modeling: The evolution of thinking about research on complex mathematical activity. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning and teaching (pp. 501–518). Mahwah, NJ: Lawrence Erlbaum.

Lester, F. K., Garofalo, J., & Kroll, D. (1989). The role of metacognition in mathematical problem solving: A study of two grade seven classes. Final report to the National Science Foundation, NSF Project No. MDR 85-50346. Bloomington: Indiana University, Mathematics Education Development Center.

Leung, A., & Bolite-Frant, J. (2015). Designing mathematical tasks: The role of tools. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education (pp. 191–225). New York: Springer.

Liljedahl, P. (2008). The AHA! experience: Mathematical contexts, pedagogical implications . Saarbrücken, Germany: VDM Verlag.

Liljedahl, P., & Allan, D. (2014). Mathematical discovery. In E. Carayannis (Ed.), Encyclopedia of creativity, invention, innovation, and entrepreneurship . New York, NY: Springer.

Liljedahl, P., & Sriraman, B. (2006). Musings on mathematical creativity. For the Learning of Mathematics, 26 (1), 20–23.

Lompscher, J. (1975). Theoretische und experimentelle Untersuchungen zur Entwicklung geistiger Fähigkeiten . Berlin: Volk und Wissen. 2. Auflage.

Lompscher, J. (1985). Die Lerntätigkeit als dominierende Tätigkeit des jüngeren Schulkindes. In L. Irrlitz, W. Jantos, E. Köster, H. Kühn, J. Lompscher, G. Matthes, & G. Witzlack (Eds.), Persönlichkeitsentwicklung in der Lerntätigkeit . Berlin: Volk und Wissen.

Mason, J., & Johnston-Wilder, S. (2006). Designing and using mathematical tasks . St. Albans: Tarquin Publications.

Mason, J., Burton, L., & Stacey, K. (1982). Thinking mathematically . Harlow: Pearson Prentice Hall.

Mayer, R. (1982). The psychology of mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 1–13). Philadelphia, PA: Franklin Institute Press.

Mevarech, Z. R., & Kramarski, B. (1997). IMPROVE: A multidimensional method for teaching mathematics in heterogeneous classrooms. American Educational Research Journal, 34 (2), 365–394.

Mevarech, Z. R., & Kramarski, B. (2003). The effects of metacognitive training versus worked-out examples on students’ mathematical reasoning. British Journal of Educational Psychology, 73 , 449–471.

Moreno-Armella, L., & Santos-Trigo, M. (2016). The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (3rd ed., pp. 595–616). New York: Taylor and Francis.

National Council of Teachers of Mathematics (NCTM). (1980). An agenda for action . Reston, VA: NCTM.

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA: National Council of Teachers of Mathematics.

Newman, J. (2000). The world of mathematics (Vol. 4). New York, NY: Dover Publishing.

Novick, L. (1988). Analogical transfer, problem similarity, and expertise. Journal of Educational Psychology: Learning, Memory, and Cognition, 14 (3), 510–520.

Novick, L. (1990). Representational transfer in problem solving. Psychological Science, 1 (2), 128–132.

Novick, L. (1995). Some determinants of successful analogical transfer in the solution of algebra word problems. Thinking & Reasoning, 1 (1), 5–30.

Novick, L., & Holyoak, K. (1991). Mathematical problem solving by analogy. Journal of Experimental Psychology, 17 (3), 398–415.

Pehkonen, E. K. (1991). Developments in the understanding of problem solving. ZDM—The International Journal on Mathematics Education, 23 (2), 46–50.

Pehkonen, E. (1997). The state-of-art in mathematical creativity. Analysis, 97 (3), 63–67.

Perels, F., Schmitz, B., & Bruder, R. (2005). Lernstrategien zur Förderung von mathematischer Problemlösekompetenz. In C. Artelt & B. Moschner (Eds.), Lernstrategien und Metakognition. Implikationen für Forschung und Praxis (pp. 153–174). Waxmann education.

Perkins, D. (2000). Archimedes’ bathtub: The art of breakthrough thinking . New York, NY: W.W. Norton and Company.

Poincaré, H. (1952). Science and method . New York, NY: Dover Publications Inc.

Pólya, G. (1945). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1949). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1954). Mathematics and plausible reasoning . Princeton: Princeton University Press.

Pólya, G. (1964). Die Heuristik. Versuch einer vernünftigen Zielsetzung. Der Mathematikunterricht , X (1), 5–15.

Pólya, G. (1965). Mathematical discovery: On understanding, learning and teaching problem solving (Vol. 2). New York, NY: Wiley.

Resnick, L., & Glaser, R. (1976). Problem solving and intelligence. In L. B. Resnick (Ed.), The nature of intelligence (pp. 230–295). Hillsdale, NJ: Lawrence Erlbaum Associates.

Rusbult, C. (2000). An introduction to design . http://www.asa3.org/ASA/education/think/intro.htm#process . Accessed January 10, 2016.

Santos-Trigo, M. (2007). Mathematical problem solving: An evolving research and practice domain. ZDM—The International Journal on Mathematics Education , 39 (5, 6): 523–536.

Santos-Trigo, M. (2014). Problem solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 496–501). New York: Springer.

Schmidt, E., & Cohen, J. (2013). The new digital age. Reshaping the future of people nations and business . NY: Alfred A. Knopf.

Schoenfeld, A. H. (1979). Explicit heuristic training as a variable in problem-solving performance. Journal for Research in Mathematics Education, 10 , 173–187.

Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.

Schoenfeld, A. H. (1985). Mathematical problem solving . Orlando, Florida: Academic Press Inc.

Schoenfeld, A. H. (1987). What’s all the fuss about metacognition? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 189–215). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York, NY: Simon and Schuster.

Schön, D. (1987). Educating the reflective practitioner . San Fransisco, CA: Jossey-Bass Publishers.

Sewerin, H. (1979): Mathematische Schülerwettbewerbe: Beschreibungen, Analysen, Aufgaben, Trainingsmethoden mit Ergebnissen . Umfrage zum Bundeswettbewerb Mathematik. München: Manz.

Silver, E. (1982). Knowledge organization and mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 15–25). Philadelphia: Franklin Institute Press.

Singer, F., Ellerton, N., & Cai, J. (2013). Problem posing research in mathematics education: New questions and directions. Educational Studies in Mathematics, 83 (1), 9–26.

Singer, F. M., Ellerton, N. F., & Cai, J. (Eds.). (2015). Mathematical problem posing. From research to practice . NY: Springer.

Törner, G., Schoenfeld, A. H., & Reiss, K. M. (2007). Problem solving around the world: Summing up the state of the art. ZDM—The International Journal on Mathematics Education, 39 (1), 5–6.

Verschaffel, L., de Corte, E., Lasure, S., van Vaerenbergh, G., Bogaerts, H., & Ratinckx, E. (1999). Learning to solve mathematical application problems: A design experiment with fifth graders. Mathematical Thinking and Learning, 1 (3), 195–229.

Wallas, G. (1926). The art of thought . New York: Harcourt Brace.

Watson, A., & Ohtani, M. (2015). Themes and issues in mathematics education concerning task design: Editorial introduction. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education, an ICMI Study 22 (pp. 3–15). NY: Springer.

Zimmermann, B. (1983). Problemlösen als eine Leitidee für den Mathematikunterricht. Ein Bericht über neuere amerikanische Beiträge. Der Mathematikunterricht, 3 (1), 5–45.

Further Reading

Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex, and setting . Buckingham, PA: Open University Press.

Borwein, P., Liljedahl, P., & Zhai, H. (2014). Mathematicians on creativity. Mathematical Association of America.

Burton, L. (1984). Thinking things through . London, UK: Simon & Schuster Education.

Feynman, R. (1999). The pleasure of finding things out . Cambridge, MA: Perseus Publishing.

Gardner, M. (1978). Aha! insight . New York, NY: W. H. Freeman and Company.

Gardner, M. (1982). Aha! gotcha: Paradoxes to puzzle and delight . New York, NY: W. H. Freeman and Company.

Gardner, H. (1993). Creating minds: An anatomy of creativity seen through the lives of Freud, Einstein, Picasso, Stravinsky, Eliot, Graham, and Ghandi . New York, NY: Basic Books.

Glas, E. (2002). Klein’s model of mathematical creativity. Science & Education, 11 (1), 95–104.

Hersh, D. (1997). What is mathematics, really? . New York, NY: Oxford University Press.

Root-Bernstein, R., & Root-Bernstein, M. (1999). Sparks of genius: The thirteen thinking tools of the world’s most creative people . Boston, MA: Houghton Mifflin Company.

Zeitz, P. (2006). The art and craft of problem solving . New York, NY: Willey.

Download references

Author information

Authors and affiliations.

Faculty of Education, Simon Fraser University, Burnaby, BC, Canada

Peter Liljedahl

Mathematics Education Department, Cinvestav-IPN, Centre for Research and Advanced Studies, Mexico City, Mexico

Manuel Santos-Trigo

Pontificia Universidad Católica del Perú, Lima, Peru

Uldarico Malaspina

Technical University Darmstadt, Darmstadt, Germany

Regina Bruder

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Peter Liljedahl .

Rights and permissions

Open Access This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.

The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.

Reprints and permissions

Copyright information

© 2016 The Author(s)

About this chapter

Liljedahl, P., Santos-Trigo, M., Malaspina, U., Bruder, R. (2016). Problem Solving in Mathematics Education. In: Problem Solving in Mathematics Education. ICME-13 Topical Surveys. Springer, Cham. https://doi.org/10.1007/978-3-319-40730-2_1

Download citation

DOI : https://doi.org/10.1007/978-3-319-40730-2_1

Published : 28 June 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-40729-6

Online ISBN : 978-3-319-40730-2

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Examples for

Mathematical Word Problems

Math word problems is one of the most complex parts of the elementary math curriculum since translating text into symbolic math is required to solve the problem. Because the Wolfram Language has powerful symbolic computation ability, Wolfram|Alpha can interpret basic mathematical word problems and give descriptive results.

Word Problems

Solve a word problem and explore related facts.

Solve a word problem:

Related examples.

The Robots That Will Change the World Are Already Among Us

Climate change more like ecosocial crisis, openmind books, scientific anniversaries, kary mullis, the genius of a scientist, the eccentricity of a celebrity, featured author, latest book, solving problems visually.

What’s the best way to approach (and successfully solve) a mathematical problem statement? Perhaps by drawing a picture? That, at least, is the conclusion of a striking new study by researchers at the Universities of Geneva and Burgundy.

It’s not a trivial assumption. It is thought that when we face a mathematical problem that contains both mathematical information (numbers and arithmetic operations) and non-mathematical information (the context of the problem and the characteristics of the entities involved), our brains process this combination of verbal and numerical information and convert it into a mental representation in order to identify the best strategy for solving it. On the other hand, more and more studies suggest that the schematic drawings that are usually made to solve this type of problem are a reflection of these mental representations.

Game 1: Not a game, an experiment

In the study, participants were asked to solve 12 simple arithmetic problems in as few steps as possible and to draw a picture that would help them understand and solve the problem.

Here are two of these problems, and we invite you to solve them in the same way: in as few steps as possible, and with a drawing to help you understand the problem.

Problem 1 : Paul has five red marbles and also has some blue marbles. In total he has eleven marbles. Julie’s marbles are green and blue. Julie has as many blue marbles as Paul and also has two fewer green marbles than Paul has red marbles. How many marbles does Julie have?

Problem 2 : Lisa takes the train during the day, travels for 5 hours and arrives at her destination at 11am. Fred got on the train at the same time as Lisa and his trip took 2 hours less. What time did Fred arrive at his destination?

Independently of the above, many studies postulate that relying on drawings, diagrams or other types of graphical representations when processing information has numerous benefits: it improves our ability to learn and remember, it helps us to understand complex concepts, it reinforces critical and scientific thinking, and it fosters a transversal and interdisciplinary interpretation. And from a mathematical point of view, using these representations makes it easier to establish the relationships between different data, to visualise the information implicit in the statement and to identify the most direct and simplest solution strategy.

Use the drawings to answer these complex and hieroglyphic questions.

A recent study goes a step further by suggesting that the verbal information in the problem statement influences the type of diagram shown and also the strategy chosen to solve the problem. More specifically, the study has found that the type of diagram preferentially chosen depends on whether the statement is cardinal or ordinal in nature.

Thus, when the context alludes to the cardinal properties of the quantities involved—the number of elements in a set—a drawing based on groupings of entities (crosses, circles, etc.) that sometimes overlap (or intersect) is usually chosen. This in turn leads to a three-step arithmetic strategy. On the other hand, when the statement of the problem focuses on the ordinal properties of numbers—the position they occupy in a set—we usually opt for drawings based on axes, graduations or intervals, which lead to a more direct and simpler one-step solution strategy.

And this is observed even when the problems are analogous from a mathematical point of view: they have the same structure, the same numerical values and can be solved with the same strategy (as in the case of the two problems in Game 1).

But perhaps the most interesting reflection is that, knowing this, it is possible to guide and train the student to apply this second type of diagram, thereby facilitating the identification of the best way to solve it.

Game 3:  A high-flying challenge

Sara wants to travel from Madrid to Tokyo. To do so, she flies first to New York, from where she takes a plane to London and from there to Tokyo.

Paul also wants to go from Madrid to Tokyo, but in his case he flies directly from Madrid to London and then takes a flight to Tokyo.

If Sara flies for a total of 27hrs 15min and Paul for 14hrs 30min, and given that the flight from New York to London takes 4hrs 45min longer than the flight from Madrid to London, and the flight from London to Tokyo takes 12 hours, how long is the flight from Madrid to New York?

And if both Sara and Paul lose only one hour at each stopover, what will the local time be when they each arrive in Tokyo if they both depart Madrid at 2pm?

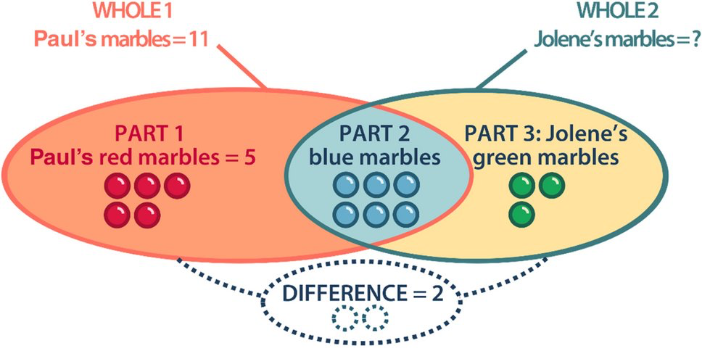
            M                                 NY    M-L + 4:45   L                    12:00 h                   T

                                                   M           L                                       12:00 h                    T 

14 hrs 30 min

The Madrid-London flight takes 2hrs 30min. New York to London is 2hrs 30min + 4hrs 45min = 7hrs 15min. And the Madrid to New York flight is 27hrs 15min – 12hrs – 7hrs 15min = 8 hours.

With this, and bearing in mind that each stopover only takes one hour:

If Sara leaves at 2pm from Madrid then: 2pm + 8hrs – 6hrs (time difference) + 1hr (at NY airport) + 7hrs 15min + 5hrs (time difference) + 1hr + 12hrs + 8hrs (time difference) = 2:15am on day 3.

In Paul’s case: 2pm + 2hrs 30min – 1hr (time difference) + 1hr + 12hrs + 8hrs (time difference) = 12:30pm on day 2.

Miguel Barral

Related publications.

• What Purpose Do the Great Mathematical Problems Serve?
• David Hilbert: The Architect of Modern Mathematics
• Magic Squares: When Art is Squared With Mathematics

More about Science

Environment, leading figures, mathematics, scientific insights, more publications about ventana al conocimiento (knowledge window), comments on this publication.

Morbi facilisis elit non mi lacinia lacinia. Nunc eleifend aliquet ipsum, nec blandit augue tincidunt nec. Donec scelerisque feugiat lectus nec congue. Quisque tristique tortor vitae turpis euismod, vitae aliquam dolor pretium. Donec luctus posuere ex sit amet scelerisque. Etiam sed neque magna. Mauris non scelerisque lectus. Ut rutrum ex porta, tristique mi vitae, volutpat urna.

Sed in semper tellus, eu efficitur ante. Quisque felis orci, fermentum quis arcu nec, elementum malesuada magna. Nulla vitae finibus ipsum. Aenean vel sapien a magna faucibus tristique ac et ligula. Sed auctor orci metus, vitae egestas libero lacinia quis. Nulla lacus sapien, efficitur mollis nisi tempor, gravida tincidunt sapien. In massa dui, varius vitae iaculis a, dignissim non felis. Ut sagittis pulvinar nisi, at tincidunt metus venenatis a. Ut aliquam scelerisque interdum. Mauris iaculis purus in nulla consequat, sed fermentum sapien condimentum. Aliquam rutrum erat lectus, nec placerat nisl mollis id. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Nam nisl nisi, efficitur et sem in, molestie vulputate libero. Quisque quis mattis lorem. Nunc quis convallis diam, id tincidunt risus. Donec nisl odio, convallis vel porttitor sit amet, lobortis a ante. Cras dapibus porta nulla, at laoreet quam euismod vitae. Fusce sollicitudin massa magna, eu dignissim magna cursus id. Quisque vel nisl tempus, lobortis nisl a, ornare lacus. Donec ac interdum massa. Curabitur id diam luctus, mollis augue vel, interdum risus. Nam vitae tortor erat. Proin quis tincidunt lorem.

Do you want to stay up to date with our new publications?

Receive the OpenMind newsletter with all the latest contents published on our website

OpenMind Books

• The Search for Alternatives to Fossil Fuels
• View all books

About OpenMind

Connect with us.

• Keep up to date with our newsletter

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.6: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 132869

• Michelle Manes
• University of Hawaii

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solve them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching  effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, How to Solve it . Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

A Problem Solving Strategy: Try Something!

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

Note that being "good at mathematics" is not about doing things right the first time. It is about figuring things out. Practice being okay with having done something incorrectly. Try to avoid using an eraser and just lightly cross out incorrect work (do not black out the entire thing). This way if it turns out that you did something useful, you still have that work to reference! If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what was left after paying Brianna. Finally, Alex saw David and gave him 1/2 of the remaining money. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

A Problem Solving Strategy: Draw a Picture

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

A Problem Solving Strategy: Make Up Numbers

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

Try this: Assume (that is, pretend) Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person.

Or try working backward: suppose Alex has some specific amount left at the end, say $10. Since he gave David half of what he had before seeing David, that means he had $20 before running into David. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

Most people want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. Instead of asking the teacher, “Is this right?”, you should be ready to justify it and say, “Here’s my answer, and here is how I got it.”

A Problem Solving Strategy: Try a Simpler Problem

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said, “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

The ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

A Problem Solving Strategy: Work Systematically

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

A Problem Solving Strategy: Use Manipulatives to Help You Investigate

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

A Problem Solving Strategy: Look for and Explain Patterns

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table. If possible, actually describe these to a friend.
• Explain and justify any of the patterns you see (if possible, actually do this with a friend). If you don't have a partner to work with, imagine they asked you, "How can you be sure the patterns will continue?"
• Expand this to find what calculation(s) you would perform to find the total number of squares on a 100 × 100 chess board.

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What progress have you made?

A Problem Solving Strategy: Find the Math, Remove the Context

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

A Problem Solving Strategy: Check Your Assumptions

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.