general form of hypothesis

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base

Methodology

How to Write a Strong Hypothesis | Steps & Examples

How to Write a Strong Hypothesis | Steps & Examples

Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.

A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .

Example: Hypothesis

Daily apple consumption leads to fewer doctor’s visits.

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Variables in hypotheses

Hypotheses propose a relationship between two or more types of variables .

An independent variable is something the researcher changes or controls.
A dependent variable is something the researcher observes and measures.

If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias will affect your results.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Prevent plagiarism. Run a free check.

Step 1. ask a question.

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2. Do some preliminary research

Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.

At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.

Step 3. Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

4. Refine your hypothesis

You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:

The relevant variables
The specific group being studied
The predicted outcome of the experiment or analysis

5. Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.

If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.

Sampling methods
Simple random sampling
Stratified sampling
Cluster sampling
Likert scales
Reproducibility

Statistics

Null hypothesis
Statistical power
Probability distribution
Effect size
Poisson distribution

Research bias

Optimism bias
Cognitive bias
Implicit bias
Hawthorne effect
Anchoring bias
Explicit bias

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved March 30, 2024, from https://www.scribbr.com/methodology/hypothesis/

Is this article helpful?

Shona McCombes

Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, unlimited academic ai-proofreading.

✔ Document error-free in 5minutes ✔ Unlimited document corrections ✔ Specialized in correcting academic texts

Bipolar Disorder
Therapy Center
When To See a Therapist
Types of Therapy
Best Online Therapy
Best Couples Therapy
Best Family Therapy
Managing Stress
Sleep and Dreaming
Understanding Emotions
Self-Improvement
Healthy Relationships
Student Resources
Personality Types
Verywell Mind Insights
2023 Verywell Mind 25
Mental Health in the Classroom
Editorial Process
Meet Our Review Board
Crisis Support

How to Write a Great Hypothesis

Hypothesis Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk, "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis, operational definitions, types of hypotheses, hypotheses examples.

Collecting Data

Frequently Asked Questions

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study.

One hypothesis example would be a study designed to look at the relationship between sleep deprivation and test performance might have a hypothesis that states: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

Forming a question
Performing background research
Creating a hypothesis
Designing an experiment
Collecting data
Analyzing the results
Drawing conclusions
Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. It is only at this point that researchers begin to develop a testable hypothesis. Unless you are creating an exploratory study, your hypothesis should always explain what you expect to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore a number of factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment do not support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk wisdom that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

Is your hypothesis based on your research on a topic?
Can your hypothesis be tested?
Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the journal articles you read . Many authors will suggest questions that still need to be explored.

To form a hypothesis, you should take these steps:

Collect as many observations about a topic or problem as you can.
Evaluate these observations and look for possible causes of the problem.
Create a list of possible explanations that you might want to explore.
After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method , falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that if something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in a number of different ways. One of the basic principles of any type of scientific research is that the results must be replicable. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. How would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

In order to measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming other people. In this situation, the researcher might utilize a simulated task to measure aggressiveness.

Hypothesis Checklist

Does your hypothesis focus on something that you can actually test?
Does your hypothesis include both an independent and dependent variable?
Can you manipulate the variables?
Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

Simple hypothesis : This type of hypothesis suggests that there is a relationship between one independent variable and one dependent variable.
Complex hypothesis : This type of hypothesis suggests a relationship between three or more variables, such as two independent variables and a dependent variable.
Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative sample of the population and then generalizes the findings to the larger group.
Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the dependent variable if you change the independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

"Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
Complex hypothesis: "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."
"Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."

Examples of a complex hypothesis include:

"People with high-sugar diets and sedentary activity levels are more likely to develop depression."
"Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

"Children who receive a new reading intervention will have scores different than students who do not receive the intervention."
"There will be no difference in scores on a memory recall task between children and adults."

Examples of an alternative hypothesis:

"Children who receive a new reading intervention will perform better than students who did not receive the intervention."
"Adults will perform better on a memory task than children."

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as case studies , naturalistic observations , and surveys are often used when it would be impossible or difficult to conduct an experiment . These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a correlational study can then be used to look at how the variables are related. This type of research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually cause another to change.

A Word From Verywell

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Some examples of how to write a hypothesis include:

"Staying up late will lead to worse test performance the next day."
"People who consume one apple each day will visit the doctor fewer times each year."
"Breaking study sessions up into three 20-minute sessions will lead to better test results than a single 60-minute study session."

The four parts of a hypothesis are:

The research question
The independent variable (IV)
The dependent variable (DV)
The proposed relationship between the IV and DV

Castillo M. The scientific method: a need for something better? . AJNR Am J Neuroradiol. 2013;34(9):1669-71. doi:10.3174/ajnr.A3401

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

Knowledge Base
Methodology
How to Write a Strong Hypothesis | Guide & Examples

How to Write a Strong Hypothesis | Guide & Examples

Published on 6 May 2022 by Shona McCombes .

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, frequently asked questions about writing hypotheses.

Variables in hypotheses

Hypotheses propose a relationship between two or more variables . An independent variable is something the researcher changes or controls. A dependent variable is something the researcher observes and measures.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Prevent plagiarism, run a free check.

Step 1: ask a question.

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2: Do some preliminary research

At this stage, you might construct a conceptual framework to identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalise more complex constructs.

Step 3: Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

Step 4: Refine your hypothesis

The relevant variables
The specific group being studied
The predicted outcome of the experiment or analysis

Step 5: Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

Step 6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis. The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

McCombes, S. (2022, May 06). How to Write a Strong Hypothesis | Guide & Examples. Scribbr. Retrieved 25 March 2024, from https://www.scribbr.co.uk/research-methods/hypothesis-writing/

Is this article helpful?

Shona McCombes

Other students also liked, operationalisation | a guide with examples, pros & cons, what is a conceptual framework | tips & examples, a quick guide to experimental design | 5 steps & examples.

Choose Your Test

Sat / act prep online guides and tips, what is a hypothesis and how do i write one.

General Education

Think about something strange and unexplainable in your life. Maybe you get a headache right before it rains, or maybe you think your favorite sports team wins when you wear a certain color. If you wanted to see whether these are just coincidences or scientific fact, you would form a hypothesis, then create an experiment to see whether that hypothesis is true or not.

But what is a hypothesis, anyway? If you’re not sure about what a hypothesis is--or how to test for one!--you’re in the right place. This article will teach you everything you need to know about hypotheses, including:

Defining the term “hypothesis”
Providing hypothesis examples
Giving you tips for how to write your own hypothesis

So let’s get started!

What Is a Hypothesis?

Merriam Webster defines a hypothesis as “an assumption or concession made for the sake of argument.” In other words, a hypothesis is an educated guess . Scientists make a reasonable assumption--or a hypothesis--then design an experiment to test whether it’s true or not. Keep in mind that in science, a hypothesis should be testable. You have to be able to design an experiment that tests your hypothesis in order for it to be valid.

As you could assume from that statement, it’s easy to make a bad hypothesis. But when you’re holding an experiment, it’s even more important that your guesses be good...after all, you’re spending time (and maybe money!) to figure out more about your observation. That’s why we refer to a hypothesis as an educated guess--good hypotheses are based on existing data and research to make them as sound as possible.

Hypotheses are one part of what’s called the scientific method . Every (good) experiment or study is based in the scientific method. The scientific method gives order and structure to experiments and ensures that interference from scientists or outside influences does not skew the results. It’s important that you understand the concepts of the scientific method before holding your own experiment. Though it may vary among scientists, the scientific method is generally made up of six steps (in order):

Observation
Asking questions
Forming a hypothesis
Analyze the data
Communicate your results

You’ll notice that the hypothesis comes pretty early on when conducting an experiment. That’s because experiments work best when they’re trying to answer one specific question. And you can’t conduct an experiment until you know what you’re trying to prove!

Independent and Dependent Variables

After doing your research, you’re ready for another important step in forming your hypothesis: identifying variables. Variables are basically any factor that could influence the outcome of your experiment . Variables have to be measurable and related to the topic being studied.

There are two types of variables: independent variables and dependent variables. I ndependent variables remain constant . For example, age is an independent variable; it will stay the same, and researchers can look at different ages to see if it has an effect on the dependent variable.

Speaking of dependent variables... dependent variables are subject to the influence of the independent variable , meaning that they are not constant. Let’s say you want to test whether a person’s age affects how much sleep they need. In that case, the independent variable is age (like we mentioned above), and the dependent variable is how much sleep a person gets.

Variables will be crucial in writing your hypothesis. You need to be able to identify which variable is which, as both the independent and dependent variables will be written into your hypothesis. For instance, in a study about exercise, the independent variable might be the speed at which the respondents walk for thirty minutes, and the dependent variable would be their heart rate. In your study and in your hypothesis, you’re trying to understand the relationship between the two variables.

Elements of a Good Hypothesis

The best hypotheses start by asking the right questions . For instance, if you’ve observed that the grass is greener when it rains twice a week, you could ask what kind of grass it is, what elevation it’s at, and if the grass across the street responds to rain in the same way. Any of these questions could become the backbone of experiments to test why the grass gets greener when it rains fairly frequently.

As you’re asking more questions about your first observation, make sure you’re also making more observations . If it doesn’t rain for two weeks and the grass still looks green, that’s an important observation that could influence your hypothesis. You'll continue observing all throughout your experiment, but until the hypothesis is finalized, every observation should be noted.

Finally, you should consult secondary research before writing your hypothesis . Secondary research is comprised of results found and published by other people. You can usually find this information online or at your library. Additionally, m ake sure the research you find is credible and related to your topic. If you’re studying the correlation between rain and grass growth, it would help you to research rain patterns over the past twenty years for your county, published by a local agricultural association. You should also research the types of grass common in your area, the type of grass in your lawn, and whether anyone else has conducted experiments about your hypothesis. Also be sure you’re checking the quality of your research . Research done by a middle school student about what minerals can be found in rainwater would be less useful than an article published by a local university.

Writing Your Hypothesis

Once you’ve considered all of the factors above, you’re ready to start writing your hypothesis. Hypotheses usually take a certain form when they’re written out in a research report.

When you boil down your hypothesis statement, you are writing down your best guess and not the question at hand . This means that your statement should be written as if it is fact already, even though you are simply testing it.

The reason for this is that, after you have completed your study, you'll either accept or reject your if-then or your null hypothesis. All hypothesis testing examples should be measurable and able to be confirmed or denied. You cannot confirm a question, only a statement!

In fact, you come up with hypothesis examples all the time! For instance, when you guess on the outcome of a basketball game, you don’t say, “Will the Miami Heat beat the Boston Celtics?” but instead, “I think the Miami Heat will beat the Boston Celtics.” You state it as if it is already true, even if it turns out you’re wrong. You do the same thing when writing your hypothesis.

Additionally, keep in mind that hypotheses can range from very specific to very broad. These hypotheses can be specific, but if your hypothesis testing examples involve a broad range of causes and effects, your hypothesis can also be broad.

The Two Types of Hypotheses

Now that you understand what goes into a hypothesis, it’s time to look more closely at the two most common types of hypothesis: the if-then hypothesis and the null hypothesis.

#1: If-Then Hypotheses

First of all, if-then hypotheses typically follow this formula:

If ____ happens, then ____ will happen.

The goal of this type of hypothesis is to test the causal relationship between the independent and dependent variable. It’s fairly simple, and each hypothesis can vary in how detailed it can be. We create if-then hypotheses all the time with our daily predictions. Here are some examples of hypotheses that use an if-then structure from daily life:

If I get enough sleep, I’ll be able to get more work done tomorrow.
If the bus is on time, I can make it to my friend’s birthday party.
If I study every night this week, I’ll get a better grade on my exam.

In each of these situations, you’re making a guess on how an independent variable (sleep, time, or studying) will affect a dependent variable (the amount of work you can do, making it to a party on time, or getting better grades).

You may still be asking, “What is an example of a hypothesis used in scientific research?” Take one of the hypothesis examples from a real-world study on whether using technology before bed affects children’s sleep patterns. The hypothesis read s:

“We hypothesized that increased hours of tablet- and phone-based screen time at bedtime would be inversely correlated with sleep quality and child attention.”

It might not look like it, but this is an if-then statement. The researchers basically said, “If children have more screen usage at bedtime, then their quality of sleep and attention will be worse.” The sleep quality and attention are the dependent variables and the screen usage is the independent variable. (Usually, the independent variable comes after the “if” and the dependent variable comes after the “then,” as it is the independent variable that affects the dependent variable.) This is an excellent example of how flexible hypothesis statements can be, as long as the general idea of “if-then” and the independent and dependent variables are present.

#2: Null Hypotheses

Your if-then hypothesis is not the only one needed to complete a successful experiment, however. You also need a null hypothesis to test it against. In its most basic form, the null hypothesis is the opposite of your if-then hypothesis . When you write your null hypothesis, you are writing a hypothesis that suggests that your guess is not true, and that the independent and dependent variables have no relationship .

One null hypothesis for the cell phone and sleep study from the last section might say:

“If children have more screen usage at bedtime, their quality of sleep and attention will not be worse.”

In this case, this is a null hypothesis because it’s asking the opposite of the original thesis!

Conversely, if your if-then hypothesis suggests that your two variables have no relationship, then your null hypothesis would suggest that there is one. So, pretend that there is a study that is asking the question, “Does the amount of followers on Instagram influence how long people spend on the app?” The independent variable is the amount of followers, and the dependent variable is the time spent. But if you, as the researcher, don’t think there is a relationship between the number of followers and time spent, you might write an if-then hypothesis that reads:

“If people have many followers on Instagram, they will not spend more time on the app than people who have less.”

In this case, the if-then suggests there isn’t a relationship between the variables. In that case, one of the null hypothesis examples might say:

“If people have many followers on Instagram, they will spend more time on the app than people who have less.”

You then test both the if-then and the null hypothesis to gauge if there is a relationship between the variables, and if so, how much of a relationship.

4 Tips to Write the Best Hypothesis

If you’re going to take the time to hold an experiment, whether in school or by yourself, you’re also going to want to take the time to make sure your hypothesis is a good one. The best hypotheses have four major elements in common: plausibility, defined concepts, observability, and general explanation.

#1: Plausibility

At first glance, this quality of a hypothesis might seem obvious. When your hypothesis is plausible, that means it’s possible given what we know about science and general common sense. However, improbable hypotheses are more common than you might think.

Imagine you’re studying weight gain and television watching habits. If you hypothesize that people who watch more than twenty hours of television a week will gain two hundred pounds or more over the course of a year, this might be improbable (though it’s potentially possible). Consequently, c ommon sense can tell us the results of the study before the study even begins.

Improbable hypotheses generally go against science, as well. Take this hypothesis example:

“If a person smokes one cigarette a day, then they will have lungs just as healthy as the average person’s.”

This hypothesis is obviously untrue, as studies have shown again and again that cigarettes negatively affect lung health. You must be careful that your hypotheses do not reflect your own personal opinion more than they do scientifically-supported findings. This plausibility points to the necessity of research before the hypothesis is written to make sure that your hypothesis has not already been disproven.

#2: Defined Concepts

The more advanced you are in your studies, the more likely that the terms you’re using in your hypothesis are specific to a limited set of knowledge. One of the hypothesis testing examples might include the readability of printed text in newspapers, where you might use words like “kerning” and “x-height.” Unless your readers have a background in graphic design, it’s likely that they won’t know what you mean by these terms. Thus, it’s important to either write what they mean in the hypothesis itself or in the report before the hypothesis.

Here’s what we mean. Which of the following sentences makes more sense to the common person?

If the kerning is greater than average, more words will be read per minute.

If the space between letters is greater than average, more words will be read per minute.

For people reading your report that are not experts in typography, simply adding a few more words will be helpful in clarifying exactly what the experiment is all about. It’s always a good idea to make your research and findings as accessible as possible.

Good hypotheses ensure that you can observe the results.

#3: Observability

In order to measure the truth or falsity of your hypothesis, you must be able to see your variables and the way they interact. For instance, if your hypothesis is that the flight patterns of satellites affect the strength of certain television signals, yet you don’t have a telescope to view the satellites or a television to monitor the signal strength, you cannot properly observe your hypothesis and thus cannot continue your study.

Some variables may seem easy to observe, but if you do not have a system of measurement in place, you cannot observe your hypothesis properly. Here’s an example: if you’re experimenting on the effect of healthy food on overall happiness, but you don’t have a way to monitor and measure what “overall happiness” means, your results will not reflect the truth. Monitoring how often someone smiles for a whole day is not reasonably observable, but having the participants state how happy they feel on a scale of one to ten is more observable.

In writing your hypothesis, always keep in mind how you'll execute the experiment.

#4: Generalizability

Perhaps you’d like to study what color your best friend wears the most often by observing and documenting the colors she wears each day of the week. This might be fun information for her and you to know, but beyond you two, there aren’t many people who could benefit from this experiment. When you start an experiment, you should note how generalizable your findings may be if they are confirmed. Generalizability is basically how common a particular phenomenon is to other people’s everyday life.

Let’s say you’re asking a question about the health benefits of eating an apple for one day only, you need to realize that the experiment may be too specific to be helpful. It does not help to explain a phenomenon that many people experience. If you find yourself with too specific of a hypothesis, go back to asking the big question: what is it that you want to know, and what do you think will happen between your two variables?

Hypothesis Testing Examples

We know it can be hard to write a good hypothesis unless you’ve seen some good hypothesis examples. We’ve included four hypothesis examples based on some made-up experiments. Use these as templates or launch pads for coming up with your own hypotheses.

Experiment #1: Students Studying Outside (Writing a Hypothesis)

You are a student at PrepScholar University. When you walk around campus, you notice that, when the temperature is above 60 degrees, more students study in the quad. You want to know when your fellow students are more likely to study outside. With this information, how do you make the best hypothesis possible?

You must remember to make additional observations and do secondary research before writing your hypothesis. In doing so, you notice that no one studies outside when it’s 75 degrees and raining, so this should be included in your experiment. Also, studies done on the topic beforehand suggested that students are more likely to study in temperatures less than 85 degrees. With this in mind, you feel confident that you can identify your variables and write your hypotheses:

If-then: “If the temperature in Fahrenheit is less than 60 degrees, significantly fewer students will study outside.”

Null: “If the temperature in Fahrenheit is less than 60 degrees, the same number of students will study outside as when it is more than 60 degrees.”

These hypotheses are plausible, as the temperatures are reasonably within the bounds of what is possible. The number of people in the quad is also easily observable. It is also not a phenomenon specific to only one person or at one time, but instead can explain a phenomenon for a broader group of people.

To complete this experiment, you pick the month of October to observe the quad. Every day (except on the days where it’s raining)from 3 to 4 PM, when most classes have released for the day, you observe how many people are on the quad. You measure how many people come and how many leave. You also write down the temperature on the hour.

After writing down all of your observations and putting them on a graph, you find that the most students study on the quad when it is 70 degrees outside, and that the number of students drops a lot once the temperature reaches 60 degrees or below. In this case, your research report would state that you accept or “failed to reject” your first hypothesis with your findings.

Experiment #2: The Cupcake Store (Forming a Simple Experiment)

Let’s say that you work at a bakery. You specialize in cupcakes, and you make only two colors of frosting: yellow and purple. You want to know what kind of customers are more likely to buy what kind of cupcake, so you set up an experiment. Your independent variable is the customer’s gender, and the dependent variable is the color of the frosting. What is an example of a hypothesis that might answer the question of this study?

Here’s what your hypotheses might look like:

If-then: “If customers’ gender is female, then they will buy more yellow cupcakes than purple cupcakes.”

Null: “If customers’ gender is female, then they will be just as likely to buy purple cupcakes as yellow cupcakes.”

This is a pretty simple experiment! It passes the test of plausibility (there could easily be a difference), defined concepts (there’s nothing complicated about cupcakes!), observability (both color and gender can be easily observed), and general explanation ( this would potentially help you make better business decisions ).

Experiment #3: Backyard Bird Feeders (Integrating Multiple Variables and Rejecting the If-Then Hypothesis)

While watching your backyard bird feeder, you realized that different birds come on the days when you change the types of seeds. You decide that you want to see more cardinals in your backyard, so you decide to see what type of food they like the best and set up an experiment.

However, one morning, you notice that, while some cardinals are present, blue jays are eating out of your backyard feeder filled with millet. You decide that, of all of the other birds, you would like to see the blue jays the least. This means you'll have more than one variable in your hypothesis. Your new hypotheses might look like this:

If-then: “If sunflower seeds are placed in the bird feeders, then more cardinals will come than blue jays. If millet is placed in the bird feeders, then more blue jays will come than cardinals.”

Null: “If either sunflower seeds or millet are placed in the bird, equal numbers of cardinals and blue jays will come.”

Through simple observation, you actually find that cardinals come as often as blue jays when sunflower seeds or millet is in the bird feeder. In this case, you would reject your “if-then” hypothesis and “fail to reject” your null hypothesis . You cannot accept your first hypothesis, because it’s clearly not true. Instead you found that there was actually no relation between your different variables. Consequently, you would need to run more experiments with different variables to see if the new variables impact the results.

Experiment #4: In-Class Survey (Including an Alternative Hypothesis)

You’re about to give a speech in one of your classes about the importance of paying attention. You want to take this opportunity to test a hypothesis you’ve had for a while:

If-then: If students sit in the first two rows of the classroom, then they will listen better than students who do not.

Null: If students sit in the first two rows of the classroom, then they will not listen better or worse than students who do not.

You give your speech and then ask your teacher if you can hand out a short survey to the class. On the survey, you’ve included questions about some of the topics you talked about. When you get back the results, you’re surprised to see that not only do the students in the first two rows not pay better attention, but they also scored worse than students in other parts of the classroom! Here, both your if-then and your null hypotheses are not representative of your findings. What do you do?

This is when you reject both your if-then and null hypotheses and instead create an alternative hypothesis . This type of hypothesis is used in the rare circumstance that neither of your hypotheses is able to capture your findings . Now you can use what you’ve learned to draft new hypotheses and test again!

Key Takeaways: Hypothesis Writing

The more comfortable you become with writing hypotheses, the better they will become. The structure of hypotheses is flexible and may need to be changed depending on what topic you are studying. The most important thing to remember is the purpose of your hypothesis and the difference between the if-then and the null . From there, in forming your hypothesis, you should constantly be asking questions, making observations, doing secondary research, and considering your variables. After you have written your hypothesis, be sure to edit it so that it is plausible, clearly defined, observable, and helpful in explaining a general phenomenon.

Writing a hypothesis is something that everyone, from elementary school children competing in a science fair to professional scientists in a lab, needs to know how to do. Hypotheses are vital in experiments and in properly executing the scientific method . When done correctly, hypotheses will set up your studies for success and help you to understand the world a little better, one experiment at a time.

What’s Next?

If you’re studying for the science portion of the ACT, there’s definitely a lot you need to know. We’ve got the tools to help, though! Start by checking out our ultimate study guide for the ACT Science subject test. Once you read through that, be sure to download our recommended ACT Science practice tests , since they’re one of the most foolproof ways to improve your score. (And don’t forget to check out our expert guide book , too.)

If you love science and want to major in a scientific field, you should start preparing in high school . Here are the science classes you should take to set yourself up for success.

If you’re trying to think of science experiments you can do for class (or for a science fair!), here’s a list of 37 awesome science experiments you can do at home

Ashley Sufflé Robinson has a Ph.D. in 19th Century English Literature. As a content writer for PrepScholar, Ashley is passionate about giving college-bound students the in-depth information they need to get into the school of their dreams.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Research Hypothesis In Psychology: Types, & Examples

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .

Hypotheses connect theory to data and guide the research process towards expanding scientific understanding

Some key points about hypotheses:

A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.

Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.

Types of Research Hypotheses

Alternative hypothesis.

The research hypothesis is often called the alternative or experimental hypothesis in experimental research.

It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.

The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).

A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:

Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.

In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.

An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and are significant in supporting the theory being investigated.

The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.

Null Hypothesis

The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.

It states results are due to chance and are not significant in supporting the idea being investigated.

The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.

Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.

This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.

Nondirectional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.

It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.

For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.

Directional Hypothesis

A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)

It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.

For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability

The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.

Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.

It means that there should exist some potential evidence or experiment that could prove the proposition false.

However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.

For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.

Can a Hypothesis be Proven?

Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.

All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.

In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.

Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.

We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.

If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.

Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.

How to Write a Hypothesis

Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.

Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).

Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:

The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.

More Examples

Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.

What is a scientific hypothesis?

It's the initial building block in the scientific method.

A girl looks at plants in a test tube for a science experiment. What's her scientific hypothesis?

Hypothesis basics

What makes a hypothesis testable.

Types of hypotheses
Hypothesis versus theory

Additional resources

Bibliography.

A scientific hypothesis is a tentative, testable explanation for a phenomenon in the natural world. It's the initial building block in the scientific method . Many describe it as an "educated guess" based on prior knowledge and observation. While this is true, a hypothesis is more informed than a guess. While an "educated guess" suggests a random prediction based on a person's expertise, developing a hypothesis requires active observation and background research.

The basic idea of a hypothesis is that there is no predetermined outcome. For a solution to be termed a scientific hypothesis, it has to be an idea that can be supported or refuted through carefully crafted experimentation or observation. This concept, called falsifiability and testability, was advanced in the mid-20th century by Austrian-British philosopher Karl Popper in his famous book "The Logic of Scientific Discovery" (Routledge, 1959).

A key function of a hypothesis is to derive predictions about the results of future experiments and then perform those experiments to see whether they support the predictions.

A hypothesis is usually written in the form of an if-then statement, which gives a possibility (if) and explains what may happen because of the possibility (then). The statement could also include "may," according to California State University, Bakersfield .

Here are some examples of hypothesis statements:

If garlic repels fleas, then a dog that is given garlic every day will not get fleas.
If sugar causes cavities, then people who eat a lot of candy may be more prone to cavities.
If ultraviolet light can damage the eyes, then maybe this light can cause blindness.

A useful hypothesis should be testable and falsifiable. That means that it should be possible to prove it wrong. A theory that can't be proved wrong is nonscientific, according to Karl Popper's 1963 book " Conjectures and Refutations ."

An example of an untestable statement is, "Dogs are better than cats." That's because the definition of "better" is vague and subjective. However, an untestable statement can be reworded to make it testable. For example, the previous statement could be changed to this: "Owning a dog is associated with higher levels of physical fitness than owning a cat." With this statement, the researcher can take measures of physical fitness from dog and cat owners and compare the two.

Types of scientific hypotheses

Elementary-age students study alternative energy using homemade windmills during public school science class.

In an experiment, researchers generally state their hypotheses in two ways. The null hypothesis predicts that there will be no relationship between the variables tested, or no difference between the experimental groups. The alternative hypothesis predicts the opposite: that there will be a difference between the experimental groups. This is usually the hypothesis scientists are most interested in, according to the University of Miami .

For example, a null hypothesis might state, "There will be no difference in the rate of muscle growth between people who take a protein supplement and people who don't." The alternative hypothesis would state, "There will be a difference in the rate of muscle growth between people who take a protein supplement and people who don't."

If the results of the experiment show a relationship between the variables, then the null hypothesis has been rejected in favor of the alternative hypothesis, according to the book " Research Methods in Psychology " (BCcampus, 2015).

There are other ways to describe an alternative hypothesis. The alternative hypothesis above does not specify a direction of the effect, only that there will be a difference between the two groups. That type of prediction is called a two-tailed hypothesis. If a hypothesis specifies a certain direction — for example, that people who take a protein supplement will gain more muscle than people who don't — it is called a one-tailed hypothesis, according to William M. K. Trochim , a professor of Policy Analysis and Management at Cornell University.

Sometimes, errors take place during an experiment. These errors can happen in one of two ways. A type I error is when the null hypothesis is rejected when it is true. This is also known as a false positive. A type II error occurs when the null hypothesis is not rejected when it is false. This is also known as a false negative, according to the University of California, Berkeley .

A hypothesis can be rejected or modified, but it can never be proved correct 100% of the time. For example, a scientist can form a hypothesis stating that if a certain type of tomato has a gene for red pigment, that type of tomato will be red. During research, the scientist then finds that each tomato of this type is red. Though the findings confirm the hypothesis, there may be a tomato of that type somewhere in the world that isn't red. Thus, the hypothesis is true, but it may not be true 100% of the time.

Scientific theory vs. scientific hypothesis

The best hypotheses are simple. They deal with a relatively narrow set of phenomena. But theories are broader; they generally combine multiple hypotheses into a general explanation for a wide range of phenomena, according to the University of California, Berkeley . For example, a hypothesis might state, "If animals adapt to suit their environments, then birds that live on islands with lots of seeds to eat will have differently shaped beaks than birds that live on islands with lots of insects to eat." After testing many hypotheses like these, Charles Darwin formulated an overarching theory: the theory of evolution by natural selection.

"Theories are the ways that we make sense of what we observe in the natural world," Tanner said. "Theories are structures of ideas that explain and interpret facts."

Read more about writing a hypothesis, from the American Medical Writers Association.
Find out why a hypothesis isn't always necessary in science, from The American Biology Teacher.
Learn about null and alternative hypotheses, from Prof. Essa on YouTube .

Encyclopedia Britannica. Scientific Hypothesis. Jan. 13, 2022. https://www.britannica.com/science/scientific-hypothesis

Karl Popper, "The Logic of Scientific Discovery," Routledge, 1959.

California State University, Bakersfield, "Formatting a testable hypothesis." https://www.csub.edu/~ddodenhoff/Bio100/Bio100sp04/formattingahypothesis.htm

Karl Popper, "Conjectures and Refutations," Routledge, 1963.

Price, P., Jhangiani, R., & Chiang, I., "Research Methods of Psychology — 2nd Canadian Edition," BCcampus, 2015.‌

University of Miami, "The Scientific Method" http://www.bio.miami.edu/dana/161/evolution/161app1_scimethod.pdf

William M.K. Trochim, "Research Methods Knowledge Base," https://conjointly.com/kb/hypotheses-explained/

University of California, Berkeley, "Multiple Hypothesis Testing and False Discovery Rate" https://www.stat.berkeley.edu/~hhuang/STAT141/Lecture-FDR.pdf

University of California, Berkeley, "Science at multiple levels" https://undsci.berkeley.edu/article/0_0_0/howscienceworks_19

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

How much does Earth weigh?

Largest gold nugget ever found in England unearthed with faulty metal detector

Space photo of the week: James Webb telescope reveals surprising starburst in ancient galaxy

What Are Examples of a Hypothesis?

Scientific Method
Chemical Laws
Periodic Table
Projects & Experiments
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

A hypothesis is an explanation for a set of observations. Here are examples of a scientific hypothesis.

Although you could state a scientific hypothesis in various ways, most hypotheses are either "If, then" statements or forms of the null hypothesis . The null hypothesis is sometimes called the "no difference" hypothesis. The null hypothesis is good for experimentation because it's simple to disprove. If you disprove a null hypothesis, that is evidence for a relationship between the variables you are examining.

Examples of Null Hypotheses

Hyperactivity is unrelated to eating sugar.
All daisies have the same number of petals.
The number of pets in a household is unrelated to the number of people living in it.
A person's preference for a shirt is unrelated to its color.

Examples of If, Then Hypotheses

If you get at least 6 hours of sleep, you will do better on tests than if you get less sleep.
If you drop a ball, it will fall toward the ground.
If you drink coffee before going to bed, then it will take longer to fall asleep.
If you cover a wound with a bandage, then it will heal with less scarring.

Improving a Hypothesis to Make It Testable

You may wish to revise your first hypothesis in order to make it easier to design an experiment to test. For example, let's say you have a bad breakout the morning after eating a lot of greasy food. You may wonder if there is a correlation between eating greasy food and getting pimples. You propose the hypothesis:

Eating greasy food causes pimples.

Next, you need to design an experiment to test this hypothesis. Let's say you decide to eat greasy food every day for a week and record the effect on your face. Then, as a control, you'll avoid greasy food for the next week and see what happens. Now, this is not a good experiment because it does not take into account other factors such as hormone levels, stress, sun exposure, exercise, or any number of other variables that might conceivably affect your skin.

The problem is that you cannot assign cause to your effect . If you eat french fries for a week and suffer a breakout, can you definitely say it was the grease in the food that caused it? Maybe it was the salt. Maybe it was the potato. Maybe it was unrelated to diet. You can't prove your hypothesis. It's much easier to disprove a hypothesis.

So, let's restate the hypothesis to make it easier to evaluate the data:

Getting pimples is unaffected by eating greasy food.

So, if you eat fatty food every day for a week and suffer breakouts and then don't break out the week that you avoid greasy food, you can be pretty sure something is up. Can you disprove the hypothesis? Probably not, since it is so hard to assign cause and effect. However, you can make a strong case that there is some relationship between diet and acne.

If your skin stays clear for the entire test, you may decide to accept your hypothesis . Again, you didn't prove or disprove anything, which is fine

Null Hypothesis Definition and Examples
What Is a Hypothesis? (Science)
What Are the Elements of a Good Hypothesis?
Understanding Simple vs Controlled Experiments
What Is a Testable Hypothesis?
What 'Fail to Reject' Means in a Hypothesis Test
Null Hypothesis Examples
How To Design a Science Fair Experiment
Scientific Method Vocabulary Terms
Scientific Hypothesis Examples
Six Steps of the Scientific Method
An Example of a Hypothesis Test
Definition of a Hypothesis
Scientific Method Flow Chart
Null Hypothesis and Alternative Hypothesis

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis ($H_0$) and an alternative hypothesis ($H_a$).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

At this point we can write hypotheses for a single mean ($\mu$), paired means($\mu_d$), a single proportion ($p$), the difference between two independent means ($\mu_1-\mu_2$), the difference between two proportions ($p_1-p_2$), a simple linear regression slope ($\beta$), and a correlation ($\rho$).
The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., $\mu_0$ and $p_0$). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., $p$ and $\mu$). The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Scientific Methods

What is Hypothesis?

We have heard of many hypotheses which have led to great inventions in science. Assumptions that are made on the basis of some evidence are known as hypotheses. In this article, let us learn in detail about the hypothesis and the type of hypothesis with examples.

A hypothesis is an assumption that is made based on some evidence. This is the initial point of any investigation that translates the research questions into predictions. It includes components like variables, population and the relation between the variables. A research hypothesis is a hypothesis that is used to test the relationship between two or more variables.

Characteristics of Hypothesis

Following are the characteristics of the hypothesis:

The hypothesis should be clear and precise to consider it to be reliable.
If the hypothesis is a relational hypothesis, then it should be stating the relationship between variables.
The hypothesis must be specific and should have scope for conducting more tests.
The way of explanation of the hypothesis must be very simple and it should also be understood that the simplicity of the hypothesis is not related to its significance.

Sources of Hypothesis

Following are the sources of hypothesis:

The resemblance between the phenomenon.
Observations from past studies, present-day experiences and from the competitors.
Scientific theories.
General patterns that influence the thinking process of people.

Types of Hypothesis

There are six forms of hypothesis and they are:

Simple hypothesis
Complex hypothesis
Directional hypothesis
Non-directional hypothesis
Null hypothesis
Associative and casual hypothesis

Simple Hypothesis

It shows a relationship between one dependent variable and a single independent variable. For example – If you eat more vegetables, you will lose weight faster. Here, eating more vegetables is an independent variable, while losing weight is the dependent variable.

Complex Hypothesis

It shows the relationship between two or more dependent variables and two or more independent variables. Eating more vegetables and fruits leads to weight loss, glowing skin, and reduces the risk of many diseases such as heart disease.

Directional Hypothesis

It shows how a researcher is intellectual and committed to a particular outcome. The relationship between the variables can also predict its nature. For example- children aged four years eating proper food over a five-year period are having higher IQ levels than children not having a proper meal. This shows the effect and direction of the effect.

Non-directional Hypothesis

It is used when there is no theory involved. It is a statement that a relationship exists between two variables, without predicting the exact nature (direction) of the relationship.

Null Hypothesis

It provides a statement which is contrary to the hypothesis. It’s a negative statement, and there is no relationship between independent and dependent variables. The symbol is denoted by “H O ”.

Associative and Causal Hypothesis

Associative hypothesis occurs when there is a change in one variable resulting in a change in the other variable. Whereas, the causal hypothesis proposes a cause and effect interaction between two or more variables.

Examples of Hypothesis

Following are the examples of hypotheses based on their types:

Consumption of sugary drinks every day leads to obesity is an example of a simple hypothesis.
All lilies have the same number of petals is an example of a null hypothesis.
If a person gets 7 hours of sleep, then he will feel less fatigue than if he sleeps less. It is an example of a directional hypothesis.

Functions of Hypothesis

Following are the functions performed by the hypothesis:

Hypothesis helps in making an observation and experiments possible.
It becomes the start point for the investigation.
Hypothesis helps in verifying the observations.
It helps in directing the inquiries in the right direction.

How will Hypothesis help in the Scientific Method?

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

Formation of question
Doing background research
Creation of hypothesis
Designing an experiment
Collection of data
Result analysis
Summarizing the experiment
Communicating the results

Frequently Asked Questions – FAQs

What is hypothesis.

A hypothesis is an assumption made based on some evidence.

Give an example of simple hypothesis?

What are the types of hypothesis.

Types of hypothesis are:

Associative and Casual hypothesis

State true or false: Hypothesis is the initial point of any investigation that translates the research questions into a prediction.

Define complex hypothesis..

A complex hypothesis shows the relationship between two or more dependent variables and two or more independent variables.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

Hypothesis Testing

Last updated
Save as PDF
Page ID 31289

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

The student’s claim: I did not cheat on the exam.
The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

Here is how the process of statistical hypothesis testing works:

We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

claim 1: The proportion of smokers at Goodheart is 0.20.
claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

Claim 1: The mean concentration in the shipment is the required 245 ppm.
Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

Claim 1: Performance on the SAT is not related to gender (males and females score the same).
Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
“The data provide enough evidence to reject claim 1 and accept claim 2”; or
“The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

A flow chart describing the process. First, we state Claim 1 and Claim 2. Claim 1 says "nothing special is going on" and is challenged by claim 2. Second, we collect relevant data and summarize it. Third, we assess how surprising it woudl be to observe data like that observed if Claim 1 is true. Fourth, we draw conclusions in context.

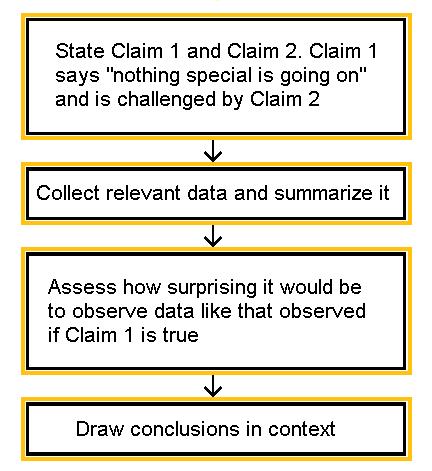
Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

Ho: The proportion of smokers at GU is 0.20.
Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

Ho: The mean concentration in the shipment is the required 245 ppm.
Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

Ho: Performance on the SAT is not related to gender (males and females score the same).
Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

Example 1: p-value = 0.106
Example 2: p-value = 0.0007
Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

Using our cutoff of 0.05, we fail to reject Ho.
Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

Using our cutoff of 0.05, we reject Ho.
Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
Let’s go back to the issue of the nature of the two types of conclusions that I can make.
Either I reject Ho (when the p-value is smaller than the significance level)
or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

Ho: The proportion of male managers hired is 0.5
Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

“The results are statistically significant” – when the p-value < α (alpha).
“The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
If p-value < 0.001, then the results are very highly statistically significant .
If p-value > 0.05, then the results are not statistically significant (NS).
If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

You have made the correct decision since the null hypothesis is false
You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

You have made the correct decision since the null hypothesis is true
You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

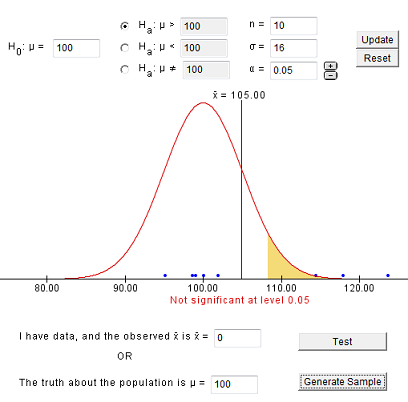
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

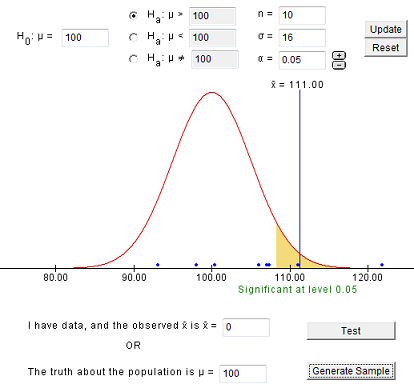
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

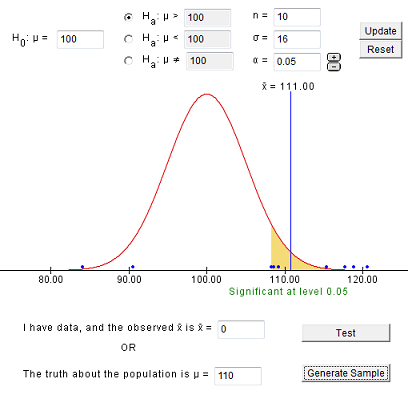
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

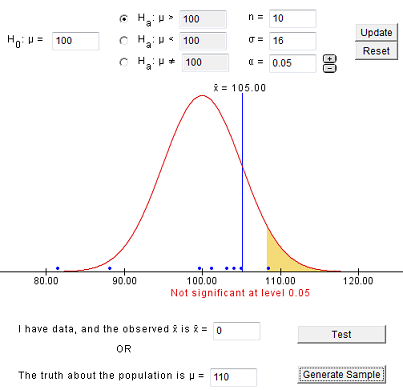
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

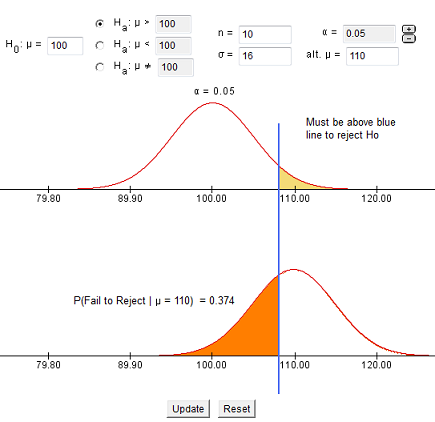
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

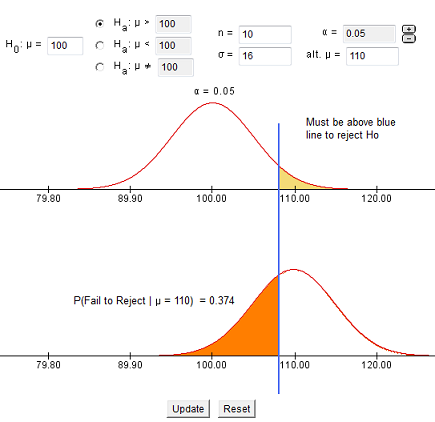
When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

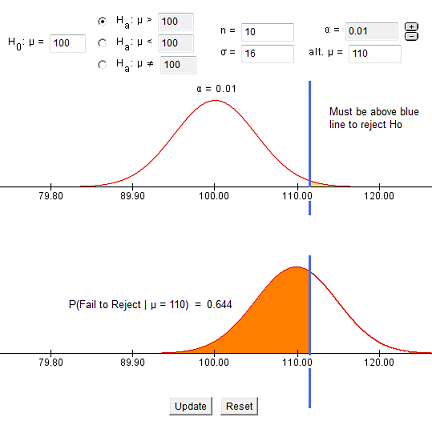
As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

Ho = The student’s claim: I did not cheat on the exam.
Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

The reason for a Type I error is random chance.
When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

Ho: p = 0.20 (No change; the repair did not help).
Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

Ho: p = 0.157 (same as among all college students in the country).
Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

Ho: p = 0.64 (No change from 2003).
Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
STEP 3: Find the p-value of the test.
STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

Ha: p < that value (like in example 1) or
Ha: p > that value (like in example 2) or
Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

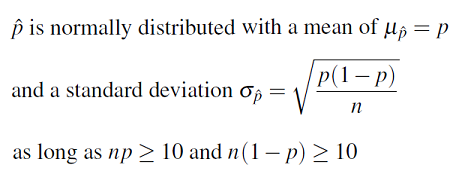
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

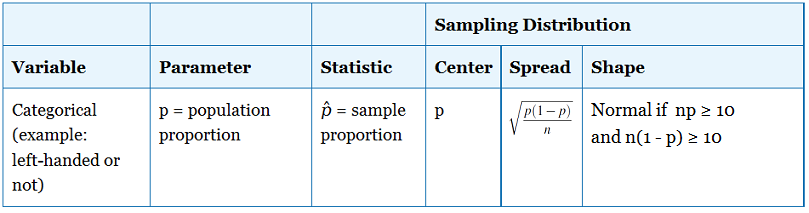
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

$\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02$

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

A normal curve representing samping distribution of p-hat assuming that p=p_0. Marked on the horizontal axis is p_0 and a particular value of p-hat. z is the difference between p-hat and p_0 measured in standard deviations (with the sign of z indicating whether p-hat is below or above p_0)

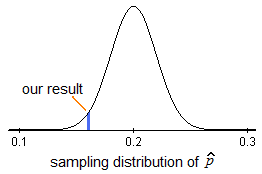
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

$z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}$

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

$\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}$

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

$\sqrt{\dfrac{0.64(1-0.64)}{n}}$.

Important Comment:

Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

$z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91$

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

$z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31$

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

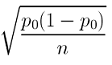
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

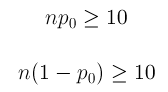
Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

$n p_{0}=400(0.2)=80 \geq 10$

$n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10$

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

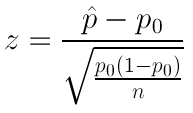
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

Conclusion: There IS enough evidence that Ha is True
Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

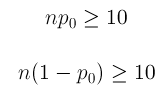
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

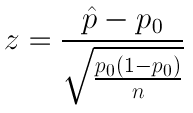
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

The effect of sample size on hypothesis testing.
Statistical significance vs. practical importance.
Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

If p 0 falls outside the confidence interval, reject Ho.
If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

If p 0 is not one of the plausible values for p, we reject Ho.
If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

$0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)$

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

Ho: p = 0.5 (the coin is fair).
Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

$0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)$

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

$0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)$

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

STEP 1: Stating the hypotheses H o and H a .
STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

Ha: μ < μ 0 (mu < mu_zero) (one-sided)
Ha: μ > μ 0 (mu > mu_zero) (one-sided)
Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
The sample is random (or at least can be considered random in context).
We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

$t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}$

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

A large circle represents the population, which is the shipment. μ represents the concentration of the chemical. The question we want to answer is "is the mean concentration the required 250ppm or not? (Assume: SD = 12)." Selected from the population is a sample of size n=100, represented by a smaller circle. x-bar for this sample is 247.

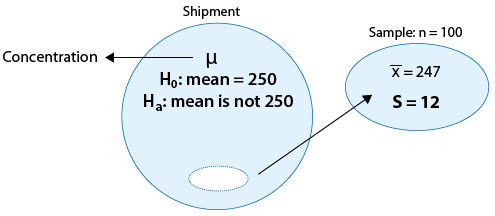
1. The hypotheses being tested are:

Ha: μ ≠ μ 0 (mu ≠ mu_zero)
Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

The sample is random
The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
The test statistic is:

$t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5$

The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
We reject the null hypothesis.
There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

The hypotheses being tested are:
Ho: μ = 72
Ha: μ ≠ 72
Where μ = population mean heart rate among college men
The conditions that allow us to use the t- test are met since:
The sample is random.
The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

$t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53$

The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

A t(56) curve, for which the horizontal axis has been labeled with t-scores of -2.5 and 2.5 . The area under the curve and to the left of -1.53 and to the right of 1.53 is the p-value.

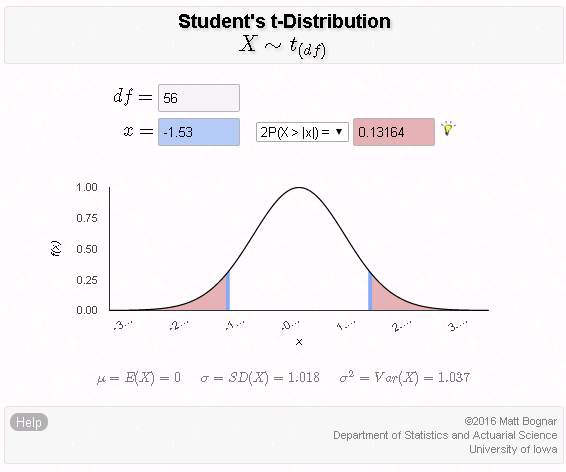
4. Making conclusions.

The p-value (0.132) is not small, indicating that the results are not significant.
We fail to reject the null hypothesis.
There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

More from M-W
To save this word, you'll need to log in. Log In

Definition of hypothesis

Did you know.

The Difference Between Hypothesis and Theory

A hypothesis is an assumption, an idea that is proposed for the sake of argument so that it can be tested to see if it might be true.

In the scientific method, the hypothesis is constructed before any applicable research has been done, apart from a basic background review. You ask a question, read up on what has been studied before, and then form a hypothesis.

A hypothesis is usually tentative; it's an assumption or suggestion made strictly for the objective of being tested.

A theory , in contrast, is a principle that has been formed as an attempt to explain things that have already been substantiated by data. It is used in the names of a number of principles accepted in the scientific community, such as the Big Bang Theory . Because of the rigors of experimentation and control, it is understood to be more likely to be true than a hypothesis is.

In non-scientific use, however, hypothesis and theory are often used interchangeably to mean simply an idea, speculation, or hunch, with theory being the more common choice.

Since this casual use does away with the distinctions upheld by the scientific community, hypothesis and theory are prone to being wrongly interpreted even when they are encountered in scientific contexts—or at least, contexts that allude to scientific study without making the critical distinction that scientists employ when weighing hypotheses and theories.

The most common occurrence is when theory is interpreted—and sometimes even gleefully seized upon—to mean something having less truth value than other scientific principles. (The word law applies to principles so firmly established that they are almost never questioned, such as the law of gravity.)

This mistake is one of projection: since we use theory in general to mean something lightly speculated, then it's implied that scientists must be talking about the same level of uncertainty when they use theory to refer to their well-tested and reasoned principles.

The distinction has come to the forefront particularly on occasions when the content of science curricula in schools has been challenged—notably, when a school board in Georgia put stickers on textbooks stating that evolution was "a theory, not a fact, regarding the origin of living things." As Kenneth R. Miller, a cell biologist at Brown University, has said , a theory "doesn’t mean a hunch or a guess. A theory is a system of explanations that ties together a whole bunch of facts. It not only explains those facts, but predicts what you ought to find from other observations and experiments.”

While theories are never completely infallible, they form the basis of scientific reasoning because, as Miller said "to the best of our ability, we’ve tested them, and they’ve held up."

proposition
supposition

hypothesis , theory , law mean a formula derived by inference from scientific data that explains a principle operating in nature.

hypothesis implies insufficient evidence to provide more than a tentative explanation.

theory implies a greater range of evidence and greater likelihood of truth.

law implies a statement of order and relation in nature that has been found to be invariable under the same conditions.

Examples of hypothesis in a Sentence

These examples are programmatically compiled from various online sources to illustrate current usage of the word 'hypothesis.' Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.

Word History

Greek, from hypotithenai to put under, suppose, from hypo- + tithenai to put — more at do

1641, in the meaning defined at sense 1a

Phrases Containing hypothesis

null hypothesis
counter - hypothesis
Whorfian hypothesis
nebular hypothesis
planetesimal hypothesis

Articles Related to hypothesis

This is the Difference Between a...

This is the Difference Between a Hypothesis and a Theory

In scientific reasoning, they're two completely different things

Dictionary Entries Near hypothesis

hypothermia

hypothesize

Cite this Entry

“Hypothesis.” Merriam-Webster.com Dictionary , Merriam-Webster, https://www.merriam-webster.com/dictionary/hypothesis. Accessed 1 Apr. 2024.

Kids Definition

Kids definition of hypothesis, medical definition, medical definition of hypothesis, more from merriam-webster on hypothesis.

Nglish: Translation of hypothesis for Spanish Speakers

Britannica English: Translation of hypothesis for Arabic Speakers

Britannica.com: Encyclopedia article about hypothesis

Subscribe to America's largest dictionary and get thousands more definitions and advanced search—ad free!

Play Quordle: Guess all four words in a limited number of tries. Each of your guesses must be a real 5-letter word.

Can you solve 4 words at once?

Word of the day.

See Definitions and Examples »

Get Word of the Day daily email!

Popular in Grammar & Usage

The tangled history of 'it's' and 'its', more commonly misspelled words, why does english have so many silent letters, your vs. you're: how to use them correctly, every letter is silent, sometimes: a-z list of examples, popular in wordplay, the words of the week - mar. 29, 10 scrabble words without any vowels, 12 more bird names that sound like insults (and sometimes are), 8 uncommon words related to love, 9 superb owl words, games & quizzes.

Play Blossom: Solve today's spelling word game by finding as many words as you can using just 7 letters. Longer words score more points.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.1: The Elements of Hypothesis Testing

Last updated
Save as PDF
Page ID 130263

Learning Objectives

To understand the logical framework of tests of hypotheses.
To learn basic terminology connected with hypothesis testing.
To learn fundamental facts about hypothesis testing.

Types of Hypotheses

A hypothesis about the value of a population parameter is an assertion about its value. As in the introductory example we will be concerned with testing the truth of two competing hypotheses, only one of which can be true.

Definition: null hypothesis and alternative hypothesis

The null hypothesis , denoted $H_0$, is the statement about the population parameter that is assumed to be true unless there is convincing evidence to the contrary.
The alternative hypothesis , denoted $H_a$, is a statement about the population parameter that is contradictory to the null hypothesis, and is accepted as true only if there is convincing evidence in favor of it.

Definition: statistical procedure

Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample.

The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions:

Reject $H_0$ (and therefore accept $H_a$), or
Fail to reject $H_0$ (and therefore fail to accept $H_a$).

The null hypothesis typically represents the status quo, or what has historically been true. In the example of the respirators, we would believe the claim of the manufacturer unless there is reason not to do so, so the null hypotheses is $H_0:\mu =75$. The alternative hypothesis in the example is the contradictory statement $H_a:\mu <75$. The null hypothesis will always be an assertion containing an equals sign, but depending on the situation the alternative hypothesis can have any one of three forms: with the symbol $<$, as in the example just discussed, with the symbol $>$, or with the symbol $\neq$. The following two examples illustrate the latter two cases.

Example $\PageIndex{1}$

A publisher of college textbooks claims that the average price of all hardbound college textbooks is $\$127.50$. A student group believes that the actual mean is higher and wishes to test their belief. State the relevant null and alternative hypotheses.

The default option is to accept the publisher’s claim unless there is compelling evidence to the contrary. Thus the null hypothesis is $H_0:\mu =127.50$. Since the student group thinks that the average textbook price is greater than the publisher’s figure, the alternative hypothesis in this situation is $H_a:\mu >127.50$.

Example $\PageIndex{2}$

The recipe for a bakery item is designed to result in a product that contains $8$ grams of fat per serving. The quality control department samples the product periodically to insure that the production process is working as designed. State the relevant null and alternative hypotheses.

The default option is to assume that the product contains the amount of fat it was formulated to contain unless there is compelling evidence to the contrary. Thus the null hypothesis is $H_0:\mu =8.0$. Since to contain either more fat than desired or to contain less fat than desired are both an indication of a faulty production process, the alternative hypothesis in this situation is that the mean is different from $8.0$, so $H_a:\mu \neq 8.0$.

In Example $\PageIndex{1}$, the textbook example, it might seem more natural that the publisher’s claim be that the average price is at most $\$127.50$, not exactly $\$127.50$. If the claim were made this way, then the null hypothesis would be $H_0:\mu \leq 127.50$, and the value $\$127.50$ given in the example would be the one that is least favorable to the publisher’s claim, the null hypothesis. It is always true that if the null hypothesis is retained for its least favorable value, then it is retained for every other value.

Thus in order to make the null and alternative hypotheses easy for the student to distinguish, in every example and problem in this text we will always present one of the two competing claims about the value of a parameter with an equality. The claim expressed with an equality is the null hypothesis. This is the same as always stating the null hypothesis in the least favorable light. So in the introductory example about the respirators, we stated the manufacturer’s claim as “the average is $75$ minutes” instead of the perhaps more natural “the average is at least $75$ minutes,” essentially reducing the presentation of the null hypothesis to its worst case.

The first step in hypothesis testing is to identify the null and alternative hypotheses.

The Logic of Hypothesis Testing

Although we will study hypothesis testing in situations other than for a single population mean (for example, for a population proportion instead of a mean or in comparing the means of two different populations), in this section the discussion will always be given in terms of a single population mean $\mu$.

The null hypothesis always has the form $H_0:\mu =\mu _0$ for a specific number $\mu _0$ (in the respirator example $\mu _0=75$, in the textbook example $\mu _0=127.50$, and in the baked goods example $\mu _0=8.0$). Since the null hypothesis is accepted unless there is strong evidence to the contrary, the test procedure is based on the initial assumption that $H_0$ is true. This point is so important that we will repeat it in a display:

The test procedure is based on the initial assumption that $H_0$ is true.

The criterion for judging between $H_0$ and $H_a$ based on the sample data is: if the value of $\overline{X}$ would be highly unlikely to occur if $H_0$ were true, but favors the truth of $H_a$, then we reject $H_0$ in favor of $H_a$. Otherwise we do not reject $H_0$.

Supposing for now that $\overline{X}$ follows a normal distribution, when the null hypothesis is true the density function for the sample mean $\overline{X}$ must be as in Figure $\PageIndex{1}$: a bell curve centered at $\mu _0$. Thus if $H_0$ is true then $\overline{X}$ is likely to take a value near $\mu _0$ and is unlikely to take values far away. Our decision procedure therefore reduces simply to:

if $H_a$ has the form $H_a:\mu <\mu _0$ then reject $H_0$ if $\bar{x}$ is far to the left of $\mu _0$;
if $H_a$ has the form $H_a:\mu >\mu _0$ then reject $H_0$ if $\bar{x}$ is far to the right of $\mu _0$;
if $H_a$ has the form $H_a:\mu \neq \mu _0$ then reject $H_0$ if $\bar{x}$ is far away from $\mu _0$ in either direction.

Think of the respirator example, for which the null hypothesis is $H_0:\mu =75$, the claim that the average time air is delivered for all respirators is $75$ minutes. If the sample mean is $75$ or greater then we certainly would not reject $H_0$ (since there is no issue with an emergency respirator delivering air even longer than claimed).

If the sample mean is slightly less than $75$ then we would logically attribute the difference to sampling error and also not reject $H_0$ either.

Values of the sample mean that are smaller and smaller are less and less likely to come from a population for which the population mean is $75$. Thus if the sample mean is far less than $75$, say around $60$ minutes or less, then we would certainly reject $H_0$, because we know that it is highly unlikely that the average of a sample would be so low if the population mean were $75$. This is the rare event criterion for rejection: what we actually observed $(\overline{X}<60)$ would be so rare an event if $\mu =75$ were true that we regard it as much more likely that the alternative hypothesis $\mu <75$ holds.

In summary, to decide between $H_0$ and $H_a$ in this example we would select a “rejection region” of values sufficiently far to the left of $75$, based on the rare event criterion, and reject $H_0$ if the sample mean $\overline{X}$ lies in the rejection region, but not reject $H_0$ if it does not.

The Rejection Region

Each different form of the alternative hypothesis Ha has its own kind of rejection region:

if (as in the respirator example) $H_a$ has the form $H_a:\mu <\mu _0$, we reject $H_0$ if $\bar{x}$ is far to the left of $\mu _0$, that is, to the left of some number $C$, so the rejection region has the form of an interval $(-\infty ,C]$;
if (as in the textbook example) $H_a$ has the form $H_a:\mu >\mu _0$, we reject $H_0$ if $\bar{x}$ is far to the right of $\mu _0$, that is, to the right of some number $C$, so the rejection region has the form of an interval $[C,\infty )$;
if (as in the baked good example) $H_a$ has the form $H_a:\mu \neq \mu _0$, we reject $H_0$ if $\bar{x}$ is far away from $\mu _0$ in either direction, that is, either to the left of some number $C$ or to the right of some other number $C′$, so the rejection region has the form of the union of two intervals $(-\infty ,C]\cup [C',\infty )$.

The key issue in our line of reasoning is the question of how to determine the number $C$ or numbers $C$ and $C′$, called the critical value or critical values of the statistic, that determine the rejection region.

Definition: critical values

The critical value or critical values of a test of hypotheses are the number or numbers that determine the rejection region.

Suppose the rejection region is a single interval, so we need to select a single number $C$. Here is the procedure for doing so. We select a small probability, denoted $\alpha$, say $1\%$, which we take as our definition of “rare event:” an event is “rare” if its probability of occurrence is less than $\alpha$. (In all the examples and problems in this text the value of $\alpha$ will be given already.) The probability that $\overline{X}$ takes a value in an interval is the area under its density curve and above that interval, so as shown in Figure $\PageIndex{2}$ (drawn under the assumption that $H_0$ is true, so that the curve centers at $\mu _0$) the critical value $C$ is the value of $\overline{X}$ that cuts off a tail area $\alpha$ in the probability density curve of $\overline{X}$. When the rejection region is in two pieces, that is, composed of two intervals, the total area above both of them must be $\alpha$, so the area above each one is $\alpha /2$, as also shown in Figure $\PageIndex{2}$.

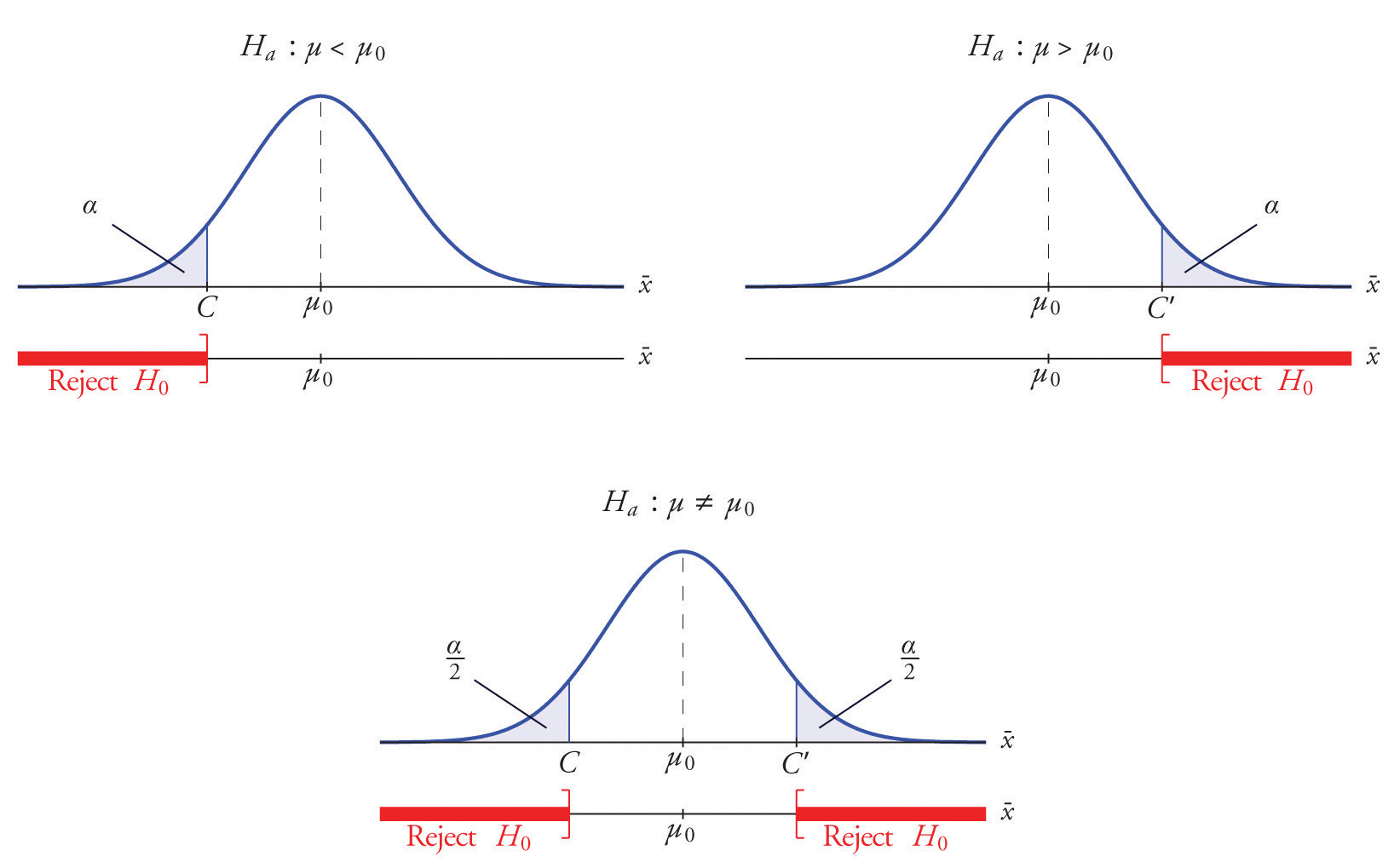
The number $\alpha$ is the total area of a tail or a pair of tails.

Example $\PageIndex{3}$

In the context of Example $\PageIndex{2}$, suppose that it is known that the population is normally distributed with standard deviation $\alpha =0.15$ gram, and suppose that the test of hypotheses $H_0:\mu =8.0$ versus $H_a:\mu \neq 8.0$ will be performed with a sample of size $5$. Construct the rejection region for the test for the choice $\alpha =0.10$. Explain the decision procedure and interpret it.

If $H_0$ is true then the sample mean $\overline{X}$ is normally distributed with mean and standard deviation

\[\begin{align} \mu _{\overline{X}} &=\mu \nonumber \\[5pt] &=8.0 \nonumber \end{align} \nonumber \]

\[\begin{align} \sigma _{\overline{X}}&=\dfrac{\sigma}{\sqrt{n}} \nonumber \\[5pt] &= \dfrac{0.15}{\sqrt{5}} \nonumber\\[5pt] &=0.067 \nonumber \end{align} \nonumber \]

Since $H_a$ contains the $\neq$ symbol the rejection region will be in two pieces, each one corresponding to a tail of area $\alpha /2=0.10/2=0.05$. From Figure 7.1.6, $z_{0.05}=1.645$, so $C$ and $C′$ are $1.645$ standard deviations of $\overline{X}$ to the right and left of its mean $8.0$:

\[C=8.0-(1.645)(0.067) = 7.89 \; \; \text{and}\; \; C'=8.0 + (1.645)(0.067) = 8.11 \nonumber \]

The result is shown in Figure $\PageIndex{3}$. α = 0.1

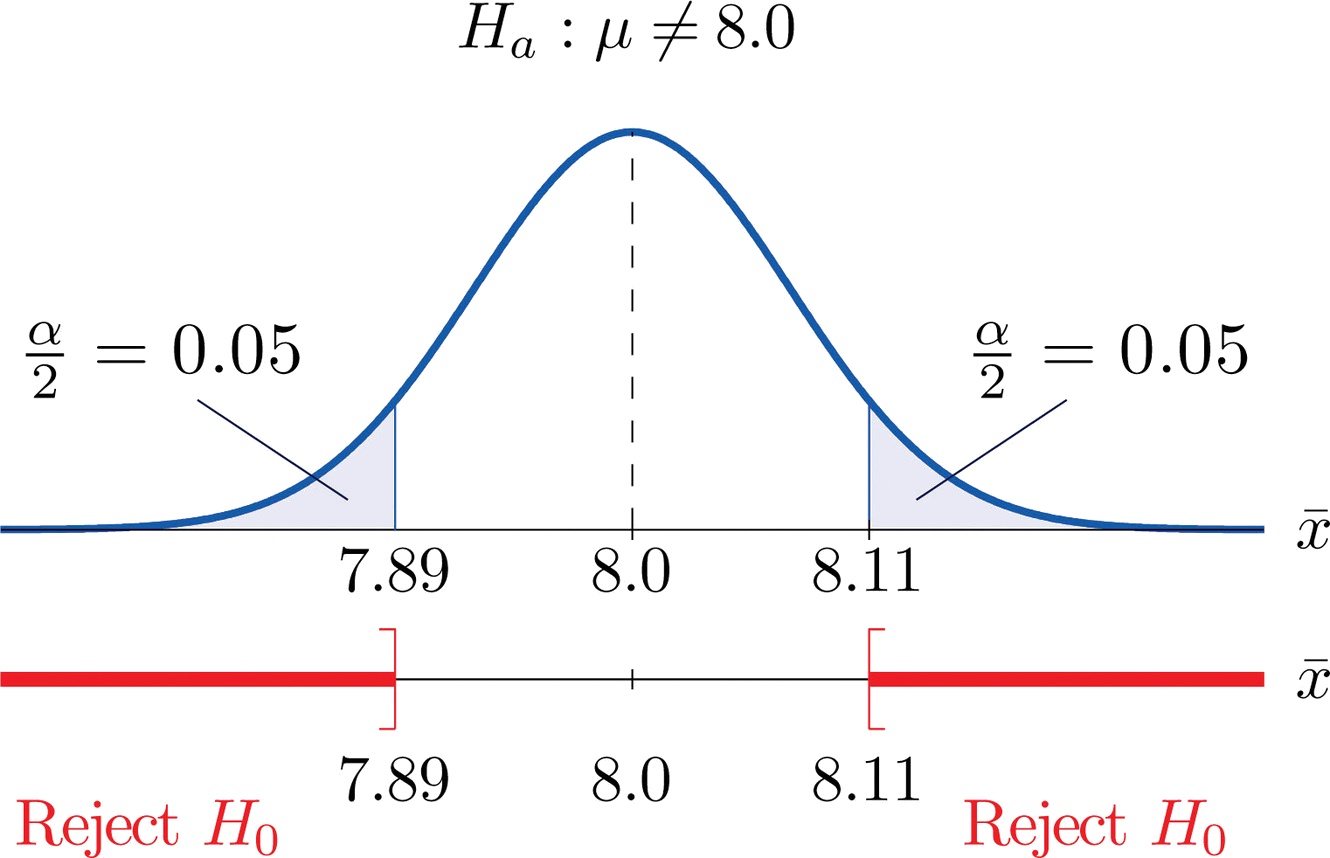
The decision procedure is: take a sample of size $5$ and compute the sample mean $\bar{x}$. If $\bar{x}$ is either $7.89$ grams or less or $8.11$ grams or more then reject the hypothesis that the average amount of fat in all servings of the product is $8.0$ grams in favor of the alternative that it is different from $8.0$ grams. Otherwise do not reject the hypothesis that the average amount is $8.0$ grams.

The reasoning is that if the true average amount of fat per serving were $8.0$ grams then there would be less than a $10\%$ chance that a sample of size $5$ would produce a mean of either $7.89$ grams or less or $8.11$ grams or more. Hence if that happened it would be more likely that the value $8.0$ is incorrect (always assuming that the population standard deviation is $0.15$ gram).

Because the rejection regions are computed based on areas in tails of distributions, as shown in Figure $\PageIndex{2}$, hypothesis tests are classified according to the form of the alternative hypothesis in the following way.

Definitions: Test classifications

If $H_a$ has the form $\mu \neq \mu _0$ the test is called a two-tailed test .
If $H_a$ has the form $\mu < \mu _0$ the test is called a left-tailed test .
If $H_a$ has the form $\mu > \mu _0$the test is called a right-tailed test .

Each of the last two forms is also called a one-tailed test .

Two Types of Errors

The format of the testing procedure in general terms is to take a sample and use the information it contains to come to a decision about the two hypotheses. As stated before our decision will always be either

reject the null hypothesis $H_0$ in favor of the alternative $H_a$ presented, or
do not reject the null hypothesis $H_0$ in favor of the alternative $H_0$ presented.

There are four possible outcomes of hypothesis testing procedure, as shown in the following table:

As the table shows, there are two ways to be right and two ways to be wrong. Typically to reject $H_0$ when it is actually true is a more serious error than to fail to reject it when it is false, so the former error is labeled “ Type I ” and the latter error “ Type II ”.

Definition: Type I and Type II errors

In a test of hypotheses:

A Type I error is the decision to reject $H_0$ when it is in fact true.
A Type II error is the decision not to reject $H_0$ when it is in fact not true.

Unless we perform a census we do not have certain knowledge, so we do not know whether our decision matches the true state of nature or if we have made an error. We reject $H_0$ if what we observe would be a “rare” event if $H_0$ were true. But rare events are not impossible: they occur with probability $\alpha$. Thus when $H_0$ is true, a rare event will be observed in the proportion $\alpha$ of repeated similar tests, and $H_0$ will be erroneously rejected in those tests. Thus $\alpha$ is the probability that in following the testing procedure to decide between $H_0$ and $H_a$ we will make a Type I error.

Definition: level of significance

The number $\alpha$ that is used to determine the rejection region is called the level of significance of the test. It is the probability that the test procedure will result in a Type I error .

The probability of making a Type II error is too complicated to discuss in a beginning text, so we will say no more about it than this: for a fixed sample size, choosing $alpha$ smaller in order to reduce the chance of making a Type I error has the effect of increasing the chance of making a Type II error . The only way to simultaneously reduce the chances of making either kind of error is to increase the sample size.

Standardizing the Test Statistic

Hypotheses testing will be considered in a number of contexts, and great unification as well as simplification results when the relevant sample statistic is standardized by subtracting its mean from it and then dividing by its standard deviation. The resulting statistic is called a standardized test statistic . In every situation treated in this and the following two chapters the standardized test statistic will have either the standard normal distribution or Student’s $t$-distribution.

Definition: hypothesis test

A standardized test statistic for a hypothesis test is the statistic that is formed by subtracting from the statistic of interest its mean and dividing by its standard deviation.

For example, reviewing Example $\PageIndex{3}$, if instead of working with the sample mean $\overline{X}$ we instead work with the test statistic

\[\frac{\overline{X}-8.0}{0.067} \nonumber \]

then the distribution involved is standard normal and the critical values are just $\pm z_{0.05}$. The extra work that was done to find that $C=7.89$ and $C′=8.11$ is eliminated. In every hypothesis test in this book the standardized test statistic will be governed by either the standard normal distribution or Student’s $t$-distribution. Information about rejection regions is summarized in the following tables:

Every instance of hypothesis testing discussed in this and the following two chapters will have a rejection region like one of the six forms tabulated in the tables above.

No matter what the context a test of hypotheses can always be performed by applying the following systematic procedure, which will be illustrated in the examples in the succeeding sections.

Systematic Hypothesis Testing Procedure: Critical Value Approach

Identify the null and alternative hypotheses.
Identify the relevant test statistic and its distribution.
Compute from the data the value of the test statistic.
Construct the rejection region.
Compare the value computed in Step 3 to the rejection region constructed in Step 4 and make a decision. Formulate the decision in the context of the problem, if applicable.

The procedure that we have outlined in this section is called the “Critical Value Approach” to hypothesis testing to distinguish it from an alternative but equivalent approach that will be introduced at the end of Section 8.3.

Key Takeaway

A test of hypotheses is a statistical process for deciding between two competing assertions about a population parameter.
The testing procedure is formalized in a five-step procedure.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Microb Biotechnol
v.15(11); 2022 Nov

On the role of hypotheses in science

Harald brüssow.

1 Laboratory of Gene Technology, Department of Biosystems, KU Leuven, Leuven Belgium

Associated Data

Scientific research progresses by the dialectic dialogue between hypothesis building and the experimental testing of these hypotheses. Microbiologists as biologists in general can rely on an increasing set of sophisticated experimental methods for hypothesis testing such that many scientists maintain that progress in biology essentially comes with new experimental tools. While this is certainly true, the importance of hypothesis building in science should not be neglected. Some scientists rely on intuition for hypothesis building. However, there is also a large body of philosophical thinking on hypothesis building whose knowledge may be of use to young scientists. The present essay presents a primer into philosophical thoughts on hypothesis building and illustrates it with two hypotheses that played a major role in the history of science (the parallel axiom and the fifth element hypothesis). It continues with philosophical concepts on hypotheses as a calculus that fits observations (Copernicus), the need for plausibility (Descartes and Gilbert) and for explicatory power imposing a strong selection on theories (Darwin, James and Dewey). Galilei introduced and James and Poincaré later justified the reductionist principle in hypothesis building. Waddington stressed the feed‐forward aspect of fruitful hypothesis building, while Poincaré called for a dialogue between experiment and hypothesis and distinguished false, true, fruitful and dangerous hypotheses. Theoretical biology plays a much lesser role than theoretical physics because physical thinking strives for unification principle across the universe while biology is confronted with a breathtaking diversity of life forms and its historical development on a single planet. Knowledge of the philosophical foundations on hypothesis building in science might stimulate more hypothesis‐driven experimentation that simple observation‐oriented “fishing expeditions” in biological research.

Short abstract

Scientific research progresses by the dialectic dialogue between hypothesis building and the experimental testing of these hypotheses. Microbiologists can rely on an increasing set of sophisticated experimental methods for hypothesis testing but the importance of hypothesis building in science should not be neglected. This Lilliput offers a primer on philosophical concepts on hypotheses in science.

INTRODUCTION

Philosophy of science and the theory of knowledge (epistemology) are important branches of philosophy. However, philosophy has over the centuries lost its dominant role it enjoyed in antiquity and became in Medieval Ages the maid of theology (ancilla theologiae) and after the rise of natural sciences and its technological applications many practising scientists and the general public doubt whether they need philosophical concepts in their professional and private life. This is in the opinion of the writer of this article, an applied microbiologist, shortsighted for several reasons. Philosophers of the 20th century have made important contributions to the theory of knowledge, and many eminent scientists grew interested in philosophical problems. Mathematics which plays such a prominent role in physics and increasingly also in other branches of science is a hybrid: to some extent, it is the paradigm of an exact science while its abstract aspects are deeply rooted in philosophical thinking. In the present essay, the focus is on hypothesis and hypothesis building in science, essentially it is a compilation what philosophers and scientists thought about this subject in past and present. The controversy between the mathematical mind and that of the practical mind is an old one. The philosopher, physicist and mathematician Pascal ( 1623 –1662a) wrote in his Pensées : “Mathematicians who are only mathematicians have exact minds, provided all things are explained to them by means of definitions and axioms; otherwise they are inaccurate. They are only right when the principles are quite clear. And men of intuition cannot have the patience to reach to first principles of things speculative and conceptional, which they have never seen in the world and which are altogether out of the common. The intellect can be strong and narrow, and can be comprehensive and weak.” Hypothesis building is an act both of intuition and exact thinking and I hope that theoretical knowledge about hypothesis building will also profit young microbiologists.

HYPOTHESES AND AXIOMS IN MATHEMATICS

In the following, I will illustrate the importance of hypothesis building for the history of science and the development of knowledge and illustrate it with two famous concepts, the parallel axiom in mathematics and the five elements hypothesis in physics.

Euclidean geometry

The prominent role of hypotheses in the development of science becomes already clear in the first science book of the Western civilization: Euclid's The Elements written about 300 BC starts with a set of statements called Definitions, Postulates and Common Notions that lay out the foundation of geometry (Euclid, c.323‐c.283 ). This axiomatic approach is very modern as exemplified by the fact that Euclid's book remained for long time after the Bible the most read book in the Western hemisphere and a backbone of school teaching in mathematics. Euclid's twenty‐three definitions start with sentences such as “1. A point is that which has no part; 2. A line is breadthless length; 3. The extremities of a line are points”; and continues with the definition of angles (“8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line”) and that of circles, triangles and quadrilateral figures. For the history of science, the 23rd definition of parallels is particularly interesting: “Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction”. This is the famous parallel axiom. It is clear that the parallel axiom cannot be the result of experimental observations, but must be a concept created in the mind. Euclid ends with five Common Notions (“1. Things which are equal to the same thing are also equal to one another, to 5. The whole is greater than the part”). The establishment of a contradiction‐free system for a branch of mathematics based on a set of axioms from which theorems were deduced was revolutionary modern. Hilbert ( 1899 ) formulated a sound modern formulation for Euclidian geometry. Hilbert's axiom system contains the notions “point, line and plane” and the concepts of “betweenness, containment and congruence” leading to five axioms, namely the axioms of Incidence (“Verknüpfung”), of Order (“Anordnung”), of Congruence, of Continuity (“Stetigkeit”) and of Parallels.

Origin of axioms

Philosophers gave various explanations for the origin of the Euclidean hypotheses or axioms. Plato considered geometrical figures as related to ideas (the true things behind the world of appearances). Aristoteles considered geometric figures as abstractions of physical bodies. Descartes perceived geometric figures as inborn ideas from extended bodies ( res extensa ), while Pascal thought that the axioms of Euclidian geometry were derived from intuition. Kant reasoned that Euclidian geometry represented a priori perceptions of space. Newton considered geometry as part of general mechanics linked to theories of measurement. Hilbert argued that the axioms of mathematical geometry are neither the result of contemplation (“Anschauung”) nor of psychological source. For him, axioms were formal propositions (“formale Aussageformen”) characterized by consistency (“Widerspruchsfreiheit”, i.e. absence of contradiction) (Mittelstrass, 1980a ).

Definitions

Axioms were also differently defined by philosophers. In Topics , Aristoteles calls axioms the assumptions taken up by one partner of a dialogue to initiate a dialectic discussion. Plato states that an axiom needs to be an acceptable or credible proposition, which cannot be justified by reference to other statements. Yet, a justification is not necessary because an axiom is an evident statement. In modern definition, axioms are methodical first sentences in the foundation of a deductive science (Mittelstrass, 1980a ). In Posterior Analytics , Aristotle defines postulates as positions which are at least initially not accepted by the dialogue partners while hypotheses are accepted for the sake of reasoning. In Euclid's book, postulates are construction methods that assure the existence of the geometric objects. Today postulates and axioms are used as synonyms while the 18th‐century philosophy made differences: Lambert defined axioms as descriptive sentences and postulates as prescriptive sentences. According to Kant, mathematical postulates create (synthesize) concepts (Mittelstrass, 1980b ). Definitions then fix the use of signs; they can be semantic definitions that explain the proper meaning of a sign in common language use (in a dictionary style) or they can be syntactic definitions that regulate the use of these signs in formal operations. Nominal definitions explain the words, while real definitions explain the meaning or the nature of the defined object. Definitions are thus essential for the development of a language of science, assuring communication and mutual understanding (Mittelstrass, 1980c ). Finally, hypotheses are also frequently defined as consistent conjectures that are compatible with the available knowledge. The truth of the hypothesis is only supposed in order to explain true observations and facts. Consequences of this hypothetical assumptions should explain the observed facts. Normally, descriptive hypotheses precede explanatory hypotheses in the development of scientific thought. Sometimes only tentative concepts are introduced as working hypotheses to test whether they have an explanatory capacity for the observations (Mittelstrass, 1980d ).

The Euclidian geometry is constructed along a logical “if→then” concept. The “if‐clause” formulates at the beginning the supposition, the “then clause” formulates the consequences from these axioms which provides a system of geometric theorems or insights. The conclusions do not follow directly from the hypothesis; this would otherwise represent self‐evident immediate conclusions. The “if‐then” concept in geometry is not used as in other branches of science where the consequences deduced from the axioms are checked against reality whether they are true, in order to confirm the validity of the hypothesis. The task in mathematics is: what can be logically deduced from a given set of axioms to build a contradiction‐free system of geometry. Whether this applies to the real world is in contrast to the situation in natural sciences another question and absolutely secondary to mathematics (Syntopicon, 1992 ).

Pascal's rules for hypotheses

In his Scientific Treatises on Geometric Demonstrations , Pascal ( 1623‐1662b ) formulates “Five rules are absolutely necessary and we cannot dispense with them without an essential defect and frequently even error. Do not leave undefined any terms at all obscure or ambiguous. Use in definitions of terms only words perfectly well known or already explained. Do not fail to ask that each of the necessary principles be granted, however clear and evident it may be. Ask only that perfectly self‐evident things be granted as axioms. Prove all propositions, using for their proof only axioms that are perfectly self‐evident or propositions already demonstrated or granted. Never get caught in the ambiguity of terms by failing to substitute in thought the definitions which restrict or define them. One should accept as true only those things whose contradiction appears to be false. We may then boldly affirm the original statement, however incomprehensible it is.”

Kant's rules on hypotheses

Kant ( 1724–1804 ) wrote that the analysis described in his book The Critique of Pure Reason “has now taught us that all its efforts to extend the bounds of knowledge by means of pure speculation, are utterly fruitless. So much the wider field lies open to hypothesis; as where we cannot know with certainty, we are at liberty to make guesses and to form suppositions. Imagination may be allowed, under the strict surveillance of reason, to invent suppositions; but these must be based on something that is perfectly certain‐ and that is the possibility of the object. Such a supposition is termed a hypothesis. We cannot imagine or invent any object or any property of an object not given in experience and employ it in a hypothesis; otherwise we should be basing our chain of reasoning upon mere chimerical fancies and not upon conception of things. Thus, we have no right to assume of new powers, not existing in nature and consequently we cannot assume that there is any other kind of community among substances than that observable in experience, any kind of presence than that in space and any kind of duration than that in time. The conditions of possible experience are for reason the only conditions of the possibility of things. Otherwise, such conceptions, although not self‐contradictory, are without object and without application. Transcendental hypotheses are therefore inadmissible, and we cannot use the liberty of employing in the absence of physical, hyperphysical grounds of explanation because such hypotheses do not advance reason, but rather stop it in its progress. When the explanation of natural phenomena happens to be difficult, we have constantly at hand a transcendental ground of explanation, which lifts us above the necessity of investigating nature. The next requisite for the admissibility of a hypothesis is its sufficiency. That is it must determine a priori the consequences which are given in experience and which are supposed to follow from the hypothesis itself.” Kant stresses another aspect when dealing with hypotheses: “It is our duty to try to discover new objections, to put weapons in the hands of our opponent, and to grant him the most favorable position. We have nothing to fear from these concessions; on the contrary, we may rather hope that we shall thus make ourselves master of a possession which no one will ever venture to dispute.”

For Kant's analytical and synthetical judgements and Difference between philosophy and mathematics (Kant, Whitehead) , see Appendices S1 and S2 , respectively.

Poincaré on hypotheses

The mathematician‐philosopher Poincaré ( 1854 –1912a) explored the foundation of mathematics and physics in his book Science and Hypothesis . In the preface to the book, he summarizes common thinking of scientists at the end of the 19th century. “To the superficial observer scientific truth is unassailable, the logic of science is infallible, and if scientific men sometimes make mistakes, it is because they have not understood the rules of the game. Mathematical truths are derived from a few self‐evident propositions, by a chain of flawless reasoning, they are imposed not only by us, but on Nature itself. This is for the minds of most people the origin of certainty in science.” Poincaré then continues “but upon more mature reflection the position held by hypothesis was seen; it was recognized that it is as necessary to the experimenter as it is to the mathematician. And then the doubt arose if all these constructions are built on solid foundations.” However, “to doubt everything or to believe everything are two equally convenient solutions: both dispense with the necessity of reflection. Instead, we should examine with the utmost care the role of hypothesis; we shall then recognize not only that it is necessary, but that in most cases it is legitimate. We shall also see that there are several kinds of hypotheses; that some are verifiable and when once confirmed by experiment become truths of great fertility; that others may be useful to us in fixing our ideas; and finally that others are hypotheses only in appearance, and reduce to definitions or to conventions in disguise.” Poincaré argues that “we must seek mathematical thought where it has remained pure‐i.e. in arithmetic, in the proofs of the most elementary theorems. The process is proof by recurrence. We first show that a theorem is true for n = 1; we then show that if it is true for n –1 it is true for n; and we conclude that it is true for all integers. The essential characteristic of reasoning by recurrence is that it contains, condensed in a single formula, an infinite number of syllogisms.” Syllogism is logical argument that applies deductive reasoning to arrive at a conclusion. Poincaré notes “that here is a striking analogy with the usual process of induction. But an essential difference exists. Induction applied to the physical sciences is always uncertain because it is based on the belief in a general order of the universe, an order which is external to us. Mathematical induction‐ i.e. proof by recurrence – is on the contrary, necessarily imposed on us, because it is only the affirmation of a property of the mind itself. No doubt mathematical recurrent reasoning and physical inductive reasoning are based on different foundations, but they move in parallel lines and in the same direction‐namely, from the particular to the general.”

Non‐Euclidian geometry: from Gauss to Lobatschewsky

Mathematics is an abstract science that intrinsically does not request that the structures described reflect a physical reality. Paradoxically, mathematics is the language of physics since the founder of experimental physics Galilei used Euclidian geometry when exploring the laws of the free fall. In his 1623 treatise The Assayer , Galilei ( 1564 –1642a) famously formulated that the book of Nature is written in the language of mathematics, thus establishing a link between formal concepts in mathematics and the structure of the physical world. Euclid's parallel axiom played historically a prominent role for the connection between mathematical concepts and physical realities. Mathematicians had doubted that the parallel axiom was needed and tried to prove it. In Euclidian geometry, there is a connection between the parallel axiom and the sum of the angles in a triangle being two right angles. It is therefore revealing that the famous mathematician C.F. Gauss investigated in the early 19th century experimentally whether this Euclidian theorem applies in nature. He approached this problem by measuring the sum of angles in a real triangle by using geodetic angle measurements of three geographical elevations in the vicinity of Göttingen where he was teaching mathematics. He reportedly measured a sum of the angles in this triangle that differed from 180°. Gauss had at the same time also developed statistical methods to evaluate the accuracy of measurements. Apparently, the difference of his measured angles was still within the interval of Gaussian error propagation. He did not publish the reasoning and the results for this experiment because he feared the outcry of colleagues about this unorthodox, even heretical approach to mathematical reasoning (Carnap, 1891 ‐1970a). However, soon afterwards non‐Euclidian geometries were developed. In the words of Poincaré, “Lobatschewsky assumes at the outset that several parallels may be drawn through a point to a given straight line, and he retains all the other axioms of Euclid. From these hypotheses he deduces a series of theorems between which it is impossible to find any contradiction, and he constructs a geometry as impeccable in its logic as Euclidian geometry. The theorems are very different, however, from those to which we are accustomed, and at first will be found a little disconcerting. For instance, the sum of the angles of a triangle is always less than two right angles, and the difference between that sum and two right angles is proportional to the area of the triangle. Lobatschewsky's propositions have no relation to those of Euclid, but are none the less logically interconnected.” Poincaré continues “most mathematicians regard Lobatschewsky's geometry as a mere logical curiosity. Some of them have, however, gone further. If several geometries are possible, they say, is it certain that our geometry is true? Experiments no doubt teaches us that the sum of the angles of a triangle is equal to two right angles, but this is because the triangles we deal with are too small” (Poincaré, 1854 ‐1912a)—hence the importance of Gauss' geodetic triangulation experiment. Gauss was aware that his three hills experiment was too small and thought on measurements on triangles formed with stars.

Poincaré vs. Einstein

Lobatschewsky's hyperbolic geometry did not remain the only non‐Euclidian geometry. Riemann developed a geometry without the parallel axiom, while the other Euclidian axioms were maintained with the exception of that of Order (Anordnung). Poincaré notes “so there is a kind of opposition between the geometries. For instance the sum of the angles in a triangle is equal to two right angles in Euclid's geometry, less than two right angles in that of Lobatschewsky, and greater than two right angles in that of Riemann. The number of parallel lines that can be drawn through a given point to a given line is one in Euclid's geometry, none in Riemann's, and an infinite number in the geometry of Lobatschewsky. Let us add that Riemann's space is finite, although unbounded.” As further distinction, the ratio of the circumference to the diameter of a circle is equal to π in Euclid's, greater than π in Lobatschewsky's and smaller than π in Riemann's geometry. A further difference between these geometries concerns the degree of curvature (Krümmungsmass k) which is 0 for a Euclidian surface, smaller than 0 for a Lobatschewsky and greater than 0 for a Riemann surface. The difference in curvature can be roughly compared with plane, concave and convex surfaces. The inner geometric structure of a Riemann plane resembles the surface structure of a Euclidean sphere and a Lobatschewsky plane resembles that of a Euclidean pseudosphere (a negatively curved geometry of a saddle). What geometry is true? Poincaré asked “Ought we then, to conclude that the axioms of geometry are experimental truths?” and continues “If geometry were an experimental science, it would not be an exact science. The geometric axioms are therefore neither synthetic a priori intuitions as affirmed by Kant nor experimental facts. They are conventions. Our choice among all possible conventions is guided by experimental facts; but it remains free and is only limited by the necessity of avoiding contradictions. In other words, the axioms of geometry are only definitions in disguise. What then are we to think of the question: Is Euclidean geometry true? It has no meaning. One geometry cannot be more true than another, it can only be more convenient. Now, Euclidean geometry is, and will remain, the most convenient, 1 st because it is the simplest and 2 nd because it sufficiently agrees with the properties of natural bodies” (Poincaré, 1854 ‐1912a).

Poincaré's book was published in 1903 and only a few years later Einstein published his general theory of relativity ( 1916 ) where he used a non‐Euclidean, Riemann geometry and where he demonstrated a structure of space that deviated from Euclidean geometry in the vicinity of strong gravitational fields. And in 1919, astronomical observations during a solar eclipse showed that light rays from a distant star were indeed “bent” when passing next to the sun. These physical observations challenged the view of Poincaré, and we should now address some aspects of hypotheses in physics (Carnap, 1891 ‐1970b).

HYPOTHESES IN PHYSICS

The long life of the five elements hypothesis.

Physical sciences—not to speak of biological sciences — were less developed in antiquity than mathematics which is already demonstrated by the primitive ideas on the elements constituting physical bodies. Plato and Aristotle spoke of the four elements which they took over from Thales (water), Anaximenes (air) and Parmenides (fire and earth) and add a fifth element (quinta essentia, our quintessence), namely ether. Ether is imagined a heavenly element belonging to the supralunar world. In Plato's dialogue Timaios (Plato, c.424‐c.348 BC a ), the five elements were associated with regular polyhedra in geometry and became known as Platonic bodies: tetrahedron (fire), octahedron (air), cube (earth), icosahedron (water) and dodecahedron (ether). In regular polyhedra, faces are congruent (identical in shape and size), all angles and all edges are congruent, and the same number of faces meet at each vertex. The number of elements is limited to five because in Euclidian space there are exactly five regular polyhedral. There is in Plato's writing even a kind of geometrical chemistry. Since two octahedra (air) plus one tetrahedron (fire) can be combined into one icosahedron (water), these “liquid” elements can combine while this is not the case for combinations with the cube (earth). The 12 faces of the dodecahedron were compared with the 12 zodiac signs (Mittelstrass, 1980e ). This geometry‐based hypothesis of physics had a long life. As late as 1612, Kepler in his Mysterium cosmographicum tried to fit the Platonic bodies into the planetary shells of his solar system model. The ether theory even survived into the scientific discussion of the 19th‐century physics and the idea of a mathematical structure of the universe dominated by symmetry operations even fertilized 20th‐century ideas about symmetry concepts in the physics of elementary particles.

Huygens on sound waves in air

The ether hypothesis figures prominently in the 1690 Treatise on Light from Huygens ( 1617‐1670 ). He first reports on the transmission of sound by air when writing “this may be proved by shutting up a sounding body in a glass vessel from which the air is withdrawn and care was taken to place the sounding body on cotton that it cannot communicate its tremor to the glass vessel which encloses it. After having exhausted all the air, one hears no sound from the metal though it is struck.” Huygens comes up with some foresight when suspecting “the air is of such a nature that it can be compressed and reduced to a much smaller space than that it normally occupies. Air is made up of small bodies which float about and which are agitated very rapidly. So that the spreading of sound is the effort which these little bodies make in collisions with one another, to regain freedom when they are a little more squeezed together in the circuit of these waves than elsewhere.”

Huygens on light waves in ether

“That is not the same air but another kind of matter in which light spreads; since if the air is removed from the vessel the light does not cease to traverse it as before. The extreme velocity of light cannot admit such a propagation of motion” as sound waves. To achieve the propagation of light, Huygens invokes ether “as a substance approaching to perfect hardness and possessing springiness as prompt as we choose. One may conceive light to spread successively by spherical waves. The propagation consists nowise in the transport of those particles but merely in a small agitation which they cannot help communicate to those surrounding.” The hypothesis of an ether in outer space fills libraries of physical discussions, but all experimental approaches led to contradictions with respect to postulated properties of this hypothetical material for example when optical experiments showed that light waves display transversal and not longitudinal oscillations.

The demise of ether

Mechanical models for the transmission of light or gravitation waves requiring ether were finally put to rest by the theory of relativity from Einstein (Mittelstrass, 1980f ). This theory posits that the speed of light in an empty space is constant and does not depend on movements of the source of light or that of an observer as requested by the ether hypothesis. The theory of relativity also provides an answer how the force of gravitation is transmitted from one mass to another across an essentially empty space. In the non‐Euclidian formulation of the theory of relativity (Einstein used the Riemann geometry), there is no gravitation force in the sense of mechanical or electromagnetic forces. The gravitation force is in this formulation simply replaced by a geometric structure (space curvature near high and dense masses) of a four‐dimensional space–time system (Carnap, 1891 ‐1970c; Einstein & Imfeld, 1956 ) Gravitation waves and gravitation lens effects have indeed been experimental demonstrated by astrophysicists (Dorfmüller et al., 1998 ).

For Aristotle's on physical hypotheses , see Appendix S3 .

PHILOSOPHICAL THOUGHTS ON HYPOTHESES

In the following, the opinions of a number of famous scientists and philosophers on hypotheses are quoted to provide a historical overview on the subject.

Copernicus' hypothesis: a calculus which fits observations

In his book Revolutions of Heavenly Spheres Copernicus ( 1473–1543 ) reasoned in the preface about hypotheses in physics. “Since the newness of the hypotheses of this work ‐which sets the earth in motion and puts an immovable sun at the center of the universe‐ has already received a great deal of publicity, I have no doubt that certain of the savants have taken great offense.” He defended his heliocentric thesis by stating “For it is the job of the astronomer to use painstaking and skilled observations in gathering together the history of the celestial movements‐ and then – since he cannot by any line of reasoning reach the true causes of these movements‐ to think up or construct whatever causes or hypotheses he pleases such that, by the assumption of these causes, those same movements can be calculated from the principles of geometry for the past and the future too. This artist is markedly outstanding in both of these respects: for it is not necessary that these hypotheses should be true, or even probable; but it is enough if they provide a calculus which fits the observations.” This preface written in 1543 sounds in its arguments very modern physics. However, historians of science have discovered that it was probably written by a theologian friend of Copernicus to defend the book against the criticism by the church.

Bacon's intermediate hypotheses

In his book Novum Organum , Francis Bacon ( 1561–1626 ) claims for hypotheses and scientific reasoning “that they augur well for the sciences, when the ascent shall proceed by a true scale and successive steps, without interruption or breach, from particulars to the lesser axioms, thence to the intermediates and lastly to the most general.” He then notes “that the lowest axioms differ but little from bare experiments, the highest and most general are notional, abstract, and of no real weight. The intermediate are true, solid, full of life, and up to them depend the business and fortune of mankind.” He warns that “we must not then add wings, but rather lead and ballast to the understanding, to prevent its jumping and flying, which has not yet been done; but whenever this takes place we may entertain greater hopes of the sciences.” With respect to methodology, Bacon claims that “we must invent a different form of induction. The induction which proceeds by simple enumeration is puerile, leads to uncertain conclusions, …deciding generally from too small a number of facts. Sciences should separate nature by proper rejections and exclusions and then conclude for the affirmative, after collecting a sufficient number of negatives.”

Gilbert and Descartes for plausible hypotheses

William Gilbert introduced in his book On the Loadstone (Gilbert, 1544‐1603 ) the argument of plausibility into physical hypothesis building. “From these arguments, therefore, we infer not with mere probability, but with certainty, the diurnal rotation of the earth; for nature ever acts with fewer than with many means; and because it is more accordant to reason that the one small body, the earth, should make a daily revolution than the whole universe should be whirled around it.”

Descartes ( 1596‐1650 ) reflected on the sources of understanding in his book Rules for Direction and distinguished what “comes about by impulse, by conjecture, or by deduction. Impulse can assign no reason for their belief and when determined by fanciful disposition, it is almost always a source of error.” When speaking about the working of conjectures he quotes thoughts of Aristotle: “water which is at a greater distance from the center of the globe than earth is likewise less dense substance, and likewise the air which is above the water, is still rarer. Hence, we hazard the guess that above the air nothing exists but a very pure ether which is much rarer than air itself. Moreover nothing that we construct in this way really deceives, if we merely judge it to be probable and never affirm it to be true; in fact it makes us better instructed. Deduction is thus left to us as the only means of putting things together so as to be sure of their truth. Yet in it, too, there may be many defects.”

Care in formulating hypotheses

Locke ( 1632‐1704 ) in his treatise Concerning Human Understanding admits that “we may make use of any probable hypotheses whatsoever. Hypotheses if they are well made are at least great helps to the memory and often direct us to new discoveries. However, we should not take up any one too hastily.” Also, practising scientists argued against careless use of hypotheses and proposed remedies. Lavoisier ( 1743‐1794 ) in the preface to his Element of Chemistry warned about beaten‐track hypotheses. “Instead of applying observation to the things we wished to know, we have chosen rather to imagine them. Advancing from one ill‐founded supposition to another, we have at last bewildered ourselves amidst a multitude of errors. These errors becoming prejudices, are adopted as principles and we thus bewilder ourselves more and more. We abuse words which we do not understand. There is but one remedy: this is to forget all that we have learned, to trace back our ideas to their sources and as Bacon says to frame the human understanding anew.”

Faraday ( 1791–1867 ) in a Speculation Touching Electric Conduction and the Nature of Matter highlighted the fundamental difference between hypotheses and facts when noting “that he has most power of penetrating the secrets of nature, and guessing by hypothesis at her mode of working, will also be most careful for his own safe progress and that of others, to distinguish that knowledge which consists of assumption, by which I mean theory and hypothesis, from that which is the knowledge of facts and laws; never raising the former to the dignity or authority of the latter.”

Explicatory power justifies hypotheses

Darwin ( 1809 –1882a) defended the conclusions and hypothesis of his book The Origin of Species “that species have been modified in a long course of descent. This has been affected chiefly through the natural selection of numerous, slight, favorable variations.” He uses a post hoc argument for this hypothesis: “It can hardly be supposed that a false theory would explain, to so satisfactory a manner as does the theory of natural selection, the several large classes of facts” described in his book.

The natural selection of hypotheses

In the concluding chapter of The Descent of Man Darwin ( 1809 –1882b) admits “that many of the views which have been advanced in this book are highly speculative and some no doubt will prove erroneous.” However, he distinguished that “false facts are highly injurious to the progress of science for they often endure long; but false views do little harm for everyone takes a salutory pleasure in proving their falseness; and when this is done, one path to error is closed and the road to truth is often at the same time opened.”

The American philosopher William James ( 1842–1907 ) concurred with Darwin's view when he wrote in his Principles of Psychology “every scientific conception is in the first instance a spontaneous variation in someone'’s brain. For one that proves useful and applicable there are a thousand that perish through their worthlessness. The scientific conceptions must prove their worth by being verified. This test, however, is the cause of their preservation, not of their production.”

The American philosopher J. Dewey ( 1859‐1952 ) in his treatise Experience and Education notes that “the experimental method of science attaches more importance not less to ideas than do other methods. There is no such thing as experiment in the scientific sense unless action is directed by some leading idea. The fact that the ideas employed are hypotheses, not final truths, is the reason why ideas are more jealously guarded and tested in science than anywhere else. As fixed truths they must be accepted and that is the end of the matter. But as hypotheses, they must be continuously tested and revised, a requirement that demands they be accurately formulated. Ideas or hypotheses are tested by the consequences which they produce when they are acted upon. The method of intelligence manifested in the experimental method demands keeping track of ideas, activities, and observed consequences. Keeping track is a matter of reflective review.”

The reductionist principle

James ( 1842‐1907 ) pushed this idea further when saying “Scientific thought goes by selection. We break the solid plenitude of fact into separate essences, conceive generally what only exists particularly, and by our classifications leave nothing in its natural neighborhood. The reality exists as a plenum. All its part are contemporaneous, but we can neither experience nor think this plenum. What we experience is a chaos of fragmentary impressions, what we think is an abstract system of hypothetical data and laws. We must decompose each chaos into single facts. We must learn to see in the chaotic antecedent a multitude of distinct antecedents, in the chaotic consequent a multitude of distinct consequents.” From these considerations James concluded “even those experiences which are used to prove a scientific truth are for the most part artificial experiences of the laboratory gained after the truth itself has been conjectured. Instead of experiences engendering the inner relations, the inner relations are what engender the experience here.“

Following curiosity

Freud ( 1856–1939 ) considered curiosity and imagination as driving forces of hypothesis building which need to be confronted as quickly as possible with observations. In Beyond the Pleasure Principle , Freud wrote “One may surely give oneself up to a line of thought and follow it up as far as it leads, simply out of scientific curiosity. These innovations were direct translations of observation into theory, subject to no greater sources of error than is inevitable in anything of the kind. At all events there is no way of working out this idea except by combining facts with pure imagination and thereby departing far from observation.” This can quickly go astray when trusting intuition. Freud recommends “that one may inexorably reject theories that are contradicted by the very first steps in the analysis of observation and be aware that those one holds have only a tentative validity.”

Feed‐forward aspects of hypotheses

The geneticist Waddington ( 1905–1975 ) in his essay The Nature of Life states that “a scientific theory cannot remain a mere structure within the world of logic, but must have implications for action and that in two rather different ways. It must involve the consequence that if you do so and so, such and such result will follow. That is to say it must give, or at least offer, the possibility of controlling the process. Secondly, its value is quite largely dependent on its power of suggesting the next step in scientific advance. Any complete piece of scientific work starts with an activity essentially the same as that of an artist. It starts by asking a relevant question. The first step may be a new awareness of some facet of the world that no one else had previously thought worth attending to. Or some new imaginative idea which depends on a sensitive receptiveness to the oddity of nature essentially similar to that of the artist. In his logical analysis and manipulative experimentation, the scientist is behaving arrogantly towards nature, trying to force her into his categories of thought or to trick her into doing what he wants. But finally he has to be humble. He has to take his intuition, his logical theory and his manipulative skill to the bar of Nature and see whether she answers yes or no; and he has to abide by the result. Science is often quite ready to tolerate some logical inadequacy in a theory‐or even a flat logical contradiction like that between the particle and wave theories of matter‐so long as it finds itself in the possession of a hypothesis which offers both the possibility of control and a guide to worthwhile avenues of exploration.”

Poincaré: the dialogue between experiment and hypothesis

Poincaré ( 1854 –1912b) also dealt with physics in Science and Hypothesis . “Experiment is the sole source of truth. It alone can teach us certainty. Cannot we be content with experiment alone? What place is left for mathematical physics? The man of science must work with method. Science is built up of facts, as a house is built of stones, but an accumulation of facts is no more a science than a heap of stones is a house. It is often said that experiments should be made without preconceived concepts. That is impossible. Without the hypothesis, no conclusion could have been drawn; nothing extraordinary would have been seen; and only one fact the more would have been catalogued, without deducing from it the remotest consequence.” Poincaré compares science to a library. Experimental physics alone can enrich the library with new books, but mathematical theoretical physics draw up the catalogue to find the books and to reveal gaps which have to be closed by the purchase of new books.

Poincaré: false, true, fruitful and dangerous hypotheses

Poincaré continues “we all know that there are good and bad experiments. The latter accumulate in vain. Whether there are hundred or thousand, one single piece of work will be sufficient to sweep them into oblivion. Bacon invented the term of an experimentum crucis for such experiments. What then is a good experiment? It is that which teaches us something more than an isolated fact. It is that which enables us to predict and to generalize. Experiments only gives us a certain number of isolated points. They must be connected by a continuous line and that is true generalization. Every generalization is a hypothesis. It should be as soon as possible submitted to verification. If it cannot stand the test, it must be abandoned without any hesitation. The physicist who has just given up one of his hypotheses should rejoice, for he found an unexpected opportunity of discovery. The hypothesis took into account all the known factors which seem capable of intervention in the phenomenon. If it is not verified, it is because there is something unexpected. Has the hypothesis thus rejected been sterile? Far from it. It has rendered more service than a true hypothesis.” Poincaré notes that “with a true hypothesis only one fact the more would have been catalogued, without deducing from it the remotest consequence. It may be said that the wrong hypothesis has rendered more service than a true hypothesis.” However, Poincaré warns that “some hypotheses are dangerous – first and foremost those which are tacit and unconscious. And since we make them without knowing them, we cannot get rid of them.” Poincaré notes that here mathematical physics is of help because by its precision one is compelled to formulate all the hypotheses, revealing also the tacit ones.

Arguments for the reductionist principle

Poincaré also warned against multiplying hypotheses indefinitely: “If we construct a theory upon multiple hypotheses, and if experiment condemns it, which of the premisses must be changed?” Poincaré also recommended to “resolve the complex phenomenon given directly by experiment into a very large number of elementary phenomena. First, with respect to time. Instead of embracing in its entirety the progressive development of a phenomenon, we simply try to connect each moment with the one immediately preceding. Next, we try to decompose the phenomenon in space. We must try to deduce the elementary phenomenon localized in a very small region of space.” Poincaré suggested that the physicist should “be guided by the instinct of simplicity, and that is why in physical science generalization so readily takes the mathematical form to state the problem in the form of an equation.” This argument goes back to Galilei ( 1564 –1642b) who wrote in The Two Sciences “when I observe a stone initially at rest falling from an elevated position and continually acquiring new increments of speed, why should I not believe that such increases take place in a manner which is exceedingly simple and rather obvious to everybody? If now we examine the matter carefully we find no addition or increment more simple than that which repeats itself always in the same manner. It seems we shall not be far wrong if we put the increment of speed as proportional to the increment of time.” With a bit of geometrical reasoning, Galilei deduced that the distance travelled by a freely falling body varies as the square of the time. However, Galilei was not naïve and continued “I grant that these conclusions proved in the abstract will be different when applied in the concrete” and considers disturbances cause by friction and air resistance that complicate the initially conceived simplicity.

Four sequential steps of discovery…

Some philosophers of science attributed a fundamental importance to observations for the acquisition of experience in science. The process starts with accidental observations (Aristotle), going to systematic observations (Bacon), leading to quantitative rules obtained with exact measurements (Newton and Kant) and culminating in observations under artificially created conditions in experiments (Galilei) (Mittelstrass, 1980g ).

…rejected by Popper and Kant

In fact, Newton wrote that he had developed his theory of gravitation from experience followed by induction. K. Popper ( 1902‐1994 ) in his book Conjectures and Refutations did not agree with this logical flow “experience leading to theory” and that for several reasons. This scheme is according to Popper intuitively false because observations are always inexact, while theory makes absolute exact assertions. It is also historically false because Copernicus and Kepler were not led to their theories by experimental observations but by geometry and number theories of Plato and Pythagoras for which they searched verifications in observational data. Kepler, for example, tried to prove the concept of circular planetary movement influenced by Greek theory of the circle being a perfect geometric figure and only when he could not demonstrate this with observational data, he tried elliptical movements. Popper noted that it was Kant who realized that even physical experiments are not prior to theories when quoting Kant's preface to the Critique of Pure Reason : “When Galilei let his globes run down an inclined plane with a gravity which he has chosen himself, then a light dawned on all natural philosophers. They learnt that our reason can only understand what it creates according to its own design; that we must compel Nature to answer our questions, rather than cling to Nature's apron strings and allow her to guide us. For purely accidental observations, made without any plan having been thought out in advance, cannot be connected by a law‐ which is what reason is searching for.” From that reasoning Popper concluded that “we ourselves must confront nature with hypotheses and demand a reply to our questions; and that lacking such hypotheses, we can only make haphazard observations which follow no plan and which can therefore never lead to a natural law. Everyday experience, too, goes far beyond all observations. Everyday experience must interpret observations for without theoretical interpretation, observations remain blind and uninformative. Everyday experience constantly operates with abstract ideas, such as that of cause and effect, and so it cannot be derived from observation.” Popper agreed with Kant who said “Our intellect does not draw its laws from nature…but imposes them on nature”. Popper modifies this statement to “Our intellect does not draw its laws from nature, but tries‐ with varying degrees of success – to impose upon nature laws which it freely invents. Theories are seen to be free creations of our mind, the result of almost poetic intuition. While theories cannot be logically derived from observations, they can, however, clash with observations. This fact makes it possible to infer from observations that a theory is false. The possibility of refuting theories by observations is the basis of all empirical tests. All empirical tests are therefore attempted refutations.”

OUTLOOK: HYPOTHESES IN BIOLOGY

Is biology special.

Waddington notes that “living organisms are much more complicated than the non‐living things. Biology has therefore developed more slowly than sciences such as physics and chemistry and has tended to rely on them for many of its basic ideas. These older physical sciences have provided biology with many firm foundations which have been of the greatest value to it, but throughout most of its history biology has found itself faced with the dilemma as to how far its reliance on physics and chemistry should be pushed” both with respect to its experimental methods and its theoretical foundations. Vitalism is indeed such a theory maintaining that organisms cannot be explained solely by physicochemical laws claiming specific biological forces active in organisms. However, efforts to prove the existence of such vital forces have failed and today most biologists consider vitalism a superseded theory.

Biology as a branch of science is as old as physics. If one takes Aristotle as a reference, he has written more on biology than on physics. Sophisticated animal experiments were already conducted in the antiquity by Galen (Brüssow, 2022 ). Alertus Magnus displayed biological research interest during the medieval time. Knowledge on plants provided the basis of medical drugs in early modern times. What explains biology's decreasing influence compared with the rapid development of physics by Galilei and Newton? One reason is the possibility to use mathematical equations to describe physical phenomena which was not possible for biological phenomena. Physics has from the beginning displayed a trend to few fundamental underlying principles. This is not the case for biology. With the discovery of new continents, biologists were fascinated by the diversity of life. Diversity was the conducting line of biological thinking. This changed only when taxonomists and comparative anatomists revealed recurring pattern in this stunning biological variety and when Darwin provided a theoretical concept to understand variation as a driving force in biology. Even when genetics and molecular biology allowed to understand biology from a few universally shared properties, such as a universal genetic code, biology differed in fundamental aspects from physics and chemistry. First, biology is so far restricted to the planet earth while the laws of physic and chemistry apply in principle to the entire universe. Second, biology is to a great extent a historical discipline; many biological processes cannot be understood from present‐day observations because they are the result of historical developments in evolution. Hence, the importance of Dobzhansky's dictum that nothing makes sense in biology except in the light of evolution. The great diversity of life forms, the complexity of processes occurring in cells and their integration in higher organisms and the importance of a historical past for the understanding of extant organisms, all that has delayed the successful application of mathematical methods in biology or the construction of theoretical frameworks in biology. Theoretical biology by far did not achieve a comparable role as theoretical physics which is on equal foot with experimental physics. Many biologists are even rather sceptical towards a theoretical biology and see progress in the development of ever more sophisticated experimental methods instead in theoretical concepts expressed by new hypotheses.

Knowledge from data without hypothesis?

Philosophers distinguish rational knowledge ( cognitio ex principiis ) from knowledge from data ( cognitio ex data ). Kant associates these two branches with natural sciences and natural history, respectively. The latter with descriptions of natural objects as prominently done with systematic classification of animals and plants or, where it is really history, when describing events in the evolution of life forms on earth. Cognitio ex data thus played a much more prominent role in biology than in physics and explains why the compilation of data and in extremis the collection of museum specimen characterizes biological research. To account for this difference, philosophers of the logical empiricism developed a two‐level concept of science languages consisting of a language of observations (Beobachtungssprache) and a language of theories (Theoriesprache) which are linked by certain rules of correspondence (Korrespondenzregeln) (Carnap, 1891 –1970d). If one looks into leading biological research journals, it becomes clear that biology has a sophisticated language of observation and a much less developed language of theories.

Do we need more philosophical thinking in biology or at least a more vigorous theoretical biology? The breathtaking speed of progress in experimental biology seems to indicate that biology can well develop without much theoretical or philosophical thinking. At the same time, one could argue that some fields in biology might need more theoretical rigour. Microbiologists might think on microbiome research—one of the breakthrough developments of microbiology research in recent years. The field teems with fascinating, but ill‐defined terms (our second genome; holobionts; gut–brain axis; dysbiosis, symbionts; probiotics; health benefits) that call for stricter definitions. One might also argue that biologists should at least consider the criticism of Goethe ( 1749–1832 ), a poet who was also an active scientist. In Faust , the devil ironically teaches biology to a young student.

“Wer will was Lebendigs erkennen und beschreiben, Sucht erst den Geist herauszutreiben, Dann hat er die Teile in seiner Hand, Fehlt, leider! nur das geistige Band.” (To docket living things past any doubt. You cancel first the living spirit out: The parts lie in the hollow of your hand, You only lack the living thing you banned).

We probably need both in biology: more data and more theory and hypotheses.

CONFLICT OF INTEREST

The author reports no conflict of interest.

FUNDING INFORMATION

No funding information provided.

Supporting information

Appendix S1

Brüssow, H. (2022) On the role of hypotheses in science . Microbial Biotechnology , 15 , 2687–2698. Available from: 10.1111/1751-7915.14141 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]

Bacon, F. (1561. –1626) Novum Organum. In: Adler, M.J. (Ed.) (editor‐in‐chief) Great books of the western world . Chicago, IL: Encyclopaedia Britannica, Inc. 2nd edition 1992 vol 1–60 (abbreviated below as GBWW) here: GBWW vol. 28: 128. [ Google Scholar ]
Brüssow, H. (2022) What is Truth – in science and beyond . Environmental Microbiology , 24 , 2895–2906. [ PubMed ] [ Google Scholar ]
Carnap, R. (1891. ‐1970a) Philosophical foundations of physics. Ch. 14 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
Carnap, R. (1891. ‐1970b) Philosophical foundations of physics. Ch. 15 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
Carnap, R. (1891. ‐1970c) Philosophical foundations of physics. Ch. 16 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
Carnap, R. (1891. ‐1970d) Philosophical foundations of physics. Ch. 27–28 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
Copernicus . (1473. ‐1543) Revolutions of heavenly spheres . GBWW , vol. 15 , 505–506. [ Google Scholar ]
Darwin, C. (1809. ‐1882a) The origin of species . GBWW , vol. 49 : 239. [ Google Scholar ]
Darwin, C. (1809. ‐1882b) The descent of man . GBWW , vol. 49 : 590. [ Google Scholar ]
Descartes, R. (1596. ‐1650) Rules for direction . GBWW , vol. 28 , 245. [ Google Scholar ]
Dewey, J. (1859. –1952) Experience and education . GBWW , vol. 55 , 124. [ Google Scholar ]
Dorfmüller, T. , Hering, W.T. & Stierstadt, K. (1998) Bergmann Schäfer Lehrbuch der Experimentalphysik: Band 1 Mechanik, Relativität, Wärme. In: Was ist Schwerkraft: Von Newton zu Einstein . Berlin, New York: Walter de Gruyter, pp. 197–203. [ Google Scholar ]
Einstein, A. (1916) Relativity . GBWW , vol. 56 , 191–243. [ Google Scholar ]
Einstein, A. & Imfeld, L. (1956) Die Evolution der Physik . Hamburg: Rowohlts deutsche Enzyklopädie, Rowohlt Verlag. [ Google Scholar ]
Euclid . (c.323‐c.283) The elements . GBWW , vol. 10 , 1–2. [ Google Scholar ]
Faraday, M. (1791. –1867) Speculation touching electric conduction and the nature of matter . GBWW , 42 , 758–763. [ Google Scholar ]
Freud, S. (1856. –1939) Beyond the pleasure principle . GBWW , vol. 54 , 661–662. [ Google Scholar ]
Galilei, G. (1564. ‐1642a) The Assayer, as translated by S. Drake (1957) Discoveries and Opinions of Galileo pp. 237–8 abridged pdf at Stanford University .
Galilei, G. (1564. ‐1642b) The two sciences . GBWW vol. 26 : 200. [ Google Scholar ]
Gilbert, W. (1544. ‐1603) On the Loadstone . GBWW , vol. 26 , 108–110. [ Google Scholar ]
Goethe, J.W. (1749. –1832) Faust . GBWW , vol. 45 , 20. [ Google Scholar ]
Hilbert, D. (1899) Grundlagen der Geometrie . Leipzig, Germany: Verlag Teubner. [ Google Scholar ]
Huygens, C. (1617. ‐1670) Treatise on light . GBWW , vol. 32 , 557–560. [ Google Scholar ]
James, W. (1842. –1907) Principles of psychology . GBWW , vol. 53 , 862–866. [ Google Scholar ]
Kant, I. (1724. –1804) Critique of pure reason . GBWW , vol. 39 , 227–230. [ Google Scholar ]
Lavoisier, A.L. (1743. ‐1794) Element of chemistry . GBWW , vol. 42 , p. 2, 6‐7, 9‐10. [ Google Scholar ]
Locke, J. (1632. ‐1704) Concerning Human Understanding . GBWW , vol. 33 , 317–362. [ Google Scholar ]
Mittelstrass, J. (1980a) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 239–241 .
Mittelstrass, J. (1980b) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 3: 307 .
Mittelstrass, J. (1980c) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 439–442 .
Mittelstrass, J. (1980d) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 2: 157–158 .
Mittelstrass, J. (1980e) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 3: 264‐267, 449.450 .
Mittelstrass, J. (1980f) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 209–210 .
Mittelstrass, J. (1980g) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 281–282 .
Pascal, B. (1623. ‐1662a) Pensées GBWW vol. 30 : 171–173. [ Google Scholar ]
Pascal, B. (1623. ‐1662b) Scientific treatises on geometric demonstrations . GBWW vol. 30 : 442–443. [ Google Scholar ]
Plato . (c.424‐c.348 BC a) Timaeus . GBWW , vol. 6 , 442–477. [ Google Scholar ]
Poincaré, H. (1854. ‐1912a) Science and hypothesis GBWW , vol. 56 : XV‐XVI, 1–5, 10–15 [ Google Scholar ]
Poincaré, H. (1854. ‐1912b) Science and hypothesis GBWW , vol. 56 : 40–52. [ Google Scholar ]
Popper, K. (1902. ‐1994) Conjectures and refutations . London and New York, 2002: The Growth of Scientific Knowledge Routledge Classics, pp. 249–261. [ Google Scholar ]
Syntopicon . (1992) Hypothesis . GBWW , vol. 1 , 576–587. [ Google Scholar ]
Waddington, C.H. (1905. –1975) The nature of life . GBWW , vol. 56 , 697–699. [ Google Scholar ]

IMAGES

15 Hypothesis Examples (2024)
How to Write a Hypothesis: The Ultimate Guide with Examples
How to Write a Strong Hypothesis in 6 Simple Steps
How to Form a Hypothesis
How to Write a Hypothesis
Research Hypothesis: Definition, Types, Examples and Quick Tips

VIDEO

A Review of the General Principles of Hypothesis Testing
General procedure for testing hypothesis ch 16 lec 5
Chapter #1 Leacture no.9 part 2 Other ways to form Hypothesis. Class 11th Biology
Step 1. Form Null Hypothesis (H_0) and Alternative Hypothesis (H_1)
#Second Quarter Week 5/ Lesson: #CONDITIONAL Statements #Hypothesis #Conclusion #If-thenStatements
How moon is form!! Gaint hypothesis!! Earth crash

COMMENTS

How to Write a Strong Hypothesis
Developing a hypothesis (with example) Step 1. Ask a question. Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project. Example: Research question.
How to Write a Great Hypothesis
What is a hypothesis and how can you write a great one for your research? A hypothesis is a tentative statement about the relationship between two or more variables that can be tested empirically. Find out how to formulate a clear, specific, and testable hypothesis with examples and tips from Verywell Mind, a trusted source of psychology and mental health information.
What is a Hypothesis
Definition: Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation. Hypothesis is often used in scientific research to guide the design of experiments ...
How to Write a Strong Hypothesis
Step 5: Phrase your hypothesis in three ways. To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable. If a first-year student starts attending more lectures, then their exam scores will improve.
What Is a Hypothesis and How Do I Write One?
This is an excellent example of how flexible hypothesis statements can be, as long as the general idea of "if-then" and the independent and dependent variables are present. #2: Null Hypotheses Your if-then hypothesis is not the only one needed to complete a successful experiment, however.
Scientific hypothesis
hypothesis. science. scientific hypothesis, an idea that proposes a tentative explanation about a phenomenon or a narrow set of phenomena observed in the natural world. The two primary features of a scientific hypothesis are falsifiability and testability, which are reflected in an "If…then" statement summarizing the idea and in the ...
Hypothesis
The hypothesis of Andreas Cellarius, showing the planetary motions in eccentric and epicyclical orbits.. A hypothesis (pl.: hypotheses) is a proposed explanation for a phenomenon.For a hypothesis to be a scientific hypothesis, the scientific method requires that one can test it. Scientists generally base scientific hypotheses on previous observations that cannot satisfactorily be explained ...
Research Hypothesis In Psychology: Types, & Examples
Examples. A research hypothesis, in its plural form "hypotheses," is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.
How to Write a Hypothesis w/ Strong Examples
Simple Hypothesis Examples. Increasing the amount of natural light in a classroom will improve students' test scores. Drinking at least eight glasses of water a day reduces the frequency of headaches in adults. Plant growth is faster when the plant is exposed to music for at least one hour per day.
What is a scientific hypothesis?
A hypothesis is usually written in the form of an if-then statement, which gives a possibility (if) and explains what may happen because of the possibility (then).
PDF Topic #6: Hypothesis
Topic #6: Hypothesis. A hypothesis is a suggested explanation of a phenomenon or reasoned proposal suggesting a possible correlation between multiple phenomena. The term derives from the ancient Greek, hypotithenai meaning "to put under" or "to suppose". The scientific method requires that one can test a scientific hypothesis.
2.4 Developing a Hypothesis
Theories and Hypotheses. Before describing how to develop a hypothesis it is imporant to distinguish betwee a theory and a hypothesis. A theory is a coherent explanation or interpretation of one or more phenomena.Although theories can take a variety of forms, one thing they have in common is that they go beyond the phenomena they explain by including variables, structures, processes, functions ...
What Are Examples of a Hypothesis?
Scientific Hypothesis Examples. By Anne Marie Helmenstine, Ph.D. If you get at least 6 hours of sleep, you will do better on tests than if you get less sleep. If you drop a ball, it will fall toward the ground. If you drink coffee before going to bed, then it will take longer to fall asleep. If you cover a wound with a bandage, then it will ...
5.2
5.2 - Writing Hypotheses. The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis ( H 0) and an alternative hypothesis ( H a ). Null Hypothesis. The statement that there is not a difference in the population (s), denoted as H 0.
What is Hypothesis
Functions of Hypothesis. Following are the functions performed by the hypothesis: Hypothesis helps in making an observation and experiments possible. It becomes the start point for the investigation. Hypothesis helps in verifying the observations. It helps in directing the inquiries in the right direction.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Hypothesis Testing
Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value, and is generally denoted by p 0. We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form: Ho: p = p 0
On the scope of scientific hypotheses
2. The scientific hypothesis. In this section, we will describe a functional and descriptive role regarding how scientists use hypotheses. Jeong & Kwon [] investigated and summarized the different uses the concept of 'hypothesis' had in philosophical and scientific texts.They identified five meanings: assumption, tentative explanation, tentative cause, tentative law, and prediction.
Hypothesis Definition & Meaning
hypothesis: [noun] an assumption or concession made for the sake of argument. an interpretation of a practical situation or condition taken as the ground for action.
8.1: The Elements of Hypothesis Testing
Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample. The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions: Reject H0. H 0. (and therefore accept Ha.
On the role of hypotheses in science
Scientific research progresses by the dialectic dialogue between hypothesis building and the experimental testing of these hypotheses. Microbiologists as biologists in general can rely on an increasing set of sophisticated experimental methods for hypothesis testing such that many scientists maintain that progress in biology essentially comes with new experimental tools.

Have a language expert improve your writing

How to Write a Strong Hypothesis | Steps & Examples

Example: Hypothesis

Table of contents

Variables in hypotheses

Prevent plagiarism. Run a free check.

Step 2. Do some preliminary research

Step 3. Formulate your hypothesis

4. Refine your hypothesis

5. Phrase your hypothesis in three ways

6. Write a null hypothesis

Cite this Scribbr article

Is this article helpful?

Shona McCombes

How to Write a Great Hypothesis

Hypothesis Format

Frequently Asked Questions

The Hypothesis in the Scientific Method

Elements of a Good Hypothesis

Hypothesis Checklist

A few examples of simple hypotheses:

Examples of a complex hypothesis include:

Examples of a null hypothesis include:

Examples of an alternative hypothesis:

Collecting Data on Your Hypothesis

Descriptive Research Methods

Experimental Research Methods

A Word From Verywell

Have a language expert improve your writing

How to Write a Strong Hypothesis | Guide & Examples

Table of contents

Variables in hypotheses

Prevent plagiarism, run a free check.

Step 2: Do some preliminary research

Step 3: Formulate your hypothesis

Step 4: Refine your hypothesis

Step 5: Phrase your hypothesis in three ways

Step 6. Write a null hypothesis

Cite this Scribbr article

Is this article helpful?

Shona McCombes

Choose Your Test

What Is a Hypothesis?

Independent and Dependent Variables

Elements of a Good Hypothesis

Writing Your Hypothesis

The Two Types of Hypotheses

#1: If-Then Hypotheses

#2: Null Hypotheses

4 Tips to Write the Best Hypothesis

#1: Plausibility

#2: Defined Concepts

#3: Observability

#4: Generalizability

Hypothesis Testing Examples

Experiment #1: Students Studying Outside (Writing a Hypothesis)

Experiment #2: The Cupcake Store (Forming a Simple Experiment)

Experiment #3: Backyard Bird Feeders (Integrating Multiple Variables and Rejecting the If-Then Hypothesis)

Experiment #4: In-Class Survey (Including an Alternative Hypothesis)

Key Takeaways: Hypothesis Writing

What’s Next?

Ask a Question Below

Improve With Our Famous Guides

Series: How to Get 800 on Each SAT Section:

Series: How to Get to 600 on Each SAT Section:

Series: How to Get 36 on Each ACT Section:

Series: How to Get to 24 on Each ACT Section:

Stay Informed

Looking for Graduate School Test Prep?

Research Hypothesis In Psychology: Types, & Examples

Some key points about hypotheses:

Types of Research Hypotheses

Null Hypothesis

Nondirectional Hypothesis

Directional Hypothesis

Falsifiability

Can a Hypothesis be Proven?

How to Write a Hypothesis

More Examples

What is a scientific hypothesis?