matrix assignment pdf

7.5 Matrices and Matrix Operations

Learning objectives.

In this section, you will:

• Find the sum and difference of two matrices.
• Find scalar multiples of a matrix.
• Find the product of two matrices.

Two club soccer teams, the Wildcats and the Mud Cats, are hoping to obtain new equipment for an upcoming season. Table 1 shows the needs of both teams.

A goal costs $300; a ball costs $10; and a jersey costs $30. How can we find the total cost for the equipment needed for each team? In this section, we discover a method in which the data in the soccer equipment table can be displayed and used for calculating other information. Then, we will be able to calculate the cost of the equipment.

Finding the Sum and Difference of Two Matrices

To solve a problem like the one described for the soccer teams, we can use a matrix , which is a rectangular array of numbers. A row in a matrix is a set of numbers that are aligned horizontally. A column in a matrix is a set of numbers that are aligned vertically. Each number is an entry , sometimes called an element, of the matrix. Matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. For example, three matrices named A , B , A , B , and C C are shown below.

Describing Matrices

A matrix is often referred to by its size or dimensions: m × n m × n indicating m m rows and n n columns. Matrix entries are defined first by row and then by column. For example, to locate the entry in matrix A A identified as a i j , a i j , we look for the entry in row i , i , column j . j . In matrix A ,   A ,   shown below, the entry in row 2, column 3 is a 23 . a 23 .

A square matrix is a matrix with dimensions n × n , n × n , meaning that it has the same number of rows as columns. The 3 × 3 3 × 3 matrix above is an example of a square matrix.

A row matrix is a matrix consisting of one row with dimensions 1 × n . 1 × n .

A column matrix is a matrix consisting of one column with dimensions m × 1. m × 1.

A matrix may be used to represent a system of equations. In these cases, the numbers represent the coefficients of the variables in the system. Matrices often make solving systems of equations easier because they are not encumbered with variables. We will investigate this idea further in the next section, but first we will look at basic matrix operations .

A matrix is a rectangular array of numbers that is usually named by a capital letter: A , B , C , A , B , C , and so on. Each entry in a matrix is referred to as a i j , a i j , such that i i represents the row and j j represents the column. Matrices are often referred to by their dimensions: m × n m × n indicating m m rows and n n columns.

Finding the Dimensions of the Given Matrix and Locating Entries

Given matrix A : A :

• ⓐ What are the dimensions of matrix A ? A ?
• ⓑ What are the entries at a 31 a 31 and a 22 ? a 22 ? A = [ 2 1 0 2 4 7 3 1 − 2 ] A = [ 2 1 0 2 4 7 3 1 − 2 ]
• ⓐ The dimensions are 3 × 3 3 × 3 because there are three rows and three columns.
• ⓑ Entry a 31 a 31 is the number at row 3, column 1, which is 3. The entry a 22 a 22 is the number at row 2, column 2, which is 4. Remember, the row comes first, then the column.

Adding and Subtracting Matrices

We use matrices to list data or to represent systems. Because the entries are numbers, we can perform operations on matrices. We add or subtract matrices by adding or subtracting corresponding entries.

In order to do this, the entries must correspond. Therefore, addition and subtraction of matrices is only possible when the matrices have the same dimensions . We can add or subtract a 3 × 3 3 × 3 matrix and another 3 × 3 3 × 3 matrix, but we cannot add or subtract a 2 × 3 2 × 3 matrix and a 3 × 3 3 × 3 matrix because some entries in one matrix will not have a corresponding entry in the other matrix.

Given matrices A A and B B of like dimensions, addition and subtraction of A A and B B will produce matrix C C or matrix D D of the same dimension.

Matrix addition is commutative.

It is also associative.

Finding the Sum of Matrices

Find the sum of A A and B , B , given

Add corresponding entries.

Adding Matrix A and Matrix B

Find the sum of A A and B . B .

Add corresponding entries. Add the entry in row 1, column 1, a 11 , a 11 , of matrix A A to the entry in row 1, column 1, b 11 , b 11 , of B . B . Continue the pattern until all entries have been added.

Finding the Difference of Two Matrices

Find the difference of A A and B . B .

We subtract the corresponding entries of each matrix.

Finding the Sum and Difference of Two 3 x 3 Matrices

Given A A and B : B :

• ⓐ Find the sum.
• ⓑ Find the difference.
• ⓐ Add the corresponding entries. A + B = [ 2 − 10 − 2 14 12 10 4 − 2 2 ] + [ 6 10 − 2 0 − 12 − 4 − 5 2 − 2 ] = [ 2 + 6 − 10 + 10 − 2 − 2 14 + 0 12 − 12 10 − 4 4 − 5 − 2 + 2 2 − 2 ] = [ 8 0 − 4 14 0 6 − 1 0 0 ] A + B = [ 2 − 10 − 2 14 12 10 4 − 2 2 ] + [ 6 10 − 2 0 − 12 − 4 − 5 2 − 2 ] = [ 2 + 6 − 10 + 10 − 2 − 2 14 + 0 12 − 12 10 − 4 4 − 5 − 2 + 2 2 − 2 ] = [ 8 0 − 4 14 0 6 − 1 0 0 ]
• ⓑ Subtract the corresponding entries. A − B = [ 2 −10 −2 14 12 10 4 −2 2 ] − [ 6 10 −2 0 −12 −4 −5 2 −2 ] = [ 2 − 6 −10 − 10 −2 + 2 14 − 0 12 + 12 10 + 4 4 + 5 −2 − 2 2 + 2 ] = [ −4 −20 0 14 24 14 9 −4 4 ] A − B = [ 2 −10 −2 14 12 10 4 −2 2 ] − [ 6 10 −2 0 −12 −4 −5 2 −2 ] = [ 2 − 6 −10 − 10 −2 + 2 14 − 0 12 + 12 10 + 4 4 + 5 −2 − 2 2 + 2 ] = [ −4 −20 0 14 24 14 9 −4 4 ]

Add matrix A A and matrix B . B .

Finding Scalar Multiples of a Matrix

Besides adding and subtracting whole matrices, there are many situations in which we need to multiply a matrix by a constant called a scalar. Recall that a scalar is a real number quantity that has magnitude, but not direction. For example, time, temperature, and distance are scalar quantities. The process of scalar multiplication involves multiplying each entry in a matrix by a scalar. A scalar multiple is any entry of a matrix that results from scalar multiplication.

Consider a real-world scenario in which a university needs to add to its inventory of computers, computer tables, and chairs in two of the campus labs due to increased enrollment. They estimate that 15% more equipment is needed in both labs. The school’s current inventory is displayed in Table 2 .

Converting the data to a matrix, we have

To calculate how much computer equipment will be needed, we multiply all entries in matrix C C by 0.15.

We must round up to the next integer, so the amount of new equipment needed is

Adding the two matrices as shown below, we see the new inventory amounts.

Thus, Lab A will have 18 computers, 19 computer tables, and 19 chairs; Lab B will have 32 computers, 40 computer tables, and 40 chairs.

Scalar Multiplication

Scalar multiplication involves finding the product of a constant by each entry in the matrix. Given

the scalar multiple c A c A is

Scalar multiplication is distributive. For the matrices A , B , A , B , and C C with scalars a a and b , b ,

Multiplying the Matrix by a Scalar

Multiply matrix A A by the scalar 3.

Multiply each entry in A A by the scalar 3.

Given matrix B , B , find −2 B −2 B where

Finding the Sum of Scalar Multiples

Find the sum 3 A + 2 B . 3 A + 2 B .

First, find 3 A , 3 A , then 2 B . 2 B .

Now, add 3 A + 2 B . 3 A + 2 B .

Finding the Product of Two Matrices

In addition to multiplying a matrix by a scalar, we can multiply two matrices. Finding the product of two matrices is only possible when the inner dimensions are the same, meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. If A A is an m × r m × r matrix and B B is an r × n r × n matrix, then the product matrix A B A B is an m × n m × n matrix. For example, the product A B A B is possible because the number of columns in A A is the same as the number of rows in B . B . If the inner dimensions do not match, the product is not defined.

We multiply entries of A A with entries of B B according to a specific pattern as outlined below. The process of matrix multiplication becomes clearer when working a problem with real numbers.

To obtain the entries in row i i of A B , A B , we multiply the entries in row i i of A A by column j j in B B and add. For example, given matrices A A and B , B , where the dimensions of A A are 2 × 3 2 × 3 and the dimensions of B B are 3 × 3 , 3 × 3 , the product of A B A B will be a 2 × 3 2 × 3 matrix.

Multiply and add as follows to obtain the first entry of the product matrix A B . A B .

• To obtain the entry in row 1, column 1 of A B , A B , multiply the first row in A A by the first column in B , B , and add. [ a 11 a 12 a 13 ] [ b 11 b 21 b 31 ] = a 11 ⋅ b 11 + a 12 ⋅ b 21 + a 13 ⋅ b 31 [ a 11 a 12 a 13 ] [ b 11 b 21 b 31 ] = a 11 ⋅ b 11 + a 12 ⋅ b 21 + a 13 ⋅ b 31
• To obtain the entry in row 1, column 2 of A B , A B , multiply the first row of A A by the second column in B , B , and add. [ a 11 a 12 a 13 ] [ b 12 b 22 b 32 ] = a 11 ⋅ b 12 + a 12 ⋅ b 22 + a 13 ⋅ b 32 [ a 11 a 12 a 13 ] [ b 12 b 22 b 32 ] = a 11 ⋅ b 12 + a 12 ⋅ b 22 + a 13 ⋅ b 32
• To obtain the entry in row 1, column 3 of A B , A B , multiply the first row of A A by the third column in B , B , and add. [ a 11 a 12 a 13 ] [ b 13 b 23 b 33 ] = a 11 ⋅ b 13 + a 12 ⋅ b 23 + a 13 ⋅ b 33 [ a 11 a 12 a 13 ] [ b 13 b 23 b 33 ] = a 11 ⋅ b 13 + a 12 ⋅ b 23 + a 13 ⋅ b 33

We proceed the same way to obtain the second row of A B . A B . In other words, row 2 of A A times column 1 of B ; B ; row 2 of A A times column 2 of B ; B ; row 2 of A A times column 3 of B . B . When complete, the product matrix will be

Properties of Matrix Multiplication

For the matrices A , B , A , B , and C C the following properties hold.

• Matrix multiplication is associative: ( A B ) C = A ( B C ) . ( A B ) C = A ( B C ) .
• Matrix multiplication is distributive: C ( A + B ) = C A + C B , ( A + B ) C = A C + B C . C ( A + B ) = C A + C B , ( A + B ) C = A C + B C .

Note that matrix multiplication is not commutative.

Multiplying Two Matrices

Multiply matrix A A and matrix B . B .

First, we check the dimensions of the matrices. Matrix A A has dimensions 2 × 2 2 × 2 and matrix B B has dimensions 2 × 2. 2 × 2. The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions 2 × 2. 2 × 2.

We perform the operations outlined previously.

• ⓐ Find A B . A B .
• ⓑ Find B A . B A .
• ⓐ As the dimensions of A A are 2 × 3 2 × 3 and the dimensions of B B are 3 × 2 , 3 × 2 , these matrices can be multiplied together because the number of columns in A A matches the number of rows in B . B . The resulting product will be a 2 × 2 2 × 2 matrix, the number of rows in A A by the number of columns in B . B . A B = [ −1 2 3 4 0 5 ]    [ 5 −1 − 4 0 2 3 ] = [ −1 ( 5 ) + 2 ( −4 ) + 3 ( 2 ) −1 ( −1 ) + 2 ( 0 ) + 3 ( 3 ) 4 ( 5 ) + 0 ( −4 ) + 5 ( 2 ) 4 ( −1 ) + 0 ( 0 ) + 5 ( 3 ) ] = [ −7 10 30 11 ] A B = [ −1 2 3 4 0 5 ]    [ 5 −1 − 4 0 2 3 ] = [ −1 ( 5 ) + 2 ( −4 ) + 3 ( 2 ) −1 ( −1 ) + 2 ( 0 ) + 3 ( 3 ) 4 ( 5 ) + 0 ( −4 ) + 5 ( 2 ) 4 ( −1 ) + 0 ( 0 ) + 5 ( 3 ) ] = [ −7 10 30 11 ]
• ⓑ The dimensions of B B are 3 × 2 3 × 2 and the dimensions of A A are 2 × 3. 2 × 3. The inner dimensions match so the product is defined and will be a 3 × 3 3 × 3 matrix. B A = [ 5 −1 −4 0 2 3 ]    [ −1 2 3 4 0 5 ] = [ 5 ( −1 ) + −1 ( 4 ) 5 ( 2 ) + −1 ( 0 ) 5 ( 3 ) + −1 ( 5 ) −4 ( −1 ) + 0 ( 4 ) −4 ( 2 ) + 0 ( 0 ) −4 ( 3 ) + 0 ( 5 ) 2 ( −1 ) + 3 ( 4 ) 2 ( 2 ) + 3 ( 0 ) 2 ( 3 ) + 3 ( 5 ) ] = [ −9 10 10 4 −8 −12 10 4 21 ] B A = [ 5 −1 −4 0 2 3 ]    [ −1 2 3 4 0 5 ] = [ 5 ( −1 ) + −1 ( 4 ) 5 ( 2 ) + −1 ( 0 ) 5 ( 3 ) + −1 ( 5 ) −4 ( −1 ) + 0 ( 4 ) −4 ( 2 ) + 0 ( 0 ) −4 ( 3 ) + 0 ( 5 ) 2 ( −1 ) + 3 ( 4 ) 2 ( 2 ) + 3 ( 0 ) 2 ( 3 ) + 3 ( 5 ) ] = [ −9 10 10 4 −8 −12 10 4 21 ]

Notice that the products A B A B and B A B A are not equal.

This illustrates the fact that matrix multiplication is not commutative.

Is it possible for AB to be defined but not BA ?

Yes, consider a matrix A with dimension 3 × 4 3 × 4 and matrix B with dimension 4 × 2. 4 × 2. For the product AB the inner dimensions are 4 and the product is defined, but for the product BA the inner dimensions are 2 and 3 so the product is undefined.

Using Matrices in Real-World Problems

Let’s return to the problem presented at the opening of this section. We have Table 3 , representing the equipment needs of two soccer teams.

We are also given the prices of the equipment, as shown in Table 4 .

We will convert the data to matrices. Thus, the equipment need matrix is written as

The cost matrix is written as

We perform matrix multiplication to obtain costs for the equipment.

The total cost for equipment for the Wildcats is $2,520, and the total cost for equipment for the Mud Cats is $3,840.

Given a matrix operation, evaluate using a calculator.

• Save each matrix as a matrix variable [ A ] , [ B ] , [ C ] , ... [ A ] , [ B ] , [ C ] , ...
• Enter the operation into the calculator, calling up each matrix variable as needed.
• If the operation is defined, the calculator will present the solution matrix; if the operation is undefined, it will display an error message.

Using a Calculator to Perform Matrix Operations

Find A B − C A B − C given

On the matrix page of the calculator, we enter matrix A A above as the matrix variable [ A ] , [ A ] , matrix B B above as the matrix variable [ B ] , [ B ] , and matrix C C above as the matrix variable [ C ] . [ C ] .

On the home screen of the calculator, we type in the problem and call up each matrix variable as needed.

The calculator gives us the following matrix.

Access these online resources for additional instruction and practice with matrices and matrix operations.

• Dimensions of a Matrix
• Matrix Addition and Subtraction
• Matrix Operations
• Matrix Multiplication

7.5 Section Exercises

Can we add any two matrices together? If so, explain why; if not, explain why not and give an example of two matrices that cannot be added together.

Can we multiply any column matrix by any row matrix? Explain why or why not.

Can both the products A B A B and B A B A be defined? If so, explain how; if not, explain why.

Can any two matrices of the same size be multiplied? If so, explain why, and if not, explain why not and give an example of two matrices of the same size that cannot be multiplied together.

Does matrix multiplication commute? That is, does A B = B A ? A B = B A ? If so, prove why it does. If not, explain why it does not.

For the following exercises, use the matrices below and perform the matrix addition or subtraction. Indicate if the operation is undefined.

A + B A + B

C + D C + D

A + C A + C

B − E B − E

C + F C + F

D − B D − B

For the following exercises, use the matrices below to perform scalar multiplication.

1 2 C 1 2 C

100 D 100 D

For the following exercises, use the matrices below to perform matrix multiplication.

For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed.

A + B − C A + B − C

4 A + 5 D 4 A + 5 D

2 C + B 2 C + B

3 D + 4 E 3 D + 4 E

C −0.5 D C −0.5 D

100 D −10 E 100 D −10 E

For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. (Hint: A 2 = A ⋅ A A 2 = A ⋅ A )

B 2 A 2 B 2 A 2

A 2 B 2 A 2 B 2

( A B ) 2 ( A B ) 2

( B A ) 2 ( B A ) 2

( A B ) C ( A B ) C

A ( B C ) A ( B C )

For the following exercises, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. Use a calculator to verify your solution.

A B C A B C

For the following exercises, use the matrix below to perform the indicated operation on the given matrix.

Using the above questions, find a formula for B n . B n . Test the formula for B 201 B 201 and B 202 , B 202 , using a calculator.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/7-5-matrices-and-matrix-operations

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.6: Matrices and Matrix Operations

• Last updated
• Save as PDF
• Page ID 15091

Learning Objectives

• Find the sum and difference of two matrices.
• Find scalar multiples of a matrix.
• Find the product of two matrices.

Two club soccer teams, the Wildcats and the Mud Cats, are hoping to obtain new equipment for an upcoming season. Table \(\PageIndex{1}\) shows the needs of both teams.

A goal costs \($300\); a ball costs \($10\); and a jersey costs \($30\). How can we find the total cost for the equipment needed for each team? In this section, we discover a method in which the data in the soccer equipment table can be displayed and used for calculating other information. Then, we will be able to calculate the cost of the equipment.

Finding the Sum and Difference of Two Matrices

To solve a problem like the one described for the soccer teams, we can use a matrix, which is a rectangular array of numbers. A row in a matrix is a set of numbers that are aligned horizontally. A column in a matrix is a set of numbers that are aligned vertically. Each number is an entry, sometimes called an element, of the matrix. Matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. For example, three matrices named \(A\), \(B\), and \(C\) are shown below.

\[ \begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}\]

A matrix is often referred to by its size or dimensions: \(m×n\) indicating \(m\) rows and \(n\) columns. Matrix entries are defined first by row and then by column. For example, to locate the entry in matrix \(A\) identified as \(a_{ij}\),we look for the entry in row \(i\),column \(j\). In matrix \(A\), shown below, the entry in row \(2\), column \(3\) is \(a_{23}\).

\[A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber\]

• A square matrix is a matrix with dimensions \(n × n\), meaning that it has the same number of rows as columns. The \(3×3\) matrix above is an example of a square matrix.
• A row matrix is a matrix consisting of one row with dimensions \(1 × n\). \[\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber\]
• A column matrix is a matrix consisting of one column with dimensions \(m × 1\). \[\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber\]

A matrix may be used to represent a system of equations. In these cases, the numbers represent the coefficients of the variables in the system. Matrices often make solving systems of equations easier because they are not encumbered with variables. We will investigate this idea further in the next section, but first we will look at basic matrix operations .

Definition: MATRICES

A matrix is a rectangular array of numbers that is usually named by a capital letter: \(A\), \(B\), \(C\),and so on. Each entry in a matrix is referred to as \(a_{ij}\),such that \(i\) represents the row and \(j\) represents the column. Matrices are often referred to by their dimensions: \(m × n\) indicating \(m\) rows and \(n\) columns.

Example \(\PageIndex{1}\): Finding the Dimensions of the Given Matrix and Locating Entries

Given matrix \(A\):

• What are the dimensions of matrix \(A\)?
• What are the entries at \(a_{31}\) and \(a_{22}\)?

\[A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber\]

• The dimensions are \(3 \times 3\) because there are three rows and three columns.
• Entry \(a_{31}\) is the number at row 3, column 1, which is \(3\). The entry \(a_{22}\) is the number at row 2, column 2, which is \(4\). Remember, the row comes first, then the column.

Adding and Subtracting Matrices

We use matrices to list data or to represent systems. Because the entries are numbers, we can perform operations on matrices. We add or subtract matrices by adding or subtracting corresponding entries. To do this, the entries must correspond. Therefore, addition and subtraction of matrices is only possible when the matrices have the same dimensions . We can add or subtract a \(3 \times 3\) matrix and another \(3 \times 3\) matrix, but we cannot add or subtract a \(2 \times 3\) matrix and a \(3 \times 3\) matrix because some entries in one matrix will not have a corresponding entry in the other matrix.

ADDING AND SUBTRACTING MATRICES

Given matrices \(A\) and \(B\) of like dimensions, addition and subtraction of \(A\) and \(B\) will produce matrix \(C\) or matrix \(D\) of the same dimension.

such that \(a_{ij}+b_{ij}=c_{ij}\)

\[A−B=D\]

such that \(a_{ij}−b_{ij}=d_{ij}\)

Matrix addition is commutative .

\[A+B=B+A\]

It is also associative .

\[(A+B)+C=A+(B+C)\]

Example \(\PageIndex{2A}\): Finding the Sum of Matrices

Find the sum of \(A\) and \(B\), given

\[A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber\]

Add corresponding entries.

\[\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber\]

Example \(\PageIndex{2B}\): Adding Matrix \(A\) and Matrix \(B\)

Find the sum of \(A\) and \(B\).

\[A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber\]

Add corresponding entries. Add the entry in row 1, column 1, \(a_{11}\), of matrix \(A\) to the entry in row 1, column 1, \(b_{11}\), of \(B\). Continue the pattern until all entries have been added.

\[\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber\]

Example \(\PageIndex{2C}\): Finding the Difference of Two Matrices

Find the difference of \(A\) and \(B\).

\(A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}\) and \(B=\begin{bmatrix}8&1\\5&4\end{bmatrix}\)

We subtract the corresponding entries of each matrix.

\[\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber\]

Example \(\PageIndex{2D}\): Finding the Sum and Difference of Two 3 x 3 Matrices

Given \(A\) and \(B\):

• Find the sum.
• Find the difference.

\[A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber\]

• Add the corresponding entries.

\[\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber\]

• Subtract the corresponding entries.

\[\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber\]

Exercise \(\PageIndex{1}\)

Add matrix \(A\) and matrix \(B\).

\[A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber\]

\[\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber\]

Finding Scalar Multiples of a Matrix

Besides adding and subtracting whole matrices, there are many situations in which we need to multiply a matrix by a constant called a scalar. Recall that a scalar is a real number quantity that has magnitude, but not direction. For example, time, temperature, and distance are scalar quantities. The process of scalar multiplication involves multiplying each entry in a matrix by a scalar. A scalar multiple is any entry of a matrix that results from scalar multiplication.

Consider a real-world scenario in which a university needs to add to its inventory of computers, computer tables, and chairs in two of the campus labs due to increased enrollment. They estimate that \(15%\) more equipment is needed in both labs. The school’s current inventory is displayed in Table \(\PageIndex{2}\).

Converting the data to a matrix, we have

\[C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber\]

To calculate how much computer equipment will be needed, we multiply all entries in matrix \(C\) by \(0.15\).

\[(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber\]

We must round up to the next integer, so the amount of new equipment needed is

\[\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber\]

Adding the two matrices as shown below, we see the new inventory amounts.

\[\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]

\[C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]

Thus, Lab A will have \(18\) computers, \(19\) computer tables, and \(19\) chairs; Lab B will have \(32\) computers, \(40\) computer tables, and \(40\) chairs.

SCALAR MULTIPLICATION

Scalar multiplication involves finding the product of a constant by each entry in the matrix. Given

\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]

the scalar multiple \(cA\) is

\[cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]

\[=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber\]

Scalar multiplication is distributive. For the matrices \(A\), \(B\),and \(C\) with scalars \(a\) and \(b\),

\[a(A+B)=aA+aB\]

\[(a+b)A=aA+bA\]

Example \(\PageIndex{3}\): Multiplying the Matrix by a Scalar

Multiply matrix \(A\) by the scalar \(3\).

\[A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber\]

Multiply each entry in \(A\) by the scalar \(3\).

\[ \begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber\]

Exercise \(\PageIndex{2}\)

Given matrix \(B\), find \(−2B\) where

\[B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber\]

\[−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber\]

Example \(\PageIndex{4}\): Finding the Sum of Scalar Multiples

Find the sum \(3A+2B\).

\[A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber\]

First, find \(3A\), then \(2B\).

\[ \begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber\]

\[ \begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber\]

Now, add \(3A+2B\).

\[ \begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber\]

Finding the Product of Two Matrices

In addition to multiplying a matrix by a scalar, we can multiply two matrices. Finding the product of two matrices is only possible when the inner dimensions are the same, meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. If \(A\) is an \(m × r\) matrix and \(B\) is an \(r × n\) matrix, then the product matrix \(AB\) is an \(m × n\) matrix. For example, the product \(AB\) is possible because the number of columns in \(A\) is the same as the number of rows in \(B\). If the inner dimensions do not match, the product is not defined.

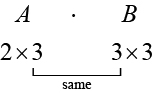
We multiply entries of \(A\) with entries of \(B\) according to a specific pattern as outlined below. The process of matrix multiplication becomes clearer when working a problem with real numbers.

To obtain the entries in row \(i\) of \(AB\), we multiply the entries in row \(i\) of \(A\) by column \(j\) in \(B\) and add. For example, given matrices \(A\) and \(B\), where the dimensions of \(A\) are \(2 \times 3\) and the dimensions of \(B\) are \(3 \times 3\),the product of \(AB\) will be a \(2 \times 3\) matrix.

\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber \]

\[B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber\]

Multiply and add as follows to obtain the first entry of the product matrix \(AB\).

\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber \]

\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber \]

\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber \]

We proceed the same way to obtain the second row of \(AB\). In other words, row 2 of \(A\) times column 1 of \(B\); row 2 of \(A\) times column 2 of \(B\); row 2 of \(A\) times column 3 of \(B\). When complete, the product matrix will be

\[AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber\]

PROPERTIES OF MATRIX MULTIPLICATION

For the matrice \(A, B\),and \(C\) the following properties hold.

• Matrix multiplication is associative : \[(AB)C=A(BC).\]
• Matrix multiplication is distributive : \[C(A+B)=CA+CB\] \[(A+B)C=AC+BC.\]

Note that matrix multiplication is not commutative.

Example \(\PageIndex{5A}\): Multiplying Two Matrices

Multiply matrix \(A\) and matrix \(B\).

\[A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber\]

First, we check the dimensions of the matrices. Matrix \(A\) has dimensions \(2 × 2\) and matrix \(B\) has dimensions \(2 × 2\). The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions \(2 × 2\).

We perform the operations outlined previously.

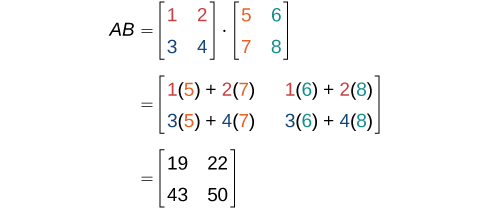
Example \(\PageIndex{5B}\): Multiplying Two Matrices

• Find \(AB\).
• Find \(BA\).

\[A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber\]

\[B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber\]

• As the dimensions of \(A\) are \(2 \times 3\) and the dimensions of \(B\) are \(3 \times 2\),these matrices can be multiplied together because the number of columns in \(A\) matches the number of rows in \(B\). The resulting product will be a \(2 \times 2\) matrix, the number of rows in \(A\) by the number of columns in \(B\).

\[ \begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber\]

• The dimensions of \(B\) are \(3 \times 2\) and the dimensions of \(A\) are \(2 \times 3\). The inner dimensions match so the product is defined and will be a \(3 \times 3\) matrix.

\[ \begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber\]

Notice that the products \(AB\) and \(BA\) are not equal.

\[AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber\]

This illustrates the fact that matrix multiplication is not commutative.

Q&A: Is it possible for AB to be defined but not BA?

Yes, consider a matrix \(A\) with dimension \(3 × 4\) and matrix \(B\) with dimension \(4 × 2\). For the product \(AB\) the inner dimensions are \(4\) and the product is defined, but for the product \(BA\) the inner dimensions are \(2\) and \(3\) so the product is undefined.

Example \(\PageIndex{6}\): Using Matrices in Real-World Problems

Let’s return to the problem presented at the opening of this section. We have Table \(\PageIndex{3}\), representing the equipment needs of two soccer teams.

We are also given the prices of the equipment, as shown in Table \(\PageIndex{4}\).

We will convert the data to matrices. Thus, the equipment need matrix is written as

\[E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber\]

The cost matrix is written as

\[C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber\]

We perform matrix multiplication to obtain costs for the equipment.

\[ \begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber\]

The total cost for equipment for the Wildcats is \($2,520\), and the total cost for equipment for the Mud Cats is \($3,840\).

How to: Given a matrix operation, evaluate using a calculator

• Save each matrix as a matrix variable \([A], [B], [C],...\)
• Enter the operation into the calculator, calling up each matrix variable as needed.
• If the operation is defined, the calculator will present the solution matrix; if the operation is undefined, it will display an error message.

Example \(\PageIndex{7}\): Using a Calculator to Perform Matrix Operations

Find \(AB−C\) given

\(A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}\), \(B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}\), and \(C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}\)

On the matrix page of the calculator, we enter matrix \(A\) above as the matrix variable \([ A ]\), matrix \(B\) above as the matrix variable \([ B ]\), and matrix \(C\) above as the matrix variable \([ C ]\).

On the home screen of the calculator, we type in the problem and call up each matrix variable as needed.

\[[A]×[B]−[C] \nonumber\]

The calculator gives us the following matrix.

\[\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber\]

Access these online resources for additional instruction and practice with matrices and matrix operations.

• Dimensions of a Matrix
• Matrix Addition and Subtraction
• Matrix Operations
• Matrix Multiplication

Key Concepts

• A matrix is a rectangular array of numbers. Entries are arranged in rows and columns.
• The dimensions of a matrix refer to the number of rows and the number of columns. A \(3×2\) matrix has three rows and two columns. See Example \(\PageIndex{1}\).
• We add and subtract matrices of equal dimensions by adding and subtracting corresponding entries of each matrix. See Example \(\PageIndex{2}\), Example \(\PageIndex{3}\), Example \(\PageIndex{4}\), and Example \(\PageIndex{5}\).
• Scalar multiplication involves multiplying each entry in a matrix by a constant. See Example \(\PageIndex{6}\).
• Scalar multiplication is often required before addition or subtraction can occur. See Example \(\PageIndex{7}\).
• Multiplying matrices is possible when inner dimensions are the same—the number of columns in the first matrix must match the number of rows in the second.
• The product of two matrices, \(A\) and \(B\),is obtained by multiplying each entry in row 1 of \(A\) by each entry in column 1 of \(B\); then multiply each entry of row 1 of \(A\) by each entry in columns 2 of \(B\),and so on. See Example \(\PageIndex{8}\) and Example \(\PageIndex{9}\).
• Many real-world problems can often be solved using matrices. See Example \(\PageIndex{10}\).
• We can use a calculator to perform matrix operations after saving each matrix as a matrix variable. See Example \(\PageIndex{11}\).

OASIS: Writing Center

Common assignments: literature review matrix, literature review matrix.

As you read and evaluate your literature there are several different ways to organize your research. Courtesy of Dr. Gary Burkholder in the School of Psychology, these sample matrices are one option to help organize your articles. These documents allow you to compile details about your sources, such as the foundational theories, methodologies, and conclusions; begin to note similarities among the authors; and retrieve citation information for easy insertion within a document.

You can review the sample matrixes to see a completed form or download the blank matrix for your own use.

• Literature Review Matrix 1 This PDF file provides a sample literature review matrix.
• Literature Review Matrix 2 This PDF file provides a sample literature review matrix.
• Literature Review Matrix Template (Word)
• Literature Review Matrix Template (Excel)

Related Resources

Didn't find what you need? Search our website or email us .

Read our website accessibility and accommodation statement .

• Previous Page: Commentary Versus Opinion
• Next Page: Professional Development Plans (PDPs)
• Office of Student Disability Services

Walden Resources

Departments.

• Academic Residencies
• Academic Skills
• Career Planning and Development
• Customer Care Team
• Field Experience
• Military Services
• Student Success Advising
• Writing Skills

Centers and Offices

• Center for Social Change
• Office of Academic Support and Instructional Services
• Office of Degree Acceleration
• Office of Research and Doctoral Services
• Office of Student Affairs

Student Resources

• Doctoral Writing Assessment
• Form & Style Review
• Quick Answers
• ScholarWorks
• SKIL Courses and Workshops
• Walden Bookstore
• Walden Catalog & Student Handbook
• Student Safety/Title IX
• Legal & Consumer Information
• Website Terms and Conditions
• Cookie Policy
• Accessibility
• Accreditation
• State Authorization
• Net Price Calculator
• Contact Walden

Walden University is a member of Adtalem Global Education, Inc. www.adtalem.com Walden University is certified to operate by SCHEV © 2024 Walden University LLC. All rights reserved.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Matrix Assignment

Related Papers

Cotton is the world’s leading cash crop, but it lags behind other major crops for marker-assisted breeding due to limited polymorphisms and a genetic bottleneck through historic domestication. This underlies a need for characterization, tagging, and utilization of existing natural polymorphisms in cotton germplasm collections. Here we report genetic diversity, population characteristics, the extent of linkage disequilibrium (LD), and association mapping of fiber quality traits using 202 microsatellite marker primer pairs in 335 G. hirsutum germplasm grown in two diverse environments, Uzbekistan and Mexico. At the significance threshold (r 2 ≥ 0.1), a genome-wide average of LD extended up to genetic distance of 25 cM in assayed cotton variety accessions. Genome wide LD at r 2 ≥ 0.2 was reduced to ~5–6 cM, providing evidence of the potential for association mapping of agronomically important traits in cotton. Results suggest linkage, selection, inbreeding, population stratification, and genetic drift as the potential LD-generating factors in cotton. In two environments, an average of ~20 SSR markers was associated with each main fiber quality traits using a unified mixed liner model (MLM) incorporating population structure and kinship. These MLM-derived significant associations were confirmed in general linear model and structured association test, accounting for population structure and permutation-based multiple testing. Several common markers, showing the significant associations in both Uzbekistan and Mexican environments, were determined. Between 7 and 43% of the MLM-derived significant associations were supported by a minimum Bayes factor at ‘moderate to strong’ and ‘strong to very strong’ evidence levels, suggesting their usefulness for marker-assisted breeding programs and overall effectiveness of association mapping using cotton germplasm resources.

Akemi Atsuko

BMC Nursing

Hanny Handiyani

Joseph Robins

Rangeland revegetation is necessary to stabilize disturbed sites and increase forage production, but frequently fails due to a variety of environmental and biotic factors. Plant breeding efforts in perennial cool-season grasses result in the development of potential cultivars that must be evaluated in multi-environment trials to determine their level of adaptation. This study evaluated 49 cultivars for stand frequency and dry matter yield over five years at five environments in the Intermountain and High Plains regions of the United States. The results were significant differences among the included cultivars for both traits across and within environments. Yet, there was also crossover genotype × environment interaction. Thus, highest performing cultivars were to some extent dependent on the environment. Hycrest II crested wheatgrass and Vavilov II Siberian wheatgrass possessed high stand frequency (>80 %) and dry matter yield (>800 kg·ha−1) across environments and within envi...

Encarnación Núñez-olivera

Natural Product Communications

Pham Hai Yen

Two new sesquiterpenes and one new bis-sesquiterpene, named dysinidins C-E (1–3) along with three known sterols, dysideasterol F, 9α,11α-epoxycholest-7-en-3β,5α,6α-triol, and 9α,11α-epoxycholest-7-en-3β,5α,6α,19-tetrol 6-acetate (4–6) were isolated from the Vietnamese marine sponge Dysidea fragilis (Montagu, 1814). Their structures were determined by 1D- and 2D-NMR spectroscopies and HR-ESI-MS, as well as by comparison with reported literature data. Compounds 4–6 were found to inhibit eight human cancer cell lines (KB, LU-1, HL-60, LNCaP, SK-Mel-2, HepG-2, MCF-7, and PC-3), with IC50 values ranging from 7.3 to 31.5 μM.

Gaetano Garfì

The use of a portable thermal camera has been applied to routine monitoring of the 2002 Etna flank eruption. The eruption started on 27 October with the opening of a field of fissures on the north and south flanks of the volcano. Abundant ash emission from the whole length of the 10 km long fissure covered the lava flow field,

Jurnal Kefarmasian Akfarindo

ajeng kumala

Kortikosteroid merupakan obat yang mempunyai khasiat dan indikasi klinis yang sangat luas, bahkan sering disebut sebagai life saving drug. Kortikosteroid merupakan obat yang sangat banyak dipakai dalam dunia kedokteran. Manfaat dari kortikosteroid cukup besar, tetapi efek samping yang tidak diharapkan cukup besar dan merugikan kesehatan. Efek samping yang cukup serius meliputi, diabetes mellitus, osteoporosis, hipertensi dan gangguan lambung. Dewasa ini penggunaan bat kortikosteroid meningkat. Banyak pasien membeli obat dari golongan kortikosteroid dalam jumlah banyak dan intensitas yang sering. Oleh sebab itu, peneliti melakukan penelitian untuk mengevaluasi pengetahuan pasien tentang obat kortikosteroid di Apotek Hs 23. Peneliti melakukan penelitian di Apotek Hs 23 karena tingkat penggunaan obat kortikosteroid tinggi. Metode penelitian yang digunakan adalah metode penelitian deskriptif non eksperimental dengan menggunakan kuesioner. Setelah data dari kuesioner terkumpul kem...

Anatolian Journal of Psychiatry

Rakesh Kumar

This paper deals with design of various controllers such as Proportional Integral Derivative (PID) controller, Internal Model Controller(IMC) and transfer function controller by using Genetic Algorithm(GA) for a non-linear liquid conical tank system. Level control of a conical tank is a complex issue because of the nonlinear nature of the tank. For each stable operating point, a First Order Process

RELATED PAPERS

Virology Journal

Muhammad Ali

Journal of Membrane Biology

L. Santella

Johannes Royset

Norasmahani Hussain

Jurnal Penataan Ruang

Alfie Zubaidah

11. mezinárodní vědecká konference. Didaktická konference 2017. 11th International Scientific Conference. Didactic Conference 2017. 1. a 2. června 2017, Brno, Česká republika

Peter Marinič

Journal of Substance Use

Seyran Naghdi

Journal of Neurosurgery

Charles Wilson

Energy Advances

Aniket Raut

Estuarine, Coastal and Shelf Science

J. Forget-Leray

Anuário Antropológico

Joao Tadeu De Andrade

Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments

Scientific Electronic Archives

Edleusa Seidel

Kamái Freire

LJMU毕业证书 利物浦约翰摩尔斯大学毕业证

RePEc: Research Papers in Economics

gonzalo iberti

Tauqir Ashraf

See More Documents Like This

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Help | Advanced Search

Computer Science > Information Retrieval

Title: lightweight embeddings for graph collaborative filtering.

Abstract: Graph neural networks (GNNs) are currently one of the most performant collaborative filtering methods. Meanwhile, owing to the use of an embedding table to represent each user/item as a distinct vector, GNN-based recommenders have inherited the long-standing defect of parameter inefficiency. As a common practice for scalable embeddings, parameter sharing enables the use of fewer embedding vectors (i.e., meta-embeddings). When assigning meta-embeddings, most existing methods are a heuristically designed, predefined mapping from each user's/item's ID to the corresponding meta-embedding indexes, thus simplifying the optimization problem into learning only the meta-embeddings. However, in the context of GNN-based collaborative filtering, such a fixed mapping omits the semantic correlations between entities that are evident in the user-item interaction graph, leading to suboptimal recommendation performance. To this end, we propose Lightweight Embeddings for Graph Collaborative Filtering (LEGCF), a parameter-efficient embedding framework dedicated to GNN-based recommenders. LEGCF innovatively introduces an assignment matrix as an extra learnable component on top of meta-embeddings. To jointly optimize these two heavily entangled components, aside from learning the meta-embeddings by minimizing the recommendation loss, LEGCF further performs efficient assignment update by enforcing a novel semantic similarity constraint and finding its closed-form solution based on matrix pseudo-inverse. The meta-embeddings and assignment matrix are alternately updated, where the latter is sparsified on the fly to ensure negligible storage overhead. Extensive experiments on three benchmark datasets have verified LEGCF's smallest trade-off between size and performance, with consistent accuracy gain over state-of-the-art baselines. The codebase of LEGCF is available in this https URL .

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .