probability distribution research papers

• Search by keyword
• Search by citation

Page 1 of 3

A generalization to the log-inverse Weibull distribution and its applications in cancer research

In this paper we consider a generalization of a log-transformed version of the inverse Weibull distribution. Several theoretical properties of the distribution are studied in detail including expressions for i...

• View Full Text

Approximations of conditional probability density functions in Lebesgue spaces via mixture of experts models

Mixture of experts (MoE) models are widely applied for conditional probability density estimation problems. We demonstrate the richness of the class of MoE models by proving denseness results in Lebesgue space...

Structural properties of generalised Planck distributions

A family of generalised Planck (GP) laws is defined and its structural properties explored. Sometimes subject to parameter restrictions, a GP law is a randomly scaled gamma law; it arises as the equilibrium la...

New class of Lindley distributions: properties and applications

A new generalized class of Lindley distribution is introduced in this paper. This new class is called the T -Lindley{ Y } class of distributions, and it is generated by using the quantile functions of uniform, expon...

Tolerance intervals in statistical software and robustness under model misspecification

A tolerance interval is a statistical interval that covers at least 100 ρ % of the population of interest with a 100(1− α ) % confidence, where ρ and α are pre-specified values in (0, 1). In many scientific fields, su...

Combining assumptions and graphical network into gene expression data analysis

Analyzing gene expression data rigorously requires taking assumptions into consideration but also relies on using information about network relations that exist among genes. Combining these different elements ...

A comparison of zero-inflated and hurdle models for modeling zero-inflated count data

Counts data with excessive zeros are frequently encountered in practice. For example, the number of health services visits often includes many zeros representing the patients with no utilization during a follo...

A general stochastic model for bivariate episodes driven by a gamma sequence

We propose a new stochastic model describing the joint distribution of ( X , N ), where N is a counting variable while X is the sum of N independent gamma random variables. We present the main properties of this gene...

A flexible multivariate model for high-dimensional correlated count data

We propose a flexible multivariate stochastic model for over-dispersed count data. Our methodology is built upon mixed Poisson random vectors ( Y 1 ,…, Y d ), where the { Y i } are conditionally independent Poisson random...

Generalized fiducial inference on the mean of zero-inflated Poisson and Poisson hurdle models

Zero-inflated and hurdle models are widely applied to count data possessing excess zeros, where they can simultaneously model the process from how the zeros were generated and potentially help mitigate the eff...

Multivariate distributions of correlated binary variables generated by pair-copulas

Correlated binary data are prevalent in a wide range of scientific disciplines, including healthcare and medicine. The generalized estimating equations (GEEs) and the multivariate probit (MP) model are two of ...

On two extensions of the canonical Feller–Spitzer distribution

We introduce two extensions of the canonical Feller–Spitzer distribution from the class of Bessel densities, which comprise two distinct stochastically decreasing one-parameter families of positive absolutely ...

A new trivariate model for stochastic episodes

We study the joint distribution of stochastic events described by ( X , Y , N ), where N has a 1-inflated (or deflated) geometric distribution and X , Y are the sum and the maximum of N exponential random variables. Mod...

A flexible univariate moving average time-series model for dispersed count data

Al-Osh and Alzaid ( 1988 ) consider a Poisson moving average (PMA) model to describe the relation among integer-valued time series data; this model, however, is constrained by the underlying equi-dispersion assumpt...

Spatio-temporal analysis of flood data from South Carolina

To investigate the relationship between flood gage height and precipitation in South Carolina from 2012 to 2016, we built a conditional autoregressive (CAR) model using a Bayesian hierarchical framework. This ...

Affine-transformation invariant clustering models

We develop a cluster process which is invariant with respect to unknown affine transformations of the feature space without knowing the number of clusters in advance. Specifically, our proposed method can iden...

Distributions associated with simultaneous multiple hypothesis testing

We develop the distribution for the number of hypotheses found to be statistically significant using the rule from Simes (Biometrika 73: 751–754, 1986) for controlling the family-wise error rate (FWER). We fin...

New families of bivariate copulas via unit weibull distortion

This paper introduces a new family of bivariate copulas constructed using a unit Weibull distortion. Existing copulas play the role of the base or initial copulas that are transformed or distorted into a new f...

Generalized logistic distribution and its regression model

A new generalized asymmetric logistic distribution is defined. In some cases, existing three parameter distributions provide poor fit to heavy tailed data sets. The proposed new distribution consists of only t...

The spherical-Dirichlet distribution

Today, data mining and gene expressions are at the forefront of modern data analysis. Here we introduce a novel probability distribution that is applicable in these fields. This paper develops the proposed sph...

Item fit statistics for Rasch analysis: can we trust them?

To compare fit statistics for the Rasch model based on estimates of unconditional or conditional response probabilities.

Exact distributions of statistics for making inferences on mixed models under the default covariance structure

At this juncture when mixed models are heavily employed in applications ranging from clinical research to business analytics, the purpose of this article is to extend the exact distributional result of Wald (A...

A new discrete pareto type (IV) model: theory, properties and applications

Discrete analogue of a continuous distribution (especially in the univariate domain) is not new in the literature. The work of discretizing continuous distributions begun with the paper by Nakagawa and Osaki (197...

Density deconvolution for generalized skew-symmetric distributions

The density deconvolution problem is considered for random variables assumed to belong to the generalized skew-symmetric (GSS) family of distributions. The approach is semiparametric in that the symmetric comp...

The unifed distribution

We introduce a new distribution with support on (0,1) called unifed. It can be used as the response distribution for a GLM and it is suitable for data aggregation. We make a comparison to the beta regression. ...

On Burr III Marshal Olkin family: development, properties, characterizations and applications

In this paper, a flexible family of distributions with unimodel, bimodal, increasing, increasing and decreasing, inverted bathtub and modified bathtub hazard rate called Burr III-Marshal Olkin-G (BIIIMO-G) fam...

The linearly decreasing stress Weibull (LDSWeibull): a new Weibull-like distribution

Motivated by an engineering pullout test applied to a steel strip embedded in earth, we show how the resulting linearly decreasing force leads naturally to a new distribution, if the force under constant stress i...

Meta analysis of binary data with excessive zeros in two-arm trials

We present a novel Bayesian approach to random effects meta analysis of binary data with excessive zeros in two-arm trials. We discuss the development of likelihood accounting for excessive zeros, the prior, a...

On ( p 1 ,…, p k )-spherical distributions

The class of ( p 1 ,…, p k )-spherical probability laws and a method of simulating random vectors following such distributions are introduced using a new stochastic vector representation. A dynamic geometric disintegra...

A new class of survival distribution for degradation processes subject to shocks

Many systems experience gradual degradation while simultaneously being exposed to a stream of random shocks of varying magnitudes that eventually cause failure when a shock exceeds the residual strength of the...

A new extended normal regression model: simulations and applications

Various applications in natural science require models more accurate than well-known distributions. In this context, several generators of distributions have been recently proposed. We introduce a new four-par...

Multiclass analysis and prediction with network structured covariates

Technological advances associated with data acquisition are leading to the production of complex structured data sets. The recent development on classification with multiclass responses makes it possible to in...

High-dimensional star-shaped distributions

Stochastic representations of star-shaped distributed random vectors having heavy or light tail density generating function g are studied for increasing dimensions along with corresponding geometric measure repre...

A unified complex noncentral Wishart type distribution inspired by massive MIMO systems

The eigenvalue distributions from a complex noncentral Wishart matrix S = X H X has been the subject of interest in various real world applications, where X is assumed to be complex matrix variate normally distribute...

Particle swarm based algorithms for finding locally and Bayesian D -optimal designs

When a model-based approach is appropriate, an optimal design can guide how to collect data judiciously for making reliable inference at minimal cost. However, finding optimal designs for a statistical model w...

Admissible Bernoulli correlations

A multivariate symmetric Bernoulli distribution has marginals that are uniform over the pair {0,1}. Consider the problem of sampling from this distribution given a prescribed correlation between each pair of v...

On p -generalized elliptical random processes

We introduce rank- k -continuous axis-aligned p -generalized elliptically contoured distributions and study their properties such as stochastic representations, moments, and density-like representations. Applying th...

Parameters of stochastic models for electroencephalogram data as biomarkers for child’s neurodevelopment after cerebral malaria

The objective of this study was to test statistical features from the electroencephalogram (EEG) recordings as predictors of neurodevelopment and cognition of Ugandan children after coma due to cerebral malari...

A new generalization of generalized half-normal distribution: properties and regression models

In this paper, a new extension of the generalized half-normal distribution is introduced and studied. We assess the performance of the maximum likelihood estimators of the parameters of the new distribution vi...

Analytical properties of generalized Gaussian distributions

The family of Generalized Gaussian (GG) distributions has received considerable attention from the engineering community, due to the flexible parametric form of its probability density function, in modeling ma...

A new Weibull- X family of distributions: properties, characterizations and applications

We propose a new family of univariate distributions generated from the Weibull random variable, called a new Weibull-X family of distributions. Two special sub-models of the proposed family are presented and t...

The transmuted geometric-quadratic hazard rate distribution: development, properties, characterizations and applications

We propose a five parameter transmuted geometric quadratic hazard rate (TG-QHR) distribution derived from mixture of quadratic hazard rate (QHR), geometric and transmuted distributions via the application of t...

A nonparametric approach for quantile regression

Quantile regression estimates conditional quantiles and has wide applications in the real world. Estimating high conditional quantiles is an important problem. The regular quantile regression (QR) method often...

Mean and variance of ratios of proportions from categories of a multinomial distribution

Ratio distribution is a probability distribution representing the ratio of two random variables, each usually having a known distribution. Currently, there are results when the random variables in the ratio fo...

The power-Cauchy negative-binomial: properties and regression

We propose and study a new compounded model to extend the half-Cauchy and power-Cauchy distributions, which offers more flexibility in modeling lifetime data. The proposed model is analytically tractable and c...

Families of distributions arising from the quantile of generalized lambda distribution

In this paper, the class of T-R { generalized lambda } families of distributions based on the quantile of generalized lambda distribution has been proposed using the T-R { Y } framework. In the development of the T - R {

Risk ratios and Scanlan’s HRX

Risk ratios are distribution function tail ratios and are widely used in health disparities research. Let A and D denote advantaged and disadvantaged populations with cdfs F ...

Joint distribution of k -tuple statistics in zero-one sequences of Markov-dependent trials

We consider a sequence of n , n ≥3, zero (0) - one (1) Markov-dependent trials. We focus on k -tuples of 1s; i.e. runs of 1s of length at least equal to a fixed integer number k , 1≤ k ≤ n . The statistics denoting the n...

Quantile regression for overdispersed count data: a hierarchical method

Generalized Poisson regression is commonly applied to overdispersed count data, and focused on modelling the conditional mean of the response. However, conditional mean regression models may be sensitive to re...

Describing the Flexibility of the Generalized Gamma and Related Distributions

The generalized gamma (GG) distribution is a widely used, flexible tool for parametric survival analysis. Many alternatives and extensions to this family have been proposed. This paper characterizes the flexib...

• ISSN: 2195-5832 (electronic)

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• J Thorac Dis
• v.10(2); 2018 Feb

A brief introduction to probability

Gioacchino di paola.

1 Office of Research, IRCCS ISMETT, Palermo, Italy;

Alessandro Bertani

2 Division of Thoracic Surgery and Lung Transplantation, Department for the Treatment and Study of Cardiothoracic Diseases and Cardiothoracic Transplantation, IRCCS ISMETT-UPMC, Palermo, Italy

Lavinia De Monte

Fabio tuzzolino.

The theory of probability has been debated for centuries: back in 1600, French mathematics used the rules of probability to place and win bets. Subsequently, the knowledge of probability has significantly evolved and is now an essential tool for statistics. In this paper, the basic theoretical principles of probability will be reviewed, with the aim of facilitating the comprehension of statistical inference. After a brief general introduction on probability, we will review the concept of the “probability distribution” that is a function providing the probabilities of occurrence of different possible outcomes of a categorical or continuous variable. Specific attention will be focused on normal distribution that is the most relevant distribution applied to statistical analysis.

Probability

A simple clinical vignette may help introducing the concept of probability.

In a clinical study, patients with claudicatio intermittens who received treatment “A” walked an average of 472 m, while patients who received treatment “B” walked 405 m. Given the difference of 67 m in favor of treatment “A”, is it possible to conclude that, based on this study, treatment “A” is better than treatment “B”? And, based on this assumption, should the doctor administer treatment “A” to his next patient with claudicatio intermittens?

The first question is a typical question involving the concept of statistical inference and, precisely, is: “what is the conclusion that we may draw from our study?”

The second question is a typical question about decision-making: what is the rationale for preferring a specific treatment over another, based on the information available in the study and other information coming from previous studies?

The answers to both questions may be provided with just a limited amount of uncertainty, although uncertainty may vary in different circumstances. If the degree of uncertainty is low, the conclusions will be strong and the decision based on the available knowledge (or evidence) will be almost certain. If the degree of uncertainty is high, the conclusions will be poor and the decision will not be based on evidence but will be only based on personal experience, instinct, or will be left to chance.

It is therefore very important to measure the degree of uncertainty, and the theory of probability provides us with the appropriate tools to do so. Probability may also be defined as the “logic of the possible” or the “logic of the uncertain”, because it has to deal with hypotheses that may not be associated with a completely true or false attestation, but just with a “possible” attestation. For example, “tomorrow will rain” is neither a true or false hypothesis, but it is only possible. For all the hypotheses that have to deal with uncertainty, the theory of probability will measure the degree of possibility of such hypothesis, and will assign to the hypothesis a certain value of probability ( 1 ).

Defining probability is useful to measure how likely it is that a given event will actually occur. The word “probability” actually belongs to spoken language and is used in different situations. Although the general concept of this word is very clear, a formal definition of probability is also useful for the physicians who are approaching statistics.

The most common definitions of probability are called the “frequentistic” and the “subjectivist” (or Bayesian). Both of them tend to measure probability with a quantitative ( 2 , 3 ) approach and to assign a value between 0 and 1 or, in term of percentage, any value between 0% and 100%. A value of 0 or 0% represents the absence of any probability that an event may occur. On the other side, a value of 1 or 100% means that the event will occur with complete certainty.

According to a “frequentistic” approach, probability is seen as the proportion (relative frequency) of times that a given event occurs in an infinite or very high number of attempts, performed in stable conditions. The relative frequency is the ratio between the number (k) of attempts with a favorable outcome and the overall number (n) of attempts: (k/n). For example, one should think about a clinical trial looking at complete clinical response after a certain medical treatment, and observe if the outcome is favorable (the patient recovered) or unfavorable (the patient did not recover). The relative frequency of response to the treatment is the ratio between the number of patients who recovered and the overall number of patients who received the treatment, (k/n).

On the other side, according to the subjectivist (Bayesian) approach, probability is defined as the degree of belief that an individual holds in respect to the occurrence of a certain event. The inspiring principle of the Bayesian approach is that all unknown quantities can be assigned a probability. In other words, every type of uncertainty can be represented in probabilistic terms. In this approach, probability is the expression of an evaluation of the event made by the researcher on the basis of the information available to him/her. For this reason, in order to translate the degree of belief into a number, the Bayesian approach introduces the concept of a “Bet scheme”. Probability is handled as the price that an individual feels appropriate to be paid in order to receive a value of 1 if the event occurs or a value of 0 if the event does not occur. The degree of belief that a person holds in respect to a certain event is subjective, and different individuals with similar or different information may reach different estimates of the probability of a given event.

Looking back to our previous clinical example, the probability that a patient recovers after receiving a certain treatment may be seen, according to the Bayesian approach, as a subjective estimate of the effect of the treatment. This estimate is based on the available information and may be presented as the risk that an individual may take within a fictional bet, during which patient recovery and its opposite (failed recovery) are being bet.

The debate on the definition of probability generated a basic set of axioms that may all reflect the properties of the concept of probability. The entire system of statistical probability is based on these three simple axioms of rules ( Table 1 ) ( 4 ).

There are also circumstances when information about a certain event may influence the estimate of probability of another event. For example, a physician may think that the probability for a certain disease to occur may be, generally speaking, very low. But, if the patient is exposed to a relevant risk factor for this disease, then the physician’s estimate of probability may change and he may think that the patient is more exposed to this particular disease. In this example, the probability of a certain event is modified after another separate event happens. This is the concept of “conditional probability”. Frequently, a cause-effect relationship between two events may be found under the concept of “conditional probability”.

Distribution of probability

In many situations, the events of interest have a natural interpretation in numerical terms. For example, let’s take into consideration a few typical outcome variables such as diastolic blood pressure, distance walked on a stress test, or the expenses of a family. In all these cases, it is useful to introduce a “random” variable among the results of the real, actual numbers. “Random” or “aleatory” refers to the uncertainty related to the specific value that the variable will receive in a given patient, in a given experiment, at a given time, etc.

In order to express and quantify the uncertainty of the possible values of the aleatory variable, we will introduce the concept of the distribution of probability. This is a mathematical model that is able to link every value of a variable to the probability that this value may be actually observed. Based on the scale used to measure the variable, we may distinguish between two different distributions of probability ( 5 , 6 ):

Probability distribution: discrete case and continuous case.

• “ Discrete distributions ” : the variable is measured with whole numerical values (for example, number of cigarettes in a period of time). Each probability is a number between 0 and 1. The sum of the probabilities of all the possible values is 1 ( Figure 1 ).

From a formal statistical standpoint, the distributions of probability are expressed by a mathematical formula called “function of density of probability”, called “ f(x) ” for continuous distributions or “ p(x)” for discrete distributions ( Figure 1 ). Table 2 shows the most common continuous and discrete distributions of probability.

Some theoretical distributions of probability are important because they match very closely the distribution of many variables that may be observed in the real world. Among others, the “normal” distribution is the one that has the most important role in inferential statistics, because many statistical techniques are based on this distribution. The “bell-shaped” curve of the normal distribution is able to describe very well data histograms of variables that are continuous and have a symmetrical distribution. This distribution is frequently used in medicine because many clinical variables may empirically present the typical shape of normal distribution. For example, the linear regression is based on this distribution.

In other cases, the shape of the distribution is not completely normal and there are mathematical transformations that can help the statistician to “normalize” the distribution of data ( 7 ).

The importance of the normal distribution should not minimize the role of other types of distribution, because many statistical models have been created in order to bypass the issues of non-normally distributed sets of data using different types of distributions. For example the generalized linear models can assess different types of the outcome distribution such as gamma, binomial, poisson distribution, etc.

Binary variables (dichotomous) are those variables where two only values are allowed to describe a phenomenon, defining two opposite situations (yes or not, alive or dead, etc.). The concept of probability may also apply to these variables, both as an aggregate property ((if a “representative” sample is considered and analyzed, the probability is the rate between the number of outcomes resulting in “yes” and the total number of the subjects of the sample) or an individual probability (the propensity or risk to fall into one specific category). Using this interpretation, probability for categorical variables may be described as well with a value between 0 and 1 and may be analyzed as the dependent variable in an appropriate regression model, for example the logistic regression model ( 7 ).

Take home messages

• Uncertainty characterizes every question of inference or decision in clinical research;
• Probability theories provide all the instruments and methodologies to measure these uncertain phenomena. In particular, probability may describe the proportion of times that a certain observation may occur in a large set of observations;
• In statistics, different inferential approaches are based on a probabilistic background: the frequentist (more widely used) and the Bayesan approach;
• The normal distribution has a pivotal role in clinical research because many variables present this type of distribution. Many statistical models are based on this distribution. Many alternatives are available for different type of distributions.

Acknowledgements

Conflicts of Interest: The authors have no conflicts of interest to declare.

A Discrete Probability Distribution and Some Applications

• Published: 16 December 2022
• Volume 20 , article number  34 , ( 2023 )

Cite this article

• Ana-Maria Acu   ORCID: orcid.org/0000-0003-1192-2281 1 &
• Ioan Rasa 2  

182 Accesses

3 Citations

Explore all metrics

This paper is concerned with the probability distribution \(a_{n,j}:=4^{-n}{2j\atopwithdelims ()j}{2n-2j\atopwithdelims ()n-j}, j=0,1,\dots ,n\) . We present basic properties of the sequence \((a_{n,j})\) : integral representations, recurrence formulas, convexity properties, bounds for the associated information potential. Two related random variables are also studied and compared from the point of view of the stochastic convex ordering and in connection with strongly convex functions. We consider a quadrature formula and investigate it with analytic and probabilistic methods. The paper contains two open problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

A probabilistic proof of some integral formulas involving the Meijer G-function

Discrete uniform and binomial distributions with infinite support

$${\varvec{(k,s)}}$$ -riemann–liouville fractional integral inequalities for continuous random variables, data availability statement.

No data were used to support this study.

Abel, U., Leviatan, D.: An Extension of Raşa’s Conjecture to q-Monotone Functions. Results Math. 75 , 180 (2020)

Article   MATH   Google Scholar  

Abel, U., Leviatan, D., Raşa, I.: Relations between the Bernstein polynomials and q-monotone functions. Results Math 77 , 239 (2022) (submitted)

Abel, U., Raşa, I.: A sharpening of a problem on Bernstein polynomials and convex functions. Math. Ineq. Appl. 21 , 773–777 (2018)

MATH   Google Scholar  

Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications (1970)

Acu, A.M., Bascanbaz-Tunca, G., Rasa, I.: Bounds for indices of coincidence and entropies. Math. Inequal. Appl. 24 (2), 307–321 (2021)

Altomare, F., Campiti, M.: Korovkin-type approximation theory and its applications. Ser. De Gruyter Stud. Math. 17 (1994)

Alzer, H.: Remarks on a convexity theorem of Rasa. Results Math. 75 , 29 (2020)

Bauer, H.: Probability Theory and Elements of Measure Theory. Holt, Rinehart and Winston, New York (1972)

Berdysheva, E.: Studying Baskakov-Durrmeyer operators and quasi-interpolants via special functions. J. Approx. Theory 149 , 131–150 (2007)

Costabile, F., Dell’Accio, F., Gualtieri, M.I.: A new approach to Bernoulli polynomials. Rend. Mat. Serie VII 26 , 1–12 (2006)

Dragomir, S.S.: Some Levin-Ste č kin’s type inequalities for operator convex functions on Hilbert spaces. https://arxiv.org/pdf/2005.04340v1.pdf

Dragomir, D.D.: Two mappings in connection to Hadamard’s inequalities. J. Math. Anal. Appl. 167 (1), 49–56 (1992)

Gould, H.W.: Combinatorical Identities—A Standardized Set of Tables Listing 500 Binomial Coefficient Summations. Morgantown (1972)

Heilmann, M., Raşa, I.: On the decomposition of Bernstein Operators. Numer. Funct. Anal. Optim. 36 (1), 72–85 (2015)

Kageyama, Y.: A new class of modified Bernstein operators. J. Approx. Theory 101 , 121–147 (1999)

Karlin, S., Novikoff, A.: Generalized convex inequalities. Pac. J. Math. 13 , 1251–1279 (1963)

Karlin, S., Studden, W.J.: Tchebycheff systems: with applications in analysis and statistics. Interscience, Interscience Publishers, New York (1966)

Komisarski, A., Rajba, T.: Muirhead inequality for convex orders and a problem of I Raşa on Bernstein polynomials. J. Math. Anal. Appl. 458 (1), 821–830 (2018)

Levin, V.I., Stečkin, S.B.: Inequalities. Am. Math. Soc. Transl. 2 (14), 1–29 (1960)

Google Scholar  

Levy, H., Myles, R.: Stochastic Dominance: Investment Decision Making Under Uncertainty, vol. 34. Springer, New York (2006)

Mrowiec, J., Rajba, T., Wasowicz, S.: A solution to the problem of Raşa connected with Bernstein polynomials. J. Math. Anal. Appl. 446 , 864–878 (2017)

Müller, A., Stoyan, D.: Comparison Methods for Stochastic Models and Risks. Wiley, New York (2002)

Nikodem, K., Rajba, T.: Ohlin and Levin-Stečkin-type results for strongly convex functions. Annales Mathematicae Silesianae 34 (1), 123–132 (2020)

Ohlin, J.: On a class of measures of dispersion with application to optimal reinsurance. ASTIN Bull. 5 , 249–266 (1969)

Article   Google Scholar  

Rajba, T.: On the Ohlin lemma for Hermite-Hadamard-Fejér type inequalities. Math. Inequal. Appl. 17 , 557–571 (2014)

Rajba, T.: On some recent applications of stochastic convex ordering theorems to some functional inequalities for convex functions: a survey. In: J. Brzdek, K. Cieplinski, Th.M. Rassias (eds.) Developments in Functional Equations and Related Topics, Springer Optimization and Its Applications, Vol. 124, Springer, Cham, Chpt. 11, pp. 231–274 (2017)

Rajba, T., Wasowicz, Sz:. Probabilistic characterization of strong convexity. Opuscula Math. 31 , 97–103 (2011)

Raşa, I.: Entropies and Heun functions associated with positive linear operators. Appl. Math. Comput. 268 , 422–431 (2015)

Raşa, I.: Convexity properties of some entropies (II). Results Math. 74 , 154 (2019)

Raşa, I.: 2. Problem, p. 164. Ann. Univ. Paedagog. Crac. Stud. Math. 13, 139- 169. In: Report of Meeting Conference on Ulam’s Type Stability, Rytro, Poland, June 2–6 (2014)

Rasa, I.: Bernstein polynomials and convexity: recent probabilistic and analytic proofs. In: The Workshop “Numerical Analysis, Approximation and Modeling”, T. Popoviciu Institute of Numerical Analysis, Cluj-Napoca, June 14, 2017. http://ictp.acad.ro/zilele-academice-clujene- (2017)

Shaked, M., Shanthikumar, J.G.: Stochastic Orders. Springer, Berlin (2006)

Szegö, G.: Orthogonal polynomials. Amer. Math. Soc. Colloq, Pub., Vol. 23, Amer. Math. Soc. Providence. R.I. (1967)

Szostok, T.: Functional inequalities involving numerical differentiation formulas of order two. Bull. Malays. Math. Sci. Soc. 41 , 2053–2066 (2018)

Download references

Acknowledgements

This work was supported by a Hasso Plattner Excellence Research Grant (LBUS-HPI-ERG-2020-07), financed by the Knowledge Transfer Center of the Lucian Blaga University of Sibiu.

Author information

Authors and affiliations.

Department of Mathematics and Informatics, Lucian Blaga University of Sibiu, Str. Dr. I. Ratiu, No.5-7, 550012, Sibiu, Romania

Ana-Maria Acu

Department of Mathematics, Faculty of Automation and Computer Science, Technical University of Cluj-Napoca, Str. Memorandumului nr. 28, 400114, Cluj-Napoca, Romania

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Ioan Rasa .

Ethics declarations

Conflicts of interest.

The authors declare no competing financial interests.

Note added in proof.

The authors remarked that inequality (10.3) can be proved using Theorem 10.1. Details will appear in a forthcoming paper.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Acu, AM., Rasa, I. A Discrete Probability Distribution and Some Applications. Mediterr. J. Math. 20 , 34 (2023). https://doi.org/10.1007/s00009-022-02243-8

Download citation

Received : 16 February 2022

Revised : 19 June 2022

Accepted : 26 November 2022

Published : 16 December 2022

DOI : https://doi.org/10.1007/s00009-022-02243-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Probability distribution
• information potential
• convexity properties
• stochastic convex ordering
• strongly convex function
• quadrature formula

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 07 August 2023

Modified generalized Weibull distribution: theory and applications

• Mustafa S. Shama 1 , 2 ,
• Amirah Saeed Alharthi 3 ,
• Fatimah A. Almulhim 4 ,
• Ahmed M. Gemeay 5 ,
• Mohammed Amine Meraou 6 ,
• Manahil SidAhmed Mustafa 7 ,
• Eslam Hussam 8 &
• Hassan M. Aljohani 3  

Scientific Reports volume  13 , Article number:  12828 ( 2023 ) Cite this article

1986 Accesses

8 Citations

Metrics details

• Mathematics and computing

This article presents and investigates a modified version of the Weibull distribution that incorporates four parameters and can effectively represent a hazard rate function with a shape resembling a bathtub. Its significance in the fields of lifetime and reliability stems from its ability to model both increasing and decreasing failure rates. The proposed distribution encompasses several well-known models such as the Weibull, extreme value, exponentiated Weibull, generalized Rayleigh, and modified Weibull distributions. The paper derives key mathematical statistics of the proposed distribution, including the quantile function, moments, moment-generating function, and order statistics density. Various mathematical properties of the proposed model are established, and the unknown parameters of the distribution are estimated using different estimation techniques. Furthermore, the effectiveness of these estimators is assessed through numerical simulation studies. Finally, the paper applies the new model and compares it with various existing distributions by analyzing two real-life time data sets.

Similar content being viewed by others

Causal machine learning for predicting treatment outcomes

Development and validation of a new algorithm for improved cardiovascular risk prediction

Principal component analysis

Introduction.

Statistical models are crucial in comprehending and predicting real-world phenomena. In numerous applications, it becomes necessary to utilize enhanced versions of well-established distributions. These new distributions offer greater flexibility when it comes to simulating real-world data with high skewness and kurtosis. Among the advantages of the new distribution is its suitability for various fields, including medical, financial, and engineering applications. Selecting the most appropriate statistical model for data analysis is both critical and challenging. For further exploration on the topic of distributions, I recommend referring to the following references: Almongy et al. 1 , Shafiq et al. 2 , and Meriem et al. 3 . These sources provide additional insights and information.

The Weibull distribution is extensively employed in the analysis of lifetime data and has demonstrated notable efficacy in capturing failure rates that display monotonic patterns. Its density shapes, which manifest as either right or left-skewed, render it well-suited for survival and reliability analysis. Nevertheless, the Weibull model is inadequate for accurately representing non-monotonic failure rates, such as those characterized by hazard functions exhibiting bathtub-shaped or upside-down bathtub-shaped patterns. To address this limitation, researchers have developed enhanced versions of the Weibull distribution that can accurately accommodate different hazard function shapes to represent complex failure models accurately. Xie and Lai 4 introduced the additive Weibull distribution, incorporating a bathtub-shaped hazard function. Bebbington et al. 5 proposed the flexible Weibull distribution, which modifies the hazard function to exhibit an increasing pattern followed by a bathtub shape. Lai et al. 6 presented a new Weibull distribution model with three parameters and a bathtub-shaped hazard function.

Notwithstanding the progress made in the field, numerous prevailing models exhibit limited flexibility and may not yield optimal fits when applied to real-world data in engineering and related domains. To address this issue, researchers have employed diverse techniques to develop alternative distributions that enhance the flexibility of existing models. One approach involves generating a new distribution by combining two cumulative hazard rate (CHR) functions through a mixture model. It can be written as below:

with \(H\left( x\right)\) denoted the cumulative hazard rate function satisfies the following conditions

\(\mathop {\lim }\limits _{x\rightarrow 0} H\left( x\right) =0\) ,

\(\mathop {\lim }\limits _{x\rightarrow \infty } H\left( x\right) =\infty\) ,

\(H\left( x\right)\) is a differentiable non-negative and non-decreasing.

By using Eq. ( 1 ), the generated cumulative density function (cdf) and probability density function (pdf) are, respectively, given by

Some generalized distributions generated according to ( 2 ) and ( 3 ) are listed in Table 1 .

Bagdonavicius and Nikulin 10 proposed an extension of the Weibull distribution, namely power generalized Weibull (PGW) distribution, and its cdf and pdf can be described as

and the relationship between cdf and pdf is given by

respectively, where \(\alpha\) and \(\theta\) are two shape parameters and \(\lambda\) is a scale parameter. PGW distribution contains constant, monotone (increasing or decreasing), bathtub-shaped, and unimodal hazard shapes. For more details about this extension, see, for example, Bagdonavicius and Nikulin 11 , Voinov et al. 12 , and Kumar and Dey 13 .

In this research article, we introduce a novel statistical model called the modified power generalized Weibull (MPGW) distribution. Four parameters characterize the MPGW distribution and exhibit several significant properties. This distribution’s probability density function (pdf) can assume different forms, including constant, monotonic (increasing or decreasing), and unimodal. Moreover, the hazard rate function (hrf) associated with the MPGW distribution can take on various shapes, such as constant, monotonic, bathtub, and upside-down bathtub.

We investigate several mathematical properties of the MPGW distribution and explore its applicability in different contexts. To estimate the model parameters, we employ various estimation techniques, including maximum likelihood estimation (MLE), the maximum product of spacing (MPS), least square estimators (LSE), and Cramer-von Mises estimators (CVE). These estimation methods enable us to determine the most suitable parameter values for the MPGW distribution based on the available data.

The proposed distribution was used in many fields of science such as engineering and bio-sciences as it can model many kinds of data because of the distribution’s great flexibility. For more details about similar papers see 12 , 14 The rest of this paper is structured as follows. Section “ The formulation of the MPGW distribution ” described the new MPGW model and provided different distributional properties. Further, numerous statistical properties for the proposed distribution were introduced in Section “ Statistical properties ”. In Section “ Estimation methods ”, we established different estimation procedures for the unknown parameters of the suggested distribution. Monte Carlo simulation studies are performed in Section “ Numerical simulation ” to compare the proposed estimators. Finally, in Section “ Real data analysis ”, two real data sets defined by the survival field are analyzed for validation purposes, and we conclude the article in Section “ Conclusion ”.

Main contribution and novelty

This research paper presents a noteworthy advancement in the field of probability distributions by introducing a novel four-parameter generalization of the Weibull distribution. The proposed generalization offers the ability to model a hazard rate function that exhibits a bathtub-shaped pattern. The bathtub-shaped hazard rate function is of great interest in various domains, as it accurately captures the characteristics of failure rates observed in certain real-world scenarios. To evaluate the efficacy of the newly proposed model, we conducted an empirical investigation using two distinct real-life time data sets. These data sets were carefully selected to encompass diverse applications and ensure the generalizability of the findings. We could assess the model’s effectiveness in practical applications by employing the proposed four-parameter generalized Weibull distribution and comparing its performance with several existing distributions. Through a comprehensive analysis of the results, valuable insights were obtained regarding the capabilities and advantages of the novel four-parameter generalized Weibull distribution when applied to real-world data sets. The comparison of the proposed model with existing distributions provided a rigorous evaluation framework, enabling a thorough understanding of its performance in different scenarios. This study contributes to the existing body of knowledge by demonstrating the applicability and usefulness of the new distribution in capturing the complexities of time-to-failure data.

The formulation of the MPGW distribution

The MPGW distribution is generated by using \(H_{1} \left( x\right)\) of the PGW distribution and \(H_{2} \left( x\right)\) of the exponential distribution in Eqs. ( 2 ) and ( 3 ). Its cdf and pdf can be defined as the following

and the relationship between cdf and pdf can be written as

where \(\theta >0\) , \(\lambda ,\alpha ,\beta \ge 0\) such that \(\lambda +\beta >0\) and \(\alpha +\beta >0\) .

The hazard rate function (hrf) of the MPGW model can be expressed as

Table 2 summarized several well-known lifetime distributions from the newly suggested distribution, which is quite flexible.

Statistical properties

In this part of the study, we provided some mathematical properties of the MPGW distribution, especially moments, skewness, kurtosis, and asymmetry.

Behavior of the pdf of the MPGW distribution

The pdf limits of the MPGW distribution are

From the pdf of the MPGW distribution, the first derivative of the pdf is

where \(\psi \left( x\right) =\left( h\left( x\right) \right) ^{2} -h\mathrm{{'} }\left( x\right)\) . It is clear that \(f\mathrm {{'} }\left( x\right)\) and \(\psi \left( x\right)\) have the same sign, and \(\psi \left( x\right)\) has not an explicit solution. Therefore, we can discuss the following special cases which depend on \(\theta\) and \(\alpha\) :

Case 1 : For \(\theta \le 1\) and \(\alpha \theta \le 1\) , \(\psi \left( x\right)\) is negative which means \(f\left( x\right)\) is decreasing in x

Case 2 : For \(\theta =1\) , \(\psi \left( x\right)\) reduces to

which has no solution for \(\alpha \le 1\) and the pdf becomes decreasing for all x .

Case 3 : For \(\alpha =1\) , \(\psi \left( x\right)\) reduces to

which has no solution for \(\theta \le 1\) and the pdf becomes decreasing for all x .

Case 4 : For \(\beta =0\) and \(\theta =1\) , \(\psi \left( x\right)\) reduces to

which has a solution for \(\alpha \mathrm {>}1\) , therefore the mode (M) becomes

Case 5 : For \(\alpha =1\) and \(\beta =0\) , \(\psi \left( x\right)\) reduces to

which has a solution for \(\theta \mathrm {>}1\) , therefore the mode becomes

Case 6 : For \(\alpha =1\) , \(\beta =0\) and \(\theta =2\) , \(\psi \left( x\right)\) reduces to

in this case, the mode becomes

For different parameter values, Fig.  1 depicts the pdf plots of MPGW distribution. The graphs show that the pdf of MPGW is decreasing and uni-modal which gives our proposed model the superiority for analyzing lifetime data.

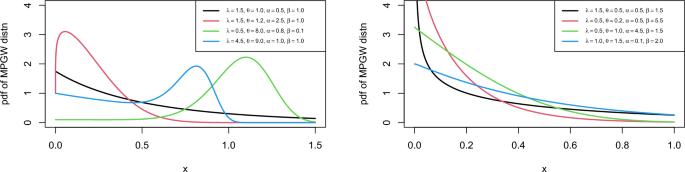
Plot for PDF of the MPGW model for different values of the parameters.

Behavior of the hazard rate function of the MPGW distribution

The hrf limits of the MPGW distribution are

The study of the shape of the hrf needs an analysis of the first derivative \(h\mathrm {{'} }\left( x\right)\) and it can be described as

where \(\eta \left( x\right) =\theta -1+\lambda \left( \alpha \theta -1\right) x^{\theta }\) . Clearly, \(h\mathrm {{'} }\left( x\right)\) and \(\eta \left( x\right)\) have the same sign and \(\eta \left( x\right)\) has critical value at the point

From \(\eta \left( x\right)\) , it can be noted that the hrf has different shapes written as:

Case1: \(\alpha \theta \mathrm {>}1\) .

If \(\theta \ge 1\) , then \(h\mathrm {{'} }\left( x\right) >0\) and \(h\left( x\right)\) are monotonically increasing.

If \(\theta \mathrm {<}1\) , then the hrf is decreasing for \(x\mathrm {<}x^{*}\) and increasing for \(x\mathrm {>}x^{*}\) . Hence, the hrf has a bathtub shape.

Case2: \(\alpha \theta \mathrm {<}1\) .

If \(\theta \le 1\) , then \(h\mathrm {{'} }\left( x\right) \mathrm {<}0\) and \(h\left( x\right)\) are monotonically decreasing.

If \(\theta \mathrm {>}1\) , this means \(\mathrm {0<}\alpha \mathrm {<}1\) and \(\mathrm {1<}\theta \mathrm {<}1/\alpha\) , then the hrf is increasing for \(x\mathrm {<}x^{*}\) and the hrf is decreasing for \(x\mathrm {>}x^{*}\) . Hence, the hrf has an upside-down bathtub shape.

Case3: \(\alpha \theta =1\) .

\(h\mathrm {{'} }\left( x\right) \mathrm {=}0\) and \(h\left( x\right)\) are constant when \(\theta\) .

\(h\mathrm {{'} }\left( x\right) >0\) and \(h\left( x\right)\) are monotonically increasing where \(\theta \mathrm {>}1\) .

\(h\mathrm {{'} }\left( x\right) \mathrm {<}0\) and \(h\left( x\right)\) are monotonically decreasing where \(\theta \mathrm {<}1\) .

Figure  2 displays the plot of hrf of MPGW model for multiple parameter values. The plots of hrf of MPGW are more efficient in modeling lifetime data.

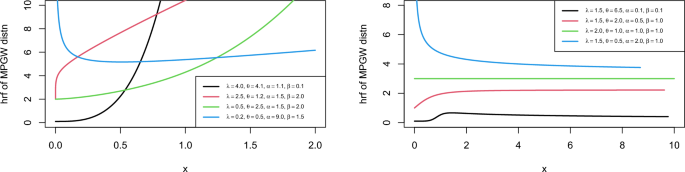
Plot for PDF of the MPGW distribution for different values of the parameters.

For any \(r\in N\) , the rth raw moment of the MPGW model can be written as

By the pdf ( 8 ) and the definition of the rth raw moment, we have

In the general case, we suppose that \(\lambda\) , \(\alpha\) and \(\beta \mathrm{>}0\) . Using the following expansion of \(\textrm{e}^{-\beta x}\) given by

then Eq. ( 12 ) is rewritten as

Let \(I\left( r,i\right) =\int _{0}^{\infty }x^{r+i} \textrm{e}^{-\left( 1+\lambda x^{\theta } \right) ^{\alpha } } dx\) and \(u=\left( 1+\lambda x^{\theta } \right) ^{\alpha }\) , we have

By using the expansion of \(\left( 1-u^{-1/\alpha } \right) ^{\left( r+i+1\right) /\theta -1}\) where \(\left| u^{-1/\alpha } \right| \mathrm{<}1\) , above integral is described as

Hence, after some algebra, we get

let \(k\left( r,i\right) =\int _{0}^{\infty }x^{r+i+\theta -1} \left( 1+\lambda x^{\theta } \right) ^{\alpha -1} \textrm{e}^{-\left( 1+\lambda x^{\theta } \right) ^{\alpha } } dx\) and \(u=\left( 1+\lambda x^{\theta } \right) ^{\alpha }\) , we have

Hence, after some algebra, we obtain

finally, substituting ( 14 ) and ( 15 ) into ( 13 ), we have

which completes the proof. \(\square\)

According to the results given in theorem 3, the mean and the variance of the proposed model, respectively, are \(\mu =\mu _{1}^{\mathrm{{'} }}\) and \(\sigma ^{2} =\mu _{2}^{\mathrm{{'} }} -\mu ^{2}\) . As well as the measures of skewness, kurtosis, and  asymmetry of the MPGW are given, respectively, by

Table 3 shows some necessary MPGW measures for various parameter combinations computed using the R program.

From the values of Table 3 it can be deduced that

If \(\alpha\) increases and for fixed \(\beta\) , \(\lambda\) and \(\theta\) , the values of Mean and Variance of the suggested MPGW model tend to decrease, while the values of \(\beta _1\) , \(\beta _2\) and \(\beta _3\) are increasing. The same result for \(\lambda\) with fixed \(\alpha\) , \(\beta\) and \(\theta\) .

For fixed values of \(\alpha\) , \(\lambda\) and \(\theta\) and for \(\beta\) augment, all values of Mean, Variance, \(\beta _1\) , \(\beta _2\) and \(\beta _3\) of the MPGW model are decrease..

The MPGW distribution is a flexible model for explaining more data sets.

Estimation methods

Here, we considered four estimation techniques for constructing the estimation of the unknown parameters for MPGW model. The determination of the estimate parameters using different procedures has been made available to various authors such as 17 , 18 , 19 .

Maximum likelihood estimation and its asymptotics

Let \(\{x_1, \ldots , x_n\}\) be a a random sample coming from MPGW \((\alpha , \beta , \lambda , \theta )\) . Then, the corresponding log-likelihood function is described by

with \(\Theta =(\alpha , \beta , \lambda , \theta )\) . Consequently, with respect to \(\alpha , \beta , \lambda\) , and \(\theta\) and by taking the derivatives of ( 16 ), we can be determined the estimates \({\hat{\alpha }}_{MLE}\) , \({\hat{\beta }}_{MLE}\) , \({\hat{\lambda }}_{MLE}\) and \({\hat{\theta }}_{MLE}\) and these estimates are given respectively by

These estimates can be solved numerically using various approach methods, including Newton Raphson, bisection, or fixed point methods.

Least square estimation

Let \(x_1,\ldots ,x_n\) be a random sample from MPGW \((\alpha , \beta , \lambda , \theta )\) and \(x_{1:n}<\cdots <x_{n:n}\) represent the order statistics of the random sample from the MPGW model. The least-square estimator (LSE) which introduced by 20 ) of \(\alpha , \beta , \lambda , \theta\) , noted by \({\hat{\alpha }}_{LSE}\) , \({\hat{\beta }}_{LSE}\) , \({\hat{\lambda }}_{LSE}\) and \({\hat{\theta }}_{LSE}\) ) can be described by minimizing

Maximum product of spacings

For \(x_1\le \cdots \le x_n\) representing the ordered statistics random sample from MPGW distribution, the maximum product of the spacings estimation (MPS) estimators of the proposed model resulted by maximizing the following equation

Cramer-von Mises minimum distance estimators

The Cramer-von Mises-type minimum distance estimators (CVEs) \({\hat{\alpha }}_{CVE}\) , \({\hat{\beta }}_{CVE}\) , \({\hat{\lambda }}_{CVE}\) and \({\hat{\theta }}_{CVE}\) of \(\alpha , \beta , \lambda , \theta\) are described respectively by minimizing

Numerical simulation

Here in this part of the work, we performed some results from simulation experiments so that you may assess how well the various estimating techniques provided in Section “ Estimation methods ” using different sample sizes, \(n = \{100, 300, 500, 700, 1000\}\) and different sets of initial parameters. After repeating the process \(K = 1000\) , we generate different random samples from the suggested model. The following algorithm can be easily used to generate samples from the MPGW distribution

Step 1: Generate u from U(0,1).

Step 2: Generate x as x is the solution of equation \(1-\textrm{e}^{1-\left( 1+\lambda x^{\theta } \right) ^{\alpha } -\beta x}=u\) .

Further, we compute the average values of biases (AB), mean square errors (MSEs), and mean relative errors (MREs) by the following equations

where \(\pmb \Theta\) =( \(\alpha , \beta , \lambda ,\theta\) ). All calculations were performed by using the R software version 4.1.2.

Tables 4 , 5 and 6 summarized the results of the simulation studies for the proposed model using the four estimation procedures. From the results, it can be concluded that as the sample size increases, all estimation methods of the proposed distribution approach to their initial guess of values. Furthermore, in all cases, the values of MSEs, and MREs tend to decrease. This ensures the consistency and asymptotically impartiality of all estimators. Additionally, by taking the MSE as an optimally criteria, we deduce that MLEs outperform alternative methods of estimate for the MPGWD.

Real data analysis

Through performing goodness-of-fit tests, we utilize two data sets to contrast the MPGW model with PGW distribution and the other four alternative existing models to see the effectiveness of the new model. The compared distributions:

Additive modified Weibull (AMW) distribution 4 with pdf defined as follows

Modified extension Weibull (MEW) distribution 21 with pdf defined as follows

Extended Weibull (EW) distribution 22 with pdf defined as follows

Flexible Weibull (FW) distribution 5 with pdf defined as follows

Kumaraswamy Weibull (KW) distribution 23 with pdf defined as follows

Beta Weibull (BW) distribution 24 with pdf defined as follows

The first data set represents the recorded remission times given in months from bladder cancer patients, reported by Lee and Wang 25 . The ordered array of the data is

The second data set considered the values of the survival times given in days of guinea pigs infected with virulent tubercle bacilli, summarized by Bjerkedal 14 . The ordered array of the data is

Table 7 recorded different statistic measures for the two proposed data sets.

To assess the validity of the proposed model, we conducted several statistical tests and computed various criterion measures. Firstly, we computed the log-likelihood function (-L), then, we employed criterion measures such as the Akaike Information Criterion ( \(\mathcal {A}_1\) ) and the Bayesian Information Criterion ( \(\mathcal {B}_1\) ) to evaluate the performance of the model further. The model that yields the minimum values of these criteria is considered to be the most appropriate for the given data set. To complement the criterion measures, we also employed various test statistics, including the Cramér-von Mises (Cr), Anderson–Darling (An), and Kolmogorov–Smirnov (KS) tests. These tests assess the model’s overall fit by comparing the observed data with the model’s predicted values. The associated p-values obtained from these tests measure the statistical significance of the differences between the observed and predicted values. By considering these criterion measures and test statistics, we can comprehensively evaluate the validity of the proposed model. The model that exhibits the best fit, as indicated by the minimum values of the criterion measures and non-significant p-values from the test statistics, can be considered the most suitable for the given data set.

Tables 8 and 9 , contain the values of criterion measure statistics for the fitted models by applying the two considered data sets. Based on these measures and along with the p -values of the proposed test statistics for each distribution, the MPGW model is the best candidate distribution for modeling the two data sets. The plots of the probability–probability (P–P) and quartile–quartile (Q–Q) of the suggested distributions using the two proposed data are shown in Figs.  3 , 4 , 5 and 6 . This figure confirms this conclusion.

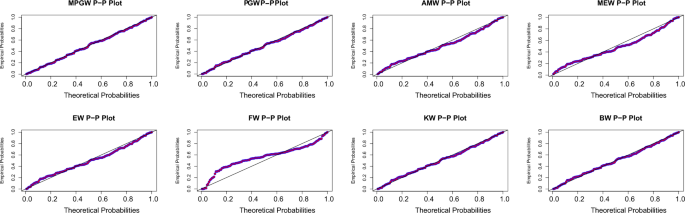
P-P plots of MPGW, GW, AMW, MEW, EW, FW, KW, and BW for the first data set.

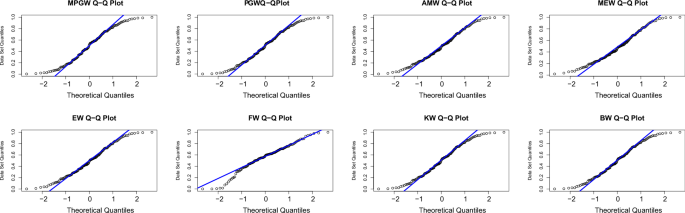
QQ plots of MPGW, GW, AMW, MEW, EW, FW, KW, and BW for the first data set.

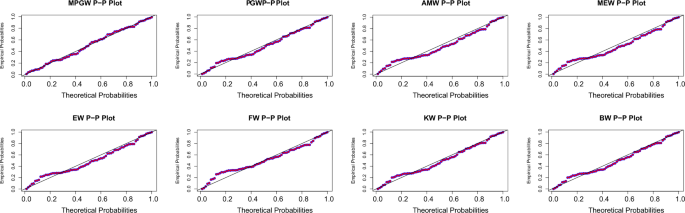
P-P plots of MPGW, GW, AMW, MEW, EW, FW, KW, and BW for the second data set.

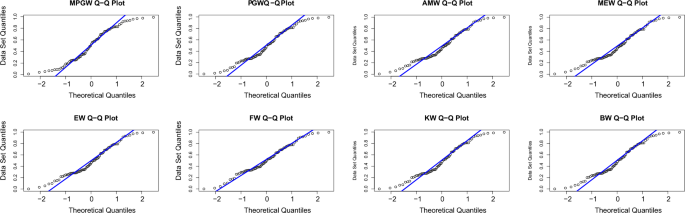
QQ plots of MPGW, GW, AMW, MEW, EW, FW, KW, and BW for the second data set.

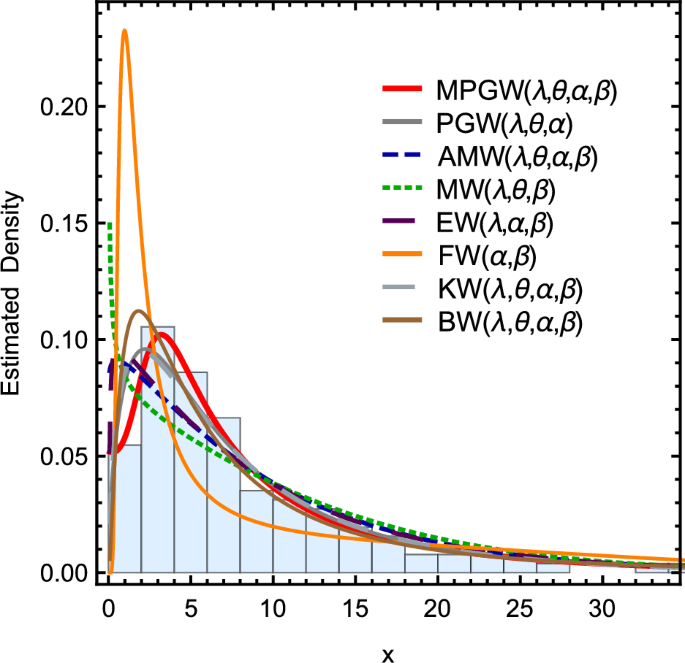
Curves of the pdfs for different fitting distributions using the first data set.

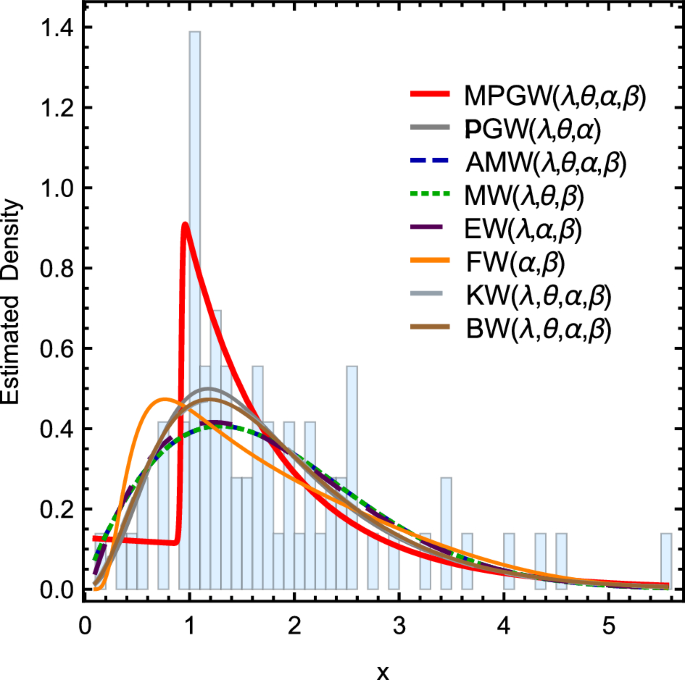
Curves of the pdfs for different fitting distributions using the second data set.

Figure 7 shows the curves of the pdfs for different fitting distributions using the first data set. Figure 8 shows the Curves of the pdfs for different fitting distributions using the second data set. Tables 10 and 11 contain The goodness of fit test for various fitting distributions by applying the first and second data sets, respectively.

This research paper introduces a novel distribution that involves compounding two cumulative hazard rate functions. We have derived a specific sub-model from the proposed distribution and established various mathematical properties related to it. We have applied four different estimation techniques to estimate the unknown parameters of our suggested model. Additionally, we have conducted simulation experiments to evaluate the effectiveness of these proposed estimation methods. Furthermore, we have analyzed two real engineering data sets to assess how well the MPGW model fits the data when compared to other well-known models. Our findings indicate that the MPGW model demonstrates a good fit to the data sets, highlighting its potential utility in practical applications.

Looking ahead, there are several potential avenues for future research. Firstly, we can extend our work to study the bivariate case and explore different properties of the proposed distribution within that context. Additionally, we can investigate the application of different censored methods, such as progressive type I, II, and hybrid censored methods, for estimating the unknown parameters of the proposed model. Moreover, we may explore the estimation of model parameters using Bayesian approaches and consider various loss functions, such as square error, Linex, and general entropy, to further enhance our understanding of the proposed model. The current study can be extended using neutrosophic statistics as future research; see 26 , 27 , 28 .

Data availability

All references exist in the paper for data used in the paper; see Lee and Wang 25 for the first real data set and Bjerkedal 14 for the second one.

Almongy, H. M., Almetwally, E. M., Aljohani, H. M., Alghamdi, A. S. & Hafez, E. H. A new extended Rayleigh distribution with applications of covid-19 data. Results Phys. 23 , 104012 (2021).

Article   PubMed   PubMed Central   Google Scholar  

Shafiq, A. et al. A new modified kies fréchet distribution: Applications of mortality rate of covid-19. Results Phys. 28 , 104638 (2021).

Meriem, B. et al. The power xlindley distribution: Statistical inference, fuzzy reliability, and covid-19 application. J. Funct. Spaces 2022 , 1–21 (2022).

Article   MathSciNet   MATH   Google Scholar  

Xie, M. & Lai, C. D. Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 52 (1), 87–93 (1996).

Article   Google Scholar  

Bebbington, M., Lai, C. D. & Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Saf. 92 (6), 719–726 (2007).

Lai, C. D., Xie, M. & Murthy, D. N. P. A modified Weibull distribution. IEEE Trans. Reliab. 52 (1), 33–37 (2003).

Almalki, S. J. & Yuan, J. A new modified Weibull distribution. Reliab. Eng. Syst. Saf. 111 , 164–170 (2013).

Sarhan, A. M. & Zaindin, M. Modified Weibull distribution. APPS Appl. Sci. 11 , 123–136 (2009).

MathSciNet   MATH   Google Scholar  

Kumar, C. S. & Nair, S. R. On some aspects of a flexible class of additive Weibull distribution. Commun. Stat.-Theory Methods 47 (5), 1028–1049 (2018).

Bagdonavicius, V. & Nikulin, M. Accelerated Life Models: Modeling and Statistical Analysis (Chapman and Hall/CRC, 2001).

Book   MATH   Google Scholar  

Bagdonavicius, V. & Nikulin, M. Chi-squared goodness-of-fit test for right censored data. Int. J. Appl. Math. Stat. 24 (1), 1–11 (2011).

MathSciNet   Google Scholar  

Voinov, V., Pya, N., Shapakov, N. & Voinov, Y. Goodness-of-fit tests for the power-generalized Weibull probability distribution. Commun. Stat.-Simul. Comput. 42 (5), 1003–1012 (2013).

Kumar, D., Dey, S. & Nadarajah, S. Extended exponential distribution based on order statistics. Commun. Stat.-Theory Methods 46 (18), 9166–9184 (2017).

Bjerkedal, T. Acquisition of resistance in guinea pies infected with different doses of virulent tubercle bacilli. Am. J. Hyg. 72 (1), 130–48 (1960).

PubMed   CAS   Google Scholar  

Nadarajah, S. & Haghighi, F. An extension of the exponential distribution. Statistics 45 (6), 543–558 (2011).

Bain, L. J. Analysis for the linear failure-rate life-testing distribution. Technometrics 16 (4), 551–559 (1974).

Meraou, M. A. & Raqab, M. Z. Statistical properties and different estimation procedures of Poisson–Lindley distribution. J. Stat. Theory Appl. 20 (1), 33–45 (2021).

Benchiha, S. A. & Al-Omari, A. I. Generalized quasi lindley distribution: Theoretical properties, estimation methods and applications. Electron. J. Appl. Stat. Anal. 14 (1) (2021)

Almetwally, E. A. & Meraou, M. A. Application of environmental data with new extension of Nadarajah–Haghighi distribution. Comput. J. Math. Stat. Sci. 1 (1), 26–41 (2022).

Google Scholar  

Swain, J. J., Venkatraman, S. & Wilson, J. R. Least-squares estimation of distribution functions in Johnson’s translation system. J. Stat. Comput. Simul. 29 (4), 271–297 (1988).

Xie, M., Tang, Y. & Goh, T. N. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 76 (3), 279–285 (2002).

Peng, X. & Yan, Z. Estimation and application for a new extended Weibull distribution. Reliab. Eng. Syst. Saf. 121 , 34–42 (2014).

Cordeiro, G. M., Ortega, E. M. M. & Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 347 (8), 1399–1429 (2010).

Lee, C., Famoye, F. & Olumolade, O. Beta-Weibull distribution: Some properties and applications to censored data. J. Mod. Appl. Stat. Methods 6 (1), 17 (2007).

Lee, E. T. & Wang, J. Statistical Methods for Survival Data Analysis Vol. 476 (Wiley, 2003).

Salem, S., Khan, Z., Ayed, H., Brahmia, A. & Amin, A. The neutrosophic lognormal model in lifetime data analysis: Properties and applications. J. Funct. Spaces 1–9 , 2021 (2021).

Vishwakarma, G. K. & Singh, A. Generalized estimator for computation of population mean under neutrosophic ranked set technique: An application to solar energy data. Comput. Appl. Math. 41 (4), 144 (2022).

Article   MathSciNet   Google Scholar  

Nayana, B. M., Anakha, K. K., Chacko, V. M., Aslam, M. & Albassam, M. A new neutrosophic model using dus-Weibull transformation with application. Complex Intell. Syst. 8 (5), 4079–4088 (2022).

Download references

Acknowledgements

The researchers would like to acknowledge the Deanship of Scientific Research, Taif University for funding this work.

Author information

Authors and affiliations.

Department of Basic Sciences, CFY, King Saud University, Riyadh, 12373, Saudi Arabia

Mustafa S. Shama

Department of Mathematics and Statistics, Osim Higher Institute of Administrative Science, Osim, 12961, Egypt

Department of Mathematics and Statistics, College of Science, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia

Amirah Saeed Alharthi & Hassan M. Aljohani

Department of Mathematical Sciences, College of Sciences, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia

Fatimah A. Almulhim

Department of Mathematics, Faculty of Science, Tanta University, Tanta, 31527, Egypt

Ahmed M. Gemeay

Laboratory of Statistics and Stochastic Processes, University of Djillali Liabes, BP 89, 22000, Sidi Bel Abbès, Algeria

Mohammed Amine Meraou

Department of Statistics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia

Manahil SidAhmed Mustafa

Department of Mathematics, Faculty of Science, Helwan University, Cairo, Egypt

Eslam Hussam

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed equally to this work.

Corresponding author

Correspondence to Eslam Hussam .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Shama, M.S., Alharthi, A.S., Almulhim, F.A. et al. Modified generalized Weibull distribution: theory and applications. Sci Rep 13 , 12828 (2023). https://doi.org/10.1038/s41598-023-38942-9

Download citation

Received : 03 April 2023

Accepted : 17 July 2023

Published : 07 August 2023

DOI : https://doi.org/10.1038/s41598-023-38942-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

The return period of heterogeneous climate data with a new invertible distribution.

• Beatriz L. Simões e Silva
• Cira E. G. Otiniano
• Eduardo Y. Nakano

Stochastic Environmental Research and Risk Assessment (2024)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

discrete probability distribution Recently Published Documents

Total documents.

• Latest Documents
• Most Cited Documents
• Contributed Authors
• Related Sources
• Related Keywords

Discrete Probability Distribution

Dynamic sampling from a discrete probability distribution with a known distribution of rates.

AbstractIn this paper, we consider several efficient data structures for the problem of sampling from a dynamically changing discrete probability distribution, where some prior information is known on the distribution of the rates, in particular the maximum and minimum rate, and where the number of possible outcomes N is large. We consider three basic data structures, the Acceptance–Rejection method, the Complete Binary Tree and the Alias method. These can be used as building blocks in a multi-level data structure, where at each of the levels, one of the basic data structures can be used, with the top level selecting a group of events, and the bottom level selecting an element from a group. Depending on assumptions on the distribution of the rates of outcomes, different combinations of the basic structures can be used. We prove that for particular data structures the expected time of sampling and update is constant when the rate distribution follows certain conditions. We show that for any distribution, combining a tree structure with the Acceptance–Rejection method, we have an expected time of sampling and update of $$O\left( \log \log {r_{max}}/{r_{min}}\right) $$ O log log r max / r min is possible, where $$r_{max}$$ r max is the maximum rate and $$r_{min}$$ r min the minimum rate. We also discuss an implementation of a Two Levels Acceptance–Rejection data structure, that allows expected constant time for sampling, and amortized constant time for updates, assuming that $$r_{max}$$ r max and $$r_{min}$$ r min are known and the number of events is sufficiently large. We also present an experimental verification, highlighting the limits given by the constraints of a real-life setting.

Development of a Discrete Probability Distribution and its application to the Pattern of Child Deaths

Discrete probability distribution prediction of image emotions with shared sparse learning, analytic univalent functions defined by generalized discrete probability distribution.

The close-to-convex analogue of a starlike functions by means of generalized discrete probability distribution and Poisson distribution was considered. Some coefficient inequalities and their connection to classical Fekete-Szego theorem are obtained. Our results provide strong connection between Geometric Function Theory and Statistics.

From the St. Petersburg paradox to the dismal theorem

AbstractThis paper aims to consider the meaning of the dismal theorem, as presented by Martin Weitzman [(2009) On modeling and interpreting the economics of catastrophic climate change. Review of Economics and Statistics91, 1–19]. The theorem states that a standard cost–benefit analysis breaks down if there is a possibility of catastrophes occurring. This result has a significant influence on debates regarding the economics of climate change. In this study, we present an intuitive similarity between the dismal theorem and the St. Petersburg paradox using a simple discrete probability distribution.

Conditional Subscore Reporting Using Iterated Discrete Convolutions

The literature showing that subscores fail to add value is vast; yet despite their typical redundancy and the frequent presence of substantial statistical errors, many stakeholders remain convinced of their necessity. This article describes a method for identifying and reporting unexpectedly high or low subscores by comparing each examinee’s observed subscore with a discrete probability distribution of subscores conditional on the examinee’s overall ability. The proposed approach turns out to be somewhat conservative due to the nature of subscores as finite sums of item scores associated with a subdomain. Thus, the method may be a compromise that satisfies score users by reporting subscore information as well as psychometricians by limiting misinterpretation, at most, to the rates of Type I and Type II error.

Discrete Probability Distribution: Binomial and Poisson Distributions

Generalized distribution and its geometric properties associated with univalent functions.

The purpose of the present paper is to introduce a generalized discrete probability distribution and obtain some results regarding moments, mean, variance, and moment generating function for this distribution. Further, we show that for specific values it reduces to various well-known distributions. Finally, we give a beautiful application of this distribution on certain analytic univalent functions.

Approximating Discrete Probability Distribution of Image Emotions by Multi-Modal Features Fusion

Existing works on image emotion recognition mainly assigned the dominant emotion category or average dimension values to an image based on the assumption that viewers can reach a consensus on the emotion of images. However, the image emotions perceived by viewers are subjective by nature and highly related to the personal and situational factors. On the other hand, image emotions can be conveyed by different features, such as semantics and aesthetics. In this paper, we propose a novel machine learning approach that formulates the categorical image emotions as a discrete probability distribution (DPD). To associate emotions with the extracted visual features, we present a weighted multi-modal shared sparse leaning to learn the combination coefficients, with which the DPD of an unseen image can be predicted by linearly integrating the DPDs of the training images. The representation abilities of different modalities are jointly explored and the optimal weight of each modality is automatically learned. Extensive experiments on three datasets verify the superiority of the proposed method, as compared to the state-of-the-art.

Export Citation Format

Share document.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

•  We're Hiring!
•  Help Center

Probability Distributions

• Most Cited Papers
• Most Downloaded Papers
• Newest Papers
• Save to Library
• Last »
• Distribution Theory Follow Following
• Order Statistics Follow Following
• Probability Theory Follow Following
• Fibonacci numbers Follow Following
• Mathematical Statistics Follow Following
• Mathematics Olympiad Follow Following
• Central Limit Theorems Follow Following
• Probability and statistics Follow Following
• Probability Distribution & Applications Follow Following
• Probability Follow Following

Enter the email address you signed up with and we'll email you a reset link.

• Academia.edu Publishing
•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

• Increase Font Size

39 Probability Distribution

1.   INTRODUCTION

In 17th century, the theory of probability was developed. The concept of probability was first developed from throwing a dice, games, tossing coins, drawing a card from a pack. In the year 1954, Antoine Gornband took an initiation to develop the probability distribution and made this area more interesting among the statisticians. In our routine life style the term probability or chance generally used. For instance, we say probably tomorrow the climate may be very hot in temperature, probably Ms.Vasanthi may come for party today, and probably you are right. These terms of possibility and probability express the same sense. But in statistics the probability has certain unique connotation unlike in Layman’s outlook.

2.   DEFINITIO N

Probability Distribution is distinct conditions of the principal sample space, with the set of all possible results of the random occurrence or happenings of the event which is generally observed. The sample space with the set of real numbers/ higher-dimensional vector space and non-numerical values are considered. For instance, the sample space of a coin flip will be either head or tail. The probability theory provides a means of getting an idea of the likelihood of occurrence of different events resulting from a random experiment in terms of quantitative measures ranging between zero and one. The probability is zero for an impossible event and one for an event which is certain to occur.

3.     PROBABILITY DISTRIBUTIONS

Probability Distributions are the record of all the values of the random variables. These variables are assumed as corresponding probabilities to create a probability distribution. Random variable doesn’t mean that all the values are different type or anything which is experimental study. These random variables are well explained with a set of results along with the well distinct probabilities for the happening of each outcomes of the explorative study or any research outcome. Here, the term random refers to the fact or statistics that the outcomes happen by chance or occurrence of events.

This can be well explained with a suitable example. For instance, the probability distribution which results in rolling of a dies in solo performance, it is discussed clearly in the below table – 1.

Table – 1: Single Fair Die

Mean, Variance, and Standard Deviation – To understand the probability distribution, it is very important to understand the mean, media, variance and standard deviation. From the following, it is very clearly specified that, how the population of the study can be distributed systematically.

Here, the definitions for population mean and variance are well defined for both the used ungrouped frequency distribution.

The above syntax can be explained by taking the population (N). This N – Population is divided by the population variance, the sample variance, which was the fair estimator for the population variance. This can be divided by n-1 for computation purpose.

After this process, you can use algebraic formulas or any equations to understand more effectively, this equation can be equivalent to:

To recollect, the probability are elongated term to the relative frequency distribution. So every frequency (f) and Population (N) [(f/N)] can be replaced by Probability (p) and Population (x) [p(x)].

This syntax can be simplified as follows:

To understand better, two formulas can be used for the last portion of variance in the mean square calculation.

The above example is worked out in the table – 2

Table – 2: Probability Distribution

The mean is xp(x) = (21/6) or 7/2 or 3.5,

Variance will be computed as follows –

=  x p(x) – x^2 p(x)

=  91/6 – (7/2)^2

=  15.17 – 12.25

The standard deviation is the square root of the variance = 1.7078

So, we can say that Probability Distribution (Pd) is a mathematical, arithmetical, numerical, statistical, geometrical function which can be stated in very simple way to make it very easy to provide the varies probabilities of occurrence of different possible happenings of the events in any experiment.

In more methodological terms, the probability distribution is a narrative of random happenings of the events which is represented in a pictorial way to understand the probabilities of occurrence of the events. The probability distribution is narrated in a bell shaped curve, with unimodal peaks at a single value. It is a Symmetrical where one side is mirror of the other which is mentioned with mean, median and mode in a bell shaped curve. (Mean=Md=Mo). The Pd is symptotic on both the left and right side of the normal bell shaped curve is asymptotic to x-axis, width is determined by quantum of amount with the variation of random variable. This is not used in all the business and it also replaced by Standardized Normal Distribution (SND) in general form.

This is a continuous distribution. It can be derived from the binomial distribution as a limiting case where n The no. of trials is very large. x & P the probability of success is close to ½. The general equation is

  f(x) = 1 e

Where the variable x lies between -∞ < x< ∞, μ & σ are called the parameters of the distribution. F(x) is called pdf of the normal distribution N( μ ,σ 2 ).The graph of the normal distribution is called the normal curve. It is bell shaped and symmetric about its mean. The two tails of the curve extend to +∞ & -∞ the curve is unimodal. The total area under the curve is 1.

EXAMPLE –

(a) A coin is tossed 3 times. Find the probability of getting 2 heads and a tail in any given order.

3.1.   Normal Random Variable/Normal Distribution (NRC/ND)

The normal random variables or distributions can be described as continuous random variables. It can be better understood by two predominant ways which is represented below -(a) Density plot – Shape : Bell

3.2.     Standard Normal Distribution (SND)

The Normal distribution with mean zero (mean=0) and standard deviation ( s /SD=1). It denotes N (0, 1). Normally we use Z to denote a standard normal random variable. It is very important to know that for what purpose we learn or understand the SND. To calculate the area under the normal curve either numerically or geometrically. Many statisticians have established tables to indicate the left tail area under the Standard Normal Curve (SNC) of any given number. Probability distributions are a elementary model in statistics. They are used both on a theoretical point and a practical point.

3.3.    Discrete Probability Distribution (DPD) –

It applicable to the scenarios where the set of possible outcomes is discrete, such as a coin toss or a roll of dice can be encoded by a discrete list of the probabilities of the outcomes, known as a probability mass function.

3.4.    Continuous Probability Distribution (CPD) –

It applicable to the scenarios where the set of possible outcomes can take on values in a continuous range (e.g., real numbers), such as the temperature on a given day) is typically described by probability density functions (with the probability of any individual outcome actually being 0). The normal distribution is a commonly encountered continuous probability distribution.

4.    Random variable

Random variable is a variable whose value is determined by the outcome of a random experiment. Random variable whose value is determined by the outcome of a random experiment is called a random variable. An example of this is the income of a randomly selected family. A random variable X is said to have the normal distribution with parameters µ and σ if its density function is given by: f(x) = 1 √ 2π σ exp (− 1 2 x − µ σ 2) (6) for −∞ < x < ∞. It can be shown that E(X) = µ and V (X) = σ 2. Thus, the normal distribution is characterized by a mean µ and a standard deviation σ.

4.1.    Discrete Random Variable

A discrete random variable is one whose set of assumed values is countable (arises from counting). Discrete random variable whose values are  countable is called a discrete random variable. An example of this is the number of cars in a parking lot at any particular time.

4.2.    Continuous Random Variable

A continuous random variable is one whose set of assumed values is uncountable (arises from measurement.).Continuous random variable that can assume any value in one or more intervals is called a continuous random variable. An example of this is the time taken by a person to travel by car from New York City to Boston.

5.   BINOMIAL DISTRIBUTION

In probability theory and statistics, the binomial distribution is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p . Such a success/failure experiment is also called a Bernoulli experiment or Bernoulli trial. In fact, when n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

An elementary example is this: roll a die ten times and count the number of 1s a outcome. Then this random number follows a binomial distribution with n = 10 and p =1/6.

For example, assume 5% of the population is green-eyed. You pick 500 people randomly. The number of green-eyed people you pick is a random variable X which follows a binomial distribution with n = 500 and p = 0.05.

6.     CONDITIONAL PROBABILITY

The conditional probability of two events A and B is P (A|B) = P ( A   and P ( B )  B )

where P (A and B) means the probability of the outcomes that events A and B have in common.

(i)   EXAMPLE –

When a die is rolled once, find the probability of getting a 4 given that an even number occurred in an earlier throw.

P (4 and an even number) = 1/6

.i.e. P (A and B) =1/6.

P (even number) =3/6 =1/2.

A bag contains 3 orange, 3 yellow and 2 white marbles. Three marbles are selected without replacement. Find the probability of selecting two yellow and a white marble.

P( 1st Y) =3/8, P( 2nd Y) = 2/7 and P( W)= 2/6

P(Y and Y and W) =P(Y) x P(Y) x P (W) = 3/8 x 2/7 x 2/6 = 1 / 28

(iii)     In a class, there are 8 girls and 6 boys. If three students are selected at random for debating, find the probability that all girls.

P (G) =8/14 and P (B) =6/14. P (1st G) =8/14, P (2nd G) 7/13 and P (3rdG) = 6/12. P (three girls) 8/14 x 7/13 x 6/12= 2/13

(iv) In how many ways can 3 drama officials be selected from 8 members?

Solution:              8 C 3 = 56 ways.

(v)   A box has 12 bulbs, of which 3 are defective. If 4 bulbs are sold, find the probability that exactly one will be defective.

P (defective bulb) = 3 C 1 and P (non-defective bulbs) = 9 C 3

3 C 1 x 9 C 3 = 3! x 9!= 252

(3 -1)!1! (9 – 3)!3!

P (4 bulbs from 12) = 12 C 4 = 495.

P (1 defective bulb and 3 okay bulbs) = 295/495=0.509.

7.     POISSON DISTRIBUTION

Poisson distribution: is a discrete probability distribution that expresses the probability of a number of events occurring in a fixed period of time if these events occur with a known average rate, and are independent of the time since the last event. The Poisson distribution arises in many situations. It is safe to say that it is one of the three most important discrete probability distributions (the other two being the uniform and the binomial distributions). The Poisson distribution can be viewed as arising from the binomial distribution or from the exponential density.

If the parameters n & p of a binomial distribution are known then we can find the distribution. But when n is large and p is very small the application of binomial distribution is very difficult. Let x be any discrete random variable which can take values 0,1,2,3….. such that the probability distribution function of x

P(x)=e -λ λx  x!

where λ is a positive constant, np = λ . This distribution is called the poisson distribution.

 Number of printing mistakes on each page of a book published by a good publisher

Number of telephone calls arriving at a telephone switch board per minute

The Poisson distribution is a common distribution used to model “count” data:

• Number of telephone calls received per hour
• Number of claims received per day by an insurance company
• Number of accidents per month at an intersection

8.   OBJECTIVES OF PROBABILITY DISTRIBUTION The core objectives of tabulation are mentioned below:

(a)To compute and interpret the expected value, variance, and standard deviation for a discrete random variable and work with probabilities involving a binomial probability distribution.

(b)To work out the probabilities involving a Poisson probability distribution,

(c)Understand the concepts of a random variable and a probability distribution.

(d) To decide the binomial distribution problems to be approximated by the Poisson distribution , to use the Poisson distribution in analyzing statistical

(e)To use the hyper geometric distribution and know how to work such problems.

9. RULES OF PROBABILITY

(a)   ADDITION RULES I. Rule – 1:

When two events A and B are mutually exclusive, then P (A or B) =P (A) +P (B)

Example –

When a is tossed, find the probability of getting a 3 or 5.

Solution: P (3) =1/6 and P (5) =1/6.

Therefore P (3 or 5) = P (3) + P (5) = 1/6+1/6 =2/6=1/3.

II. Rule – 2:

If A and B are two events that are NOT mutually exclusive, then P (A or B) = P (A)

+   P (B) – P (A and B), where A and B means the number of outcomes that event A and B have in common.

When a card is drawn from a pack of 52 cards, find the probability that the card is a 10 or a heart.

P (10) = 4/52 and P (heart) =13/52

P (10 that is Heart) = 1/52

P (A or B) = P (A) +P (B) – P (A and B) = 4/52 _ 13/52 – 1/52 = 16/52.

(b) MULTIPLICATION RULES

I.  Rule – 1: For two independent events A and B, then P (A and B) = P (A) x P (B).

Determine the probability of obtaining a 5 on a die and a tail on a coin in one throw.

Solution: P (5) =1/6 and P (T) =1/2.

P (5 and T) = P (5) x P (T) = 1/6 x ½= 1/12.

II.  Rule – 2:

When to events are dependent, the probability of both events occurring is P(A and  B)=P(A) x P(B|A), where P(B|A) is the probability that event B occurs given that  event A has already occurred.

Example – Find  the  probability  of  obtaining  two  Aces  from  a  pack  of  52  cards  without  replacement.

P( Ace) =2/52 and P( second Ace if NO replacement) = 3/51

Therefore P (Ace and Ace) = P(Ace) x P( Second Ace) = 4/52 x 3/51 = 1/221

10. MERITS OF PROBABILITY DISTRIBUTION

Merits of probability distribution and benefits of theoretical or probability distribution

• Where the calculation of observed distribution is not possible.
• Sometime observed base distribution’s calculation is not possible due to impossibility at that place we can calculate probability distribution.
• Helpful in forecasting – Probability distribution isvery helpful for forecasting and on this basis we can estimate our future and make good plans for our business.
• Helpful in Comparison – It can compare it with observed or real distribution and evaluate our efficiency of work.
• LIMITATIONS OF PROBABILITY DISTRIBUTION
• Probability distribution cannot be correlated
• Probability distribution cannot be viewed in chart form or in any statistical view
• The data cannot be extract data from probability distribution or it cannot include in the reports
• It is excluded from sensitivity analyses or charts.
• Probability distribution doesn’t support the Latin Hypercube sampling

To summaries, the probability has become one of the basic tools of statistics. Sometimes statistical analysis becomes paralyzed without the theorem of probability. Probability of a given event is defined as the expected frequency of occurrence of the event among events of a like sort. According to basic economic theory, people wish to maximize their expected utility. In order to do so they should integrate the likelihood (i.e. probability) and the possible outcomes (good or bad). This means that people maximize their utility based on their perceived importance of probabilities and outcomes.

• https://www.merriam-webster.com/dictionary/probability
• http://whatis.techtarget.com/definition/probability
• http://www.itl.nist.gov/div898/handbook/eda/section3/eda361.htm
• http://study.com/academy/lesson/probability-distribution-definition-formula-example.html
• https://www.intmath.com/counting-probability/11-probability-distributions-concepts.php
• https://onlinecourses.science.psu.edu/stat200/node/34
• https://www.thoughtco.com/probability-distribution-3126569
• https://people.richland.edu/james/lecture/m170/ch06-prb.html
• https://www.utdallas.edu/~scniu/OPRE-6301/documents/Important_Probability_Distributions.pdf
• http://www.ce.memphis.edu/7012/pdf%20files/Discrete_notes.pdf
• https://cran.r-project.org/web/packages/IPSUR/vignettes/IPSUR.pdf
• http://www.itl.nist.gov/div898/handbook/eda/section3/eda3661.htm
• http://study.com/academy/lesson/probability-distribution-definition-formula-example.html http://www.itl.nist.gov/div898/handbook/eda/section3/eda36.htm
• https://www.slideshare.net/bijayabnanda/ls-bs-9probability-concept-and-probability-distribution
• https://www.wyzant.com/resources/lessons/math/statistics_and_probability/probability_dis tributions