problem solving involving trigonometric identities

7.1 Solving Trigonometric Equations with Identities

Learning objectives.

In this section, you will:

• Verify the fundamental trigonometric identities.
• Simplify trigonometric expressions using algebra and the identities.

In espionage movies, we see international spies with multiple passports, each claiming a different identity. However, we know that each of those passports represents the same person. The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression. Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation.

In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.

Verifying the Fundamental Trigonometric Identities

Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equations. In fact, we use algebraic techniques constantly to simplify trigonometric expressions. Basic properties and formulas of algebra, such as the difference of squares formula and the perfect squares formula, will simplify the work involved with trigonometric expressions and equations. We already know that all of the trigonometric functions are related because they all are defined in terms of the unit circle. Consequently, any trigonometric identity can be written in many ways.

To verify the trigonometric identities, we usually start with the more complicated side of the equation and essentially rewrite the expression until it has been transformed into the same expression as the other side of the equation. Sometimes we have to factor expressions, expand expressions, find common denominators, or use other algebraic strategies to obtain the desired result. In this first section, we will work with the fundamental identities: the Pythagorean Identities , the even-odd identities, the reciprocal identities, and the quotient identities.

We will begin with the Pythagorean Identities (see Table 1 ), which are equations involving trigonometric functions based on the properties of a right triangle. We have already seen and used the first of these identifies, but now we will also use additional identities.

The second and third identities can be obtained by manipulating the first. The identity 1 + cot 2 θ = csc 2 θ 1 + cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine.

Prove: 1 + cot 2 θ = csc 2 θ 1 + cot 2 θ = csc 2 θ

Similarly, 1 + tan 2 θ = sec 2 θ 1 + tan 2 θ = sec 2 θ can be obtained by rewriting the left side of this identity in terms of sine and cosine. This gives

The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle and determine whether the identity is odd or even. (See Table 2 ).

Recall that an odd function is one in which f (− x ) = − f ( x ) f (− x ) = − f ( x ) for all x x in the domain of f . f . The sine function is an odd function because sin ( − θ ) = − sin θ . sin ( − θ ) = − sin θ . The graph of an odd function is symmetric about the origin. For example, consider corresponding inputs of π 2 π 2 and − π 2 . − π 2 . The output of sin ( π 2 ) sin ( π 2 ) is opposite the output of sin ( − π 2 ) . sin ( − π 2 ) . Thus,

This is shown in Figure 2 .

Recall that an even function is one in which

The graph of an even function is symmetric about the y- axis. The cosine function is an even function because cos ( − θ ) = cos θ . cos ( − θ ) = cos θ . For example, consider corresponding inputs π 4 π 4 and − π 4 . − π 4 . The output of cos ( π 4 ) cos ( π 4 ) is the same as the output of cos ( − π 4 ) . cos ( − π 4 ) . Thus,

See Figure 3 .

For all θ θ in the domain of the sine and cosine functions, respectively, we can state the following:

• Since sin (− θ ) = − sin θ , sin (− θ ) = − sin θ , sine is an odd function.
• Since, cos (− θ ) = cos θ , cos (− θ ) = cos θ , cosine is an even function.

The other even-odd identities follow from the even and odd nature of the sine and cosine functions. For example, consider the tangent identity, tan (− θ ) = −tan θ . tan (− θ ) = −tan θ . We can interpret the tangent of a negative angle as tan (− θ ) = sin ( − θ ) cos (− θ ) = − sin θ cos θ = − tan θ . tan (− θ ) = sin ( − θ ) cos (− θ ) = − sin θ cos θ = − tan θ . Tangent is therefore an odd function, which means that tan ( − θ ) = − tan ( θ ) tan ( − θ ) = − tan ( θ ) for all θ θ in the domain of the tangent function .

The cotangent identity, cot ( − θ ) = − cot θ , cot ( − θ ) = − cot θ , also follows from the sine and cosine identities. We can interpret the cotangent of a negative angle as cot ( − θ ) = cos ( − θ ) sin ( − θ ) = cos θ − sin θ = − cot θ . cot ( − θ ) = cos ( − θ ) sin ( − θ ) = cos θ − sin θ = − cot θ . Cotangent is therefore an odd function, which means that cot ( − θ ) = − cot ( θ ) cot ( − θ ) = − cot ( θ ) for all θ θ in the domain of the cotangent function .

The cosecant function is the reciprocal of the sine function, which means that the cosecant of a negative angle will be interpreted as csc ( − θ ) = 1 sin ( − θ ) = 1 − sin θ = − csc θ . csc ( − θ ) = 1 sin ( − θ ) = 1 − sin θ = − csc θ . The cosecant function is therefore odd.

Finally, the secant function is the reciprocal of the cosine function, and the secant of a negative angle is interpreted as sec ( − θ ) = 1 cos ( − θ ) = 1 cos θ = sec θ . sec ( − θ ) = 1 cos ( − θ ) = 1 cos θ = sec θ . The secant function is therefore even.

To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities.

The next set of fundamental identities is the set of reciprocal identities , which, as their name implies, relate trigonometric functions that are reciprocals of each other. See Table 3 .

The final set of identities is the set of quotient identities , which define relationships among certain trigonometric functions and can be very helpful in verifying other identities. See Table 4 .

The reciprocal and quotient identities are derived from the definitions of the basic trigonometric functions.

Summarizing Trigonometric Identities

The Pythagorean Identities are based on the properties of a right triangle.

The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.

The reciprocal identities define reciprocals of the trigonometric functions.

The quotient identities define the relationship among the trigonometric functions.

Graphing the Equations of an Identity

Graph both sides of the identity cot θ = 1 tan θ . cot θ = 1 tan θ . In other words, on the graphing calculator, graph y = cot θ y = cot θ and y = 1 tan θ . y = 1 tan θ .

See Figure 4 .

We see only one graph because both expressions generate the same image. One is on top of the other. This is a good way to confirm an identity verified with analytical means. If both expressions give the same graph, then they are most likely identities.

Given a trigonometric identity, verify that it is true.

• Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
• Look for opportunities to factor expressions, square a binomial, or add fractions.
• Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
• If these steps do not yield the desired result, try converting all terms to sines and cosines.

Verifying a Trigonometric Identity

Verify tan θ cos θ = sin θ . tan θ cos θ = sin θ .

We will start on the left side, as it is the more complicated side:

This identity was fairly simple to verify, as it only required writing tan θ tan θ in terms of sin θ sin θ and cos θ . cos θ .

Verify the identity csc θ cos θ tan θ = 1. csc θ cos θ tan θ = 1.

Verifying the Equivalency Using the Even-Odd Identities

Verify the following equivalency using the even-odd identities:

Working on the left side of the equation, we have

Verifying a Trigonometric Identity Involving sec 2 θ

Verify the identity sec 2 θ − 1 sec 2 θ = sin 2 θ sec 2 θ − 1 sec 2 θ = sin 2 θ

As the left side is more complicated, let’s begin there.

There is more than one way to verify an identity. Here is another possibility. Again, we can start with the left side.

In the first method, we used the identity sec 2 θ = tan 2 θ + 1 sec 2 θ = tan 2 θ + 1 and continued to simplify. In the second method, we split the fraction, putting both terms in the numerator over the common denominator. This problem illustrates that there are multiple ways we can verify an identity. Employing some creativity can sometimes simplify a procedure. As long as the substitutions are correct, the answer will be the same.

Show that cot θ csc θ = cos θ . cot θ csc θ = cos θ .

Creating and Verifying an Identity

Create an identity for the expression 2 tan θ sec θ 2 tan θ sec θ by rewriting strictly in terms of sine.

There are a number of ways to begin, but here we will use the quotient and reciprocal identities to rewrite the expression:

Verifying an Identity Using Algebra and Even/Odd Identities

Verify the identity:

Let’s start with the left side and simplify:

Verify the identity sin 2 θ − 1 tan θ sin θ − tan θ = sin θ + 1 tan θ . sin 2 θ − 1 tan θ sin θ − tan θ = sin θ + 1 tan θ .

Verifying an Identity Involving Cosines and Cotangents

Verify the identity: ( 1 − cos 2 x ) ( 1 + cot 2 x ) = 1. ( 1 − cos 2 x ) ( 1 + cot 2 x ) = 1.

We will work on the left side of the equation.

Using Algebra to Simplify Trigonometric Expressions

We have seen that algebra is very important in verifying trigonometric identities, but it is just as critical in simplifying trigonometric expressions before solving. Being familiar with the basic properties and formulas of algebra, such as the difference of squares formula, the perfect square formula, or substitution, will simplify the work involved with trigonometric expressions and equations.

For example, the equation ( sin x + 1 ) ( sin x − 1 ) = 0 ( sin x + 1 ) ( sin x − 1 ) = 0 resembles the equation ( x + 1 ) ( x − 1 ) = 0 , ( x + 1 ) ( x − 1 ) = 0 , which uses the factored form of the difference of squares. Using algebra makes finding a solution straightforward and familiar. We can set each factor equal to zero and solve. This is one example of recognizing algebraic patterns in trigonometric expressions or equations.

Another example is the difference of squares formula, a 2 − b 2 = ( a − b ) ( a + b ) , a 2 − b 2 = ( a − b ) ( a + b ) , which is widely used in many areas other than mathematics, such as engineering, architecture, and physics. We can also create our own identities by continually expanding an expression and making the appropriate substitutions. Using algebraic properties and formulas makes many trigonometric equations easier to understand and solve.

Writing the Trigonometric Expression as an Algebraic Expression

Write the following trigonometric expression as an algebraic expression: 2 cos 2 θ + cos θ − 1. 2 cos 2 θ + cos θ − 1.

Notice that the pattern displayed has the same form as a standard quadratic expression, a x 2 + b x + c . a x 2 + b x + c . Letting cos θ = x , cos θ = x , we can rewrite the expression as follows:

This expression can be factored as ( 2 x − 1 ) ( x + 1 ) . ( 2 x − 1 ) ( x + 1 ) . If it were set equal to zero and we wanted to solve the equation, we would use the zero factor property and solve each factor for x . x . At this point, we would replace x x with cos θ cos θ and solve for θ . θ .

Rewriting a Trigonometric Expression Using the Difference of Squares

Rewrite the trigonometric expression: 4 cos 2 θ − 1. 4 cos 2 θ − 1.

Notice that both the coefficient and the trigonometric expression in the first term are squared, and the square of the number 1 is 1. This is the difference of squares. Thus,

If this expression were written in the form of an equation set equal to zero, we could solve each factor using the zero factor property. We could also use substitution like we did in the previous problem and let cos θ = x , cos θ = x , rewrite the expression as 4 x 2 − 1 , 4 x 2 − 1 , and factor ( 2 x − 1 ) ( 2 x + 1 ) . ( 2 x − 1 ) ( 2 x + 1 ) . Then replace x x with cos θ cos θ and solve for the angle.

Rewrite the trigonometric expression: 25 − 9 sin 2 θ . 25 − 9 sin 2 θ .

Simplify by Rewriting and Using Substitution

Simplify the expression by rewriting and using identities:

We can start with the Pythagorean identity.

Now we can simplify by substituting 1 + cot 2 θ 1 + cot 2 θ for csc 2 θ . csc 2 θ . We have

Use algebraic techniques to verify the identity: cos θ 1 + sin θ = 1 − sin θ cos θ . cos θ 1 + sin θ = 1 − sin θ cos θ .

(Hint: Multiply the numerator and denominator on the left side by 1 − sin θ . ) 1 − sin θ . )

Access these online resources for additional instruction and practice with the fundamental trigonometric identities.

• Fundamental Trigonometric Identities
• Verifying Trigonometric Identities

7.1 Section Exercises

We know g ( x ) = cos x g ( x ) = cos x is an even function, and f ( x ) = sin x f ( x ) = sin x and h ( x ) = tan x h ( x ) = tan x are odd functions. What about G ( x ) = cos 2 x , F ( x ) = sin 2 x , G ( x ) = cos 2 x , F ( x ) = sin 2 x , and H ( x ) = tan 2 x ? H ( x ) = tan 2 x ? Are they even, odd, or neither? Why?

Examine the graph of f ( x ) = sec x f ( x ) = sec x on the interval [ − π , π ] . [ − π , π ] . How can we tell whether the function is even or odd by only observing the graph of f ( x ) = sec x ? f ( x ) = sec x ?

After examining the reciprocal identity for sec t , sec t , explain why the function is undefined at certain points.

All of the Pythagorean Identities are related. Describe how to manipulate the equations to get from sin 2 t + cos 2 t = 1 sin 2 t + cos 2 t = 1 to the other forms.

For the following exercises, use the fundamental identities to fully simplify the expression.

sin x cos x sec x sin x cos x sec x

sin ( − x ) cos ( − x ) csc ( − x ) sin ( − x ) cos ( − x ) csc ( − x )

tan x sin x + sec x cos 2 x tan x sin x + sec x cos 2 x

csc x + cos x cot ( − x ) csc x + cos x cot ( − x )

cot t + tan t sec ( − t ) cot t + tan t sec ( − t )

3 sin 3 t csc t + cos 2 t + 2 cos ( − t ) cos t 3 sin 3 t csc t + cos 2 t + 2 cos ( − t ) cos t

− tan ( − x ) cot ( − x ) − tan ( − x ) cot ( − x )

− sin ( − x ) cos x sec x csc x tan x cot x − sin ( − x ) cos x sec x csc x tan x cot x

1 + tan 2 θ csc 2 θ + sin 2 θ + 1 sec 2 θ 1 + tan 2 θ csc 2 θ + sin 2 θ + 1 sec 2 θ

( tan x csc 2 x + tan x sec 2 x ) ( 1 + tan x 1 + cot x ) − 1 cos 2 x ( tan x csc 2 x + tan x sec 2 x ) ( 1 + tan x 1 + cot x ) − 1 cos 2 x

1 − cos 2 x tan 2 x + 2 sin 2 x 1 − cos 2 x tan 2 x + 2 sin 2 x

For the following exercises, simplify the first trigonometric expression by writing the simplified form in terms of the second expression.

tan x + cot x csc x ; cos x tan x + cot x csc x ; cos x

sec x + csc x 1 + tan x ; sin x sec x + csc x 1 + tan x ; sin x

cos x 1 + sin x + tan x ; cos x cos x 1 + sin x + tan x ; cos x

1 sin x cos x − cot x ; cot x 1 sin x cos x − cot x ; cot x

1 1 − cos x − cos x 1 + cos x ; csc x 1 1 − cos x − cos x 1 + cos x ; csc x

( sec x + csc x ) ( sin x + cos x ) − 2 − cot x ; tan x ( sec x + csc x ) ( sin x + cos x ) − 2 − cot x ; tan x

1 csc x − sin x ; sec x  and  tan x 1 csc x − sin x ; sec x  and  tan x

1 − sin x 1 + sin x − 1 + sin x 1 − sin x ; sec x  and  tan x 1 − sin x 1 + sin x − 1 + sin x 1 − sin x ; sec x  and  tan x

tan x ; sec x tan x ; sec x

sec x ; cot x sec x ; cot x

sec x ; sin x sec x ; sin x

cot x ; sin x cot x ; sin x

cot x ; csc x cot x ; csc x

For the following exercises, verify the identity.

cos x − cos 3 x = cos x sin 2 x cos x − cos 3 x = cos x sin 2 x

cos x ( tan x − sec ( − x ) ) = sin x − 1 cos x ( tan x − sec ( − x ) ) = sin x − 1

1 + sin 2 x cos 2 x = 1 cos 2 x + sin 2 x cos 2 x = 1 + 2 tan 2 x 1 + sin 2 x cos 2 x = 1 cos 2 x + sin 2 x cos 2 x = 1 + 2 tan 2 x

( sin x + cos x ) 2 = 1 + 2 sin x cos x ( sin x + cos x ) 2 = 1 + 2 sin x cos x

cos 2 x − tan 2 x = 2 − sin 2 x − sec 2 x cos 2 x − tan 2 x = 2 − sin 2 x − sec 2 x

For the following exercises, prove or disprove the identity.

1 1 + cos x − 1 1 − cos ( − x ) = − 2 cot x csc x 1 1 + cos x − 1 1 − cos ( − x ) = − 2 cot x csc x

csc 2 x ( 1 + sin 2 x ) = cot 2 x csc 2 x ( 1 + sin 2 x ) = cot 2 x

( sec 2 ( − x ) − tan 2 x tan x ) ( 2 + 2 tan x 2 + 2 cot x ) − 2 sin 2 x = cos 2 x ( sec 2 ( − x ) − tan 2 x tan x ) ( 2 + 2 tan x 2 + 2 cot x ) − 2 sin 2 x = cos 2 x

tan x sec x sin ( − x ) = cos 2 x tan x sec x sin ( − x ) = cos 2 x

sec ( − x ) tan x + cot x = − sin ( − x ) sec ( − x ) tan x + cot x = − sin ( − x )

1 + sin x cos x = cos x 1 + sin ( − x ) 1 + sin x cos x = cos x 1 + sin ( − x )

For the following exercises, determine whether the identity is true or false. If false, find an appropriate equivalent expression.

cos 2 θ − sin 2 θ 1 − tan 2 θ = sin 2 θ cos 2 θ − sin 2 θ 1 − tan 2 θ = sin 2 θ

3 sin 2 θ + 4 cos 2 θ = 3 + cos 2 θ 3 sin 2 θ + 4 cos 2 θ = 3 + cos 2 θ

sec θ + tan θ cot θ + cos θ = sec 2 θ sec θ + tan θ cot θ + cos θ = sec 2 θ

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Precalculus 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions
• Section URL: https://openstax.org/books/precalculus-2e/pages/7-1-solving-trigonometric-equations-with-identities

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Forgot password? New user? Sign up

Existing user? Log in

Fundamental Trigonometric Identities - Problem Solving (Easy)

Already have an account? Log in here.

• Brilliant Mathematics
• A Former Brilliant Member
• Tirthankar Mazumder
• Sravanth C.

When working with trigonometric identities, it may be useful to keep the following tips in mind:

• Draw a picture illustrating the problem if it involves only the basic trigonometric functions.
• If the problem expresses an identity between trigonometric functions, try working on one side of the identity to write the trigonometric functions from one side in terms of trigonometric functions on the other side.
• Use the Pythagorean identities to compute values in the trigonometric identity.
• Multiply rational expressions by conjugates in order to take advantage of the Pythagorean identities .
• Add rational expressions by finding common denominators.

Fundamental Formulas

Specific values, pythagorean identities, symmetry properties, periodicity identities, complementary angle identities, double-angle formulas, sum and difference formulas, triple-angle formulas, half-angle tangent formulas, power reduction identities, product-to-sum formulas, sum-to-product formulas, fundamental trigonometric identities - problem solving (basic), fundamental trigonometric identities - problem solving (intermediate), additional problems.

The fundamental period of the graphs of \(\sin x, \cos x, \csc x, \sec x \) is \(2\pi,\) while the fundamental period of the graphs of \( \tan x, \cot x \) is \(\pi\).

Pythagorean identities:

\[\begin{eqnarray} \sin^2 A + \cos^2 A &=& 1 \\ \tan^2 A + 1 &=& \sec^2 A \\ \cot^2 A + 1 &=& \csc^2 A. \end{eqnarray} \]

Compound angle formulas:

\[\begin{eqnarray} \sin(A\pm B) &=& \sin A \cos B \pm \cos A \sin B \\ \cos(A\pm B) &=& \cos A \cos B \mp \sin A \sin B \\ \tan(A\pm B) &=& \frac{ \tan A \pm \tan B } { 1 \mp \tan A \tan B }. \end{eqnarray} \]

You may find the following table useful:

\[ \begin{array} {| c | c | c | c | c | c |} \hline \theta & 0^\circ & \frac{\pi}{6} = 30^\circ & \frac{\pi}{4} = 45^\circ & \frac{\pi}{3} = 60^\circ & \frac{\pi}{2} = 90^\circ\\ \hline \sin \theta & \frac {\sqrt{0}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{4}} {2} \\ \hline \cos \theta & \frac {\sqrt{4}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{0}} {2}\\ \hline \tan \theta & 0 & \frac { 1}{\sqrt{3} } & 1 & \sqrt{3} & \infty \\ \hline \end{array}\]

For any angle \(\theta,\) we have

\[\begin{align} \cos^2 \theta + \sin^2 \theta &= 1 \\ 1 + \tan^2 \theta &= \sec^2 \theta \\ \cot^2 \theta + 1 &= \csc^2 \theta. \end{align}\]

\[\begin{align} \cos(-\theta) &= \cos \theta \\ \sin(-\theta) &= -\sin \theta\\ \tan(-\theta) &= -\tan \theta\\ \cot(-\theta) &= -\cot \theta\\ \csc(-\theta) &= -\csc \theta\\ \sec(-\theta) &= \sec \theta. \end{align}\]

\[\begin{align} \sin \theta &=\sin(\theta+2\pi) &\quad \csc \theta &=\csc(\theta+2\pi)\\ \cos \theta &=\cos(\theta+2\pi) &\quad \sec \theta &=\sec(\theta+2\pi)\\ \tan \theta &=\tan(\theta+\pi) &\quad \cot \theta &=\cot(\theta+\pi). \end{align}\]

\[ \begin{align} \cos \theta & = \sin \left( \frac{\pi}{2} - \theta \right) \\ \sin \theta &= \cos \left( \frac{\pi}{2}-\theta \right) \\ \cot \theta & = \tan \left( \frac{\pi}{2} - \theta \right) \\ \csc \theta & = \sec \left( \frac{\pi}{2} - \theta \right). \end{align}\]

\[\begin{align} \sin 2 \theta &= 2\sin \theta \cos \theta \\\\ \cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ &= 2\cos^2 \theta - 1\\ &= 1 - 2\sin^2 \theta \\\\ \tan 2\theta &= \frac{2\tan \theta}{1 - \tan^2 \theta}. \end{align} \]

\[\begin{align} \sin(x+y) &= \sin x \cos y + \cos x \sin y \\ \sin(x-y) &= \sin x \cos y - \cos x \sin y \\\\ \cos(x+y) &= \cos x \cos y − \sin x \sin y \\ \cos(x-y) &= \cos x \cos y + \sin x \sin y \\\\ \tan(x+y) &= \dfrac{\tan x + \tan y}{1 - \tan x \tan y} \\ \tan(x-y) &= \dfrac{\tan x - \tan y}{1 + \tan x \tan y}. \end{align} \]

\[\begin{align} \sin 3 \theta &= 3 \sin \theta - 4 \sin ^3 \theta \\ \cos 3\theta &= 4 \cos ^ 3 \theta - 3 \cos \theta. \end{align} \]

\[\sin\theta=\frac{2\tan\frac{\theta}{2}}{1+\tan^{2}\frac{\theta}{2}} \\ \cos\theta=\frac{1-\tan^{2}\frac{\theta}{2}}{1+\tan^{2}\frac{\theta}{2}} \\ \tan\theta=\frac{2\tan\frac{\theta}{2}}{1-\tan^{2}\frac{\theta}{2}}.\]

\[\begin{align} \sin^2 \theta &=\frac{1}{2}(1-\cos 2\theta) \\ \cos^2 \theta &=\frac{1}{2}(1+\cos 2\theta). \end{align} \]

\[\begin{align} \cos x \cos y & = \frac{1}{2} \big(\cos (x - y) + \cos(x+ y) \big) \\ \sin x \cos y &= \frac{1}{2} \big(\sin (x- y) + \sin(x + y) \big) \\ \cos x \sin y &= \frac{1}{2} \big(\sin (x + y) - \sin(x - y) \big)\\ \sin x \sin y &= \frac{1}{2} \big(\cos (x - y) - \cos(x + y) \big). \end{align}\]

\[\begin{align} \sin x+\sin y & =2\sin\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right) \\ \cos x+\cos y &=2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right). \\ \end{align}\]

If \(\sin x = \cos x = 0.2\), what is the value of \(\cos 2x?\) ANSWER Because the Pythagorean identity \( \sin^2 x + \cos^2 x = 1 \) is not fulfilled, there is no solution of \(x\) and thus there is no possible value for \(\cos 2x \). \(_\square\)

If \(\sin \theta = \frac45\) and \(\theta\) is not in the first quadrant, then find the value of \(\cos \theta\). ANSWER Sine is positive only in the first and second quadrants but \(\theta\) is not in the first quadrant, so definitely \(\theta\) must lie in the second quadrant where \(\cos \theta < 0:\) \[\begin{align} \sin^2 \theta + \cos^2 \theta & = 1 \\ \cos^2 \theta & = 1 - \sin^2 \theta \\ & = 1 - \dfrac{16}{25} = \dfrac{9}{25} \\ \Rightarrow \cos \theta & = \pm \dfrac35 \\ \Rightarrow \cos \theta & = - \dfrac35.\ _\square \qquad (\text{since } \cos \theta < 0) \\ \end{align}\]

If \(\sec \theta + \tan \theta = \frac23\), find the value of \(\sin \theta\) and determine the quadrant in which \(\theta\) lies. ANSWER We know that \(\sec^2 \theta - \tan^2 \theta = 1 \implies \sec \theta - \tan \theta - \frac{1}{\sec \theta + \tan \theta} = \dfrac{1}{\hspace{2mm} \frac23\hspace{2mm} } = \frac32\). By adding, \((\sec \theta + \tan \theta) + (\sec \theta - \tan \theta) = \frac23 + \frac32 \implies 2 \sec \theta = \frac{13}{6} \implies \sec \theta = \frac{13}{12}\). By subtracting, \((\sec \theta + \tan \theta) - (\sec \theta - \tan \theta) = \frac23 - \frac32 \implies 2 \tan \theta = \frac{-5}{6} \implies \tan \theta = \frac{-5}{12}\). From this we get to know that \(\sec \theta\) is positive and \(\tan \theta\) is negative. This is only possible when \(\theta\) lies in the fourth quadrant . Therefore, \( \sin \theta = \frac{\tan \theta}{\sec \theta} = \frac{-5}{13}.\) \(_\square\)

Find the value of \(2\big(\sin^6 \theta + \cos^6 \theta\big) - 3\big(\sin^4 \theta + \cos^4 \theta\big)\). ANSWER We have \[\begin{align} 2\big(\sin^6 \theta + \cos^6 \theta\big) - 3\big(\sin^4 \theta + \cos^4 \theta\big) & = 2\left[\big(\sin^2 \theta\big)^3 + \big(\cos^2 \theta\big)^3\right] - 3\left[\big(\sin^2 \theta\big)^2 + \big(\cos^2 \theta\big)^2\right] \\ & = 2\left[\big(\sin^2 \theta + \cos^2 \theta\big)^3 - 3\sin^2 \theta \cos^2 \theta\big(\sin^2 \theta + \cos^2 \theta\big)\right] - 3\left[\big(\sin^2 \theta + \cos^2 \theta\big)^2 - \sin^2 \theta \cos^2 \theta\right] \\ & = 2\big(1 - 3\sin^2 \theta \cos^2 \theta\big) - 3\big(1 - 2\sin^2 \theta \cos^2 \theta\big) \\ & = 2 - 3 \\ & = -1.\ _\square \end{align}\]

Find the value of \(\,(\tan \theta + \cot \theta)^2 \) \(\ \sec^2 \theta + \csc^2 \theta.\) ANSWER We have \(\begin{align} 1.\ (\tan \theta + \cot \theta)^2 & = \tan^2 \theta + \cot^2 \theta + 2\tan \theta \cot \theta \\ & = \tan^2 \theta + \cot^2 \theta + 2 \\ & = \big(1 + \tan^2 \theta\big) + \big(1 + \cot^2 \theta\big) \\ & = \sec^2 \theta + \csc^2 \theta \end{align}\) \(\begin{align} 2.\ \sec^2 \theta + \csc^2 \theta & = \dfrac{1}{\cos^2 \theta} + \dfrac{1}{\sin^2 \theta} \\ \\ & = \dfrac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta \cdot \cos^2 \theta} \\ \\ & = \dfrac{1}{\sin^2 \theta \cdot \cos^2 \theta} \\ \\ & = \sec^2 \theta \cdot \csc^2 \theta.\ _\square \end{align}\)

In this summary, we collect all of the trigonometric identities that are useful to know for problem-solving.

Find the value of \(\sin^2 \frac{\pi}{10} + \sin^2 \frac{4\pi}{10} + \sin^2 \frac{6 \pi}{10} + \sin^2 \frac{9 \pi}{10}\). ANSWER We have \[\begin{align} \sin^2 \dfrac{\pi}{10} + \sin^2 \dfrac{4\pi}{10} + \sin^2 \dfrac{6 \pi}{10} + \sin^2 \dfrac{9 \pi}{10} &=\sin^2 \left(\dfrac{\pi}{10}\right) + \sin^2 \left( \dfrac{\pi}{2} - \dfrac{\pi}{10} \right) + \sin^2 \left(\dfrac{\pi}{2} + \dfrac{\pi}{10} \right) + \sin^2 \left(\pi - \dfrac{\pi}{10} \right) \\ &=\underbrace{\sin^2 \dfrac{\pi}{10} + \cos^2 \dfrac{\pi}{10}}_{1} + \underbrace{\cos^2 \dfrac{\pi}{10} + \sin^2 \dfrac{\pi}{10}}_{1} \\ &=1 + 1 \\ &= 2.\ _\square \end{align}\]

Find the value of \(\cot \frac{\pi}{16} \times \cot \frac{2 \pi}{16} \times \cot \frac{3 \pi}{16} \times \cdots \times \cot \frac{7 \pi}{16}\). ANSWER We have \[\begin{align} \cot \dfrac{\pi}{16} \cdot \cot \dfrac{2 \pi}{16} \cdot \cot \dfrac{3 \pi}{16} \times \cdots \times \cot \dfrac{7 \pi}{16} &=\left(\cot \dfrac{\pi}{16} \cdot \cot \dfrac{7 \pi}{16}\right) \cdot \left(\cot \dfrac{2 \pi}{16} \cdot \cot \dfrac{6 \pi}{16} \right) \cdot \left(\cot \dfrac{3 \pi}{16} \cdot \cot \dfrac{5 \pi}{16} \right) \cdot \cot \dfrac{4 \pi}{16} \\ &=\left(\cot \dfrac{\pi}{16} \cdot \cot \Big(\dfrac{\pi}{2} - \dfrac{\pi}{16}\Big)\right) \cdot \left(\cot \dfrac{2 \pi}{16} \cdot \cot \Big(\dfrac{\pi}{2} - \dfrac{2\pi}{16} \Big)\right) \cdot \left(\cot \dfrac{3 \pi}{16} \cdot \cot \Big(\dfrac{\pi}{2} - \dfrac{3\pi}{16} \Big)\right) \cdot \cot \dfrac{\pi}{4} \\ &=\underbrace{\left(\cot \dfrac{\pi}{16} \cdot \tan \dfrac{\pi}{16}\right)}_{1} \cdot \underbrace{\left(\cot \dfrac{2 \pi}{16} \cdot \tan \dfrac{2\pi}{16} \right)}_{1} \cdot \underbrace{\left(\cot \dfrac{3 \pi}{16} \cdot \tan \dfrac{3\pi}{16} \right)}_{1} \cdot 1 \\ &= 1.\ _\square \end{align}\]

If \(3 \sin \theta + 4 \cos \theta = 5\), then find the value of \(4 \sin \theta - 3 \cos \theta\). ANSWER Given \(3 \sin \theta + 4 \cos \theta = 5,\) let \(4\sin \theta - 3\cos \theta = a\). On squaring and adding both these equations, we get \[\begin{align} 5^2 & = (3\sin \theta + 4 \cos \theta)^2 \\ a^2 & = (4\sin \theta - 3\cos \theta)^2 \\ \\ 5^2 + a^2 & = (3\sin \theta + 4 \cos \theta)^2 + (4\sin \theta - 3\cos \theta)^2 \\ a^2 + 25 & = 9\sin^2 \theta + 16\cos^2 \theta + 24\sin\theta\cos\theta + 16\sin^2\theta + 9\cos^2\theta - 24\sin\theta\cos\theta \\ a^2 + 25 & = 25(\sin^2 \theta + \cos^2 \theta) \\ a^2 + 25 & = 25 \\ a & = 0 \\ \\ \Rightarrow 4\sin\theta - 3\cos\theta & = 0.\ _\square \end{align}\]

If \(\cos \theta + \sin \theta = \sqrt{2} \cos \theta\), find the value of \(\cos \theta - \sin \theta\). ANSWER Given \(\cos \theta + \sin \theta = \sqrt{2}\cos \theta,\) we have \(\big(\sqrt{2} - 1\big)\cos\theta = \sin\theta\). On multiplying both the sides with \(\big(\sqrt2 + 1\big),\) we get \[\begin{align} \big(\sqrt2 + 1\big)\big(\sqrt2 - 1\big)\cos\theta & = \big(\sqrt2 + 1\big)\sin \theta \\ (2 - 1)\cos\theta & = \sqrt2 \sin\theta + \sin\theta \\ \\ \Rightarrow \cos\theta - \sin\theta & = \sqrt2 \sin\theta.\ _\square \end{align}\]

Given that \(\cos{35°}=\alpha\), express \(\sin{2015^\circ}\) in terms of \(\alpha\).

This problem is part of the set 2015 Countdown Problems.

Find the value of

\[\frac{\cos^4 75^{\circ}+\sin^4 75^{\circ}+3\sin^2 75^{\circ}\cos^2 75^{\circ}}{\cos^6 75^{\circ}+\sin^6 75^{\circ}+4\sin^2 75^{\circ}\cos^2 75^{\circ}}.\]

\[\cos 5x=a \cos^5 x+b \cos^3 x+c \cos x\]

If \(a, b,\) and \(c\) are constants that satisfy the trigonometric identity above, find the value of \(c.\)

If \(x\) and \(y\) are acute angles such that

\[ \frac {\sin x}{\sin y } = \frac {1}{2}, \quad \frac {\cos x}{\cos y } = \frac 3 2 , \]

what is \( \tan^2 (x+y)?\)

Problem Loading...

Note Loading...

Set Loading...

PROBLEMS ON TRIGONOMETRIC IDENTITIES WITH SOLUTIONS

Problem 1 : 

Prove : 

(1 - cos 2  θ)csc 2  θ = 1

Let A = (1 - cos 2  θ)csc 2  θ and B = 1.

A = (1 - cos 2  θ)csc 2  θ

Since sin 2  θ + cos 2  θ = 1 , we have  

sin 2  θ = 1 - cos 2  θ

Then, 

A = sin 2  θ  ⋅  csc 2  θ

A = B   (Proved)

Problem 2 : 

Since sin 2  θ + cos 2  θ = 1 , we have  

cos 2  θ = 1 - sin 2  θ

Problem 3 : 

t an θ sin θ + cos θ = sec θ

Let A =  t an θ sin θ + cos θ  and B = sec θ.

A =  t an θ sin θ + cos θ

Problem 4 : 

(1 - cos θ)(1 + cos θ)(1 + cot 2 θ) = 1

Let A = (1 - cos θ)(1 + cos θ)(1 + cot 2 θ) = 1 and B = 1.

A =  (1 - cos θ)(1 + cos θ)(1 + cot 2 θ)

A =  (1 - cos 2 θ)(1 + cot 2 θ)

A =  sin 2 θ  ⋅  (1 + cot 2 θ)

A =  sin 2 θ  + sin 2 θ  ⋅  cot 2 θ

A = sin 2  θ + cos 2  θ

Problem 5 : 

cot θ + tan θ = sec θ csc θ

Let A =  cot θ + tan θ and B = sec θ csc θ.

A = cot θ + tan θ

A = csc θ  sec θ

A = sec  θ csc θ

A = B    (Proved)

Problem 6 : 

A = sin θ + cos  θ  

Problem 7 : 

t an 4  θ  + t an 2  θ  = sec 4  θ  - sec 2  θ

Let A =  t an 4  θ  + t an 2  θ and B = sec 4  θ  + sec 2  θ.

A =  t an 4  θ  + tan 2  θ

A =  t an 2  θ  (tan 2  θ  + 1)

We know that,

t an 2  θ = sec 2  θ - 1

t an 2  θ + 1 = sec 2  θ 

A = (sec 2  θ  - 1)(sec 2  θ )

A = sec 4  θ  - sec 2  θ

Problem 8 : 

Problem 9 : 

A = (sec  θ – t an θ ) 2

Problem 10 : 

A = B    (Proved)

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Honors Algebra 2 Solving Logarithmic Equations

Apr 11, 24 09:06 PM

Honors Algebra 2 Solving Exponential Equations

Apr 11, 24 07:50 PM

Sinusoidal Function

Apr 10, 24 11:49 PM

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

11 Solving Trigonometric Equations with Identities

Learning objectives.

In this section, you will:

• Verify the fundamental trigonometric identities.
• Simplify trigonometric expressions using algebra and the identities.

In espionage movies, we see international spies with multiple passports, each claiming a different identity. However, we know that each of those passports represents the same person. The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression. Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation.

In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.

Verifying the Fundamental Trigonometric Identities

Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equations. In fact, we use algebraic techniques constantly to simplify trigonometric expressions. Basic properties and formulas of algebra, such as the difference of squares formula and the perfect squares formula, will simplify the work involved with trigonometric expressions and equations. We already know that all of the trigonometric functions are related because they all are defined in terms of the unit circle. Consequently, any trigonometric identity can be written in many ways.

To verify the trigonometric identities, we usually start with the more complicated side of the equation and essentially rewrite the expression until it has been transformed into the same expression as the other side of the equation. Sometimes we have to factor expressions, expand expressions, find common denominators, or use other algebraic strategies to obtain the desired result. In this first section, we will work with the fundamental identities: the Pythagorean identities , the even-odd identities, the reciprocal identities, and the quotient identities.

We will begin with the Pythagorean identities (see (Figure) ), which are equations involving trigonometric functions based on the properties of a right triangle. We have already seen and used the first of these identifies, but now we will also use additional identities.

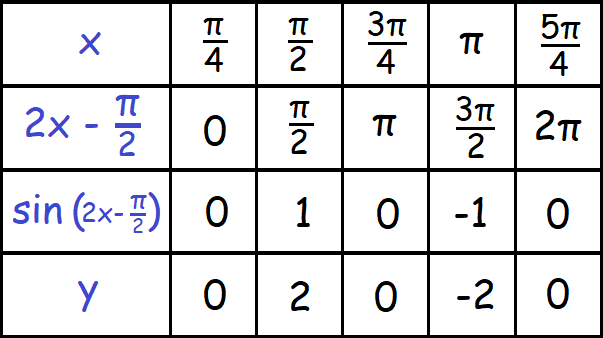
Recall that we determined which trigonometric functions are odd and which are even. The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle. (See (Figure) ).

This is shown in (Figure 2) .

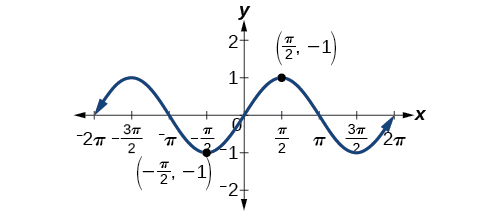
Recall that an even function is one in which

See (Figure 3) .

To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities.

The next set of fundamental identities is the set of reciprocal identities, which, as their name implies, relate trigonometric functions that are reciprocals of each other. See (Figure) . Recall that we first encountered these identities when defining trigonometric functions from right angles in Right Angle Trigonometry .

The final set of fundamental identities is the set of quotient identities , which define relationships among certain trigonometric functions and can be very helpful in verifying other identities. See (Figure) .

The reciprocal and quotient identities are derived from the definitions of the basic fundamental trigonometric functions.

Summarizing Fundamental Trigonometric Identities

The Pythagorean identities are based on the properties of a right triangle.

The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.

The reciprocal identities define reciprocals of the trigonometric functions.

The quotient identities define the relationship among the trigonometric functions.

Graphing the Equations of an Identity

See (Figure 4) .

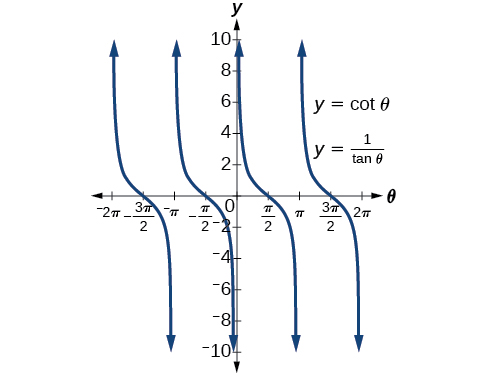
We see only one graph because both expressions generate the same image. One is on top of the other. This is a good way to confirm an identity verified with analytical means. If both expressions give the same graph, then they are most likely identities.

Given a trigonometric identity, verify that it is true.

• Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
• Look for opportunities to factor expressions, square a binomial, multiply by the conjugate, or add fractions.
• Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
• If these steps do not yield the desired result, try converting all terms to sines and cosines.

Verifying a Trigonometric Identity

We will start on the left side, as it is the more complicated side:

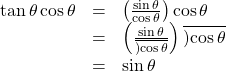
Verifying the Equivalency Using the Even-Odd Identities

Verify the following equivalency using the even-odd identities:

Working on the left side of the equation, we have

Verifying a Trigonometric Identity Involving sec 2 θ

As the left side is more complicated, let’s begin there.

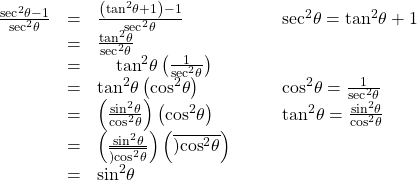
There is more than one way to verify an identity. Here is another possibility. Again, we can start with the left side.

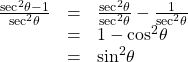
Creating and Verifying an Identity

There are a number of ways to begin, but here we will use the quotient and reciprocal identities to rewrite the expression:

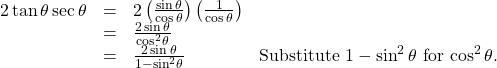
Verifying an Identity Using Algebra and Even/Odd Identities

Verify the identity:

Let’s start with the left side and simplify:

Verifying an Identity Involving Cosines and Cotangents

We will work on the left side of the equation.

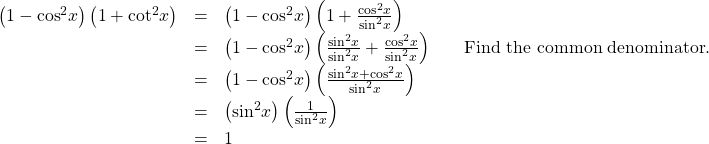
Using Algebra to Simplify Trigonometric Expressions

We have seen that algebra is very important in verifying trigonometric identities, but it is just as critical in simplifying trigonometric expressions before solving. Being familiar with the basic properties and formulas of algebra, such as the difference of squares formula, the perfect square formula, or substitution, will simplify the work involved with trigonometric expressions and equations.

Writing the Trigonometric Expression as an Algebraic Expression

Factor a Trigonometric Expression Using the Difference of Squares

Notice that both the coefficient and the trigonometric expression in the first term are squared, and in the second term the square of the number 1 is 1. This is the difference of squares.

Simplify by Rewriting and Using Substitution

Simplify the expression by rewriting and using identities:

We can start with the Pythagorean identity.

Access these online resources for additional instruction and practice with the fundamental trigonometric identities.

• Fundamental Trigonometric Identities
• Verifying Trigonometric Identities

Key Equations

Key concepts.

• There are multiple ways to represent a trigonometric expression. Verifying the identities illustrates how expressions can be rewritten to simplify a problem.
• Graphing both sides of an identity will verify it. See (Figure) .
• Simplifying one side of the equation to equal the other side is another method for verifying an identity. See (Figure) and (Figure) .
• The approach to verifying an identity depends on the nature of the identity. It is often useful to begin on the more complex side of the equation. See (Figure) .
• We can create an identity and then verify it. See (Figure) .
• Verifying an identity may involve algebra with the fundamental identities. See (Figure) and (Figure) .
• Algebraic techniques can be used to simplify trigonometric expressions. We use algebraic techniques throughout this text, as they consist of the fundamental rules of mathematics. See (Figure) , (Figure) , and (Figure) .

Section Exercises

For the following exercises, use the fundamental identities to fully simplify the expression.

For the following exercises, simplify the first trigonometric expression by writing the simplified form in terms of the second expression.

For the following exercises, verify the identity.

Answers will vary. Sample proof:

For the following exercises, prove or disprove the identity.

Proved with negative and Pythagorean identities

For the following exercises, determine whether the identity is true or false. If false, find an appropriate equivalent expression.

Trigonometry Copyright © 2015 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Module 9: Trigonometric Identities and Equations

Solving trigonometric equations, learning outcomes.

• Solve equations involving a single trigonometric function.
• Solve trigonometric equations using a calculator.
• Solve trigonometric equations that involve factoring.
• Solve trigonometric equations using fundamental identities.
• Solve trigonometric equations with multiple angles.
• Solve right triangle problems.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is [latex]2\pi [/latex]. In other words, every [latex]2\pi [/latex] units, the y- values repeat. If we need to find all possible solutions, then we must add [latex]2\pi k[/latex], where [latex]k[/latex] is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is [latex]2\pi :[/latex]

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Example 1: Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation [latex]\cos \theta =\frac{1}{2}[/latex].

From the unit circle , we know that

[latex]\begin{gathered}\cos \theta =\frac{1}{2} \\ \theta =\frac{\pi }{3},\frac{5\pi }{3} \end{gathered}[/latex]

These are the solutions in the interval [latex]\left[0,2\pi \right][/latex]. All possible solutions are given by

[latex]\theta =\frac{\pi }{3}\pm 2k\pi \text{ and }\theta =\frac{5\pi }{3}\pm 2k\pi [/latex]

where [latex]k[/latex] is an integer.

Example 2: Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation [latex]\sin t=\frac{1}{2}[/latex].

Solving for all possible values of t means that solutions include angles beyond the period of [latex]2\pi [/latex]. From the unit circle, we can see that the solutions are [latex]t=\frac{\pi }{6}[/latex] and [latex]t=\frac{5\pi }{6}[/latex]. But the problem is asking for all possible values that solve the equation. Therefore, the answer is

[latex]t=\frac{\pi }{6}\pm 2\pi k\text{ and }t=\frac{5\pi }{6}\pm 2\pi k[/latex]

How To: Given a trigonometric equation, solve using algebra.

• Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
• Substitute the trigonometric expression with a single variable, such as [latex]x[/latex] or [latex]u[/latex].
• Solve the equation the same way an algebraic equation would be solved.
• Substitute the trigonometric expression back in for the variable in the resulting expressions.
• Solve for the angle.

Example 3: Solve the Trigonometric Equation in Linear Form

Solve the equation exactly: [latex]2\cos \theta -3=-5,0\le \theta <2\pi [/latex].

[latex]\begin{gathered}2\cos \theta -3=-5 \\ \cos \theta =-2 \\ \cos \theta =-1 \\ \theta =\pi \end{gathered}[/latex]

Solve exactly the following linear equation on the interval [latex]\left[0,2\pi \right):2\sin x+1=0[/latex].

[latex]x=\frac{7\pi }{6},\frac{11\pi }{6}[/latex]

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Example 4: Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation [latex]\sin \theta =0.8[/latex], where [latex]\theta [/latex] is in radians.

Make sure mode is set to radians. To find [latex]\theta [/latex], use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the [latex]{\sin }^{-1}[/latex] function. What is shown on the screen is [latex]{\sin}^{-1}[/latex](. The calculator is ready for the input within the parentheses. For this problem, we enter [latex]{\sin }^{-1}\left(0.8\right)[/latex], and press ENTER. Thus, to four decimals places,

[latex]{\sin }^{-1}\left(0.8\right)\approx 0.9273[/latex]

This is the solution in quadrant I. There is also a solution in quadrant II. To find this we subtract [latex]/pi - 0.9273 \approx 2.2143 [/latex]

The general solution is

[latex]\theta \approx 0.9273\pm 2\pi k \text{ and } \theta \approx 2.2143 \pm 2\pi k[/latex]

The angle measurement in degrees is

[latex]\begin{align} \theta &\approx {53.1}^{\circ } \\ \theta &\approx {180}^{\circ }-{53.1}^{\circ } \\ &\approx {126.9}^{\circ } \end{align}[/latex]

Analysis of the Solution

Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using [latex]\pi -\theta [/latex].

Example 5: Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation [latex]\sec \theta =-4[/latex], giving your answer in radians.

We can begin with some algebra.

[latex]\begin{gathered}\sec \theta =-4\\ \frac{1}{\cos \theta }=-4\\ \cos \theta =-\frac{1}{4}\end{gathered}[/latex]

Check that the MODE is in radians. Now use the inverse cosine function.

[latex]\begin{gathered}{\cos }^{-1}\left(-\frac{1}{4}\right)\approx 1.8235 \\ \theta \approx 1.8235+2\pi k \end{gathered}[/latex]

Since [latex]\frac{\pi }{2}\approx 1.57[/latex] and [latex]\pi \approx 3.14[/latex], 1.8235 is between these two numbers, thus [latex]\theta \approx \text{1}\text{.8235}[/latex] is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine.

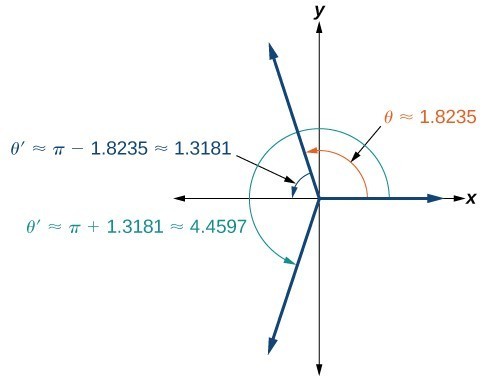
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi -\text{1}\text{.8235}\approx \text{1}\text{.3181}\text{.}[/latex] The other solution in quadrant III is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi +\text{1}\text{.3181}\approx \text{4}\text{.4597}\text{.}[/latex]

The solutions are [latex]\theta \approx 1.8235\pm 2\pi k[/latex] and [latex]\theta \approx 4.4597\pm 2\pi k[/latex].

Solve [latex]\cos \theta =-0.2[/latex].

[latex]\theta \approx 1.7722\pm 2\pi k[/latex] and [latex]\theta \approx 4.5110\pm 2\pi k[/latex]

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle. We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is [latex]\pi [/latex], not [latex]2\pi [/latex]. Further, the domain of tangent is all real numbers with the exception of odd integer multiples of [latex]\frac{\pi }{2}[/latex], unless, of course, a problem places its own restrictions on the domain.

Example 6: Solving a Problem Involving a Single Trigonometric Function

Solve the problem exactly: [latex]2{\sin }^{2}\theta -1=0,0\le \theta <2\pi [/latex].

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate [latex]\sin \theta [/latex]. Then we will find the angles.

[latex]\begin{gathered}2{\sin }^{2}\theta -1=0 \\ 2{\sin }^{2}\theta =1 \\ {\sin }^{2}\theta =\frac{1}{2} \\ \sqrt{{\sin }^{2}\theta }=\pm \sqrt{\frac{1}{2}} \\ \sin \theta =\pm \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2} \\ \theta =\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4} \end{gathered}[/latex]

Example 7: Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: [latex]\csc \theta =-2,0\le \theta <4\pi [/latex].

We want all values of [latex]\theta [/latex] for which [latex]\csc \theta =-2[/latex] over the interval [latex]0\le \theta <4\pi [/latex].

[latex]\begin{gathered}\csc \theta =-2 \\ \frac{1}{\sin \theta }=-2 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6},\frac{19\pi }{6},\frac{23\pi }{6} \end{gathered}[/latex]

As [latex]\sin \theta =-\frac{1}{2}[/latex], notice that all four solutions are in the third and fourth quadrants.

Example 8: Solving an Equation Involving Tangent

Solve the equation exactly: [latex]\tan \left(\theta -\frac{\pi }{2}\right)=1,0\le \theta <2\pi [/latex].

Recall that the tangent function has a period of [latex]\pi [/latex]. On the interval [latex]\left[0,\pi \right)[/latex], and at the angle of [latex]\frac{\pi }{4}[/latex], the tangent has a value of 1. However, the angle we want is [latex]\left(\theta -\frac{\pi }{2}\right)[/latex]. Thus, if [latex]\tan \left(\frac{\pi }{4}\right)=1[/latex], then

[latex]\begin{gathered}\theta -\frac{\pi }{2}=\frac{\pi }{4}\\ \theta =\frac{3\pi }{4}\pm k\pi \end{gathered}[/latex]

Over the interval [latex]\left[0,2\pi \right)[/latex], we have two solutions:

[latex]\theta =\frac{3\pi }{4}\text{ and }\theta =\frac{3\pi }{4}+\pi =\frac{7\pi }{4}[/latex]

Find all solutions for [latex]\tan x=\sqrt{3}[/latex].

[latex]\frac{\pi }{3}\pm \pi k[/latex]

Example 9: Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation [latex]2\left(\tan x+3\right)=5+\tan x,0\le x<2\pi [/latex].

We can solve this equation using only algebra. Isolate the expression [latex]\tan x[/latex] on the left side of the equals sign.

[latex]\begin{gathered} 2\left(\tan x\right)+2\left(3\right) =5+\tan x \\ 2\tan x+6 =5+\tan x \\ 2\tan x-\tan x =5 - 6 \\ \tan x =-1\end{gathered}[/latex]

There are two angles on the unit circle that have a tangent value of [latex]-1:\theta =\frac{3\pi }{4}[/latex] and [latex]\theta =\frac{7\pi }{4}[/latex].

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as [latex]x[/latex] or [latex]u[/latex]. If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Example 10: Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: [latex]{\cos }^{2}\theta +3\cos \theta -1=0,0\le \theta <2\pi[/latex].

We begin by using substitution and replacing cos [latex]\theta[/latex] with [latex]x[/latex]. It is not necessary to use substitution, but it may make the problem easier to solve visually. Let [latex]\cos \theta =x[/latex]. We have

[latex]{x}^{2}+3x - 1=0[/latex]

The equation cannot be factored, so we will use the quadratic formula [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex].

[latex]\begin{align} x&=\frac{-3\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-1\right)}}{2}&=\frac{-3\pm \sqrt{13}}{2} \end{align}[/latex]

Replace [latex]x[/latex] with [latex]\cos \theta[/latex], and solve. Thus,

[latex]\begin{gathered} \cos \theta =\frac{-3\pm \sqrt{13}}{2}\theta ={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right)\end{gathered}[/latex]

Note that only the + sign is used. This is because we get an error when we solve [latex]\theta ={\cos }^{-1}\left(\frac{-3-\sqrt{13}}{2}\right)[/latex] on a calculator, since the domain of the inverse cosine function is [latex]\left[-1,1\right][/latex]. However, there is a second solution:

[latex]\begin{align}\theta &={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 1.26 \end{align}[/latex]

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

[latex]\begin{align}\theta &=2\pi -{\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 5.02 \end{align}[/latex]

Example 11: Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: [latex]2{\sin }^{2}\theta -5\sin \theta +3=0,0\le \theta \le 2\pi[/latex].

Using grouping, this quadratic can be factored. Either make the real substitution, [latex]\sin \theta =u[/latex], or imagine it, as we factor:

[latex]\begin{gathered}2{\sin }^{2}\theta -5\sin \theta +3=0 \\ \left(2\sin \theta -3\right)\left(\sin \theta -1\right)=0 \end{gathered}[/latex]

Now set each factor equal to zero.

[latex]\begin{gathered}2\sin \theta -3=0 \\ 2\sin \theta =3 \\ \sin \theta =\frac{3}{2} \\ \text{ } \\ \sin \theta -1=0 \\ \sin \theta =1 \end{gathered}[/latex]

Next solve for [latex]\theta :\sin \theta \ne \frac{3}{2}[/latex], as the range of the sine function is [latex]\left[-1,1\right][/latex]. However, [latex]\sin \theta =1[/latex], giving the solution [latex]\theta =\frac{\pi }{2}[/latex].

Make sure to check all solutions on the given domain as some factors have no solution.

Solve [latex]{\sin }^{2}\theta =2\cos \theta +2,0\le \theta \le 2\pi[/latex]. [Hint: Make a substitution to express the equation only in terms of cosine.]

[latex]\cos \theta =-1,\theta =\pi [/latex]

Example 12: Solving a Trigonometric Equation Using Algebra

Solve exactly:

[latex]2{\sin }^{2}\theta +\sin \theta =0;0\le \theta <2\pi[/latex]

This problem should appear familiar as it is similar to a quadratic. Let [latex]\sin \theta =x[/latex]. The equation becomes [latex]2{x}^{2}+x=0[/latex]. We begin by factoring:

[latex]\begin{gathered}2{x}^{2}+x=0\\ x\left(2x+1\right)=0\end{gathered}[/latex]

Set each factor equal to zero.

[latex]\begin{gathered}x=0 \\ 2x+1=0 \\ x=-\frac{1}{2} \end{gathered}[/latex]

Then, substitute back into the equation the original expression [latex]\sin \theta[/latex] for [latex]x[/latex]. Thus,

[latex]\begin{gathered}\sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]

The solutions within the domain [latex]0\le \theta <2\pi[/latex] are [latex]\theta =0,\pi ,\frac{7\pi }{6},\frac{11\pi }{6}[/latex].

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

[latex]\begin{gathered}2{\sin }^{2}\theta +\sin \theta =0 \\ \sin \theta \left(2\sin \theta +1\right)=0 \\ \sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ 2\sin \theta +1=0 \\ 2\sin \theta =-1 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]

We can see the solutions on the graph in Figure 3. On the interval [latex]0\le \theta <2\pi[/latex], the graph crosses the x- axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

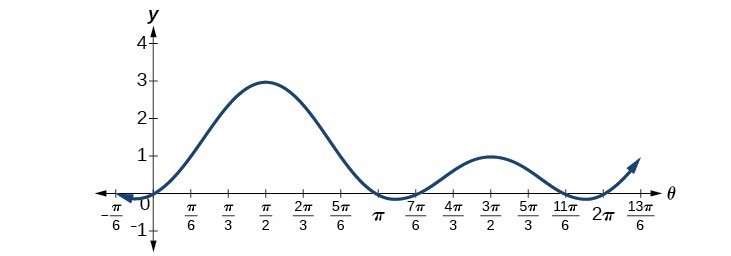
We can verify the solutions on the unit circle in Sum and Difference Identities as well.

Example 13: Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: [latex]2{\sin }^{2}\theta -3\sin \theta +1=0,0\le \theta <2\pi[/latex].

We can factor using grouping. Solution values of [latex]\theta[/latex] can be found on the unit circle:

[latex]\begin{gathered}\left(2\sin \theta -1\right)\left(\sin \theta -1\right)=0 \\ 2\sin \theta -1=0 \\ \sin \theta =\frac{1}{2} \\ \theta =\frac{\pi }{6},\frac{5\pi }{6} \\ \text{ } \\ \sin \theta =1 \\ \theta =\frac{\pi }{2} \end{gathered}[/latex]

Solve the quadratic equation [latex]2{\cos }^{2}\theta +\cos \theta =0[/latex].

[latex]\frac{\pi }{2},\frac{2\pi }{3},\frac{4\pi }{3},\frac{3\pi }{2}[/latex]

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Example 14: Use Identities to Solve an Equation

Use identities to solve exactly the trigonometric equation over the interval [latex]0\le x<2\pi [/latex].

[latex]\cos x\cos \left(2x\right)+\sin x\sin \left(2x\right)=\frac{\sqrt{3}}{2}[/latex]

Notice that the left side of the equation is the difference formula for cosine.

[latex]\begin{align} \cos x\cos \left(2x\right)+\sin x\sin \left(2x\right)&=\frac{\sqrt{3}}{2} \\ \cos \left(x - 2x\right)&=\frac{\sqrt{3}}{2}&& \text{Difference formula for cosine} \\ \cos \left(-x\right)&=\frac{\sqrt{3}}{2}&& \text{Use the negative angle identity}. \\ \cos x&=\frac{\sqrt{3}}{2}\end{align}[/latex]

From the unit circle in Sum and Difference Identities, we see that [latex]\cos x=\frac{\sqrt{3}}{2}[/latex] when [latex]x=\frac{\pi }{6},\frac{11\pi }{6}[/latex].

Example 15: Solving the Equation Using a Double-Angle Formula

Solve the equation exactly using a double-angle formula: [latex]\cos \left(2\theta \right)=\cos \theta [/latex].

We have three choices of expressions to substitute for the double-angle of cosine. As it is simpler to solve for one trigonometric function at a time, we will choose the double-angle identity involving only cosine:

[latex]\begin{gathered}\cos \left(2\theta \right)=\cos \theta \\ 2{\cos }^{2}\theta -1=\cos \theta \\ 2{\cos }^{2}\theta -\cos \theta -1=0 \\ \left(2\cos \theta +1\right)\left(\cos \theta -1\right)=0 \\ 2\cos \theta +1=0 \\ \cos \theta =-\frac{1}{2} \\ \text{ } \\ \cos \theta -1=0 \\ \cos \theta =1 \end{gathered}[/latex]

So, if [latex]\cos \theta =-\frac{1}{2}[/latex], then [latex]\theta =\frac{2\pi }{3}\pm 2\pi k[/latex] and [latex]\theta =\frac{4\pi }{3}\pm 2\pi k[/latex]; if [latex]\cos \theta =1[/latex], then [latex]\theta =0\pm 2\pi k[/latex].

Example 16: Solving an Equation Using an Identity

Solve the equation exactly using an identity: [latex]3\cos \theta +3=2{\sin }^{2}\theta ,0\le \theta <2\pi [/latex].

If we rewrite the right side, we can write the equation in terms of cosine:

[latex]\begin{align} 3 cos\theta +3& ={2 sin}^{2}\theta \\ 3 cos\theta +3& =2\left(1-{\text{cos}}^{2}\theta \right) \\ 3 cos\theta +3& =2 - 2{\cos }^{2}\theta \\ 2{\cos }^{2}\theta +3 cos\theta +1& =0 \\ \left(2 cos\theta +1\right)\left(\cos \theta +1\right)& =0 \\ 2 cos\theta +1& =0 \\ \cos \theta & =-\frac{1}{2} \\ \theta & =\frac{2\pi }{3},\frac{4\pi }{3} \\ \text{ } \\ \cos \theta +1& =0 \\ \cos \theta & =-1 \\ \theta & =\pi\end{align}[/latex]

Our solutions are [latex]\theta =\frac{2\pi }{3},\frac{4\pi }{3},\pi [/latex].

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as [latex]\sin \left(2x\right)[/latex] or [latex]\cos \left(3x\right)[/latex]. When confronted with these equations, recall that [latex]y=\sin \left(2x\right)[/latex] is a horizontal compression by a factor of 2 of the function [latex]y=\sin x[/latex]. On an interval of [latex]2\pi [/latex], we can graph two periods of [latex]y=\sin \left(2x\right)[/latex], as opposed to one cycle of [latex]y=\sin x[/latex]. This compression of the graph leads us to believe there may be twice as many x -intercepts or solutions to [latex]\sin \left(2x\right)=0[/latex] compared to [latex]\sin x=0[/latex]. This information will help us solve the equation.

Example 17: Solving a Multiple Angle Trigonometric Equation

Solve exactly: [latex]\cos \left(2x\right)=\frac{1}{2}[/latex] on [latex]\left[0,2\pi \right)[/latex].

We can see that this equation is the standard equation with a multiple of an angle. If [latex]\cos \left(\alpha \right)=\frac{1}{2}[/latex], we know [latex]\alpha [/latex] is in quadrants I and IV. While [latex]\theta ={\cos }^{-1}\frac{1}{2}[/latex] will only yield solutions in quadrants I and II, we recognize that the solutions to the equation [latex]\cos \theta =\frac{1}{2}[/latex] will be in quadrants I and IV.

Therefore, the possible angles are [latex]\theta =\frac{\pi }{3}[/latex] and [latex]\theta =\frac{5\pi }{3}[/latex]. So, [latex]2x=\frac{\pi }{3}[/latex] or [latex]2x=\frac{5\pi }{3}[/latex], which means that [latex]x=\frac{\pi }{6}[/latex] or [latex]x=\frac{5\pi }{6}[/latex]. Does this make sense? Yes, because [latex]\cos \left(2\left(\frac{\pi }{6}\right)\right)=\cos \left(\frac{\pi }{3}\right)=\frac{1}{2}[/latex].

Are there any other possible answers? Let us return to our first step.

In quadrant I, [latex]2x=\frac{\pi }{3}[/latex], so [latex]x=\frac{\pi }{6}[/latex] as noted. Let us revolve around the circle again:

[latex]\begin{align} 2x&=\frac{\pi }{3}+2\pi \\ &=\frac{\pi }{3}+\frac{6\pi }{3} \\ &=\frac{7\pi }{3} \end{align}[/latex]

so [latex]x=\frac{7\pi }{6}[/latex].

One more rotation yields

[latex]\begin{align} 2x&=\frac{\pi }{3}+4\pi \\ &=\frac{\pi }{3}+\frac{12\pi }{3} \\ &=\frac{13\pi }{3} \end{align}[/latex]

[latex]x=\frac{13\pi }{6}>2\pi [/latex], so this value for [latex]x[/latex] is larger than [latex]2\pi [/latex], so it is not a solution on [latex]\left[0,2\pi \right)[/latex].

In quadrant IV, [latex]2x=\frac{5\pi }{3}[/latex], so [latex]x=\frac{5\pi }{6}[/latex] as noted. Let us revolve around the circle again:

[latex]\begin{align}2x&=\frac{5\pi }{3}+2\pi \\ &=\frac{5\pi }{3}+\frac{6\pi }{3} \\ &=\frac{11\pi }{3}\end{align}[/latex]

so [latex]x=\frac{11\pi }{6}[/latex].

[latex]\begin{align}2x&=\frac{5\pi }{3}+4\pi \\ &=\frac{5\pi }{3}+\frac{12\pi }{3} \\ &=\frac{17\pi }{3} \end{align}[/latex]

[latex]x=\frac{17\pi }{6}>2\pi [/latex], so this value for [latex]x[/latex] is larger than [latex]2\pi [/latex], so it is not a solution on [latex]\left[0,2\pi \right)[/latex].

Our solutions are [latex]x=\frac{\pi }{6},\frac{5\pi }{6},\frac{7\pi }{6},\text{and }\frac{11\pi }{6}[/latex]. Note that whenever we solve a problem in the form of [latex]\sin \left(nx\right)=c[/latex], we must go around the unit circle [latex]n[/latex] times.

Solving Right Triangle Problems

We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem . We begin with the familiar Pythagorean Theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], and model an equation to fit a situation.

Example 18: Using the Pythagorean Theorem to Model an Equation

Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.

One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)?

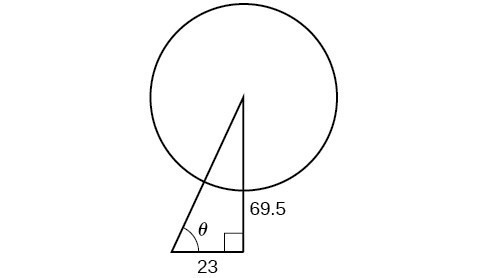
Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.

[latex]\begin{gathered}{a}^{2}+{b}^{2}={c}^{2} \\ {\left(23\right)}^{2}+{\left(69.5\right)}^{2}\approx 5359 \\ \sqrt{5359}\approx 73.2\text{ m}\end{gathered}[/latex]

The angle of elevation is [latex]\theta [/latex], formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.

[latex]\begin{align}\tan \theta &=\frac{69.5}{23} \\ {\tan }^{-1}\left(\frac{69.5}{23}\right)&\approx 1.2522 \\ &\approx {71.69}^{\circ } \end{align}[/latex]

The angle of elevation is approximately [latex]{71.7}^{\circ }[/latex], and the length of the cable is 73.2 meters.

Example 19: Using the Pythagorean Theorem to Model an Abstract Problem

OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.

For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “ a” feet from the wall, the length of the ladder will be 4 a feet.

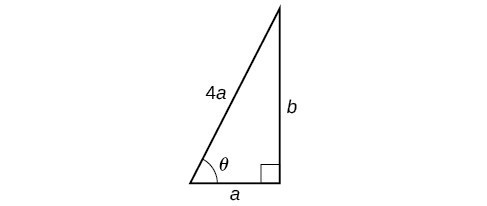
The side adjacent to [latex]\theta [/latex] is a and the hypotenuse is [latex]4a[/latex]. Thus,

[latex]\begin{gathered}\cos \theta =\frac{a}{4a}=\frac{1}{4} \\ {\cos }^{-1}\left(\frac{1}{4}\right)\approx {75.5}^{\circ } \end{gathered}[/latex]

The elevation of the ladder forms an angle of [latex]{75.5}^{\circ }[/latex] with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:

[latex]\begin{gathered}{a}^{2}+{b}^{2}={\left(4a\right)}^{2} \\ {b}^{2}={\left(4a\right)}^{2}-{a}^{2} \\ {b}^{2}=16{a}^{2}-{a}^{2} \\ {b}^{2}=15{a}^{2} \\ b=\sqrt{15}a \end{gathered}[/latex]

Thus, the ladder touches the wall at [latex]\sqrt{15}a[/latex] feet from the ground.

Key Concepts

• When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution.
• Equations involving a single trigonometric function can be solved or verified using the unit circle.
• We can also solve trigonometric equations using a graphing calculator.
• Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc.
• We can also use the identities to solve trigonometric equation.
• We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval.
• Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions.
• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Problems on Trigonometric Identities | Word Problems Involving Trigonometric Identities

Check problems on trigonometric identities along with the solutions. Find the step by step procedure to know the trigonometric identities problems. Refer to all the solutions present in the below sections to prepare for the exam. Scroll down the page to get the Trigonometric Identities Word Problems and study material. Know the various formulae involved in solving trigonometric identities below. Assess your knowledge level taking the help of the Practice Problems on Trigonometric Identities available.

Also, Read:

• Worksheet on Trigonometric Identities
• Trigonometrical Ratios Table

The angle of inclination from a point on the ground 30 feet away to the top of Lakeland’s Armington Clocktower is 60°. Find the height of the clock tower which is nearest to the foot?

As given in the question,

The angle of inclination (θ) = 60°

The height from the ground(a) = 30 feet

To find the height of the Clocktower to the nearest foot, we use the formula

tan θ = h/a

tan 60° = h / 30

h = 30 tan 60°

h = 9.60 ≅ 10 feet

Therefore, the height of the clocktower to the nearest foot is 10 feet.

Hence, the final solution is 10 feet.

Mary wants to determine the California redwood tree height, there are two sightings available from the ground which one is 200 feet directly behind the other. If the angles of inclination (Θ) are 45° and 30° respectively, how tall is the tree to the nearest foot?

Length at which trees are slighting = 200

The angle of inclinations = 45° and 30°

To find the inclination on the first tree, we apply the Pythagorean theorem,

tan 45° = h/x

h = x tan 45° is the (1) equation

tan 30° = h/(200+x)

h = (200 + x) tan 30 is the (2) equation

From both the equations,

x tan 45° = (200 + x) tan 30°

x tan 45° = 200 tan 30° + x tan 30°

x tan 45° – x tan 30° = 200 tan 30

Divide the equation with tan 45° – tan 30°

x (tan 45° – tan 30°) / tan 45° – tan 30° = 200 tan 30° / tan 45° – tan 30°

x = 273.21 feet

h = 273.21 tan 45

h = 273. 21 feet

h ≅ 273 feet

Therefore, the height of the tree to the nearest foot = 273 feet

Thus, the final solution = 273 feet

A tree that is standing vertically on the level ground casts the 120 foot long shadow. The angle of elevation from the end of the shadow of the top of the tree is 21.4°. Find the height of the tree to the nearest foot?

Length of the foot-long shadow = 120

The inclination of the tree = 21.4°

To find the height of the tree to the nearest foot, we apply the Pythagorean theorem

tan θ = 0/a

tan 214° = h/120

h = 120 tan 214°

h ≅ 47 feet

The height of the tree to the nearest foot = 47 feet

Thus, the final solution is 47 feet

The broadcast tower which is for the radio station WSAZ (“Carl” and “Jeff”‘s home of algebra) has 2 enormous flashing red lights on it. Of the 2 enormous flashing lights, one is at the very top and the other one is few feet below the top. From that point to the base of the tower it is 5000 feet away from level ground, the top light angle of elevation is 7.970° and the light angle of elevation of the second light is 7.125°. Find the distance between the nearest foot and the lights.

Height of the tower = 5000 feet

The angle of elevation of top light = 7.970

The angle of elevation of second light = 7.125°

To find the distance between the nearest foot and the lights, we have to use the Pythagorean theorem

tan θ = h/5000

h = 5000 tan 7.97°

tan β = h-x/5000

h-x = 5000 tan (7.125)°

x = h – 5000 tan (7.125)°

x = 5000 tan 7.97° – 5000 tan 7.125°

x = 5000 (tan 7.97° – tan 7.125°)

x = 75.04 feet

x ≅ 75  feet

Therefore, 75 feet is the distance between the nearest foot and the lights

Thus, the final solution is 75 feet.

Find the solution of tan (θ) = sin (θ) sec (θ)?

sinθ/ cosθ = sinθ secθ

sinθ. (1/cosθ) = sinθ secθ

sinθ secθ = sinθ secθ

tanθ = sinθ secθ

= sinθ(1/cosθ)

= sinθ/cosθ

∴ Hence it is proved

Prove that (sec(θ)-tan(θ))(sec(θ)+tan(θ))=1

sec²(θ)-tan²(θ)=1

1/cos²(θ)-sin²(θ)/cos(θ)=1

(1-sin²(θ))/cos²(θ)=1

cos²(θ)/cos²(θ)=1

(1-sin²(θ))/cos²(θ)

1/cos²(θ)-sin²(θ)/cos²(θ)=sec²(θ)-tan²(θ)

(sec(θ)-tan(θ))(sec(θ)+tan(θ))

Therefore, (sec(θ)-tan(θ))(sec(θ)+tan(θ)) = 1

∴Hence, it is proved

Prove that sec(θ)/(1-tan(θ))=1/(cos(θ)-sin(θ))

1/((cos(θ)-sin(θ)).1/cos(θ).1/cos(θ)

(1/cos(θ))/((cos(θ)-sin(θ))-(cos(θ))=sec(θ)/(1-tan(θ))

Therefore, sec(θ)/(1-tan(θ))=1/(cos(θ)-sin(θ))

Problem 8 :

An aeroplane over the Pacific sights an atoll at a 20° angle of depression. If the plane is 435 ma above water, how many kilometres is it from a point 435m directly above the centre of a troll?

The angle of depression = 20°

Height of the plane above water = 435ma

Height above the centre of a troll = 435m

To find the kilometers, we use the pythegorean theorem

tan 20° = 435/x

x = 435/tan20°

x = 1.195 km

Therefore, 1.195 kilometres is it from a point 435m directly above the centre of a troll

Thus, the final solution is 1.195 kilometres

The force F (in pounds)on the back of a person when he or she bends over an acute angle θ (in degrees) is given by F = 0.2W sin(θ + 70)/sin12° where w is the weight in pounds of the person

a) Simplify the formula or F.

b) Find the force on the back of a person where an angle of 30° weight is 50 pounds if he bends an angle of 30°

c) How many pounds should a person weigh for his book to endure a force of 400 lbs if he bends 40°?

a. F = 0.2W sin (θ + 90)/sin 12°

= 0.2W [sinθ cos 90 + cosθ sin90]/sin 12°

= 0.2W [θ(sinθ) + (cosθ) (1)]/sin 12°

= 0.2W [0 + cosθ]/sin 12°

F = 0.2W(cosθ)/sin 12°

The value of F is 0.2W(cosθ)/sin 12°

b. W = 50, θ = 30°, F=?

F = 0.2W cosθ/sin 12°

F = 0.2 (50) (cos30°)/sin 12°

The force on the back of a person wherein the angle of 30e weight is 50 pounds if he bends an angle of 30° is 41.45

c. F = 400, θ = 40°, W = ?

400 = 0.2(w)(cos 40°)/sin 12°

400(sin 12°)/0.2 cos 40 = 0.2 (w) (cos 40°)/0.2 cos40°

Therefore, the weigh for his book to endure a force of 400 lbs if he bends 40° is 542.82 pounds

Problem 10:

An observer standing on the top of vertical cliff pots a house in the adjacent valley at an angle of depression of 12°. The cliff is 60m tall. How far is the house from the base of the cliff?

The angle of depression = 12°

Height of the cliff = 60m

To find, the distance of the house from the base of the cliff, we apply the Pythagorean theorem

tan 12° = 60/x

x = 60/tan 12°

282m is the distance of the house from the base of the cliff

Hence, the final solution is 282m

Problem 11:

Building A and B are across the street from each other which is 35m apart. From the point on the roof of building A, the angle of elevation of the top of building B is 24°, the angle of depression of the base of building B is 34° How tall is each building?

The angle of elevation of the top of the building = 24°

The angle of depression of the base of the building = 34°

The distance of both buildings = 35m

To find the height of each building, we apply the Pythagoras theorem,

tan 24° = c/35

tan 56° = 35/a

A is 23.6m tall

B is 39.2m tall

Therefore, the height of building A is 23.6m tall

The height of building B is 39.2m tall

Thus the final solution is 23.6m, 39.2m

Problem 12:

In Johannesburg in June, the daily low temperature is usually around 3°C, and the daily temperature is around 18°. The temperature is typically halfway between the daily high and daily low at 10 am and 10 pm. and the highest temperatures are in the afternoon. Find out the trigonometric function which models the temperature T in Johannesburg t hours after midnight?

As per the question,

To determine the trigonometric model, the temperature ‘T’ which is Celsius degree and the temperature in axis and then right over here is time in hours. To think about the range of temperatures, the daily temperature is around 3-degree celsius and the highest is 18°. The midpoint between 18 and 3 is 10.5 (21 divided by 2)

Let F(t) is the temperature t hours after 10 am

F(t) = 7.5sin(2Π/24 t) + 10.5

T (t) = 7.5sin (Π/12(t-10)) + 10.5

T(10) = F(0) where T(10) is temperature at 10 pm

F(0) is the temperature at 10 am

Therefore, T(10) = F(0) is the trigonometric function that models the temperature T in Johannesburg t hours after midnight

Problem 13:

A ladder is 6 meters long and reaches the wall at a point of 5m from the ground. What is the angle which the ladder will make with the wall?

Let θ be the inclination of the ladder which it makes with the wall

Length of the ladder = 6m

The distance at which the ladder touches the wall = 5m

The angle at which the ladder will make with the wall

cos θ = 5/6

θ = cos¯¹ (5/6)

Problem 14:

The acceleration of the piston is given by a = 5.0(sinωt + cos2ωt). At what positive values of ωt less than 2Π does a = 0?

Let ωt be the crank angle(product of time and angular velocity) in piston acceleration, a be the accelaration of a piston.

a = 5.0(sinωt + cos2ωt)

0 = 5.0(sinωt + cos2ωt)

0 = sinωt + cos2ωt

0 = sinωt + 1 – 2sin²ωt

2sin²ωt – sinωt – 1 = 0

(2sinωt + 1) (sinωt – 1) = 0

2sinωt + 1 = 0

2sinωt = -1

sinωt = -1/2

ωt = sin¯¹(-1/2)

ωt = (7π/6, 11π/6)

sinωt – 1 = 0

ωt = sin¯¹(1)

{π/2, 7π/6, 11π/6}

Problem 15:

A lighthouse at sea level is 34 mi from a boat. It is known that the top of the lighthouse is 42.5mi from the boat. Find the angle of depression from the top of the lighthouse.

Let θ be the angle of inclination from the top of the lighthouse to the boat

Let x be the horizontal distance from the base of the lighthouse to the boat, and

r be the distance from the top of the lighthouse to the boat.

The length of the lighthouse at sea level = 34 mi

The distance of the top lighthouse from the boat = 42.5 mi

To find the angle of depression from the top of the lighthouse, we apply the Pythagorean theorem

cosθ = 34/42.5

θ = cos¯¹(34/42.5)

Leave a Comment Cancel Reply

You must be logged in to post a comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 10 (Old)

Course: class 10 (old)   >   unit 8.

• Intro to Pythagorean trigonometric identities
• Converting between trigonometric ratios example: write all ratios in terms of sine
• Evaluating expressions using basic trigonometric identities
• Trigonometric identity example proof involving sec, sin, and cos
• Trigonometric identity example proof involving sin, cos, and tan
• Trigonometric identity example proof involving all the six ratios

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Pythagorean
• Angle Sum/Difference
• Double Angle
• Multiple Angle
• Negative Angle
• Sum to Product
• Product to Sum
• Proving Identities
• Trigonometric Equations
• Trig Inequalities
• Evaluate Functions
• Conversions

Most Used Actions

Number line.

• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• prove\:\cot(2x)=\frac{1-\tan^2(x)}{2\tan(x)}
• prove\:\csc(2x)=\frac{\sec(x)}{2\sin(x)}
• prove\:\frac{\sin(3x)+\sin(7x)}{\cos(3x)-\cos(7x)}=\cot(2x)
• prove\:\frac{\csc(\theta)+\cot(\theta)}{\tan(\theta)+\sin(\theta)}=\cot(\theta)\csc(\theta)
• prove\:\cot(x)+\tan(x)=\sec(x)\csc(x)

trigonometric-identity-proving-calculator

• Spinning The Unit Circle (Evaluating Trig Functions ) If you’ve ever taken a ferris wheel ride then you know about periodic motion, you go up and down over and over...

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Solving Trigonometric Equations with Identities

• Last updated
• Save as PDF
• Page ID 13870

• David Lippman & Melonie Rasmussen
• The OpenTextBookStore

In the last chapter, we solved basic trigonometric equations. In this section, we explore the techniques needed to solve more complicated trig equations. Building from what we already know makes this a much easier task.

Consider the function \(f(x)=2x^{2} +x\). If you were asked to solve \(f(x)=0\), it requires simple algebra:

\[2x^{2} +x=0\nonumber\]Factor \[x(2x+1)=0\nonumber\]Giving solutions \[x = 0\text{ or }x = -\dfrac{1}{2}\nonumber\]

Similarly, for \(g(t)=\sin (t)\), if we asked you to solve \(g(t)=0\), you can solve this using unit circle values:

\[\sin (t)=0\text{ for }t=0, \pi , 2\pi\text{ and so on.}\nonumber\]

Using these same concepts, we consider the composition of these two functions:

\[f(g(t))=2(\sin (t))^{2} +(\sin (t))=2\sin ^{2} (t)+\sin (t)\nonumber\]

This creates an equation that is a polynomial trig function. With these types of functions, we use algebraic techniques like factoring and the quadratic formula, along with trigonometric identities and techniques, to solve equations.

As a reminder, here are some of the essential trigonometric identities that we have learned so far:

DefinitionS: IDENTITIES

Pythagorean Identities

\[\cos ^{2} (t)+\sin ^{2} (t)=1\quad 1+\cot ^{2} (t)=\csc ^{2} (t)\quad 1+\tan ^{2} (t)=\sec ^{2} (t)\]

Negative Angle Identities

\[\sin (-t)=-\sin (t)\quad \cos (-t)=\cos (t)\quad \tan (-t)=-\tan (t)\]

\[\csc (-t)=-\csc (t)\quad \sec (-t)=\sec (t)\quad \cot (-t)=-\cot (t)\]

Reciprocal Identities

\[\sec (t)=\dfrac{1}{\cos (t)}\quad \csc (t)=\dfrac{1}{\sin (t)}\quad \tan (t)=\dfrac{\sin (t)}{\cos (t)}\quad \cot (t)=\dfrac{1}{\tan (t)}\]

Example \(\PageIndex{1}\)

Solve \(2\sin ^{2} (t)+\sin (t)=0\) for all solutions with \(0\le t<2\pi\).

This equation kind of looks like a quadratic equation, but with sin( t ) in place of an algebraic variable (we often call such an equation “quadratic in sine”). As with all quadratic equations, we can use factoring techniques or the quadratic formula. This expression factors nicely, so we proceed by factoring out the common factor of sin(\(t\)):

\[\sin (t)\left(2\sin (t)+1\right)=0\nonumber\]

Using the zero product theorem, we know that the product on the left will equal zero if either factor is zero, allowing us to break this equation into two cases:

\[\sin (t)=0\text{ or }2\sin (t)+1=0\nonumber\]

\[\sin (t)=0\nonumber\] \[2\sin (t)+1=0\nonumber\] \[t = 0\text{ or }t = \pi\nonumber\] \[\sin (t)=-\dfrac{1}{2}\nonumber\] \[t=\dfrac{7\pi }{6}\text{ or }t=\dfrac{11\pi }{6}\nonumber\]

Together, this gives us four solutions to the equation on \(0\le t<2\pi\):

\[t=0,\pi ,\dfrac{7\pi }{6} ,\dfrac{11\pi }{6}\nonumber\]

We could check these answers are reasonable by graphing the function and comparing the zeros.

Example \(\PageIndex{2}\)

Solve \(3\sec ^{2} (t)-5\sec (t)-2=0\) for all solutions with \(0\le t<2\pi\).

Since the left side of this equation is quadratic in secant, we can try to factor it, and hope it factors nicely.

If it is easier to for you to consider factoring without the trig function present, consider using a substitution \(u=\sec (t)\), resulting in \(3u^{2} -5u-2=0\), and then try to factor:

\[3u^{2} -5u-2=(3u+1)(u-2)\nonumber\]

Undoing the substitution,

\[(3\sec (t)+1)(\sec (t)-2)=0\nonumber\]

Since we have a product equal to zero, we break it into the two cases and solve each separately.

\[3\sec (t)+1=0\nonumber\]Isolate the secant \[\sec (t)=-\dfrac{1}{3}\nonumber\]Rewrite as a cosine \[\dfrac{1}{\cos (t)} =-\dfrac{1}{3}\nonumber\]Invert both sides \[\cos (t)=-3\nonumber\]

Since the cosine has a range of [-1, 1], the cosine will never take on an output of -3. There are no solutions to this case.

Continuing with the second case,

These are the only two solutions on the interval.

By utilizing technology to graph \(f(t)=3\sec ^{2} (t)-5\sec (t)-2\), a look at a graph confirms there are only two zeros for this function on the interval [0, 2 \(\pi\)), which assures us that we didn’t miss anything.

Exercise \(\PageIndex{1}\)

Solve \(2\sin ^{2} (t)+3\sin (t)+1=0\) for all solutions with \(0\le t<2\pi\).

Factor as \[\left(2\sin (t)+1\right)\left(\sin (t)+1\right)=0\nonumber\] \[2\sin (t)+1=0\text{ at }t=\dfrac{7\pi }{6} ,\dfrac{11\pi }{6}\nonumber\] \[\sin (t)+1=0\text{ at }t=\dfrac{3\pi }{2}\nonumber\] \[t=\dfrac{7\pi }{6} ,\dfrac{3\pi }{2} ,\dfrac{11\pi }{6}\nonumber\]

When solving some trigonometric equations, it becomes necessary to first rewrite the equation using trigonometric identities. One of the most common is the Pythagorean Identity, \(\sin ^{2} (\theta )+\cos ^{2} (\theta )=1\) which allows you to rewrite \(\sin ^{2} (\theta )\) in terms of \(\cos ^{2} (\theta )\) or vice versa,

Alternate Forms of the Pythagorean Identity

\[\begin{array}{l} {\sin ^{2} (\theta )=1-\cos ^{2} (\theta )} \\ {\cos ^{2} (\theta )=1-\sin ^{2} (\theta )} \end{array}\]

These identities become very useful whenever an equation involves a combination of sine and cosine functions.

Example \(\PageIndex{3}\)

Solve \(2\sin ^{2} (t)-\cos (t)=1\) for all solutions with \(0\le t<2\pi\).

Since this equation has a mix of sine and cosine functions, it becomes more complicated to solve. It is usually easier to work with an equation involving only one trig function. This is where we can use the Pythagorean Identity.

\[2\sin ^{2} (t)-\cos (t)=1\nonumber\]Using \(\sin ^{2} (\theta )=1-\cos ^{2} (\theta )\) \[2\left(1-\cos ^{2} (t)\right)-\cos (t)=1\nonumber\]Distributing the 2 \[2-2\cos ^{2} (t)-\cos (t)=1\nonumber\]

Since this is now quadratic in cosine, we rearrange the equation so one side is zero and factor.

\[-2\cos ^{2} (t)-\cos (t)+1=0\nonumber\]Multiply by -1 to simplify the factoring \[2\cos ^{2} (t)+\cos (t)-1=0\nonumber\]Factor \[\left(2\cos (t)-1\right)\left(\cos (t)+1\right)=0\nonumber\]

This product will be zero if either factor is zero, so we can break this into two separate cases and solve each independently.

\[2\cos (t)-1=0\text{ or }\cos (t)+1=0\nonumber\] \[\cos (t)=\dfrac{1}{2}\text{ or }\cos (t)=-1\nonumber\] \[t=\dfrac{\pi }{3}\text{ or }t=\dfrac{5\pi }{3}\text{ or }t=\pi\nonumber\]

Exercise \(\PageIndex{3}\)

Solve \(2\sin ^{2} (t)=3\cos (t)\) for all solutions with \(0\le t<2\pi\).

\[2\left(1-\cos ^{2} (t)\right)=3\cos (t)\nonumber\] \[2\cos ^{2} (t)+3\cos (t)-2=0\nonumber\] \[\left(2\cos (t)-1\right)\left(\cos (t)+2\right)=0\nonumber\] \(\cos (t)+2=0\) has no solutions \(2\cos (t)-1=0\) at \(t=\dfrac{\pi }{3} ,\dfrac{5\pi }{3}\)

In addition to the Pythagorean Identity, it is often necessary to rewrite the tangent, secant, cosecant, and cotangent as part of solving an equation.

Example \(\PageIndex{4}\)

Solve \(\tan (x)=3\sin (x)\) for all solutions with \(0\le x<2\pi\).

With a combination of tangent and sine, we might try rewriting tangent

\[\tan (x)=3\sin (x)\nonumber\] \[\dfrac{\sin (x)}{\cos (x)} =3\sin (x)\nonumber\]Multiplying both sides by cosine \[\sin (x)=3\sin (x)\cos (x) \nonumber\]

At this point, you may be tempted to divide both sides of the equation by sin(\(x\)).

Resist the urge . When we divide both sides of an equation by a quantity, we are assuming the quantity is never zero. In this case, when sin(\(x\)) = 0 the equation is satisfied, so we’d lose those solutions if we divided by the sine.

To avoid this problem, we can rearrange the equation so that one side is zero (You technically can divide by sin( x ), as long as you separately consider the case where sin( x ) = 0. Since it is easy to forget this step, the factoring approach used in the example is recommended.).

\[\sin (x)-3\sin (x)\cos (x)=0\nonumber\]Factoring out sin(\(x\)) from both parts \[\sin (x)\left(1-3\cos (x)\right)=0 \nonumber\]

From here, we can see we get solutions when \(\sin (x)=0\) or \(1-3\cos (x)=0\).

Using our knowledge of the special angles of the unit circle,

\[\sin (x)=0\text{ when }x = 0\text{ or }x = \pi\nonumber\]

For the second equation, we will need the inverse cosine.

\[1-3\cos (x)=0\nonumber\] \[\cos (x)=\dfrac{1}{3}\nonumber\]Using our calculator or technology \[x=\cos ^{-1} \left(\dfrac{1}{3} \right)\approx 1.231\nonumber\]Using symmetry to find a second solution \[x=2\pi -1.231=5.052 \nonumber\]

We have four solutions on \(0 \le x<2\pi\):

\[x = 0, 1.231, \quad\pi , 5.052\nonumber\]

Solve \(\sec (\theta )=2\cos (\theta )\) to find the first four positive solutions.

\[\dfrac{1}{\cos (\theta )} =2\cos (\theta )\nonumber\] \[\dfrac{1}{2} =\cos ^{2} (\theta )\nonumber\] \[\cos (\theta )=\pm \sqrt{\dfrac{1}{2} } =\pm \dfrac{\sqrt{2} }{2}\nonumber\] \[\theta =\dfrac{\pi }{4} ,\dfrac{3\pi }{4} ,\dfrac{5\pi }{4} ,\dfrac{7\pi }{4}\nonumber\]

Example \(\PageIndex{5}\)

Solve \(\dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left(\theta \right)\) for all solutions with \(0\le \theta <2\pi\).

\[\dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left(\theta \right)\nonumber\] Using the reciprocal identities \[4\cos ^{2} (\theta )+3\cos (\theta )=2\dfrac{1}{\tan (\theta )} \tan (\theta )\nonumber\] Simplifying \[4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)=2\nonumber\] Subtracting 2 from each side \[4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)-2=0\nonumber\]

This does not appear to factor nicely so we use the quadratic formula, remembering that we are solving for cos( \(\theta\) ).

\[\cos (\theta )=\dfrac{-3\pm \sqrt{3^{2} -4(4)(-2)} }{2(4)} =\dfrac{-3\pm \sqrt{41} }{8}\nonumber\]

Using the negative square root first,

\[\cos (\theta )=\dfrac{-3-\sqrt{41} }{8} =-1.175\nonumber\]

This has no solutions, since the cosine can’t be less than -1.

Using the positive square root,

\[\cos (\theta )=\dfrac{-3+\sqrt{41} }{8} =0.425\nonumber\] \[\theta =\cos ^{-1} \left(0.425\right)=1.131\nonumber\] By symmetry, a second solution can be found \[\theta =2\pi -1.131=5.152\nonumber\]

Important Topics of This Section

• Review of Trig Identities
• Solving Trig Equations
• By Factoring
• Using the Quadratic Formula
• Utilizing Trig Identities to simplify