
- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.


9.3: Solve Quadratic Equations by Completing the Square
- Last updated
- Save as PDF
- Page ID 5176

Learning Objectives
By the end of this section, you will be able to:
- Complete the square of a binomial expression
- Solve quadratic equations of the form \(x^{2}+bx+c=0\) by completing the square
- Solve quadratic equations of the form \(ax^{2}+bx+c=0\) by completing the square
Before you get started, take this readiness quiz.
- Expand: \((x+9)^{2}\). If you missed this problem, review Example 5.32.
- Factor \(y^{2}-14 y+49\). If you missed this problem, review Example 6.9.
- Factor \(5 n^{2}+40 n+80\). If you missed this problem, review Example 6.14.
So far we have solved quadratic equations by factoring and using the Square Root Property. In this section, we will solve quadratic equations by a process called completing the square , which is important for our work on conics later.
Complete the Square of a Binomial Expression
In the last section, we were able to use the Square Root Property to solve the equation \((y-7)^{2}=12\) because the left side was a perfect square.
\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)
We also solved an equation in which the left side was a perfect square trinomial, but we had to rewrite it the form \((x−k)^{2}\) in order to use the Square Root Property.
\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)
What happens if the variable is not part of a perfect square? Can we use algebra to make a perfect square?
Let’s look at two examples to help us recognize the patterns.
\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)
We restate the patterns here for reference.
Definition \(\PageIndex{1}\): Binomial Squares Pattern
If \(a\) and \(b\) are real numbers,
We can use this pattern to “make” a perfect square.
We will start with the expression \(x^{2}+6 x\). Since there is a plus sign between the two terms, we will use the \((a+b)^{2}\) pattern, \(a^{2}+2 a b+b^{2}=(a+b)^{2}\).
We ultimately need to find the last term of this trinomial that will make it a perfect square trinomial. To do that we will need to find \(b\). But first we start with determining \(a\). Notice that the first term of \(x^{2}+6x\) is a square, \(x^{2}\). This tells us that \(a=x\).
What number, \(b\) , when multiplied with \(2x\) gives \(6x\)? It would have to be \(3\), which is \(\frac{1}{2}(6)\). So \(b=3\).
Now to complete the perfect square trinomial, we will find the last term by squaring \(b\), which is \(3^{2}=9\).
We can now factor.
So we found that adding \(9\) to \(x^{2}+6 x\) ‘completes the square’, and we write it as \((x+3)^{2}\).
Howto: Complete a Square of \(x^{2}+bx\)
- Identify \(b\), the coefficient of \(x\).
- Find \(\left(\frac{1}{2} b\right)^{2}\), the number to complete the square.
- Add the\(\left(\frac{1}{2} b\right)^{2}\) to \(x^{2}+bx\).
- Factor the perfect square trinomial, writing it as a binomial squared.
Example \(\PageIndex{1}\)
Complete the square to make a perfect square trinomial. Then write the result as a binomial squared.
- \(x^{2}-26 x\)
- \(y^{2}-9 y\)
- \(n^{2}+\frac{1}{2} n\)
Exercise \(\PageIndex{1}\)
- \(a^{2}-20 a\)
- \(m^{2}-5 m\)
- \(p^{2}+\frac{1}{4} p\)
- \((a-10)^{2}\)
- \(\left(b-\frac{5}{2}\right)^{2}\)
- \(\left(p+\frac{1}{8}\right)^{2}\)
Exercise \(\PageIndex{2}\)
- \(b^{2}-4 b\)
- \(n^{2}+13 n\)
- \(q^{2}-\frac{2}{3} q\)
- \((b-2)^{2}\)
- \(\left(n+\frac{13}{2}\right)^{2}\)
- \(\left(q-\frac{1}{3}\right)^{2}\)
Solve Quadratic Equations of the Form \(x^{2}+bx+c=0\) by Completing the Square
In solving equations, we must always do the same thing to both sides of the equation. This is true, of course, when we solve a quadratic equation by completing the square too. When we add a term to one side of the equation to make a perfect square trinomial, we must also add the same term to the other side of the equation.
For example, if we start with the equation \(x^{2}+6x=40\), and we want to complete the square on the left, we will add 9 to both sides of the equation.
Now the equation is in the form to solve using the Square Root Property ! Completing the square is a way to transform an equation into the form we need to be able to use the Square Root Property.
Example \(\PageIndex{2}\) How to Solve a Quadratic Equation of the Form \(x^{2}+bx+x=0\) by Completing the Square
Solve by completing the square: \(x^{2}+8x=48\).
Exercise \(\PageIndex{3}\)
Solve by completing the square: \(x^{2}+4 x=5\).
\(x=-5, x=-1\)
Exercise \(\PageIndex{4}\)
Solve by completing the square: \(y^{2}−10y=−9\).
\(y=1, y=9\)
The steps to solve a quadratic equation by completing the square are listed here.
Solve a Quadratic Equation of the Form \(x^{2}+bx+c=0\) by Completing the Square
- Isolate the variable terms on one side and the constant terms on the other.
- Find \(\left(\frac{1}{2} \cdot b\right)^{2}\), the number needed to complete the square. Add it to both sides of the equation.
- Factor the perfect square trinomial, writing it as a binomial squared on the left and simplify by adding the terms on the right
- Use the Square Root Property.
- Simplify the radical and then solve the two resulting equations.
- Check the solutions.
When we solve an equation by completing the square, the answers will not always be integers.
Example \(\PageIndex{3}\)
Solve by completing the square: \(x^{2}+4 x=-21\).
Exercise \(\PageIndex{5}\)
Solve by completing the square: \(y^{2}-10 y=-35\).
\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)
Exercise \(\PageIndex{6}\)
Solve by completing the square: \(z^{2}+8 z=-19\).
\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)
In the previous example, our solutions were complex numbers. In the next example, the solutions will be irrational numbers.
Example \(\PageIndex{4}\)
Solve by completing the square: \(y^{2}-18 y=-6\).
Another way to check this would be to use a calculator. Evaluate \(y^{2}−18y\) for both of the solutions. The answer should be \(−6\).
Exercise \(\PageIndex{7}\)
Solve by completing the square: \(x^{2}-16 x=-16\).
\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)
Exercise \(\PageIndex{8}\)
Solve by completing the square: \(y^{2}+8 y=11\).
\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)
We will start the next example by isolating the variable terms on the left side of the equation.
Example \(\PageIndex{5}\)
Solve by completing the square: \(x^{2}+10 x+4=15\).
Exercise \(\PageIndex{9}\)
Solve by completing the square: \(a^{2}+4 a+9=30\).
\(a=-7, a=3\)
Exercise \(\PageIndex{10}\)
Solve by completing the square: \(b^{2}+8 b-4=16\).
\(b=-10, b=2\)
To solve the next equation, we must first collect all the variable terms on the left side of the equation. Then we proceed as we did in the previous examples.

Example \(\PageIndex{6}\)
Solve by completing the square: \(n^{2}=3 n+11\).
Exercise \(\PageIndex{11}\)
Solve by completing the square: \(p^{2}=5 p+9\).
\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)
Exercise \(\PageIndex{12}\)
Solve by completing the square: \(q^{2}=7 q-3\).
\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)
Notice that the left side of the next equation is in factored form. But the right side is not zero. So, we cannot use the Zero Product Property since it says “If \(a⋅b=0\), then \(a=0\) or \(b=0\).” Instead, we multiply the factors and then put the equation into standard form to solve by completing the square.
Example \(\PageIndex{7}\)
Solve by completing the square: \((x-3)(x+5)=9\).
Exercise \(\PageIndex{13}\)
Solve by completing the square: \((c-2)(c+8)=11\).
\(c=-9, c=3\)
Exercise \(\PageIndex{14}\)
Solve by completing the square: \((d-7)(d+3)=56\).
\(d=11, d=-7\)
Solve Quadratic Equations of the Form \(ax^{2}+bx+c=0\) by Completing the Square
The process of completing the square works best when the coefficient of \(x^{2}\) is \(1\), so the left side of the equation is of the form \(x^{2}+bx+c\). If the \(x^{2}\) term has a coefficient other than \(1\), we take some preliminary steps to make the coefficient equal to \(1\).
Sometimes the coefficient can be factored from all three terms of the trinomial. This will be our strategy in the next example.
Example \(\PageIndex{8}\)
Solve by completing the square: \(3 x^{2}-12 x-15=0\).
To complete the square, we need the coefficient of \(x^{2}\) to be one. If we factor out the coefficient of \(x^{2}\) as a common factor, we can continue with solving the equation by completing the square.
Exercise \(\PageIndex{15}\)
Solve by completing the square: \(2 m^{2}+16 m+14=0\).
\(m=-7, m=-1\)
Exercise \(\PageIndex{16}\)
Solve by completing the square: \(4 n^{2}-24 n-56=8\).
\(n=-2, n=8\)
To complete the square, the coefficient of the \(x^{2}\) must be \(1\). When the leading coefficient is not a factor of all the terms, we will divide both sides of the equation by the leading coefficient! This will give us a fraction for the second coefficient. We have already seen how to complete the square with fractions in this section.
Example \(\PageIndex{9}\)
Solve by completing the square: \(2 x^{2}-3 x=20\).
To complete the square we need the coefficient of \(x^{2}\) to be one. We will divide both sides of the equation by the coefficient of \(x^{2}\). Then we can continue with solving the equation by completing the square.
Exercise \(\PageIndex{17}\)
Solve by completing the square: \(3 r^{2}-2 r=21\).
\(r=-\frac{7}{3}, r=3\)
Exercise \(\PageIndex{18}\)
Solve by completing the square: \(4 t^{2}+2 t=20\).
\(t=-\frac{5}{2}, t=2\)
Now that we have seen that the coefficient of \(x^{2}\) must be \(1\) for us to complete the square, we update our procedure for solving a quadratic equation by completing the square to include equations of the form \(a x^{2}+b x+c=0\).
Howto: Solve a Quadratic Equation of the Form \(a x^{2}+b x+c=0\) by Completing the Square
- Divide by aa to make the coefficient of \(x^{2}\) term \(1\).
Example \(\PageIndex{10}\)
Solve by completing the square: \(3 x^{2}+2 x=4\).
Again, our first step will be to make the coefficient of \(x^{2}\) one. By dividing both sides of the equation by the coefficient of \(x^{2}\), we can then continue with solving the equation by completing the square.
Exercise \(\PageIndex{19}\)
Solve by completing the square: \(4 x^{2}+3 x=2\).
\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)
Exercise \(\PageIndex{20}\)
Solve by completing the square: \(3 y^{2}-10 y=-5\).
\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)
Access these online resources for additional instruction and practice with completing the square.
- Completing Perfect Square Trinomials
- Completing the Square 1
- Completing the Square to Solve Quadratic Equations
- Completing the Square to Solve Quadratic Equations: More Examples
- Completing the Square 4
Key Concepts
- Binomial Squares Pattern If \(a\) and \(b\) are real numbers,
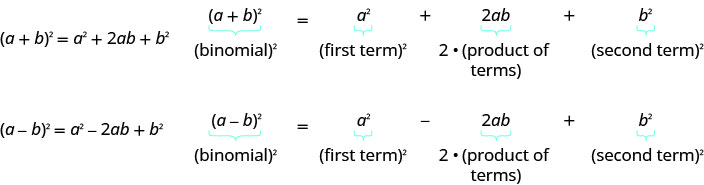
- Add the \(\left(\frac{1}{2} b\right)^{2}\) to \(x^{2}+bx\)
- Rewrite the trinomial as a binomial square
- Divide by \(a\) to make the coefficient of \(x^{2}\) term \(1\).
- Factor the perfect square trinomial, writing it as a binomial squared on the left and simplify by adding the terms on the right.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: Algebra 1 > Unit 14
- Solve by completing the square: Integer solutions
- Solve by completing the square: Non-integer solutions
- Solve equations by completing the square
- Worked example: completing the square (leading coefficient ≠ 1)
- Completing the square
- Solving quadratics by completing the square: no solution
- Proof of the quadratic formula
- Solving quadratics by completing the square
Completing the square review
- Quadratic formula proof review
What is completing the square?
- Rewrite quadratics as perfect squares
- Completing the square 1
- Completing the square 2
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

IMAGES
VIDEO
COMMENTS
Solve by completing the square: x2 + 8x = 48. Solution: Step 1: Isolate the variable terms on one side and the constant terms on the other. This equation has all the variables on the left. x2 + bx c x2 + 8x = 48. Step 2: Find (1 2 ⋅ b)2, the number to complete the square. Add it to both sides of the equation.
x 2 + 10 x = − 24. We complete the square by taking half of the coefficient of our x term, squaring it, and adding it to both sides of the equation. Since the coefficient of our x term is 10 , half of it would be 5 , and squaring it gives us 25 . x 2 + 10 x + 25 = − 24 + 25. We can now rewrite the left side of the equation as a squared term.