two tailed hypothesis testing examples

Statistics Made Easy

Two-Tailed Hypothesis Tests: 3 Example Problems

In statistics, we use hypothesis tests to determine whether some claim about a population parameter is true or not.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter = ≤, ≥ some value

H A (Alternative Hypothesis): Population parameter <, >, ≠ some value

There are two types of hypothesis tests:

One-tailed test : Alternative hypothesis contains either < or > sign
Two-tailed test : Alternative hypothesis contains the ≠ sign

In a two-tailed test , the alternative hypothesis always contains the not equal ( ≠ ) sign.

This indicates that we’re testing whether or not some effect exists, regardless of whether it’s a positive or negative effect.

Check out the following example problems to gain a better understanding of two-tailed tests.

Example 1: Factory Widgets

Suppose it’s assumed that the average weight of a certain widget produced at a factory is 20 grams. However, one engineer believes that a new method produces widgets that weigh less than 20 grams.

To test this, he can perform a one-tailed hypothesis test with the following null and alternative hypotheses:

H 0 (Null Hypothesis): μ = 20 grams
H A (Alternative Hypothesis): μ ≠ 20 grams

This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The engineer believes that the new method will influence widget weight, but doesn’t specify whether it will cause average weight to increase or decrease.

To test this, he uses the new method to produce 20 widgets and obtains the following information:

n = 20 widgets
x = 19.8 grams
s = 3.1 grams

Plugging these values into the One Sample t-test Calculator , we obtain the following results:

t-test statistic: -0.288525
two-tailed p-value: 0.776

Since the p-value is not less than .05, the engineer fails to reject the null hypothesis.

He does not have sufficient evidence to say that the true mean weight of widgets produced by the new method is different than 20 grams.

Example 2: Plant Growth

Suppose a standard fertilizer has been shown to cause a species of plants to grow by an average of 10 inches. However, one botanist believes a new fertilizer causes this species of plants to grow by an average amount different than 10 inches.

To test this, she can perform a one-tailed hypothesis test with the following null and alternative hypotheses:

H 0 (Null Hypothesis): μ = 10 inches
H A (Alternative Hypothesis): μ ≠ 10 inches

This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The botanist believes that the new fertilizer will influence plant growth, but doesn’t specify whether it will cause average growth to increase or decrease.

To test this claim, she applies the new fertilizer to a simple random sample of 15 plants and obtains the following information:

n = 15 plants
x = 11.4 inches
s = 2.5 inches
t-test statistic: 2.1689
two-tailed p-value: 0.0478

Since the p-value is less than .05, the botanist rejects the null hypothesis.

She has sufficient evidence to conclude that the new fertilizer causes an average growth that is different than 10 inches.

Example 3: Studying Method

A professor believes that a certain studying technique will influence the mean score that her students receive on a certain exam, but she’s unsure if it will increase or decrease the mean score, which is currently 82.

To test this, she lets each student use the studying technique for one month leading up to the exam and then administers the same exam to each of the students.

She then performs a hypothesis test using the following hypotheses:

H 0 : μ = 82
H A : μ ≠ 82

This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The professor believes that the studying technique will influence the mean exam score, but doesn’t specify whether it will cause the mean score to increase or decrease.

To test this claim, the professor has 25 students use the new studying method and then take the exam. He collects the following data on the exam scores for this sample of students:

t-test statistic: 3.6586
two-tailed p-value: 0.0012

Since the p-value is less than .05, the professor rejects the null hypothesis.

She has sufficient evidence to conclude that the new studying method produces exam scores with an average score that is different than 82.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing What is a Directional Hypothesis? When Do You Reject the Null Hypothesis?

Published by Zach

What Is a Two-Tailed Test?

Understanding a two-tailed test, special considerations, two-tailed vs. one-tailed test.

Two-Tailed Test FAQs
Corporate Finance
Financial Analysis

What Is a Two-Tailed Test? Definition and Example

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Investopedia / Joules Garcia

A two-tailed test, in statistics, is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values. It is used in null-hypothesis testing and testing for statistical significance . If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.

Key Takeaways

In statistics, a two-tailed test is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater or less than a range of values.
It is used in null-hypothesis testing and testing for statistical significance.
If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.
By convention two-tailed tests are used to determine significance at the 5% level, meaning each side of the distribution is cut at 2.5%.

A basic concept of inferential statistics is hypothesis testing , which determines whether a claim is true or not given a population parameter. A hypothesis test that is designed to show whether the mean of a sample is significantly greater than and significantly less than the mean of a population is referred to as a two-tailed test. The two-tailed test gets its name from testing the area under both tails of a normal distribution , although the test can be used in other non-normal distributions.

A two-tailed test is designed to examine both sides of a specified data range as designated by the probability distribution involved. The probability distribution should represent the likelihood of a specified outcome based on predetermined standards. This requires the setting of a limit designating the highest (or upper) and lowest (or lower) accepted variable values included within the range. Any data point that exists above the upper limit or below the lower limit is considered out of the acceptance range and in an area referred to as the rejection range.

There is no inherent standard about the number of data points that must exist within the acceptance range. In instances where precision is required, such as in the creation of pharmaceutical drugs, a rejection rate of 0.001% or less may be instituted. In instances where precision is less critical, such as the number of food items in a product bag, a rejection rate of 5% may be appropriate.

A two-tailed test can also be used practically during certain production activities in a firm, such as with the production and packaging of candy at a particular facility. If the production facility designates 50 candies per bag as its goal, with an acceptable distribution of 45 to 55 candies, any bag found with an amount below 45 or above 55 is considered within the rejection range.

To confirm the packaging mechanisms are properly calibrated to meet the expected output, random sampling may be taken to confirm accuracy. A simple random sample takes a small, random portion of the entire population to represent the entire data set, where each member has an equal probability of being chosen.

For the packaging mechanisms to be considered accurate, an average of 50 candies per bag with an appropriate distribution is desired. Additionally, the number of bags that fall within the rejection range needs to fall within the probability distribution limit considered acceptable as an error rate. Here, the null hypothesis would be that the mean is 50 while the alternate hypothesis would be that it is not 50.

If, after conducting the two-tailed test, the z-score falls in the rejection region, meaning that the deviation is too far from the desired mean, then adjustments to the facility or associated equipment may be required to correct the error. Regular use of two-tailed testing methods can help ensure production stays within limits over the long term.

Be careful to note if a statistical test is one- or two-tailed as this will greatly influence a model's interpretation.

When a hypothesis test is set up to show that the sample mean would be only higher than the population mean, this is referred to as a one-tailed test . A formulation of this hypothesis would be, for example, that "the returns on an investment fund would be at least x%." One-tailed tests could also be set up to show that the sample mean could be only less than the population mean. The key difference from a two-tailed test is that in a two-tailed test, the sample mean could be different from the population mean by being either higher or lower than it.

If the sample being tested falls into the one-sided critical area, the alternative hypothesis will be accepted instead of the null hypothesis. A one-tailed test is also known as a directional hypothesis or directional test.

A two-tailed test, on the other hand, is designed to examine both sides of a specified data range to test whether a sample is greater than or less than the range of values.

Example of a Two-Tailed Test

As a hypothetical example, imagine that a new stockbroker , named XYZ, claims that their brokerage fees are lower than that of your current stockbroker, ABC) Data available from an independent research firm indicates that the mean and standard deviation of all ABC broker clients are $18 and $6, respectively.

A sample of 100 clients of ABC is taken, and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and the sample standard deviation is $6, can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?

H 0 : Null Hypothesis: mean = 18
H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)
Rejection region: Z <= - Z 2.5 and Z>=Z 2.5 (assuming 5% significance level, split 2.5 each on either side).
Z = (sample mean – mean) / (std-dev / sqrt (no. of samples)) = (18.75 – 18) / (6/(sqrt(100)) = 1.25

This calculated Z value falls between the two limits defined by: - Z 2.5 = -1.96 and Z 2.5 = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker. Therefore, the null hypothesis cannot be rejected. Alternatively, the p-value = P(Z< -1.25)+P(Z >1.25) = 2 * 0.1056 = 0.2112 = 21.12%, which is greater than 0.05 or 5%, leads to the same conclusion.

How Is a Two-Tailed Test Designed?

A two-tailed test is designed to determine whether a claim is true or not given a population parameter. It examines both sides of a specified data range as designated by the probability distribution involved. As such, the probability distribution should represent the likelihood of a specified outcome based on predetermined standards.

What Is the Difference Between a Two-Tailed and One-Tailed Test?

A two-tailed hypothesis test is designed to show whether the sample mean is significantly greater than or significantly less than the mean of a population. The two-tailed test gets its name from testing the area under both tails (sides) of a normal distribution. A one-tailed hypothesis test, on the other hand, is set up to show only one test; that the sample mean would be higher than the population mean, or, in a separate test, that the sample mean would be lower than the population mean.

What Is a Z-score?

A Z-score numerically describes a value's relationship to the mean of a group of values and is measured in terms of the number of standard deviations from the mean. If a Z-score is 0, it indicates that the data point's score is identical to the mean score whereas Z-scores of 1.0 and -1.0 would indicate values one standard deviation above or below the mean. In most large data sets, 99% of values have a Z-score between -3 and 3, meaning they lie within three standard deviations above and below the mean.

San Jose State University. " 6: Introduction to Null Hypothesis Significance Testing ."

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

Two-Tailed Hypothesis Tests: 3 Example Problems

In statistics, we use hypothesis tests to determine whether some claim about a population parameter is true or not.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter = ≤, ≥ some value

H A (Alternative Hypothesis): Population parameter , ≠ some value

There are two types of hypothesis tests:

One-tailed test : Alternative hypothesis contains either or > sign
Two-tailed test : Alternative hypothesis contains the ≠ sign

In a two-tailed test , the alternative hypothesis always contains the not equal ( ≠ ) sign.

This indicates that we’re testing whether or not some effect exists, regardless of whether it’s a positive or negative effect.

Check out the following example problems to gain a better understanding of two-tailed tests.

Example 1: Factory Widgets

Suppose it’s assumed that the average weight of a certain widget produced at a factory is 20 grams. However, one engineer believes that a new method produces widgets that weigh less than 20 grams.

To test this, he can perform a one-tailed hypothesis test with the following null and alternative hypotheses:

H 0 (Null Hypothesis): μ = 20 grams
H A (Alternative Hypothesis): μ ≠ 20 grams

To test this, he uses the new method to produce 20 widgets and obtains the following information:

n = 20 widgets
x = 19.8 grams
s = 3.1 grams

Plugging these values into the One Sample t-test Calculator , we obtain the following results:

t-test statistic: -0.288525
two-tailed p-value: 0.776

Since the p-value is not less than .05, the engineer fails to reject the null hypothesis.

He does not have sufficient evidence to say that the true mean weight of widgets produced by the new method is different than 20 grams.

Example 2: Plant Growth

To test this, she can perform a one-tailed hypothesis test with the following null and alternative hypotheses:

H 0 (Null Hypothesis): μ = 10 inches
H A (Alternative Hypothesis): μ ≠ 10 inches

To test this claim, she applies the new fertilizer to a simple random sample of 15 plants and obtains the following information:

n = 15 plants
x = 11.4 inches
s = 2.5 inches
t-test statistic: 2.1689
two-tailed p-value: 0.0478

Since the p-value is less than .05, the botanist rejects the null hypothesis.

She has sufficient evidence to conclude that the new fertilizer causes an average growth that is different than 10 inches.

Example 3: Studying Method

To test this, she lets each student use the studying technique for one month leading up to the exam and then administers the same exam to each of the students.

She then performs a hypothesis test using the following hypotheses:

H 0 : μ = 82
H A : μ ≠ 82

To test this claim, the professor has 25 students use the new studying method and then take the exam. He collects the following data on the exam scores for this sample of students:

t-test statistic: 3.6586
two-tailed p-value: 0.0012

Since the p-value is less than .05, the professor rejects the null hypothesis.

She has sufficient evidence to conclude that the new studying method produces exam scores with an average score that is different than 82.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing What is a Directional Hypothesis? When Do You Reject the Null Hypothesis?

Statistics vs. Probability: What’s the Difference?

One sample z-test calculator, related posts, how to normalize data between -1 and 1, how to interpret f-values in a two-way anova, how to create a vector of ones in..., vba: how to check if string contains another..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to find the mode of a histogram..., how to find quartiles in even and odd..., how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

Hypothesis Testing for Means & Proportions

1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

Type i and type ii errors.

All Modules

Z score Table

t score Table

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.

Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);

H 1 : Research hypothesis (investigator's belief); α =0.05

Step 2. Select the appropriate test statistic.

The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

Step 3. Set up decision rule.

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value. In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.
The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Standard normal distribution with lower tail at -1.645 and alpha=0.05

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Standard normal distribution with two tails

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

Step 4. Compute the test statistic.

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

Step 5. Conclusion.

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .

Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

Step 3. Set up decision rule.

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05. Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

The most common reason for a Type II error is a small sample size.

return to top | previous page | next page

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability > unit 12.

Hypothesis testing and p-values

One-tailed and two-tailed tests

Z-statistics vs. T-statistics
Small sample hypothesis test
Large sample proportion hypothesis testing

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
Collect data in a way designed to test the hypothesis.
Perform an appropriate statistical test .
Decide whether to reject or fail to reject your null hypothesis.
Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Prevent plagiarism. Run a free check.

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

an estimate of the difference in average height between the two groups.
a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved April 15, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

MA121: Introduction to Statistics

Setting Up Hypotheses

One- and two-tailed tests, learning objectives.

Define Type I and Type II errors
Interpret significant and non-significant differences
Explain why the null hypothesis should not be accepted when the effect is not significant

In the James Bond case study, Mr. Bond was given 16 trials on which he judged whether a martini had been shaken or stirred. He was correct on 13 of the trials. From the binomial distribution , we know that the probability of being correct 13 or more times out of 16 if one is only guessing is 0.0106. Figure 1 shows a graph of the binomial distribution. The red bars show the values greater than or equal to 13. As you can see in the figure, the probabilities are calculated for the upper tail of the distribution. A probability calculated in only one tail of the distribution is called a " one-tailed probability ".

Figure 1. The binomial distribution. The upper (right-hand) tail is red.

Figure 2. The binomial distribution. Both tails are red.

Should the one-tailed or the two-tailed probability be used to assess Mr. Bond's performance? That depends on the way the question is posed. If we are asking whether Mr. Bond can tell the difference between shaken or stirred martinis, then we would conclude he could if he performed either much better than chance or much worse than chance. If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which. Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability.

On the other hand, if our question is whether Mr. Bond is better than chance at determining whether a martini is shaken or stirred, we would use a one-tailed probability. What would the one-tailed probability be if Mr. Bond were correct on only 3 of the 16 trials? Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting 3 or more correct out of 16. This is a very high probability and the null hypothesis would not be rejected.

You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data. Statistical tests that compute one-tailed probabilities are called one-tailed tests ; those that compute two-tailed probabilities are called two-tailed tests . Two-tailed tests are much more common than one-tailed tests in scientific research because an outcome signifying that something other than chance is operating is usually worth noting. One-tailed tests are appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction. For example, consider an experiment designed to test the efficacy of a treatment for the common cold. The researcher would only be interested in whether the treatment was better than a placebo control. It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless.

Some have argued that a one-tailed test is justified whenever the researcher predicts the direction of an effect. The problem with this argument is that if the effect comes out strongly in the non-predicted direction, the researcher is not justified in concluding that the effect is not zero. Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.

The Open University
Guest user / Sign out
Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

4.2 Two-tailed tests

Hypotheses that have an equal (=) or not equal (≠) supposition (sign) in the statement are called non-directional hypotheses . In non-directional hypotheses, the researcher is interested in whether there is a statistically significant difference or relationship between two or more variables, but does not have any specific expectation about which group or variable will be higher or lower. For example, a non-directional hypothesis might be: ‘There is a difference in the preference for brand X between male and female consumers.’ In this hypothesis, the researcher is interested in whether there is a statistically significant difference in the preference for brand X between male and female consumers, but does not have a specific prediction about which gender will have a higher preference. The researcher may conduct a survey or experiment to collect data on the brand preference of male and female consumers and then use statistical analysis to determine whether there is a significant difference between the two groups.

Non-directional hypotheses are also known as two-tailed hypotheses. The term ‘two-tailed’ comes from the fact that the statistical test used to evaluate the hypothesis is based on the assumption that the difference or relationship could occur in either direction, resulting in two ‘tails’ in the probability distribution. Using the coffee foam example (from Activity 1), you have the following set of hypotheses:

H 0 : µ = 1cm foam

H a : µ ≠ 1cm foam

In this case, the researcher can reject the null hypothesis for the mean value that is either ‘much higher’ or ‘much lower’ than 1 cm foam. This is called a two-tailed test because the rejection region includes outcomes from both the upper and lower tails of the sample distribution when determining a decision rule. To give an illustration, if you set alpha level (α) equal to 0.05, that would give you a 95% confidence level. Then, you would reject the null hypothesis for obtained values of z 1.96 (you will look at how to calculate z-scores later in the course).

This can be plotted on a graph as shown in Figure 7.

A two-tailed test shown in a symmetrical graph reminiscent of a bell

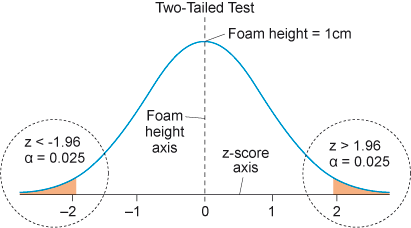
A symmetrical graph reminiscent of a bell. The x-axis is labelled ‘z-score’ and the y-axis is labelled ‘probability density’. The x-axis increases in increments of 1 from -2 to 2.

The top of the bell-shaped curve is labelled ‘Foam height = 1cm’. The graph circles the rejection regions of the null hypothesis on both sides of the bell curve. Within these circles are two areas shaded orange: beneath the curve from -2 downwards which is labelled z 1.96 and α = 0.025.

In a two-tailed hypothesis test, the null hypothesis assumes that there is no significant difference or relationship between the two groups or variables, and the alternative hypothesis suggests that there is a significant difference or relationship, but does not specify the direction of the difference or relationship.

When performing a two-tailed test, you need to determine the level of significance, which is denoted by alpha (α). The value of alpha, in this case, is 0.05. To perform a two-tailed test at a significance level of 0.05, you need to divide alpha by 2, giving a significance level of 0.025 for each distribution tail (0.05/2 = 0.025). This is done because the two-tailed test is looking for significance in either tail of the distribution. If the calculated test statistic falls in the rejection region of either tail of the distribution, then the null hypothesis is rejected and the alternative hypothesis is accepted. In this case, the researcher can conclude that there is a significant difference or relationship between the two groups or variables.

Assuming that the population follows a normal distribution, the tail located below the critical value of z = –1.96 (in a later section, you will discuss how this value was determined) and the tail above the critical value of z = +1.96 each represent a proportion of 0.025. These tails are referred to as the lower and upper tails, respectively, and they correspond to the extreme values of the distribution that are far from the central part of the bell curve. These critical values are used in a two-tailed hypothesis test to determine whether to reject or fail to reject the null hypothesis. The null hypothesis represents the default assumption that there is no significant difference between the observed data and what would be expected under a specific condition.

If the calculated test statistic falls within the critical values, then the null hypothesis cannot be rejected at the 0.05 level of significance. However, if the calculated test statistic falls outside the critical values (orange-coloured areas in Figure 7), then the null hypothesis can be rejected in favour of the alternative hypothesis, suggesting that there is evidence of a significant difference between the observed data and what would be expected under the specified condition.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.3 hypothesis testing examples.

Example: Right-Tailed Test
Example: Left-Tailed Test
Example: Two-Tailed Test

Brinell Hardness Scores

An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:

The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:

H 0 : μ = 170 H A : μ > 170

The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

Descriptive Statistics

$\mu$: mean of Brinelli

Null hypothesis H₀: $\mu$ = 170 Alternative hypothesis H₁: $\mu$ > 170

The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.

If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):

t distribution graph for df = 24 and a right tailed test of .05 significance level

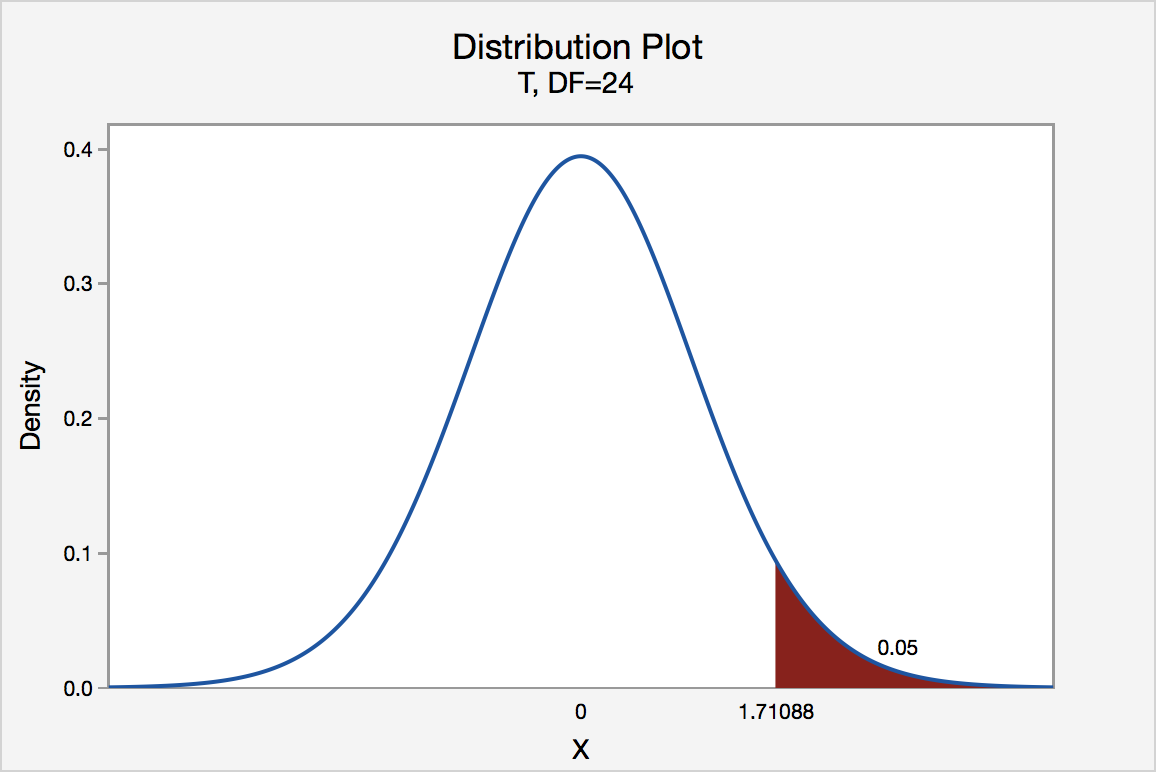
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:

t distribution graph of right tailed test showing the p-value of 0117 for a t-value of 1.22

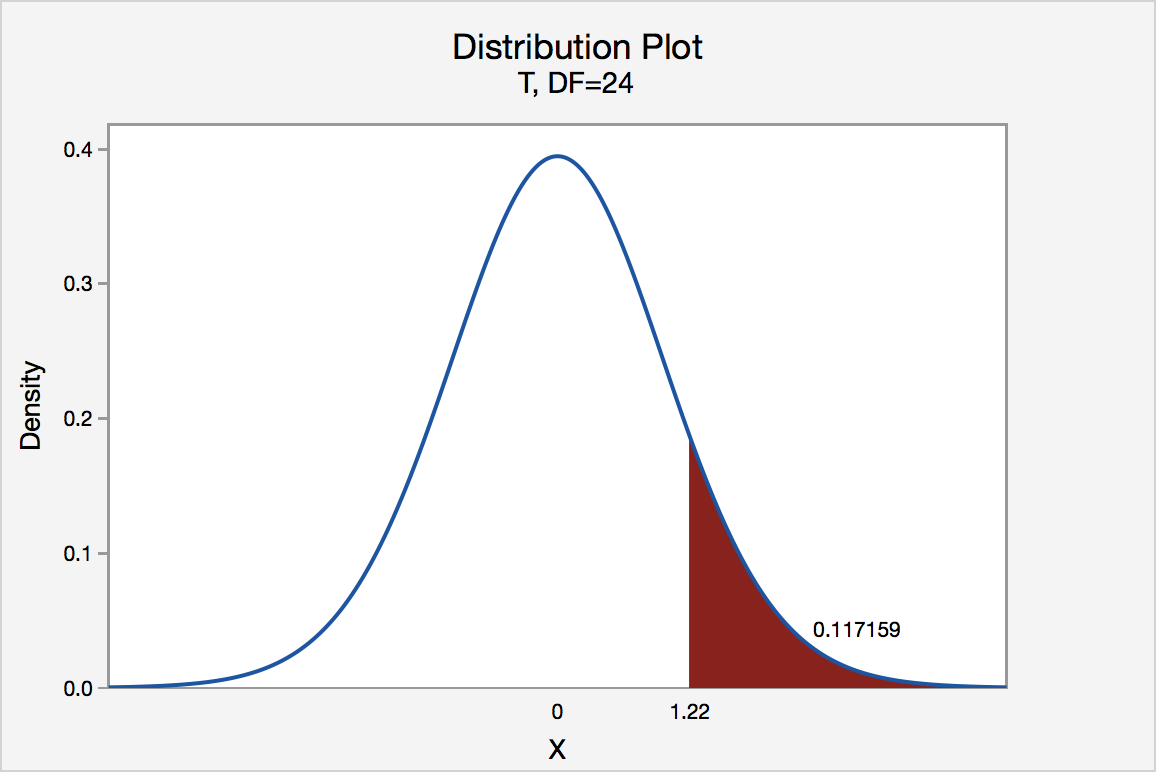
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than $\alpha$ = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Height of Sunflowers

A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:

The biologist's hypotheses are:

H 0 : μ = 15.7 H A : μ < 15.7

The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:

$\mu$: mean of Height

Null hypothesis H₀: $\mu$ = 15.7 Alternative hypothesis H₁: $\mu$ < 15.7

The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.

Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."

If the biologist set her significance level $\alpha$ at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3

Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:

t-distribution for left tailed test with significance level of 0.05 shown in left tail

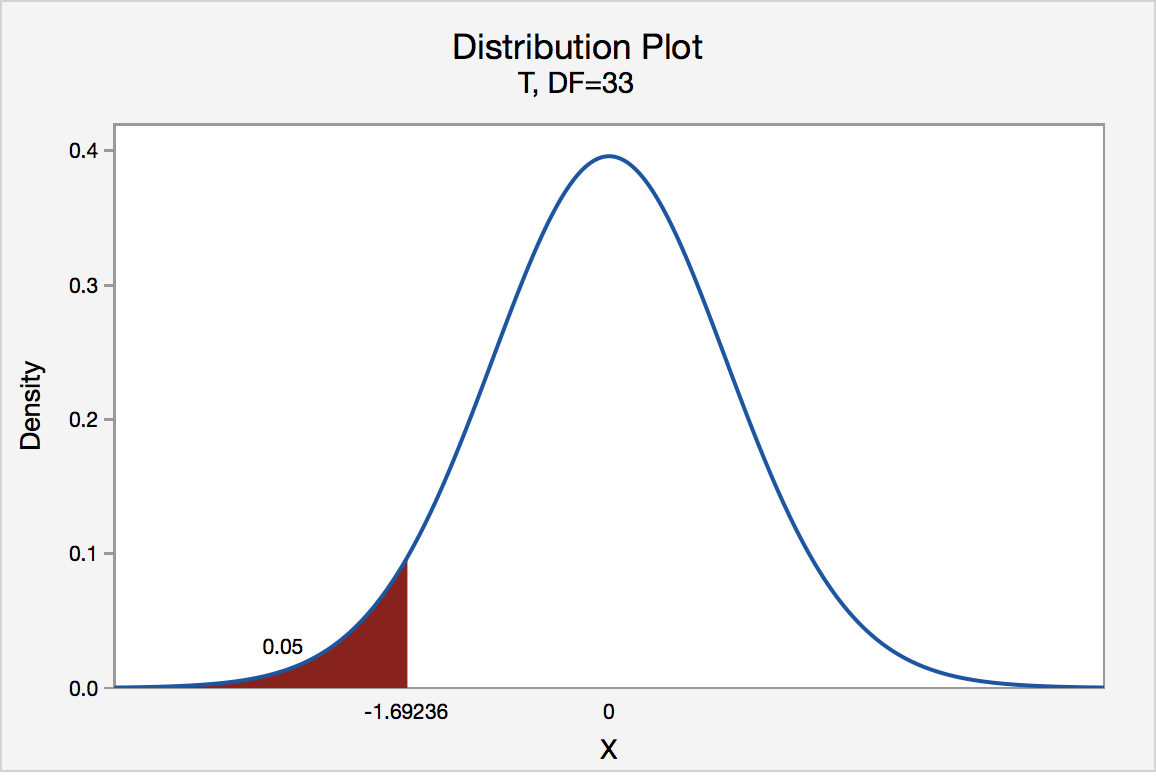
In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than $\alpha$ = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

t-distribution graph for left tailed test with a t-value of -4.60 and left tail area of 0.000

Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Gum Thickness

A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:

The quality control specialist's hypotheses are:

H 0 : μ = 7.5 H A : μ ≠ 7.5

The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

$\mu$: mean of Thickness

Null hypothesis H₀: $\mu$ = 7.5 Alternative hypothesis H₁: $\mu \ne$ 7.5

The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.

If the quality control specialist sets his significance level $\alpha$ at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):

t-distribution graph of two tails with a significance level of .05 and t values of -2.2616 and 2.2616

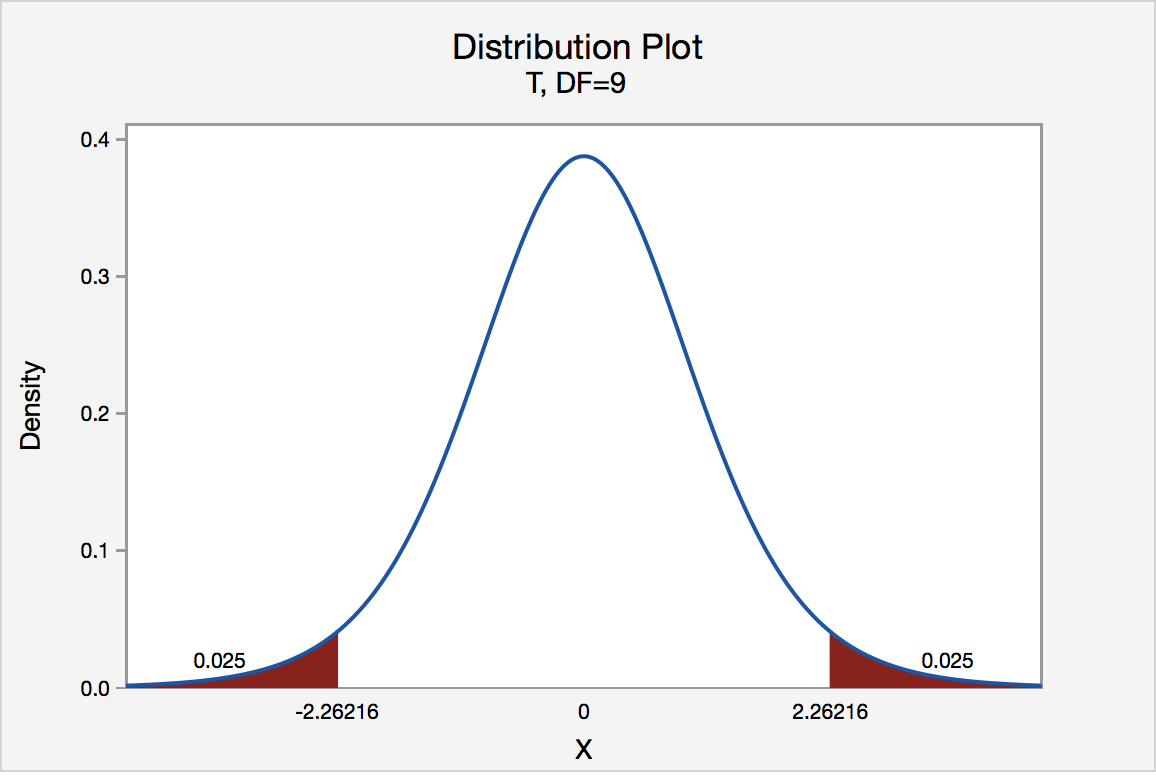
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.

If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:

t-distribution graph for a two tailed test with t values of -1.54 and 1.54, the corresponding p-values are 0.0789732 on both tails

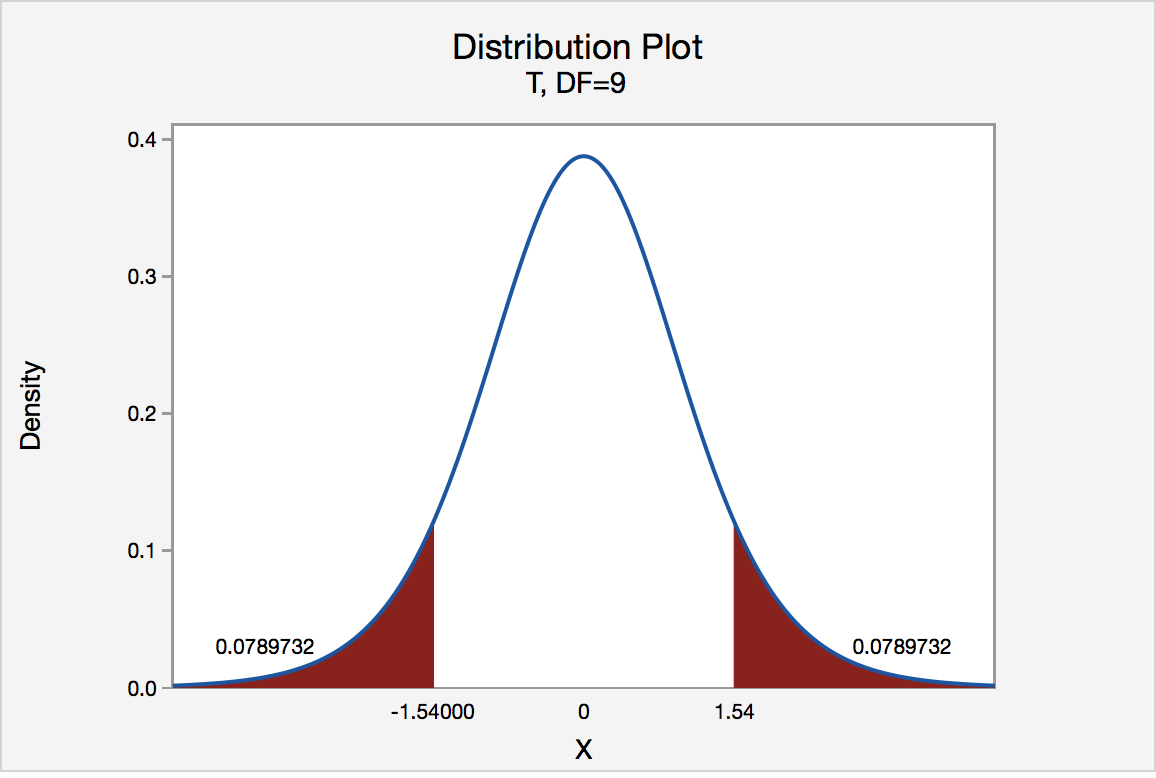
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than $\alpha$ = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.

Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean $\mu$. The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a mean (two tailed).

A population mean is an average of value a population.

Hypothesis tests are used to check a claim about the size of that population mean.

Hypothesis Testing a Mean

The following steps are used for a hypothesis test:

Check the conditions
Define the claims
Decide the significance level
Calculate the test statistic

For example:

Population : Nobel Prize winners
Category : Age when they received the prize.

And we want to check the claim:

"The average age of Nobel Prize winners when they received the prize is not 60"

By taking a sample of 30 randomly selected Nobel Prize winners we could find that:

The mean age in the sample ($\bar{x}$) is 62.1
The standard deviation of age in the sample ($s$) is 13.46

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

The sample is randomly selected
The population data is normally distributed
Sample size is large enough

A moderately large sample size, like 30, is typically large enough.

In the example, the sample size was 30 and it was randomly selected, so the conditions are fulfilled.

Note: Checking if the data is normally distributed can be done with specialized statistical tests.

2. Defining the Claims

We need to define a null hypothesis ($H_{0}$) and an alternative hypothesis ($H_{1}$) based on the claim we are checking.

The claim was:

In this case, the parameter is the mean age of Nobel Prize winners when they received the prize ($\mu$).

The null and alternative hypothesis are then:

Null hypothesis : The average age was 60.

Alternative hypothesis : The average age is not 60.

Which can be expressed with symbols as:

$H_{0}$: $\mu = 60 $

$H_{1}$: $\mu \neq 60 $

This is a ' two-tailed ' test, because the alternative hypothesis claims that the proportion is different from the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

3. Deciding the Significance Level

The significance level ($\alpha$) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

$\alpha = 0.1$ (10%)
$\alpha = 0.05$ (5%)
$\alpha = 0.01$ (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population mean is:

$\displaystyle \frac{\bar{x} - \mu}{s} \cdot \sqrt{n} $

$\bar{x}-\mu$ is the difference between the sample mean ($\bar{x}$) and the claimed population mean ($\mu$).

$s$ is the sample standard deviation .

$n$ is the sample size.

In our example:

The claimed ($H_{0}$) population mean ($\mu$) was $ 60 $

The sample mean ($\bar{x}$) was $62.1$

The sample standard deviation ($s$) was $13.46$

The sample size ($n$) was $30$

So the test statistic (TS) is then:

$\displaystyle \frac{62.1-60}{13.46} \cdot \sqrt{30} = \frac{2.1}{13.46} \cdot \sqrt{30} \approx 0.156 \cdot 5.477 = \underline{0.855}$

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic.

With R use built-in math and statistics functions to calculate the test statistic.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

The critical value approach compares the test statistic with the critical value of the significance level.
The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level ($\alpha$).

For a population mean test, the critical value (CV) is a T-value from a student's t-distribution .

This critical T-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population proportion is different from 60, the rejection region is split into both the left and right tail:

The student's t-distribution is adjusted for the uncertainty from smaller samples.

This adjustment is called degrees of freedom (df), which is the sample size $(n) - 1$

In this case the degrees of freedom (df) is: $30 - 1 = \underline{29} $

Choosing a significance level ($\alpha$) of 0.05, or 5%, we can find the critical T-value from a T-table , or with a programming language function:

Note: Because this is a two-tailed test the tail area ($\alpha$) needs to be split in half (divided by 2).

With Python use the Scipy Stats library t.ppf() function find the T-Value for an $\alpha$/2 = 0.025 at 29 degrees of freedom (df).

With R use the built-in qt() function to find the t-value for an $\alpha$/ = 0.025 at 29 degrees of freedom (df).

Using either method we can find that the critical T-Value is $\approx \underline{-2.045}$

For a two-tailed test we need to check if the test statistic (TS) is smaller than the negative critical value (-CV), or bigger than the positive critical value (CV).

If the test statistic is smaller than the negative critical value, the test statistic is in the rejection region .

If the test statistic is bigger than the positive critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis ($H_{0}$).

Here, the test statistic (TS) was $\approx \underline{0.855}$ and the critical value was $\approx \underline{-2.045}$

Here is an illustration of this test in a graph:

Since the test statistic is between the critical values we keep the null hypothesis.

This means that the sample data does not support the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data does not support the claim that "The average age of Nobel Prize winners when they received the prize is not 60" at a 5% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level ($\alpha$), we reject the null hypothesis ($H_{0}$).

The test statistic was found to be $ \approx \underline{0.855} $

For a population proportion test, the test statistic is a T-Value from a student's t-distribution .

Because this is a two-tailed test, we need to find the P-value of a T-value bigger than 0.855 and multiply it by 2 .

The student's t-distribution is adjusted according to degrees of freedom (df), which is the sample size $(30) - 1 = \underline{29}$

We can find the P-value using a T-table , or with a programming language function:

With Python use the Scipy Stats library t.cdf() function find the P-value of a T-value bigger than 0.855 for a two tailed test at 29 degrees of freedom (df):

With R use the built-in pt() function find the P-value of a T-Value bigger than 0.855 for a two tailed test at 29 degrees of freedom (df):

Using either method we can find that the P-value is $\approx \underline{0.3996}$

This tells us that the significance level ($\alpha$) would need to be smaller 0.3996, or 39.96%, to reject the null hypothesis.

This P-value is bigger than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is kept at all of these significance levels.

The sample data does not support the claim that "The average age of Nobel Prize winners when they received the prize is not 60" at a 10%, 5%, or 1% significance level .

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a two tailed hypothesis test for a mean.

Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean different from 60.

With R use built-in math and statistics functions find the P-value for a two tailed hypothesis test for a mean.

Left-Tailed and Two-Tailed Tests

This was an example of a left tailed test, where the alternative hypothesis claimed that parameter is smaller than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

Right-Tailed Test
Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Two Tailed Hypothesis

In the vast realm of scientific inquiry, the two-tailed hypothesis holds a special place, serving as a compass for researchers exploring possibilities in two opposing directions. Instead of predicting a specific direction of the relationship between variables, it remains open to outcomes on both ends of the spectrum. Understanding how to craft such a hypothesis, enriched with insights and nuances, can elevate the robustness of one’s research. Delve into its world, discover thesis statement examples, learn the art of its formulation, and grasp tips to master its intricacies.

What is Two Tailed Hypothesis? – Definition

A two-tailed hypothesis, also known as a non-directional hypothesis , is a type of hypothesis used in statistical testing that predicts a relationship between variables without specifying the direction of the relationship. In other words, it tests for the possibility of the relationship in both directions. This approach is used when a researcher believes there might be a difference due to the experiment but doesn’t have enough preliminary evidence or basis to predict a specific direction of that difference.

What is an example of a Two Tailed hypothesis statement?

Let’s consider a study on the impact of a new teaching method on student performance:

Hypothesis Statement : The new teaching method will have an effect on student performance.

Notice that the hypothesis doesn’t specify whether the effect will be positive or negative (i.e., whether student performance will improve or decline). It’s open to both possibilities, making it a two-tailed hypothesis.

Two Tailed Hypothesis Statement Examples

The two-tailed hypothesis, an essential tool in research, doesn’t predict a specific directional outcome between variables. Instead, it posits that an effect exists, without specifying its nature. This approach offers flexibility, as it remains open to both positive and negative outcomes. Below are various examples from diverse fields to shed light on this versatile research method. You may also be interested to browse through our other one-tailed hypothesis .

Sleep and Cognitive Ability : Sleep duration affects cognitive performance in adults.
Dietary Fiber and Digestion : Consumption of dietary fiber influences digestion rates.
Exercise and Stress Levels : Engaging in physical activity impacts stress levels.
Vitamin C and Immunity : Intake of Vitamin C has an effect on immunity strength.
Noise Levels and Concentration : Ambient noise levels influence individual concentration ability.
Artificial Sweeteners and Appetite : Consumption of artificial sweeteners affects appetite.
UV Light and Skin Health : Exposure to UV light influences skin health.
Coffee Intake and Sleep Quality : Consuming coffee has an effect on sleep quality.
Air Pollution and Respiratory Issues : Levels of air pollution impact respiratory health.
Meditation and Blood Pressure : Practicing meditation affects blood pressure readings.
Pet Ownership and Loneliness : Having a pet influences feelings of loneliness.
Green Spaces and Mental Wellbeing : Exposure to green spaces impacts mental health.
Music Tempo and Heart Rate : Listening to music of varying tempos affects heart rate.
Chocolate Consumption and Mood : Eating chocolate has an effect on mood.
Social Media Usage and Self-Esteem : The frequency of social media usage influences self-esteem.
E-reading and Eye Strain : Using e-readers affects eye strain levels.
Vegan Diets and Energy Levels : Following a vegan diet influences daily energy levels.
Carbonated Drinks and Tooth Decay : Consumption of carbonated drinks has an effect on tooth decay rates.
Distance Learning and Student Engagement : Engaging in distance learning impacts student involvement.
Organic Foods and Health Perceptions : Consuming organic foods influences perceptions of health.
Urban Living and Stress Levels : Living in urban environments affects stress levels.
Plant-Based Diets and Cholesterol : Adopting a plant-based diet impacts cholesterol levels.
Virtual Reality Training and Skill Acquisition : Using virtual reality for training influences the rate of skill acquisition.
Video Game Play and Hand-Eye Coordination : Playing video games has an effect on hand-eye coordination.
Aromatherapy and Sleep Quality : Using aromatherapy impacts the quality of sleep.
Bilingualism and Cognitive Flexibility : Being bilingual affects cognitive flexibility.
Microplastics and Marine Health : The presence of microplastics in oceans influences marine organism health.
Yoga Practice and Joint Health : Engaging in yoga has an effect on joint health.
Processed Foods and Metabolism : Consuming processed foods impacts metabolic rates.
Home Schooling and Social Skills : Being homeschooled influences the development of social skills.
Smartphone Usage and Attention Span : Regular smartphone use affects attention spans.
E-commerce and Consumer Trust : Engaging with e-commerce platforms influences levels of consumer trust.
Work-from-Home and Productivity : The practice of working from home has an effect on productivity levels.
Classical Music and Plant Growth : Exposing plants to classical music impacts their growth rate.
Public Transport and Community Engagement : Using public transport influences community engagement levels.
Digital Note-taking and Memory Retention : Taking notes digitally affects memory retention.
Acoustic Music and Relaxation : Listening to acoustic music impacts feelings of relaxation.
GMO Foods and Public Perception : Consuming GMO foods influences public perception of food safety.
LED Lights and Eye Comfort : Using LED lights affects visual comfort.
Fast Fashion and Consumer Satisfaction : Engaging with fast fashion brands influences consumer satisfaction levels.
Diverse Teams and Innovation : Working in diverse teams impacts the level of innovation.
Local Produce and Nutritional Value : Consuming local produce affects its nutritional value.
Podcasts and Language Acquisition : Listening to podcasts influences the speed of language acquisition.
Augmented Reality and Learning Efficiency : Using augmented reality in education has an effect on learning efficiency.
Museums and Historical Interest : Visiting museums impacts interest in history.
E-books vs. Physical Books and Reading Retention : The type of book, whether e-book or physical, affects memory retention from reading.
Biophilic Design and Worker Well-being : Implementing biophilic designs in office spaces influences worker well-being.
Recycled Products and Consumer Preference : Using recycled materials in products impacts consumer preferences.
Interactive Learning and Critical Thinking : Engaging in interactive learning environments affects the development of critical thinking skills.
High-Intensity Training and Muscle Growth : Participating in high-intensity training has an effect on muscle growth rate.
Pet Therapy and Anxiety Levels : Engaging with therapy animals influences anxiety levels.
3D Printing and Manufacturing Efficiency : Implementing 3D printing in manufacturing affects production efficiency.
Electric Cars and Public Adoption Rates : Introducing more electric cars impacts the rate of public adoption.
Ancient Architectural Study and Modern Design Inspiration : Studying ancient architecture influences modern design inspirations.
Natural Lighting and Productivity : The amount of natural lighting in a workspace affects worker productivity.
Streaming Platforms and Traditional TV Viewing : The rise of streaming platforms has an effect on traditional TV viewing habits.
Handwritten Notes and Conceptual Understanding : Taking notes by hand influences the depth of conceptual understanding.
Urban Farming and Community Engagement : Implementing urban farming practices impacts levels of community engagement.
Influencer Marketing and Brand Loyalty : Collaborating with influencers affects brand loyalty among consumers.
Online Workshops and Skill Enhancement : Participating in online workshops influences skill enhancement.
Virtual Reality and Empathy Development : Using virtual reality experiences influences the development of empathy.
Gardening and Mental Well-being : Engaging in gardening activities affects overall mental well-being.
Drones and Wildlife Observation : The use of drones impacts the accuracy of wildlife observations.
Artificial Intelligence and Job Markets : The introduction of artificial intelligence in industries has an effect on job availability.
Online Reviews and Purchase Decisions : Reading online reviews influences purchase decisions for consumers.
Blockchain Technology and Financial Security : Implementing blockchain technology affects financial transaction security.
Minimalism and Life Satisfaction : Adopting a minimalist lifestyle influences levels of life satisfaction.
Microlearning and Long-term Retention : Engaging in microlearning practices impacts long-term information retention.
Virtual Teams and Communication Efficiency : Operating in virtual teams has an effect on the efficiency of communication.
Plant Music and Growth Rates : Exposing plants to specific music frequencies influences their growth rates.
Green Building Practices and Energy Consumption : Implementing green building designs affects overall energy consumption.
Fermented Foods and Gut Health : Consuming fermented foods impacts gut health.
Digital Art Platforms and Creative Expression : Using digital art platforms influences levels of creative expression.
Aquatic Therapy and Physical Rehabilitation : Engaging in aquatic therapy has an effect on the rate of physical rehabilitation.
Solar Energy and Utility Bills : Adopting solar energy solutions influences monthly utility bills.
Immersive Theatre and Audience Engagement : Experiencing immersive theatre performances affects audience engagement levels.
Podcast Popularity and Radio Listening Habits : The rise in podcast popularity impacts traditional radio listening habits.
Vertical Farming and Crop Yield : Implementing vertical farming techniques has an effect on crop yields.
DIY Culture and Craftsmanship Appreciation : The rise of DIY culture influences public appreciation for craftsmanship.
Crowdsourcing and Solution Innovation : Utilizing crowdsourcing methods affects the innovativeness of solutions derived.
Urban Beekeeping and Local Biodiversity : Introducing urban beekeeping practices impacts local biodiversity levels.
Digital Nomad Lifestyle and Work-Life Balance : Adopting a digital nomad lifestyle affects perceptions of work-life balance.
Virtual Tours and Tourism Interest : Offering virtual tours of destinations influences interest in real-life visits.
Neurofeedback Training and Cognitive Abilities : Engaging in neurofeedback training has an effect on various cognitive abilities.
Sensory Gardens and Stress Reduction : Visiting sensory gardens impacts levels of stress reduction.
Subscription Box Services and Consumer Spending : The popularity of subscription box services influences overall consumer spending patterns.
Makerspaces and Community Collaboration : Introducing makerspaces in communities affects collaboration levels among members.
Remote Work and Company Loyalty : Adopting long-term remote work policies impacts employee loyalty towards the company.
Upcycling and Environmental Awareness : Engaging in upcycling activities influences levels of environmental awareness.
Mixed Reality in Education and Engagement : Implementing mixed reality tools in education affects student engagement.
Microtransactions in Gaming and Player Commitment : The presence of microtransactions in video games impacts player commitment and longevity.
Floating Architecture and Sustainable Living : Adopting floating architectural solutions influences perceptions of sustainable living.
Edible Packaging and Waste Reduction : Introducing edible packaging in markets has an effect on overall waste reduction.
Space Tourism and Interest in Astronomy : The advent of space tourism influences the general public’s interest in astronomy.
Urban Green Roofs and Air Quality : Implementing green roofs in urban settings impacts the local air quality.
Smart Mirrors and Fitness Consistency : Using smart mirrors for workouts affects consistency in fitness routines.
Open Source Software and Technological Innovation : Promoting open-source software has an effect on the rate of technological innovation.
Microgreens and Nutrient Intake : Consuming microgreens influences nutrient intake.
Aquaponics and Sustainable Farming : Implementing aquaponic systems impacts perceptions of sustainable farming.
Esports Popularity and Physical Sport Engagement : The rise of esports affects engagement in traditional physical sports.

Two Tailed Hypothesis Statement Examples in Research

In academic research, a two-tailed hypothesis is versatile, not pointing to a specific direction of effect but remaining open to outcomes on both ends of the spectrum. Such hypothesis aim to determine if a particular variable affects another, without specifying how. Here are examples tailored to research scenarios.

Interdisciplinary Collaboration and Innovation : Engaging in interdisciplinary collaborations impacts the degree of innovation in research findings.
Open Access Journals and Citation Rates : Publishing in open-access journals influences the citation rates of the papers.
Research Grants and Publication Quality : Receiving larger research grants affects the quality of resulting publications.
Laboratory Environment and Data Accuracy : The physical conditions of a research laboratory impact the accuracy of experimental data.
Peer Review Process and Research Integrity : The stringency of the peer review process influences the overall integrity of published research.
Researcher Mobility and Knowledge Transfer : The mobility of researchers between institutions affects the rate of knowledge transfer.
Interdisciplinary Conferences and Networking Opportunities : Attending interdisciplinary conferences impacts the depth and breadth of networking opportunities.
Qualitative Methods and Research Depth : Incorporating qualitative methods in research affects the depth of findings.
Data Visualization Tools and Research Comprehension : Utilizing advanced data visualization tools influences the comprehension of complex research data.
Collaborative Tools and Research Efficiency : The adoption of modern collaborative tools impacts research efficiency and productivity.

Two Tailed Testing Hypothesis Statement Examples

In hypothesis testing , a two-tailed test examines the possibility of a relationship in both directions. Unlike one-tailed tests, it doesn’t anticipate a specific direction of the relationship. The following are examples that encapsulate this approach within varied testing scenarios.

Load Testing and Website Speed : Conducting load testing on a website influences its loading speed.
A/B Testing and Conversion Rates : Implementing A/B testing affects the conversion rates of a webpage.
Drug Efficacy Testing and Patient Recovery : Testing a new drug’s efficacy impacts patient recovery rates.
Usability Testing and User Engagement : Conducting usability testing on an app influences user engagement metrics.
Genetic Testing and Disease Prediction : Utilizing genetic testing affects the accuracy of disease prediction.
Water Quality Testing and Contaminant Levels : Performing water quality tests influences our understanding of contaminant levels.
Battery Life Testing and Device Longevity : Conducting battery life tests impacts claims about device longevity.
Product Safety Testing and Recall Rates : Implementing rigorous product safety tests affects the rate of product recalls.
Emissions Testing and Pollution Control : Undertaking emissions testing on vehicles influences pollution control measures.
Material Strength Testing and Product Durability : Testing the strength of materials affects predictions about product durability.

How do you know if a hypothesis is two-tailed?

To determine if a hypothesis is two-tailed, you must look at the nature of the prediction. A two-tailed hypothesis is neutral concerning the direction of the predicted relationship or difference between groups. It simply predicts a difference or relationship without specifying whether it will be positive, negative, greater, or lesser. The hypothesis tests for effects in both directions.

What is one-tailed and two-tailed Hypothesis test with example?

In hypothesis testing, the choice between a one-tailed and a two-tailed test is determined by the nature of the research question.

One-tailed hypothesis: This tests for a specific direction of the effect. It predicts the direction of the relationship or difference between groups. For example, a one-tailed hypothesis might state: “The new drug will reduce symptoms more effectively than the standard treatment.”

Two-tailed hypothesis: This doesn’t specify the direction. It predicts that there will be a difference, but it doesn’t forecast whether the difference will be positive or negative. For example, a two-tailed hypothesis might state: “The new drug will have a different effect on symptoms compared to the standard treatment.”

What is a two-tailed hypothesis in psychology?

In psychology, a two-tailed hypothesis is frequently used when researchers are exploring new areas or relationships without a strong prior basis to predict the direction of findings. For instance, a psychologist might use a two-tailed hypothesis to explore whether a new therapeutic method has different outcomes than a traditional method, without predicting whether the outcomes will be better or worse.

What does a two-tailed alternative hypothesis look like?

A two-tailed alternative hypothesis is generally framed to show that a parameter is simply different from a certain value, without specifying the direction of the difference. Using mathematical notation, for a population mean (μ) and a proposed value (k), the two-tailed hypothesis would look like: H1: μ ≠ k.

How do you write a Two-Tailed hypothesis statement? – A Step by Step Guide

Identify the Variables: Start by identifying the independent and dependent variables you want to study.
Formulate a Relationship: Consider the potential relationship between these variables without setting a direction.
Avoid Directional Language: Words like “increase”, “decrease”, “more than”, or “less than” should be avoided as they point to a one-tailed hypothesis.
Keep it Simple: The statement should be clear, concise, and to the point.
Use Neutral Language: For instance, words like “affects”, “influences”, or “has an impact on” can be used to indicate a relationship without specifying a direction.
Finalize the Statement: Once the relationship is clear in your mind, form a coherent sentence that describes the relationship between your variables.

Tips for Writing Two Tailed Hypothesis

Start Broad: Given that you’re not seeking a specific direction, it’s okay to start with a broad idea.
Be Objective: Avoid letting any biases or expectations shape your hypothesis.
Stay Informed: Familiarize yourself with existing research on the topic to ensure your hypothesis is novel and not inadvertently directional.
Seek Feedback: Share your hypothesis with colleagues or mentors to ensure it’s indeed non-directional.
Revisit and Refine: As with any research process, be open to revisiting and refining your hypothesis as you delve deeper into the literature or collect preliminary data.

AI Generator

Text prompt

Instructive
Professional

10 Examples of Public speaking

20 Examples of Gas lighting

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

10.E: Hypothesis Testing with Two Samples (Exercises)

Last updated
Save as PDF
Page ID 1149

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

10.1: Introduction

10.2: two population means with unknown standard deviations.

Use the following information to answer the next 15 exercises: Indicate if the hypothesis test is for

independent group means, population standard deviations, and/or variances known
independent group means, population standard deviations, and/or variances unknown
matched or paired samples
single mean
two proportions
single proportion

Exercise 10.2.3

It is believed that 70% of males pass their drivers test in the first attempt, while 65% of females pass the test in the first attempt. Of interest is whether the proportions are in fact equal.

Exercise 10.2.4

A new laundry detergent is tested on consumers. Of interest is the proportion of consumers who prefer the new brand over the leading competitor. A study is done to test this.

Exercise 10.2.5

A new windshield treatment claims to repel water more effectively. Ten windshields are tested by simulating rain without the new treatment. The same windshields are then treated, and the experiment is run again. A hypothesis test is conducted.

Exercise 10.2.6

The known standard deviation in salary for all mid-level professionals in the financial industry is $11,000. Company A and Company B are in the financial industry. Suppose samples are taken of mid-level professionals from Company A and from Company B. The sample mean salary for mid-level professionals in Company A is $80,000. The sample mean salary for mid-level professionals in Company B is $96,000. Company A and Company B management want to know if their mid-level professionals are paid differently, on average.

Exercise 10.2.7

The average worker in Germany gets eight weeks of paid vacation.

Exercise 10.2.8

According to a television commercial, 80% of dentists agree that Ultrafresh toothpaste is the best on the market.

Exercise 10.2.9

It is believed that the average grade on an English essay in a particular school system for females is higher than for males. A random sample of 31 females had a mean score of 82 with a standard deviation of three, and a random sample of 25 males had a mean score of 76 with a standard deviation of four.

independent group means, population standard deviations and/or variances unknown

Exercise 10.2.10

The league mean batting average is 0.280 with a known standard deviation of 0.06. The Rattlers and the Vikings belong to the league. The mean batting average for a sample of eight Rattlers is 0.210, and the mean batting average for a sample of eight Vikings is 0.260. There are 24 players on the Rattlers and 19 players on the Vikings. Are the batting averages of the Rattlers and Vikings statistically different?

Exercise 10.2.11

In a random sample of 100 forests in the United States, 56 were coniferous or contained conifers. In a random sample of 80 forests in Mexico, 40 were coniferous or contained conifers. Is the proportion of conifers in the United States statistically more than the proportion of conifers in Mexico?

Exercise 10.2.12

A new medicine is said to help improve sleep. Eight subjects are picked at random and given the medicine. The means hours slept for each person were recorded before starting the medication and after.

Exercise 10.2.13

It is thought that teenagers sleep more than adults on average. A study is done to verify this. A sample of 16 teenagers has a mean of 8.9 hours slept and a standard deviation of 1.2. A sample of 12 adults has a mean of 6.9 hours slept and a standard deviation of 0.6.

Exercise 10.2.14

Varsity athletes practice five times a week, on average.

Exercise 10.2.15

A sample of 12 in-state graduate school programs at school A has a mean tuition of $64,000 with a standard deviation of $8,000. At school B, a sample of 16 in-state graduate programs has a mean of $80,000 with a standard deviation of $6,000. On average, are the mean tuitions different?

Exercise 10.2.16

A new WiFi range booster is being offered to consumers. A researcher tests the native range of 12 different routers under the same conditions. The ranges are recorded. Then the researcher uses the new WiFi range booster and records the new ranges. Does the new WiFi range booster do a better job?

Exercise 10.2.17

A high school principal claims that 30% of student athletes drive themselves to school, while 4% of non-athletes drive themselves to school. In a sample of 20 student athletes, 45% drive themselves to school. In a sample of 35 non-athlete students, 6% drive themselves to school. Is the percent of student athletes who drive themselves to school more than the percent of nonathletes?

Use the following information to answer the next three exercises: A study is done to determine which of two soft drinks has more sugar. There are 13 cans of Beverage A in a sample and six cans of Beverage B. The mean amount of sugar in Beverage A is 36 grams with a standard deviation of 0.6 grams. The mean amount of sugar in Beverage B is 38 grams with a standard deviation of 0.8 grams. The researchers believe that Beverage B has more sugar than Beverage A, on average. Both populations have normal distributions.

Exercise 10.2.18

Are standard deviations known or unknown?

Exercise 10.2.19

What is the random variable?

The random variable is the difference between the mean amounts of sugar in the two soft drinks.

Exercise 10.2.20

Is this a one-tailed or two-tailed test?

Use the following information to answer the next 12 exercises: The U.S. Center for Disease Control reports that the mean life expectancy was 47.6 years for whites born in 1900 and 33.0 years for nonwhites. Suppose that you randomly survey death records for people born in 1900 in a certain county. Of the 124 whites, the mean life span was 45.3 years with a standard deviation of 12.7 years. Of the 82 nonwhites, the mean life span was 34.1 years with a standard deviation of 15.6 years. Conduct a hypothesis test to see if the mean life spans in the county were the same for whites and nonwhites.

Exercise 10.2.21

Is this a test of means or proportions?

Exercise 10.2.22

State the null and alternative hypotheses.

$H_{0}$: __________
$H_{a}$: __________

Exercise 10.2.23

Is this a right-tailed, left-tailed, or two-tailed test?

Exercise 10.2.24

In symbols, what is the random variable of interest for this test?

Exercise 10.2.25

In words, define the random variable of interest for this test.

the difference between the mean life spans of whites and nonwhites

Exercise 10.2.26

Which distribution (normal or Student's t ) would you use for this hypothesis test?

Exercise 10.2.27

Explain why you chose the distribution you did for Exercise .

This is a comparison of two population means with unknown population standard deviations.

Exercise 10.2.28

Calculate the test statistic and $p\text{-value}$.

Exercise 10.2.29

Sketch a graph of the situation. Label the horizontal axis. Mark the hypothesized difference and the sample difference. Shade the area corresponding to the $p\text{-value}$.

This is a horizontal axis with arrows at each end. The axis is labeled p'N - p'ND

Check student’s solution.

Exercise 10.2.30

Find the $p\text{-value}$.

Exercise 10.2.31

At a pre-conceived $\alpha = 0.05$, what is your:

Reason for the decision:
Conclusion (write out in a complete sentence):
Reject the null hypothesis
$p\text{-value} < 0.05$
There is not enough evidence at the 5% level of significance to support the claim that life expectancy in the 1900s is different between whites and nonwhites.

Exercise 10.2.32

Does it appear that the means are the same? Why or why not?

DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in Appendix E . Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.

If you are using a Student's t -distribution for a homework problem in what follows, including for paired data, you may assume that the underlying population is normally distributed. (When using these tests in a real situation, you must first prove that assumption, however.)

The mean number of English courses taken in a two–year time period by male and female college students is believed to be about the same. An experiment is conducted and data are collected from 29 males and 16 females. The males took an average of three English courses with a standard deviation of 0.8. The females took an average of four English courses with a standard deviation of 1.0. Are the means statistically the same?

A student at a four-year college claims that mean enrollment at four–year colleges is higher than at two–year colleges in the United States. Two surveys are conducted. Of the 35 two–year colleges surveyed, the mean enrollment was 5,068 with a standard deviation of 4,777. Of the 35 four-year colleges surveyed, the mean enrollment was 5,466 with a standard deviation of 8,191.

Subscripts: 1: two-year colleges; 2: four-year colleges

$H_{0}: \mu_{1} \geq \mu_{2}$
$H_{a}: \mu_{1} < \mu_{2}$
$\bar{X}_{1} - \bar{X}_{2}$ is the difference between the mean enrollments of the two-year colleges and the four-year colleges.
Student’s- t
test statistic: -0.2480
$p\text{-value}: 0.4019$
Alpha: 0.05
Decision: Do not reject
Reason for Decision: $p\text{-value} > \alpha$
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean enrollment at four-year colleges is higher than at two-year colleges.

At Rachel’s 11 th birthday party, eight girls were timed to see how long (in seconds) they could hold their breath in a relaxed position. After a two-minute rest, they timed themselves while jumping. The girls thought that the mean difference between their jumping and relaxed times would be zero. Test their hypothesis.

Mean entry-level salaries for college graduates with mechanical engineering degrees and electrical engineering degrees are believed to be approximately the same. A recruiting office thinks that the mean mechanical engineering salary is actually lower than the mean electrical engineering salary. The recruiting office randomly surveys 50 entry level mechanical engineers and 60 entry level electrical engineers. Their mean salaries were $46,100 and $46,700, respectively. Their standard deviations were $3,450 and $4,210, respectively. Conduct a hypothesis test to determine if you agree that the mean entry-level mechanical engineering salary is lower than the mean entry-level electrical engineering salary.

Subscripts: 1: mechanical engineering; 2: electrical engineering

$\bar{X}_{1} - \bar{X}_{2}$ is the difference between the mean entry level salaries of mechanical engineers and electrical engineers.
$t_{108}$
test statistic: $t = -0.82$
$p\text{-value}: 0.2061$
$\alpha: 0.05$
Decision: Do not reject the null hypothesis.
Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the mean entry-level salaries of mechanical engineers is lower than that of electrical engineers.

Marketing companies have collected data implying that teenage girls use more ring tones on their cellular phones than teenage boys do. In one particular study of 40 randomly chosen teenage girls and boys (20 of each) with cellular phones, the mean number of ring tones for the girls was 3.2 with a standard deviation of 1.5. The mean for the boys was 1.7 with a standard deviation of 0.8. Conduct a hypothesis test to determine if the means are approximately the same or if the girls’ mean is higher than the boys’ mean.

Use the information from [link] to answer the next four exercises.

Using the data from Lap 1 only, conduct a hypothesis test to determine if the mean time for completing a lap in races is the same as it is in practices.

$H_{0}: \mu_{1} = \mu_{2}$

$H_{a}: \mu_{1} \neq \mu_{2}$

$\bar{X}_{1} - \bar{X}_{2}$ is the difference between the mean times for completing a lap in races and in practices.
$t_{20.32}$
test statistic: –4.70
$p\text{-value}: 0.0001$
Decision: Reject the null hypothesis.
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean time for completing a lap in races is different from that in practices.

Repeat the test in Exercise 10.83, but use Lap 5 data this time.

Repeat the test in Exercise 10.83, but this time combine the data from Laps 1 and 5.

is the difference between the mean times for completing a lap in races and in practices.
$t_{40.94}$
test statistic: –5.08
$p\text{-value}: 0$
Reason for Decision: $p\text{-value} < \alpha$

In two to three complete sentences, explain in detail how you might use Terri Vogel’s data to answer the following question. “Does Terri Vogel drive faster in races than she does in practices?”

Use the following information to answer the next two exercises. The Eastern and Western Major League Soccer conferences have a new Reserve Division that allows new players to develop their skills. Data for a randomly picked date showed the following annual goals.

Conduct a hypothesis test to answer the next two exercises.

The exact distribution for the hypothesis test is:

the normal distribution
the Student's t -distribution
the uniform distribution
the exponential distribution

If the level of significance is 0.05, the conclusion is:

There is sufficient evidence to conclude that the W Division teams score fewer goals, on average, than the E teams
There is insufficient evidence to conclude that the W Division teams score more goals, on average, than the E teams.
There is insufficient evidence to conclude that the W teams score fewer goals, on average, than the E teams score.
Unable to determine

Suppose a statistics instructor believes that there is no significant difference between the mean class scores of statistics day students on Exam 2 and statistics night students on Exam 2. She takes random samples from each of the populations. The mean and standard deviation for 35 statistics day students were 75.86 and 16.91. The mean and standard deviation for 37 statistics night students were 75.41 and 19.73. The “day” subscript refers to the statistics day students. The “night” subscript refers to the statistics night students. A concluding statement is:

There is sufficient evidence to conclude that statistics night students' mean on Exam 2 is better than the statistics day students' mean on Exam 2.
There is insufficient evidence to conclude that the statistics day students' mean on Exam 2 is better than the statistics night students' mean on Exam 2.
There is insufficient evidence to conclude that there is a significant difference between the means of the statistics day students and night students on Exam 2.
There is sufficient evidence to conclude that there is a significant difference between the means of the statistics day students and night students on Exam 2.

Researchers interviewed street prostitutes in Canada and the United States. The mean age of the 100 Canadian prostitutes upon entering prostitution was 18 with a standard deviation of six. The mean age of the 130 United States prostitutes upon entering prostitution was 20 with a standard deviation of eight. Is the mean age of entering prostitution in Canada lower than the mean age in the United States? Test at a 1% significance level.

Test: two independent sample means, population standard deviations unknown.

Random variable:

\[\bar{X}_{1} - \bar{X}_{2}\]

Distribution: $H_{0}: \mu_{1} = \mu_{2} H_{a}: \mu_{1} < \mu_{2}$ The mean age of entering prostitution in Canada is lower than the mean age in the United States.

This is a normal distribution curve with mean equal to zero. A vertical line near the tail of the curve to the left of zero extends from the axis to the curve. The region under the curve to the left of the line is shaded representing p-value = 0.0157.

Graph: left-tailed

$p\text{-value}: 0.0151$

Decision: Do not reject $H_{0}$.

Conclusion: At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean age of entering prostitution in Canada is lower than the mean age in the United States.

A powder diet is tested on 49 people, and a liquid diet is tested on 36 different people. Of interest is whether the liquid diet yields a higher mean weight loss than the powder diet. The powder diet group had a mean weight loss of 42 pounds with a standard deviation of 12 pounds. The liquid diet group had a mean weight loss of 45 pounds with a standard deviation of 14 pounds.

Suppose a statistics instructor believes that there is no significant difference between the mean class scores of statistics day students on Exam 2 and statistics night students on Exam 2. She takes random samples from each of the populations. The mean and standard deviation for 35 statistics day students were 75.86 and 16.91, respectively. The mean and standard deviation for 37 statistics night students were 75.41 and 19.73. The “day” subscript refers to the statistics day students. The “night” subscript refers to the statistics night students. An appropriate alternative hypothesis for the hypothesis test is:

$\mu_{day} > \mu_{night}$
$\mu_{day} < \mu_{night}$
$\mu_{day} = \mu_{night}$
$\mu_{day} \neq \mu_{night}$

10.3: Two Population Means with Known Standard Deviations

Use the following information to answer the next five exercises. The mean speeds of fastball pitches from two different baseball pitchers are to be compared. A sample of 14 fastball pitches is measured from each pitcher. The populations have normal distributions. Table shows the result. Scouters believe that Rodriguez pitches a speedier fastball.

Exercise 10.3.2

The difference in mean speeds of the fastball pitches of the two pitchers

Exercise 10.3.3

Exercise 10.3.4

What is the test statistic?

Exercise 10.3.5

What is the $p\text{-value}$?

Exercise 10.3.6

At the 1% significance level, we can reject the null hypothesis. There is sufficient data to conclude that the mean speed of Rodriguez’s fastball is faster than Wesley’s.

Use the following information to answer the next five exercises. A researcher is testing the effects of plant food on plant growth. Nine plants have been given the plant food. Another nine plants have not been given the plant food. The heights of the plants are recorded after eight weeks. The populations have normal distributions. The following table is the result. The researcher thinks the food makes the plants grow taller.

Exercise 10.3.7

Is the population standard deviation known or unknown?

Exercise 10.3.8

Subscripts: 1 = Food, 2 = No Food

$H_{a}: \mu_{1} > \mu_{2}$

Exercise 10.3.9

Exercise 10.3.10

Draw the graph of the $p\text{-value}$.

This is a normal distribution curve with mean equal to zero. The values 0 and 0.1 are labeled on the horiztonal axis. A vertical line extends from 0.1 to the curve. The region under the curve to the right of the line is shaded to represent p-value = 0.0198.

Exercise 10.3.11

At the 1% significance level, what is your conclusion?

Use the following information to answer the next five exercises. Two metal alloys are being considered as material for ball bearings. The mean melting point of the two alloys is to be compared. 15 pieces of each metal are being tested. Both populations have normal distributions. The following table is the result. It is believed that Alloy Zeta has a different melting point.

Exercise 10.3.12

Subscripts: 1 = Gamma, 2 = Zeta

Exercise 10.3.13

Is this a right-, left-, or two-tailed test?

Exercise 10.3.14

Exercise 10.3.15

Exercise 10.3.16

There is sufficient evidence to reject the null hypothesis. The data support that the melting point for Alloy Zeta is different from the melting point of Alloy Gamma.

DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in [link] . Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.

If you are using a Student's t -distribution for one of the following homework problems, including for paired data, you may assume that the underlying population is normally distributed. (When using these tests in a real situation, you must first prove that assumption, however.)

A study is done to determine if students in the California state university system take longer to graduate, on average, than students enrolled in private universities. One hundred students from both the California state university system and private universities are surveyed. Suppose that from years of research, it is known that the population standard deviations are 1.5811 years and 1 year, respectively. The following data are collected. The California state university system students took on average 4.5 years with a standard deviation of 0.8. The private university students took on average 4.1 years with a standard deviation of 0.3.

Parents of teenage boys often complain that auto insurance costs more, on average, for teenage boys than for teenage girls. A group of concerned parents examines a random sample of insurance bills. The mean annual cost for 36 teenage boys was $679. For 23 teenage girls, it was $559. From past years, it is known that the population standard deviation for each group is $180. Determine whether or not you believe that the mean cost for auto insurance for teenage boys is greater than that for teenage girls.

Subscripts: 1 = boys, 2 = girls

$H_{0}: \mu_{1} \leq \mu_{2}$
The random variable is the difference in the mean auto insurance costs for boys and girls.
test statistic: $z = 2.50$
$p\text{-value}: 0.0062$
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean cost of auto insurance for teenage boys is greater than that for girls.

A group of transfer bound students wondered if they will spend the same mean amount on texts and supplies each year at their four-year university as they have at their community college. They conducted a random survey of 54 students at their community college and 66 students at their local four-year university. The sample means were $947 and $1,011, respectively. The population standard deviations are known to be $254 and $87, respectively. Conduct a hypothesis test to determine if the means are statistically the same.

Some manufacturers claim that non-hybrid sedan cars have a lower mean miles-per-gallon (mpg) than hybrid ones. Suppose that consumers test 21 hybrid sedans and get a mean of 31 mpg with a standard deviation of seven mpg. Thirty-one non-hybrid sedans get a mean of 22 mpg with a standard deviation of four mpg. Suppose that the population standard deviations are known to be six and three, respectively. Conduct a hypothesis test to evaluate the manufacturers claim.

Subscripts: 1 = non-hybrid sedans, 2 = hybrid sedans

The random variable is the difference in the mean miles per gallon of non-hybrid sedans and hybrid sedans.
test statistic: 6.36
Reason for decision: $p\text{-value} < \alpha$
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean miles per gallon of non-hybrid sedans is less than that of hybrid sedans.

A baseball fan wanted to know if there is a difference between the number of games played in a World Series when the American League won the series versus when the National League won the series. From 1922 to 2012, the population standard deviation of games won by the American League was 1.14, and the population standard deviation of games won by the National League was 1.11. Of 19 randomly selected World Series games won by the American League, the mean number of games won was 5.76. The mean number of 17 randomly selected games won by the National League was 5.42. Conduct a hypothesis test.

One of the questions in a study of marital satisfaction of dual-career couples was to rate the statement “I’m pleased with the way we divide the responsibilities for childcare.” The ratings went from one (strongly agree) to five (strongly disagree). Table contains ten of the paired responses for husbands and wives. Conduct a hypothesis test to see if the mean difference in the husband’s versus the wife’s satisfaction level is negative (meaning that, within the partnership, the husband is happier than the wife).

$H_{0}: \mu_{d} = 0$

$H_{a}: \mu_{d} < 0$

The random variable $X_{d}$ is the average difference between husband’s and wife’s satisfaction level.
test statistic: $t = –1.86$
$p\text{-value}: 0.0479$
Check student’s solution
Decision: Reject the null hypothesis, but run another test.
Conclusion: This is a weak test because alpha and the p -value are close. However, there is insufficient evidence to conclude that the mean difference is negative.

10.4: Comparing Two Independent Population Proportions

Use the following information for the next five exercises. Two types of phone operating system are being tested to determine if there is a difference in the proportions of system failures (crashes). Fifteen out of a random sample of 150 phones with OS 1 had system failures within the first eight hours of operation. Nine out of another random sample of 150 phones with OS 2 had system failures within the first eight hours of operation. OS 2 is believed to be more stable (have fewer crashes) than OS 1 .

Exercise 10.4.2

Exercise 10.4.3

$P'_{OS_{1}} - P'_{OS_{2}} =$ difference in the proportions of phones that had system failures within the first eight hours of operation with OS 1 and OS 2 .

Exercise 10.4.4

Exercise 10.4.5

Exercise 10.4.6

What can you conclude about the two operating systems?

Use the following information to answer the next twelve exercises. In the recent Census, three percent of the U.S. population reported being of two or more races. However, the percent varies tremendously from state to state. Suppose that two random surveys are conducted. In the first random survey, out of 1,000 North Dakotans, only nine people reported being of two or more races. In the second random survey, out of 500 Nevadans, 17 people reported being of two or more races. Conduct a hypothesis test to determine if the population percents are the same for the two states or if the percent for Nevada is statistically higher than for North Dakota.

Exercise 10.4.7

proportions

Exercise 10.4.8

$H_{0}$: _________
$H_{a}$: _________

Exercise 10.4.9

Is this a right-tailed, left-tailed, or two-tailed test? How do you know?

right-tailed

Exercise 10.4.10

What is the random variable of interest for this test?

Exercise 10.4.11

In words, define the random variable for this test.

The random variable is the difference in proportions (percents) of the populations that are of two or more races in Nevada and North Dakota.

Exercise 10.4.12

Exercise 10.4.13

Explain why you chose the distribution you did for the Exercise 10.56 .

Our sample sizes are much greater than five each, so we use the normal for two proportions distribution for this hypothesis test.

Exercise 10.4.14

Calculate the test statistic.

Exercise 10.4.15

Sketch a graph of the situation. Mark the hypothesized difference and the sample difference. Shade the area corresponding to the $p\text{-value}$.

Exercise 10.4.16

Exercise 10.4.17

Reject the null hypothesis.
$p\text{-value} < \alpha$
At the 5% significance level, there is sufficient evidence to conclude that the proportion (percent) of the population that is of two or more races in Nevada is statistically higher than that in North Dakota.

Exercise 10.4.18

Does it appear that the proportion of Nevadans who are two or more races is higher than the proportion of North Dakotans? Why or why not?

If you are using a Student's t -distribution for one of the following homework problems, including for paired data, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, however.)

A recent drug survey showed an increase in the use of drugs and alcohol among local high school seniors as compared to the national percent. Suppose that a survey of 100 local seniors and 100 national seniors is conducted to see if the proportion of drug and alcohol use is higher locally than nationally. Locally, 65 seniors reported using drugs or alcohol within the past month, while 60 national seniors reported using them.

We are interested in whether the proportions of female suicide victims for ages 15 to 24 are the same for the whites and the blacks races in the United States. We randomly pick one year, 1992, to compare the races. The number of suicides estimated in the United States in 1992 for white females is 4,930. Five hundred eighty were aged 15 to 24. The estimate for black females is 330. Forty were aged 15 to 24. We will let female suicide victims be our population.

$H_{0}: P_{W} = P_{B}$
$H_{a}: P_{W} \neq P_{B}$
The random variable is the difference in the proportions of white and black suicide victims, aged 15 to 24.
normal for two proportions
test statistic: –0.1944
$p\text{-value}: 0.8458$
Reason for decision: $p\text{-value} > \alpha$
Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportions of white and black female suicide victims, aged 15 to 24, are different.

Elizabeth Mjelde, an art history professor, was interested in whether the value from the Golden Ratio formula, $\left(\frac{(larger + smaller dimension}{larger dimension}\right)$ was the same in the Whitney Exhibit for works from 1900 to 1919 as for works from 1920 to 1942. Thirty-seven early works were sampled, averaging 1.74 with a standard deviation of 0.11. Sixty-five of the later works were sampled, averaging 1.746 with a standard deviation of 0.1064. Do you think that there is a significant difference in the Golden Ratio calculation?

A recent year was randomly picked from 1985 to the present. In that year, there were 2,051 Hispanic students at Cabrillo College out of a total of 12,328 students. At Lake Tahoe College, there were 321 Hispanic students out of a total of 2,441 students. In general, do you think that the percent of Hispanic students at the two colleges is basically the same or different?

Subscripts: 1 = Cabrillo College, 2 = Lake Tahoe College

$H_{0}: p_{1} = p_{2}$
$H_{a}: p_{1} \neq p_{2}$
The random variable is the difference between the proportions of Hispanic students at Cabrillo College and Lake Tahoe College.
test statistic: 4.29
$p\text{-value}: 0.00002$
Reason for decision: p -value < alpha
Conclusion: There is sufficient evidence to conclude that the proportions of Hispanic students at Cabrillo College and Lake Tahoe College are different.

Use the following information to answer the next three exercises. Neuroinvasive West Nile virus is a severe disease that affects a person’s nervous system . It is spread by the Culex species of mosquito. In the United States in 2010 there were 629 reported cases of neuroinvasive West Nile virus out of a total of 1,021 reported cases and there were 486 neuroinvasive reported cases out of a total of 712 cases reported in 2011. Is the 2011 proportion of neuroinvasive West Nile virus cases more than the 2010 proportion of neuroinvasive West Nile virus cases? Using a 1% level of significance, conduct an appropriate hypothesis test.

“2011” subscript: 2011 group.
“2010” subscript: 2010 group
a test of two proportions
a test of two independent means
a test of a single mean
a test of matched pairs.

An appropriate null hypothesis is:

$p_{2011} \leq p_{2010}$
$p_{2011} \geq p_{2010}$
$\mu_{2011} \leq \mu_{2010}$
$p_{2011} > p_{2010}$

The $p\text{-value}$ is 0.0022. At a 1% level of significance, the appropriate conclusion is

There is sufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is less than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
There is insufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is more than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
There is insufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is less than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
There is sufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is more than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.

Researchers conducted a study to find out if there is a difference in the use of eReaders by different age groups. Randomly selected participants were divided into two age groups. In the 16- to 29-year-old group, 7% of the 628 surveyed use eReaders, while 11% of the 2,309 participants 30 years old and older use eReaders.

Test: two independent sample proportions.

Random variable: $p′_{1} - p′_{2}$

Distribution:

The proportion of eReader users is different for the 16- to 29-year-old users from that of the 30 and older users.

Graph: two-tailed

This is a normal distribution curve with mean equal to zero. Both the right and left tails of the curve are shaded. Each tail represents 1/2(p-value) = 0.0017.

$p\text{-value}: 0.0033$

Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that the proportion of eReader users 16 to 29 years old is different from the proportion of eReader users 30 and older.

are considered obese if their body mass index (BMI) is at least 30. The researchers wanted to determine if the proportion of women who are obese in the south is less than the proportion of southern men who are obese. The results are shown in Table . Test at the 1% level of significance.

Two computer users were discussing tablet computers. A higher proportion of people ages 16 to 29 use tablets than the proportion of people age 30 and older. Table details the number of tablet owners for each age group. Test at the 1% level of significance.

Test: two independent sample proportions

$H_{a}: p_{1} > p_{2}$

A higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.

Graph: right-tailed

This is a normal distribution curve with mean equal to zero. A vertical line near the tail of the curve to the right of zero extends from the axis to the curve. The region under the curve to the right of the line is shaded representing p-value = 0.2354.

$p\text{-value}: 0.2354$

Decision: Do not reject the $H_{0}$.

Conclusion: At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that a higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.

A group of friends debated whether more men use smartphones than women. They consulted a research study of smartphone use among adults. The results of the survey indicate that of the 973 men randomly sampled, 379 use smartphones. For women, 404 of the 1,304 who were randomly sampled use smartphones. Test at the 5% level of significance.

While her husband spent 2½ hours picking out new speakers, a statistician decided to determine whether the percent of men who enjoy shopping for electronic equipment is higher than the percent of women who enjoy shopping for electronic equipment. The population was Saturday afternoon shoppers. Out of 67 men, 24 said they enjoyed the activity. Eight of the 24 women surveyed claimed to enjoy the activity. Interpret the results of the survey.

Subscripts: 1: men; 2: women

$H_{0}: p_{1} \leq p_{2}$
$P'_{1} - P\_{2}$ is the difference between the proportions of men and women who enjoy shopping for electronic equipment.
test statistic: 0.22
$p\text{-value}: 0.4133$
Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportion of men who enjoy shopping for electronic equipment is more than the proportion of women.

We are interested in whether children’s educational computer software costs less, on average, than children’s entertainment software. Thirty-six educational software titles were randomly picked from a catalog. The mean cost was $31.14 with a standard deviation of $4.69. Thirty-five entertainment software titles were randomly picked from the same catalog. The mean cost was $33.86 with a standard deviation of $10.87. Decide whether children’s educational software costs less, on average, than children’s entertainment software.

Joan Nguyen recently claimed that the proportion of college-age males with at least one pierced ear is as high as the proportion of college-age females. She conducted a survey in her classes. Out of 107 males, 20 had at least one pierced ear. Out of 92 females, 47 had at least one pierced ear. Do you believe that the proportion of males has reached the proportion of females?

$P'_{1} - P\_{2}$ is the difference between the proportions of men and women that have at least one pierced ear.
test statistic: –4.82
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportions of males and females with at least one pierced ear is different.

Use the data sets found in [link] to answer this exercise. Is the proportion of race laps Terri completes slower than 130 seconds less than the proportion of practice laps she completes slower than 135 seconds?

"To Breakfast or Not to Breakfast?" by Richard Ayore

In the American society, birthdays are one of those days that everyone looks forward to. People of different ages and peer groups gather to mark the 18th, 20th, …, birthdays. During this time, one looks back to see what he or she has achieved for the past year and also focuses ahead for more to come.

If, by any chance, I am invited to one of these parties, my experience is always different. Instead of dancing around with my friends while the music is booming, I get carried away by memories of my family back home in Kenya. I remember the good times I had with my brothers and sister while we did our daily routine.

Every morning, I remember we went to the shamba (garden) to weed our crops. I remember one day arguing with my brother as to why he always remained behind just to join us an hour later. In his defense, he said that he preferred waiting for breakfast before he came to weed. He said, “This is why I always work more hours than you guys!”

And so, to prove him wrong or right, we decided to give it a try. One day we went to work as usual without breakfast, and recorded the time we could work before getting tired and stopping. On the next day, we all ate breakfast before going to work. We recorded how long we worked again before getting tired and stopping. Of interest was our mean increase in work time. Though not sure, my brother insisted that it was more than two hours. Using the data in Table , solve our problem.

$H_{a}: \mu_{d} > 0$
The random variable $X_{d}$ is the mean difference in work times on days when eating breakfast and on days when not eating breakfast.
test statistic: 4.8963

$p\text{-value}: 0.0004$

Reason for Decision:$p\text{-value} < \alpha$
Conclusion: At the 5% level of significance, there is sufficient evidence to conclude that the mean difference in work times on days when eating breakfast and on days when not eating breakfast has increased.

10.5: Matched or Paired Samples

Use the following information to answer the next five exercises. A study was conducted to test the effectiveness of a software patch in reducing system failures over a six-month period. Results for randomly selected installations are shown in Table . The “before” value is matched to an “after” value, and the differences are calculated. The differences have a normal distribution. Test at the 1% significance level.

Exercise 10.5.4

the mean difference of the system failures

Exercise 10.5.5

Exercise 10.5.6

Exercise 10.5.7

Exercise 10.5.8

What conclusion can you draw about the software patch?

With a $p\text{-value} 0.0067$, we can reject the null hypothesis. There is enough evidence to support that the software patch is effective in reducing the number of system failures.

Use the following information to answer next five exercises. A study was conducted to test the effectiveness of a juggling class. Before the class started, six subjects juggled as many balls as they could at once. After the class, the same six subjects juggled as many balls as they could. The differences in the number of balls are calculated. The differences have a normal distribution. Test at the 1% significance level.

Exercise 10.5.9

Exercise 10.5.10

Exercise 10.5.11

What is the sample mean difference?

Exercise 10.5.12

This is a normal distribution curve with mean equal to zero. The values 0 and 1.67 are labeled on the horiztonal axis. A vertical line extends from 1.67 to the curve. The region under the curve to the right of the line is shaded to represent p-value = 0.0021.

Exercise 10.5.13

What conclusion can you draw about the juggling class?

Use the following information to answer the next five exercises. A doctor wants to know if a blood pressure medication is effective. Six subjects have their blood pressures recorded. After twelve weeks on the medication, the same six subjects have their blood pressure recorded again. For this test, only systolic pressure is of concern. Test at the 1% significance level.

Exercise 10.5.14

$H_{0}: \mu_{d} \geq 0$

Exercise 10.5.15

Exercise 10.5.16

Exercise 10.5.17

Exercise 10.5.18

What is the conclusion?

We decline to reject the null hypothesis. There is not sufficient evidence to support that the medication is effective.

Bringing It Together

Use the following information to answer the next ten exercises. indicate which of the following choices best identifies the hypothesis test.

independent group means, population standard deviations and/or variances known

Exercise 10.5.19

A powder diet is tested on 49 people, and a liquid diet is tested on 36 different people. The population standard deviations are two pounds and three pounds, respectively. Of interest is whether the liquid diet yields a higher mean weight loss than the powder diet.

Exercise 10.5.20

A new chocolate bar is taste-tested on consumers. Of interest is whether the proportion of children who like the new chocolate bar is greater than the proportion of adults who like it.

Exercise 10.5.21

Exercise 10.5.22

A football league reported that the mean number of touchdowns per game was five. A study is done to determine if the mean number of touchdowns has decreased.

Exercise 10.5.23

A study is done to determine if students in the California state university system take longer to graduate than students enrolled in private universities. One hundred students from both the California state university system and private universities are surveyed. From years of research, it is known that the population standard deviations are 1.5811 years and one year, respectively.

Exercise 10.5.24

According to a YWCA Rape Crisis Center newsletter, 75% of rape victims know their attackers. A study is done to verify this.

Exercise 10.5.25

According to a recent study, U.S. companies have a mean maternity-leave of six weeks.

Exercise 10.5.26

A recent drug survey showed an increase in use of drugs and alcohol among local high school students as compared to the national percent. Suppose that a survey of 100 local youths and 100 national youths is conducted to see if the proportion of drug and alcohol use is higher locally than nationally.

Exercise 10.5.27

A new SAT study course is tested on 12 individuals. Pre-course and post-course scores are recorded. Of interest is the mean increase in SAT scores. The following data are collected:

Exercise 10.5.28

University of Michigan researchers reported in the Journal of the National Cancer Institute that quitting smoking is especially beneficial for those under age 49. In this American Cancer Society study, the risk (probability) of dying of lung cancer was about the same as for those who had never smoked.

Exercise 10.5.29

Lesley E. Tan investigated the relationship between left-handedness vs. right-handedness and motor competence in preschool children. Random samples of 41 left-handed preschool children and 41 right-handed preschool children were given several tests of motor skills to determine if there is evidence of a difference between the children based on this experiment. The experiment produced the means and standard deviations shown Table . Determine the appropriate test and best distribution to use for that test.

Two independent means, normal distribution
Two independent means, Student’s-t distribution
Matched or paired samples, Student’s-t distribution
Two population proportions, normal distribution

Exercise 10.5.30

A golf instructor is interested in determining if her new technique for improving players’ golf scores is effective. She takes four (4) new students. She records their 18-hole scores before learning the technique and then after having taken her class. She conducts a hypothesis test. The data are as Table .

a test of two independent means.
a test of two proportions.
a test of a single mean.
a test of a single proportion.

If you are using a Student's t -distribution for the homework problems, including for paired data, you may assume that the underlying population is normally distributed. (When using these tests in a real situation, you must first prove that assumption, however.)

Ten individuals went on a low–fat diet for 12 weeks to lower their cholesterol. The data are recorded in Table . Do you think that their cholesterol levels were significantly lowered?

$p\text{-value} = 0.1494$

At the 5% significance level, there is insufficient evidence to conclude that the medication lowered cholesterol levels after 12 weeks.

Use the following information to answer the next two exercises. A new AIDS prevention drug was tried on a group of 224 HIV positive patients. Forty-five patients developed AIDS after four years. In a control group of 224 HIV positive patients, 68 developed AIDS after four years. We want to test whether the method of treatment reduces the proportion of patients that develop AIDS after four years or if the proportions of the treated group and the untreated group stay the same.

Let the subscript $t =$ treated patient and $ut =$ untreated patient.

The appropriate hypotheses are:

$H_{0}: p_{t} < p_{ut}$ and $H_{a}: p_{t} \geq p_{ut}$
$H_{0}: p_{t} \leq p_{ut}$ and $H_{a}: p_{t} > p_{ut}$
$H_{0}: p_{t} = p_{ut}$ and $H_{a}: p_{t} \neq p_{ut}$
$H_{0}: p_{t} = p_{ut}$ and $H_{a}: p_{t} < p_{ut}$

If the $p\text{-value}$ is 0.0062 what is the conclusion (use $\alpha = 0.05$)?

The method has no effect.
There is sufficient evidence to conclude that the method reduces the proportion of HIV positive patients who develop AIDS after four years.
There is sufficient evidence to conclude that the method increases the proportion of HIV positive patients who develop AIDS after four years.
There is insufficient evidence to conclude that the method reduces the proportion of HIV positive patients who develop AIDS after four years.

Use the following information to answer the next two exercises. An experiment is conducted to show that blood pressure can be consciously reduced in people trained in a “biofeedback exercise program.” Six subjects were randomly selected and blood pressure measurements were recorded before and after the training. The difference between blood pressures was calculated (after - before) producing the following results: $\bar{x}_{d} = -10.2$ $s_{d} = 8.4$. Using the data, test the hypothesis that the blood pressure has decreased after the training.

The distribution for the test is:

$N(-10.2, 8.4)$
$N\left(-10.2, \frac{8.4}{\sqrt{6}}\right)$

If $\alpha = 0.05$, the $p\text{-value}$ and the conclusion are

0.0014; There is sufficient evidence to conclude that the blood pressure decreased after the training.
0.0014; There is sufficient evidence to conclude that the blood pressure increased after the training.
0.0155; There is sufficient evidence to conclude that the blood pressure decreased after the training.
0.0155; There is sufficient evidence to conclude that the blood pressure increased after the training.

A golf instructor is interested in determining if her new technique for improving players’ golf scores is effective. She takes four new students. She records their 18-hole scores before learning the technique and then after having taken her class. She conducts a hypothesis test. The data are as follows.

The correct decision is:

Reject $H_{0}$.
Do not reject the $H_{0}$.

A local cancer support group believes that the estimate for new female breast cancer cases in the south is higher in 2013 than in 2012. The group compared the estimates of new female breast cancer cases by southern state in 2012 and in 2013. The results are in Table .

Test: two matched pairs or paired samples ( t -test)

Random variable: $\bar{X}_{d}$

Distribution: $t_{12}$

$H_{0}: \mu_{d} = 0 H_{a}: \mu_{d} > 0$

The mean of the differences of new female breast cancer cases in the south between 2013 and 2012 is greater than zero. The estimate for new female breast cancer cases in the south is higher in 2013 than in 2012.

Decision: Reject $H_{0}$

Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that there was a higher estimate of new female breast cancer cases in 2013 than in 2012.

A traveler wanted to know if the prices of hotels are different in the ten cities that he visits the most often. The list of the cities with the corresponding hotel prices for his two favorite hotel chains is in Table. Test at the 1% level of significance.

A politician asked his staff to determine whether the underemployment rate in the northeast decreased from 2011 to 2012. The results are in Table.

Test: matched or paired samples ( t -test)

Difference data: $\{–0.9, –3.7, –3.2, –0.5, 0.6, –1.9, –0.5, 0.2, 0.6, 0.4, 1.7, –2.4, 1.8\}$

Random Variable: $\bar{X}_{d}$

Distribution: $H_{0}: \mu_{d} = 0 H_{a}: \mu_{d} < 0$

The mean of the differences of the rate of underemployment in the northeastern states between 2012 and 2011 is less than zero. The underemployment rate went down from 2011 to 2012.

Graph: left-tailed.

$p\text{-value}: 0.1207$

Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that there was a decrease in the underemployment rates of the northeastern states from 2011 to 2012.

10.6: Hypothesis Testing for Two Means and Two Proportions

IMAGES

Hypothesis Testing: Upper, Lower, and Two Tailed Tests
Hypothesis Testing Example Two Sample t-Test
What Is a Two-Tailed Test? Definition and Example / STATISTICAL TABLES
p-value (Two tailed test) : Solved Example 2
Two Tailed Test Tutorial
PPT

VIDEO

1 tailed and 2 tailed Hypothesis
Lecture 53: One tailed and two tailed test and Testing hypothesis about mean
Evaluating One Tailed Hypothesis Testing at Different Critical Values
CRITICAL VALUE APPROACH TO TWO TAILED HYPOTHESIS TESTING L 151
One & Two-Tailed Test With Examples
Sta301 Lecture 38 Hypothesis Testing Part1

COMMENTS

Two-Tailed Hypothesis Tests: 3 Example Problems
H0 (Null Hypothesis): μ = 20 grams. HA (Alternative Hypothesis): μ ≠ 20 grams. This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal "≠" sign. The engineer believes that the new method will influence widget weight, but doesn't specify whether it will cause average weight to ...
One-Tailed and Two-Tailed Hypothesis Tests Explained
Two-tailed hypothesis tests are also known as nondirectional and two-sided tests because you can test for effects in both directions. When you perform a two-tailed test, you split the significance level percentage between both tails of the distribution. In the example below, I use an alpha of 5% and the distribution has two shaded regions of 2. ...
What Is a Two-Tailed Test? Definition and Example
Two-Tailed Test: A two-tailed test is a statistical test in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values ...
Two-Tailed Hypothesis Tests: 3 Example Problems
To test this, he can perform a one-tailed hypothesis test with the following null and alternative hypotheses: H 0 (Null Hypothesis): μ = 20 grams; H A (Alternative Hypothesis): μ ≠ 20 grams; This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal "≠" sign. The engineer believes that ...
Two Tailed Test: Definition, Examples
This video explains the difference between one and two tailed tests: For example, let's say you were running a z test with an alpha level of 5% (0.05). In a one tailed test, the entire 5% would be in a single tail. But with a two tailed test, that 5% is split between the two tails, giving you 2.5% (0.025) in each tail.
Hypothesis Testing
So let's perform the step -1 of hypothesis testing which is: Specify the Null (H0) and Alternate (H1) hypothesis. Null hypothesis (H0): The null hypothesis here is what currently stated to be true about the population. In our case it will be the average height of students in the batch is 100. H0 : μ = 100.
Hypothesis Testing: Upper-, Lower, and Two Tailed Tests
The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645. The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05.
One-tailed and two-tailed tests (video)
A one tailed test does not leave more room to conclude that the alternative hypothesis is true. The benefit (increased certainty) of a one tailed test doesn't come free, as the analyst must know "something more", which is the direction of the effect, compared to a two tailed test. ( 3 votes)
Hypothesis testing: One-tailed and two-tailed tests
At this point, you might use a statistical test, like unpaired or 2-sample t-test, to see if there's a significant difference between the two groups' means. Typically, an unpaired t-test starts with two hypotheses. The first hypothesis is called the null hypothesis, and it basically says there's no difference in the means of the two groups.
11.4: One- and Two-Tailed Tests
The one-tailed hypothesis is rejected only if the sample proportion is much greater than $0.5$. The alternative hypothesis in the two-tailed test is $\pi \neq 0.5$. In the one-tailed test it is $\pi > 0.5$. You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data.
Hypothesis Testing
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
Two-Tailed Test in Statistics
A two-tailed hypothesis test example: A machine is used to fill bags with coffee, and each bag is 1 kg. A randomly selected sample of 30 bags has a mean weight of 1.01 kg with a standard deviation ...
S.3.2 Hypothesis Testing (P-Value Approach)
Two-Tailed. In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead of equaling -2.5.The P-value for conducting the two-tailed test H 0: μ = 3 versus H A: μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean ...
Setting Up Hypotheses: One- and Two-Tailed Tests
The one-tailed hypothesis is rejected only if the sample proportion is much greater than 0.5 0.5. The alternative hypothesis in the two-tailed test is n ≠ 0.5 n ≠ 0.5. In the one-tailed test it is π > 0.5 π > 0.5. You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data.
Data analysis: hypothesis testing: 4.2 Two-tailed tests
The term 'two-tailed' comes from the fact that the statistical test used to evaluate the hypothesis is based on the assumption that the difference or relationship could occur in either direction, resulting in two 'tails' in the probability distribution. Using the coffee foam example (from Activity 1), you have the following set of ...
S.3.3 Hypothesis Testing Examples
If the biologist set her significance level $\alpha$ at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3. Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis.
Statistics
The test statistic is used to decide the outcome of the hypothesis test. The test statistic is a standardized value calculated from the sample. The formula for the test statistic (TS) of a population mean is: x ¯ − μ s ⋅ n. x ¯ − μ is the difference between the sample mean ( x ¯) and the claimed population mean ( μ ).
PDF Two Samples Hypothesis Testing
• In a previous learning module, we discussed how to perform hypothesis tests for a single variable x. • Here, we extend the concept of hypothesis testing to the comparison of two variables x A and x B. Two Samples Hypothesis Testing when n is the same for the two Samples . Two-tailed paired samples hypothesis test: • In engineering ...
Two Tailed Hypothesis
What is one-tailed and two-tailed Hypothesis test with example? In hypothesis testing, the choice between a one-tailed and a two-tailed test is determined by the nature of the research question. One-tailed hypothesis: This tests for a specific direction of the effect. It predicts the direction of the relationship or difference between groups.
One- and two-tailed tests
In coin flipping, the null hypothesis is a sequence of Bernoulli trials with probability 0.5, yielding a random variable X which is 1 for heads and 0 for tails, and a common test statistic is the sample mean (of the number of heads) ¯. If testing for whether the coin is biased towards heads, a one-tailed test would be used - only large numbers of heads would be significant.
10.E: Hypothesis Testing with Two Samples (Exercises)
Use the following information to answer the next 15 exercises: Indicate if the hypothesis test is for. independent group means, population standard deviations, and/or variances known. independent group means, population standard deviations, and/or variances unknown. matched or paired samples. single mean.

Two-Tailed Hypothesis Tests: 3 Example Problems

Example 1: Factory Widgets

Example 2: Plant Growth

Example 3: Studying Method

Additional Resources

Published by Zach

What Is a Two-Tailed Test?

What Is a Two-Tailed Test? Definition and Example

Key Takeaways

Example of a Two-Tailed Test

How Is a Two-Tailed Test Designed?

What Is the Difference Between a Two-Tailed and One-Tailed Test?

What Is a Z-score?

Two-Tailed Hypothesis Tests: 3 Example Problems

Example 1: Factory Widgets

Example 2: Plant Growth

Example 3: Studying Method

Additional Resources

Statistics vs. Probability: What’s the Difference?

Hypothesis Testing for Means & Proportions

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

Statistics and probability

One-tailed and two-tailed tests

Want to join the conversation?

Video transcript

Have a language expert improve your writing

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Table of contents

Prevent plagiarism. Run a free check.

Cite this Scribbr article

Is this article helpful?

Rebecca Bevans

MA121: Introduction to Statistics

Setting Up Hypotheses

My OpenLearn Profile

About this free course

4.2 Two-tailed tests

User Preferences

Keyboard Shortcuts

Brinell Hardness Scores

Descriptive Statistics

Height of Sunflowers

Gum Thickness

Statistics Tutorial

Hypothesis Testing a Mean

1. Checking the Conditions

2. Defining the Claims

3. Deciding the Significance Level

4. Calculating the Test Statistic

5. Concluding

The Critical Value Approach

The P-Value Approach

Calculating a P-Value for a Hypothesis Test with Programming

Left-Tailed and Two-Tailed Tests

COLOR PICKER

Contact Sales

Report Error

Top Tutorials

Two Tailed Hypothesis

What is Two Tailed Hypothesis? – Definition

What is an example of a Two Tailed hypothesis statement?

Two Tailed Hypothesis Statement Examples

Two Tailed Hypothesis Statement Examples in Research

Two Tailed Testing Hypothesis Statement Examples

How do you know if a hypothesis is two-tailed?

What is one-tailed and two-tailed Hypothesis test with example?

What is a two-tailed hypothesis in psychology?

What does a two-tailed alternative hypothesis look like?

How do you write a Two-Tailed hypothesis statement? – A Step by Step Guide

Tips for Writing Two Tailed Hypothesis

AI Generator

10.E: Hypothesis Testing with Two Samples (Exercises)

10.1: Introduction

10.3: Two Population Means with Known Standard Deviations

10.4: Comparing Two Independent Population Proportions

10.5: Matched or Paired Samples

Bringing It Together

10.6: Hypothesis Testing for Two Means and Two Proportions

IMAGES

VIDEO