assignment fill in the blank exercise 15.03

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

15.2: Exercises

• Last updated
• Save as PDF
• Page ID 52800

• Laird C. Sheldahl
• Mt. Hood Community College

LAB 15 EXERCISES \(\PageIndex{1}\)

Identify the 3 major components of a hematocrit:

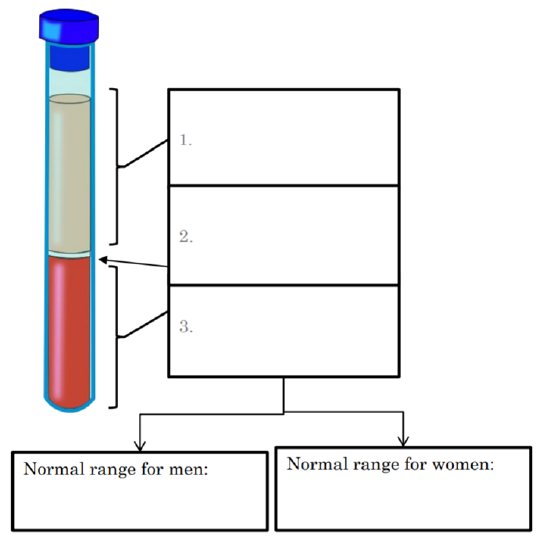
Match the following items to their location: Albumin, Erythrocytes, Glucose, Chloride, Antibodies, Platelets, Monocytes, Neutrophils, Fibrinogen

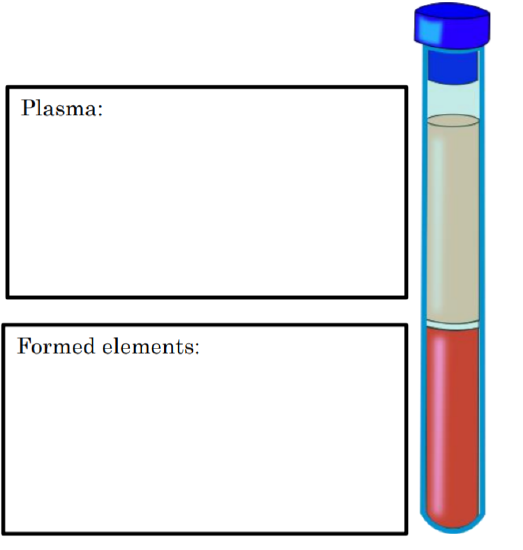
LAB 15 EXERCISES \(\PageIndex{2}\)

Blood cell identification.

Identify the formed elements by their picture below:

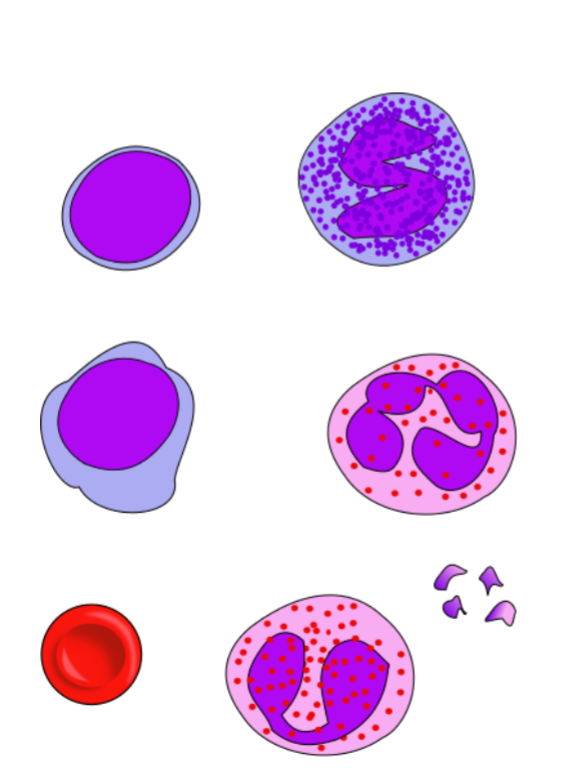
Label the image below

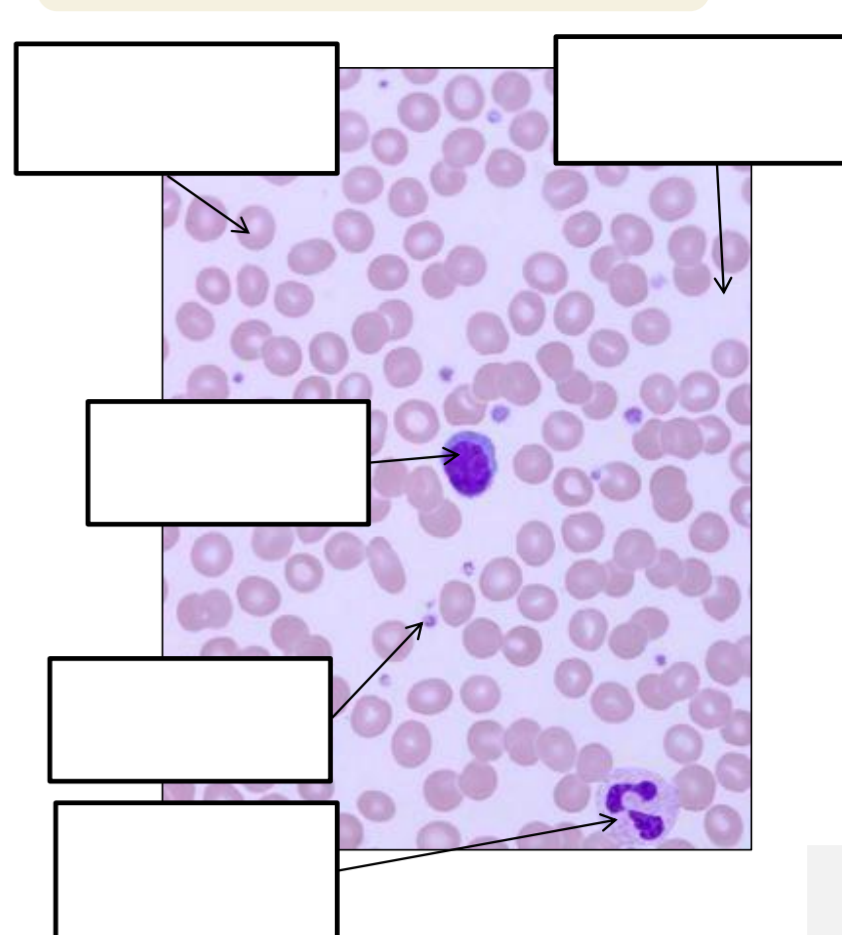
Fill in the Following Table

LAB 15 EXERCISES \(\PageIndex{3}\)

1.     Obtain a slide of blood from the slide box at your table.

2.     Follow the checklist above to set up your slide for viewing.

3.     View the slide on the objective which provides the best view (400X). Find the representative object.

4.     In the circle below the name, draw a representative sample of the blood cell, taking care to correctly and clearly draw their true shape in the slide. Draw your structures proportionately to their size in your microscope’s field of view.

Repeat this for each of the blood cell types seen below

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

15.E: Microbial Mechanisms of Pathogenicity (Exercises)

• Last updated
• Save as PDF
• Page ID 8330

15.1: Characteristics of Infectious Diseases

In an infection, a microorganism enters a host and begins to multiply. Some infections cause disease, which is any deviation from the normal function or structure of the host. Signs of a disease are objective and are measured. Symptoms of a disease are subjective and are reported by the patient. Diseases can either be noninfectious (due to genetics and environment) or infectious (due to pathogens).

Multiple Choice

Which of the following would be a sign of an infection?

• muscle aches

Which of the following is an example of a noncommunicable infectious disease?

• infection with a respiratory virus
• food poisoning due to a preformed bacterial toxin in food
• skin infection acquired from a dog bite
• infection acquired from the stick of a contaminated needle

During an oral surgery, the surgeon nicked the patient’s gum with a sharp instrument. This allowed Streptococcus , a bacterium normally present in the mouth, to gain access to the blood. As a result, the patient developed bacterial endocarditis (an infection of the heart). Which type of disease is this?

Which period is the stage of disease during which the patient begins to present general signs and symptoms?

• convalescence

A communicable disease that can be easily transmitted from person to person is which type of disease?

Fill in the Blank

A difference between an acute disease and chronic disease is that chronic diseases have an extended period of __________.

A person steps on a rusty nail and develops tetanus. In this case, the person has acquired a(n) __________ disease.

noncommunicable

Short Answer

Brian goes to the hospital after not feeling well for a week. He has a fever of 38 °C (100.4 °F) and complains of nausea and a constant migraine. Distinguish between the signs and symptoms of disease in Brian’s case.

Critical Thinking

Two periods of acute disease are the periods of illness and period of decline. (a) In what way are both of these periods similar? (b) In terms of quantity of pathogen, in what way are these periods different? (c) What initiates the period of decline?

In July 2015, a report 1 was released indicating the gram-negative bacterium Pseudomonas aeruginosa was found on hospital sinks 10 years after the initial outbreak in a neonatal intensive care unit. P. aeruginosa usually causes localized ear and eye infections but can cause pneumonia or septicemia in vulnerable individuals like newborn babies. Explain how the current discovery of the presence of this reported P. aeruginosa could lead to a recurrence of nosocomial disease.

15.2: How Pathogens Cause Disease

Koch’s postulates are used to determine whether a particular microorganism is a pathogen. Molecular Koch’s postulates are used to determine what genes contribute to a pathogen’s ability to cause disease. Virulence, the degree to which a pathogen can cause disease, can be quantified by calculating either the ID50 or LD50 of a pathogen on a given population. Primary pathogens are capable of causing pathological changes associated with disease in a healthy individual.

Which of the following is a pathogen that could not be identified by the original Koch’s postulates?

• Staphylococcus aureus
• Pseudomonas aeruginosa
• Human immunodeficiency virus
• Salmonella enterica serovar Typhimurium

Pathogen A has an ID 50 of 50 particles, pathogen B has an ID 50 of 1,000 particles, and pathogen C has an ID 50 of 1 × 10 6 particles. Which pathogen is most virulent?

Which of the following choices lists the steps of pathogenesis in the correct order?

• invasion, infection, adhesion, exposure
• adhesion, exposure, infection, invasion
• exposure, adhesion, invasion, infection
• disease, infection, exposure, invasion

A(n) __________ pathogen causes disease only when conditions are favorable for the microorganism because of transfer to an inappropriate body site or weakened immunity in an individual.

opportunistic

The concentration of pathogen needed to kill 50% of an infected group of test animals is the __________.

A(n) __________ infection is a small region of infection from which a pathogen may move to another part of the body to establish a second infection.

Cilia, fimbriae, and pili are all examples of structures used by microbes for __________.

Diseases that involve biofilm-producing bacteria are of serious concern. They are not as easily treated compared with those involving free-floating (or planktonic) bacteria. Explain three reasons why biofilm formers are more pathogenic.

A microbiologist has identified a new gram-negative pathogen that causes liver disease in rats. She suspects that the bacterium’s fimbriae are a virulence factor. Describe how molecular Koch’s postulates could be used to test this hypothesis.

Acupuncture is a form of alternative medicine that is used for pain relief. Explain how acupuncture could facilitate exposure to pathogens.

15.3: Virulence Factors

Virulence factors contribute to a pathogen’s ability to cause disease. Exoenzymes and toxins allow pathogens to invade host tissue and cause tissue damage. Exoenzymes are classified according to the macromolecule they target and exotoxins are classified based on their mechanism of action. Bacterial toxins include endotoxin and exotoxins. Endotoxin is the lipid A component of the LPS of the gram-negative cell envelope. Exotoxins are proteins secreted mainly by gram-positive bacteria.

Which of the following would be a virulence factor of a pathogen?

• a surface protein allowing the pathogen to bind to host cells
• a secondary host the pathogen can infect
• a surface protein the host immune system recognizes
• the ability to form a provirus

You have recently identified a new toxin. It is produced by a gram-negative bacterium. It is composed mostly of protein, has high toxicity, and is not heat stable. You also discover that it targets liver cells. Based on these characteristics, how would you classify this toxin?

• superantigen

Which of the following applies to hyaluronidase?

• It acts as a spreading factor.
• It promotes blood clotting.
• It is an example of an adhesin.
• It is produced by immune cells to target pathogens.

Phospholipases are enzymes that do which of the following?

• degrade antibodies
• promote pathogen spread through connective tissue.
• degrade nucleic acid to promote spread of pathogen
• degrade cell membranes to allow pathogens to escape phagosomes

The glycoprotein adhesion gp120 on HIV must interact with __________ on some immune cells as the first step in the process of infecting the cell.

Adhesins are usually located on __________ of the pathogen and are composed mainly of __________ and __________.

surface; proteins; sugars

The Shiga and diphtheria toxins target __________ in host cells.

protein synthesis

Antigenic __________ is the result of reassortment of genes responsible for the production of influenza virus spike proteins between different virus particles while in the same host, whereas antigenic __________ is the result of point mutations in the spike proteins.

shift; drift

Two types of toxins are hemolysins and leukocidins. (a) How are these toxins similar? (b) How do they differ?

Imagine that a mutation in the gene encoding the cholera toxin was made. This mutation affects the A-subunit, preventing it from interacting with any host protein. (a) Would the toxin be able to enter into the intestinal epithelial cell? (b) Would the toxin be able to cause diarrhea?

15.4: Aseptic Techniques

Fungal and parasitic pathogens use pathogenic mechanisms and virulence factors that are similar to those of bacterial pathogens. Fungi initiate infections through the interaction of adhesins with receptors on host cells. Some fungi produce toxins and exoenzymes involved in disease production and capsules that provide protection of phagocytosis. Protozoa adhere to target cells through complex mechanisms and can cause cellular damage through release of cytopathic substances.

Which of the following is a major virulence factor for the fungal pathogen Cryptococcus?

• collagenase

Which of the following pathogens undergoes antigenic variation to avoid immune defenses?

• Cryptococcus

Candida can invade tissue by producing the exoenzymes __________ and __________.

protease and phospholipase

The larval form of Schistosoma mansoni uses a __________ to help it gain entry through intact skin.

Describe the virulence factors associated with the fungal pathogen Aspergillus.

Explain how helminths evade the immune system.

• 1 C. Owens. “ P. aeruginosa survives in sinks 10 years after hospital outbreak.” 2015. http://www.healio.com/infectious-disease/nosocomial-infections/news/online/%7B5afba909-56d9-48cc-a9b0-ffe4568161e8%7D/p-aeruginosa-survives-in-sinks-10-years-after-hospital-outbreak

Past Simple and Continuous (15.03.10)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

15.2E: Exercises for Section 15.2

• Last updated
• Save as PDF
• Page ID 67163

• Gilbert Strang & Edwin “Jed” Herman

1) The region \(D\) bounded by \(y = x^3, \space y = x^3 + 1, \space x = 0,\) and \(x = 1\) as given in the following figure.

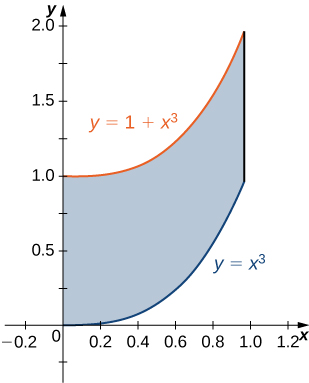
a. Classify this region as vertically simple (Type I) or horizontally simple (Type II).

b. Find the area of the region \(D\).

c. Find the average value of the function \(f(x,y) = 3xy\) on the region graphed in the previous exercise.

2) The region \(D\) bounded by \(y = \sin x, \space y = 1 + \sin x, \space x = 0\), and \(x = \frac{\pi}{2}\) as given in the following figure.

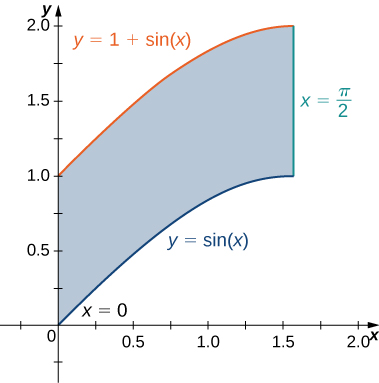
c. Find the average value of the function \(f(x,y) = \cos x\) on the region \(D\).

3) The region \(D\) bounded by \(x = y^2 - 1\) and \(x = \sqrt{1 - y^2}\) as given in the following figure.

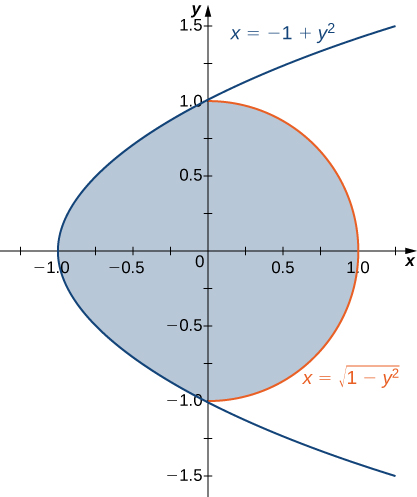
b. Find the volume of the solid under the graph of the function \(f(x,y) = xy + 1\) and above the region \(D\).

4) The region \(D\) bounded by \(y = 0, \space x = -10 + y,\) and \(x = 10 - y\) as given in the following figure.

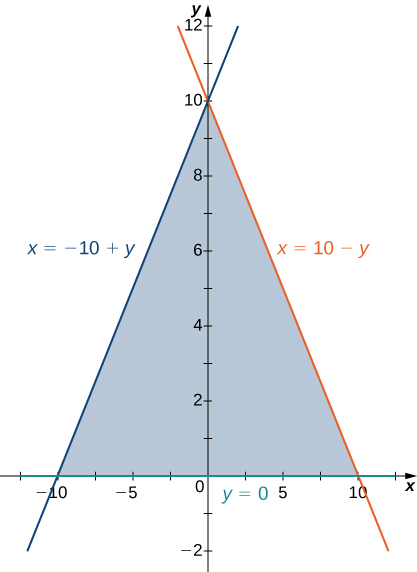
b. Find the volume of the solid under the graph of the function \(f(x,y) = x + y\) and above the region in the figure from the previous exercise.

5) The region \(D\) bounded by \(y = 0, \space x = y - 1, \space x = \frac{\pi}{2}\) as given in the following figure.

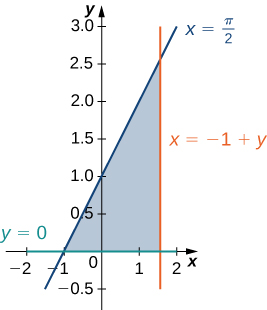
Classify this region as vertically simple (Type I) or horizontally simple (Type II).

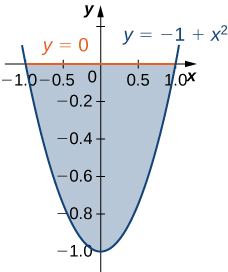
6) The region \(D\) bounded by \(y = 0\) and \(y = x^2 - 1\) as given in the following figure.

7) Let \(D\) be the region bounded by the curves of equations \(y = \cos x\) and \(y = 4 - x^2\) and the \(x\)-axis. Explain why \(D\) is neither of Type I nor II.

8) Let \(D\) be the region bounded by the curves of equations \(y = x, \space y = -x\) and \(y = 2 - x^2\). Explain why \(D\) is neither of Type I nor II.

In exercises 9 - 14, evaluate the double integral \(\displaystyle \iint_D f(x,y) \,dA\) over the region \(D\).

9) \(f(x,y) = 1\) and

\(D = \big\{(x,y)| \, 0 \leq x \leq \frac{\pi}{2}, \space \sin x \leq y \leq 1 + \sin x \big\}\)

10) \(f(x,y) = 2\) and

\(D = \big\{(x,y)| \, 0 \leq y \leq 1, \space y - 1 \leq x \leq \arccos y \big\}\)

11) \(f(x,y) = xy\) and

\(D = \big\{(x,y)| \, -1 \leq y \leq 1, \space y^2 - 1 \leq x \leq \sqrt{1 - y^2} \big\}\)

12) \(f(x,y) = \sin y\) and \(D\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((3,0)\)

13) \(f(x,y) = -x + 1\) and \(D\) is the triangular region with vertices \((0,0), \space (0,2)\), and \((2,2)\)

14) \(f(x,y) = 2x + 4y\) and

\(D = \big\{(x,y)|\, 0 \leq x \leq 1, \space x^3 \leq y \leq x^3 + 1 \big\}\)

In exercises 15 - 20, evaluate the iterated integrals.

15) \(\displaystyle \int_0^1 \int_{2\sqrt{x}}^{2\sqrt{x}+1} (xy + 1) \,dy \space dx\)

16) \(\displaystyle \int_0^3 \int_{2x}^{3x} (x + y^2) \,dy \space dx\)

17) \(\displaystyle \int_1^2 \int_{-u^2-1}^{-u} (8 uv) \,dv \space du\)

18) \(\displaystyle \int_e^{e^2} \int_{\ln u}^2 (v + \ln u) \,dv \space du\)

19) \(\displaystyle \int_0^{1/2} \int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}} 4 \,dx \space dy\)

20) \(\displaystyle \int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} (2x + 4y^3) \,dx \space dy\)

21) Let \(D\) be the region bounded by \(y = 1 - x^2, \space y = 4 - x^2\), and the \(x\)- and \(y\)-axes.

a. Show that \(\displaystyle \iint_D x\,dA = \int_0^1 \int_{1-x^2}^{4-x^2} x \space dy \space dx + \int_1^2 \int_0^{4-x^2} x \space dy \space dx\) by dividing the region \(D\) into two regions of Type I.

b. Evaluate the integral \(\displaystyle \iint_D x \,dA.\)

22) Let \(D\) be the region bounded by \(y = 1, \space y = x, \space y = \ln x\), and the \(x\)-axis.

a. Show that \(\displaystyle \iint_D y^2 \,dA = \int_{-1}^0 \int_{-x}^{2-x^2} y^2 dy \space dx + \int_0^1 \int_x^{2-x^2} y^2 dy \space dx\) by dividing the region \(D\) into two regions of Type I, where \(D = \big\{(x,y)\,|\,y \geq x, y \geq -x, \space y \leq 2-x^2\big\}\).

b. Evaluate the integral \(\displaystyle \iint_D y^2 \,dA.\)

23) Let \(D\) be the region bounded by \(y = x^2\), \(y = x + 2\), and \(y = -x\).

a. Show that \(\displaystyle \iint_D x \, dA = \int_0^1 \int_{-y}^{\sqrt{y}} x \space dx \space dy + \int_1^4 \int_{y-2}^{\sqrt{y}} x \space dx \space dy\) by dividing the region \(D\) into two regions of Type II, where \(D = \big\{(x,y)\,|\,y \geq x^2, \space y \geq -x, \space y \leq x + 2\big\}\).

24) The region \(D\) bounded by \(x = 0, y = x^5 + 1\), and \(y = 3 - x^2\) is shown in the following figure. Find the area \(A(D)\) of the region \(D\).

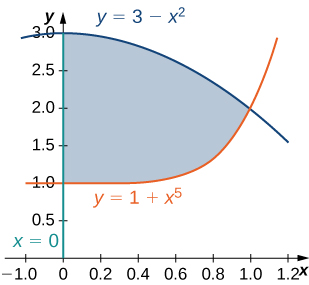
25) The region \(D\) bounded by \(y = \cos x, \space y = 4 + \cos x\), and \(x = \pm \frac{\pi}{3}\) is shown in the following figure. Find the area \(A(D)\) of the region \(D\).

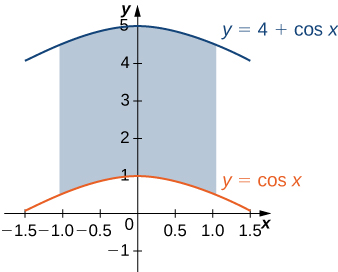
26) Find the area \(A(D)\) of the region \(D = \big\{(x,y)| \, y \geq 1 - x^2, y \leq 4 - x^2, \space y \geq 0, \space x \geq 0 \big\}\).

27) Let \(D\) be the region bounded by \( y = 1, \space y = x, \space y = \ln x\), and the \(x\)-axis. Find the area \(A(D)\) of the region \(D\).

28) Find the average value of the function \(f(x,y) = \sin y\) on the triangular region with vertices \((0,0), \space (0,3)\), and \((3,0)\).

29) Find the average value of the function \(f(x,y) = -x + 1\) on the triangular region with vertices \((0,0), \space (0,2)\), and \((2,2)\).

In exercises 30 - 33, change the order of integration and evaluate the integral.

30) \(\displaystyle \int_{-1}^{\pi/2} \int_0^{x+1} \sin x \, dy \, dx\)

31) \(\displaystyle \int_0^1 \int_{x-1}^{1-x} x \, dy \, dx\)

32) \(\displaystyle \int_{-1}^0 \int_{-\sqrt{y+1}}^{\sqrt{y+1}} y^2 dx \space dy\)

33) \(\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy\)

34) The region \(D\) is shown in the following figure. Evaluate the double integral \(\displaystyle \iint_D (x^2 + y) \,dA\) by using the easier order of integration.

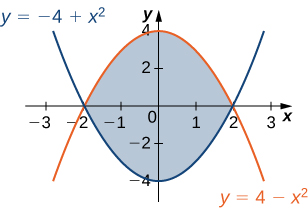
35) The region \(D\) is shown in the following figure. Evaluate the double integral \(\displaystyle \iint_D (x^2 - y^2) \,dA\) by using the easier order of integration.

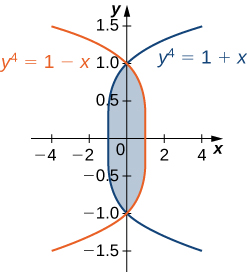
36) Find the volume of the solid under the surface \(z = 2x + y^2\) and above the region bounded by \(y = x^5\) and \(y = x\).

37) Find the volume of the solid under the plane \(z = 3x + y\) and above the region determined by \(y = x^7\) and \(y = x\).

38) Find the volume of the solid under the plane \(z = 3x + y\) and above the region bounded by \(x = \tan y, \space x = -\tan y\), and \(x = 1\).

39) Find the volume of the solid under the surface \(z = x^3\) and above the plane region bounded by \(x = \sin y, \space x = -\sin y\), and \(x = 1\).

40) Let \(g\) be a positive, increasing, and differentiable function on the interval \([a,b]\). Show that the volume of the solid under the surface \(z = g'(x)\) and above the region bounded by \(y = 0, \space y = g(x), \space x = a\), and \(x = b\) is given by \(\frac{1}{2}(g^2 (b) - g^2 (a))\).

41) Let \(g\) be a positive, increasing, and differentiable function on the interval \([a,b]\) and let \(k\) be a positive real number. Show that the volume of the solid under the surface \(z = g'(x)\) and above the region bounded by \(y = g(x), \space y = g(x) + k, \space x = a\), and \(x = b\) is given by \(k(g(b) - g(a)).\)

42) Find the volume of the solid situated in the first octant and determined by the planes \(z = 2\), \(z = 0, \space x + y = 1, \space x = 0\), and \(y = 0\).

43) Find the volume of the solid situated in the first octant and bounded by the planes \(x + 2y = 1\), \(x = 0, \space z = 4\), and \(z = 0\).

44) Find the volume of the solid bounded by the planes \(x + y = 1, \space x - y = 1, \space x = 0, \space z = 0\), and \(z = 10\).

45) Find the volume of the solid bounded by the planes \(x + y = 1, \space x - y = 1, \space x + y = -1\space x - y = -1, \space z = 1\), and \(z = 0\)

46) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the planes \(x + y + z = 1\) and \(x + y + 2z = 1\) respectively, and let \(S\) be the solid situated between \(S_1, \space S_2, \space x = 0\), and \(y = 0\).

• Find the volume of the solid \(S_1\).
• Find the volume of the solid \(S_2\).
• Find the volume of the solid \(S\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).

47) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the planes \(2x + 2y + z = 2\) and \(x + y + z = 1\) respectively, and let \(S\) be the solid situated between \(S_1, \space S_2, \space x = 0\), and \(y = 0\).

48) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the plane \(x + y + z = 2\) and under the sphere \(x^2 + y^2 + z^2 = 4\), respectively. If the volume of the solid \(S_2\) is \(\frac{4\pi}{3}\) determine the volume of the solid \(S\) situated between \(S_1\) and \(S_2\) by subtracting the volumes of these solids.

49) Let \(S_1\) and \(S_2\) be the solids situated in the first octant under the plane \(x + y + z = 2\) and bounded by the cylinder \(x^2 + y^2 = 4\), respectively.

• Find the volume of the solid \(S\) situated between \(S_1\) and \(S_2\) by subtracting the volumes of the solids \(S_1\) and \(S_2\).

50) [T] The following figure shows the region \(D\) bounded by the curves \(y = \sin x, \space x = 0\), and \(y = x^4\). Use a graphing calculator or CAS to find the \(x\)-coordinates of the intersection points of the curves and to determine the area of the region \(D\). Round your answers to six decimal places.

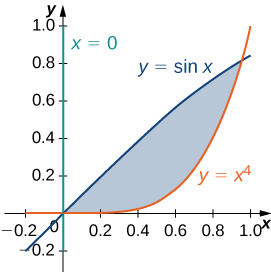
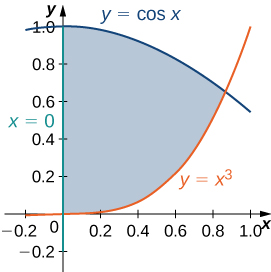
51) [T] The region \(D\) bounded by the curves \(y = \cos x, \space x = 0\), and \(y = x^3\) is shown in the following figure. Use a graphing calculator or CAS to find the \(x\)-coordinates of the intersection points of the curves and to determine the area of the region \(D\). Round your answers to six decimal places.

52) Suppose that \((X,Y)\) is the outcome of an experiment that must occur in a particular region \(S\) in the \(xy\)-plane. In this context, the region \(S\) is called the sample space of the experiment and \(X\) and \(Y\) are random variables. If \(D\) is a region included in \(S\), then the probability of \((X,Y)\) being in \(D\) is defined as \(P[(X,Y) \in D] = \iint_D p(x,y)dx \space dy\), where \(p(x,y)\) is the joint probability density of the experiment. Here, \(p(x,y)\) is a nonnegative function for which \(\iint_S p(x,y) dx \space dy = 1\). Assume that a point \((X,Y)\) is chosen arbitrarily in the square \([0,3] \times [0,3]\) with the probability density

\[p(x,y) = \frac{1}{9} (x,y) \in [0,3] \times [0,3],\nonumber \]

\[p(x,y) = 0 \space \text{otherwise}\nonumber \]

Find the probability that the point \((X,Y)\) is inside the unit square and interpret the result.

53) Consider \(X\) and \(Y\) two random variables of probability densities \(p_1(x)\) and \(p_2(x)\), respectively. The random variables \(X\) and \(Y\) are said to be independent if their joint density function is given by \(p_(x,y) = p_1(x)p_2(y)\). At a drive-thru restaurant, customers spend, on average, 3 minutes placing their orders and an additional 5 minutes paying for and picking up their meals. Assume that placing the order and paying for/picking up the meal are two independent events \(X\) and \(Y\). If the waiting times are modeled by the exponential probability densities

\[p_1(x) = \frac{1}{3}e^{-x/3} \space x\geq 0,\nonumber \]

\[p_1(x) = 0 \space \text{otherwise}\nonumber \]

\[p_2(y) = \frac{1}{5} e^{-y/5} \space y \geq 0\nonumber \]

\[p_2(y) = 0 \space \text{otherwise}\nonumber \]

respectively, the probability that a customer will spend less than 6 minutes in the drive-thru line is given by \(P[X + Y \leq 6] = \iint_D p(x,y) dx \space dy\), where \(D = {(x,y)|x \geq 0, \space y \geq 0, \space x + y \leq 6}\). Find \(P[X + Y \leq 6]\) and interpret the result.

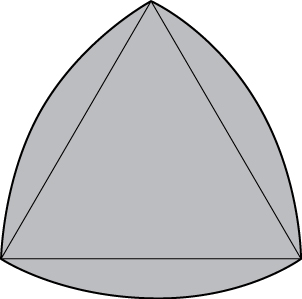
54) [T] The Reuleaux triangle consists of an equilateral triangle and three regions, each of them bounded by a side of the triangle and an arc of a circle of radius s centered at the opposite vertex of the triangle. Show that the area of the Reuleaux triangle in the following figure of side length \(s\) is \(\frac{s^2}{2}(\pi - \sqrt{3})\).

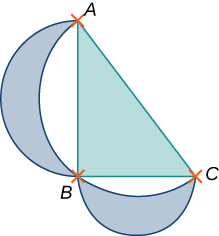
55) [T] Show that the area of the lunes of Alhazen , the two blue lunes in the following figure, is the same as the area of the right triangle \(ABC.\) The outer boundaries of the lunes are semicircles of diameters \(AB\) and \(AC\) respectively, and the inner boundaries are formed by the circumcircle of the triangle \(ABC\).

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Chi-Square Test of Independence | Formula, Guide & Examples

Chi-Square Test of Independence | Formula, Guide & Examples

Published on May 30, 2022 by Shaun Turney . Revised on June 22, 2023.

A chi-square (Χ 2 ) test of independence is a nonparametric hypothesis test . You can use it to test whether two categorical variables are related to each other.

The city decides to test two interventions: an educational flyer (pamphlet) or a phone call. They randomly select 300 households and randomly assign them to the flyer, phone call, or control group (no intervention). They’ll use the results of their experiment to decide which intervention to use for the whole city.

Table of contents

What is the chi-square test of independence, chi-square test of independence hypotheses, when to use the chi-square test of independence, how to calculate the test statistic (formula), how to perform the chi-square test of independence, when to use a different test, practice questions, other interesting articles, frequently asked questions about the chi-square test of independence.

A chi-square (Χ 2 ) test of independence is a type of Pearson’s chi-square test . Pearson’s chi-square tests are nonparametric tests for categorical variables. They’re used to determine whether your data are significantly different from what you expected.

You can use a chi-square test of independence, also known as a chi-square test of association, to determine whether two categorical variables are related. If two variables are related, the probability of one variable having a certain value is dependent on the value of the other variable.

The chi-square test of independence calculations are based on the observed frequencies, which are the numbers of observations in each combined group.

The test compares the observed frequencies to the frequencies you would expect if the two variables are unrelated. When the variables are unrelated, the observed and expected frequencies will be similar.

Contingency tables

When you want to perform a chi-square test of independence, the best way to organize your data is a type of frequency distribution table called a contingency table .

A contingency table, also known as a cross tabulation or crosstab, shows the number of observations in each combination of groups. It also usually includes row and column totals.

They reorganize the data into a contingency table:

They also visualize their data in a bar graph:

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The chi-square test of independence is an inferential statistical test, meaning that it allows you to draw conclusions about a population based on a sample . Specifically, it allows you to conclude whether two variables are related in the population.

Like all hypothesis tests, the chi-square test of independence evaluates a null and alternative hypothesis. The hypotheses are two competing answers to the question “Are variable 1 and variable 2 related?”

• Null hypothesis ( H 0 ): Variable 1 and variable 2 are not related in the population; The proportions of variable 1 are the same for different values of variable 2.
• Alternative hypothesis ( H a ): Variable 1 and  variable 2 are related in the population; The proportions of variable 1 are not the same for different values of  variable 2.

You can use the above sentences as templates. Replace variable 1 and variable 2 with the names of your variables.

• Null hypothesis ( H 0 ): Whether a household recycles and the type of intervention they receive are not related in the population; The proportion of households that recycle is the same for all interventions.
• Alternative hypothesis ( H a ):  Whether a household recycles and the type of intervention they receive are related in the population; The proportion of households that recycle is not the same for all interventions.

Expected values

A chi-square test of independence works by comparing the observed and the expected frequencies. The expected frequencies are such that the proportions of one variable are the same for all values of the other variable.

You can calculate the expected frequencies using the contingency table. The expected frequency for row r and column c is:

The following conditions are necessary if you want to perform a chi-square goodness of fit test:

• Chi-square tests of independence are usually performed on binary or nominal variables. They are sometimes performed on ordinal variables, although generally only on ordinal variables with fewer than five groups.
• The sample was random l y selected from the population .
• There are a minimum of five observations expected in each combined group.
• They want to test a hypothesis about the relationships between two categorical variables: whether a household recycles and the type of intervention.
• They recruited a random sample of 300 households.
• There are a minimum of five observations expected in each combined group. The smallest expected frequency is 12.57.

Pearson’s chi-square (Χ 2 ) is the test statistic for the chi-square test of independence:

• Χ 2 is the chi-square test statistic
• Σ is the summation operator (it means “take the sum of”)
• O is the observed frequency
• E is the expected frequency

The chi-square test statistic measures how much your observed frequencies differ from the frequencies you would expect if the two variables are unrelated. It is large when there’s a big difference between the observed and expected frequencies ( O − E in the equation).

Follow these five steps to calculate the test statistic:

Step 1: Create a table

Create a table with the observed and expected frequencies in two columns.

Step 2: Calculate O − E

In a new column called “ O −   E ”, subtract the expected frequencies from the observed frequencies.

Step 3: Calculate ( O – E ) 2

In a new column called “( O −   E ) 2 ”, square the values in the previous column.

Step 4: Calculate ( O − E ) 2 / E

In a final column called “(O − E) 2 / E”, divide the previous column by the expected frequencies.

Step 5: Calculate Χ 2

Finally, add up the values of the previous column to calculate the chi-square test statistic (Χ2).

Prevent plagiarism. Run a free check.

If the test statistic is big enough then you should conclude that the observed frequencies are not what you’d expect if the variables are unrelated. But what counts as big enough?

We compare the test statistic to a critical value from a chi-square distribution to decide whether it’s big enough to reject the null hypothesis that the two variables are unrelated. This procedure is called the chi-square test of independence.

Follow these steps to perform a chi-square test of independence (the first two steps have already been completed for the recycling example):

Step 1: Calculate the expected frequencies

Use the contingency table to calculate the expected frequencies following the formula:

Step 2: Calculate chi-square

Use the Pearson’s chi-square formula to calculate the test statistic :

Step 3: Find the critical chi-square value

You can find the critical value in a chi-square critical value table or using statistical software. You need to known two numbers to find the critical value:

• The degrees of freedom ( df ): For a chi-square test of independence, the df is (number of variable 1 groups − 1) * (number of variable 2 groups − 1).
• Significance level (α): By convention, the significance level is usually .05.

Step 4: Compare the chi-square value to the critical value

Is the test statistic big enough to reject the null hypothesis? Compare it to the critical value to find out.

Critical value = 5.99

Step 5: Decide whether to reject the null hypothesis

• The data allows you to reject the null hypothesis that the variables are unrelated and provides support for the alternative hypothesis that the variables are related.
• The data doesn’t allow you to reject the null hypothesis that the variables are unrelated and doesn’t provide support for the alternative hypothesis that the variables are related.

There is a significant difference between the observed frequencies and the frequencies expected if the two variables were unrelated ( p < .05). This suggests that the proportion of households that recycle is not the same for all interventions.

Step 6: Follow up with post hoc tests (optional)

If there are more than two groups in either of the variables and you rejected the null hypothesis, you may want to investigate further with post hoc tests. A post hoc test is a follow-up test that you perform after your initial analysis.

Similar to a one-way ANOVA with more than two groups, a significant difference doesn’t tell you which groups’ proportions are significantly different from each other.

One post hoc approach is to compare each pair of groups using chi-square tests of independence and a Bonferroni correction. A Bonferroni correction is when you divide your original significance level (usually .05) by the number of tests you’re performing.

• Since there are two intervention groups and two outcome groups for each test, there is (2 − 1) * (2 − 1) = 1 degree of freedom.
• There are three tests, so the significance level with a Bonferroni correction applied is α = .05 / 3 = .016.
• For a test of significance at α = .016 and df = 1, the Χ 2 critical value is 5.803.
• The chi-square value is greater than the critical value for the pamphlet vs control and phone call vs. control tests.

Based on these findings, the city concludes that a significantly greater proportion of households recycled after receiving a pamphlet or phone call compared to the control.

Several tests are similar to the chi-square test of independence, so it may not always be obvious which to use. The best choice will depend on your variables, your sample size, and your hypotheses.

When to use the chi-square goodness of fit test

There are two types of Pearson’s chi-square test. The chi-square test of independence is one of them, and the chi-square goodness of fit test is the other. The math is the same for both tests—the main difference is how you calculate the expected values.

You should use the chi-square goodness of fit test when you have one categorical variable and you want to test a hypothesis about its distribution .

When to use Fisher’s exact test

If you have a small sample size ( N < 100), Fisher’s exact test is a better choice. You should especially opt for Fisher’s exact test when your data doesn’t meet the condition of a minimum of five observations expected in each combined group.

When to use McNemar’s test

You should use McNemar’s test when you have a closely-related pair of categorical variables that each have two groups. It allows you to test whether the proportions of the variables are equal. This test is most often used to compare before and after observations of the same individuals.

When to use a G test

A G test and a chi-square test give approximately the same results. G tests can accommodate more complex experimental designs than chi-square tests. However, the tests are usually interchangeable and the choice is mostly a matter of personal preference.

One reason to prefer chi-square tests is that they’re more familiar to researchers in most fields.

Do you want to test your knowledge about the chi-square goodness of fit test? Download our practice questions and examples with the buttons below.

Download Word doc Download Google doc

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Statistical power
• Descriptive statistics
• Degrees of freedom
• Pearson correlation
• Null hypothesis

Methodology

• Double-blind study
• Case-control study
• Research ethics
• Data collection
• Hypothesis testing
• Structured interviews

Research bias

• Hawthorne effect
• Unconscious bias
• Recall bias
• Halo effect
• Self-serving bias
• Information bias

You can use the CHISQ.TEST() function to perform a chi-square test of independence in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value.

You can use the chisq.test() function to perform a chi-square test of independence in R. Give the contingency table as a matrix for the “x” argument. For example:

m = matrix(data = c(89, 84, 86, 9, 8, 24), nrow = 3, ncol = 2)

chisq.test(x = m)

The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence .

A chi-square distribution is a continuous probability distribution . The shape of a chi-square distribution depends on its degrees of freedom , k . The mean of a chi-square distribution is equal to its degrees of freedom ( k ) and the variance is 2 k . The range is 0 to ∞.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Chi-Square Test of Independence | Formula, Guide & Examples. Scribbr. Retrieved April 9, 2024, from https://www.scribbr.com/statistics/chi-square-test-of-independence/

Is this article helpful?

Shaun Turney

Other students also liked, chi-square (χ²) tests | types, formula & examples, chi-square (χ²) distributions | definition & examples, chi-square goodness of fit test | formula, guide & examples, what is your plagiarism score.

• Online Class
• Ask Doubt on Whatsapp
• Search Doubtnut

Complete Solutions to ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Fill in the blank of chapter WORK, ENERGY AND POWER of Class 12 book with complete answers and questions

Work is said to be negative when angle between force and displacement lies between _________ and __________ .

If the particle moves opposite to the conservative field, work done by the field will be ________ and so change in potential energy will be _________, i.e. potential energy wil ________ .

ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Fill in the blank questions and complete solutions for chapter WORK, ENERGY AND POWER of FIIT JEE PHYSICS (HINGLISH) of Class 12

All Exercises from FIITJEE Class 12 PHYSICS WORK, ENERGY AND POWER

• ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I)
• ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I) (ASSERTION REASONING TYPE)
• ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-II)
• ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Fill in the blank
• ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Numerical
• ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) Short Answer Type Question
• ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-I) True or False Type Questions
• ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-II & III)
• COMPREHENSIONS ( Comprehension-I)
• COMPREHENSIONS ( Comprehension-II)
• Illustration
• MATRIX MATCH TYPE
• NUMERICAL BASED QUESTIONS
• SOLVED PROBLEMS ( OBJECTIVE)
• SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
• SOLVED PROBLEMS (SUBJECTIVE )