class 10 ch 1 case study maths

Class 10 Maths Case Study Questions of Chapter 1 Real Numbers

Post author: studyrate
Post published:
Post category: class 10th
Post comments: 0 Comments

Case study Questions in the Class 10 Mathematics Chapter 1 are very important to solve for your exam. Class 10 Maths Chapter 1 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving Class 10 Maths Case Study Questions Chapter 1 Real Numbers

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Real Numbers Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers

Case Study/Passage-Based Questions

Case Study 1: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. (i) For what value of n, 4 n ends in 0?

Answer: (d) no value of n

(ii) If a is a positive rational number and n is a positive integer greater than 1, then for what value of n, a n is a rational number?

Answer: (c) for all n > 1

(iii) If x and yare two odd positive integers, then which of the following is true?

Answer: (d) both (a) and (b)

(iv) The statement ‘One of every three consecutive positive integers is divisible by 3’ is

Answer: (a) always true

(v) If n is any odd integer, then n2 – 1 is divisible by

Answer: (d) 8

Case Study 2: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.

(i) If two positive integers x and y are expressible in terms of primes as x =p 2 q 3 and y=p 3 q, then which of the following is true? (a) HCF = pq 2 x LCM (b) LCM = pq 2 x HCF (c) LCM = p 2 q x HCF (d) HCF = p 2 q x LCM

Answer: (b) LCM = pq2 x HCF

ii) A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p? (a) p is odd (b) p is even (c) p is not prime (d) both (b) and (c)

Answer: (d) both (b) and (c)

(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17

Answer: (d) 17

(iv) Find the least positive integer that on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500

Answer: (b) 12599

(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9

Answer: (a) 3

Case Study 3: Real numbers are an essential concept in mathematics that encompasses both rational and irrational numbers. Rational numbers are those that can be expressed as fractions, where the numerator and denominator are integers and the denominator is not zero. Examples of rational numbers include integers, decimals, and fractions. On the other hand, irrational numbers are those that cannot be expressed as fractions and have non-terminating and non-repeating decimal expansions. Examples of irrational numbers include √2, π (pi), and e. Real numbers are represented on the number line, which extends infinitely in both positive and negative directions. The set of real numbers is closed under addition, subtraction, multiplication, and division, making it a fundamental number system used in various mathematical operations and calculations.

Which numbers can be classified as rational numbers? a) Fractions b) Integers c) Decimals d) All of the above Answer: d) All of the above

What are rational numbers? a) Numbers that can be expressed as fractions b) Numbers that have non-terminating decimal expansions c) Numbers that extend infinitely in both positive and negative directions d) Numbers that cannot be expressed as fractions Answer: a) Numbers that can be expressed as fractions

What are examples of irrational numbers? a) √2, π (pi), e b) Integers, decimals, fractions c) Numbers with terminating decimal expansions d) Numbers that can be expressed as fractions Answer: a) √2, π (pi), e

How are real numbers represented? a) On the number line b) In complex mathematical formulas c) In algebraic equations d) In geometric figures Answer: a) On the number line

What operations are closed under the set of real numbers? a) Addition, subtraction, multiplication b) Subtraction, multiplication, division c) Addition, multiplication, division d) Addition, subtraction, multiplication, division Answer: d) Addition, subtraction, multiplication, division

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 1 Real Numbers with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Real Numbers Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

Class 10 Science Topper’s Answer Sheet Latest PDF Download FREE

Assertion reason questions class 10 science chapter 3 metals and non-metals, case study questions class 10 science chapter 11 the human eye and the colourful world, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 10 Maths Chapter 1 Real Numbers

Last modified on: 10 months ago
Reading Time: 7 Minutes

Question 1:

HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.

(ii) A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p? (a) p is odd (b) p is even (c) p is not prime (d) both (b) and (c)

(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17

(iv) Find the least positive integer which on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500

(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9

Question 2:

To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.

(i) What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B? (a) 144 (b) 128 (c) 288 (d) 272

(ii) If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is (a) 2 (b) 4 (c) 6 (d) 8

(iii) 36 can be expressed as a product of its primes as (a) (b) (c) (d)

(iv) 7 is a (a) Prime number (b) Composite number (c) Neither prime nor composite (d) None of the above

(v) If p and q are positive integers such that p = a and q= b, where a , b are prime numbers, then the LCM (p, q) is (a) ab (b) a 2 b 2 (c) a 3 b 2 (d) a 3 b 3

✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

CBSE Expert

CBSE Class 10 Maths: Case Study Questions of Chapter 1 Real Numbers PDF Download

Case study Questions in the Class 10 Mathematics Chapter 1 are very important to solve for your exam. Class 10 Maths Chapter 1 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 1 Real Numbers

Real Numbers Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers

Case Study/Passage-Based Questions

Question 1:

Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. (i) For what value of n, 4 n ends in 0?

Answer: (d) no value of n

(ii) If a is a positive rational number and n is a positive integer greater than 1, then for what value of n, a n is a rational number?

Answer: (c) for all n > 1

(iii) If x and yare two odd positive integers, then which of the following is true?

Answer: (d) both (a) and (b)

(iv) The statement ‘One of every three consecutive positive integers is divisible by 3’ is

Answer: (a) always true

(v) If n is any odd integer, then n2 – 1 is divisible by

Answer: (d) 8

Question 2:

Answer: (b) LCM = pq2 x HCF

Answer: (d) both (b) and (c)

(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17

Answer: (d) 17

(iv) Find the least positive integer that on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500

Answer: (b) 12599

(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9

Answer: (a) 3

Download India's best Exam Preparation App Now.

Key Features

Revision Notes
Important Questions
Previous Years Questions
Case-Based Questions
Assertion and Reason Questions

No thanks, I’m not interested!

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

Case Study on Real Numbers Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Real Numbers Class 10 Maths can use this page to download the PDF file.

The case study questions on Real Numbers are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Real Numbers case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Real Numbers Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Real Numbers, therefore, they prepared a set of solutions along with the case study questions on Real Numbers.

The case study on Real Numbers Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Real Numbers case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Real Numbers Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Real Numbers case study questions on Class 10 Maths - all those major reasons are discussed below:

To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Real Numbers Case study questions as it will help better prepare for the Class 10 board exam preparation.
Develop Problem-Solving Skills: Class 10 Maths Real Numbers case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
Understand Real-Life Applications: Several Real Numbers Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Real Numbers as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Real Numbers?

Students can choose their own way to answer Case Study on Real Numbers Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Real Numbers Case Study questions.

Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Real Numbers questions quickly.
Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Real Numbers Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Real Numbers?

A few essential things to know to solve Case Study Questions on Class 10 Real Numbers are -

Basic Formulas of Real Numbers: One of the most important things to know to solve Case Study Questions on Class 10 Real Numbers is to learn about the basic formulas or revise them before solving the case-based questions on Real Numbers.
To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Real Numbers case study questions.
Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Real Numbers Class 10 Maths?

Use Selfstudys.com to find Case Study on Real Numbers Class 10 Maths. For ease, here is a step-wise procedure to download the Real Numbers Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Real Numbers. To help others reach this page let them know these steps:

Open Selfstudys.com on your computer/laptop or Smartphone
Once the website gets loaded, click on the navigation button

Case Study on Real Numbers Class 10 Maths, Maths Case Study on Real Numbers Class 10, Class 10 Maths Case Study on Real Numbers, Real Numbers Case Study for Class 10 Maths, Case Study on Real Numbers Class 10 Maths with Solutions, Real Numbers Case Study Questions, Case Study Questions on Real Numbers, Case Study Questions on Class 10 Real Numbers

Find CBSE from the given menu

Click on Case Study

Choose Class 10
Search Maths and then navigate to the Real Numbers Class 10 Maths Case Study

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

One Last Step...

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

NCERT Solutions
NCERT Solutions for Class 10
NCERT Solutions for Class 10 Maths
Chapter 1: Real Numbers

NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

NCERT Solutions Class 10 Maths Chapter 1 Real Numbers are provided here. These solutions are prepared by our expert faculty to help students in their board exam preparations. They solve and provide the NCERT Solutions for Maths to aid the students in solving the problems easily. They also focus on preparing the solutions in such a way that it is easy to understand for the students. A detailed and step-wise explanation is given for each question given in the exercises of NCERT books.

Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 1 Real Numbers

Download most important questions for class 10 maths chapter – 1 real numbers.

Answers to the questions present in Real Numbers are given in the first chapter of Maths Solutions of NCERT Class 10. Here, students are introduced to several important concepts that will be useful for those who wish to pursue mathematics as a subject in their Class 11. Based on these solutions of Class 10 NCERT , students can prepare for their upcoming board exam. These solutions are helpful as they are in accordance with the CBSE Syllabus for 2023-24.

Chapter 1 Real Numbers
Chapter 2 Polynomials
Chapter 3 Pair of Linear Equations in Two Variables
Chapter 4 Quadratic Equations
Chapter 5 Arithmetic Progressions
Chapter 6 Triangles
Chapter 7 Coordinate Geometry
Chapter 8 Introduction to Trigonometry
Chapter 9 Some Applications of Trigonometry
Chapter 10 Circles
Chapter 11 Constructions
Chapter 12 Areas Related to Circles
Chapter 13 Surface Areas and Volumes
Chapter 14 Statistics
Chapter 15 Probability
Exercise 1.1 Chapter 1 Real Numbers
Exercise 1.2 Chapter 1 Real Numbers
Exercise 1.3 Chapter 1 Real Numbers
Exercise 1.4 Chapter 1 Real Numbers

Download PDF of NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

carouselExampleControls111

Previous Next

Access Answers to NCERT Class 10 Maths Chapter 1 – Real Numbers

Exercise 1.1 page: 7.

1. Use Euclid’s division algorithm to find the HCF of:

i. 135 and 225

ii. 196 and 38220

iii. 867 and 255

As you can see from the question, 225 is greater than 135. Therefore, by Euclid’s division algorithm, we have,

225 = 135 × 1 + 90

Now, remainder 90 ≠ 0, thus again using division lemma for 90, we get,

135 = 90 × 1 + 45

Again, 45 ≠ 0, repeating the above step for 45, we get,

90 = 45 × 2 + 0

The remainder is now zero, so our method stops here. Since, in the last step, the divisor is 45, therefore, HCF (225,135) = HCF (135, 90) = HCF (90, 45) = 45.

Hence, the HCF of 225 and 135 is 45.

In this given question, 38220>196, therefore the by applying Euclid’s division algorithm and taking 38220 as divisor, we get,

38220 = 196 × 195 + 0

We have already got the remainder as 0 here. Therefore, HCF(196, 38220) = 196.

Hence, the HCF of 196 and 38220 is 196.

As we know, 867 is greater than 255. Let us apply now Euclid’s division algorithm on 867, to get,

867 = 255 × 3 + 102

Remainder 102 ≠ 0, therefore taking 255 as divisor and applying the division lemma method, we get,

255 = 102 × 2 + 51

Again, 51 ≠ 0. Now 102 is the new divisor, so repeating the same step we get,

102 = 51 × 2 + 0

The remainder is now zero, so our procedure stops here. Since, in the last step, the divisor is 51, therefore, HCF (867,255) = HCF(255,102) = HCF(102,51) = 51.

Hence, the HCF of 867 and 255 is 51.

2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.

Let a be any positive integer and b = 6. Then, by Euclid’s algorithm, a = 6q + r, for some integer q ≥ 0, and r = 0, 1, 2, 3, 4, 5, because 0≤r<6.

Now substituting the value of r, we get,

If r = 0, then a = 6q

Similarly, for r= 1, 2, 3, 4 and 5, the value of a is 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5, respectively.

If a = 6q, 6q+2, 6q+4, then a is an even number and divisible by 2. A positive integer can be either even or odd Therefore, any positive odd integer is of the form of 6q+1, 6q+3 and 6q+5, where q is some integer.

3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?

Number of army contingent members = 616

Number of army band members = 32

If the two groups have to march in the same column, we have to find out the highest common factor between the two groups. HCF(616, 32), gives the maximum number of columns in which they can march.

By using Euclid’s algorithm to find their HCF, we get,

Since, 616>32, therefore,

616 = 32 × 19 + 8

Since, 8 ≠ 0, therefore, taking 32 as new divisor, we have,

32 = 8 × 4 + 0

Now we have got remainder as 0, therefore, HCF (616, 32) = 8.

Hence, the maximum number of columns in which they can march is 8.

4. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Let x be any positive integer and y = 3.

By Euclid’s division algorithm, then,

x = 3q + r for some integer q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.

Therefore, x = 3q, 3q+1 and 3q+2

Now as per the question given, by squaring both the sides, we get,

x 2 = (3q) 2 = 9q 2 = 3 × 3q 2

Let 3q 2 = m

Therefore, x 2 = 3m ……………………..(1)

x 2 = (3q + 1) 2 = (3q) 2 +1 2 +2×3q×1 = 9q 2 + 1 +6q = 3(3q 2 +2q) +1

Substitute, 3q 2 +2q = m, to get,

x 2 = 3m + 1 ……………………………. (2)

x 2 = (3q + 2) 2 = (3q) 2 +2 2 +2×3q×2 = 9q 2 + 4 + 12q = 3 (3q 2 + 4q + 1)+1

Again, substitute, 3q 2 +4q+1 = m, to get,

x 2 = 3m + 1…………………………… (3)

Hence, from equation 1, 2 and 3, we can say that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

x = 3q+r, where q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.

Therefore, putting the value of r, we get,

Now, by taking the cube of all the three above expressions, we get,

Case (i): When r = 0, then,

x 2 = (3q) 3 = 27q 3 = 9(3q 3 )= 9m; where m = 3q 3

Case (ii): When r = 1, then,

x 3 = (3q+1) 3 = (3q) 3 +1 3 +3×3q×1(3q+1) = 27q 3 +1+27q 2 +9q

Taking 9 as common factor, we get,

x 3 = 9(3q 3 +3q 2 +q)+1

Putting = m, we get,

Putting (3q 3 +3q 2+ q) = m, we get ,

Case (iii): When r = 2, then,

x 3 = (3q+2) 3 = (3q) 3 +2 3 +3×3q×2(3q+2) = 27q 3 +54q 2 +36q+8

x 3 =9(3q 3 +6q 2 +4q)+8

Putting (3q 3 +6q 2 +4q) = m, we get ,

Therefore, from all the three cases explained above, it is proved that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

Exercise 1.2 Page: 11

1. Express each number as a product of its prime factors:

By taking the LCM of 140, we will get the product of its prime factor.

Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 2 2 ×5×7

By Taking the LCM of 156, we will get the product of its prime factor.

Hence, 156 = 2 × 2 × 13 × 3 × 1 = 2 2 × 13 × 3

By taking the LCM of 3825, we will get the product of its prime factor.

Hence, 3825 = 3 × 3 × 5 × 5 × 17 × 1 = 3 2 ×5 2 ×17

By Taking the LCM of 5005, we will get the product of its prime factor.

Hence, 5005 = 5 × 7 × 11 × 13 × 1 = 5 × 7 × 11 × 13

By taking the LCM of 7429, we will get the product of its prime factor.

Hence, 7429 = 17 × 19 × 23 × 1 = 17 × 19 × 23

2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.

(i) 26 and 91

(ii) 510 and 92

(iii) 336 and 54

Expressing 26 and 91 as product of its prime factors, we get,

26 = 2 × 13 × 1

91 = 7 × 13 × 1

Therefore, LCM (26, 91) = 2 × 7 × 13 × 1 = 182

And HCF (26, 91) = 13

Verification

Now, product of 26 and 91 = 26 × 91 = 2366

And product of LCM and HCF = 182 × 13 = 2366

Hence, LCM × HCF = product of the 26 and 91.

Expressing 510 and 92 as product of its prime factors, we get,

510 = 2 × 3 × 17 × 5 × 1

92 = 2 × 2 × 23 × 1

Therefore, LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460

And HCF (510, 92) = 2

Now, product of 510 and 92 = 510 × 92 = 46920

And Product of LCM and HCF = 23460 × 2 = 46920

Hence, LCM × HCF = product of the 510 and 92.

Expressing 336 and 54 as product of its prime factors, we get,

336 = 2 × 2 × 2 × 2 × 7 × 3 × 1

54 = 2 × 3 × 3 × 3 × 1

Therefore, LCM(336, 54) = = 3024

And HCF(336, 54) = 2×3 = 6

Now, product of 336 and 54 = 336 × 54 = 18,144

And product of LCM and HCF = 3024 × 6 = 18,144

Hence, LCM × HCF = product of the 336 and 54.

3. Find the LCM and HCF of the following integers by applying the prime factorisation method.

(i) 12, 15 and 21

(ii) 17, 23 and 29

(iii) 8, 9 and 25

Writing the product of prime factors for all the three numbers, we get,

HCF(12,15,21) = 3

LCM(12,15,21) = 2 × 2 × 3 × 5 × 7 = 420

HCF(17,23,29) = 1

LCM(17,23,29) = 17 × 23 × 29 = 11339

HCF(8,9,25)=1

LCM(8,9,25) = 2×2×2×3×3×5×5 = 1800

4. Given that HCF (306, 657) = 9, find LCM (306, 657).

Solution: As we know that,

HCF×LCM=Product of the two given numbers

9 × LCM = 306 × 657

LCM = (306×657)/9 = 22338

Hence, LCM(306,657) = 22338

5. Check whether 6 n can end with the digit 0 for any natural number n.

Solution: If the number 6 n ends with the digit zero (0), then it should be divisible by 5, as we know any number with unit place as 0 or 5 is divisible by 5.

Prime factorization of 6 n = (2×3) n

Therefore, the prime factorization of 6 n doesn’t contain prime number 5.

Hence, it is clear that for any natural number n, 6 n is not divisible by 5, and thus it proves that 6 n cannot end with the digit 0 for any natural number n.

6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.

Solution: By the definition of composite number, we know, if a number is composite, then it means it has factors other than 1 and itself. Therefore, for the given expression;

7 × 11 × 13 + 13

Taking 13 as common factor, we get,

=13(7×11×1+1) = 13(77+1) = 13×78 = 13×3×2×13

Hence, 7 × 11 × 13 + 13 is a composite number.

Now let’s take the other number,

7 × 6 × 5 × 4 × 3 × 2 × 1 + 5

Taking 5 as a common factor, we get,

=5(7×6×4×3×2×1+1) = 5(1008+1) = 5×1009

Hence, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.

7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?

Solution: Since, Both Sonia and Ravi move in the same direction and at the same time, the method to find the time when they will be meeting again at the starting point is LCM of 18 and 12.

Therefore, LCM(18,12) = 2×3×3×2×1=36

Hence, Sonia and Ravi will meet again at the starting point after 36 minutes.

Exercise 1.3 Page: 14

1. Prove that √ 5 is irrational.

Solutions: Let us assume, that √ 5 is rational number.

i.e. √ 5 = x/y (where, x and y are co-primes)

Squaring both the sides, we get,

(y √ 5) 2 = x 2

⇒5y 2 = x 2 ……………………………….. (1)

Thus, x 2 is divisible by 5, so x is also divisible by 5.

Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get,

5y 2 = (5k) 2

⇒y 2 = 5k 2

is divisible by 5 it means y is divisible by 5.

Clearly, x and y are not co-primes. Thus, our assumption about √ 5 is rational is incorrect.

Hence, √ 5 is an irrational number.

2. Prove that 3 + 2√5 + is irrational.

Solutions: Let us assume 3 + 2 √ 5 is rational.

Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y

Rearranging, we get,

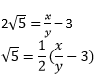
Since, x and y are integers, thus,

Therefore, √ 5 is also a rational number. But this contradicts the fact that √ 5 is irrational.

So, we conclude that 3 + 2 √ 5 is irrational.

3. Prove that the following are irrationals:

(iii) 6 + √ 2

Let us assume 1/√2 is rational.

Then we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y

Since, x and y are integers, thus, √2 is a rational number, which contradicts the fact that √2 is irrational.

Hence, we can conclude that 1/√2 is irrational.

Let us assume 7√5 is a rational number.

Then we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y

Since, x and y are integers, thus, √5 is a rational number, which contradicts the fact that √5 is irrational.

Hence, we can conclude that 7√5 is irrational.

Let us assume 6 +√2 is a rational number.

Then we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y⋅

√2 = (x/y) – 6

Since, x and y are integers, thus (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number.

Hence, we can conclude that 6 +√2 is irrational.

Exercise 1.4 Page: 17

1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2 3 5 2 ) (vii) 129/(2 2 5 7 7 5 ) (viii) 6/15 (ix) 35/50 (x) 77/210

Note: If the denominator has only factors of 2 and 5 or in the form of 2 m ×5 n then it has terminating decimal expansion.

If the denominator has factors other than 2 and 5 then it has a non-terminating decimal expansion.

(i) 13/3125

Factorizing the denominator, we get,

3125 = 5 × 5 × 5 × 5 × 5 = 5 5

Since, the denominator has only 5 as its factor, 13/3125 has a terminating decimal expansion.

8 = 2×2×2 = 2 3

Since, the denominator has only 2 as its factor, 17/8 has a terminating decimal expansion.

(iii) 64/455

455 = 5×7×13

Since, the denominator is not in the form of 2 m × 5 n , thus 64/455 has a non-terminating decimal expansion.

(iv) 15/ 1600

1600 = 2 6 ×5 2

Since, the denominator is in the form of 2 m × 5 n , thus 15/1600 has a terminating decimal expansion.

343 = 7×7×7 = 7 3 Since, the denominator is not in the form of 2 m × 5 n thus 29/343 has a non-terminating decimal expansion.

(vi)23/(2 3 5 2 )

Clearly, the denominator is in the form of 2 m × 5 n .

Hence, 23/ (2 3 5 2 ) has a terminating decimal expansion.

(vii) 129/(2 2 5 7 7 5 )

As you can see, the denominator is not in the form of 2 m × 5 n .

Hence, 129/ (2 2 5 7 7 5 ) has a non-terminating decimal expansion.

(viii) 6/15

Since, the denominator has only 5 as its factor, thus, 6/15 has a terminating decimal expansion.

35/50 = 7/10

Factorising the denominator, we get,

Since, the denominator is in the form of 2 m × 5 n thus, 35/50 has a terminating decimal expansion.

77/210 = (7× 11)/ (30 × 7) = 11/30

30 = 2 × 3 × 5

As you can see, the denominator is not in the form of 2 m × 5 n .Hence, 77/210 has a non-terminating decimal expansion.

2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

13/3125 = 0.00416

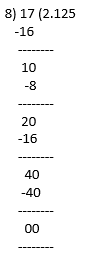
17/8 = 2.125

(iii) 64/455 has a non terminating decimal expansion

(iv)15/ 1600

15/1600 = 0.009375

(v) 29/ 343 has a non terminating decimal expansion

(vi)23/ (2 3 5 2 ) = 23/(8×25)= 23/200

23/ (2 3 5 2 ) = 0.115

(vii) 129/ (2 2 5 7 7 5 ) has a non terminating decimal expansion

(viii) 6/15 = 2/5

(ix) 35/50 = 7/10

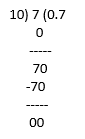
35/50 = 0.7

(x) 77/210 has a non-terminating decimal expansion.

3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?

(i) 43.123456789

(ii) 0.120120012000120000. . .

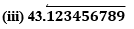
Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.

Since, it has non-terminating and non- repeating decimal expansion, it is an irrational number.

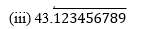
Since it has non-terminating but repeating decimal expansion, it is a rational number in the form of p/q and q has factors other than 2 and 5.

NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers

Real Number is one of the important topics in Maths, and it has a weightage of 6 marks in Class 10 (Unit – Number Systems) Maths board exams. The average number of questions asked in this chapter is usually 3. Three questions were asked from this chapter in the previous year board examination (2018).

One out of three questions in part A (1 mark).
One out of three questions in part B (2 marks).
One out of three questions in part C (3 marks).

This chapter talks about

Euclid’s Division Algorithm
The Fundamental Theorem of Arithmetic
Revisiting Rational & Irrational Numbers
Decimal Expansions

List of Exercises in Class 10 Maths Chapter 1: Exercise 1.1 Solutions 5 Questions ( 4 long, 1 short) Exercise 1.2 Solutions 7 Questions ( 4 long, 3 short) Exercise 1.3 Solutions 3 Questions ( 3 short) Exercise 1.4 Solutions 3 Questions ( 3 short)

Real Numbers is introduced in Class 9, and this is discussed in further detail in Class 10. NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers provides the answers to the questions present in this chapter. The chapter discusses real numbers and their applications. The divisibility of integers using Euclid’s division algorithm says that any positive integer a can be divided by another positive integer b such that the remainder will be smaller than b. On the other hand, The Fundamental Theorem of Arithmetic works on the multiplication of positive integers.

The chapter starts with the introduction of real numbers in section 1.1, followed by two very important topics in sections 1.2 and 1.3

Euclid’s Division Algorithm – It includes 5 questions based on Theorem 1.1 – Euclid’s Division Lemma.
The Fundamental Theorem of Arithmetic – Explore the applications of this topic which talks about the multiplication of positive integers, through solutions of the 7 problems in Exercise 1.2.

Next, it discusses the following topics, which were introduced in Class 9.

Revisiting Rational & Irrational Numbers – In this, the solutions for 3 problems in Exercise 1.3 are given, which also use the topic in the last Exercise 1.2.
Decimal Expansions – It explores when the decimal expansion of a rational number is terminating and when it is recurring. It includes a total of 3 problems with sub-parts in Exercise 1.4

Key Features of NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

These NCERT Solutions help you solve and revise the updated CBSE syllabus of Class 10 for 2023-24.
After going through the stepwise solutions given by our subject expert teachers, you will be able to score more marks.
It follows NCERT guidelines which help in preparing the students competently.
It contains all the important questions from the examination point of view.

Disclaimer –

Dropped Topics –

1.2 Euclid’s division lemma 1.5 Revisiting rational numbers and their decimal Expansions

Frequently Asked Questions on NCERT Solutions for Class 10 Maths Chapter 1

What are the main topics covered in the ncert solutions for class 10 maths chapter 1, how many exercises are there in ncert solutions for class 10 maths chapter 1, are ncert solutions for class 10 maths chapter 1 important from the exam point of view, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

It’s helping a lot in tenth Thanks byjus

Byju’s is quite helpful for giving a clear knowledge to new students of promoted class. The best study materials are published in the website make students to succeed.

Share Share

Register with BYJU'S & Download Free PDFs

Trial Class

Class 10 Notes
9th IT CODE 402
10th IT CODE 402
10th Hindi Grammar MCQ
9th Hindi Grammar MCQ

Case Study Questions Class 10 Maths with Solutions PDF Download

case study questions class 10 maths pdf, case study questions class 10 maths with solutions, case study questions class 10 maths cbse chapter wise pdf download, how to solve case-based question in maths.

First of all, a student needs to read the complete passage thoroughly. Then start solving the question
After reading the question try to understand from which topics the question is asked. and try to remember all the concepts of that topic.
Sometimes the question is very tricky and you will find it very difficult to understand. In that case, Read the question and passage again and again.
After solving the answer check your answer with the options given.
Remember, write only answering your answer book

Link to Download Case-Study Questions of class 10

Communication Skills Class 9 Notes

Communication Skills Class 10 Notes PDF

Information Technology Code 402 Class 10 Solutions

Set-1 | Padbandh MCQ Questions Class 10 - CBSE 2022

Top 50+ MCQ on Communication Skills Class 10 for TERM 1- 2022 | IT Code 402

TERM 1 MCQ | Communication Skills Class 10 Questions and Answers

Information Technology Code 402 Class 10 Notes 2023

Menu footer widget.

CBSE Case Study Questions for Class 10 Maths Real Numbers Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 10 Maths Real Numbers in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 10 Maths Real Numbers PDF

Mcq set 1 -, mcq set 2 -, checkout our case study questions for other chapters.

Chapter 2: Polynomials Case Study Questions
Chapter 3: Pair of Linear Equations in Two Variables Case Study Questions
Chapter 4: Quadratic Equation Case Study Questions
Chapter 5: Arithmetic Progressions Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Contact Form

myCBSEguide

Mathematics
Case Study Class 10...

Case Study Class 10 Maths Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Now, CBSE will ask only subjective questions in class 10 Maths case studies. But if you search over the internet or even check many books, you will get only MCQs in the class 10 Maths case study in the session 2022-23. It is not the correct pattern. Just beware of such misleading websites and books.

We advise you to visit CBSE official website ( cbseacademic.nic.in ) and go through class 10 model question papers . You will find that CBSE is asking only subjective questions under case study in class 10 Maths. We at myCBSEguide helping CBSE students for the past 15 years and are committed to providing the most authentic study material to our students.

Here, myCBSEguide is the only application that has the most relevant and updated study material for CBSE students as per the official curriculum document 2022 – 2023. You can download updated sample papers for class 10 maths .

First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.

Class 10 Maths has the following chapters.

Real Numbers Case Study Question
Polynomials Case Study Question
Pair of Linear Equations in Two Variables Case Study Question
Quadratic Equations Case Study Question
Arithmetic Progressions Case Study Question
Triangles Case Study Question
Coordinate Geometry Case Study Question
Introduction to Trigonometry Case Study Question
Some Applications of Trigonometry Case Study Question
Circles Case Study Question
Area Related to Circles Case Study Question
Surface Areas and Volumes Case Study Question
Statistics Case Study Question
Probability Case Study Question

Format of Maths Case-Based Questions

CBSE Class 10 Maths Case Study Questions will have one passage and four questions. As you know, CBSE has introduced Case Study Questions in class 10 and class 12 this year, the annual examination will have case-based questions in almost all major subjects. This article will help you to find sample questions based on case studies and model question papers for CBSE class 10 Board Exams.

Maths Case Study Question Paper 2023

Here is the marks distribution of the CBSE class 10 maths board exam question paper. CBSE may ask case study questions from any of the following chapters. However, Mensuration, statistics, probability and Algebra are some important chapters in this regard.

Case Study Question in Mathematics

Here are some examples of case study-based questions for class 10 Mathematics. To get more questions and model question papers for the 2021 examination, download myCBSEguide Mobile App .

Case Study Question – 1

In the month of April to June 2022, the exports of passenger cars from India increased by 26% in the corresponding quarter of 2021–22, as per a report. A car manufacturing company planned to produce 1800 cars in 4th year and 2600 cars in 8th year. Assuming that the production increases uniformly by a fixed number every year.

Find the production in the 1 st year.
Find the production in the 12 th year.
Find the total production in first 10 years. OR In which year the total production will reach to 15000 cars?

Case Study Question – 2

In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.

Find the distance between Lucknow (L) to Bhuj(B).
If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P) OR Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).

Case Study Question – 3

Find the distance PA.
Find the distance PB
Find the width AB of the river. OR Find the height BQ if the angle of the elevation from P to Q be 30 o .

Case Study Question – 4

What is the length of the line segment joining points B and F?
The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
What are the coordinates of the point on y axis equidistant from A and G? OR What is the area of area of Trapezium AFGH?

Case Study Question – 5

The school auditorium was to be constructed to accommodate at least 1500 people. The chairs are to be placed in concentric circular arrangement in such a way that each succeeding circular row has 10 seats more than the previous one.

If the first circular row has 30 seats, how many seats will be there in the 10th row?
For 1500 seats in the auditorium, how many rows need to be there? OR If 1500 seats are to be arranged in the auditorium, how many seats are still left to be put after 10 th row?
If there were 17 rows in the auditorium, how many seats will be there in the middle row?

Case Study Question – 6

$class 10 ch 1 case study maths$

Draw a neat labelled figure to show the above situation diagrammatically.

$class 10 ch 1 case study maths$

What is the speed of the plane in km/hr.

How to Solve Case-Based Questions?

Questions based on a given case study are normally taken from real-life situations. These are certainly related to the concepts provided in the textbook but the plot of the question is always based on a day-to-day life problem. There will be all subjective-type questions in the case study. You should answer the case-based questions to the point.

What are Class 10 competency-based questions?

Competency-based questions are questions that are based on real-life situations. Case study questions are a type of competency-based questions. There may be multiple ways to assess the competencies. The case study is assumed to be one of the best methods to evaluate competencies. In class 10 maths, you will find 1-2 case study questions. We advise you to read the passage carefully before answering the questions.

Case Study Questions in Maths Question Paper

CBSE has released new model question papers for annual examinations. myCBSEguide App has also created many model papers based on the new format (reduced syllabus) for the current session and uploaded them to myCBSEguide App. We advise all the students to download the myCBSEguide app and practice case study questions for class 10 maths as much as possible.

Case Studies on CBSE’s Official Website

CBSE has uploaded many case study questions on class 10 maths. You can download them from CBSE Official Website for free. Here you will find around 40-50 case study questions in PDF format for CBSE 10th class.

10 Maths Case Studies in myCBSEguide App

You can also download chapter-wise case study questions for class 10 maths from the myCBSEguide app. These class 10 case-based questions are prepared by our team of expert teachers. We have kept the new reduced syllabus in mind while creating these case-based questions. So, you will get the updated questions only.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

CBSE Class 10 Maths Sample Paper 2020-21
Class 12 Maths Case Study Questions
CBSE Reduced Syllabus Class 10 (2020-21)
Class 10 Maths Basic Sample Paper 2024
How to Revise CBSE Class 10 Maths in 3 Days
CBSE Practice Papers 2023
Class 10 Maths Sample Papers 2024
Competency Based Learning in CBSE Schools

Save my name, email, and website in this browser for the next time I comment.

New QB365-SLMS
NEET Materials
JEE Materials
Banking first yr Materials
TNPSC Materials
DIPLOMA COURSE Materials
5th Standard Materials
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

CBSE 10th Standard Maths Subject Polynomials Case Study Questions With Solution 2021

By QB365 on 21 May, 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams

QB365 - Question Bank Software

10th Standard CBSE

Final Semester - June 2015

Case Study Questions

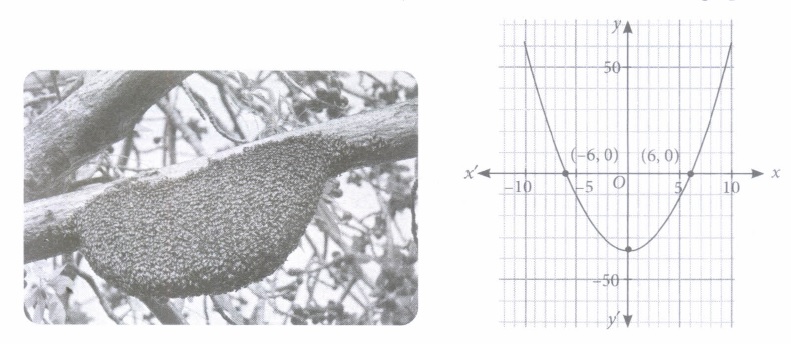
(ii) The expression of the polynomial represented by the graph is

(iii) Find the value of the polynomial represented by the graph when x = 6.

(iv) The sum of zeroes of the polynomial x 2 + 2x - 3 is

(v) If the sum of zeroes of polynomial at 2 + 5t + 3a is equal to their product, then find the value of a.

(ii) Find the value of $\alpha$ + $\beta$ + $\alpha$ $\beta$ .

(iii) The value of p(2) is

(iv) If $\alpha$ and $\beta$ are zeroes of $x^{2}+x-2, \text { then } \frac{1}{\alpha}+\frac{1}{\beta}=$

(v) If sum of zeroes of $q(x)=k x^{2}+2 x+3 k$ is equal to their product, then k =

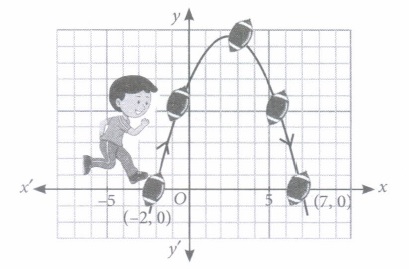
(ii) The axis of symmetry of the given parabola is

(iii) The zeroes of the polynomial, represented in the given graph, are

(iv) Which of the following polynomial has -2 and -3 as its zeroes?

(v) For what value of 'x', the value of the polynomial $f(x)=(x-3)^{2}+9 \text { is } 9 ?$

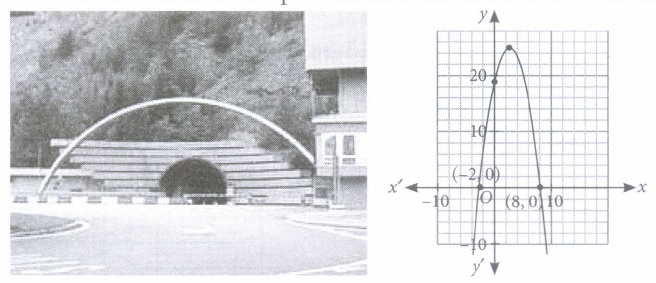
(ii) What will be the expression of the polynomial given in diagram?

(iii) What is the value of the polynomial, represented by the graph, when x = 4?

(iv) If the tunnel is represented by x 2 + 3x - 2, then its zeroes are

(v) If one zero is 4 and sum of zeroes is -3, then representation of tunnel as a polynomial is

(ii) The sum of product of zeroes taken two at a time is

(iii) Product of zeroes of polynomial p(x) is

(iv) The value of the polynomial p(x), when x = 4 is

(v) If $\alpha,\beta,\gamma$ are the zeroes of a polynomial g(x) such that $\alpha+\beta+\gamma=3, \alpha \beta+\beta \gamma+\gamma \alpha=-16$ and $\alpha \beta \gamma=-48$ then, g(x) =

*****************************************

Cbse 10th standard maths subject polynomials case study questions with solution 2021 answer keys.

(i) (b): Graph of a quadratic polynomial is a parabolic in shape. (ii) (c): Since the graph of the polynomial cuts the x-axis at (-6,0) and (6, 0). So, the zeroes of polynomial are -6 and 6. $\therefore$ Required polynomial is p(x) = x 2 - (-6 + 6)x + (-6)(6) = x 2 - 36 (iii) (c) : We have, p(x) = x 2 - 36 Now, p( 6) = 62 - 36 = 36 - 36 = 0 (iv) (b): Letf (x) = x 2 + 2x - 3. Then, $\text { Sum of zeroes }=-\frac{\text { coefficient of } x}{\text { coefficient of } x^{2}}=-\frac{(2)}{1}=-2$ (v) (d): The given polynomial is at 2 + 5t + 3a Given, sum of zeroes = product of zeroes. $\Rightarrow \quad \frac{-5}{a}=\frac{3 a}{a} \Rightarrow a=\frac{-5}{3}$

(i) (b): Given, a and $\beta$ are the zeroes of $p(x)=x^{2}-24 x+128$ $\text { Putting } p(x)=0 \text { , we get }$ $ x^{2}-8 x-16 x+128=0 $ $\Rightarrow x(x-8)-16(x-8)=0 $ $\Rightarrow (x-8)(x-16)=0 \Rightarrow x=8 \text { or } x=16 $ $\therefore \alpha=8, \beta=16$ (ii) (c) : $\alpha+\beta+\alpha \beta =8+16+(8)(16) =24+128=152 $ (iii) (d) : $p(2)=2^{2}-2 4(2)+128=4-48+128=84$ (iv) (a): Since a and $\beta$ are zeroes of $x^{2}+x-2$ $\therefore \quad \alpha+\beta=-1 \text { and } \alpha \beta=-2 $ $\text { Now, } \frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{-1}{-2}=\frac{1}{2}$ (v) (c): Sum of zeroes $=\frac{-2}{k}$ Product of zeroes $=\frac{3 k}{k}=3$ According to question, we have $\frac{-2}{k}=3$ $\Rightarrow \quad k=\frac{-2}{3}$

(i) (b): The shape of the path of the soccer ball is a parabola. (ii) (c): The axis of symmetry of the given curve is a line parallel to y-axis. (iii) (a): The zeroes of the polynomial, represented in the given graph, are -2 and 7, since the curve cuts the x-axis at these points. (iv) (d): A polynomial having zeroes -2 and -3 is $p(x)=x^{2}-(-2-3) x+(-2)(-3)=x^{2}+5 x+6$ (v) (c): We have $f(x)=(x-3)^{2}+9$ $\text { Now, } 9=(x-3)^{2}+9 $ $\Rightarrow(x-3)^{2}=0 \Rightarrow x-3=0 \Rightarrow x=3$

(i) (a): Since, the graph intersects the x-axis at two points, namely x = 8, -2. So, 8, - 2 are the zeroes of the given polynomial. (ii) (b): The expression of the polynomial given in diagram is $-x^{2}+6 x+16$ (iii) (c) : Let $p(x)=-x^{2}+6 x+16$ $\text { When } x=4, p(4)=-4^{2}+6 \times 4+16=24$ (iv) (d): Let $f(x)=-x^{2}+3 x-2$ Now, consider $f(x)=0 \Rightarrow-x^{2}+3 x-2=0$ $\begin{aligned} &\Rightarrow x^{2}-3 x+2=0 \Rightarrow(x-2)(x-1)=0\\ &\Rightarrow x=1,2 \text { are its zeroes. } \end{aligned}$ (v) (b): Let a and $\beta$ are the zeroes of the required polynomial. Given $\alpha + \beta = - 3$ If $\alpha$ = 4, then $\beta$ = -7 $\therefore \quad \text { Representation of tunnel is }-x^{2}-3 x+28 \text { . }$

(i) (c): For finding $\alpha,\beta,$ $\gamma$ consider p(x) = 0 $\Rightarrow \quad x^{3}-18 x^{2}+95 x-150=0 $ $\Rightarrow \quad(x-3)\left(x^{2}-15 x+50\right)=0 $ $\Rightarrow \quad(x-3)(x-5)(x-10)=0 \Rightarrow x=10 \text { or } x=5 \text { or } x=3 $ $\text { Thus } \alpha=10, \beta=5 \text { and } \gamma=3$ (ii) (d): Here $\alpha=10, \beta=5 \text { and } \gamma=3$ $\therefore$ Sum of product of zeroes taken two at a time $\begin{array}{l} =\alpha \beta+\beta \gamma+\gamma \alpha=(10)(5)+(5)(3)+(3)(10) \\ =50+15+30=95 \end{array}$ (iii) (a): Product of zeroes of polynomial p(x) = $\alpha\beta\gamma$ = (10) (5) (3) = 150 (iv) (b): We have $p(x)=x^{3}-18 x^{2}+95 x-150$ $\begin{array}{l} \text { Now, } p(4)=4^{3}-18(4)^{2}+95(4)-150 \\ =64-288+380-150=6 \end{array}$ (v) (d): $g(x)=x^{3}-(\alpha+\beta+\gamma) x^{2} +(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma $ $\Rightarrow g(x)=x^{3}-3 x^{2}-16 x-(-48)=x^{3}-3 x^{2}-16 x+48$

Related 10th Standard CBSE Maths Materials

10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

Privacy Policy
Terms and Conditions

Web Stories

Tuesday, September 21, 2021

Case study based questions class 10 chapter 1 real numbers cbse board term 1 with answer key.

Hello students, Welcome to Maths Easy Institute.

Please do not enter any spam link in the comment box.

Warning: Do Not Copy!

Blog Archives

Best Books for IIT JEE
Best Colleges Of India
class 10 Case Study Based questions
Class 10 Maths MCQ
Class 11 Maths Case Study Questions
Class 11 Maths MCQ
Class 12 Math Case Study questions
Class 12 Maths MCQ
JEE MAIN MCQ
Maths Strategy JEE
News for Students

Blog Archive

► April (3)
► March (2)
► February (1)
► January (5)
► December (9)
► November (5)
► October (6)
Class 10 Maths Case Study Based Questions Chapter ...
Case Study Based Questions Class 10 Chapter 1 Real...
[Video] Indian Statistical (ISI) Institute Admissi...
[Video] Last 10 days MATHS Strategy for JEE MAIN G...
► April (4)
► March (3)
► October (2)
► September (7)
► August (2)
► July (4)

Class 10 Maths Chapter 1 MCQ

Class 10 Maths Chapter 1 Real Numbers MCQ (Multiple Choice Objective Questions) with answers and complete explanation case study type questions for the first term examination 2024-25. The answers of 10th Maths Chapter 1 MCQ are given with explanation, so that students can understand easily. This page of Class 10 Maths MCQ contains the questions released by CBSE as well as extra questions for practice.

Case Study – 1

What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?

Factors of 32 = 2 х 2 х 2 х 2 х 2 = 2⁵ Factors of 36 = 2 х 2 х 3 х 3 = 2² х 3² LCM of 32 and 36 = 2⁵ х 3² = 32 х 9 = 288 Hence, the correct option is (C).

View Answer

If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32, 36) is

Factors of 32 = 2 х 2 х 2 х 2 х 2 = 2⁵ Factors of 36 = 2 х 2 х 3 х 3 = 2² х 3² LCM of 32 and 36 = 2⁵ х 3² = 32 х 9 = 288 HCF (32, 36) = (32 х 36) / LCM = (32 х 36) / 288 = 4 Hence, the correct option is (B).

36 can be expressed as a product of its primes as

Factors of 36 = 2 х 2 х 3 х 3 = 2² х 3² Hence, the correct option is (A).

7 х 11 х 13 х 15 + 15 is a

7 х 11 х 13 х 15 + 15 = 15 х (7 х 11 х 13 + 1) = 15 х (Integer) It has more than two factor. So, it is a composite number. Hence, the correct option is (B).

If p and q are positive integers such that p = ab² and q = a²b, where a, b are prime numbers, then the LCM (p, q) is

p = ab² q = a²b LCM = highest powers of common factors of ab² and a²b = a²b² Hence, the correct option is (B).

Case Study – 2

A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English, and Mathematics are 60, 84, and 108 respectively.

Class 10 Maths Chapter 1 Real Numbers MCQ

In each room the same number of participants are to be seated and all of them being in the same subject, hence maximum number participants that can accommodated in each room are

Factors of 60 = 2 х 2 х 3 х 5 = 2² х 3 х 5 Factors of 84 = 2 х 2 х 3 х 7 = 2² х 3 х 7 Factors of 108 = 2 х 2 х 3 х 3 х 3 = 2² х 3³ HCF of 60, 84, and 108 = 2² х 3 = 12 Hence, the correct option is (B).

What is the minimum number of rooms required during the event?

Factors of 60 = 2 х 2 х 3 х 5 = 2² х 3 х 5 Factors of 84 = 2 х 2 х 3 х 7 = 2² х 3 х 7 Factors of 108 = 2 х 2 х 3 х 3 х 3 = 2² х 3³ HCF of 60, 84, and 108 = 2² х 3 = 12 Number of room required for Hindi participants = 60/12 = 5 Number of room required for English participants = 84/12 = 7 Number of room required for Mathematics participants = 108/12 = 9 Total number of room required = 5 + 7 + 9 = 21 Hence, the correct option is (D).

The LCM of 60, 84, and 108 is

Factors of 60 = 2 х 2 х 3 х 5 = 2² х 3 х 5 Factors of 84 = 2 х 2 х 3 х 7 = 2² х 3 х 7 Factors of 108 = 2 х 2 х 3 х 3 х 3 = 2² х 3³ LCM of 60, 84, and 108 = 2² х 3³ х 5 х 7 = 4 х 27 х 5 х 7 = 3780 Hence, the correct option is (A).

The product of HCF and LCM of 60, 84, and 108 is

Factors of 60 = 2 х 2 х 3 х 5 = 2² х 3 х 5 Factors of 84 = 2 х 2 х 3 х 7 = 2² х 3 х 7 Factors of 108 = 2 х 2 х 3 х 3 х 3 = 2² х 3³ HCF of 60, 84, and 108 = 2² х 3 = 12 LCM of 60, 84, and 108 = 2² х 3³ х 5 х 7 = 4 х 27 х 5 х 7 = 3780 Product of HCF and LCM of 60, 84, and 108 = 12 х 3780 = 45360 Hence, the correct option is (D).

108 can be expressed as a product of its primes as

Factors of 108 = 2 х 2 х 3 х 3 х 3 = 2² х 3³ Hence, the correct option is (D).

Case Study – 3

Rohit Singh is a worker in a petrol pump. He along with the other co-workers, use to transfer petrol from tanker to storage. On Monday, there were two tankers containing 850 litres and 680 litres of petrol respectively.

Case study based MCQ for 10th Maths chapter 1

What is the maximum capacity of a container which can measure the petrol of either tanker in exact number of time?

The maximum capacity of the container is the HCF of 850 and 680. Factors of 850 = 2 х 5 х 5 х 17 = 2 х 5² х 17 Factors of 680 = 2 х 2 х 2 х 5 х 17 = 2³ х 5 х 17 HCF of 850 and 680 = 2 х 5 х 17 = 170 Hence, the correct option is (C).

If the product of two positive integers is equal to the product of their HCF and LCM is true then, the LCM (850, 680) is

Factors of 850 = 2 х 5 х 5 х 17 = 2 х 5² х 17 Factors of 680 = 2 х 2 х 2 х 5 х 17 = 2³ х 5 х 17 HCF of 850 and 680 = 2 х 5 х 17 = 170 LCM (850, 680) = (850 х 680) / HCF = (850 х 680) / 170 = 3400 Hence, the correct option is (D).

680 can be expressed as a product of its primes as

Factors of 680 = 2 х 2 х 2 х 5 х 17 = 2³ х 5 х 17 Hence, the correct option is (C).

2 х 3 х 5 х 11 х 17 + 11 is a

2 х 3 х 5 х 11 х 17 + 11 = 11 х (2 х 3 х 5 х 17 + 1) = 11 х (Integer) It has more than two factor. So, it is a composite number. Hence, the correct option is (B).

If p and q are positive integers such that p = a³b² and q = a²b³, where a, b are prime numbers, then the LCM (p, q) is

p = a³b² q = a²b³ LCM = highest powers of common factors of a³b² and a²b³ = a³b³ Hence, the correct option is (B).

Case Study – 4

A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience. Observe the following factor tree and answer the following:

Class 10 Maths Case study MCQ Factor tree

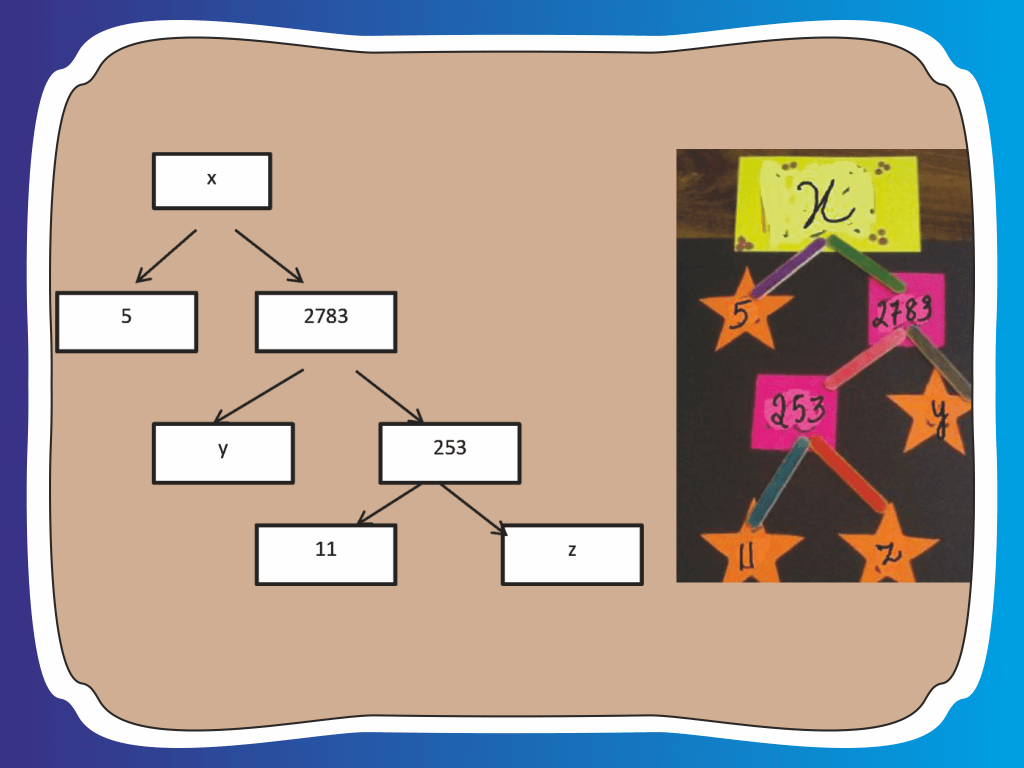
What will be the value of x?

X = 5 х 2783 = 13915 Hence, the correct option is (B).

What will be the value of y?

Y = 2783/253 = 11 Hence, the correct option is (C).

What will be the value of z?

Z = 253/11 = 23 Hence, the correct option is (B).

According to Fundamental Theorem of Arithmetic 13915 is a

Because 13915 can be written into the product of primes. 13915 = 5 х 11 х 11 х 23 = 5 х 11² х 23 Hence, the correct option is (A).

The prime factorisation of 13915 is

13915 = 5 х 11 х 11 х 23 = 5 х 11² х 23 Hence, the correct option is (C).

Case Study – 5

We all know that morning walk is good for health. In a morning walk, three friends Anjali, Sofia, and Angelina step of together. There steps measure 80 cm, 85 cm, and 90 cm. respectively.

What is the minimum distance each should walk so that they can cover the distance in complete steps?

The minimum distance covered by each in complete steps must be the LCM of 80 cm, 85 cm, and 90 cm. Factors of 80 = 2 х 2 х 2 х 2 х 5 = 2⁴ х 5 Factors of 85 = 5 х 17 Factors of 90 = 2 х 3 х 3 х 5 = 2 х 3² х 5 LCM of 80, 85, and 90 = 2² х 3² х 5 х 17 = 12240 Now, 12240 cm = 122 m 40 cm Hence, the correct option is (B).

What is the minimum number of steps taken by any of the three friends, when they meet again?

Factors of 80 = 2 х 2 х 2 х 2 х 5 = 2⁴ х 5 Factors of 85 = 5 х 17 Factors of 90 = 2 х 3 х 3 х 5 = 2 х 3² х 5 LCM of 80, 85, and 90 = 2² х 3² х 5 х 17 = 12240 The step size of Angelina is maximum among these three. So, she will take minimum number of steps to cover the same distance. Number of steps = 12240/90 = 136 Hence, the correct option is (D).

The HCF of 80, 85, and 90 is

Factors of 80 = 2 х 2 х 2 х 2 х 5 = 2⁴ х 5 Factors of 85 = 5 х 17 Factors of 90 = 2 х 3 х 3 х 5 = 2 х 3² х 5 HCF of 80, 85, and 90 = 5 Hence, the correct option is (A).

The product of HCF and LCM of 80, 85, and 90 is

Factors of 80 = 2 х 2 х 2 х 2 х 5 = 2⁴ х 5 Factors of 85 = 5 х 17 Factors of 90 = 2 х 3 х 3 х 5 = 2 х 3² х 5 HCF of 80, 85, and 90 = 5 LCM of 80, 85, and 90 = 2² х 3² х 5 х 17 = 12240 Therefore, the product of HCF and LCM of 80, 85, and 90 = 12240 х 5 = 61200 Hence, the correct option is (C).

90 can be expressed as a product of its primes as

Factors of 108 = 2 х 3 х 3 х 5 = 2 х 3² х 5 Hence, the correct option is (D).

Class 10 Maths Chapter 1 MCQ are given below. There are total of 5 questions with four choices. Only one option is correct and the explanation of correct answer is given below the questions. Every time the students will get a new set of five questions with different levels of questions. For any further discussion, please join the Discussion Forum.

HCF of 210 and 55 is

Given integer are 210 & 55, clearly 210>55, applying Euclid’s division lemma to 210 & 55, we get 210 = 55 × 3 + 45, applying division lemma till remainder will be 0. 55 =45×1 +10 45 = 10×4 +5 10 = 5×2 +0 Hence HCF is 5

Largest number which divides 60 and 75, leaving remainders 8 and 10 respectively, is

This means 60 – 8 = 52 and 75 – 10 = 65, are completely divided by a integer. Therefore, we have to find the HCF of 52 and 65.. According to Euclid’s Division Lemma, 65 = 52 × 1 +13 and 52 = 13 × 4 + 0, Hence 13 is HCF.

The decimal expansion of the rational number 14587/250 will terminate after

The factors of denominator 250 = 2 × 5 × 5 × 5. There are three factors of 5, that is why it will terminate after three decimal places. [Always more number of factors will be considered, whether it is 5 or 2, does not matter.] By dividing actually 14587 by 250 we get the quotient as 58.348.

If HCF (16, y) = 8 and LCM (16, y) = 48, then the value of y is

We know that: HCF × LCM = 16 × y So, 8 × 48 = 16 × y y = 8 × 48/16 = 24

The smallest rational number by which 1/3 should be multiplied so that its decimal expansion terminates after one place of decimal, is

1/3 × 3/10 = 1/10 = 0.1

Discuss in Forum
Visit for Revision

What are the important topics in Class 10 Maths Chapter 1 MCQ?

Euclid’ division lemma and the Fundamental Theorem of Arithmetic are the two main topics in 10th Maths chapter 1 Real Numbers. Now questions are designed on the basis of case study. So practice MCQ questions based on daily life events which will be more helpful in CBSE exams.

In which of the four exercise of 10th Maths Chapter 1, are Case Study MCQ asked?

There are questions from each exercise of Chapter 1 of 10th Maths, but most of the MCQs can be formed from Exercise 1.4. Now CBSE introduces the questions based on CASE STUDY which may be asked from any section of class 10 Maths chapter 1.

How many MCQ are required to be perfect in Chapter 1 of Class 10 Maths?

If your concepts are clear, the MCQs provide more confidence in that section. More practice means more to retain and better understanding with the concepts of topics.

How many questions from Chapter 1 of Class 10 Maths asked in CBSE Board?

There is no classification of number of questions from the different chapters. There may be one, more than one or none from Chapter 1 Real Numbers of Class 10 Maths.

We are adding more questions frequently, so that students can have a good practice of Class 10 Maths Chapters. If you have suggestion or feedback about this page or website improvement, you are welcome. Important questions with solutions and answers will be added very soon for each chapter of class 10 Maths.

Download NCERT Books and Offline Apps 2024-25 based on new CBSE Syllabus. Ask your doubts related to NIOS or CBSE Board and share your knowledge with your friends and other users through Discussion Forum.

Class 6 Maths
Class 6 Science
Class 6 Social Science
Class 6 English
Class 7 Maths
Class 7 Science
Class 7 Social Science
Class 7 English
Class 8 Maths
Class 8 Science
Class 8 Social Science
Class 8 English
Class 9 Maths
Class 9 Science
Class 9 Social Science
Class 9 English
Class 10 Maths
Class 10 Science
Class 10 Social Science
Class 10 English
Class 11 Maths
Class 11 Computer Science (Python)
Class 11 English
Class 12 Maths
Class 12 English
Class 12 Economics
Class 12 Accountancy
Class 12 Physics
Class 12 Chemistry
Class 12 Biology
Class 12 Computer Science (Python)
Class 12 Physical Education
GST and Accounting Course
Excel Course
Tally Course
Finance and CMA Data Course
Payroll Course

Interesting

Learn English
Learn Excel
Learn Tally
Learn GST (Goods and Services Tax)
Learn Accounting and Finance
GST Tax Invoice Format
Accounts Tax Practical
Tally Ledger List
GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 1 Class 10 Real Numbers

Click on any of the links below to start learning from Teachoo ...

Updated for NCERT 2023-2024 Book.

Answers to all exercise questions and examples are solved for Chapter 1 Class 10 Real numbers. Solutions of all these NCERT Questions are explained in a step-by-step easy to understand manner

In this chapter, we will study

What is a Real Number
What is Euclid's Division Lemma , and
How to find HCF (Highest Common Factor) using Euclid's Division Algorithm
Then, we study Fundamental Theorem of Arithmetic, which is basically Prime Factorisation
And find HCF and LCM using Prime Factorisation
We also use the formula of HCF and LCM of two numbers a and b HCF × LCM = a × b
Then, we see what is an Irrational Number
and Prove numbers irrational (Like Prove √ 2, √ 3 irrational)
We revise our concepts about Decimal Expansion (Terminating, Non-Terminating Repeating, Non Terminating Non Repeating)
And find out Decimal Expansion of numbers without performing long division

Click on an NCERT Exercise below to get started.

Or you can also check the Concepts from the concept Wise. The chapter is divided into concepts, and first each concept is explained. And then, the questions of the concept is solved, from easy to difficult. This is the Teachoo way of learning.

You can check the concepts by clicking on a link below Concept Wise.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

Bihar Board

RBSE Result 2024

Srm university.

Goa Board Result 2024
Maharashtra HSC Result
Maharashtra SSC Result
RBSE 10th Result 2024
RBSE 12th Result 2024
CBSE Board Result 2024
Shiv Khera Special
Education News
Web Stories
Current Affairs
नए भारत का नया उत्तर प्रदेश
School & Boards
College Admission
Govt Jobs Alert & Prep
GK & Aptitude
CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 3 - Pair of Linear Equations in Two Variables (Published by CBSE)

Cbse's question bank on case study for class 10 maths chapter 3 is available here. these questions will be very helpful to prepare for the cbse class 10 maths exam 2022..

Case study questions are going to be new for CBSE Class 10 students. These are the competency-based questions that are completely new to class 10 students. To help students understand the format of the questions, CBSE has released a question bank on case study for class 10 Maths. Students must practice with these questions to get familiarised with the concepts and logic used in the case study and understand how to answers them correctly. You may check below the case study questions for CBSE Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables. You can also check the right answer at the end of each question.

Check Case Study Questions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables

CASE STUDY-1:

1. If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?

2. How many questions did he guess?

3. If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?

4. If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?

Let the no of questions whose answer is known to the student x and questions attempted by cheating be y

x – 1/4y =90

solving these two

x = 96 and y = 24

1. He answered 96 questions correctly.

2. He attempted 24 questions by guessing.

3. Marks = 80- ¼ 0f 40 =70

4. x – 1/4 of (120 – x) = 95

5x = 500, x = 100

CASE STUDY-2:

Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.

Based on the above information, answer the following questions:

1. Form the pair of linear equations in two variables from this situation.

2. Find the length of the outer boundary of the layout.

3. Find the area of each bedroom and kitchen in the layout.

4. Find the area of living room in the layout.

5. Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m.

1. Area of two bedrooms= 10x sq.m

Area of kitchen = 5y sq.m

10x + 5y = 95

Also, x + 2+ y = 15

2. Length of outer boundary = 12 + 15 + 12 + 15 = 54m

3. On solving two equation part(i)

x = 6m and y = 7m

area of bedroom = 5 x 6 = 30m

area of kitchen = 5 x 7 = 35m

4. Area of living room = (15 x 7) – 30 = 105 – 30 = 75 sq.m

5. Total cost of laying tiles in the kitchen = Rs50 x 35 = Rs1750

Case study-3 :

It is common that Governments revise travel fares from time to time based on various factors such as inflation ( a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations:

Situation 1: In city A, for a journey of 10 km, the charge paid is Rs 75 and for a journey of 15 km, the charge paid is Rs 110.

Situation 2: In a city B, for a journey of 8km, the charge paid is Rs91 and for a journey of 14km, the charge paid is Rs 145.

Refer situation 1

1. If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is

a) x + 10y =110, x + 15y = 75

b) x + 10y = 75, x + 15y = 110

c) 10x + y = 110, 15x + y = 75

d) 10x + y = 75, 15x + y = 110

Answer: b) x + 10y = 75, x + 15y = 110

2. A person travels a distance of 50km. The amount he has to pay is

Answer: c) Rs.355

Refer situation 2

3. What will a person have to pay for travelling a distance of 30km?

Answer: b) Rs.289

4. The graph of lines representing the conditions are: (situation 2)

Answer: (iii)

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check Board Result 2024 for Class 10 and Class 12 like CBSE Board Result , UP Board Result , Bihar Board Result , MP Board Result , Rajasthan Board Result and Other States Boards.

RBSE 12th रिजल्ट 2024
RBSE रिजल्ट 2024
TS TET Hall Ticket 2024
Goa SSC Result 2024
SSC GD Result 2024
GBSHSE SSC Result 2024
SSC Result 2024 Goa
CDS 2 Notification 2024
results.gbshsegoa.net Result 2024
CBSE 10th Result 2024
CBSE Study Material
CBSE Class 10

Latest Education News

Rajasthan Board 5th, 8th Result 2024: RBSE Class 5, 8 Results Expected Soon, Check Your Scores Online at rajshaladarpan.nic.in

[LIVE] RBSE 10th, 12th Result 2024: राजस्थान बोर्ड 10वीं, 12वीं रिजल्ट पर बड़ा अपडेट, जल्द rajresults.nic.in पर एक्टिव होगा Direct Link

CUET Exam Analysis 2024, May 15: Check Detailed Paper Review, Difficulty Level, and Good Attempts

MSBSHSE Result 2024 LIVE: Maharashtra Board SSC, HSC Results Date, Time Soon at mahresult.nic.in, Check Direct Link and Past Year's Trends

JAC 8th, 9th, 11th Result 2024 Date And Time Soon, Get Latest Updates Here

Only 1 Out Of 10 Can Find The Umbrella Hidden Among Ostriches in 11 Seconds. Test Your IQ!

TS TET Hall Ticket Download 2024 Today: Direct Link to Telangana TSTET Admit Card at tstet2024.aptonline.in

Netherlands T20 World Cup Squad 2024: Complete List of Team Players and Name

CUET UG Question Paper 2024, May 15: Download Question Paper PDF (SET A, B, C, D)

MPSC SI PT Date 2024 Out For Sub Inspector Posts at mpsc.gov.in: Check Detailed Schedule

CUET UG Answer May 15, 2024: Download Set Wise Answer Sheet PDF

UGC NET June 2024: Registration Deadline Extended Till May 19, Apply Online Link

Namibia T20 World Cup Squad 2024: Complete List of Team Players and Name

Rajasthan BSTC Pre Deled Online Form 2024: राजस्थान प्रीडीएलएड प्रवेश परीक्षा के लिए आवेदन शुरू, ये रहा ऑफिसियल लिंक

[चेक] Most Runs In IPL 2024: दिलचस्प हो गयी है Orange Cap की रेस, Virat टॉप पर

IPL 2024 Live Streaming: मोबाइल या टीवी कहां और कैसे देखें आज के आईपीएल का LIVE टेलीकास्ट?

CUET UG Exam Analysis 2024: All Days Shift Wise Paper Review, Difficulty Level

CUET UG Answer May 16, 2024: Download Set Wise Answer Sheet PDF

Rajasthan Board Result 2024 LIVE: RBSE Class 10th and 12th Results Official Notice Likely to be Released Today at rajeduboard.rajasthan.gov.in, Check Latest Updates

SGPGI Nursing Officer Recruitment 2024: नर्सिंग ऑफिसर के 1683 पदों पर निकली भर्ती, जानें कैसे करें Apply

IMAGES

CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments Worksheet
NCERT Solutions Class 10 Maths
Class 10 Maths Chapter 1 MCQ (Case Study Based for 2023-24) Answers
NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1 Real Numbers
Case study based questions class 10
CBSE MATHS CLASS 10 CH-1

VIDEO

Class 10
Class 10 Maths
Class 11 Maths Most Important Questions From NCERT
Class 10 Maths Answer Key 2024
Case Study for Class 11 Maths
Class 10th Maths Chapter 1

COMMENTS

CBSE Class 10 Maths Case Study Questions for Class 10 Maths Chapter 1
Case Study Questions for Class 10 Maths Chapter 1 - Real Numbers To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library.
Class 10 Maths Case Study Questions of Chapter 1 Real Numbers
Show Answer. (v) If A, B and C are three rational numbers such that 85C - 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by. (a) 3. (b) 6. (c) 7. (d) 9. Show Answer. Case Study 3: Real numbers are an essential concept in mathematics that encompasses both rational and irrational numbers.
PDF Real Numbers- Case Study Case Study 1
1. b) 13915 2. c) 11 3. b) 23 4. a) composite number 5. c) POLYNOMIALS- CASE STUDY CASE STUDY 1: The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be ...
CBSE Class 10 Maths Case Study Questions PDF
Download Case Study Questions for Class 10 Mathematics to prepare for the upcoming CBSE Class 10 Final Exam of 2022-23. These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 10 so that they can score 100% on Boards. ... Class 10 Maths Syllabus 2024 Chapter-1 Real Numbers ...
CBSE Class 10 Maths Case Study : Case Study With Solutions
CBSE Board has introduced the case study questions for the ongoing academic session 2021-22. The board will ask the paper on the basis of a different exam pattern which has been introduced this year where 50% syllabus is occupied for MCQ for Term 1 exam. Selfstudys has provided below the chapter-wise questions for CBSE Class 10 Maths.
Case Study Questions for Class 10 Maths Chapter 1 Real Numbers
Case Study Questions for Class 10 Maths Chapter 1 Real Numbers. Question 1: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM. Based on the above information answer ...
CBSE Class 10 Maths: Case Study Questions of Chapter 1 ...
Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers. Case Study/Passage-Based Questions. Question 1: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions ...
Case Study Class 10 Maths Questions and Answers (Download PDF)
Students referring to the Class 10 Maths Case Study Questions And Answers Pdf from Selfstudys will find these features:-. Accurate answers of all the Case-based questions given in the PDF. Case Study class 10 Maths solutions are prepared by subject experts referring to the CBSE Syllabus of class 10. Free to download in Portable Document Format ...
CBSE 10th Standard Maths Real Number Case Study Questions With Solution
CBSE 10th Standard Maths Subject Real Number Case Study Questions With Solution 2021 Answer Keys. Case Study Questions. (i) (d) : For a number to end in zero it must be divisible by 5, but 4 n = 22 n is never divisible by 5. So, 4 n never ends in zero for any value of n. (ii) (c) : We know that product of two rational numbers is also a rational ...
Case Study on Real Numbers Class 10 Maths PDF
Students looking for Case Study on Real Numbers Class 10 Maths can use this page to download the PDF file. The case study questions on Real Numbers are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Real Numbers case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 ...
NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers
Key Features of NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers. These NCERT Solutions help you solve and revise the updated CBSE syllabus of Class 10 for 2023-24. After going through the stepwise solutions given by our subject expert teachers, you will be able to score more marks.
Case Study Questions Class 10 Maths with Solutions PDF Download
Case Study Questions Class 10 Maths PDF. In class 10 Board Exam 2021, You will find a new type of case-based questions. This is for the first time when you are going to face these type of questions in the board examination. CBSE has introduced these types of questions to better understand each chapter of class 10 maths.
CBSE Case Study Questions for Class 10 Maths Real Numbers Free PDF
Level 1. First, learn to sit for at least 2 hours at a stretch. Level 2. Solve every question of NCERT by hand, without looking at the solution. Level 3. Solve NCERT Exemplar (if available) Level 4. Sit through chapter wise FULLY INVIGILATED TESTS. Level 5.
Case Study Based Questions class 10 maths
Welcome to CBSE Worldz. In this video we will be discussing CBSE class 10 maths case study based questions officially provided by CBSE Board on its website.I...
Case Study Class 10 Maths Questions
First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.
CBSE 10th Standard Maths Polynomials Case Study Questions With Solution
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams ... study questions,10th mathsPolynomials case study questions with answer key,chapter ...
Case Study Based Questions Class 10 Chapter 1 Real Numbers ...
Class 10 Maths Case Study Based Questions Chapter ... Class 10 Maths Case Study Based Questions Chapter ... Case Study Based Questions Class 10 Chapter 1 Real... [Video] Indian Statistical (ISI) Institute Admissi... [Video] Last 10 days MATHS Strategy for JEE MAIN G... April (4) March (3) 2020 (15)
Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 1
R S Aggarwal and V Aggarwal Solutions for Class 10 Maths CBSE Chapter 1: Get free access to Real Numbers Class 10 Solutions which includes all the exercises with solved solutions. ... T S Grewal Solutions for class 11 commerce; Study Materials. CBSE. CBSE Sample Papers. CBSE Sample Papers for Class 6; ... But in this case, LCM ≠ k × HCF ...
Class 10 Maths Chapter 1 MCQ
Class 10 Maths Chapter 1 Real Numbers MCQ (Multiple Choice Objective Questions) with answers and complete explanation case study type questions for the first term examination 2024-25. The answers of 10th Maths Chapter 1 MCQ are given with explanation, so that students can understand easily.
Chapter 1 Class 10 Real Numbers
Updated for NCERT 2023-2024 Book. Answers to all exercise questions and examples are solved for Chapter 1 Class 10 Real numbers. Solutions of all these NCERT Questions are explained in a step-by-step easy to understand manner. In this chapter, we will study. Click on an NCERT Exercise below to get started.
CBSE Class 10 Maths Case Study Questions for Chapter 10
Case study questions are helpful for the preparation of the Class 10 Maths Exam 2021-2022. Case Study Questions for Class 10 Maths Chapter 10 - Circles. CASE STUDY 1: A Ferris wheel (or a big ...
CBSE Class 10 Maths Case Study Questions for Chapter 2
1. In the standard form of quadratic polynomial, ax2 + bx + c, a, b and c are. a) All are Polynomials. b) All are rational numbers. c) 'a' is a non zero real number and b and c are any ...
2024 AP Exam Dates
2024 AP Exam Dates. The 2024 AP Exams will be administered in schools over two weeks in May: May 6-10 and May 13-17. AP coordinators are responsible for notifying students when and where to report for the exams. Early testing or testing at times other than those published by College Board is not permitted under any circumstances.
CBSE Class 10 Maths Case Study Questions for Chapter 3
Check Case Study Questions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables CASE STUDY-1: A test consists of 'True' or 'False' questions.

Class 10 Maths Case Study Questions of Chapter 1 Real Numbers

Real Numbers Case Study Questions With Answers

You Might Also Like

Class 10 Science Topper’s Answer Sheet Latest PDF Download FREE

Case Study Questions for Class 10 Maths Chapter 1 Real Numbers

Download CBSE Books

Leave a Reply Cancel reply

Discover more from Gurukul of Excellence

CBSE Class 10 Maths: Case Study Questions of Chapter 1 Real Numbers PDF Download

Real Numbers Case Study Questions With answers

Leave a Comment Cancel reply

Download India's best Exam Preparation App Now.

Case Study on Real Numbers Class 10 Maths PDF

Case Study on Real Numbers Class 10 Maths with Solutions in PDF

Why Solve Real Numbers Case Study Questions on Class 10 Maths?

How to Answer Case Study Questions on Real Numbers?

What to Know to Solve Case Study Questions on Class 10 Real Numbers?

Where to Find Case Study on Real Numbers Class 10 Maths?

One Last Step...

NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 1 Real Numbers

Download PDF of NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

Access Answers to NCERT Class 10 Maths Chapter 1 – Real Numbers

Exercise 1.2 Page: 11

Exercise 1.3 Page: 14

Exercise 1.4 Page: 17

NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers

Key Features of NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers

Frequently Asked Questions on NCERT Solutions for Class 10 Maths Chapter 1

Register with BYJU'S & Download Free PDFs

Case Study Questions Class 10 Maths with Solutions PDF Download

Link to Download Case-Study Questions of class 10

Communication Skills Class 9 Notes

Communication Skills Class 10 Notes PDF

Information Technology Code 402 Class 10 Solutions

Set-1 | Padbandh MCQ Questions Class 10 - CBSE 2022

Top 50+ MCQ on Communication Skills Class 10 for TERM 1- 2022 | IT Code 402

TERM 1 MCQ | Communication Skills Class 10 Questions and Answers

Information Technology Code 402 Class 10 Notes 2023

CBSE Case Study Questions for Class 10 Maths Real Numbers Free PDF

CBSE Case Study Questions for Class 10 Maths Real Numbers PDF

How should I study for my upcoming exams?

Contact Form

Case Study Class 10 Maths Questions

myCBSEguide App

Format of Maths Case-Based Questions

Maths Case Study Question Paper 2023

Case Study Question in Mathematics

Case Study Question – 1

Case Study Question – 2

Case Study Question – 3

Case Study Question – 4

Case Study Question – 5

Case Study Question – 6

More Case Study Questions

How to Solve Case-Based Questions?

What are Class 10 competency-based questions?

Case Study Questions in Maths Question Paper

Case Studies on CBSE’s Official Website

10 Maths Case Studies in myCBSEguide App

Related Posts

Leave a Comment

CBSE 10th Standard Maths Subject Polynomials Case Study Questions With Solution 2021

QB365 - Question Bank Software

*****************************************

Related 10th Standard CBSE Maths Materials

Class VI to XII

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

Tuesday, September 21, 2021

Warning: Do Not Copy!

Blog Archive

Class 10 Maths Chapter 1 MCQ

Case Study – 1

What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?

If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32, 36) is

36 can be expressed as a product of its primes as

7 х 11 х 13 х 15 + 15 is a

If p and q are positive integers such that p = ab² and q = a²b, where a, b are prime numbers, then the LCM (p, q) is

Case Study – 2