the quadratic assignment problem

Analysis of Algorithms
Backtracking
Dynamic Programming
Divide and Conquer
Geometric Algorithms
Mathematical Algorithms
Pattern Searching
Bitwise Algorithms
Branch & Bound
Randomized Algorithms
Solve Coding Problems
Introduction to Exact Cover Problem and Algorithm X
Transform and Conquer Technique
Preemptive Priority CPU Scheduling Algorithm
Introduction to Grover's Algorithm
Art Gallery Problem
Implementation of Exact Cover Problem and Algorithm X using DLX
Representation Change in Transform and Conquer Technique
How to develop an Algorithm from Scratch | Develop Algorithmic Thinking
Approximation Algorithms
Algorithm definition and meaning
What Does Big O(N^2) Complexity Mean?
How to write a Pseudo Code?
What are Objects in Programming?
Order of removal in Josephus problem in O(N logN)
Can ChatGPT be used to solve Competitive Coding Problems?
Difference between Data Structures and Algorithms
How Data Structures can be used to achieve Efficient Memory Utilization
Difference between Deterministic and Non-deterministic Algorithms
Merge Sort Tree with point update using Policy Based Data Structure

Quadratic Assignment Problem (QAP)

The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.

The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.

The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.

The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.

There are various types of algorithms for different problem structures, such as:

Precise algorithms
Approximation algorithms
Metaheuristics like genetic algorithms and simulated annealing
Specialized algorithms

Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.

Facilities cost matrix:

Flow matrix:

To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.

The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.

The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.

To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.

Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.

Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.

Please Login to comment...

10 YouTube Alternatives to Stream Music Online in 2024
12 Best Paint 3D Alternatives in 2024
10 Best Pixlr Alternatives for Android in 2024 [Free + Paid]
Bougie Definition and Usage Examples
30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

1 Introduction
2.1 Koopmans-Beckman Mathematical Formulation
2.2.1 Parameters
2.3.1 Optimization Problem
2.4 Computational Complexity
2.5 Algorithmic Discussions
2.6 Branch and Bound Procedures
2.7 Linearizations
3.1 QAP with 3 Facilities
4.1 Inter-plant Transportation Problem
4.2 The Backboard Wiring Problem
4.3 Hospital Layout
4.4 Exam Scheduling System
5 Conclusion
6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

$F=(F_{ij})$

Inner Product

$A,B$

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

$F_{i,j}(X_{\phi }DX_{\phi }^{T})_{i,j}$

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

$\min _{X\in P}\langle F,XDX^{T}\rangle$

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

Dynamic Program
Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

$min\sum _{i=1}^{n}\sum _{j=1}^{n}c{_{\phi (i)\phi (j)}}+\sum _{i=1}^{n}b{_{\phi (i)}}$

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

$D={\begin{bmatrix}0&5&6\\5&0&3.6\\6&3.6&0\end{bmatrix}}$

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

$E=\left\{E_{1},E_{2},...,E_{n}\right\}$

as well as a set of r points

$P_{1},P_{2},...,P_{r}$

In his paper he derives the below formula:

$min\sum _{1\leq i\leq j\leq n}^{}C_{ij}(d_{s(i)s(j))})$

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

$min\sum _{i,j}\sum _{k,q}f_{ik}d_{jq}y_{ij}y_{kq}$

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

$n!$

↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

The Quadratic Assignment Problem : Theory and Algorithms

Available online.

SpringerLink

At the library

Stanford libraries, more options.

Find it at other libraries via WorldCat
Contributors

Description

Creators/contributors, contents/summary.

Preface. List of Figures. List of Tables.
1. Problem Statement and Complexity Aspects.
2. Exact Algorithms and Lower Bounds.
3. Heuristics and Asymptotic Behavior.
4. QAPs on Specially Structured Matrices.
5. Two More Restricted Versions of the QAP.
6. QAPs Arising as Optimization Problems in Graphs.
7. On the Biquadratic Assignment Problem (BIQAP). References. Notation Index. Subject Index.
(source: Nielsen Book Data)

Bibliographic information

Stanford Home
Maps & Directions
Search Stanford
Emergency Info
Terms of Use
Non-Discrimination
Accessibility

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

We're Hiring!
Help Center

The Quadratic Assignment Problem

Related Papers

Encyclopedia of Optimization

Panos Pardalos

Panos M Pardalos

Abstract This paper aims at describing the state of the art on quadratic assignment problems (QAPs). It discusses the most important developments in all aspects of the QAP such as linearizations, QAP polyhedra, algorithms to solve the problem to optimality, heuristics, polynomially solvable special cases, and asymptotic behavior.

Güneş Erdoğan

The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we analyze the binary structure of the QAP and present new IP formulations. We focus on “flow-based” formulations, strengthen the formulations with valid inequalities, and report computational experience with a branch-and-cut algorithm. Next, we present new classes of instances of the QAP that can be completely or partially reduced to the Linear Assignment Problem and give procedures to check whether or not an instance is an element of one of these classes. We also identify classes of instances of the Koopmans-Beckmann form of the QAP that are solvable in polynomial time. Lastly, we present a strong lower bound based on Bender’s decomposition.

Cesar Beltran-Royo

Pesquisa Operacional

Paulo Boaventura Netto

We investigate the classical Gilmore-Lawler lower bound for the quadratic assignment problem. We provide evidence of the difficulty of improving the Gilmore-Lawler bound and develop new bounds by means of optimal reduction schemes. Computational results are reported indicating that the new lower bounds have advantages over previous bounds and can be used in a branch-and-bound type algorithm for the quadratic assignment problem.

Computers & Operations Research

Ricardo P M Ferreira

Ilyes Beltaef

RELATED PAPERS

Paulo Gonçalves

Dennis Heffley

Franz Rendl

Vittorio Maniezzo

New ideas in optimization

Marco Dorigo

Álvaro M. Valdebenito B.

Journal of Combinatorial Optimization

Madalina Drugan

Ali Safari Mamaghani

Informs Journal on Computing

Dushyant Sharma

Mathematics of Operations Research

Discrete Applied Mathematics

catherine roucairol

IEEE Transactions on Knowledge and Data Engineering

Cut Latifah

European Journal of Operational Research

Bernard Mans

Teodor Crainic

Applied Mathematical Sciences

Hassan Mishmast Nehi

Panos M Pardalos , John Mitchell

Paulo Boaventura-Netto

Ajay Bidyarthy

Yugoslav Journal of …

Journal of Industrial Engineering International

Hossein Karimi

NURDIYANA JAMIL

Ajith Abraham

IEEE Transactions on Information Theory

David Malah

Tansel Dökeroğlu

Matteo Fischetti

Sunderesh Heragu

Computer Science > Artificial Intelligence

Title: where the really hard quadratic assignment problems are: the qap-sat instances.

Abstract: The Quadratic Assignment Problem (QAP) is one of the major domains in the field of evolutionary computation, and more widely in combinatorial optimization. This paper studies the phase transition of the QAP, which can be described as a dramatic change in the problem's computational complexity and satisfiability, within a narrow range of the problem parameters. To approach this phenomenon, we introduce a new QAP-SAT design of the initial problem based on submodularity to capture its difficulty with new features. This decomposition is studied experimentally using branch-and-bound and tabu search solvers. A phase transition parameter is then proposed. The critical parameter of phase transition satisfaction and that of the solving effort are shown to be highly correlated for tabu search, thus allowing the prediction of difficult instances.

Submission history

Access paper:.

Download PDF
HTML (experimental)
Other Formats

References & Citations

Google Scholar
Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Combinatorial Programming: Methods and Applications pp 351–360 Cite as

The Quadratic Assignment Problem: A Brief Review

E. L. Lawler 3
Conference paper

273 Accesses

1 Citations

Part of the book series: NATO Advanced Study Institutes Series ((ASIC,volume 19))

The quadratic assignment problem, its applications, and various exact and inexact procedures for its solution are briefly reviewed. Certain special cases of the one-dimensional module placement problem, itself a special case of the quadratic assignment problem, are surveyed.

Assignment Problem
Permutation Matrix
Placement Problem
Quadratic Assignment Problem
Presidential Candidate

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The preparation of this paper was supported in part by the U.S. Air Force Office of Scientific Research, Grant AFOSR-71–2076.

This is a preview of subscription content, log in via an institution .

Buying options

Available as PDF
Read on any device
Instant download
Own it forever
Compact, lightweight edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Unable to display preview. Download preview PDF.

D. Adolphson and T.C. Hu, “Optimal Linear Ordering,” SIAM J. Appl. Math. 25 (1973), 403–423.

Article MathSciNet MATH Google Scholar

P.S. Davis and T.L. Ray, “A Branch-Bound Algorithm for the Capacitated Facilities Location Problem,” Naval Res. Logistics Qtrly 16 (1969), 331–344.

MATH Google Scholar

M.A. Efroymson and T.L. Ray, “A Branch-Bound Algorithm for Plant Location,” Opns. Res. 14 (1966), 361–368.

Article Google Scholar

J.N. Gavert and N.V. Plyter, “The Optimal Assignment of Facilities to Locations by Branch and Bound,” Opns.Res. 14 (1966), 210–232.

P.C. Gilmore, “Optimal and Sub-optimal Algorithms for the Quadratic Assignment Problem,” SIAM J. Appl. Math. 10 (1962), 305–313.

R.H. Glaser, “A Quasi-Simplex Method for Designing Suboptimal Packages for Electronic Building Blocks,” Proc. 1959 Computer Applic. Symp. , Armour Res. Found., Ill. Inst. Tech., 100–111.

Google Scholar

R.E. Gomory and T.C. Hu, “Multi-Terminal Network Flows,” SIAM J. Appl. Math. 9 (1961), 551–570.

G.W. Graves and A.B. Whinston, “An Algorithm for the Quadratic Assignment Problem,” Mgt. Sci. 16 (1970), 453–471.

Article MATH Google Scholar

S.A. Graciano, “Branch and Bound Solutions to the Capacitated Plant Location Problem,” Opns. Res. 17 (1969), 1005–1016.

M. Hanan and J.M. Kurtzberg, “A Review of the Placement and Quadratic Assignment Problems,” SIAM Rev. 14 (1972), 324–342.

G. Henry, “Recherche d’un Reseau de Depots Optimum,” Reuve Francaise d’informatique et de Recherche Operationnelle 2 (1968), 61–70.

F.S. Hillier and M.M. Connors, “Quadratic Assignment Problem Algorithms and the Location of Indivisible Facilities,” Mgt. Sci. 13 (1966), 42–57.

W.A. Horn, “Single Machine Job Sequencing with Treelike Precedence Ordering and Linear Delay Penalties,” SIAM J. Appl. Math. 23 (1972), 189–202.

R.M. Karp, “Reducibility Among Combinatorial Problems,” in Complexity of Computer Computations , R.E. Miller and J.W. Thatcher, eds., Plenum Press, N.Y., 1972, 85–104.

R.M. Karp, A.C. McKellar, C.K. Wong, “Near-Optimal Solutions to a 2-Dimensional Placement Problem,” IBM Research Tech. Report RC4740, February 1974.

U.R. Kodres, “Geometrical Positioning of Circuit Elements in a Computer,” Conf. Paper 1172 , AIEE Fall General Mtg., Oct. 1959.

T.C. Koopmans and M.J. Beckmann, “Assignment Problems and the Location of Economic Activities,” Econometrica 25 (1957), 52–75.

Article MathSciNet Google Scholar

A.H. Land, “A Problem of Assignment with Inter-related Costs,” Opnl. Res. Qtrly 14 (1963), 185–199.

E.L. Lawler, “The Quadratic Assignment Problem,” Mgt. Sci. 9 (1963), 586–589.

P.M. Morse, “Optimal Linear Ordering of Information Items,” Opns. Res. 20 (1972), 741–751.

C.E. Nugent, T.E. Vollman and J. Ruml, “An Experimental Comparison of Techniques for the Assignment of Facilities to Locations,” Opns. Res. 16 (1968), 150–173.

V.R. Pratt, “An N log N Algorithm to Distribute N Records Optimally in a Sequential Access File,” in Complexity of Computer Computations , R.E. Miller and J.W. Thatcher, eds., Plenum Press, N.Y., 1972, 111–118.

T.C. Raymond, “A Method for Optimizing Circuit Module Placement,” IBM Tech. Disclosure Bull. 13 (1970), 274–276.

J. Sidney, Ph.D. dissertation, University of Michigan, Ann Arbor, 1971.

K. Spielberg, “Plant Location with Generalized Search Origin,” Mgt. Sci. 16 (1969), 165–178.

L. Steinberg, “The Backboard Wiring Problem: A Placement Algorithm,” SIAM Rev. 3 (1961), 37–50.

Download references

Author information

Authors and affiliations.

Department of Electrical Engineering and Computer Sciences, The University of California, Berkeley, CA, USA

E. L. Lawler

You can also search for this author in PubMed Google Scholar

Editor information

Editors and affiliations.

Université de Paris, France

B. Roy ( Professeur et Conseiller Scientifique ) ( Professeur et Conseiller Scientifique )

SEMA, France

Rights and permissions

Reprints and permissions

Copyright information

About this paper

Cite this paper.

Lawler, E.L. (1995). The Quadratic Assignment Problem: A Brief Review. In: Roy, B. (eds) Combinatorial Programming: Methods and Applications. NATO Advanced Study Institutes Series, vol 19. Springer, Dordrecht. https://doi.org/10.1007/978-94-011-7557-9_20

Download citation

DOI : https://doi.org/10.1007/978-94-011-7557-9_20

Publisher Name : Springer, Dordrecht

Print ISBN : 978-94-011-7559-3

Online ISBN : 978-94-011-7557-9

eBook Packages : Springer Book Archive

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

View all journals
My Account Login
Explore content
About the journal
Publish with us
Sign up for alerts
Open access
Published: 12 March 2024

Short-depth QAOA circuits and quantum annealing on higher-order ising models

Elijah Pelofske ORCID: orcid.org/0000-0003-2673-796X 1 ,
Andreas Bärtschi 1 &
Stephan Eidenbenz 1

npj Quantum Information volume 10 , Article number: 30 ( 2024 ) Cite this article

376 Accesses

1 Altmetric

Metrics details

Computational science
Quantum information
Quantum simulation

We present a direct comparison between QAOA (Quantum Alternating Operator Ansatz), and QA (Quantum Annealing) on 127 qubit problem instances. QAOA with p = 1, 2 rounds is executed on the 127 qubit heavy-hex graph gate-model quantum computer ibm_washington, using on-device grid-searches for angle finding, and QA is executed on two Pegasus-chip D-Wave quantum annealers. The problems are random Ising models whose connectivity matches heavy-hex graphs and the Pegasus graph connectivity, and optionally include hardware-compatible cubic terms ( Z Z Z terms). The QAOA circuits are heavily optimized and of extremely short depth, with a CNOT depth of 6 per round, which allows whole chip usage of the heavy-hex lattice. QAOA and QA are both compared against simulated annealing and the optimal solutions are computed exactly using CPLEX. The noiseless mean QAOA expectation values for p = 1, 2 are computed using classical light-cone based simulations. We find QA outperforms QAOA on the evaluated devices.

Drug design on quantum computers

Raffaele Santagati, Alan Aspuru-Guzik, … Clemens Utschig-Utschig

De novo design of protein structure and function with RFdiffusion

Joseph L. Watson, David Juergens, … David Baker

Exploring the frontiers of condensed-phase chemistry with a general reactive machine learning potential

Shuhao Zhang, Małgorzata Z. Makoś, … Justin S. Smith

Introduction

The Quantum Alternating Operator Ansatz (QAOA) is a hybrid quantum-classical algorithm for sampling combinatorial optimization problems 1 , 2 , 3 , the parameterized quantum component of which is executed on a programmable gate-based universal quantum computer. The Quantum Approximate Optimization Algorithm 4 , 5 is the original algorithm of this type, which was then generalized to the Quantum Alternating Operator Ansatz algorithm 1 under the same acronym of QAOA. The classical component of QAOA involves learning the best parameters of the circuit to obtain low energy solutions of the combinatorial optimization problem.

Quantum annealing (QA) in the transverse field Ising model is a model of quantum computation that utilizes quantum fluctuations to search for ground state solutions of a combinatorial optimization problem, that is encoded as a Hamiltonian 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 . D-Wave quantum annealers are programmable hardware implementations of quantum annealing that use superconducting flux qubits 14 , 15 , 16 , 17 , which can be programmed by a user by specifying an Ising model that maps to the hardware graph. For the experiments in this paper, we use the IBM Quantum programmable fixed-frequency superconducting transmon qubit 18 device ibm_washington , which has a heavy-hex connectivity graph 19 with 127 qubits.

Both QAOA and Quantum Annealing are based on the adiabatic theorem, and in particular Adiabatic Quantum Computation. Both algorithms are implementing a type of adiabatic evolution, both algorithms aim to sample optimal solutions of combinatorial optimization problems, and both algorithms are being actively studied for demonstrating advantage over classical heuristics as quantum heuristic samplers for optimization problems 20 , 21 . The exact characteristics of how both QA and QAOA will scale to large system sizes, especially on noisy hardware, is currently not fully understood 22 , 23 , 24 . There is evidence that QAOA may be more difficult for classical computers to simulate than quantum annealing, which could make it a viable candidate for quantum advantage 25 . Therefore it is of interest to investigate differences between QAOA and QA and determine how these algorithms scale—both for large problem sizes and for larger QAOA rounds, or annealing times in the case of QA 26 , 27 , 28 , 29 , 30 , 31 . There have been a limited number of studies that directly compare Quantum Annealing and the QAOA algorithm 32 , 33 , 34 , 35 , 36 (or even more generally, gate model quantum computing and QA 37 ), which in part motivates the direct comparison of the two protocols presented in this research. With respect to large QAOA implementations, there have been experiments that used up to 40 qubits 38 , 27 qubits 39 , and 23 qubits 40 . There have also been QAOA experiments which used circuit depths up to 148 41 and 159 42 .

Because both QA and QAOA address combinatorial optimization problems, it is of considerable interest to experimentally and theoretically evaluate both algorithms. QAOA has been evaluated for a number of problems, including portfolio optimization 41 , maximum cut 40 , 43 , 44 , 45 , 46 , 47 , 48 , 49 , maximum k-vertex cover 2 , maximum independent set 50 , the knapsack problem 51 , and the Sherrington-Kirkpatrick model 40 , 44 , 52 . QA has been experimentally applied to a wide variety of problems, including semiprime factorization 53 , 54 , 55 , 56 , 57 , graph coloring 58 , 59 , clustering 60 , the Sherrington-Kirkpatrick model 61 , and portfolio optimization 62 , 63 , 64 . See refs. 9 , 10 for quantum annealing reviews. Both QAOA and QA have been used to simulate properties of magnetic systems 24 , 65 , 66 , 67 , 68 , 69 .

We perform a comparison between two different algorithms (QA on two D-Wave processors and QAOA on an IBM Quantum processor), on instances of two sets of combinatorial optimization problems.

Instances with linear and quadratic terms, which can be described as a graph.

Instances with linear, quadratic and cubic terms, which can be described as a hypergraph.

Every instance is individually compared across the two algorithms/devices. Instances from (1) are native to the connectivity of both devices. Instances from (2) are non-native to the connectivity of either device (in the case of QAOA, the hypergraph instances are not native to the circuit model quantum computer because there are no hardware-native 3-qubit gates), and compiled using slack variable order reduction (which itself is hardware-native) and QAOA circuit optimization, respectively. This article is a significant extension of ref. 36 . The enumerated contributions of this article are as follows:

We define a class of higher-order Ising model problems that have an interaction connectivity that matches the native IBM Quantum heavy-hex connectivity as well as onto D-Wave’s Pegasus connectivity, allowing the two algorithms and technologies to be compared. Adding optimization terms that are higher than quadratic has not been studied in QAOA NISQ experiments and circuit constructions. We randomly generate and sample 10 different instances of these Ising models, each for cubic and quadratic maximum degree. The cubic (higher-order) Ising models are not native to the heavy-hex connectivity graph by definition since the cubic terms are hyper-edges and the heavy-hex graph is composed only of edges and nodes, however we choose the cubic terms so that they match the underlying heavy-hex hardware graph, and can be very very efficiently implemented in the QAOA circuit (with no two-qubit gate overhead).

We design optimized QAOA circuits for these Ising problems that are short depth (CNOT depth of 6, both for the quadratic and cubic Ising models), thus allowing the use of the entire chip of the ibm_washington with 127 qubits for QAOA. Remarkably, the optimized QAOA circuits require only a single additional layer of single qubit rotations for addressing the cubic terms. This hardware compatible, geometrically local, problem type allows the QAOA circuits to be implemented in a NISQ-friendly way, not requiring SWAP networks for long range variable interactions. This choice is highly intentional because it allows a direct comparison between QAOA and QA. We limit the experiments to two QAOA rounds because the computation quality at two rounds is approximately the same as at one round (due to device error rates). These experiments are the largest QAOA experiments, with respect to number of qubits, performed on a quantum computer to date – to the best of our knowledge. There have been QAOA circuits executed on current quantum computers with higher gate count and higher number of rounds, e.g. refs. 38 , 39 , 40 , 41 , 42 , 70 , 71 .

So as to solve the Ising models with cubic terms on D-Wave Quantum Annealing hardware, we order-reduce the Ising model instances to quadratic problems carefully ensuring that a scalable mapping to the Pegasus lattice remains viable and we then instantiate these problems on two different D-Wave machines.

The quantum annealing implementation uses the Transverse field driving Hamiltonian as the initial state, and the QAOA implementation uses the Transverse field mixer. This ensures that the comparison between the two algorithms is as fair as possible, since there are many other possible variants of both algorithms.

We put significant optimization efforts into both the QAOA and QA experiments. In particular, for QAOA on IBM Quantum, we perform angle optimization and test digital dynamical decoupling (DDD). For running QA on D-Wave processors, we vary the forward anneal schedule with symmetric pauses.

In order to better assess the quality of the obtained NISQ results, we calculate theoretical results for the optimum solutions of the problem Ising models using CPLEX, and the classical heuristic simulated annealing (giving a solution spectrum); we also calculate the theoretical means of the solution quality achieved by (noise-free) QAOA for 1 and 2 rounds, as well as expectation values for random solutions.

The experiments on the NISQ devices of solving the same problem set are the key method for us to answer what the state-of-the-art is in QA and QAOA performance in a fair comparison. Our main insights are the following:

Quantum Annealing on D-Wave clearly outperforms QAOA on the ibm_washington . In particular, QA finds significantly better minimum energy solutions as well as better average solutions found on all Ising problems studied

QA finds optimum or very nearly optimum solutions for all problems and longer annealing times work the best.

QAOA runs on IBM Quantum find solutions that are significantly worse than those found by QA, but they are better than random sampling. QAOA solutions from ibm_washington are on average significantly worse than the theoretical noise-free QAOA expectation values.

The optimal QAOA angles show pronounced parameter concentration – this parameter concentration is observed even between the Ising models with and without geometrically-local higher order terms. These results are consistent for the classically computed QAOA results as well as for the actual IBM Quantum hardware runs. The finding of parameter concentration on this ensemble of random Ising problems is consistent with previous QAOA simulations and empirical results on other problem types.

Digital dynamical decoupling, for the specific gate sequences we chose, improves performance for QAOA only for two rounds and cubic Ising problems, whereas it actually leads to poorer performance in all other cases.

In Section “Methods” the QAOA and QA hardware implementations are detailed. Section “Results” details the experimental results and how the two algorithms compare. Section “Methods” concludes with what the results show. The figures in this article were generated using a combination of plotly 72 , matplotlib 73 , 74 , networkx 75 , and Qiskit 76 in Python 3.

Section “Background” gives background on the QAOA and Quantum Annealing algorithms. Section “Theory” describes the custom Ising models, the QAOA circuits to sample the Ising models, and the embedding of the Ising models onto the D-Wave quantum annealers. Section “Experiments” details all of the experimental results.

QAOA general overview

For a combinatorial optimization problem over inputs z ∈ {+1, −1} n , let $C(z):{\{+1,-1\}}^{n}\to {\mathbb{R}}$ be the objective function from Eqs. ( 4 ), ( 5 ). For a minimization problem, the goal is to find a variable assignment vector z for which C ( z ) is minimized. The QAOA algorithm consists of the following components:

an initial state $\left\vert \psi \right\rangle$ ,

a phase separating Cost Hamiltonian H C , which is derived from C ( z ) by replacing all spin variables z i by Pauli-Z operators ${\sigma }_{i}^{z}$

a mixing Hamiltonian H M ; in our case, we use the standard transverse field mixer, which is the sum of the Pauli-X operators ${\sigma }_{i}^{x}$

an integer p ≥1, the number of rounds to run the algorithm (also referred to as the number of layers ),

two real vectors $\overrightarrow{\gamma }=({\gamma }_{1},...,{\gamma }_{p})$ and $\overrightarrow{\beta }=({\beta }_{1},...,{\beta }_{p})$ , each with length p .

The QAOA algorithm consists of first preparing the initial state $\left\vert \psi \right\rangle$ , and then applying p rounds of the alternating simulation of the phase separating Hamiltonian and the mixing Hamiltonian:

Within reach round, H C is applied first, which separates the basis states of the state vector by phases e − i γ C ( z ) . H M then provides parameterized interference between solutions of different cost values. After p rounds, the state $\vert \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ is measured in the computational basis and returns a sample solution z of cost value C ( z ) with probability $| \langle y| \overrightarrow{\gamma },\overrightarrow{\beta }\rangle {| }^{2}$ .

The goal when using QAOA is to prepare the state $\vert \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ from which we can sample a variable assignment vector y with high cost value f ( y ). Therefore, to use QAOA the task is to find angles $\overrightarrow{\gamma }$ and $\overrightarrow{\beta }$ such that the expectation value $\langle \overrightarrow{\gamma },\overrightarrow{\beta }| {H}_{C}| \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ is large ( − H C for minimization problems). In the limit p → ∞ , QAOA is effectively a Trotterization of of the Quantum Adiabatic Algorithm, and in general as we increase p we expect to see a corresponding increase in the probability of sampling the optimal solution. The challenge is the classical outer loop component of finding good angles (not necessarily optimal) $\overrightarrow{\gamma }$ and $\overrightarrow{\beta }$ for all rounds p , which has a high computational cost as p increases 29 , 71 .

There are a growing number of QAOA variants including GM-QAOA 77 , ST-QAOA 78 , CD-QAOA 79 , Th-QAOA 80 , RQAOA 81 , warm start QAOA 82 , 83 , 84 , 85 , FUNC-QAOA 86 , FQAOA 87 , FKL-QAOA 88 , HLZ-QAOA 88 , DC-QAOA 89 , and multi-angle QAOA 90 , 91 , but here we do not use any of these QAOA variants instead we use the standard transverse-field mixer implementation, which makes the comparison consistent with the D-Wave quantum annealing devices that use a transverse field driving Hamiltonian for the initial state.

Variational quantum algorithms, including QAOA, have been a subject of interest in quantum algorithms research in large part because of the problem domains that variational algorithms can address (such as combinatorial optimization) 92 . The primary challenge in variational quantum algorithms is the classical component of parameter selection which has not been solved and is even more difficult when noise is present in the computation 93 . Typically, for small scale experiments the optimal angles for QAOA are computed exactly (up to numerical simulation precision) for small problem instances 33 , 94 . For this class of Ising models, it is not known whether there exist analytically optimal QAOA angles (for some problem types analytically optimal solutions have been found 95 ). Therefore, our angle finding approach consists of a reasonably high-resolution gridsearch without knowing good angles a-priori. We note that a fine gridsearch scales exponentially with the number of QAOA rounds p , and is therefore not practical for higher round QAOA 2 , 4 . Classically computing good angles is computationally intensive, especially with the introduction of cubic terms. In our specific case of the class of sparse Ising models defined in Section “Theory”, it is possible due to the geometric locality of the problem instances to classically simulate the mean energy expectation values computed by QAOA (at least for p = 1 and p = 2), albeit at significant computational cost for the high-resolution angle gridsearch; Section “Classical Simulation of QAOA” details how this can be accomplished.

Quantum annealing general overview

Quantum annealing uses quantum fluctuations to search for the ground state of a Ising model of interest. Quantum annealing, in the case of the transverse field Ising model as implemented on D-Wave hardware, is explicitly described by the system given in Eq. ( 2 ) below. The state begins at time zero purely in the easy-to-prepare ground state of the transverse field Hamiltonian ${\sum }_{i}{\sigma }_{i}^{x}$ , and then over the course of the anneal (parameterized by the annealing time ) the user programmed Ising problem is applied according the function B ( s ). Together, A ( s ) and B ( s ) define the anneal schedules of the annealing process, and s is referred to as the anneal fraction . The standard anneal schedule that is used is a linear interpolation between s = 0 and s = 1.

The adiabatic theorem states that if changes to the Hamiltonian of the system are sufficiently slow, then the system will remain in the ground state of problem Hamiltonian (up until the state is classically measured), thereby providing a computational mechanism for finding the ground state of combinatorial optimization problems. The user programmed Ising problem H i s i n g , acting on n qubits, is defined in Eq. ( 3 ). Combined, the quadratic terms and the linear terms define the optimization problem instance that quantum annealing samples. As with QAOA, the objective of quantum annealing is to find the variable assignment vector z that minimizes the cost function that has the form of Eq. ( 3 ).

Ising model problem instances

Table 1 shows that the D-Wave quantum annealers have more available qubits than ibm_washington . The additional qubits available on the quantum annealers will allow us to embed multiple problem instances in parallel onto the chips. The current IBM Quantum devices have a hardware connectivity graph referred to as a heavy-hex lattice 19 . The current D-Wave quantum annealers have three different families of hardware connectivity graphs – Chimera 96 , 97 , 98 , Pegasus 96 , 99 , and Zephyr 100 . For this direct comparison we target the Pegasus connectivity devices. The two current D-Wave quantum annealers with Pegasus hardware connectivity graphs have chip id names Advantage_system6.1 and Advantage_system4.1 . Among the current quantum annealing hardware that is available, the Zephyr Z 4 and Chimera C 16 hardware graph devices are either not large enough or dense enough in order to instantiate the problem embeddings, whereas the P 16 Pegasus chip devices are large enough and dense enough for the problem instances to be embedded directly. Therefore, for a direct QAOA and QA comparison we create Ising problems with connectivities that map directly onto both the logical heavy-hex lattice of the IBM Quantum device for the QAOA circuits as well as onto the P 16 Pegasus connectivity of the quantum annealers. For a fair comparison, we need to define problems that can be instantiated on all three of the devices in Table 1 . In particular, we want these implementations to not be unfairly costly in terms of implementation overhead. For example, we do not want to introduce unnecessary qubit swapping in the QAOA circuit because that would introduce larger circuit depths, which would introduce more decoherence in the computation. We also want to avoid minor embedding the problems onto the quantum annealers because there are an additional set of problems introduced with minor embedding, including chain break resolution algorithms 101 , the large ferromagnetic chain strength dominating the programmed energy scale on the chip 102 , and suppressed ground state sampling 103 (especially for non-calibrated chains).

As an additional dimension to push boundaries of the state-of-the-art in quantum optimization, we introduce higher-order terms , specifically cubic Z Z Z interactions 104 , 105 , 106 , 107 , which could be viewed as 3-body (or multi-body) interacting terms, or hypergraphs, or p-spin Ising models 108 , 109 , 110 , 111 , 112 , 113 , 114 , 115 , 116 , 117 , 118 (the exact terminology varies throughout the literature on this topic). The introduction of higher order terms offers a way to increase the complexity of the problems, because more terms need to be addressed by the solver, while keeping the total number of variables the same. The introduction of higher order terms into the Ising models we wish to sample for the direct QAOA and QA comparison requires both QAOA and QA to handle these geometrically local higher order variable interactions, which is an additional test on the capability of both algorithms. Importantly, QAOA can naturally handle higher-order terms, which is a notable feature of the algorithm that has only been explored in a few previous studies 119 , 120 , 121 , 122 , 123 . Because D-Wave quantum annealing hardware only natively supports Ising models with linear and quadratic terms, implementing higher-order terms requires introducing auxiliary variables for the purpose of performing order reduction to obtain a problem structure that is comprised of only linear and quadratic terms that match the hardware graph, but whose optimal variable assignments (not including the auxiliary variables) are exactly the same as the optimal variable assignments of the original high order polynomial 9 , 53 , 124 , 125 , 126 , 127 . Note that the term HUBO (Higher-order Unconstrained Binary Optimization) problem 107 , 121 , 126 , 127 , 128 is also used when referring to these types of combinatorial optimization problems which contain higher order terms, however HUBO is specifically for problems where the variable type is binary, and the Ising models we defined for these experiments have variables which are spins (e.g. + 1, − 1).

Taking each of these characteristics into account, we create a class of random problems that respect the native device hardware connectivity graphs, as described in Table 1 . The problem instances we will be considering are Ising problems defined on the hardware connectivity graph of the heavy hex lattice of the device, which for these experiments will be ibm_washington . For a vector z = ( z 0 , …, z n −1 ) ∈ {+1, −1} n we define

Equation ( 4 ) defines the class of random Ising models with cubic terms that we wish to minimize as follows. Any heavy hex lattice is a bipartite graph with vertices V = {0, …, n − 1} bipartitioned as V = V 2 ⊔ V 3 , where V 3 consists of vertices with a maximum degree of 3 (shown in Fig. 1 (left) as the dark gray nodes), and V 2 consists of vertices with a maximum degree of 2 (shown in Fig. 1 (left) as the light gray nodes). E ⊂ V 2 × V 3 is the edge set representing available two qubit gates (in this case CNOTs where we choose targets i ∈ V 2 and controls j ∈ V 3 ). W is the set of vertices in V 2 that all have degree exactly equal to 2. n 1 is a function that gives the qubit (variable) index of the first of the two neighbors of a degree-2 node and n 2 provides the qubit (variable) index of the second of the two neighbors of any degree-2 node. Thus d v , d i , j , and ${d}_{l,{n}_{1}(l),{n}_{2}(l)}$ are all coefficients representing the random selection of the linear, quadratic, and cubic coefficients, respectively. These coefficients could be drawn from any distribution – in this paper we draw the coefficients from { + 1, − 1} with probability 0.5. Combined, any vector of variable states z can be evaluated given this objective function formulation of Eq. ( 4 ).

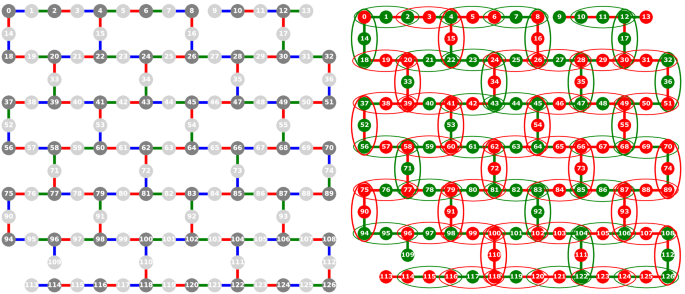
(left) ibm_washington graph connectivity, where qubits are connected by CNOT (also referred to as cx ) gates. There are two missing graph edges from the ibm_washington lattice, with respect to the logical lattice, between qubits 8-9 and 109-114. The total number of qubits (nodes) is 127. The edges of the hardware graph are three colored (red, blue, and green) such that no node shares two or more edges with the same color. The node colorings of light and dark gray show that the heavy hex lattice is bipartite (meaning it can be partitioned into two disjoint sets). The three edge coloring is consistent with the QAOA circuit construction in Fig. 2 . (right) Example of a single random cubic problem instance (see Eq. ( 4 )) on the ibm_washington graph. The linear and quadratic terms are shown using two distinct colors (red and green). The nodes and edges colored red denote a weight of − 1 and the nodes and edges colored green denote a weight of + 1. The cubic terms are represented by ovals around the three qubits which define the cubic variable interactions -- these terms could also be referred to as Z Z Z terms, or hyperedges represented by the closed curve around each set of 3 qubits. Like the linear and quadratic terms, the color of the oval representing the cubic terms represents the sign of the weight on the terms, where green is + 1 and red is − 1. The quadratic problem instances (Eq. ( 5 )) would be defined only by the randomly weighted nodes and edges, with no cubic terms. All cubic problem instances contain exactly 127 linear terms, 142 quadratic terms, and 69 cubic terms. All quadratic problem instances contain exactly 127 linear terms, 142 quadratic terms.

Equation ( 5 ) defines the class of Ising problem that are the same as Eq. ( 4 ), except without any cubic terms; in particular this class of problems are easier since the problem is comprised of only linear and quadratic terms. Both of the Ising models defined by Eqs. ( 5 ), ( 4 ) are intended to be minimization combinatorial optimization problems, where the aim is to find the global optimal solution of these Ising models.

The heavy hex connectivity of ibm_washington , along with an overlay showing one of the random problem instances defined on ibm_washington , is shown in Fig. 1 . The edge set E shows a 3-edge-coloring due to Kőnig’s line coloring theorem, which we will make use of in the QAOA Section “Theory”.

Each term coefficient is sampled from { + 1, − 1} with the goals of mitigating control error sources on the NISQ devices, making the problem definition very clear, and to make the problems still reasonably difficult to sample. Because all of these Ising models are random spin glasses, although fitting a very specific connectivity structure, it is expected that there will be a small number of degenerate ground states. However, we do not specifically compute all of the degenerate ground states, or even how many degenerate ground states exist. We leave further inquiries on the properties of the sampling of degenerate ground states for these specific Ising models, such as how fairly the degenerate ground states are sampled 33 , 129 , 130 , to future research.

For the remainder of the article, the problem instances defined in Eq. ( 4 ) will be referred to as the cubic class of problems, meaning that the highest degree variable terms present in the problem are Z Z Z terms. The problem instances defined in Eq. ( 5 ) will be referred to as the quadratic class of problems, meaning that the highest degree variable terms present in the model are two variable terms. For all experiments, we randomly generate 10 cubic Ising models and 10 quadratic Ising models with the goal of providing a reasonable ensemble of different problems to compare against each other, and importantly to discern if there are significant differences that occur between different random instances of the same problem type.

Implementing ising model QAOA circuits on IBM quantum Heavy-Hex connectivity

Figure 2 describes the short depth QAOA circuit construction for sampling a geometrically local hardware-compatible higher order Ising problem instance, described in Section “Theory”. This algorithm can be applied to any heavy-hex lattice connectivity, which allows for executing the QAOA circuits on the 127 variable instances on the IBM Quantum ibm_washington backend (or more generally), any heavy-hex hardware connectivity graph quantum computer. This particular QAOA circuit could be viewed as a type of Hardware Efficient Ansatz (HEA) 131 , 132 , 133 , but is applied to QAOA, not general Variational Quantum Algorithms (VQA’s), and is restricted to a very particular form of random Ising model (defined in Section “Theory”) that itself is hardware specific.

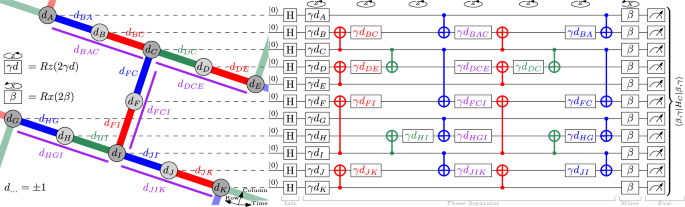
(Left) The problem instance is a hardware-native bipartite graph with an arbitrary 3-edge-coloring given by Kőnig’s line coloring theorem. Figure 1 (left) shows a 3-edge-coloring and bipartite shading consistent with this figure. The purple lines denote the cubic terms.(right) Any quadratic term (colored edge) gives rise to a combination of two CNOTs and a Rz-rotation in the phase separator, giving a CNOT depth of 6 due to the degree-3 nodes. When targeting the degree-2 nodes with the CNOT gates, these constructions can be nested, leading to no overhead when implementing the three-qubit terms: these always have a degree-2 node in the middle (see Eq. ( 4 )). For the problem instances without cubic terms, the QAOA circuit construction can simply disregard the purple single qubit rotations.

For considering the angle parameter searchspace, note that each quadratic and each cubic problem instance has the property that all its samples will have the same parity as each term contributes either + 1 or − 1. Therefore, for any objective value C (i.e. either C 1 ( x ) or C 2 ( x )), we have C = 2 k + parity and thus

Therefore, increasing the angle γ by π only adds a global phase, and hence γ has a periodicity of π which is why the angle range of (0, π ) was chosen to perform the grid-search within (although for example $\left[\frac{-\pi }{2},\frac{\pi }{2}\right)$ would also work). The same reasoning applies to β . Furthermore, there is an additional symmetry that can be used: Applying the two angle sequences of

β = ( β 0 , β 1 , …, β p ), and γ = ( γ 0 , γ 1 , …, γ p )

− β = ( − β 0 , − β 1 , …, − β p ), and − γ = ( − γ 0 , − γ 1 , …, − γ p )

Give the same expectation values because they are mirror symmetric. This means that the search space can be cut in half; in this case we chose to divide the last β p angle in half so as to take advantage of this mirror symmetry and reduce the angle search space. Therefore, for both quadratic and cubic problem instances, the QAOA angle ranges used are ${\gamma }_{1},\ldots ,{\gamma }_{p}\in \left[0,\pi \right)$ and ${\beta }_{1},\ldots ,{\beta }_{p-1}\in \left[0,\pi \right),{\beta }_{p}\in \left[0,\frac{\pi }{2}\right)$ where p is the number of QAOA rounds. The search ranges we use are not 0 and π inclusive. The halving of the angle search space for β applies when p = 1.

For optimizing the angles using the naive grid search for p = 1, β 0 is varied over 60 linearly spaced angles $\in [0,\frac{\pi }{2}]$ and γ 0 is varied over 120 linearly spaced angles ∈ [0, π ]. For a comparable resolution gridsearch for p = 2, β 1 is varied over 5 linearly spaced angles $\in [0,\frac{\pi }{2}]$ and γ 0 , γ 1 , and β 0 are varied over 11 linearly spaced angles ∈ [0, π ]. Therefore, for p = 2 the angle gridsearch uses 6655 separate circuit executions (for each of the 10 problem instances), and for p = 1 the angle gridsearch uses 7200 separate circuit executions. Each circuit execution measures 10, 000 samples with the goal of obtaining a highly robust distribution for each angle combination.

Implementing ising models on D-wave pegasus connectivity

In order to execute the Ising models of Eqs. ( 4 ) and ( 5 ) on D-Wave quantum annealers, the primary challenge is that the higher-order (i.e., cubic) terms will need to have order reduction techniques applied to them so as to decompose the cubic terms into linear and quadratic terms 9 , 53 , 124 , 125 , 126 . This order reduction will result in using additional variables, usually called auxiliary or slack variables, in addition to additional edges (quadratic terms) that allow those new auxiliary variables and the existing discrete optimization problem variables to interact. Figure 3 shows the mapping of the Ising models onto a logical Pegasus P 16 hardware connectivity graph, in particular showing the order reduction procedure which makes use of two alternating order reductions using auxiliary variables with different connectivities. The alternating order reduction’s are required to fit an entire problem instance Ising model (defined on a heavy-hex hardware graph) with cubic terms onto the D-Wave hardware graph(s). The order reduction procedure outlined in Fig. 3 allows for direct embedding of the order reduced polynomials onto the hardware graph, regardless of whether the cubic term coefficient is + 1 or − 1. This order reduction ensures that the ground state(s) of the cubic term are also the ground states of the order reduced Ising model. Additionally, this order reduction ensures that for every excited state of the cubic term, there are no slack variable assignments which result in the original variables having an energy less than or equal to the ground state of the original cubic term. This order reduction procedure allows any problem in the form of Eq. ( 4 ) to be mapped natively to Pegasus quantum annealing hardware which accepts problems with the form of Eq. ( 3 ). Importantly, this procedure does not require minor-embedding (e.g. use of chains of physical qubits to represent a logical variable), even including the auxiliary variables. Constructing the embeddings of the order reduced higher order terms onto Pegasus requires alternating between two valid cubic reductions (both of which are shown in Fig. 3 ); we found this was not possible to do using only a single cubic order reduction formulation. When evaluating the cost value of a sample measured by the quantum annealing processor, the energy is computed on the original polynomial meaning that the auxiliary variable states are not used when computing the energy. Supplementary Note 8 contains detailed truth tables for the order reductions, as well as the exact polynomials that describe the order reduction. We do not claim that these order reductions are optimal for hardware-native ± Z Z Z term reduction on a Pegasus hardware graph, but they are the best manual embeddings that we found.

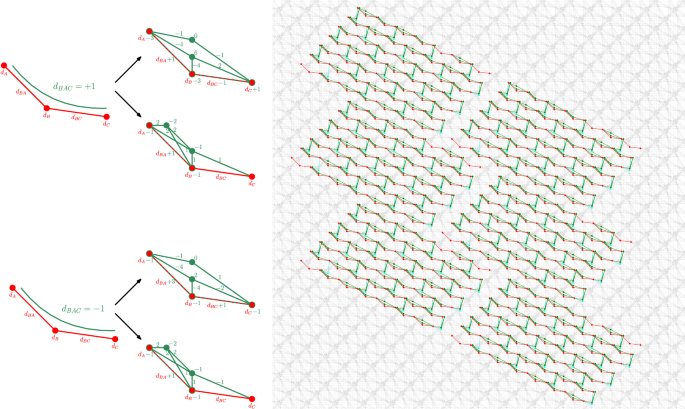
(left) Two different embeddings for cubic + 1/ − 1 terms onto D-Wave’s Pegasus connectivity. Each embedding needs two slack variable qubits, shown as green circles with the numbers indicating the weights d of the slack variables and their connections as well as changes to the original weights of the variables involved in the cubic term. Our overall embedding alternates between these two cubic term embeddings. Any embedding with only one slack variable needs a 4-clique between the slack and the three original variables, which is not possible to embed for consecutive cubic terms. This order reduction scheme introduces two auxiliary variables per cubic term, meaning that for the cubic Ising models the auxiliary qubit overhead is exactly 69 ⋅ 2 = 138. (right) Embedding structures of the cubic problem instances embedded in parallel (independently) 6 times onto the logical Pegasus P 16 hardware connectivity graph. The visual view of this graph has been slightly partitioned so that not all of the outer parts of the Pegasus chip are drawn. The light gray qubits and couplers indicate unused hardware regions. The cyan coloring on nodes and edges denote the vertical qubits and CNOTs on the ibm_washington hardware graph (see Fig. 1) . The red coloring on nodes and edges denote the horizontal lines of qubits and CNOTs on ibm_washington . The green nodes and edges denote the order reduction auxiliary variables. Note that in problem tiling on Pegasus, the top right hand and lower left hand qubits are not present on the ibm_washington lattice, but for the purposes of generating the embeddings these extra qubits are filled in to complete the heavy hex lattice embedding. The embedding structure for quadratic problems is identical to this embedding, with the exception that there are no auxiliary (green) variables.

For the purpose of mitigating local biases and errors that may occur on the QA processor chip, and in order to get more problem samples for the same QPU time, the other strategy that is employed is to embed multiple independent problem instances onto the hardware graph and thus be able to execute several instances in the same annealing cycle(s). This technique is referred to as parallel quantum annealing 126 , 134 , 135 or tiling 136 . Note that the concept of parallel quantum annealing has analogous ideas in the circuit model quantum computing paradigm, which are generally referred to as multi-programming 137 , 138 , 139 , 140 , or parallel circuit execution 141 , 142 , or circuit concurrency 143 . Figure 3 (right) shows the parallel embeddings on a logical Pegasus hardware graph. Because some of the logical embeddings may use a qubit or coupler that is missing or defect on the actual hardware (see Fig. 4 for a rendering that highlights such hardware), less than 6 parallel instances can be tiled onto the chips to be executed at the same time. For Advantage_system4.1 , 2 independent embeddings of the cubic problem instances could be created without encountering missing hardware and 3 independent embeddings of the quadratic problem instances could be created. For Advantage_system6.1 , 3 independent embeddings of the cubic problem instances could be created and 5 independent embeddings of the quadratic problem instances could be created. The structure of the heavy-hex lattice onto Pegasus can be visually seen in Fig. 3 ; the horizontal heavy-hex lines (Fig. 1) are mapped to diagonal Pegasus qubit lines that run from top left to bottom right of the square Pegasus hardware graph rendering. Then the vertical heavy-hex qubits are mapped to QA qubits in between diagonal lines.

Pegasus hardware connectivity graph ( P 16 ) renderings with the missing hardware drawn in red nodes and edges for the Advantage_system4.1 D-Wave chip (left) and the Advantage_system6.1 D-Wave chip (right).

Experiments

Comparing qaoa, quantum annealing (qa), simulated annealing (sa), and random samples.

Figure 5 plots 2 histograms, one for 2 out of the 10 minimization cubic problem instances. As a baseline comparison, the energy distribution histograms contain the objective functions of random samples—these are computed with binomial probability of 0.5 for selecting + 1 or − 1. Each histogram contains a distribution showing 10, 000 random samples, the best angle choices found (experimentally) for p = 1 and p = 2 QAOA with and without dynamical decoupling, the QA results from two D-Wave quantum annealers (which contain between 500 and 2500 samples, depending on the problem and device), 1000 samples from simulated annealing, and the mean expectation values for the best angle choices of QAOA computed exactly. We make the following eight observations from these plots: Fig. 5

Shows that the random samples are clearly separated from the QAOA energy distributions – although there is overlap.

The QA distribution is clearly distinct from the QAOA distribution, and performs much better.

The experimental QAOA distributions are roughly half-way between the exact QAOA simulation (which was computed classically) and random samples.

The four different QAOA implementations performed very similarly – their distributions have very high overlap and differences in the performance is marginal. For the purpose of showing exactly which of the QAOA methods performed better across the 10 problems, Table 2 shows a confusion matrix type representation of what methods had better mean energy distributions (for the best QAOA angle choice) compared to the other methods. In Table 2 , we can see that digital dynamical decoupling improves the p = 2 QAOA computation noticeably for the best angle combination found during the gridsearch. Supplementary Note 7 contains a more detailed comparison of the full spectrum of QAOA energy computations with and without dynamical decoupling.

The exact QAOA simulations show that a zero noise quantum computation of QAOA would not achieve the same mean energy found by the two quantum annealers. However, it could be the case that the lower energy tails of such a QAOA computation would be able to find the optimal solution or at least get close.

Although this will be observed in more detail in Section “Experiments”, the optimal angle choices (computed experimentally) show parameter concentration – i.e. even though the 10 problems are different, the best QAOA angles across the problems are similar if not identical.

QA and simulated annealing are comparable but typically simulated annealing has a slightly better mean energy.

Advantage_system6.1 consistently has slightly higher (lower quality) mean energy than Advantage_system4.1 .

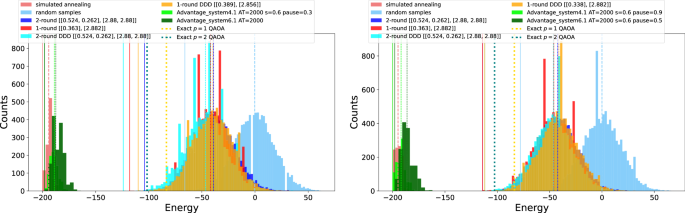
Here the energies being plotted are the full energy spectrum for the parameters that gave the minimum mean energy across the parameter grid searches performed across the QA and QAOA parameters. The optimal parameter combination is given in the figure legend. For QA parameters, the annealing time in microseconds, the forward anneal schedule (symmetric) pause fraction, and anneal fraction, are given in the legend. If the QA parameter in the legend is only an annealing time that denotes that the optimal annealing schedule was the default linear interpolation. For the QAOA angle parameters, the format is [ β , γ ], and are rounded to 3 decimal places. The mean for the energy distributions is marked with vertical dashed lines and the minimum energy found in each dataset is marked with solid vertical lines. If there are multiple parameter combinations that result in the same mean energy, one of those parameter combinations is chosen arbitrarily to plot. The best mean energy found across the possible angle combinations from the exact (classical) QAOA simulations (described in Section “Classical Simulation of QAOA”) are marked with vertical thick dotted lines; those energy means show what QAOA could sample theoretically if there was no noise in the computation. These two plots are intended to be representative of the other 8 cubic Ising models – the remaining Ising model sample distributions are shown in Supplementary Note 1 .

Figure 6 , similar to Fig. 5 , shows 2 histograms, but now for the 2 out of the 10 minimization quadratic problem instances that contain no higher order terms. The set of observations made about Fig. 5 also apply to Fig. 6 with a few exceptions. First, Table 3 shows the confusion matrix-style representation of how the four QAOA methods compared against each other, but now for the quadratic problems. Table 3 shows that, as opposed to Table 2 , digital dynamical decoupling does not help as much as it did for the cubic problems, at least for the best angle combinations. Supplementary Note 7 shows a more detailed analysis of the comparison between QAOA circuits with and without dynamical decoupling. This observed difference in how useful dynamical decoupling was for the best angles could be due to the cubic problem instances having greater circuit depth, thus having more idle qubit time in the computation which dynamical decoupling can help to mitigate errors on. Second, these problems were considerably easier for both simulated annealing and quantum annealing to sample the optimal solution of. As a result, the energy distributions for both QA and SA are concentrated near the optimal solutions and there are not clear visual differences between the two distributions.

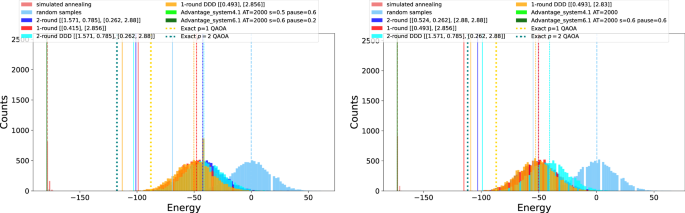
Here the energies being plotted are the full energy spectrum for the parameters that gave the minimum mean energy across the parameter grid searches performed across the QA and QAOA parameters. The optimal parameter combination is given in the figure legend. For QA parameters, the annealing time in microseconds, the forward anneal schedule (symmetric) pause fraction, and anneal fraction, are given in the legend. For the QAOA angle parameters, the format is [ β , γ ], and are rounded to 3 decimal places. The mean for each dataset is marked with vertical dashed lines and the minimum energy found in each dataset is marked with solid vertical lines. The best mean energy found across the possible angle combinations from the exact (classical) QAOA simulations (described in Section “Classical Simulation of QAOA”) are marked with vertical thick dotted lines; those energy means show what QAOA could sample theoretically if there was no noise in the computation. These two plots are intended to be representative of the other 8 quadratic Ising models - the remaining Ising model sample distributions are shown in Supplementary Note 1 .

A notable comparison point that is not highlighted in these experiment plots is the total amount of computation time required to execute these experiments. Approximately 120 minutes of QPU access time was used for all D-Wave quantum annealing experiments. Approximately 16500 minutes of QPU time was used for all QAOA experiments. These estimates do not include queue times. The QPU time consumed for QAOA is entirely due to the high resolution parameter gridsearch that is performed, which used more parameters than the QA experiments. The QAOA gridsearch using more parameters than QA is important because it is necessary in order for QAOA to perform as expected (e.g., theoretically for the solution quality to improve as a function of p ) that good parameters are found, whereas for QA (since it is a specialized computation) reasonably good optimization can occur across a wide range of parameter choices.

Optimal solution sampling

One important detail that is not fully represented in Figs. 5 , 6 is whether any of the methods were able to sample the optimal solutions of the problems, and if so how frequently. In the case of QAOA, it is clear that it never sampled the optimal solution(s) because the plots have visual indicators for those minimum energies. Table 4 details the minimum energies found for each of the solver methods along with the optimal minimum energy, computed using CPLEX (see Section “Simulated Annealing and CPLEX implementations”). CPLEX does not provide information on degenerate ground states, if they exist, and therefore here degenerate ground states or how those states are sampled is not considered—only whether the optimal energy was found or not. Table 4 shows that both simulated annealing and quantum annealing are able to sample the optimal solutions for all 10 quadratic problems. Simulated annealing is also able to sample the ground state solution for all 10 cubic problems, and quantum annealing is able to sample the ground state solution for 6 out of the 10 cubic problems.

Importantly, the implementations of quantum annealing, simulated annealing, and CPLEX, all required the use of order-reduction techniques for the cubic Ising models (as opposed to QAOA which can handle the higher order terms natively in the algorithm without auxiliary terms). This means the SA, QA, and CPLEX solutions all use auxiliary variables in their implementation. When reporting the objective function evaluations (e.g. energy), these auxiliary terms are not included in the objective function computation. The objective function computations are always performed strictly on the variable assignments found for the original variables (not auxiliary variables from the order reduction), defined by Eqs. ( 4 ), ( 5 ).

Quantum annealing schedule tuning

Figure 7 shows the QA pause anneal schedule energy landscapes for a quadratic problem and a cubic problem. It is clear that longer annealing times have a better energy (objective function value), and more uniform. Shorter annealing times, in particular 10 microseconds, shows a more pronounced difference across the energy landscape where it becomes clear that pauses at an anneal fraction of s = 0.1 and s = 0.9 produce equally poor solution quality and pauses around s = 0.5 produce better solution quality.

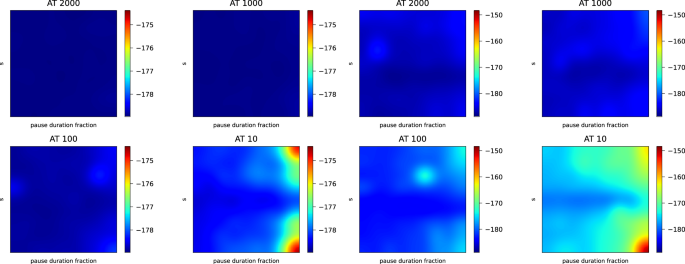
Each individual heatmap is plotting the mean sample energy found among the N anneal samples for that problem and device ( N can vary, see Section “Theory”) where the y-axis is the anneal fraction s at which the forward anneal pause occurs and the x-axis is the fraction of the anneal time that was spent in that pause at the anneal fraction s . Both the x and y-axis range is 0.1, 0.2, …, 0.8, 0.9. Each cluster of 4 heatmaps are performing the same grid search over anneal fraction and pause duration fraction, but repeated over the annealing times of 2000, 1000, 100, and 10 microseconds (shown the individual heatmap titles). The left four heatmaps are QA results for one quadratic problem instance, while the right four heatmaps are QA results for one cubic problem instance, both executed on Advantage_system4.1 . The heatmaps show that there is a consistent low energy region slightly below s = 0.5 for any pause duration and for all annealing times. Longer annealing times clearly result in lower energy results.

Figure 8 (right) shows some energy distributions for one of the cubic problems across different annealing times. The smallest and largest annealing times available on the two D-Wave quantum annealers. This plot shows that there is consistent trend towards longer annealing times performing better, however there is also a diminishing return on energy improvement as a function of annealing time as the mean energy distribution approaches the optimal solution. Figure 8 (left) shows the same histogram distribution of energies as a function of annealing times for one of the quadratic problem instances. The energy distributions for the other 18 problems are very similar to these two arbitrarily chosen plots.

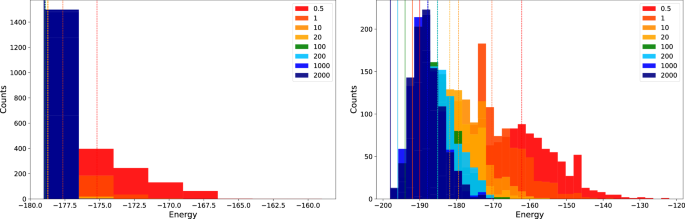
The annealing times were varied (annealing time in microseconds shown in legend) to show how the energy distribution changes as a function of annealing time. These histograms, while only the energies of a single one out of the 10 problem instances, are representative of the behavior of the other nine problem instances. Mean energy is marked with dashed vertical lines, and the minimum energy is marked with solid vertical lines. Notice that there is a clear improvement in solution quality as the anneal times get longer.

QAOA angle tuning

Figure 9 shows the experimentally computed 1 round QAOA parameter search space, and classically computed search space for one of the cubic Ising models. Figure 10 shows the same results, but for one of the quadratic Ising models. Figures in Supplementary Note 2 show that the optimal QAOA angles found in the angle gridsearch across the remaining 9 random problem instances are very similar, if not identical at the level of grid resolution we selected. This type of result has been observed for other classes of random combinatorial optimization problems, such as maximum cut and the Sherrington-Kirkpatrick model 40 , 52 , 144 , 145 , 146 , 147 . If this behavior is consistent for large classes of combinatorial optimization problems then this could partially alleviate the hardness of the angle finding problem by allowing a single computation of optimal angles to be applied to any number of problems that fall into that class, and could potentially assist with angle finding for higher round QAOA. Supplementary Note 3 shows volumetric p = 2 representations of the angle search spaces.

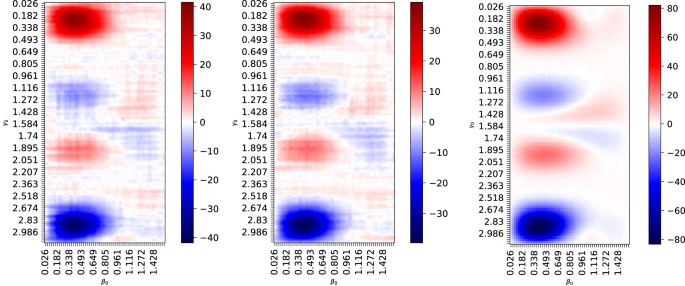
Note that the ideal classical objective function values are approximately 2 times that of the experimentally computed values.

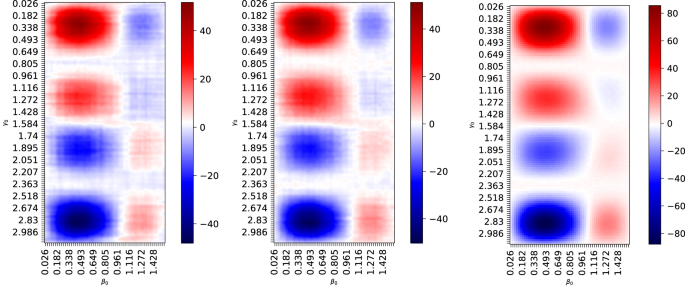
Classical simulation of QAOA results

As described in Section “Classical Simulation of QAOA” it is possible for HPC resources to simulate the studied QAOA circuits for p = 1, 2. At least, it is possible to simulate the ideal mean expectation values for arbitrary angles. Figures 9 , 10 , in addition to showing the experimental results, also plot the ideal mean expectation values for the p = 1 QAOA circuits, for one quadratic and one cubic Ising model. Additional plots in Supplementary Note 2 show the classically computed p = 1 parameter search space for the remaining quadratic and cubic problem instances. The mean energy for the best angle combinations, computed exactly, are also shown as part of the histograms in Figs. 5 , 6 . These plots should be compared against the ensemble of plots in Supplementary Note 2 , where two things are clear. First, the trends of the landscape computed on the NISQ computer are very similar to the trends in the exact energy landscape—e.g. there are no obvious biases or lost local minima/maxima not found by the quantum hardware results. Second, the optimal angle combinations result in a significantly worse mean expectation value (energy) on ibm_washington ; compared to the exact QAOA simulation, the hardware energies get approximately 50% to the ideal computation. Interestingly, this is also true for the angle symmetries that result in the highest expectation values (which in this case we do not want since it is a minimization problem). Specifically, the experimental energies are symmetric and the highest expectation values are also approximately 50% of what the exact classical simulations show could be sampled for those angle choices.

An observation that has not been made before for QAOA sampling combinatorial optimization problems is that adding in higher order terms to the Ising models (e.g. going from the quadratic instances to the cubic instances) does not substantially change the angle search space. In other words, the parameter concentration held as higher order terms were added or removed. This can be seen especially clearly in Figs. 9 , 10 , and is also shown in the extensive NISQ computer experimental plots in Supplementary Note 2 . The exact shape of the energy landscape does change when the higher order terms are added, but the best parameter combination region is nearly identical. This gives evidence that parameter concentration may be transferable across problem instances even when adding or removing higher order terms.

The Figures in Supplementary Note 5 examine detailed (normalized) differences in the experimentally computed p = 1 QAOA energy landscapes on ibm_washington , compared to the ideal classical mean energy QAOA simulations. Note that such a comparison could be made for p = 2, but representing the high dimensional search space (such as the plots in Supplementary Note 3 ) becomes difficult to meaningfully visually convey.

This paper has presented state of the art QAOA results, in particular the largest QAOA experimental demonstration to date, which enabled a direct comparison against quantum annealing. This is also one of the largest quantum system simulations performed on a circuit model quantum computer to date, using approximately 3000 circuit instructions on 127 qubits. Specifically we found the following:

Quantum annealing finds lower energy solutions compared to QAOA, and is able to sample the optimal solution at least once for all 10 quadratic problems and 6 out of the 10 cubic problems.

QAOA samples all of the Ising model instances better than random sampling

The short depth QAOA circuit can be applied to heavy hex lattices of any size, which means that as heavy hex hardware improves these short depth QAOA circuits can be used.

Dynamical decoupling can help improve the quality of computation on NISQ computers, even for relatively short depth QAOA circuits. However, as observed in other empirical results the improvements are not uniform – and in particular for p = 1 dynamical decoupling did not improve the computation.

Consistent with empirical results on other problems, we observed parameter concentration for both p = 1 and p = 2 QAOA circuits. This is encouraging since it indicates that for some classes of similar problem instance it may be possible to develop good heuristics for angle selection for high-round QAOA. This result is consistent with other similar classes of random combinatorial optimization problems.

The exact classical simulation of QAOA showed that the experimental QAOA p = 1 energy landscapes computed on ibm_washington were not biased in particular regions, but overall performed significantly worse (roughly one half) than the theoretical performance.

Figures 5 , 6 hint at a possible future research direction involving the selection of good QAOA angles at higher rounds. This observation is that the best found β 0 and γ 0 in the gridsearch are usually similar—because the p = 2 gridsearch was not as granular as the p = 1 gridsearch, this similarity is not always highly apparent. This suggests that it may be possible to extrapolate good angle choices for high round QAOA, using the best angles found at p = 1. This type of extrapolation technique has been used in other studies for studying the scaling of QAOA using classical simulation 30 . Additionally, we have seen evidence that the addition of the higher order terms does not substantially change the concentration of good QAOA angles. This then leads to the natural question of how far this extends to higher order terms beyond cubic terms, and whether QAOA parameter concentration holds for classes combinatorial optimization problems where higher order terms are added to a fixed underlying connectivity structure. Parameter concentration for QAOA on problems which contain higher order terms is very under-investigated, and would be an interesting topic of future research.

Because of the increasing availability of NISQ computers with increasing qubit count (now with hundreds of qubits), we encourage the algorithmic development of optimized short depth circuits alongside experimental evaluation of these shallow circuits on full hardware lattices. Both the QAOA circuit construction algorithm and the QA embedding algorithm that we have outlined are scalable to larger lattice sizes—as are the problem instances that match those hardware graphs. This means that these algorithms can be used in the future as hardware improves and increases in scale.

Although here we used an angle gridsearch for the QAOA implementation, this is not scalable to high round QAOA. High round QAOA needs to be experimentally evaluated as the hardware and algorithms improve, since it is known that QAOA will need to be executed at reasonably high rounds (not low rounds such as p = 1 and p = 2) so as to provide meaningful computations for combinatorial optimization 148 , 149 . Therefore an important future research topic is to utilize more scalable angle finding algorithms for high round QAOA on quantum computers. The class of Ising models we have introduced in this research would allow high round QAOA computation on a large number of qubits, as IBM Quantum hardware continues to improve.

The capability of QAOA to natively accept higher order terms seems to be under-utilized when evaluating QAOA capabilities, both numerically in ideal simulations, and on NISQ computers. As a future research direction, we encourage further testing of QAOA on problem types which contain higher order terms.

Sections “Dynamical Decoupling for QAOA Circuits” and “IBM Quantum Processor QAOA Circuit Execution” define the QAOA circuit execution and parameters on the ibm_washington processor. Section “Classical Simulation of QAOA” describe the lightcone classical simulation of mean QAOA expectation values for depths p = 1 and p = 2. Section “D-Wave Quantum Annealing Processor Parameter Optimizations” describes the D-Wave quantum annealer parameter optimizations. Section “Simulated Annealing and CPLEX implementations” describes the simulated annealing and CPLEX implementation.

Dynamical decoupling for QAOA circuits

With the goal of mitigating decoherence on idle qubits, digital dynamical decoupling (DDD) is tested on all QAOA circuits, for both p = 1 and p = 2. Dynamical Decoupling is an open loop quantum control error suppression technique for mitigating decoherence on idle qubits 150 , 151 , 152 , 153 , 154 , 155 . Dynamical decoupling can be implemented with pulse level quantum control, and digital dynamical decoupling can be implemented with circuit level gate instructions comprised of sequences of identity gates 154 . Digital dynamical decoupling is an approximation of pulse level dynamical decoupling, and in this case we use the Qiskit 76 dynamical decoupling pass to insert the digital gate sequences, but with circuit delays so that the circuit is scheduled to work as intended on the device. Dynamical decoupling has been experimentally demonstrated to be useful in certain computations for superconducting qubit quantum processors including IBM Quantum devices 156 , 157 , 158 , 159 , 160 , 161 . Dynamical decoupling in particular could applicable for high round QAOA circuits because the circuits can be relatively sparse and therefore have idle qubits 156 . Dynamical decoupling is not always effective at consistently reducing errors during computation (for example because of other control errors present on the device 153 , 156 , 161 ), and therefore the raw QAOA circuits are compared against the QAOA circuits with dynamical decoupling in Section “Results”. So as to apply the dynamical decoupling sequences to the OpenQASM 162 QAOA circuits, the PadDynamicalDecoupling 163 method from Qiskit 76 is used, with the pulse_alignment parameter specified based on the ibm_washington backend properties. The circuit scheduling algorithm that is used for inserting the digital dynamical decoupling sequences is ALAP, which schedules the stop time of instructions as late as possible 164 . There are other scheduling algorithms that could be applied which may perform better. There are different DDD gate sequences that can be applied, including Pauli Y, Y or Pauli X, X gate sequences. Because the X Pauli gate is already a native gate of ibm_washington , the two Pauli X gate X, X DDD sequence is used for simplicity. The X-X sequence is expected to typically mitigate time correlated dephasing noise 165 .

Because of the magnitude error rates on current NISQ hardware, utilizing as many error mitigation strategies as possible would be ideal for these experiments. Unfortunately, other error mitigation strategies are either not scalable to large system sizes, such as measurement error mitigation requiring an exponential number of circuit executions 166 , or are intended to provide error mitigated expectation values and therefore do not provide variable assignments, such as Zero Noise Extrapolation (ZNE) 154 , 167 , 168 , 169 . For this direct comparison of QA and QAOA, we aim to obtain the variable assignments for the solutions to the combinatorial optimization problems, and therefore do not utilize quantum error mitigation algorithms that use classical post processing.

IBM quantum processor QAOA circuit execution

The variable states for the optimization problems are either { + 1, − 1}, but the IBM Quantum circuit measurement states are either 0 or 1. Therefore once the measurements are made on the QAOA circuits, for each variable in each sample the variable states are mapped as follows: 0 ↦ 1, 1 ↦ − 1. When executing circuits on the superconducting transom qubit ibm_washington , circuits are batched into jobs where each job is composed of a group of at most 250 circuits. The maximum number of circuits for a job on ibm_washington is 300, but we use 250 circuits per job so as to reduce backend job errors related to the size of jobs. Grouping circuits into jobs reduces the total amount of compute time required to prepare and measure each circuit. When submitting the circuits to the backend, they are all first locally transpiled using Qiskit 76 with optimization_level=3 and targeting the exact hardware connectivity graph used to define the Ising models (see Fig. 1) . This transpilation adapts the gateset to the ibm_washington native gateset, and the transpiler optimization attempts to simplify the circuit where possible. The QAOA circuit execution on ibm_washington spanned several months, and therefore the backend software versions were not consistent. The backend software versions of ibm_washington that were used for all of the QAOA experiments are: 1.3.7 , 1.3.8 , 1.3.13 , 1.3.14 , 1.3.15 , 1.3.17 , 1.3.19 , 1.3.22 , 1.4.0 , 1.5.1 , 1.5.2 , 1.5.3 , 1.5.4 , 1.5.5 , 1.6.0 .

Example Qiskit QAOA circuit drawings are given in Supplementary Note 4 . When these QAOA circuits are compiled, the total number of instructions used (not including delay gates) is approximately 3000 depending on the compilation routine and β , γ angles used. Importantly, many of the single qubit gate operations used in these compiled circuits are rz gates, which are virtual gates 170 , meaning that they are executed at the software level and have an error rate of 0.

Aggregated T1 and T2 coherence times and randomized benchmarking calibration 171 , 172 gate error rates on ibm_washington during the execution of these QAOA circuits is given in Supplementary Note 6 .

Classical simulation of QAOA

Because the problem instance Ising models are defined on a relatively sparse graph, and because we run only 1 and 2 rounds, it is possible to classically simulate the mean QAOA energy landscape (for an arbitrary set of angles β , γ ) for both quadratic and cubic problem instances. This is an improvement over ref. 36 where no classical simulation was performed on the cubic Ising models, but this method as we propose it does not provide a mechanism to compute a distribution of expectation values (e.g. with some shot noise), instead it provides only a mechanism to compute the mean expectation value for any β , γ combination. The key observation is that we can simulate portions of the overall QAOA circuit applied to a subset of the problem instances to compute the mean expectation value for a single term (e.g. a linear, quadratic, or cubic term). By linearity of expectation, you can compute the cumulative sum of the mean energy for each of the terms in the problem instance. This provides a mechanism to compute the overall mean energy for a problem instance, given some angles β , γ . Note however that this only provides the mean expectation values for any given β , γ , but it does not provide an objective function distribution and it does not provide variable assignment solutions for the given optimization problem. Therefore, this simulation method will allow us to verify and compare against the NISQ experimental results. For highly entangled problems though, this would still be intractable to simulate. However, for the heavy hex lattice problems it is only required that those qubits be simulated that interact with the specific term in question. More rounds leads to more interactions for each term, and variable interactions (e.g. entanglement) are defined by both quadratic and cubic terms. Figure 11 shows the subgraph of the problem instances, for a single cubic problem instance, which interact with the specific cubic term (which, in this example, is formed by the qubits 23, 22, 24) for p = 2 QAOA. This lightcone of interacting terms contains 27 qubits, which is possible to simulate using HPC resources. However, if p = 3 QAOA was used or if the problem instance had denser long range interactions, then the simulation would be considerably harder and potentially intractable. p = 2 rounds applied to a cubic problem instance is the hardest of the problems to simulate; p = 1 is easier to simulate, in that it uses fewer qubits, as are simulations of the quadratic problems.

Since this subgraph contains 27 qubits (nodes), it is possible to directly classically simulate all of the linear, quadratic, and cubic term components for all of the problem instances by classically simulating the sub-circuit which contains all of the interacting terms in this 27 qubit light-cone (none of the other terms which are outside of this subgraphs).

The procedure is to enumerate over all of the terms, either in a quadratic or cubic , and compute the neighborhood of qubits that interact with that term (this is dependent on how many rounds are used), extract all terms (linear quadratic, and optionally cubic depending on the problem) that are strictly within this neighborhood of qubits, and then execute the QAOA circuit construction algorithm (see Fig. 2 ) in order to create a QAOA circuit specifically for that neighborhood of terms. Next, execute that full QAOA circuit using many shots (in this case 10, 000) and measure only the states of the qubits for that specific term. The expectation value for each of those shots is computed, and the mean energy is recorded. This is then repeated for all other terms in the problem instance, thus giving a cumulative mean expectation value. Lastly, this entire procedure is iterated over for the discrete angle search space—specifically the exact same angle search space that is evaluated experimentally on ibm_washington and that is described in Section “Theory”.

There are two optimizations to this method which we do not explore in this study, but that could potentially be used for future improved simulations:

There are classical simulation methods, such as stabilizer decompositions 173 , or tensor networks, which could be used to approximately simulate the full entanglement lightcone of these Ising models for QAOA rounds greater than 2.

The lightcone of entanglement for individual terms in these Ising models does not include all of the gate operations performed in the QAOA circuit subgraph, and in particular many gate operations within each Ising term entanglement lightcone could be removed in order to speed up classical computations of each sub-circuit.

D-wave quantum annealing processor parameter optimizations

With the aim to optimize the quantum annealing parameters, similar to the QAOA angle gridsearch, a gridsearch over forward anneal schedules with pauses is performed. Figure 12 visually shows all of forward annealing schedules with pauses that are used for this schedule optimization. Pausing the anneal at the appropriate spot can provide higher chances of sampling the ground state 108 , 174 , 175 , 176 . Importantly the annealing times used in these schedule are also optimized for, but are not shown in the figure since the schedules can be scaled to different annealing times. The total number of QA parameters that are varied are 9 anneal fractions, 9 pause durations, and 4 different annealing times (10, 100, 1000, 2000 microseconds). Therefore, the total number of parameter combinations that are considered in the grid search is 324. 2000 microseconds is the longest annealing time available on the current D-Wave quantum annealers. The number of anneals sampled for each D-Wave job was either 500 a series of 250 anneal jobs (this was dependent on the maximum total QPU time that could be used per job). The annealing times and the anneal schedules were varied in a simple grid search. Readout and programming thermalization times are both set to 0 microseconds. All other parameters are set to default, with the exception of the modified annealing schedule.

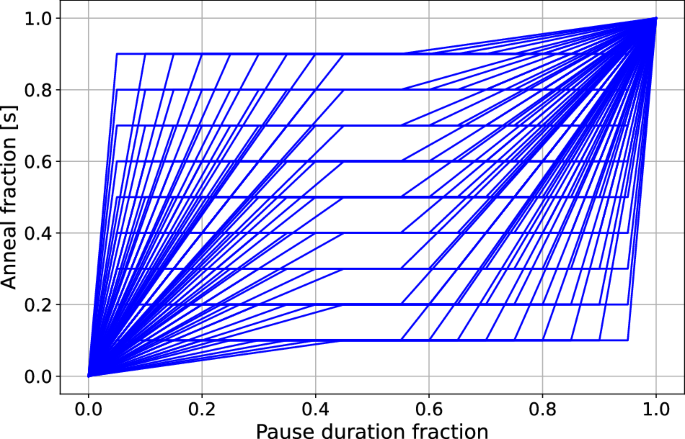
The symmetric pause inserted into the normal linearly interpolated schedule defining the A ( s ) and B ( s ) functions can provide better ground state sampling probability. The anneal fraction at which this pause occurs is varied between 0.1 and 0.9 in steps of 0.1. The pause duration, as a fraction of the total annealing time, is also varied between 0.1 and 0.9 in steps of 0.1. Although not shown in this figure, the annealing times are also varied between 10, 100, 1000, and 2000 microseconds. Although not shown, linearly interpolated anneal schedules are also executed on both QA devices and all problem instances using an annealing time of 0.5, 1, 10, 20, 100, 200, 1000, 2000 ms.

Simulated annealing and CPLEX implementations

For the purpose of providing a reasonable basis of comparison, the 10 cubic instances and 10 quadratic instances are also solved exactly using CPLEX 177 , and sampled using simulated annealing. Knowing the exact, optimum solutions tells us whether either QAOA or QA were able to find the optimal solutions. Simulated annealing is a well-known general purpose classical heuristic 178 that provides a good comparison point for heuristic quantum algorithms 23 . The simulated annealing implementation we use is the D-Wave systems SDK package 179 , using all default settings and generating 1000 samples per problem instance.

Applying simulated annealing to the quadratic problem instances is straightforward since there are only linear and quadratic terms. The simulated annealing implementation we used does not natively handle higher order terms though, and therefore the cubic problem instances could not sampled natively. Instead, the cubic instances required an order reduction scheme—similar to the quantum annealing implementation (Section “Theory”). Since the connectivity is not constrained for using simulated annealing we use an order reduction method available in the D-Wave systems SDK package dimod 180 . This method is called make_quadratic , which can take any higher spin or binary polynomial and transform it into linear and quadratic terms, at the cost of introducing additional auxiliary variables 181 . This method requires the specification of a strength term that defines the cost function penalty for breaking a product constraint in the order reduced Ising model. If the order reduction strength is too small, the ground states of the order reduced term problem will not match the ground states of the original problem. Typically, using a strength that is equal to the maximum of the absolute values of all problem coefficients produces order reduced problems that match the ground state of the original problem 126 . Because the maximum absolute value of all coefficients is 1, a penalty strength of 2 is used so as to construct order reduced Ising models so that simulated annealing can be run on the cubic Ising model problem instances.

The CPLEX solver was used by converting the spin variables into binary variables so that it could be solved as a Mixed Integer Quadratic Programming (MIQP) problem. Adapting the linear terms h and quadratic terms J into this binary form is possible, the exact formulation is given in Eq. ( 6 ) where all x i variables are binary. This is sufficient for adapting the quadratic problem instances to be solved exactly using CPLEX. However, for the cubic problem instances, CPLEX does not support higher order variable terms. Therefore, the same dimod order reduction method that was used for simulated annealing is also applied for all cubic problem instances. Equation ( 6 ) allows CPLEX to evaluate the objective function of Eqs. ( 5 ) (or Eq. ( 4 ) after order reduction) by specifying the variables in the domain of {0, 1}, but the objective function computation is evaluated correctly because the variables are first transformed into spins { + 1, − 1}.

After CPLEX has found the optimal variable assignment in terms of {0, 1} variables, the variable states are mapped 1 ↦ 1 and 0 ↦ − 1. This mapping then allows the original objective functions (Eq. ( 5 ) or Eq. ( 4 )) to be evaluated using the optimal spin variable assignments.

We also utilize CPLEX to find the maximum energy variable assignment for all of the Ising models. For the quadratic Ising models, this can be done using the maximize CPLEX method instead of the minimize method used to find the lowest energy state. For the higher order Ising models, this needs to be done by first inverting the sign of all of the polynomial coefficients, then performing the dimod order reduction of the higher order terms, and then minimizing the order-reduced polynomial. This is necessary for the higher order Ising models because the order reduction technique is correct for ground states, but not necessarily correct for excited states.

Data availability

Code, data, and additional figures are available in a public Github repository https://github.com/lanl/QAOA_vs_QA .

Code availability

Hadfield, S. et al. From the quantum approximate optimization algorithm to a quantum alternating operator Ansatz. Algorithms 12 , 34 (2019).

Article MathSciNet Google Scholar

Cook, J., Eidenbenz, S. & Bärtschi, A. The quantum alternating operator Ansatz on maximum k-Vertex cover. In IEEE International Conference on Quantum Computing and Engineering QCE’20 , 83–92 (2020). https://doi.org/10.1109/QCE49297.2020.00021 .

Wang, Z., Rubin, N. C., Dominy, J. M. & Rieffel, E. G. X Y mixers: Analytical and numerical results for the quantum alternating operator ansatz. Phys. Rev. A 101 , 012320 (2020).

Article ADS MathSciNet CAS Google Scholar

Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv preprint (2014). https://doi.org/10.48550/arXiv.1411.4028 .

Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm Applied to a Bounded Occurrence Constraint Problem. arXiv preprint (2015). https://doi.org/10.48550/arXiv.1412.6062 .

Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. Quantum computation by adiabatic evolution. arXiv preprint (2000). https://doi.org/10.48550/arXiv.quant-ph/0001106 .

Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse ising model. Phys. Rev. E 58 , 5355–5363 (1998).

Article ADS CAS Google Scholar

Das, A. & Chakrabarti, B. K. Quantum annealing and analog quantum computation. Rev. Mod. Phys. 80 , 1061 (2008).

Article ADS MathSciNet Google Scholar

Hauke, P., Katzgraber, H. G., Lechner, W., Nishimori, H. & Oliver, W. D. Perspectives of quantum annealing: methods and implementations. Rep. Prog. Phys. 83 , 054401 (2020).

Article ADS CAS PubMed Google Scholar

Yarkoni, S., Raponi, E., Bäck, T. & Schmitt, S. Quantum annealing for industry applications: Introduction and review. Rep. Prog. Phys. 85 , 104001 (2022).

Morita, S. & Nishimori, H. Mathematical foundation of quantum annealing. J. Math. Phys. 49 , 125210 (2008).

Santoro, G. E. & Tosatti, E. Optimization using quantum mechanics: Quantum annealing through adiabatic evolution. J. Phys. A: Math. Gen. 39 , R393 (2006).

Finnila, A. B., Gomez, M., Sebenik, C., Stenson, C. & Doll, J. D. Quantum annealing: A new method for minimizing multidimensional functions. Chem. Phys. Lett. 219 , 343–348 (1994).

Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473 , 194–198 (2011).

Lanting, T. et al. Entanglement in a quantum annealing processor. Phys. Rev. X 4 , 021041 (2014).

Google Scholar

Boixo, S., Albash, T., Spedalieri, F. M., Chancellor, N. & Lidar, D. A. Experimental signature of programmable quantum annealing. Nat. Commun. 4 , 2067 (2013).

Article ADS PubMed Google Scholar

King, A. D. et al. Coherent quantum annealing in a programmable 2000-qubit Ising chain. Nat. Phys. 18 , 1324–1328 (2022).

Article CAS Google Scholar

Chow, J. M. et al. Simple all-microwave entangling gate for fixed-frequency superconducting qubits. Phys. Rev. Lett. 107 , 080502 (2011).

Chamberland, C., Zhu, G., Yoder, T. J., Hertzberg, J. B. & Cross, A. W. Topological and subsystem codes on low-degree graphs with flag qubits. Phys. Rev. X 10 , 011022 (2020).

CAS Google Scholar

Tasseff, B. et al. On the emerging potential of quantum annealing hardware for combinatorial optimization. arXiv preprint (2022). https://doi.org/10.48550/arXiv.2210.04291 .

Sanders, Y. R. et al. Compilation of fault-tolerant quantum heuristics for combinatorial optimization. PRX Quantum 1 , 020312 (2020).

Article Google Scholar

Lotshaw, P. C. et al. Scaling quantum approximate optimization on near-term hardware. Sci. Rep. 12 , 12388 (2022).

Article ADS CAS PubMed PubMed Central Google Scholar

Albash, T. & Lidar, D. A. Demonstration of a scaling advantage for a quantum annealer over simulated annealing. Phys. Rev. X 8 , 031016 (2018).

King, A. D. et al. Scaling advantage over path-integral Monte Carlo in quantum simulation of geometrically frustrated magnets. Nat. Commun. 12 , 1113 (2021).

Farhi, E. & Harrow, A. W. Quantum supremacy through the quantum approximate optimization algorithm. arXiv preprint (2019). https://doi.org/10.48550/arXiv.1602.07674 .

Brady, L. T., Baldwin, C. L., Bapat, A., Kharkov, Y. & Gorshkov, A. V. Optimal protocols in quantum annealing and quantum approximate optimization algorithm problems. Phys. Rev. Lett. 126 , 070505 (2021).

Article ADS MathSciNet CAS PubMed Google Scholar

Willsch, M., Willsch, D., Jin, F., De Raedt, H. & Michielsen, K. Benchmarking the quantum approximate optimization algorithm. Quantum Inf. Process. 19 , 197 (2020).

Sack, S. H. & Serbyn, M. Quantum annealing initialization of the quantum approximate optimization algorithm. Quantum 5 , 491 (2021).

Golden, J., Bärtschi, A., Eidenbenz, S. & O’Malley, D. Numerical Evidence for Exponential Speed-up of QAOA over Unstructured Search for Approximate Constrained Optimization. In IEEE International Conference on Quantum Computing and Engineering QCE’23 , 496–505 (2023). https://doi.org/10.1109/QCE57702.2023.00063 .

Golden, J., Bärtschi, A., O’Malley, D. & Eidenbenz, S. The Quantum Alternating Operator Ansatz for Satisfiability Problems. In IEEE International Conference on Quantum Computing and Engineering QCE’23 , 307–312 (2023). https://doi.org/10.1109/QCE57702.2023.00042 .

Binkowski, L., Koßmann, G., Ziegler, T. & Schwonnek, R. Elementary Proof of QAOA Convergence. arXiv preprint (2023). https://doi.org/10.48550/arXiv.2302.04968 .

Lubinski, T. et al. Optimization Applications as Quantum Performance Benchmarks. arXiv preprint (2024). https://doi.org/10.48550/arXiv.2302.02278 .

Pelofske, E., Golden, J., Bärtschi, A., O’Malley, D. & Eidenbenz, S. Sampling on NISQ Devices: “Who’s the Fairest One of All?”. In IEEE International Conference on Quantum Computing and Engineering QCE’21 , 207–217 (2021). https://doi.org/10.1109/qce52317.2021.00038 .

Ushijima-Mwesigwa, H. et al. Multilevel combinatorial optimization across quantum architectures. ACM Trans. Quantum Comput. 2 , 1:1–1:29 (2021).

Streif, M. & Leib, M. Comparison of QAOA with quantum and simulated annealing. arXiv preprint (2019). https://doi.org/10.48550/arXiv.1901.01903 .

Pelofske, E., Bärtschi, A. & Eidenbenz, S. Quantum Annealing vs. QAOA: 127 Qubit Higher-Order Ising Problems on NISQ Computers. In International Conference on High Performance Computing ISC HPC’23 , 240–258 (2023). https://doi.org/10.1007/978-3-031-32041-5_13 .

Suau, A. et al. Single-Qubit Cross Platform Comparison of Quantum Computing Hardware. In IEEE International Conference on Quantum Computing and Engineering QCE’23 , 1369–1377 (2023). https://doi.org/10.1109/QCE57702.2023.00155 .

Pagano, G. et al. Quantum approximate optimization of the long-range ising model with a trapped-ion quantum simulator. Proc. Natl. Acad. Sci. 117 , 25396–25401 (2020).

Article ADS MathSciNet CAS PubMed PubMed Central Google Scholar

Weidenfeller, J. et al. Scaling of the quantum approximate optimization algorithm on superconducting qubit based hardware. Quantum 6 , 870 (2022).

Harrigan, M. P. et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 17 , 332–336 (2021).

Herman, D. et al. Constrained optimization via quantum Zeno dynamics. Commun. Phys. 6 , 219 (2023).

Niroula, P. et al. Constrained quantum optimization for extractive summarization on a trapped-ion quantum computer. Sci. Rep. 12 , 17171 (2022).

Zhou, L., Wang, S.-T., Choi, S., Pichler, H. & Lukin, M. D. Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices. Phys. Rev. X 10 , 021067 (2020).

Basso, J., Farhi, E., Marwaha, K., Villalonga, B. & Zhou, L. The quantum approximate optimization algorithm at high depth for maxcut on large-girth regular graphs and the Sherrington-Kirkpatrick Model. In 17th Conference on the Theory of Quantum Computation, Communication and Cryptography TQC’22 (2022). https://doi.org/10.4230/LIPICS.TQC.2022.7 .

Wang, Z., Hadfield, S., Jiang, Z. & Rieffel, E. G. Quantum approximate optimization algorithm for MaxCut: A fermionic view. Phys. Rev. A 97 , 022304 (2018).

Crooks, G. E. Performance of the quantum approximate optimization algorithm on the maximum cut problem. arXiv preprint (2018). https://doi.org/10.48550/arXiv.1811.08419 .

Guerreschi, G. G. & Matsuura, A. Y. QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci. Rep. 9 , 6903 (2019).

Marwaha, K. Local classical MAX-CUT algorithm outperforms p = 2 QAOA on high-girth regular graphs. Quantum 5 , 437 (2021).

Hastings, M. B. Classical and quantum bounded depth approximation algorithms. Quantum Inf. Comput. 19 , 1116–1140 (2019).

MathSciNet Google Scholar

Saleem, Z. H. Max independent set and quantum alternating operator Ansatz. Int. J. Quantum Inf. 18 , 2050011 (2020).

de la Grand’rive, P. D. & Hullo, J.-F. Knapsack Problem variants of QAOA for battery revenue optimisation. arXiv preprint (2019). https://doi.org/10.48550/arXiv.1908.02210 .

Farhi, E., Goldstone, J., Gutmann, S. & Zhou, L. The quantum approximate optimization algorithm and the Sherrington-Kirkpatrick model at infinite size. Quantum 6 , 759 (2022).

Jiang, S., Britt, K. A., McCaskey, A. J., Humble, T. S. & Kais, S. Quantum annealing for prime factorization. Sci. Rep. 8 , 17667 (2018).

Article ADS PubMed PubMed Central Google Scholar

Ji, X., Wang, B., Hu, F., Wang, C. & Zhang, H. New advanced computing architecture for cryptography design and analysis by D-Wave quantum annealer. Tsinghua Sci. Technol. 27 , 751–759 (2022).

Dridi, R. & Alghassi, H. Prime factorization using quantum annealing and computational algebraic geometry. Sci. Rep. 7 , 43048 (2017).

Peng, W. et al. Factoring larger integers with fewer qubits via quantum annealing with optimized parameters. Sci. China Phys., Mech. Astron. 62 , 60311 (2019).

Article ADS Google Scholar

Warren, R. H. Factoring on a quantum annealing computer. Quantum Inf. Comput. 19 , 252–261 (2019).

Titiloye, O. & Crispin, A. Quantum annealing of the graph coloring problem. Discret. Optim. 8 , 376–384 (2011).

Kwok, J. & Pudenz, K. Graph coloring with quantum annealing. arXiv preprint (2020). https://doi.org/10.48550/arXiv.2012.04470 .

Kumar, V., Bass, G., Tomlin, C. & Dulny, J. Quantum annealing for combinatorial clustering. Quantum Inf. Process. 17 , 39 (2018).

Venturelli, D. et al. Quantum optimization of fully connected spin glasses. Phys. Rev. X 5 , 031040 (2015).

Grant, E., Humble, T. S. & Stump, B. Benchmarking quantum annealing controls with portfolio optimization. Phys. Rev. Appl. 15 , 014012 (2021).

Rosenberg, G. et al. Solving the optimal trading trajectory problem using a quantum annealer. IEEE J. Sel. Top. Signal Process. 10 , 1053–1060 (2016).

Venturelli, D. & Kondratyev, A. Reverse quantum annealing approach to portfolio optimization problems. Quantum Mach. Intell. 1 , 17–30 (2019).

Lotshaw, P. C. et al. Simulations of frustrated ising Hamiltonians with quantum approximate optimization. Philos. Trans. R. Soc. A 381 , 20210414 (2022).

Harris, R. et al. Phase transitions in a programmable quantum spin glass simulator. Science 361 , 162–165 (2018).

King, A. D., Nisoli, C., Dahl, E. D., Poulin-Lamarre, G. & Lopez-Bezanilla, A. Qubit spin ice. Science 373 , 576–580 (2021).

Zhou, S., Green, D., Dahl, E. D. & Chamon, C. Experimental realization of classical ${{\mathbb{z}}}_{2}$ spin liquids in a programmable quantum device. Phys. Rev. B 104 , L081107 (2021).

King, A. D. et al. Quantum annealing simulation of out-of-equilibrium magnetization in a spin-chain compound. PRX Quantum 2 , 030317 (2021).

Shaydulin, R. & Pistoia, M. QAOA with N ⋅ p ≥200. In IEEE International Conference on Quantum Computing and Engineering QCE’23 , 1074–1077 (2023). https://doi.org/10.1109/QCE57702.2023.00121 .

Pelofske, E., Bärtschi, A., Golden, J. & Eidenbenz, S. High-Round QAOA for MAX k-SAT on Trapped Ion NISQ Devices. In IEEE International Conference on Quantum Computing and Engineering QCE’23 , 506–517 (2023). https://doi.org/10.1109/QCE57702.2023.00064 .

Inc., P. T. Collaborative data science (2015). https://plot.ly .

Caswell, T. A. et al. matplotlib/matplotlib.

Hunter, J. D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 9 , 90–95 (2007).

Hagberg, A. A., Schult, D. A. & Swart, P. J. Exploring network structure, dynamics, and function using networkX. In 7th Python in Science Conference SciPy’08 , 11–15 (2008). https://www.osti.gov/biblio/960616 .

Qiskit contributors. Qiskit: An Open-source Framework for Quantum Computing (2023).

Bärtschi, A. & Eidenbenz, S. Grover Mixers for QAOA: Shifting complexity from mixer design to state preparation. In IEEE International Conference on Quantum Computing and Engineering QCE’20 , 72–82 (2020). https://doi.org/10.1109/QCE49297.2020.00020 .

Wurtz, J. & Love, P. J. Classically optimal variational quantum algorithms. IEEE Trans. Quantum Eng. 2 , 3104107 (2021).

Wurtz, J. & Love, P. J. Counterdiabaticity and the quantum approximate optimization algorithm. Quantum 6 , 635 (2022).

Golden, J., Bärtschi, A., O’Malley, D. & Eidenbenz, S. Threshold-based quantum optimization. In IEEE International Conference on Quantum Computing and Engineering QCE’21 , 137–147 (2021). https://doi.org/10.1109/QCE52317.2021.00030 .

Bravyi, S., Kliesch, A., Koenig, R. & Tang, E. Obstacles to variational quantum optimization from symmetry protection. Phys. Rev. Lett. 125 , 260505 (2020).

Egger, D. J., Mareček, J. & Woerner, S. Warm-starting quantum optimization. Quantum 5 , 479 (2021).

Tate, R., Farhadi, M., Herold, C., Mohler, G. & Gupta, S. Bridging classical and quantum with SDP initialized warm-starts for QAOA. ACM Trans. Quantum Comput. 4 , 9:1–9:39 (2023).

Cain, M., Farhi, E., Gutmann, S., Ranard, D. & Tang, E. The QAOA gets stuck starting from a good classical string. arXiv preprint (2023). https://doi.org/10.48550/arXiv.2207.05089 .

Beaulieu, D. & Pham, A. Max-cut Clustering Utilizing Warm-Start QAOA and IBM Runtime. arXiv preprint (2021). https://doi.org/10.48550/arXiv.2108.13464 .

Bakó, B., Glos, A., Salehi, z. & Zimborás, Z. Near-optimal circuit design for variational quantum optimization. arXiv preprint (2024). https://doi.org/10.48550/arXiv.2209.03386 .

Yoshioka, T., Sasada, K., Nakano, Y. & Fujii, K. Fermionic quantum approximate optimization algorithm. Phys. Rev. Res. 5 , 023071 (2023).

Caha, L., Kliesch, A. & Koenig, R. Twisted hybrid algorithms for combinatorial optimization. Quantum Sci. Technol. 7 , 045013 (2022).

Li, J., Alam, M. & Ghosh, S. Large-scale quantum approximate optimization via divide-and-conquer. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 42 , 1852–1860 (2023).

Herrman, R., Lotshaw, P. C., Ostrowski, J., Humble, T. S. & Siopsis, G. Multi-angle quantum approximate optimization algorithm. Sci. Rep. 12 , 6781 (2022).

Shi, K. et al. Multi-Angle QAOA Does Not Always Need All Its Angles. In IEEE/ACM 7th Symposium on Edge Computing SEC’22 (2022). https://doi.org/10.1109/SEC54971.2022.00062 .

Cerezo, M. et al. Variational quantum algorithms. Nat. Rev. Phys. 3 , 625–644 (2021).

Wang, S. et al. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun. 12 , 6961 (2021).

Zhu, Y. et al. Multi-round QAOA and advanced mixers on a trapped-ion quantum computer. Quantum Sci. Technol. 8 , 015007 (2022).

Rabinovich, D., Sengupta, R., Campos, E., Akshay, V. & Biamonte, J. Progress towards analytically optimal angles in quantum approximate optimisation. Mathematics 10 , 2601 (2022).

Zbinden, S., Bärtschi, A., Djidjev, H. & Eidenbenz, S. Embedding Algorithms for Quantum Annealers with Chimera and Pegasus Connection Topologies. In International Conference on High Performance Computing ISC HPC’20 , 187–206 (2020). https://doi.org/10.1007/978-3-030-50743-5_10 .

Boothby, T., King, A. D. & Roy, A. Fast clique minor generation in Chimera qubit connectivity graphs. Quantum Inf. Process. 15 , 495–508 (2016).

Patton, R., Schuman, C. & Potok, T. et al. Efficiently embedding qubo problems on adiabatic quantum computers. Quantum Inf. Process. 18 , 117 (2019).

Dattani, N., Szalay, S. & Chancellor, N. Pegasus: The second connectivity graph for large-scale quantum annealing hardware. arXiv preprint (2019). https://doi.org/10.48550/arXiv.1901.07636 .

DWave NetworkX Zephyr Graph. https://web.archive.org/web/20230000000000*/https://docs.ocean.dwavesys.com/en/stable/docs_dnx/reference/generated/dwave_networkx.zephyr_graph.html . Accessed: 2023-10-14.

Grant, E. & Humble, T. S. Benchmarking embedded chain breaking in quantum annealing. Quantum Sci. Technol. 7 , 025029 (2022).

Marshall, J., Mossi, G. & Rieffel, E. G. Perils of embedding for quantum sampling. Phys. Rev. A 105 , 022615 (2022).

Könz, M.Embedding penalties for quantum hardware architectures and performance of simulated quantum annealing. Ph.D. thesis, ETH Zürich (2019). https://doi.org/10.3929/ethz-b-000439876 .

Tseng, C. H. et al. Quantum simulation of a three-body-interaction Hamiltonian on an NMR quantum computer. Phys. Rev. A 61 , 012302 (1999).

Chancellor, N., Zohren, S. & Warburton, P. A. Circuit design for multi-body interactions in superconducting quantum annealing systems with applications to a scalable architecture. npj Quantum Inf. 3 , 21 (2017).

Katzgraber, H. G., Bombin, H. & Martin-Delgado, M. A. Error threshold for color codes and random three-body ising models. Phys. Rev. Lett. 103 , 090501 (2009).

Gilbert, V., Rodriguez, J., Louise, S. & Sirdey, R. Solving Higher Order Binary Optimization Problems on NISQ Devices: Experiments and Limitations. In 23rd International Conference on Computational Science ICCS’23 , 224–232 (Springer, 2023). https://doi.org/10.1007/978-3-031-36030-5_18 .

Passarelli, G., Cataudella, V. & Lucignano, P. Improving quantum annealing of the ferromagnetic p -spin model through pausing. Phys. Rev. B 100 , 024302 (2019).

Passarelli, G., Yip, K.-W., Lidar, D. A., Nishimori, H. & Lucignano, P. Reverse quantum annealing of the p -spin model with relaxation. Phys. Rev. A 101 , 022331 (2020).

Passarelli, G., Cataudella, V., Fazio, R. & Lucignano, P. Counterdiabatic driving in the quantum annealing of the p -spin model: A variational approach. Phys. Rev. Res. 2 , 013283 (2020).

Krzakala, F. & Zdeborová, L. Performance of simulated annealing in p-spin glasses. J. Phys.: Conf. Ser. 473 , 012022 (2013).

Yamashiro, Y., Ohkuwa, M., Nishimori, H. & Lidar, D. A. Dynamics of reverse annealing for the fully connected p -spin model. Phys. Rev. A 100 , 052321 (2019).

Passarelli, G., De Filippis, G., Cataudella, V. & Lucignano, P. Dissipative environment may improve the quantum annealing performances of the ferromagnetic p -spin model. Phys. Rev. A 97 , 022319 (2018).

Matsuura, S., Nishimori, H., Vinci, W., Albash, T. & Lidar, D. A. Quantum-annealing correction at finite temperature: Ferromagnetic p -spin models. Phys. Rev. A 95 , 022308 (2017).

Susa, Y., Imoto, T. & Matsuzaki, Y. Nonstoquastic catalyst for bifurcation-based quantum annealing of the ferromagnetic p -spin model. Phys. Rev. A 107 , 052401 (2023).

Matsuura, S., Nishimori, H., Vinci, W. & Lidar, D. A. Nested quantum annealing correction at finite temperature: p -spin models. Phys. Rev. A 99 , 062307 (2019).

Susa, Y. et al. Quantum annealing of the p -spin model under inhomogeneous transverse field driving. Phys. Rev. A 98 , 042326 (2018).

Seki, Y. & Nishimori, H. Quantum annealing with antiferromagnetic fluctuations. Phys. Rev. E 85 , 051112 (2012).

Campbell, C. & Dahl, E. QAOA of the Highest Order. In IEEE 19th International Conference on Software Architecture Companion ICSA-C’22 , 141–146 (2022). https://doi.org/10.1109/ICSA-C54293.2022.00035 .

Basso, J., Gamarnik, D., Mei, S. & Zhou, L. Performance and limitations of the QAOA at constant levels on large sparse hypergraphs and spin glass models. In IEEE 63rd Annual Symposium on Foundations of Computer Science FOCS’22 , 335–343 (2022). https://doi.org/10.1109/FOCS54457.2022.00039 .

Fakhimi, R., Validi, H., Hicks, I. V., Terlaky, T. & Zuluaga, L. F. Quantum-inspired formulations for the Max k-cut Problem. ISE Technical Report 21T-007 2021).

Glos, A., Krawiec, A. & Zimborás, Z. Space-efficient binary optimization for variational quantum computing. npj Quantum Inf. 8 , 39 (2022).

Tabi, Z. et al. Quantum Optimization for the Graph Coloring Problem with Space-Efficient Embedding. In IEEE International Conference on Quantum Computing and Engineering QCE’20 (2020). https://doi.org/10.1109/qce49297.2020.00018 .

Valiante, E., Hernandez, M., Barzegar, A. & Katzgraber, H. G. Computational overhead of locality reduction in binary optimization problems. Computer Phys. Commun. 269 , 108102 (2021).

Article MathSciNet CAS Google Scholar

Ishikawa, H. Transformation of general binary MRF minimization to the first-order case. IEEE Trans. Pattern Anal. Mach. Intell. 33 , 1234–1249 (2011).

Article PubMed Google Scholar

Pelofske, E., Hahn, G., O’Malley, D., Djidjev, H. N. & Alexandrov, B. S. Quantum annealing algorithms for boolean tensor networks. Sci. Rep. 12 , 8539 (2022).

Pelofske, E., Hahn, G., O’Malley, D., Djidjev, H. N. & Alexandrov, B. S. Boolean hierarchical tucker networks on quantum annealers. In 13th International Conference on Large-Scale Scientific Computing LSSC’21 , 351–358 (Springer, 2022). https://doi.org/10.1007/978-3-030-97549-4_40 .

Jun, K. & Lee, H. HUBO formulations for solving the eigenvalue problem. Results Control Optim. 11 , 100222 (2023).

Könz, M. S., Mazzola, G., Ochoa, A. J., Katzgraber, H. G. & Troyer, M. Uncertain fate of fair sampling in quantum annealing. Phys. Rev. A 100 , 030303 (2019).

Mandrà, S., Zhu, Z. & Katzgraber, H. G. Exponentially biased ground-state sampling of quantum annealing machines with transverse-field driving Hamiltonians. Phys. Rev. Lett. 118 , 070502 (2017).

Leone, L., Oliviero, S. F. E., Cincio, L. & Cerezo, M. On the practical usefulness of the Hardware Efficient Ansatz. arXiv preprint (2022). https://doi.org/10.48550/arXiv.2211.01477 .

Nakaji, K. & Yamamoto, N. Expressibility of the alternating layered ansatz for quantum computation. Quantum 5 , 434 (2021).

Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549 , 242–246 (2017).

Pelofske, E., Hahn, G. & Djidjev, H. N. Parallel quantum annealing. Sci. Rep. 12 , 4499 (2022).

Pelofske, E., Hahn, G. & Djidjev, H. N. Solving larger maximum clique problems using parallel quantum annealing. Quantum Inf. Process. 22 , 219 (2023).

DWave Tiling. https://web.archive.org/web/20230000000000*/https://dwave-systemdocs.readthedocs.io/en/samplers/reference/composites/tiling.html . Accessed: 2023-10-14.

Ash-Saki, A., Alam, M. & Ghosh, S. Analysis of Crosstalk in NISQ Devices and Security Implications in Multi-Programming Regime. In ACM/IEEE International Symposium on Low Power Electronics and Design ISLPED’20 , ISLPED ’20, 25–30 (2020). https://doi.org/10.1145/3370748.3406570 .

Das, P., Tannu, S. S., Nair, P. J. & Qureshi, M. A Case for Multi-Programming Quantum Computers. In 52nd Annual IEEE/ACM International Symposium on Microarchitecture MICRO-52 , 291–303 (2019). https://doi.org/10.1145/3352460.3358287 .

Niu, S. & Todri-Sanial, A. Multi-programming cross platform benchmarking for quantum computing hardware. arXiv preprint (2022). https://doi.org/10.48550/arXiv.2206.03144 .

Ohkura, Y., Satoh, T. & Van Meter, R. Simultaneous execution of quantum circuits on current and near-future NISQ systems. IEEE Trans. Quantum Eng. 3 , 2500210 (2022).

Niu, S. & Todri-Sanial, A. How Parallel Circuit Execution Can Be Useful for NISQ Computing? In Conference & Exhibition on Design, Automation & Test in Europe DATE’22 , 1065–1070 (2022). https://doi.org/10.23919/DATE54114.2022.9774512 .

Mineh, L. & Montanaro, A. Accelerating the variational quantum eigensolver using parallelism. Quantum Sci. Technol. 8 , 035012 (2023).

Resch, S. et al. Accelerating Variational Quantum Algorithms Using Circuit Concurrency. arXiv preprint (2021). https://doi.org/10.48550/arXiv.2109.01714 .

Lee, X., Saito, Y., Cai, D. & Asai, N. Parameters fixing strategy for quantum approximate optimization algorithm. In IEEE International Conference on Quantum Computing and Engineering QCE’21 , 10–16 (2021). https://doi.org/10.1109/QCE52317.2021.00016 .

Galda, A., Liu, X., Lykov, D., Alexeev, Y. & Safro, I. Transferability of optimal QAOA parameters between random graphs. In IEEE International Conference on Quantum Computing and Engineering QCE’21 , 171–180 (2021). https://doi.org/10.1109/QCE52317.2021.00034 .

Akshay, V., Rabinovich, D., Campos, E. & Biamonte, J. Parameter concentration in quantum approximate optimization. Phys. Rev. A 104 , L010401 (2021).

Wurtz, J. & Lykov, D. Fixed-angle conjectures for the quantum approximate optimization algorithm on regular MaxCut graphs. Phys. Rev. A 104 , 052419 (2021).

Farhi, E., Gamarnik, D. & Gutmann, S. The quantum approximate optimization algorithm needs to see the whole graph: A typical case. arXiv preprint (2020). https://doi.org/10.48550/arXiv.2004.09002 .

Farhi, E., Gamarnik, D. & Gutmann, S. The quantum approximate optimization algorithm needs to see the whole graph: Worst case examples. arXiv preprint (2020). https://doi.org/10.48550/arXiv.2005.08747 .

Viola, L. & Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 58 , 2733–2744 (1998).

Suter, D. & Álvarez, G. A. Colloquium: Protecting quantum information against environmental noise. Rev. Mod. Phys. 88 , 041001 (2016).

Viola, L., Knill, E. & Lloyd, S. Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82 , 2417–2421 (1999).

Ahmed, M. A. A., Álvarez, G. A. & Suter, D. Robustness of dynamical decoupling sequences. Phys. Rev. A 87 , 042309 (2013).

LaRose, R. et al. Mitiq: A software package for error mitigation on noisy quantum computers. Quantum 6 , 774 (2022).

Charles, C. et al. Simulating ${{\mathbb{Z}}}_{2}$ lattice gauge theory on a quantum computer. Phys. Rev. D. 108 , 074503 (2023).

Niu, S. & Todri-Sanial, A. Effects of dynamical decoupling and pulse-level optimizations on IBM quantum computers. IEEE Trans. Quantum Eng. 3 , 3102510 (2022).

Ezzell, N., Pokharel, B., Tewala, L., Quiroz, G. & Lidar, D. A. Dynamical decoupling for superconducting qubits: A performance survey. Phys. Rev. Appl. 20 , 064027 (2023).

Pokharel, B., Anand, N., Fortman, B. & Lidar, D. A. Demonstration of fidelity improvement using dynamical decoupling with superconducting qubits. Phys. Rev. Lett. 121 , 220502 (2018).

Pokharel, B. & Lidar, D. Better-than-classical Grover search via quantum error detection and suppression. arXiv preprint (2022). https://doi.org/10.48550/arXiv.2211.04543 .

Kim, Y. et al. Scalable error mitigation for noisy quantum circuits produces competitive expectation values. Nat. Phys. 19 , 752–759 (2023).

Jurcevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Sci. Technol. 6 , 025020 (2021).

Cross, A. W., Bishop, L. S., Smolin, J. A. & Gambetta, J. M. Open quantum assembly language. arXiv preprint (2017). https://doi.org/10.48550/arXiv.1707.03429 .

Qiskit Transpiler Pad DynamicalDecoupling. https://web.archive.org/web/20230000000000*/https://qiskit.org/documentation/locale/bn_BN/stubs/qiskit.transpiler.passes.PadDynamicalDecoupling.html . Accessed: 2023-10-14.

Qiskit Transpiler Passes. https://web.archive.org/web/20230000000000*/https://qiskit.org/documentation/apidoc/transpiler_passes.html . Accessed: 2023-10-14.

Mitiq digital dynamical decoupling. https://web.archive.org/web/20230000000000*/https://mitiq.readthedocs.io/en/latest/guide/ddd-5-theory.html . Accessed: 2023-10-14.

Maciejewski, F. B., Zimborás, Z. & Oszmaniec, M. Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum 4 , 257 (2020).

Li, Y. & Benjamin, S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7 , 021050 (2017).

Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567 , 491–495 (2019).

Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119 , 180509 (2017).

Article ADS MathSciNet PubMed Google Scholar

McKay, D. C., Wood, C. J., Sheldon, S., Chow, J. M. & Gambetta, J. M. Efficient Z gates for quantum computing. Phys. Rev. A 96 , 022330 (2017).

Magesan, E., Gambetta, J. M. & Emerson, J. Characterizing quantum gates via randomized benchmarking. Phys. Rev. A 85 , 042311 (2012).

Harper, R., Hincks, I., Ferrie, C., Flammia, S. T. & Wallman, J. J. Statistical analysis of randomized benchmarking. Phys. Rev. A 99 , 052350 (2019).

Bravyi, S. et al. Simulation of quantum circuits by low-rank stabilizer decompositions. Quantum 3 , 181 (2019).

Marshall, J., Venturelli, D., Hen, I. & Rieffel, E. G. Power of pausing: Advancing understanding of thermalization in experimental quantum annealers. Phys. Rev. Appl. 11 , 044083 (2019).

Chen, H. & Lidar, D. A. Why and when pausing is beneficial in quantum annealing. Phys. Rev. Appl. 14 , 014100 (2020).

Izquierdo, Z. G. et al. Advantage of pausing: Parameter setting for quantum annealers. Phys. Rev. Appl. 18 , 054056 (2022).

Cplex, I. I. V12.10.0 : User’s manual for CPLEX. Int. Bus. Mach. Corp. 46 , 157 (2019).

Kirkpatrick, S., Gelatt Jr, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220 , 671–680 (1983).

DWave Simulated Annealing. https://web.archive.org/web/20230000000000*/https://github.com/dwavesystems/dwave-neal . Accessed: 2023-10-14.

DWave Dimod Package. https://web.archive.org/web/20230000000000*/https://github.com/dwavesystems/dimod . Accessed: 2023-10-14.

DWave dimod make-quadratic. https://web.archive.org/web/20230000000000*/https://docs.ocean.dwavesys.com/en/stable/docs_dimod/reference/generated/dimod.make_quadratic.html . Accessed: 2023-10-14.

Download references

Acknowledgements

This work was supported by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). Research presented in this article was supported by the NNSA’s Advanced Simulation and Computing Beyond Moore’s Law Program at Los Alamos National Laboratory. The research presented in this article was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number 20220656ER and 20210114ER. This research used resources provided by the Darwin testbed at Los Alamos National Laboratory (LANL) which is funded by the Computational Systems and Software Environments subprogram of LANL’s Advanced Simulation and Computing program (NNSA/DOE). We acknowledge the use of IBM Quantum services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team. We thank the IBM Quantum team for technical support on the IBM Quantum systems throughout this project. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. This work has been assigned the LANL technical report number LA-UR-23-22023.

Author information

Authors and affiliations.

Los Alamos National Laboratory, CCS-3 Information Sciences, Los Alamos, NM, USA

Elijah Pelofske, Andreas Bärtschi & Stephan Eidenbenz

You can also search for this author in PubMed Google Scholar

Contributions

E.P. ran all experiments, analyzed the data, and drafted the manuscript. A.B. conceived of the core idea and developed the QAOA circuits and QA order reduction algorithm. S.E. supervised the project and the project methodology. All authors contributed to the experimental design and all authors reviewed and revised the manuscript.

Corresponding authors

Correspondence to Elijah Pelofske or Andreas Bärtschi .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplemental materials appendix, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Pelofske, E., Bärtschi, A. & Eidenbenz, S. Short-depth QAOA circuits and quantum annealing on higher-order ising models. npj Quantum Inf 10 , 30 (2024). https://doi.org/10.1038/s41534-024-00825-w

Download citation

Received : 23 March 2023

Accepted : 26 February 2024

Published : 12 March 2024

DOI : https://doi.org/10.1038/s41534-024-00825-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

Explore articles by subject
Guide to authors
Editorial policies

IMAGES

PPT
PPT
Quadratic Equation Worksheet With Answers
PPT
PPT
Quadratic Assignment Problem Example

VIDEO

My favorite quadratic solving method
Important Question on Quadratic Equations 😲 Can you solve this ⚡ #ytshorts #maths #practice
Quadratic Function
Quadratic equation practice problem
Solve The Quadratic Problem
Quadratic Type Review

COMMENTS

Quadratic assignment problem
The quadratic assignment problem ( QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann. [1] There are a set of n facilities and a set of n locations.
PDF The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the
Quadratic Assignment Problem (QAP)
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance ...
Quadratic assignment problem
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize ...
The Quadratic Assignment Problem
Abstract. The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the cost being a function of the distance and flow between the ...
A comprehensive review of quadratic assignment problem: variants
The quadratic assignment problem (QAP) has considered one of the most significant combinatorial optimization problems due to its variant and significant applications in real life such as scheduling, production, computer manufacture, chemistry, facility location, communication, and other fields. QAP is NP-hard problem that is impossible to be solved in polynomial time when the problem size ...
The Quadratic Assignment Problem
The quadratic assignment problem (QAP) is considered one of the most difficult optimization problems to solve optimally. The QAP is a combinatorial optimization problem stated for the first time by Koopmans and Beckmann ().Early papers on the subject include Gilmore (), Pierce and Crowston (), Lawler (), and Love and Wong ().The problem is defined as follows.
The Quadratic Assignment Problem : Theory and Algorithms
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization problem which is (still) attractive from many ...
The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization problem which is (still) attractive from many ...
the Quadratic Assignment Problem
The quadratic assignment problem (QAP) is arguably one of the hardest NP-hard discrete optimization problems. Problems of dimension greater than 25 are still considered to be large scale. Current successful solution techniques use branch-and-bound methods, which rely on obtaining strong and inexpensive bounds.
The Quadratic Assignment Problem : Theory and Algorithms
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...
The Quadratic Assignment Problem: Theory and Algorithms
An algorithm for generating quadratic assignment problem (QAP) instances with known provably optimal solution which generalizes some existing algorithms based on the iterative selection of triangles only and produces a set of instances which can be produced by the algorithm. Expand. 14. Highly Influenced.
(PDF) The Quadratic Assignment Problem
The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we ...
Quadratic Assignment Problem
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time. The QAP can be viewed as a natural extension of the linear assignment problem (LAP; cf. also ...
The Quadratic Assignment Problem: An Analysis of Applications and
A wide variety of practical problems in design, planning, and management can be formulated as quadratic assignment problems, and this paper discusses this class of problem. Since algorithms for producing optimal solutions to such problems are computationally infeasible for all but small problems of this type, heuristic techniques must usually ...
A survey for the quadratic assignment problem
The quadratic assignment problem (QAP), one of the most difficult problems in the NP-hard class, models many real-life problems in several areas such as facilities location, parallel and distributed computing, and combinatorial data analysis. Combinatorial optimization problems, such as the traveling salesman problem, maximal clique and graph ...
PDF arXiv:1908.04522v1 [math.OC] 13 Aug 2019
The quadratic assignment problem (QAP) is a classical mathematical model for location theory, which is used to model the location problem of allocating nfa-cilities to nlocations while minimizing the quadratic objective coming from the distance between the locations and the ow between the facilities. The standard
The Quadratic Assignment Problem
Abstract. This paper presents a formulation of the quadratic assignment problem, of which the Koopmans-Beckmann formulation is a special case. Various applications for the formulation are discussed. The equivalence of the problem to a linear assignment problem with certain additional constraints is demonstrated. A method for calculating a lower ...
The Quadratic Assignment Problem
This paper presents a formulation of the quadratic assignment problem, of which the Koopmans-Beckmann formulation is a special case. Various applications for the formulation are discussed. The equivalence of the problem to a linear assignment problem with certain additional constraints is demonstrated. A method for calculating a lower bound on the cost function is presented, and this forms the ...
The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...
On the quadratic assignment problem
On the quadratic assignment problem 97 These values minimise EEi*j (cij -,uj)2 etc. and are sifriilar but not identical to those in [6]). lbl. This is the largest value obtained for L(a, /3) using the subgradient algorithm. itl. The number of iterations of the subgradient algorithm needed to reach lbl. (The approach of Bazaraa and Goode [2] was ...
PDF the Quadratic Assignment Problem
travelling salesman problem, graph isomorphism and graph packing problem [1]. The QAP problem has been shown to be NP-hard [2], hence several approaches have been used to solve this problem. Intensive studies on quadratic assignment problems produced many algorithms over the last few decades. For a survey on these methods, see [3,4].
[2403.02783] Where the Really Hard Quadratic Assignment Problems Are
The Quadratic Assignment Problem (QAP) is one of the major domains in the field of evolutionary computation, and more widely in combinatorial optimization. This paper studies the phase transition of the QAP, which can be described as a dramatic change in the problem's computational complexity and satisfiability, within a narrow range of the problem parameters. To approach this phenomenon, we ...
The Quadratic Assignment Problem: A Brief Review
The quadratic assignment problem, its applications, and various exact and inexact procedures for its solution are briefly reviewed. Certain special cases of the one-dimensional module placement problem, itself a special case of the quadratic assignment problem, are surveyed.
Short-depth QAOA circuits and quantum annealing on higher ...
p = 2 rounds applied to a cubic problem instance is the hardest of the problems to simulate; p = 1 is easier to simulate, in that it uses fewer qubits, as are simulations of the quadratic problems.

Quadratic Assignment Problem (QAP)

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Quadratic assignment problem

Introduction

Theory, Methodology, and/or Algorithmic Discussions

Quadratic Assignment Problem Formulation

Inner Product

Optimization Problem

Computational Complexity

Algorithmic Discussions

Branch and Bound Procedures

Linearizations

Numerical Example

Applications

The Backboard Wiring Problem

Hospital Layout

Exam Scheduling System

The Quadratic Assignment Problem : Theory and Algorithms

At the library

Description

Bibliographic information

The Quadratic Assignment Problem

Related Papers

RELATED PAPERS

RELATED TOPICS

Computer Science > Artificial Intelligence

Submission history

References & Citations

BibTeX formatted citation

Bibliographic and Citation Tools

arXivLabs: experimental projects with community collaborators

The Quadratic Assignment Problem: A Brief Review

Buying options

Author information

Editor information

Rights and permissions

Copyright information

About this paper

Download citation

Share this paper

Short-depth QAOA circuits and quantum annealing on higher-order ising models

Similar content being viewed by others

Drug design on quantum computers

De novo design of protein structure and function with RFdiffusion

Exploring the frontiers of condensed-phase chemistry with a general reactive machine learning potential

Introduction

QAOA general overview

Quantum annealing general overview

Ising model problem instances

Implementing ising model QAOA circuits on IBM quantum Heavy-Hex connectivity

Implementing ising models on D-wave pegasus connectivity

Experiments

Optimal solution sampling

Quantum annealing schedule tuning

QAOA angle tuning

Classical simulation of QAOA results

Dynamical decoupling for QAOA circuits

IBM quantum processor QAOA circuit execution

Classical simulation of QAOA

D-wave quantum annealing processor parameter optimizations

Simulated annealing and CPLEX implementations

Data availability

Code availability

Acknowledgements

Author information

Contributions

Corresponding authors

Ethics declarations

Additional information

Supplementary information

About this article

Share this article

Quick links

IMAGES

VIDEO

COMMENTS