hypothesis testing for p value

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P -value is large, say more than \(\alpha\), then it is "likely."

If the P -value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than \(\alpha\), then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
• Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to \(\alpha\). If the P -value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than \(\alpha\), do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

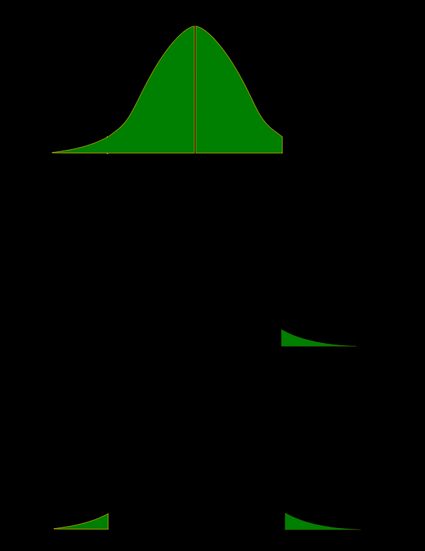
The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

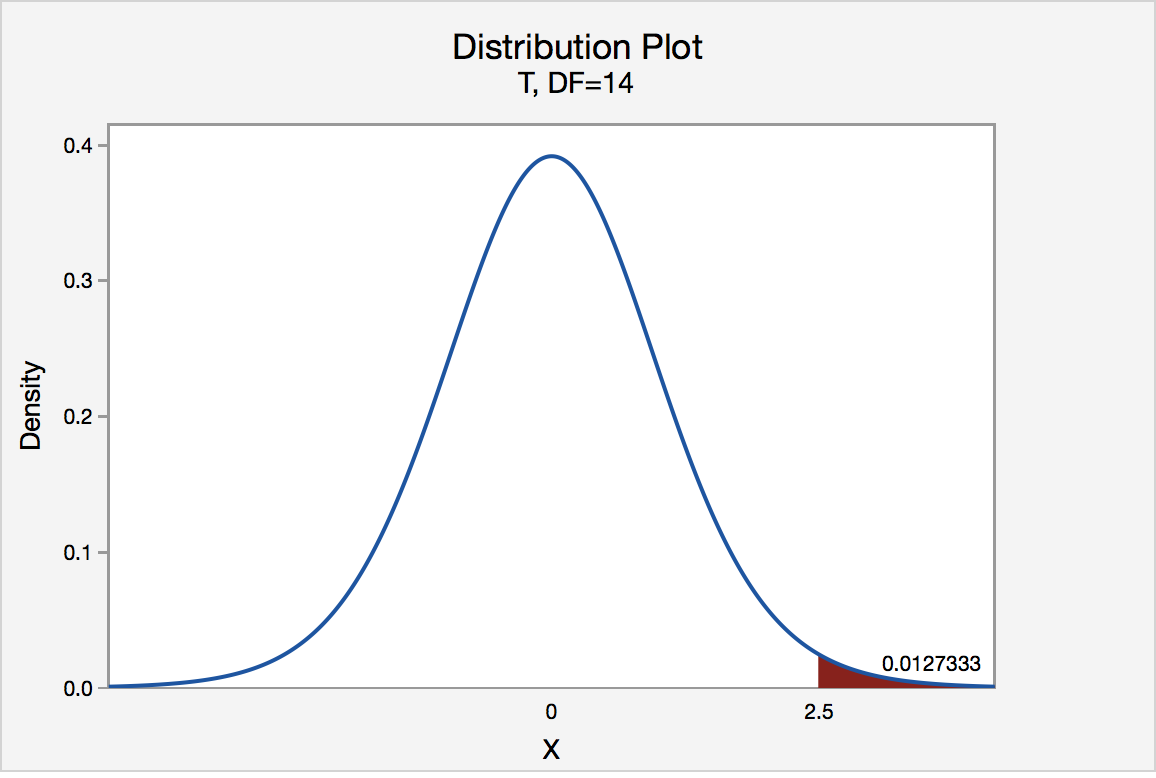
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

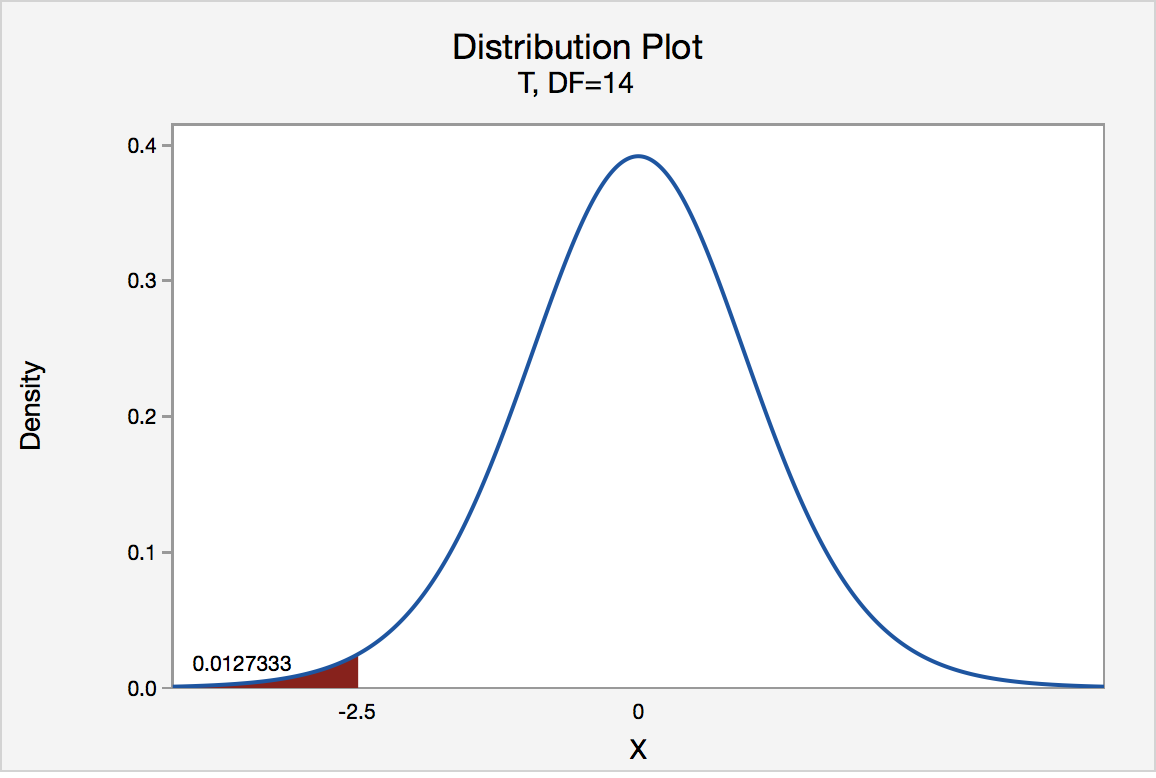
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

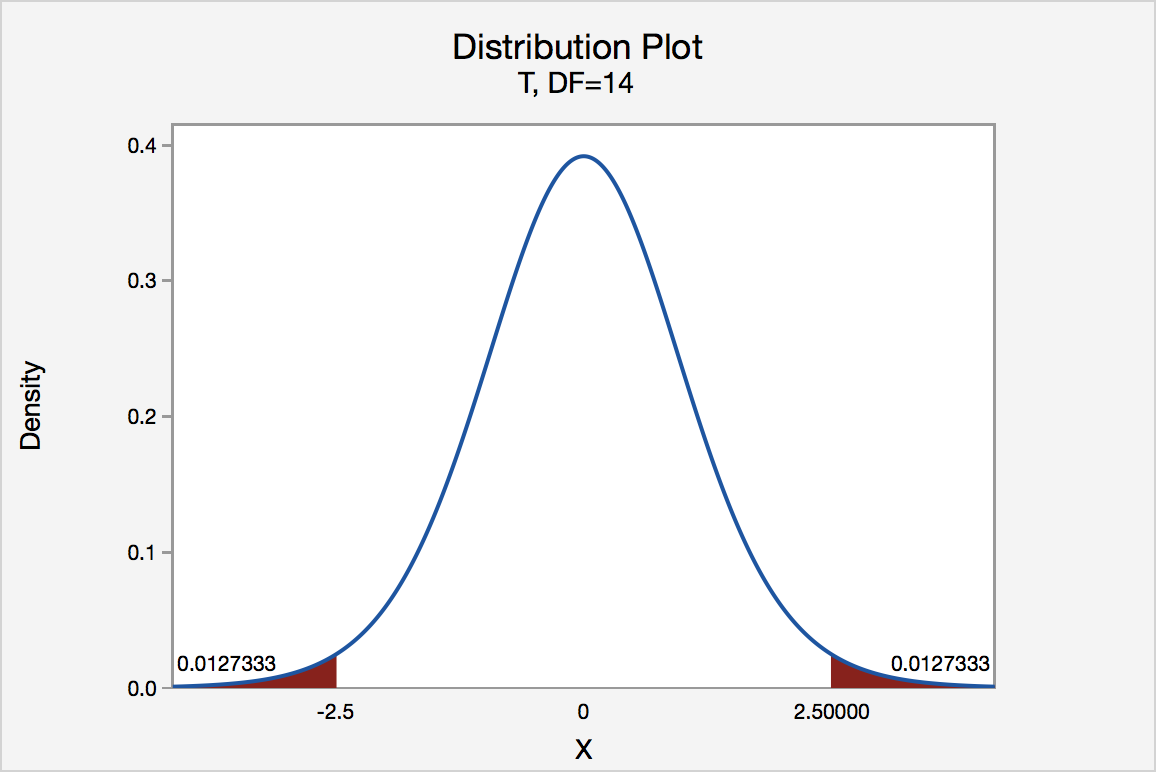
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than \(\alpha\) = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

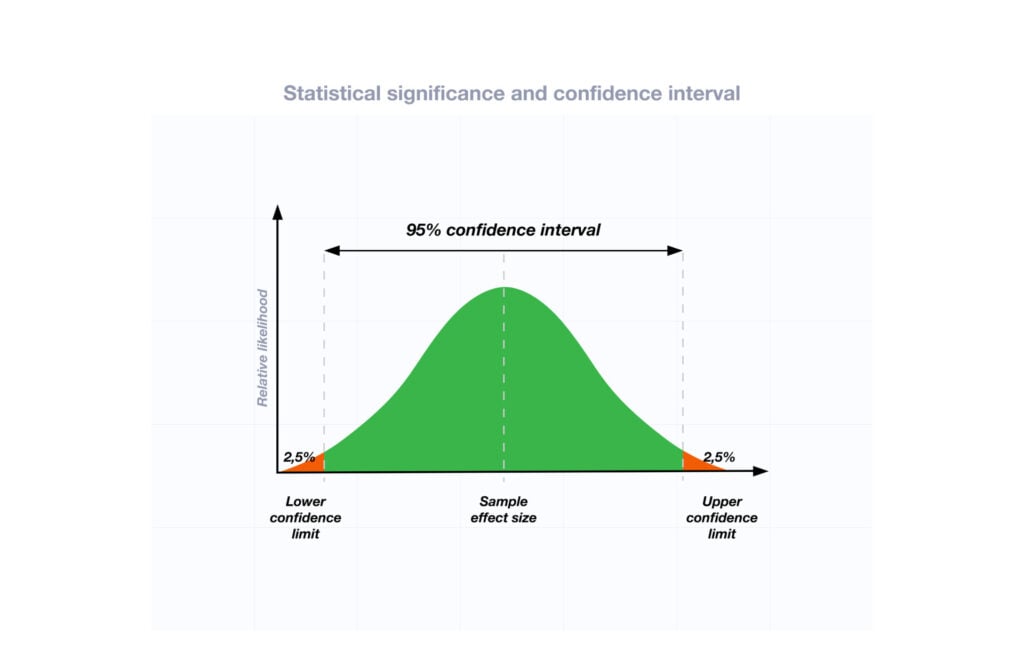
Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

P-Value And Statistical Significance: What It Is & Why It Matters

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

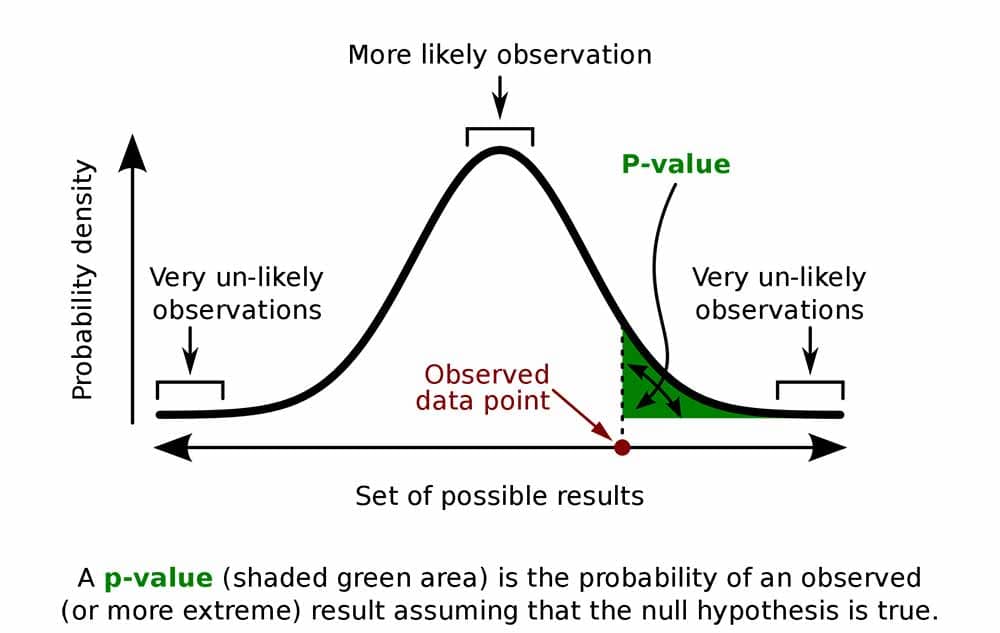
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.5: Critical values, p-values, and significance level

• Last updated
• Save as PDF
• Page ID 7117

• Foster et al.
• University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

A low probability value casts doubt on the null hypothesis. How low must the probability value be in order to conclude that the null hypothesis is false? Although there is clearly no right or wrong answer to this question, it is conventional to conclude the null hypothesis is false if the probability value is less than 0.05. More conservative researchers conclude the null hypothesis is false only if the probability value is less than 0.01. When a researcher concludes that the null hypothesis is false, the researcher is said to have rejected the null hypothesis. The probability value below which the null hypothesis is rejected is called the α level or simply \(α\) (“alpha”). It is also called the significance level. If α is not explicitly specified, assume that \(α\) = 0.05.

The significance level is a threshold we set before collecting data in order to determine whether or not we should reject the null hypothesis. We set this value beforehand to avoid biasing ourselves by viewing our results and then determining what criteria we should use. If our data produce values that meet or exceed this threshold, then we have sufficient evidence to reject the null hypothesis; if not, we fail to reject the null (we never “accept” the null).

There are two criteria we use to assess whether our data meet the thresholds established by our chosen significance level, and they both have to do with our discussions of probability and distributions. Recall that probability refers to the likelihood of an event, given some situation or set of conditions. In hypothesis testing, that situation is the assumption that the null hypothesis value is the correct value, or that there is no effect. The value laid out in H0 is our condition under which we interpret our results. To reject this assumption, and thereby reject the null hypothesis, we need results that would be very unlikely if the null was true. Now recall that values of z which fall in the tails of the standard normal distribution represent unlikely values. That is, the proportion of the area under the curve as or more extreme than \(z\) is very small as we get into the tails of the distribution. Our significance level corresponds to the area under the tail that is exactly equal to α: if we use our normal criterion of \(α\) = .05, then 5% of the area under the curve becomes what we call the rejection region (also called the critical region) of the distribution. This is illustrated in Figure \(\PageIndex{1}\).

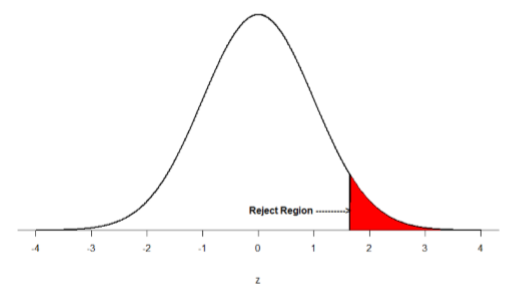
The shaded rejection region takes us 5% of the area under the curve. Any result which falls in that region is sufficient evidence to reject the null hypothesis.

The rejection region is bounded by a specific \(z\)-value, as is any area under the curve. In hypothesis testing, the value corresponding to a specific rejection region is called the critical value, \(z_{crit}\) (“\(z\)-crit”) or \(z*\) (hence the other name “critical region”). Finding the critical value works exactly the same as finding the z-score corresponding to any area under the curve like we did in Unit 1. If we go to the normal table, we will find that the z-score corresponding to 5% of the area under the curve is equal to 1.645 (\(z\) = 1.64 corresponds to 0.0405 and \(z\) = 1.65 corresponds to 0.0495, so .05 is exactly in between them) if we go to the right and -1.645 if we go to the left. The direction must be determined by your alternative hypothesis, and drawing then shading the distribution is helpful for keeping directionality straight.

Suppose, however, that we want to do a non-directional test. We need to put the critical region in both tails, but we don’t want to increase the overall size of the rejection region (for reasons we will see later). To do this, we simply split it in half so that an equal proportion of the area under the curve falls in each tail’s rejection region. For \(α\) = .05, this means 2.5% of the area is in each tail, which, based on the z-table, corresponds to critical values of \(z*\) = ±1.96. This is shown in Figure \(\PageIndex{2}\).

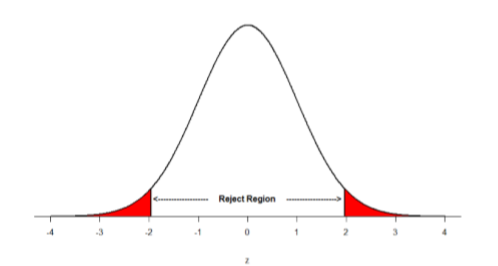
Thus, any \(z\)-score falling outside ±1.96 (greater than 1.96 in absolute value) falls in the rejection region. When we use \(z\)-scores in this way, the obtained value of \(z\) (sometimes called \(z\)-obtained) is something known as a test statistic, which is simply an inferential statistic used to test a null hypothesis. The formula for our \(z\)-statistic has not changed:

\[z=\dfrac{\overline{\mathrm{X}}-\mu}{\bar{\sigma} / \sqrt{\mathrm{n}}} \]

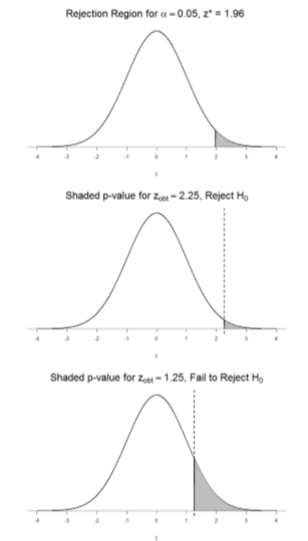
To formally test our hypothesis, we compare our obtained \(z\)-statistic to our critical \(z\)-value. If \(\mathrm{Z}_{\mathrm{obt}}>\mathrm{Z}_{\mathrm{crit}}\), that means it falls in the rejection region (to see why, draw a line for \(z\) = 2.5 on Figure \(\PageIndex{1}\) or Figure \(\PageIndex{2}\)) and so we reject \(H_0\). If \(\mathrm{Z}_{\mathrm{obt}}<\mathrm{Z}_{\mathrm{crit}}\), we fail to reject. Remember that as \(z\) gets larger, the corresponding area under the curve beyond \(z\) gets smaller. Thus, the proportion, or \(p\)-value, will be smaller than the area for \(α\), and if the area is smaller, the probability gets smaller. Specifically, the probability of obtaining that result, or a more extreme result, under the condition that the null hypothesis is true gets smaller.

The \(z\)-statistic is very useful when we are doing our calculations by hand. However, when we use computer software, it will report to us a \(p\)-value, which is simply the proportion of the area under the curve in the tails beyond our obtained \(z\)-statistic. We can directly compare this \(p\)-value to \(α\) to test our null hypothesis: if \(p < α\), we reject \(H_0\), but if \(p > α\), we fail to reject. Note also that the reverse is always true: if we use critical values to test our hypothesis, we will always know if \(p\) is greater than or less than \(α\). If we reject, we know that \(p < α\) because the obtained \(z\)-statistic falls farther out into the tail than the critical \(z\)-value that corresponds to \(α\), so the proportion (\(p\)-value) for that \(z\)-statistic will be smaller. Conversely, if we fail to reject, we know that the proportion will be larger than \(α\) because the \(z\)-statistic will not be as far into the tail. This is illustrated for a one-tailed test in Figure \(\PageIndex{3}\).

When the null hypothesis is rejected, the effect is said to be statistically significant. For example, in the Physicians Reactions case study, the probability value is 0.0057. Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected. It is very important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what “significant” usually means. When an effect is significant, you can have confidence the effect is not exactly zero. Finding that an effect is significant does not tell you about how large or important the effect is. Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough. Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.

p-value Calculator

What is p-value, how do i calculate p-value from test statistic, how to interpret p-value, how to use the p-value calculator to find p-value from test statistic, how do i find p-value from z-score, how do i find p-value from t, p-value from chi-square score (χ² score), p-value from f-score.

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

• Non-symmetric case: chi-squared distribution:

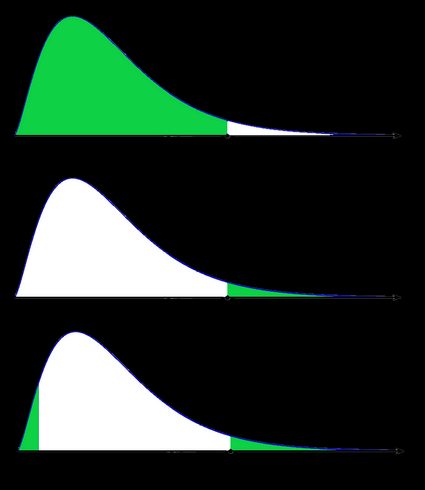
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level .

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

Frequency distribution

Moneyline odds, plant spacing.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

Summary and Analysis of Extension Program Evaluation in R

Salvatore S. Mangiafico

Search Rcompanion.org

• Purpose of this Book
• Author of this Book
• Statistics Textbooks and Other Resources
• Why Statistics?
• Evaluation Tools and Surveys
• Types of Variables
• Descriptive Statistics
• Confidence Intervals
• Basic Plots

Hypothesis Testing and p-values

• Reporting Results of Data and Analyses
• Choosing a Statistical Test
• Independent and Paired Values
• Introduction to Likert Data
• Descriptive Statistics for Likert Item Data
• Descriptive Statistics with the likert Package
• Confidence Intervals for Medians
• Converting Numeric Data to Categories
• Introduction to Traditional Nonparametric Tests
• One-sample Wilcoxon Signed-rank Test
• Sign Test for One-sample Data
• Two-sample Mann–Whitney U Test
• Mood’s Median Test for Two-sample Data
• Two-sample Paired Signed-rank Test
• Sign Test for Two-sample Paired Data
• Kruskal–Wallis Test
• Mood’s Median Test
• Friedman Test
• Scheirer–Ray–Hare Test
• Aligned Ranks Transformation ANOVA
• Nonparametric Regression and Local Regression
• Nonparametric Regression for Time Series
• Introduction to Permutation Tests
• One-way Permutation Test for Ordinal Data
• One-way Permutation Test for Paired Ordinal Data
• Permutation Tests for Medians and Percentiles
• Association Tests for Ordinal Tables
• Measures of Association for Ordinal Tables
• Introduction to Linear Models
• Using Random Effects in Models
• What are Estimated Marginal Means?
• Estimated Marginal Means for Multiple Comparisons
• Factorial ANOVA: Main Effects, Interaction Effects, and Interaction Plots
• p-values and R-square Values for Models
• Accuracy and Errors for Models
• Introduction to Cumulative Link Models (CLM) for Ordinal Data
• Two-sample Ordinal Test with CLM
• Two-sample Paired Ordinal Test with CLMM
• One-way Ordinal Regression with CLM
• One-way Repeated Ordinal Regression with CLMM
• Two-way Ordinal Regression with CLM
• Two-way Repeated Ordinal Regression with CLMM
• Introduction to Tests for Nominal Variables
• Confidence Intervals for Proportions
• Goodness-of-Fit Tests for Nominal Variables
• Association Tests for Nominal Variables
• Measures of Association for Nominal Variables
• Tests for Paired Nominal Data
• Cochran–Mantel–Haenszel Test for 3-Dimensional Tables
• Cochran’s Q Test for Paired Nominal Data
• Models for Nominal Data
• Introduction to Parametric Tests
• One-sample t-test
• Two-sample t-test
• Paired t-test
• One-way ANOVA
• One-way ANOVA with Blocks
• One-way ANOVA with Random Blocks
• Two-way ANOVA
• Repeated Measures ANOVA
• Correlation and Linear Regression
• Advanced Parametric Methods
• Transforming Data
• Normal Scores Transformation
• Regression for Count Data
• Beta Regression for Percent and Proportion Data
• An R Companion for the Handbook of Biological Statistics

Initial comments

Traditionally when students first learn about the analysis of experiments, there is a strong focus on hypothesis testing and making decisions based on p -values. Hypothesis testing is important for determining if there are statistically significant effects.  However, readers of this book should not place undo emphasis on p -values. Instead, they should realize that p -values are affected by sample size, and that a low p -value does not necessarily suggest a large effect or a practically meaningful effect.  Summary statistics, plots, effect size statistics, and practical considerations should be used. The goal is to determine: a) statistical significance, b) effect size, c) practical importance.  These are all different concepts, and they will be explored below.

Statistical inference

Most of what we’ve covered in this book so far is about producing descriptive statistics: calculating means and medians, plotting data in various ways, and producing confidence intervals.  The bulk of the rest of this book will cover statistical inference:  using statistical tests to draw some conclusion about the data.  We’ve already done this a little bit in earlier chapters by using confidence intervals to conclude if means are different or not among groups.

As Dr. Nic mentions in her article in the “References and further reading” section, this is the part where people sometimes get stumped.  It is natural for most of us to use summary statistics or plots, but jumping to statistical inference needs a little change in perspective.  The idea of using some statistical test to answer a question isn’t a difficult concept, but some of the following discussion gets a little theoretical.  The video from the Statistics Learning Center in the “References and further reading” section does a good job of explaining the basis of statistical inference.

One important thing to gain from this chapter is an understanding of how to use the p -value, alpha , and decision rule to test the null hypothesis.  But once you are comfortable with that, you will want to return to this chapter to have a better understanding of the theory behind this process.

Another important thing is to understand the limitations of relying on p -values, and why it is important to assess the size of effects and weigh practical considerations.

Packages used in this chapter

The packages used in this chapter include:

The following commands will install these packages if they are not already installed:

if(!require(lsr)){install.packages("lsr")}

Hypothesis testing

The null and alternative hypotheses.

The statistical tests in this book rely on testing a null hypothesis, which has a specific formulation for each test.  The null hypothesis always describes the case where e.g. two groups are not different or there is no correlation between two variables, etc.

The alternative hypothesis is the contrary of the null hypothesis, and so describes the cases where there is a difference among groups or a correlation between two variables, etc.

Notice that the definitions of null hypothesis and alternative hypothesis have nothing to do with what you want to find or don't want to find, or what is interesting or not interesting, or what you expect to find or what you don’t expect to find.  If you were comparing the height of men and women, the null hypothesis would be that the height of men and the height of women were not different.  Yet, you might find it surprising if you found this hypothesis to be true for some population you were studying.  Likewise, if you were studying the income of men and women, the null hypothesis would be that the income of men and women are not different, in the population you are studying.  In this case you might be hoping the null hypothesis is true, though you might be unsurprised if the alternative hypothesis were true.  In any case, the null hypothesis will take the form that there is no difference between groups, there is no correlation between two variables, or there is no effect of this variable in our model.

p -value definition

Most of the tests in this book rely on using a statistic called the p -value to evaluate if we should reject, or fail to reject, the null hypothesis.

Given the assumption that the null hypothesis is true , the p -value is defined as the probability of obtaining a result equal to or more extreme than what was actually observed in the data.

We’ll unpack this definition in a little bit.

Decision rule

The p -value for the given data will be determined by conducting the statistical test.

This p -value is then compared to a pre-determined value alpha .  Most commonly, an alpha value of 0.05 is used, but there is nothing magic about this value.

If the p -value for the test is less than alpha , we reject the null hypothesis.

If the p -value is greater than or equal to alpha , we fail to reject the null hypothesis.

Coin flipping example

For an example of using the p -value for hypothesis testing, imagine you have a coin you will toss 100 times.  The null hypothesis is that the coin is fair—that is, that it is equally likely that the coin will land on heads as land on tails.  The alternative hypothesis is that the coin is not fair.  Let’s say for this experiment you throw the coin 100 times and it lands on heads 95 times out of those hundred.  The p -value in this case would be the probability of getting 95, 96, 97, 98, 99, or 100 heads, or 0, 1, 2, 3, 4, or 5 heads, assuming that the null hypothesis is true . 

This is what we call a two-sided test, since we are testing both extremes suggested by our data:  getting 95 or greater heads or getting 95 or greater tails.  In most cases we will use two sided tests.

You can imagine that the p -value for this data will be quite small.  If the null hypothesis is true, and the coin is fair, there would be a low probability of getting 95 or more heads or 95 or more tails.

Using a binomial test, the p -value is < 0.0001.

(Actually, R reports it as < 2.2e-16, which is shorthand for the number in scientific notation, 2.2 x 10 -16 , which is 0.00000000000000022, with 15 zeros after the decimal point.)

Assuming an alpha of 0.05, since the p -value is less than alpha , we reject the null hypothesis.  That is, we conclude that the coin is not fair.

binom.test(5, 100, 0.5)

Exact binomial test number of successes = 5, number of trials = 100, p-value < 2.2e-16 alternative hypothesis: true probability of success is not equal to 0.5

Passing and failing example

As another example, imagine we are considering two classrooms, and we have counts of students who passed a certain exam.  We want to know if one classroom had statistically more passes or failures than the other.

In our example each classroom will have 10 students.  The data is arranged into a contingency table.

Classroom   Passed   Failed A          8       2 B          3       7

We will use Fisher’s exact test to test if there is an association between Classroom and the counts of passed and failed students.  The null hypothesis is that there is no association between Classroom and Passed/Failed , based on the relative counts in each cell of the contingency table.

Input =("  Classroom  Passed  Failed  A          8       2  B          3       7 ") Matrix = as.matrix(read.table(textConnection(Input),                    header=TRUE,                    row.names=1)) Matrix 

  Passed Failed A      8      2 B      3      7

fisher.test(Matrix)

Fisher's Exact Test for Count Data p-value = 0.06978

The reported p -value is 0.070.  If we use an alpha of 0.05, then the p -value is greater than alpha , so we fail to reject the null hypothesis.  That is, we did not have sufficient evidence to say that there is an association between Classroom and Passed/Failed .

More extreme data in this case would be if the counts in the upper left or lower right (or both!) were greater. 

Classroom   Passed   Failed A          9       1 B          3       7 Classroom   Passed   Failed A          10      0 B           3      7 and so on, with Classroom B...

In most cases we would want to consider as "extreme" not only the results when Classroom A has a high frequency of passing students, but also results when Classroom B has a high frequency of passing students.  This is called a two-sided or two-tailed test.  If we were only concerned with one classroom having a high frequency of passing students, relatively, we would instead perform a one-sided test.  The default for the fisher.test function is two-sided, and usually you will want to use two-sided tests.

Classroom   Passed   Failed A          2       8 B          7       3 Classroom   Passed   Failed A          1       9 B          7       3 Classroom   Passed   Failed A          0       10 B          7        3 and so on, with Classroom B...

In both cases, "extreme" means there is a stronger association between Classroom and Passed/Failed .

Theory and practice of using p -values

Wait, does this make any sense.

Recall that the definition of the p -value is:

The astute reader might be asking herself, “If I’m trying to determine if the null hypothesis is true or not, why would I start with the assumption that the null hypothesis is true?  And why am I using a probability of getting certain data given that a hypothesis is true?  Don’t I want to instead determine the probability of the hypothesis given my data?”

The answer is yes , we would like a method to determine the likelihood of our hypothesis being true given our data, but we use the Null Hypothesis Significance Test approach since it is relatively straightforward, and has wide acceptance historically and across disciplines.

In practice we do use the results of the statistical tests to reach conclusions about the null hypothesis.

Technically, the p -value says nothing about the alternative hypothesis.  But logically, if the null hypothesis is rejected, then its logical complement, the alternative hypothesis, is supported.  Practically, this is how we handle significant p -values, though this practical approach generates disapproval in some theoretical circles.

Statistics is like a jury?

Note the language used when testing the null hypothesis.  Based on the results of our statistical tests, we either reject the null hypothesis, or fail to reject the null hypothesis.

This is somewhat similar to the approach of a jury in a trial.  The jury either finds sufficient evidence to declare someone guilty, or fails to find sufficient evidence to declare someone guilty. 

Failing to convict someone isn’t necessarily the same as declaring someone innocent.  Likewise, if we fail to reject the null hypothesis, we shouldn’t assume that the null hypothesis is true.  It may be that we didn’t have sufficient samples to get a result that would have allowed us to reject the null hypothesis, or maybe there are some other factors affecting the results that we didn’t account for.  This is similar to an “innocent until proven guilty” stance.

Errors in inference

For the most part, the statistical tests we use are based on probability, and our data could always be the result of chance.  Considering the coin flipping example above, if we did flip a coin 100 times and came up with 95 heads, we would be compelled to conclude that the coin was not fair.  But 95 heads could happen with a fair coin strictly by chance.

We can, therefore, make two kinds of errors in testing the null hypothesis:

•  A Type I error occurs when the null hypothesis really is true, but based on our decision rule we reject the null hypothesis.  In this case, our result is a false positive ; we think there is an effect (unfair coin, association between variables, difference among groups) when really there isn’t.  The probability of making this kind error is alpha , the same alpha we used in our decision rule.

•  A Type II error occurs when the null hypothesis is really false, but based on our decision rule we fail to reject the null hypothesis.  In this case, our result is a false negative ; we have failed to find an effect that really does exist.  The probability of making this kind of error is called beta .

The following table summarizes these errors.

                            Reality                             ___________________________________ Decision of Test             Null is true             Null is false Reject null hypothesis      Type I error           Correctly                              (prob. = alpha)          reject null                                                      (prob. = 1 – beta) Retain null hypothesis      Correctly               Type II error                              retain null             (prob. = beta)                              (prob. = 1 – alpha)

Statistical power

The statistical power of a test is a measure of the ability of the test to detect a real effect.  It is related to the effect size, the sample size, and our chosen alpha level. 

The effect size is a measure of how unfair a coin is, how strong the association is between two variables, or how large the difference is among groups.  As the effect size increases or as the number of observations we collect increases, or as the alpha level increases, the power of the test increases.

Statistical power in the table above is indicated by 1 – beta , and power is the probability of correctly rejecting the null hypothesis.

An example should make these relationship clear.  Imagine we are sampling a large group of 7 th grade students for their height.  That is, the group is the population, and we are sampling a sub-set of these students.  In reality, for students in the population, the girls are taller than the boys, but the difference is small (that is, the effect size is small), and there is a lot of variability in students’ heights.  You can imagine that in order to detect the difference between girls and boys that we would have to measure many students.  If we fail to sample enough students, we might make a Type II error.  That is, we might fail to detect the actual difference in heights between sexes.

If we had a different experiment with a larger effect size—for example the weight difference between mature hamsters and mature hedgehogs—we might need fewer samples to detect the difference.

Note also, that our chosen alpha plays a role in the power of our test, too.  All things being equal, across many tests, if we decrease our alph a, that is, insist on a lower rate of Type I errors, we are more likely to commit a Type II error, and so have a lower power.  This is analogous to a case of a meticulous jury that has a very high standard of proof to convict someone.  In this case, the likelihood of a false conviction is low, but the likelihood of a letting a guilty person go free is relatively high.

The 0.05 alpha value is not dogma

The level of alpha is traditionally set at 0.05 in some disciplines, though there is sometimes reason to choose a different value.

One situation in which the alpha level is increased is in preliminary studies in which it is better to include potentially significant effects even if there is not strong evidence for keeping them.  In this case, the researcher is accepting an inflated chance of Type I errors in order to decrease the chance of Type II errors.

Imagine an experiment in which you wanted to see if various environmental treatments would improve student learning.  In a preliminary study, you might have many treatments, with few observations each, and you want to retain any potentially successful treatments for future study.  For example, you might try playing classical music, improved lighting, complimenting students, and so on, and see if there is any effect on student learning.  You might relax your alpha value to 0.10 or 0.15 in the preliminary study to see what treatments to include in future studies.

On the other hand, in situations where a Type I, false positive, error might be costly in terms of money or people’s health, a lower alpha can be used, perhaps, 0.01 or 0.001.  You can imagine a case in which there is an established treatment for cancer, and a new treatment is being tested.  Because the new treatment is likely to be expensive and to hold people’s lives in the balance, a researcher would want to be very sure that the new treatment is more effective than the established treatment.  In reality, the researchers would not just lower the alpha level, but also look at the effect size, submit the research for peer review, replicate the study, be sure there were no problems with the design of the study or the data collection, and weigh the practical implications.

The 0.05 alpha value is almost dogma

In theory, as a researcher, you would determine the alpha level you feel is appropriate.  That is, the probability of making a Type I error when the null hypothesis is in fact true. 

In reality, though, 0.05 is almost always used in most fields for readers of this book.  Choosing a different alpha value will rarely go without question.  It is best to keep with the 0.05 level unless you have good justification for another value, or are in a discipline where other values are routinely used.

Practical advice

One good practice is to report actual p -values from analyses.  It is fine to also simply say, e.g. “The dependent variable was significantly correlated with variable A ( p < 0.05).”  But I prefer when possible to say, “The dependent variable was significantly correlated with variable A ( p = 0.026).

It is probably best to avoid using terms like “marginally significant” or “borderline significant” for p -values less than 0.10 but greater than 0.05, though you might encounter similar phrases.  It is better to simply report the p -values of tests or effects in straight-forward manner.  If you had cause to include certain model effects or results from other tests, they can be reported as e.g., “Variables correlated with the dependent variable with p < 0.15 were A , B , and C .”

Is the p -value every really true?

Considering some of the examples presented, it may have occurred to the reader to ask if the null hypothesis is ever really true.   For example, in some population of 7 th graders, if we could measure everyone in the population to a high degree of precision, then there must be some difference in height between girls and boys.  This is an important limitation of null hypothesis significance testing.  Often, if we have many observations, even small effects will be reported as significant.  This is one reason why it is important to not rely too heavily on p -values, but to also look at the size of the effect and practical considerations.  In this example, if we sampled many students and the difference in heights was 0.5 cm, even if significant, we might decide that this effect is too small to be of practical importance, especially relative to an average height of 150 cm.  (Here, the difference would be  0.3% of the average height).

Effect sizes and practical importance

Practical importance and statistical significance.

It is important to remember to not let p -values be the only guide for drawing conclusions.  It is equally important to look at the size of the effects you are measuring, as well as take into account other practical considerations like the costs of choosing a certain path of action.

For example, imagine we want to compare the SAT scores of two SAT preparation classes with a t -test.

Class.A = c(1500, 1505, 1505, 1510, 1510, 1510, 1515, 1515, 1520, 1520) Class.B = c(1510, 1515, 1515, 1520, 1520, 1520, 1525, 1525, 1530, 1530) t.test(Class.A, Class.B)

Welch Two Sample t-test t = -3.3968, df = 18, p-value = 0.003214 mean of x mean of y      1511      1521

The p -value is reported as 0.003, so we would consider there to be a significant difference between the two classes ( p < 0.05).

But we have to ask ourselves the practical question, is a difference of 10 points on the SAT large enough for us to care about?  What if enrolling in one class costs significantly more than the other class?  Is it worth the extra money for a difference of 10 points on average?

Sizes of effects

It should be remembered that p -values do not indicate the size of the effect being studied.  It shouldn’t be assumed that a small p -value indicates a large difference between groups, or vice-versa. 

For example, in the SAT example above, the p -value is fairly small, but the size of the effect (difference between classes) in this case is relatively small (10 points, especially small relative to the range of scores students receive on the SAT).

In converse, there could be a relatively large size of the effects, but if there is a lot of variability in the data or the sample size is not large enough, the p -value could be relatively large. 

In this example, the SAT scores differ by 100 points between classes, but because the variability is greater than in the previous example, the p -value is not significant.

Class.C = c(1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500) Class.D = c(1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600) t.test(Class.C, Class.D)

Welch Two Sample t-test t = -1.4174, df = 18, p-value = 0.1735 mean of x mean of y      1290      1390

boxplot(cbind(Class.C, Class.D))

p -values and sample sizes

It should also be remembered that p -values are affected by sample size.   For a given effect size and variability in the data, as the sample size increases, the p -value is likely to decrease.  For large data sets, small effects can result in significant p -values.

As an example, let’s take the data from Class.C and Class.D and double the number of observations for each without changing the distribution of the values in each, and rename them Class.E and Class.F .

Class.E = c(1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500,             1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500) Class.F = c(1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600,             1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600) t.test(Class.E, Class.F)

Welch Two Sample t-test t = -2.0594, df = 38, p-value = 0.04636 mean of x mean of y      1290      1390

boxplot(cbind(Class.E, Class.F))

Notice that the p -value is lower for the t -test for Class.E and Class.F than it was for Class.C and Class.D .  Also notice that the means reported in the output are the same, and the box plots would look the same.

Effect size statistics

One way to account for the effect of sample size on our statistical tests is to consider effect size statistics.  These statistics reflect the size of the effect in a standardized way, and are unaffected by sample size.

An appropriate effect size statistic for a t -test is Cohen’s d .  It takes the difference in means between the two groups and divides by the pooled standard deviation of the groups.  Cohen’s d equals zero if the means are the same, and increases to infinity as the difference in means increases relative to the standard deviation.

In the following, note that Cohen’s d is not affected by the sample size difference in the Class.C / Class.D and the Class.E /  Class.F examples.

library(lsr) cohensD(Class.C, Class.D,         method = "raw")

cohensD(Class.E, Class.F,         method = "raw")

Effect size statistics are standardized so that they are not affected by the units of measurements of the data.  This makes them interpretable across different situations, or if the reader is not familiar with the units of measurement in the original data.  A Cohen’s d of 1 suggests that the two means differ by one pooled standard deviation.  A Cohen’s d of 0.5 suggests that the two means differ by one-half the pooled standard deviation.

For example, if we create new variables— Class.G and Class.H —that are the SAT scores from the previous example expressed as a proportion of a 1600 score, Cohen’s d will be the same as in the previous example.

Class.G = Class.E / 1600 Class.H = Class.F / 1600 Class.G Class.H cohensD(Class.G, Class.H,         method="raw")

Good practices for statistical analyses

Statistics is not like a trial.

When analyzing data, the analyst should not approach the task as would a lawyer for the prosecution.  That is, the analyst should not be searching for significant effects and tests, but should instead be like an independent investigator using lines of evidence to find out what is most likely to true given the data, graphical analysis, and statistical analysis available.

The problem of multiple p -values

One concept that will be in important in the following discussion is that when there are multiple tests producing multiple p -values, that there is an inflation of the Type I error rate.  That is, there is a higher chance of making false-positive errors.

This simply follows mathematically from the definition of alpha .  If we allow a probability of 0.05, or 5% chance, of making a Type I error for any one test, as we do more and more tests, the chances that at least one of them having a false positive becomes greater and greater.

p -value adjustment

One way we deal with the problem of multiple p -values in statistical analyses is to adjust p -values when we do a series of tests together (for example, if we are comparing the means of multiple groups).

Don’t use Bonferroni adjustments

There are various p -value adjustments available in R.  In some cases, we will use FDR, which stands for false discovery rate , and in R is an alias for the Benjamini and Hochberg method.  There are also cases in which we’ll use Tukey range adjustment to correct for the family-wise error rate. 

Unfortunately, students in analysis of experiments courses often learn to use Bonferroni adjustment for p -values.  This method is simple to do with hand calculations, but is excessively conservative in most situations, and, in my opinion, antiquated.

There are other p -value adjustment methods, and the choice of which one to use is dictated either by which are common in your field of study, or by doing enough reading to understand which are statistically most appropriate for your application.

Preplanned tests

The statistical tests covered in this book assume that tests are preplanned for their p -values to be accurate.  That is, in theory, you set out an experiment, collect the data as planned, and then say “I’m going to analyze it with kind of model and do these post-hoc tests afterwards”, and report these results, and that’s all you would do.

Some authors emphasize this idea of preplanned tests.  In contrast is an exploratory data analysis approach that relies upon examining the data with plots and using simple tests like correlation tests to suggest what statistical analysis makes sense.

If an experiment is set out in a specific design, then usually it is appropriate to use the analysis suggested by this design.

p -value hacking

It is important when approaching data from an exploratory approach, to avoid committing p -value hacking.  Imagine the case in which the researcher collects many different measurements across a range of subjects.  The researcher might be tempted to simply try different tests and models to relate one variable to another, for all the variables.  He might continue to do this until he found a test with a significant p -value.

But this would be a form of p -value hacking.

Because an alpha value of 0.05 allows us to make a false-positive error five percent of the time, finding one p -value below 0.05 after several successive tests may simply be due to chance.

Some forms of p -value hacking are more egregious.  For example, if one were to collect some data, run a test, and then continue to collect data and run tests iteratively until a significant p -value is found.

Publication bias

A related issue in science is that there is a bias to publish, or to report, only significant results.  This can also lead to an inflation of the false-positive rate.  As a hypothetical example, imagine if there are currently 20 similar studies being conducted testing a similar effect—let’s say the effect of glucosamine supplements on joint pain.  If 19 of those studies found no effect and so were discarded, but one study found an effect using an alpha of 0.05, and was published, is this really any support that glucosamine supplements decrease joint pain?

Clarification of terms and reporting on assignments

"statistically significant".

In the context of this book, the term "significant" means "statistically significant". 

Whenever the decision rule finds that p < alpha , the difference in groups, the association, or the correlation under consideration is then considered "statistically significant" or "significant". 

No effect size or practical considerations enter into determining whether an effect is “significant” or not.  The only exception is that test assumptions and requirements for appropriate data must also be met in order for the p -value to be valid.

What you need to consider :

 •  The null hypothesis

 •  p , alpha , and the decision rule,

 •  Your result.  That is, whether the difference in groups, the association, or the correlation is significant or not.

What you should report on your assignments:

•  The p -value

•  The conclusion, e.g. "There was a significant difference in the mean heights of boys and girls in the class." It is best to preface this with the "reject" or "fail to reject" language concerning your decision about the null hypothesis.

“Size of the effect” / “effect size”

In the context of this book, I use the term "size of the effect" to suggest the use of summary statistics to indicate how large an effect is.  This may be, for example the difference in two medians.  I try reserve the term “effect size” to refer to the use of effect size statistics. This distinction isn’t necessarily common.

Usually you will consider an effect in relation to the magnitude of measurements.  That is, you might look at the difference in medians as a percent of the median of one group or of the global median.  Or, you might look at the difference in medians in relation to the range of answers.  For example, a one-point difference on a 5-point Likert item.  Counts might be expressed as proportions of totals or subsets.

What you should report on assignments :

 •  The size of the effect.  That is, the difference in medians or means, the difference in counts, or the  proportions of counts among groups.

 •  Where appropriate, the size of the effect expressed as a percentage or proportion.

•  If there is an effect size statistic—such as r , epsilon -squared, phi , Cramér's V , or Cohen's d —:  report this and its interpretation (small, medium, large), and incorporate this into your conclusion.

"Practical" / "Practical importance"

If there is a significant result, the question of practical importance asks if the difference or association is large enough to matter in the real world.

If there is no significant result, the question of practical importance asks if the a difference or association is large enough to warrant another look, for example by running another test with a larger sample size or that controls variability in observations better.

•  Your conclusion as to whether this effect is large enough to be important in the real world.

•  The context, explanation, or support to justify your conclusion.

•  In some cases you might include considerations that aren't included in the data presented.  Examples might include the cost of one treatment over another, including time investment, or whether there is a large risk in selecting one treatment over another (e.g., if people's lives are on the line).

A few of xkcd comics

Significant.

xkcd.com/882/

Null hypothesis

xkcd.com/892/

xkcd.com/1478/

Experiments, sampling, and causation

Types of experimental designs, experimental designs.

A true experimental design assigns treatments in a systematic manner.  The experimenter must be able to manipulate the experimental treatments and assign them to subjects.  Since treatments are randomly assigned to subjects, a causal inference can be made for significant results.  That is, we can say that the variation in the dependent variable is caused by the variation in the independent variable.

For interval/ratio data, traditional experimental designs can be analyzed with specific parametric models, assuming other model assumptions are met.  These traditional experimental designs include:

•  Completely random design

•  Randomized complete block design

•  Factorial

•  Split-plot

•  Latin square

Quasi-experiment designs

Often a researcher cannot assign treatments to individual experimental units, but can assign treatments to groups.  For example, if students are in a specific grade or class, it would not be practical to randomly assign students to grades or classes.  But different classes could receive different treatments (such as different curricula).  Causality can be inferred cautiously if treatments are randomly assigned and there is some understanding of the factors that affect the outcome.

Observational studies

In observational studies, the independent variables are not manipulated, and no treatments are assigned.  Surveys are often like this, as are studies of natural systems without experimental manipulation.  Statistical analysis can reveal the relationships among variables, but causality cannot be inferred.  This is because there may be other unstudied variables that affect the measured variables in the study.

Good sampling practices are critical for producing good data.  In general, samples need to be collected in a random fashion so that bias is avoided.

In survey data, bias is often introduced by a self-selection bias.  For example, internet or telephone surveys include only those who respond to these requests.  Might there be some relevant difference in the variables of interest between those who respond to such requests and the general population being surveyed?  Or bias could be introduced by the researcher selecting some subset of potential subjects, for example only surveying a 4-H program with particularly cooperative students and ignoring other clubs.  This is sometimes called “convenience sampling”.

In election forecasting, good pollsters need to account for selection bias and other biases in the survey process.  For example, if a survey is done by landline telephone, those being surveyed are more likely to be older than the general population of voters, and so likely to have a bias in their voting patterns.

Plan ahead and be consistent

It is sometimes necessary to change experimental conditions during the course of an experiment.  Equipment might fail, or unusual weather may prevent making meaningful measurements.

But in general, it is much better to plan ahead and be consistent with measurements. 

Consistency

People sometimes have the tendency to change measurement frequency or experimental treatments during the course of a study.  This inevitably causes headaches in trying to analyze data, and makes writing up the results messy.  Try to avoid this.

Controls and checks

If you are testing an experimental treatment, include a check treatment that almost certainly will have an effect and a control treatment that almost certainly won’t.  A control treatment will receive no treatment and a check treatment will receive a treatment known to be successful.  In an educational setting, perhaps a control group receives no instruction on the topic but on another topic, and the check group will receive standard instruction.

Including checks and controls helps with the analysis in a practical sense, since they serve as standard treatments against which to compare the experimental treatments.  In the case where the experimental treatments have similar effects, controls and checks allow you say, for example, “Means for the all experimental treatments were similar, but were higher than the mean for control, and lower than the mean for check treatment.”

Include alternate measurements

It often happens that measuring equipment fails or that a certain measurement doesn’t produce the expected results.  It is therefore helpful to include measurements of several variables that can capture the potential effects.  Perhaps test scores of students won’t show an effect, but a self-assessment question on how much students learned will.

Include covariates

Including additional independent variables that might affect the dependent variable is often helpful in an analysis.  In an educational setting, you might assess student age, grade, school, town, background level in the subject, or how well they are feeling that day.

The effects of covariates on the dependent variable may be of interest in itself.  But also, including co-variates in an analysis can better model the data, sometimes making treatment effects more clear or making a model better meet model assumptions.

Optional discussion: Alternative methods to the Null Hypothesis Significance Test

The nhst controversy.

Particularly in the fields of psychology and education, there has been much criticism of the null hypothesis significance test approach.  From my reading, the main complaints against NHST tend to be:

•  Students and researchers don’t really understand the meaning of p -values.

•  p -values don’t include important information like confidence intervals or parameter estimates.

•  p -values have properties that may be misleading, for example that they do not represent effect size, and that they change with sample size.

•  We often treat an alpha of 0.05 as a magical cutoff value.

Personally, I don’t find these to be very convincing arguments against the NHST approach. 

The first complaint is in some sense pedantic:  Like so many things, students and researchers learn the definition of p -values at some point and then eventually forget.  This doesn’t seem to impact the usefulness of the approach.

The second point has weight only if researchers use only p -values to draw conclusions from statistical tests.  As this book points out, one should always consider the size of the effects and practical considerations of the effects, as well present finding in table or graphical form, including confidence intervals or measures of dispersion.  There is no reason why parameter estimates, goodness-of-fit statistics, and confidence intervals can’t be included when a NHST approach is followed.

The properties in the third point also don’t count much as criticism if one is using p -values correctly.  One should understand that it is possible to have a small effect size and a small p -value, and vice-versa.  This is not a problem, because p -values and effect sizes are two different concepts.  We shouldn’t expect them to be the same.  The fact that p -values change with sample size is also in no way problematic to me.  It makes sense that when there is a small effect size or a lot of variability in the data that we need many samples to conclude the effect is likely to be real.

(One case where I think the considerations in the preceding point are commonly problematic is when people use statistical tests to check for the normality or homogeneity of data or model residuals.  As sample size increases, these tests are better able to detect small deviations from normality or homoscedasticity.  Too many people use them and think their model is inappropriate because the test can detect a small effect size, that is, a small deviation from normality or homoscedasticity).

The fourth point is a good one.  It doesn’t make much sense to come to one conclusion if our p -value is 0.049 and the opposite conclusion if our p -value is 0.051.  But I think this can be ameliorated by reporting the actual p -values from analyses, and relying less on p -values to evaluate results.

Overall it seems to me that these complaints condemn poor practices that the authors observe: not reporting the size of effects in some manner; not including confidence intervals or measures of dispersion; basing conclusions solely on p -values; and not including important results like parameter estimates and goodness-of-fit statistics.

Alternatives to the NHST approach

Estimates and confidence intervals.

One approach to determining statistical significance is to use estimates and confidence intervals.  Estimates could be statistics like means, medians, proportions, or other calculated statistics.  This approach can be very straightforward, easy for readers to understand, and easy to present clearly.

Bayesian approach

The most popular competitor to the NHST approach is Bayesian inference.  Bayesian inference has the advantage of calculating the probability of the hypothesis given the data , which is what we thought we should be doing in the “Wait, does this make any sense?” section above.  Essentially it takes prior knowledge about the distribution of the parameters of interest for a population and adds the information from the measured data to reassess some hypothesis related to the parameters of interest.  If the reader will excuse the vagueness of this description, it makes intuitive sense.  We start with what we suspect to be the case, and then use new data to assess our hypothesis.

One disadvantage of the Bayesian approach is that it is not obvious in most cases what could be used for legitimate prior information.  A second disadvantage is that conducting Bayesian analysis is not as straightforward as the tests presented in this book.

References and further reading

[Video]  “Understanding statistical inference” from Statistics Learning Center (Dr. Nic). 2015. www.youtube.com/watch?v=tFRXsngz4UQ .

[Video]  “Hypothesis tests, p-value” from Statistics Learning Center (Dr. Nic). 2011. www.youtube.com/watch?v=0zZYBALbZgg .

[Video]   “Understanding the p-value” from Statistics Learning Center (Dr. Nic). 2011.

www.youtube.com/watch?v=eyknGvncKLw .

[Video]  “Important statistical concepts: significance, strength, association, causation” from Statistics Learning Center (Dr. Nic). 2012. www.youtube.com/watch?v=FG7xnWmZlPE .

“Understanding statistical inference” from Dr. Nic. 2015. Learn and Teach Statistics & Operations Research. creativemaths.net/blog/understanding-statistical-inference/ .

“Basic concepts of hypothesis testing” in McDonald, J.H. 2014. Handbook of Biological Statistics . www.biostathandbook.com/hypothesistesting.html .

“Hypothesis testing” , section 4.3, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .

“Hypothesis Testing with One Sample”, sections 9.1–9.2 in Openstax. 2013. Introductory Statistics . openstax.org/textbooks/introductory-statistics .

"Proving causation" from Dr. Nic. 2013. Learn and Teach Statistics & Operations Research. creativemaths.net/blog/proving-causation/ .

[Video]   “Variation and Sampling Error” from Statistics Learning Center (Dr. Nic). 2014. www.youtube.com/watch?v=y3A0lUkpAko .

[Video]   “Sampling: Simple Random, Convenience, systematic, cluster, stratified” from Statistics Learning Center (Dr. Nic). 2012. www.youtube.com/watch?v=be9e-Q-jC-0 .

“Confounding variables” in McDonald, J.H. 2014. Handbook of Biological Statistics . www.biostathandbook.com/confounding.html .

“Overview of data collection principles” , section 1.3, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .

“Observational studies and sampling strategies” , section 1.4, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .

“Experiments” , section 1.5, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .

Exercises F

1.  Which of the following pair is the null hypothesis?

A) The number of heads from the coin is not different from the number of tails.

B) The number of heads from the coin is different from the number of tails.

2.  Which of the following pair is the null hypothesis?

A) The height of boys is different than the height of girls.

B) The height of boys is not different than the height of girls.

3.  Which of the following pair is the null hypothesis?

A) There is an association between classroom and sex.  That is, there is a difference in counts of girls and boys between the classes.

B) There is no association between classroom and sex.  That is, there is no difference in counts of girls and boys between the classes.

4.  We flip a coin 10 times and it lands on heads 7 times.  We want to know if the coin is fair.

a.  What is the null hypothesis?

b.  Looking at the code below, and assuming an alpha of 0.05,

What do you decide (use the reject or fail to reject language)?

c.  In practical terms, what do you conclude?

binom.test(7, 10, 0.5)

Exact binomial test number of successes = 7, number of trials = 10, p-value = 0.3438

5.  We measure the height of 9 boys and 9 girls in a class, in centimeters.  We want to know if one group is taller than the other.

c.  In practical terms, what do you conclude?  Address the practical importance of the results.

Girls = c(152, 150, 140, 160, 145, 155, 150, 152, 147) Boys  = c(144, 142, 132, 152, 137, 147, 142, 144, 139) t.test(Girls, Boys)

Welch Two Sample t-test t = 2.9382, df = 16, p-value = 0.009645 mean of x mean of y  150.1111  142.1111

mean(Boys) sd(Boys) quantile(Boys)

mean(Girls) sd(Girls) quantile(Girls) boxplot(cbind(Girls, Boys))

6. We count the number of boys and girls in two classrooms.  We are interested to know if there is an association between the classrooms and the number of girls and boys.  That is, does the proportion of boys and girls differ statistically across the two classrooms?

Classroom   Girls   Boys A          13       7 B           5      15

Input =("  Classroom  Girls  Boys  A          13       7  B           5      15 ") Matrix = as.matrix(read.table(textConnection(Input),                    header=TRUE,                    row.names=1)) fisher.test(Matrix)

Fisher's Exact Test for Count Data p-value = 0.02484

Matrix rowSums(Matrix) colSums(Matrix) prop.table(Matrix,            margin=1)    ### Proportions for each row barplot(t(Matrix),         beside = TRUE,         legend = TRUE,         ylim   = c(0, 25),         xlab   = "Class",         ylab   = "Count")

7. Why should you not rely solely on p -values to make a decision in the real world?  (You should have at least two reasons.)

8. Create your own example to show the importance of considering the size of the effect . Describe the scenario: what the research question is, and what kind of data were collected.  You may make up data and provide real results, or report hypothetical results.

9. Create your own example to show the importance of weighing other practical considerations . Describe the scenario: what the research question is, what kind of data were collected, what statistical results were reached, and what other practical considerations were brought to bear.

10. What is 5e-4 in common decimal notation?

©2016 by Salvatore S. Mangiafico. Rutgers Cooperative Extension, New Brunswick, NJ.

Non-commercial reproduction of this content, with attribution, is permitted. For-profit reproduction without permission is prohibited.

If you use the code or information in this site in a published work, please cite it as a source.  Also, if you are an instructor and use this book in your course, please let me know.   My contact information is on the About the Author of this Book page.

Mangiafico, S.S. 2016. Summary and Analysis of Extension Program Evaluation in R, version 1.20.05, revised 2023. rcompanion.org/handbook/ . (Pdf version: rcompanion.org/documents/RHandbookProgramEvaluation.pdf .)

• Search Search Please fill out this field.

What Is P-Value?

Understanding p-value.

• P-Value in Hypothesis Testing

The Bottom Line

• Corporate Finance
• Financial Analysis

P-Value: What It Is, How to Calculate It, and Why It Matters

Yarilet Perez is an experienced multimedia journalist and fact-checker with a Master of Science in Journalism. She has worked in multiple cities covering breaking news, politics, education, and more. Her expertise is in personal finance and investing, and real estate.

In statistics, a p-value is a number that indicates how likely you are to obtain a value that is at least equal to or more than the actual observation if the null hypothesis is correct.

The p-value serves as an alternative to rejection points to provide the smallest level of significance at which the null hypothesis would be rejected. A smaller p-value means stronger evidence in favor of the alternative hypothesis.

P-value is often used to promote credibility for studies or reports by government agencies. For example, the U.S. Census Bureau stipulates that any analysis with a p-value greater than 0.10 must be accompanied by a statement that the difference is not statistically different from zero. The Census Bureau also has standards in place stipulating which p-values are acceptable for various publications.

Key Takeaways

• A p-value is a statistical measurement used to validate a hypothesis against observed data.
• A p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true.
• The lower the p-value, the greater the statistical significance of the observed difference.
• A p-value of 0.05 or lower is generally considered statistically significant.
• P-value can serve as an alternative to—or in addition to—preselected confidence levels for hypothesis testing.

Jessica Olah / Investopedia

P-values are usually found using p-value tables or spreadsheets/statistical software. These calculations are based on the assumed or known probability distribution of the specific statistic tested. P-values are calculated from the deviation between the observed value and a chosen reference value, given the probability distribution of the statistic, with a greater difference between the two values corresponding to a lower p-value.

Mathematically, the p-value is calculated using integral calculus from the area under the probability distribution curve for all values of statistics that are at least as far from the reference value as the observed value is, relative to the total area under the probability distribution curve.

The calculation for a p-value varies based on the type of test performed. The three test types describe the location on the probability distribution curve: lower-tailed test, upper-tailed test, or two-tailed test .

In a nutshell, the greater the difference between two observed values, the less likely it is that the difference is due to simple random chance, and this is reflected by a lower p-value.

The P-Value Approach to Hypothesis Testing

The p-value approach to hypothesis testing uses the calculated probability to determine whether there is evidence to reject the null hypothesis. The null hypothesis, also known as the conjecture, is the initial claim about a population (or data-generating process). The alternative hypothesis states whether the population parameter differs from the value of the population parameter stated in the conjecture.

In practice, the significance level is stated in advance to determine how small the p-value must be to reject the null hypothesis. Because different researchers use different levels of significance when examining a question, a reader may sometimes have difficulty comparing results from two different tests. P-values provide a solution to this problem.

Even a low p-value is not necessarily proof of statistical significance, since there is still a possibility that the observed data are the result of chance. Only repeated experiments or studies can confirm if a relationship is statistically significant.

For example, suppose a study comparing returns from two particular assets was undertaken by different researchers who used the same data but different significance levels. The researchers might come to opposite conclusions regarding whether the assets differ.

If one researcher used a confidence level of 90% and the other required a confidence level of 95% to reject the null hypothesis, and if the p-value of the observed difference between the two returns was 0.08 (corresponding to a confidence level of 92%), then the first researcher would find that the two assets have a difference that is statistically significant , while the second would find no statistically significant difference between the returns.

To avoid this problem, the researchers could report the p-value of the hypothesis test and allow readers to interpret the statistical significance themselves. This is called a p-value approach to hypothesis testing. Independent observers could note the p-value and decide for themselves whether that represents a statistically significant difference or not.

Example of P-Value

An investor claims that their investment portfolio’s performance is equivalent to that of the Standard & Poor’s (S&P) 500 Index . To determine this, the investor conducts a two-tailed test.

The null hypothesis states that the portfolio’s returns are equivalent to the S&P 500’s returns over a specified period, while the alternative hypothesis states that the portfolio’s returns and the S&P 500’s returns are not equivalent—if the investor conducted a one-tailed test , the alternative hypothesis would state that the portfolio’s returns are either less than or greater than the S&P 500’s returns.

The p-value hypothesis test does not necessarily make use of a preselected confidence level at which the investor should reset the null hypothesis that the returns are equivalent. Instead, it provides a measure of how much evidence there is to reject the null hypothesis. The smaller the p-value, the greater the evidence against the null hypothesis.

Thus, if the investor finds that the p-value is 0.001, there is strong evidence against the null hypothesis, and the investor can confidently conclude that the portfolio’s returns and the S&P 500’s returns are not equivalent.

Although this does not provide an exact threshold as to when the investor should accept or reject the null hypothesis, it does have another very practical advantage. P-value hypothesis testing offers a direct way to compare the relative confidence that the investor can have when choosing among multiple different types of investments or portfolios relative to a benchmark such as the S&P 500.

For example, for two portfolios, A and B, whose performance differs from the S&P 500 with p-values of 0.10 and 0.01, respectively, the investor can be much more confident that portfolio B, with a lower p-value, will actually show consistently different results.

Is a 0.05 P-Value Significant?

A p-value less than 0.05 is typically considered to be statistically significant, in which case the null hypothesis should be rejected. A p-value greater than 0.05 means that deviation from the null hypothesis is not statistically significant, and the null hypothesis is not rejected.

What Does a P-Value of 0.001 Mean?

A p-value of 0.001 indicates that if the null hypothesis tested were indeed true, then there would be a one-in-1,000 chance of observing results at least as extreme. This leads the observer to reject the null hypothesis because either a highly rare data result has been observed or the null hypothesis is incorrect.

How Can You Use P-Value to Compare 2 Different Results of a Hypothesis Test?

If you have two different results, one with a p-value of 0.04 and one with a p-value of 0.06, the result with a p-value of 0.04 will be considered more statistically significant than the p-value of 0.06. Beyond this simplified example, you could compare a 0.04 p-value to a 0.001 p-value. Both are statistically significant, but the 0.001 example provides an even stronger case against the null hypothesis than the 0.04.

The p-value is used to measure the significance of observational data. When researchers identify an apparent relationship between two variables, there is always a possibility that this correlation might be a coincidence. A p-value calculation helps determine if the observed relationship could arise as a result of chance.

U.S. Census Bureau. “ Statistical Quality Standard E1: Analyzing Data .”

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices