problem solving about proportion

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Proportions

Last Updated: February 24, 2023

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 91,270 times.

What is the "vertical" way to solve a proportion?

How can I solve a proportion with the "horizontal" method?

How do I solve a proportion step by step by cross-multiplying?

How do you find the missing value in a proportion with a table of ratios?

• Each column in this table represents a fraction. All of the fractions in this table are equal to each other.

• The two answers are the same, which means your answer is correct.

How do you solve percent proportions?

How do you solve proportions algebraically?

• You can change the left hand side of the equation, as long as you do the same math to the right hand side.

• To get rid of the fraction on the left, multiply both sides by 27:

How do you solve a proportion with a variable on both sides?

• Warning : This is a difficult example. If you haven't learned about quadratic equations yet, you might want to skip this part.

• You can now solve this as a quadratic equation , using any method that you've learned.

Proportions Calculator, Practice Problems, and Answers

Community Q&A

• The algebraic method above works with any proportion. But for a specific proportion, there is often a faster way to use algebra to find the answer. As you learn more algebra, this will get easier. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ http://www.mathvillage.info/node/72
• ↑ https://www.youtube.com/watch?v=nwsDiID7UtQ
• ↑ https://www.youtube.com/watch?v=Uo8HgcyfRFI
• ↑ https://www.purplemath.com/modules/ratio2.htm

About This Article

To solve proportions, start by taking the numerator, or top number, of the fraction you know and multiplying it with the denominator, or bottom number, of the fraction you don’t know. Next, take that number and divide it by the denominator of the fraction you know. Now you can replace x with this final number. For example, to figure out “x” in the problem 3/4 = x/8, multiply 3 x 8 to get 24, then divide 24 / 4 to get 6, or the value of x. To learn how to use proportions to determine percentages, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

John Almacen

Nov 10, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Proportion word problems

It is very important to notice that if the ratio on the left is a ratio of number of liters of water to number of lemons, you have to do the same ratio on the right before you set them equal. 

More interesting proportion word problems

Check this site if you want to solve more proportion word problems.

Ratio word problems

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

6.5 Solve Proportions and their Applications

Learning objectives.

By the end of this section, you will be able to:

• Use the definition of proportion
• Solve proportions
• Solve applications using proportions
• Write percent equations as proportions
• Translate and solve percent proportions

Be Prepared 6.11

Before you get started, take this readiness quiz.

Simplify: 1 3 4 . 1 3 4 . If you missed this problem, review Example 4.44 .

Be Prepared 6.12

Solve: x 4 = 20 . x 4 = 20 . If you missed this problem, review Example 4.99 .

Be Prepared 6.13

Write as a rate: Sale rode his bike 24 24 miles in 2 2 hours. If you missed this problem, review Example 5.63 .

Use the Definition of Proportion

In the section on Ratios and Rates we saw some ways they are used in our daily lives. When two ratios or rates are equal, the equation relating them is called a proportion .

A proportion is an equation of the form a b = c d , a b = c d , where b ≠ 0 , d ≠ 0 . b ≠ 0 , d ≠ 0 .

The proportion states two ratios or rates are equal. The proportion is read “ a “ a is to b , b , as c c is to d ”. d ”.

The equation 1 2 = 4 8 1 2 = 4 8 is a proportion because the two fractions are equal. The proportion 1 2 = 4 8 1 2 = 4 8 is read “ 1 “ 1 is to 2 2 as 4 4 is to 8 ”. 8 ”.

If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion 20 students 1 teacher = 60 students 3 teachers 20 students 1 teacher = 60 students 3 teachers we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.

Example 6.40

Write each sentence as a proportion:

• ⓐ 3 3 is to 7 7 as 15 15 is to 35 . 35 .
• ⓑ 5 5 hits in 8 8 at bats is the same as 30 30 hits in 48 48 at-bats.
• ⓒ $1.50 $1.50 for 6 6 ounces is equivalent to $2.25 $2.25 for 9 9 ounces.

Try It 6.79

• ⓐ 5 5 is to 9 9 as 20 20 is to 36 . 36 .
• ⓑ 7 7 hits in 11 11 at-bats is the same as 28 28 hits in 44 44 at-bats.
• ⓒ $2.50 $2.50 for 8 8 ounces is equivalent to $3.75 $3.75 for 12 12 ounces.

Try It 6.80

• ⓐ 6 6 is to 7 7 as 36 36 is to 42 . 42 .
• ⓑ 8 8 adults for 36 36 children is the same as 12 12 adults for 54 54 children.
• ⓒ $3.75 $3.75 for 6 6 ounces is equivalent to $2.50 $2.50 for 4 4 ounces.

Look at the proportions 1 2 = 4 8 1 2 = 4 8 and 2 3 = 6 9 . 2 3 = 6 9 . From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?

To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross product because of the cross formed. If, and only if, the given proportion is true, that is, the two sides are equal, then the cross products of a proportion will be equal.

Cross Products of a Proportion

For any proportion of the form a b = c d , a b = c d , where b ≠ 0 , d ≠ 0 , b ≠ 0 , d ≠ 0 , its cross products are equal.

Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are both equal, we have a proportion.

Example 6.41

Determine whether each equation is a proportion:

• ⓐ 4 9 = 12 28 4 9 = 12 28
• ⓑ 17.5 37.5 = 7 15 17.5 37.5 = 7 15

To determine if the equation is a proportion, we find the cross products. If they are equal, the equation is a proportion.

Since the cross products are not equal, 28 · 4 ≠ 9 · 12 , 28 · 4 ≠ 9 · 12 , the equation is not a proportion.

Since the cross products are equal, 15 · 17.5 = 37.5 · 7 , 15 · 17.5 = 37.5 · 7 , the equation is a proportion.

Try It 6.81

• ⓐ 7 9 = 54 72 7 9 = 54 72
• ⓑ 24.5 45.5 = 7 13 24.5 45.5 = 7 13

Try It 6.82

• ⓐ 8 9 = 56 73 8 9 = 56 73
• ⓑ 28.5 52.5 = 8 15 28.5 52.5 = 8 15

Solve Proportions

To solve a proportion containing a variable, we remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality .

Example 6.42

Solve: x 63 = 4 7 . x 63 = 4 7 .

Try It 6.83

Solve the proportion: n 84 = 11 12 . n 84 = 11 12 .

Try It 6.84

Solve the proportion: y 96 = 13 12 . y 96 = 13 12 .

When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions.

We can find the cross products of the proportion and then set them equal. Then we solve the resulting equation using our familiar techniques.

Example 6.43

Solve: 144 a = 9 4 . 144 a = 9 4 .

Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.

Another method to solve this would be to multiply both sides by the LCD, 4 a . 4 a . Try it and verify that you get the same solution.

Try It 6.85

Solve the proportion: 91 b = 7 5 . 91 b = 7 5 .

Try It 6.86

Solve the proportion: 39 c = 13 8 . 39 c = 13 8 .

Example 6.44

Solve: 52 91 = −4 y . 52 91 = −4 y .

Try It 6.87

Solve the proportion: 84 98 = −6 x . 84 98 = −6 x .

Try It 6.88

Solve the proportion: −7 y = 105 135 . −7 y = 105 135 .

Solve Applications Using Proportions

The strategy for solving applications that we have used earlier in this chapter, also works for proportions, since proportions are equations. When we set up the proportion , we must make sure the units are correct—the units in the numerators match and the units in the denominators match.

Example 6.45

When pediatricians prescribe acetaminophen to children, they prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of the child’s weight. If Zoe weighs 80 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

You could also solve this proportion by setting the cross products equal.

Try It 6.89

Pediatricians prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 60 pounds?

Try It 6.90

For every 1 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?

Example 6.46

One brand of microwave popcorn has 120 120 calories per serving. A whole bag of this popcorn has 3.5 3.5 servings. How many calories are in a whole bag of this microwave popcorn?

Try It 6.91

Marissa loves the Caramel Macchiato at the coffee shop. The 16 16 oz. medium size has 240 240 calories. How many calories will she get if she drinks the large 20 20 oz. size?

Try It 6.92

Yaneli loves Starburst candies, but wants to keep her snacks to 100 100 calories. If the candies have 160 160 calories for 8 8 pieces, how many pieces can she have in her snack?

Example 6.47

Josiah went to Mexico for spring break and changed $325 $325 dollars into Mexican pesos. At that time, the exchange rate had $1 $1 U.S. is equal to 12.54 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?

Try It 6.93

Yurianna is going to Europe and wants to change $800 $800 dollars into Euros. At the current exchange rate, $1 $1 US is equal to 0.738 0.738 Euro. How many Euros will she have for her trip?

Try It 6.94

Corey and Nicole are traveling to Japan and need to exchange $600 $600 into Japanese yen. If each dollar is 94.1 94.1 yen, how many yen will they get?

Write Percent Equations As Proportions

Previously, we solved percent equations by applying the properties of equality we have used to solve equations throughout this text. Some people prefer to solve percent equations by using the proportion method. The proportion method for solving percent problems involves a percent proportion. A percent proportion is an equation where a percent is equal to an equivalent ratio.

For example, 60% = 60 100 60% = 60 100 and we can simplify 60 100 = 3 5 . 60 100 = 3 5 . Since the equation 60 100 = 3 5 60 100 = 3 5 shows a percent equal to an equivalent ratio, we call it a percent proportion . Using the vocabulary we used earlier:

Percent Proportion

The amount is to the base as the percent is to 100 . 100 .

If we restate the problem in the words of a proportion, it may be easier to set up the proportion:

We could also say:

First we will practice translating into a percent proportion. Later, we’ll solve the proportion.

Example 6.48

Translate to a proportion. What number is 75% 75% of 90 ? 90 ?

If you look for the word "of", it may help you identify the base.

Try It 6.95

Translate to a proportion: What number is 60% 60% of 105 ? 105 ?

Try It 6.96

Translate to a proportion: What number is 40% 40% of 85 ? 85 ?

Example 6.49

Translate to a proportion. 19 19 is 25% 25% of what number?

Try It 6.97

Translate to a proportion: 36 36 is 25% 25% of what number?

Try It 6.98

Translate to a proportion: 27 27 is 36% 36% of what number?

Example 6.50

Translate to a proportion. What percent of 27 27 is 9 ? 9 ?

Try It 6.99

Translate to a proportion: What percent of 52 52 is 39 ? 39 ?

Try It 6.100

Translate to a proportion: What percent of 92 92 is 23 ? 23 ?

Translate and Solve Percent Proportions

Now that we have written percent equations as proportions, we are ready to solve the equations.

Example 6.51

Translate and solve using proportions: What number is 45% 45% of 80 ? 80 ?

Try It 6.101

Translate and solve using proportions: What number is 65% 65% of 40 ? 40 ?

Try It 6.102

Translate and solve using proportions: What number is 85% 85% of 40 ? 40 ?

In the next example, the percent is more than 100 , 100 , which is more than one whole. So the unknown number will be more than the base.

Example 6.52

Translate and solve using proportions: 125% 125% of 25 25 is what number?

Try It 6.103

Translate and solve using proportions: 125% 125% of 64 64 is what number?

Try It 6.104

Translate and solve using proportions: 175% 175% of 84 84 is what number?

Percents with decimals and money are also used in proportions.

Example 6.53

Translate and solve: 6.5% 6.5% of what number is $1.56 ? $1.56 ?

Try It 6.105

Translate and solve using proportions: 8.5% 8.5% of what number is $3.23 ? $3.23 ?

Try It 6.106

Translate and solve using proportions: 7.25% 7.25% of what number is $4.64 ? $4.64 ?

Example 6.54

Translate and solve using proportions: What percent of 72 72 is 9 ? 9 ?

Try It 6.107

Translate and solve using proportions: What percent of 72 72 is 27 ? 27 ?

Try It 6.108

Translate and solve using proportions: What percent of 92 92 is 23 ? 23 ?

Section 6.5 Exercises

Practice makes perfect.

In the following exercises, write each sentence as a proportion.

4 4 is to 15 15 as 36 36 is to 135 . 135 .

7 7 is to 9 9 as 35 35 is to 45 . 45 .

12 12 is to 5 5 as 96 96 is to 40 . 40 .

15 15 is to 8 8 as 75 75 is to 40 . 40 .

5 5 wins in 7 7 games is the same as 115 115 wins in 161 161 games.

4 4 wins in 9 9 games is the same as 36 36 wins in 81 81 games.

8 8 campers to 1 1 counselor is the same as 48 48 campers to 6 6 counselors.

6 6 campers to 1 1 counselor is the same as 48 48 campers to 8 8 counselors.

$9.36 $9.36 for 18 18 ounces is the same as $2.60 $2.60 for 5 5 ounces.

$3.92 $3.92 for 8 8 ounces is the same as $1.47 $1.47 for 3 3 ounces.

$18.04 $18.04 for 11 11 pounds is the same as $4.92 $4.92 for 3 3 pounds.

$12.42 $12.42 for 27 27 pounds is the same as $5.52 $5.52 for 12 12 pounds.

In the following exercises, determine whether each equation is a proportion.

7 15 = 56 120 7 15 = 56 120

5 12 = 45 108 5 12 = 45 108

11 6 = 21 16 11 6 = 21 16

9 4 = 39 34 9 4 = 39 34

12 18 = 4.99 7.56 12 18 = 4.99 7.56

9 16 = 2.16 3.89 9 16 = 2.16 3.89

13.5 8.5 = 31.05 19.55 13.5 8.5 = 31.05 19.55

10.1 8.4 = 3.03 2.52 10.1 8.4 = 3.03 2.52

In the following exercises, solve each proportion.

x 56 = 7 8 x 56 = 7 8

n 91 = 8 13 n 91 = 8 13

49 63 = z 9 49 63 = z 9

56 72 = y 9 56 72 = y 9

5 a = 65 117 5 a = 65 117

4 b = 64 144 4 b = 64 144

98 154 = −7 p 98 154 = −7 p

72 156 = −6 q 72 156 = −6 q

a −8 = −42 48 a −8 = −42 48

b −7 = −30 42 b −7 = −30 42

2.6 3.9 = c 3 2.6 3.9 = c 3

2.7 3.6 = d 4 2.7 3.6 = d 4

2.7 j = 0.9 0.2 2.7 j = 0.9 0.2

2.8 k = 2.1 1.5 2.8 k = 2.1 1.5

1 2 1 = m 8 1 2 1 = m 8

1 3 3 = 9 n 1 3 3 = 9 n

In the following exercises, solve the proportion problem.

Pediatricians prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Jocelyn, who weighs 45 45 pounds?

Brianna, who weighs 6 6 kg, just received her shots and needs a pain killer. The pain killer is prescribed for children at 15 15 milligrams (mg) for every 1 1 kilogram (kg) of the child’s weight. How many milligrams will the doctor prescribe?

At the gym, Carol takes her pulse for 10 10 sec and counts 19 19 beats. How many beats per minute is this? Has Carol met her target heart rate of 140 140 beats per minute?

Kevin wants to keep his heart rate at 160 160 beats per minute while training. During his workout he counts 27 27 beats in 10 10 seconds. How many beats per minute is this? Has Kevin met his target heart rate?

A new energy drink advertises 106 106 calories for 8 8 ounces. How many calories are in 12 12 ounces of the drink?

One 12 12 ounce can of soda has 150 150 calories. If Josiah drinks the big 32 32 ounce size from the local mini-mart, how many calories does he get?

Karen eats 1 2 1 2 cup of oatmeal that counts for 2 2 points on her weight loss program. Her husband, Joe, can have 3 3 points of oatmeal for breakfast. How much oatmeal can he have?

An oatmeal cookie recipe calls for 1 2 1 2 cup of butter to make 4 4 dozen cookies. Hilda needs to make 10 10 dozen cookies for the bake sale. How many cups of butter will she need?

Janice is traveling to Canada and will change $250 $250 US dollars into Canadian dollars. At the current exchange rate, $1 $1 US is equal to $1.01 $1.01 Canadian. How many Canadian dollars will she get for her trip?

Todd is traveling to Mexico and needs to exchange $450 $450 into Mexican pesos. If each dollar is worth 12.29 12.29 pesos, how many pesos will he get for his trip?

Steve changed $600 $600 into 480 480 Euros. How many Euros did he receive per US dollar?

Martha changed $350 $350 US into 385 385 Australian dollars. How many Australian dollars did she receive per US dollar?

At the laundromat, Lucy changed $12.00 $12.00 into quarters. How many quarters did she get?

When she arrived at a casino, Gerty changed $20 $20 into nickels. How many nickels did she get?

Jesse’s car gets 30 30 miles per gallon of gas. If Las Vegas is 285 285 miles away, how many gallons of gas are needed to get there and then home? If gas is $3.09 $3.09 per gallon, what is the total cost of the gas for the trip?

Danny wants to drive to Phoenix to see his grandfather. Phoenix is 370 370 miles from Danny’s home and his car gets 18.5 18.5 miles per gallon. How many gallons of gas will Danny need to get to and from Phoenix? If gas is $3.19 $3.19 per gallon, what is the total cost for the gas to drive to see his grandfather?

Hugh leaves early one morning to drive from his home in Chicago to go to Mount Rushmore, 812 812 miles away. After 3 3 hours, he has gone 190 190 miles. At that rate, how long will the whole drive take?

Kelly leaves her home in Seattle to drive to Spokane, a distance of 280 280 miles. After 2 2 hours, she has gone 152 152 miles. At that rate, how long will the whole drive take?

Phil wants to fertilize his lawn. Each bag of fertilizer covers about 4,000 4,000 square feet of lawn. Phil’s lawn is approximately 13,500 13,500 square feet. How many bags of fertilizer will he have to buy?

April wants to paint the exterior of her house. One gallon of paint covers about 350 350 square feet, and the exterior of the house measures approximately 2000 2000 square feet. How many gallons of paint will she have to buy?

Write Percent Equations as Proportions

In the following exercises, translate to a proportion.

What number is 35% 35% of 250 ? 250 ?

What number is 75% 75% of 920 ? 920 ?

What number is 110% 110% of 47 ? 47 ?

What number is 150% 150% of 64 ? 64 ?

45 45 is 30% 30% of what number?

25 25 is 80% 80% of what number?

90 90 is 150% 150% of what number?

77 77 is 110% 110% of what number?

What percent of 85 85 is 17 ? 17 ?

What percent of 92 92 is 46 ? 46 ?

What percent of 260 260 is 340 ? 340 ?

What percent of 180 180 is 220 ? 220 ?

In the following exercises, translate and solve using proportions.

What number is 65% 65% of 180 ? 180 ?

What number is 55% 55% of 300 ? 300 ?

18% 18% of 92 92 is what number?

22% 22% of 74 74 is what number?

175% 175% of 26 26 is what number?

250% 250% of 61 61 is what number?

What is 300% 300% of 488 ? 488 ?

What is 500% 500% of 315 ? 315 ?

17% 17% of what number is $7.65 ? $7.65 ?

19% 19% of what number is $6.46 ? $6.46 ?

$13.53 $13.53 is 8.25% 8.25% of what number?

$18.12 $18.12 is 7.55% 7.55% of what number?

What percent of 56 56 is 14 ? 14 ?

What percent of 80 80 is 28 ? 28 ?

What percent of 96 96 is 12 ? 12 ?

What percent of 120 120 is 27 ? 27 ?

Everyday Math

Mixing a concentrate Sam bought a large bottle of concentrated cleaning solution at the warehouse store. He must mix the concentrate with water to make a solution for washing his windows. The directions tell him to mix 3 3 ounces of concentrate with 5 5 ounces of water. If he puts 12 12 ounces of concentrate in a bucket, how many ounces of water should he add? How many ounces of the solution will he have altogether?

Mixing a concentrate Travis is going to wash his car. The directions on the bottle of car wash concentrate say to mix 2 2 ounces of concentrate with 15 15 ounces of water. If Travis puts 6 6 ounces of concentrate in a bucket, how much water must he mix with the concentrate?

Writing Exercises

To solve “what number is 45% 45% of 350 ” 350 ” do you prefer to use an equation like you did in the section on Decimal Operations or a proportion like you did in this section? Explain your reason.

To solve “what percent of 125 125 is 25 ” 25 ” do you prefer to use an equation like you did in the section on Decimal Operations or a proportion like you did in this section? Explain your reason.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Prealgebra 2e
• Publication date: Mar 11, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra-2e/pages/6-5-solve-proportions-and-their-applications

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Proportions: Word Problems

Ratios Proportions Proportionality Solving Word Problems Similar Figures Sun's Rays / Parts

Many "proportion" word problems can be solved using other methods, so they may be familiar to you. For instance, if you've learned about straight-line equations, then you've learned about the slope of a straight line, and how this slope is sometimes referred to as being "rise over run".

But that word "over" gives a hint that, yes, we're talking about a fraction. And this means that "rise over run" can be discussed within the context of proportions.

Content Continues Below

MathHelp.com

You are installing rain gutters across the back of your house. The directions say that the gutters should decline katex.render("\\small{ \\bm{\\color{green}{ \\frac{1}{4} }}}", typed01); 1 / 4 inch for every four feet of lateral run. The gutters will be spanning thirty-seven feet. How much lower than the starting point (that is, how much lower than the high end) should the low end of the gutters be?

Rain gutters have to be slightly sloped so the rainwater will drain toward and then down the downspout. As I go from the high end of the guttering to the low end, for every four-foot length that I go sideways, the gutters should decline [be lower by] one-quarter inch. So how much must the guttering decline over the thirty-seven foot span? I'll set up the proportion, using " d " to stand for the distance I'm needing to find.

There is a variable in only one part of my proportion, so I can use the shortcut method to solve.

d = [(37)(1/4)]/4

For convenience sake (because my tape measure isn't marked in decimals), I'll convert this answer to mixed-number form:

Advertisement

As is always the case with "solving" exercises, we can check our answers by plugging them back into the original problem. In this case, we can verify the size of the "drop" from one end of the house to the other by checking the products of the means and the extremes (that is, by confirming that the cross-multiplications match) of the completed proportion:

(1/4)/4 = 2.3125/37

Converting the "one-fourth" to " 0.25 ", we get:

(0.25)(37) = 9.25

(4)(2.3125) = 9.25

Since the values match, then the proportionality must have been solved correctly, and the solution must be right.

Biologists need to know roughly how many fish live in a certain lake, but they don't want to stress or otherwise harm the fish by draining or dragnetting the lake. Instead, they let down small nets in a few different spots around the lake, catching, tagging, and releasing 96 fish. A week later, after the tagged fish have had a chance to mix thoroughly with the general population, the biologists come back and let down their nets again. They catch 72 fish, of which 4 are tagged. Assuming that the catch is representative, how many fish live in the lake?

As far as I know, biologists and park managers actually use this technique for estimating populations. The idea is that, after allowing enough time (it is hoped) for the tagged fish to circulate throughout the lake, these fish will then be evenly mixed in with the total population. When the researchers catch some fish later, the ratio of tagged fish in the sample to untagged is representative of the ratio of the 96 fish that they tagged with the total population.

I'll use " f " to stand for the total number of fish in the lake, and set up my ratios with the numbers of "tagged" fish on top. Then I'll set up and solve the proportion:

Because the variable is in only one part of the proportion, I can use the shortcut method to solve.

f = [(96)(72)]/4

This tells me that the estimated population is:

about 1,728 fish

Another type of "proportion" word problem is unit conversion, which looks like this:

How many feet per second are equivalent to 60 mph?

To complete this exercise, I will need conversion factors, which are just ratios. (If you're doing this kind of problem, then you should have access — in your textbook or in a handout, for instance — to basic conversion factors. If not, then your instructor is probably expecting that you have these factors memorized.)

I'll set everything up in a long multiplication so that the units cancel :

88 feet per second

Take note of how I set up the conversion factors for my multiplicate (above) in not-necessarily-standard ways. For instance, one usually says "sixty minutes in an hour", not "one hour in sixty minutes". So why did I enter the hour-minute conversion factor (in the second line of my computations above) as "one hour per sixty minutes"?

Because doing so lined up the fractions so that the unit of "hours" in my conversion factor would cancel off with the "hours" in the original " 60 miles per hour". This cancelling-units thing is an important technique, and you should review it further if you are not comfortable with it.

A particular cookie recipe calls for 225 grams of flour for one batch of thirty cookies. Jade would like to make as many cookies as possible for the upcoming block party, and flour is his only constraint (he's got loads of sugar, eggs, etc). If he has 1.206 kilograms of flour, and assuming that all cookies are the same size, approximately how many cookies can he make? (Round to an appropriate whole number.)

I've got two elements here for my proportion: grams of flour and number of cookies. I got to "grams" first when reading the exercise, so I'll put "grams" on top in my proportion.

Since the relationship is given to me in terms of grams, not kilograms, I'll need to convert Jade's on-hand measure to " 1,206 grams, also. I'll use " c " to stand for the number that I'm trying to figure out for "cookies".

(grams)/(cookies): 225/30 = 1206/ c

Since I have an unknown in only one spot in this proportion, I can use the shortcut method to solve.

c = [(1206)(30)]/225

c = 36180/225

Ohhh! Now I see why the instructions said to round to an "appropriate" whole number: Jade can only make whole cookies; the "point-eight" of a cookie will be an undersized niblet that he'll eat before heading to the party.

While normally I'd round this number up to get my whole-number answer, in this case I need to round down ; in other words, in this context (namely, of all the cookies being the same size), I have to ignore the fractional portion (that is, the point-eight decimal part) to get the desired answer.

160 cookies

Kumar lives in Croatia, and is visiting relatives in India. The current exchange rate is one Euro ( €1 ) to 80.45 Indian rupees ( ₹80.45 ). He wants to buy a gift for them, which costs ₹3,759 . How many Euros will this gift cost him? (State your answer accurate to two decimal places.)

They've given me an exchange rate, which is, effectively, just another conversion factor, like the "miles per hour" exercise above. So I'll set up my proportion, with Euros on top, and will use e to stand for the number of Euros he'll need.

(Euros)/(Rupees): 1/80.45 = e /3759

I'll use the shortcut method to solve:

e = [(3759)(1)]/80.45

e = 46.72467371...

Rounding to two decimal places, Kumar will be spending:

€46.72

Other than for the rate-conversion exercise above, we've been able to solve all of the proportions by the shortcut method. You will likely find this to be the case in your homework, also. But it is always possible that you'll get a question where you'll be better off using cross-multiplication instead.

George has heard from two different sources about the pay range at a particular company. One source says that the ratio of lowest pay to highest pay is 3 : 7 . The other source says that the top earner annually makes about $57,000 more than the lowest earner. What are the approximate salaries for the highest and lowest earners? (Round to the nearest thousand.)

I know that the ratio is 3 : 7 , so I'll be using the fraction 3/7 for one side of my proportion. If the lowest pay rate, in thousands of dollars, is L , then the highest is L  + 57 . My proportion is:

(lowest)/(highest): 3/7 = L /( L + 57)

Because there are variables in two of the parts of this proportion, the shortcut method won't be as useful as cross-multiplication to clear all the fractions. So I'll cross-multiply:

3/7 = L /( L + 57)

3( L + 57) = 7 L

3 L + 171 = 7 L

Remembering that I dropped the trailing zeroes and am counting by thousands, the above number means that the lowest salary is (rounded to the nearest thousand) approximately $43,000 . Then the highest salary, being around $57K more, is approximately $100,000 .

lowest: $43,000 highest: $100,000

URL: https://www.purplemath.com/modules/ratio5.htm

Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Home / United States / Math Classes / 7th Grade Math / Writing and Solving Proportions

Writing and Solving Proportions

A proportion is an equation that states that two ratios are equivalent. We can perform operations on proportions, just l ike we do with normal equations. Here we will learn to perform operations on proportions and the steps involved in solving them. ...Read More Read Less

About Proportions in Math

What are Proportions?

Writing proportions as fractions, using operations to solve proportions, solved examples.

• Frequently Asked Questions

Proportions are mathematical equations that are used to relate equivalent ratios. Two ratios having different antecedents and consequents can have the same value. This relation can be expressed with the help of proportions. Let us consider the ratios \( 2:5 \)  and \( 8:20 \) . When we simplify the ratio \( 8:20 \) , we obtain \( 2:5 \) . This implies that \( 2:5 \)  and \( 8:20 \)  are equivalent ratios. 

In other words, these ratios are in proportion. If \( a:b \)  and \( c:d \) are equivalent ratios, we can express the relation as \( a:b::c:d \) , where the ‘ \( ~::~ \) ’ sign is used to express proportion. So, we can state the proportion in the example that was just observed as, \( 2:5 :: 8:20 \) .

We have learned that a ratio is a comparison of two quantities having the same unit. We also compare two quantities using fractions. Hence, a ratio can also be written as a fraction. For example, we can write the ratio \( a:b \)  as \( \frac{a}{b} \) and \( c:d \)  as \( \frac{c}{d} \) .

Similarly, we can write a proportion as a fraction. Instead of writing \( 2:5::8:20 \) , we can write the proportion as \( \frac{2}{5} = \frac{8}{20} \)   , and this makes it easier to perform operations on proportions to solve for unknown values.

Since a proportion is basically an equation, we can perform operations on them to find unknown values. We can use operations like addition, subtraction, multiplication, and division to solve a proportion. In most cases, we only need to use multiplication and division. Let’s consider a proportion in which one of the values is unknown. 

For example, \( \frac{5}{8} = \frac{x}{40} \)

Use basic math operations to solve this equation. Begin by removing the denominator from both sides.

\( \frac{5 \times 8}{8} = \frac{x \times 8}{40} \)            [Multiply both sides by \( 8 \)]

\( 5 = \frac{x}{5} \)                    [Simplify]

\( 5 \times 5 = \frac{x\times 5}{5} \)          [Multiply both sides by \( 5 \)]

\( 25 = x \)                   [ Simplify]      

Hence, the value of \( x \) is \( 25 \). 

Similarly, we can use a combination of mathematical operations to solve proportions.

Example 1: Use math operations to find the value of \( x \) in the expression, \( \frac{3}{7} = \frac{x}{28} \) .

Solution:  

To find the value of \( x \) , simplify the equation.

\( \frac{3}{7} = \frac{x}{28} \)                    [Write the equation]

\( \frac{3 \times 7}{7} = \frac{x \times 7}{28} \)              [Multiply both sides by \( 7 \)]

\( 3 = \frac{x}{4} \)                      [Simplify]

\( 3 \times 4 = \frac{x \times 4}{4} \)            [Multiply both sides by \( 4 \)]

\( 12 = x \)                    [Simplify]

So, the value of \( x \) is \( 12 \).

Example 2: Solve the proportion to find the unknown value: \( 15:y :: 25:55 \) .

The proportion is \( 15:y :: 25:55 \) and this expression can also be written as \( \frac{15}{y} = \frac{25}{55} \)

To find the value of \( y \) , simplify the equation.

\( \frac{15}{y} = \frac{25}{55} \)                   [Write the proportion]

\( \frac{y}{15} = \frac{55}{25} \)                    [Taking reciprocal of both sides]

\( \frac{y \times 15}{15} = \frac{55 \times 15}{25} \)           [Multiplying both sides by \( 15 \)]

\( y = \frac{11 \times 15}{55} \)                  [Simplify]

\( y = 11 \times 3 \)                [Simplify]

\( y = 33 \)                      [Multiply]

Hence, the unknown value, \( y \) is \( 33 \).

Example 3: An athlete can run \( 100 \) meters in \( 11 \) seconds. If she runs at a constant pace, how long will she take to run \( 800 \) meters?

Time taken by the athlete to cover \( 100 \) meters \( = 11 \) seconds

Let us assume the time taken by the athlete to cover \( 800 \) meters \( = x \) seconds

Since her speed is constant, the ratio of distance and time in both cases is in proportion. 

\( \frac{100}{11} = \frac{800}{x} \)                      [Write the above condition in proportion]

\( \frac{11}{100} = \frac{x}{800} \)                      [Taking reciprocal of both sides]

\( \frac{11 \times 100}{100} = \frac{x \times 100}{800} \)              [Multiplying both sides by \( 100 \)]

\( 11 = \frac{x}{8} \)                          [Simplify]

\( x = 88 \)                            [Multiplying both sides by \( 8 \)]

Hence, the athlete will take \( 88 \) seconds to run \( 800 \) meters.

Are ratios related to proportions?

Yes, a proportion is an equation that states that two ratios are equivalent. So, we can say that proportions are directly related to ratios.

Can we perform mathematical operations on proportions?

Since proportions are basically mathematical equations, we can perform all the mathematical operations on them, just like we do with a normal mathematical equation.

How do we solve a proportion?

We can solve a proportion to find the unknown value by performing mathematical operations on them. The goal is to isolate the unknown value on one side of the equation. Thus, by solving the equation, we will get the value of the unknown on the other side of the equation.

Check out our other courses

Grades 1 - 12

Level 1 - 10

Proportions

Proportion says that two ratios (or fractions) are equal.

We see that 1-out-of-3 is equal to 2-out-of-6

The ratios are the same, so they are in proportion.

Example: Rope

A rope's length and weight are in proportion.

When 20m of rope weighs 1kg , then:

• 40m of that rope weighs 2kg
• 200m of that rope weighs 10kg

20 1 = 40 2

When shapes are "in proportion" their relative sizes are the same.

Example: International paper sizes (like A3, A4, A5, etc) all have the same proportions:

So any artwork or document can be resized to fit on any sheet. Very neat.

Working With Proportions

NOW, how do we use this?

Example: you want to draw the dog's head ... how long should it be?

Let us write the proportion with the help of the 10/20 ratio from above:

? 42 = 10 20

Now we solve it using a special method:

Multiply across the known corners, then divide by the third number

And we get this:

? = (42 × 10) / 20 = 420 / 20 = 21

So you should draw the head 21 long.

Using Proportions to Solve Percents

A percent is actually a ratio! Saying "25%" is actually saying "25 per 100":

25% = 25 100

We can use proportions to solve questions involving percents.

The trick is to put what we know into this form:

Part Whole = Percent 100

Example: what is 25% of 160 ?

The percent is 25, the whole is 160, and we want to find the "part":

Part 160 = 25 100

Multiply across the known corners, then divide by the third number:

Part = (160 × 25) / 100 = 4000 / 100 = 40

Answer: 25% of 160 is 40.

Note: we could have also solved this by doing the divide first, like this:

Part = 160 × (25 / 100) = 160 × 0.25 = 40

Either method works fine.

We can also find a Percent:

Example: what is $12 as a percent of $80 ?

Fill in what we know:

$12 $80 = Percent 100

Multiply across the known corners, then divide by the third number. This time the known corners are top left and bottom right:

Percent = ($12 × 100) / $80 = 1200 / 80 = 15%

Answer: $12 is 15% of $80

Or find the Whole:

Example: The sale price of a phone was $150, which was only 80% of normal price. What was the normal price?

$150 Whole = 80 100

Whole = ($150 × 100) / 80 = 15000 / 80 = 187.50

Answer: the phone's normal price was $187.50

Using Proportions to Solve Triangles

We can use proportions to solve similar triangles.

Example: How tall is the Tree?

Sam tried using a ladder, tape measure, ropes and various other things, but still couldn't work out how tall the tree was.

But then Sam has a clever idea ... similar triangles!

Sam measures a stick and its shadow (in meters), and also the shadow of the tree, and this is what he gets:

Now Sam makes a sketch of the triangles, and writes down the "Height to Length" ratio for both triangles:

Height: Shadow Length:     h 2.9 m = 2.4 m 1.3 m

h = (2.9 × 2.4) / 1.3 = 6.96 / 1.3 = 5.4 m (to nearest 0.1)

Answer: the tree is 5.4 m tall.

And he didn't even need a ladder!

The "Height" could have been at the bottom, so long as it was on the bottom for BOTH ratios, like this:

Let us try the ratio of "Shadow Length to Height":

Shadow Length: Height:     2.9 m h = 1.3 m 2.4 m

It is the same calculation as before.

A "Concrete" Example

Ratios can have more than two numbers !

For example concrete is made by mixing cement, sand, stones and water.

A typical mix of cement, sand and stones is written as a ratio, such as 1:2:6 .

We can multiply all values by the same amount and still have the same ratio.

10:20:60 is the same as 1:2:6

So when we use 10 buckets of cement, we should use 20 of sand and 60 of stones.

Example: you have just put 12 buckets of stones into a mixer, how much cement and how much sand should you add to make a 1:2:6 mix?

Let us lay it out in a table to make it clearer:

You have 12 buckets of stones but the ratio says 6.

That is OK, you simply have twice as many stones as the number in the ratio ... so you need twice as much of everything to keep the ratio.

Here is the solution:

And the ratio 2:4:12 is the same as 1:2:6 (because they show the same relative sizes)

So the answer is: add 2 buckets of Cement and 4 buckets of Sand. (You will also need water and a lot of stirring....)

Why are they the same ratio? Well, the 1:2:6 ratio says to have :

• twice as much Sand as Cement ( 1 : 2 :6)
• 6 times as much Stones as Cement ( 1 :2: 6 )

In our mix we have:

• twice as much Sand as Cement ( 2 : 4 :12)
• 6 times as much Stones as Cement ( 2 :4: 12 )

So it should be just right!

That is the good thing about ratios. You can make the amounts bigger or smaller and so long as the relative sizes are the same then the ratio is the same.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 1

Worked example: solving proportions.

• Solving proportions
• Writing proportions example
• Writing proportions
• Proportion word problem: cookies
• Proportion word problem: hot dogs
• Proportion word problems

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Algebra: Ratio Word Problems

Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Algebra Lessons

In these lessons, we will learn how to solve ratio word problems that have two-term ratios or three-term ratios.

Ratio problems are word problems that use ratios to relate the different items in the question.

The main things to be aware about for ratio problems are:

• Change the quantities to the same unit if necessary.
• Write the items in the ratio as a fraction .
• Make sure that you have the same items in the numerator and denominator.

Ratio Problems: Two-Term Ratios

Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?

Solution: Step 1: Assign variables: Let x = number of red sweets.

Step 2: Solve the equation. Cross Multiply 3 × 120 = 4 × x 360 = 4 x

Answer: There are 90 red sweets.

Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?

Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = number of blue marbles for Jane 20 – x = number red marbles for Jane

Step 2: Solve the equation

Cross Multiply 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x

John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.

Answer: John has 4 more blue marbles than Jane.

How To Solve Word Problems Using Proportions?

This is another word problem that involves ratio or proportion.

Example: A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?

How To Solve Proportion Word Problems?

When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.

• Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
• Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank? 3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?

Ratio problems: Three-term Ratios

Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?

Solution: Step 1: Assign variables: Let x = amount of corn

Step 2: Solve the equation Cross Multiply 2 × x = 3 × 5 2 x = 15

Answer: The mixture contains 7.5 pounds of corn.

Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?

Solution: Step 1: Assign variables: Let x = number of red shirts and y = number of green shirts

Step 2: Solve the equation Cross Multiply 3 × 20 = x × 4 60 = 4 x x = 15

5 × 20 = y × 4 100 = 4 y y = 25

The total number of shirts would be 15 + 25 + 20 = 60

Answer: There are 60 shirts.

Algebra And Ratios With Three Terms

Let’s study how algebra can help us think about ratios with more than two terms.

Example: There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: Applications of Proportions

• Last updated
• Save as PDF
• Page ID 48873

• Denny Burzynski & Wade Ellis, Jr.
• College of Southern Nevada via OpenStax CNX

Learning Objectives

• solve proportion problems using the five-step method

The Five-Step Method

In [link] we noted that many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specified numbers and one unknown number represented by a letter.

The first and most important part of solving a proportion problem is to deter­mine, by careful reading, what the unknown quantity is and to represent it with some letter.

The Five-Step Method The five-step method for solving proportion problems:

• By careful reading, determine what the unknown quantity is and represent it with some letter. There will be only one unknown in a problem.
• Identify the three specified numbers.
• Determine which comparisons are to be made and set up the proportion.
• Solve the proportion (using the methods of [link] ).
• Interpret and write a conclusion in a sentence with the appropriate units of measure.

Step 1 is extremely important. Many problems go unsolved because time is not taken to establish what quantity is to be found.

When solving an applied problem, always begin by determining the unknown quantity and representing it with a letter.

Problem Solving

Sample Set A

On a map, 2 inches represents 25 miles. How many miles are represented by 8 inches?

Step 1: The unknown quantity is miles. Let \(x =\) number of miles represented by 8 inches

Step 2: The three specified numbers are 2 inches 25 miles 8 inches

Step 3: The comparisons are 2 inches to 25 miles \(\to \dfrac{\text{2 inches}}{\text{25 miles}}\) 8 inches to \(x\) miles \(\to \dfrac{\text{8 inches}}{\text{x miles}}\) Proportions involving ratios and rates are more readily solved by suspending the units while doing the computations. \(\dfrac{2}{25} = \dfrac{8}{x}\)

Step 4: \(\dfrac{2}{25} = \dfrac{8}{x}\) Perform the cross multiplication. \(\begin{array} {rcl} {2 \cdot x} & = & {8 \cdot 25} \\ {2 \cdot x} & = & {200 \ \ \ \ \ \ \ \text{Divide 200 by 2.}} \\ {x} & = & {\dfrac{200}{2}} \\ {x} & = & {100} \end{array}\) In step 1, we let \(x\) represent the number of miles. So, \(x\) represents 100 miles.

Step 5: If 2 inches represents 25 miles, then 8 inches represents 100 miles.

An acid solution is composed of 7 parts water to 2 parts acid. How many parts of water are there in a solution composed of 20 parts acid?

Step 1: The unknown quantity is the number of parts of water. Let \(x =\) number of parts of water.

Step 2: The three specified numbers are 7 parts water 2 parts acid 20 parts acid

Step 3: The comparisons are 7 parts water to 2 parts acid \(\to \dfrac{7}{2}\) \(n\) parts water to 20 parts acid \(\to \dfrac{n}{20}\) \(\dfrac{7}{2} = \dfrac{n}{20}\)

Step 4: \(\dfrac{7}{2} = \dfrac{n}{20}\) Perform the cross multiplication. \(\begin{array} {rcl} {7 \cdot 20} & = & {2 \cdot n} \\ {140} & = & {2 \cdot n \ \ \ \text{Divide 140 by 2.}} \\ {\dfrac{140}{2}} & = & {n} \\ {70} & = & {n} \end{array}\) In step 1, we let \(n\) represent the number of parts of water. So, \(n\) represents 70 parts of water.

Step 5: 7 parts water to 2 parts acid indicates 70 parts water to 20 parts acid.

A 5-foot girl casts a \(3 \dfrac{1}{3}\) foot shadow at a particular time of the day. How tall is a person who casts a 3-foot shadow at the same time of the day?

Step 1: The unknown quantity is the height of the person. Let \(h = \text{ height of the preson.}\)

Step 2: The three specified numbers are 5 feet ( height of girl) 3\(\dfrac{1}{3}\) feet (length of shadow) 3 feet (length of shadow)

Step 3: The comparisons are 5-foot girl is to \(3 \dfrac{1}{3}\) foot shadow \(\to \dfrac{5}{3 \dfrac{1}{3}}\) \(h\)-foot person is to 3-foot shadow \(\to \dfrac{h}{3}\) \(\dfrac{5}{3\dfrac{1}{3}} = \dfrac{h}{3}\)

\(\begin{array} {rcl} {\dfrac{5}{3\dfrac{1}{3}}} & = & {\dfrac{h}{3}} \\ {5 \cdot 3} & = & {3 \dfrac{1}{3} \cdot h} \\ {15} & = & {\dfrac{10}{3} \cdot h \ \ \ \ \text{Divide 15 by } \dfrac{10}{3}} \\ {\dfrac{15}{\dfrac{10}{3}}} & = & {h} \\ {\dfrac{\begin{array} {c} {^3} \\ {\cancel{15}} \end{array}}{1} \cdot \dfrac{3}{\begin{array} {c} {\cancel{10}} \\ {^2} \end{array}}} & = & {h} \\ {\dfrac{9}{2}} & = & {h} \\ {h} & = & {4 \dfrac{1}{2}} \end{array}\)

Step 5: A person who casts a 3-foot shadow at this particular time of the day is \(4 \dfrac{1}{2}\) feet tall.

The ratio of men to women in a particular town is 3 to 5. How many women are there in the town if there are 19,200 men in town?

Step 1: The unknown quantity is the number of women in town. Let \(x =\) number of women in town.

Step 2: The three specified numbers are 3 5 19,200

Step 3: The comparisons are 3 men to 5 women \(\to \dfrac{3}{5}\) 19,200 men to \(x\) women \(\to \dfrac{19,200}{x}\) \(\dfrac{3}{5} = \dfrac{19,200}{x}\)

\(\begin{array} {rcl} {\dfrac{3}{5}} & = & {\dfrac{19,200}{x}} \\ {3 \cdot x} & = & {19,200 \cdot 5} \\ {3 \cdot x} & = & {96,000} \\ {x} & = & {\dfrac{96,000}{3}} \\ {x} & = & {32,000} \end{array}\)

Step 5: There are 32,000 women in town.

The rate of wins to losses of a particular baseball team is \(\dfrac{9}{2}\). How many games did this team lose if they won 63 games?

Step 1: The unknown quantity is the number of games lost. Let \(n =\) number of games lost.

Step 2: Since \(\dfrac{9}{2} \to\) means 9 wins to 2 losses, the three specified numbers are 9 (wins) 2 (losses) 63 (wins)

Step 3: The comparisons are 9 wins to 2 losses \(\to \dfrac{9}{2}\) 63 wins to \(n\) losses \(\to \dfrac{63}{n}\) \(\dfrac{9}{2} = \dfrac{63}{n}\)

\(\begin{array} {rcl} {\dfrac{9}{2}} & = & {\dfrac{63}{n}} \\ {9 \cdot n} & = & {2 \cdot 63} \\ {9 \cdot n} & = & {126} \\ {n} & = & {\dfrac{126}{9}} \\ {n} & = & {14} \end{array}\)

Step 5: This team had 14 losses.

Practice Set A

Solve each problem.

On a map, 3 inches represents 100 miles. How many miles are represented by 15 inches?

An alcohol solution is composed of 14 parts water to 3 parts alcohol. How many parts of alcohol are in a solution that is composed of 112 parts water?

24 parts of alcohol

A \(5 \dfrac{1}{2}\)-foot woman casts a 7-foot shadow at a particular time of the day. How long of a shadow does a 3-foot boy cast at that same time of day?

\(3 \dfrac{9}{11}\) feet

The rate of houseplants to outside plants at a nursery is 4 to 9. If there are 384 houseplants in the nursery, how many outside plants are there?

864 outside plants

The odds for a particular event occurring are 11 to 2. (For every 11 times the event does occur, it will not occur 2 times.) How many times does the event occur if it does not occur 18 times?

The event occurs 99 times.

The rate of passing grades to failing grades in a particular chemistry class is 7272 . If there are 21 passing grades, how many failing grades are there?

6 failing grades

For the following 20 problems, use the five-step method to solve each problem.

Exercise \(\PageIndex{1}\)

On a map, 4 inches represents 50 miles. How many inches represent 300 miles?

Exercise \(\PageIndex{2}\)

On a blueprint for a house, 2 inches represents 3 feet. How many inches represent 10 feet?

Exercise \(\PageIndex{3}\)

A model is built to \(\dfrac{2}{15}\) scale. If a particular part of the model measures 6 inches, how long is the actual structure?

Exercise \(\PageIndex{4}\)

An acid solution is composed of 5 parts acid to 9 parts of water. How many parts of acid are there in a solution that contains 108 parts of water?

Exercise \(\PageIndex{5}\)

An alloy contains 3 parts of nickel to 4 parts of silver. How much nickel is in an alloy that con­tains 44 parts of silver?

Exercise \(\PageIndex{6}\)

The ratio of water to salt in a test tube is 5 to 2. How much salt is in a test tube that contains 35 ml of water?

Exercise \(\PageIndex{7}\)

The ratio of sulfur to air in a container is \(\dfrac{4}{45}\). How many ml of air are there in a container that contains 207 ml of sulfur?

Exercise \(\PageIndex{8}\)

A 6-foot man casts a 4-foot shadow at a particu­lar time of the day. How tall is a person that casts a 3-foot shadow at that same time of the day?

Exercise \(\PageIndex{9}\)

A \(5\dfrac{1}{2}\)-foot woman casts a \(1\dfrac{1}{2}\)-foot shadow at a particular time of the day. How long a shadow does her \(3\dfrac{1}{2}\)-foot niece cast at the same time of the day?

\(\dfrac{21}{22}\) feet

Exercise \(\PageIndex{10}\)

A man, who is 6 feet tall, casts a 7-foot shadow at a particular time of the day. How tall is a tree that casts an 84-foot shadow at that same time of the day?

Exercise \(\PageIndex{11}\)

The ratio of books to shelves in a bookstore is 350 to 3. How many books are there in a store that has 105 shelves?

Exercise \(\PageIndex{12}\)

The ratio of algebra classes to geometry classes at a particular community college is 13 to 2. How many geometry classes does this college offer if it offers 13 algebra classes?

Exercise \(\PageIndex{13}\)

The odds for a particular event to occur are 16 to 3. If this event occurs 64 times, how many times would you predict it does not occur?

Exercise \(\PageIndex{14}\)

The odds against a particular event occurring are 8 to 3. If this event does occur 64 times, how many times would you predict it does not occur?

Exercise \(\PageIndex{15}\)

The owner of a stationery store knows that a 1-inch stack of paper contains 300 sheets. The owner wishes to stack the paper in units of 550 sheets. How many inches tall should each stack be?

\(1\dfrac{5}{6}\)

Exercise \(\PageIndex{16}\)

A recipe that requires 6 cups of sugar for 15 serv­ings is to be used to make 45 servings. How much sugar will be needed?

Exercise \(\PageIndex{17}\)

A pond loses \(7\dfrac{1}{2}\) gallons of water every 2 days due to evaporation. How many gallons of water are lost, due to evaporation, in \(\dfrac{1}{2}\) day?

\(1\dfrac{7}{8}\)

Exercise \(\PageIndex{18}\)

A photograph that measures 3 inches wide and \(4\dfrac{1}{2}\) inches high is to be enlarged so that it is 5 inches wide. How high will it be?

Exercise \(\PageIndex{19}\)

If 25 pounds of fertilizer covers 400 square feet of grass, how many pounds will it take to cover 500 square feet of grass?

\(31 \dfrac{1}{4}\)

Exercise \(\PageIndex{20}\)

Every \(\dfrac{1}{2}\) teaspoons of a particular multiple vitamin, in granular form, contains 0.65 the mini­mum daily requirement of vitamin C. How many teaspoons of this vitamin are required to supply 1.25 the minimum daily requirement?

Exercises for Review

Exercise \(\PageIndex{21}\)

Find the product, \(818 \cdot 0\).

Exercise \(\PageIndex{22}\)

Determine the missing numerator: \(\dfrac{8}{15} = \dfrac{N}{90}\).

Exercise \(\PageIndex{23}\)

Find the value of \(\dfrac{\dfrac{3}{10} + \dfrac{4}{12}}{\dfrac{19}{20}}\).

\(\dfrac{2}{3}\)

Exercise \(\PageIndex{24}\)

Subtract 0.249 from the sum of 0.344 and 0.612.

Exercise \(\PageIndex{25}\)

Solve the proportion: \(\dfrac{6}{x} = \dfrac{36}{30}\).

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Ratio Problem Solving

Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.

There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio problem solving?

Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer. 

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods we can use when given certain pieces of information.

When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation. 

For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

We use the ratio to divide 40 sweets into 8 equal parts. 

Then we multiply each part of the ratio by 5.

3 x 5:5 x 5 = 15:25

This means that Charlie will get 15 sweets and David will get 25 sweets.

• Dividing ratios

Step-by-step guide: Dividing ratios (coming soon)

Ratios and fractions (proportion problems)

We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.

Simplifying and equivalent ratios

• Simplifying ratios

Equivalent ratios

Units and conversions ratio questions

Units and conversions are usually equivalent ratio problems (see above).

• If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
• The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.

Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.

Top tip: if you are converting units, always write the units in your ratio.

Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .

Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Explain how to do ratio problem solving

Ratio problem solving worksheet

Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on ratio

Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• How to work out ratio  
• Ratio to fraction
• Ratio scale
• Ratio to percentage

Ratio problem solving examples

Example 1: part:part ratio.

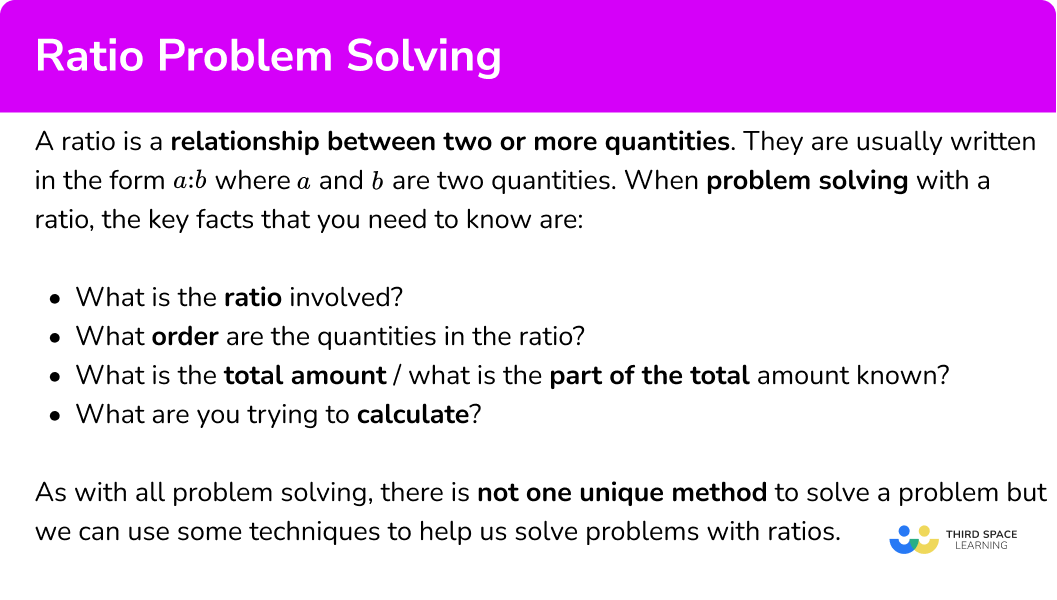
Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?

Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?

Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).

We could write this as

Where the letter above each part of the ratio links to the question.

We know that 465 students have school dinner.

2 Know what you are trying to calculate.

From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.

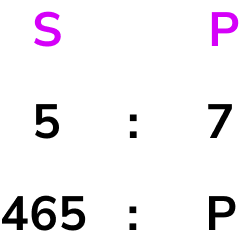
We need to find the value of p.

3 Use prior knowledge to structure a solution.

We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.

So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

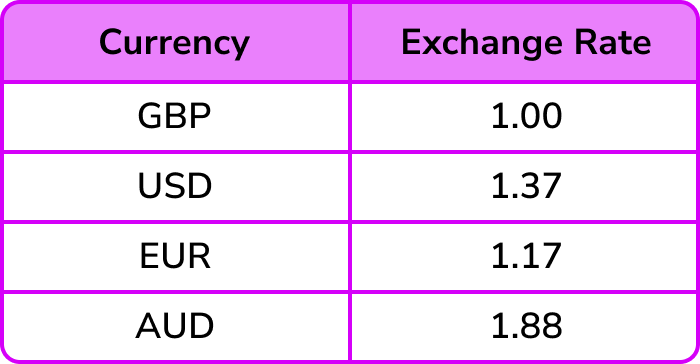
Use the table above to convert £520 (GBP) to Euros € (EUR).

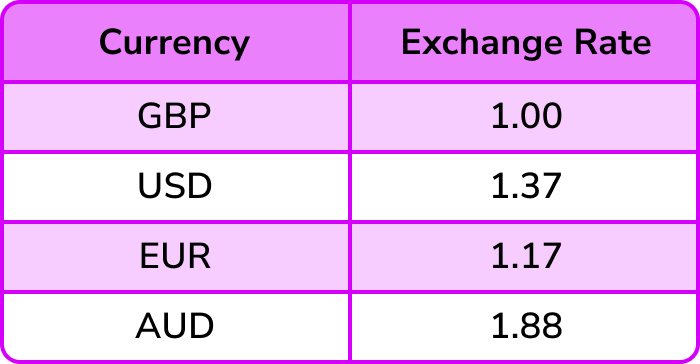
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).

The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state

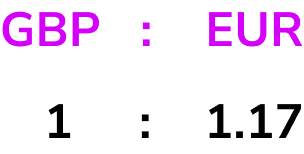
We know that we have £520.

We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520 = €608.40.

Example 3: writing a ratio 1:n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.

Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.

2l = 2000ml

So we can also express the ratio as 500:2000 which will help us in later steps.

We want to simplify the ratio 500:2000 into the form 1:n.

We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

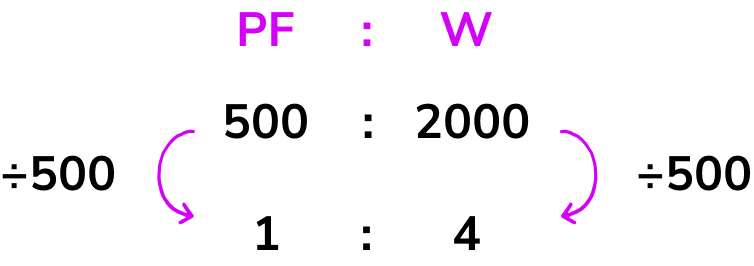
So the ratio of plant food to water in the form 1:n is 1:4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?

We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have

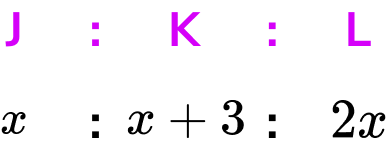
We also know that Luke receives £8.

We want to calculate the total amount of pocket money for the three siblings.

We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.

Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

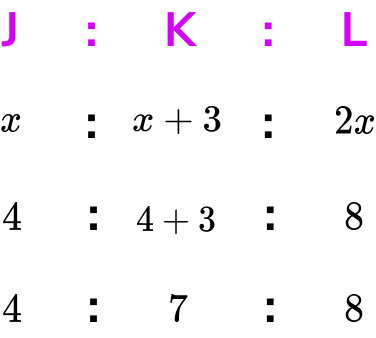
The total amount of pocket money is therefore 4+7+8=£19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colours of counters in a bag.

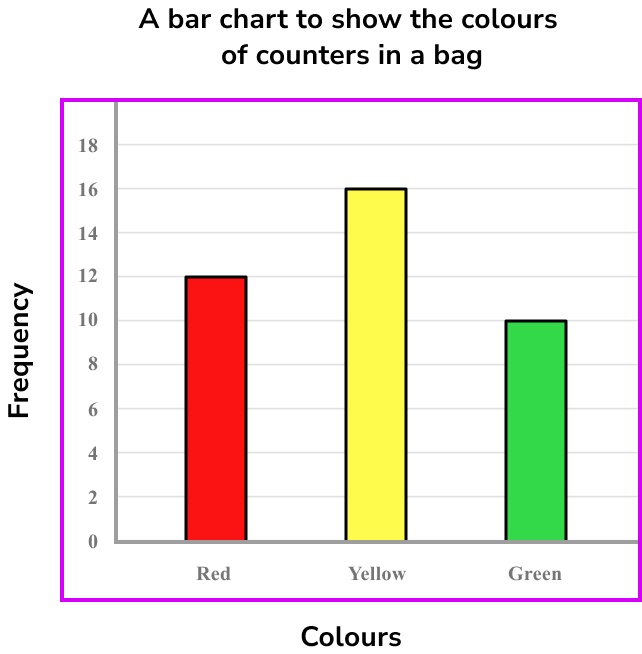
Express this data as a ratio in its simplest form.

From the bar chart, we can read the frequencies to create the ratio.

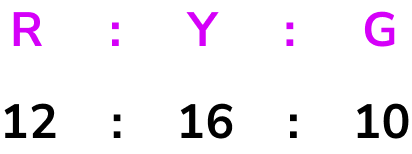
We need to simplify this ratio.

To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}

HCF (12,16,10) = 2

Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .

Example 6: combining two ratios

Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .

We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.

Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.

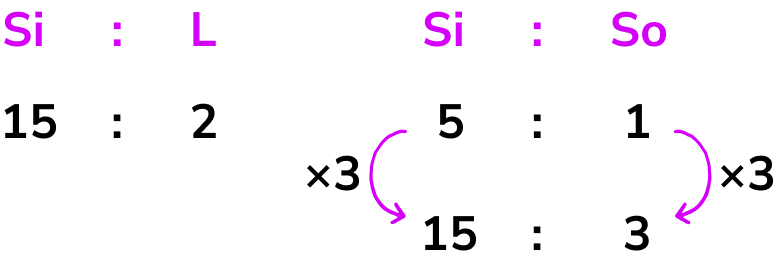
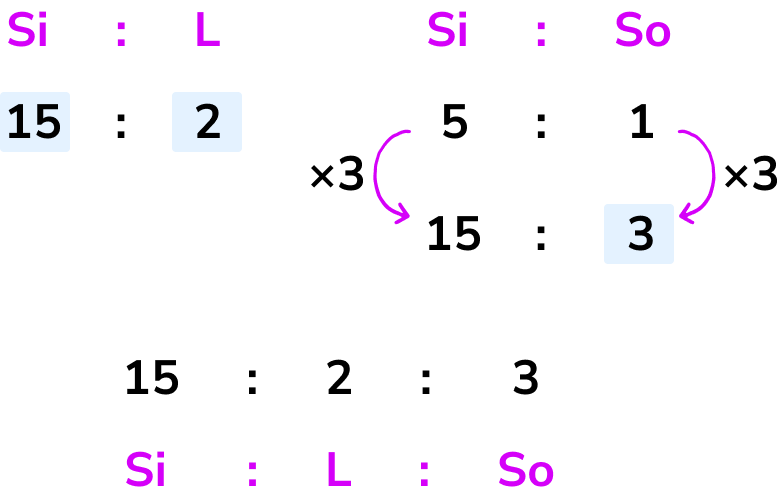
We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.

Example 7: using bar modelling

India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?

We know that the initial ratio is 5:2 and that India has three more parts than Beau.

We want to find the original quantity.

Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if we can find out this value, we can then find the total quantity.

From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.

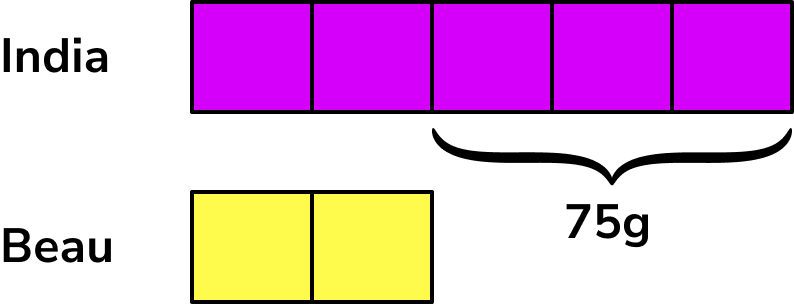
We can find the value of one share by working out 75 \div 3=25g.

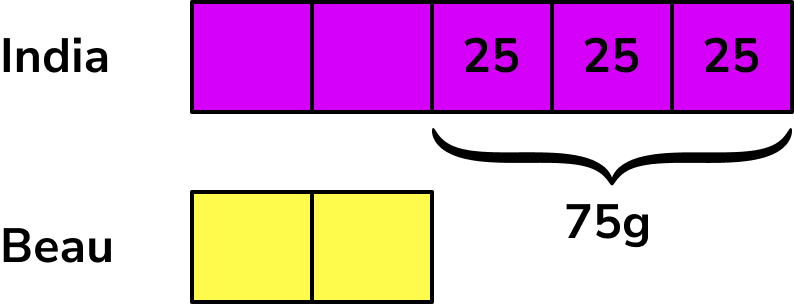
We can fill in each share to be 25g.

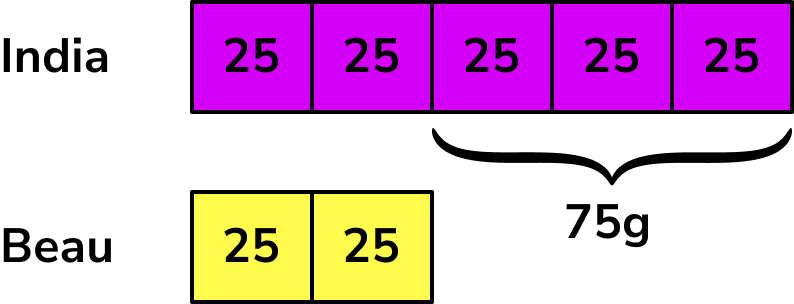
Adding up each share, we get

India = 5 \times 25=125g

Beau = 2 \times 25=50g

The total amount of popcorn was 125+50=175g.

Common misconceptions

• Mixing units

Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.

• Ratio written in the wrong order

For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.

• Ratios and fractions confusion

Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

• Counting the number of parts in the ratio, not the total number of shares

For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.

• Ratios of the form \bf{1:n}

The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.

4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.

5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.

Ratio problem solving GCSE questions

1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.

Write this in the form 1gram:n where n represents the number of water molecules in standard form.

2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.

Calculate the length of the plank of wood.

5-3=2 \ parts = 36cm so 1 \ part = 18cm

3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.

(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.

Learning checklist

You have now learned how to:

• Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
• Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
• Make and use connections between different parts of mathematics to solve problems

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Ratio: Problem Solving Textbook Exercise

Click here for questions, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024