symbolic representation definition in math

• Skip to main content

Welcome, Fellow Math Enthusiast! I’m so happy you’re here!

• Counting & Cardinality
• Addition & Subtraction
• Multiplication & Division
• Place Value & Base Ten
• Measurement & Data
• Geometry & Fractions
• Vocabulary & Discourse
• Math Manipulatives
• Classroom Management
• Classroom Organization
• Holidays & Seasonal
• Social-Emotional Learning
• Privacy Policy
• Terms of Use
• SHOP RESOURCES
• BECOME A MEMBER
• Search this website

Teaching with Jillian Starr

teaching little stars to shine brightly

Grab Your FREE Gift

Addition Centers Freebie

Looking for fun and engaging centers to help your students practice their addition fact fluency? Be sure to grab these freebies!

Mathematical Representations Series Part 3: Symbolic Representation

Welcome back to our deep dive into mathematical representations! Today, we are taking a look at symbolic representations and how we can translate between symbolic, concrete, and visual representations. First, let’s do a two-sentence recap of this series so far:

We have already focused on concrete representations and the immense value of manipulatives, as well as the range of visual representations we want to encourage with our students. We are centering our conversation around Lesh’s Translation Model, which encompasses the range of ways we represent our thinking, and stresses the importance of making connections between representations.

Symbolic Representation

Now, that we’re all caught up, let’s take a peek at Symbolic Representations. You may have heard it called Abstract Representation, especially if you’re familiar with the Concrete-Pictorial-Abstract model (also called CRA model).

So what are symbolic representations? Well, symbolic representation is when mathematical symbols (like numerals and operation signs) are used to show a mathematical concept. They are using symbolic, mathematical language to express their understanding of a math concept.

Let’s go back to the example from concrete representation . In that example, the student used 5 yellow counters, and 4 red counters to concretely show their understanding of 5 + 4 = 9.

Then in their visual representation , they were able to create a sketch of their concrete representation. This was our first example of translating between two different representations (connecting visual to concrete).

Now, we can support students even further by helping them represent their understanding with symbols. Here the student counts the collection of five counters and writes the numeral “5” below it. They do the same for the four counters.

Finally, they count all of the counters together and write down “9”. We can help them with the operations symbols if needed, showing that “+” means that we are putting the 5 and the 4 together and that the “=” means “4+5” has the same value as “9”.

When we guide students to using numerals and operations, they are connecting their manipulatives, their sketches, AND the symbolic representation. This is such a powerful move to help deepen student understanding!

Connecting Two Symbolic Representations

It’s a fairly straightforward representation, but how do abstract representations connect to themselves in Lesh’s translation model? 

Well, this student actually wanted to write 4 + 4 +1 because that is how they solved the problem. They knew 4 + 4 = 8, so 4 + 5 = 9 because it’s 4 + 4 + 1 more. Understanding that both expressions can describe the same concept is just one example of how to translate within the symbolic representation.

What’s Up Next?

This series is going to dive deep into each of the representations discussed in Lesh’s Translation Model, and then we are going to put it all together so we can make a big impact on your math teaching this year.

If you missed Part One about Concrete Representations or Part Two about Visual Representations , check them out so you have all of the info you need before we move on!

Addition & Subtraction Resources

You May Also Enjoy These Posts:

Reader Interactions

Leave a comment.

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Ready to go deeper?

JOIN MEANINGFUL MATH

hello I'm Jillian

I’m so happy you’re here. I want every child to feel confident in their math abilities, and that happens when every teacher feels confident in their ability to teach math.

In my fifteen years of teaching, I sought every opportunity to learn more about teaching math. I wanted to know HOW students develop math concepts, just like I had been taught how students learn to read. I want every teacher to experience the same math transformation I did, and have the confidence to teach any student that steps foot in their classroom. I’m excited to be alongside you in your math journey!

Follow Me on Instagram!

• Subscriber Services
• For Authors
• Publications
• Archaeology
• Art & Architecture
• Bilingual dictionaries
• Classical studies
• Encyclopedias
• English Dictionaries and Thesauri
• Language reference
• Linguistics
• Media studies
• Medicine and health
• Names studies
• Performing arts
• Science and technology
• Social sciences
• Society and culture
• Overview Pages
• Subject Reference
• English Dictionaries
• Bilingual Dictionaries

Recently viewed (0)

• Save Search
• Share This Facebook LinkedIn Twitter

Related Content

Related overviews.

See all related overviews in Oxford Reference »

More Like This

Show all results sharing these subjects:

symbolic representation

Quick reference.

A form of knowledge representation in which arbitrary symbols or structures are used to stand for the things that are represented, and the representations therefore do not resemble the things that they represent. Natural language (apart from onomatopoeic expressions) is the most familiar example of symbolic representation. Also called propositional representation . Compare analogue (2). [From Greek symbolon a token + -ikos of, relating to, or resembling]

From:   symbolic representation   in  A Dictionary of Psychology »

Subjects: Science and technology — Psychology

Related content in Oxford Reference

Reference entries, symbolic representation n..

View all related items in Oxford Reference »

Search for: 'symbolic representation' in Oxford Reference »

• Oxford University Press

PRINTED FROM OXFORD REFERENCE (www.oxfordreference.com). (c) Copyright Oxford University Press, 2023. All Rights Reserved. Under the terms of the licence agreement, an individual user may print out a PDF of a single entry from a reference work in OR for personal use (for details see Privacy Policy and Legal Notice ).

date: 27 April 2024

• Cookie Policy
• Privacy Policy
• Legal Notice
• Accessibility
• [66.249.64.20|81.177.182.159]
• 81.177.182.159

Character limit 500 /500

What Does Symbolic Representation Mean in Math? Relations!

Symbolic representation in mathematics refers to the use of symbols to denote numbers, operations, relations, or functions, simplifying the communication and processing of mathematical ideas and problems.

Symbolic representation in mathematics is the practice of using symbols to express mathematical ideas.

Symbols can represent numbers (like ‘1’ or ‘π’), operations (such as ‘+’ for addition or ‘−’ for subtraction), relations (like ‘=’ for equality or ‘≤’ for less than or equal to), or functions (such as ‘f(x)’ for a function named ‘f’ of the variable ‘x’).

This system allows for concise and clear communication of mathematical concepts, making it easier to work with complex equations and theorems.

• Example: The quadratic formula x = (-b ± √(b²-4ac)) / (2a) uses symbols to represent the solution to a quadratic equation.

Symbolic representation is the backbone of mathematical communication, offering clarity and precision in a universal language.

Table of Contents

Key Takeaway

Overview of symbolic representations in mathematics, origins of symbolic representation.

One might trace the origins of symbolic representation in mathematics back to ancient civilizations such as the Babylonians and Egyptians. These early mathematicians developed numerical systems and notations to record and perform calculations.

The Babylonians, for instance, used a base-60 positional notation, while the Egyptians employed hieroglyphs for numerals. These systems laid the foundation for symbolic representation in mathematics, enabling the manipulation of abstract concepts and quantities.

As civilizations advanced, so did their mathematical notations. The Greeks introduced symbols for unknowns and variables, a crucial development in the evolution of algebra.

The use of symbolic representation continued to progress through the Middle Ages and the Renaissance, eventually leading to the formalized algebraic notation we use today.

Understanding the historical origins of symbolic representation provides insight into the development of mathematical thought and the power of abstract representation.

Fundamental Principles of Symbolic Notation

The use of symbolic notation in math is essential for communicating abstract concepts and ensuring precision in mathematical language.

Understanding the fundamental principles of symbolic notation allows for the representation and manipulation of mathematical ideas in a concise and efficient manner.

Symbolic Notation in Math

Symbolic notation in math is a fundamental tool for representing mathematical concepts and operations concisely and precisely. It allows mathematicians to communicate complex ideas in a compact form, aiding in the understanding and manipulation of mathematical principles.

The fundamental principles of symbolic notation include:

• Conciseness : Symbolic notation condenses complex mathematical ideas into compact forms, simplifying the expression of concepts.
• Precision : It enables precise representation of mathematical operations and relationships, reducing ambiguity in mathematical communication.
• Flexibility : Symbolic notation allows for the manipulation and transformation of mathematical expressions, facilitating problem-solving and analysis.
• Universality : It provides a universal language for expressing mathematical ideas, transcending linguistic and cultural barriers.

Understanding symbolic notation is crucial for effectively communicating abstract mathematical concepts, as it forms the basis for expressing and interpreting mathematical ideas.

Next, let’s explore how symbolic notation aids in communicating abstract concepts.

Communicating Abstract Concepts

Communicating abstract concepts through fundamental principles of symbolic notation is essential for conveying complex mathematical ideas concisely and precisely in a professional style of writing.

Symbolic notation allows mathematicians to represent intricate concepts in a compact and standardized form, facilitating efficient communication and understanding.

Utilizing symbolic representation enables the expression of relationships, operations, and structures in a universal language, transcending linguistic barriers and aiding in the dissemination of mathematical knowledge.

To emphasize the significance of symbolic notation, consider the following table:

This table underscores the fundamental principles of symbolic notation, highlighting its role in effectively communicating abstract mathematical concepts.

Mathematical Language Precision

In professional mathematical discourse, achieving precision in language is paramount for effectively conveying complex concepts through symbolic notation.

Mathematical language precision is based on fundamental principles of symbolic notation, which include:

• Consistency : Ensuring uniform use of symbols and notation throughout a mathematical argument or proof.
• Clarity : Clearly defining the meaning of each symbol or notation used to avoid ambiguity.
• Concision : Using the most succinct and precise language possible to convey mathematical ideas.
• Rigor : Maintaining strict adherence to logical reasoning and mathematical rules when using symbolic representation.

Symbolic Representation in Algebra

Within algebra, symbolic representation involves expressing mathematical relationships and operations using letters, symbols, and mathematical notation. Instead of using specific numbers, algebraic expressions and equations use symbols to represent quantities.

This allows for generalization and the ability to solve problems for any value of the variables involved.

For example, instead of writing a specific equation like 2x + 5 = 11, algebra uses the symbolic representation of the equation as ax + b = c, where a, b, and c represent any numbers.

This abstraction enables mathematicians to work with a wide range of problems and develop general rules and principles that apply across various scenarios.

Understanding symbolic representation in algebra is crucial for solving complex equations and real-world problems.

This leads us to the subsequent section about the role of symbols in mathematical equations.

Role of Symbols in Mathematical Equations

Playing a crucial role in expressing mathematical relationships and operations, symbols in mathematical equations allow for abstraction and generalization.

They serve as a compact and efficient way to represent complex mathematical ideas, making it easier for mathematicians to communicate and work with various mathematical concepts.

The role of symbols in mathematical equations can be understood through the following points:

• Clarity : Symbols help in making mathematical expressions clear and concise.
• Flexibility : They allow for the manipulation of mathematical entities in a flexible manner.
• Generalization : Symbols aid in formulating general rules and principles that apply across different contexts.
• Efficiency : The use of symbols simplifies complex calculations and problem-solving processes.

Understanding the role of symbols in mathematical equations is essential for grasping the language of mathematics and its applications.

Symbolic Representation in Calculus

Symbolic representation plays a crucial role in calculus, particularly in the context of derivatives and integrals.

In calculus, symbolic notations are used to represent various mathematical concepts and operations, allowing for concise and precise expressions of complex mathematical ideas.

Understanding the use of symbolic representation in calculus is essential for effectively solving problems and analyzing mathematical functions.

Calculus and Symbolic Notations

Studying calculus involves utilizing symbolic notations to represent mathematical concepts and relationships. Symbolic representation in calculus is essential for expressing and manipulating complex ideas in a concise and standardized manner.

Here are some key aspects of calculus that rely on symbolic notations:

• Functions and Their Derivatives : Symbolic notations, such as f’(x) and dy/dx, represent the derivatives of functions, enabling the precise analysis of their rates of change.
• Integration : Symbolic representation, like ∫f(x) dx, is used to denote the process of finding the accumulation of quantities and the area under curves.
• Limits : Notations such as lim(x→a) f(x) are crucial for defining the behavior of functions as they approach specific values.
• Differential Equations : Symbolic representation is fundamental for expressing relationships between a function and its derivatives in various applications.

Understanding these symbolic notations is crucial for mastering the concepts of calculus and their applications in diverse fields. In the subsequent section, we will delve into ‘symbolic representation in derivatives.’

Symbolic Representation in Derivatives

Utilizing symbolic notations in calculus, particularly in the context of derivatives, is fundamental for expressing and analyzing the rates of change of functions and their broader applications in mathematics and other fields.

In the table below, we illustrate some common symbolic representations used in derivatives:

Understanding and manipulating these symbolic representations is crucial for solving problems in calculus and its applications.

The symbolic notation allows for concise and precise communication of derivative concepts and plays a significant role in advanced mathematics, physics, engineering, and other fields. Transitioning to the subsequent section, we will delve into ‘integrals and symbolic notation’.

Integrals and Symbolic Notation

The use of symbolic notation in calculus extends to integrals, enabling precise representation and analysis of the accumulation of quantities and their applications across various fields of mathematics and science.

• Antiderivative : The symbolic representation of integrals allows for the determination of antiderivatives, providing a reverse process to differentiation.
• Area Under a Curve : Integrals symbolically represent the area under a curve, facilitating the calculation of complex shapes and regions.
• Accumulation of Quantities : Symbolic notation in integrals helps in understanding the accumulation of quantities over an interval, such as distance traveled or total mass.
• Applications in Science : Symbolic representation in integrals is crucial in physics, engineering, and other sciences, where it is used to analyze concepts like work, energy, and fluid dynamics.

Applications of Symbolic Notation in Geometry

Geometry’s applications of symbolic notation allow for precise and concise representation of geometric concepts and relationships.

Symbols such as angles, lines, and shapes are used to express properties and theorems, making complex ideas easier to understand and work with.

For instance, using symbolic notation, the Pythagorean theorem can be succinctly expressed as a^2 + b^2 = c^2, where ‘a’ and ‘b’ denote the lengths of the triangle’s two shorter sides, and ‘c’ represents the length of the hypotenuse.

Additionally, geometric formulas, such as those for area and volume, can be compactly denoted using symbolic representation, aiding in calculations and problem-solving.

Symbolic notation in geometry streamlines communication and problem-solving, allowing mathematicians, scientists, and engineers to efficiently work with and understand complex geometric relationships and properties.

What are the similarities and differences between symbolic representation in math and in art?

In both math and art, symbolic representation plays a crucial role. It helps convey complex ideas in a simplified manner. However, the main difference lies in their purpose – math uses symbols to represent quantitative relationships, while symbolic representation in art is used to convey emotions, narratives, and abstract concepts.

Advantages of Symbolic Representation in Mathematics

Symbolic representation in mathematics offers a concise and precise means of expressing complex concepts and relationships, facilitating efficient problem-solving and communication within the field.

The advantages of symbolic representation in mathematics include:

• Clarity : Symbolic representation can simplify complex ideas, making them easier to understand and work with.
• Efficiency : It allows for more efficient manipulation of mathematical expressions, leading to streamlined problem-solving processes.
• Generality : Symbols can represent general formulas and concepts, making them applicable to a wide range of specific cases.
• Consistency : Symbolic representation helps maintain consistency in mathematical reasoning and communication, reducing the likelihood of errors.

These advantages make symbolic representation a powerful tool in the practice and understanding of mathematics.

Symbolic representation in mathematics has its origins in ancient civilizations and is based on fundamental principles of notation.

It plays a crucial role in algebra, calculus, and geometry, allowing for complex mathematical concepts to be expressed concisely and accurately.

While some may argue that symbolic notation can be confusing or difficult to understand, its advantages in simplifying and generalizing mathematical ideas far outweigh any potential drawbacks.

Similar Posts

What Is the Symbolic Meaning of Darkness? Fear!

What is the Symbolic Meaning of a Shamrock: Luck!

The Symbolic Meaning of Signs and Subjects Is Called

What Is the Symbolic Meaning of the Valley of Ashes?

What Is the Symbolic Meaning of the Mockingbird? Purity!

What Is the Symbolic Meaning of a Rainbow? Hope!

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Please log in to save materials. Log in

• Resource Library
• 6th Grade Mathematics
• Inequalities

Education Standards

Maryland college and career ready math standards.

Learning Domain: Expressions and Equations

Standard: Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.

Common Core State Standards Math

Cluster: Reason about and solve one-variable equations and inequalities

Balance Scale A

Balance scale b, balance scale c, balancing the scale, equal to, greater than, or less than, symbolic representation.

Lesson Overview

Students use weights to represent equal and unequal situations on a balance scale and represent them symbolically.

Key Concepts

• An equation is a statement that shows that two expressions are equivalent. An equal sign (=) is used between the two expressions to indicate that they are equivalent. You can think of the two expressions as being “balanced.”
• An inequality is a statement that shows that two expressions are unequal. The symbols for “greater than” (>) and “less than” (<) are used to indicate which expression has the greater or lesser value. In an inequality, you can think of the two expressions as being “unbalanced.”

Goals and Learning Objectives

• Explore a balance scale as a model for equations and inequalities.
• Understand that an equation states that two expressions are equivalent using an equal sign (=).
• Understand that an inequality states that one expression is greater than (>) or is less than (<) another expression.
• Use the equal sign (=) and the greater than (>) and less than (<) symbols with rational numbers.

History of Scales

Lesson guide.

Have students read the text about the history of the balance scale and discuss what they know about scales with their partner.

The history of balance scales begins in ancient Egypt, possibly as far back as 5000 BCE. The Egyptians used balance scales to compare the weights of goods. They placed goods on each side of the scale; when the scale became balanced, they knew that the weights of the goods were equal.

• What type of scales have you used, or seen someone else use, to measure things?
• How are the scales you've used similar to, or different from, the balance scale?

• Think about places you visit, like the grocery store or the doctor's office. Have you seen scales there?
• Scales are used to measure weight. What are some of the things we weigh?

Have students look at the Balancing the Scale interactive. Demonstrate how to put 2 and 3 on the left side of the scale.

Ask students: What number(s) do you need to place on the right side of the scale in order to balance the scale? Have students turn and talk to their partners about the question, and then try to balance the scale. After a few minutes, have students share and discuss their findings with the class. When several responses have been verbalized, discuss the definition of equation. Then ask students to represent the balance scale using an equation.

Ask students: How can you make the scale unbalanced so that the left side is heavier than the right side? Have students unbalance the scale and share what they did. Then discuss the definition of inequality. Ask students to represent the unbalanced scale using an inequality.

Possible Answers

• 5; 4 and 1; or 2 and 3
• 2 + 3 = 5; 2 + 3 = 4 + 1; or 2 + 3 = 2 + 3
• Answers will vary.
• Possible answer: 2 + 3 > 3

Balance Scales

• An equation consists of two equivalent expressions that are linked by an equal sign (=).
• An inequality consists of two nonequivalent expressions that are linked by a less than sign (<) or a greater than sign (>).

Using the Balance Scale interactive, place the numbers 2 and 3 on the left side of the scale.

• What number(s) do you need to place on the right side of the scale in order to balance the scale?
• Write an equation to represent the balanced scale.
• Now, “unbalance” the scale so that what is on the left side is greater than what is on the right side.
• Write an inequality to represent the unbalanced scale.

INTERACTIVE: Balancing the Scale

Math Mission

Discuss the Math Mission. Students will set up balanced and unbalanced scales and represent the scales using equations and inequalities.

Set up balanced and unbalanced scales, and represent the scales using equations and inequalities.

Equations and Inequalities

Have students work in pairs on these problems.

ELL: For this task, encourage students to explain their ideas to one another. Math language must be used. Encourage the use of English without discouraging students from using their primary language.

Mathematical Practices

Mathematical Practice 7: Look for and make use of structure.

Look for students who have ideas that help them relate the equal sign (=) and the inequality symbols (< and >) to the tilt of the scale.

Interventions

Student does not understand the task.

• Reread the instructions. Ask your partner for help.
• What does a balanced scale look like?
• What does an unbalanced scale look like?

Student does not know how to write an equation or an inequality to represent the scale.

• What is the value of the left side of the scale? The right side?
• Is the scale balanced or unbalanced?
• What sign can you use to represent a balanced scale?
• What symbols can you use to represent an unbalanced scale?
• What does the < symbol mean?
• What does the > symbol mean?

Student has a solution.

• Explain your strategy for setting up the balance scale.
• Explain how your equation [inequality] represents your balance scale. 

SWDL Check for understanding by asking students to restate new terms or concepts in their own words, as well as any directions they will need to follow during the lesson. Students should be able to explain the relationship between a balanced equation and an unbalanced inequality.

• Answers will vary. A balanced scale that has two numbers on each side, using four different numbers: 1 + 5 = 2 + 4
• A modified scale from the previous step with the right side less than the left side: 1 + 5 > 1 + 4
• An unbalanced scale with one number on one side and two numbers on the other side: 6 > 2 + 1
• A modified scale from the previous step that is balanced: 6 = 5 + 1
• An unbalanced scale that has three numbers on one side and two numbers on the other side, such that the side with the two numbers is greater than the side with the three numbers: 1 + 2 + 3 < 4 + 5
• A modified scale from the previous step that is balanced: 1 + 2 + 3 = 1 + 5
• A modified scale from the previous step that has the same number added on each side: 1 + 2 + 3 + 4 = 1 + 5 + 4. The scale remains balanced after placing the same number on each side.

Set up numbers on both sides of the scale to match the descriptions below. After you set up each scale, write the equation or inequality that represents the scale.

• Use Balance Scale A to set up a balanced scale (both sides equal) that has two numbers on both sides, using four different numbers.
• Modify your scale from the previous step to make the right side less than the left side.
• Use Balance Scale B to set up an unbalanced scale with one number on one side and two numbers on the other side.
• Modify your scale from the previous step to make it balanced.
• Use Balance Scale C to set up an unbalanced scale that has three numbers on one side and two numbers on the other side, such that the side with two numbers is greater than the side with the three numbers.
• Modify your scale again by placing the same number on both sides. What happens?

INTERACTIVE: Balance Scale A

INTERACTIVE: Balance Scale B

INTERACTIVE: Balance Scale C

• If the scale is balanced, write an equation.
• If the scale is not balanced, write an inequality.

Prepare a Presentation

Preparing for ways of thinking.

Look for students who understand that a balanced scale can be represented with an equation and an unbalanced scale can be represented with an inequality statement. Identify different solutions to share in the Ways of Thinking discussion. Make note of students who are having trouble so you can address any misconceptions in the Ways of Thinking discussion.

• Presentations will vary.

Challenge Problem

The Challenge Problem reuses the interactive Balance Scale B. Instruct students to ignore the directions in the interactive, and to use the scale to complete the directions given in the Challenge Problem.

• No, if you add the same amount to each side of an unbalanced scale, the scale will remain unbalanced.
• Choose one equation or inequality that you created in the Balance Scale interactives that you think is particularly interesting.
• Use this equation/inequality to explain your understanding of equations and/or inequalities. In your explanation, refer to the corresponding scale you created using the interactive.

NOTE: Ignore the instructions in the interactive and follow the steps below.

• Place a number on the left side of the scale.
• Place a different number on the right side.
• Is there any one number you can now add on both sides that will balance the scale? Explain.
• An equation consists of two equivalent expressions that are linked by an equal sign.

Make Connections

Have students share their presentations. Review the following points as students share their work:

• Point out different ways students set up a balanced scale that has two numbers on each side, using four different numbers. Ask students why each representation of the scale uses an equation.
• Discuss the different ways students modified the scale to make the right side less than the left side. Some students may have added to the left side, while others may have taken away from the right side. Compare the different inequality statements that represent these approaches. Why do they all use the > symbol?
• Look for different ways of setting up an unbalanced scale with one number on one side and two numbers on the other side. Some students may have the one number greater than the two numbers; other students may have the one number less than the two numbers. Discuss the different inequality statements and how they represent the unbalanced scales. Have students who have devised a way of knowing which inequality symbol to use share their strategies.
• Then discuss how to make an unbalanced scale balanced. What do you need to do to make a scale balanced? Students may have added to one side or taken away from a side. Compare the different representations of the balanced scale. What is similar? (They all use an equal sign.)
• Then have students compare different strategies for finding two numbers that are greater than three numbers and how the unbalanced scale is represented using an inequality statement.
• Be sure at the end of the discussion that students understand the meanings of equation and inequality and how they are modeled using a scale.

Have students who completed the Challenge Problem explain why it is impossible to add the same number to each side of an unbalanced scale to balance the scale. Demonstrate using the Balance Scale B interactive.

ELL: When selecting a group of students to present in the Ways of Thinking section, ensure students present a topic they are confident about. Have students draw diagrams or demonstrate their knowledge in some other way than through verbal language alone.

Performance Task

Ways of thinking: make connections.

Take notes as your classmates explain their understanding of equations and inequalities.

As your classmates present, ask questions such as:

• Should the pointed side of the inequality sign point to the greater or lesser number?
• How does the equation or inequality you wrote represent the balance scale you made?
• What can you do to an unbalanced scale to balance it? How can you represent the balanced scale using an equation or an inequality?
• What can you do to a balanced scale to make the right side greater than the left side? How can you represent this scale using an equation or an inequality?

Equal to, Greater Than, or Less Than?

As students complete these problems, look for students who may be struggling with fraction and decimal concepts, operations, or negative numbers. Pair those students with students who have been successful with these concepts.

SWD: Students with disabilities may have difficulty working with decimals and fractions, especially when applying decimals and fractions to inequalities. If students demonstrate difficulty to the point of frustration, provide direct instruction on the basics for adding decimals and fractions.

Mathematics

As you go over the answers to these problems, encourage students who used mathematical reasoning, properties, or estimation to share their thinking processes.

For example:

• For 5 + 7 ☐ 8 + 12, I saw immediately that 5 + 7 was 12, so 8 + 12 must be greater. Therefore, 5 + 7 < 8 + 12.
• For 1 3 ☐ 1 5 , I knew that if a whole were divided into 3 pieces, each piece would be greater than if that whole were divided into 5 pieces. Therefore, 1 3 > 1 5 .
• For 5.4 + 2.06 ☐ 8 + 0.3, I knew the left side was less than 8, so it had to be less than the right side. Therefore, 5.4 + 2.06 < 8 + 0.3.
• For 9.8 + 6.7 + 0.4 ☐ 6.7 + 9.8 + 0.4, I knew that the two expressions were equal because of the commutative property of addition. Therefore, 9.8 + 6.7 + 0.4 = 6.7 + 9.8 + 0.4.
• For 1 2 ☐ 1 4 + 1 3 , I knew that 1 2 = 1 4 + 1 4 , and I knew 1 3 was greater than 1 4 . Therefore, 1 2 < 1 4 + 1 3 .

a. = b. < c. > d. < e. = f. < g. = h. < i. < j. >

• Place =, >, or < in the boxes in the equations and inequalities.

INTERACTIVE: Equal to, Greater Than, or Less Than?

A Possible Summary

A statement that shows that two expressions are equal to one another is an equation. You can use an equal sign (=) to show that the expressions are equal. A statement that shows that two expressions are unequal is an inequality statement; an inequality statement specifies which expression has the greater value (or lesser value). You can use the less than (<) or greater than (>) symbols to show which expression is less than or greater than the other.

Formative Assessment

Summary of the math: equations and inequalities.

Write a summary about equations and inequalities based on what you learned today.

Check your summary:

• Do you explain the difference between an equation and an inequality?
• Do you explain the meaning of the signs <, >, and =?

Reflect On Your Work

Have each student write a quick reflection before the end of the class. Review the reflections to learn if students understand how equations and inequalities can be represented using a balance scale.

Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.

A balance scale helps me understand equations and inequalities because …

Writing the Symbolic Representation of a Function (Graph → Symbolic)

Let's get started.

You will learn to represent functions in different forms and use your graphing calculator to find equations that match different graphs. 

TEKS Standards and Student Expectations

A(2) Linear functions, equations, and inequalities. The student applies the mathematical process standards when using properties of linear functions to write and represent in multiple ways, with and without technology, linear equations, inequalities, and systems of equations. The student is expected to:

A(2)(C) write linear equations in two variables given a table of values, a graph, and a verbal description

A(7) Quadratic functions and equations. The student applies the mathematical process standards when using graphs of quadratic functions and their related transformations to represent in multiple ways and determine, with and without technology, the solutions to equations. The student is expected to:

A(7)(A) graph quadratic functions on the coordinate plane and use the graph to identify key attributes, if possible, including x -intercept, y -intercept, zeros, maximum value, minimum values, vertex, and the equation of the axis of symmetry

Resource Objective(s)

Given the graph of a linear or quadratic function, the student will write the symbolic representation of the function.

Essential Questions

What are the different forms of linear functions?

How can a graphing calculator be used to match a graph to a linear equation?

How is a quadratic equation different from a linear equation? 

• Linear Function
• Quadratic Equation

Slope-Intercept Form

Introduction.

This table shows the three different ways to represent linear functions .

We’ll first look at slope-intercept form . Remember that the slope is the rise over the run (i.e., the change in y -value over the change in x -value.)

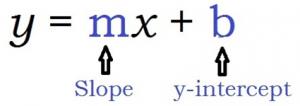
To review slope-intercept form, use this  linked interactive activity . Move the sliders one at a time to change the slope (the y -intercept). After you have experimented with the activity, answer the questions below.

Using a Calculator with Slope-Intercept Form

Even the best mathematicians need ways to check their work. We’re going to use the graphing calculator to make sure we have the correct answer.

If you need a graphing calculator, you can use an online calculator here .

Which equation best describes the following graph?

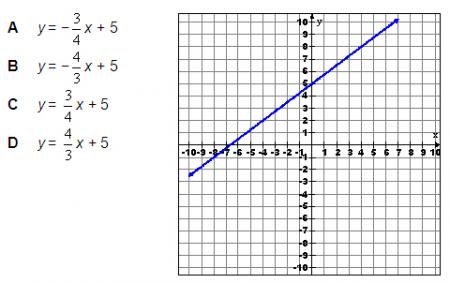
If you are not sure of the answer, you can use your calculator three different ways to double check. You should learn all three methods because there will be times when one of the methods will not be obvious.

We will try option C:  y =  3/4 x   + 5.

Method 1: Match the Graph

You can use your graphing calculator to look at a graph of an equation by following these steps:

• Enter the equation.
• Graph the equation.

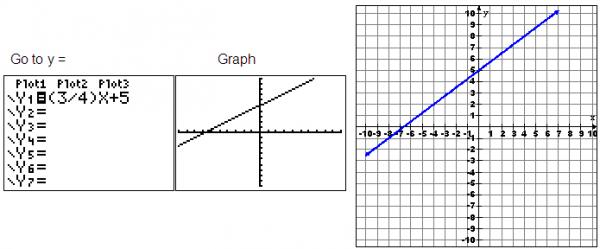
The graph on the calculator looks similar to the given graph, but we can’t be sure.  We certainly can tell the line is increasing. Options A and B are definitely wrong because they have a negative slope.

Method 2: Match the Graph to the Table

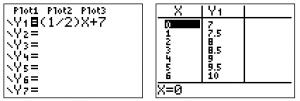
You can also use your graphing calculator to match the table of values from an equation by following these steps:

• Use 2nd Graph to view the table.

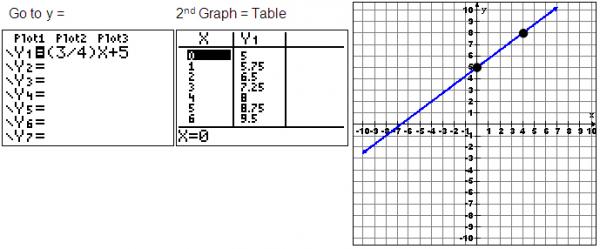
You can see that the two points (0, 5) and (4, 8) are on the line and in the table.

Method 3: Match Points on a Graph Using TRACE

You can also use the graphing calculator to find points on the line using the following steps:

• Press the TRACE button and type x -values that are on the line.

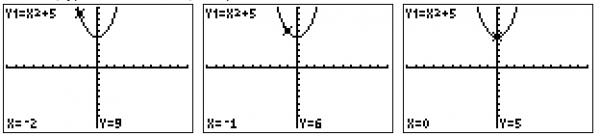
We can see that the point (-4, 2) is on the graph, so we'll use the TRACE button to find where x equals -4.

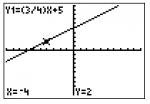
The point is on the line. Just to be sure, we will try another point at (-8, -1)

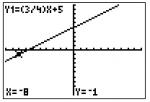
This point is also on the line.  Now we know that option C is correct.

Standard Form Equations and Practice

What if the equation is not in slope-intercept form? This is a standard form equation.

Ax + By = C

You can manipulate the equation, so you can use the graphing calculator to check your answer .

Forms of Linear Equations

To change a standard form equation to a slope-intercept form, you must isolate the variable y on the left side of the equation.

You can review the steps to change an equation from standard form to slope-intercept form in these 2 examples.

Example 1: Standard form to slope-intercept form .

Example 2: Standard form to slope-intercept form .

The following is a typical question you might see that has answer choices in standard form.

Which equation best describes the graph shown below?

A )   x   -    2 y   =   14   B )   x   -    2 y   =   -  14   C )   x   +   2 y   =   14   D )   x   +   2 y   =   -  14

Solving each equation for y , the equations are:

A )   y = 1 2 x   -   7 B )   y = 1 2 x   +   7 C )   y   =   - 1 2 x   +   7 D )   y =   - 1 2 x   -   7

It seems that the right equation is option B .

When we enter the equation in to the graphing calculator under Y=, we see the following results.

According to this, the points (0, 7), (2, 8) (4, 9) and (6, 10) should all be points on the graph. To check this, we substitute the x - and y -values from these points into x − 2 y = −14.

We know B is correct!

Here is how you know an answer is wrong:

Option D is incorrect because the points (0, 7), (2, 8) (4, 9) and (6, 10) will not satisfy the equation x + 2 y = −14.

Quadratic Functions and Practice

Next we will look at writing equations for quadratic functions. This is the form of a quadratic function.

y   =   a x 2   +   b x   +   c

Quadratic functions are parabolas and either have a U-shape or a mountain shape. Parabolas with a positive "a" value have a U-shape, and those with a negative "a" value have a mountain shape.

In addition, you know how to use a calculator to check for the correct answer, so you can input these equations in the equation editor (Y=) as well.

Which quadratic equation best represents the parabola shown below?

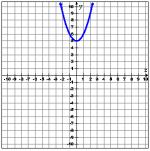
You can test each of the answer choices by using your graphing calculator to eliminate obviously wrong answers.

• Enter the equation in Y=.

Each graph looks like this.

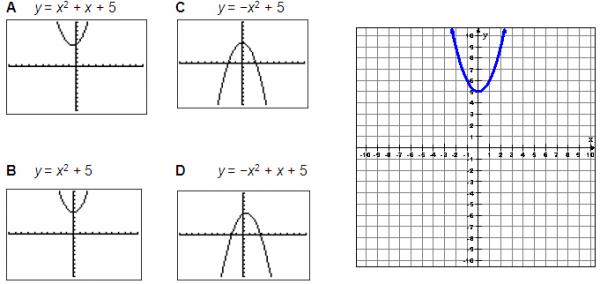
Options  C and D are obviously wrong because they are facing down. 

Now we can look at the table values for the remaining graphs. The graph we were given contains the points (-2, 9), (-1, 6), (0, 5), (1, 6), and (2, 9). Use the TABLE.

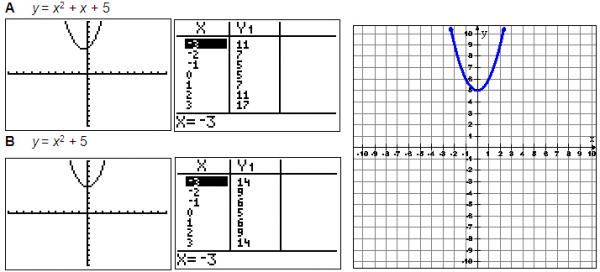
Now you can confidently pick option  B as your answer.

Remember, you can also use the TRACE key to check points on the graph. Press TRACE, type in the x -value, and press ENTER.

Vocabulary Activity

Journal activity.

Copy and paste the link code above.

Related Items

On Visual and Symbolic Representations

• Conference paper
• Cite this conference paper

• L. E. Moreno Armella 3 &
• Ana Isabel Sacristán 3  

Part of the book series: NATO ASI Series ((NATO ASI F,volume 138))

316 Accesses

Activities intended to enhance the theoretical framework and the methodology of mathematical education have intensified during the last decade. We have witnessed, for instance, the publication of diverse cognitive and epistemological studies - in both books and journals - converging to constructivist stances. See [6], [9]. However, it is still necessary to try to make clear in our own work, the meaning of the terms we are using. At present, the general discussion involves the mise en scene of Representation Theory in the context of computers.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Eisenberg T., Dreyfus, T. (1986). On visual versus analytical thinking in mathematics. Proceedings PME-10, London.

Google Scholar  

Gardiner, T. (1984). Human Activity: The soft underbelly of mathematics? The Mathematical Intelligencer, 6(3), 22–27.

Article   MathSciNet   Google Scholar  

Hallett, D. H. (1991). Visualisation and Calculus Reform. In: Zimmermann W., Cunningham, S. (eds), Visualization in Teaching and Learning Mathematics. MAA Note Series.

Mandelbrot, B. (1992). Fractals and the rebirth of experimental mathematics. Foreword to: Peitgen, H.-O., Jürgens H., Saupe, D. Fractals for the Classroom, Vol. 1. New York: Springer-Verlag.

Moreno, L. (1992). Calculus: A historical and didactic perspective. HPM-Meeting, Toronto.

Nesher P., Kilpatrik, J. (eds) (1990). Mathematics and Cognition, ICMI Study Series. Cambridge Univ. Press.

Piaget J., García, R. (1989). Psychogenesis and the History of Science. (translated into English by Helga Fieder). New York: Columbia University Press.

Sfard, A. (1991). On the dual nature of mathematical conceptions. Educational Studies in Mathematics, 22, 1–36.

Tall, D. (ed) (1991). Advanced Mathematical Thinking. Kluwer Academic Publishers.

Tall D., Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, vol 11, 271–284.

Download references

Author information

Authors and affiliations.

Departamento de Matemática Educativa, CINVESTAV-IPN, Dakota 379, Col. Nápoles;, C.P 03810, México D.F., Mexico

L. E. Moreno Armella & Ana Isabel Sacristán

You can also search for this author in PubMed   Google Scholar

Editor information

Editors and affiliations.

Department of Mathematics, Statistics and Computing Institute of Education, University of London, London, WC1H 0AL, UK

Rosamund Sutherland

Mathematics Faculty, The Open University, Milton Keynes, MK7 6AA, UK

Rights and permissions

Reprints and permissions

Copyright information

© 1995 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper.

Moreno Armella, L.E., Sacristán, A.I. (1995). On Visual and Symbolic Representations. In: Sutherland, R., Mason, J. (eds) Exploiting Mental Imagery with Computers in Mathematics Education. NATO ASI Series, vol 138. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-57771-0_12

Download citation

DOI : https://doi.org/10.1007/978-3-642-57771-0_12

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-642-63350-8

Online ISBN : 978-3-642-57771-0

eBook Packages : Springer Book Archive

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.4: Analyzing Symbolic Arguments

• Last updated
• Save as PDF
• Page ID 92958

• David Lippman
• Pierce College via The OpenTextBookStore

Our previous work with statements and truth tables allows us to analyze and to evaluate arguments using logic. Here, the word argument is not used in the sense that two or more people disagree with each other. Rather, argument is used in the sense of trying to make a convincing case that something must be true using ideas of logic.

The everyday notion of an argument is that it is used to convince us to believe something. An argument is formed with two components: a set of premises and a conclusion . The thing that we are being encouraged to believe is the conclusion, while the premises are the statements offered as supporting evidence for the conclusion that we want to make.

Here are some examples of arguments.

\(\begin{array} {ll} \text{Premise 1:} & \text{If I do not have to go to summer school, then I will get an internship.} \\ \text{Premise 2:} & \text{I have to go to summer school.} \\ \text{Conclusion:} & \text{I won’t get an internship.} \end{array}\)

\(\begin{array} {ll} \text{Premise 1:} & \text{I studied or I failed the class.} \\ \text{Premise 2:} & \text{I did not fail the class.} \\ \text{Conclusion:} & \text{I studied.} \end{array}\)

To give an argument is to give some premises in support of a conclusion. But suppose that you are given an argument for some conclusion such as the in the previous examples. How can you tell whether that argument is a good argument or bad argument? Our goal in this section will be to analyze an argument to determine whether or not it is a "good" argument.

For an argument to be "good," the truth of an argument’s premises must guarantee the conclusion occurs. If this is the case, we will say that the argument is valid . When the truth of an argument’s premises fails to guarantee the conclusion, we will say that the argument is invalid .

Valid Argument

An argument is valid if its conclusion necessarily follows from the premises. Otherwise, the argument is invalid.

For the conclusion of an argument to necessarily follow from the premises, it means that the symbolic statement

[ Premise 1 \(\wedge\) Premise 2 ] \(\rightarrow\) Conclusion

is always true for all possible truth values of the simple statements involved. You might recall that these types of statements are known as tautologies. If at least one truth value of this symbolic statement is false, then the argument is invalid. Sometimes, this type of argument is called a fallacy .

It is important to note here that if an argument is valid, it only means that conclusion necessarily follows from the premises. It does not mean that conclusion is true.

Arguments can be analyzed using truth tables.

Analyzing Arguments Using Truth Tables

To analyze an argument with a truth table:

• Represent each of the premises symbolically
• Create a conditional statement, joining all the premises to form the antecedent, and using the conclusion as the consequent.
• Create a truth table for the statement. If it is always true, then the argument is valid.

Consider the argument

\(\begin{array} {ll} \text{Premise 1:} & \text{If you bought bread, then you went to the store.} \\ \text{Premise 2:} & \text{You bought bread.} \\ \text{Conclusion:} & \text{You went to the store.} \end{array}\)

While this example is fairly obviously a valid argument, we can analyze it using a truth table by representing each of the premises symbolically. We can then form a conditional statement showing that the premises together imply the conclusion. If the truth table is a tautology (always true), then the argument is valid.

We’ll let \(b\) represent “ you bought bread ” and \(s\) represent “ you went to the store ”. Then, the argument becomes

\(\begin{array} {ll} \text{Premise 1:} & b \rightarrow s \\ \text{Premise 2:} & b \\ \text{Conclusion:} & s \end{array}\)

To test the validity, we look at whether the combination of both premises implies the conclusion. Is it true that \([(b \rightarrow s) \wedge b] \rightarrow s ?\)

\(\begin{array}{|c|c|c|c|c|} \hline b & s & b \rightarrow s & (b \rightarrow s) \wedge b & {[(b \rightarrow s) \wedge b] \rightarrow s} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T \rightarrow T = T} & \mathrm{T \wedge T = T} & \mathrm{T \rightarrow T = T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T \rightarrow F = F} & \mathrm{F \wedge T = F} & \mathrm{F \rightarrow F = T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F \rightarrow T = T} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow T = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F \rightarrow F = T} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow F = T} \\ \hline \end{array}\)

The last column of the truth table shows that \([(b \rightarrow s) \wedge b] \rightarrow s\) is always true. This is a tautology, and so the argument is valid. Based on these premises, it is correct to conclude " You went to the store."

The next two examples revisit the arguments presented in Example 1 and Example 2. Let's determine whether the arguments presented there were examples of valid or invalid reasoning.

Determine whether the argument is valid or invalid:

We’ll let \(p\) represent “ I go to summer school ” and \(q\) represent “ I will get an internship ”. In symbolic form, the argument becomes

\(\begin{array} {ll} \text{Premise 1:} & \sim p \rightarrow q \\ \text{Premise 2:} & p \\ \text{Conclusion:} & \sim q \end{array}\)

Form a truth table to find the truth values for \([( \sim p \rightarrow q) \wedge p] \rightarrow \; \sim q \).

\(\begin{array}{|c|c|c|c|c|c|c|} \hline p & q & \sim p & \sim q & \sim p \rightarrow q & (\sim p \rightarrow q) \wedge p & {[( \sim p \rightarrow q) \wedge p] \rightarrow \; \sim q } \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F \rightarrow T = T} & \mathrm{T \wedge T = T} & \mathrm{T \rightarrow F = F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F \rightarrow F = T} & \mathrm{T \wedge T = T} & \mathrm{T \rightarrow T = T}\\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T \rightarrow T = T} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow F = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T \rightarrow F = F} & \mathrm{F \wedge F = F} & \mathrm{F \rightarrow T = T}\\ \hline \end{array}\)

One truth value for \([( \sim p \rightarrow q) \wedge p] \rightarrow \; \sim q \) in the last column of the table is False, while the remaining truth values are True. This is not a tautology, and so the argument is invalid. Based on these premises, it is not correct to conclude " I won't get an internship."

Let \(s=\) I studied and \(f=\) I failed the class.

The premises and conclusion can be stated as:

\(\begin{array} {ll} \text{Premise 1:} & s \vee f \\ \text{Premise 2:} & \sim f \\ \text{Conclusion:} & s \end{array}\)

Form a truth table to find the truth values for \([(s \vee f) \wedge \sim f] \rightarrow s .\)

\(\begin{array}{|c|c|c|c|c|} \hline s & f & s \vee f & \sim f & (s \vee f) \; \wedge \sim f & {[(s \vee f) \; \wedge \sim f] \rightarrow s} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T \vee T =T} & \mathrm{F} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow T = T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T \vee F =T} & \mathrm{T} & \mathrm{T \wedge T = T} & \mathrm{T \rightarrow T = T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F \vee T =T} & \mathrm{F} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow F = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F \vee F = F} & \mathrm{T} & \mathrm{F \wedge T = F} & \mathrm{F \rightarrow F = T} \\ \hline \end{array}\)

All truth values for \([(s \vee f) \wedge \sim f] \rightarrow s \) in the last column of the table are True. This is a tautology, and so the argument is valid. Based on these premises, it is correct to conclude " I studied."

Try it Now 1

Determine whether the argument is valid:

\(\begin{array} {ll} \text{Premise 1:} & \text{If I have a shovel, I can dig a hole.} \\ \text{Premise 2:} & \text{I dug a hole.} \\ \text{Conclusion:} & \text{Therefore, I had a shovel.} \end{array}\)

Let \(S=\) have a shovel and \(D=\) dig a hole. Premise 1 is equivalent to \(S \rightarrow D\). Premise 2 is \(D\). The conclusion is \(S\). We are testing \([(S \rightarrow D) \wedge D] \rightarrow S\).

\(\begin{array}{|c|c|c|c|c|} \hline S & D & S \rightarrow D & (S \rightarrow D) \wedge D & {[(S \rightarrow D) \wedge D] \rightarrow S} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

This is not a tautology, and so this is an invalid argument. It is not correct to conclude "I had a shovel."

The final example follows the same process of using a truth table to analyze an argument for validity. However, this argument contains 3 simple statements, and its truth table is a bit more complex.

\(\begin{array} {ll} \text{Premise 1:} & \text{If I go to the mall, then I’ll buy new jeans.} \\ \text{Premise 2:} & \text{If I buy new jeans, I’ll buy a shirt to go with it.} \\ \text{Conclusion:} & \text{If I go to the mall, I’ll buy a shirt.} \end{array}\)

Let \(m=\) I go to the mall , \(j=\) I buy jeans , and \(s=\) I buy a shirt .

\(\begin{array} {ll} \text{Premise 1:} & m \rightarrow j \\ \text{Premise 2:} & j \rightarrow s \\ \text{Conclusion:} & m \rightarrow s \end{array}\)

We can construct a truth table for \([(m \rightarrow j) \wedge(j \rightarrow s)] \rightarrow(m \rightarrow s) .\) Try to recreate each step to verify how the truth table was constructed.

\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline m & j & s & m \rightarrow j & j \rightarrow s & (m \rightarrow j) \wedge(j \rightarrow s) & m \rightarrow s & {[(m \rightarrow j) \wedge(j \rightarrow s)] \rightarrow(m \rightarrow s)} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \end{array}\)

From the final column of the truth table, all truth values for \([(m \rightarrow j) \wedge(j \rightarrow s)] \rightarrow(m \rightarrow s)\) are True. This is a tautology, and so the argument is valid. Based on these premises, it is correct to conclude " If I go to the mall, I'll buy a shirt."

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

20.2: Concrete, representational/visual/Pictorial, and abstract/symbolic models

• Last updated
• Save as PDF
• Page ID 87591

Table of Contents

• Concrete, representational and abstracts models of math.
• Questioning used in mathematics.
• Teaching Math Vocabulary
• Building Math Fluency
• Error Analysis

This next section contains excerpts from the National Center on Intensive Intervention. (2016). Principles for designing intervention in mathematics. Washington, DC: Office of Special Education, U.S. Department of Education and is in the pubic domain.

Special education instructors, math interventionists, and others working with students who struggle with mathematics may find this guide helpful. The strategies presented in this guide should be used in conjunction with teaching guides developed for specific mathematical concepts. Specific topics covered include the following:

Explicit, Systematic Instruction (aka Direct Instruction)- Chapter 4 •Effective Questioning in the math classroom (questioning was introduced in chapter 9) •Concrete, Representational/Visual/Pictorial, Abstract/Symbolic Models •Teaching Mathematical Vocabulary and Symbols •Fluency Building •Error Analysis

Concrete, Representational/Visual/Pictorial, and Abstract/Symbolic Models

Using multiple representations to teach mathematics allows students to understand mathematics conceptually, often as a result of developing or “seeing” an algorithm or strategy on their own. By building strong conceptual understanding, students are able to better generalize skills and understand algorithms (Gersten et al., 2009; Jones, Inglis, Gilmore, & Evans, 2013; Miller & Hudson, 2007). Moving through each phase is essential for every skill area, not just for early foundational skills (Jayanthi et al., 2008; National Mathematics Advisory Panel, 2008; Stein, Kinder, Silbert, & Carnine, 2005; Woodward, 2006). A description of the three phases follows.

1. Concrete: In this phase, students use three-dimensional manipulatives to solve problems and to gain a better conceptual understanding of a concept. Examples of manipulatives include counting bears, snap cubes, base-10 blocks, real or plastic money, clocks, fraction tiles, geoboards, Algeblocks, algebra tiles, and others. It is helpful to use a variety of manipulatives (if possible) to teach concepts so that students can generalize the concept being taught. Using an assortment of manipulatives is not always possible, however; some concepts can only be taught using a specific manipulative. It is important to note that although students may demonstrate proper use of a manipulative, this does not mean that they understand the concepts behind use of the manipulative. Explicit instruction and student verbalizations, such as explaining the concept or demonstrating use of the manipulative while they verbally describe the mathematical procedure, should accompany all manipulative use.

2. Representational/Visual/Pictorial: Students use two-dimensional pictures, drawings, or diagrams to solve problems. These pictures, drawings, or diagrams may be given to the students, or they may draw them when presented with a problem. These representations should be used to connect and solve the same concepts previously taught using concrete objects. Representational models also may be presented virtually through websites or tablet applications. With a virtual representation, students move the image with a mouse or with their hands.

3. Abstract/Symbolic: During this phase, students are expected to solve problems through the use of numbers and symbols rather than with the use of concrete objects or visual representations. Students are often expected to memorize facts and algorithms as well as to build fluency.

Following is an example that demonstrates use of the three phases to solve the problem 4 + 5: