case study on simple harmonic motion

15.1 Simple Harmonic Motion

Learning objectives.

By the end of this section, you will be able to:

• Define the terms period and frequency
• List the characteristics of simple harmonic motion
• Explain the concept of phase shift
• Write the equations of motion for the system of a mass and spring undergoing simple harmonic motion
• Describe the motion of a mass oscillating on a vertical spring

When you pluck a guitar string, the resulting sound has a steady tone and lasts a long time ( Figure 15.2 ). The string vibrates around an equilibrium position, and one oscillation is completed when the string starts from the initial position, travels to one of the extreme positions, then to the other extreme position, and returns to its initial position. We define periodic motion to be any motion that repeats itself at regular time intervals, such as exhibited by the guitar string or by a child swinging on a swing. In this section, we study the basic characteristics of oscillations and their mathematical description.

Period and Frequency in Oscillations

In the absence of friction, the time to complete one oscillation remains constant and is called the period ( T ) . Its units are usually seconds, but may be any convenient unit of time. The word ‘period’ refers to the time for some event whether repetitive or not, but in this chapter, we shall deal primarily in periodic motion, which is by definition repetitive.

A concept closely related to period is the frequency of an event. Frequency ( f ) is defined to be the number of events per unit time. For periodic motion, frequency is the number of oscillations per unit time. The relationship between frequency and period is

The SI unit for frequency is the hertz (Hz) and is defined as one cycle per second :

A cycle is one complete oscillation .

Example 15.1

Determining the frequency of medical ultrasound.

Solve to find

Significance

Characteristics of simple harmonic motion.

A very common type of periodic motion is called simple harmonic motion (SHM) . A system that oscillates with SHM is called a simple harmonic oscillator .

Simple Harmonic Motion

In simple harmonic motion, the acceleration of the system, and therefore the net force, is proportional to the displacement and acts in the opposite direction of the displacement.

A good example of SHM is an object with mass m attached to a spring on a frictionless surface, as shown in Figure 15.3 . The object oscillates around the equilibrium position, and the net force on the object is equal to the force provided by the spring. This force obeys Hooke’s law F s = − k x , F s = − k x , as discussed in a previous chapter.

If the net force can be described by Hooke’s law and there is no damping (slowing down due to friction or other nonconservative forces), then a simple harmonic oscillator oscillates with equal displacement on either side of the equilibrium position, as shown for an object on a spring in Figure 15.3 . The maximum displacement from equilibrium is called the amplitude ( A ) . The units for amplitude and displacement are the same but depend on the type of oscillation. For the object on the spring, the units of amplitude and displacement are meters.

What is so significant about SHM? For one thing, the period T and frequency f of a simple harmonic oscillator are independent of amplitude. The string of a guitar, for example, oscillates with the same frequency whether plucked gently or hard.

Two important factors do affect the period of a simple harmonic oscillator. The period is related to how stiff the system is. A very stiff object has a large force constant ( k ) , which causes the system to have a smaller period. For example, you can adjust a diving board’s stiffness—the stiffer it is, the faster it vibrates, and the shorter its period. Period also depends on the mass of the oscillating system. The more massive the system is, the longer the period. For example, a heavy person on a diving board bounces up and down more slowly than a light one. In fact, the mass m and the force constant k are the only factors that affect the period and frequency of SHM. To derive an equation for the period and the frequency, we must first define and analyze the equations of motion. Note that the force constant is sometimes referred to as the spring constant .

Equations of SHM

Consider a block attached to a spring on a frictionless table ( Figure 15.4 ). The equilibrium position (the position where the spring is neither stretched nor compressed) is marked as x = 0 x = 0 . At the equilibrium position, the net force is zero.

Work is done on the block to pull it out to a position of x = + A , x = + A , and it is then released from rest. The maximum x -position ( A ) is called the amplitude of the motion. The block begins to oscillate in SHM between x = + A x = + A and x = − A , x = − A , where A is the amplitude of the motion and T is the period of the oscillation. The period is the time for one oscillation. Figure 15.5 shows the motion of the block as it completes one and a half oscillations after release. Figure 15.6 shows a plot of the position of the block versus time. When the position is plotted versus time, it is clear that the data can be modeled by a cosine function with an amplitude A and a period T . The cosine function cos θ cos θ repeats every multiple of 2 π , 2 π , whereas the motion of the block repeats every period T . However, the function cos ( 2 π T t ) cos ( 2 π T t ) repeats every integer multiple of the period. The maximum of the cosine function is one, so it is necessary to multiply the cosine function by the amplitude A .

Recall from the chapter on rotation that the angular frequency equals ω = d θ d t ω = d θ d t . In this case, the period is constant, so the angular frequency is defined as 2 π 2 π divided by the period, ω = 2 π T ω = 2 π T .

The equation for the position as a function of time x ( t ) = A cos ( ω t ) x ( t ) = A cos ( ω t ) is good for modeling data, where the position of the block at the initial time t = 0.00 s t = 0.00 s is at the amplitude A and the initial velocity is zero. Often when taking experimental data, the position of the mass at the initial time t = 0.00 s t = 0.00 s is not equal to the amplitude and the initial velocity is not zero. Consider 10 seconds of data collected by a student in lab, shown in Figure 15.7 .

The data in Figure 15.7 can still be modeled with a periodic function, like a cosine function, but the function is shifted to the right. This shift is known as a phase shift and is usually represented by the Greek letter phi ( ϕ ) ( ϕ ) . The equation of the position as a function of time for a block on a spring becomes

This is the generalized equation for SHM where t is the time measured in seconds, ω ω is the angular frequency with units of inverse seconds, A is the amplitude measured in meters or centimeters, and ϕ ϕ is the phase shift measured in radians ( Figure 15.8 ). It should be noted that because sine and cosine functions differ only by a phase shift, this motion could be modeled using either the cosine or sine function.

The velocity of the mass on a spring, oscillating in SHM, can be found by taking the derivative of the position equation:

Because the sine function oscillates between –1 and +1, the maximum velocity is the amplitude times the angular frequency, v max = A ω v max = A ω . The maximum velocity occurs at the equilibrium position ( x = 0 ) ( x = 0 ) when the mass is moving toward x = + A x = + A . The maximum velocity in the negative direction is attained at the equilibrium position ( x = 0 ) ( x = 0 ) when the mass is moving toward x = − A x = − A and is equal to − v max − v max .

The acceleration of the mass on the spring can be found by taking the time derivative of the velocity:

The maximum acceleration is a max = A ω 2 a max = A ω 2 . The maximum acceleration occurs at the position ( x = − A ) ( x = − A ) , and the acceleration at the position ( x = − A ) ( x = − A ) and is equal to a max a max .

Summary of Equations of Motion for SHM

In summary, the oscillatory motion of a block on a spring can be modeled with the following equations of motion:

Here, A is the amplitude of the motion, T is the period, ϕ ϕ is the phase shift, and ω = 2 π T = 2 π f ω = 2 π T = 2 π f is the angular frequency of the motion of the block.

Example 15.2

Determining the equations of motion for a block and a spring.

Work is done on the block, pulling it out to x = + 0.02 m . x = + 0.02 m . The block is released from rest and oscillates between x = + 0.02 m x = + 0.02 m and x = −0.02 m . x = −0.02 m . The period of the motion is 1.57 s. Determine the equations of motion.

All that is left is to fill in the equations of motion:

The Period and Frequency of a Mass on a Spring

One interesting characteristic of the SHM of an object attached to a spring is that the angular frequency, and therefore the period and frequency of the motion, depend on only the mass and the force constant, and not on other factors such as the amplitude of the motion. We can use the equations of motion and Newton’s second law ( F → net = m a → ) ( F → net = m a → ) to find equations for the angular frequency, frequency, and period.

Consider the block on a spring on a frictionless surface. There are three forces on the mass: the weight, the normal force, and the force due to the spring. The only two forces that act perpendicular to the surface are the weight and the normal force, which have equal magnitudes and opposite directions, and thus sum to zero. The only force that acts parallel to the surface is the force due to the spring, so the net force must be equal to the force of the spring:

Substituting the equations of motion for x and a gives us

Cancelling out like terms and solving for the angular frequency yields

The angular frequency depends only on the force constant and the mass, and not the amplitude. The angular frequency is defined as ω = 2 π / T , ω = 2 π / T , which yields an equation for the period of the motion:

The period also depends only on the mass and the force constant. The greater the mass, the longer the period. The stiffer the spring, the shorter the period. The frequency is

Vertical Motion and a Horizontal Spring

When a spring is hung vertically and a block is attached and set in motion, the block oscillates in SHM. In this case, there is no normal force, and the net effect of the force of gravity is to change the equilibrium position. Consider Figure 15.9 . Two forces act on the block: the weight and the force of the spring. The weight is constant and the force of the spring changes as the length of the spring changes.

When the block reaches the equilibrium position, as seen in Figure 15.9 , the force of the spring equals the weight of the block, F net = F s − m g = 0 F net = F s − m g = 0 , where

From the figure, the change in the position is Δ y = y 0 − y 1 Δ y = y 0 − y 1 and since − k ( − Δ y ) = m g − k ( − Δ y ) = m g , we have

If the block is displaced and released, it will oscillate around the new equilibrium position. As shown in Figure 15.10 , if the position of the block is recorded as a function of time, the recording is a periodic function.

If the block is displaced to a position y , the net force becomes F net = k ( y 0 − y ) − m g = 0 F net = k ( y 0 − y ) − m g = 0 . But we found that at the equilibrium position, m g = k Δ y = k y 0 − k y 1 m g = k Δ y = k y 0 − k y 1 . Substituting for the weight in the equation yields

Recall that y 1 y 1 is just the equilibrium position and any position can be set to be the point y = 0.00 m . y = 0.00 m . So let’s set y 1 y 1 to y = 0.00 m . y = 0.00 m . The net force then becomes

This is just what we found previously for a horizontally sliding mass on a spring. The constant force of gravity only served to shift the equilibrium location of the mass. Therefore, the solution should be the same form as for a block on a horizontal spring, y ( t ) = A cos ( ω t + ϕ ) . y ( t ) = A cos ( ω t + ϕ ) . The equations for the velocity and the acceleration also have the same form as for the horizontal case. Note that the inclusion of the phase shift means that the motion can actually be modeled using either a cosine or a sine function, since these two functions only differ by a phase shift.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/15-1-simple-harmonic-motion

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.1: Simple Harmonic Motion

• Last updated
• Save as PDF
• Page ID 2883

A Foucault pendulum is a pendulum suspended from a long wire, that is sustained in motion over long periods. Due to the axial rotation of the Earth, the plane of motion of the pendulum shifts at a rate and direction dependent on its latitude: clockwise in the Northern Hemisphere and counterclockwise in the Southern Hemisphere. At the poles the plane rotates once per day, while at the equator it does not rotate at all.

Simple Harmonic Motion

Many objects vibrate or oscillate – an object on the end of a spring, a tuning fork, the balance wheel of a watch, a pendulum, the strings of a guitar or a piano. When we speak of a vibration or oscillation, we mean the motion of an object that repeats itself, back and forth, over the same path. This motion is also known as simple harmonic motion , often denoted as SHM.

A useful design for examining SHM is an object attached to the end of a spring and laid on a surface. The surface supports the object so its weight (the force of gravity) doesn’t get involved in the forces. The spring is considered to be weightless.

The position shown in the illustration is the equilibrium position . This position is the middle, where the spring is not exerting any force either to the left or to the right. If the object is pulled to the right, the spring will be stretched and exert a restoring force to return to the weight to the equilibrium position. Similarly, if the object is pushed to the left, the spring will be compressed and will exert a restoring force to return the object to its original position. The magnitude of the restoring force, F, in either case must be directly proportional to the distance, x, the spring has been stretched or compressed. (A spring must be chosen that obeys this requirement.)

F=−kx

In the equation above, the constant of proportionality is called the spring constant . The spring constant is represented by k and its units are N/m. This equation is accurate as long as the spring is not compressed to the point that the coils touch nor stretched beyond elasticity.

Suppose the spring is compressed a distance x=A, and then released. The spring exerts a force on the mass pushing it toward the equilibrium position. When the mass is at the maximum displacement position, velocity is zero because the mass is changing direction. At the position of maximum displacement, the restoring force is at its greatest - the acceleration of the mass will be greatest. As the mass moves toward the equilibrium position, the displacement decreases, so the restoring force decreases and the acceleration decreases. When the mass reaches the equilibrium position, there is no restoring force. The acceleration, therefore, is zero, but the mass is moving at its highest velocity. Because of its inertia, the mass will continue past the equilibrium position, and stretch the string. As the spring is stretched further, the displacement increases, the restoring force increases, the acceleration toward the equilibrium position increases, and the velocity decreases. Eventually, when the mass reaches its maximum displacement on this side of the equilibrium position, the velocity has returned to zero and the restoring force and acceleration have returned to the maximum. In a frictionless system, the mass would oscillate forever, but in a real system, friction gradually reduces the motion until the mass returns to the equilibrium position and motion stops.

Imagine an object moving in uniform circular motion. Remember the yo-yo we spin over our heads? In your mind, turn the circle so that you are looking at it on edge; imagine you are eight feet tall, and the yo-yo's circle is exactly at eye level. The object will move back forth in the same way that a mass moves in SHM. It moves consistently from the far left to the far right until you stop spinning the yo-yo. Another example is to imagine a glowing light bulb riding a merry-go-round at night. You are sitting in a chair at some distance from the merry-go-round so that the only part of the system that is visible to you is the light bulb. The movement of the light will appear to you to be back and forth in simple harmonic motion. Circular motion and simple harmonic motion have a lot in common.

The greatest displacement of the mass from the equilibrium position is called the amplitude of the motion. One cycle refers to the complete to-and-fro motion that starts at some position, goes all the way to one side, then all the way to the other side, and returns to the original position. The period , T, is the time required for one cycle and the frequency , f, is the number of cycles that occur in exactly 1.00 second. The frequency, in this case, is the reciprocal of the period.

When a 500. kg crate of cargo is placed in the bed of a pickup truck, the truck’s springs compress 4.00 cm. Assume the springs act as a single spring.

Example 11.1.1

What is the spring constant for the truck springs?

k=F/x=(500. kg)(9.80 m/s2)/0.0400 m=1.23×105 N/m

Example 11.1.2

How far with the springs compress if 800. kg of cargo is placed in the truck bed?

x=F/k=(800. kg)(9.80 m/s 2 )/1.23×105 N/m=0.064 m=6.4 cm

Explore how the mass of the box (m) affects the distance the spring stretches (x) using the PLIX Interactive below:

Interactive Element

• Simple harmonic motion occurs in many situations, including an object of the end of a spring, a tuning fork, a pendulum, and strings on a guitar or piano.
• A mass oscillating on a horizontal spring is often used to analyze SHM.
• The restoring force for a mass oscillating on a horizontal spring is related to the displacement of the mass from its equilibrium position, F=−kx.
• SHM is related to uniform circular motion when the uniform circular motion is viewed in one dimension.
• If a spring has a spring constant of 1.00 × 10 3 N/m, what is the restoring force when the mass has been displaced 20.0 cm?

Explore More

Use this resource to answer the questions that follow.

• What is the graph produced by a swinging pendulum's motion graphed over time?
• How does the Exploratorium demonstrate the relationship between simple harmonic motion and circular motion? Is it convincing?
• Why don't the pendulums all swing at the same rate?

Additional Resources

Study Guide: Harmonic Motion Study Guide

Videos: Introduction to Harmonic Motion - Overview

Real World Application: The Vibrating Chair

PLIX: Play, Learn, Interact, eXplore: Simple Harmonic Motion

• Simple Harmonic Motion

We see different kinds of motion every day. For example, the motion of the hands of a clock, motion of the wheels of a car, etc. Did you ever notice that these types of motion keep repeating themselves? Well, such motions are periodic in nature, and, one such type of periodic motion is simple harmonic motion (S.H.M.). But, what is S.H.M.? Let’s find out.

Suggested Videos

Periodic motion and oscillations.

Periodic motion is the motion that repeats itself in equal intervals of time. Now,   we need to know what periodic motion is, so as to understand simple harmonic motion.

We see many examples of periodic motion in our day-to-day life. For example, the motion of the hands of a clock is a periodic motion, the rocking of a cradle, swinging on a swing, leaves of a tree moving to and fro due to wind breeze, and so on.

In these examples, the particle performs the same set of movements again and again in a periodic motion, and oscillation is one such set of movements. Simple Harmonic Motion is a great example of an oscillatory motion.

Browse more Topics under Oscillations

• Damped S.H.M.
• Forced S.H.M.
• Force Law for S.H.M.
• Velocity and Acceleration in S.H.M.
• Some Systems executing S.H.M.
• Energy in S.H.M.
• Periodic and Oscillatory Motion

Download the Cheat Sheet of Oscillations below

Simple Harmonic Motion (S.H.M.)

Simple Harmonic Motion Definition – Simple harmonic motion is the motion in which the object moves to and fro along a line.

For instance, Have you seen a pendulum? When we swing it, it moves to and fro along the same line. These movements are  oscillations . Oscillations of a pendulum are an example of simple harmonic motion.

Now, consider there is a spring that is fixed at one end. When there is no force applied to it, it is at its equilibrium position. Now,

• If we pull it outwards, there is a force exerted by the string that is directed towards the equilibrium position
• And, if we push the spring inwards, there is a force exerted by the string towards the equilibrium position

In each case, we can see that the force exerted by the spring is towards the equilibrium position, this force is called the restoring force. Now, let the force be F and the displacement of the string from the equilibrium position be x.

Therefore, the restoring force will be F= – kx (the negative sign indicates that the force is in the opposite direction). Here, k is the constant called the force constant. Its unit is N/m in S.I. system and dynes/cm in C.G.S. system.

Learn how to calculate Energy in Simple Harmonic Motion  here

Linear Simple Harmonic Motion

Definition – The linear periodic motion of a body in which the restoring force is always directed towards the equilibrium position or mean position and its magnitude is directly proportional to the displacement from the equilibrium position. Also, all simple harmonic motions are periodic in nature, but all periodic motions are not simple harmonic motions.

Now, take the previous example of the string. Let its mass be m. The acceleration of the body will be,

Here, k/m = ω 2   ( ω is the angular frequency of the body)

Learn the difference between Linear and Damped Simple Harmonic Motion  here

Concepts of Simple Harmonic Motion (S.H.M)

• Amplitude : The maximum displacement of a particle from its equilibrium position or mean position is its amplitude, and its direction is always away from the mean or equilibrium position. Its S.I. unit is the meter, and the dimensions are [L 1 M 0 T 0 ].
• Period : The time taken by a particle to complete one oscillation is its period. Therefore, the period of S.H.M. is the least time after which the motion will repeat itself. Thus, the motion will repeat itself after nT, where, n is an integer.
• Frequency : Frequency of S.H.M. is the number of oscillations that a particle performs per unit time. The S.I. unit of frequency is hertz or r.p.s(rotations per second), and its dimensions are [L 0 M 0 T -1 ].
• Phase : Phase of S.H.M. is its state of oscillation, and the magnitude and direction of displacement of particles represent the phase. Epoch(α) is the phase at the beginning of the motion.

Learn how to find Velocity and Acceleration of Simple Harmonic Motion  here

Note: The period of simple harmonic motion does not depend on amplitude or energy or the phase constant.

Difference between Periodic and Simple Harmonic Motion

Learn the difference between Periodic and Oscillatory Motion here .

Solved Questions for You

Q: Assertion(A): In simple harmonic motion, the motion is to and fro and periodic Reason(R): Velocity of the particle V = ω√A 2 – x 2   where x is displacement as measured from the extreme position Chose the right answer:

• Both a and B are true and R is the correct explanation of A.
• Both A and B are true and R is not the correct explanation of A.
• A is true, and R is false.
• A is false, and R is true.

Solution:   c) A is true and R is false. In V = ω√A 2 – x 2 ,   x measured from the mean position, not from the extreme position, and SHM involves to and fro periodic motion.

Customize your course in 30 seconds

Which class are you in.

Oscillations

• Pulse Amplitude Modulation
• Periodic Function
• Oscillatory Motion
• Some Systems Executing Simple Harmonic Motion
• Force Law for Simple Harmonic Motion
• Velocity and Acceleration in Simple Harmonic Motion
• Energy in Simple Harmonic Motion

2 responses to “Energy in Simple Harmonic Motion”

very helpful

It was so much helping. Thank u for that. 👍

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

• IIT JEE Study Material
• Simple Harmonic Motion Shm

Simple Harmonic Motion (SHM)

What is simple harmonic motion.

A Simple Harmonic Motion , or SHM, is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position. The direction of this restoring force is always towards the mean position. The acceleration of a particle executing simple harmonic motion is given by a(t) = -ω 2  x(t). Here, ω is the angular velocity of the particle.

Download Complete Chapter Notes of Simple Harmonic Motion Download Now

Table of Contents

• Difference between Simple Harmonic, Periodic and Oscillation Motion

Types of Simple Harmonic Motion

• General Terms
• Differential Equation
• Angular SHM
• Quantitative Analysis
• Necessary Conditions
• Energy in SHM
• Geometrical Interpretations
• Horizontal Phasor

Simple Harmonic, Periodic and Oscillation Motion

Simple harmonic motion can be described as an oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion.

All the Simple Harmonic Motions are oscillatory and also periodic, but not all oscillatory motions are SHM. Oscillatory motion is also called the harmonic motion of all the oscillatory motions, wherein the most important one is Simple Harmonic Motion (SHM).

In this type of oscillatory motion, displacement, velocity and acceleration, and force vary (w.r.t time) in a way that can be described by either sine (or) the cosine functions collectively called sinusoids.

• Simple Pendulum Concepts
• Spring-Mass System

The study of Simple Harmonic Motion is very useful and forms an important tool in understanding the characteristics of sound waves, light waves and alternating currents. Any oscillatory motion which is not simple harmonic can be expressed as a superposition of several harmonic motions of different frequencies.

Difference between Periodic, Oscillation and Simple Harmonic Motion

Periodic motion.

• A motion repeats itself after an equal interval of time. For example, uniform circular motion.
• There is no equilibrium position.
• There is no restoring force.
• There is no stable equilibrium position.

Oscillation Motion

• To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of the equilibrium (or) mean position is an oscillatory motion.
• It is a kind of periodic motion bounded between two extreme points. For example, the o scillation of a simple pendulum, spring-mass system.
• The object will keep on moving between two extreme points about a fixed point is called the mean position (or) equilibrium position along any path (the path is not a constraint).
• There will be a restoring force directed towards the equilibrium position (or) mean position.
• In an oscillatory motion, the net force on the particle is zero at the mean position.
• The mean position is a stable equilibrium position.

Simple Harmonic Motion or SHM

• It is a special case of oscillation, along with a straight line between the two extreme points (the path of SHM is a constraint).
• The path of the object needs to be a straight line.
• The mean position in Simple Harmonic Motion is a stable equilibrium.

Conditions for SHM

The SHM, or Simple Harmonic Motion, can be classified into two types:

Linear Simple Harmonic Motion

When a particle moves to and fro about a fixed point (called equilibrium position) along with a straight line , then its motion is called linear Simple Harmonic Motion.

For example, the spring-mass system.

Conditions for Linear SHM

The restoring force or acceleration acting on the particle should always be proportional to the displacement of the particle and directed towards the equilibrium position.

• \(\begin{array}{l}\overrightarrow{x}- \text{displacement of particle from equilibrium position}\end{array} \)
• \(\begin{array}{l}\overrightarrow{F}- \text{Restoring force}\end{array} \)
• \(\begin{array}{l}\overrightarrow{a}- \text{acceleration}\end{array} \)

Angular Simple Harmonic Motion

When a system oscillates angular long with respect to a fixed axis, then its motion is called angular simple harmonic motion.

Conditions to Execute Angular SHM

The restoring torque (or) angular acceleration acting on the particle should always be proportional to the angular displacement of the particle and directed towards the equilibrium position.

Τ ∝ θ or α ∝ θ

• Τ – Torque
• α – Angular acceleration
• θ – Angular displacement

Simple Harmonic Motion Key Terms

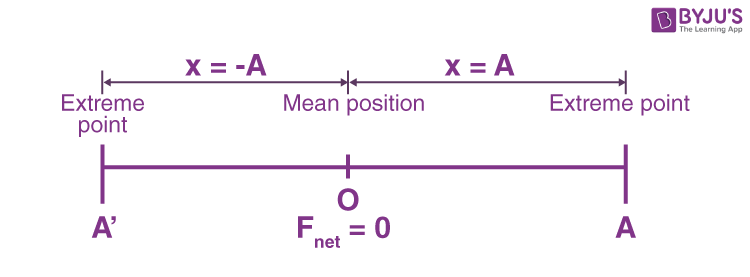
Mean position.

The point at which net force acting on the particle is zero.

From the mean position, the force acting on the particle is

Conditions at Mean Position

The force acting on the particle is negative of the displacement. So, this point of equilibrium will be a stable equilibrium.

Amplitude in SHM

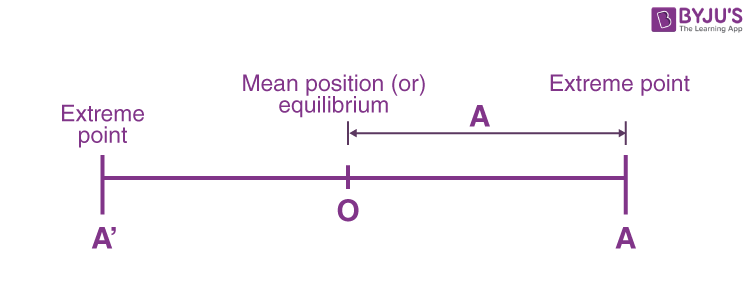
It is the maximum displacement of the particle from the mean position.

Time Period and Frequency of SHM

The minimum time after which the particle keeps on repeating its motion is known as the time period, or the shortest time taken to complete one oscillation is also defined as the time period.

Frequency:  The number of oscillations per second is defined as the  frequency .

Frequency = 1/T and, angular frequency ω = 2πf = 2π/T

Phase in SHM

The phase of a vibrating particle at any instant is the state of the vibrating or oscillating particle regarding its displacement and direction of vibration at that particular instant.

The expression and position of a particle as a function of time.

x = A sin (ωt + Φ)

Where (ωt + Φ) is the phase of the particle, the phase angle at time t = 0 is known as the initial phase.

Phase Difference 

The difference in total phase angles of two particles executing simple harmonic motion with respect to the mean position is known as the phase difference. Two vibrating particles are said to be in the same phase; the phase difference between them is an even multiple of π.

ΔΦ = nπ where n = 0, 1, 2, 3, . . . . .

Two vibrating particles are said to be in opposite phases if the phase difference between them is an odd multiple of π.

ΔΦ = (2n + 1) π where n = 0, 1, 2, 3, . . . . .

Simple Harmonic Motion Equation and Its Solution

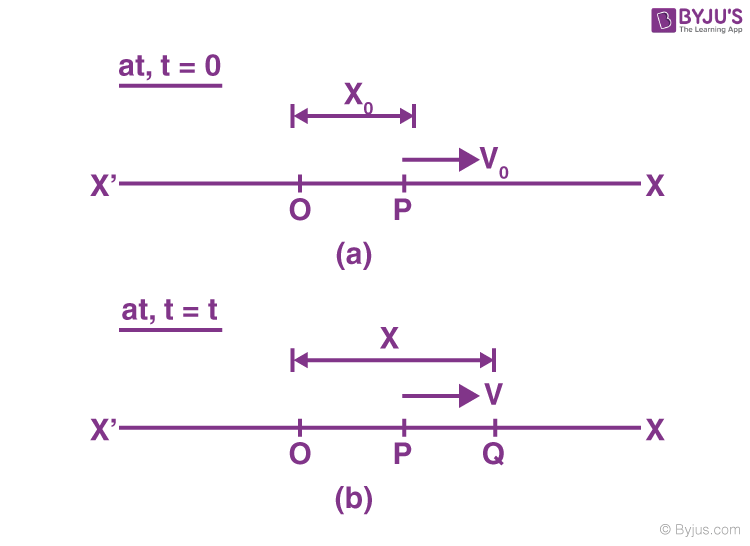
Consider a particle of mass (m) executing Simple Harmonic Motion along a path x o x; the mean position at O. Let the speed of the particle be v 0 when it is at position p (at a distance no from O).

At t = 0, the particle at P (moving towards the right)

At t = t, the particle is at Q (at a distance x from O)

With a velocity (v).

K – is a positive constant

d 2 x/dt 2 + ω 2 x = 0, which is the differential equation for linear Simple Harmonic Motion.

Solutions of Differential Equations of SHM

The differential equation for the Simple Harmonic Motion has the following solutions:

• \(\begin{array}{l}x=A\sin \omega \,t\end{array} \) (This solution when the particle is in its mean position point (O) in figure (a)
• \(\begin{array}{l}{{x}_{0}}=A\sin \phi\end{array} \) (When the particle is at the position & (not at mean position) in figure (b)
• \(\begin{array}{l}x=A\sin \left( \omega t+\phi \right)\end{array} \) (When the particle at Q at in figure (b) (any time t).

These solutions can be verified by substituting these x values in the above differential equation for the linear simple harmonic motion.

Angular Simple Harmonic Motion

A body free to rotate about an axis can make angular oscillations. For example, a photo frame or a calendar suspended from a nail on the wall. If it is slightly pushed from its mean position and released, it makes angular oscillations.

Conditions for an Angular Oscillation to be Angular SHM

The body must experience a net torque that is restored in nature. If the angle of oscillation is small, this restoring torque will be directly proportional to the angular displacement.

Τ ∝ – θ

Τ = – kθ

α = – kθ

This is the differential equation of an angular Simple Harmonic Motion . The solution of this equation is the angular position of the particle with respect to time.

Then the angular velocity,

θ 0 – Amplitude of the angular SHM

• Simple pendulum
• Seconds pendulum
• The physical pendulum
• Torsional pendulum

Quantitative Analysis of SHM

Let us consider a particle executing Simple Harmonic Motion between A and A 1 about passing through the mean position (or) equilibrium position (O). Its analysis is as follows

SHM about Position O

Equation of Position of a Particle as a Function of Time

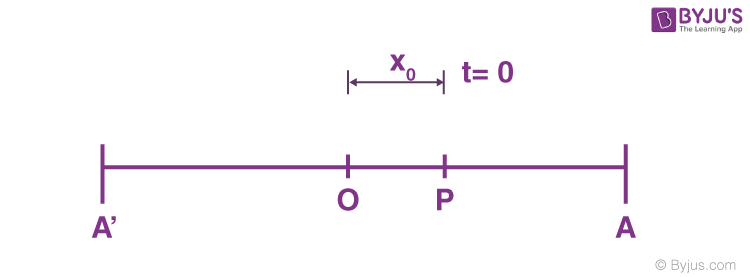
Let us consider a particle, which is executing SHM at time t = 0, and the particle is at a distance from the equilibrium position.

Necessary Conditions for Simple Harmonic Motion

• \(\begin{array}{l}\overrightarrow{F}\propto -\overrightarrow{x}\end{array} \)
• \(\begin{array}{l}\overrightarrow{a}\propto -\overrightarrow{x}\end{array} \)
• \(\begin{array}{l}\overrightarrow{a}=-{{\omega }^{2}}x\end{array} \)
• \(\begin{array}{l}\overrightarrow{a}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}\end{array} \)
• \(\begin{array}{l}\overrightarrow{a}=v\frac{dv}{dx}=-{{\omega }^{2}}x\end{array} \)
• \(\begin{array}{l}\int\limits_{0}^{v}{vdv}=\int\limits_{0}^{x}{-{{\omega }^{2}}xdx}\end{array} \)
• \(\begin{array}{l}\frac{{{v}^{2}}}{2}=\frac{-{{\omega }^{2}}{{x}^{2}}}{2}+c….(1)\end{array} \)

Some conditions we know:

At point A v = 0 [ x = A] the equation (1) becomes

Sub the value of C in equation (1)

Where v is the velocity of the particle executing simple harmonic motion from the definition of instantaneous velocity

x = Asin ( ωt + Φ) . . . . . (3)

Equation (3) – Equation of the position of a particle as a function of time.

Case 1: If at t = 0

The particle at x = x0

Φ is the initial phase of the particle.

Case 2: If at t = 0

The particle at x = 0

Case 3:  If the particle is at one of its extreme positions, x = A at t = 0

So, the value can be anything depending upon the position of the particle at t = 0. That is why it is called the initial phase of the particle.

Now, if we see the equation of the position of the particle with respect to time,

π/2 = x = A sin ( ωt + Φ)

sin (ωt + Φ) is the periodic function, whose period is T = 2π/ω

Which can be anything, sine function or cosine function

Time Period of SHM

The coefficient of t is ω.

So, the time period T = 2π/ω

ω =2π/T = 2πf

ωt = Angular frequency of SHM

From the expression of particle position as a function of time:

The Velocity of a Particle Executing Simple Harmonic Motion

Velocity in SHM is given by v = dx/dt,

Since x = A sin ωt

On squaring both sides,

The curve between displacement and velocity of a particle executing the simple harmonic motion is an ellipse.

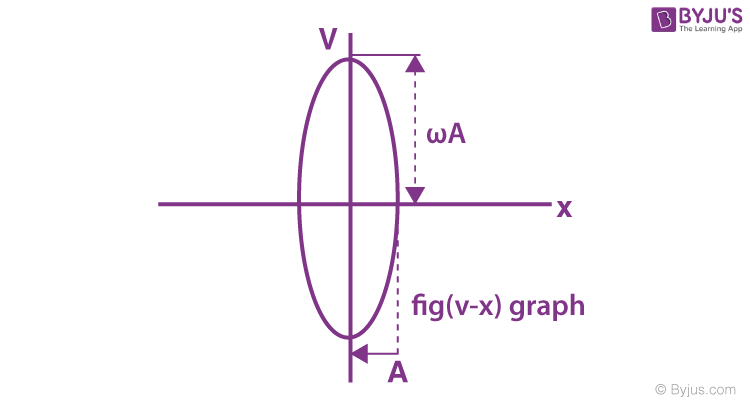
When ω = 1, then the curve between v and x will be circular.

Acceleration in SHM

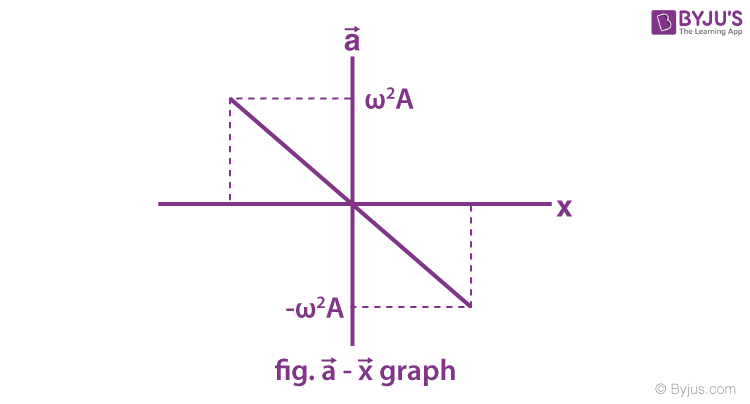
Hence, the expression for displacement, velocity and acceleration in linear simple harmonic motion is

• x = A sin ( ωt + Φ)
• \(\begin{array}{l}v = A\omega \cos \left( \omega t+\phi \right)=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}\end{array} \) and
• \(\begin{array}{l}a = -A{{\omega }^{2}}\sin \left( \omega t+\phi \right)=-{{\omega }^{2}}x\end{array} \)

Energy in Simple Harmonic Motion (SHM)

The system that executes SHM is called the harmonic oscillator.

F = -kx, where k = mω 2 .

Kinetic Energy of a Particle in SHM

Potential energy of shm.

The total work done by the restoring force in displacing the particle from (x = 0) (mean position) to x = x:

When the particle has been displaced from x to x + dx, the work done by restoring force is

dw = F dx = -kx dx

Potential Energy = -(work done by restoring force)

Total Mechanical Energy of the Particle Executing SHM

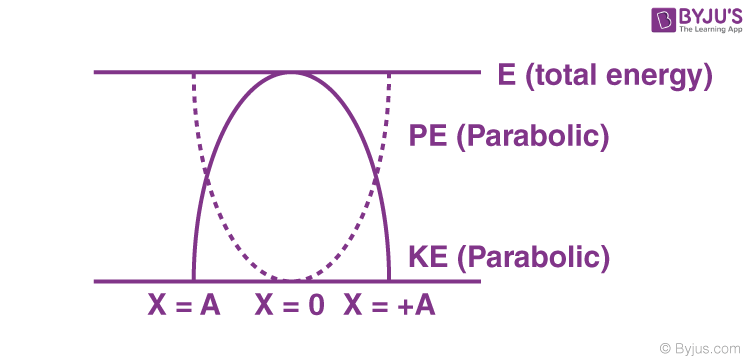
E = KE + PE

Hence, the particle’s total energy in SHM is constant, independent of the instantaneous displacement.

⇒ Relationship between kinetic energy , potential energy and time in Simple Harmonic Motion at t = 0, when x = ±A.

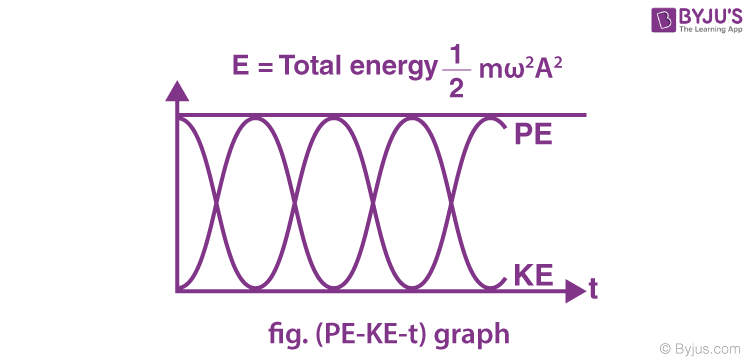
⇒ Variation of kinetic energy and potential energy in Simple Harmonic Motion with displacement.

Geometrical Interpretation of Simple Harmonic Motion

If a particle is moving with uniform speed along the circumference of a circle, then the straight line motion of the foot of the perpendicular drawn from the particle on the diameter of the circle is called simple harmonic motion.

SHM as a Projection of Circular Motion

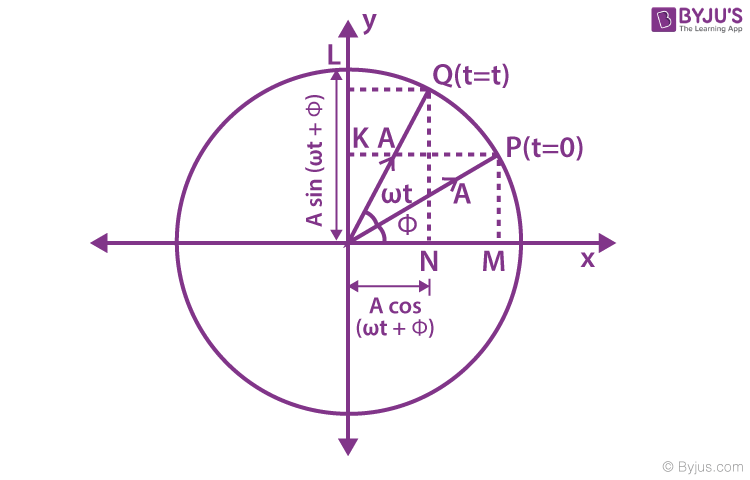
The particle is at position P at t = 0 and revolves along a circle with a constant angular velocity (ω). The projection of P on the diameter along the x-axis (M). At the later time (t), the particle is at Q. Now, its projection on the diameter along the x-axis is N.

As the particle P revolves around in a circle anti-clockwise, its projection M follows it up, moving back and forth along the diameter, such that the displacement of the point of projection at any time (t) is the x-component of the radius vector (A).

x = A cos ( ωt + Φ) . . . . . . . (1)

y = A sin ( ωt + Φ) . . . . . (2)

Thus, we see that the uniform circular motion is the combination of two mutually perpendicular linear harmonic oscillations.

It implies that P is under uniform circular motion, (M and N) and (K and L) are performing simple harmonic motion about O with the same angular speed ω as that of P.

P is under uniform circular motion, which will have centripetal acceleration along A (radius vector).

It can be resolved into two components:

• \(\begin{array}{l}{{a}_{N}}=A{{\omega }^{2}}{{\sin }^{2}}\left( \omega t+\phi \right)\end{array} \)
• \(\begin{array}{l}{{a}_{L}}=A{{\omega }^{2}}{{\cos }^{2}}\left( \omega t+\phi \right)\end{array} \)

a N and a L acceleration correspond to the points N and L, respectively.

In the above discussion, the foot of the projection on the x-axis is called a horizontal phasor.

Similarly, the foot of the perpendicular on the y-axis is called the vertical phasor. We already know the vertical and horizontal phasor will execute the simple harmonic motion of amplitude A and angular frequency ω. The phases of the two SHMs differ by π/2.

Video Lessons

Simple harmonic motion short notes.

Simple Harmonic Motion (SHM) – JEE Concept

Angular SHM (Simple Harmonic Motion)

What Is Energy in SHM?

Graphical Representation of SHM

Simple Harmonic Motion – Top 12 Most Important and Expected JEE Questions

Waves and Simple Harmonic Motion Important Questions

Problem-solving Strategy in Horizontal Phasor

• Let us assume a circle of radius equal to the amplitude of SHM.
• Assume a particle rotating in a circular path moving with constant same as that of simple harmonic motion in the clockwise direction.
• The angle made by the particle at t = 0 with the upper vertical axis is equal to φ (phase constant).
• The horizontal component of the velocity of a particle gives you the velocity of a particle performing the simple harmonic motion.
• The component of the acceleration of a particle in the horizontal direction is equal to the acceleration of the particle performing SHM. [In uniform circular acceleration centripetal only a c = ω 2 A].

Frequently Asked Questions on Simple Harmonic Motion

What is a simple harmonic motion.

Simple harmonic motion is a periodic motion in which the particle acceleration is directly proportional to its displacement and is directed towards the mean position.

What is the formula for restoring force in SHM?

The restoring force is given by the formula F = -kx The negative sign shows that the force is in the opposite direction. k is the force constant. x is the displacement of the string from the equilibrium position.

Mention the difference between harmonic motion and simple harmonic motion.

The harmonic motion is when the restoring force is proportional to the ​displacement but in opposite directions. Simple Harmonic Motion is a harmonic motion with a constant amplitude and the same frequency.

What is damped simple harmonic motion?

The periodic motion of gradually decreasing amplitude is called the damped simple harmonic motion.

What is the displacement of the particle executing simple harmonic motion?

Distance travelled by the particle from its mean position at any instant is called the displacement of the particle executing simple harmonic motion.

At what points is the energy entirely kinetic and entirely potential in simple harmonic motion?

At the mean position, the energy is entirely kinetic energy. At the extreme position, the energy is entirely potential energy.

What is the phase difference between displacement and acceleration of the particle executing simple harmonic motion?

The phase difference between displacement and acceleration of the particle executing simple harmonic motion is π radian.

What is meant by the amplitude of simple harmonic motion?

The maximum displacement of the particle is called the amplitude of motion.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

24.2: Simple Harmonic Motion

• Last updated
• Save as PDF
• Page ID 88077

• Julio Gea-Banacloche
• University of Arkansas via University of Arkansas Libraries

A particularly important kind of oscillatory motion is called simple harmonic motion. This is what happens when the restoring force is linear in the displacement from the equilibrium position: that is to say, in one dimension, if \(x_0\) is the equilibrium position, the restoring force has the form

\[ F=-k\left(x-x_{0}\right) \label{eq:11.2} .\]

We are familiar with this from Hooke’s “law” for an ideal spring (see Chapter 19 ). So, an object attached to an ideal, massless spring, as in the figure below, should perform simple harmonic motion. This kind of oscillation is distinguished by the following characteristics:

• The position as a function of time, \(x(t)\), is a sinusoidal function.
• The period of the oscillations does not depend on their amplitude (by “amplitude” we mean the maximum displacement from the equilibrium position).

What this second property means is that, for instance, with reference to Figure \(\PageIndex{1}\), you can displace the mass a distance \(A\), or \(A/2\), or \(A/3\), or whatever you choose, and the period (and frequency) of the resulting oscillations will be the same regardless. (This means, actually, that if you displace it farther it has to end up moving faster, to cover the larger distance in the same time.)

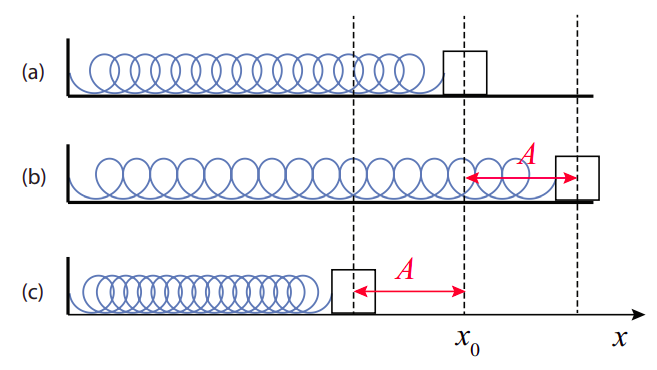
Since we know that “Hooke’s law” is actually just an approximation, valid only provided that the spring is not compressed or stretched too much, we expect that in real life the “ideal” simple harmonic motion properties I have listed above will only hold approximately, as well; so, in fact, if you stretch a spring too much you will get a different period, eventually, than if you stay in the “linear,” Hooke’s law regime. This is a general characteristic of most physical systems: simple harmonic motion only happens for relatively small oscillations, but “relatively small” can still be fairly large sometimes, and even as an approximation it is often an extremely valuable one.

The other distinctive characteristic of simple harmonic motion is that the position function is sinusoidal, by which I mean a sine or a cosine. Thus, for example, if the mass in Figure \(\PageIndex{1}\) is released from rest at \(t\) = 0, and the position \(x\) is measured from the equilibrium position \(x_0\) (that is, the point \(x = x_0\) is taken as the origin of coordinates), the function \(x(t)\) will be

\[ x(t)=A \cos (\omega t) \label{eq:11.3} \]

where the quantity \(\omega\), known as the oscillator’s angular frequency , is given by

\[ \omega=\sqrt{\frac{k}{m}} \label{eq:11.4} .\]

Here, \(k\) is the spring constant, and \(m\) the mass of the object (remember the spring is assumed to be massless). I will prove that Equation (\ref{eq:11.3}), together with (\ref{eq:11.4}), satisfy Newton’s second law of motion for this system in a moment; first, however, I need to say a couple of things about \(\omega\). You’ll recall that we have used this symbol before, in Chapter 6 , to represent the angular velocity of a particle moving in a circle (or, more generally, of any rotating object). Why bring it up again now for an apparently completely different purpose?

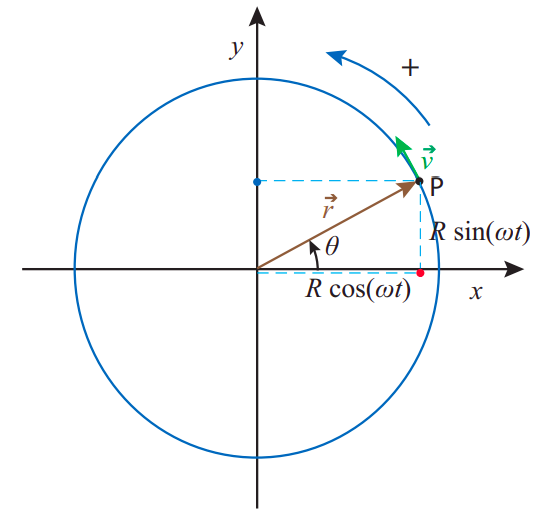
The answer is that there is a very close relationship between simple harmonic motion and circular motion with constant speed, as Figure \(\PageIndex{2}\) illustrates: as the point P rotates with constant angular velocity \(\omega\), its projection onto the \(x\) axis (the red dot in the figure) performs simple harmonic motion with angular frequency \(\omega\) (and amplitude \(R\)). (Of course, there is nothing special about the \(x\) axis; the projection on any other axis will also perform simple harmonic motion with the same angular frequency; for example, the blue dot on the figure.)

If the angular velocity of the particle in Figure \(\PageIndex{2}\) is constant, then its “orbital period” (the time needed to complete one revolution) will be \(T = 2\pi/\omega\), and this will also be the period of the associated harmonic motion (the time it takes for the motion to repeat itself). You can see this directly from Equation (\ref{eq:11.3}): if you increase the time \(t\) by \(2\pi/\omega\), you get the same value of \(x\):

\[ x\left(t+\frac{2 \pi}{\omega}\right)=A \cos \left[\omega\left(t+\frac{2 \pi}{\omega}\right)\right]=A \cos (\omega t+2 \pi)=A \cos (\omega t)=x(t) \label{eq:11.5} .\]

Since the frequency \(f\) of an oscillator is equal to 1/\(T\), this gives us the following relationship between \(f\) and \(\omega\):

\[ f=\frac{1}{T}=\frac{\omega}{2 \pi} \label{eq:11.6} .\]

One way to tell whether one is talking about an oscillator’s frequency (\(f\)) or its angular frequency (\(\omega\))—apart from the different symbols, of course—is to pay attention to the units. The frequency \(f\) is usually given in hertz, whereas the angular frequency \(\omega\) is always given in radians per second. Apart from the factor of \(2\pi\), they are, of course, completely equivalent; sometimes one is just more convenient than the other. On the other hand, the only way to tell whether \(\omega\) is a harmonic oscillator’s angular frequency or the angular velocity of something moving in a circle is from the context. (In this chapter, of course, it will always be the former).

Let us go back now to Equation \ref{eq:11.3} for our block-on-a-spring system. The derivative with respect to time will give us the block’s velocity. This is a simple application of the chain rule of calculus:

\[ v(t)=\frac{d x}{d t}=-\omega A \sin (\omega t) \label{eq:11.7} .\]

Another derivative will then give us the acceleration:

\[ a(t)=\frac{d v}{d t}=-\omega^{2} A \cos (\omega t) \label{eq:11.8} .\]

Note that the acceleration is always proportional to the position, only with the opposite sign. The proportionality constant is \(\omega^2\). Since the force exerted by the spring on the block is \(F = −kx\) (because we are measuring the position from the equilibrium position \(x_0\)), Newton’s second law, \(F = ma\), gives us

\[ ma = -kx \label{eq:11.9} \]

and you can check for yourself that this will be satisfied if \(x\) is given by Equation (\ref{eq:11.3}), \(a\) is given by Equation (\ref{eq:11.8}), and \(\omega\) is given by Equation (\ref{eq:11.4}).

The expression (\ref{eq:11.4}) for \(\omega\) is typical of what we find for many different kinds of oscillators: the restoring force (here represented by the spring constant \(k\)) and the object’s inertia (\(m\)) together determine the frequency of the motion, acting in opposite directions: a larger restoring force means a higher frequency (faster oscillations) whereas a larger inertia means a lower frequency (slower oscillations—a more “sluggish” response).

The position, velocity and acceleration graphs for the motion (\ref{eq:11.3}) are shown in Figure \(\PageIndex{3}\) below. You may want to pay attention to some of their main features. For instance, the position and the velocity are what we call “90\(^{\circ}\) out of phase”: one is maximum (or minimum) when the other one is zero. The acceleration, on the other hand, is “180\(^{\circ}\) out of phase” (that is to say, in complete opposition) with the position. As a result of that, all combinations of signs for \(a\) and \(v\) are possible: the object may be moving to the right with positive or negative acceleration (depending on which side of the origin it’s on), and likewise when it is moving to the left.

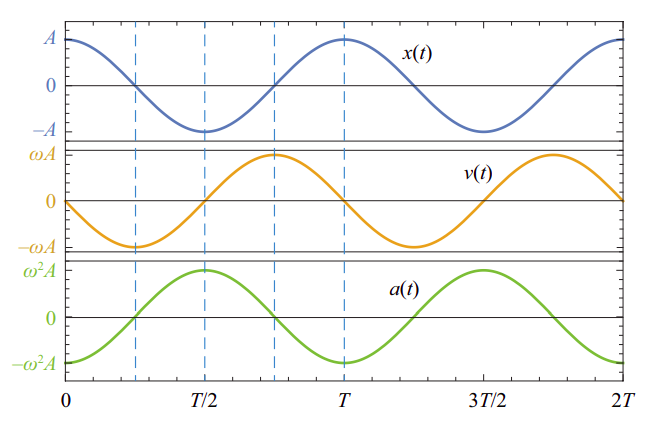
Since the time we choose as \(t\) = 0 is arbitrary, the function in Equation (\ref{eq:11.3}) (which assumes that \(t\) = 0 is when the object’s displacement is maximum and positive) is clearly not the most general formula for simple harmonic motion. Another way to see this is to realize that we could have started the motion differently. For instance, we could have hit the block with a sharp, “impulsive” force, lasting only a very short time, so it would have acquired a substantial velocity before it could have moved very far from its initial (equilibrium) position. In such a case, the motion would be better described by a sine function, such as \(x(t) = A \sin(\omega t)\), which is zero at \(t\) = 0 but whose derivative (the object’s velocity) is maximum at that time.

If we stick to using cosines, for definiteness, then the most general equation for the position of a simple harmonic oscillator is as follows:

\[ x(t)=A \cos (\omega t+\phi) \label{eq:11.10} \]

where \(\phi\) is what we call a “phase angle,” that allows us to match the function to the initial conditions—by which I mean, the object’s initial position and velocity. Specifically, you can see, by setting \(t\) = 0 in Equation (\ref{eq:11.10}) and its derivative, that the initial position and velocity of the motion described by Equation (\ref{eq:11.10}) are

\begin{align} x_{i}&=A \cos \phi \nonumber \\ v_{i}&=-\omega A \sin \phi \label{eq:11.11}. \end{align}

Conversely, if you are given \(x_i\) and \(v_i\), you can use Eqs. (\ref{eq:11.11}) to determine \(A\) and \(\phi\), which is what you need to know in order to use Equation (\ref{eq:11.10}) (note that the angular frequency, \(\omega\), does not depend on the initial conditions—it is always the same regardless of how you choose to start the motion). Specifically, you can verify that Eqs. (\ref{eq:11.11}) imply the following:

\[ A^{2}=x_{i}^{2}+\frac{v_{i}^{2}}{\omega^{2}} \label{eq:11.12} \]

and then, once you know \(A\), you can get \(\phi\) from either \(x_i = A \cos \phi\) or \(v_i = −\omega A \sin \phi\) (in fact, since the inverse sine and inverse cosine are both multivalued functions, you should use both equations, to make sure you get the correct sign for \(\phi\)).

Energy in Simple Harmonic Motion

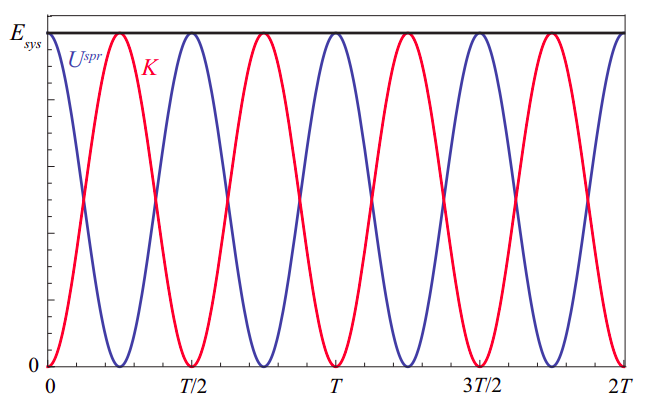
Equation (\ref{eq:11.11}) above actually follows from the conservation of energy principle for a harmonic oscillator. Consider again the mass on the spring in Figure \(\PageIndex{2}\). Its kinetic energy is clearly \(K = \frac{1}{2}mv^2\), whereas the potential energy in the spring is \(\frac{1}{2}kx^2\). Using Equation (\ref{eq:11.10}) and its derivative, we have

\begin{align} U^{s p r} &=\frac{1}{2} k A^{2} \cos ^{2}(\omega t+\phi) \nonumber \\ K &=\frac{1}{2} m \omega^{2} A^{2} \sin ^{2}(\omega t+\phi) \label{eq:11.13}. \end{align}

Recalling Equation (\ref{eq:11.4}), note that \(\omega^2 = k/m\), so if you substitute this in the second equation above, you can see that the amplitude of both the potential and the kinetic energy is the same, namely, \(\frac{1}{2}kA^2\). Since, for any angle \(\theta\), it is always true that \(\cos^2 \theta + \sin^2 \theta = 1\), we find

\[ E_{s y s}=U^{s p r}+K=\frac{1}{2} k A^{2}=\frac{1}{2} m \omega^{2} A^{2} \label{eq:11.14} \]

so the total energy of the system is constant (independent of time), at it should be, in the absence of dissipation. Figure \(\PageIndex{4}\) shows how the potential and kinetic energies oscillate in opposition, so one is maximum whenever the other is minimum. It also shows that they oscillate twice as fast as the oscillator itself: for example, the potential energy is maximum both when the displacement is maximum (spring maximally stretched) and when it is minimum (spring maximally compressed). Similarly, the kinetic energy is maximum when the oscillator passes through the equilibrium position, regardless of whether it is moving to the left or to the right.

Harmonic Oscillator Subject to an External, Constant Force

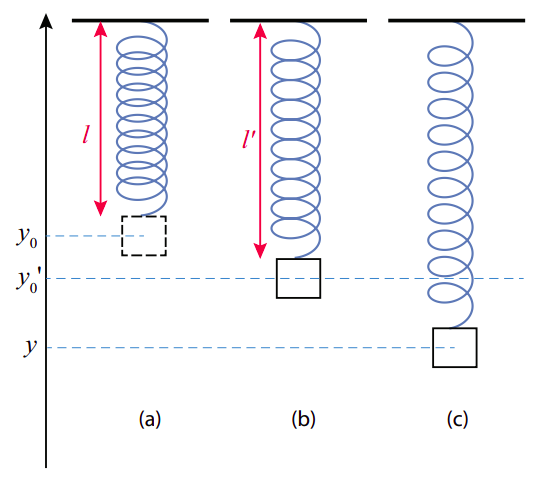
Consider a mass hanging from an ideal spring suspended from the ceiling, as in Figure \(\PageIndex{5}\) below (next page). Supposed the relaxed length of the spring is \(l\), such that, in the absence of gravity, the object’s equilibrium position would be at the height \(y_0\) shown in figure \(\PageIndex{5}\)(a). In the presence of gravity, of course, the spring needs to stretch, to balance the object’s weight, and so the actual equilibrium position for the system will be \(y^{\prime}_0\), as shown in figure \(\PageIndex{5}\)(b). The upwards force from the spring at that point will be \(-k\left(y_{0}^{\prime}-y_{0}\right)\), and to balance gravity we must have

\[ -k\left(y_{0}^{\prime}-y_{0}\right)-m g=0 \label{eq:11.15} .\]

Suppose that we now stretch the spring beyond this new equilibrium position, so the mass is now at a height \(y\) (figure \(\PageIndex{5}\)(c)). What happens then? The net upwards force will be \(-k\left(y-y_{0}\right)-m g\), but using Equation (\ref{eq:11.15}) this can be rewritten as

\[ F_{n e t}=-k\left(y-y_{0}\right)-m g=-k( y - \left[ \frac{mg}{k}+y_0'\right])-mg=-ky+mg+ky_0'-mg=-k\left(y-y_{0}^{\prime}\right) \label{eq:11.16} .\]

This is a remarkable result, because the force of gravity has disappeared completely from the final expression. Basically, the system behaves as if it consisted of just a spring of constant \(k\) with equilibrium length \(l^{\prime}=l+y_{0}-y_{0}^{\prime}\), and no gravity . In other words, the only thing gravity does is to change the equilibrium position, so that if you now displace the mass, it will oscillate around \(y_{0}^{\prime}\) instead of around \(y_0\). The oscillation’s period and frequency are the same as if the spring was horizontal.

Although I have established this here for the specific case where the oscillator involves a spring, and the external force is gravity, this is a completely general result, valid for any simple harmonic oscillator, since for such a system the restoring force will always be a linear function of the displacement (which is all that is required for the math to work). As long as the external force is constant, the frequency of the oscillations will not be affected, and only the equilibrium position will change. In an example at the end of the chapter (under “Advanced Topics”) I will show you how you can make use of this to calculate the effect of friction on the horizontal mass-spring combination in Figure \(\PageIndex{1}\).

One thing you need to keep in mind, however, is that when the oscillator is subjected to an external force, as was the case here, its energy will not , in general, remain constant (unlike what we saw in the previous subsection "Energy in Simple Harmonic Motion"), since the external force will be doing work on the system as it oscillates. If the external force is constant, and does not change direction, this work will be positive half the time, and negative half the time. If it is kinetic friction, then of course it will change direction every half cycle, and the work will be negative all the time.

In the case shown in Figure \(\PageIndex{5}\), the external force is gravity, which we know to be a conservative force, so the energy that will be conserved will be the total energy of the system that includes the oscillation and the Earth, and hence also the gravitational potential energy (for which we can use here the familiar form \(U^G = mgy\)):

\[ E_{\text {osc+earth }}=U^{s p r}+K+U^{G}=\frac{1}{2}\left(y-y_{0}\right)^{2}+\frac{1}{2} m v^{2}+m g y=\text { const } \label{eq:11.17} .\]

The reason it is no longer possible to combine the terms \(U^{spr} + K\) into the constant \(\frac{1}{2} kA^2\), as in Equation (\ref{eq:11.14}), is that now we have

\begin{align} &y(t)=y_{0}^{\prime}+A \cos (\omega t+\phi) \nonumber \\ &v(t)=-\omega A \sin (\omega t+\phi) \label{eq:11.18} \end{align}

so the oscillations are centered around the new equilibrium position \(y_{0}^{\prime}\), but the spring energy is not zero at that point: it is zero at \(y = y_0\) instead. You can check for yourself, however, that if you substitute Eqs. (\ref{eq:11.18}) into Equation (\ref{eq:11.17}), and make use of the fact that \(k\left(y_{0}^{\prime}-y_{0}\right)=-m g\) (Equation (\ref{eq:11.15})), you do indeed get a constant, as you should.