mean free path case study

• Electric Charge
• Mean Free Path

Concept of mean free path

In a gaseous system, the molecules never move in a straight path without interruptions. This is because they collide with each other and change speed and direction. Between every two collisions, a molecule travels a path length. The mean free path is the average of all path lengths between collisions. In this article, we will derive an expression for the mean free path.

What is Mean Free Path?

A gas molecule’s mean free path λ is its average path length between collisions.

Mathematically the mean free path can be represented as follows:

Let’s look at the motion of a gas molecule inside an ideal gas; a typical molecule inside an ideal gas will abruptly change its direction and speed as it collides elastically with other molecules of the same gas. Though between the collisions, the molecule will move in a straight line at some constant speed, this is applicable for all the molecules in the gas.

It is difficult to measure or describe this random motion of gas molecules thus, we attempt to measure its mean free path λ.

As its name says, λ is the average distance travelled by any molecule between collisions, we expect λ to vary inversely with N/V, which is the number of molecules per unit volume or the density of molecules because if there are more molecules, more are the chances of them colliding with each other hence reducing the mean free path, and also λ would be inversely proportional to the diameter d of the molecules, because if the molecules were point masses, then they would never collide with each other, thus larger the molecule smaller the mean free path. It should be proportional to π times the diameter square and not the diameter itself because we consider the circular cross-section and not the diameter itself. Click on the links provided below to read more about the speed of the gas molecules

• Derivation of Kinetic Theory of Gas Molecules
• RMS Speed of Gas Molecules

Derivation of Mean Free Path

We will derive the equation using the following assumptions, let’s assume that the molecule is spherical, and the collision occurs when one molecule hits the other. Only the molecule we are going to study will be in motion, and the rest molecules will be stationary.

Let’s consider our single-molecule to have a diameter of d and all the other molecules to be points this does not change our criteria for collision. As our single-molecule moves through the gas, it sweeps out a short cylinder of cross-section area π d 2 between successive collisions. For a small-time t, it will move a distance of vt where v is the velocity of the molecule, now if we sweep this cylinder, we will get a volume of π d 2 *vt, so the number of point molecules inside this volume will give us the number of collisions the molecule might have.

Since N/V is the number of molecules per unit volume, the number of molecules in the cylinder will be N/V multiplied by the volume of the cylinder, i.e. πd 2 vt, and the mean free path can be derived as follows,

We have approximated the equation because we have assumed that all the particles are stationary with respect to the particle we are studying. In fact, all the molecules are moving relative to each other, we have cancelled two velocities in the above equation, but actually, the v in the numerator is the  average velocity and v In the denominator is relative velocity hence they both differ from each other with a factor √ 2. Therefore, the final equation would be,

The mean free path at sea level is 0.1 micrometres.

Mean Free Path Factors

Following are the mean free path factors :

• Radius of molecule
• Number of molecules
• Temperature, pressure, etc

Recommended Video

Frequently Asked Questions – FAQs

What are the mean free path factors, what are the assumptions of the kinetic theory of gases.

• The collision of molecules with themselves or walls will be an elastic collision.
• The momentum is conserved.
• Kinetic energy will be conserved.

What is the SI unit of temperature?

What is the unit of molar mass, define average velocity..

Stay tuned to BYJU’S and Fall in Love with Learning!

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Chapter 2: Vectors and Scalars

Chapter 3: motion along a straight line, chapter 4: motion in two or three dimensions, chapter 5: newton's laws of motion, chapter 6: application of newton's laws of motion, chapter 7: work and kinetic energy, chapter 8: potential energy and energy conservation, chapter 9: linear momentum, impulse and collisions, chapter 10: rotation and rigid bodies, chapter 11: dynamics of rotational motions, chapter 12: equilibrium and elasticity, chapter 13: fluid mechanics, chapter 14: gravitation, chapter 15: oscillations, chapter 16: waves, chapter 17: sound, chapter 18: temperature and heat, chapter 19: the kinetic theory of gases, chapter 20: the first law of thermodynamics, chapter 21: the second law of thermodynamics, chapter 22: electric charges and fields, chapter 23: gauss's law, chapter 24: electric potential, chapter 25: capacitance, chapter 26: current and resistance, chapter 27: direct-current circuits, chapter 28: magnetic forces and fields, chapter 29: sources of magnetic fields, chapter 30: electromagnetic induction, chapter 31: inductance, chapter 32: alternating-current circuits, chapter 33: electromagnetic waves.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

Consider N gas molecules with radius r moving randomly with speed v in a cylindrical volume V . When one molecule collides with another molecule, the distance between their centers is 2 r .

Imagine a cylinder with a radius of 2 r , with an axis parallel to the molecule's velocity. When the molecule travels for a small time interval and collides inside the cylinder, the number of collisions per unit time can be determined.

Using the average relative velocity equation, the collisions for all the moving molecules per unit time can be determined.

The reciprocal of the equation gives the average time between collisions, known as the mean free time.

Meanwhile, the mean free path of a gas molecule is the product of the molecule's speed and the average time between collisions. By substituting the terms, the mean free path can be determined, which is inversely proportional to the number of molecules per unit volume and the cross-sectional area of the molecule.

Recalling the ideal-gas equation and substituting the terms, the macroscopic properties of the gas can be obtained.

19.10: Mean free path and Mean free time

Consider the gas molecules in a cylinder. They move in a random motion as they collide with each other and change speed and direction. The average of all the path lengths between collisions is known as the "mean free path."

The mean free path varies inversely with the density of the molecules because when there are more molecules inside a volume, they have a greater chance of colliding with each other, thus reducing the mean free path. Additionally, the mean free path is inversely related to the diameter of the molecules because if they were point masses, they would never collide. Thus, larger molecules are associated with a shorter mean free path.

The gas expands when the temperature increases under constant pressure; thus, the average distance between molecules and the mean free path increases. However, when the pressure is increased at a constant temperature, the gas compresses, leading to a decrease in the mean free path. The mean free path can be defined as the product of the average speed and the mean free time, where the mean free time is the average time between collisions.

Consider argon atoms with a molar mass of 39.9 g/mol moving randomly in a cylinder at a temperature of 273 K and a pressure of 1 atm. Taking the radius of an argon atom to be 1.70 × 10 -10 m, determine the mean free time for argon atoms.

To solve the problem, first identify the known and unknown quantities, and convert them into SI units.

Secondly, recall the RMS speed equation for gas molecules. By substituting the values, the RMS speed can be determined as follows:

Lastly, recall the mean free time equation. By substituting the values, the mean free time can be determined as follows:

• Young, H.D and Freedman, R.A. (2012). University Physics with Modern Physics . San Francisco, CA: Pearson. Pp. 630
• OpenStax. (2019). University Physics Vol. 1 . [Web version]. Retrieved from https://openstax.org/books/college-physics-2e/pages/13-4-kinetic-theory-atomic-and-molecular-explanation-of-pressure-and-temperature

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

• Mean Free Path

Mean free path refers to the average distance that a moving particle travels between successive collisions or impacts. Furthermore, the successive collisions result in modification of the moving particle’s energy or direction or any other particle properties. Moreover, the moving particle here refers to a molecule, an atom, or a photon.

Introduction to Mean Free Path

In the field of radiography, the pencil beam of mono-energetic photon shall have a mean free path. Furthermore, this mean free path is the average travelling distance of a photon between collisions with the target material’s atoms. Moreover, this means that the free path is dependent on the material as well as the energy of the photons.

In electronics, a charge carrier’s mean free path of electrons in a metal is proportional to the electrical mobility. Furthermore, electrical mobility is a value that has a direct relation to the electrical conductivity .

How do we Measure Mean Free Path?

Let’s consider the motion of a gas molecule that is present inside an ideal gas. Furthermore, a typical molecule inside an ideal gas will change its direction and speed in an abrupt fashion. This is because its collision takes place elastically with other molecules of the same gas.

The molecule between the collisions shall move at a constant speed in a straight line. Most noteworthy, this is applicable for all the gas’s molecules.

Measuring this random motion of gas molecules is certainly difficult.  Therefore, one must try to measure its mean free path λ.

The symbol λ represents the average distance that a molecule travels between collisions. Furthermore, one can expect λ to vary inversely with N/V, which happens to be the number of molecules per unit volume or the density of the molecules.

Formula of Mean Free Path

Mathematically, representation of the mean free path can take place as follows:

λ = \(\frac{1}{\sqrt{2}\pi d^{2}\frac{N}{V}}\)

Derivation of the Formula of Mean Free Path

The derivation of the equation will make use of certain assumptions. Consider the molecule to be spherical. Furthermore, the collision takes place when one molecule hits the other. Moreover, the focus here is on the molecule that is in motion while the rest are stationary.

Assume the diameter of a single-molecule to be d. Furthermore, consider the single-molecule to move via the gas.

As such, it shall sweep out a short cylinder. Moreover, the cross-section area of this short cylinder is πd 2 .

Between the successive collisions, it will move a distance of vt for time t. Here, v happens to be the velocity of the molecule. Most noteworthy, one would attain the volume of πd 2 *vt on sweeping this cylinder.

Therefore, the number of collisions the molecule might have can be determined by the number of point molecules inside this volume.

Certainly, N/V is the number of molecules per unit volume. Therefore, the number of molecule in the cylinder will be N/V multiplied by the volume of cylinder i.e.πd 2 vt. As such, the derivation of mean free path can take place as follows,

λ = length of path during the time t/number of collision in time r ≈ \(\frac{vt}{\pi d^{2}vt\frac{N}{V}}\) = \(\frac{1}{\pi d^{2}\frac{N}{V}}\)

The approximation of the equation has taken place because it has been assumed that all the particles are stationary in relation to the particle under consideration. Most noteworthy, there is a movement of all the molecules relative to each other.

There has been the cancellation of two velocities in the above equation. Moreover, v in the numerator represents the average velocity while v in the denominator represents the relative velocity. As such, there is a difference between both with a factor \(\sqrt{2}\).

Most importantly, the final equation is,

λ = \ (\frac{1}{\sqrt{2}\pi d^{2}\frac{N}{V}}\)

FAQs For Mean Free Path

Question 1: What is the relation between the mean free path and temperature?

Answer 1: The relation between the mean free path and temperature is that there is a display of linear proportionality from the mean free path to the temperature.

Question 2: Explain the mean free path in electronics?

Answer 2: In electronics, charge carrier’s mean free path in metal is proportional to the electrical mobility.

Customize your course in 30 seconds

Which class are you in.

• Distance and Displacement

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

• Open access
• Published: 07 May 2020

A mean free path approach to the micro/nanochannel gas flows

• Jianfei Xie 1  

Advances in Aerodynamics volume  2 , Article number:  11 ( 2020 ) Cite this article

4073 Accesses

5 Citations

Metrics details

We investigate the gas flows near to solid surfaces in terms of the local spatial variation in the molecular mean free path (MFP). Molecular dynamics (MD) is the appropriate scientific tool for obtaining molecularly-accurate dynamic information in micro and nano-scale gas flows, and has been used to evaluate the molecular mean free path of gases. In the calibration procedure, the viscosity of a gas in the homogeneous case can be recovered in our MD simulations and reach good agreement with the theoretical prediction and data from NIST. In surface-bounded gas flows, if the collisions between gas molecules and walls are counted, a spatially-varying mean free path is presented, and for the first time we have observed that the distribution of the free paths deviates from the exponential one and spikes appear in their distributions at larger Kn, i.e. in the transition flow regime. Based on elementary kinetic theory, the effective viscosity of the gas derived from the mean free path has been incorporated into the framework of the continuum-fluid dynamics equations, and micro-Couette flows are performed to demonstrate this potential application.

1 Introduction

The Knudsen number (Kn) is usually adopted to quantify the deviation from the continuum behaviour in gas flows, i.e. the traditional index of the degree of rarefaction, and is defined as the ratio of the molecular mean free path (MFP) of gases to the characteristic dimension of the flow. The features of a gas flow are known to vary significantly depending on the value of Kn. For example, a gas flow at Kn = 1 may either refer to a low pressure condition and thus a large MFP in high altitude atmosphere (i.e. spaceship flying environments) or a higher pressure flow in very small channels (i.e. shale gas recovery [ 1 , 2 ]). Incidentally, the free molecular flow (i.e. Kn >10) in nano devices can be observed even at standard temperature and pressure (STP).

The physics of gas flows in rarefied regimes can significantly deviate from the continuum-based Navier-Stokes-Fourier (NSF) descriptions. Furthermore, fluid dynamics usually involve the motion of gases near the surface of a solid body, i.e. the Knudsen layer, in which the flow is in the local thermodynamic non-equilibrium state [ 3 , 4 ] and the standard NSF breaks down [ 5 , 6 ]. Thus Lockerby et al. [ 7 ] suggested to incorporate, rather than directly model, Knudsen layer effects within the conventional continuum-based fluid dynamics equations. This aim can be achieved by capturing the Knudsen layer structure within the NSF framework by scaling the stress/strain-rate relation in terms of correction functions. In the past decade, various researchers had proposed several different scaling functions for the rarefied gas flows: wall function [ 6 ], Kn-dependent functions [ 8 ], power-law scaling [ 9 ], and recently developed double power series [ 10 , 11 ]. These scaling functions come from the curve-fitting of kinetic theory or the direct simulation Monte Carlo (DSMC) calculations, and can provide the effective gas viscosity, which varies as a function of the normal wall distance. The primary advantage of the scaling constitutive relation is that it enables us efficiently to incorporate the rarefied effects within the NSF framework by paying less computational cost than the discrete velocity method (DVM) [ 12 , 13 ] and DSMC [ 14 ].

While the above mentioned scaling functions are derived from kinetic theory or DSMC data, it is still highly desirable to explore other case-specific scaling laws by counting gas-wall interactions (i.e. physical walls), allowing the scaling constitutive relation to be extended to complex flows such as the shale gas (i.e. polyatomic molecules) and the evaporation process of hydrocarbon fuel droplets (i.e. chain-like molecules) [ 15 – 17 ]. The novelty of this paper is to explore the potential of a molecular MFP-based scaling constitutive relation, which can be incorporated into the framework of continuum-based fluid dynamics equations to capture the effects that deviate from the equilibrium state such as the Knudsen layer in near-wall regions. In next section, we will introduce a procedure to evaluate the molecular MFP of gases bounded by solid surfaces in molecular dynamics simulations. Section 3 will present the spatial variation of MFP in micro/nano-channels, i.e. the effect of solid walls on the MFP, and illustrate the variation of the gas viscosity (i.e. effective viscosity) in near-wall regions. Importantly, a MFP-based scaling constitutive relation is applied in micro-Couette flows. Conclusions are drawn in Section 4 .

2 Assessment of MFP

2.1 kinetic prediction.

The molecular mean free path (MFP) is of great importance and fundamental in gas dynamics. Based on elementary kinetic theory arguments [ 18 – 21 ], the MFP for a gas composed of hard spheres is given by:

or a general expression in terms of the gas viscosity μ given by [ 20 ]:

where m is the molecular mass, d is the molecular diameter, ρ is the density of the gas, T is the gas temperature, and k B is the Boltzmann constant. Equation ( 1 ) assumes that the gas is dilute and spatially homogeneous. When the gas is bounded by solid walls, i.e. spatially-inhomogeneous cases, however, the expression in Eq. ( 1 ) needs to be revised to consider the collisions between gas molecules and solid walls.

Stops [ 22 ] first derived a space-dependent expression for the MFP of gas molecules leaving a wall, distributed according to the diffusive Lambert’s cosine law of reflection; three decades later, Guo et al. [ 23 ] extended the Stops’ model for MFP of gases in micro-channels; more recently, Abramov [ 24 ] has introduced a new expression for the MFP in confined geometries by replacing the cosine law with the equilibrium Maxwellian to give

where y = z / λ 0 , z is the normal distance from the wall, λ 0 the nominal MFP, and E 1 ( y ) is the exponential integral function, i.e. \(E_{1}(y)=\int _{y}^{\infty }{e^{-z}}/{z}\, \mathrm {d}z\) . Beside its kinetic-theoretical interest, a space-dependent expression for the MFP could be of practical relevance and has been used to propose scaling laws for the viscosity of a gas in near-wall regions [ 23 – 26 ].

2.2 Direct evaluation

Interestingly, the molecular MFP can also be calculated by averaging recorded individual free paths in molecular dynamics (MD) simulations [ 25 – 29 ]. MD simulations of the rarefied gas flows not only tackle the motion of gas molecules, but model the gas-surface interactions such as gas adsorption [ 30 , 31 ]. The distances travelled by gas molecules between every two successive collisions are calculated in MD simulations. In the present study, the monatomic gas argon (Ar) molecules are used. The molecules move according to Newton’s second law, and the intermolecular interactions between molecules are modelled through the Lennard-Jones (LJ) potential [ 31 , 32 ]:

where U is the intermolecular potential, r ij is the intermolecular distance, ε is the energy parameter, σ is the molecular diameter, and r c is the cutoff distance. For a micro-channel gas flow, we choose our wall atoms to be platinum (Pt), and the gas-wall (Ar-Pt) interaction is also modelled with the Lennard-Jones potential. The equations of motion are integrated using a velocity Verlet algorithm with a time step of Δ t =0.002 τ , where the characteristic time unit is \(\tau = {\sigma _{Ar}}\sqrt {m_{Ar} \left / \varepsilon _{Ar}\right.}=2.15 \times 10^{-12} \) s. The parameters and their values that were used in our MD simulations are summarised in Table I of [ 33 ].

For the measurement of individual free paths in MD, as shown in Fig.  1 , we set a condition to judge the occurrence of a collision event between gas molecules: if the distance between two gas molecules is equal to or less than the collision diameter, i.e. r ij ≤ σ col , where σ col is the collision diameter, the two molecules have collided and we stop recording the free paths of the involved molecules. Because the Lennard-Jones potential is used, the two molecules can still move closer to each other and the distance between them can be smaller than the collision diameter, i.e. r ij < σ col . So the finite time spent during collisions must be excluded when calculating the individual free paths. We therefore restart recording the free paths when the distance between the molecules is larger than the collision diameter, i.e. when r ij > σ col . In this procedure, the counter for recording the individual molecular free path is switched on after the last collision between two molecules and it is not switched off until the next collision. In addition, collisions between gas molecules and wall atoms are also counted: if the gas molecule approaches to the wall and has crossed a virtual plane that is placed σ col away from the walls, i.e. r z ≤ σ col or r z ≥( H − σ col ), where r z and H are the coordinate of gas molecules in the z direction and distance between two solid walls, respectively, we say it has collided with the wall (see Fig.  1 ) and stop recording its free path. The procedures of MD simulations and the treatment of bounding solid surfaces can be found in [ 33 ].

Schematic of the calculation of individual free paths in molecular dynamics (MD) simulations: the parameters l and v are the individual free path and velocity of molecules, respectively; r ij is the distance between two molecules, σ col is the collision diameter which is used to determine the collision event; Δ t is the time step in MD, and n is the number of time steps between two successive collisions of the i th molecule. It should be noted that x and y are orthogonal coordinate directions (i.e. the walls are oriented along the xy -plane) and the distance between the walls is along z direction

3 Results and discussion

3.1 recovering the viscosity of gases.

In order to demonstrate the capacity of our MD technique, we first recover the viscosity of a gas in a homogeneous case using the equilibrium Green-Kubo approach [ 34 , 35 ] via

where V is the volume of the system, and the time integration is the ensemble average of the auto-correlation of the stress tensor P xz . Using this, the gas viscosity has been calculated for temperatures ranging from 273 K to 473 K at a pressure of 1 atm , and the results are shown in Table  1 ; the viscosities obtained in our MD simulations reach good agreement with the theoretical prediction of a Lennard-Jones (LJ) fluid [ 36 , 37 ] as well as with the data for argon from National Institute of Science and Technology (NIST, http://webbook.nist.gov/chemistry/fluid/ ).

It is worth noticing that, in principle, a temperature-dependent collision diameter could also be defined based on the Chapman-Enskog expression of the viscosity for a gas composed of hard spheres [ 36 ]:

where d h is also called the molecular diameter of hard sphere in kinetic theory. The dependence of the collision diameter on the temperature predicted by Eq. ( 6 ) is shown in Fig.  2 by using the values of viscosity from NIST and the viscosity of Lennard-Jones (LJ) fluids [ 36 , 37 ]. In both cases, it can be seen that the relationship is roughly linear and the collision diameter also decreases as the gas temperature increases. However, the collision diameters predicted based on Eq. ( 6 ) significantly differ from the one obtained in MD: the change of collision diameter as the gas temperature is insignificant in MD simulations; but in both hard-sphere gas and LJ fluids the molecular diameter significantly depends on the gas temperature indicating a variable hard-sphere (VHS) model that is commonly used in kinetic theory.

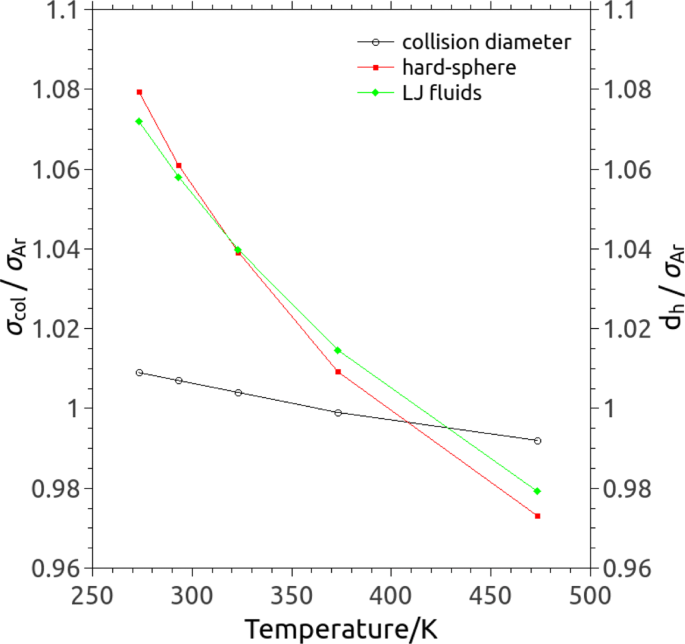
Collision diameter σ col (open circles) and molecular diameter for a hard-sphere gas d h (filled red squares) vary as a function of the gas temperature, and they are normalised by the molecular diameter in MD σ Ar =3.405×10 −10 m. By using Eq. ( 6 ) the prediction based on the viscosity of Lennard-Jones (LJ) fluids (filled green diamonds) [ 36 , 37 ] is also included for comparison. It can be seen that quasi-linear (i.e. MD simulations) or roughly linear (i.e. the hard-sphere gas) relationship exists in explored gas temperatures

3.2 Assessing the MFP in micro/nano-channels

We now consider a stationary gas confined in micro/nano-channels at STP, as shown in Fig.  1 , and evaluate the MFPs using MD simulations. In the channel x and y are orthogonal coordinates, and the two solid walls are parallel and oriented along the xy -plane with periodic boundary conditions imposed along the x and y directions. We simulate cases with different distances between the two parallel walls in the z -direction (i.e. the gap across the channel), varying from 20 λ 0 to λ 0 /2, where λ 0 is the nominal MFP given by Eq. ( 1 ). These correspond to Kn ranging from 0.05 to 2.0. For Kn = 0.05, there are 137,952 gas molecules in the micro-channel; as Kn increases (i.e. the channel height decreases), the number of gas molecules decreases accordingly. The spatial variation of the MFP is obtained by assigning the individual free paths to small constant-width bins that divide the space in the z -direction [ 26 , 27 , 29 ]. We have investigated the bin-independence of MFP results by varying the number of bins from 100 to 2000. It is found that the MFP profiles across the channel do not significantly change beyond 500 bins for Kn = 0.2, 1000 bins for Kn = 0.1, and 2000 bins for Kn = 0.05. These correspond to the same bin width in each case. The MD results reported below use these numbers of bins.

We first investigate the influence of a solid wall on the MFP by analysing the probability distribution of the individual free paths across the channel. In elementary kinetic theory, the free path distribution of gas molecules is claimed to be exponential in a homogeneous system (i.e. the gas is non-bounded by the solid surfaces) and it had been validated in our previous study [ 33 ]. However, the free path of gas molecules can be terminated at the wall in confined geometries (i.e. an inhomogeneous case), and a power-law distribution of the free paths had been reported in rarefied gases [ 27 ]. Therefore, to consider the effect of solid walls, we measure the free path distribution of gas molecules in micro/nano-channels. Our previous study showed that the free path distributions are still exponential at small Kn (i.e. in the upper slip and early transition regimes) [ 33 ]. As Kn increases ( ∼ 0.5), as shown in Fig. 3 , spikes are observed in distributions of the free paths, and move to the small free paths. The spikes may be caused by the gas molecules hitting the solid walls and get significant at higher Kn (i.e. in small channels narrower than λ 0 ). As reviewed in section 1 , gas flows at large Kn originally refer to the low pressure conditions in high altitude atmosphere and large mean free paths are expected. On the other hand, the transition flow (i.e. 0.1 < Kn <10) in micro/nano confinements can also be observed at STP, and as shown in Fig.  3 , the free path distribution of gas molecules is dominated by small free paths. Note that the distributions of free paths presented in Fig.  3 are different from the ones in [ 33 ], which measured the free path distributions of gas molecules in the central bins of channels.

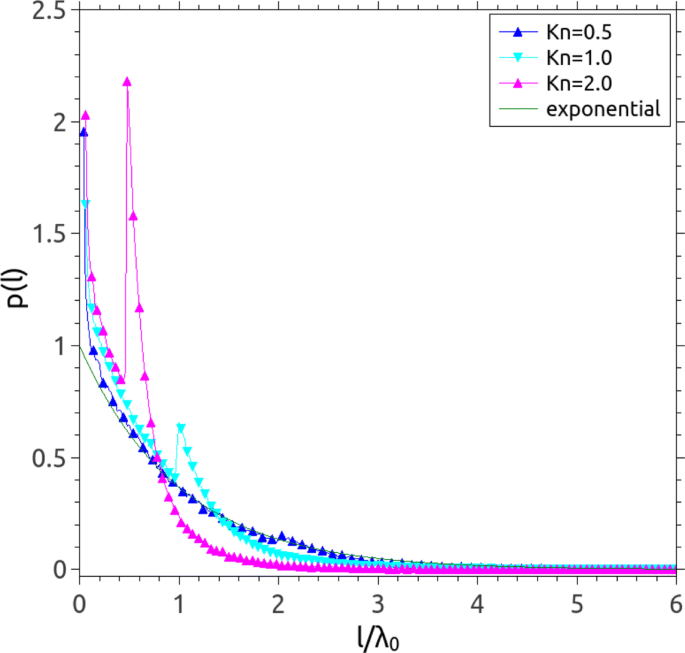
Probability density distribution of the individual free paths of gas molecules in channels with heights decreasing from 2 λ 0 to λ 0 /2, corresponding to Kn increasing from 0.5 to 2.0. The green solid line is the exponential distribution

It should be stressed that some studies argued that the MFP should be defined as the averaged distance travelled by gas molecules between two successive collisions with other gas molecules only, and that collisions between gas molecules and wall atoms or gas molecules adsorbed on the surface should not be taken into account when evaluating individual free paths [ 28 ]. With such a definition, a constant and isotropic MFP would be expected. Compared to the decrease of MFP at the walls when gas-wall collisions are counted, our previous MD predicted a constant MFP when gas-wall collisions were disregarded [ 33 ], whatever kind of walls (i.e. specular or diffusive) were utilised. Collisions between the gas and bounding surfaces can be encompassed in the concept of the MFP, and the resulting spatial variation of the MFP may help in understanding transport of gases in Knudsen layers near solid surfaces.

Apart from the spatial variation, the system MFP of a gas in the micro/nanochannel is also calculated in our MD simulations, and as shown in Fig.  4 , it varies as a function of Kn. An exponential decay fit can be expressed as λ s (Kn)/ λ 0 = 0.255 + 0.784 exp(-Kn/1.122), and we find that the system MFP deceases with increasing Kn (i.e. decreasing H ) but approaches to λ 0 if Kn → 0. Perumanath Dharmapalan et al. [ 29 , 38 ] also observed the variation of the system MFP as a function of the channel height, but their MFPs in nanochannels (height varying from 6 nm to 16 nm) are only several nanometres, which are much smaller than ours. Barisik and Beskok [ 28 ] used a fixed Kn ( ∼ 1.14) by changing both the channel height and gas density, and their data reaches reasonable agreement with our calculated system MFPs.

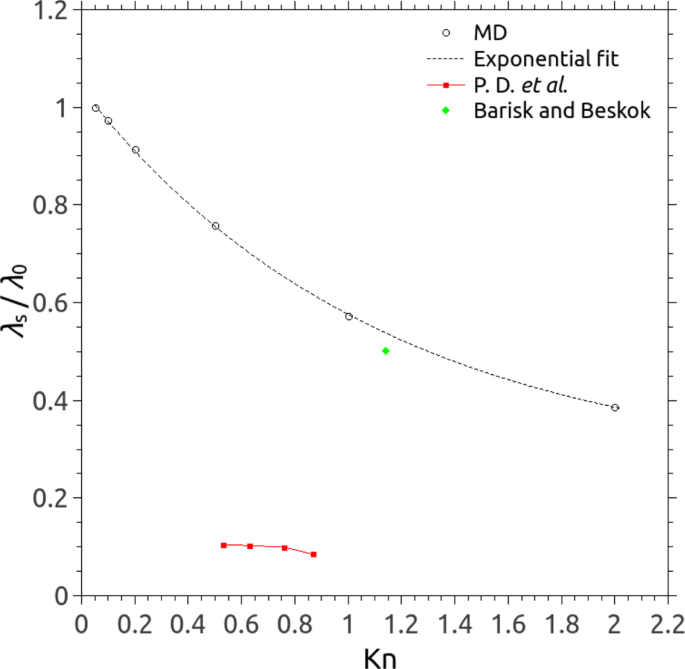
The system MFP of a gas varies as the function of Kn using MD (open circles): λ s and λ 0 are the system MFP and the nominal MFP, respectively. An exponential fit can be expressed as λ s (Kn)/ λ 0 = 0.255 + 0.784 exp(-Kn/1.122) (the dotted line). The system MFPs in nanochanels obtained in MD simulations by Barisik and Beskok [ 28 ] (filled green diamond) and Perumanath Dharmapalan et al [ 29 ] (filled red squares) are also shown for comparison. Note that Kn was kept a constant by changing both the density of gas and channel height in [ 28 ], and the range of the channel height varied only from 6 nm to 16 nm in [ 29 ]

3.3 Scaling constitutive relation in near-wall regions

It is well known that the standard fluid dynamics equations are no longer valid in the Knudsen layer. However, their range of validity can be extended by introducing the modified constitutive relation [ 23 , 25 , 39 , 40 ]. To summarise the scaling functions in the literature, we propose a general form of the scaling law for the constitutive relation in one-dimensional flow case (it can be easily extended to the three-dimensional case) as follows:

where Ψ ( z ) is an expression of the higher order non-linear correction terms, which vary with the chosen curve-fitting function such as the wall function from kinetic theory [ 6 ] or power-law function from DSMC [ 9 , 41 ]; u is the velocity of gas flows, τ is the shear stress, and μ is the viscosity of gases. It should be noted that the higher order non-linear correction terms are only considered when the non-equilibrium effect becomes significant or plays an important role in the flow region such as the Knudsen layer. Otherwise, Eq. ( 7 ) reduces to the linear constitutive relation in the framework of continuum-fluid dynamics equations when Ψ ( z ) vanishes.

In the extended hydrodynamic models, the effective gas viscosity that varies with the normal distance to the nearest solid wall can be expressed by:

where μ 0 is the nominal viscosity of the gas. We also find it convenient to recast the expression for the effective viscosity into an expression for the MFP of the gas. In elementary kinetic theory [ 18 , 36 ], the gas viscosity is proportional to the MFP. As a result, the spatial variation of MFP can be used to define a phenomenological scaling law for the viscosity of gases near any solid surfaces:

For example, based on Eq. ( 3 ), Abramov [ 24 , 42 ] proposed a geometry-dependent viscosity; Dongari et al. [ 27 ] introduced a power-law based effective viscosity in rarefied gases; To et al. [ 26 ] also reported the local viscosity which varied with the MFP. According to the MFP-based scaling law, Guo et al. straightforwardly pointed out that the gas viscosity \(\mu \rightarrow {\frac {1}{2}}\mu _{0}\) at the wall ( z =0) if the distance between two plates becomes infinity (i.e. Kn → 0 in Kramers’ problem); Fichman and Hetsroni [ 43 ] gave a fixed effective gas viscosity \(\mu _{e}={\frac {1}{2}}\mu _{0}\) in the whole Knudsen layer by considering the interactions between gas molecules and the wall (i.e. momentum exchange events). Apart from the MFP-based scaling law, Lockerby et al. [ 6 ] predicted an effective gas viscosity of 0.59 μ 0 at the solid surface when they used a wall-function expression in the constitutive relation; Reese et al. [ 44 ] generalised the scaling function to give the effective gas viscosity of 0.62 μ 0 at the wall. However, Lilley and Sader [ 9 ] contradicted these claims, and demonstrated that the flow exhibits a striking power-law dependence on distance from the solid surface and the effective gas viscosity at the surface should be zero due to the singularity of velocity gradient. Later Lockerby and Reese [ 41 ] revisited their scaling law and proposed an exponential scaling function, which results in the zero-viscosity of the gas at the wall. All values of the gas viscosity at the wall predicted by different scaling laws are summarised in Table  2 , and the expressions for different scaling functions can be found in Table I of [ 45 ].

Comparison of the gas viscosity in micro/nano-channels predicted by different scaling functions in Eq. ( 8 ) and by using Eq. ( 9 ) (as given by MD) illustrates that: all scaling functions have overpredicted the gas viscosity, particularly in the Knudsen layer; the generalised model proposed by Reese et al. [ 44 ] agrees well with the wall-function expression [ 6 ] except a larger gas viscosity at the wall; the power-law model introduced by Lilley and Sader [ 9 ] can only predict the gas viscosity within the Knudsen layer of one-MFP thickness, but it may fail when Kn varies. As can be seen in Fig.  5 , the MFP-based gas viscosity also varies near the solid surface and decreases with increasing Kn. Our previous study has already applied the linear-response relationship (i.e. Newtonian’s law) to calculate the gas viscosity and validate the MFP-based scaling function [ 33 ].

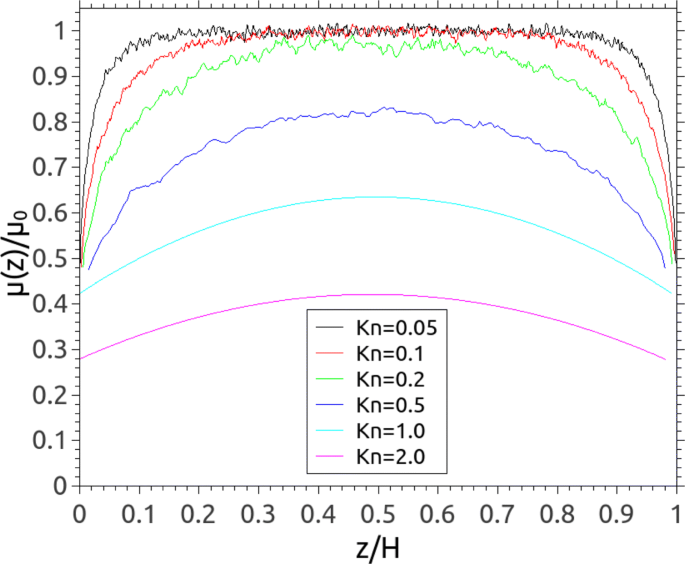
Spatial variation of the MFP-based viscosity of gases in micro/nanomicrochannels. Note that the viscosity is normalised by the nominal value μ 0

Although the Knudsen layer also affects the relationship between heat flux and temperature gradient, we restrict our attention to its effect on the stress/strain-rate relationship in the present study. Figure  6 a shows the uniform distribution of the shear stress P xz across the channel but reduction at the wall due to the strong gas-wall interactions. It also illustrates that the shear stress P xz in the bulk increases with increasing Kn, which is consistent with the prediction by Lockerby et al. [ 41 , 46 ]. We would like to point out that the greater value of the shear stress at the wall reported by Tu et al. [ 47 ] may be caused by counting the volume of gas within the bin close to the wall (i.e. part of wall atoms included) when sampling the properties of a gas across the channel in their MD simulations. Figure  6 b indicates the distribution of the strain rate across the channel. It can be seen that the strain rate also increases as Kn increases and the larger gradient of the strain rate has been observed in near-wall regions. It indicates that the gas viscosity varies near a solid surface and decreases with increasing Kn, which was theoretically predicted by Fei et al. [ 48 ] in terms of the Green-Kubo relation. We also observe that the gas viscosity at the wall reduces almost to half value it has in the bulk, i.e. 49% for Kn = 0.05, 48% for Kn = 0.1, 44% for Kn = 0.2 and 48% for Kn = 0.5.

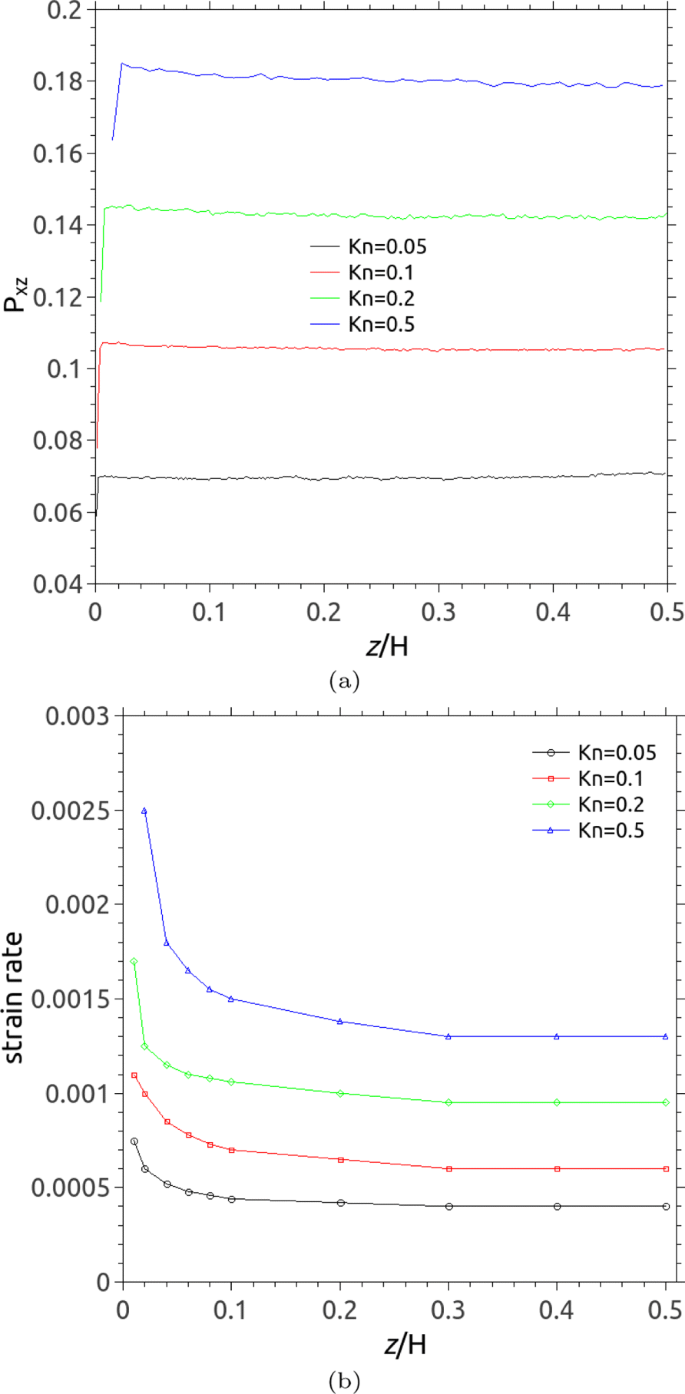
Local shear stress and strain rate in micro-Couette flows using MD for Kn = 0.05, 0.1, 0.2 and 0.5: a the shear stress P xz normal to the solid wall; b the strain rate in the xz panel. The data is plotted for only half the channel (i.e. above one of the surfaces)

It can be concluded that the MFP-based scaling law provides important insight into the use of the local viscosity of gas in near-wall regions, particularly in the Knudsen layer. Additionally, the thickness of the Knudsen layer is also measured and defined as the distance from the solid surface at which the stain rate reaches within 5% of the Navier-Stokes value [ 6 ]. Figure  7 presents the comparison of the Knudsen layer thickness between our MD simulations and other data: augmented Burnett approach gives the minimum thickness ( ∼ λ 0 ); regularised Burnett method estimates the maximum thickness ( ∼ 5 λ 0 ); and our MD results reach good agreement with the data of BGK Burnett approach in Kramers’ problem ( ∼ 2 λ 0 ), i.e. Kn →0.

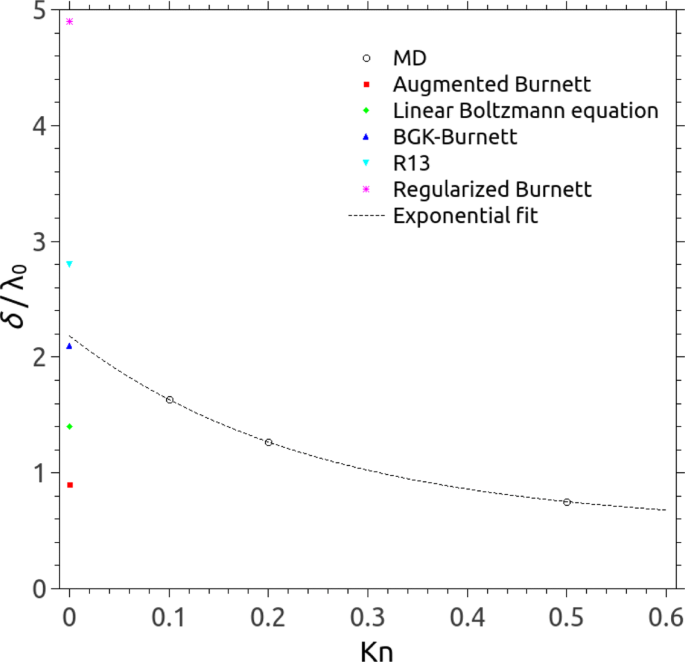
Thickness of the Knudsen layer predicted by different approaches: MD (open circles), Augmented Burnett (red filled squares) [ 49 ], Linear Boltzmann equation (green filled diamonds) [ 20 ], BGK-Burnett (blue filled triangles) [ 50 ], R13 (filled downtriangles) [ 51 ], and Regularised Burnett (pink stars) [ 52 ]. The dashed line refers to an exponential fit for our MD measurement. Note that the thickness of the Knudsen layer is normalised by the nominal MFP λ 0 and is related to the Kramers’ problem, i.e. Kn →0 presented in the literature

3.4 Application of MFP to non-equilibrium gas flows

In order to explore the potential application of the spatially-varying MFP, we discuss a MFP-based scaling solution for a non-equilibrium flow. According to the relation for the MFP given by Eq. ( 3 ), the viscosity of gases can be scaled in the same manner, i.e. Eq. ( 9 ). We assume that the temperature of the gas flow varies insignificantly, i.e. an isothermal and incompressible flow. Considering a variable viscosity, the Navier-Stokes velocity equation for the shear flow reduces to [ 24 ]:

where u 0 is the velocity of top and bottom walls which move in opposite directions along the x axis, and the local viscosity of gases across the channel μ ( z ) is given by Eq. ( 9 ). The solution for the shear flow (i.e. micro-Couette flow) derived from the MFP-based scaling law is illustrated in Fig.  8 with Kn ranging from 0.05 to 0.2. Without loss of generality, the wall-dependent MFP in Eq. ( 3 ) proposed by Abramov [ 24 ] has also been used to scale the gas viscosity.

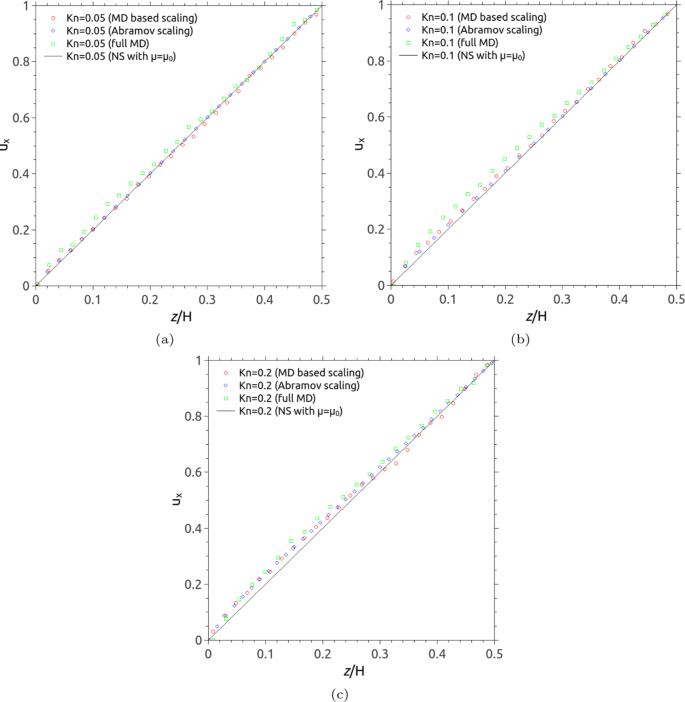
Velocity profiles of the micro-Couette gas flow for: a Kn = 0.05; b Kn = 0.1; and c Kn = 0.2. Open circles (red) and diamonds (blue) are based on the scaling laws from MFP in MD results and Abramov [ 24 ], respectively; open squares (green) refer to the full MD simulations results; the solid line refers to the Navier-Stokes solution with a constant viscosity. The data is plotted for only half the channel (i.e. above one of the surfaces) and the velocity is rescaled by half of the value for shearing walls

Apart from the scaling constitutive solution, our MD results for the profile of the cross-channel gas velocity have been presented in Fig.  8 for comparison. Note that the no-slip velocity boundary condition is used in the scaling constitutive solution and the possibly different velocity of the wall itself is disregarded for the sake of argument [ 24 ]. For the purpose of comparing the scaling constitutive solution and MD-computed velocity profiles, we remove the velocity slip at the solid wall in MD simulations by subtracting its zero-distance value from the velocity profiles. The Navier-Stokes solution with a constant viscosity, moreover, has been included for comparison. Figure  8 indicates that good agreement between two scaling constitutive solutions with variable viscosity and MD results has reached up to the early transition region (i.e. Kn ∼ 0.2). However, the Navier-Stokes solution with a constant viscosity fails to capture the non-equilibrium gas flow in the Knudsen layer. The MFP-based scaling constitutive relation can accredit us to capture the non-equilibrium flow near any solid surfaces.

In the scaling or extended constitutive relation, the non-equilibrium gas flow in the Knudsen layer is much more sensitive to the slip coefficient at the solid surface and it has still been an open question. This tenet, together with the second-order constitutive and velocity slip and temperature jump models [ 40 , 45 ], may need further investigation in rarefied or micro/nano scale gas flows and it is beyond the scope of this paper.

4 Conclusion

The molecular mean free path (MFP) in a gas has been evaluated by using molecular dynamics (MD). In a spatially-homogeneous case, we obtained good agreement of the gas viscosities between our MD results and LJ fluids/NIST data. In micro-channels (spatially-inhomogeneous cases) we found that the MFP at the walls reduces smoothly to half of its bulk value, as long as the collisions between the gas and the wall are accounted for. If it is used as a tool to scale transport properties near to bounding surfaces as a simple way to describe Knudsen layers, then a definition that counts gas-wall collisions should be preferred.

Evaluations of the molecular MFP of gases open up an exciting new direction: explicitly connecting the governing gas/gas and gas/surface interactions at a molecular scale to the continuum-fluid dynamics in the bulk. Based on elementary kinetic theory, the MFP-based scaling law has been proposed to obtain the local gas viscosity and the spatial variation of the gas viscosity as a function of the perpendicular distance from the solid surface has been implemented to the framework of continuum-fluid dynamics equations.

While we also presented the application of a spatially-varying MFP model to micro/nano-channel flows (i.e. micro-Couette flows), with the aim of developing greater understanding of transport behaviour in near-wall regions, our detailed investigations into the Knudsen layer near a solid surface have illustrated the capacity of this MFP-based scaling constitutive relation to capture the non-equilibrium gas flows. It is recommended that an extended MFP approach will be applicable to develop a higher order hydrodynamic model of the transport of gases in highly-confined geometries in the future.

Availability of data and materials

All data and materials are available upon request.

Darabi H, Ettehad A, Javadpour F, Sepehrnoori K (2012) Gas flow in ultra-tight shale strata. J Fluid Mech 710:641–658.

Article   MathSciNet   MATH   Google Scholar  

Wu L, Ho MT, Germanou L, Gu X-J, Liu C, Xu K, Zhang Y (2017) On the apparent permeability of porous media in rarefied gas flows. J Fluid Mech 822:398–417.

Zhang J, John B, Pfeiffer M, Fei F, Wen D (2019) Particle-based hybrid and multiscale methods for nonequilibrium gas flows. Adv Aerodyn 1:12.

Article   Google Scholar  

Fei F, Zhang J, Li J, Liu Z (2020) A unified stochastic particle Bhatnagar-Gross-Krook method for multiscale gas flows. J Comput Phys 400:108972.

Article   MathSciNet   Google Scholar  

Reese JM, Gallis MA, Lockerby DA (2003) New directions in fluid dynamics: non-equilibrium aerodynamic and microsystem flows. Phil Trans R Soc Lond A Math Phys Eng Sci 361:2967–2988.

Lockerby DA, Reese JM, Gallis MA (2005) Capturing the Knudsen layer in continuum-fluid models of nonequilibrium gas flows. AIAA J 43:1391–1393.

Lockerby DA, Reese JM, Gallis MA (2005) The usefulness of higher-order constitutive relations for describing the Knudsen layer. Phys Fluids 17:109902.

Article   MATH   Google Scholar  

Cercignani C, Frangi A, Lorenzani S, Vigna B (2007) BEM approaches and simplified kinetic models for the analysis of damping in deformable MEMS. Eng Anal Bound Elem 31:451–457.

Lilley CR, Sader JE (2007) Velocity gradient singularity and structure of the velocity profile in the Knudsen layer according to the Boltzmann equation. Phys Rev E 76:026315.

Li W, Luo L-S, Shen J (2015) Accurate solution and approximations of the linearized BGK equation for steady Couette flow. Comput Fluids 111:18–32.

Jiang S, Luo L-S (2016) Analysis and accurate numerical solutions of the integral equation derived from the linearized BGKW equation for the steady Couette flow. J Comput Phys 316:416–434.

Mieussens L (2000) Discrete-Velocity Models and Numerical Schemes for the Boltzmann-BGK Equation in Plane and Axisymmetric Geometries. J Comput Phys 162:429–466.

Mieussens L (2001) Convergence of a discrete-velocity model for the Boltzmann-BGK equation. Comput Math Appl 41:83–96.

Bird GA (1994) Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Oxford University Press, Oxford.

Google Scholar  

Cao B-Y, Xie J-F, Sazhin SS (2011) Molecular dynamics study on evaporation and condensation of n-dodecane at liquid-vapor phase equilibria. J Chem Phys 134:164309.

Xie J-F, Sazhin SS, Cao B-Y (2011) Molecular dynamics study of the processes in the vicinity of the n-dodecane vapour/liquid interface. Phys Fluids 23:112104.

Xie J-F, Sazhin SS, Cao B-Y (2012) Molecular dynamics study of condensation/evaporation and velocity distribution of n-dodecane at liquid-vapour phase equilibria. J Therm Sci Technol 7:288–300.

Kennard EH (1938) Kinetic Theory of Gases. McGraw-Hill Book Company, Inc., New York and London.

Patterson GN (1956) Molecular Flow of Gases. Wiley, New York.

Book   MATH   Google Scholar  

Cercignani C (1990) Mathematical Methods in Kinetic Theory. Plenum Press, New York and London.

Kremer GM (2010) An Introduction to the Boltzmann Equation and Transport Processes in Gases. Springer, Berlin, Heidelberg.

Stops DW (1970) The mean free path of gas molecules in the transition regime. J Phys D Appl Phys 3:685–696.

Guo ZL, Shi BC, Zheng CG (2007) An extended Navier-Stokes formulation for gas flows in the Knudsen layer near a wall. Europhys Lett 80:24001.

Abramov RV (2018) Gas Near a Wall: Shortened Mean Free Path, Reduced Viscosity, and the Manifestation of the Knudsen Layer in the Navier–Stokes Solution of a Shear Flow. J Nonlinear Sci 28:833–845.

Arlemark EJ, Dadzie SK, Reese JM (2010) An extension to the Navier-Stokes equations to incorporate gas molecular collisions with boundaries. J Heat Tran 132:041006.

To QD, Léonard C, Lauriat G (2015) Free-path distribution and Knudsen-layer modeling for gaseous flows in the transition regime. Phys Rev E 91:023015.

Dongari N, Zhang Y, Reese JM (2011) Molecular free path distribution in rarefied gases. J Phys D Appl Phys 44:125502.

Barisik M, Beskok A (2015) Molecular free paths in nanoscale gas flows. Microfluid Nanofluid 18:1365–1371.

Hari SPD, Prabha SK, Sathian SP (2015) The effect of characteristic length on mean free path for confined gases. Phys A Stat Mech Appl 437:68–74.

Xie J-F, Cao B-Y (2016) Nanochannel flow past permeable walls via molecular dynamics. AIP Adv 6:075307.

Xie J-F, Cao B-Y (2017) Effect of various surface conditions on nanochannel flows past permeable walls. Mol Simul 43:65–75.

Xie J-F, Cao B-Y (2017) Fast nanofluidics by travelling surface waves. Microfluid Nanofluid 21(7):111.

Xie J, Borg MK, Gibelli L, Henrich O, Lockerby DA, Reese JM (2019) Effective mean free path and viscosity of confined gases. Phys Fluids 31:072002.

Zhang L, Greenfield ML (2007) Relaxation time, diffusion, and viscosity analysis of model asphalt systems using molecular simulation. J Chem Phys 127:194502.

Feng Y, Goree J, Liu B (2011) Green-Kubo relation for viscosity tested using experimental data for a two-dimensional dusty plasma. Phys Rev E 84:046412.

Chapman S, Cowling TG (1970) The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction and diffusion in gases. Cambridge University Press, Cambridge.

MATH   Google Scholar  

Neufeld PD, Janzen A, Aziz R (1972) Empirical equations to calculate 16 of the transport collision integrals ω ( l , s ) ∗ for the Lennard-Jones (12-6) potential. J Chem Phys 57:1100–1102.

Prabha SK, Sreehari PD, Murali GM, Sathian SP (2013) The effect of system boundaries on the mean free path for confined gases. AIP Adv 3:102107.

O’Hare L, Scanlon TJ, Emerson DR, Reese JM (2008) Evaluating constitutive scaling models for application to compressible microflows. Int J Heat Mass Tran 51:1281–1292.

Myong RS (2016) Theoretical description of the gaseous Knudsen layer in Couette flow based on the second-order constitutive and slip-jump models. Phys Fluids 28:012002.

Lockerby DA, Reese JM (2008) On the modelling of isothermal gas flows at the microscale. J Fluid Mech 604:235–261.

Abramov RV (2017) Diffusive Boltzmann equation, its fluid dynamics, Couette flow and Knudsen layers. Phys A Stat Mech Appl 484:532–557.

Fichman M, Hetsroni G (2005) Viscosity and slip velocity in gas flow in microchannels. Phys Fluids 17:123102.

Reese JM, Zheng Y, Lockerby DA (2007) Computing the Near-Wall Region in Gas Micro- and Nanofluidics: Critical Knudsen Layer Phenomena. J Comput Theor Nanosci 4:807–813.

Guo Z, Qin J, Zheng C (2014) Generalized second-order slip boundary condition for nonequilibrium gas flows. Phys Rev E 89:013021.

Lockerby DA, Reese JM (2003) High-resolution Burnett simulations of micro Couette flow and heat transfer. J Comput Phys 188(2):333–347.

Tu C, Qian L, Bao F, Yan W (2017) Local effective viscosity of gas in nano-scale channels. Eur J Mech B/Fluids 64:55–59.

Fei F, Fan J, Jiang J (2012) Solid wall effect on the transport coefficients of gases. Sci China Phys Mech Astron 55:927–932.

Zhong X, Maccormack RW, Chapman DR (1993) Stabilization of the Burnett equations and application to hypersonicflows. AIAA J 31:1036–1043.

Balakrishnan R (2004) An approach to entropy consistency in second-order hydrodynamic equations. J Fluid Mech 503:201–245.

Struchtrup H, Torrilhon M (2003) Regularization of Grad’s 13 moment equations: Derivation and linear analysis. Phys Fluids 15:2668.

Jin S, Slemrod M (2001) Regularization of the Burnett Equations via Relaxation. J Stat Phys 103:1009–1033.

Download references

Acknowledgements

JX would like to thank Professor Jason Reese, who proposed this subject to the author and passed away due to a sudden illness in March 2019.

The work was financially supported by the UK’s Engineering and Physical Sciences Research Council (EPSRC) via grant no. EP/N016602/1.

Author information

Authors and affiliations.

Department of Mechanical Engineering, University of Derby, Derby, DE22 3AW, United Kingdom

Jianfei Xie

You can also search for this author in PubMed   Google Scholar

Contributions

JX read and approved the final manuscript.

Corresponding author

Correspondence to Jianfei Xie .

Ethics declarations

Competing interests.

The author declares that he has no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Xie, J. A mean free path approach to the micro/nanochannel gas flows. Adv. Aerodyn. 2 , 11 (2020). https://doi.org/10.1186/s42774-020-00035-w

Download citation

Received : 13 February 2020

Accepted : 15 April 2020

Published : 07 May 2020

DOI : https://doi.org/10.1186/s42774-020-00035-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Rarefied gas
• Mean free path
• Effective viscosity
• Molecular dynamics

The mean free time and the mean free path: exact expressions for an (approximately) ideal gas

• Regular Article
• Published: 07 September 2023
• Volume 138 , article number  791 , ( 2023 )

Cite this article

• Mohammad Khorrami   ORCID: orcid.org/0000-0002-2524-5237 1  

64 Accesses

Explore all metrics

The order of magnitudes for the mean free time and the mean free path corresponding to classical (nearly) ideal gases are easy to estimate. The exact values, however, are a little trickier to calculate. To do so, more careful definitions are needed, and one should carefully calculate averages of functions of particle velocities. These are done, and compared with the simpler less-accurate results which are usually used.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

Data sharing not applicable to this article as no data sets were generated or analysed during the current study.

F. Reif, Fundamentals of Statistical and Thermal Physics , extended ninth edn. (Waveland Press, Long Grove, 2010)

Google Scholar  

R.L. Liboff, Kinetic Theory: Classical, Quantum, and Relativistic Descriptions , 3rd edn. (Springer, Berlin, 2003)

K. Huang, Introduction to Statistical Physics (Taylor & Francis, Milton Park, 2001)

Book   MATH   Google Scholar  

S.J. Blundell, K.M. Blundell, Concepts in Thermal Physics , 2nd edn. (Oxford University Press, Oxford, 2010)

MATH   Google Scholar  

C. Kittel, H. Kroemer, Thermal Physics , 2nd edn. (W. H. Freeman and Company, New York, 2000)

G.F. Mazenko, Nonequilibrium Statistical Mechanics (Wiley-VCH, Weinheim, 2006)

F.S. Crawford, Waves (McGraw Hill, New York, 1968)

J. Wu, Am. J. Phys. 58 , 694 (1990)

Article   ADS   Google Scholar  

K. Huang, Statistical Mechanics , 2nd edn. (Wiley, Hoboken, 1987)

F. Reif, Statistical Physics (McGraw-Hill, New York, 1975)

J. Walker, Halliday & Resnick Fundamentals of Physics , extended elevnth edn. (Wiley, Hoboken, 2018)

W. Feller, An Introduction to Probability Theory and Its Applications , 3rd edn. (Wiley, Hoboken, 1968)

A.N. Gorban, H.P. Sargsyan, H.A. Wahab, Math. Model. Nat. Phenom. 6 , 184 (2011)

Article   MathSciNet   Google Scholar  

M. Hamada, P. de Anna, Transp. Porous Med. 146 , 463 (2023)

Article   Google Scholar  

L. van den Berg, M.C.M. van Loosdrecht, M.K. de Kreuk, Biotechnol. Bioeng. 118 , 1273 (2020)

M.J. Assael, K.D. Antoniadis, I.N. Metaxa, S.K. Mylona, J.-A.M. Assael, J. Wu, M. Hu, Int. J. Thermophys. 36 , 3083 (2015)

Ch.D. Chliatzou, M.J. Assael, K.D. Antoniadis, M.L. Huber, W.A. Wakeham, J. Phys. Chem. Ref. 47 , 033104 (2018)

ADS   Google Scholar  

L. Qiu, X.H. Zheng, P. Yue, J. Zhu, D.W. Tang, Y.J. Dong, Y.L. Peng, Int. J. Therm. Sci. 89 , 185 (2015)

X. Xiao, D. Rowland, S.Z.S. Al Ghafri, E.F. May, J. Phys. Chem. Ref. 49 , 013101 (2020)

K. Trachenko, V.V. Brazhkin, Sci. Adv. (2020). https://doi.org/10.1126/sciadv.aba3747

E.J. Maginn, R.A. Messerly, D.J. Carlson, D.R. Roe, J.R. Elliott, Living J. Comp. Mol. Sci. 1 , 6324 (2018)

M. Bešter-Rogač, D. Habe, Acta Chim. Slov. 53 , 391 (2006)

N. Doppelhammer, N. Pellens, J. Martens, C.E.A. Kirschhock, B. Jakoby, E.K. Reichel, ACS Sens. 5 , 3392 (2020)

M. Petrowsky, R. Frech, J. Phys. Chem. B 113 , 5996 (2009)

N.W. Ashcroft, N.D. Mermin, Solid State Physics (Harcourt College Publishers, Fort Worth, 1976)

R.K. Pathria, Statistical Mechanics , 3rd edn. (Elsevier, Amsterdam, 2011)

Download references

Acknowledgements

This work was supported by the research council of the Alzahra University.

Author information

Authors and affiliations.

Department of Fundamental Physics, Faculty of Physics, Alzahra University, Tehran, Iran

Mohammad Khorrami

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Mohammad Khorrami .

Ethics declarations

Conflict of interest.

The author reports there are no competing interests to declare.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Khorrami, M. The mean free time and the mean free path: exact expressions for an (approximately) ideal gas. Eur. Phys. J. Plus 138 , 791 (2023). https://doi.org/10.1140/epjp/s13360-023-04414-2

Download citation

Received : 01 August 2023

Accepted : 24 August 2023

Published : 07 September 2023

DOI : https://doi.org/10.1140/epjp/s13360-023-04414-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

Determination of mean free path for energy loss and surface oxide film thickness using convergent beam electron diffraction and thickness mapping: a case study using Si and P91 steel

Affiliation.

• 1 Institute of Materials and Engineering Science, ANSTO, PMB 1, Menai, NSW 2234, Australia. [email protected]
• PMID: 17204066
• DOI: 10.1111/j.1365-2818.2006.01690.x

Determining transmission electron microscope specimen thickness is an essential prerequisite for carrying out quantitative microscopy. The convergent beam electron diffraction method is highly accurate but provides information only on the small region being probed and is only applicable to crystalline phases. Thickness mapping with an energy filter is rapid, maps an entire field of view and can be applied to both crystalline and amorphous phases. However, the thickness map is defined in terms of the mean free path for energy loss (lambda), which must be known in order to determine the thickness. Convergent beam electron diffraction and thickness mapping methods were used to determine lambda for two materials, Si and P91 steel. These represent best- and worst-case scenario materials, respectively, for this type of investigation, owing to their radically different microstructures. The effects of collection angle and the importance of dynamical diffraction contrast are also examined. By minimizing diffraction contrast effects in thickness maps, reasonably accurate (+/-15%) values of lambda were obtained for P91 and accuracies of +/-5% were obtained for Si. The correlation between the convergent beam electron diffraction-derived thickness and the log intensity ratios from thickness maps also permits estimation of the thickness of amorphous layers on the upper and lower surfaces of transmission electron microscope specimens. These estimates were evaluated for both Si and P91 using cross-sectional transmission electron microscopy and were found to be quite accurate.

Talk to our experts

1800-120-456-456

• Mean Free Path Factors

Concept of Mean Free Path

According to Classius, every gas comprises an infinite number of molecules that are perfectly elastic spheres. 

The size of the gas molecules is tiny as compared to the distance between them. 

Further, the molecules of a gas in the state of never-ending, speedy, and random motion; undergo perfectly elastic collisions with one another. 

As the molecules exert no force on one another except during collision, the free path travelled between two successive collisions will be a linear path with invariant velocity. 

Therefore, the path of a single molecule consists of a series of short zig-zag paths of different lengths. 

(Image will be uploaded soon)

These paths of varying lengths are called free paths of the molecules, and their mean is called the mean free path. 

Let’s talk about the free path of molecules.

We presume in the kinetic theory of gases that the gas molecules are in constant motion, which means they are colliding with each other and with the walls of the container. This type of collision is elastic by nature. 

Let’s say, in Fig, there is ‘n’ number of molecules.

Now, focus on molecule A inside the gas, which is in a random motion and continuously collides with all the other molecules one by one. 

Molecule A collides with another molecule B, with C and then with D.

When molecule A collides with molecule B, then it is the first collision. Thereafter, it collides with C, which is the second collision, then with D, which is the third collision, and then with E, which is the fourth collision. Thus, it keeps on colliding with all the molecules. 

Consider the distance between the first and the second collision be λ 1 and the distance between the second and the third collision be  λ 2 , then the distance between the third and fourth collision

(Image will be uploaded soon)  

Here, λ 1 , λ 2 , and λ 3 are free paths i.e The path between each collision is free. 

So, at λ 1 , molecule A after colliding with molecule B got the first free path, at  λ 2 , after colliding with molecule C, it got another free path and so on. 

Since no collisions occur between any two collisions, the path is free between each collision. 

Therefore, we can say that the free path is the distance between the two consecutive collisions like λ 1 , which is the free path. Similarly, λ 2 is another free path and so.

Mean Free Path 

We just understood the concept of a free path of molecules. Now, if we wish to find the average of these free paths, we get the mean of the free paths, which is represented as λ 1 = First free path      

λ 2   = Second free path        

λ 3     = Third free path 

λ n = nth free path. 

So, Mean free path formula is:          

λmean = ( λ 1 +  λ 2 +  λ 3 +.....+ λ n )/n.

Define Mean Free Path  

We can define the mean free path as the average distance between the two consecutive collisions. 

Here, the distance between the molecules may vary, sometimes they would be separated at a large distance, sometimes close to each other, sometimes collisions will happen early, and sometimes collisions may take time. We need an average of the overall conditions.

Mean Free Path in Physics

Consider a gas comprising ‘n’ number of molecules scattered inside the container.

Assume molecule A, colliding with all other molecules. 

Now, construct a cylinder of length ‘1 m’, and, imagine, whichever molecule, a molecule A collides with, is inside this cylinder. 

This means molecule A doesn’t collide with all the molecules, rather only with those packed in the cylinder. 

Let us assume that all the molecules travel in a straight line, including the molecule A.

(Image to be added soon)

As this molecule A starts moving in a straight line, it won’t collide with the molecules in and around the cylinder shown in Fig

(image to be added soon)

Now, a question comes in our mind; if the distance between the two molecules is larger, a molecule A would pass between them without a collision. However, if it passes between the molecules that are close to each other, there will be a collision.

Let’s Understand This is a Better Way

Consider the diameter of molecule A as ‘d’, and the space required for it to pass through the molecules inside the cylinder without any collision between the molecules is also ‘d’. Now, it is for sure, if the molecules inside the cylinder are close to each other, then, definitely, there will be a collision between A and these molecules; however, molecules completely outside this imaginary cylinder of diameter ‘2d’ won’t collide with A.

Now, the number of molecules per unit volume = n(n molecules in 1 m 3 volume)

No of molecules inside the cylinder = πd 2 x 1= πd 2 * 1

No of collisions in traveling distance of 1 m  = πd 2 * n

So, in 1 collision = 1/πd 2 * n distance, which is the mean free path.

Factors Affecting the Mean Free Path

The different factors affecting the mean free path are density, number of molecules, the radius of the molecules and other physical factors including temperature, pressure and all. 

Density - It simply measures the fraction of the mass of an object to its volume. As the density increases, molecules come closer and collide, thus reducing the mean free path. Similarly, as the density decreases, the molecules loosen up and more mean free paths appear. Therefore, density is inversely proportional to the mean free path. For eg, when air is compressed, the air molecules only get less space to roam around which will cause a collision. 

The number of molecules - An increase in the number of molecules can result in more collisions and will decrease the mean free path. 

The radius of the molecule - A rise in the radius of the molecules leads to the extension of the area it occupies and can touch the neighbouring molecules giving decreasing effect on the mean free path. For eg, heating pushes an increase in the kinesthetic energy of molecule particles and will steer to an expansion in the radius of the molecules creating collisions followed by a decrease in free mean paths. 

Other physical factors - Pressure is one important factor that can regulate the free mean path. If the pressure among the molecules increases, the average speed between the molecules increases and thus collision happens. So the increase in pressure will decrease the free mean path. 

Every factor is an integral of the free mean path and the interconnections between them stem the outcomes. 

Here pressure and temperature have a great relationship concerning the mean free path. 

As you have studied from the 11th NCERT Texts, Gay Luccas’ Law explains that the pressure of a given amount of gas is directly proportional to its’ temperature,

interconnection between the factors of the mean free path.  

Motion of Molecules 

If there are enough mean free paths, then the moment of the gas molecules will be fast and free, ie; it will possess random motion. However, if a mean free path is being created by releasing any of the factors, then the molecules would show diffusive motion since the molecules are getting rapid freedom and the moment is from an area of higher concentration to lower concentration. Diffusion is basically the intermixing of particles or molecules. This is the reason why keeping the volume constant. This law is self-sufficient to showcase the bond between temperature and pressure, thereby giving an idea about the i we get the cooking smell from the kitchen.  This can be in contrast with another motion called ballistic motion. The molecules or particles mostly tend to move in a zig-zag motion. 

Imagine what would have happened if these molecules were tightly packed? They would have never had any motions! Because of the distance that the molecules have before their successive collisions, motions like diffusion could occur. Not only that, they in turn are helpful in the transportation of matter, thermal energy and much more.

Mean Free Path in Ions 

It is important to know the relative distance between ions to understand and calculate various physical properties and spatial information respectively. So let us take a brief look at the relationship between ions and the mean free path.

Ions are a bunch of atoms that take shape when an atom loses its stability by the loss or gain of proton or electron. Ions are used in water purification and many other things. Mean free path helps us to analyse the distance from which negative ions can be extracted and the relative prominence of several collisions. There are many more crucial findings and concepts pertaining to the mean free path. You will study them in higher classes.

Different matters will have different mean free paths, depending on their type of gas, density, volume etc. For eg, the mean free path in hydrogen is longer than in deuterium. Thus, the chaotic motions of these spherical and elastic molecules in gas can actually teach and be useful for many purposes. 

FAQs on Mean Free Path Factors

1. How Do You Increase the Mean Free Path?

The mean free path is the average distance a molecule travels between collisions, which means the farther the molecules are, the more will be the free path. If the density of the gas increases, the molecules run into each other, decreasing the free path.Thus, it’s necessary to keep the molecules apart to increase the mean free path.

The mean free path formula is given by,

                 λ = RT/√2πd 2 N A P

2. How Does Temperature Affect the Mean Free Path?

According to the kinetic theory of gases, on increasing the temperature, molecules run fastly; however, the distance or the mean free path remains constant, and only the meantime of collision decreases.

Therefore, we can say that the mean free path is independent of the temperature.

3. Which Has the Maximum Value of the Mean Free Path?

The molecule possessing a small size will have a maximum mean free path.

4. What Is Meant by Collision Frequency?

Collision frequency is the repetitive time interval in which on average molecular collisions take place. It is denoted by letter Z. Its formula is given as:

Z = 1/f = T

5. What is molecular collision?

The concept of the molecular collision was proposed by  Max Trautz in 1916 and William Lewis in 1918. It gives us a subjective elaboration on the phenomenon of a chemical reaction and why the reaction rate differs from different reactions. The collision theory states that when suitable particles of the reactant hit each other, only a certain percentage of the collisions cause any noticeable or significant chemical change; these successful changes are called successful collisions. The collisions should be energy-packed, also called the activation energy in order to break the preexisting bonds and form new ones while colliding. This gives out the reactions. An increase in the concentration of reactant particles or other physical chattels like temperature brings more collisions and more collisions increase the rate of reactions.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Chapter 6.7: Mean Free Path

• Last updated
• Save as PDF
• Page ID 43253

Learning Objective

• The mean free path is the average distance traveled by a moving molecule between collisions.

Introduction

Imagine gas leaking out of a pipe. It would take a while for the gas to diffuse and spread into the environment. This is because gas molecules collide with each other, causing them to change in speed and direction. Therefore, they can never move in a straight path without interruptions. Between every two consecutive collisions, a gas molecule travels a straight path. The average distance of all the paths of a molecule is the mean free path.

Gas molecules do not diffuse nearly as rapidly as their very high speeds might suggest. If molecules actually moved through a room at hundreds of miles per hour, we would detect odors faster than we hear sound. Instead, it can take several minutes for us to detect an aroma because molecules are traveling in a medium with other gas molecules. Because gas molecules collide as often as 10 10 times per second, changing direction and speed with each collision, they do not diffuse across a room in a straight line, as illustrated schematically in Figure 6.7.1 The average distance traveled by a molecule between collisions is the mean free path The average distance traveled by a molecule between collisions. . The denser the gas, the shorter the mean free path; conversely, as density decreases, the mean free path becomes longer because collisions occur less frequently. At 1 atm pressure and 25°C, for example, an oxygen or nitrogen molecule in the atmosphere travels only about 6.0 × 10 −8 m (60 nm) between collisions. In the upper atmosphere at about 100 km altitude, where gas density is much lower, the mean free path is about 10 cm; in space between galaxies, it can be as long as 1 × 10 10 m (about 6 million miles).

Figure 6.7.1 The Path of a Single Particle in a Gas Sample The frequent changes in direction are the result of collisions with other gas molecules and with the walls of the container.

Calculations

In reality, the mean free path cannot be calculated by taking the average of all the paths because it is impossible to know the distance of each path traveled by a molecule. However, we can calculate it from the average speed (\(\langle c \rangle\)) of the molecule divided by the collision frequency (\(Z\)). The formula for this is:

\[\lambda = \dfrac{\langle c \rangle}{Z} \tag{6.7.1} \]

Because \(Z\) is equal to \(1/ t\), where \(t\) is the average time between collisions, the formula can also be:

\[\begin{eqnarray} \lambda &=& \dfrac{\langle c \rangle}{\dfrac{1}{t}} \\ &=& \langle c \rangle \times t \end{eqnarray} \tag{6.7.2} \]

In addition, because

\[\lambda = \sqrt{2} \pi d^2 \langle c \rangle (N/V) \tag{6.7.3} \]

• \(d\) is the diameter of the molecule and
• (\(N/V\)) is the density,

The formula can be further modified to:

\[ \begin{eqnarray} l &=& \dfrac{\langle c \rangle}{\sqrt{2} \pi d^2 \langle c \rangle \dfrac{N}{V}} \\ &=& \dfrac{1}{\sqrt{2} \pi d^2 \dfrac{N}{V}} \end{eqnarray} \tag{6.7.4} \]

Factors affecting mean free path

• Increasing the number of molecules or decreasing the volume causes density to increase. This decreases the mean free path.
• Radius of molecule: Increasing the radii of the molecules decreases the space between them, causing them to run into each other more often. Therefore, the mean free path decreases.
• Pressure, temperature, and other factors that affect density can indirectly affect mean free path.

Practice Problems

• A gas has an average speed of 10 m/s and a collision frequency of 10 s -1 . What is its mean free path?
• A gas has an average speed of 10 m/s and an average time of 0.1 s between collisions. What is its mean free path?
• A gas has a density of 10 particles m -3 and a molecular diameter of 0.1 m. What is its mean free path?
• A gas in a 1 m 3 container has a molecular diameter of 0.1 m. There are 10 molecules. What is its mean free path?
• A gas has a molecular diameter of 0.1 m. It also has a mean free path of 2.25 m. What is its density?
• l = <c> / = 10 m/s / 10 s^(-1) = 1 m
• l = <c> X (average time between collisions) = 10 m/s X 0.1 s = 1 m

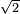
• Chang, Raymond. Physical Chemistry for the Biosciences. California: University Science Books, 2005.
• Atkins, Peter and Julio de Paula. Physical Chemistry for the Life Sciences. New York: Oxford University Press, 2006.

Contributors

• Tho Nguyen, Michael Dai