definition of hypothesis in physics

• Scientific Methods

What is Hypothesis?

We have heard of many hypotheses which have led to great inventions in science. Assumptions that are made on the basis of some evidence are known as hypotheses. In this article, let us learn in detail about the hypothesis and the type of hypothesis with examples.

A hypothesis is an assumption that is made based on some evidence. This is the initial point of any investigation that translates the research questions into predictions. It includes components like variables, population and the relation between the variables. A research hypothesis is a hypothesis that is used to test the relationship between two or more variables.

Characteristics of Hypothesis

Following are the characteristics of the hypothesis:

• The hypothesis should be clear and precise to consider it to be reliable.
• If the hypothesis is a relational hypothesis, then it should be stating the relationship between variables.
• The hypothesis must be specific and should have scope for conducting more tests.
• The way of explanation of the hypothesis must be very simple and it should also be understood that the simplicity of the hypothesis is not related to its significance.

Sources of Hypothesis

Following are the sources of hypothesis:

• The resemblance between the phenomenon.
• Observations from past studies, present-day experiences and from the competitors.
• Scientific theories.
• General patterns that influence the thinking process of people.

Types of Hypothesis

There are six forms of hypothesis and they are:

• Simple hypothesis
• Complex hypothesis
• Directional hypothesis
• Non-directional hypothesis
• Null hypothesis
• Associative and casual hypothesis

Simple Hypothesis

It shows a relationship between one dependent variable and a single independent variable. For example – If you eat more vegetables, you will lose weight faster. Here, eating more vegetables is an independent variable, while losing weight is the dependent variable.

Complex Hypothesis

It shows the relationship between two or more dependent variables and two or more independent variables. Eating more vegetables and fruits leads to weight loss, glowing skin, and reduces the risk of many diseases such as heart disease.

Directional Hypothesis

It shows how a researcher is intellectual and committed to a particular outcome. The relationship between the variables can also predict its nature. For example- children aged four years eating proper food over a five-year period are having higher IQ levels than children not having a proper meal. This shows the effect and direction of the effect.

Non-directional Hypothesis

It is used when there is no theory involved. It is a statement that a relationship exists between two variables, without predicting the exact nature (direction) of the relationship.

Null Hypothesis

It provides a statement which is contrary to the hypothesis. It’s a negative statement, and there is no relationship between independent and dependent variables. The symbol is denoted by “H O ”.

Associative and Causal Hypothesis

Associative hypothesis occurs when there is a change in one variable resulting in a change in the other variable. Whereas, the causal hypothesis proposes a cause and effect interaction between two or more variables.

Examples of Hypothesis

Following are the examples of hypotheses based on their types:

• Consumption of sugary drinks every day leads to obesity is an example of a simple hypothesis.
• All lilies have the same number of petals is an example of a null hypothesis.
• If a person gets 7 hours of sleep, then he will feel less fatigue than if he sleeps less. It is an example of a directional hypothesis.

Functions of Hypothesis

Following are the functions performed by the hypothesis:

• Hypothesis helps in making an observation and experiments possible.
• It becomes the start point for the investigation.
• Hypothesis helps in verifying the observations.
• It helps in directing the inquiries in the right direction.

How will Hypothesis help in the Scientific Method?

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

• Formation of question
• Doing background research
• Creation of hypothesis
• Designing an experiment
• Collection of data
• Result analysis
• Summarizing the experiment
• Communicating the results

Frequently Asked Questions – FAQs

What is hypothesis.

A hypothesis is an assumption made based on some evidence.

Give an example of simple hypothesis?

What are the types of hypothesis.

Types of hypothesis are:

• Associative and Casual hypothesis

State true or false: Hypothesis is the initial point of any investigation that translates the research questions into a prediction.

Define complex hypothesis..

A complex hypothesis shows the relationship between two or more dependent variables and two or more independent variables.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Theories, Hypotheses and Models

• Last updated
• Save as PDF
• Page ID 19359

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

For the purpose of this textbook (and science in general), we introduce a distinction in what we mean by “theory”, “hypothesis”, and by “model”. We will consider a “theory” to be a set of statements (or an equation) that gives us a broad description, applicable to several phenomena and that allows us to make verifiable predictions. For example, Chloë’s Theory ( \(t \propto \sqrt{h}\) ) can be considered a theory. Specifically, we do not use the word theory in the context of “I have a theory about this...”

A “hypothesis” is a consequence of the theory that one can test. From Chloë’s Theory, we have the hypothesis that an object will take \(\sqrt{2}\) times longer to fall from \(1\:\text{m}\) than from \(2\:\text{m}\) . We can formulate the hypothesis based on the theory and then test that hypothesis. If the hypothesis is found to be invalidated by experiment, then either the theory is incorrect, or the hypothesis is not consistent with the theory.

A “model” is a situation-specific description of a phenomenon based on a theory , that allows us to make a specific prediction. Using the example from the previous section, our theory would be that the fall time of an object is proportional to the square root of the drop height, and a model would be applying that theory to describe a tennis ball falling by \(4.2\) m. From the model, we can form a testable hypothesis of how long it will take the tennis ball to fall that distance. It is important to note that a model will almost always be an approximation of the theory applied to describe a particular phenomenon. For example, if Chloë’s Theory is only valid in vacuum, and we use it to model the time that it take for an object to fall at the surface of the Earth, we may find that our model disagrees with experiment. We would not necessarily conclude that the theory is invalidated, if our model did not adequately apply the theory to describe the phenomenon (e.g. by forgetting to include the effect of air drag).

This textbook will introduce the theories from Classical Physics, which were mostly established and tested between the seventeenth and nineteenth centuries. We will take it as given that readers of this textbook are not likely to perform experiments that challenge those well-established theories. The main challenge will be, given a theory, to define a model that describes a particular situation, and then to test that model. This introductory physics course is thus focused on thinking of “doing physics” as the task of correctly modeling a situation.

Emma's Thoughts

What’s the difference between a model and a theory?

“Model” and “Theory” are sometimes used interchangeably among scientists. In physics, it is particularly important to distinguish between these two terms. A model provides an immediate understanding of something based on a theory.

For example, if you would like to model the launch of your toy rocket into space, you might run a computer simulation of the launch based on various theories of propulsion that you have learned. In this case, the model is the computer simulation, which describes what will happen to the rocket. This model depends on various theories that have been extensively tested such as Newton’s Laws of motion, Fluid dynamics, etc.

• “Model”: Your homemade rocket computer simulation
• “Theory”: Newton’s Laws of motion, Fluid dynamics

With this analogy, we can quickly see that the “model” and “theory” are not interchangeable. If they were, we would be saying that all of Newton’s Laws of Motion depend on the success of your piddly toy rocket computer simulation!

Exercise \(\PageIndex{2}\)

Models cannot be scientifically tested, only theories can be tested.

What is a scientific hypothesis?

It's the initial building block in the scientific method.

Hypothesis basics

What makes a hypothesis testable.

• Types of hypotheses
• Hypothesis versus theory

Additional resources

Bibliography.

A scientific hypothesis is a tentative, testable explanation for a phenomenon in the natural world. It's the initial building block in the scientific method . Many describe it as an "educated guess" based on prior knowledge and observation. While this is true, a hypothesis is more informed than a guess. While an "educated guess" suggests a random prediction based on a person's expertise, developing a hypothesis requires active observation and background research. 

The basic idea of a hypothesis is that there is no predetermined outcome. For a solution to be termed a scientific hypothesis, it has to be an idea that can be supported or refuted through carefully crafted experimentation or observation. This concept, called falsifiability and testability, was advanced in the mid-20th century by Austrian-British philosopher Karl Popper in his famous book "The Logic of Scientific Discovery" (Routledge, 1959).

A key function of a hypothesis is to derive predictions about the results of future experiments and then perform those experiments to see whether they support the predictions.

A hypothesis is usually written in the form of an if-then statement, which gives a possibility (if) and explains what may happen because of the possibility (then). The statement could also include "may," according to California State University, Bakersfield .

Here are some examples of hypothesis statements:

• If garlic repels fleas, then a dog that is given garlic every day will not get fleas.
• If sugar causes cavities, then people who eat a lot of candy may be more prone to cavities.
• If ultraviolet light can damage the eyes, then maybe this light can cause blindness.

A useful hypothesis should be testable and falsifiable. That means that it should be possible to prove it wrong. A theory that can't be proved wrong is nonscientific, according to Karl Popper's 1963 book " Conjectures and Refutations ."

An example of an untestable statement is, "Dogs are better than cats." That's because the definition of "better" is vague and subjective. However, an untestable statement can be reworded to make it testable. For example, the previous statement could be changed to this: "Owning a dog is associated with higher levels of physical fitness than owning a cat." With this statement, the researcher can take measures of physical fitness from dog and cat owners and compare the two.

Types of scientific hypotheses

In an experiment, researchers generally state their hypotheses in two ways. The null hypothesis predicts that there will be no relationship between the variables tested, or no difference between the experimental groups. The alternative hypothesis predicts the opposite: that there will be a difference between the experimental groups. This is usually the hypothesis scientists are most interested in, according to the University of Miami .

For example, a null hypothesis might state, "There will be no difference in the rate of muscle growth between people who take a protein supplement and people who don't." The alternative hypothesis would state, "There will be a difference in the rate of muscle growth between people who take a protein supplement and people who don't."

If the results of the experiment show a relationship between the variables, then the null hypothesis has been rejected in favor of the alternative hypothesis, according to the book " Research Methods in Psychology " (​​BCcampus, 2015). 

There are other ways to describe an alternative hypothesis. The alternative hypothesis above does not specify a direction of the effect, only that there will be a difference between the two groups. That type of prediction is called a two-tailed hypothesis. If a hypothesis specifies a certain direction — for example, that people who take a protein supplement will gain more muscle than people who don't — it is called a one-tailed hypothesis, according to William M. K. Trochim , a professor of Policy Analysis and Management at Cornell University.

Sometimes, errors take place during an experiment. These errors can happen in one of two ways. A type I error is when the null hypothesis is rejected when it is true. This is also known as a false positive. A type II error occurs when the null hypothesis is not rejected when it is false. This is also known as a false negative, according to the University of California, Berkeley . 

A hypothesis can be rejected or modified, but it can never be proved correct 100% of the time. For example, a scientist can form a hypothesis stating that if a certain type of tomato has a gene for red pigment, that type of tomato will be red. During research, the scientist then finds that each tomato of this type is red. Though the findings confirm the hypothesis, there may be a tomato of that type somewhere in the world that isn't red. Thus, the hypothesis is true, but it may not be true 100% of the time.

Scientific theory vs. scientific hypothesis

The best hypotheses are simple. They deal with a relatively narrow set of phenomena. But theories are broader; they generally combine multiple hypotheses into a general explanation for a wide range of phenomena, according to the University of California, Berkeley . For example, a hypothesis might state, "If animals adapt to suit their environments, then birds that live on islands with lots of seeds to eat will have differently shaped beaks than birds that live on islands with lots of insects to eat." After testing many hypotheses like these, Charles Darwin formulated an overarching theory: the theory of evolution by natural selection.

"Theories are the ways that we make sense of what we observe in the natural world," Tanner said. "Theories are structures of ideas that explain and interpret facts." 

• Read more about writing a hypothesis, from the American Medical Writers Association.
• Find out why a hypothesis isn't always necessary in science, from The American Biology Teacher.
• Learn about null and alternative hypotheses, from Prof. Essa on YouTube .

Encyclopedia Britannica. Scientific Hypothesis. Jan. 13, 2022. https://www.britannica.com/science/scientific-hypothesis

Karl Popper, "The Logic of Scientific Discovery," Routledge, 1959.

California State University, Bakersfield, "Formatting a testable hypothesis." https://www.csub.edu/~ddodenhoff/Bio100/Bio100sp04/formattingahypothesis.htm  

Karl Popper, "Conjectures and Refutations," Routledge, 1963.

Price, P., Jhangiani, R., & Chiang, I., "Research Methods of Psychology — 2nd Canadian Edition," BCcampus, 2015.‌

University of Miami, "The Scientific Method" http://www.bio.miami.edu/dana/161/evolution/161app1_scimethod.pdf  

William M.K. Trochim, "Research Methods Knowledge Base," https://conjointly.com/kb/hypotheses-explained/  

University of California, Berkeley, "Multiple Hypothesis Testing and False Discovery Rate" https://www.stat.berkeley.edu/~hhuang/STAT141/Lecture-FDR.pdf  

University of California, Berkeley, "Science at multiple levels" https://undsci.berkeley.edu/article/0_0_0/howscienceworks_19

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Bizarre evolutionary roots of Africa's iconic upside-down baobab trees revealed

Snake Island: The isle writhing with vipers where only Brazilian military and scientists are allowed

Newfound autoimmune syndrome tied to COVID-19 can trigger deadly lung scarring

Most Popular

• 2 'It was not a peaceful crossing': Hannibal's troops linked to devastating fire 2,200 years ago in Spain
• 3 Snake Island: The isle writhing with vipers where only Brazilian military and scientists are allowed
• 4 Newfound 'glitch' in Einstein's relativity could rewrite the rules of the universe, study suggests
• 5 Scientists prove 'quantum theory' that could lead to ultrafast magnetic computing
• 5 Alien 'Dyson sphere' megastructures could surround at least 7 stars in our galaxy, new studies suggest

A hypothesis (plural hypothesis) is a proposed clarification for a phenomenon. For a hypothesis to be logical speculation. These are the logical strategy necessitate that one can test it. Researchers for the most part base logical hypothesis on past perceptions that can’t sufficiently be clarified with the accessible logical hypothesis.

Despite the fact that the word “hypothesis” is regularly in use. Equivalently, a logical hypothesis isn’t equivalent to a scientific hypothesis. A working hypothesis is a temporarily acknowledged hypothesis proposed for additional exploration, in a cycle starting with an informed estimate or thought.

                                                                                             Hypothesis

In its antiquated utilization, hypothesis alluded to an outline of the plot of an old-style dramatization. The English word hypothesis comes from the antiquated Greek word hypothesis. Its exacting or etymological sense is “putting or setting under”. Henceforth in broad use has numerous different implications including “assumption”.

In Common Utilization

In common utilization, a hypothesis alludes to a temporary thought whose legitimacy requires assessment. For legitimate assessment, the composer of a hypothesis needs to characterize particulars in operational terms. A hypothesis requires more work by the scientist to either affirm or negate it. At the appointed time, an affirmed hypothesis may turn out to be important for a hypothesis. At times may develop to turn into a hypothesis itself.

Regularly, a logical hypothesis has the type of numerical model. Sometimes, however not generally, one can likewise plan them as existential proclamations. Expressing that some specific case of the phenomenon under assessment has some trademark and causal clarifications. This has the overall type of explanations, expressing that each case of the specific trademark.

In Innovative Science

In innovative science, a hypothesis is useful to define temporary thoughts inside a business setting. The figured hypothesis is then assessed where either the hypothesis is demonstrated to be “valid” or “bogus”. It is through an undeniable nature or falsifiability-arranged test.

Any valuable hypothesis will empower forecasts by thinking (counting deductive thinking). It may foresee the result of an analysis in a research centre setting or the perception of wonder in nature. The forecast may likewise conjure measurements and just discussion about probabilities. Karl Popper, following others, has contended that a hypothesis must be falsifiable. One can’t view a suggestion or hypothesis as logical on the off chance that it doesn’t concede the chance of being indicated bogus. Different thinkers of science have dismissed the model of falsifiability or enhanced it with other measures.

For example, undeniable nature for e.g., verificationism or soundness like affirmation comprehensive quality. The logical technique includes experimentation, to test the capacity of some hypothesis to satisfactorily address the inquiry under scrutiny. Conversely, liberated perception isn’t as liable to bring up unexplained issues or open issues in science. As it would the plan of a pivotal trial to test the hypothesis. A psychological test may likewise be utilized to test the hypothesis too.

In outlining a hypothesis, the examiner must not right now know the result of a test. It remains sensibly under proceeding with examination. Just in such cases does the analysis, test or study conceivably increment the likelihood of indicating the reality of a hypothesis.

If the specialist definitely knows the result, it considers an “outcome”. The scientist ought to have just thought about this while detailing the hypothesis. On the off chance that one can’t survey the expectations by perception or by experience. The hypothesis should be tried by others giving perceptions. For instance, another innovation or hypothesis may make the essential trials practical.

Characteristics of Hypothesis

Following are the characteristics of the hypothesis:

• The theory ought to be clear and exact to believe it to be solid.
• If the hypothesis is a social theory, at that point it ought to express the connection between factors.
• The theory must be explicit and ought to have scope for leading more tests.
• The method of clarification of the theory must be basic and it should likewise be perceived that the straightforwardness of the hypothesis isn’t identified with its essentialness.

Sources of Hypothesis

Following are the sources of the hypothesis:

• The likeness between the wonder.
• Observations from past investigations, present-day encounters and from the contenders.
• Scientific hypothesis.
• General designs that impact the considering cycle individuals.

Types of Hypothesis

There are six forms of the hypothesis and they are:

• Simple hypothesis
• Complex hypothesis
• Directional hypothesis
• Non-directional hypothesis
• Null hypothesis
• Associative and casual hypothesis

Simple Hypothesis

It shows a connection between one ward variable and a solitary autonomous variable. For instance, If you eat more vegetables, you will get in shape quicker. Here, eating more vegetables is a free factor, while getting more fit is the needy variable.

Complex Hypothesis

It shows the connection between at least two ward factors and at least two autonomous factors. Eating more vegetables and natural products prompts weight reduction. May be sparkling skin, diminishes the danger of numerous infections, for example, coronary illness, hypertension and a few diseases.

Directional Hypothesis

It shows how an analyst is scholarly and focused on a specific result. The connection between the factors can likewise foresee its inclination. For instance, kids matured four years eating appropriate food over a five-year time frame are having higher IQ levels than youngsters not having a legitimate dinner. This shows the impact and course of impact.

Non-directional Hypothesis

It is utilized when there is no theory included. It is an explanation that a relationship exists between two factors, without foreseeing the specific nature (course) of the relationship.

Null Hypothesis

It gives the explanation which is in opposition to the theory. It’s a negative assertion, and there is no connection between autonomous and subordinate factors. The image is indicated by “HO”.

Associative and Causal Hypothesis

Acquainted hypothesis happens when there is an adjustment in one variable bringing about an adjustment in the other variable. Though, the causal hypothesis proposes a circumstances and logical results connection between at least two factors.

Examples of Hypothesis

Following are the examples of the hypothesis according to their types:

• Consumption of sweet beverages consistently prompts weight is a case of a straightforward theory.
• All lilies have a similar number of petals is a case of an invalid hypothesis.
• If an individual gets 7 hours of rest, at that point he will feel less weakness than if he dozens less.

FAQs about Hypothesis

Q.1. Write a short note on the term hypothesis.

Answer: A hypothesis (plural hypothesis) is a proposed clarification for a phenomenon. For a hypothesis to be logical speculation. The logical strategy necessitates that one can test it. Researchers for the most part base logical hypothesis on past perceptions that can’t sufficiently be clarified with the accessible logical hypotheses. Despite the fact that the words “hypothesis” and “hypothesis” are regularly utilized equivalently, a logical hypothesis isn’t equivalent to a scientific hypothesis.

Q.2. What are the functions of the Hypothesis?

Answer: Following are the functions performed by the hypothesis:

• Hypothesis helps in mentioning an objective fact and tests conceivable.
• It turns into the beginning point for the formal examination.
• Hypothesis helps in checking the perceptions.
• It helps in coordinating the requests in the correct ways.

Q.3. How will Hypothesis help in Scientific Method?

Answer: Scientists use theory to put down their considerations coordinating how the test would happen. Following are the means that are engaged with the logical strategy:

• Formation of inquiry
• Doing foundation research
• Creation of hypothesis
• Designing an investigation
• Collection of information
• Result examination
• Summarizing the trial
• Communicating the outcomes

Customize your course in 30 seconds

Which class are you in.

• Statistical Physics
• Physics Diagrams
• Constants In Physics
• Quantum Physics
• Electron Spin
• Bridge Construction
• Physics Symbols
• Murphy’s Law
• Difference Between in Physics

2 responses to “Difference Between in Physics”

I want to prepare for nda

I want to prepare physics for x group exam

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

• Privacy Policy

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

• Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
• Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
• Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
• Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
• Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
• Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

• Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
• Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
• Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
• Education : “Implementing a new teaching method will result in higher student achievement scores.”
• Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
• Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
• Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

• In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
• In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
• I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

• Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
• Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
• Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
• Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
• Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
• Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
• Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

• Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
• Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
• Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
• Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
• Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
• Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

• Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
• May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
• May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
• Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
• Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
• May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Theories, Hypotheses, and Laws: Definitions, examples, and their roles in science

by Anthony Carpi, Ph.D., Anne E. Egger, Ph.D.

Listen to this reading

Did you know that the idea of evolution had been part of Western thought for more than 2,000 years before Charles Darwin was born? Like many theories, the theory of evolution was the result of the work of many different scientists working in different disciplines over a period of time.

A scientific theory is an explanation inferred from multiple lines of evidence for some broad aspect of the natural world and is logical, testable, and predictive.

As new evidence comes to light, or new interpretations of existing data are proposed, theories may be revised and even change; however, they are not tenuous or speculative.

A scientific hypothesis is an inferred explanation of an observation or research finding; while more exploratory in nature than a theory, it is based on existing scientific knowledge.

A scientific law is an expression of a mathematical or descriptive relationship observed in nature.

Imagine yourself shopping in a grocery store with a good friend who happens to be a chemist. Struggling to choose between the many different types of tomatoes in front of you, you pick one up, turn to your friend, and ask her if she thinks the tomato is organic . Your friend simply chuckles and replies, "Of course it's organic!" without even looking at how the fruit was grown. Why the amused reaction? Your friend is highlighting a simple difference in vocabulary. To a chemist, the term organic refers to any compound in which hydrogen is bonded to carbon. Tomatoes (like all plants) are abundant in organic compounds – thus your friend's laughter. In modern agriculture, however, organic has come to mean food items grown or raised without the use of chemical fertilizers, pesticides, or other additives.

So who is correct? You both are. Both uses of the word are correct, though they mean different things in different contexts. There are, of course, lots of words that have more than one meaning (like bat , for example), but multiple meanings can be especially confusing when two meanings convey very different ideas and are specific to one field of study.

• Scientific theories

The term theory also has two meanings, and this double meaning often leads to confusion. In common language, the term theory generally refers to speculation or a hunch or guess. You might have a theory about why your favorite sports team isn't playing well, or who ate the last cookie from the cookie jar. But these theories do not fit the scientific use of the term. In science, a theory is a well-substantiated and comprehensive set of ideas that explains a phenomenon in nature. A scientific theory is based on large amounts of data and observations that have been collected over time. Scientific theories can be tested and refined by additional research , and they allow scientists to make predictions. Though you may be correct in your hunch, your cookie jar conjecture doesn't fit this more rigorous definition.

All scientific disciplines have well-established, fundamental theories . For example, atomic theory describes the nature of matter and is supported by multiple lines of evidence from the way substances behave and react in the world around us (see our series on Atomic Theory ). Plate tectonic theory describes the large scale movement of the outer layer of the Earth and is supported by evidence from studies about earthquakes , magnetic properties of the rocks that make up the seafloor , and the distribution of volcanoes on Earth (see our series on Plate Tectonic Theory ). The theory of evolution by natural selection , which describes the mechanism by which inherited traits that affect survivability or reproductive success can cause changes in living organisms over generations , is supported by extensive studies of DNA , fossils , and other types of scientific evidence (see our Charles Darwin series for more information). Each of these major theories guides and informs modern research in those fields, integrating a broad, comprehensive set of ideas.

So how are these fundamental theories developed, and why are they considered so well supported? Let's take a closer look at some of the data and research supporting the theory of natural selection to better see how a theory develops.

Comprehension Checkpoint

• The development of a scientific theory: Evolution and natural selection

The theory of evolution by natural selection is sometimes maligned as Charles Darwin 's speculation on the origin of modern life forms. However, evolutionary theory is not speculation. While Darwin is rightly credited with first articulating the theory of natural selection, his ideas built on more than a century of scientific research that came before him, and are supported by over a century and a half of research since.

• The Fixity Notion: Linnaeus

Figure 1: Cover of the 1760 edition of Systema Naturae .

Research about the origins and diversity of life proliferated in the 18th and 19th centuries. Carolus Linnaeus , a Swedish botanist and the father of modern taxonomy (see our module Taxonomy I for more information), was a devout Christian who believed in the concept of Fixity of Species , an idea based on the biblical story of creation. The Fixity of Species concept said that each species is based on an ideal form that has not changed over time. In the early stages of his career, Linnaeus traveled extensively and collected data on the structural similarities and differences between different species of plants. Noting that some very different plants had similar structures, he began to piece together his landmark work, Systema Naturae, in 1735 (Figure 1). In Systema , Linnaeus classified organisms into related groups based on similarities in their physical features. He developed a hierarchical classification system , even drawing relationships between seemingly disparate species (for example, humans, orangutans, and chimpanzees) based on the physical similarities that he observed between these organisms. Linnaeus did not explicitly discuss change in organisms or propose a reason for his hierarchy, but by grouping organisms based on physical characteristics, he suggested that species are related, unintentionally challenging the Fixity notion that each species is created in a unique, ideal form.

• The age of Earth: Leclerc and Hutton

Also in the early 1700s, Georges-Louis Leclerc, a French naturalist, and James Hutton , a Scottish geologist, began to develop new ideas about the age of the Earth. At the time, many people thought of the Earth as 6,000 years old, based on a strict interpretation of the events detailed in the Christian Old Testament by the influential Scottish Archbishop Ussher. By observing other planets and comets in the solar system , Leclerc hypothesized that Earth began as a hot, fiery ball of molten rock, mostly consisting of iron. Using the cooling rate of iron, Leclerc calculated that Earth must therefore be at least 70,000 years old in order to have reached its present temperature.

Hutton approached the same topic from a different perspective, gathering observations of the relationships between different rock formations and the rates of modern geological processes near his home in Scotland. He recognized that the relatively slow processes of erosion and sedimentation could not create all of the exposed rock layers in only a few thousand years (see our module The Rock Cycle ). Based on his extensive collection of data (just one of his many publications ran to 2,138 pages), Hutton suggested that the Earth was far older than human history – hundreds of millions of years old.

While we now know that both Leclerc and Hutton significantly underestimated the age of the Earth (by about 4 billion years), their work shattered long-held beliefs and opened a window into research on how life can change over these very long timescales.

• Fossil studies lead to the development of a theory of evolution: Cuvier

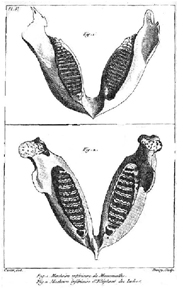
Figure 2: Illustration of an Indian elephant jaw and a mammoth jaw from Cuvier's 1796 paper.

With the age of Earth now extended by Leclerc and Hutton, more researchers began to turn their attention to studying past life. Fossils are the main way to study past life forms, and several key studies on fossils helped in the development of a theory of evolution . In 1795, Georges Cuvier began to work at the National Museum in Paris as a naturalist and anatomist. Through his work, Cuvier became interested in fossils found near Paris, which some claimed were the remains of the elephants that Hannibal rode over the Alps when he invaded Rome in 218 BCE . In studying both the fossils and living species , Cuvier documented different patterns in the dental structure and number of teeth between the fossils and modern elephants (Figure 2) (Horner, 1843). Based on these data , Cuvier hypothesized that the fossil remains were not left by Hannibal, but were from a distinct species of animal that once roamed through Europe and had gone extinct thousands of years earlier: the mammoth. The concept of species extinction had been discussed by a few individuals before Cuvier, but it was in direct opposition to the Fixity of Species concept – if every organism were based on a perfectly adapted, ideal form, how could any cease to exist? That would suggest it was no longer ideal.

While his work provided critical evidence of extinction , a key component of evolution , Cuvier was highly critical of the idea that species could change over time. As a result of his extensive studies of animal anatomy, Cuvier had developed a holistic view of organisms , stating that the

number, direction, and shape of the bones that compose each part of an animal's body are always in a necessary relation to all the other parts, in such a way that ... one can infer the whole from any one of them ...

In other words, Cuvier viewed each part of an organism as a unique, essential component of the whole organism. If one part were to change, he believed, the organism could not survive. His skepticism about the ability of organisms to change led him to criticize the whole idea of evolution , and his prominence in France as a scientist played a large role in discouraging the acceptance of the idea in the scientific community.

• Studies of invertebrates support a theory of change in species: Lamarck

Jean Baptiste Lamarck, a contemporary of Cuvier's at the National Museum in Paris, studied invertebrates like insects and worms. As Lamarck worked through the museum's large collection of invertebrates, he was impressed by the number and variety of organisms . He became convinced that organisms could, in fact, change through time, stating that

... time and favorable conditions are the two principal means which nature has employed in giving existence to all her productions. We know that for her time has no limit, and that consequently she always has it at her disposal.

This was a radical departure from both the fixity concept and Cuvier's ideas, and it built on the long timescale that geologists had recently established. Lamarck proposed that changes that occurred during an organism 's lifetime could be passed on to their offspring, suggesting, for example, that a body builder's muscles would be inherited by their children.

As it turned out, the mechanism by which Lamarck proposed that organisms change over time was wrong, and he is now often referred to disparagingly for his "inheritance of acquired characteristics" idea. Yet despite the fact that some of his ideas were discredited, Lamarck established a support for evolutionary theory that others would build on and improve.

• Rock layers as evidence for evolution: Smith

In the early 1800s, a British geologist and canal surveyor named William Smith added another component to the accumulating evidence for evolution . Smith observed that rock layers exposed in different parts of England bore similarities to one another: These layers (or strata) were arranged in a predictable order, and each layer contained distinct groups of fossils . From this series of observations , he developed a hypothesis that specific groups of animals followed one another in a definite sequence through Earth's history, and this sequence could be seen in the rock layers. Smith's hypothesis was based on his knowledge of geological principles , including the Law of Superposition.

The Law of Superposition states that sediments are deposited in a time sequence, with the oldest sediments deposited first, or at the bottom, and newer layers deposited on top. The concept was first expressed by the Persian scientist Avicenna in the 11th century, but was popularized by the Danish scientist Nicolas Steno in the 17th century. Note that the law does not state how sediments are deposited; it simply describes the relationship between the ages of deposited sediments.

Figure 3: Engraving from William Smith's 1815 monograph on identifying strata by fossils.

Smith backed up his hypothesis with extensive drawings of fossils uncovered during his research (Figure 3), thus allowing other scientists to confirm or dispute his findings. His hypothesis has, in fact, been confirmed by many other scientists and has come to be referred to as the Law of Faunal Succession. His work was critical to the formation of evolutionary theory as it not only confirmed Cuvier's work that organisms have gone extinct , but it also showed that the appearance of life does not date to the birth of the planet. Instead, the fossil record preserves a timeline of the appearance and disappearance of different organisms in the past, and in doing so offers evidence for change in organisms over time.

• The theory of evolution by natural selection: Darwin and Wallace

It was into this world that Charles Darwin entered: Linnaeus had developed a taxonomy of organisms based on their physical relationships, Leclerc and Hutton demonstrated that there was sufficient time in Earth's history for organisms to change, Cuvier showed that species of organisms have gone extinct , Lamarck proposed that organisms change over time, and Smith established a timeline of the appearance and disappearance of different organisms in the geological record .

Figure 4: Title page of the 1859 Murray edition of the Origin of Species by Charles Darwin.

Charles Darwin collected data during his work as a naturalist on the HMS Beagle starting in 1831. He took extensive notes on the geology of the places he visited; he made a major find of fossils of extinct animals in Patagonia and identified an extinct giant ground sloth named Megatherium . He experienced an earthquake in Chile that stranded beds of living mussels above water, where they would be preserved for years to come.

Perhaps most famously, he conducted extensive studies of animals on the Galápagos Islands, noting subtle differences in species of mockingbird, tortoise, and finch that were isolated on different islands with different environmental conditions. These subtle differences made the animals highly adapted to their environments .

This broad spectrum of data led Darwin to propose an idea about how organisms change "by means of natural selection" (Figure 4). But this idea was not based only on his work, it was also based on the accumulation of evidence and ideas of many others before him. Because his proposal encompassed and explained many different lines of evidence and previous work, they formed the basis of a new and robust scientific theory regarding change in organisms – the theory of evolution by natural selection .

Darwin's ideas were grounded in evidence and data so compelling that if he had not conceived them, someone else would have. In fact, someone else did. Between 1858 and 1859, Alfred Russel Wallace , a British naturalist, wrote a series of letters to Darwin that independently proposed natural selection as the means for evolutionary change. The letters were presented to the Linnean Society of London, a prominent scientific society at the time (see our module on Scientific Institutions and Societies ). This long chain of research highlights that theories are not just the work of one individual. At the same time, however, it often takes the insight and creativity of individuals to put together all of the pieces and propose a new theory . Both Darwin and Wallace were experienced naturalists who were familiar with the work of others. While all of the work leading up to 1830 contributed to the theory of evolution , Darwin's and Wallace's theory changed the way that future research was focused by presenting a comprehensive, well-substantiated set of ideas, thus becoming a fundamental theory of biological research.

• Expanding, testing, and refining scientific theories
• Genetics and evolution: Mendel and Dobzhansky

Since Darwin and Wallace first published their ideas, extensive research has tested and expanded the theory of evolution by natural selection . Darwin had no concept of genes or DNA or the mechanism by which characteristics were inherited within a species . A contemporary of Darwin's, the Austrian monk Gregor Mendel , first presented his own landmark study, Experiments in Plant Hybridization, in 1865 in which he provided the basic patterns of genetic inheritance , describing which characteristics (and evolutionary changes) can be passed on in organisms (see our Genetics I module for more information). Still, it wasn't until much later that a "gene" was defined as the heritable unit.

In 1937, the Ukrainian born geneticist Theodosius Dobzhansky published Genetics and the Origin of Species , a seminal work in which he described genes themselves and demonstrated that it is through mutations in genes that change occurs. The work defined evolution as "a change in the frequency of an allele within a gene pool" ( Dobzhansky, 1982 ). These studies and others in the field of genetics have added to Darwin's work, expanding the scope of the theory .

• Evolution under a microscope: Lenski

More recently, Dr. Richard Lenski, a scientist at Michigan State University, isolated a single Escherichia coli bacterium in 1989 as the first step of the longest running experimental test of evolutionary theory to date – a true test meant to replicate evolution and natural selection in the lab.

After the single microbe had multiplied, Lenski isolated the offspring into 12 different strains , each in their own glucose-supplied culture, predicting that the genetic make-up of each strain would change over time to become more adapted to their specific culture as predicted by evolutionary theory . These 12 lines have been nurtured for over 40,000 bacterial generations (luckily bacterial generations are much shorter than human generations) and exposed to different selective pressures such as heat , cold, antibiotics, and infection with other microorganisms. Lenski and colleagues have studied dozens of aspects of evolutionary theory with these genetically isolated populations . In 1999, they published a paper that demonstrated that random genetic mutations were common within the populations and highly diverse across different individual bacteria . However, "pivotal" mutations that are associated with beneficial changes in the group are shared by all descendants in a population and are much rarer than random mutations, as predicted by the theory of evolution by natural selection (Papadopoulos et al., 1999).

• Punctuated equilibrium: Gould and Eldredge

While established scientific theories like evolution have a wealth of research and evidence supporting them, this does not mean that they cannot be refined as new information or new perspectives on existing data become available. For example, in 1972, biologist Stephen Jay Gould and paleontologist Niles Eldredge took a fresh look at the existing data regarding the timing by which evolutionary change takes place. Gould and Eldredge did not set out to challenge the theory of evolution; rather they used it as a guiding principle and asked more specific questions to add detail and nuance to the theory. This is true of all theories in science: they provide a framework for additional research. At the time, many biologists viewed evolution as occurring gradually, causing small incremental changes in organisms at a relatively steady rate. The idea is referred to as phyletic gradualism , and is rooted in the geological concept of uniformitarianism . After reexamining the available data, Gould and Eldredge came to a different explanation, suggesting that evolution consists of long periods of stability that are punctuated by occasional instances of dramatic change – a process they called punctuated equilibrium .

Like Darwin before them, their proposal is rooted in evidence and research on evolutionary change, and has been supported by multiple lines of evidence. In fact, punctuated equilibrium is now considered its own theory in evolutionary biology. Punctuated equilibrium is not as broad of a theory as natural selection . In science, some theories are broad and overarching of many concepts, such as the theory of evolution by natural selection; others focus on concepts at a smaller, or more targeted, scale such as punctuated equilibrium. And punctuated equilibrium does not challenge or weaken the concept of natural selection; rather, it represents a change in our understanding of the timing by which change occurs in organisms , and a theory within a theory. The theory of evolution by natural selection now includes both gradualism and punctuated equilibrium to describe the rate at which change proceeds.

• Hypotheses and laws: Other scientific concepts

One of the challenges in understanding scientific terms like theory is that there is not a precise definition even within the scientific community. Some scientists debate over whether certain proposals merit designation as a hypothesis or theory , and others mistakenly use the terms interchangeably. But there are differences in these terms. A hypothesis is a proposed explanation for an observable phenomenon. Hypotheses , just like theories , are based on observations from research . For example, LeClerc did not hypothesize that Earth had cooled from a molten ball of iron as a random guess; rather, he developed this hypothesis based on his observations of information from meteorites.

A scientist often proposes a hypothesis before research confirms it as a way of predicting the outcome of study to help better define the parameters of the research. LeClerc's hypothesis allowed him to use known parameters (the cooling rate of iron) to do additional work. A key component of a formal scientific hypothesis is that it is testable and falsifiable. For example, when Richard Lenski first isolated his 12 strains of bacteria , he likely hypothesized that random mutations would cause differences to appear within a period of time in the different strains of bacteria. But when a hypothesis is generated in science, a scientist will also make an alternative hypothesis , an explanation that explains a study if the data do not support the original hypothesis. If the different strains of bacteria in Lenski's work did not diverge over the indicated period of time, perhaps the rate of mutation was slower than first thought.

So you might ask, if theories are so well supported, do they eventually become laws? The answer is no – not because they aren't well-supported, but because theories and laws are two very different things. Laws describe phenomena, often mathematically. Theories, however, explain phenomena. For example, in 1687 Isaac Newton proposed a Theory of Gravitation, describing gravity as a force of attraction between two objects. As part of this theory, Newton developed a Law of Universal Gravitation that explains how this force operates. This law states that the force of gravity between two objects is inversely proportional to the square of the distance between those objects. Newton 's Law does not explain why this is true, but it describes how gravity functions (see our Gravity: Newtonian Relationships module for more detail). In 1916, Albert Einstein developed his theory of general relativity to explain the mechanism by which gravity has its effect. Einstein's work challenges Newton's theory, and has been found after extensive testing and research to more accurately describe the phenomenon of gravity. While Einstein's work has replaced Newton's as the dominant explanation of gravity in modern science, Newton's Law of Universal Gravitation is still used as it reasonably (and more simply) describes the force of gravity under many conditions. Similarly, the Law of Faunal Succession developed by William Smith does not explain why organisms follow each other in distinct, predictable ways in the rock layers, but it accurately describes the phenomenon.

Theories, hypotheses , and laws drive scientific progress

Theories, hypotheses , and laws are not simply important components of science, they drive scientific progress. For example, evolutionary biology now stands as a distinct field of science that focuses on the origins and descent of species . Geologists now rely on plate tectonics as a conceptual model and guiding theory when they are studying processes at work in Earth's crust . And physicists refer to atomic theory when they are predicting the existence of subatomic particles yet to be discovered. This does not mean that science is "finished," or that all of the important theories have been discovered already. Like evolution , progress in science happens both gradually and in short, dramatic bursts. Both types of progress are critical for creating a robust knowledge base with data as the foundation and scientific theories giving structure to that knowledge.

Table of Contents

• Theories, hypotheses, and laws drive scientific progress

Activate glossary term highlighting to easily identify key terms within the module. Once highlighted, you can click on these terms to view their definitions.

Activate NGSS annotations to easily identify NGSS standards within the module. Once highlighted, you can click on them to view these standards.

Advertisement

Three Famous Hypotheses and How They Were Tested

• Share Content on Facebook
• Share Content on LinkedIn
• Share Content on Flipboard
• Share Content on Reddit
• Share Content via Email

Key Takeaways

• Ivan Pavlov's experiment demonstrated conditioned responses in dogs.
• Pavlov's work exemplifies the scientific method, starting with a hypothesis about conditioned responses and testing it through controlled experiments.
• Pavlov's findings not only advanced an understanding of animal physiology but also laid foundational principles for behaviorism, a major school of thought in psychology that emphasizes the study of observable behaviors.

Coho salmon ( Oncorhynchus kisutch ) are amazing fish. Indigenous to the Pacific Northwest, they begin their lives in freshwater streams and then relocate to the open ocean. But when a Coho salmon reaches breeding age, it'll return to the waterway of its birth , sometimes traveling 400 miles (644 kilometers) to get there.

Enter the late Arthur Davis Hasler. While an ecologist and biologist at the University of Wisconsin, he was intrigued by the question of how these creatures find their home streams. And in 1960, he used a Hypothesis-Presentation.pdf">basic tenet of science — the hypothesis — to find out.

So what is a hypothesis? A hypothesis is a tentative, testable explanation for an observed phenomenon in nature. Hypotheses are narrow in scope — unlike theories , which cover a broad range of observable phenomena and draw from many different lines of evidence. Meanwhile, a prediction is a result you'd expect to get if your hypothesis or theory is accurate.

So back to 1960 and Hasler and those salmon. One unverified idea was that Coho salmon used eyesight to locate their home streams. Hasler set out to test this notion (or hypothesis). First, he rounded up several fish who'd already returned to their native streams. Next, he blindfolded some of the captives — but not all of them — before dumping his salmon into a faraway stretch of water. If the eyesight hypothesis was correct, then Hasler could expect fewer of the blindfolded fish to return to their home streams.

Things didn't work out that way. The fish without blindfolds came back at the same rate as their blindfolded counterparts. (Other experiments demonstrated that smell, and not sight, is the key to the species' homing ability.)

Although Hasler's blindfold hypothesis was disproven, others have fared better. Today, we're looking at three of the best-known experiments in history — and the hypotheses they tested.

Ivan Pavlov and His Dogs (1903-1935)

Isaac newton's radiant prisms (1665), robert paine's revealing starfish (1963-1969).

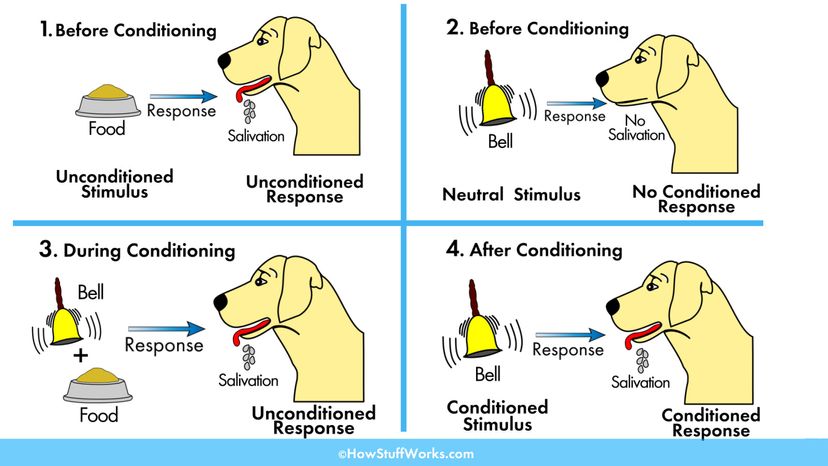
The Hypothesis : If dogs are susceptible to conditioned responses (drooling), then a dog who is regularly exposed to the same neutral stimulus (metronome/bell) before it receives food will associate this neutral stimulus with the act of eating. Eventually, the dog should begin to drool at a predictable rate when it encounters said stimulus — even before any actual food is offered.

The Experiment : A Nobel Prize-winner and outspoken critic of Soviet communism, Ivan Pavlov is synonymous with man's best friend . In 1903, the Russian-born scientist kicked off a decades-long series of experiments involving dogs and conditioned responses .

Offer a plate of food to a hungry dog and it'll salivate. In this context, the stimulus (the food) will automatically trigger a particular response (the drooling). The latter is an innate, unlearned reaction to the former.

By contrast, the rhythmic sound of a metronome or bell is a neutral stimulus. To a dog, the noise has no inherent meaning and if the animal has never heard it before, the sound won't provoke an instinctive reaction. But the sight of food sure will .

So when Pavlov and his lab assistants played the sound of the metronome/bell before feeding sessions, the researchers conditioned test dogs to mentally link metronomes/bells with mealtime. Due to repeated exposure, the noise alone started to make the dogs' mouths water before they were given food.

According to " Ivan Pavlov: A Russian Life in Science " by biographer Daniel P. Todes, Pavlov's big innovation here was his discovery that he could quantify the reaction of each pooch by measuring the amount of saliva it generated. Every canine predictably drooled at its own consistent rate when he or she encountered a personalized (and artificial) food-related cue.

Pavlov and his assistants used conditioned responses to look at other hypotheses about animal physiology, as well. In one notable experiment, a dog was tested on its ability to tell time . This particular pooch always received food when it heard a metronome click at the rate of 60 strokes per minute. But it never got any food after listening to a slower, 40-strokes-per-minute beat. Lo and behold, Pavlov's animal began to salivate in response to the faster rhythm — but not the slower one . So clearly, it could tell the two rhythmic beats apart.

The Verdict : With the right conditioning — and lots of patience — you can make a hungry dog respond to neutral stimuli by salivating on cue in a way that's both predictable and scientifically quantifiable.

The Hypothesis : If white sunlight is a mixture of all the colors in the visible spectrum — and these travel at varying wavelengths — then each color will refract at a different angle when a beam of sunlight passes through a glass prism.

The Experiments : Color was a scientific mystery before Isaac Newton came along. During the summer of 1665, he started experimenting with glass prisms from the safety of a darkened room in Cambridge, England.

He cut a quarter-inch (0.63-centimeter) circular hole into one of the window shutters, allowing a single beam of sunlight to enter the place. When Newton held up a prism to this ray, an oblong patch of multicolored light was projected onto the opposite wall.

This contained segregated layers of red, orange, yellow, green, blue, indigo and violet light. From top to bottom, this patch measured 13.5 inches (33.65 centimeters) tall, yet it was only 2.6 inches (6.6 centimeters) across.

Newton deduced that these vibrant colors had been hiding within the sunlight itself, but the prism bent (or "refracted") them at different angles, which separated the colors out.

Still, he wasn't 100 percent sure. So Newton replicated the experiment with one small change. This time, he took a second prism and had it intercept the rainbow-like patch of light. Once the refracted colors entered the new prism, they recombined into a circular white sunbeam. In other words, Newton took a ray of white light, broke it apart into a bunch of different colors and then reassembled it. What a neat party trick!

The Verdict : Sunlight really is a blend of all the colors in the rainbow — and yes, these can be individually separated via light refraction.

The Hypothesis : If predators limit the populations of the organisms they attack, then we'd expect the prey species to become more common after the eradication of a major predator.

The Experiment : Meet Pisaster ochraceus , also known as the purple sea star (or the purple starfish if you prefer).

Using an extendable stomach , the creature feeds on mussels, limpets, barnacles, snails and other hapless victims. On some seaside rocks (and tidal pools) along the coast of Washington state, this starfish is the apex predator.

The animal made Robert Paine a scientific celebrity. An ecologist by trade, Paine was fascinated by the environmental roles of top predators. In June 1963, he kicked off an ambitious experiment along Washington state's Mukkaw Bay. For years on end, Paine kept a rocky section of this shoreline completely starfish-free.

It was hard work. Paine had to regularly pry wayward sea stars off "his" outcrop — sometimes with a crowbar. Then he'd chuck them into the ocean.

Before the experiment, Paine observed 15 different species of animals and algae inhabiting the area he decided to test. By June 1964 — one year after his starfish purge started — that number had dropped to eight .

Unchecked by purple sea stars, the barnacle population skyrocketed. Subsequently, these were replaced by California mussels , which came to dominate the terrain. By anchoring themselves to rocks in great numbers, the mussels edged out other life-forms. That made the outcrop uninhabitable to most former residents: Even sponges, anemones and algae — organisms that Pisaster ochraceus doesn't eat — were largely evicted.

All those species continued to thrive on another piece of shoreline that Paine left untouched. Later experiments convinced him that Pisaster ochraceus is a " keystone species ," a creature who exerts disproportionate influence over its environment. Eliminate the keystone and the whole system gets disheveled.

The Verdict : Apex predators don't just affect the animals that they hunt. Removing a top predator sets off a chain reaction that can fundamentally transform an entire ecosystem.

Contrary to popular belief, Pavlov almost never used bells in his dog experiments. Instead, he preferred metronomes, buzzers, harmoniums and electric shocks.

Frequently Asked Questions

How can a hypothesis become a theory, what's the difference between a hypothesis and a prediction.

Please copy/paste the following text to properly cite this HowStuffWorks.com article:

1.1 Physics: An Introduction

Learning objectives.

By the end of this section, you will be able to:

• Explain the difference between a principle and a law.
• Explain the difference between a model and a theory.

The physical universe is enormously complex in its detail. Every day, each of us observes a great variety of objects and phenomena. Over the centuries, the curiosity of the human race has led us collectively to explore and catalog a tremendous wealth of information. From the flight of birds to the colors of flowers, from lightning to gravity, from quarks to clusters of galaxies, from the flow of time to the mystery of the creation of the universe, we have asked questions and assembled huge arrays of facts. In the face of all these details, we have discovered that a surprisingly small and unified set of physical laws can explain what we observe. As humans, we make generalizations and seek order. We have found that nature is remarkably cooperative—it exhibits the underlying order and simplicity we so value.

It is the underlying order of nature that makes science in general, and physics in particular, so enjoyable to study. For example, what do a bag of chips and a car battery have in common? Both contain energy that can be converted to other forms. The law of conservation of energy (which says that energy can change form but is never lost) ties together such topics as food calories, batteries, heat, light, and watch springs. Understanding this law makes it easier to learn about the various forms energy takes and how they relate to one another. Apparently unrelated topics are connected through broadly applicable physical laws, permitting an understanding beyond just the memorization of lists of facts.

The unifying aspect of physical laws and the basic simplicity of nature form the underlying themes of this text. In learning to apply these laws, you will, of course, study the most important topics in physics. More importantly, you will gain analytical abilities that will enable you to apply these laws far beyond the scope of what can be included in a single book. These analytical skills will help you to excel academically, and they will also help you to think critically in any professional career you choose to pursue. This module discusses the realm of physics (to define what physics is), some applications of physics (to illustrate its relevance to other disciplines), and more precisely what constitutes a physical law (to illuminate the importance of experimentation to theory).

Science and the Realm of Physics

Science consists of the theories and laws that are the general truths of nature as well as the body of knowledge they encompass. Scientists are continually trying to expand this body of knowledge and to perfect the expression of the laws that describe it. Physics is concerned with describing the interactions of energy, matter, space, and time, and it is especially interested in what fundamental mechanisms underlie every phenomenon. The concern for describing the basic phenomena in nature essentially defines the realm of physics .

Physics aims to describe the function of everything around us, from the movement of tiny charged particles to the motion of people, cars, and spaceships. In fact, almost everything around you can be described quite accurately by the laws of physics. Consider a smart phone ( Figure 1.3 ). Physics describes how electricity interacts with the various circuits inside the device. This knowledge helps engineers select the appropriate materials and circuit layout when building the smart phone. Next, consider a GPS system. Physics describes the relationship between the speed of an object, the distance over which it travels, and the time it takes to travel that distance. GPS relies on precise calculations that account for variations in the Earth's landscapes, the exact distance between orbiting satellites, and even the effect of a complex occurrence of time dilation. Most of these calculations are founded on algorithms developed by Gladys West, a mathematician and computer scientist who programmed the first computers capable of highly accurate remote sensing and positioning. When you use a GPS device, it utilizes these algorithms to recognize where you are and how your position relates to other objects on Earth.

Applications of Physics

You need not be a scientist to use physics. On the contrary, knowledge of physics is useful in everyday situations as well as in nonscientific professions. It can help you understand how microwave ovens work, why metals should not be put into them, and why they might affect pacemakers. (See Figure 1.4 and Figure 1.5 .) Physics allows you to understand the hazards of radiation and rationally evaluate these hazards more easily. Physics also explains the reason why a black car radiator helps remove heat in a car engine, and it explains why a white roof helps keep the inside of a house cool. Similarly, the operation of a car’s ignition system as well as the transmission of electrical signals through our body’s nervous system are much easier to understand when you think about them in terms of basic physics.

Physics is the foundation of many important disciplines and contributes directly to others. Chemistry, for example—since it deals with the interactions of atoms and molecules—is rooted in atomic and molecular physics. Most branches of engineering are applied physics. In architecture, physics is at the heart of structural stability, and is involved in the acoustics, heating, lighting, and cooling of buildings. Parts of geology rely heavily on physics, such as radioactive dating of rocks, earthquake analysis, and heat transfer in the Earth. Some disciplines, such as biophysics and geophysics, are hybrids of physics and other disciplines.

Physics has many applications in the biological sciences. On the microscopic level, it helps describe the properties of cell walls and cell membranes ( Figure 1.6 and Figure 1.7 ). On the macroscopic level, it can explain the heat, work, and power associated with the human body. Physics is involved in medical diagnostics, such as x-rays, magnetic resonance imaging (MRI), and ultrasonic blood flow measurements. Medical therapy sometimes directly involves physics; for example, cancer radiotherapy uses ionizing radiation. Physics can also explain sensory phenomena, such as how musical instruments make sound, how the eye detects color, and how lasers can transmit information.

It is not necessary to formally study all applications of physics. What is most useful is knowledge of the basic laws of physics and a skill in the analytical methods for applying them. The study of physics also can improve your problem-solving skills. Furthermore, physics has retained the most basic aspects of science, so it is used by all of the sciences, and the study of physics makes other sciences easier to understand.

Models, Theories, and Laws; The Role of Experimentation

The laws of nature are concise descriptions of the universe around us; they are human statements of the underlying laws or rules that all natural processes follow. Such laws are intrinsic to the universe; humans did not create them and so cannot change them. We can only discover and understand them. Their discovery is a very human endeavor, with all the elements of mystery, imagination, struggle, triumph, and disappointment inherent in any creative effort. (See Figure 1.8 and Figure 1.9 .) The cornerstone of discovering natural laws is observation; science must describe the universe as it is, not as we may imagine it to be.

We all are curious to some extent. We look around, make generalizations, and try to understand what we see—for example, we look up and wonder whether one type of cloud signals an oncoming storm. As we become serious about exploring nature, we become more organized and formal in collecting and analyzing data. We attempt greater precision, perform controlled experiments (if we can), and write down ideas about how the data may be organized and unified. We then formulate models, theories, and laws based on the data we have collected and analyzed to generalize and communicate the results of these experiments.

A model is a representation of something that is often too difficult (or impossible) to display directly. While a model is justified with experimental proof, it is only accurate under limited situations. An example is the planetary model of the atom in which electrons are pictured as orbiting the nucleus, analogous to the way planets orbit the Sun. (See Figure 1.10 .) We cannot observe electron orbits directly, but the mental image helps explain the observations we can make, such as the emission of light from hot gases (atomic spectra). Physicists use models for a variety of purposes. For example, models can help physicists analyze a scenario and perform a calculation, or they can be used to represent a situation in the form of a computer simulation. A theory is an explanation for patterns in nature that is supported by scientific evidence and verified multiple times by various groups of researchers. Some theories include models to help visualize phenomena, whereas others do not. Newton’s theory of gravity, for example, does not require a model or mental image, because we can observe the objects directly with our own senses. The kinetic theory of gases, on the other hand, is a model in which a gas is viewed as being composed of atoms and molecules. Atoms and molecules are too small to be observed directly with our senses—thus, we picture them mentally to understand what our instruments tell us about the behavior of gases.

A law uses concise language to describe a generalized pattern in nature that is supported by scientific evidence and repeated experiments. Often, a law can be expressed in the form of a single mathematical equation. Laws and theories are similar in that they are both scientific statements that result from a tested hypothesis and are supported by scientific evidence. However, the designation law is reserved for a concise and very general statement that describes phenomena in nature, such as the law that energy is conserved during any process, or Newton’s second law of motion, which relates force, mass, and acceleration by the simple equation F = m a F = m a . A theory, in contrast, is a less concise statement of observed phenomena. For example, the Theory of Evolution and the Theory of Relativity cannot be expressed concisely enough to be considered a law. The biggest difference between a law and a theory is that a theory is much more complex and dynamic. A law describes a single action, whereas a theory explains an entire group of related phenomena. And, whereas a law is a postulate that forms the foundation of the scientific method, a theory is the end result of that process.

Less broadly applicable statements are usually called principles (such as Pascal’s principle, which is applicable only in fluids), but the distinction between laws and principles often is not carefully made.

Models, Theories, and Laws

Models, theories, and laws are used to help scientists analyze the data they have already collected. However, often after a model, theory, or law has been developed, it points scientists toward new discoveries they would not otherwise have made.

The models, theories, and laws we devise sometimes imply the existence of objects or phenomena as yet unobserved. These predictions are remarkable triumphs and tributes to the power of science. It is the underlying order in the universe that enables scientists to make such spectacular predictions. However, if experiment does not verify our predictions, then the theory or law is wrong, no matter how elegant or convenient it is. Laws can never be known with absolute certainty because it is impossible to perform every imaginable experiment in order to confirm a law in every possible scenario. Physicists operate under the assumption that all scientific laws and theories are valid until a counterexample is observed. If a good-quality, verifiable experiment contradicts a well-established law, then the law must be modified or overthrown completely.

The study of science in general and physics in particular is an adventure much like the exploration of uncharted ocean. Discoveries are made; models, theories, and laws are formulated; and the beauty of the physical universe is made more sublime for the insights gained.

The Scientific Method

Ibn al-Haytham (sometimes referred to as Alhazen), a 10th-11th century scientist working in Cairo, significantly advanced the understanding of optics and vision. But his contributions go much further. In demonstrating that previous approaches were incorrect, he emphasized that scientists must be ready to reject existing knowledge and become "the enemy" of everything they read; he expressed that scientists must trust only objective evidence. Al-Haytham emphasized repeated experimentation and validation, and acknowledged that senses and predisposition could lead to poor conclusions. His work was a precursor to the scientific method that we use today.

As scientists inquire and gather information about the world, they follow a process called the scientific method . This process typically begins with an observation and question that the scientist will research. Next, the scientist typically performs some research about the topic and then devises a hypothesis. Then, the scientist will test the hypothesis by performing an experiment. Finally, the scientist analyzes the results of the experiment and draws a conclusion. Note that the scientific method can be applied to many situations that are not limited to science, and this method can be modified to suit the situation.

Consider an example. Let us say that you try to turn on your car, but it will not start. You undoubtedly wonder: Why will the car not start? You can follow a scientific method to answer this question. First off, you may perform some research to determine a variety of reasons why the car will not start. Next, you will state a hypothesis. For example, you may believe that the car is not starting because it has no engine oil. To test this, you open the hood of the car and examine the oil level. You observe that the oil is at an acceptable level, and you thus conclude that the oil level is not contributing to your car issue. To troubleshoot the issue further, you may devise a new hypothesis to test and then repeat the process again.

The Evolution of Natural Philosophy into Modern Physics

Physics was not always a separate and distinct discipline. It remains connected to other sciences to this day. The word physics comes from Greek, meaning nature. The study of nature came to be called “natural philosophy.” From ancient times through the Renaissance, natural philosophy encompassed many fields, including astronomy, biology, chemistry, physics, mathematics, and medicine. Over the last few centuries, the growth of knowledge has resulted in ever-increasing specialization and branching of natural philosophy into separate fields, with physics retaining the most basic facets. (See Figure 1.11 , Figure 1.12 , and Figure 1.13 .) Physics as it developed from the Renaissance to the end of the 19th century is called classical physics . It was transformed into modern physics by revolutionary discoveries made starting at the beginning of the 20th century.

Classical physics is not an exact description of the universe, but it is an excellent approximation under the following conditions: Matter must be moving at speeds less than about 1% of the speed of light, the objects dealt with must be large enough to be seen with a microscope, and only weak gravitational fields, such as the field generated by the Earth, can be involved. Because humans live under such circumstances, classical physics seems intuitively reasonable, while many aspects of modern physics seem bizarre. This is why models are so useful in modern physics—they let us conceptualize phenomena we do not ordinarily experience. We can relate to models in human terms and visualize what happens when objects move at high speeds or imagine what objects too small to observe with our senses might be like. For example, we can understand an atom’s properties because we can picture it in our minds, although we have never seen an atom with our eyes. New tools, of course, allow us to better picture phenomena we cannot see. In fact, new instrumentation has allowed us in recent years to actually “picture” the atom.

Limits on the Laws of Classical Physics

For the laws of classical physics to apply, the following criteria must be met: Matter must be moving at speeds less than about 1% of the speed of light, the objects dealt with must be large enough to be seen with a microscope, and only weak gravitational fields (such as the field generated by the Earth) can be involved.

Some of the most spectacular advances in science have been made in modern physics. Many of the laws of classical physics have been modified or rejected, and revolutionary changes in technology, society, and our view of the universe have resulted. Like science fiction, modern physics is filled with fascinating objects beyond our normal experiences, but it has the advantage over science fiction of being very real. Why, then, is the majority of this text devoted to topics of classical physics? There are two main reasons: Classical physics gives an extremely accurate description of the universe under a wide range of everyday circumstances, and knowledge of classical physics is necessary to understand modern physics.

Modern physics itself consists of the two revolutionary theories, relativity and quantum mechanics. These theories deal with the very fast and the very small, respectively. Relativity must be used whenever an object is traveling at greater than about 1% of the speed of light or experiences a strong gravitational field such as that near the Sun. Quantum mechanics must be used for objects smaller than can be seen with a microscope. The combination of these two theories is relativistic quantum mechanics, and it describes the behavior of small objects traveling at high speeds or experiencing a strong gravitational field. Relativistic quantum mechanics is the best universally applicable theory we have. Because of its mathematical complexity, it is used only when necessary, and the other theories are used whenever they will produce sufficiently accurate results. We will find, however, that we can do a great deal of modern physics with the algebra and trigonometry used in this text.

Check Your Understanding

A friend tells you they have learned about a new law of nature. What can you know about the information even before your friend describes the law? How would the information be different if your friend told you they had learned about a scientific theory rather than a law?

Without knowing the details of the law, you can still infer that the information your friend has learned conforms to the requirements of all laws of nature: it will be a concise description of the universe around us; a statement of the underlying rules that all natural processes follow. If the information had been a theory, you would be able to infer that the information will be a large-scale, broadly applicable generalization.

PhET Explorations

Equation grapher.

Learn about graphing polynomials. The shape of the curve changes as the constants are adjusted. View the curves for the individual terms (e.g. y = bx y = bx ) to see how they add to generate the polynomial curve.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/1-1-physics-an-introduction

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• More from M-W
• To save this word, you'll need to log in. Log In

Definition of hypothesis

Did you know.

The Difference Between Hypothesis and Theory

A hypothesis is an assumption, an idea that is proposed for the sake of argument so that it can be tested to see if it might be true.

In the scientific method, the hypothesis is constructed before any applicable research has been done, apart from a basic background review. You ask a question, read up on what has been studied before, and then form a hypothesis.

A hypothesis is usually tentative; it's an assumption or suggestion made strictly for the objective of being tested.

A theory , in contrast, is a principle that has been formed as an attempt to explain things that have already been substantiated by data. It is used in the names of a number of principles accepted in the scientific community, such as the Big Bang Theory . Because of the rigors of experimentation and control, it is understood to be more likely to be true than a hypothesis is.

In non-scientific use, however, hypothesis and theory are often used interchangeably to mean simply an idea, speculation, or hunch, with theory being the more common choice.

Since this casual use does away with the distinctions upheld by the scientific community, hypothesis and theory are prone to being wrongly interpreted even when they are encountered in scientific contexts—or at least, contexts that allude to scientific study without making the critical distinction that scientists employ when weighing hypotheses and theories.

The most common occurrence is when theory is interpreted—and sometimes even gleefully seized upon—to mean something having less truth value than other scientific principles. (The word law applies to principles so firmly established that they are almost never questioned, such as the law of gravity.)

This mistake is one of projection: since we use theory in general to mean something lightly speculated, then it's implied that scientists must be talking about the same level of uncertainty when they use theory to refer to their well-tested and reasoned principles.

The distinction has come to the forefront particularly on occasions when the content of science curricula in schools has been challenged—notably, when a school board in Georgia put stickers on textbooks stating that evolution was "a theory, not a fact, regarding the origin of living things." As Kenneth R. Miller, a cell biologist at Brown University, has said , a theory "doesn’t mean a hunch or a guess. A theory is a system of explanations that ties together a whole bunch of facts. It not only explains those facts, but predicts what you ought to find from other observations and experiments.”

While theories are never completely infallible, they form the basis of scientific reasoning because, as Miller said "to the best of our ability, we’ve tested them, and they’ve held up."

• proposition
• supposition

hypothesis , theory , law mean a formula derived by inference from scientific data that explains a principle operating in nature.

hypothesis implies insufficient evidence to provide more than a tentative explanation.

theory implies a greater range of evidence and greater likelihood of truth.

law implies a statement of order and relation in nature that has been found to be invariable under the same conditions.

Examples of hypothesis in a Sentence

These examples are programmatically compiled from various online sources to illustrate current usage of the word 'hypothesis.' Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.

Word History

Greek, from hypotithenai to put under, suppose, from hypo- + tithenai to put — more at do

1641, in the meaning defined at sense 1a

Phrases Containing hypothesis

• counter - hypothesis
• nebular hypothesis
• null hypothesis
• planetesimal hypothesis
• Whorfian hypothesis

Articles Related to hypothesis

This is the Difference Between a...

This is the Difference Between a Hypothesis and a Theory

In scientific reasoning, they're two completely different things

Dictionary Entries Near hypothesis

hypothermia

hypothesize

Cite this Entry

“Hypothesis.” Merriam-Webster.com Dictionary , Merriam-Webster, https://www.merriam-webster.com/dictionary/hypothesis. Accessed 19 May. 2024.

Kids Definition

Kids definition of hypothesis, medical definition, medical definition of hypothesis, more from merriam-webster on hypothesis.

Nglish: Translation of hypothesis for Spanish Speakers

Britannica English: Translation of hypothesis for Arabic Speakers

Britannica.com: Encyclopedia article about hypothesis

Subscribe to America's largest dictionary and get thousands more definitions and advanced search—ad free!

Can you solve 4 words at once?

Word of the day.

See Definitions and Examples »

Get Word of the Day daily email!

Popular in Grammar & Usage

More commonly misspelled words, your vs. you're: how to use them correctly, every letter is silent, sometimes: a-z list of examples, more commonly mispronounced words, how to use em dashes (—), en dashes (–) , and hyphens (-), popular in wordplay, the words of the week - may 17, birds say the darndest things, a great big list of bread words, 10 scrabble words without any vowels, 12 more bird names that sound like insults (and sometimes are), games & quizzes.

• Previous Article
• Next Article

The importance of hypothesis

• Open the PDF for in another window
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Bernard Lightman; The importance of hypothesis. Physics Today 1 December 2020; 73 (12): 56–57. https://doi.org/10.1063/PT.3.4637

Download citation file:

• Ris (Zotero)
• Reference Manager

Some history of science studies are groundbreaking because they examine a previously neglected topic. Others are innovative in their use of new archival material. Still others use well-known sources to tell a new story about subjects previously tackled by scholars. Henry M. Cowles’s The Scientific Method: An Evolution of Thinking from Darwin to Dewey falls into the last category. His novel account provides a big-picture look at the development of the scientific method across the natural, medical, and social sciences in both Britain and the US during the 19th century.

Charles Darwin’s study in his home, Down House, outside London.

Cowles argues that Charles Darwin’s evolutionary theory birthed an entirely new concept of the scientific method that shaped the thinking of biologists, anthropologists, neurologists, philosophers, psychologists, and educators in the late 19th century. He begins by stating flatly on the first page that “there is no such thing as the scientific method, and there never was.” While that may seem to be an unpromising start for a book examining the history of the scientific method, Cowles’s intention is to identify the history of the scientific method as a powerful myth.

According to The Scientific Method, a significant development in that history took place in the early 19th century, when philosophers and scientists such as John Stuart Mill, William Whewell, and John Herschel increasingly emphasized the role of hypothesis in the scientific method and rejected the notion that it could only lead to wild speculation. Darwin picked up on the importance of hypothesis, but he broke with the earlier figures by placing it within an evolutionary framework. For Darwin, Cowles argues, both species and theories evolved through a process of trial and error.

The testing of hypotheses was an integral part of the competition between scientific theories. Cowles shows how Darwin’s theory of pangenesis, put forward in his The Variation of Animals and Plants Under Domestication (1868), was not an aberration. It was reminiscent of Darwin’s unpublished early theorizing (1836–44) about evolution. Darwin believed that an integral part of the scientific method was formulating bold ideas that helped explain a variety of phenomena.

British figures from various disciplines subsequently embraced the notion that science and nature used the same method; they applied it explicitly to an understanding of how science evolved. For example, in his account of mental evolution, Herbert Spencer sought to construct a reflexive natural history of the mind that would include science as an object of study. Science itself became a tool used by the adaptive mind to cope with a constantly evolving world. Neurologists like William Benjamin Carpenter and John Hughlings Jackson and anthropologists like Edward Burnett Tylor explored the ramifications of the concept of the scientific method for their respective disciplines.

Halfway through the book, Cowles shifts his focus to the US to follow the development of Darwin’s insight in the field of evolutionary psychology. He begins by depicting the meetings of the Metaphysical Club, an informal discussion group of philosophers that met in Cambridge, Massachusetts, during the 1870s, and uses them to discuss the importance of hypothesis and the nature of science to American thought. (Curiously, Cowles does not compare the Metaphysical Club to its British counterpart, the Metaphysical Society, even though such a comparison would serve as a way to transport his readers across the Atlantic.) The section examines philosophers and psychologists such as Charles Peirce, William James, Edward Thorndike, G. Stanley Hall, Ernest Lindley, and John Dewey.

As Cowles argues on page 185, studies of animal intelligence in comparative psychology “expanded outward to new minds and turned inward in new ways simultaneously, seeking the source of their scientific thinking in observable animal behaviors.” Psychologists began to study children in the hope that they would reveal the developmental roots of human reasoning. After discussing John Dewey’s interest in experimentalism, Cowles concludes by outlining how the school of psychology Dewey founded, functionalism, became the dominant line of thought in the US by the end of the 19th century.

The Scientific Method is an absorbing read that illuminates the history of the natural and social sciences in Britain and the US. It features nuanced readings of important scientific figures from a new perspective. Well-argued, accessible, and based on extensive research, Cowles’s hypothesis about the transformation of the scientific method by evolutionary theory should win the struggle for existence in Darwin’s “tangled bank” of scholarship on 19th-century science.

Bernard Lightman is distinguished research professor of humanities at York University in Toronto.

Citing articles via

• Online ISSN 1945-0699
• Print ISSN 0031-9228
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Talk to our experts

1800-120-456-456

Hypothesis: An Introduction

You must have heard about hypotheses that led to several achievements in scientific inventions. A hypothesis is a milestone in any research; it is the point of the research where we propose an analysis. The hypothesis of any research corresponds to the assumptions we conclude from the evidence gathered. The hypothesis consists of the points or the concepts that are proven successful. Now, let us learn about what exactly a hypothesis means and the type of hypothesis along with examples.

What is Hypothesis?

An assumption that is made based on some limited evidence collected is known as a hypothesis. It is the beginning point of study that translates research questions into predictions that might or might not be true. It depends on the variables and population used, also the relation between the variables. The hypothesis used to test the relationship between two or multiple variables is known as the research hypothesis.

Hypothesis Properties

The properties of the hypothesis are as follows:

It should be empirically tested irrespective of being right or wrong.

It should establish the relationship between the variables that are considered.

It must be specific, clear, and precise.

It should possess the scope for future studies and be capable of conducting more tests.

It should be capable of testing it in a reasonable time and it must be reliable.

Types of Hypothesis

Hypothesis can be classified as follows:

Null Hypothesis

Simple hypothesis

Directional hypothesis

Complex hypothesis

Non-directional hypothesis

Causal and associative hypothesis

It states that one variable doesn't affect the other variables being studied. A null hypothesis asserts that two factors or groups are independent of each other and that some traits of a population or process are identical. To contradict or invalidate the null hypothesis, we must assess the likelihood of the alternative hypothesis in addition to the null hypothesis.

Simple Hypothesis

There are two types of variables i.e, dependent and independent variables. A simple hypothesis shows the relationship between the dependent and independent variables. For example, if you pump petrol into your bike, you can go for long rides. Here bike is the dependent variable and petrol is the independent one.

Directional Hypothesis

A directional hypothesis is a researcher's prediction of a positive or negative change, relationship, or difference between two variables in a population. This statement is often supported by prior research, a widely established theory, considerable experience, or relevant literature.

For example, students who do proper revision and assignments could score more marks than the students who skipped. Here, we already know the process and its impact on the outcome. This is what we call a directional hypothesis.

Complex Hypothesis

The complex hypothesis shows the relationship that comes between two or more dependent and independent variables. For example, if you pump petrol in your bike, you can go for long rides, also you become an expert in riding a bike, you explore more places and come across new things.

Non-directional Hypothesis

There is no theory for this kind. Unlike the directional hypothesis, there are no predictions. We can say there is a relation between the variables but prediction and nature are unknown.

Causal and Associative Hypothesis

If there is a change in one variable and as a result, it affects the other variable, then we say it is associative. Meanwhile, the causal hypothesis comes into play when the cause and effect interaction occurs between two or more variables.

Sources of Hypothesis

The major sources of hypothesis are:

Scientific theories

Personal experience and conclusion arrived

Studies that underwent in the past

The resemblances between the phenomena, that is the pattern observed in common

Common thoughts and thinking

Functions of Hypothesis

The functions of hypothesis are as follows:

It tells us the specific aspects of studies we investigate. It provides study with focus.

The cnstruction of the hypothesis led to objectivity in the investigation

It helps to formulate the theory for the research work and sort out what is wrong and right.

It filters out the data that have to be collected for the work.

Hypothesis Examples

Some examples of hypotheses are as follows

Consumption of tobacco led to cancer, which is an example of a simple hypothesis.

If a person does work out daily, his/her skin, body, and mind remain healthy and fresh, which is an example of a directional hypothesis.

If you consume tobacco it not only causes cancer, but also affects your brain, turns your lips black, etc.

Role of Hypothesis in the Scientific Method

Experimental designing

Predicting results

Background research

Question formation

Data collection

Verification of results

Concluding the experiment

Being a future reference for the further studies

Role of hypothesis in the scientific method

In conclusion, it can be understood that a hypothesis is an assumption that researchers make on the basis of the limited evidence collected. It is the starting point of study that translates research questions into predictions. The various types of hypotheses include Null Hypothesis, Simple hypothesis, Directional hypothesis, Complex hypothesis, Non-directional hypothesis, and Causal and associative hypothesis. We proceed with our research or experiments according to the hypothesis we design.

FAQs on Hypothesis

1. Why is a hypothesis important?

Hypothesis plays an important role in any research project; it's a stepping stone to proving a theory. Hypothesis serves in establishing a connection to the underlying theory and particular research subject. It helps in data processing and evaluates the reliability and validity of the study. It offers a foundation or supporting evidence to demonstrate the accuracy of the study. A hypothesis allows researchers not only to get a relationship between variables, but also to predict a relationship based on theoretical guidelines and/or empirical proof.

2. How do I write a hypothesis?

Writing a good hypothesis starts before you even begin to type. Like several tasks, preparation is vital, thus you begin first by conducting analysis yourself, and reading all you can regarding the subject that you decide to do research on. From there, you’ll gain the information you need to know , where your focus within the subject will lie. Keep in mind that a hypothesis may be a prediction of the relationship that exists between 2 or more variables. The hypothesis should be straightforward and concise , the result should be predictable , clear and with no assumptions about the reader's knowledge.

3. What are a few examples of hypotheses?

Consumption of drugs leads to depression is an example of a simple hypothesis. If a person has a proper diet plan, his/her skin, body, and mind remain healthy and fresh. This is an example of a directional hypothesis. If you consume drugs it not only causes depression, but also affects your brain, leads to addiction, etc. If you pump petrol in your bike, you can go for long rides, also you become an expert in riding a bike, you explore more places and come across new things.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Microb Biotechnol
• v.15(11); 2022 Nov

On the role of hypotheses in science

Harald brüssow.

1 Laboratory of Gene Technology, Department of Biosystems, KU Leuven, Leuven Belgium

Associated Data

Scientific research progresses by the dialectic dialogue between hypothesis building and the experimental testing of these hypotheses. Microbiologists as biologists in general can rely on an increasing set of sophisticated experimental methods for hypothesis testing such that many scientists maintain that progress in biology essentially comes with new experimental tools. While this is certainly true, the importance of hypothesis building in science should not be neglected. Some scientists rely on intuition for hypothesis building. However, there is also a large body of philosophical thinking on hypothesis building whose knowledge may be of use to young scientists. The present essay presents a primer into philosophical thoughts on hypothesis building and illustrates it with two hypotheses that played a major role in the history of science (the parallel axiom and the fifth element hypothesis). It continues with philosophical concepts on hypotheses as a calculus that fits observations (Copernicus), the need for plausibility (Descartes and Gilbert) and for explicatory power imposing a strong selection on theories (Darwin, James and Dewey). Galilei introduced and James and Poincaré later justified the reductionist principle in hypothesis building. Waddington stressed the feed‐forward aspect of fruitful hypothesis building, while Poincaré called for a dialogue between experiment and hypothesis and distinguished false, true, fruitful and dangerous hypotheses. Theoretical biology plays a much lesser role than theoretical physics because physical thinking strives for unification principle across the universe while biology is confronted with a breathtaking diversity of life forms and its historical development on a single planet. Knowledge of the philosophical foundations on hypothesis building in science might stimulate more hypothesis‐driven experimentation that simple observation‐oriented “fishing expeditions” in biological research.

Short abstract

Scientific research progresses by the dialectic dialogue between hypothesis building and the experimental testing of these hypotheses. Microbiologists can rely on an increasing set of sophisticated experimental methods for hypothesis testing but the importance of hypothesis building in science should not be neglected. This Lilliput offers a primer on philosophical concepts on hypotheses in science.

INTRODUCTION

Philosophy of science and the theory of knowledge (epistemology) are important branches of philosophy. However, philosophy has over the centuries lost its dominant role it enjoyed in antiquity and became in Medieval Ages the maid of theology (ancilla theologiae) and after the rise of natural sciences and its technological applications many practising scientists and the general public doubt whether they need philosophical concepts in their professional and private life. This is in the opinion of the writer of this article, an applied microbiologist, shortsighted for several reasons. Philosophers of the 20th century have made important contributions to the theory of knowledge, and many eminent scientists grew interested in philosophical problems. Mathematics which plays such a prominent role in physics and increasingly also in other branches of science is a hybrid: to some extent, it is the paradigm of an exact science while its abstract aspects are deeply rooted in philosophical thinking. In the present essay, the focus is on hypothesis and hypothesis building in science, essentially it is a compilation what philosophers and scientists thought about this subject in past and present. The controversy between the mathematical mind and that of the practical mind is an old one. The philosopher, physicist and mathematician Pascal ( 1623 –1662a) wrote in his Pensées : “Mathematicians who are only mathematicians have exact minds, provided all things are explained to them by means of definitions and axioms; otherwise they are inaccurate. They are only right when the principles are quite clear. And men of intuition cannot have the patience to reach to first principles of things speculative and conceptional, which they have never seen in the world and which are altogether out of the common. The intellect can be strong and narrow, and can be comprehensive and weak.” Hypothesis building is an act both of intuition and exact thinking and I hope that theoretical knowledge about hypothesis building will also profit young microbiologists.

HYPOTHESES AND AXIOMS IN MATHEMATICS

In the following, I will illustrate the importance of hypothesis building for the history of science and the development of knowledge and illustrate it with two famous concepts, the parallel axiom in mathematics and the five elements hypothesis in physics.

Euclidean geometry

The prominent role of hypotheses in the development of science becomes already clear in the first science book of the Western civilization: Euclid's The Elements written about 300 BC starts with a set of statements called Definitions, Postulates and Common Notions that lay out the foundation of geometry (Euclid,  c.323‐c.283 ). This axiomatic approach is very modern as exemplified by the fact that Euclid's book remained for long time after the Bible the most read book in the Western hemisphere and a backbone of school teaching in mathematics. Euclid's twenty‐three definitions start with sentences such as “1. A point is that which has no part; 2. A line is breadthless length; 3. The extremities of a line are points”; and continues with the definition of angles (“8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line”) and that of circles, triangles and quadrilateral figures. For the history of science, the 23rd definition of parallels is particularly interesting: “Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction”. This is the famous parallel axiom. It is clear that the parallel axiom cannot be the result of experimental observations, but must be a concept created in the mind. Euclid ends with five Common Notions (“1. Things which are equal to the same thing are also equal to one another, to 5. The whole is greater than the part”). The establishment of a contradiction‐free system for a branch of mathematics based on a set of axioms from which theorems were deduced was revolutionary modern. Hilbert ( 1899 ) formulated a sound modern formulation for Euclidian geometry. Hilbert's axiom system contains the notions “point, line and plane” and the concepts of “betweenness, containment and congruence” leading to five axioms, namely the axioms of Incidence (“Verknüpfung”), of Order (“Anordnung”), of Congruence, of Continuity (“Stetigkeit”) and of Parallels.

Origin of axioms

Philosophers gave various explanations for the origin of the Euclidean hypotheses or axioms. Plato considered geometrical figures as related to ideas (the true things behind the world of appearances). Aristoteles considered geometric figures as abstractions of physical bodies. Descartes perceived geometric figures as inborn ideas from extended bodies ( res extensa ), while Pascal thought that the axioms of Euclidian geometry were derived from intuition. Kant reasoned that Euclidian geometry represented a priori perceptions of space. Newton considered geometry as part of general mechanics linked to theories of measurement. Hilbert argued that the axioms of mathematical geometry are neither the result of contemplation (“Anschauung”) nor of psychological source. For him, axioms were formal propositions (“formale Aussageformen”) characterized by consistency (“Widerspruchsfreiheit”, i.e. absence of contradiction) (Mittelstrass,  1980a ).

Definitions

Axioms were also differently defined by philosophers. In Topics , Aristoteles calls axioms the assumptions taken up by one partner of a dialogue to initiate a dialectic discussion. Plato states that an axiom needs to be an acceptable or credible proposition, which cannot be justified by reference to other statements. Yet, a justification is not necessary because an axiom is an evident statement. In modern definition, axioms are methodical first sentences in the foundation of a deductive science (Mittelstrass,  1980a ). In Posterior Analytics , Aristotle defines postulates as positions which are at least initially not accepted by the dialogue partners while hypotheses are accepted for the sake of reasoning. In Euclid's book, postulates are construction methods that assure the existence of the geometric objects. Today postulates and axioms are used as synonyms while the 18th‐century philosophy made differences: Lambert defined axioms as descriptive sentences and postulates as prescriptive sentences. According to Kant, mathematical postulates create (synthesize) concepts (Mittelstrass,  1980b ). Definitions then fix the use of signs; they can be semantic definitions that explain the proper meaning of a sign in common language use (in a dictionary style) or they can be syntactic definitions that regulate the use of these signs in formal operations. Nominal definitions explain the words, while real definitions explain the meaning or the nature of the defined object. Definitions are thus essential for the development of a language of science, assuring communication and mutual understanding (Mittelstrass,  1980c ). Finally, hypotheses are also frequently defined as consistent conjectures that are compatible with the available knowledge. The truth of the hypothesis is only supposed in order to explain true observations and facts. Consequences of this hypothetical assumptions should explain the observed facts. Normally, descriptive hypotheses precede explanatory hypotheses in the development of scientific thought. Sometimes only tentative concepts are introduced as working hypotheses to test whether they have an explanatory capacity for the observations (Mittelstrass,  1980d ).

The Euclidian geometry is constructed along a logical “if→then” concept. The “if‐clause” formulates at the beginning the supposition, the “then clause” formulates the consequences from these axioms which provides a system of geometric theorems or insights. The conclusions do not follow directly from the hypothesis; this would otherwise represent self‐evident immediate conclusions. The “if‐then” concept in geometry is not used as in other branches of science where the consequences deduced from the axioms are checked against reality whether they are true, in order to confirm the validity of the hypothesis. The task in mathematics is: what can be logically deduced from a given set of axioms to build a contradiction‐free system of geometry. Whether this applies to the real world is in contrast to the situation in natural sciences another question and absolutely secondary to mathematics (Syntopicon,  1992 ).

Pascal's rules for hypotheses

In his Scientific Treatises on Geometric Demonstrations , Pascal ( 1623‐1662b ) formulates “Five rules are absolutely necessary and we cannot dispense with them without an essential defect and frequently even error. Do not leave undefined any terms at all obscure or ambiguous. Use in definitions of terms only words perfectly well known or already explained. Do not fail to ask that each of the necessary principles be granted, however clear and evident it may be. Ask only that perfectly self‐evident things be granted as axioms. Prove all propositions, using for their proof only axioms that are perfectly self‐evident or propositions already demonstrated or granted. Never get caught in the ambiguity of terms by failing to substitute in thought the definitions which restrict or define them. One should accept as true only those things whose contradiction appears to be false. We may then boldly affirm the original statement, however incomprehensible it is.”

Kant's rules on hypotheses

Kant ( 1724–1804 ) wrote that the analysis described in his book The Critique of Pure Reason “has now taught us that all its efforts to extend the bounds of knowledge by means of pure speculation, are utterly fruitless. So much the wider field lies open to hypothesis; as where we cannot know with certainty, we are at liberty to make guesses and to form suppositions. Imagination may be allowed, under the strict surveillance of reason, to invent suppositions; but these must be based on something that is perfectly certain‐ and that is the possibility of the object. Such a supposition is termed a hypothesis. We cannot imagine or invent any object or any property of an object not given in experience and employ it in a hypothesis; otherwise we should be basing our chain of reasoning upon mere chimerical fancies and not upon conception of things. Thus, we have no right to assume of new powers, not existing in nature and consequently we cannot assume that there is any other kind of community among substances than that observable in experience, any kind of presence than that in space and any kind of duration than that in time. The conditions of possible experience are for reason the only conditions of the possibility of things. Otherwise, such conceptions, although not self‐contradictory, are without object and without application. Transcendental hypotheses are therefore inadmissible, and we cannot use the liberty of employing in the absence of physical, hyperphysical grounds of explanation because such hypotheses do not advance reason, but rather stop it in its progress. When the explanation of natural phenomena happens to be difficult, we have constantly at hand a transcendental ground of explanation, which lifts us above the necessity of investigating nature. The next requisite for the admissibility of a hypothesis is its sufficiency. That is it must determine a priori the consequences which are given in experience and which are supposed to follow from the hypothesis itself.” Kant stresses another aspect when dealing with hypotheses: “It is our duty to try to discover new objections, to put weapons in the hands of our opponent, and to grant him the most favorable position. We have nothing to fear from these concessions; on the contrary, we may rather hope that we shall thus make ourselves master of a possession which no one will ever venture to dispute.”

For Kant's analytical and synthetical judgements and Difference between philosophy and mathematics (Kant, Whitehead) , see Appendices  S1 and S2 , respectively.

Poincaré on hypotheses

The mathematician‐philosopher Poincaré ( 1854 –1912a) explored the foundation of mathematics and physics in his book Science and Hypothesis . In the preface to the book, he summarizes common thinking of scientists at the end of the 19th century. “To the superficial observer scientific truth is unassailable, the logic of science is infallible, and if scientific men sometimes make mistakes, it is because they have not understood the rules of the game. Mathematical truths are derived from a few self‐evident propositions, by a chain of flawless reasoning, they are imposed not only by us, but on Nature itself. This is for the minds of most people the origin of certainty in science.” Poincaré then continues “but upon more mature reflection the position held by hypothesis was seen; it was recognized that it is as necessary to the experimenter as it is to the mathematician. And then the doubt arose if all these constructions are built on solid foundations.” However, “to doubt everything or to believe everything are two equally convenient solutions: both dispense with the necessity of reflection. Instead, we should examine with the utmost care the role of hypothesis; we shall then recognize not only that it is necessary, but that in most cases it is legitimate. We shall also see that there are several kinds of hypotheses; that some are verifiable and when once confirmed by experiment become truths of great fertility; that others may be useful to us in fixing our ideas; and finally that others are hypotheses only in appearance, and reduce to definitions or to conventions in disguise.” Poincaré argues that “we must seek mathematical thought where it has remained pure‐i.e. in arithmetic, in the proofs of the most elementary theorems. The process is proof by recurrence. We first show that a theorem is true for n  = 1; we then show that if it is true for n –1 it is true for n; and we conclude that it is true for all integers. The essential characteristic of reasoning by recurrence is that it contains, condensed in a single formula, an infinite number of syllogisms.” Syllogism is logical argument that applies deductive reasoning to arrive at a conclusion. Poincaré notes “that here is a striking analogy with the usual process of induction. But an essential difference exists. Induction applied to the physical sciences is always uncertain because it is based on the belief in a general order of the universe, an order which is external to us. Mathematical induction‐ i.e. proof by recurrence – is on the contrary, necessarily imposed on us, because it is only the affirmation of a property of the mind itself. No doubt mathematical recurrent reasoning and physical inductive reasoning are based on different foundations, but they move in parallel lines and in the same direction‐namely, from the particular to the general.”

Non‐Euclidian geometry: from Gauss to Lobatschewsky

Mathematics is an abstract science that intrinsically does not request that the structures described reflect a physical reality. Paradoxically, mathematics is the language of physics since the founder of experimental physics Galilei used Euclidian geometry when exploring the laws of the free fall. In his 1623 treatise The Assayer , Galilei ( 1564 –1642a) famously formulated that the book of Nature is written in the language of mathematics, thus establishing a link between formal concepts in mathematics and the structure of the physical world. Euclid's parallel axiom played historically a prominent role for the connection between mathematical concepts and physical realities. Mathematicians had doubted that the parallel axiom was needed and tried to prove it. In Euclidian geometry, there is a connection between the parallel axiom and the sum of the angles in a triangle being two right angles. It is therefore revealing that the famous mathematician C.F. Gauss investigated in the early 19th century experimentally whether this Euclidian theorem applies in nature. He approached this problem by measuring the sum of angles in a real triangle by using geodetic angle measurements of three geographical elevations in the vicinity of Göttingen where he was teaching mathematics. He reportedly measured a sum of the angles in this triangle that differed from 180°. Gauss had at the same time also developed statistical methods to evaluate the accuracy of measurements. Apparently, the difference of his measured angles was still within the interval of Gaussian error propagation. He did not publish the reasoning and the results for this experiment because he feared the outcry of colleagues about this unorthodox, even heretical approach to mathematical reasoning (Carnap,  1891 ‐1970a). However, soon afterwards non‐Euclidian geometries were developed. In the words of Poincaré, “Lobatschewsky assumes at the outset that several parallels may be drawn through a point to a given straight line, and he retains all the other axioms of Euclid. From these hypotheses he deduces a series of theorems between which it is impossible to find any contradiction, and he constructs a geometry as impeccable in its logic as Euclidian geometry. The theorems are very different, however, from those to which we are accustomed, and at first will be found a little disconcerting. For instance, the sum of the angles of a triangle is always less than two right angles, and the difference between that sum and two right angles is proportional to the area of the triangle. Lobatschewsky's propositions have no relation to those of Euclid, but are none the less logically interconnected.” Poincaré continues “most mathematicians regard Lobatschewsky's geometry as a mere logical curiosity. Some of them have, however, gone further. If several geometries are possible, they say, is it certain that our geometry is true? Experiments no doubt teaches us that the sum of the angles of a triangle is equal to two right angles, but this is because the triangles we deal with are too small” (Poincaré,  1854 ‐1912a)—hence the importance of Gauss' geodetic triangulation experiment. Gauss was aware that his three hills experiment was too small and thought on measurements on triangles formed with stars.

Poincaré vs. Einstein

Lobatschewsky's hyperbolic geometry did not remain the only non‐Euclidian geometry. Riemann developed a geometry without the parallel axiom, while the other Euclidian axioms were maintained with the exception of that of Order (Anordnung). Poincaré notes “so there is a kind of opposition between the geometries. For instance the sum of the angles in a triangle is equal to two right angles in Euclid's geometry, less than two right angles in that of Lobatschewsky, and greater than two right angles in that of Riemann. The number of parallel lines that can be drawn through a given point to a given line is one in Euclid's geometry, none in Riemann's, and an infinite number in the geometry of Lobatschewsky. Let us add that Riemann's space is finite, although unbounded.” As further distinction, the ratio of the circumference to the diameter of a circle is equal to π in Euclid's, greater than π in Lobatschewsky's and smaller than π in Riemann's geometry. A further difference between these geometries concerns the degree of curvature (Krümmungsmass k) which is 0 for a Euclidian surface, smaller than 0 for a Lobatschewsky and greater than 0 for a Riemann surface. The difference in curvature can be roughly compared with plane, concave and convex surfaces. The inner geometric structure of a Riemann plane resembles the surface structure of a Euclidean sphere and a Lobatschewsky plane resembles that of a Euclidean pseudosphere (a negatively curved geometry of a saddle). What geometry is true? Poincaré asked “Ought we then, to conclude that the axioms of geometry are experimental truths?” and continues “If geometry were an experimental science, it would not be an exact science. The geometric axioms are therefore neither synthetic a priori intuitions as affirmed by Kant nor experimental facts. They are conventions. Our choice among all possible conventions is guided by experimental facts; but it remains free and is only limited by the necessity of avoiding contradictions. In other words, the axioms of geometry are only definitions in disguise. What then are we to think of the question: Is Euclidean geometry true? It has no meaning. One geometry cannot be more true than another, it can only be more convenient. Now, Euclidean geometry is, and will remain, the most convenient, 1 st because it is the simplest and 2 nd because it sufficiently agrees with the properties of natural bodies” (Poincaré,  1854 ‐1912a).

Poincaré's book was published in 1903 and only a few years later Einstein published his general theory of relativity ( 1916 ) where he used a non‐Euclidean, Riemann geometry and where he demonstrated a structure of space that deviated from Euclidean geometry in the vicinity of strong gravitational fields. And in 1919, astronomical observations during a solar eclipse showed that light rays from a distant star were indeed “bent” when passing next to the sun. These physical observations challenged the view of Poincaré, and we should now address some aspects of hypotheses in physics (Carnap,  1891 ‐1970b).

HYPOTHESES IN PHYSICS

The long life of the five elements hypothesis.

Physical sciences—not to speak of biological sciences — were less developed in antiquity than mathematics which is already demonstrated by the primitive ideas on the elements constituting physical bodies. Plato and Aristotle spoke of the four elements which they took over from Thales (water), Anaximenes (air) and Parmenides (fire and earth) and add a fifth element (quinta essentia, our quintessence), namely ether. Ether is imagined a heavenly element belonging to the supralunar world. In Plato's dialogue Timaios (Plato,  c.424‐c.348 BC a ), the five elements were associated with regular polyhedra in geometry and became known as Platonic bodies: tetrahedron (fire), octahedron (air), cube (earth), icosahedron (water) and dodecahedron (ether). In regular polyhedra, faces are congruent (identical in shape and size), all angles and all edges are congruent, and the same number of faces meet at each vertex. The number of elements is limited to five because in Euclidian space there are exactly five regular polyhedral. There is in Plato's writing even a kind of geometrical chemistry. Since two octahedra (air) plus one tetrahedron (fire) can be combined into one icosahedron (water), these “liquid” elements can combine while this is not the case for combinations with the cube (earth). The 12 faces of the dodecahedron were compared with the 12 zodiac signs (Mittelstrass,  1980e ). This geometry‐based hypothesis of physics had a long life. As late as 1612, Kepler in his Mysterium cosmographicum tried to fit the Platonic bodies into the planetary shells of his solar system model. The ether theory even survived into the scientific discussion of the 19th‐century physics and the idea of a mathematical structure of the universe dominated by symmetry operations even fertilized 20th‐century ideas about symmetry concepts in the physics of elementary particles.

Huygens on sound waves in air

The ether hypothesis figures prominently in the 1690 Treatise on Light from Huygens ( 1617‐1670 ). He first reports on the transmission of sound by air when writing “this may be proved by shutting up a sounding body in a glass vessel from which the air is withdrawn and care was taken to place the sounding body on cotton that it cannot communicate its tremor to the glass vessel which encloses it. After having exhausted all the air, one hears no sound from the metal though it is struck.” Huygens comes up with some foresight when suspecting “the air is of such a nature that it can be compressed and reduced to a much smaller space than that it normally occupies. Air is made up of small bodies which float about and which are agitated very rapidly. So that the spreading of sound is the effort which these little bodies make in collisions with one another, to regain freedom when they are a little more squeezed together in the circuit of these waves than elsewhere.”

Huygens on light waves in ether

“That is not the same air but another kind of matter in which light spreads; since if the air is removed from the vessel the light does not cease to traverse it as before. The extreme velocity of light cannot admit such a propagation of motion” as sound waves. To achieve the propagation of light, Huygens invokes ether “as a substance approaching to perfect hardness and possessing springiness as prompt as we choose. One may conceive light to spread successively by spherical waves. The propagation consists nowise in the transport of those particles but merely in a small agitation which they cannot help communicate to those surrounding.” The hypothesis of an ether in outer space fills libraries of physical discussions, but all experimental approaches led to contradictions with respect to postulated properties of this hypothetical material for example when optical experiments showed that light waves display transversal and not longitudinal oscillations.

The demise of ether

Mechanical models for the transmission of light or gravitation waves requiring ether were finally put to rest by the theory of relativity from Einstein (Mittelstrass,  1980f ). This theory posits that the speed of light in an empty space is constant and does not depend on movements of the source of light or that of an observer as requested by the ether hypothesis. The theory of relativity also provides an answer how the force of gravitation is transmitted from one mass to another across an essentially empty space. In the non‐Euclidian formulation of the theory of relativity (Einstein used the Riemann geometry), there is no gravitation force in the sense of mechanical or electromagnetic forces. The gravitation force is in this formulation simply replaced by a geometric structure (space curvature near high and dense masses) of a four‐dimensional space–time system (Carnap,  1891 ‐1970c; Einstein & Imfeld,  1956 ) Gravitation waves and gravitation lens effects have indeed been experimental demonstrated by astrophysicists (Dorfmüller et al.,  1998 ).

For Aristotle's on physical hypotheses , see Appendix  S3 .

PHILOSOPHICAL THOUGHTS ON HYPOTHESES

In the following, the opinions of a number of famous scientists and philosophers on hypotheses are quoted to provide a historical overview on the subject.

Copernicus' hypothesis: a calculus which fits observations

In his book Revolutions of Heavenly Spheres Copernicus ( 1473–1543 ) reasoned in the preface about hypotheses in physics. “Since the newness of the hypotheses of this work ‐which sets the earth in motion and puts an immovable sun at the center of the universe‐ has already received a great deal of publicity, I have no doubt that certain of the savants have taken great offense.” He defended his heliocentric thesis by stating “For it is the job of the astronomer to use painstaking and skilled observations in gathering together the history of the celestial movements‐ and then – since he cannot by any line of reasoning reach the true causes of these movements‐ to think up or construct whatever causes or hypotheses he pleases such that, by the assumption of these causes, those same movements can be calculated from the principles of geometry for the past and the future too. This artist is markedly outstanding in both of these respects: for it is not necessary that these hypotheses should be true, or even probable; but it is enough if they provide a calculus which fits the observations.” This preface written in 1543 sounds in its arguments very modern physics. However, historians of science have discovered that it was probably written by a theologian friend of Copernicus to defend the book against the criticism by the church.

Bacon's intermediate hypotheses

In his book Novum Organum , Francis Bacon ( 1561–1626 ) claims for hypotheses and scientific reasoning “that they augur well for the sciences, when the ascent shall proceed by a true scale and successive steps, without interruption or breach, from particulars to the lesser axioms, thence to the intermediates and lastly to the most general.” He then notes “that the lowest axioms differ but little from bare experiments, the highest and most general are notional, abstract, and of no real weight. The intermediate are true, solid, full of life, and up to them depend the business and fortune of mankind.” He warns that “we must not then add wings, but rather lead and ballast to the understanding, to prevent its jumping and flying, which has not yet been done; but whenever this takes place we may entertain greater hopes of the sciences.” With respect to methodology, Bacon claims that “we must invent a different form of induction. The induction which proceeds by simple enumeration is puerile, leads to uncertain conclusions, …deciding generally from too small a number of facts. Sciences should separate nature by proper rejections and exclusions and then conclude for the affirmative, after collecting a sufficient number of negatives.”

Gilbert and Descartes for plausible hypotheses

William Gilbert introduced in his book On the Loadstone (Gilbert,  1544‐1603 ) the argument of plausibility into physical hypothesis building. “From these arguments, therefore, we infer not with mere probability, but with certainty, the diurnal rotation of the earth; for nature ever acts with fewer than with many means; and because it is more accordant to reason that the one small body, the earth, should make a daily revolution than the whole universe should be whirled around it.”

Descartes ( 1596‐1650 ) reflected on the sources of understanding in his book Rules for Direction and distinguished what “comes about by impulse, by conjecture, or by deduction. Impulse can assign no reason for their belief and when determined by fanciful disposition, it is almost always a source of error.” When speaking about the working of conjectures he quotes thoughts of Aristotle: “water which is at a greater distance from the center of the globe than earth is likewise less dense substance, and likewise the air which is above the water, is still rarer. Hence, we hazard the guess that above the air nothing exists but a very pure ether which is much rarer than air itself. Moreover nothing that we construct in this way really deceives, if we merely judge it to be probable and never affirm it to be true; in fact it makes us better instructed. Deduction is thus left to us as the only means of putting things together so as to be sure of their truth. Yet in it, too, there may be many defects.”

Care in formulating hypotheses

Locke ( 1632‐1704 ) in his treatise Concerning Human Understanding admits that “we may make use of any probable hypotheses whatsoever. Hypotheses if they are well made are at least great helps to the memory and often direct us to new discoveries. However, we should not take up any one too hastily.” Also, practising scientists argued against careless use of hypotheses and proposed remedies. Lavoisier ( 1743‐1794 ) in the preface to his Element of Chemistry warned about beaten‐track hypotheses. “Instead of applying observation to the things we wished to know, we have chosen rather to imagine them. Advancing from one ill‐founded supposition to another, we have at last bewildered ourselves amidst a multitude of errors. These errors becoming prejudices, are adopted as principles and we thus bewilder ourselves more and more. We abuse words which we do not understand. There is but one remedy: this is to forget all that we have learned, to trace back our ideas to their sources and as Bacon says to frame the human understanding anew.”

Faraday ( 1791–1867 ) in a Speculation Touching Electric Conduction and the Nature of Matter highlighted the fundamental difference between hypotheses and facts when noting “that he has most power of penetrating the secrets of nature, and guessing by hypothesis at her mode of working, will also be most careful for his own safe progress and that of others, to distinguish that knowledge which consists of assumption, by which I mean theory and hypothesis, from that which is the knowledge of facts and laws; never raising the former to the dignity or authority of the latter.”

Explicatory power justifies hypotheses

Darwin ( 1809 –1882a) defended the conclusions and hypothesis of his book The Origin of Species “that species have been modified in a long course of descent. This has been affected chiefly through the natural selection of numerous, slight, favorable variations.” He uses a post hoc argument for this hypothesis: “It can hardly be supposed that a false theory would explain, to so satisfactory a manner as does the theory of natural selection, the several large classes of facts” described in his book.

The natural selection of hypotheses

In the concluding chapter of The Descent of Man Darwin ( 1809 –1882b) admits “that many of the views which have been advanced in this book are highly speculative and some no doubt will prove erroneous.” However, he distinguished that “false facts are highly injurious to the progress of science for they often endure long; but false views do little harm for everyone takes a salutory pleasure in proving their falseness; and when this is done, one path to error is closed and the road to truth is often at the same time opened.”

The American philosopher William James ( 1842–1907 ) concurred with Darwin's view when he wrote in his Principles of Psychology “every scientific conception is in the first instance a spontaneous variation in someone'’s brain. For one that proves useful and applicable there are a thousand that perish through their worthlessness. The scientific conceptions must prove their worth by being verified. This test, however, is the cause of their preservation, not of their production.”

The American philosopher J. Dewey ( 1859‐1952 ) in his treatise Experience and Education notes that “the experimental method of science attaches more importance not less to ideas than do other methods. There is no such thing as experiment in the scientific sense unless action is directed by some leading idea. The fact that the ideas employed are hypotheses, not final truths, is the reason why ideas are more jealously guarded and tested in science than anywhere else. As fixed truths they must be accepted and that is the end of the matter. But as hypotheses, they must be continuously tested and revised, a requirement that demands they be accurately formulated. Ideas or hypotheses are tested by the consequences which they produce when they are acted upon. The method of intelligence manifested in the experimental method demands keeping track of ideas, activities, and observed consequences. Keeping track is a matter of reflective review.”

The reductionist principle

James ( 1842‐1907 ) pushed this idea further when saying “Scientific thought goes by selection. We break the solid plenitude of fact into separate essences, conceive generally what only exists particularly, and by our classifications leave nothing in its natural neighborhood. The reality exists as a plenum. All its part are contemporaneous, but we can neither experience nor think this plenum. What we experience is a chaos of fragmentary impressions, what we think is an abstract system of hypothetical data and laws. We must decompose each chaos into single facts. We must learn to see in the chaotic antecedent a multitude of distinct antecedents, in the chaotic consequent a multitude of distinct consequents.” From these considerations James concluded “even those experiences which are used to prove a scientific truth are for the most part artificial experiences of the laboratory gained after the truth itself has been conjectured. Instead of experiences engendering the inner relations, the inner relations are what engender the experience here.“

Following curiosity

Freud ( 1856–1939 ) considered curiosity and imagination as driving forces of hypothesis building which need to be confronted as quickly as possible with observations. In Beyond the Pleasure Principle , Freud wrote “One may surely give oneself up to a line of thought and follow it up as far as it leads, simply out of scientific curiosity. These innovations were direct translations of observation into theory, subject to no greater sources of error than is inevitable in anything of the kind. At all events there is no way of working out this idea except by combining facts with pure imagination and thereby departing far from observation.” This can quickly go astray when trusting intuition. Freud recommends “that one may inexorably reject theories that are contradicted by the very first steps in the analysis of observation and be aware that those one holds have only a tentative validity.”

Feed‐forward aspects of hypotheses

The geneticist Waddington ( 1905–1975 ) in his essay The Nature of Life states that “a scientific theory cannot remain a mere structure within the world of logic, but must have implications for action and that in two rather different ways. It must involve the consequence that if you do so and so, such and such result will follow. That is to say it must give, or at least offer, the possibility of controlling the process. Secondly, its value is quite largely dependent on its power of suggesting the next step in scientific advance. Any complete piece of scientific work starts with an activity essentially the same as that of an artist. It starts by asking a relevant question. The first step may be a new awareness of some facet of the world that no one else had previously thought worth attending to. Or some new imaginative idea which depends on a sensitive receptiveness to the oddity of nature essentially similar to that of the artist. In his logical analysis and manipulative experimentation, the scientist is behaving arrogantly towards nature, trying to force her into his categories of thought or to trick her into doing what he wants. But finally he has to be humble. He has to take his intuition, his logical theory and his manipulative skill to the bar of Nature and see whether she answers yes or no; and he has to abide by the result. Science is often quite ready to tolerate some logical inadequacy in a theory‐or even a flat logical contradiction like that between the particle and wave theories of matter‐so long as it finds itself in the possession of a hypothesis which offers both the possibility of control and a guide to worthwhile avenues of exploration.”

Poincaré: the dialogue between experiment and hypothesis

Poincaré ( 1854 –1912b) also dealt with physics in Science and Hypothesis . “Experiment is the sole source of truth. It alone can teach us certainty. Cannot we be content with experiment alone? What place is left for mathematical physics? The man of science must work with method. Science is built up of facts, as a house is built of stones, but an accumulation of facts is no more a science than a heap of stones is a house. It is often said that experiments should be made without preconceived concepts. That is impossible. Without the hypothesis, no conclusion could have been drawn; nothing extraordinary would have been seen; and only one fact the more would have been catalogued, without deducing from it the remotest consequence.” Poincaré compares science to a library. Experimental physics alone can enrich the library with new books, but mathematical theoretical physics draw up the catalogue to find the books and to reveal gaps which have to be closed by the purchase of new books.

Poincaré: false, true, fruitful and dangerous hypotheses

Poincaré continues “we all know that there are good and bad experiments. The latter accumulate in vain. Whether there are hundred or thousand, one single piece of work will be sufficient to sweep them into oblivion. Bacon invented the term of an experimentum crucis for such experiments. What then is a good experiment? It is that which teaches us something more than an isolated fact. It is that which enables us to predict and to generalize. Experiments only gives us a certain number of isolated points. They must be connected by a continuous line and that is true generalization. Every generalization is a hypothesis. It should be as soon as possible submitted to verification. If it cannot stand the test, it must be abandoned without any hesitation. The physicist who has just given up one of his hypotheses should rejoice, for he found an unexpected opportunity of discovery. The hypothesis took into account all the known factors which seem capable of intervention in the phenomenon. If it is not verified, it is because there is something unexpected. Has the hypothesis thus rejected been sterile? Far from it. It has rendered more service than a true hypothesis.” Poincaré notes that “with a true hypothesis only one fact the more would have been catalogued, without deducing from it the remotest consequence. It may be said that the wrong hypothesis has rendered more service than a true hypothesis.” However, Poincaré warns that “some hypotheses are dangerous – first and foremost those which are tacit and unconscious. And since we make them without knowing them, we cannot get rid of them.” Poincaré notes that here mathematical physics is of help because by its precision one is compelled to formulate all the hypotheses, revealing also the tacit ones.

Arguments for the reductionist principle

Poincaré also warned against multiplying hypotheses indefinitely: “If we construct a theory upon multiple hypotheses, and if experiment condemns it, which of the premisses must be changed?” Poincaré also recommended to “resolve the complex phenomenon given directly by experiment into a very large number of elementary phenomena. First, with respect to time. Instead of embracing in its entirety the progressive development of a phenomenon, we simply try to connect each moment with the one immediately preceding. Next, we try to decompose the phenomenon in space. We must try to deduce the elementary phenomenon localized in a very small region of space.” Poincaré suggested that the physicist should “be guided by the instinct of simplicity, and that is why in physical science generalization so readily takes the mathematical form to state the problem in the form of an equation.” This argument goes back to Galilei ( 1564 –1642b) who wrote in The Two Sciences “when I observe a stone initially at rest falling from an elevated position and continually acquiring new increments of speed, why should I not believe that such increases take place in a manner which is exceedingly simple and rather obvious to everybody? If now we examine the matter carefully we find no addition or increment more simple than that which repeats itself always in the same manner. It seems we shall not be far wrong if we put the increment of speed as proportional to the increment of time.” With a bit of geometrical reasoning, Galilei deduced that the distance travelled by a freely falling body varies as the square of the time. However, Galilei was not naïve and continued “I grant that these conclusions proved in the abstract will be different when applied in the concrete” and considers disturbances cause by friction and air resistance that complicate the initially conceived simplicity.

Four sequential steps of discovery…

Some philosophers of science attributed a fundamental importance to observations for the acquisition of experience in science. The process starts with accidental observations (Aristotle), going to systematic observations (Bacon), leading to quantitative rules obtained with exact measurements (Newton and Kant) and culminating in observations under artificially created conditions in experiments (Galilei) (Mittelstrass,  1980g ).

…rejected by Popper and Kant

In fact, Newton wrote that he had developed his theory of gravitation from experience followed by induction. K. Popper ( 1902‐1994 ) in his book Conjectures and Refutations did not agree with this logical flow “experience leading to theory” and that for several reasons. This scheme is according to Popper intuitively false because observations are always inexact, while theory makes absolute exact assertions. It is also historically false because Copernicus and Kepler were not led to their theories by experimental observations but by geometry and number theories of Plato and Pythagoras for which they searched verifications in observational data. Kepler, for example, tried to prove the concept of circular planetary movement influenced by Greek theory of the circle being a perfect geometric figure and only when he could not demonstrate this with observational data, he tried elliptical movements. Popper noted that it was Kant who realized that even physical experiments are not prior to theories when quoting Kant's preface to the Critique of Pure Reason : “When Galilei let his globes run down an inclined plane with a gravity which he has chosen himself, then a light dawned on all natural philosophers. They learnt that our reason can only understand what it creates according to its own design; that we must compel Nature to answer our questions, rather than cling to Nature's apron strings and allow her to guide us. For purely accidental observations, made without any plan having been thought out in advance, cannot be connected by a law‐ which is what reason is searching for.” From that reasoning Popper concluded that “we ourselves must confront nature with hypotheses and demand a reply to our questions; and that lacking such hypotheses, we can only make haphazard observations which follow no plan and which can therefore never lead to a natural law. Everyday experience, too, goes far beyond all observations. Everyday experience must interpret observations for without theoretical interpretation, observations remain blind and uninformative. Everyday experience constantly operates with abstract ideas, such as that of cause and effect, and so it cannot be derived from observation.” Popper agreed with Kant who said “Our intellect does not draw its laws from nature…but imposes them on nature”. Popper modifies this statement to “Our intellect does not draw its laws from nature, but tries‐ with varying degrees of success – to impose upon nature laws which it freely invents. Theories are seen to be free creations of our mind, the result of almost poetic intuition. While theories cannot be logically derived from observations, they can, however, clash with observations. This fact makes it possible to infer from observations that a theory is false. The possibility of refuting theories by observations is the basis of all empirical tests. All empirical tests are therefore attempted refutations.”

OUTLOOK: HYPOTHESES IN BIOLOGY

Is biology special.

Waddington notes that “living organisms are much more complicated than the non‐living things. Biology has therefore developed more slowly than sciences such as physics and chemistry and has tended to rely on them for many of its basic ideas. These older physical sciences have provided biology with many firm foundations which have been of the greatest value to it, but throughout most of its history biology has found itself faced with the dilemma as to how far its reliance on physics and chemistry should be pushed” both with respect to its experimental methods and its theoretical foundations. Vitalism is indeed such a theory maintaining that organisms cannot be explained solely by physicochemical laws claiming specific biological forces active in organisms. However, efforts to prove the existence of such vital forces have failed and today most biologists consider vitalism a superseded theory.

Biology as a branch of science is as old as physics. If one takes Aristotle as a reference, he has written more on biology than on physics. Sophisticated animal experiments were already conducted in the antiquity by Galen (Brüssow, 2022 ). Alertus Magnus displayed biological research interest during the medieval time. Knowledge on plants provided the basis of medical drugs in early modern times. What explains biology's decreasing influence compared with the rapid development of physics by Galilei and Newton? One reason is the possibility to use mathematical equations to describe physical phenomena which was not possible for biological phenomena. Physics has from the beginning displayed a trend to few fundamental underlying principles. This is not the case for biology. With the discovery of new continents, biologists were fascinated by the diversity of life. Diversity was the conducting line of biological thinking. This changed only when taxonomists and comparative anatomists revealed recurring pattern in this stunning biological variety and when Darwin provided a theoretical concept to understand variation as a driving force in biology. Even when genetics and molecular biology allowed to understand biology from a few universally shared properties, such as a universal genetic code, biology differed in fundamental aspects from physics and chemistry. First, biology is so far restricted to the planet earth while the laws of physic and chemistry apply in principle to the entire universe. Second, biology is to a great extent a historical discipline; many biological processes cannot be understood from present‐day observations because they are the result of historical developments in evolution. Hence, the importance of Dobzhansky's dictum that nothing makes sense in biology except in the light of evolution. The great diversity of life forms, the complexity of processes occurring in cells and their integration in higher organisms and the importance of a historical past for the understanding of extant organisms, all that has delayed the successful application of mathematical methods in biology or the construction of theoretical frameworks in biology. Theoretical biology by far did not achieve a comparable role as theoretical physics which is on equal foot with experimental physics. Many biologists are even rather sceptical towards a theoretical biology and see progress in the development of ever more sophisticated experimental methods instead in theoretical concepts expressed by new hypotheses.

Knowledge from data without hypothesis?

Philosophers distinguish rational knowledge ( cognitio ex principiis ) from knowledge from data ( cognitio ex data ). Kant associates these two branches with natural sciences and natural history, respectively. The latter with descriptions of natural objects as prominently done with systematic classification of animals and plants or, where it is really history, when describing events in the evolution of life forms on earth. Cognitio ex data thus played a much more prominent role in biology than in physics and explains why the compilation of data and in extremis the collection of museum specimen characterizes biological research. To account for this difference, philosophers of the logical empiricism developed a two‐level concept of science languages consisting of a language of observations (Beobachtungssprache) and a language of theories (Theoriesprache) which are linked by certain rules of correspondence (Korrespondenzregeln) (Carnap,  1891 –1970d). If one looks into leading biological research journals, it becomes clear that biology has a sophisticated language of observation and a much less developed language of theories.

Do we need more philosophical thinking in biology or at least a more vigorous theoretical biology? The breathtaking speed of progress in experimental biology seems to indicate that biology can well develop without much theoretical or philosophical thinking. At the same time, one could argue that some fields in biology might need more theoretical rigour. Microbiologists might think on microbiome research—one of the breakthrough developments of microbiology research in recent years. The field teems with fascinating, but ill‐defined terms (our second genome; holobionts; gut–brain axis; dysbiosis, symbionts; probiotics; health benefits) that call for stricter definitions. One might also argue that biologists should at least consider the criticism of Goethe ( 1749–1832 ), a poet who was also an active scientist. In Faust , the devil ironically teaches biology to a young student.

“Wer will was Lebendigs erkennen und beschreiben, Sucht erst den Geist herauszutreiben, Dann hat er die Teile in seiner Hand, Fehlt, leider! nur das geistige Band.” (To docket living things past any doubt. You cancel first the living spirit out: The parts lie in the hollow of your hand, You only lack the living thing you banned).

We probably need both in biology: more data and more theory and hypotheses.

CONFLICT OF INTEREST

The author reports no conflict of interest.

FUNDING INFORMATION

No funding information provided.

Supporting information

Appendix S1

Brüssow, H. (2022) On the role of hypotheses in science . Microbial Biotechnology , 15 , 2687–2698. Available from: 10.1111/1751-7915.14141 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]

• Bacon, F. (1561. –1626) Novum Organum. In: Adler, M.J. (Ed.) (editor‐in‐chief) Great books of the western world . Chicago, IL: Encyclopaedia Britannica, Inc. 2nd edition 1992 vol 1–60 (abbreviated below as GBWW) here: GBWW vol. 28: 128. [ Google Scholar ]
• Brüssow, H. (2022) What is Truth – in science and beyond . Environmental Microbiology , 24 , 2895–2906. [ PubMed ] [ Google Scholar ]
• Carnap, R. (1891. ‐1970a) Philosophical foundations of physics. Ch. 14 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
• Carnap, R. (1891. ‐1970b) Philosophical foundations of physics. Ch. 15 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
• Carnap, R. (1891. ‐1970c) Philosophical foundations of physics. Ch. 16 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
• Carnap, R. (1891. ‐1970d) Philosophical foundations of physics. Ch. 27–28 . Basic Books, Inc., New York, 1969. [ Google Scholar ]
• Copernicus . (1473. ‐1543) Revolutions of heavenly spheres . GBWW , vol. 15 , 505–506. [ Google Scholar ]
• Darwin, C. (1809. ‐1882a) The origin of species . GBWW , vol. 49 : 239. [ Google Scholar ]
• Darwin, C. (1809. ‐1882b) The descent of man . GBWW , vol. 49 : 590. [ Google Scholar ]
• Descartes, R. (1596. ‐1650) Rules for direction . GBWW , vol. 28 , 245. [ Google Scholar ]
• Dewey, J. (1859. –1952) Experience and education . GBWW , vol. 55 , 124. [ Google Scholar ]
• Dorfmüller, T. , Hering, W.T. & Stierstadt, K. (1998) Bergmann Schäfer Lehrbuch der Experimentalphysik: Band 1 Mechanik, Relativität, Wärme. In: Was ist Schwerkraft: Von Newton zu Einstein . Berlin, New York: Walter de Gruyter, pp. 197–203. [ Google Scholar ]
• Einstein, A. (1916) Relativity . GBWW , vol. 56 , 191–243. [ Google Scholar ]
• Einstein, A. & Imfeld, L. (1956) Die Evolution der Physik . Hamburg: Rowohlts deutsche Enzyklopädie, Rowohlt Verlag. [ Google Scholar ]
• Euclid . (c.323‐c.283) The elements . GBWW , vol. 10 , 1–2. [ Google Scholar ]
• Faraday, M. (1791. –1867) Speculation touching electric conduction and the nature of matter . GBWW , 42 , 758–763. [ Google Scholar ]
• Freud, S. (1856. –1939) Beyond the pleasure principle . GBWW , vol. 54 , 661–662. [ Google Scholar ]
• Galilei, G. (1564. ‐1642a) The Assayer, as translated by S. Drake (1957) Discoveries and Opinions of Galileo pp. 237–8 abridged pdf at Stanford University .
• Galilei, G. (1564. ‐1642b) The two sciences . GBWW vol. 26 : 200. [ Google Scholar ]
• Gilbert, W. (1544. ‐1603) On the Loadstone . GBWW , vol. 26 , 108–110. [ Google Scholar ]
• Goethe, J.W. (1749. –1832) Faust . GBWW , vol. 45 , 20. [ Google Scholar ]
• Hilbert, D. (1899) Grundlagen der Geometrie . Leipzig, Germany: Verlag Teubner. [ Google Scholar ]
• Huygens, C. (1617. ‐1670) Treatise on light . GBWW , vol. 32 , 557–560. [ Google Scholar ]
• James, W. (1842. –1907) Principles of psychology . GBWW , vol. 53 , 862–866. [ Google Scholar ]
• Kant, I. (1724. –1804) Critique of pure reason . GBWW , vol. 39 , 227–230. [ Google Scholar ]
• Lavoisier, A.L. (1743. ‐1794) Element of chemistry . GBWW , vol. 42 , p. 2, 6‐7, 9‐10. [ Google Scholar ]
• Locke, J. (1632. ‐1704) Concerning Human Understanding . GBWW , vol. 33 , 317–362. [ Google Scholar ]
• Mittelstrass, J. (1980a) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 239–241 .
• Mittelstrass, J. (1980b) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 3: 307 .
• Mittelstrass, J. (1980c) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 439–442 .
• Mittelstrass, J. (1980d) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 2: 157–158 .
• Mittelstrass, J. (1980e) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 3: 264‐267, 449.450 .
• Mittelstrass, J. (1980f) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 209–210 .
• Mittelstrass, J. (1980g) Enzyklopädie Philosophie und Wissenschaftstheorie Bibliographisches Institut Mannheim, Wien, Zürich B.I. Wissenschaftsverlag Vol. 1: 281–282 .
• Pascal, B. (1623. ‐1662a) Pensées GBWW vol. 30 : 171–173. [ Google Scholar ]
• Pascal, B. (1623. ‐1662b) Scientific treatises on geometric demonstrations . GBWW vol. 30 : 442–443. [ Google Scholar ]
• Plato . (c.424‐c.348 BC a) Timaeus . GBWW , vol. 6 , 442–477. [ Google Scholar ]
• Poincaré, H. (1854. ‐1912a) Science and hypothesis GBWW , vol. 56 : XV‐XVI, 1–5, 10–15 [ Google Scholar ]
• Poincaré, H. (1854. ‐1912b) Science and hypothesis GBWW , vol. 56 : 40–52. [ Google Scholar ]
• Popper, K. (1902. ‐1994) Conjectures and refutations . London and New York, 2002: The Growth of Scientific Knowledge Routledge Classics, pp. 249–261. [ Google Scholar ]
• Syntopicon . (1992) Hypothesis . GBWW , vol. 1 , 576–587. [ Google Scholar ]
• Waddington, C.H. (1905. –1975) The nature of life . GBWW , vol. 56 , 697–699. [ Google Scholar ]

Hypothesis, Model, Theory, and Law

Dorling Kindersley / Getty Images

• Physics Laws, Concepts, and Principles
• Quantum Physics
• Important Physicists
• Thermodynamics
• Cosmology & Astrophysics
• Weather & Climate

• M.S., Mathematics Education, Indiana University
• B.A., Physics, Wabash College

In common usage, the words hypothesis, model, theory, and law have different interpretations and are at times used without precision, but in science they have very exact meanings.

Perhaps the most difficult and intriguing step is the development of a specific, testable hypothesis. A useful hypothesis enables predictions by applying deductive reasoning, often in the form of mathematical analysis. It is a limited statement regarding the cause and effect in a specific situation, which can be tested by experimentation and observation or by statistical analysis of the probabilities from the data obtained. The outcome of the test hypothesis should be currently unknown, so that the results can provide useful data regarding the validity of the hypothesis.

Sometimes a hypothesis is developed that must wait for new knowledge or technology to be testable. The concept of atoms was proposed by the ancient Greeks , who had no means of testing it. Centuries later, when more knowledge became available, the hypothesis gained support and was eventually accepted by the scientific community, though it has had to be amended many times over the year. Atoms are not indivisible, as the Greeks supposed.

A model is used for situations when it is known that the hypothesis has a limitation on its validity. The Bohr model of the atom , for example, depicts electrons circling the atomic nucleus in a fashion similar to planets in the solar system. This model is useful in determining the energies of the quantum states of the electron in the simple hydrogen atom, but it is by no means represents the true nature of the atom. Scientists (and science students) often use such idealized models  to get an initial grasp on analyzing complex situations.

Theory and Law

A scientific theory or law represents a hypothesis (or group of related hypotheses) which has been confirmed through repeated testing, almost always conducted over a span of many years. Generally, a theory is an explanation for a set of related phenomena, like the theory of evolution or the big bang theory . 

The word "law" is often invoked in reference to a specific mathematical equation that relates the different elements within a theory. Pascal's Law refers an equation that describes differences in pressure based on height. In the overall theory of universal gravitation developed by Sir Isaac Newton , the key equation that describes the gravitational attraction between two objects is called the law of gravity .

These days, physicists rarely apply the word "law" to their ideas. In part, this is because so many of the previous "laws of nature" were found to be not so much laws as guidelines, that work well within certain parameters but not within others.

Scientific Paradigms

Once a scientific theory is established, it is very hard to get the scientific community to discard it. In physics, the concept of ether as a medium for light wave transmission ran into serious opposition in the late 1800s, but it was not disregarded until the early 1900s, when Albert Einstein proposed alternate explanations for the wave nature of light that did not rely upon a medium for transmission.

The science philosopher Thomas Kuhn developed the term scientific paradigm to explain the working set of theories under which science operates. He did extensive work on the scientific revolutions that take place when one paradigm is overturned in favor of a new set of theories. His work suggests that the very nature of science changes when these paradigms are significantly different. The nature of physics prior to relativity and quantum mechanics is fundamentally different from that after their discovery, just as biology prior to Darwin’s Theory of Evolution is fundamentally different from the biology that followed it. The very nature of the inquiry changes.

One consequence of the scientific method is to try to maintain consistency in the inquiry when these revolutions occur and to avoid attempts to overthrow existing paradigms on ideological grounds.

Occam’s Razor

One principle of note in regards to the scientific method is Occam’s Razor (alternately spelled Ockham's Razor), which is named after the 14th century English logician and Franciscan friar William of Ockham. Occam did not create the concept—the work of Thomas Aquinas and even Aristotle referred to some form of it. The name was first attributed to him (to our knowledge) in the 1800s, indicating that he must have espoused the philosophy enough that his name became associated with it.

The Razor is often stated in Latin as:

entia non sunt multiplicanda praeter necessitatem

or, translated to English:

entities should not be multiplied beyond necessity

Occam's Razor indicates that the most simple explanation that fits the available data is the one which is preferable. Assuming that two hypotheses presented have equal predictive power, the one which makes the fewest assumptions and hypothetical entities takes precedence. This appeal to simplicity has been adopted by most of science, and is invoked in this popular quote by Albert Einstein:

Everything should be made as simple as possible, but not simpler.

It is significant to note that Occam's Razor does not prove that the simpler hypothesis is, indeed, the true explanation of how nature behaves. Scientific principles should be as simple as possible, but that's no proof that nature itself is simple.

However, it is generally the case that when a more complex system is at work there is some element of the evidence which doesn't fit the simpler hypothesis, so Occam's Razor is rarely wrong as it deals only with hypotheses of purely equal predictive power. The predictive power is more important than the simplicity.

Edited by Anne Marie Helmenstine, Ph.D.

• Scientific Hypothesis, Model, Theory, and Law
• Theory Definition in Science
• The Basics of Physics in Scientific Study
• A Brief History of Atomic Theory
• Einstein's Theory of Relativity
• What Is a Paradigm Shift?
• Wave Particle Duality and How It Works
• Oversimplification and Exaggeration Fallacies
• Hypothesis Definition (Science)
• Kinetic Molecular Theory of Gases
• Scientific Method
• Understanding Cosmology and Its Impact
• The History of Gravity
• The Copenhagen Interpretation of Quantum Mechanics
• Geological Thinking: Method of Multiple Working Hypotheses
• Tips on Winning the Debate on Evolution

Hypothesis n., plural: hypotheses [/haɪˈpɑːθəsɪs/] Definition: Testable scientific prediction

Table of Contents

What Is Hypothesis?

A scientific hypothesis is a foundational element of the scientific method . It’s a testable statement proposing a potential explanation for natural phenomena. The term hypothesis means “little theory” . A hypothesis is a short statement that can be tested and gives a possible reason for a phenomenon or a possible link between two variables . In the setting of scientific research, a hypothesis is a tentative explanation or statement that can be proven wrong and is used to guide experiments and empirical research.

It is an important part of the scientific method because it gives a basis for planning tests, gathering data, and judging evidence to see if it is true and could help us understand how natural things work. Several hypotheses can be tested in the real world, and the results of careful and systematic observation and analysis can be used to support, reject, or improve them.

Researchers and scientists often use the word hypothesis to refer to this educated guess . These hypotheses are firmly established based on scientific principles and the rigorous testing of new technology and experiments .

For example, in astrophysics, the Big Bang Theory is a working hypothesis that explains the origins of the universe and considers it as a natural phenomenon. It is among the most prominent scientific hypotheses in the field.

“The scientific method: steps, terms, and examples” by Scishow:

Biology definition: A hypothesis  is a supposition or tentative explanation for (a group of) phenomena, (a set of) facts, or a scientific inquiry that may be tested, verified or answered by further investigation or methodological experiment. It is like a scientific guess . It’s an idea or prediction that scientists make before they do experiments. They use it to guess what might happen and then test it to see if they were right. It’s like a smart guess that helps them learn new things. A scientific hypothesis that has been verified through scientific experiment and research may well be considered a scientific theory .

Etymology: The word “hypothesis” comes from the Greek word “hupothesis,” which means “a basis” or “a supposition.” It combines “hupo” (under) and “thesis” (placing). Synonym:   proposition; assumption; conjecture; postulate Compare:   theory See also: null hypothesis

Characteristics Of Hypothesis

A useful hypothesis must have the following qualities:

• It should never be written as a question.
• You should be able to test it in the real world to see if it’s right or wrong.
• It needs to be clear and exact.
• It should list the factors that will be used to figure out the relationship.
• It should only talk about one thing. You can make a theory in either a descriptive or form of relationship.
• It shouldn’t go against any natural rule that everyone knows is true. Verification will be done well with the tools and methods that are available.
• It should be written in as simple a way as possible so that everyone can understand it.
• It must explain what happened to make an answer necessary.
• It should be testable in a fair amount of time.
• It shouldn’t say different things.

Sources Of Hypothesis

Sources of hypothesis are:

• Patterns of similarity between the phenomenon under investigation and existing hypotheses.
• Insights derived from prior research, concurrent observations, and insights from opposing perspectives.
• The formulations are derived from accepted scientific theories and proposed by researchers.
• In research, it’s essential to consider hypothesis as different subject areas may require various hypotheses (plural form of hypothesis). Researchers also establish a significance level to determine the strength of evidence supporting a hypothesis.
• Individual cognitive processes also contribute to the formation of hypotheses.

One hypothesis is a tentative explanation for an observation or phenomenon. It is based on prior knowledge and understanding of the world, and it can be tested by gathering and analyzing data. Observed facts are the data that are collected to test a hypothesis. They can support or refute the hypothesis.

For example, the hypothesis that “eating more fruits and vegetables will improve your health” can be tested by gathering data on the health of people who eat different amounts of fruits and vegetables. If the people who eat more fruits and vegetables are healthier than those who eat less fruits and vegetables, then the hypothesis is supported.

Hypotheses are essential for scientific inquiry. They help scientists to focus their research, to design experiments, and to interpret their results. They are also essential for the development of scientific theories.

Types Of Hypothesis

In research, you typically encounter two types of hypothesis: the alternative hypothesis (which proposes a relationship between variables) and the null hypothesis (which suggests no relationship).

Simple Hypothesis

It illustrates the association between one dependent variable and one independent variable. For instance, if you consume more vegetables, you will lose weight more quickly. Here, increasing vegetable consumption is the independent variable, while weight loss is the dependent variable.

Complex Hypothesis

It exhibits the relationship between at least two dependent variables and at least two independent variables. Eating more vegetables and fruits results in weight loss, radiant skin, and a decreased risk of numerous diseases, including heart disease.

Directional Hypothesis

It shows that a researcher wants to reach a certain goal. The way the factors are related can also tell us about their nature. For example, four-year-old children who eat well over a time of five years have a higher IQ than children who don’t eat well. This shows what happened and how it happened.

Non-directional Hypothesis

When there is no theory involved, it is used. It is a statement that there is a connection between two variables, but it doesn’t say what that relationship is or which way it goes.

Null Hypothesis

It says something that goes against the theory. It’s a statement that says something is not true, and there is no link between the independent and dependent factors. “H 0 ” represents the null hypothesis.

Associative and Causal Hypothesis

When a change in one variable causes a change in the other variable, this is called the associative hypothesis . The causal hypothesis, on the other hand, says that there is a cause-and-effect relationship between two or more factors.

Examples Of Hypothesis

Examples of simple hypotheses:

• Students who consume breakfast before taking a math test will have a better overall performance than students who do not consume breakfast.
• Students who experience test anxiety before an English examination will get lower scores than students who do not experience test anxiety.
• Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone, is a statement that suggests that drivers who talk on the phone while driving are more likely to make mistakes.

Examples of a complex hypothesis:

• Individuals who consume a lot of sugar and don’t get much exercise are at an increased risk of developing depression.
• Younger people who are routinely exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces, according to a new study.
• Increased levels of air pollution led to higher rates of respiratory illnesses, which in turn resulted in increased costs for healthcare for the affected communities.

Examples of Directional Hypothesis:

• The crop yield will go up a lot if the amount of fertilizer is increased.
• Patients who have surgery and are exposed to more stress will need more time to get better.
• Increasing the frequency of brand advertising on social media will lead to a significant increase in brand awareness among the target audience.

Examples of Non-Directional Hypothesis (or Two-Tailed Hypothesis):

• The test scores of two groups of students are very different from each other.
• There is a link between gender and being happy at work.
• There is a correlation between the amount of caffeine an individual consumes and the speed with which they react.

Examples of a null hypothesis:

• Children who receive a new reading intervention will have scores that are different than students who do not receive the intervention.
• The results of a memory recall test will not reveal any significant gap in performance between children and adults.
• There is not a significant relationship between the number of hours spent playing video games and academic performance.

Examples of Associative Hypothesis:

• There is a link between how many hours you spend studying and how well you do in school.
• Drinking sugary drinks is bad for your health as a whole.
• There is an association between socioeconomic status and access to quality healthcare services in urban neighborhoods.

Functions Of Hypothesis

The research issue can be understood better with the help of a hypothesis, which is why developing one is crucial. The following are some of the specific roles that a hypothesis plays: (Rashid, Apr 20, 2022)

• A hypothesis gives a study a point of concentration. It enlightens us as to the specific characteristics of a study subject we need to look into.
• It instructs us on what data to acquire as well as what data we should not collect, giving the study a focal point .
• The development of a hypothesis improves objectivity since it enables the establishment of a focal point.
• A hypothesis makes it possible for us to contribute to the development of the theory. Because of this, we are in a position to definitively determine what is true and what is untrue .

How will Hypothesis help in the Scientific Method?

• The scientific method begins with observation and inquiry about the natural world when formulating research questions. Researchers can refine their observations and queries into specific, testable research questions with the aid of hypothesis. They provide an investigation with a focused starting point.
• Hypothesis generate specific predictions regarding the expected outcomes of experiments or observations. These forecasts are founded on the researcher’s current knowledge of the subject. They elucidate what researchers anticipate observing if the hypothesis is true.
• Hypothesis direct the design of experiments and data collection techniques. Researchers can use them to determine which variables to measure or manipulate, which data to obtain, and how to conduct systematic and controlled research.
• Following the formulation of a hypothesis and the design of an experiment, researchers collect data through observation, measurement, or experimentation. The collected data is used to verify the hypothesis’s predictions.
• Hypothesis establish the criteria for evaluating experiment results. The observed data are compared to the predictions generated by the hypothesis. This analysis helps determine whether empirical evidence supports or refutes the hypothesis.
• The results of experiments or observations are used to derive conclusions regarding the hypothesis. If the data support the predictions, then the hypothesis is supported. If this is not the case, the hypothesis may be revised or rejected, leading to the formulation of new queries and hypothesis.
• The scientific approach is iterative, resulting in new hypothesis and research issues from previous trials. This cycle of hypothesis generation, testing, and refining drives scientific progress.

Importance Of Hypothesis

• Hypothesis are testable statements that enable scientists to determine if their predictions are accurate. This assessment is essential to the scientific method, which is based on empirical evidence.
• Hypothesis serve as the foundation for designing experiments or data collection techniques. They can be used by researchers to develop protocols and procedures that will produce meaningful results.
• Hypothesis hold scientists accountable for their assertions. They establish expectations for what the research should reveal and enable others to assess the validity of the findings.
• Hypothesis aid in identifying the most important variables of a study. The variables can then be measured, manipulated, or analyzed to determine their relationships.
• Hypothesis assist researchers in allocating their resources efficiently. They ensure that time, money, and effort are spent investigating specific concerns, as opposed to exploring random concepts.
• Testing hypothesis contribute to the scientific body of knowledge. Whether or not a hypothesis is supported, the results contribute to our understanding of a phenomenon.
• Hypothesis can result in the creation of theories. When supported by substantive evidence, hypothesis can serve as the foundation for larger theoretical frameworks that explain complex phenomena.
• Beyond scientific research, hypothesis play a role in the solution of problems in a variety of domains. They enable professionals to make educated assumptions about the causes of problems and to devise solutions.

Research Hypotheses: Did you know that a hypothesis refers to an educated guess or prediction about the outcome of a research study?

It’s like a roadmap guiding researchers towards their destination of knowledge. Just like a compass points north, a well-crafted hypothesis points the way to valuable discoveries in the world of science and inquiry.

Choose the best answer. 

Send Your Results (Optional)

Further Reading

• RNA-DNA World Hypothesis
• BYJU’S. (2023). Hypothesis. Retrieved 01 Septermber 2023, from https://byjus.com/physics/hypothesis/#sources-of-hypothesis
• Collegedunia. (2023). Hypothesis. Retrieved 1 September 2023, from https://collegedunia.com/exams/hypothesis-science-articleid-7026#d
• Hussain, D. J. (2022). Hypothesis. Retrieved 01 September 2023, from https://mmhapu.ac.in/doc/eContent/Management/JamesHusain/Research%20Hypothesis%20-Meaning,%20Nature%20&%20Importance-Characteristics%20of%20Good%20%20Hypothesis%20Sem2.pdf
• Media, D. (2023). Hypothesis in the Scientific Method. Retrieved 01 September 2023, from https://www.verywellmind.com/what-is-a-hypothesis-2795239#toc-hypotheses-examples
• Rashid, M. H. A. (Apr 20, 2022). Research Methodology. Retrieved 01 September 2023, from https://limbd.org/hypothesis-definitions-functions-characteristics-types-errors-the-process-of-testing-a-hypothesis-hypotheses-in-qualitative-research/#:~:text=Functions%20of%20a%20Hypothesis%3A&text=Specifically%2C%20a%20hypothesis%20serves%20the,providing%20focus%20to%20the%20study.

©BiologyOnline.com. Content provided and moderated by Biology Online Editors.

Last updated on September 8th, 2023

You will also like...

Gene Action – Operon Hypothesis

Water in Plants

Growth and Plant Hormones

Sigmund Freud and Carl Gustav Jung

Population Growth and Survivorship

Related articles....

RNA-DNA World Hypothesis?

On Mate Selection Evolution: Are intelligent males more attractive?

Actions of Caffeine in the Brain with Special Reference to Factors That Contribute to Its Widespread Use

Dead Man Walking