lesson 8 1 volume of cylinders (homework practice)

Addition (Basic)

Addition (Multi-Digit)

Algebra & Pre-Algebra

Comparing Numbers

Daily Math Review

Division (Basic)

Division (Long Division)

Hundreds Charts

Measurement

Multiplication (Basic)

Multiplication (Multi-Digit)

Order of Operations

Place Value

Probability

Skip Counting

Subtraction

Telling Time

Word Problems (Daily)

More Math Worksheets

Reading Comprehension

Reading Comprehension Gr. 1

Reading Comprehension Gr. 2

Reading Comprehension Gr. 3

Reading Comprehension Gr. 4

Reading Comprehension Gr. 5

Reading Comprehension Gr. 6

Reading & Writing

Reading Worksheets

Cause & Effect

Fact & Opinion

Fix the Sentences

Graphic Organizers

Synonyms & Antonyms

Writing Prompts

Writing Story Pictures

Writing Worksheets

More ELA Worksheets

Consonant Sounds

Vowel Sounds

Consonant Blends

Consonant Digraphs

Word Families

More Phonics Worksheets

Early Literacy

Build Sentences

Sight Word Units

Sight Words (Individual)

More Early Literacy

Punctuation

Subjects and Predicates

More Grammar Worksheets

Spelling Lists

Spelling Grade 1

Spelling Grade 2

Spelling Grade 3

Spelling Grade 4

Spelling Grade 5

Spelling Grade 6

More Spelling Worksheets

Chapter Books

Charlotte's Web

Magic Tree House #1

Boxcar Children

More Literacy Units

Animal (Vertebrate) Groups

Butterfly Life Cycle

Electricity

Matter (Solid, Liquid, Gas)

Simple Machines

Space - Solar System

More Science Worksheets

Social Studies

Maps (Geography)

Maps (Map Skills)

More Social Studies

Mother's Day

Father's Day

More Holiday Worksheets

Puzzles & Brain Teasers

Brain Teasers

Logic:  Addition Squares

Mystery Graph Pictures

Number Detective

Lost in the USA

More Thinking Puzzles

Teacher Helpers

Teaching Tools

Award Certificates

More Teacher Helpers

Pre-K and Kindergarten

Alphabet (ABCs)

Numbers and Counting

Shapes (Basic)

More Kindergarten

Worksheet Generator

Word Search Generator

Multiple Choice Generator

Fill-in-the-Blanks Generator

More Generator Tools

Full Website Index

Volume of a Cylinder

The worksheets below can be used to help teach students how to calculate the volumes of cylinders. The basic level worksheets do not include decimal measurements. The advanced level includes decimals and/or fractional measurements.

Level: Basic

Logged in members can use the Super Teacher Worksheets filing cabinet to save their favorite worksheets.

Quickly access your most used files AND your custom generated worksheets!

Please login to your account or become a member and join our community today to utilize this helpful feature.

Level : Advanced

From this page you can download a collection of worksheets on calculating the volumes of rectangular prisms.

Sample Worksheet Images

PDF with answer key:

PDF no answer key:

Volume of Cylinders

A cylinder is a solid with two congruent circles joined by a curved surface.

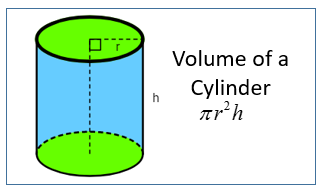
In the above figure, the radius of the circular base is r and the height is h.

The volume of the cylinder is the area of the base × height. Since the base is a circle and the area of a circle is πr 2 then the volume of the cylinder is πr 2 × h.

Volume of cylinder = πr 2 h

Surface Area of cylinder = 2πr 2 + 2πrh

Calculate the volume of a cylinder where:

a) the area of the base is 30 cm 2 and the height is 6 cm. b) the radius of the base is 14 cm and the height is 10 cm.

Sometimes you may be required to calculate the volume of a hollow cylinder or tube or pipe.

Volume of hollow cylinder: = πR 2 h – πr 2 h = πh (R 2 – r 2 )

The figure shows a section of a metal pipe. Given the internal radius of the pipe is 2 cm, the external radius is 2.4 cm and the length of the pipe is 10 cm. Find the volume of the metal used.

Solution: The cross section of the pipe is a ring: Area of ring = [ π (2.4) 2 – π (2) 2 ]= 1.76 π cm 2

These videos show how to solve word problems about cylinders.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Volume of a Cylinder Lesson Plan

In this lesson, students will learn how to find the volume of a cylinder. Students will review the volume of rectangular prisms and area of circles. Then, students will make connections between rectangular prisms, circles, and cylinders to help them find the volume of a cylinder. You can expect this lesson with practice to take one `45`-minute class period.

ByteLearn gives students targeted feedback and hints based on their specific mistakes

Preview step-by-step-help

Students will be able to find the volume of a cylinder.

• Teacher slideshow
• Online Practice

How to Teach Finding the Volume of a Cylinder

Before having students find the volume of a cylinder, you will want to review what they already know about circles and volume. Later as we discover the formula for volume of a cylinder, the knowledge of volume of a rectangular prism and area of a circle will be helpful.

Copy these Google Slides for free

When reviewing these problems, it’s important to ensure students understand that the volume of any regular prism is the area of the base times the height. If needed, use the first problem for reference. Students should also understand how to find the area of a circle, either rounded or written in terms of `pi`. For some students, you may need to reinforce how to write their answer in terms of `pi`.

Introducing cylinders

Ask students to write down `5` things they know about a cylinder. Also, ask them to make a drawing of an object that looks like a cylinder.  Let students share what they wrote with the class and make a list on the board. This will help you capture their current understanding and build on it. It will also help to make connections to real-world objects.

Discover the formula for volume of a cylinder

Present a cylinder to students and ask them to figure out how they can find the volume of a cylinder. Students should work in pairs to do this.

It is quite likely that a bunch of students might come up with an informal way for finding the volume of a cylinder. They might not be able to use the right words, but discovering an informal formula will help them make sense of the actual formula. 

Students are likely to see that the base and height of the cylinder are like those of the rectangular prism - but instead of a rectangle as a base, you now have a circle as a base. They are likely to reason that in a rectangular prism, we multiplied the area of the base by the height - it might make sense to do the same in a cylinder!

Vocabulary and formula

Students are now ready to understand the formula of a cylinder as it is traditionally presented. Use the same cylinder as you did earlier so that they see the connections. 

Now work through an example with the class. The first problem could have scaffolding that will make it simpler for students to find the volume of the cylinder.

Class practice

Work through one more problem with the class - this time, with less scaffolding. You could ask students to leave their answers in terms of `\pi` for now, so it is easier to check which values were multiplied. Remind students that the units for volume are cubed.

Encourage students to focus on the formula as “base area `\times` height” because it will help them when they have to find the volume of more unusual prisms in high school. Helping solidify that “base area” will change based on the prism can help reduce students’ confusion later, but some students may still prefer to think of the formula as `V =\pi r^2h`.

Possible misconceptions

It is important to recognize that some students may not square their radius correctly, or they will multiply the height and radius before squaring. By allowing students time to work on the problem and then compare their answers with a partner or table group, you may find that students are able to correct each other with minor misconceptions. 

Finding volume of a cylinder given diameter

Now, introduce a complication - show a cylinder with the diameter given. Give students time to work through the problem.

Students can review their answers with a partner or table group. As students are working, you may notice that some students do not immediately recognize they were given the diameter first instead. Although this misconception will need to be addressed, see if students can correct each other when comparing answers. 

Example given a description

Though this example is not significantly different in terms of the information given, it might confuse some students. If students are stuck, encourage them to draw a cylinder and annotate the figure with the given measurements. If students aren’t sure how to draw one, you can let them know they just draw two ovals with a gap and parallel to each other, then connect the outer edges.

Volume of a Cylinder Practice

Now it’s time for some independent practice! You can assign a ByteLearn online practice to your class using the link below. Students will get immediate feedback and step-by-step help if they need it. Set a due date and allow students to finish the assignment for homework. Once complete, you’ll see detailed reports of students who may need additional support, students who are ready for a challenge, and other interesting insights!

View this practice

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Go Math Grade 8 Answer Key Chapter 13 Volume

Gather all the Go Math Grade 8 Questions and answers along with the explanations are provided for all the students. The best math practice will come with the Go Math Grade 8 Answer Key Chapter 13 Volume. Everyday learning is easy with the practice of the Go Math Grade 8 Chapter 13 Volume Solution Key. Get a free pdf of Go Math Grade 8 Answer Key now to practice maths offline. Be the first to grab your HMH Go Math Grade 8 Answer Key and read all the questions of maths.

Go Math Grade 8 Chapter 13 Volume Answer Key

Refer to Go Math Grade 8 Answer Key Chapter 13 Volume for answers and explanations. It is very easy to get good marks in the exam by practicing with the help of Go Math Grade 8 Solution Key. Top-ranked student’s first choice is Go Math Grade 8 Answer Key Chapter 13 Volume. Learn and practice the maths in the best way using Go Math Grade 8 Answer Key.

Lesson 1: Volume of Cylinders

• Volume of Cylinders – Page No. 402
• Volume of Cylinders – Page No. 403
• Volume of Cylinders – Page No. 404

Lesson 2: Volume of Cones

• Volume of Cones – Page No. 408
• Volume of Cones – Page No. 409
• Volume of Cones – Page No. 410

Lesson 3: Volume of Spheres

• Volume of Spheres – Page No. 414
• Volume of Spheres – Page No. 415
• Volume of Spheres – Page No. 416

Model Quiz :

• Model Quiz – Page No. 417
• Mixed Review – Page No. 418

Guided Practice – Volume of Cylinders – Page No. 402

Question 1. Vocabulary Describe the bases of a cylinder. Type below: ____________

Answer: The ends of a cylinder are the bases of the cylinder of the two flat surfaces.

Explanation: Number of inch cubes that fit in the base of the cylinder = 61 Number of inch cubes that fit in the length of the cylinder = 7 The volume of cylinder = base area x height V= 61 x 7 V = 427 cubic units. Volume of each cube = 1 in³ Volume of cylinder = 427in³

Answer: The volume of the cylinder is approximately 1695.6 m 3 . 1695.6m³

Explanation: V = πr²h V = π . 6² . 15 V = 3.14 × 36 × 15 V = 1695.6m³

Question 4. A Japanese odaiko is a very large drum that is made by hollowing out a section of a tree trunk. A museum in Takayama City has three odaikos of similar size carved from a single tree trunk. The largest measures about 2.7 meters in both diameter and length, and weighs about 4.5 metric tons. Using the volume formula for a cylinder, approximate the volume of the drum to the nearest tenth. The radius of the drum is about _____ m. The volume of the drum is about _____ m 3 . The radius of the drum is about ___________ m The volume of the drum is about ___________ m 3

Answer: The radius of the drum is about 1.35 m. The volume of the drum is about 15.5 m 3 .

Explanation: Diameter of base of drum = 2.7 m The radius of the base of the drum = 2.7/2 R = 1.35 m The volume of cylinder = πr²h Height (h) = 2.7 m Radius (R) = 1.35 m Volume = 3.14 × (1.35) × 2.7 V = 15.4511 m³ V = 15.5 m³

ESSENTIAL QUESTION CHECK-IN

Question 5. How do you find the volume of a cylinder? Describe which measurements of a cylinder you need to know. Type below: ____________

Answer: The volume of the cylinder is = πr²h

Explanation: We need to find the radius of the base, r, and the height of the cylinder, h. The volume of the cylinder is = πr²h

13.1 Independent Practice – Volume of Cylinders – Page No. 403

Find the volume of each figure. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Answer: 569.9 cm³

Explanation: Radius of base = 11 cm Height of cylinder = 1.5 cm The volume of the cylinder = πr²h V = 3.14 × (11)² × 1.5 V = 569.91 V = 569.9 cm³

Answer: 1205.8 in³

Explanation: Radius of base = 4 in Height of cylinder = 24 in The volume of cylinder = πr²h V = 3.14 × (4)² × 24 V = 1205.76 V = 1205.8 in³

Answer: 1256 m³

Explanation: Radius of base = 5 m Height of cylinder = 16 m The volume of the cylinder = πr²h V = 3.14 × (5)² × 16 V = 1256 V = 1256 m³

Answer: 942 in³

Explanation: Diameter of base = 10 in Radius of base = 5 in Height of cylinder = 12 in The volume of the cylinder = πr²h V = 3.14 × (5)² × 12 V = 942 in³

Question 10. A cylinder has a radius of 4 centimeters and a height of 40 centimeters. _________ cm 3

Answer: 2009.6 cm³

Explanation: Radius of base = 4 cm Height of cylinder = 40 cm The volume of cylinder = πr²h V = 3.14 × (4)² × 40 V = 2009.6 cm³

Question 11. A cylinder has a radius of 8 meters and a height of 4 meters. _________ m 3

Answer: 803.8 m³

Explanation: The radius of base = 8 m Height of cylinder = 4 m The volume of the cylinder = πr²h V = 3.14 × (8)² × 4 V = 803.84 m³ V = 803.8 m³

Round your answer to the nearest tenth, if necessary. Use 3.14 for π.

Question 12. The cylindrical Giant Ocean Tank at the New England Aquarium in Boston is 24 feet deep and has a radius of 18.8 feet. Find the volume of the tank. _________ ft 3

Answer: 26635.2 ft³

Explanation: The base radius of the tank = 18.8 ft Depth of the tank in the ocean = 24 ft The volume of the cylinder = πr²h V = 3.14 × (18.8)² × 24 V = 3.14 × 354.44 × 24 V = 26635.2384 ft³ V = 26635.2 ft³

Question 13. A standard-size bass drum has a diameter of 22 inches and is 18 inches deep. Find the volume of this drum. _________ in 3

Answer: 6838.9 in³

Explanation: The base diameter of the drum = 22 in Base radius of the drum = 22/2 = 11 in Depth of the bass drum = 18 in The volume of the bass drum = πr²h V = 3.14 × (11)² × 18 V = 3.14 × 121 × 18 V = 6838.92 in³ V = 6838.9 in³

Question 14. Grain is stored in cylindrical structures called silos. Find the volume of a silo with a diameter of 11.1 feet and a height of 20 feet. _________ ft 3

Answer: 1934.4 ft³

Explanation: Base diameter of silo = 11.1 ft Base radius of the silo = 11.1/2 = 5.55 ft Depth of the silo = 20 ft Volume of the silo = πr²h V = 3.14 × (5.55)² × 18 V = 3.14 × 30.8025 × 18 V = 1934.397 ft³ V = 1934.4 ft³

Question 15. The Frank Erwin Center, or “The Drum,” at the University of Texas in Austin can be approximated by a cylinder that is 120 meters in diameter and 30 meters in height. Find its volume. _________ m 3

Answer: 339120 m³

Explanation: Base diameter of the drum = 120 m Base radius of the drum = 120/2 = 60 m Height of the drum = 30 m Volume of the drum = πr²h V = 3.14 × (60)² × 30 V = 3.14 × 3600 × 30 V = 339120 m³

Volume of Cylinders – Page No. 404

Question 16. A barrel of crude oil contains about 5.61 cubic feet of oil. How many barrels of oil are contained in 1 mile (5280 feet) of a pipeline that has an inside diameter of 6 inches and is completely filled with oil? How much is “1 mile” of oil in this pipeline worth at a price of $100 per barrel? __________ barrels $ __________

Answer: 184.7 barrels $18470

Explanation: Volume of barrel = 5.61 cubic feet Length of the pipe = 1 mile = 5280 feet Diameter of the pipe = 6 inches = 0.5 feet Radius of the pipe = 6/2 inches = 3 inches = 0.25 feet Volume of oil in the pipe = πr²h = 3.14 × (0.25)² × 5280 = 1036.2 cubic feet Number of barrels in the pipe = 1036.2/5.61 = 184.7 barrels Cost of one barrel = $100 Cost of 184.7 barrels =184.7 × $100 = $18470

Answer: 57.697 in³

Explanation: The length of the pan = 12 in The diameter of the pan = 3.5 in Radius = 3.5/2 = 1.75 in The volume of uncooked dough = Half the volume of the full cylinder of the above dimensions. = (πr²h)/2 = (3.14 × (1.75)² × 12)/2 = 115.395/2 = 57.697 in³

FOCUS ON HIGHER ORDER THINKING

Question 18. Explain the Error A student said the volume of a cylinder with a 3-inch diameter is two times the volume of a cylinder with the same height and a 1.5-inch radius. What is the error? Type below: _______________

Answer: The volume of the cylinder of 3 in is four times the volume of the new cylinder of radius 1.5 in

Explanation: The volume of a cylinder is directly proportional to the square of the radius of the cylinder. The volume does not depend on the radius linearly. Volume = πr²h V1 = π(3)²h V2 = π(1.5)²h V1/V2 = (π(3)²h)/(π(1.5)²h) V1/V2 = 4 V1 = 4V2

Volume of Cylinders and Cones Mini Quiz Answer Key Question 19. Communicate Mathematical Ideas Explain how you can find the height of a cylinder if you know the diameter and the volume. Include an example with your explanation. Type below: _______________

Answer: Let the diameter be D. Radius r = D/2 Volume = πr²h Volume = π(D/2)²h V = π((D)²/4)h h = 4V/π(D)² To find the height of a cylinder with diameter D = 2 m Let the volume be 10 m³ h = 4V/π(D)² h = (4 × 10)/(3.14 × 2²) h = 3.18 m³

Question 20. Analyze Relationships Cylinder A has a radius of 6 centimeters. Cylinder B has the same height and a radius half as long as cylinder A. What fraction of the volume of cylinder A is the volume of cylinder B? Explain. Fraction: \(\frac{□}{□}\)

Answer: \(\frac{VA}{4}\)

Explanation: rA = 6 cm rB = half of the radius of cylinder A = 3 cm hA = hB VA = πrA²h VB = πrB²h VA/VB = (πrA²h)/(πrB²h) VA/VB = 6²/3² = 36/9 = 4 Thus VB = VA/4

Guided Practice – Volume of Cones – Page No. 408

Answer: 150 in³

Explanation: In the question, the area of the base of the cylinder, B = 45 in² Height of the cylinder, h = 10 inch Volume of the cylinder, V cylinder = B × h = 45 × 10 = 450 inch³ Volume of the cone, V Cone = 1/3 V cylinder =1/3(450 inch) = 150 inch³ So, the volume of the cone is Vcone = 150 in³

Volume of Cylinders and Cones Mini Quiz Answer Key Question 2. A cone and a cylinder have congruent heights and bases. The volume of the cone is 18 m 3 . What is the volume of the cylinder? Explain. _________ m 3

Answer: 54 m 3

Explanation: The volume of the cone is 18 m 3 . Vcone = 1/3 Vcylinder Vcylinder = 3Vcone Vcylinder = 3.18 Vcylinder = 54 m 3

Find the volume of each cone. Round your answer to the nearest tenth if necessary. Use 3.14 for π.

Answer: 65.94 ft³

Explanation: the diameter of the cone is 6ft. so, the radius of the cone is 3ft. the height of the cone is 7ft. the volume of the cone = 1/3 × πr²h = 1/3 × 3.14 × 3² × 7 = 65.94 ft³

Answer: 113982in³

Explanation: The radius is 33inch and the height is 100 inch Volume of the cone = 1/3 × πr²h = 1/3 × π(33)²100 = 113982in³

Question 5. Gretchen made a paper cone to hold a gift for a friend. The paper cone was 15 inches high and had a radius of 3 inches. Find the volume of the paper cone to the nearest tenth. Use 3.14 for π. _________ in 3

Answer: 141.3in³

Explanation: the radius of the cone is 3inch and the height of the cone is 15inch. Volume of the cone = 1/3 × πr²h = 1/3 × π(3)² × 15 = 141.3in³

Question 6. A cone-shaped building is commonly used to store sand. What would be the volume of a cone-shaped building with a diameter of 50 meters and a height of 20 meters? Round your answer to the nearest tenth. Use 3.14 for π. _________ m 3

Answer: 13083.33 m³

Explanation: The diameter of the cone is 50 meters. So, the radius of the cone is 25 meters. The height of the cone is 20 meters. Volume of the cone = 1/3 × πr²h = 1/3 × π(25)² × 20 = 13083.33 m³

Question 7. How do you find the volume of a cone? Type below: ____________

Answer: V cone = 1/3 V cylinder V cone = 1/3 πr²h

13.2 Independent Practice – Volume of Cones – Page No. 409

Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Answer: 410.3 mm³

Explanation: Radius r = 7 mm height = 8 mm Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(7)²(8) Volume = 410.29 mm³ Volume = 410.3 mm³

Answer: 25.1 in 3

Explanation: Radius r = 2 in Height = 6 in Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(2)²(6) Volume = 25.12 in 3 Volume = 25.1 in 3

Lesson 2 Extra Practice Volume of Cones Answers Key Question 10. A cone has a diameter of 6 centimeters and a height of 11.5 centimeters. _________ cm 3

Answer: 108.3 cm 3

Explanation: Diameter of base = 6 cm Radius = 6/2 cm = 3 cm Height = 11.5 cm Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(3)² (11.5) Volume = 108.33 cm 3 Volume = 108.3 cm 3

Question 11. A cone has a radius of 3 meters and a height of 10 meters. _________ m 3

Answer: 94.2 m 3

Explanation: Radius r = 3 m Height = 10 m Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(3)²(10) Volume = 94.2 m 3

Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 12. Antonio is making mini waffle cones. Each waffle cone is 3 inches high and has a radius of \(\frac{3}{4}\) inch. What is the volume of a waffle cone? _________ in 3

Answer: 1.8 in 3

Explanation: Radius = 3/4 in Radius r = 0.75 in Height = 3 in Volume of each waffle cone = 1/3 πr²h Volume = 1/3 (3.14) (0.75)² (3) Volume = 1.76625 in 3 Volume = 1.8 in 3

Question 13. A snack bar sells popcorn in cone-shaped containers. One container has a diameter of 8 inches and a height of 10 inches. How many cubic inches of popcorn does the container hold? _________ in 3

Answer: 167.5 in 3

Explanation: Diameter of base = 8 in Radius = 8/2 in = 4 in Height = 10 in Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (4)² (10) Volume = 167.466 in 3 Volume = 167.5 in 3

Question 14. A volcanic cone has a diameter of 300 meters and a height of 150 meters. What is the volume of the cone? _________ m 3

Answer: 3534291.7 m 3

Explanation: Diameter of base = 300 m Radius = 300/2 m = 150 m Height = 150 m Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (150)² (150) Volume = 3534291.735 m 3 Volume = 3534291.7 m 3

The volume of Cones Answers Key Question 15. Multistep Orange traffic cones come in a variety of sizes. Approximate the volume, in cubic inches, of a traffic cone that has a height of 2 feet and a diameter of 10 inches. Use 3.14 for π. _________ in 3

Answer: 628 in³

Explanation: The radius of the cone is Diameter/2 = 10/2 = 5 The height of the cone is 2 ft = 2 . 12 = 24 in Vcone = 1/3 πr²h Vcone = 1/3 (3.14) (5)² (24) Vcone = 628 in³

Find the missing measure for each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 16. radius = _______ height = 6 in. volume = 100.48 in3 _________ in.

Answer: radius = 4 in. 4 in.

Explanation: Let radius be R. Height = 6 in Volume = 100.4 in Volume of cone = 1/3 πr²h √(3v/hπ) = R √((3 × 100.48)/(18.84)) = R √(301.44/18.84) = R R = √(16) R = 4 in

Question 17. diameter = 6 cm height = _______ volume = 56.52 cm 3 _______ cm

Answer: height = 6 cm h = 6 cm

Explanation: Let height be h Diameter = 6 cm Radius = 6/2 = 3 cm Volume = 56.52 cm Volume of cone = 1/3 πr²h (3V/r²h) = h (3 × 56.52)/(3² × 3.14) = h 169.56/28.26 = h h = 6 cm

Question 18. The diameter of a cone-shaped container is 4 inches, and its height is 6 inches. How much greater is the volume of a cylinder-shaped container with the same diameter and height? Round your answer to the nearest hundredth. Use 3.14 for π. Type below: ____________

Answer: The volume of the cylinder is 50.24 in³ greater than the volume of the cone.

Explanation: The diameter of a cone, d = 4 inch radius of a cone, r = d/2 = 4/2 = 2 inches height of a cone, h = 6 inches. So, the volume of a cone, V cone = 1/3 πr²h = 1/3 (3.14) (2)² (6) = 25.12 in³ And the volume of a cylinder with the same diameter and height, V cylinder = πr²h = (3.14) (2)² (6) = 75.36 in³ The volume of the cylinder is 50.24 in³ greater than the volume of the cone.

FOCUS ON HIGHER ORDER THINKING – Volume of Cones – Page No. 410

Question 19. Alex wants to know the volume of sand in an hourglass. When all the sand is in the bottom, he stands a ruler up beside the hourglass and estimates the height of the cone of sand. a. What else does he need to measure to find the volume of sand? ____________

Answer: To find the volume of the sand, he needs to measure the radius of the base of the hourglass.

Question 19. b. Make a Conjecture If the volume of sand is increasing at a constant rate, is the height increasing at a constant rate? Explain. ____________

Answer: The volume of the cone is linearly proportional to the height of the cone. Therefore, if the volume is increasing at a constant rate, the height is also increasing at a constant rate.

Question 20. Problem Solving The diameter of a cone is x cm, the height is 18 cm, and the volume is 301.44 cm 3 . What is x? Use 3.14 for π. ________ cm

Answer: 8 cm

Explanation: V cone = 1/3 πr²h 301.44 = 1/3 . 3.14 . r² . 18 r² = 904.32/56.52 r² = 16 r = 4 cm The diameter of the circle is twice its radius, therefore x = 2 . r x = 2 . 4 x = 8 cm

Question 21. Analyze Relationships A cone has a radius of 1 foot and a height of 2 feet. How many cones of liquid would it take to fill a cylinder with a diameter of 2 feet and a height of 2 feet? Explain. ________ cones

Answer: 3 cones

Explanation: The diameter of the base of the cylinder is 2 feet, which means that its radius is 1 foot. Its height is 2 feet. The volume of this cylinder is V cylinder = πr²h V cylinder = (3.14) (1)² (2) V cylinder = 6.28 The radius of the cone is 1 foot and the height of the cone is 2 feet. The volume of the cone is: V cone = 1/3 πr²h V cone = 1/3 (3.14) (1)² (2) V cone = 1/3 × 6.28 V cone = 1/3 . V cylinder V cone = 2.09 It would take 3 cones of liquid to fill the cylinder.

Question 22. Critique Reasoning Herb knows that the volume of a cone is one third that of a cylinder with the same base and height. He reasons that a cone with the same height as a given cylinder but 3 times the radius should therefore have the same volume as the cylinder, since \(\frac{1}{3}\) ⋅ 3 = 1. Is Herb correct? Explain. ____________

Answer: The volume of the given cylinder is V cylinder = πr²h The volume of the cone with the same height h as a given cylinder but 3 times the radius r is V cone = 1/3 π(3r)²h V cone = 3 πr²h V cone = 3 V cylinder As we can see, Herb is not correct. The volume of the cone is not equal to the volume of the cylinder. But it is three times the volume of the cylinder.

Guided Practice – Volume of Spheres – Page No. 414

Question 1. Vocabulary A sphere is a three-dimensional figure with all points _____ from the center. Type below: ____________

Answer: A sphere is a three-dimensional figure with all points at equal distances from the center.

Lesson 13.2 Volume of Cones Practice and Problem Solving a/b Answers Question 2. Vocabulary The _____ is the distance from the center of a sphere to a point on the sphere. Type below: ____________

Answer: radius

Explanation: The radius is the distance from the center f the sphere to a point on the sphere

Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Answer: 4.12 in 3

Explanation: V = 4/3πr³ V = 4/3 (3.14) (1)³ V = 4.12 in 3

Answer: 4186.7 cm³

Explanation: Diameter = 20 cm Radius r = 20/2 = 10 cm Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (10)³ Volume = 4186.66 cm³ Volume = 4186.7 cm³

Question 5. A sphere has a radius of 1.5 feet. _______ ft 3

Answer: 14.1 ft³

Explanation: Radius r = 1.5 ft The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (1.5)³ Volume = 14.13 ft³ Volume = 14.1 ft³

Question 6. A sphere has a diameter of 2 yards. _______ yd 3

Answer: 4.2 yd³

Explanation: Diameter = 2 yards Radius r = 2/2 yards Radius r = 1 yd Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (1)³ Volume = 4.1866 yd³ Volume = 4.2 yd³

Question 7. A baseball has a diameter of 2.9 inches. Find the volume of the baseball. Round your answer to the nearest tenth if necessary. Use 3.14 for π. _______ in 3

Answer: 12.8 in³

Explanation: Diameter of baseball = 2.9 in Radius r = 2.9/2 in Radius of baseball = 1.45 in The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (1.45)³ Volume = 12.763 in³ Volume = 12.8 in³

Lesson 13.3 Volume of Spheres Practice and Problem Solving a/b Question 8. A basketball has a radius of 4.7 inches. What is its volume to the nearest cubic inch? Use 3.14 for π. _______ in 3

Answer: 1304 in³

Explanation: Radius of baseball = 4.7 in The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (4.7)³ Volume = 1304.0168 in³ Volume = 1304 in³

Answer: The volume of the cylinder is V cylinder = πr²h Since the ball touches the bottom, top, and sides, then the height of the cylinder will be equal to 2r. V cylinder = πr²(2r) = 2πr³ On the other hand, the volume of the sphere is V sphere = 4/3 πr³ The volume of the empty space inside the cylindrical box is found by subtracting the volume of the sphere from the volume of the cylinder V cylinder – V sphere = 2πr³ – 4/3 πr³ = (2 – 4/3)πr³ = 2/3πr³

Question 9. b. Find an expression for the volume of the cubic box. Type below: _______________

Answer: The volume of a cube with side a is V cube = a³ Since the ball touches the bottom, top, and sides, then the side of the cube will be equal to 2r. V cube = (2r)³ V cube = 8r³

Question 9. c. About what portion of the space inside the cubic box is empty? Explain Type below: _______________

Answer: The volume of the empty space inside the cubical box is found by subtracting the volume of the sphere from the volume of the cube: V cube – V sphere = 8r³ – 4/3 πr³ = (8 – 4/3π)r³ = (8 – 4.2)r³ = 3.8r³

Question 10. Explain the steps you use to find the volume of a sphere. Type below: _______________

Answer: Step 1: The radius of the sphere is found out. Step 2: The volume of the sphere is 4/3 πr³; where R is the radius. Step 3: Put the value of radius in the equation of volume. Step 4: Calculate the volume.

13.3 Independent Practice – Volume of Spheres – Page No. 415

Question 11. radius of 3.1 meters _______ m 3

Answer: 124.7 m³

Explanation: The volume of the sphere with a radius of 3.1 meter is 4/3 πr³ V = 4/3 . (3.14) . (3.1)³ V = 124.7 m³

Question 12. diameter of 18 inches _______ in 3

Answer: 3052.1 in³

Explanation: The diameter of the sphere is 18 inches, which means that its radius is 9 inches. The volume of the sphere is V = 4/3 πr³ V = 4/3 . (3.14) . (9)³ V = 3052.08 in³ V = 3052.1 in³

Volume of Cylinders Cones and Spheres Iready Answers Question 13. r = 6 in. _______ in 3

Answer: 904.3 in³

Explanation: The volume of the sphere with a radius of 6 inches is V = 4/3 πr³ V = 4/3 (3.14) (6)³ V = 904.32 V = 904.3 in³

Question 14. d = 36 m _______ m 3

Answer: 24416.6 m³

Explanation: d = 36 m radius r = 36/2 = 18 m Volume = 4/3 πr³ = 4/3 (3.14) (18)³ = 24416.64 Volume = 24416.6 m³

Answer: 5572.5 cm³

Explanation: The volume of the sphere with a radius of 11 centimeters is V = 4/3 πr³ V = 4/3 (3.14) (11)³ V = 5572.5 cm³

Answer: 8.2 feet³

Explanation: The diameter of the sphere is 2.5 feet, which means that its radius is 1.25 feet. The volume of the sphere is V = 4/3 πr³ V = 4/3 . (3.14) . (1.25)³ V = 8.2 feet³

The eggs of birds and other animals come in many different shapes and sizes. Eggs often have a shape that is nearly spherical. When this is true, you can use the formula for a sphere to find their volume.

Question 17. The green turtle lays eggs that are approximately spherical with an average diameter of 4.5 centimeters. Each turtle lays an average of 113 eggs at one time. Find the total volume of these eggs, to the nearest cubic centimeter. _______ cm 3

Answer: 5389 cm³

Explanation: The diameter of an egg (sphere) is 4.5 centimeters, which means that its radius is 2.25 centimeters. The volume of a single egg is V = 4/3 πr³ V = 4/3 (3.14) (2.25)³ V = 47.68875 cm³ Therefore, the total volume of 113 eggs is 113 . V = 113(47.68875) = 5388.82875 = 5389 cm³

Question 18. Hummingbirds lay eggs that are nearly spherical and about 1 centimeter in diameter. Find the volume of an egg. Round your answer to the nearest tenth. _______ cm 3

Answer: 0.5 cm³

Explanation: The diameter of an egg (sphere) is 1 centimeter, which means that its radius is 0.5 centimeters. The volume of a single egg is V = 4/3 πr³ V = 4/3 (3.14) (0.5)³ V = 0.5 cm³

Question 19. Fossilized spherical eggs of dinosaurs called titanosaurid sauropods were found in Patagonia. These eggs were 15 centimeters in diameter. Find the volume of an egg. Round your answer to the nearest tenth. _______ cm 3

Answer: 1766.25 cm³

Explanation: Diameter of an egg = 15 cm Its radius = 15/2 = 7.5 cm Volume = 4/3 πr³ V = 4/3 (3.14) (7.5)³ V = 1766.25 cm³

Volume and Surface Area of Spheres Question 20. Persevere in Problem Solving An ostrich egg has about the same volume as a sphere with a diameter of 5 inches. If the eggshell is about \(\frac{1}{12}\) inch thick, find the volume of just the shell, not including the interior of the egg. Round your answer to the nearest tenth. _______ in 3

Answer: 6.8 in³

Explanation: Diameter including the eggshell = 5 + (2 . 1/2) = (5 + 1/6) in = 5.166 in Radius including eggshell = 5.166/2 = 2.5833 in Volume = 4/3 πr³ Volume = 4/3 (3.14) (2.5833)³ =72.176 in³ Volume with shell = 72.2 in³ Radius excluding shell = 5/2 = 2.5 in Volume = 4/3 (3.14) (2.5)³ = 65.416 in³ Volume (without shell) = 65.4 in³ Volume of shell = Total volume – Inner Volume = 72.2 – 65.4 = 6.8 in³

Answer: 5/3πr³

Explanation: The radius of the hemisphere = r The radius of cylinder = r Height of cylinder = r Step 1: Find the formula for the volume of a hemisphere The volume of hemisphere = 4/3 π/2 r³ = 2/3πr³ Step 2: Find the formula for the volume of a cylinder The volume of the cylinder = πr²h =πr³ Step 3: Add both the volume expressions: Total volume = 2/3πr³ + πr³ = 5/3πr³

Volume of Spheres – Page No. 416

Question 22. Critical Thinking Explain what happens to the volume of a sphere if you double the radius. Type below: _____________

Answer: Let Radius = r Volume V1 = 4/3πr³ Radius = 2r Volume V2 = 4/3π(2r)³ = 8 . 4/3πr³ = 8 V1 = 8(initial volume) By doubling the radius of the sphere we make the volume 8 times the initial value.

Answer: 12.3 in³

Explanation: Radius of the ball = 1.25 inch Height of the cylinder = (2 × 1.25) × 3 = (2.5) × 3 = 7.5 in radius of base of cylinder = 1.25 in. Volume of cylinder = πr²h = (3.14) (1.25)² (7.5) = 36.7968 = 36.8 in³ Volume of a ball (all three) = 3 × 4/3πr³ = 4 (3.14) (1.25)³ = 24.53125 in³ = 24.5 in³ Volume of empty space = Volume of cylinder – Volume of ball = 36.8 – 24.5 = 12.3 in³

Question 24. Critique Reasoning A sphere has a radius of 4 inches, and a cube-shaped box has an edge length of 7.5 inches. J.D. says the box has a greater volume, so the sphere will fit in the box. Is he correct? Explain. _____________

Answer: The volume of sphere = 4/3πr³ = 4/3 (3.14) (4)³ = 267.9466 = 268 The volume of cube = (7.5)³ = 421.875 =421.9 The volume of cube > Volume of a sphere But the base of the cube has an area of (7.5 × 7.5) = 56.25 while the cross-action area of the sphere. πr² = (3.14) (4)² = 50.24 The cross-section area of the cube is less than that of a sphere. thus J.D. is wrong and the ball (sphere) will not fit in the cube.

Question 25. Critical Thinking Which would hold the most water: a bowl in the shape of a hemisphere with radius r, a cylindrical glass with radius r and height r, or a cone-shaped drinking cup with radius r and height r? Explain. _____________

Answer: The volume of a sphere with radius r is V sphere = 4/3πr³ Therefore, the volume of a hemisphere is V hemisphere = V sphere/2 V hemisphere = 2/3πr³ The volume of a cylinder with radius r and height r is V cylinder = πr²h V cylinder = πr³ The volume of a cone with radius r and height r is V cone = 1/3πr²h V cone = 1/3πr³ V cone < V hemisphere < V cylinder Therefore, the cylindrical glass with radius r and height r will hold the most water.

8th Grade Review for Volume of Cylinders, Cones, and Spheres Answer Key Question 26. Analyze Relationships Hari has models of a sphere, a cylinder, and a cone. The sphere’s diameter and the cylinder’s height are the same, 2r. The cylinder has radius r. The cone has diameter 2r and height 2r. Compare the volumes of the cone and the sphere to the volume of the cylinder. Type below: _____________

Answer: Radius of sphere = 2r/2 = r Volume of sphere = 4/3πr³ The radius of cylinder = r Height of cylinder = 2r volume of cylinder = πr²(2r) V cylinder = 2πr³ Radius of cone = 2r/2 = r Height of cone = 2r Volume of cone = 1/3 πr²(2r) V cone = 2/3πr³ Volume of cylinder > Volume of sphere > Volume of cone 2πr³ > 4/3πr³ > 2/3πr³

Question 27. A spherical helium balloon that is 8 feet in diameter can lift about 17 pounds. What does the diameter of a balloon need to be to lift a person who weighs 136 pounds? Explain. _______ feet

Answer: Diameter of ballon = 8 ft Weight it could lift = 17 pound Volume = 4/3 π(8/2)³ = 4³(4π/3) 4³/x(4π/3) = 17/36 1/x = 1/8 × 3/4π × 1/48 x = 4π/3 . 4³ . 2³ x = 4/3. π . 8³ The volume of ballon which can lift 136 pounds is equal to 4/3. π . 8³ The radius of that ballon = 8ft Diameter = 8 . 2 = 16 ft

Ready to Go On ? – Model Quiz – Page No. 417

13.1 Volume of Cylinders

Find the volume of each cylinder. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Answer: 904.8 ft³

Explanation: Radius of base = 6 ft Height of cylinder = 8 ft The volume of cylinder = πr²h Volume = (3.14) (6)² (8) Volume = 904.77 ft³ Volume = 904.8 ft³

Volume of Cylinders, Cones, and Spheres Iready Answers Question 2. A can of juice has a radius of 4 inches and a height of 7 inches. What is the volume of the can? _______ in 3

Answer: 351.7 in³

Explanation: Radius if cylindrical can = 4 in Height of cylindrical can = 7 in The volume of cylinder = πr²h Volume = (3.14) (4)² (7) Volume = 351.68 in³ Volume = 351.7 in³

13.2 Volume of Cones

Answer: 565.2 cm³

Explanation: Radius of base of cone = 6 cm Height of cone = 15 cm Volume of cone = 1/3πr²h Volume = 1/3 (3.14) (4)² (7) Volume = 565.2 cm³

Answer: 3014.4 in³

Explanation: The radius of the base of cone = 12 in Height of cone = 20 in The volume of cone = 1/3πr²h Volume = 1/3 (3.14) (12)² (20) Volume = 3014.4 in³

13.3 Volume of Spheres

Answer: 113 in³

Explanation: Radius of sphere = 3 ft Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (3)³ Volume = 113.04 ft³ Volume = 113 in³

Answer: 1149.8 cm³

Explanation: Diameter = 13 cm Radius = 13/2 cm = 6.5 cm Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (6.5)³ Volume = 1149.7633 cm³ Volume = 1149.8 cm³

ESSENTIAL QUESTION

Question 7. What measurements do you need to know to find the volume of a cylinder? a cone? a sphere? Type below: ___________

Answer: Sphere: To find the volume of the sphere, the radius is to be measured. Cylinder: To measure the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder. Cone: To calculate the volume of the cone, we need to calculate the base radius of the base of the cone along with the height of the cone.

Explanation: The volume of sphere = 4/3 πr³ Sphere: For finding the volume of the sphere, the radius is to be measured The volume of Cylinder = πr²h Cylinder: To calculate the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder The volume of Cone = 1/3 πr²h Cone: To calculate the volume of the cone, we need to measure the base radius of the base of the cone along with the height of the cone

Selected Response – Mixed Review – Page No. 418

Question 1. The bed of a pickup truck measures 4 feet by 8 feet. To the nearest inch, what is the length of the longest thin metal bar that will lie flat in the bed? Options: a. 11 ft 3 in. b. 10 ft 0 in. c. 8 ft 11 in. d. 8 ft 9 in.

Answer: d. 8 ft 9 in.

Explanation: The length of the longest thin metal bar that will lie flat in the bed’s equal to the length of the bed’s hypotenuse. Let a = 4 and b = 8. Using the Pythagorean Theorem a² + b² = c² 4² + 8² = c² 16 + 64 = c² 80 = c² Rounding the length of the hypotenuse to the nearest tenth of a foot c = 8.9 ft Therefore, the length of the longest thin metal bar that will lie flat in the bed is 8 ft. 9 in.

Answer: c. 1,091.6 cubic yards

Explanation: Diameter of the base of the cylinder = 11.4 yd Radius = 11.4/2 yd = 5.7 yd Height = 10.7 ys Volume of cylinder = πr²h Volume = (3.14) (5.7)² (10.7) Volume = 1091.599 yd³ Volume = 1091.6 yd³

Question 3. Rhett made mini waffle cones for a birthday party. Each waffle cone was 3.5 inches high and had a radius of 0.8 inches. What is the volume of each cone to the nearest hundredth? Options: a. 1.70 cubic inches b. 2.24 cubic inches c. 2.34 cubic inches d. 8.79 cubic inches

Answer: c. 2.34 cubic inches

Explanation: Height of each waffle cone = 3.5 in Radius of base = 0.8 in Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (0.8)² (3.5) Volume = 2.344533 in³ Volume = 2.34 in³

Question 4. What is the volume of a cone that has a height of 17 meters and a base with a radius of 6 meters? Use 3.14 for π and round to the nearest tenth. Options: a. 204 cubic meters b. 640.6 cubic meters c. 2,562.2 cubic meters d. 10,249 cubic meters

Answer: b. 640.6 cubic meters

Explanation: Height of the cone = 17 m Radius of base = 6 m Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (6)² (17) Volume = 640.56 m³ Volume = 640.6 m³

Answer: b. 5,572.5 cubic centimeters

Explanation: Diameter of the base of the sphere = 22 cm Radius = 22/2 yd = 11 cm Volume of sphere = 4/3 πr³ Volume = 4/3 (3.14) (11)³ Volume = 5572.4533 cm³ Volume = 5572.5 cm³

Answer: 8.574 cm³

Explanation: The radius of the cylinder as well as the hemisphere = 1.6 cm Height = 6.2 cm the volume of the hemisphere = 2/3 πr³ the volume of the hemisphere = 2/3 (3.14) (1.6)³ the volume of the hemisphere = 8.574 cm³

Question 6. b. What is the volume of the cylinder? _______ cm 3

Answer: 49.838 cm³

Explanation: The volume of cylinder = πr²h = (3.14) (1.6)² (6.2) = 49.838 cm³

Question 6. c. What is the volume of the whole figure? _______ cm 3

Answer: 58.4 cm³

Explanation: Total volume = Volume of cylinder + volume of a hemisphere Total volume = 8.574 cm³ + 49.838 cm³ Total volume = 58.4 cm³

Conclusion:

Download Go Math Grade 8 Answer Key Chapter 13 Volume for free of cost. Self-study is also possible with the help of HMH Go Math Grade 8 Solution Key. Begin your practice now by referring to Go Math Grade 8 Chapter 13 Volume Solution Key. Every student love to practice maths with the help of the Go Math Grade 8 Solution Key. Each and every problem is explained in a detailed way to help the students to practice in the best way.

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 8th grade   >   Unit 5

• Cylinder volume & surface area
• Volume of cylinders
• Volume of a sphere
• Volume of spheres
• Volume of a cone
• Volume of cones

Volume of cylinders, spheres, and cones word problems

• Geometry: FAQ
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

volume of cylinder practice

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Volume of cylinder practice

Volume of Cylinders Notes & Practice | + Interactive Notebook Pages

Volume of Cylinders Missing Dimensions Notes & Practice (Distance Learning)

• Easel Activity

Volume of Cylinders Word Problem Practice PLUS Critical Writing

Volume of a Cylinder Practice Problems/Engaging Questions

Volume of Cylinders , Cones, & Spheres NOTES & Practice

Volume of Cylinders Task Cards | Math Center Practice Activity

Volume of Cylinders Notes & Practice | Guided Notes | + Interactive Notebook

Volume of Cylinders & Prisms: Notes & Practice

Volume of Prisms, Cylinders , Pyramids, Cones, and Spheres notes & practice

Volume of a Cylinder , Cone, and Sphere - 3 Practice Worksheets 8.G.C.9

Surface Area and Volume of Prisms, Cylinders , and Spheres Notes and Practice

Volume of Cylinders , Cones, & Spheres Practice Worksheet 8.7A

Volume of Composite Figures with Cylinders , Cones & Spheres | Printable Practice

Volume of a Cylinder Practice Activities - Print & Digital

• Google Apps™

Volume of Cylinders , Cones, & Spheres Sketch Notes & Practice

Volume of a Cone, Cylinder , and Sphere - Free Practice or Quiz - 8.G.C.9

Volume of Cylinders Guided Notes & Practice

Circumference, Area, and Volume of Circles & Cylinders Practice

Math Modeling Volume of Sphere, Cylinder , Pyramid, Cone, Practice Word Problems

Volume of Cylinders Notes and Practice

Volume of Cylinders , Cones, and Spheres Bundle (Notes & Practice )

Volume of 3D Shapes Practice Worksheet - Prisms Cylinders Pyramids Cones Spheres

Volume of Prisms, Cylinders , Pyramids, and Cones - Practice Puns

Volume of Prisms, Cylinders , and Pyramids - Practice Puns

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

Mrs. Smith's Class

“it is not that i'm so smart. but i stay with the questions much longer.” ~ albert einstein, unit 8 – volume and surface area.

Wed. January 14 Lesson: ASSIGNMENT REVIEW DAY – In-Class Assignment TOMORROW! Homework:  Unit 8 Assignment Review Questions ;  Unit 8 Assignment Review (SOLUTIONS)

Tues. January 13 Lesson:  Surface Area of Cylinders, Spheres, and Cones (Lesson Notes) Homework: Surface Area of Cylinders, Spheres, and Cones (Homeworkd w Solutions)

Mon. January 12 Lesson:  Surface Area of Prisms & Pyramids (Lesson Notes) Homework: Surface Area of Prisms & Pyramids (HOMEWORK w Answers)

Fri. January 9 Lesson:  Volume of Cylinders, Cones, & Spheres (Lesson Notes) Homework: Volume of Cylinders, Cones, & Spheres (Handout & Worksheet)

Thurs. January 8 Lesson: Culminating Activity Work Period – DUE THIS FRIDAY JAN. 9

Wed. January 7 Lesson:  Volume of Prisms & Pyramids (Lesson Notes) Homework: Volume of Prisms & Pyramids (HOMEWORK)

Tues. January 6 Lesson: Imperial Conversions (Lesson Notes) Homework: Imperial System (Homework)

Mon. January 5 Lesson: Metric System (Lesson Notes) Homework: Metric Conversion Worksheet

Leave a Reply

You must be logged in to post a comment.

• View Calendar

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Lesson 1 Homework Practice Volume Of Cylinders

Lesson 1 Homework Practice Volume Of Cylinders - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Answers lessons 12 1 and 12 2 name date period 8, Lesson 47 prisms and cylinders, Volumes of cylinders, , Practice a 10 6 volume of prisms and cylinders, Surface area prisms cylinders l1es1, By the mcgraw hill companies all rights, Lesson 47 prisms and cylinders.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Answers (Lessons 12-1 and 12-2) NAME DATE PERIOD 8 in.

2. lesson 47: prisms and cylinders, 3. 7.2 volumes of cylinders, 5. practice a 10-6 volume of prisms and cylinders, 6. surface area: prisms & cylinders l1es1, 7. copyright by the mcgraw-hill companies, inc. all rights ..., 8. lesson 47: prisms and cylinders.

• Notifications 0

• Add Friend ($5)

As a registered member you can:

• View all solutions for free
• Request more in-depth explanations for free
• Ask our tutors any math-related question for free
• Email your homework to your parent or tutor for free
• Grade 8 HMH Go Math - Answer Keys

Explanation:

A can of juice has a radius of 4 inches and a height of 7 inches. What is the volume of the can?

13.2 Volume of Cones

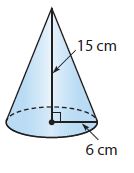
Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for \(\pi\).

13.3 Volume of Spheres

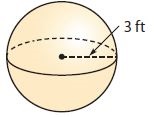
Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for \(\pi\).

ESSENTIAL QUESTION

What measurements do you need to know to find the volume of a cylinder? a cone? a sphere?

• Type below:

Yes, email page to my online tutor. ( if you didn't add a tutor yet, you can add one here )

Thank you for doing your homework!

Submit Your Question