linear regression with hypothesis test

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.2.1: Hypothesis Test for Linear Regression

• Last updated
• Save as PDF
• Page ID 34850

• Rachel Webb
• Portland State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

To test to see if the slope is significant we will be doing a two-tailed test with hypotheses. The population least squares regression line would be \(y = \beta_{0} + \beta_{1} + \varepsilon\) where \(\beta_{0}\) (pronounced “beta-naught”) is the population \(y\)-intercept, \(\beta_{1}\) (pronounced “beta-one”) is the population slope and \(\varepsilon\) is called the error term.

If the slope were horizontal (equal to zero), the regression line would give the same \(y\)-value for every input of \(x\) and would be of no use. If there is a statistically significant linear relationship then the slope needs to be different from zero. We will only do the two-tailed test, but the same rules for hypothesis testing apply for a one-tailed test.

We will only be using the two-tailed test for a population slope.

The hypotheses are:

\(H_{0}: \beta_{1} = 0\) \(H_{1}: \beta_{1} \neq 0\)

The null hypothesis of a two-tailed test states that there is not a linear relationship between \(x\) and \(y\). The alternative hypothesis of a two-tailed test states that there is a significant linear relationship between \(x\) and \(y\).

Either a t-test or an F-test may be used to see if the slope is significantly different from zero. The population of the variable \(y\) must be normally distributed.

F-Test for Regression

An F-test can be used instead of a t-test. Both tests will yield the same results, so it is a matter of preference and what technology is available. Figure 12-12 is a template for a regression ANOVA table,

where \(n\) is the number of pairs in the sample and \(p\) is the number of predictor (independent) variables; for now this is just \(p = 1\). Use the F-distribution with degrees of freedom for regression = \(df_{R} = p\), and degrees of freedom for error = \(df_{E} = n - p - 1\). This F-test is always a right-tailed test since ANOVA is testing the variation in the regression model is larger than the variation in the error.

Use an F-test to see if there is a significant relationship between hours studied and grade on the exam. Use \(\alpha\) = 0.05.

T-Test for Regression

If the regression equation has a slope of zero, then every \(x\) value will give the same \(y\) value and the regression equation would be useless for prediction. We should perform a t-test to see if the slope is significantly different from zero before using the regression equation for prediction. The numeric value of t will be the same as the t-test for a correlation. The two test statistic formulas are algebraically equal; however, the formulas are different and we use a different parameter in the hypotheses.

The formula for the t-test statistic is \(t = \frac{b_{1}}{\sqrt{ \left(\frac{MSE}{SS_{xx}}\right) }}\)

Use the t-distribution with degrees of freedom equal to \(n - p - 1\).

The t-test for slope has the same hypotheses as the F-test:

Use a t-test to see if there is a significant relationship between hours studied and grade on the exam, use \(\alpha\) = 0.05.

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Linear regression hypothesis testing: Concepts, Examples

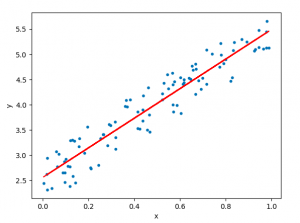
In relation to machine learning , linear regression is defined as a predictive modeling technique that allows us to build a model which can help predict continuous response variables as a function of a linear combination of explanatory or predictor variables. While training linear regression models, we need to rely on hypothesis testing in relation to determining the relationship between the response and predictor variables. In the case of the linear regression model, two types of hypothesis testing are done. They are T-tests and F-tests . In other words, there are two types of statistics that are used to assess whether linear regression models exist representing response and predictor variables. They are t-statistics and f-statistics. As data scientists , it is of utmost importance to determine if linear regression is the correct choice of model for our particular problem and this can be done by performing hypothesis testing related to linear regression response and predictor variables. Many times, it is found that these concepts are not very clear with a lot many data scientists. In this blog post, we will discuss linear regression and hypothesis testing related to t-statistics and f-statistics . We will also provide an example to help illustrate how these concepts work.

Table of Contents

What are linear regression models?

A linear regression model can be defined as the function approximation that represents a continuous response variable as a function of one or more predictor variables. While building a linear regression model, the goal is to identify a linear equation that best predicts or models the relationship between the response or dependent variable and one or more predictor or independent variables.

There are two different kinds of linear regression models. They are as follows:

• Simple or Univariate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and one predictor or independent variable. The form of the equation that represents a simple linear regression model is Y=mX+b, where m is the coefficients of the predictor variable and b is bias. When considering the linear regression line, m represents the slope and b represents the intercept.
• Multiple or Multi-variate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and more than one predictor or independent variable. The form of the equation that represents a multiple linear regression model is Y=b0+b1X1+ b2X2 + … + bnXn, where bi represents the coefficients of the ith predictor variable. In this type of linear regression model, each predictor variable has its own coefficient that is used to calculate the predicted value of the response variable.

While training linear regression models, the requirement is to determine the coefficients which can result in the best-fitted linear regression line. The learning algorithm used to find the most appropriate coefficients is known as least squares regression . In the least-squares regression method, the coefficients are calculated using the least-squares error function. The main objective of this method is to minimize or reduce the sum of squared residuals between actual and predicted response values. The sum of squared residuals is also called the residual sum of squares (RSS). The outcome of executing the least-squares regression method is coefficients that minimize the linear regression cost function .

The residual e of the ith observation is represented as the following where [latex]Y_i[/latex] is the ith observation and [latex]\hat{Y_i}[/latex] is the prediction for ith observation or the value of response variable for ith observation.

[latex]e_i = Y_i – \hat{Y_i}[/latex]

The residual sum of squares can be represented as the following:

[latex]RSS = e_1^2 + e_2^2 + e_3^2 + … + e_n^2[/latex]

The least-squares method represents the algorithm that minimizes the above term, RSS.

Once the coefficients are determined, can it be claimed that these coefficients are the most appropriate ones for linear regression? The answer is no. After all, the coefficients are only the estimates and thus, there will be standard errors associated with each of the coefficients.  Recall that the standard error is used to calculate the confidence interval in which the mean value of the population parameter would exist. In other words, it represents the error of estimating a population parameter based on the sample data. The value of the standard error is calculated as the standard deviation of the sample divided by the square root of the sample size. The formula below represents the standard error of a mean.

[latex]SE(\mu) = \frac{\sigma}{\sqrt(N)}[/latex]

Thus, without analyzing aspects such as the standard error associated with the coefficients, it cannot be claimed that the linear regression coefficients are the most suitable ones without performing hypothesis testing. This is where hypothesis testing is needed . Before we get into why we need hypothesis testing with the linear regression model, let’s briefly learn about what is hypothesis testing?

Train a Multiple Linear Regression Model using R

Before getting into understanding the hypothesis testing concepts in relation to the linear regression model, let’s train a multi-variate or multiple linear regression model and print the summary output of the model which will be referred to, in the next section. 

The data used for creating a multi-linear regression model is BostonHousing which can be loaded in RStudioby installing mlbench package. The code is shown below:

install.packages(“mlbench”) library(mlbench) data(“BostonHousing”)

Once the data is loaded, the code shown below can be used to create the linear regression model.

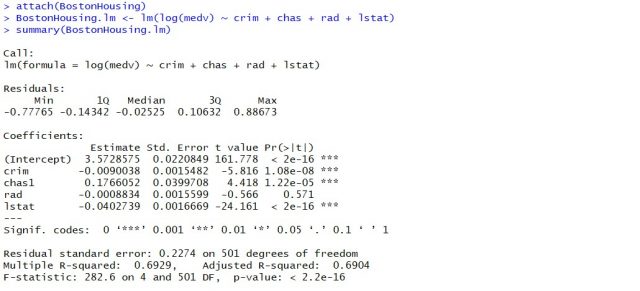
attach(BostonHousing) BostonHousing.lm <- lm(log(medv) ~ crim + chas + rad + lstat) summary(BostonHousing.lm)

Executing the above command will result in the creation of a linear regression model with the response variable as medv and predictor variables as crim, chas, rad, and lstat. The following represents the details related to the response and predictor variables:

• log(medv) : Log of the median value of owner-occupied homes in USD 1000’s
• crim : Per capita crime rate by town
• chas : Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
• rad : Index of accessibility to radial highways
• lstat : Percentage of the lower status of the population

The following will be the output of the summary command that prints the details relating to the model including hypothesis testing details for coefficients (t-statistics) and the model as a whole (f-statistics) 

Hypothesis tests & Linear Regression Models

Hypothesis tests are the statistical procedure that is used to test a claim or assumption about the underlying distribution of a population based on the sample data. Here are key steps of doing hypothesis tests with linear regression models:

• Hypothesis formulation for T-tests: In the case of linear regression, the claim is made that there exists a relationship between response and predictor variables, and the claim is represented using the non-zero value of coefficients of predictor variables in the linear equation or regression model. This is formulated as an alternate hypothesis. Thus, the null hypothesis is set that there is no relationship between response and the predictor variables . Hence, the coefficients related to each of the predictor variables is equal to zero (0). So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis for each test states that a1 = 0, a2 = 0, a3 = 0 etc. For all the predictor variables, individual hypothesis testing is done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. Thus, if there are, say, 5 features, there will be five hypothesis tests and each will have an associated null and alternate hypothesis.
• Hypothesis formulation for F-test : In addition, there is a hypothesis test done around the claim that there is a linear regression model representing the response variable and all the predictor variables. The null hypothesis is that the linear regression model does not exist . This essentially means that the value of all the coefficients is equal to zero. So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis states that a1 = a2 = a3 = 0.
• F-statistics for testing hypothesis for linear regression model : F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0. F-statistics is calculated as a function of sum of squares residuals for restricted regression (representing linear regression model with only intercept or bias and all the values of coefficients as zero) and sum of squares residuals for unrestricted regression (representing linear regression model). In the above diagram, note the value of f-statistics as 15.66 against the degrees of freedom as 5 and 194. 
• Evaluate t-statistics against the critical value/region : After calculating the value of t-statistics for each coefficient, it is now time to make a decision about whether to accept or reject the null hypothesis. In order for this decision to be made, one needs to set a significance level, which is also known as the alpha level. The significance level of 0.05 is usually set for rejecting the null hypothesis or otherwise. If the value of t-statistics fall in the critical region, the null hypothesis is rejected. Or, if the p-value comes out to be less than 0.05, the null hypothesis is rejected.
• Evaluate f-statistics against the critical value/region : The value of F-statistics and the p-value is evaluated for testing the null hypothesis that the linear regression model representing response and predictor variables does not exist. If the value of f-statistics is more than the critical value at the level of significance as 0.05, the null hypothesis is rejected. This means that the linear model exists with at least one valid coefficients. 
• Draw conclusions : The final step of hypothesis testing is to draw a conclusion by interpreting the results in terms of the original claim or hypothesis. If the null hypothesis of one or more predictor variables is rejected, it represents the fact that the relationship between the response and the predictor variable is not statistically significant based on the evidence or the sample data we used for training the model. Similarly, if the f-statistics value lies in the critical region and the value of the p-value is less than the alpha value usually set as 0.05, one can say that there exists a linear regression model.

Why hypothesis tests for linear regression models?

The reasons why we need to do hypothesis tests in case of a linear regression model are following:

• By creating the model, we are establishing a new truth (claims) about the relationship between response or dependent variable with one or more predictor or independent variables. In order to justify the truth, there are needed one or more tests. These tests can be termed as an act of testing the claim (or new truth) or in other words, hypothesis tests.
• One kind of test is required to test the relationship between response and each of the predictor variables (hence, T-tests)
• Another kind of test is required to test the linear regression model representation as a whole. This is called F-test.

While training linear regression models, hypothesis testing is done to determine whether the relationship between the response and each of the predictor variables is statistically significant or otherwise. The coefficients related to each of the predictor variables is determined. Then, individual hypothesis tests are done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. If at least one of the null hypotheses is rejected, it represents the fact that there exists no relationship between response and that particular predictor variable. T-statistics is used for performing the hypothesis testing because the standard deviation of the sampling distribution is unknown. The value of t-statistics is compared with the critical value from the t-distribution table in order to make a decision about whether to accept or reject the null hypothesis regarding the relationship between the response and predictor variables. If the value falls in the critical region, then the null hypothesis is rejected which means that there is no relationship between response and that predictor variable. In addition to T-tests, F-test is performed to test the null hypothesis that the linear regression model does not exist and that the value of all the coefficients is zero (0). Learn more about the linear regression and t-test in this blog – Linear regression t-test: formula, example .

Recent Posts

• Machine Learning Lifecycle: Data to Deployment Example - May 12, 2024
• Autoencoder vs Variational Autoencoder (VAE): Differences, Example - May 12, 2024
• Linear Regression T-test: Formula, Example - May 7, 2024

Ajitesh Kumar

One response.

Very informative

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Search for:
• Excellence Awaits: IITs, NITs & IIITs Journey

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Machine Learning Lifecycle: Data to Deployment Example
• Autoencoder vs Variational Autoencoder (VAE): Differences, Example
• Linear Regression T-test: Formula, Example
• Feature Engineering in Machine Learning: Python Examples
• Feature Selection vs Feature Extraction: Machine Learning

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

Linear regression - Hypothesis testing

by Marco Taboga , PhD

This lecture discusses how to perform tests of hypotheses about the coefficients of a linear regression model estimated by ordinary least squares (OLS).

Table of contents

Normal vs non-normal model

The linear regression model, matrix notation, tests of hypothesis in the normal linear regression model, test of a restriction on a single coefficient (t test), test of a set of linear restrictions (f test), tests based on maximum likelihood procedures (wald, lagrange multiplier, likelihood ratio), tests of hypothesis when the ols estimator is asymptotically normal, test of a restriction on a single coefficient (z test), test of a set of linear restrictions (chi-square test), learn more about regression analysis.

The lecture is divided in two parts:

in the first part, we discuss hypothesis testing in the normal linear regression model , in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors;

in the second part, we show how to carry out hypothesis tests in linear regression analyses where the hypothesis of normality holds only in large samples (i.e., the OLS estimator can be proved to be asymptotically normal).

We also denote:

We now explain how to derive tests about the coefficients of the normal linear regression model.

It can be proved (see the lecture about the normal linear regression model ) that the assumption of conditional normality implies that:

How the acceptance region is determined depends not only on the desired size of the test , but also on whether the test is:

one-tailed (only one of the two things, i.e., either smaller or larger, is possible).

For more details on how to determine the acceptance region, see the glossary entry on critical values .

The F test is one-tailed .

A critical value in the right tail of the F distribution is chosen so as to achieve the desired size of the test.

Then, the null hypothesis is rejected if the F statistics is larger than the critical value.

In this section we explain how to perform hypothesis tests about the coefficients of a linear regression model when the OLS estimator is asymptotically normal.

As we have shown in the lecture on the properties of the OLS estimator , in several cases (i.e., under different sets of assumptions) it can be proved that:

These two properties are used to derive the asymptotic distribution of the test statistics used in hypothesis testing.

The test can be either one-tailed or two-tailed . The same comments made for the t-test apply here.

Like the F test, also the Chi-square test is usually one-tailed .

The desired size of the test is achieved by appropriately choosing a critical value in the right tail of the Chi-square distribution.

The null is rejected if the Chi-square statistics is larger than the critical value.

Want to learn more about regression analysis? Here are some suggestions:

R squared of a linear regression ;

Gauss-Markov theorem ;

Generalized Least Squares ;

Multicollinearity ;

Dummy variables ;

Selection of linear regression models

Partitioned regression ;

Ridge regression .

How to cite

Please cite as:

Taboga, Marco (2021). "Linear regression - Hypothesis testing", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/linear-regression-hypothesis-testing.

Most of the learning materials found on this website are now available in a traditional textbook format.

• F distribution
• Beta distribution
• Conditional probability
• Central Limit Theorem
• Binomial distribution
• Mean square convergence
• Delta method
• Almost sure convergence
• Mathematical tools
• Fundamentals of probability
• Probability distributions
• Asymptotic theory
• Fundamentals of statistics
• About Statlect
• Cookies, privacy and terms of use
• Loss function
• Almost sure
• Type I error
• Precision matrix
• Integrable variable
• To enhance your privacy,
• we removed the social buttons,
• but don't forget to share .

Teach yourself statistics

Hypothesis Test for Regression Slope

This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y .

The test focuses on the slope of the regression line

Y = Β 0 + Β 1 X

where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of the independent variable, and Y is the value of the dependent variable.

If we find that the slope of the regression line is significantly different from zero, we will conclude that there is a significant relationship between the independent and dependent variables.

Test Requirements

The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.

• The dependent variable Y has a linear relationship to the independent variable X .
• For each value of X, the probability distribution of Y has the same standard deviation σ.
• The Y values are independent.
• The Y values are roughly normally distributed (i.e., symmetric and unimodal ). A little skewness is ok if the sample size is large.

The test procedure consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

If there is a significant linear relationship between the independent variable X and the dependent variable Y , the slope will not equal zero.

H o : Β 1 = 0

H a : Β 1 ≠ 0

The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use a linear regression t-test (described in the next section) to determine whether the slope of the regression line differs significantly from zero.

Analyze Sample Data

Using sample data, find the standard error of the slope, the slope of the regression line, the degrees of freedom, the test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.

SE = s b 1 = sqrt [ Σ(y i - ŷ i ) 2 / (n - 2) ] / sqrt [ Σ(x i - x ) 2 ]

• Slope. Like the standard error, the slope of the regression line will be provided by most statistics software packages. In the hypothetical output above, the slope is equal to 35.

t = b 1 / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

The local utility company surveys 101 randomly selected customers. For each survey participant, the company collects the following: annual electric bill (in dollars) and home size (in square feet). Output from a regression analysis appears below.

Is there a significant linear relationship between annual bill and home size? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

H o : The slope of the regression line is equal to zero.

H a : The slope of the regression line is not equal to zero.

• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a linear regression t-test to determine whether the slope of the regression line differs significantly from zero.

We get the slope (b 1 ) and the standard error (SE) from the regression output.

b 1 = 0.55       SE = 0.24

We compute the degrees of freedom and the t statistic, using the following equations.

DF = n - 2 = 101 - 2 = 99

t = b 1 /SE = 0.55/0.24 = 2.29

where DF is the degrees of freedom, n is the number of observations in the sample, b 1 is the slope of the regression line, and SE is the standard error of the slope.

• Interpret results . Since the P-value (0.0242) is less than the significance level (0.05), we cannot accept the null hypothesis.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.2 - the general linear f-test, the general linear f-test section  .

The " general linear F-test " involves three basic steps, namely:

• Define a larger  full model . (By "larger," we mean one with more parameters.)
• Define a smaller reduced model . (By "smaller," we mean one with fewer parameters.)
• Use an F- statistic to decide whether or not to reject the smaller reduced model in favor of the larger full model.

As you can see by the wording of the third step, the null hypothesis always pertains to the reduced model, while the alternative hypothesis always pertains to the full model.

The easiest way to learn about the general linear test is to first go back to what we know, namely the simple linear regression model. Once we understand the general linear test for the simple case, we then see that it can be easily extended to the multiple-case model. We take that approach here.

The Full Model Section  

The " full model ", which is also sometimes referred to as the " unrestricted model ," is the model thought to be most appropriate for the data. For simple linear regression, the full model is:

\(y_i=(\beta_0+\beta_1x_{i1})+\epsilon_i\)

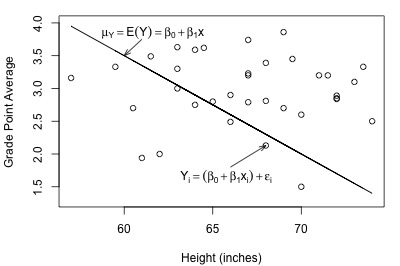
Here's a plot of a hypothesized full model for a set of data that we worked with previously in this course (student heights and grade point averages):

And, here's another plot of a hypothesized full model that we previously encountered (state latitudes and skin cancer mortalities):

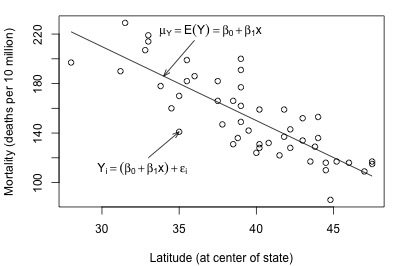
In each plot, the solid line represents what the hypothesized population regression line might look like for the full model. The question we have to answer in each case is "does the full model describe the data well?" Here, we might think that the full model does well in summarizing the trend in the second plot but not the first.

The Reduced Model Section  

The " reduced model ," which is sometimes also referred to as the " restricted model ," is the model described by the null hypothesis \(H_{0}\). For simple linear regression, a common null hypothesis is \(H_{0} : \beta_{1} = 0\). In this case, the reduced model is obtained by "zeroing out" the slope \(\beta_{1}\) that appears in the full model. That is, the reduced model is:

\(y_i=\beta_0+\epsilon_i\)

This reduced model suggests that each response \(y_{i}\) is a function only of some overall mean, \(\beta_{0}\), and some error \(\epsilon_{i}\).

Let's take another look at the plot of student grade point average against height, but this time with a line representing what the hypothesized population regression line might look like for the reduced model:

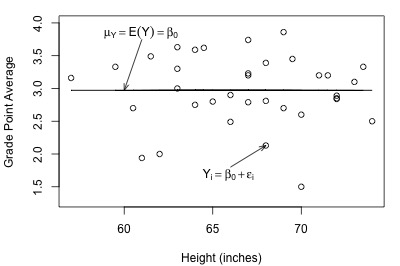
Not bad — there (fortunately?!) doesn't appear to be a relationship between height and grade point average. And, it appears as if the reduced model might be appropriate in describing the lack of a relationship between heights and grade point averages. What does the reduced model do for the skin cancer mortality example?

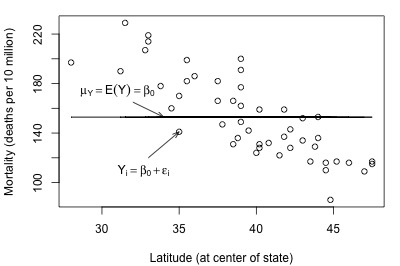
It doesn't appear as if the reduced model would do a very good job of summarizing the trend in the population.

F-Statistic Test Section  

How do we decide if the reduced model or the full model does a better job of describing the trend in the data when it can't be determined by simply looking at a plot? What we need to do is to quantify how much error remains after fitting each of the two models to our data. That is, we take the general linear test approach:

• Obtain the least squares estimates of \(\beta_{0}\) and \(\beta_{1}\).
• Determine the error sum of squares, which we denote as " SSE ( F )."
• Obtain the least squares estimate of \(\beta_{0}\).
• Determine the error sum of squares, which we denote as " SSE ( R )."

Recall that, in general, the error sum of squares is obtained by summing the squared distances between the observed and fitted (estimated) responses:

\(\sum(\text{observed } - \text{ fitted})^2\)

Therefore, since \(y_i\) is the observed response and \(\hat{y}_i\) is the fitted response for the full model :

\(SSE(F)=\sum(y_i-\hat{y}_i)^2\)

And, since \(y_i\) is the observed response and \(\bar{y}\) is the fitted response for the reduced model :

\(SSE(R)=\sum(y_i-\bar{y})^2\)

Let's get a better feel for the general linear F-test approach by applying it to two different datasets. First, let's look at the Height and GPA data . The following plot of grade point averages against heights contains two estimated regression lines — the solid line is the estimated line for the full model, and the dashed line is the estimated line for the reduced model:

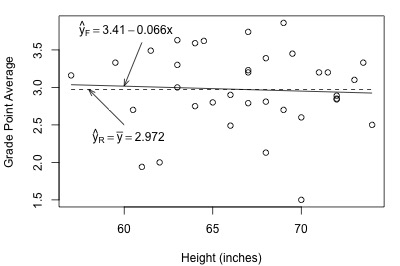
As you can see, the estimated lines are almost identical. Calculating the error sum of squares for each model, we obtain:

\(SSE(F)=\sum(y_i-\hat{y}_i)^2=9.7055\)

\(SSE(R)=\sum(y_i-\bar{y})^2=9.7331\)

The two quantities are almost identical. Adding height to the reduced model to obtain the full model reduces the amount of error by only 0.0276 (from 9.7331 to 9.7055). That is, adding height to the model does very little in reducing the variability in grade point averages. In this case, there appears to be no advantage in using the larger full model over the simpler reduced model.

Look what happens when we fit the full and reduced models to the skin cancer mortality and latitude dataset :

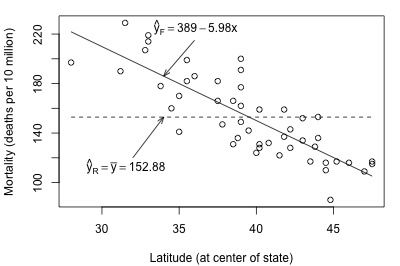
Here, there is quite a big difference between the estimated equation for the full model (solid line) and the estimated equation for the reduced model (dashed line). The error sums of squares quantify the substantial difference in the two estimated equations:

\(SSE(F)=\sum(y_i-\hat{y}_i)^2=17173\)

\(SSE(R)=\sum(y_i-\bar{y})^2=53637\)

Adding latitude to the reduced model to obtain the full model reduces the amount of error by 36464 (from 53637 to 17173). That is, adding latitude to the model substantially reduces the variability in skin cancer mortality. In this case, there appears to be a big advantage in using the larger full model over the simpler reduced model.

Where are we going with this general linear test approach? In short:

• The general linear test involves a comparison between SSE ( R ) and SSE ( F ).
• If SSE ( F ) is close to SSE ( R ), then the variation around the estimated full model regression function is almost as large as the variation around the estimated reduced model regression function. If that's the case, it makes sense to use the simpler reduced model.
• On the other hand, if SSE ( F ) and SSE ( R ) differ greatly, then the additional parameter(s) in the full model substantially reduce the variation around the estimated regression function. In this case, it makes sense to go with the larger full model.

How different does SSE ( R ) have to be from SSE ( F ) in order to justify using the larger full model? The general linear F -statistic:

\(F^*=\left( \dfrac{SSE(R)-SSE(F)}{df_R-df_F}\right)\div\left( \dfrac{SSE(F)}{df_F}\right)\)

helps answer this question. The F -statistic intuitively makes sense — it is a function of SSE ( R )- SSE ( F ), the difference in the error between the two models. The degrees of freedom — denoted \(df_{R}\) and \(df_{F}\) — are those associated with the reduced and full model error sum of squares, respectively.

We use the general linear F -statistic to decide whether or not:

• to reject the null hypothesis \(H_{0}\colon\) The reduced model
• in favor of the alternative hypothesis \(H_{A}\colon\) The full model

In general, we reject \(H_{0}\) if F * is large — or equivalently if its associated P -value is small.

The test applied to the simple linear regression model Section  

For simple linear regression, it turns out that the general linear F -test is just the same ANOVA F -test that we learned before. As noted earlier for the simple linear regression case, the full model is:

and the reduced model is:

Therefore, the appropriate null and alternative hypotheses are specified either as:

• \(H_{0} \colon y_i = \beta_{0} + \epsilon_{i}\)
• \(H_{A} \colon y_i = \beta_{0} + \beta_{1} x_{i} + \epsilon_{i}\)
• \(H_{0} \colon \beta_{1} = 0 \)
• \(H_{A} \colon \beta_{1} ≠ 0 \)

The degrees of freedom associated with the error sum of squares for the reduced model is n -1, and:

\(SSE(R)=\sum(y_i-\bar{y})^2=SSTO\)

The degrees of freedom associated with the error sum of squares for the full model is n -2, and:

\(SSE(F)=\sum(y_i-\hat{y}_i)^2=SSE\)

Now, we can see how the general linear F -statistic just reduces algebraically to the ANOVA F -test that we know:

Can be rewritten by substituting...

\(\begin{aligned} &&df_{R} = n - 1\\  &&df_{F} = n - 2\\ &&SSE(R)=SSTO\\&&SSE(F)=SSE\end{aligned}\)

\(F^*=\left( \dfrac{SSTO-SSE}{(n-1)-(n-2)}\right)\div\left( \dfrac{SSE}{(n-2)}\right)=\frac{MSR}{MSE}\)

That is, the general linear F -statistic reduces to the ANOVA F -statistic:

\(F^*=\dfrac{MSR}{MSE}\)

For the student height and grade point average example:

\( F^*=\dfrac{MSR}{MSE}=\dfrac{0.0276/1}{9.7055/33}=\dfrac{0.0276}{0.2941}=0.094\)

For the skin cancer mortality example:

\( F^*=\dfrac{MSR}{MSE}=\dfrac{36464/1}{17173/47}=\dfrac{36464}{365.4}=99.8\)

The P -value is calculated as usual. The P -value answers the question: "what is the probability that we’d get an F* statistic as large as we did if the null hypothesis were true?" The P -value is determined by comparing F * to an F distribution with 1 numerator degree of freedom and n -2 denominator degrees of freedom. For the student height and grade point average example, the P -value is 0.761 (so we fail to reject \(H_{0}\) and we favor the reduced model), while for the skin cancer mortality example, the P -value is 0.000 (so we reject \(H_{0}\) and we favor the full model).

Example 6-2: Alcohol and muscle Strength Section  

Does alcoholism have an effect on muscle strength? Some researchers (Urbano-Marquez, et al , 1989) who were interested in answering this question collected the following data ( Alcohol Arm data ) on a sample of 50 alcoholic men:

• x = the total lifetime dose of alcohol ( kg per kg of body weight) consumed
• y = the strength of the deltoid muscle in the man's non-dominant arm

The full model is the model that would summarize a linear relationship between alcohol consumption and arm strength. The reduced model, on the other hand, is the model that claims there is no relationship between alcohol consumption and arm strength.

• \(H_0 \colon y_i = \beta_0 + \epsilon_i \)
• \(H_A \colon y_i = \beta_0 + \beta_{1}x_i + \epsilon_i\)
• \(H_0 \colon \beta_1 = 0\)
• \(H_A \colon \beta_1 ≠ 0\)

Upon fitting the reduced model to the data, we obtain:

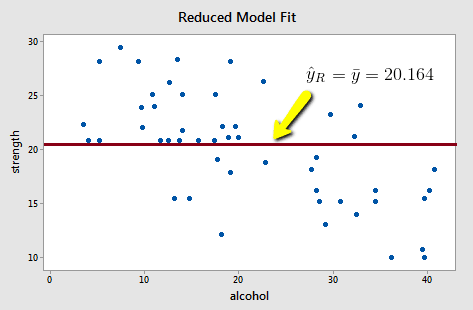
\(SSE(R)=\sum(y_i-\bar{y})^2=1224.32\)

Note that the reduced model does not appear to summarize the trend in the data very well.

Upon fitting the full model to the data, we obtain:

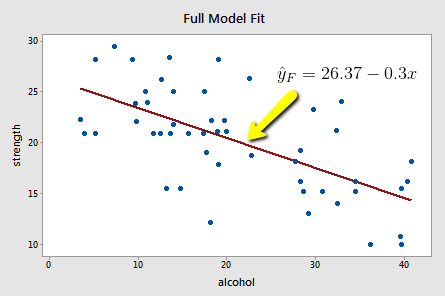
\(SSE(F)=\sum(y_i-\hat{y}_i)^2=720.27\)

The full model appears to describe the trend in the data better than the reduced model.

The good news is that in the simple linear regression case, we don't have to bother with calculating the general linear F -statistic. Minitab does it for us in the ANOVA table.

Click on the light bulb to see the error in the full and reduced models.

Analysis of Variance

As you can see, Minitab calculates and reports both SSE ( F ) — the amount of error associated with the full model — and SSE ( R ) — the amount of error associated with the reduced model. The F -statistic is:

\( F^*=\dfrac{MSR}{MSE}=\dfrac{504.04/1}{720.27/48}=\dfrac{504.04}{15.006}=33.59\)

and its associated P -value is < 0.001 (so we reject \(H_{0}\) and favor the full model). We can conclude that there is a statistically significant linear association between lifetime alcohol consumption and arm strength.

This concludes our discussion of our first aside from the general linear F-test. Now, we move on to our second aside from sequential sums of squares.

Statistics Made Easy

Understanding the t-Test in Linear Regression

Linear regression is used to quantify the relationship between a predictor variable and a response variable.

Whenever we perform linear regression, we want to know if there is a statistically significant relationship between the predictor variable and the response variable.

We test for significance by performing a t-test for the regression slope. We use the following null and alternative hypothesis for this t-test:

• H 0 : β 1 = 0 (the slope is equal to zero)
• H A : β 1 ≠ 0 (the slope is not equal to zero)

We then calculate the test statistic as follows:

• t = b  / SE b
• b : coefficient estimate
• SE b : standard error of the coefficient estimate

If the p-value that corresponds to t is less than some threshold (e.g. α = .05) then we reject the null hypothesis and conclude that there is a statistically significant relationship between the predictor variable and the response variable.

The following example shows how to perform a t-test for a linear regression model in practice.

Example: Performing a t-Test for Linear Regression

Suppose a professor wants to analyze the relationship between hours studied and exam score received for 40 of his students.

He performs simple linear regression using hours studied as the predictor variable and exam score received as the response variable.

The following table shows the results of the regression model:

To determine if hours studied has a statistically significant relationship with final exam score, we can perform a t-test.

We use the following null and alternative hypothesis for this t-test:

• H 0 : β 1 = 0 (the slope for hours studied is equal to zero)
• H A : β 1 ≠ 0 (the slope for hours studied is not equal to zero)
• t = 1.117 / 1.025

The p-value that corresponds to t = 1.089 with df = n-2 = 40 – 2 = 38 is 0.283 .

Note that we can also use the T Score to P Value Calculator to calculate this p-value:

Since this p-value is not less than .05, we fail to reject the null hypothesis.

This means that hours studied does not have a statistically significant relationship between final exam score.

Additional Resources

The following tutorials offer additional information about linear regression:

Introduction to Simple Linear Regression Introduction to Multiple Linear Regression How to Interpret Regression Coefficients How to Interpret the F-Test of Overall Significance in Regression

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

One Reply to “Understanding the t-Test in Linear Regression”

if I t-test a regression vs another regression instead vs zero, ie a slope vs another slope, do I need to compare against a t crit of n – 4?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

I have read and agree to the terms & conditions

What is the purpose and significance of the t-test in linear regression analysis?

Table of Contents

The t-test is a statistical tool used in linear regression analysis to determine the significance of the relationship between two variables. It helps to determine whether the observed relationship between the dependent and independent variables is statistically significant or if it occurred by chance. This is important in understanding the strength and direction of the relationship between the variables, and it helps to make informed decisions on the variables to include in the regression model. Additionally, the t-test allows for the identification of any potential errors or flaws in the data, ensuring the accuracy and validity of the regression results. Overall, the t-test is a crucial tool in linear regression analysis as it helps to assess the significance of the relationship between variables and aids in making sound and reliable conclusions.

Understanding the t-Test in Linear Regression

Linear regression is used to quantify the relationship between a predictor variable and a response variable.

Whenever we perform linear regression, we want to know if there is a statistically significant relationship between the predictor variable and the response variable.

We test for significance by performing a t-test for the regression slope. We use the following null and alternative hypothesis for this t-test:

• H 0 : β 1 = 0 (the slope is equal to zero)
• H A : β 1 ≠ 0 (the slope is not equal to zero)

We then calculate the test statistic as follows:

• t = b  / SE b
• b : coefficient estimate
• SE b : standard error of the coefficient estimate

If the p-value that corresponds to t is less than some threshold (e.g. α = .05) then we reject the null hypothesis and conclude that there is a statistically significant relationship between the predictor variable and the response variable.

The following example shows how to perform a t-test for a linear regression model in practice.

Example: Performing a t-Test for Linear Regression

Suppose a professor wants to analyze the relationship between hours studied and exam score received for 40 of his students.

He performs simple linear regression using hours studied as the predictor variable and exam score received as the response variable.

The following table shows the results of the regression model:

To determine if hours studied has a statistically significant relationship with final exam score, we can perform a t-test.

We use the following null and alternative hypothesis for this t-test:

• H 0 : β 1 = 0 (the slope for hours studied is equal to zero)
• H A : β 1 ≠ 0 (the slope for hours studied is not equal to zero)
• t = 1.117 / 1.025

The p-value that corresponds to t = 1.089 with df = n-2 = 40 – 2 = 38 is 0.283 .

Note that we can also use the to calculate this p-value:

Since this p-value is not less than .05, we fail to reject the null hypothesis.

This means that hours studied does not have a statistically significant relationship between final exam score.

Additional Resources

The following tutorials offer additional information about linear regression:

Related terms:

• 1. Customer Segmentation in Marketing: Companies often use cluster analysis to group customers based on their demographics, behavior, and preferences. This helps them tailor their marketing strategies and target specific customer segments. 2. Disease Clustering in Healthcare: Cluster analysis is used in healthcare to identify patterns and clusters of diseases in a population. This can help in understanding the spread of diseases and developing targeted prevention and treatment methods. 3. Fraud Detection in Banking: Banks and financial institutions use cluster analysis to identify patterns of fraudulent activities and detect anomalies in transactions. This helps in preventing fraud and protecting customers’ financial assets. 4. Image and Text Clustering in Social Media: Social media platforms use cluster analysis to group similar images, videos, and text posts together. This helps in organizing and recommending relevant content to users based on their interests and preferences. 5. Crime Analysis in Law Enforcement: Police departments use cluster analysis to identify high-crime areas and patterns of criminal activities. This helps in deploying resources effectively and preventing crime in specific areas.
• What is the meaning and significance of P-values and statistical significance in statistical analysis?
• What is a Residuals vs. Leverage Plot? (Definition & Example) A Residuals vs. Leverage Plot is a graphical representation used in regression analysis to assess the influence of individual data points on the overall model fit. It plots the standardized residuals (vertical axis) against the leverage values (horizontal axis) for each data point in the dataset. The standardized residual represents the difference between the observed and predicted values, divided by the standard error of the regression. It helps identify unusual observations or outliers that may have a significant impact on the regression model. The leverage value, on the other hand, measures how much influence a data point has on the estimated regression coefficients. It is calculated based on the distance of a data point from the center of the predictor variables. In a Residuals vs. Leverage Plot, a data point with a high leverage value and a large standardized residual indicates that it has a significant impact on the model fit. This can be due to extreme values or influential observations that are not well represented by the model. An example of a Residuals vs. Leverage Plot is shown below: [Image of a Residuals vs. Leverage Plot] In this example, the outliers are represented by the data points with high standardized residuals and leverage values, as they deviate significantly from the overall pattern of the data. These points may need to be further investigated and potentially excluded from the model if they are found to be influential.
• What is the difference between statistical significance and practical significance?
• What is the purpose of classification and regression trees and how are they used in data analysis?
• What is the purpose of Bartlett’s Test of Sphericity and how is it used in statistical analysis?
• What is the F-test of overall significance in regression and how can it be understood?
• How can multiple linear regression be used for predictive analysis in Excel?
• What is the significance of the message “glm.fit: fitted probabilities numerically 0 or 1 occurred” in statistical analysis?
• What is the significance of the F-value and p-value in ANOVA and how do they help interpret the results of the analysis?