linear hypothesis in statistics

Linear regression - Hypothesis testing

by Marco Taboga , PhD

This lecture discusses how to perform tests of hypotheses about the coefficients of a linear regression model estimated by ordinary least squares (OLS).

Table of contents

Normal vs non-normal model

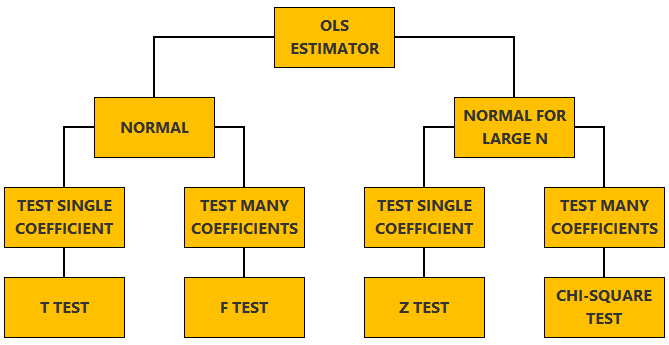
The linear regression model, matrix notation, tests of hypothesis in the normal linear regression model, test of a restriction on a single coefficient (t test), test of a set of linear restrictions (f test), tests based on maximum likelihood procedures (wald, lagrange multiplier, likelihood ratio), tests of hypothesis when the ols estimator is asymptotically normal, test of a restriction on a single coefficient (z test), test of a set of linear restrictions (chi-square test), learn more about regression analysis.

The lecture is divided in two parts:

in the first part, we discuss hypothesis testing in the normal linear regression model , in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors;

in the second part, we show how to carry out hypothesis tests in linear regression analyses where the hypothesis of normality holds only in large samples (i.e., the OLS estimator can be proved to be asymptotically normal).

We also denote:

We now explain how to derive tests about the coefficients of the normal linear regression model.

It can be proved (see the lecture about the normal linear regression model ) that the assumption of conditional normality implies that:

How the acceptance region is determined depends not only on the desired size of the test , but also on whether the test is:

one-tailed (only one of the two things, i.e., either smaller or larger, is possible).

For more details on how to determine the acceptance region, see the glossary entry on critical values .

The F test is one-tailed .

A critical value in the right tail of the F distribution is chosen so as to achieve the desired size of the test.

Then, the null hypothesis is rejected if the F statistics is larger than the critical value.

In this section we explain how to perform hypothesis tests about the coefficients of a linear regression model when the OLS estimator is asymptotically normal.

As we have shown in the lecture on the properties of the OLS estimator , in several cases (i.e., under different sets of assumptions) it can be proved that:

These two properties are used to derive the asymptotic distribution of the test statistics used in hypothesis testing.

The test can be either one-tailed or two-tailed . The same comments made for the t-test apply here.

Like the F test, also the Chi-square test is usually one-tailed .

The desired size of the test is achieved by appropriately choosing a critical value in the right tail of the Chi-square distribution.

The null is rejected if the Chi-square statistics is larger than the critical value.

Want to learn more about regression analysis? Here are some suggestions:

R squared of a linear regression ;

Gauss-Markov theorem ;

Generalized Least Squares ;

Multicollinearity ;

Dummy variables ;

Selection of linear regression models

Partitioned regression ;

Ridge regression .

How to cite

Please cite as:

Taboga, Marco (2021). "Linear regression - Hypothesis testing", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/linear-regression-hypothesis-testing.

Most of the learning materials found on this website are now available in a traditional textbook format.

• F distribution
• Beta distribution
• Conditional probability
• Central Limit Theorem
• Binomial distribution
• Mean square convergence
• Delta method
• Almost sure convergence
• Mathematical tools
• Fundamentals of probability
• Probability distributions
• Asymptotic theory
• Fundamentals of statistics
• About Statlect
• Cookies, privacy and terms of use
• Loss function
• Almost sure
• Type I error
• Precision matrix
• Integrable variable
• To enhance your privacy,
• we removed the social buttons,
• but don't forget to share .

The Linear Model and Hypothesis

A General Unifying Theory

• © 2015
• George Seber 0

Department of Statistics, The University of Auckland, Auckland, New Zealand

You can also search for this author in PubMed   Google Scholar

• Provides a concise and unique overview of hypothesis testing in four important statistical subject areas: linear and nonlinear models, multivariate analysis, and large sample theory
• Shows that all hypotheses are linear or asymptotically so, and that all the basic models are exact or asymptotically linear normal models. This means that the concept of orthogonality in analysis variance can be extended to other models, and the three standard methods of hypothesis testing, namely the likelihood ratio test, the Wald test and the Score (Lagrange Multiplier) test, can be shown to be asymptotically equivalent for the various models
• Uses a geometrical approach utilizing the ideas of orthogonal projections and idempotent matrices. It avoids some of the complications involved with finding ranks of matrices and provides a simpler and more intuitive approach to the subject matter
• Includes supplementary material: sn.pub/extras

Part of the book series: Springer Series in Statistics (SSS)

39k Accesses

18 Citations

2 Altmetric

This is a preview of subscription content, log in via an institution to check access.

Access this book

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Other ways to access

Licence this eBook for your library

Institutional subscriptions

Table of contents (12 chapters)

Front matter, preliminaries.

• George A. F. Seber

The Linear Hypothesis

Hypothesis testing, inference properties, testing several hypotheses, enlarging the model, nonlinear regression models, multivariate models, large sample theory: constraint-equation hypotheses, large sample theory: freedom-equation hypotheses, multinomial distribution, back matter.

• Analysis of variance
• Goodness-of-fit test.
• Hypothesis tests
• Lagrange multiplier test
• Large sample tests
• Likelihood ratio test
• Linear models
• Missing observations
• Multinomial distribution
• Multivariate hypothesis testing
• Orthogonal projections
• Separable hypotheses
• Simultaneous confidence intervals

About this book

This book provides a concise and integrated overview of hypothesis testing in four important subject areas, namely linear and nonlinear models, multivariate analysis, and large sample theory. The approach used is a geometrical one based on the concept of projections and their associated idempotent matrices, thus largely avoiding the need to involvematrix ranks. It is shown that all the hypotheses encountered are either linear or asymptotically linear, and that all the underlying models used are either exactly or asymptotically linear normal models. This equivalence can be used, for example, to extend the concept of orthogonality to other models in the analysis of variance, and to show that the asymptotic equivalence of the likelihood ratio, Wald, and Score (Lagrange Multiplier) hypothesis tests generally applies.

“The book deals with the classical topic of multivariate linear models. … the monograph is a consistent, logical and comprehensive treatment of the theory of linear models aimed at scientists who already have a good knowledge of the subject and are well trained in application of matrix algebra.” (Jurgita Markeviciute, zbMATH 1371.62002, 2017)

“This monograph is a welcome update of the author's 1966 book. It contains a wealth of material and will be of interest to graduate students, teachers, and researchers familiar with the 1966 book.” (William I. Notz, Mathematical Reviews, June, 2016)

Authors and Affiliations

George Seber

About the author

George Seber is an Emeritus Professor of Statistics at Auckland University, New Zealand. He is an elected Fellow of the Royal Society of New Zealand, recipient of their Hector medal in Information Science, and recipient of an international Distinguished Statistical Ecologist Award. He has authored or coauthored 16 books and 90 research articles on a wide variety of topics including linear and nonlinear models, multivariate analysis, matrix theory for statisticians, large sample theory, adaptive sampling, genetics, epidemiology, and statistical ecology.

Bibliographic Information

Book Title : The Linear Model and Hypothesis

Book Subtitle : A General Unifying Theory

Authors : George Seber

Series Title : Springer Series in Statistics

DOI : https://doi.org/10.1007/978-3-319-21930-1

Publisher : Springer Cham

eBook Packages : Mathematics and Statistics , Mathematics and Statistics (R0)

Copyright Information : Springer International Publishing Switzerland 2015

Hardcover ISBN : 978-3-319-21929-5 Published: 16 October 2015

Softcover ISBN : 978-3-319-34917-6 Published: 23 August 2016

eBook ISBN : 978-3-319-21930-1 Published: 08 October 2015

Series ISSN : 0172-7397

Series E-ISSN : 2197-568X

Edition Number : 1

Number of Pages : IX, 205

Topics : Statistical Theory and Methods , Statistics for Social Sciences, Humanities, Law

• Publish with us

Policies and ethics

• Find a journal
• Track your research

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

3.6 - the general linear test.

This is just a general representation of an F -test based on a full and a reduced model. We will use this frequently when we look at more complex models.

Let's illustrate the general linear test here for the single factor experiment:

First we write the full model, \(Y_{ij} = \mu + \tau_i + \epsilon_{ij}\) and then the reduced model, \(Y_{ij} = \mu + \epsilon_{ij}\) where you don't have a \(\tau_i\) term, you just have an overall mean, \(\mu\). This is a pretty degenerate model that just says all the observations are just coming from one group. But the reduced model is equivalent to what we are hypothesizing when we say the \(\mu_i\) would all be equal, i.e.:

\(H_0 \colon \mu_1 = \mu_2 = \dots = \mu_a\)

This is equivalent to our null hypothesis where the \(\tau_i\)'s are all equal to 0.

The reduced model is just another way of stating our hypothesis. But in more complex situations this is not the only reduced model that we can write, there are others we could look at.

The general linear test is stated as an F ratio:

\(F=\dfrac{(SSE(R)-SSE(F))/(dfR-dfF)}{SSE(F)/dfF}\)

This is a very general test. You can apply any full and reduced model and test whether or not the difference between the full and the reduced model is significant just by looking at the difference in the SSE appropriately. This has an F distribution with ( df R - df F), df F degrees of freedom, which correspond to the numerator and the denominator degrees of freedom of this F ratio.

Let's take a look at this general linear test using Minitab...

Example 3.5: Cotton Weight Section  

Remember this experiment had treatment levels 15, 20, 25, 30, 35 % cotton weight and the observations were the tensile strength of the material.

The full model allows a different mean for each level of cotton weight %.

We can demonstrate the General Linear Test by viewing the ANOVA table from Minitab:

STAT > ANOVA > Balanced ANOVA

The \(SSE(R) = 636.96\) with a \(dfR = 24\), and \(SSE(F) = 161.20\) with \(dfF = 20\). Therefore:

\(F^\ast =\dfrac{(636.96-161.20)/(24-20)}{161.20/20}\)

This demonstrates the equivalence of this test to the F -test. We now use the General Linear Test (GLT) to test for Lack of Fit when fitting a series of polynomial regression models to determine the appropriate degree of polynomial.

We can demonstrate the General Linear Test by comparing the quadratic polynomial model (Reduced model), with the full ANOVA model (Full model). Let \(Y_{ij} = \mu + \beta_{1}x_{ij} + \beta_{2}x_{ij}^{2} + \epsilon_{ij}\) be the reduced model, where \(x_{ij}\) is the cotton weight percent. Let \(Y_{ij} = \mu + \tau_i + \epsilon_{ij}\) be the full model.

The General Linear Test - Cotton Weight Example (no sound)

The video above shows the SSE ( R ) = 260.126 with dfR = 22 for the quadratic regression model. The ANOVA shows the full model with SSE ( F ) = 161.20 with dfF = 20.

Therefore the GLT is:

\(\begin{eqnarray} F^\ast &=&\dfrac{(SSE(R)-SSE(F))/(dfR-dfF)}{SSE(F)/dfF} \nonumber\\ &=&\dfrac{(260.126-161.200)/(22-20)}{161.20/20}\nonumber\\ &=&\dfrac{98.926/2}{8.06}\nonumber\\ &=&\dfrac{49.46}{8.06}\nonumber\\&=&6.14 \nonumber \end{eqnarray}\)

We reject \(H_0\colon \) Quadratic Model and claim there is Lack of Fit if \(F^{*} > F_{1}-\alpha (2, 20) = 3.49\).

Therefore, since 6.14 is > 3.49 we reject the null hypothesis of no Lack of Fit from the quadratic equation and fit a cubic polynomial. From the viewlet above we noticed that the cubic term in the equation was indeed significant with p -value = 0.015.

We can apply the General Linear Test again, now testing whether the cubic equation is adequate. The reduced model is:

\(Y_{ij} = \mu + \beta_{1}x_{ij} + \beta_{2}x_{ij}^{2} + \beta_{3}x_{ij}^{3} + \epsilon_{ij}\)

and the full model is the same as before, the full ANOVA model:

\(Y_ij = \mu + \tau_i + \epsilon_{ij}\)

The General Linear Test is now a test for Lack of Fit from the cubic model:

\begin{aligned} F^{*} &=\frac{(\operatorname{SSE}(R)-\operatorname{SSE}(F)) /(d f R-d f F)}{\operatorname{SSE}(F) / d f F} \\ &=\frac{(195.146-161.200) /(21-20)}{161.20 / 20} \\ &=\frac{33.95 / 1}{8.06} \\ &=4.21 \end{aligned}

We reject if \(F^{*} > F_{0.95} (1, 20) = 4.35\).

Therefore we do not reject \(H_A \colon\) Lack of Fit and conclude the data are consistent with the cubic regression model, and higher order terms are not necessary.

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Linear hypothesis

A statistical hypothesis according to which the mean $ a $ of an $ n $- dimensional normal law $ N _ {n} ( a , \sigma ^ {2} I ) $( where $ I $ is the unit matrix), lying in a linear subspace $ \Pi ^ {s} \subset \mathbf R ^ {n} $ of dimension $ s < n $, belongs to a linear subspace $ \Pi ^ {r} \subset \Pi ^ {s} $ of dimension $ r < s $.

Many problems of mathematical statistics can be reduced to the problem of testing a linear hypothesis, which is often stated in the following so-called canonical form. Let $ X = ( X _ {1} \dots X _ {n} ) $ be a normally distributed vector with independent components and let $ {\mathsf E} X _ {i} = a _ {i} $ for $ i = 1 \dots s $, $ {\mathsf E} X _ {i} = 0 $ for $ i = s + 1 \dots n $ and $ {\mathsf D} X _ {i} = \sigma ^ {2} $ for $ i = 1 \dots n $, where the quantities $ a _ {1} \dots a _ {s} $ are unknown. Then the hypothesis $ H _ {0} $, according to which

$$ a _ {1} = \dots = a _ {r} = 0 ,\ \ r < s < n , $$

is the canonical linear hypothesis.

Example. Let $ Y _ {1} \dots Y _ {n} $ and $ Z _ {1} \dots Z _ {m} $ be $ n + m $ independent random variables, subject to normal distributions $ N _ {1} ( a , \sigma ^ {2} ) $ and $ N _ {1} ( b , \sigma ^ {2} ) $, respectively, where the parameters $ a $, $ b $, $ \sigma ^ {2} $ are unknown. Then the hypothesis $ H _ {0} $: $ a = b = 0 $ is the linear hypothesis, while a hypothesis $ a = a _ {0} $, $ b = b _ {0} $ with $ a _ {0} \neq b _ {0} $ is not linear.

However, such a linear hypothesis $ a = a _ {0} $, $ b = b _ {0} $ with $ a _ {0} \neq b _ {0} $ does correspond to a linear hypothesis concerning the means of the transformed quantities $ Y _ {i} ^ \prime = Y _ {i} - a _ {0} $, $ Z _ {i} ^ \prime = Z _ {i} - b _ {0} $.

• This page was last edited on 5 June 2020, at 22:17.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3.4: Hypothesis Test for Simple Linear Regression

• Last updated
• Save as PDF
• Page ID 28708

We will now describe a hypothesis test to determine if the regression model is meaningful; in other words, does the value of \(X\) in any way help predict the expected value of \(Y\)?

Simple Linear Regression ANOVA Hypothesis Test

Model Assumptions

• The residual errors are random and are normally distributed.
• The standard deviation of the residual error does not depend on \(X\)
• A linear relationship exists between \(X\) and \(Y\)
• The samples are randomly selected

Test Hypotheses

\(H_o\):  \(X\) and \(Y\) are not correlated   

\(H_a\):  \(X\) and \(Y\) are correlated   

\(H_o\):  \(\beta_1\) (slope) = 0   

\(H_a\):  \(\beta_1\) (slope) ≠ 0

Test Statistic

\(F=\dfrac{M S_{\text {Regression }}}{M S_{\text {Error }}}\)

\(d f_{\text {num }}=1\)

\(d f_{\text {den }}=n-2\)

Sum of Squares

\(S S_{\text {Total }}=\sum(Y-\bar{Y})^{2}\)

\(S S_{\text {Error }}=\sum(Y-\hat{Y})^{2}\)

\(S S_{\text {Regression }}=S S_{\text {Total }}-S S_{\text {Error }}\)

In simple linear regression, this is equivalent to saying “Are X an Y correlated?”

In reviewing the model, \(Y=\beta_{0}+\beta_{1} X+\varepsilon\), as long as the slope (\(\beta_{1}\)) has any non‐zero value, \(X\) will add value in helping predict the expected value of \(Y\). However, if there is no correlation between X and Y, the value of the slope (\(\beta_{1}\)) will be zero. The model we can use is very similar to One Factor ANOVA.

The Results of the test can be summarized in a special ANOVA table:

Example: Rainfall and sales of sunglasses

Design : Is there a significant correlation between rainfall and sales of sunglasses?

Research Hypothese s:

\(H_o\):  Sales and Rainfall are not correlated      \(H_o\):  1 (slope) = 0

\(H_a\):  Sales and Rainfall are correlated      \(H_a\):  1 (slope) ≠ 0

Type I error would be to reject the Null Hypothesis and \(t\) claim that rainfall is correlated with sales of sunglasses, when they are not correlated. The test will be run at a level of significance (\(\alpha\)) of 5%.

The test statistic from the table will be \(\mathrm{F}=\dfrac{\text { MSRegression }}{\text { MSError }}\). The degrees of freedom for the numerator will be 1, and the degrees of freedom for denominator will be 5‐2=3.  

Critical Value for \(F\) at  \(\alpha\)of 5% with \(df_{num}=1\) and \(df_{den}=3} is 10.13.  Reject \(H_o\) if \(F >10.13\). We will also run this test using the \(p\)‐value method with statistical software, such as Minitab.  

Data/Results

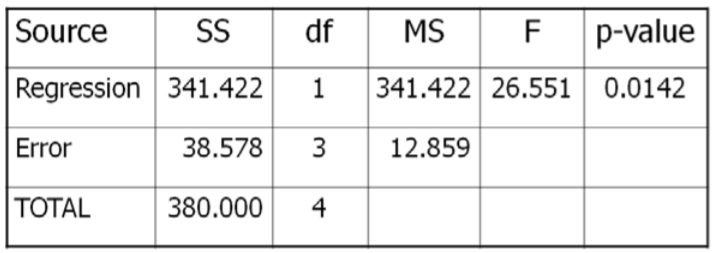
\(F=341.422 / 12.859=26.551\), which is more than the critical value of 10.13, so Reject \(H_o\). Also, the \(p\)‐value = 0.0142 < 0.05 which also supports rejecting \(H_o\).  

Sales of Sunglasses and Rainfall are negatively correlated.

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Linear regression hypothesis testing: Concepts, Examples

In relation to machine learning , linear regression is defined as a predictive modeling technique that allows us to build a model which can help predict continuous response variables as a function of a linear combination of explanatory or predictor variables. While training linear regression models, we need to rely on hypothesis testing in relation to determining the relationship between the response and predictor variables. In the case of the linear regression model, two types of hypothesis testing are done. They are T-tests and F-tests . In other words, there are two types of statistics that are used to assess whether linear regression models exist representing response and predictor variables. They are t-statistics and f-statistics. As data scientists , it is of utmost importance to determine if linear regression is the correct choice of model for our particular problem and this can be done by performing hypothesis testing related to linear regression response and predictor variables. Many times, it is found that these concepts are not very clear with a lot many data scientists. In this blog post, we will discuss linear regression and hypothesis testing related to t-statistics and f-statistics . We will also provide an example to help illustrate how these concepts work.

Table of Contents

What are linear regression models?

A linear regression model can be defined as the function approximation that represents a continuous response variable as a function of one or more predictor variables. While building a linear regression model, the goal is to identify a linear equation that best predicts or models the relationship between the response or dependent variable and one or more predictor or independent variables.

There are two different kinds of linear regression models. They are as follows:

• Simple or Univariate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and one predictor or independent variable. The form of the equation that represents a simple linear regression model is Y=mX+b, where m is the coefficients of the predictor variable and b is bias. When considering the linear regression line, m represents the slope and b represents the intercept.
• Multiple or Multi-variate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and more than one predictor or independent variable. The form of the equation that represents a multiple linear regression model is Y=b0+b1X1+ b2X2 + … + bnXn, where bi represents the coefficients of the ith predictor variable. In this type of linear regression model, each predictor variable has its own coefficient that is used to calculate the predicted value of the response variable.

While training linear regression models, the requirement is to determine the coefficients which can result in the best-fitted linear regression line. The learning algorithm used to find the most appropriate coefficients is known as least squares regression . In the least-squares regression method, the coefficients are calculated using the least-squares error function. The main objective of this method is to minimize or reduce the sum of squared residuals between actual and predicted response values. The sum of squared residuals is also called the residual sum of squares (RSS). The outcome of executing the least-squares regression method is coefficients that minimize the linear regression cost function .

The residual e of the ith observation is represented as the following where [latex]Y_i[/latex] is the ith observation and [latex]\hat{Y_i}[/latex] is the prediction for ith observation or the value of response variable for ith observation.

[latex]e_i = Y_i – \hat{Y_i}[/latex]

The residual sum of squares can be represented as the following:

[latex]RSS = e_1^2 + e_2^2 + e_3^2 + … + e_n^2[/latex]

The least-squares method represents the algorithm that minimizes the above term, RSS.

Once the coefficients are determined, can it be claimed that these coefficients are the most appropriate ones for linear regression? The answer is no. After all, the coefficients are only the estimates and thus, there will be standard errors associated with each of the coefficients.  Recall that the standard error is used to calculate the confidence interval in which the mean value of the population parameter would exist. In other words, it represents the error of estimating a population parameter based on the sample data. The value of the standard error is calculated as the standard deviation of the sample divided by the square root of the sample size. The formula below represents the standard error of a mean.

[latex]SE(\mu) = \frac{\sigma}{\sqrt(N)}[/latex]

Thus, without analyzing aspects such as the standard error associated with the coefficients, it cannot be claimed that the linear regression coefficients are the most suitable ones without performing hypothesis testing. This is where hypothesis testing is needed . Before we get into why we need hypothesis testing with the linear regression model, let’s briefly learn about what is hypothesis testing?

Train a Multiple Linear Regression Model using R

Before getting into understanding the hypothesis testing concepts in relation to the linear regression model, let’s train a multi-variate or multiple linear regression model and print the summary output of the model which will be referred to, in the next section. 

The data used for creating a multi-linear regression model is BostonHousing which can be loaded in RStudioby installing mlbench package. The code is shown below:

install.packages(“mlbench”) library(mlbench) data(“BostonHousing”)

Once the data is loaded, the code shown below can be used to create the linear regression model.

attach(BostonHousing) BostonHousing.lm <- lm(log(medv) ~ crim + chas + rad + lstat) summary(BostonHousing.lm)

Executing the above command will result in the creation of a linear regression model with the response variable as medv and predictor variables as crim, chas, rad, and lstat. The following represents the details related to the response and predictor variables:

• log(medv) : Log of the median value of owner-occupied homes in USD 1000’s
• crim : Per capita crime rate by town
• chas : Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
• rad : Index of accessibility to radial highways
• lstat : Percentage of the lower status of the population

The following will be the output of the summary command that prints the details relating to the model including hypothesis testing details for coefficients (t-statistics) and the model as a whole (f-statistics) 

Hypothesis tests & Linear Regression Models

Hypothesis tests are the statistical procedure that is used to test a claim or assumption about the underlying distribution of a population based on the sample data. Here are key steps of doing hypothesis tests with linear regression models:

• Hypothesis formulation for T-tests: In the case of linear regression, the claim is made that there exists a relationship between response and predictor variables, and the claim is represented using the non-zero value of coefficients of predictor variables in the linear equation or regression model. This is formulated as an alternate hypothesis. Thus, the null hypothesis is set that there is no relationship between response and the predictor variables . Hence, the coefficients related to each of the predictor variables is equal to zero (0). So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis for each test states that a1 = 0, a2 = 0, a3 = 0 etc. For all the predictor variables, individual hypothesis testing is done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. Thus, if there are, say, 5 features, there will be five hypothesis tests and each will have an associated null and alternate hypothesis.
• Hypothesis formulation for F-test : In addition, there is a hypothesis test done around the claim that there is a linear regression model representing the response variable and all the predictor variables. The null hypothesis is that the linear regression model does not exist . This essentially means that the value of all the coefficients is equal to zero. So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis states that a1 = a2 = a3 = 0.
• F-statistics for testing hypothesis for linear regression model : F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0. F-statistics is calculated as a function of sum of squares residuals for restricted regression (representing linear regression model with only intercept or bias and all the values of coefficients as zero) and sum of squares residuals for unrestricted regression (representing linear regression model). In the above diagram, note the value of f-statistics as 15.66 against the degrees of freedom as 5 and 194. 
• Evaluate t-statistics against the critical value/region : After calculating the value of t-statistics for each coefficient, it is now time to make a decision about whether to accept or reject the null hypothesis. In order for this decision to be made, one needs to set a significance level, which is also known as the alpha level. The significance level of 0.05 is usually set for rejecting the null hypothesis or otherwise. If the value of t-statistics fall in the critical region, the null hypothesis is rejected. Or, if the p-value comes out to be less than 0.05, the null hypothesis is rejected.
• Evaluate f-statistics against the critical value/region : The value of F-statistics and the p-value is evaluated for testing the null hypothesis that the linear regression model representing response and predictor variables does not exist. If the value of f-statistics is more than the critical value at the level of significance as 0.05, the null hypothesis is rejected. This means that the linear model exists with at least one valid coefficients. 
• Draw conclusions : The final step of hypothesis testing is to draw a conclusion by interpreting the results in terms of the original claim or hypothesis. If the null hypothesis of one or more predictor variables is rejected, it represents the fact that the relationship between the response and the predictor variable is not statistically significant based on the evidence or the sample data we used for training the model. Similarly, if the f-statistics value lies in the critical region and the value of the p-value is less than the alpha value usually set as 0.05, one can say that there exists a linear regression model.

Why hypothesis tests for linear regression models?

The reasons why we need to do hypothesis tests in case of a linear regression model are following:

• By creating the model, we are establishing a new truth (claims) about the relationship between response or dependent variable with one or more predictor or independent variables. In order to justify the truth, there are needed one or more tests. These tests can be termed as an act of testing the claim (or new truth) or in other words, hypothesis tests.
• One kind of test is required to test the relationship between response and each of the predictor variables (hence, T-tests)
• Another kind of test is required to test the linear regression model representation as a whole. This is called F-test.

While training linear regression models, hypothesis testing is done to determine whether the relationship between the response and each of the predictor variables is statistically significant or otherwise. The coefficients related to each of the predictor variables is determined. Then, individual hypothesis tests are done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. If at least one of the null hypotheses is rejected, it represents the fact that there exists no relationship between response and that particular predictor variable. T-statistics is used for performing the hypothesis testing because the standard deviation of the sampling distribution is unknown. The value of t-statistics is compared with the critical value from the t-distribution table in order to make a decision about whether to accept or reject the null hypothesis regarding the relationship between the response and predictor variables. If the value falls in the critical region, then the null hypothesis is rejected which means that there is no relationship between response and that predictor variable. In addition to T-tests, F-test is performed to test the null hypothesis that the linear regression model does not exist and that the value of all the coefficients is zero (0). Learn more about the linear regression and t-test in this blog – Linear regression t-test: formula, example .

Recent Posts

• Model Parallelism vs Data Parallelism: Examples - April 11, 2024
• Model Complexity & Overfitting in Machine Learning: How to Reduce - April 10, 2024
• 6 Game-Changing Features of ChatGPT’s Latest Upgrade - April 9, 2024

Ajitesh Kumar

One response.

Very informative

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Search for:
• Excellence Awaits: IITs, NITs & IIITs Journey

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Model Parallelism vs Data Parallelism: Examples
• Model Complexity & Overfitting in Machine Learning: How to Reduce
• 6 Game-Changing Features of ChatGPT’s Latest Upgrade
• Self-Prediction vs Contrastive Learning: Examples
• Free IBM Data Sciences Courses on Coursera

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

Linear Hypothesis Tests

Most regression output will include the results of frequentist hypothesis tests comparing each coefficient to 0. However, in many cases, you may be interested in whether a linear sum of the coefficients is 0. For example, in the regression

You may be interested to see if \(GoodThing\) and \(BadThing\) (both binary variables) cancel each other out. So you would want to do a test of \(\beta_1 - \beta_2 = 0\).

Alternately, you may want to do a joint significance test of multiple linear hypotheses. For example, you may be interested in whether \(\beta_1\) or \(\beta_2\) are nonzero and so would want to jointly test the hypotheses \(\beta_1 = 0\) and \(\beta_2=0\) rather than doing them one at a time. Note the and here, since if either one or the other is rejected, we reject the null.

Keep in Mind

• Be sure to carefully interpret the result. If you are doing a joint test, rejection means that at least one of your hypotheses can be rejected, not each of them. And you don’t necessarily know which ones can be rejected!
• Generally, linear hypothesis tests are performed using F-statistics. However, there are alternate approaches such as likelihood tests or chi-squared tests. Be sure you know which on you’re getting.
• Conceptually, what is going on with linear hypothesis tests is that they compare the model you’ve estimated against a more restrictive one that requires your restrictions (hypotheses) to be true. If the test you have in mind is too complex for the software to figure out on its own, you might be able to do it on your own by taking the sum of squared residuals in your original unrestricted model (\(SSR_{UR}\)), estimate the alternate model with the restriction in place (\(SSR_R\)) and then calculate the F-statistic for the joint test using \(F_{q,n-k-1} = ((SSR_R - SSR_{UR})/q)/(SSR_{UR}/(n-k-1))\).

Also Consider

• The process for testing a nonlinear combination of your coefficients, for example testing if \(\beta_1\times\beta_2 = 1\) or \(\sqrt{\beta_1} = .5\), is generally different. See Nonlinear hypothesis tests .

Implementations

Linear hypothesis test in R can be performed for most regression models using the linearHypothesis() function in the car package. See this guide for more information.

Tests of coefficients in Stata can generally be performed using the built-in test command.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

17 Introduction to Hypothesis Testing

Jenna Lehmann

What is Hypothesis Testing?

Hypothesis testing is a big part of what we would actually consider testing for inferential statistics. It’s a procedure and set of rules that allow us to move from descriptive statistics to make inferences about a population based on sample data. It is a statistical method that uses sample data to evaluate a hypothesis about a population.

This type of test is usually used within the context of research. If we expect to see a difference between a treated and untreated group (in some cases the untreated group is the parameters we know about the population), we expect there to be a difference in the means between the two groups, but that the standard deviation remains the same, as if each individual score has had a value added or subtracted from it.

Steps of Hypothesis Testing

The following steps will be tailored to fit the first kind of hypothesis testing we will learn first: single-sample z-tests. There are many other kinds of tests, so keep this in mind.

• Null Hypothesis (H0): states that in the general population there is no change, no difference, or no relationship, or in the context of an experiment, it predicts that the independent variable has no effect on the dependent variable.
• Alternative Hypothesis (H1): states that there is a change, a difference, or a relationship for the general population, or in the context of an experiment, it predicts that the independent variable has an effect on the dependent variable.

• Critical Region: Composed of the extreme sample values that are very unlikely to be obtained if the null hypothesis is true. Determined by alpha level. If sample data fall in the critical region, the null hypothesis is rejected, because it’s very unlikely they’ve fallen there by chance.
• After collecting the data, we find the sample mean. Now we can compare the sample mean with the null hypothesis by computing a z-score that describes where the sample mean is located relative to the hypothesized population mean. We use the z-score formula.
• We decided previously what the two z-score boundaries are for a critical score. If the z-score we get after plugging the numbers in the aforementioned equation is outside of that critical region, we reject the null hypothesis. Otherwise, we would say that we failed to reject the null hypothesis.

Regions of the Distribution

Because we’re making judgments based on probability and proportion, our normal distributions and certain regions within them come into play.

The Critical Region is composed of the extreme sample values that are very unlikely to be obtained if the null hypothesis is true. Determined by alpha level. If sample data fall in the critical region, the null hypothesis is rejected, because it’s very unlikely they’ve fallen there by chance.

These regions come into play when talking about different errors.

A Type I Error occurs when a researcher rejects a null hypothesis that is actually true; the researcher concludes that a treatment has an effect when it actually doesn’t. This happens when a researcher unknowingly obtains an extreme, non-representative sample. This goes back to alpha level: it’s the probability that the test will lead to a Type I error if the null hypothesis is true.

A result is said to be significant or statistically significant if it is very unlikely to occur when the null hypothesis is true. That is, the result is sufficient to reject the null hypothesis. For instance, two means can be significantly different from one another.

Factors that Influence and Assumptions of Hypothesis Testing

Assumptions of Hypothesis Testing:

• Random sampling: it is assumed that the participants used in the study were selected randomly so that we can confidently generalize our findings from the sample to the population.
• Independent observation: two observations are independent if there is no consistent, predictable relationship between the first observation and the second. The value of σ is unchanged by the treatment; if the population standard deviation is unknown, we assume that the standard deviation for the unknown population (after treatment) is the same as it was for the population before treatment. There are ways of checking to see if this is true in SPSS or Excel.
• Normal sampling distribution: in order to use the unit normal table to identify the critical region, we need the distribution of sample means to be normal (which means we need the population to be distributed normally and/or each sample size needs to be 30 or greater based on what we know about the central limit theorem).

Factors that influence hypothesis testing:

• The variability of the scores, which is measured by either the standard deviation or the variance. The variability influences the size of the standard error in the denominator of the z-score.
• The number of scores in the sample. This value also influences the size of the standard error in the denominator.

Test statistic: indicates that the sample data are converted into a single, specific statistic that is used to test the hypothesis (in this case, the z-score statistic).

Directional Hypotheses and Tailed Tests

In a directional hypothesis test , also known as a one-tailed test, the statistical hypotheses specify with an increase or decrease in the population mean. That is, they make a statement about the direction of the effect.

The Hypotheses for a Directional Test:

• H0: The test scores are not increased/decreased (the treatment doesn’t work)
• H1: The test scores are increased/decreased (the treatment works as predicted)

Because we’re only worried about scores that are either greater or less than the scores predicted by the null hypothesis, we only worry about what’s going on in one tail meaning that the critical region only exists within one tail. This means that all of the alpha is contained in one tail rather than split up into both (so the whole 5% is located in the tail we care about, rather than 2.5% in each tail). So before, we cared about what’s going on at the 0.025 mark of the unit normal table to look at both tails, but now we care about 0.05 because we’re only looking at one tail.

A one-tailed test allows you to reject the null hypothesis when the difference between the sample and the population is relatively small, as long as that difference is in the direction that you predicted. A two-tailed test, on the other hand, requires a relatively large difference independent of direction. In practice, researchers hypothesize using a one-tailed method but base their findings off of whether the results fall into the critical region of a two-tailed method. For the purposes of this class, make sure to calculate your results using the test that is specified in the problem.

Effect Size

A measure of effect size is intended to provide a measurement of the absolute magnitude of a treatment effect, independent of the size of the sample(s) being used. Usually done with Cohen’s d. If you imagine the two distributions, they’re layered over one another. The more they overlap, the smaller the effect size (the means of the two distributions are close). The more they are spread apart, the greater the effect size (the means of the two distributions are farther apart).

Statistical Power

The power of a statistical test is the probability that the test will correctly reject a false null hypothesis. It’s usually what we’re hoping to get when we run an experiment. It’s displayed in the table posted above. Power and effect size are connected. So, we know that the greater the distance between the means, the greater the effect size. If the two distributions overlapped very little, there would be a greater chance of selecting a sample that leads to rejecting the null hypothesis.

This chapter was originally posted to the Math Support Center blog at the University of Baltimore on June 11, 2019.

Math and Statistics Guides from UB's Math & Statistics Center Copyright © by Jenna Lehmann is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Choosing the Right Statistical Test | Types & Examples

Choosing the Right Statistical Test | Types & Examples

Published on January 28, 2020 by Rebecca Bevans . Revised on June 22, 2023.

Statistical tests are used in hypothesis testing . They can be used to:

• determine whether a predictor variable has a statistically significant relationship with an outcome variable.
• estimate the difference between two or more groups.

Statistical tests assume a null hypothesis of no relationship or no difference between groups. Then they determine whether the observed data fall outside of the range of values predicted by the null hypothesis.

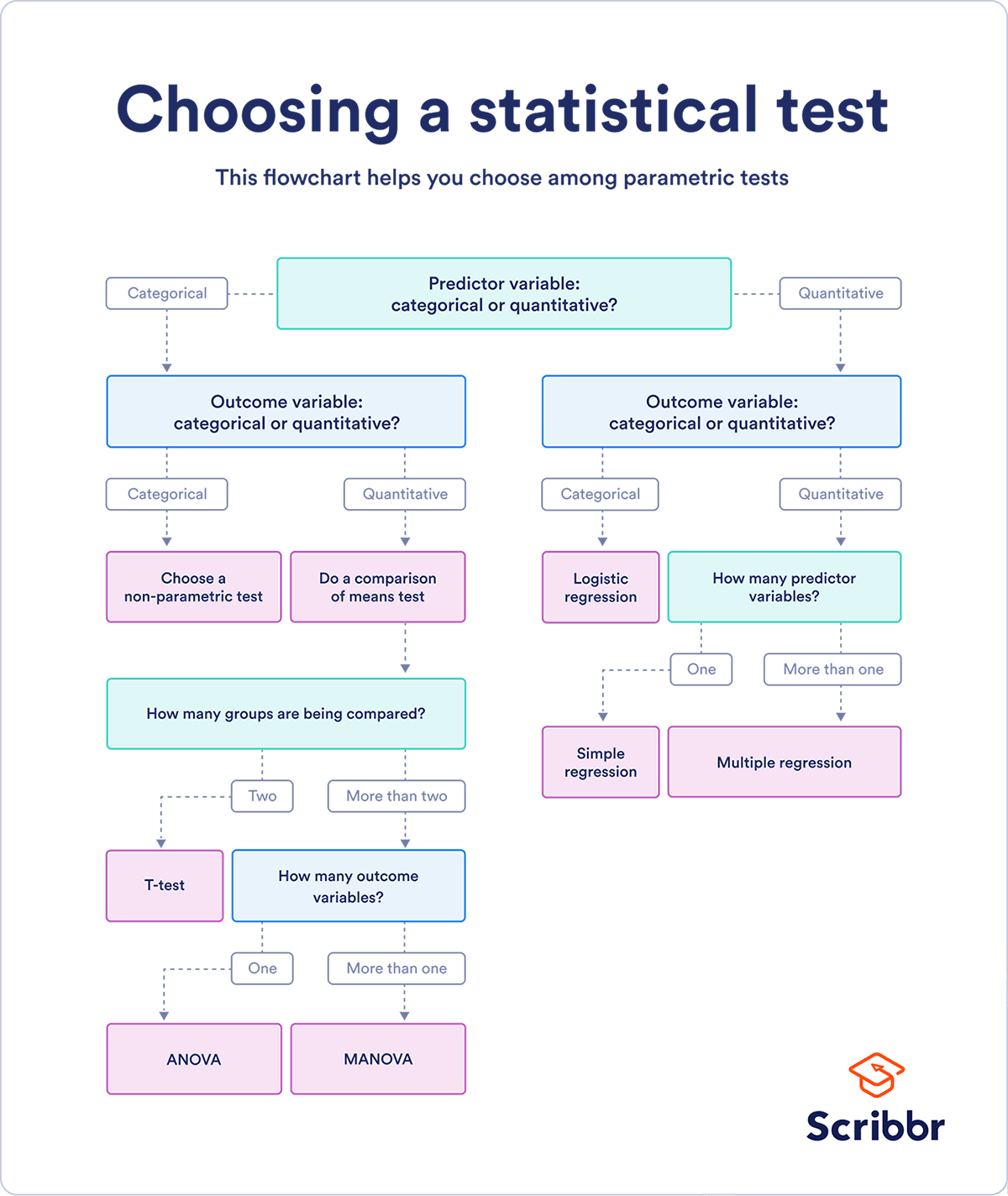
If you already know what types of variables you’re dealing with, you can use the flowchart to choose the right statistical test for your data.

Statistical tests flowchart

Table of contents

What does a statistical test do, when to perform a statistical test, choosing a parametric test: regression, comparison, or correlation, choosing a nonparametric test, flowchart: choosing a statistical test, other interesting articles, frequently asked questions about statistical tests.

Statistical tests work by calculating a test statistic – a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship.

It then calculates a p value (probability value). The p -value estimates how likely it is that you would see the difference described by the test statistic if the null hypothesis of no relationship were true.

If the value of the test statistic is more extreme than the statistic calculated from the null hypothesis, then you can infer a statistically significant relationship between the predictor and outcome variables.

If the value of the test statistic is less extreme than the one calculated from the null hypothesis, then you can infer no statistically significant relationship between the predictor and outcome variables.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

You can perform statistical tests on data that have been collected in a statistically valid manner – either through an experiment , or through observations made using probability sampling methods .

For a statistical test to be valid , your sample size needs to be large enough to approximate the true distribution of the population being studied.

To determine which statistical test to use, you need to know:

• whether your data meets certain assumptions.
• the types of variables that you’re dealing with.

Statistical assumptions

Statistical tests make some common assumptions about the data they are testing:

• Independence of observations (a.k.a. no autocorrelation): The observations/variables you include in your test are not related (for example, multiple measurements of a single test subject are not independent, while measurements of multiple different test subjects are independent).
• Homogeneity of variance : the variance within each group being compared is similar among all groups. If one group has much more variation than others, it will limit the test’s effectiveness.
• Normality of data : the data follows a normal distribution (a.k.a. a bell curve). This assumption applies only to quantitative data .

If your data do not meet the assumptions of normality or homogeneity of variance, you may be able to perform a nonparametric statistical test , which allows you to make comparisons without any assumptions about the data distribution.

If your data do not meet the assumption of independence of observations, you may be able to use a test that accounts for structure in your data (repeated-measures tests or tests that include blocking variables).

Types of variables

The types of variables you have usually determine what type of statistical test you can use.

Quantitative variables represent amounts of things (e.g. the number of trees in a forest). Types of quantitative variables include:

• Continuous (aka ratio variables): represent measures and can usually be divided into units smaller than one (e.g. 0.75 grams).
• Discrete (aka integer variables): represent counts and usually can’t be divided into units smaller than one (e.g. 1 tree).

Categorical variables represent groupings of things (e.g. the different tree species in a forest). Types of categorical variables include:

• Ordinal : represent data with an order (e.g. rankings).
• Nominal : represent group names (e.g. brands or species names).
• Binary : represent data with a yes/no or 1/0 outcome (e.g. win or lose).

Choose the test that fits the types of predictor and outcome variables you have collected (if you are doing an experiment , these are the independent and dependent variables ). Consult the tables below to see which test best matches your variables.

Parametric tests usually have stricter requirements than nonparametric tests, and are able to make stronger inferences from the data. They can only be conducted with data that adheres to the common assumptions of statistical tests.

The most common types of parametric test include regression tests, comparison tests, and correlation tests.

Regression tests

Regression tests look for cause-and-effect relationships . They can be used to estimate the effect of one or more continuous variables on another variable.

Comparison tests

Comparison tests look for differences among group means . They can be used to test the effect of a categorical variable on the mean value of some other characteristic.

T-tests are used when comparing the means of precisely two groups (e.g., the average heights of men and women). ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults).

Correlation tests

Correlation tests check whether variables are related without hypothesizing a cause-and-effect relationship.

These can be used to test whether two variables you want to use in (for example) a multiple regression test are autocorrelated.

Non-parametric tests don’t make as many assumptions about the data, and are useful when one or more of the common statistical assumptions are violated. However, the inferences they make aren’t as strong as with parametric tests.

Prevent plagiarism. Run a free check.

This flowchart helps you choose among parametric tests. For nonparametric alternatives, check the table above.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient
• Null hypothesis

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Statistical tests commonly assume that:

• the data are normally distributed
• the groups that are being compared have similar variance
• the data are independent

If your data does not meet these assumptions you might still be able to use a nonparametric statistical test , which have fewer requirements but also make weaker inferences.

A test statistic is a number calculated by a  statistical test . It describes how far your observed data is from the  null hypothesis  of no relationship between  variables or no difference among sample groups.

The test statistic tells you how different two or more groups are from the overall population mean , or how different a linear slope is from the slope predicted by a null hypothesis . Different test statistics are used in different statistical tests.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Discrete and continuous variables are two types of quantitative variables :

• Discrete variables represent counts (e.g. the number of objects in a collection).
• Continuous variables represent measurable amounts (e.g. water volume or weight).

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Choosing the Right Statistical Test | Types & Examples. Scribbr. Retrieved April 15, 2024, from https://www.scribbr.com/statistics/statistical-tests/

Is this article helpful?

Rebecca Bevans

Other students also liked, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, normal distribution | examples, formulas, & uses, what is your plagiarism score.