hypothesis testing formula t test

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

An Introduction to t Tests | Definitions, Formula and Examples

Published on January 31, 2020 by Rebecca Bevans . Revised on June 22, 2023.

A t test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from one another.

• The null hypothesis ( H 0 ) is that the true difference between these group means is zero.
• The alternate hypothesis ( H a ) is that the true difference is different from zero.

Table of contents

When to use a t test, what type of t test should i use, performing a t test, interpreting test results, presenting the results of a t test, other interesting articles, frequently asked questions about t tests.

A t test can only be used when comparing the means of two groups (a.k.a. pairwise comparison). If you want to compare more than two groups, or if you want to do multiple pairwise comparisons, use an   ANOVA test  or a post-hoc test.

The t test is a parametric test of difference, meaning that it makes the same assumptions about your data as other parametric tests. The t test assumes your data:

• are independent
• are (approximately) normally distributed
• have a similar amount of variance within each group being compared (a.k.a. homogeneity of variance)

If your data do not fit these assumptions, you can try a nonparametric alternative to the t test, such as the Wilcoxon Signed-Rank test for data with unequal variances .

Prevent plagiarism. Run a free check.

When choosing a t test, you will need to consider two things: whether the groups being compared come from a single population or two different populations, and whether you want to test the difference in a specific direction.

One-sample, two-sample, or paired t test?

• If the groups come from a single population (e.g., measuring before and after an experimental treatment), perform a paired t test . This is a within-subjects design .
• If the groups come from two different populations (e.g., two different species, or people from two separate cities), perform a two-sample t test (a.k.a. independent t test ). This is a between-subjects design .
• If there is one group being compared against a standard value (e.g., comparing the acidity of a liquid to a neutral pH of 7), perform a one-sample t test .

One-tailed or two-tailed t test?

• If you only care whether the two populations are different from one another, perform a two-tailed t test .
• If you want to know whether one population mean is greater than or less than the other, perform a one-tailed t test.
• Your observations come from two separate populations (separate species), so you perform a two-sample t test.
• You don’t care about the direction of the difference, only whether there is a difference, so you choose to use a two-tailed t test.

The t test estimates the true difference between two group means using the ratio of the difference in group means over the pooled standard error of both groups. You can calculate it manually using a formula, or use statistical analysis software.

T test formula

The formula for the two-sample t test (a.k.a. the Student’s t-test) is shown below.

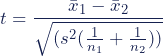
In this formula, t is the t value, x 1 and x 2 are the means of the two groups being compared, s 2 is the pooled standard error of the two groups, and n 1 and n 2 are the number of observations in each of the groups.

A larger t value shows that the difference between group means is greater than the pooled standard error, indicating a more significant difference between the groups.

You can compare your calculated t value against the values in a critical value chart (e.g., Student’s t table) to determine whether your t value is greater than what would be expected by chance. If so, you can reject the null hypothesis and conclude that the two groups are in fact different.

T test function in statistical software

Most statistical software (R, SPSS, etc.) includes a t test function. This built-in function will take your raw data and calculate the t value. It will then compare it to the critical value, and calculate a p -value . This way you can quickly see whether your groups are statistically different.

In your comparison of flower petal lengths, you decide to perform your t test using R. The code looks like this:

Download the data set to practice by yourself.

Sample data set

If you perform the t test for your flower hypothesis in R, you will receive the following output:

The output provides:

• An explanation of what is being compared, called data in the output table.
• The t value : -33.719. Note that it’s negative; this is fine! In most cases, we only care about the absolute value of the difference, or the distance from 0. It doesn’t matter which direction.
• The degrees of freedom : 30.196. Degrees of freedom is related to your sample size, and shows how many ‘free’ data points are available in your test for making comparisons. The greater the degrees of freedom, the better your statistical test will work.
• The p value : 2.2e-16 (i.e. 2.2 with 15 zeros in front). This describes the probability that you would see a t value as large as this one by chance.
• A statement of the alternative hypothesis ( H a ). In this test, the H a is that the difference is not 0.
• The 95% confidence interval . This is the range of numbers within which the true difference in means will be 95% of the time. This can be changed from 95% if you want a larger or smaller interval, but 95% is very commonly used.
• The mean petal length for each group.

When reporting your t test results, the most important values to include are the t value , the p value , and the degrees of freedom for the test. These will communicate to your audience whether the difference between the two groups is statistically significant (a.k.a. that it is unlikely to have happened by chance).

You can also include the summary statistics for the groups being compared, namely the mean and standard deviation . In R, the code for calculating the mean and the standard deviation from the data looks like this:

flower.data %>% group_by(Species) %>% summarize(mean_length = mean(Petal.Length), sd_length = sd(Petal.Length))

In our example, you would report the results like this:

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Chi square test of independence
• Statistical power
• Descriptive statistics
• Degrees of freedom
• Pearson correlation
• Null hypothesis

Methodology

• Double-blind study
• Case-control study
• Research ethics
• Data collection
• Hypothesis testing
• Structured interviews

Research bias

• Hawthorne effect
• Unconscious bias
• Recall bias
• Halo effect
• Self-serving bias
• Information bias

A t-test is a statistical test that compares the means of two samples . It is used in hypothesis testing , with a null hypothesis that the difference in group means is zero and an alternate hypothesis that the difference in group means is different from zero.

A t-test measures the difference in group means divided by the pooled standard error of the two group means.

In this way, it calculates a number (the t-value) illustrating the magnitude of the difference between the two group means being compared, and estimates the likelihood that this difference exists purely by chance (p-value).

Your choice of t-test depends on whether you are studying one group or two groups, and whether you care about the direction of the difference in group means.

If you are studying one group, use a paired t-test to compare the group mean over time or after an intervention, or use a one-sample t-test to compare the group mean to a standard value. If you are studying two groups, use a two-sample t-test .

If you want to know only whether a difference exists, use a two-tailed test . If you want to know if one group mean is greater or less than the other, use a left-tailed or right-tailed one-tailed test .

A one-sample t-test is used to compare a single population to a standard value (for example, to determine whether the average lifespan of a specific town is different from the country average).

A paired t-test is used to compare a single population before and after some experimental intervention or at two different points in time (for example, measuring student performance on a test before and after being taught the material).

A t-test should not be used to measure differences among more than two groups, because the error structure for a t-test will underestimate the actual error when many groups are being compared.

If you want to compare the means of several groups at once, it’s best to use another statistical test such as ANOVA or a post-hoc test.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). An Introduction to t Tests | Definitions, Formula and Examples. Scribbr. Retrieved March 25, 2024, from https://www.scribbr.com/statistics/t-test/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, what is your plagiarism score.

• Math Formulas
• T Test Formula

T-Test Formula

The t-test is any statistical hypothesis test in which the test statistic follows a Student’s t-distribution under the null hypothesis. It can be used to determine if two sets of data are significantly different from each other, and is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known.

T-test uses means and standard deviations of two samples to make a comparison. The formula for T-test is given below:

\begin{array}{l}\qquad t=\frac{\bar{X}_{1}-\bar{X}_{2}}{s_{\bar{\Delta}}} \\ \text { where } \\ \qquad s_{\bar{\Delta}}=\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}} \\ \end{array}

Where, \(\begin{array}{l}\overline{x}\end{array} \) = Mean of first set of values \(\begin{array}{l}\overline{x}_{2}\end{array} \)  = Mean of second set of values \(\begin{array}{l}S_{1}\end{array} \)   = Standard deviation of first set of values \(\begin{array}{l}S_{2}\end{array} \)   = Standard deviation of second set of values \(\begin{array}{l}n_{1}\end{array} \)   = Total number of values in first set \(\begin{array}{l}n_{2}\end{array} \)   = Total number of values in second set.

The formula for standard deviation is given by:

Where, x = Values given \(\begin{array}{l}\overline{x}\end{array} \) = Mean n = Total number of values.

T-Test Solved Examples

Question 1: Find the t-test value for the following two sets of values: 7, 2, 9, 8 and 1, 2, 3, 4?

Formula for standard deviation:  \(\begin{array}{l}S=\sqrt{\frac{\sum\left(x-\overline{x}\right)^{2}}{n-1}}\end{array} \)

Number of terms in first set:  \(\begin{array}{l}n_{1}\end{array} \) = 4

Mean for first set of data: \(\begin{array}{l}\overline{x}_{1}\end{array} \) = 6.5

Construct the following table for standard deviation:

Standard deviation for the first set of data: S 1 = 3.11

Number of terms in second set: n 2 = 4

Standard deviation for first set of data: \(\begin{array}{l}S_{2}\end{array} \) = 1.29

Formula for t-test value:

t = 2.3764 = 2.36 (approx)

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

t-test Calculator

When to use a t-test, which t-test, how to do a t-test, p-value from t-test, t-test critical values, how to use our t-test calculator, one-sample t-test, two-sample t-test, paired t-test, t-test vs z-test.

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

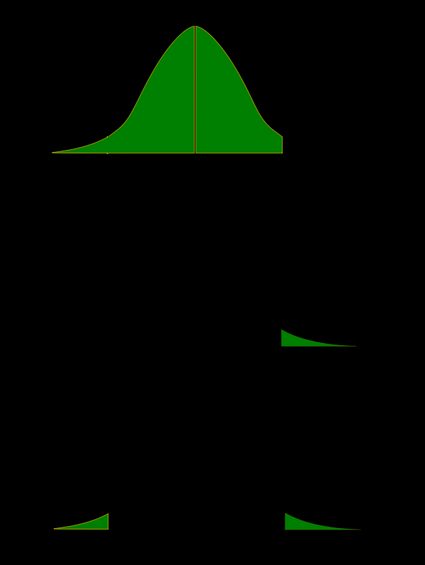
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

Bertrand's paradox

Confusion matrix, plant spacing, secretary problem (valentine's day).

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

• Search Search Please fill out this field.

What Is a T-Test?

Understanding the t-test, using a t-test, which t-test to use.

• T-Test FAQs
• Fundamental Analysis

T-Test: What It Is With Multiple Formulas and When To Use Them

Read how this calculation can be used for hypothesis testing in statistics

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

A t-test is an inferential statistic used to determine if there is a significant difference between the means of two groups and how they are related. T-tests are used when the data sets follow a normal distribution and have unknown variances, like the data set recorded from flipping a coin 100 times.

The t-test is a test used for hypothesis testing in statistics and uses the t-statistic, the t-distribution values, and the degrees of freedom to determine statistical significance.

Key Takeaways

• A t-test is an inferential statistic used to determine if there is a statistically significant difference between the means of two variables.
• The t-test is a test used for hypothesis testing in statistics.
• Calculating a t-test requires three fundamental data values including the difference between the mean values from each data set, the standard deviation of each group, and the number of data values.
• T-tests can be dependent or independent.

Investopedia / Sabrina Jiang

A t-test compares the average values of two data sets and determines if they came from the same population. In the above examples, a sample of students from class A and a sample of students from class B would not likely have the same mean and standard deviation. Similarly, samples taken from the placebo-fed control group and those taken from the drug prescribed group should have a slightly different mean and standard deviation.

Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement. It assumes a null hypothesis that the two means are equal.

Using the formulas, values are calculated and compared against the standard values. The assumed null hypothesis is accepted or rejected accordingly. If the null hypothesis qualifies to be rejected, it indicates that data readings are strong and are probably not due to chance.

The t-test is just one of many tests used for this purpose. Statisticians use additional tests other than the t-test to examine more variables and larger sample sizes. For a large sample size, statisticians use a  z-test . Other testing options include the chi-square test and the f-test.

Consider that a drug manufacturer tests a new medicine. Following standard procedure, the drug is given to one group of patients and a placebo to another group called the control group. The placebo is a substance with no therapeutic value and serves as a benchmark to measure how the other group, administered the actual drug, responds.

After the drug trial, the members of the placebo-fed control group reported an increase in average life expectancy of three years, while the members of the group who are prescribed the new drug reported an increase in average life expectancy of four years.

Initial observation indicates that the drug is working. However, it is also possible that the observation may be due to chance. A t-test can be used to determine if the results are correct and applicable to the entire population.

Four assumptions are made while using a t-test. The data collected must follow a continuous or ordinal scale, such as the scores for an IQ test, the data is collected from a randomly selected portion of the total population, the data will result in a normal distribution of a bell-shaped curve, and equal or homogenous variance exists when the standard variations are equal.

T-Test Formula

Calculating a t-test requires three fundamental data values. They include the difference between the mean values from each data set, or the mean difference, the standard deviation of each group, and the number of data values of each group.

This comparison helps to determine the effect of chance on the difference, and whether the difference is outside that chance range. The t-test questions whether the difference between the groups represents a true difference in the study or merely a random difference.

The t-test produces two values as its output: t-value and degrees of freedom . The t-value, or t-score, is a ratio of the difference between the mean of the two sample sets and the variation that exists within the sample sets.

The numerator value is the difference between the mean of the two sample sets. The denominator is the variation that exists within the sample sets and is a measurement of the dispersion or variability.

This calculated t-value is then compared against a value obtained from a critical value table called the T-distribution table. Higher values of the t-score indicate that a large difference exists between the two sample sets. The smaller the t-value, the more similarity exists between the two sample sets.

A large t-score, or t-value, indicates that the groups are different while a small t-score indicates that the groups are similar.

Degrees of freedom refer to the values in a study that has the freedom to vary and are essential for assessing the importance and the validity of the null hypothesis. Computation of these values usually depends upon the number of data records available in the sample set.

Paired Sample T-Test

The correlated t-test, or paired t-test, is a dependent type of test and is performed when the samples consist of matched pairs of similar units, or when there are cases of repeated measures. For example, there may be instances where the same patients are repeatedly tested before and after receiving a particular treatment. Each patient is being used as a control sample against themselves.

This method also applies to cases where the samples are related or have matching characteristics, like a comparative analysis involving children, parents, or siblings.

The formula for computing the t-value and degrees of freedom for a paired t-test is:

T = mean 1 − mean 2 s ( diff ) ( n ) where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom \begin{aligned}&T=\frac{\textit{mean}1 - \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\&\textbf{where:}\\&\textit{mean}1\text{ and }\textit{mean}2=\text{The average values of each of the sample sets}\\&s(\text{diff})=\text{The standard deviation of the differences of the paired data values}\\&n=\text{The sample size (the number of paired differences)}\\&n-1=\text{The degrees of freedom}\end{aligned} ​ T = ( n ) ​ s ( diff ) ​ mean 1 − mean 2 ​ where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom ​

Equal Variance or Pooled T-Test

The equal variance t-test is an independent t-test and is used when the number of samples in each group is the same, or the variance of the two data sets is similar.

The formula used for calculating t-value and degrees of freedom for equal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 n 1 + n 2 − 2 × 1 n 1 + 1 n 2 where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value} = \frac{ mean1 - mean2 }{\frac {(n1 - 1) \times var1^2 + (n2 - 1) \times var2^2 }{ n1 +n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets}\\&var1 \text{ and } var2 = \text{Variance of each of the sample sets}\\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = n 1 + n 2 − 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 ​ × n 1 1 ​ + n 2 1 ​ ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = n1 + n2 - 2 \\ &\textbf{where:}\\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set ​

Unequal Variance T-Test

The unequal variance t-test is an independent t-test and is used when the number of samples in each group is different, and the variance of the two data sets is also different. This test is also called Welch's t-test.

The formula used for calculating t-value and degrees of freedom for an unequal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( v a r 1 n 1 + v a r 2 n 2 ) where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)}}}\\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets} \\&var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = ( n 1 v a r 1 ​ + n 2 v a r 2 ​ ) ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = ( v a r 1 2 n 1 + v a r 2 2 n 2 ) 2 ( v a r 1 2 n 1 ) 2 n 1 − 1 + ( v a r 2 2 n 2 ) 2 n 2 − 1 where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = \frac{ \left ( \frac{ var1^2 }{ n1 } + \frac{ var2^2 }{ n2 } \right )^2 }{ \frac{ \left ( \frac{ var1^2 }{ n1 } \right )^2 }{ n1 - 1 } + \frac{ \left ( \frac{ var2^2 }{ n2 } \right )^2 }{ n2 - 1}} \\ &\textbf{where:}\\ &var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 − 1 ( n 1 v a r 1 2 ​ ) 2 ​ + n 2 − 1 ( n 2 v a r 2 2 ​ ) 2 ​ ( n 1 v a r 1 2 ​ + n 2 v a r 2 2 ​ ) 2 ​ where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

The following flowchart can be used to determine which t-test to use based on the characteristics of the sample sets. The key items to consider include the similarity of the sample records, the number of data records in each sample set, and the variance of each sample set.

Image by Julie Bang © Investopedia 2019

Example of an Unequal Variance T-Test

Assume that the diagonal measurement of paintings received in an art gallery is taken. One group of samples includes 10 paintings, while the other includes 20 paintings. The data sets, with the corresponding mean and variance values, are as follows:

Though the mean of Set 2 is higher than that of Set 1, we cannot conclude that the population corresponding to Set 2 has a higher mean than the population corresponding to Set 1.

Is the difference from 19.4 to 21.6 due to chance alone, or do differences exist in the overall populations of all the paintings received in the art gallery? We establish the problem by assuming the null hypothesis that the mean is the same between the two sample sets and conduct a t-test to test if the hypothesis is plausible.

Since the number of data records is different (n1 = 10 and n2 = 20) and the variance is also different, the t-value and degrees of freedom are computed for the above data set using the formula mentioned in the Unequal Variance T-Test section.

The t-value is -2.24787. Since the minus sign can be ignored when comparing the two t-values, the computed value is 2.24787.

The degrees of freedom value is 24.38 and is reduced to 24, owing to the formula definition requiring rounding down of the value to the least possible integer value.

One can specify a level of probability (alpha level, level of significance,  p ) as a criterion for acceptance. In most cases, a 5% value can be assumed.

Using the degree of freedom value as 24 and a 5% level of significance, a look at the t-value distribution table gives a value of 2.064. Comparing this value against the computed value of 2.247 indicates that the calculated t-value is greater than the table value at a significance level of 5%. Therefore, it is safe to reject the null hypothesis that there is no difference between means. The population set has intrinsic differences, and they are not by chance.

How Is the T-Distribution Table Used?

The T-Distribution Table is available in one-tail and two-tails formats. The former is used for assessing cases that have a fixed value or range with a clear direction, either positive or negative. For instance, what is the probability of the output value remaining below -3, or getting more than seven when rolling a pair of dice? The latter is used for range-bound analysis, such as asking if the coordinates fall between -2 and +2.

What Is an Independent T-Test?

The samples of independent t-tests are selected independent of each other where the data sets in the two groups don’t refer to the same values. They may include a group of 100 randomly unrelated patients split into two groups of 50 patients each. One of the groups becomes the control group and is administered a placebo, while the other group receives a prescribed treatment. This constitutes two independent sample groups that are unpaired and unrelated to each other.

What Does a T-Test Explain and How Are They Used?

A t-test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment has an effect on the population of interest, or whether two groups are different from one another.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

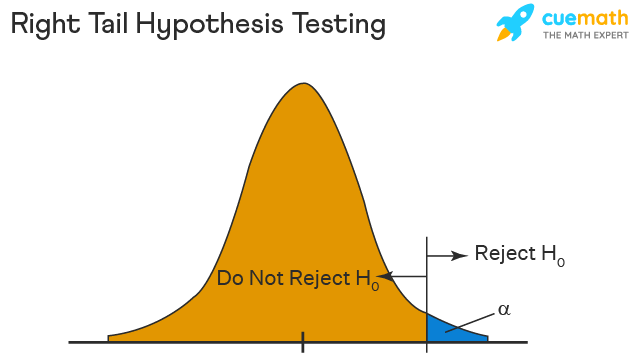
Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

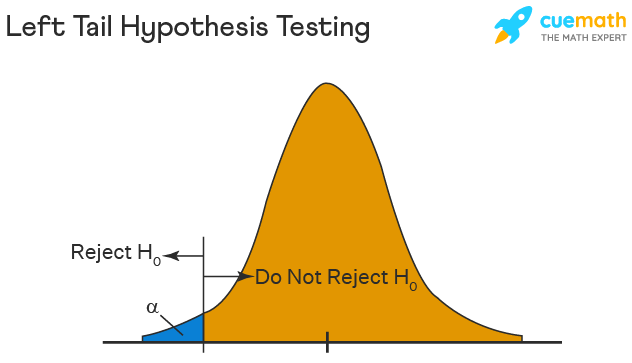
Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

• Maths Notes Class 12
• NCERT Solutions Class 12
• RD Sharma Solutions Class 12
• Maths Formulas Class 12
• Maths Previous Year Paper Class 12
• Class 12 Syllabus
• Class 12 Revision Notes
• Physics Notes Class 12
• Chemistry Notes Class 12
• Biology Notes Class 12
• What are the rational numbers between 3 and 5?
• In how many ways a committee of 3 can be made from a total of 10 members?
• Which kind of angle is between the smallest and the largest?
• How many bit strings of length 9 have exactly 4 0's?
• What are non negative real numbers?
• Is 0.5 a whole number?
• What is 2i equal to?
• What are the six trigonometry functions?
• What is the magnitude of the complex number 3 - 2i?
• What are the uses of arithmetic mean?
• How to find the ratio in which a point divides a line?
• Evaluate sin 35° sin 55° - cos 35° cos 55°
• If tan (A + B) = √3 and tan (A – B) = 1/√3, 0° B, then find A and B
• How to find the vertex angle?
• What is the most likely score from throwing two dice?
• If two numbers a and b are even, then prove that their sum a + b is even
• State whether Every whole number is a natural number or not
• How to convert a complex number to exponential form?
• What happens when you subtract two negatives?

T-Test in Statistics

T-Test is a method used in statistics to derive some conclusions for a population which is based upon some sample data using values of means and variances. Here, a population refers to the entities or a group of entities that are in our study of interest. And, the sample data is a subset of the population that we use to draw conclusions about the population as a whole. 

For example, if we want to know the average weight of mangoes grown on a farm, the population would consist of all the mangoes that grew on the farm. However, it would be time-consuming to weigh each mango. Instead, we could take a sample of mangoes from trees at different locations on the farm and use their weights to make inferences about the average weight of all the mangoes grown on the farm.

T-Test Definition

The T-test can be defined as a statistical method that uses some formulae, depending upon the analysis that is required to be carried out, to compare the average values of two data sets. It helps us to determine whether the data sets belong to the same population or not. This comparison is often called a T-test.

T-Test Formula

There is no specific formula for T-Test, as it is divided into various types such as One Samples T-Test, Independent Samples T-test, etc. which are used as per the need. The formula used in each type is defined under the specific headings. The formula allows us to calculate a T-value which helps to make a comparison between the data sets.

Value of T-Test

The value obtained by substituting required values to the t-test formula is called the t-value. A larger T-value implies that the sets belong to a different population, while a smaller T-value implies that they belong to the same population. The formula is comprised of the values of mean, standard deviation and variance of the data sets under consideration.

How to Calculate T Value in T-Test

To calculate T-value in T-Test, we can use the following steps:

Step 1: To perform a T-test, two hypotheses namely the null hypothesis and the alternative hypothesis are defined which have different meanings for different types of T-tests. Step 2: And, a value for the level of significance is defined which signifies the probability of making a Type I error, which implies the rejection of the null hypothesis while it is actually true. Commonly used values of level of significance are 0.05 (5%) and 0.01 (1%). Step 3: A higher significance level, such as α = 0.05, provides a higher tolerance for Type I errors, meaning that it is more likely to reject the null hypothesis even when it is true. Step 4: On the other hand, a lower significance level, such as α = 0.01, reduces the risk of Type I errors but it may increase the chances of accepting the null hypothesis when it is actually false, resulting in a Type II error.

Types of T-Test

Let us take a look at each type of T-test and the procedure to perform them, one by one, as follows:

• One Sample T-test
• Independent Samples T-test
• Paired Samples T-test

Let’s discuss these types in detail as follows:

One Sample T-Test

As the name implies, this test is used when we have one data set for a sample and we need to determine whether this data set belongs to a particular population or not. The mean value for the population data must be known in this case. The formula to determine T-value, in this case, is as follows:

t = (x̄ – μ) / (σ / √n) Where, t is the t-value, x̄ is the Sample mean, μ is the Population mean, σ is the Sample standard deviation, and n is the Sample size.

Steps to Calculate T Value One Sample T-Test 

To perform the One Sample T-test, the steps listed below are generally followed:

Step 1: State a null hypothesis and an alternative hypothesis. The null hypothesis assumes that the sample mean and the known population mean (μ) are equal, while the other assumes that the sample mean is different from the population mean. Step 2: Define values for the level of significance (α) and the degree of freedom (df). The degree of freedom equals (n – 1) for this case. Step 3: Calculate the t-value using the formula stated above by putting all the known values of the sample mean (x̄), sample standard deviation (σ), the population mean (μ), and the sample size (n). Step 4: Determine the associated p-value with the t-value using a t-distribution table. Step 5: Compare the p-value to the level of significance. If the p-value is less than the level of significance, reject the null hypothesis and conclude that the sample mean is significantly different from the population mean. Otherwise, conclude that there is no significant difference between the sample mean and the population mean.

Independent Samples T-Test

As the name suggests, an Independent samples T-test is used when we need to compare the statistical means of two independent samples or groups. It helps us determine whether there is a significant difference between the means of the two groups. If there is a significant difference, it suggests that the groups likely have different population means; otherwise, they have the same population means. For example, when an investigation aims to determine if there is a significant difference in the mean scores between athletes who follow a specific training camp (Team A) and those who do not (Team B), an independent samples t-test can be conducted.

This test is performed using either of two assumptions made about variances of the samples, one assumes equal variances for the sample and the other assumes unequal variances for the samples.

Unequal Variances T-Test

Under this test, variances of two groups considered are assumed to be equal. This is appropriate when we are uncertain about the variances of the two groups considered. The formula to calculate T-value, in this case, is as follows:

t = (x̄ 1 – x̄ 2 ) / √((σ 1 2 /n 1 ) + (σ 2 2 /n 2 )) Where, x̄ 1 is the sample mean of Group 1, x̄ 2 is the sample mean of Group 2, σ 1 is the sample standard deviation of Group 1, σ 2 is the sample standard deviation of Group 2, n 1 is the sample size of Group 1, and n 2 sample size of Group 2.

Equal Variance T-Test

Under this test, variances of two groups considered are assumed to be equal. This is appropriate when we have some assurance about variances of data considered to be equal. The formula to calculate T-value, in this case, is similar to the above formula with a slight change that σ 1 = σ 2 = σ.

t = (x̄ 1 – x̄ 2 ) / √(σ 2 (1/n 1 + 1/n 2 )) Where, x̄ 1 is the sample mean of Group 1, x̄ 2 is the sample mean of Group 2, σ is the standard deviation of both groups, n 1 is the sample size of Group 1, and n 2 sample size of Group 2.

T Test for Independent Samples

The steps listed below are generally followed to perform this test:

Step 1: State a null hypothesis and an alternate hypothesis. The null hypothesis assumes that the means of the two groups are equal (x̄ 1 = x̄ 2 ), while the other assumes that the means of the two groups are significantly different (x̄ 1 ≠ x̄ 2 ). Step 2: Define the values for the level of significance (α) and the degrees of freedom (df). The degree of freedom equals (n 1 + n 2 – 2) in this case. Step 3: Calculate the t-value from the formula defined above after obtaining the required data related to each group. Step 4: Find the critical t-value from a t-distribution table with the corresponding degrees of freedom and level of significance. Step 5: If the calculated t-value is greater than the critical t-value, then reject the null hypothesis. This indicates that there is a significant difference between the means of the two groups. Otherwise, the null hypothesis is not rejected. And, this suggests that there is no significant difference between the means of the two groups.

Paired Samples T-Test

The Paired samples t-test is used when we want to compare the means of two related groups or samples. For example, we may use this test to compare the average scores of the players of an athletics team before and after a training program. To calculate the t-value in this case, the following formula is used,

t = (x̄ d – μ d ) / (σ d / √n) Where: t is the t-value, x̄ d is the sample mean of the differences between the paired observations, μ d isthe population mean difference, σ d is the sample standard deviation of the differences, n is the number of paired observations.

Steps for Paired Samples T-Test

Following are the steps to perform this type of T-test:

Step 1: State the null hypothesis which assumes that there is no significant difference between the statistical means of the paired observations (μ d = 0) while the alternative hypothesis assumes that there is a significant difference between the statistical means of the paired observations (μ d ≠ 0). Step 2: Match each observation in one group with a corresponding observation in the other group. Step 3: Calculate the differences between each paired observation and then, calculate the mean of the differences (x̄ d ), and the sample standard deviation of the differences (σ d ). Furthermore, calculate the t-value from the formula. Step 4: Obtain the critical t-value from a t-distribution table corresponding to the chosen level of significance (α) and degree of freedom (df). The degree of freedom (df) equals (n – 1) in this case. Step 5: If the calculated t-value is greater than the critical t-value, then reject the null hypothesis. This indicates a significant difference in the sample before and after the intervention. Otherwise, it can be concluded that there is no significant difference in the sample before and after the intervention.

T-Distribution Table

A T-Distribution table is used to obtain a critical t-value that is used as a reference to the calculated t-value for obtaining further results. Critical t-value depends on values of the level of significance and degrees of freedom. A concise form of the table for critical t-values is as follows for your reference:

Solved Problems of T-Test Formula

Problem 1: Determine whether the average weight of a sample of 20 mangoes is significantly different from the population’s average weight of 70 grams. The sample mean weight is 70.55 grams, and the sample standard deviation is 2.82 grams. Use one sample T-test.

To perform a T-test, first of all, we define two hypotheses: Null hypothesis: The sample mean weight of mangoes is equal to the known population mean. (i.e., 70 grams). Alternative hypothesis: The sample mean weight of mangoes is not equal to the known mean value. Then, determine the degrees of freedom (d f ): d f = n – 1 = 20 – 1 = 19 and define the level of significance(α) as 0.05 for this case. Next, determine the t-value from the formula, t = (70.55 – 70) / (2.82 / √20) ⇒ t ≈ 1.041 From the t-distribution table, we find 1.041 < 2.093. (i.e. p-value for α = 0.05). So, the null hypothesis is true. Thus, we conclude that the sample does not vary significantly from the population.

Problem 2: Determine if there is a significant difference in the average scores between the two teams. The following data is given:  Team A: Score: 65, 68, 70, 63, 67 Team B: Score: 62, 66, 69, 64, 68

According to the question, we come to know that we need to perform an Independent Samples T-test. Set up the null hypothesis and alternative hypothesis: Null hypothesis: The means of the two groups are equal (μ A = μ B ). Alternative hypothesis: The means of the two groups are not equal (μ A ≠ μ B ). Next, we calculate the sample means (x̄ A and x̄ B ) and sample standard deviations (σ A and σ B ): Team A: Sample size (n A ) = 5 Sample mean (x̄ A ) = (65 + 68 + 70 + 63 + 67) / 5 = 66.6 Sample standard deviation (σ A ) ≈ 2.607 Team B: Sample size (n B ) = 5 Sample mean (x̄ B ) = (62 + 66 + 69 + 64 + 68) / 5 = 65.8 Sample standard deviation (σ B ) ≈ 2.588 Now, we calculate the t-value using the formula: t = (x̄ A – x̄ B ) / √((σ A 2 / n A ) + (σ B 2 / n B )) ⇒ t = (66.6 – 65.8) / √{(2.607 2 /5) + (2.588 2 /5)} ⇒ t ≈ 0.296 Then, determine the degrees of freedom (df):  df = n A + n B – 2 = 5 + 5 – 2 = 8  and set the level of significance as 0.05.  From the table, we get the critical t-value as 2.306. As the calculated t-value is less than the critical t-value, we conclude that the null hypothesis is not rejected, which suggests that there is no significant difference between the average scores of the two teams.

Problem 3: You need to assess the effectiveness of a new teaching scheme by comparing the test scores of the same group of students before and after the implementation of the scheme. The following data is given: Before scores: 76, 88, 65, 56, 76 After scores: 85, 95, 75, 60, 81 Determine if there is a significant difference in the average test scores before and after the implementation of the scheme.

Here, we need to perform a Paired Samples T-test, as we need to compare data of the same sample. Set up the null hypothesis and alternative hypothesis: Null hypothesis: The population mean difference between the before and after scores are zero (μ d = 0). Alternative hypothesis: The population mean difference between the before and after scores is not zero (μ d ≠ 0). Next, calculate the differences between the paired observations: Difference (d) = After score – Before score d 1 = 85 – 76 = 9 d 2 = 95 – 88 = 7 d 3 = 75 – 65 = 10 d 4 = 60 – 56 = 4 d 5 = 81 – 76 = 5 Now, calculate the sample mean (x̄d) and sample standard deviation (σ d ) of the differences: Sample size (n) = 5 Sample mean (x̄ d ) = (d 1 + d 2 + d 3 + d 4 + d 5 ) / 5 = (9 + 7 + 10 + 4 + 5) / 5 = 7 Sample standard deviation (σ d ) ≈ 2.828 Then, calculate the t-value using the formula: t = (x̄ d – μ d ) / (σ d / √n)  ⇒ t = (7 – 0) / (2.828 / √5) ⇒ t ≈ 5.535 Next, calculate the value of degrees of freedom (df):  df = n – 1 = 5 – 1 = 4.  And, define the level of significance(α) as 0.05.  Now, from the t-distribution table, we find that the critical t-value is 2.776. As the calculated t-value is greater than the critical t-value ( 5.535 > 2.776), thus, the null hypothesis is rejected. And we conclude that there is a significant difference in the average test scores before and after the implementation of the scheme.

FAQs on T-Test Formula

Q1: what is a t-test in statistics.

T-Test is the test in tatistics to derive some conclusions for a population which is based upon some sample data using values of means and variances. 

Q2: When is a T-Test used?

The test is basically used to determine whether there is any significant difference in the statistical means of two samples of the data considered. The purpose to determine this can be to check if a sample data set belongs to the population data set, or if there is an effect of any variation on the data values before or after any specific treatment/intervention.

Q3: What are the Different Types of T-Tests?

There are three types of T-tests that are used as per the situation, listed as follows: One-sample T-test: It is used when we need to compare the mean of a single sample to a known (or assumed) population mean value. Independent T-test: It is used when we need to compare the means of two independent groups. Paired T-test: It is used to compare the means of two related or paired groups.

Q4: What does the T-Value obtain from the T-Test Formula Indicate?

The t-value indicates the magnitude of the difference between the means relative to the variability within the groups. A larger t-value suggests a greater difference between the means.

Q5: Are there any Assumptions related to Sample Data in Performing a T-Test on it?

The t-test assumes that the data within each group are normally distributed, the variances of the two groups are equal (in the case of an independent t-test), the observations are independent, and the data points represent their respective populations.

Q6: What are the Limitations of the T-Test?

The t-test assumes that the data meet the assumptions of normality, independence, and equal variances (in the case of an independent t-test). If these assumptions are not true, it can lead to inaccurate or misleading results. Also, the test is sensitive to outliers, and may not give accurate results for small sample sizes.

Please Login to comment...

• Maths-Class-12
• Mathematics
• School Learning
• WhatsApp To Launch New App Lock Feature
• Top Design Resources for Icons
• Node.js 21 is here: What’s new
• Zoom: World’s Most Innovative Companies of 2024
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.4: Hypothesis Test Examples for Proportions

• Last updated
• Save as PDF
• Page ID 11533

• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\).
• The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
• If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• \(H_{a}\) never has a symbol that contains an equal sign.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

Full Hypothesis Test Examples

Example \(\PageIndex{7}\)

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

\(H_{0}: p = 0.50\)  \(H_{a}: p \neq 0.50\)

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: \(P′ =\) the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for P′ , the estimated proportion.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P(p′ < 0.47 or p′ > 0.53) = 0.5485\nonumber \]

where \[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the \(p\text{-value})\: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(p'\) is 0.53 or more OR 0.47 or less (see the graph in Figure).

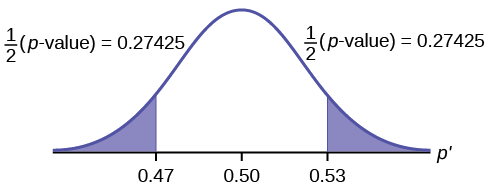
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.

\(p′ = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \(p′\) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)

Compare \(\alpha\) and the \(p\text{-value}\):

Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).

Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The \(p\text{-value}\) can easily be calculated.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(\(z\) = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{7}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

• \(H_{0} : p = 0.85\)
• \(H_{a}: p \neq 0.85\)
• \(p = 0.7554\)

Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example \(\PageIndex{8}\)

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Set up the Hypothesis Test:

\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)

Determine the distribution needed:

The random variable is \(P′ =\) proportion of households that have three cell phones.

The distribution for the hypothesis test is \(P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)\)

Exercise 9.6.8.2

a. The value that helps determine the \(p\text{-value}\) is \(p′\). Calculate \(p′\).

a. \(p' = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.

\(x = 43, n = 150\)

\(p′ = 43150\)

Exercise 9.6.8.3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise 9.6.8.4

c. What is the level of significance?

c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).

Exercise 9.6.8.5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the \(p\text{-value}\).

d. \(p\text{-value} = 0.7216\)

Exercise 9.6.8.6

e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.

e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise \(\PageIndex{8}\)

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: p = 0.92\)
• \(H_{a}: p < 0.92\)
• \(p\text{-value} = 0.0046\)

Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

• Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(p′\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{9}\)

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

\(H_{0}: p \leq 0.25\)   \(H_{a}: p > 0.25\)

In words, CLEARLY state what your random variable \(\bar{X}\) or \(P′\) represents.

\(P′ =\) The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Test Statistic: \(z = 2.3163\)

Calculate the \(p\text{-value}\) using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).

Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

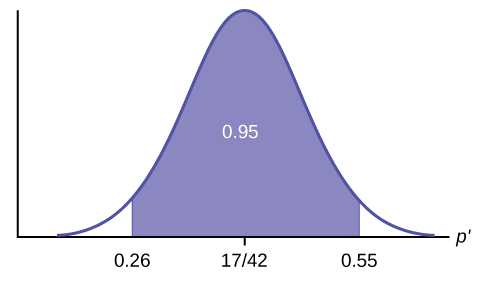
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example \(\PageIndex{11}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

• \(H_{0}: p \leq 0.00034\)
• \(H_{a}: p > 0.00034\)

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• We will be testing a sample proportion with \(x = 172\) and \(n = 420,019\). The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\), two independent outcomes, and a fixed probability of success \(p = 0.00034\). Thus we will be able to generalize our results to the population.

Figure 9.6.11.

Figure 9.6.12.

• Since the \(p\text{-value} = 0.0073\) is greater than our alpha value \(= 0.005\), we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example \(\PageIndex{12}\)

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the four-step plan.

• We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
• \(H_{0}: p = 0.00078\)
• \(H_{a}: p \neq 0.00078\)

Figure 9.6.13.

Figure 9.6.14.

• Since the \(p\text{-value}\), \(p = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at http://www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Statistics Made Easy

Paired Samples t-test: Definition, Formula, and Example

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

This tutorial explains the following:

• The motivation for performing a paired samples t-test.
• The formula to perform a paired samples t-test.
• The assumptions that should be met to perform a paired samples t-test.
• An example of how to perform a paired samples t-test.

Paired Samples t-test: Motivation

A paired samples t-test is commonly used in two scenarios:

1. A measurement is taken on a subject before and after some treatment – e.g. the max vertical jump of college basketball players is measured before and after participating in a training program.

2. A measurement is taken under two different conditions  – e.g. the response time of a patient is measured on two different drugs.

In both cases we are interested in comparing the mean measurement between two groups in which each observation in one sample can be paired with an observation in the other sample.

Paired Samples t-test: Formula

A paired samples t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

t = x diff  / (s diff /√n)

• x diff :  sample mean of the differences
• s:  sample standard deviation of the differences
• n:  sample size (i.e. number of pairs)

If the p-value that corresponds to the test statistic t with (n-1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Paired Samples t-test: Assumptions

For the results of a paired samples t-test to be valid, the following assumptions should be met:

• The participants should be selected randomly from the population.
• The differences between the pairs should be approximately normally distributed.
• There should be no extreme outliers in the differences.

Paired Samples t-test : Example

Suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of college basketball players.

To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month.

To determine whether or not the training program actually had an effect on max vertical jump, we will perform a paired samples t-test at significance level α = 0.05 using the following steps:

Step 1: Calculate the summary data for the differences.

• x diff :  sample mean of the differences =  -0.95
• s:  sample standard deviation of the differences =  1.317
• n:  sample size (i.e. number of pairs) =  20

Step 2: Define the hypotheses.

We will perform the paired samples t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

t = x diff  / (s diff /√n)  = -0.95 / (1.317/ √ 20) =  -3.226

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -3.226 and degrees of freedom = n-1 = 20-1 = 19 is  0.00445 .

Step 5: Draw a conclusion.

Since this p-value is less than our significance level α = 0.05, we reject the null hypothesis. We have sufficient evidence to say that the mean max vertical jump of players is different before and after participating in the training program.

Note:  You can also perform this entire paired samples t-test by simply using the Paired Samples t-test Calculator .

Additional Resources

The following tutorials explain how to perform a paired samples t-test using different statistical programs:

How to Perform a Paired Samples t-Test in Excel How to Perform a Paired Samples t-test in SPSS How to Perform a Paired Samples t-test in Stata How to Perform a Paired Samples t-test on a TI-84 Calculator How to Perform a Paired Samples t-test in R How to Perform a Paired Samples t-Test in Python How to Perform a Paired Samples t-Test by Hand

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *