problem solving using equations

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Solving equations & inequalities

About this unit, linear equations with variables on both sides.

• Why we do the same thing to both sides: Variable on both sides (Opens a modal)
• Intro to equations with variables on both sides (Opens a modal)
• Equations with variables on both sides: 20-7x=6x-6 (Opens a modal)
• Equation with variables on both sides: fractions (Opens a modal)
• Equation with the variable in the denominator (Opens a modal)
• Equations with variables on both sides Get 3 of 4 questions to level up!
• Equations with variables on both sides: decimals & fractions Get 3 of 4 questions to level up!

Linear equations with parentheses

• Equations with parentheses (Opens a modal)
• Reasoning with linear equations (Opens a modal)
• Multi-step equations review (Opens a modal)
• Equations with parentheses Get 3 of 4 questions to level up!
• Equations with parentheses: decimals & fractions Get 3 of 4 questions to level up!
• Reasoning with linear equations Get 3 of 4 questions to level up!

Analyzing the number of solutions to linear equations

• Number of solutions to equations (Opens a modal)
• Worked example: number of solutions to equations (Opens a modal)
• Creating an equation with no solutions (Opens a modal)
• Creating an equation with infinitely many solutions (Opens a modal)
• Number of solutions to equations Get 3 of 4 questions to level up!
• Number of solutions to equations challenge Get 3 of 4 questions to level up!

Linear equations with unknown coefficients

• Linear equations with unknown coefficients (Opens a modal)
• Why is algebra important to learn? (Opens a modal)
• Linear equations with unknown coefficients Get 3 of 4 questions to level up!

Multi-step inequalities

• Inequalities with variables on both sides (Opens a modal)
• Inequalities with variables on both sides (with parentheses) (Opens a modal)
• Multi-step inequalities (Opens a modal)
• Using inequalities to solve problems (Opens a modal)
• Multi-step linear inequalities Get 3 of 4 questions to level up!
• Using inequalities to solve problems Get 3 of 4 questions to level up!

Compound inequalities

• Compound inequalities: OR (Opens a modal)
• Compound inequalities: AND (Opens a modal)
• A compound inequality with no solution (Opens a modal)
• Double inequalities (Opens a modal)
• Compound inequalities examples (Opens a modal)
• Compound inequalities review (Opens a modal)
• Solving equations & inequalities: FAQ (Opens a modal)
• Compound inequalities Get 3 of 4 questions to level up!

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Solving equations

Here you will learn about solving equations, including linear and quadratic algebraic equations, and how to solve them.

Students will first learn about solving equations in grade 8 as a part of expressions and equations, and again in high school as a part of reasoning with equations and inequalities.

What is solving an equation?

Solving equations is a step-by-step process to find the value of the variable. A variable is the unknown part of an equation, either on the left or right side of the equals sign. Sometimes, you need to solve multi-step equations which contain algebraic expressions.

To do this, you must use the order of operations, which is a systematic approach to equation solving. When you use the order of operations, you first solve any part of an equation located within parentheses. An equation is a mathematical expression that contains an equals sign.

For example,

\begin{aligned}y+6&=11\\\\ 3(x-3)&=12\\\\ \cfrac{2x+2}{4}&=\cfrac{x-3}{3}\\\\ 2x^{2}+3&x-2=0\end{aligned}

There are two sides to an equation, with the left side being equal to the right side. Equations will often involve algebra and contain unknowns, or variables, which you often represent with letters such as x or y.

You can solve simple equations and more complicated equations to work out the value of these unknowns. They could involve fractions, decimals or integers.

Common Core State Standards

How does this relate to 8 th grade and high school math?

• Grade 8 – Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
• High school – Reasoning with Equations and Inequalities (HSA.REI.B.3) Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.

[FREE] Solving Equations Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations. 15 questions with answers to identify areas of strength and support!

How to solve equations

In order to solve equations, you need to work out the value of the unknown variable by adding, subtracting, multiplying or dividing both sides of the equation by the same value.

• Combine like terms .
• Simplify the equation by using the opposite operation to both sides.
• Isolate the variable on one side of the equation.

Solving equations examples

Example 1: solve equations involving like terms.

Solve for x.

Combine like terms.

Combine the q terms on the left side of the equation. To do this, subtract 4q from both sides.

The goal is to simplify the equation by combining like terms. Subtracting 4q from both sides helps achieve this.

After you combine like terms, you are left with q=9-4q.

2 Simplify the equation by using the opposite operation on both sides.

Add 4q to both sides to isolate q to one side of the equation.

The objective is to have all the q terms on one side. Adding 4q to both sides accomplishes this.

After you move the variable to one side of the equation, you are left with 5q=9.

3 Isolate the variable on one side of the equation.

Divide both sides of the equation by 5 to solve for q.

Dividing by 5 allows you to isolate q to one side of the equation in order to find the solution. After dividing both sides of the equation by 5, you are left with q=1 \cfrac{4}{5} \, .

Example 2: solve equations with variables on both sides

Combine the v terms on the same side of the equation. To do this, add 8v to both sides.

7v+8v=8-8v+8v

After combining like terms, you are left with the equation 15v=8.

Simplify the equation by using the opposite operation on both sides and isolate the variable to one side.

Divide both sides of the equation by 15 to solve for v. This step will isolate v to one side of the equation and allow you to solve.

15v \div 15=8 \div 15

The final solution to the equation 7v=8-8v is \cfrac{8}{15} \, .

Example 3: solve equations with the distributive property

Combine like terms by using the distributive property.

The 3 outside the parentheses needs to be multiplied by both terms inside the parentheses. This is called the distributive property.

\begin{aligned}& 3 \times c=3 c \\\\ & 3 \times(-5)=-15 \\\\ &3 c-15-4=2\end{aligned}

Once the 3 is distributed on the left side, rewrite the equation and combine like terms. In this case, the like terms are the constants on the left, –15 and –4. Subtract –4 from –15 to get –19.

Simplify the equation by using the opposite operation on both sides.

The goal is to isolate the variable, c, on one side of the equation. By adding 19 to both sides, you move the constant term to the other side.

\begin{aligned}& 3 c-19+19=2+19 \\\\ & 3 c=21\end{aligned}

Isolate the variable to one side of the equation.

To solve for c, you want to get c by itself.

Dividing both sides by 3 accomplishes this.

On the left side, \cfrac{3c}{3} simplifies to c, and on the right, \cfrac{21}{3} simplifies to 7.

The final solution is c=7.

As an additional step, you can plug 7 back into the original equation to check your work.

Example 4: solve linear equations

Combine like terms by simplifying.

Using steps to solve, you know that the goal is to isolate x to one side of the equation. In order to do this, you must begin by subtracting from both sides of the equation.

\begin{aligned} & 2x+5=15 \\\\ & 2x+5-5=15-5 \\\\ & 2x=10 \end{aligned}

Continue to simplify the equation by using the opposite operation on both sides.

Continuing with steps to solve, you must divide both sides of the equation by 2 to isolate x to one side.

\begin{aligned} & 2x \div 2=10 \div 2 \\\\ & x= 5 \end{aligned}

Isolate the variable to one side of the equation and check your work.

Plugging in 5 for x in the original equation and making sure both sides are equal is an easy way to check your work. If the equation is not equal, you must check your steps.

\begin{aligned}& 2(5)+5=15 \\\\ & 10+5=15 \\\\ & 15=15\end{aligned}

Example 5: solve equations by factoring

Solve the following equation by factoring.

Combine like terms by factoring the equation by grouping.

Multiply the coefficient of the quadratic term by the constant term.

2 x (-20) = -40

Look for two numbers that multiply to give you –40 and add up to the coefficient of 3. In this case, the numbers are 8 and –5 because 8 x -5=–40, and 8+–5=3.

Split the middle term using those two numbers, 8 and –5. Rewrite the middle term using the numbers 8 and –5.

2x^2+8x-5x-20=0

Group the terms in pairs and factor out the common factors.

2x^2+8x-5x-20=2x(x + 4)-5(x+4)=0

Now, you’ve factored the equation and are left with the following simpler equations 2x-5 and x+4.

This step relies on understanding the zero product property, which states that if two numbers multiply to give zero, then at least one of those numbers must equal zero.

Let’s relate this back to the factored equation (2x-5)(x+4)=0

Because of this property, either (2x-5)=0 or (x+4)=0

Isolate the variable for each equation and solve.

When solving these simpler equations, remember that you must apply each step to both sides of the equation to maintain balance.

\begin{aligned}& 2 x-5=0 \\\\ & 2 x-5+5=0+5 \\\\ & 2 x=5 \\\\ & 2 x \div 2=5 \div 2 \\\\ & x=\cfrac{5}{2} \end{aligned}

\begin{aligned}& x+4=0 \\\\ & x+4-4=0-4 \\\\ & x=-4\end{aligned}

The solution to this equation is x=\cfrac{5}{2} and x=-4.

Example 6: solve quadratic equations

Solve the following quadratic equation.

Combine like terms by factoring the quadratic equation when terms are isolated to one side.

To factorize a quadratic expression like this, you need to find two numbers that multiply to give -5 (the constant term) and add to give +2 (the coefficient of the x term).

The two numbers that satisfy this are -1 and +5.

So you can split the middle term 2x into -1x+5x: x^2-1x+5x-5-1x+5x

Now you can take out common factors x(x-1)+5(x-1).

And since you have a common factor of (x-1), you can simplify to (x+5)(x-1).

The numbers -1 and 5 allow you to split the middle term into two terms that give you common factors, allowing you to simplify into the form (x+5)(x-1).

Let’s relate this back to the factored equation (x+5)(x-1)=0.

Because of this property, either (x+5)=0 or (x-1)=0.

Now, you can solve the simple equations resulting from the zero product property.

\begin{aligned}& x+5=0 \\\\ & x+5-5=0-5 \\\\ & x=-5 \\\\\\ & x-1=0 \\\\ & x-1+1=0+1 \\\\ & x=1\end{aligned}

The solutions to this quadratic equation are x=1 and x=-5.

Teaching tips for solving equations

• Use physical manipulatives like balance scales as a visual aid. Show how you need to keep both sides of the equation balanced, like a scale. Add or subtract the same thing from both sides to keep it balanced when solving. Use this method to practice various types of equations.
• Emphasize the importance of undoing steps to isolate the variable. If you are solving for x and 3 is added to x, subtracting 3 undoes that step and isolates the variable x.
• Relate equations to real-world, relevant examples for students. For example, word problems about tickets for sports games, cell phone plans, pizza parties, etc. can make the concepts click better.
• Allow time for peer teaching and collaborative problem solving. Having students explain concepts to each other, work through examples on whiteboards, etc. reinforces the process and allows peers to ask clarifying questions. This type of scaffolding would be beneficial for all students, especially English-Language Learners. Provide supervision and feedback during the peer interactions.

Easy mistakes to make

• Forgetting to distribute or combine like terms One common mistake is neglecting to distribute a number across parentheses or combine like terms before isolating the variable. This error can lead to an incorrect simplified form of the equation.
• Misapplying the distributive property Incorrectly distributing a number across terms inside parentheses can result in errors. Students may forget to multiply each term within the parentheses by the distributing number, leading to an inaccurate equation.
• Failing to perform the same operation on both sides It’s crucial to perform the same operation on both sides of the equation to maintain balance. Forgetting this can result in an imbalanced equation and incorrect solutions.
• Making calculation errors Simple arithmetic mistakes, such as addition, subtraction, multiplication, or division errors, can occur during the solution process. Checking calculations is essential to avoid errors that may propagate through the steps.
• Ignoring fractions or misapplying operations When fractions are involved, students may forget to multiply or divide by the common denominator to eliminate them. Misapplying operations on fractions can lead to incorrect solutions or complications in the final answer.

Related math equations lessons

• Math equations
• Rearranging equations
• How to find the equation of a line
• Solve equations with fractions
• Linear equations
• Writing linear equations
• Substitution
• Identity math
• One step equation

Practice solving equations questions

1. Solve 4x-2=14.

Add 2 to both sides.

Divide both sides by 4.

2. Solve 3x-8=x+6.

Add 8 to both sides.

Subtract x from both sides.

Divide both sides by 2.

3. Solve 3(x+3)=2(x-2).

Expanding the parentheses.

Subtract 9 from both sides.

Subtract 2x from both sides.

4. Solve \cfrac{2 x+2}{3}=\cfrac{x-3}{2}.

Multiply by 6 (the lowest common denominator) and simplify.

Expand the parentheses.

Subtract 4 from both sides.

Subtract 3x from both sides.

5. Solve \cfrac{3 x^{2}}{2}=24.

Multiply both sides by 2.

Divide both sides by 3.

Square root both sides.

6. Solve by factoring:

Use factoring to find simpler equations.

Set each set of parentheses equal to zero and solve.

x=3 or x=10

Solving equations FAQs

The first step in solving a simple linear equation is to simplify both sides by combining like terms. This involves adding or subtracting terms to isolate the variable on one side of the equation.

Performing the same operation on both sides of the equation maintains the equality. This ensures that any change made to one side is also made to the other, keeping the equation balanced and preserving the solutions.

To handle variables on both sides of the equation, start by combining like terms on each side. Then, move all terms involving the variable to one side by adding or subtracting, and simplify to isolate the variable. Finally, perform any necessary operations to solve for the variable.

To deal with fractions in an equation, aim to eliminate them by multiplying both sides of the equation by the least common denominator. This helps simplify the equation and make it easier to isolate the variable. Afterward, proceed with the regular steps of solving the equation.

The next lessons are

• Inequalities
• Types of graph
• Coordinate plane

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Module 4: Equations and Inequalities

Using formulas to solve problems, learning outcomes.

• Set up a linear equation involving distance, rate, and time.
• Find the dimensions of a rectangle given the area.
• Find the dimensions of a box given information about its side lengths.

Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region, [latex]A=LW[/latex]; the perimeter of a rectangle, [latex]P=2L+2W[/latex]; and the volume of a rectangular solid, [latex]V=LWH[/latex]. When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.

Example: Solving an Application Using a Formula

It takes Andrew 30 minutes to drive to work in the morning. He drives home using the same route, but it takes 10 minutes longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?

This is a distance problem, so we can use the formula [latex]d=rt[/latex], where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.

First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or [latex]\frac{1}{2}[/latex] h at rate [latex]r[/latex]. His drive home takes 40 min, or [latex]\frac{2}{3}[/latex] h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance [latex]d[/latex]. A table, such as the one below, is often helpful for keeping track of information in these types of problems.

Write two equations, one for each trip.

As both equations equal the same distance, we set them equal to each other and solve for r .

We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.

The distance between home and work is 20 mi.

Analysis of the Solution

Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for [latex]r[/latex].

On Saturday morning, it took Jennifer 3.6 hours to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 hours to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?

45 [latex]\frac{\text{mi}}{\text{h}}[/latex]

Example: Solving a Perimeter Problem

The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft. greater than the width. What are the dimensions of the patio?

The perimeter formula is standard: [latex]P=2L+2W[/latex]. We have two unknown quantities, length and width. However, we can write the length in terms of the width as [latex]L=W+3[/latex]. Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides as shown below.

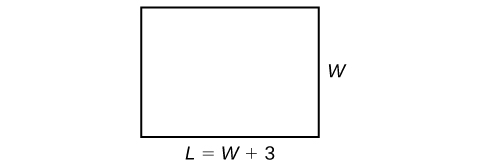
Now we can solve for the width and then calculate the length.

The dimensions are [latex]L=15[/latex] ft and [latex]W=12[/latex] ft.

Find the dimensions of a rectangle given that the perimeter is [latex]110[/latex] cm. and the length is 1 cm. more than twice the width.

L = 37 cm, W = 18 cm

Example: Solving an Area Problem

The perimeter of a tablet of graph paper is 48 in. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.

The standard formula for area is [latex]A=LW[/latex]; however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.

We know that the length is 6 in. more than the width, so we can write length as [latex]L=W+6[/latex]. Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.

Now, we find the area given the dimensions of [latex]L=15[/latex] in. and [latex]W=9[/latex] in.

The area is [latex]135[/latex] in 2 .

A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft 2 of new carpeting should be ordered?

Example: Solving a Volume Problem

Find the dimensions of a shipping box given that the length is twice the width, the height is [latex]8[/latex] inches, and the volume is 1,600 in. 3 .

The formula for the volume of a box is given as [latex]V=LWH[/latex], the product of length, width, and height. We are given that [latex]L=2W[/latex], and [latex]H=8[/latex]. The volume is [latex]1,600[/latex] cubic inches.

The dimensions are [latex]L=20[/latex] in., [latex]W=10[/latex] in., and [latex]H=8[/latex] in.

Note that the square root of [latex]{W}^{2}[/latex] would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.

Contribute!

Improve this page Learn More

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Question ID 52436. Authored by : Edward Wicks. License : CC BY: Attribution . License Terms : IMathAS Community License CC- BY + GPL
• Question ID 7679. Authored by : Tyler Wallace. License : CC BY: Attribution . License Terms : IMathAS Community License CC- BY + GPL
• Question ID 1688. Authored by : WebWork-Rochester. License : CC BY: Attribution . License Terms : IMathAS Community License CC- BY + GPL

Problem solving with equations

Solving a task usually consists of finding the value of some quantity by logical reasoning and calculations. For example, find the speed, time, distance, mass of an object, or amount of something.

Such a task can be solved by using an equation. To do this, the desired value is denoted by a variable, then by logical reasoning the equation is composed and solved. After solving the equation, you check to see if the solution to the equation satisfies the conditions of the task.

Writing expressions containing the unknown

The solution of the task is accompanied by the composition of the equation to this task. At the initial stage of studying tasks it is desirable to learn to make up letter expressions describing this or that situation in life. This stage is not complicated and can be studied in the process of solving the task itself.

Consider a few situations that can be written down using a mathematical expression.

Task 1. The father is x years old. Mom is two years younger. The son is three times younger than the father. Write the age of each using expressions.

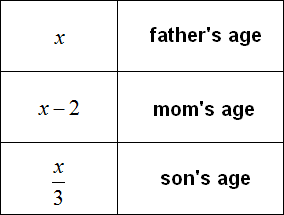
Task 2. Father is x years old, mother is 2 years younger than father. Son is 3 times younger than father, daughter is 3 times younger than mother. Write the age of each using expressions.

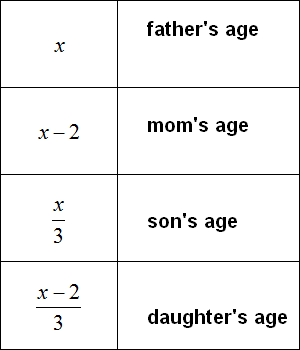
Task 3. Father is x years old, mother is 3 years younger than father. The son is 3 times younger than the father, the daughter is 3 times younger than the mother. How old are each of them if the total age of the father, mother, son, and daughter is 92?

In this task, in addition to writing down the expressions, we need to calculate the age of each family member.

First, write down the age of each family member using expressions. We will take the age of the father as the variable x, and then use that variable to make the rest of the expressions:

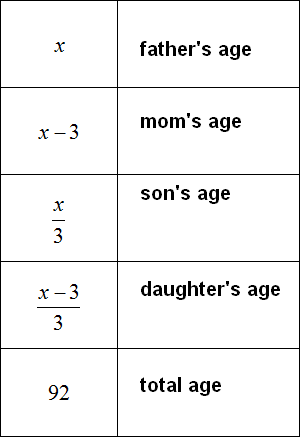
Now let's determine the age of each family member. To do this, we need to make and solve an equation. We have all the components of the equation ready. The only thing left to do is to put them together.

The total age of 92 was obtained by adding the ages of the father, mother, son and daughter:

father + mother + son + daughter = 92

For each age, we made up a mathematical expression. These expressions will be the components of our equation. Let's assemble our equation according to this diagram and the table above. That is, replace the words father, mother, son, daughter with their corresponding expression in the table:

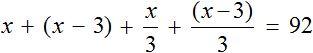
The expression corresponding to mom's age x - 3 was put in brackets for clarity.

Now let's solve the resulting equation. To begin with, you can open the brackets where you can:

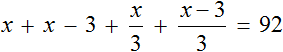
To free the equation from fractions, multiply both parts by 3

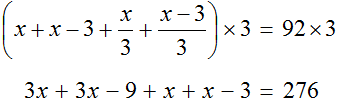
Solve the resulting equation using the known identity transformations:

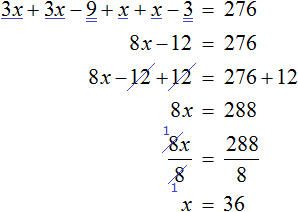
We found the value of variable x. This variable was responsible for the age of the father. So the age of the father is 36 years old.

Knowing the age of the father, we can calculate the ages of the other family members. To do this, substitute the value of variable x in those expressions that correspond to the age of a particular family member.

The task said that my mother is 3 years younger than my father. We denoted her age by the expression x - 3. The value of the variable x is now known, and to calculate mom's age, substitute the found value 36 instead of x in the expression x - 3

x - 3 = 36 - 3 = 33 years old mom.

The age of the other family members is determined similarly:

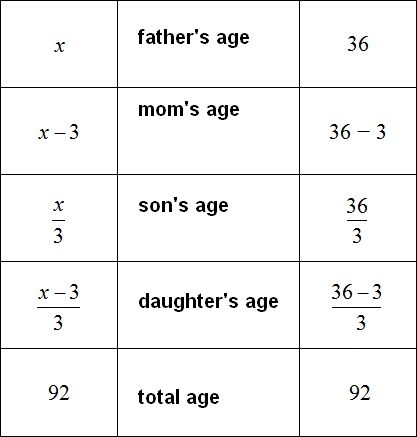
Task 4. A kilogram of caviar costs x dollars. Write an expression that calculates how many kilograms of caviar you can buy for $300.

Task 5. x dollars was used to buy 5 kilograms of strawberries. Write an expression that calculates how many dollars one kilogram of strawberries costs.

Task 6. Tom, John, and Leo went to the cafeteria during recess and bought a large pizza and a glass of fresh juice. The large pizza cost x dollars and the coffee cost $15. Determine the cost of the pizza if you know that $120 was paid for everything?

Of course, this task is simple and can be solved without resorting to an equation. To do this, subtract the cost of three glasses of juice from $120 (15 × 3), and divide the result by 3

But our goal is to make an equation to the task and solve this equation. So, the cost of a large pizza is x dollars. Only three of them were bought. So if we increase the cost by three times, we get an expression describing how many dollars were paid for the three large pizzas.

3x — the cost of three large pizzas

And the cost of three glasses of juice can be written as 15 × 3. 15 is the cost of one glass of juice, and 3 is the multiplier (Tom, John, and Leo) that triples that cost.

Under the terms of the task, $120 is paid for everything. We already have an approximate scheme of what needs to be done:

Cost of three large pizzas + cost of three glasses of fresh juice = $120

The expressions describing the cost of three pizzas and three glasses of juice are ready. These are expressions 3x and 15 × 3. Use the scheme to make an equation and solve it:

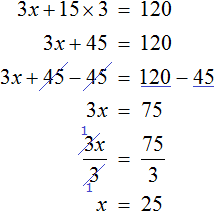
So, the cost of one large pizza is $25.

The task is solved correctly only if the equation to it is written correctly. Unlike ordinary equations by which we learn to find the roots, problem-solving equations have their own specific application. Each component of such an equation can be described in verbal form. When making an equation, it is imperative that we understand why we are including one component or another and why it is needed.

You must also remember that after solving the equation, the left-hand side will have to equal the right-hand side. The equation composed must not contradict this idea.

Let's imagine that the equation is a scale with two bowls and a screen showing the state of the scale.

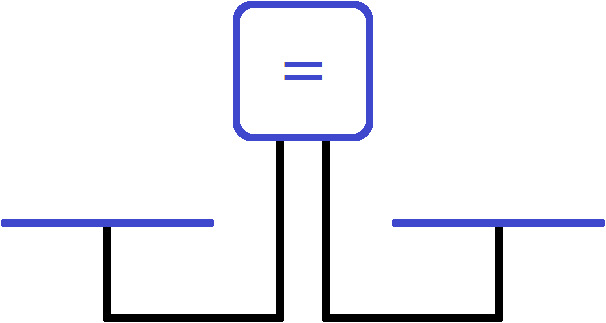
At this point, the screen shows an equal sign. It is clear why the left bowl is equal to the right bowl - there is nothing on the scales. The state of the scales and the absence of anything on the bowls will be recorded with the following equality:

Put a watermelon on the left side of the scale:

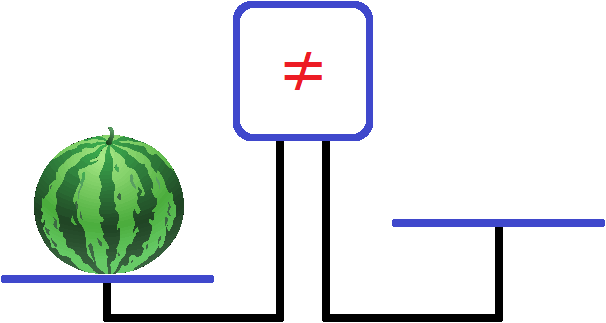
The left bowl outweighed the right bowl and the screen sounded an alarm, showing a not equal sign ( ≠ ). This sign indicates that the left bowl is not equal to the right bowl.

Now let's try to solve the problem. Let's find out how much the watermelon on the left bowl weighs. But how can we find this out? Our scales are only for checking if the left bowl is equal to the right one.

Equations come to the rescue. Recall that an equation contains a variable whose value must be found. The scale in this case is the equation itself, and the mass of the watermelon is the variable, the value of which needs to be found. Our goal is to get this equation right. That is, to align the scales so that we can calculate the mass of the watermelon.

To level the scales, we can put some heavy object on the right-hand bowl. For example, let's put a weight of 7 kilograms there.

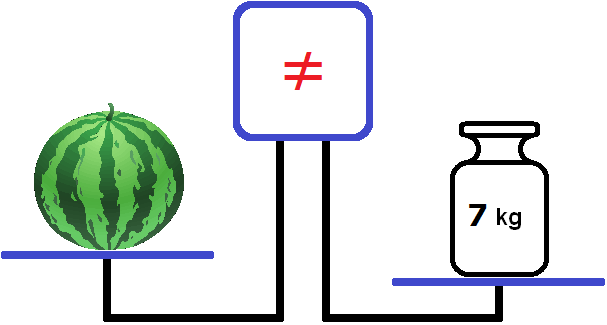
Now the right bowl outweighs the left bowl. The screen still shows that the bowls are not equal.

Let's try to put a weight of 4 kg on the left bowl

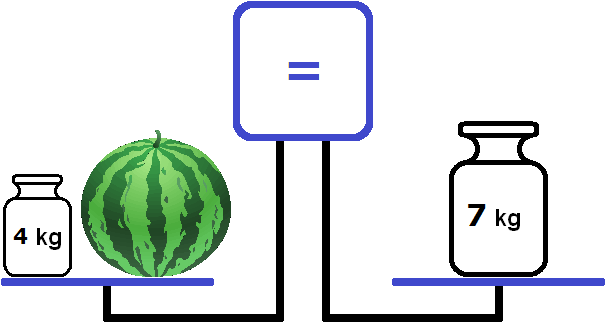
Now the scales are aligned. In the picture you can see that the left bowl is at the level of the right bowl. And the screen shows an equal sign. This sign says that the left bowl is equal to the right bowl.

So we got an equation - an equality that contains the unknown. The left bowl is the left side of the equation, consisting of the components 4 and the variable x (watermelon mass), and the right bowl is the right side of the equation, consisting of the component 7.

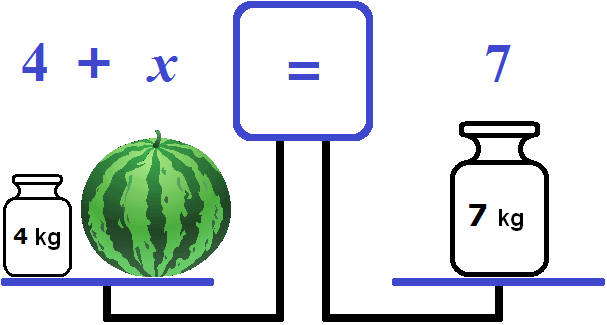
Well, it's not hard to guess that the root of the equation 4 + x = 7 is 3. So the mass of the watermelon is 3 kg.

The same is true for the other tasks. To find some unknown value, various elements are added to the left or right side of the equation: terms, multipliers, expressions. In school tasks, these elements may already be given. All that remains is to structure them correctly and construct the equation. In this example, we were trying weights of different weights to calculate the mass of the watermelon.

Naturally, the data given in the task must first be reduced to a form in which they can be included in the equation.

Consider the following task. The father's age is equal to the age of the son and daughter together. The son is twice as old as the daughter and twenty years younger than the father. How old are each?

The daughter's age can be denoted by x. If the son is twice as old as the daughter, his age will be denoted by 2x. The condition of the problem says that together the age of the daughter and the son are equal to the age of the father. So the father's age will be denoted by the sum x + 2x

In the expression x + 2x you can give like terms. Then the age of the father will be denoted as 3x

Now let's make an equation. We need to get an equation where we can find the unknown x. Let's use weights. On the left hand side put the age of the father (3x), and on the right hand side put the age of the son (2x)

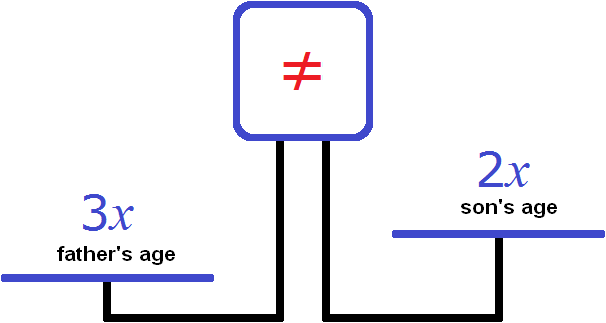
It is clear why the left bowl outweighs the right and why the screen shows the sign ( ≠ ). After all, it is logical that the age of the father is greater than the age of the son.

But we need to equalize the scales to be able to calculate the unknown x. To do this we need to add some number to the right-hand scale. What exact number is given in the task. The condition said that the son is 20 years younger than his father. So 20 years is the number to put on the scale.

The scales will even out if we add these 20 years to the right side of the scale. In other words, raise the son to the age of the father.

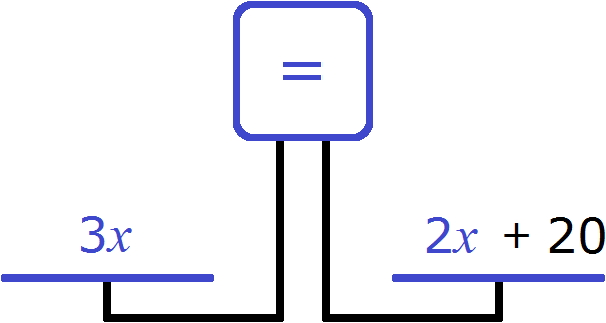
Now the scales are aligned. We got the equation 3x = 2x + 20, which is easy to solve:

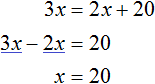
At the beginning of this task, we used the variable x to represent our daughter's age. Now we found the value of this variable. The daughter is 20 years old.

Next, it was said that the son is two years older than the daughter, so the son is (20 × 2), that is, 40 years old.

Finally, let's calculate the age of the father. It was said in the problem that he is equal to the sum of the ages of the son and daughter, that is, (20 + 40) years old.

Let's return to the middle of the task and note one point. When we put the age of the father and the age of the son on the scale, the left cup outweighed the right

But we solved this problem by adding another 20 years to the right-hand scale. As a result, the scales aligned and we got the equality 3x = 2x + 20

But we could not add those 20 years to the right cup, but subtract them from the left. We would have obtained equality and in that case

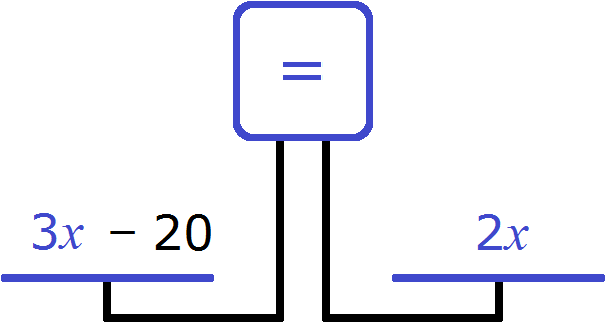
This time you get the equation 3x -20 = 2x. The root of the equation is still 20

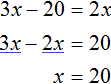
That is, the equations 3x = 2x + 20 and 3x -20 = 2x are equipotent. And we remember that equal equations have the same roots. If you look closely at these two equations, you can see that the second equation is obtained by moving the number 20 from the right side to the left side with the opposite sign. And this action, as stated in the previous lesson, does not change the roots of the equation.

Also note that at the beginning of the task, the ages of each family member could be given by other expressions.

Let's solve this equation

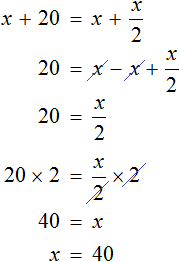
In other words, the task can be solved by different methods. So you should not be discouraged if you cannot solve a particular problem. But you should keep in mind that there are the easiest ways to solve the problem. It is possible to get to the city center by different routes, but there is always the most convenient, fastest and safest route.

Examples of problem solving

Task 1. There are a total of 30 notebooks in two packs. If two notebooks were moved from the first stack to the second stack, the first stack would contain twice as many notebooks as the second stack. How many notebooks were in each pack?

Denote by x the number of notebooks that were in the first stack. If the total number of notebooks was 30, and the variable x is the number of notebooks in the first stack, then the number of notebooks in the second stack will be denoted by the expression 30 - x. That is, from the total number of notebooks we subtract the number of notebooks in the first stack, and thus we obtain the number of notebooks in the second stack.

Further it is said that if you move two notebooks from the first pack to the second pack, there will be twice as many notebooks in the first pack. So let's remove two notebooks from the first stack

and add these two notebooks to the second pack

The expressions from which we will compose the equation now take the following form:

Let's try to make an equation out of the available expressions. Put both stacks of notebooks on the scales

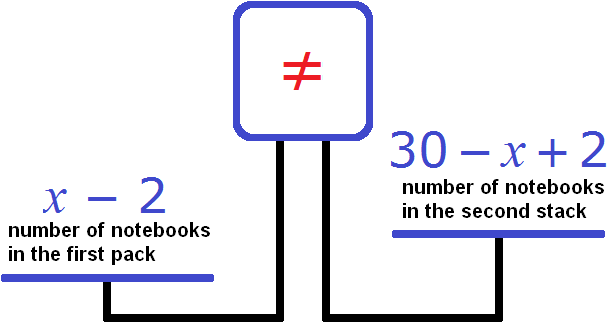
The left bowl is heavier than the right one. This is because the problem statement says that after taking two notebooks from the first stack and putting them into the second stack, the number of notebooks in the first stack became twice as many as in the second stack.

To equalize the scales and get the equation, let's double the right-hand side. To do this, multiply it by 2

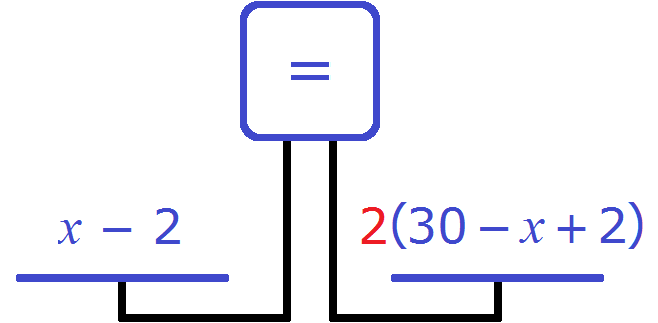
We obtain the equation x-2 = 2(30 - x +2) . Solve this equation:

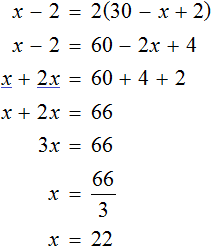
We denoted the first packet by the variable x. Now we have found its value. The variable x is 22. So there were 22 notebooks in the first stack.

And we denoted the second tutu by the expression 30 - x, and since the value of the variable x is now known, we can calculate the number of notebooks in the second tutu. It is equal to 30 - 22, i.e. 8 pieces.

Task 2. Two people were peeling potatoes. One peeled two potatoes per minute and the other peeled three potatoes. Together they peeled 400 pieces. How long did each work, if the second worked 25 minutes longer than the first?

Denote by x the time the first person worked. Since the second person worked 25 minutes longer than the first person, his time will be denoted by x + 25

The first worker peeled 2 potatoes per minute, and since he worked x minutes, he peeled a total of 2x potatoes.

The second person peeled three potatoes per minute, and since he worked x + 25 minutes, he peeled a total of 3(x + 25) potatoes.

Together they peeled 400 potatoes

From the available components let us make and solve the equation. The left side of the equation will be the potatoes peeled by each person, and the right side will be their sum:

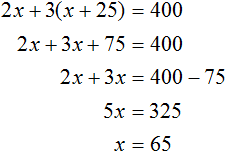
At the beginning of this task, we used the variable x to denote the working time of the first person. Now we found the value of this variable. The first person worked for 65 minutes.

And the second person worked x + 25 minutes, and since the value of the variable x is now known, we can calculate the working time of the second person - it is 65 + 25, that is, 90 minutes.

The task from the Russian algebra textbook . (Their currency is rubles and kopecks (like dollars and cents))

Of the varieties of tea is a mixture of 32 kg. A kilogram of the first grade costs 8 rubles, and the second grade 6 rubles. 50 kop. How many kilos of both varieties, if a kilo of mixture costs (no profit and loss) 7 rubles. 10 kop.

Denote by x the mass of first grade tea. Then the mass of second grade tea will be denoted by the expression 32 - x

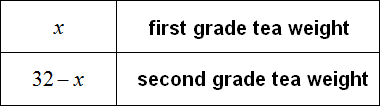
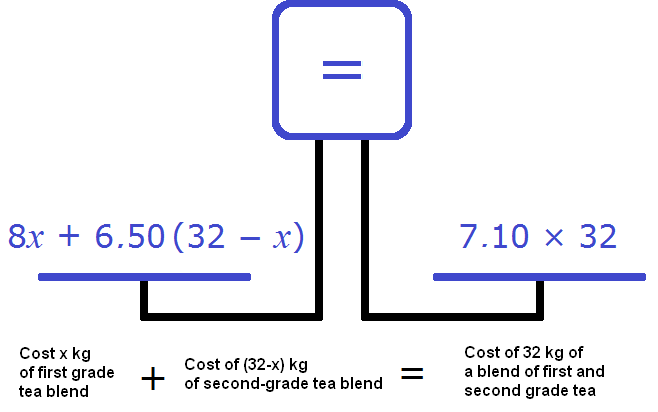
A kilogram of first grade tea costs 8 rubles. If you multiply these eight rubles by the number of kilograms of first grade tea, you can find out how many rubles it cost x kilograms of first grade tea.

A kg of second class tea costs 6 roubles. 50 kopecks. If the price is 6 rubles. 50 kopecks times 32 - x, we will find out how much it cost 32 - x kg of tea of the second sort.

The condition says that a kilogram of mixture costs 7 rubles. 10 kopecks. All in all 32 kg of the mixture were produced. Multiply 7 rubles. 10 kopecks by 32 we can find out how much 32 kg of the mixture costs.

The expressions from which we will make the equation now take the following form:

Let's try to make an equation out of the available expressions. Let's put the cost of mixtures of first and second grade teas on the left scale, and on the right scale let's put the cost of 32 kg of mixture, i.e. the total cost of the mixture, which includes both varieties of tea:

We get the equation 8x + 6.50(32 - x) = 7.10 * 32 . Let's solve it:

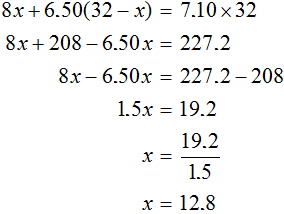
At the beginning of this task, we used the variable x to denote the mass of the first grade tea. Now we have found the value of this variable. The variable x is 12.8. This means that 12.8 kg of first grade tea was used to make the mixture.

We have used the expression 32 - x to represent the mass of second-grade tea, and since the value of the variable x is now known, we can calculate the mass of second-grade tea. It is 32 - 12.8, i.e. 19.2. This means that 19.2 kg of second grade tea were used to prepare the mixture.

Some tasks may involve topics that a person may not have studied. This task is one of those tasks. It touches on the concepts of distance, speed, and time. Accordingly, to solve such a problem, it is necessary to have an idea of the things mentioned in the problem. In our case, it is necessary to know what represents distance, speed and time.

In the task we need to find the distances of the two roads. We have to make an equation that will allow us to calculate these distances.

Let's remember how distance, speed, and time are interrelated. Each of these quantities can be described using a letter equation:

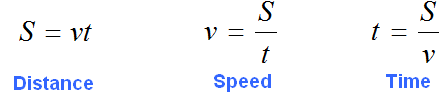
We will use the right side of one of these equations to make our own equation. To find out which one, go back to the text of the problem and pay attention to the following point:

Now let's make an equation out of the available expressions

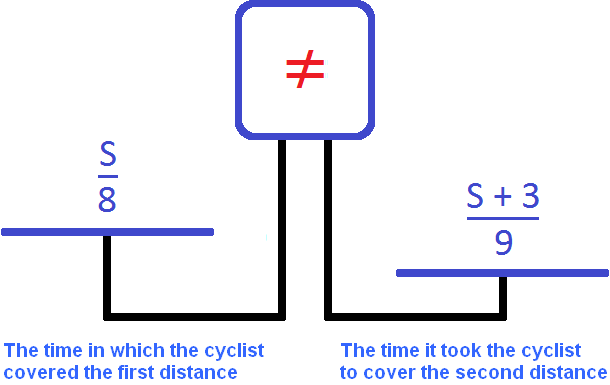
Through the variable S we denoted the distance of the first road. Now we have found the value of this variable. The variable S is 15. So the distance of the first road is 15 km.

And the distance of the second road is S + 3. Since the value of the variable S is now known, we can calculate the distance of the second road. This distance is equal to the sum of 15 + 3, that is 18 km.

Task 4. Two cars walk along the highway at the same speed. If the first increases the speed by 10 km/h, and the second decreases the speed by 10 km/h, then the first car will pass the same distance in 2 h as the second car did in 3 h. At what speed are the cars traveling?

Denote by v the speed of each car. Further in the problem there are hints: increase the speed of the first car by 10 km/h, and decrease the speed of the second car by 10 km/h. Let us use this hint

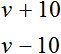
Further it is said that at such speeds (increased and decreased by 10 km/h) the first car will cover the same distance in 2 hours as the second car did in 3 hours. The phrase "as much" can be understood as "the distance traveled by the first car will be equal to the distance traveled by the second car" .

The distance, as we remember, is determined by the formula S = vt. We are interested in the right part of this letter equation - it will allow us to make an equation containing the variable v.

So, at speed v + 10 km/h, the first car will travel 2(v+10) km and the second car will travel 3(v - 10) km. Under this condition, the cars will travel the same distance, so it is sufficient to connect the two expressions with an equal sign to obtain the equation. Then we obtain the equation 2(v+10) = 3(v - 10). Solve it:

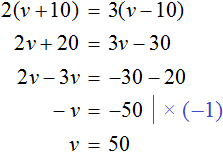
In the task condition it was said that the cars go at the same speed. We denoted this speed by the variable v. Now we have found the value of this variable. The variable v is 50. So the speed of both cars was 50 km/h.

Task 5. In 9 hours along the river the ship travels the same distance as in 11 hours against the stream. Find the boat's own speed if the speed of the river flow is 2 km/h.

Denote by v the boat's own speed. The speed of the river flow is 2 km/h. The speed of the ship along the river will be v + 2 km/h, and against the current - (v - 2) km/h.

The statement of the task says that the boat takes the same distance in 9 hours upstream as it took 11 hours upstream. The phrase "the same distance" can be understood as "the distance traveled by the ship upstream in 9 hours is equal to the distance traveled by the ship against the river in 11 hours". That is, the distances will be the same.

The distance is determined by the formula S = vt. Let's use the right part of this letter equation to make our own equation.

So, the boat will travel 9(v + 2) km in 9 hours upstream, and 11(v - 2) km in 11 hours upstream. Since both expressions describe the same distance, let's equate the first expression to the second one. The resulting equation is 9(v + 2) = 11(v - 2) 

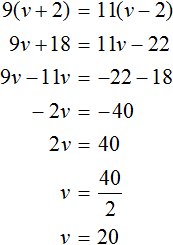
So the proper speed of the motorboat is 20 km/h.

When solving tasks, it is a useful habit to determine in advance on which set the solution is sought.

Suppose that in the task we needed to find the time in which the pedestrian travels the specified path. We denoted the time by the variable t, then made an equation containing this variable and found its value.

We know from practice that the time of motion of an object can take both integer and fractional values, for example 2 h, 1.5 h, and 0.5 h. Then we can say that the solution of this problem is searched for on the set of rational numbers Q, because each value of 2 h, 1.5 h, 0.5 h can be represented as a fraction.

So after you denote an unknown quantity by a variable, it is useful to specify which set this quantity belongs to. In our example, time t belongs to the set of rational numbers Q

You can also introduce a restriction for the variable t, stating that it can only take positive values. Indeed, if an object has spent a certain amount of time on the path, then this time cannot be negative. Therefore next to the expression t ∈ Q we specify that its value must be greater than zero:

t  ∈  R , t  > 0

If by solving the equation we get a negative value for the variable t, then we can conclude that the problem is solved incorrectly, because this solution will not satisfy the condition t ∈ Q, t > 0.

Another example. If we were solving a task that required us to find the number of people to do a particular job, we would denote this number by the variable x. In such a task the solution would be searched for on the set of natural numbers

x  ∈ N

Indeed, the number of people is a whole number, e.g., 2 people, 3 people, 5 people. But not 1.5 (one whole person and half a person) or 2.3 (two whole persons and three tenths of a person).

Here we could specify that the number of people must be greater than zero, but the numbers included in the set of natural numbers N are themselves positive and greater than zero. In this set there are no negative numbers and no number 0. Therefore the expression x > 0 can be omitted. 

Task 6. A team of 2.5 times as many painters as carpenters arrived to repair a school. Soon the foreman added four more painters to the brigade, and transferred two carpenters to another site. As a result, there were four times as many painters as carpenters in the brigade. How many painters and how many carpenters were in the brigade originally

Denote by x the carpenters who arrived initially for repairs.

The number of carpenters is an integer greater than zero. Therefore let us specify that x belongs to the set of natural numbers

x  ∈ N

There were 2.5 times more painters than carpenters. Therefore, the number of painters will be denoted as 2.5x.

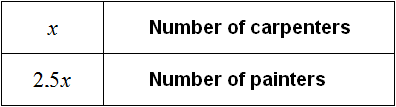
It goes on to say that the foreman included four more painters in the crew, and transferred two carpenters to another site. Let's do the same for our expressions. Reduce the number of carpenters by 2

And the number of painters will increase by 4

Now the number of carpenters and painters will be denoted by the following expressions:

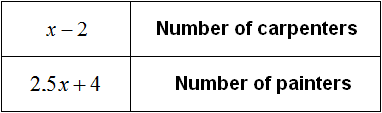
Let's try to make an equation out of the available expressions:

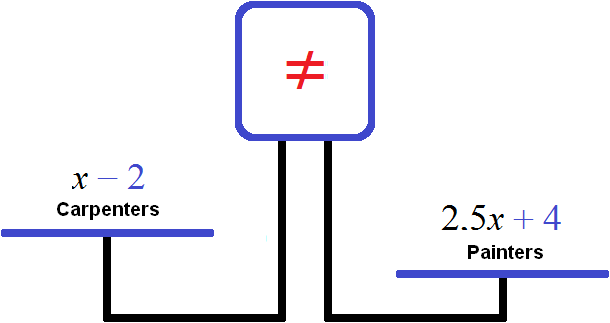
The right bowl is larger because after adding four more painters to the brigade and moving two carpenters to another site, the number of painters in the brigade is 4 times more than the number of carpenters. To equalize the scales, you need to quadruple the left bowl:

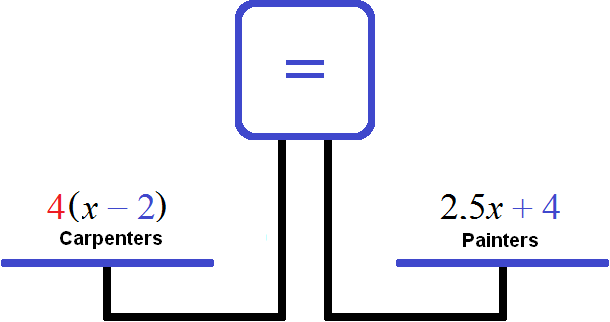
The variable x was used to represent the original number of carpenters. Now we have found the value of this variable.  The variable x is equal to 8. So there were 8 carpenters in the team originally.

The number of painters was expressed as 2.5x, and since the value of the variable x is now known, we can calculate the number of painters, which is 2.5 × 8, that is, 20.

Go back to the beginning of the task and make sure that the condition x ∈ N is satisfied. The variable x is 8, and the elements of the set of natural numbers N are all numbers starting with 1, 2, 3 and so on to infinity. The same set includes the number 8, which we found.

8  ∈ N

The same can be said of the number of painters. The number 20 belongs to the set of natural numbers:

20  ∈ N

To understand the essence of the task and to correctly compose the equation, it is not necessary to use the model of scales with bowls. You can use other models: segments, tables, diagrams. You can come up with your own model, which would describe the essence of the task well.

Task 9. 30% of the milk was poured out of the can. This left 14 liters of milk in the can. How many liters of milk was in the can originally?

We need to find the original number of liters in the can. Let's represent the number of liters as a line and sign this line as X

It is said that 30% of the milk was poured out of the beaker. Let's draw an approximate figure of 30%

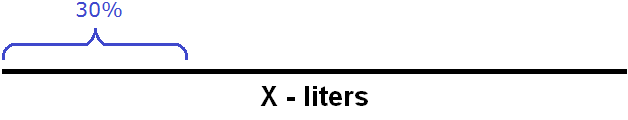
A percentage is, by definition, one hundredth of something. If 30% of the milk is poured, the other 70% is left in the can. This 70% is the 14 liters in the problem. Let's draw a picture of the remaining 70%

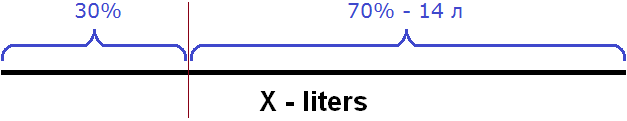
Now you can make an equation. Recall how to find the percentage of a number. To do this, the total amount of something is divided by 100 and the result is multiplied by the number of percentages you are looking for. Note that 14 liters, which is 70 percent, can be obtained in the same way: the original number of liters X divided by 100 and the result multiplied by 70. Equate all this to the number 14

Or get a simpler equation: write 70% as 0.70, then multiply by X and equate that expression to 14

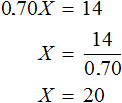
So originally there were 20 liters of milk in the can.

Task 9. Two alloys of gold and silver are taken. One has the quantity of these metals in the ratio of 1 : 9, and the other 2 : 3. How much of each alloy do you need to take to get 15 kg of a new alloy in which the gold and silver would be 1 : 4?

Let's first try to find out how much gold and silver will be contained in 15 kg of the new alloy. The task says that the content of these metals should be 1 : 4, that is, one part of the alloy should contain gold, and four parts should contain silver. Then the total number of parts in the alloy will be 1 + 4 = 5, and the mass of one part will be 15 : 5 = 3 kg.

Let's determine how much gold is contained in 15 kg of the alloy. To do this, multiply 3 kg by the number of parts of gold:

3 kg × 1 = 3 kg

Let's determine how much silver will be contained in 15 kg of alloy:

3 kg × 4 = 12 kg

So an alloy with a mass of 15 kg will contain 3 kg of gold and 12 kg of silver. Now let's go back to the original alloys. We have to use each of them. Denote by x the mass of the first alloy, and the mass of the second alloy can be denoted by 15 - x

Express in percentages all the ratios given in the problem and fill in the following table with them:

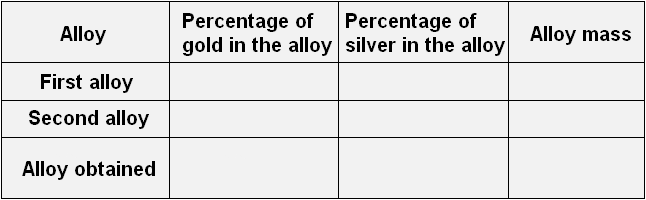
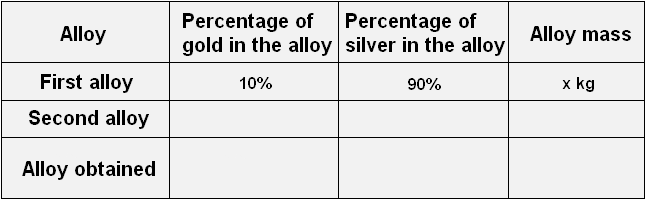
Let's transfer these data to the table. Let's enter 10% in the first line in the column "percentage of gold in the alloy" , 90% in the first line in the column "percentage of silver in the alloy" , and in the last column "mass of the alloy" we will enter the variable x, because that is how we designated the mass of the first alloy:

Let's transfer these data to the table. Let's enter 40% in the second line in the column "percentage of gold in the alloy", 60% in the second line in the column "percentage of silver in the alloy", and in the last column "mass of the alloy" let's enter the expression 15 - x, because that is how we denoted the mass of the second alloy:

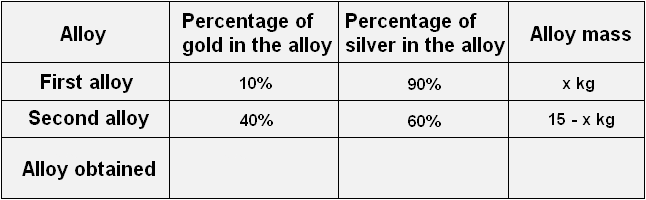
Now you can use this table to make equations. Recall the tasks of concentration, alloys, and mixtures . If we separately add up the gold of both alloys and equate this sum to the mass of gold of the resulting alloy, we can find out what the value of x equals.

Further, for convenience we will express percentages in decimals.

The first alloy had 0.10x gold and the second alloy had 0.40(15 - x) gold. Then the mass of gold in the resulting alloy will be the sum of the masses of gold of the first and second alloys and this mass is 20% of the new alloy. And 20% of the new alloy is 3 kg of gold, calculated earlier. The resulting equation is 0.10x + 0.40(15 - x) = 3 . Let us solve this equation:

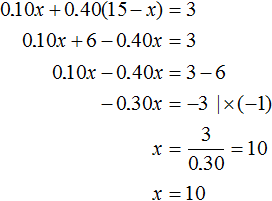
Initially we denoted by x the mass of the first alloy. Now we have found the value of this variable. The variable x is 10. And the mass of the second alloy we denoted by 15 - x, and since the value of the variable x is now known, we can calculate the mass of the second alloy, it is equal to 15 - 10 = 5 kg.

So in order to obtain a new alloy with a mass of 15 kg in which gold and silver would be 1 : 4, we would have to take 10 kg of the first alloy and 5 kg of the second alloy.

The equation could also be made using the second column of the resulting table. Then we would get the equation 0.90x + 0.60(15 - x) = 12 . The root of this equation is also 10.

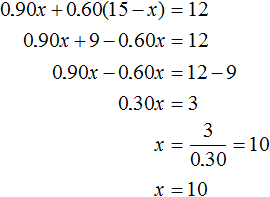
Task 10. There is an ore from two layers with copper grades of 6% and 11%. How much poor ore must be taken to get 20 tons with a copper content of 8% when mixed with the rich ore?

Denote by x the mass of poor ore. Since 20 tons of ore are to be obtained, 20 - x will be taken from the rich ore. Since the copper content in the poor ore is 6%, x tons of ore will contain 0.06x tons of copper. The rich ore has a copper content of 11%, and 20 - x tons of rich ore will contain 0.11(20 - x) tons of copper.

The resulting 20 tons of ore should have a copper content of 8%. This means that 20 tons of ore will contain 20 × 0.08 = 1.6 tons of copper.

Add 0.06x and 0.11(20 - x) and equate the sum to 1.6. We obtain the equation 0.06x + 0.11(20 - x) = 1.6

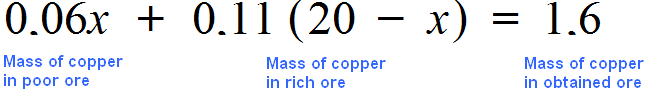
Let's solve this equation:

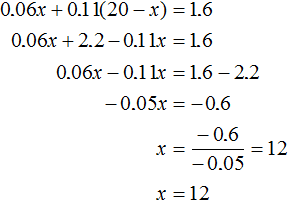
So, to get 20 tons of ore with 8% copper content, you need to take 12 tons of poor ore. The rich ore will be taken 20 - 12 = 8 tons.

Task 11. By increasing the average speed from 250 to 300 meters/minute, the athlete began to run the distance 1 minute faster. What is the length of the distance?

The length of the course (or distance of the course) can be described by the following letter equation:

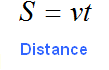
Let's use the right side of this equation to make our own equation. Initially, the athlete ran the distance at a speed of 250 meters per minute. At this speed, the length of the course would be described by the expression 250t

Then, the athlete increased her speed to 300 metres per minute. At this speed, the length of the course would be described by the expression 300t

Note that the length of the course is a constant. Whether the athlete increases her speed or decreases it, the length of the distance will remain the same.

This allows us to equate 250t with 300t, since both describe the same length.

250 t = 300 t

But the problem says that at a speed of 300 meters per minute, the athlete began to run the distance 1 minute faster. In other words, at 300 meters per minute, the running time will decrease by one. Therefore, in the equation 250t = 300t on the right hand side, the time should be reduced by one:

We get the simplest equation. Let's solve it:

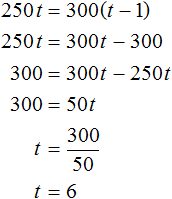
At a speed of 250 meters per minute, the athlete runs the distance in 6 minutes. Knowing the speed and time, you can determine the length of the course:

S = 250 × 6 = 1500 m

And at 300 meters per minute, the athlete runs the distance in t - 1, that is, in 5 minutes. As stated earlier, the length of the distance does not change:

S  = 300 × 5 = 1500 m

Task 12. A rider catches up with a pedestrian 15 km ahead of him. In how many hours will the rider catch up with the pedestrian, if the first rides 10 km every hour and the second rides only 4 km?

This task is a motion task . It can be solved by determining the speed of approach and dividing the initial distance between the rider and the pedestrian by that speed.

The speed of convergence is determined by subtracting the slower speed from the faster speed:

10 km/h - 4 km/h = 6 km/h (approach speed)

With each hour, the distance of 15 kilometers will decrease by 6 kilometers. To find out when it is completely shortened (when the rider catches up with the pedestrian), divide 15 by 6

15 : 6 = 2,5 h

2.5 hours is two whole hours and a half hour. And half an hour is 30 minutes. So the rider will catch up with the pedestrian in two hours and 30 minutes.

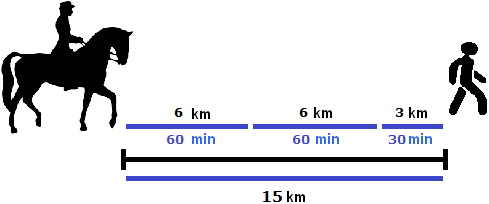
Let's solve this problem using an equation.

Assume that the pedestrian and the rider set out from the same place. The pedestrian left before the rider and managed to cover 15 km

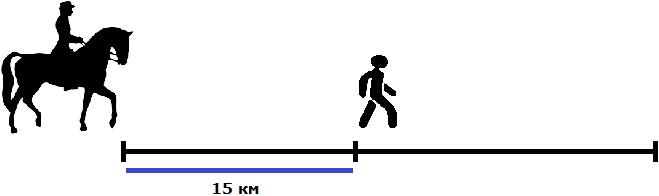
After that, the rider followed him on the road at a speed of 10 km/h. The speed of the pedestrian is only 4 km/h. This means that in some time the rider will catch up with the pedestrian. We need to find this time.

When the rider catches up with the pedestrian it will mean that they have traveled the same distance together. The distance traveled by the rider and the pedestrian is described by the following equation:

Let us use the right side of this equation to make our own equation.

The distance traveled by the rider will be described by the expression 10t. Since the pedestrian went ahead of the rider and managed to cover 15 km, the distance traveled by him will be described by the expression 4t + 15.

By the time the rider catches up with the pedestrian, they have both traveled the same distance. This allows us to equate the distances traveled by the rider and the pedestrian:

Tasks for independent decision

Train speeds in this problem are measured in kilometers per hour. Therefore, convert the 45 min specified in the problem to hours. 45 min is 0.75 h

Denote the time it takes for the freight train to arrive in the city by the variable t . Since the passenger train arrives in this city 0.75 h faster, its travel time will be denoted by the expression t −  0,75

The passenger train covered 48(t-0.75) km, and the freight train 36t km. Since we are talking about the same distance, let us equate the first expression with the second one. The resulting equation is 48(t - 0.75) = 36t. Solve it:

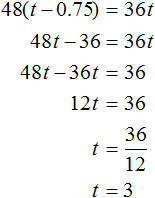
Now calculate the distance between the cities. To do this, multiply the speed of the freight train (36 km/h) by its travel time t. The value of the variable t is now known - it is equal to three hours

36 × 3 = 108 km

You can also use the speed of the passenger train to calculate the distance. But in this case the value of the variable t should be reduced by 0.75 because the passenger train spent 0.75 h less time

48 × (3 − 0,75) = 144 − 36 = 108 km

Answer: The distance between the cities is 108 km.

Let t be the time after which the cars meet. Then the first car at the time of the meeting will have traveled 65t km, and the second 60t km. Add these distances and equate them to 150. We get the equation 65t + 60t = 150

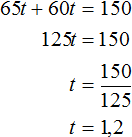
The value of the variable t is 1.2. So the cars met after 1.2 hours.

Answer: the cars met after 1.2 hours.

Let x be the number of workers in the first workshop. The second workshop had three times as many workers as the first workshop, so the number of workers in the second workshop can be denoted by the expression 3x. The third workshop had 15 fewer workers than the second workshop. Therefore, the number of workers in the third workshop can be denoted by the expression 3x - 15.

The task says that the total number of workers was 685. Therefore we can add the expressions x, 3x, 3x - 15 and equate that sum to the number 685. The result is x + 3x + (3x - 15) = 685

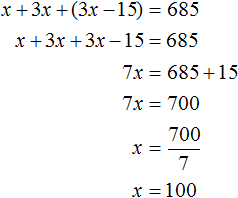
The variable x was used to denote the number of workers in the first workshop. Now we have found the value of this variable, it is 100. So there were 100 workers in the first workshop.

The second workshop had 3x workers, so 3 × 100 = 300. And the third workshop had 3x - 15, so 3 × 100 - 15 = 285

Answer: In the first shop there were 100 workers, in the second - 300, in the third - 285.

Let x motors be repaired by the first workshop. Then the second workshop had to repair 18 - x motors.

Since the first workshop fulfilled its plan by 120%, that means it repaired 1.2x motors . And the second repair shop fulfilled its plan by 125%, so it repaired 1.25(18 - x) motors.

The problem says that 22 motors were repaired. Therefore we can add the expressions 1.2x and 1.25(18 - x) , then equate that sum to the number 22. The resulting equation is 1.2x + 1.25(18 - x) = 22

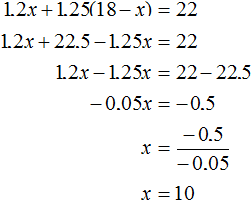
The variable x was used to denote the number of motors to be repaired by the first workshop. Now we have found the value of this variable, it is 10. So the first workshop had to repair 10 motors.

The expression 18 - x represents the number of motors to be repaired by the second workshop. So the second workshop had to repair 18 - 10 = 8 motors.

Answer: The first workshop was to repair 10 engines and the second workshop was to repair 8 engines..

Let x dollars was the price of the product before the price increase. If the price increased by 30%, it means that it increased by $0.30x dollars. After the price increase, the product began to cost $91. Add x to 0.30x and equate that sum to 91. As a result we get the equation x + 0.30x = 91

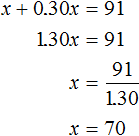
So before the price increase, the product cost $70.

Answer: Before the price increase, the product cost $70.

Let x be the initial number. Increase it by 25%. We obtain the expression x + 0.25x. Given the like terms, we obtain x + 0.25x = 1.25x.

Find what part of the original number x is from the new number 1.25x

If the new number 1.25x is 100%, and the original number x is 80% of it, then reducing the new number by 20% you can get the original number x>

Answer: to get the original number, the new number must be reduced by 20%.

Let x be the original number. Increase it by 20%. We obtain the expression x + 0.20x. Equate this sum to the number 144, so we obtain the equation x + 0.20x = 144

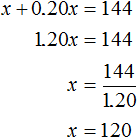
Answer: the original value of the number is 120.

Let x be the original number. Decrease it by 10%. We obtain the expression x - 0.10x. Equate this difference to the number 45, so we get the equation x - 0.10x = 45

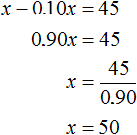
Answer: the original value of the number is 50.

Let x be the original price of the album. Decrease this price by 15%, we get x - 0.15x. Reduce the price by another $15, so we get x - 0.15x - 15. After these reductions, the album now costs $19. Equate the expression x - 0.15x - 15 to the number 19, we get the equation x - 0.15x - 15 = 19

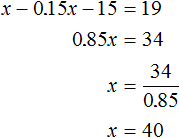
Answer: The original album price is $40.

If 80% of the mass is lost, the remaining 20% will account for 4 tons of hay. Let x tons of grass be required to produce 4 tons of hay. If 4 tons will account for 20% of the grass, then we can make the equation:

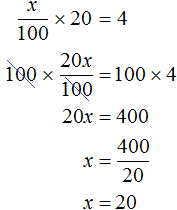
Answer: to get 4 tons of hay, you need to cut 20 tons of grass.

Let x kg of 20% salt solution be added to 1 kg of 10% salt solution.

1 kg of 10% salt solution contains 0.1 kg of salt. And x kg of 20% salt solution contains 0.20x kg of salt.

After adding x kg of the 20% solution, the new solution will contain 0.12(1 + x) kg of salt. We add 0.1 and 0.20x, then equate that sum to 0.12(1 + x). The resulting equation is 0.1 + 0.20x = 0.12(1 + x)

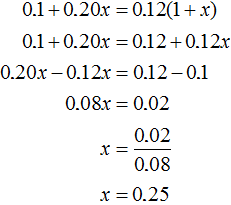
Answer: to get a 12% salt solution, you need to add 0.25 kg of 20% solution to 1 kg of 10% solution.

Let x kg of the first solution be taken. Since 25 kg of solution must be prepared, the mass of the second solution can be denoted by the expression 25 - x.

The first solution will contain 0.20x kg of salt, and the second solution will contain 0.30(25 - x) kg of salt. The resulting solution contains 25 × 0.252 = 6.3 kg of salt. Add the expressions 0.20x and 0.30(25 - x), then equate that sum to 6.3. The resulting equation is

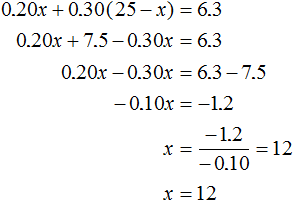
So the first solution should take 12 kg, and the second 25 - 12 = 13 kg.

Answer: the first solution should take 12 kg, and the second 13 kg.

• Basic theory of equation
• Proportions: exercises

Add comment

Name (required)

E-mail (required, but will not display)

Notify me of follow-up comments

• You are here:  
• Home >>
• 49. Problem solving with equations
• 2. Basic operations
• 3. Expressions
• 4. Substitutions in expressions
• 5. Place value for beginners
• 6. Multiplication
• 7. Division
• 8. Order of operations
• Basic Laws of Math
• 9. Basic Laws of Math
• 10. Divisors and multiples
• 11. GCD and LCM
• 12. Fractions
• 13. Actions with fractions
• 14. Mixed numbers
• 15. Comparing Fractions
• 16. Units of Measurement
• 17. Ways to use fractions
• 18. Decimals
• 19. Operations with decimals
• 20. Using decimals
• 21. Rounding numbers
• 22. Repeating Decimals
• 23. Unit conversion
• Ratios & Proportion
• 25. Proportion
• 26. Distance, speed, time
• 27. Direct and inverse proportions
• 28. What are percentages?
• Additional topic & Number line
• 29. Negative numbers
• 30. Absolute value or modulus
• 31. What is a set?
• 32. Adding and subtracting integers
• 33. Multiplication and division of integers
• Rational numbers
• 34. Rational numbers
• 35. Comparing rational numbers
• 36. Adding and subtracting rational numbers
• 37. Multiplying and dividing rational numbers
• 38. More information about fractions
• 39. Algebraic expressions
• 40. Taking out a common factor
• 41. Expanding brackets
• 42. Simple math problems
• 43. Tasks on fractions
• 44. Percent worksheets for practice
• 45. Speed, distance, time tasks
• 46. Productivity problem
• 47. Statistics in Math
• 48. Basic theory of equation
• 50. Proportions: exercises
• 51. Systems of linear equations
• 52. Introduction to Inequalities
• 53. Systems of linear inequalities with one variable
• 54. Set Operations | Union | Intersection
• 55. Power with a natural exponent
• 56. Power with integer exponent
• 57. Perimeter, area and volume
• 58. Monomials
• 59. Polynomials
• 60. Reduced multiplication formulas
• 61. Polynomial decomposition
• 62. Dividing polynomials
• 63. Identical transformations of polynomials
• 64. Square root
• 65. Algorithm for extracting the square root
• 66. Quadratic equation
• 67. A quadratic equation with an even second coefficient
• 68. Viette's Theorem
• 69. Factoring a trinomial using decomposition
• 70. More about modules
• 71. Absolute value equations
• 72. Solving equations with module by method of intervals
• 73. Inequalities with module
• 74. Solving inequalities with module by method intervals
• 75. Square root from both parts of an equation
• Functions and graphs
• 76. What is a function?
• 77. Linear function and its graph
• 78. Power function
• 79. Direct Proportion and its Graph
• 80. Function y=x² and its graph
• 81. Function y = √x its properties and graph
• 82. Function y=k*x² its properties and graph
• 83. Function y=k/x its properties and graph
• 84. Graphical solution of equations and inequalities
• coming soon... (new lessons every month)

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

The equations section of QuickMath allows you to solve and plot virtually any equation or system of equations. In most cases, you can find exact solutions to your equations. Even when this is not possible, QuickMath may be able to give you approximate solutions to almost any level of accuracy you require. It also contains a number of special commands for dealing with quadratic equations.

The Solve command can be uses to solve either a single equation for a single unknown from the basic solve page or to simultaneously solve a system of many equations in many unknowns from the advanced solve page . The advanced command allows you to specify whether you want approximate numerical answers as well as exact ones, and how many digits of accuracy (up to 16) you require. It also allows you to eliminate certain variables from the equations.

Go to the Solve page

The Plot command, from the Graphs section, will plot any function of two variables. In order to plot a single function of x, go to the basic equation plotting page , where you can enter the equation and specify the upper and lower limits on x that you want the graph to be plotted for. The advanced plotting page allows you to plot up to 6 equations on the one graph, each with their own color. It also gives you control over such things as whether or not to show the axes, where the axes should be located, what the aspect ratio of the plot should be and what the range of the dependent variable should be. All equations can be given in the explicit y = f(x) form or the implicit g(x,y) = c form.

Go to the Equation Plotting page

The Quadratics page contains 13 separate commands for dealing with the most common questions concerning quadratics. It allows you to : factor a quadratic function (by two different methods); solve a quadratic equation by factoring the quadratic, using the quadratic formula or by completing the square; rewrite a quadratic function in a different form by completing the square; calculate the concavity, x-intercepts, y-intercept, axis of symmetry and vertex of a parabola; plot a parabola; calculate the discriminant of a quadratic equation and use the discriminant to find the number of roots of a quadratic equation. Each command generates a complete and detailed custom-made explanation of all the steps needed to solve the problem.

Go to the Quadratics page

Introduction to Equations

By an equation we mean a mathematical sentence that states that two algebraic expressions are equal. For example, a (b + c) =ab + ac, ab = ba, and x 2 -1 = (x-1)(x+1) are all equations that we have been using. We recall that we defined a variable as a letter that may be replaced by numbers out of a given set, during a given discussion. This specified set of numbers is sometimes called the replacement set. In this chapter we will deal with equations involving variables where the replacement set, unless otherwise specified, is the set of all real numbers for which all the expressions in the equation are defined.

If an equation is true after the variable has been replaced by a specific number, then the number is called a solution of the equation and is said to satisfy it. Obviously, every solution is a member of the replacement set. The real number 3 is a solution of the equation 2x-1 = x+2, since 2*3-1=3+2. while 1 is a solution of the equation (x-1)(x+2) = 0. The set of all solutions of an equation is called the solution set of the equation.

In the first equation above {3} is the solution set, while in the second example {-2,1} is the solution set. We can verify by substitution that each of these numbers is a solution of its respective equation, and we will see later that these are the only solutions.

A conditional equation is an equation that is satisfied by some numbers from its replacement set and not satisfied by others. An identity is an equation that is satisfied by all numbers from its replacement set.

Example 1 Consider the equation 2x-1 = x+2

The replacement set here is the set of all real numbers. The equation is conditional since, for example, 1 is a member of the replacement set but not of the solution set.

Example 2 Consider the equation (x-1)(x+1) =x 2 -1 The replacement set is the set of all real numbers. From our laws of real numbers if a is any real number, then (a-1)(a+1) = a 2 -1 Therefore, every member of the replacement set is also a member of the solution set. Consequently this equation is an identity.  

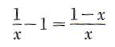
The replacement set for this equation is the set of real numbers except 0, since 1/x and (1- x)/x are not defined for x = 0. If a is any real number in the replacement set, then

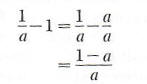
Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

Illustrative Mathematics Grade 7, Unit 6, Lesson 11: Using Equations to Solve Problems

Learning Targets:

• I can solve story problems by drawing and reasoning about a tape diagram or by writing and solving an equation.

Related Pages Illustrative Math Grade 7

Lesson 11: Using Equations to Solve Problems

Let’s use tape diagrams, equations, and reasoning to solve problems.

Illustrative Math Unit 7.6, Lesson 11 (printable worksheets)

Lesson 11 Summary

Many problems can be solved by writing and solving an equation. Here is an example: Clare ran 4 miles on Monday. Then for the next six days, she ran the same distance each day. She ran a total of 22 miles during the week. How many miles did she run on each of the 6 days? One way to solve the problem is to represent the situation with an equation, 4 + 6x = 22, where x represents the distance, in miles, she ran on each of the 6 days. Solving the equation gives the solution to this problem. 4 + 6x = 22 6x = 18 x = 3

Lesson 11.1 Remember Tape Diagrams

• Write a story that could be represented by this tape diagram.
• Write an equation that could be represented by this tape diagram.

Lesson 11.2 At the Fair

• Tyler is making invitations to the fair. He has already made some of the invitations, and he wants to finish the rest of them within a week. He is trying to spread out the remaining work, to make the same number of invitations each day. Tyler draws a diagram to represent the situation. a. Explain how each part of the situation is represented in Tyler’s diagram: How many total invitations Tyler is trying to make. How many invitations he has made already. How many days he has to finish the invitations. b. How many invitations should Tyler make each day to finish his goal within a week? Explain or show your reasoning. c. Use Tyler’s diagram to write an equation that represents the situation. Explain how each part of the situation is represented in your equation. d. Show how to solve your equation.
• Noah and his sister are making prize bags for a game at the fair. Noah is putting 7 pencil erasers in each bag. His sister is putting in some number of stickers. After filling 3 of the bags, they have used a total of 57 items. a. Explain how the diagram represents the situation. b. Noah writes the equation 3(x + 7) = 57 to represent the situation. Do you agree with him? Explain your reasoning. c. How many stickers is Noah’s sister putting in each prize bag? Explain or show your reasoning.
• A family of 6 is going to the fair. They have a coupon for $1.50 off each ticket. If they pay $46.50 for all their tickets, how much does a ticket cost without the coupon? Explain or show your reasoning. If you get stuck, consider drawing a diagram or writing an equation.

Lesson 11.3 Running Around

Priya, Han, and Elena, are members of the running club at school.

• Priya was busy studying this week and ran 7 fewer miles than last week. She ran 9 times as far as Elena ran this week. Elena only had time to run 4 miles this week. a. How many miles did Priya run last week? b. Elena wrote the equation 1/9 (x + 7) = 4 to describe the situation. She solved the equation by multiplying each side by 9 and then adding 7 to each side. How does her solution compare to the way you found Priya’s miles?
• One day last week, 6 teachers joined 5/7 of the members of the running club in an after-school run. Priya counted a total of 31 people running that day. How many members does the running club have?
• Priya and Han plan a fundraiser for the running club. They begin with a balance of -80 because of expenses. In the first hour of the fundraiser they collect equal donations from 9 parents, which brings their balance to -44. How much did each parent give?
• The running club uses the money they raised to pay for a trip to a canyon. At one point during a run in the canyon, the students are at an elevation of 128 feet. After descending at a rate of 50 feet per minute, they reach an elevation of -472 feet. How long did the descent take?

Are you ready for more?

Let x be the amount of money he had before performing at the fairs. 2x - 30 + 3x - 54 + 4x - 72 = 48 9x - 156 = 48 9x = 48 + 156 9x = 204 x = 22.67

Lesson 11 Practice Problems

• Find the value of each variable. a. a · 3 = -30 b. -9 · b = 45 c. -89 · 12 = c d. d · 88 = -88,000
• Match each equation to its solution and to the story it describes. Stories:
• The temperature is -7. Since midnight the temperature tripled and then rose 5 degrees. What was temperature at midnight?
• Jada has 7 pink roses and some white roses. She gives all of them away: 5 roses to each of her 3 favorite teachers. How many white roses did she give away?
• A musical instrument company reduced the time it takes for a worker to build a guitar. Before the reduction it took 5 hours. Now in 7 hours they can build 3 guitars. By how much did they reduce the time it takes to build each guitar?
• A club puts its members into 5 groups for an activity. After 7 students have to leave early, there are only 3 students left to finish the activity. How many students were in each group?
• The baby giraffe weighed 132 pounds at birth. He gained weight at a steady rate for the first 7 months until his weight reached 538 pounds. How much did he gain each month?
• Six teams are out on the field playing soccer. The teams all have the same number of players. The head coach asks for 2 players from each team to come help him move some equipment. Now there are 78 players on the field. Write and solve an equation whose solution is the number of players on each team.
• A small town had a population of 960 people last year. The population grew to 1200 people this year. By what percentage did the population grow?
• The gas tank of a truck holds 30 gallons. The gas tank of a passenger car holds 50% less. How many gallons does it hold?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics .

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

How to solve your equation, solving equations video lessons.

• Solving Simple Equations

Need more problem types? Try MathPapa Algebra Calculator

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Use a Problem-Solving Strategy

• Last updated
• Save as PDF
• Page ID 15136

Learning Objectives

By the end of this section, you will be able to:

• Approach word problems with a positive attitude
• Use a problem-solving strategy for word problems
• Solve number problems

Before you get started, take this readiness quiz.

• Translate “6 less than twice x ” into an algebraic expression. If you missed this problem, review Exercise 1.3.43 .
• Solve: \(\frac{2}{3}x=24\). If you missed this problem, review Exercise 2.2.10 .
• Solve: \(3x+8=14\). If you missed this problem, review Exercise 2.3.1 .

Approach Word Problems with a Positive Attitude

“If you think you can… or think you can’t… you’re right.”—Henry Ford

The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion? How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below (Figure \(\PageIndex{1}\))?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in Figure \(\PageIndex{2}\) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!

Use a Problem-Solving Strategy for Word Problems

We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.

Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.

USE A PROBLEM-SOLVING STRATEGY TO SOLVE WORD PROBLEMS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Example \(\PageIndex{1}\)

Pilar bought a purse on sale for \($18\), which is one-half of the original price. What was the original price of the purse?

Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.

Let p = the original price of the purse.

Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

In this problem, the words “what was the original price of the purse” tell us what we need to find.

Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.

Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.

Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.

Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.

Step 6. Check the answer in the problem to make sure it makes sense. We solved the equation and found that \(p=36\),which means “the original price” was \($36\).

If this were a homework exercise, our work might look like this:

Pilar bought a purse on sale for \($18\), which is one-half the original price. What was the original price of the purse?

Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”

Try It \(\PageIndex{2}\)

Joaquin bought a bookcase on sale for \($120\), which was two-thirds of the original price. What was the original price of the bookcase?

Try It \(\PageIndex{3}\)

Two-fifths of the songs in Mariel’s playlist are country. If there are \(16\) country songs, what is the total number of songs in the playlist?

Let’s try this approach with another example.

Example \(\PageIndex{4}\)

Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were \(11\) girls in the study group. How many boys were in the study group?

Try It \(\PageIndex{5}\)

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was \(3\) more than twice the number of notebooks. He bought \(7\) textbooks. How many notebooks did he buy?

Try It \(\PageIndex{6}\)

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed \(22\) Sudoku puzzles. How many crossword puzzles did he do?

Solve Number Problems

Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.

Example \(\PageIndex{7}\)

The difference of a number and six is \(13\). Find the number.

Try It \(\PageIndex{8}\)

The difference of a number and eight is \(17\). Find the number.

Try It \(\PageIndex{9}\)

The difference of a number and eleven is \(−7\). Find the number.

Example \(\PageIndex{10}\)

The sum of twice a number and seven is \(15\). Find the number.

Try It \(\PageIndex{11}\)

The sum of four times a number and two is \(14\). Find the number.

Try It \(\PageIndex{12}\)

The sum of three times a number and seven is \(25\). Find the number.

​​​​​​ Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

Example \(\PageIndex{13}\)

One number is five more than another. The sum of the numbers is 21. Find the numbers.

Try It \(\PageIndex{14}\)

One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.

Try It \(\PageIndex{15}\)

The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.

Example \(\PageIndex{16}\)

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

Try It \(\PageIndex{17}\)

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

Try It \(\PageIndex{18}\)

The sum of two numbers is \(−18\). One number is \(40\) more than the other. Find the numbers.

Example \(\PageIndex{19}\)

One number is ten more than twice another. Their sum is one. Find the numbers.

Try It \(\PageIndex{20}\)

One number is eight more than twice another. Their sum is negative four. Find the numbers.

\(-4,\; 0\)

Try It \(\PageIndex{21}\)

One number is three more than three times another. Their sum is \(−5\). Find the numbers.

\(-3,\; -2\)

Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:

\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]

Notice that each number is one more than the number preceding it. So if we define the first integer as \(n\), the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\). \[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Example \(\PageIndex{22}\)

The sum of two consecutive integers is \(47\). Find the numbers.

Try It \(\PageIndex{23}\)

The sum of two consecutive integers is 95. Find the numbers.

Try It \(\PageIndex{24}\)

The sum of two consecutive integers is −31. Find the numbers.

Example \(\PageIndex{25}\)

Find three consecutive integers whose sum is −42.

Try It \(\PageIndex{26}\)

Find three consecutive integers whose sum is −96.

-33, -32, -31

Try It \(\PageIndex{27}\)

Find three consecutive integers whose sum is −36.

-13, -12, -11

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]

Notice each integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). \[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers \(77\), \(79\), and \(81\).

\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]

\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2.

Example \(\PageIndex{28}\)

Find three consecutive even integers whose sum is 84.

\[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]

Try It \(\PageIndex{29}\)

Find three consecutive even integers whose sum is 102.

Try It \(\PageIndex{30}\)

Find three consecutive even integers whose sum is −24.

−10,−8,−6

Example \(\PageIndex{31}\)

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

Try It \(\PageIndex{32}\)

According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,500. This was $1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?

Try It \(\PageIndex{33}\)

U.S. Census data shows that the median price of new home in the United States in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

USING EQUATIONS TO SOLVE PROBLEMS

To solve real world problems, we can use the relationship between the quantities and form equations which represent the situation given in the problem.

Then, we can use these equations to solve the problems.

Example 1 :

Juanita is scrapbooking. She usually completes about 9 pages per hour. One night last week she completed pages 23 through 47 in 2.5 hours. Did she work at her average rate ?

Analyze Information :

Identify the important information.

• Worked for 2.5 hours

• Starting page: 23

• Ending page: 47

• Scrapbooking rate: 9 pages per hour

Formulate a Plan :

• Solve an equation to find the number of pages Juanita can expect to complete.

• Compare the number of pages Juanita can expect to complete with the number of pages she actually completed.

Solve : 

Let n represent the number of pages Juanita can expect to complete in 2.5 hours if she works at her average rate of 9 pages per hour.

Write an equation.

Since we are trying to solve for "n", we have to get rid of 2.5 which divides n in the above equation.

To get rid of 2.5 in the above equation, we have to multiply by 2.5 on both sides.  

2.5 x (n/2.5) = 2.5 x 9

Juanita can expect to complete 22.5 pages in 2.5 hours.

Juanita completed pages 23 through 47, a total of 25 pages.

Because 25 > 22.5, she worked faster than her expected rate.

Justify and Evaluate :

We used an equation to find the number of pages Juanita could expect to complete in 2.5 hours if she worked at her average rate.

We found that she could complete 22.5 pages.

Since 22.5 pages is less than the 25 pages Juanita completed, she worked faster than her average rate.

The answer makes sense, because Juanita completed 25 pages in 2.5 hours, which is equivalent to a rate of 10 pages in 1 hour.

Since 10 > 9, we know that she worked faster than her average rate.

Example 2 :

Tion divides his baseball cards equally among himself, his brother, and  3 friends. He has 9 cards left. How many does he give away ? Write and  solve an equation to solve the problem. Tell what the variable represents. 

• Baseballs cards are equally divided among five people. (Tion, his brother and 3 of his friends) 

• When cards are divided equally among five people, Tion has 9 cards left. So each one gets 9 cards. 

• Solve an equation to find the number of cards that  Tion had initially.

• Subtract 9 from the cards that Tion had initially to find the number of cards he gave away. 

Let n represent the number of cards that Tion had initially.

Since we are trying to solve for "n", we have to get rid of 5 which divides n in the above equation.

To get rid of 5 in the above equation, we have to multiply by 5 on both sides.  

5 x (n/5) = 5 x 9

Therefore, Tion had 45 baseball cards initially. 

We used an equation to find the number of baseball cards that Tion had initially.  

We found that  the number of baseball cards that Tion had initially is 45   

The answer makes sense, because when we divide 45 by 5, we get 9 that Tion has left. 

After dividing 45 cards equally among five people including himself,  Tion has left with 9 cards.

Then the number of cards he gave away is

The variable we have taken to solve this problem is "n". And this variable "n" represents the number of baseball cards that Tion had initially.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

How to Find a Limit Using a Table

Apr 09, 24 08:44 PM

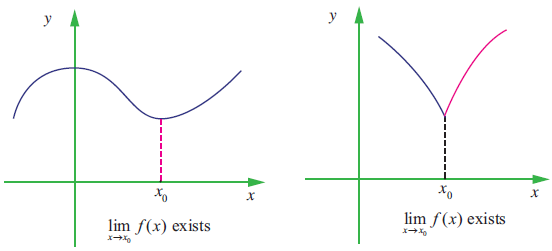
Evaluating Logarithms Worksheet

Apr 09, 24 09:30 AM

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

Help | Advanced Search

Mathematics > Numerical Analysis

Title: optimization methods for solving matrix equations.

Abstract: In this paper, we focus on using optimization methods to solve matrix equations by transforming the problem of solving the Sylvester matrix equation or continuous algebraic Riccati equation into an optimization problem. Initially, we use a constrained convex optimization method (CCOM) to solve the Sylvester matrix equation with $\ell_{2,1}$-norm, where we provide a convergence analysis and numerical examples of CCOM; however, the results show that the algorithm is not efficient. To address this issue, we employ classical quasi-Newton methods such as DFP and BFGS algorithms to solve the Sylvester matrix equation and present the convergence and numerical results of the algorithm. Additionally, we compare these algorithms with the CG algorithm and AR algorithm, and our results demonstrate that the presented algorithms are effective. Furthermore, we propose a unified framework of the alternating direction multiplier method (ADMM) for directly solving the continuous algebraic Riccati equation (CARE), and we provide the convergence and numerical results of ADMM. Our experimental results indicate that ADMM is an effective optimization algorithm for solving CARE. Finally, to improve the effectiveness of the optimization method for solving Riccati equation, we propose the Newton-ADMM algorithm framework, where the outer iteration of this method is the classical Newton method, and the inner iteration involves using ADMM to solve Lyapunov matrix equations inexactly. We also provide the convergence and numerical results of this algorithm, which our results demonstrate are more efficient than ADMM for solving CARE.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Search Cornell

Class Roster

Section menu.

• Toggle Navigation
• Summer 2024
• Spring 2024
• Winter 2024
• Archived Rosters

Last Updated

• Schedule of Classes - April 9, 2024 7:33PM EDT
• Course Catalog - April 9, 2024 7:07PM EDT

MATH 2940 Linear Algebra for Engineers

Course description.

Course information provided by the Courses of Study 2023-2024 . Courses of Study 2024-2025 is scheduled to publish mid-June.

Linear algebra and its applications. Topics include: matrices, determinants, vector spaces, eigenvalues and eigenvectors, orthogonality and inner product spaces; applications include brief introductions to difference equations, Markov chains, and systems of linear ordinary differential equations. May include computer use in solving problems.

When Offered Fall, Spring, Summer.

Prerequisites/Corequisites Prerequisite: MATH 1920. Forbidden Overlaps Forbidden Overlap: due to an overlap in content, students will receive credit for only one course in the following group: MATH 2210, MATH 2230, MATH 2310, MATH 2940.

Distribution Category (MQR-AS, SMR-AS)

Comments Taking MATH 2930 and MATH 2940 simultaneously is not recommended. For guidance in selecting an appropriate course, please consult First Steps in Math.

View Enrollment Information

  Regular Academic Session.   Choose one lecture and one discussion.

Credits and Grading Basis

4 Credits Stdnt Opt (Letter or S/U grades)

Class Number & Section Details

 3276 MATH 2940   LEC 001

Meeting Pattern

• MWF 10:10am - 11:00am To Be Assigned
• Aug 26 - Dec 9, 2024

Instructors

To be determined. There are currently no textbooks/materials listed, or no textbooks/materials required, for this section. Additional information may be found on the syllabus provided by your professor.

For the most current information about textbooks, including the timing and options for purchase, see the Cornell Store .

Additional Information

Instruction Mode: In Person Co-enrollment in a one-credit Academic Excellence Workshop (ENGRG 1094) is an option for undergraduates who wish to enhance their understanding of the course material.

 3277 MATH 2940   LEC 002

• MWF 12:20pm - 1:10pm To Be Assigned

 3278 MATH 2940   DIS 201

• W 3:35pm - 4:25pm To Be Assigned

Instruction Mode: In Person

 5811 MATH 2940   DIS 202

• W 7:30pm - 8:20pm To Be Assigned

 9234 MATH 2940   DIS 203

• W 8:35pm - 9:25pm To Be Assigned

 3279 MATH 2940   DIS 204

• R 8:00am - 8:50am To Be Assigned

 3280 MATH 2940   DIS 205

• R 9:05am - 9:55am To Be Assigned

 3281 MATH 2940   DIS 206

• R 10:10am - 11:00am To Be Assigned

 3282 MATH 2940   DIS 207

• R 12:20pm - 1:10pm To Be Assigned

 3283 MATH 2940   DIS 208

 3284 MATH 2940   DIS 209

• R 1:25pm - 2:15pm To Be Assigned

 3285 MATH 2940   DIS 210

 3286 MATH 2940   DIS 211

• R 2:30pm - 3:20pm To Be Assigned

 3287 MATH 2940   DIS 212

• R 3:35pm - 4:25pm To Be Assigned

 3288 MATH 2940   DIS 213

• F 8:00am - 8:50am To Be Assigned

 3289 MATH 2940   DIS 214

• F 9:05am - 9:55am To Be Assigned

 3290 MATH 2940   DIS 215

• F 11:15am - 12:05pm To Be Assigned

 5329 MATH 2940   DIS 216

 5330 MATH 2940   DIS 217

• F 1:25pm - 2:15pm To Be Assigned

 5331 MATH 2940   DIS 218

 9708 MATH 2940   DIS 219

• F 2:30pm - 3:20pm To Be Assigned

 9709 MATH 2940   DIS 220

 9710 MATH 2940   DIS 221

• F 3:35pm - 4:25pm To Be Assigned

Or send this URL:

Available Syllabi

About the class roster.

The schedule of classes is maintained by the Office of the University Registrar . Current and future academic terms are updated daily . Additional detail on Cornell University's diverse academic programs and resources can be found in the Courses of Study . Visit The Cornell Store for textbook information .

Please contact [email protected] with questions or feedback.

If you have a disability and are having trouble accessing information on this website or need materials in an alternate format, contact [email protected] for assistance.

Cornell University ©2024

Element differential method for contact problems with non-conforming contact discretization

• Original Article
• Published: 09 April 2024

Cite this article

• Wei-Long Fan 1 ,
• Xiao-Wei Gao   ORCID: orcid.org/0000-0001-5818-4058 1 , 2 ,
• Yong-Tong Zheng 3 ,
• Bing-Bing Xu 4 &
• Hai-Feng Peng 1  

In this paper, a new strong-form numerical method, the element differential method (EDM) is employed to solve two- and three-dimensional contact problems without friction. When using EDM, one can obtain the system of equations by directly differentiating the shape functions of Lagrange isoparametric elements for characterizing physical variables and geometry without the variational principle or any integration. Non-uniform contact discretization is used to enhance contact conditions, which avoids performing identical discretization along the contact surfaces of two contact objects. Two methods for imposing contact constraints are proposed. One method imposes Neumann boundary conditions on the contact surface, whereas the other directly applies the contact constraints as collocation equations for the nodes within the contact zone. The accuracy of the two methods is similar, but the multi-point constraints method does not increase the degrees of freedom of the system equations during the iteration process. The results of four numerical examples have verified the accuracy of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The authors state that all the data necessary to replicate the results are presented in the manuscript. Relevant parts of the code can be shared by contacting the corresponding author.

Johnson KL (1985) Contact mechanics. Cambridge University Press, Cambridge

Book   Google Scholar  

Hertz H (1882) Study on the contact of elastic solids. J Reine Angew Math 92:156–171

Article   MathSciNet   Google Scholar  

Bozorgmehri B, Obrezkov LP, Harish AB et al (2023) A contact description for continuum beams with deformable arbitrary cross-section. Finite Elements Anal Des. https://doi.org/10.1016/j.finel.2022.103863

Gay Neto A, de Pimenta P, M, Wriggers P (2018) Contact between spheres and general surfaces. Comput Methods Appl Mech Eng 328:686–716

Liu GR, Gu YT (2005) An introduction to meshfree methods and their programming. Springer-Verlag, Berlin/Heidelberg

Google Scholar  

Simo JC, Wriggers P, Taylor RL (1985) A perturbed Lagrangian formulation for the finite element solution of contact problems. Comput Methods Appl Mech Eng 50(2):163–180

Wriggers P (2006) Computational contact mechanics. Springer, Berlin

Dandekar BW, Conant RJ (1992) An efficient equation solver for frictional contact problems using the boundary integral equation formulation. Commun Appl Numer Methods 8:171–178

Article   Google Scholar  

Man KW, Aliabadi MH, Rooke DP (1993) BEM frictional contact analysis: load incremental technique. Comput Struct 47:893–905

Li G, Belytschko T (2001) Element-free Galerkin method for contact problems in metal forming analysis. Eng Comput 18(1/2):62–78

Chen J-S, Wang H-P (2000) New boundary condition treatments in meshfree computation of contact problems. Comput Methods Appl Mech Eng 187(3–4):441–468

Belgacem FB, Maday Y (1994) A spectral element methodology tuned to parallel implementations. Comput Methods Appl Mech Eng 116(1–4):59–67

Belhachmi Z, Bernardi C (1994) Resolution of fourth-order problems by the mortar element method. Comput Methods Appl Mech Eng 116(1–4):53–58

Maday Y, Mavriplis C, Patera A (1988) Nonconforming mortar element methods: application to spectral discretizations (No.NASA-CR-181729)

Wohlmuth BI (2001) Iterative solvers based on domain decomposition. In: Discretization methods and iterative solvers based on domain decomposition. Lecture Notes in Computational Science and Engineering, vol. 17. Springer, Berlin, Heidelberg

Puso MA, Laursen TA (2004) A mortar segment-to-segment contact method for large deformation solid mechanics. Comput Methods Appl Mech Eng 193(6–8):601–629

Farah P, Popp A, Wall WA (2015) Segment-based vs. element-based integration for mortar methods in computational contact mechanics. Comput Mech 55:209–228

Belgacem FB, Hild P, Laborde P (1998) The mortar finite element method for contact problems. Math Comput Model 28(4–8):263–271

McDevitt T, Laursen T (2000) A mortar-finite element formulation for frictional contact problems. Int J Numer Methods Eng 48(10):1525–1547

Puso MA (2004) A 3D mortar method for solid mechanics. Int J Numer Methods Eng 59:315–336

Yang B, Laursen TA, Meng X (2005) Two dimensional mortar contact methods for large deformation frictional sliding. Int J Numer Methods Eng 62(9):1183–1225

Kim TY, Dolbow J, Laursen T (2007) A mortared finite element method for frictional contact on arbitrary interfaces. Comput Mech 39(3):223–235

Khater AH, Temsah RS, Hassan MM (2008) A Chebyshev spectral collocation method for solving burgers’ type equations. J Comput Appl Math 222(2):333–350

Haq S, Hussain A, Uddin M (2011) RBFs meshless method of lines for the numerical solution of time-dependent nonlinear coupled partial differential equations. Appl Mat 2(4):414–423

Liu GR, Zhang J, Li H, Lam KY, Kee BBT (2006) Radial point interpolation based finite difference method for mechanics problems. Int J Numer Methods Eng 68(7):728–754

Fantuzzi N, Tornabene F, Viola E, Ferreira AJM (2014) A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape. Meccanica 49(10):2503–2542

Wen PH, Cao P, Korakianitis T (2014) Finite block method in elasticity. Eng Anal Bound Elem 46:116–125

Li M, Wen PH (2014) Finite block method for transient heat conduction analysis in functionally graded media. Int J Numer Methods Eng. 99(5):372–390

Li M, Lei M, Munjiza A, Wen PH (2015) Frictional contact analysis of functionally graded materials with Lagrange finite block method. Int J Numer Methods Eng 103(6):391–412

Almasi A, Kim T-Y, Song J-H (2022) Strong form meshfree collocation method for frictional contact between a rigid pile and an elastic foundation. Eng Comput 39(1):791–807

De Lorenzis L, Evans J, Hughes TJ, Reali A (2015) Isogeometric collocation: Neumann boundary conditions and contact. Comput Methods Appl Mech Eng 284:21–54

Kruse R, Nguyen-Thanh N, De Lorenzis L, Hughes TJ (2015) Isogeometric collocation for large deformation elasticity and frictional contact problems. Comput Methods Appl Mech Eng 296:73–112

Zheng YT, Gao XW, Liu YJ (2023) Numerical modelling of braided ceramic fiber seals by using element differential method. Compos Struct 304:116461

Gao XW, Huang SZ, Cui M, Ruan B, Zhu QH, Yang K, Lv J, Peng HF (2017) Element differential method for solving general heat conduction problems. Int J Heat Mass Transf 115:882–894

Gao XW, Li ZY, Yang K et al (2018) Element differential method and its application in thermal-mechanical problems. Int J Numer Methods Eng 113:82–108

Lv J, Shao MJ, Cui M, Gao XW (2019) An efficient collocation approach for piezoelectric problems based on the element differential method. Compos Struct 230:111483

Jiang WW, Gao XW, Xu BB, Lv J (2023) Static and forced vibration analysis of layered piezoelectric functionally graded structures based on element differential method. Appl Math Comput 437:127548

MathSciNet   Google Scholar  

Zheng YT, Gao XW, Lv J, Peng HF (2020) Weak-form element differential method for solving mechanics and heat conduction problems with abruptly changed boundary conditions. Int J Numer Methods Eng 121:3722–3741

Jean M (1999) The non-smooth contact dynamics method. Comput Methods Appl Mech Eng 177(3):235–257

Hughes TJR (1987) The finite element method: linear static and dynamic finite element analysis. Prentice-Hall, New Jersey

Shu X, Zhang J, Han L et al (2016) A surface-to-surface scheme for 3D contact problems by boundary face method. Eng Anal Bound Elem 70:23–30

Download references

This work was supported by the National Natural Science Foundation of China (12072064,12272081) and the Natural Science Foundation of Liaoning Province, China (2022-MS-138).

Author information

Authors and affiliations.

School of Mechanics and Aerospace Engineering, Dalian University of Technology, Dalian, 116024, China

Wei-Long Fan, Xiao-Wei Gao & Hai-Feng Peng

State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, 116024, China

Xiao-Wei Gao

School of Infrastructure Engineering, Nanchang University, Nanchang, 330031, China

Yong-Tong Zheng

Institute of Continuum Mechanics, Leibniz University Hannover, Hannover, Germany

Bing-Bing Xu

You can also search for this author in PubMed   Google Scholar

Corresponding authors

Correspondence to Xiao-Wei Gao or Hai-Feng Peng .

Ethics declarations

Conflict of interest.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

1.1 The description of symbols and abbreviations

The symbols and abbreviations used in this paper:

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Fan, WL., Gao, XW., Zheng, YT. et al. Element differential method for contact problems with non-conforming contact discretization. Engineering with Computers (2024). https://doi.org/10.1007/s00366-024-01963-7

Download citation

Received : 19 July 2023

Accepted : 22 February 2024

Published : 09 April 2024

DOI : https://doi.org/10.1007/s00366-024-01963-7

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Element differential method
• Strong-form formulation
• Point collocation method
• Contact problems
• Non-conforming contact discretization
• Find a journal
• Publish with us
• Track your research

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Solution approximation of fractional boundary value problems and convergence analysis using AA-iterative scheme

• Mujahid Abbas 1,2 , 
• Cristian Ciobanescu 3 , 
• Muhammad Waseem Asghar 4 ,  ,  , 
• Andrew Omame 5,6
• 1. Department of Mechanical Engineering Science, Faculty of Engineering and the Built Environment, University of Johannesburg, Johannesburg, South Africa
• 2. Department of Medical Research, China Medical University, Taichung 404, Taiwan
• 3. Department of Mathematics and Informatics, National University of Science and Technology Politehnica Bucharest, Bucharest 060042, Romania
• 4. Department of Mathematics, Government College University Lahore, Lahore 54000, Pakistan
• 5. Department of Mathematics, Federal University of Technology, Owerri, Nigeria
• 6. Abdus Salam School of Mathematical Sciences, Lahore 54000, Pakistan
• Received: 18 January 2024 Revised: 18 March 2024 Accepted: 22 March 2024 Published: 09 April 2024

MSC : 37C25, 47H09, 47H10

• Full Text(HTML)
• Download PDF

Addressing the boundary value problems of fractional-order differential equations hold significant importance due to their applications in various fields. The aim of this paper was to approximate solutions for a class of boundary value problems involving Caputo fractional-order differential equations employing the AA-iterative scheme. Moreover, the stability and data dependence results of the iterative scheme were given for a certain class of mappings. Finally, a numerical experiment was illustrated to support the results presented herein. The results presented in this paper extend and unify some well-known comparable results in the existing literature.

• AA iteration ,
• boundary value problems ,
• fractional differential equation ,
• stability ,
• data dependence

Citation: Mujahid Abbas, Cristian Ciobanescu, Muhammad Waseem Asghar, Andrew Omame. Solution approximation of fractional boundary value problems and convergence analysis using AA-iterative scheme[J]. AIMS Mathematics, 2024, 9(5): 13129-13158. doi: 10.3934/math.2024641

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding author: Email: [email protected] ; 

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 8 ) PDF downloads( 1 ) Cited by( 0 )

Figures and Tables

Figures( 4 )  /  Tables( 1 )

Associated material

Other articles by authors.

• Mujahid Abbas
• Cristian Ciobanescu
• Muhammad Waseem Asghar
• Andrew Omame

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1. $ k _{n} = \frac{2n^{2}+n-1}{n^{3}+4n^{2}-1}, $ $ o _{n} = \frac{(n-1)^{2}}{n^{3}+2n+1} $, $ w_{n} = \frac{2n^{4}-1}{n^{7}+n^{4}+3} $
• Figure 2. $ k_{n} = \frac{2n^{2}+n}{n^{5}+7n+11}, $ $ o_{n} = \frac{n-1}{n^{2}+2n+1} $, $ w_{n} = \frac{2n^{2}-1}{n^{3}+2n+1} $
• Figure 3. $ k_{n} = \frac{n^{2}+n}{n^{2}+4n+7}, $ $ o_{n} = \frac{n+1}{n^{2}+n+1} $, $ w_{n} = \frac{n^{2}+1}{n^{2}+n+7} $
• Figure 4. $ k_{n} = \frac{n^{2}+n}{n^{2}+4n+2}, $ $ o _{n} = \frac{n+1}{n^{3}+n-1} $, $ w_{n} = \frac{n^{2}+1}{n^{5}+n+7} $

How do i equation a string

i am making a random number generator that does math. for example, we got generated numbers 1,5,2 and -,* then it concats it to 1-5*2 trying to achieve it to work and solve the math problem.

Just use loadstring:

Note: You need to turn on the loadstring property in serverscriptservice and I’m pretty sure this only works on the server, though I could be wrong.

Like the previous post stated loadstring is an option although it invites unwelcome security vulnerabilities if handed improperly.

A method of parsing strings is leveraging infix and postfix parsers. A typical arithmetic sequence such as 2 + 5 / 7 is said to be in “infix” notation. This can be converted into what is called “postfix” notation, which can be evaluated through methods such as the shunting-yard algorithm.

You can use what’s called a stack to parse postfix notation. A stack is basically an array where the first item in is the last item out (LIFO). Think of it like stacking plates; the bottom place can only be accessed once all of the plates on top are removed, or “popped”, from the stack. This method does require you to assign precedence to your operators, however (PEMDAS/BODMAS/whatever).

As in returns just the string, not something that performs the math? Assuming you have two lists

you could do something like this, it’s not optimized but it’ll return as long of an equation as can be combined from the number of operators and operands

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&