research proposal in abstract algebra

Including number theory, algebraic geometry, and combinatorics

We have large groups of researchers active in number theory and algebraic geometry, as well as many individuals who work in other areas of algebra: groups, noncommutative rings, Lie algebras and Lie super-algebras, representation theory, combinatorics, game theory, and coding.

Chairs: George Bergman and Tony Feng

Algebra Faculty, Courses, Dissertations

Senate faculty, graduate students, visiting faculty, meet our faculty, george m. bergman, richard e. borcherds, sylvie corteel, david eisenbud, edward frenkel, vadim gorin, mark d. haiman, robin c. hartshorne, tsit-yuen lam (林節玄), hannah k. larson, hendrik w. lenstra, jr., ralph mckenzie, david nadler, andrew p. ogg, arthur e. ogus, martin olsson, alexander paulin, nicolai reshetikhin, john l. rhodes, marc a. rieffel, thomas scanlon, vera serganova.

1 of 2 Grid: People (Current page)
2 of 2 Grid: People
next › Grid: People
last » Grid: People

Abstract Algebra: Theory and Applications

(4 reviews)

Thomas W. Judson, Stephen F. Austin State University

ISBN 13: 9781944325022

Publisher: University of Puget Sound

Language: English

Formats Available

Conditions of use.

Free Documentation License (GNU) Free Documentation License (GNU)

Learn more about reviews.

Reviewed by Malik Barrett, Assistant Professor, Earlham College on 6/24/19

Judson covers all of the basics one expects to see in an undergraduate algebra sequence. That is, some review from discrete math/intro to proofs (chapters 1-2), and elementary group theory including chapters on matrix groups, group structure,... read more

Comprehensiveness rating: 5 see less

The coverage of ring theory is slimmer, but still relatively "complete" for a semester of undergraduate study. Three chapters on rings, one on lattices, a chapter reviewing linear algebra, and three chapters on field theory with an eye towards three classical applications of Galois theory. I will note here that Judson avoids generators and relations.

The coverage is all fairly standard, with excepting the definition of Galois group (see accuracy), and the referencing system in the HTML version is extremely convenient. For example, Judson leverages HTML so that proofs are collapsed (but can be expanded) which allows him to clean up the presentation of each section and include full proofs of earlier results when useful as references. The index uses a similar approach, choosing to display a collapsed link to the first paragraph in which the term is used, which is often a formal definition. There are no pages displayed, but there is a google search bar to scan the book with. Given the searchability, the index style is an interesting choice.

Since Judson includes _a lot_ of Sage which he uses to expand, clarify, or apply theory from the text, a fairly standard presentation of the theory, and includes hints/solutions to selected exercises, the textbook is very comprehensive.

Content Accuracy rating: 4

I've noticed very few outright errors in the text proper. However, of primary note is Judson's non-standard (in my experience) definition of Galois group as the automorphism group Aut(E/F) of an arbitrary field extension E/F. He defines this before he's defined fixed fields (ala Artin), or normal/separable extensions. All of the exercises use this definition as well, and so I chose to (mostly) avoid the chapter on Galois theory in favor of a more standard presentation.

There _are_ some errors in the exercises, however, like the inclusion of unnecessary or irrelevant parts, or typos. But I came across very few of these in my problem sets.

Relevance/Longevity rating: 5

Modern applications are sprinkled throughout the text that informs the students of the value of the material beyond theoretical. Judson does this in practical ways given that Sage is such a big component of the book, and so there are many exercises and descriptions that stress this relevance.

Clarity rating: 4

Judson's writing is direct and effective. I find his style clean and easy to follow. However, there are instances where there are big jumps between what some beginning exercises assume and what was presented explicitly in the chapter which confused many of my students. For instance, there is a dearth of examples of how to compute minimal polynomials and extension degrees (and the subtleties involved), and so the instructor has to provide the strategies necessary to solve parts of the first two problems.

Consistency rating: 5

The book is consistent in language, tone, and style. The only inconsistencies I've noticed involve the occasional definition appearing inline (usually in a sentence motivating the definition) instead of set aside in a text box. Defined terms _are_ still shown in bold, though. Still, it can make it hard to locate the precise definition quickly by scanning the section, but happens so rarely I won't detract a point.

Modularity rating: 5

Judson is very direct, and so his chapters are very focused. Moreover, many sections are punctuated, perhaps including no more than several definitions and propositions along with a historical note. So it's quite easy to divide the material into tight, bite-sized portions along the sections of the book, with a few exceptions, i.e., sections that run -much- longer and denser than average, like the section on field automorphisms.

Many sections and some chapters are written in a way that relies minimally on previous material which allows one to omit them or change the order of presentation without too much fuss. For instance, it's easy to cover the material on matrix groups and symmetry (chapter 12) right after the intro coverage of groups (chapter 3) if you want more concrete examples. Or omit the chapters on integral domains (with some minimal adjustment), lattices, and linear algebra if one is making a push to fields and Galois theory.

Organization/Structure/Flow rating: 5

The text has a relatively linear progression, with some exceptions. The exceptions aren't detractions, though, and allow for modularity or digressions to applications.

Interface rating: 5

The UI of the text is amazingly clean and efficient. Google search makes scanning the book quick and easy, the collapsible table of contents and the sidebar makes jumping around in the text simple. Sage can be run on the page itself making the Sage section quite effective. One can even right-click on rendered LaTeX, like tables, and copy the underlying code (which is super convenient for Cayley tables).

Grammatical Errors rating: 5

I recall no major grammatical errors.

Cultural Relevance rating: 5

Judson sticks to the math, so the text is pretty impersonal. Even the historical notes are fact-based accounts.

I used the book for a year-long algebra sequence and was fairly happy with the outcome. Beyond the first two sections of the Galois theory chapter being too non-standard for my tastes, I had few complaints and will very likely use the text again. The problem bank is also very good and they generally complement the material from the chapters quite well.

Reviewed by Andrew Misseldine, Assistant Professor, Southern Utah University on 6/19/18

This textbook is recommended for a upper division undergraduate course on abstract algebra and contains enough materials to cover a two-semester sequence, with particular emphasis placed on groups, rings, and fields. The group theory contains all the main topics of undergraduate algebra, including subgroups, cosets, normal subgroups, quotient groups, homomorphisms, and isomorphism theorems and introduces students to the important families of groups, with a particular emphasis on finite groups, such as cyclic, abelian, dihedral, permutation, and matrix groups. The textbook also includes more advanced topics such as structure of finite abelian groups, solvable groups, group actions, and Sylow Theory. The coverage of rings is equally comprehensive including the important topics of ideals, domains, fields, homomorphisms, polynomials, factorization, field extensions, and Galois Theory. The book is accompanied with a comprehensive index of topics and notation as well of solutions to selected exercises.

Content Accuracy rating: 5

The content of the textbook is very accurate, mathematically sound, and there are only a few errors throughout. The few errors which still exist can be reported to the author via email who appears to be very welcoming to suggestions or corrections from others. The author updates the textbook annually with corrections and additions.

This textbook follows the classical approach to teaching groups, rings, and fields to undergraduate and will retain its value throughout the years as the theory and examples will not be changing. It is possible that some of the applications included, mostly related to computer science, could eventually become obsolete as new techniques are discovered, but this will probably not be too consequential to this text which is a math book and not a compute science textbook. The applications of algebra can still be interesting and motivating to the reader even if they are not the state-of-the-art. The author updates the textbook annually with corrections and is very welcoming to suggestions or corrections from others.

Overall, the textbook is very clear to read for those readers with the appropriate background of set theory, logic, and linear algebra. Proofs are particularly easy to follow and are well-written. The only real struggle here is in the homework exercises. Occasionally, the assumptions of the homework are not explicit which can lead to confusion for the student. This is often the fault that the exercises are collected for the entire chapter and not for individual sections. It can sometimes be a chore for instructors to assign regular homework because they might unintentionally assign an exercise which only involves vocabulary from an early section but whose proofs required theory from later in the chapter.

The author is consistent in his approach to both the theory and applications of abstract algebra, which matches in style many available textbooks on abstract algebra. In particular, the book's definitions and names of important theorems are in harmony with the greater body of algebraists. It is also consistent with its notation, although sometimes this notations deviates from the more popular notations and often fails to mention alternative notations used by others. A comprehensive notation index is included with references to the original introduction of the notation in the text. Regrettably, no similar glossary of terms exists except the index, which is should be sufficient for most readers.

Modularity rating: 4

The textbook is divided into chapters, sections, and subsections, with exercises and supplementary materials placed in the back of each chapter or at the end of the book. These headings and subheadings lead themselves naturally to how an instructor might parse the course material into regular lectures, but, dependent of the amount of detail desired by the instructor, these subsections do not often produce 50-minute lectures. The textbook's preface includes a dependency chart to help an instructor decide on the order of topics if time restricts complete coverage of the topics. The textbook could be easily adapted for a two semester sequence with the first semester covering groups and the second covering rings and fields or a single semester course which introduces both groups and rings while skipping the more advanced topics. The application chapters/sections can easily be included into the course or omitted from the course based upon the instructor's interest and background with virtually no interruption to the students. Some chapters include a section of "Additional Exercises" which include exercises about topic not covered in the textbook but adjacent to the topics introduced. Although these sections are prefaced by some explanation of the exploratory topic, rarely are these topics thorough explained which might leave student grossly confused and require the instructor to supplement the textbook on any exercises assigned from here.

All sections follow the basic template of first introducing new definitions followed by examples, theorems, and proofs (although counterexamples are included, the presentation could benefit from additional counterexamples) and further definitions, examples, and theory are introduced as appropriate. Each chapter is concluded with a historical note, exercises for students, and references and suggested readings. Additionally, each chapter includes a section about programming in Sage relevant to the chapter contents with accompanying exercise, but this section is only available in the online version, not the downloadable or print versions. The first chapters review prerequisite materials including set theory and integers, which can be skipped by those students with a sufficient background without any loss. This book takes a "group-first" approach to introductory abstract algebra with rings, fields, vector spaces, and Boolean algebras introduced later. Throughout the textbook, in addition to the examples and theory, there are several practical applications of abstract algebra with a particular emphasis on computer science, such as cryptography and coding theory. These application sections/chapters can be easily included into the course without much extra preparation for the instructor or omitted at no real disruption to the student.

This textbook was authored using PreTeXt, which designed for typesetting mathematical documents and allow them to be converted into multiple formats. This textbook is available in an online, downloadable pdf, and print version. All three versions have solid format, especially in regard to the mathematical typesetting and graphics. The online version is available in both English and Spanish, where the interface and readability are equally of high quality.

The textbook appears to be absent of regular grammatical or mathematical errors, although a few might be present. The few errors which still might exist can be reported to the author via email who appears to be very welcoming to suggestions or corrections from others. The author updates the textbook annually with corrections and additions. For the purposes of this review, the English version of the textbook was reviewed. The reviewed makes no claim about the quality of the grammar of the Spanish version which was translated by Antonio Behn from the author's original English version.

Culture is not really a concern for theoretical mathematics textbooks which focuses almost entire on mathematical content knowledge and theory and not so much on people or their relationships. The textbook is devoid of culturally insensitive of offensive materials. Many chapters end with historical notes about mathematicians who helped to develop the chapter's materials. These notes typically follow the traditional Western European narrative of abstract algebra's development and is fairly homogeneous. Efforts could be made to include a more diverse and international history of algebra beyond Europe. For example, there is no historical note about the Chinese Remainder Theorem other than a sentence to explain why its name includes the word "Chinese." The textbook, originally written in English, now includes a complete Spanish edition, which is a massive effort for any textbook to be more inclusive.

This has been one of my absolute favorite textbooks for teaching abstract algebra. In fact, I think Judson's book is a golden standard for what a high-quality, mathematical OER textbook should be. It has created using the very impressive PreTeXt. In addition to the different formats, this book includes SAGE exercises. It has enough material to fill the usual two-semester course in undergraduate abstract algebra.

Reviewed by Nicolae Anghel, Associate Professor, University of North Texas on 4/11/17

This is a two-in-one book: a theoretical part and a computational part. Initially the OTL contained a 2014 version of the book, which only made tangential reference to the SAGE computational system. I downloaded from the author’s website the full, 2016 version, which eventually was also made into the OTL default. The theoretical part of the book is certainly adequately comprehensive, covering evenly the proposed material, and being supported by judiciously chosen exercises. The computational part also seems to me comprehensive enough, however one should not take my word for it as this side exceeds my areas of expertise and interest.

The parts that I checked, at random, were very accurate, so I have no reason to believe that the book was not entirely accurate. However, only after testing the book in the classroom, which I intend to do soon, can I certify this aspect.

The material is highly relevant for any serious discussion on math curriculum, and will live as long as mankind does.

Clarity rating: 5

For me as instructor the book was very clear, however keep in mind that this was not the first source for learning the material. Things may be different for a beginning student, who sees the material for the first time. Again, a judgment on this should be postponed until testing the book in the classroom.

The book is consistent throughout, all the topics being covered thoroughly and meaningfully.

I have no substantive comments on this topic.

The book, maybe a little too long for its own good, is divided into 23 chapters. The flow is natural, and builds on itself. The structure of each chapter is the same: After adequately presenting the material (conceptual definitions, theorems, examples), it proceeds to exercises, sometimes historical notes, references and further readings, to conclude with a substantial computational (based on SAGE syntax) discussion of the material, also including SAGE exercises. The applications to cryptography and coding theory highlight the practical importance of the material. I particularly liked the selection of exercises.

Another big advantage of a free book is that the student does not have to print all of it, certainly not all of it at the same time. This is a big plus, since with commercial books most of the time a student buys a book and only a fraction of it is needed in a course.

Written in a conversational, informal style the book is by and large free of grammatical errors. There are about a dozen minor mistakes, such as concatenated words or repeated words.

The historical vignettes are sweet. Maybe adding pictures of the mathematicians involved would not be a bad thing.

I liked the book, but I like more the concept of free access to theoretical and practical knowledge. Best things in life should essentially be free: air, water, …, education. I will make an effort to use open textbooks whenever possible.

Reviewed by Daniel Hernández, Assistant Professor, University of Kansas on 8/21/16

This book is introductory, and covers the basic of groups, rings, fields, and vector spaces. In addition, it also includes material on some interesting applications (e.g., public key cryptography). In terms of covering a lot of topics, the book is certainly comprehensive, and contains enough material for at least a year-long course for undergraduate math majors. A "dependency chart" in the preface should be very useful when deciding on what path to take through the text.

One noteworthy feature of this book is that it incorporates the open-source algebra program Sage. While the .pdf copy I found through the OTN website only included a not-very-serious discussion of Sage at the end of most exercise sets, the online textbook found at

http://abstract.pugetsound.edu/aata/

appears to contain a much more substantial discussion of how to use Sage to explore the ideas in this book. I admit that I didn't explore this feature very much.

Though I have not checked every detail (the book is quite long!), there do not appear to be any major errors.

The topics covered here are basic, and will therefore not require any real updates.

The book is also written in such a way that it should be easy to include new sections of applications.

I would say that this this book is well-written. The style is somewhat informal, and there are plenty of illustrative examples throughout the text. The first chapter also contains a brief discussion of what it means to write and read a mathematical proof, and gives many useful suggestions for beginners.

Through I didn't read every proof, in the ones I did look at, the arguments convey the key ideas without saying too much. The author also maintains the good habit of explicitly recalling what has been proved, and pointing out what remains to be done. In my experience, it is this sort of mid-proof "recap" is helpful for beginners.

The terminology in this text is standard, and appears to be consistent.

Each chapter is broken up into subsections, which makes it easy to for students to read, and for instructors to assign reading. In addition, this book covers modular arithmetic, which makes it even more "modular" in my opinion!

Organization/Structure/Flow rating: 4

It seems like there is no standard way to present this material. While the author's choices are perfectly fine, my personal bias would have been to discuss polynomial rings and fields earlier in the text.

The link on page v to

abstract.pugetsound.edu

appears to be broken.

My browser also had some issues when browsing the Sage-related material on the online version of this text, but this may be a personal problem.

I did not notice any major grammatical errors.

I'm not certain that this question is appropriate for a math textbook. On the other hand, I'll take this as an opportunity to note that the historical notes that appear throughout are a nice touch.

The problem sets appear to be substantial and appropriate for a strong undergraduate student. Also, many sections contain problems that are meant to be solved by writing a computer program, which might be of interest for students studying computer science.

I am also slightly concerned that the book is so long that students may find it overwhelming and hard to sift through.

Preliminaries
The Integers
Cyclic Groups
Permutation Groups
Cosets and Lagrange's Theorem
Introduction to Cryptography
Algebraic Coding Theory
Isomorphisms
Normal Subgroups and Factor Groups
Homomorphisms
Matrix Groups and Symmetry
The Structure of Groups
Group Actions
The Sylow Theorems
Polynomials
Integral Domains
Lattices and Boolean Algebras
Vector Spaces
Finite Fields
Galois Theory

Ancillary Material

About the book.

This text is intended for a one- or two-semester undergraduate course in abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many science, engineering, and computer science students are now electing to minor in mathematics. Though theory still occupies a central role in the subject of abstract algebra and no student should go through such a course without a good notion of what a proof is, the importance of applications such as coding theory and cryptography has grown significantly.

Until recently most abstract algebra texts included few if any applications. However, one of the major problems in teaching an abstract algebra course is that for many students it is their first encounter with an environment that requires them to do rigorous proofs. Such students often find it hard to see the use of learning to prove theorems and propositions; applied examples help the instructor provide motivation.

This text contains more material than can possibly be covered in a single semester. Certainly there is adequate material for a two-semester course, and perhaps more; however, for a one-semester course it would be quite easy to omit selected chapters and still have a useful text. The order of presentation of topics is standard: groups, then rings, and finally fields. Emphasis can be placed either on theory or on applications. A typical one-semester course might cover groups and rings while briefly touching on field theory, using Chapters 1 through 6, 9, 10, 11, 13 (the first part), 16, 17, 18 (the first part), 20, and 21. Parts of these chapters could be deleted and applications substituted according to the interests of the students and the instructor. A two-semester course emphasizing theory might cover Chapters 1 through 6, 9, 10, 11, 13 through 18, 20, 21, 22 (the first part), and 23. On the other hand, if applications are to be emphasized, the course might cover Chapters 1 through 14, and 16 through 22. In an applied course, some of the more theoretical results could be assumed or omitted. A chapter dependency chart appears below. (A broken line indicates a partial dependency.)

About the Contributors

Thomas W. Judson, Associate Professor, Department of Mathematics and Statistics, Stephen F. Austin State University. PhD University of Oregon.

Contribute to this Page

abstract algebra Recently Published Documents

Total documents.

Latest Documents
Most Cited Documents
Contributed Authors
Related Sources
Related Keywords

Basic Abstract Algebra

An introduction to abstract algebra, brief talk on ideological and political teaching in abstract algebra, how mathematicians assign homework problems in abstract algebra courses, an invitation to abstract algebra, verifying non-isomorphism of groups.

The concept of isomorphism is central to group theory, indeed to all of abstract algebra. Two groups {G, *} and {H, ο}are said to be isomorphic to each other if there exists a set bijection α from G onto H, such that $$\left( {a\;*\;b} \right)\alpha = \left( a \right)\alpha \; \circ \;(b)\alpha $$ for all a, b ∈ G. This can be illustrated by what is usually known as a commutative diagram:

On the Exponential Diophantine Equation (132m) + (6r + 1)n = z2

Nowadays, mathematicians are very interested in discovering new and advanced methods for determining the solution of Diophantine equations. Diophantine equations are those equations that have more unknowns than equations. Diophantine equations appear in astronomy, cryptography, abstract algebra, coordinate geometry and trigonometry. Congruence theory plays an important role in finding the solution of some special type Diophantine equations. The absence of any generalized method, which can handle each Diophantine equation, is challenging for researchers. In the present paper, the authors have discussed the existence of the solution of exponential Diophantine equation (132m) + (6r + 1)n = Z2, where m, n, r, z are whole numbers. Results of the present paper show that the exponential Diophantine equation (132m) + (6r + 1)n = Z2, where m, n, r, z are whole numbers, has no solution in the whole number.

Abstract Algebra

Ring hypothesis is one of the pieces of the theoretical polynomial math that has been thoroughly used in pictures. Nevertheless, ring hypothesis has not been associated with picture division. In this paper, we propose another rundown of similarity among pictures using rings and the entropy work. This new record was associated as another stopping standard to the Mean Shift Iterative Calculation with the goal to accomplish a predominant division. An examination on the execution of the calculation with this new ending standard is finished. In spite of the fact that ring hypothesis and class hypothesis from the start sought after assorted direction it turned out during the 1970s – that the investigation of functor groupings furthermore reveals new plots for module hypothesis.

(m, n)-Ideals in Semigoups Based on Int-Soft Sets

Algebraic structures play a prominent role in mathematics with wide ranging applications in many disciplines such as theoretical physics, computer sciences, control engineering, information sciences, coding theory, and topological spaces. This provides sufficient motivation to researchers to review various concepts and results from the realm of abstract algebra in the broader framework of fuzzy setting. In this paper, we introduce the notions of int-soft m , n -ideals, int-soft m , 0 -ideals, and int-soft 0 , n -ideals of semigroups by generalizing the concept of int-soft bi-ideals, int-soft right ideals, and int-soft left ideals in semigroups. In addition, some of the properties of int-soft m , n -ideal, int-soft m , 0 -ideal, and int-soft 0 , n -ideal are studied. Also, characterizations of various types of semigroups such as m , n -regular semigroups, m , 0 -regular semigroups, and 0 , n -regular semigroups in terms of their int-soft m , n -ideals, int-soft m , 0 -ideals, and int-soft 0 , n -ideals are provided.

A transition to abstract algebra

Export citation format, share document.

Forgot password? New user? Sign up

Existing user? Log in

Abstract Algebra

Already have an account? Log in here.

Abstract algebra is a broad field of mathematics, concerned with algebraic structures such as groups , rings , vector spaces , and algebras . On the 12-hour clock, $9+4=1$, rather than 13 as in usual arithmetic

Roughly speaking, abstract algebra is the study of what happens when certain properties of number systems are abstracted out; for instance, altering the definitions of the basic arithmetic operations result in a structure known as a ring, so long as the operations are consistent.

For example, the 12-hour clock is an example of such an object, where the arithmetic operations are redefined to use modular arithmetic (with modulus 12). An even further level of abstraction--where only one operation is considered--allows the clock to be understood as a group. In either case, the abstraction is useful because many properties can be understood without needing to consider the specific structure at hand, which is especially important when considering the relationship(s) between structures; the concept of a group isomorphism is an example.

Levels of Abstraction in Abstract Algebra

Group theory.

Ring Theory

Other Applications of Abstract Algebra

It is possible to abstract away practically all of the properties found in the "usual" number systems, the tradeoff being that the resulting object--known as a magma (which consists of a set and a binary operation, that need not satisfy any properties other than closure)--is simply too general to be interesting. On the other extreme, it is possible to abstract out practically no properties, which allows for many results to be found, but the resulting object (the usual number systems) is too specific to solve more general problems.

Most of abstract algebra is dedicated to objects that have a reasonable balance between generality and structure, most notably groups and rings (discussed in more detail below) in which most of the basic properties of arithmetic are maintained, but their specifics are left free. Still, some higher levels of abstraction are occasionally useful; quasigroups , for instance, are related to Latin squares , and monoids are often used in computer science and are simple examples of categories .

Main article: Group theory The possible moves on a Rubik's cube form a (very large) group . Group theory is useful as an abstract notion of symmetry , which makes it applicable to a wide range of areas: the relationship between the roots of a polynomial (as in Galois theory ) and the solution methods to the Rubik's cube are both prominent examples.

Informally, a group is a set equipped with a binary operation $\circ$, so that operating on any two elements of the group also produces an element of the group. For example, the integers form a group under addition, and the nonzero real numbers form a group under multiplication. The $\circ$ operation needs to satisfy a number of properties analogous to the ones it satisfies for these "normal" number systems: it should be associative (which essentially means that the order of operations doesn't matter), and there should be an identity element (0 in the first example above, and 1 in the second). More formally, a group is a set equipped with an operation $\cdot$ such that the following axioms hold; note that $\cdot$ does not necessarily refer to multiplication; rather, it should be viewed as a function on two variables (indeed, $\cdot$ can even refer to addition):

Group Axioms 1) Associativity. For any $x, y, z \in G $, we have $ (x \cdot y) \cdot z = x \cdot (y \cdot z) $. 2) Identity. There exists an $ e \in G $, such that $ e \cdot x = x \cdot e = x $ for any $x \in G $. We say that $e$ is an identity element of $G$. 3) Inverse. For any $x \in G$, there exists a $y \in G$ such that $x \cdot y = e = y \cdot x $. We say that $y$ is an inverse of $x$.

It is also worth noting the closure axiom for emphasis, as it is important to verify closure when working with subgroups (groups contained entirely within another):

4) Closure. For any $x, y \in G $, $x*y $ is also in $G$.

Additional examples of groups include

$\mathbb{Z}_n$, the set of integers $\{0, 1, \ldots, n-1\}$ with the operation addition modulo $n$
$S_n$, the set of permutations of $\{1, 2, \ldots, n\}$ with the operation of composition .

$S_3$ is worth special note as an example of a group that is not commutative , meaning that $a \cdot b = b \cdot a$ does not generally hold. Formally speaking, $S_3$ is nonabelian (an abelian group is one in which the operation is commutative). When the operation is not clear from context, groups are written in the form $(\text{set}, \text{op})$; e.g. the nonzero reals equipped with multiplication can be written as $(\mathbb{R}^*, \cdot)$.

Much of group theory (and abstract algebra in general) is centered around the concept of a group homomorphism , which essentially means a mapping from one group to another that preserves the structure of the group. In other words, the mapping of the product of two elements should be the same as the product of the two mappings; intuitively speaking, the product of two elements should not change under the mapping. Formally, a homomorphism is a function $\phi: G \rightarrow H$ such that

\[\phi(g_1) \cdot_H \phi(g_2) = \phi(g_1 \cdot_G g_2),\]

where $\cdot_H$ is the operation on $H$ and $\cdot_G$ is the operation on $G$. For example, $\phi(g) = g \pmod n$ is an example of a group homomorphism from $\mathbb{Z}$ to $\mathbb{Z}_n$. The concept of potentially differing operations is necessary; for example, $\phi(g)=e^g$ is an example of a group homomorphism from $(\mathbb{R},+)$ to $(\mathbb{R}^{*},\cdot)$.

Main article: Ring theory

Rings are one of the lowest level of abstraction, essentially obtained by overwriting the addition and multiplication functions simultaneously (compared to groups, which uses only one operation). Thus a ring is--in some sense--a combination of multiple groups, as a ring can be viewed as a group over either one of its operations. This means that the analysis of groups is also applicable to rings, but rings have additional properties to work with (the tradeoff being that rings are less general and require more conditions).

The definition of a ring is similar to that of a group, with the extra condition that the distributive law holds as well:

A ring is a set $ R $ together with two operations $ + $ and $ \cdot $ satisfying the following properties (ring axioms): (1) $ R $ is an abelian group under addition. That is, $ R$ is closed under addition, there is an additive identity (called $ 0 $), every element $a\in R$ has an additive inverse $-a\in R $, and addition is associative and commutative. (2) $ R $ is closed under multiplication, and multiplication is associative: $\forall a,b\in R\quad a.b\in R\\ \forall a,b,c\in R\quad a\cdot ( b\cdot c ) =( a\cdot b ) \cdot c.$ (3) Multiplication distributes over addition: $\forall a,b,c\in R\\ a\cdot \left( b+c \right) =a\cdot b+a\cdot c\quad \text{ and }\quad \left( b+c \right) \cdot a=b\cdot a+c\cdot a.$ A ring is usually denoted by $\left( R,+,. \right) $ and often it is written only as $R$ when the operations are understood.

For example, the integers $\mathbb{Z}$ form a ring, as do the integers modulo $n$ $($denoted by $\mathbb{Z}_n).$ Less obviously, the square matrices of a given size also form a ring; this ring is noncommutative. Commutative ring theory, or commutative algebra, is much better understood than noncommutative rings are.

As in groups, a ring homomorphism can be defined as a mapping preserving the structure of both operations.

Rings are used extensively in algebraic number theory , where " integers " are reimagined as slightly different objects (for example, Gaussian integers ), and the effect on concepts such as prime factorization is analyzed. Of particular interest is the fundamental theorem of arithmetic , which involves the concept of unique factorization; in other rings, this may not hold, such as

\[6 = 2 \cdot 3 = \big(1+\sqrt{-5}\big)\big(1-\sqrt{-5}\big).\]

Theory developed in this field solves problems ranging from sum of squares theorems to Fermat's last theorem .

Abstract algebra also has heavy application in physics and computer science through the analysis of vector spaces . For example, the Fourier transform and differential geometry both have vector spaces as their underlying structures; in fact, the Poincare conjecture is (roughly speaking) a statement about whether the fundamental group of a manifold determines if the manifold is a sphere.

Related to vector spaces are modules , which are essentially identical to vector spaces but defined over a ring rather than over a field (and are thus more general). Modules are heavily related to representation theory , which views the elements of a group as linear transformations of a vector space; this is desirable to make an abstract object (a group) somewhat more concrete, in the sense that the group is better understood by translating it into a well-understood object in linear algebra (as matrices can be viewed as linear transformations, and vice versa).

The relationships between various algebraic structures are formalized using category theory .

Group Theory Introduction

Problem Loading...

Note Loading...

Set Loading...

Customer Reviews
Extended Essays
IB Internal Assessment
Theory of Knowledge
Literature Review
Dissertations
Essay Writing
Research Writing
Assignment Help
Capstone Projects
College Application
Online Class

How to Write an Abstract for Research Proposal

by Antony W

December 13, 2021

An abstract in a research proposal summarizes the main aspect of the assignment in a given sequence in 300 words or less. It highlights the purpose of the study, the research problem, design of the study, findings, summary of your interpretations and conclusions.

For what it’s worth, the abstract of your research proposal should give a clear and concise elaboration of the major aspects of an issue you’ve investigated.

In this guide, you’ll learn how to write an abstract for any research proposal. We’ll look at why an abstract is important, the types of abstracts, writing style, and what to avoid when it comes to writing an abstract for your research proposal.

Types of Abstracts for a Research Proposal

There are four types of abstracts that you can write for a research proposal:

Critical abstract
Descriptive abstract
Informative abstract
Highlight abstract

1. Critical abstract

A critical abstract in a research proposal describes the primary findings and gives a solid judgment on the validity, completeness, and reliability of the study. It’s your responsibility as a researcher to evaluate your work and then compare it with already existing work on the same subject.

Because a critical abstract includes an additional commentary, it tends to longer. Often, the length falls between 400 and 500 words. However, do keep in mind that this type of an abstract is very are, which means your instructor may never ask you to write a critical abstract for your research proposal.

2. Highlight Abstract

A highlight abstract is a piece of writing that can’t stand independent of its associated document. It uses incomplete and leading remarks, with the primary goal of grabbing the attention of the reader to the study.

Professors have made it clear that a highlight abstract is not by itself a true abstract to use in a research proposal. Since it cannot stand on its away separate from the associated article, it’s unlikely that your teacher will ask you to use it in academic writing.

3. Descriptive abstract

A descriptive abstract gives a short description of the research proposal. It may include purpose, method, and the scope of the research, and it’s often 100 words or less in length. Some people consider it to be an outline of the research proposal rather than an actual abstract for the document.

While a descriptive abstract describes the type of information a reader will find in a research proposal, it neither critics the work nor provides results and conclusion of the study.

4. Informative Abstract

Many abstracts in academic writing are informative. They don’t analyze the study or investigation that you propose, but they explain a research project in a way that they can stand independently. In other words, an informative abstract gives an explanation for the main arguments, evidence, and significant results.

In addition to featuring purpose, method, and scope, an informative abstract also include the results, conclusion, as well as the recommendation of the author. As for the length, an informative abstract should not be more than 300 words.

How to Write an Abstract for a Research Proposal

Of the four type of abstracts that we’ve discussed above, an informative abstract is what you’ll need to write in your research proposal. Writing an abstract for a research proposal isn’t difficult at all. You only need to know what to write and how to write it, and you’re good to get started.

1. Write in Active Voice

First, use active voice when writing an abstract for your research proposal. However, this doesn’t mean you should avoid passive voice in entirety. If you find that some sentences can’t make sense unless with passive sentence construction, feel free to bend this rule somewhat.

Second, make sure your sentences are concise and complete. Refrain from using ambiguous words. Keep the language simple instead.

Lastly, never use present or future tense to write an abstract for a research proposal. You’re reporting a study that you’ve already conducted and therefore writing in past sense makes the most sense.

Your abstract should come immediately after the title page. Write in block format without paragraph indentations. The abstract should not be more than 300 words long and the page should not have a number. The word “Abstract” in your research proposal should be center aligned in the page, unless otherwise stated.

In addition to these formatting rules, the last sentence of your abstract should summarize the application to practice or the conclusions of your study. In the case where it seems appropriate, you might want follow this by statement that suggests a need for additional research.

3. Time to Write the Abstract

There are no hard rules on when to write an abstract for a research proposal. Some students choose to write the section first while others choose to write it last. We strongly recommend that you write the abstract last because it’s a summary of the whole paper. You can also write it in the beginning if you’ve already outlined your draft and know what you want to talk about even before you start writing.

Your informative abstract is subject to frequent changes as you work on your paper, and that holds whether you write the section first or last. Be flexible and tweak this part of the assignment as necessary. Also, make sure you report statistical findings in parentheses.

Read abstract to be sure the summary of the study agrees with what you’ve written in your proposal. As we mentioned earlier, this section is subject to change depending on the direction your research takes. So make sure you identify and correct any anomalies if any.

Mistakes to Avoid When Writing an Abstract for Research Proposal

To wind up this guide, here are some of the most common mistakes that you should avoid when writing an abstract for your research proposal:

Avoid giving a lengthy background
Don’t include citations to other people’s work
An abstract shouldn’t include a table, figure, image, or any kind of illustration
Don’t include terms that are difficult to understand

About the author

Antony W is a professional writer and coach at Help for Assessment. He spends countless hours every day researching and writing great content filled with expert advice on how to write engaging essays, research papers, and assignments.

Math Careers

Search form

MAA Centennial
Spotlight: Archives of American Mathematics
MAA Officers
MAA to the Power of New
Council and Committees
MAA Code of Conduct
Policy on Conflict of Interest
Statement about Conflict of Interest
Recording or Broadcasting of MAA Events
Policy for Establishing Endowments and Funds
Avoiding Implicit Bias
Copyright Agreement
Principal Investigator's Manual
Planned Giving
The Icosahedron Society
Our Partners
Advertise with MAA
Employment Opportunities
Staff Directory
2022 Impact Report
In Memoriam
Membership Categories
Become a Member
Membership Renewal
MERCER Insurance
MAA Member Directories
New Member Benefits
The American Mathematical Monthly
Mathematics Magazine
The College Mathematics Journal
How to Cite
Communications in Visual Mathematics
About Convergence
What's in Convergence?
Convergence Articles
Mathematical Treasures
Portrait Gallery
Paul R. Halmos Photograph Collection
Other Images
Critics Corner
Problems from Another Time
Conference Calendar
Guidelines for Convergence Authors
Math Horizons
Submissions to MAA Periodicals
Guide for Referees
Scatterplot
Math Values
MAA Book Series
MAA Press (an imprint of the AMS)
MAA Library Recommendations
Additional Sources for Math Book Reviews
About MAA Reviews
Mathematical Communication
Information for Libraries
Author Resources
MAA MathFest
Proposal and Abstract Deadlines
MAA Policies
Invited Paper Session Proposals
Contributed Paper Session Proposals
Panel, Poster, Town Hall, and Workshop Proposals
Minicourse Proposals
MAA Section Meetings
Virtual Programming
Joint Mathematics Meetings
Calendar of Events
MathFest Programs Archive
MathFest Abstract Archive
Historical Speakers
Information for School Administrators
Information for Students and Parents
Registration
Getting Started with the AMC
AMC Policies
AMC Administration Policies
Important AMC Dates
Competition Locations
Invitational Competitions
Putnam Competition Archive
AMC International
Curriculum Inspirations
Sliffe Award
MAA K-12 Benefits
Mailing List Requests
Statistics & Awards
Submit an NSF Proposal with MAA
MAA Distinguished Lecture Series
Common Vision
CUPM Curriculum Guide
Instructional Practices Guide
Möbius MAA Placement Test Suite
META Math Webinar May 2020
Progress through Calculus
Survey and Reports
"Camp" of Mathematical Queeries
DMEG Awardees
National Research Experience for Undergraduates Program (NREUP)
Neff Outreach Fund Awardees
Tensor SUMMA Grants
Tensor Women & Mathematics Grants
Grantee Highlight Stories
"Best Practices" Statements
CoMInDS Summer Workshop 2023
MAA Travel Grants for Project ACCCESS
2024 Summer Workshops
Minority Serving Institutions Leadership Summit
Previous Workshops
Frequently Asked Questions
Course Resources
Industrial Math Case Studies
Participating Faculty
2020 PIC Math Student Showcase
Previous PIC Math Workshops on Data Science
Dates and Locations
Past Programs
Leadership Team
Support Project NExT
Section NExT
Section Officers Meeting History
Preparations for Section Meetings
Bylaws Template
Editor Lectures Program
MAA Section Lecturer Series
Officer Election Support
Section Awards
Section Liaison Programs
Section Visitors Program
Expense Reimbursement
Guidelines for Bylaw Revisions
Guidelines for Local Arrangement Chair and/or Committee
Guidelines for Section Webmasters
MAA Logo Guidelines
MAA Section Email Policy
Section Newsletter Guidelines
Statement on Federal Tax ID and 501(c)3 Status
Communication Support
Guidelines for the Section Secretary and Treasurer
Legal & Liability Support for Section Officers
Section Marketing Services
Section in a Box
Subventions and Section Finances
Web Services
Joining a SIGMAA
Forming a SIGMAA
History of SIGMAA
SIGMAA Officer Handbook
MAA Connect
Meetings and Conferences for Students
Opportunities to Present
Information and Resources
MAA Undergraduate Student Poster Session
Undergraduate Research Resources
MathFest Student Paper Sessions
Research Experiences for Undergraduates
Student Poster Session FAQs
High School
A Graduate School Primer
Reading List
Student Chapters
Awards Booklets
Carl B. Allendoerfer Awards
Regulations Governing the Association's Award of The Chauvenet Prize
Trevor Evans Awards
Paul R. Halmos - Lester R. Ford Awards
Merten M. Hasse Prize
George Pólya Awards
David P. Robbins Prize
Beckenbach Book Prize
Euler Book Prize
Daniel Solow Author’s Award
Henry L. Alder Award
Deborah and Franklin Tepper Haimo Award
Certificate of Merit
Gung and Hu Distinguished Service
JPBM Communications Award
Meritorious Service
MAA Award for Inclusivity
T. Christine Stevens Award
Dolciani Award Guidelines
Morgan Prize Information
Selden Award Eligibility and Guidelines for Nomination
Selden Award Nomination Form
AMS-MAA-SIAM Gerald and Judith Porter Public Lecture
Etta Zuber Falconer
Hedrick Lectures
James R. C. Leitzel Lecture
Pólya Lecturer Information
Putnam Competition Individual and Team Winners
D. E. Shaw Group AMC 8 Awards & Certificates
Maryam Mirzakhani AMC 10 A Awards & Certificates
Two Sigma AMC 10 B Awards & Certificates
Jane Street AMC 12 A Awards & Certificates
Akamai AMC 12 B Awards & Certificates
High School Teachers
MAA Social Media

David R. Finston and Patrick J. Morandi

Table of Contents

Many students in our abstract algebra courses are frustrated with the abstract nature of the standard presentations of this subject matter. Furthermore, students often perceive this course as irrelevant for their future careers. In Abstract Algebra: Structure and Application , Finston and Morandi intend to develop the structures and basic theorems of modern algebra through applications that have relevance to the students’ daily lives. Some of these applications include identification numbers like zip codes and UPCs, error-correcting codes, linear codes, ruler and compass constructions, cyclic codes, cryptography, and wallpaper patterns.

I have witnessed the struggle which motivated the authors to write this text in my own Abstract Algebra class. Students are now attending college in the belief that a college degree should provide direct training for a future career. Students want to know that it is worth their time to learn the material covered in a specific course. Often instructors get the question “When will I ever use this?” I still argue that the mathematics courses students are required to take will train them to take everyday problems and organize the information so they are able to use logic and previously developed theories to determine a solution. Sometimes, however, and especially in more abstract classes, it is useful to illustrate how others have used the material they are studying in practice.

The inclusion of examples such as Fermat’s Little Theorem allows instructors to argue that a theorem proven more than 350 years ago, well before the time of computers and the internet, is used today to protect our financial information when making purchases online. This shows students that sometimes applications are not readily available; but it is still useful to study this material because you never know what will be useful a few years down the road.

While I agree with the necessity of providing motivation for this course material, I think that the theory should motivate the examples, rather than the examples motivating the theory. At least for my students, that works better. That is why I teach undergraduate abstract algebra out of Abstract Algebra: an Introduction by Thomas W. Hungerford. This textbook is presented in a more traditional format but still contains many of the same applications presented in Finston and Morandi’s book.

When choosing between the two texts it is important to keep in mind your target audience. Finston and Morandi both described their typical student; one describes their students as math majors and secondary education mathematics majors, while the other’s students are pre-service or in-service teachers. For the vast majority of their students this will be their final abstract algebra course. The heavy emphasis on applications with the substantially less rigorous presentation of theory might make more sense for this audience. They delve deeper, providing more in-depth examples than what is provided in Hungerford. However the trade-off is a loss of the unifying themes of Abstract Algebra. The text does not emphasize the patterns that exist between various algebraic structures. Instead it seems often times theory is provided as an afterthought to explain why an application works.

In my own classroom I have fewer students planning to be future teachers, and far more students planning to go on to graduate school or into industry. For this population I think it is still important to motivate theory through the inclusion of applications, but developing a firm understanding of the structure and basic theorems of modern algebra is essential. For this population of students I believe Hungerford’s more traditional approach is better. Both books, however, do an excellent job of introducing students to the theory of abstract algebra and its applications. I believe students need to see how theory, even in a more abstract form, can be used in their everyday lives.

Ellen Ziliak is an Assistant Professor of mathematics at Benedictine University in Lisle IL. Her training is in computational group theory. More recently she has become interested in ways to introduce undergraduate students to research in abstract algebra through applications.

See the table of contents in pdf format .

Dummy View - NOT TO BE DELETED

MAA Publications

Periodicals
MAA History
Policies and Procedures
Support MAA
Member Discount Programs
Propose a Session
MathFest Archive
Putnam Competition
AMC Resources
Curriculum Resources
Outreach Initiatives
Professional Development
Communities

Connect with MAA

Mathematical Association of America P: (800) 331-1622 F: (240) 396-5647 Email: [email protected]

Terms of Use
Privacy Policy
Mobile Version

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base
Starting the research process
How to Write a Research Proposal | Examples & Templates

How to Write a Research Proposal | Examples & Templates

Published on October 12, 2022 by Shona McCombes and Tegan George. Revised on November 21, 2023.

A research proposal describes what you will investigate, why it’s important, and how you will conduct your research.

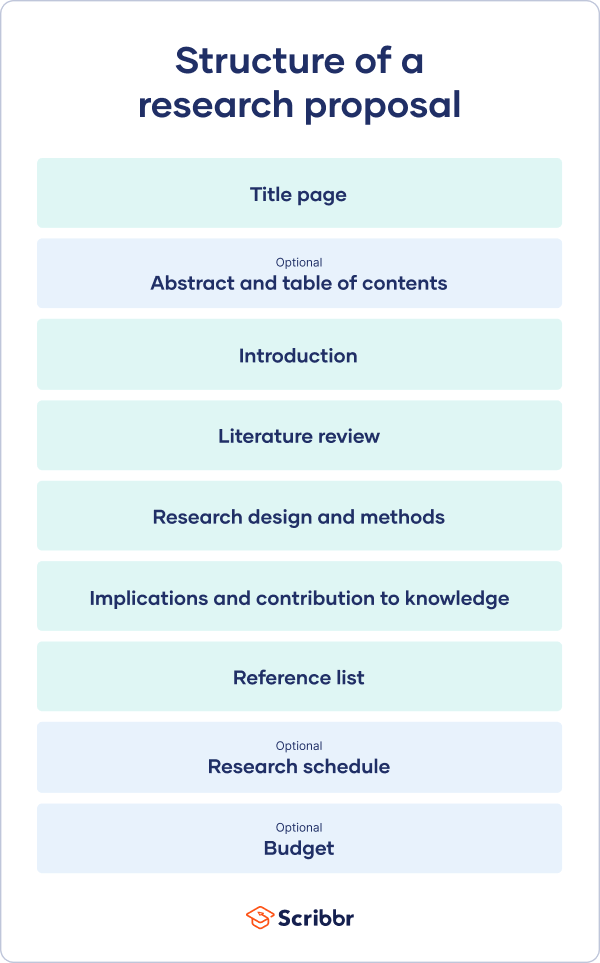
The format of a research proposal varies between fields, but most proposals will contain at least these elements:

Introduction

Literature review.

Research design

Reference list

While the sections may vary, the overall objective is always the same. A research proposal serves as a blueprint and guide for your research plan, helping you get organized and feel confident in the path forward you choose to take.

Research proposal purpose, research proposal examples, research design and methods, contribution to knowledge, research schedule, other interesting articles, frequently asked questions about research proposals.

Academics often have to write research proposals to get funding for their projects. As a student, you might have to write a research proposal as part of a grad school application , or prior to starting your thesis or dissertation .

In addition to helping you figure out what your research can look like, a proposal can also serve to demonstrate why your project is worth pursuing to a funder, educational institution, or supervisor.

Research proposal length

The length of a research proposal can vary quite a bit. A bachelor’s or master’s thesis proposal can be just a few pages, while proposals for PhD dissertations or research funding are usually much longer and more detailed. Your supervisor can help you determine the best length for your work.

One trick to get started is to think of your proposal’s structure as a shorter version of your thesis or dissertation , only without the results , conclusion and discussion sections.

Download our research proposal template

Prevent plagiarism. Run a free check.

Writing a research proposal can be quite challenging, but a good starting point could be to look at some examples. We’ve included a few for you below.

Example research proposal #1: “A Conceptual Framework for Scheduling Constraint Management”
Example research proposal #2: “Medical Students as Mediators of Change in Tobacco Use”

Like your dissertation or thesis, the proposal will usually have a title page that includes:

The proposed title of your project
Your supervisor’s name
Your institution and department

The first part of your proposal is the initial pitch for your project. Make sure it succinctly explains what you want to do and why.

Your introduction should:

Introduce your topic
Give necessary background and context
Outline your problem statement and research questions

To guide your introduction , include information about:

Who could have an interest in the topic (e.g., scientists, policymakers)
How much is already known about the topic
What is missing from this current knowledge
What new insights your research will contribute
Why you believe this research is worth doing

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

Academic style
Vague sentences
Style consistency

See an example

As you get started, it’s important to demonstrate that you’re familiar with the most important research on your topic. A strong literature review shows your reader that your project has a solid foundation in existing knowledge or theory. It also shows that you’re not simply repeating what other people have already done or said, but rather using existing research as a jumping-off point for your own.

In this section, share exactly how your project will contribute to ongoing conversations in the field by:

Comparing and contrasting the main theories, methods, and debates
Examining the strengths and weaknesses of different approaches
Explaining how will you build on, challenge, or synthesize prior scholarship

Following the literature review, restate your main objectives . This brings the focus back to your own project. Next, your research design or methodology section will describe your overall approach, and the practical steps you will take to answer your research questions.

To finish your proposal on a strong note, explore the potential implications of your research for your field. Emphasize again what you aim to contribute and why it matters.

For example, your results might have implications for:

Improving best practices
Informing policymaking decisions
Strengthening a theory or model
Challenging popular or scientific beliefs
Creating a basis for future research

Last but not least, your research proposal must include correct citations for every source you have used, compiled in a reference list . To create citations quickly and easily, you can use our free APA citation generator .

Some institutions or funders require a detailed timeline of the project, asking you to forecast what you will do at each stage and how long it may take. While not always required, be sure to check the requirements of your project.

Here’s an example schedule to help you get started. You can also download a template at the button below.

Download our research schedule template

If you are applying for research funding, chances are you will have to include a detailed budget. This shows your estimates of how much each part of your project will cost.

Make sure to check what type of costs the funding body will agree to cover. For each item, include:

Cost : exactly how much money do you need?
Justification : why is this cost necessary to complete the research?
Source : how did you calculate the amount?

To determine your budget, think about:

Travel costs : do you need to go somewhere to collect your data? How will you get there, and how much time will you need? What will you do there (e.g., interviews, archival research)?
Materials : do you need access to any tools or technologies?
Help : do you need to hire any research assistants for the project? What will they do, and how much will you pay them?

If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.

Methodology

Sampling methods
Simple random sampling
Stratified sampling
Cluster sampling
Likert scales
Reproducibility

Statistics

Null hypothesis
Statistical power
Probability distribution
Effect size
Poisson distribution

Research bias

Optimism bias
Cognitive bias
Implicit bias
Hawthorne effect
Anchoring bias
Explicit bias

Once you’ve decided on your research objectives , you need to explain them in your paper, at the end of your problem statement .

Keep your research objectives clear and concise, and use appropriate verbs to accurately convey the work that you will carry out for each one.

I will compare …

A research aim is a broad statement indicating the general purpose of your research project. It should appear in your introduction at the end of your problem statement , before your research objectives.

Research objectives are more specific than your research aim. They indicate the specific ways you’ll address the overarching aim.

A PhD, which is short for philosophiae doctor (doctor of philosophy in Latin), is the highest university degree that can be obtained. In a PhD, students spend 3–5 years writing a dissertation , which aims to make a significant, original contribution to current knowledge.

A PhD is intended to prepare students for a career as a researcher, whether that be in academia, the public sector, or the private sector.

A master’s is a 1- or 2-year graduate degree that can prepare you for a variety of careers.

All master’s involve graduate-level coursework. Some are research-intensive and intend to prepare students for further study in a PhD; these usually require their students to write a master’s thesis . Others focus on professional training for a specific career.

Critical thinking refers to the ability to evaluate information and to be aware of biases or assumptions, including your own.

Like information literacy , it involves evaluating arguments, identifying and solving problems in an objective and systematic way, and clearly communicating your ideas.

The best way to remember the difference between a research plan and a research proposal is that they have fundamentally different audiences. A research plan helps you, the researcher, organize your thoughts. On the other hand, a dissertation proposal or research proposal aims to convince others (e.g., a supervisor, a funding body, or a dissertation committee) that your research topic is relevant and worthy of being conducted.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

McCombes, S. & George, T. (2023, November 21). How to Write a Research Proposal | Examples & Templates. Scribbr. Retrieved April 8, 2024, from https://www.scribbr.com/research-process/research-proposal/

Is this article helpful?

Shona McCombes

Other students also liked, how to write a problem statement | guide & examples, writing strong research questions | criteria & examples, how to write a literature review | guide, examples, & templates, unlimited academic ai-proofreading.

✔ Document error-free in 5minutes ✔ Unlimited document corrections ✔ Specialized in correcting academic texts

How It Works
PhD thesis writing
Master thesis writing
Bachelor thesis writing
Dissertation writing service
Dissertation abstract writing
Thesis proposal writing
Thesis editing service
Thesis proofreading service
Thesis formatting service
Coursework writing service
Research paper writing service
Architecture thesis writing
Computer science thesis writing
Engineering thesis writing
History thesis writing
MBA thesis writing
Nursing dissertation writing
Psychology dissertation writing
Sociology thesis writing
Statistics dissertation writing
Buy dissertation online
Write my dissertation
Cheap thesis
Cheap dissertation
Custom dissertation
Dissertation help
Pay for thesis
Pay for dissertation
Senior thesis
Write my thesis

100+ Amazing Algebra Topics for Research Papers

Many students seek algebra topics when writing research papers in this mathematical field. Algebra is the study field that entails studying mathematical symbols and rules for their manipulation. Algebra is the unifying thread for most mathematics, including solving elementary equations to learning abstractions like rings, groups, and fields.

In most cases, people use algebra when unsure about the exact numbers. Therefore, they replace those numbers with letters. In business, algebra helps with sales prediction. While many students dislike mathematics, avoiding algebra research paper topics is almost impossible at an advanced study level.

Therefore, this article lists topics to consider when writing a research paper in this academic field. It’s helpful because many learners struggle to find suitable topics when writing research papers in this field.

How to Write Theses on Advanced Algebra Topics

A thesis on an algebra topic is an individual project that the learner writes after investigating and studying a specific idea. Here’s a step-by-step guide for writing a thesis on an algebra topic.

Pick a topic: Start by selecting a title for your algebra thesis. Your topic should relate to your research interests and your supervisor’s guidelines. Investigate your topic: Once you’ve chosen a topic, research it extensively to know the relevant theories, formulas, and texts. Your thesis should be an extension of a particular topic’s analysis and a report on your research. Write the thesis: Once you’ve explored the topic extensively, start writing your paper. Your dissertation should have an abstract, an introduction, the body, and a conclusion.

The abstract should summarise your thesis’ aims, scope, and conclusions. The introduction should introduce the topic, size, and significance while providing relevant literature and outlining the logical structure. The body should have several chapters with details and proofs of numerical implementations, while the conclusion should restate your main arguments and tell readers the effects. Also, it should suggest future work.

College Algebra Topics

You may need topics to consider if you’re in college and want to write an algebra research paper. Here’s a list of titles worth considering for your essay.

Exploring the relationship between Rubik’s cube and the group theory
Comparing the relationship between various equation systems
Finding the most appropriate way to solve mathematical word problems
Investigating the distance formula and its origin
Exploring the things you can achieve with determinants
Explaining what “domain” and “range” mean in algebra
A two-dimension analysis of the Gram-Schmidt process
Exploring the differences between eigenvalues and eigenvectors
What the Cramer’s rule states, and why does it matter
Describing the Gaussian elimination
Provide an induction-proof example
Describe the uses of F-algebras
Understanding the number problems in algebra
What’s the essence of abstract algebra?
Investigating Fermat’s last theorem peculiarities
Exploring the algebra essentials
Investigating the relationship between geometry and algebra

These are exciting topics in college algebra. However, writing a winning paper about any of them requires careful research and analysis. Therefore, prepare to spend sufficient time working on any of these titles.

Cool Topics in Algebra

Perhaps, you want to write about an excellent topic in this mathematical field. If so, consider the following ideas for your algebra paper.

Discussing a differential equation with illustrations
Describing and analysing the Noetherian ring
Explain the commutative ring from an algebra viewpoint
Describe the Artin-Weddderburn theorem
Studying the Jacobson density theorem
Describe the four properties of any binary operation from an algebra viewpoint
A detailed analysis of the unary operator
Analysing the Abel-Ruffini theorem
Monomorphisms versus Epimorphisms: Contrast and comparison
Discus Morita duality with algebraic structures in mind
Nilpotent versus Idempotent in Ring theory

Pick any idea from this list and develop it into a research topic. Your educator will love your paper and award you a good grade if you research it and write an informative essay.

Linear Algebra Topics

Linear algebra covers vector spaces and the linear mapping between them. Linear equation systems have unknowns, and mathematicians use vectors and matrices to represent them. Here are exciting topics in linear algebra to consider for your research paper.

Decomposition of singular value
Investigating linear independence and dependence
Exploring projections in linear algebra
What are linear transformations in linear algebra?
Describe positive definite matrices
What are orthogonal matrices?
Describe Euclidean vector spaces with examples
Explain how you can solve equation systems with matrices
Determinants versus matrix inverses
Describe mathematical operations using matrices
Functional analysis of linear algebra
Exploring linear algebra and its fundamentals

These are some of the exciting project topics in linear algebra. Nevertheless, prepare sufficient resources and time to investigate any of these titles to write a winning paper.

Pre Algebra Topics

Are you interested in a pre-algebra research topic? If so, this category has some of the most exciting ideas to explore.

Investigating the importance of pre-algebra
The best way to start pre-algebra for a beginner
Pre-algebra and algebra- Which is the hardest and why?
Core lessons in pre-algebra
What follows pre-algebra?
The first things to learn in pre-algebra
Investigating the standard form in pre-algebra
Provide pre-algebra examples using the basic rules to evaluate expressions
Differentiate pre-algebra and algebra
Describe five pre-algebra formulas

Consider exploring any of these ideas if you’re interested in pre-algebra. Nevertheless, choose a title you’re comfortable with to develop a winning paper.

Intermediate Algebra Topics for Research

Perhaps, you’re interested in intermediate algebra. If so, consider any of these ideas for your research paper.

Reviewing absolute value and real numbers
Investigating real numbers’ operations
Exploring the cube and square roots of real numbers
Analysing algebraic formulas and expressions
What are the rules of scientific notation and exponents?
How to solve a linear inequality with a single variable
Exploring relations, functions, and graphics from an algebraic viewpoint
Investigating linear systems with two variables and solutions
How to solve a linear system with two variables
Exploring linear systems applications with two variables
How to solve a linear system with three variables
Gaussian elimination and matrices
How to simplify a radical expression
How to add and subtract a radical expression
How to multiply and divide a radical expression
How to extract a square root and complete the square
Investigating quadratic functions and graphs
How to solve a polynomial and rational inequality
How to solve logarithmic and exponential equations
Exploring arithmetic series and sequences

These are exciting topics in intermediate algebra to consider for research papers. Nevertheless, learners should prepare to solve equations in their work.

Algebra Topics High School Students Can Explore

Are you in high school and want to explore algebra? If yes, consider these topics for your research, they could be a great coursework help to you.

Crucial principles and formulas to embrace when solving a matrix
Ways to create charts on a firm’s financial analysis for the past five years
How to find solutions to finance and mathematical gaps
Ways to solve linear equations
What is a linear equation- Provide examples
Describe the substitution and elimination methods for solving equations
How to solve logarithmic equations
What are partial fractions?
Describe linear inequalities with examples
How to solve a quadratic equation by factoring
How to solve a quadratic equation by formula
How to solve a quadratic equation with a square completion method
How to frame a worksheet for a quadratic equation
Explain the relationship between roots and coefficients
Describe rational expressions and ways to simplify them
Describe a cubic equation roots
What is the greatest common factor- Provide examples
What is the least common multiple- Provide examples
Describe the remainder theorem with examples

Explore any of these titles for your high school paper. However, pick a title you’re comfortable working with from the beginning to the end to make your work easier.

Advanced Topics in Algebra and Geometry

Maybe you want to explore something more advanced in your paper. In that case, the following list has advanced topics in geometry and algebra worth considering.

Arithmetical structures and their algorithmic aspects
Fractional thermoentropy spaces in topological quantum fields
Fractional thermoentripy spaces in large-scale systems
Eigenpoints configurations
Investigating the higher dimension aperiodic domino problem
Exploring math anxiety, executive functions, and math performance
Coherent quantiles and lifting elements
Absolute values extension on two subfields
Reviewing the laws of form and Majorana fermions
Studying the specialisation and rational maps degree
Investigating mathematical-pedagogical knowledge of prospective teachers in ECD programs
The adeles I model theory
Exploring logarithmic vector fields, arrangements, and divisors’ freeness
How to reconstruct curves from Hodge classes
Investigating Eigen points configuration

These are advanced topics in algebra and geometry worth investigating. However, please prepare to explore your topic extensively to write a strong essay.

Abstract Algebra Topics

Most people study abstract algebra in college. If you’re interested in research in this area, consider these topics for your project.

Describe abstract algebra applications
Why is abstract algebra essential?
Describe ring theory and its application
What is group theory, and why does it matter?
Describe the critical conceptual algebra levels
Describe the fundamental theorem of the finite Abelian groups
Describe Sylow’s theorems
What is Polya counting?
Describe the RSA algorithm
What are the homomorphisms and ideals of Rings?
Describe integral domains and factorisation
Describe Boolean algebra and its importance
State and explain Cauchy’s Theorem- Why is it important?

This algebra topics list is not exhaustive. You can find more ideas worth exploring in your project. Nevertheless, pick an idea you will work with comfortably to deliver a winning paper.

Get Professional Math Homework Help!

Perhaps, you don’t have the time to find accurate algebra homework solutions. Maybe you need math thesis help from an expert. If so, you’ve no reason to search further. Our thesis writing services in USA can help you write a winning assignment. We offer custom help with math assignments at cheap prices.

If you want to get a quality algebra dissertation without sweating, place an order with us. We’re an online team providing homework help to students across educational levels. We guarantee you a top-notch service once you approach us, saying, “Please do my math assignment.” We’re fast and can beat even a tight deadline without compromising quality. And whether you’re in high school, university, or college, we will write a paper that will compel your teacher to award you the best grade in your class. Contact us now!

Article Contents

1 introduction, 2 blob algebras and soergel calculus for |$\tilde {a}_1$|, 3 isomorphism theorems, 4 restriction of |$ \delta ^{ {{\mathbb {b}}}}_{ n}(\lambda ) $| to |$ {\mathbb {t}\mathbb {l}_{n}}$|, 5 determination of |$ c_i(x,y)$|, 6 characterization of |$ c_i(x,y)$| in terms of bruhat order on |$w$|, 7 graded jantzen filtrations and sum formulas.

< Previous

Graded Sum Formula for ~ A 1 -Soergel Calculus and the Nil-Blob Algebra

Article contents
Figures & tables
Supplementary Data

Marcelo Hernández Caro, Steen Ryom-Hansen, Graded Sum Formula for ~ A 1 -Soergel Calculus and the Nil-Blob Algebra, International Mathematics Research Notices , Volume 2024, Issue 7, April 2024, Pages 5923–5962, https://doi.org/10.1093/imrn/rnad287

Permissions Icon Permissions

We study the representation theory of the Soergel calculus algebra |$ {{ \tilde {A}_w^{{\mathbb {C}}}}}:= \mbox {End}_{ {{\mathcal {D}}}_{(W,S)}} (\underline {w}) $| over |$ {\mathbb {C}}$| in type |$ \tilde {A}_1$|⁠ . We generalize the recent isomorphism between the nil-blob algebra |$ {{\mathbb {N}\mathbb {B}}_n}$| and a diagrammatically defined subalgebra |$ {A}_w^{{\mathbb {C}}}$| of |${{ \tilde {A}_w^{{\mathbb {C}}}}}$| to deal with the two-parameter blob algebra. Under this generalization, the two parameters correspond to the two simple roots for |$ \tilde {A}_1$|⁠ . Using this, together with calculations involving the Jones-Wenzl idempotents for the Temperley-Lieb subalgebra of |$ {{\mathbb {N}\mathbb {B}}_n}$|⁠ , we obtain a concrete diagonalization of the matrix of the bilinear form on the cell module |$ \Delta _w(v) $| for |$ {{ \tilde {A}_w^{{\mathbb {C}}}}} $|⁠ . The entries of the diagonalized matrices turn out to be products of roots for |$ \tilde {A}_1$|⁠ . We use this to study Jantzen-type filtrations of |$ \Delta _w(v) $| for |$ {{ \tilde {A}_w^{{\mathbb {C}}}}}$|⁠ . We show that, at an enriched Grothendieck group level, the corresponding sum formula has terms |$ \Delta _w(s_{\alpha }v)[ l(s_{\alpha }v)- l(v)] $|⁠ , where |$ [ \cdot ] $| denotes grading shift.

Cellular algebras were introduced by Graham and Lehrer in 1994 in the paper [ 15 ] as a framework for studying the non-semisimple representation theory of many finite dimensional algebras,

The motivating examples for cellular algebras were the Iwahori-Hecke algebras of type |$ A_n $| and Temperley-Lieb algebras, but it has since been realized that many other finite dimensional algebras fit into this framework. For a cellular algebra one has a family of cell modules |$ \{ \Delta (\lambda ) \}$|⁠ , endowed with bilinear forms |$ \langle \cdot , \cdot \rangle _ \lambda $|⁠ , that together control the representation theory of the algebra in question. Unfortunately, the concrete analysis of these bilinear forms is in general difficult, but in this paper we give a non-trivial cellular algebra over |$ {\mathbb {C}} $| for which the bilinear forms |$ \langle \cdot , \cdot \rangle _ \lambda $| can in fact be diagonalized over an integral form of the algebra, thus solving all relevant questions concerning them, and therefore, by cellular algebra theory, concerning the representation theory of the algebra itself.

Our cellular algebra has two origins. Firstly, it arises in the diagrammatic Soergel calculus of the Coxeter system |$ (W,S) $| of type |$ \tilde {A}_1 $| as the endomorphism algebra |$ \tilde {A}_w^{{\mathbb {C}}}:= \mbox {End} ({w}) $| of |$ w:= {\color {red}{ s}}{\color {blue}{ t}}{\color {red}{ s}}{\color {blue}{ t}} \cdots $| of length |$n $|⁠ , where |$ S= \{ {\color {red}{ s}}, {\color {blue}{ t}} \} $|⁠ . An approach to Soergel calculus of universal Coxeter groups, in particular of type |$ \tilde {A}_1 $|⁠ , has been developed recently by Elias and Libedinsky in [ 10 ]; see also [ 8 ]. For type |$ \tilde {A}_1 $| this approach involves the two-colour Temperley-Lieb algebra but unfortunately the two-colour Temperley-Lieb algebra only captures the degree zero part of |$ \tilde {A}_w^{{\mathbb {C}}} $|⁠ , whereas our interests lie in the full grading on |$ \tilde {A}_w^{{\mathbb {C}}} $|⁠ .

The second origin of our cellular algebra is as a certain idempotent truncation |$\mathbb {N}\mathbb {B}_{n-1} $| of Martin and Saleur’s blob-algebra from [ 28 ]. In [ 26 ] the algebras |$ \tilde {A}_w^{{\mathbb {C}}} $| and |$\mathbb {N}\mathbb {B}_{n-1} $| were studied extensively and in particular presentations in terms of generators and relations were found for each of them. Using this it was shown that there is an isomorphism |$ {A}^{{\mathbb {C}}}_w \cong \mathbb {N}\mathbb {B}_{n-1} $| where |$ A_w^{{\mathbb {C}}} $| is a natural diagrammatically defined subalgebra of |$ \tilde {A}^{{\mathbb {C}}}_w $|⁠ , whose dimension is half the dimension of |$ \tilde {A}^{{\mathbb {C}}}_w $|⁠ . On the other hand, we show in this paper that the representation theory of |$ \tilde {A}^{{\mathbb {C}}}_w $| can be completely recovered from the representation theory of |$ A_w^{{\mathbb {C}}} $|⁠ .

An important feature of |$ \tilde {A}_w^{{\mathbb {C}}} $| and |$ \mathbb {N}\mathbb {B}_{n-1} $|⁠ , and in fact of all cellular algebras appearing in this paper, is the fact that they are |$ {\mathbb {Z}} $| -graded algebras, with explicitly given degree functions defined in terms of the diagrams. They are |${\mathbb {Z}}$| -graded cellular in the sense of Hu and Mathas; see [ 20 ].

In this paper our first new result is a construction of integral forms |$ {A}_w $| and |$ {{\mathbb {B}}^{x,y}_{n-1}} $| for |$ {A}^{{\mathbb {C}}}_w $| and |$ \mathbb {N}\mathbb {B}_{n-1} $| over the two-parameter polynomial algebra |$ R:= {\mathbb C}[x,y] $| and a lift of the isomorphism |$ {A}^{{\mathbb {C}}}_w \cong \mathbb {N}\mathbb {B}_{n-1} $| to |$ {A}_w \cong {{\mathbb {B}}^{x,y}_{n-1}} $|⁠ . The integral form |$ A_w $| is in fact already implicit in the setup for Soergel calculus, using the dual geometric realization of the Coxeter group |$ W $| of type |$ \tilde {A}_1$|⁠ . Under this realization, the parameters |$ x $| and |$ y $| correspond to the two simple roots for |$W$|⁠ . The integral form for |$ \mathbb {N}\mathbb {B}_{n-1} $| is also a well-known object, since it is simply the two-parameter blob-algebra |$ {{\mathbb {B}}^{x,y}_{n-1}}$| with blob-parameter |$ x $| and marked loop parameter |$ y $|⁠ . Thus, the novelty of our result lies primarily in the isomorphism between these integral forms, which on the other hand has the quite surprising consequence of rendering a Coxeter group theoretical meaning to the two blob algebra parameters for |$ {{\mathbb {B}}^{x,y}_{n-1}}$|⁠ , since they become nothing but the simple roots for |$ W $|⁠ .

Our main interests lies in the representation theory of |$ A_w $| which via the above isomorphism is equivalent to the representation theory of |$ {{\mathbb {B}}^{x,y}_{n-1}}$|⁠ . For several reasons the representation theory of |$ {{\mathbb {B}}^{x,y}_{n-1}}$| is more convenient to handle. Both algebras are cellular algebras with diagrammatically defined cellular bases, but the straightening rules for expanding the product of two cellular basis elements in terms of the cellular basis are easier in the |$ {{\mathbb {B}}^{x,y}_{n-1}}$| setting. Secondly, there is a natural Temperley-Lieb subalgebra |$ {\mathbb {T}\mathbb {L}_{n-1}}$| of |$ {{\mathbb {B}}^{x,y}_{n-1}}$| whose associated restriction functor |$ \textrm {Res} $| is very useful for our purposes. We show in section 4 of our paper that |$ \textrm {Res} $| maps a cell module |$ \Delta ^{{\mathbb {B}}}_{n-1}(\lambda ) $| for |$ {{\mathbb {B}}^{x,y}_{n-1}}$| to a module with a cell module filtration for |$ {\mathbb {T}\mathbb {L}_{n-1}}$| and that the sections of this filtration induce a diagonalization of the bilinear form |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n-1,\lambda } $| on |$ \Delta ^{{\mathbb {B}}}_{n-1}(\lambda ) $|⁠ .

This work is partially motivated by the paper [ 36 ] by the second author in which a diagonalization of the bilinear form for the cell module for |$ \tilde {A}_w $| is obtained, in fact the results of [ 36 ] are valid for a general Coxeter system. Unfortunately, as was already mentioned in [ 36 ], the diagonalization process in that paper does not work over |$R$| itself, but only over the fraction field |$ Q $| of |$R$|⁠ , since it relies on certain Jucys-Murphy elements for |$ A_w $| that are of degree 2, and not 0. As a consequence the |${\mathbb {Z}}$| -graded structure on the cell module for |$ \tilde {A}_w $| breaks down under the diagonalization process in [ 36 ]. The diagonalization process of the present paper, however, which is based on the Jones-Wenzl idempotents that are of degree 0, resolves this problem at least for type |$\tilde {A}_1$|⁠ .

The layout of the paper is as follows. In the next section we introduce the notation that shall be used throughout the paper and recall the various algebras that play a role throughout: the Temperley-Lieb algebra |$ {\mathbb {T}\mathbb {L}_{n}}$|⁠ , the blob algebra |$ {{\mathbb {B}}^{x,y}_n} $|⁠ , the nil-blob algebra |$ {{\mathbb {N}\mathbb {B}}_n}$| and the Soergel algebra |$ \tilde {A}_w$|⁠ . We also recall how each of them fits into the cellular algebra language. In section 3 we introduce the subalgebra |$ {A}_w $| of |$ \tilde {A}_w $| and show the isomorphism |$ {{\mathbb {B}}^{x,y}_{n-1}} \cong {A}_w $| that was mentioned above. We also show how the cellular algebra structure on |$ \tilde {A}_w $| induces a cellular structure on |$ {A}_w $| and that there is an isomorphism |$ \Delta ^{ {{\mathbb {B}}}}_{n-1}(\lambda ) \cong \Delta _w(v)$| between the respective cell modules for |$ {{\mathbb {B}}^{x,y}_{n-1}} $| and |${A}_w$|⁠ . In section 4 we consider a natural filtration of |$\textrm {Res} \Delta ^{ {{\mathbb {B}}}}_{n}(\lambda ) $| where |$\textrm {Res} $| is the restriction functor from |$ { {{\mathbb {B}}^{x,y}_{n-1}}} $| -modules to |$ { {\mathbb {T}\mathbb {L}_{n-1}}} $| -modules. We show that the Jones-Wenzl idempotents |$ {\textbf {JW}_k} $| for |$ {\mathbb {T}\mathbb {L}_{k}} $| where |$ k \le n-1 $| can be used to construct sections for this filtration and to diagonalize the bilinear form |$ \langle \cdot , \cdot \rangle _{n-1, \lambda }^{{\mathbb {B}}} $| on |$\Delta ^{ {{\mathbb {B}}}}_{n-1}(\lambda )$|⁠ . In section 5 we prove the key Theorems 5.1 and 5.2 , that were already mentioned above. They allow us to give concrete expressions for the diagonal elements of the matrix for |$ \langle \cdot , \cdot \rangle _{n-1, \lambda }^{{\mathbb {B}}}$|⁠ , which, as already mentioned, turn out to be products of positive roots |$ \alpha $| for |$W$|⁠ . In section 6 we give a description of the reflections |$ s_{\alpha } $| in |$ W $| that correspond to the positive roots of section 5 . Finally, in section 7 we use the results of the previous sections to give the graded Jantzen filtration with corresponding graded sum formula.

The authors wish to express their gratitude to P. Wedrich for useful conversations and for pointing out that the nil-blob algebra and the dotted Temperley-Lieb algebra are the same. They also wish to thank the two anonymous referees for detailed reports that greatly helped improving the presentation and accuracy of the paper.

In this paper we shall consider several diagram algebras. Possibly the oldest and most studied diagram algebra is the Temperley-Lieb algebra. It arose in statistical mechanics in the seventies. In the present paper we shall use the following variation of it.

Definition 2.1. The Temperley-Lieb algebra |$ {\mathbb {T}\mathbb {L}_{n}}$| with loop-parameter |$ -2$| is the |$R$| -algebra on the generators |${\mathbb {U}}_1, \ldots , {\mathbb {U}}_{n-1} $| subject to the relations $$ \begin{align} {\mathbb{U}}_i^2 & = - 2 {\mathbb{U}}_i & & \mbox{if}\ 1\leq i < n\end{align}$$ (2.3) $$ \begin{align} {\mathbb{U}}_i{\mathbb{U}}_j{\mathbb{U}}_i & ={\mathbb{U}}_i & & \mbox{if}\ |i-j|=1\end{align}$$ (2.4) $$ \begin{align} {\mathbb{U}}_i{\mathbb{U}}_j& = {\mathbb{U}}_j{\mathbb{U}}_i & & \mbox{if}\ |i-j|>1 {{.}}\end{align}$$ (2.5)

The blob algebra was introduced by Martin and Saleur in [ 28 ], as a a way of considering boundary conditions in the statistical mechanical model of the Temperley-Lieb algebra. Since its introduction, the blob algebra has been the subject of much research activity in mathematics as well as physics; see for example [ 14 ], [ 27 ], [ 29 ], [ 31 ], [ 32 ], [ 33 ], [ 34 ]. In this paper, we shall use the following variation of it.

Definition 2.2. The two-parameter blob algebra |$ {{\mathbb {B}}^{x,y}_n}$|⁠ , or more precisely the blob algebra with loop-parameter |$ -2$|⁠ , marked loop parameter |$ y $| and blob-parameter |$ x $|⁠ , is the |$R$| -algebra on the generators |${\mathbb {U}}_0,{\mathbb {U}}_1, \ldots , {\mathbb {U}}_{n-1} $| subject to the relations $$ \begin{align} {\mathbb{U}}_i^2 & = - 2 {\mathbb{U}}_i & & \mbox{if } 1\leq i < n\end{align}$$ (2.6) $$ \begin{align} {\mathbb{U}}_i{\mathbb{U}}_j{\mathbb{U}}_i & ={\mathbb{U}}_i & & \mbox{if } |i-j|=1 \mbox{ and } i,j>0\end{align}$$ (2.7) $$ \begin{align} {\mathbb{U}}_i{\mathbb{U}}_j& = {\mathbb{U}}_j{\mathbb{U}}_i & & \mbox{if } |i-j|>1\end{align}$$ (2.8) $$ \begin{align} {\mathbb{U}}_1{\mathbb{U}}_0{\mathbb{U}}_1& = y {\mathbb{U}}_1 & &\end{align}$$ (2.9) $$ \begin{align} {\mathbb{U}}_0^2& = x {\mathbb{U}}_0 {{.}} &&\end{align}$$ (2.10)

Just as is the case for |$ {{\mathbb {N}\mathbb {B}}_n}$|⁠ , one easily checks that |$ {{\mathbb {B}}^{x,y}_n} $| is a |$ {\mathbb {Z}}$| -graded algebra.

The rules |$ \textrm {deg}({\mathbb {U}}_i) = 0 $| for |$ i> 0 $| and |$ \textrm {deg}({\mathbb {U}}_0) = 2 $| define a (non-negative) |$ {\mathbb {Z}}$| -grading on |$ {{\mathbb {B}}^{x,y}_n}$|⁠ .

The relations are easily seen to be homogeneous with respect to |$\textrm {deg} $|⁠ .

All algebras considered in the present paper fit into the general language of cellular algebras , introduced by Graham and Lehrer.

Definition 2.4. Let |$ \mathcal {A} $| be a finite dimensional algebra over a commutative ring |$ \Bbbk $| with unity. Then a cellular basis structure for |$\mathcal {A}$| consists of a triple |$ (\Lambda , {\textrm {Tab}}, C ) $| such that |$ \Lambda $| is a poset, |$\textrm {Tab} $| is a function on |$ \Lambda $| with values in finite sets and |$ C:\coprod _{\lambda \in \Lambda } {\textrm {Tab}}(\lambda ) \times {\textrm {Tab}}(\lambda ) \rightarrow \mathcal {A}$| is an injection such that $$ \begin{align*} & \{ C_{st}^{\lambda} \, |\, s,t \in {\textrm{Tab}}(\lambda), \, \lambda \in \Lambda \} \end{align*}$$ is a |$ \Bbbk $| -basis for |$\mathcal {A} $|⁠ : the cellular basis for |$ \mathcal {A}$|⁠ . The rule |$ (C_{st}^{\lambda })^{\ast }:= C_{ts}^{\lambda }$| defines a |$ \Bbbk $| -linear antihomomorphism of |$\mathcal {A}$| and the structure constants for |$\mathcal {A}$| with respect to |$ \{ C_{st}^{\lambda } \}$| satisfy the following condition with respect to the partial order: for all |$ a \in \mathcal {A} $| we have $$ \begin{align*} & a C_{st}^{\lambda} = \sum_{u \in \textrm{Tab}(\lambda)} r_{usa} C_{ut}^{\lambda} + \mbox{ lower terms} \end{align*}$$ where lower terms means a linear combination of |$ C^{\mu }_{ab} $| where |$ \mu < \lambda $| and where |$ r_{usa} \in {{ \Bbbk }} $|⁠ .

The above triple |$ (\Lambda _n, {\textrm {Tab}}, C ) $| makes |$ {\mathbb {T}\mathbb {L}_{n}}$| into a cellular algebra.

This follows directly from the definitions.

With this notation we have the following Theorem.

The above triple |$ (\Lambda _{\pm n}, {\textrm {Tab}}, C ) $| makes |$ {{\mathbb {B}}^{x,y}_n}$| into a cellular algebra.

This also follows directly from the definitions.

Let |$ \Delta _n^{ {\mathbb {T}\mathbb {L}}}(\lambda ) $| be the cell module for |$ {\mathbb {T}\mathbb {L}_{n}}$|⁠ . Then |$ \Delta _n^{ {\mathbb {T}\mathbb {L}}}(\lambda ) $| is free over |$ R $| with basis |$ \{ \overline {C}_{s t_{\lambda }}\, | \, s \in {\textrm {Tab}}(\lambda ) \} $| where |$ \overline {C}_{s t_{\lambda }}:= {C}_{s t_{\lambda }} + A^{< \lambda } $|⁠ . A similar statement holds for |$ \Delta _n^{ {{\mathbb {B}}}}(\lambda ) $|⁠ .

This follows from the algorithm given in the proof Theorem 2.5 of [ 26 ].

Our definition ( 2.24 ) of the cell modules for |$ {\mathbb {T}\mathbb {L}_{n}} $| and |$ {{\mathbb {B}}^{x,y}_n} $| differs slightly from the definition given in [ 15 ], but in view of the Theorem the two definitions coincide.

We now come to Soergel calculus. In [ 26 ], an isomorphism |$ {A}_w \cong {{\mathbb {N}\mathbb {B}}_n}$| was established, where |$ {A}_w $| is the endomorphism algebra of a Bott-Samelson object in the Soergel calculus of type |$\tilde {A}_1$|⁠ . We aim at generalizing this result to an isomorphism involving |$ {{\mathbb {B}}^{x,y}_n}$|⁠ .

Let us now briefly explain the definition of the diagrammatic Soergel category |$ {{{\mathcal {D}}}}_{(W,S)} $| for our choices. Let |$ {\textbf {exp}} $| be the set of expressions over |$ S $|⁠ , that is words |$ \underline {w}= s_{i_1} s_{i_1} \cdots s_{i_N} $| in the alphabet |$ S $|⁠ . We consider the empty expression |$ \underline {w} = \emptyset $| to be an element of |$ {\textbf {exp}} $|⁠ .

For |$ f \in R $| and |$ D $| a Soergel diagram, the product |$ f D$| is defined as the diagram obtained from |$ D $| by replacing the polynomial |$ g$| of the leftmost region of |$D$| by |$fg$|⁠ . The multiplication |$ D_1 D_2 $| of diagrams |$ D_1 $| and |$ D_2 $| is given by vertical concatenation with |$ D_2 $| on top of |$ D_1$|⁠ , where regions containing two polynomials are replaced by the same regions, but containing the product of these polynomials. The monoidal structure is given by horizontal concatenation. There is a natural |$ {\mathbb {Z}}$| -grading on |$ {{{\mathcal {D}}}}_{(W,S)} $|⁠ , extending the grading on |$ R $|⁠ , in which dots, that is the first two diagrams in ( 2.32 ) have degree |$ 1$|⁠ , and the trivalents, that is the last two diagrams in ( 2.32 ), have degree |$-1$|⁠ .

We define |$ {{\mathcal {D}}}^{{\mathbb {C}}}_{(W,S)} $| to be the category obtained from |$ {{{\mathcal {D}}}}_{(W,S)} $| by adding relation ( 2.38 ).

It is shown in [ 11 ] that there is an equivalence between |$ {{{\mathcal {D}}}}_{(W,S)} $| and the category of Soergel bimodules for |$ (W,S) $|⁠ . It induces an equivalence between |$ {{\mathcal {D}}}^{{\mathbb {C}}}_{(W,S)} $| and the category of Soergel modules.

The following Theorem is fundamental for this paper.

There is a homomorphism of |$ R $| -algebras |$ \varphi : {{\mathbb {B}}^{x,y}_{n-1}} \rightarrow \tilde {A}_w$| given by |$\mathbb {U}_i\mapsto U_i $| for |$ i = 0, 1, \ldots , n-2$|⁠ .

For general |$(W,S)$| there is a, somewhat unwieldy, recursive procedure for constructing an |$ R$| -basis for the morphisms |$ \mbox {Hom}_{{{\mathcal {D}}}} ( \underline {x}, \underline {y} ) $|⁠ , for any |$ \underline {x}, \underline {y} \in {\textbf {exp}} $|⁠ . It is a diagrammatic version of Libedinsky’s double leaves basis for Soergel bimodules and the basis elements are also called double leaves. For |$ W $| the infinite dihedral group, there is however a non-recursive description of the double leaves basis that was used extensively in [ 26 ], and that also plays an important role in the present paper.

The double leaves diagram basis elements for |$\tilde {A}_{w}$| are built up from top and bottom ‘half-diagrams’, similarly to Temperley-Lieb and blob diagrams. Let us explain these half-diagrams.

The fundamental result concerning double leaves is the fact that they form an |$R$| -basis for |$\tilde {A}_w$|⁠ . In fact, a stronger Theorem holds. Let |$ \tilde {\Lambda }_{{w}}:= \{ v \in W | v \le w \} $|⁠ , endowed with poset structure via the Bruhat order <. For |$ v \in \tilde {\Lambda }_{w} $| let |$ {\textrm {Tab}}_w(v ) $| be the set of light leaves for |$ \tilde {A}_w $| defining |$ v$| in the above sense, and for |$ D_1, D_2 \in {\textrm {Tab}}_w(v ) $| let |$ C_{D_1, D_2}^{v} \in \tilde {A}_w $| be the double leaf obtained by gluing as above. We now have the following Theorem.

The triple |$ ( \tilde {\Lambda }_{{w}}, {\textrm {Tab}}_w(v), C) $| defines a cellular basis structure on |$ \tilde {A}_w$|⁠ .

See [ 25 ] and [ 11 ].

Following [ 26 ], we now introduce |$ A_w \subseteq \tilde {A}_w$| as follows.

Let |$ A_w $| be the span in |$ \tilde {A}_w$| of all double leaves with empty zone C, or equivalently, |$ A_w $| is the free |$ R$| -module with basis given by the double leaves of empty zone C.

Our next Theorem is an analogue of Theorem 3.8 and Corollary 3.9 of [ 26 ], although the proofs of parts |$\textbf {b)}$| and |$\textbf {c)}$| of the Theorem are different from the proofs of the corresponding statements in [ 26 ], since the algebras considered in [ 26 ] are |$ {\mathbb {C}} $| -algebras whereas the algebras in the present paper are |$R$| -algebras. Therefore, in the present article some extra care is necessary since nonzero coefficients of |$ R $| need not be invertible. Moreover, the arguments in [ 26 ] depend on the linear algebra fact that injective linear transformations |$ f: V \rightarrow W $| between vector spaces |$ V $| and |$ W $| of the same finite dimension are isomorphisms. The analogous statement is false for free |$ R$| -modules, which is the main reason why the proofs of the present paper are different from the ones in [ 26 ].

The cardinality of double leaves of empty zone C is |$ \binom {2n}{n}$| and so |${A}_w$| is free over |$ R$| of rank |$ {{\textrm {rk }}}\, A_w = {{\textrm {rk }}}\, {{\mathbb {B}}^{x,y}_n} = {{2n}\choose{n}}$|⁠ .

|${A}_w$| is an |$ R$| -algebra. It is the subalgebra of |$\tilde {A}_w$| generated by |$U_0, U_1, \ldots , U_{n-2}$|⁠ .

The homomorphism |$ \varphi : {{\mathbb {B}}^{x,y}_{n-1}} \rightarrow \tilde {A}_w$| from Theorem 3.1 induces an isomorphism |$ \varphi : {{\mathbb {B}}^{x,y}_{n-1}} \rightarrow {A}_w$|⁠ .

To show |$\textbf {a)}$| we first note that the cardinality of the set of double leaves of empty zone C is given by Definition 3.7 in [ 26 ] and Theorem 3.8 |$\textbf {c)}$| in [ 26 ], and so the statements about |$ A_w $| are a direct consequence of Definition 3.3 and ( 2.17 ).

In order to prove |$\textbf {b)}$| we define |$ {A}_w^{\prime }$| to be the subalgebra of |$ \tilde {A}_w $| generated by |$U_0, U_1, \ldots , U_{n-2}$| and must show that |$ {A}^{\prime }_w = {A}_w $|⁠ . We first show that |$ {A}^{\prime }_w \supseteq {A}_w $|⁠ .

In fact, once we have the right number of birdcages in zone A, we can use successive multiplications of the types given in ( 3.18 ), to obtain any combination of desired birdcage lengths, as opposed to ( 3.17 ) that always produces degenerate birdcages.

Now in ( 3.16 ), we must also break the symmetry with respect to birdcage lengths in zone B. But in order to break this symmetry we proceed just as we did in the last step for zone A, applying ( 3.18 ) successively, adjusting the lengths of the relevant birdcages until they are as desired.

In order to prove the other inclusion |$ {A}^{\prime }_w \subseteq {A}_w $| we need to change the argument of the corresponding statement in [ 26 ] since it, as already mentioned, depends on dimension arguments in linear algebra (over |$ {\mathbb {C}} $|⁠ ).

We first observe that |$ U_i \in {A}_w $| for |$ i =0,1,\ldots , n-2 $|⁠ . Hence, to show |$ {A}^{\prime }_w \subseteq {A}_w $| it is enough to verify that |$ {A}_w $| is invariant under left and right multiplication by the |$ U_i$| ’s.

Let therefore |$ D$| be a diagram for |$ {A}_w $|⁠ . We first choose |$ i> 0 $| and proceed to give a description of the effect of multiplying |$ U_i $| below on |$ D $|⁠ , that is we describe |$ U_i D$| in terms of |$ D$|⁠ . Let |$ l_1, l_2 $| and |$ l_3 $| be the arcs in |$ D $| that has bottom boundary points |$ i, i+1 $| and |$ i+2$| of |$ D$|⁠ , respectively. Without loss of generality we may assume that |$ l_1 $| and |$ l_3 $| are red, and that |$ l_2 $| is blue. Recall that an arc |$ l $| of |$ D $| is a boundary dot arc if one of its vertices is a dot and the other one is a boundary point.

There are a few remaining cases to consider, but they are all small variations of the cases already studied and so we leave them to the reader.

Finally, we observe that the description of the right multiplication |$ D U_i $| is completely analogous to the description of |$ U_i D $|⁠ , and so we have concluded the proof of |$\textbf {b)}$|⁠ .

We now give an alternative proof of |$ {A}^{\prime }_w \subseteq {A}_w $|⁠ , adapting the proof in [ 26 ] and using one of the main results in [ 11 ]. Let |$ Q $| be the quotient field of |$ R $| and let |$ Q{A}_w:= Q \otimes _R {A}_w $|⁠ , |$ Q{A}^{\prime }_w:= Q \otimes _R {A}^{\prime }_w $| and |$ Q {{\mathbb {B}}^{x,y}_{n-1}} = Q \otimes _R {{\mathbb {B}}^{x,y}_{n-1}}$|⁠ . Since |$ A_w $| and |$ {{\mathbb {B}}^{x,y}_{n-1}} $| are torsion free |$R$| -modules, in fact even free, we may view |$ A_w $| and |$ {{\mathbb {B}}^{x,y}_{n-1}}$| as |$R$| -submodules of |$ Q{A}_w $| and |$ Q {{\mathbb {B}}^{x,y}_{n-1}}$|⁠ , via the map |$ D \mapsto 1 \otimes _R D $|⁠ . Similarly, we may view |$ A^{\prime }_w $| as an |$R$| -submodule of |$ Q{A}^{\prime }_w $|⁠ , since |$ {A}^{\prime }_w $| is torsion free, being a submodule of the free |$ R$| -module |$ \tilde {A}_w $|⁠ .

Now the inclusion |$ {A}_w \subseteq {A}^{\prime }_w $| induces an inclusion |$ Q {A}_w \subseteq Q {A}^{\prime }_w $|⁠ , since |$ Q \otimes _R ( \cdot ) $| is an exact functor, and the surjection |$ \varphi : {{\mathbb {B}}^{x,y}_{n-1}} \twoheadrightarrow A^{\prime }_w $| induces a surjection |$ Q {{\mathbb {B}}^{x,y}_{n-1}} \twoheadrightarrow Q A^{\prime }_w $|⁠ . Combining this with |$\textbf {a)}$|⁠ , we deduce that |$ Q {A}_w = Q {A}^{\prime }_w $| since both are |$Q$| -vector spaces of the same dimension |$ {2n}\choose{n}$|⁠ .

We remark that, in a suitable sense, the alternative proof of |$\textbf {b)}$| is equivalent to the first proof, since the arguments in [ 11 ], that hold in the setting of a general Coxeter system |$(W,S) $|⁠ , depend on a case-by-case similar to the one carried out in our first proof.

To prove |$\textbf {c)}$| we argue essentially as in [ 26 ], although a little extra care has to be exercised since the algebras are defined over a commutative ring rather than a field. But by ( 2.17 ), |$\textbf {a)}$| and |$\textbf {b)}$| we have that |$ \varphi $| is a surjective homomorphism between free |$R$| -modules of the same finite rank. On the other hand, |$ R $| is a commutative ring with 1 and so indeed |$ \varphi $| is an isomorphism, as follows from Vasconcelos’ Theorem; see [ 39 ]. The proof of the Theorem is finished.

The triple |$ ( \Lambda _{w}, {\textrm {Tab}}_w(v), C) $| defines a cellular basis structure on |$ {A}_w$|⁠ .

By part |$\textbf {b})$| of Theorem 3.4 we know that |$ A_w $| is a subalgebra of |$ \tilde {A}_{w} $| and so the Theorem follows immediately from Theorem 3.5 and the fact that for |$ D_1, D_2 \in {\textrm {Tab}}_w(v ) $| and |$ v \in \tilde {\Lambda }_{w}$| we have that |$ C_{D_1 D_2} ^v $| belongs to |$ A_w $| if and only if |$ v \in {\Lambda }_{w}$|⁠ .

By Theorem 3.4 we know that |$ {{\mathbb {B}}^{x,y}_{n-1}} \cong A_w $| and from Theorem 2.6 and Theorem 3.5 we know that both algebras are cellular. It now seems plausible that the corresponding cell modules are isomorphic as well. This is however not automatic since the cellular structure on a cellular algebra is not unique. Our next aim is to show that the cell modules are indeed isomorphic.

For this we first need to establish a poset isomorphism |$ \psi : \Lambda _{w} \cong \Lambda _{ {{\pm } ( n-1)}} $|⁠ . The sets |$ \Lambda _{w} $| and |$ \Lambda _{ {{\pm } ( n-1)}} $| are both of cardinality |$ n $| and the respective order relations are both total, so there is in fact a unique choice of |$ \psi $|⁠ . It is given by the following Lemma, where |$ l(\cdot ) $| is the usual Coxeter length function on |$ W$|⁠ .

|$ \Delta _w(v) $| is free over |$ R $| with basis |$ \{ \overline {C}_{D, D_{v}}\, | \, D \in {\textrm {Tab}}_w(v) \} $| where |$ \overline {C}_{D, D_{v}}:= {C}_{D, D_{v}} + A^{< v} $|⁠ .

This follows from the algorithm given in the proof of Theorem Theorem 3.4 .

We then finally obtain the main result of this section.

Suppose that |$ \varphi (\lambda ) = v $|⁠ . Then the isomorphism |$ \varphi : {{\mathbb {B}}^{x,y}_{n-1}} \rightarrow {A}_w$| induces an isomorphism |$ \varphi : \Delta ^{ {{\mathbb {B}}}}_{n-1}(\lambda ) \rightarrow \Delta _w(v)$| of cell modules.

Since |$ \varphi (C_\lambda ) = C_v $| we have that |$ \varphi $| induces ideal isomorphisms |$ A^{\lambda } \cong A^v $| and |$ A^{< \lambda } \cong A^{< v}$| and hence |$ A^{\lambda } /A^{< \lambda } \cong A^v / A^{< v} $|⁠ . But from this we deduce that |$ \Delta _w(v) $| and |$ \Delta ^{ {{\mathbb {B}}}}_{n-1}(\lambda ) $| are isomorphic under |$ \varphi $|⁠ , as claimed.

For a general cellular algebra |$ \mathcal {A}$| over |$ \Bbbk $| with cell modules |$ \{ \Delta (\lambda ) \, | \, \lambda \in \Lambda \} $| there is a canonical bilinear form |$ \langle \cdot , \cdot \rangle _{\lambda } $| on |$ \Delta (\lambda ) $| that plays an important role for the representation theory of |$ \mathcal {A}$|⁠ . Let |$ \Lambda _0 = \{\lambda \in \Lambda \, | \, \langle \cdot , \cdot \rangle _{\lambda }\neq 0 \} $| and define for |$ \lambda \in \Lambda _0 $| the |$ \mathcal {A}$| -module |$ L(\lambda ):= {{\Delta }}(\lambda ) / \textrm {rad} \langle \cdot , \cdot \rangle _{\lambda } $| where |$ \textrm {rad} $| is the radical of |$ \langle \cdot , \cdot \rangle _{\lambda } $| in the usual sense of bilinear forms. It is an |$ \mathcal {A}$| -submodule of |$ \Delta (\lambda ) $| because |$ \langle \cdot , \cdot \rangle _{\lambda } $| is |$ \mathcal {A} $| -invariant, that is |$ \langle xy, z \rangle _{\lambda } = \langle x, y^{\ast } z \rangle _{\lambda } $| for all |$ x \in \mathcal {A} $| and |$ y, z \in \Delta (\lambda ) $|⁠ , where |$ \ast $| is the antihomomorphism of |$\mathcal {A} $| given in Definition 2.4 . In the case where |$ \Bbbk $| is a field, the |$ \mathcal {A} $| -modules in the set |$ \{ L(\lambda ) \, | \, \lambda \in \Lambda _0 \} $| are all irreducible, and each |$ \mathcal {A} $| -irreducible module occurs exactly once in the set; see Theorem 3.4 in [ 15 ].

Let |$ \langle \cdot , \cdot \rangle ^w_{n, v} $| be the bilinear form on |$ \Delta _{w}(v) $| and let |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n-1, \lambda } $| be the bilinear form on |$ \Delta ^{ {{\mathbb {B}}}}_{n-1}(\lambda ) $|⁠ . Then we have the following Theorem.

Theorem 3.9. |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n-1, \lambda } $| and |$ \langle \cdot , \cdot \rangle ^w_{n, v} $| are equivalent under |$ \varphi $|⁠ , in other words $$ \begin{align}& \langle \varphi(s), \varphi(t) \rangle^w_{n, v} = \langle s, t \rangle^{{\mathbb{B}}}_{n-1, \lambda} \, \, \, \mbox{for } s,t \in \Delta^{ {{\mathbb{B}}}}_{n-1}(\lambda)\end{align}$$ (3.39) where |$ \varphi (\lambda ) = v$|⁠ .

Proof. A bilinear and invariant form |$ \langle \cdot , \cdot \rangle $| on |$ \Delta _w(v) $| corresponds to an |$ A_w$| -homomorphism |$ \Delta ^{ {{\mathbb {B}}}}_{ n-1}(\lambda ) \rightarrow \Delta _{ n-1}^{ {{\mathbb {B}}}, \ast }(\lambda )$| where |$ \Delta ^{ {{\mathbb {B}}}, \ast }_{ n-1}(\lambda ) $| is the dual of |$ \Delta ^{ {{\mathbb {B}}}}_{ n-1}(\lambda )$|⁠ . For |$ Q $| the fraction field of |$ R$| and |$\overline {Q} $| its algebraic closure we set |$ \Delta ^{\overline {Q}}_{ n-1}(\lambda ):= \Delta ^{ {{\mathbb {B}}}}_{ n-1}(\lambda ) \otimes _R \overline {Q} $|⁠ . Then |$ \Delta ^{\overline {Q}}_{ n-1}(\lambda ) $| is irreducible and so by Schur’s Lemma |$ \Delta ^{\overline {Q}}_{ n-1}(\lambda ) \rightarrow \Delta _{ n-1}^{\overline {Q},\ast }(\lambda )$| is unique up to a scalar. Hence, |$ \langle \cdot , \cdot \rangle $| is unique up to a scalar |$ \mu $|⁠ , that is $$ \begin{align}& \langle \psi(a), \psi(b) \rangle^{{\mathbb{B}}}_{n-1, \lambda} = \mu \langle a, b \rangle^w_{n, v} \, \, \, \mbox{for } a,b \in \Delta_{w, v}(\lambda)\end{align}$$ (3.40) But using |$ a=b = C_v$|⁠ , one checks that |$ \mu =1$| and so the Theorem follows.

The purpose of the present paper is to study the form |$ \langle \cdot , \cdot \rangle ^w_{n, v} $|⁠ . In view of Theorem 3.9 , we can instead study the form |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n-1, \lambda } $|⁠ , which turns out to be easier to handle.

As already mentioned, there is an embedding |$ {\mathbb {T}\mathbb {L}_{n}} \subseteq {{\mathbb {B}}^{x,y}_n} $| which at the diagrammatic level is an embedding of Temperley-Lieb diagrams in blob diagrams. This gives rise to a restriction functor |$\textrm {Res} = \textrm {Res}^{ {{\mathbb {B}}^{x,y}_n}}_ {\mathbb {T}\mathbb {L}_{n}} $| from |$ { {{\mathbb {B}}^{x,y}_n}} $| -modules to |$ { {\mathbb {T}\mathbb {L}_{n}}} $| -modules. In this section we study the application of |$\textrm {Res} $| on |$ \Delta ^{ {{\mathbb {B}}}}_{ n}(\lambda ) $|⁠ .

In terms of these identifications the action of |$ D \in {{\mathbb {B}}^{x,y}_n}$| (resp. |$D \in {\mathbb {T}\mathbb {L}_{n}}$|⁠ ) on |$ D_1 \in \Delta _n^{\mathbb {B}}(\lambda ) $| (resp. |$ D_1 \in \Delta _n^ {\mathbb {T}\mathbb {L}}(\lambda )) $| is given by concatenation with |$D_1$| on top of |$D$|⁠ , followed by the same reduction process of extra blobs and internal loops, marked or unmarked, that we gave for |$ {{\mathbb {B}}^{x,y}_n}$| (resp. |$ {\mathbb {T}\mathbb {L}_{n}}$|⁠ ) itself. If the result of this does not belong to the span of half-diagrams for |$ \Delta _n^{\mathbb {B}}(\lambda ) $| (resp. |$ \Delta _n^ {\mathbb {T}\mathbb {L}}(\lambda ) $|⁠ ), we have |$DD_1 = 0.$|

The following result is the analogue of Lemma 8.2 from [ 9 ].

|$ { {\mathcal {F}}}^i(\lambda ) $| is a |$ {\mathbb {T}\mathbb {L}_{n}}$| -submodule of |$ \textrm {Res} \Delta ^{ {{\mathbb {B}}}}_n(\lambda ) $|⁠ .

b) There is a homomorphism of |$ {\mathbb {T}\mathbb {L}_{n}}$| -modules |$\pi _i: { {\mathcal {F}}}^i(\lambda ) \rightarrow \Delta ^{ {\mathbb {T}\mathbb {L}}}_n(|\lambda |+2i) $| that induces an isomorphism $$ \begin{align}& \overline{\pi}_i: { {\mathcal{F}}}^i(\lambda)/ { {\mathcal{F}}}^{i-1}(\lambda) \cong \Delta^{ {\mathbb{T}\mathbb{L}}}_n(|\lambda|+2i) { {{.}}}\end{align}$$ (4.4)

Lemma 4.2. Let |$\pi _i: { {\mathcal {F}}}^i(\lambda ) \rightarrow \Delta ^{ {\mathbb {T}\mathbb {L}}}_n(|\lambda |+2i) $| be the homomorphism from Lemma 4.1 . We have that $$ \begin{align}& \pi_i( e_{i}^{\lambda} ) = \pi_i( f_{i}^{\lambda} ) {{.}}\end{align}$$ (4.15)

We have |$ (e_j^{\lambda })^{\ast } {\mathbb {T}\mathbb {L}_{n}} f_i^{\lambda }=0 $| for |$ j <i$|⁠ .

We have |$ \langle { {\mathcal {F}}}^{i-1}(\lambda ), S_i(\lambda ) \rangle ^{ {{\mathbb {B}}}}_{n,\lambda } =0 $|⁠ .

We have |$ S_i(\lambda ) \cap { {\mathcal {F}}}^{i-1}(\lambda ) =0$|⁠ .

The |$ {\mathbb {T}\mathbb {L}_{n}}$| -modules |$S_i(\lambda ) $| and |$ \Delta ^{ {\mathbb {T}\mathbb {L}}}_n(|\lambda | +2i) $| are isomorphic.

Corollary 4.4. Set as before |$ k:= \dfrac {n - | \lambda |}{2}$|⁠ . Then, with respect to |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n,\lambda } $|⁠ , there is an orthogonal direct sum decomposition of |$\textrm {Res} \, \Delta ^{ {{\mathbb {B}}}}_n(\lambda ) $|⁠ , as follows $$ \begin{align}& \textrm{Res} \,\Delta^{ {{\mathbb{B}}}}_n(\lambda) = S_1(\lambda) \oplus \ldots \oplus S_k(\lambda) {{.}}\end{align}$$ (4.26)

Proof. Combining Lemma 4.2 with |$ \textbf {c}) $| of Theorem 4.3 , we get that $$ \begin{align}& \textrm{Res}\, { {\mathcal{F}}}^{i}(\lambda) = S_i(\lambda) \oplus { {\mathcal{F}}}^{i-1}(\lambda)\end{align}$$ (4.27) and the Corollary follows by induction on this formula.

The purpose of this section is to calculate the |$ c_i(x,y)$| ’s from ( 4.28 ) and ( 4.30 ). This is the key calculation of the paper. Quite surprisingly, the result turns out to be given in terms of nice expressions involving the positive roots for |$W$|⁠ .

With this notation we can now formulate the following Theorem.

b) Let |$ c_i(x,y) $| be as in ( 4.28 ) and ( 4.30 ). Then up to multiplication by a nonzero scalar in |${\mathbb {C}}$|⁠ , we have that $$ \begin{align}& c_i(x,y) = ( \alpha_{x,\lambda +2 }\, \alpha_{x,\lambda +3} \cdots \alpha_{x,\lambda +i+1} ) \alpha_{y,1} \, \alpha_{y,2} \cdots \alpha_{y,i}\end{align}$$ (5.5) (where, as before, the product is set equal to |$1 $| if |$i=0$|⁠ ).

We now consider the situation where |$ \lambda < 0$|⁠ . We have the following Theorem.

b) Let |$ c_i(x,y) $| be as in ( 4.28 ) and ( 4.30 ). Then up to multiplication by a nonzero scalar in |${\mathbb {C}}$|⁠ , we have that $$ \begin{align}& c_i(x,y) = \left( \alpha_{x,1 } \, \alpha_{x,2} \cdots \alpha_{x,i+1} \right) \alpha_{y,1+|\lambda|} \, \alpha_{y,2+|\lambda|} \cdots \alpha_{y,i+|\lambda|}\end{align}$$ (5.33) (where, as before, the product is set equal to |$x $| if |$i=0$|⁠ ).

The proof is essentially the same as the proof of Theorem 5.1 . We leave the details to the reader.

We saw in the Theorems 5.1 and 5.2 that |$ c_i(x,y) $| has a factorization in terms of roots for |$W$|⁠ . In this section we describe the reflections in |$ W$| that correspond to these roots. It turns out that these reflections can be described nicely in terms of the Bruhat order on |$W$|⁠ .

For our |$W$|⁠ , the reflections |$ s_{x,i} $| and |$ s_{y,i} $| for the roots |$ \alpha _{x,i} $| and |$\alpha _{y,i} $| are given by the formulas of the following Lemma.

Lemma 6.1. Let |$ \alpha _{x,i} $| and |$ \alpha _{y,i} $| be the positive roots for |$ W $| introduced in ( 5.1 ) and let |$ s_{x,i} $| and |$ s_{y,i} $| be the associated reflections, for |$ i=1,2, \ldots $| Then we have that $$ \begin{align}& s_{x,i} = ({\color{red} s} {\color{blue}{t}})^{i-1} {\color{red} s}, \, \, \, \, \, \, \, \, \, \, \, \, s_{y,i} = {\color{blue}{t}} ({\color{red} s} {\color{blue}{t}})^{i-1} {{.}}\end{align}$$ (6.2)

This is immediate from ( 5.1 ) and the definitions.

We now have the following Lemma.

a) Suppose that |$ \lambda \ge 0$|⁠ . Then the set of reflections |$ s_{\alpha } $| in |$W $| satisfying |$ v < s_{\alpha } v \le w $| is exactly $$ \begin{align}& \{ s_{x,\lambda +2 }, \, s_{x,\lambda +3}, \, \cdots \,, s_{x,\lambda +k+1} \} \cup \{ s_{y,1}, \, s_{y,2}, \cdots, s_{y,k} \}\end{align}$$ (6.3) obtained by transforming the roots of the factors of ( 5.4 ) to reflections.
b) Suppose that |$ \lambda < 0$|⁠ . Then the set of reflections |$ s_{\alpha } $| in |$W $| satisfying |$ v < s_{\alpha } v \le w $| is exactly $$ \begin{align}& \{ s_{x,1 }, \, s_{x,2}, \, \cdots \,, s_{x,k+1} \} \cup \{ s_{y,1 + | \lambda| }, \, s_{y, 2 + | \lambda|}, \cdots, s_{y,k + | \lambda|} \}\end{align}$$ (6.4) obtained by transforming the roots of the factors of ( 5.32 ) to reflections.

In this final section we study the representation theory of |$ \tilde {A}_w $| and its specialization |$ \tilde {A}_w^{{\mathbb {C}}}:= \tilde {A}_w \otimes _R \mathbb {\mathbb {C}} $|⁠ , where the |$ R $| -algebra structure on |$ {\mathbb {C}} $| is given by mapping |$ \alpha ^\vee _ {\color{red} s} $| and |$ \alpha ^\vee _{\color{blue}{t}} $| to |$ 0$|⁠ . Note that |$ \tilde {A}_w^{{\mathbb {C}}} $| has already been studied in the literature, in fact for general |$ (W,S) $| for example in [ 36 ] or in [ 33 ].

As already mentioned, |$\tilde {A}_w $| is a cellular algebra and hence also |$ \tilde {A}_w^{{\mathbb {C}}} $| is a cellular algebra, with cell modules |$ \Delta _w^{{\mathbb {C}}}(y ):= \Delta _w(y) \otimes _R {\mathbb {C}}$| for |$ y \in \tilde {\Lambda }_w$|⁠ . Moreover, as already indicated, |$ \tilde {A}_w $| and |$ \tilde {A}_w^{{\mathbb {C}}} $| are |$ {\mathbb {Z}}$| -graded algebras with degree function |$ \deg $| given in ( 2.10 ). In fact they are graded cellular algebras, that is they fit into the following definition first formulated by Hu and Mathas; see [ 20 ].

Suppose that |$ \Bbbk $| is a commutative ring with identity and that |$ \mathcal {A} $| is a |$ \Bbbk $| -algebra which is cellular on the triple |$ (\Lambda , {\textrm {Tab}}, C ) $|⁠ . Suppose moreover that |$ \mathcal {A} $| is a |$ {\mathbb {Z}}$| -graded algebra via |$ { \mathcal {A}} = \oplus _{i \in {\mathbb {Z}}} A_i $|⁠ . Then we say that |$ \mathcal {A} $| is a |${\mathbb {Z}}$| -graded cellular algebra if for each |$ \lambda \in \Lambda $| there is a function |$ \deg : \textrm {Tab}(\lambda ) \rightarrow {\mathbb {Z}}$| such that for |$ {\mathfrak {s}}, {\mathfrak {t}} \in \textrm {Tab}(\lambda ) $| we have that |$ C_{{\mathfrak {s}} {\mathfrak {t}}} \in \mathcal {A}_{ \deg ({\mathfrak {s}}) + \deg ( {\mathfrak {t}})} $|⁠ .

We shall in general refer to |${\mathbb {Z}}$| -graded cellular algebras simply as graded cellular algebras .

We shall use the notation |$ \tilde {A}_w^{gr} $| and |$ \tilde {A}_w^{gr, {\mathbb {C}}} $| when referring to |$ \tilde {A}_w $| and |$ \tilde {A}_w^{ {\mathbb {C}}} $| as graded cellular algebras and similarly, for |$ v \in \tilde {\Lambda }_w$|⁠ , we shall use the notation |$ \Delta _w^{gr}(v ) $| and |$ \Delta _w^{gr, {\mathbb {C}}}(v ) $| for the graded cell modules for |$ \tilde { A}_w^{gr} $| and |$ \tilde {A}_w^{gr, {\mathbb {C}}} $|⁠ . On the blob-algebra side, we shall use the notation |$ {{\mathbb {B}}^{gr, x,y}_n}$| and |$ {{\mathbb {N}\mathbb {B}_n^{gr}}} $| for |$ {{\mathbb {B}}^{x,y}_n} $| and |$ {{\mathbb {N}\mathbb {B}}_n} $|⁠ , when viewed as graded cellular algebras, and shall for |$ \lambda \in \Lambda _{ {{\pm n}}} $| use the notation |$ \Delta _n^{gr, {{\mathbb {B}}}}( \lambda ) $| and |$ \Delta _n^{gr, {{\mathbb {B}}}, {\mathbb {C}}}(\lambda ) $| for the graded cell modules for |$ {{\mathbb {B}}^{gr, x,y}_n}$| and |$ {{\mathbb {N}\mathbb {B}_n^{gr}}} $|⁠ .

The proof of Theorem 3.4 shows that |$ {{\mathbb {B}}^{gr, x,y}_{n-1}} \cong A_w^{gr} $| and so also |$ {{\mathbb {N}\mathbb {B}_{n-1}^{gr}}} \cong A_w^{gr,{\mathbb {C}}} $|⁠ . Recall the map |$ \varphi : \Lambda _{ \pm (n-1)} \rightarrow \Lambda _{w} $| from Lemma 3.6 Then, similarly, the proof of Theorem 3.8 shows that |$ \Delta ^{gr, {{\mathbb {B}}}}_{n-1}(\lambda ) \cong \Delta ^{gr}_w(v)$| where |$ \varphi (\lambda ) = v $| and so also |$ \Delta ^{gr, {{\mathbb {B}}}, {\mathbb {C}}}_{n-1}(\lambda ) \cong \Delta ^{gr, {\mathbb {C}}}_w(v)$|⁠ . However, for |$ v $| not belonging to the image of |$ \varphi $|⁠ , that is for |$ v \in {\Lambda }^c_{w} $|⁠ , see ( 3.33 ), we need to work a little bit to get an analogous description of |$ \Delta ^{gr}_w(v) $| and |$ \Delta ^{gr, {\mathbb {C}}}_w(v) $|⁠ .

For |$ v= \varphi (\lambda ) $| we have that |$\Delta ^{gr}_w(v) \cong \Delta ^{gr, {{\mathbb {B}}}}_{n-1}(\lambda ) $|⁠ .

For |$ v \in \Lambda _w^c $| set |$ v_1:= v s^{\prime } $|⁠ , that is |$ l(v_1) = l(v) +1 $|⁠ . Then |$\Delta ^{gr}_w(v) \cong \Delta ^{gr}_w(v_1 )[1] \cong \Delta ^{gr, {{\mathbb {B}}}}_{n-1}(\lambda )[1] $| where |$ \varphi (\lambda ) = v_1 $|⁠ .

a) Suppose that |$ \lambda \in \Lambda _{ {{\pm (n-1)}}} $| with |$\lambda \ge 0 $|⁠ . Then $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}}(\lambda) = {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}, {\mathbb{C}}}(\lambda) = \sum_{i=0}^{\frac{n-1-\lambda}{2}} {{\textrm{rk }}}\, \Delta_{n-1}^{ {\mathbb{T}\mathbb{L}}}(\lambda+2i) q^{2i} {{.}}\end{align}$$ (7.5)
b) Suppose that |$ \lambda \in \Lambda _{ {{\pm (n-1)}}} $| with |$ \lambda < 0 $|⁠ . Then $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}}(\lambda) = {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}, {\mathbb{C}}}(\lambda) = q {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}}(-\lambda) {{.}}\end{align}$$ (7.6)

This follows immediately from Lemma 4.1 .

For |$ \lambda \in \Lambda _{ {{\pm (n-1)}}} $| let |$ \{b_1, b_2, \ldots , b_m \} $| be the |$ R $| -basis for |$ \Delta _{n-1}^{ {\mathbb {B}}}(\lambda ) $| obtained from ( 4.30 ) and Theorem 5.1 if |$ \lambda \ge 0 $| or from Theorem 5.2 if |$ \lambda <0 $|⁠ . According to these Theorems |$ \langle b_i, b_i \rangle ^{{\mathbb {B}}}_{n-1,\lambda } $| is a product of positive roots for |$ W$| and so |$ \{b_1, b_2, \ldots , b_m \} $| consists of homogeneous elements since |$ \langle \cdot , \cdot \rangle ^{{\mathbb {B}}}_{n-1,\lambda } $| is homogeneous. The degree of |$ b_i $| is equal to number of roots appearing in |$ \langle b_i, b_i \rangle ^{{\mathbb {B}}}_{n-1,\lambda } $| according to Theorem 5.1 and 5.2 .

Theorem 7.4. Supposing that |$ v = \varphi (\lambda ) $| and that |$ v < s_{\alpha } v \le w $| we have that $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, \alpha }(\lambda) = {{\textrm{rk}_q }}\, \Delta^{gr}_{w}(s_{\alpha}v) [l(s_{\alpha} v)-l(v)] {{.}}\end{align}$$ (7.9) Otherwise, if |$ v < s_{\alpha } v \le w $| is not satisfied, we have |$ \Delta _{n-1}^{gr, \alpha }(\lambda ) =0$|⁠ .

Proof. Let |$ k:= \frac {n-1-\lambda }{2}$|⁠ . Let us first consider the case where |$ \lambda \ge 0 $| and |$ \alpha = \alpha _{y,i}$| for some |$ i=1,2, \ldots , k $|⁠ , hence |$ s_{\alpha } = {\color{blue}{t}} ({\color{red} s} {\color{blue}{t}})^{i-1} $|⁠ ; see Lemma 6.2 . By Lemma 7.2 we have that |$\Delta ^{gr, {{\mathbb {B}}}}_{n-1}(\lambda ) \cong \Delta ^{gr}_w(v) $|⁠ . The distinct roots |$ \alpha _{x,j} $| and |$ \alpha _{y,j} $| are irreducible and unassociated elements of |$ R $| and so it follows from the description in Theorem 5.1 of the matrix |$M_{n-1, \lambda }^{{\mathbb {B}}} $| in ( 4.30 ) that $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta^{gr, \alpha}_{n-1}(\lambda) = \sum_{j=i}^{k} {{\textrm{rk }}}\, \Delta_{n-1}^{ {\mathbb{T}\mathbb{L}}}(\lambda+2j) q^{2j } = q^{2i} \sum_{j=0}^{k-i } {{\textrm{rk }}}\, \Delta_{n-1}^{ {\mathbb{T}\mathbb{L}}}(\lambda+2i + 2j) q^{2j } {{.}}\end{align}$$ (7.10) Using Lemma 7.3 and Lemma 3.6 we get that ( 7.10 ) is equal to $$ \begin{align}& q^{2i} {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}}(\lambda+2i ) = q^{2i-1} {{\textrm{rk}_q }}\, \Delta_{n-1}^{gr, {\mathbb{B}}}(-\lambda-2i ) = q^{2i-1} {{\textrm{rk}_q }}\, \Delta^{gr}_w({\color{blue}{t}} ({\color{red} s} {\color{blue}{t}})^{i-1}v) = q^{2i-1} {{\textrm{rk}_q }}\, \Delta^{gr}_w( s_{\alpha}v) {{.}}\end{align}$$ (7.11) But |$ v $| begins with |${ s} $| since |$ \lambda \ge 0 $| and so the last expression of ( 7.11 ) is |$ {{\textrm {rk}_q }}\, \Delta ^{gr}_w( s_{\alpha }v) [l(s_{\alpha } v)-l(v)] $| which shows the Theorem in this case. For an illustration of |$ s_{\alpha } v $|⁠ , see ( 6.5 ). Let us now consider the case where still |$ \lambda \ge 0$|⁠ , but |$ \alpha = \alpha _{x,\lambda + 1 + i }$| and hence |$ s_{\alpha } = ({\color{red} s} {\color{blue}{t}})^{\lambda +i} {\color{red} s}$|⁠ ; see Lemma 6.2 . Then |$ \alpha $| appears in the same blocks as |$ \alpha _{y,i} $| did in the previous case, and so we get from ( 7.10 ) and ( 7.11 ) that $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta^{gr, \alpha}_{n-1}(\lambda) = q^{2i-1} {{\textrm{rk}_q }}\, \Delta^{gr}_{w}({\color{blue}{t}} ({\color{red} s} {\color{blue}{t}})^{i-1}v) = q^{2i} {{\textrm{rk}_q }}\, \Delta^{gr}_w( ({\color{red} s} {\color{blue}{t}})^{i}v)\end{align}$$ (7.12) where we used Lemma 3.6 and b) of Lemma 7.3 for the second equality. On the other hand, writing |$ v= u s^{\prime } $| with |$ l(u)+1 = l(v) $| we get from Lemma 6.2 and b) of Lemma 7.2 that $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta^{gr}_w( s_{\alpha} v) = {{\textrm{rk}_q }}\, \Delta^{gr}_w( ({\color{red} s} {\color{blue}{t}})^{i}u) = q {{\textrm{rk}_q }}\, \Delta^{gr}_w( ({\color{red} s} {\color{blue}{t}})^{i}v) {{.}}\end{align}$$ (7.13) Comparing ( 7.12 ) and ( 7.13 ) we get $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta^{gr, \alpha}_{n-1}(\lambda) = q^{2i-1} {{\textrm{rk}_q }}\, \Delta^{gr}_w( s_{\alpha} v) = {{\textrm{rk}_q }}\, \Delta^{gr}_w( s_{\alpha} v) [l(s_{\alpha} v)-l(v)]\end{align}$$ (7.14) which shows the Theorem in this case as well. The remaining cases of the Theorem are proved with similar techniques.

Theorem 7.5. Let |$ \alpha $| be a positive root for |$ W$|⁠ . If |$ v < s_{\alpha } v \le w $| then $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{w}^{gr, \alpha }(v) = {{\textrm{rk}_q }}\, \Delta^{gr}_{w}(s_{\alpha}v) [l(s_{\alpha} v)-l(v)]\end{align}$$ (7.16) and otherwise |$ \Delta _{w}^{gr, \alpha }(v) =0$|⁠ .

Proof. As already mentioned, if |$ v \in \Lambda _w $| the result follows immediately from Theorem 7.4 , so let us assume that |$ v \in \Lambda _w^c$|⁠ . As before we write |$ \underline {w} = \underline {w}_1s^{\prime } $|⁠ , where |$ s^{\prime } $| is the last |$S$| -generator of |$ \underline {w}$| and set |$ v_1 = v s^{\prime }$|⁠ . Then |$ l(v_1) = l(v)+1$| and |$ v_1 \in \Lambda _w$|⁠ . Let |$D$| be a diagram basis element for |$\Delta _{w}(v) $|⁠ . Then |$ D $| has nonempty zone C and we define |$ D_1 $| to be the diagram basis element for |$\Delta _{w}(v_1) $| which is obtained from |$ D$| by making the last non-hanging birdcage, corresponding to zone C, hanging. Then |$ D \mapsto D_1 $| is a bijection between the diagram basis for |$\Delta _{w}(v) $| and the diagram basis for |$\Delta _{w}(v_1) $|⁠ . On the other hand, using the definition of the bilinear forms we have that $$ \begin{align}& \langle D, C \rangle^w_{n, v} = v(\alpha^{\prime}) \langle D_1, C_1 \rangle^w_{n, v_1}\end{align}$$ (7.17) where |$ \alpha ^{\prime } $| is the root corresponding to |$ s^{\prime } $| and so the matrix for |$ \langle \cdot , \cdot \rangle ^w_{n, v} $| has the diagonalized form |$ v(\alpha ^{\prime }) M_{n-1, \lambda }^{{\mathbb {B}}} $| where |$ \lambda = \varphi (v_1) $|⁠ . We now assume that |$ \lambda \ge 0 $| such that |$ M_{n-1, \lambda }^{{\mathbb {B}}} $| is given by Theorem 5.1 . One then checks that |$ v(\alpha ^{\prime }) = \alpha _{x, \lambda +1}$|⁠ . Moreover, the set of reflections |$ s_{\alpha } $| in |$W $| satisfying |$ v < s_{\alpha } v \le w $| is the union of |$ s_{x,\lambda +1} $| with the set of reflections |$ s_{\alpha } $| satisfying |$ v_1 < s_{\alpha } v_1 \le w $|⁠ , and hence, in view of Lemma 6.2 , it is equal to $$ \begin{align}& \{ s_{x,\lambda +1}, s_{x,\lambda +2 }, \, s_{x,\lambda +3}, \, \cdots \,, s_{x,\lambda +k+1} \} \cup \{ s_{y,1}, \, s_{y,2}, \cdots, s_{y,k} \}\end{align}$$ (7.18) which is exactly the set of reflections obtained by transforming the roots of the factors of the diagonal elements of of |$ v(\alpha ^{\prime }) M_{n-1, \lambda }^{{\mathbb {B}}} $| to reflections. Let us now show ( 7.16 ). If |$ \alpha $| is a factor of a diagonal element of |$ M_{n-1, \lambda }^{{\mathbb {B}}}$| we are reduced to the previous case treated in Theorem 7.4 , as follows $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{w}^{gr, \alpha }(v) = q {{\textrm{rk}_q }}\, \Delta^{gr, \alpha}_{n-1}(\lambda) = q {{\textrm{rk}_q }}\, \Delta^{gr}_{w}(s_{\alpha}v_1) [l(s_{\alpha} v_1)-l(v_1)] = {{\textrm{rk}_q }}\, \Delta^{gr}_{w}(s_{\alpha}v) [l(s_{\alpha} v)-l(v)]\end{align}$$ (7.19) where we used Lemma 7.2 for the last step. On the other hand, if |$ \alpha = \alpha _{x,\lambda +1} $| we have that |$ s_{\alpha } v_1=v $| and so we get $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{w}^{gr, \alpha }(v) = q {{\textrm{rk}_q }}\, \Delta^{gr}_{n-1}(\lambda) = {{\textrm{rk}_q }}\, \Delta^{gr}_{w}(s_{\alpha}v_1) [l(s_{\alpha} v)-l(v)]\end{align}$$ (7.20) which shows ( 7.16 ) in this case as well. The cases where |$ \lambda < 0 $| are treated with similar techniques.

|$ \Delta ^{gr, \alpha }_{w}(v) $| is free over |$ R $| and hence we get immediately a specialized version of Theorem 7.5 .

Corollary 7.6. Defining |$ \Delta ^{gr, \alpha , {\mathbb {C}}}_{w}(v):= \Delta ^{gr, \alpha }_{w}(v) \otimes _R {\mathbb {C}} $| we have that $$ \begin{align}& {{\textrm{rk}_q }}\, \Delta_{w}^{gr, \alpha, {\mathbb{C}} }(v) = {{\textrm{rk}_q }}\, \Delta^{gr, {\mathbb{C}}}_{w}(s_{\alpha}v) [l(s_{\alpha} v)-l(v)] {{.}}\end{align}$$ (7.21)

|$ \Delta ^{gr, {\mathbb {C}}}_{w}(v) / \Delta ^{gr, 1, {\mathbb {C}}}_{w}(v) $| is irreducible or zero.

b) The following graded analogue of Jantzen’s sum formula holds $$ \begin{align}& \sum_{k>0} {{\textrm{rk}_q }}\, \Delta_{w}^{gr, k, {\mathbb{C}} }(v) = \sum_{\substack{ \alpha > 0 \\ v <s_{\alpha} v \le w}} {{\textrm{rk}_q }}\, \Delta^{gr, {\mathbb{C}}}_{w}(s_{\alpha}v) [l(s_{\alpha} v)-l(v)]\end{align}$$ (7.24) where |$ \alpha> 0 $| refers to the positive roots of |$ W$|⁠ .

As pointed out in the introduction, analogues of ungraded Jantzen filtrations with associated sum formulas exist in many module categories of Lie type and give information on the irreducible modules for the category in question. But although graded representation theories in Lie theory have been known for a long time and would be very useful for calculating decomposition numbers, to our knowledge graded sum formulas have so far not been available. The virtue of Corollary 7.7 is to show the possible form of graded sum formulas in graded representation theory.

It should be noted that in the present |$ {{\mathbb {N}\mathbb {B}}_n} $| -situation, the irreducible modules can be read off from Theorem 5.1 and Theorem 5.2 and are in fact Temperley-Lieb cell modules. See also [ 32 ] for a different approach to this.

We believe that the equalities in Theorem 7.5 and Corollary 7.6 are valid on module level, but have so far not been able to prove so. But in the remainder of the article we indicate how to generalize them to enriched Grothendieck group level. The methods for this are essentially generalizations to the graded case of the methods in [ 36 ], where the corresponding ungraded case is treated.

Let |$ \mathcal {A} $| be a graded cellular algebra over |$ {\mathbb {C}} $|⁠ . Let |$ \langle \mathcal {A}\textrm {-mod} \rangle _{q} $| be the enriched Grothendieck group for |$ \mathcal {A}$|⁠ , that is |$ \langle \mathcal {A}\textrm {-mod} \rangle _{q} $| is the Abelian group generated by symbols |$ \langle M \rangle _q $|⁠ , for |$ M $| running over the modules in |$ \langle \mathcal {A}\textrm {-mod} \rangle _{q} $|⁠ , subject to the relations |$ \langle M \rangle _q = \langle M_1 \rangle _q + \langle M_2 \rangle _q $| whenever there is a short exact sequence |$ 0 \rightarrow M_1 \rightarrow M \rightarrow M_2 \rightarrow 0$| in |$ \langle \mathcal {A}\textrm {-mod} \rangle _{q} $|⁠ . The grading shift in |$ \mathcal {A}-\textrm {mod} $| induces a grading shift in |$ \langle \mathcal {A}\textrm {-mod} \rangle _{q} $| via |$ \langle M \rangle _q[ k]:= \langle M [k] \rangle _q$| and so we get a |$ {\mathbb {Z}}[q, q^{-1}] $| -structure on |$ \mathcal {A}\textrm {-mod} $| via |$ \langle M \rangle _q +\langle N \rangle _q:= \langle M \oplus N \rangle _q$| and |$ q^{k} \langle M \rangle _q:= \langle M \rangle _q[k]$|⁠ .

The following is a natural generalization of the definition of a cellular category, see [ 41 ], to the |$ {\mathbb {Z}}$| -graded case.

Definition 7.8. Let |$ \Bbbk $| be a commutative ring with identity and let |$ \mathcal {C} $| be a |$ \Bbbk $| -linear |$\mathbb Z$| -graded category, that is for objects |$ m,n $| in |$ \mathcal {C} $| we have a decomposition $$ \begin{align}& \textrm{Hom}_{\mathcal{C}}(m,n) = \oplus_{i \in {\mathbb{Z}}}\textrm{Hom}_{\mathcal{C}}(m,n)_i {{.}}\end{align}$$ (7.25) Suppose that |$ \mathcal {C} $| is endowed with a duality |$ \ast $|⁠ . Then |$ \mathcal {C} $| is called a |${\mathbb {Z}}$| -graded cellular category if there exists a poset |$ \Lambda $| and for each |$ \lambda \in \Lambda $| and each object |$ n $| in |$ \mathcal {C} $| a finite set |$ \textrm {Tab}(n, \lambda ) $| which is decomposed as |$ \textrm {Tab}(n, \lambda ) = \mathbin {\cdot\kern-5pt\cup}_{ i \in {\mathbb {Z}}}\textrm {Tab}(n, \lambda )_i $| together with a map |$ \textrm {Tab}(m, \lambda ) \times \textrm {Tab}(n, \lambda ) \rightarrow \textrm {Hom}_{\mathcal {C}}(m,n), (S,T) \mapsto C_{ST}^{\lambda } $|⁠ , satisfying |$ C_{ST}^{\lambda } \in \textrm {Hom}_{\mathcal {C}}(m,n)_{i+j} $| if |$ S \in \textrm {Tab}(n, \lambda )_i $| and |$ T \in \textrm {Tab}(n, \lambda )_j $|⁠ . These data satisfy that |$(C_{ST}^{\lambda })^{\ast } = C_{TS}^{\lambda }$| and that $$ \begin{align} & \{ C_{ST}^{\lambda} | S \in \textrm{Tab}(m, \lambda), T \in \textrm{Tab}(n, \lambda), \lambda \in \Lambda \}\ \textrm{is a homogeneous}\ \Bbbk\textrm{-basis for}\ Hom_{\mathcal{C}}(m,n) \end{align}$$ (7.26) and for all |$ a \in Hom_{\mathcal {C}}(n,p)_i, S \in \textrm {Tab}(m, \lambda )_j, T \in \textrm {Tab}(n, \lambda )_k $| $$ \begin{align}& a C_{ST}^{\lambda} = \sum_{ S^{\prime} \in \textrm{Tab}(p, \lambda)_{i+j}} r_{a}(S^{\prime}, S) C_{ S^{\prime}, T}^{\lambda} \mbox{ mod} A^{\lambda}_{i+j+k}\end{align}$$ (7.27) where |$ A^{\lambda } $| is the span of |$\{ C_{ST}^{\mu } | \mu < \lambda , S \in \textrm {Tab}(m, \mu ), T \in \textrm {Tab}(p,\mu ) \} $|⁠ .

Let |$ \mathcal {C} $| be a graded cellular category and let |$ A $| be a finite subset of the objects for |$ \mathcal {C}$|⁠ . Define for |$ \lambda \in \Lambda $| the set |$ \textrm {Tab}(\lambda ):= \cup _{ n \in A} \textrm {Tab}(n, \lambda ) $|⁠ . Let for |$ S \in \textrm {Tab}(\lambda ), T \in \textrm {Tab}(\lambda ) $| the element |$ C_{ST}^{\lambda } \in \textrm {End}_{\mathcal {C}}(A) $| be defined as the inclusion of |$ C_{ST}^{\lambda } \in \textrm {Hom}_{\mathcal {C}}(m,n) $| in |$ \textrm {End}_{\mathcal {C}}(A) $|⁠ . Then these data define a graded cellular algebra structure on |$ \textrm {End}_{\mathcal {C}}(A) $|⁠ .

Just as in the ungraded case considered in [ 36 ], this follows immediately from the definitions.

For a general Coxeter system |$(W,S)$|⁠ , it was shown in [ 11 ] that the diagrammatic Soergel categories |$ {{{\mathcal {D}}}}_{(W,S)} $| and |$ {\mathcal D}_{(W,S)}^{{\mathbb {C}}} $|⁠ , see Definition 2.10 and Remark 2.11 , are graded cellular categories in the sense of Definition 7.8 .

Let us indicate the ingredients that make the categories |$ {{{\mathcal {D}}}}_{(W,S)} $| and |$ {{\mathcal {D}}}^{{\mathbb {C}}}_{(W,S)} $|⁠ , see Definition 2.10 and Remark 2.11 , fit into Definition 7.8 , for our choice of |$ (W,S) $|⁠ . In case of |$ {{{\mathcal {D}}}}_{(W,S)} $|⁠ , we use for |$ \Bbbk $| the ring |$ R $|⁠ , and for the objects and morphisms we use the objects and morphisms given in Definition 2.10 . For the poset |$ \Lambda $| we use |$ W$| itself, endowed with the Bruhat order poset structure. For |$ \underline {w} \in {\textbf {exp}} $| starting with |$ {\color{red} s} $| and in reduced form, that is |$ \underline {w} = w $|⁠ , we use for |$ \textrm {Tab}(\underline {w}, v) $| the set of birdcages |$ \textrm {Tab}_w(v) $|⁠ . For |$ \underline {w} \in {\textbf {exp}} $| starting with |$ {\color{blue}{t}} $| and in reduced form, we use for |$ \textrm {Tab}_w(v) $| the corresponding set of birdcages |$ \textrm {Tab}_w(v) $|⁠ . For |$ \underline {w} \in {\textbf {exp}} $| a general object in |$ {{{\mathcal {D}}}}_{(W,S)} $| not in reduced form, we use the general light leaves construction from [ 11 ]. Since we do not need the details of this construction we skip it at this point. In case of |$ {{\mathcal {D}}}^{{\mathbb {C}}}_{(W,S)} $| we use the same ingredients as for |$ {{{\mathcal {D}}}}_{(W,S)} $|⁠ , except that for |$ \Bbbk $| we replace |$ R $| by |$ {\mathbb {C}}$|⁠ .

We now have the following Theorem, which is our main reason for changing to the categorical setting.

|$ \tilde {A}_{W_0}^{gr, {\mathbb {C}}}$| is a graded quasi-hereditary algebra over |$ {\mathbb {C}} $|⁠ .

The proof of Theorem 8.5 in [ 36 ], corresponding to the ungraded setting, carries over to the present graded setting.

|$ \Phi : \langle \tilde {A}_{W_0}^{gr, {\mathbb {C}}}-\textrm {mod} \rangle _{q} \rightarrow \oplus _{ \underline {z} \in \underline {W}_0} {\mathbb {Z}}[q, q^{-1}] $| is an isomorphism of |$ {\mathbb {Z}}[q,q^{-1}] $| -modules.

Since |$ \langle \tilde {A}_{W_0}^{gr, {\mathbb {C}}}-\textrm {mod} \rangle _{q} $| and |$ \oplus _{ \underline {z} \in \underline {W}_0} {\mathbb {Z}}[q, q^{-1}] $| are free |$ {\mathbb {Z}}[q, q^{-1}] $| -modules of the same rank, it is enough to show that |$ \Phi $| is surjective, by Vasconcelos’ Theorem once again; see [ 39 ]. Let |$ f = \sum _{ \underline {z} \in \underline {W}_0 } f_{ \underline {z}} \in \oplus _{ \underline {z} \in W_0 } {\mathbb {Z}}[q, q^{-1}] $| and choose |$ f_{ \underline {z}_0} $| nonzero and |$ \underline {z}_0 $| minimal with respect to this condition. The |$ \underline {z}_0 $| ’th component of |$ \Phi ( \langle \Delta ^{gr, {\mathbb {C}}}_{W_0}(z_0) \rangle _q) $| is |$ {{\textrm {rk}_{z_0, q} }}\,( \Delta _{ z_0}( z_0)) =1 $| and so the |$ {z}_0 $| ’th component of |$ \Phi ( f_{ \underline {z}_0} \langle \Delta ^{gr, {\mathbb {C}}}_{W_0}(z_0) \rangle _q) $| is |$ f_{ \underline {z}_0} $|⁠ . On the other hand, the |$z$| ’th component of |$ \Phi ( \Delta ^{gr, {\mathbb {C}}}_{W_0}(z_0)) $| is |$ {{\textrm {rk}_{z, q} }}\, \langle \Delta _{ z}( z_0) \rangle _q $| which is nonzero only if |$ z_0 \le z $|⁠ . Hence, we can use induction on |$ f - \Phi ( f_{ \underline {z}_0} \langle \Delta ^{gr, {\mathbb {C}}}_{W_0}(z_0) \rangle _q) $| and get that |$ f \in \textrm {im} \Phi $|⁠ , as claimed.

We can now prove the promised Grothendieck group extension of Corollary 7.6 .

Corollary 7.12. For |$ v \in W_0 $| we have |$ \Delta ^{gr, \alpha ,{\mathbb {C}}} _{W_0}(v) = 0 $| unless |$ w \ge s_{\alpha } v> v $|⁠ . If |$ w \ge s_{\alpha } v> v $| then $$ \begin{align}& \langle \Delta^{gr, \alpha, {\mathbb{C}}}_{W_0}(v) \rangle_q = \langle \Delta^{gr, {\mathbb{C}}}_{W_0}(s_{\alpha}v )[l(s_{\alpha}v) -l(v)] \rangle_q {{.}}\end{align}$$ (7.37)

We apply |$ \Phi $| to ( 7.37 ) and check that both sides are equal. Using ( 7.35 ) and Corollary 7.6 we get that the |$\underline {z}$| ’th component of the left-hand side is |$ {{\textrm {rk}_q }}\, \Delta ^{gr, {\mathbb {C}}}_{z}(s_{\alpha }v) [l(s_{\alpha } v)-l(v)] $| which by definition of |$ \Phi $| coincides with the right-hand side. We then use Theorem 7.11 to conclude the proof.

Corollary 7.13. The following graded analogue of Jantzen’s sum formula holds: $$ \begin{align}& \sum_{k>0} \langle \Delta_{W_0}^{gr, k, {\mathbb{C}} }(v) \rangle_q = \sum_{\substack{ \alpha > 0 \\ v <s_{\alpha} v \le w}} \langle \Delta^{gr, {\mathbb{C}}}_{W_0}(s_{\alpha}v)[l(s_{\alpha}v) -l(v)] \rangle_q {{.}}\end{align}$$ (7.40)

Supported in part by beca ANID-PFCHA/Doctorado Nacional/2019-21190827 and FONDECYT [grant 1221112].

Andersen , H. H. “ A sum formula for tilting filltrations .” J. Pure Appl. Algebra 152 ( 2000 ): 17 – 40 . https://doi.org/10.1016/S0022-4049(99)00141-3 .

Google Scholar

Andersen , H. H. “ Filtrations of cohomology modules for Chevalley groups .” Annales scientifiques de l’É.N.S. 4e série, tome 16 , n |$^{\circ }$|⁠ . 4 ( 1983 ): 495 – 528 .

Andersen , H. H. , J. C. Jantzen , and W. Soergel . Representations of quantum groups at a p -th root of unity and of semisimple groups in characteristic p : independence of p . Astérisque , Vol. 220 . Paris : Société Mathématique de France , 1994, p. 321 .

Google Preview

Beilinson , A. , V. Ginzburg , and W. Soergel . “ Koszul duality patterns in representation theory .” J. Amer. Math. Soc. 9 , no. 2 ( 1996 ): 473 – 527 . https://doi.org/10.1090/S0894-0347-96-00192-0 .

Bowman , C. , A. Cox , and A. Hazi . “ Path isomorphisms between quiver Hecke and diagrammatic Bott-Samelson endomorphism algebras.” arXiv:2005.02825, to appear in Adv. Math .

Bowman , C. , A. Cox , A. Hazi , and D. Michailidis . “ Path combinatorics and light leaves for quiver Hecke algebras .” Math. Z. 300 , no. 3 ( 2022 ): 2167 – 203 . https://doi.org/10.1007/s00209-021-02829-0 .

Brundan , J. , and A. Kleshchev . “ Blocks of cyclotomic Hecke algebras and Khovanov-Lauda algebras .” Invent. Math. 178 ( 2009 ): 451 – 84 . https://doi.org/10.1007/s00222-009-0204-8 .

Burrull , G. , N. Libedinsky , and P. Sentinelli . “ P-Jones-Wenzl idempotents .” Adv. Math. 352 ( 2019 ): 246 – 64 . https://doi.org/10.1016/j.aim.2019.06.005 .

Cox , A. , J. Graham , and P. Martin . “ The blob algebra in positive characteristic .” J. Algebra 266 , no. 2 ( 2003 ): 584 – 635 . https://doi.org/10.1016/S0021-8693(03)00260-6 .

Elias , B. , and N. Libedinsky . “ Indecomposable Soergel bimodules for universal Coxeter groups With an appendix by Ben Webster .” Trans. Amer. Math. Soc. 369 , no. 6 ( 2017 ): 3883 – 910 .

Elias , B. , and G. Williamson . “ Soergel calculus .” Represent. Theory 20 ( 2016 ): 295 – 374 . https://doi.org/10.1090/ert/481 .

Ehrig , M. , and C. Stroppel . “ Koszul gradings on Brauer algebras .” Int. Math. Res. Notices 2016 , no. 13 ( 2016 ): 3970 – 4011 . https://doi.org/10.1093/imrn/rnv267 .

Fiebig , P. , and M. Lanini . “ The combinatorial category of Andersen, Jantzen and Soergel and filtered moment graph sheaves .” Abh. Math. Semin. Univ. Hamb. 86 , no. 2 ( 2016 ): 203 – 12 . https://doi.org/10.1007/s12188-016-0133-6 .

Gainutdinov , A. M. , J. L. Jacobsen , H. Saleur , and R. Vasseur . “ A physical approach to the classification of indecomposable Virasoro representations from the blob algebra .” Nuclear Phys. B Proc. Suppl. 873 , no. 3 ( 2013 ): 614 – 81 . https://doi.org/10.1016/j.nuclphysb.2013.04.017 .

Graham , J. J. , and G. I. Lehrer . “ Cellular algebras .” Invent. Math. 123 ( 1996 ): 1 – 34 . https://doi.org/10.1007/BF01232365 .

Graham , J. J. , and G. I. Lehrer . “ The representation theory of affine Temperley-Lieb algebras .” Enseign. Math., II. Sér . 44 , no. 3-4 ( 1998 ): 173 – 218 .

Hazi , A. , P. Martin , and A. Parker . “ Indecomposable tilting modules for the blob algebra .” J. Algebra 568 ( 2021 ): 273 – 313 . https://doi.org/10.1016/j.jalgebra.2020.09.042 .

Hogancamp , M. , D. E. V. Rose , and P. Wedrich . “A Kirby color for Khovanov homology.” arXiv:2210.05640, to appear in J. Eur. Math. Soc .

Hu , J. “ BGG Category |$\mathcal {O}$| and |$\mathbb {Z}$| -Graded Representation Theory .” East China Normal University Scientific Reports , Vol. 16. Forty Years of Algebraic Groups, Algebraic Geometry, and Representation Theory in China .

Hu , J. , and A. Mathas . “ Graded cellular bases for the cyclotomic Khovanov-Lauda-Rouquier algebras of type a .” Adv. Math. 225 ( 2010 ): 598 – 642 . https://doi.org/10.1016/j.aim.2010.03.002 .

Humphreys , J. E. Reflection Groups and Coxeter Groups , volume 29 of Cambridge Studies in Advanced Mathematics . Cambridge : Cambridge University Press , 1990 , https://doi.org/10.1017/CBO9780511623646 .

Humphreys , J. Representations of Semisimple Lie Algebras in the BGG Category O , Vol. 94 . Providence, R.I. : American Mathematical Society , 2008 Graduate Studies in Mathematics ISBN 978-0-8218-4678-0 .

Jones , V. F. R. “ Index for subfactors .” Invent. Math. 72 , no. 1 ( 1983 ): 1 – 25 . https://doi.org/10.1007/BF01389127 .

Khovanov , M. , and A. Lauda . “ A diagrammatic approach to categorification of quantum groups I .” Represent. Theory 13 ( 2009 ): 309 – 47 . https://doi.org/10.1090/S1088-4165-09-00346-X .

Libedinsky , N. “ Gentle introduction to Soergel bimodules I: the basics .” Sao Paulo J. Math. Sci. 13 , no. 2 ( 2019 ): 499 – 538 . https://doi.org/10.1007/s40863-019-00136-5 .

Lobos , D. , D. Plaza , and S. Ryom-Hansen . “ The nil-blob algebra: an incarnation of type |$\widetilde {A}_1$| Soergel calculus and of the truncated blob algebra .” J. Algebra 570 ( 2021 ): 297 – 365 .

Lobos , D. and Ryom-Hansen , S. Graded cellular basis and Jucys-murphy elements for generalized blob algebras , J. Pure Appl. Algebra 224 ( 7 ) ( 2020 ): 106277, 1 – 40 .

Martin , P. P. , and H. Saleur . “ The blob algebra and the periodic Temperley-Lieb algebra .” Lett. Math. Phys. 30 ( 1994 ): 189 – 206 . https://doi.org/10.1007/BF00805852 .

Martin , P. P. , and D. Woodcock . “ On the structure of the blob algebra .” J. Algebra 225 , no. 2 ( 2000 ): 957 – 88 . https://doi.org/10.1006/jabr.1999.7948 .

Mathas , A. “ Positive Jantzen sum formulas for cyclotomic Hecke algebras .” Math. Z. 301 , no. 3 ( 2022 ): 2617 – 58 . https://doi.org/10.1007/s00209-021-02957-7 .

Michailidis , D. “ Bases and BGG resolutions of simple modules of Temperley-Lieb algebras of type B .” Internat. Math. Res. Notices 2022 , no. 12 ( 2022 ): 9357 – 412 . https://doi.org/10.1093/imrn/rnab003 .

Plaza , D. “ Graded decomposition numbers for the blob algebra .” J. Algebra 394 ( 2013 ): 182 – 206 . https://doi.org/10.1016/j.jalgebra.2013.07.017 .

Plaza , D. “ Graded cellularity and the monotonicity conjecture .” J. Algebra 473 ( 2017 ): 324 – 51 . https://doi.org/10.1016/j.jalgebra.2016.10.040 .

Plaza , D. , and S. Ryom-Hansen . “ Graded cellular bases for Temperley-Lieb algebras of type a and B .” J. Algebraic Combin. 40 , no. 1 ( 2014 ): 137 – 77 . https://doi.org/10.1007/s10801-013-0481-6 .

Russell , H. “ The Bar-Natan skein module of the solid torus and the homology of |$\left (n,n\right )$| springer varieties .” Geom. Dedicata 142 ( 2009 ): 71 – 89 .

Ryom-Hansen , S. “ Jucys-murphy elements for Soergel bimodules .” J. Algebra 551 ( 2020 ): 154 – 90 . https://doi.org/10.1016/j.jalgebra.2020.01.016 .

Shan , P. “ Graded decomposition matrices of |$v$| -Schur algebras via Jantzen filtration .” Represent. Theory 16 ( 2012 ): 212 – 69 . https://doi.org/10.1090/S1088-4165-2012-00416-2 .

Stroppel , C. “ Category |$\mathcal {O}$| : Gradings and Translation Functors .” J. Algebra 268 , no. 1 ( 2003 ): 301 – 26 . https://doi.org/10.1016/S0021-8693(03)00308-9 .

Vasconcelos , W. V. “ On finitely generated flat modules .” Trans. Amer. Math. Soc. 138 ( 1969 ): 505 – 12 . https://doi.org/10.1090/S0002-9947-1969-0238839-5 .

Wenzl , H. “ On sequences of projections .” C. R. Math. Rep. Acad. Sci. Can. 9 , no. 1 ( 1987 ): 5 – 9 .

Westbury , B. W. “ Invariant tensors and cellular categories .” J. Algebra 321 , no. 11 ( 2009 ): 3563 – 7 . https://doi.org/10.1016/j.jalgebra.2008.07.004 .

Email alerts

Citing articles via.

Recommend to your Library

Affiliations

Online ISSN 1687-0247
Print ISSN 1073-7928
About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Viola V. Madsen

Customer Reviews

Team of Essay Writers

What is a good essay writing service?

Oddly enough, but many people still have not come across a quality service. A large number of users fall for deceivers who take their money without doing their job. And some still fulfill the agreements, but very badly.

A good essay writing service should first of all provide guarantees:

confidentiality of personal information;
for the terms of work;
for the timely transfer of the text to the customer;
for the previously agreed amount of money.

The company must have a polite support service that will competently advise the client, answer all questions and support until the end of the cooperation. Also, the team must get out of conflict situations correctly.

It is necessary to have several payment methods on the site to make it easier for the client to transfer money.

And of course, only highly qualified writers with a philological education should be present in the team, who will not make spelling and punctuation errors in the text, checking all the information and not stealing it from extraneous sites.

IMAGES

Contemporary Abstract Algebra
ABSTRACT ALGEBRA 3RD EDITION PDF
17 Research Proposal Examples (2024)
Lecture1: Abstract algebra-Group theory
[PDF] Abstract Algebra by Thomas Hungerford eBook
(PDF) Research Abstract

VIDEO

Congrats
Abstract algebra : Group Theory: Groups and Subgroups جبر مجرد نظرية الزمر
Abstract Algebra # Examples Group Theory # class 08
Abstract Algebra # Group Theory # class 03
Writing Abstract of Research Proposal
Abstract Algebra # Examples of Group Theory # class 06

COMMENTS

45628 PDFs
Mar 2023. Ivo Da Silva Knopp. Vinicius Linder. Explore the latest full-text research PDFs, articles, conference papers, preprints and more on ABSTRACT ALGEBRA. Find methods information, sources ...
PDF Abstract Algebra
5.1 Algebra A. This course o ers what we feel is a standard model for a rst-semester Abstract Algebra course suitable for nearly every college or university. We feel some tension between the breadth of a rst course that includes both groups and rings and the depth of one that focuses only on groups or only on rings.
Algebra
We have large groups of researchers active in number theory and algebraic geometry, as well as many individuals who work in other areas of algebra: groups, noncommutative rings, Lie algebras and Lie super-algebras, representation theory, combinatorics, game theory, and coding. Chairs: George Bergman and Tony Feng.
(PDF) An Abstract Algebra Story
Because the adequate application of the proof techniques learned in algebra lessons to the problems improves the students' reasoning and inference skills. However, research shows that abstract ...
PhD Applied Mathematics Research project proposal
Abstract. PhD in Applied Mathematics - Research Proposal Scope of the research project: development of a game theory-based mathematical model for an autonomous machine decision-making system, with ...
Abstract Algebra: Theory and Applications
This text is intended for a one- or two-semester undergraduate course in abstract algebra. Traditionally, these courses have covered the theoretical aspects of groups, rings, and fields. However, with the development of computing in the last several decades, applications that involve abstract algebra and discrete mathematics have become increasingly important, and many science, engineering ...
A Friendly Introduction to Abstract Algebra
This is a "groups first" textbook for the first course in undergraduate abstract algebra, pitched at a rather elementary level and assuming no prior exposure to proof-based mathematics. It begins with sections on proof techniques and sets, proceeds through elementary group theory (up to quotient groups and the isomorphism theorems), and ...
PDF GRADUATE/QUALIFIER LINEAR ALGEBRA: COMMENTS AND A PROPOSAL Overview
For this reason, Abstract Algebra and Linear Algebra were taught and had qualifying exams written by faculty whose main research interests were in algebra and they had large numbers of students who were doing so also. I am not an algebraist, but I think about linear algebra, have done some research in linear algebra, and teach linear algebra a lot.
PDF What Group Theory Can Do for You: From Magmas to Abstract Thinking in
comprehensive overlook of all the covered topics of abstract within the new math reform can be found in [22]. 3. Historical and Contemporary Ideas on Teaching Abstract Algebra In this section, we present and discuss didactical ideas and research on the topic of teaching abstract algebra. We will highlight both the work of researchers from the ...
abstract algebra Latest Research Papers
Abstract Algebra. Ring hypothesis is one of the pieces of the theoretical polynomial math that has been thoroughly used in pictures. Nevertheless, ring hypothesis has not been associated with picture division. In this paper, we propose another rundown of similarity among pictures using rings and the entropy work.
Abstract Algebra
Abstract algebra is a broad field of mathematics, concerned with algebraic structures such as groups, rings, vector spaces, and algebras. Roughly speaking, abstract algebra is the study of what happens when certain properties of number systems are abstracted out; for instance, altering the definitions of the basic arithmetic operations result in a structure known as a ring, so long as the ...
PDF INCREASING STUDENT LEARNING IN MATHEMATICS WITH THE USE OF ...
An Action Research Proposal Submitted to the Graduate Faculty of the School of ... Saint Xavier University Chicago, Illinois May 2009. i ABSTRACT Three teacher researchers conducted this action research project to increase their 54 high ... The project included 40 high school students enrolled in either Algebra 1-2 or Geometry classes, from ...
How to Write an Abstract for Research Proposal
Your abstract should come immediately after the title page. Write in block format without paragraph indentations. The abstract should not be more than 300 words long and the page should not have a number. The word "Abstract" in your research proposal should be center aligned in the page, unless otherwise stated.
Abstract Algebra: Structure and Application
In Abstract Algebra: Structure and Application, Finston and Morandi intend to develop the structures and basic theorems of modern algebra through applications that have relevance to the students' daily lives. Some of these applications include identification numbers like zip codes and UPCs, error-correcting codes, linear codes, ruler and ...
How to Write an Abstract
An abstract is a short summary of a longer work (such as a thesis, dissertation or research paper). The abstract concisely reports the aims and outcomes of your research, so that readers know exactly what your paper is about. ... Writing a book or research proposal; Applying for research grants; It's easiest to write your abstract last, ...
PDF How to Write an Abstract Proposal
An abstract is a brief summary of a completed research/innovation project. What should an abstract include? An abstract should include the following components: 1. Background: What is the motivation behind the research? Provide a short paragraph that details the background information. 2. Objectives: What problem are you attempting to solve ...
How to Write a Research Proposal
Research proposal examples. Writing a research proposal can be quite challenging, but a good starting point could be to look at some examples. We've included a few for you below. Example research proposal #1: "A Conceptual Framework for Scheduling Constraint Management".
100-Plus Exciting Algebra Topics for Research Papers
Linear algebra covers vector spaces and the linear mapping between them. Linear equation systems have unknowns, and mathematicians use vectors and matrices to represent them. Here are exciting topics in linear algebra to consider for your research paper. Decomposition of singular value. Investigating linear independence and dependence.
Research Proposal: A Treatise on Subtropical Algebra
3 Prior Research Due to the algebraic nature of this topic, pertinent coursework might include Abstract Algebra I/II and Galois Theory. It is straightforward to show that min and max distribute over one another, which is analogous to the distributivity of intersections and unions over one another. For this reason,
Designing and analysing a teaching proposal about linear algebra
Abstract. In this paper we propose a new strategy of dialogue between theories, considering a semiotic cognitive analysis and a praxeological analysis. We examine the implementation of a teaching and learning sequence for introducing eigentheory in a linear algebra course taught during the first year of an engineering degree programme.
Graded Sum Formula for ~ A1-Soergel Calculus and the Nil-Blob Algebra
1 Introduction. Cellular algebras were introduced by Graham and Lehrer in 1994 in the paper [] as a framework for studying the non-semisimple representation theory of many finite dimensional algebras,The motivating examples for cellular algebras were the Iwahori-Hecke algebras of type |$ A_n $| and Temperley-Lieb algebras, but it has since been realized that many other finite dimensional ...
Research Proposal In Abstract Algebra
Jason. 10 Customer reviews. offers three types of essay writers: the best available writer aka. standard, a top-level writer, and a premium essay expert. Every class, or type, of an essay writer has its own pros and cons. Depending on the difficulty of your assignment and the deadline, you can choose the desired type of writer to fit in your ...

Algebra Faculty, Courses, Dissertations

Abstract Algebra: Theory and Applications

Formats Available

Table of Contents

Ancillary Material

About the Contributors

Contribute to this Page

abstract algebra Recently Published Documents

Basic Abstract Algebra

On the Exponential Diophantine Equation (132m) + (6r + 1)n = z2

Abstract Algebra

(m, n)-Ideals in Semigoups Based on Int-Soft Sets

A transition to abstract algebra

Abstract Algebra

Levels of Abstraction in Abstract Algebra

Other Applications of Abstract Algebra

How to Write an Abstract for Research Proposal

Search form

You are here

David R. Finston and Patrick J. Morandi

Dummy View - NOT TO BE DELETED

MAA Publications

Connect with MAA

Have a language expert improve your writing

How to Write a Research Proposal | Examples & Templates

Introduction

Reference list

Table of contents

Research proposal length

Prevent plagiarism. Run a free check.

Receive feedback on language, structure, and formatting

Cite this Scribbr article

Is this article helpful?

Shona McCombes

100+ Amazing Algebra Topics for Research Papers

How to Write Theses on Advanced Algebra Topics

College Algebra Topics

Cool Topics in Algebra

Linear Algebra Topics

Pre Algebra Topics

Intermediate Algebra Topics for Research

Algebra Topics High School Students Can Explore

Advanced Topics in Algebra and Geometry

Abstract Algebra Topics

Get Professional Math Homework Help!

Leave a Reply Cancel reply

Article Contents

Graded Sum Formula for ~ A 1 -Soergel Calculus and the Nil-Blob Algebra

Email alerts

Affiliations

This Feature Is Available To Subscribers Only

Team of Essay Writers

What is a good essay writing service?

IMAGES

VIDEO

COMMENTS