negate the original hypothesis and conclusion

A free service from Mattecentrum

If-then statement

• Logical correct I
• Logical correct II

When we previously discussed inductive reasoning we based our reasoning on examples and on data from earlier events. If we instead use facts, rules and definitions then it's called deductive reasoning.

We will explain this by using an example.

If you get good grades then you will get into a good college.

The part after the "if": you get good grades - is called a hypotheses and the part after the "then" - you will get into a good college - is called a conclusion.

Hypotheses followed by a conclusion is called an If-then statement or a conditional statement.

This is noted as

$$p \to q$$

This is read - if p then q.

A conditional statement is false if hypothesis is true and the conclusion is false. The example above would be false if it said "if you get good grades then you will not get into a good college".

If we re-arrange a conditional statement or change parts of it then we have what is called a related conditional.

Our conditional statement is: if a population consists of 50% men then 50% of the population must be women.

If we exchange the position of the hypothesis and the conclusion we get a converse statemen t: if a population consists of 50% women then 50% of the population must be men.

$$q\rightarrow p$$

If both statements are true or if both statements are false then the converse is true. A conditional and its converse do not mean the same thing

If we negate both the hypothesis and the conclusion we get a inverse statemen t: if a population do not consist of 50% men then the population do not consist of 50% women.

$$\sim p\rightarrow \: \sim q$$

The inverse is not true juest because the conditional is true. The inverse always has the same truth value as the converse.

We could also negate a converse statement, this is called a contrapositive statemen t:  if a population do not consist of 50% women then the population do not consist of 50% men.

$$\sim q\rightarrow \: \sim p$$

The contrapositive does always have the same truth value as the conditional. If the conditional is true then the contrapositive is true.

A pattern of reaoning is a true assumption if it always lead to a true conclusion. The most common patterns of reasoning are detachment and syllogism.

If we turn of the water in the shower, then the water will stop pouring.

If we call the first part p and the second part q then we know that p results in q. This means that if p is true then q will also be true. This is called the law of detachment and is noted:

$$\left [ (p \to q)\wedge p \right ] \to q$$

The law of syllogism tells us that if p → q and q → r then p → r is also true.

This is noted:

$$\left [ (p \to q)\wedge (q \to r ) \right ] \to (p \to r)$$

If the following statements are true:

If we turn of the water (p), then the water will stop pouring (q). If the water stops pouring (q) then we don't get wet any more (r).

Then the law of syllogism tells us that if we turn of the water (p) then we don't get wet (r) must be true.

Video lesson

Write a converse, inverse and contrapositive to the conditional

"If you eat a whole pint of ice cream, then you won't be hungry"

• Angles, parallel lines and transversals
• Congruent triangles
• More about triangles
• Inequalities
• Mean and geometry
• The converse of the Pythagorean theorem and special triangles
• Properties of parallelograms
• Common types of transformation
• Transformation using matrices
• Basic information about circles
• Inscribed angles and polygons
• Advanced information about circles
• Parallelogram, triangles etc
• The surface area and the volume of pyramids, prisms, cylinders and cones
• SAT Overview
• ACT Overview

Understanding the Inverse Statement | Explained with Examples and Significance

Inverse statement, the inverse statement is a logical statement that is formed by negating both the hypothesis and the conclusion of an original conditional statement.

The inverse statement is a logical statement that is formed by negating both the hypothesis and the conclusion of an original conditional statement.

In general, a conditional statement consists of two parts: the hypothesis and the conclusion. The hypothesis is the “if” part of the statement, and the conclusion is the “then” part. For example, consider the conditional statement:

“If it is raining, then the ground is wet.”

To form the inverse statement, we simply negate both the hypothesis and the conclusion of the original statement. In this case, the inverse statement would be:

“If it is not raining, then the ground is not wet.”

The key idea in the inverse statement is that if the original statement is true, then the inverse statement may or may not be true. The truth value of the inverse is independent of the original statement. So, if the original statement is true, the inverse statement can be either true or false, and if the original statement is false, the inverse can also be either true or false.

It’s important to note that the inverse statement is not always logically equivalent to the original conditional statement. In other words, the truth value of the inverse statement does not always match the truth value of the original statement. However, if both the original statement and its inverse are true or both are false, then they are logically equivalent.

More Answers:

Error 403 The request cannot be completed because you have exceeded your quota . : quotaExceeded

Recent Posts

Ramses ii a prominent pharaoh and legacy of ancient egypt.

Ramses II (c. 1279–1213 BCE) Ramses II, also known as Ramses the Great, was one of the most prominent and powerful pharaohs of ancient Egypt.

Formula for cyclic adenosine monophosphate & Its Significance

Is the formula of cyclic adenosine monophosphate (cAMP) $ce{C_{10}H_{11}N_{5}O_{6}P}$ or $ce{C_{10}H_{12}N_{5}O_{6}P}$? Does it matter? The correct formula for cyclic adenosine monophosphate (cAMP) is $ce{C_{10}H_{11}N_{5}O_{6}P}$. The

Development of a Turtle Inside its Egg

How does a turtle develop inside its egg? The development of a turtle inside its egg is a fascinating process that involves several stages and

The Essential Molecule in Photosynthesis for Energy and Biomass

Why does photosynthesis specifically produce glucose? Photosynthesis is the biological process by which plants, algae, and some bacteria convert sunlight, carbon dioxide (CO2), and water

How the Human Body Recycles its Energy Currency

Source for “The human body recycles its body weight of ATP each day”? The statement that “the human body recycles its body weight of ATP

Don't Miss Out! Sign Up Now!

Sign up now to get started for free!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.12: Converse, Inverse, and Contrapositive Statements

• Last updated
• Save as PDF
• Page ID 2145

Conditional statements drawn from an if-then statement.

Converse, Inverse, and Contrapositive

Consider the statement: If the weather is nice, then I’ll wash the car. We can rewrite this statement using letters to represent the hypothesis and conclusion.

\(p=the\: weather \:is \:nice \qquad q=I'll \:wash \:the \:car\)

Now the statement is: if \(p\), then \(q\), which can also be written as \(p\rightarrow q\).

We can also make the negations, or “nots,” of \(p\) and \(q\). The symbolic version of "not p" is \(\sim p.

\(\sim p=the \:weather \:is \:not \:nice \qquad \sim q=I \:won't \:wash \:the \:car\)

Using these “nots” and switching the order of \(p\) and \(q\), we can create three new statements.

\(Converse \qquad q\rightarrow p \qquad \underbrace{If\: I\: wash\: the\: car}_\text{q}, \underbrace{then\: the \:weather \:is \: nice}_\text{p}\).

\(Inverse \qquad \sim p\rightarrow \sim q \qquad \underbrace{If\: the\: weather\: is \:not \:nice}_\text{p}, \underbrace{\:then \:I \:won't \:wash \:the \:car}_\text{q}\).

\(Contrapositive \qquad \sim q\rightarrow \sim p \qquad \underbrace{If\: I \:don't \:wash \:the \:car}_\text{q}, \underbrace{then the weather is not nice}_\text{p}\).

If the “if-then” statement is true, then the contrapositive is also true. The contrapositive is logically equivalent to the original statement. The converse and inverse may or may not be true. When the original statement and converse are both true then the statement is a biconditional statement . In other words, if \(p\rightarrow q\) is true and \(q\rightarrow p\) is true, then \(p \leftrightarrow q\) (said “\(p\) if and only if \(q\)”).

What if you were given a conditional statement like "If I walk to school, then I will be late"? How could you rearrange and/or negate this statement to form new conditional statements?

Example \(\PageIndex{1}\)

If \(n>2\), then \(n^{2}>4\).

Find the converse, inverse, and contrapositive. Determine if each resulting statement is true or false. If it is false, find a counterexample.

The original statement is true.

\(\underline{Converse}\): If \(n^{2}>4\), then \(n>2\).

False. If \(n^{2}=9\), \(n=−3\: or \: 3\). \((−3)^{2}=9\)

\(\underline{Inverse}\): If \(n\leq 2\), then \(n^{2}\leq 4\).

False. If \(n=−3\), then \(n^{2}=9\).

\(\underline{Contrapositive}\): If \(n^{2}\leq 4\), then \(n\leq 2\).

True. The only \(n^{2}\leq 4\) is 1 or 4. \(\sqrt{1}=\pm 1\) and\(\sqrt{4}=\pm 2\), which are both less than or equal to 2.

Example \(\PageIndex{2}\)

If I am at Disneyland, then I am in California.

\(\underline{Converse}\): If I am in California, then I am at Disneyland.

False. I could be in San Francisco.

\(\underline{Inverse}\): If I am not at Disneyland, then I am not in California.

False. Again, I could be in San Francisco.

\(\underline{Contrapositive}\): If I am not in California, then I am not at Disneyland.

True. If I am not in the state, I couldn't be at Disneyland.

Notice for the converse and inverse we can use the same counterexample.

Example \(\PageIndex{3}\)

Rewrite as a biconditional statement: Any two points are collinear.

This statement can be rewritten as:

Two points are on the same line if and only if they are collinear. Replace the “if-then” with “if and only if” in the middle of the statement.

Example \(\PageIndex{4}\)

Any two points are collinear.

First, change the statement into an “if-then” statement:

If two points are on the same line, then they are collinear.

\(\underline{Converse}\): If two points are collinear, then they are on the same line. True.

\(\underline{Inverse}\): If two points are not on the same line, then they are not collinear. True.

\(\underline{Contrapositive}\): If two points are not collinear, then they do not lie on the same line. True.

Example \(\PageIndex{5}\)

The following is a true statement:

\(m\angle ABC>90^{\circ}\) if and only if \(\angle ABC\) is an obtuse angle.

Determine the two true statements within this biconditional.

Statement 1: If \(m\angle ABC>90^{\circ}\), then \(\angle ABC\) is an obtuse angle.

Statement 2: If \(\angle ABC\) is an obtuse angle, then \(m\angle ABC>90^{\circ}\).

For questions 1-4, use the statement:

If \(AB=5\) and \(BC=5\), then \(B\) is the midpoint of \(\overline{AC}\).

• Is this a true statement? If not, what is a counterexample?
• Find the converse of this statement. Is it true?
• Find the inverse of this statement. Is it true?
• Find the contrapositive of this statement. Which statement is it the same as?

Find the converse of each true if-then statement. If the converse is true, write the biconditional statement.

• An acute angle is less than \(90^{\circ}\).
• If you are at the beach, then you are sun burnt.
• If \(x>4\), then \(x+3>7\).

For questions 8-10, determine the two true conditional statements from the given biconditional statements.

• A U.S. citizen can vote if and only if he or she is 18 or more years old.
• A whole number is prime if and only if its factors are 1 and itself.
• \(2x=18\) if and only if \(x=9\).

Review (Answers)

To see the Review answers, open this PDF file and look for section 2.4.

Additional Resources

Interactive Element

Video: Converse, Inverse and Contrapositive of a Conditional Statement Principles - Basic

Activities: Converse, Inverse, and Contrapositive Discussion Questions

Study Aids: Conditional Statements Study Guide

Practice: Converse, Inverse, and Contrapositive Statements

Real World: Converse Inverse Contrapositive

Logic Laws: Converse, Inverse, Contrapositive & Counterexample

Logical statements

Logical statements  are utterances that can be tested for truth or falsity. The phrase, "Jennifer's white birds" is not a logical statement because it lacks meaning. The phrase, "Jennifer is best at magic" is not logical because it is an opinion; it is not testable. The phrase, "Jennifer wears dresses every Tuesday" is logical because it can be tested. Either she wears dresses on Tuesdays or she does not.

Humans are not born to be logical. Most humans do not begin to learn logic until they are around 10 years old. Logic is a learned mathematical skill, a method of ferreting out truth using specific steps and formal structures. Some of those structures of formal logic are converse, inverse, contrapositive, and counterexample statements.

Logical statements must be tested to be valid. For example, one of the two statements below is logical in that they can be tested for its truthfulness. One is an opinion, which cannot be tested for truthfulness:

Cuban food tastes best.

Jennifer is a man.

The first statement is an opinion and is neither logical nor factual; it cannot be tested to be true. We know the second statement can be tested for its truthfulness. The second statement is logical but not factual.

Logic statement examples

Which of these phrases or utterances is a logical statement? Remember, it need not be true, just testable.

Mint chocolate chip ice cream is delicious.

Jennifer is a woman.

3 penguins and 2 water buffalo

Fricasé de Pollo is a type of Cuban food.

Statements 2 and 4 are logical statements; statement 1 is an opinion, and statement 3 is a fragment with no logical meaning.

Four testable types of logical statements are  converse, inverse, contrapositive, and counterexample statements . They can produce logical equivalence for the original statement, but they do not  necessarily  produce logical equivalence.

Logical equivalence

Suppose instead of writing an opinion for our first statement and a logical but not factual second statement, we wrote:

Jennifer is alive.

Living women eat food.

We can use these statements to form a  conditional statement  with a hypothesis and a conclusion:

If Jennifer is alive, then Jennifer eats food.

This type of if-then statement is the heart of logic. We can immediately see that the two statements result in a true conditional statement. Here is Jennifer; she is alive; she eats food (and we already know she likes Cuban food).

A  logical equivalence  recasts the same hypothesis and conclusion as a negative statement that produces the same result:

If Jennifer does not eat food, then Jennifer is not alive.

These statements have logical equivalence because they contain the same content and arrive at the same result. Statements with logical equivalence are either both true or both false.

Converse statements

The original if-then conditional statement was:

Switching the hypothesis for the conclusion provides the  converse statement :

If Jennifer eats food, then Jennifer is alive.

We have the same words, but the order of the two parts has changed. Has the truth of the conditional statement changed? In this case, the statement is still true, but it would not have to be true.

Switching the conclusion for the hypothesis does not  automatically  prove the logical conditional statement, so the converse statement could be true  or  false.

Inverse statements

A logical  inverse statement  negates both the hypothesis and the conclusion. Again, our original, conditional statement was:

By carefully making the hypothesis negative and then negating the conclusion, we create the inverse statement:

The inverse statement may or  may not  be true.

Let's compare the converse and inverse statements to see if we can make any judgments about them:

Converse: If Jennifer eats food, then Jennifer is alive.

Inverse: If Jennifer is not alive, then Jennifer does not eat food.

Both of those produce true statements. Neither would have to produce a true statement, but in this case they did. It is not possible for one to produce a true statement and the other to produce a false statement.

We now know these three facts about converse and inverse statements:

If one is true, the other statement is true.

If one statement is false, the other is false.

Converse and inverse statements are logically equivalent to one another.

Contrapositive statements

If the converse reverses a statement and the inverse negates it, could we do both? Could we flip  and  negate the statement?

Our original conditional statement was:

To create the logical  contrapositive statement , we negate the hypothesis and the conclusion and then we also switch them:

If the conditional statement is true, then the logical contrapositive statement is true. If the logical contrapositive statement is false, then the conditional statement itself is also false. They have logical equivalence.

Counterexamples

If you can find a substitute that tests the logical validity of the statement (but not its factual accuracy), you know the claim is not always true and is therefore not logically valid.

We need only find one instance, called a  counterexample , where the conditions set out in our arguments are not valid:

Original statement: If Jennifer is alive, then Jennifer eats food.

Contrapositive: If Jennifer does not eat food, then Jennifer is not alive.

We would need to find a single example of one of these conditions, any one of which would be a counterexample:

A living woman who does not eat food, or

A woman who eats food but who is not alive, or

A nonliving woman who eats food, or

A woman who does not eat food but who is alive

If we can find such an example, even a single example, in which the premises are valid but the conclusions are false, we would have a counterexample showing the original argument is invalid.

Surely you can see - leaving out zombies and vampires and other imaginary creatures - that we cannot produce a counterexample for any of our logical statements; our argument is valid.

The logical result of all this work with converse, inverse, contrapositive, and counterexample logical statements is, we learn that Jennifer is a living, breathing woman who eats.

And she likes Cuban food!

Get in touch with us

Are you sure you want to logout?

Please select your grade.

• Earth and space

Conditional Statement

Key concepts.

• Write definitions as conditional statements
• Verify statements
• Write the converse, inverse and the contrapositive of the conditional statement
• Write definitions as biconditional statements

Definition 

A conditional statement is a logical statement that has two parts, a hypothesis and a conclusion. When a conditional statement is written in if-then form , the “if” part contains the hypothesis, and the “then” part contains the conclusion . 

Here is an example: 

Re-write a Statement in if-then form 

Example 1 :

Re-write the conditional statement in if-then form.  

• All birds have feathers.  
• Two angles are supplementary if they are a linear pair. 

First, identify the hypothesis and the conclusion . When you rewrite the statement in if-then form, you may need to reword the hypothesis or conclusion. 

1. All birds have feathers . 

If an animal is a bird, then it has feathers.  

2. Two angles are supplementary if they are a linear pair.  

If two angles are a linear pair, then they are supplementary.  

Negation and Verifying Statements 

The negation of a statement is the opposite of the original statement. Notice that Statement 2 is already negative, so its negation is positive. 

Statement 1: The ball is red. Statement 2: The cat is not black. 

Statement 2: The cat is not black. Negation 2: The cat is black.  

Verifying Statements 

Conditional statements can be true or false. To show that a conditional statement is true, you must prove that the conclusion is true every time the hypothesis is true. To show that a conditional statement is false, you need to give only one counterexample. 

Related Conditionals 

To write the converse of a conditional statement, exchange the hypothesis and conclusion .  

To write the inverse of a conditional statement, negate both the hypothesis and the conclusion. To write the contrapositive , first, write the converse and then negate both the hypothesis and the conclusion. 

Write four related conditional statements 

Example 2:   

Write the if-then form, the converse, the inverse, and the contrapositive of the conditional statement “Guitar players are musicians.” Decide whether each statement is true or false . 

Solution:  

If-then form: If you are a guitar player, then you are a musician. 

True, guitars players are musicians. 

Converse: If you are a musician, then you are a guitar player. 

False, not all musicians play the guitar. 

Inverse: If you are not guitar player, then you are not a musician. 

False, even if you don’t play a guitar, you can still be a musician. 

Contrapositive: If you are not a musician, then you are not a guitar player. 

True, a person who is not a musician cannot be a guitar player. 

Equivalent Statements  

A conditional statement and its contrapositive are either both true or both false. Similarly, the converse and inverse of a conditional statement are either both true or both false. Pairs of statements such as these are called equivalent statements . In general, when two statements are both true or both false, they are called equivalent statements. 

You can write a definition as a conditional statement in if-then form or as its converse. Both the conditional statement and its converse are true. For example, consider the definition of perpendicular lines . 

Perpendicular Lines

If two lines intersect to form a right angle, then they are perpendicular lines . 

The definition can also be written using the converse:  

If two lines are perpendicular lines, then they intersect to form a right angle. 

You can write “line l is perpendicular to line m” as l ⊥ m. 

Use Definitions 

Decide whether each statement about the diagram is true. Explain your answer using the definitions you have learned. 

• −𝐀𝐂 ↔ ⊥ 𝐁𝐃 ↔ 
• ∠𝐀𝐄𝐁 and ∠𝐂𝐄𝐁 are a linear pair. 
• →−𝐄𝐀→ and →−𝐄𝐁→ are opposite rays. 

This statement is true. The right angle symbol in the diagram indicates that the lines intersect to form a right angle. So you can say the lines are perpendicular. 

This statement is true. By definition, if the noncommon sides of adjacent angles are opposite rays, then the angles are opposite rays, then the angles are a linear pair. Because

𝐄𝐀 → and →−𝐄𝐂→ are opposite rays,

∠𝐀𝐄𝐁 and ∠𝐂𝐄𝐁 are a linear pair.   

This statement is false. Point E does not lie on the same line as A and B, so the rays are not opposite rays. 

Bi-conditional Statements 

Definition  .

When a conditional statement and its converse are both true, you can write them as a single biconditional statement . A biconditional statement is a statement that contains the phrase “if and only if.”  

Any valid definition can be written as a biconditional statement. 

Write a Bi-conditional 

Example 4:   

Write the definition of perpendicular lines as a biconditional. 

Definition: If two lines intersect to form a right angle, then they are perpendicular.  

Converse: If two lines perpendicular, then they intersect to form a right angle.  

Biconditional: Two lines are perpendicular, if and only if they intersect to form a right angle.  

Question 1 : 

Rewrite the conditional statement in if-then form. 

Only people who are registered are allowed to vote.  

If one is allowed to vote, then one is registered.  

Question 2 :

Write the if-then form, the converse, the inverse, and the contrapositive of the following statement. 

3x + 10 = 16, because x = 2.  

If-then form:  

If 3x + 10 = 16, then x = 2.  

If x = 2, then 3x + 10 = 16.  

If 3x + 10 is not equal to 16, then x is not equal to 2.  

Contrapositive: 

If x is not equal to 2, then 3x + 10 is not equal to 16.  

Question 3 :

Decide whether the statement is true or false. If false, provide a counterexample. 

If a polygon has five sides, then it is a regular pentagon.  

False statement 

Counterexample: If a polygon has five sides of unequal length, then it is not a regular pentagon. The sides of a regular pentagon should be equal in length.  

Question 4 :

Rewrite the definition as a biconditional statement. 

An angle with a measure between 90 degrees and 180 degrees is called obtuse.  

An angle is called obtuse if and only if it measures between 90 degrees and 180 degrees.  

Key Concepts Covered  

• To write a conditional statement in if-then form, find the hypothesis and then the conclusion.  

• Converse: To write the converse of a conditional statement, exchange the hypothesis and conclusion. 
• Inverse: To write the inverse of a conditional statement, negate both the hypothesis and the conclusion. 
• Contrapositive: To write the contrapositive, first write the converse and then negate both the hypothesis and the conclusion.  
• When two statements are both true or both false, they are called equivalent statements . 
• A biconditional statement is a statement that contains the phrase “if and only if.” 
• In triangle ABC, AD is a median. If the area of ΔABD is 15 cm sq. then find the area of ΔABC.
• ABCD is a parallelogram and BPC is a triangle with P falling on AD. If the area of parallelogram ABCD= 26 cm 2 , find the area of triangle BPC.
• PQRS is a parallelogram and PQT is a triangle with T falling on RS. If area of triangle PQT = 18 cm 2 , then find the area of parallelogram PQRS.
• ABCD is a parallelogram where E is a point on AD. Area of ΔBCE = 21 cm 2 . If CD = 6 cm, then find the length of AF.
• The area of triangle ABC is 15 cm sq. If ΔABC and a parallelogram ABPD are on the same base and between the same parallel lines then what is the area of parallelogram ABPD.
• The area of parallelogram PQRS is 88 cm sq. A perpendicular from S is drawn to intersect PQ at M. If SM = 8 cm, then find the length of PQ.
• Amy needs to order a shade for a triangular-shaped window that has a base of 6 feet and a height of 4 feet. What is the area of the shade?
• Monica has a triangular piece of fabric. The height of the triangle is 15 inches and the triangle’s base is 6 inches. Monica says that the area of the fabric is 90 square inches. What error did Monica make? Explain your answer.
• The sixth-grade art students are making a mosaic using tiles in the shape of right triangle. The two sides that meet to form a right angle are 3 centimeters and 5 centimeters long. If there are 200 tiles in the mosaic, what is the area of the mosaic?
• A parallelogram with area 301 has a base of 35. What is its height?

Related topics

Addition and Multiplication Using Counters & Bar-Diagrams

Introduction: We can find the solution to the word problem by solving it. Here, in this topic, we can use 3 methods to find the solution. 1. Add using counters 2. Use factors to get the product 3. Write equations to find the unknown. Addition Equation: 8+8+8 =? Multiplication equation: 3×8=? Example 1: Andrew has […]

Dilation: Definitions, Characteristics, and Similarities

Understanding Dilation A dilation is a transformation that produces an image that is of the same shape and different sizes. Dilation that creates a larger image is called enlargement. Describing Dilation Dilation of Scale Factor 2 The following figure undergoes a dilation with a scale factor of 2 giving an image A’ (2, 4), B’ […]

How to Write and Interpret Numerical Expressions?

Write numerical expressions What is the Meaning of Numerical Expression? A numerical expression is a combination of numbers and integers using basic operations such as addition, subtraction, multiplication, or division. The word PEMDAS stands for: P → Parentheses E → Exponents M → Multiplication D → Division  A → Addition S → Subtraction         Some examples […]

System of Linear Inequalities and Equations

Introduction: Systems of Linear Inequalities: A system of linear inequalities is a set of two or more linear inequalities in the same variables. The following example illustrates this, y < x + 2…………..Inequality 1 y ≥ 2x − 1…………Inequality 2 Solution of a System of Linear Inequalities: A solution of a system of linear inequalities […]

Other topics

How to Find the Area of Rectangle?

How to Solve Right Triangles?

Ways to Simplify Algebraic Expressions

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Understanding Logical Statements

Learning Objectives

• Identify the hypothesis and conclusion in a logical statement.
• Determine whether mathematical statements involving linear, quadratic, absolute value expressions, equations, or inequalities are always, sometimes, or never true.
• Use counterexamples to show that a statement is false, and recognize that a single counterexample is sufficient.

Introduction

Logic is an essential part of the study of mathematics. Much of mathematics is concerned with the characteristics of numbers and other mathematical objects (such as geometric figures or variables), and being able to make decisions about what must be true based on known characteristics and other facts is vital.

The Parts of a Logical Statement

A logical statement A statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesis The part of a logical statement that provides the premise on which the conclusion is based. In a statement “If `x` then `y` ,” the hypothesis is `x` . , which is the premise or set of facts that we start with, and the conclusion The part of a logical statement that provides the result or consequences of the hypothesis. In a statement “If `x` then `y` ,” the conclusion is `y` . , which is the new fact that we can infer when the hypothesis is true. (Note: If you've used hypothesis in science class, you've probably noticed that this is a fairly different definition. Be careful not to get confused!)

Consider this statement:

If you go outside without any rain gear or cover when it’s pouring rain, you will get wet.

Here, the hypothesis is “you go outside without any rain gear or cover when it’s pouring rain.” The hypothesis must be completely true before we can use the statement to infer anything new from it. What does this statement say about someone who doesn’t go outside? About someone who uses an umbrella? About what happens to someone when it’s not pouring rain? Nothing. This statement doesn't apply to anyone in those cases.

The conclusion of this statement is “you will get wet.” Suppose it’s raining, and someone walks outside, and doesn't have any rain gear or other kind of cover—what will happen? All the parts of the hypothesis have been met, so—if the statement is true—we can infer that the person is going to get wet. It certainly seems reasonable that they would!

Note that in this example, if the hypothesis isn’t true, the person still could get wet. On a sunny day with no rain, someone might go outside to wash his car and get sprayed by the hose. Someone else might go swimming, and then they would really get wet! The statement says nothing when the hypothesis is false. It's only helpful when the hypothesis is true.

Not all logical statements are written as “If (something is true) then (something else is true).” To identify the hypothesis and conclusion, you may need to try to rewrite a statement in an “if-then” format.

Logical statements can also be about mathematics, of course! Anything that lets us infer a new fact about something mathematical from given information is a logical statement. For example, “The diagonals of a rectangle have the same length” is a logical statement. The hypothesis is the part that can help us if we know it’s true. When could this statement be useful?

With algebraic statements, the hypothesis is often an assumption about what values are allowed for a variable. For example, you might have seen a statement like “ `a + b = b + a` , where `a`  and `b` are real numbers.” Let's treat this equation as a logical statement:

Testing for Truth

Critical thinking is important, not just in mathematics but in everyday life. Have you ever heard someone make a statement and then thought, “Wait. Is that true?” Sometimes people have reasons for thinking something is true even though it isn’t. Determining if a statement is true is a great skill to have!

When determining if a statement is true, most people start by looking for examples A situation that suggests a logical statement may be true. , which are situations for which the statement does turn out to be true (both the hypothesis and the conclusion are true). A more powerful situation to find, if one exists, is a counterexample A situation that provides evidence that a logical statement is false. , a situation for which the statement turns out to be false (the hypothesis is true, but the conclusion is false). Why are counterexamples so powerful?

Consider a person who sees the moon many times at night and then thinks: I’ve never seen the moon during the day. The person might then make the statement, “The moon only comes out at night.” As an if-then statement, this is the same as “If the moon is out, then it’s night.” We can all probably think of many times when we saw the moon out, and it was nighttime. These are examples, situations when the statement was true.

But in fact, the statement is not always true, and we only need to see the moon during the day once —only one counterexample—to know that the statement is not true. Many, many examples cannot prove the statement is true, but we only need one counterexample to prove it’s not!

For a given statement, then, we have three possibilities:

So how can we be sure if something is true (or never true for that matter), if we can’t rely on lots of examples? With algebraic statements, sometimes we can turn to a graph for help:

Another way to decide if something is always, sometimes, or never true is reasoning from other things we know are true. We can start with something we know is true and try to create the original statement. Let’s try this with the same example above:

When we try to put together logical arguments like that, the biggest problem can be knowing where to start. There's a good chance our first attempt(s) will run into a dead end, and we'll need to start over. Practice does make it easier. Sometimes it helps to work backward: start by assuming the conclusion is true, try to think of a related statement known to be true (or false), and then connect them. Let’s take one last look at the example above:

Another way to test the truth of a statement is to look for counterexamples. Graphs can help us there, too:

Although we know  `|-x| = -x` is not always true if `x` is any real number, we also know that it is sometimes true. In fact, we can specify when it’s true—using the graph from the example, we can see it’s true when `x<=0` . We can use that fact to create a new statement:

If `x<=0` , then `|-x| = -x` .

Because of the narrower hypothesis, this statement is always true.

Special Cases

When we look for examples, and particularly for counterexamples, there are some special cases that are easy to overlook. Keeping these cases in mind is often very helpful. Look through some special cases and consider if any of them provides a counterexample for this statement: “When two numbers are multiplied, the product is larger than each of the factors.”

Here are some more examples. Consider the special cases above as you read through these.

Logical statements have two parts, a hypothesis that presents facts that the statement needs to be true, and a conclusion that presents a new fact we can infer when the hypothesis is true.

For a statement to be always true, there must be no counterexamples for which the hypothesis is true and the conclusion is false. If there are examples for which the statement is true, but there are also counterexamples, then the statement is sometimes true. These sometimes true statements can be made into always true statements by changing the hypothesis. A statement is never true if there are no examples for which both the hypothesis and the conclusion are true. When looking for counterexamples and examples, there are some special cases (such as negative numbers and fractions) that should be considered.

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11th Grade Math
• 12th Grade Math
• Trigonometry
• Physics Tutoring
• Guitar Lessons
• Piano Lessons
• Foreign Languages
• Study Skills
• ADHD & Learning Disabilities
• Summer Tutoring
• College Planning
• School Support
• SAT and ACT Online
• Own a Franchise

Converse, Inverse, and Contrapositive of a Conditional Statement

Conditional Statement Definitions and Examples

GET TUTORING NEAR ME!

By submitting the following form, you agree to Club Z!'s Terms of Use and Privacy Policy

A conditional statement is a statement in mathematics that declares two values or sets of values to be equivalent under specific conditions. The converse, inverse, and contrapositive of a conditional statement are three ways to restate the original statement in order to better understand it. In this blog post, we will explore the Converse, Inverse, and Contrapositive of a Conditional Statement. We will look at how each one is used to restate the original statement and what benefits they offer in terms of understanding the statement.

What is a conditional statement?

A conditional statement is a statement in which one proposition is asserted to be true if and only if another proposition is also true. For example, the statement “If it rains, then the ground will be wet” is a conditional statement. The first proposition (“it rains”) is called the antecedent, while the second proposition (“the ground will be wet”) is called the consequent.

What is the converse of a conditional statement?

The converse of a conditional statement is the result of reversing the hypothesis and conclusion of the original statement. In other words, the converse of “If A, then B” is “If B, then A.” The converse is not necessarily true – it can be false or true. For example, the converse of “If it rains, then the ground is wet” would be “If the ground is wet, then it rains.” This is not always true because there are other ways for the ground to become wet (e.g., dew, sprinklers).

What is the inverse of a conditional statement?

The inverse of a conditional statement is the statement formed by reversing the hypothesis and conclusion of the original statement. For example, the inverse of the conditional statement “If it rains, then the grass will be wet” is “If the grass is not wet, then it did not rain.”

What is the contrapositive of a conditional statement?

If the contrapositive of a conditional statement is true, then the conditional statement is false. The contrapositive of a conditional statement is formed by reversing the order of the elements in the original statement and negating both the hypothesis and conclusion. For example, the contrapositive of “If it rains, then the ground will be wet” is “If the ground is not wet, then it will not rain.”

How to use the converse, inverse, and contrapositive of a conditional statement

If you know how to use the conditional statement, then you can easily understand its converse, inverse, and contrapositive. The converse of the conditional statement is “If A, then B.” The inverse of the conditional statement is “If not A, then not B.” The contrapositive of the conditional statement is “If not B, then not A.”

Here is an example:

Suppose we have a conditional statement such as “If it rains tomorrow, I will go to the movies.”

The converse of this would be “If I go to the movies tomorrow, it will rain.” The inverse would be “If it does not rain tomorrow, I will not go to the movies.” The contrapositive would be “If I do not go to the movies tomorrow, it will not rain.”

The Converse, Inverse, and Contrapositive of a Conditional Statement are all important concepts to understand when studying mathematics. The Converse of a statement is the reverse of the original statement, the Inverse is the negation of both the hypothesis and conclusion, and the Contrapositive is the inverse of the converse. These three concepts are critical to understanding mathematical proofs and solving problems.

We guarantee you’ll find the right tutor, or we’ll cover the first hour of your lesson.

Testimonials

Club Z! has connected me with a tutor through their online platform! This was exactly the one-on-one attention I needed for my math exam. I was very pleased with the sessions and ClubZ’s online tutoring interface.

My son was suffering from low confidence in his educational abilities. I was in need of help and quick. Club Z! assigned Charlotte (our tutor) and we love her! My son’s grades went from D’s to A’s and B’s.

I’ve been using Club Z’s online classrooms to receive some help and tutoring for 2 of my college classes. I must say that I am very impressed by the functionality and ease of use of their online App. Working online with my tutor has been a piece of cake. Thanks Z.

Jonathan is doing really well in all of his classes this semester, 5 A’s & 2 B’s (he has a computer essentials class instead of PLC). In his Algebra class that Nathan is helping him with he has an A+.

Sarah is very positive, enthusiastic and encourages my daughter to do better each time she comes. My daughter’s grade has improved, we are very grateful for Sarah and that she is tutoring our daughter. Way to go ClubZ!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

17.6: Truth Tables: Conditional, Biconditional

• Last updated
• Save as PDF
• Page ID 34287

• David Lippman
• Pierce College via The OpenTextBookStore

We discussed conditional statements earlier, in which we take an action based on the value of the condition. We are now going to look at another version of a conditional, sometimes called an implication, which states that the second part must logically follow from the first.

Conditional

A conditional is a logical compound statement in which a statement \(p\), called the antecedent, implies a statement \(q\), called the consequent.

A conditional is written as \(p \rightarrow q\) and is translated as "if \(p\), then \(q\)".

The English statement “If it is raining, then there are clouds is the sky” is a conditional statement. It makes sense because if the antecedent “it is raining” is true, then the consequent “there are clouds in the sky” must also be true.

Notice that the statement tells us nothing of what to expect if it is not raining; there might be clouds in the sky, or there might not. If the antecedent is false, then the consquent becomes irrelevant.

Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. The website says that if you pay for expedited shipping, you will receive the jersey by Friday. In what situation is the website telling a lie?

There are four possible outcomes:

1) You pay for expedited shipping and receive the jersey by Friday

2) You pay for expedited shipping and don’t receive the jersey by Friday

3) You don’t pay for expedited shipping and receive the jersey by Friday

4) You don’t pay for expedited shipping and don’t receive the jersey by Friday

Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. The first outcome is exactly what was promised, so there’s no problem with that. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping; maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping.

It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. Remember, though, that if the antecedent is false, we cannot make any judgment about the consequent. The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.

A friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?

1) You upload the picture and lose your job

2) You upload the picture and don’t lose your job

3) You don’t upload the picture and lose your job

4) You don’t upload the picture and don’t lose your job

There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong. Even if you didn’t upload the picture and lost your job anyway, your friend never said that you were guaranteed to keep your job if you didn’t upload the picture; you might lose your job for missing a shift or punching your boss instead.

In traditional logic, a conditional is considered true as long as there are no cases in which the antecedent is true and the consequent is false.

Truth table for the conditional

\(\begin{array}{|c|c|c|} \hline p & q & p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Again, if the antecedent \(p\) is false, we cannot prove that the statement is a lie, so the result of the third and fourth rows is true.

Construct a truth table for the statement \((m \wedge \sim p) \rightarrow r\)

We start by constructing a truth table with 8 rows to cover all possible scenarios. Next, we can focus on the antecedent, \(m \wedge \sim p\).

\(\begin{array}{|c|c|c|} \hline m & p & r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline m & p & r & \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

Now we can create a column for the conditional. Because it can be confusing to keep track of all the Ts and \(\mathrm{Fs}\), why don't we copy the column for \(r\) to the right of the column for \(m \wedge \sim p\) ? This makes it a lot easier to read the conditional from left to right.

\(\begin{array}{|c|c|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

When \(m\) is true, \(p\) is false, and \(r\) is false- -the fourth row of the table-then the antecedent \(m \wedge \sim p\) will be true but the consequent false, resulting in an invalid conditional; every other case gives a valid conditional.

If you want a real-life situation that could be modeled by \((m \wedge \sim p) \rightarrow r\), consider this: let \(m=\) we order meatballs, \(p=\) we order pasta, and \(r=\) Rob is happy. The statement \((m \wedge \sim p) \rightarrow r\) is "if we order meatballs and don't order pasta, then Rob is happy". If \(m\) is true (we order meatballs), \(p\) is false (we don't order pasta), and \(r\) is false (Rob is not happy), then the statement is false, because we satisfied the antecedent but Rob did not satisfy the consequent.

For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.

Related Statments

The original conditional is \(\quad\) "if \(p,\) then \(q^{\prime \prime} \quad p \rightarrow q\)

The converse is \(\quad\) "if \(q,\) then \(p^{\prime \prime} \quad q \rightarrow p\)

The inverse is \(\quad\) "if not \(p,\) then not \(q^{\prime \prime} \quad \sim p \rightarrow \sim q\)

The contrapositive is "if not \(q,\) then not \(p^{\prime \prime} \quad \sim q \rightarrow \sim p\)

Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.

The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.

The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.

The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.

Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.

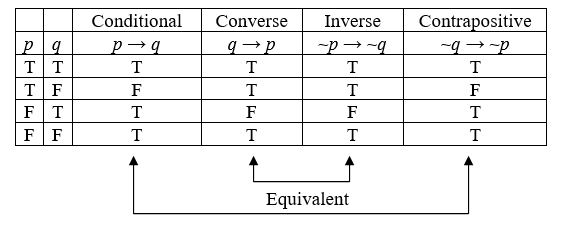
Equivalence

A conditional statement and its contrapositive are logically equivalent.

The converse and inverse of a conditional statement are logically equivalent.

In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.

Be aware that symbolic logic cannot represent the English language perfectly. For example, we may need to change the verb tense to show that one thing occurred before another.

Suppose this statement is true: “If I eat this giant cookie, then I will feel sick.” Which of the following statements must also be true?

• If I feel sick, then I ate that giant cookie.
• If I don’t eat this giant cookie, then I won’t feel sick.
• If I don’t feel sick, then I didn’t eat that giant cookie.
• This is the converse, which is not necessarily true. I could feel sick for some other reason, such as drinking sour milk.
• This is the inverse, which is not necessarily true. Again, I could feel sick for some other reason; avoiding the cookie doesn’t guarantee that I won’t feel sick.
• This is the contrapositive, which is true, but we have to think somewhat backwards to explain it. If I ate the cookie, I would feel sick, but since I don’t feel sick, I must not have eaten the cookie.

Notice again that the original statement and the contrapositive have the same truth value (both are true), and the converse and the inverse have the same truth value (both are false).

Try it Now 5

“If you microwave salmon in the staff kitchen, then I will be mad at you.” If this statement is true, which of the following statements must also be true?

• If you don’t microwave salmon in the staff kitchen, then I won’t be mad at you.
• If I am not mad at you, then you didn’t microwave salmon in the staff kitchen.
• If I am mad at you, then you microwaved salmon in the staff kitchen.

Choice b is correct because it is the contrapositive of the original statement.

Consider the statement “If you park here, then you will get a ticket.” What set of conditions would prove this statement false?

• You don’t park here and you get a ticket.
• You don’t park here and you don’t get a ticket.
• You park here and you don’t get a ticket.

The first two statements are irrelevant because we don’t know what will happen if you park somewhere else. The third statement, however contradicts the conditional statement “If you park here, then you will get a ticket” because you parked here but didn’t get a ticket. This example demonstrates a general rule; the negation of a conditional can be written as a conjunction: “It is not the case that if you park here, then you will get a ticket” is equivalent to “You park here and you do not get a ticket.”

The Negation of a Conditional

The negation of a conditional statement is logically equivalent to a conjunction of the antecedent and the negation of the consequent.

\(\sim(p \rightarrow q)\) is equivalent to \(p \wedge \sim q\)

Which of the following statements is equivalent to the negation of “If you don’t grease the pan, then the food will stick to it” ?

• I didn’t grease the pan and the food didn’t stick to it.
• I didn’t grease the pan and the food stuck to it.
• I greased the pan and the food didn’t stick to it.
• This is correct; it is the conjunction of the antecedent and the negation of the consequent. To disprove that not greasing the pan will cause the food to stick, I have to not grease the pan and have the food not stick.
• This is essentially the original statement with no negation; the “if…then” has been replaced by “and”.
• This essentially agrees with the original statement and cannot disprove it.

Try it Now 6

“If you go swimming less than an hour after eating lunch, then you will get cramps.” Which of the following statements is equivalent to the negation of this statement?

• I went swimming more than an hour after eating lunch and I got cramps.
• I went swimming less than an hour after eating lunch and I didn’t get cramps.
• I went swimming more than an hour after eating lunch and I didn’t get cramps.

Choice b is equivalent to the negation; it keeps the first part the same and negates the second part.

In everyday life, we often have a stronger meaning in mind when we use a conditional statement. Consider “If you submit your hours today, then you will be paid next Friday.” What the payroll rep really means is “If you submit your hours today, then you will be paid next Friday, and if you don’t submit your hours today, then you won’t be paid next Friday.” The conditional statement if t , then p also includes the inverse of the statement: if not t , then not p . A more compact way to express this statement is “You will be paid next Friday if and only if you submit your timesheet today.” A statement of this form is called a biconditional .

Biconditional

A biconditional is a logical conditional statement in which the antecedent and consequent are interchangeable.

A biconditional is written as \(p \leftrightarrow q\) and is translated as " \(p\) if and only if \(q^{\prime \prime}\).

Because a biconditional statement \(p \leftrightarrow q\) is equivalent to \((p \rightarrow q) \wedge(q \rightarrow p),\) we may think of it as a conditional statement combined with its converse: if \(p\), then \(q\) and if \(q\), then \(p\). The double-headed arrow shows that the conditional statement goes from left to right and from right to left. A biconditional is considered true as long as the antecedent and the consequent have the same truth value; that is, they are either both true or both false.

Truth table for the biconditional

\(\begin{array}{|c|c|c|} \hline p & q & p \leftrightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Notice that the fourth row, where both components are false, is true; if you don’t submit your timesheet and you don’t get paid, the person from payroll told you the truth.

Suppose this statement is true: “The garbage truck comes down my street if and only if it is Thursday morning.” Which of the following statements could be true?

• It is noon on Thursday and the garbage truck did not come down my street this morning.
• It is Monday and the garbage truck is coming down my street.
• It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
• This cannot be true. This is like the second row of the truth table; it is true that I just experienced Thursday morning, but it is false that the garbage truck came.
• This cannot be true. This is like the third row of the truth table; it is false that it is Thursday, but it is true that the garbage truck came.
• This could be true. This is like the fourth row of the truth table; it is false that it is Thursday, but it is also false that the garbage truck came, so everything worked out like it should.

Try it Now 7

Suppose this statement is true: “I wear my running shoes if and only if I am exercising.” Determine whether each of the following statements must be true or false.

• I am exercising and I am not wearing my running shoes.
• I am wearing my running shoes and I am not exercising.
• I am not exercising and I am not wearing my running shoes.

Choices a & b are false; c is true.

Create a truth table for the statement \((A \vee B) \leftrightarrow \sim C\)

Whenever we have three component statements, we start by listing all the possible truth value combinations for \(A, B,\) and \(C .\) After creating those three columns, we can create a fourth column for the antecedent, \(A \vee B\). Now we will temporarily ignore the column for \(C\) and focus on \(A\) and \(B\), writing the truth values for \(A \vee B\).

\(\begin{array}{|c|c|c|} \hline A & B & C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline A & B & C & A \vee B \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

Next we can create a column for the negation of \(C\). (Ignore the \(A \vee B\) column and simply negate the values in the \(C\) column.)

\(\begin{array}{|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Finally, we find the truth values of \((A \vee B) \leftrightarrow \sim C\). Remember, a biconditional is true when the truth value of the two parts match, but it is false when the truth values do not match.

\(\begin{array}{|c|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

To illustrate this situation, suppose your boss needs you to do either project \(A\) or project \(B\) (or both, if you have the time). If you do one of the projects, you will not get a crummy review ( \(C\) is for crummy). So \((A \vee B) \leftrightarrow \sim C\) means "You will not get a crummy review if and only if you do project \(A\) or project \(B\)." Looking at a few of the rows of the truth table, we can see how this works out. In the first row, \(A, B,\) and \(C\) are all true: you did both projects and got a crummy review, which is not what your boss told you would happen! That is why the final result of the first row is false. In the fourth row, \(A\) is true, \(B\) is false, and \(C\) is false: you did project \(A\) and did not get a crummy review. This is what your boss said would happen, so the final result of this row is true. And in the eighth row, \(A, B\), and \(C\) are all false: you didn't do either project and did not get a crummy review. This is not what your boss said would happen, so the final result of this row is false. (Even though you may be happy that your boss didn't follow through on the threat, the truth table shows that your boss lied about what would happen.)