hypothesis testing two parameters

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10: Hypothesis Testing with Two Samples

• Last updated
• Save as PDF
• Page ID 699

You have learned to conduct hypothesis tests on single means and single proportions. You will expand upon that in this chapter. You will compare two means or two proportions to each other. The general procedure is still the same, just expanded. To compare two means or two proportions, you work with two groups. The groups are classified either as independent or matched pairs. Independent groups consist of two samples that are independent, that is, sample values selected from one population are not related in any way to sample values selected from the other population. Matched pairs consist of two samples that are dependent. The parameter tested using matched pairs is the population mean. The parameters tested using independent groups are either population means or population proportions.

• 10.1: Prelude to Hypothesis Testing with Two Samples This chapter deals with the following hypothesis tests: Independent groups (samples are independent) Test of two population means. Test of two population proportions. Matched or paired samples (samples are dependent) Test of the two population proportions by testing one population mean of differences.
• 10.2: Two Population Means with Unknown Standard Deviations The comparison of two population means is very common. A difference between the two samples depends on both the means and the standard deviations. Very different means can occur by chance if there is great variation among the individual samples.
• 10.3: Two Population Means with Known Standard Deviations Even though this situation is not likely (knowing the population standard deviations is not likely), the following example illustrates hypothesis testing for independent means, known population standard deviations.
• 10.4: Comparing Two Independent Population Proportions Comparing two proportions, like comparing two means, is common. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions.
• 10.5: Matched or Paired Samples When using a hypothesis test for matched or paired samples, the following characteristics should be present: Simple random sampling is used. Sample sizes are often small. Two measurements (samples) are drawn from the same pair of individuals or objects. Differences are calculated from the matched or paired samples. The differences form the sample that is used for the hypothesis test. Either the matched pairs have differences that come from a population that is normal or the number of difference
• 10.6: Hypothesis Testing for Two Means and Two Proportions (Worksheet) A statistics Worksheet: The student will select the appropriate distributions to use in each case. The student will conduct hypothesis tests and interpret the results.
• 10.E: Hypothesis Testing with Two Samples (Exercises) These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved April 12, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

What is a Hypothesis Test for 2 Samples?

Searching the internet for a definition of hypothesis testing for 2 samples brings back a lot of different results. Most of them are a little different. The definitions you will find online usually are disjointed, covering hypothesis testing for independent means, paired means, and proportions. Instead of giving one uniform definition, we’ll take a look at key components that are common to all of the tests, and then some of the specific components and notation.

The Basic Idea

The appearance of these hypothesis tests (in the real world) will be very similar to the tests that we see with one sample. In fact, the examples of hypothesis tests that were in the previous introduction include tests for one sample as well as two samples. The basic structure of these hypothesis tests are very similar to the ones we saw before. You have a problem, hypothesis, data collection, some computations, results or conclusions. Some of the notation will be slightly different. These examples below are the same ones we presented in the previous introduction, but here we are highlighting the two-sample variations. The examples with bolded terms are the ones that use 2 samples.

Some Examples of Hypothesis Tests

Example 1: agility testing in youth football (soccer)players; evaluating reliability, validity, and correlates of newly developed testing protocols.

Reactive agility (RAG)and change of direction speed (CODS) were analyzed in 13U and 15U youth soccer players. “ Independent samples t-test indicated significant differences between U13 and U15 in S10 (t-test: 3.57, p < 0.001), S20M (t-test: 3.13, p < 0.001), 20Y (t-test: 4.89, p < 0.001), FS_RAG (t-test: 3.96, p < 0.001), and FS_CODS (t-test: 6.42, p < 0.001), with better performance in U15. Starters outperformed non-starters in most capacities among U13, but only in FS_RAG among U15 (t-test: 1.56, p < 0.05).”

Most of this might seem like gibberish for now, but essentially the two groups were analyzed and compared, with significant differences observed between the groups. This is a hypothesis test for 2 means, independent samples.

Source: https://pubmed.ncbi.nlm.nih.gov/31906269/

Example 2: Manual therapy in the treatment of carpal tunnel syndrome in diabetic patients: A randomized clinical trial

Thirty diabetic patients with carpal tunnel syndrome were split up into two groups. One received physiotherapy modality and the other received manual therapy. “ Paired t-test revealed that all of the outcome measures had a significant change in the manual therapy group, whereas only the VAS and SSS changed significantly in the modality group at the end of 4 weeks. Independent t-test showed that the variables of SSS, FSS and MNT in the manual therapy group improved significantly greater than the modality group.”

This is a hypothesis test for matched pairs, sometimes known as 2 means, dependent samples.

Source: https://pubmed.ncbi.nlm.nih.gov/30197774/

Example 3: Omega-3 fatty acids decreased irritability of patients with bipolar disorder in an add-on, open label study

“The initial mean was 63.51 (SD 34.17), indicating that on average, subjects were irritable for about six of the previous ten days. The mean for the last recorded percentage was less than half of the initial score: 30.27 (SD 34.03). The decrease was found to be statistically significant using a paired sample t-test (t = 4.36, 36 df, p < .001).”

Source: https://nutritionj.biomedcentral.com/articles/10.1186/1475-2891-4-6

Example 4: Evaluating the Efficacy of COVID-19 Vaccines

“We reduced all values of vaccine efficacy by 30% to reflect the waning of vaccine efficacy against each endpoint over time. We tested the null hypothesis that the vaccine efficacy is 0% versus the alternative hypothesis that the vaccine efficacy is greater than 0% at the nominal significance level of 2.5%.”

Source: https://www.medrxiv.org/content/10.1101/2020.10.02.20205906v2.full

Example 5: Social Isolation During COVID-19 Pandemic. Perceived Stress and Containment Measures Compliance Among Polish and Italian Residents

“The Polish group had a higher stress level than the Italian group (mean PSS-10 total score 22,14 vs 17,01, respectively; p < 0.01). There was a greater prevalence of chronic diseases among Polish respondents. Italian subjects expressed more concern about their health, as well as about their future employment. Italian subjects did not comply with suggested restrictions as much as Polish subjects and were less eager to restrain from their usual activities (social, physical, and religious), which were more often perceived as “most needed matters” in Italian than in Polish residents.”

Even though the test wording itself does not explicitly state the tests we will study, this is a comparison of means from two different groups, so this is a test for two means, independent samples.

Source: https://www.frontiersin.org/articles/10.3389/fpsyg.2021.673514/full

Example 6: A Comparative Analysis of Student Performance in an Online vs. Face-to-Face Environmental Science Course From 2009 to 2016

“The independent sample t-test showed no significant difference in student performance between online and F2F learners with respect to gender [t(145) = 1.42, p = 0.122].”

Once again, a test of 2 means, independent samples.

Source: https://www.frontiersin.org/articles/10.3389/fcomp.2019.00007/full

But what does it all mean?

That’s what comes next. The examples above span a variety of different types of hypothesis tests. Within this chapter we will take a look at some of the terminology, formulas, and concepts related to Hypothesis Testing for 2 Samples.

Key Terminology and Formulas

Hypothesis: This is a claim or statement about a population, usually focusing on a parameter such as a proportion (%), mean, standard deviation, or variance. We will be focusing primarily on the proportion and the mean.

Hypothesis Test: Also known as a Significance Test or Test of Significance , the hypothesis test is the collection of procedures we use to test a claim about a population.

Null Hypothesis: This is a statement that the population parameter (such as the proportion, mean, standard deviation, or variance) is equal to some value. In simpler terms, the Null Hypothesis is a statement that “nothing is different from what usually happens.” The Null Hypothesis is usually denoted by [latex]H_{0}[/latex], followed by other symbols and notation that describe how the parameter from one population or group is the same as the parameter from another population or group.

Alternative Hypothesis: This is a statement that the population parameter (such as the proportion, mean, standard deviation, or variance) is somehow different the value involved in the Null Hypothesis. For our examples, “somehow different” will involve the use of [latex] [/latex], or [latex]\neq[/latex]. In simpler terms, the Alternative Hypothesis is a statement that “something is different from what usually happens.” The Alternative Hypothesis is usually denoted by [latex]H_{1}[/latex], [latex]H_{A}[/latex], or [latex]H_{a}[/latex], followed by other symbols and notation that describe how the parameter from one population or group is different from the parameter from another population or group.

Significance Level: We previous learned about the significance level as the “left over” stuff from the confidence level. This is still true, but we will now focus more on the significance level as its own value, and we will use the symbol alpha, [latex]\alpha[/latex]. This looks like a lowercase “a,” or a drawing of a little fish. The significance level [latex]\alpha[/latex] is the probability of rejecting the null hypothesis when it is actually true (more on what this means in the next section). The common values are still similar to what we had previously, 1%, 5%, and 10%. We commonly write these as decimals instead, 0.01, 0.05, and 0.10.

Test Statistic:  One of the key components of a hypothesis test is what we call a  test statistic . This is a calculation, sort of like a z-score, that is specific to the type of test being conducted. The idea behind a test statistic, relating it back to science projects, would be like calculations from measurements that were taken. In this chapter we will address the test statistic for 2 proportions, 2 means (independent samples), and matched pairs (2 means from dependent samples). The formulas are listed in the table below:

What the different symbols mean:

Critical Region: The critical region , also known as the rejection region , is the area in the normal (or other) distribution in which we reject the null hypothesis. Think of the critical region  like a target area that you are aiming for. If we are able to get a value in this region, it means we have evidence for the claim.

Critical Value: These are like special z-scores for us; the critical value  (or values, sometimes there are two) separates the critical region from the rest of the distribution. This is the non-target part, or what we are not aiming for. If our value is in this region, we do not have evidence for the claim.

P-Value: This is a special value that we compute. If we assume the null hypothesis is true, the p-value represents the probability that a test statistic is at least as extreme as the one we computed from our sample data; for us the test statistics would be either [latex]z[/latex] or [latex]t[/latex].

Decision Rule for Hypothesis Testing:  There are a few ways we can arrive at our decision with a hypothesis test. We can arrive at our conclusion by using confidence intervals, critical values (also known as traditional method), and using p-values. Relating this to a science project, the decision rule would be what we take into consideration to arrive at our conclusion. When we make our decision, the wording will sound a little strange. We’ll say things like “we have enough evidence to reject the null hypothesis” or “there is insufficient evidence to reject the null hypothesis.”

Decision Rule with Critical Values:  If the test statistic is in the critical region, we have enough evidence to reject the null hypothesis. We can also say we have sufficient evidence to support the claim. If the test statistic is not in the critical region, we fail to reject the null hypothesis. We can also say we do not have sufficient evidence to support the claim.

Decision Rule with P-Values: If the p-value is less than or equal to the significance level, we have enough evidence to reject the null hypothesis. We can also say we have sufficient evidence to support the claim. If the p-value is greater than the significance level, we fail to reject the null hypothesis. We can also say we do not have sufficient evidence to support the claim.

More About Hypotheses

Writing the Null and Alternative Hypothesis can be tricky. Here are a few examples of claims followed by the respective hypotheses:

Basic Statistics Copyright © by Allyn Leon is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

A Guide on Data Analysis

14 hypothesis testing.

Error types:

Type I Error (False Positive):

• Reality: nope
• Diagnosis/Analysis: yes

Type II Error (False Negative):

• Reality: yes
• Diagnosis/Analysis: nope

Power: The probability of rejecting the null hypothesis when it is actually false

Always written in terms of the population parameter ( \(\beta\) ) not the estimator/estimate ( \(\hat{\beta}\) )

Sometimes, different disciplines prefer to use \(\beta\) (i.e., standardized coefficient), or \(\mathbf{b}\) (i.e., unstandardized coefficient)

\(\beta\) and \(\mathbf{b}\) are similar in interpretation; however, \(\beta\) is scale free. Hence, you can see the relative contribution of \(\beta\) to the dependent variable. On the other hand, \(\mathbf{b}\) can be more easily used in policy decisions.

\[ \beta_j = \mathbf{b} \frac{s_{x_j}}{s_y} \]

Assuming the null hypothesis is true, what is the (asymptotic) distribution of the estimator

\[ \begin{aligned} &H_0: \beta_j = 0 \\ &H_1: \beta_j \neq 0 \end{aligned} \]

then under the null, the OLS estimator has the following distribution

\[ A1-A3a, A5: \sqrt{n} \hat{\beta_j} \sim N(0,Avar(\sqrt{n}\hat{\beta}_j)) \]

• For the one-sided test, the null is a set of values, so now you choose the worst case single value that is hardest to prove and derive the distribution under the null

\[ \begin{aligned} &H_0: \beta_j\ge 0 \\ &H_1: \beta_j < 0 \end{aligned} \]

then the hardest null value to prove is \(H_0: \beta_j=0\) . Then under this specific null, the OLS estimator has the following asymptotic distribution

\[ A1-A3a, A5: \sqrt{n}\hat{\beta_j} \sim N(0,Avar(\sqrt{n}\hat{\beta}_j)) \]

14.1 Types of hypothesis testing

\(H_0 : \theta = \theta_0\)

\(H_1 : \theta \neq \theta_0\)

How far away / extreme \(\theta\) can be if our null hypothesis is true

Assume that our likelihood function for q is \(L(q) = q^{30}(1-q)^{70}\) Likelihood function

Log-Likelihood function

Figure from ( Fox 1997 )

typically, The likelihood ratio test (and Lagrange Multiplier (Score) ) performs better with small to moderate sample sizes, but the Wald test only requires one maximization (under the full model).

14.2 Wald test

\[ \begin{aligned} W &= (\hat{\theta}-\theta_0)'[cov(\hat{\theta})]^{-1}(\hat{\theta}-\theta_0) \\ W &\sim \chi_q^2 \end{aligned} \]

where \(cov(\hat{\theta})\) is given by the inverse Fisher Information matrix evaluated at \(\hat{\theta}\) and q is the rank of \(cov(\hat{\theta})\) , which is the number of non-redundant parameters in \(\theta\)

Alternatively,

\[ t_W=\frac{(\hat{\theta}-\theta_0)^2}{I(\theta_0)^{-1}} \sim \chi^2_{(v)} \]

where v is the degree of freedom.

Equivalently,

\[ s_W= \frac{\hat{\theta}-\theta_0}{\sqrt{I(\hat{\theta})^{-1}}} \sim Z \]

How far away in the distribution your sample estimate is from the hypothesized population parameter.

For a null value, what is the probability you would have obtained a realization “more extreme” or “worse” than the estimate you actually obtained?

Significance Level ( \(\alpha\) ) and Confidence Level ( \(1-\alpha\) )

• The significance level is the benchmark in which the probability is so low that we would have to reject the null
• The confidence level is the probability that sets the bounds on how far away the realization of the estimator would have to be to reject the null.

Test Statistics

• Standardized (transform) the estimator and null value to a test statistic that always has the same distribution
• Test Statistic for the OLS estimator for a single hypothesis

\[ T = \frac{\sqrt{n}(\hat{\beta}_j-\beta_{j0})}{\sqrt{n}SE(\hat{\beta_j})} \sim^a N(0,1) \]

\[ T = \frac{(\hat{\beta}_j-\beta_{j0})}{SE(\hat{\beta_j})} \sim^a N(0,1) \]

the test statistic is another random variable that is a function of the data and null hypothesis.

• T denotes the random variable test statistic
• t denotes the single realization of the test statistic

Evaluating Test Statistic: determine whether or not we reject or fail to reject the null hypothesis at a given significance / confidence level

Three equivalent ways

Critical Value

• Confidence Interval

For a given significance level, will determine the critical value \((c)\)

• One-sided: \(H_0: \beta_j \ge \beta_{j0}\)

\[ P(T<c|H_0)=\alpha \]

Reject the null if \(t<c\)

• One-sided: \(H_0: \beta_j \le \beta_{j0}\)

\[ P(T>c|H_0)=\alpha \]

Reject the null if \(t>c\)

• Two-sided: \(H_0: \beta_j \neq \beta_{j0}\)

\[ P(|T|>c|H_0)=\alpha \]

Reject the null if \(|t|>c\)

Calculate the probability that the test statistic was worse than the realization you have

\[ \text{p-value} = P(T<t|H_0) \]

\[ \text{p-value} = P(T>t|H_0) \]

\[ \text{p-value} = P(|T|<t|H_0) \]

reject the null if p-value \(< \alpha\)

Using the critical value associated with a null hypothesis and significance level, create an interval

\[ CI(\hat{\beta}_j)_{\alpha} = [\hat{\beta}_j-(c \times SE(\hat{\beta}_j)),\hat{\beta}_j+(c \times SE(\hat{\beta}_j))] \]

If the null set lies outside the interval then we reject the null.

• We are not testing whether the true population value is close to the estimate, we are testing that given a field true population value of the parameter, how like it is that we observed this estimate.
• Can be interpreted as we believe with \((1-\alpha)\times 100 \%\) probability that the confidence interval captures the true parameter value.

With stronger assumption (A1-A6), we could consider Finite Sample Properties

\[ T = \frac{\hat{\beta}_j-\beta_{j0}}{SE(\hat{\beta}_j)} \sim T(n-k) \]

• This above distributional derivation is strongly dependent on A4 and A5
• T has a student t-distribution because the numerator is normal and the denominator is \(\chi^2\) .
• Critical value and p-values will be calculated from the student t-distribution rather than the standard normal distribution.
• \(n \to \infty\) , \(T(n-k)\) is asymptotically standard normal.

Rule of thumb

if \(n-k>120\) : the critical values and p-values from the t-distribution are (almost) the same as the critical values and p-values from the standard normal distribution.

if \(n-k<120\)

• if (A1-A6) hold then the t-test is an exact finite distribution test
• if (A1-A3a, A5) hold, because the t-distribution is asymptotically normal, computing the critical values from a t-distribution is still a valid asymptotic test (i.e., not quite the right critical values and p0values, the difference goes away as \(n \to \infty\) )

14.2.1 Multiple Hypothesis

test multiple parameters as the same time

• \(H_0: \beta_1 = 0\ \& \ \beta_2 = 0\)
• \(H_0: \beta_1 = 1\ \& \ \beta_2 = 0\)

perform a series of simply hypothesis does not answer the question (joint distribution vs. two marginal distributions).

The test statistic is based on a restriction written in matrix form.

\[ y=\beta_0+x_1\beta_1 + x_2\beta_2 + x_3\beta_3 + \epsilon \]

Null hypothesis is \(H_0: \beta_1 = 0\) & \(\beta_2=0\) can be rewritten as \(H_0: \mathbf{R}\beta -\mathbf{q}=0\) where

• \(\mathbf{R}\) is a \(m \times k\) matrix where m is the number of restrictions and \(k\) is the number of parameters. \(\mathbf{q}\) is a \(k \times 1\) vector
• \(\mathbf{R}\) “picks up” the relevant parameters while \(\mathbf{q}\) is a the null value of the parameter

\[ \mathbf{R}= \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} \right), \mathbf{q} = \left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right) \]

Test Statistic for OLS estimator for a multiple hypothesis

\[ F = \frac{(\mathbf{R\hat{\beta}-q})\hat{\Sigma}^{-1}(\mathbf{R\hat{\beta}-q})}{m} \sim^a F(m,n-k) \]

\(\hat{\Sigma}^{-1}\) is the estimator for the asymptotic variance-covariance matrix

• if A4 holds, both the homoskedastic and heteroskedastic versions produce valid estimator
• If A4 does not hold, only the heteroskedastic version produces valid estimators.

When \(m = 1\) , there is only a single restriction, then the \(F\) -statistic is the \(t\) -statistic squared.

\(F\) distribution is strictly positive, check F-Distribution for more details.

14.2.2 Linear Combination

Testing multiple parameters as the same time

\[ \begin{aligned} H_0&: \beta_1 -\beta_2 = 0 \\ H_0&: \beta_1 - \beta_2 > 0 \\ H_0&: \beta_1 - 2\times\beta_2 =0 \end{aligned} \]

Each is a single restriction on a function of the parameters.

Null hypothesis:

\[ H_0: \beta_1 -\beta_2 = 0 \]

can be rewritten as

\[ H_0: \mathbf{R}\beta -\mathbf{q}=0 \]

where \(\mathbf{R}\) =(0 1 -1 0 0) and \(\mathbf{q}=0\)

14.2.3 Estimate Difference in Coefficients

There is no package to estimate for the difference between two coefficients and its CI, but a simple function created by Katherine Zee can be used to calculate this difference. Some modifications might be needed if you don’t use standard lm model in R.

14.2.4 Application

14.2.5 nonlinear.

Suppose that we have q nonlinear functions of the parameters \[ \mathbf{h}(\theta) = \{ h_1 (\theta), ..., h_q (\theta)\}' \]

The,n, the Jacobian matrix ( \(\mathbf{H}(\theta)\) ), of rank q is

\[ \mathbf{H}_{q \times p}(\theta) = \left( \begin{array} {ccc} \frac{\partial h_1(\theta)}{\partial \theta_1} & ... & \frac{\partial h_1(\theta)}{\partial \theta_p} \\ . & . & . \\ \frac{\partial h_q(\theta)}{\partial \theta_1} & ... & \frac{\partial h_q(\theta)}{\partial \theta_p} \end{array} \right) \]

where the null hypothesis \(H_0: \mathbf{h} (\theta) = 0\) can be tested against the 2-sided alternative with the Wald statistic

\[ W = \frac{\mathbf{h(\hat{\theta})'\{H(\hat{\theta})[F(\hat{\theta})'F(\hat{\theta})]^{-1}H(\hat{\theta})'\}^{-1}h(\hat{\theta})}}{s^2q} \sim F_{q,n-p} \]

14.3 The likelihood ratio test

\[ t_{LR} = 2[l(\hat{\theta})-l(\theta_0)] \sim \chi^2_v \]

Compare the height of the log-likelihood of the sample estimate in relation to the height of log-likelihood of the hypothesized population parameter

This test considers a ratio of two maximizations,

\[ \begin{aligned} L_r &= \text{maximized value of the likelihood under $H_0$ (the reduced model)} \\ L_f &= \text{maximized value of the likelihood under $H_0 \cup H_a$ (the full model)} \end{aligned} \]

Then, the likelihood ratio is:

\[ \Lambda = \frac{L_r}{L_f} \]

which can’t exceed 1 (since \(L_f\) is always at least as large as \(L-r\) because \(L_r\) is the result of a maximization under a restricted set of the parameter values).

The likelihood ratio statistic is:

\[ \begin{aligned} -2ln(\Lambda) &= -2ln(L_r/L_f) = -2(l_r - l_f) \\ \lim_{n \to \infty}(-2ln(\Lambda)) &\sim \chi^2_v \end{aligned} \]

where \(v\) is the number of parameters in the full model minus the number of parameters in the reduced model.

If \(L_r\) is much smaller than \(L_f\) (the likelihood ratio exceeds \(\chi_{\alpha,v}^2\) ), then we reject he reduced model and accept the full model at \(\alpha \times 100 \%\) significance level

14.4 Lagrange Multiplier (Score)

\[ t_S= \frac{S(\theta_0)^2}{I(\theta_0)} \sim \chi^2_v \]

where \(v\) is the degree of freedom.

Compare the slope of the log-likelihood of the sample estimate in relation to the slope of the log-likelihood of the hypothesized population parameter

14.5 Two One-Sided Tests (TOST) Equivalence Testing

This is a good way to test whether your population effect size is within a range of practical interest (e.g., if the effect size is 0).

Forgot password? New user? Sign up

Existing user? Log in

Hypothesis Testing

Already have an account? Log in here.

A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.

The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the \(p\)-value to the level of significance (a chosen target). If the \(p\)-value is less than or equal to the level of significance, then the null hypothesis is rejected.

When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.

Definitions and Methodology

Hypothesis test and confidence intervals.

In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.

The null hypothesis \((\)denoted \(H_0)\) is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis \((\)denoted \(H_1).\) Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted \(\alpha\), which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted \(\beta\), which is also its probability of occurrence. Also, \(\alpha\) is known as the significance level , and \(1-\beta\) is known as the power of the test. \(H_0\) \(\textbf{is true}\)\(\hspace{15mm}\) \(H_0\) \(\textbf{is false}\) \(\textbf{Reject}\) \(H_0\)\(\hspace{10mm}\) Type I error Correct Decision \(\textbf{Reject}\) \(H_1\) Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The \(p\)-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.

Methodologies: Given an estimator \(\hat \theta\) of a population statistic \(\theta\), following a probability distribution \(P(T)\), computed from a sample \(\mathcal{S},\) and given a significance level \(\alpha\) and test statistic \(t^*,\) define \(H_0\) and \(H_1;\) compute the test statistic \(t^*.\) \(p\)-value Approach (most prevalent): Find the \(p\)-value using \(t^*\) (right-tailed). If the \(p\)-value is at most \(\alpha,\) reject \(H_0\). Otherwise, reject \(H_1\). Critical Value Approach: Find the critical value solving the equation \(P(T\geq t_\alpha)=\alpha\) (right-tailed). If \(t^*>t_\alpha\), reject \(H_0\). Otherwise, reject \(H_1\). Note: Failing to reject \(H_0\) only means inability to accept \(H_1\), and it does not mean to accept \(H_0\).

Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05:\) Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu>200\). Since our values are normally distributed, the test statistic is \(z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09\). Using a standard normal distribution, we find that our \(p\)-value is approximately \(0.001\). Since the \(p\)-value is at most \(\alpha=0.05,\) we reject \(H_0\). Therefore, we can conclude that the test shows sufficient evidence to support the claim that \(\mu\) is larger than \(200\) mg/dL.

If the sample size was smaller, the normal and \(t\)-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.

Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05\) and the \(t\)-distribution with 24 degrees of freedom: Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu\neq 200\). Using the \(t\)-distribution, the test statistic is \(t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54\). Using a \(t\)-distribution with 24 degrees of freedom, we find that our \(p\)-value is approximately \(2(0.068)=0.136\). We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the \(p\)-value is larger than \(\alpha=0.05,\) we fail to reject \(H_0\). Therefore, the test does not show sufficient evidence to support the claim that \(\mu\) is not equal to \(200\) mg/dL.

The complement of the rejection on a two-tailed hypothesis test (with significance level \(\alpha\)) for a population parameter \(\theta\) is equivalent to finding a confidence interval \((\)with confidence level \(1-\alpha)\) for the population parameter \(\theta\). If the assumption on the parameter \(\theta\) falls inside the confidence interval, then the test has failed to reject the null hypothesis \((\)with \(p\)-value greater than \(\alpha).\) Otherwise, if \(\theta\) does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate \((\)with \(p\)-value at most \(\alpha).\)

• Statistics (Estimation)
• Normal Distribution
• Correlation
• Confidence Intervals

Problem Loading...

Note Loading...

Set Loading...

Hypothesis Testing Framework

Now that we've seen an example and explored some of the themes for hypothesis testing, let's specify the procedure that we will follow.

Hypothesis Testing Steps

The formal framework and steps for hypothesis testing are as follows:

• Identify and define the parameter of interest
• Define the competing hypotheses to test
• Set the evidence threshold, formally called the significance level
• Generate or use theory to specify the sampling distribution and check conditions
• Calculate the test statistic and p-value
• Evaluate your results and write a conclusion in the context of the problem.

We'll discuss each of these steps below.

Identify Parameter of Interest

First, I like to specify and define the parameter of interest. What is the population that we are interested in? What characteristic are we measuring?

By defining our population of interest, we can confirm that we are truly using sample data. If we find that we actually have population data, our inference procedures are not needed. We could proceed by summarizing our population data.

By identifying and defining the parameter of interest, we can confirm that we use appropriate methods to summarize our variable of interest. We can also focus on the specific process needed for our parameter of interest.

In our example from the last page, the parameter of interest would be the population mean time that a host has been on Airbnb for the population of all Chicago listings on Airbnb in March 2023. We could represent this parameter with the symbol $\mu$. It is best practice to fully define $\mu$ both with words and symbol.

Define the Hypotheses

For hypothesis testing, we need to decide between two competing theories. These theories must be statements about the parameter. Although we won't have the population data to definitively select the correct theory, we will use our sample data to determine how reasonable our "skeptic's theory" is.

The first hypothesis is called the null hypothesis, $H_0$. This can be thought of as the "status quo", the "skeptic's theory", or that nothing is happening.

Examples of null hypotheses include that the population proportion is equal to 0.5 ($p = 0.5$), the population median is equal to 12 ($M = 12$), or the population mean is equal to 14.5 ($\mu = 14.5$).

The second hypothesis is called the alternative hypothesis, $H_a$ or $H_1$. This can be thought of as the "researcher's hypothesis" or that something is happening. This is what we'd like to convince the skeptic to believe. In most cases, the desired outcome of the researcher is to conclude that the alternative hypothesis is reasonable to use moving forward.

Examples of alternative hypotheses include that the population proportion is greater than 0.5 ($p > 0.5$), the population median is less than 12 ($M < 12$), or the population mean is not equal to 14.5 ($\mu \neq 14.5$).

There are a few requirements for the hypotheses:

• the hypotheses must be about the same population parameter,
• the hypotheses must have the same null value (provided number to compare to),
• the null hypothesis must have the equality (the equals sign must be in the null hypothesis),
• the alternative hypothesis must not have the equality (the equals sign cannot be in the alternative hypothesis),
• there must be no overlap between the null and alternative hypothesis.

You may have previously seen null hypotheses that include more than an equality (e.g. $p \le 0.5$). As long as there is an equality in the null hypothesis, this is allowed. For our purposes, we will simplify this statement to ($p = 0.5$).

To summarize from above, possible hypotheses statements are:

$H_0: p = 0.5$ vs. $H_a: p > 0.5$

$H_0: M = 12$ vs. $H_a: M < 12$

$H_0: \mu = 14.5$ vs. $H_a: \mu \neq 14.5$

In our second example about Airbnb hosts, our hypotheses would be:

$H_0: \mu = 2100$ vs. $H_a: \mu > 2100$.

Set Threshold (Significance Level)

There is one more step to complete before looking at the data. This is to set the threshold needed to convince the skeptic. This threshold is defined as an $\alpha$ significance level. We'll define exactly what the $\alpha$ significance level means later. For now, smaller $\alpha$s correspond to more evidence being required to convince the skeptic.

A few common $\alpha$ levels include 0.1, 0.05, and 0.01.

For our Airbnb hosts example, we'll set the threshold as 0.02.

Determine the Sampling Distribution of the Sample Statistic

The first step (as outlined above) is the identify the parameter of interest. What is the best estimate of the parameter of interest? Typically, it will be the sample statistic that corresponds to the parameter. This sample statistic, along with other features of the distribution will prove especially helpful as we continue the hypothesis testing procedure.

However, we do have a decision at this step. We can choose to use simulations with a resampling approach or we can choose to rely on theory if we are using proportions or means. We then also need to confirm that our results and conclusions will be valid based on the available data.

Required Condition

The one required assumption, regardless of approach (resampling or theory), is that the sample is random and representative of the population of interest. In other words, we need our sample to be a reasonable sample of data from the population.

Using Simulations and Resampling

If we'd like to use a resampling approach, we have no (or minimal) additional assumptions to check. This is because we are relying on the available data instead of assumptions.

We do need to adjust our data to be consistent with the null hypothesis (or skeptic's claim). We can then rely on our resampling approach to estimate a plausible sampling distribution for our sample statistic.

Recall that we took this approach on the last page. Before simulating our estimated sampling distribution, we adjusted the mean of the data so that it matched with our skeptic's claim, shown in the code below.

We'll see a few more examples on the next page.

Using Theory

On the other hand, we could rely on theory in order to estimate the sampling distribution of our desired statistic. Recall that we had a few different options to rely on:

• the CLT for the sampling distribution of a sample mean
• the binomial distribution for the sampling distribution of a proportion (or count)
• the Normal approximation of a binomial distribution (using the CLT) for the sampling distribution of a proportion

If relying on the CLT to specify the underlying sampling distribution, you also need to confirm:

• having a random sample and
• having a sample size that is less than 10% of the population size if the sampling is done without replacement
• having a Normally distributed population for a quantitative variable OR
• having a large enough sample size (usually at least 25) for a quantitative variable
• having a large enough sample size for a categorical variable (defined by $np$ and $n(1-p)$ being at least 10)

If relying on the binomial distribution to specify the underlying sampling distribution, you need to confirm:

• having a set number of trials, $n$
• having the same probability of success, $p$ for each observation

After determining the appropriate theory to use, we should check our conditions and then specify the sampling distribution for our statistic.

For the Airbnb hosts example, we have what we've assumed to be a random sample. It is not taken with replacement, so we also need to assume that our sample size (700) is less than 10% of our population size. In other words, we need to assume that the population of Chicago Airbnbs in March 2023 was at least 7000. Since we do have our (presumed) population data available, we can confirm that there were at least 7000 Chicago Airbnbs in the population in 2023.

Additionally, we can confirm that normality of the sampling distribution applies for the CLT to apply. Our sample size is more than 25 and the parameter of interest is a mean, so this meets our necessary criteria for the normality condition to be valid.

With the conditions now met, we can estimate our sampling distribution. From the CLT, we know that the distribution for the sample mean should be $\bar{X} \sim N(\mu, \frac{\sigma}{\sqrt{n}})$.

Now, we face our next challenge -- what to plug in as the mean and standard error for this distribution. Since we are adopting the skeptic's point of view for the purpose of this approach, we can plug in the value of $\mu_0 = 2100$. We also know that the sample size $n$ is 700. But what should we plug in for the population standard deviation $\sigma$?

When we don't know the value of a parameter, we will generally plug in our best estimate for the parameter. In this case, that corresponds to plugging in $\hat{\sigma}$, or our sample standard deviation.

Now, our estimated sampling distribution based on the CLT is: $\bar{X} \sim N(2100, 41.4045)$.

If we compare to our corresponding skeptic's sampling distribution on the last page, we can confirm that the theoretical sampling distribution is similar to the simulated sampling distribution based on resampling.

Assumptions not met

What do we do if the necessary conditions aren't met for the sampling distribution? Because the simulation-based resampling approach has minimal assumptions, we should be able to use this approach to produce valid results as long as the provided data is representative of the population.

The theory-based approach has more conditions, and we may not be able to meet all of the necessary conditions. For example, if our parameter is something other than a mean or proportion, we may not have appropriate theory. Additionally, we may not have a large enough sample size.

• First, we could consider changing approaches to the simulation-based one.
• Second, we might look at how we could meet the necessary conditions better. In some cases, we may be able to redefine groups or make adjustments so that the setup of the test is closer to what is needed.
• As a last resort, we may be able to continue following the hypothesis testing steps. In this case, your calculations may not be valid or exact; however, you might be able to use them as an estimate or an approximation. It would be crucial to specify the violation and approximation in any conclusions or discussion of the test.

Calculate the evidence with statistics and p-values

Now, it's time to calculate how much evidence the sample contains to convince the skeptic to change their mind. As we saw above, we can convince the skeptic to change their mind by demonstrating that our sample is unlikely to occur if their theory is correct.

How do we do this? We do this by calculating a probability associated with our observed value for the statistic.

For example, for our situation, we want to convince the skeptic that the population mean is actually greater than 2100 days. We do that by calculating the probability that a sample mean would be as large or larger than what we observed in our actual sample, which was 2188 days. Why do we need the larger portion? We use the larger portion because a sample mean of 2200 days also provides evidence that the population mean is larger than 2100 days; it isn't limited to exactly what we observed in our sample. We call this specific probability the p-value.

That is, the p-value is the probability of observing a test statistic as extreme or more extreme (as determined by the alternative hypothesis), assuming the null hypothesis is true.

Our observed p-value for the Airbnb host example demonstrates that the probability of getting a sample mean host time of 2188 days (the value from our sample) or more is 1.46%, assuming that the true population mean is 2100 days.

Test statistic

Notice that the formal definition of a p-value mentions a test statistic . In most cases, this word can be replaced with "statistic" or "sample" for an equivalent statement.

Oftentimes, we'll see that our sample statistic can be used directly as the test statistic, as it was above. We could equivalently adjust our statistic to calculate a test statistic. This test statistic is often calculated as:

$\text{test statistic} = \frac{\text{estimate} - \text{hypothesized value}}{\text{standard error of estimate}}$

P-value Calculation Options

Note also that the p-value definition includes a probability associated with a test statistic being as extreme or more extreme (as determined by the alternative hypothesis . How do we determine the area that we consider when calculating the probability. This decision is determined by the inequality in the alternative hypothesis.

For example, when we were trying to convince the skeptic that the population mean is greater than 2100 days, we only considered those sample means that we at least as large as what we observed -- 2188 days or more.

If instead we were trying to convince the skeptic that the population mean is less than 2100 days ($H_a: \mu < 2100$), we would consider all sample means that were at most what we observed - 2188 days or less. In this case, our p-value would be quite large; it would be around 99.5%. This large p-value demonstrates that our sample does not support the alternative hypothesis. In fact, our sample would encourage us to choose the null hypothesis instead of the alternative hypothesis of $\mu < 2100$, as our sample directly contradicts the statement in the alternative hypothesis.

If we wanted to convince the skeptic that they were wrong and that the population mean is anything other than 2100 days ($H_a: \mu \neq 2100$), then we would want to calculate the probability that a sample mean is at least 88 days away from 2100 days. That is, we would calculate the probability corresponding to 2188 days or more or 2012 days or less. In this case, our p-value would be roughly twice the previously calculated p-value.

We could calculate all of those probabilities using our sampling distributions, either simulated or theoretical, that we generated in the previous step. If we chose to calculate a test statistic as defined in the previous section, we could also rely on standard normal distributions to calculate our p-value.

Evaluate your results and write conclusion in context of problem

Once you've gathered your evidence, it's now time to make your final conclusions and determine how you might proceed.

In traditional hypothesis testing, you often make a decision. Recall that you have your threshold (significance level $\alpha$) and your level of evidence (p-value). We can compare the two to determine if your p-value is less than or equal to your threshold. If it is, you have enough evidence to persuade your skeptic to change their mind. If it is larger than the threshold, you don't have quite enough evidence to convince the skeptic.

Common formal conclusions (if given in context) would be:

• I have enough evidence to reject the null hypothesis (the skeptic's claim), and I have sufficient evidence to suggest that the alternative hypothesis is instead true.
• I do not have enough evidence to reject the null hypothesis (the skeptic's claim), and so I do not have sufficient evidence to suggest the alternative hypothesis is true.

The only decision that we can make is to either reject or fail to reject the null hypothesis (we cannot "accept" the null hypothesis). Because we aren't actively evaluating the alternative hypothesis, we don't want to make definitive decisions based on that hypothesis. However, when it comes to making our conclusion for what to use going forward, we frame this on whether we could successfully convince someone of the alternative hypothesis.

A less formal conclusion might look something like:

Based on our sample of Chicago Airbnb listings, it seems as if the mean time since a host has been on Airbnb (for all Chicago Airbnb listings) is more than 5.75 years.

Significance Level Interpretation

We've now seen how the significance level $\alpha$ is used as a threshold for hypothesis testing. What exactly is the significance level?

The significance level $\alpha$ has two primary definitions. One is that the significance level is the maximum probability required to reject the null hypothesis; this is based on how the significance level functions within the hypothesis testing framework. The second definition is that this is the probability of rejecting the null hypothesis when the null hypothesis is true; in other words, this is the probability of making a specific type of error called a Type I error.

Why do we have to be comfortable making a Type I error? There is always a chance that the skeptic was originally correct and we obtained a very unusual sample. We don't want to the skeptic to be so convinced of their theory that no evidence can convince them. In this case, we need the skeptic to be convinced as long as the evidence is strong enough . Typically, the probability threshold will be low, to reduce the number of errors made. This also means that a decent amount of evidence will be needed to convince the skeptic to abandon their position in favor of the alternative theory.

p-value Limitations and Misconceptions

In comparison to the $\alpha$ significance level, we also need to calculate the evidence against the null hypothesis with the p-value.

The p-value is the probability of getting a test statistic as extreme or more extreme (in the direction of the alternative hypothesis), assuming the null hypothesis is true.

Recently, p-values have gotten some bad press in terms of how they are used. However, that doesn't mean that p-values should be abandoned, as they still provide some helpful information. Below, we'll describe what p-values don't mean, and how they should or shouldn't be used to make decisions.

Factors that affect a p-value

What features affect the size of a p-value?

• the null value, or the value assumed under the null hypothesis
• the effect size (the difference between the null value under the null hypothesis and the true value of the parameter)
• the sample size

More evidence against the null hypothesis will be obtained if the effect size is larger and if the sample size is larger.

Misconceptions

We gave a definition for p-values above. What are some examples that p-values don't mean?

• A p-value is not the probability that the null hypothesis is correct
• A p-value is not the probability that the null hypothesis is incorrect
• A p-value is not the probability of getting your specific sample
• A p-value is not the probability that the alternative hypothesis is correct
• A p-value is not the probability that the alternative hypothesis is incorrect
• A p-value does not indicate the size of the effect

Our p-value is a way of measuring the evidence that your sample provides against the null hypothesis, assuming the null hypothesis is in fact correct.

Using the p-value to make a decision

Why is there bad press for a p-value? You may have heard about the standard $\alpha$ level of 0.05. That is, we would be comfortable with rejecting the null hypothesis once in 20 attempts when the null hypothesis is really true. Recall that we reject the null hypothesis when the p-value is less than or equal to the significance level.

Consider what would happen if you have two different p-values: 0.049 and 0.051.

In essence, these two p-values represent two very similar probabilities (4.9% vs. 5.1%) and very similar levels of evidence against the null hypothesis. However, when we make our decision based on our threshold, we would make two different decisions (reject and fail to reject, respectively). Should this decision really be so simplistic? I would argue that the difference shouldn't be so severe when the sample statistics are likely very similar. For this reason, I (and many other experts) strongly recommend using the p-value as a measure of evidence and including it with your conclusion.

Putting too much emphasis on the decision (and having a significant result) has created a culture of misusing p-values. For this reason, understanding your p-value itself is crucial.

Searching for p-values

The other concern with setting a definitive threshold of 0.05 is that some researchers will begin performing multiple tests until finding a p-value that is small enough. However, with a p-value of 0.05, we know that we will have a p-value less than 0.05 1 time out of every 20 times, even when the null hypothesis is true.

This means that if researchers start hunting for p-values that are small (sometimes called p-hacking), then they are likely to identify a small p-value every once in a while by chance alone. Researchers might then publish that result, even though the result is actually not informative. For this reason, it is recommended that researchers write a definitive analysis plan to prevent performing multiple tests in search of a result that occurs by chance alone.

Best Practices

With all of this in mind, what should we do when we have our p-value? How can we prevent or reduce misuse of a p-value?

• Report the p-value along with the conclusion
• Specify the effect size (the value of the statistic)
• Define an analysis plan before looking at the data
• Interpret the p-value clearly to specify what it indicates
• Consider using an alternate statistical approach, the confidence interval, discussed next, when appropriate

Lesson 7: Comparing Two Population Parameters

So far in our course, we have only discussed measurements taken in one variable for each sampling unit. This is referred to as univariate data. In this lesson, we are going to talk about measurements taken in two variables for each sampling unit. This is referred to as bivariate data.

Often when there are two measurements taken on the same sampling unit, one variable is the response variable and the other is the explanatory variable. The explanatory variable can be seen as the indicator of which population the sampling unit comes from. It helps to be able to identify which is the response and which is the explanatory variable.

In this lesson, here are some of the cases we will consider:

Two-Sample Cases

Categorical - taken from two distinct groups

Sex and whether they smoke

Consider a case where we measure sex and whether they smoke. In this case, the response variable is categorical, and the explanatory variable is also categorical.

• Response variable : Yes or No to the Question “Do you smoke?”
• Explanatory variable : Sex (Female or Male)

Quantitative - taken from two distinct groups

GPA and the current degree level of a student

In this case, the response variable is quantitative, and the explanatory variable is categorical.

• Response variable : GPA
• Explanatory variable : Graduate or Undergraduate

Quantitative - taken twice from each subject (paired)

Dieting and the participant's weight before and after

In this case, the response is quantitative, and we will show later why there is no explanatory variable.

• Response variable : Weight
• Explanatory variable : Diet

Categorical - taken twice from each subject (paired)

To begin, just as we did previously, one has to first decide whether the problem you are investigating requires the analysis of categorical or quantitative data. In other words, you need to identify your response variable and determine the type of variable. Next, one has to determine if the two measurements are from independent samples or dependent samples.

You will find that much of what we discuss will be an extension of our previous lessons on confidence intervals and hypothesis testing for one-proportion and one-mean. We will want to check the necessary conditions in order to use the distributions as before. If conditions are satisfied, we calculate the specific test statistic and again compare this to a critical value (rejection region approach) or find the probability of observing this test statistic or one more extreme (p-value approach). The decision process will be the same as well: if the test statistic falls in the rejection region, we will reject the null hypothesis; if the p -value is less than the preset level of significance, we will reject the null hypothesis. The interpretation of confidence intervals in support of the hypothesis decision will also be familiar:

• if the interval does not contain the null hypothesis value, then we will reject the null hypothesis;
• if the interval contains the null hypothesis value, then we will fail to reject the null hypothesis.

One departure we will take from our previous lesson on hypothesis testing is how we will treat the null value. In the previous lesson, the null value could vary. In this lesson, when comparing two proportions or two means, we will use a null value of 0 (i.e., "no difference").

For example, \(\mu_1-\mu_2=0\) would mean that \(\mu_1=\mu_2\), and there would be no difference between the two population parameters. Similarly for two population proportions.

Although we focus on the difference equalling zero, it is possible to test for specific values of the difference using the methods presented. However, most applications research only for a difference in the parameters (i.e., the difference is less than, greater than, or not equal to zero).

We will start by comparing two independent population proportions, move to compare two independent population means, from there to paired population means, and ending with the comparison of two independent population variances.

• Compare two population proportions using confidence intervals and hypothesis tests.
• Distinguish between independent data and paired data for when analyzing means.
• Compare two means from independent samples using confidence intervals and hypothesis tests when the variances are assumed equal.
• Compare two means from independent samples using confidence intervals and hypothesis tests when the variances are assumed unequal.
• Compare two means from dependent samples using confidence intervals and hypothesis tests.
• Compare two population variances using a hypothesis test.

7.1 - Difference of Two Independent Normal Variables

In the previous Lessons, we learned about the Central Limit Theorem and how we can apply it to find confidence intervals and use it to develop hypothesis tests. In this section, we will present a theorem to help us continue this idea in situations where we want to compare two population parameters.

As we mentioned before, when we compare two population means or two population proportions, we consider the difference between the two population parameters. In other words, we consider either \(\mu_1-\mu_2\) or \(p_1-p_2\).

We present the theory here to give you a general idea of how we can apply the Central Limit Theorem. We intentionally leave out the mathematical details.

Let \(X\) have a normal distribution with mean \(\mu_x\), variance \(\sigma^2_x\), and standard deviation \(\sigma_x\).

Let \(Y\) have a normal distribution with mean \(\mu_y\), variance \(\sigma^2_y\), and standard deviation \(\sigma_y\).

If \(X\) and \(Y\) are independent, then \(X-Y\) will follow a normal distribution with mean \(\mu_x-\mu_y\), variance \(\sigma^2_x+\sigma^2_y\), and standard deviation \(\sqrt{\sigma^2_x+\sigma^2_y}\).

The idea is that, if the two random variables are normal, then their difference will also be normal. This is wonderful but how can we apply the Central Limit Theorem?

If \(X\) and \(Y\) are normal, we know that \(\bar{X}\) and \(\bar{Y}\) will also be normal. If \(X\) and \(Y\) are not normal but the sample size is large, then \(\bar{X}\) and \(\bar{Y}\) will be approximately normal (applying the CLT). Using the theorem above, then \(\bar{X}-\bar{Y}\) will be approximately normal with mean \(\mu_1-\mu_2\).

This is great! This theory can be applied when comparing two population proportions, and two population means. The details are provided in the next two sections.

7.2 - Comparing Two Population Proportions

Introduction.

When we have a categorical variable of interest measured in two populations, it is quite often that we are interested in comparing the proportions of a certain category for the two populations.

Let’s consider the following example.

Example: Received $100 by Mistake

Males and females were asked about what they would do if they received a $100 bill by mail, addressed to their neighbor, but wrongly delivered to them. Would they return it to their neighbor? Of the 69 males sampled, 52 said "yes" and of the 131 females sampled, 120 said "yes."

Does the data indicate that the proportions that said "yes" are different for male and female? How do we begin to answer this question?

If the proportion of males who said “yes, they would return it” is denoted as \(p_1\) and the proportion of females who said “yes, they would return it” is denoted as \(p_2\), then the following equations indicate that \(p_1\) is equal to \(p_2\).

\(p_1-p_2=0\) or \(\dfrac{p_1}{p_2}=1\)

We would need to develop a confidence interval or perform a hypothesis test for one of these expressions.

Moving forward

There may be other ways of setting up these equations such that the proportions are equal. We choose the difference due to the theory discussed in the last section. Under certain conditions, the sampling distribution of \(\hat{p}_1\), for example, is approximately normal and centered around \(p_1\). Similarly, the sampling distribution of \(\hat{p}_2\) is approximately normal and centered around \(p_2\). Their difference, \(\hat{p}_1-\hat{p}_2\), will then be approximately normal and centered around \(p_1-p_2\), which we can use to determine if there is a difference.

In the next subsections, we explain how to use this idea to develop a confidence interval and hypothesis tests for \(p_1-p_2\).

7.2.1 - Confidence Intervals

In this section, we begin by defining the point estimate and developing the confidence interval based on what we have learned so far.

The point estimate for the difference between the two population proportions, \(p_1-p_2\), is the difference between the two sample proportions written as \(\hat{p}_1-\hat{p}_2\).

We know that a point estimate is probably not a good estimator of the actual population. By adding some amount of error to this point estimate, we can create a confidence interval as we did with one sample parameters.

Derivation of the Confidence Interval

Consider two populations and label them as population 1 and population 2. Take a random sample of size \(n_1\) from population 1 and take a random sample of size \(n_2\) from population 2. If we consider them separately,

If \(n_1p_1\ge 5\) and \(n_1(1-p_1)\ge 5\), then \(\hat{p}_1\) will follow a normal distribution with...

\begin{array}{rcc}  \text{Mean:}&&p_1 \\ \text{ Standard Error:}&& \sqrt{\dfrac{p_1(1-p_1)}{n_1}} \\ \text{Estimated Standard Error:}&& \sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}} \end{array}

\begin{array}{rcc}  \text{Mean:}&&p_2 \\ \text{ Standard Error:}&& \sqrt{\dfrac{p_2(1-p_2)}{n_2}} \\ \text{Estimated Standard Error:}&& \sqrt{\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \end{array}

Using the theory introduced previously, if \(n_1p_1\), \(n_1(1-p_1)\), \(n_2p_2\), and \(n_2(1-p_2)\) are all greater than five and we have independent samples, then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) is approximately normal with...

\begin{array}{rcc}  \text{Mean:}&&p_1-p_2 \\ \text{ Standard Error:}&& \sqrt{\dfrac{p_1(1-p_1)}{n_1}+\dfrac{p_2(1-p_2)}{n_2}} \\ \text{Estimated Standard Error:}&& \sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \end{array}

Putting these pieces together, we can construct the confidence interval for \(p_1-p_2\). Since we do not know \(p_1\) and \(p_2\), we need to check the conditions using \(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\). If these conditions are satisfied, then the confidence interval can be constructed for two independent proportions.

The \((1-\alpha)100\%\) confidence interval of \(p_1-p_2\) is given by:

\(\hat{p}_1-\hat{p}_2\pm z_{\alpha/2}\sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\)

Example 7-1: Received $100 by Mistake

Males and females were asked about what they would do if they received a $100 bill by mail, addressed to their neighbor, but wrongly delivered to them. Would they return it to their neighbor? Of the 69 males sampled, 52 said "yes" and of the 131 females sampled, 120 said "yes."

Find a 95% confidence interval for the difference in proportions for males and females who said "yes."

Let’s let sample one be males and sample two be females. Then we have:

Checking conditions we see that \(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five so our conditions are satisfied.

Using the formula above, we get:

\begin{array}{rcl} \hat{p}_1-\hat{p}_2 &\pm &z_{\alpha/2}\sqrt{\dfrac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\dfrac{\hat{p}_2(1-\hat{p}_2)}{n_2}}\\ \dfrac{52}{69}-\dfrac{120}{131}&\pm &1.96\sqrt{\dfrac{\frac{52}{69}\left(1-\frac{52}{69}\right)}{69}+\dfrac{\frac{120}{131}(1-\frac{120}{131})}{131}}\\ -0.1624 &\pm &1.96 \left(0.05725\right)\\ -0.1624 &\pm &0.1122\  or \  (-0.2746, -0.0502)\\ \end{array}

We are 95% confident that the difference of population proportions of males who said "yes" and females who said "yes" is between -0.2746 and -0.0502.

Based on both ends of the interval being negative, it seems like the proportion of females who would return it is higher than the proportion of males who would return it.

We will discuss how to find the confidence interval using Minitab after we examine the hypothesis test for two proportion. Minitab calculates the test and the confidence interval at the same time.

Caution!  What happens if we defined \(\hat{p}_1\) to be the proportion of females and \(\hat{p}_2\) for the proportion of males? If you follow through the calculations, you will find that the confidence interval will differ only in sign. In other words, if female was \(\hat{p}_1\), the interval would be 0.0502 to 0.2746. It still shows that the proportion of females is higher than the proportion of males.

7.2.2 - Hypothesis Testing

Derivation of the test.

We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test will follow the same six steps we learned in the previous Lesson although they are not explicitly stated.

We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval. One major difference in the hypothesis test is the null hypothesis and assuming the null hypothesis is true.

For a test for two proportions, we are interested in the difference. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:

\(H_0\colon p_1-p_2=0\)

Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\). Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).

We take this into account by finding an estimate for this \(p^*\) using the two sample proportions. We can calculate an estimate of \(p^*\) using the following formula:

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)

This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).

Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.

\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...will follow a standard normal distribution.

Finally, we can develop our hypothesis test for \(p_1-p_2\).

Null: \(H_0\colon p_1-p_2=0\)

Possible Alternatives:

\(H_a\colon p_1-p_2\ne0\)

\(H_a\colon p_1-p_2>0\)

\(H_a\colon p_1-p_2<0\)

Conditions:

\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five

The test statistic is:

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).

The critical values, rejection regions, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one sample proportion.

Example 7-2: Received $100 by Mistake

Let's continue with the question that was asked previously.

Males and females were asked about what they would do if they received a $100 bill by mail, addressed to their neighbor, but wrongly delivered to them. Would they return it to their neighbor? Of the 69 males sampled, 52 said “yes” and of the 131 females sampled, 120 said “yes.”

Does the data indicate that the proportions that said “yes” are different for males and females at a 5% level of significance? Conduct the test using the p-value approach.

• Using Minitab

Again, let’s define males as sample 1.

The conditions are all satisfied as we have shown previously.

The null and alternative hypotheses are:

\(H_0\colon p_1-p_2=0\) vs \(H_a\colon p_1-p_2\ne 0\)

The test statistic:

\(n_1=69\), \(\hat{p}_1=\frac{52}{69}\)

\(n_2=131\), \(\hat{p}_2=\frac{120}{131}\)

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}=\dfrac{52+120}{69+131}=\dfrac{172}{200}=0.86\)

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}=\dfrac{\dfrac{52}{69}-\dfrac{120}{131}}{\sqrt{0.86(1-0.86)\left(\frac{1}{69}+\frac{1}{131}\right)}}=-3.1466\)

The p-value of the test based on the two-sided alternative is:

\(\text{p-value}=2P(Z>|-3.1466|)=2P(Z>3.1466)=2(0.0008)=0.0016\)

Since our p-value of 0.0016 is less than our significance level of 5%, we reject the null hypothesis. There is enough evidence to suggest that proportions of males and females who would return the money are different.

  Minitab: Inference for Two Proportions with Independent Samples

To conduct inference for two proportions with an independent sample in Minitab...

The following window will appear. In the drop-down choose ‘Summarized data’ and entered the number of events and trials for both samples.

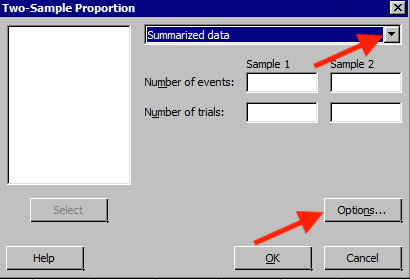
You should get the following output for this example:

Test and CI for Two Proportions

Difference = p (1) - p (2)

Estimate for difference: -0.162407

95% CI for difference: (-0.274625, -0.0501900)

Test for difference = 0 (vs  ≠ 0): Z = -3.15 P-Value = 0.002 (Use this!)

Fisher's exact test: P-Value = 0.003 (Ignore the Fisher's exact test. This test uses a different method to calculate a test statistic from the Z-test we have learned in this lesson.)

Ignore the Fisher's p -value! The p -value highlighted above is calculated using the methods we learned in this lesson. The Fisher's test uses a different method than what we explained in this lesson to calculate a test statistic and p -value. This method incorporates a log of the ratio of observed to expected values. It's just a different technique that is more complicated to do by-hand. Minitab automatically includes both results in its output.

In 1980, of 750 men 20-34 years old, 130 were found to be overweight. Whereas, in 1990, of 700 men, 20-34 years old, 160 were found to be overweight.

At the 5% significance level, do the data provide sufficient evidence to conclude that, for men 20-34 years old, a higher percentage were overweight in 1990 than 10 years earlier? Conduct the test using the p-value approach.

Let’s define 1990 as sample 1.

\(H_0\colon p_1-p_2=0\) vs \(H_a\colon p_1-p_2>0\)

\(n_1=700\), \(\hat{p}_1=\frac{160}{700}\)

\(n_2=750\), \(\hat{p}_2=\frac{130}{750}\)

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}=\dfrac{160+130}{700+750}=\dfrac{290}{1450}=0.2\)

The conditions are all satisfied: \(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than 5.

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}=\dfrac{\dfrac{160}{700}-\dfrac{130}{750}}{\sqrt{0.2(1-0.2)\left(\frac{1}{700}+\frac{1}{750}\right)}}=2.6277\)

The p-value of the test based on the right-tailed alternative is:

\(\text{p-value}=P(Z>2.6277)=0.0043\)

Since our p-value of 0.0043 is less than our significance level of 5%, we reject the null hypothesis. There is enough evidence to suggest that the proportion of males overweight in 1990 is greater than the proportion in 1980.

  Using Minitab

To conduct inference for two proportions with independent samples in Minitab...

• Choose Stat > Basic Statistics > 2 proportions
• Choose Options

Select "Difference < hypothesized difference" for 'Alternative Hypothesis.

You should get the following output.

Estimate for difference: -0.0552381

95% upper bound for difference: -0.0206200

Test for difference = 0 (vs < 0): Z = -2.63 P-Value = 0.004

Fisher's exact test: P-Value = 0.005 (Ignore the Fisher's exact test)

7.3 - Comparing Two Population Means

In this section, we are going to approach constructing the confidence interval and developing the hypothesis test similarly to how we approached those of the difference in two proportions.

There are a few extra steps we need to take, however. First, we need to consider whether the two populations are independent. When considering the sample mean, there were two parameters we had to consider, \(\mu\) the population mean, and \(\sigma\) the population standard deviation. Therefore, the second step is to determine if we are in a situation where the population standard deviations are the same or if they are different.

Independent and Dependent Samples

It is important to be able to distinguish between an independent sample or a dependent sample.

The following are examples to illustrate the two types of samples.

Example 7-3: Gas Mileage

We want to compare the gas mileage of two brands of gasoline. Describe how to design a study involving...

• independent sample Answer: Randomly assign 12 cars to use Brand A and another 12 cars to use Brand B.
• dependent samples Answer: Using 12 cars, have each car use Brand A and Brand B. Compare the differences in mileage for each car.
• Design involving independent samples
• Design involving dependent samples
• Answer: Randomly assign half of the subjects to taste Coke and the other half to taste Pepsi.

Answer: Allow all the subjects to rate both Coke and Pepsi. The drinks should be given in random order. The same subject's ratings of the Coke and the Pepsi form a paired data set.

• We randomly select 20 males and 20 females and compare the average time they spend watching TV. Is this an independent sample or paired sample?
• We randomly select 20 couples and compare the time the husbands and wives spend watching TV. Is this an independent sample or paired sample?
• Answer: Independent Sample

Answer: Paired sample

The two types of samples require a different theory to construct a confidence interval and develop a hypothesis test. We consider each case separately, beginning with independent samples.

7.3.1 - Inference for Independent Means

Two-cases for independent means.

As with comparing two population proportions, when we compare two population means from independent populations, the interest is in the difference of the two means. In other words, if \(\mu_1\) is the population mean from population 1 and \(\mu_2\) is the population mean from population 2, then the difference is \(\mu_1-\mu_2\). If \(\mu_1-\mu_2=0\) then there is no difference between the two population parameters.

If each population is normal, then the sampling distribution of \(\bar{x}_i\) is normal with mean \(\mu_i\), standard error \(\dfrac{\sigma_i}{\sqrt{n_i}}\), and the estimated standard error \(\dfrac{s_i}{\sqrt{n_i}}\), for \(i=1, 2\).

Using the Central Limit Theorem, if the population is not normal, then with a large sample, the sampling distribution is approximately normal.

The theorem presented in this Lesson says that if either of the above are true, then \(\bar{x}_1-\bar{x}_2\) is approximately normal with mean \(\mu_1-\mu_2\), and standard error \(\sqrt{\dfrac{\sigma^2_1}{n_1}+\dfrac{\sigma^2_2}{n_2}}\).

However, in most cases, \(\sigma_1\) and \(\sigma_2\) are unknown, and they have to be estimated. It seems natural to estimate \(\sigma_1\) by \(s_1\) and \(\sigma_2\) by \(s_2\). When the sample sizes are small, the estimates may not be that accurate and one may get a better estimate for the common standard deviation by pooling the data from both populations if the standard deviations for the two populations are not that different.

Given this, there are two options for estimating the variances for the independent samples:

• Using pooled variances
• Using unpooled (or unequal) variances

When to use which? When we are reasonably sure that the two populations have nearly equal variances, then we use the pooled variances test. Otherwise, we use the unpooled (or separate) variance test.

7.3.1.1 - Pooled Variances

Confidence intervals for \(\boldsymbol{\mu_1-\mu_2}\): pooled variances.

When we have good reason to believe that the variance for population 1 is equal to that of population 2, we can estimate the common variance by pooling information from samples from population 1 and population 2.

An informal check for this is to compare the ratio of the two sample standard deviations. If the two are equal , the ratio would be 1, i.e. \(\frac{s_1}{s_2}=1\). However, since these are samples and therefore involve error, we cannot expect the ratio to be exactly 1. When the sample sizes are nearly equal (admittedly "nearly equal" is somewhat ambiguous, so often if sample sizes are small one requires they be equal), then a good Rule of Thumb to use is to see if the ratio falls from 0.5 to 2. That is, neither sample standard deviation is more than twice the other.

If this rule of thumb is satisfied, we can assume the variances are equal. Later in this lesson, we will examine a more formal test for equality of variances.

• Let \(n_1\) be the sample size from population 1 and let \(s_1\) be the sample standard deviation of population 1.
• Let \(n_2\) be the sample size from population 2 and \(s_2\) be the sample standard deviation of population 2.

Then the common standard deviation can be estimated by the pooled standard deviation:

\(s_p=\sqrt{\dfrac{(n_1-1)s_1^2+(n_2-1)s^2_2}{n_1+n_2-2}}\)

If we can assume the populations are independent, that each population is normal or has a large sample size, and that the population variances are the same, then it can be shown that...

\(t=\dfrac{\bar{x}_1-\bar{x_2}-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\)

follows a t-distribution with \(n_1+n_2-2\) degrees of freedom.

Now, we can construct a confidence interval for the difference of two means, \(\mu_1-\mu_2\).

where \(t_{\alpha/2}\) comes from a t-distribution with \(n_1+n_2-2\) degrees of freedom.

Hypothesis Tests for \(\boldsymbol{\mu_1-\mu_2}\): The Pooled t-test

Now let's consider the hypothesis test for the mean differences with pooled variances.

\(H_0\colon\mu_1-\mu_2=0\)

\(H_a\colon \mu_1-\mu_2\ne0\)

\(H_a\colon \mu_1-\mu_2>0\)

\(H_a\colon \mu_1-\mu_2<0\)

The assumptions/conditions are:

• The populations are independent
• The population variances are equal
• Each population is either normal or the sample size is large.

The test statistic is...

\(t^*=\dfrac{\bar{x}_1-\bar{x}_2-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\)

And \(t^*\) follows a t-distribution with degrees of freedom equal to \(df=n_1+n_2-2\).

The p-value, critical value, rejection region, and conclusion are found similarly to what we have done before.

Example 7-4: Comparing Packing Machines

In a packing plant, a machine packs cartons with jars. It is supposed that a new machine will pack faster on the average than the machine currently used. To test that hypothesis, the times it takes each machine to pack ten cartons are recorded. The results, ( machine.txt ), in seconds, are shown in the tables.

\(\bar{x}_1=42.14, \text{s}_1= 0.683\)

\(\bar{x}_2=43.23, \text{s}_2= 0.750\)

Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster?

• Hypothesis Test
• Confidence Interval

Are these independent samples? Yes, since the samples from the two machines are not related.

Are these large samples or a normal population?

We have \(n_1\lt 30\) and \(n_2\lt 30\). We do not have large enough samples, and thus we need to check the normality assumption from both populations. Let's take a look at the normality plots for this data:

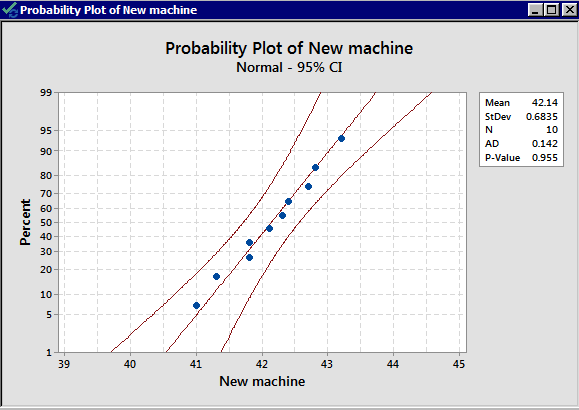
From the normal probability plots, we conclude that both populations may come from normal distributions. Remember the plots do not indicate that they DO come from a normal distribution. It only shows if there are clear violations. We should proceed with caution.

Do the populations have equal variance? No information allows us to assume they are equal. We can use our rule of thumb to see if they are “close.” They are not that different as \(\dfrac{s_1}{s_2}=\dfrac{0.683}{0.750}=0.91\) is quite close to 1. This assumption does not seem to be violated.

We can thus proceed with the pooled t -test.

Let \(\mu_1\) denote the mean for the new machine and \(\mu_2\) denote the mean for the old machine.

The null hypothesis is that there is no difference in the two population means, i.e.

\(H_0\colon \mu_1-\mu_2=0\)

The alternative is that the new machine is faster, i.e.

The significance level is 5%. Since we may assume the population variances are equal, we first have to calculate the pooled standard deviation:

\begin{align} s_p&=\sqrt{\frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n_1+n_2-2}}\\ &=\sqrt{\frac{(10-1)(0.683)^2+(10-1)(0.750)^2}{10+10-2}}\\ &=\sqrt{\dfrac{9.261}{18}}\\ &=0.7173 \end{align}

\begin{align} t^*&=\dfrac{\bar{x}_1-\bar{x}_2-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\\ &=\dfrac{42.14-43.23}{0.7173\sqrt{\frac{1}{10}+\frac{1}{10}}}\\&=-3.398 \end{align}

The alternative is left-tailed so the critical value is the value \(a\) such that \(P(T<a)=0.05\), with \(10+10-2=18\) degrees of freedom. The critical value is -1.7341. The rejection region is \(t^*<-1.7341\).

Our test statistic, -3.3978, is in our rejection region, therefore, we reject the null hypothesis. With a significance level of 5%, we reject the null hypothesis and conclude there is enough evidence to suggest that the new machine is faster than the old machine.

To find the interval, we need all of the pieces. We calculated all but one when we conducted the hypothesis test. We only need the multiplier. For a 99% confidence interval, the multiplier is \(t_{0.01/2}\) with degrees of freedom equal to 18. This value is 2.878.

The interval is:

\(\bar{x}_1-\bar{x}_2\pm t_{\alpha/2}s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\)

\((42.14-43.23)\pm 2.878(0.7173)\sqrt{\frac{1}{10}+\frac{1}{10}}\)

\(-1.09\pm 0.9232\)

The 99% confidence interval is (-2.013, -0.167).

We are 99% confident that the difference between the two population mean times is between -2.012 and -0.167.

  Minitab: 2-Sample t-test - Pooled

The following steps are used to conduct a 2-sample t-test for pooled variances in Minitab.

• Choose Stat > Basic Statistics > 2-Sample t .

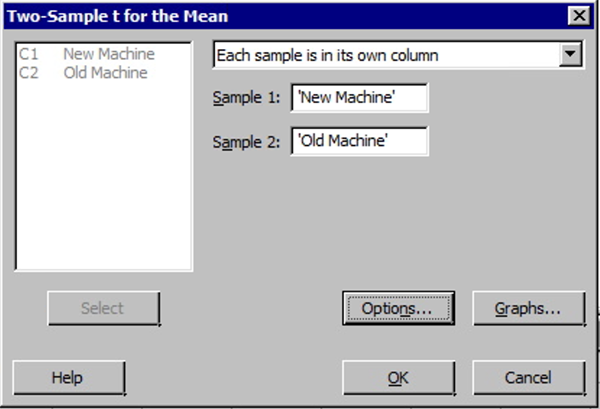
• Select the Options button and enter the desired 'confidence level', 'null hypothesis value' (again for our class this will be 0), and select the correct 'alternative hypothesis' from the drop-down menu. Finally, check the box for 'assume equal variances'. This latter selection should only be done when we have verified the two variances can be assumed equal.

The Minitab output for the packing time example:

Two-Sample T-Test and CI: New Machine, Old Machine

μ 1 : mean of New Machine

μ 2 : mean of Old Machine

Difference: μ 1 - μ 2

Equal variances are assumed for this analysis.

Descriptive Statistics

Estimation for difference.

Alternative hypothesis

H 1 : μ 1 - μ 2 < 0

7.3.1.2 - Unpooled Variances

When the assumption of equal variances is not valid, we need to use separate, or unpooled, variances. The mathematics and theory are complicated for this case and we intentionally leave out the details.

We still have the following assumptions:

If the assumptions are satisfied, then

\(t^*=\dfrac{\bar{x}_1-\bar{x_2}-0}{\sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}}\)

will have a t-distribution with degrees of freedom

\(df=\dfrac{(n_1-1)(n_2-1)}{(n_2-1)C^2+(1-C)^2(n_1-1)}\)

where \(C=\dfrac{\frac{s^2_1}{n_1}}{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}\).

Where \(t_{\alpha/2}\) comes from the t-distribution using the degrees of freedom above.

Minitab ®

Minitab: unpooled t-test.

To perform a separate variance 2-sample, t -procedure use the same commands as for the pooled procedure EXCEPT we do NOT check box for 'Use Equal Variances.'

• Choose Stat > Basic Statistics > 2-sample t
• Select the Options box and enter the desired 'Confidence level,' 'Null hypothesis value' (again for our class this will be 0), and select the correct 'Alternative hypothesis' from the drop-down menu.

For some examples, one can use both the pooled t-procedure and the separate variances (non-pooled) t -procedure and obtain results that are close to each other. However, when the sample standard deviations are very different from each other, and the sample sizes are different, the separate variances 2-sample t -procedure is more reliable.

Example 7-5: Grade Point Average

Independent random samples of 17 sophomores and 13 juniors attending a large university yield the following data on grade point averages ( student_gpa.txt ):

At the 5% significance level, do the data provide sufficient evidence to conclude that the mean GPAs of sophomores and juniors at the university differ?

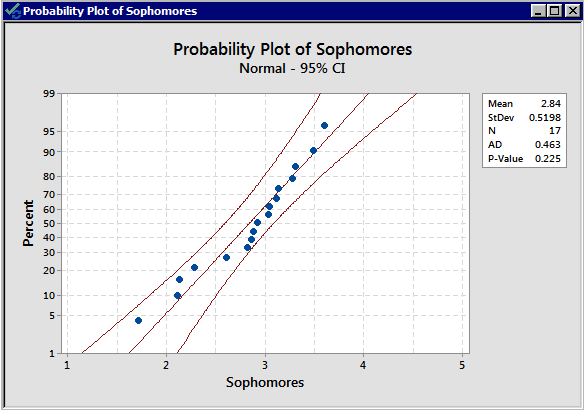
There is no indication that there is a violation of the normal assumption for both samples. As before, we should proceed with caution.

Now, we need to determine whether to use the pooled t-test or the non-pooled (separate variances) t -test. The summary statistics are:

The standard deviations are 0.520 and 0.3093 respectively; both the sample sizes are small, and the standard deviations are quite different from each other. We, therefore, decide to use an unpooled t -test.

\(H_0\colon \mu_1-\mu_2=0\) vs \(H_a\colon \mu_1-\mu_2\ne0\)

The significance level is 5%. Perform the 2-sample t -test in Minitab with the appropriate alternative hypothesis.

Remember, the default for the 2-sample t-test in Minitab is the non-pooled one. Minitab generates the following output.

Two sample T for sophomores vs juniors

95% CI for mu sophomore - mu juniors: (-0.45, 0.173)

T-Test mu sophomore = mu juniors (Vs no =): T = -0.92

P = 0.36 DF = 26

Since the p-value of 0.36 is larger than \(\alpha=0.05\), we fail to reject the null hypothesis.

At 5% level of significance, the data does not provide sufficient evidence that the mean GPAs of sophomores and juniors at the university are different.

95% CI for mu sophomore- mu juniors is;

(-0.45, 0.173)

We are 95% confident that the difference between the mean GPA of sophomores and juniors is between -0.45 and 0.173.

7.3.2 - Inference for Paired Means

When we developed the inference for the independent samples, we depended on the statistical theory to help us. The theory, however, required the samples to be independent. What can we do when the two samples are not independent, i.e., the data is paired?

Consider an example where we are interested in a person’s weight before implementing a diet plan and after. Since the interest is focusing on the difference, it makes sense to “condense” these two measurements into one and consider the difference between the two measurements. For example, if instead of considering the two measures, we take the before diet weight and subtract the after diet weight. The difference makes sense too! It is the weight lost on the diet.

When we take the two measurements to make one measurement (i.e., the difference), we are now back to the one sample case! Now we can apply all we learned for the one sample mean to the difference (Cool!)

The Confidence Interval for the Difference of Paired Means, \(\mu_d\)

When we consider the difference of two measurements, the parameter of interest is the mean difference, denoted \(\mu_d\). The mean difference is the mean of the differences. We are still interested in comparing this difference to zero.

Suppose we have two paired samples of size \(n\):

\(x_1, x_2, …., x_n\) and \(y_1, y_2, … , y_n\)

Their difference can be denoted as:

\(d_1=x_1-y_1, d_2=x_2-y_2, …., d_n=x_n-y_n\)

The sample mean of the differences is:

\(\bar{d}=\frac{1}{n}\sum_{i=1}^n d_i\)

Denote the sample standard deviation of the differences as \(s_d\).

If \(\bar{d}\) is normal (or the sample size is large), the sampling distribution of \(\bar{d}\) is (approximately) normal with mean \(\mu_d\), standard error \(\dfrac{\sigma_d}{\sqrt{n}}\), and estimated standard error \(\dfrac{s_d}{\sqrt{n}}\).

At this point, the confidence interval will be the same as that of one sample.

\(\bar{d}\pm t_{\alpha/2}\frac{s_d}{\sqrt{n}}\)

where \(t_{\alpha/2}\) comes from \(t\)-distribution with \(n-1\) degrees of freedom

Example 7-6: Zinc Concentrations

Trace metals in drinking water affect the flavor and an unusually high concentration can pose a health hazard. Ten pairs of data were taken measuring zinc concentration in bottom water and surface water ( zinc_conc.txt ).

Does the data suggest that the true average concentration in the bottom water is different than that of surface water? Construct a confidence interval to address this question.

Zinc concentrations

In this example, the response variable is concentration and is a quantitative measurement. The explanatory variable is location (bottom or surface) and is categorical. The two populations (bottom or surface) are not independent. Therefore, we are in the paired data setting. The parameter of interest is \(\mu_d\).

Find the difference as the concentration of the bottom water minus the concentration of the surface water.

Since the problem did not provide a confidence level, we should use 5%.

To use the methods we developed previously, we need to check the conditions. The problem does not indicate that the differences come from a normal distribution and the sample size is small (n=10). We should check, using the Normal Probability Plot to see if there is any violation. First, we need to find the differences.

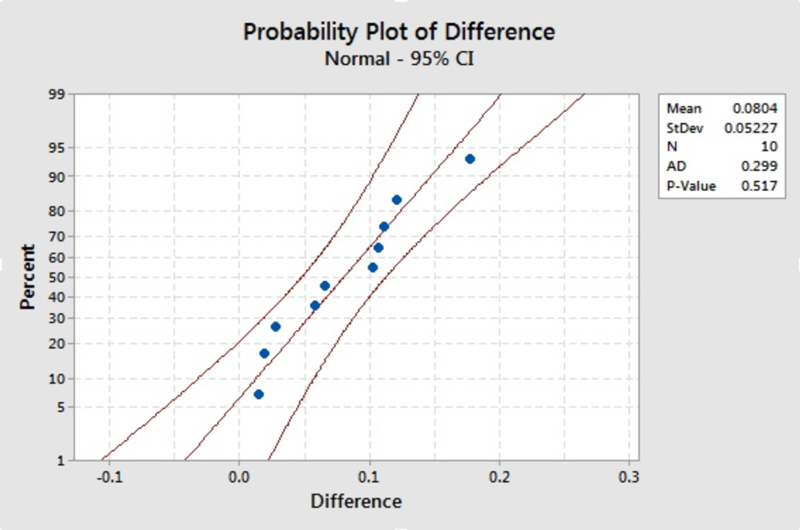
All of the differences fall within the boundaries, so there is no clear violation of the assumption. We can proceed with using our tools, but we should proceed with caution.

We need all of the pieces for the confidence interval. The sample mean difference is \(\bar{d}=0.0804\) and the standard deviation is \(s_d=0.0523\). For practice, you should find the sample mean of the differences and the standard deviation by hand. With \(n-1=10-1=9\) degrees of freedom, \(t_{0.05/2}=2.2622\).

The 95% confidence interval for the mean difference, \(\mu_d\) is:

\(\bar{d}\pm t_{\alpha/2}\dfrac{s_d}{\sqrt{n}}\)

\(0.0804\pm 2.2622\left( \dfrac{0.0523}{\sqrt{10}}\right)\)

(0.04299, 0.11781)

We are 95% confident that the population mean difference of bottom water and surface water zinc concentration is between 0.04299 and 0.11781.

If there is no difference between the means of the two measures, then the mean difference will be 0. Since 0 is not in our confidence interval, then the means are statistically different (or statistical significant or statistically different).

Note! Minitab will calculate the confidence interval and a hypothesis test simultaneously. We demonstrate how to find this interval using Minitab after presenting the hypothesis test.

Hypothesis Test for the Difference of Paired Means, \(\mu_d\)

In this section, we will develop the hypothesis test for the mean difference for paired samples. As we learned in the previous section, if we consider the difference rather than the two samples, then we are back in the one-sample mean scenario.

The possible null and alternative hypotheses are:

\(H_0\colon \mu_d=0\)

\(H_a\colon \mu_d\ne 0\)

\(H_a\colon \mu_d>0\)

\(H_a\colon \mu_d<0\)

We still need to check the conditions and at least one of the following need to be satisfied:

• The differences of the paired follow a normal distribution
• The sample size is large, \(n>30\).

If at least one is satisfied then...

\(t^*=\dfrac{\bar{d}-0}{\frac{s_d}{\sqrt{n}}}\)

Will follow a t-distribution with \(n-1\) degrees of freedom.

The same process for the hypothesis test for one mean can be applied. The test for the mean difference may be referred to as the paired t-test or the test for paired means.

Example 7-7: Zinc Concentrations - Hypothesis Test

Recall the zinc concentration example. Does the data suggest that the true average concentration in the bottom water exceeds that of surface water? Conduct this test using the rejection region approach. ( zinc_conc.txt ).

If we find the difference as the concentration of the bottom water minus the concentration of the surface water, then null and alternative hypotheses are:

\(H_0\colon \mu_d=0\) vs \(H_a\colon \mu_d>0\)

Note! If the difference was defined as surface - bottom, then the alternative would be left-tailed.

The desired significance level was not stated so we will use \(\alpha=0.05\).

The assumptions were discussed when we constructed the confidence interval for this example. Remember although the Normal Probability Plot for the differences showed no violation, we should still proceed with caution.

The next step is to find the critical value and the rejection region. The critical value is the value \(a\) such that \(P(T>a)=0.05\). Using the table or software, the value is 1.8331. For a right-tailed test, the rejection region is \(t^*>1.8331\).

Recall from the previous example, the sample mean difference is \(\bar{d}=0.0804\) and the sample standard deviation of the difference is \(s_d=0.0523\). Therefore, the test statistic is:

\(t^*=\dfrac{\bar{d}-0}{\frac{s_d}{\sqrt{n}}}=\dfrac{0.0804}{\frac{0.0523}{\sqrt{10}}}=4.86\)

The value of our test statistic falls in the rejection region. Therefore, we reject the null hypothesis. With a significance level of 5%, there is enough evidence in the data to suggest that the bottom water has higher concentrations of zinc than the surface level.

Minitab ®  – Paired t-Test

You can use a paired t -test in Minitab to perform the test. Alternatively, you can perform a 1-sample t -test on difference = bottom - surface.

• Choose Stat > Basic Statistics > Paired t
• Click Options to specify the confidence level for the interval and the alternative hypothesis you want to test. The default null hypothesis is 0.

Zinc Concentrations Example

The Minitab output for paired T for bottom - surface is as follows:

Paired T for bottom - surface

95% lower bound for mean difference: 0.0505

T-Test of mean difference = 0 (vs > 0): T-Value = 4.86 P-Value = 0.000

Note! In Minitab, if you choose a lower-tailed or an upper-tailed hypothesis test, an upper or lower confidence bound will be constructed, respectively, rather than a confidence interval.

Using the p -value to draw a conclusion about our example:

p -value = 0.000 < 0.05

Reject \(H_0\) and conclude that bottom zinc concentration is higher than surface zinc concentration.

Additional Notes

• For the zinc concentration problem, if you do not recognize the paired structure, but mistakenly use the 2-sample t -test treating them as independent samples, you will not be able to reject the null hypothesis. This demonstrates the importance of distinguishing the two types of samples. Also, it is wise to design an experiment efficiently whenever possible.
• What if the assumption of normality is not satisfied? Considering a nonparametric test would be wise.

7.4 - Comparing Two Population Variances

So far, we considered inference to compare two proportions and inference to compare two means. In this section, we will present how to compare two population variances.

Why would we want to compare two population variances? There are many situations, such as in quality control problems, where you may want to choose the process with smaller variability for a variable of interest.

One of the essential steps of a test to compare two population variances is for checking the equal variances assumption if you want to use the pooled variances. Many people use this test as a guide to see if there are any clear violations, much like using the rule of thumb.

When we introduce inference for two parameters before, we started with the sampling distribution. We will not do this here. The details of this test are left out. We will simply present how to use it.

F-Test to Compare Two Population Variances

To compare the variances of two quantitative variables, the hypotheses of interest are:

\(H_0\colon \dfrac{\sigma^2_1}{\sigma^2_2}=1\)

\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}\ne1\)

\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}>1\)

\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}<1\)

The last two alternatives are determined by how you arrange your ratio of the two sample statistics.

We will rely on Minitab to conduct this test for us. Minitab offers three (3) different methods to test equal variances.

• The F -test : This test assumes the two samples come from populations that are normally distributed.
• Bonett's test : this assumes only that the two samples are quantitative.
• Levene's test : similar to Bonett's in that the only assumption is that the data is quantitative. Best to use if one or both samples are heavily skewed, and your two sample sizes are both under 20.

Bonett’s test and Levene’s test are both considered nonparametric tests. In our case, since the tests we will be considering are based on a normal distribution, we are expecting to use the F -test. Again, we will need to confirm this by plotting our sample data (i.e., using a probability plot).

Caution!  To use the F-test, the samples must come from a normal distribution. The Central Limit Theorem applies to sample means, not to the data. Therefore, if the sample size is large, it does not mean we can assume the data come from a normal distribution.

Example 7-8: Comparing Packing Time Variances

Using the data in the packaging time from our previous discussion on two independent samples, we want to check whether it is reasonable to assume that the two machines have equal population variances.

Recall that the data are given below as ( machine.txt ):

  Minitab: F-test to Compare Two Population Variances

In Minitab...

• Choose Stat  >  Basic Statistics  >  2 Variances  and complete the dialog boxes.
• In the dialog box, check 'Use test and confidence intervals based on normal distribution' when we are confident the two samples come from a normal distribution.

Notes on using Minitab :

• Minitab will compare the two variances using the popular F-test method.
• If we only have summarized data (e.g. the sample sizes and sample variances or sample standard deviations), then the two variance test in Minitab will only provide an F-test.
• Minitab will use the Bonett and Levene test that are more robust tests when normality is not assumed.
• Minitab calculates the ratio based on Sample 1 divided by Sample 2.

The Minitab Output for the test for equal variances is as follows (a graph is also given in the output that provides confidence intervals and p -value for the test. This is not shown here):

Test and CI for Two Variances: New machine, Old machine

σ 1 : standard deviation of New machine

σ 2 : standard deviation of Old machine

Ratio: σ 1 /σ 2

F method was used. This method is accurate for normal data only.

Ratio of standard deviations

Null hypothesis

Significance level

H 0 : σ 1 /σ 2 =1

H 1 : σ 1 /σ 2 ≠1

How do we interpret the Minitab output?

Note that \(S_{new}=0.683\) and \(s_{old}=0.750\) The test statistic \(F\) is computed as...

\(F=\dfrac{s^2_{new}}{s^2_{old}}=0.83\)

The p -value provided is that for the alternative selected i.e. two-sided. If the alternative were one sided, for example if our alternative in the above example was "ratio less than 1", then the p -value would be half the reported p -value for the two-sided test, or 0.393.

Minitab provided the results only from the F -test since we checked the box to assume normal distribution. Regardless, the hypotheses would be the same for any of the test options and the decision method is the same: if the p -value is less than alpha, we reject the null and conclude the two population variances are not equal. Otherwise, if the p -value is large (i.e. greater than alpha) then we fail to reject the null and can assume the two population variances are equal.

In this example, the p -value for the F -test is very large (larger than 0.1). Therefore, we fail to reject the null hypothesis and conclude that there is not enough evidence to conclude the variances are different.

Note!  Remember, if there is doubt about normality, the better choice is to NOT use the F -test. You need to check whether the normal assumption holds before you can use the F -test since the F -test is very sensitive to departure from the normal assumption.

7.5 - Lesson 7 Summary

In this Lesson, we discussed how to compare population parameters from two samples. It is important to recognize which parameters are of interest. Once we identify the parameters, there are different approaches based on what we can assume about the samples.

We compared two population proportions for independent samples by developing the confidence interval and the hypothesis test for the difference between the two population proportions.

Next, we discussed how to compare two population means. The approach for inference is different if the samples are paired or independent. For two independent samples, we presented two cases based on whether or not we can assume the population variances are the same.

Finally, we discussed a test for comparing two sample variances from independent samples using the F-test.

In this Lesson, we considered the cases where the response is either qualitative or quantitative, and the explanatory variable is qualitative (categorical). In the next Lesson, we will present the case where both the response and the explanatory variable are qualitative.

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Module 8: Inference for One Proportion

Hypothesis testing (1 of 5), learning outcomes.

• When testing a claim, distinguish among situations involving one population mean, one population proportion, two population means, or two population proportions.
• Given a claim about a population, determine null and alternative hypotheses.

Introduction

In inference, we use a sample to draw a conclusion about a population. Two types of inference are the focus of our work in this course:

• Estimate a population parameter with a confidence interval.
• Test a claim about a population parameter with a hypothesis test.

We can also use samples from two populations to compare those populations. In this situation, the two types of inference focus on differences in the parameters.

• Estimate a difference in population parameters with a confidence interval.
• Test a claim about a difference in population parameters with a hypothesis test.

In “Estimating a Population Proportion,” we learned to estimate a population proportion using a confidence interval. For example, we estimated the proportion of all Tallahassee Community College students who are female and the proportion of all American adults who used the Internet to obtain medical information in the previous month. We will revisit confidence intervals in future modules.

Now we look more carefully at how to test a claim with a hypothesis test. Statistical investigations begin with research questions. We begin our discussion of hypothesis tests with research questions that require us to test a claim. Later we look at how a claim becomes a hypothesis.

Research Questions about Testing Claims

Let’s revisit some of the research questions from examples in the module Types of Statistical Studies and Producing Data that involve testing a claim.

Is the average course load for community college students less than 12 semester hours? This question contains a claim about a population mean. The question contains information about the population, the variable, and the parameter. The population is all community college students. The variable is course load in semester hours . It is quantitative, so the parameter is a mean. The claim is, “The mean course load for all community college students is less than 12 semester hours.”

Do the majority of community college students qualify for federal student loans? This question contains a claim about a population proportion and information about the population, the variable, and the parameter. The population is all community college students. The variable is Qualify for federal student loan (yes or no). It is categorical, so the parameter is a proportion. The claim is, “The proportion of community college students who qualify is greater than 0.5” (a majority means more than half, or 0.5).

In community colleges, do female students and male students have different mean GPAs? This question contains a claim that compares two population means. Again, we see information about the populations, the variable, and the parameters. The two populations are female community college students and male community college students. The variable is GPA . It is quantitative, so the parameters are means. The claim is, “The mean GPA for female community college students is different from the mean GPA for male community college students.” Notice that the claim compares the two population means, but there is no claim about the numeric value of either mean.

Are college athletes more likely than nonathletes to receive academic advising? This question contains a claim that compares two population proportions: college athletes and college students who are not athletes. The variable is Receive academic advising (yes or no). The variable is categorical, so the parameters are proportions. The claim is, “The proportion of all college athletes who receive academic advising is greater than the proportion of all nonathletes in college who receive academic advising.” Notice that the claim compares two population proportions, but there is no claim about the numeric value of either proportion.

In the case of testing a claim about a single population parameter, we compare it to a numeric value. In the case of testing a claim about two population parameters, we compare them to each other.

Identify the type of claim in each research question below.

Next Steps: Forming Hypotheses

We already know that in inference we use a sample to draw a conclusion about a population. If the research question contains a claim about the population, we translate the claim into two related hypotheses.

The null hypothesis is a hypothesis about the value of the parameter. The null hypothesis relates to our work in Linking Probability to Statistical Inference where we drew a conclusion about a population parameter on the basis of the sampling distribution. We started with an assumption about the value of the parameter, then used a simulation to simulate the selection of random samples from a population with this parameter value. Or we used the parameter value in a mathematical model to describe the center and spread of the sampling distribution. The null hypothesis gives the value of the parameter that we will use to create the sampling distribution. In this way, the null hypothesis states what we assume to be true about the population.

The alternative hypothesis usually reflects the claim in the research question about the value of the parameter. The alternative hypothesis says the parameter is “greater than” or “less than” or “not equal to” the value we assume to true in the null hypothesis.

Stating Hypotheses

Here are the hypotheses for the research questions from the previous example. The null hypothesis is abbreviated H 0 . The alternative hypothesis is abbreviated H a .

Is the average course load for community college students less than 12 semester hours?

• H 0 : The mean course load for community college students is equal to 12 semester hours.
• H a : The mean course load for community college students is less than 12 semester hours.

Do the majority of community college students qualify for federal student loans?

• H 0 : The proportion of community college students who qualify for federal student loans is 0.5.
• H a : The proportion of community college students who qualify for federal student loans is greater than 0.5.

When the research question contains a claim that compares two populations, the null hypothesis states that the parameters are equal. We will see in Modules 9 and 10 that we translate the null hypothesis into a statement about “no difference” in parameter values. We revisit this idea in more depth later.

In community colleges, do female students and male students have different mean GPAs?

• H 0 : In community colleges, female and male students have the same mean GPAs.
• H a : In community colleges, female and male students have different mean GPAs.

Are college athletes more likely than nonathletes to receive academic advising?

• H 0 : In colleges, the proportion of athletes who receive academic advising is equal to the proportion of nonathletes who receive academic advising.
• H a : In colleges, the proportion of athletes who receive academic advising is greater than the proportion of nonathletes who receive academic advising.

Here are some general observations about null and alternative hypotheses.

• The hypotheses are competing claims about the parameter or about the comparison of parameters.
• Both hypotheses are statements about the same population parameter or same two population parameters.
• The null hypothesis contains an equal sign.
• The alternative hypothesis is always an inequality statement. It contains a “less than” or a “greater than” or a “not equal to” symbol.
• In a statistical investigation, we determine the research question, and thus the hypotheses, before we collect data.

The process of forming hypotheses, collecting data, and using the data to draw a conclusion about the hypotheses is called hypothesis testing .

Contribute!

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Estimation and Hypothesis Testing

• Living reference work entry
• First Online: 14 August 2020
• Cite this living reference work entry

• Pamela A. Shaw 3 &
• Michael A. Proschan 4  

247 Accesses

1 Citations

This chapter presents basic elements of parameter estimation and hypothesis testing. The reader will learn how to form confidence intervals for the mean, and more generally, how to calculate confidence intervals for the one parameter setting and for the difference between two groups. Principles of hypothesis testing are detailed, including the choice of the null and alternative hypotheses, the significance level, and implications for choosing a one-sided versus two-sided test. The p-value is defined and a discussion of controversies that have arisen over its use are included. After reading this chapter, the reader will have a better understanding of the necessary steps to set up a hypothesis test and make valid inference about the quantity of interest. Other topics in this chapter include exact hypothesis tests, which may be preferable for small sample settings, and the choice of a parametric versus nonparametric test. The chapter also includes a brief discussion of the implications of multiple comparisons on hypothesis testing and considerations of hypothesis testing in the setting of noninferiority trials.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Institutional subscriptions

Berry SM, Carlin BP, Lee JJ, Muller P (2010) Bayesian adaptive methods for clinical trials. CRC Press, Boca Raton

Book   Google Scholar  

Cardiac Arrhythmia Suppression Trial (CAST) Investigators (1989) Preliminary report: effect of encainide and flecainide on mortality in a randomized trial of arrhythmia suppression after myocardial infarction. NEJM 321(6):406–412

Article   Google Scholar  

Casella G, Berger RL (2002) Statistical inference. Duxbury, Pacific Grove

MATH   Google Scholar  

Cox DR (1972) Regression models and life-tables. Journal of the Royal Statistical Society: Series B (Methodological) 34(2):187–202

MathSciNet   MATH   Google Scholar  

Fisher RA (1925) Statistical methods for research workers. Oliver and Boyd, Edinburgh

Friedman LM, Bristow JD, Hallstrom A et al (1993) Data monitoring in the cardiac arrhythmia suppression trial. Online J Curr Clin Trials, Doc. No. 79 [5870 words; 53 paragraphs]

Google Scholar  

Hackshaw A, Kirkwood A (2011) Interpreting and reporting clinical trials with results of borderline significance. BMJ 343:d3340

Hochberg Y, Tamhane AC (1987) Multiple comparison procedures. Wiley, Hoboken

Hosmer DW Jr, Lemeshow S, May S (2011) Applied survival analysis: regression modeling of time-to-event data. Wiley, Hoboken

Kyriacou DN (2016) The enduring evolution of the p value. JAMA 315(11):1113–1115

Lin DY, Dai L, Cheng G et al (2016) On confidence intervals for the hazard ratio in randomized clinical trials. Biometrics 72(4):1098–1102

Article   MathSciNet   Google Scholar  

Lurie P, Wolfe SM (1997) Unethical trials of interventions to reduce perinatal transmission of the human immunodeficiency virus in developing countries. NEJM 337(12):853–856

Rosner B (2015) Fundamentals of biostatistics. Brooks/Cole, Boston

Wendl MC (2016) Pseudonymous fame. Science 351(6280):1406–1406

Download references

Author information

Authors and affiliations.

University of Pennsylvania Perelman School of Medicine, Philadelphia, PA, USA

Pamela A. Shaw

National Institute of Allergy and Infectious Diseases, Bethesda, MD, USA

Michael A. Proschan

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Pamela A. Shaw .

Editor information

Editors and affiliations.

Samuel Oschin Comprehensive Cancer Insti, WEST HOLLYWOOD, CA, USA

Steven Piantadosi

Bloomberg School of Public Health, Johns Hopkins Center for Clinical Trials Bloomberg School of Public Health, Baltimore, MD, USA

Curtis L. Meinert

Section Editor information

Department of Biostatistics and Bioinformatics, Basic Science Division, Duke University School of Medicine, Durham, NC, USA

Stephen L. George

The Johns Hopkins Center for Clinical Trials and Evidence Synthesis, Johns Hopkins University, Baltimore, MD, USA

Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this entry

Cite this entry.

Shaw, P.A., Proschan, M.A. (2020). Estimation and Hypothesis Testing. In: Piantadosi, S., Meinert, C.L. (eds) Principles and Practice of Clinical Trials. Springer, Cham. https://doi.org/10.1007/978-3-319-52677-5_114-1

Download citation

DOI : https://doi.org/10.1007/978-3-319-52677-5_114-1

Received : 09 June 2020

Accepted : 06 July 2020

Published : 14 August 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-52677-5

Online ISBN : 978-3-319-52677-5

eBook Packages : Springer Reference Mathematics Reference Module Computer Science and Engineering

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.