writing systems of equations homework 5

Writing Systems of Equations: Explanation, Review, and Examples

• The Albert Team
• Last Updated On: March 30, 2022

Just like the English language can be translated into other languages, we can also translate it into the language of math. Many words we use every day can imply different mathematical operations. For example, “total” might indicate the equal sign, and “increase by” could mean the addition symbol. Being able to translate from English into math allows us to turn words into equations. Keep reading to see how this works for writing systems of equations .

What is a System of Equations?

Before we start writing systems of equations, let’s make sure we know what a system of equations is. A system of equations is simply two or more equations that share the same variables. In Algebra 1, you will mainly focus on systems with two equations and two variables.

The two variables you likely know best are x and y . You may be wondering, why x and y ? The axes of a coordinate plane are the x -axis and y -axis. So, the x and y in the equations represent the x and y coordinates on a graph. When you solve a system of equations with two variables, it is your goal to find the point — (x,y) — where the two graphs intersect. This point of intersection is the solution to the system of equations.

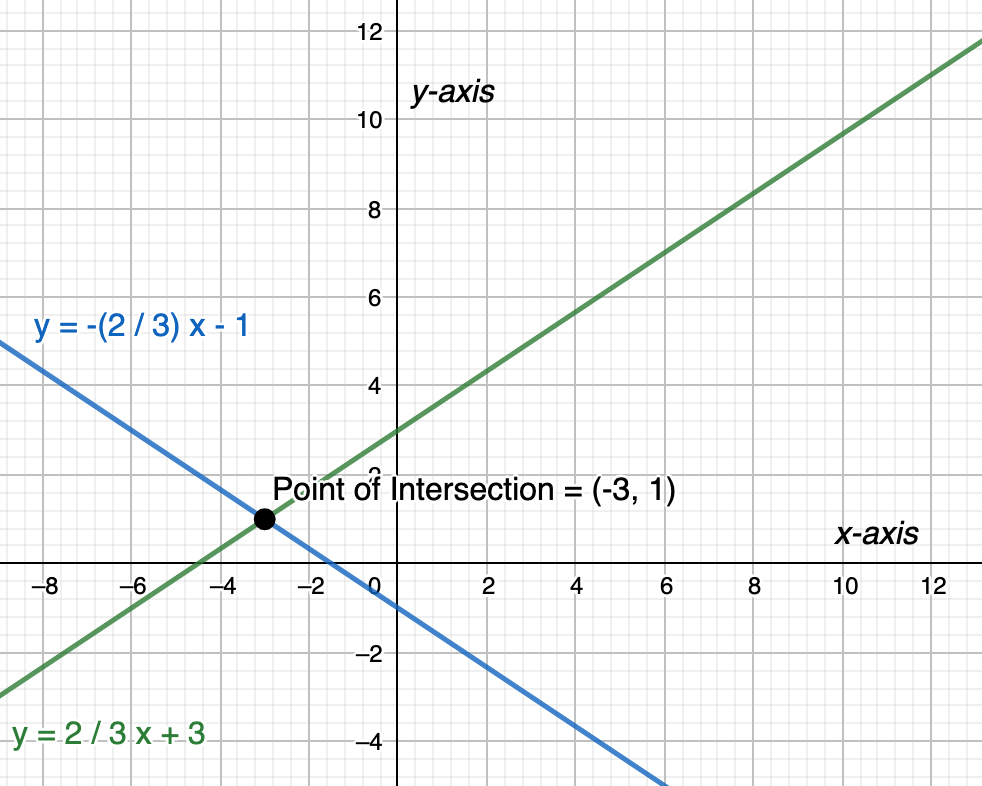
You might also notice that most systems of equations you solve in Algebra 1 are systems of two linear equations. To review linear equations and their many different forms, check out the Albert blog post Forms of Linear Equations .

Looking ahead: What if you have three equations and three variables, making a three-variable system of equations? You will need a third axis, the z -axis.

Examples of Systems of Equations

Did you know that there are multiple ways to represent a system of equations? The four main ways you will see a system of equations represented are by its equations (algebra), a table (numbers), a graph (visual), and a verbal description (words). Let’s take a look at what each form looks like using a system of two linear equations:

Equation (algebra) form:

y=3x+1  

Table (numbers) form:

Graph (visual) form:

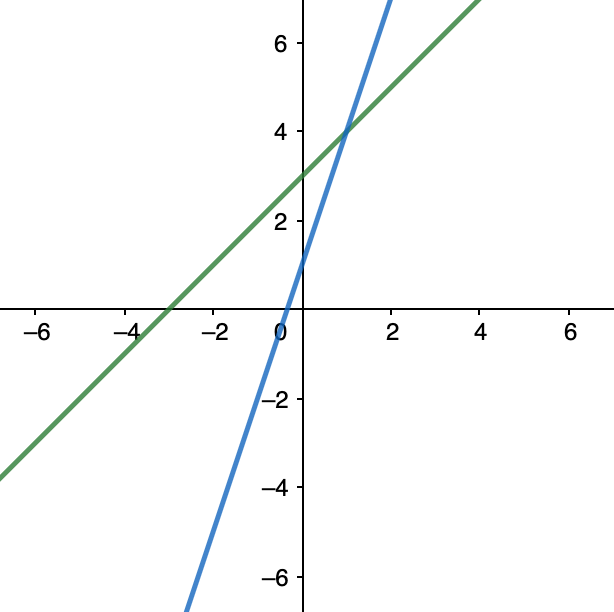
Verbal Description (words) form:

Now that we have explored the different ways to represent a system of linear equations, we will see how to write a system of linear equations. The following sections of this post will investigate how to write the equation form of a system of equations from a table, a graph, and a verbal description or what your teacher probably calls word problems.

How to Write a System of Equations

Writing systems of equations from a table.

Writing a system of linear equations from a table is just like writing a linear equation from a table. However, this time we will be writing two equations . Let’s remember the two things you need to calculate from the table to write a linear equation: 1) the slope and 2) the y -intercept. If you are lucky, the y -intercept will be in the table. If not, then there is a little more work to do, but you can still do it!

Let’s look at the table below to practice writing a system of linear equations from a table:

Notice there is only one x row while there are two y rows because our table is showing a system of TWO equations. We can separate this table into two tables, one for each equation:

Now we need to apply our writing linear equation skills and calculate the slope and the y -intercept from each table. Remember, the slope-intercept form of an equation is y=mx +b , where m represents the slope and b represents the y -intercept.

You can find the slope of the first table by calculating the ratio of the change in y values to the change in x values using two points from the table, such as (-2, 0) and (1, 2) :

Now, we need to use a point in the table to calculate the y -intercept. Let’s use the point ( -2, 0) . Substitute -2 for x , 0 for y , and \frac{2}{3} for m in the equation and solve for b .

Now that we know the slope and y -intercept, we can write our first equation: 

We can use this same process to write the second equation in our system. First, calculate the slope as the ratio of the change in y values to the change in x values between two points, such as (1, -8) and (4, -11) :

And once more, we can calculate the y -intercept by substituting a point — such as (1, -8) – into our equation and solving for b .

So, our second equation is y_2= -x-7 . We can now write our system of equations for the given table:

If you are having trouble writing linear equations using a table or two points, then check out these Albert blogs to help: How to Find Slope and Slope-Intercept Form .

Writing Systems of Equations from a Graph

Writing a system of linear equations from a graph is like writing a system from a table. We need to identify the slope and the y -intercept of each line in the graph to write our system of equations.

Let’s look at the graph given below to practice writing a system of linear equations from a graph:

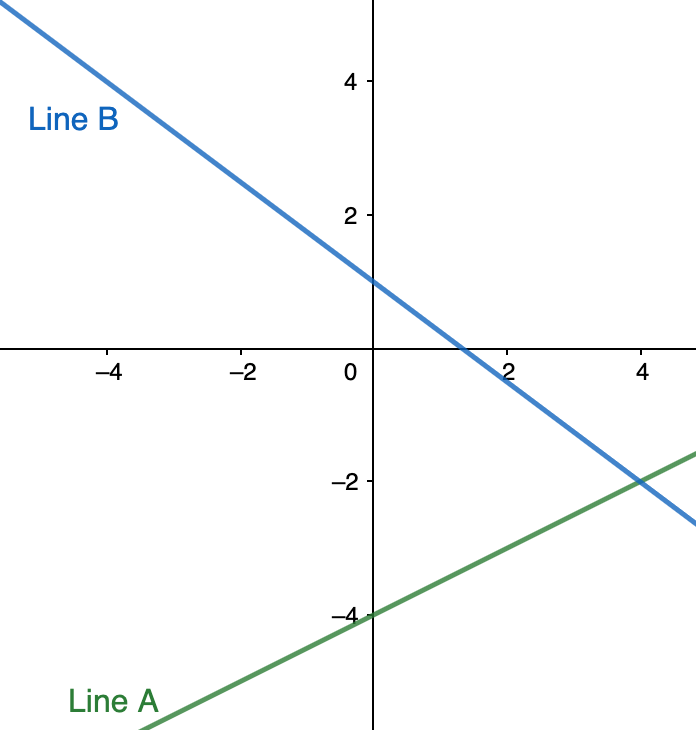
Starting with line A, let’s calculate the slope. We can use the slope formula and the points (0, -4) and (4, -2) to find the slope:

Let’s repeat this process with two points from line B, such as (0, 1) and (4, -2) :

Next, we can identify the y -intercepts of each line from the graph. Remember, the y -intercept is always where the line crosses the y -axis and where the {x} coordinate is {0} :

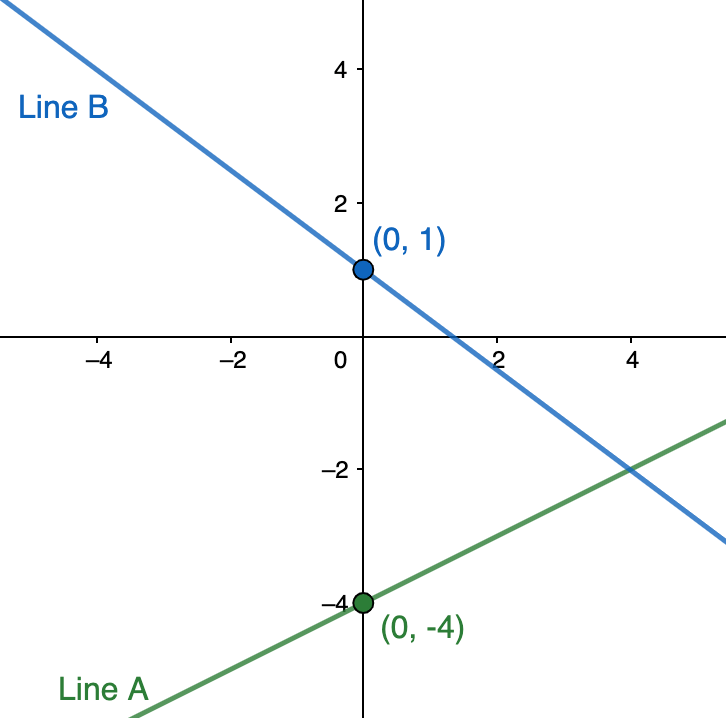
So, the y -intercept of line A is -4 and the y -intercept of line B is 1 . Now we can substitute the slopes and y -intercepts of our two lines into equations in the form y=mx+b to create our system:

If you are having trouble writing linear equations using a graph or two points, then check out these Albert blogs to help: How to Find Slope and Slope-Intercept Form .

Writing Systems of Equations from Word Problems

When writing systems of equations from word problems, it is important to create a list of common translations from words to their equivalent math operations. If you haven’t done this in class yet, here is a table to get you started:

To practice writing systems of equations from word problems, let’s take a look at the following two examples:

Example 1: At the end of a basketball game, your team’s final score was 53 points. You know that the team scored 23 baskets altogether. Some baskets were worth 2 points, and others were worth 3 points. Surprisingly, no one made it to the free-throw line. Write a system of equations to represent this situation.

Step 1: Write down what you know from the problem .

• the team scored 53 points
• a total of 23 baskets were scored

Step 2: Write down all the unknowns of the situation.

• number of 2 -point baskets 
• number of 3 -point baskets

Step 3: Define your variables.

This is a crucial step that can feel overwhelming. However, if you have identified the words in the word problem that tell you what is unknown, you now have your variable definitions. Remember, a variable represents an unknown.

• x : number of 2 -point baskets
• y : number of 3 -point baskets

Step 4: Write mathematical sentences using your variables (unknowns) and the given information. 

Notice that the important information identified represents totals or a final score. These values will go after the equal sign. You need to figure out how your variables (unknowns) relate to the final score and the total number of baskets. Let’s take a look:

• The number of 2 -point baskets and the number of 3 -point baskets is a total of 23 baskets scored.
• 2 times the number of 2 -point baskets and 3 times the number of 3 -point baskets equals a final score of 53 points.

Step 5: Translate your math sentences into equations.

Remember to use the table above and look for words that can translate to a math operation.

• 2x + 3y = 53

Step 6: Write your system of equations for the word problem.

Example 2: Two numbers have a difference of 7 , and when combined, their sum is 33 . Write a system of equations to represent this situation.

• two numbers have a difference of 7
• the same two numbers combine to a sum of 33

Since the two numbers have a difference, one number must be larger, and one number must be smaller.

• the value of the smaller number
• the value of the greater number
• x : smaller number
• y : larger number

Notice there are multiple words in the original problem that can be translated to math operations: the word difference means to subtract (minus) and the words sum and combine mean to add. Let’s take a look:

• Larger number minus the smaller number is a difference of 7 .
• Larger number combined with the smaller number is a sum of 33 .

For more practice writing systems of equations from word problems, check out this video example .

Writing Systems of Equations: Keys to Remember

• A system of equations is when you have two or more equations that share the same variables.
• Four ways to represent a system of equations are by its equations (algebra), a table (numbers), a graph (visual), and a verbal description (words). 
• To write a system of linear equations from a table or graph, you must calculate the slope and the y -intercept.
• To write a system of linear equations from a word problem, you need to translate the words into math sentences to create equations.

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

Interested in a school license?

Bring Albert to your school and empower all teachers with the world's best question bank for: ➜ SAT® & ACT® ➜ AP® ➜ ELA, Math, Science, & Social Studies aligned to state standards ➜ State assessments Options for teachers, schools, and districts.

5.2 Solving Systems of Equations by Substitution

Learning objectives.

By the end of this section, you will be able to:

• Solve a system of equations by substitution
• Solve applications of systems of equations by substitution

Be Prepared 5.4

Before you get started, take this readiness quiz.

Simplify −5 ( 3 − x ) −5 ( 3 − x ) . If you missed this problem, review Example 1.136 .

Be Prepared 5.5

Simplify 4 − 2 ( n + 5 ) 4 − 2 ( n + 5 ) . If you missed this problem, review Example 1.123 .

Be Prepared 5.6

Solve for y y : 8 y − 8 = 32 − 2 y 8 y − 8 = 32 − 2 y If you missed this problem, review Example 2.34 .

Be Prepared 5.7

Solve for x x : 3 x − 9 y = −3 3 x − 9 y = −3 If you missed this problem, review Example 2.65 .

Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.

In this section, we will solve systems of linear equations by the substitution method.

Solve a System of Equations by Substitution

We will use the same system we used first for graphing.

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.

We’ll fill in all these steps now in Example 5.13 .

Example 5.13

How to solve a system of equations by substitution.

Solve the system by substitution. { 2 x + y = 7 x − 2 y = 6 { 2 x + y = 7 x − 2 y = 6

Try It 5.25

Solve the system by substitution. { −2 x + y = −11 x + 3 y = 9 { −2 x + y = −11 x + 3 y = 9

Try It 5.26

Solve the system by substitution. { x + 3 y = 10 4 x + y = 18 { x + 3 y = 10 4 x + y = 18

Solve a system of equations by substitution.

• Step 1. Solve one of the equations for either variable.
• Step 2. Substitute the expression from Step 1 into the other equation.
• Step 3. Solve the resulting equation.
• Step 4. Substitute the solution in Step 3 into one of the original equations to find the other variable.
• Step 5. Write the solution as an ordered pair.
• Step 6. Check that the ordered pair is a solution to both original equations.

If one of the equations in the system is given in slope–intercept form, Step 1 is already done! We’ll see this in Example 5.14 .

Example 5.14

Solve the system by substitution.

{ x + y = −1 y = x + 5 { x + y = −1 y = x + 5

The second equation is already solved for y . We will substitute the expression in place of y in the first equation.

Try It 5.27

Solve the system by substitution. { x + y = 6 y = 3 x − 2 { x + y = 6 y = 3 x − 2

Try It 5.28

Solve the system by substitution. { 2 x − y = 1 y = −3 x − 6 { 2 x − y = 1 y = −3 x − 6

If the equations are given in standard form, we’ll need to start by solving for one of the variables. In this next example, we’ll solve the first equation for y .

Example 5.15

Solve the system by substitution. { 3 x + y = 5 2 x + 4 y = −10 { 3 x + y = 5 2 x + 4 y = −10

We need to solve one equation for one variable. Then we will substitute that expression into the other equation.

Try It 5.29

Solve the system by substitution. { 4 x + y = 2 3 x + 2 y = −1 { 4 x + y = 2 3 x + 2 y = −1

Try It 5.30

Solve the system by substitution. { − x + y = 4 4 x − y = 2 { − x + y = 4 4 x − y = 2

In Example 5.15 it was easiest to solve for y in the first equation because it had a coefficient of 1. In Example 5.16 it will be easier to solve for x .

Example 5.16

Solve the system by substitution. { x − 2 y = −2 3 x + 2 y = 34 { x − 2 y = −2 3 x + 2 y = 34

We will solve the first equation for x x and then substitute the expression into the second equation.

Try It 5.31

Solve the system by substitution. { x − 5 y = 13 4 x − 3 y = 1 { x − 5 y = 13 4 x − 3 y = 1

Try It 5.32

Solve the system by substitution. { x − 6 y = −6 2 x − 4 y = 4 { x − 6 y = −6 2 x − 4 y = 4

When both equations are already solved for the same variable, it is easy to substitute!

Example 5.17

Solve the system by substitution. { y = −2 x + 5 y = 1 2 x { y = −2 x + 5 y = 1 2 x

Since both equations are solved for y , we can substitute one into the other.

Try It 5.33

Solve the system by substitution. { y = 3 x − 16 y = 1 3 x { y = 3 x − 16 y = 1 3 x

Try It 5.34

Solve the system by substitution. { y = − x + 10 y = 1 4 x { y = − x + 10 y = 1 4 x

Be very careful with the signs in the next example.

Example 5.18

Solve the system by substitution. { 4 x + 2 y = 4 6 x − y = 8 { 4 x + 2 y = 4 6 x − y = 8

We need to solve one equation for one variable. We will solve the first equation for y .

Try It 5.35

Solve the system by substitution. { x − 4 y = −4 −3 x + 4 y = 0 { x − 4 y = −4 −3 x + 4 y = 0

Try It 5.36

Solve the system by substitution. { 4 x − y = 0 2 x − 3 y = 5 { 4 x − y = 0 2 x − 3 y = 5

In Example 5.19 , it will take a little more work to solve one equation for x or y .

Example 5.19

Solve the system by substitution. { 4 x − 3 y = 6 15 y − 20 x = −30 { 4 x − 3 y = 6 15 y − 20 x = −30

We need to solve one equation for one variable. We will solve the first equation for x .

Since 0 = 0 is a true statement, the system is consistent. The equations are dependent. The graphs of these two equations would give the same line. The system has infinitely many solutions.

Try It 5.37

Solve the system by substitution. { 2 x − 3 y = 12 −12 y + 8 x = 48 { 2 x − 3 y = 12 −12 y + 8 x = 48

Try It 5.38

Solve the system by substitution. { 5 x + 2 y = 12 −4 y − 10 x = −24 { 5 x + 2 y = 12 −4 y − 10 x = −24

Look back at the equations in Example 5.19 . Is there any way to recognize that they are the same line?

Let’s see what happens in the next example.

Example 5.20

Solve the system by substitution. { 5 x − 2 y = −10 y = 5 2 x { 5 x − 2 y = −10 y = 5 2 x

The second equation is already solved for y , so we can substitute for y in the first equation.

Since 0 = −10 is a false statement the equations are inconsistent. The graphs of the two equation would be parallel lines. The system has no solutions.

Try It 5.39

Solve the system by substitution. { 3 x + 2 y = 9 y = − 3 2 x + 1 { 3 x + 2 y = 9 y = − 3 2 x + 1

Try It 5.40

Solve the system by substitution. { 5 x − 3 y = 2 y = 5 3 x − 4 { 5 x − 3 y = 2 y = 5 3 x − 4

Solve Applications of Systems of Equations by Substitution

We’ll copy here the problem solving strategy we used in the Solving Systems of Equations by Graphing section for solving systems of equations. Now that we know how to solve systems by substitution, that’s what we’ll do in Step 5.

How to use a problem solving strategy for systems of linear equations.

• Step 1. Read the problem. Make sure all the words and ideas are understood.
• Step 2. Identify what we are looking for.
• Step 3. Name what we are looking for. Choose variables to represent those quantities.
• Step 4. Translate into a system of equations.
• Step 5. Solve the system of equations using good algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

Some people find setting up word problems with two variables easier than setting them up with just one variable. Choosing the variable names is easier when all you need to do is write down two letters. Think about this in the next example—how would you have done it with just one variable?

Example 5.21

The sum of two numbers is zero. One number is nine less than the other. Find the numbers.

Try It 5.41

The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.

Try It 5.42

The sum of two number is −6. One number is 10 less than the other. Find the numbers.

In the Example 5.22 , we’ll use the formula for the perimeter of a rectangle, P = 2 L + 2 W .

Example 5.22

The perimeter of a rectangle is 88. The length is five more than twice the width. Find the length and the width.

Try It 5.43

The perimeter of a rectangle is 40. The length is 4 more than the width. Find the length and width of the rectangle.

Try It 5.44

The perimeter of a rectangle is 58. The length is 5 more than three times the width. Find the length and width of the rectangle.

For Example 5.23 we need to remember that the sum of the measures of the angles of a triangle is 180 degrees and that a right triangle has one 90 degree angle.

Example 5.23

The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.

We will draw and label a figure.

Try It 5.45

The measure of one of the small angles of a right triangle is 2 more than 3 times the measure of the other small angle. Find the measure of both angles.

Try It 5.46

The measure of one of the small angles of a right triangle is 18 less than twice the measure of the other small angle. Find the measure of both angles.

Example 5.24

Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 plus $15 for each training session. Option B would pay her $10,000 + $40 for each training session. How many training sessions would make the salary options equal?

Try It 5.47

Geraldine has been offered positions by two insurance companies. The first company pays a salary of $12,000 plus a commission of $100 for each policy sold. The second pays a salary of $20,000 plus a commission of $50 for each policy sold. How many policies would need to be sold to make the total pay the same?

Try It 5.48

Kenneth currently sells suits for company A at a salary of $22,000 plus a $10 commission for each suit sold. Company B offers him a position with a salary of $28,000 plus a $4 commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?

Access these online resources for additional instruction and practice with solving systems of equations by substitution.

• Instructional Video-Solve Linear Systems by Substitution
• Instructional Video-Solve by Substitution

Section 5.2 Exercises

Practice makes perfect.

In the following exercises, solve the systems of equations by substitution.

{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6

{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7

{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4

{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4

{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3

{ −2 x + 2 y = 6 y = −3 x + 1 { −2 x + 2 y = 6 y = −3 x + 1

{ 2 x + 3 y = 3 y = − x + 3 { 2 x + 3 y = 3 y = − x + 3

{ 2 x + 5 y = −14 y = −2 x + 2 { 2 x + 5 y = −14 y = −2 x + 2

{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2

{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2

{ 3 x − 2 y = 6 y = 2 3 x + 2 { 3 x − 2 y = 6 y = 2 3 x + 2

{ −3 x − 5 y = 3 y = 1 2 x − 5 { −3 x − 5 y = 3 y = 1 2 x − 5

{ 2 x + y = 10 − x + y = −5 { 2 x + y = 10 − x + y = −5

{ −2 x + y = 10 − x + 2 y = 16 { −2 x + y = 10 − x + 2 y = 16

{ 3 x + y = 1 −4 x + y = 15 { 3 x + y = 1 −4 x + y = 15

{ x + y = 0 2 x + 3 y = −4 { x + y = 0 2 x + 3 y = −4

{ x + 3 y = 1 3 x + 5 y = −5 { x + 3 y = 1 3 x + 5 y = −5

{ x + 2 y = −1 2 x + 3 y = 1 { x + 2 y = −1 2 x + 3 y = 1

{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15

{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20

{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4

{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4

{ y = 2 x − 8 y = 3 5 x + 6 { y = 2 x − 8 y = 3 5 x + 6

{ y = − x − 1 y = x + 7 { y = − x − 1 y = x + 7

{ 4 x + 2 y = 8 8 x − y = 1 { 4 x + 2 y = 8 8 x − y = 1

{ − x − 12 y = −1 2 x − 8 y = −6 { − x − 12 y = −1 2 x − 8 y = −6

{ 15 x + 2 y = 6 −5 x + 2 y = −4 { 15 x + 2 y = 6 −5 x + 2 y = −4

{ 2 x − 15 y = 7 12 x + 2 y = −4 { 2 x − 15 y = 7 12 x + 2 y = −4

{ y = 3 x 6 x − 2 y = 0 { y = 3 x 6 x − 2 y = 0

{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0

{ 2 x + 16 y = 8 − x − 8 y = −4 { 2 x + 16 y = 8 − x − 8 y = −4

{ 15 x + 4 y = 6 −30 x − 8 y = −12 { 15 x + 4 y = 6 −30 x − 8 y = −12

{ y = −4 x 4 x + y = 1 { y = −4 x 4 x + y = 1

{ y = − 1 4 x x + 4 y = 8 { y = − 1 4 x x + 4 y = 8

{ y = 7 8 x + 4 −7 x + 8 y = 6 { y = 7 8 x + 4 −7 x + 8 y = 6

{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11

In the following exercises, translate to a system of equations and solve.

The sum of two numbers is 15. One number is 3 less than the other. Find the numbers.

The sum of two numbers is 30. One number is 4 less than the other. Find the numbers.

The sum of two numbers is −26. One number is 12 less than the other. Find the numbers.

The perimeter of a rectangle is 50. The length is 5 more than the width. Find the length and width.

The perimeter of a rectangle is 60. The length is 10 more than the width. Find the length and width.

The perimeter of a rectangle is 58. The length is 5 more than three times the width. Find the length and width.

The perimeter of a rectangle is 84. The length is 10 more than three times the width. Find the length and width.

The measure of one of the small angles of a right triangle is 14 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 26 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles.

Maxim has been offered positions by two car dealers. The first company pays a salary of $10,000 plus a commission of $1,000 for each car sold. The second pays a salary of $20,000 plus a commission of $500 for each car sold. How many cars would need to be sold to make the total pay the same?

Jackie has been offered positions by two cable companies. The first company pays a salary of $ 14,000 plus a commission of $100 for each cable package sold. The second pays a salary of $20,000 plus a commission of $25 for each cable package sold. How many cable packages would need to be sold to make the total pay the same?

Amara currently sells televisions for company A at a salary of $17,000 plus a $100 commission for each television she sells. Company B offers her a position with a salary of $29,000 plus a $20 commission for each television she sells. How many televisions would Amara need to sell for the options to be equal?

Mitchell currently sells stoves for company A at a salary of $12,000 plus a $150 commission for each stove he sells. Company B offers him a position with a salary of $24,000 plus a $50 commission for each stove he sells. How many stoves would Mitchell need to sell for the options to be equal?

Everyday Math

When Gloria spent 15 minutes on the elliptical trainer and then did circuit training for 30 minutes, her fitness app says she burned 435 calories. When she spent 30 minutes on the elliptical trainer and 40 minutes circuit training she burned 690 calories. Solve the system { 15 e + 30 c = 435 30 e + 40 c = 690 { 15 e + 30 c = 435 30 e + 40 c = 690 for e e , the number of calories she burns for each minute on the elliptical trainer, and c c , the number of calories she burns for each minute of circuit training.

Stephanie left Riverside, California, driving her motorhome north on Interstate 15 towards Salt Lake City at a speed of 56 miles per hour. Half an hour later, Tina left Riverside in her car on the same route as Stephanie, driving 70 miles per hour. Solve the system { 56 s = 70 t s = t + 1 2 { 56 s = 70 t s = t + 1 2 .

• ⓐ for t t to find out how long it will take Tina to catch up to Stephanie.
• ⓑ what is the value of s s , the number of hours Stephanie will have driven before Tina catches up to her?

Writing Exercises

Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6

ⓐ by graphing. ⓑ by substitution. ⓒ Which method do you prefer? Why?

Solve the system of equations { 3 x + y = 12 x = y − 8 { 3 x + y = 12 x = y − 8 by substitution and explain all your steps in words.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra-2e/pages/5-2-solving-systems-of-equations-by-substitution

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Illustrative Mathematics Grade 8, Unit 4, Lesson 15: Writing Systems of Equations

Learning Targets:

• I can write a system of equations from a real-world situation.

Related Pages Illustrative Math Grade 8

Lesson 15: Writing Systems of Equations

Let’s write systems of equations from real-world situations.

Illustrative Math Unit 8.4, Lesson 15 (printable worksheets)

Lesson 15 Summary

Lesson 15.1 How Many Solutions? Matching

Match each system of equations with the number of solutions the system has.

Lesson 15.2 Situations and Systems

For each situation:

• Create a system of equations.
• Then, without solving, interpret what the solution to the system would tell you about the situation.
• Lin’s family is out for a bike ride when her dad stops to take a picture of the scenery. He tells the rest of the family to keep going and that he’ll catch up. Lin’s dad spends 5 minutes taking the photo and then rides at 0.24 miles per minute until he meets up with the rest of the family further along the bike path. Lin and the rest were riding at 0.18 miles per minute.
• Noah is planning a kayaking trip. Kayak Rental A charges a base fee of $15 plus $4.50 per hour. Kayak Rental B charges a base fee of $12.50 plus $5 per hour.
• Diego is making a large batch of pastries. The recipe calls for 3 strawberries for every apple. Diego used 52 fruits all together.
• Flour costs $0.80 per pound and sugar costs $0.50 per pound. An order of flour and sugar weighs 15 pounds and costs $9.00.

Lesson 15.3 Solving Systems Practice

Here is a lot of systems of equations:

• Without solving, identify 3 systems that you think would be the least difficult for you to solve and 3 systems you think would be the most difficult. Be prepared to explain your reasoning.
• Choose 4 systems to solve. At least one should be from your “least difficult” list and one should be from your “most difficult” list.

Lesson 15 Practice Problems

• Kiran and his cousin work during the summer for a landscaping company. Kiran’s cousin has been working for the company longer, so his pay is 30% more than Kiran’s. Last week his cousin worked 27 hours, and Kiran worked 23 hours. Together, they earned $493.85. What is Kiran’s hourly pay? Explain or show your reasoning.
• Decide which story can be represented by the system of equations y = x + 6 and x + y = 100. Explain your reasoning. a. Diego’s teacher writes a test worth 100 points. There are 6 more multiple choice questions than short answer questions. b. Lin and her younger cousin measure their heights. They notice that Lin is 6 inches taller, and their heights add up to exactly 100 inches.
• Clare and Noah play a game in which they earn the same number of points for each goal and lose the same number of points for each penalty. Clare makes 6 goals and 3 penalties, ending the game with 6 points. Noah earns 8 goals and 9 penalties and ends the game with -22 points. a. Write a system of equations that describes Clare and Noah’s outcomes. Use to represent the number of points for a goal and to represent the number of points for a penalty. b. Solve the system. What does your solution mean?
• a. Estimate the coordinates of the point where the two lines meet. b. Choose two equations that make up the system represented by the graph. c. Solve the system of equations and confirm the accuracy of your estimate.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics .

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: Solve Systems of Equations by Graphing

• Last updated
• Save as PDF
• Page ID 30519

Learning Objectives

By the end of this section, you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Determine the number of solutions of linear system
• Solve applications of systems of equations by graphing

Before you get started, take this readiness quiz.

• For the equation \(y=\frac{2}{3}x−4\) ⓐ is (6,0) a solution? ⓑ is (−3,−2) a solution? If you missed this problem, review Example 2.1.1 .
• Find the slope and y-intercept of the line 3x−y=12. If you missed this problem, review Example 4.5.7 .
• Find the x- and y-intercepts of the line 2x−3y=12. If you missed this problem, review Example 4.3.7 .

Determine Whether an Ordered Pair is a Solution of a System of Equations

In the section on Solving Linear Equations and Inequalities we learned how to solve linear equations with one variable. Remember that the solution of an equation is a value of the variable that makes a true statement when substituted into the equation. Now we will work with systems of linear equations , two or more linear equations grouped together.

Definition: SYSTEM OF LINEAR EQUATIONS

When two or more linear equations are grouped together, they form a system of linear equations.

We will focus our work here on systems of two linear equations in two unknowns. Later, you may solve larger systems of equations.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

\[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]

A linear equation in two variables, like 2 x + y = 7, has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) that make both equations true. These are called the solutions to a system of equations .

Definition: SolutionS OF A SYSTEM OF EQUATIONS

Solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ).

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Let’s consider the system below:

\[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]

Is the ordered pair (2,−1) a solution?

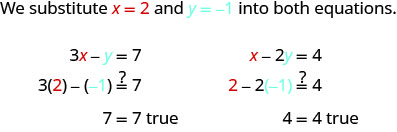
The ordered pair (2, −1) made both equations true. Therefore (2, −1) is a solution to this system.

Let’s try another ordered pair. Is the ordered pair (3, 2) a solution?

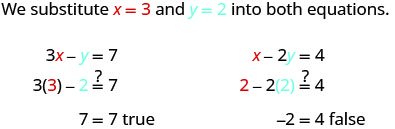
The ordered pair (3, 2) made one equation true, but it made the other equation false. Since it is not a solution to both equations, it is not a solution to this system.

Example \(\PageIndex{1}\)

Determine whether the ordered pair is a solution to the system: \(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)

• (−2,−1)
• (−4,−3)

\(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)

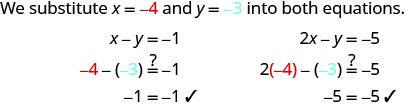
Try It \(\PageIndex{2}\)

Determine whether the ordered pair is a solution to the system: \(\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}\)

• (1,−3)

Try It \(\PageIndex{3}\)

Determine whether the ordered pair is a solution to the system: \(\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}\)

• (2,−2)
• (−2,2)

Solve a System of Linear Equations by Graphing

In this chapter we will use three methods to solve a system of linear equations. The first method we’ll use is graphing. The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

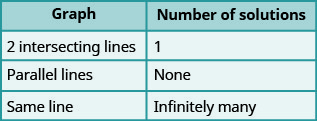
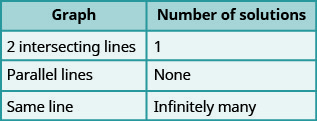
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions , have no solutions and for other equations, called identities , all numbers are solutions. Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown in Figure \(\PageIndex{1}\):

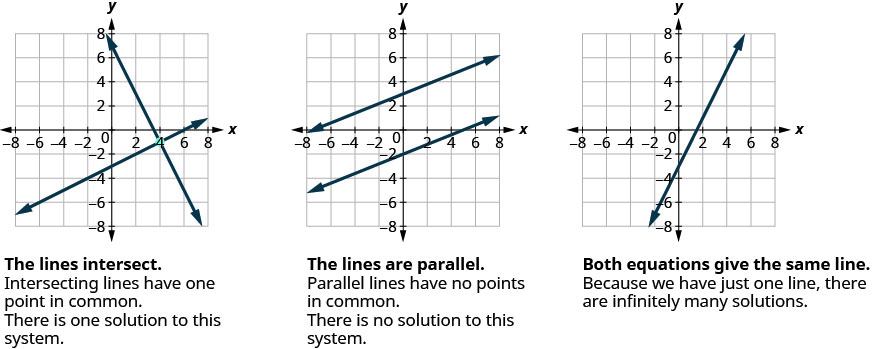
For the first example of solving a system of linear equations in this section and in the next two sections, we will solve the same system of two linear equations. But we’ll use a different method in each section. After seeing the third method, you’ll decide which method was the most convenient way to solve this system.

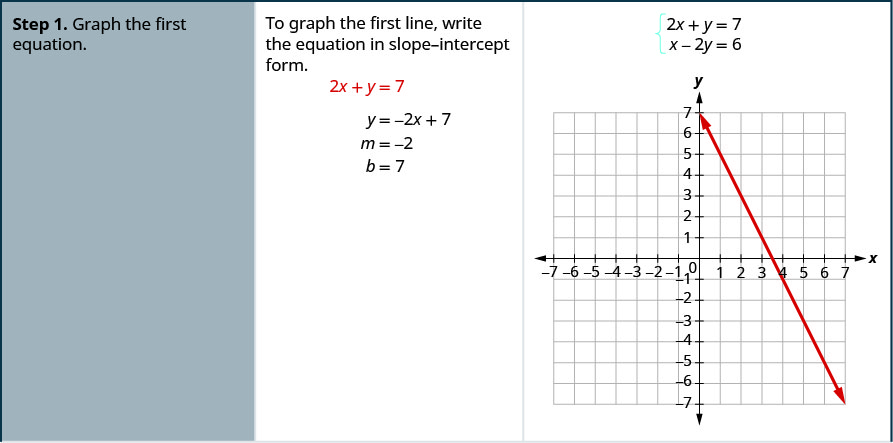
Example \(\PageIndex{4}\): How to Solve a System of Linear Equations by Graphing

Solve the system by graphing: \(\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}\)

Try It \(\PageIndex{5}\)

Solve each system by graphing: \(\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}\)

Try It \(\PageIndex{6}\)

Solve each system by graphing: \(\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}\)

The steps to use to solve a system of linear equations by graphing are shown below.

TO SOLVE A SYSTEM OF LINEAR EQUATIONS BY GRAPHING.

• Graph the first equation.
• Graph the second equation on the same rectangular coordinate system.
• Determine whether the lines intersect, are parallel, or are the same line.
• If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.
• If the lines are parallel, the system has no solution.
• If the lines are the same, the system has an infinite number of solutions.

Example \(\PageIndex{7}\)

Solve the system by graphing: \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)

Both of the equations in this system are in slope-intercept form, so we will use their slopes and y -intercepts to graph them. \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)

Try It \(\PageIndex{8}\)

Solve the system by graphing: \(\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}\)

(−2,−2)

Try It \(\PageIndex{9}\)

Solve the system by graphing: \(\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}\)

Both equations in Example \(\PageIndex{7}\) were given in slope–intercept form. This made it easy for us to quickly graph the lines. In the next example, we’ll first re-write the equations into slope–intercept form.

Example \(\PageIndex{10}\)

Solve the system by graphing: \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)

We’ll solve both of these equations for \(y\) so that we can easily graph them using their slopes and y -intercepts. \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)

Try It \(\PageIndex{11}\)

Solve each system by graphing: \(\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}\)

Try It \(\PageIndex{12}\)

Solve each system by graphing: \(\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}\)

(5,−4)

Usually when equations are given in standard form, the most convenient way to graph them is by using the intercepts. We’ll do this in Example \(\PageIndex{13}\).

Example \(\PageIndex{13}\)

Solve the system by graphing: \(\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}\)

We will find the x - and y -intercepts of both equations and use them to graph the lines.

Try It \(\PageIndex{14}\)

Solve each system by graphing: \(\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}\)

Try It \(\PageIndex{15}\)

Solve each system by graphing: \(\begin{cases}{x+y=2} \\ {x−y=8}\end{cases}\)

(5,−3)

Do you remember how to graph a linear equation with just one variable? It will be either a vertical or a horizontal line.

Example \(\PageIndex{16}\)

Solve the system by graphing: \(\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}\)

Try It \(\PageIndex{17}\)

Solve each system by graphing: \(\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}\)

(9,−1)

Try It \(\PageIndex{18}\)

Solve each system by graphing: \(\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}\)

(4,−6)

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example \(\PageIndex{19}\)

Solve the system by graphing: \(\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\)

Try It \(\PageIndex{20}\)

Solve each system by graphing: \(\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}\)

no solution

Try It \(\PageIndex{21}\)

Solve each system by graphing: \(\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}\)

Example \(\PageIndex{22}\)

Solve the system by graphing: \(\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}\)

Try It \(\PageIndex{23}\)

Solve each system by graphing: \(\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}\)

infinitely many solutions

Try It \(\PageIndex{24}\)

Solve each system by graphing: \(\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}\)

If you write the second equation in Example \(\PageIndex{22}\) in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident. Coincident lines have the same slope and same y -intercept.

COINCIDENT LINES

Coincident lines have the same slope and same y -intercept.

Determine the Number of Solutions of a Linear System

There will be times when we will want to know how many solutions there will be to a system of linear equations, but we might not actually have to find the solution. It will be helpful to determine this without graphing.

We have seen that two lines in the same plane must either intersect or are parallel. The systems of equations in Example \(\PageIndex{4}\) through Example \(\PageIndex{18}\) all had two intersecting lines. Each system had one solution.

A system with parallel lines, like Example \(\PageIndex{19}\), has no solution. What happened in Example \(\PageIndex{22}\)? The equations have coincident lines , and so the system had infinitely many solutions.

We’ll organize these results in Figure \(\PageIndex{2}\) below:

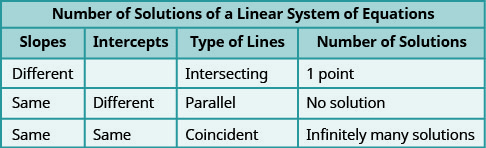
Parallel lines have the same slope but different y -intercepts. So, if we write both equations in a system of linear equations in slope–intercept form, we can see how many solutions there will be without graphing! Look at the system we solved in Example \(\PageIndex{19}\).

\(\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}\)

The two lines have the same slope but different y -intercepts. They are parallel lines.

Figure \(\PageIndex{3}\) shows how to determine the number of solutions of a linear system by looking at the slopes and intercepts.

Let’s take one more look at our equations in Example \(\PageIndex{19}\) that gave us parallel lines.

\[\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\]

When both lines were in slope-intercept form we had:

\[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]

Do you recognize that it is impossible to have a single ordered pair (x,y) that is a solution to both of those equations?

We call a system of equations like this an inconsistent system . It has no solution.

A system of equations that has at least one solution is called a consistent system .

CONSISTENT AND INCONSISTENT SYSTEMS

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

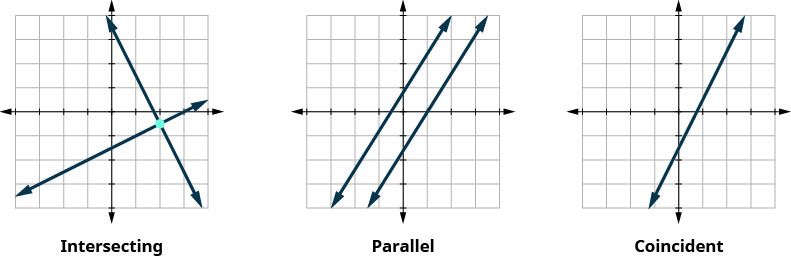
We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent equations , they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations , we get coincident lines.

INDEPENDENT AND DEPENDENT EQUATIONS

Two equations are independent if they have different solutions.

Two equations are dependent if all the solutions of one equation are also solutions of the other equation.

Let’s sum this up by looking at the graphs of the three types of systems. See Figure \(\PageIndex{4}\) and Figure \(\PageIndex{5}\).

Example \(\PageIndex{25}\)

Without graphing, determine the number of solutions and then classify the system of equations: \(\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}\)

\(\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \text{slope–intercept form.} \\  && 6x-2y =&12 \\  && -2y =& -6x - 12 \\  &&\frac{-2y}{-2}=& \frac{-6x + 12}{-2}\\  &&y=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same and y-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

Try It \(\PageIndex{26}\)

Without graphing, determine the number of solutions and then classify the system of equations.

\(\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}\)

no solution, inconsistent, independent

Try It \(\PageIndex{27}\)

\(\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}\)

Example \(\PageIndex{28}\)

Without graphing, determine the number of solutions and then classify the system of equations: \(\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}\)

\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are  different, the lines intersect.}\end{array}\)

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

Try It \(\PageIndex{29}\)

\(\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}\)

one solution, consistent, independent

Try It \(\PageIndex{30}\)

\(\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}\)

Example \(\PageIndex{31}\)

Without graphing, determine the number of solutions and then classify the system of equations. \(\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}\)

\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and same y-intercept and so the lines are coincident.}\end{array}\)

A system of equations whose graphs are coincident lines has infinitely many solutions and is consistent and dependent.

Try It \(\PageIndex{32}\)

\(\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}\)

infinitely many solutions, consistent, dependent

Try It \(\PageIndex{33}\)

\(\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}\)

Solve Applications of Systems of Equations by Graphing

We will use the same problem solving strategy we used in Math Models to set up and solve applications of systems of linear equations. We’ll modify the strategy slightly here to make it appropriate for systems of equations.

USE A PROBLEM SOLVING STRATEGY FOR SYSTEMS OF LINEAR EQUATIONS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose variables to represent those quantities.
• Translate into a system of equations.
• Solve the system of equations using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Step 5 is where we will use the method introduced in this section. We will graph the equations and find the solution.

Example \(\PageIndex{34}\)

Sondra is making 10 quarts of punch from fruit juice and club soda. The number of quarts of fruit juice is 4 times the number of quarts of club soda. How many quarts of fruit juice and how many quarts of club soda does Sondra need?

Step 1. Read the problem.

Step 2. Identify what we are looking for.

We are looking for the number of quarts of fruit juice and the number of quarts of club soda that Sondra will need.

Step 3. Name what we are looking for. Choose variables to represent those quantities.

  Let f= number of quarts of fruit juice.     c= number of quarts of club soda

Step 4. Translate into a system of equations.

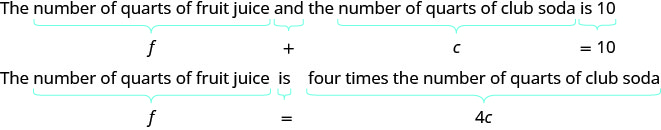
We now have the system. \(\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}\)

Step 5. Solve the system of equations using good algebra techniques.

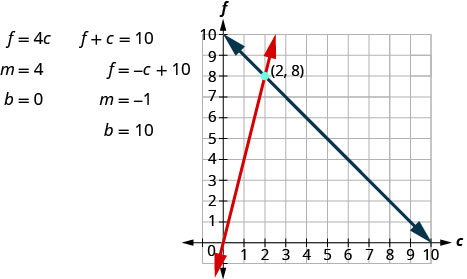
The point of intersection (2, 8) is the solution. This means Sondra needs 2 quarts of club soda and 8 quarts of fruit juice.

Step 6. Check the answer in the problem and make sure it makes sense.

Does this make sense in the problem?

Yes, the number of quarts of fruit juice, 8 is 4 times the number of quarts of club soda, 2.

Yes, 10 quarts of punch is 8 quarts of fruit juice plus 2 quarts of club soda.

Step 7. Answer the question with a complete sentence.

Sondra needs 8 quarts of fruit juice and 2 quarts of soda.

Try It \(\PageIndex{35}\)

Manny is making 12 quarts of orange juice from concentrate and water. The number of quarts of water is 3 times the number of quarts of concentrate. How many quarts of concentrate and how many quarts of water does Manny need?

Manny needs 3 quarts juice concentrate and 9 quarts water.

Try It \(\PageIndex{36}\)

Alisha is making an 18 ounce coffee beverage that is made from brewed coffee and milk. The number of ounces of brewed coffee is 5 times greater than the number of ounces of milk. How many ounces of coffee and how many ounces of milk does Alisha need?

Alisha needs 15 ounces of coffee and 3 ounces of milk.

Access these online resources for additional instruction and practice with solving systems of equations by graphing.

• Instructional Video Solving Linear Systems by Graphing
• Instructional Video Solve by Graphing

Key Concepts

• Identify the solution to the system. If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system. If the lines are parallel, the system has no solution. If the lines are the same, the system has an infinite number of solutions.
• Check the solution in both equations.

• Skip to main content
• Skip to primary sidebar

CLICK HERE TO LEARN ABOUT MTM ALL ACCESS MEMBERSHIP FOR GRADES 6-ALGEBRA 1

Maneuvering the Middle

Student-Centered Math Lessons

3 Steps to Mastering Systems of Equations

Is there anything more satisfying than solving a system of equations problem? That might be the nerdiest sentence ever published on this blog, but it is true! I loved learning systems of equations as a student, and I loved teaching it as a teacher. Let’s jump into the 3 methods for mastering systems of equations.

This post is full, so be on the lookout for part 2 where we will discuss various systems activities for your classroom.

Vertical Alignment

Solving systems of equations starts in 8th grade and carries on being explicitly taught in Algebra 2. If you are an 8th grade teacher, you aren’t exactly starting from scratch.

Students will need to be proficient at:

• Solving for a single variable ( in this case y ) and graphing lines in slope-intercept form (for solving by graphing)
• Rational number operations (for elimination and substitution)
• Combining like terms and distributing (for substitution)

If your students aren’t up to speed with these skills, don’t fret! There is plenty of time to refresh and practice as you introduce systems of equations. I mention this to remind you that students will not be able to solve systems of equations problems without this foundation, so give your students time + practice!

System of Equations Overview

We can often jump in with the methods to solve so quickly that we don’t properly explain what we are solving for apart from saying x and y.

Remind students daily (or even before every problem) that solving systems means we are looking for a solution that makes both equations true! Then reinforce that this is where the lines will intersect on a graph.

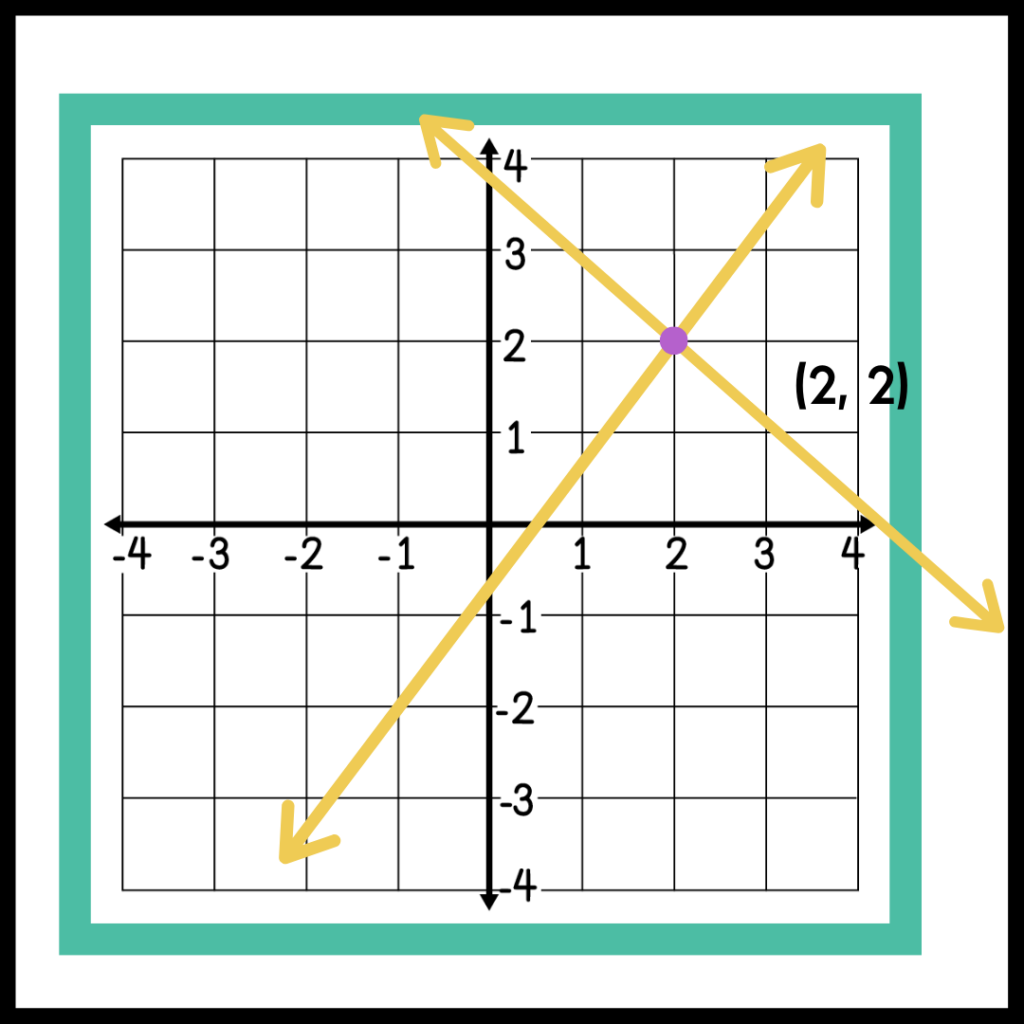
Let’s dive into each method for solving systems of equations. 

The method that I recommend starting with is solving systems of equations by graphing. Due to its visual nature, I find that it makes the abstract nature of solving 2 equations more concrete.

As you introduce this skill, start with the basics of a single line . Remind and reinforce that any point that exists on that single line is a solution to that equation! You can ask students to choose a point on the line, plug in the x and y values, and show them that the equation is a true statement! You can also do the opposite – have students choose and plug in a point that is not on the line to prove that it is not a solution to the equation.

Then you can move to the conclusion that the intersection of two lines is a solution to the system of equations! When students find the point of intersection, plug that point into both equations to find that it is a solution for both equations! (Wow! I am getting pretty excited writing about this!)

Other tips:

• If there was ever time to have your 8th grade or Algebra 1 students move their bodies around, it is this! Arms crossing for one solution, arms parallel for no solution, and arms overlapping for infinitely many solutions. 
• Students often get stuck with how to graph vertical and horizontal lines, such as y = 3 or x = 2. It is helpful to say it as a sentence, “The y-values will always be equal to 5.” Students can plot 2-3 points with a y-value of 3 and visually see that it will be a horizontal line that also intersects the y-axis at 3.

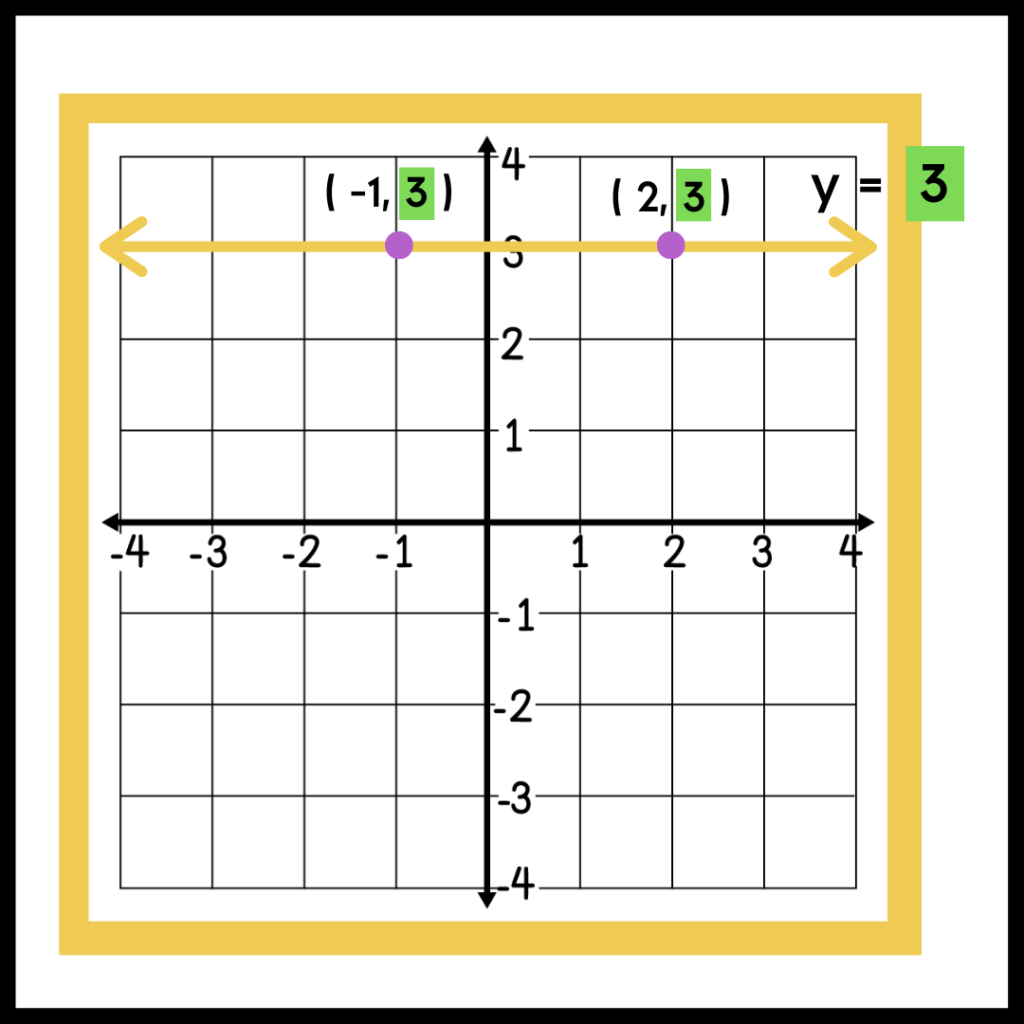
• Students will have to be proficient at solving for y! In fact, I wrote an entire blog post for this specific skill here .

Substitution

It is my recommendation that substitution is going to require a minimum of 2 days. For it to be done well, I recommend building a strong conceptual foundation of what substitution is before trying to actually solve anything by substituting.

I love these two ideas that I found while researching this topic. This first idea I can attribute to a teacher’s explanation in a Facebook Thread (I am going to summarize with bullet points to make it easier to follow):

• Write a whole number on the board.
• Ask students to write down as many different equivalent expressions of that number
• If the number is 6, then: 3(2), 4+2, 7-1 and so on. 
• Make the point that expressions can look different but still be equivalent.
• Next, add variables. x=6, then: x=3+3 and x=3(2).
• Now have students substitute their expressions for x: 3+3 = 3(2).

This blog post breaks down in painstaking detail how a visual aid (stars) makes substitution more concrete. While I used a similar technique with colored Post-it Notes , I think you will benefit from reading this teacher’s methodology. 

Other Tips:

• One solution, no solution, infinitely many solutions will still pop up in substitution, so be sure to review. If variables cancel out and the remaining statement is true, the system has infinitely many solutions. Example: 2=2. If variables cancel out and the remaining statement is false, the system has no solution. Example: 2=/=3.
• Distributing and managing negative signs is going to be a common error. Demonstrate and remind students that they can check their work by just plugging solutions in! This goes for elimination too!
• If you need a fun, no-prep, and free activity for substitution, I recommend playing this “Who Wants to Be a Millionaire” style game as a class.

Elimination

This is my personal favorite – maybe it is because I like when standard form actually comes in handy!  I am hesitant to admit that I did not know why the elimination method worked until I wrote this post, so I want to share what I learned.

The Additional Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. 

For any expressions, a, b, c, and d,

Then a+c = b+d

Whenever I present that type of information to my students, I prefer to give a few examples with numbers.

So let’s says a = 2, b = 2, c = 1, and d = 1

Then 2+1 = 2+1

If you didn’t follow that, perhaps this color coded image will make more sense?

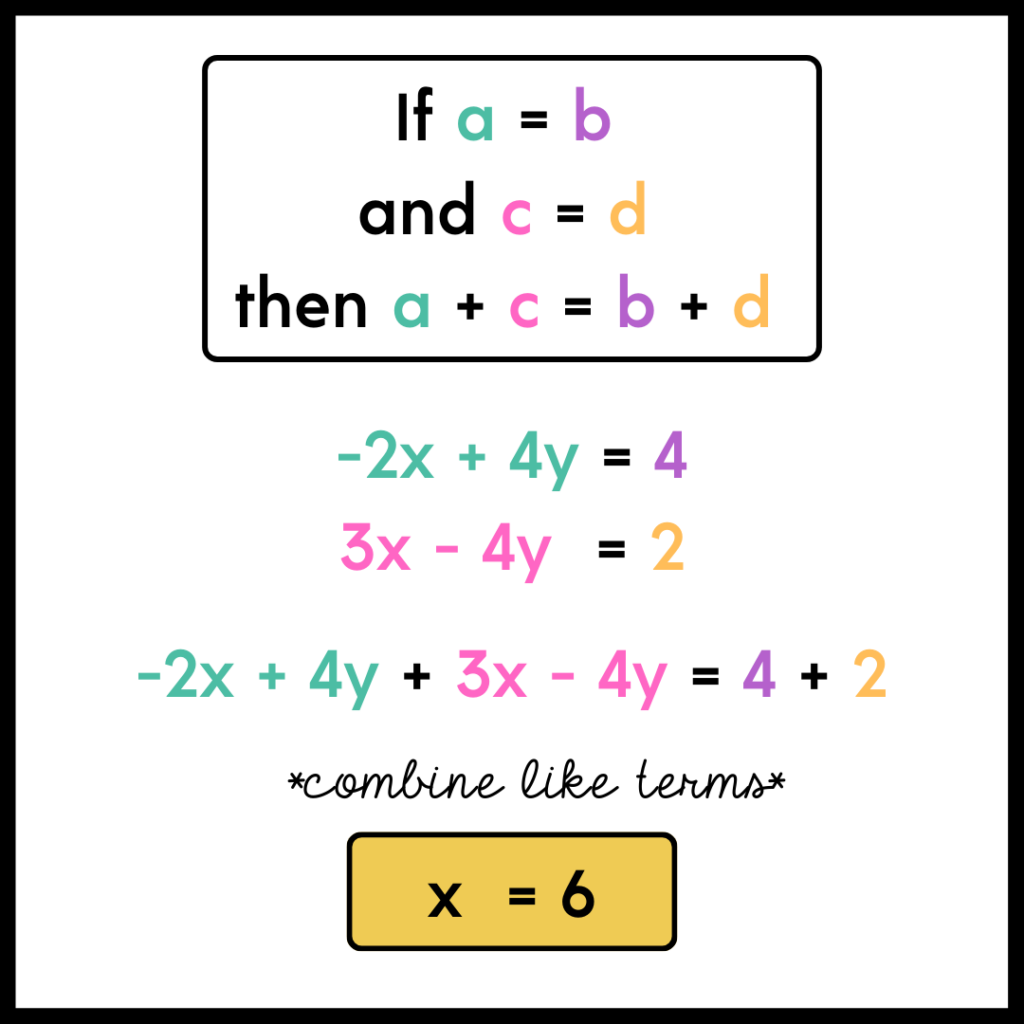
• Students seem to prefer elimination to substitution! I would give students the opportunity to practice changing y = mx+b into standard form. 
• Provide lots of practice multiplying to clear the fractions.
• Don’t forget to go back and solve for the other variable. This is why you should save elimination for after substitution. 

 What tips would you add to solving the system of equations?

Pi Day Classroom Activities

Check out these related products from my shop.