homework 4 zeros of functions answer key

Algebra Function Worksheets with Answer Keys

Feel free to download and enjoy these free worksheets on functions and relations .Each one has model problems worked out step by step, practice problems, as well as challenge questions at the sheets end. Plus each one comes with an answer key.

• Domain and Range (Algebra 1)
• Functions vs Relations (distinguish function from relation, state domain etc..) (Algebra 2)
• Evaluating Functions (Algebra 2)
• 1 to 1 Functions (Algebra 2)
• Composition of Functions (Algebra 2)
• Inverse Functions Worksheet (Algebra 2)
• Operations With Functions (Algebra 2)
• Functions Review Worksheet (Algebra 2)

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

4.1 Linear Functions

m = 4 − 3 0 − 2 = 1 − 2 = − 1 2 ; m = 4 − 3 0 − 2 = 1 − 2 = − 1 2 ; decreasing because m < 0. m < 0.

y = − 7 x + 3 y = − 7 x + 3

H ( x ) = 0.5 x + 12.5 H ( x ) = 0.5 x + 12.5

Possible answers include ( − 3 , 7 ) , ( − 3 , 7 ) , ( − 6 , 9 ) , ( − 6 , 9 ) , or ( − 9 , 11 ) . ( − 9 , 11 ) .

( 16 , 0 ) ( 16 , 0 )

• ⓐ f ( x ) = 2 x ; f ( x ) = 2 x ;
• ⓑ g ( x ) = − 1 2 x g ( x ) = − 1 2 x

y = – 1 3 x + 6 y = – 1 3 x + 6

4.2 Modeling with Linear Functions

ⓐ C ( x ) = 0.25 x + 25 , 000 C ( x ) = 0.25 x + 25 , 000 ⓑ The y -intercept is ( 0 , 25 , 000 ) ( 0 , 25 , 000 ) . If the company does not produce a single doughnut, they still incur a cost of $25,000.

ⓐ 41,100 ⓑ 2020

21.57 miles

4.3 Fitting Linear Models to Data

54 ° F 54 ° F

150.871 billion gallons; extrapolation

4.1 Section Exercises

Terry starts at an elevation of 3000 feet and descends 70 feet per second.

d ( t ) = 100 − 10 t d ( t ) = 100 − 10 t

The point of intersection is ( a , a ) . ( a , a ) . This is because for the horizontal line, all of the y y coordinates are a a and for the vertical line, all of the x x coordinates are a . a . The point of intersection is on both lines and therefore will have these two characteristics.

y = 3 5 x − 1 y = 3 5 x − 1

y = 3 x − 2 y = 3 x − 2

y = − 1 3 x + 11 3 y = − 1 3 x + 11 3

y = − 1.5 x − 3 y = − 1.5 x − 3

perpendicular

f ( 0 ) = − ( 0 ) + 2 f ( 0 ) = 2 y − int : ( 0 , 2 ) 0 = − x + 2 x − int : ( 2 , 0 ) f ( 0 ) = − ( 0 ) + 2 f ( 0 ) = 2 y − int : ( 0 , 2 ) 0 = − x + 2 x − int : ( 2 , 0 )

h ( 0 ) = 3 ( 0 ) − 5 h ( 0 ) = − 5 y − int : ( 0 , − 5 ) 0 = 3 x − 5 x − int : ( 5 3 , 0 ) h ( 0 ) = 3 ( 0 ) − 5 h ( 0 ) = − 5 y − int : ( 0 , − 5 ) 0 = 3 x − 5 x − int : ( 5 3 , 0 )

− 2 x + 5 y = 20 − 2 ( 0 ) + 5 y = 20 5 y = 20 y = 4 y − int : ( 0 , 4 ) − 2 x + 5 ( 0 ) = 20 x = − 10 x − int : ( − 10 , 0 ) − 2 x + 5 y = 20 − 2 ( 0 ) + 5 y = 20 5 y = 20 y = 4 y − int : ( 0 , 4 ) − 2 x + 5 ( 0 ) = 20 x = − 10 x − int : ( − 10 , 0 )

Line 1: m = –10 Line 2: m = –10 Parallel

Line 1: m = –2 Line 2: m = 1 Neither

Line 1 :   m = – 2       Line 2 :   m = – 2       Parallel Line 1 :   m = – 2       Line 2 :   m = – 2       Parallel

y = 3 x − 3 y = 3 x − 3

y = − 1 3 t + 2 y = − 1 3 t + 2

y = − 5 4 x + 5 y = − 5 4 x + 5

y = 3 x − 1 y = 3 x − 1

y = − 2.5 y = − 2.5

y = 3 y = 3

x = − 3 x = − 3

Linear, g ( x ) = − 3 x + 5 g ( x ) = − 3 x + 5

Linear, f ( x ) = 5 x − 5 f ( x ) = 5 x − 5

Linear, g ( x ) = − 25 2 x + 6 g ( x ) = − 25 2 x + 6

Linear, f ( x ) = 10 x − 24 f ( x ) = 10 x − 24

f ( x ) = − 58 x + 17.3 f ( x ) = − 58 x + 17.3

• ⓐ a = 11,900 , b = 1000.1 a = 11,900 , b = 1000.1
• ⓑ q ( p ) = 1000 p – 100 q ( p ) = 1000 p – 100

y = − 16 3 y = − 16 3

x = a x = a

y = d c – a x – a d c – a y = d c – a x – a d c – a

y = 100 x – 98 y = 100 x – 98

x < 1999 201 , x > 1999 201 x < 1999 201 , x > 1999 201

$45 per training session.

The rate of change is 0.1. For every additional minute talked, the monthly charge increases by $0.1 or 10 cents. The initial value is 24. When there are no minutes talked, initially the charge is $24.

The slope is –400. this means for every year between 1960 and 1989, the population dropped by 400 per year in the city.

4.2 Section Exercises

Determine the independent variable. This is the variable upon which the output depends.

To determine the initial value, find the output when the input is equal to zero.

6 square units

20.01 square units

P ( t ) = 75 , 000 + 2500 t P ( t ) = 75 , 000 + 2500 t

(–30, 0) Thirty years before the start of this model, the town had no citizens. (0, 75,000) Initially, the town had a population of 75,000.

Ten years after the model began

W ( t ) = 0.5 t + 7.5 W ( t ) = 0.5 t + 7.5

( − 15 , 0 ) ( − 15 , 0 ) : The x -intercept is not a plausible set of data for this model because it means the baby weighed 0 pounds 15 months prior to birth. ( 0 , 7 . 5 ) ( 0 , 7 . 5 ) : The baby weighed 7.5 pounds at birth.

At age 5.8 months

C ( t ) = 12 , 025 − 205 t C ( t ) = 12 , 025 − 205 t

( 58 . 7 , 0 ) : ( 58 . 7 , 0 ) : In roughly 59 years, the number of people inflicted with the common cold would be 0. ( 0 , 12 , 0 25 ) ( 0 , 12 , 0 25 ) Initially there were 12,025 people afflicted by the common cold.

y = − 2 t +180 y = − 2 t +180

In 2070, the company’s profit will be zero.

y = 3 0 t − 3 00 y = 3 0 t − 3 00

(10, 0) In the year 1990, the company’s profits were zero

During the year 1933

• ⓐ 696 people
• ⓒ 174 people per year
• ⓓ 305 people
• ⓔ P(t) = 305 + 174t
• ⓕ 2,219 people
• ⓐ C(x) = 0.15x + 10
• ⓑ The flat monthly fee is $10 and there is a $0.15 fee for each additional minute used

P(t) = 190t + 4,360

• ⓐ R ( t ) = − 2 . 1 t   +   16 R ( t ) = − 2 . 1 t   +   16
• ⓑ 5.5 billion cubic feet
• ⓒ During the year 2017

More than 133 minutes

More than $42,857.14 worth of jewelry

More than $66,666.67 in sales

4.3 Section Exercises

When our model no longer applies, after some value in the domain, the model itself doesn’t hold.

We predict a value outside the domain and range of the data.

The closer the number is to 1, the less scattered the data, the closer the number is to 0, the more scattered the data.

61.966 years

Interpolation. About 60 ° F . 60 ° F .

This value of r indicates a strong negative correlation or slope, so C This value of r indicates a strong negative correlation or slope, so C

This value of r indicates a weak negative correlation, so B This value of r indicates a weak negative correlation, so B

Yes, trend appears linear because r = 0. 985 r = 0. 985 and will exceed 12,000 near midyear, 2016, 24.6 years since 1992.

y = 1 . 64 0 x + 13 . 8 00 , y = 1 . 64 0 x + 13 . 8 00 , r = 0. 987 r = 0. 987

y = − 0.962 x + 26.86 ,       r = − 0.965 y = − 0.962 x + 26.86 ,       r = − 0.965

y = − 1 . 981 x + 6 0. 197; y = − 1 . 981 x + 6 0. 197; r = − 0. 998 r = − 0. 998

y = 0. 121 x − 38.841 , r = 0.998 y = 0. 121 x − 38.841 , r = 0.998

( −2 , −6 ) , ( 1 , −12 ) , ( 5 , −20 ) , ( 6 , −22 ) , ( 9 , −28 ) ; ( −2 , −6 ) , ( 1 , −12 ) , ( 5 , −20 ) , ( 6 , −22 ) , ( 9 , −28 ) ; Yes, the function is a good fit.

( 189 .8 , 0 ) ( 189 .8 , 0 ) If 18,980 units are sold, the company will have a profit of zero dollars.

y = 0.00587 x + 1985 .4 1 y = 0.00587 x + 1985 .4 1

y = 2 0. 25 x − 671 . 5 y = 2 0. 25 x − 671 . 5

y = − 1 0. 75 x + 742 . 5 0 y = − 1 0. 75 x + 742 . 5 0

Review Exercises

y = − 3 x + 26 y = − 3 x + 26

y = 2 x − 2 y = 2 x − 2

Not linear.

( –9 , 0 ) ; ( 0 , –7 ) ( –9 , 0 ) ; ( 0 , –7 )

Line 1: m = − 2 ; m = − 2 ; Line 2: m = − 2 ; m = − 2 ; Parallel

y = − 0.2 x + 21 y = − 0.2 x + 21

More than 250

y = − 3 00 x + 11 , 5 00 y = − 3 00 x + 11 , 5 00

• ⓑ 100 students per year
• ⓒ P ( t ) = 1 00 t + 17 00 P ( t ) = 1 00 t + 17 00

Extrapolation

y = − 1.294 x + 49.412 ;   r = − 0.974 y = − 1.294 x + 49.412 ;   r = − 0.974

Practice Test

y = −1.5x − 6

y = −2x − 1

Perpendicular

(−7, 0); (0, −2)

y = −0.25x + 12

Slope = −1 and y-intercept = 6

y = 875x + 10,625

• ⓑ dropped an average of 46.875, or about 47 people per year
• ⓒ y = −46.875t + 1250

In early 2018

y = 0.00455x + 1979.5

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/chapter-4

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

MATH 1111 - College Algebra: 4.1 Finding Zeros of Polynomial Functions

• 1.1 Sets and Set Operations
• 1.2 Linear Equations and Inequalities
• 1.3 Systems of Linear Equations
• 1.4 Polynomials; Operations with Polynomials
• 1.5 Factoring Polynomials
• 1.6 Quadratic Equations
• 1.7 Rational Expressions and Equations
• 1.8 Complex Numbers
• 2.1 Cartesian Coordinates/Relations
• 2.2 Intro to Functions
• 2.3 Operations with Functions
• 2.4 Graph of Functions
• 3.1 Linear Functions
• 3.2 Quadratic Functions and Quadratic Inequalities

4.1 Finding Zeros of Polynomial Functions

• 4.2 Graphing Polynomial Functions
• 4.3 Rational Functions
• 4.4 Rational Inequalities
• 5.1 Composition of Functions
• 5.2 Inverse Functions
• 5.3 Introduction to Exponential and Logarithmic Functions

At the end of this section students will be able to:

• Use synthetic division to divide polynomials
• Evaluate polynomials using the Remainder Theorem
• Use the Factor Theorem to factor polynomials
• Use the Rational Zeros Theorem in finding possible zeros of a polynomial with integers coefficients
• Determine all zeros of a polynomial function with real coefficients

Required Reading

3.2 The Factor Theorem and the Remainder Theorem

Stitz-Zeager College Algebra   - pages  257-264

3.3 Real Zeros of Polynomials

Stitz-Zeager College Algebra  - pages  269-270

Practice Exercises

The Factor Theorem and the Remainder Theorem

Stitz-Zeager College Algebra  - pages 265-266

Answers to practice exercises can be found on pages 267-268.

Real Zeros of Polynomials

Stitz-Zeager College Algebra  - pages 280

Answers to practice exercises can be found on pages 283.

Supplemental Resources

Synthetic Division and the Remainder and Factor Theorems  (tutorial):  West Texas A&M University Virtual Math Lab (College Algebra Tutorial 37)

Zeros of Polynomial Functions   (tutorial):  West Texas A&M University Virtual Math Lab (College Algebra Tutorial 38)

Synthetic Division:

Evaluating Polynomials Using the Remainder Theorem:

Finding All Zeros of A Polynomial Function:

• << Previous: Module 4
• Next: 4.2 Graphing Polynomial Functions >>
• Last Updated: Apr 2, 2024 2:52 PM
• URL: https://libguides.gcsu.edu/math1111

Math Worksheets Land

Math Worksheets For All Ages

• Math Topics
• Grade Levels

Finding Zeros of Polynomial Functions Worksheets

We can transform equations of interest into equivalent equations that have one side equal to zero. So, if we can get that one side to be equal to zero, we can solve it for other cases as well. The zero of polynomials is very helpful because it allows use to determine the root. When you are able to rearrange an equation to perform this and then couple it with a well-known formula, you can usually solve for the value of any unknown variables within it. This is especially helpful for solving quadratics. These worksheets and lessons help students locate and understand how to find a root of a polynomial. These are values of x or y that cause the polynomial to equal zero.

Aligned Standard: HSA-APR.B.3

• Zero Products Step-by-step Lesson - We show you an effective means for determine the possible values for a product that equals zero.
• Guided Lesson - Working through these types of problems will give you a great deal of time to understand the rearrangement of equations.
• Guided Lesson Explanation - We go over the concept of Zero Product Properties and how they relate to finding missing variable values.
• Practice Worksheet - Work away at this skills by tackling ten nicely developed problems.
• Matching Worksheet - We used f as every variable to make it much more challenging. Different variable would have just made it too easy.
• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

This is a true fundamental skill that students need to master for higher grade level work.

• Homework 1 - We know that the Zero Product Property states that for all real numbers a and b: If ab = 0, then a = 0 or b = 0
• Homework 2 - According to the Zero Product Property, if (t - 62) (t - 17) = 0, then (t - 62) must be 0 or (t - 17) must be 0.
• Homework 3 - Solve for p and write your answers as whole numbers in the simplest form.

Practice Worksheets

Some of the addends in here are huge on purpose.

• Practice 1 - Write your final outcome in the simplest form.
• Practice 2 - Where does d equal zero?
• Practice 3 - Solve for b and write your answers as whole numbers in the simplest form.

Math Skill Quizzes

See if you think version 3 is challenging? I got asked to make that version slightly easier. I'm not sure why.

• Quiz 1 - Find the values of g (g – 12) (g – 45) = 0
• Quiz 2 - We use large integers here.
• Quiz 3 - Get everything in one side.

How to Identify Zeros of Binomials?

Let us first determine what root or a zero of a polynomial is. The root of the polynomial means that by solving a function, you will get a non-zero answer. This value is called the root of a function. However, if by solving a function, your answer is 0, then that means you get no value for solving it.

Now, a binomial function means that in a given equation, two unknowns are present. Now, we will find out how we can identify a zero in a binomial equation. Let us take an example of y = x 2 + 2x - 15. First, we need to solve the equation to find out its roots. Let us consider y as zero for solving this problem.

x 2 + 2x – 15 = 0, x 2 + 5x - 3x - 15 = 0, (x + 5) (x - 3) = 0

Now, if we write the last equation separately, then, we get: (x + 5) = 0, (x - 3) = 0

Both separate equations can be solved as roots, so by placing the constants from the left-hand side of the equal sign to the right-hand-side, the signs will change. The resultant values will be:

x = 3, x = -5

If we look at it objectively, the binomial equation had two zeros and two roots. Similarly, we can solve other binomial equations as well.

How Do You Find the Zeros of a Polynomial?

The easiest way to do this is to factor the polynomial into linear factors but is not always applicable. Always begin by listing all the possible rational zeroes by using the Rational Zero Theorem. We then apply an available synthetic division operations to see if we have any other potential contenders. If it is a 0, it is in the running otherwise it is not. You can continue on with this until you form a quadratic and then determine any remaining zeroes with the quadratic formula.

Get Access to Answers, Tests, and Worksheets

Become a paid member and get:

• Answer keys to everything
• Unlimited access - All Grades
• 64,000 printable Common Core worksheets, quizzes, and tests
• Used by 1000s of teachers!

Worksheets By Email:

Get Our Free Email Now!

We send out a monthly email of all our new free worksheets. Just tell us your email above. We hate spam! We will never sell or rent your email.

Thanks and Don't Forget To Tell Your Friends!

I would appreciate everyone letting me know if you find any errors. I'm getting a little older these days and my eyes are going. Please contact me, to let me know. I'll fix it ASAP.

• Privacy Policy
• Other Education Resource

© MathWorksheetsLand.com, All Rights Reserved

• (512) 464- 6491 (classroom)
• [email protected]
• McNeil HS Home Page
• Home Access Center (Student Grades)
• Class Information:
• Parent Letter-Precalculus
• Parent Letter-Calculus

Precalculus

Mrs. Snow's Math

McNeil High School

Notes are intended to compliment the current text in use at McNeil High School Precalculus, Enhanced with Graphing Utilities, Texas Edition By Michael Sullivan and Michael Sullivan, III

FALL SEMESTER

Fundamentals

MATHXL FOR SCHOOL – where to find it on line and where are all the assignments!

Algebra II Review Annotated Notes

Chapter 2:  Functions and Their Graphs All assignments are due at the start of the next class period.  The first assignments of this school year will be completed on paper: 

Current assignments are currently not available on Mathxl, the precalculus online homework program.  For full credit, use separate paper:   please write your full name, class period, and identify the assignment with chapter.section number.  Write out each problem, show all work and circle the answer.

Lesson 2.1 and Lesson 2.2 Functions and 2.2 The Graph of a Function Mathxl Homework 2.1 and 2.2 Solutions 2.1 2.2 Mathxl -Textbook Homework 2.3 and 2.4 Solutions Textbook 2.3 and 2.4 Mathxl – Textbook Homework 2.5 Solutions 2.5 Annotated Notes Video Lesson 2.1 and 2.2 Lesson 2.3 and Lesson 2.4 Properties of Functions,   2.4  Piecewise and Greatest Integer Functions Annotated Notes 2.3 and 2.4 Video Lesson 2.3 and 2.4 Lesson 2.5   Graphing Techniques:  Transformations Annotated Notes 2.5 Video Lesson 2.5 In-class Transformation Practice Annotated Transformation Practice mrssnowsmath.com/…/chapter2review.2023r.pdf 2.5 Homework Worksheet Chapter 2 Review Review Solutions  

Chapter 4:  Polynomial and Rational Functions

Lesson 4.1  Polynomial Functions and Model Annotated Notes Video Lesson 4.1 Lesson 4.2 The Real Zeros of a Polynomial Function Lesson 4.3 Complex Zeros; Fundamental Theorem of Algebra Annotated Notes 4.2 and 4.3 Video Lesson 4.2 and 4.3 Lesson 4.4 and Lesson 4.5  4.4 Properties of Rational Functions and.4.5 The Graphs of a Rational Function Annotated Notes 4.4 and 4.5 Video Lesson 4.4 and 4.5 Lesson 4.6 Polynomial and Rational Inequalities Annotated Notes 4.6 Video Lesson 4.6 Chapter 4 Spiral Ch 2 Review    Updated 9/2023 Spiral Review Solutions    

Chapter 6 Trigonometric Functions

Quizlet Links: Sine, Cosine, and Tangent Radian Values Practice with radians from the unit circle; flashcards and more Unit Circle practice page   2 unit circles for drill practice

Lesson 6.1 and 6.2 Part 1 Angles and Their Measure, The Unit Circle Annotated Notes 6.1 And 6.2 Part 1 Video Lesson 6.1 and 6.2 part 1 Lesson 6.1 and 6.2 Part 2 Trigonometric Functions: Unit Circle Approach Annotated Notes 6.1 and 6-2 Part2 Video Lesson 6.1 and 6.2 part 2 2 Unit Circles   Practice Form Lesson 6.3 Properties of the Trigonometric Functions Annotated Notes Video Lesson 6.3 Review 6.1-6.3 Chapter 6.1-6.3 Review Solutions   

Unit Circle Chart – In Order Lesson 6.4 Graphs of the Sine and Cosine Functions Annotated Notes 6.4 Video Lesson 6.4 Worksheet6.4 Lesson 6.5   Graphs of Secant and Cosecant Functions Annotated Notes 6.5 Part 1 Lesson 6.5 Graphs of Tangent and Cotangent Functions Annotated Notes 6.5 Part 2 Worksheet 6.5    Worksheet for: secant, Cosecant, Tangent and Cotangent Functions Video Lesson 6.5    this covers both part 1 and part 2:  Secant, Cosecant, Tangent and Cotangent Functions Lesson 6.6 Phase Shift Annotated Notes 6.6 Video Lesson 6.6 Worksheet 6.6 Lesson 8.5   Simple Harmonic Motion Annotated Notes 8.5 Video Lesson 8.5   “The Ferris Wheel Problem”   Video showing Simple Harmonic Motion Spiral Review 6.1-6.6, 8.5   Spiral Review Solutions

Lesson 5.1 and Lesson 5.2 Composite Functions and One-to-One Functions, Inverse Functions Annotated Notes 5.1 and 5.2 Video Lesson 5.1 and 5.2

Lesson 7.1 and 7.2   The Inverse Sine, Cosine, and Tangent Functions and The Inverse Trigonometric Function, Continued 7.1 and 7.2 Annotated Notes Video Lesson 7.1 Extra Examples Lesson 7.3 Trigonometric Equations Annotated Notes 7.3 Video Lesson 7.3 Review 5.1-5.2  and 7.1-7.3 Review 7.1-7.3 Solutions (revised 11/2/2019)

Unit Circle Sine, Cosine and Tangent values – Quizlet     link to a quizlet that has flash cards for our unit circle values.  The “Learn” link will quiz you with the flash cards out of order.

Trigonometric Identities Reference Sheet The first page will need to be memorized! Lesson 7.4 Trigonometric Identities Annotated Notes 7.4 Video Lesson 7.4 Worksheet Proofs Trig Identities   fall 2022 we are only doing the odd problems.  The even are available for additional practice Lesson 7.5 Sum and Difference Formulas Annotated Notes 7.5 Video Lesson 7.5 Lesson 7.6 Double-angle and Half-angle Formulas Annotated Notes 7.6 Video Lesson 7.6 Review Spiral 5.1-2, 7.1-3 7.4-7.5 Review Answers    Corrected!

 Chapter 10

Lesson 10.1 and 10.2 Conics and the Parabola Annotated Notes 10.1 and 10.2 Video Lesson 10.1 and 10.2

Lesson 10.3 The Ellipse Annota te d Notes 10.3 Lesson 10.4 The Hyperbola Annotated Notes 10.4 Lesson 10.7 Plane Curves and Parametric Equations Annotated Notes 10.7

Fall Final Exam Review Fall Final Exam solutions

GUIDELINE FOR NOTECARD

This link will take you to an excel spreadsheet that will allow you to take your averages for either fall or spring semester and see what you need for the grading period or final to pass class.  This is designed for the grading cycles at McNeil High School. “WHAT IF…”GRADE CHECK  for Fall and Spring Semesters

SPRING SEMESTER 

Chapter 8 Lesson 8.1 Right Triangle Trigonometry; Applications Annotated Notes 8.1 Video 8.1 Trigonometry Applications Worksheet Lesson 8.2 The Law of Sines Lesson 8.2 The Ambiguous Case Example Annotated Notes 8.2 Video 8.2 Lesson 8.3 The Law of Cosines Lesson 8.4 Area of a Triangle Annotated Notes 8.3 and 8.4 Video 8.3 and 8.4 Review Chapter 8 Review Chapter  Solutions  

Lesson 8.5 Simple Harmonic Motion (presented in the fall with Chapter 6) Annotated Notes 8.5 are located with Chapter 6

Chapter 9 Lesson 9.1 Polar Coordinates Annotated Notes 9.1 Video Lesson 9.1 Lesson 9.2 Polar Equations and Graphs Annotated Notes .9.2 Video Lesson 9.2 Limacon Examples Polar Graph Paper Lesson 9.4 Vectors Video Lesson 9.4 Annotated Notes 9.4 9.4 Static Equilibrium Problem #19 example Lesson 9.5 The Dot Product Annotated Notes 9.5 Video Lesson 9.5 Spiral Ch 8 and 9 Re view Spiral Review Solutions

Chapter 5 and 11.5 Lesson5.3 Exponential Functions Annotated Notes 5.3  and corrected Video Lesson 5.3 Lesson 5.4 Logarithmic Functions  and Lesson 5.5 Properties of Logarithms Annotated Notes 5.4 and 5.5 V ideo Lesson 5.4 Video Lesson 5.5

Lesson 5.6 Logarithmic and Exponential Equations Annotated Notes 5.6 Video Lesson 5.6 Lesson 5.7 and Lesson 5.8 Financial Models   and  Exponential Growth and Decay Models Annotated Notes 5.7 and 5.8 Video Lesson 5.7  Video Lesson 5.8 Chapter 5 Review  Review Solutions Chapter 5

Extra Lessons 11.5 and Rational Expressions Addition and Subtraction of Rational Expressions Annotated Notes Video Lesson Addition and Subtraction of Rational Expressions Multiplication and Division of Rational Expressions  Annotated Notes Video Lesson Multiplication and Division of Rational Expressions

Lesson 11.5 Partial Fraction Decomposition Annotated Notes 11.5 Video Lesson 11.5 https://www.youtube.com/watch?v=8lSCAY15BdQ

Chapter  12 Lesson 12.1 Sequences Annotated Notes 12.1 Video Lesson Lesson 12.2 Arithmetic Sequences Annotated Notes 12.2 Video Lesson Lesson 12.3   Geometric Sequences Lesson 12.3 Lecture Notes modified for voice over lecture Annotated Notes 12.3 Video Lesson Lesson 12.4 Mathematical Induction Lesson 12.4 Lecture Notes modified for voice over lecture Annotated Notes 12.4 Video Lesson 12.4 Homework Worksheet Lesson 12.5  The Binomial Theorem Lesson 12.5 Lecture Notes modified for voice over lecture Annotated Notes 12.5 Video Lesson Review Chapter 12    

Solutions Review Ch 12 and 11.5   if you want credit for the review, make sure you show your work,  copying these answers will result in a 0%

Chapter 14 –  A Preview of Calculus  

Lesson 14.1 Finding Limits Using Tables and Graphs Annotated Notes 14.1 *    Video Lecture 14.1 14.1 Worksheet

Lesson 14.2 Algebra Techniques for Finding Limits *    Video Lecture 14.2 Annotated Notes 14.2 14.2 Worksheet

Lesson 14.3  The Tangent Problem:  The Derivative Annotated Notes 14.3 *     Video Lecture 14.3 14.3 Worksheet Helpful videos for visualizing secant lines morphing into a tangent line: The Tangent Line and the Derivative   an 11 minute video, all is very good, the definition by derivative starts at 4 minutes. Applet:  Ordinary Derivative by Limit Definition   as an interactive applet to let the student see as the distance between points goes to zero,  the secant line becomes the tangent line.

Lesson 14.4  Limits at Infinity Annotated Notes 14.4 14.4 Worksheet *    Video Lecture 14.4

Lesson 14.5 The Area Problem:  The Integral Annotated Notes 14.5 14.5 Worksheet *    Video Lecture 14.5

Solutions to Chapter 14 practice problems

14.3, problem #7: correct answer is f'(x)=-5

Spiral Review Chapter 14 and Chapter 12 -remember, no work no credit!! Review Ch 12 and 14 Solutions

Note Card For Precalculus Final All students, whether exempting the final exam or not,  are required to complete the Final Exam Review.  Work must be shown for credit.   Spring Final Exam Review Spring Final Review Solutions

Other Notes

Intro to Calculus Lesson on Derivatives and Integration Annotated Notes Derivatives Worksheet #1 – Product and Quotient Rules Worksheet #2 – Chain Rule Chain Rule Notes Worksheet #3 – Integrals Integral Notes

This link will take you to an excel spreadsheet that will allow you to take your averages for either fall or spring semester and see what you need for the grading period or final to pass class.  This is designed for the grading cycles at McNeil High School. “WHAT IF…”GRADE CHECK for 2020-2021 School Year

Maze - Find the Zeros of a Polynomial Functions (Level 4)

What educators are saying

Also included in.

Description

This activity is a good review of understanding how to "Find the zeros of Polynomial Functions" . There are 17 questions provided. From start to end, the student will be able to answer 15 questions out of the 17 provided to get to the end of the maze.

The polynomial functions are:

☑ SOME Polynomial Functions are given in factored form with 2, 3, 4, or 5 linear factors of the form (x ± #). ..... (x is a factor in some questions)

☑ SOME Polynomial Functions need to be factored out (See Below for Factoring Techniques)

☑ The Leading coefficient of x is NOT 1 .

☑ The multiplicity of some factors is more than 1

☑ The zeros are Integers & Fractions

Factoring Techniques of this Maze are:

☑ Factor GCF

☑ Factor Difference of Two Squares

☑ Factor Quadratic Form

☑ Factor by Grouping

☑ Factor Trinomials (a is 1 or others)

Students would need to find the zeros by setting each factor equals to zero and isolate the x. The purpose behind this maze is to strengthen the ability of my students to finding the zeros given the factored form of Polynomial Functions AND factor a given polynomials to find the zero when a is not 1.

Please take a look at the preview and let me know if you have any questions via Q&A.

A SUGGESTED STEP-BY-STEP Answer Key is Included in this Maze

These mazes will work very well with the first part of section 5.2 in Pearson Common Core Textbook and could be used as a homework.

AN INTERACTIVE DIGITAL VERSION OF THIS ACTIVITY IS SOLD SEPARATELY AT MY STORE HERE

This maze could be used as: a way to check for understanding, a review, recap of the lesson, pair-share, cooperative learning, exit ticket, entrance ticket, homework, individual practice, when you have time left at the end of a period, beginning of the period (as a warm up or bell work), before a quiz on the topic, and more.

You may also like:

☑ LEVEL 1 Finding Zeros of Polynomial Functions

☑ LEVEL 2 Finding Zeros of Polynomial Functions

☑ LEVEL 3 Finding Zeros of Polynomial Functions

☑ LEVEL 5 Finding Zeros of Polynomial Functions

☑ Find Zeros & Write Polynomial Functions

FOLLOW ME FOR MORE MAZES ON THIS TOPIC & OTHER TOPICS

☺Would love to hear your feedback☺. Please don't forget to come back and rate this product when you have a chance. You will also earn TPT credits. Enjoy and I ☺Thank You☺ for visiting my ☺Never Give Up On Math☺ store!!!

© Never Give Up On Math 2017

This product is intended for personal use in one classroom only. For use in multiple classrooms, please purchase additional licenses.

☺ HAVE A WONDERFUL DAY ☺

Questions & Answers

Never give up on math.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Graphs of Polynomial Functions

• Last updated
• Save as PDF
• Page ID 15069

Learning Objectives

• Recognize characteristics of graphs of polynomial functions.
• Use factoring to find zeros of polynomial functions.
• Identify zeros and their multiplicities.
• Determine end behavior.
• Understand the relationship between degree and turning points.
• Graph polynomial functions.
• Use the Intermediate Value Theorem.

The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in Table \(\PageIndex{1}\).

The revenue can be modeled by the polynomial function

\[R(t)=−0.037t^4+1.414t^3−19.777t^2+118.696t−205.332\]

where \(R\) represents the revenue in millions of dollars and \(t\) represents the year, with \(t=6\) corresponding to 2006. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. We have already explored the local behavior of quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.

Recognizing Characteristics of Graphs of Polynomial Functions

Polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. Figure \(\PageIndex{1}\) shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.

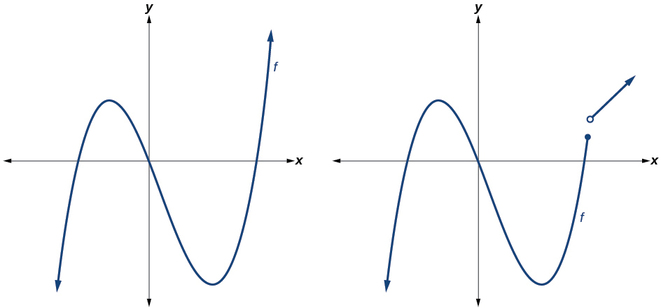
Example \(\PageIndex{1}\): Recognizing Polynomial Functions

Which of the graphs in Figure \(\PageIndex{2}\) represents a polynomial function?

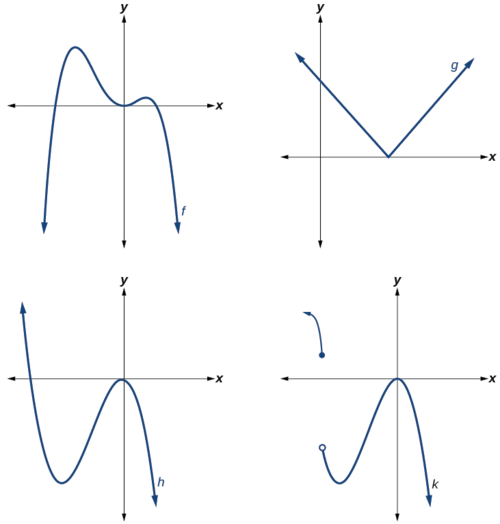
• The graphs of \(f\) and \(h\) are graphs of polynomial functions. They are smooth and continuous .
• The graphs of \(g\) and \(k\) are graphs of functions that are not polynomials. The graph of function \(g\) has a sharp corner. The graph of function \(k\) is not continuous.

Do all polynomial functions have as their domain all real numbers?

• Yes. Any real number is a valid input for a polynomial function.

Using Factoring to Find Zeros of Polynomial Functions

Recall that if \(f\) is a polynomial function, the values of \(x\) for which \(f(x)=0\) are called zeros of \(f\). If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros.

We can use this method to find x-intercepts because at the x-intercepts we find the input values when the output value is zero. For general polynomials, this can be a challenging prospect. While quadratics can be solved using the relatively simple quadratic formula, the corresponding formulas for cubic and fourth-degree polynomials are not simple enough to remember, and formulas do not exist for general higher-degree polynomials. Consequently, we will limit ourselves to three cases in this section:

The polynomial can be factored using known methods: greatest common factor and trinomial factoring. The polynomial is given in factored form. Technology is used to determine the intercepts.

HOwTO: Given a polynomial function \(f\), find the x-intercepts by factoring

• Set \(f(x)=0\).
• Factor out any common monomial factors.
• Factor any factorable binomials or trinomials.
• Set each factor equal to zero and solve to find the x-intercepts.

Example \(\PageIndex{2}\): Finding the x-Intercepts of a Polynomial Function by Factoring

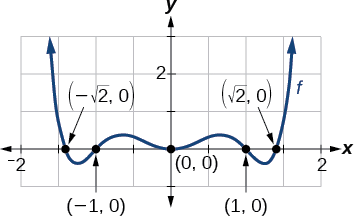
Find the x-intercepts of \(f(x)=x^6−3x^4+2x^2\).

We can attempt to factor this polynomial to find solutions for \(f(x)=0\).

\[\begin{align*} x^6−3x^4+2x^2&=0 & &\text{Factor out the greatest common factor.} \\ x^2(x^4−3x^2+2)&=0 & &\text{Factor the trinomial.} \\ x^2(x^2−1)(x^2−2)&=0 & &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\] .

This gives us five x-intercepts: \((0,0)\), \((1,0)\), \((−1,0)\), \((\sqrt{2},0)\),and \((−\sqrt{2},0)\) (Figure \(\PageIndex{3}\)). We can see that this is an even function.

Example \(\PageIndex{3}\): Finding the x-Intercepts of a Polynomial Function by Factoring

Find the x-intercepts of \(f(x)=x^3−5x^2−x+5\).

Find solutions for \(f(x)=0\) by factoring.

\[\begin{align*} x^3−5x^2−x+5&=0 &\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

There are three x-intercepts: \((−1,0)\), \((1,0)\), and \((5,0)\) (Figure \(\PageIndex{4}\)).

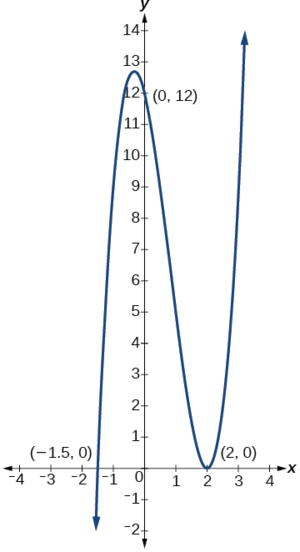
Example \(\PageIndex{4}\): Finding the y- and x-Intercepts of a Polynomial in Factored Form

Find the y- and x-intercepts of \(g(x)=(x−2)^2(2x+3)\).

The y-intercept can be found by evaluating \(g(0)\).

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) \\ &=12 \end{align*}\]

So the y-intercept is \((0,12)\).

The x-intercepts can be found by solving \(g(x)=0\).

\[(x−2)^2(2x+3)=0\]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

So the x-intercepts are \((2,0)\) and \(\left(−\dfrac{3}{2},0\right)\).

We can always check that our answers are reasonable by using a graphing calculator to graph the polynomial as shown in Figure \(\PageIndex{5}\).

Example \(\PageIndex{5}\): Finding the x-Intercepts of a Polynomial Function Using a Graph

Find the x-intercepts of \(h(x)=x^3+4x^2+x−6\).

This polynomial is not in factored form, has no common factors, and does not appear to be factorable using techniques previously discussed. Fortunately, we can use technology to find the intercepts. Keep in mind that some values make graphing difficult by hand. In these cases, we can take advantage of graphing utilities.

Looking at the graph of this function, as shown in Figure \(\PageIndex{6}\), it appears that there are x-intercepts at \(x=−3,−2, \text{ and }1\).

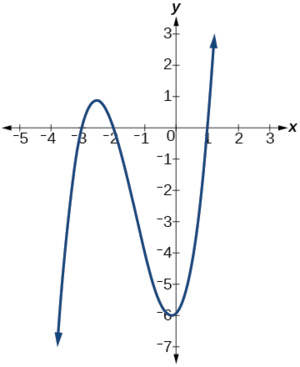
We can check whether these are correct by substituting these values for \(x\) and verifying that \[h(−3)=h(−2)=h(1)=0. \nonumber\]

Since \(h(x)=x^3+4x^2+x−6\), we have:

\[ \begin{align*} h(−3)&=(−3)^3+4(−3)^2+(−3)−6=−27+36−3−6=0 \\[4pt] h(−2) &=(−2)^3+4(−2)^2+(−2)−6 =−8+16−2−6=0 \\[4pt] h(1)&=(1)^3+4(1)^2+(1)−6=1+4+1−6=0 \end{align*}\]

Each x-intercept corresponds to a zero of the polynomial function and each zero yields a factor, so we can now write the polynomial in factored form.

\[\begin{align*} h(x)&=x^3+4x^2+x−6 \\ &=(x+3)(x+2)(x−1) \end{align*}\]

Exercise \(\PageIndex{1}\)

Find the y-and x-intercepts of the function \(f(x)=x^4−19x^2+30x\).

• y-intercept \((0,0)\);
• x-intercepts \((0,0)\), \((–5,0)\), \((2,0)\), and \((3,0)\)

Identifying Zeros and Their Multiplicities

Graphs behave differently at various x-intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and bounce off. Suppose, for example, we graph the function

\[f(x)=(x+3)(x−2)^2(x+1)^3.\]

Notice in Figure \(\PageIndex{7}\) that the behavior of the function at each of the x-intercepts is different.

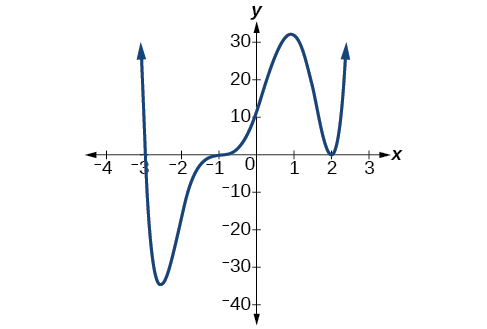
The x-intercept −3 is the solution of equation \((x+3)=0\). The graph passes directly through thex-intercept at \(x=−3\). The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.

The x-intercept 2 is the repeated solution of equation \((x−2)^2=0\). The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree 2), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept.

\[(x−2)^2=(x−2)(x−2)\]

The factor is repeated, that is, the factor \((x−2)\) appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity . The zero associated with this factor, \(x=2\), has multiplicity 2 because the factor \((x−2)\) occurs twice.

The x-intercept −1 is the repeated solution of factor \((x+1)^3=0\).The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function \(f(x)=x^3\). We call this a triple zero, or a zero with multiplicity 3.

For zeros with even multiplicities, the graphs touch or are tangent to the x-axis. For zeros with odd multiplicities, the graphs cross or intersect the x-axis. See Figure \(\PageIndex{8}\) for examples of graphs of polynomial functions with multiplicity 1, 2, and 3.

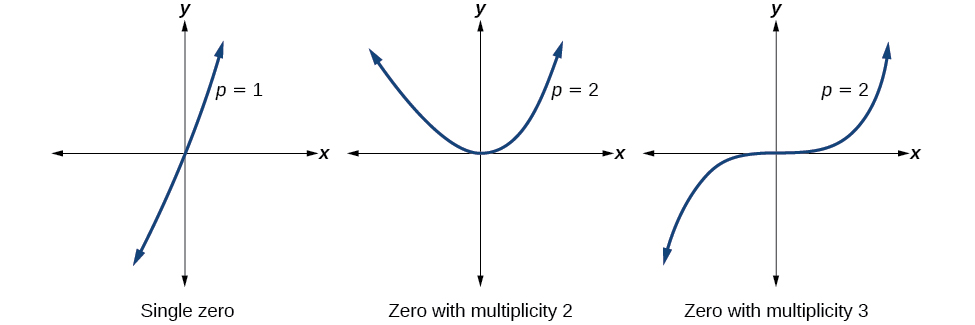
For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the x-axis.

For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the x-axis.

Graphical Behavior of Polynomials at x-Intercepts

If a polynomial contains a factor of the form \((x−h)^p\), the behavior near the x-intercepth is determined by the power \(p\). We say that \(x=h\) is a zero of multiplicity \(p\).

The graph of a polynomial function will touch the x-axis at zeros with even multiplicities. The graph will cross the x-axis at zeros with odd multiplicities.

The sum of the multiplicities is the degree of the polynomial function.

HOWTO: Given a graph of a polynomial function of degree \(n\), identify the zeros and their multiplicities

• If the graph crosses the x-axis and appears almost linear at the intercept, it is a single zero.
• If the graph touches the x-axis and bounces off of the axis, it is a zero with even multiplicity.
• If the graph crosses the x-axis at a zero, it is a zero with odd multiplicity.
• The sum of the multiplicities is \(n\).

Example \(\PageIndex{6}\): Identifying Zeros and Their Multiplicities

Use the graph of the function of degree 6 in Figure \(\PageIndex{9}\) to identify the zeros of the function and their possible multiplicities.

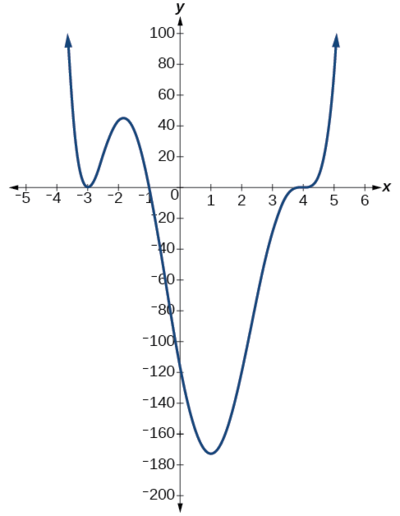
The polynomial function is of degree \(n\). The sum of the multiplicities must be \(n\).

Starting from the left, the first zero occurs at \(x=−3\). The graph touches the x-axis, so the multiplicity of the zero must be even. The zero of −3 has multiplicity 2.

The next zero occurs at \(x=−1\). The graph looks almost linear at this point. This is a single zero of multiplicity 1.

The last zero occurs at \(x=4\).The graph crosses the x-axis, so the multiplicity of the zero must be odd. We know that the multiplicity is likely 3 and that the sum of the multiplicities is likely 6.

Exercise \(\PageIndex{2}\)

Use the graph of the function of degree 5 in Figure \(\PageIndex{10}\) to identify the zeros of the function and their multiplicities.

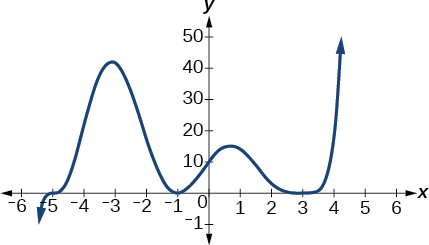
Figure \(\PageIndex{10}\): Graph of a polynomial function with degree 5.

The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity.

Determining End Behavior

As we have already learned, the behavior of a graph of a polynomial function of the form

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\]

will either ultimately rise or fall as \(x\) increases without bound and will either rise or fall as \(x\) decreases without bound. This is because for very large inputs, say 100 or 1,000, the leading term dominates the size of the output. The same is true for very small inputs, say –100 or –1,000.

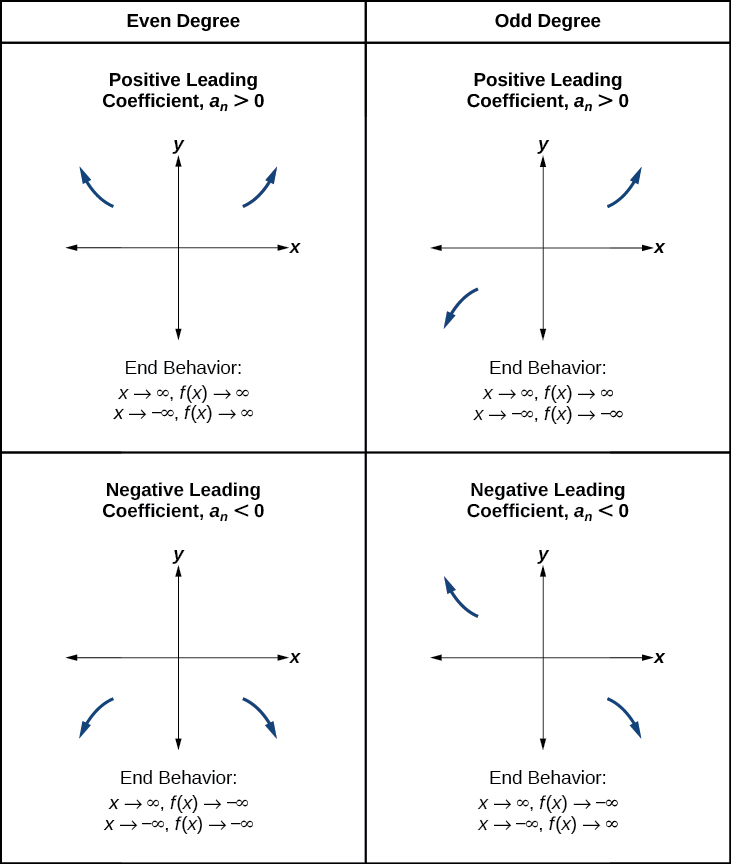
Recall that we call this behavior the end behavior of a function. As we pointed out when discussing quadratic equations, when the leading term of a polynomial function, \(a_nx^n\), is an even power function, as \(x\) increases or decreases without bound, \(f(x)\) increases without bound. When the leading term is an odd power function, as \(x\) decreases without bound, \(f(x)\) also decreases without bound; as \(x\) increases without bound, \(f(x)\) also increases without bound. If the leading term is negative, it will change the direction of the end behavior. Figure \(\PageIndex{11}\) summarizes all four cases.

Understanding the Relationship between Degree and Turning Points

In addition to the end behavior, recall that we can analyze a polynomial function’s local behavior. It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). Look at the graph of the polynomial function \(f(x)=x^4−x^3−4x^2+4x\) in Figure \(\PageIndex{12}\). The graph has three turning points.

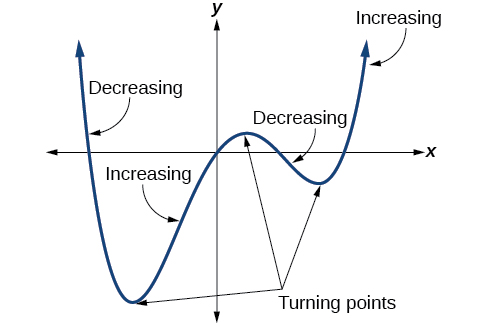
This function \(f\) is a 4th degree polynomial function and has 3 turning points. The maximum number of turning points of a polynomial function is always one less than the degree of the function.

Definition: Interpreting Turning Points

A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). A polynomial of degree \(n\) will have at most \(n−1\) turning points.

Example \(\PageIndex{7}\): Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function

Find the maximum number of turning points of each polynomial function.

• \(f(x)=−x^3+4x^5−3x^2+1\)
• \(f(x)=−(x−1)^2(1+2x^2)\)

a. \(f(x)=−x^3+4x^5−3x^2+1\)

First, rewrite the polynomial function in descending order: \(f(x)=4x^5−x^3−3x^2+1\)

Identify the degree of the polynomial function. This polynomial function is of degree 5.

The maximum number of turning points is \(5−1=4\).

b. \(f(x)=−(x−1)^2(1+2x^2)\)

First, identify the leading term of the polynomial function if the function were expanded.

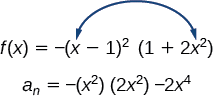
Then, identify the degree of the polynomial function. This polynomial function is of degree 4.

The maximum number of turning points is \(4−1=3\).

Graphing Polynomial Functions

We can use what we have learned about multiplicities, end behavior, and turning points to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.

Howto: Given a polynomial function, sketch the graph

• Find the intercepts.
• Check for symmetry. If the function is an even function, its graph is symmetrical about the y-axis, that is, \(f(−x)=f(x)\). If a function is an odd function, its graph is symmetrical about the origin, that is, \(f(−x)=−f(x)\).
• Use the multiplicities of the zeros to determine the behavior of the polynomial at the x-intercepts.
• Determine the end behavior by examining the leading term.
• Use the end behavior and the behavior at the intercepts to sketch a graph.
• Ensure that the number of turning points does not exceed one less than the degree of the polynomial.
• Optionally, use technology to check the graph.

Example \(\PageIndex{8}\): Sketching the Graph of a Polynomial Function

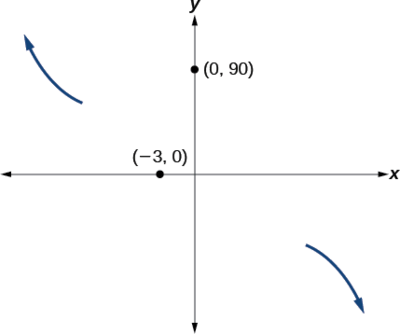
Sketch a graph of \(f(x)=−2(x+3)^2(x−5)\).

This graph has two x-intercepts. At \(x=−3\), the factor is squared, indicating a multiplicity of 2. The graph will bounce at this x-intercept. At \(x=5\),the function has a multiplicity of one, indicating the graph will cross through the axis at this intercept.

The y-intercept is found by evaluating \(f(0)\).

\[\begin{align*} f(0)&=−2(0+3)^2(0−5) \\ &=−2⋅9⋅(−5) \\ &=90 \end{align*}\]

The y-intercept is \((0,90)\).

Additionally, we can see the leading term, if this polynomial were multiplied out, would be \(−2x3\), so the end behavior is that of a vertically reflected cubic, with the outputs decreasing as the inputs approach infinity, and the outputs increasing as the inputs approach negative infinity. See Figure \(\PageIndex{13}\).

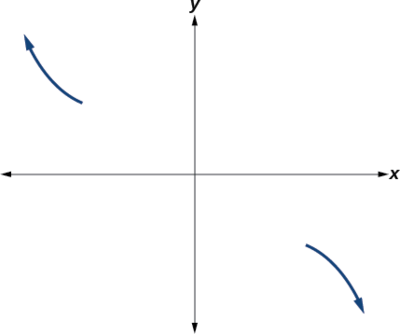
To sketch this, we consider that:

• As \(x{\rightarrow}−{\infty}\) the function \(f(x){\rightarrow}{\infty}\),so we know the graph starts in the second quadrant and is decreasing toward the x-axis.
• Since \(f(−x)=−2(−x+3)^2(−x–5)\) is not equal to \(f(x)\), the graph does not display symmetry.
• At \((−3,0)\), the graph bounces off of thex-axis, so the function must start increasing.
• At \((0,90)\), the graph crosses the y-axis at the y-intercept. See Figure \(\PageIndex{14}\).

Somewhere after this point, the graph must turn back down or start decreasing toward the horizontal axis because the graph passes through the next intercept at \((5,0)\). See Figure \(\PageIndex{15}\).

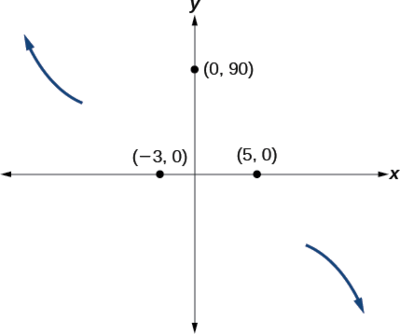
As \(x{\rightarrow}{\infty}\) the function \(f(x){\rightarrow}−{\infty}\),

so we know the graph continues to decrease, and we can stop drawing the graph in the fourth quadrant.

Using technology, we can create the graph for the polynomial function, shown in Figure \(\PageIndex{16}\), and verify that the resulting graph looks like our sketch in Figure \(\PageIndex{15}\).

Exercise \(\PageIndex{8}\)

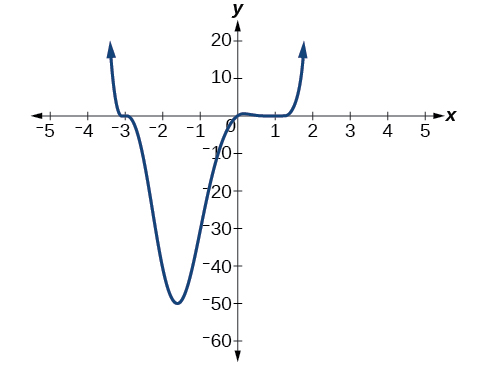
Sketch a graph of \(f(x)=\dfrac{1}{4}x(x−1)^4(x+3)^3\).

Using the Intermediate Value Theorem

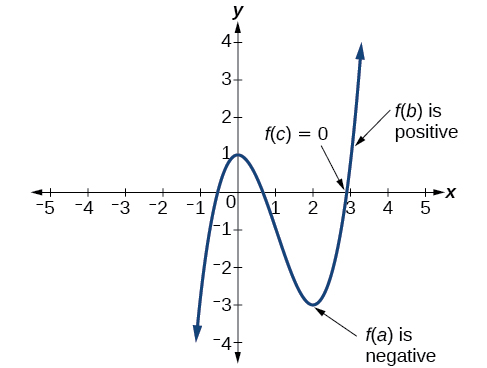
In some situations, we may know two points on a graph but not the zeros. If those two points are on opposite sides of the x-axis, we can confirm that there is a zero between them. Consider a polynomial function \(f\) whose graph is smooth and continuous. The Intermediate Value Theorem states that for two numbers \(a\) and \(b\) in the domain of \(f\),if \(a<b\) and \(f(a){\neq}f(b)\),then the function \(f\) takes on every value between \(f(a)\) and \(f(b)\). We can apply this theorem to a special case that is useful in graphing polynomial functions. If a point on the graph of a continuous function \(f\) at \(x=a\) lies above the x-axis and another point at \(x=b\) lies below thex-axis, there must exist a third point between \(x=a\) and \(x=b\) where the graph crosses the x-axis. Call this point \((c,f(c))\).This means that we are assured there is a solution \(c\) where \(f(c)=0\).

In other words, the Intermediate Value Theorem tells us that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis. Figure \(\PageIndex{18}\) shows that there is a zero between \(a\) and \(b\).

Definition: Intermediate Value Theorem

Let \(f\) be a polynomial function. The Intermediate Value Theorem states that if \(f(a)\) and \(f(b)\) have opposite signs, then there exists at least one value \(c\) between \(a\) and \(b\) for which \(f(c)=0\).

Example \(\PageIndex{9}\): Using the Intermediate Value Theorem

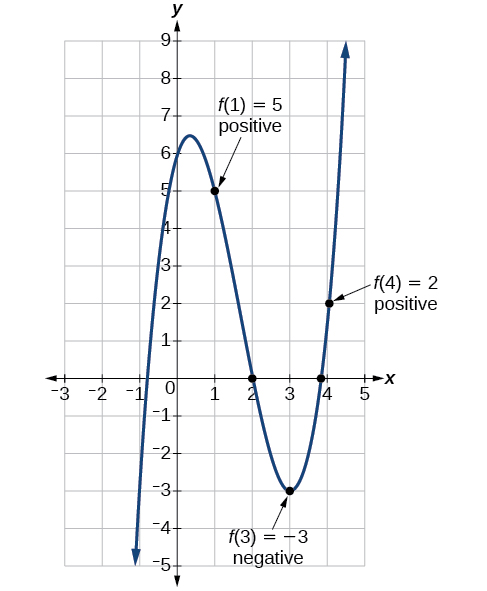
Show that the function \(f(x)=x^3−5x^2+3x+6\) has at least two real zeros between \(x=1\) and \(x=4\).

As a start, evaluate \(f(x)\) at the integer values \(x=1,\;2,\;3,\; \text{and }4\) (Table \(\PageIndex{2}\)).

We see that one zero occurs at \(x=2\). Also, since \(f(3)\) is negative and \(f(4)\) is positive, by the Intermediate Value Theorem, there must be at least one real zero between 3 and 4.

We have shown that there are at least two real zeros between \(x=1\) and \(x=4\).

We can also see on the graph of the function in Figure \(\PageIndex{19}\) that there are two real zeros between \(x=1\) and \(x=4\).

Exercise \(\PageIndex{4}\)

Show that the function \(f(x)=7x^5−9x^4−x^2\) has at least one real zero between \(x=1\) and \(x=2\).

Because \(f\) is a polynomial function and since \(f(1)\) is negative and \(f(2)\) is positive, there is at least one real zero between \(x=1\) and \(x=2\).

Writing Formulas for Polynomial Functions

Now that we know how to find zeros of polynomial functions, we can use them to write formulas based on graphs. Because a polynomial function written in factored form will have an x-intercept where each factor is equal to zero, we can form a function that will pass through a set of x-intercepts by introducing a corresponding set of factors.

Note: Factored Form of Polynomials

If a polynomial of lowest degree \(p\) has horizontal intercepts at \(x=x_1,x_2,…,x_n\), then the polynomial can be written in the factored form: \(f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}\) where the powers \(p_i\) on each factor can be determined by the behavior of the graph at the corresponding intercept, and the stretch factor \(a\) can be determined given a value of the function other than the x-intercept.

• Identify the x-intercepts of the graph to find the factors of the polynomial.
• Examine the behavior of the graph at the x-intercepts to determine the multiplicity of each factor.
• Find the polynomial of least degree containing all the factors found in the previous step.
• Use any other point on the graph (the y-intercept may be easiest) to determine the stretch factor.

Example \(\PageIndex{10}\): Writing a Formula for a Polynomial Function from the Graph

Write a formula for the polynomial function shown in Figure \(\PageIndex{20}\).

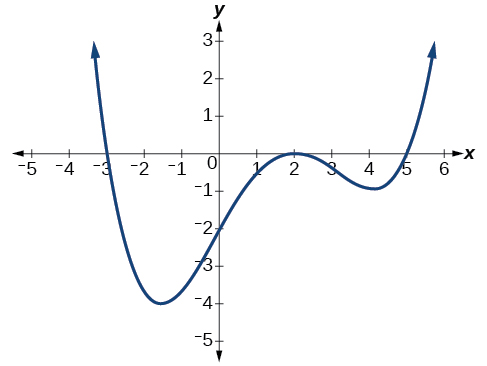
This graph has three x-intercepts: \(x=−3,\;2,\text{ and }5\). The y-intercept is located at \((0,2)\).At \(x=−3\) and \( x=5\), the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear. At \(x=2\), the graph bounces at the intercept, suggesting the corresponding factor of the polynomial will be second degree (quadratic). Together, this gives us

\[f(x)=a(x+3)(x−2)^2(x−5)\]

To determine the stretch factor, we utilize another point on the graph. We will use the y-intercept \((0,–2)\), to solve for \(a\).

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

The graphed polynomial appears to represent the function \(f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)\).

Exercise \(\PageIndex{5}\)

Given the graph shown in Figure \(\PageIndex{21}\), write a formula for the function shown.

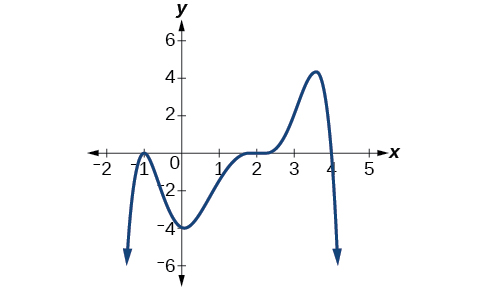
\(f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)\)

Using Local and Global Extrema

With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph.

Each turning point represents a local minimum or maximum. Sometimes, a turning point is the highest or lowest point on the entire graph. In these cases, we say that the turning point is a global maximum or a global minimum . These are also referred to as the absolute maximum and absolute minimum values of the function.

Note: Local and Global Extrema

A local maximum or local minimum at \(x=a\) (sometimes called the relative maximum or minimum, respectively) is the output at the highest or lowest point on the graph in an open interval around \(x=a\).If a function has a local maximum at \(a\), then \(f(a){\geq}f(x)\)for all \(x\) in an open interval around \(x=a\). If a function has a local minimum at \(a\), then \(f(a){\leq}f(x)\)for all \(x\) in an open interval around \(x=a\).

A global maximum or global minimum is the output at the highest or lowest point of the function. If a function has a global maximum at \(a\), then \(f(a){\geq}f(x)\) for all \(x\). If a function has a global minimum at \(a\), then \(f(a){\leq}f(x)\) for all \(x\).

We can see the difference between local and global extrema in Figure \(\PageIndex{22}\).

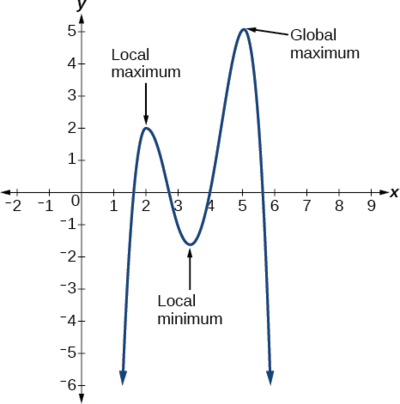
No. Only polynomial functions of even degree have a global minimum or maximum. For example, \(f(x)=x\) has neither a global maximum nor a global minimum.

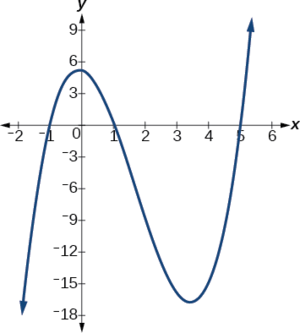
Example \(\PageIndex{11}\): Using Local Extrema to Solve Applications

An open-top box is to be constructed by cutting out squares from each corner of a 14 cm by 20 cm sheet of plastic then folding up the sides. Find the size of squares that should be cut out to maximize the volume enclosed by the box.

We will start this problem by drawing a picture like that in Figure \(\PageIndex{23}\), labeling the width of the cut-out squares with a variable, \(w\).

Notice that after a square is cut out from each end, it leaves \(a(14−2w)\) cm by \((20−2w)\) cm rectangle for the base of the box, and the box will be \(w\) cm tall. This gives the volume

\[\begin{align*} V(w)&=(20−2w)(14−2w)w \\ &=280w−68w^2+4w^3 \end{align*}\]

Notice, since the factors are \(20–2w\), \(14–2w\), and \(w\), the three zeros are \(10, \,7,\) and \(0,) respectively. Because a height of \(0\) cm is not reasonable, we consider the only the zeros \(10\) and \(7.\) The shortest side is \(14\) and we are cutting off two squares, so values \(w\) may take on are greater than zero or less than \(7.\) This means we will restrict the domain of this function to \(0<w<7\).Using technology to sketch the graph of \(V(w)\) on this reasonable domain, we get a graph like that in Figure \(\PageIndex{24}\). We can use this graph to estimate the maximum value for the volume, restricted to values for \(w\) that are reasonable for this problem—values from 0 to 7.

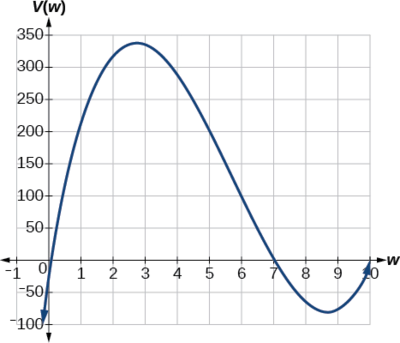
From this graph, we turn our focus to only the portion on the reasonable domain, \([0, 7]\). We can estimate the maximum value to be around 340 cubic cm, which occurs when the squares are about 2.75 cm on each side. To improve this estimate, we could use advanced features of our technology, if available, or simply change our window to zoom in on our graph to produce Figure \(\PageIndex{25}\).

From this zoomed-in view, we can refine our estimate for the maximum volume to about 339 cubic cm, when the squares measure approximately 2.7 cm on each side.

Use technology to find the maximum and minimum values on the interval \([−1,4]\) of the function \(f(x)=−0.2(x−2)^3(x+1)^2(x−4)\).

The minimum occurs at approximately the point \((0,−6.5)\), and the maximum occurs at approximately the point \((3.5,7)\).

Key Concepts

• Polynomial functions of degree 2 or more are smooth, continuous functions.
• To find the zeros of a polynomial function, if it can be factored, factor the function and set each factor equal to zero.
• Another way to find the x-intercepts of a polynomial function is to graph the function and identify the points at which the graph crosses the x-axis.
• The multiplicity of a zero determines how the graph behaves at the x-intercepts.
• The graph of a polynomial will cross the horizontal axis at a zero with odd multiplicity.
• The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity.
• The end behavior of a polynomial function depends on the leading term.
• The graph of a polynomial function changes direction at its turning points.
• A polynomial function of degree \(n\) has at most \(n−1\) turning points.
• To graph polynomial functions, find the zeros and their multiplicities, determine the end behavior, and ensure that the final graph has at most \(n−1\) turning points.
• Graphing a polynomial function helps to estimate local and global extremas.
• The Intermediate Value Theorem tells us that if \(f(a)\) and \(f(b)\) have opposite signs, then there exists at least one value \(c\) between \(a\) and \(b\) for which \(f(c)=0\).

global maximum highest turning point on a graph; \(f(a)\) where \(f(a){\geq}f(x)\) for all \(x\).

global minimum lowest turning point on a graph; \(f(a)\) where \(f(a){\leq}f(x)\) for all \(x\).

Intermediate Value Theorem for two numbers \(a\) and \(b\) in the domain of \(f\), if \(a<b\) and \(f(a){\neq}f(b)\), then the functionf takes on every value between \(f(a)\) and \(f(b)\); specifically, when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis

multiplicity the number of times a given factor appears in the factored form of the equation of a polynomial; if a polynomial contains a factor of the form \((x−h)^p\), \(x=h\) is a zero of multiplicity \(p\).