hypothesis testing of proportion calculator

• 1-800-234-2933
• [email protected]

Hypothesis Testing for a proportion Calculator

How does the Hypothesis Testing for a proportion Calculator work?

What 2 formulas are used for the hypothesis testing for a proportion calculator, what 6 concepts are covered in the hypothesis testing for a proportion calculator.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Subjects

Top Categories

• Trigonometry
• Pre-Algebra
• Pre-Calculus
• Post a Math Problem

Single Proportion Hypothesis Test Calculator

Use the calculator below to analyze the results of a single proportion hypothesis test. Enter your null hypothesis's proportion, sample proportion, sample size, test type, and significance level.

You will find a description of how to conduct a hypothesis test of a proportion below the calculator.

Define the z-test

Sample proportion under the null distribution, conducting single proportion hypothesis tests.

A hypothesis test of a sample proportion can help you make inferences about the population from which you drew it. It is a tool to determine what is probably true about an event or phenomena.

Testing a Proportion

For the results of a hypothesis test to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Binary Outcomes - When conducting a hypothesis test for a proportion, each sample point should consist of only one of two outcomes. We often label one outcome a “success” and one outcome a “failure,” but it does not matter which of the two outcomes gets which label.
• Success-Failure Rate - Your sample size should be large enough that under the null hypothesis proportion you are likely to see at least 10 “success” and 10 “failures.” For example, if you have null hypothesis proportion with a 10% or 0.1 “success” rate, then you would need a sample of 100 [10 = 100 * 10%] to have a large enough sample to meet this condition. This condition helps ensure that the sampling distribution from which you collect your sample reasonably follows the Normal Distribution.
• Simple Random Sampling - You should collect your sample with simple random sampling. This type of sampling requires that every occurrence of a category or event in a population has an equal chance of being selected when taking a sample.
• Sample-to-Population Ratio - The population should be much larger than the sample you collect. As a rule-of-thumb, the sample size should represent no more than 5% of the population.

You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test for a proportion.

The null hypothesis, is a skeptical claim that you would like to test. It is defined by a hypothesized proportion, which is often labeled P 0 .

The alternative hypothesis represents an alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

Before conducting a hypothesis test, you must determine a reasonable significance level , α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of P ≠ P 0 requires a two-tail test.
• One-tail tests place the rejection region entirely on one side of the null distribution i.e. to the right or left tail of the null sampling distribution. For example, in a one-tail test evaluating if the sampling distribution is above the null sampling distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. P > P 0 and P < P 0 alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, α, and collecting your sample, you are ready to analyze your hypothesis.

Sample proportions follow the Normal Distribution with the following parameters (i.e. numbers that define the distribution):

• The Population Proportion, P - The population proportion is assumed to be the proportion given by the null hypothesis in a single proportion hypothesis test.
• The Standard Error, SE - The standard error can be computed as follows: SE = sqrt((P x (1 - P))/ n), with n being the sample size. It defines how sample proportions are expected to vary around the null hypothesis's proportion given the sample size and under the assumption that the null hypothesis is true.

In a single proportion hypothesis test, we calculate the probability that we would observe the sample proportion, p, assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the z-score as follows: z = (p - P) / SE

The z-score is a test statistic that tells us how far our observation is from the null hypothesis's proportion under the null distribution. Using any z-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the z-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for a proportion is sometimes known as a z-test because of the use of a z-score in analyzing results.

If we find the probability is below the significance level, we reject the null hypothesis.

The conclusion of a hypothesis test for a proportion is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample proportion is the true population proportion. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.

A hypothesis test is simply a way to look at a sample and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for a Proportion

Let’s say you are the Marketing Director of a software company. You have set up a demo request page on your website, and you believe that 40% of visitors to that page will request a demo.

You decide to test your claim that 40% of visitors to the demo page will request a demo. So, you decide to run a hypothesis test for a proportion with a sample size of 500 visitors. Let’s go through the steps you would take to run the test.

• Check the conditions - Your test consists of binary outcomes (i.e. request demo and not request demo), your sample size is large enough to meet the success-failure condition but not too large to violate the sample-to-population ratio condition, and you collect your sample using simple random sampling . So, your test satisfies the conditions for a z-test of a single proportion.
• State Your Hypothesis - Your null hypothesis is that the true proportion of visitors requesting a demo equals 40%, formally stated P = 40%. Your alternate hypothesis is that the true proportion of vistors requesting a demo does not equal 40%, formally stated P ≠ 40%.
• Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is two-tail test, you will evaluate if your sample proportion would occur at the upper or lower 2.5% [2.5% = 5%/2] of the null distribution.
• Analyze Your Sample - You collect your samle (which you do after steps 1-3). You find that the proportion of visitors request a demo in your sample is 44%. Using the calculator above, you find that a sample proportion of 44% would results in a z-score of 1.83 under the null distribution, which translates to a p-value of 6.79%.
• Interpret Your Results - Since your p-value of 6.79% is greater than the significance level of 5%, you do not have sufficient evidence to reject the null hypothesis.

In this example, you found that you cannot reject your original claim that 40% of your demo webpage vistors request demos. The test does not guarantee that your 40% figure is correct, but it does give you confidence that you do not have sufficient evidence to say otherwise.

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Teach yourself statistics

Hypothesis Test for a Proportion

This lesson explains how to conduct a hypothesis test of a proportion, when the following conditions are met:

• The sampling method is simple random sampling .
• Each sample point can result in just two possible outcomes. We call one of these outcomes a success and the other, a failure.
• The sample includes at least 10 successes and 10 failures.
• The population size is at least 20 times as big as the sample size.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample z-test to determine whether the hypothesized population proportion differs significantly from the observed sample proportion.

Analyze Sample Data

Using sample data, find the test statistic and its associated P-Value.

σ = sqrt[ P * ( 1 - P ) / n ]

z = (p - P) / σ

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a z-score, use the Normal Distribution Calculator to assess the probability associated with the z-score. (See sample problems at the end of this lesson for examples of how this is done.)

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two hypothesis testing examples illustrate how to conduct a hypothesis test of a proportion. The first problem involves a a two-tailed test; the second problem, a one-tailed test.

Sample Size Calculator

As you probably noticed, the process of testing a hypothesis about a proportion can be complex. Stat Trek's Sample Size Calculator can do the same job quickly and easily. When you need to test a hypothesis, consider using the Sample Size Calculator. The calculator is free. It can found in the Stat Trek main menu under the Stat Tools tab. Or you can tap the button below.

Problem 1: Two-Tailed Test

The CEO of a large electric utility claims that 80 percent of his 1,000,000 customers are very satisfied with the service they receive. To test this claim, the local newspaper surveyed 100 customers, using simple random sampling. Among the sampled customers, 73 percent say they are very satisified. Based on these findings, can we reject the CEO's hypothesis that 80% of the customers are very satisfied? Use a 0.05 level of significance.

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.

Null hypothesis: P = 0.80

Alternative hypothesis: P ≠ 0.80

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method, shown in the next section, is a one-sample z-test .

σ = sqrt [(0.8 * 0.2) / 100]

σ = sqrt(0.0016) = 0.04

z = (p - P) / σ = (.73 - .80)/0.04 = -1.75

where P is the hypothesized value of population proportion in the null hypothesis, p is the sample proportion, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the z-score is less than -1.75 or greater than 1.75. We use the Normal Distribution Calculator to find P(z < -1.75) = 0.04. Since the standard normal distribution is symmetric with a mean of zero, we know that P(z > 1.75) = 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.

• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the sample included at least 10 successes and 10 failures, and the population size was at least 10 times the sample size.

Problem 2: One-Tailed Test Suppose the previous example is stated a little bit differently. Suppose the CEO claims that at least 80 percent of the company's 1,000,000 customers are very satisfied. Again, 100 customers are surveyed using simple random sampling. The result: 73 percent are very satisfied. Based on these results, should we accept or reject the CEO's hypothesis? Assume a significance level of 0.05.

Null hypothesis: P >= 0.80

Alternative hypothesis: P < 0.80

σ = sqrt[ P * ( 1 - P ) / n ] = sqrt [(0.8 * 0.2) / 100]

• Interpret results . Since the P-value (0.04) is less than the significance level (0.05), we cannot accept the null hypothesis.

This calculator runs a one sample proportion test for a given sample data set and specified null and alternative hypotheses. In the fields below enter the sample size \(n\) and the number of scores with the trait of interest, \(f\).

Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. It must be between the values 0 and 1. Indicate whether your alternative hypothesis involves one-tail or two-tails. If it is a one-tailed test, then you need to indicate whether it is a positive (right tail) test or a negative (left tail) test.

Enter an \(\alpha\) value for the hypothesis test. This is the Type I error rate for your hypothesis test. It also determines the confidence level \(100 \times (1-\alpha)\) for a confidence interval. The confidence interval is based on the normal distribution, which is an approximation.

Press the Run Test button and a table summarizing the computations and conclusions will appear below.

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a proportion.

A population proportion is the share of a population that belongs to a particular category .

Hypothesis tests are used to check a claim about the size of that population proportion.

Hypothesis Testing a Proportion

The following steps are used for a hypothesis test:

• Check the conditions
• Define the claims
• Decide the significance level
• Calculate the test statistic

For example:

• Population : Nobel Prize winners
• Category : Born in the United States of America

And we want to check the claim:

" More than 20% of Nobel Prize winners were born in the US"

By taking a sample of 40 randomly selected Nobel Prize winners we could find that:

10 out of 40 Nobel Prize winners in the sample were born in the US

The sample proportion is then: \(\displaystyle \frac{10}{40} = 0.25\), or 25%.

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

• The sample is randomly selected
• Being in the category
• Not being in the category
• 5 members in the category
• 5 members not in the category

In our example, we randomly selected 10 people that were born in the US.

The rest were not born in the US, so there are 30 in the other category.

The conditions are fulfilled in this case.

Note: It is possible to do a hypothesis test without having 5 of each category. But special adjustments need to be made.

2. Defining the Claims

We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.

The claim was:

In this case, the parameter is the proportion of Nobel Prize winners born in the US (\(p\)).

The null and alternative hypothesis are then:

Null hypothesis : 20% of Nobel Prize winners were born in the US.

Alternative hypothesis : More than 20% of Nobel Prize winners were born in the US.

Which can be expressed with symbols as:

\(H_{0}\): \(p = 0.20 \)

\(H_{1}\): \(p > 0.20 \)

This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

Advertisement

3. Deciding the Significance Level

The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

• \(\alpha = 0.1\) (10%)
• \(\alpha = 0.05\) (5%)
• \(\alpha = 0.01\) (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population proportion is:

\(\displaystyle \frac{\hat{p} - p}{\sqrt{p(1-p)}} \cdot \sqrt{n} \)

\(\hat{p}-p\) is the difference between the sample proportion (\(\hat{p}\)) and the claimed population proportion (\(p\)).

\(n\) is the sample size.

In our example:

The claimed (\(H_{0}\)) population proportion (\(p\)) was \( 0.20 \)

The sample size (\(n\)) was \(40\)

So the test statistic (TS) is then:

\(\displaystyle \frac{0.25-0.20}{\sqrt{0.2(1-0.2)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.2(0.8)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.16}} \cdot \sqrt{40} \approx \frac{0.05}{0.4} \cdot 6.325 = \underline{0.791}\)

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic for a proportion.

With R use the built-in prop.test() function to calculate the test statistic for a proportion.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).

For a population proportion test, the critical value (CV) is a Z-value from a standard normal distribution .

This critical Z-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population proportion is more than 20%, the rejection region is in the right tail:

Choosing a significance level (\(\alpha\)) of 0.05, or 5%, we can find the critical Z-value from a Z-table , or with a programming language function:

Note: The functions find the Z-value for an area from the left side.

To find the Z-value for a right tail we need to use the function on the area to the left of the tail (1-0.05 = 0.95).

With Python use the Scipy Stats library norm.ppf() function find the Z-value for an \(\alpha\) = 0.05 in the right tail.

With R use the built-in qnorm() function to find the Z-value for an \(\alpha\) = 0.05 in the right tail.

Using either method we can find that the critical Z-value is \(\approx \underline{1.6449}\)

For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).

If the test statistic is bigger than the critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).

Here, the test statistic (TS) was \(\approx \underline{0.791}\) and the critical value was \(\approx \underline{1.6449}\)

Here is an illustration of this test in a graph:

Since the test statistic was smaller than the critical value we do not reject the null hypothesis.

This means that the sample data does not support the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 5% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).

The test statistic was found to be \( \approx \underline{0.791} \)

For a population proportion test, the test statistic is a Z-Value from a standard normal distribution .

Because this is a right tailed test, we need to find the P-value of a Z-value bigger than 0.791.

We can find the P-value using a Z-table , or with a programming language function:

Note: The functions find the P-value (area) to the left side of Z-value.

To find the P-value for a right tail we need to subtract the left area from the total area: 1 - the output of the function.

With Python use the Scipy Stats library norm.cdf() function find the P-value of a Z-value bigger than 0.791:

With R use the built-in pnorm() function find the P-value of a Z-value bigger than 0.791:

Using either method we can find that the P-value is \(\approx \underline{0.2145}\)

This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.2145, or 21.45%, to reject the null hypothesis.

This P-value is bigger than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is kept at all of these significance levels.

The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 10%, 5%, or 1% significance level .

Note: It may still be true that the real population proportion is more than 20%.

But there was not strong enough evidence to support it with this sample.

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a proportion.

Here, the sample size is 40, the occurrences are 10, and the test is for a proportion bigger than 0.20.

With R use the built-in prop.test() function find the P-value for a right tailed hypothesis test for a proportion.

Note: The conf.level in the R code is the reverse of the significance level.

Here, the significance level is 0.05, or 5%, so the conf.level is 1-0.05 = 0.95, or 95%.

Left-Tailed and Two-Tailed Tests

This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

• Left-Tailed Test
• Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

Other calculators ...

Free statistical calculators, test for one proportion calculator, description.

The Test for one proportion can be used to test the hypothesis that an observed proportion is equal to a pre-specified proportion.

This test is not performed on data in the data table, but on statistics you enter in a dialog box.

Required input

Computational notes.

The significance level, or P-value, is calculated using a general z-test (Altman, 1991):

where p is the observed proportion; p exp is the Null hypothesis (or expected) proportion; and se ( p ) is the standard error of the expected proportion:

The P-value is the area of the normal distribution that falls outside ± z (see Values of the Normal distribution table).

If the P-value is less than 0.05, the hypothesis that the observed proportion is equal to the pre-specified proportion value is rejected, and the alternative hypothesis that there is a significant difference between the two proportions can be accepted.

Confidence interval

MedCalc calculates the "exact" Clopper-Pearson confidence interval for the observed proportion (Clopper & Pearson, 1934; Fleis et al., 2003).

How to cite this page

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.5 - hypothesis testing for two-sample proportions.

We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group.

These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing for two groups. If this starts to get a little confusion, just skim over it for a general understanding! Remember we can rely on the software to do the calculations for us, but it is good to have a basic understanding of the logic!

We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval.

For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:

\(H_0\colon p_1-p_2=0\)

Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\).

Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).

We take this into account by finding an estimate for this \(p^*\) using the two-sample proportions. We can calculate an estimate of \(p^*\) using the following formula:

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)

This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).

Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.

\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...will follow a standard normal distribution.

Finally, we can develop our hypothesis test for \(p_1-p_2\).

Hypothesis Testing for Two-Sample Proportions

Conditions :

\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five

Test Statistic:

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).

The critical values, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one-sample proportion.

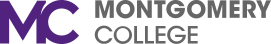
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

9 Inference for the Proportion

• SUBEDI Calc

1. SUBEDI CALCULATORS

Inference for the Proportion new window

Hypothesis testing for the proportion using either data or sample statistics from one sample or two samples . Option to include confidence interval in the results.

Calculator Screenshot

2. LibreTEXT CALCULATORS

Hypothesis Test for a Population Proportion new window

Hypothesis Test for Two Proportions new window

3. Ti 83/84+

Statistics Calculators Copyright © 2021 by Ram Subedi is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Z-test for Two Proportions

Instructions: This calculator conducts a Z-test for two population proportions (\(p_1\) and \(p_2\)), Please select the null and alternative hypotheses, type the significance level, the sample sizes, the number of favorable cases (or the sample proportions) and the results of the z-test will be displayed for you:

When Do You Use a Z-test for Two Proportions?

More about the z-test for two proportions so you can better understand the results yielded by this solver: A z-test for two proportions is a hypothesis test that attempts to make a claim about the population proportions p 1 and p 2 . Specifically, we are interested in assessing whether or not it is reasonable to claim that p 1 = p 2 , using sample information. The Z-test for two proportions has two non-overlapping hypotheses, the null and the alternative hypothesis.

What are the null and alternative hypotheses for the z-test for two proportions?

The null hypothesis is a statement about the population parameter which indicates no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for two population proportions are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

What is the z-test formula in this case?

The formula for a z-statistic for two population proportions is

where \(\bar p = \frac{X_1+X_2}{n_1+n_2}\) corresponds to the pooled proportion (Notice that in the above z test for proportions formula, we get in the denominator something like our "best guess" of what the population proportion is from information from the two samples, assuming that the null hypothesis of equality of proportions is true). The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

The Case for one population proportion

In case you only have one sample proportion (so you are testing for one population proportion), you should use our z-test for one proportion calculator , which specifically addresses that case.

Related Calculators

log in to your account

Reset password.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

33: Hypothesis Test and Confidence Interval Calculator- Difference Between Population Proportions

• Last updated
• Save as PDF
• Page ID 8621

• Larry Green
• Lake Tahoe Community College

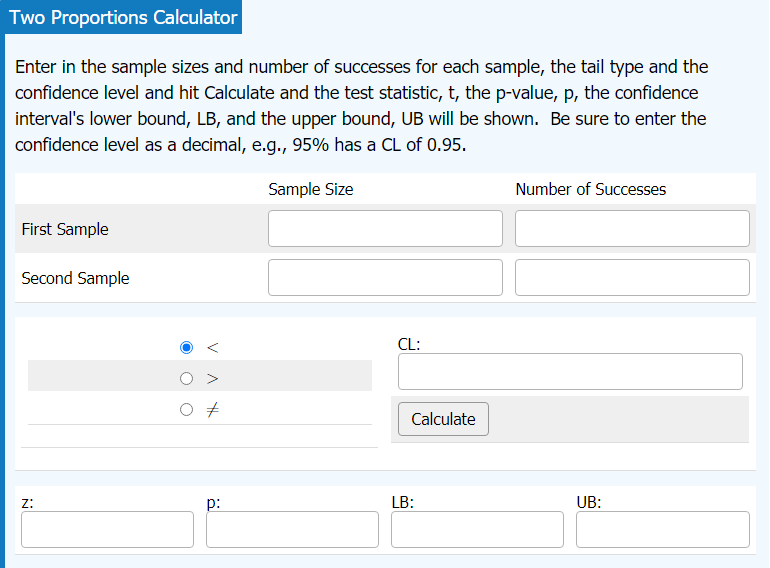
Two Proportions Calculator

Enter in the sample sizes and number of successes for each sample, the tail type and the confidence level and hit Calculate and the test statistic, t, the p-value, p, the confidence interval's lower bound, LB, and the upper bound, UB will be shown.  Be sure to enter the confidence level as a decimal, e.g., 95% has a CL of 0.95.

Back to the Calculator Menu

Statistics Made Easy

Two Proportion Z-Test Calculator

• p = total pooled proportion
• p 1 = sample 1 proportion
• p 2 = sample 2 proportion
• n 1 = sample 1 size
• n 2 = sample 2 size

z-statistic: 0.31917

p-value (one-tailed): 0.37480

p-value (two-tailed): 0.74960

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Two sample proportion test calculator

Calcualate h effect size, reporting results in apa style, two proportion z test calculator, what is the continuity correction, should i use the continuity correction, when using continuity correction, confidence interval statistics formula, assumptions, required sample data, calculators.