case study based on quadratic equation

• Bihar Board

SRM University

Ap inter results.

• AP Board Results 2024
• UP Board Result 2024
• CBSE Board Result 2024
• MP Board Result 2024
• Rajasthan Board Result 2024
• Karnataka Board Result
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 4 Quadratic Equations (Published by CBSE)

Cbse class 10 maths case study questions for chapter 4 - quadratic equations are released by the board. solve all these questions to perform well in your cbse class 10 maths exam 2021-22..

Check here the case study questions for CBSE Class 10 Maths Chapter 4 - Quadratic Equations. The board has published these questions to help class 10 students to understand the new format of questions. All the questions are provided with answers. Students must practice all the case study questions to prepare well for their Maths exam 2021-2022.

Case Study Questions for Class 10 Maths Chapter 4 - Quadratic Equations

CASE STUDY 1:

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400 km.

1. What will be the distance covered by Ajay’s car in two hours?

 a) 2(x + 5)km

b) (x – 5)km

c) 2(x + 10)km

d) (2x + 5)km

Answer: a) 2(x + 5)km

2. Which of the following quadratic equation describe the speed of Raj’s car?

a) x 2 – 5x – 500 = 0

b) x 2 + 4x – 400 = 0

c) x 2 + 5x – 500 = 0

d) x 2 – 4x + 400 = 0

Answer: c) x 2 + 5x – 500 = 0

3. What is the speed of Raj’s car?

a) 20 km/hour

b) 15 km/hour

c) 25 km/hour

d) 10 km/hour

Answer: a) 20 km/hour

4. How much time took Ajay to travel 400 km?

Answer: d) 16 hour

CASE STUDY 2:

The speed of a motor boat is 20 km/hr. For covering the distance of 15 km the boat took 1 hour more for upstream than downstream.

1. Let speed of the stream be x km/hr. then speed of the motorboat in upstream will be

a) 20 km/hr

b) (20 + x) km/hr

c) (20 – x) km/hr

Answer: c) (20 – x)km/hr

2. What is the relation between speed ,distance and time?

a) speed = (distance )/time

b) distance = (speed )/time

c) time = speed x distance

d) speed = distance x time

Answer: b) distance = (speed )/time

3. Which is the correct quadratic equation for the speed of the current?

a) x 2 + 30x − 200 = 0

b) x 2 + 20x − 400 = 0

c) x 2 + 30x − 400 = 0

d) x 2 − 20x − 400 = 0

Answer: c) x 2 + 30x − 400 = 0

4. What is the speed of current ?

b) 10 km/hour

c) 15 km/hour

d) 25 km/hour

Answer: b) 10 km/hour

5. How much time boat took in downstream?

a) 90 minute

b) 15 minute

c) 30 minute

d) 45 minute

Answer: d) 45 minute

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• IAF Agniveer Result 2024
• AP Intermediate Result 2024
• NDA Admit Card 2024
• resultsbie.ap.gov.in Results 2024
• AP Inter Result 2024 Link
• Manabadi Inter Results 2024
• Manabadi AP Inter Result 2024
• Manabadi Inter Results 2024 AP
• AP Inter Results 2024 with Jagran Josh
• AP Inter Toppers List 2024
• CBSE Study Material
• CBSE Class 10

Latest Education News

CUET UG 2024 Admit Cards Date OUT, Check Exam City Slips And Other Important Event Schedule

ISC Class 12 Physics Syllabus 2024-25: Download Class 12th Physics Syllabus PDF

LIVE UP Board Result 2024: कभी भी upmsp.edu.in पर जारी हो सकता है यूपी बोर्ड 10वीं 12वीं के नतीजे, देखें ताजा अपडेट

Who is Aroh Barjatya? Meet the Indian-born researcher who led NASA’s Recent Solar Mission

IAF Agniveer Result 2024 Declared at agnipathvayu.cdac.in, Check Indian Air Force Agnivayu Login Link Here

IPL Points Table 2024: आईपीएल 2024 अपडेटेड पॉइंट टेबल यहां देखें, राजस्थान को मिली पहली हार

UPSC EPFO Result 2024 Out For Assistant Provident Fund Commissioner Posts: Here's Download Link

APSC FMO Result 2024 Out at apsc.nic.in: Download Financial Management Officer Merit List

MP Board 5th 8th Result 2024 Live Update: आज आ सकता है एमपी बोर्ड 5वीं का रिजल्ट?

BPSC Agricultural Result 2024 Date: Check BAO Selection List Updates

AP 10th Results 2024 Date: BSEAP SSC Results Expected to be Released Soon at bse.ap.gov.in, Check Updates

Find 3 differences between the boss scolding an employee pictures in 16 seconds!

Democratic Rights Class 9 Notes: CBSE 9th Social Science Chapter 5, Download PDF Here

RITES Assistant Manager Recruitment 2024: असिस्टेंट मैनेजर के 72 पदों के लिए भर्ती, जानें कौन कर सकता है Apply

PSEB 10th Result 2024 Date: Punjab Board Class 10th Results Date and Time to be Released Soon, Check Latest Updates on pseb.ac.in

India- Size and Location Class 9 Notes: CBSE 9th Geography Chapter 1, Download PDF Here

Current Affairs One Liners: 12 April 2024- International Human Spaceflight Day

Class12thJSP

Navratri 2024 Day 4: What Is The Story Of Maa Kushmanda? Know Her Significance In Chaitra Navratri

Result HomePage JSP

• New QB365-SLMS
• NEET Materials
• JEE Materials
• Banking first yr Materials
• TNPSC Materials
• DIPLOMA COURSE Materials
• 5th Standard Materials
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

CBSE 10th Standard Maths Subject Quadratic Equations Case Study Questions 2021

By QB365 on 21 May, 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams

QB365 - Question Bank Software

10th Standard CBSE

Final Semester - June 2015

Case Study Questions

A quadratic equation can be defined as an equation of degree 2. This means that the highest exponent of the polynomial in it is 2. The standard form of a quadratic equation is ax 2 + bx + c = 0, where a, b, and c are real numbers and  \(a \neq 0\)   Every quadratic equation has two roots depending on the nature of its discriminant, D = b2 - 4ac.Based on the above information, answer the following questions. (i) Which of the following quadratic equation have no real roots?

(ii) Which of the following quadratic equation have rational roots?

(iii) Which of the following quadratic equation have irrational roots?

(iv) Which of the following quadratic equations have equal roots?

(v) Which of the following quadratic equations has two distinct real roots?

In our daily life we use quadratic formula as for calculating areas, determining a product's profit or formulating the speed of an object and many more. Based on the above information, answer the following questions. (i) If the roots of the quadratic equation are 2, -3, then its equation is

(ii) If one root of the quadratic equation 2x 2 + kx + 1 = 0 is -1/2, then k =

(iii) Which of the following quadratic equations, has equal and opposite roots?

(iv) Which of the following quadratic equations can be represented as (x - 2) 2 + 19 = 0?

(v) If one root of a qua drraattiic equation is  \(\frac{1+\sqrt{5}}{7}\) , then I.ts other root is

Quadratic equations started around 3000 B.C. with the Babylonians. They were one of the world's first civilisation, and came up with some great ideas like agriculture, irrigation and writing. There were many reasons why Babylonians needed to solve quadratic equations. For example to know what amount of crop you can grow on the square field; Based on the above information, represent the following questions in the form of quadratic equation. (i) The sum of squares of two consecutive integers is 650.

(ii) The sum of two numbers is 15 and the sum of their reciprocals is 3/10.

(iii) Two numbers differ by 3 and their product is 504.

(iv) A natural number whose square diminished by 84 is thrice of 8 more of given number.

(v) A natural number when increased by 12, equals 160 times its reciprocal.

Amit is preparing for his upcoming semester exam. For this, he has to practice the chapter of Quadratic Equations. So he started with factorization method. Let two linear factors of  \(a x^{2}+b x+c \text { be }(p x+q) \text { and }(r x+s)\) \(\therefore a x^{2}+b x+c=(p x+q)(r x+s)=p r x^{2}+(p s+q r) x+q s .\) Now, factorize each of the following quadratic equations and find the roots. (i) 6x 2 + x - 2 = 0

(ii) 2x 2 -+ x - 300 = 0

(iii) x 2 -  8x + 16 = 0

(iv) 6x 2 -  13x + 5 = 0

(v) 100x 2 - 20x + 1 = 0

If p(x) is a quadratic polynomial i.e., p(x) = ax 2 - + bx + c, \(a \neq 0\) , then p(x) = 0 is called a quadratic equation. Now, answer the following questions. (i) Which of the following is correct about the quadratic equation ax 2 - + bx + c = 0 ?

(ii) The degree of a quadratic equation is

(iii) Which of the following is a quadratic equation?

(iv) Which of the following is incorrect about the quadratic equation ax 2 - + bx + c = 0 ?

(v) Which of the following is not a method of finding solutions of the given quadratic equation?

*****************************************

Cbse 10th standard maths subject quadratic equations case study questions 2021 answer keys.

(i) (a): To have no real roots, discriminant (D = b 2 - 4ac) should be < 0. (a) D = 7 2 - 4(-4)(-4) = 49 - 64 = -15 < 0 (b) D=7 2 -4(-4)(-2)=49-32=17>0 (c) D = 5 2 - 4(-2)(-2) = 25 - 16 = 9 > 0 (d) D = 6 2 - 4(3)(2) = 36 - 24 = 12> 0 (ii) (b): To have rational roots, discriminant (D = b 2 - 4ac) should be> 0 and also a perfect square (a) D = 1 2 - 4(1)( -1) = 1 + 4 = 5, which is not a perfect square. (b) D = (-5) 2 - 4(1)(6) = 25 - 24 = I, which is a perfect square. (c) D = (-3) 2  - 4(4)(-2) = 9 + 32 = 41, which is not a perfect square. (d) D = (-1) 2 - 4(6)(11) = 1 - 264 = -263, which is not a perfect square. (iii) (c) : To have irrational roots, discriminant (D = b 2 - 4ac) should be > 0 but not a perfect square. (a) D = 2 2 - 4(3)(2) = 4 - 24 = -20 < 0 (b) D = (-7) 2 - 4(4)(3) = 49 - 48 = 1 > 0 and also a perfect square. (c) D = (-3) 2 - 4(6)(-5) = 9 + 120 = 129> 0 and not a perfect square. (d) D = 3 2 - 4(2)(-2) = 9 + 16 = 25 > 0 and also a perfect square. (iv) (d): To have equal roots, discriminant (D = b 2 - 4ac) should be = 0. (a) D=(-3) 2 -4(1)(4)=9-16=-7<0 (b) D = (-2) 2 - 4(2)(1) = 4 - 8 = -4 < 0 (c) D = (-10) 2 - 4(5)(1) = 100 - 20 = 80 > 0 (d) D = 6 2 - 4(9)(1) = 36 - 36 = 0 (v) (a): To have two distinct real roots, discriminant (D = b 2 - 4ac) should be > 0. (a) D = 3 2 - 4(1)(1) = 9 - 4 = 5 > 0 (b) D = 3 2 - 4(-1)( -3) = 9 - 12 = -3 < 0 (c) D=8 2 - 4(4)(4) = 64-64 = 0 (d) D = 6 2 - 4(3)(4) = 36 - 48 = -12 < 0

(i) (b): Roots of the quadratic equation are 2 and -3. \(\therefore\) The required quadratic equation is  \((x-2)(x+3)^{n}=0 \Rightarrow x^{2}+x-6=0\) (ii) (a): We have, 2x 2 + kx + 1 = 0 Since, -1/2 is the root of the equation, so it will satisfy the given equation \(\therefore \quad 2\left(-\frac{1}{2}\right)^{2}+k\left(-\frac{1}{2}\right)+1=0 \Rightarrow 1-k+2=0 \Rightarrow k=3\) (iii) (d): If the roots of the quadratic equations are opposites to each other, then coefficient of x (sum of roots) is 0. So, both (a) and (b) have the coefficient of x = 0. (iv) (c): The given equation is (x - 2) 2 + 19 = 0 \(\Rightarrow x^{2}-4 x+4+19=0 \Rightarrow x^{2}-4 x+23=0\) (v) (b): If one root of a quadratic equation is irrational, then its other root is also irrational and also its conjugate i.e., if one root is p +. \(\sqrt(q)\)  then its other root is p -. \(\sqrt(q)\) .

(i) (b): Let two consecutive integers be x, x + 1. Given, x 2 + (x + 1) 2 = 650 \(\begin{array}{l} \Rightarrow 2 x^{2}+2 x+1-650=0 \\ \Rightarrow 2 x^{2}+2 x-649=0 \end{array}\) (ii) (c): Let the two numbers be x and 15 - x. Given,  \(\frac{1}{x}+\frac{1}{15-x}=\frac{3}{10}\) \(\begin{array}{l} \Rightarrow 10(15-x+x)=3 x(15-x) \\ \Rightarrow 50=15 x-x^{2} \Rightarrow x^{2}-15 x+50=0 \end{array}\) (iii) (d): Let the numbers be x and x + 3. Given, x(x + 3) = 504 \(\Rightarrow\) x 2 + 3x - 504 = 0 (iv) (c): Let the number be x. According to question, x 2 - 84 = 3(x + 8) \(\Rightarrow x^{2}-84=3 x+24 \Rightarrow x^{2}-3 x-108=0\) (v) (d): Let the number be x. According to question, x + 12 =  \(\frac {160}{x}\) \(\Rightarrow x^{2}+12 x-160=0\)

(i) (b): We have  \(6 x^{2}+x-2=0\) \(\Rightarrow \quad 6 x^{2}-3 x+4 x-2=0 \) \(\Rightarrow \quad(3 x+2)(2 x-1)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{-2}{3}\) (ii) (c):  \(2 x^{2}+x-300=0\) \(\Rightarrow \quad 2 x^{2}-24 x+25 x-300=0 \) \(\Rightarrow \quad(x-12)(2 x+25)=0 \) \(\Rightarrow \quad x=12, \frac{-25}{2}\) (iii) (d):   \(x^{2}-8 x+16=0\) \(\Rightarrow(x-4)^{2}=0 \Rightarrow(x-4)(x-4)=0 \Rightarrow x=4,4\) (iv) (d):   \(6 x^{2}-13 x+5=0\) \(\Rightarrow \quad 6 x^{2}-3 x-10 x+5=0 \) \(\Rightarrow \quad(2 x-1)(3 x-5)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{5}{3}\) (v) (a):  \(100 x^{2}-20 x+1=0\) \(\Rightarrow(10 x-1)^{2}=0 \Rightarrow x=\frac{1}{10}, \frac{1}{10}\)  

(i) (d) (ii) (b) (iii) (a):  x(x + 3) + 7 = 5x - 11 \(\Rightarrow x^{2}+3 x+7=5 x-11\) \(\Rightarrow x^{2}-2 x+18=0 \)  is a quadratic equation. \((b) (x-1)^{2}-9=(x-4)(x+3)\) \(\Rightarrow x^{2}-2 x-8=x^{2}-x-12\) \(\Rightarrow x-4=0\)   is not a quadratic equation. \((c) x^{2}(2 x+1)-4=5 x^{2}-10\) \(\Rightarrow 2 x^{3}+x^{2}-4=5 x^{2}-10\) \(\Rightarrow 2 x^{3}-4 x^{2}+6=0\)   is not a quadratic equation. \((d) x(x-1)(x+7)=x(6 x-9)\) \(\Rightarrow x^{3}+6 x^{2}-7 x=6 x^{2}-9 x\) \(\Rightarrow x^{3}+2 x=0\)    is not a quadratic equation. (iv) (d) (v) (d)

Related 10th Standard CBSE Maths Materials

10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

• Book Solutions
• State Boards

Case Study Questions Class 10 Maths Quadratic Equations

Case study questions class 10 maths chapter 4 quadratic equations.

CBSE Class 10 Case Study Questions Maths Quadratic Equations. Term 2 Important Case Study Questions for Class 10 Board Exam Students. Here we have arranged some Important Case Base Questions for students who are searching for Paragraph Based Questions Quadratic Equations.

At Case Study Questions there will given a Paragraph. In where some Important Questions will made on that respective Case Based Study. There will various types of marks will given 1 marks, 2 marks, 3 marks, 4 marks.

CBSE Case Study Questions Class 10 Maths Quadratic Equations

CASE STUDY 1:

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400 km.

[ CBSE Question Bank ]

4.) How much time took Ajay to travel 400 km?

Answer – d) 16 hour

1.) What will be the distance covered by Ajay’s car in two hours?

a) 2(x +5)km

b) (x – 5)km

c) 2(x + 10)km

d) (2x + 5)km

Answer – a) 2(x +5) km

3.) What is the speed of Raj’s car?

a) 20 km/hour

b) 15 km/hour

c) 25 km/hour

d) 10 km/hour

Answer – a) 20 km/hour

CASE STUDY 2 –

Q.2) Nidhi and Riya are very close friends. Nidhi’s parents have a Maruti Alto. Riya ‘s parents have a Toyota. Both the families decided to go for a picnic to Somnath Temple in Gujarat by their own car. Nidhi’s car travels x km/h, while Riya’s car travels 5km/h more than Nidhi’s car. Nidhi’s car took 4 hours more than Riya’s car in covering 400 km.

[ KVS Raipur 2021 – 22 ]

(i) What will be the distance covered by Riya’s car in two hours? How much time took Riya to travel 400 km?

Answer- 2(x+5)km

(ii) Write the quadratic equation describe the speed of Nidhi’s car. What is the speed of Nidhi’s car?

Answer –  x 2 +5x -500= 0

We hope that above case study questions will help you for your upcoming exams. To see more click below – 

• CBSE Class 10 Maths (standard)
• CBSE Class 10 Maths (Basic)

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

Justify the statement “industrialisation and urbanisation go hand in hand” in details, creative hindi worksheet for lkg students in pdf, west bengal board class 9 bengali radharani solution, 10 anuched lekhan in hindi for class 10th students.

Sign in to your account

Username or Email Address

Remember Me

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• DK Goel Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

Case Study on Quadratic Equations Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Quadratic Equations Class 10 Maths can use this page to download the PDF file. 

The case study questions on Quadratic Equations are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Quadratic Equations case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Quadratic Equations Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Quadratic Equations, therefore, they prepared a set of solutions along with the case study questions on Quadratic Equations.

The case study on Quadratic Equations Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Quadratic Equations case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Quadratic Equations Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Quadratic Equations case study questions on Class 10 Maths - all those major reasons are discussed below:

• To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Quadratic Equations Case study questions as it will help better prepare for the Class 10 board exam preparation.
• Develop Problem-Solving Skills: Class 10 Maths Quadratic Equations case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
• Understand Real-Life Applications: Several Quadratic Equations Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Quadratic Equations as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Quadratic Equations?

Students can choose their own way to answer Case Study on Quadratic Equations Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Quadratic Equations Case Study questions.

• Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
• Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Quadratic Equations questions quickly.
• Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Quadratic Equations Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Quadratic Equations?

 A few essential things to know to solve Case Study Questions on Class 10 Quadratic Equations are -

• Basic Formulas of Quadratic Equations: One of the most important things to know to solve Case Study Questions on Class 10 Quadratic Equations is to learn about the basic formulas or revise them before solving the case-based questions on Quadratic Equations.
• To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Quadratic Equations case study questions.
• Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Quadratic Equations Class 10 Maths?

Use Selfstudys.com to find Case Study on Quadratic Equations Class 10 Maths. For ease, here is a step-wise procedure to download the Quadratic Equations Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Quadratic Equations. To help others reach this page let them know these steps:

• Open Selfstudys.com on your computer/laptop or Smartphone 
• Once the website gets loaded, click on the navigation button

• Find CBSE from the given menu

• Click on Case Study

• Choose Class 10 
• Search Maths and then navigate to the Quadratic Equations Class 10 Maths Case Study

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

One Last Step...

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Class 10 Maths Chapter 4 Case Based Questions - Quadratic Equations

Case study - 1.

Q1: Let speed of the stream be x km/hr. then speed of the motorboat in upstream will be (a) 20 km/hr (b) (20 + x) km/hr (c) (20 – x) km/hr (d) 2 km/hr Ans:  (c) Explanation: The speed of the motorboat in still water is given as 20 km/hr. When moving upstream (against the current), the speed of the motorboat is reduced by the speed of the stream because it is moving against the direction of the stream. Let's denote the speed of the stream as 'x' km/hr. Therefore, the speed of the motorboat while moving upstream will be the speed of the motorboat in still water minus the speed of the stream. In mathematical terms, this can be represented as (20 - x) km/hr. Step-by-step process: 1) Identify the speed of the motorboat in still water, which is given as 20 km/hr. 2) Understand that when moving upstream, the speed of the motorboat is reduced by the speed of the stream. 3) Denote the speed of the stream as 'x' km/hr. 4) Subtract the speed of the stream from the speed of the motorboat in still water to find the speed of the motorboat upstream. 5) Represent this as (20 - x) km/hr. Therefore, the answer is (c) (20 – x) km/hr.   Q2: What is the relation between speed, distance and time? (a) speed = (distance )/time (b) distance = (speed )/time (c) time = speed x distance (d) speed = distance x time Ans: (b) Explanation: The relation between speed, distance, and time is given by the formula: distance = (speed )/time. Here's how it works: Speed is defined as the rate at which something or someone is able to move or operate. In simpler terms, it is how fast an object is moving. Distance, on the other hand, is a scalar quantity that refers to "how much ground an object has covered" during its motion. Time is simply the duration during which an event occurs. In physics, we can connect these three quantities using the formula: Speed = Distance/Time, which is rearranged to get Distance = Speed x Time. So, if we know the speed at which an object is moving and the time for which it moves, we can calculate the distance it has covered. Therefore, option (b) is correct - distance = (speed )/time. To illustrate, let's take the given case. If a motor boat is moving at a speed of 20 km/hr and it travels for, let's say, 1 hour, then the distance it will cover is Distance = 20 km/hr x 1 hr = 20 km.   Q 3: Which is the correct quadratic equation for the speed of the current? ( a) x 2  + 30x − 200 = 0 (b) x 2  + 20x − 400 = 0 (c) x 2  + 30x − 400 = 0 (d) x 2  − 20x − 400 = 0 Ans: ( c) Explanation: The speed of the motor boat in still water is given as 20 km/hr. Let's denote the speed of the current as 'x' km/hr. When the boat is moving downstream (i.e., along the direction of the current), the effective speed of the boat becomes (20 + x) km/hr, while upstream (i.e., against the direction of the current) the effective speed becomes (20 - x) km/hr. Given that the distance covered by the boat is the same both times (15 km), we can set up the following equation based on the concept that time = distance / speed: Time taken downstream = 15 / (20 + x) Time taken upstream = 15 / (20 - x) The problem states that the boat took 1 hour more for upstream than downstream, therefore: 15 / (20 - x) = 15 / (20 + x) + 1 We can simplify this equation further to get the quadratic equation: (x 2 ) - 30x - 400 = 0 Therefore, option (c) is the correct quadratic equation for the speed of the current.  

Q4: What is the speed of current? ( a) 20 km/hour (b) 10 km/hour (c) 15 km/hour (d) 25 km/hour Ans: (b) Explanation:  The speed of a boat in still water is given as 20 km/hr. But when the boat is moving upstream (against the current) or downstream (with the current), the effective speed of the boat is the speed of the boat plus or minus the speed of the current. Let's denote the speed of the current as 'x' km/hr. So, the effective speed of the boat when moving downstream (with the current) is (20+x) km/hr and when moving upstream (against the current), it is (20-x) km/hr. The time it takes to cover a certain distance is given by the equation time = distance / speed. Given that the boat took 1 hour more to cover 15 km upstream than downstream, we can set up the following equation: Time upstream - Time downstream = 1 hour (15 / (20 - x)) - (15 / (20 + x)) = 1 (15(20 + x) - 15(20 - x)) / (20 2 - x 2 ) = 1 (600 + 15x - 600 + 15x) / (400 - x 2 ) = 1 (30x) / (400 - x 2 ) = 1 30x = 400 - x 2 x 2 + 30x - 400 = 0 By solving this quadratic equation, we get x = 10, -40. Since speed cannot be negative, we discard -40. So, the speed of the current is 10 km/hr. Hence, the answer is (b) 10 km/hr.   Q5: How much time boat took in downstream? (a) 90 minute (b) 15 minute (c) 30 minute (d) 45 minute Ans:  (d) Explanation: The speed of the boat in still water is given as 20 km/hr. Let's denote the speed of the current as 'c' km/hr. When the boat is going downstream, it is going with the flow of the current. So, the effective speed of the boat is (20+c) km/hr. When the boat is going upstream, it is going against the current. So, the effective speed of the boat is (20-c) km/hr. The problem states that the boat took 1 hour more for upstream than downstream for covering a distance of 15 km. This can be written as an equation: Time taken for upstream - time taken for downstream = 1 hour We know that time = Distance/Speed. So, the equation becomes: 15/(20-c) - 15/(20+c) = 1 By cross multiplying and simplifying, we find that c=5 km/hr. Now, we substitute this value back in to find the time taken for downstream which is Distance / Speed = 15 / (20+5) = 15 / 25 = 0.6 hours. Converting 0.6 hours into minutes (since 1 hour = 60 minutes), we get 0.6 * 60 = 36 minutes. The closest answer to 36 minutes is 45 minutes. Therefore, the answer is (d) 45 minutes.  

Case Study - 2

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400 km.

Q1: What will be the distance covered by Ajay’s car in two hours? (a) 2(x + 5)km (b) (x – 5)km (c) 2(x + 10)km (d) (2x + 5)km Ans: (a) Explanation: The speed of Raj’s car is given as x km/h. Ajay’s car travels at a speed that is 5 km/h faster than Raj's car. Therefore, the speed of Ajay’s car is (x+5) km/h. Distance is calculated by multiplying speed by time. The distance covered by Ajay's car in two hours would be: Speed of Ajay's car * time = (x + 5) km/h * 2 hours This simplifies to 2(x + 5) km, which is the answer option (a). Q2: Which of the following quadratic equation describe the speed of Raj’s car? (a) x 2  – 5x – 500 = 0 (b) x 2 + 4x – 400 = 0 (c) x 2  + 5x – 500 = 0 (d) x 2 – 4x + 400 = 0 Ans:  (c) Q3: What is the speed of Raj’s car? (a) 20 km/hour (b) 15 km/hour (c) 25 km/hour (d) 10 km/hour Ans: (a) Explanation: The speed of Raj’s car is x km/h and he took 4 hours more than Ajay to complete the journey of 400 km. Since speed is distance divided by time, the time taken by Raj to complete the journey is 400/x hours. Ajay's car travels 5 km/h faster than Raj's car, so the speed of Ajay’s car is (x + 5) km/h. The time taken by Ajay to complete the journey is 400/(x + 5) hours. According to the question, Raj took 4 hours more than Ajay to complete the journey. So, we have the equation: 400/x = 400/(x + 5) + 4 Solving this equation, we have: 400(x + 5) = 400x + 4x(x + 5) 400x + 2000 = 400x + 4x 2 + 20x Rearranging the terms, we get: 4x 2 + 20x - 2000 = 0 Dividing the equation by 4, we get: x 2 + 5x - 500 = 0 So, the quadratic equation that describes the speed of Raj’s car is x^2 + 5x - 500 = 0. Hence, the correct answer is (c).   Q4: How much time took Ajay to travel 400 km? (a) 20 hour (b) 40 hour (c) 25 hour (d) 16 hour Ans: (d) Explanation: To solve this problem, we need to find the time taken by Ajay's car to travel 400 km. Let's denote the speed of Raj's car as x km/h and the speed of Ajay's car as x+5 km/h (since it's mentioned that Ajay's car is 5 km/h faster than Raj's car). The formula for time is distance divided by speed. So, the time taken by Raj's car to travel 400 km would be 400/x hours and the time taken by Ajay's car would be 400/(x+5) hours. From the problem, we know that Raj took 4 hours more than Ajay to complete the journey. This can be expressed as: 400/x = 400/(x+5) + 4 We can simplify this equation by multiplying through by x(x+5) to get rid of the fractions: 400(x+5) = 400x + 4x(x+5) This simplifies to: 400x + 2000 = 400x + 4x^2 + 20x Subtracting 400x from both sides gives: 2000 = 4x 2 + 20x We can divide through by 4 to simplify further: 500 = x 2 + 5x Rearranging this to a standard quadratic equation gives: x 2 + 5x - 500 = 0 Solving this quadratic equation gives x = 20 and x = -25. Since a speed can't be negative, we discard the -25 solution. So, the speed of Raj's car is 20 km/h and the speed of Ajay's car is 25 km/h. Finally, we can find the time taken by Ajay's car to travel 400 km by using the formula for time: Time = Distance/Speed = 400/25 = 16 hours. Therefore, the answer is (d) 16 hours.  

Top Courses for Class 10

Shortcuts and tricks, viva questions, past year papers, important questions, video lectures, objective type questions, study material, practice quizzes, previous year questions with solutions, sample paper, extra questions, mock tests for examination, semester notes.

Case Based Questions: Quadratic Equations Free PDF Download

Importance of case based questions: quadratic equations, case based questions: quadratic equations notes, case based questions: quadratic equations class 10, study case based questions: quadratic equations on the app, welcome back, create your account for free.

Forgot Password

Unattempted tests, change country.

Real World Examples of Quadratic Equations

A Quadratic Equation looks like this:

Quadratic equations pop up in many real world situations!

Here we have collected some examples for you, and solve each using different methods:

• Factoring Quadratics
• Completing the Square
• Graphing Quadratic Equations
• The Quadratic Formula
• Online Quadratic Equation Solver

Each example follows three general stages:

• Take the real world description and make some equations
• Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones

When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...

... and a Quadratic Equation tells you its position at all times!

Example: Throwing a Ball

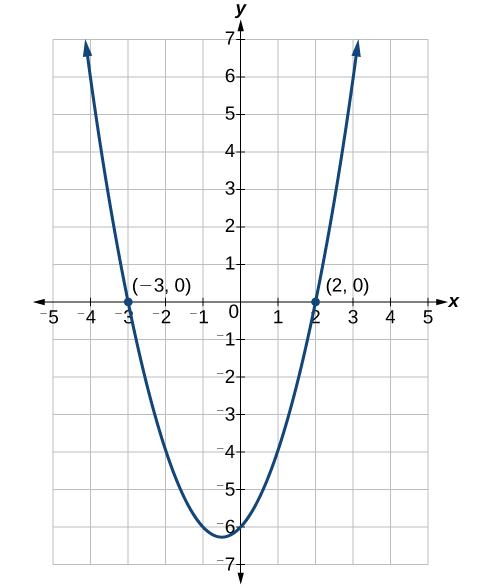
A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.

Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)

Add them up and the height h at any time t is:

h = 3 + 14t − 5t 2

And the ball will hit the ground when the height is zero:

3 + 14t − 5t 2 = 0

Which is a Quadratic Equation !

In "Standard Form" it looks like:

−5t 2 + 14t + 3 = 0

It looks even better when we multiply all terms by −1 :

5t 2 − 14t − 3 = 0

Let us solve it ...

There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :

ac = −15 , and b = −14 .

The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15

By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)

The "t = −0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

Here is the graph of the Parabola h = −5t 2 + 14t + 3

It shows you the height of the ball vs time

Some interesting points:

(0,3) When t=0 (at the start) the ball is at 3 m

(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.

(3,0) says that at 3 seconds the ball is at ground level.

Also notice that the ball goes nearly 13 meters high.

Note: You can find exactly where the top point is!

The method is explained in Graphing Quadratic Equations , and has two steps:

Find where (along the horizontal axis) the top occurs using −b/2a :

• t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

Example: New Sports Bike

You have designed a new style of sports bicycle!

Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

Based on similar bikes, you can expect sales to follow this "Demand Curve":

Where "P" is the price.

For example, if you set the price:

• at $0, you just give away 70,000 bikes
• at $350, you won't sell any bikes at all
• at $300 you might sell 70,000 − 200×300 = 10,000 bikes

So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

Profit = −200P 2 + 92,000P − 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square .

Solve: −200P 2 + 92,000P − 8,400,000 = 0

Step 1 Divide all terms by -200

Step 2 Move the number term to the right side of the equation:

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900

Step 4 Take the square root on both sides of the equation:

Step 5 Subtract (-230) from both sides (in other words, add 230):

What does that tell us? It says that the profit is ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

It is exactly half way in-between! At $230

And here is the graph:

The best sale price is $230 , and you can expect:

• Unit Sales = 70,000 − 200 x 230 = 24,000
• Sales in Dollars = $230 x 24,000 = $5,520,000
• Costs = 700,000 + $110 x 24,000 = $3,340,000
• Profit = $5,520,000 − $3,340,000 = $2,180,000

A very profitable venture.

Example: Small Steel Frame

Your company is going to make frames as part of a new product they are launching.

The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2

The inside of the frame has to be 11 cm by 6 cm

What should the width x of the metal be?

Area of steel before cutting:

Area of steel after cutting out the 11 × 6 middle:

Let us solve this one graphically !

Here is the graph of 4x 2 + 34x :

The desired area of 28 is shown as a horizontal line.

The area equals 28 cm 2 when:

x is about −9.3 or 0.8

The negative value of x make no sense, so the answer is:

x = 0.8 cm (approx.)

Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.

There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:

• Let x = the boat's speed in the water (km/h)
• Let v = the speed relative to the land (km/h)

Because the river flows downstream at 2 km/h:

• when going upstream, v = x−2 (its speed is reduced by 2 km/h)
• when going downstream, v = x+2 (its speed is increased by 2 km/h)

We can turn those speeds into times using:

time = distance / speed

(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x−2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2) (x+2) :

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x 2 −4) = 15x+30 + 15x−30

Bring everything to the left and simplify:

3x 2 − 30x − 12 = 0

It is a Quadratic Equation!

Let us solve it using the Quadratic Formula :

Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0

Solve 3x 2 - 30x - 12 = 0

Answer: x = −0.39 or 10.39 (to 2 decimal places)

x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Example: Resistors In Parallel

Two resistors are in parallel, like in this diagram:

The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.

What are the values of the two resistors?

The formula to work out total resistance "R T " is:

1 R T   =   1 R 1 + 1 R 2

In this case, we have R T = 2 and R 2 = R 1 + 3

1 2   =   1 R 1 + 1 R 1 +3

To get rid of the fractions we can multiply all terms by 2R 1 (R 1 + 3) and then simplify:

Yes! A Quadratic Equation!

Let us solve it using our Quadratic Equation Solver .

• Enter 1, −1 and −6
• And you should get the answers −2 and 3

R 1 cannot be negative, so R 1 = 3 Ohms is the answer.

The two resistors are 3 ohms and 6 ohms.

Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.

Quadratic equations are also needed when studying lenses and curved mirrors.

And many questions involving time, distance and speed need quadratic equations.

CBSE Case Study Questions for Class 10 Maths Quadratic Equation Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 10 Maths Quadratic Equation  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 10 Maths Quadratic Equation PDF

Checkout our case study questions for other chapters.

• Chapter 2: Polynomials Case Study Questions
• Chapter 3: Pair of Linear Equations in Two Variables Case Study Questions
• Chapter 5: Arithmetic Progressions Case Study Questions
• Chapter 6: Triangles Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Privacy Policy

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

The quadratic formula, understanding the quadratic formula.

• Worked example: quadratic formula (example 2)
• Worked example: quadratic formula (negative coefficients)
• Quadratic formula
• Using the quadratic formula: number of solutions
• Number of solutions of quadratic equations
• Quadratic formula review
• Discriminant review

Worked example

• a ‍   is the coefficient in front of x 2 ‍   , so here a = 1 ‍   (note that a ‍   can’t equal 0 ‍   -- the x 2 ‍   is what makes it a quadratic).
• b ‍   is the coefficient in front of the x ‍   , so here b = 4 ‍   .
• c ‍   is the constant, or the term without any x ‍   next to it, so here c = − 21 ‍   .

What does the solution tell us?

Second worked example, tips when using the quadratic formula.

• Be careful that the equation is arranged in the right form: a x 2 + b x + c = 0 ‍   or it won’t work!
• Make sure you take the square root of the whole ( b 2 − 4 a c ) ‍   , and that 2 a ‍   is the denominator of everything above it
• Watch your negatives: b 2 ‍   can’t be negative, so if b ‍   starts as negative, make sure it changes to a positive since the square of a negative or a positive is a positive
• Keep the + / − ‍   and always be on the look out for TWO solutions
• If you use a calculator, the answer might be rounded to a certain number of decimal places. If asked for the exact answer (as usually happens) and the square roots can’t be easily simplified, keep the square roots in the answer, e.g. 2 − 10 2 ‍   and 2 + 10 2 ‍  
• Practice using the quadratic formula .
• Watch Sal do an example:
• Prove the quadratic formula:

Study Guides > College Algebra: Co-requisite Course

Quadratic equations, learning objectives.

• Use the zero product principle to solve quadratic equations that can be factored
• Identify solutions to quadratic equations on a graph
• Use the square root property to solve a quadratic equation
• Complete the square to solve a quadratic equation
• Write a quadratic equation in standard form and identify the values of a , b , and c in a standard form quadratic equation.
• Use the Quadratic Formula to find solutions of a quadratic equation, (rational, irrational and complex)

The Zero-Product Property and Quadratic Equations

Solving quadratics with a leading coefficient of 1, reminder: given a quadratic equation with the leading coefficient of 1, factor it..

• Find two numbers whose product equals c and whose sum equals b .
• Use those numbers to write two factors of the form [latex]\left(x+k\right)\text{ or }\left(x-k\right)[/latex], where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and [latex]-2[/latex], the factors are [latex]\left(x+1\right)\left(x - 2\right)[/latex].
• Solve using the zero-product property by setting each factor equal to zero and solving for the variable.

Answer: Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property. [latex]\begin{array}{l}{x}^{2}-9=0\hfill \\ \left(x - 3\right)\left(x+3\right)=0\hfill \\ \hfill \\ \left(x - 3\right)=0\hfill \\ x=3\hfill \\ \hfill \\ \left(x+3\right)=0\hfill \\ x=-3\hfill \end{array}[/latex] The solutions are [latex]x=3[/latex] and [latex]x=-3[/latex].

 Solving Quadratics with a Leading Coefficient of [latex]\ne1[/latex]

• With the quadratic in standard form, [latex]a{x}^{2}+bx+c=0[/latex], multiply [latex]a\cdot c[/latex].
• Find two numbers whose product equals [latex]ac[/latex] and whose sum equals [latex]b[/latex].
• Rewrite the equation replacing the [latex]bx[/latex] term with two terms using the numbers found in step 1 as coefficients of x.
• Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
• Factor out the expression in parentheses.
• Set the expressions equal to zero and solve for the variable.

Answer: This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out [latex]-x[/latex] from all of the terms and then proceed with grouping. [latex]\begin{array}{l}-3{x}^{3}-5{x}^{2}-2x=0\hfill \\ -x\left(3{x}^{2}+5x+2\right)=0\hfill \end{array}[/latex] Use grouping on the expression in parentheses. [latex]\begin{array}{l}-x\left(3{x}^{2}+3x+2x+2\right)=\hfill&0\hfill \\ -x\left[3x\left(x+1\right)+2\left(x+1\right)\right]=\hfill&0\hfill \\ -x\left(3x+2\right)\left(x+1\right)=\hfill&0\hfill \end{array}[/latex] Now, we use the zero-product property. Notice that we have three factors. [latex]\begin{array}{l}-x\hfill&=0\hfill \\ x\hfill&=0\hfill \\ 3x+2\hfill&=0\hfill \\ x\hfill&=-\frac{2}{3}\hfill \\ x+1\hfill&=0\hfill \\ x\hfill&=-1\hfill \end{array}[/latex] The solutions are [latex]x=0[/latex], [latex]x=-\frac{2}{3}[/latex], and [latex]x=-1[/latex].

Solve a Quadratic Equation by the Square Root Property

The square root property.

[latex]\begin{array}{l}x^{2}=9\\\,\,\,x=\pm\sqrt{9}\\\,\,\,x=\pm3\end{array}[/latex]

[latex]10x^{2}+5=85[/latex]

[latex]10x^{2}=80[/latex]

[latex] \begin{array}{l}{{x}^{2}}=8\\\,\,\,x=\pm \sqrt{8}\\\,\,\,\,\,\,=\pm \sqrt{(4)(2)}\\\,\,\,\,\,\,=\pm \sqrt{4}\sqrt{2}\\\,\,\,\,\,\,=\pm 2\sqrt{2}\end{array}[/latex]

[latex]\left(x-2\right)^{2}-50=0[/latex]

[latex]\begin{array}{r}\left(x-2\right)^{2}=50\,\,\,\,\,\,\,\,\,\,\\x-2=\pm\sqrt{50}\end{array}[/latex]

[latex] \begin{array}{l}x=2\pm \sqrt{50}\\\,\,\,\,=2\pm \sqrt{(25)(2)}\\\,\,\,\,=2\pm \sqrt{25}\sqrt{2}\\\,\,\,\,=2\pm 5\sqrt{2}\end{array}[/latex]

Solve a Quadratic Equation by Completing the Square

Answer: First notice that the [latex]x^{2}[/latex] term and the constant term are both perfect squares. [latex-display]\begin{array}{l}9x^{2}=\left(3x\right)^{2}\\\,\,\,16=4^{2}\end{array}[/latex-display] Then notice that the middle term (ignoring the sign) is twice the product of the square roots of the other terms. [latex-display]24x=2\left(3x\right)\left(4\right)[/latex-display] A trinomial in the form [latex]r^{2}-2rs+s^{2}[/latex] can be factored as [latex](r–s)^{2}[/latex]. In this case, the middle term is subtracted, so subtract r and s and square it to get [latex](r–s)^{2}[/latex]. [latex-display]\begin{array}{c}\,\,\,r=3x\\s=4\\9x^{2}-24x+16=\left(3x-4\right)^{2}\end{array}[/latex-display]

Steps for Completing The Square

• Given a quadratic equation that cannot be factored, and with [latex]a=1[/latex], first add or subtract the constant term to the right side of the equal sign. [latex]{x}^{2}+4x=-1[/latex]
• Multiply the b term by [latex]\frac{1}{2}[/latex] and square it. [latex]\begin{array}{l}\frac{1}{2}\left(4\right)=2\hfill \\ {2}^{2}=4\hfill \end{array}[/latex]
• Add [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to both sides of the equal sign and simplify the right side. We have [latex]\begin{array}{l}{x}^{2}+4x+4=-1+4\hfill \\ {x}^{2}+4x+4=3\hfill \end{array}[/latex]
• The left side of the equation can now be factored as a perfect square. [latex]\begin{array}{l}{x}^{2}+4x+4=3\hfill \\ {\left(x+2\right)}^{2}=3\hfill \end{array}[/latex]
• Use the square root property and solve. [latex]\begin{array}{l}\sqrt{{\left(x+2\right)}^{2}}=\pm \sqrt{3}\hfill \\ x+2=\pm \sqrt{3}\hfill \\ x=-2\pm \sqrt{3}\hfill \end{array}[/latex]
• The solutions are [latex]x=-2+\sqrt{3}[/latex], [latex]x=-2-\sqrt{3}[/latex].

[latex]\begin{array}{r}x^{2}-12x=4\,\,\,\,\,\,\,\,\\b=-12\end{array}[/latex]

[latex]\begin{array}{l}x^{2}-12x+36=4+36\\x^{2}-12x+36=40\end{array}[/latex]

[latex]\left(x-6\right)^{2}=40[/latex]

[latex] x-6=\pm\sqrt{40}[/latex]

[latex] \begin{array}{l}x=6\pm \sqrt{40}\\\,\,\,\,=6\pm \sqrt{4}\sqrt{10}\\\,\,\,\,=6\pm 2\sqrt{10}\end{array}[/latex]

Answer: First, move the constant term to the right side of the equal sign. [latex]{x}^{2}-3x=5[/latex] Identify b .[latex]b=-3[/latex] Then, take [latex]\frac{1}{2}[/latex] of the b term and square it. [latex]\begin{array}{l}\frac{1}{2}\left(-3\right)=-\frac{3}{2}\hfill \\ {\left(-\frac{3}{2}\right)}^{2}=\frac{9}{4}\hfill \end{array}[/latex] Add the result to both sides of the equal sign. [latex]\begin{array}{l}\text{ }{x}^{2}-3x+{\left(-\frac{3}{2}\right)}^{2}=5+{\left(-\frac{3}{2}\right)}^{2}\hfill \\ {x}^{2}-3x+\frac{9}{4}=5+\frac{9}{4}\hfill \end{array}[/latex] Factor the left side as a perfect square and simplify the right side. [latex]{\left(x-\frac{3}{2}\right)}^{2}=\frac{29}{4}[/latex] Use the square root property and solve. [latex]\begin{array}{l}\sqrt{{\left(x-\frac{3}{2}\right)}^{2}}\hfill&=\pm \sqrt{\frac{29}{4}}\hfill \\ \left(x-\frac{3}{2}\right)\hfill&=\pm \frac{\sqrt{29}}{2}\hfill \\ x\hfill&=\frac{3}{2}\pm \frac{\sqrt{29}}{2}\hfill \end{array}[/latex] The solutions are [latex]x=\frac{3}{2}+\frac{\sqrt{29}}{2}[/latex], [latex]x=\frac{3}{2}-\frac{\sqrt{29}}{2}[/latex].

[latex]\begin{array}{c}x^{2}+16x=-64\\b=16\end{array}[/latex]

[latex]\begin{array}{l}x^{2}+16x+64=-64+64\\x^{2}+16x+64=0\end{array}[/latex]

[latex]\left(x+8\right)^{2}=0[/latex]

[latex]x+8=0[/latex]

[latex]x=-8[/latex]

The Quadratic Formula

• First, move the constant term to the right side of the equal sign: [latex]a{x}^{2}+bx=-c[/latex]
• As we want the leading coefficient to equal 1, divide through by a : [latex]{x}^{2}+\frac{b}{a}x=-\frac{c}{a}[/latex]
• Then, find [latex]\frac{1}{2}[/latex] of the middle term, and add [latex]{\left(\frac{1}{2}\frac{b}{a}\right)}^{2}=\frac{{b}^{2}}{4{a}^{2}}[/latex] to both sides of the equal sign: [latex]{x}^{2}+\frac{b}{a}x+\frac{{b}^{2}}{4{a}^{2}}=\frac{{b}^{2}}{4{a}^{2}}-\frac{c}{a}[/latex]
• Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction: [latex]{\left(x+\frac{b}{2a}\right)}^{2}=\frac{{b}^{2}-4ac}{4{a}^{2}}[/latex]
• Now, use the square root property, which gives [latex]\begin{array}{l}x+\frac{b}{2a}=\pm \sqrt{\frac{{b}^{2}-4ac}{4{a}^{2}}}\hfill \\ x+\frac{b}{2a}=\frac{\pm \sqrt{{b}^{2}-4ac}}{2a}\hfill \end{array}[/latex]
• Finally, add [latex]-\frac{b}{2a}[/latex] to both sides of the equation and combine the terms on the right side. Thus, [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex]

Solving a Quadratic Equation using the Quadratic Formula

• Put the equation in standard form first.
• Identify the coefficients, a , b, and c. Be careful to include negative signs if the bx or c terms are subtracted.
• Carefully substitute the values noted in step 2 into the equation. To avoid needless errors, use parentheses around each number input into the formula.
• Simplify as much as possible.
• Use the [latex]\pm[/latex] in front of the radical to separate the solution into two values: one in which the square root is added, and one in which it is subtracted .
• Simplify both values to get the possible solutions.

[latex]\begin{array}{r}x^{2}+4x=5\,\,\,\\x^{2}+4x-5=0\,\,\,\\\\a=1,b=4,c=-5\end{array}[/latex]

[latex] \begin{array}{r}{{x}^{2}}\,\,\,+\,\,\,4x\,\,\,-\,\,\,5\,\,\,=\,\,\,0\\\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\a{{x}^{2}}\,\,\,+\,\,\,bx\,\,\,+\,\,\,c\,\,\,=\,\,\,0\end{array}[/latex]

[latex] \begin{array}{l}\\x=\frac{-4\pm \sqrt{{{(4)}^{2}}-4(1)(-5)}}{2(1)}\end{array}[/latex]

[latex]x=\frac{-4\pm\sqrt{16+20}}{2}[/latex]

[latex] x=\frac{-4\pm \sqrt{36}}{2}[/latex]

[latex] x=\frac{-4\pm 6}{2}[/latex]

[latex]\begin{array}{c}x=\frac{-4+6}{2}=\frac{2}{2}=1\\\\\text{or}\\\\x=\frac{-4-6}{2}=\frac{-10}{2}=-5\end{array}[/latex]

[latex]\begin{array}{l}x^{2}-2x=6x-16\\x^{2}-2x-6x+16=0\\x^{2}-8x+16=0\end{array}[/latex]

[latex] \begin{array}{r}{{x}^{2}}\,\,\,-\,\,\,8x\,\,\,+\,\,\,16\,\,\,=\,\,\,0\\\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\a{{x}^{2}}\,\,\,+\,\,\,bx\,\,\,+\,\,\,\,c\,\,\,\,=\,\,\,0\end{array}[/latex]

[latex]\begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-(-8)\pm \sqrt{{{(-8)}^{2}}-4(1)(16)}}{2(1)}\end{array}[/latex]

[latex] x=\frac{8\pm \sqrt{64-64}}{2}[/latex]

[latex] x=\frac{8\pm \sqrt{0}}{2}=\frac{8}{2}=4[/latex]

[latex]\begin{array}{r}x^{2}-2x=6x-16\,\,\,\,\,\\\left(4\right)^{2}-2\left(4\right)=6\left(4\right)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Quadratic equations with complex solutions

[latex]2x^2+3x+6=0[/latex]

Using the quadratic formula to solve this equation, we first identify a, b, and c.

[latex]a = 2,b = 3,c = 6[/latex]

We can place a, b and c into the quadratic formula and simplify to get the following result:

[latex]x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, x=-\frac{3}{4}-\frac{\sqrt{-39}}{4}[/latex]

Up to this point, we would have said that [latex]\sqrt{-39}[/latex] is not defined for real numbers and determine that this equation has no solutions.  But, now that we have defined the square root of a negative number, we can also define a solution to this equation as follows.

[latex]x=-\frac{3}{4}+i\frac{\sqrt{39}}{4}, x=-\frac{3}{4}-i\frac{\sqrt{39}}{4}[/latex]

In the following example we will work through the process of solving a quadratic equation with complex solutions. Take note that we be simplifying complex numbers - so if you need a review of how to rewrite the square root of a negative number as an imaginary number, now is a good time.

Use the quadratic formula to solve [latex]{x}^{2}+x+2=0[/latex].

Answer: First, we identify the coefficients: [latex]a=1,b=1[/latex], and [latex]c=2[/latex]. Substitute these values into the quadratic formula. [latex]\begin{array}{l}x\hfill&=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}\hfill \\\hfill&=\frac{-\left(1\right)\pm \sqrt{{\left(1\right)}^{2}-\left(4\right)\cdot \left(1\right)\cdot \left(2\right)}}{2\cdot 1}\hfill \\\hfill&=\frac{-1\pm \sqrt{1 - 8}}{2}\hfill \\ \hfill&=\frac{-1\pm \sqrt{-7}}{2}\hfill \\\hfill&=\frac{-1\pm i\sqrt{7}}{2}\hfill \end{array}[/latex] Now we can separate the expression [latex]\frac{-1\pm i\sqrt{7}}{2}[/latex] into two solutions: [latex-display]-\frac{1}{2}+\frac{ i\sqrt{7}}{2}[/latex-display] [latex-display]-\frac{1}{2}-\frac{ i\sqrt{7}}{2}[/latex-display]   The solutions to the equation are [latex]x=\frac{-1+i\sqrt{7}}{2}[/latex] and [latex]x=\frac{-1-i\sqrt{7}}{2}[/latex] or [latex]x=\frac{-1}{2}+\frac{i\sqrt{7}}{2}[/latex] and [latex]x=\frac{-1}{2}-\frac{i\sqrt{7}}{2}[/latex].

[latex]\begin{array}{l}x^{2}+x=-x-3\\x^{2}+2x+3=0\end{array}[/latex]

[latex]a=1, b=2, c=3[/latex]

Substitute values for a, b, c into the quadratic formula.

[latex]\begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-2\pm \sqrt{{{(2)}^{2}}-4(1)(3)}}{2(1)}\end{array}[/latex]

[latex]\displaystyle x=\frac{-2\pm \sqrt{-8}}{2}[/latex]

Rewrite the radical of a negative number in terms of the imaginary unit [latex]i[/latex]

[latex]\displaystyle x=\frac{-2\pm i\sqrt{8}}{2}[/latex]

[latex]\displaystyle x=\frac{-2\pm 2i\sqrt{2}}{2}[/latex]

[latex]x=-1 \pm i\sqrt{2}[/latex]

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .
• Quadratic Formula Application - Time for an Object to Hit the Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
• Quadratic Formula Application - Determine the Width of a Border. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .

CC licensed content, Shared previously

• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution . License terms: Download for free at : http://cnx.org/contents/ [email protected] :1/Preface.
• Ex: Solve a Quadratic Equation Using Factor By Grouping. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Ex: Factor and Solve Quadratic Equation - Trinomial a = -1. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution .
• Ex 1: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Ex 2: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright .
• Ex 1: Completing the Square - Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright .
• Ex 2: Completing the Square - Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Ex2: Quadratic Formula - Two Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
• Ex: Quadratic Formula - Two Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution .
• Question ID#31110. Authored by: Wallace,Tyler, mb Sousa,James. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

CBSE Expert

CBSE Class 10 Maths Case Study Questions PDF

Download Case Study Questions for Class 10 Mathematics to prepare for the upcoming CBSE Class 10 Final Exam. These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 10 so that they can score 100% on Boards.

CBSE Class 10 Mathematics Exam 2024  will have a set of questions based on case studies in the form of MCQs. The CBSE Class 10 Mathematics Question Bank on Case Studies, provided in this article, can be very helpful to understand the new format of questions. Share this link with your friends.

Table of Contents

Chapterwise Case Study Questions for Class 10 Mathematics

Inboard exams, students will find the questions based on assertion and reasoning. Also, there will be a few questions based on case studies. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

The above  Case studies for Class 10 Maths will help you to boost your scores as Case Study questions have been coming in your examinations. These CBSE Class 10 Mathematics Case Studies have been developed by experienced teachers of cbseexpert.com for the benefit of Class 10 students.

• Class 10th Science Case Study Questions
• Assertion and Reason Questions of Class 10th Science
• Assertion and Reason Questions of Class 10th Social Science

Class 10 Maths Syllabus 2024

Chapter-1  real numbers.

Starting with an introduction to real numbers, properties of real numbers, Euclid’s division lemma, fundamentals of arithmetic, Euclid’s division algorithm, revisiting irrational numbers, revisiting rational numbers and their decimal expansions followed by a bunch of problems for a thorough and better understanding.

Chapter-2  Polynomials

This chapter is quite important and marks securing topics in the syllabus. As this chapter is repeated almost every year, students find this a very easy and simple subject to understand. Topics like the geometrical meaning of the zeroes of a polynomial, the relationship between zeroes and coefficients of a polynomial, division algorithm for polynomials followed with exercises and solved examples for thorough understanding.

Chapter-3  Pair of Linear Equations in Two Variables

This chapter is very intriguing and the topics covered here are explained very clearly and perfectly using examples and exercises for each topic. Starting with the introduction, pair of linear equations in two variables, graphical method of solution of a pair of linear equations, algebraic methods of solving a pair of linear equations, substitution method, elimination method, cross-multiplication method, equations reducible to a pair of linear equations in two variables, etc are a few topics that are discussed in this chapter.

Chapter-4  Quadratic Equations

The Quadratic Equations chapter is a very important and high priority subject in terms of examination, and securing as well as the problems are very simple and easy. Problems like finding the value of X from a given equation, comparing and solving two equations to find X, Y values, proving the given equation is quadratic or not by knowing the highest power, from the given statement deriving the required quadratic equation, etc are few topics covered in this chapter and also an ample set of problems are provided for better practice purposes.

Chapter-5  Arithmetic Progressions

This chapter is another interesting and simpler topic where the problems here are mostly based on a single formula and the rest are derivations of the original one. Beginning with a basic brief introduction, definitions of arithmetic progressions, nth term of an AP, the sum of first n terms of an AP are a few important and priority topics covered under this chapter. Apart from that, there are many problems and exercises followed with each topic for good understanding.

Chapter-6  Triangles

This chapter Triangle is an interesting and easy chapter and students often like this very much and a securing unit as well. Here beginning with the introduction to triangles followed by other topics like similar figures, the similarity of triangles, criteria for similarity of triangles, areas of similar triangles, Pythagoras theorem, along with a page summary for revision purposes are discussed in this chapter with examples and exercises for practice purposes.

Chapter-7  Coordinate Geometry

Here starting with a general introduction, distance formula, section formula, area of the triangle are a few topics covered in this chapter followed with examples and exercises for better and thorough practice purposes.

Chapter-8  Introduction to Trigonometry

As trigonometry is a very important and vast subject, this topic is divided into two parts where one chapter is Introduction to Trigonometry and another part is Applications of Trigonometry. This Introduction to Trigonometry chapter is started with a general introduction, trigonometric ratios, trigonometric ratios of some specific angles, trigonometric ratios of complementary angles, trigonometric identities, etc are a few important topics covered in this chapter.

Chapter-9  Applications of Trigonometry

This chapter is the continuation of the previous chapter, where the various modeled applications are discussed here with examples and exercises for better understanding. Topics like heights and distances are covered here and at the end, a summary is provided with all the important and frequently used formulas used in this chapter for solving the problems.

Chapter-10  Circle

Beginning with the introduction to circles, tangent to a circle, several tangents from a point on a circle are some of the important topics covered in this chapter. This chapter being practical, there are an ample number of problems and solved examples for better understanding and practice purposes.

Chapter-11  Constructions

This chapter has more practical problems than theory-based definitions. Beginning with a general introduction to constructions, tools used, etc, the topics like division of a line segment, construction of tangents to a circle, and followed with few solved examples that help in solving the exercises provided after each topic.

Chapter-12  Areas related to Circles

This chapter problem is exclusively formula based wherein topics like perimeter and area of a circle- A Review, areas of sector and segment of a circle, areas of combinations of plane figures, and a page summary is provided just as a revision of the topics and formulas covered in the entire chapter and also there are many exercises and solved examples for practice purposes.

Chapter-13  Surface Areas and Volumes

Starting with the introduction, the surface area of a combination of solids, the volume of a combination of solids, conversion of solid from one shape to another, frustum of a cone, etc are to name a few topics explained in detail provided with a set of examples for a better comprehension of the concepts.

Chapter-14  Statistics

In this chapter starting with an introduction, topics like mean of grouped data, mode of grouped data, a median of grouped, graphical representation of cumulative frequency distribution are explained in detail with exercises for practice purposes. This chapter being a simple and easy subject, securing the marks is not difficult for students.

Chapter-15  Probability

Probability is another simple and important chapter in examination point of view and as seeking knowledge purposes as well. Beginning with an introduction to probability, an important topic called A theoretical approach is explained here. Since this chapter is one of the smallest in the syllabus and problems are also quite easy, students often like this chapter

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

• Mathematics CBSE
• Quadratic Equations
• Nature of Roots

12. Case study: Nature of roots

Exercise condition:.

• 2 x 2 − 4 x + 390 = 0
• 2 x 2 − 4 x − 390 = 0
• 2 x 2 + 4 x − 390 = 0
• 2 x 2 + 4 x + 390 = 0
• \(ax^2 - bx + c = 0\)
• \(ax^2 + bx + c = 0\)
• \(ax^2 + bx = c\)
• \(ax^2 + ax + c = 0\)
• \(b^2 - 4ac = 0\)
• \(b^2 - 4ac \le 0\)
• \(b^2 - 4ac < 0\)
• \(b^2 - 4ac > 0\)

Journal of Mathematics Education © Education for All December 2011, Vol. 4, No. 2, pp. 1-16

Mathematical Knowledge for Teaching Algebraic Routines: A Case Study of Solving Quadratic Equations

Xuhui Li California State University at Long Beach

This paper describes the sequence of mathematical practices that a teacher designed and enacted during three consecutive lessons about four algebraic routines for solving quadratic equations, and focuses on the mathematical knowledge that is entailed in the teacher’s actions and decisions. Among the three domains of mathematical knowledge for teaching (MKT), the teacher’s knowledge of the equation solving routines played the most crucial role in shaping the lessons and potentially promoting mathematical proficiency in a balanced approach. The findings suggest that mathematics teacher preparation and professional development programs should provide more opportunities for teachers to revisit in-depth the features and applicability of various mathematical routines, and develop skills in making instructional decisions that would balance all domains of teachers’ MKT, teacher beliefs, and other factors related to proficiency in algebraic routines.

Key words: mathematical knowledge for teaching, algebraic routines, quadratic equations, mathematical proficiency

The last decade has witnessed mathematics education researchers’ tremendous interests and efforts in conceptualizing and assessing the kinds of mathematical knowledge that teachers draw upon or need to acquire for effective teaching (Adler & Davis, 2006; Ball, 1999, 2000; Ball & Bass, 2000, 2003; Ball, Bass, Hill, & Schilling, 2005; Ball, Lubienski, & Mewborn, 2001; Ball, Thames, & Phelps, 2008; Cuoco, 2001; Davis & Simmt, 2006; Ferrini- Mundy & Findell, 2001; Hill, Ball, & Schilling, 2004, 2008; Ma, 1999; Moreira & David, 2008; Stylianides & Ball, 2008). The entire body of such knowledge has been typically phrased as mathematical knowledge for teaching (MKT). A number of the systematic explorations focused specifically on MKT in school algebra (Artigue, Assude, Grugeon, & Lenfant, 2001; Ferrini-Mundy, Burrill, Floden, & Sandow, 2003; Ferrini-Mundy, McCrory, & Senk, 2006; Heid, 2007), and proposed theoretical frameworks and developed preliminary assessment instruments. Consider the foundational role and high-stake status of algebra in the school mathematics curriculum. However, more research is needed for researchers and mathematics teacher

2 Mathematical Knowledge for Teaching educators to deepen their understanding and design more robust assessments of MKT in regard to school algebra. Because modern school algebra is a complex and evolving entity that involves multiple, and often competing, conceptions, focuses, and approaches (Chazan, 2000, 2008; Kieran, 2007; Kilpatrick & Izsák, 2008), research on algebra-related MKT would have to go beyond the overarching features of algebra and address the unique characteristics and dynamics of individual algebraic topics, strands, or types of activities. In recent years the researcher has focused his work on a particular content theme in algebra – basic routines and procedures, which include the algebraic rules, algorithms, and formulas that can be applied to given inputs and yield desired outcomes through finite steps (e.g., the distributive property of multiplication over addition and its extensions, such as the so-called FOIL formula (a + b)(c + d) = ac + ad + bc + bd and identities (a + b)2 = a2 + 2ab + b2 and (a + b)(a – b) = a2 – b2; various established methods or formulas for solving linear and quadratic equations, such as the balancing and backtracking methods, factoring, completing the square, and the quadratic formula ). Algebraic routines and procedures are closely tied to the five interwoven essential strands of mathematical proficiency (Kilpatrick, Swafford, & Findell, 2001), in particular, conceptual understanding, procedural fluency, and strategic competence. Ideally, these strands are interdependent and are to be developed simultaneously in balanced ways. In practice, however, there lacks a consensus among mathematics educators on the distinctions and relationships between conceptual and procedural knowledge (De Jong & Ferguson-Hessler, 1996; Hiebert, 1986; Li, 2007; Star, 2000, 2005). Consequently, the twin goals of developing procedural fluency and conceptual understanding are often viewed as competing for attention and priority in school mathematics (Kilpatrick, Swafford, & Findell, 2001), which in turn creates a false dichotomy (Wu, 1999). Mathematics teachers with distinct beliefs and MKT regarding these strands may likely approach algebraic routines with different goals and teaching strategies. Hence, studying the kinds of MKT used in teaching algebraic routines would help researchers and teacher educators to evaluate the depth and breadth of individual mathematics teachers’ own conceptions of the routines and best ways of teaching and learning them, and make better sense of teachers’ instructional preferences, design, reasoning, and decision-making. Such studies would also potentially identify the most crucial features of MKT that could support effective teaching and facilitate balanced and substantial growth in students’ algebraic proficiencies, including the most recent emphasis on developing reasoning and sense making skills (Graham, Cuoco, & Zimmermann, 2010; National Council of Teachers of Mathematics, 2010).

Research Objective and Question

In previous studies (Li, 2007, 2008, 2009), the researcher measured secondary school mathematics teachers’ MKT in algebraic equation solving based on teacher participants’ written responses to an assessment instrument and data generated from follow-up interviews. In a current study on MKT, the researcher looked into an individual mathematics teacher’s daily instructional activities in actual school and classroom settings to search for traces and indications of MKT. Through this case study, the researcher expected to generate richer, more subtle, and more authentic details of individual teachers’ MKT that is demonstrated in and has influence on the teachers’ pedagogical routines reasoning in teaching algebraic routines. Specifically, the researcher chose quadratic equation solving as the algebraic routine to focus on, and attempted to answer the following questions: What MKT is entailed in a mathematics teacher’s instructional design and enactment, when the teacher is teaching an algebraic routine (such as solving quadratic equations) and aims to develop multiple strands of mathematical proficiency simultaneously among students?

Conceptual Framework

In building a tentative framework for MKT for his own studies, the researcher compared a variety of existing theoretical perspectives on MKT, including the most influential ones proposed by Shulman (1986a, 1986b, 1987), Ball, Thames, and Phelps (2008), and Thames and Ball (2010). Three common core domains of knowledge emerged during this process, which resemble very much the three dimensions of teachers’ professional knowledge for teaching algebra, epistemological, cognitive, and didactic (Artigue, Assule, Grugeon, & Lenfant, 2001), and the three components of teachers’ mathematical knowledge base, mathematics content, student epistemology, and pedagogy (Harel & Lim, 2004). These three domains were adapted by the researcher to establish his own framework for MKT, and they were described as follows: 1. Knowledge of the mathematical subject matter: teachers’ knowledge of the mathematical content in its subject matter forms (interrelated concepts, processes, properties, methods, and sequences of reasoning), both as an academic discipline and as a course of study. 2. Knowledge of pedagogical representations: teachers’ knowledge of the pedagogical form of the mathematical content, as presented by instructional media (e.g., textbooks, manipulatives, visual aids, and electronic technologies) and through various teaching strategies. Such content is the intermediate product when the subject matter is being unpacked, linked, reorganized, and tailored by the teachers through particular sequences of curriculum units and topics, as well as the uses of various examples, metaphors, models, explanations, questions, tasks, tools, and technologies, etc.

4 Mathematical Knowledge for Teaching

3. Knowledge of learners’ conceptions: teachers’ knowledge of the cognitive forms of the mathematical content, i.e., learners’ mental representations of the mathematics subject matter, which results from learners’ interactions with the subject matter, the teacher, other learners, instructional technologies, and other factors in the learning environment. The researcher believes that these domains of knowledge would evolve along with the growth in teachers’ mathematics learning experiences and teaching expertise, in teacher preparation and professional development programs, and in their daily teaching practices. These domains of knowledge would be cognitive entities existing in teachers’ mental registry. They have major impact on, and could also be reflected by, teachers’ instructional design and decision making. Meanwhile, these knowledge domains would likely be constantly modified or refined during teachers’ daily interactions with curricular content, learners, and school context. Such beliefs have underlain the entire research design, implementation, and analysis processes.

Methods Context and Participant

The study took place in one of the largest and most diverse school districts in California. The teacher who participated in the case study, Mary (pseudonym), teaches mathematics at an urban high school in the district. According to the latest profile, student population in the school includes 43.5% Hispanic, 30.7 % white, 12.5 % African-American, and 9.5% Asian. Over 17 primary languages are spoken in the homes of the students. Nearly half of the students are on a free or reduced lunch program. At the time of the study, Mary had taught high school mathematics for 8 years, and was the leader of the mathematics department in her school. She was chosen for this study because of her experiences and success in working with ethnically and economically diverse students to learn mathematics.

Data Collection

In the Fall of 2010, the researcher observed three consecutive 90-minute lessons taught by Mary in her 9th grade algebra class, which will be named Lessons 1, 2, and 3, respectively, from the rest of this paper. In these lessons, Mary introduced the quadratic formula for solving quadratic equations, addressed various aspects of this method, and compared it to other methods. Four main sources of data were collected in Mary’s class: (1) teaching videos of the three lessons; (2) classroom observation notes; (3) artifacts used by Mary or her students, including lesson plans, presentation slides and transparencies, handouts, worksheets, and student work, etc.; and (4) semi- structured interviews conducted with Mary and audiotaped right after each lesson.

Prior to the data collection process, human subject research applications were approved by the Institutional Research Board at the researcher’s institution and by the school district. Informed consent forms were signed by and collected from Mary and the parents or guardians of all students in Mary’s class.

Data Analysis

During data analysis, the classroom teaching videos and the interview audiotapes were first transcribed. Both the transcripts and the observation notes then underwent two rounds of coding. The first round focused on the various pedagogical moves that Mary made in the three lessons surrounding the methods for solving quadratic equations. The rationale for this initial analysis is that teachers’ actions in response to teaching tasks are places where teachers’ knowledge in action can be identified (Marcus & Chazan, 2010). Codes were categorized and compiled into themes such using representations, making connections and making justifications, which overlap with the five mathematical processes addressed by NCTM (2000). The researcher named these themes as mathematical practices since they are in essence very similar to those mathematical practices defined in by the Common Core State Standards Initiative (2010). They are physical or mental actions that can be carried out by both teachers and students. As pedagogical moves, they are more closely tied to the focal mathematics topic (in this case, routines for solving quadratic equations) than those general instructional activities or strategies such as selecting tasks, asking questions, orchestrating discussions, or coordinating group work. The second round of coding was based on the conceptual framework for MKT presented earlier. The researcher first related each of the mathematical practices identified in the first round of coding to one of the three domains of knowledge in the framework, then unpacked and coded the specific MKT entailed in each of the practices. Afterward the researcher combed through all transcripts and notes searching for other evidence and indications of MKT. In the last step of data analysis, the researcher examined all artifacts to triangulate with the themes which emerged from the observation and interview data.

Results and Findings

Mathematical Practices Staged in the Lessons

Throughout the three lessons, Mary had engaged her class into seven mathematical practices which are mostly sequential: Representations. In Lesson 1, Mary introduced the quadratic formula to her class by employing four kinds of representations in a row: symbolic,

6 Mathematical Knowledge for Teaching verbal, rhythmic, and metaphorical. She first presented the formula for the general form of quadratic equations, ax2 + bx + c = 0, then asked a student to read the formula aloud, and asked the entire class to sing the formula as a rhythm: “x equals negative b, plus or minus the square root, b squared minus 4ac, all over 2a.”. She also told the story of The Sad Little Bee three times as a phonetic cue: The bee is sad (negative), and he is feeling wishy-washy, maybe he will go or maybe he won’t (plus or minus). It’s about going to the radical party. He’s feeling a little squared, about the four awesome cheerleaders. The entire party was over, however, by 2am.

Exemplifications. The above four representations were followed immediately by five examples of solving quadratic equations through which Mary demonstrated in detail how to identify the coefficients a, b, and c, substitute them into the formula, and carry out the numerical computations. These examples were well selected to cover several different situations: (1) the leading coefficient a equals 1 versus (2) a is a whole number greater than 1, and (3) the linear coefficient b is zero versus (4) b is non-zero. In the first 55 minutes of Lesson 3, Mary led the class through a second and more comprehensive round of exemplifications, going over seven different equations and demonstrated in detail how one or more of the four basic methods (factoring, complete the square, the quadratic formula, and graphing) are used to solve each of these equations. These practices prepared the class for discussion on the features of the four methods at the very end. Derivation. In Lesson 2, Mary spent nearly one hour out of the total 90 minutes on the derivation and justification of the quadratic formula. She provided the students with a handout that compares side-by-side the 14 parallel steps of the completing the square procedure when it was applied to two problem situations: (1) solving the specific quadratic equation 3x2 + 7x + 2 = 0, and (2) transforming the general quadratic equation ax2 + bx + c = 0 step-by-step to induce the quadratic formula. Justifications. To make sure her students were familiar with and understood the derivation of the quadratic formula, Mary went further to ask the class to justify each of the 14 demonstrated steps. As a preparation, she first let the students turn to the back of the handout which showed six mathematical properties and processes (complete the square, factor, subtraction property of equality, find common denominators, division property of equality, and taking the square root of both sides), and use these to explain six steps selected among the 14. Afterward, she asked the class to turn back to the side with the 14 parallel steps and justify the rationale of each step. Connections. The derivation and justification activities provided an opportunity through which Mary’s students could realize the relationship and connections between the quadratic formula and other foundational properties

Li 7 and methods, such as completing the square. She didn’t require the students to reconstruct the derivation process on their own, but did expect them to understand the fact that, despite the seemingly different outlooks and levels of sophistication of the two procedures (numerical vs. symbolic), solving specific quadratic equations by completing the square and deriving the general quadratic formula actually follow the exact same procedure and both are based on the same set of mathematical properties and processes. Applications. During the last 15 minutes of Lesson 1 and the last 20 minutes of Lesson 2, Mary asked her students to work in pairs and use all four methods (factoring, complete the square, the quadratic formula, and graphing) to solve assigned quadratic equations. Her goal appeared to be that her students not only became fluent with each of these methods but also understood them better in terms of their similarities and differences. Together with the comprehensive exemplifications during the first hour in Lesson 3, these applications and contrasts that occurred across two lessons laid the foundation for the class’ final discussion on the features of the four methods. Comparisons. In the last 35 minutes of Lesson 3, Mary initiated a whole class discussion on the strengths and limitations of the four methods. After eliciting preferences and comparisons from the class, she summarized the typical situations in which one of these methods would work better: (1) use graphing if the graph of the trinomial is already given; (2) use factoring if the lead coefficient a equals 1 and the trinomial is “composite” (reducible); (3) use completing the square if a is 1 and the trinomial is “prime” (irreducible); and (4) use the quadratic formula if a is not 1 and the trinomial is prime. Right afterward she went through three specific examples with her students. Her goal here was to provide the students with some general guidelines on choosing the best method for solving a given quadratic equation. She briefly touched on two of the five features of mathematics algorithms (Kilpatrick, Swafford, & Findell, 2001): (1) generality, e.g., the quadratic formula works for any quadratic equation while factoring doesn’t if integral coefficients are desired in the linear factors; and (2) efficiency, e.g., the factoring method would typically work faster than completing the square.

MKT Entailed in the Mathematical Practices The mathematical practices identified in Mary’s three lessons provided an important venue for the three domains of mathematical knowledge she utilized to surface. Her conversations with the researcher during the post- observation interviews offered further information on her MKT. Knowledge of the mathematical subject matter. Mary’s knowledge of the subject matter was reflected mainly through five of the mathematical practices she enacted: application, derivation, justification, connection, and comparison. During the practices and the interviews, Mary demonstrated a solid understanding of the quadratic formula in terms of the following three aspects:

8 Mathematical Knowledge for Teaching

1. She was able to apply the formula competently to solving various kinds of quadratic equations. She understood that one has to write a given equation into the standard form before substituting the coefficients in the formula, and to correctly perform the numerical computations one needs to follow the order of operations and apply basic properties of fractions and radicals. 2. She was very familiar with the derivation process of the formula, including the underlying mathematical property of each step, as well as the connections between the formula and other methods for solving quadratic equations. 3. She knows clearly about some of the basic features of the quadratic formula (e.g., generality or applicability, accuracy, and efficiency) in comparison with other methods. She understood that the quadratic formula is most general and applicable in solving quadratic equations, and in turn shared this knowledge to her students: It works on everything, under any conditions, and makes it easy and beautiful. It’s fabulous. At the end of the day it would solve everything. Meanwhile, she understood and paid attention to the limitations of the other three methods. She believed it is important to convey these to her students, as an alternative way to convince them the importance of the quadratic formula: There are actually some really great reasons to memorize this [formula]… If I’m gonna graph a quadratic equation and find the roots, it’s a lot of work, and often times the roots are not integers , the graphing won’t land on pretty numbers, they land on yucky numbers, we can’t read on the graph…… Sometimes factoring is just a pain. It’s easy if they are factorable, but what if they are prime? You can’t even use this [factoring method]…… And then completing the square is a bit grove, the problem with completing the square is when the first coefficient is not 1. If the coefficient A is not 1, then completing the square is a pain. Knowledge of pedagogical representations. Mary’s knowledge of pedagogical representations was mainly entailed in two of the mathematical practices: representations and exemplifications. Together with her understanding of the subject matter, and influenced by her considerations on students’ learning characteristics and preferences, Mary first drew upon her knowledge of various representations of the quadratic formula and other methods: song, storyline, color coding, and other visual effects, which she believed would be suitable and helpful to students with different learning preferences. The examples and exercises Mary provided to her class covered three basic types of quadratic equations, which could prove that she had a quite complete picture of the entire landscape of solving quadratic equations in the algebra curriculum.

Knowledge of learners’ conceptions. Compared to her first two domains of MKT that were just discussed, Mary’s knowledge of learners’ conceptions was not as directly visible through the lens of the mathematical practices. Instead, her knowledge and considerations of her students’ prior knowledge, skills, and learning preferences were identified mainly through the interviews, and maybe in combination with a few instructional activities in the lessons: 1. At the beginning of each lesson she always provided a short review of concepts or skills covered in previous sections, as a preparation for studying in the current lesson. She was fully aware of the fact that solving quadratic equations is a complicated task that requires students’ proficiency in arithmetic and linear expressions and equations. 2. In Lesson 1 she asked the students to read the quadratic formula aloud, sing it as a rhythm, and tell the story of The Sad Little Bee, because she believed the purely symbolic derivation of the formula could be overwhelming or challenging to many students, whereas those verbal and rhythmic representations and activities would make it a lot more joyful and easier for the students to remember the formula. Students should like this because “it uses different memory devices”. 3. With multiple examples and a series of exercises, she spent quite some time on demonstrating how to use the quadratic formula and what to pay attention to in carrying out the arithmetic computations step-by-step, which indicated that she was very knowledgeable of the various mistakes her students may make and the typical difficulties they would encounter in the calculations.

The Dynamics of MKT

Among the three domains of MKT demonstrated in Mary’s teaching, her knowledge of the subject matter (i.e., the quadratic formula and other methods for solving quadratic equations) appeared to be solid and comprehensive. Together with her strong beliefs on the importance of facilitating students’ conceptual understanding, her knowledge of those algebraic routines exerted most influences on her design and enactment of the three lessons. Since she truly understood the entire derivation process of the quadratic formula and its step-by-step justifications, and recognized the importance of the derivations and justifications, she was willing to spend much time helping her students to become familiar with these aspects of the formula. Similarly, based on her own clear insights in the features and applicabilities of the four methods for solving quadratic equations, and her preference on efficiency, she was both willing and feeling comfortable to lead the whole-class discussion on these matters. Meanwhile, her lesson planning and teaching were also influenced by her knowledge of and past experiences with her students’ learning characteristics

10 Mathematical Knowledge for Teaching and preferences. The constant review of previously studied foundational concepts and methods, introducing the quadratic formula with multiple representations, and detailed demonstrations of the execution of the quadratic formula on various examples, are all evidence of such knowledge and its influence. Further, her knowledge of student learning in turn activated her third domain of MKT, knowledge of pedagogical representations - various ways to present and familiarize with the formula, and basic types of examples and exercises that could capture the nature of the formula and demonstrate the various applications of the formula.

Discussion and Implications

The three lessons taught by Mary provide an example of a mathematics teacher’s attempt in teaching algebraic routines in ways that address both the conceptual and the procedural aspects of the routines. The MKT utilized by Mary shaped her design and enactment of the various mathematical practices which in turn created a positive learning environment that had potentials in facilitating conceptual understanding, procedural fluency, and strategic competence. Since only three lessons were observed and analyzed, it is unclear whether and when these aspects of mathematical proficiency could all be achieved simultaneously and effectively by the students. At the end of the third lesson, it was unknown to what extent the students in Mary’s class had retained the conceptual underpinnings of the formula (derivation and justifications) and the features of all four methods for solving quadratic equations. It was obvious, though, that the majority of the students still needed more time to achieve fluency in applying the quadratic formula and to develop the kind of strategic flexibility that Mary expected. Simultaneously developing students’ conceptual understanding, procedural fluency, and strategic competence in algebraic routines could be a fairly long and complex process. A teacher’s solid MKT lays the foundation for effective teaching and learning, but may not be easily transformed into productive learning and expected outcomes in proficiency. Some major variants are involved during this transformation process. One of the variants is the relative strengths of the three domains of a teacher’s MKT. How these three domains of knowledge interact among themselves and how they collectively influence a teacher’s thinking and decision making are worth further investigations. For instance, Mary’s knowledge of the subject matter weighed more in her teaching than the other two domains of knowledge. Had she not understood the routines as in depth but instead had richer knowledge in pedagogical representations and student learning with respect to the routines, would she have come up with a different set of goals, focuses, and strategies and subsequently taught the lessons differently? And if the answer is yes, then how?

Another variant is a teacher’s beliefs on mathematical proficiency, such as the nature and criteria for mathematical proficiency, the relationship among various aspects of proficiency, and how proficiency could or should be developed. How is a teacher’s MKT of algebraic routines related to and interacting with her or his beliefs on proficiency? In Mary’s case, her solid knowledge of the algebraic routines went hand-in-hand with her beliefs in pursuing conceptual understanding, which led to her attempt in developing students’ procedural fluency and strategic competency based upon their conceptual understanding of the routines. Had she valued procedural automaticity more than anything else, several situations could have happened: she might have completely skipped the derivation, justifications, and comparisons, and focused more on the representations or applications; she might have simply let her students memorize the formula and then go through repeated practices until reaching procedural fluency; or, she might have told her students that all methods are good so they can choose whatever method they like to solve a given quadratic equation. A more fundamental question is how to distinguish between a teacher’s MKT and beliefs, or, when certain beliefs a teacher hold could be considered as part of her or his MKT. Not all teacher beliefs merit the label of knowledge (Feiman-Nemser & Floden, 1986). Following Plato’s definition of knowledge as justified true beliefs (Theaetetus), Li (2007) identified five main sources of justification for knowledge claims: mathematical criteria, educational policies, educational theories or perspectives, collective experiences, and individual experiences and contexts. In Mary’s case, her beliefs on building procedural fluency upon conceptual understanding and strategic competency could be well justified by the standard-based curriculum movement and state mathematics curriculum framework. In contrast, some of her notions about student learning characteristics and ways of presenting the algebraic routines appeared to be justifiable mostly by her personal teaching experiences. Whether these conceptions and strategies can become substantial knowledge claims that are easily shared by other fellow teachers and yield wider impacts on student learning, would largely depend on how well they match the policy, theory, and local educational settings that the other teachers are in. Overall, there are multiple indicators of effective mathematics teaching (An & Wu, 2007) which may not always be attainable simultaneously. In making instructional designs and decisions to facilitate student learning, a mathematics teacher explicitly or implicitly puts varying preferences on her or his three domains of MKT, and assigns different interpretations and weights on the various mathematical strands of mathematical proficiency. Further, due to limited time and resources, the teacher may also have to constantly find compromises among personal MKT, the instructional demands from developing proficiency, and other variants such as policy and assessment requirements, district and school settings, diverse student characteristics and needs, and her or his personal beliefs, goals, expectations, and experiences.

12 Mathematical Knowledge for Teaching

A major implication of the study is that mathematics teacher preparation and professional development activities should address two crucial themes regarding teaching mathematical routines for proficiency. On the one hand, more emphasis needs to be put on the features and applicability of the various algorithms and strategies for carrying out a fundamental procedure in school mathematics: why, when, and how these algorithms and strategies work, in what cases they would work the best, when they would not work well, and how to compare them and choose the optimal one both in general and in a specific problem context. Scholars have summarized these features as transparency, efficiency, generality, precision, and simplicity (Kilpatrick, Swafford, & Findell, 2001) and provided suggestions for instructions. On the other hand, since teachers would have varying strengths and preferences across the three basic domains of mathematical knowledge for teaching routines, and teachers’ knowledge and beliefs with varying sources and degrees of justification would exert different impacts on teaching, mathematics teacher preparation and professional development should not only aim at strengthening teachers’ MKT in all three domains, but also help teachers to develop the insights, skills, and flexibilities that are needed to make well-informed, thoroughly-reasoned, and balanced decisions in promoting mathematical proficiency among all mathematics learners. The kinds of MKT revealed this study may better to be phrased as mathematical knowledge teachers draw upon in teaching, as they are observed empirically only from individual teachers’ work on a particular mathematics topic with students in individual classrooms. The analysis and synthesis of these kinds of knowledge were certainly not meant to be exhaustive. Future studies should involve other teachers with distinct backgrounds, experiences, and classroom settings and teaching other types of mathematical routines. Only in doing so may we be able to ultimately generate and describe a more comprehensive body of mathematical knowledge that the majority of mathematics educators would collectively agree as essential for effectively teaching mathematical routines for proficiency.

An, S., & Wu, Z. (2007). What is the effective mathematics lesson? Journal of People’s Education of China. 549, 44-47 Adler, J., & Davis, Z. (2006). Opening another black box: Researching mathematics for teaching in mathematics teacher education. Journal for Research in Mathematics Education, 37(4), 270-296. Ball, D. L. (1999). Crossing boundaries to examine the mathematics entailed in elementary teaching. In T. Lam (Ed.), Contemporary Mathematics, 243. 15-36. Providence, ST: American Mathematical Society. Ball, D. L., & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J.

Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83-104). Westport, CT: Ablex. Ball, D. L. & Bass, H. (2003). Towards a practice-based theory of mathematical knowledge for teaching. In B. Davis & E. Simmt (Eds.), Proceedings of the 2002 annual meeting of the Canadian Mathematics Education Study Group (pp. 3-14). Edmonton, AB: CMESG/GCEDM. Ball, D.L., Bass, H., Hill, H., & Schilling, S. (2005, February). Developing measures of mathematical knowledge for teaching. Presentation at Teachers Development Group Leadership Seminar, Mathematics Professional Development, Portland, OR,. Ball, D. L., Lubienski, S., & Mewborn, D. (2001). Research on teaching mathematics: The unsolved problem of teachers’ mathematical knowledge. In V. Richardson (Ed.), Handbook of research on teaching (4th ed., pp. 433-456). New York: Macmillan. Conference Board of the Mathematical Sciences. (2001). The mathematical education of teachers. Providence, RI: American Mathematical Society and Mathematical Association of America. Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407. Chazan, D. (2000). Beyond formulas in mathematics and teaching: Dynamics of the high school algebra classrooms. New York: Teachers College. Chazan, D. (2008). The shifting landscape of school algebra in the United States. In C. Greenes & R. Rubenstein (Eds.), Algebra and Algebraic Thinking in School Mathematics (pp. 19-33). 70th Yearbook of the National Council of Teachers of Mathematics. NCTM: Reston, VA. Common Core State Standards Initiative. (2010). Common core state standards for mathematics. Retrieved from http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf Cuoco, A. (2001). Mathematics for teaching. Notices of the American Mathematical Society, 48 (2), 68-74. Davis, B., & Simmt, E. (2006). Mathematics-for-teaching: An ongoing investigation of the mathematics that teachers (need to) know. Educational Studies in Mathematics, 61(3), 293-319. Ed-Data. (2011). Profile of Long Beach Unified school district, Fiscal Year 2009-2010. Retrieved from http://www.ed- data.k12.ca.us/Navigation/fsTwoPanel.asp?bottom=%2Fprofile.asp%3Fl evel%3D06%26reportNumber%3D16 Feiman-Nemser S., & Floden R.E. (1986). The cultures of teaching. In M.C. Wittrock (Ed.), Handbook of research on teaching, (3rd edition, pp. 505- 526). New York: Macmillan. Ferrini-Mundy, J., & Findell, B. (2001). The mathematical education of prospective teachers of secondary school mathematics. CUPM

14 Mathematical Knowledge for Teaching

Discussion papers about mathematics and the mathematical sciences in 2010: What should students know? Washington, DC: MAA. Ferrini-Mundy, J., Burrill, G., Floden, R., & Sandow, D. (2003, April). Teacher knowledge for teaching school algebra: Challenges in developing an analytical framework. Paper presented at the annual meeting of the American Educational Research Association, Chicago, IL. Ferrini-Mundy, J., McCrory, R., & Senk, S. (2006, Month). Knowledge of algebra teaching: Framework, item development, and pilot results. Paper presented Research symposium at the research presession of NCTM annual meeting. St. Louis, MO. Goldhaber, D. D., & Brewer, D. J. (2000). Does teacher certification matter? High school teacher certification status and student achievement. Educational Evaluation and Policy Analysis, 22, 129-145. Graham, K., Cuoco, A., & Zimmermann, G. (2010). Focus in high school mathematics: Reasoning and sense making in algebra. Reston, VA: National Council of Teachers of Mathematics. Harel, G., & Lim, K. H. (2004). Mathematics teachers’ knowledge base: Preliminary results. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway. Heid, M. K. (2007, May). Mathematical knowledge for teaching algebra: Recommendations, research, and relationship to practice. Presentation at California Algebra Forum. Hill, H. C., Schilling, S. G., & Ball, D. L. (2004). Developing measures of teachers’ mathematics knowledge for teaching. The Elementary School Journal, 105(1), 12-30. Hiebert, J. (1986). Conceptual and procedural knowledge: The case of mathematics. Hillsdale, NJ: Erlbaum. Kieran, C. (2007). Learning and teaching algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In F. K. lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 707–62). Charlotte, N.C.: Information Age Publishing; Reston, Va. National Council of Teachers of Mathematics. Kilpatrick, J., & Izsák, A. (2008). A history of algebra in the school curriculum. In C. Greenes & R. Rubenstein (Eds.), Algebra and algebraic thinking in school mathematics (pp. 3-18). 70th Yearbook of the National Council of Teachers of Mathematics. NCTM: Reston, VA. Kilpatrick, J., Swafford, J., & Findell, B. (Eds.) (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press. Kennedy, M. M. (1997). Defining optimal knowledge for teaching science and mathematics. (Research Monograph No. 10). Madison, WI: National Institute for Science Education. Li, X. (2007). An investigation of secondary school algebra teachers' mathematical knowledge for teaching algebraic equation solving

(Doctoral dissertation). The University of Texas at Austin. Available electronically from http : / /hdl .handle .net /2152 /3337. Li, X. (2008, January). Patterns in and justifications for mathematics teachers’ use of knowledge in context. Presentation at the 12th annual conference of the Association of Mathematics Teacher Educators, Tulsa, OK. Li, X. (2009, April). Mathematics teachers’ preferential uses of knowledge for teaching algebra and the intervention of personal perceptions and experiences. Presentation at the annual meeting of the American Education Research Association, San Diego, CA. Ma, L. (1999). Knowing and teaching elementary school mathematics: Teachers' understanding of fundamental mathematics in China and US. Mahwah, NJ: Erlbaum. Marcus, R., & Chazan, D. (2010). Teachers’ knowledge of mathematics in action: Helping students think about solving equations in the one- variable -first algebra curriculum. In R. Leikin & R. Zaskis (Eds.), Learning through teaching: Developing mathematics teachers' knowledge and expertise in practice (pp. 169-187). New York: Springer. Monk, D. H. (1994). Subject area preparation of secondary mathematics and science teachers and student achievement. Economics of Education Review, 13(2), 125-145. National Council of Teachers of Mathematics. (2000). Principles and standardsfor school mathematics. Reston, VA. National Council of Teachers of Mathematics. (2010). Focus in high school mathematics: Reasoning and sense making. Reston, VA. Rowan, B., Chiang, F. S., & Miller, R. J. (1997). Using research on employee’s performance to study the effects of teachers on student achievement. Sociology of Education, 70, 256-284. Shulman, S. L. (1986a). Those who understand: Knowledge growth in teaching. Educational Researcher, 4-14. Shulman, S. L. (1986b). Paradigms and research programs in the study of teaching: A contemporary perspective. In Wittrock, M. C. (Ed), Handbook of research on teaching (pp. 3-36). City, ST: Macmillan Publishing Company. Shulman, S. L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57 (1). 1-22. Star, J. R. (2000). Levels of competence in procedural skills. In B. Fishman & S. O'Connor-Divelbiss (Eds.), Proceedings of fourth international Conference of the Learning Sciences (pp. 78-79). Mahwah, NJ: Erlbaum Star, J. R. (2005). Reconceptualizing procedural knowledge. Journal for Research in Mathematics Education, 36(5), 404-411. Stylianides, A. J., & Ball, D. L. (2008). Understanding and describing mathematical knowledge for teaching: knowledge about proof for engaging students in the activity of proving. Journal of Mathematics Teacher Education. issue and pages missing

16 Mathematical Knowledge for Teaching

Thames, M. H.,& Ball, D. L. (2010). What mathematical knowledge does teaching require? Knowing mathematics in and for teaching. Teaching Children Mathematics, 17(4), 220-225. Wu, H. H. (1999). Basic skills versus conceptual understanding: A bogus dichotomy in mathematics Education. American Educator 11(4), 307-332

Author: Xuhui Li California State University at Long Beach, USA. [email protected]