hypothesis test on slope of regression line

Teach yourself statistics

Hypothesis Test for Regression Slope

This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y .

The test focuses on the slope of the regression line

Y = Β 0 + Β 1 X

where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of the independent variable, and Y is the value of the dependent variable.

If we find that the slope of the regression line is significantly different from zero, we will conclude that there is a significant relationship between the independent and dependent variables.

Test Requirements

The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.

• The dependent variable Y has a linear relationship to the independent variable X .
• For each value of X, the probability distribution of Y has the same standard deviation σ.
• The Y values are independent.
• The Y values are roughly normally distributed (i.e., symmetric and unimodal ). A little skewness is ok if the sample size is large.

The test procedure consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

If there is a significant linear relationship between the independent variable X and the dependent variable Y , the slope will not equal zero.

H o : Β 1 = 0

H a : Β 1 ≠ 0

The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use a linear regression t-test (described in the next section) to determine whether the slope of the regression line differs significantly from zero.

Analyze Sample Data

Using sample data, find the standard error of the slope, the slope of the regression line, the degrees of freedom, the test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.

SE = s b 1 = sqrt [ Σ(y i - ŷ i ) 2 / (n - 2) ] / sqrt [ Σ(x i - x ) 2 ]

• Slope. Like the standard error, the slope of the regression line will be provided by most statistics software packages. In the hypothetical output above, the slope is equal to 35.

t = b 1 / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

The local utility company surveys 101 randomly selected customers. For each survey participant, the company collects the following: annual electric bill (in dollars) and home size (in square feet). Output from a regression analysis appears below.

Is there a significant linear relationship between annual bill and home size? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

H o : The slope of the regression line is equal to zero.

H a : The slope of the regression line is not equal to zero.

• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a linear regression t-test to determine whether the slope of the regression line differs significantly from zero.

We get the slope (b 1 ) and the standard error (SE) from the regression output.

b 1 = 0.55       SE = 0.24

We compute the degrees of freedom and the t statistic, using the following equations.

DF = n - 2 = 101 - 2 = 99

t = b 1 /SE = 0.55/0.24 = 2.29

where DF is the degrees of freedom, n is the number of observations in the sample, b 1 is the slope of the regression line, and SE is the standard error of the slope.

• Interpret results . Since the P-value (0.0242) is less than the significance level (0.05), we cannot accept the null hypothesis.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

15.1 - a test for the slope.

Once again we've already done the bulk of the theoretical work in developing a hypothesis test for the slope parameter \(\beta\) of a simple linear regression model when we developed a \((1-\alpha)100\%\) confidence interval for \(\beta\). We had shown then that:

\(T=\dfrac{\hat{\beta}-\beta}{\sqrt{\frac{MSE}{\sum(x_i-\bar{x})^2}}}\)

follows a \(t_{n-2}\) distribution. Therefore, if we're interested in testing the null hypothesis:

\(H_0:\beta=\beta_0\)

against any of the alternative hypotheses:

\(H_A:\beta \neq \beta_0\), \(H_A:\beta < \beta_0\), \(H_A:\beta > \beta_0\)

we can use the test statistic:

\(t=\dfrac{\hat{\beta}-\beta_0}{\sqrt{\frac{MSE}{\sum(x_i-\bar{x})^2}}}\)

and follow the standard hypothesis testing procedures. Let's take a look at an example.

Example 15-1 Section  

In alligators' natural habitat, it is typically easier to observe the length of an alligator than it is the weight. This data set contains the log weight (\(y\)) and log length (\(x\)) for 15 alligators captured in central Florida. A scatter plot of the data suggests that there is a linear relationship between the response \(y\) and the predictor \(x\). Therefore, a wildlife researcher is interested in fitting the linear model:

\(Y_i=\alpha+\beta x_i+\epsilon_i\)

to the data. She is particularly interested in testing whether there is a relationship between the length and weight of alligators. At the \(\alpha=0.05\) level, perform a test of the null hypothesis \(H_0:\beta=0\) against the alternative hypothesis \(H_A:\beta \neq 0\).

The easiest way to perform the hypothesis test is to let Minitab do the work for us! Under the Stat menu, selecting Regression, and then Regression, and specifying the response logW (for log weight) and the predictor logL (for log length), we get:

The regression equation is logW = - 8.48 + 3.43 logL

Analysis of Variance

Easy as pie! Minitab tells us that the test statistic is \(t=25.80\) (in blue ) with a \(p\)-value (0.000) that is less than 0.001. Because the \(p\)-value is less than 0.05, we reject the null hypothesis at the 0.05 level. There is sufficient evidence to conclude that the slope parameter does not equal 0. That is, there is sufficient evidence, at the 0.05 level, to conclude that there is a linear relationship, among the population of alligators, between the log length and log weight.

Of course, since we are learning this material for just the first time, perhaps we could go through the calculation of the test statistic at least once. Letting Minitab do some of the dirtier calculations for us, such as calculating:

\(\sum(x_i-\bar{x})^2=0.8548\)

as well as determining that \(MSE=0.015\) and that the slope estimate = 3.4311, we get:

\(t=\dfrac{\hat{\beta}-\beta_0}{\sqrt{\frac{MSE}{\sum(x_i-\bar{x})^2}}}=\dfrac{3.4311-0}{\sqrt{0.015/0.8548}}=25.9\)

which is the test statistic that Minitab calculated... well, with just a bit of round-off error.

Advanced High School Statistics: Second Edition, with updates based on AP© Statistics Course Framework

David M Diez, Mine Çetinkaya-Rundel, Leah Dorazio, Christopher D Barr

Section 8.3 Inference for the slope of a regression line

Here we encounter our last confidence interval and hypothesis test procedures, this time for making inferences about the slope of the population regression line. We can use this to answer questions such as the following:

Is the unemployment rate a significant linear predictor for the loss of the President's party in the House of Representatives?

On average, how much less in college gift aid do students receive when their parents earn an additional $1000 in income?

Subsection 8.3.1 Learning objectives

Recognize that the slope of the sample regression line is a point estimate and has an associated standard error.

Be able to read the results of computer regression output and identify the quantities needed for inference for the slope of the regression line, specifically the slope of the sample regression line, the \(SE\) of the slope, and the degrees of freedom.

State and verify whether or not the conditions are met for inference on the slope of the regression line based using the \(t\)-distribution.

Carry out a complete confidence interval procedure for the slope of the regression line.

Carry out a complete hypothesis test for the slope of the regression line.

Distinguish between when to use the \(t\)-test for the slope of a regression line and when to use the matched pairs \(t\)-test for a mean of differences.

Subsection 8.3.2 The role of inference for regression parameters

Previously, we found the equation of the regression line for predicting gift aid from family income at Elmhurst College. The slope, \(b\text{,}\) was equal to \(-0.0431\text{.}\) This is the slope for our sample data. However, the sample was taken from a larger population. We would like to use the slope computed from our sample data to estimate the slope of the population regression line.

The equation for the population regression line can be written as

Here, \(\alpha\) and \(\beta\) represent two model parameters, namely the \(y\)-intercept and the slope of the true or population regression line. (This use of \(\alpha\) and \(\beta\) have nothing to do with the \(\alpha\) and \(\beta\) we used previously to represent the probability of a Type I Error and Type II Error!) The parameters \(\alpha\) and \(\beta\) are estimated using data. We can look at the equation of the regression line calculated from a particular data set:

and see that \(a\) and \(b\) are point estimates for \(\alpha\) and \(\beta\text{,}\) respectively. If we plug in the values of \(a\) and \(b\text{,}\) the regression equation for predicting gift aid based on family income is:

The slope of the sample regression line, \(-0.0431\text{,}\) is our best estimate for the slope of the population regression line, but there is variability in this estimate since it is based on a sample. A different sample would produce a somewhat different estimate of the slope. The standard error of the slope tells us the typical variation in the slope of the sample regression line and the typical error in using this slope to estimate the slope of the population regression line.

We would like to construct a 95% confidence interval for \(\beta\text{,}\) the slope of the population regression line. As with means, inference for the slope of a regression line is based on the \(t\)-distribution.

Inference for the slope of a regression line.

Inference for the slope of a regression line is based on the \(t\)-distribution with \(n-2\) degrees of freedom, where \(n\) is the number of paired observations.

Once we verify that conditions for using the \(t\)-distribution are met, we will be able to construct the confidence interval for the slope using a critical value \(t^{\star}\) based on \(n-2\) degrees of freedom. We will use a table of the regression summary to find the point estimate and standard error for the slope.

Subsection 8.3.3 Conditions for the least squares line

Conditions for inference in the context of regression can be more complicated than when dealing with means or proportions.

Inference for parameters of a regression line involves the following assumptions:

Linearity. The true relationship between the two variables follows a linear trend. We check whether this is reasonable by examining whether the data follows a linear trend. If there is a nonlinear trend (e.g. left panel of Figure 8.3.1 ), an advanced regression method from another book or later course should be applied.

Nearly normal residuals. For each \(x\)-value, the residuals should be nearly normal. When this assumption is found to be unreasonable, it is usually because of outliers or concerns about influential points. An example which suggestions non-normal residuals is shown in the second panel of Figure 8.3.1 . If the sample size \(n\ge 30\text{,}\) then this assumption is not necessary.

Constant variability. The variability of points around the true least squares line is constant for all values of \(x\text{.}\) An example of non-constant variability is shown in the third panel of Figure 8.3.1 .

Independent. The observations are independent of one other. The observations can be considered independent when they are collected from a random sample or randomized experiment. Be careful of data collected sequentially in what is called a time series . An example of data collected in such a fashion is shown in the fourth panel of Figure 8.3.1 .

We see in Figure 8.3.1 , that patterns in the residual plots suggest that the assumptions for regression inference are not met in those four examples. In fact, identifying nonlinear trends in the data, outliers, and non-constant variability in the residuals are often easier to detect in a residual plot than in a scatterplot.

We note that the second assumption regarding nearly normal residuals is particularly difficult to assess when the sample size is small. We can make a graph, such as a histogram, of the residuals, but we cannot expect a small data set to be nearly normal. All we can do is to look for excessive skew or outliers. Outliers and influential points in the data can be seen from the residual plot as well as from a histogram of the residuals.

Conditions for inference on the slope of a regression line.

The data is collected from a random sample or randomized experiment.

The residual plot appears as a random cloud of points and does not have any patterns or significant outliers that would suggest that the linearity, nearly normal residuals, constant variability, or independence assumptions are unreasonable.

Subsection 8.3.4 Constructing a confidence interval for the slope of a regression line

We would like to construct a confidence interval for the slope of the regression line for predicting gift aid based on family income for all freshmen at Elmhurst college.

Do conditions seem to be satisfied? We recall that the 50 freshmen in the sample were randomly chosen, so the observations are independent. Next, we need to look carefully at the scatterplot and the residual plot.

Always check conditions.

Do not blindly apply formulas or rely on regression output; always first look at a scatterplot or a residual plot. If conditions for fitting the regression line are not met, the methods presented here should not be applied.

The scatterplot seems to show a linear trend, which matches the fact that there is no curved trend apparent in the residual plot. Also, the standard deviation of the residuals is mostly constant for different \(x\) values and there are no outliers or influential points. There are no patterns in the residual plot that would suggest that a linear model is not appropriate, so the conditions are reasonably met. We are now ready to calculate the 95% confidence interval.

Example 8.3.4 .

Construct a 95% confidence interval for the slope of the regression line for predicting gift aid from family income at Elmhurst college.

As usual, the confidence interval will take the form:

The point estimate for the slope of the population regression line is the slope of the sample regression line: \(-0.0431\text{.}\) The standard error of the slope can be read from the table as 0.0108. Note that we do not need to divide 0.0108 by the square root of \(n\) or do any further calculations on 0.0108; 0.0108 is the \(SE\) of the slope. Note that the value of \(t\) given in the table refers to the test statistic, not to the critical value \(t^{\star}\text{.}\) To find \(t^{\star}\) we can use a \(t\)-table. Here \(n=50\text{,}\) so \(df=50-2=48\text{.}\) Using a \(t\)-table, we round down to row \(df=40\) and we estimate the critical value \(t^{\star}=2.021\) for a 95% confidence level. The confidence interval is calculated as:

Note: \(t^{\star}\) using exactly 48 degrees of freedom is equal to 2.01 and gives the same interval of \((-0.065,\ -0.021)\text{.}\)

Example 8.3.5 .

Intepret the confidence interval in context. What can we conclude?

We are 95% confident that the slope of the population regression line, the true average change in gift aid for each additional $1000 in family income, is between \(-$0.065\) thousand dollars and \(-$0.021\) thousand dollars. That is, we are 95% confident that, on average, when family income is $1000 higher, gift aid is between $21 and $65 lower .

Because the entire interval is negative, we have evidence that the slope of the population regression line is less than 0. In other words, we have evidence that there is a significant negative linear relationship between gift aid and family income.

Constructing a confidence interval for the slope of regression line.

To carry out a complete confidence interval procedure to estimate the slope of the population regression line \(\beta\text{,}\)

Identify : Identify the parameter and the confidence level, C%.

The parameter will be a slope of the population regression line, e.g. the slope of the population regression line relating air quality index to average rainfall per year for each city in the United States.

Choose : Choose the correct interval procedure and identify it by name.

Here we use choose the \(t\)-interval for the slope .

Check : Check conditions for using a \(t\)-interval for the slope.

Data come from a random sample or randomized experiment.

The residual plot shows no pattern implying that a linear model is reasonable. More specifically, the residuals should be independent, nearly normal (or \(n\ge 30\)), and have constant standard deviation.

Calculate : Calculate the confidence interval and record it in interval form.

\(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\text{,}\) \(df = n - 2\)

point estimate: the slope \(b\) of the sample regression line

\(SE\) of estimate: \(SE\) of slope (find using computer output)

\(t^{\star}\text{:}\) use a \(t\)-distribution with \(df = n-2\) and confidence level C

Conclude : Interpret the interval and, if applicable, draw a conclusion in context.

We are C% confident that the true slope of the regression line, the average change in [y] for each unit increase in [x], is between and . If applicable, draw a conclusion based on whether the interval is entirely above, is entirely below, or contains the value 0.

Example 8.3.7 .

The regression summary below shows statistical software output from fitting the least squares regression line for predicting head length from total length for 104 brushtail possums. The scatterplot and residual plot are shown above.

Construct a 95% confidence interval for the slope of the regression line. Is there convincing evidence that there is a positive, linear relationship between head length and total length? Use the five step framework to organize your work.

Identify : The parameter of interest is the slope of the population regression line for predicting head length from body length. We want to estimate this at the 95% confidence level.

Choose : Because the parameter to be estimated is the slope of a regression line, we will use the \(t\)-interval for the slope.

Check : These data come from a random sample. The residual plot shows no pattern. In general, the residuals have constant standard deviation and there are no outliers or influential points. Also \(n=104\ge 30\) so some skew in the residuals would be acceptable. A linear model is reasonable here.

Calculate : We will calculate the interval: \(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\)

We read the slope of the sample regression line and the corresponding \(SE\) from the table. The point estimate is \(b = 0.57290\text{.}\) The \(SE\) of the slope is 0.05933, which can be found next to the slope of 0.57290. The degrees of freedom is \(df=n-2=104-2=102\text{.}\) As before, we find the critical value \(t^{\star}\) using a \(t\)-table (the \(t^{\star}\) value is not the same as the \(T\)-statistic for the hypothesis test). Using the \(t\)-table at row \(df = 100\) (round down since 102 is not on the table) and confidence level 95%, we get \(t^{\star}=1.984\text{.}\)

So the 95% confidence interval is given by:

Conclude : We are 95% confident that the slope of the population regression line is between 0.456 and 0.691. That is, we are 95% confident that the true average increase in head length for each additional cm in total length is between 0.456mm and 0.691mm. Because the interval is entirely above 0, we do have evidence of a positive linear association between the head length and body length for brushtail possums.

Subsection 8.3.5 Calculator: the linear regression \(t\)-interval for the slope

We will rely on regression output from statistical software when constructing confidence intervals for the slope of a regression line. We include calculator instructions here simply for completion.

TI-84: T-interval for \(\beta\).

Use STAT , TESTS , LinRegTInt .

Choose STAT .

Right arrow to TESTS .

Down arrow and choose G: LinRegTInt .

This test is not built into the TI-83.

Let Xlist be L1 and Ylist be L2 . (Don't forget to enter the \(x\) and \(y\) values in L1 and L2 before doing this interval.)

Let Freq be 1 .

Enter the desired confidence level.

Leave RegEQ blank.

Choose Calculate and hit ENTER , which returns:

Subsection 8.3.6 Midterm elections and unemployment

Elections for members of the United States House of Representatives occur every two years, coinciding every four years with the U.S. Presidential election. The set of House elections occurring during the middle of a Presidential term are called midterm elections. In America's two-party system, one political theory suggests the higher the unemployment rate, the worse the President's party will do in the midterm elections.

To assess the validity of this claim, we can compile historical data and look for a connection. We consider every midterm election from 1898 to 2018, with the exception of those elections during the Great Depression. Figure 8.3.8 shows these data and the least-squares regression line:

We consider the percent change in the number of seats of the President's party (e.g. percent change in the number of seats for Republicans in 2018) against the unemployment rate.

Examining the data, there are no clear deviations from linearity, the constant variance condition, or the normality of residuals. While the data are collected sequentially, a separate analysis was used to check for any apparent correlation between successive observations; no such correlation was found.

Checkpoint 8.3.9 .

The data for the Great Depression (1934 and 1938) were removed because the unemployment rate was 21% and 18%, respectively. Do you agree that they should be removed for this investigation? Why or why not?  1 

There is a negative slope in the line shown in Figure 8.3.8 . However, this slope (and the y-intercept) are only estimates of the parameter values. We might wonder, is this convincing evidence that the “true” linear model has a negative slope? That is, do the data provide strong evidence that the political theory is accurate? We can frame this investigation as a statistical hypothesis test:

\(\beta = 0\text{.}\) The true linear model has slope zero.

\(\beta \lt 0\text{.}\) The true linear model has a slope less than zero. The higher the unemployment, the greater the loss for the President's party in the House of Representatives.

We would reject \(H_0\) in favor of \(H_A\) if the data provide strong evidence that the slope of the population regression line is less than zero. To assess the hypotheses, we identify a standard error for the estimate, compute an appropriate test statistic, and identify the p-value. Before we calculate these quantities, how good are we at visually determining from a scatterplot when a slope is significantly less than or greater than 0? And why do we tend to use a 0.05 significance level as our cutoff? Try out the following activity which will help answer these questions.

Testing for the slope using a cutoff of 0.05.

What does it mean to say that the slope of the population regression line is significantly greater than 0? And why do we tend to use a cutoff of \(\alpha = 0.05\text{?}\) This 5-minute interactive task will explain: www.openintro.org/why05

Subsection 8.3.7 Understanding regression output from software

The residual plot shown in Figure 8.3.10 shows no pattern that would indicate that a linear model is inappropriate. Therefore we can carry out a test on the population slope using the sample slope as our point estimate. Just as for other point estimates we have seen before, we can compute a standard error and test statistic for \(b\text{.}\) The test statistic \(T\) follows a \(t\)-distribution with \(n-2\) degrees of freedom.

Hypothesis tests on the slope of the regression line.

Use a \(t\)-test with \(n - 2\) degrees of freedom when performing a hypothesis test on the slope of a regression line.

We will rely on statistical software to compute the standard error and leave the explanation of how this standard error is determined to a second or third statistics course. Table 8.3.11 shows software output for the least squares regression line in Figure 8.3.8 . The row labeled unemp represents the information for the slope, which is the coefficient of the unemployment variable.

Example 8.3.12 .

What do the first column of numbers in the regression summary represent?

The entries in the first column represent the least squares estimates for the \(y\)-intercept and slope, \(a\) and \(b\) respectively. Using this information, we could write the equation for the least squares regression line as

where \(y\) in this case represents the percent change in the number of seats for the president's party, and \(x\) represents the unemployment rate.

We previously used a test statistic \(T\) for hypothesis testing in the context of means. Regression is very similar. Here, the point estimate is \(b=-0.8897\text{.}\) The \(SE\) of the estimate is 0.8350, which is given in the second column, next to the estimate of \(b\text{.}\) This \(SE\) represents the typical error when using the slope of the sample regression line to estimate the slope of the population regression line.

The null value for the slope is 0, so we now have everything we need to compute the test statistic. We have:

This value corresponds to the \(T\)-score reported in the regression output in the third column along the unemp row.

Example 8.3.14 .

In this example, the sample size \(n=27\text{.}\) Identify the degrees of freedom and p-value for the hypothesis test.

The degrees of freedom for this test is \(n-2\text{,}\) or \(df = 27-2 = 25\text{.}\) We could use a table or a calculator to find the probability of a value less than -1.07 under the \(t\)-distribution with 25 degrees of freedom. However, the two-side p-value is given in Table 8.3.11 , next to the corresponding \(t\)-statistic. Because we have a one-sided alternate hypothesis, we take half of this. The p-value for the test is \(\frac{0.2961}{2}=0.148\text{.}\)

Because the p-value is so large, we do not reject the null hypothesis. That is, the data do not provide convincing evidence that a higher unemployment rate is associated with a larger loss for the President's party in the House of Representatives in midterm elections.

Don't carelessly use the p-value from regression output.

The last column in regression output often lists p-values for one particular hypothesis: a two-sided test where the null value is zero. If your test is one-sided and the point estimate is in the direction of \(H_A\text{,}\) then you can halve the software's p-value to get the one-tail area. If neither of these scenarios match your hypothesis test, be cautious about using the software output to obtain the p-value.

Hypothesis test for the slope of regression line.

To carry out a complete hypothesis test for the claim that there is no linear relationship between two numerical variables, i.e. that \(\beta=0\text{,}\)

Identify : Identify the hypotheses and the significance level, \(\alpha\text{.}\)

\(H_0\text{:}\) \(\beta = 0\)

\(H_A\text{:}\) \(\beta \ne 0\text{;}\) \(H_A\text{:}\) \(\beta > 0\text{;}\) or \(H_A\text{:}\) \(\beta \lt 0\)

Choose : Choose the correct test procedure and identify it by name.

Here we choose the \(t\)-test for the slope .

Check : Check conditions for using a \(t\)-test for the slope.

The residual plot shows no pattern implying that a linear model is reasonable. More specifically, the residuals should be independent, nearly normal (or \(n\ge 30\)),and have constant standard deviation.

Calculate : Calculate the \(t\)-statistic, \(df\text{,}\) and p-value.

\(T= \frac{\text{ point estimate } - \text{ null value } }{SE \text{ of estimate } }\text{,}\) \(df=n-2\)

null value: 0

p-value = (based on the \(t\)-statistic, the \(df\text{,}\) and the direction of \(H_A\))

Conclude : Compare the p-value to \(\alpha\text{,}\) and draw a conclusion in context.

If the p-value is \(\lt \alpha\text{,}\) reject \(H_0\text{;}\) there is sufficient evidence that [\(H_A\) in context].

If the p-value is \(> \alpha\text{,}\) do not reject \(H_0\text{;}\) there is not sufficient evidence that [\(H_A\) in context].

Example 8.3.15 .

The regression summary below shows statistical software output from fitting the least squares regression line for predicting gift aid based on family income for 50 freshman students at Elmhurst College. The scatterplot and residual plot were shown in Figure 8.3.2 .

Do these data provide convincing evidence that there is a negative, linear relationship between family income and gift aid? Carry out a complete hypothesis test at the 0.05 significance level. Use the five step framework to organize your work.

Identify : We will test the following hypotheses at the \(\alpha=0.05\) significance level.

\(H_0\text{:}\) \(\beta = 0\text{.}\) There is no linear relationship.

\(H_A\text{:}\) \(\beta \lt 0\text{.}\) There is a negative linear relationship.

Here, \(\beta\) is the slope of the population regression line for predicting gift aid from family income at Elmhurst College.

Choose : Because the hypotheses are about the slope of a regression line, we choose the \(t\)-test for a slope.

Check : The data come from a random sample. Also, the residual plot shows that the residuals have constant variance and no outliers or influential points (and \(n=50\ge 30\)). The lack of any pattern in the residual plot indicates that a linear model is appropriate.

Calculate : We will calculate the \(t\)-statistic, degrees of freedom, and the p-value.

We read the slope of the sample regression line and the corresponding \(SE\) from the table.

The point estimate is: \(b = -0.04307\text{.}\)

The \(SE\) of the slope is: \(SE = 0.01081\text{.}\)

Because \(H_A\) uses a less than sign (\(\lt\)), meaning that it is a lower-tail test, the p-value is the area to the left of \(t=-3.985\) under the \(t\)-distribution with \(50-2=48\) degrees of freedom. The p-value = \(\frac{1}{2}(0.000229)\approx 0.0001\text{.}\)

Conclude : The p-value of 0.0001 is \(\lt 0.05\text{,}\) so we reject \(H_0\text{;}\) there is sufficient evidence that there is a negative linear relationship between family income and gift aid at Elmhurst College.

Subsection 8.3.8 Calculator: the \(t\)-test for the slope

When performing this type of inference, we generally make use of regression output that provides us with the necessary quantities: \(b\) and \(SE \text{ of } {b}\text{.}\) The calculator functions below require knowing all of the data and are, therefore, rarely used. We describe them here for the sake of completion.

TI-83/84: Linear regression T-test on \(\beta\).

Use STAT , TESTS , LinRegTTest .

Down arrow and choose F:LinRegTTest . (On TI-83 it is E:LinRegTTest ).

Let Xlist be L1 and Ylist be L2 . (Don't forget to enter the \(x\) and \(y\) values in L1 and L2 before doing this test.)

Choose \(\ne\text{,}\) \(\lt\text{,}\) or \(>\) to correspond to \(H_A\text{.}\)

Casio fx-9750GII: Linear regression T-test on \(\beta\).

Navigate to STAT ( MENU button, then hit the 2 button or select STAT ).

Enter your data into 2 lists.

Select TEST ( F3 ), t ( F2 ), and REG ( F3 ).

If needed, update the sidedness of the test and the XList and YList lists. The Freq should be set to 1 .

Hit EXE , which returns:

Example 8.3.16 .

Why does the calculator test include the symbol \(\rho\) when choosing the direction of the alternate hypothesis?

Recall the we used the letter \(r\) to represent correlation. The Greek letter \(\rho=0\) represents the correlation for the entire population. The slope \(b=r\frac{s_y}{s_x}\text{.}\) If the slope of the population regression line is zero, the correlation for the population must also be zero. For this reason, the \(t\)-test for \(\beta=0\) is equivalent to a test for \(\rho=0\text{.}\)

Subsection 8.3.9 Which inference procedure to use for paired data?

In Subsection 7.2.5 , we looked at a set of paired data involving the price of textbooks for UCLA courses at the UCLA Bookstore and on Amazon. The left panel of Figure 8.3.17 shows the difference in price (UCLA Bookstore \(-\) Amazon) for each book. Because we have two data points on each textbook, it also makes sense to construct a scatterplot, as seen in the right panel of Figure 8.3.17 .

Example 8.3.18 .

What additional information does the scatterplot provide about the price of textbooks at UCLA Bookstore and on Amazon?

With a scatterplot, we see the relationship between the variables. We can see when UCLA Bookstore price is larger, whether Amazon price tends to be larger. We can consider the strength of the correlation and we can plot the linear regression equation.

Example 8.3.19 .

Which test should we do if we want to check whether:

prices for textbooks for UCLA courses are higher at the UCLA Bookstore than on Amazon

there is a significant, positive linear relationship between UCLA Bookstore price and Amazon price?

In the first case, we are interested in whether the differences (UCLA Bookstore \(-\) Amazon) are, on average, greater than 0, so we would do a matched pairs \(t\)-test for a mean of differences. In the second case, we are interested in whether the slope is significantly greater than 0, so we would do a \(t\)-test for the slope of a regression line.

Likewise, a matched pairs \(t\)-interval for a mean of differences would provide an interval of reasonable values for mean of the differences for all UCLA textbooks, whereas a \(t\)-interval for the slope would provide an interval of reasonable values for the slope of the regression line for all UCLA textbooks.

Inference for paired data.

A matched pairs \(t\)-interval or \(t\)-test for a mean of differences only makes sense when we are asking whether, on average, one variable is greater than another (think histogram of the differences). A \(t\)-interval or \(t\)-test for the slope of a regression line makes sense when we are interested in the linear relationship between them (think scatterplot).

Example 8.3.20 .

Previously, we looked at the relationship betweeen body length and head length for bushtail possums. We also looked at the relationship between gift aid and family income for freshmen at Elmhurst College. Could we do a matched pairs \(t\)-test in either of these scenarios?

We have to ask ourselves, does it make sense to ask whether, on average, body length is greater than head length? Similarly, does it make sense to ask whether, on average, gift aid is greater than family income? These don't seem to be meaningful research questions; a matched pairs \(t\)-test for a mean of differences would not be useful here.

Checkpoint 8.3.21 .

A teacher gives her class a pretest and a posttest. Does this result in paired data? If so, which hypothesis test should she use?  2 

Subsection 8.3.10 Section summary

In Chapter 6 , we used a \(\chi^2\) test of independence to test for association between two categorical variables. In this section, we test for association/correlation between two numerical variables.

We use the slope \(b\) as a point estimate for the slope \(\beta\) of the population regression line. The slope of the population regression line is the true increase/decrease in \(y\) for each unit increase in \(x\text{.}\) If the slope of the population regression line is 0, there is no linear relationship between the two variables.

Under certain assumptions, the sampling distribution of \(b\) is normal and the distribution of the standardized test statistic using the standard error of the slope follows a \(t\) -distribution with \(n-2\) degrees of freedom.

When there is \((x, y)\) data and the parameter of interest is the slope of the population regression line, e.g. the slope of the population regression line relating air quality index to average rainfall per year for each city in the United States:

Estimate \(\beta\) at the C% confidence level using a \(t\)-interval for the slope .

Test \(H_0\text{:}\) \(\beta=0\) at the \(\alpha\) significance level using a \(t\)-test for the slope .

The conditions for the \(t\)-interval and \(t\)-test for the slope of a regression line are the same.

The confidence interval and test statistic are calculated as follows:

Confidence interval:  \(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\text{,}\) or

Test statistic: \(T = \frac{\text{ point estimate } - \text{ null value } }{SE\ \text{ of estimate } }\) and p-value

\(df = n-2\)

If the confidence interval for the slope of the population regression line estimates the true average increase in the \(y\)-variable for each unit increase in the \(x\)-variable.

The \(t\)-test for the slope and the matched pairs \(t\)-test for a mean of differences both involve paired , numerical data. However, the \(t\)-test for the slope asks if the two variables have a linear relationship , specifically if the slope of the population regression line is different from 0. The matched pairs \(t\)-test for a mean of differences, on the other hand, asks if the two variables are in some way the same , specifically if the mean of the population differences is 0.

Exercises 8.3.11 Exercises

1 . body measurements, part iv..

The scatterplot and least squares summary below show the relationship between weight measured in kilograms and height measured in centimeters of 507 physically active individuals.

Describe the relationship between height and weight.

Write the equation of the regression line. Interpret the slope and intercept in context.

Do the data provide strong evidence that an increase in height is associated with an increase in weight? State the null and alternative hypotheses, report the p-value, and state your conclusion.

The correlation coefficient for height and weight is 0.72. Calculate \(R^2\) and interpret it in context.

(a) The relationship is positive, moderate-to-strong, and linear. There are a few outliers but no points that appear to be influential.

(b) \(\widehat{\text{weight} = -105.0113 + 1.0176 \times \text{height}\text{.}\) Slope: For each additional centimeter in height, the model predicts the average weight to be 1.0176 additional kilograms (about 2.2 pounds). Intercept: People who are 0 centimeters tall are expected to weigh -105.0113 kilograms. This is obviously not possible. Here, the \(y\)- intercept serves only to adjust the height of the line and is meaningless by itself.

(c) \(H_{0}:\) The true slope coefficient of height is zero \((\beta_{1} = 0)\text{.}\) \(H_{A}:\) The true slope coefficient of height is different than zero \((\beta_{1} \ne 0)\text{.}\) The p-value for the two-sided alternative hypothesis \((\beta_{1} \ne 0)\) is incredibly small, so we reject \(H_{0}\text{.}\) The data provide convincing evidence that height and weight are positively correlated. The true slope parameter is indeed greater than 0.

(d) \(R^2 = 0.72^2 = 0.52\text{.}\) Approximately 52% of the variability in weight can be explained by the height of individuals.

2 . Beer and blood alcohol content.

Many people believe that gender, weight, drinking habits, and many other factors are much more important in predicting blood alcohol content (BAC) than simply considering the number of drinks a person consumed. Here we examine data from sixteen student volunteers at Ohio State University who each drank a randomly assigned number of cans of beer. These students were different genders, and they differed in weight and drinking habits. Thirty minutes later, a police officer measured their blood alcohol content (BAC) in grams of alcohol per deciliter of blood.  3  The scatterplot and regression table summarize the findings.

Describe the relationship between the number of cans of beer and BAC.

Do the data provide strong evidence that drinking more cans of beer is associated with an increase in blood alcohol? State the null and alternative hypotheses, report the p-value, and state your conclusion.

The correlation coefficient for number of cans of beer and BAC is 0.89. Calculate \(R^2\) and interpret it in context.

Suppose we visit a bar, ask people how many drinks they have had, and also take their BAC. Do you think the relationship between number of drinks and BAC would be as strong as the relationship found in the Ohio State study?

3 . Spouses, Part II.

The scatterplot below summarizes womens' heights and their spouses' heights for a random sample of 170 married women in Britain, where both partners' ages are below 65 years. Summary output of the least squares fit for predicting spouse's height from the woman's height is also provided in the table.

Is there strong evidence in this sample that taller women have taller spouses? State the hypotheses and include any information used to conduct the test.

Write the equation of the regression line for predicting the height of a woman's spouse based on the woman's height.

Interpret the slope and intercept in the context of the application.

Given that \(R^2 = 0.09\text{,}\) what is the correlation of heights in this data set?

You meet a married woman from Britain who is 5'9" (69 inches). What would you predict her spouse's height to be? How reliable is this prediction?

You meet another married woman from Britain who is 6'7" (79 inches). Would it be wise to use the same linear model to predict her spouse's height? Why or why not?

(a) \(H_{0}: \beta_{1} = 0\text{;}\) \(H_{A}: \beta_{1} \ne 0\text{.}\) The p-value, as reported in the table, is incredibly small and is smaller than 0.05, so we reject \(H_{0}\text{.}\) The data provide convincing evidence that womens' and spouses' heights are positively correlated.

(b) \(\widehat{\text{height}}_{S} = 43.5755 + 0.2863 \times \text{height}_W\text{.}\)

(c) Slope: For each additional inch in woman's height, the spouse's height is expected to be an additional 0.2863 inches, on average. Intercept: Women who are 0 inches tall are predicted to have spouses who are 43.5755 inches tall. The intercept here is meaningless, and it serves only to adjust the height of the line.

(d) The slope is positive, so \(r\) must also be positive. \(r= \sqrt{0.09} = 0.30\)

(e) 63.2612. Since \(R^2\) is low, the prediction based on this regression model is not very reliable.

(f) No, we should avoid extrapolating.

4 . Urban homeowners, Part II.

Exercise 8.2.11.13 gives a scatterplot displaying the relationship between the percent of families that own their home and the percent of the population living in urban areas. Below is a similar scatterplot, excluding District of Columbia, as well as the residuals plot. There were 51 cases.

For these data, \(R^2 = 0.28\text{.}\) What is the correlation? How can you tell if it is positive or negative?

Examine the residual plot. What do you observe? Is a simple least squares fit appropriate for these data?

5 . Murders and poverty, Part II.

Exercise 8.2.11.9 presents regression output from a model for predicting annual murders per million from percentage living in poverty based on a random sample of 20 metropolitan areas. The model output is also provided below.

What are the hypotheses for evaluating whether poverty percentage is a significant predictor of murder rate?

State the conclusion of the hypothesis test from part (a) in context of the data.

Calculate a 95% confidence interval for the slope of poverty percentage, and interpret it in context of the data.

Do your results from the hypothesis test and the confidence interval agree? Explain.

(a) \(H_{0}: \beta_{1} = 0\text{;}\) \(H_{A}: \beta_{1} \ne 0\)

(b) The p-value for this test is approximately 0, therefore we reject \(H_{0}\text{.}\) The data provide convincing evidence that poverty percentage is a significant predictor of murder rate.

(c) \(n = 20\text{;}\) \(df = 18\text{;}\) \(T^{*}_{18} = 2.10\text{;}\) \(2.559 \pm 2.10 \times 0.390 = (1.74, 3.378)\text{;}\) For each percentage point poverty is higher, murder rate is expected to be higher on average by 1.74 to 3.378 per million.

(d) Yes, we rejected \(H_{0}\) and the confidence interval does not include 0.

6 . Babies.

Is the gestational age (time between conception and birth) of a low birth-weight baby useful in predicting head circumference at birth? Twenty-five low birth-weight babies were studied at a Harvard teaching hospital; the investigators calculated the regression of head circumference (measured in centimeters) against gestational age (measured in weeks). The estimated regression line is

What is the predicted head circumference for a baby whose gestational age is 28 weeks?

The standard error for the coefficient of gestational age is 0.35, which is associated with \(df=23\text{.}\) Does the model provide strong evidence that gestational age is significantly associated with head circumference?

Statistics Made Easy

How to Perform t-Test for Slope of Regression Line in R

Whenever we perform simple linear regression , we end up with the following estimated regression equation:

ŷ = b 0 + b 1 x

We typically want to know if the slope coefficient, b 1 , is statistically significant.

To determine if b 1  is statistically significant, we can perform a t-test with the following test statistic:

• t = b 1 / se(b 1 )
• se(b 1 ) represents the standard error of b 1 .

We can then calculate the p-value that corresponds to this test statistic with n-2 degrees of freedom.

If the p-value is less than some threshold (e.g. α = .05) then we can conclude that the slope coefficient is different than zero.

In other words, there is a statistically significant relationship between the predictor variable and the response variable in the model.

The following example shows how to perform a t-test for the slope of a regression line in R.

Example: Performing a t-Test for Slope of Regression Line in R

Suppose we have the following data frame in R that contains information about the hours studied and final exam score received by 12 students in some class:

Suppose we would like to fit a simple linear regression model to determine if there is a statistically significant relationship between hours studied and exam score.

We can use the lm() function in R to fit this regression model:

From the model output, we can see that the estimated regression equation is:

Exam score = 67.7685 + 2.7037(hours)

To test if the slope coefficient is statistically significant, we can calculate the t-test statistic as:

• t = 2.7037 / 0.7456

The p-value that corresponds to this t-test statistic is shown in the column called Pr(> |t|) in the output.

The p-value turns out to be 0.00464 .

Since this p-value is less than 0.05, we conclude that the slope coefficient is statistically significant.

In other words, there is a statistically significant relationship between the number of hours studied and the final score that a student receives on the exam.

Additional Resources

The following tutorials explain how to perform other common tasks in R:

How to Perform Simple Linear Regression in R How to Perform Multiple Linear Regression in R How to Interpret Regression Output in R

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3.4: Hypothesis Test for Simple Linear Regression

• Last updated
• Save as PDF
• Page ID 28708

We will now describe a hypothesis test to determine if the regression model is meaningful; in other words, does the value of \(X\) in any way help predict the expected value of \(Y\)?

Simple Linear Regression ANOVA Hypothesis Test

Model Assumptions

• The residual errors are random and are normally distributed.
• The standard deviation of the residual error does not depend on \(X\)
• A linear relationship exists between \(X\) and \(Y\)
• The samples are randomly selected

Test Hypotheses

\(H_o\):  \(X\) and \(Y\) are not correlated   

\(H_a\):  \(X\) and \(Y\) are correlated   

\(H_o\):  \(\beta_1\) (slope) = 0   

\(H_a\):  \(\beta_1\) (slope) ≠ 0

Test Statistic

\(F=\dfrac{M S_{\text {Regression }}}{M S_{\text {Error }}}\)

\(d f_{\text {num }}=1\)

\(d f_{\text {den }}=n-2\)

Sum of Squares

\(S S_{\text {Total }}=\sum(Y-\bar{Y})^{2}\)

\(S S_{\text {Error }}=\sum(Y-\hat{Y})^{2}\)

\(S S_{\text {Regression }}=S S_{\text {Total }}-S S_{\text {Error }}\)

In simple linear regression, this is equivalent to saying “Are X an Y correlated?”

In reviewing the model, \(Y=\beta_{0}+\beta_{1} X+\varepsilon\), as long as the slope (\(\beta_{1}\)) has any non‐zero value, \(X\) will add value in helping predict the expected value of \(Y\). However, if there is no correlation between X and Y, the value of the slope (\(\beta_{1}\)) will be zero. The model we can use is very similar to One Factor ANOVA.

The Results of the test can be summarized in a special ANOVA table:

Example: Rainfall and sales of sunglasses

Design : Is there a significant correlation between rainfall and sales of sunglasses?

Research Hypothese s:

\(H_o\):  Sales and Rainfall are not correlated      \(H_o\):  1 (slope) = 0

\(H_a\):  Sales and Rainfall are correlated      \(H_a\):  1 (slope) ≠ 0

Type I error would be to reject the Null Hypothesis and \(t\) claim that rainfall is correlated with sales of sunglasses, when they are not correlated. The test will be run at a level of significance (\(\alpha\)) of 5%.

The test statistic from the table will be \(\mathrm{F}=\dfrac{\text { MSRegression }}{\text { MSError }}\). The degrees of freedom for the numerator will be 1, and the degrees of freedom for denominator will be 5‐2=3.  

Critical Value for \(F\) at  \(\alpha\)of 5% with \(df_{num}=1\) and \(df_{den}=3} is 10.13.  Reject \(H_o\) if \(F >10.13\). We will also run this test using the \(p\)‐value method with statistical software, such as Minitab.  

Data/Results

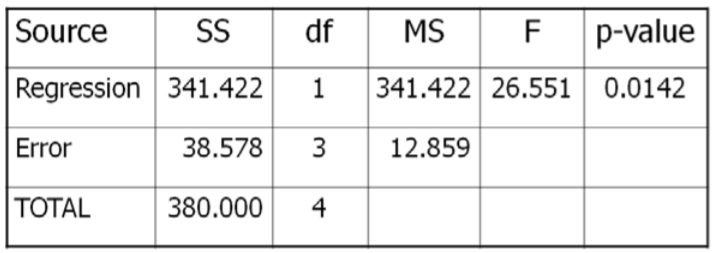
\(F=341.422 / 12.859=26.551\), which is more than the critical value of 10.13, so Reject \(H_o\). Also, the \(p\)‐value = 0.0142 < 0.05 which also supports rejecting \(H_o\).  

Sales of Sunglasses and Rainfall are negatively correlated.

How to Test the Significance of a Regression Slope

Suppose we have the following dataset that shows the square feet and price of 12 different houses:

We want to know if there is a significant relationship between square feet and price.

To get an idea of what the data looks like, we first create a scatterplot with  square feet  on the x-axis and  price  on the y-axis:

We can clearly see that there is a positive correlation between square feet and price. As square feet increases, the price of the house tends to increase as well.

However, to know if there is a statistically significant relationship between square feet and price, we need to run a simple linear regression.

So, we run a simple linear regression using  square feet  as the predictor and  price  as the response and get the following output:

Whether you run a simple linear regression in Excel, SPSS, R, or some other software, you will get a similar output to the one shown above.

Recall that a simple linear regression will produce the line of best fit, which is the equation for the line that best “fits” the data on our scatterplot. This line of best fit is defined as:

  ŷ = b 0  + b 1 x 

where ŷ is the predicted value of the response variable, b 0  is the y-intercept, b 1  is the regression coefficient, and x is the value of the predictor variable.

The value for b 0  is given by the coefficient for the intercept, which is 47588.70.

The value for b 1  is given by the coefficient for the predictor variable  Square Feet , which is 93.57.

Thus, the line of best fit in this example is  ŷ = 47588.70+ 93.57x

Here is how to interpret this line of best fit:

• b 0 :  When the value for square feet is zero, the average expected value for price is $47,588.70. (In this case, it doesn’t really make sense to interpret the intercept, since a house can never have zero square feet)
• b 1 :  For each additional square foot, the average expected increase in price is $93.57. 

So, now we know that for each additional square foot, the average expected increase in price is $93.57.

To find out if this increase is statistically significant, we need to conduct a hypothesis test for B 1 or construct a confidence interval for B 1 .

Note : A hypothesis test and a confidence interval will always give the same results.

Constructing a Confidence Interval for a Regression Slope

To construct a confidence interval for a regression slope, we use the following formula:

Confidence Interval = b 1   +/-  (t 1-∝/2, n-2 ) * (standard error of b 1 )

•   b 1  is the slope coefficient given in the regression output
• (t 1-∝/2, n-2 ) is the t critical value for confidence level 1-∝ with n-2 degrees of freedom where  n  is the total number of observations in our dataset
• (standard error of b 1 ) is the standard error of b 1  given in the regression output

For our example, here is how to construct a 95% confidence interval for B 1 :

• b 1  is 93.57 from the regression output.
• Since we are using a 95% confidence interval, ∝ = .05 and n-2 = 12-2 = 10, thus t .975, 10  is 2.228 according to the t-distribution table
• (standard error of b 1 ) is 11.45 from the regression output

Thus, our 95% confidence interval for B 1  is:

93.57  +/-  (2.228) * (11.45) = (68.06 , 119.08)

This means we are 95% confident that the true average increase in price for each additional square foot is between $68.06 and $119.08.

Notice that $0 is not in this interval, so the relationship between square feet and price is statistically significant at the 95% confidence level.

Conducting a Hypothesis Test for a Regression Slope

To conduct a hypothesis test for a regression slope, we follow the standard five steps for any hypothesis test :

Step 1. State the hypotheses. 

The null hypothesis (H0): B 1 = 0

The alternative hypothesis: (Ha): B 1 ≠ 0

Step 2. Determine a significance level to use.

Since we constructed a 95% confidence interval in the previous example, we will use the equivalent approach here and  choose to use a .05 level of significance.

Step 3. Find the test statistic and the corresponding p-value.

In this case, the test statistic is t  =  coefficient  of b 1 / standard error of b 1 with n-2 degrees of freedom.  We can find these values from the regression output:

Using the   T Score to P Value Calculator   with a t score of 6.69 with 10 degrees of freedom and a two-tailed test, the p-value =  0.000 .

Step 4. Reject or fail to reject the null hypothesis.

Since the p-value is less than our significance level of .05, we reject the null hypothesis.

Step 5. Interpret the results. 

Since we rejected the null hypothesis, we have sufficient evidence to say that the true average increase in price for each additional square foot is not zero.

How to Remove Duplicate Rows in R so None are Left

How to load the analysis toolpak in excel, related posts, three-way anova: definition & example, two sample z-test: definition, formula, and example, one sample z-test: definition, formula, and example, how to find a confidence interval for a..., an introduction to the exponential distribution, an introduction to the uniform distribution, the breusch-pagan test: definition & example, population vs. sample: what’s the difference, introduction to multiple linear regression, dunn’s test for multiple comparisons.