model drawing for problem solving

• Events Calendar
• Constitution
• 2024 Conference
• Upcoming Events
• Past Events
• Professional Development Grant
• Ena Gross Professional Development Scholarship
• First Timers Grant
• Affiliates Grant
• Edward A. Anderson Scholarship
• Math Educator of the Year
• Math Beauty Contest
• Model Drawing for Problem Solving
• Classcraft: Warriors and Healers and Mages, Oh My!
• Malawi & Mathematics Education
• Capacity to Generalize: Connections for Future Mathematics Specialists
• Let's Get Real: Effective Number Talks in Algebra I
• Manipulate and Engage the Geometry Class
• Inquiry: Ready, Set, Go
• Blended Learning Tools
• The Shape of Ordered Pairs Connecting Graphing to Big Ideas
• Get Moving in Secondary Math
• How Much Should I Save for Retirement? Modeling Series in Spreadsheets
• Influencing Students' Beliefs about Math
• Problem Solving Strategies in Mathematics

Model Drawing for Math Problem Solving

Model Drawing is a highly effective method for solving Math questions that involve fractions and remainders. Drawing bar models allows your child to visualise the relationship between “Part” vs “Whole” clearly.

In this tutorial, we look at two questions taken from 2021 Prelim papers to help you learn how to use model drawing.

But before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

The first question is taken from the Tao Nan School Paper 2 and is worth 2 marks. This is a basic fraction question that can be solved using model drawing.

The key concept is that half of 3 units (3u) is $3. Since Alan used 7 units of his allowance on food, he had 3 units left.

He spent half of the remaining 3 units, and he had $3 left. This means the other half of the 3 units is $3. To visualize this, a model drawing is necessary.

Step 1: Visualisation – Model the provided information

The first part of the model drawing is a long bar to represent the number of units. Alan’s allowance at first was 10 units, meaning the bar must have 10 equal parts.

Then, indicate the number of units spent on food (F). In this example, that is 7 units.

Alan spent half of his remaining allowance on stationary items. In the model drawing above, his remaining allowance is 3 units. However, 3 units cannot be split into half directly.

So, we have to split the middle unit into 2 halves to indicate that he spent half of his allowance on stationary (S). The other half would then be $3.

Because one unit has been split into 2 halves, we have to split all the remaining units into 2 parts as well. This ensures that there are equal units throughout.

Step 2: Start solving the question

Since 3 units (3u) = $3, then 1 unit (1u) is $1. Because we’ve split every unit into 2 parts, Alan’s allowance will not be 10 units anymore. It will be 20 instead.

Make sure that your child or student uses the new total units when solving this type of question using model drawing.

Naturally, 20 units would be $20, and this is the final answer to this question.

This is a more complex question taken from the Catholic High School Paper 2, and it is worth 3 marks.

Since 3 4 of the fruits were removed, 1 4 of the fruits were left. That means 1 8 of the apples and 30 pears = 1 8 of the total number of fruits.

Step 1: Visualisation

Begin model drawing and split the bar into five equal groups.

Explanation : 5 was the original denominator, indicating the total number of fruits.

Out of 5 units, 4 were apples (A) and the rest were pears (P). Indicate that as shown in the worksheet below:

There were 4 units of apples. However, 1 8 of the apples were left. In this case, we can't indicate 1 8 right away. So, we have to split the 4 units into 2 groups.

To ensure that all units are the same, we also split the unit representing the pears. Now we have 10 units in total. Next, shade the unit that represents the number of apples left.

There were 30 pairs left, and we do not know how many units that represents. So, we shade a random part of the unit to indicate these remaining pears.

The two shaded portions represent 1 4 of the total, and the unshaded portion would naturally be 3 4 of the fruits that were removed.

Based on the shaded areas, 7 units (7u) of apples and 2 units (2u) minus 30 pears were removed.

This means that 7u and 2u - 30 is 3 4 of the total number of fruits. So, the shaded 1u of apples + 30 would be 1 4 of the total number of fruits. The equation forms of this information would be as follows:

To make a fair comparison during model drawing, ensure that the values on the right-hand side of both equations are the same. To convert 1 4 into 3 4 , multiply the entire equation by 3.

The above effectively means that 9u – 30 is actually the same as 3u + 90. So, write that in another equation.

This point gets a bit tricky because your child may not yet learn to change the sign from positive to negative or vice versa when changing sides.

So, draw another smaller model representing 9u – 30. When we remove 30 from 9u, we are left with the length shown below the smaller model:

The length indicated in the second bar is also the same as 3u + 90. That means the portion between the end of 3u and the rest of the bar makes up 6 units (6u).

Therefore, 6u is 90 + 30, which would give us 120. Once this visualisation is done, you can write it in an equation form.

From here, you can determine the value of 1 unit which is 20. However, the question asked for the number of fruits that were in the box at first.

At first, we used a denominator of 5. So, our model drawing had 5 parts. However, each unit was split into 2 parts, making the new total units 10. That gives us a total of 200 fruits, and that is the final answer to this question.

I hope this tutorial was easy for you to follow, especially the second question. We used the method of elimination in simultaneous equations to solve the second question, but we did so in a way where P6 students can understand.

You might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

If you have any questions or suggestions, please leave them in the comments below.

You can also watch the full Model Drawing video tutorial here:

To Your Child’s Success,

Ms Elaine Wee Math and Science Specialist Jimmy Maths and Grade Solution Learning Centre

Does your child need help in his or her studies?

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success.  Here are the services we provide:

– Live Zoom lessons

– EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths, and weaknesses through personalized digital worksheets.

– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialize in English, Math, and Science subjects.

You can see our fees and schedules here >> https://gradesolution.com.sg/schedule/

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>  https://jimmymaths.com/our-courses/

• PRIMARY SCHOOL
• SECONDARY SCHOOL
• LOGIN / REGISTER

Modeling Word Problems

Using models is a critical step in helping students transition from concrete manipulative work with word problems to the abstract step of generating an equation to solve contextual problems. By learning to use simple models to represent key mathematical relationships in a word problem, students can more easily make sense of word problems, recognize both the number relationships in a given problem and connections among types of problems, and successfully solve problems with the assurance that their solutions are reasonable.

Why is modeling word problems important?

Mr. Alexander and teachers from his grade level team were talking during their Professional Learning Community (PLC) meeting about how students struggle with word problems. Everyone felt only a few of their students seem to be able to quickly generate the correct equation to solve the problem. Many students just seem to look for some numbers and do something with them, hoping they solve the problem.

Mr. Alexander had recently learned about using modeling for word problems in a workshop he had attended.  He began to share the model diagrams with his teammates and they were excited to see how students might respond to this approach. They even practiced several model diagrams among themselves as no one had ever learned to use models with word problems. Since part of their PLC work freed them up to observe lessons in each others' rooms, they decided they would watch Mr. Alexander introduce modeling to his students. 

So, two days later they gathered in Mr. Alexander's room for the math lesson. Mr. Alexander presented the following problem:

Lily and her brother, Scotty, were collecting cans for the recycling drive. One weekend they collected 59 cans and the next weekend they collected 85 cans.  How many cans were collected in all?

Mr. Alexander went over the problem and drew a rectangular bar divided into two parts on the board, explaining that each part of the rectangle was for the cans collected on one of the weekends and the bracket indicated how many cans were collected in all. Reviewing the problem, Mr. Alexander asked students what was not known, and where the given numbers would go and why. This resulted in the following bar model:

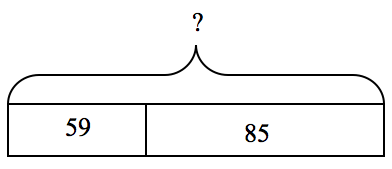
The class then discussed what equations made sense given the relationship of the numbers in the bar model. This time many students wrote the equation, 59 + 85 = ?, and solved the problem. In their discussion after the lesson, Mr. Alexander's teammates mentioned that they noticed a much higher degree of interest and confidence in problem solving when Mr. Alexander introduced the bar model. Everyone noticed that many more students were successful in solving problems once modeling was introduced and encouraged. As the class continued to do more word problems, the diagrams appeared to be a helpful step in scaffolding success with word problems.

Knowledge can be represented both linguistically and nonlinguistically. An increase in nonlinguistic representations allows students to better recall knowledge and has a strong impact on student achievement (Marzano, et. al., 2001, Section 5). In classic education research, Bruner (1961) identified three modes of learning:  enactive (manipulating concrete objects), iconic (pictures or diagrams), and symbolic (formal equation).  The iconic stage, using pictures and diagrams, is an important bridge to abstracting mathematical ideas using the symbols of an equation. Research has also validated that students need to see an idea in multiple representations in order to identify and represent the common core (Dienes, undated). For word problems involving the operation of addition, students need to experience several types of problems to generalize that when two parts are joined they result in a total or a quantity that represents the whole. Whether the items are bears, balloons, or cookies no longer matters as the students see the core idea of two subsets becoming one set. Dienes discovered that this abstraction is only an idea; therefore it is hard to represent. Diagrams can capture the similarity students notice in addition/joining problems where both addends are known and the total or whole is the unknown.  Diagrams will also be useful for missing addend situations. Like Bruner, Dienes saw diagrams as an important bridge to abstracting and formalizing mathematical ideas.  

Along with Bruner and Dienes, Skemp (1993) identified the critical middle step in moving from a real-life situation to the abstractness of an equation. While students need to experience many real-life situations they will get bogged down with the "noise" of the problem such as names, locations, kinds of objects, and other details. It is the teacher's role to help students sort through the noise to capture what matters most for solving the problem. A diagram can help students capture the numerical information in a problem, and as importantly, the relationship between the numbers, e.g. Do we know both the parts, or just one of the parts and the whole? Are the parts similar in size, or is one larger than the other? Once students are comfortable with one kind of diagram, they can think about how to relate it to a new situation. A student who has become proficient with using a part-part-whole bar model diagram when the total or whole is unknown, (as in the collecting cans problem in Mr. Alexander's class), cannot only use the model in other part-part-whole situations, but can use it in new situations, for example, a missing addend situation. Given several missing addend situations, students may eventually generalize that these will be subtractive situations, solvable by either a subtraction or adding on equation.

The work of Bruner, Dienes and Skemp informed the development of computation diagrams in some elementary mathematics curriculum materials in the United States. Interestingly, it also informed the development of curriculum in Singapore, as they developed the "Thinking Schools, Thinking Nation" era of reforming their educational model and instructional strategies (Singapore Ministry of Education, 1997). The bar model is a critical part of "Singapore Math."  It is used and extended across multiple grades to capture the relationships within mathematical problems. Singapore has typically scored near the top of the world on international assessments, a possible indicator of the strong impact of including the visual diagram step to represent and solve mathematical problems.

What is modeling word problems?

Models at any level can vary from simple to complex, realistic to representational. Young students often solve beginning word problems, acting them out, and modeling them with the real objects of the problem situation, e.g. teddy bears or toy cars. Over time they expand to using representational drawings, initially drawing pictures that realistically portray the items in a problem, and progressing to multi-purpose representations such as circles or tally marks. After many concrete experiences with real-life word problems involving joining and separating, or multiplying and dividing objects, teachers can transition students to inverted-V and bar model drawings which are multi-purpose graphic organizers tied to particular types of word problems.

Modeling Basic Number Relationships

Simple diagrams, sometimes known as fact triangles, math mountains, situation diagrams, or representational diagrams have appeared sporadically in some curriculum materials. But students' problem solving and relational thinking abilities would benefit by making more routine use of these diagrams and models.

Young children can begin to see number relationships that exist within a fact family through the use of a model from which they derive equations. An inverted-V is one simple model that helps students see the addition/subtraction relationships in a fact family, and can be used with word problems requiring simple joining and separating. The inverted-V model can be adapted for multiplication and division fact families. For addition, students might think about the relationships among the numbers in the inverted-V in formal terms, addend and sum , or in simpler terms, part and total , as indicated in the diagrams below.

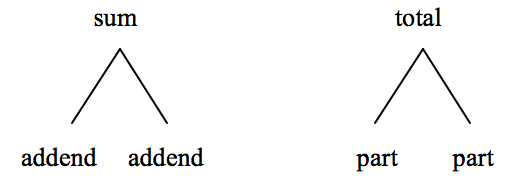
A specific example for a given sum of 10 would be the following, depending on which element of the problem is unknown.

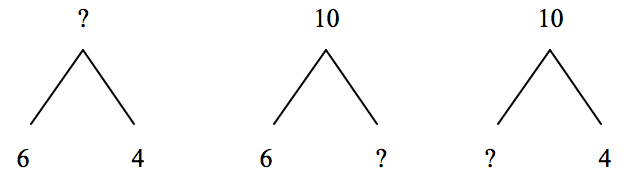
      6 + 4 = ?                   6 + ? = 10                       ? + 4 = 1

         4 + 6 = ?                 10 - 6 = ?                       10 - 4 = ?

While often used with fact families, and the learning of basic facts, inverted-V diagrams can also work well with solving word problems. Students need to think about what they know and don't know in a word problem - are both the parts known, or just one of them?  By placing the known quantities correctly into the inverted-V diagram, students are more likely to determine a useful equation for solving the problem, and see the result as reasonable for the situation. For example, consider the following problem:

Zachary had 10 train cars. Zachary gave 3 train cars to his brother. How many train cars does Zachary have now? 

Students should determine they know how many Zachary started with ( total or whole ), and how many he gave away ( part of the total ). So, they need to find out how many are left ( other part of the total ). The following inverted-V diagram represents the relationships among the numbers of this problem:

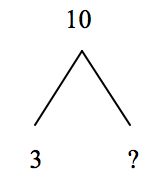
3 + ? = 10 or 10 - 3 = ?, so Zachary had 7 train cars left.

As students move on to multiplication and division, the inverted-V model can still be utilized in either the repeated addition or multiplicative mode. Division situations do not require a new model; division is approached as the inverse of multiplication or a situation when one of the factors is unknown.

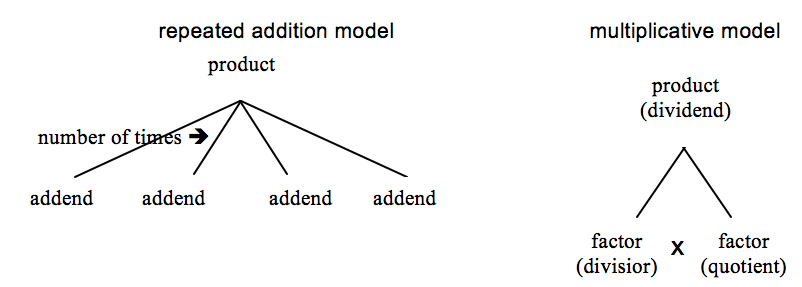
Again, the inverted-V diagram can be useful in solving multiplication and division word problems. For example, consider the following problem:

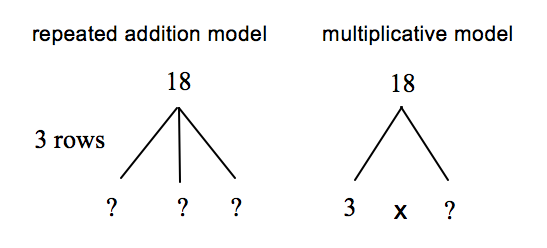
Phong planted 18 tomato plants in 3 rows. If each row had the same number of plants, how many plants were in each row?   

Students can see that they know the product and the number OF rows. The number IN A row is unknown. Either diagram below may help solve this problem, convincing students that 6 in a row is a reasonable answer.

While the inverted-V diagram can be extended to multi-digit numbers, it has typically been used with problems involving basic fact families. Increasing the use of the inverted-V model diagram should heighten the relationship among numbers in a fact family making it a useful, quick visual for solving simple word problems with the added benefit of using and increasing the retention of basic facts.

Models and Problem Types for Computation

As children move to multi-digit work, teachers can transition students to bar model drawings, quick sketches that help students see the relationships among the important numbers in a word problem and identify what is known and unknown in a situation. 

With bar models the relationships among numbers in all these types of problems becomes more transparent, and helps bridge student thinking from work with manipulatives and drawing pictures to the symbolic stage of writing an equation for a situation. With routine use of diagrams and well-facilitated discussions by teachers, student will begin to make sense of the parts of a word problem and how the parts relate to each other.

Part-Part-Whole Problems. Part-Part-Whole problems are useful with word problems that are about sets of things, e.g. collections. They are typically more static situations involving two or more subsets of a whole set. Consider the problem,

Cole has 11 red blocks and 16 blue blocks. How many blocks does Cole have in all?

Students may construct a simple rectangle with two parts to indicate the two sets of blocks that are known (parts/addends). It is not important to have the parts of the rectangle precisely proportional to the numbers in the problem, but some attention to their relative size can aid in solving the problem. The unknown in this problem is how many there are altogether (whole/total/sum), indicated by a bracket (or an inverted-V) above the bar, indicating the total of the 2 sets of blocks. The first bar model below reflects the information in the problem about Cole's blocks. 

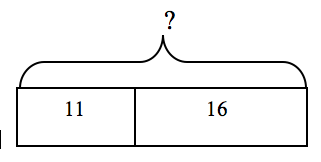
11 + 16 = ?  so Cole has 27 blocks in all.

A similar model would work for a problem where the whole amount is known, but one of the parts (a missing addend) is the unknown. For example:

Cole had 238 blocks. 100 of them were yellow. If all Cole's blocks are either blue or yellow, how many were blue? 

The following bar model would be useful in solving this problem.

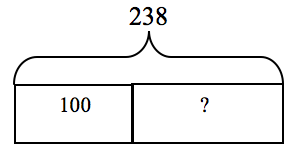
100 + ? = 238 or 238 - 100 = ? so Cole has 138 blue blocks.

The answer has to be a bit more than 100 because 100 + 100 is 200 but the total here is 238 so the blue blocks have to be a bit more than 100.

The part-part-whole bar model can easily be expanded to large numbers, and other number types such as fractions and decimals. Consider the problem:

Leticia read 7 ½ books for the read-a-thon.She wants to read 12 books in all. How many more books does she have to read?   

The first diagram below reflects this problem. Any word problem that can be thought of as parts and wholes is responsive to bar modeling diagrams. If a problem has multiple addends, students just draw enough parts in the bar to reflect the number of addends or parts, and indicate whether one of the parts, or the whole/sum, is the unknown, as shown in the second figure below.

     12 - 7 ½ = ? or  7 ½ + ? = 12 so Leticia needs to read 4 ½ more books.

Join (Addition) and Separate (Subtraction) Problems.

Consider this joining problem:

Maria had $20.  She got $11 more dollars for babysitting.  How much money does she have now?

Students can identify that the starting amount of $20 is one of the parts, $11 is another part (the additive amount), and the unknown is the sum/whole amount, or how much money she has now. The first diagram below helps represent this problem.   

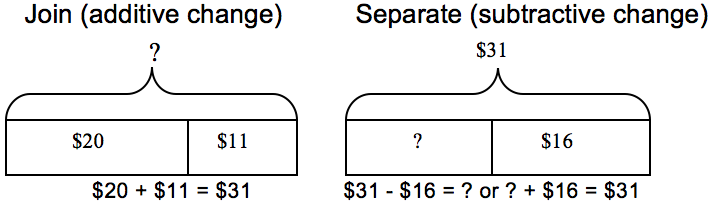
Consider the related subtractive situation:

Maria had $31.  She spent some of her money on a new CD.  Maria now has $16 left.

The second diagram above represents this situation. Students could use the model to help them identify that the total or sum is now $31, one of the parts (the subtractive change) is unknown, so the other part is the $16 she has left. 

Comparison Problems. Comparison problems have typically been seen as difficult for children. This may partially be due to an emphasis on subtraction as developed in word problems that involve "take away" situations rather than finding the "difference" between two numbers. Interestingly, studies in countries that frequently use bar models have determined that students do not find comparison problems to be much more difficult than part-part-whole problems (Yeap, 2010, pp. 88-89). 

A double bar model can help make comparison problems less mysterious. Basically, comparison problems involve two quantities (either one quantity is greater than the other one, or they are equal), and a difference between the quantities. Two bars, one representing each quantity, can be drawn with the difference being represented by the dotted area added onto the lesser amount. For example, given the problem:

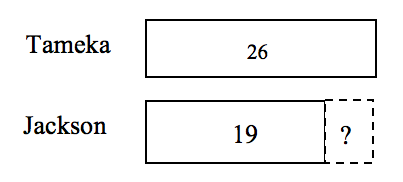
Tameka rode on 26 county fair rides. Her friend, Jackson, rode on 19 rides. How many more rides did Tameka ride on than Jackson?

Students might generate the comparison bars diagram shown below, where the greater quantity, 26, is the longer bar. The dotted section indicates the difference between Jackson's and Tameka's quantities, or how much more Tameka had than Jackson, or how many more rides Jackson would have had to have ridden to have the same number of rides as Tameka.

26 - 19 = ?  or  19 + ? = 26; the difference is 7 so Tameka rode 7 more rides.

Comparison problems express several differently worded relationships. If Tameka rode 7 more rides than Jackson, Jackson rode 7 fewer rides than Tameka.  Variations of the double bar model diagram can make differently worded relationships more visual for students. It is often helpful for students to recognize that at some point both quantities have the same amount, as shown in the model below by the dotted line draw up from the end of the rectangle representing the lesser quantity. But one of the quantities has more than that, as indicated by the area to the right of the dotted line in the longer bar. The difference between the quantities can be determined by subtracting 19 from 26, or adding up from 19 to 26 and getting 7, meaning 26 is 7 more than 19 or 19 is 7 less than 26.

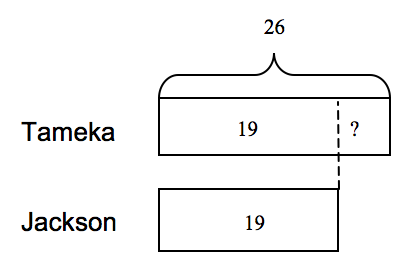
Comparison word problems are especially problematic for English Learners as the question can be asked several ways. Modifying the comparison bars may make the questions more transparent. Some variations in asking questions about the two quantities of rides that Tameka and Jackson rode might be:  

• How many more rides did Tameka ride than Jackson?
• How many fewer rides did Jackson go on than Tameka?
• How many more rides would Jackson have had to ride to have ridden the same number of rides as Tameka?
• How many fewer rides would Tameka have had to ride to have ridden the same number of rides as Jackson?

Comparisons may also be multiplicative. Consider the problem:

Juan has 36 CDs in his collection. This is 3 times the amount of CDs that his brother, Marcos, has. How many CDs does Marcos have?  

In this situation, students would construct a bar model, shown below on the left, with 3 parts. Students could divide the 36 into 3 equal groups to show the amount that is to be taken 3 times to create 3 times as many CDs for Juan.

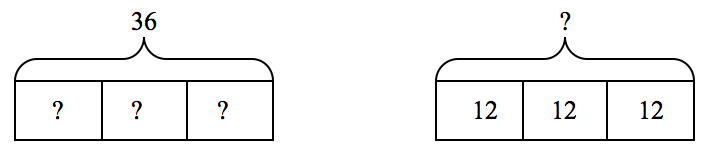
  36 ¸ 3 = ? or  3 x ? = 36             12 + 12 + 12 = ? (or 3 x 12 = ?)

so Marcos has 12 CDs.                    so Juan has 36 CDs.

A similar model can be used if the greater quantity is unknown, but the lesser quantity, and the multiplicative relationship are both known. If the problem was:

Juan has some CDs. He has 3 times as many CDs as Marcos who has 12 CDs. How many CDs does Juan have?

As seen in the diagram above on the right, students could put 12 in a box to show the number of CDs Marcos has; then duplicate that 3 times to sow that Juan has 3 times as many CDs. Then the total number that Juan has would be the sum of those 3 parts. 

Multiplication and Division Problems. The same model used for multiplicative comparisons will also work for basic multiplication word problems, beginning with single digit multipliers. Consider the problem:

Alana had 6 packages of gum. Each package holds 12 pieces of gum. How many pieces of gum does Alana have in all?

The following bar model uses a repeated addition view of multiplication to visualize the problem.

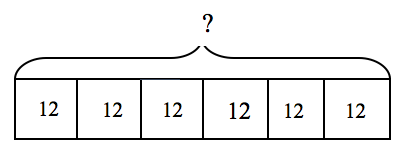
12 + 12 + 12 + 12 + 12 + 12 = 72 (or 6 x 12 = 72)

so Alana has 72 pieces of gum.

As students move into multi-digit multipliers, they can use a model that incorporates an ellipsis to streamline the bar model. For example:

Sam runs 32 km a day during April to get ready for a race. If Sam runs every day of the month, how many total kilometers did he run in April?

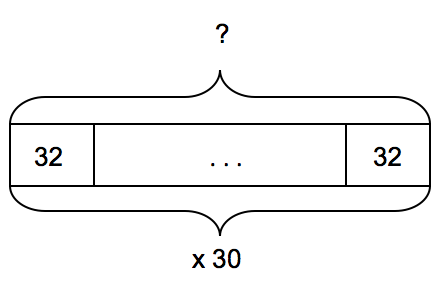
30 x 32 km = 30 x 30 km + 30 x 2 km = 960 km

Sam ran 960 km during the 30 days of April.

Since division is the inverse of multiplication, division word problems will utilize the multiplicative bar model where the product (dividend) is known, but one of the factors (divisor or quotient) is the unknown. 

Problems Involving Rates, Fractions, Percent & Multiple Steps. As students progress through the upper grades, they can apply new concepts and multi-step word problems to bar model drawings. Skemp (1993) identified the usefulness of relational thinking as critical to mathematical development. A student should be able to extend their thinking based on models they used earlier, by relating and adapting what they know to new situations. 

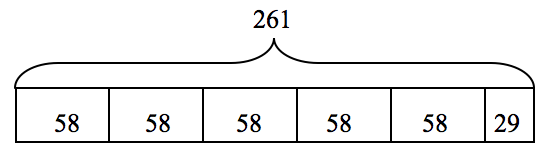
Consider this rate and distance problem:

Phong traveled 261 miles to see her grandmother. She averaged 58 mph. How long did it take her to get to her grandmother's house?

The following model builds off of the part-part-whole model using a repeated addition format for multiplication and division. It assumes that students have experience with using the model for division problems whose quotients are not just whole numbers. As they build up to (or divide) the total of 261 miles, they calculate that five 58's will represent 5 hours of travel, and the remaining 29 miles would be represented by a half box, so the solution is it would take Phong 5½ hours of driving time to get to her grandmother's house.

Even a more complex rate problem can be captured with a combination of similar models.  Consider this problem: 

Sue and her friend Anne took a trip together.  Sue drove the first 2/5 of the trip and Anne drove 210 miles for the last 3/5 of the trip.  Sue averaged 60 mph and Anne averaged 70 mph.  How long did the trip take them?

There are several ways students might combine or modify a basic bar model. One solution might be the following, where the first unknown is how many miles Sue drove. A bar divided into fifths represents how to calculate the miles Sue drove. Since we know that the 210 miles Anne drove is 3/5 of the total trip, each one of Anne's boxes, each representing 1/5 of the trip, is 70 miles. Therefore, Sue drove two 70 mile parts, or 140 miles, to equal 2/5 of the total trip.

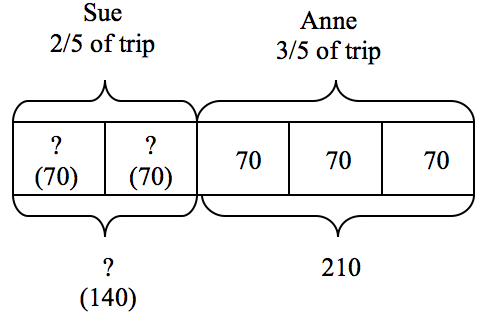
The diagram now needs to be extended to show how to calculate the number of hours. Anne's 210 mile segment, divided by her 70 mph rate will take 3 hours, as recorded on the following extension of the diagram. Sue's distance of 140 miles now needs to be divided into 60 mph segments to determine her driving time of 2 1/3 hours.  So, the total trip of 350 miles would take 5 1/3 hours of driving time, considering the two driving rates. 

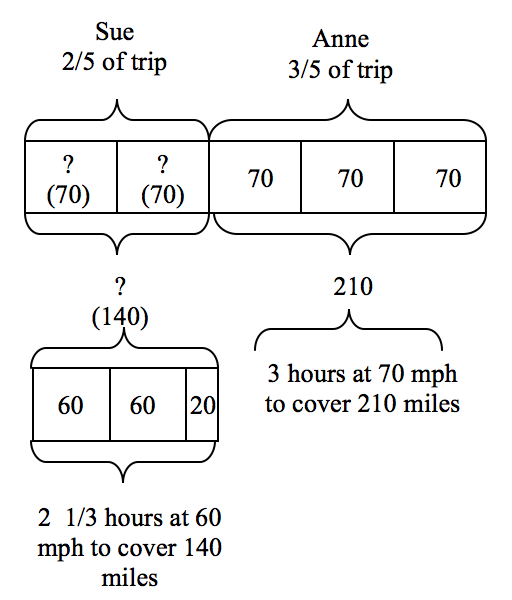
Certainly, a foundation of using simple bar model drawings needs to be well developed in early grades for students to extend diagrams with understanding in later grades. The Sue and Anne rate-time-distance problem would not be the place to begin using bar models!  But, by building on work in earlier grades with models, this extended model makes the mathematics of this complex problem more transparent, and helps students think through the steps. 

Consider a simpler multi-step problem:

Roberto purchased 5 sports drinks at $1.25 each. Roberto gave the cashier $20. How much change did he get back?

Again, there may be student variations when they begin to extend the use of diagrams in multi-step or more complex problems.  Some students might use two diagrams at once, as show below on the left.  Others may indicate computation within one diagram, as shown in the diagram on the right.

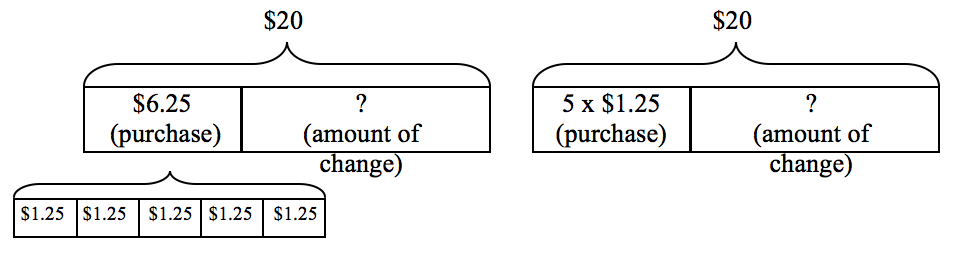
With routine experience with bar modeling, students can extend the use of the models to problems involving relationships that can be expressed with variables.  Consider this simple problem that could be represented algebraically:

Callan and Avrielle collected a total of 190 bugs for a science project.  Callan collected 10 more bugs than Avrielle.  How many bugs did Callan collect?

Let n equal the number of bugs Avrielle collected, and n + 10 equal the number of bugs Callan collected.  The following model might be created by students:

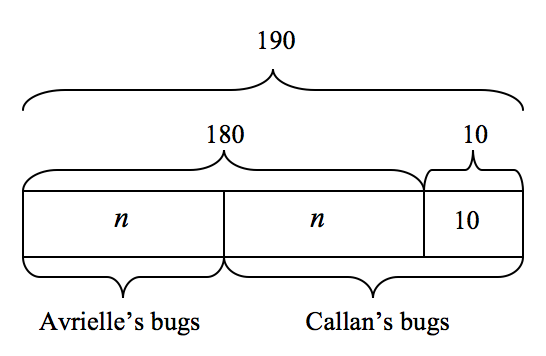
Since n + n = 180 (or 2 n = 180), n = 90.  Therefore, Callan collected 90 + 10 or 100 bugs and Avrielle collected 90 bugs for a total of 190 bugs collected together.

Planning and Instruction

How do I intentionally plan for and use modeling?

If modeling is not a way you learned to identify the important information and numerical relationships in word problems, you may want to review some of the resources on problem types (see Carpenter's book in References and Resources section below), or bar modeling (see books by Forsten, Walker, or Yeap in the References and Resources section below).  You may also want to practice the different types of models.  Decide which are most accessible for your students, and start with introducing one model at a time, helping students determine what is unknown in the problem, and where that unknown and the other numerical information should be placed in the bar model.  A question mark, box, or a variable can be used for the unknown.  As students become comfortable with that model, introduce, and compare and contrast a second model with the known model. 

You might introduce bar model drawings, or inverted-V diagrams, when there is a unit in your curriculum that contains several word problems.  If word problems are sporadic in your curriculum, you might introduce a "Word-Problem-of-the-Day" format where students solve a problem, or cluster of related problems, each day. 

To emphasize model drawings, you might have students take a set of problems, and classify them as to which model would help them solve the problem, or do a matching activity between word problems and model drawings.  Ask students to explain why a particular equation matches a model and would be useful in finding the solution.  Another activity is to present a bar model with some numerical information and an unknown.  Then ask students to write a word problem that could logically be solved using that model.  Ask students to explain why the word problem created matches a diagram well.  As students use models for solving word problems, they may generate different equations to solve a problem even though their models are the same.  Plan for class discussions where students may discuss why there can be different equations from the same bar model. 

Several studies have shown that students who can visualize a word problem through modeling increase their problem solving ability and accuracy.  This has been particularly documented in Singapore and other high performing countries where bar modeling is used extensively across grades.  Students are more likely to solve problems correctly when they incorporate bar model drawings.  On difficult problems, students who have been able to easily generate equations with simple problems often find that bar model drawings are especially helpful in increasing accuracy as problems increase in difficulty or involve new concepts (Yeap, 2010, pp. 87-89).

TALK:  Reflection and Discussion

• Are there particular types of word problems that your students solve more easily than others?  What characterizes these problems?
• Identify some basic facts with which your students struggle.  How could you incorporate those facts into word problems, and how might the use of the inverted-V model help?
• How do bar model drawings help extract and represent the mathematical components and numerical relationships of a word problem?
• With which type of word problems would you begin to show your students the use of bar model drawings?

DO:  Action Plans

• Select several story problems from your curriculum, MCA sample test items, or the Forsten, Walker, or Yeap resources on bar model drawing. Practice creating a bar model for several problems.  Compare your models with others in your grade level, team, or PLC group.  Practice until you feel comfortable with various model drawings.
• Investigate the types of multiplication and division problems, and how bar models can be used with different types such as measurement and partitive division, arrays, equal groups, rates.  The Carpenter resource may be helpful.
• Select some problems from your curriculum that are of a similar type.  Which bar model would be helpful in solving this type of problem?  Practice using the model yourself with several problems of this type.  How will you introduce the model to your students?
• Identify some basic facts with which your students struggle.  Craft some rich word problems utilizing these fact families.  Introduce the inverted-V diagrams with the word problems to make sense of the information in the word problem, and discuss strategies for solving the problems.
• Initiate a "Word-Problem-of-the-Day".  Students might want to keep problem solving notebooks.  Begin with problems of a particular type, and show students how to use a bar model to represent the information in a problem.  Cluster several problems of a given type during the week.  What improvements do you see in student selection of appropriate equations, accuracy of solutions, and ability to estimate or justify their answers as they increase the use of bar models to solve the word problems?  A quick way to disseminate the "Word-Problem-of-the-Day" is to duplicate the problem on each label on a sheet of address labels.  Students can just peel off the daily problem, add it to their problem solving notebook or a sheet of paper and solve away.
• When your district is doing a curriculum materials review, advocate to include a criteria that requires the use of visual models in helping students make sense of mathematical problems. 
• Watch some of the videos of students using models on the Powerful Practices CD (see Carpenter and Romberg in References and Resources Section). 

References and Resources

Bruner, J. S. (1961). The act of discovery.  Harvard Educational Review, 31, pp. 21-32, in Yeap, Ban Har. (2010). Bar modeling:  A problem solving tool.  Singapore: Marshall Cavendish Education. 

Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L. & Empson, S. B. (1999). Children's mathematics: Cognitively guided instruction.  Portsmouth, NH:  Heinemann.  (Book and CD)

Carpenter, T. P. & Romberg. T. A. (2004). Modeling, generalization, and justification in mathematics cases, in Powerful practices in mathematics & science.  Madison, WI:  National Center for Improving Student Learning and Achievement in Mathematics and Science.  www.wcer.wisc.edu/ncisla   (Booklet and CD)

Dienes, Z. (undated). Zoltan Dienes' six-state theory of learning mathematics. Retrieved from http://www.zoltandienes.com

Forsten, C. (2009). Step-by-step model drawing:  Solving math problems the Singapore way.  Peterborough, NH: SDE:  Crystal Spring Books.  http:// www.crystalspringsbooks.com

Hoven, J. & Garelick, B. (2007). Singapore math: Simple or complex? Educational Leadership, 65 (3), 28-31.

Leinwand, S. (2009). Accessible mathematics: 10 instructional shifts that raise student achievement.  Portsmouth, NH:  Heinemann.

Marzano, R. J., Norford, J. S., Paynter, D. E., Pickering, D. J., & Gaddy, B. B. (2001).   A handbook for classroom instruction that works.  Alexandria, VA:  Association for Supervision and Curriculum Development.

Singapore Ministry of Education. (1997). Retrieved http://moe.gov.sg

Skemp, R. R. (January, 1993). "Theoretical foundations of problem solving: A position paper."  University of Warwick. Retrieved from http://www.grahamtall.co.uk/skemp/sail/theops.html

Walker, L. (2010). Model drawing for challenging word problems:  Finding solutions the Singapore way.   Peterborough, NH: SDE:  Crystal Spring Books.  http:// www.crystalspringsbooks.com

Yeap, B. H. (2010). Bar modeling:  A problem solving tool.  Singapore: Marshall Cavendish Education.  http:// www.singaporemath.com

Model method drawing acts as a double-edged sword for solving inconsistent word problems

• Open access
• Published: 23 April 2022
• Volume 111 , pages 29–45, ( 2022 )

Cite this article

You have full access to this open access article

• Björn B. de Koning 1 ,
• Anton J. H. Boonen 2 ,
• Joran Jongerling 1 , 3 ,
• Floryt van Wesel 4 &
• Menno van der Schoot 4  

3232 Accesses

2 Citations

2 Altmetric

Explore all metrics

Drawing bar diagrams has been shown to improve performance on mathematical word problems wherein the relational keyword is consistent with the required arithmetic operation. This study extends this by testing the effectiveness of bar diagram drawing for word problems with an inconsistent keyword-arithmetic operation mapping. Seventy-five fifth graders solved consistent and inconsistent word problems while encouraged to draw bar diagrams. For each word problem, we assessed problem type (consistent/inconsistent), performance (correct/incorrect), and bar diagrams (accurate/inaccurate/no drawing). Overall, bar diagram drawing was associated with increased performance on both consistent and inconsistent word problems, but the strongest benefits of drawing were found for inconsistent word problems. For inconsistent word problems, bar diagram accuracy was more clearly related to performance (accurate bar diagrams related to correct answers, but inaccurate ones to incorrect answers) than for consistent word problems. We conclude that bar diagram drawing provides an effective graphical support for solving inconsistent word problems.

Similar content being viewed by others

Uncovering the interplay between drawings, mental representations, and arithmetic problem-solving strategies in children and adults

Hippolyte Gros, Jean-Pierre Thibaut & Emmanuel Sander

The role of relational preference in word-problem solving in 6- to 7-year-olds

Elien Vanluydt, Lieven Verschaffel & Wim Van Dooren

Different complex word problems require different combinations of cognitive skills

Anselm R. Strohmaier, Frank Reinhold, … Kristina Reiss

Avoid common mistakes on your manuscript.

Contemporary mathematics education increasingly relies on word problem-solving (Boonen et al., 2016 ). Word problems are mathematical exercises describing real-life situations in connected text of a few sentences to a paragraph in length instead of in mathematical notation (Rasmussen & King, 2000 ; Timmermans et al., 2007 ). Notwithstanding the assumed benefits of word problems regarding students’ motivation and connection with realistic contexts and personal experiences (e.g., van den Heuvel-Panhuizen, 2003 ), a significant number of students struggle, or even fail, to accurately solve word problems (e.g., De Koning et al., 2017 ; van der Schoot et al., 2009 ). Consequently, researchers have started to develop and test remedying problem solving strategies and instructional approaches that offer textual guidance (e.g., De Koning et al., 2017 ) or serve as graphical aids (e.g., Dewolf et al., 2017 ). In the present study, we focus on one specific type of graphical approach that has recently attracted a considerable amount of attention from researchers and educational practitioners: the model method. Specifically, our aim was to investigate whether model method drawing supports problem solving performance to a similar extent in word problems that differ in their consistency (i.e., relational term consistent vs. inconsistent with the required mathematical operation).

1 The model method

The model method is a graphical approach for supporting word problem-solving that originated in Singapore as part of the primary mathematics curriculum reform (Kho, 1987 ; Ng & Lee, 2009 ) and is increasingly used in various other countries worldwide such as the Netherlands (Kaur, 2019 ). The core feature of the model method is that children are taught to draw a bar diagram to represent the known and unknown mathematical quantities, as well as their relations, of a word problem (Kho, 1987 ; Ng, 2004 ). Specifically, children are encouraged to graphically depict the problem situation that is hidden in the word problem text by representing the relationship(s) among the quantities externally in the form of rectangles. So, all information explicitly or implicitly presented in the word problem is captured in a series of rectangles (i.e., a bar diagram) where each rectangle represents a different variable (and its quantity) from the word problem. The bar diagram thereby serves as a “visual analogue” (Ng & Lee, 2009 , p. 62; also see Ng & Lee, 2005 ) in that it contains all relevant variables, quantities, and relations from a word problem that are needed to solve the word problem. In this sense, the model method targets what is most fundamental for the word problem solution, namely constructing a representation of the situation described in the word problem (e.g., De Corte et al., 1985 ; Ng & Lee, 2009 ). Prior research has indeed shown that the model method is a powerful graphical strategy to support word problem solving in various types of word problems including algebraic routine problems (Ng & Lee, 2009 ), arithmetic routine problems (Ng & Lee, 2005 ), and non-routine problems (Ho & Lowrie, 2014 ) as well as for different types of learners including those with learning disabilities (Sharp & Dennis, 2017 ) and lower mathematical skills (Goh, 2009 ; Poh, 2007 ).

2 The model method focuses on consistent word problems

Interestingly, so far, prior research on the use (by students and teachers) and instructional effectiveness of the model method has been characterized by an exclusive focus on consistent word problems (e.g., Lee, Khng, Ng, & Ng Lan Kong, 2013 ; Ng & Lee, 2005 , 2009 ) while ignoring their inconsistent counterparts (for example, of consistent and inconsistent word problems, see Table 1 ). In consistent word problems, the required mathematical operation can be derived straightforwardly from the word problem because the words used in the word problem steer towards the mathematical operation that is needed to solve the problem. Look, for example, at Table 1 which shows a compare word problem, one of the most well-known types of word problems in which the consistency of the language used in a word problem is investigated. In a compare word problem, one needs to compute the quantity of a variable by comparing the information given about the relative magnitude of two quantities where one variable serves as the referent set and another variable as the comparison set (Boonen et al., 2016 ; De Koning et al., 2017 ; Verschaffel et al., 1992 ). For the consistent compare problem, the relational keyword “less than” is used to indicate the comparative relationship between the (quantities of) variables in the first and second sentences and is consistent in that the relational keyword in the second sentence aligns with the required mathematical operation which is addition. For solving consistent compare problems, the problem solver simply can rely on the numbers and the comparative keyword(s) given in the text to compute the answer. There is no need to internally or externally represent the described problem situation capturing all solution-relevant elements to come to the correct answer.

In inconsistent word problems, the required mathematical operation cannot directly be derived from the word problem text because the language used in the word problem steers towards an inappropriate mathematical operation. To illustrate, in the inconsistent compare word problem presented in Table 1 , “less than” primes a subtraction operation while an addition operation is required. This has to do with the pronominal reference (That is…) at the beginning of the second sentence which refers back to the quantity expressed in the first sentence and thus requires a reversal of the arithmetic operation that needs to be performed. In this case, a correct solution to the word problem requires the problem solver to engage in additional cognitive processing conducive to the construction of a mental representation of the problem situation (Hegarty et al., 1995 ; Kintsch & Greeno, 1985 ). Especially Kintsch and Greeno’s ( 1985 ) schema theory sheds helpful light on how the language consistency of word problems relates to mental representation processes. According to this theory, the key to solving a word problem is to translate the problem statement into a mental representation of the base type of mathematical situation that is embedded in the problem (and on the basis of which the required arithmetic operations can be planned and executed). To build an effective mental representation, problem solvers above all need to derive the correct relations between the solution-relevant elements from the text base of the word problem. In doing so, they have to utilize top-down comprehension processes to organize the text base, exclude irrelevant information, infer missing information, and most relevantly here, deal with inconsistent relational statements (Kintsch & Greeno, 1985 ). If problem solvers do not sufficiently engage in these cognitive processes when constructing a mental representation of the situation described in the word problem or do not construct a mental representation at all, and therefore do not reverse the addition operation to the subtraction operation, they commit a reversal error and most likely will solve the word problem incorrectly (Lewis & Mayer, 1987 ; Schumacher & Fuchs, 2012 ).

A robust finding in word problem-solving research that is relevant here is that word problems containing consistent language are solved correctly more often than those with inconsistent language (i.e., consistency effect, Lewis & Mayer, 1987 ; van der Schoot et al., 2009 ). Connecting this to the model method research conducted so far, it appears that past studies involving compare word problems, such as those by Lee et al. ( 2013 ) and Ng and Lee ( 2005 , 2009 ), and other types of word problems (e.g., fraction problems; Sharp & Dennis, 2017 ), did not yet test the efficacy of the model method for solving inconsistent word problems even though inconsistent problems in particular may benefit from additional support to accurately represent and solve the word problem.

Also at the theoretical level, no explicit attention is given to the suitability of the model method to provide representational support for solving inconsistent word problems: “The theoretical model we present is for consistent-language compare word problems that require the construction of a single model drawing….” (Ng & Lee, 2009 , p. 289/290). According to this theoretical model, which draws on the above discussed processing model for word problem solving by Kintsch and Greeno ( 1985 ), solving word problems with the model method consists of three phases. In the text phase, the text presented in the word problem is read with the aim to identify the variables, quantities, and relations that are given as well as what is unknown and is to be found. For the consistent word problem presented in Table 1 , this would mean that the store names, prices, and relational keyword are identified. In the structural phase, the text information is represented graphically in the form of rectangles where each rectangle represents a specific piece of information identified in the text (e.g., quantity of 45 euros for the variable jeans at the store Bijenkorf). Hence, there is continuous coordination between the text phase and the structural phase: if one piece of information is represented (e.g., step 1: top rectangle in Fig.  1 representing the price at Bijenkorf), one returns to the text for representing the next piece of information (e.g., step 2: bottom rectangle in Fig.  1 representing the price at C&A). The comparative relation between the two variables in a compare word problem is used to determine how to draw the two rectangles. For example, for the consistent word problem depicted in Table 1 , the relational keyword “less than” makes that the quantity of the second variable is smaller (expressed as a shorter rectangle) than that of the first variable (expressed as a longer rectangle), as is illustrated in Fig.  1 . The structural phase is completed if all pieces of information are combined into a series of rectangles (i.e., bar diagram). In the procedural-symbolic phase, the bar diagram drawn in the previous phase is used as a basis to formulate the mathematical equation that needs to be solved and the mathematical operations are carried out to solve the problem. Together, the theoretical model assumes that going through these three phases in an iterative manner to graphically depict the word problem helps to represent and solve consistent word problems.

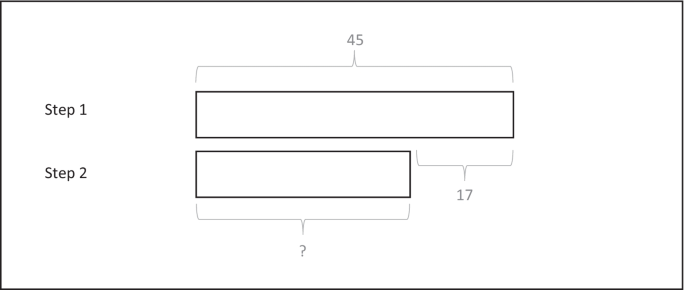
Bar model drawing accurately representing the relations of the consistent word problem presented in Table 1

3 Extending the model method to inconsistent word problems

Although one might be tempted to assume that what works for consistent word problems will probably also work for inconsistent word problems, previous research has indicated that the same instructional support may impact consistent and inconsistent word problems differently (e.g., De Koning et al., 2017 ). Based on the assumptions of the abovementioned theoretical account, the continuous interactions between one’s thought processes and drawing using the model method might be especially helpful for solving inconsistent word problems: the solution-relevant elements identified in the text (text phase) form the basis for the drawing process, while engaging in model method drawing in turn helps problem solvers to reflect on the problem situation (structural phase) such that it reshapes one’s interpretation of the word problem, helps to see through relations that they were not aware of before, encourages them to consider additional pieces of information, and things alike (all text phase), which is then again externalized in a revised drawing (construction phase). In other words, graphically representing the word problem text influences one’s cognitive representation of the problem situation and hence the mathematical operation that one considers appropriate for the word problem.

In case of inconsistent word problems, this would mean that model method drawing would serve a crucial function in that it helps the problem solver to re-analyze and critically reflect on the word problem text. Such cognitive consequences of having to graphically externalize the solution-relevant elements and their relations are thought to support the representation process (cf. van Meter, Aleksic, Schwarz, & Garner, 2006 ) and are therefore likely to contribute to the realization that in an inconsistent compare word problem, the comparative keyword steers towards an inappropriate mathematical operation. These interactions between drawing and cognitive processing are supposed to help problem solvers to reverse the comparative keyword to an appropriate arithmetic operation and hence to arrive at the correct solution on inconsistent word problems. If we apply this to the inconsistent word problem presented in Table 1 , problem solvers first identify the relevant elements in an inconsistent word problem and then graphically represent the variable presented in the first sentence in a bar diagram (see Fig.  2 , step 1). Subsequently, they use the textual information and the drawing to determine how to mentally and graphically represent the variable presented in the second sentence in relation to the first variable. If this processing results in the realization that the relational keyword “less than” needs to be reversed to an addition operation, a longer rectangle is drawn for the second variable (see Fig.  2 , step 2).

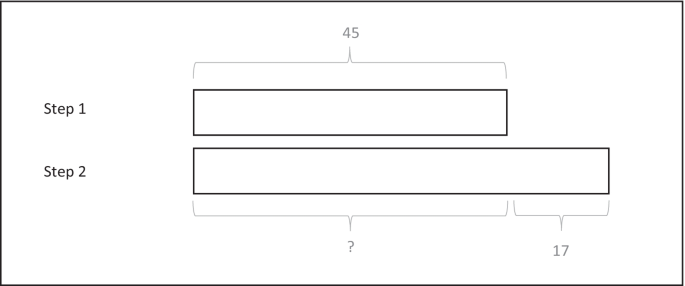
Bar model drawing accurately representing the relations of the inconsistent word problem presented in Table 1

The above is in line with previous research showing that self-generated drawing has a positive effect on mathematics performance for tasks like word problem solving (e.g., Boonen et al., 2016 ) and solving mathematical modelling problems (e.g., Rellensman, Schukajlow & Leopold, 2020 ). Comparable beneficial effects of drawing have been reported outside the mathematical domain such as in the comprehension of science topics from text (e.g., Schwamborn et al., 2010 ). Recent lines of research on the role of drawing in word problem-solving have focused on various aspects related to drawing such as the effects of strategic knowledge about drawing (i.e., students’ views on the characteristics of a drawing that fit a given problem), the type of drawing (e.g., situational vs. mathematical; number lines, diagrams), and the accuracy of drawing (i.e., the correctness of representation of the relevant objects and relations, including the correct labeling of the drawing with numbers) on word problem solving performance (e.g., Chu et al., 2017 ; Csíkos et al., 2012 ; Gvozdic & Sander, 2020 ; Krawitz & Schukajlow, 2020 ; Munez et al., 2013 ; Ott, 2020 ; Rellensmann et al., 2019 , 2020 ). For the present study, particularly, the research on the accuracy of drawing is relevant as this work shows that benefits of drawing for word problem solving are strongly related to the accuracy of the drawing with more accurate drawings correlating with better word problem solving performance (e.g., De Bock et al., 1998 ).

Also in using the model method, the drawing of accurate bar diagrams appears crucial for word problem-solving performance. Yan ( 2002 ) and Ng and Lee ( 2009 ), for example, demonstrated that the errors students made in solving word problems were less likely to arise from computational problems (cf. De Corte et al., 1985 ), but rather were due to students experiencing problems with drawing an accurate bar diagram. Particularly, problems with understanding the word problem, determining the solution steps with help of the model method, and deciding what the correct model is to be drawn, should be have been indicated as hindrances to solving word problems (Goh, 2009 ; Ng & Lee, 2009 ). This makes clear that understanding the relations between the different pieces of information and drawing an accurate bar diagram that corresponds to this are critical for the model method to be successful, although it does not guarantee that a correct answer is given (Ho & Lowrie, 2014 ). Given that such relational processing is most relevant for solving inconsistent word problems, it seems plausible that the accuracy of the drawn bar diagram is most critical in inconsistent word problems. In consistent word problems, a correct answer may be given without drawing a (correct) bar diagram as the appropriate mathematical procedure can be read off directly from the problem text and the construction of a representation is not a prerequisite (Hegarty et al., 1995 ). In other words, drawing no or an inaccurate bar diagram likely hinders word problem-solving performance most in inconsistent word problems. By taking into account both consistent and inconsistent word problems as well as the accuracy of the drawn bar diagram, the present study contributes to better understanding of the use and effectiveness of the model method and extends previous research on (accuracy of) drawing in word problem solving (e.g., Krawitz & Schukajlow, 2020 ).

4 The present study

In this study, we addressed the question of whether the positive effects of bar model drawing on consistent compare word problem performance can also be found for inconsistent compare word problems. The study was conducted among fifth-grade primary school children who attended a school that used the model method as an instructional approach in their mathematics curriculum. The children completed a set of consistent and inconsistent compare word problems and they were encouraged to use the model method while they solved the word problems. Both the word problems and the drawn bar diagrams were scored for accuracy. Given that prior research has indicated a positive influence of model method drawing on solving consistent word problems (e.g., Ng & Lee, 2009 ), we expected that drawing a correct bar diagram would be positively associated with problem-solving performance on consistent word problems and would yield a slightly higher number of correctly solved consistent word problems than when no or an inaccurate bar diagram was drawn. For inconsistent word problems, we expected the accuracy of the drawn bar diagram to have a more pronounced influence. Assuming that drawing a bar diagram supports one’s understanding of the problem situation described in the word problem text, a relatively higher number of accurate bar diagrams than inaccurate bar diagrams or no bar diagrams were expected and these accurately drawn bar diagrams were expected to be more likely associated with a correct answer on an inconsistent word problem than when drawing no or an inaccurate bar diagram.

5.1 Participants

The participants were 75 fifth-grade children (46 boys, M age  = 9.70 years, SD age  = 0.03; 29 girls, M age  = 9.83 years, SD age  = 0.35) from three regular primary schools located in the Netherlands. The participating schools used the instructional method Rekenwonders for teaching mathematics; this method is the only Dutch mathematics method that uses the model method as the core problem-solving approach in mathematics instruction. This means that all participating children were familiar with schematically representing mathematical exercises according to the model method and had experience using it for solving mathematical tasks. All children participated voluntarily and received a small gift as an appreciation for their participation. Children’s parents provided informed consent based on printed information about the purpose of the study.

5.2 Materials

The inconsistency task was used for assessing word problem-solving performance. This task is a well-established and frequently used instrument for measuring one’s proficiency in solving arithmetic word problems (Daroczy et al., 2015 ). The inconsistency task used in this study contained 24 one-step compare word problems (available at https://osf.io/fnxzj/ ) that were based on van der Schoot et al. ( 2009 ). Each compare word problem was presented in Dutch and consisted of three sentences. The first sentence presented an assignment statement in which the value of the first variable was expressed (e.g., At the Bijenkorf, a sweater costs 45 euros.). The second sentence contained a relational statement expressing the value of the second variable in relation to the first variable (e.g., At the C&A, a sweater costs 17 euros less than at the Bijenkorf). The third sentence asked participants to indicate the price of the second variable (e.g., How much will you pay at C&A?).

In half of the compare word problems (i.e., 12 problems), the relational keyword used in the second sentence (“more/less than”) was consistent with the required mathematical operation, whereas in the other half, the relational keyword was inconsistent with it. In consistent compare word problems (see Table 1 ), the relation between the values of the first and second variables is explicitly and unambiguously indicated in the first two sentences. This makes that the relational keyword in the second sentence (e.g., less than) primes the appropriate arithmetic operation (e.g., subtraction). In inconsistent compare word problems (see Table 1 ), the second sentence contains a pronominal reference relating the value of the second variable to the value of the first variable from the first sentence (e.g., That is 17 euros less than at the C&A). Hence, in inconsistent compare word problems, the relational keyword (e.g., less than) primes an inappropriate arithmetic operation (e.g., subtraction) instead of the required arithmetic operation (e.g., addition).

To ensure comparability across all compare word problems, we applied several rules derived from prior research (e.g., Boonen et al., 2016 ; De Koning et al., 2017 ; van der Schoot et al., 2009 ). The rules were tailored to our sample in consultation with the children’s teachers so that all compare word problems could be solved by every child. This was done to reduce the possibility that the execution of the required arithmetic operations would be a determining factor in students’ word problem solving. This resulted in the following rules: (1) answers to each problem always required a subtraction or addition operation, (2) answers and numerical values in the problems contained no fractions or negative numbers, (3) numerical values occurred only once in the same problem, (4) answers to each problem were between 13 and 75, and (5) numerical values in consistent and inconsistent word problems were matched for magnitude.

Three versions of paper-and-pencil booklets were created that each contained 24 (12 consistent, 12 inconsistent) compare word problems. Each page of the booklet contained (1) one compare word problem followed by a text box in which participants could write their answer (top half of the page) and (2) an empty box in which participants could draw their schematic representation (i.e., bar model) of the compare word problem (bottom half of the page). In all three versions, the problems were presented in a random order while taking into account that problems of the same type were not presented more than two times consecutively. The versions differed in the order in which the problems were presented. The internal consistency of the inconsistency task (all consistent and inconsistent word problems together) as used in the present study was high (Cronbach’s α = 0.87).

5.3 Procedure

The experiment took place in the children’s classroom at their school and was conducted by three trained research assistants in a single session. The research assistants told the children that they were expected to complete a booklet of arithmetic word problems. They verbally instructed the children to complete the problems as they would normally do and encouraged them once to schematically represent each problem by drawing a bar model in the indicated box to help them solve that problem (note that the word problem booklet did not contain additional drawing prompts). There was no practice with drawing because children were already familiar with bar model drawing from their regular lessons. It was explicitly mentioned that their word problem-solving performance would not be graded, but that they still should try to perform to the best of their abilities. After having placed the children’s desks in a test situation (all desks separated from each other, lined up in separate rows), the booklets were distributed. After all children had received a booklet (one of the three randomly assigned versions) and had filled out their demographic information (i.e., age, gender) on the first page, they were told to start solving the problems. Children were given 60 min to individually complete the booklet and could do something for themselves (e.g., reading, drawing) when they were done. At the end of the experiment, all booklets were collected and children were given a small gift.

5.4 Data-analysis

For each compare word problem in the inconsistency task, it was known whether it was a consistent or inconsistent word problem because of the “word problem type” (consistent vs. inconsistent; an independent variable in the study). Each word problem was additionally scored for the following aspects: (1) word problem performance (the dependent variable), which was determined by indicating for each word problem whether the provided answer was correct (yielding 1 point) or incorrect (yielding 0 points), and (2) bar diagram (the second independent variable in the study), which was determined for each word problem by categorizing the drawing as “no bar diagram”, “accurate bar diagram”, or “inaccurate bar diagram”. The category “no bar diagram” was assigned if no drawing was made for solving the compare word problem. A drawing was categorized as “accurate bar diagram” if a complete bar diagram was drawn in which all values and relations expressed in the compare word problem were correctly represented. If a bar diagram drawing incorrectly represented (or missed) one or more values and/or relations, it was coded as an “inaccurate bar diagram”. Please note that we did not subdivide further into number and type of errors within this category as we were primarily interested in the accuracy of the drawn bar diagrams and wanted to avoid ending up with (too) many categories containing just a few instances of bar diagram drawings that would be difficult to interpret. For the scoring of (1) and (2), there were no missing values. A randomly selected subset of 50 bar diagram drawings was coded by two independent raters. Given that the inter-rater reliability of these coded drawings was high (Cohen’s Kappa [κ] = 0.96), the remaining bar diagram drawings were coded by one rater.

We ran multilevel logistic regressions using the lme4 R-package (Bates et al., 2015 ) to see how word problem type, bar diagram, and the interaction between word problem type and bar diagram were related to word problem performance, while correcting for nesting within students. Specifically, we ran (1) an intercept only model to determine the amount of variability between participants in word problem performance, (2) a model with the main effects of bar diagram and word problem type on word problem performance, and (3) a model with the main effects of bar diagram and word problem type as well as their interaction. In these analyses, word problem type was a dummy variable (0 = consistent, 1 = inconsistent) and bar diagram was included using two dummies that compare an inaccurate drawing to the no drawing condition (dummy 1) and an accurate drawing against no drawing (dummy 2). In multilevel logistic regression models, R-squared can be defined in different ways due to the presence of multiple variance components. Here we use the pseudo-R-squared as implemented by Nakagawa and Schielzeth ( 2013 ) which gives an estimate of the total variance explained on all levels in the model. This statistic should be interpreted with caution, however, since there is no proper estimator for explained variance in multilevel logistic regression models that works well all the time and for all purposes. Pairwise comparisons between all possible conditions were corrected for inflated type I error rates using the Sidak correction to prevent inflated type I error rates. All analyses were run in R version 3.6.1 (R Core Team, 2019 ); see https://osf.io/fnxzj/ for the annotated R code.

6.1 Descriptive information

Participants produced a bar diagram drawing in 904 (50.99%) out of the total number of 1773 word problems: 644 (71.23%) were identified as an accurate bar diagram drawing and 260 (28.77%) were categorized as an inaccurate bar diagram drawing. The category “no bar diagram drawing” contained 869 cases (49.01%). For consistent word problems, out of the 889 consistent word problems in 453 (50.98%) of the cases, a bar diagram was drawn, whereas in 436 (49.04%) of the cases, no bar diagram was drawn. If a bar diagram was drawn, in 385 (84.99%) of the cases, an accurate bar diagram was drawn, whereas in 68 (15.01%) of the cases, an inaccurate bar diagram was produced. For inconsistent word problems, out of the 884 inconsistent word problems in 451 (51.02%) of the cases, a bar diagram was drawn, whereas in 433 (48.98%) of the cases, no bar diagram was drawn. If a bar model was drawn, in 259 (57.43%) of the cases, an accurate bar model was drawn, but in 192 (42.57%) cases, an inaccurate bar diagram was produced. Participants’ performance on each consistent and inconsistent compare word problem (i.e., correct vs. incorrect) subdivided into the type of bar diagram drawing they had produced (i.e., none, accurate, inaccurate) for that compare word problem is depicted in Fig.  3 .

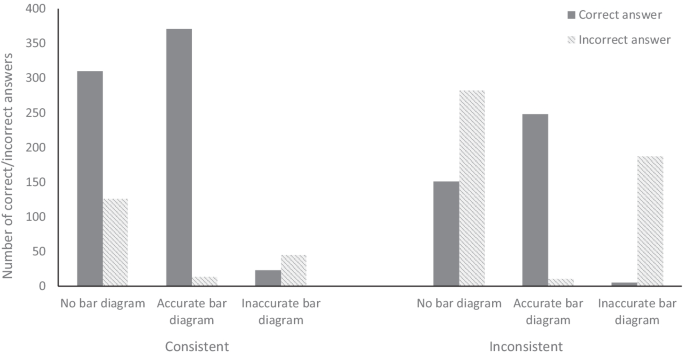
Number of correctly and incorrectly solved consistent (left) and inconsistent (right) word problems in each bar diagram category (no, accurate, inaccurate)

6.2 Statistical testing

An intercept only model showed that 26.7% of the total variance in accuracy of word problem solving was on the student level. The pseudo-R 2 of this model is equal to 0.27.

Next, we ran the main effects model to test the overall effect of word problem type and bar diagram on word problem performance. Results showed that there was a significant effect of word problem type with fewer correct answers being given on inconsistent word problems than on consistent word problems, b =  − 1.93, se = 0.162, p  < 0.001. The probability of a right answer is 83.2% for consistent problems compared to 41.7% for inconsistent ones. In other words, we obtained a consistency effect (e.g., Lewis & Mayer, 1987 ; van der Schoot et al., 2009 ). There was also a significant effect of bar diagram: fewer correct answers were given when an inaccurate bar diagram was drawn than when no bar diagram was drawn, b =  − 2.36, se = 0.417, p  < 0.001; more correct answers were given when an accurate bar diagram was drawn than when no bar diagram was drawn, b = 4.76, se = 0.425, p  < 0.001; and more correct answers were given when an accurate bar diagram was drawn than when an incorrect bar diagram was drawn, b = 7.12, se = 0.507, p  < 0.001 (all after correction for multiple testing using the Sidak correction). The pseudo-R 2 of this model is equal to 0.77, and the probability of a correct answer for the no bar diagram, incorrect bar diagram, and accurate bar diagram was 45.8%, 7.4%, and 99.0%, respectively.

Results of the model that takes into account the interaction between word problem type and bar drawing showed that there was a significant interaction between these two factors, Χ 2 diff (2) = 23.41, p  < 0.001. The pseudo-R 2 of this model is equal to 0.77. When no bar diagram was drawn, there were more incorrect answers on inconsistent word problems than on consistent word problems, b =  − 2.07, se = 0.184, p  < 0.001. Drawing an inaccurate bar diagram resulted in more incorrect answers on inconsistent word problems than on consistent word problems and this difference was larger than when no bar diagram was drawn, b =  − 3.27, se = 0.594, p  < 0.001. There were no significant differences in word problem-solving performance between consistent and inconsistent word problems when an accurate bar diagram was drawn, b =  − 0.06, se = 0.442, p  = 0.887. If no bar diagram was drawn, the probability of a correct response for consistent and inconsistent problems is 70.4% and 23.1%, respectively. If a wrong bar diagram was drawn, these probabilities are 26.9% and 1.4%, respectively, while the probability of a correct response for consistent and inconsistent problems is 98.9% and 98.8% when an accurate bar diagram is drawn. An additional sensitivity analysis with students’ performance on a standardized mathematics test (Cito mathematics) as a control variable showed that adding mathematics performance to the analysis did not change this pattern of results. Together, our results show that when an inaccurate bar diagram is drawn, poorer performance is obtained on both consistent and inconsistent word problems, yet inaccurate drawing appears most disadvantageous for inconsistent word problems (also see Table 2 ). For inconsistent word problems, an all-or-nothing picture emerged: if an accurate bar diagram was drawn, there was a close to 100% accuracy in word problem-solving performance, while if an inaccurate bar diagram was drawn, word problem-solving performance accuracy was close to zero.

7 Discussion

This study investigated the extent to which drawing a bar diagram affects problem-solving performance for compare word problems. We were particularly interested in whether drawing a bar diagram can improve performance on inconsistent compare word problems and how this compares to drawing bar diagrams on consistent compare word problems. Overall, results showed that producing accurate bar diagrams benefited problem-solving performance on both consistent and inconsistent word problems relative to drawing inaccurate bar diagrams or not drawing. This is in line with our predictions and confirms previous findings showing that bar diagram drawing supports problem-solving success in consistent word problems (e.g., Ng & Lee, 2009 ). An important contribution our study makes is that we show that drawing bar diagrams can also support word problem-solving performance on inconsistent word problems.

7.1 The “all-or-nothing” of drawing for inconsistent word problems

The results of our study show that there is a positive impact of drawing bar diagrams on both consistent and inconsistent word problems, with effects of drawing being the most pronounced on inconsistent word problems. It is important to consider that, as hypothesized, this positive impact strongly depends on the accuracy of the drawn bar diagram, which is in line with earlier research showing that the accuracy (or quality) of drawing influences word problem-solving performance (e.g., Krawitz & Schukajlow, 2020 ; Ott, 2020 ; Rellensmann et al., 2019 , 2020 ). That is, bar diagram drawing is mostly supportive to problem solving on inconsistent word problems if an accurate bar diagram is drawn. For inconsistent word problems, drawing resulted in an accurate bar diagram and subsequently in a correct answer in a large majority of the cases. Such a high percentage of correct problem solutions was not realized when no bar diagrams were drawn, indicating a benefit of engaging in drawing accurate bar diagrams. However, if an inaccurate bar diagram was drawn, which occurred relatively less often than accurate drawings, this hardly ever was accompanied with a correct answer. In fact, the chance of a correct answer after drawing an inaccurate diagram was only 2.60%, whereas this chance for consistent word problems was 33.82%. Together, when controlling for students’ mathematical abilities, drawing accurate bar diagrams has a positive impact on word problem solving performance, whereas drawing inaccurate bar diagrams has a detrimental effect on word problem-solving performance, and both effects are more pronounced for inconsistent word problems. This suggests that drawing a bar diagram for inconsistent word problems resembles an “all-or-nothing” principle where the accuracy of the drawn bar diagram (i.e., accurate vs. inaccurate) is tightly coupled with the correctness of the answer on the word problem (i.e., correct vs. incorrect answer).

Our interpretation of this is that the “all” (i.e., association between accurate bar diagrams and correct problem solutions) represents a situation where the instruction to draw encouraged students to reflect on their mental processes. Being confronted with the expectation to draw a bar diagram likely stimulated students to invest mental resources to more critically analyze the word problem and their approach to solve the problem. The engagement in cognitive activities such as identifying and relating the key variables in the word problem has proven to be associated with word problem solving success (e.g., Daroczy et al., 2015 ; van der Schoot et al., 2009 ). Several studies indicate that such deeper-level thinking strategies are particularly supportive for improving performance on inconsistent word problems (e.g., De Koning et al., 2017 ). In this scenario, students are therefore more likely to reverse the arithmetic operation (e.g., subtraction) primed by the relational keyword (e.g., less than) to the appropriate arithmetic operation (e.g., addition). Consequently, their chance to solve an inconsistent word problem correctly is improved.

In contrast, the “nothing” (i.e., association between inaccurate bar diagrams and incorrect problem solutions) in our view reflects students’ attempts to solve an inconsistent word problem while they are insufficiently investing mental resources to accurately mentally represent the described problem situation. That is, they do not take the requirement to draw as an opportunity to carefully and critically analyze the word problem (or may not succeed in this) resulting in the typical reversal error (Schumacher & Fuchs, 2012 ) that underlies the lower performance on inconsistent word problems. By externalizing these thought processes in a bar diagram (e.g., making one bar longer instead of shorter than the other), the drawing likely visually reinforces students’ inadequate problem-solving approach. Students may perceive this as confirmation that they used an appropriate problem solving approach and do not additionally engage in the deeper cognitive processes required to correctly solve the word problem. This could explain why drawing inaccurate bar diagrams resulted in lower problem-solving performance than not drawing, as without drawing such a visual reinforcement is not available to prevent students from engaging in additional cognitive processing.

For consistent word problems, the relation between bar model drawing and problem-solving success has less of such an all-or-nothing character. The overall pattern of findings indicates that accurate bar diagram drawings most likely coincide with a correct answer on a consistent word problem, more so than respectively not drawing or drawing inaccurate bar diagrams. However, in contrast to inconsistent word problems, on consistent word problems, there were relatively fewer inaccurate bar diagrams but such inaccurate drawings resulted in a correct answer more often than was the case for inconsistent word problems. This suggests that potential harmful effects of drawing an inaccurate bar diagram (e.g., visual reinforcement) are less likely to occur when solving consistent word problems. This is related to the fact that consistent word problems may be solved by relying on a rather superficial problem-solving strategy (Hegarty et al., 1995 ). For example, to solve consistent word problems, students may simply concentrate on the numbers and relational keyword given in the word problem, and without engaging in deeper cognitive processing, arrive at the correct answer. If students in this situation attempt to draw a bar diagram for the consistent problem because they were expected to do so, their drawing might be inaccurate for several reasons. For example, students might insufficiently master the model method approach resulting in a poorly worked out model (which is unlikely in this study because we tested a sample that was familiar with this method) or they might not finish the drawing because it is not needed to correctly answer the word problem. Additionally, when students draw an inaccurate bar diagram and still are able to provide a correct answer, it is possible that students might have noticed the mismatch between the inaccurate bar diagram and the situation described in the word problem. This may have triggered them to mentally adjust their representation of the word problem and mentally execute the required arithmetic computation to provide the correct answer without additionally changing the initially drawn bar diagram. Although these interpretations, as well as the ones provided for inconsistent word problems, appear plausible, they need confirmation in future work that extends the current study with a close examination of the actual problem-solving process. This may provide insight into the extent to which and in what ways cognitive processing and drawing bar diagrams influence each other.

7.2 Implications

We can tentatively draw a number of educational implications from our results. These implications, which need further ratification, are intended to inform teachers and educational designers about some issues related to drawing bar diagrams during word problem solving. First, asking students to draw a bar diagram during word problem solving improves performance on both consistent and inconsistent word problems. Yet, benefits of drawing compared to not drawing are larger for inconsistent than for consistent word problems. Additionally, it should be noted that the implication that drawing has comparable effects on problem-solving performance for students of varying mathematical abilities should be treated with caution given that we did not have sufficient power to perform interaction analyses, and thus needs corroborating evidence from future studies. Second, our results suggest that carefully analyzing an inconsistent word problem before or during drawing—presumably elicited by the requirement to draw—supports creating accurate bar diagrams and improves problem-solving performance. Third, it appeared that once an inaccurate bar diagram was drawn for an inconsistent word problem, it was unlikely that students were able and/or willing to arrive at the correct problem solution. Therefore, using drawing as a control mechanism for the correctness of an answer is likely to be ineffective when solving inconsistent word problems, at least without feedback on the accuracy of the given answer and/or the drawing and prompts to reflect on their problem-solving approach. Fourth, simply indicating that students should draw bar diagrams while solving word problems does not guarantee that they will create a drawing nor that they create accurate drawings. It would therefore be advisable to complement this instruction with explicit guidance in how to draw and/or to increase the likelihood that students perceive drawing as processing support rather than as optional. For example, a to-be-completed bar diagram could be presented together with the word problem such that students only have to insert the numbers at the right location or, as a more complex variant, are required to draw the second bar and decide whether this should be longer or shorter than the already given bar. A considerable amount of research has shown that using partially completed problems where students need to complete some key solution steps results in fewer errors, increased motivation, and shorter solution times than when having to solve the problem without such guidance (cf. completion effect, Sweller et al., 2011 ).

8 Conclusion

The present study shows that bar diagram drawing is an effective approach to support word problem-solving performance, particularly for inconsistent word problems. This is a promising finding given that with inconsistent word problems learners typically fail to convert the given relation keyword into the appropriate arithmetic operation. Our results indicate that this high probable conversion error can be prevented to a large extent by engaging in externally visualizing the problem situation in a bar diagram. With this, the current study contributes to an emerging line of research aimed at improving the performance on inconsistent word problems, which thus far has only concentrated on testing the efficacy of verbal/linguistic approaches (De Koning & van der Schoot, 2019 ; De Koning et al., 2017 ); here we add to this research by showing that a graphical approach to processing inconsistent word problems can support problem-solving success.

Bates, D., Maechler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67 (1), 1–48. https://doi.org/10.18637/jss.v067.i01

Article   Google Scholar  

Boonen, A. J. H., De Koning, B. B., Jolles, J., & van der Schoot, M. (2016). Word problem solving in contemporary math education: A plea for reading comprehension skills training. Frontiers in Psychology: Educational Psychology, 7 , 191. https://doi.org/10.3389/fpsyg.2016.00191

Chu, J., Rittle-Johnson, B., & Fyfe, E. R. (2017). Diagrams benefit symbolic problem-solving. British Journal of Educational Psychology, 87 (2), 273–287. https://doi.org/10.1111/bjep.12149

Csíkos, C., Szitányi, J., & Kelemen, R. (2012). The effects of using drawings in developing young children’s mathematical word problem solving: A design experiment with third-grade Hungarian students. Educational Studies in Mathematics, 81 (1), 47–65. https://doi.org/10.1007/s10649-011-9360-z

Daroczy, G., Wolska, M., Meurers, W. D., & Nuerk, H.-C. (2015). Word problems: A review of linguistic and numerical factors contributing to their difficulty. Frontiers in Psychology, 6 , 348. https://doi.org/10.3389/fpsyg.2015.00348

De Bock, D., Verschaffel, L., & Janssens, D. (1998). The predominance of the linear model in secondary school students’ solutions of word problems involving length and area of similar plane figures. Educational Studies in Mathematics, 35 , 65–83. https://doi.org/10.1023/A:1003151011999

De Corte, E., Verschaffel, L., & De Win, L. (1985). The influence of rewording verbal problems on children’s problem representations and solutions. Journal of Educational Psychology, 77 , 460–470. https://doi.org/10.1037/0022-0663.77.4.460

De Koning, B. B., & van der Schoot (2019). Can “you” make a difference? Investigating whether perspective-taking improves performance on inconsistent mathematical word problems. Applied Cognitive Psychology . https://doi.org/10.1002/acp.3555

De Koning, B. B., Boonen, A. J. H., & van der Schoot, M. (2017). The consistency effect in word problem solving is effectively reduced through verbal instruction. Contemporary Educational Psychology, 49 , 121–129. https://doi.org/10.1016/j.cedpsych.2017.01.006

Dewolf, T., Van Dooren, W., & Verschaffel, L. (2017). Can visual aids in representational illustrations help pupils to solve mathematical word problems more realistically? European Journal of Psychology of Education, 32 , 335–351. https://doi.org/10.1007/s10212-016-0308-7

Goh, S. P. (2009). Primary Five pupils’ difficulties in using the model method for solving complex relational word problems (Unpublished master dissertation). National Institute of Education, Nanyang Technological University.

Gvozdic, K., & Sander, E. (2020). Learning to be an opportunistic word problem solver: Going beyond informal solving strategies. ZDM-Mathematics Education, 52 (1), 111–123. https://doi.org/10.1007/s11858-019-01114-z

Hegarty, M., Mayer, R. E., & Monk, C. A. (1995). Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. Journal of Educational Psychology, 87 , 18–32. https://doi.org/10.1037/0022-0663.87.1.18

Ho, S. Y., & Lowrie, T. (2014). The model method: Students’ performance and its effectiveness. The Journal of Mathematical Behavior, 35 , 87–100. https://doi.org/10.1016/j.jmathb.2014.06.002

Kaur, B. (2019). The why, what and how of the ‘Model’ method: A tool for representing and visualising relationships when solving whole number arithmetic word problems. ZDM-Mathematics Education, 51 , 151–168. https://doi.org/10.1007/s11858-018-1000-y

Kho, T. H. (1987). Mathematical models for solving arithmetic problems . In Proceedings of the 4th Southeast Asian conference on mathematics education (ICMI-SEAMS), Volume 4 (pp. 345–351). Singapore: Institute of Education.

Kintsch, W., & Greeno, J. G. (1985). Understanding and solving word arithmetic problems. Psychological Review, 92 , 109–129. https://doi.org/10.1037/0033-295X.92.1.109

Krawitz, J., & Schukajlow, S. (2020). When can making a drawing hinder problem solving? Effect of the drawing strategy on linear overgeneralizations and problem solving. Frontiers in Psychology, 11 , 506. https://doi.org/10.3389/fpsyg.2020.00506

Lee, K., Khng, K. H., Ng, S. F., Kong, N. L., & J. (2013). Longer bars for bigger numbers? Children’s usage and understanding of graphical representations of algebraic problems. Frontline Learning Research, 1 , 81–96. https://doi.org/10.14786/flr.v1i1.49

Lewis, A. B., & Mayer, R. E. (1987). Students’ miscomprehension of relational statements in arithmetic word problems. Journal of Educational Psychology, 79 , 363–371. https://doi.org/10.1037/00220663.79.4.363

Munez, D., Orrantia, J., & Rosales, J. (2013). The effect of external representations on compare word problems: Supporting mental model construction. The Journal of Experimental Education, 81 (3), 337–355. https://doi.org/10.1080/00220973.2012.715095

Nakagawa, S., & Schielzeth, H. (2013). A general and simple method for obtaining R 2 from generalized linear mixed-effects models. Methods in Ecology and Evolution, 4 , 133–142. https://doi.org/10.1111/j.2041210x.2012.00261.x

Ng, S. F. (2004). Developing algebraic thinking in early grades: Case study of the Singapore primary mathematics curriculum. The Mathematics Educator, 8 , 39–59.

Google Scholar  

Ng, S. F., & Lee, K. (2005). How primary five pupils use the model method to solve word problems. The Mathematics Educator, 9 , 60–83.

Ng, S. F., & Lee, K. (2009). The model method: Singapore children’s tool for representing and solving algebraic word problems. Journal for Research in Mathematics Education , 40, 282–313. www.jstor.org/stable/40539338

Ott, B. (2020). Learner-generated graphic representations for word problems: An intervention and evaluation study in grade 3. Educational Studies in Mathematics, 105 , 91–113. https://doi.org/10.1007/s10649-020-09978-9

Poh, B. K. (2007). Model method: Primary three pupils’ ability to use models for representing and solving word problems (Unpublished master dissertation) . National Institute of Education, Nanyang Technological University.

Rasmussen, C. L., & King, K. D. (2000). Locating starting points in differential equations: A realistic mathematics education approach. International Journal of Mathematical Education in Science and Technology, 31 , 161–172. https://doi.org/10.1080/002073900287219

R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing , Vienna, Austria. https://www.R-project.org/ .

Rellensmann, J., Schukajlow, S., & Leopold, C. (2020). Measuring and investigating strategic knowledge about drawing to solve geometry modelling problems. ZDM-Mathematics Education, 52 , 97–110. https://doi.org/10.1007/s11858-019-01085-1

Rellensmann, J., Schukajlow, S., & Leopold, C. (2019). Measuring and investigating strategic knowledge about drawing to solve geometry modelling problems. ZDM-Mathematics Education, 52 , 97–110. https://doi.org/10.1007/s11858-019-01085-1

Schumacher, R. F., & Fuchs, L. S. (2012). Does understanding relational terminology mediate effects of intervention on compare word problem? Journal of Experimental Child Psychology, 111 , 607–628. https://doi.org/10.1016/j.jecp.2011.12.001

Schwamborn, A., Mayer, R. E., Thillmann, H., Leopold, C., & Leutner, D. (2010). Drawing as a generative activity and drawing as a prognostic activity. Journal of Educational Psychology, 102 , 872–879. https://doi.org/10.1037/a0019640

Sharp, E., & Dennis, M. S. (2017). Model drawing strategy for fraction word problem solving of fourth-grade students with learning disabilities. Remedial and Special Education, 38 , 181–192. https://doi.org/10.1177/0741932516678823

Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive load theory . Springer.

Book   Google Scholar  

Timmermans, R. E., Van Lieshout, E. C. D. M., & Verhoeven, L. (2007). Gender related effects of contemporary math instruction for low performers on problem-solving behavior. Learning and Instruction, 17 , 42–54. https://doi.org/10.1016/j.learninstruc.2006.11.005

Van den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54 , 9–35. https://doi.org/10.1023/B:EDUC.0000005212.03219.dc

van der Schoot, M., Bakker-Arkema, A. H., Horsley, T. M., & Van Lieshout, E. C. D. M. (2009). The consistency effect depends on markedness in less successful but not successful problem solvers: An eye movement study in primary school children. Contemporary Educational Psychology, 34 , 58–66. https://doi.org/10.1016/j.cedpsych.2008.07.002

van Meter, P., Aleksic, M., Schwartz, A., & Garner, J. (2006). Learner-generated drawing as a strategy for learning from content area text. Contemporary Educational Psychology, 31 , 142–166. https://doi.org/10.1016/j.cedpsych.2005.04.001

Verschaffel, L., De Corte, E., & Pauwels, A. (1992). Solving compare problems: An eye movement test of Lewis and Mayer’s consistency hypothesis. Journal of Educational Psychology, 84 , 85–94. https://doi.org/10.1037/0022-0663.84.1.85

Yan, K. C. (2002). The model method in Singapore. The Mathematics Educator, 6 , 47–64.

Download references

Author information

Authors and affiliations.

Department of Psychology, Education, and Child Studies, Erasmus School of Social and Behavioral Sciences, Erasmus University Rotterdam, Burgemeester Oudlaan 50, 3062 PA, Rotterdam, The Netherlands

Björn B. de Koning & Joran Jongerling

Theo Thijssen Institute, Faculty of Education, Utrecht University of Applied Sciences, Padualaan 97, 3584 CH, Utrecht, The Netherlands

Anton J. H. Boonen

Department of Methodology and Statistics, Tilburg School of Social and Behavioral Sciences, Tilburg University, Simon Building, Professor Cobbenhagenlaan, 5037 AB, Tilburg, The Netherlands

Joran Jongerling

Department of Educational and Family Studies, Section Educational Studies, Faculty of Behavioral and Movement Sciences & LEARN! Institute, Vrije Universiteit Amsterdam, Van der Boechorststraat 1, 1081 BT, Amsterdam, The Netherlands

Floryt van Wesel & Menno van der Schoot

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Björn B. de Koning .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

de Koning, B.B., Boonen, A.J.H., Jongerling, J. et al. Model method drawing acts as a double-edged sword for solving inconsistent word problems. Educ Stud Math 111 , 29–45 (2022). https://doi.org/10.1007/s10649-022-10150-8

Download citation

Accepted : 15 March 2022

Published : 23 April 2022

Issue Date : September 2022

DOI : https://doi.org/10.1007/s10649-022-10150-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Arithmetic word problem solving
• Consistency effect
• Model method
• Compare problems
• Find a journal
• Publish with us
• Track your research

• Education & Teaching
• Schools & Teaching
• Instruction Methods
• Mathematics

Enjoy fast, free delivery, exclusive deals, and award-winning movies & TV shows with Prime Try Prime and start saving today with fast, free delivery

Amazon Prime includes:

Fast, FREE Delivery is available to Prime members. To join, select "Try Amazon Prime and start saving today with Fast, FREE Delivery" below the Add to Cart button.

• Cardmembers earn 5% Back at Amazon.com with a Prime Credit Card.
• Unlimited Free Two-Day Delivery
• Streaming of thousands of movies and TV shows with limited ads on Prime Video.
• A Kindle book to borrow for free each month - with no due dates
• Listen to over 2 million songs and hundreds of playlists
• Unlimited photo storage with anywhere access

Important:  Your credit card will NOT be charged when you start your free trial or if you cancel during the trial period. If you're happy with Amazon Prime, do nothing. At the end of the free trial, your membership will automatically upgrade to a monthly membership.

Buy new: #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-whole { font-size: 28px !important; } #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-fraction, #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-symbol { top: -0.75em; font-size: 13px; } $24.48 $ 24 . 48 FREE delivery: Tuesday, April 9 on orders over $35.00 shipped by Amazon. Ships from: Amazon Sold by: ASELStore

Return this item for free.

Free returns are available for the shipping address you chose. You can return the item for any reason in new and unused condition: no shipping charges

• Go to your orders and start the return
• Select the return method

Save with Used - Good #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-whole { font-size: 28px !important; } #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-fraction, #buybox .a-accordion .a-accordion-active .a-price[data-a-size=l].reinventPriceAccordionT2 .a-price-symbol { top: -0.75em; font-size: 13px; } $17.95 $ 17 . 95 FREE delivery: Friday, April 5 on orders over $35.00 shipped by Amazon. Ships from: Amazon Sold by: Krak Dogz Distribution

Other sellers on amazon.

Image Unavailable

• Sorry, this item is not available in
• Image not available
• To view this video download Flash Player

Step by Step Model Drawing: Solving Word Problems the Singapore Way

Purchase options and add-ons, frequently bought together.

Customers who viewed this item also viewed

Special offers and product promotions

Product description.

Step-by-Step Model Drawing explains how this powerful problem-solving strategy from Singapore bridges the gap between the concrete and the abstract (the algorithm) by representing number relationships pictorially. This resource demonstrates exactly how teachers can guide their students through model-drawing solutions to a wide variety of word problems. Educators will discover crystal-clear ways to teach everything from simple addition to fractions, decimals, ratio, rate, and percent; they'll even explore sample problems that provide a pictorial bridge to algebra. Plus you will find practice problems-with full solutions-to help students perfect their new skills. (1-6) 144 pp. This resource demonstrates exactly how teachers can guide their students through model-drawing solutions to a wide variety of word problems. Step-by-Step Model Drawing explains how this powerful problem-solving strategy from Singapore bridges the gap between the concrete and the abstract (the algorithm) by representing number relationships pictorially.

Product details

• Language ‏ : ‎ English
• Product Dimensions ‏ : ‎ 10.7 x 8.4 x 0.4 inches; 14.4 ounces
• Our Recommended age ‏ : ‎ 6 - 12 years
• Manufacturer recommended age ‏ : ‎ 6 - 6 years
• Item model number ‏ : ‎ ELP402696
• Date First Available ‏ : ‎ December 30, 2009
• Manufacturer ‏ : ‎ Essential Learning Products
• ASIN ‏ : ‎ 1934026964
• Best Sellers Rank: #510 in Math Teaching Materials

Product information

Technical details, additional information, what's in the box, looking for specific info, customer reviews.

Customer Reviews, including Product Star Ratings help customers to learn more about the product and decide whether it is the right product for them.

To calculate the overall star rating and percentage breakdown by star, we don’t use a simple average. Instead, our system considers things like how recent a review is and if the reviewer bought the item on Amazon. It also analyzed reviews to verify trustworthiness.

• Sort reviews by Top reviews Most recent Top reviews

Top reviews from the United States

There was a problem filtering reviews right now. please try again later..

Top reviews from other countries

• Amazon Newsletter
• About Amazon
• Accessibility
• Sustainability
• Press Center
• Investor Relations
• Amazon Devices
• Amazon Science
• Start Selling with Amazon
• Sell apps on Amazon
• Supply to Amazon
• Protect & Build Your Brand
• Become an Affiliate
• Become a Delivery Driver
• Start a Package Delivery Business
• Advertise Your Products
• Self-Publish with Us
• Host an Amazon Hub
• › See More Ways to Make Money
• Amazon Visa
• Amazon Store Card
• Amazon Secured Card
• Amazon Business Card
• Shop with Points
• Credit Card Marketplace
• Reload Your Balance
• Amazon Currency Converter
• Your Account
• Your Orders
• Shipping Rates & Policies
• Amazon Prime
• Returns & Replacements
• Manage Your Content and Devices
• Recalls and Product Safety Alerts
• Conditions of Use
• Privacy Notice
• Consumer Health Data Privacy Disclosure
• Your Ads Privacy Choices

Common Problem-Solving Models & How to Use Them

Problem – solving models are step-by-step processes that provide a framework for addressing challenges. Problems arise in every facet of life. From work. to home. to friends and family, problems and conflicts can make life difficult and interfere with our physical and mental well-being. Understanding how to approach problems when they arise and implementing problem-solving techniques can make the journey through a problem less onerous on ourselves and those around us.

By building a structured problem-solving process, you can begin to build muscle memory by repeatedly practicing the same approach, and eventually, you may even begin to find yourself solving complex problems . Building a problem-solving model for each of the situations where you may encounter a problem can give you a path forward, even when the most difficult of problems arise.

This article will explore the concept of problem-solving models and dive into examples of such models and how to use them. It will also outline the benefits of implementing a problem-solving model in each area of life and why these problem-solving methods can have a large impact on your overall well-being. The goal of this article is to help you identify effective problem-solving strategies and develop critical thinking to generate solutions for any problem that comes your way.

Problem-Solving Model Defined

The first step in creating a problem-solving plan is to understand what we mean when we say problem-solving models. A problem-solving model is a step-by-step process that helps a team identify and effectively solve problems that they may encounter. This problem-solving approach gives the team the muscle memory and guide to address a conflict and resolve disputes quickly and effectively.

There are common problem-solving models that many teams have implemented, but there is also the freedom to shape a method to fit the needs of a specific situation. These models often rely on various problem-solving techniques to identify the root cause of the issue and find the best solution. This article will explore some common problem-solving models as well as general problem-solving techniques to help a team engage with and solve problems effectively.

Benefits of Implementing Problem-Solving Models

Before we discuss the exact models for problem-solving, it can be helpful to discuss why problem-solving models are beneficial in the first place. There are a variety of benefits to having a plan in place when a problem arises, but a few important benefits are listed below.

Guide Posts

When a team encounters a problem and has a guide for how to approach and solve the problem, it can be a relief to know that they have a process to fall back on when the issue cannot be resolved quickly from the beginning. A problem-solving strategy will serve as a guide for the parties to know which steps to take next and how to identify the appropriate solution.

It can also clarify when the issue needs to stay within the team, and when the issue needs to be escalated to someone in a position with more authority. It can also help the entire team solve complex problems without creating an issue out of the way the team solves the problem. It gives the team a blueprint to work from and encourages them to find a good solution.

Creative Solutions That Last

When the team or family has a way to fall back on to solve a problem, it takes some of the pressure off of coming up with the process and allows the parties to focus on identifying the relevant information and coming up with various potential solutions to the issue. By using a problem-solving method, the parties can come up with different solutions and find common ground with the best solution. This can be stifled if the team is too focused on figuring out how to solve the problem.

Additionally, the solutions that the parties come up with through problem-solving tools will often address the root cause of the issue and stop the team from having to revisit the same problem over and over again. This can lead to overall productivity and well-being and help the team continue to output quality work. By encouraging collaboration and creativity, a problem-solving technique will often keep solving problems between the parties moving forward and possibly even address them before they show up.

Common Models to Use in the Problem-Solving Process

Several models can be applied to a complex problem and create possible solutions. These range from common and straightforward to creative and in-depth to identify the most effective ways to solve a problem. This section will discuss and break down the problem-solving models that are most frequently used.

Standard Problem-Solving Process

When you search for a problem-solving technique, chances are you will find the standard model for saving problems. This model identifies and uses several important steps that will often be used in other models as well, so it can be helpful to begin the model-building process with an understanding of this model as a base. Other models often draw from this process and adapt one or more of the steps to help create additional options. Each of these steps works to accomplish a specific goal in furtherance of a solution.

Define the Problem

The first step in addressing a problem is to create a clear definition of the issue at hand. This will often require the team to communicate openly and honestly to place parameters around the issue. As the team defines the problem, it will be clear what needs to be solved and what pieces of the conflict are ancillary to the major issue. It helps to find the root causes of the issue and begin a process to address that rather than the symptoms of the problem. The team can also create a problem statement, which outlines the parameters of the problem and what needs to be fixed.

In addition to open and honest communication, other techniques can help to identify the root cause and define the problem. This includes a thorough review of the processes and steps that are currently used in the task and whether any of those steps are directly or indirectly causing the problem.

This includes reviewing how tasks are done, how communication is shared, and the current partners and team members that work together to identify if any of those are part of the issue. It is also the time to identify if some of the easy fixes or new tools would solve the problem and what the impact would be.

It is also important to gain a wide understanding of the problem from all of the people involved. Many people will have opinions on what is going on, but it is also important to understand the facts over the opinions that are affecting the problem. This can also help you identify if the problem is arising from a boundary or standard that is not being met or honored. By gathering data and understanding the source of the problem, the process of solving it can begin.

Generate Solutions

The next step in the basic process is to generate possible solutions to the problem. At this step, it is less important to evaluate how each of the options will play out and how they may change the process and more important to identify solutions that could address the issue. This includes solutions that support the goals of the team and the task, and the team can also identify short and long-term solutions.

The team should work to brainstorm as many viable solutions as possible to give them the best options to consider moving forward. They cannot pick the first solution that is proposed and consider it a successful problem-solving process.

Evaluate and Select

After a few good options have been identified, the next step is to evaluate the options and pick the most viable option that also supports the goals of the team or organization. This includes looking at each of the possible solutions and determining how they would either encourage or hinder the goals and standards of the team. These should evaluated without bias toward the solution proposed or the person putting forward the solution. Additionally, the team should consider both actual outcomes that have happened in the past and predicted instances that may occur if the solution is chosen.

Each solution should be evaluated by considering if the solution would solve the current problem without causing additional issues, the willingness of the team to buy in and implement the solution, and the actual ability of the team to implement the solution.

Participation and honesty from all team members will make the process go more smoothly and ensure that the best option for everyone involved is selected. Once the team picks the option they would like to use for the specific problem, they should clearly define what the solution is and how it should be implemented. There should also be a strategy for how to evaluate the effectiveness of the solution.

Implement the Solution and Follow Up

Once a solution is chosen, a team will often assume that the work of solving problems is complete. However, the final step in the basic model is an important step to determine if the matter is resolved or if additional options are needed. After the solution has been implemented by the team, the members of the team must provide feedback and identify any potential obstacles that may have been missed in the decision-making process.

This encourages long-term solutions for the problem and helps the team to continue to move forward with their work. It also gives the team a sense of ownership and an example of how to evaluate an idea in the future.

If the solution is not working the way that it should, the team will often need to adapt the option, or they may get to the point where they scrap the option and attempt another. Solving a problem is not always a linear process, and encouraging reform and change within the process will help the team find the answer to the issues that they face.

GROW Method

Another method that is similar to the standard method is the G.R.O.W. method. This method has very similar steps to the standard method, but the catchiness of the acronym helps a team approach the problem from the same angle each time and work through the method quickly.

The first step in the method is to identify a goal, which is what the “g” stands for in “grow.” To establish a goal, the team will need to look at the issues that they are facing and identify what they would like to accomplish and solve through the problem-solving process. The team will likely participate in conversations that identify the issues that they are facing and what they need to resolve.

The next step is to establish the current reality that the group is facing. This helps them to determine where they currently are and what needs to be done to move them forward. This can help the group establish a baseline for where they started and what they would like to change.

The next step is to find any obstacles that may be blocking the group from achieving their goal. This is where the main crux of the issues that the group is facing will come out. This is also helpful in giving the group a chance to find ways around these obstacles and toward a solution.

Way Forward

After identifying the obstacles and potential ways to avoid them, the group will then need to pick the best way to move forward and approach their goal together. Here, they will need to create steps to move forward with that goal.

Divide and Conquer

Another common problem-solving method is the divide-and-conquer method. Here, instead of the entire team working through each step of the process as a large group, they split up the issue into smaller problems that can be solved and have individual members or small groups work through the smaller problems. Once each group is satisfied with the solution to the problem, they present it to the larger group to consider along with the other options.

This process can be helpful if there is a large team attempting to solve a large and complex problem. It is also beneficial because it can be used in teams with smaller, specialized teams within it because it allows each smaller group to focus on what they know best.

However, it does encourage the parties to shy away from collaboration on the overall issue, and the different solutions that each proposes may not be possible when combined and implemented.

For this reason, it is best to use this solution when approaching complex problems with large teams and the ability to combine several problem-solving methods into one.

Six Thinking Hats

The Six Thinking Hats theory is a concept designed for a team with a lot of differing conflict styles and problem-solving techniques. This method was developed to help sort through the various techniques that people may use and help a team find a solution that works for everyone involved. It helps to organize thinking and lead the conversation to the best possible solution.

Within this system, there are six different “hats” that identify with the various aspects of the decision-making process: the overall process, idea generation, intuition and emotions, values, information gathering, and caution or critical thinking. The group agrees to participate in the process by agreeing on which of the hats the group is wearing at a given moment. This helps set parameters and expectations around what the group is attempting to achieve at any moment.

This system is particularly good in a group with different conflict styles or where people have a hard time collecting and organizing their thoughts. It can be incredibly beneficial for complex problems with many moving parts. It can also help groups identify how each of the smaller sections relates to the big picture and help create new ideas to answer the overall problem.

However, it can derail if the group focuses too heavily or for too long on one of the “hats.” The group should ensure that they have a facilitator to guide them through the process and ensure that each idea and section is considered adequately.

Trial and Error

The trial and error process takes over the evaluation and selection process and instead chooses to try out each of the alternatives to determine what the best option would be. It allows the team to gather data on each of the options and how they apply practically. It also provides the ability for the team to have an example of each possible answer to help a decision-maker determine what the best option is.

Problem-solving methods that focus on trial and error can be helpful when a team has a simple problem or a lot of time to test potential solutions, gather data, and determine an answer to the issue.

It can also be helpful when the team has a sense of the best guess for a solution but wants to test it out to determine if the data supports that option, or if they have several viable options and would like to identify the best one. However, it can be incredibly time-consuming to test each of the options and evaluate how they went. Time can often be saved by evaluating each option and selecting the best to test.

Other Problem-Solving Skills

In addition to the methods outlined above, other problem-solving skills can be used regardless of the model that is used. These techniques can round out the problem-solving process and help address either specific steps in the overall method or alter the step in some way to help it fit a specific situation.

Ask Good Questions

One of the best ways to work through any of the problem-solving models is to ask good questions. This will help the group find the issue at the heart of the problem and address that issue rather than the symptoms. The best questions will also help the group find viable solutions and pick the solution that the group can use to move forward. The more creative the questions , the more likely that they will produce innovative solutions.

Take a Step Back

Occasionally, paying attention to a problem too much can give the group tunnel vision and harm the overall processes that the group is using. Other times, the focus can lead to escalations in conflict. When this happens, it can be helpful to set aside the problem and give the group time to calm down. Once they have a chance to reconsider the options and how they apply, they can approach the issue with a new sense of purpose and determination. This can lead to additional creative solutions that may help the group find a new way forward.

Final Thoughts

Problem-solving can be a daunting part of life. However, with a good problem-solving method and the right techniques, problems can be addressed well and quickly. Applying some of these options outlined in this article can give you a head start in solving your next problem and any others that arise.

To learn more about problem-solving models, problem-solving activities, and more, contact ADR Times !

Must-read Articles:

• Recent Posts

• How Long After Mediation Will I Get My Money? - March 19, 2024
• Understanding the Judicial Estoppel Doctrine - March 12, 2024
• Compromise Conflict Style: At A Glance - March 12, 2024

Please use the browser's LEFT ARROW to return to this page

These lessons are free for online use., copyright © 2005 www.thesingaporemaths.com, email us at: [email protected].

Posted Mar 29, 2024

At 2:23 PM UTC

The company said Grok 1.5 , the first release since open-sourcing the model , performed significantly better in coding and math-related reasoning than its previous version. xAI’s testing showed Grok 1.5 outdid models like Claude 2, Gemini Pro 1.5, and GPT-4 in some problem-solving benchmarks.

Grok 1.5 will be available to early users of the model on X soon.

Sam Bankman-Fried is still gambling

20 years of gmail, bill maher expands podcast operation with a controversial host, leaked images reveal microsoft’s white disc-less xbox series x console, the xiaomi 14 ultra is a photography nerd’s dream, more from this stream the entire story of twitter / x under elon musk, elon musk has a new pay-to-play x premium gambit., judge tosses elon musk’s x lawsuit against anti-hate group, is this what x will look like on a smart tv, here’s the elon musk interview that got don lemon’s show canceled.

• Member Home
• My Bookmarks

Problem Solving Series: Part/Whole Problems for Model Drawings

Oct 27, 2017

In this post, we move from just talking about math problems like we were doing in Kindergarten, into the 1st grade classroom where kids are able to answer a variety of part/whole problems.

As we’ve talked about in the previous two posts in this series ( Intro to Model Drawings and The Early Years ), model drawings have different names: bar models, tape diagrams and model drawings. These are great comprehension strategies to help students learn to decode what questions are asking. 

Part/whole problems comprise one fifth of the type of problems students will encounter in elementary school. These problems often will use all operations (addition, subtraction, multiplication, division) and will even extend to missing addends, 3-part part/whole problems and multi-step part/whole problems. A child in 1st grade will learn part/whole problems with addition, subtraction, and missing addends, as well as 2-part part/whole problems and the addition of a third character into the story problem.

Let’s start with a typical problem:

If Shannon has 8 pieces of an orange, and Suzy has 5 pieces of oranges, how many do they have altogether?

Teachers often want to use individual unifix cubes to represent the problem. With this level of a problem, individual cubes are fine, but after a while, the quantities in problems will continue to get larger. Maybe instead of 5, Suzy might have 26 pieces of something and her friend might have 42. These numbers become much more challenging to represent individually.

In a typical 1st grade classroom, we like to scaffold as much as possible so students start to understand that, not only do numbers and words have a connection to the real world, but there are words that ask them to do specific operations. In the first blog , we talked about how , sometimes we see T-charts with plus/minus, multiply/divide on the wall, and we train kids to watch out for certain language in a story problem that will trigger an action. These are ok for part/whole problems because those are typically what is being asked. But as soon as you get asked more than one step, “altogether” might not mean that you just add the two numbers.

Types of Part/Whole Problems

Part/Whole Addition. Start by labelling the who or the what. Then have the kids use a starting line to actually build their bar for their bar drawing. You technically don’t have to do the drawing until you get to comparison bars, but it’s nice to have in a scenario like this:

Shannon has 5 pieces of candy, and Sarah has 9 pieces of candy. How many pieces of candy do they have all together?

We start by labelling the candy (the what), then draw the bar model to represent how many Shannon has and how many Sarah has. We can actually chunk the bar, so if Shannon only had five, we can put the line a little bit to the left to make the bar larger for Sarah, who has nine. At the top, we would label who has 5 and who has 9 pieces of candy. And our question mark would be at the end.

For this type of problem, the quantities can get up quite a bit higher, but the bar graph is non-proportional so will work regardless of the number quantity. For example, Shannon might have 52 pieces of candy after Halloween, but Sarah has 92. How many altogether? The model drawing will look similar, but it will simply contain higher numbers.

Part/Whole Subtraction. When we do a part/whole subtraction problem, we typically use a diagonal slash to say that something was taken away in the problem. Let’s look at a scenario:

Shannon has 14 pieces of candy and her brother Patrick ate 3 pieces. How many pieces of candy does Shannon have left?

This is similar to part/whole addition in that we still identify the who (Shannon) and the what (Shannon’s candy). At the end of the individual bar, we would put the total, since we know it equals 14. Since her brother ate some, we’re going to proportion the bar, put a diagonal slash through it to say that he actually ate three pieces. At the top, we’re going to label that part “eaten,” and put a question mark for how many are left.

This can also definitely ramp up much higher. For example, after Halloween, Shannon had 126 pieces of candy, and she at 42 of the pieces. How many are left? When we get to more complex problems, there will also be some problems with missing addends. The thing to remember is that we only represent in the model drawing the things that the problem is actually saying. Even if they want to write the answer in the box, the idea is that the model drawing is a drawing of just what the words are asking in order to  help kids decode them.

Kids in upper grades can also do lots of part/whole problems with addition and subtraction, but they’ll use higher numbers and might also include more steps.

The best app to use for part/whole addition and subtraction is ThinkingBlocks.com via the Math Playground. This site has many videos showing part/whole addition and subtraction, as well as missing addends. Check out our resource page for the link and for all more model drawing resources.

Part/Whole Multiplication.

Here’s a sample problem:

1 spider has 8 legs. How many legs do 5 spiders have?

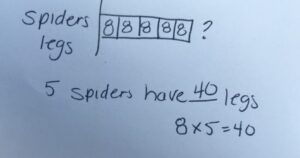
Multiplication can get more complex very easily, using bigger numbers or having kids divide. Remember, during the computation phase, kids will have different ways to figure out 5 groups of 8 and they can do all kinds of things, but ultimately we want the model drawings to look a certain way so they start to understand what a part/whole multiplication problem looks like.

Part/Whole Division Problems.

This type of problems have their own unique appearance.

I looked out and saw 40 spider legs. One spider has 8 legs, so how many spiders do I see in all?

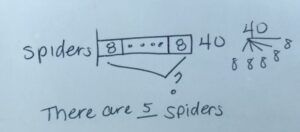
The Bottom Line

In essence, when we look at part/whole problems, although they look very simplistic, they’re the foundation of what students need to understand to continue. Many of our part/whole problems can become very complex by using larger numbers, requiring kids to divide by larger groups, add or subtract and become three-part problems.

You can find a range of problems on Thinkingblocks.com. I f you want to do multiplication and division, click on the multiplication/division section. You’re looking at part/whole problems or you can select two-part problems to make things more complex. The idea is when problems become harder, you want all of these to be on one model drawing for a child to figure out how to go about solving these problems. 

The most important thing to remember is to be using our journal templates ( PreK/K and Simple ) as well as our Step-by-Step Model Drawing poster . For continued resources to help you with model drawing, we highly recommend our Step-by-Step Model Drawing book, as well as our 1st-6th grade series of model drawing books . These give you really great problems, as well as an answer key. So if you’re new to model drawings, you’ll want to be able to use these as a support to help you.

Eventually, as you become better at finding part/whole problems, you’ll be able to enter this process into any math series or any story problem that you’re using. Remember that these problems can become much more complex, so it’s much better for students (even older students!) go down to easier problems, and then help them work their way up.

Check out our problem solving kits here. You’ll notice that we always provide a teacher with the model drawing book for the grade below to help them scaffold for students that are learning.

I can’t tell you how powerful this problem solving process is for schools that in our Math Initiative project . Many of our schools start learning problem solving through model drawing in 1st grade and can go all the way up through 8th grade. There are students taking our state test that were actually using the model drawing process because the poster was up in the classroom, they were consistently provided with instruction in using the process with all different types of problems, and they were also given the student step-by-step checklist. Consistency is the key. When students are working on problems five days a week (in grades 2-5), and students start to understand the early development of model drawing. Even in the second semester of the 1st grade year, it really helps students as problems become more complex and math continues.

Join us next week for a look at comparison bars!

Comment on our blog if you’ve been using model drawings! We want to hear what they’ve done for you as an adult learner, as well as for your students!

Word problems, featured products.

• Track Orders
• Shopping Bag

*Addition , *Subtraction , *Word Problems , Audience - Lower Elementary (K-2) , Series - Problem Solving | 0 comments

Related Posts

Screening for Numeracy Development

Dec 5, 2022

Ever feel like the years are flying by and standing still at the same time? Usually, it’s children that help us feel this odd sensation, but I also can’t believe it’s been TEN years since I first created my numeracy screeners!Ten years ago, I developed a set of...

Rekenrek Activities for Numeracy Development

Feb 28, 2022

This little-known math tool, the rekenrek, is a star when it comes to numeracy development!

Using Place Value Discs in the Math Classroom

Jan 27, 2022

I have all these place value discs - How am I supposed to use them across different areas of my mathematical instruction?? This is a question that we get from a lot of teachers and we know that having a Math Salad Bar full of tools but not knowing how to implement...